Prerpints.org logo
Preprint
Article

A Reversible Spherical Geometric Conversion of Protein Backbone Structure Coordinate Matrix to Three Independent Vectors of ρ, θ and φ

Altmetrics

Downloads

236

Views

155

Comments

0

supplementary.pdf (1.66MB )

Wei Li  *

This version is not peer-reviewed

Submitted:

07 April 2024

Posted:

08 April 2024

You are already at the latest version

Alerts
Abstract
Due to the vast conformational space proteins can adopt, accurate and efficient prediction of protein structure remains still a challenging task, coupled with the intricacies of interatomic interactions and the limitations of current computational models in effectively navigating this complex molecular landscape. Additionally, the lack of comprehensive experimental data for all protein structures further exacerbates the difficulty in reliable machine learning-based prediction of the three-dimensional conformations of the proteios building block of life. Geometrically, Cartesian coordinate system (CCS, X, Y and Z) and spherical coordinate system (SCS, ρ, θ and φ) are two interconvertible coordinate systems, and are like two sides of one coin. Since the beginning of Protein Data Bank (PDB) in 1971, CCS has been the default approach to specify atomic positions with X, Y and Z in PDB. In this manuscript, therefore, I present a novel method for the reversible spherical geometric conversion of protein backbone structure coordinate matrices to three independent vectors: ρ, θ and φ. This reversible conversion facilitates lossless extraction of essential structural features from protein backbone structural data, enabling the development of advanced novel algorithms for protein structure prediction in future. In short, this inter-atomic SCS approach offers a comprehensive yet efficient means of representing protein backbone geometry, leveraging spherical coordinates to capture spatial relationships in a compact and intuitive inter-atomic manner, and to provide a robust framework for reversible feature extraction for the ongoing efforts in advancing the field of protein structure prediction, the holy grail of computational structural biology.
Keywords: 
Subject: Biology and Life Sciences  -   Biophysics

1. Introduction

Protein structure prediction is the computational task of determining the three-dimensional structure of a protein from its amino acid sequence. This process is crucial for understanding protein function, interactions, and designing novel therapeutics [1,2,3,4,5,6,7,8]. By definition, accurate prediction of protein structure from its amino acid sequence is a formidable challenge in computational structural biology, with profound implications for understanding biological function and designing novel therapeutics [9,10,11,12]. Over the past decade, numerous computational methods have been developed to tackle this problem, ranging from physics-based simulations to machine learning approaches. For instance, physics-based simulations utilize principles of molecular mechanics and dynamics to simulate folding pathways, while homology modeling (e.g., algorithms such as PSI-BLAST, HHblits, and HMMER) leverages evolutionary relationships between proteins to infer structures [13,14,15,16,17,18,19,20]. Of recent further interest, machine learning techniques, particularly deep learning, have emerged as powerful tools for predicting protein structures by learning patterns from large datasets [4,21,22,23,24,25,26,27,28,29,30]. Recent advancements in deep learning, exemplified by AlphaFold, have revolutionized protein structure prediction. Deep learning models, particularly convolutional neural networks (CNNs) and recurrent neural networks (RNNs), have shown remarkable performance in predicting protein structures directly from amino acid sequences. AlphaFold, for instance, integrates multiple sequence alignment (MSA) with a deep learning architecture to accurately predict protein structures, outperforming traditional methods in terms of accuracy and speed [31,32,33,34,35,36,37,38,39]. Moreover, hybrid approaches that integrate multiple methods are also gaining traction, aiming to combine the strengths of different approaches for improved accuracy and efficiency [40,41,42,43].
In particular, the key for machine learning-based protein structure prediction is the extraction of essential structural features from protein data, which serve as the basis for predicting the three-dimensional arrangement of atoms in a protein molecule [44,45,46,47,48,49,50,51,52,53]. Take AlphaFold for example, which is an artificial intelligence system developed by DeepMind, a subsidiary of Alphabet Inc. (Google’s parent company). Here’s a simplified explanation of how AlphaFold works:
  • Input data: AlphaFold takes the primary sequence of amino acids that make up a protein as input. This sequence is derived from the genetic code.
  • Homology detection: AlphaFold starts by comparing the target protein sequence to a large database of known protein structures to identify proteins with similar sequences. This process is known as homology detection. If similar structures are found, they can provide valuable clues about the structure of the target protein.
  • Multiple sequence alignment (MSA): After identifying similar sequences, AlphaFold aligns them with the target sequence to create a multiple sequence alignment (MSA). This step helps identify conserved regions in the protein sequence, which are likely to correspond to important structural elements.
  • Structure prediction: Using the MSA and other relevant data, AlphaFold employs deep learning techniques, particularly deep neural networks, to predict the 3D structure of the target protein. The neural network is trained on a diverse set of protein structures to learn the complex relationships between amino acid sequences and their corresponding 3D structures.
  • Model refinement: AlphaFold then refines the initial predicted structures through iterative optimization techniques to improve accuracy and consistency. This refinement process helps correct any errors and inconsistencies in the predicted structure.
  • Output: The final output of AlphaFold is a predicted 3D model of the protein’s structure, including the positions of individual atoms. This model provides valuable insights into the protein’s function, interactions with other molecules, and potential implications for drug discovery and other applications [54,55,56,57,58,59,60].
Overall, AlphaFold combines advanced machine learning algorithms with biological insights to accurately predict protein structures, significantly advancing our understanding of biology and opening new avenues for drug discovery and biotechnology. While current algorithms in protein structure prediction have made significant strides, particularly with the advent of machine learning techniques, enhanced sampling methods, and improved force fields [61,62,63,64,65,66,67,68], further improvement in protein structure prediction algorithms is necessary for several reasons:
  • Accuracy for large proteins and complexes [69,70,71]: while current algorithms perform reasonably well for small to medium-sized proteins, accurately predicting the structures of large proteins or protein complexes remains challenging. Improvements are needed to capture the intricacies of these larger systems, including domain-domain interactions and conformational changes.
  • Conformational flexibility [53,72,73]: Proteins exhibit conformational flexibility, adopting multiple states with different structural conformations. Current algorithms often struggle to accurately predict these flexible regions or transitions between states. Enhancements in sampling techniques and modeling approaches are needed to better capture and predict protein flexibility.
  • Computational Efficiency [74,75]: High-resolution protein structure prediction often requires substantial computational resources and time. Improvements in algorithm efficiency and scalability are necessary to enable broader application and faster turnaround times for protein structure prediction tasks [76,77,78,79,80,81,82,83].

2. Motivation

Protein is life’s proteios building block, experimental determination of protein structure is critical to understand how they perform their functions [21]. Since the establishment of PDB in 1971 [84,85,86,87,88], protein structure has been described using Cartesian coordinates, i.e., X, Y and Z, to specify atomic positions [89]. Geometrically, Cartesian coordinate system (CCS, X, Y and Z) and spherical coordinate system (SCS, ρ , θ and ϕ ) are two interconvertible coordinate systems (Figure 1), and are like two sides of one coin [89]. Therefore, in this manuscript, I put forward an inter-atomic spherical coordinate system (IASCS) approach to redefine protein structure with ρ , θ and ϕ [89] for the reversible spherical geometric conversion of protein backbone structure coordinate matrices into three independent vectors: ρ , θ , and ϕ .
Unlike traditional Cartesian coordinates, which represent a protein’s backbone geometry in terms of its x, y, and z coordinates, the approach here leverages spherical coordinates to capture the inherent curvature (i.e., structural features [90]) of protein backbone structures more intuitively. By transforming the Cartesian coordinate matrix into spherical coordinates, this approach effectively decouple the spatial information into radial distance ( ρ ), polar angle ( θ ), and azimuthal angle ( ϕ ), providing a more natural representation of the protein’s backbone conformation [91]. In light of the fact that protein backbone structure consists of a network of covalently bonded atoms, the radial distance ( ρ ) here represents the equilibrium atomic bond length, which is defined as the inter-nuclear distance at which the system energy minimum occurs [92,93,94].

3. Materials and Methods

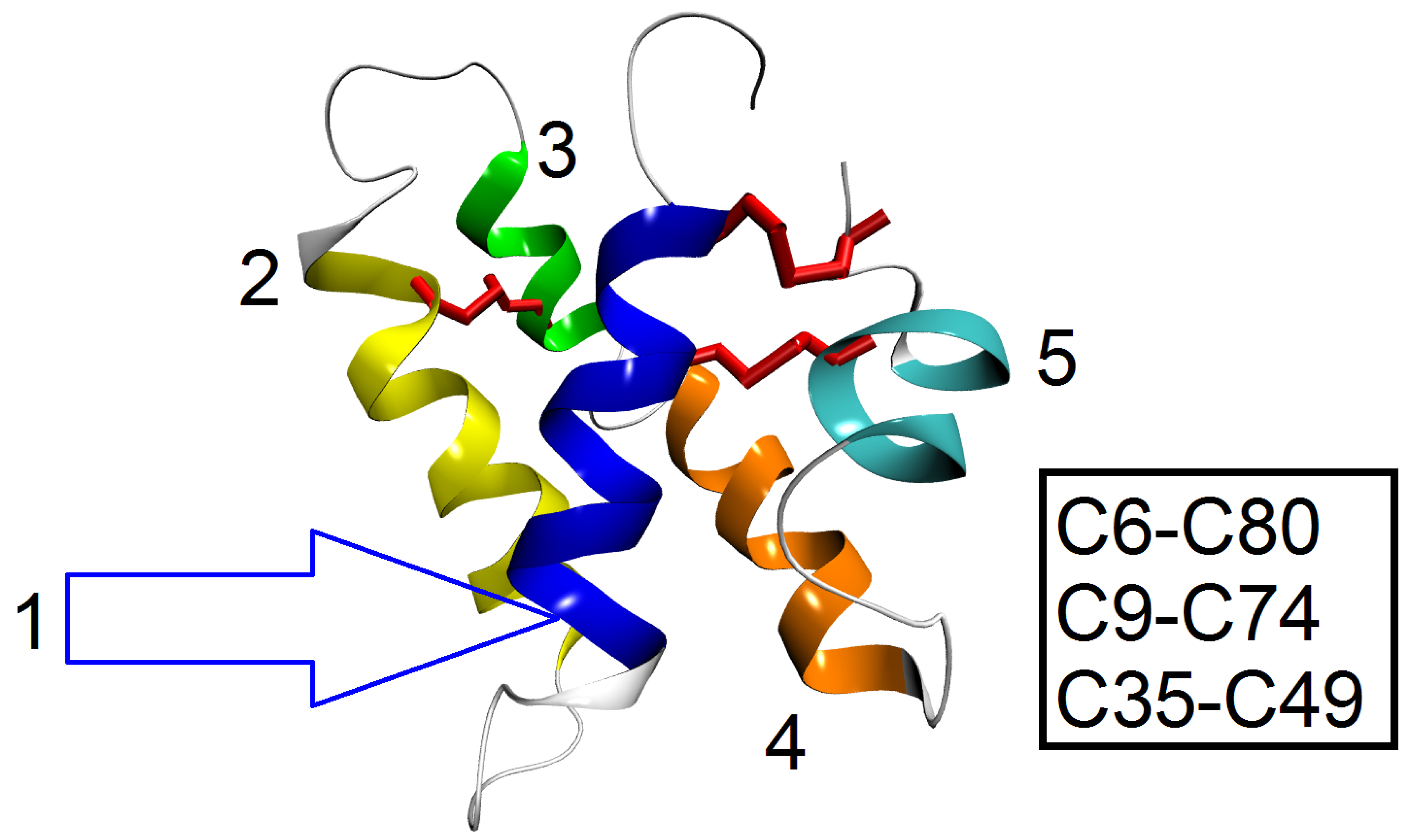
3.1. Redefining Protein Backbone Structure with ρ , θ and ϕ : Caenopore-5 as an Example

To illustrate the redefinition of protein backbone structure with ρ , θ and ϕ , this article takes Caenopore-5 as an example, whose three-dimensional structure has been experimentally determined by liquid-state NMR spectroscopy [95,96,97]. As is a member of the pore-forming toxin family found in the nematode Caenorhabditis elegans, Caenopore-5 is characterized by a primary amino acid sequence (Figure 2) rich in hydrophobic residues, facilitating its insertion into lipid membranes [95,96].
>2JSA_1|Chain A|Saposin-like protein family protein 5|Caenorhabditis elegans (6239) [95,96,98]
MSGSHHHHHHSSGIEGRGRSALSCQMCELVVKKYEGSADKDANVIKKDFDAECKKLFHTIPFGTRECDHYVNSKVDPIIHELEGGTAPKDVCTKLNECP
Structurally, Caenopore-5 typically adopts a helical conformation, forming oligomeric pores upon interaction with lipid bilayers, with five helices stabilized by three disulfide bridges between Cys6 and Cys80, and between Cys9 and Cys74, and between Cys35 and Cys49, as shown in Figure 3. Functionally, Caenopore-5 exhibits potent antimicrobial activity, playing a crucial role in the nematode’s innate immune defense against pathogens [95,96,98]. As the three-dimensional structure of Caenopore-5 was experimentally determined by liquid-state NMR spectroscopy [95,96], the structural model deposited in PDB [85] is an NMR ensemble of 15, instead of 1, structural models calculated using experimentally recorded NMR data. As a result, the redefinition of the backbone structure of Caenopore-5 with ρ , θ and ϕ is illustrated for all 15 structural models of Caenopore-5 [95,96,98].

3.2. Redefining Protein Backbone Structure with ρ , θ and ϕ : How?

In light of the geometric interconvertibility of CCS and SCS (Figure 1) [89], a local SCS (LSCS) approach was proposed in as an alternative to the default half-a-century-old CCS approach and a global SCS (GSCS) approach proposed a decade ago [89,100]. Since the LSCS approach takes into account the whole inter-atomic covalent bonding network of protein, it is referred to as an inter-atomic SCS (IASCS) approach below.
First, to define an inter-atomic spherical coordinate system (IASCS) approach to redefine protein structure with ρ , θ and ϕ [89] for the reversible spherical geometric conversion of protein backbone structure coordinate matrices into three independent vectors: ρ , θ , and ϕ , a short peptide with five amino acids (Figure 4) is used here as an example. Specifically, the whole inter-atomic covalent bonding network of the backbone of the short peptide (Figure 4) is defined sequentially as below:
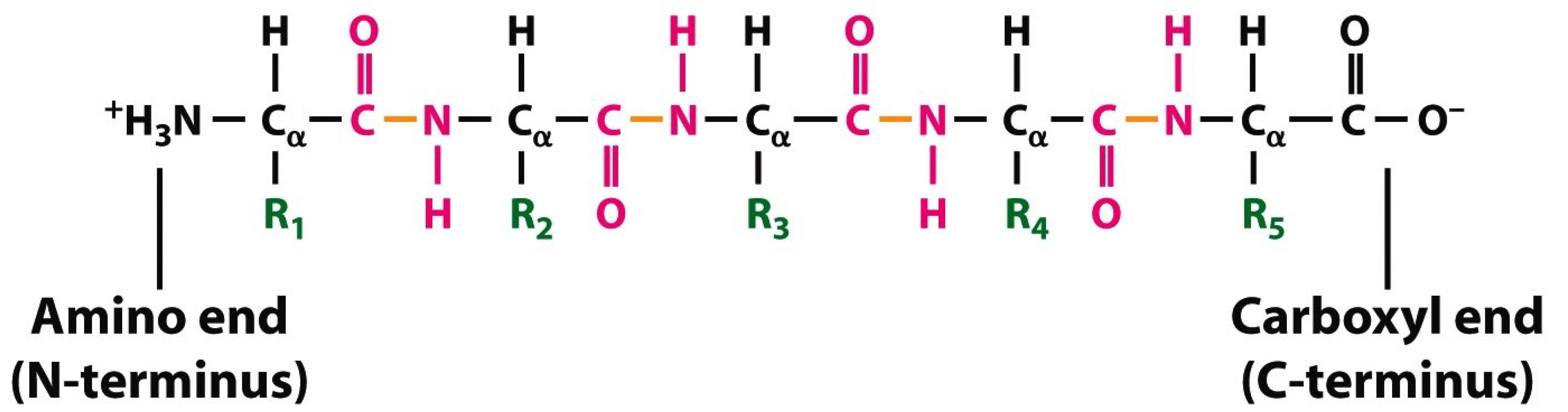
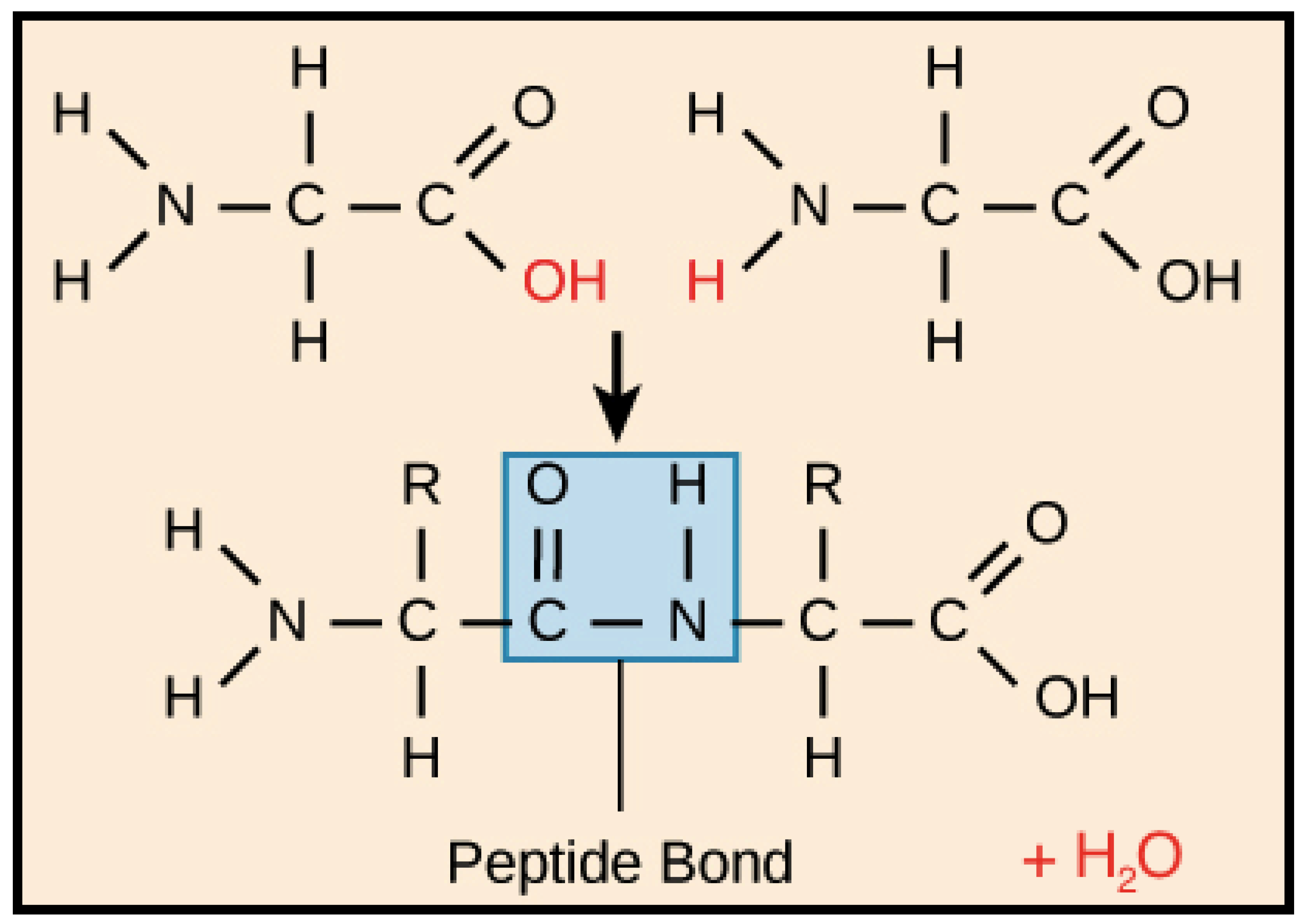
  • the covalent bond between N-terminal amide nitrogen atom (Atom_initial in the IASCS coordinate system) of the first residue of the short peptide with five amino acids (Figure 4) and three N-terminal amide hydrogen atoms (Atom_finals in the IASCS coordinate system) of the backbone of the first residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between N-terminal amide nitrogen atom (Atom_initial in the IASCS coordinate system) of the first residue of the short peptide with five amino acids (Figure 4) and carbon α(Cα, Atom_final in the IASCS coordinate system) of the backbone of the first residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between carbon α(Cα, Atom_initial in the IASCS coordinate system) of the first residue of the short peptide with five amino acids (Figure 4) and hydrogen α(Hα, Atom_final in the IASCS coordinate system) of the backbone of the first residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between carbon α(Cα, Atom_initial in the IASCS coordinate system) of the first residue of the short peptide with five amino acids (Figure 4) and carbonyl carbon (Atom_final in the IASCS coordinate system) of the backbone of the first residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between carbonyl carbon (Atom_initial in the IASCS coordinate system) of the first residue of the short peptide with five amino acids (Figure 4) and carbonyl oxygen (the double-bonded oxygen atom, Atom_final in the IASCS coordinate system) of the backbone of the first residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between carbonyl carbon (Atom_initial in the IASCS coordinate system) of the first residue of the short peptide with five amino acids (Figure 4) and the amide nitrogen atom (Atom_final in the IASCS coordinate system) of the second residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between the amide nitrogen atom (Atom_initial in the IASCS coordinate system) of the second residue of the short peptide with five amino acids (Figure 4) and the amide hydrogen atom (Atom_final in the IASCS coordinate system) of the backbone of the second residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between N-terminal amide nitrogen atom (Atom_initial in the IASCS coordinate system) of the second residue of the short peptide with five amino acids (Figure 4) and carbon α(Cα, Atom_final in the IASCS coordinate system) of the backbone of the second residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between carbon α(Cα, Atom_initial in the IASCS coordinate system) of the second residue of the short peptide with five amino acids (Figure 4) and hydrogen α(Hα, Atom_final in the IASCS coordinate system) of the backbone of the second residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between carbon α(Cα, Atom_initial in the IASCS coordinate system) of the second residue of the short peptide with five amino acids (Figure 4) and carbonyl carbon (Atom_final in the IASCS coordinate system) of the backbone of the second residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between carbonyl carbon (Atom_initial in the IASCS coordinate system) of the second residue of the short peptide with five amino acids (Figure 4) and carbonyl oxygen (the double-bonded oxygen atom, Atom_final in the IASCS coordinate system) of the backbone of the second residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between carbonyl carbon (Atom_initial in the IASCS coordinate system) of the second residue of the short peptide with five amino acids (Figure 4) and the amide nitrogen atom (Atom_final in the IASCS coordinate system) of the third residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between the amide nitrogen atom (Atom_initial in the IASCS coordinate system) of the third residue of the short peptide with five amino acids (Figure 4) and the amide hydrogen atom (Atom_final in the IASCS coordinate system) of the backbone of the third residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between N-terminal amide nitrogen atom (Atom_initial in the IASCS coordinate system) of the third residue of the short peptide with five amino acids (Figure 4) and carbon α(Cα, Atom_final in the IASCS coordinate system) of the backbone of the third residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between carbon α(Cα, Atom_initial in the IASCS coordinate system) of the third residue of the short peptide with five amino acids (Figure 4) and hydrogen α(Hα, Atom_final in the IASCS coordinate system) of the backbone of the third residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between carbon α(Cα, Atom_initial in the IASCS coordinate system) of the third residue of the short peptide with five amino acids (Figure 4) and carbonyl carbon (Atom_final in the IASCS coordinate system) of the backbone of the third residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between carbonyl carbon (Atom_initial in the IASCS coordinate system) of the third residue of the short peptide with five amino acids (Figure 4) and carbonyl oxygen (the double-bonded oxygen atom, Atom_final in the IASCS coordinate system) of the backbone of the third residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between carbonyl carbon (Atom_initial in the IASCS coordinate system) of the third residue of the short peptide with five amino acids (Figure 4) and the amide nitrogen atom (Atom_final in the IASCS coordinate system) of the fourth residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between the amide nitrogen atom (Atom_initial in the IASCS coordinate system) of the fourth residue of the short peptide with five amino acids (Figure 4) and the amide hydrogen atom (Atom_final in the IASCS coordinate system) of the backbone of the fourth residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between N-terminal amide nitrogen atom (Atom_initial in the IASCS coordinate system) of the fourth residue of the short peptide with five amino acids (Figure 4) and carbon α(Cα, Atom_final in the IASCS coordinate system) of the backbone of the fourth residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between carbon α(Cα, Atom_initial in the IASCS coordinate system) of the fourth residue of the short peptide with five amino acids (Figure 4) and hydrogen α(Hα, Atom_final in the IASCS coordinate system) of the backbone of the fourth residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between carbon α(Cα, Atom_initial in the IASCS coordinate system) of the fourth residue of the short peptide with five amino acids (Figure 4) and carbonyl carbon (Atom_final in the IASCS coordinate system) of the backbone of the fourth residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between carbonyl carbon (Atom_initial in the IASCS coordinate system) of the fourth residue of the short peptide with five amino acids (Figure 4) and carbonyl oxygen (the double-bonded oxygen atom, Atom_final in the IASCS coordinate system) of the backbone of the fourth residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between carbonyl carbon (Atom_initial in the IASCS coordinate system) of the fourth residue of the short peptide with five amino acids (Figure 4) and the amide nitrogen atom (Atom_final in the IASCS coordinate system) of the fifth residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between the amide nitrogen atom (Atom_initial in the IASCS coordinate system) of the fifth residue of the short peptide with five amino acids (Figure 4) and the amide hydrogen atom (Atom_final in the IASCS coordinate system) of the backbone of the fifth residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between N-terminal amide nitrogen atom (Atom_initial in the IASCS coordinate system) of the fifth residue of the short peptide with five amino acids (Figure 4) and carbon α(Cα, Atom_final in the IASCS coordinate system) of the backbone of the fifth residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between carbon α(Cα, Atom_initial in the IASCS coordinate system) of the fifth residue of the short peptide with five amino acids (Figure 4) and hydrogen α(Hα, Atom_final in the IASCS coordinate system) of the backbone of the fifth residue of the short peptide with five amino acids (Figure 4);
  • the covalent bond between carbon α(Cα, Atom_initial in the IASCS coordinate system) of the fifth residue of the short peptide with five amino acids (Figure 4) and carbonyl carbon (Atom_final in the IASCS coordinate system) of the backbone of the fifth residue of the short peptide with five amino acids (Figure 4);
  • the covalent double bond between carbonyl carbon (Atom_initial in the IASCS coordinate system) of the fifth residue of the short peptide with five amino acids (Figure 4) and carbonyl oxygen (the double-bonded oxygen atom, Atom_final in the IASCS coordinate system) of the backbone of the fifth residue of the short peptide with five amino acids (Figure 4);
  • the covalent single bond between carbonyl carbon (Atom_initial in the IASCS coordinate system) of the fifth residue of the short peptide with five amino acids (Figure 4) and the carboxyl carboxyl hydroxyl oxygen atom (Atom_final in the IASCS coordinate system) of the fifth residue of the short peptide with five amino acids (Figure 4);
For further extraction of structural features from the backbones of proteins, this article also puts forward an approach to redefine the backbone peptide bond connecting pattern with ρ , θ and ϕ . As shown in Figure 5, a peptide bond is formed by dehydration, which is the removal of the carboxyl hydroxyl on one amino acid and one hydrogen atom on the amine end of another amino acid. Specifically, the whole inter-atomic peptide bonding network of the backbone of the short peptide (Figure 4) is defined sequentially as below:
  • the peptide bond (Figure 5) as formed between R1 and R2 of the short peptide with five amino acids (Figure 4);
  • the peptide bond (Figure 5) as formed between R2 and R3 of the short peptide with five amino acids (Figure 4);
  • the peptide bond (Figure 5) as formed between R3 and R4 of the short peptide with five amino acids (Figure 4);
  • the peptide bond (Figure 5) as formed between R4 and R5 of the short peptide with five amino acids (Figure 4);
Thus, with the IASCS coordinate system defined above for the backbone of protein structure in place, for CCS, GSCS and IASCS, their main differences are summarized below:
  • CCS requires three parameters (X, Y and Z) for all atoms to construct a protein backbone structural model.
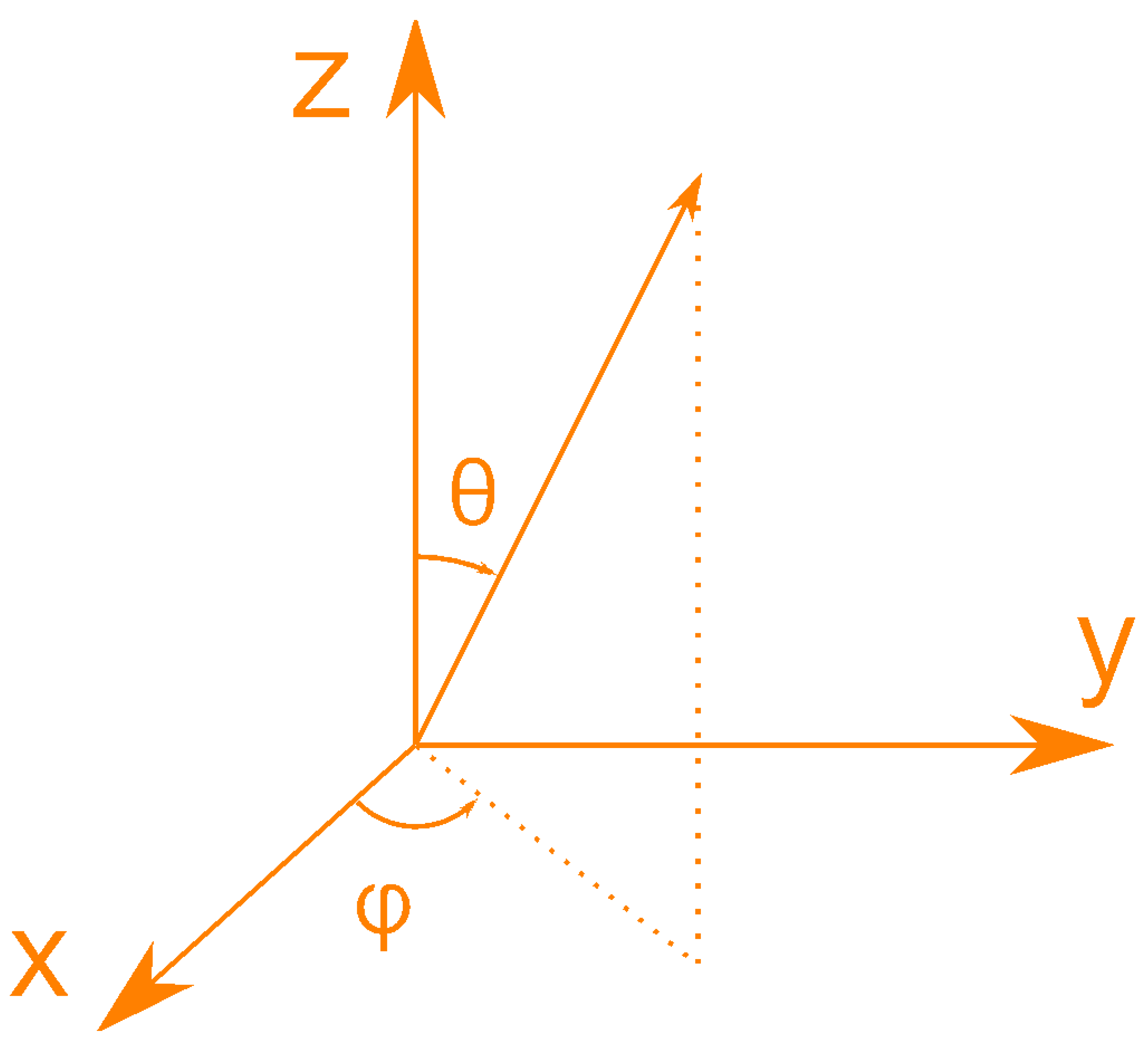
  • GSCS requires three parameters (R, θ and ϕ ) for all atoms to construct a protein structural model, because GSCS takes the centroid of the protein molecule as origin, where R is used to signify the distance between the centroid (an imaginary point) and any atom of the protein.
  • IASCS requires two parameters ( θ and ϕ ) to construct a protein structural model, because
    (a)
    IASCS takes into account the fact that protein backbone structure essentially is a network of covalently bonded atoms.
    (b)
    IASCS defines ρ as the equilibrium inter-atomic covalent bond length [92,93].
    (c)
    For a protein with unknown structure, our knowledge of its X, Y and Z is zero, which is untrue of our knowledge of its ρ [92,93].
  • Neither CCS nor GSCS take into account the inter-atomic covalent bonding network of protein backbone structures.

4. Results

In short, this article puts forward a reversible spherical geometric conversion method, which offers a promising approach for extracting essential structural features from protein backbone coordinate matrices by transforming Cartesian coordinates into spherical coordinates represented by radial distance ( ρ ), polar angle ( θ ), and azimuthal angle ( ϕ ). Specifically, the extraction of essential structural features from the backbone of all 15 structural models of Caenopore-5 [95,96,98] inculde:
  • the distribution pattern of the lengths ( ρ ) of 477 covalent bonds of the backbone of Caenopore-5 [95,96,98] as reversibly extracted from the 15 NMR structural models of the three-dimensional NMR ensemble of Caenopore-5 (PDB ID: 2JSA) [95,96,98], as shown by Figure 6;
  • the distribution pattern of the azimuthal angle ( θ ) of 477 covalent bonds of the backbone of Caenopore-5 [95,96,98] as reversibly extracted from the 15 NMR structural models of the three-dimensional NMR ensemble of Caenopore-5 (PDB ID: 2JSA) [95,96,98], as shown by Figure 7;
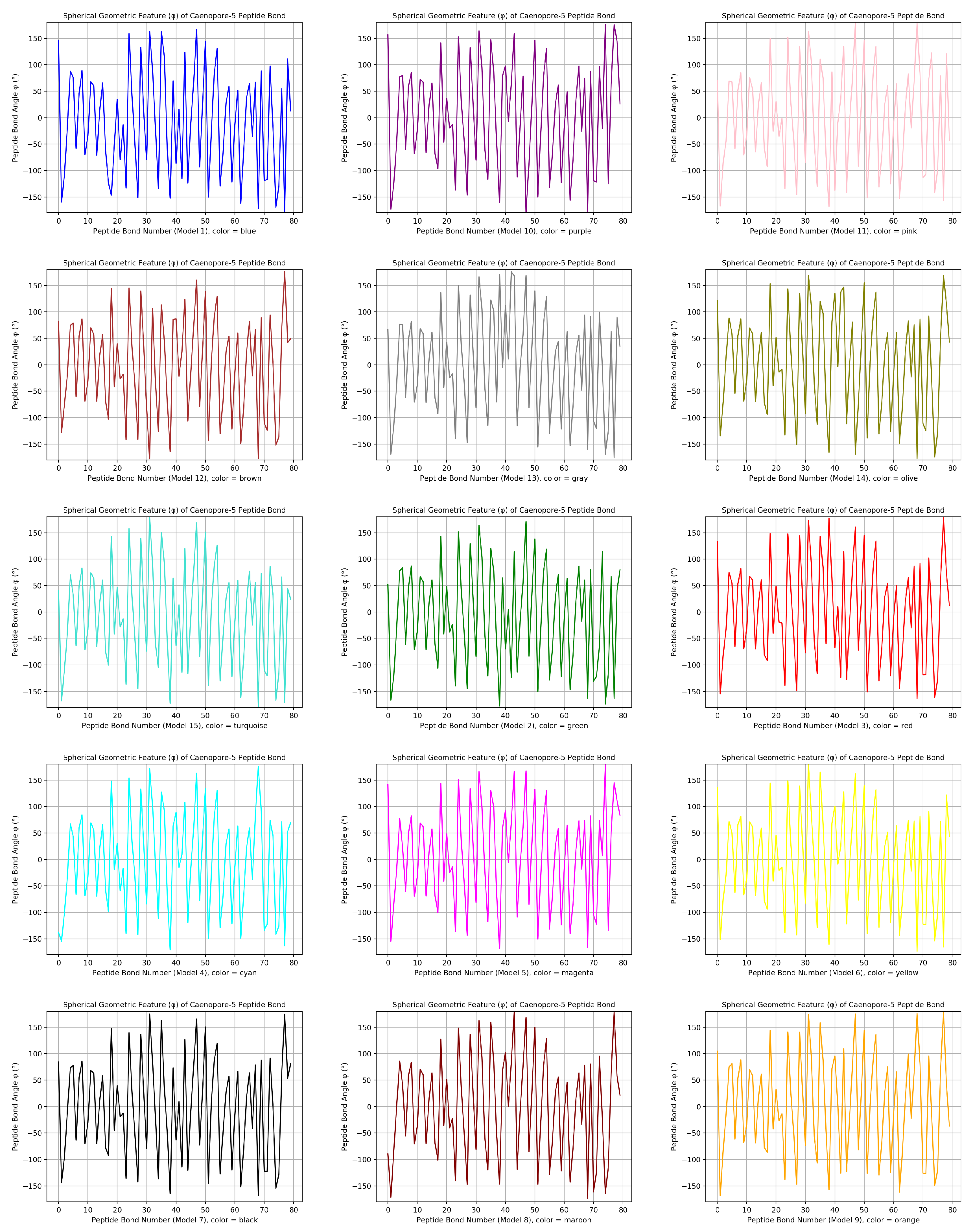
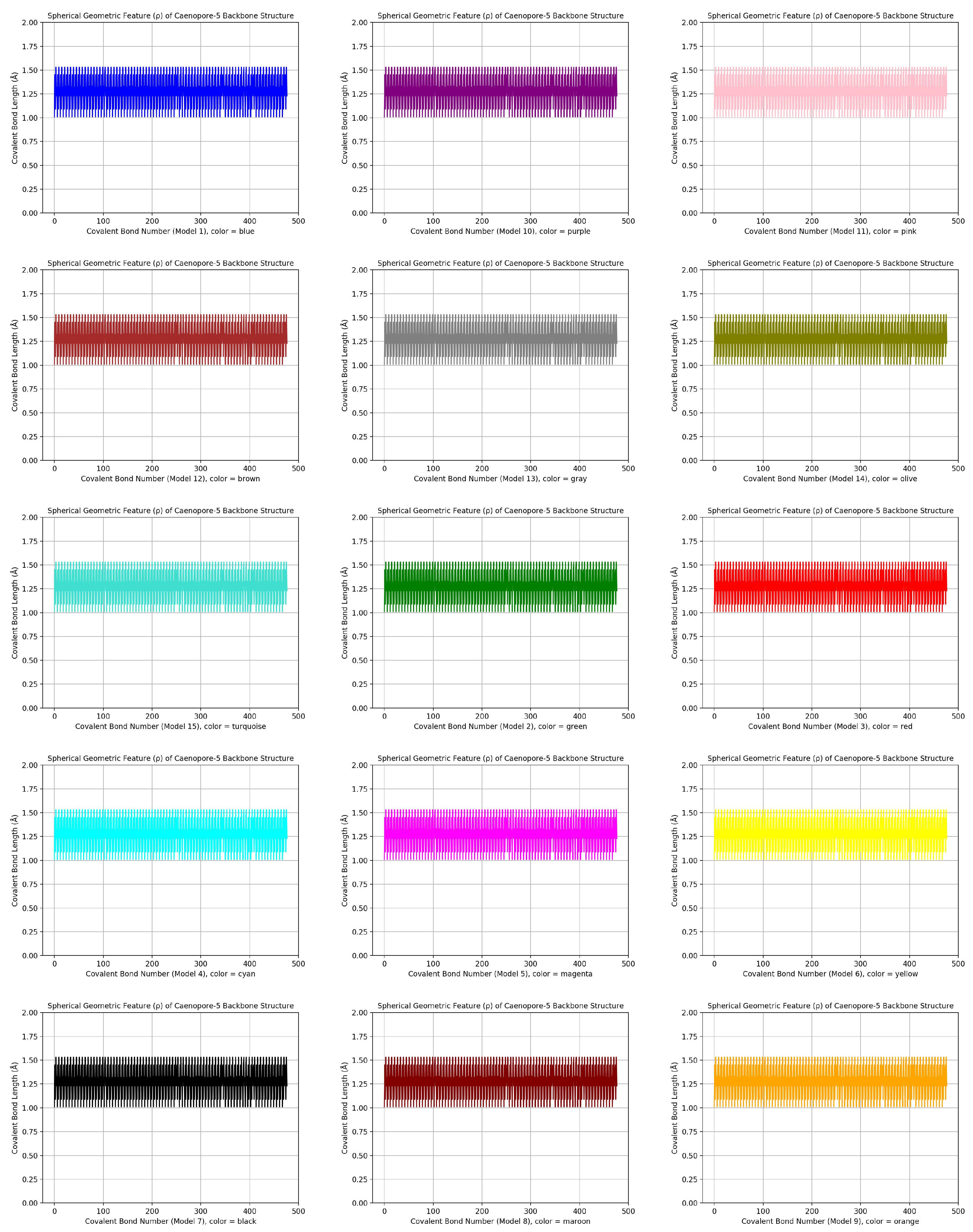
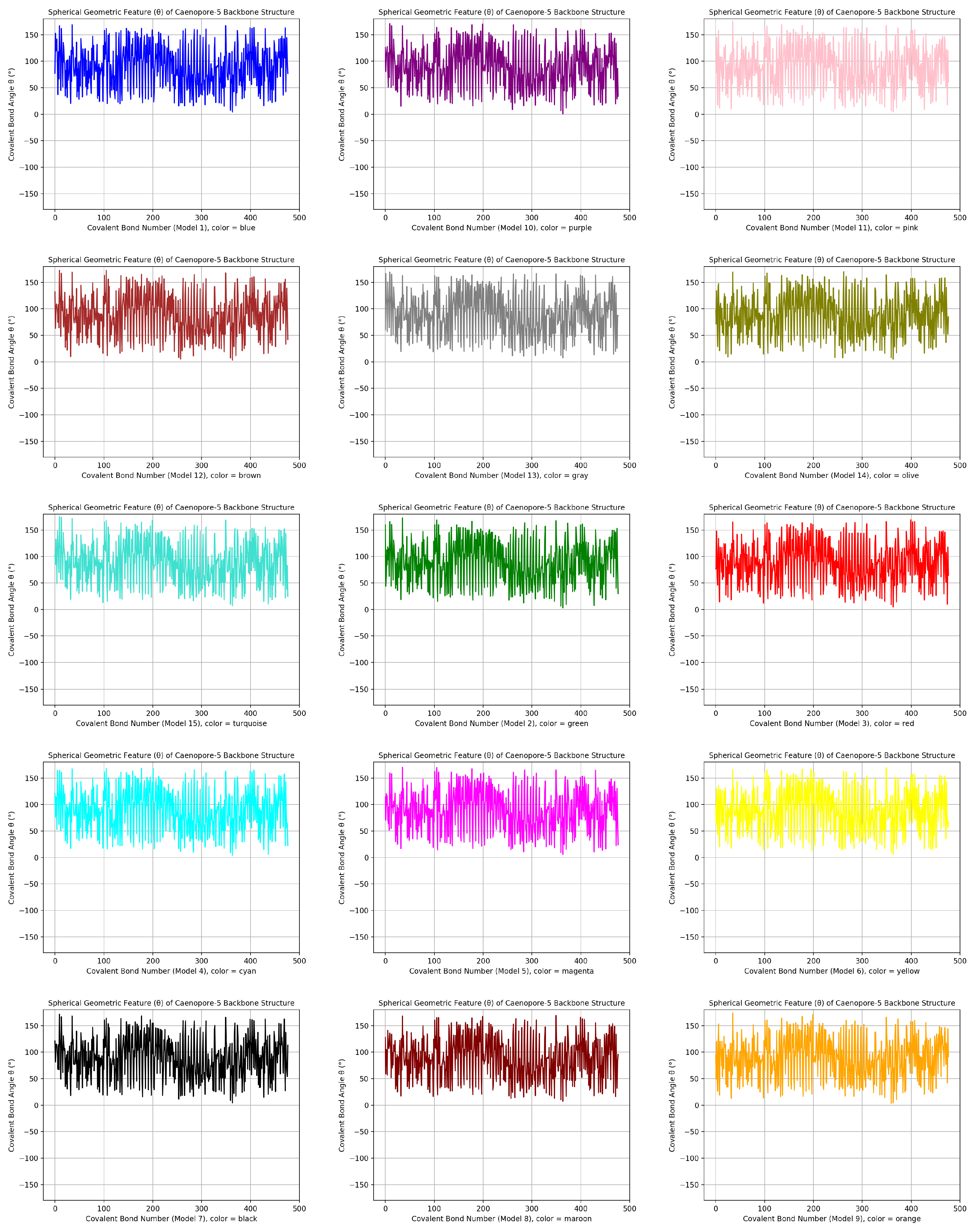
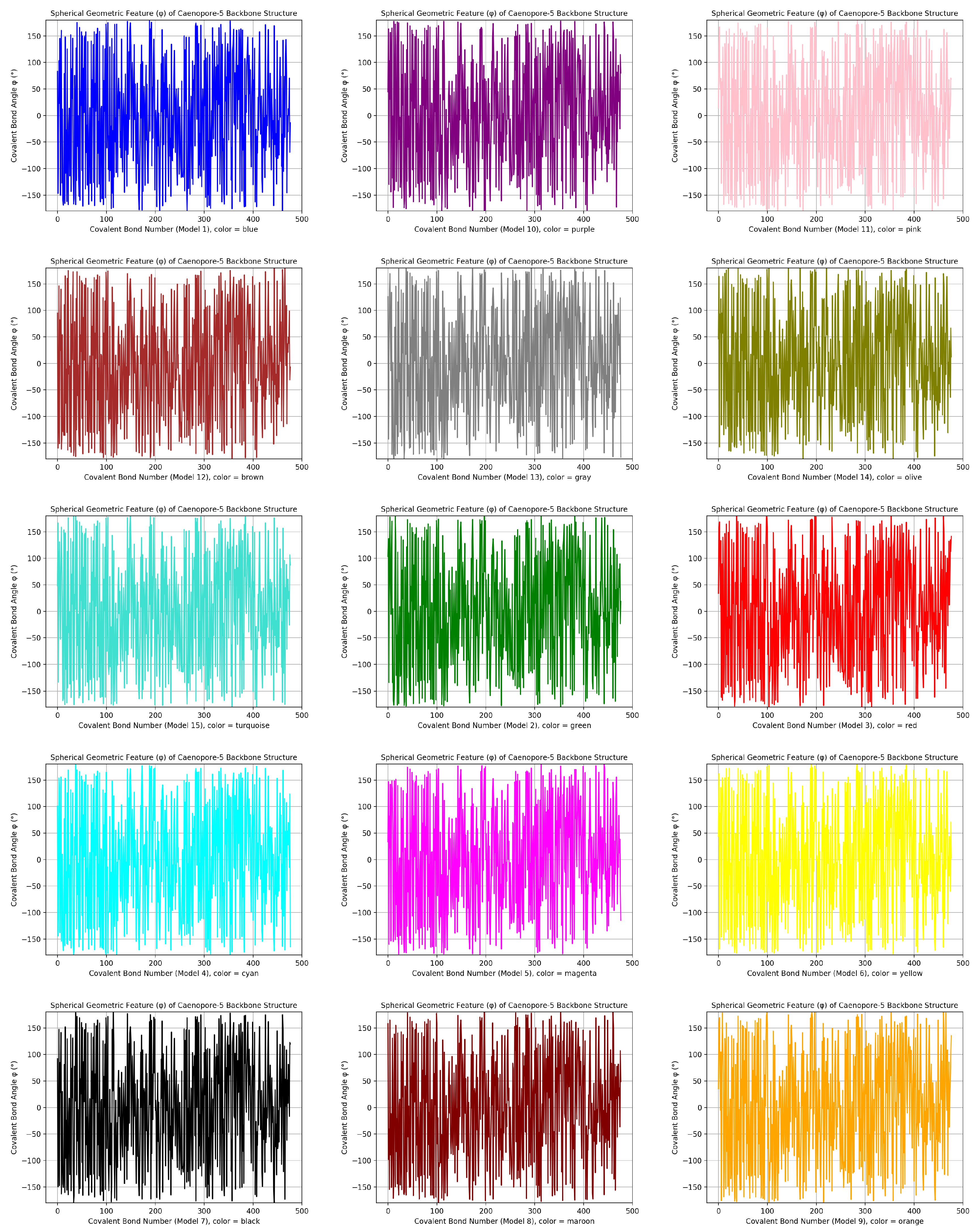
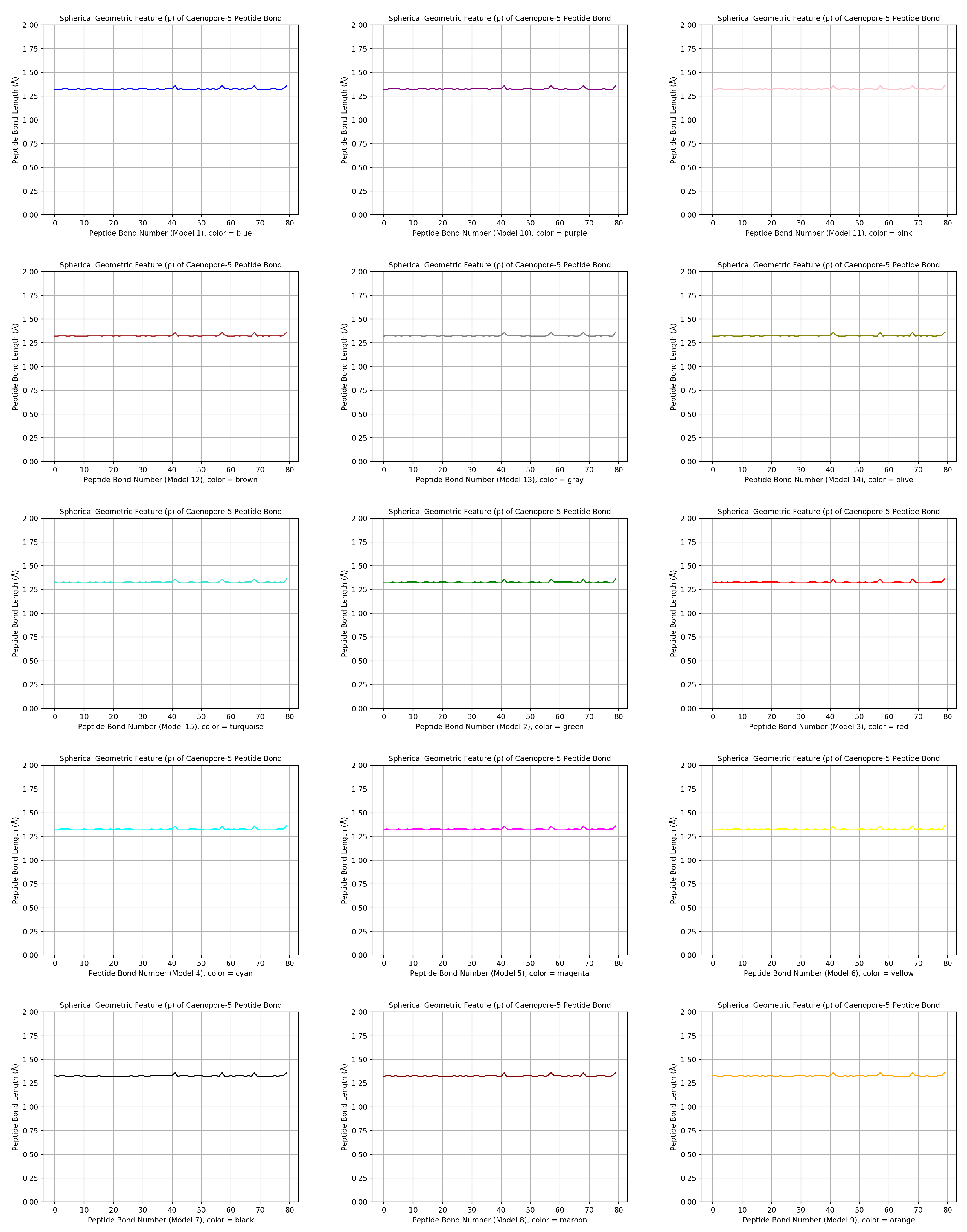
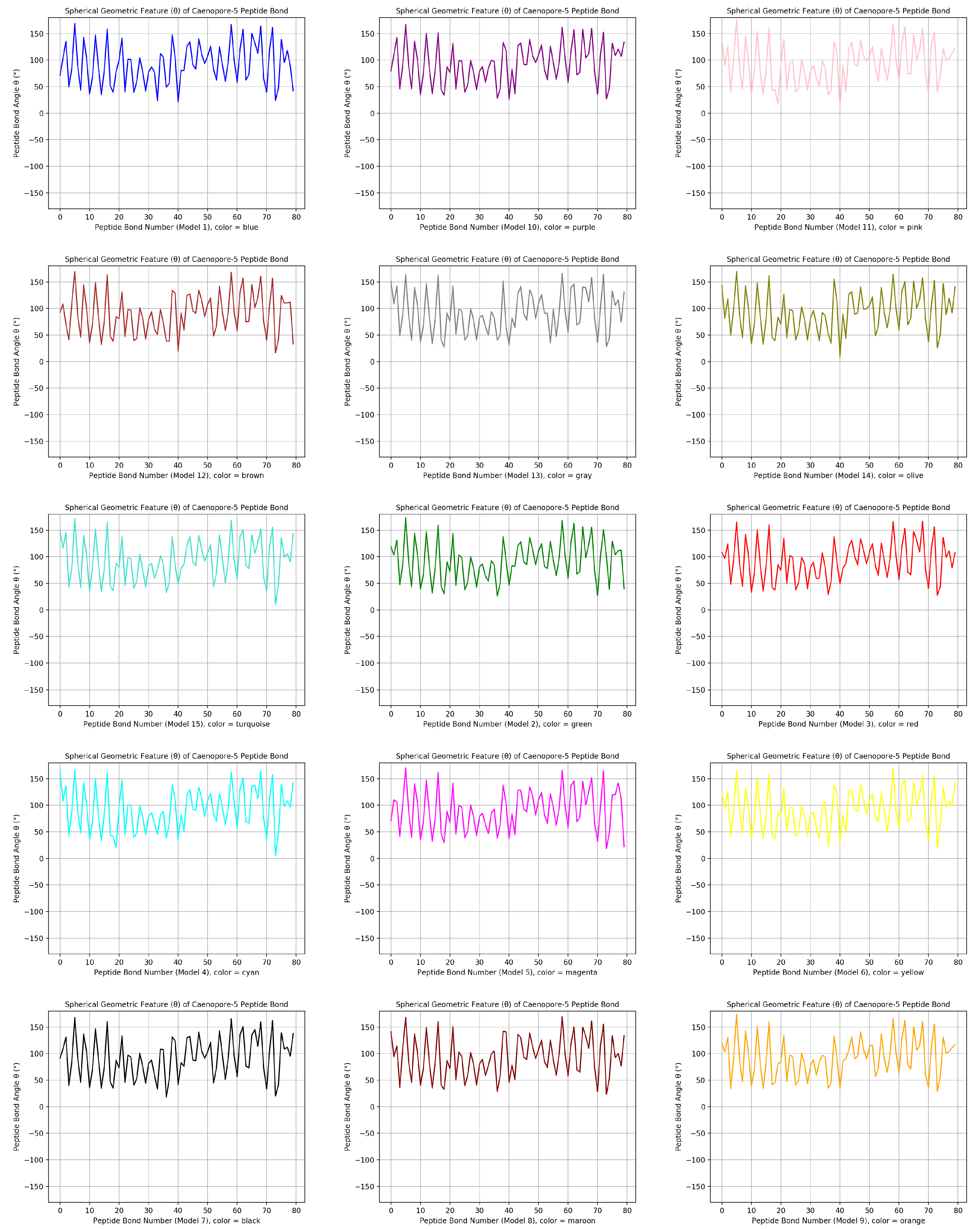
  • the distribution pattern of the polar angle (also known as the zenith angle, ϕ ) of 477 covalent bonds of the backbone of Caenopore-5 [95,96,98] as reversibly extracted from the 15 NMR structural models of the three-dimensional NMR ensemble of Caenopore-5 (PDB ID: 2JSA) [95,96,98], as shown by Figure 8;
  • the distribution pattern of the lengths ( ρ ) of 80 peptide bonds (Figure 5) of Caenopore-5 [95,96,98] as reversibly extracted from the 15 NMR structural models of the three-dimensional NMR ensemble of Caenopore-5 (PDB ID: 2JSA) [95,96,98], as shown by Figure 9;
  • the distribution pattern of the azimuthal angle ( θ ) of 80 peptide bonds (Figure 5) of Caenopore-5 [95,96,98] as reversibly extracted from the 15 NMR structural models of the three-dimensional NMR ensemble of Caenopore-5 (PDB ID: 2JSA) [95,96,98], as shown by Figure 10;
  • the distribution pattern of the polar angle (also known as the zenith angle, ϕ ) of 80 peptide bonds (Figure 5) of Caenopore-5 [95,96,98] as reversibly extracted from the 15 NMR structural models of the three-dimensional NMR ensemble of Caenopore-5 (PDB ID: 2JSA) [95,96,98], as shown by Figure 11;
In the broader context, this work contributes to the ongoing efforts in advancing the field of computational biology and protein structure prediction as the proposed IASCS (i.e., the local ρ - θ - ϕ approach) opens up new avenues for research in feature extraction and protein structure prediction algorithm design, paving the way for more accurate and efficient prediction of protein structures:
  • the reversible nature of the spherical geometric conversion ensures that no information is lost during the geometric coordinate transformation process, preserving the fidelity of the original protein backbone structure and ensuring that it is able to be reconstructed using the extracted IASCS features (local ρ , θ and ϕ values). This feature is crucial for maintaining prediction accuracy and enabling further analysis of the extracted structural features for its future application in protein structure prediction [13,14,15,16,17,18,101].
  • the compact representation offered by spherical coordinates with Caenopore-5 as an example enhances computational efficiency, making our method suitable for large-scale (for both PDB and AlphaFoldDB) protein structure prediction tasks for the entire protein molecular space [47,102,103,104,105,106,107,108,109].
  • lastly, the intuitive nature of spherical coordinates also aids in the interpretation of structural features, potentially offering insights into the underlying principles governing protein folding and function [16,110,111,112,113,114,115,116,117,118].

5. Conclusion

In conclusion, the reversible spherical geometric conversion method presented in this manuscript offers a promising approach for extracting essential structural features [119] from protein backbone coordinate matrices [120]. By transforming Cartesian coordinates into spherical coordinates represented by radial distance ( ρ ), polar angle ( θ ), and azimuthal angle ( ϕ ), our method provides a more intuitive representation of protein geometry. This approach facilitates the design of algorithms for protein structure prediction by enabling the extraction of meaningful structural features [10,121,122,123,124,125,126].

6. Discussion

To date, while ∼ 217,966 experimental structures and ∼ 1,068,577 computed structures represent a big fraction of the entire protein molecular space [21,102,127], accurate computational approaches are still needed to address this gap and to enable large-scale structural bioinformatics [21]. Three years ago, with the advent of AlphaFold2 and RosettaFold [21,22,23,128,129], 2021 saw a big step forward in the development of protein structure prediction (PSP) [130,131,132,133]. While the progresses in PSP have ebbed and flowed historically, the past two years saw dramatic advances driven by the increasing neuralization [22] of PSP algorithms, whereby computations previously based on energy models and sampling procedures are replaced by neural networks [134,135,136,137,138,139,140,141,142,143,144,145,146].
As discussed previously in [89], distance is the data which is plugged into neuralized [22] algorithms to build a structural model of a protein. To improve the quality of the model, algorithm and data are like two sides of one coin. Geometrically, CCS and SCS are like two sides of one coin, too. Focusing on the improvement of algorithms (e.g., neuralization [22]) alone is probably not enough, unless we flip the coin over and take a look at the other side, i.e., data and IASCS, which allow us to extract two spherical structural features ( θ and ϕ ) from any protein with experimentally determined structure [147,148,149,150,151]. With the redefinition of protein backbone structure with ρ , θ and ϕ here, future work may involve exploring extensions of the spherical geometric conversion method to incorporate additional structural information, such as side-chain interactions and solvent accessibility, including the design of side chain placement algorithms with improved performance. Additionally, further validation on experimentally determined protein structures and comparison with existing methods will help assess the robustness and generalizability of the ρ - θ - ϕ approach [89,152].

Ethical statement:

No ethical approval is required.

Declaration of generative AI and AI-assisted technologies in the writing process

During the preparation of this work, the author used OpenAI’s ChatGPT in order to improve the readability of the manuscript, and to make it as concise and short as possible. After using this tool, the author reviewed and edited the content as needed and takes full responsibility for the content of the publication.

Author Contributions

Conceptualization, W.L.; methodology, W.L.; software, W.L.; validation, W.L.; formal analysis, W.L.; investigation, W.L.; resources, W.L.; data duration, W.L.; writing–original draft preparation, W.L.; writing–review and editing, W.L.; visualization, W.L.; supervision, W.L.; project administration, W.L.; funding acquisition, not applicable.

Funding

This research received no external funding.

Acknowledgments

I thank the whole structural biology community, whose continued contribution is priceless to our continued understanding, both structural and functional, of the proteios building block of life.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. van Keulen, S.C.; Bonvin, A.M.J.J. Improving the quality of co-evolution intermolecular contact prediction with DisVis. Proteins: Structure, Function, and Bioinformatics 2023, 91, 1407–1416. [Google Scholar] [CrossRef] [PubMed]
  2. Hess, R.; Faessler, J.; Yun, D.; Saleh, D.; Grosch, J.H.; Schwab, T.; Hubbuch, J. Antibody sequence-based prediction of pH gradient elution in multimodal chromatography. Journal of Chromatography A 2023, 1711, 464437. [Google Scholar] [CrossRef] [PubMed]
  3. Tesei, G.; Trolle, A.I.; Jonsson, N.; Betz, J.; Knudsen, F.E.; Pesce, F.; Johansson, K.E.; Lindorff-Larsen, K. Conformational ensembles of the human intrinsically disordered proteome. Nature 2024, 626, 897–904. [Google Scholar] [CrossRef] [PubMed]
  4. Zhao, H.; Du, H.; Zhao, S.; Chen, Z.; Li, Y.; Xu, K.; Liu, B.; Cheng, X.; Wen, W.; Li, G.; Chen, G.; Zhao, Z.; Qiu, G.; Liu, P.; Zhang, T.J.; Wu, Z.; Wu, N. SIGMA leverages protein structural information to predict the pathogenicity of missense variants. Cell Reports Methods 2024, 4, 100687. [Google Scholar] [CrossRef] [PubMed]
  5. El Badaoui, L.; Barr, A.J. Analysis of Receptor-Type Protein Tyrosine Phosphatase Extracellular Regions with Insights from AlphaFold. International Journal of Molecular Sciences 2024, 25, 820. [Google Scholar] [CrossRef] [PubMed]
  6. Meller, A.; De Oliveira, S.; Davtyan, A.; Abramyan, T.; Bowman, G.R.; van den Bedem, H. Discovery of a cryptic pocket in the AI-predicted structure of PPM1D phosphatase explains the binding site and potency of its allosteric inhibitors. Frontiers in Molecular Biosciences 2023, 10. [Google Scholar] [CrossRef] [PubMed]
  7. Huber, S.T.; Jakobi, A.J. Structural biology of microbial gas vesicles: historical milestones and current knowledge. Biochemical Society Transactions 2024, 52, 205–215. [Google Scholar] [CrossRef] [PubMed]
  8. Gordon, C.H.; Hendrix, E.; He, Y.; Walker, M.C. AlphaFold Accurately Predicts the Structure of Ribosomally Synthesized and Post-Translationally Modified Peptide Biosynthetic Enzymes. Biomolecules 2023, 13, 1243. [Google Scholar] [CrossRef] [PubMed]
  9. Huang, B.; Kong, L.; Wang, C.; Ju, F.; Zhang, Q.; Zhu, J.; Gong, T.; Zhang, H.; Yu, C.; Zheng, W.M.; Bu, D. Protein Structure Prediction: Challenges, Advances, and the Shift of Research Paradigms. Genomics, Proteomics & Bioinformatics 2023, 21, 913–925. [Google Scholar] [CrossRef]
  10. Koehler Leman, J.; Künze, G. Recent Advances in NMR Protein Structure Prediction with ROSETTA. International Journal of Molecular Sciences 2023, 24, 7835. [Google Scholar] [CrossRef]
  11. Rachitskii, P.; Kruglov, I.; Finkelstein, A.V.; Oganov, A.R. Protein structure prediction using the evolutionary algorithm USPEX. Proteins: Structure, Function, and Bioinformatics 2023, 91, 933–943. [Google Scholar] [CrossRef] [PubMed]
  12. Wuyun, Q.; Chen, Y.; Shen, Y.; Cao, Y.; Hu, G.; Cui, W.; Gao, J.; Zheng, W. Recent Progress of Protein Tertiary Structure Prediction. Molecules 2024, 29, 832. [Google Scholar] [CrossRef] [PubMed]
  13. Hameduh, T.; Mokry, M.; Miller, A.D.; Heger, Z.; Haddad, Y. Solvent Accessibility Promotes Rotamer Errors during Protein Modeling with Major Side-Chain Prediction Programs. Journal of Chemical Information and Modeling 2023, 63, 4405–4422. [Google Scholar] [CrossRef] [PubMed]
  14. Wu, T.; Guo, Z.; Cheng, J. Atomic protein structure refinement using all-atom graph representations and SE(3)-equivariant graph transformer. Bioinformatics 2023, 39. [Google Scholar] [CrossRef] [PubMed]
  15. Schafer, J.W.; Porter, L.L. Evolutionary selection of proteins with two folds. Nature Communications 2023, 14. [Google Scholar] [CrossRef] [PubMed]
  16. Zhang, Z.; Gao, S.; Lei, Z.; Xiong, R.; Cheng, J. Pareto Dominance Archive and Coordinated Selection Strategy-Based Many-Objective Optimizer for Protein Structure Prediction. IEEE/ACM Transactions on Computational Biology and Bioinformatics 2023, 20, 2328–2340. [Google Scholar] [CrossRef] [PubMed]
  17. Du, K.; Huang, H. Development of anti-PD-L1 antibody based on structure prediction of AlphaFold2. Frontiers in Immunology 2023, 14. [Google Scholar] [CrossRef] [PubMed]
  18. Mutz, P.; Resch, W.; Faure, G.; Senkevich, T.G.; Koonin, E.V.; Moss, B. Exaptation of Inactivated Host Enzymes for Structural Roles in Orthopoxviruses and Novel Folds of Virus Proteins Revealed by Protein Structure Modeling. mBio 2023, 14. [Google Scholar] [CrossRef] [PubMed]
  19. Biasini, M.; Bienert, S.; Waterhouse, A.; Arnold, K.; Studer, G.; Schmidt, T.; Kiefer, F.; Cassarino, T.G.; Bertoni, M.; Bordoli, L.; Schwede, T. SWISS-MODEL: modelling protein tertiary and quaternary structure using evolutionary information. Nucleic Acids Research 2014, 42, W252–W258. [Google Scholar] [CrossRef] [PubMed]
  20. Webb, B.; Sali, A. Protein Structure Modeling with MODELLER. In Methods in Molecular Biology; Springer US, 2020; pp. 239–255.
  21. Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; Bridgland, A.; Meyer, C.; Kohl, S.A.A.; Ballard, A.J.; Cowie, A.; Romera-Paredes, B.; Nikolov, S.; Jain, R.; Adler, J.; Back, T.; Petersen, S.; Reiman, D.; Clancy, E.; Zielinski, M.; Steinegger, M.; Pacholska, M.; Berghammer, T.; Bodenstein, S.; Silver, D.; Vinyals, O.; Senior, A.W.; Kavukcuoglu, K.; Kohli, P.; Hassabis, D. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef] [PubMed]
  22. AlQuraishi, M. Machine learning in protein structure prediction. Current Opinion in Chemical Biology 2021, 65, 1–8. [Google Scholar] [CrossRef] [PubMed]
  23. AlQuraishi, M. AlphaFold at CASP13. Bioinformatics 2019, 35, 4862–4865. [Google Scholar] [CrossRef] [PubMed]
  24. Djulbegovic, M.; Taylor Gonzalez, D.J.; Antonietti, M.; Uversky, V.N.; Shields, C.L.; Karp, C.L. Intrinsic disorder may drive the interaction of PROS1 and MERTK in uveal melanoma. International Journal of Biological Macromolecules 2023, 250, 126027. [Google Scholar] [CrossRef] [PubMed]
  25. Yang, S.; Gong, W.; Zhou, T.; Sun, X.; Chen, L.; Zhou, W.; Li, C. emPDBA: protein-DNA binding affinity prediction by combining features from binding partners and interface learned with ensemble regression model. Briefings in Bioinformatics 2023, 24. [Google Scholar] [CrossRef] [PubMed]
  26. Choudhury, J.; Yonezawa, K.; Anu, A.; Shimizu, N.; Chaudhuri, B. SAXS/WAXS data of conformationally flexible ribose binding protein. Data in Brief 2024, 52, 109932. [Google Scholar] [CrossRef]
  27. Qi, H.; Yu, T.; Yu, W.; Liu, C. Drug–target affinity prediction with extended graph learning-convolutional networks. BMC Bioinformatics 2024, 25. [Google Scholar] [CrossRef] [PubMed]
  28. Reggiano, G.; Lugmayr, W.; Farrell, D.; Marlovits, T.C.; DiMaio, F. Residue-level error detection in cryoelectron microscopy models. Structure 2023, 31, 860–869.e4. [Google Scholar] [CrossRef] [PubMed]
  29. Ravnik, V.; Jukič, M.; Bren, U. Identifying Metal Binding Sites in Proteins Using Homologous Structures, the MADE Approach. Journal of Chemical Information and Modeling 2023, 63, 5204–5219. [Google Scholar] [CrossRef] [PubMed]
  30. Szikszai, M.; Magnus, M.; Sanghi, S.; Kadyan, S.; Bouatta, N.; Rivas, E. RNA3DB: A structurally-dissimilar dataset split for training and benchmarking deep learning models for RNA structure prediction 2024. [CrossRef]
  31. Garcia-Pardo, J.; Badaczewska-Dawid, A.E.; Pintado-Grima, C.; Iglesias, V.; Kuriata, A.; Kmiecik, S.; Ventura, S. A3DyDB: exploring structural aggregation propensities in the yeast proteome. Microbial Cell Factories 2023, 22. [Google Scholar] [CrossRef] [PubMed]
  32. Sassanarakkit, S.; Peerapen, P.; Thongboonkerd, V. OxaBIND: A tool for identifying oxalate-binding domain(s)/motif(s) in protein(s). International Journal of Biological Macromolecules 2023, 243, 125275. [Google Scholar] [CrossRef]
  33. Kumar, A.; Kaynak, B.T.; Dorman, K.S.; Doruker, P.; Jernigan, R.L. Predicting allosteric pockets in protein biological assemblages. Bioinformatics 2023, 39. [Google Scholar] [CrossRef] [PubMed]
  34. Kamga Youmbi, F.I.; Kengne Tchendji, V.; Tayou Djamegni, C. P-FARFAR2: A multithreaded greedy approach to sampling low-energy RNA structures in Rosetta FARFAR2. Computational Biology and Chemistry 2023, 104, 107878. [Google Scholar] [CrossRef] [PubMed]
  35. Kurniawan, J.; Ishida, T. Comparing Supervised Learning and Rigorous Approach for Predicting Protein Stability upon Point Mutations in Difficult Targets. Journal of Chemical Information and Modeling 2023, 63, 6778–6788. [Google Scholar] [CrossRef] [PubMed]
  36. Nikam, R.; Yugandhar, K.; Gromiha, M.M. Deep learning-based method for predicting and classifying the binding affinity of protein-protein complexes. Biochimica et Biophysica Acta (BBA) - Proteins and Proteomics 2023, 1871, 140948. [Google Scholar] [CrossRef] [PubMed]
  37. Guo, Z.; Wang, Y.; Ou, G. Utilizing the scale-invariant feature transform algorithm to align distance matrices facilitates systematic protein structure comparison. Bioinformatics 2024, 40. [Google Scholar] [CrossRef] [PubMed]
  38. Hatano, Y.; Ishihara, T.; Onodera, O. Accuracy of a machine learning method based on structural and locational information from AlphaFold2 for predicting the pathogenicity of TARDBP and FUS gene variants in ALS. BMC Bioinformatics 2023, 24. [Google Scholar] [CrossRef] [PubMed]
  39. Manfredi, M.; Savojardo, C.; Martelli, P.L.; Casadio, R. ISPRED-SEQ: Deep Neural Networks and Embeddings for Predicting Interaction Sites in Protein Sequences. Journal of Molecular Biology 2023, 435, 167963. [Google Scholar] [CrossRef]
  40. Lichtinger, S.M.; Biggin, P.C. Tackling Hysteresis in Conformational Sampling: How to Be Forgetful with MEMENTO. Journal of Chemical Theory and Computation 2023, 19, 3705–3720. [Google Scholar] [CrossRef] [PubMed]
  41. Schweke, H.; Pacesa, M.; Levin, T.; Goverde, C.A.; Kumar, P.; Duhoo, Y.; Dornfeld, L.J.; Dubreuil, B.; Georgeon, S.; Ovchinnikov, S.; Woolfson, D.N.; Correia, B.E.; Dey, S.; Levy, E.D. An atlas of protein homo-oligomerization across domains of life. Cell 2024, 187, 999–1010.e15. [Google Scholar] [CrossRef] [PubMed]
  42. King, J.E.; Koes, D.R. Interpreting forces as deep learning gradients improves quality of predicted protein structures. Biophysical Journal 2023. [Google Scholar] [CrossRef] [PubMed]
  43. Boadu, F.; Cao, H.; Cheng, J. Combining protein sequences and structures with transformers and equivariant graph neural networks to predict protein function. Bioinformatics 2023, 39, i318–i325. [Google Scholar] [CrossRef] [PubMed]
  44. Brixi, G.; Ye, T.; Hong, L.; Wang, T.; Monticello, C.; Lopez-Barbosa, N.; Vincoff, S.; Yudistyra, V.; Zhao, L.; Haarer, E.; Chen, T.; Pertsemlidis, S.; Palepu, K.; Bhat, S.; Christopher, J.; Li, X.; Liu, T.; Zhang, S.; Petersen, L.; DeLisa, M.P.; Chatterjee, P. SaLT&PepPr is an interface-predicting language model for designing peptide-guided protein degraders. Communications Biology 2023, 6. [Google Scholar] [CrossRef]
  45. Mulvaney, T.; Kretsch, R.C.; Elliott, L.; Beton, J.G.; Kryshtafovych, A.; Rigden, D.J.; Das, R.; Topf, M. CASP15 cryo-EM protein and RNA targets: Refinement and analysis using experimental maps. Proteins: Structure, Function, and Bioinformatics 2023, 91, 1935–1951. [Google Scholar] [CrossRef]
  46. Edmunds, N.S.; Alharbi, S.M.A.; Genc, A.G.; Adiyaman, R.; McGuffin, L.J. Estimation of model accuracy in CASP15 using the ModFOLDdock server. Proteins: Structure, Function, and Bioinformatics 2023, 91, 1871–1878. [Google Scholar] [CrossRef] [PubMed]
  47. Song, Y.; Zhang, C.; Omenn, G.S.; O’Meara, M.J.; Welch, J.D. Predicting the Structural Impact of Human Alternative Splicing 2023. [CrossRef]
  48. Maloney, A.; Joseph, S. Validating the EMCV IRES Secondary Structure with Structure–Function Analysis. Biochemistry 2023, 63, 107–115. [Google Scholar] [CrossRef]
  49. Shanker, S.; Sanner, M.F. Predicting Protein–Peptide Interactions: Benchmarking Deep Learning Techniques and a Comparison with Focused Docking. Journal of Chemical Information and Modeling 2023, 63, 3158–3170. [Google Scholar] [CrossRef] [PubMed]
  50. Han, S.R.; Park, M.; Kosaraju, S.; Lee, J.; Lee, H.; Lee, J.H.; Oh, T.J.; Kang, M. Evidential deep learning for trustworthy prediction of enzyme commission number. Briefings in Bioinformatics 2023, 25. [Google Scholar] [CrossRef]
  51. Nikam, R.; Yugandhar, K.; Gromiha, M.M. DeepBSRPred: deep learning-based binding site residue prediction for proteins. Amino Acids 2022, 55, 1305–1316. [Google Scholar] [CrossRef] [PubMed]
  52. Mikhaylov, V.; Brambley, C.A.; Keller, G.L.; Arbuiso, A.G.; Weiss, L.I.; Baker, B.M.; Levine, A.J. Accurate modeling of peptide-MHC structures with AlphaFold. Structure 2024, 32, 228–241. [Google Scholar] [CrossRef]
  53. Meller, A.; Kelly, D.; Smith, L.G.; Bowman, G.R. Toward physics-based precision medicine: Exploiting protein dynamics to design new therapeutics and interpret variants. Protein Science 2024, 33. [Google Scholar] [CrossRef] [PubMed]
  54. Li, W. Structural and Functional Consequences of the SMA-Linked Missense Mutations of the Survival Motor Neuron Protein: A Brief Update. In Novel Aspects on Motor Neuron Disease [Working Title]; IntechOpen, 2019.
  55. Li, W. Inter-Molecular Electrostatic Interactions Stabilizing the Structure of the PD-1/PD-L1 Axis: A Structural Evolutionary Perspective 2020.
  56. Li, W. Calcium Channel Trafficking Blocker Gabapentin Bound to the α-2-δ-1 Subunit of Voltage-Gated Calcium Channel: A Computational Structural Investigation 2020.
  57. Li, W. Structural Identification of the Electrostatic Hot Spots for Severe Acute Respiratory Syndrome Coronavirus Spike Protein to Be Complexed with Its Receptor ACE2 and Its Neutralizing Antibodies 2020.
  58. Li, W. Strengthening Semaglutide-GLP-1R Binding Affinity via a Val27-Arg28 Exchange in the Peptide Backbone of Semaglutide: A Computational Structural Approach. Journal of Computational Biophysics and Chemistry 2021, 20, 495–499. [Google Scholar] [CrossRef]
  59. Li, W. Delving deep into the structural aspects of a furin cleavage site inserted into the spike protein of SARS-CoV-2: A structural biophysical perspective. Biophysical Chemistry 2020, 264, 106420. [Google Scholar] [CrossRef]
  60. Li, W. Delving Deep into the Structural Aspects of the BPro28-BLys29 Exchange in Insulin Lispro: A Structural Biophysical Lesson 2020.
  61. Jänes, J.; Beltrao, P. Deep learning for protein structure prediction and design—progress and applications. Molecular Systems Biology 2024, 20, 162–169. [Google Scholar] [CrossRef]
  62. Kim, Y.; Kwon, J. AttSec: protein secondary structure prediction by capturing local patterns from attention map. BMC Bioinformatics 2023, 24. [Google Scholar] [CrossRef] [PubMed]
  63. Zhang, Y.; Li, S.; Meng, K.; Sun, S. Machine Learning for Sequence and Structure-Based Protein–Ligand Interaction Prediction. Journal of Chemical Information and Modeling 2024, 64, 1456–1472. [Google Scholar] [CrossRef] [PubMed]
  64. Ooka, K.; Arai, M. Accurate prediction of protein folding mechanisms by simple structure-based statistical mechanical models. Nature Communications 2023, 14. [Google Scholar] [CrossRef] [PubMed]
  65. Peng, C.X.; Liang, F.; Xia, Y.H.; Zhao, K.L.; Hou, M.H.; Zhang, G.J. Recent Advances and Challenges in Protein Structure Prediction. Journal of Chemical Information and Modeling 2023, 64, 76–95. [Google Scholar] [CrossRef] [PubMed]
  66. Leemann, M.; Sagasta, A.; Eberhardt, J.; Schwede, T.; Robin, X.; Durairaj, J. Automated benchmarking of combined protein structure and ligand conformation prediction. Proteins: Structure, Function, and Bioinformatics 2023, 91, 1912–1924. [Google Scholar] [CrossRef] [PubMed]
  67. Versini, R.; Sritharan, S.; Aykac Fas, B.; Tubiana, T.; Aimeur, S.Z.; Henri, J.; Erard, M.; Nüsse, O.; Andreani, J.; Baaden, M.; Fuchs, P.; Galochkina, T.; Chatzigoulas, A.; Cournia, Z.; Santuz, H.; Sacquin-Mora, S.; Taly, A. A Perspective on the Prospective Use of AI in Protein Structure Prediction. Journal of Chemical Information and Modeling 2023, 64, 26–41. [Google Scholar] [CrossRef] [PubMed]
  68. Jiao, P.; Wang, B.; Wang, X.; Liu, B.; Wang, Y.; Li, J. Struct2GO: protein function prediction based on graph pooling algorithm and AlphaFold2 structure information. Bioinformatics 2023, 39. [Google Scholar] [CrossRef] [PubMed]
  69. Wu, J.; Yan, Z.; Li, Z.; Qian, X.; Lu, S.; Dong, M.; Zhou, Q.; Yan, N. Structure of the voltage-gated calcium channel CaV1.1 at 3.6 Å resolution. Nature 2016, 537, 191–196. [Google Scholar] [CrossRef] [PubMed]
  70. Zhao, Y.; Huang, G.; Wu, J.; Wu, Q.; Gao, S.; Yan, Z.; Lei, J.; Yan, N. Molecular Basis for Ligand Modulation of a Mammalian Voltage-Gated Ca2+ Channel. Cell 2019, 177, 1495–1506.e12. [Google Scholar] [CrossRef] [PubMed]
  71. Catterall, W.A. Structure and Regulation of Voltage-Gated Ca2+ Channels. Annual Review of Cell and Developmental Biology 2000, 16, 521–555. [Google Scholar] [CrossRef] [PubMed]
  72. Farmer, J.; Kanwal, F.; Nikulsin, N.; Tsilimigras, M.; Jacobs, D. Statistical Measures to Quantify Similarity between Molecular Dynamics Simulation Trajectories. Entropy 2017, 19, 646. [Google Scholar] [CrossRef]
  73. Zheng, L.; Shi, S.; Sun, X.; Lu, M.; Liao, Y.; Zhu, S.; Zhang, H.; Pan, Z.; Fang, P.; Zeng, Z.; Li, H.; Li, Z.; Xue, W.; Zhu, F. MoDAFold: a strategy for predicting the structure of missense mutant protein based on AlphaFold2 and molecular dynamics. Briefings in Bioinformatics 2024, 25. [Google Scholar] [CrossRef] [PubMed]
  74. Verdicchio, M.; Teijeiro Barjas, C. , Introduction to High-Performance Computing. In High Performance Computing for Drug Discovery and Biomedicine; Springer US, 2023; p. 15–29. [CrossRef]
  75. Heifetz, A. , Accelerating COVID-19 Drug Discovery with High-Performance Computing. In High Performance Computing for Drug Discovery and Biomedicine; Springer US, 2023; p. 405–411. [CrossRef]
  76. Jing, X.; Wu, F.; Luo, X.; Xu, J. Single-sequence protein structure prediction by integrating protein language models. Proceedings of the National Academy of Sciences 2024, 121. [Google Scholar] [CrossRef] [PubMed]
  77. Moussad, B.; Roche, R.; Bhattacharya, D. The transformative power of transformers in protein structure prediction. Proceedings of the National Academy of Sciences 2023, 120. [Google Scholar] [CrossRef] [PubMed]
  78. Fang, Y.; Jiang, Y.; Wei, L.; Ma, Q.; Ren, Z.; Yuan, Q.; Wei, D.Q. DeepProSite: structure-aware protein binding site prediction using ESMFold and pretrained language model. Bioinformatics 2023, 39. [Google Scholar] [CrossRef] [PubMed]
  79. Harini, K.; Sekijima, M.; Gromiha, M.M. PRA-Pred: Structure-based prediction of protein-RNA binding affinity. International Journal of Biological Macromolecules 2024, 259, 129490. [Google Scholar] [CrossRef]
  80. Oda, T. Improving protein structure prediction with extended sequence similarity searches and deep-learning-based refinement in CASP15. Proteins: Structure, Function, and Bioinformatics 2023, 91, 1712–1723. [Google Scholar] [CrossRef] [PubMed]
  81. Xu, X.; Duan, R.; Zou, X. Template-guided method for protein–ligand complex structure prediction: Application to CASP15 protein–ligand studies. Proteins: Structure, Function, and Bioinformatics 2023, 91, 1829–1836. [Google Scholar] [CrossRef] [PubMed]
  82. Cen, L.P.; Ng, T.K.; Ji, J.; Lin, J.W.; Yao, Y.; Yang, R.; Dong, G.; Cao, Y.; Chen, C.; Yao, S.Q.; Wang, W.Y.; Huang, Z.; Qiu, K.; Pang, C.P.; Liu, Q.; Zhang, M. Artificial Intelligence-based database for prediction of protein structure and their alterations in ocular diseases. Database 2023, 2023. [Google Scholar] [CrossRef] [PubMed]
  83. Tripathi, A.; Mondal, R.; Lahiri, T.; Chaurasiya, D.; Pal, M.K. TemPred: A Novel Protein Template Search Engine to Improve Protein Structure Prediction. IEEE/ACM Transactions on Computational Biology and Bioinformatics 2023, 20, 2112–2121. [Google Scholar] [CrossRef] [PubMed]
  84. Crystallography: Protein Data Bank. Nature New Biology 1971, 233, 223–223. [CrossRef]
  85. Berman, H.; Henrick, K.; Nakamura, H. Announcing the worldwide Protein Data Bank. Nature Structural & Molecular Biology 2003, 10, 980–980. [Google Scholar]
  86. Bonvin, A.M.J.J. 50 years of PDB: a catalyst in structural biology. Nature Methods 2021, 18, 448–449. [Google Scholar] [CrossRef] [PubMed]
  87. Wu, D.; Cui, F.; Jernigan, R.; Wu, Z. PIDD: database for Protein Inter-atomic Distance Distributions. Nucleic Acids Research 2007, 35, D202–D207. [Google Scholar] [CrossRef] [PubMed]
  88. Li, W. Visualising the Experimentally Uncharted Territories of Membrane Protein Structures inside Protein Data Bank 2020.
  89. Li, W. A Local Spherical Coordinate System Approach to Protein 3D Structure Description 2020.
  90. Li, W. Two Achilles’ Heels of the Ebolavirus Glycoprotein? 2020.
  91. Broz, M.; Jukič, M.; Bren, U. Naive Prediction of Protein Backbone Phi and Psi Dihedral Angles Using Deep Learning. Molecules 2023, 28, 7046. [Google Scholar] [CrossRef] [PubMed]
  92. Batsanov, S. Calculation of van der Waals radii of atoms from bond distances. Journal of Molecular Structure: THEOCHEM 1999, 468, 151–159. [Google Scholar] [CrossRef]
  93. Caine, B.A.; Bronzato, M.; Popelier, P.L.A. Experiment stands corrected: accurate prediction of the aqueous pKa values of sulfonamide drugs using equilibrium bond lengths. Chemical Science 2019, 10, 6368–6381. [Google Scholar] [CrossRef] [PubMed]
  94. Li, W. NMR-Observed Atomic Bond Length Stability Supports a Dimensionality Shift in Protein Main Chain 3D Structure Description and Representation. Current Research Bioorganic Organic Chemistry 2018. [Google Scholar]
  95. Mysliwy, J.; Dingley, A.J.; Stanisak, M.; Jung, S.; Lorenzen, I.; Roeder, T.; Leippe, M.; Grötzinger, J. Caenopore-5: The three-dimensional structure of an antimicrobial protein from Caenorhabditis elegans. Dev. Comp. Immunol. 2010, 34, 323–330. [Google Scholar] [CrossRef]
  96. Roeder, T.; Stanisak, M.; Gelhaus, C.; Bruchhaus, I.; Grötzinger, J.; Leippe, M. Caenopores are antimicrobial peptides in the nematode Caenorhabditis elegans instrumental in nutrition and immunity. Dev. Comp. Immunol. 2010, 34, 203–209. [Google Scholar] [CrossRef] [PubMed]
  97. Li, W. Gravity-driven pH adjustment for site-specific protein pKa measurement by solution-state NMR. Measurement Science and Technology 2017, 28, 127002. [Google Scholar] [CrossRef]
  98. Li, W. Characterising the interaction between caenopore-5 and model membranes by NMR spectroscopy and molecular dynamics simulations. PhD thesis, University of Auckland, 2016.
  99. Humphrey, W.; Dalke, A.; Schulten, K. VMD: visual molecular dynamics. Journal of Molecular Graphics 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
  100. Reyes, V.M. Representation of protein 3D structures in spherical (ρ, ϕ, θ) coordinates and two of its potential applications. Interdisciplinary Sciences: Computational Life Sciences 2011, 3. [Google Scholar]
  101. Plonski, A.P.; Reed, S.M. Assessing protein homology models with docking reproducibility. Journal of Molecular Graphics and Modelling 2023, 121, 108430. [Google Scholar] [CrossRef]
  102. Li, W.; Vottevor, G. Towards a Truly General Intermolecular Binding Affinity Calculator for Drug Discovery and Design 2023. [CrossRef]
  103. Lategan, F.A.; Schreiber, C.; Patterton, H.G. SeqPredNN: a neural network that generates protein sequences that fold into specified tertiary structures. BMC Bioinformatics 2023, 24. [Google Scholar] [CrossRef] [PubMed]
  104. Chu, L.; Ruffolo, J.A.; Harmalkar, A.; Gray, J.J. Flexible protein–protein docking with a multitrack iterative transformer. Protein Science 2024, 33. [Google Scholar] [CrossRef] [PubMed]
  105. Matveev, E.V.; Safronov, V.V.; Ponomarev, G.V.; Kazanov, M.D. Predicting Structural Susceptibility of Proteins to Proteolytic Processing. International Journal of Molecular Sciences 2023, 24, 10761. [Google Scholar] [CrossRef] [PubMed]
  106. Udupa, A.; Kotha, S.R.; Staller, M.V. Commonly asked questions about transcriptional activation domains. Current Opinion in Structural Biology 2024, 84, 102732. [Google Scholar] [CrossRef] [PubMed]
  107. Badaczewska-Dawid, A.; Wróblewski, K.; Kurcinski, M.; Kmiecik, S. Structure prediction of linear and cyclic peptides using CABS-flex. Briefings in Bioinformatics 2024, 25. [Google Scholar] [CrossRef] [PubMed]
  108. Guillon, C.; Robert, X.; Gouet, P. “It’s Only a Model”: When Protein Structure Predictions Need Experimental Validation, the Case of the HTLV-1 Tax Protein. Pathogens 2024, 13, 241. [Google Scholar] [CrossRef] [PubMed]
  109. Waksman, T.; Astin, E.; Fisher, S.R.; Hunter, W.N.; Bos, J.I.B. Computational Prediction of Structure, Function, and Interaction of Myzus persicae (Green Peach Aphid) Salivary Effector Proteins. Molecular Plant-Microbe Interactions® 2024, 37, 338–346. [Google Scholar] [CrossRef] [PubMed]
  110. Li, W. How do SMA-linked mutations of SMN1 lead to structural/functional deficiency of the SMA protein? PLOS ONE 2017, 12, e0178519. [Google Scholar] [CrossRef] [PubMed]
  111. Segura, J.; Rose, Y.; Bi, C.; Duarte, J.; Burley, S.K.; Bittrich, S. RCSB Protein Data Bank: visualizing groups of experimentally determined PDB structures alongside computed structure models of proteins. Frontiers in Bioinformatics 2023, 3. [Google Scholar] [CrossRef]
  112. Gupta, K. In silico structural and functional characterization of hypothetical proteins from Monkeypox virus. Journal of Genetic Engineering and Biotechnology 2023, 21, 46. [Google Scholar] [CrossRef]
  113. Sawa, T.; Moriwaki, Y.; Jiang, H.; Murase, K.; Takayama, S.; Shimizu, K.; Terada, T. Comprehensive computational analysis of the SRK–SP11 molecular interaction underlying self-incompatibility in Brassicaceae using improved structure prediction for cysteine-rich proteins. Computational and Structural Biotechnology Journal 2023, 21, 5228–5239. [Google Scholar] [CrossRef] [PubMed]
  114. Kosugi, T.; Ohue, M. Design of Cyclic Peptides Targeting Protein–Protein Interactions Using AlphaFold. International Journal of Molecular Sciences 2023, 24, 13257. [Google Scholar] [CrossRef]
  115. Ertelt, M.; Mulligan, V.K.; Maguire, J.B.; Lyskov, S.; Moretti, R.; Schiffner, T.; Meiler, J.; Schoeder, C.T. Combining machine learning with structure-based protein design to predict and engineer post-translational modifications of proteins. PLOS Computational Biology 2024, 20, e1011939. [Google Scholar] [CrossRef]
  116. Li, S.; Tian, T.; Zhang, Z.; Zou, Z.; Zhao, D.; Zeng, J. PocketAnchor: Learning structure-based pocket representations for protein-ligand interaction prediction. Cell Systems 2023, 14, 692–705. [Google Scholar] [CrossRef] [PubMed]
  117. Davidson, R.B.; Coletti, M.; Gao, M.; Piatkowski, B.; Sreedasyam, A.; Quadir, F.; Weston, D.J.; Schmutz, J.; Cheng, J.; Skolnick, J.; Parks, J.M.; Sedova, A. Predicted structural proteome of Sphagnum divinum and proteome-scale annotation. Bioinformatics 2023, 39. [Google Scholar] [CrossRef] [PubMed]
  118. Guzmán-Vega, F.J.; González-Álvarez, A.C.; Peña-Guerra, K.A.; Cardona-Londoño, K.J.; Arold, S.T. Leveraging AI Advances and Online Tools for Structure-Based Variant Analysis. Current Protocols 2023, 3. [Google Scholar] [CrossRef] [PubMed]
  119. Li, W. Structurally Observed Electrostatic Features of the COVID-19 Coronavirus-Related Experimental Structures inside Protein Data Bank: A Brief Update 2020.
  120. Li, W. Extracting the Interfacial Electrostatic Features from Experimentally Determined Antigen and/or Antibody-Related Structures inside Protein Data Bank for Machine Learning-Based Antibody Design 2020.
  121. Jeppesen, M.; André, I. Accurate prediction of protein assembly structure by combining AlphaFold and symmetrical docking. Nature Communications 2023, 14. [Google Scholar] [CrossRef] [PubMed]
  122. Varadi, M.; Tsenkov, M.; Velankar, S. Challenges in bridging the gap between protein structure prediction and functional interpretation. Proteins: Structure, Function, and Bioinformatics. [CrossRef]
  123. Xia, Y.; Zhao, K.; Liu, D.; Zhou, X.; Zhang, G. Multi-domain and complex protein structure prediction using inter-domain interactions from deep learning. Communications Biology 2023, 6. [Google Scholar] [CrossRef]
  124. Camponeschi, C.; Righino, B.; Pirolli, D.; Semeraro, A.; Ria, F.; De Rosa, M.C. Prediction of CD44 Structure by Deep Learning-Based Protein Modeling. Biomolecules 2023, 13, 1047. [Google Scholar] [CrossRef] [PubMed]
  125. Lee, J.W.; Won, J.H.; Jeon, S.; Choo, Y.; Yeon, Y.; Oh, J.S.; Kim, M.; Kim, S.; Joung, I.; Jang, C.; Lee, S.J.; Kim, T.H.; Jin, K.H.; Song, G.; Kim, E.S.; Yoo, J.; Paek, E.; Noh, Y.K.; Joo, K. DeepFold: enhancing protein structure prediction through optimized loss functions, improved template features, and re-optimized energy function. Bioinformatics 2023, 39. [Google Scholar] [CrossRef] [PubMed]
  126. Kryshtafovych, A.; Schwede, T.; Topf, M.; Fidelis, K.; Moult, J. Critical assessment of methods of protein structure prediction (CASP)—Round XV. Proteins: Structure, Function, and Bioinformatics 2023, 91, 1539–1549. [Google Scholar] [CrossRef] [PubMed]
  127. Li, W. Towards a General Intermolecular Binding Affinity Calculator 2022. [CrossRef]
  128. Baek, M.; DiMaio, F.; Anishchenko, I.; Dauparas, J.; Ovchinnikov, S.; Lee, G.R.; Wang, J.; Cong, Q.; Kinch, L.N.; Schaeffer, R.D.; Millán, C.; Park, H.; Adams, C.; Glassman, C.R.; DeGiovanni, A.; Pereira, J.H.; Rodrigues, A.V.; van Dijk, A.A.; Ebrecht, A.C.; Opperman, D.J.; Sagmeister, T.; Buhlheller, C.; Pavkov-Keller, T.; Rathinaswamy, M.K.; Dalwadi, U.; Yip, C.K.; Burke, J.E.; Garcia, K.C.; Grishin, N.V.; Adams, P.D.; Read, R.J.; Baker, D. Accurate prediction of protein structures and interactions using a three-track neural network. Science 2021, 373, 871–876. [Google Scholar] [CrossRef] [PubMed]
  129. Yang, J.; Anishchenko, I.; Park, H.; Peng, Z.; Ovchinnikov, S.; Baker, D. Improved protein structure prediction using predicted interresidue orientations. Proceedings of the National Academy of Sciences 2020, 117, 1496–1503. [Google Scholar] [CrossRef] [PubMed]
  130. AlQuraishi, M. A watershed moment for protein structure prediction. Nature 2020, 577, 627–628. [Google Scholar] [CrossRef] [PubMed]
  131. Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.; Žídek, A.; Nelson, A.W.R.; Bridgland, A.; Penedones, H.; Petersen, S.; Simonyan, K.; Crossan, S.; Kohli, P.; Jones, D.T.; Silver, D.; Kavukcuoglu, K.; Hassabis, D. Improved protein structure prediction using potentials from deep learning. Nature 2020, 577, 706–710. [Google Scholar] [CrossRef] [PubMed]
  132. Hey, T.; Butler, K.; Jackson, S.; Thiyagalingam, J. Machine learning and big scientific data. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2020, 378, 20190054. [Google Scholar] [CrossRef] [PubMed]
  133. Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.; Žídek, A.; Nelson, A.W.R.; Bridgland, A.; Penedones, H.; Petersen, S.; Simonyan, K.; Crossan, S.; Kohli, P.; Jones, D.T.; Silver, D.; Kavukcuoglu, K.; Hassabis, D. Protein structure prediction using multiple deep neural networks in the 13th Critical Assessment of Protein Structure Prediction (CASP13). Proteins: Structure, Function, and Bioinformatics 2019, 87, 1141–1148. [Google Scholar] [CrossRef] [PubMed]
  134. Pinheiro, F.; Santos, J.; Ventura, S. AlphaFold and the amyloid landscape. Journal of Molecular Biology 2021, 167059. [Google Scholar] [CrossRef] [PubMed]
  135. Ruff, K.M.; Pappu, R.V. AlphaFold and Implications for Intrinsically Disordered Proteins. Journal of Molecular Biology 2021, 167208. [Google Scholar] [CrossRef] [PubMed]
  136. Higgins, M.K. Can We AlphaFold Our Way Out of the Next Pandemic? Journal of Molecular Biology 2021, 167093. [Google Scholar] [CrossRef] [PubMed]
  137. Fersht, A.R. AlphaFold: A Personal Perspective on the Impact of Machine Learning. Journal of Molecular Biology 2021, 167088. [Google Scholar] [CrossRef] [PubMed]
  138. Zweckstetter, M. NMR hawk-eyed view of AlphaFold2 structures. Protein Science 2021. [Google Scholar] [CrossRef] [PubMed]
  139. Strodel, B. Energy Landscapes of Protein Aggregation and Conformation Switching in Intrinsically Disordered Proteins. Journal of Molecular Biology 2021, 167182. [Google Scholar] [CrossRef] [PubMed]
  140. Ayoub, R.; Lee, Y. Protein structure search to support the development of protein structure prediction methods. Proteins: Structure, Function, and Bioinformatics 2021, 89, 648–658. [Google Scholar] [CrossRef] [PubMed]
  141. Tunyasuvunakool, K.; Adler, J.; Wu, Z.; Green, T.; Zielinski, M.; Žídek, A.; Bridgland, A.; Cowie, A.; Meyer, C.; Laydon, A.; Velankar, S.; Kleywegt, G.J.; Bateman, A.; Evans, R.; Pritzel, A.; figurnov, M.; Ronneberger, O.; Bates, R.; Kohl, S.A.A.; Potapenko, A.; Ballard, A.J.; Romera-Paredes, B.; Nikolov, S.; Jain, R.; Clancy, E.; Reiman, D.; Petersen, S.; Senior, A.W.; Kavukcuoglu, K.; Birney, E.; Kohli, P.; Jumper, J.; Hassabis, D. Highly accurate protein structure prediction for the human proteome. Nature 2021, 596, 590–596. [Google Scholar] [CrossRef] [PubMed]
  142. Simpkin, A.J.; filomeno Sánchez Rodríguez.; Mesdaghi, S.; Kryshtafovych, A. Rigden, D.J. Evaluation of model refinement in CASP14. Proteins, Structure, Function, and Bioinformatics 2021.
  143. Diwan, G.D.; Gonzalez-Sanchez, J.C.; Apic, G.; Russell, R.B. Next Generation Protein Structure Predictions and Genetic Variant Interpretation. Journal of Molecular Biology 2021, 167180. [Google Scholar] [CrossRef] [PubMed]
  144. Abriata, L.A.; Peraro, M.D. State-of-the-art web services for de novo protein structure prediction. Briefings in Bioinformatics 2020, 22. [Google Scholar]
  145. Billings, W.M.; Morris, C.J.; Corte, D.D. The whole is greater than its parts: ensembling improves protein contact prediction. Scientific Reports 2021, 11. [Google Scholar] [CrossRef] [PubMed]
  146. Layer, G.; Reichelt, J.; Jahn, D.; Heinz, D.W. Structure and function of enzymes in heme biosynthesis. Protein Science 2010, 19, 1137–1161. [Google Scholar] [CrossRef] [PubMed]
  147. McBride, J.M.; Polev, K.; Abdirasulov, A.; Reinharz, V.; Grzybowski, B.A.; Tlusty, T. AlphaFold2 Can Predict Single-Mutation Effects. Physical Review Letters 2023, 131. [Google Scholar] [CrossRef] [PubMed]
  148. Karelina, M.; Noh, J.J.; Dror, R.O. How accurately can one predict drug binding modes using AlphaFold models? eLife 2023, 12. [Google Scholar] [CrossRef]
  149. Jambrich, M.A.; Tusnady, G.E.; Dobson, L. How AlphaFold2 shaped the structural coverage of the human transmembrane proteome. Scientific Reports 2023, 13. [Google Scholar] [CrossRef] [PubMed]
  150. Perlinska, A.P.; Niemyska, W.H.; Gren, B.A.; Bukowicki, M.; Nowakowski, S.; Rubach, P.; Sulkowska, J.I. AlphaFold predicts novel human proteins with knots. Protein Science 2023, 32. [Google Scholar] [CrossRef] [PubMed]
  151. Manalastas-Cantos, K.; Adoni, K.R.; Pfeifer, M.; Märtens, B.; Grünewald, K.; Thalassinos, K.; Topf, M. Modeling Flexible Protein Structure With AlphaFold2 and Crosslinking Mass Spectrometry. Molecular & Cellular Proteomics 2024, 23, 100724. [Google Scholar] [CrossRef]
  152. Li, W. Half-a-century Burial of ρ, θ and φ in PDB 2021. [CrossRef]
Preprints 103306 g001
Figure 1. Geometrically, CCS (X, Y and Z) and SCS ( ρ , θ and ϕ ) are like two sides of one coin, and are both applicable in the specifications of atomic positions to define protein structure [89].
Figure 1. Geometrically, CCS (X, Y and Z) and SCS ( ρ , θ and ϕ ) are like two sides of one coin, and are both applicable in the specifications of atomic positions to define protein structure [89].
Preprints 103306 g001
Preprints 103306 g002
Figure 2. Amino acid sequence and secondary structure of Caenopore-5 [95,96,98].
Figure 2. Amino acid sequence and secondary structure of Caenopore-5 [95,96,98].
Preprints 103306 g002
Preprints 103306 g003
Figure 3. The three-dimensional NMR structure of Caenopore-5 (PDB ID: 2JSA) stabilized by three disulfide bonds (red sticks) [95,96,98]. This figure is prepared by VMD [99].
Figure 3. The three-dimensional NMR structure of Caenopore-5 (PDB ID: 2JSA) stabilized by three disulfide bonds (red sticks) [95,96,98]. This figure is prepared by VMD [99].
Preprints 103306 g003
Preprints 103306 g004
Figure 4. Chemical structure of a short peptide with five amino acids as an example to illustrate the redefinition of protein structure with ρ , θ and ϕ [89] for the reversible spherical geometric conversion of protein backbone structure coordinate matrices into three independent vectors: ρ , θ , and ϕ .
Figure 4. Chemical structure of a short peptide with five amino acids as an example to illustrate the redefinition of protein structure with ρ , θ and ϕ [89] for the reversible spherical geometric conversion of protein backbone structure coordinate matrices into three independent vectors: ρ , θ , and ϕ .
Preprints 103306 g004
Preprints 103306 g005
Figure 5. The formation of a peptide bond, which is the bond between the carbonyl carbon and the nitrogen in the amide fragment.
Figure 5. The formation of a peptide bond, which is the bond between the carbonyl carbon and the nitrogen in the amide fragment.
Preprints 103306 g005
Preprints 103306 g006
Figure 6. The distribution pattern of the lengths ( ρ ) of 477 covalent bonds of the backbone of Caenopore-5 [95,96,98] as reversibly extracted from the 15 NMR structural models of the three-dimensional NMR ensemble of Caenopore-5 (PDB ID: 2JSA) [95,96,98].
Figure 6. The distribution pattern of the lengths ( ρ ) of 477 covalent bonds of the backbone of Caenopore-5 [95,96,98] as reversibly extracted from the 15 NMR structural models of the three-dimensional NMR ensemble of Caenopore-5 (PDB ID: 2JSA) [95,96,98].
Preprints 103306 g006
Preprints 103306 g007
Figure 7. The distribution pattern of the azimuthal angle ( θ ) of 477 covalent bonds of the backbone of Caenopore-5 [95,96,98] as reversibly extracted from the 15 NMR structural models of the three-dimensional NMR ensemble of Caenopore-5 (PDB ID: 2JSA) [95,96,98].
Figure 7. The distribution pattern of the azimuthal angle ( θ ) of 477 covalent bonds of the backbone of Caenopore-5 [95,96,98] as reversibly extracted from the 15 NMR structural models of the three-dimensional NMR ensemble of Caenopore-5 (PDB ID: 2JSA) [95,96,98].
Preprints 103306 g007
Preprints 103306 g008
Figure 8. The distribution pattern of the polar angle (also known as the zenith angle, ϕ ) of 477 covalent bonds of the backbone of Caenopore-5 [95,96,98] as reversibly extracted from the 15 NMR structural models of the three-dimensional NMR ensemble of Caenopore-5 (PDB ID: 2JSA) [95,96,98].
Figure 8. The distribution pattern of the polar angle (also known as the zenith angle, ϕ ) of 477 covalent bonds of the backbone of Caenopore-5 [95,96,98] as reversibly extracted from the 15 NMR structural models of the three-dimensional NMR ensemble of Caenopore-5 (PDB ID: 2JSA) [95,96,98].
Preprints 103306 g008
Preprints 103306 g009
Figure 9. The distribution pattern of the lengths ( ρ ) of 80 peptide bonds (Figure 5) of Caenopore-5 [95,96,98] as reversibly extracted from the 15 NMR structural models of the three-dimensional NMR ensemble of Caenopore-5 (PDB ID: 2JSA) [95,96,98].
Figure 9. The distribution pattern of the lengths ( ρ ) of 80 peptide bonds (Figure 5) of Caenopore-5 [95,96,98] as reversibly extracted from the 15 NMR structural models of the three-dimensional NMR ensemble of Caenopore-5 (PDB ID: 2JSA) [95,96,98].
Preprints 103306 g009
Preprints 103306 g010
Figure 10. The distribution pattern of the azimuthal angle ( θ ) of 80 peptide bonds (Figure 5) of Caenopore-5 [95,96,98] as reversibly extracted from the 15 NMR structural models of the three-dimensional NMR ensemble of Caenopore-5 (PDB ID: 2JSA) [95,96,98].
Figure 10. The distribution pattern of the azimuthal angle ( θ ) of 80 peptide bonds (Figure 5) of Caenopore-5 [95,96,98] as reversibly extracted from the 15 NMR structural models of the three-dimensional NMR ensemble of Caenopore-5 (PDB ID: 2JSA) [95,96,98].
Preprints 103306 g010
Preprints 103306 g011
Figure 11. The distribution pattern of the polar angle (also known as the zenith angle, ϕ ) of 80 peptide bonds (Figure 5) of Caenopore-5 [95,96,98] as reversibly extracted from the 15 NMR structural models of the three-dimensional NMR ensemble of Caenopore-5 (PDB ID: 2JSA) [95,96,98].
Figure 11. The distribution pattern of the polar angle (also known as the zenith angle, ϕ ) of 80 peptide bonds (Figure 5) of Caenopore-5 [95,96,98] as reversibly extracted from the 15 NMR structural models of the three-dimensional NMR ensemble of Caenopore-5 (PDB ID: 2JSA) [95,96,98].
Preprints 103306 g011
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated