Optical Color Image Encryption Algorithm Based on Two‐Dimensional Quantum Walking (OCT)

The Double Random Phase Encoding (DRPE) image encryption method has garnered significant attention in color image processing and optical encryption, thanks to its parallel encryption of R, G, B. However, DRPE-based color image encryption faces two challenges. Firstly, it disregards the correlation of R, G, and B, compromising the encrypted image's robustness. Secondly, DRPE schemes relying on Discrete Fourier Transform (DFT) and Discrete Fractional Fourier Transform (DFRFT) are vulnerable to linear attacks, such as Known Plaintext Attack (KPA) and Chosen Plaintext Attack (CPA). Quantum walk stands out as a remarkable tool for designing modern cryptographic mechanisms, offering resistance to potential attacks from both classical and quantum computers.Therefore, this study presents an optical color image encryption algorithm that combines two-dimensional quantum walk with 24-bit plane permutation, dubbed OCT. This approach employs pseudo-random numbers generated by Two-Dimensional Quantum Walking (TDQW) for phase modulation in DRPE and scrambles the encrypted image's real and imaginary parts using the Generalized Arnold Transform. The 24-bit plane permutation helps reduce correlation of the R, G, B, while the Generalized Arnold Transform bolsters DRPE's resistance to linear attacks. By incorporating TDQW, the key space is significantly expanded. Experimental results validate the effectiveness and security of proposed method.

Keywords:

Subject: Computer Science and Mathematics - Security Systems

1. Introduction

As network and information technologies advance, digital image security faces considerable risks during storage., transmission, and reception, prompting cryptography to emerge as an effective means of safeguarding images [1,2]. In comparison to grayscale images, color images offer richer information. Optical image encryption, with its benefits of parallelism and flexibility, enables concurrent encryption of the R, G, B of color images, drawing growing interest from researchers [3,4].

In the realm of optical image encryption, various optical encryption techniques have been proposed, including full-phase encryption [5], amplitude-based encryption [6], and polarization encoding encryption [7,8].Among various techniques, the Fractional Fourier Transform (FrFT) is frequently used to manipulate polarization information in the time domain [9,10,11], whereas the Optical Fourier Transform (OFT) finds application in the encoding process [12,13]. OFT typically consists of two cascaded lenses, and cascaded phase structures are one of the most commonly used optical structures in light field modulation. This structure was first applied to the Double Random Phase Encoding (DRPE) system by Javidi et al. in 1996. DRPE modulates waves by introducing two random phase masks to scramble both spatial and frequency domains, resulting in ciphertext without white noise [14,15]. Currently, DRPE has become one of the most commonly used and effective optical encryption schemes [16,17].

Thanks to the parallelism inherent in DRPE, the three components of R, G, and B can all be encrypted concurrently. Faragallah O’s proposed algorithm involves encrypting the R, G, B of a color image three times independently [18]. Nonetheless, because of the strong correlation among the R, G, B, the color image remains susceptible to potential attacks. [19]. Wang Yonghui put forth an optical single-channel color image encryption approach rooted in chaotic fingerprint phase masks and diffraction imaging. Here, the fingerprint, which produces random phase masks, doubles as the encryption key.dividing the color pure image into equal blocks using lasers and then converting the electrical signals into optical signals using an optical transmitter (light source) [20].Independently encrypting the R, G, B three times in color images does not provide adequate defense against attacks, as stated in the existing literature [15,18], color encryption systems based on DRPE have exposed the following two key issues.

Issue 1: Ignoring the correlation of R, G, B will lead to decreased robustness of the encrypted image. It has been demonstrated that reducing the correlation values between R, G, B can effectively decrease the correlation of DRPE images, thereby enhancing the robustness of the encryption system [21,22].

Issue 2: The DRPE system itself is susceptible to linear analysis attacks. This linear transformation allows two random phase masks (RPMs) to be guessed through Known Plaintext Attack (KPA)/Chosen Plaintext Attack (CPA)/Ciphertext-Only Attack (COA), consuming significantly fewer resources compared to brute force attacks [21,22].

To tackle Issue 1, Yildirim M proposed a DRPE scheme based on chaotic system-based sub-block image swapping [23], and another DRPE scheme based on chaotic system ,DNA encoding algorithm [24]. These schemes [23,24] reduce the the correlation of R, G, B and have been experimentally demonstrated to possess good robustness. However, they overlook the issue of weak linear analysis capability of DRPE,result Issue 2. Further analysis [23,24] reveals that while these schemes demonstrate a significant improvement in robustness by reducing the correlation of R, G, B, they do not conduct in-depth analysis. Lowering the correlation of R, G, B effectively disrupts the {0, 1} bit sequence values of the pixel’s three categorized R, G, B. This paper hypothesizes that directly scrambling the bits of a color image would disrupt the {0, 1} sequence values and reduce the correlation at the bit level, thereby potentially enhancing the image’s robustness. The experiments conducted in this paper ultimately validate this hypothesis.

To tackle Issue 2, numerous scholars have explored nonlinear optical image encryption methods. Qin W and colleagues introduced a cutting-edge secure nonlinear cryptosystem in the Fourier transform domain, leveraging phase truncation techniques. This effectively addressed the linear vulnerabilities present in the DRPE system [25], but it was later deciphered by Wang X et al. [26].In addition, Li Ming put forth an attack scheme targeting a specific type of DRPE encryption systems that rely on scrambling and diffusion. This scheme can efficiently breach DRPE encryption systems employing scrambling and diffusion mechanisms [27].Zhou Qingming and colleagues presented a novel optical image encryption method that relies on dual-channel detection and deep learning. This approach involves training neural networks to establish the mapping relationship between RM images and their corresponding plaintext saliency images, aiming to identify the optimal RM. While this scheme demonstrates good performance, it demands a significant amount of time [28].Singh P and team strengthened the DRPE system’s resilience against statistical analysis attacks by incorporating nonlinear terms [29].

This paper draws inspiration from the theories of nonlinear chaotic systems and nonlinear S-boxes, exploring the possibility of incorporating nonlinear correlation algorithms into DRPE to enhance its resistance against linear attacks.Consequently, the OCT (Optical Color Image Encryption) scheme was put forth, with an improved DRPE serving as the core encryption algorithm. Two-dimensional quantum walk is employed to optimize the optical encryption algorithm, further enhancing the encryption effectiveness and security. Experimental results indicate that the proposed scheme not only lowers the correlation among the R, G, and B components but also reinforces the DRPE system’s immunity to linear attacks, specifically CPA and KPA.

The main contributions of this paper are as follows:

(I) The analysis reveals that the increased robustness of encrypted images after reducing the correlation of R, G, B stems from the enhanced robustness achieved by lowering the correlation between the 24-bit plane layers. Therefore, the paper proposes a scheme utilizing 24-bit plane permutation to reduce the correlation of R, G, B in color images.

(II) The paper introduces the generalized Arnold transformation to independently permute the real and imaginary parts of the complex matrix obtained after DRPE encryption. Experimental results demonstrate that this approach effectively enhances resistance against linear analysis attacks such as CPA and KPA.

(III) The incorporation of two-dimensional quantum walk into the optical image encryption scheme is presented.It is noted that two-dimensional quantum walk exhibits better randomness compared to chaotic systems.

The subsequent sections of this paper are structured as follows: In Section 2, author introduce Two-Dimensional Quantum Walk (TDQW) and Double Random Phase Encoding (DRPE) image encryption. Section 3 offers comprehensive details about the various components and experimental steps of the image encryption system. Section 4 showcases simulation results, evaluates security performance, and conducts a comparative analysis. Lastly, Section 5 summarizes the entire paper.

2. Preliminaries

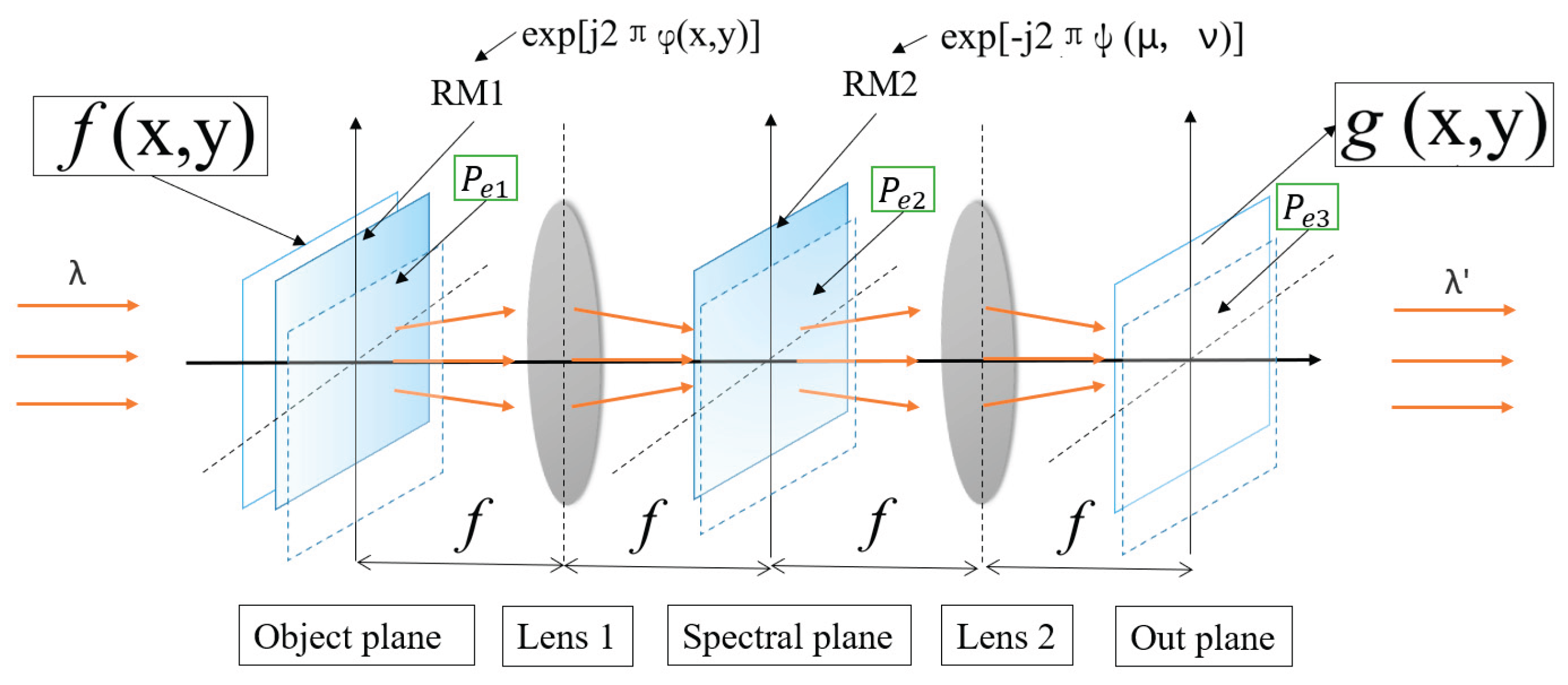
2.1. Double Random Phase Encoding

Abd-El-Atty B[16],In 1995,Javidi and Refregier first proposed DRPE system composed of four Focal-length lenses (4-f), which is a brand-new image encryption technology [14,15]. In 2020, Abd-El-Atty B proposed a new encryption method based on quantum walks (AQW) and DRPE technology, introducing quantum walks into optical image encryption [19].Image encryption and decryption are achieved through the Fourier transform utilizing lenses., as shown in Figure 1. This chapter will introduce the basic principle and method of computer simulation of Double Random Phase optical image encryption. The common 4f system is realized in Figure 1,RM1() represents mask 1,represents the original image,Lens1’s front focal plane is ,RM1() and is coherent .Collimated light of unit amplitude on the front focal plane Vertical illumination. In another random phase mask RM2 () in the FT plane .After IFT of Lens2,Lens2 rear focal plane been for of the encrypted image, as shown in equation (1):

g (x, y) = {F F T}^{- 1} {F F T {f (x, y) \cdot e^{j 2 π φ (x, y)}} \cdot e^{j 2 π ψ (μ, ν)}}

(1)

Among the equation(1),

f (x, y)

representing the original image,

g (x, y)

representing encrypted images,

F F T {\cdot}

and

{F F T}^{- 1} {\cdot}

are FT and IFT,

e^{j 2 π φ (x, y)}

and

e^{j 2 π ψ (μ, ν)}

are two random phase plates.In the equation

φ (x, y)

and

ψ (μ, ν)

,The selection of values

(x, y)

and

(μ, ν)

in is determined by the random number generator, whose values are randomly distributed among

[0,1]

.Therefore, these are two independent random white noises. Similarly, the decryption formula is as follows equation (2):

f ‘ (x, y) = {F F T}^{- 1} {F F T {g (x, y) \cdot e^{- j 2 π φ (x, y)}} \cdot e^{- j 2 π ψ (μ, ν)}}

(2)

Among the equation(2),

f ‘ (x, y)

is decrypt image, the other elements are consistent with the encryption process described above, and it is evident that the decryption process is essentially the reverse of the encryption operation.

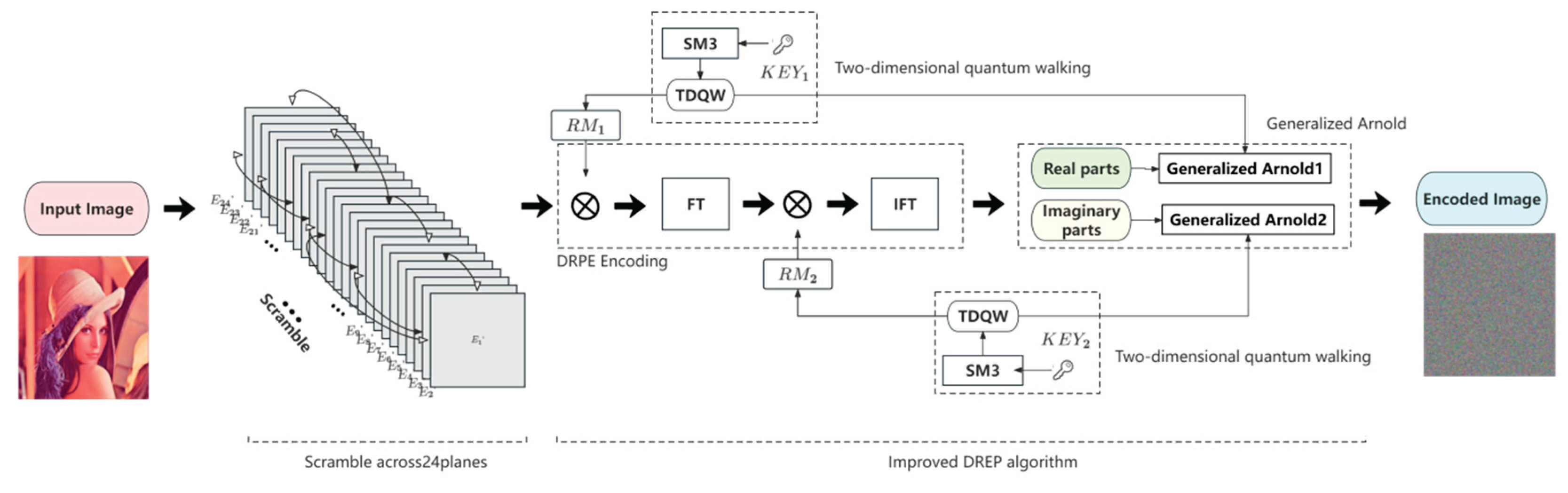
2.2. Improved DREP

Generalized Arnold Transform algorithm is an extension and improvement of Arnold algorithm, which was used in image encryption by Sun, Gege, et al. in 2024 [30].Discrete generalized Arnold mapping transformation formula and inverse transformation formula can be expressed as equation (3) and equation (4), where a and b are real numbers.

x_{n}, y_{n} \in [0,1)

In Guodong Ye’s scheme, generalized Arnold introduces chaotic system to initialize a and b to be real numbers, which solves the periodicity problem of Arnold algorithm. In order to improve DRPE’s ability to resist KPA and CPA, this paper uses two-dimensional quantum walk to initialize the selection matrix of a and b in generalized Arnold, and introduces it into DRPE scheme.

g (x, y)

is the image after Fourier transformation, the pixels of the encrypted image are complex, equation (5).

(\begin{matrix} x_{n + 1} \\ y_{n + 1} \end{matrix}) = [\begin{matrix} 1 & b \\ a & 1 + a b \end{matrix}] (\begin{matrix} x_{n} \\ y_{n} \end{matrix}) m o d (N);

(3)

(\begin{matrix} x_{n + 1} \\ y_{n + 1} \end{matrix}) = [\begin{matrix} 1 + a b & - b \\ - a & 1 \end{matrix}] (\begin{matrix} x_{n} \\ y_{n} \end{matrix}) m o d (N)

(4)

p i x e l Z = γ + δ_{i} .

(5)

Wherein

p i x e l Z

is a complex pixel, consisting of real and imaginary parts, satisfying the equation

|p i x e l Z| = \sqrt{γ^{2} + δ^{2}}

γ

represents the real part,

δ

indicate imaginary part. will

g (x, y)

.The optical encryption image (plural form) is decomposed into real matrix

‖γ‖

and imaginary matrix

‖δ‖

, and then generalized Arnold transformation is applied separately. Obtain the real matrix

{‖γ‖}^{‘}

and imaginary matrix

‖δ‖

after generalized Arnold transformation.The transformed real matrix and imaginary matrix are combined into a complex matrix

g ‘ (x, y)

,which represents Arnold encryption image. Therefore, from equation (5), the improved DRPE equation can be derived as equation (6):

g^{’} (x, y) = I F T \{F T \{f (x, y) \cdot {R M}_{1}\} \cdot {R M}_{2}\} \cdot A r n o l d .

(6)

In equation (6), FT is used to express

F F T

,IFT is used to express

{F F T}^{- 1}

{R M}_{1}

for

e^{j 2 π φ (x, y)}

{R M}_{2}

for

e^{j 2 π ψ (μ, ν)}

. The encryption algorithm is described by Table 1, where X represents the random sequence generated by the TDQW,img_fft represents the random sequence to be encrypted.

g (x, y)

,img_complex is encrypted

g ‘ (x, y)

2.3. Two Dimensional Quantum Walking (TDQW)

In some cases, chaotic systems may exhibit periodic orbits, which renders them partially predictable to attackers with computational capabilities [31]. Unlike chaotic systems, the essence of quantum walk lies in the unique properties of microscopic particles. These quantum particles exhibit wave-particle duality, meaning they can simultaneously exist in vastly different wave and particle states [18]. In quantum image encryption methods, the principles of quantum, including the inherent unpredictability and quantum entanglement, are utilized to achieve theoretically absolute security during data transmission [31]. Since Aharonov et al.’s groundbreaking research on quantum walks in 1993, this field has garnered significant attention in academia [32]. Among them, one-dimensional quantum walk serves as a quantum extension of classical random walks, while two-dimensional quantum walk further generalizes this concept. In classical random walks, each step of the walker is influenced by random step lengths and directions, resulting in a degree of uncertainty. However, two-dimensional discrete quantum walk differs in that it combines position space and coin space, collectively constructing the state space of quantum walkers.

TDQW is utilized by Hao et al. in 2022 for image encryption [31], denoted as

U

, extends the concept of a one-dimensional discrete quantum walk. The state space for quantum wandering encompasses both position space (

S

) and coin space (

C

). Typically, the entire system can be represented as

U = S \cdot (C ⨂ I)

. A TDQW system comprises a walker

U

, two coin evolution

C

, and an observation set. The coin space, represented by a two-dimensional Hilbert space

H_{c}

, characterizes the coin’s state on the x-axis , while

H_{c_{x}}

and

H_{c_{y}}

depict the coin’s state on the y-axis. Both

H_{c} = H_{c_{x}} {\otimes H}_{c_{y}}

are included.

The evolution operator of quantum wandering consists of conditional transfer operator and coin operator. coin operator

\hat{C}

{\hat{C}}_{x}

and

{\hat{C}}_{y}

In this paper, we take the coin operator as Hadamard operator, as shown in equation (7)(8)(9).

{\hat{C}}_{x} = {\hat{H}}_{x} = \frac{1}{\sqrt{2}} ({|0⟩}_{c x} ⟨0| + {|0⟩}_{c x} ⟨1| + {|1⟩}_{c x} ⟨0| - {|1⟩}_{c x} ⟨1|)

(7)

{\hat{C}}_{y} = {\hat{H}}_{y} = \frac{1}{\sqrt{2}} ({|0⟩}_{c y} ⟨0| + {|0⟩}_{c y} ⟨1| + {|1⟩}_{c y} ⟨0| - {|1⟩}_{c y} ⟨1|)

(8)

\forall x \in S, p \in P (f), n f |f^{n} (x)| - |f^{n} (y)| = 0

(9)

The transition operator

\hat{S}

{\hat{S}}_{x}

and

{\hat{S}}_{y}

composition, which determines the position of motion. The operator S taking one step to the left is shown in formula (10), and taking one step to the right is shown in formula (11):

{\hat{S}}_{x} = {|0⟩}_{c x} ⟨0| ⨂ \sum_{i} {|i + 1⟩}_{p x} ⟨i| + {|1⟩}_{c x} ⟨1| ⨂ \sum_{i} {|i - 1⟩}_{p x} ⟨i|

(10)

{\hat{S}}_{y} = {|0⟩}_{c y} ⟨0| ⨂ \sum_{j} {|j + 1⟩}_{p y} ⟨j| + {|1⟩}_{c y} ⟨1| ⨂ \sum_{j} {|j - 1⟩}_{p y} ⟨j|

(11)

The probability amplitude of TDQW is described using Fourier integration’s smooth phase method. This involves converting the walker’s time domain space to the frequency domain through Fourier transformation. After t steps, the discrete quantum state can be determined using a specific formula (12).R or L means the walker goes to the right or left,F or B means walker goes to forward or backward.Where

k \in [- π, π], x = y = \{2,4, 6 \dots M * N\}, t = 10^{5}, k = π / 6

,under the conditions,The probability of TDQW proposed by Hao et al. is shown in Figure 2.

μ_{t} = P (X_{t} = x, Y_{t} = y) = \sum_{i = R}^{L} \sum_{j = B}^{F} {| Ψ_{i} (x, t) Ψ_{j} (y, t) |}^{2}

(12)

2.4. Bit Layer Scrambling

In optical color image encryption schemes by Yildirim M [23,24], Faragallah O [18], Liu [13], with cross-layer permutation enhancing chaos. Faragallah O showed that reducing RGB component correlation can boost encryption robustness [18]. This paper delves into Faragallah O’s algorithm, revealing that the key to this robustness lies in minimizing correlation among the color image’s 24-bit plane layers.

Initially, RGB 3-plane scrambling alters the histogram, but peaks and patterns may persist, leaving some image features detectable. However, 24-bit layer scrambling disrupts every pixel bit, erasing all original distribution patterns. The resulting histogram is uniform, lacking discernible peaks or patterns, thwarting histogram-based attacks Figure 3(c). Compared to Yildirim M and Liu’s methods Figure (b), this 24-bit scrambling offers superior resistance to analysis Figure 3(c).

3. Encryption Algorithm and Decryption Algorithm

3.1. Encryption Algorithm

Owing to its sensitivity to initial conditions and its chaotic dynamical characteristics, quantum walks have become increasingly useful in modern cryptographic systems [32]. Because of the excellent properties of Two-Dimensional Quantum Walks (TDQW) [31], this paper proposes a new optical image encryption method based on TDQW. TDQW is employed to generate permutation and diffusion images, thus realizing two random masks for the DRPE process. The overall encryption process in Figure 4, and the encryption algorithm is described in Table 2. The specific steps are as follows:

Step 1: The color picture is hashed using the SM3 national secret algorithm to derive a unique picture key, termed "sm-key". This key is subsequently employed to initialize the TDQW system for generating random numbers.

Step 2:Set the initial values x, y, k, t for the TDQW system. Additionally, there are three conditions that must be met, as illustrated by the equation.(13).Sm-key as TDQW initial value, generate three random number sequence X, X 2, X 3.

\begin{matrix} \{\begin{matrix} 1 - 2 {(\frac{x + y}{t})}^{2} > 0 \\ t is odd and x + y is odd \\ t is even and x + y is even \end{matrix} \end{matrix}

(13)

Step 3: Convert RGB color image to 24-layer bit matrix img_matrix, using X sorted index pairs.The img_matrix of the 24 layers is scrambled, and then put into the S-box to obtain the encrypted image img_encoding24.

Step 4: First,use TDQW to generate X2 and X3 to initialize the two phases RM1 and RM2 for DRPE.Second, The image imgEncoding24 is put into DRPE system for FT and ITF encryption process to obtain image encryptionIm.

Step 5: First,use two-dimensional quantum walk to generate X2 and X3 to initialize the parameter selection matrix of generalized Arnold.Second, the encryptionIm image is split into a real matrix and an imaginary matrix.Third use Generalized Arnold scrambling two matrix , finally get encryptionArnoldIm.The encryptionArnoldIm is the final encryption image.The whole process can be expressed as equation(14).

g^{’} (x, y) = I F T \{F T \{f (x, y) \cdot 24 B i t \cdot {R M}_{1}\} \cdot {R M}_{2}\} \cdot A r n o l d .

(14)

Table 2. Color Image encryption Algorithm.

3.2. Decryption Algorithm

The decryption process is essentially the reverse of the encryption method depicted in Figure 5.The decryption formula is shown in equation(15). The steps are as follows:

Step 1:Set initial values and control parameters x, y, k, t of TDQW.Sm-key as TDQW’s initial value, generate three random number sequence X, X 2, X 3.

Step 2: First,use the TDQW to generateX2 and X3 and initialize the parameter selection matrix of generalized Arnold.Second,the ArnoldIm is divided into a real matrix and an imaginary matrix, and inverse scrambling is performed using inverse Arnold transformation to obtain encryptionIm.Third,the encryptionIm is be used the Input of next step.

Step 3: First,use the TDQW to generate X2 and X3 and initialize the two phases IRM1 (

{R M}_{1}^{- 1}

) and IRM2 (

{R M}_{2}^{- 1}

).Second, introduce the encryptionIm image into the DRPE decoding system, and undergo the FT and ITF encryption processes to obtain the image imgEncoding24.

Step 4:First, insert imgEncoding24 into the I_S-box to obtain imgEncoding24’. Second, utilize X sorted index pairs to perform inverse scrambling on the 24-layer bit matrix of imgEncoding24’ to acquire img_matrix, and then integrate the bit matrix of img_matrix into an RGB color image, resulting in the Decoded image

f (x, y)

f (x, y) = I F T {F T {g^{’} (x, y) \cdot I A r n o l d} \cdot {R M}_{2}^{- 1}} \cdot {R M}_{1}^{- 1} \cdot I 24 B i t .

(15)

Figure 5. Overall decryption flow chart.

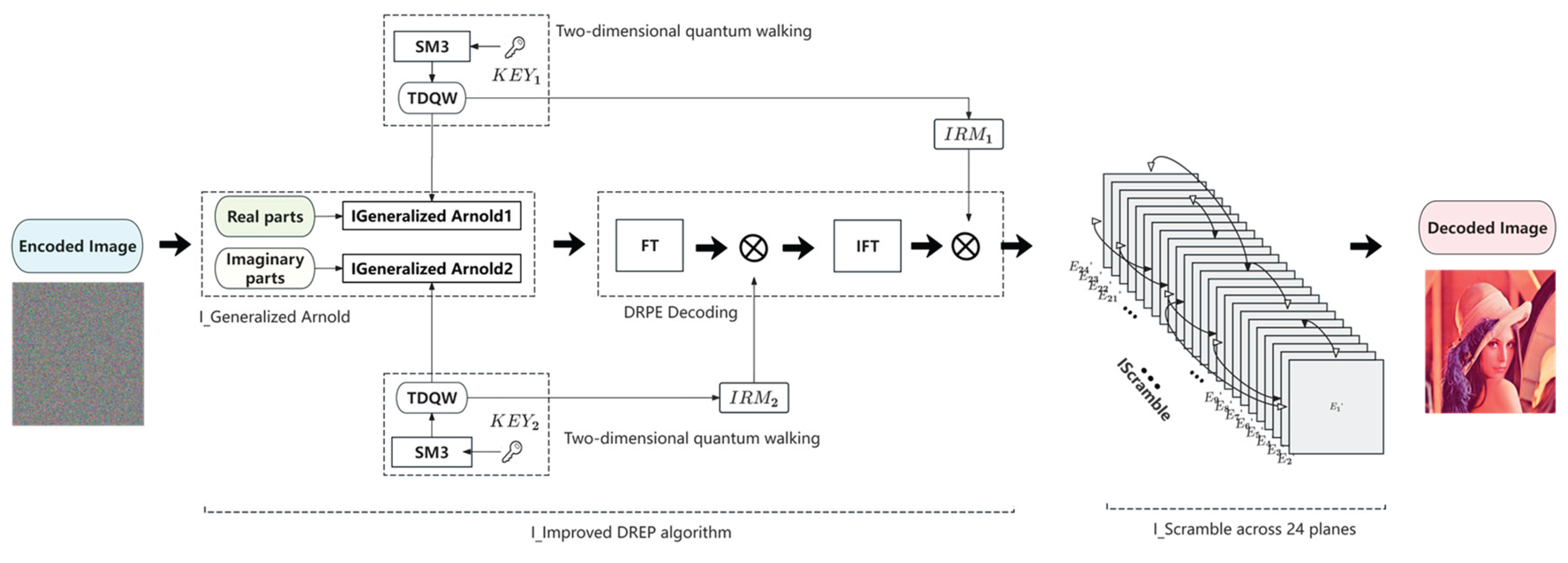
4. Numerical Simulation and Performance Analysis

The experimental conditions in this chapter are:MATLAB R2021b , Win10, i5- 11260H@2.60GHz. The color images of 512*512 "Lena","Mandril","Papper" are tested. The encryption and decryption are shown in Figure 6.

4.1. Correlation Analysis

Correlation analysis involves assessing the correlation coefficients of adjacent pixels in three directions: horizontal, vertical, and diagonal. From the pixel value matrix of the image, N pairs of neighboring pixels are chosen at random and labeled as

C_{A B}

The correlation coefficient is calculated as shown in equation (16), where

A_{n}

B_{n}

represents pixel values of neighboring pixels,

\bar{A}

\bar{B}

.N pairs

A_{n}

B_{n}

average pixel of pixels,

C_{A B} \in

[-1, 1],

C_{A B} = \frac{\sum_{n = 1}^{N} (A_{n} - \bar{A}) (B_{n} - \bar{B})}{\sqrt{\sum_{n = 1}^{N} {(A_{n} - \bar{A})}^{2} \sum_{n = 1}^{N} {(B_{n} - \bar{B})}^{2}}} .

(16)

From three color images ("Lena", "Mandril", "Pappe") of plain RGB pixels, as well as 24-bit plane scrambled and OCT encrypted RGB pixels, we randomly calculated 2000 pairs of RGB pixels. This process was repeated 100 times, and the mean values are presented in Table 3. For direct visualization, we also provide a correlation distribution map between the plaintext "Lena" and its ciphertext. Figure 7 illustrates horizontal, vertical, and diagonal correlations. A more dispersed distribution of adjacent pixels indicates better image encryption quality. Figure 7 displays this distribution. Our experiments reveal that the OCT algorithm effectively resists statistical analysis.

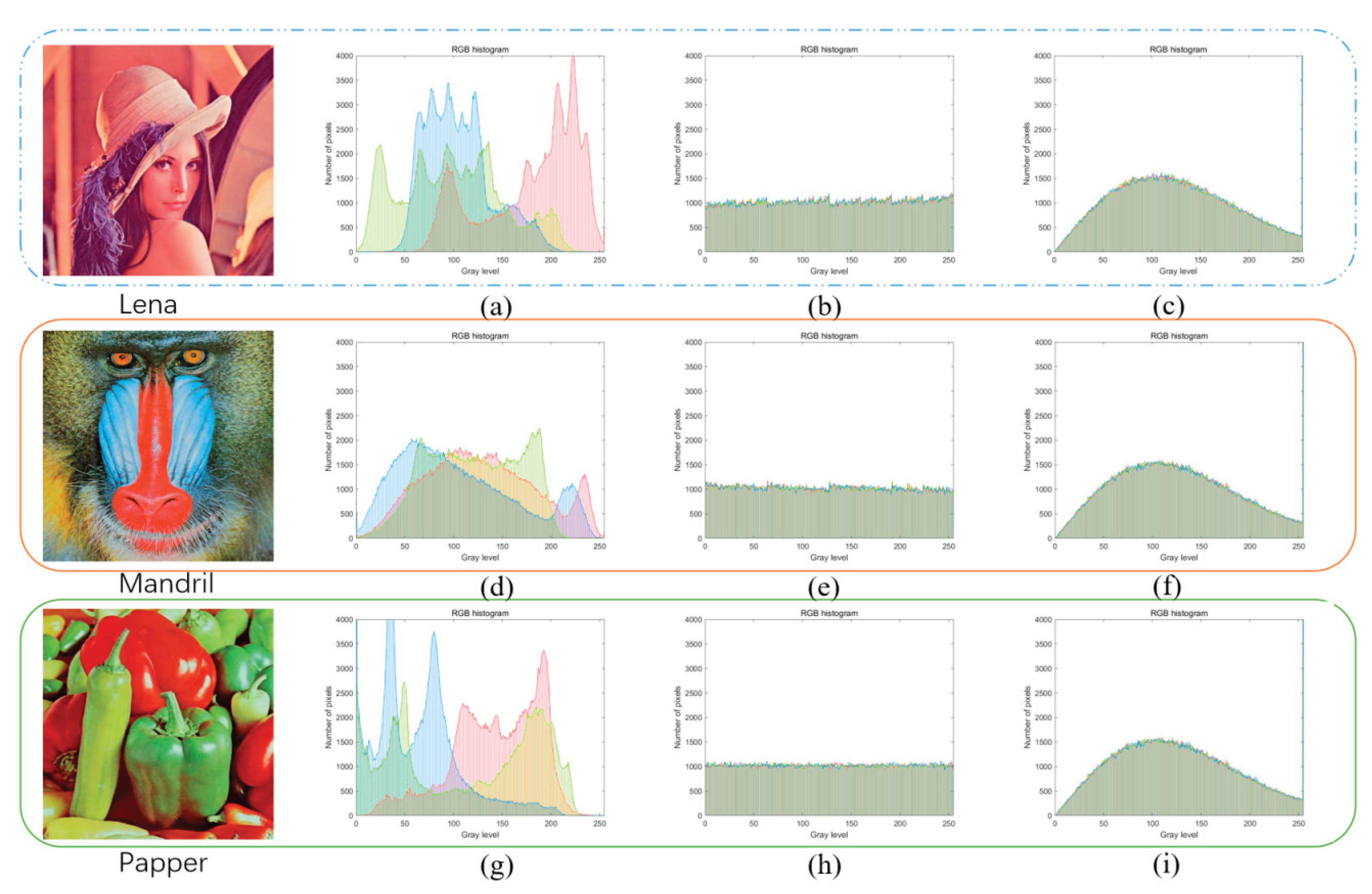
4.2. Histogram

A histogram illustrates the gray distribution of an image by statistically evaluating the frequency of occurrence for each pixel’s gray value. Histogram takes pixel value as horizontal axis and corresponding pixel number as vertical axis to form histogram. Digital image pixels are discrete, and their value range is usually limited to 0 to 255. The more uniform histogram proves that the encryption is better. Figure 8 shows color image "Lena", encrypted image after 24-bit plane scrambling, The experimental results show that OCT has a strong ability to resist statistical analysis.

4.3. Information Entropy

Information entropy, a crucial statistical measure, reflects the average information content in an image

H (m)

as equation (17), where it represents the probability of random events (pixels). An entropy closer to 8 indicates better randomness and uniformity. Table 4 shows the average entropy of original images ("Lena", "Pepper", "Baboon") and the encrypted images using OCT.

H (m) = - \sum_{i = 0}^{2^{N} - 1} p (m_{i}) \log_{2} p (m_{i}) .

(17)

Figure 7. Correlation diagram;(a),(b) and (c) are respectively correlation diagrams of R,G,B channels of "Lena";(d),(e) and (f) are respectively correlation diagrams of R,G,B channels of encrypted image after 24-bit plane replacement;(h),(i) and (j) are respectively correlation diagrams of R,G,B channels of encrypted image after OCT.

Figure 8. Histogram;(a)(d)(g) are respectively"Lena","Mandril","Papper",RGB tri-plane histogram of image;(b)(e)(h) RGB tri-plane histogram of 24-bit plane permutation;(c)(f)(i) RGB tri-plane histogram after OCT encryption.

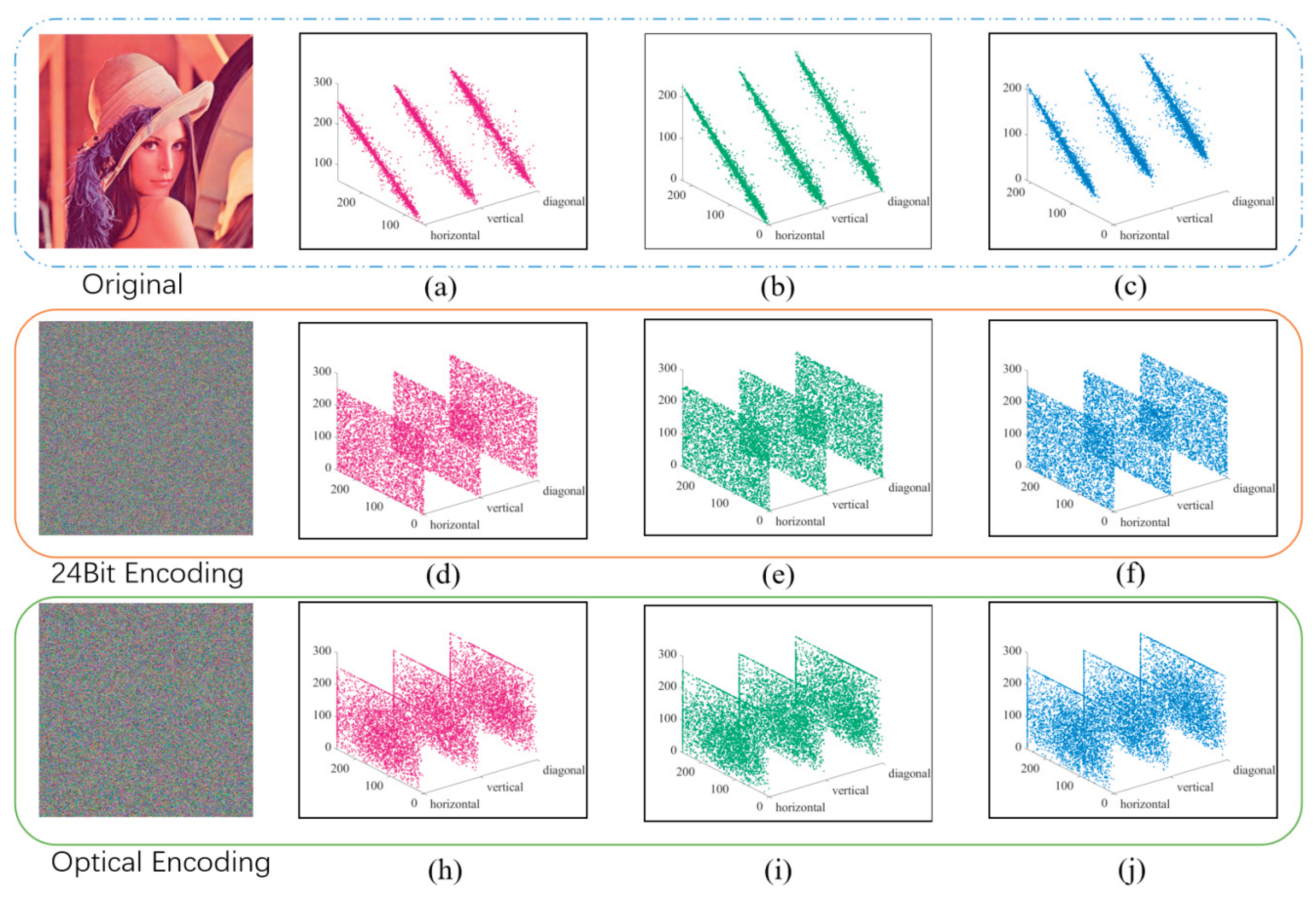
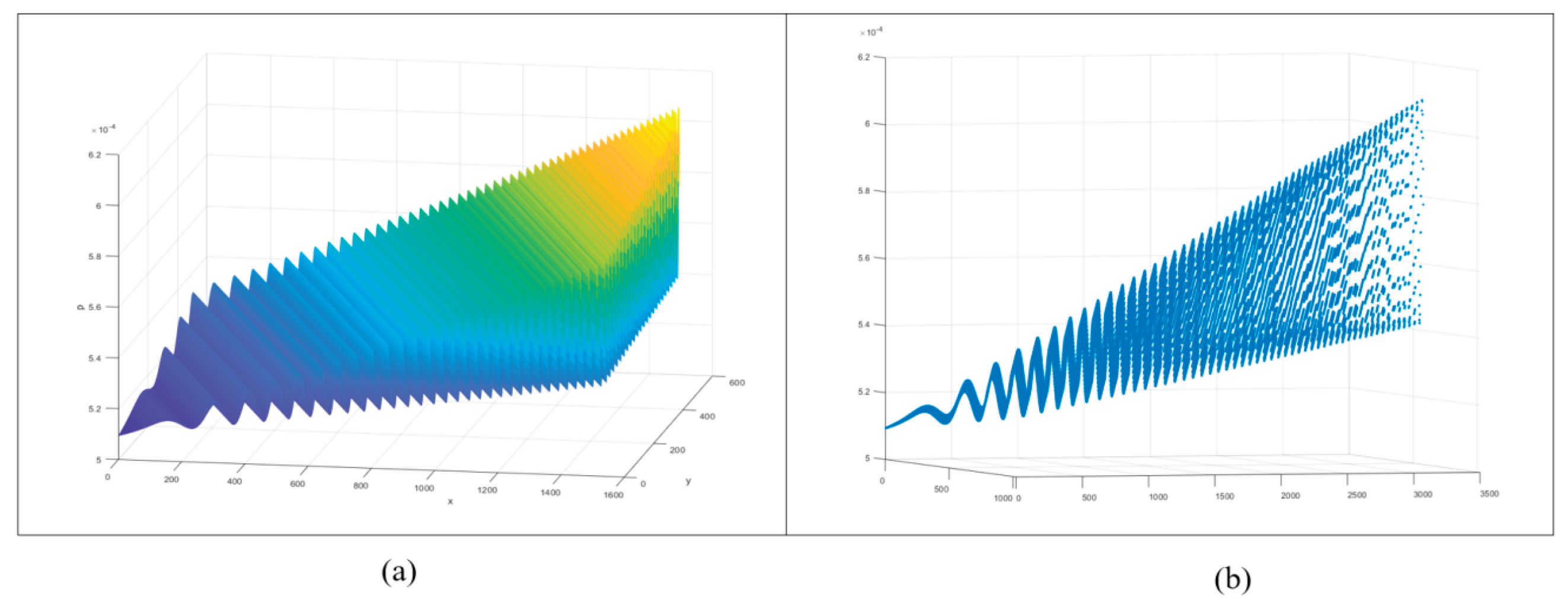
4.4. Key Space and Key Sensitivity

In the field of cryptanalysis, there is a highly respected Kerckhoff hypothesis [33]. This hypothesis holds that the attacker has mastered all the details of the encryption algorithm except the key when cracking. In other words, the encryption algorithm is transparent and open to the attacker. Only when the key space is large enough can it effectively resist potential brute force attacks. Generally, it is considered to be larger than

2^{100}

The key space is secure [34].Owing to the boundaryless characteristic of two-dimensional quantum walks, the theoretical key space is rendered infinite, such that the key space equals ∞, but is constrained by the computational accuracy of the computer, assuming that the accuracy is

10^{- 16}

.The system has

10^{128}

space, which is considered sufficient for optical image cryptography [35].

An efficient cryptosystem should recognize the variations of key parameters. This paper evaluate the image response to small variations of key parameters (sm-key, x, y, k1, t1, k2, t2, k3, t3).The parameters k1,k2,k3 changed

10^{- 13}

in this experiment, parametert1,t2,t3 changed by 1 bit, parameter sm-key changed by 1 bit, to the result of Figure 9. As observed from Figure 9, although the key undergoes minimal changes, the outcome of image decryption varies significantly. This substantial disparity between the original image and the image obtained after altering the key underscores the remarkable sensitivity of the key.

4.5. Known Plaintext Attack (KPA Attack)

The proposed scheme is evaluated for known plaintext attack (KPA) [36]. In this attack, the attacker knows the input plaintext

f (x, y)

, ciphertext

g (x, y)

in advance.In the standard DREP algorithm, RM2 can be derived from equation (19) provided that RM1 is known, as specified in equation (18).

g (x, y) = I F T {F T {f (x, y) \cdot R M 1} \cdot R M 2}

(18)

RM 2 \frac{F T \{g (x, y)\}}{F T \{f (x, y) \cdot R M 1\}} .

(19)

{R M 2}^{’} = \frac{F T \{g (x, y)\}}{F T \{f (x, y) \cdot 24 B i t \cdot {R M 1}^{’}\} \cdot A r n o l d} .

(20)

When applying the same algorithm to assess the OCT scheme, it becomes apparent that equation (14) cannot produce equation (20), which is not possible to obtain

{R M 2}^{’}

. The simulation outcomes for the OCT scheme under the KPA test are exhibited in Figure 10. Specifically, Figure 10(a) depicts an image encrypted using the conventional DRPE scheme, while Figure 10(b) illustrates the decryption of the DRPE-encrypted image employing the KPA algorithm. Figure 10(c) showcases an image encrypted via the OCT scheme, and Figure 10(d) presents the decrypted image of the OCT scheme using the KPA algorithm. Notably, the decrypted image in Figure 10(d) appears noisy and does not divulge any discernible information about the original image. Based on these findings, it is evident that the OCT scheme demonstrates resistance against the KPA.

4.6. Chosen Plaintext Attack (CPA Attack)

In DRPE, the Dirac function is chosen as the plaintext, as shown in equation (21).DRPE is vulnerable to CPA attacks [3]. The 512 ×512 Dirac function is shown in Figure 11(a), and its three-dimensional representation is shown in Figure 11(b). When the Dirac function is used instead of the input image, the encryption process of DRPE scheme follows equation (21)(22).

δ = \{\begin{matrix} 1, x = 0, y = 0 . \\ 0, o t h e r w u s e . \end{matrix}

(21)

{δ_{g (x, y)} |}_{C P A} = I F T \{F T \{δ (x, y) \cdot {R M}_{1}\} \cdot {R M}_{2}\}

(22)

The Dirac encryption

{δ_{g (x, y)} |}_{C P A}

,Dirac images

δ (x, y)

,plaintext encrypted image

g (x, y)

are known,Based on that,

f (x, y) \cdot {R M}_{1}

can be derived from equation (23).

f (x, y) \cdot {R M}_{1} = I F T (\frac{F T (g (x, y))}{F T ({δ_{g (x, y)} |}_{C P A})}) .

(23)

Therefore, in the DRPE scheme, the Dirac function is used as the selected plaintext image and any input image can be deciphered. Now, the same mechanism is applied to the proposed OCT scheme. In the OCT scheme, when the input image is replaced by the Dirac delta function during encryption, the equation is rewritten as equation (24):

{δ_{g (x, y)} |}_{C P A} = I F T \{F T \{δ (x, y) \cdot 24 B i t \cdot {R M}_{1}\} \cdot {R M}_{2}\} \cdot A r n o l d .

(24)

From equation(24), note that since we do not know

24 B i t

and

A r n o l d

information.Therefore, in this case, the key information is also encrypted, and the plaintext selected based on Dirac delta function cannot crack the key information. Therefore, compared with the traditional DRPE scheme, the proposed scheme has higher security. The simulation results of OCT scheme tested by CPA are shown in Figure 11.

In order to demonstrate the system’s ability to resist CPA, two key indicators, NPCR (Number of Pixels Changed Rate) and UACI (Unified Average Changing Intensity), can be adopted. Both NPCR and UACI describe the differences between the encrypted image AttackE after being attacked and the encrypted image E of the plaintext image without being attacked. They are calculated as shown in formulas (25) and (26), respectively.

N P C R = \frac{\sum_{i, j} D (i, j)}{2^{2 n}} \times 100 %, w h e r e D (i, j) = \{\begin{matrix} 0, e_{1} (i, j) = e_{2} (i, j) \\ 1, e_{1} (i, j) \neq e_{2} (i, j) \end{matrix}

(25)

U A C I = \frac{1}{2^{2 n}} [\sum_{i, j} \frac{|e_{1} (i, j) - e_{2} (i, j)|}{255}] \times 100 %

(26)

Comparing the AttackE with CPA and E’ without CPA for the three images of "Lena", "Mandril", and "Papper", the result can obtain Table 5.In a 256-level grayscale image, the theoretical expected values are 99.6094% and 33.4635%, respectively. The data in Table 3.7 demonstrates that the results obtained from various test images closely approximate these theoretical values, providing strong evidence of the excellent plaintext sensitivity exhibited by the encryption algorithm.

4.7. Noise and Shear Attack Test

Noise exists in most data channels and can easily damage or cause loss of data. Therefore, a well-designed cryptosystem should be capable of effectively preventing these attacks. To verify the impact of noise attacks, Gaussian Noise (GN) of 0.01, 0.1, 0.2, and 0.5, as well as Salt and Pepper Noise (SPN), were introduced. The results are presented in Figure 12. When the algorithm is subjected to 0.5 intensity of SPN and 0.5 intensity of GN, the decrypted Lena portrait remains clearly visible. This indicates that the scheme possesses strong resistance to noise attacks.

To assess the effect of cropping attacks on image decryption, encrypted and decrypted color images were derived by subjecting the cipher images of R, G, B to varying intensities. Figure 13(a), (b), and (c) exhibit the encrypted and decrypted color images subsequent to the loss of 50% data in the R, G, and B planes, correspondingly. Figure 13(d), (e), and (f) display the outcomes when 100% of the data is lost in the R, G, and B planes, respectively. Figure 13(g), (h), and (i) illustrate situations where one plane loses all its data while another loses 50% data. Figure 13(j), (k), and (l) illustrate situations where two planes each lose 100% of their data. Lastly, Figure 13(m), (n), and (o) show cases where two planes lose 100% of their data and one plane loses 50%. Despite losing two color planes (66.66% of the data), the decrypted Lena portrait remains clearly visible in the decrypted image. This demonstrates that the proposed scheme exhibits excellent resistance to cropping attacks.

(g)SPN=0.2;(h)SPN=0.5.

4.8. Comparisons of Correlation Coefficient

Compare the original image, the encrypted image of 24-bit plane permutation, and the optically encrypted image after OCT encryption in terms of correlation, entropy, and key space with other schemes, as shown in Table 5. The results show that OCT has better effect than other methods in correlation, entropy and key space.

Table 6. Comparisons of correlation coefficient.

REF.#	Cor.R	Cor.G	Cor.B	Entropy.R	Entropy.G	Entropy.B	Key space
Original	0.9794	0.9909	0.9745	7.3484	7.5866	7.0930	-
[18]	−0.00006	0.0367	0.0247	7.7771	7.7190	7.7150	-
[23]	-0.0016	-0.0077	-0.0002	7.9968(Modulo and XOR )
[24]	-0.0014	0.0023	0.0015	7.9988(DNA)			-
[22]	-0.0053	-0.0012	0.005	7.9973			2³⁷²
[13]	-0.0119	-0.0087	-0.0045	7.7317	7.7864	7.6481	(10¹⁵)¹⁶
Bit24	0.00133	0.00191	-0.0036	7.9994	7.9994	7.9993	∞
OCT	-0.00177	-0.00168	-0.000499	7.7590	7.7503	7.7514	∞
Theoretical value	0	0	0	8	8	8	∞

5. Conclusions

This paper presents a color Double Random Phase Encoding (DRPE) scheme named OCT, which is founded upon 24-bit plane scrambling and Two-Dimensional Quantum Walking (TDQW). The introduction of TDQW significantly expands the key space. Furthermore, the paper analyzes that the fundamental reason for enhancing image robustness lies in reducing RGB correlation, which essentially aims to decrease the correlation of the 24-bit plane.The paper devises a method to minimize the correlation of the 24-bit plane and introduces an advanced DRPE system for image encryption. Through assessments involving correlation, entropy, histogram, clipping, and noise attacks, it is demonstrated that OCT exhibits an exceptional encryption effect. Additionally, KPA and CPA analyses are conducted to confirm OCT’s resistance against linear attacks.

References

Zhang, Y.; Chen, A.; Tang, Y.; et al. plain-text-related image encryption algorithm based on perceptron-like network. Inf. Sci. 2020, 526, 180–202. [Google Scholar] [CrossRef]
Hu, W.W.; Zhou, R.G.; Luo, J.; et al. Quantum image encryption algorithm based on Arnold scrambling and wavelet transforms. Quantum Inf. Process. 2020, 19, 1–29. [Google Scholar] [CrossRef]
Farah, M.A.B.; Farah, A.; Farah, T. An image encryption scheme based on a new hybrid chaotic map and optimized substitution box. Nonlinear Dyn. 2020, 99, 3041–3064. [Google Scholar] [CrossRef]
Trujillo-Toledo, D.A.; López-Bonilla, O.R.; García-Guerrero, E.E.; et al. Real-time RGB image encryption for IoT applications using enhanced sequences from chaotic maps. Chaos Solitons Fractals 2021, 153, 111506. [Google Scholar] [CrossRef]
Xiong, Y.; Wang, Y. Cryptoanalysis on the optical image encryption scheme based on full phase encoding and equal modulus decomposition. Appl. Opt. 2022, 61, 2743–2749. [Google Scholar] [CrossRef]
Inoue, K.; Cho, M. Amplitude based keyless optical encryption system using deep neural network. J. Vis. Commun. Image Represent. 2021, 79, 103251. [Google Scholar] [CrossRef]
Guo, X.; Zhong, J.; Li, B.; et al. Full-color holographic display and encryption with full-polarization degree of freedom. Adv. Mater. 2022, 34, 2103192. [Google Scholar] [CrossRef]
Wang, H.L.; Ma, H.F.; Cui, T.J. A Polarization-Modulated Information Metasurface for Encryption Wireless Communications. Adv. Sci. 2022, 9, 2204333. [Google Scholar] [CrossRef]
Abuturab, M.R.; Alfalou, A. Multiple color image fusion, compression, and encryption using compressive sensing, chaotic-biometric keys, and optical fractional Fourier transform. Opt. Laser Technol. 2022, 151, 108071. [Google Scholar] [CrossRef]
Zhang, Y.; Zhang, L.; Zhong, Z.; et al. Hyperchaotic image encryption using phase-truncated fractional Fourier transform and DNA-level operation. Opt. Lasers Eng. 2021, 143, 106626. [Google Scholar] [CrossRef]
Li, Y.M.; Wei, D.; Zhang, L. Double-encrypted watermarking algorithm based on cosine transform and fractional Fourier transform in invariant wavelet domain. Inf. Sci. 2021, 551, 205–227. [Google Scholar] [CrossRef]
Peng, D.; Huang, Z.; Liu, Y.; et al. Optical coherence encryption with structured random light. PhotoniX 2021, 2, 1–15. [Google Scholar] [CrossRef] [PubMed]
Liu, Q.; Liu, L. Color image encryption algorithm based on DNA coding and double chaos system. IEEE Access 2020, 8, 83596–83610. [Google Scholar] [CrossRef]
Javidi, B.; Zhang, G.; Li, J. Experimental demonstration of the random phase encoding technique for image encryption and security verification. Opt. Eng. 1996, 35, 2506–2512. [Google Scholar] [CrossRef]
Javidi, B.; Sergent, A.; Zhang, G.; et al. Fault tolerance properties of a double phase encoding encryption technique. Opt. Eng. 1997, 36, 992–998. [Google Scholar] [CrossRef]
Jeong, O.; Moon, I. Adaptive transfer learning-based cryptanalysis on double random phase encoding. Opt. Laser Technol. 2024, 168, 109916. [Google Scholar] [CrossRef]
Zhang, R.; Xiao, D. Double image encryption scheme based on compressive sensing and double random phase encoding. Mathematics 2022, 10, 1242. [Google Scholar] [CrossRef]
Faragallah, O.S.; Afifi, A.; Elashry, I.F.; et al. Efficient optical double image cryptosystem using chaotic mapping-based Fresnel transform. Opt. Quantum Electron. 2021, 53, 305. [Google Scholar] [CrossRef]
Abd-El-Atty, B.; Iliyasu, A.M.; Alanezi, A.; et al. Optical image encryption based on Quantum walks. Opt. Lasers Eng. 2021, 138, 106403. [Google Scholar] [CrossRef]
Wang, Y.; et al. Optical single-channel color image encryption based on chaotic fingerprint phase mask and diffractive imaging. Appl. Opt. 2023, 62.4, 1009–1018. [Google Scholar] [CrossRef]
Hu, W.; Dong, Y. Quantum color image encryption based on a novel 3D chaotic system. J. Appl. Phys. 2022, 131, 114402. [Google Scholar] [CrossRef]
Tian, P.; Su, R. A Novel Virtual Optical Image Encryption Scheme Created by Combining Chaotic S-Box with Double Random Phase Encoding. Sensors 2022, 22, 5325. [Google Scholar] [CrossRef] [PubMed]
Yildirim, M. A color image encryption scheme reducing the correlations between R, G, B components. Optik 2021, 237, 166728. [Google Scholar] [CrossRef]
Yildirim, M. Optical color image encryption scheme with a novel DNA encoding algorithm based on a chaotic circuit. Chaos Solitons Fractals 2022, 155, 111631. [Google Scholar] [CrossRef]
Qin, W.; Peng, X. Asymmetric cryptosystem based on phase-truncated Fourier transforms. Opt. Lett. 2010, 35, 118–120. [Google Scholar] [CrossRef] [PubMed]
Wang, X.; Zhao, D. A special attack on the asymmetric cryptosystem based on phase-truncated Fourier transforms. Opt. Commun. 2012, 285, 1078–1081. [Google Scholar] [CrossRef]
Li, M.; et al. On the security of image cryptosystems using DRPE based on scrambling and diffusion. Opt. Quantum Electron. 2024, 56.2, 241. [Google Scholar] [CrossRef]
Zhou, Q.; et al. Optical image encryption based on two-channel detection and deep learning. Opt. Lasers Eng. 2023, 162, 107415. [Google Scholar] [CrossRef]
Singh, P.; Kumar, R.; Yadav, A.K.; et al. Security analysis and modified attack algorithms for a nonlinear optical cryptosystem based on DRPE. Optics and Lasers in Engineering, 2021, 139, 106501.
Sun, G.; et al. A novel optical video cryptosystem based on improved 3D arnold transform in gyrator domains. Opt. Laser Technol. 2024, 168, 109891. [Google Scholar] [CrossRef]
Hao, W.; Zhang, T.; Chen, X.; et al. A hybrid NEQR image encryption cryptosystem using two-dimensional Quantum walks and Quantum coding. Signal Process. 2023, 205, 108890. [Google Scholar] [CrossRef]
Aharonov, D.; Ambainis, A.; Kempe, J.; et al. Quantum walks on graphs[C]//Proceedings of the thirty-third annual ACM symposium on Theory of computing. 2001: 50-59.
Simonson, S. Public Key Cryptography. MAA NOTES 2005, 68, 109. [Google Scholar]
Farah, M.A.B.; Farah, A.; Farah, T. An image encryption scheme based on a new hybrid chaotic map and optimized substitution box. Nonlinear Dyn. 2020, 99, 3041–3064. [Google Scholar] [CrossRef]
Zhang, Y. A unified image cryptography based on a perceptron-like network. The Visual Computer, 2022: 1-16.
Man, Z.; Li, J.; Di, X., et al. Double image encryption algorithm based on neural network and chaos. Chaos, solitons & fractals, 2021, 152, 111318.

Figure 1. Double random phase encoding(DREP) .

Figure 2. Two-dimensional quantum walk.(a) continuous probability distribution;(b) three-dimensional discrete probability distribution.

Figure 3. Histogram analysis.(a)"Lena" Original RGB three-plane histogram analysis,(b)RGB three-plane scrambling histogram analysis,(c)24bit layer scrambling three-plane histogram analysis.

Figure 4. Overall encryption flow chart.

Figure 6. Schematic diagram of encrypted and decrypted images;(a),(e), and (f) are plaintext images of "Lena","Mandril", and "Papper";(b),(f),(j) are encrypted images after 24-bit plane permutation;(c),(g),(k) are encrypted images after OCT;(d)(h)(r) are decrypted images of "Lena","Mandril","Papper".

Figure 9. Effect of decryption of images with different keys "Lena".(a) is the correct key decryption diagram, and (b)(c)(d)(e)(f)(g)(h) are the images decrypted with the wrong keys.

Figure 10. Known plaintext attack (KPA analysis):(a) Encrypt images using DRPE scheme;(b)KPA algorithm decrypts image;(c) OCT scheme encrypts image;(d) KPA algorithm OCT decrypts image.

Figure 11. Chosen plaintext attack (CPA attack).(a)Dirac delta function;(b) Dirac delta function of three-dimensional map;(c) encrypting DREP image with CPA;(d) decrypting DREP image with CPA;(e) encrypting OCT image with CPA algorithm;(f) decrypting OCT image with CPA method.

Figure 12. Noise attack;(a)GN=0.01;(b)GN=0.1;(c)GN=0.2;(d)GN=0.5;(e)SPN= 0.01;(f)SPN=0.1;.

Figure 13. Shear Attack.

Table 1. Improved DRPE Algorithm.

Table 3. Correlation analysis.

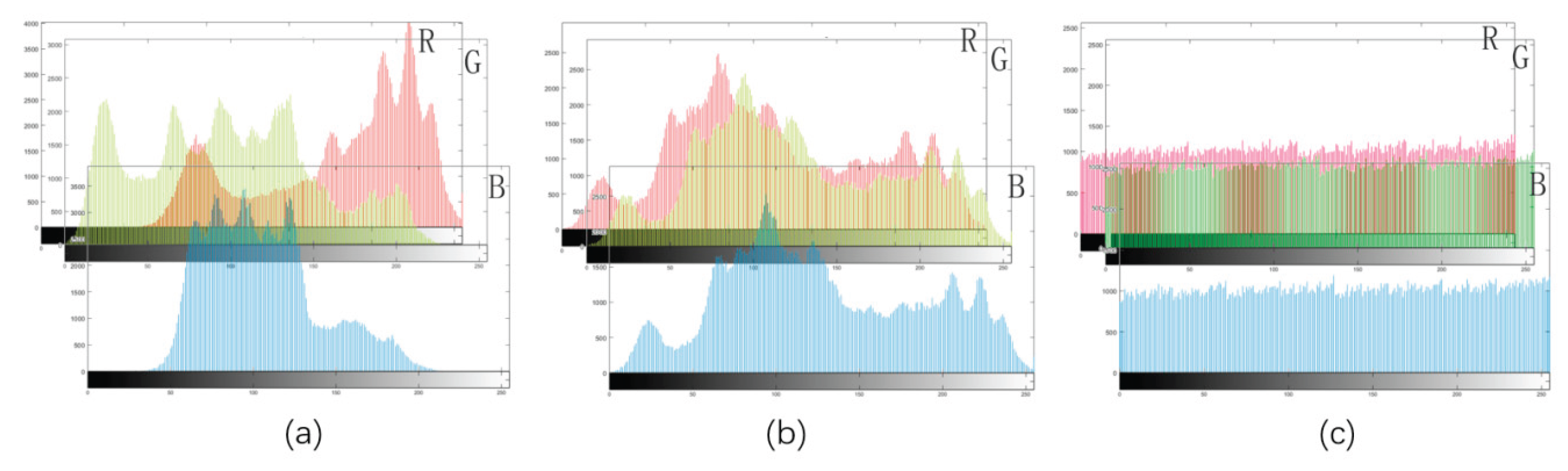
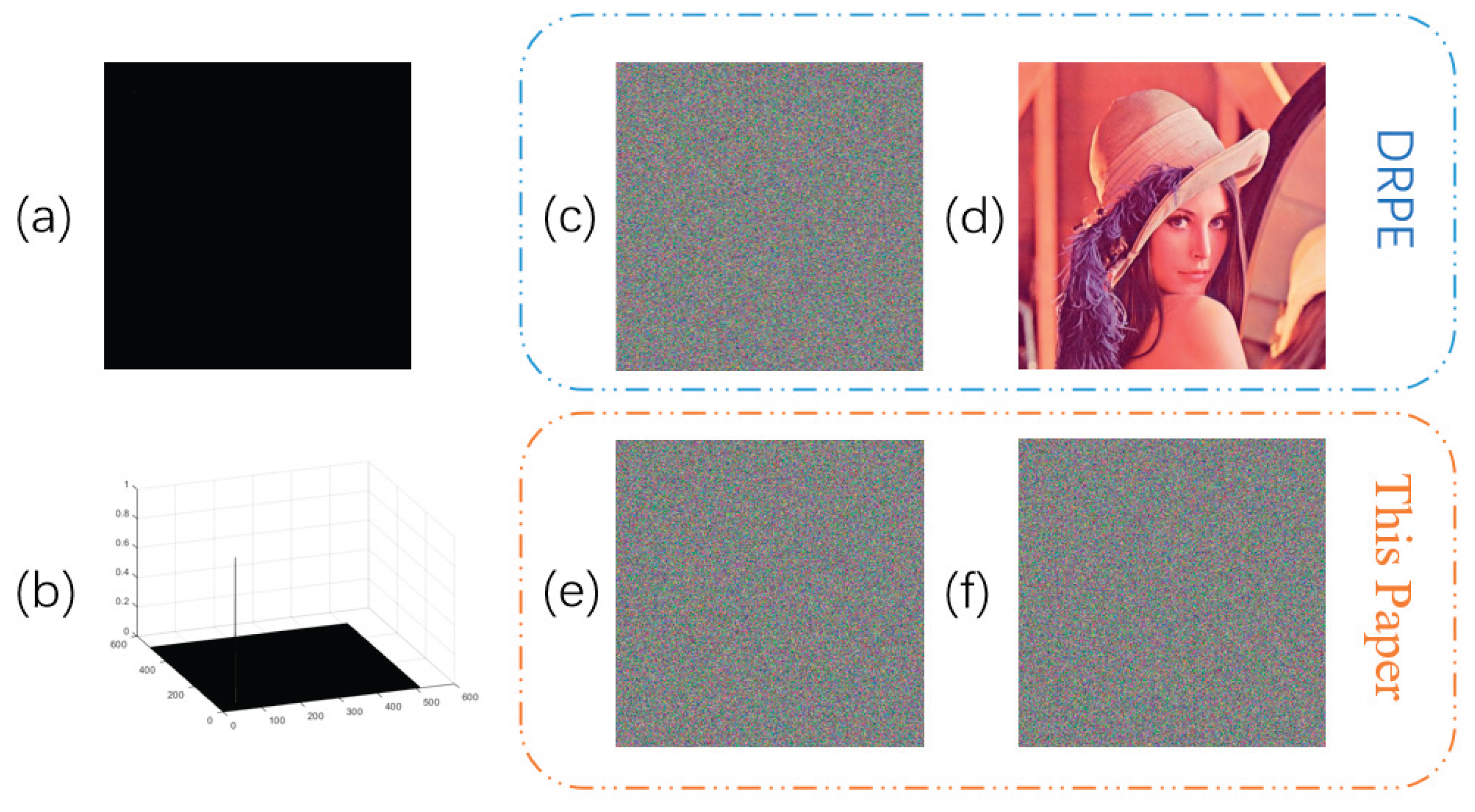
Fig	Correlation.R			Correlation.G			Correlation.B
Fig	H	V	D	H	V	D	H	V	D
Figure 6(a)	0.9811	0.9811	0.9677	0.9830	0.9703	0.9516	0.9592	0.9362	0.8999
Figure 6(b)	-0.0075	-0.0083	0.0036	-0.0050	0.0003	-0.0052	-0.0016	0.0020	-0.0140
Figure 6(c)	0.0006	-0.0023	-0.0016	-0.0004	-0.0017	-0.0019	-0.0003	0.0009	0.0020
Figure 6(e)	0.7707	0.8563	0.7524	0.7465	0.8443	0.7311	0.8567	0.9081	0.8369
Figure 6(f)	-0.0097	0.0236	-0.0036	0.0086	-0.0125	0.0015	0.0051	-0.0084	-0.0230
Figure 6(g)	0.0025	0.0074	0.0019	0.0026	-0.0014	0.0070	0.0275	0.0036	-0.0025
Figure 6(i)	0.9772	0.9738	0.9587	0.9920	0.9892	0.9800	0.9749	0.9691	0.9427
Figure 6(j)	0.0013	-0.0037	0.0045	0.0191	0.0066	-0.002	-0.0036	0.0200	-0.0058
Figure 6(k)	-0.0101	0.0055	-0.0030	-0.0320	0.0003	0.0040	-0.0059	0.0016	0.0248

Table 4. Average information entropy.

Numble	Lena			Mandril			Papper
	Figure 6(a)	Figure 6(b)	Figure 6(c)	Figure 6(e)	Figure 6(f)	Figure 6(g)	Figure 6(i)	Figure 6(j)	Figure 6(k)
Entropy.R	7.3484	7.9994	7.7590	7.7593	7.9994	7.7249	7.3484	7.9994	7.7191
Entropy.G	7.5866	7.9994	7.7503	7.4594	7.9993	7.7222	7.5866	7.9994	7.7215
Entropy.B	7.0930	7.9992	7.7514	7.7556	7.9994	7.7213	7.093	7.9992	7.7209

Table 5. The value of NPCR and UACI.

Numble	Lena			Mandril			Papper
	R	G	B	R	G	B	R	G	B
UACI	99.6217	99.6016	99.5987	99.6033	99.5867	99.5865	99.5986	99.5879	99.5942
NPCR	33.6643	33.3611	33.3695	33.5258	33.3890	33.3780	33.4928	33.3977	33.4915

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer