Prerpints.org logo
Preprint
Article

Study on the Relationship between Strength and Failure Area of Concrete Specimens under Complex Loading Conditions

Altmetrics

Downloads

84

Views

16

Comments

0

This version is not peer-reviewed

Submitted:

10 April 2024

Posted:

11 April 2024

You are already at the latest version

Alerts
Abstract
Based on the dynamic strength variation mechanism of concrete under complex loading conditions, two approaches were devised: numerical testing and CT scanning, guided by the principle of minimizing energy dissipation. A methodology for calculating concrete's failure area and measuring its strength was developed. The analysis delves into the mechanisms behind failure patterns and variations in concrete specimen strength, focusing on crack initiation, development, and the resultant failure surface formed by crack propagation, along with the stress distribution in concrete specimens subjected to diverse loading conditions. Through evaluating the strength and computed failure area of concrete specimens, it is evident that the loading method influences both the strength and failure area of concrete specimens. In general, a larger failure area correlates with a higher measured strength.
Keywords: 
Subject: Engineering  -   Architecture, Building and Construction

1. Introduction

Early research on the dynamic strength of concrete under uniaxial compression mainly adopts the drop hammer method and hydraulic loading method, which are representative of the achievements made by Watstein [1], Takeda et al [2], Atchley et al [3]. and the maximum strain rate is 10m/s. The results show that the dynamic compressive strength of concrete increases with the increase of loading rate under uniaxial compression. Split Hopkinson Pressure Bar (SHPB) technology is the most effective method to measure the correlation characteristics of concrete materials under high strain rates. Hopkinson first proposed this technology in 1914. At present, the strain rate of concrete materials can be measured in the range of 10-1m/s to 103m/s. Malvar et al [4].Tedesco et al [5].Bischoff et al [6].and Kepaczko et al [7]. have obtained some recognized test results. In order to obtain the uniaxial tensile strength of concrete under the action of high strain rate, it is necessary to test the SHPB splitpull test, which is relatively difficult. According to the obtained test results [8,9], the uniaxial dynamic tensile strength also increases with the continuous increase of the loading rate, and its growth rate and increase range are larger than the value of the uniaxial compressive dynamic strength relative to the static strength.In recent years, many scholars at home and abroad have studied the strength of concrete and lithologic materials from the perspective of energy, and have made some achievements [10,11,12,13,14].
The mechanical property of concrete, known as strength, remains constant regardless of external conditions. It is a widely recognized fact that concrete specimens exhibit varying tensile, compressive, shear, torsional, and bending strengths when measured. Additionally, the enhancement of static and dynamic tensile and compressive strengths also differs. [15,16,17]. Under uniform external loading, changes in specimen height, effective cross-sectional area, and cross-section shape result in proportional fluctuations in measured strength. This raises inquiries regarding the origins of these differences, whether they arise from variances in concrete strength definitions, testing methodologies, or underlying factors. Studies confirm that concrete's tensile strength remains intrinsic and constant, irrespective of external circumstances. However, the typically measured strength aligns with the stress condition of the concrete specimen. Diverse stress conditions yield varying levels of specimen damage, discrepancies in crack surface areas, and unique forms of specimen failure.
To explore the correlation between concrete specimen strength and failure patterns amidst complex stress conditions, the author investigated the stress state, strength, crack initiation process, failure surface morphology, and failure area of concrete specimens under varied loading conditions via physical CT experiments and numerical simulations. The methodology for determining concrete specimen strength under diverse stress states and computing the failure area is outlined, with concrete strength being characterized by the failure area observed.

2. Methodology

To ascertain the strength of concrete specimens subjected to tensile, compressive, torsional, and bending loads, following the principle of minimizing energy dissipation [18], the uniaxial stress-strain relationship of concrete is expressed as a function with damage variables g [ D ( ε ) ] [19], namely:
ε = σ g [ D ( ε ) ] E 0
Where E0 is the initial elastic modulus, which damages with the change of strain, and D is the damage variable.
When the concrete specimen is subjected to external work, the inelastic principal strain εs is energy consumption, then the ratio of the energy consumption rate of the concrete unit at the time of failure to the peak stress of the concrete under uniaxial action fi2 is:
∑ i = 1 3 Φ i f i 2 = ∑ i = 1 3 Φ σ i ε s f i 2
σ i i = 1 , 2 , 3 is the principal stress at this point at the beginning, ε s i is the inelastic principal strain, the stress-strain relationship during damage energy dissipation is:
{ ε 1 ε 2 ε 3 } = ( 1 E 0 + 1 g E 0 ) [ 1 − λ − λ − λ 1 − λ − λ − λ 1 ] { σ 1 σ 2 σ 3 }
Where λ is the Poisson ratio of concrete, and
{ ε s 1 ε s 2 ε s 3 } = 1 g E 0 [ 1 − λ − λ − λ 1 − λ − λ − λ 1 ] { σ 1 σ 2 σ 3 }
When the test piece is damaged, there are:
{ ε s 1 f 1 = − 1 g 2 E 0 [ σ 1 f 1 − λ ( σ 2 f 2 + σ 3 f 3 ) ] ε s 2 f 2 = − 1 g 2 E 0 [ σ 2 f 2 − λ ( σ 1 f 1 + σ 3 f 3 ) ] ε s 3 f 3 = − 1 g 2 E 0 [ σ 3 f 3 − λ ( σ 2 f 2 + σ 1 f 1 ) ]
The failure energy dissipation process is an irreversible process, and the corresponding increase of inelastic strain is also irreversible. Therefore, the expression of energy dissipation rate of concrete failure when formula 5 is brought into formula 2 is as follows:
∑ i = 1 3 Φ i f i 2 = − 1 g 2 E 0 [ σ 1 2 f 1 2 + σ 2 2 f 2 2 + σ 3 2 f 3 2 − 2 λ ( σ 1 f 1 + σ 2 f 2 + σ 3 f 3 ) ]
The triaxial strength criterion expression of concrete is set as follows:
According to the principle of minimum energy dissipation [12], the stress conditions that should be satisfied in the damage energy dissipation are:
∂ ∑ i = 1 3 Φ i f i 2 + λ * F ∂ σ i = 0 , i = 1 , 2 , 3
λ * is the Lagrange multiplier, substituting formula 6 into:
{ ∂ F ∂ σ 1 = 1 g 2 E 0 λ * ( 2 σ 1 f 1 2 − 2 λ 1 f 1 ) ∂ F ∂ σ 2 = 1 g 2 E 0 λ * ( 2 σ 2 f 2 2 − 2 λ 1 f 2 ) ∂ F ∂ σ 3 = 1 g 2 E 0 λ * ( 2 σ 3 f 3 2 − 2 λ 1 f 3 )
Substituting equation 7 into the equation gives:
d F = ∂ F ∂ σ 1 d σ 1 + ∂ F ∂ σ 2 d σ 2 + ∂ F ∂ σ 3 d σ 3
Points earned:
F ( σ 1 , σ 2 , σ 3 ) = 1 g 2 E 0 [ σ 1 2 f 1 2 + σ 2 2 f 2 2 + σ 3 2 f 3 2 − 2 λ ( σ 1 f 1 + σ 2 f 2 + σ 3 f 3 ) + c ]
Order:
A = σ 1 2 f 1 2 + σ 2 2 f 2 2 + σ 3 2 f 3 2 − 2 λ ( σ 1 f 1 + σ 2 f 2 + σ 3 f 3 )
Then:
A = − λ * E 0 g 2 c
When acting under uniaxial stress, A = 1 the general form of the unified failure criterion for the concrete specimen unit is obtained as
σ 1 2 f 1 2 + σ 2 2 f 2 2 + σ 3 2 f 3 2 − 2 λ ( σ 1 f 1 + σ 2 f 2 + σ 3 f 3 ) = 1
For the whole concrete specimen under uniaxial tension and compression, Formula 13 is satisfied, so it can be judged that the strength of the concrete specimen is its peak stress.
When the stress of each element satisfies formula 13, the element will fail.

3. Calculation Model

In the mesoscopic study of concrete materials, in order to study the evolution process of cracks, two paths are carried out, namely physical test and numerical test. At present, a typical physical experiment is CT test. The study examines the failure modes, stress distribution, failure surfaces, and energy per unit area of concrete specimens subjected to tension, compression, torsion, and bending loads, based on the different failure modes of concrete under various loading conditions. Table 1 provides the concrete specimen used in the research.

3.1. Loading Condition

Table 2 is the loading condition control table, which lists various loading conditions in the system and their corresponding control parameters in detail.

3.2. Failure Criterion

In the numerical loading analysis, a double-broken line damage evolution model was employed to replicate the gradual decrease in elastic modulus, resulting in the failure of certain elements due to strength issues.
A double-broken line damage evolution model was used in the numerical loading analysis to mimic the progressive decline in elastic modulus, leading to the failure of specific elements due to strength concerns. In ANSYS numerical calculation, the destruction area is the area of the kill unit multiplied by the number of kill units. The shape of the element is tetrahedron, and the area of the element is the surface area of the tetrahedron.

3.3. The Solving Process of Numerical Calculation

While loading, if an element's maximum tensile strain exceeds the material's ultimate tensile strain, the element's stiffness is compromised. This indicates that as the load increases, the elastic modulus of the element follows a double-line damage law. Solving the static equilibrium equation for the element necessitates an incremental method due to its nonlinearity. Since the extent of damage to the elastic modulus changes as the load increases, the solution process necessitates constant iterations for damage, resulting in a significant computational workload.
The static equilibrium equation of step i of a unit is:
K i { u i } = { p i }
The balance equation loaded to step i+1 is:
K i + 1 { u i + 1 } = { p i + 1 }
From equation 14 subtract equation 15, we obtain:
K i { Δ u } = { Δ p } − Δ K { u i + 1 }
K i is the stiffness matrix for step i, { u i } is the node displacement, and { p i } is the load matrix.
where, Δ K = K i + 1 − K i , { Δ p } = { p i + 1 } − { p i } , { Δ u } = { u i + 1 } − { u i } .
Following Lemaitre's strain equivalence principle, the stress of a material can be represented by its effective stress without causing damage to the material. This paper focuses solely on considering damage to the elastic modulus, without accounting for the influence of Poisson's ratio on material damage. By introducing the damage variable d ( ε ) for the elastic modulus, the post-damage elastic modulus is denoted as E = [ 1 − d ( ε ) ] E 0 . The change in the damage variable with strain is illustrated in the elastic double-break line damage model.
D = { 0 ε max < ε 0 1 − η − λ η − 1 ε 0 ε max + 1 − λ η − 1 ε 0 < ε max < ε r 1 − λ ε 0 ε max ε r < ε max < ε u 1 ε u < ε max
λ is the residual strength coefficient; ε 0 is the main tensile strain of the element when the stress reaches the tensile strength; ε r is the residual strain of the unit corresponding to the tensile residual strength: ε r = η ε 0 ; η is the residual strain coefficient, and the value range of each phase of concrete materials is usually 1 < η < 5 . Where the ultimate tensile strain is calculated as ε u = ξ ε 0 ξ η , ξ is the ultimate strain coefficient; ε max is the maximum value of the principal tension strain of the element during loading. In the damage evolution equation (17), η take 5, and ξ 10 as elements; λ take 0.1. When the maximum tensile strain ( ε max ) of the unit in damage 1 is within ε 0 and ε r , the set of units that undergo the first progressive stage of damage occurs. Unit damage 2 is the set of units where the damage of the second progressive stage occurs when the maximum tensile strain in the interface ( ε max ) unit is within the range of ε r and ε u , and the unit is gradually transformed from damage 1 to damage 2, and the damaged unit is gradually transformed into the killing unit.
Δ K = ∑ [ d θ ( ε i θ ) − d θ ( ε i + 1 θ ) ] K 0 θ = − ∑ Δ d θ ( ε ) K 0 θ )
Where, Δ d θ ε is the incremental variable of the unit damage, and K 0 θ is the unit stiffness matrix when the unit is not loaded.
K i { Δ u } = { Δ p } + ∑ Δ d θ ( ε ) K 0 θ { u i + 1 }
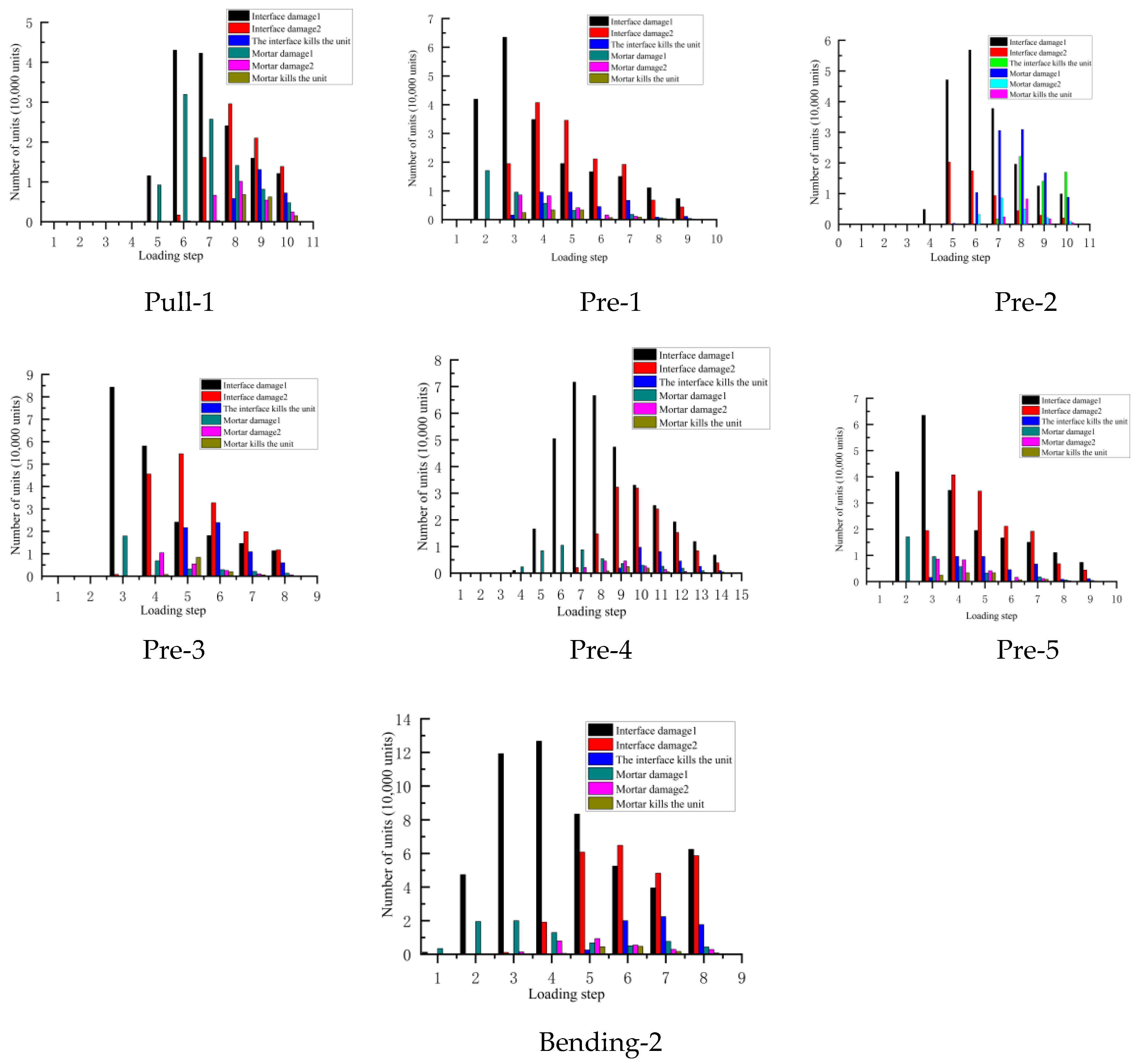
Iterative solution { u i + 1 } is obtained. Figure 1 shows the damage unit of the computing unit.

3.4. Numerical Analysis of Failure Area of Specimens under Different Stress States

The number and strength of damaged units obtained are summarized in Table 3.
The failure area of specimens under various loading conditions is obtained from large to small as Pre-1~Pre-5, and the sizes are as follows: 21.98e3mm2, 20.82e3mm2, 17.24e3mm2, 9.39e3mm2, 9.37e3mm2, 3.36e3mm2和1.00e3mm2.
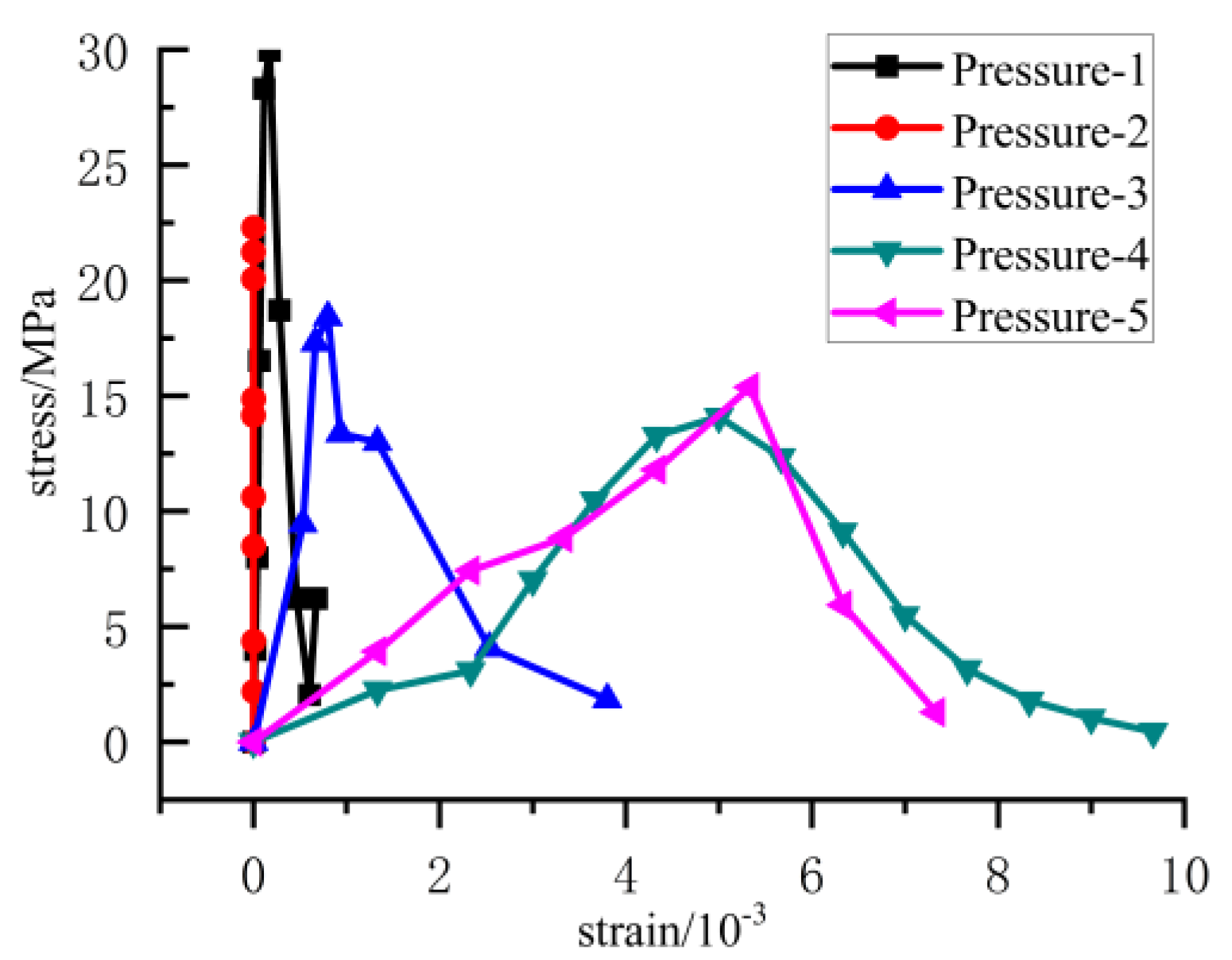
As shown in Figure 2, the peak stress and strength of compressive concrete specimens Pre-1, Pre-2, Pre-3, Pre-4 and Pre-5 are 29.96MPa, 22.29MPa, 18.41MPa, 14.10MPa and 15.37MPa, respectively. With the decrease of length-diameter ratio, the strength of the specimen decreases.
By the same method, the strength of Pull-1 and Bending 2 was 7.56MPa and 6.2MPa respectively.
Based on the data presented above, it's evident that specimens with larger failure areas exhibit higher strengths, showcasing a direct correlation between strength and failure area. The macroscopic failure area varies under different loading conditions due to the distinct stress states experienced by the unit. Concrete specimens subjected to different stress states exhibit diverse failure forms, crack patterns, and propagation directions, leading to variations in their failure areas. Additionally, the energy released during failure differs among specimens, influencing their strengths, such as Pull-1, Pre-1, Pre-5, and Twist-1 specimens. Conversely, when subjected to different loading conditions, specimens with identical failure forms, crack types, development paths, and failure areas exhibit consistent failure energies, resulting in equivalent strengths, such as Pull-1, Pre-3, and Bending-1 specimens. This suggests that the measured strength of concrete specimens under varied loading conditions is associated with their respective failure areas, which differ based on the stress states experienced by the concrete specimens.
When the concrete specimen with the change of length-diameter ratio is under pressure, its failure energy and failure area are also different due to the different stress state, so the strength of the concrete specimen under pressure is affected by the size effect.
No matter how the loading method of the tensile failure of the concrete specimen, such as under bending and uniaxial tensile action, the stress state of the two is similar, both are tensile failure, the damage area is the same, and the damage area and the damage energy are the same, so the strength is very close. Therefore, the tensile strength of concrete is a stable value, which is not affected by the loading method, size effect, and load size.
Therefore, the difference of measured strength of concrete specimens under different loading conditions is essentially affected by the failure area, and further, it is determined by the stress state in which it is located.

4. Failure Area Analysis of CT Test under Complex Loading Conditions

Applying the second law of thermodynamics and the principle of energy conservation, the CT test of concrete primarily examines static tension and static pressure specimens from an energetic perspective. The analysis focuses on delineating the connection between the compressive and tensile strength of concrete and the characteristics of the failure surface.

4.1. Calculation of Failure Area in CT Test of Concrete Specimen under Static Tension and Static Pressure

Based on the crack theory computed using CT images and experimental observations, the alteration in the average CT number within the statistical area results from the variation in the average CT number within the crack area before and after cracking. In other words, the change in the average CT number of S D is equivalent to the change in the average CT number of S 0 .
S D = H 0 − H i 1000 + H i S 0
H 0 and H i represent the CT values at different points or specific statistical areas during the initial stress stage and at a particular stress stage, respectively. S 0 denotes the statistical region's area before the crack appears, while S D represents the damaged area.
There are two kinds of specimens, namely, the primary small specimen and the secondary wet sieve large specimen. The small specimen size is Φ60mm×120mm cylindrical concrete specimen, and the secondary wet sieve large specimen size is Φ50mm×300mm cylindrical concrete specimen, and the age is 10 months.The chosen test equipment was the Philips 16-slice spiral CT located at Renhe Hospital of China Three Gorges University, with a resolution of 512×512. Both static pull and dynamic pull methods were utilized during testing. The CT examination primarily targeted specimens of specific sizes, with conc-042, conc-043, and conc-044 undergoing static tension testing, while conc-066 was subjected to static pressure testing.

4.1.1. Failure Area Analysis under Tension

Conc-042 (CT2), conc-043 (CT3), and conc-044 (CT4) were the subjects of investigation. As the load increased, concrete specimens exhibited the initiation, propagation, and penetration of cracks, including macroscopic ones. When subjected to static tensile load, a type I tensile crack developed, aligning nearly perpendicular to the primary tensile stress direction, resulting in a relatively flat failure surface across the specimen's cross-section. The failure surface of CT2, CT3 and CT4 is approximately circular, S L = 0 . 002826 m 2 .

4.1.2. Failure Area Analysis under Pressure

Under static pressure, most of the cracks into longitudinal distribution, and rich development, crack through the fracture surface into a cone, generally will not pass through the aggregate, after the formation of the main crack of the specimen, there is still a certain residual strength, from the formation of the crack to the specimen damage for a long time, static pressure failure for obvious softening phenomenon, the formation of type II shear crack.
Furthermore, the failure surface area of the conc-66 specimen equals the number of elements within the crack zone multiplied by the area of the resolved elements. According to the computed crack of CT image, S D = 0 . 2605 m 2 .

4.2. Analysis of Failure Forms and Strength of Concrete Specimens in CT Tests under Static Tension and Static Pressure

Failure surfaces in all cases propagate along one or two principal cracks perpendicular to the main tensile stress direction, leading to instantaneous, brittle failure where the concrete specimens lose their tensile strength entirely, measured at 2.95 MPa, 3.30 MPa, and 3.50 MPa, respectively. However, in the conc-066 compression specimen test, residual strength is observed post-failure, measuring 32 MPa, accompanied by an extensive failure area. Compression induces a relatively complex stress state, resulting in the development of failure surfaces along multiple cracks, characterized by rough new surfaces post-failure, slag detachment, and extensive specimen destruction. Comparing tensile and compressive CT test results reveals variations in material damage variables due to the differing stress states within concrete under tension and compression. Concrete, being a three-phase composite material with distinct bearing capacities of aggregate, mortar, and interface, exhibits contrasting crack initiation, expansion, penetration, and failure processes in tension and compression. Both stress states involve spherical stress and deviator stress tensors. In tensile failure, the positive spherical stress component, along with the deviator stress component, facilitates microcrack development. Conversely, in concrete under shear and compression, the negative spherical stress component, alongside deviator stress, induces damage, leading to varied material forces, crack initiation locations, development directions, damage forms, areas, and energy storage capacities, ultimately affecting strength. Specimens with larger failure areas exhibit greater strength.

5. A Theoretical Framework is Proposed to Understand the Relationship between the Strength of Concrete and Its Failure area under Various Loading Conditions

Drawing from research on the factors influencing strength, this analysis delves into the diverse strength exhibited by concrete specimens under varying loading conditions. The explored strength theory posits that the concrete's strength is dictated by both the stress state of the specimens and the testing apparatus. While the current examination does not delve into the influence of the testing equipment, it underscores the direct impact of the stress state on crack formation, propagation, and the resultant failure surface morphology. Comparisons among concrete specimens under different loading scenarios—tensile, compressive, bending, and torsion—highlight how distinct stress states yield varied crack initiation, progression, propagation, and failure patterns. In essence, the study investigates the energy expended during failure and concrete strength from the perspective of macroscopic physical phenomena—the failure surface. It aims to characterize concrete strength based on the energy perspective inherent in failure area assessment.
The relationship between the strength of tensile, compressive (long pressure, medium pressure, short pressure), bending and torsion specimens was studied, and the relationship between the basic strength of concrete specimens was used as the basis to determine the order of the strength of concrete materials as follows: short pressure, torsion, medium pressure, long pressure, bending and tension specimens. The bending strength, long pressure strength and tensile strength are close to each other, because their stress states are the same during failure, and they are all the through failure of tensile and opening cracks. Short pressure is the through failure of sliding crack, which is manifested as shear failure. The medium pressure failure is the connection of complex cracks composed of open and slip cracks, and the failure is both tensile and shear. The torsional crack is broken through by tearing type crack, and it is damaged by three-dimensional shear.
Following the principle of minimum potential energy, the actual displacement minimizes the total potential energy, signifying that the entire structure's potential energy aligns with the displacement post-failure of the concrete specimen. Various failure modes of the concrete specimen under different loading conditions are documented, and the areas of several typical failure surfaces under tension, compression (longitudinal, lateral, and transverse), bending, and torsion are computed. The order of the area of the failure surface from large to small is: S p ( 1 ) , S T , S p ( 3 ) , S p ( 5 ) , S B and S L .
It is assumed that the concrete specimen is linear elastic failure in the process of failure, and the energy provided by the system is converted into the energy consumed by the specimen to produce the unit failure surface in the unit area of crack propagation. From the theoretical point of view, it is believed that no matter how the loading method is, the stress state of the concrete specimen determines its failure form and failure area, and the energy consumed by the failure is related to the size of the failure surface. When the failure surface of the concrete specimen is generated, the upper and lower two new surfaces are formed, and the energy consumed per unit failure surface is twice the surface energy of the concrete material per unit area. The surface energy γ of the material is the inherent mechanical properties of the material, that is, R = 2 γ . According to the result of unit failure energy U = R S , under different load conditions, the failure energy of concrete specimens is proportional to the failure area. The greater the failure area during specimen failure, the more energy is absorbed from the external environment, resulting in increased energy consumption by the specimen. Therefore, the breakdown and consumption of concrete materials are sorted from large to small: short pressure, torsion, medium pressure, long pressure, bending and tension.
It is found that the order of failure area and strength of all specimens is completely consistent. Therefore, this paper concluded that the strength of concrete specimens is related to the failure area, and the stress state of the specimen determines the failure form of the specimen, that is, the failure area formed by different failure forms is different, and the size of the failure area determines the size of its strength.

6. Conclusion

Expanding on the analysis of concrete specimen failures across diverse loading conditions, the ranking of strength and failure area is reinforced through numerical tests and CT tests. Investigating the correlation between failure area and energy reveals a direct proportionality between the two.
Analyzing the failure area and strength of numerical test specimens Pre-1 to Pre-5, Pull-1, and Bending 2 uncovers a clear correlation between larger failure areas and greater strength. This correlation primarily arises from variations in stress distribution across different specimen materials, leading to distinct damage characteristics in their elastic modulus. The progression of micro-crack initiation, growth, expansion, and eventual penetration into macroscopic cracks differs, resulting in diverse failure modes and areas among the various specimens. As a result, the energy consumption on the failure surface of the specimens differs, resulting in strength variations.
The same principle applies to both compression and tension specimens tested using CT. While under load, the paths of crack initiation and development vary, resulting in unique crack evolution patterns and failure areas for each specimen. The failure area of the compression specimen notably exceeds that of the tension specimen, resulting in higher failure energy and greater strength for the compression specimen. This difference primarily arises from the varying internal stress distribution of concrete materials during tensile cracking and shear compression.
Concrete specimen failure involves the disruption of material continuity, creating a new surface. As concrete fractures, a fresh surface is exposed, requiring energy to overcome the material's surface energy per unit area. Thus, as the specimen's failure area increases, it consumes more strain energy stored in the material, absorbing additional energy from its surroundings. The specimen's ability to perform external work, reflecting its load-bearing capacity, corresponds with the material's strength: stronger materials exhibit greater capacity for external work.
In summary, under the loading condition of concrete specimens, the failure area is closely related to the strength, and the failure area is proportional to the energy consumed during the failure process. The larger the failure area, the more energy consumed and the greater the strength.

Author Contributions

Funding acquisition, Xinyu Liang; Methodology, Xinyu Liang; Software, Xinyu Liang and Wenhai Li; Writing – original draft, Xinyu Liang, Wenhai Li and Zengbiao Wu; Writing – review & editing, Xinyu Liang.

Funding

This research was funded by [National Natural Science Youth Fund] grant number [51909204] and [Natural science research project in Shanxi Province] grant number [20220302121321]awarded to Xinyu Liang.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Acknowledgments

The authors also thank the anonymous reviewers for their helpful comments and suggestions.

Conflicts of Interest

The authors declare that they have no known competing financial interests orpersonal relationships that could have appeared to influence the work reported in this paper.

References

  1. Watstein DO(1953).Effect of straining rate on the compressive strength and elastic properties of concrete. ACI Materials Journal,49(8):729~744. [CrossRef]
  2. Takeda J, Tachikawa H(1962).The mechanical properties of several kinds of concrete at compressive,tensile, and flexural tests in high rates of loading. Transactions of the Japan Architect Institute,77:1~6.
  3. Atchley B L, Furr H L(1967).Strength and energy absorption capabilities of plain concrete under dynamic and static loading. ACI Materials Journal, 64:745~756. [CrossRef]
  4. Malvar L J, Ross C A(1998).Effects of strain rate on concrete strength. ACI Materials Journal, 95:735-739. [CrossRef]
  5. Tedesco J W, Powell J C, Ross C A, et al(1997).A strain~rate~dependent concrete material model for ADINA. Computers and Structures, 64(5/6):1053~1067. [CrossRef]
  6. Bischoff P H,Perry S H(1991).Compressive behaviour of concrete at high strain rates.Materials and Structures, 24:425~450. [CrossRef]
  7. Klepaczko J R,Brara A(2001).An experimental method for dynamic tensile testing of concrete by spa. International Journal of Impact Engineering, 25:387~409.
  8. Cadoni E,Labibes K,Albertini C,at el(2001).Strain~rate effect on the tensile behaviour of concrete at different relative humidity levels [J]. Materials and Structures, 34:21~26. [CrossRef]
  9. Lambert D E,Ross C A(2000).Strain rate effects on dynamic fracture and strength. International Journal of Impact Engineering, 24(10):985~998. [CrossRef]
  10. Akdag, S.; Karakus, M.; Nguyen, G.D.; Taheri, A.; Bruning, T(2021). Evaluation of the propensity of strain burst in brittle granite based on post-peak energy analysis. Undergr. Space, 6, 1–11. [CrossRef]
  11. Munoz, H.; Taheri, A.; Chanda, E.K(2016). Rock Drilling Performance Evaluation by an Energy Dissipation Based Rock Brittleness Index. Rock Mech. Rock Eng. 49, 3343–3355. [CrossRef]
  12. Shen, J.; Arruda MR, T.; Pagani(2023). A. Concrete damage analysis based on higher-order beam theories using fracture energy regularization. Mech. Adv. Mater. Struct., 30, 4582–4596. [CrossRef]
  13. Zeng,Ming-Hui, Wu,Zhi-Min; Zheng, Jian-Jun; Yu, Rena C(2023).A mesoscopic numerical method for fracture energy of concrete. Fatigue & Fracture OF Engineering Materials & Structures. 46(7) : 2380-2395. [CrossRef]
  14. Wang, Jie ;Wang, Mingyang ;Tao, Junlin(2023).The Effects of Stochastic Circular Pores on Splitting Tensile Behavior of Concrete Based on the Multifractal Theory. Fractal And Fractional. 7(7). [CrossRef]
  15. Sun, Bi ;Chen, Rui ;Ping, Yang ;Zhu, Zhende ;Wu, Nan(2022). Study on Axial Tensile Strain Rate Effect on Concrete Based on Experimental Investigation and Numerical Simulation. Materials. 15(15) : 5164. [CrossRef]
  16. Slowik, Marta ;Akram, Amanda(2022).Length Effect at Testing Splitting Tensile Strength of Concrete. Materials. 15(1) : 250. [CrossRef]
  17. WANG YanPeng;LI Jie(2022).Stochastic fatigue damage model for concrete under complex stress states. Science China(Technological Sciences). 65(11) : 2641-2648. [CrossRef]
  18. Zhou, Z.B. Principle of Minimum Energy Consumption and Its Application; Science Press: Beijing, China, 2001. [Google Scholar]
  19. Wang, Yu-Shuang ;Wu, Jian-Ying(2023).An energy-based elastoplastic damage model for concrete at high temperatures. International Journal Of Damage Mechanics. 32(4) : 485-518. [CrossRef]
Preprints 103613 g001
Figure 1. The unit number of material damage figure.
Figure 1. The unit number of material damage figure.
Preprints 103613 g001
Preprints 103613 g002
Figure 2. The stress-strain figure of the specimens under compression.
Figure 2. The stress-strain figure of the specimens under compression.
Preprints 103613 g002
Table 1. Model of concrete specimens under different loading conditions.
Table 1. Model of concrete specimens under different loading conditions.
Specimen model Pull-1 Pre-(1) Pre-(2) Pre-(3) Pre-(4) Pre-(5) Bending-2
（R×H）mm/
(L×B×H)mm		 30×120 30×30 30×60 30×120 30×180 30×300 53×53×159
Table 2. The loading table of displacement control.
Table 2. The loading table of displacement control.
model Pull-1 Pre-1 Pre-2 Pre-3 Pre-4 Pre-5 Bending-2
Displacement loading/mm 0.01 0.01 0.08 0.16 0.16 0.16 0.01
0.03 0.012 0.12 0.28 0.28 0.2 0.02
0.06 0.016 0.16 0.4 0.36 0.24 0.03
0.08 0.022 0.2 0.52 0.44 0.28 0.04
0.10 0.028 0.28 0.64 0.52 0.4 0.05
0.12 0.04 0.34 0.76 0.60 0.76 0.06
0.13 0.052 0.4 0.88 0.68 1.14 0.07
0.14 0.064 0.52 —— 0.76 —— 0.08
0.15 0.076 0.64 —— 0.84 —— 0.09
—— 0.088 —— —— 0.92 —— 0.10
—— —— —— —— 1.0 —— 0.11
—— —— —— —— 1.08 —— 0.12
—— —— —— —— 1.16 —— ——
Table 3. strength and failure unit the different samples.
Table 3. strength and failure unit the different samples.
model Pull-1 Pre-1 Pre-2 Pre-3 Pre-4 Pre-5 Bending-2
strength（MPa） 7.56 29.78 22.2877 18.4091 14.0984 15.3780 6.2
Number of broken units Sj:34069
Jm:11033
45102		 Sj:14892
Jm: 26356
41248		 Sj:12041
Jm:62898
74939		 Sj:13002
Jm:46391
59393		 Sj:36110
Jm: 27792
63902		 Sj:12041
Jm:62674
74715		 SJ:3088
Jm:14442
17530
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated