Prerpints.org logo
Preprint
Article

YOLOv8-Mu: An Improved YOLOv8 Underwater Detector Based on Large Kernel Block and Multi-branch Heavy Parameterization Module

Altmetrics

Downloads

196

Views

119

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

10 April 2024

Posted:

11 April 2024

You are already at the latest version

Alerts
Abstract
Underwater visual detection technology plays a pivotal role in fields such as marine exploration. With the increasing demand for underwater monitoring, the quest for efficient and reliable methods for underwater target recognition has become particularly significant. To address this requirement, this study developed an innovative underwater object detection architecture based on YOLOv8, named YOLOv8-MU, aimed at significantly enhancing detection accuracy.By integrating the LarK module proposed in UniRepLKNet to optimize the backbone network, YOLOv8-MU aims to achieve a larger receptive field without increasing the model’s depth. Further, this research introduces C2fSTR, an innovative method that combines Swin Transformer with the C2f module. Additionally, we have incorporated the SPPFCSPC_EMA module, which combines Cross-Stage Partial Fast Spatial Pyramid Pooling (SPPFCSPC) with attention mechanisms, significantly improving the detection accuracy and robustness of various biological targets. Moreover, by introducing a fusion block based on DAMO-YOLO into the neck of the model, we further enhanced the model’s capability in multi-scale feature extraction. Finally, the adoption of the MPDIoU loss function, designed around vertex distance, effectively tackles the challenges of localization accuracy and boundary clarity in underwater organism detection. Experimental results on the URPC2019 dataset demonstrate that the YOLOv8-MU model achieved an mAP@0.5 of 78.4%, marking improvements of 5.6%, 1.1%, and 4.0% over YOLOv5s, YOLOv7, and YOLOv8n respectively, indicating the leading performance (SOTA) of this method. On the other hand, further evaluation on the URPC2020 dataset confirmed the generalization capability of the YOLOv8-MU architecture, with its mAP@0.5 reaching 80.4%, surpassing various models including YOLOv5x and YOLOv8n, showcasing the wide applicability of our proposed improved model architecture.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

In the exploration and management of marine resources, accurate detection and localization of underwater resources are essential for their sustainable utilization. This area of application is extensive, encompassing, but not limited to, monitoring marine ecosystems [1], exploring underwater historical sites [2], and assessing the health of aquaculture [2]. To address the challenges posed by the limitations of traditional detection methods and the complexity of marine environments, this study investigates the use of intelligent sensors and automation technologies, such as Autonomous Underwater Vehicles (AUVs), underwater positioning and navigation systems, wireless underwater communication systems, and Remotely Operated Vehicles (ROVs), for efficient underwater exploration. These advanced technological approaches not only enable direct observation of the deep sea but also facilitate the precise mapping of seafloor topography and the accurate identification of various marine organisms through integrated smart sensors, including sonar systems and high-resolution cameras. Faced with the phenomena of light absorption and scattering in underwater environments, as well as the diversity of marine life forms, this research adopts an improved YOLOv8 [4] deep learning architecture to further enhance the model’s feature extraction and recognition capabilities, especially by incorporating intelligent algorithms to bolster the model’s adaptability and perceptual range in complex underwater settings. Moreover, considering the importance of clear target boundaries for accurate localization, we also focus on improving image boundary clarity through deep learning techniques, thereby increasing the accuracy of detection.
In the field of computer vision, selecting an appropriate receptive field size is crucial for enhancing the performance of neural networks. This is because only the image content falling within the receptive field of a neuron can activate that neuron, thus influencing the final processing outcome. Therefore, when designing networks, it is imperative to ensure that their receptive fields are sufficiently broad to encompass all important regions of the image. Deep Convolutional Neural Networks (CNNs) have demonstrated outstanding capabilities in handling complex visual tasks, where adjusting parameters such as network depth and convolutional kernel size to modulate the network’s receptive field has become a common strategy for improving prediction accuracy. This is particularly crucial in applications requiring dense predictions such as semantic image segmentation [5][6], stereo vision analysis [7], and optical flow estimation [8], as these tasks rely on a comprehensive understanding of the extensive context surrounding each pixel to ensure no critical information is overlooked. In this study, we adopted the innovative LarK Block from UniRepLKNet [9], which extends the model’s receptive field by leveraging large kernel blocks without the need to increase network layers, effectively enhancing the network’s ability to capture details. This approach enables the network to gain a broader context without adding computational complexity, thereby improving its recognition and understanding capabilities in complex scenes.
The intricate diversity of marine ecosystems and the morphological variations among organisms pose significant challenges to underwater detection technologies. In the ever-changing marine environment, the visual characteristics of aquatic organisms undergo varying degrees of change, complicating the task of accurate detection. While traditional Transformer models [10] can partially address these challenges, their complex structures demand substantial computational resources and extensive training data, making model optimization quite challenging. In contrast, the Swin Transformer [11] introduces a hierarchical attention mechanism to improve upon traditional transformer architectures. By limiting attention computations within individual windows, it effectively reduces processing overhead while enhancing the model’s ability to handle distant information, thereby improving the quality of feature capture. This is particularly beneficial for enhancing the accuracy and robustness of detecting various types and sizes of underwater organisms.
Furthermore, the newly developed Cross-Stage Partial Fast Spatial Pyramid Pooling (SPPFCSPC) module [12] offers new possibilities for feature extraction and integration in object detection tasks. This technology enables effective feature fusion across multiple scales, thereby optimizing detection performance. In conjunction with this technology, we introduce an innovative non-dimensional multi-scale attention mechanism—Efficient Multi-scale Attention (EMA) [13]. This mechanism further optimizes feature processing within the SPPFCSPC framework, referred to as SPPFCSPC_EMA, enabling the model to flexibly handle and integrate information from different levels, significantly enhancing the overall performance of the model in handling complex underwater biological detection tasks. Through the application of this approach, we aim to enhance the performance of underwater biological detection technology to better address the diversity and challenges of the marine environment.
To enhance the performance of the network in handling highly complex detection tasks, we introduce an improved Fusion Block based on the DAMO-YOLO model, which incorporates reparameterization and dense connection strategies [14]. This design optimizes the information flow between layers of the network, endowing it with the capability to identify and localize targets through richer feature representations. The innovation in this architecture addresses the challenges posed by complex detection environments, particularly in maintaining the accuracy and stability of the network amidst the diversity and complexity of features. With the design of the Fusion Block, the YOLOv8 network can more effectively extract and integrate multi-scale features, significantly improving the performance of object detection. The integration of techniques within the Fusion block provides a comprehensive means of reinforcement for the YOLOv8 network, enabling it to handle and parse complex detection scenes more accurately. This improvement not only directly enhances the accuracy of detection but also fosters the development of more efficient and scalable object detection models.
One common challenge encountered during image acquisition in underwater environments is the blurring caused by motion, resulting in loss of clarity in object contours and texture details [15]. When dealing with such images, traditional loss functions often struggle to achieve the desired accuracy in object localization and boundary recognition, leading to blurred boundaries and positioning errors. To overcome this issue, the MPDIoU loss function based on vertex distance is employed to strengthen the limitations of IoU loss [16]. This method enhances the adaptability to underwater targets with indistinct boundaries, thereby improving the accuracy of object detection and the overall robustness of the system. Through this improvement, the common challenges of positioning accuracy and boundary clarity in underwater biological detection tasks are effectively addressed.
In this study, we have conducted crucial optimizations on the YOLOv8 object detection framework to enhance the detection accuracy of underwater targets. The innovations of this paper mainly focus on the following aspects:
  • Firstly, we introduced the LarK Block from UniRepLKNet into the backbone network, replacing some C2f modules, aiming to achieve higher detection performance and a more lightweight network structure. Furthermore, we proposed the C2fSTR module, inspired by the Swin Transformer, to enhance the accuracy and robustness of detecting different types and scales of biological targets. Simultaneously, in the neck network of YOLOv8, we replaced the C2f module with Fusion Block to strengthen the network’s feature representation and perception abilities.
  • Additionally, We have also introduced the EMA attention mechanism based on the SPPFCSPC module, forming the SPPFCSPC_EMA module. This module can effectively extract and integrate features from different scales, significantly improving the recognition capability of multi-scale targets.
  • Finally, to enhance the model’s localization accuracy and boundary recognition capability in underwater object detection, we have adopted the MPDIOU loss function. This novel loss function greatly enhances the detection accuracy of the model, enabling our improved version of the YOLOv8 model to demonstrate excellent performance in underwater target detection tasks.
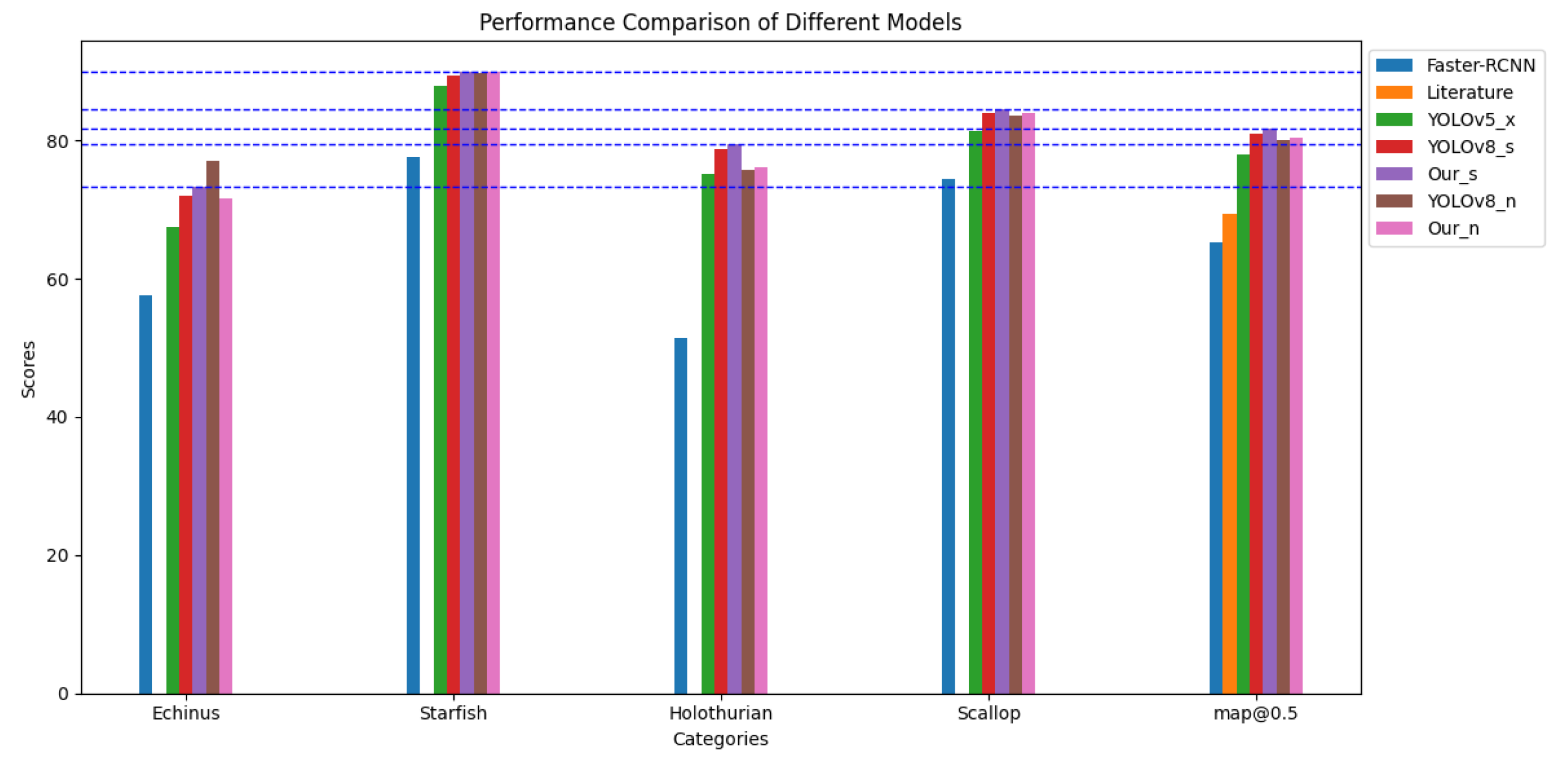
Experimental results on the URPC2019 and URPC2020 datasets demonstrate that the proposed YOLOv8-MU model achieves higher detection accuracy, with mAP@0.5 scores of 78.4% and 80.4%, respectively. These scores represent an improvement of 4.0% and 0.4% over the original YOLOv8.
The remainder of this paper is organized as follows: Section 2 reviews related work, while the proposed YOLOv8-MU and experimental analysis are presented in Section 3 and Section 4, respectively. Section 5 concludes our contributions to this paper and discusses future work.

2. Related Work

2.1. Object Detection

Object detection technology is mainly divided into two types: one-stage and two-stage object detection. Two-stage object detection first generates candidate region boxes and then classifies and regresses these boxes to determine the location, size, and category of the target. Common two-stage object detection algorithms include the R-CNN family, such as R-CNN[17] and Faster R-CNN[18]. Current research is focused on improving models in the R-CNN family to make them more efficient and accurate. For example, Zeng et al.[19] proposed an underwater object detection algorithm based on Faster R-CNN and adversarial networks, enhancing the robustness and rapid detection capability of the detector. Song et al.[20] proposed an underwater object detection method based on an enhanced R-CNN detection framework to address challenges such as uneven illumination, low contrast, occlusion, and camouflage of aquatic organisms in underwater environments. Hsia et al.[21]combined Mask R-CNN, data augmentation (DA), and discrete wavelet transform (DWT) to propose an intelligent retail product detection algorithm, improving the detection of overlooked objects.
One-stage object detection directly processes the entire image and simultaneously predicts the location, size, and category of the target through regression methods to improve detection efficiency. Common one-stage object detection algorithms include the YOLO family, SSD, and RetinaNet. For example, the YOLO series of algorithms achieve rapid detection by dividing the image into grids and predicting bounding boxes and classification confidences for each grid. The YOLO series has undergone multiple iterations and improvements: YOLOv1[22] addressed the shortcomings of two-stage detection networks. YOLOv2[23] added batch normalization layers after each convolutional layer and eliminated the use of dropout. YOLOv3[24] introduced the residual module Darknet-53 and the feature pyramid network FPN, resulting in significant improvements. The backbone network of YOLOv4[25] is based on CSPDarknet53, using cross-stage partial connections (CSP) to facilitate information flow between different layers. YOLOv5[26] introduced multi-scale prediction, automated hyperparameter optimization, and a more efficient model structure, leading to improvements in both speed and accuracy. YOLOv6[27], YOLOv7[28], and YOLOv8[4] added many technologies on the basis of previous versions. There are also many improvements to the YOLO series to achieve more efficient detection performance. For example, Li et al.[29] proposed an improved YOLOv8 algorithm that integrates innovative modules from the real-time detection transformer (RT-DETR) to address the occlusion problem in underwater fish target detection. The algorithm, trained on an occlusion dataset using an exclusion loss function specifically designed for occlusion scenarios, significantly improved detection accuracy. Additionally, SSD[30] uses a pyramid structure to classify and regress locations on multiple feature maps, making it more suitable for handling objects of different sizes. RetinaNet[31] introduces focal loss and a feature pyramid network to address the disparity between foreground and background classes, achieving higher accuracy.
In summary, two-stage object detection performs better in terms of accuracy but is slower in speed; whereas one-stage object detection has an advantage in speed but may lack in accuracy. In practical applications, the choice between these methods depends on the specific requirements for detection speed and accuracy.

2.2. Transformer

In the field of Natural Language Processing (NLP), the Transformer model has become a mainstream technology, widely recognized for its capabilities in understanding and generating text. Over time, researchers have begun to explore the application of Transformer architectures in the field of Computer Vision (CV), aiming to enhance the efficiency and accuracy of image-related tasks. In early attempts, Transformers were employed as enhanced decoders to optimize model performance. For instance, Yang et al. [32] developed the TransPose model, which directly processed features extracted by Convolutional Neural Networks (CNNs) to model global relationships in images and effectively capture dependencies between key points. On the other hand, Mao et al. [33] designed the Poseur method, utilizing lightweight Transformer decoders to achieve higher detection accuracy and computational efficiency.
Furthermore, Transformers have also been successfully applied to a broader range of image processing tasks. For example, the Vision Transformer (ViT) is a groundbreaking example that directly applies Transformer architectures to tasks such as image classification. Xu et al. [34] demonstrated the transferability of knowledge between different models and the flexibility of models through the ViTPose project. Recent research advances indicate that combining attention mechanisms from Transformers with object detection networks can lead to significant performance improvements. For instance, Wang et al. [35] integrated the SimAM attention module into the YOLO-BS network to improve the accuracy of detecting large coal blocks, helping to reduce congestion in underground conveyor systems. Similarly, BoTNet [35] introduced the BoT module with a self-attention mechanism, which optimizes and accelerates the training process of small networks by simulating the behavior of large networks, thereby effectively extracting and integrating features at different scales.
Based on these advanced observations and innovations, this study plans to integrate attention mechanisms and Transformer modules into the YOLOv8 network architecture to further enhance the model’s performance in various object detection tasks. This introduction aims to leverage the powerful global information modeling capabilities of Transformers to pave the way for improving the efficiency and accuracy of image recognition and processing tasks.

2.3. SPP

In the research of machine vision and object recognition, the Spatial Pyramid Pooling (SPP) module and its improved versions, such as Spatial Pyramid Pooling - Fast (SPPF), Simplified SPPF (SimSPPF), Atrous Spatial Pyramid Pooling (ASPP), Spatial Pyramid Pooling, Cross Stage Partial Channel (SPPCSPC), and SPPFCSPC, have been widely utilized to improve the accuracy of object detection. These modules effectively address the problem caused by differences in input image sizes, avoiding image distortion. The initial concept of the SPP module was proposed by He et al. [37], aiming to overcome the challenge of inconsistent sizes. Subsequently, to further improve processing speed, the SPPF [26] and SimSPPF [27] modules were developed successively. Additionally, Chen et al. introduced the ASPP module [38] in the DeepLabv2 semantic segmentation model, which enhances the recognition capability of multiscale objects by capturing information at different scales through parallel dilated convolutions. The SPPCSPC module [28] achieves performance improvement by optimizing parameters and reducing computational complexity without expanding the receptive field.
In recent years, attention mechanisms have been introduced into object detection networks to enhance the model’s ability to detect small objects in complex scenes. For example, Wu et al. [39] proposed an Effective Multiscale Attention (EMA) mechanism based on multiscale feature fusion, which automatically adjusts the weight distribution in feature maps to focus more on key areas of the image. This is particularly effective for accurately identifying small objects in complex environments. Given this, this study plans to integrate these improved SPP modules and attention mechanisms into the YOLOv8 network architecture, aiming to further optimize the performance of the network in various object detection tasks.

2.4. IoU Loss

In the research field of object detection, localization, and tracking, precise regression of bounding boxes is crucial. In recent years, localization loss functions, represented by Intersection over Union (IoU) loss [40] and its derivative versions [41,42,43,44], have played a central role in improving the accuracy of bounding box regression. These types of loss functions optimize the model by evaluating the overlap between predicted bounding boxes and actual bounding boxes, effectively mitigating the impact of aspect ratio variations on detection performance. However, IoU loss has certain limitations. For instance, when the predicted box and the ground truth box do not overlap, the IoU value remains zero, failing to reflect the actual distance between them. Additionally, in cases where the IoU is the same, it cannot distinguish between positional differences.
To address these challenges, several studies have proposed various improvements to IoU loss, including Generalized IoU (GIoU), Distance-IoU (DIoU), CIoU, Efficient IoU (EIoU), and Wise-IoU (WIoU). GIoU loss overcomes the issue of traditional IoU calculation resulting in zero by introducing the concept of the minimum enclosing rectangle, although it may lead to smaller gradients and slower convergence in some scenarios [41] . DIoU loss enhances the model’s sensitivity to position by considering the distance between the center points of predicted and ground truth boxes, but it does not involve shape matching [42]. CIoU loss builds upon this by incorporating the difference in aspect ratios, although it may cause training instability in certain circumstances despite improving shape matching accuracy. EIoU loss balances the relationship between simple and hard samples by introducing separate consistency and focal losses, thereby enhancing the stability and efficiency of the model [43]. WIoU loss further enhances the model’s performance and robustness through a dynamic non-monotonic static focus mechanism (FM) [44].
In general, these variants of IoU loss effectively improves the accuracy of bounding box regression and the robustness of models by introducing mechanisms in loss calculation that consider the distance between predicted and ground truth boxes, differences in position center points, consistency of aspect ratios, and handling of samples with varying difficulty levels. In practice, selecting the appropriate variant of the loss function tailored to specific object detection tasks is a key strategy for optimizing detection performance.

3. Methodology

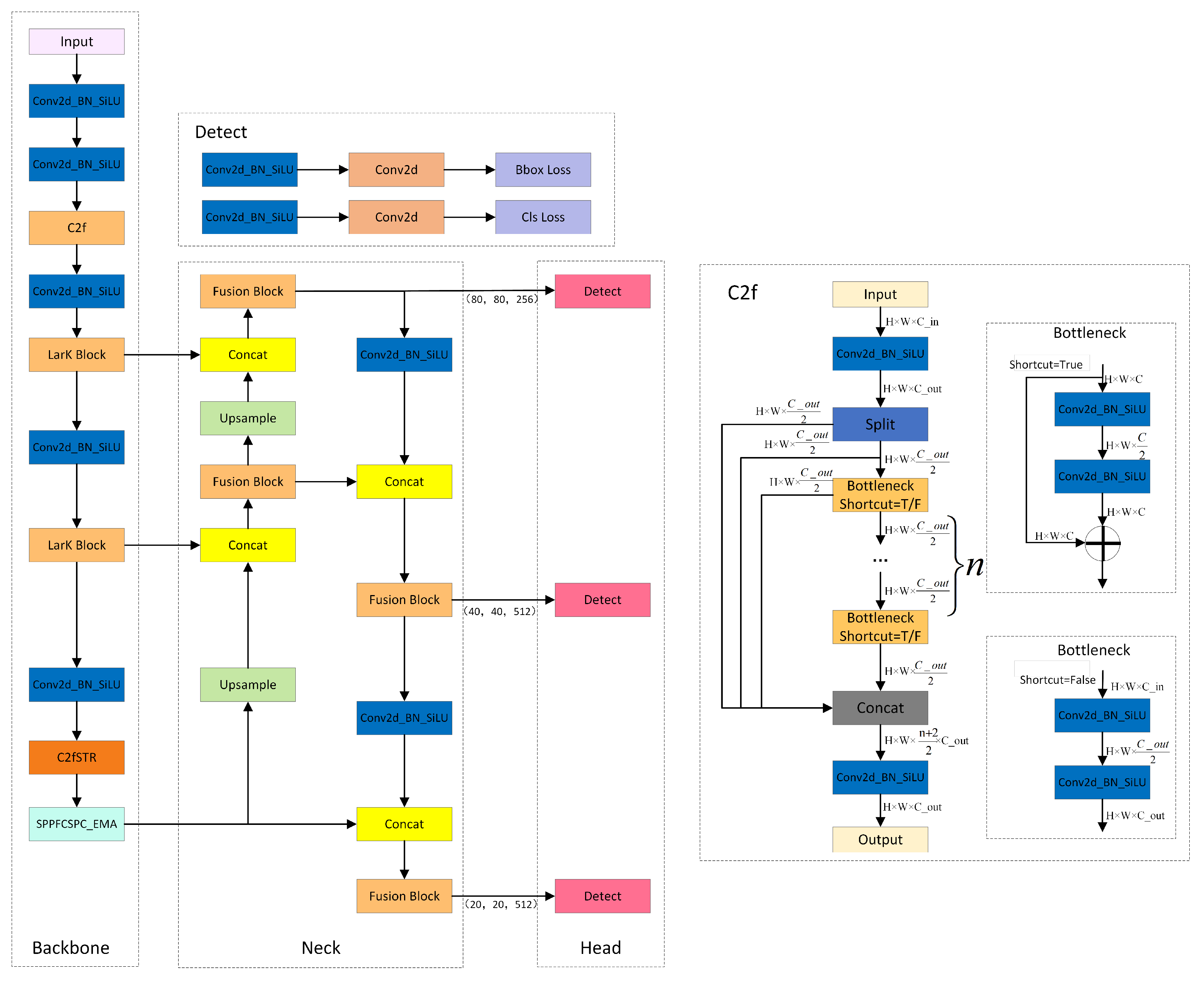
Although the YOLOv8 model has achieved significant results in the field of object detection, there are still some limitations. Firstly, the model’s receptive field during the detection process is relatively limited. At the same time, the feature representation and perception capabilities of the YOLOv8 network need enhancement. Secondly, the diversity of marine life, along with its myriad forms and shapes, poses challenges to the accuracy and robustness of target detection. Lastly, the common absorption and scattering effects of water on light often result in inadequate clarity of target boundary information, hindering precise localization. To address these issues, we designed YOLOv8-MU, as shown in Figure 1.

3.1. LarK Block

The Convolutional Neural Network (ConvNet) with large kernels has shown remarkable performance in capturing sparse patterns and generating high-quality features, but there is still considerable room for exploration in its architectural design. While the Transformer model has demonstrated powerful versatility across multiple domains, it still faces some challenges and limitations in terms of computational efficiency, memory requirements, interpretability, and optimization. To address these limitations, we introduce the LarK Block from UniRepLKNet into our model [9], as depicted in Figure 2. It leverages the advantages of large-kernel convolution, allowing us to achieve a larger receptive field without increasing model depth. This implies that by using larger convolutional kernels, the Large Kernel Block can capture more contextual information without the need to add more network layers. This represents a key advantage of large-kernel convolution, enabling the network to capture richer features.
As illustrated in Figure 2, the block utilizing Dilated Reparam Block is referred to as a Large Kernel Block (LarK Block), while those employing DWconv are termed Small Kernel Block (SmaK Block). The Dilated Reparam Block is proposed based on equivalent transformation, aiming to enhance feature extraction by combining a non-sparse large-kernel convolutional layer with multiple sparse small-kernel convolutional layers. The key hyperparameters of this method include the size of the large kernel K, the size of parallel convolutional layers k, and the sparsity rate r. Assuming there are four parallel layers with K=9, r=(1,2,3,4), and k=(5,3,3,3). To utilize a larger K, more layers can be enhanced by increasing the kernel size or expanding the sparsity rate. For instance, when K=13, five layers are employed with k=(5,7,3,3,3) and r=(1,2,3,4,5), resulting in equivalent kernel sizes of (5,13,7,9,11) respectively. During the inference stage, to transform the Dilated Reparam Block into a large-kernel transformation layer, each batch normalization (BN) layer is first merged into the preceding transformation layer. Then, each layer with dilation rate r > 1 is transformed into Equation(1), and all generated kernels are added together with appropriate zero-padding. The Dilated Reparam Block utilizes dilated small-kernel convolutional layers to enhance the non-dilated large-kernel layers. From a parameter perspective, these dilated layers are equivalent to non-dilated convolutional layers with larger sparse kernels, enabling the entire block to be effectively transformed into a single large-kernel convolutional layer.
W ′ = conv_transpose2d ( W , I , stride = r )
The Large Kernel Block is primarily integrated into the middle and upper layers of the model to enhance the depth and expressive capability of the model when using large kernel convolutional layers. This enhancement is achieved by stacking multiple SE Block (Squeeze-and-Excitation Block) to deepen the model and utilize 3x3 convolutional layers to extract more complex spatial patterns. Conversely, the Small Kernel Block is used when adding more layers to the model, aiming to increase the depth of the model and extract more complex spatial patterns. We note that besides capturing small-scale patterns, enhancing the ability of large kernel blocks to capture sparse patterns may result in higher-quality features. The demand for capturing this pattern aligns perfectly with the mechanism of dilated convolution [9]. From the perspective of a sliding window, a dilated convolutional layer with a dilation rate of r will scan the input channels to capture spatial patterns, where the distance between each interested pixel and its neighboring pixels is r - 1. Therefore, we adopt dilated convolutional layers parallel to the large kernel and sum their outputs.

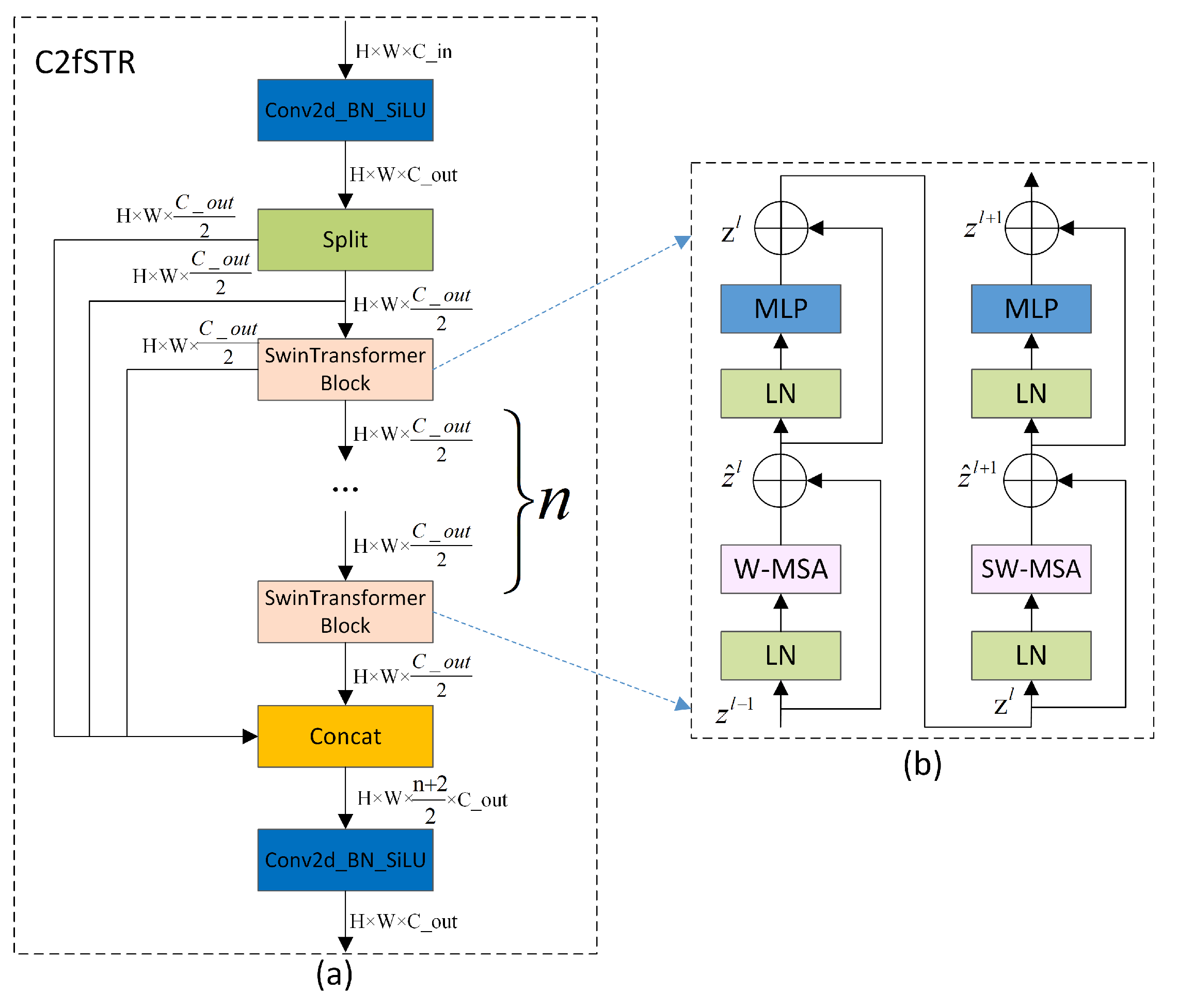
3.2. C2fSTR

The proposed C2fSTR in this paper modifies the original YOLOv8 architecture’s C2f module using the Swin Transformer Block[11]. Compared to the original C2f module, the modified C2fSTR module facilitates better interaction between strong feature maps and fully utilizes target background information, thereby enhancing the accuracy and robustness of object detection under complex background conditions. Figure 3.(a) illustrates the structure of the C2fSTR.
The C2fSTR consists of two modules. One is the Conv module, which consists of a Conv2d with a kernel size of 1×1 and a stride of 1, followed by batch normalization and the Silu activation function. The role of the convolution module is to reduce the length and width of the feature map while expanding the dimensionality. The other module is the Swin Transformer Block, which comprises a linear layer (LN), shifted window multi-head self-attention (SW-MSA), and feedforward MLP (MLP). The structure includes n Swin Transformer modules. The function of the Swin Transformer Block is to reduce the computational complexity of the multi-head attention mechanism and expand the range of information interaction. Its structure is illustrated in Figure 3.(b).
Traditional Transformers typically compute attention globally, leading to high computational complexity. The computational complexity of the multi-head attention mechanism is proportional to the square of the size of the feature map. To reduce the computational complexity of the multi-head attention mechanism and expand the range of information interaction, in the Swin Transformer, the feature map is divided into windows. Each window undergoes window-based multi-head self-attention computation followed by shifted window-based multi-head self-attention computation, enabling mutual communication between windows [47]. The computation of consecutive Swin Transformer blocks is as Equation(2):
z ^ l = W − MSA LN z l − 1 + z l − 1 , z l = MLP LN z ^ l + z ^ l , z ^ l + 1 = SW-MSA LN z l + z l , z l + 1 = MLP LN z ^ l + 1 + z ^ l + 1 .
where z ^ l and z l represent the output features of the (S)W-MSA and MLP modules of block l, respectively; W-MSA and SW-MSA represent window-based multi-head self-attention using regular and shifted window partitioning configurations, respectively.
In this way, Swin Transformer effectively reduces the computational burden by confining attention computation within each window. However, object recognition and localization in images depend on the feature information of the global background. The information interaction in Swin Transformer is limited to individual windows and shifted windows, capturing only local details of the target, while global background information is difficult to obtain[48]. To achieve more extensive information interaction and simultaneously obtain both global background and local detail information, we apply the Swin Transformer Block to C2f, replacing the Darknetbottleneck and forming the C2fSTR feature backbone system. This combined strategy enables comprehensive information interaction, effectively capturing rich spatial details, and significantly improving the model’s accuracy in object detection in complex backgrounds.

3.3. SPPFCSPC_EMA

As shown in Figure 4, YOLOv8-MU replaces the SPPF module in YOLOv8 with the SPPFCSPC module and introduces multiple convolutions and concatenation techniques to extract and fuse features at different scales, expanding the receptive field of the model and thereby improving model accuracy. Additionally, we have introduced the EMA module, whose parallel processing and self-attention strategy significantly improve the model’s performance and optimize feature representation. By combining the SPPFCSPC and EMA modules to form the SPPFCSPC_EMA module, not only are the model’s accuracy, efficiency, and robustness enhanced, but the model’s performance is further improved while maintaining efficiency.
The SPPFCSPC module integrates two submodules: SPP and fully connected spatial pyramid convolution (FCSPC)[49]. SPP, as a pooling layer, can handle input feature maps of different scales, effectively detecting both small and large targets. FCSPC is an improved convolutional layer aimed at optimizing the representation of feature maps to enhance detection performance. By performing multi-scale spatial pyramid pooling on the input feature map, the SPP module captures information about targets and scenes at different scales[37]. Subsequently, the FCSPC module convolves the different scale feature maps output by the SPP module and divides the input feature map into blocks. These blocks are pooled and concatenated, followed by convolution operations, to enhance the model’s receptive field and retain key feature information, thereby improving the model’s accuracy[49]. The SPPFCSPC module is an optimization of SPPCSPC based on the SPPF concept, reducing the computational requirements for the pooling layer’s output by connecting three independent pooling operations, and improving the speed and detection accuracy of dense targets without changing the receptive field[50]. The results produced by this pooling method are comparable to those obtained using larger pooling kernels, thus optimizing the training and inference speed of the model. The calculation formula for the pooling part is as Equation (3):
S 1 ( R ) = MaxPool k = 5 p = 2 ( R ) S 2 S 1 = MaxPool k = 5 p = 2 S 1 S 3 S 2 = MaxPool k = 5 p = 2 S 2 S 4 = S 1 ⊛ S 2 ⊛ S 3
Where R represents the input feature layer, S 1 represents the pooling layer result of the smallest pooling kernel, S 2 represents the pooling layer result of the medium-sized pooling kernel, S 3 represents the pooling layer result of the largest pooling kernel, S 4 represents the final output result, and ⊛ represents tensor concatenation.
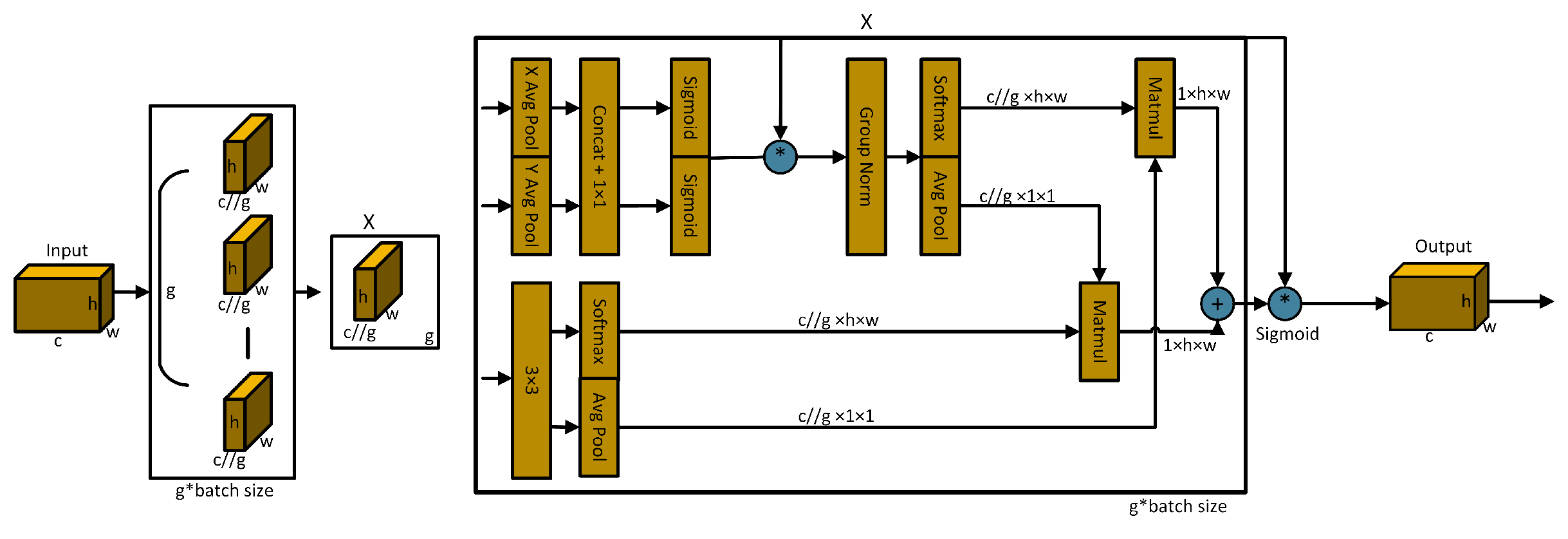
The EMA[13] mechanism employs three parallel pathways, including two 1×1 branches and one 3×3 branch, to enhance the processing capability of spatial information. In the 1×1 branches, global spatial information is extracted through two-dimensional global average pooling, and the Softmax function is utilized to ensure computational efficiency. The output of the 3×3 branch is directly adjusted to align with the corresponding dimensional structure before the joint activation mechanism, which combines channel features as shown in Equation(4). An initial spatial attention map is generated through matrix dot product operations, integrating spatial information of different scales within the same processing stage. Furthermore, 2D global average pooling embeds global spatial information into the 3×3 branch, producing a second spatial attention map that preserves precise spatial location information. Finally, the output feature maps within each group are further processed through the Sigmoid function [51]. As illustrated in Figure 5., the design of EMA aims to assist the model in capturing the interactions between features at different scales, thereby enhancing the performance of the model.
z c = 1 H × W ∑ j ∑ i x c ( i , j )
Here, z c represents the output related to the c-th channel. The primary purpose of this output is to encode global information, thereby capturing and modeling long-range dependencies.
Therefore, the overall formula for the SPPFCSPC_EMA module is as shown in Equation(5):
z c = 1 H × W ∑ j ∑ i S 4 ( i , j )

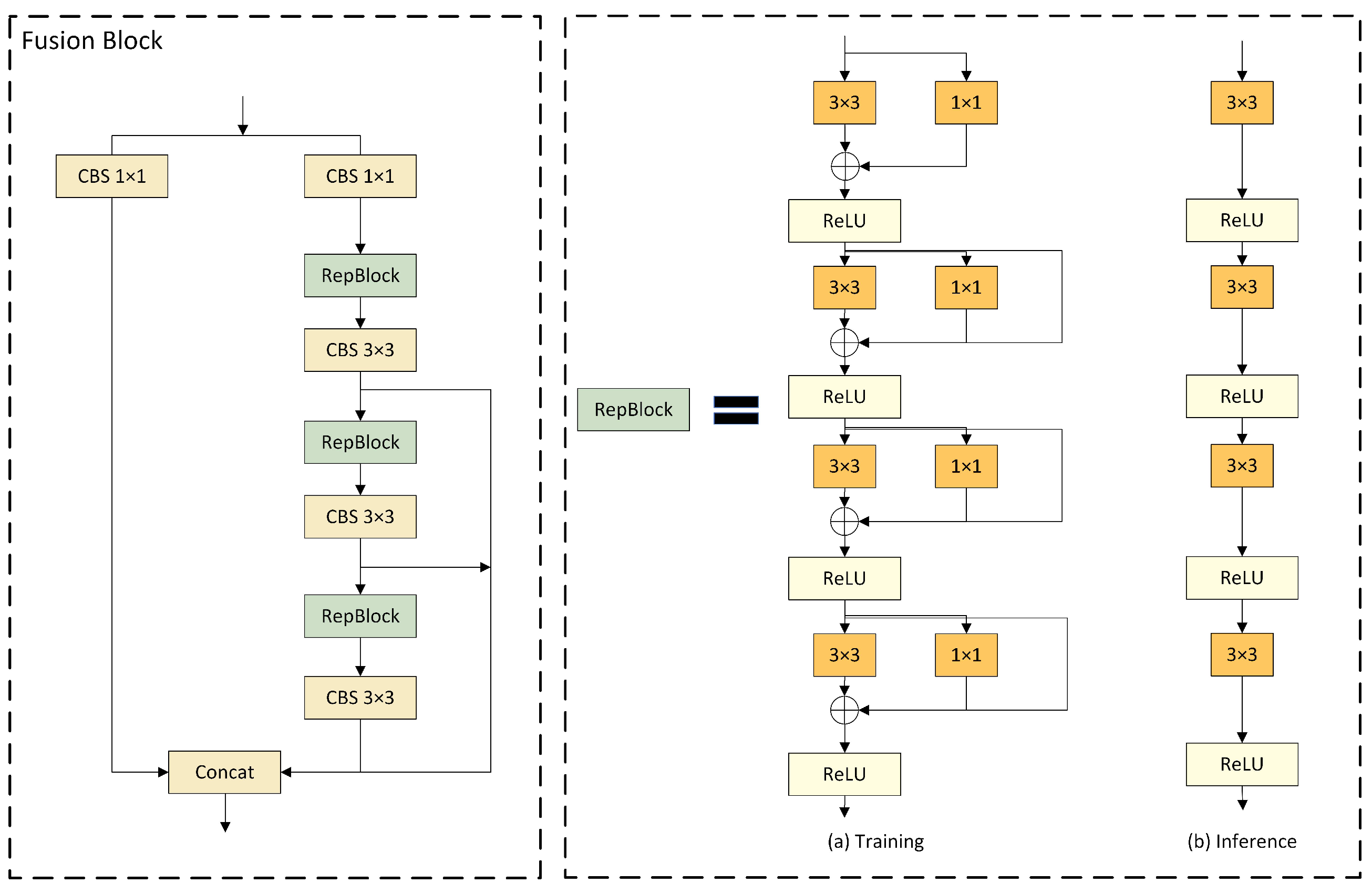
3.4. Fusion Block

DAMO-YOLO has improved the efficiency of node stacking operations and optimized feature fusion by introducing a specially designed Fusion Block. Inspired by this, we replaced the C2f module in the neck network with the Fusion Block to enhance the fusion capability of multi-scale features. As illustrated in Figure 6, the architecture of Fusion Block commences with channel number adjustment on two parallel branches through 1 × 1 CBS, followed by the incorporation of the concept of feature aggregation from the Efficient Layer Aggregation Network (ELAN) [52] into the subsequent branch, comprised of multiple RepBlocks and 3 × 3 CBS. This design leverages strategies such as CSPNet [53], reparameterization mechanism, and multi-layer aggregation to effectively promote rich gradient flow information at various levels. Furthermore, the introduction of the reparameterized convolutional module has significantly enhanced performance.
In the model, four gradient path fusion blocks are utilized, each splitting the input feature map into two streams. One stream is directly connected to the output, while the other undergoes channel reduction, cross-level edge processing, and convolutional reparameterization before further dividing into three gradient paths from this stream. Ultimately, all paths are merged into the output feature map. This design segments the gradient flow paths, introducing variability in the gradient information as it moves through the network, effectively facilitating a richer flow of gradient information.
As for Figure 6, RepBlock is designed to employ different network structures during the training and inference phases through the use of reparameterization techniques, thereby achieving efficient model training and rapid inference speed [54]. Following the recommendations of RepVGG, we optimized the parameter structure, clearly segregating the multi-branch used during the training phase from the single-branch used during the inference phase. During the training process, RepBlock adopts a complex structure containing multiple parallel branches, which extract features through 3x3 convolutions, 1x1 convolutions, and Batch Normalization (BN). This design is intended to enhance the representational capacity of the model. During inference, these multi-branch structures are converted into a single, more streamlined 3x3 convolutional layer through structural reparameterization, eliminating the branch structure to increase inference speed and reduce memory consumption of the model.
The conversion from a multi-branch to a single-branch architecture is primarily motivated by three considerations. Firstly, from the perspective of speed, models reparameterized for inference demonstrate a significant acceleration in inference speed. This not only expedites the model inference process but also enhances the practicality of model deployment. Secondly, regarding memory consumption, the multi-branch model necessitates allocating memory individually for each branch to store its computational results, leading to substantial memory usage. Adopting a single-path model significantly reduces the demand for memory. Lastly, in terms of model flexibility, the multi-branch model is constrained by the requirement that the input and output channels for each branch remain consistent, posing challenges to model modifications and optimizations. In contrast, the single-path model is not subject to such limitations, thereby increasing the flexibility of model adjustments.

3.5. MPDIOU

Existing boundary box regression loss functions, such as CIoU, although considering multiple factors, may still encounter inaccurate localization and blurred boundary issues when dealing with complex scenarios where target boundary information is unclear, affecting the regression accuracy. Given the intricate underwater environment and limited lighting conditions, the boundary information of target objects is often inadequate, posing challenges for traditional loss functions to adapt effectively. Inspired by the geometric properties of a horizontal rectangle, Ma et al. [16] designed a novel boundary box regression loss function based on the minimum point distance L MPD I o U . We incorporated this function, referred to as MPDIoU, into our model to evaluate the similarity between predicted and ground-truth boundary boxes. Compared to existing loss functions, MPDIoU not only better accommodates blurred boundary scenarios and enhances object detection accuracy but also accelerates model convergence and reduces redundant computational overhead, thereby improving the localization and boundary precision for underwater organism detection.
The calculation process of MPDIoU is as follows: Assume ( x 1 gt , y 1 gt ) and ( x 2 gt , y 2 gt ) represent the coordinates of the top-left and bottom-right points of the ground truth box, respectively; ( x 2 pd , y 2 pd ) and ( x 1 pd , y 1 pd ) represent the coordinates of the top-left and bottom-right points of the predicted box, respectively. Parameters w and h represent the width and height of the input image, respectively. The formulas for the ground truth box and the predicted box are: d 1 2 = x 1 p d − x 1 g t 2 + y 1 p d − y 1 g t 2 and d 2 2 = x 2 p d − x 2 g t 2 + y 2 p d − y 2 g t 2 .
Subsequently, the final L MPD I o U can be calculated using Equations (6) and (7) based on d 1 and d 2 .
MPD I o U = A ∩ B A ∪ B − d 1 2 w 2 + h 2 − d 2 2 w 2 + h 2
L MPD I o U = 1 − MPD I o U
The MPDIoU loss function optimizes the similarity measurement between two bounding boxes, enabling it to adapt to scenarios involving both overlapping and non-overlapping bounding box regression. Moreover, all components of the existing bounding box regression loss functions can be represented using four-point coordinates, as shown in Equations (8)-(10).
| C | = max ( x 2 g t , x 2 p d ) − min ( x 1 g t , x 1 p d ) × max ( y 2 g t , y 2 p d ) − min ( y 1 g t , y 1 p d )
x c g t = x 1 g t + x 2 g t 2 , y c g t = y 1 g t + y 2 g t 2 , x c p d = x 1 p d + x 2 p d 2 , y c p d = y 1 p d + y 2 p d 2
w g t = x 2 g t − x 1 g t , h g t = y 2 g t − y 1 g t , w p d = x 2 p d − x 1 p d , h p d = y 2 p d − y 1 p d
where | C | represents the area of the smallest bounding rectangle encompassing both the ground truth and predicted boxes. The center coordinates of the ground truth and predicted boxes are denoted by ( x c gt , y c gt ) and ( x c pd , y c pd ) , respectively, while their widths and heights are represented by and , respectively. Through Equations (8)-(10), we can calculate the non-overlapping area, the distance between center points, and the deviation in width and height. This method not only ensures comprehensiveness but also simplifies the computational process. Therefore, in the localization loss part of the YOLOv8-MU model, we choose to use the MPDIoU function to calculate the loss, to enhance the model’s localization accuracy and efficiency.

4. Experimental Details

4.1. Benchmark Testing and Implementation Details

4.1.1. Dataset

In this study, the dataset used to validate the effectiveness of our optimized model is URPC20191, a publicly available dataset for underwater object detection. It includes five different categories of aquatic life: sea cucumbers, sea urchins, scallops, starfish, and seaweed, with a total of 3765 training samples and 942 validation samples. Examples of dataset images are shown in the first row of Figure 7. Additionally, we conducted detection experiments on the URPC20202 dataset. Similar to URPC2019, URPC2020 is also an underwater dataset, but it differs in that it contains only four different categories: sea cucumbers, sea urchins, scallops, and starfish, with a total of 4200 training samples and 800 validation samples. Examples of dataset images are shown in the second row of Figure 7. We will validate the feasibility of our model on these two datasets.

4.1.2. Environment Configuration and Parameter Settings

The experiments in this study were conducted on the Ubuntu operating system, utilizing the PyTorch deep learning framework. The experimental setup includes the parallel computing platform and programming model developed by NVIDIA, the Python programming language, and server processors released by Intel. The performance of different GPUs and the size of RAM significantly impact our experimental results. Therefore, we maintained a consistent experimental environment throughout our entire experiment process. The specific configuration is shown in Table 1.
To enhance the persuasiveness of the experiments, we conducted experiments based on the original YOLOv8 model, during which a series of parameter adjustments were made and multiple experimental tests were conducted. Ultimately, we determined that some of the main hyperparameters for all experiments would adopt the settings consistent with Table 1 . A larger batch size can speed up training, so we set it to 16. In terms of loss calculation, we continue YOLOv8’s approach of combining Classification Loss, Bounding Box Regression Loss, and Distribution Focal Loss, with the weights of the three losses being 7.5, 0.5, and 1.5, respectively, to optimize the model. In addition, momentum and weight decay are important hyperparameters for optimizing the model, with detailed settings available in Table 2.

4.1.3. Evaluation Criteria

Evaluating the quality of YOLO models requires a comprehensive consideration of speed, accuracy, applicability, robustness, and cost, among other factors, with varying focus points in different use scenarios. For the URPC series datasets, this study primarily focuses on the accuracy of the improved YOLOv8 model. We assess the model’s accuracy by calculating and comparing the Average Precision (AP) for each class and the Mean Average Precision (mAP). Additionally, we examine the impact of Floating Point Operations(FLOPs) and the number of Parameters (Para) on model accuracy to verify the superiority of our improved YOLOv8 model.
The calculation of the AP value is related to the calculation and integration of the Precision-Recall curve. First, it is necessary to calculate the Precision and Recall values using Equations (11) and (12), where TP, FP, and FN represent True Positive, False Positive, and False Negative. True Positive is the number of positive samples predicted as positive by the model; False Positive is the number of negative samples predicted as positive by the model; False Negative is the number of positive samples predicted as negative by the model. Subsequently, the Average Precision for each category is calculated according to Equation (13). To reflect the performance of the model on the entire dataset, the mAP’s value is calculated according to Equation (14). In the calculation of mAP, we take the value at IOU of 0.5 and write it as mAP@0.5, which means that detection is considered successful only when the intersection part of the true box and our predicted box is greater than 50%.
Precision = T P ( T P + F P )
Recall = T P ( T P + F N )
A P = ∫ 0 1 P ( R ) d R
m A P = 1 N ∑ i = 1 n A P i

4.2. Comparative Experiments

4.2.1. Experiments on URPC2019

We first conducted a literature search or experiments on the performance of various models on the URPC2019 dataset, including the Boosting R-CNN model, which introduces the idea of reinforcement learning to improve Faster R-CNN, the YOLOv3 model, YOLOv5 series models, YOLOv7 model, YOLOv8 series models, and our optimized YOLOv8 model. The experimental data is shown in Table 3. We also plotted two bar graphs with different horizontal axes, Figure 8. and Figure 9. to provide a more intuitive comparison of the performance of each model.
After our observation and analysis, we can find that the optimized model performs better than the other models, especially since the optimization on the AP values of each category is more obvious. Particularly in the detection of the Waterweeds category, the data performance is quite prominent, with an AP value increase of 25.2% compared to the traditional Boosting RCNN model. The AP value is also only slightly lower than that of the YOLOv3 model when compared to the YOLO series models, and there is an increase of nearly 20% compared to the baseline model YOLOv8n. This indicates that the improved YOLOv8 model has overcome the difficulties faced by other models in detecting the Waterweeds category, demonstrating a unique advantage in enhancing the AP value for the individual category of Waterweeds.
Furthermore, upon analyzing the mAP@0.5 values, we found that the YOLOv8-MU model also demonstrates superior performance in terms of overall dataset detection accuracy. The mAP@0.5 of YOLOv8-MU is the highest in Table 3, reaching 78.4%, which is an improvement of 8.2% compared to the traditional Boosting RCNN model and an increase of 4% compared to the baseline model YOLOv8n. It is closest to the YOLOv3 model but shows an improvement. The main reason is that although the AP value of YOLOv8-MU in the Waterweeds category is lower than that of YOLOv3, YOLOv8-MU has higher detection accuracy in the remaining four categories compared to YOLOv3. This also verifies the effectiveness of YOLOv8-MU in improving the overall detection accuracy of the URPC2019 dataset.
In deep learning models, a relatively lower number of parameters and FLOPs can reduce the model’s computational complexity and size, enhancing its performance and applicability in practical applications. For this reason, we specifically plotted the bar graphs shown in Figure 10. and Figure 11. based on Table 3. to compare the number of parameters and FLOPs among various models. It can be seen that although the number of parameters and FLOPs of our optimized model, YOLOv8-MU, has increased compared to the baseline model YOLOv8n, they are still reduced compared to other models. This proves that our model achieves the effect of making the model lightweight.
To more intuitively demonstrate the advantages of our optimized YOLOv8 model’s detection performance, we extracted and compared the detection results of different models on the URPC2019 dataset, as shown in Figure 12. Our model outperforms other models in both precision and recall. As can be seen clearly in rows 1 to 4, our optimized model did not detect any targets beyond the Ground_Truth, indicating our model has high precision. In the result, images of rows 5 to 8, both YOLOv5s and YOLOv8n have the same issue, failing to detect all targets in the Ground_Truth and missing some targets, while our model exhibits high recall. This sufficiently demonstrates the effectiveness of our optimized YOLOv8 model in detecting the URPC2019 dataset.

4.2.2. Experiments on URPC2020

On the URPC2020 dataset, which is part of the same series as URPC2019, we also conducted a series of experiments. The results are presented in Table 4, and based on these results, we plotted bar graphs with different horizontal axes, Figure 13. and Figure 14. We observed that on the URPC2020 dataset, compared to URPC2019, there are only 4 biological categories, missing the Waterweeds category which performs well in AP values for a single category, resulting in a small improvement in detection performance relative to other models, but enough to reflect the advantages of our model. We compared the experimental results of Faster-RCNN, Literature, YOLOv5x, and YOLOv8n with our model Our_n and found that the mAP@0.5 score of our improved model is higher than that of the other models. Additionally, we compared YOLOv8s with Ours to demonstrate the high efficiency of our improved model in terms of detection accuracy.

4.3. Ablation Study

4.3.1. Comparison of the Effectiveness of LarK Block at Different Positions

Table 5. compares the impact of using the LarK Block to replace different positions of C2f in the backbone on the accuracy, the number of parameters, and computational complexity of the model on the URPC2019 dataset for various marine life categories. Among them, the model with the middle two C2f in the backbone replaced by LarK Block performed the best, achieving an mAP@0.5 of 75.5%, with the smallest number of parameters, similar to the model that modifies only the last C2f, and with FLOPs at a medium level. In contrast, the model that modifies only the last C2f, although having the least number of parameters and the lowest computational complexity, experienced a decrease in accuracy compared to the original YOLOv8n. The accuracy of other models with different modification positions was also lower than that of the original YOLOv8n. Therefore, in subsequent research, we adopted the model that replaces the middle two C2f with LarK Block, as it ensures higher accuracy while improving the speed of the object detection model with a smaller modification to the network.

4.3.2. Comparison of the effectiveness of C2fSTR at different positions

Table 6. compares the impact of using C2fSTR to replace different positions of C2f in the backbone on the accuracy, the number of parameters, and computational complexity of the model on the URPC2019 dataset for various marine life categories. Among them, the model with the last C2f in the backbone replaced by C2fSTR performed the best, achieving an mAP@0.5 of 75.2%, with the smallest computational load and the fastest speed. In contrast, the model that replaces all C2f had a decrease in accuracy, with an mAP@0.5 of only 73.8%. Other models with different modification positions, although all having an mAP@0.5 higher than YOLOv8n, did not perform as well as the model that modifies only the last C2f in terms of computational load and speed. Therefore, in subsequent research, we adopted the model that replaces the last C2f with C2fSTR, as it ensures the highest accuracy while also achieving the best computational efficiency and speed.

4.3.3. Comparison of the effectiveness of Fusion Block at different positions

Table 7. shows the impact of using Fusion Block to replace different positions of C2f in the neck on the accuracy, the number of parameters, and computational complexity of the model on the URPC2019 dataset for various marine life categories. Among them, the model with all C2f in the neck replaced by Fusion Block performed the best, achieving an mAP@0.5 of 74.7%, although its number of parameters and computational complexity are not the lowest, its accuracy is the highest. In comparison, the models that modify the last three C2f and the middle two C2f, although having smaller parameter counts and lower computational complexity, have mAP@0.5 values of only 74.1% and 73.5% respectively, which are 0.3% and 0.9% lower than YOLOv8n. Modifications at other positions also failed to surpass the accuracy of the model that modifies all C2f. Therefore, in subsequent research, we adopted the model that replaces all C2f with Fusion Block, as it achieves higher target detection accuracy.

4.3.4. Analysis of the effectiveness of other modules

In this section, we take the original YOLOv8 as the base and gradually add or remove components included in our model to explore the contribution of each component to the overall performance of the system model, thereby demonstrating their effectiveness in improving YOLOv8. We conducted multiple ablation experiments, and by analyzing Table 8. , we can see that different combinations of modules have varying effects on the performance of the YOLOv8 model.
In the process of optimizing the YOLOv8 model, we first added five modules individually, and the mAP@0.5 values obtained were all improved compared to the original YOLOv8, with the improvement effects ranked from largest to smallest as LarK Block, SPPFCSPC_EMA, C2fSTR, Fusion Block, and MPDIoU. It can be seen that the use of the LarK Block module alone resulted in the highest increase in mAP@0.5, which is 1.1%. This indicates that all five modules have a positive impact on optimizing the detection accuracy of YOLOv8.
When these modules are used in combination, the mAP@0.5 also increases, and the increase in mAP@0.5 is generally greater compared to when each module is used individually. The best combination is when LarK Block, SPPFCSPC_EMA, C2fSTR, Fusion Block, and MPDIoU are used simultaneously, achieving the highest mAP@0.5 of 78.4%, which is an increase of 4.0% compared to the original YOLOv8. In summary, based on the experimental results, the simultaneous use of LarK Block, SPPFCSPC_EMA, C2fSTR, Fusion Block, and MPDIoU can achieve the best performance improvement. These results provide guidance for the design and configuration of optimized object detection systems.

4.4. Result Analysis

To verify the effectiveness of our improved YOLOv8-MU model, we analyzed the training result plots on the URPC2020 dataset. As can be seen from Figure 15., in both the training and validation sets, the real-time loss value of the YOLOv8-MU model smoothly decreases with the increase of epochs and eventually converges. Especially in the validation set, the Classification Loss is more stable compared to the Bounding Box Regression Loss and Distribution Focal Loss, indicating that the YOLOv8-MU model has good performance in classifying target categories. At the same time, observing the changes in accuracy, recall, mAP@0.5, and mAP@0.5:0.95 values, all show an upward trend and good convergence, demonstrating that YOLOv8-MU has good performance in object detection.
Figure 16 shows the normalized confusion matrix for the experimental results of our model on the URPC2020 dataset, from which the predictive effectiveness of the model can be visualized. Each row of the matrix represents the actual category, and each column represents the predicted category. The diagonal elements reflect the prediction accuracy of each category in the URPC2020 dataset, while the off-diagonal elements show the prediction situation between different categories. The results indicate that, the YOLOv8-MU model has high prediction accuracy for the categories in the URPC2020 dataset, with a low error rate, fully demonstrating the effectiveness of YOLOv8-MU on this URPC2020 dataset.
The Precision-Recall (PR) curve is a common method for evaluating the performance of binary classifiers. In this curve, the horizontal axis represents recall, and the vertical axis represents precision. Precision and recall are two commonly used metrics for evaluating the performance of classifiers. The PR curve shows the trade-off between precision and recall at different thresholds. Generally, we hope that the classifier has both high precision and high recall, so the closer the PR curve is to the top-right corner, the better the performance of the classifier. As can be seen in Figure 17. , our model performs well on the URPC2020 dataset, with the overall PR curve being closer to the top-right corner, indicating good performance of our model.

5. Conclusions and Future Work

In this research, we have successfully developed and validated an advanced underwater organism detection framework, YOLOv8-MU, which significantly enhances the model’s detection accuracy. By substituting the original backbone network structure with the LarK Block from UniRepLKNet, we achieved a larger receptive field without increasing the model’s depth. Integrating the Swin Transformer block into the C2f module further strengthened the model’s capability for learning and generalizing features of various underwater organisms. Combining the multi-scale attention module EMA with SPPFCSPC significantly improved detection accuracy and robustness for multi-scale targets. Introducing a Fusion Block into the neck network enhanced the model’s capability in feature extraction and integration across different scales. The adoption of the MPDIoU loss function, optimized through vertex distance design, effectively resolved issues related to target localization and boundary precision, thereby improving detection accuracy. Validation on the URPC2019 and URPC2020 datasets demonstrated that the YOLOv8-MU model achieved mAP@0.5 scores of 78.4% and 80.4%, respectively, marking improvements of 4.0% and 0.4% over the YOLOv8n model. These achievements not only prove the effectiveness of our proposed improvements but also provide new research directions and practical foundations for the development of target detection technologies in complex environments. Future work will focus on strengthening interdisciplinary collaboration with marine biology and ecological conservation fields. Through ongoing research and innovation, we anticipate further enhancements in the performance of underwater organism detection technology, contributing to the research and protection of marine ecosystems.

Author Contributions

Conceptualization, J.Z. ; methodology, X.Z. and J.Z.; software, J.C., X.J. and X.Z. ; validation, X.J., X.Z. and J.C.; formal analysis, X.J.; investigation, J.C.; resources, J.Z.; data curation, X.Z. ; writing—original draft preparation, X.J., X.Z. and J.C., and Y.Z.; writing—review and editing, J.Z.; visualization, X.J. ; supervision, J.Z.; project administration, J.Z.; funding acquisition, J.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the college student innovation and entrepreneurship project of Hainan University(Hdcxcyxm201704) and Hainan Provincial Natural Science Foundation of China (623RC449)

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The datasets generated during and/or analyzed during the current study are available from the corresponding authors upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Selvaraj, J.J.; Rosero-Henao, L.V.; Cifuentes-Ossa, M.A. Projecting Future Changes in Distributions of Small-Scale Pelagic Fisheries of the Southern Colombian Pacific Ocean. Heliyon 2022, 8, e08975. [Google Scholar] [CrossRef] [PubMed]
  2. Shen, R.; Zhao, Y.; Cheng, H.; Hu, S.; Chen, S.; Ge, S. Surface-Related Multiples Elimination for Waterborne GPR Data. Remote Sens. 2023, 15, 3250. [Google Scholar] [CrossRef]
  3. Hu, J.; Zhao, D.; Zhang, Y.; Zhou, C.; Chen, W. (2021). Real-time nondestructive fish behavior detecting in mixed polyculture system using deep-learning and low-cost devices. Expert Systems with Applications 2021, 178, 115051. [Google Scholar] [CrossRef]
  4. Jocher, G. YOLOv8 by Ultralytics. 2023. Available online: https://github.com/ultralytics/ultralytics (accessed on 15 February 2023).
  5. Wang, H.; Hu, J.; Xue, R.; Liu, Y.; Pan, G. Thangka Image Segmentation Method Based on Enhanced Receptive Field. IEEE Access 2022, 10, 89687–89695. [Google Scholar] [CrossRef]
  6. Chen, X.; Li, Z.; Jiang, J.; Han, Z.; Deng, S.; Li, Z.; Fang, T.; Huo, H.; Li, Q.; Liu, M. Adaptive Effective Receptive Field Convolution for Semantic Segmentation of VHR Remote Sensing Images. IEEE Trans. Geosci. Remote Sensing 2021, 59, 26357–26365. [Google Scholar] [CrossRef]
  7. Zhu, Z.; Huang, C.; Xia, M.; Xu, B.; Fang, H.; Huang, Z. RFRFlow: Recurrent Feature Refinement Network for Optical Flow Estimation. IEEE Sensors J 2023, 23, 26357–26365. [Google Scholar] [CrossRef]
  8. Zhai, M.; Xiang, X.; Lv, N.; Masroor Ali, S.; El Saddik, A. SKFlow: Optical Flow Estimation Using Selective Kernel Networks. IEEE Access 2019, 7, 98854–98865. [Google Scholar] [CrossRef]
  9. Ding, X.; Zhang, Y.; Ge, Y.; Zhao, S.; Song, L.; Yue, X.; Shan, Y. Unireplknet: A universal perception large-kernel convnet for audio, video, point cloud, time-series and image recognition. arXiv 2023, arXiv:2311.15599. [Google Scholar]
  10. Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Advances in neural information processing systems 2017, 30, 30. [Google Scholar]
  11. Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV); IEEE: Montreal, QC, Canada, October, 2021; pp. 9992–10002. [Google Scholar]
  12. Yan, J.; Zhou, Z.; Zhou, D.; Su, B.; Xuanyuan, Z.; Tang, J.; Lai, Y.; Chen, J.; Liang, W. Underwater Object Detection Algorithm Based on Attention Mechanism and Cross-Stage Partial Fast Spatial Pyramidal Pooling. Front. Mar. Sci., 2022, 9, 1056300.
  13. Ouyang, D.; He, S.; Zhang, G.; Luo, M.; Guo, H.; Zhan, J.; Huang, Z. Efficient Multi-Scale Attention Module with Cross-Spatial Learning. In Proceedings of the ICASSP 2023 - 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); IEEE, June.
  14. Xu, X.; Jiang, Y.; Chen, W.; Huang, Y.; Zhang, Y.; Sun, X. DAMO-YOLO: A Report on Real-Time Object Detection Design. arXiv 2022, arXiv:2211.15444. [Google Scholar]
  15. Pei, Y.; Huang, Y.; Zou, Q.; Zhang, X.; Wang, S. Effects of Image Degradation and Degradation Removal to CNN-Based Image Classification. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 1239–1253. [Google Scholar] [CrossRef] [PubMed]
  16. Siliang, M.; Yong, X. MPDIoU: A Loss for Efficient and Accurate Bounding Box Regression. arXiv 2023, arXiv:2307.07662. [Google Scholar]
  17. Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition; IEEE, June 2014.
  18. Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017; 39, 1137–1149. [Google Scholar]
  19. Zeng, L.; Sun, B.; Zhu, D. Underwater Target Detection Based on Faster R-CNN and Adversarial Occlusion Network. Engineering Applications of Artificial Intelligence, 2021; 100, 104190. [Google Scholar]
  20. Song, P.; Li, P.; Dai, L.; Wang, T.; Chen, Z. Boosting R-CNN: Reweighting R-CNN Samples by RPN’s Error for Underwater Object Detection. Neurocomputing, 2023; 530, 150–164. [Google Scholar]
  21. Hsia, C.-H.; Chang, T.-H.W.; Chiang, C.-Y.; Chan, H.-T. Mask R-CNN with New Data Augmentation Features for Smart Detection of Retail Products. Applied Sciences, 2022; 12, 2902. [Google Scholar]
  22. Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); IEEE, June 2016.
  23. Redmon, J.; Farhadi, A. YOLO9000: Better, Faster, Stronger. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); IEEE, July 2017. [CrossRef]. [Google Scholar]
  24. Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
  25. Bochkovskiy, A.; Wang, C.Y.; Liao, H.Y.M. Yolov4: Optimal speed and accuracy of object detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
  26. Jocher, G. YOLOv5 by Ultralytics. 2022. Available online: https://github.com/ultralytics/yolov5 (accessed on 22 December 2022).
  27. Li, C.; Li, L.; Jiang, H.; Weng, K.; Geng, Y.; Li, L.; Ke, Z.; Li, Q.; Cheng, M.; Nie, W.; et al. YOLOv6: A Single-Stage Object Detection Framework for Industrial Applications 2022. arXiv, 2022; arXiv:2209.02976. [Google Scholar]
  28. Wang, C.-Y.; Bochkovskiy, A.; Liao, H.-Y.M. YOLOv7: Trainable Bag-of-Freebies Sets New State-of-the-Art for Real-Time Object Detectors. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); IEEE, June 2023.[CrossRef]. [Google Scholar]
  29. Li, E.; Wang, Q.; Zhang, J.; Zhang, W.; Mo, H.; Wu, Y. Fish Detection under Occlusion Using Modified You Only Look Once v8 Integrating Real-Time Detection Transformer Features. Applied Sciences 2023, 13, 12645. [Google Scholar] [CrossRef]
  30. Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.-Y.; Berg, A.C. SSD: Single Shot MultiBox Detector. In Lecture Notes in Computer Science ; Springer International Publishing, 2016; pp. 21–37 ISBN 978-3-319-46448-0.
  31. Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollar, P. Focal Loss for Dense Object Detection. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV); IEEE, October 2017.[CrossRef ]. [Google Scholar]
  32. Yang, S.; Quan, Z.; Nie, M.; Yang, W. TransPose: Keypoint Localization via Transformer. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV); IEEE: Montreal, QC, Canada, October, 2021; pp. 11782–11792. [Google Scholar]
  33. Mao, W.; Ge, Y.; Shen, C.; Tian, Z.; Wang, X.; Wang, Z.; den Hengel, A.v. Poseur: Direct Human Pose Regression with Transformers. In Proceedings of the European Conference on Computer Vision; Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 72–88. [Google Scholar]
  34. Xu, Y.; Zhang, J.; Zhang, Q.; Tao, D. ViTPose: Simple Vision Transformer Baselines for Human Pose Estimation. Adv. Neural Inf.Process. Syst. 2022, 35, 38571–38584. [Google Scholar]
  35. Wang, Y.; Guo, W.; Zhao, S.; Xue, B.; Zhang, W.; Xing, Z. A Big Coal Block Alarm Detection Method for Scraper Conveyor Based on YOLO-BS. Sensors. 2022, 22, 9052. [Google Scholar] [CrossRef]
  36. Srinivas, A.; Lin, T.-Y.; Parmar, N.; Shlens, J.; Abbeel, P.; Vaswani, A. Bottleneck Transformers for Visual Recognition. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); IEEE: Nashville, TN, USA, June, 2021; pp. 16514–16524. [Google Scholar]
  37. He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition. In; 2014; Vol. 8691, pp. 346–361.
  38. Chen, L. C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A. L. (2017). Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40(4), 834–848. [Google Scholar] [CrossRef]
  39. Wu, T.; Dong, Y. YOLO-SE: Improved YOLOv8 for Remote Sensing Object Detection and Recognition. Applied Sciences 2023, 13, 12977. [Google Scholar] [CrossRef]
  40. Yu, J.; Jiang, Y.; Wang, Z.; Cao, Z.; Huang, T. UnitBox: An Advanced Object Detection Network. In Proceedings of the Proceedings of the 24th ACM international conference on Multimedia; October; 2016; pp. 516–520. [Google Scholar]
  41. Rezatofighi, H.; Tsoi, N.; Gwak, J.; Sadeghian, A.; Reid, I.; Savarese, S. Generalized Intersection Over Union: A Metric and a Loss for Bounding Box Regression. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); IEEE: Long Beach, CA, USA, June, 2019; pp. 658–666. [Google Scholar]
  42. Zheng, Z.; Wang, P.; Liu, W.; Li, J.; Ye, R.; Ren, D. Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression. AAAI 2020, 34, 12993–13000. [Google Scholar] [CrossRef]
  43. Zhang, Y. F.; Ren, W.; Zhang, Z.; Jia, Z.; Wang, L.; Tan, T. (2022). Focal and efficient IOU loss for accurate bounding box regression. Neurocomputing 2022, 506, 146–157. [Google Scholar] [CrossRef]
  44. Tong, Z.; Chen, Y.; Xu, Z.; Yu, R. Wise-iou: Bounding box regression loss with dynamic focusing mechanism. arXiv, 2023; arXiv:2301.10051. [Google Scholar]
  45. Hu, J.; Shen, L.; Sun, G. (2018)Squeeze-and-excitationnetworks. In Proceedings of the IEEE conference on computer vision and pattern recognition 7132–7141.
  46. Ioffe, S.; Szegedy, C. (2015, June). Batch normalization: Accelerating deep network training by reducing internal covariate shift. In International conference on machine learning (pp. 448-456). pmlr.
  47. Mahaadevan, V.C.; Narayanamoorthi, R.; Gono, R.; Moldrik, P. Automatic Identifier of Socket for Electrical Vehicles Using SWIN-Transformer and SimAM Attention Mechanism-Based EVS YOLO. IEEE Access 2023, 11, 111238–111254. [Google Scholar] [CrossRef]
  48. Hui, Y.; Wang, J.; Li, B. STF-YOLO: A Small Target Detection Algorithm for UAV Remote Sensing Images Based on Improved SwinTransformer and Class Weighted Classification Decoupling Head. Measurement 2024, 224, 113936. [Google Scholar] [CrossRef]
  49. Yang, H.; Min, Z.; Zhang, Y.; Wang, Z.; Jiang, D. (2021, October). An improved model-free finite control set predictive power control for PWM rectifiers. In 2021 IEEE Energy Conversion Congress and Exposition (ECCE) (pp. 3425-3429). IEEE.
  50. Xie, S.; Sun, H. Tea-YOLOv8s: A Tea Bud Detection Model Based on Deep Learning and Computer Vision. Sensors 2023, 23, 6576. [Google Scholar] [CrossRef]
  51. Hao, W.; Ren, C.; Han, M.; Zhang, L.; Li, F.; Liu, Z. Cattle Body Detection Based on YOLOv5-EMA for Precision Livestock Farming. Animals 2023, 13, 3535. [Google Scholar] [CrossRef]
  52. Wang, C.Y.; Liao, H.Y.M.; Yeh, I.H. Designing Network Design Strategies Through Gradient Path Analysis. arXiv 2022, arXiv:2211.04800. [Google Scholar]
  53. Wang, C.-Y.; Mark Liao, H.-Y.; Wu, Y.-H.; Chen, P.-Y.; Hsieh, J.-W.; Yeh, I.-H. CSPNet: A New Backbone That Can Enhance Learning Capability of CNN. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW); IEEE: Seattle, WA, USA, June, 2020; pp. 1571–1580. [Google Scholar]
  54. Zhang, J.; Chen, H.; Yan, X.; Zhou, K.; Zhang, J.; Zhang, Y.; Jiang, H.; Shao, B. An Improved YOLOv5 Underwater Detector Based on an Attention Mechanism and Multi-Branch Reparameterization Module. Electronics 2023, 12(12), 2597. [Google Scholar] [CrossRef]
  55. Zhang, X.; Fang, X.; Pan, M.; Yuan, L.; Zhang, Y.; Yuan, M.; Lv, S.; Yu, H. A Marine Organism Detection Framework Based on the Joint Optimization of Image Enhancement and Object Detection. Sensors 2021, 21, 7205. [Google Scholar] [CrossRef]
  56. Zhang, J.; Zhang, J.; Zhou, K.; Zhang, Y.; Chen, H.; Yan, X. An Improved YOLOv5-Based Underwater Object-Detection Framework. Sensors 2023, 23, 3693. [Google Scholar] [CrossRef]
1
http://www.urpc.org.cn/index.html
2
http://www.urpc.org.cn/index.html
Preprints 103570 g001
Figure 1. The structure of YOLOv8-MU. It consists of Backbone, Neck, and Head, including detailed structures of C2f and Detect.
Figure 1. The structure of YOLOv8-MU. It consists of Backbone, Neck, and Head, including detailed structures of C2f and Detect.
Preprints 103570 g001
Preprints 103570 g002
Figure 2. The structural design of UniRepLKNet. The LarK Block consists of a Dilated Reparam Block, SE Block [45], Feed-Forward Network (FFN), and Batch Normalization (BN) [46] layers. The only difference between the SmaK block and the LarK Block is that the former uses a depth-wise 3×3 convolutional layer to replace the Dilated Reparam layer of the latter. The stages are connected by downsampling blocks, which are implemented by stride-2 dense 3×3 convolutional layers.
Figure 2. The structural design of UniRepLKNet. The LarK Block consists of a Dilated Reparam Block, SE Block [45], Feed-Forward Network (FFN), and Batch Normalization (BN) [46] layers. The only difference between the SmaK block and the LarK Block is that the former uses a depth-wise 3×3 convolutional layer to replace the Dilated Reparam layer of the latter. The stages are connected by downsampling blocks, which are implemented by stride-2 dense 3×3 convolutional layers.
Preprints 103570 g002
Preprints 103570 g003
Figure 3. (a) The structure of C2fSTR; (b) Two consecutive Swin Transformer Blocks (represented by Equation (1)). W-MSA and SW-MSA are multi-head self-attention modules, employing regular and shifted window configurations, respectively.
Figure 3. (a) The structure of C2fSTR; (b) Two consecutive Swin Transformer Blocks (represented by Equation (1)). W-MSA and SW-MSA are multi-head self-attention modules, employing regular and shifted window configurations, respectively.
Preprints 103570 g003
Preprints 103570 g004
Figure 4. The structure of SPPFCSPC_EMA. SPPFCSPC performs a series of convolutions on the feature map, followed by max-pooling and fusion over four receptive fields (one 3 × 3 and three 7 × 7). After further convolution, it is fused with the original feature map, and finally combined with EMA to form the SPPFCSPC_EMA module. (Conv: convolution; MaxPool2d: max pooling).
Figure 4. The structure of SPPFCSPC_EMA. SPPFCSPC performs a series of convolutions on the feature map, followed by max-pooling and fusion over four receptive fields (one 3 × 3 and three 7 × 7). After further convolution, it is fused with the original feature map, and finally combined with EMA to form the SPPFCSPC_EMA module. (Conv: convolution; MaxPool2d: max pooling).
Preprints 103570 g004
Preprints 103570 g005
Figure 5. Schematic diagram of EMA. Here, ’g’ denotes grouping, ’X Avg Pool’ represents 1D horizontal global pooling, and ’Y Avg Pool’ represents 1D vertical global pooling.
Figure 5. Schematic diagram of EMA. Here, ’g’ denotes grouping, ’X Avg Pool’ represents 1D horizontal global pooling, and ’Y Avg Pool’ represents 1D vertical global pooling.
Preprints 103570 g005
Preprints 103570 g006
Figure 6. Structure diagram of the Fusion Block, which includes a schematic diagram of the RepBlock. (a) represents the model structure used during training, (b) represents the model structure used during inference
Figure 6. Structure diagram of the Fusion Block, which includes a schematic diagram of the RepBlock. (a) represents the model structure used during training, (b) represents the model structure used during inference
Preprints 103570 g006
Preprints 103570 g007
Figure 7. Example images from the URPC2019 and URPC2020 datasets.
Figure 7. Example images from the URPC2019 and URPC2020 datasets.
Preprints 103570 g007
Preprints 103570 g008
Figure 8. Performance comparison of various models on the URPC2019 dataset.
Figure 8. Performance comparison of various models on the URPC2019 dataset.
Preprints 103570 g008
Preprints 103570 g009
Figure 9. Performance comparison of various models on the URPC2019 dataset.
Figure 9. Performance comparison of various models on the URPC2019 dataset.
Preprints 103570 g009
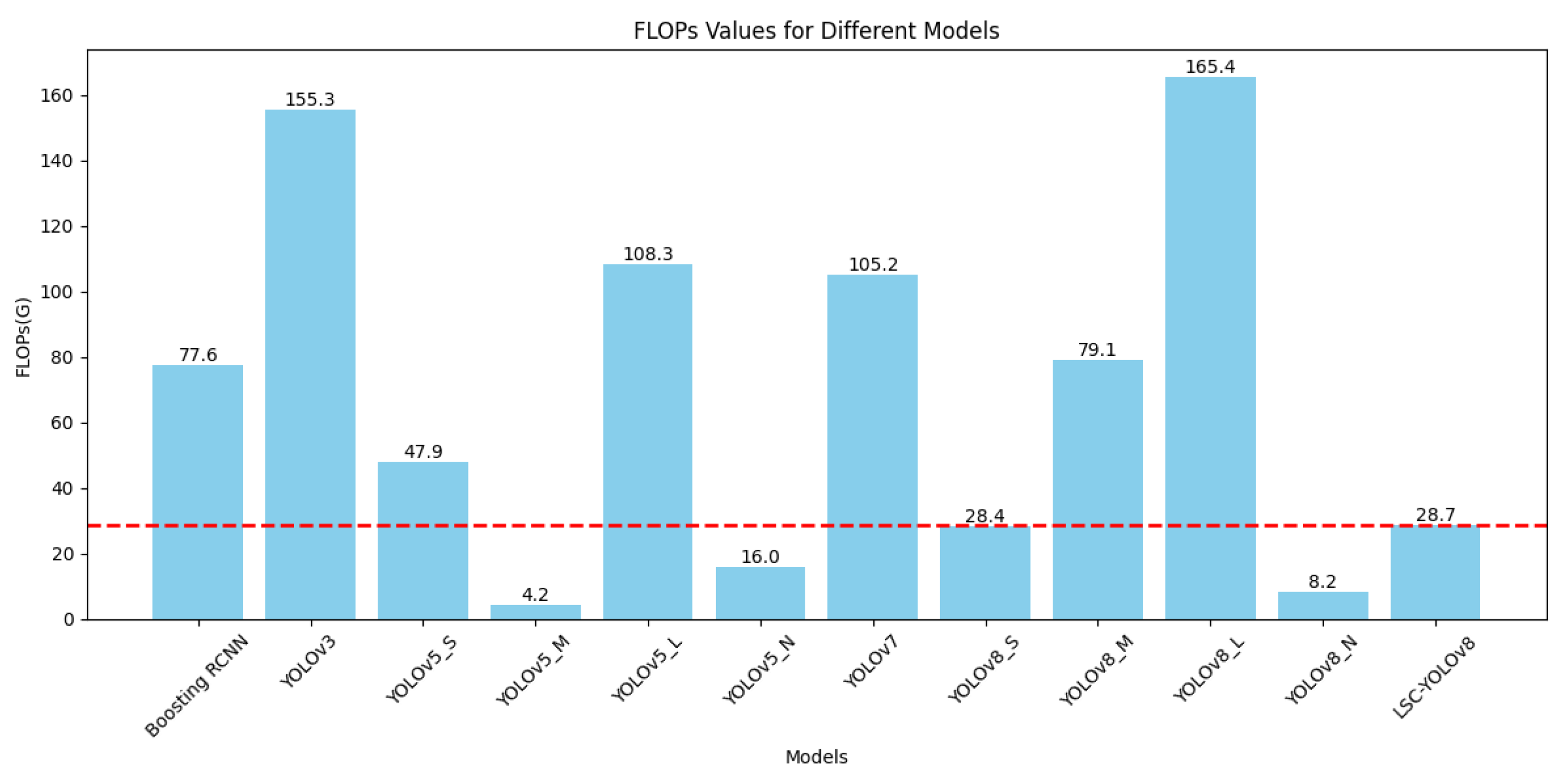
Preprints 103570 g010
Figure 10. Bar graph comparison of FLOPs for various models on the URPC2019 dataset.
Figure 10. Bar graph comparison of FLOPs for various models on the URPC2019 dataset.
Preprints 103570 g010
Preprints 103570 g011
Figure 11. Bar graph comparison of the number of parameters for various models on the URPC2019 dataset.
Figure 11. Bar graph comparison of the number of parameters for various models on the URPC2019 dataset.
Preprints 103570 g011
Preprints 103570 g012
Figure 12. Comparison of target detection results between different models.
Figure 12. Comparison of target detection results between different models.
Preprints 103570 g012
Preprints 103570 g013
Figure 13. Performance comparison of various models on the URPC2020 dataset.
Figure 13. Performance comparison of various models on the URPC2020 dataset.
Preprints 103570 g013
Preprints 103570 g014
Figure 14. Performance comparison of various models on the URPC2020 dataset.
Figure 14. Performance comparison of various models on the URPC2020 dataset.
Preprints 103570 g014
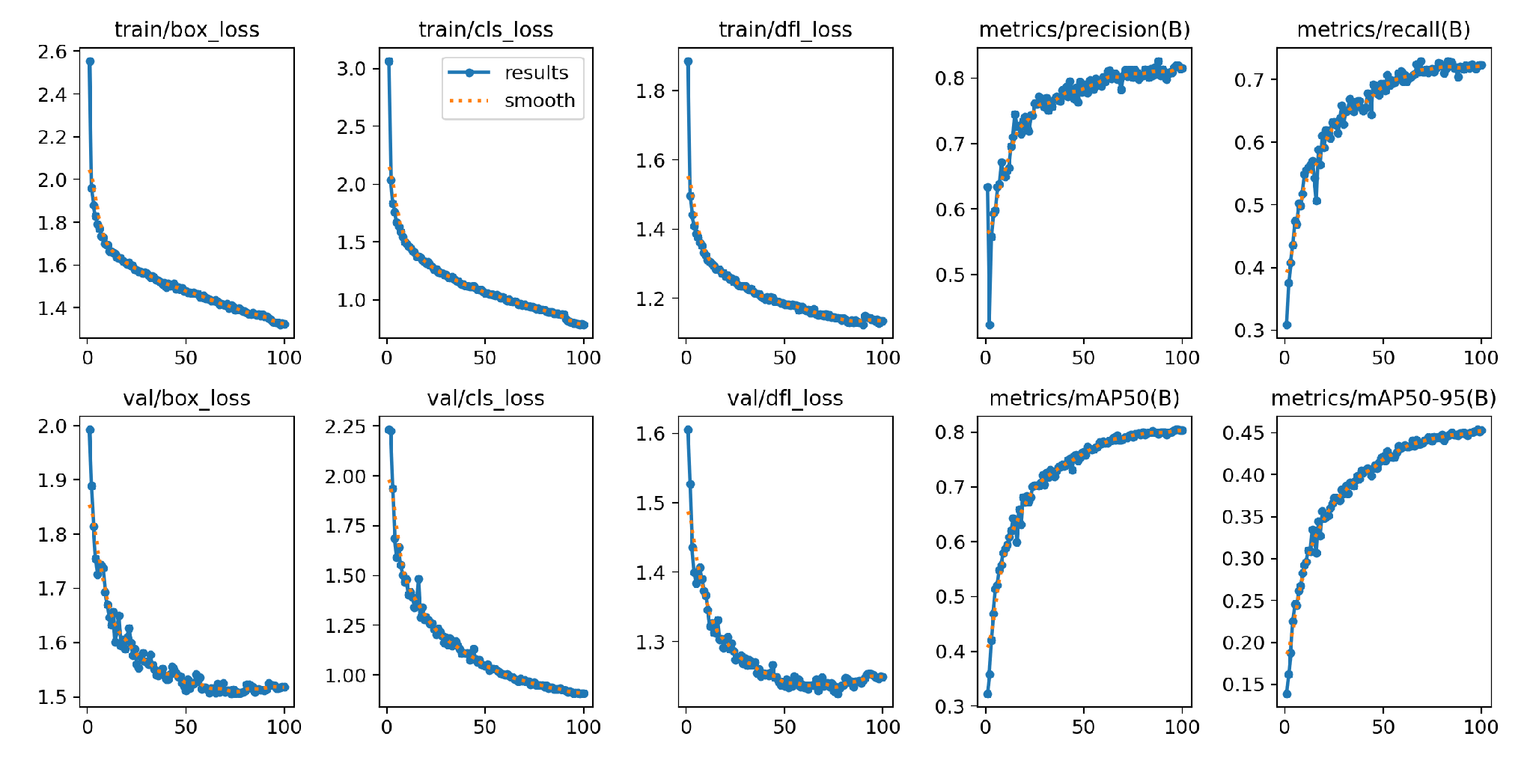
Preprints 103570 g015
Figure 15. Results of the YOLOv8-MU model on the URPC2020 dataset.
Figure 15. Results of the YOLOv8-MU model on the URPC2020 dataset.
Preprints 103570 g015
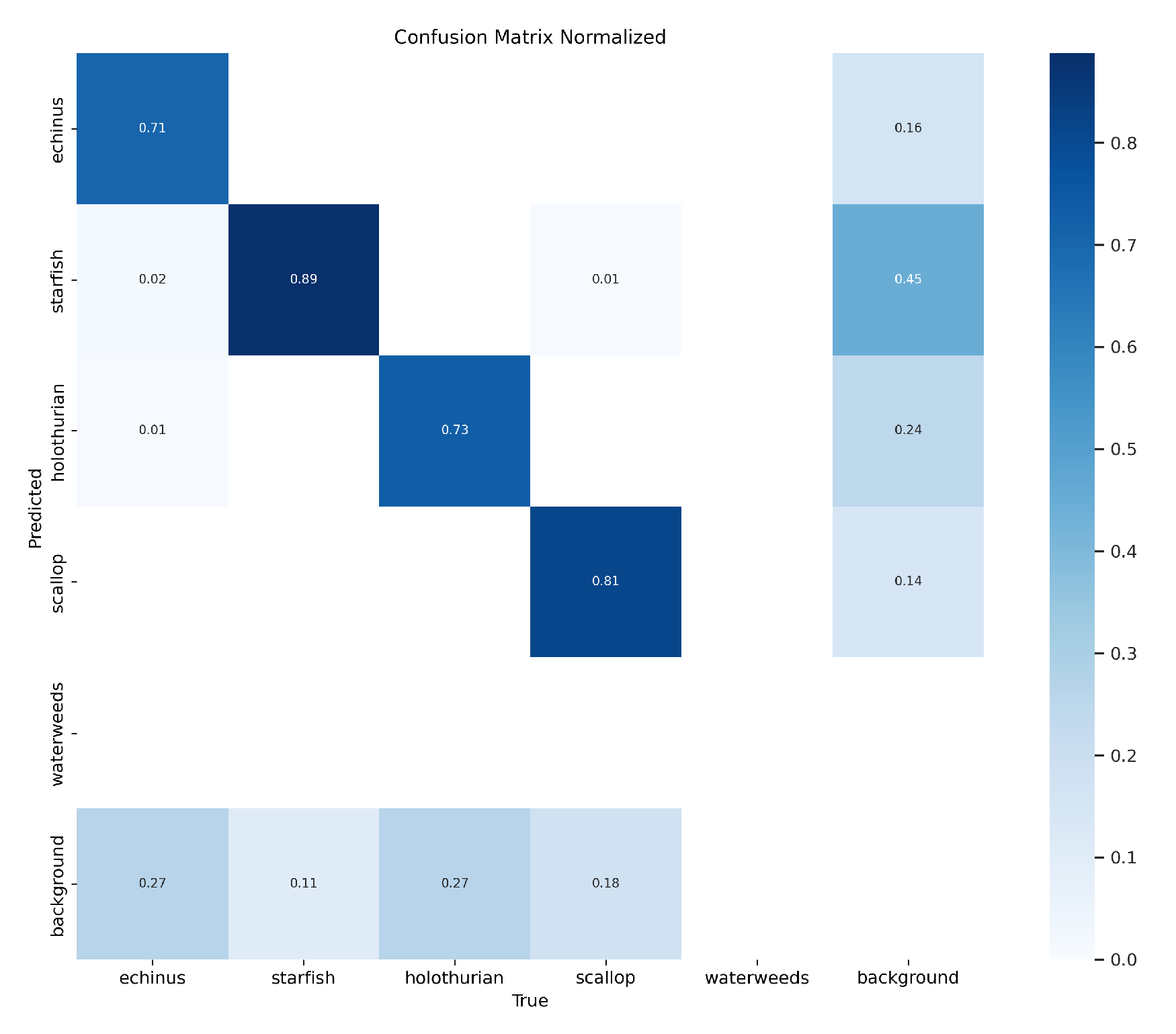
Preprints 103570 g016
Figure 16. Confusion matrix of the YOLOv8-MU model on the URPC2020 datasets.
Figure 16. Confusion matrix of the YOLOv8-MU model on the URPC2020 datasets.
Preprints 103570 g016
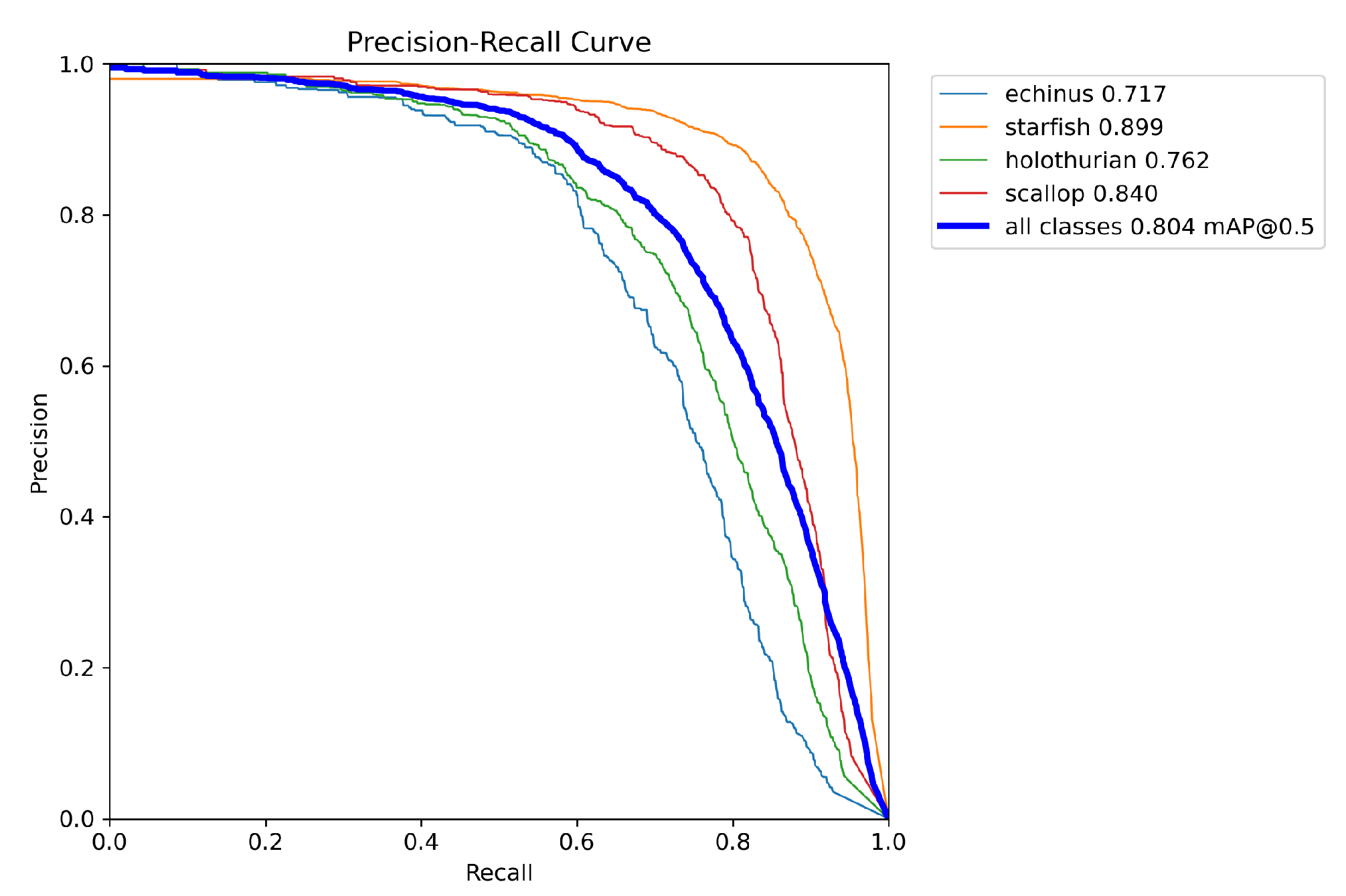
Preprints 103570 g017
Figure 17. PR curve of the YOLOv8-MU model on the URPC2020 dataset.
Figure 17. PR curve of the YOLOv8-MU model on the URPC2020 dataset.
Preprints 103570 g017
Table 1. Experimental Environment Configuration.
Table 1. Experimental Environment Configuration.
Parameters Setup
Ubuntu 20.04
PyTorch 1.11.0
Python3 3.8
CUDA 11.3
CPU 12 vCPU Intel(R) Xeon(R) Platinum 8255C CPU @ 2.50GHz
GPU RTX 3090(24GB) × 1
RAM 43GB
Table 2. Settings of Some Hyperparameters During Training.
Table 2. Settings of Some Hyperparameters During Training.
Parameters Setup
Epoch 100
Batch size 16
NMS IoU 0.7
Image Size 640×640
Initial Learning Rate 1 × 10 − 2
Final Learning Rate 1 × 10 − 2
Momentum 0.937
Weight Decay 0.005
Table 3. Performance comparison of the YOLOv8-MU model with other models on the URPC2019 dataset.
Table 3. Performance comparison of the YOLOv8-MU model with other models on the URPC2019 dataset.
Model AP(%) mAP@0.5 (%) Para (M) FLOPs(G)
Echinus Starfish Holothurian Scallop Waterweeds
Boosting RCNN[20] 89.2 86.7 72.2 76.4 26.6 70.2 45.9 77.6
YOLOv3 89.6 86.8 73.6 82.6 57.8 78.1 61.5 155.3
YOLOv5s 92.0 88.1 75.2 84.5 24.2 72.8 20.9 47.9
YOLOv5m 91.9 86.3 58.4 71.8 17.6 62.5 1.8 4.2
YOLOv5ł 92.4 89.1 73.6 82.8 36.6 74.6 46.2 108.3
YOLOv5n 92.4 89.3 74.7 83.8 28.4 73.7 7.0 16.0
YOLOv7 92.6 90.0 78.5 85.6 39.6 77.3 37.2 105.2
YOLOv8s 91.3 89.0 75.2 84.9 32.1 74.5 11.1 28.4
YOLOv8m 90.9 89.5 76.9 85.7 28.1 74.2 25.9 79.1
YOLOv8l 90.9 90.4 77.1 84.8 27.0 74.0 43.6 165.4
YOLOv8n 91.7 89.2 76.1 82.8 32.3 74.4 3.0 8.2
YOLOv8-MU 91.9 89.3 75.8 83.5 51.5 78.4 5.7 28.7
Table 4. Performance comparison of the YOLOv8-MU model with other models on the URPC2020 dataset.
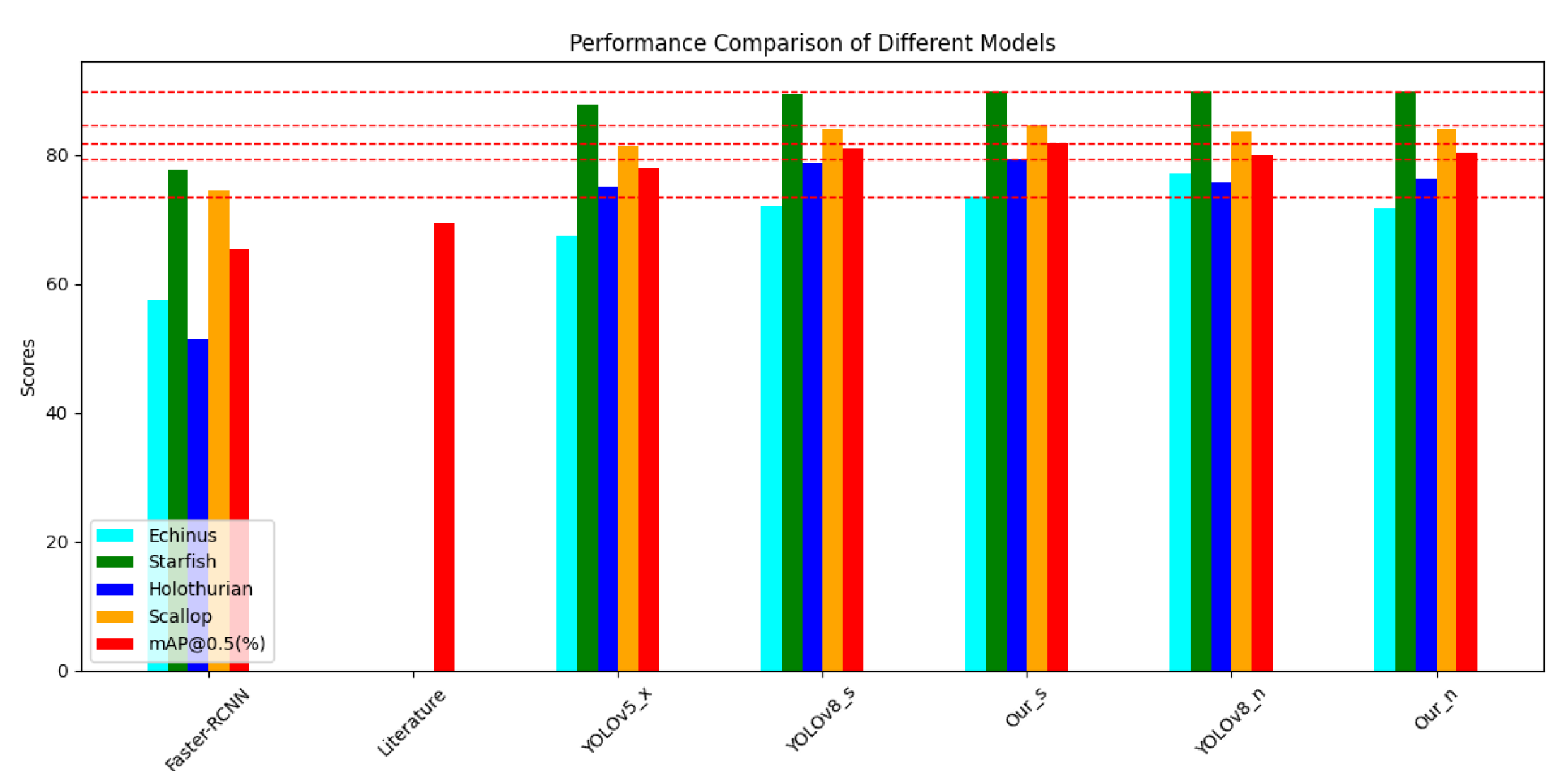
Table 4. Performance comparison of the YOLOv8-MU model with other models on the URPC2020 dataset.
Model AP(%) mAP@0.5 (%)
Echinus Starfish Holothurian Scallop
Faster-RCNN[55] 57.5 77.7 51.4 74.5 65.3
Literature[56] - - - - 69.4
YOLOv5x[55] 67.5 87.9 75.1 81.4 78.0
YOLOv8s 72.0 89.4 78.7 83.9 81.0
Ours 73.4 89.9 79.4 84.5 81.7
YOLOv8n 77.1 89.8 75.7 83.6 80.0
Ourn 71.7 89.9 76.2 84.0 80.4
Table 5. Parameter comparison of replacing C2f with LarK Block at different positions in the backbone.
Table 5. Parameter comparison of replacing C2f with LarK Block at different positions in the backbone.
Location of LarK Block AP(%) mAP@0.5 (%) Para (M) FLOPs(G)
Echinus Starfish Holothurian Scallop Waterweeds
All 91.5 88.0 73.5 82.1 35.8 74.2 3.4 9.7
The last three 91.8 88.8 73.0 82.6 30.1 73.3 3.4 9.3
The last two 90.7 88.8 75.2 82.8 29.4 73.4 3.4 8.7
The last one 91.7 89.5 75.6 83.6 28.9 73.9 3.2 8.2
The middle two 92.2 89.4 76.4 84.6 34.7 75.5 3.2 9.2
Table 6. Parameter comparison of replacing C2f with C2fSTR at different positions in the backbone.
Table 6. Parameter comparison of replacing C2f with C2fSTR at different positions in the backbone.
Location of LarK Block AP(%) mAP@0.5 (%) Para (M) FLOPs(G)
Echinus Starfish Holothurian Scallop Waterweeds
All 90.5 89.1 73.6 82.1 33.8 73.8 3.0 30.9
The last three 90.9 88.6 75.5 82.3 36.2 74.7 3.0 29.9
The last two 90.4 88.9 75.4 82.8 35.0 74.5 3.0 27.8
The last one 91.4 88.9 75.7 82.4 37.6 75.2 2.9 18.1
The middle two 91.6 89.0 73.2 81.9 38.4 74.8 3.1 20.0
Table 7. Parameter comparison of replacing C2f with Fusion Block at different positions in the neck.
Table 7. Parameter comparison of replacing C2f with Fusion Block at different positions in the neck.
Location of LarK Block AP(%) mAP@0.5 (%) Para (M) FLOPs(G)
Echinus Starfish Holothurian Scallop Waterweeds
All 91.5 89.7 75.7 84.0 32.6 74.7 3.95 16.5
The last three 92.2 89.6 75.6 83.8 29.1 74.1 3.8 15.8
The last two 91.8 89.1 75.7 83.1 32.9 74.5 2.9 8.4
The last one 92.0 88.8 75.3 83.3 33.5 74.6 2.7 7.8
The middle two 92.1 89.9 75.3 83.2 26.9 73.5 2.9 8.4
Table 8. Demonstration of the effectiveness of each module in YOLOv8-MU;“✓” indicates that we used this module.
Table 8. Demonstration of the effectiveness of each module in YOLOv8-MU;“✓” indicates that we used this module.
Module mAP@0.5 (%)
Lark Block C2fSTR SPPFCSPC_EMA Fusion Block MPDIOU
74.4
✓ 75.5
✓ 75.2
✓ 75.3
✓ 74.7
✓ 74.6
✓ ✓ 75.6
✓ ✓ 75.7
✓ ✓ 75.6
✓ ✓ 75.6
✓ ✓ 75.7
✓ ✓ 75.4
✓ ✓ 75.6
✓ ✓ 75.5
✓ ✓ ✓ 75.8
✓ ✓ ✓ 76.3
✓ ✓ ✓ 75.8
✓ ✓ ✓ 75.8
✓ ✓ ✓ 75.9
✓ ✓ ✓ 76.0
✓ ✓ ✓ ✓ 76.0
✓ ✓ ✓ ✓ 76.5
✓ ✓ ✓ ✓ 77.6
✓ ✓ ✓ ✓ 76.4
✓ ✓ ✓ ✓ ✓ 78.4
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated