Prerpints.org logo
Preprint
Article

A High-Speed Multichannel Electrochemical Impedance Spectroscopy System Using Broadband Multi-Sine Binary Perturbation for Retired Li-Ion Batteries of EVs

Altmetrics

Downloads

110

Views

54

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 April 2024

Posted:

11 April 2024

You are already at the latest version

Alerts
Abstract
Retired Electric vehicles (EVs) batteries are reused in second life energy storage applications. However, the overall performance of repurposed energy storage system (ESS) is limited by the unevenness of individual batteries use in it. Therefore, battery grading is required for optimal performance of ESS. Electrochemical impedance spectroscopy (EIS) based evaluation of battery aging is a promising way to grade lithium-ion batteries. However, it is not practical to measure impedance of mass retired batteries due to high complexity and slowness. In this paper, a broadband multi-sine binary signal (MSBS) perturbation integrated with multichannel EIS system is presented to measure impedance spectra for high-speed aging evaluation of lithium-ion batteries or modules. The measurement speed is multi-times higher than conventional EIS with single-channel configuration. The broadband MSBS is validated with reference sinusoidal sweep perturbation and corresponding root-mean-square error (RMSE) analysis is performed. Moreover, the accuracy of the presented multichannel EIS system is validated by impedance spectra measurement of Samsung INR18650-29E batteries and comparing it with those measured with commercial EIS instrument. A chi-squared error under 0.641% is obtained for all 8-channels. Since the non-linearity of battery has significant impact on quality of impedance spectra. Therefore, Kronig-Kramer (KK) transform validation is also performed.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Nowadays, lithium-ion batteries are widely used in various technologies easing our daily life. It is well known that high power and energy density, high charge-discharge efficiency and low cost of lithium-ion batteries have made them as a first-hand choice for electric mobility, portable electronics, and energy storage system (ESS) [1,2]. However, performance of lithium-ion batteries is being stumbled by unpredictable battery degradation [3]. Therefore, accurate estimation of battery state of health (SOH) and remaining useful life (RUL) are important to avoid accidental capacity fading and failure [4]. For lithium-ion batteries used in electric vehicles (EVs); capacity drop below 80% is consider end of life (EOL) [5]. However, these batteries can still store a significant amount of energy and can be used in repurposed or less demand application [6]. Since, it is well-known that optimal operation of repurposed system is highly dependent on similar characteristics of individual batteries used in it. Therefore, battery aging is a crucial indicator in recycling industry to decide whether a battery should be use in repurposed second life application such as ESS or recycled as a scrap [7,8]. Conventionally, microscopic phenomena modelling such as active material loss, solid electrolyte interface (SEI) and lithium-ion plating are in practice to forecast the battery state [9,10,11]. However, modelling each phenomenon is unscalable. Alternative way is measuring the AC impedance and relating it to the battery aging evaluation without modelling the actual degradation processes [12]. Electrochemical impedance spectroscopy (EIS) is a powerful tool to measure AC impedance. The battery is usually perturbed through minuscule excitation signal over a wide frequency range to measure the battery voltage and current response [13,14]. The impedance data obtained through EIS contain diverse information about battery electrochemical reaction, material properties and other interfacial phenomena [15]. Further, aging evaluation is performed by fitting the impedance spectrum to an equivalent circuit model (ECM). The extracted ECM parameters reflect the degradation mechanisms occurring inside the battery [16]. In conventional EIS, a sweep excitation is used which perturbs the battery for one frequency at a time [17]. Since it is well known that low frequencies take longer time. Additionally, multi-cycles are required to make the measurement results less prone to error. Therefore, sweep excitation has high complexity and longer measurement time, and it is not applicable for aging evaluation of mass retired EVs battery. Moreover, longer perturbation is more prone to environmental disturbances, drifts, and uncertainties in impedance measurement [18]. To address the longer measurement time and complexity of conventional EIS, broadband excitation is a desirable solution with short measurement time which increase the capability of EIS to be applied for aging evaluation on large scale. The class of broadband perturbation signal for high-speed impedance measurement consists of multi-sine [19] and pseudorandom sequences (PRS) [20]. Multi-sine is a combined signal of harmonically related sinusoids and further classified into different types. They can have linear, random, quasi logarithmic and logarithmic frequency distribution [21]. The energy of combined signal is distributed equally among the frequency spectra. However, combining frequency components without modification results higher amplitude and CF. Since, excitation signal with large amplitude and CF can drive a battery beyond linear-time-invariant (LTI) boundaries [22]. Therefore, perturbation amplitude should be limited for linear and steady-state operation of battery under test. Schroeder, Newman, and Littlewood proposed analytical methods to optimize CF of multi-sine by inserting suitable initial phases [23]. Among them, Schroeder gives good results for flat frequency distribution. However, there is no improvement in CF for logarithmic frequency distribution, instead it gets worse [24]. There are some deterministic CF optimization strategies for random or logarithmic distributed spectra with their own limitations and complexities [25,26,27]. Another class of broadband excitation is PRS which are further classified into pseudo random binary sequences (PRBS) and ternary signals. Since, the PRS can be limited to minimum two or three levels [28]. Therefore, they are simple and easy to generate using a low-cost DSP. However, PRS contain linearly distributed frequencies spectra, and the frequencies of interest are not selectable. Unlike sweep excitation, the energy is divided among equally spaced harmonics which reduces the signal-to noise ratio (SNR) and corresponding accuracy of measurement results [29]. Although, SNR can be increased by adjusting the sequence length or increasing the PRS amplitude, but it causes impedance deviation due non-linearity [30]. A broadband multi-sine binary signal (MSBS) is an attractive solution for random and logarithmic frequency distribution. They are two-level signal obtained through direct binarization of multi-sine. Therefore, it inherent the advantages of both multi-sine and PRS such as selectable frequencies of interest, simple to generate and lower CF (1.0) respectively. Since, frequency components are selectable, therefore the SNR of MSBS is good in comparison with that of PRS. Although, direct binarization of CMSS introduce extra harmonics in resulting binary signal. However, the desired frequencies can be accurately extracted through digital lock-in amplifier (DLIA) algorithm. In this work, a high-speed multichannel EIS system is developed which measures the impedance spectrums of eight batteries simultaneously. A broadband MSBS is presented to perturb the batteries. The proposed system is implemented on a 180 by 135mm PCB which make it compact and portable compared to commercially available instruments. A low-cost STM32 DSP is used to generate the MSBS perturbation. The impedance measurement time is drastically reduced through presented broadband perturbation and multichannel EIS setup. The validity of presented MSBS is carried out through experiments and comparing the results with sinusoidal sweep and other broadband perturbation schemes. The multichannel EIS system accuracy is verified through chi-squared error analysis with reference commercial EIS instrument. A linear Kronig-Kramer (KK) transform is used to validate the quality of obtained impedance spectra [31]. In last, the ECM parameters of batteries are estimated by fitting algorithms. This paper is organized as: Overview of conventional EIS and interpretation of impedance spectra is discussed under section II, various excitation scheme used for AC impedance measurement are explained in section III, architecture of proposed high-speed multichannel EIS system is discussed in section IV, experimental validation is explained in section V, and the work is concluded in the last section.

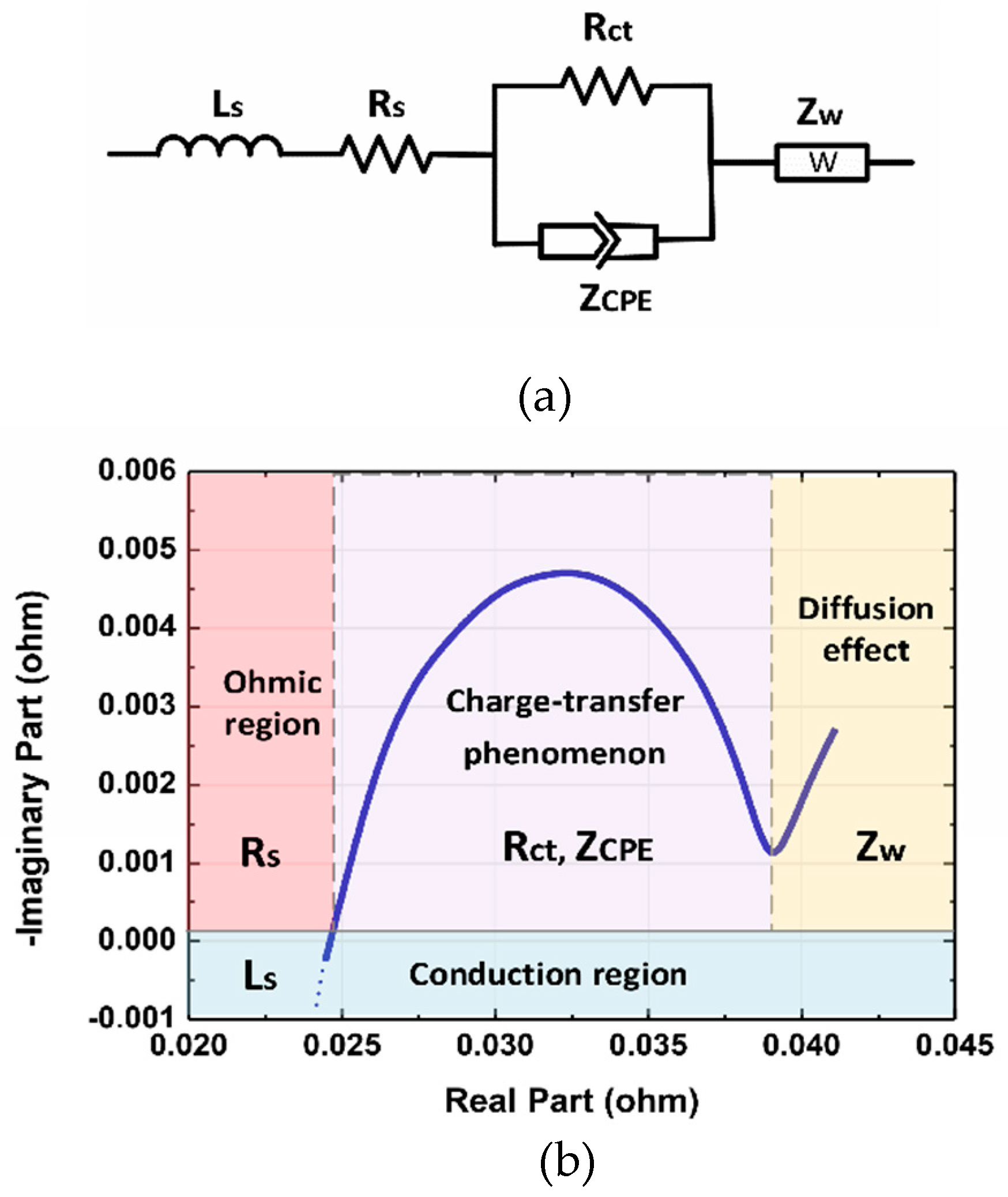
2. Overview of Conventional EIS and Interpretation of Impedance Spectra

The measurement setup for an EIS in galvanostatic excitation is to perturb the battery with predetermined current and measure the battery response. In conventional EIS, sweep excitation is applied to determine the impedance spectrum of a battery [18,19]. The impedance is measured for individual perturbation frequency one after another. Since, the energy is concentrated only on single excitation frequency at a time. Therefore, SNR and correspondingly the quality of measurement result is good. However, due large measurement time, the conventional EIS is not practical for aging evaluation of mass retired batteries. Therefore, simplified EIS such as using square signal perturbation instead of sine-sweep, but still the measurement approach is slow [32]. Thus, there is clear gap to introduce advance EIS approaches for high-speed and quality impedance measurement of a battery. The battery impedance resists the flow of current and responsible for voltage drops by connecting the load. It is well known that battery impedance is a function of frequency and for EIS it is expressed as follows.
Z ω = V ( ω ) I ( ω )
where 𝜔 is the angular frequency, Z(𝜔) is impedance, V(𝜔) and I(𝜔) are the voltage and current response of a battery respectively.
The impedance spectrum of battery is usually represented through Nyquist impedance plot as shown in Figure 1b. It is curve fitted to related ECM as shown in Figure 1a and corresponding ECM parameters are extracted. These parameters are further analyzed to get useful information about internal electrochemical processes, capacity, SOH, and aging of the battery [14]. Moreover, they are useful in maintaining the in-service battery performance, aging evaluation of retired batteries and grading them for repurposing.
In Figure 1b, the Nyquist impedance plot is divided into four regions. The nearly vertical part at high frequency (several kHz) shows the inductive region caused by battery current collector and conduction of connecting wires. The intersect on the real axis indicates the ohmic resistance possessed by the electrodes, electrolyte, and terminal contacts. The semicircle (s) are formed at medium frequency range, it is due to charge transfer phenomenon occurs at the electrode surface. The low frequency region (mHz) describes the Li+ solid-state diffusion occurs between the electrodes which is expressed by Warburg impedance in ECM. Further, the shape of impedance spectrum varies with the temperature, SOC, SOH, and aging of the battery [7]. As the temperature rises, the impedance of the battery decreases due to acceleration of chemical reaction. However, high temperature speed-up the degradation processes which after all increase the impedance [16]. As the SOC of the battery changes correspondingly impedance also varies. Battery impedance increases with battery degradation due to formation of SEI layer, current collector corrosion, depletion of electrolyte and various other phenomena [8].

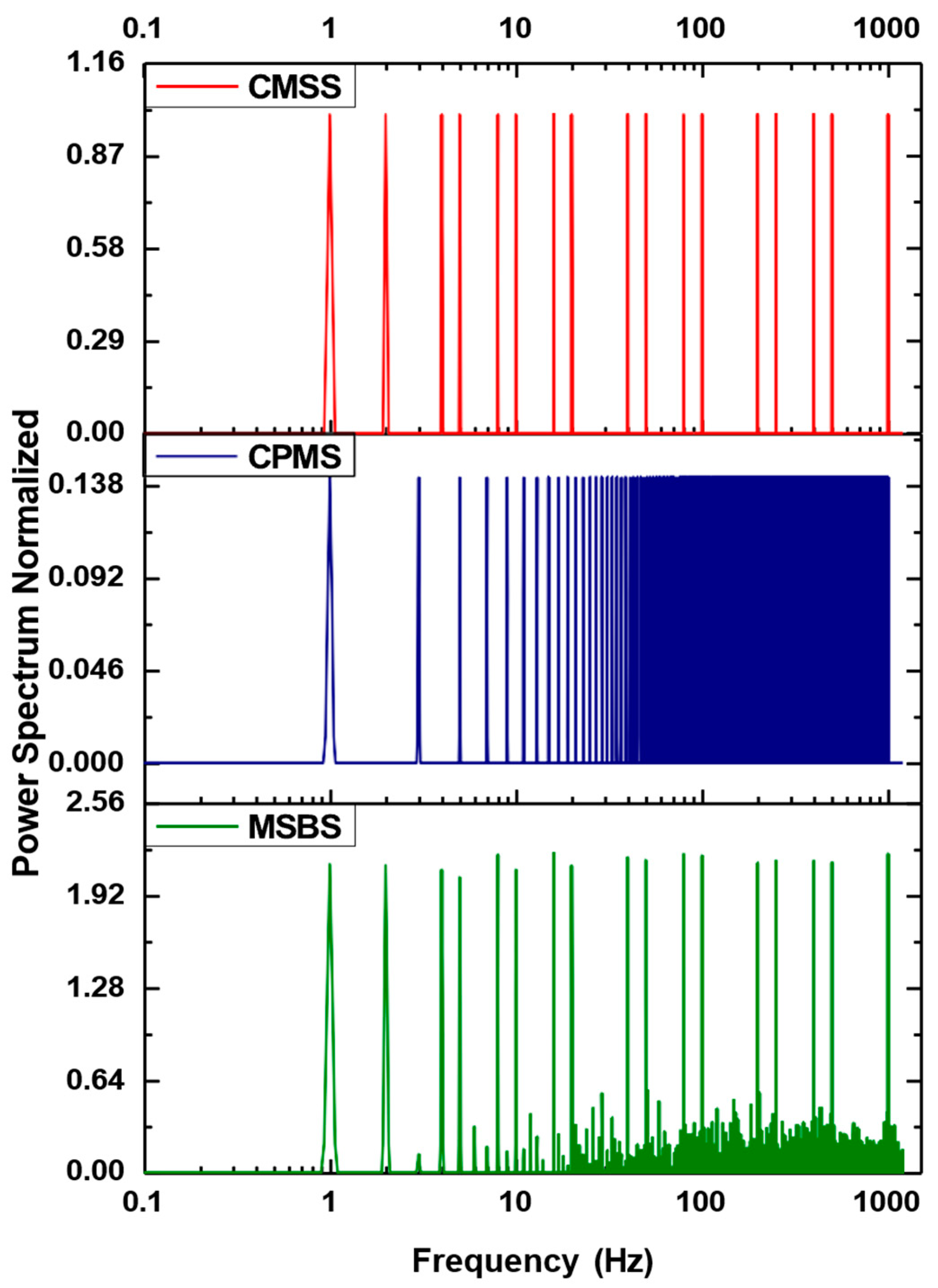
3. Broadband Excitations for EIS

Broadband excitations are widely used in system identification. All the frequencies of interest are excited in a combined signal which shortened the measurement time. However, some essential conditions should be considered while using particularly broadband excitation signal. To get valid impedance spectra of any electrochemical system, it should fulfil the property of linearity, causality, and stability. These properties can be satisfied by applying appropriate excitation signal. In EIS for batteries, linearity means that amplitude and phase response should be independent of perturbation signal amplitude. However, this condition cannot be strictly satisfied due to non-linear charge transfer and diffusion effects in batteries. To minimize the impact of non-linearity, the magnitude of voltage response should be less than 25mV at room temperature [21]. For lithium-ion batteries, an amplitude should be limited under 10mV [33]. However, impedance deviation observed due non-linearity effect for 10mV amplitude is very small which make it very restrictive [34]. Therefore, some higher values can be used for better SNR. In galvanostatic excitation, the amplitude of perturbation current should be selected according with the impedance of the battery so that voltage response of a battery should stay within a linear operating range (under 25mV). The excitation current amplitude should be adjusted according to the battery impedance to reduce the impacts of non-linearity. The second required condition is causality, which practically means that the battery response for measuring impedance spectra is only caused by the applied perturbation. More specifically the noise level is low, no response at t < 0, and measurements are repeatable. The last requirement is stability, which means that state of a battery during measurement should not change significantly, e.g., the change in battery SOC should be less than 1% [33]. As the perturbation time for broadband signals is short compared to sweep excitation. Therefore, broadband perturbations are more advantageous to avoid momentary changes and more likely to maintain battery steady state. In multi-sine signals, the frequency components are selectable. Since, the EIS goal is to extract information about physical and internal electrochemical processes of the battery in frequency domain. However, the internal phenomena occurring inside battery are not equally distributed over the impedance spectrum. The ohmic effect, charge transfer processes, solid state diffusion and SEI occurs at different frequency band which are partially overlapped [17]. In sweep excitation, enough time can be afforded, and a dense frequency distribution can be selected. However, only useful frequency content can be included in combined signal due to finite power of excitation signal. In multi-sine perturbation, usually 10, 6 and 3 per decade frequency distribution is included to cover the entire perturbation band [23]. Unlike PRS, the signal power is distributed only on limited numbers of selected frequency components which suppress the impact of noise and increase the accuracy of measured impedance spectrum. Therefore, no filtering is required for EIS results using multi-sine perturbation [21,22]. Moreover, the back-end impedance computation burden is also low compared to using PRS excitation. The multi-sine signals are further classified into various types which are briefly discussed in following subsections.

3.1. CMSS

These signals are obtained by adding harmonically related sinusoids with adjustable amplitudes. The primary advantage of CMSS is system response is measured at multiple discrete frequencies of interest simultaneously which drastically reduce the measurement time.
x t = ∑ k − 0 N A k . sin ⁡ 2 π f k t
Where N is the sinusoidal component to be combined, A k and f k is the amplitude and frequency of respective frequency component.
As previously mentioned, the number of harmonically related sinusoids are limited by overall amplitude and finite power of combined signal represented by (3). The drawback of CMSS is highest CF which may drive the battery response to non-linear operating region. Moreover, clipping of perturbation could occur if the controlling circuit is not able source the desired amplitude of excitation.
P = 1 T 0 ∫ 0 T 0 ∑ k = 0 N A k . sin ⁡ 2 π f k t
Where P is the average power of CMSS and T 0 is the time period of fundamental frequency component.

3.2. CPMS

CPMS are modified form of CMSS with optimized and lower CF. The optimization of CF is performed using direct analytical methods such Schroeder, Newman, and Littlewood [26,27]. For CMSS with equidistant or linear frequency distribution, initial phases are calculated using Schroeder approach to adjust the peaks and obtain an optimized CF.
x t = ∑ k − 0 N A k . sin ⁡ 2 π f k t + Φ k
Φ k = ( k − k 2 ) N
C F = | x t P e a k | 1 T 0 ( ∫ 0 T 0 ∑ k = 0 N A k . sin ⁡ 2 π f k t 2 d t
Where (4) represents the Schroeder analytical equation, 𝜙𝑘 are the Schroeder phases expressed in (5). CF is represented by (6) which is equal to peak value divided by root-mean-square (RMS) value.
The drawback of direct optimization strategies is that CF can be optimized only for linear distributed CMSS. For random and logarithmic frequency distribution, the CF doesn’t improve and sometimes gets even worse [28].

3.3. MSBS

MSBS is a two-level signal obtained through direct mapping of CMSS to an equivalent binary level. The multi-sine signal is clipped at average value, the amplitude instantaneous value greater than average is mapped to binary high (+A) and less than average is mapped to binary low (-A). The mapping of CMSS into MSBS is represented by (7). The resulted MSBS signal inherent both the advantages of PRS and multi-sine signals. Since it is a two-level signal which simplify the generation algorithms and hardware. The CF is equal to that of PRS (CF=1.0), and the frequencies of interest are selectable. Some additional harmonics appears along with frequencies of interest in the FFT of MSBS. However, the appeared harmonics have small amplitude and 70 to 85 % of signal power can be concentrated desired frequencies [14]. The MSBS generation using (7) is represented by block diagram shown in Figure 2. It is implemented in LabVIEW, the resulted MSBS signal is converted to look-up array for coding in DSP.
M S B S t = s i g n ∑ k = 0 N A k . sin ⁡ 2 π n N k  
In Figure 3, the normalized power spectrums of CMSS, CPMS and MSBS are given. The power spectrums are normalized with respect to CMSS for relative analysis. The CMSS and MSBS signal contain 17 frequencies components ranging from 1 Hz to 1kHz. The values of frequencies are: 1, 2, 4, 8, 10, 16, 20, 40, 50, 80, 100, 200, 250, 400, and 1kHz. The CPMS based on Schroeder phases insertion and having optimal CF as compared to CMSS is constructed of linear distributed frequencies. In given CPMS, 500 harmonics are included between 1 Hz to 1kHz with 2 Hz frequency step. The reason behind such dense frequency distribution is to measure impedance at lower frequency range and observe the battery electrochemical phenomena occurs in lower frequency range (≤ 10 Hz). The power spectrum equation of CMSS and CPMS is obtained using (8) as:
P C M S S ,   C P M S =   ∑ k = 0 N A k 2 2
Where 𝐴𝑘 are the amplitudes and N is number of frequencies component. The respective power spectrum of MSBS approximated is given by (9):
P M S B S ( k ) =   ∑ k = 0 N A k + S u b _ H a r m o n i c s
S N R = P S i g n a l P N o i s e
The SNR of MSBS is approximately double to that of CMSS. It is observed from the normalized power spectrum given in Figure 3 that for similar numbers of frequency components (N), the amplitude of MSBS can be decreased by a factor of 1 2 to get same SNR with that of CMSS. This increases the flexibility in designing the amplitude of MSBS. Moreover, the frequency content (N) which can be accommodated for a given amplitude and SNR is larger than CMSS. Since, the CPMS power is divided among linearly distributed frequency components which are quite large in number compared to MSBS. Therefore, the SNR of CPMS for a given frequency component is multi-times smaller than MSBS. Although the SNR can be increased by increasing the amplitude or limiting the frequency density of CPMS. However, it will become more prone to non-linearity for higher amplitude, and not able to properly measure impedance spectrum in lower frequency region by limiting frequency density.

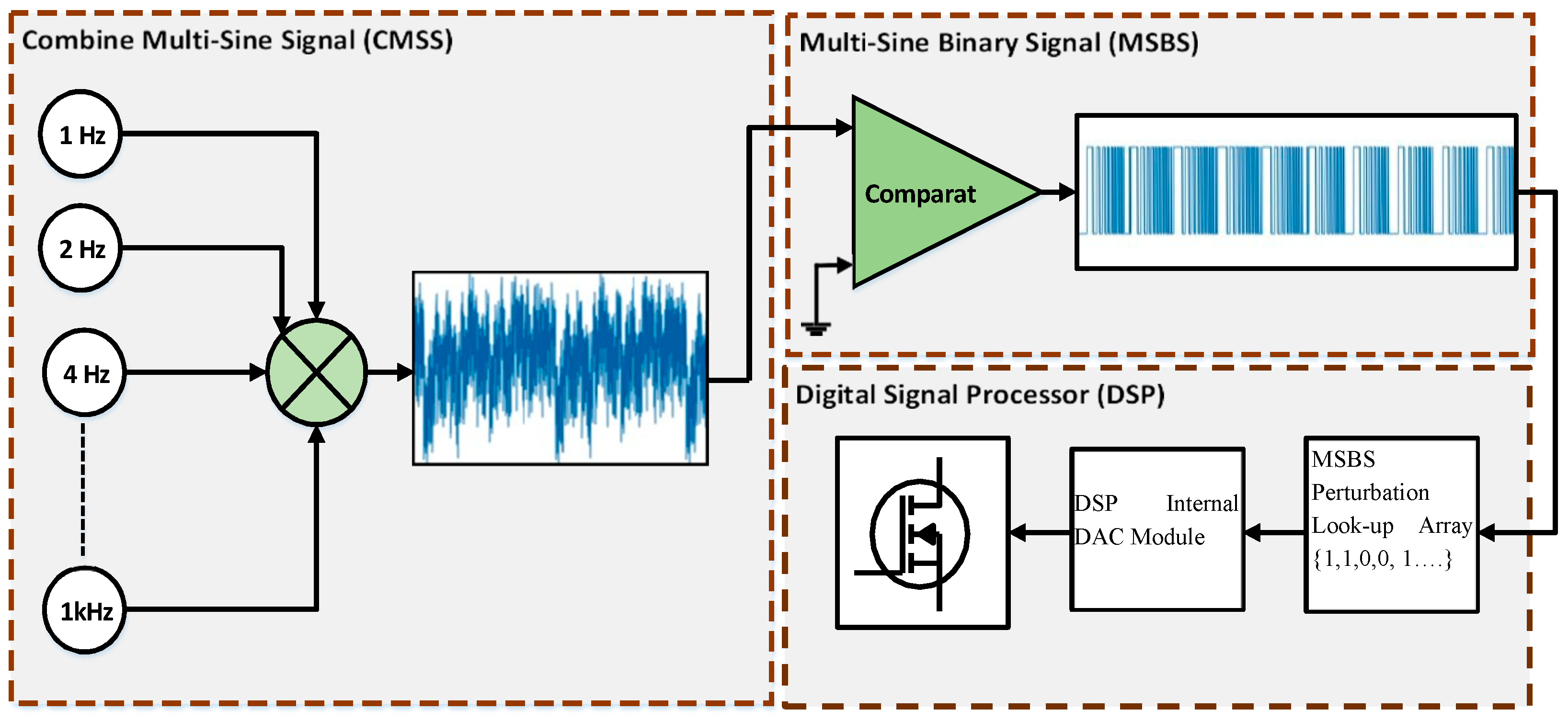
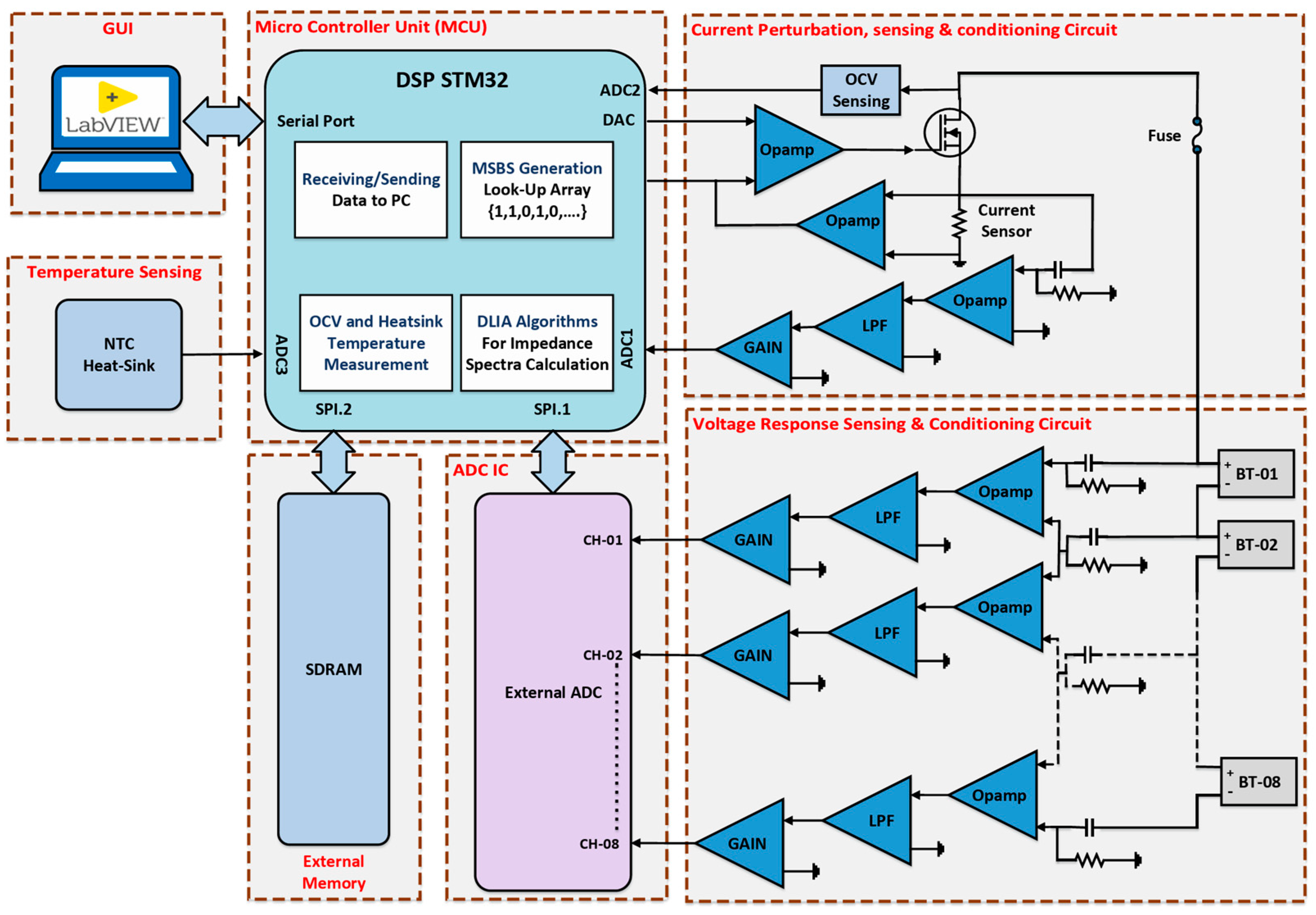
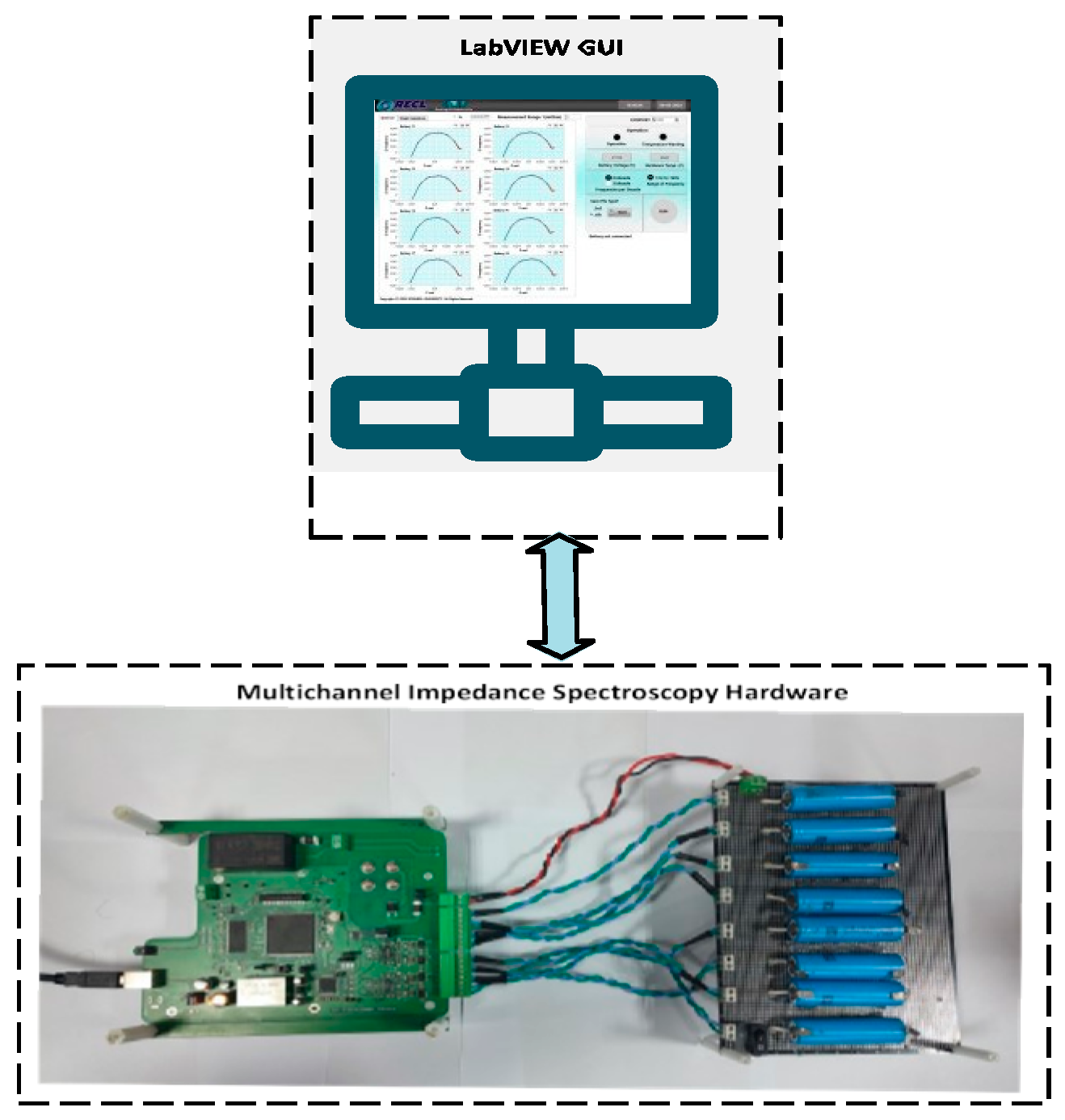
4. Architecture of Presented High-Speed Multichannel EIS System

The block diagram of proposed high-speed multichannel EIS system is shown in Figure 4. A low-cost MCU manufactured by STMicroelectronics having Arm cortex-M7 processor, two 12-bits built-in DACs, three 16-bit ADCs, dual mode quad SPI memory interface, 2 MBs programmable flash, communication peripherals and low power consumption is selected. To make the design compact and simple, the MSBS reference perturbation signal is generated using internal DAC. The reference perturbation signal is used to control the discharging of the battery through a high-precision current-sink based on voltage-controlled current source arrangement. The perturbation current magnitude through the MOSFET is controlled through feedback from drain to gate. Since, there is 2 MB flash memory in the selected MCU. Therefore, as mentioned in previous section, the presented MSBS is programmed as a look-up array in DSP and the internal DAC is used to produce the corresponding analogue perturbation reference signal represented by (9).
V ( t ) M S B S = V m . s i g n [ ∑ k = 0 N A k . sin ⁡ 2 π f k t + V m 2 ]
Where V m is the amplitude of perturbation reference signal and V m 2   is the DC offset because the battery is perturbed in discharging mode. The presented EIS system perturbs eight batteries/modules simultaneously using broadband MSBS for all frequencies of interest. Similarly, the current and voltage responses of all batteries are measured at the same time using bipolar 16-bit 8 channel external ADC IC (AD7606) manufactured by Analog Devices. Therefore, the proposed EIS system drastically reduces the measured time using broadband MSBS and 8-channel configurations.
The batteries perturbation responses are sensed and measured using sensing and conditioning circuit which consists of high precision current sensors, high pass passive filter, active low pass filters, and gain amplifiers. The responses read by external ADC IC are transmitted to DSP which process them to calculate impedance spectrums of respective batteries.
The impedance calculations for all channels are carried out using DLIA algorithms implemented in DSP. In first part, the measured broadband batteries responses are demodulated by mixing with reference frequencies signals. The magnitudes and phases of respective responses are obtained after passing the demodulated battery response through a low pass filter. These magnitudes and phases of voltages and current responses are used to determine the impedance spectrum for each battery.
The flowchart of DSP codes for proposed EIS system along with graphical user interface (GUI) developed in LabVIEW is shown in Figure 5. The GUI generates control command for a given EIS test by decoding the user setting which is further send to the hardware. Once the DSP receive the control command from the GUI, it is decoded, and EIS test begins with corresponding user setting. The DSP generates reference broadband MSBS reference signal to perturb the batteries. Perturbation responses of battery are recorded, and the data is saved in external SDRAM. The impedance spectrum for all 8 batteries is calculated and the data is sent to the PC. The impedance spectrum data received by the GUI is decoded, plotted on respective channel plots, and saved in excel and text file for further analysis.

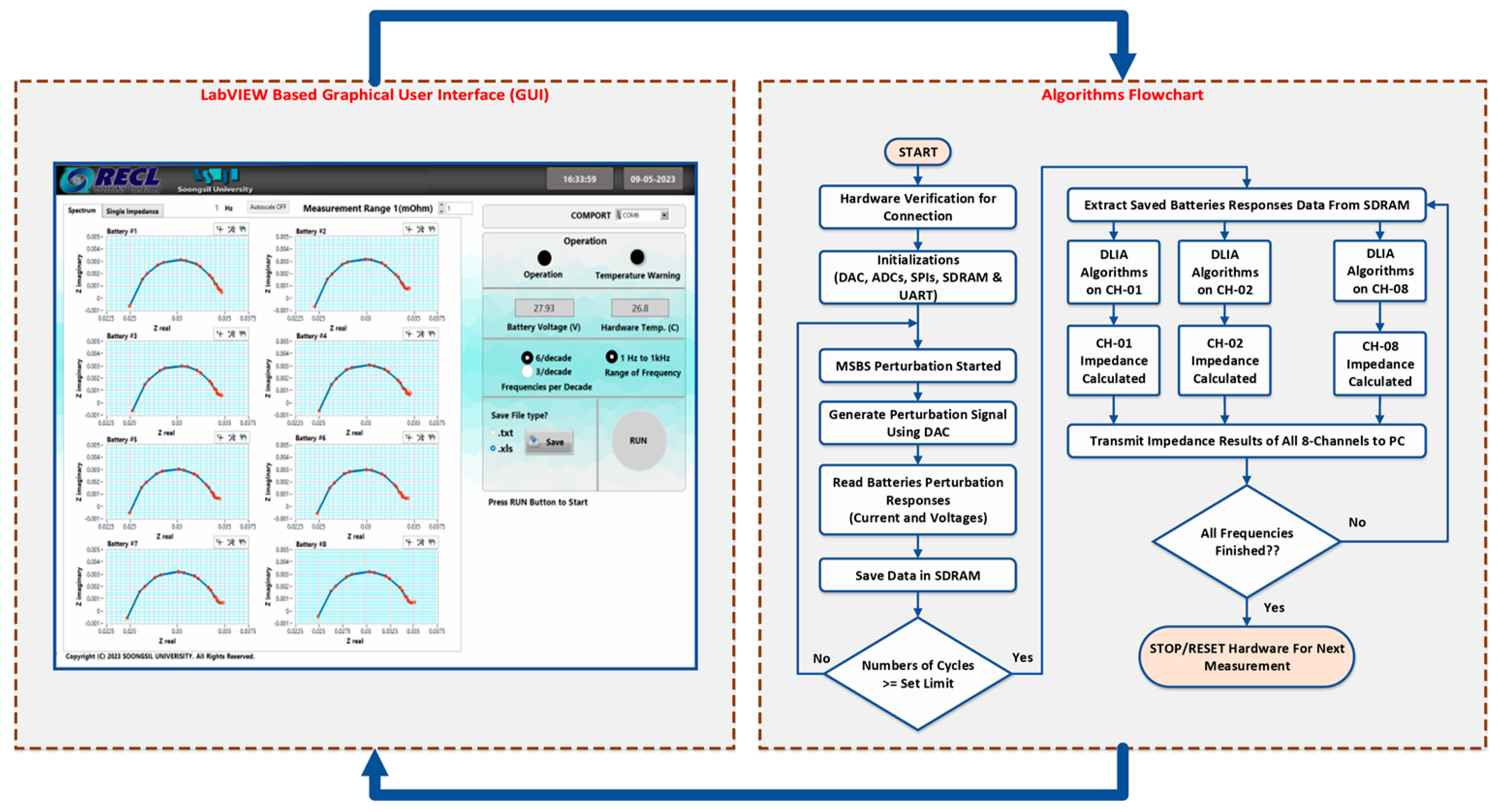
5. Experimental Validation and Discussion

During the first group of experiments, the sinusoidal sweep and multi-sine perturbation such as CMSS, CPMS and presented MSBS are applied to the lithium-ion Samsung INR18650 battery to validate the presented MSBS perturbation. In second group of experiments, the validation of proposed high -speed multichannel EIS system is carried out by comparing measurement results with that of commercial EIS instrument. KK transform is used to verify the compliance of impedance spectra with LTI criteria. The specifications of given batteries are shown in Table 1. Before the experiment, batteries were equally charged according to the specifications of manufacturer. The open circuit voltage (OCV) recorded was 3.50 V for each battery. Moreover, batteries were relaxed for 2 hr prior to the experiment to stabilize and reach thermal equilibrium.

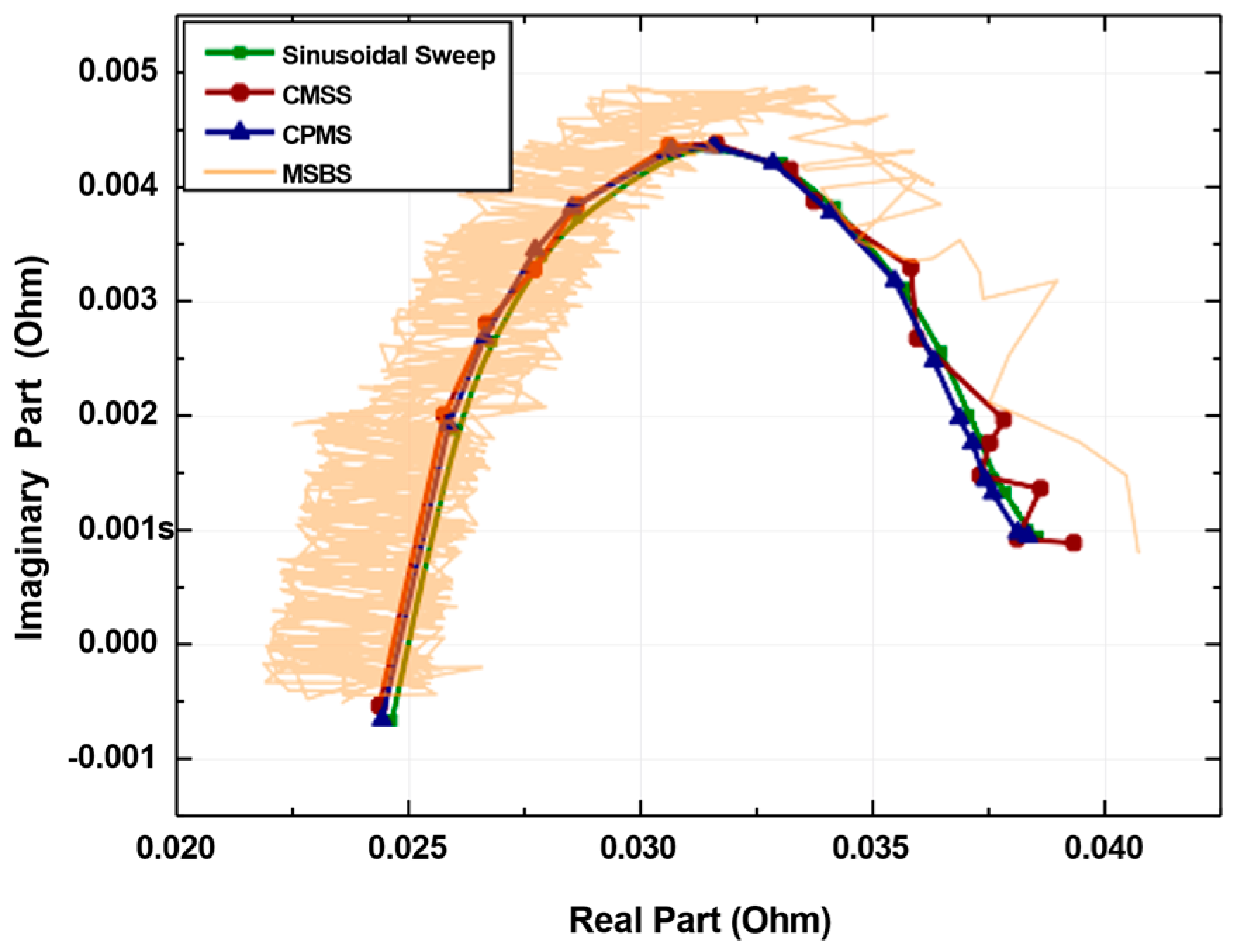
5.1. Sinusoidal Sweep, CMSS, CPMS and Presented MSBS Comparison

For validation of presented broadband MSBS for impedance spectroscopy, a comparison with sinusoidal sweep, CMSS, and CPMS is carried out. The parameters of each perturbation signal are listed in Table 2. The peak-to-peak amplitude is kept to 1.0 App for all the perturbation. The aim for same value of perturbation amplitude is to validate that which broadband signal have better SNR and root mean square error (RMSE) compared to sinusoidal sweep perturbation. Moreover, for given perturbation current, the voltage response of a battery will be less than 25mV which ensure the linearity condition. Lastly, 5 cycles of broadband perturbation are used for stable battery response measurement.
R M S E = 1 N ∑ k = 0 N | z r k − z m k z r k | 2
Where z r is the reference measurement results obtained through sinusoidal perturbation, z m is the measured impedance results through broadband perturbations. Since, the CPMS have linear distribution with 500 measurement impedance points compared to sinusoidal sweep perturbation is logarithmically distributed with 17 measurement points. Therefore, curve fitted impedance curve is used for calculating RMSE.
The results of the experiment obtained are shown in Figure 6. The Nyquist impedance plot of CMSS shows zig zag measurement for lower frequencies. It is due to low SNR and unwanted impact of noise. Similarly, the impedance spectrum of CPMS is quite zig zag with large deviation compared to actual values. Therefore, additional filtering technique is also required to get some meaningful results for further analysis. On the other hand, the Nyquist curve of presented MSBS perturbation is smooth and almost coinciding with that of sinusoidal sweep perturbation. The RMSE of the CMSS, CPMS and presented MSBS is given in the Table 3. It is observed that for same amplitude (1.0 App) of combined perturbation signal, the MSBS shows lowest RMSE of 0.51% w.r.t reference sinusoidal sweep perturbation. Hence, this analysis verifies the validity and accuracy of MSBS compared to CMSS and CPMS.

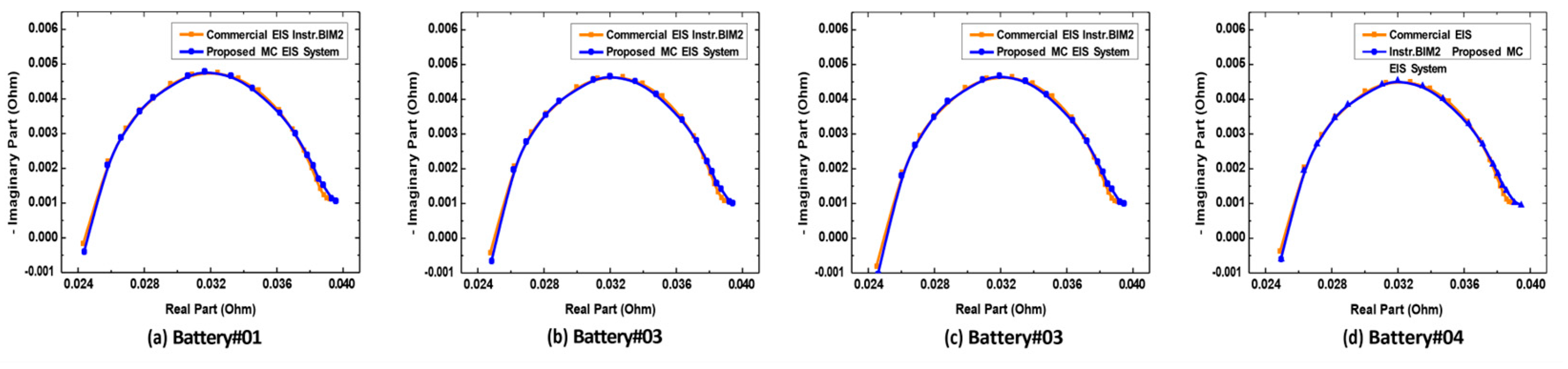
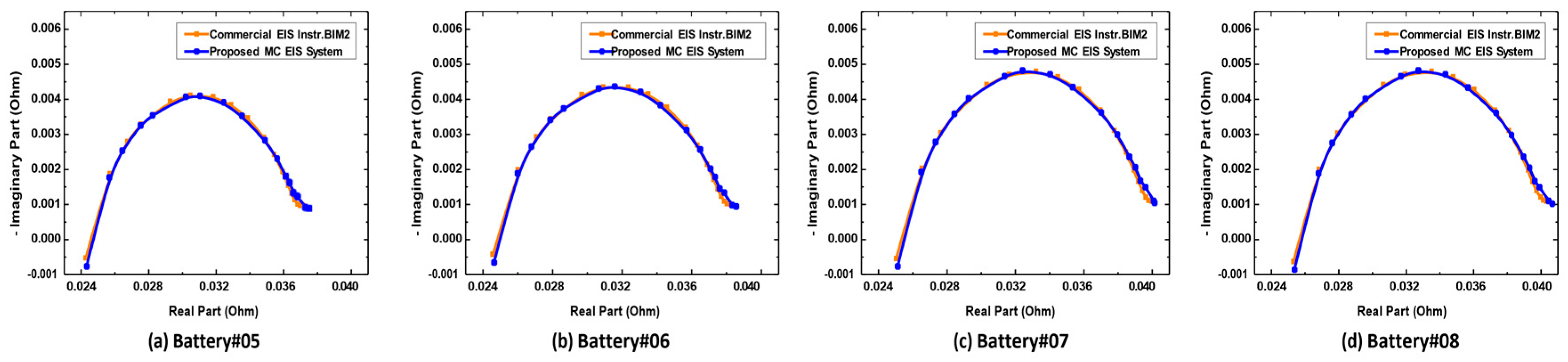
5.2. Validation of Presented Multi-Channel Fast EIS System Using Commercial EIS Instrument

The validation of proposed high-speed multi-channel EIS system is carried out by comparing the results with that of commercial EIS instrument named “BIM2” developed by BRS Messtechnik [35]. The experimental setup of the proposed EIS system is shown in Figure 7. A battery module which consists of eight lithium-ion Samsung INR18650-29E batteries connected in series are used to perform the validation experiment. The impedance spectrum of each battery is obtained simultaneously, and the results are display on the LabVIEW based GUI open in laptop. Four-wire kelvin connection is used for batteries connection with proposed high-speed multichannel EIS system which reduce the effect of unwanted noise, interference, and minimized the impact of contact resistances. The experiment is performed by clicking the RUN button on LabVIEW based GUI. Since, the MSBS is for very short interval of time and the batteries are in steady state. Therefore, the impedance spectrum of each battery is also measured through BIM2 just after the earlier experiment. The measurement frequency range of BIM2 selected is from 1 Hz to 1kHz and frequency distribution of 6 per decade. However, the excitation frequencies of BIM2 and presented MSBS are not all same, rather some frequencies are equal while other are not. The impedance spectrums obtained through presented EIS system and commercial EIS instrument are shown in Figure 8 and Figure 9. It is observed that impedance spectrums obtained through proposed system are well coincide with that of BIM2. The chi-squared analysis of each battery impedance spectrum is performed, and the respective results are shown in Table 4. The values of chi-squared error lie under 0.641% which verify the accuracy of the proposed high speed multichannel EIS system.

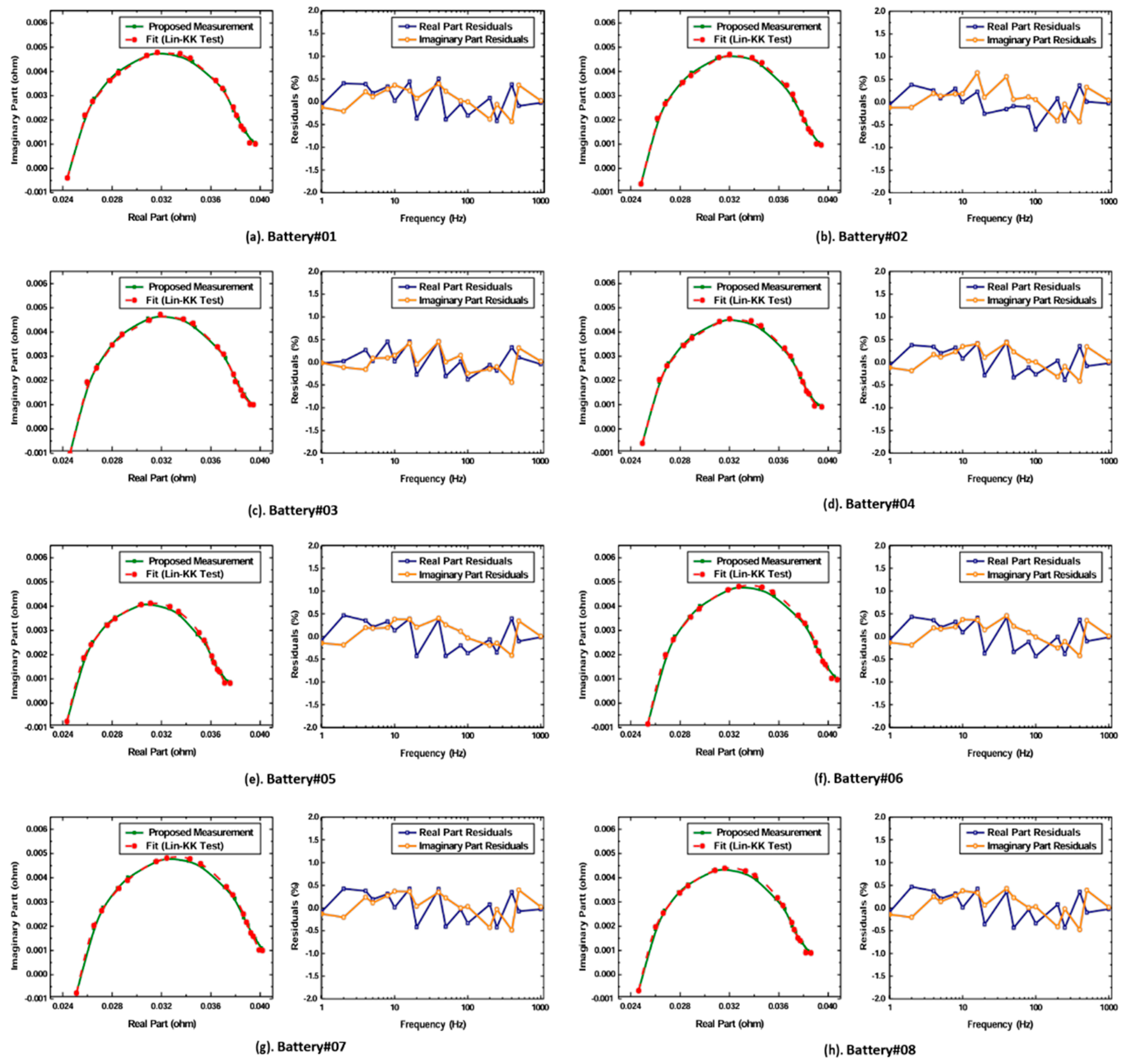
5.3. Validation of Impedance Spectra through KK Transform

The validity of obtained impedance spectra by applying the presented MSBS perturbation are also analyzed through KK transform. It describes the relation of real and imaginary component of impedance spectra obtain from a linear-time- invariant (LTI) system. The relation of real and imaginary component of impedance is given by [31]:
Z R e ω =   2 π ∫ 0 ∞ ω ′ .   Z I m ( ω ′ ) ω 2 − ω ′ 2 d ω ′
Z I m ω = − 2 π ∫ 0 ∞ ω .   Z I m ( ω ′ ) ω 2 − ω ′ 2 d ω ′
Equation (13) and (14) are the theoretically derived relations for KK transform which ranges from 0 to infinite frequency limit. However, an EIS test cannot be performed up to infinite frequency range. Therefore, Voigt circuit is used which consists of passive elements and the spectrum is obtained from it will be KK compliance. The impedance expression governed by Voigt circuit with logarithmically distributed fixed time constant (𝜏𝑘) is represented by (15).
z ^ ω = R o h m + ∑ k = 0 M R k 1 + j ω τ k
In case of any physical meaningfulness, an additional inductor or capacitor can be added, or if the frequency range of measured impedance spectrum is small compared to full impedance spectrum of the system. The reproducibility of impedance spectrum measurement is judged through corresponding residuals of the real and imaginary component as shown by (16) and (17). KK compliance test is a useful tool which validate how well the impedance spectrum data can be linear fitted and guarantee its usability for battery state estimation.
∆ R e ω = Z R e ω − Z ^ R e ω | Z ω |
∆ I m ω = Z I m ω − Z ^ I m ω | Z ω |
The Lin-KK software developed by Karlsruhe Institute of Technology (KIT) is used for robust validation of KK- compliance test [36]. This tool is based on fitting the impedance spectra to a linearized Voigt circuit having multiple RC elements. Residuals of real and imaginary components are between measured and fitted data. The residual should be less than 0.5% for validity of measurement under the conditions for an LTI system. An impedance spectrum data is valid if the residuals are random or white noise distribution. However, the data is corrupted if the residuals follow some clear trace. The validity of impedance spectrum through KK compliance test guarantees its usability for state-estimation of a battery. The KK-compliance test of impedance spectra of Samsung INR18650 batteries obtained through proposed high-speed Equation (13) and (14) are the theoretically derived relations for KK transform which ranges from 0 to infinite frequency limit. However, an EIS test cannot be performed up to infinite multichannel EIS system is performed. The fitted impedance spectra and corresponding residuals are shown in Figure 10. All the residuals are random, unbiased (no time variance), and less than 0.5% which validate the presented broadband MSBS perturbation and high-speed multichannel EIS system.

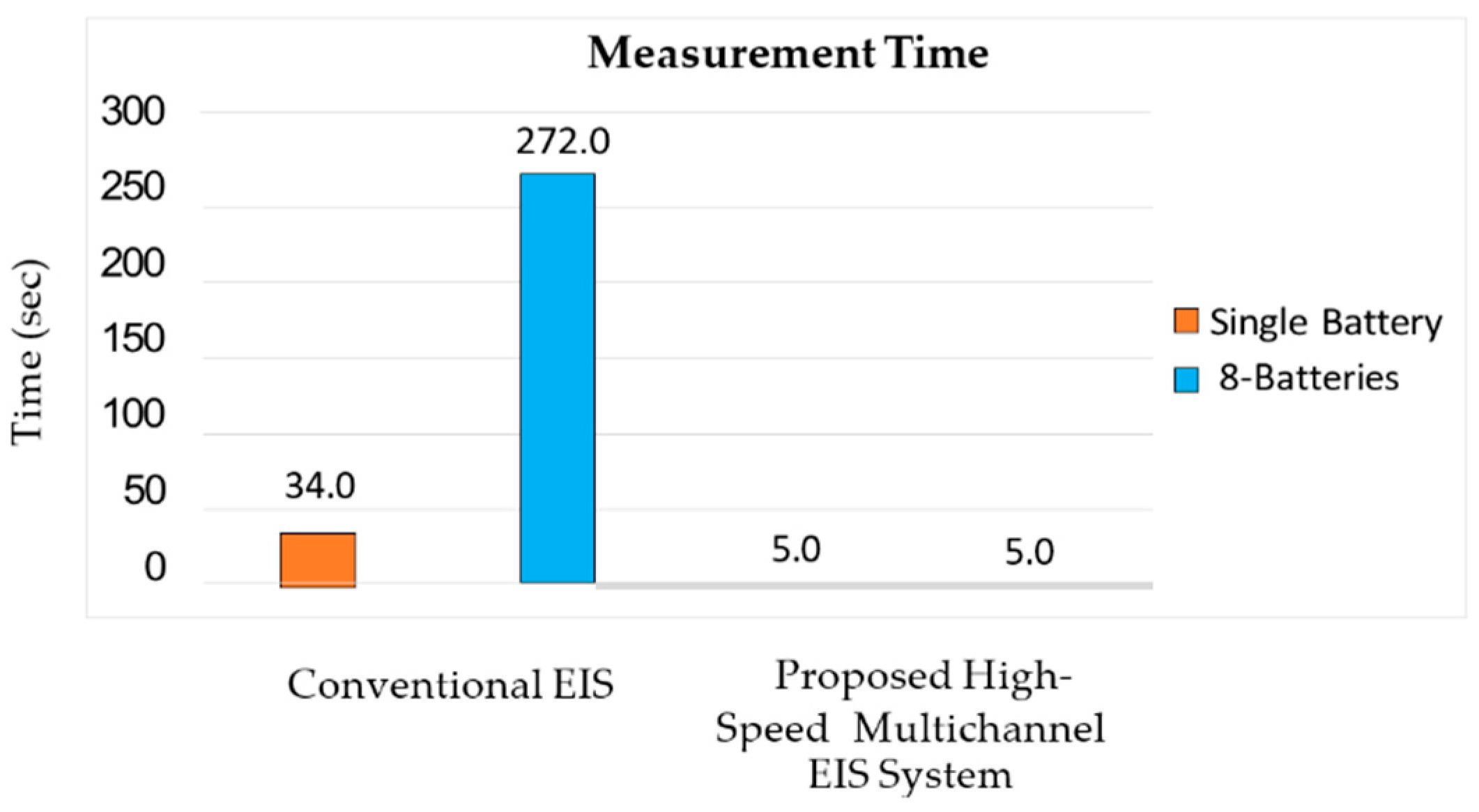
5.4. Measurement speed comparison with sinusoidal sweep perturbation

In this section, measurement speed of proposed high-speed multichannel EIS system is analyzed. The presented EIS system has two advantages over conventional EIS.
  • Broadband MSBS perturbation is used instead of sinusoidal sweep excitation to shorten the measurement.
  • 8-channels configuration is used which further decrease the measurement time and increase the capability by simultaneously measuring the impedance spectrums of eight individual batteries or eight battery modules with overall voltage less than 100 V.
The measurement speed experiment is performed under same conditions for both conventional EIS and presented EIS system as shown in Table 5.
The time period of MSBS is 1.0 sec, however for accurate measurement of impedance spectra, 5 cycles perturbation is applied. It should be noted that conventional EIS is a single channel configuration using sinusoidal sweep perturbation. The conventional EIS requires perturbation time of 34.0 sec for single battery. It means that 272.0 sec are required to measure impedance spectra of eight batteries using conventional EIS. While proposed EIS system needs only 5.0 sec for measuring response of eight batteries. Therefore, the measurement speed of developed high-speed multichannel EIS system is multi- times faster than conventional EIS with single channel configuration and using sweep perturbation.
Preprints 103649 g011
Figure 11. Measurement time comparison of conventional EIS and proposed high-speed multichannel EIS system for 8-batteries impedance spectra measurement.
Figure 11. Measurement time comparison of conventional EIS and proposed high-speed multichannel EIS system for 8-batteries impedance spectra measurement.
Preprints 103649 g011

6. Conclusion

In this paper, broadband perturbations are discussed with corresponding consideration for high-speed impedance measurement of lithium-ion batteries. After validation of multi-sine signals with reference sinusoidal sweep, the impedance spectrum of MSBS well coincide with reference measurement by having lowest RMSE of 0.51%. The MSBS is a two-level signal, having less complexity compared to sinusoidal sweep, CMSS, and CPMS. It can be easily generated through a low- cost DSP. Moreover, the frequencies of interest are selectable with lower CF=1.0. Further, MSBS allows to use lower amplitude value compared to CMSS and CPMS which reduces the impacts of non-linearity. A high-speed multichannel EIS system is developed which uses MSBS to perturb the batteries. The validation is performed with that of commercial EIS instrument and chi-square error analysis shows an error under 0.641% which validate the accuracy of proposed EIS system. Moreover, to validate the impedance spectra to be used for battery-state estimation, KK compliance tests are performed. The obtained residuals plots validate the performance of MSBS and proposed high-speed multichannel EIS system. Since, the proposed EIS system possess two advantages over conventional EIS, using broadband MSBS perturbation and 8-channels measurement configuration which drastically lowers the measurement time. Therefore, measurement speed of developed EIS system is multi-times faster than conventional EIS. In view of aforementioned aspects, the proposed high- speed multichannel EIS system is a valid solution for mass testing and grading of retired EVs batteries. Further work is in progress to integrate it with battery management system (BMS) for online SOH and aging estimation.

Author Contributions

M.S. wrote the original draft manuscript and implemented the prototype of the proposed method and revised the manuscript; W.C. reviewed the manuscript and supervised the research. All authors have read and agreed to the published version of the manuscript.

Funding

This research has been funded by the National Research Foundation (NRF) of the Republic of Korea (Grant No. NRF2021R1A2C1011504 “Research on the High-Speed Multichannel Impedance Spectroscopy Technique for Battery Performance Evaluation”).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. A. El Mejdoubi, H. Chaoui, H. Gualous, P. Van Den Bossche, N. Omar and J. Van Mierlo, "Lithium-Ion Batteries Health Prognosis Considering Aging Conditions," in IEEE Transactions on Power Electronics, vol. 34, no. 7, pp. 6834-6844, July 2019. [CrossRef]
  2. Q. Shi, Z. Jiang, Z. Wang, X. Shao and L. He, "State of Charge Estimation by Joint Approach With Model-Based and Data-Driven Algorithm for Lithium-Ion Battery," in IEEE Transactions on Instrumentation and Measurement, vol. 71, pp. 1-10, 2022, Art no. 3000610. [CrossRef]
  3. S. S. Afshari, S. Cui, X. Xu and X. Liang, "Remaining Useful Life Early Prediction of Batteries Based on the Differential Voltage and Differential Capacity Curves," in IEEE Transactions on Instrumentation and Measurement, vol. 71, pp. 1-9, 2022, Art no. 6500709. [CrossRef]
  4. S. Bamati and H. Chaoui, "Lithium-Ion Batteries Long Horizon Health Prognostic Using Machine Learning," in IEEE Transactions on Energy Conversion, vol. 37, no. 2, pp. 1176-1186, June 2022. [CrossRef]
  5. I. Sanz-Gorrachategui et al., "Remaining Useful Life Estimation for LFP Cells in Second-Life Applications," in IEEE Transactions on Instrumentation and Measurement, vol. 70, pp. 1-10, 2021, Art no. 2505810. [CrossRef]
  6. Alexander Farmann, Wladislaw Waag, Andrea Marongiu, Dirk Uwe Sauer,Critical review of on-board capacity estimation techniques for lithium-ion batteries in electric and hybrid electric vehicles, Journal of Power Sources, Volume 281, 2015, Pages 114-130, ISSN 0378-7753. [CrossRef]
  7. R. Xiong, Y. Zhang, J. Wang, H. He, S. Peng and M. Pecht, "Lithium-Ion Battery Health Prognosis Based on a Real Battery Management System Used in Electric Vehicles," in IEEE Transactions on Vehicular Technology, vol. 68, no. 5, pp. 4110-4121, May 2019. [CrossRef]
  8. D. Liu, W. Xie, H. Liao and Y. Peng, "An Integrated Probabilistic Approach to Lithium-Ion Battery Remaining Useful Life Estimation," in IEEE Transactions on Instrumentation and Measurement, vol. 64, no. 3, pp. 660- 670, March 2015. [CrossRef]
  9. J. Vetter, P. Novák, M.R. Wagner, C. Veit, K.-C. Möller, J.O. Besenhard, M. Winter, M. Wohlfahrt-Mehrens, C. Vogler, A. Hammouche, Ageing mechanisms in lithium-ion batteries, Journal of Power Sources, Volume 147, Issues 1–2, 2005, Pages 269-281, ISSN 0378- 7753. [CrossRef]
  10. Y. Gao et al., "Health-Aware Multiobjective Optimal Charging Strategy With Coupled Electrochemical-Thermal-Aging Model for Lithium-Ion Battery," in IEEE Transactions on Industrial Informatics, vol. 16, no. 5, pp. 3417-3429, May 2020. [CrossRef]
  11. S. J. Moura, J. L. Stein and H. K. Fathy, "Battery-Health Conscious Power Management in Plug-In Hybrid Electric Vehicles via Electrochemical Modeling and Stochastic Control," in IEEE Transactions on Control Systems Technology, vol. 21, no. 3, pp. 679-694, May 2013. [CrossRef]
  12. Q. Zhang, C. -G. Huang, H. Li, G. Feng and W. Peng, "Electrochemical Impedance Spectroscopy Based State-of-Health Estimation for Lithium- Ion Battery Considering Temperature and State-of-Charge Effect," in IEEE Transactions on Transportation Electrification, vol. 8, no. 4, pp. 4633-4645, Dec. 2022. [CrossRef]
  13. Nina Meddings, Marco Heinrich, Frédéric Overney, Jong-Sook Lee, Vanesa Ruiz, Emilio Napolitano, Steffen Seitz, Gareth Hinds, Rinaldo Raccichini, Miran Gaberšček, Juyeon Park,Application of electrochemical impedance spectroscopy to commercial Li-ion cells: A review, Journal of Power Sources, Volume 480, 2020, 228742, ISSN 0378-7753. [CrossRef]
  14. A. Fischer, A. Y. Kallel and O. Kanoun, "Comparative Study of Excitation Signals for Microcontroller-based EIS Measurement on Li-Ion Batteries," 2021 International Workshop on Impedance Spectroscopy (IWIS), Chemnitz, Germany, 2021, pp. 44-47. [CrossRef]
  15. Q. Zhang, C. -G. Huang, H. Li, G. Feng and W. Peng, "Electrochemical Impedance Spectroscopy Based State-of-Health Estimation for Lithium- Ion Battery Considering Temperature and State-of-Charge Effect," in IEEE Transactions on Transportation Electrification, vol. 8, no. 4, pp. 4633-4645, Dec. 2022. [CrossRef]
  16. Z. Xia and J. A. Abu Qahouq, "Evaluation of Parameter Variations of Equivalent Circuit Model of Lithium-ion Battery under Different SOH Conditions," 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 2020, pp. 1519-1523. [CrossRef]
  17. Stefan Skoog, Sandeep David, Parameterization of linear equivalent circuit models over wide temperature and SOC spans for automotive lithium-ion cells using electrochemical impedance spectroscopy, Journal of Energy Storage, Volume 14, Part 1, 2017, Pages 39-48, ISSN 2352-152X. [CrossRef]
  18. E. Din, C. Schaef, K. Moffat and J. T. Stauth, "A Scalable Active Battery Management System With Embedded Real-Time Electrochemical Impedance Spectroscopy," in IEEE Transactions on Power Electronics, vol. 32, no. 7, pp. 10.1109/TPEL.2016.2607519. 5688-5698, July 2017. [CrossRef]
  19. Robert R. Richardson, Peter T. Ireland, David A. Howey, Battery internal temperature estimation by combined impedance and surface temperature measurement, Journal of Power Sources, Volume 265, 2014, Pages 254- 261, ISSN 0378-7753. [CrossRef]
  20. H. Zappen, F. Ringbeck, and D. Sauer, “Application of Time-Resolved Multi-Sine Impedance Spectroscopy for Lithium-Ion Battery Characterization,” Batteries, vol. 4, no. 4, p. 64, Dec. 2018. [CrossRef]
  21. J. Sihvo, D. -I. Stroe, T. Messo and T. Roinila, "Fast Approach for Battery Impedance Identification Using Pseudo-Random Sequence Signals," in IEEE Transactions on Power Electronics, vol. 35, no. 3, pp. 2548-2557, March 2020. [CrossRef]
  22. A. Y. Kallel and O. Kanoun, "A Crest-Factor Optimization Algorithm for Multisine Signals based on the Evolutionary Role Playing Game Theory," 2021 International Workshop on Impedance Spectroscopy (IWIS), Chemnitz, Germany, 2021, pp. 131-136. [CrossRef]
  23. M. Schroeder, "Synthesis of low-peak-factor signals and binary sequences with low autocorrelation (Corresp.)," in IEEE Transactions on Information Theory, vol. 16, no. 1, pp. 85-89, January 1970. [CrossRef]
  24. Ojarand, Jaan & Min, Mart. (2017). Recent Advances in Crest Factor Minimization of Multisine. Elektronika ir Elektrotechnika. 23. [CrossRef]
  25. A. Van Den Bos, "A new method for synthesis of low-peak-factor signals," in IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 35, no. 1, pp. 120-122, January 1987. [CrossRef]
  26. Yang, Yuxiang & Zhang, Fu & Tao, Kun & Sanchez, Benjamin & Wen, He & Teng, Zhaosheng. (2015). An improved crest factor minimization algorithm to synthesize multisines with arbitrary spectrum. Physiological Measurement. 36. [CrossRef]
  27. E. Van der Ouderaa, J. Schoukens and J. Renneboog, "Peak factor minimization of input and output signals of linear systems," in IEEE Transactions on Instrumentation and Measurement, vol. 37, no. 2, pp. 207- 212, June 1988. [CrossRef]
  28. J. Sihvo, T. Messo, T. Roinila, R. Luhtala and D. I. Stroe, "Online identification of internal impedance of Li-ion battery cell using ternary- sequence injection," 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 2018, pp. 2705-2711. [CrossRef]
  29. T. Roinila and T. Messo, "Online Grid-Impedance Measurement Using Ternary-Sequence Injection," in IEEE Transactions on Industry Applications, vol. 54, no. 5, pp. 5097-5103, Sept.-Oct. 2018. [CrossRef]
  30. M. T. Talat and A. H. Khawaja, "Li-Ion Battery Parameter Identification Using Pseudo Random Noise," 2019 15th International Conference on Emerging Technologies (ICET), Peshawar, Pakistan, 2019, pp. 1-5. [CrossRef]
  31. M. Schönleber, D. Klotz, E. Ivers-Tiffée, A Method for Improving the Robustness of linear Kramers-Kronig Validity Tests, Electrochimica Acta, Volume 131, 2014, Pages 20-27, ISSN 0013-4686. [CrossRef]
  32. R. Al Nazer, V. Cattin, P. Granjon, M. Montaru and M. Ranieri, "Broadband Identification of Battery Electrical Impedance for HEVs," in IEEE Transactions on Vehicular Technology, vol. 62, no. 7, pp. 2896-2905, Sept. 2013. [CrossRef]
  33. E. Barsoukov and J. R. Macdonald. Impedance spectroscopy: Theory, experiment, and applications. Second edition. 2005. isbn: 0-471-64749-7.
  34. Koch, R. and Jossen, A. and Kanoun, “On-line Electrochemical Impedance Spectroscopy for Lithium-Ion Battery Systems” Universitätsbibliothek der TU München, 2017.
  35. https://www.brs-messtechnik.de/produktuebersicht-de (accessed on 22 November 2023).
  36. Karlsruhe Institute of Technology. Lin-KK Software Tool. Available online: https://www.iam.kit.edu/et/english/Lin-KK.php (accessed on 12 December 2023).
Preprints 103649 g001
Figure 1. (a) Equivalent Circuit Model (ECM) (b) Nyquist impedance plot of Samsung INR18650.
Figure 1. (a) Equivalent Circuit Model (ECM) (b) Nyquist impedance plot of Samsung INR18650.
Preprints 103649 g001
Preprints 103649 g002
Figure 2. Block diagram for MSBS generation.
Figure 2. Block diagram for MSBS generation.
Preprints 103649 g002
Preprints 103649 g003
Figure 3. Normalized power spectrums of broadband perturbation.
Figure 3. Normalized power spectrums of broadband perturbation.
Preprints 103649 g003
Preprints 103649 g004
Figure 4. Block diagram of High-Speed Multichannel EIS System.
Figure 4. Block diagram of High-Speed Multichannel EIS System.
Preprints 103649 g004
Preprints 103649 g005
Figure 5. Algorithms flowchart and LabVIEW based GUI.
Figure 5. Algorithms flowchart and LabVIEW based GUI.
Preprints 103649 g005
Preprints 103649 g006
Figure 6. Nyquist impedance plot using sine-sweep, CMSS, CPMS and presented MSBS perturbation.
Figure 6. Nyquist impedance plot using sine-sweep, CMSS, CPMS and presented MSBS perturbation.
Preprints 103649 g006
Preprints 103649 g007
Figure 7. Experimental Setup.
Figure 7. Experimental Setup.
Preprints 103649 g007
Preprints 103649 g008
Figure 8. Nyquist impedance plots comparison obtained through proposed high-speed multichannel EIS system and commercial EIS instrument "BIM2"(Battery 01 – 04).
Figure 8. Nyquist impedance plots comparison obtained through proposed high-speed multichannel EIS system and commercial EIS instrument "BIM2"(Battery 01 – 04).
Preprints 103649 g008
Preprints 103649 g009
Figure 9. Nyquist impedance plots comparison obtained through proposed high-speed multichannel EIS system and commercial EIS instrument "BIM2"(Battery 05 – 08).
Figure 9. Nyquist impedance plots comparison obtained through proposed high-speed multichannel EIS system and commercial EIS instrument "BIM2"(Battery 05 – 08).
Preprints 103649 g009
Preprints 103649 g010
Figure 10. KK-compliance validation of obtained impedance spectra and respective residuals.
Figure 10. KK-compliance validation of obtained impedance spectra and respective residuals.
Preprints 103649 g010
Table 1. Specification of Battery used Experiment.
Table 1. Specification of Battery used Experiment.
Battery Model Nominal Voltage OCV Capacity
Samsung INR18650-29E 3.65 V 3.50 2.850 Ah
Table 2. Perturbation Signals Parameters.
Table 2. Perturbation Signals Parameters.
Parameter Sinusoidal Sweep CMSS CPMS MSBS
Frequency range 1 Hz to 1kHz
Sampling frequency 40kHz
Frequency components 17 17 500 17
Frequency distribution random random linear random
Pk to Pk Current 1.0 A
Length in time 60.0 sec 1.0 sec 1.0 sec 1.0 sec
Table 3. Percentage RMSE of CMSS, CPMS, and MSBS compared to reference sinusoidal sweep perturbation.
Table 3. Percentage RMSE of CMSS, CPMS, and MSBS compared to reference sinusoidal sweep perturbation.
Method CMSS CPMS MSBS
RMSE % 7.68 % 24.53 % 0.51 %
Table 4. Chi-Squared error analysis for impedance spectra of Samsung INR18650-29E.
Table 4. Chi-Squared error analysis for impedance spectra of Samsung INR18650-29E.
S. No R-Chi Squared Chi-Squared Error (%)
Battery-01 3.28×10−5 0.572
Battery-02 3.54×10−5 0.594
Battery-03 3.78×10−5 0.641
Battery-04 3.94×10−5 0.628
Battery-05 3.18×10−5 0.563
Battery-06 3.09×10−5 0.556
Battery-07 3.32×10−5 0.576
Battery-08 3.41×10−5 0.583
Table 5. Conventional and proposed high-speed multichannel EIS system measurement time comparison.
Table 5. Conventional and proposed high-speed multichannel EIS system measurement time comparison.
Parameter Conventional EIS Developed high- speed multichannel EIS system
Perturbation type Sinusoidal Sweep MSBS
Frequency range 1 Hz to 1kHz 1 Hz to 1kHz
Frequency components 17 17
Measurement Time
Single Battery 34.0 sec 5.0 sec
Eight (8) Batteries 272.0 sec 5.0 sec
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated