Prerpints.org logo
Preprint
Article

An Enhanced Ageing Model for Solid-State Batteries

Altmetrics

Downloads

128

Views

103

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

11 April 2024

Posted:

15 April 2024

You are already at the latest version

Alerts
Abstract
The emphasis in the automotive industry towards sustainable mobility has led to a significant interest in hybrid-electric propulsion systems with high energy density batteries. Addressing the needs of this strategy, the battery market is exploring new technologies to improve the safety and lifespan of electric vehicles. To this end, there is a focus on the all-solid-state battery (ASSB) technology for its cycle capabilities. Filling the current void in the literature pertaining to accurate ageing models for ASSBs, in this work, we present an enhanced version of the numerical ageing model, originally developed for liquid electrolyte based batteries, to forecast the development of the solid electrolyte interface layer that is the major cause of battery capacity fading. The model has been tested on prototype batteries and reveals an accuracy of 99%. The capacity fade in ASSBs has been investigated under different conditions, and the enhanced ageing model has been validated using experimental data from these batteries. The findings suggest that there is potential for solid-state batteries to be commercialized, although significant work is needed to match the manufacturing level of lithium-ion batteries with liquid electrolytes.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

Improved energy efficiency and advances in renewable energy are essential to achieve zero emissions. With advances in these areas, a significant reduction in CO2 emissions can be accomplished in the transport sector. This sector, as indicated by the 2021 IEA study, is currently contributing nearly 24 % of the total CO2 emissions around the globe. 72 % [1] of this comes from passenger cars. This demands a consistent effort towards the decarbonization of the transport sector and energy generation via renewable energy. In response to this, electric vehicles (EVs) are rapidly permeating the market, proposing themselves as an alternative to conventional internal combustion engines (ICEs) vehicles. Despite their raising sales numbers, EVs in their current state are not a robust solution for a definite move towards sustainable mobility. That is due to the fact that in terms of life cycle assessment (LCA), commencing from the raw materials and the production to the end of life and recycling, EVs are not a definitive answer compared to ICE-driven vehicles. This assertion is primarily related to the CO2 level adduced by the battery manufacturing, which represents nearly 40 % of the emissions emanating from the manufacturing of the EVs [2]. Further, current Li-Ion batteries (LIBs) require high production costs and suffer from a limited lifespan, posing a serious environmental problem. Needless to say, extending the battery’s lifespan is of crucial importance for the electrification of the transport sector. To this end, one of the most promising battery design is the all solid-state lithium-ion battery (ASSB). The substitution of the liquid electrolyte with a solid electrolyte provides a significant improvement in the safety, energy density and cycle performance of the battery [3,4,5,6]. With this immense potential, from a computational modeling perspective, to design new and novel ASSBs, there is an urgent need to develop advanced ageing models that can be used to analyze the next generation ASSBs. However, as in the case of LIBs, the precise ageing mechanism in ASSBs is still largely unknown. Recent investigations confirm how ASSBs behaviour can be deeply affected by the solid electrolyte interface (SEI) formation [7,8], an evident similarity with LIBs, accounting for as much as 50 % of the battery’s capacity fading [9,10,11,12].
The SEI layer was originally identified and published by Peled in 1979 [13].This layer is a consequence of specific reduction and oxidation reactions on the electrode surface. More precisely, when the cathode’s potential is lower and/or the anode’s potential is higher than the electrolyte’s HOMO (highest occupied molecular orbital) and/or LUMO (lowest unoccupied molecular orbital), the electrolyte molecules are oxidized and/or reduced on the electrode surface, respectively. The products of these oxidation and reduction reactions will contribute to the formation of the SEI layer [9,14,15]. It must be noted that the operating environment of a battery, such as the loaded voltage, current, and temperature, affect these HOMO/LUMO windows. The SEI production processes deconstruct the electrolyte molecules and deplete active Li-ions, leading to capacity fading [16]. A SEI layer that is appropriately designed, inhibits electron tunneling and electrolyte diffusion at the electrode-electrolyte contact. This reduces the rate of SEI generation and reduction processes, and thus the rate of capacity fading [9]. A typical SEI layer consists of the following sections: (I) an inorganic inner layer that is closer to the electrode contact and is only permeable for Li-ions. (II) A highly permeable organic outer layer that is closer to the electrolyte interface and enables the transit of electrolyte molecules as well as Li-ions. In ASSBs, the first layer has similar thermodynamic and kinetic properties as in presence of a liquid electrolyte and covers a passivating function towards the anode [7,8]. On the other hand, the second layer can be thermodynamically unstable [8], especially when a lithium anode is implemented, and will facilitate the continuous growth of the SEI layer during the operation of the battery. Consequently, characterization and comprehension of the SEI layer’s formation mechanisms and transport properties are crucial to improving ASSBs’ longevity.
Given that some of the SEI formation reactions take place at picosecond (ps) timescales, they cannot be investigated using the traditional experimental methods. Hence, multi-scale multi-physics modeling, which includes a combination of Quantum Mechanics (QM) calculations, Molecular Dynamics (MD) simulations, and Macro-Scale mathematical modeling, is implemented by researchers to study these mechanisms. In solid-state batteries, various aspects pertaining to the growth of the SEI layer are largely unknown because of its complex structure and unstable formation process [17]. Specifically, the main constraint stems from the absence of knowledge on the diffusion coefficient equation in the SEI layer, an issue that is also found in LIBs [18,19,20]. In the absence of an accurate mathematical formulation, Deng et al.[21] hypothesized a constant diffusion coefficient in their reduced order model. A more advanced pseudo-two dimensional model has been proposed for ASSBs that continues to implement a fixed value for the diffusion coefficient over the anode active materials [22].
Clearly, there is a void in the current literature with regards to an accurate description of the diffusion mechanism in the SEI layer. Addressing this gap, this work aims at developing a model for solid-state batteries where a detailed diffusion equation is incorporated into the macro-scale model. The mathematical formulation presented in this work for ASSBs is inspired by our recent proposition for the liquid electrolyte-based LIBs [23]. More precisely, the model proposed in this work is an adaptation of the one developed by Ekström and Lindbergh [24], i.e., a macro-scale continuum mathematical model that quantifies the influence of SEI layer on the ageing of LIBs with a graphite anode material. Their model is a blend of kinetic and transport control systems and employs a constant diffusion coefficient. Additionally, their model requires three lumped fitting parameters, which are substituted in the equations rather than variables such as a diffusion coefficient. These parameters enhance the accuracy of the model with respect to the experimental data over a variety of temperature and concentration values. However, a major drawback of their model is that it needs to be tuned using battery-specific experimental data for investigating a battery design. Further, the fitting parameters will vary with the material of the LIBs, forbidding us from a computational study of new and unique materials in LIBs. Improving upon their model, in our earlier work [16], we utilized a combination of QM calculations and MD simulations to propose a temperature- and Li-ion concentration-dependent equation for the diffusion coefficient for every crystal structure in the inner section of the SEI layer. Subsequently, to precisely represent the physics within the SEI layer, the macro-scale mathematical model was equipped with a single equation for the diffusion coefficient. Specifically, the diffusion coefficient equation in our earlier work [16] was integrated into the macro-scale mathematical model (MSMM) from Ekström and Lindbergh [24] that is utilized in commercialized engineering application software, i.e., Comsol Multiphysics, to examine capacity fading of LIBs. In implementing an anologous version in this research for the ASSBs, our formulation is validated with respect to the experimental data of ASSB, predicting the battery’s behaviour for a specific temperature under multiple discharging conditions. Adapting the Ekström and Lindbergh MSMM for ASSB, we present a model with just two simplified fitting parameters, omitting the most complex parameter in the original model. The updated formulation compensates for the influence of temperature and concentration on ageing. As part of model validation, it was employed to study the formation of SEI layers and the consequent capacity fading as a function of time and initial SOC, for an extended range of temperature and concentration conditions.
It must be noted that our earlier model for LIBs was designed for batteries that used graphite anode [23]. However, in ASSBs, there is an acute shortage of experimental data on batteries with these anodes. This is because these anodes have been proven to not work efficiently with solid electrolytes [25,26,27]. Specifically, it has been shown that there is a loss of contact between the solid electrolyte and this anode. Consequently, a large part of the battery research in the past years has been focused on the use of the so-called "soft" electrolytes. The study by Kobayashi [28], the one under our scrutiny, describes the adoption of graphite as an anode in conjunction with two classes of solid polymer electrolytes, a "soft" one and a "hard" one. This work focuses on the "soft" polymer, that will be addressed as "SPE1". The experimental tests from the literature correspond to a 2032 half coin cell with the architecture [Graphite|SPE1|Li], and a prototype pouch cell [Graphite|SPE1|LiFePO4]. In the coin cell case, Li is employed as the counter electrode to permit Li intercalation in the graphite anode. An additional and significant outcome of this study is the validation of the developed model through a real driving cycle, comparing the model’s ageing data with the LIB experimental one.

2. The Theoretical Method and Computational Details

In ordinary LIBs, the inorganic inner layer consists of Li2CO3, LiF and Li2O[8,16,29]. On the other hand, the organic outer layer is made of dilithium ethylene glycol dicarbonate (Li2EDC) and ROLi (R depends on the solvent). The inner layer is mainly composed of fixed materials which do not depend on the electrolyte composition. This is where the diffusion mechanism is deeply investigated and highlighted in order to integrate it with the single-particle model previously described for SEI formation. Experimental research has established that Li2CO3 is an outcome of the conversion reaction of CoCO3 upon Li-ion insertion, when ethylene carbonate is present in the liquid electrolyte. However, Li2CO3 is thermodynamically unstable and will reduce to Li2C2 and Li2O[30]. Also, Li2C2 will participate in other processes and create Li+, C2H2, and C[31]. Hence, Li2CO3 cannot be viewed as a permanent element in the inner area of the SEI layer. In case of ASSBs, the equivalent inner layer composition is confirmed to have LiF and Li2O [7,17,28]. The diffusion equation of Li ions through the crystal structure of the SEI layer can be achieved by implementing a modified version of the Ahrrenius law (Eq.2), where the Li diffusion coefficient is a function of the concentration (C) and temperature (T). The total diffusion coefficient can be computed with the following relation[16]:
D t = δ Li 2 O D Li 2 O + δ LiF D LiF ,
where δ i and Di are the fraction of the surface area and the diffusion coefficient of the ith component, respectively. Additionally, for each species the diffusion coefficient can be computed as a function of temperature and concentration, implementing a modified version of the Arrhenius law:
D i ( C , T ) = D 0 e x p − A 0 E B ( C ) k b T .
In the above equation, A 0 and D 0 are component dependent constants. Also, EB stands for the energy barrier which can be expressed as a function of concentration as:
E B ( C L i ) = a 2 C L i + 2 + a 1 C L i + + a 0 ,
where the dependent constants, a0, a1, a2, are summarized in Table 1.
Since an actual measurement of the fractional surface area of the individual constituents in the SEI layer would be extremely complex [16], the following formulation has been employed in this work:
ω i = m i m Li 2 O + m LiF ,
δ L i 2 O = ω L i 2 O ω L i 2 O + ρ L i 2 O ρ L i F ω L i F and δ L i F = ω L i F ω L i F + ρ L i F ρ L i 2 O ω L i 2 O O ,
In the above equations, m, L, ω and ρ are the mass, thickness, mass fraction, and density of the material i (in this case, Li2O and LiF), respectively.

2.1. A Mathematical Model for Ageing

An enhanced version of the Ekström and Lindbergh model, compatible with a solid-state battery is proposed in this research. The model predicts battery ageing by utilizing data on the SEI growth rate, significantly improving the model’s accuracy. In particular, we provide a zero-dimensional model that employs a galvanostatic mode in battery cycling, eliminating the need to define a positive electrode or electrolyte. In this model, the accumulated charge (QSEI (C)), which is lost in ASSBs due to the SEI layer formation processes, is computed as follows:
d Q S E I d t = − I S E I ,
where I S E I (A) is the current of the parasitic reactions involved in the SEI layer formation. It can be expressed as the sum of the currents flowing through the surfaces that are entirely covered by the intact or cracked SEI layer. The mathematical derivation of I S E I , presented in the [Appendix]Appendix, yields to the following expression:
I S E I = − 1 + H K c r d J I 1 C exp α F η S E I R T + f J Q S E I I 1 C ,
where I S E I and I 1 C are the currents through the cracked parts and 1 C-rate charging current, respectively. Further, the original model of Ekström and Lindbergh incorporate the following three lumped fitting parameters:
J = ϵ c o v I 0 I 1 C ,
f = τ c o v V I 1 C 2 ϵ c o v 1 − ϵ c o v C D F A 2 ,
H = a c r d ϵ c o v .
The parameters in these equations are described in the nomenclature section. Collectively, these parameters compensate for the lack of information on the growth of the SEI layer and the ageing processes. Further, these fitting parameters must be calibrated for each new battery cell and/or operational condition.
As stated previously, the SEI layer comprises of various materials and crystal structures, namely, Li2O and LiF, that allow the diffusion of electrolyte solvent molecules and Li-ions, that are of different sizes and have different charge values. This implies a wide variation in the diffusion coefficients in these constituent structures, that will be governed by the operating temperatures and concentration conditions. Unfortunately, with experimental data for the complex diffusion and reaction processes, Equations (8-10) for J , f , and H are adopted for better accuracy and agreement with the experimental data. Since the accumulation of Li-ions increases the gradient of the charge distribution in the SEI layer, it increases the electron leakage, increasing I 0 . On the other hand, a higher diffusion coefficient will decrease the gradient of Li-ions in the SEI layer. In other words, I 0 is inversely proportional to DT [23]. Therefore, in this work, modifying Equation 8, we employed the following expression for J that uses a material constant ( J 0 ) and DT:
J = J 0 D T
In this equation, D D T is as defined in Equation (1). J 0 , a material constant, is set to a value of 2.2 × 10 − 15 m 2 s . Thus, with this definition, the lumped fitted parameter (J), defined in Equation (8) is eliminated from the new model. Similarly, updated expressions for f and H parameters were obtained as follows: The parameters f and H were tuned using the experimental data of Kobayashi et al. [28]. Specifically, the values were tuned to the experimental condition of charge/discharge cycling with 1/8 C-rate and 1/16 C-rate load currents at 60C. In doing so, the value of J is as prescribed in Equation 11. The tuned values are reported in Table 2.
Although the equation for the diffusion coefficient (Equation (1)) employs the same formulation for all diffusing particles, it appropriately considers the effects of different concentrations, temperatures, and crystal structures on the diffusion coefficient and SEI formation. In the forthcoming section, we demonstrate that our proposed model is able to predict the experimental data with a high degree of accuracy and forecast the ASSB behavior under diverse situations, thereby validating the new formulation that requires just two fitting parameters. Furthermore, after accounting for capacity fading due to Li-ion loss during SEI formation, the relative capacity (RC) can be determined as follows:
RC = Q batt , 0 − Q S E l Q batt , 0 ,
where Q batt , 0 is the initial battery capacity. Additionally, the thickness of the SEI layer can be expressed as:
s = Q S E I V 1 − ϵ c o v A .
The initial charge accumulation (QSEI) is set to zero at t = 0 , and the relative capacity RC is accordingly set to 100 %. The relative capacity for the previously highlighted ageing scenario is evaluated over a period of 200 days, employing the enhanced Ekström and Lindbergh model, and the results are then compared with the experimental data. Further, a parametric analysis has been conducted, supported by evidence and insights from the literature.

3. Results and Discussion

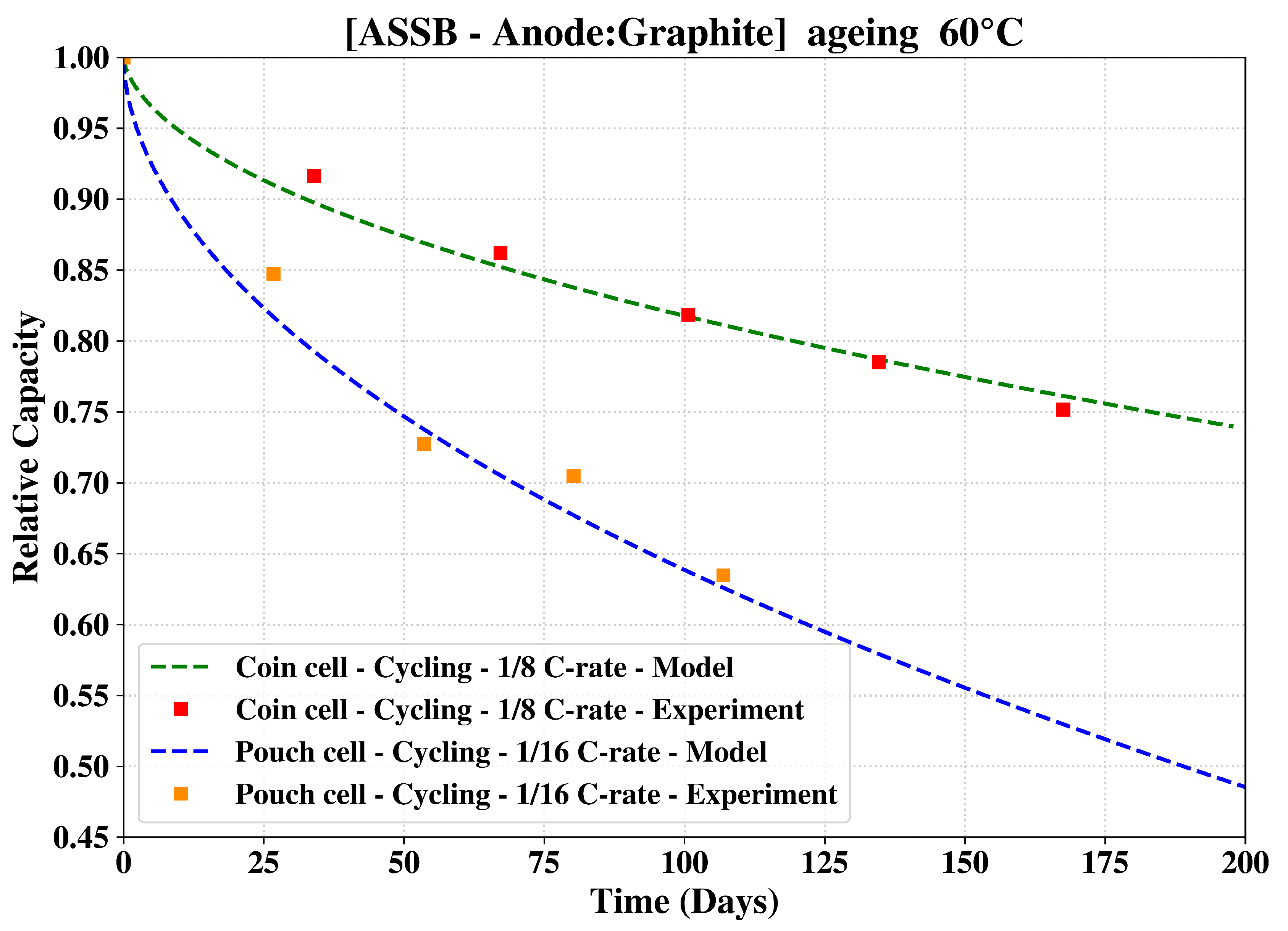
Model Validation: Due to the lack of sufficient experimental data, we investigated the capacity fade as a function of time for one temperature. The outcome of the investigation is presented in Figure 1. The results show that the enhanced MSMM is capable of forecasting a capacity fade in good agreement with the experimental data. Experimental data are from a custom 2032 coin cell whose specific capacity is retrieved from the reference battery.
Furthermore, to demonstrate the ability of the model to adapt to different geometries and cathode composition, the MSMM is calibrated with an upgraded set of f and H values reported in Table 2, and tested for the ASSB pouch cell made by Kobayashi et al. [28] (see Figure 1). As seen in this figure, there is an excellent agreement with the experimental data with an R 2 value of 0.99 in both cases.
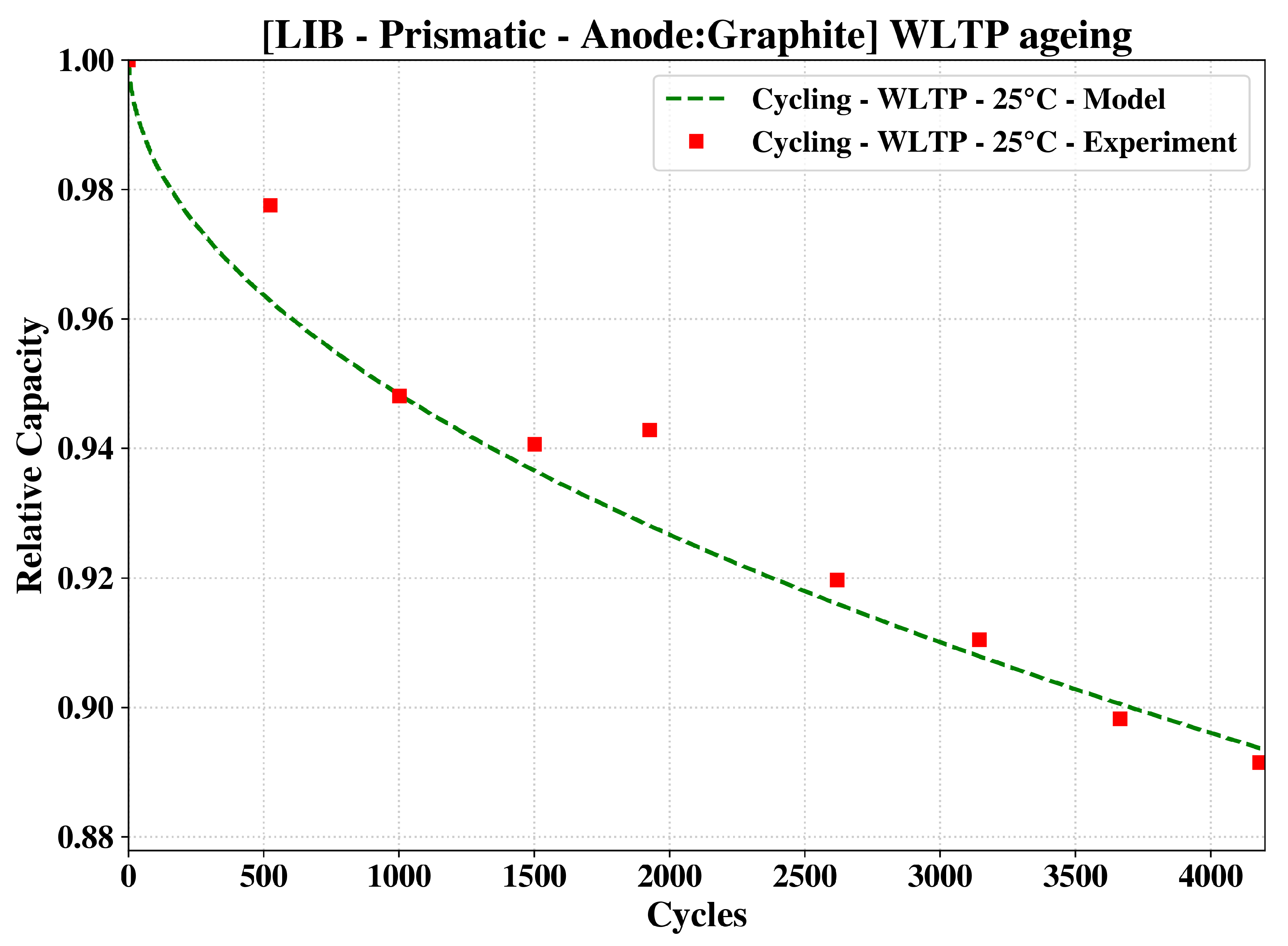
Additionally, we also applied our enhanced model to a LIB 63 Ah NMC-LMO (Nickel-Manganese-Cobalt - Lithium Nickel Manganese Cobalt Oxide) battery examined through a Worldwide Harmonised Light Vehicle Test Procedure (WLTP) cycle in literature[32]. The testing current profile is retrieved by applying a backward modeling approach to the vehicle data. The predictions from our model along with the experimental data of Micari et al. [33] is shown in Figure 2. As seen in this figure, there is an excellent agreement between our model and the experimental data.
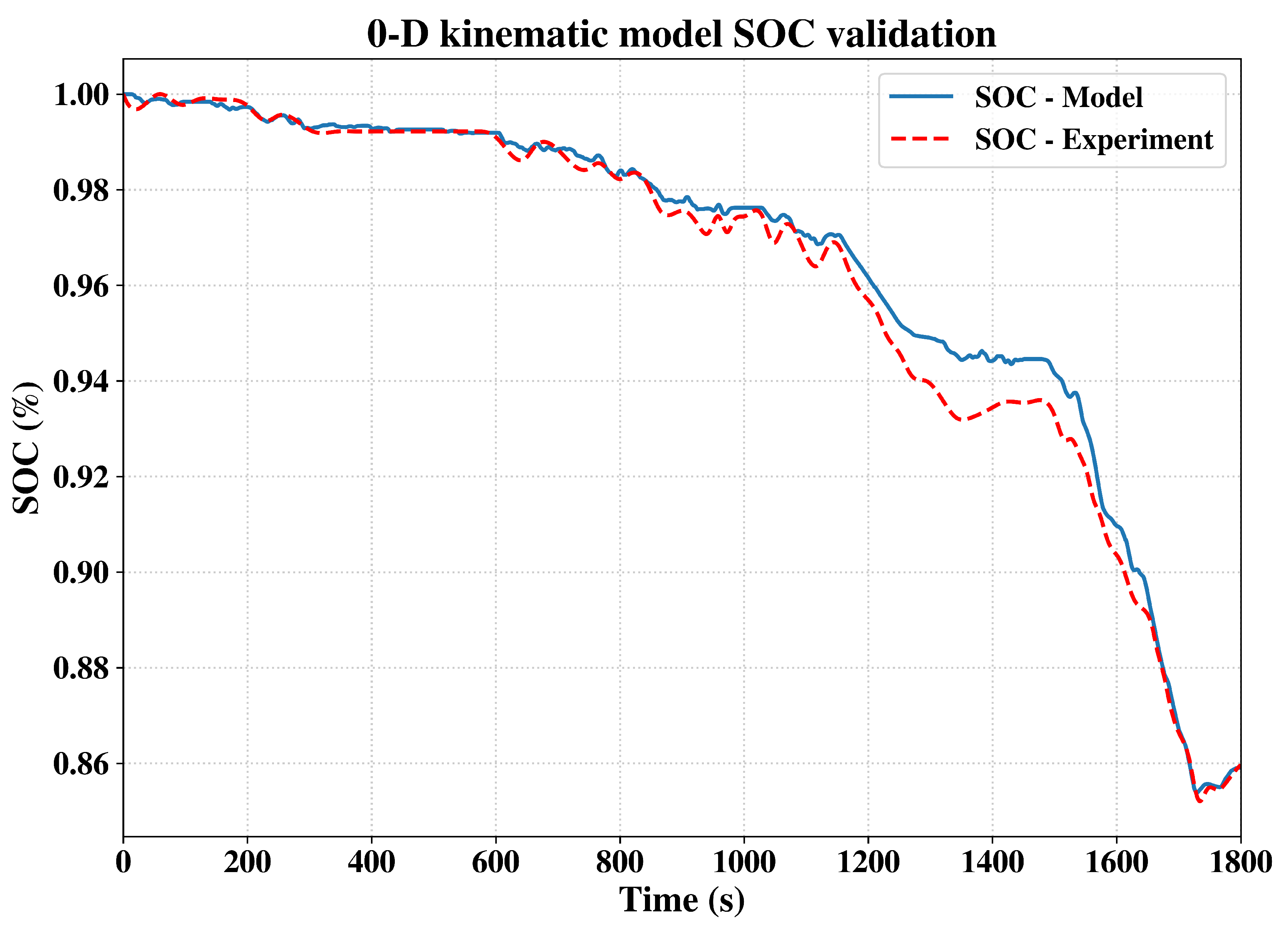
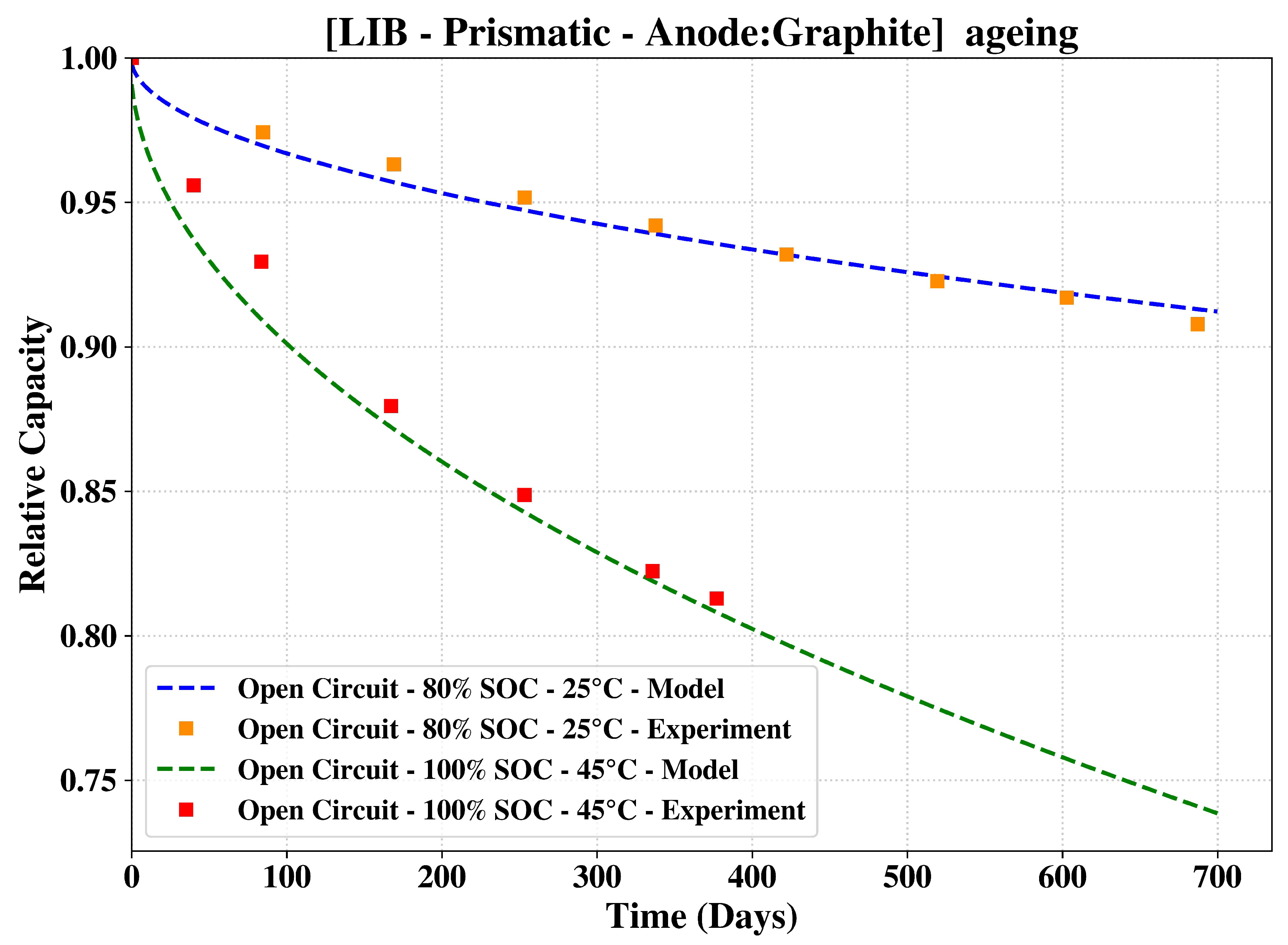
To further establish the accuracy and thereby the validity of our model, we studied the open-circuit storage conditions and a driving cycle test using our model. The results from these evaluations are presented in Figure 3 and Figure 4. To match the experimental data, the values of f and H were retuned for the two operating temperatures of 25C and 45C (Table 3.
As seen in Figure 4, the WLTP results are extremely satisfactory. A certain amount of divergence is registered in the first 2000 cycles because of the oscillatory nature of the experimental data [32]. To summarize, the determination of coefficient is reported in Table 4.
Parametric Analysis:
The validated model has been used to evaluate the ageing process of the ASSB coin cell at different operating conditions.
In absence of data for additional temperatures, the following temperature-dependent linear profile was assumed for the parameters f and H:
f ( T ) = f 0 T + f 1 ,
H ( T ) = H 0 T + H 1 ,
where f0 and H0 are summarized in Table 5. The choice of this linear profile is based on our earlier work [23] where we successfully applied an analogous model to study the effect of temperature on LFP commercial battery, assuming a linear temperature-dependent function for the parameters f and H. It must be noted that the values highlighted in our prior work[23] were for liquid electrolyte based batteries and as such would not be applicable to ASSBs. In fact, with those constants, the produced results were not feasible and in the 40-50 C range they did not demonstrate sufficient sensitiveness to temperature variation. Hence, with the intent of forecasting a reliable trend for the ASSB capacity fade, the linear profile coefficients, f 0 , f 1 and H 1 were re-tuned (see Table 5). The value of H 0 was the same as in our earlier model [23].
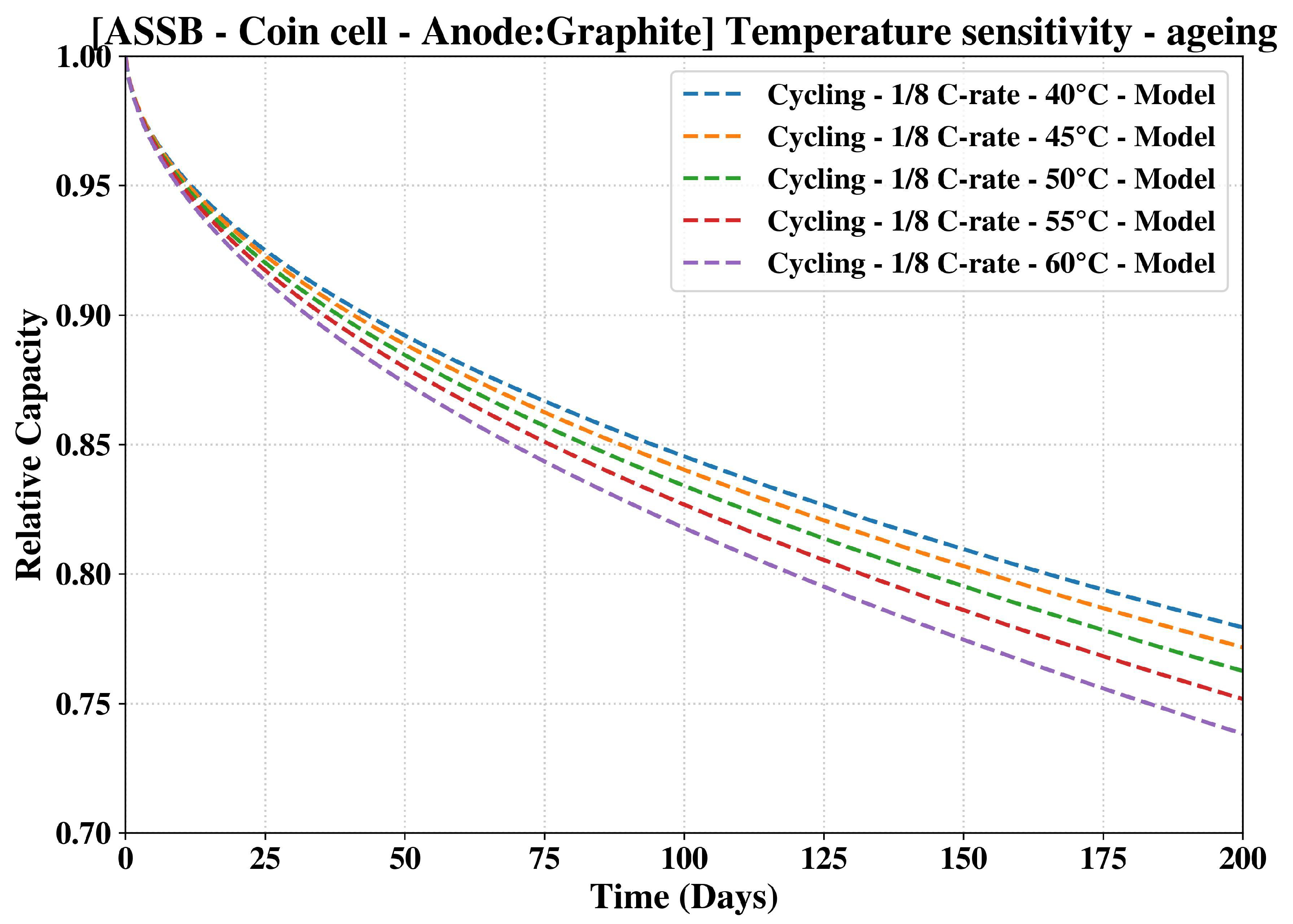
First, the ASSB cycling capabilities were analyzed for various temperature levels. The battery performance was evaluated within a range limited by the available experimental data. Specifically, the effect of temperature in the range of [ 40 ∘ C , 60 ∘ C ] on the ageing of a battery cycling at 1 / 8 C rate has been evaluated, and the results are summarized in Figure 5.
As seen in this figure, lowering the operating temperature significantly retards the ageing of a battery. 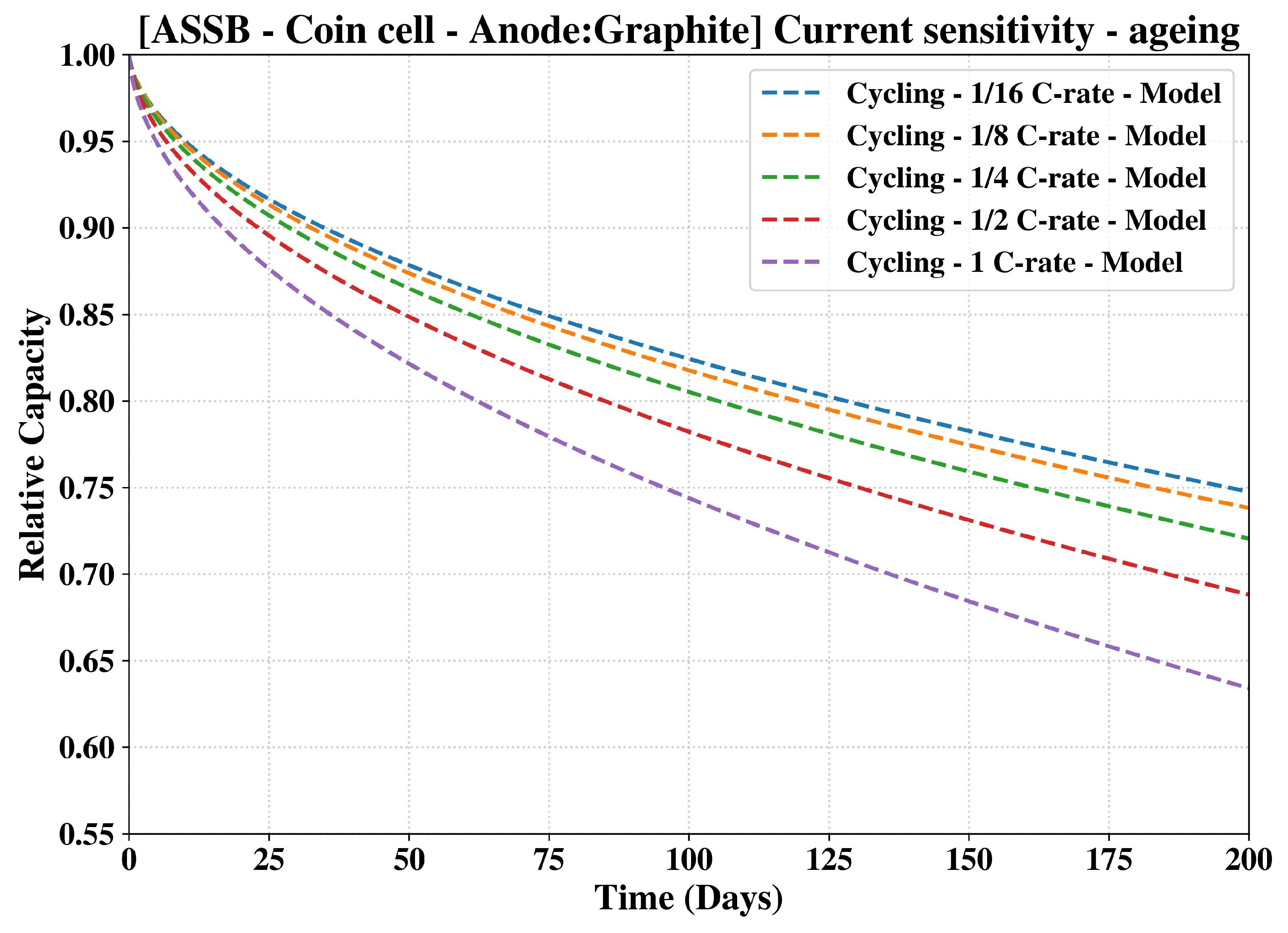Though we expect a higher lithiation temperature to not only enhance the ionic conductivity of the SPE but also mitigate the mechanical stress due to the softening effect, there is evidence in the literature that a raise in the temperature has a deleterious effect on solid polymer electrolyte, accelerating the ageing process [34]. Our trends are in excellent agreement with these propositions. A similar result is obtained when the model is applied to study the effect on the battery cycling at 1C rate, the theoretical upper limit value at which the enhanced model has been properly tested and validated (see Figure 6). Comparing the ageing results from the different c-rates shown in Figure 6, it is clear that the raise of the operating c-rate has a detrimental effect on the ageing of the solid-state battery. Once again, this is in agreement with the experimental work of Fang et al. [35]. More precisely, their results indicated a 10% increase in capacity loss when they raised the continuous discharging rate of 1C.
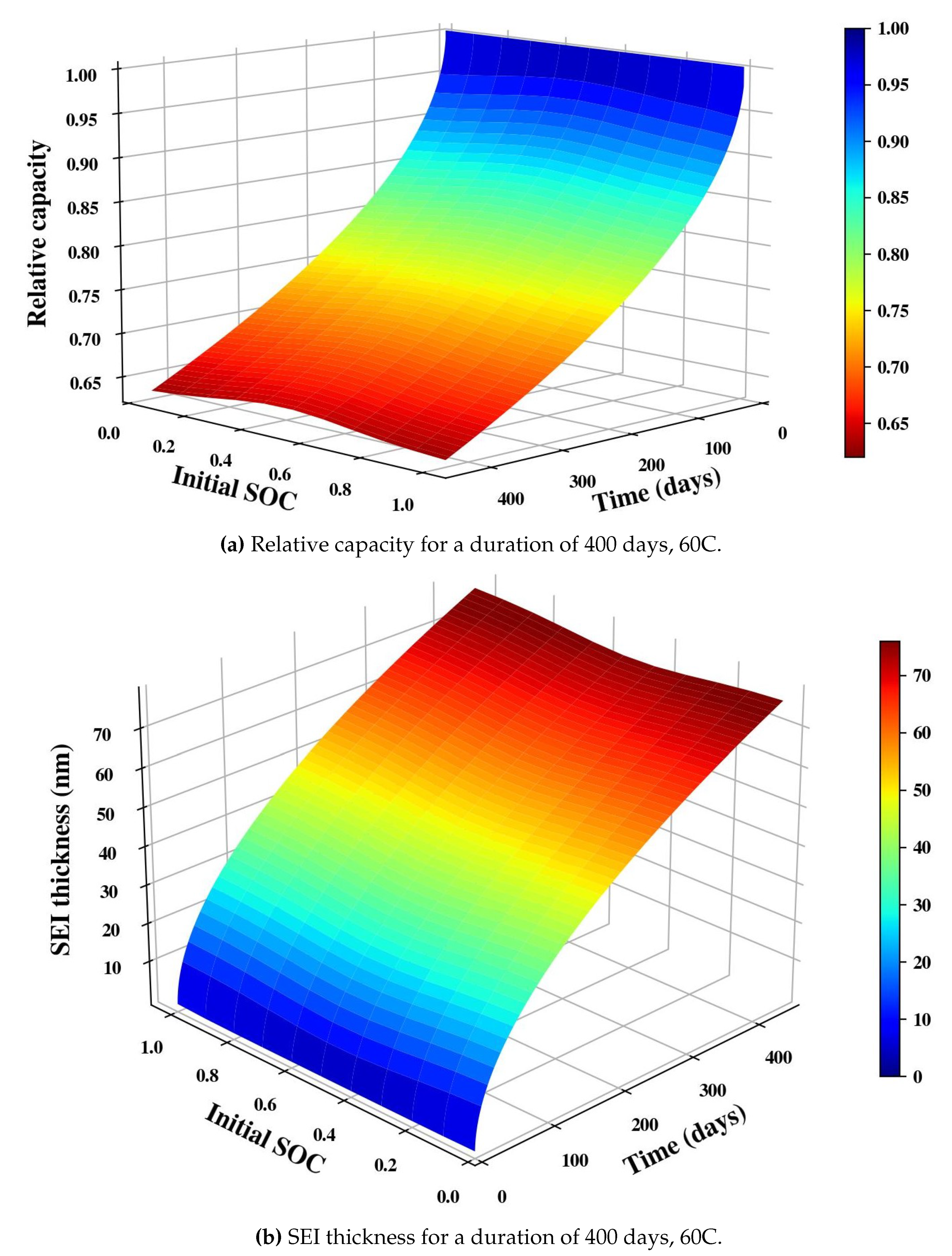
In Figure 7a, the relative capacity is computed for an extended range of initial SOC. The slowest ageing rate was recorded near 50% SOC. However, the initial SOC has a minor influence on the rate of capacity loss with respect to the LIB case. This is due to the higher operating temperature which mitigates the initial SOC leverage, a tendency consistent with our previous observations [23].
We also investigated the growth of SEI layer that grows rapidly in the battery. As shown in Figure 7b, in the ASSB coin cell, the maximum layer thickness was 79 nm at the extremes of the SOC window. At 50% SOC, the SEI layer thickness is about 75 nm. This lack of variation in the thickness is consistent with the findings of Kobayashi et al. [28], who stated that unlike the liquid electrolyte systems, the SEI formation occurs over a wider voltage region in the SPE systems. Note that the SEI formation process is more evident in ASSB because of the high difference in reactivity between the SPE and the graphite anode [28].

4. Further Investigations

We have reported the efficacy of an enhanced model applied to LIBs evaluated with a fast-varying discharge rate and to solid-state batteries. In the latter instance, implementing only two fitting parameters allows estimating the ASSB’s electrochemical performance for diverse temperatures and concentrations. Nevertheless, it impels us to acquire new experimental evidence to absolutely validate our model. Furthermore, in the macro-scale model we have assumed the same diffusion profile through the whole SEI layer for all the particles [23], which could explain for both battery technologies the slight divergence from experimental data. On the ASSB’s side, an additional factor to be addressed concerns the composition of the SEI layer. Specifically, the outer SEI layer, whose species are significantly reliant on the solid electrolyte composition, has to be examined as it could experience an uncontrolled expansion. Hence, additional research is needed to gain a better understanding of the SEI layer and to provide a diffusion equation that gathers the effects of particle charge and size, and contact resistance for ASSBs, on the diffusion coefficient and SEI species.

5. Conclusion

We have presented an adaptation to solid-state batteries of the macroscale model previously developed [23]. The calibration of the two modified lumped fitting parameters in conjunction with the upgraded equation of DT (Equation 1) is shown to adequately predict the ASSB capacity decay as a function of time. This model is validated with regard to experimental data at a single temperature under charge/discharge cycling with 1/8 C-rate load current ageing condition. Additionally, acting only on the two lumped parameters allows adjusting the model for a different ASSB geometry and cathode composition. The model estimates a capacity fade trend in solid agreement with actual data in the instance of an ASSB pouch cell cycled with a 1/16 C-rate charge/discharge load current. Further, the upgraded model can also determine the SEI formation rate as a function of temperature and Li-ion concentration. The LIBs analysis instead gave further insights; in this case, the model is verified at a specific temperature for multiple ageing conditions: (I) open circuit state at 80% and 100% SOC, (II) WLTP cycling with a fast-varying load current. As a conclusion, the macroscale model, whose fitting parameters must be evaluated only for each different operational temperature, poses itself as a solid computational tool for accurately predicting the LIBs’ electrochemical performance and conducting a primary study on ASSBs; for the latter, this could be beneficial in the selection of optimal materials.

Author Contributions

Conceptualization, S. S.; methodology, P.S. and A.L.; software, P.S. and A.L.; validation, P.S. and A.L.; formal analysis, P.S. and A.L.; investigation, P.S. and A.L.; resources, S.S.; writing—original draft preparation, P.S. and A.L.; writing—review and editing, S.S.; supervision, S.S.; project administration, S.S.; funding acquisition, S.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by NSERC-Canada through the Discovery grants program (grant number RGPIN-2022-04988).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

There is no new data in this research. All results are from simulations.

Acknowledgments

The authors are grateful to the reviewers for their constructive criticism to improve this manuscript. The research has been partially funded by NSERC-Canada through the Discovery grants program.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
Index Description
cov Areas covered by an microporous SEI layer
crd Areas where the SEI layer has cracked
ical Intercalating reaction
neg negative electrode
SEI SEI layer or SEI layer forming reaction
s Solid (Electrode) phase
l Liquid (Electrolyte) phase
Symbol Unit Description
a c r d 1 Proportionality factor
A m 2 Electrode surface area
C m o l m 3 Reactant concentration of SEI formation
C b a t t 1 Relative capacity
D i m 2 s Diffusion coefficient
E e q , i V Equilibrium potential
f 1 Lumped fitting parameter
F C m o l Faraday’s constant, 96485
I 0 A Exchange current
I 1 C A 1C charge/discharge current
I k i n A Kinetic current
I l i m A Limiting current
I l o a d A Applied current on the battery
J 1 Lumped fitting parameter
H 1 Lumped fitting parameter
Q b a t t . 0 C Initial battery capacity
Q n e g C Charge stored in the negative electrode
Q S E I C Charge lost to SEI forming reactions
R J m o l K Molar gas constant, 8.3145
s m SEI layer thickness
T k Temperature
V m 3 C Coulombic volume for forming the SEI
x 1 Stoichiometric coefficient in LixC6
α 1 Transfer coefficient
ϵ i 1 Porosity
η i V Over-potential
Φ i V Potential of i phase
τ i 1 Tortuosity

Appendix A

The entire current through a SEI layer can be expressed as:
I S E I = I c o v + I c r d
where I c o v and I c r d are the currents through the covered and cracked parts, respectively.
In addition, I cov ( or crd ) can be written relying on a first-order mass transfer limiting current through a Nernst boundary layer as:
I c o v ( o r c r d ) = I k i n , c o v ( or crd ) 1 + I k i n , c o v ( o r c r d ) I lim . cov ( o r c r d ) .
In the reported equation, I kin , cov ( or crd ) (A) is the kinetic current, and I lim is the highest current of the SEI formation, restricted by the mass transport. These currents can be computed as:
I kin , cov ( o r c r d ) = − ϵ cov ( o r c r d d I 0 exp − α η S E I F R T
where I 0 and η S E I are the exchange current and the over potential of the SEI formation reaction, respectively. The remaining symbols and notations are outlined in the nomenclature section. Further, ϵ c r d and ϵ c o v are calculated as:
ϵ c r d = a c r d K c r d ,
ϵ c o v = 1 − ϵ c r d ,
where K c r d and a c r d are the expansion factor and a dimensionless proportionality factor, respectively. Moreover, for K c r d , we have:
K cra = − 2 I ical I 1 C I ical < 0 and x < 0.3 0 I ical < 0 and 0.3 ⩽ x ⩽ 0.7 − I ical I 1 C I kcal < 0 and 0.7 ⩽ x 0 I kcal ⩾ 0
The over potential of the SEI formation reaction can be obtained by imposing the SEI reaction equilibrium potential ( E e q , S E l ) to zero and calculating the difference between the electrode potential Φ s and electrolyte potential Φ l as follows:
η S E I = Φ s − Φ l − E e q , S E I
It must be specified that the liquid phase potential is directly linked to the intercalation reaction’s equilibrium potential E e q , i c a l and the relative over potential, η i c a l , and can be expressed as:
Φ l = − E eq , ical + η ical .
By inverting the Butler-Volmer equation, the relationship between the over potential and the intercalation current can be reported as:
η ical = R T 0.5 F arcsinh I ical 2 k ical I 1 C ( ( 1 − x ) x ) 0.5 ,
where x and I ical are the SOC and intercalation current of the anode, respectively. I 1 C is the battery’s nominal 1 C charge, and k ical is the proportionality constant chosen to provide the over potential. In the Nernst boundary layer, the limiting current density and the accumulated SEI layer thickness are inversely connected:
I lim . cov ( or crd ) = − ϵ cov ( or crd ) C D cov ( or crd ) F A s
where C, F, and A are the concentration, Faraday’s constant, and electrode surface area, respectively. D cov ( or crd ) is inversely related to the tortuosity of the layer as:
D cov ( or crd ) = D T τ c o v .
To conclude, to attenuate the error and improve the accuracy of the model, Ekström and Lindbergh [24] proposed the following three lumped fitting parameters as:
J = ϵ c o v I 0 I 1 C ,
f = τ c o v V I 1 C 2 ϵ c o v 1 − ϵ c o v C D F A 2 ,
H = a c r d ϵ c o v .

References

  1. International, E.A.
  2. Shafique, M.; Azam, A.; Rafiq, M.; Luo, X. Life cycle assessment of electric vehicles and internal combustion engine vehicles: A case study of Hong Kong. Research in Transportation Economics 2022, 91, 101112. [Google Scholar] [CrossRef]
  3. Janek, J.; Zeier, W.G. A solid future for battery development. Nature Energy 2016 1:9 2016, 1, 1–4. [Google Scholar] [CrossRef]
  4. Kato, Y.; Hori, S.; Saito, T.; Suzuki, K.; Hirayama, M.; Mitsui, A.; Yonemura, M.; Iba, H.; Kanno, R. High-power all-solid-state batteries using sulfide superionic conductors. Nature Energy 2016, 1, 16030. [Google Scholar] [CrossRef]
  5. Kim, J.G.; Son, B.; Mukherjee, S.; Schuppert, N.; Bates, A.; Kwon, O.; Choi, M.J.; Chung, H.Y.; Park, S. A review of lithium and non-lithium based solid state batteries. Journal of Power Sources 2015, 282, 299–322. [Google Scholar] [CrossRef]
  6. Park, K.H.; Kaup, K.; Assoud, A.; Zhang, Q.; Wu, X.; Nazar, L.F. High-Voltage Superionic Halide Solid Electrolytes for All-Solid-State Li-Ion Batteries. ACS Energy Letters, 2020; 533–539. [Google Scholar] [CrossRef]
  7. Leung, K.; Soto, F.; Hankins, K.; Balbuena, P.B.; Harrison, K.L. Stability of Solid Electrolyte Interphase Components on Lithium Metal and Reactive Anode Material Surfaces. The Journal of Physical Chemistry C 2016, 120, 6302–6313. [Google Scholar] [CrossRef]
  8. Banerjee, A.; Wang, X.; Fang, C.; Wu, E.A.; Meng, Y.S. Interfaces and Interphases in All-Solid-State Batteries with Inorganic Solid Electrolytes. Chemical Reviews 2020, 120, 6878–6933. [Google Scholar] [CrossRef] [PubMed]
  9. Wang, A.; Kadam, S.; Li, H.; Shi, S.; Qi, Y. Review on modeling of the anode solid electrolyte interphase (SEI) for lithium-ion batteries. npj Computational Materials 2018, 4, 1–26. [Google Scholar] [CrossRef]
  10. Novák, P.; Joho, F.; Imhof, R.; Panitz, J.C.; Haas, O. In situ investigation of the interaction between graphite and electrolyte solutions. Journal of Power Sources 1999, 81-82, 212–216. [Google Scholar] [CrossRef]
  11. Electroreduction of graphite in LiClO4-ethylene carbonate electrolyte. Characterization of the passivating layer by transmission electron microscopy and Fourier-transform infrared spectroscopy. Journal of Power Sources 1996, 63, 33–39. [Google Scholar] [CrossRef]
  12. Fong, R.; von Sacken, U.; Dahn, J.R. Studies of Lithium Intercalation into Carbons Using Nonaqueous Electrochemical Cells. Journal of The Electrochemical Society 1990, 137, 2009–2013. [Google Scholar] [CrossRef]
  13. Peled, E. The Electrochemical Behavior of Alkali and Alkaline Earth Metals in Nonaqueous Battery Systems: The Solid Electrolyte Interphase Model. Journal of The Electrochemical Society 1979, 126, 2047. [Google Scholar] [CrossRef]
  14. Xu, K. Nonaqueous Liquid Electrolytes for Lithium-Based Rechargeable Batteries. Chemical Reviews 2004, 104, 4303–4418. [Google Scholar] [CrossRef]
  15. Plett, G.L. Battery management systems. Volume II, Equivalent-circuit methods. p. 329.
  16. Lanjan, A.; Moradi, Z.; Srinivasan, S. Multiscale Investigation of the Diffusion Mechanism within the Solid-Electrolyte Interface Layer: Coupling Quantum Mechanics, Molecular Dynamics, and Macroscale Mathematical Modeling. ACS Applied Materials and Interfaces 2021, 13, 42220–42229. [Google Scholar] [CrossRef] [PubMed]
  17. Multi-scale Imaging of Solid-State Battery Interfaces: From Atomic Scale to Macroscopic Scale. Chem 2020, 6, 2199–2218. [CrossRef]
  18. CHRISTENSEN, J.; NEWMAN, J. A mathematical model for the lithium-ion negative electrode solid electrolyte interphase. Journal of the Electrochemical Society 2004, 151, A1977–A1988. [Google Scholar] [CrossRef]
  19. Deng, J.; Wagner, G.J.; Muller, R.P. Phase Field Modeling of Solid Electrolyte Interface Formation in Lithium Ion Batteries. Journal of the Electrochemical Society 2013, 160, A487–A496. [Google Scholar] [CrossRef]
  20. Liu, L.; Park, J.; Lin, X.; Sastry, A.M.; Lu, W. A thermal-electrochemical model that gives spatial-dependent growth of solid electrolyte interphase in a Li-ion battery. Journal of power sources 2014, 268, 482–490. [Google Scholar] [CrossRef]
  21. Deng, Z.; Hu, X.; Lin, X.; Xu, L.; Li, J.; Guo, W. A Reduced-Order Electrochemical Model for All-Solid-State Batteries. IEEE Transactions on Transportation Electrification 2021, 7, 464–473. [Google Scholar] [CrossRef]
  22. Toghyani, S.; Baakes, F.; Zhang, N.; Kühnelt, H.; Cistjakov, W.; Krewer, U. Model-Based Design of High Energy All-Solid-State Li Batteries with Hybrid Electrolytes. Journal of The Electrochemical Society 2022, 169, 040550. [Google Scholar] [CrossRef]
  23. Lanjan, A.; Srinivasan, S. An Enhanced Battery Aging Model Based on a Detailed Diffusing Mechanism in the SEI Layer. ECS Advances 2022, 1, 030504. [Google Scholar] [CrossRef]
  24. Ekström, H.; Lindbergh, G. A Model for Predicting Capacity Fade due to SEI Formation in a Commercial Graphite/LiFePO 4 Cell. Journal of The Electrochemical Society 2015, 162, A1003–A1007. [Google Scholar] [CrossRef]
  25. Huu, N.; Phuc, H.; Hikima, K.; Muto, H.; Matsuda, A. Recent developments in materials design for all-solid-state Li-S batteries. [CrossRef]
  26. Otoyama, M.; Sakuda, A.; Hayashi, A.; Tatsumisago, M. Optical microscopic observation of graphite composite negative electrodes in all-solid-state lithium batteries. Solid State Ionics 2018, 323, 123–129. [Google Scholar] [CrossRef]
  27. Otoyama, M.; Kowada, H.; Sakuda, A.; Tatsumisago, M.; Hayashi, A. Operando Confocal Microscopy for Dynamic Changes of Li + Ion Conduction Path in Graphite Electrode Layers of All-Solid-State Batteries. The Journal of Physical Chemistry Letters 2020, 11, 900–904. [Google Scholar] [CrossRef] [PubMed]
  28. Kobayashi, Y.; Seki, S.; Mita, Y.; Ohno, Y.; Miyashiro, H.; Charest, P.; Guerfi, A.; Zaghib, K. High reversible capacities of graphite and SiO/graphite with solvent-free solid polymer electrolyte for lithium-ion batteries. Journal of Power Sources 2008, 185, 542–548. [Google Scholar] [CrossRef]
  29. Cresce, A.V.; Russell, S.M.; Baker, D.R.; Gaskell, K.J.; Xu, K. In situ and quantitative characterization of solid electrolyte interphases. Nano Letters 2014, 14, 1405–1412. [Google Scholar] [CrossRef] [PubMed]
  30. McShane, E.J.; McShane, E.J.; Colclasure, A.M.; Brown, D.E.; Brown, D.E.; Konz, Z.M.; Konz, Z.M.; Smith, K.; McCloskey, B.D.; McCloskey, B.D. Quantification of Inactive Lithium and Solid-Electrolyte Interphase Species on Graphite Electrodes after Fast Charging. ACS Energy Letters 2020, 5, 2045–2051. [Google Scholar] [CrossRef]
  31. Cabras, L.; Oancea, V.; Salvadori, A. A novel two-mechanism model for all solid state Li-ion batteries: review and comparisons 2021. [2104.05424v2].
  32. Micari, S.; Foti, S.; Testa, A.; De Caro, S.; Sergi, F.; Andaloro, L.; Aloisio, D.; Leonardi, S.G.; Napoli, G. Effect of WLTP CLASS 3B Driving Cycle on Lithium-Ion Battery for Electric Vehicles. Energies 2022, Vol. 15, Page 6703 2022, 15, 6703. [Google Scholar] [CrossRef]
  33. Micari, S.; Foti, ·.S.; Testa, ·.A.; De Caro, ·.S.; Sergi, ·.F.; Andaloro, ·.L.; Aloisio, ·.D.; Napoli, ·.G. Reliability assessment and lifetime prediction of Li-ion batteries for electric vehicles. Electrical Engineering 2022, 104, 165–177. [Google Scholar] [CrossRef]
  34. He, Y.; Li, S.; Zhou, S.; Hu, H. Mechanical Integrity Degradation and Control of All-Solid-State Lithium Battery with Physical Aging Poly (Vinyl Alcohol)-Based Electrolyte. Polymers 2020, 12, 1886. [Google Scholar] [CrossRef] [PubMed]
  35. Fang, X.; He, Y.; Fan, X.; Zhang, D.; Hu, H. Modeling and Simulation in Capacity Degradation and Control of All-Solid-State Lithium Battery Based on Time-Aging Polymer Electrolyte. Polymers 2021, 13, 1206. [Google Scholar] [CrossRef]
Preprints 103714 g001
Figure 1. The relative capacity over a duration of 200 days at 60C for the coin cell (cycling at 1/8 C-rate) and the pouch cell (1/16 C-rate). The experimental data are from Kobayashi et al. [28].
Figure 1. The relative capacity over a duration of 200 days at 60C for the coin cell (cycling at 1/8 C-rate) and the pouch cell (1/16 C-rate). The experimental data are from Kobayashi et al. [28].
Preprints 103714 g001
Preprints 103714 g002
Figure 2. A comparison of the SOC values predicted by the vehicle model with the experimental data of Micari et al.[33], for the WLTP cycles.
Figure 2. A comparison of the SOC values predicted by the vehicle model with the experimental data of Micari et al.[33], for the WLTP cycles.
Preprints 103714 g002
Preprints 103714 g003
Figure 3. Relative capacity over a duration of 700 days at 25C and 45C for a LIB-NMC-LMO-Prismatic battery. The experimental data is from Micari et al. [32].
Figure 3. Relative capacity over a duration of 700 days at 25C and 45C for a LIB-NMC-LMO-Prismatic battery. The experimental data is from Micari et al. [32].
Preprints 103714 g003
Preprints 103714 g004
Figure 4. The relative capacity over a duration of 4184 WLTP cycles at 25C for a LIB-NMC-LMO-Prismatic battery. The experimental data is from Micari et al. [32].
Figure 4. The relative capacity over a duration of 4184 WLTP cycles at 25C for a LIB-NMC-LMO-Prismatic battery. The experimental data is from Micari et al. [32].
Preprints 103714 g004
Preprints 103714 g005
Figure 5. Temperature sensitivity analysis - Relative capacity over a duration of 200 days.
Figure 5. Temperature sensitivity analysis - Relative capacity over a duration of 200 days.
Preprints 103714 g005
Preprints 103714 g006
Figure 6. Current sensitivity analysis - Relative capacity over a duration of 200 days at 60C.
Figure 6. Current sensitivity analysis - Relative capacity over a duration of 200 days at 60C.
Preprints 103714 g006
Preprints 103714 g007
Figure 7. The relative capacity and SEI thickness for different operating conditions in a ASSB.
Figure 7. The relative capacity and SEI thickness for different operating conditions in a ASSB.
Preprints 103714 g007
Table 1. Coefficients of the second-degree polynomial described in Equation (3) for Li 2 O and LiF [16].
Table 1. Coefficients of the second-degree polynomial described in Equation (3) for Li 2 O and LiF [16].
a 0 [eV] a 1 [eV] a 2 [eV]
Li 2 O 3.9488 − 8.9294 12.0460
LiF 1.9886 − 2.5607 3.5237
Table 2. Parameters for the modified MSMM ageing model for ASSBs.
Table 2. Parameters for the modified MSMM ageing model for ASSBs.
ASSB format Temperature f H
Coin cell 60C 1.5 x 10 5 3.5
Pouch cell 60C 3.4 x 10 4 2.5
Table 3. Parameters for the modified MSMM ageing model for LIBs.
Table 3. Parameters for the modified MSMM ageing model for LIBs.
Temperature f H
25 C 3.1 x 10 6 74.8
45 C 4.9 x 10 5 42.1
Table 4. V . R 2 values of the estimated relative capacity using the the modified MSMM models with respect to the experimental data.
Table 4. V . R 2 values of the estimated relative capacity using the the modified MSMM models with respect to the experimental data.
Temperature Operational condition R 2 value using MSMM
25 ∘ C Open Circuit - 80% SOC 0.99
45 ∘ C Open Circuit - 100% SOC 0.98
25 ∘ C WLTP 0.96
Table 5. The constants in Eqs. 14-15
Table 5. The constants in Eqs. 14-15
f 0 [ 1 K ] f 1 H 0 [ 1 K ] H 1
− 4.5 × 10 3 1.7 × 10 6 − 0.14 50.1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated