1. Introduction
On Dec. 31 2019, the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) causing coronavirus disease (COVID-19) was discovered in Wuhan in China. The virus has spread rapidly around the world and as of Apr. 21 2020 there were more than 2.3 million confirmed cases and a total of 162.000 deaths [
1]. Currently, the virus has infected more than 775 million people and caused the deaths of 7 million worldwide [
2]. Despite the high number of recorded deaths, the World Health Organization estimates the total number of deaths directly or indirectly from COVID-19 to be 14.9 million people [
3], three times higher than recorded.
The symptoms of COVID-19 can be divided into three categories being common symptoms such as fever, cough, tiredness and loss of taste or smell, less common symptoms such as sore throat, headache, myalgia and diarrhea, and the critical symptoms which are dyspnea, loss of speech, mobility or confusion and chest pain [
4]. Despite having several symptoms, a large proportion of infected people do not experience them. According to Wang et al. [
5] the proportion of asymptomatic people may represent about a third or a fifth of the total number of cases.
Although infected individuals develop mild or moderate disease and recover without hospitalization, a proportion of those infected may have severe symptoms, requiring hospitalization or intensive care unit (ICU) treatment.
To ensure the prevention of COVID-19, it is crucial to implement effective measures of detection, isolation and immediate medical care for infected people, in order to contain the spread of the virus [
6,
7,
8,
9]. This approach has proved effective in combating the spread of COVID-19. It is worth noting that, in addition to overloading the health system, the spread of the virus can have considerable economic impacts [
10]. The costs associated with treating infected patients put significant pressure on health systems, especially in regions with limited resources [
10]. Infected patients may require a diverse range of medical resources, from hospitalization in wards and ITUs to specialized interventions [
11,
12].
Among the various tests available to detect the disease, the reverse transcription polymerase chain reaction (RT-PCR) test, which detects the genetic material of the virus, is considered the gold standard for detecting COVID-19 and is carried out by collecting nasopharyngeal and/or oropharyngeal secretions [
13]. Although RT-PCR has high analytical specificity, its diagnostic sensitivity is limited, especially in the early stages of infection, when the viral concentration may not be high enough to produce accurate results, leading to possible false negative results [
14,
15,
16,
17]. In addition, SARS-CoV-2 is an RNA virus prone to mutations, and since the beginning of the spread of the virus we have seen the emergence of several variants with different replication capacities and clinical manifestations [
18]. Furthermore, the test has some limitations for testing patients on a large scale, requiring certified laboratories, expensive equipment and trained personnel, as well as the delay in obtaining results [
19,
20]. These limitations become even more serious in countries with limited resources, such as underdeveloped countries [
21].
In addition to the RT-PCR mentioned above, computed tomography (CT) and X-ray have also been proposed to aid in the detection of COVID-19, playing a powerful role in detecting and judging the progression of the disease [
22,
23,
24,
25,
26,
27]. However, these tests are not efficient for the proper management of patients and the control of the spread of the virus, as their sensitivity and specificity are higher only in advanced stages of COVID-19 or other diseases [
28,
29,
30], as these tests detect characteristics associated with COVID-19, such as lesions and lung inflammation, when the disease is already at an advanced stage of lung involvement. This is because the virus needs to replicate and cause significant damage to the lungs before changes are visible on the images. In addition, these exams subject patients to significant doses of ionizing radiation, which can pose major health risks [
31,
32].
Currently, machine learning has been an important tool to help doctors diagnose various diseases [
33,
34], including COVID-19 [
35,
36,
37]. Studies have made use of this technology to detect COVID-19, either through images such as x-rays or CT scans, or through laboratory tests [
38,
39,
40], since many clinical studies have shown hematological changes in infected patients [
41,
42,
43,
44]. While others focus on analyzing how these parameters vary throughout the course of the disease and their relationship with more serious clinical outcomes [
45,
46,
47]. Given the need for efficient and more accurate diagnoses in the early stages of COVID-19, the relevant attributes of laboratory tests can be used to train machine learning algorithms, making it possible to predict the risk and evolution of the disease, as well as the early classification of infected patients. It is worth noting that laboratory tests have the advantage of being relatively more accessible in terms of cost compared to RT-PCR and imaging tests such as x-rays and CT scans, as well as avoiding exposure to radiation. This approach, based on hematological evaluations, could enable its use on a large scale, with specialist algorithms, which is especially relevant for developing countries with limited resources to carry out RT-PCR tests on the entire population, thus avoiding adverse social and economic impacts.
Several studies in the literature have used machine learning to detect COVID-19 from laboratory tests. One of the first articles, by Wu et al. [
35], used the Random Forest (RF) algorithm with data collected from hospitals in China, achieving an AUC-ROC of 0.9926 in predicting patients with COVID-19. However, the model underperformed when tested with external samples. The authors Batista et al. [
48] used data collected in a hospital in São Paulo, Brazil, and trained five algorithms for the detection of COVID-19 patients, Support Vector Machine (SVM) and RF were the ones that showed the best results, with an AUC-ROC of 0.847.
Sun et al. [
36] employed the SVM algorithm to predict severe or critical cases of COVID-19 with patient data from a clinical center in China, obtaining a sensitivity of 77.5%, specificity of 78.4% and AUC-ROC of 0.9757. Tordjman et al. [
49] developed a strategy using binary logistic regression (LR) to estimate the probability of a patient being diagnosed with COVID-19 before RT-PCR, achieving an AUC-ROC of 0.918, with sensitivity and specificity of 79% and 90%, respectively. Yang et al. [
50] created a model using routine laboratory tests of patients at a medical center in the United States, and among the models tested, the Gradient Boosting Decision Tree (GBDT) obtained the best performance with an AUC-ROC of 0.854 in the internal validation and 0.838 in the external validation.
Joshi et al. [
51] developed a decision support tool using LR to predict COVID-19 negative patients. The model achieved AUC-ROC of 0.78 for Stanford Health Care data, with AUC-ROC ranging from 0.75 to 0.81 at other centers. Goodman-Meza et al. [
52] combined the probabilities of several algorithms to detect COVID-19 patients, achieving an AUC-ROC of 0.91 after adding certain tests such as ferritin, CRP and LDH. AlJame et al. [
53] proposed ERLX, a model that stacks algorithms such as extremely randomized trees (ET), RF, LR and Extreme Gradient Boosting (XGB) to diagnose COVID-19 patients from blood tests, obtaining an AUC-ROC of 0.9938. Brinati et al. [
21] proposed a model capable of predicting which patients were or were not infected with COVID-19, using data from patients admitted to the San Raffaele Hospital in Italy. Among the various algorithms tested, RF obtained the best performance, achieving an AUC-ROC of 0.84, sensitivity of 92% and specificity of 65%.
Alakus and Turkoglu [
54] used a dataset containing hematological and biochemical attributes of patients from the Hospital Israelita Albert Einstein in São Paulo, Brazil, to train six deep learning architectures, with the aim of detecting patients with COVID-19. The best performance was obtained with Long Short-Term Memory (LSTM), achieving AUC-ROC of 0.625 in cross-validation and AUC-ROC of 0.90 in hold-out validation. Kukar et al. [
55] created Smart Blood Analytics (SBA), a model for diagnosing COVID-19 from blood tests using algorithms such as RF, Deep Neural Network (DNN) and XGB. The best result with an AUC-ROC of 0.97 was obtained by XGB.
Using patient data from the Kepler University Hospital in Linz, Austria, Tschoellitsch et al. [
56] applied the RF algorithm to predict the RT-PCR result using blood tests, achieving an AUC-ROC of 0.74. Soltan et al. [
57] trained three models to identify COVID-19 patients in emergency departments and verify the need for hospitalization from patient data from Oxford University Hospitals in the UK. The best performance was obtained with XGB, achieving AUC-ROC of 0.939 in detecting patients and 0.94 in predicting hospitalization.
Cabitza et al. [
58] evaluated several algorithms, including RF, Naive Bayes (NB), LR, SVM and KNN, to predict COVID-19 patients using data from patients admitted to the San Raphael Hospital in Italy. The models achieved AUC-ROC between 0.74 and 0.90, and during internal-external validation, they obtained AUC-ROC between 0.75 and 0.78. Alves et al. [
59] developed a decision tree-based model to aid in the diagnosis of COVID-19 and provide explanations to healthcare teams, achieving AUC-ROC of 0.87, sensitivity of 67% and specificity of 91%. Rahman et al. [
60] created the QCoVSML model, which uses stacked machine learning and a nomogram scoring system to detect COVID-19 based on biomarkers. Seven different datasets were used, and the combined model achieved an AUC-ROC of 0.96 and accuracy of 91.45%. There are many other studies that make use of laboratory tests and demonstrate the ability of machine learning algorithms to assist in medical decision-making, speeding up the diagnosis of the disease.
Although the algorithms used have achieved promising results, it is essential to recognize that they have some limitations, especially those based on backpropagation. According to Grossberg [
61], these limitations include offline training, catastrophic forgetting, slow learning and sensitivity to outliers. To overcome these problems, Grossberg [
62] developed Adaptive Resonance Theory (ART), which is described in detail in
Section 2.
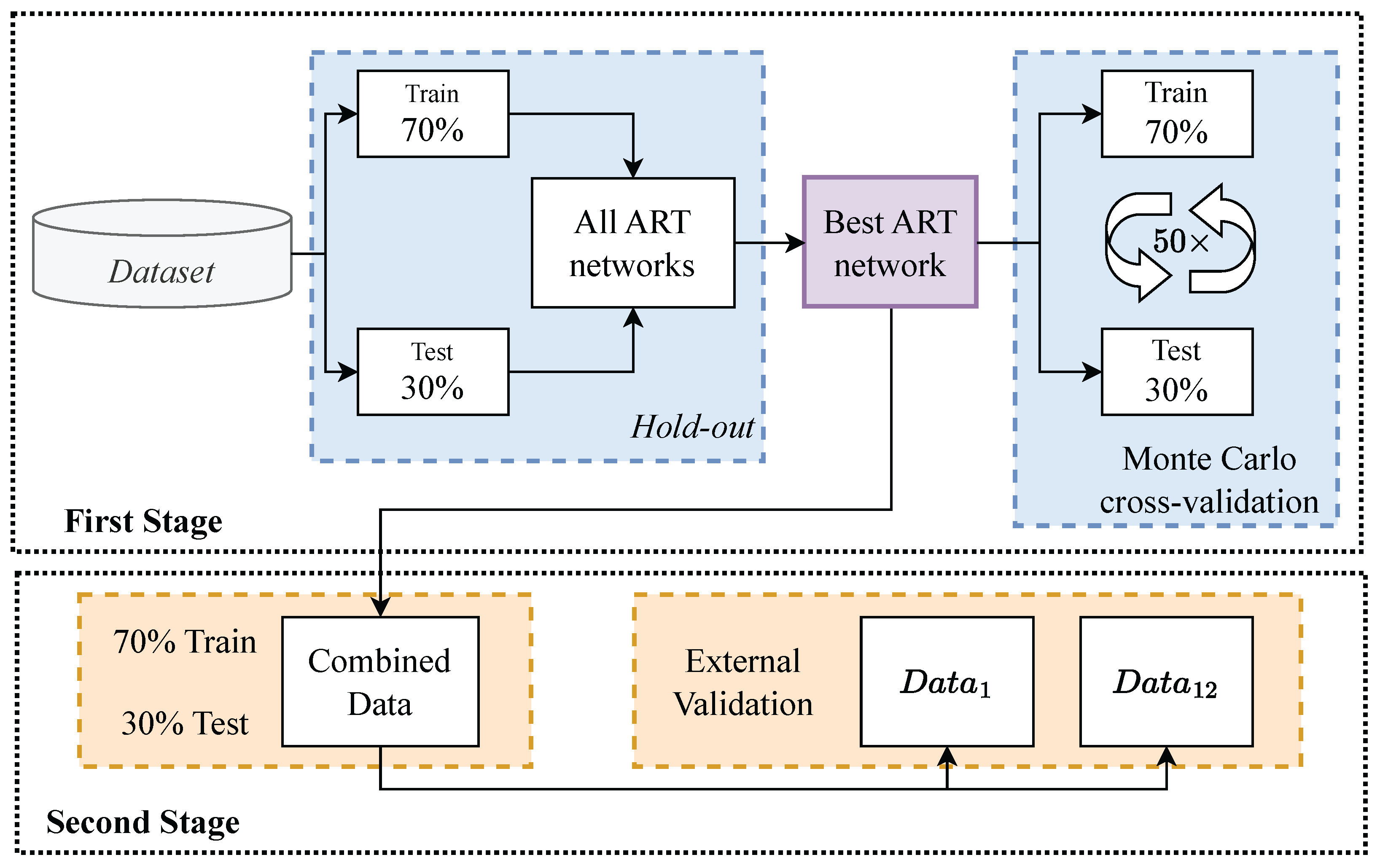
Therefore, this article presents the use of neural networks based on Adaptive Resonance Theory (ART) for the classification of COVID-19, using laboratory tests (blood tests) in order to improve the detection of infected patients. Comparisons were made between seven different ART architectures, including online training algorithms. The most successful architecture was subjected to a dataset containing laboratory tests from patients from different countries. This aspect is of paramount importance, as it allows us to evaluate the algorithm’s ability to detect relevant patterns and characteristics in data from different sources, thus increasing its usefulness in a global detection context.
2. Adaptive Resonance Theory
Developed Adaptive resonance theory in order to solve the stability-plasticity dilemma [
63], such a dilemma can be understood as the ability of the network to remain able to adapt or group input patterns, and continue learning even with the inclusion of new patterns, without catastrophically forgetting its past knowledge Carpenter and Grossberg [
64], this being a fundamental characteristic of ART family networks.
The first architecture based on this theory was developed by Grossberg [
62] and named Grossberg Network (GN), in 1987, the ART1 network was created with the purpose of binary grouping patterns and was based on the GN network of Grossberg [
64]. In the same year, Carpenter and Grossberg [
65] improved ART1 creating ART2. This new network had the purpose of processing patterns with binary or continuous values. Considering the need to solve problems with analog input patterns, in 1991 Carpenter et al. [
66], based on ART1 [
64], developed the ART Fuzzy neural network (
Figure 1), which employs the fuzzy min operator (∧) in place of the intersection operator (∩) present in ART1 network. The first ART network with supervised training was developed by Carpenter et al. [
67] and has two interconnected ART modules, the ART
module receives and processes the input pattern. In contrast, the ART
module receives the desired response for the presented pattern, and the Inter-ART module is in charge of performing the “matching” between the two ART modules. The following year Carpenter et al. [
68] presented the Fuzzy ARTMAP that also has supervised training. However, its calculations are based on Fuzzy Logic [
69].
Different ART network architectures have been tested in order to find the one that best classifies the data. These architectures have different characteristics, whether in their topology (cluster geometry), training method (supervised or unsupervised) or online learning capacity (Continuous Training), these characteristics appear in isolation or combined in the models to optimize data classification. The networks used in this study were:
Self-expanding Fuzzy ART Neural Network [
66]
Self-Expanding Euclidean ART neural network [
70]
Self-Expanding Fuzzy ARTMAP neural network [
68]
Self-expanding Fuzzy ART neural network with Continuous Training [
71]
Self-expanding Euclidean ART neural network with Continuous Training [
71,
72]
Self-expanding Fuzzy ARTMAP neural network with Continuous Training [
71]
Self-expanding Euclidean ARTMAP neural network with Continuous Training [
73]
In these architectures, some parameters play a fundamental role in controlling the functioning of the model, namely , and . The parameter, also known as the learning rate (), is crucial, indicating the extent to which new patterns will influence the category when the weights are updated in the next training cycle. The parameter, or training rate (), regulates the speed of training, with lower values indicating a slower process and values close to 1 implying faster training. Finally, the parameter, or vigilance parameter (), plays a crucial role in determining the degree of similarity required to create a new category. These parameters are essential for adjusting the network’s dynamics and adapting it effectively to the input data.
2.1. ART - Unsupervised
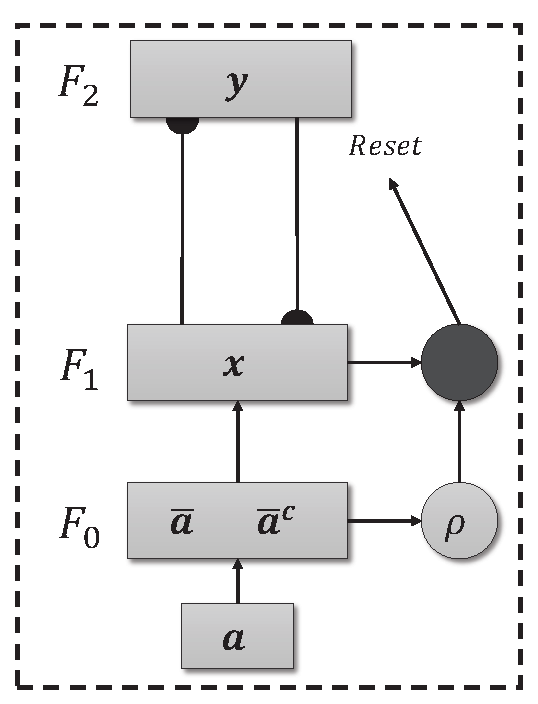
Unsupervised ART models are effective in environments where the training data does not need to be labeled. The model’s independence from labels allows it to autonomously explore the complexity of the data and identify relevant patterns. The basic architecture of an ART network can be seen in
Figure 1, and consists of three levels, the F
comparison level, the F
recognition level and the F
level responsible for pre-processing the data, in which the input data is normalized and encoded (Fuzzy Topology). In addition, there is a reset mechanism responsible for controlling the degree of similarity of the patterns associated with the same category.
It is worth noting that, although they adopt an unsupervised approach, labels are assigned to each cluster after the model has been trained. This process is explained in detail in
Section 3.4.
Algorithm 1: Algorithm ART. |
|
Input: Input data, parameters [, , (Fuzzy)]
Output: Cluster
- 1:
procedure - 2:
if Topology for Fuzzy then
- 3:
Normalize and encode the input data by Equation ( 1) and 2
- 4:
end if
- 5:
while Data for training exists do
- 6:
Calculate the distance or similarity between the input data and all existing clusters - 7:
Equation ( 3) or Equation ( 7) - 8:
while not finding a cluster to allocate the data do
- 9:
Select the cluster according to the equation Equation ( 4) or Equation ( 8) - 10:
if the Equation ( 5) or Equation ( 9) is satisfied then
- 11:
Update the weights according to Equation ( 6) or Equation ( 10) - 12:
else
- 13:
Remove the category from the search process - 14:
end if
- 15:
The data will be allocated to the current cluster - 16:
end while
- 17:
end while
- 18:
end procedure
|
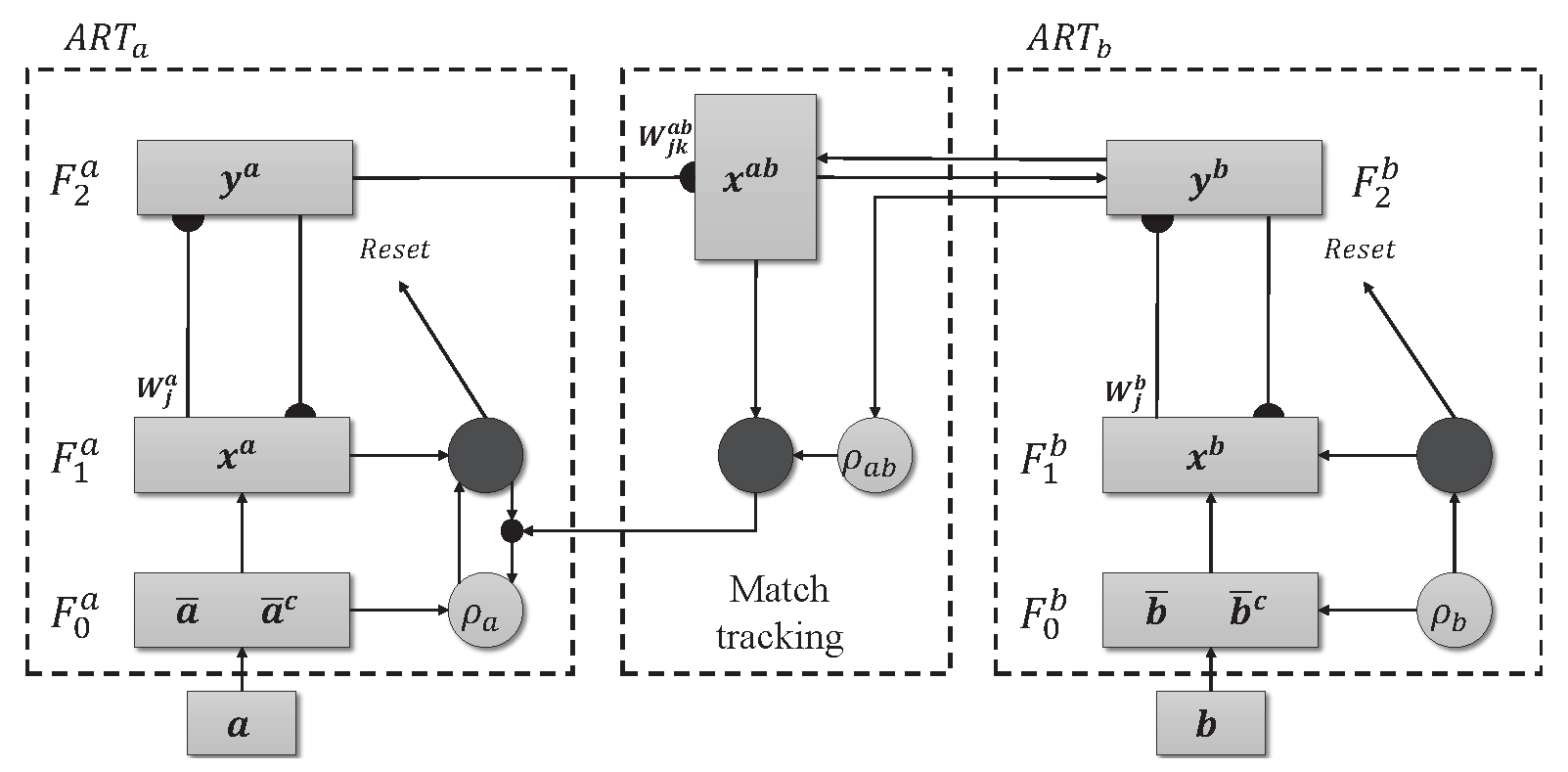
2.2. ARTMAP - Supervised
The ARTMAP model with supervised learning is made up of two ART modules, ART
and ART
, as shown in
Figure 2. Unlike their unsupervised counterparts, these modules do not operate in the dark. They use both the input data and the corresponding labels, providing guidance during training. Furthermore, ARTMAP doesn’t just passively accept information. It actively searches for meaningful connections. The inter-ART associative memory module is responsible for checking whether there is a match between the input patterns and the output. The vigilant match-tracking mechanism minimizes prediction errors and maximizes the model’s ability to generalize. The weight matrices associated with the ART
(
), ART
(
) and Inter-ART (
) modules are initialized with values equal to 1, indicating the absence of active categories. However, as training takes place, there is resonance between the input patterns and the output, causing specific categories to be activated. This dynamic activation process allows ARTMAP to learn and adapt in a controlled manner.
Although it is a powerful architecture, it is a model sensitive to noise in the labels due to supervised learning, accuracy can be compromised if the labels are inaccurate or noisy.
|
Algorithm 2: ARTMAP algorithm. |
|
Input: Input data, parameters [, , (Fuzzy)]
Output: Cluster
- 1:
procedure - 2:
if Topology for Fuzzy then
- 3:
Normalize and encode the input data by Equation ( 1) and 2
- 4:
end if
- 5:
while Data for training exists do
- 6:
Module B
- 7:
Calculate the distance or similarity between the input data and all existing clusters - 8:
Equation ( 3) or Equation ( 7) - 9:
while not finding a cluster to allocate the data do
- 10:
Select cluster according to Equation ( 4) or Equation ( 8) - 11:
if the Equation ( 5) or Equation ( 9) is met then
- 12:
Update the weights of module B according to Equation ( 6) or Equation ( 10) - 13:
else
- 14:
Remove the category from the search process - 15:
end if
- 16:
end while
- 17:
Module A
- 18:
Calculate the distance or similarity between the input data and all existing clusters - 19:
Equation ( 3) or Equation ( 7) - 20:
while not finding a cluster to allocate the data do
- 21:
Select cluster according to Equation ( 4) or Equation ( 8) - 22:
if the Equation ( 5) or Equation ( 9) is met then
- 23:
Inter-ART module
- 24:
if The category found by module A matches the category of module B then
- 25:
Update the weights of module A (Equation ( 6) or Equation ( 10)) and Inter-ART - 26:
else
- 27:
Remove the category from the search process and increase the vigilance parameter of module A - 28:
end if
- 29:
else
- 30:
Remove the category from the search process - 31:
end if
- 32:
end while
- 33:
The data will be allocated to the current cluster - 34:
end while
- 35:
end procedure
|
2.3. Fuzzy Topology in ART Networks
In the fuzzy topology, ART networks use the fuzzy logic connectives developed by [
69]. These connectives are used both to assess the similarity between input patterns and in the vigilance test. Furthermore, in this topology the data needs to be normalized and coded by complement as specified by Equation (
1) and (
2), in order to avoid the proliferation of categories [
68].
The Equation (
3) in turn is responsible for checking the similarity between the input pattern and the existing categories, the winning category will be the one with the greatest similarity to the input data as seen in the Equation (
4). The
j index refers to the cluster in which the calculations are being performed, while the
J index identifies the winning category in this process.
Resonance occurs if the vigilance criterion given by Equation (
5) is met. This process acts as a filter preventing the unbridled creation of categories. It ensures that only significantly different patterns trigger the formation of new categories, preventing the network from becoming full of redundant categories. The
parameter sets the threshold for this filter, determining the level of similarity required between an input pattern and the existing categories for the network to accept it or not within the cluster.
When resonance is achieved, the network starts a weight adjustment process, as detailed in Equation (
6). In this way, the weights associated with the winning category are modified to accommodate the new pattern.
By using fuzzy logic in the network calculations, together with normalization and complement coding, the clusters take the form of hyperrectangles, giving flexibility to the complexity of the input patterns.
2.4. Euclidean Topology in ART Networks
By adopting Euclidean topology, ART networks use Euclidean distance as a metric to measure the proximity between input patterns and existing categories. As a result, the network generates hyperspheres centered on the cluster representing the class, instead of hyperectangles. This approach eliminates the need to normalize and encode the input vector, thus reducing computational costs [
72]. The Equation (
7) indicates how the distance between the input pattern and the existing clusters is calculated. The category chosen is the one with the smallest distance according to Equation (
8), in contrast to the fuzzy approach, where the choice is based on maximum activation.
The vigilance criterion will be given by Equation (
9) and follows a similar pattern to that used in fuzzy topology, as detailed above in
Section 2.3.
Another change is in the Equation (
10) responsible for the network’s learning process. Here, the weight matrix (
) is updated according to a weighted combination of the input pattern (
) and the previous weight matrix (
), controlled by the
parameter.
2.5. Self-Expanding Mechanism
The self-expanding mechanism proposed by Moreno [
71,
72] starts training the network by adopting the first pattern as the center of the first cluster and expands according to the need to create new clusters, i.e. as the new input patterns do not fit into the pre-existing categories, a new cluster is created to allocate that pattern. This modification reduces the processing time and, consequently, the computational expense [
71,
72], as it only checks the similarity of active clusters, unlike traditional architectures, in which similarity is checked with all clusters, including inactive ones. Furthermore, when inputting data that is incompatible with any of the existing clusters, the network starts a new cluster with the new pattern that is not in resonance with the input data and the empty cluster. These changes do not alter the stability of the network or compromise its ability to recognize new information in the training data.
|
Algorithm 3: Self-expansion mechanism algorithm. |
|
Require: Initialization of the weight matrix with the first pattern
- 1:
procedure - 2:
if The surveillance criterion is not met (Equation ( 5) or Equation ( 9)) then
- 3:
if There are categories to be checked then
- 4:
Remove the current category from the search process and search again - 5:
else
- 6:
Create a new cluster to allocate the current data - 7:
The weight for this cluster will be the input pattern itself - 8:
end if
- 9:
end if
- 10:
end procedure
|
2.6. Continuous Training in ART Neural Networks
The continuous training strategy enables networks to learn online and continuously so that prediction and training are carried out constantly, making them more efficient. This approach eliminates the need to restart training when incorporating new data, resulting in a network that constantly adjusts to changes in the environment. The inclusion of this module in ART networks is only possible due to their characteristics of stability and plasticity [
72]. With online learning, there is no need to restart training when new data becomes available; this module allows new patterns to be added to the network’s memory permanently [
72].
In order to incorporate this module, the network needs to have temporary and definitive categories, a necessary process so that data that appears rarely is not incorporated into the network’s memory. In addition, two new parameters are added: the first, called the permanence parameter (
), defines the number of patterns needed for a temporary category to become definitive. The second, called the novelty index (
), checks for the need to update the weights of the definitive category, discarding information that is not very relevant to the network, avoiding overloading the network’s memory [
72]. Whenever a pattern belongs to a temporary cluster, resonance will occur; on the other hand, if the category to which the pattern belongs is definitive, resonance will only occur if the distance/similarity between the entry and the center of the category is greater than the parameter (
) [
72].
Thus, Equation (
3) and Equation (
7) are calculated for their respective topologies, for both temporary and permanent categories. The selection process remains the same. If the chosen category is definitive and passes the surveillance criterion, resonance will only occur if the condition imposed by Equation (
11) (Fuzzy) or Equation (
12) (Euclidean) is met, i.e. resonance will only occur if the pattern is significantly different.
5. Conclusion
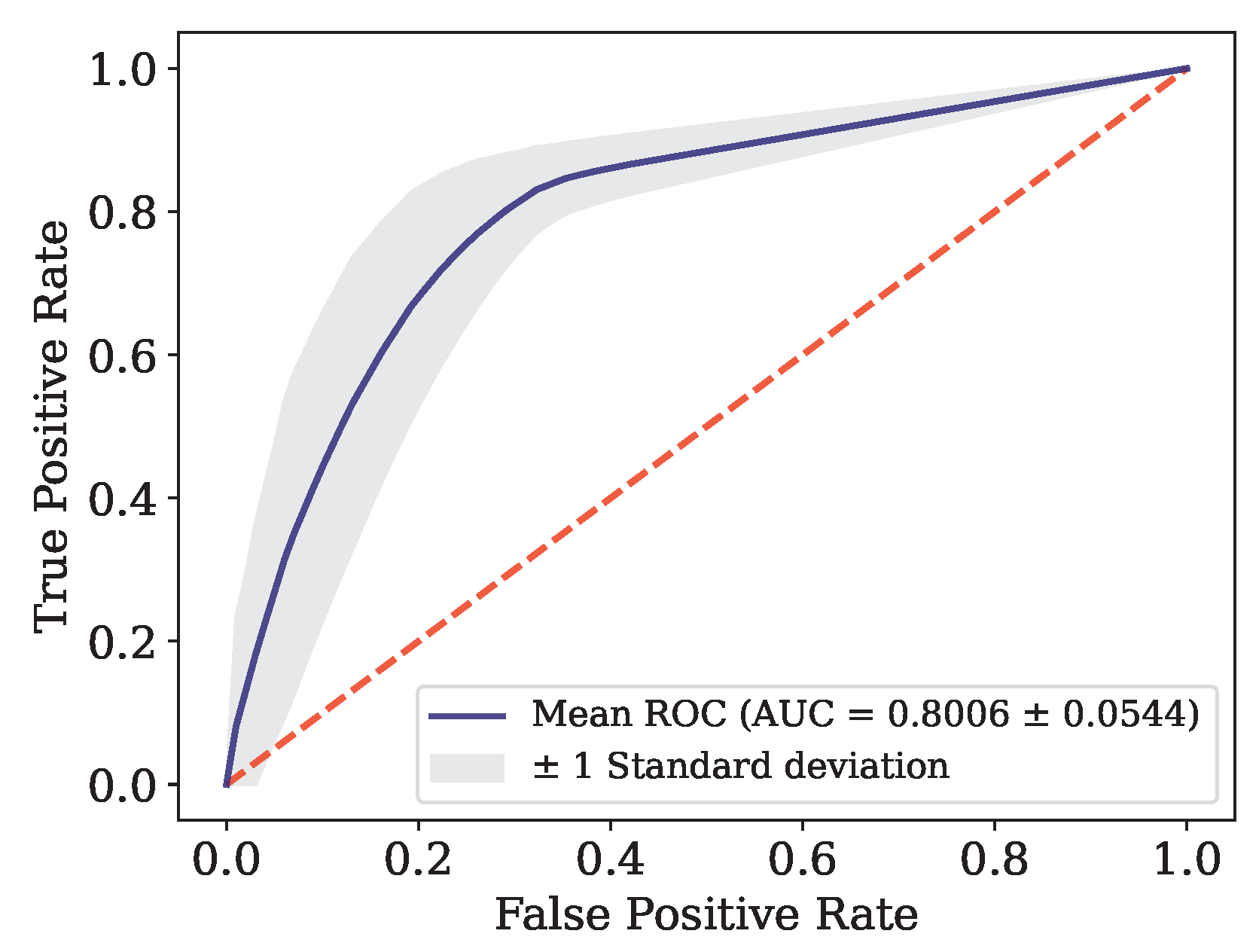
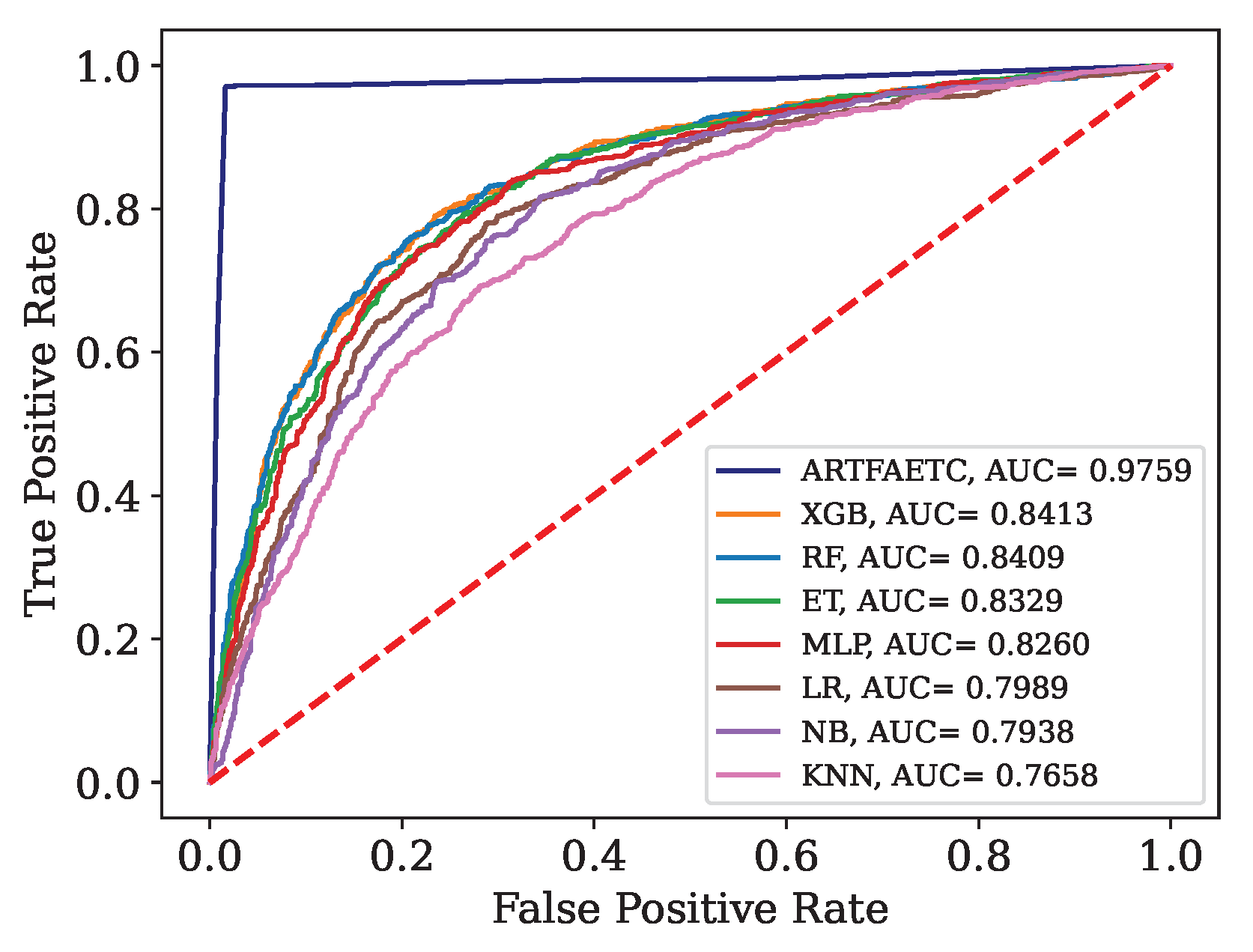
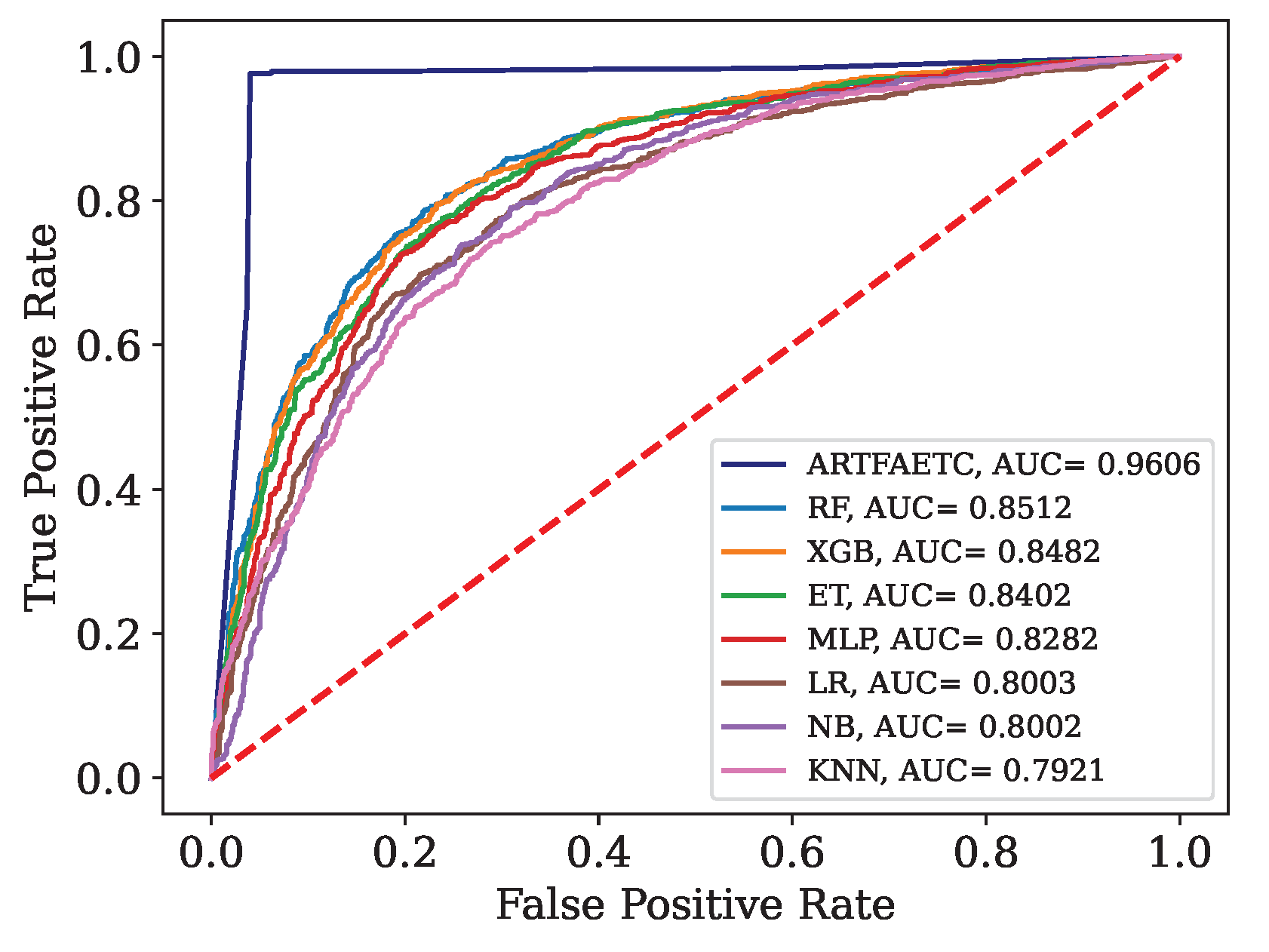
This article presents the results obtained by neural networks based on Adaptive Resonance Theory (ART) for the classification of COVID-19, using laboratory tests (blood tests) in order to correctly classify infected and healthy patients. A comparison was made between seven different ART architectures, including online training algorithms. The most successful architecture was subjected to a dataset made up of laboratory tests from patients in different countries. When comparing the results of the first stage, it can be seen that the self-expanding fuzzy ART network with continuous training (SE Fuzzy ART CT) and the self-expanding Euclidean ART network with continuous training (SE Euclidean ART CT) outperformed the other ART networks implemented. In addition, in some cases, the networks outperformed the DNN and CNN deep learning models frequently used in the literature. The SE Fuzzy ART CT obtained an AUC of 0.8501 for Data, 0.9481 for Data and 0.8962 for Data. When considering computational time, the self-expanding ART neural networks with continuous training were more efficient in the three data sets tested.
In the second stage, the self-expanding SE Fuzzy ART CT that won out in the first stage was subjected to a data set from various hospitals in four countries. This network was compared with traditional algorithms in the literature, maintaining an excellent performance that significantly outperformed all traditional models. Even during external validation with data from a different country to that included in the training, validating its generalization capacity.
In addition to the superior results compared to most of the models analyzed, the networks used do not face the main problems associated with traditional algorithms, such as slow learning, catastrophic forgetting and off-line training. Thus, these results highlight the potential of networks based on adaptive resonance theory, such as SE Fuzzy ART CT and SE Euclidean ART CT, as highly effective and reliable tools to aid in the detection of COVID-19, reducing the false negative rate of RT-PCR or even as a viable solution for detection in places with limited resources or underdeveloped countries.
Despite the promising results obtained by the ART networks, in future studies we intend to reduce the size of the data sets, selecting the most significant attributes to detect healthy and COVID-19 patients, and we can also add more information to aid classification, such as the use of imaging tests or symptoms. In addition, it is possible to make some adjustments to the models to improve the quality of the classification, such as modifying the normalization used, extending the research to the parameter, using the k-Fold cross-validation method as a way of validating and evaluating the model’s generalization capacity.
Figure 1.
Fuzzy ART Architecture.
Figure 1.
Fuzzy ART Architecture.
Figure 2.
Architecture ARTMAP.
Figure 2.
Architecture ARTMAP.
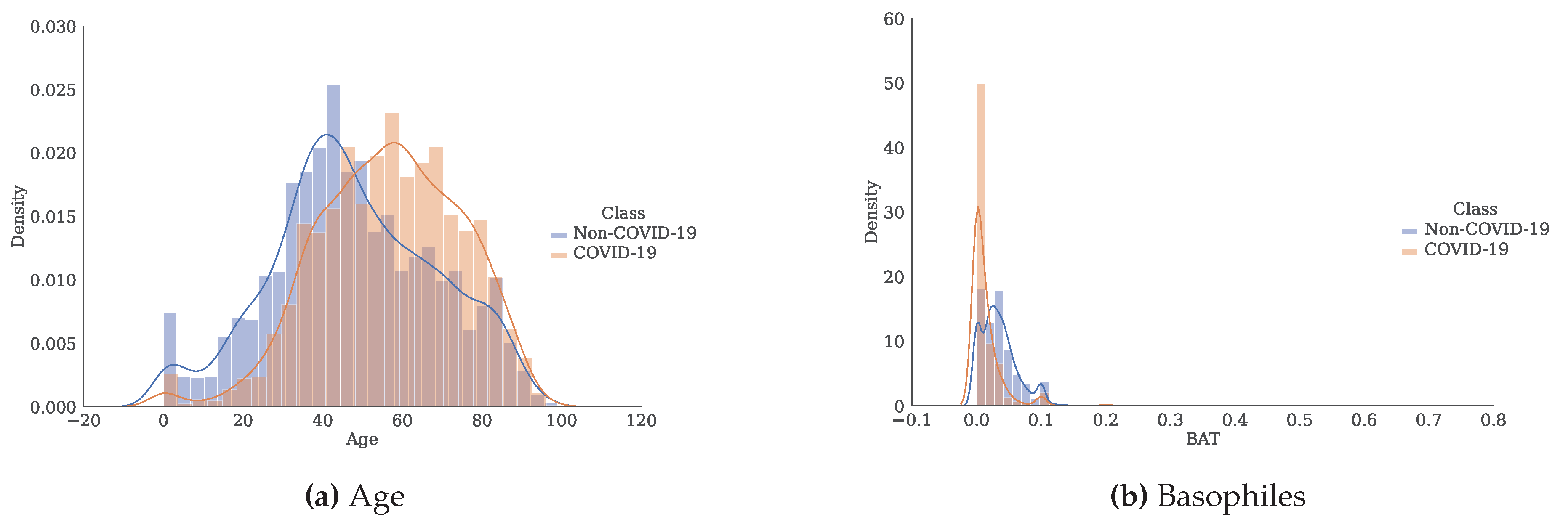
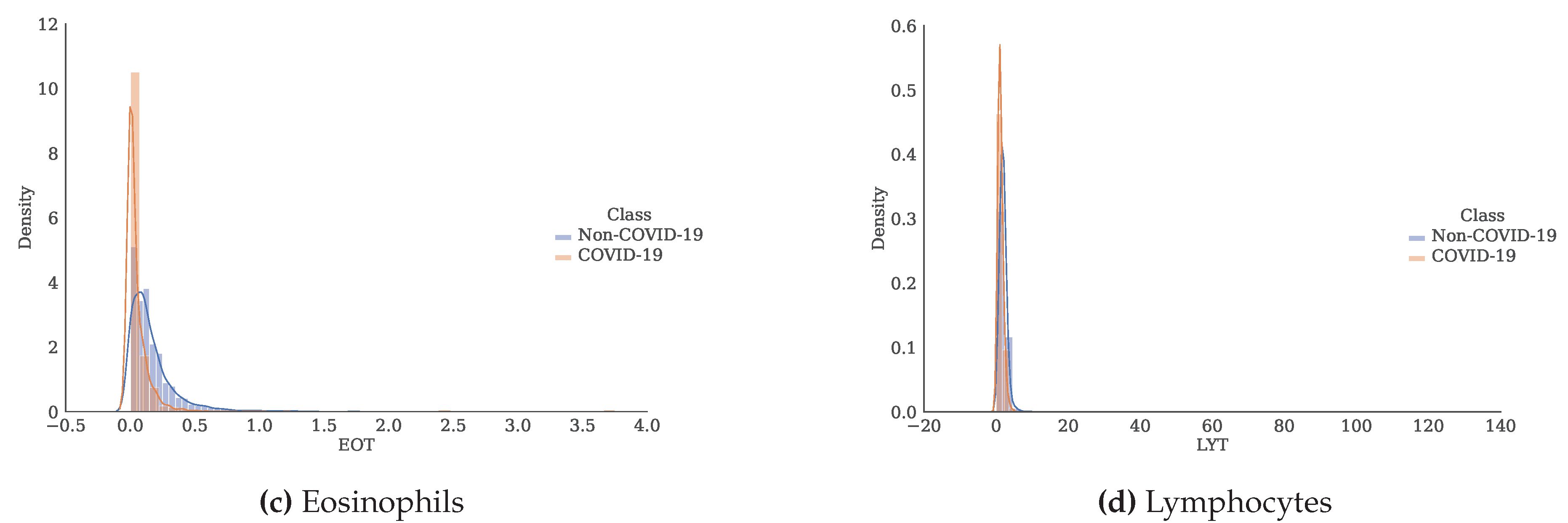
Figure 3.
Histogram and estimate of the probability density function for each of the attributes separated by class.
Figure 3.
Histogram and estimate of the probability density function for each of the attributes separated by class.
Figure 4.
Validation Overview.
Figure 4.
Validation Overview.
Figure 5.
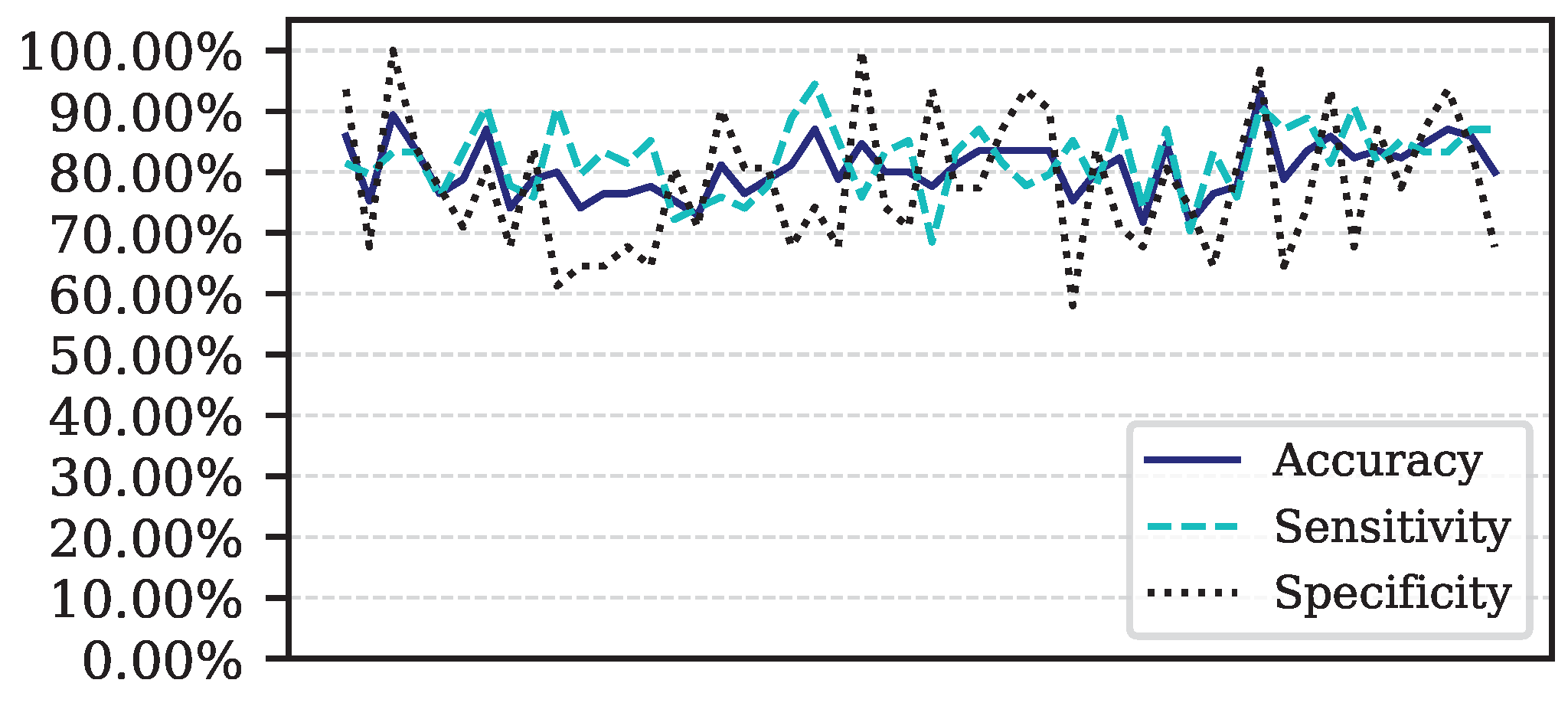
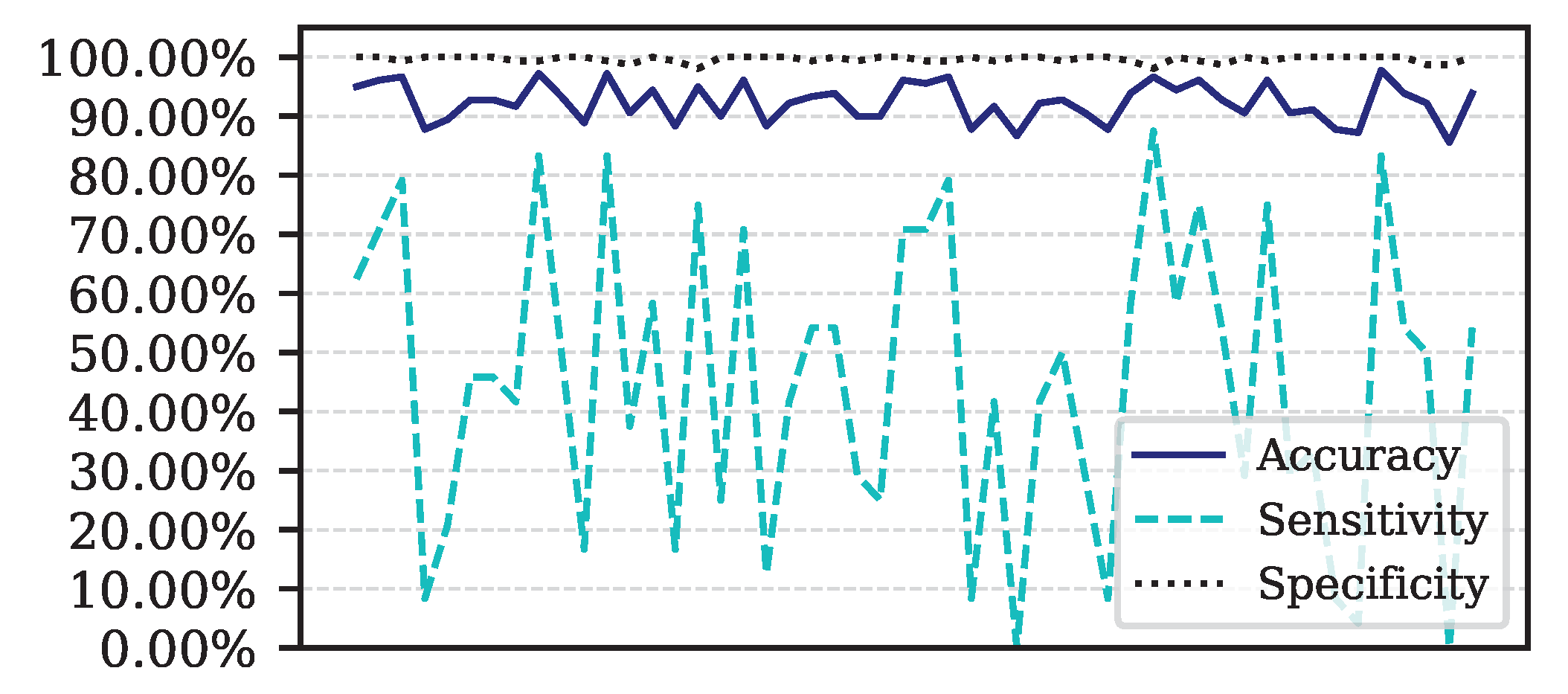
Performance for each of the 50 iterations of the Monte Carlo cross-validation for the Data.
Figure 5.
Performance for each of the 50 iterations of the Monte Carlo cross-validation for the Data.
Figure 6.
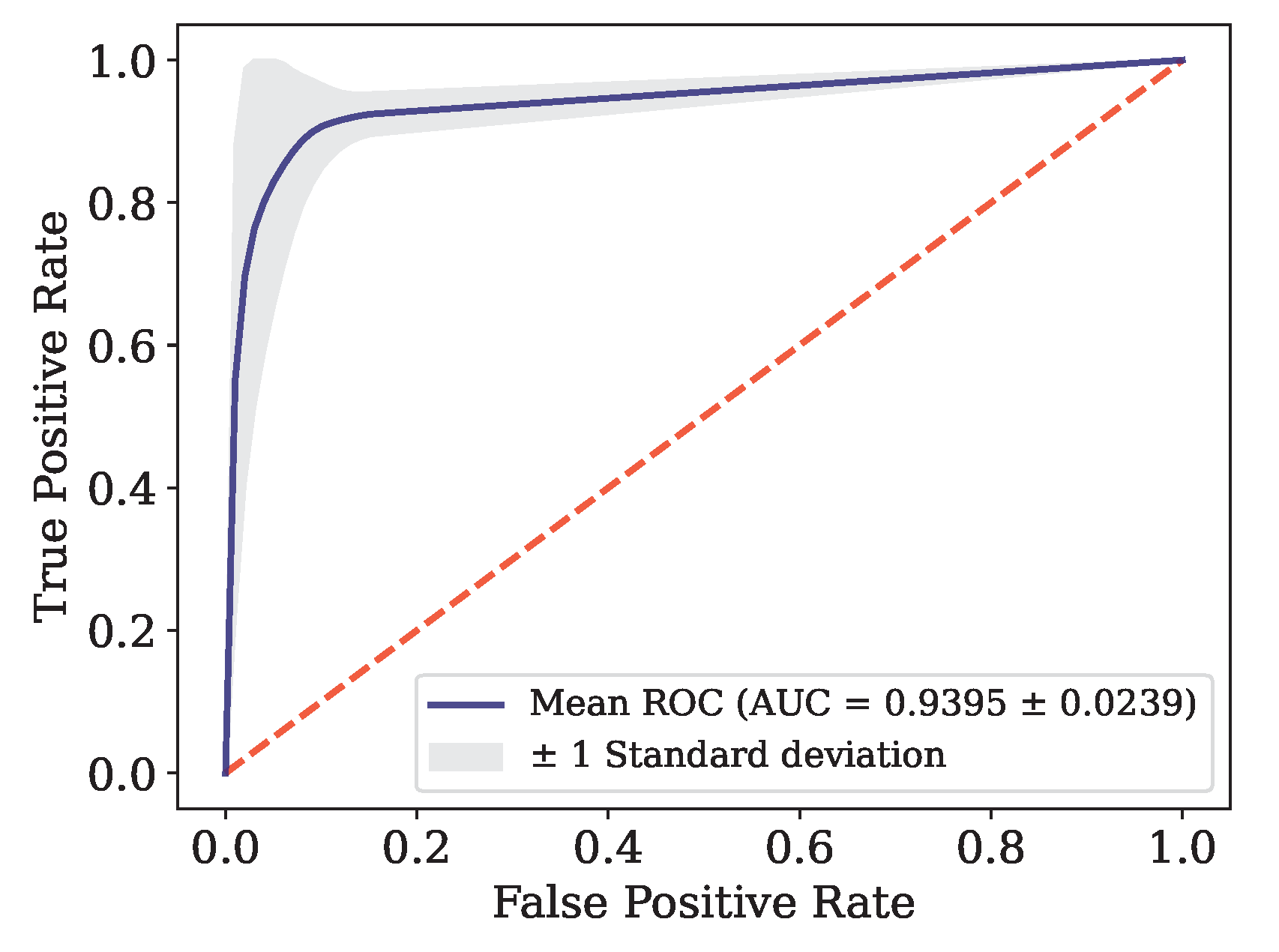
ROC curve for Data.
Figure 6.
ROC curve for Data.
Figure 7.
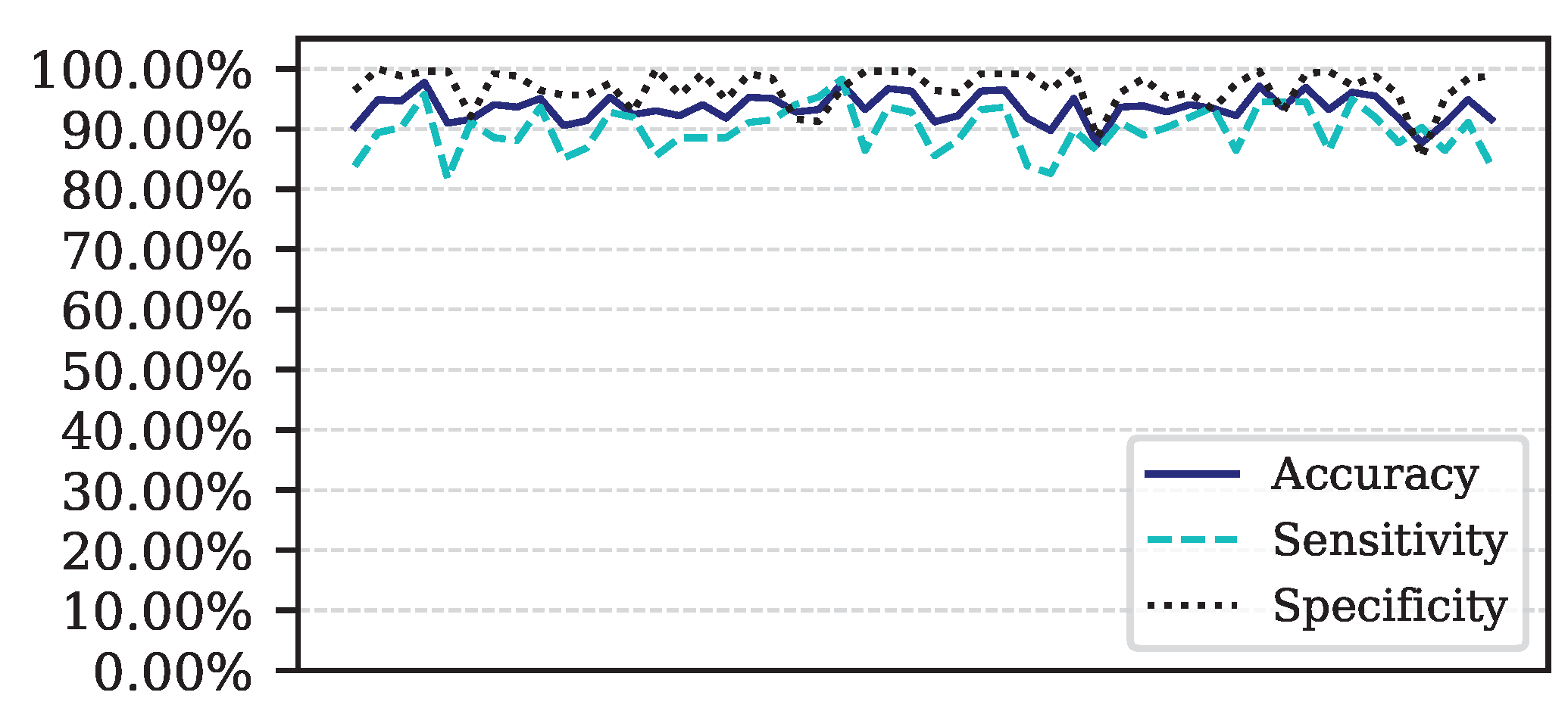
Performance for each of the 50 iterations of the Monte Carlo cross-validation for the Data.
Figure 7.
Performance for each of the 50 iterations of the Monte Carlo cross-validation for the Data.
Figure 8.
ROC Curve for Data.
Figure 8.
ROC Curve for Data.
Figure 9.
Performance for each of the 50 iterations of the Monte Carlo cross-validation for the Data.
Figure 9.
Performance for each of the 50 iterations of the Monte Carlo cross-validation for the Data.
Figure 10.
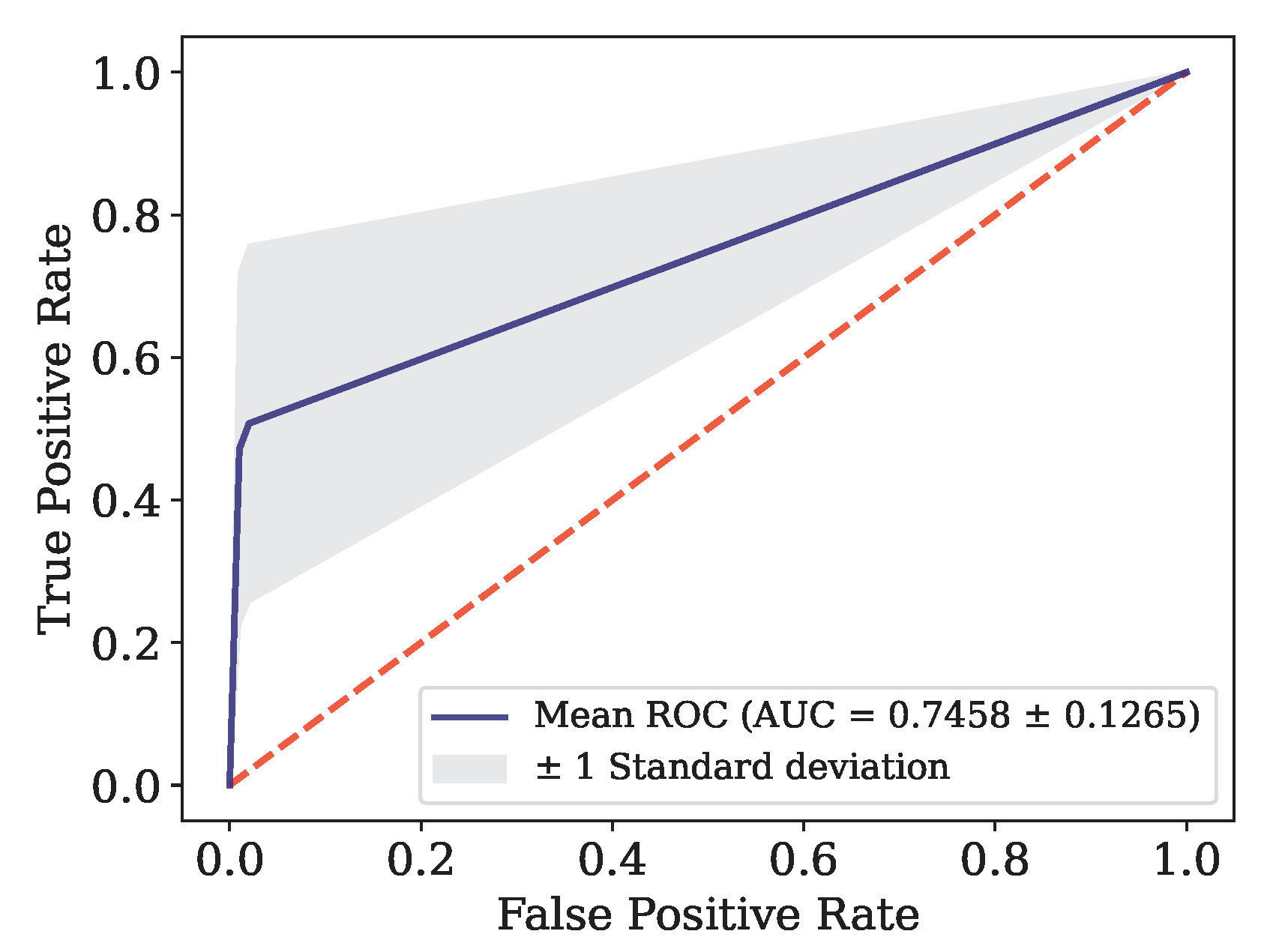
ROC curve for Data.
Figure 10.
ROC curve for Data.
Figure 11.
ROC curve and AUC for the combined data set.
Figure 11.
ROC curve and AUC for the combined data set.
Figure 12.
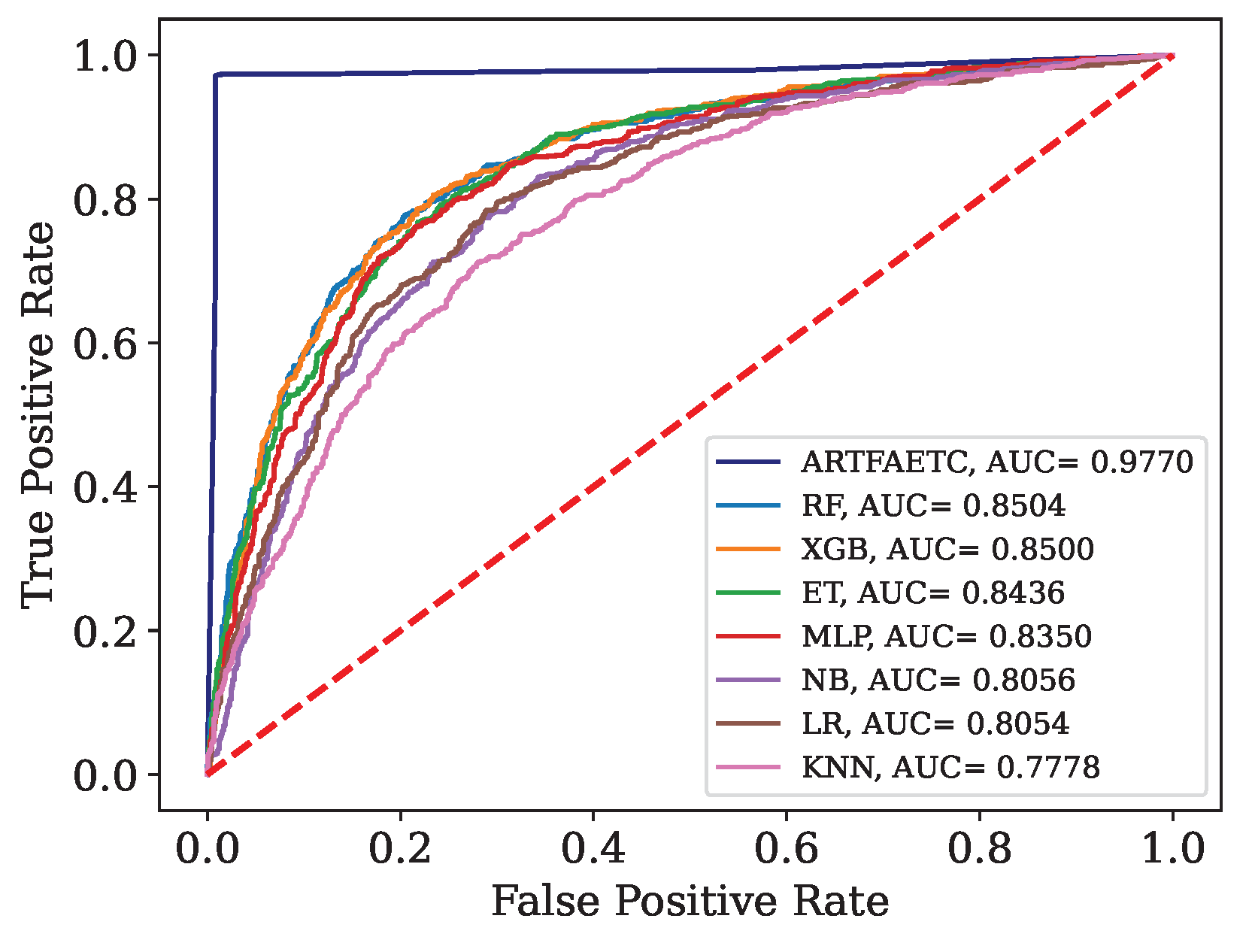
ROC curve and AUC obtained by each model trained with the combined data and validated by Dados.
Figure 12.
ROC curve and AUC obtained by each model trained with the combined data and validated by Dados.
Figure 13.
ROC curve and AUC obtained by each model trained with the combined data and validated by Data.
Figure 13.
ROC curve and AUC obtained by each model trained with the combined data and validated by Data.
Table 1.
Amount of data and features.
Table 1.
Amount of data and features.
| Available in: |
Name |
Country |
Features |
Positive |
Negative |
| [21] |
Data
|
Italy |
14 |
177 |
102 |
| [58] |
Data
|
Italy |
35 |
786 |
838 |
| [54] |
Data
|
Brazil |
19 |
80 |
520 |
| [74] |
Data
|
Italy |
22 |
163 |
174 |
| [74] |
Data
|
Italy |
22 |
104 |
145 |
| [74] |
Data
|
Italy |
22 |
118 |
106 |
| [74] |
Data
|
Brazil |
23 |
334 |
11 |
| [74] |
Data
|
Brazil |
23 |
352 |
949 |
| [74] |
Data
|
Brazil |
23 |
375 |
1960 |
| [74] |
Data
|
Ethiopia |
24 |
200 |
0 |
| [74] |
Data
|
Spain |
24 |
78 |
42 |
Table 2.
Attributes present in the data.
Table 2.
Attributes present in the data.
| Data |
Attributes |
| Data
|
Alanine Aminotransferase, Aspartate Aminotransferase, Basophils, Class, Eosinophils, Gamma GT, Gender, Age, Lactate Dehydrogenase, Leukocytes, Lymphocytes, Monocytes, Neutrophils, C-Reactive Protein, Platelets |
| Data
|
Alanine Aminotransferase, Aspartate Aminotransferase, Basophils (10), Basophils (%), Calcium, Average Corpuscular Hemoglobin Concentration, Creatine Kinase, Class, Creatinine, Eosinophils (10), Eosinophils (%), Alkaline Phosphatase, Gamma GT, Gender, Glucose, Average Corpuscular Hemoglobin, RBC, Hematocrit, Hemoglobin, Age, Lactate Dehydrogenase, Leukocytes, Lymphocytes (10), Lymphocytes (%), Monocytes (10), Monocytes (%), Neutrophils, Neutrophils (%), C-reactive protein, Platelets, Potassium, Suspected COVID-19, Urea, Mean Corpuscular Volume, Mean Platelet Volume |
| Data
|
Alanine Aminotransferase, Aspartate Aminotransferase, Basophils, Class, Creatinine, Eosinophils, Serum glucose, RBC, Hematocrit, Hemoglobin, Age, Leukocytes, Lymphocytes, Monocytes, Neutrophils, C-reactive protein, Platelets, Potassium, Sodium, urea |
Table 3.
Average and standard deviation of attributes.
Table 3.
Average and standard deviation of attributes.
| Attributes |
Data
|
Data
|
Data
|
Data
|
Data
|
Data
|
Data
|
Data
|
| Age |
60,55 |
54,38 |
66,35 |
60,53 |
54,40 |
47,01 |
42,87 |
59,73 |
| |
± 19,6 |
± 25,0 |
± 18,5 |
± 20,2 |
± 15,5 |
± 17,4 |
± 17,0 |
± 13,1 |
| BA (%) |
0,34 |
0,46 |
0,18 |
0,32 |
0,30 |
0,52 |
0,48 |
0,29 |
| |
± 0,3 |
± 0,4 |
± 0,4 |
± 0,3 |
± 0,3 |
± 0,3 |
± 0,3 |
± 0,4 |
| BAT |
0,02 |
0,03 |
0,02 |
0,02 |
0,02 |
0,03 |
0,03 |
0,04 |
| |
± 0,04 |
± 0,04 |
± 0,05 |
± 0,04 |
± 0,03 |
± 0,02 |
± 0,02 |
± 0,1 |
| EO (%) |
0,83 |
1,23 |
0,74 |
0,60 |
1,05 |
2,30 |
2,27 |
0,62 |
| |
± 1,6 |
± 2,1 |
± 1,6 |
± 1,2 |
± 1,6 |
± 2,4 |
± 2,5 |
± 1,1 |
| EOT |
0,06 |
0,09 |
0,06 |
0,05 |
0,06 |
0,15 |
0,17 |
0,08 |
| |
± 0,1 |
± 0,2 |
± 0,1 |
± 0,1 |
± 0,1 |
± 0,2 |
± 0,2 |
± 0,3 |
| HCT |
39,41 |
37,77 |
38,20 |
39,67 |
40,75 |
41,47 |
41,18 |
39,96 |
| |
± 5,6 |
± 7,4 |
± 6,3 |
± 6,1 |
± 5,0 |
± 4,0 |
± 4,1 |
± 7,9 |
| HGB |
13,21 |
12,86 |
13,21 |
13,11 |
13,74 |
13,82 |
14,11 |
13,36 |
| |
± 2,0 |
± 2,7 |
± 2,3 |
± 2,2 |
± 1,9 |
± 1,5 |
± 1,5 |
± 3,2 |
| LY (%) |
18,54 |
21,90 |
16,56 |
18,30 |
23,14 |
31,10 |
27,57 |
7,58 |
| |
± 11,1 |
± 14,5 |
± 11,6 |
± 11,9 |
± 11,4 |
± 11,2 |
± 11,0 |
± 7,1 |
| LYT |
1,37 |
1,84 |
1,63 |
1,82 |
1,31 |
2,01 |
2,00 |
0,77 |
| |
± 1,0 |
± 4,9 |
± 6,3 |
± 6,1 |
± 1,0 |
± 1,9 |
± 0,9 |
± 0,6 |
| MCH |
29,20 |
30,41 |
29,62 |
29,51 |
29,60 |
29,37 |
29,59 |
29,58 |
| |
± 2,7 |
± 2,9 |
± 3,1 |
± 2,4 |
± 1,9 |
± 1,9 |
± 1,8 |
± 2,8 |
| MCHC |
33,47 |
33,98 |
34,49 |
33,00 |
33,68 |
33,31 |
34,25 |
33,09 |
| |
± 1,4 |
± 1,4 |
± 1,5 |
± 1,3 |
± 1,1 |
± 1,1 |
± 1,0 |
± 2,0 |
| MCV |
87,22 |
89,44 |
85,72 |
89,41 |
87,90 |
88,19 |
86,39 |
88,69 |
| |
± 7,1 |
± 7,4 |
± 8,0 |
± 6,5 |
± 5,1 |
± 5,1 |
± 4,7 |
± 8,3 |
| MO (%) |
7,76 |
8,86 |
7,17 |
8,13 |
9,64 |
9,29 |
8,64 |
5,74 |
| |
± 3,9 |
± 4,7 |
± 3,9 |
± 5,0 |
± 4,4 |
± 3,7 |
± 3,2 |
± 8,2 |
| MOT |
0,62 |
0,73 |
0,64 |
0,64 |
0,56 |
0,59 |
0,63 |
0,63 |
| |
± 0,5 |
± 0,9 |
± 0,4 |
± 0,3 |
± 0,3 |
± 0,3 |
± 0,3 |
± 0,8 |
| NE (%) |
72,50 |
67,54 |
75,03 |
72,48 |
65,78 |
56,79 |
61,02 |
85,77 |
| |
± 13,3 |
± 17,2 |
± 14,2 |
± 14,5 |
± 14,1 |
± 12,4 |
± 12,4 |
± 12,7 |
| NET |
6,47 |
5,62 |
7,47 |
6,76 |
4,35 |
3,92 |
4,82 |
11,60 |
| |
± 4,5 |
± 4,3 |
± 4,9 |
± 4,3 |
± 3,1 |
± 2,1 |
± 2,4 |
± 8,5 |
| PLT |
234,49 |
204,00 |
220,23 |
218,00 |
199,81 |
246,96 |
239,92 |
268,69 |
| |
± 94,9 |
± 113,7 |
± 90,0 |
± 84,8 |
± 73,4 |
± 70,3 |
± 64,6 |
± 146,8 |
| RBC |
4,55 |
4,25 |
4,49 |
4,46 |
4,65 |
4,72 |
4,78 |
4,46 |
| |
± 0,7 |
± 0,9 |
± 0,8 |
± 0,8 |
± 0,7 |
± 0,5 |
± 0,5 |
± 0,9 |
| WBC |
8,69 |
8,31 |
9,81 |
9,53 |
6,30 |
6,70 |
7,66 |
14,18 |
| |
± 4,7 |
± 7,1 |
± 8,0 |
± 7,5 |
± 3,5 |
± 3,0 |
± 2,7 |
± 17,8 |
| BA: Basophils; BAT: Basophil Count; EO: Eosinophils; EOT: Eosinophil Count; HCT: Hematocrit; HGB: Hemoglobin; LY: Lymphocytes; LYT: Lymphocyte Count; MCH: Mean Corpuscolar Hemoglobin; MCHC: Mean Corpuscular Hemoglobin Concentration; MCV: Mean Corpuscular Volume; MO: Monocytes; MOT: Monocyte Count; NE: Neutrophils; NET: Neutrophil Count; PLT: Platelets; RBC: Red Blood Cells |
Table 4.
Selection of attributes by different methods.
Table 4.
Selection of attributes by different methods.
| Attributes |
p-value MW |
VIF |
Attributes |
p-value MW |
VIF |
| Age |
0.0000 |
1.4213 |
MCHC |
0.0000 |
10.5313 |
| BA (%) |
0.0000 |
2.8222 |
MCV |
0.3976 |
81.7446 |
| BAT |
0.0000 |
2.6595 |
MO (%) |
0.7285 |
12.1883 |
| EO (%) |
0.0000 |
10.5956 |
MOT |
0.0000 |
2.8672 |
| EOT |
0.0000 |
7.2687 |
NE (%) |
0.0000 |
140.5236 |
| HCT |
0.0003 |
400.5673 |
NET |
0.0000 |
5.4626 |
| HGB |
0.0137 |
351.4449 |
PLT |
0.0627 |
1.2310 |
| LY (%) |
0.0000 |
100.8982 |
RBC |
0.0007 |
59.8770 |
| LYT |
0.0000 |
2.1397 |
WBC |
0.0000 |
3.8370 |
| MCH |
0.0136 |
105.2796 |
|
|
|
Table 5.
Interpretation of AUC Values.
Table 5.
Interpretation of AUC Values.
| Range |
Result |
Range |
Result |
| 0.5 – 0.6 |
Bad |
0.7 – 0.8 |
Acceptable |
| 0.8 – 0.9 |
Good |
> 0.9 |
Excellent |
Table 6.
Results obtained by each model for Data.
Table 6.
Results obtained by each model for Data.
| Model |
ACC |
Se |
Sp |
MCC |
| SE Fuzzy ART |
0.800 |
0.870 |
0.670 |
0.561 |
| SE Euclidean ART |
0.706 |
0.759 |
0.613 |
0.370 |
| SE Fuzzy ARTMAP |
0.835 |
0.870 |
0.774 |
0.645 |
| SE Fuzzy ART CT |
0.871 |
0.926 |
0.774 |
0.717 |
| SE Euclidean ART CT |
0.741 |
0.778 |
0.677 |
0.450 |
| SE Fuzzy ARTMAP CT |
0.800 |
0.759 |
0.871 |
0.608 |
| SE Euclidean ARTMAP CT |
0.635 |
0.778 |
0.387 |
0.176 |
Table 7.
Average result after Monte Carlo cross-validation for Data.
Table 7.
Average result after Monte Carlo cross-validation for Data.
| Metrics |
Average result (CI 95%) |
| ACC |
0.8061 (0.7932 – 0.8191) |
| Se |
0.8211 (0.8049 – 0.8373) |
| Sp |
0.7800 (0.7495 – 0.8105) |
| MCC |
0.6555 (0.6264 – 0.6846) |
| F
|
0.8679 (0.8569 – 0.8788) |
Table 8.
Results obtained by each model for Data.
Table 8.
Results obtained by each model for Data.
| Model |
ACC |
Se |
Sp |
MCC |
| SE Fuzzy ART |
0.750 |
0.746 |
0.754 |
0.500 |
| SE Euclidean ART |
0.727 |
0.691 |
0.762 |
0.454 |
| SE Fuzzy ARTMAP |
0.783 |
0.792 |
0.774 |
0.566 |
| SE Fuzzy ART CT |
0.984 |
0.970 |
0.996 |
0.967 |
| SE Euclidean ART CT |
0.781 |
0.547 |
1.000 |
0.619 |
| SE Fuzzy ARTMAP CT |
0.738 |
0.712 |
0.762 |
0.474 |
| SE Euclidean ARTMAP CT |
0.697 |
0.712 |
0.683 |
0.394 |
Table 9.
Average result after Monte Carlo cross-validation for Data.
Table 9.
Average result after Monte Carlo cross-validation for Data.
| Metrics |
Average result (CI 95%) |
| ACC |
0.9348 (0.9282 – 0.9413) |
| Se |
0.8992 (0.8885 – 0.9098) |
| Sp |
0.9682 (0.9594 – 0.9770) |
| MCC |
0.8721 (0.8592 – 0.8850) |
| F
|
0.9301 (0.9231 – 0.9371) |
Table 10.
Results obtained by each model for Data.
Table 10.
Results obtained by each model for Data.
| Model |
ACC |
Se |
Sp |
MCC |
| SE Fuzzy ART |
0.889 |
0.208 |
0.994 |
0.382 |
| SE Euclidean ART |
0.878 |
0.500 |
0.936 |
0.452 |
| SE Fuzzy ARTMAP |
0.867 |
0.375 |
0.942 |
0.359 |
| SE Fuzzy ART CT |
0.944 |
0.583 |
1.000 |
0.740 |
| SE Euclidean ART CT |
0.972 |
0.792 |
1.000 |
0.876 |
| SE Fuzzy ARTMAP CT |
0.889 |
0.458 |
0.955 |
0.468 |
| SE Euclidean ARTMAP CT |
0.872 |
0.458 |
0.936 |
0.417 |
Table 11.
Average result after Monte Carlo cross-validation for the Data.
Table 11.
Average result after Monte Carlo cross-validation for the Data.
| Metrics |
Average result (CI 95%) |
| ACC |
0.9265 (0.9180 – 0.9350) |
| Se |
0.4714 (0.4045 – 0.5382) |
| Sp |
0.9965 (0.9951 – 0.9979) |
| MCC |
0.6195 (0.5656 – 0.6734) |
| F
|
0.5924 (0.5268 – 0.6580) |
Table 12.
Comparison of the results for each data set.
Table 12.
Comparison of the results for each data set.
| Author |
Model |
Data |
Partition |
ACC |
Se |
Sp |
MCC |
F-Score |
AUC |
| This study |
SE Fuzzy ART |
Data
|
70–30 |
0.8000 |
0.8704 |
0.6774 |
0.5610 |
0.8468 |
0.7739 |
| |
SE Euclidean ART |
Data
|
70–30 |
0.7059 |
0.7593 |
0.6129 |
0.3697 |
0.7664 |
0.6861 |
| |
SE Fuzzy ARTMAP |
Data
|
70–30 |
0.8353 |
0.8704 |
0.7742 |
0.6446 |
0.8704 |
- |
| |
SE Fuzzy ART CT |
Data
|
70–30 |
0.8706 |
0.9259 |
0.7742 |
0.7170 |
0.9009 |
0.8501 |
| |
SE Euclidean ART CT |
Data
|
70–30 |
0.7412 |
0.7778 |
0.6774 |
0.4496 |
0.7925 |
0.7276 |
| |
SE Fuzzy ARTMAP CT |
Data
|
70–30 |
0.8000 |
0.7593 |
0.8710 |
0.6078 |
0.8283 |
- |
| |
SE Euclidean ARTMAP CT |
Data
|
70–30 |
0.6353 |
0.7778 |
0.3871 |
0.1763 |
0.7304 |
- |
| |
SE Fuzzy ART CT |
Data
|
Monte Carlo |
0.8061 |
0.8211 |
0.7800 |
0.6555 |
0.8679 |
0.8006 |
| [93] |
ET |
Data
|
4-Fold |
0.8000 |
0.7500 |
0.9444 |
0.6133 |
0.8478 |
0.7710 |
| |
DNN |
Data
|
4-Fold |
0.9211 |
0.9614 |
0.8456 |
0.8250 |
0.9388 |
0.9220 |
| |
TWRF |
Data
|
70-30 |
0.8600 |
0.9500 |
0.7500 |
- |
- |
- |
| [21] |
RF |
Data
|
80-20 |
0.8200 |
0.9200 |
0.6500 |
- |
- |
0.8400 |
| This study |
SE Fuzzy ART |
Data
|
70–30 |
0.7500 |
0.7459 |
0.7540 |
0.4996 |
0.7426 |
0.7499 |
| |
SE Euclidean ART |
Data
|
70–30 |
0.7275 |
0.6907 |
0.7619 |
0.4540 |
0.7102 |
0.7263 |
| |
SE Fuzzy ARTMAP |
Data
|
70–30 |
0.7828 |
0.7924 |
0.7738 |
0.5659 |
0.7792 |
- |
| |
SE Fuzzy ART CT |
Data
|
70–30 |
0.9836 |
0.9703 |
0.9960 |
0.9674 |
0.9828 |
0.9481 |
| |
SE Euclidean ART CT |
Data
|
70–30 |
0.7807 |
0.5466 |
1.000 |
0.6194 |
0.7068 |
0.7733 |
| |
SE Fuzzy ARTMAP CT |
Data
|
70–30 |
0.7377 |
0.7119 |
0.7619 |
0.4745 |
0.7241 |
- |
| |
SE Euclidean ARTMAP CT |
Data
|
70–30 |
0.6967 |
0.7119 |
0.6828 |
0.3942 |
0.6942 |
- |
| |
SE Fuzzy ART CT |
Data
|
Monte Carlo |
0.9348 |
0.8992 |
0.9682 |
0.8721 |
0.9301 |
0.9395 |
| [93] |
ET |
Data
|
4-Fold |
0.8498 |
0.8788 |
0.8221 |
0.7012 |
0.8509 |
0.8510 |
| |
DNN |
Data
|
4-Fold |
0.9316 |
0.9327 |
0.9302 |
0.8633 |
0.9263 |
0.9320 |
| [58] |
KNN |
Data
|
hold-out |
0.8600 |
0.8000 |
0.9200 |
- |
- |
0.8700 |
| This study |
SE Fuzzy ART |
Data
|
70–30 |
0.8889 |
0.2083 |
0.9936 |
0.3824 |
0.3333 |
0.6010 |
| |
SE Euclidean ART |
Data
|
70–30 |
0.8778 |
0.5000 |
0.9359 |
0.4524 |
0.5217 |
0.7179 |
| |
SE Fuzzy ARTMAP |
Data
|
70–30 |
0.8667 |
0.3750 |
0.9423 |
0.3595 |
0.4286 |
- |
| |
SE Fuzzy ART CT |
Data
|
70–30 |
0.9444 |
0.5833 |
1.0000 |
0.7404 |
0.7368 |
0.7917 |
| |
SE Euclidean ART CT |
Data
|
70–30 |
0.9722 |
0.7917 |
1.0000 |
0.8758 |
0.8837 |
0.8962 |
| |
SE Fuzzy ARTMAP CT |
Data
|
70–30 |
0.8889 |
0.4583 |
0.9551 |
0.4685 |
0.5238 |
- |
| |
SE Euclidean ARTMAP CT |
Data
|
70–30 |
0.8722 |
0.4583 |
0.9359 |
0.4175 |
0.4889 |
- |
| |
SE Euclidean ART CT |
Data
|
Monte Carlo |
0.9265 |
0.4714 |
0.9965 |
0.6195 |
0.5924 |
0.7458 |
| [93] |
ET |
Data
|
4-Fold |
0.9200 |
0.7143 |
0.9301 |
0.4530 |
0.4545 |
0.6590 |
| |
DNN |
Data
|
4-Fold |
0.9333 |
0.7705 |
0.9547 |
0.6904 |
0.7249 |
0.8597 |
| [54] |
LSTM |
Data
|
10-Fold |
0.8666 |
0.9942 |
- |
- |
0.9189 |
0.6250 |
| |
CNN-LSTM |
Data
|
80–20 |
0.9230 |
0.9368 |
- |
- |
0.9300 |
0.9000 |
|
SE: Self-Expanding; CT: Continuous Training; ET: Extremely Randomized Trees; DNN: Deep Neural Network; RF: Random Forest; TWRF: Three-way Random Forest; KNN: K Nearest neighbors; LSTM: Long short-term memory; CNN: Convolutional Neural Networks. |
Table 13.
Computational time (in seconds) for each dataset.
Table 13.
Computational time (in seconds) for each dataset.
| Model |
Data
|
Data
|
Data
|
| SE Fuzzy ART CT |
1.25 |
6.34 |
5.14 |
| SE Euclidean ART CT |
1.22 |
0.62 |
1.67 |
| DNN |
20.2 |
40.32 |
21.01 |
Table 14.
Results obtained by each model for the combined data set.
Table 14.
Results obtained by each model for the combined data set.
| Model |
SE Fuzzy ART CT |
KNN |
RF |
MLP |
LR |
ET |
XGB |
NB |
| ACC |
0.9828 |
0.7277 |
0.7931 |
0.7825 |
0.7617 |
0.7748 |
0.7333 |
0.7429 |
| Se |
0.9667 |
0.5986 |
0.7014 |
0.6806 |
0.6389 |
0.5806 |
0.8722 |
0.6806 |
| Sp |
0.9920 |
0.8019 |
0.8458 |
0.8411 |
0.8323 |
0.8866 |
0.6534 |
0.7788 |
| F-Score |
0.9762 |
0.6162 |
0.7123 |
0.6955 |
0.6619 |
0.6531 |
0.7048 |
0.6590 |
| MCC |
0.9628 |
0.4059 |
0.5510 |
0.5267 |
0.4790 |
0.4988 |
0.5076 |
0.4536 |
Table 15.
Results obtained by each model trained with the combined data and validated with Dados.
Table 15.
Results obtained by each model trained with the combined data and validated with Dados.
| Model |
SE Fuzzy ART CT |
KNN |
RF |
MLP |
LR |
ET |
XGB |
NB |
|
0.9770 |
0.7169 |
0.7834 |
0.7724 |
0.7547 |
0.7633 |
0.7308 |
0.7331 |
|
0.9661 |
0.5834 |
0.6813 |
0.6625 |
0.6286 |
0.5609 |
0.8595 |
0.6637 |
|
0.9838 |
0.7991 |
0.8462 |
0.8400 |
0.8323 |
0.8879 |
0.6515 |
0.7759 |
| F-Score |
0.9698 |
0.6110 |
0.7057 |
0.6893 |
0.6614 |
0.6436 |
0.7087 |
0.6547 |
|
0,9513 |
0,3903 |
0,5355 |
0,5112 |
0,4714 |
0,4838 |
0,5076 |
0,4374 |
Table 16.
Results obtained by each model trained with the combined data and validated by Dados.
Table 16.
Results obtained by each model trained with the combined data and validated by Dados.
| Modelo |
SE Fuzzy ART CT |
KNN |
RF |
MLP |
LR |
ET |
XGB |
NB |
|
0,9645 |
0,7326 |
0,7863 |
0,7699 |
0,7539 |
0,7654 |
0,7326 |
0,7370 |
|
0,9710 |
0,6388 |
0,7168 |
0,6901 |
0,6589 |
0,6042 |
0,8796 |
0,7101 |
|
0,9601 |
0,7947 |
0,8323 |
0,8227 |
0,8168 |
0,8722 |
0,6352 |
0,7548 |
| F-Score |
0,9561 |
0,6556 |
0,7278 |
0,7050 |
0,6809 |
0,6725 |
0,7239 |
0,6827 |
|
0,9266 |
0,4377 |
0,5522 |
0,5168 |
0,4817 |
0,5011 |
0,5090 |
0,4597 |