Prerpints.org logo
Preprint
Article

Valuation of Currency Option based on Uncertain Fractional Differential Equation

Altmetrics

Downloads

103

Views

19

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

15 April 2024

Posted:

16 April 2024

You are already at the latest version

Alerts
Abstract
Uncertain fractional differential equation (UFDE) is an excellent tool for describing complicated dynamic systems. This paper analyzes the valuation problems of currency option based on UFDE under optimistic value criterion. Firstly, an uncertain fractional currency model is formulated to describe the dynamics of foreign exchange rate. Then, the pricing formulae of European, American and Asian currency option are obtained under optimistic value criterion, respectively. Finally, numerical simulations are provided to illustrate the validity of our theoretical results.
Keywords: 
Subject: Computer Science and Mathematics  -   Applied Mathematics

1. Introduction

A currency option is a contract that offers its holder the entitlement to purchase a certain amount of foreign currency with a predetermined exchange rate at maturity or within the validity period. This kind of option not only has the characteristic of nonlinear profits, it also has the functions of investment, hedging and risk avoidance. Compared to traditional forward foreign exchange contract, currency option is a more flexible derivative. The first development of pricing currency option may be traced back to the study of Garman and Kohlhagen (1983). They assumed that the exchange rate followed a geometric Brownian motion and derived the pricing formula of European currency option. Despite the popularity of Garman and Kohlhagen (G-K) model, there were still some inconsistencies in the model. From then on, many methodologies of pricing currency option were introduced by modifying G-K model, such as Baldeauxa et al. (2015), Lian and Chen (2022). Considering the fluctuation of interest rate over time, Grabbe (1983) assumed that both interest rates and exchange rate to be stochastic and constructed a new pricing model for currency option. Motivated by this idea, many scholars gave numerous extensions of Grabbe model, such as Carr and Wu (2007), Van and Pelsser (2011).
As mentioned above, the previous studies on currency option pricing are based on probability theory. A precondition of using probabilistic theory is that the distribution function is close enough to the frequency in the future, but numerous empirical studies show that the real world is far from frequency stability. This fact makes the distribution function obtained in practice usually deviate from the frequency. Based on this situation, we cannot but rely on the belief degrees of domain experts for each indeterminate event. To deal with belief degree reasonably, Liu (2007) established uncertainty theory based on normality, duality, subadditivity and product axioms. Nowadays it has become a branch of axiomatic mathematics to simulate human uncertainty and received wide applications.
Owing to some antinomies in random theory (Liu 2013), uncertain financial theory on the basis of uncertain differential equations (UDEs, Liu 2008) emerges as the times require. If the underlying stock price followed a geometric Liu process, Liu (2009) presented an uncertain stock model and derived its European option pricing formulas. Afterwards, Liu et al. (2015) applied UDE to model exchange rate and first put forward an uncertain currency model. Shen and Yao (2016) extended this model to a mean-reverting currency model and derived the corresponding currency option prices. Considering the fierce drifts of exchange rate, Ji and Wu (2017) provided a currency exchange rate model with jumps. Li and Sheng (2022) gave an uncertain exponential currency model and calculated the currency option prices. For the recent research on uncertain finance, readers can refer to references (Deng and Qin 2021; Yan et al. 2022; Jin et al. 2023).
These models are built on the differential equations of first order. In realistic financial markets, the future asset price not only relies on the current price, but it also correlates with the past condition. Different from integer-order differential equations, fractional differential equations (FDEs) have the characteristics of long memory and non-locality, which can better model the fluctuations of asset prices. Zhu (2015) first introduced uncertain factors into FDEs and presented the definition of UFDE. Then, Lu and Zhu (2019) put forward the concept of α -path and gave an efficient numerical method. Based on UFDE, Lu et al. (2019a) presented a new type of uncertain stock model and calculated its European option prices. Lu et al. (2019b) discussed the prices of Asian option under uncertain fractional stock model. Following that, Liu et al. (2022) used UFDE to describe exchange rate and proposed an uncertain fractional currency model. In addition, other financial problems were also discussed based on UFDE, such as barrier option (Jin et al. 2021), barrier swaption (Lu et al. 2022), and vulnerable option (Lei et al. 2023).
Because of the possibility of drastic fluctuation in asset price, investors would not always take expected value criteria as their sole investment guideline. Instead, they usually consider the best case at a certain confidence level. Based on the analysis above, this paper will study the valuation issues of currency option under optimistic criterion based on UFDE. To the best of our knowledge, the research on this topic has not yet been done. This paper is structured as follows. Section 2 reviews some useful results on UFDE and an uncertain fractional currency model. Section 3 presents a new currency model and computes the prices of European, American and Asian currency option based on optimistic value criterion, respectively. Section 4 performs numerical examples to illustrate our theoretical results. Section 5 provides a concise conclusion.

2. Preliminaries

In this part, we recall some important results on UFDE and an uncertain fractional currency model. For more information about uncertainty theory, readers may refer to Liu (2015) for a better understanding. Unless stated otherwise, the fractional order p is always assumed to satisfy n − 1 < p ≤ n ,   n ∈ N + .

2.1. UFDE with Caputo Type

Zhu (2015) proposed two kinds of UFDEs: Riemann-Liouville type and Caputo type. As previously discussed (Ford and Simpson 2001; Diethelm et al. 2002), Caputo fractional derivative is more appropriate to model uncertain dynamic systems than Riemann-Liouville derivative. Thus, this paper only focuses on the Caputo type of UFDE.
Definition 2.1 
(Zhu 2015) Assume g 1 , g 2 are two functions defined on 0 , + ∞ × R and C t is a Liu process. Then
  c D p Y t = g 1 t , Y t + g 2 t , Y t d C t d t
is called the UFDE of Caputo type.
Definition 2.2 
(Lu et al. 2019a) Assume g 1 , g 2 are two functions defined on 0 , + ∞ × R Then the solution of the related equation with initial conditions
  c D p Y t = g 1 ( t , Y t ) + g 2 ( t , Y t ) d C t d t Y ( l ) ( 0 ) = y l , l = 0 , 1 , … , n − 1
is an uncertain process Y t that satisfies
Y t = ∑ l = 0 n − 1 y l t l Γ ( l + 1 ) + 1 Γ ( p ) ∫ 0 t ( t − v ) p − 1 g 1 ( v , Y v ) d v + 1 Γ ( p ) ∫ 0 t ( t − v ) p − 1 g 2 ( v , Y v ) d C v .
Definition 2.3 
(Lu and Zhu 2019) An UFDE (2) is considered to have an α -path Y t   α ( 0 < α < 1 ) if it is the solution of the associated FDE
  c D p Y t   α = g 1 ( t , Y t   α ) + g 2 ( t , Y t   α ) γ − 1 ( α ) , Y ( l ) ( 0 ) = y l , l = 0 , 1 , … , n − 1
where γ − 1 α = 3 π ln α 1 − α .
Theorem 2.1 
(Lu and Zhu 2019) Assume UFDE (2) has a solution  Y t  and  α -  path  Y t   α  Then
M Y t ≤ Y t   α , ∀ t = α ,
M Y t > Y t   α , ∀ t = 1 − α .
Moreover,  Y t  has an inverse uncertainty distribution (IUD)
I t   − 1 α = Y t   α .
Theorem 2.2 
(Jin et al. 2019) Assume UFDE (2) has a solution  Y t  and  α -  path  Y t   α  Then the supremum sup 0 ≤ t ≤ T H ( Y t )  has an IUD
Ψ T   − 1 ( α ) = sup 0 ≤ t ≤ T H ( Y t   α ) ζ T   − 1 ( α ) = sup 0 ≤ t ≤ T H ( Y t   1 − α ) ,
where  H ( y )  is a strictly increasing (decreasing) function.
Theorem 2.3 
(Jin et al. 2020) Assume UFDE (2) has a solution  Y t  and  α -  path  Y t   α  Then the integral  ∫ 0 T H ( Y t ) d t  has an IUD
Ψ T   − 1 ( α ) = ∫ 0 T H ( Y t   α ) d t ζ T   − 1 ( α ) = ∫ 0 T H ( Y t   1 − α ) d t ,
where  H ( y )  is a strictly increasing (decreasing) function.

2.2. Uncertain Fractional Currency Model

In realistic financial markets, the future exchange rate not only relies on the current value, it also correlates with the past state. Unlike integer order differential equation, FDE provides an excellent tool to reflect the memory and hereditary properties of exchange rate. Assume X t and Y t are the domestic riskless currency and foreign riskless currency, respectively, and that foreign exchange rate Z t obeys an UFDE of Caputo type, Liu et al. (2022) introduced an uncertain fractional currency model
d X t = r d X t d t d Y t = r f Y t d t D c   p Z t = a Z t + b Z t d C t d t Z t l   t = 0 = z l , l = 0 , 1 , … , n − 1
where r d and r f denote the domestic interest rate and foreign interest rate, respectively, a and b are the drift and diffusion of foreign exchange rate, respectively, and C t is a canonical Liu process.

3. Currency Option Pricing

In real financial markets, investors would not always take expected value criteria as their sole guideline due to the possibility of drastic fluctuation in asset price. Based on the confidence in the change trend of future asset price, investors usually consider the maximum benefit at a certain confidence level. Lu et al. (2019b) first introduced the idea of VaR into the research of option pricing and discussed the valuation of Asian option based on optimistic criterion. Motivated by these ideas, this section studies the prices of currency option under optimistic criterion.

3.1. Mean-Reverting Uncertain Fractional Currency Model

In model (10), Liu et al. (2022) analyzed the short-run fluctuations in exchange rate. However, the actual exchange rate oscillates periodically around a certain level in a long run. Considering this situation, we present a mean-reverting currency model for the long term
d X t = r d X t d t d Y t = r f Y t d t D c   p Z t = a − b Z t + c d C t d t Z t l   t = 0 = z l , l = 0 , 1 , … , n − 1
where a , b , c > 0 ,   b is the reversion rate, a / b is the average exchange rate, c is the exchange rate’s volatility.

3.2. European Currency Option

Suppose a European currency option’s striking price is K and that maturity date is T . Set f 1 in domestic currency as the contract price. At initial time 0, the investor pays f 1 for purchasing this contract and receives the maximum benefit at time T based on optimistic criterion [ ( Z T − K ) + ] sup ( δ ) , where δ is the confidence level. Hence, the investor obtains the net return at time 0
− f 1 + exp − r d T [ ( Z T − K ) + ] sup ( δ ) .
On the other hand, the bank obtains profit f 1 for selling this contract at time 0, and pays 1 − K Z T + sup δ in foreign currency at time T . Hence, the bank can receive the net earning at time 0
f 1 − Z 0 exp − r f T 1 − K Z T + sup δ .
It follows from the fair price principle that the definition of a European currency option price is given as follows.
Definition 3.1 
Assuming that a European currency option’s striking price is K and maturity date is T . Then the option price under confidence level δ based on optimistic criterion is
f 1 = 1 2 exp − r d T Z T − K + sup δ + Z 0 2 exp − r f T 1 − K Z T + sup δ .
Theorem 3.1 
Suppose a European currency option for model (11) has a striking price  K  and that its expiration time is  T .  Then the option price under confidence level  δ  based on optimistic value criteria is
f 1 = 1 2 exp − r d T Ψ T − 1 ( 1 − δ ) − K + + Z 0 2 exp − r f T 1 − K Ψ T − 1 ( 1 − δ ) + ,
where  Ψ T − 1 1 − δ = ∑ l = 0 n − 1 z l T l E p , ( l + 1 ) − b T p + a + c 3 π ln 1 − δ δ T p E p , ( p + 1 ) − b T p ,
E x , y q = ∑ u = 0 ∞ q u Γ u x + y .
Proof. 
Based on Lu and Zhu (2019), we get the IUD of foreign exchange rate Z t
Ψ t   − 1 α = Z t α = ∑ l = 0 n − 1 z l t l E p , ( l + 1 ) − b t p + a + c 3 π ln α 1 − α t p E p , ( p + 1 ) − b t p .
According to the definition of optimistic value for uncertain variable, we get
Z T − K + sup δ = sup η ≥ 0 η Μ Z T − K + ≥ η ≥ δ = sup η > 0 η Μ Z T − K ≥ η ≥ δ ∨ 0 = sup η > 0 η 1 − Μ Z T < K + η ≥ δ ∨ 0 = sup η > 0 η 1 − Ψ T K + η ≥ δ ∨ 0 = sup η > 0 η Ψ T K + η ≤ 1 − δ ∨ 0 = sup η > 0 η Ψ T − 1 Ψ T K + η ≤ Ψ T − 1 1 − δ ∨ 0 = sup η > 0 η K + η ≤ Ψ T − 1 1 − δ ∨ 0 = sup η > 0 η η ≤ Ψ T − 1 1 − δ − K ∨ 0 = Ψ T − 1 1 − δ − K + .
By use of the similar method, we can get
1 − K Z T + sup δ = sup ξ ≥ 0 ξ Μ 1 − K Z T + ≥ ξ ≥ δ = sup ξ > 0 ξ Μ 1 − K Z T ≥ ξ ≥ δ ∨ 0 = sup ξ > 0 ξ Μ ( 1 − ξ ) Z T ≥ K ≥ δ ∨ 0 = sup 0 < ξ < 1 ξ Μ Z T ≥ K 1 − ξ ≥ δ ∨ 0 = sup 0 < ξ < 1 ξ 1 − Μ Z T < K 1 − ξ ≥ δ ∨ 0 = sup 0 < ξ < 1 ξ 1 − Ψ T K 1 − ξ ≥ δ ∨ 0 = sup 0 < ξ < 1 ξ Ψ T K 1 − ξ ≤ 1 − δ ∨ 0 = sup 0 < ξ < 1 ξ Ψ T − 1 Ψ T K 1 − ξ ≤ Ψ T − 1 1 − δ ∨ 0 = sup 0 < ξ < 1 ξ K 1 − ξ ≤ Ψ T − 1 1 − δ ∨ 0 = sup 0 < ξ < 1 ξ ξ ≤ 1 − K Ψ T − 1 1 − δ ∨ 0 = 1 − K Ψ T − 1 1 − δ + .
It follows from Definition 3.1 that we finally have
f 1 = 1 2 exp − r d T Z T − K + sup δ + Z 0 2 exp − r f T 1 − K Z T + sup δ = 1 2 exp − r d T Ψ T − 1 ( 1 − δ ) − K + + Z 0 2 exp − r f T 1 − K Ψ T − 1 ( 1 − δ ) + ,
where Ψ T − 1 1 − δ = ∑ l = 0 n − 1 z l T l E p , ( l + 1 ) − b T p + a + c 3 π ln 1 − δ δ T p E p , ( p + 1 ) − b T p .
Hence, the result (13) is proved. ☐

3.3. American Currency Option

Suppose an American currency option’s striking price is K and that maturity date is T . Set f 2 in domestic currency as the contract price. At time 0, the investor pays f 2 for purchasing this contract and receives the maximum benefit based on optimistic value criterion sup 0 ≤ t ≤ T exp ( − r d t ) ( Z t − K ) + sup ( δ ) , where δ is the confidence level. Hence, the investor obtains the net return at time 0
− f 2 + sup 0 ≤ t ≤ T exp ( − r d t ) ( Z t − K ) + sup ( δ ) .
Meanwhile, the bank obtains profit f 2 for selling this contract at time 0, and pays sup 0 ≤ t ≤ T exp − r f t Z 0 1 − K Z t + sup δ . Hence, the bank can receive the net earning at time 0
f 2 − sup 0 ≤ t ≤ T exp − r f t Z 0 1 − K Z t + sup δ .
It follows from the fair price principle that the definition of an American currency option price is given as follows.
Definition 3.2 
Assuming that an American currency option’s striking price is K and maturity date is T . Then the option price under confidence level δ based on optimistic criterion is
f 2 = 1 2 sup 0 ≤ t ≤ T exp ( − r d t ) ( Z t − K ) + sup ( δ ) + Z 0 2 sup 0 ≤ t ≤ T exp ( − r f t ) 1 − K Z t + sup ( δ ) .
Theorem 3.2 
Suppose that an American currency option of model (11) has a striking price K and its maturity date is  T . Then the option price under confidence level  δ  based on optimistic value criteria is
f 2 = 1 2 sup 0 ≤ t ≤ T exp ( − r d t ) Ψ t − 1 ( 1 − δ ) − K + + Z 0 2 sup 0 ≤ t ≤ T exp ( − r f t ) 1 − K Ψ t − 1 ( 1 − δ ) + ,
where  Ψ t − 1 1 − δ = ∑ l = 0 n − 1 z l t l E p , ( l + 1 ) − b t p + a + c 3 π ln 1 − δ δ t p E p , ( p + 1 ) − b t p .
Proof. 
Based on Lu and Zhu (2019), we can easily obtain that Z t has an IUD
Ψ t   − 1 α = Z t α = ∑ l = 0 n − 1 z l t l E p , ( l + 1 ) − b t p + a + c 3 π ln α 1 − α t p E p , ( p + 1 ) − b t p .
It follows from Theorem 2.2 that the IUD of sup 0 ≤ t ≤ T exp ( − r d t ) ( Z t − K ) + is
φ T − 1 ( α ) = sup 0 ≤ t ≤ T exp ( − r d t ) Ψ t − 1 ( α ) − K + ,
and the IUD of sup 0 ≤ t ≤ T exp ( − r f t ) 1 − K Z t + is
Ω T − 1 ( α ) = sup 0 ≤ t ≤ T exp ( − r f t ) 1 − K Ψ t − 1 ( α ) + .
According to the definition of optimistic value for uncertain variable, we have
sup 0 ≤ t ≤ T exp ( − r d t ) ( Z t − K ) + sup ( δ ) = sup ϖ ≥ 0 ϖ Μ sup 0 ≤ t ≤ T exp ( − r d t ) ( Z t − K ) + ≥ ϖ ≥ δ = sup ϖ ≥ 0 ϖ 1 − Μ sup 0 ≤ t ≤ T exp ( − r d t ) ( Z t − K ) + < ϖ ≥ δ = sup ϖ ≥ 0 ϖ 1 − φ T ϖ ≥ δ = sup ϖ ≥ 0 ϖ φ T ϖ ≤ 1 − δ = sup ϖ ≥ 0 ϖ φ T − 1 φ T ϖ ≤ φ T − 1 1 − δ = sup ϖ ≥ 0 ϖ ϖ ≤ φ T − 1 ( 1 − δ ) = φ T − 1 ( 1 − δ ) .
By use of the similar method, we can get
sup 0 ≤ t ≤ T exp − r f t 1 − K Z t + sup δ = sup β ≥ 0 β Μ sup 0 ≤ t ≤ T exp − r f t 1 − K Z t + ≥ β ≥ δ = sup β ≥ 0 β 1 − Μ sup 0 ≤ t ≤ T exp − r f t 1 − K Z t + < β ≥ δ = sup β ≥ 0 β 1 − Ω T ( β ) ≥ δ = sup β ≥ 0 β Ω T ( β ) ≤ 1 − δ = sup β ≥ 0 β Ω T − 1 Ω T ( β ) ≤ Ω T − 1 1 − δ = sup β ≥ 0 β β ≤ Ω T − 1 1 − δ = Ω T − 1 1 − δ .
It follows from Definition 3.2 that we finally have
f 2 = 1 2 sup 0 ≤ t ≤ T exp ( − r d t ) ( Z t − K ) + sup ( δ ) + Z 0 2 sup 0 ≤ t ≤ T exp ( − r f t ) 1 − K Z t + sup ( δ ) = 1 2 φ T − 1 ( 1 − δ ) + Z 0 2 Ω T − 1 ( 1 − δ ) = 1 2 sup 0 ≤ t ≤ T exp ( − r d t ) Ψ t − 1 ( 1 − δ ) − K + + Z 0 2 sup 0 ≤ t ≤ T exp ( − r f t ) 1 − K Ψ t − 1 ( 1 − δ ) + ,
where Ψ t − 1 1 − δ = ∑ l = 0 n − 1 z l t l E p , ( l + 1 ) − b t p + a + c 3 π ln 1 − δ δ t p E p , ( p + 1 ) − b t p .
Hence, the result (15) is proved. ☐

3.4. Asian Currency Option

Suppose an Asian currency option’s striking price is K and that maturity date is T . Set f 3 in domestic currency as the contract price. At initial time 0, the investor pays f 3 for purchasing this contract and receives the maximum benefit at time T based on optimistic criterion 1 T ∫ 0 T Z t d t − K + sup ( δ ) , where δ is the confidence level. Hence, the investor obtains the net return at time 0
− f 3 + exp − r d T 1 T ∫ 0 T Z t d t − K + sup ( δ ) .
On the other hand, the bank obtains profit f 3 for selling this contract at time 0, and pays 1 − K / 1 T ∫ 0 T Z t d t + sup δ in foreign currency at time T . Hence, the bank can receive the net earning at time 0
f 3 − Z 0 exp − r f T 1 − K / 1 T ∫ 0 T Z t d t + sup δ .
It follows from the fair price principle that the definition of an Asian currency option price is given as follows.
Definition 3.3 
Assuming that an Asian currency option’s striking price is K and maturity date is T . Then the option price under confidence level δ based on optimistic criterion is
f 3 = 1 2 exp − r d T 1 T ∫ 0 T Z t d t − K + sup δ + Z 0 2 exp − r f T 1 − K / 1 T ∫ 0 T Z t d t + sup δ .
Theorem 3.3 
Suppose an Asian currency option for model (11) has a striking price  K  and that its expiration time is  T . Then the option price under confidence level  δ based on optimistic value criteria is
f 3 = 1 2 exp − r d T I T − 1 ( 1 − δ ) − K + + Z 0 2 exp − r f T 1 − K I T − 1 ( 1 − δ ) + ,
where  I T − 1 1 − δ = ∑ l = 0 n − 1 z l T l E p , ( l + 2 ) − b T p + a + c 3 π ln 1 − δ δ T p E p , ( p + 2 ) − b T p .
Proof. 
Based on Lu and Zhu (2019), we can easily obtain that Z t has an IUD
Ψ t   − 1 α = Z t α = ∑ l = 0 n − 1 z l t l E p , ( l + 1 ) − b t p + a + c 3 π ln α 1 − α t p E p , ( p + 1 ) − b t p .
It follows from Theorem 2.3 that the IUD of 1 T ∫ 0 T Z t d t is
I T − 1 α = 1 T ∫ 0 T Z t α d t = 1 T ∫ 0 T ∑ l = 0 n − 1 z l t l E p , ( l + 1 ) − b t p + a + c 3 π ln α 1 − α t p E p , ( p + 1 ) − b t p d t = ∑ l = 0 n − 1 z l T l E p , ( l + 2 ) − b T p + a + c 3 π ln α 1 − α T p E p , ( p + 2 ) − b T p .
According to the definition of optimistic value for uncertain variable, we have
1 T ∫ 0 T Z t d t − K + sup δ = sup τ ≥ 0 τ Μ 1 T ∫ 0 T Z t d t − K + ≥ τ ≥ δ = sup τ > 0 τ Μ 1 T ∫ 0 T Z t d t − K ≥ τ ≥ δ ∨ 0 = sup τ > 0 τ 1 − Μ 1 T ∫ 0 T Z t d t < K + τ ≥ δ ∨ 0 = sup τ > 0 τ 1 − I T K + τ ≥ δ ∨ 0 = sup τ > 0 τ I T K + τ ≤ 1 − δ ∨ 0 = sup τ > 0 τ I T − 1 I T K + τ ≤ I T − 1 ( 1 − δ ) ∨ 0 = sup τ > 0 τ K + τ ≤ I T − 1 1 − δ ∨ 0 = sup τ > 0 τ τ ≤ I T − 1 1 − δ − K ∨ 0 = I T − 1 1 − δ − K + .
By use of the similar method, we can get
1 − K / 1 T ∫ 0 T Z t d t + sup δ = sup υ ≥ 0 υ M 1 − K / 1 T ∫ 0 T Z t d t + ≥ υ ≥ δ = sup υ > 0 υ M 1 − K / 1 T ∫ 0 T Z t d t ≥ υ ≥ δ ∨ 0 = sup υ > 0 υ M ( 1 − υ ) 1 T ∫ 0 T Z t d t ≥ K ≥ δ ∨ 0 = sup 0 < υ < 1 υ M 1 T ∫ 0 T Z t d t ≥ K 1 − υ ≥ δ ∨ 0 = sup 0 < υ < 1 υ 1 − M 1 T ∫ 0 T Z t d t < K 1 − υ ≥ δ ∨ 0 = sup 0 < υ < 1 υ 1 − I T K 1 − υ ≥ δ ∨ 0 = sup 0 < υ < 1 υ I T K 1 − υ ≤ 1 − δ ∨ 0 = sup 0 < υ < 1 υ I T − 1 I T K 1 − υ ≤ I T − 1 ( 1 − δ ) ∨ 0 = sup 0 < υ < 1 υ K 1 − υ ≤ I T − 1 ( 1 − δ ) ∨ 0 = sup 0 < υ < 1 υ υ ≤ 1 − K I T − 1 1 − δ ∨ 0 = 1 − K I T − 1 1 − δ + .
It follows from Definition 3.3 that we finally have
f 3 = 1 2 exp − r d T 1 T ∫ 0 T Z t d t − K + sup δ + Z 0 2 exp − r f T 1 − K / 1 T ∫ 0 T Z t d t + sup δ = 1 2 exp − r d T I T − 1 ( 1 − δ ) − K + + Z 0 2 exp − r f T 1 − K I T − 1 ( 1 − δ ) + ,
where I T − 1 1 − δ = ∑ l = 0 n − 1 z l T l E p , ( l + 2 ) − b T p + a + c 3 π ln 1 − δ δ T p E p , ( p + 2 ) − b T p .
Hence, the result (17) is proved. ☐

4. Numerical Experiments

This section provides numerical examples to further explain our theoretical results.
Example 4.1 
Assume r d = 0.05 , r f = 0.04 , a = 6 , b = 1 , c = 0.1 , z 0 = 4 , z 1 = 0.5 ,   K = 5 ,   T = 1. By use of the pricing formula (13), we calculate the price of European currency option with different order p   0 < p ≤ 2  and δ  under optimistic criterion, as presented in Table 1.
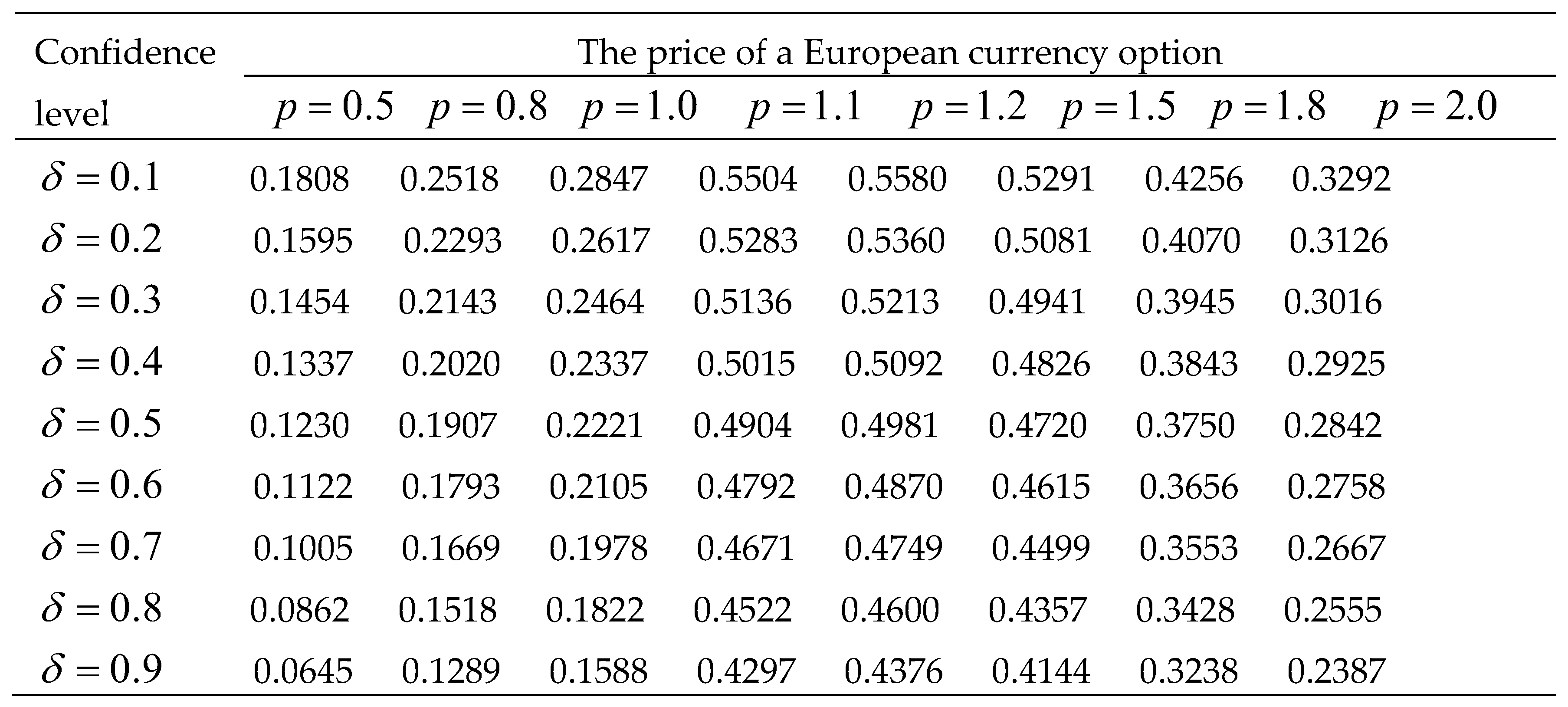
From Table 1, we first discover when confidence level  δ  remains unchanged, the price  f 1  is increasing about  p  when  p ∈ 0 , 1.2 , but it is decreasing when  p ∈ 1.2 , 2 .  The price jumps when  p  converts 1 into 1.1, and this is because instantaneous growth rate of exchange rate  z 1  works at this time. Meanwhile, we find the price  f 1  decreases with the increase of confidence level  δ  when  p  is fixed, which is in accord with the real financial markets: the more confident investors are in the future change of exchange rate, the less willing they are to spend more to diminish latent risks.
Table 1. The price f 1 with different confidence level δ and order p .
Table 1. The price f 1 with different confidence level δ and order p .
Preprints 103939 i001
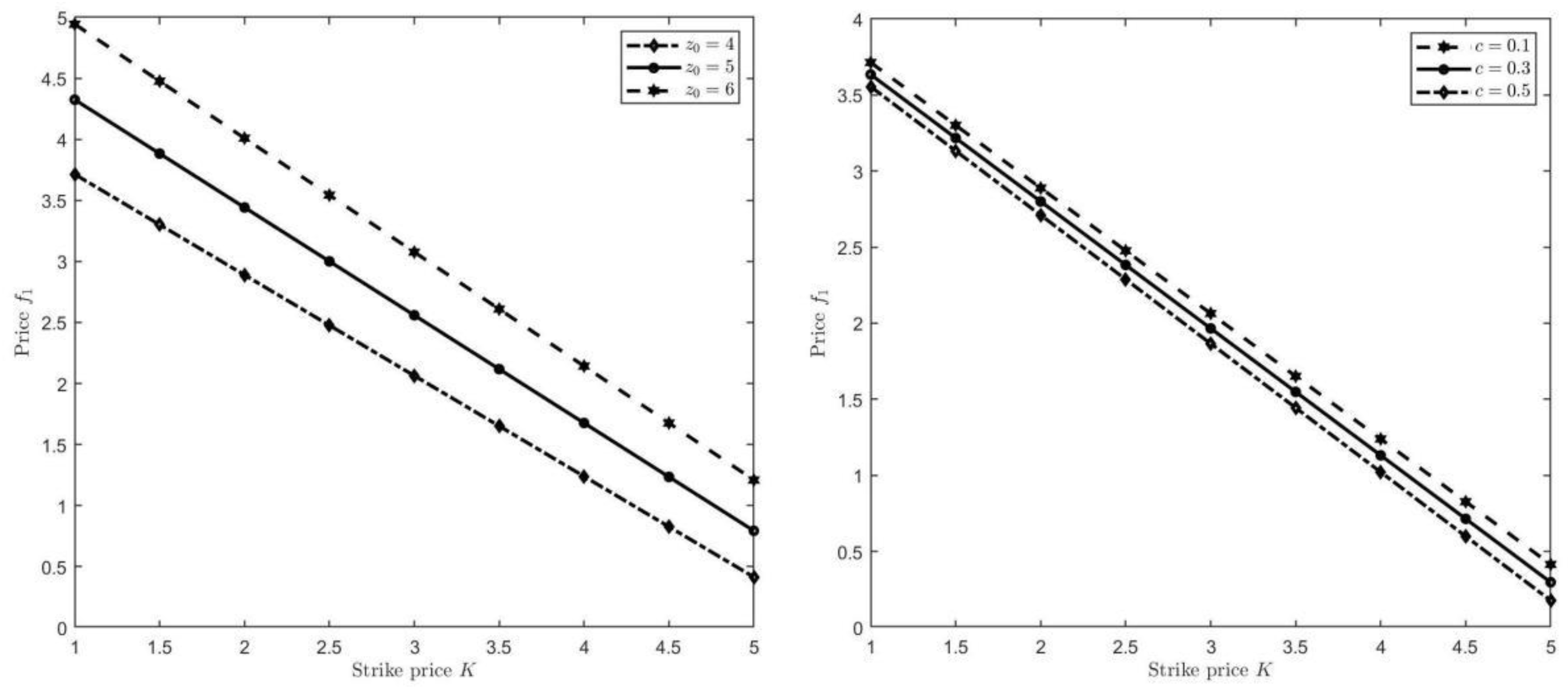
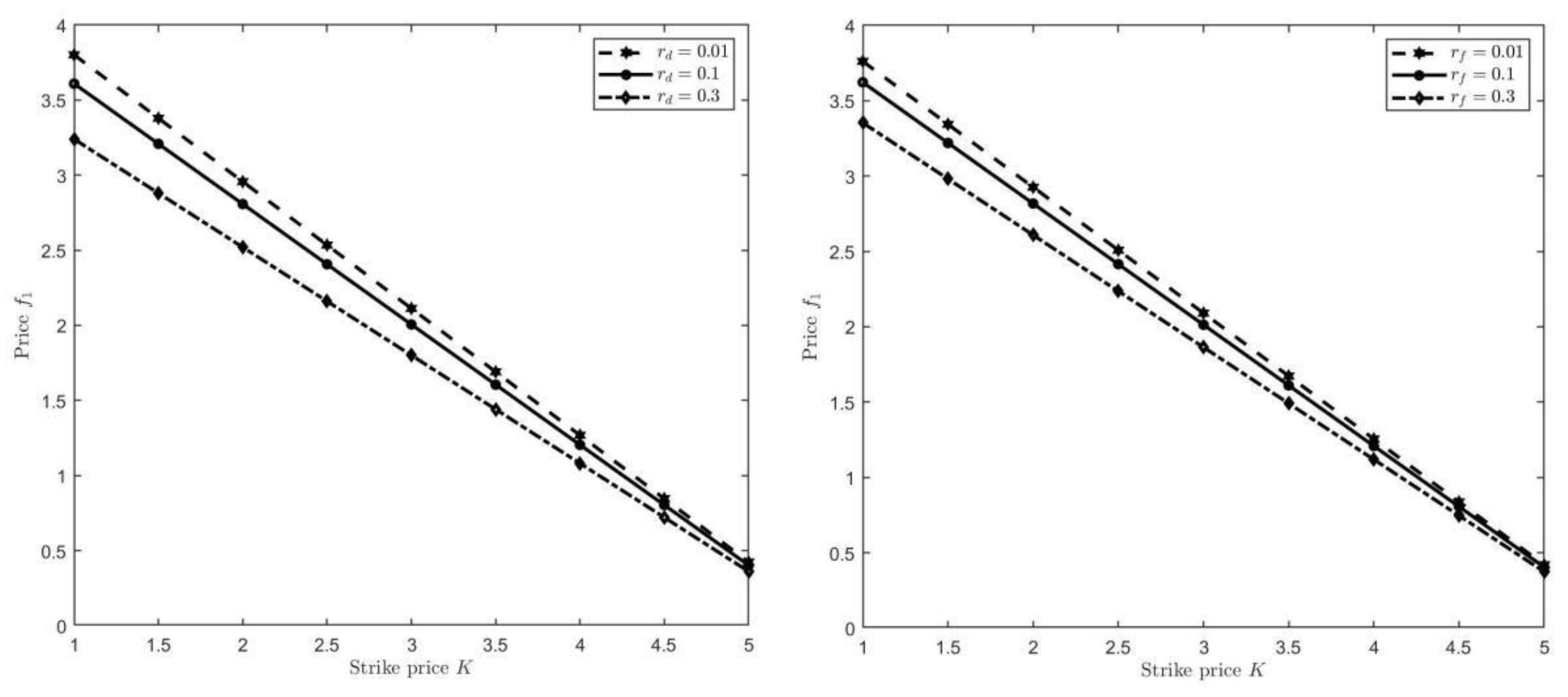
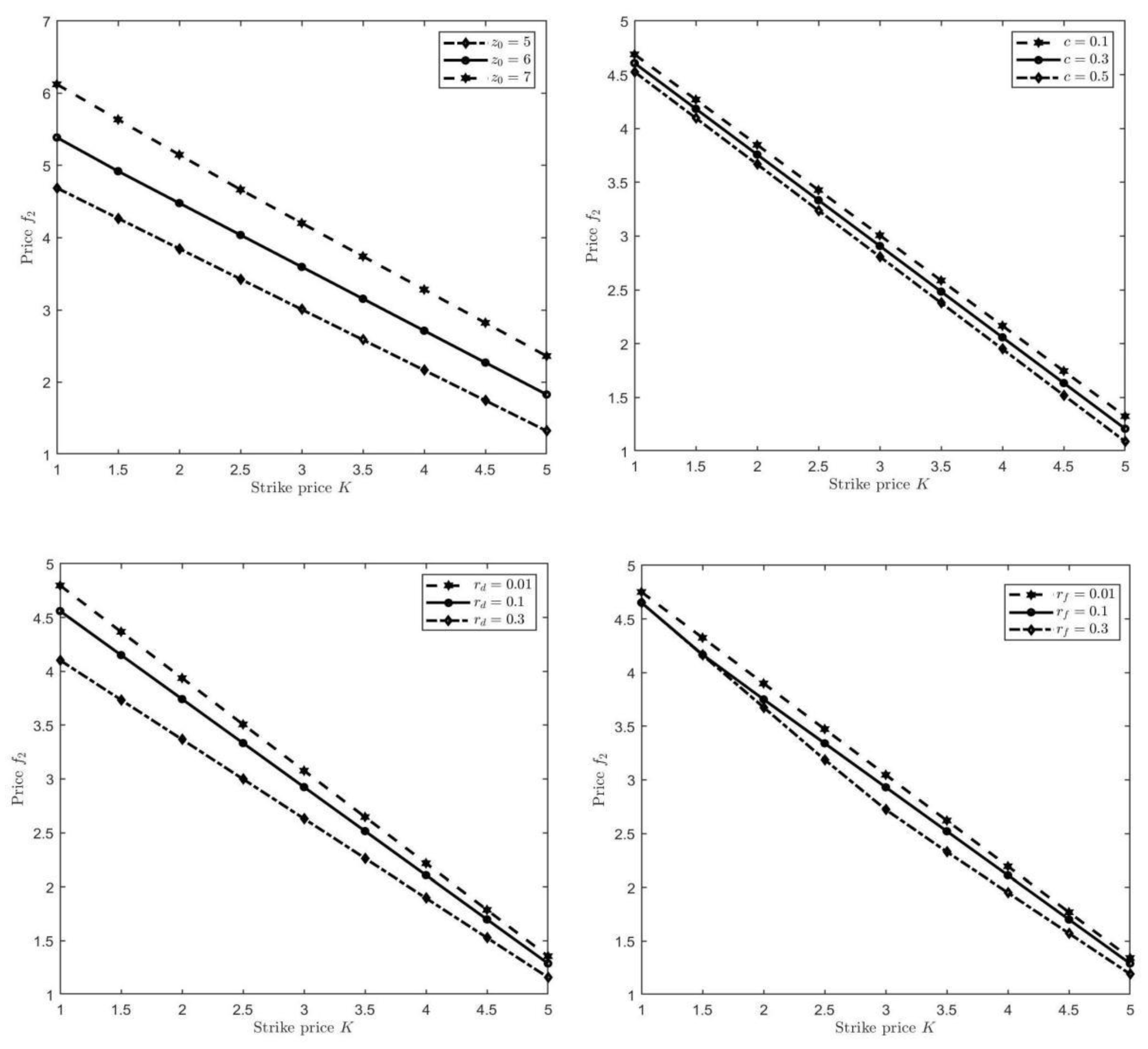
Furthermore, we discuss the properties of the option price  f 1  with regard to some parameters  K , z 0 , c , r d , r f .  It is worth noting that when we analyze the sensitivity of one parameter on the price  f 1 , other parameters keep unchanged. According to Figure 1, we notice that  f 1 is increasing monotonically concerning  z 0 ,  while it is decreasing with respect to  K , c , r d , r f ,  respectively. These results coincide with the realities in financial market, which proves the accuracy of our results.
Example 4.2 
Assume r d = 0.05 , r f = 0.04 , a = 6 , b = 0.8 , c = 0.1 , z 0 = 5 , z 1 = 0.5 , K = 6 , T = 1. By use of the pricing formula (15), we calculate the price of American currency option with different order p 0 < p ≤ 2 and δ under optimistic criterion, as presented in Table 2.
From Table 2, we first discover that when confidence level δ remains unchanged, the price f 2 is monotonously increasing about p when p ∈ 0 , 1 , but it is monotonously decreasing when p ∈ 1 , 2 . The price jumps when p converts 1 into 1.1, and this is because instantaneous growth rate of exchange rate z 1 works at this time. Meanwhile, we find the price f 2 decreases with the increase of confidence level δ when p is fixed, which is in accord with the real financial markets: the more confident investors are in the future change of exchange rate, the less willing they are to spend more to diminish latent risks.
Table 2. The price f 2 with different confidence level δ and order p .
Table 2. The price f 2 with different confidence level δ and order p .
Preprints 103939 i002
Furthermore, we discuss the properties of the option price f 2 with regard to some parameters K , z 0 , c , r d , r f . It is worth noting that when we analyze the sensitivity of one parameter on the price f 2 , other parameters keep unchanged. According to Figure 2, we notice that f 2 is increasing monotonically concerning z 0 , while it is decreasing with respect to K , c , r d , r f , respectively. These results coincide with the realities in financial market, which again proves the accuracy and effectiveness of our results.
Example 4.3 
Assume r d = 0.05 , r f = 0.04 , a = 6 , b = 0.8 ,   c = 0.2 ,   z 0 = 5 , z 1 = 0.5 , K = 5 ,   T = 1.  By use of the pricing formula (17), we calculate the price of Asian currency option with different order  p   0 < p ≤ 2 and δ under optimistic criterion, as presented in Table 3.
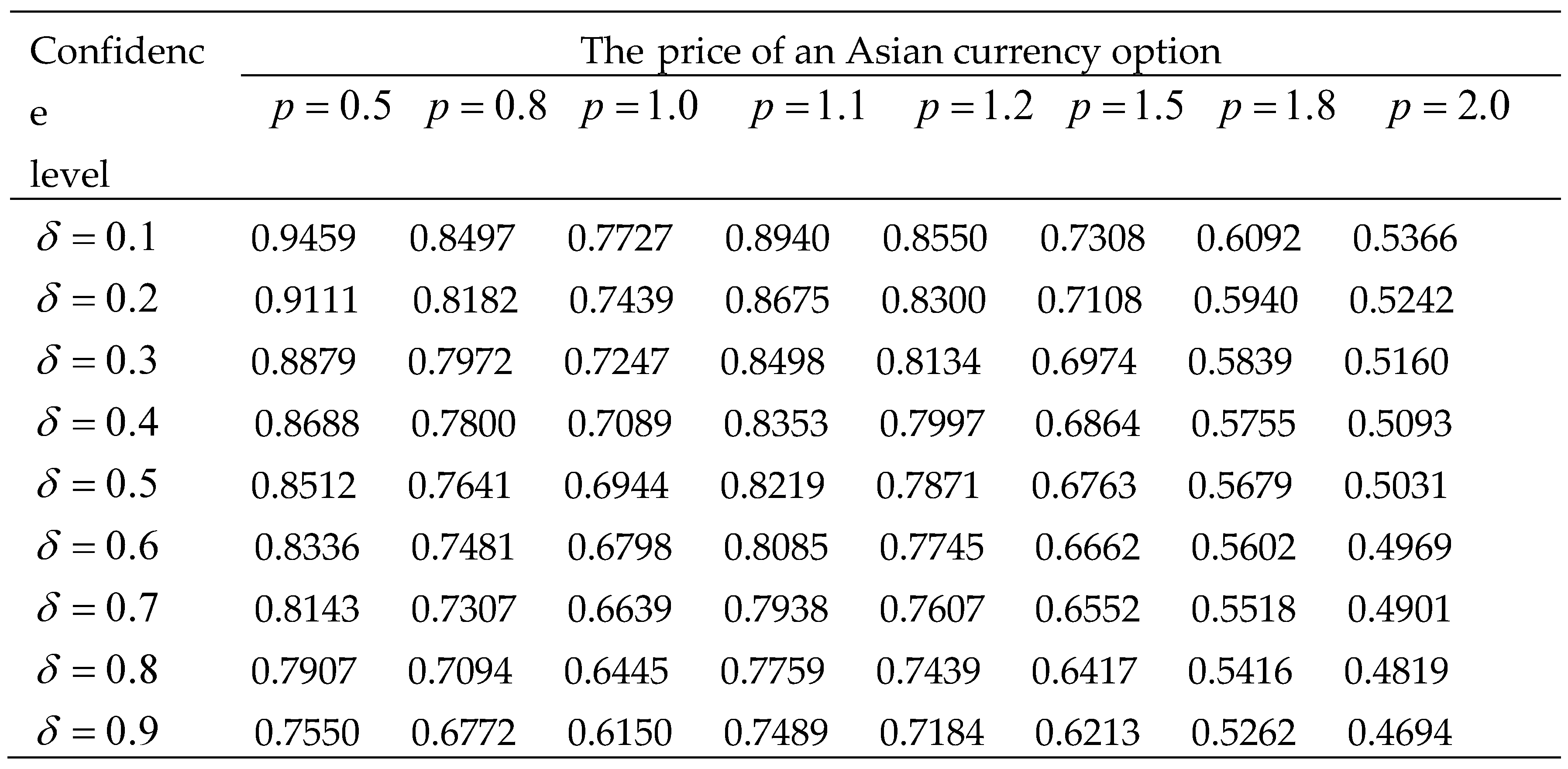
Table 3. The price f 3 with different confidence level δ and order p .
Table 3. The price f 3 with different confidence level δ and order p .
Preprints 103939 i003
From Table 3, we first discover that when confidence level δ remains unchanged, the price f 3 decreases as the order p increases in 0 , 1 and 1 , 2 , respectively. The price jumps when p converts 1 into 1.1, and this is because instantaneous growth rate of exchange rate z 1 works at this time. Meanwhile, we find the price f 3 decreases with the increase of confidence level δ when p is fixed, which is in accord with the real financial markets: the more confident investors are in the future change of exchange rate, the less willing they are to spend more to diminish latent risks.
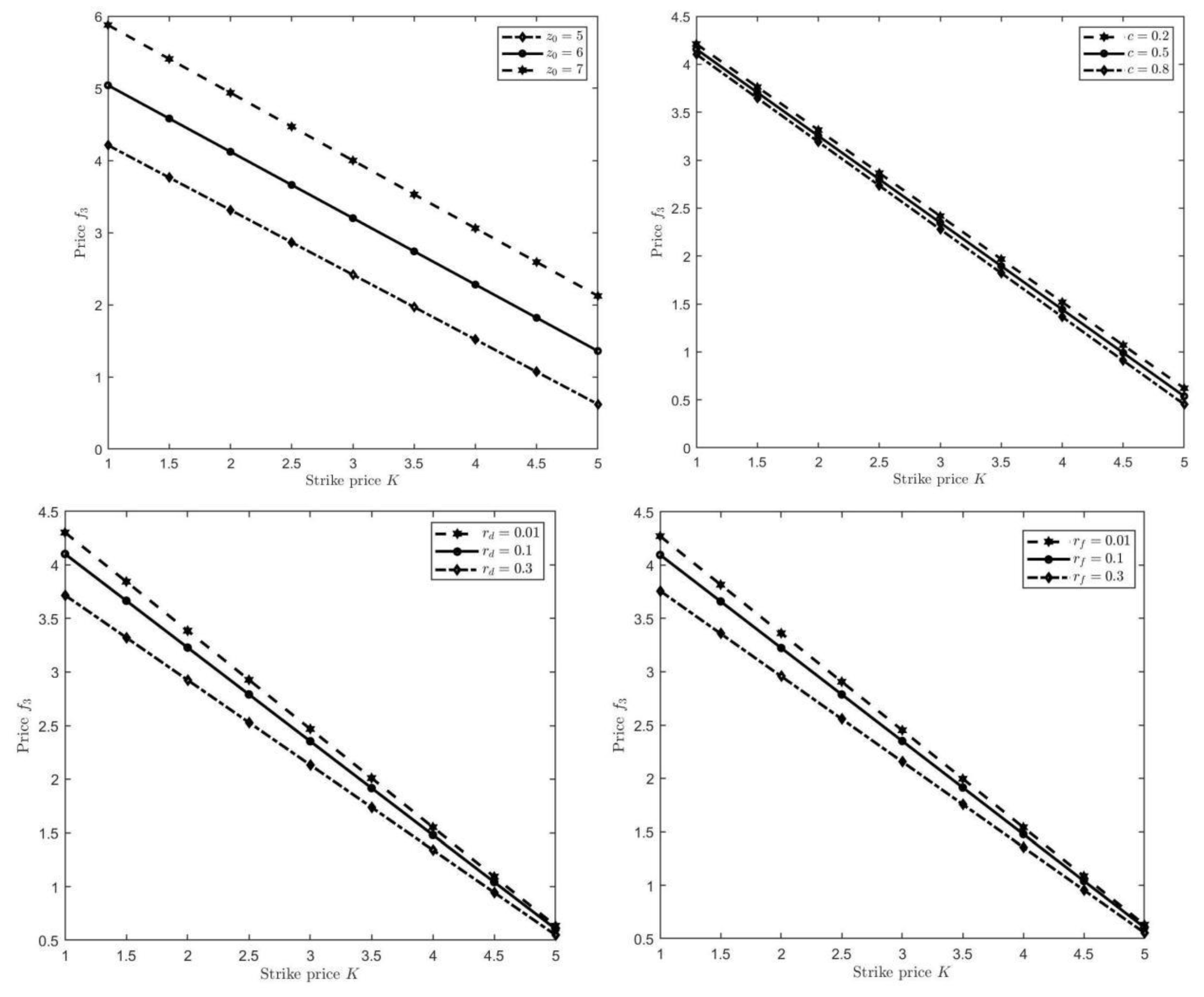
Furthermore, we discuss the properties of the option price f 3 with regard to some parameters K , z 0 , c , r d , r f . It is worth noting that when we analyze the sensitivity of one parameter on the price f 3 , other parameters keep unchanged. According to Figure 3, we notice that f 3 is increasing monotonically concerning z 0 , while it is decreasing with respect to K , c , r d , r f , respectively. These results coincide with the realities in financial market, which again proves the accuracy and effectiveness of our results.

5. Conclusions

This paper analyzed the valuation issues of currency option under optimistic value criterion. An uncertain fractional currency model with mean-reverting process based on UFDE was proposed. After that, by means of rigorous derivations, we verified the pricing formulae of currency option for the presented model. Finally, the sensitivity analyses of different parameters on the option prices were provided.

Author Contributions

Conceptualization, W.W. and D.R.; Methodology, W.W.; Software, W.W. and X.X.; Validation, W.W., D.R. and X.X.; Formal Analysis, D.R.; Investigation, W.W.; Writing- Original Draft Preparation, W.W.; Writing-Review & Editing, W.W. and D.R.; Supervision, D.R.; Funding Acquisition, X.X. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (Grant No. 12201451) and Youth Science Foundation of Shanxi Province (Grant No. 20210302124532).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Baldeauxa J, Grasselli M, Platene E (2015) Pricing currency derivatives under the benchmark approach. J Bank Finance 53:34-48.
  2. Carr P, Wu L (2007) Stochastic skew in currency options. J Financ Econ 86:213-247.
  3. Diethelm K, Ford N, Freed A (2002) A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dynam 29:3-22.
  4. Deng J, Qin Z (2021) On Parisian option pricing for uncertain currency model. Chaos Soliton Fract 143:110561.
  5. Ford N, Simpson A (2001) The numerical solution of fractional differential equations: Speed versus accuracy. Numer Algorithms 26(4):333-346.
  6. Garman M, Kohlhagen S (1983) Foreign currency option values. J Int Money Finance 2:231-237.
  7. Grabbe J (1983) The pricing of call and put options on foreign exchange. J Int Money Finance 2:239-253.
  8. Ji X, Wu H (2017) A currency exchange rate model with jumps in uncertain environment. Soft Comput 21(18):5507-5514.
  9. Jin T, Sun Y, Zhu Y (2019) Extreme values for solution to uncertain fractional differential equation and application to American option pricing model. Physica A 534:122357.
  10. Jin T, Sun Y, Zhu Y (2020) Time integral about solution of an uncertain fractional order differential equation and application to zero-coupon bond model. Appl Math Comput 372:124991.
  11. Jin T, Ding H, Xia H, Bao J (2021) Reliability index and Asian barrier option pricing formulas of the uncertain fractional first-hitting time model with Caputo type. Chaos Soliton Fract 142: 110409.
  12. Jin T, Li F, Peng H, Li B, Jiang D (2023) Uncertain barrier swaption pricing problem based on the fractional differential equation in Caputo sense. Soft Comput 27(16):11587- 11602.
  13. Liu B (2007) Uncertainty theory, 2nd edn. Springer-Verlag, Berlin.
  14. Liu B (2008) Fuzzy process, hybrid process and uncertain process. J Uncertain Syst 2(1):3-16.
  15. Liu B (2009) Some research problems in uncertainty theory. J Uncertain Syst 3(1):3-10.
  16. Liu B (2013) Toward uncertain finance theory. J Uncertain Anal Appl 1:1-15.
  17. Liu B (2015) Uncertainty theory, 4th edn. Springer-Verlag, Berlin.
  18. Liu Y, Chen X, Ralescu D (2015) Uncertain currency model and currency option pricing. Int J Intell Syst 30(1):40-51.
  19. Lu Z, Zhu Y (2019) Numerical approach for solution to an uncertain fractional differential equation. Appl Math Comput 343:137-148.
  20. Lu Z, Yan H, Zhu Y (2019a) European option pricing model based on uncertain fractional differential equation. Fuzzy Optim Decis Mak 18:199-217.
  21. Lu Z, Zhu Y, Li B (2019b) Critical value-based Asian option pricing model for uncertain financial markets. Physica A 525:694-703.
  22. Liu Q, Jin T, Zhu M, Tian C, Li F, Jiang D (2022) Uncertain currency option pricing based on the fractional differential equation in the Caputo sense. Fractal Fract 6:407.
  23. Li X, Sheng Y (2022) Uncertain exponential currency model and currency option pricing. Soft Comput 26(24):13369-13380.
  24. Lu J, Yang X, Tian M (2022) Barrier swaption pricing formulae of mean-reverting model in uncertain environment. Chaos Soliton Fract 160:112203.
  25. Lian Y, Chen J (2022) Foreign exchange option pricing under regime switching with asymmetrical jumps. Financ Res Lett 46:102294.
  26. Lei Z, Zhou Q, Wu W, Wang Z (2023) Vulnerable European call option pricing based on uncertain.
  27. fractional differential equation. J Syst Sci Complex 36(1):328-359.
  28. Shen Y, Yao K (2016) A mean-reverting currency model in an uncertain environment. Soft Comput 20(10):4131-4138.
  29. Van H, Pelsser A (2011) Generic pricing of FX, inflation and stock options under stochastic interest rates and stochastic volatility. Quant Finance 11(5):665-691.
  30. Yan X, Yang X, Zhang P, Zhang Z (2022) A new stock loan problem based on the mean-reverting equation in an uncertain environment. Soft Comput 26(6):2741-2750.
  31. Zhu Y (2015) Uncertain fractional differential equations and an interest rate model. Math Method Appl Sci 38(15):3359-3368.
Preprints 103939 g001aPreprints 103939 g001b
Figure 1. The price f 1  with different K on various other parameters while p = 1.5 ,   δ = 0.9 .
Figure 1. The price f 1  with different K on various other parameters while p = 1.5 ,   δ = 0.9 .
Preprints 103939 g001aPreprints 103939 g001b
Preprints 103939 g002
Figure 2. The price f 2 with different K on various other parameters while p = 1.5 ,   δ = 0.9 .
Figure 2. The price f 2 with different K on various other parameters while p = 1.5 ,   δ = 0.9 .
Preprints 103939 g002
Preprints 103939 g003
Figure 3. The price f 3 with different confidence level δ with different K on various other parameters while p = 1.5 ,   δ = 0.9 .
Figure 3. The price f 3 with different confidence level δ with different K on various other parameters while p = 1.5 ,   δ = 0.9 .
Preprints 103939 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated