Submitted:
17 April 2024
Posted:
17 April 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction

1.1. The Literature Survey
1.2. The Fundamental Theoretical Considerations
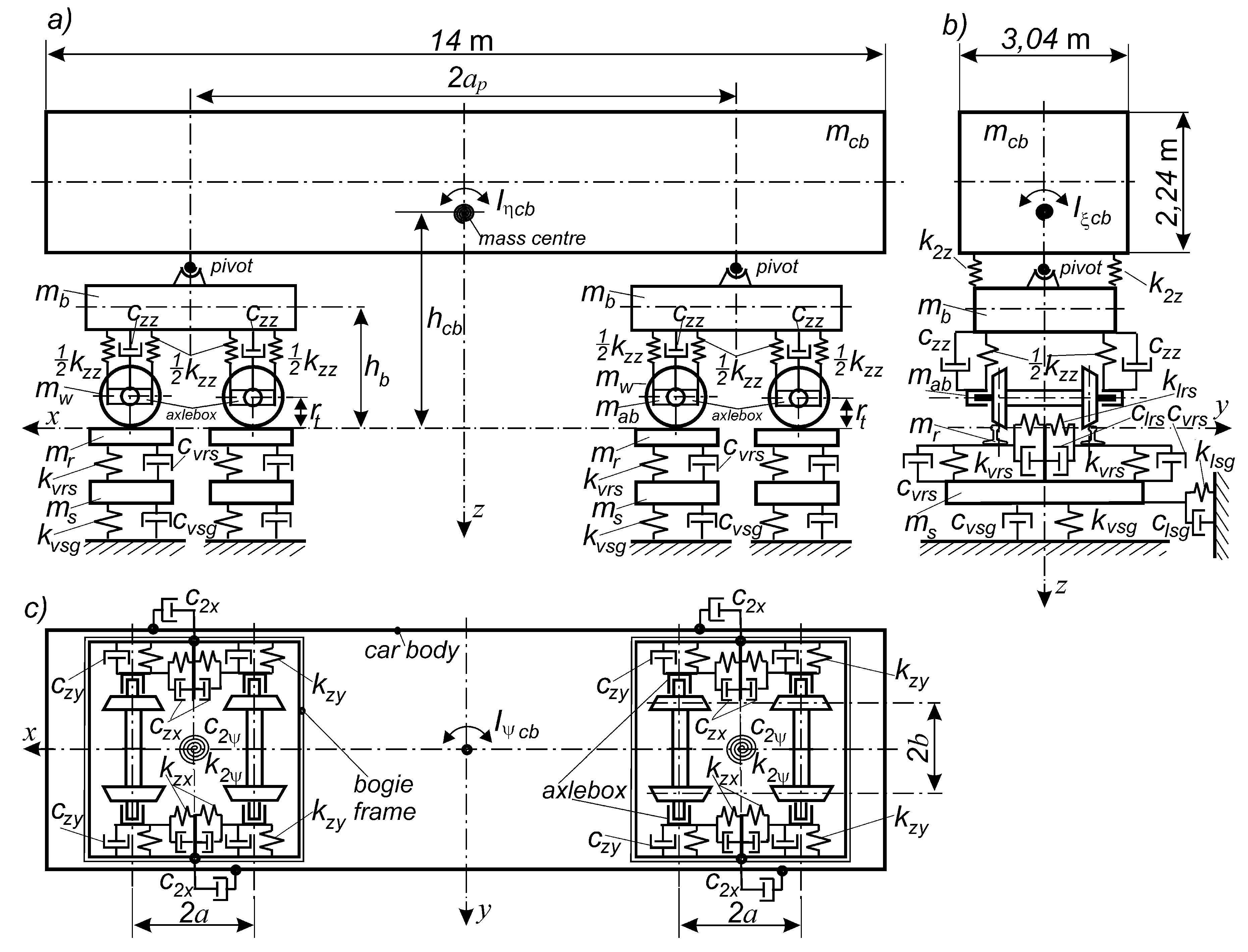
2. The Approach to Stability and the Corresponding Model
3. The Method of Research
4. Results of the Research
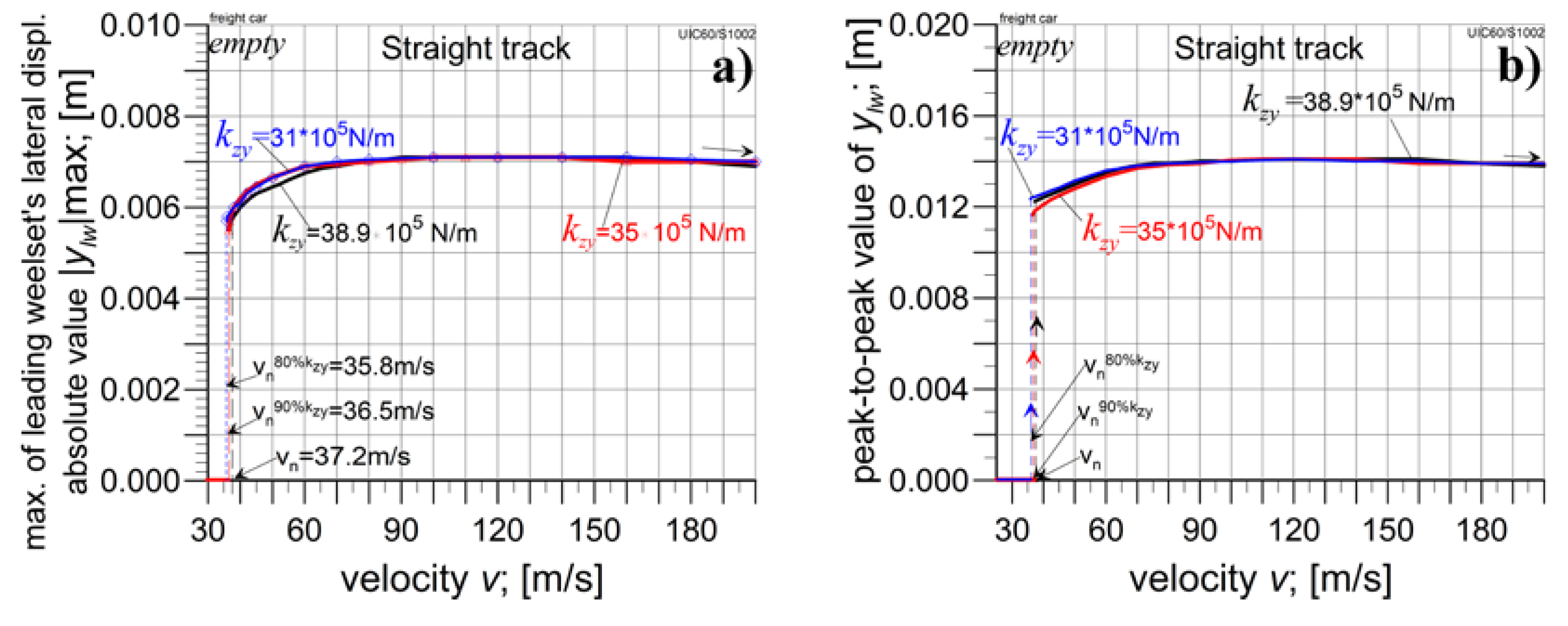
4.1. The Empty Car Analysis
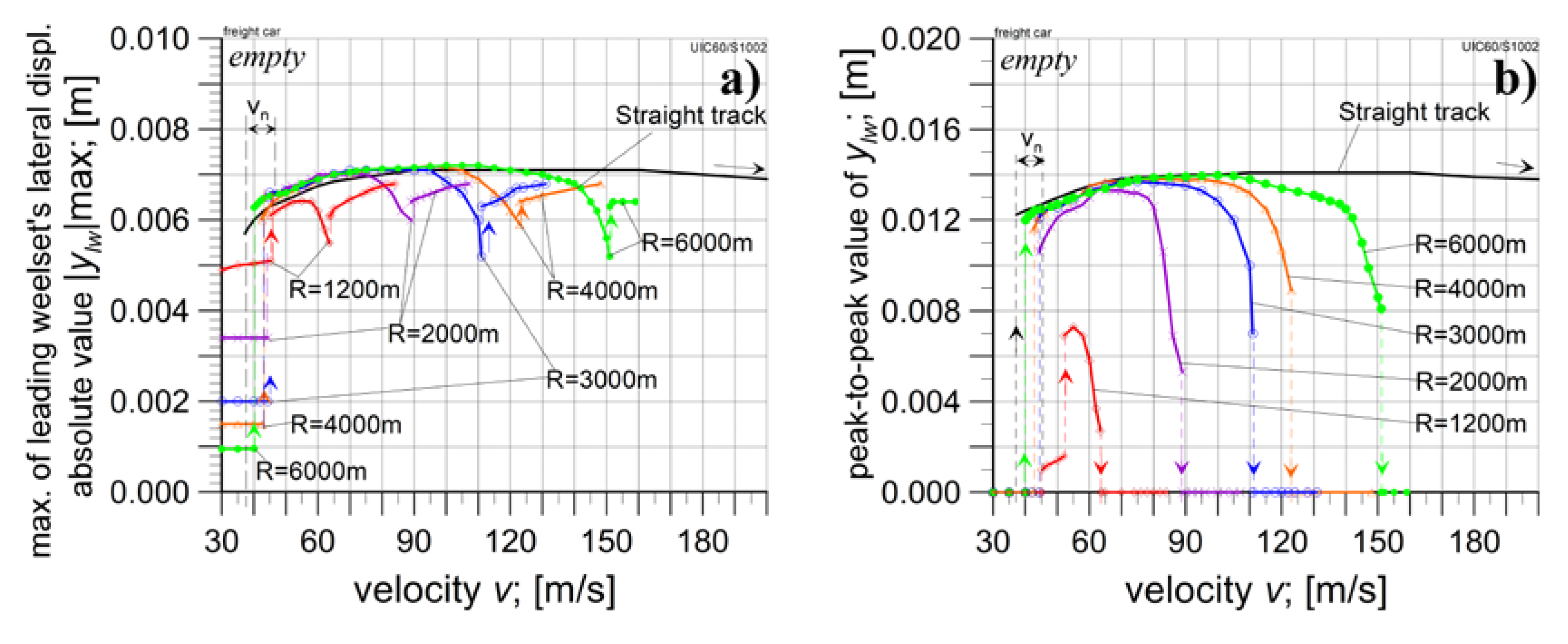
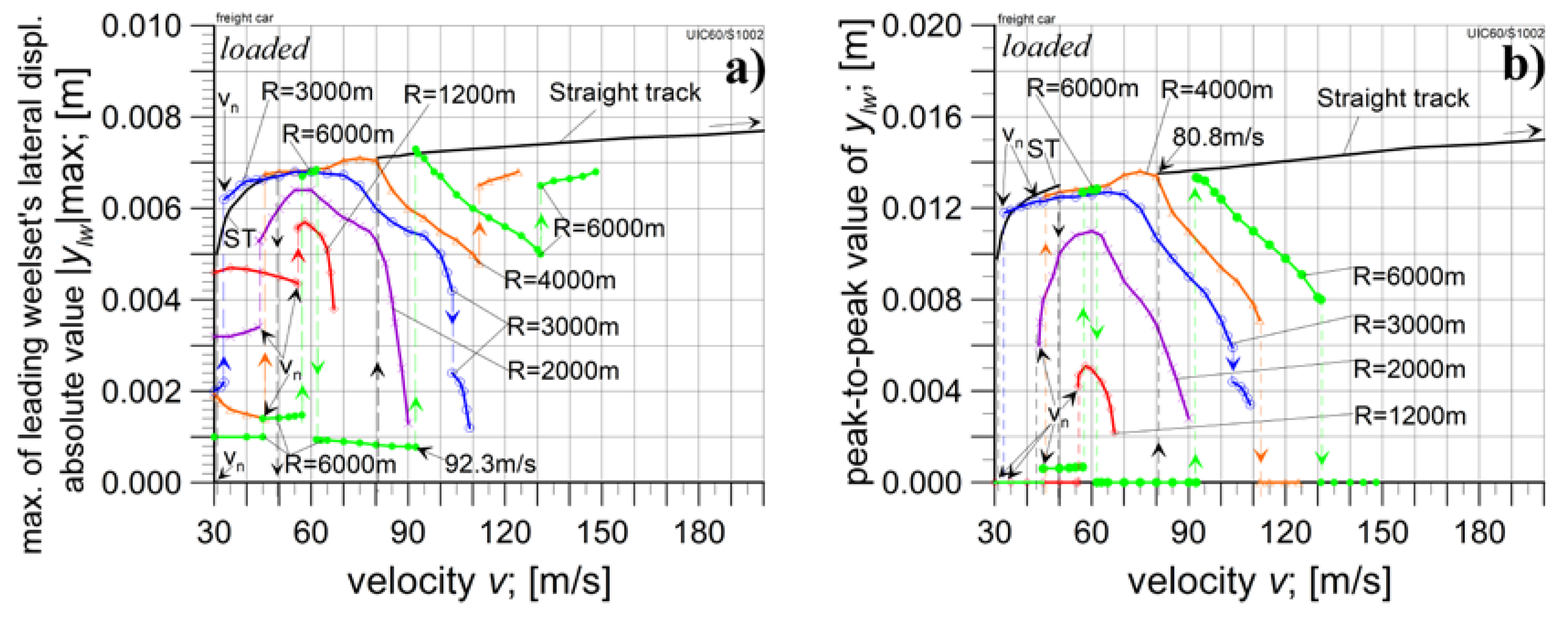
4.2. The Loaded Car Analysis
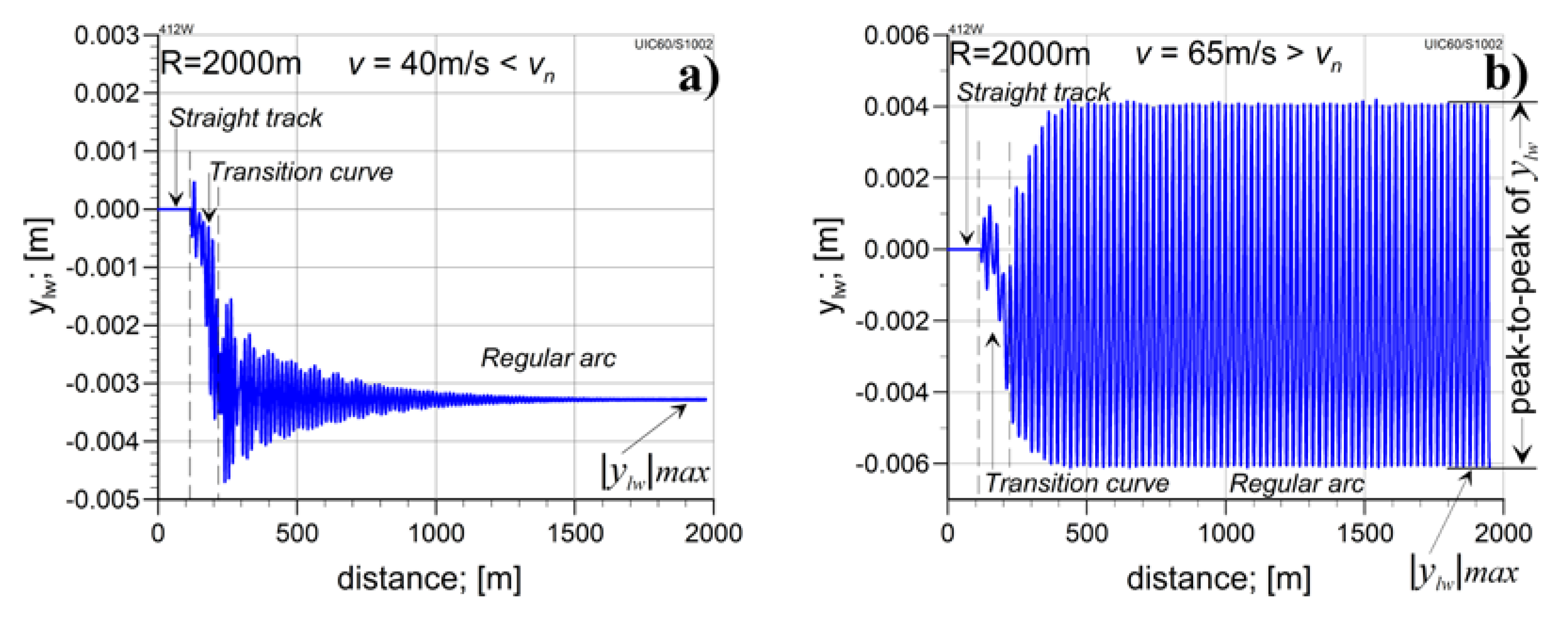
4.2.1. The Analysis in Straight Track
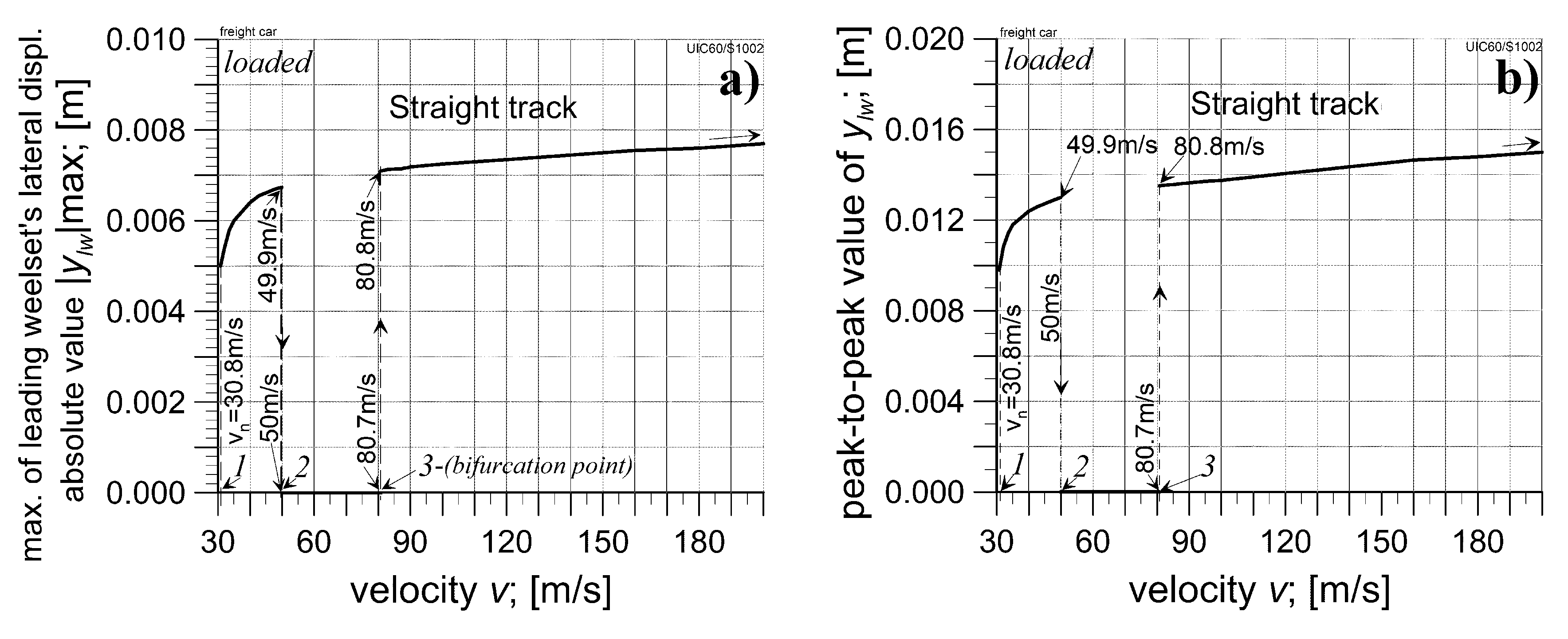
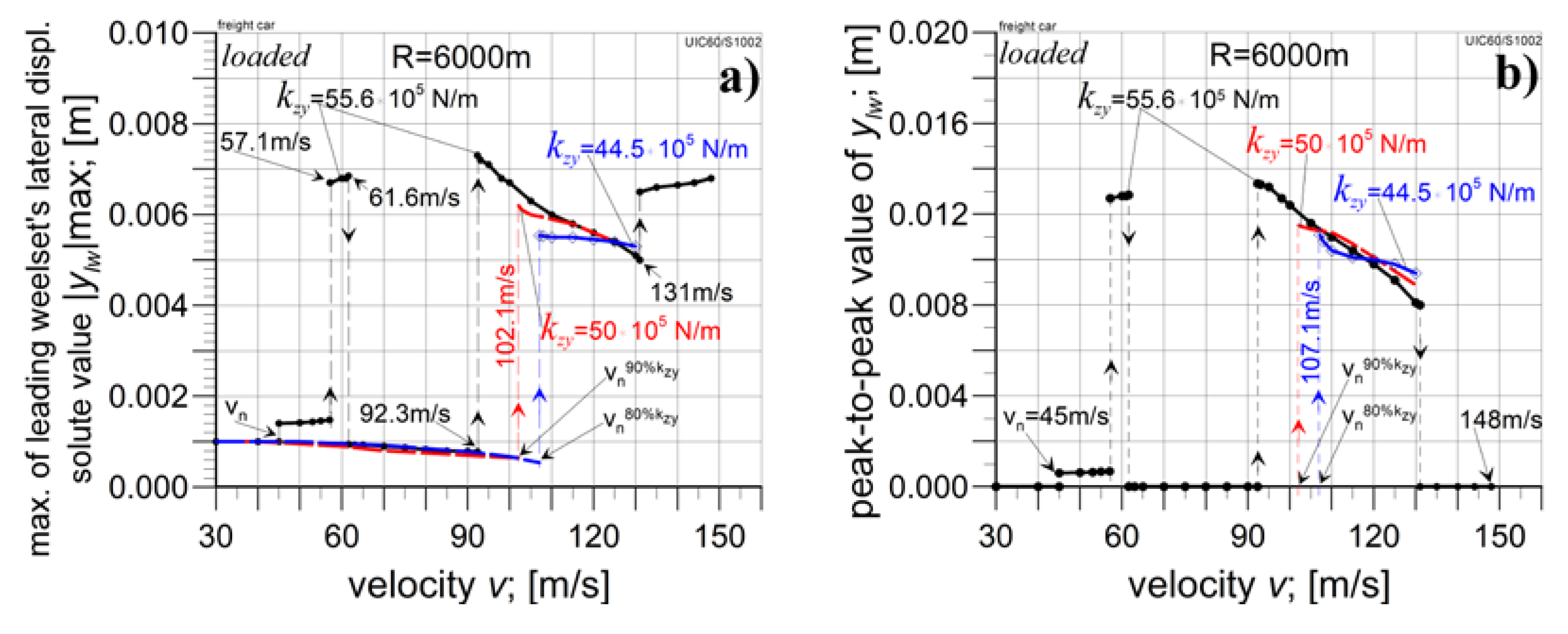
4.2.1. The Analysis in Curved Tracks
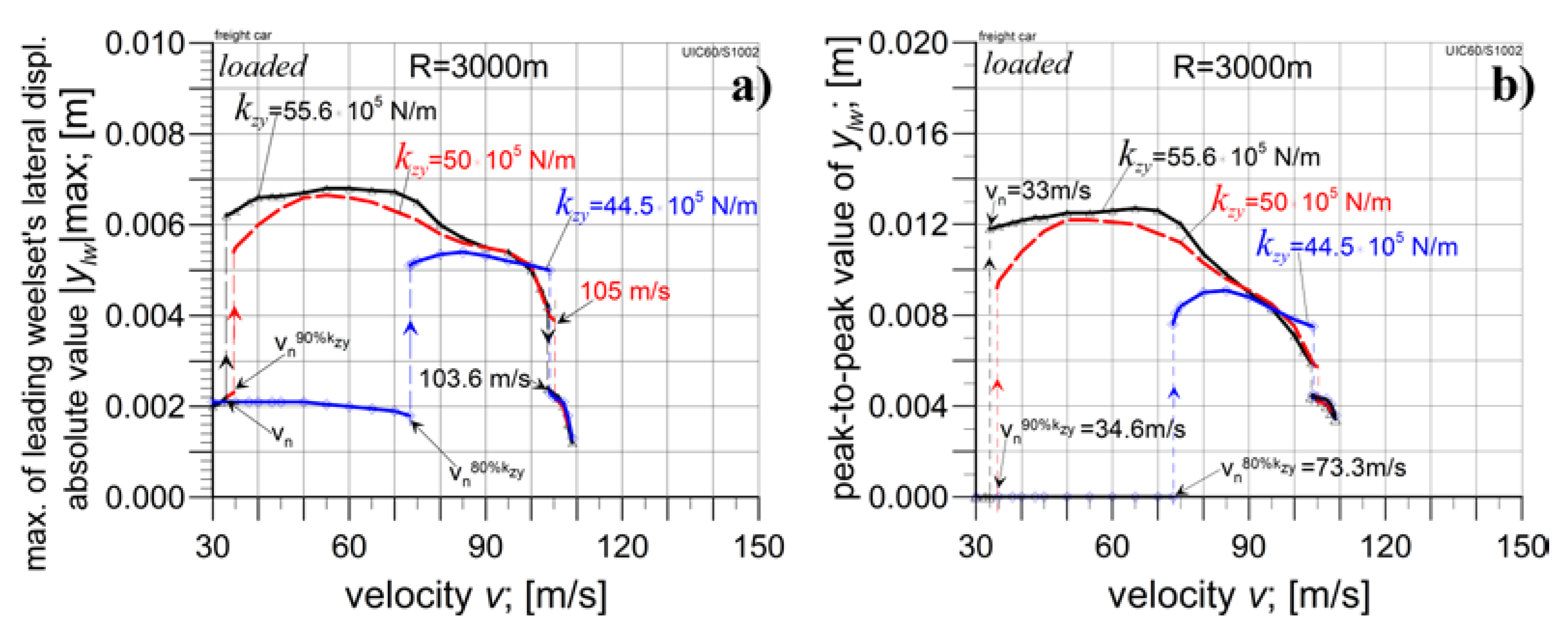
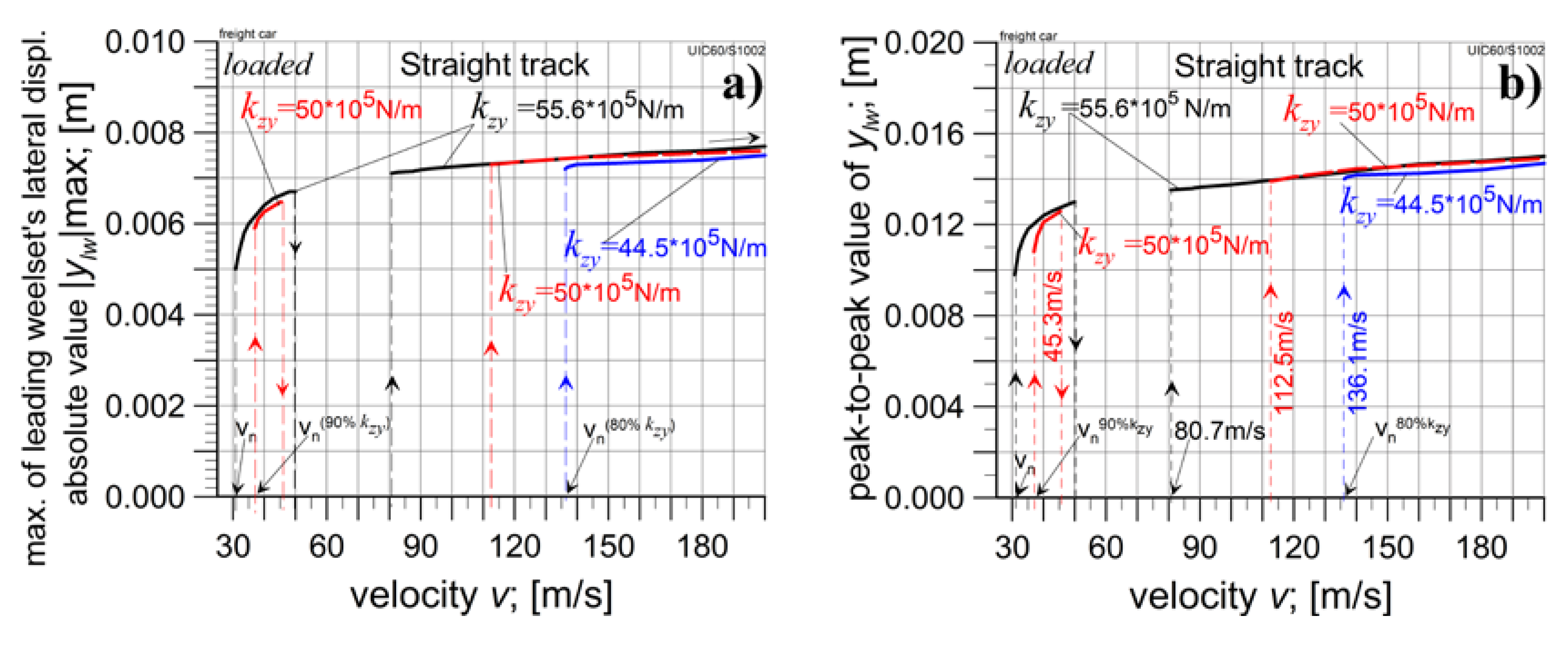
4.3. The Empty Car Analysis for Reduced kzy Value
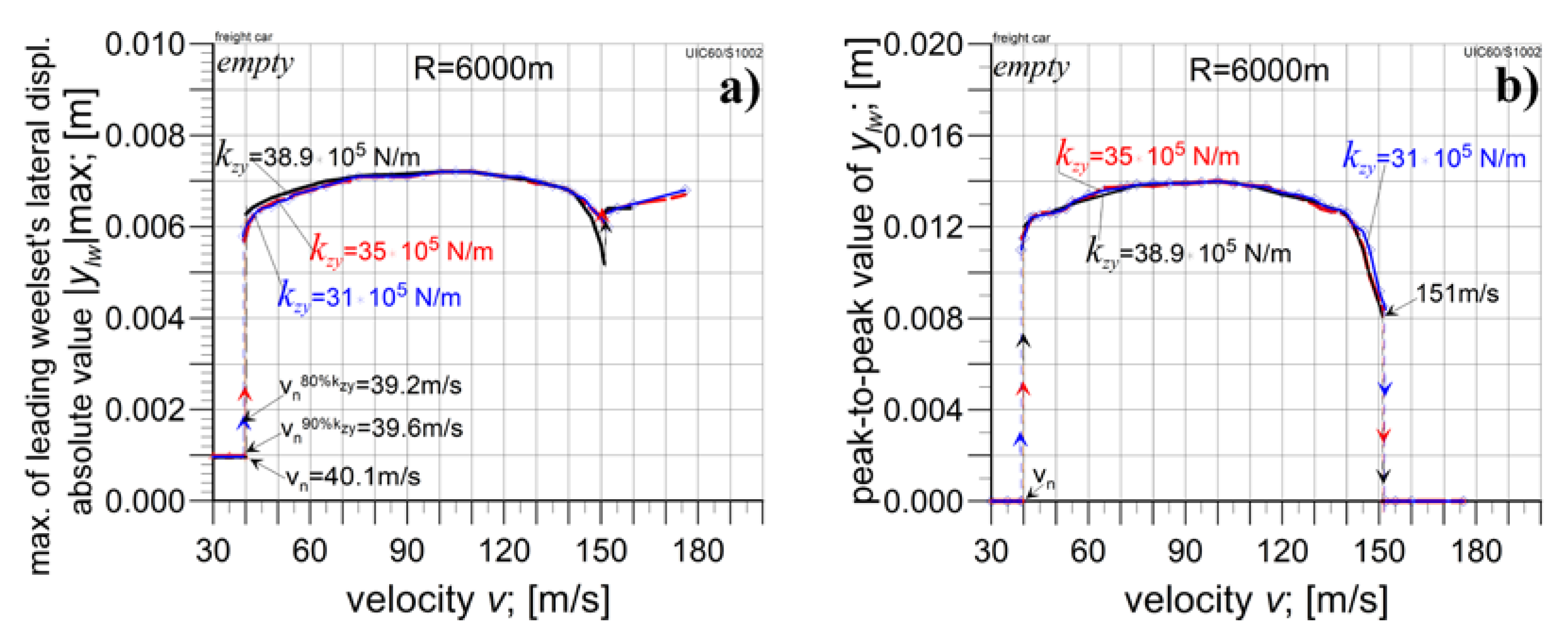

5. Conclusions
Funding
Author Contributions
Institutional Review Board Statement
Conflicts of Interest
Appendix A
| Notation | Description | Unit | Value | |
|---|---|---|---|---|
| empty | loaded | |||
| mcb | Vehicle body mass | kg | 11 000 | 72 000 |
| mb | Bogie frame mass | kg | 1 600 | |
| mw | Wheelset mass | kg | 1 400 | |
| mab | Axlebox mass | kg | 100 | |
| Icb | Body moment inertia; longitudinal axis | kg⋅m2 | 17 300 | 90 055 |
| Icb | Body moment inertia; lateral axis | kg⋅m2 | 188 500 | 1 210 606 |
| Icb | Body moment inertia; vertical axis | kg⋅m2 | 188 140 | 1 231 450 |
| Ib | Bogie frame inertia moment; longitudinal axis | kg⋅m2 | 790 | |
| Ib | Bogie frame inertia moment; lateral axis | kg⋅m2 | 1 000 | |
| Ib | Bogie frame inertia moment; vertical axis | kg⋅m2 | 1 090 | |
| Iw | Wheelset inertia moment; longitudinal axis | kg⋅m2 | 747 | |
| Iw | Wheelset inertia moment; lateral axis | kg⋅m2 | 131 | |
| Iw | Wheelset inertia moment; vertical axis | kg⋅m2 | 747 | |
| kzz | Vertical stiffness of the primary suspension | kN/m | 1 017 | 2 280 |
| kzy | Lateral stiffness of the primary suspension | kN/m | 3 890 | 5 560 |
| kzx | Longitudinal stiffness of the primary suspension | kN/m | 12 000 | 12 000 |
| czz | Vertical damping of the primary suspension | kN⋅s/m | 7 | 123.3 |
| czy | Lateral damping of the primary suspension | kN⋅s/m | 42 | 138 |
| czx | Longitudinal damping of the primary suspension | kN⋅s/m | 100 | |
| k2z | Vertical stiffness of the bogie frame – car body side bearer | kN/m | 22 500 | |
| c2x | Longitudinal damping on the bogie frame – car body side bearer | kN⋅s/m | 6 | 10 |
| k2 | Torsional stiffness between bogie frame and car body | kN⋅m/rad | 20 | |
| c2 | Torsional damping between bogie frame and car body | kN⋅m⋅s/rad | 0.5 | |
| ap | Half of bogie’s pivot-pivot distance | m | 4.5 | |
| a | Semi-wheel base | m | 0.9 | |
| tc | Semi-tape circle distance | m | 0.75 | |
| hb | Vertical distance between bogie frame centre mass and track plane | m | 0.69 | |
| hcb | Vertical distance between car body centre mass and track plane | m | 1.5 | 1.87 |
| rt | Wheel rolling radius | m | 0.46 | |
References
- Zboinski, K.; Golofit-Stawinska, M. Dynamics of a Rail Vehicle in Transition Curve above Critical Velocity with Focus on Hunting Motion Considering the Review of History of the Stability Studies. Energies 2024, 17, 967. [CrossRef]
- Zboinski, K.; Golofit-Stawinska, M. Investigation into nonlinear phenomena for various railway vehicles in transition curves at velocities close to critical one. Nonlinear Dyn. 2019, 98, 1555–1601. [CrossRef]
- Zboinski, K.; Golofit-Stawinska, M. Determination and Comparative Analysis of Critical Velocity for Five Objects of Railway Vehicle Class. Sustainability 2022, 14, 6649. [CrossRef]
- Csiba, J. Bogie type anniversary: the bogie type Y25 is over 50 years. Proceedings of the 10th International Conference On Railway Bogies And Running Gears, Budapest, 12-15 September, 2016, 253-262.
- Pagaimo, J.; Magalheas, H.; Costa, J.N.; Ambrosio, J. Derailment study of railway cargo vehicle using a response surface methodology. Vehicle System Dynamics 60(1), 309-334, 2022.
- Zboiński, K.; Dusza, M. Self-exciting vibrations and Hopf’s bifurcation in non-linear stability analysis of rail vehicles in curved track. European Journal of Mechanics - Part A/Solids, 29(2), 190–203, 2010.
- Zboiński, K.; Dusza, M. Extended study of rail vehicle lateral stability in a curved track. Vehicle System Dynamics 49(5), 789–810, 2011.
- Zboiński, K.; Dusza, M. Bifurcation analysis of 4-axle rail vehicle models in a curved track. Nonlinear Dynamics 89(2), 863–885, 2017, ISSN 0924-090X. [CrossRef]
- Bustos, A.; Tomas-Rodriguez, M.; Rubio, H.; Castejon, C. On the nonlinear hunting stability of a high-speed train boogie, Nonlinear Dynamics, 111, 2059–2078, 2023. [CrossRef]
- Xiao, F.; Hu, J.; Zhu, P. et al. A method of three-dimensional stability region and ideal roll angle to improve vehicle stability. Nonlinear Dynamics 111, 2353–2377, 2023. [CrossRef]
- Sun, J.; Meli, E.; Song, X.; Chi, M.; Jiao, W.; Jiang, Y. A novel measuring system for high-speed railway vehicles hunting monitoring able to predict wheelset motion and wheel/rail contact characteristics, Vehicle System Dynamics, 61(6), 1621-1643, 2023. [CrossRef]
- Umemoto, J.; Yabuno H. Parametric and self-excited oscillation produced in railway wheelset due to mass imbalance and large wheel tread angle, Nonlinear Dynamics, 111:4087–4106, 2023. [CrossRef]
- Seth, S., Kudra, G., Wasilewski, G. et al. Study the bifurcations of a 2DoF mechanical impacting system. Nonlinear Dynamics 112, 1713–1728, 2024. [CrossRef]
- Margazoglou, G.; Magri, L. Stability analysis of chaotic systems from data. Nonlinear Dynamics 111, 8799–8819, 2023. [CrossRef]
- Guo J.; Shi H.; Luo R.; Zeng J. Bifurcation analysis of a railway wheelset with nonlinear wheel–rail contact, Nonlinear Dynamics, 104, 989–1005, 2021. [CrossRef]
- Ge P.; Wie X.; Liu J.; Cao H. Bifurcation of a modified railway wheelset model with nonlinear equivalent conicity and wheel-rail force, Nonlinear Dynamics, 102, 79–100, 2020. [CrossRef]
- Yang, C.; Huang, Y.; Li, F. Influence of Curve Geometric Parameters on Dynamic Interactions of Side-Frame Cross-Braced Bogie. Proceedings ICRT 2021, Second International Conference on Rail Transportation, ASCE Library 2022.
- Chernysheva, Y.; Gorskiy, A. Methods Proposed for Analysis of Vibrations of Railway Cars. In: Manakov, A.,Edigarian, A. (eds) International Scientific Siberian Transport Forum TransSiberia - 2021. TransSiberia 2021. Lecture Notes in Networks and Systems, vol 402. Springer, Cham., 2022. [CrossRef]
- Skerman, D.; Colin Cole, C.; Spiryagin, M. (2022) Determining the critical speed for hunting of three-piece freight bogies: practice versus simulation approaches, Vehicle System Dynamics, 60(10), 3314-3335. [CrossRef]
- Pandey M., B. Bhattacharya B.; Effect of bolster suspension parameters of three-piece freight bogie on the lateral frame force, International Journal of Rail Transportation, 8(1), 45-65, 2020. [CrossRef]
- Sun J.; Chi M.; Jin X.; Liang S.; Wang J.; Li W. (2021) Experimental and numerical study on carbody hunting of electric locomotive induced by low wheel–rail contact conicity, Vehicle System Dynamics, 59(2), 203-223, 2021. [CrossRef]
- Shvets A.O.: Dynamic interaction of a freight car body and a three-piece bogie during axle load increase, Vehicle System Dynamics, 60(10), 3291-3313, 2022. [CrossRef]
- Guo J.; Zhang G.; Shi, H.; Zeng J. Small amplitude bogie hunting identification method for high-speed trains based on machine learning, Vehicle System Dynamics, Published online 19 Jun 2023. [CrossRef]
- He, S.;E. Jonsson, E.; Martins, J.R.R.A. Adjoint-based limit cycle oscillation instability sensitivity and suppression. Nonlinear Dynamics 111, 3191–3205, 2023. [CrossRef]
- Wang, X.; Lu, Z.; Wen, J.; Wie, J.; Wang, Z. Kinematics modelling and numerical investigation on the hunting oscillation of wheel-rail nonlinear geometric contact system, Nonlinear Dynamics 107, 2075–2097, 2022. [CrossRef]
- Knothe, K.; Böhm, F. History of Stability of Railway and Road Vehicles. Vehicle System Dynamics 31, 283-323,1999.
- Kass-Petersen, C.; True H. A bifurcation analysis of nonlinear oscillations in railway vehicles. Vehicle System Dynamics 13, 655-665, 1984.
- True, H. On the theory of nonlinear dynamics and its applications in vehicle systems dynamics. Vehicle System Dynamics 31, 393-421, 1999.
- Iwnicki, S. (ed.). Handbook of railway vehicle dynamics. CRC Press Inc. 2006.
- Shabana, A. A.; Zaazaa, K. E.; Sugiyama, H. Railroad Vehicle Dynamics: A Computatio-nal Approach. 2008, Taylor & Francis LLC and the CRC.
- Piotrowski, J.; Pazdzierniak, P.; Adamczewski, T. Curving dynamics of freight wagon with one- and two-dimensional friction damping. Proc. Of the 10th Mini Conference on Vehicle System Dynamics, Identification and Anomalies. Ed. Zobory I. Budapest 6-8 November 2006, 215-222.
- Bruni, S.; Vinolas, J.; Berg, M.; Polach, O.; Stichel, S. Modeling of suspension components in a rail vehicle dynamics context. Vehicle System Dynamics 49(7), 1021-1072, 2011.
- Evans, J.; Berg, M. Challenges in simulation of rail vehicle dynamics. Vehicle System Dynamics 47(8), 1023-1048, 2009.
- Kalker, J. J. A fast algorithm for the simplified theory of rolling contact. Vehicle System Dynamics 11, 1-13, 1982.
- Piotrowski, J. Kalker’s algorithm Fastsim solves tangential contact problems with slip-dependent friction and friction anisotropy. Vehicle System Dynamics 48(7), 869-889, 2010.
- Bogusz, W. Technical stability (in Polish Stateczność techniczna). PWN, 1972, Warsaw.
- Dusza, M. Rail vehicle model possibility of safe motion analysis in the overcritical velocity range. Proceedings of the 11th International Conference on Railway Bogies and Running Gears, Ed. Istvan Zobory, Department of Rolling Stock, SSME/GTE, ISBN 978-963-9058-42-2, Budapest, 2020, 159-168.
| Curve radius; R [m] | 1200 | 2000 | 3000 | 4000 | 6000 | ∞ |
| Superelevation; h [m] | 0.150 | 0.130 | 0.110 | 0.077 | 0.051 | 0 |
| Curve radius R [m] | 1200 | 2000 | 3000 | 4000 | 6000 | ∞ |
|---|---|---|---|---|---|---|
| Empty; vn [m/s] | 45.2 | 44.4 | 44.4 | 42.6 | 40.1 | 37.2 |
| Loaded; vn [m/s] | 55.8 | 43.7 | 33 | 45.6 | 45 | 30.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





