Prerpints.org logo
Preprint
Article

Viscoelastic Hertzian Impact — Feature Article

Altmetrics

Downloads

89

Views

19

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

17 April 2024

Posted:

17 April 2024

You are already at the latest version

Alerts
Abstract
The problem of normal impact of a rigid sphere onto a Maxwell viscoelastic solid half-space is considered. The first-order asymptotic solution is constructed in the framework of Hunter’s model of viscoelastic impact [Hunter, S. C., 1957. Energy absorbed by elastic waves during impact. Journal of the Mechanics and Physics of Solids, 5(3), 162–171.]. In particular, simple analytical approximations have been derived for the maximum contact force and the time to achieve it. A linear regression method is suggested for evaluating the instantaneous elastic modulus and the mean relaxation time from a set of experimental data collected for different impactors and impact velocities.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

In his ground-laying paper [1] on the frictionless local contact of elastic solids, Heinrich Hertz estimated the half-duration of the normal dissipationless impact as
t m 0 = τ m 0 w m 0 V 0 , τ m 0 = ∫ 0 1 d ξ 1 − ξ 5 / 2 ,
where V 0 is the initial relative velocity of approach, and w m 0 is the maximum value of the contact approach (evaluated from the initial contact moment).
Hertz’s theory of elastic impact can be represented as the initial-value problem for the second-order nonlinear differential equation
m d 2 w d t 2 = − k w 3 / 2 , w | t = 0 = 0 , d w d t | t = 0 = V 0 ,
where w is the contact approach measured from the time, t, of initial contact, m is the equivalent mass, k is the stiffness coefficient in Hertz’s contact law F = k w 3 / 2 , and F is the contact force (reaction).
In the case of collision between two elastic spheres (see Figure 1a), the equivalent mass is given by m = m 1 m 2 / ( m 1 + m 2 ) , whereas the stiffness coefficient k = ( 4 / 3 ) E * R is determined in terms of the equivalent radius, R, and the effective elastic modulus, E * , defined as
1 R = 1 R 1 + 1 R 2 , 1 E * = 1 − ν 1 2 E 1 + 1 − ν 2 2 E 2 .
From Eqs. (2), the equation of energy conservation follows in the form
m 2 V 0 2 − d w d t 2 = 2 5 k w 5 / 2 ,
which determines the maximum contact approach
w m 0 = 5 m k 2 / 5 V 0 2 4 / 5 ,
achieved at the time moment t = t m when d w / d t = 0 .
The same Hertzian equations (1)–(5) also apply in the case of impact of a rigid sphere of mass m onto an elastic half-space (see Figure 1b), as Eqs. (6) allow a passage to the limit as E 1 → ∞ and R 2 → ∞ . We recall that Hertz’s theory of frictionless contact assumes that the contact is developed in the framework of the linear theory of elasticity, the elastic bodies are assumed to be isotropic and homogeneous, the contact is local in a sense that the initial contact occurs at a single point only and the elastic half-space approximation applies for evaluating the contact stresses by neglecting the effect of global contact geometry [2].
It should be noted that some of the Hertz model’s restrictions can be relaxed. For instance, in a routine manner Willis [3] extended Hertz’s theory of impact to anisotropic bodies, using his solution for the problem of local frictionless contact. By utilizing Bondareva’s solution [4] for a heavy elastic sphere on a rigid plane, Villaggio [5] showed that the global contact geometry effect slightly increases the contact duration, compared with that predicted by the classical Hertz’s theory. The inertia effect revealing itself in the impact energy loss due to the elastic wave radiation in the impact problem for an elastic half-space (Figure 1b) was estimated by Hunter [6] (see also [7,8]) based on the analytical solution obtained by Miller and Pursey [9] for the elastic wave energy radiated by a rigid disk vibrating on the half-space surface. It is pertinent to note here that the excitation of the half-space surface by a spherical impact was considered in [10].
Hertz’s theory of impact predicts the unit coefficient of restitution, e, the symmetry of loading/unloading contact process, and the duration of impact, t c 0 , to be equal twice the time t m 0 to the maximum of the contact approach w m 0 . It was shown by Hunter [6] and Deresiewicz [11] that the variation of the contact approach as a function of the time of contact can be well approximated by the simple formula
w ≈ w m 0 sin π t t c 0 , t c 0 = 2 t m 0 .
The classical Hertz impact theory has been given substantial experimental verification [12] and, in particular, was extended to the frictional impact of anisotropic nonlinear elastic solids [13] and power-graded viscoelastic solids [14] as well as to tangential (oblique) impact [15,16,17] and impact with adhesion [18,19].
It is known [20,21] that the coefficient of restitution in collision of two perfectly elastic bodies equals unit (that is, e = 1 ), if the time of impact well exceeds the time needed for elastic waves to traverse either body. That is why, the impact configuration shown in Figure 1b primarily differs from that shown in Figure 1a by the presence of the energy dissipation (absorption [6]) mechanism due to the vibrational energy radiated into the massive substrate when elastic waves propagate to the infinity.
Energy dissipation in the Hertzian impact between two spherical solids (Figure 1a) can be associated with the effects of plastic deformation or internal friction among others [21]. A phenomenological approach (see, e.g., [22,23]) leads to the dissipative contact model
F = k w 3 / 2 + χ w β w ˙ ,
where w ˙ = d w / d t is the relative contact velocity, β is a dimensionless constant, and χ denotes the hysteresis damping factor. As a rule, the coefficient χ is interpreted in terms of the coefficient of restitution [24]. By adopting a constitutive law similar to the Kelvin–Voigt model σ z r = 2 μ 0 ε z r + 2 η ε ˙ z r , where η is the viscosity coefficient, Goldobin et al. [25] arrived at Eq. (7) with β = 1 / 2 and χ being proportional to a linear combination of the shear and bulk viscosity coefficients (see also [26,27]).
The impact problem becomes exceedingly hard if colliding solids are assumed to possess time-dependent mechanical properties. The Hertz impact problem for a rigid spherical indenter and a viscoelastic half-space was first considered by Hunter [28], who complemented the analytical solution by Lee and Radok [29] for the Hertzian quasi-static contact problem with monotonically increasing contact by the solution when the contact radius possesses a single maximum, which is the case in impact problems. In the special case of a Maxwell solid, Hunter obtained the first-order perturbation approximations for the coefficient of restitution, e, and the impact duration, t c . Later, Forney [30] questioned Hunter’s result about the impact duration. To date, this issue remains unresolved.
The case of a Kelvin–Voigt solid was considered by Khusid [31] (see also [14]) who obtained some numerical results for the impact duration and the coefficient of restitution. A systematic review of modeling linear and non-linear viscoelastic contact problems was recently given by Wang el al. [32].
In what follows, we consider the normal impact of a rigid sphere on an isotropic viscoelastic half-space with a constant Poisson’s ratio, ν , and a hereditary constitutive law
σ z r ( t ) = 2 ∫ 0 − t μ ( t − t ′ ) d ϵ z r ( t ′ ) d t ′ d t ′ ,
where μ ( t ) is the shear relaxation modulus, and 0 − indicates the instant immediately before the initial point of contact.
In his first-order perturbation analysis of the viscoelastic Hertzian impact, Aksel [33] applied the viscoelastic constitutive law in the form
σ z r ( t ) = 2 μ 0 ϵ z r ( t ) + 2 ∫ 0 t μ ^ ( t ′ ) ϵ z r ( t − t ′ ) d t ′ ,
where μ 0 = μ ( 0 ) is the instantaneous shear modulus, μ ^ ( t ) = d μ ( t ) / d t is the viscoelastic relaxation kernel, and it is tentatively assumed that ϵ z r ( t ) = 0 for t < 0 .
The problem of material parameters identification by means of impact tests was considered in a number of experimental studies [34,35,36,37]. Kren and Naumov [38] formulated the problem of determining the relaxation function μ ( t ) from the spherical impact loading history (impactor velocity, V ( t ) , contact force, F ( t ) , and contact approach, w ( t ) ) without a priori adopting any material’s model. However, the problem with the Kren–Naumov method is that the Lee–Radok solution [29], which is valid only for the loading contact stage, was incorrectly applied for the unloading stage as well. It is still to note here that the approximation that utilizes for the restitution phase the same form of the equation of motion derived for compression is sometimes used for the sake of simplicity [39,40].

2. Hunter’s Model of the Viscoelastic Impact

2.1. Viscoelastic Hertzian Impact

For the sake of simplicity, we consider the single impactor configuration (Figure 1b) and start with Newton’s second law and the initial conditions
m d 2 w d t 2 = − F , w | t = 0 = 0 , d w d t | t = 0 = V 0 ,
where F is the contact reaction.
Assuming a constant Poisson’s ratio ν and neglecting inertia effects in the viscoelastic half-space target, the Hertzian elastic solution can be generalized as follows [28,29]:
F ( t ) = 8 3 ( 1 − ν ) R ∫ 0 t μ ( t − t ′ ) d d t ′ a 3 ( t ′ ) d t ′ ,
w ( t ) = a 2 ( t ) R , t ≤ t m .
Here, μ ( t ) is the shear relaxation modulus that describes the material’s response to an instantaneous unit shear deformation, a ( t ) is the contact radius as a function of time t. It is clear that Eq. (12) is the Hertzian relation between the contact radius a and the contact approach w.
From Eqs. (10)–(12), it follows that
m d 2 w d t 2 = − 8 R 3 ( 1 − ν ) ∫ 0 t μ ( t − t ′ ) d d t ′ w 3 / 2 ( t ′ ) d t ′ .
It should be remembered that in the loading stage, the Lee–Radok solution (11), (12) as well as Eq. (13) are valid until the time moment, t m , of maximum penetration, w m , which, in view of Eq. (12), coincides with the moment of maximum contact radius, a m , and therefore, with the moment when the impactor velocity vanishes, i.e.,
a m = a ( t m ) , w m = w ( t m ) , d w d t | t = t m = 0 .
In the unloading stage ( t m < t < t c ), Hunter’s solution is given in terms of the function t 1 ( t ) that solves the equation a ( t ) = a ( t 1 ) for t > t m and t 1 < t m . Namely, the contact reaction is given by
F ( t ) = 8 3 ( 1 − ν ) R ∫ 0 t 1 ( t ) μ ( t − t ′ ) d d t ′ a 3 ( t ′ ) d t ′ ,
whereas Eq. (12) is replaced with the following relation [28]:
R w ( t ) = a 2 ( t ) − ∫ t m t μ − 1 ( t − t ′ ) d d t ′ ∫ . t 1 ( t ′ ) t ′ μ ( t ′ − t ′ ′ ) d d t ′ ′ a 2 ( t ′ ′ ) d t ′ ′ d t ′ .
Here, μ − 1 ( t ) is the shear creep compliance (we keep the notation from [28]).

2.2. Impact for a Maxwell Solid

The reciprocal relaxation and creep functions for a Maxwell solid are
μ ( t ) = μ 0 exp ( − η t ) , μ − 1 ( t ) = 1 μ 0 ( 1 + η t ) ,
where μ 0 is the instantaneous shear modulus, and η is an inverse relaxation time.
The substitution of ( 17 ) 1 into Eq. (13), in view of the initial conditions (10), leads to the differential equation
d 2 w d t 2 + η d w d t − V 0 = − 8 R μ 0 3 ( 1 − ν ) m w 3 / 2 , t < t m ,
which is an exact result.
However, in the unloading (or withdrawal) stage, the application of Eqs. (17) allows to reduce Eq. (16) to a complicated nonlinear differential equation for t 1 ( t ) . Nevertheless, by utilizing the simple approximation t 1 ≈ 2 t m − t , Hunter derived the resulting governing differential equation
d 2 w d t 2 − η 3 d w d t + V 0 = − 8 R μ 0 3 ( 1 − ν ) m w 3 / 2 , t > t m ,
which is amendable to analytical treatment, but constitutes an approximate result.
Let us introduce the auxiliary function
w = a 2 ( t ) R , t ≥ t m ,
which is related to the contact approach by the equation
d w d t = exp − 2 η ( t − t m ) d d t a 2 ( t ) R .
We note that, in view of (12) and (20), the solution of Eq. (19) is subject to the boundary conditions (or the initial conditions for the withdrawal stage)
w | t = t m = w | t = t m , d w d t | t = t m = 0 ,
The contact duration t c is determined by the condition w ( t c ) = 0 , when the contact shrinks down.
In the dimensionless variables
ω = a 2 ( t ) R w m 0 , τ = V 0 t w m 0 , τ m = V 0 t m w m 0 , ε = η w m 0 V 0 ,
where w m 0 is given by (5) with k being replaced by 8 R μ 0 / [ 3 ( 1 − ν ) ] , Eqs. (18) and (19) become
d 2 ω d τ 2 + ε d ω d τ − 1 = − 5 4 ω 3 / 2 , τ < τ m , ω | τ = 0 = 0 , d ω d τ | τ = 0 = 1 ,
d 2 ω d τ 2 − ε 3 d ω d τ + 1 = − 5 4 ω 3 / 2 , τ m < τ , ω | τ = τ m = ω m , d ω d τ | τ = τ m = 0 ,
where τ m is the time-like point for which the solution to Eq. (24) first yields d ω / d τ = 0 , and the corresponding value of ω ( τ m ) will be denoted by ω m .

2.3. Asymptotic Solution for the Loading Stage

The problem with Forney’s critique [30] of Hunter’s approximate solution is in the integral decomposition representation
τ m = ∫ 0 ω m d ω ω ˙ = ∫ 0 1 d ω ω ˙ + ∫ 1 ω m d ω ω ˙ ,
where ω ˙ = d ω / d τ , because the function ω cannot be regarded as a perturbation of the limit ( ε = 0 ) elastic solution ω 0 ( τ ) that is defined only on the interval [ 0 , τ m 0 ] , where τ m 0 is the dimensionless Hertzian half duration of impact. At the same time, the second integral on the right-hand side of Eq. (26) refers to the interval ω ∈ ( 1 , ω m ) , which corresponds to τ ∈ ( τ m 0 , τ m ) , that is outside the interval of validity of the limit solution.
That is why, we will make use of the formula
τ m = ∫ 1 0 d ω υ = − ∫ 0 1 ω ′ ( υ ) d υ υ ,
where ω is regarded as a function of υ ∈ [ 0 , 1 ] , ω ′ ( υ ) is its derivative, and υ decreases from 1 to 0 as τ increases from 0 to τ m .
By setting υ = d ω / d τ and d 2 ω / d τ 2 = d υ / d τ = υ d υ / d ω , we reduce Eq. (24) to the first-order differential equation
d ω d υ = − υ ( 5 / 4 ) ω 3 / 2 + ε ( υ − 1 ) , υ ∈ ( 0 , 1 ) .
The first-order approximate solution to Eq. (28) subject to the boundary condition ω | υ = 1 = 0 is given by
ω ≃ ω 0 + ε ω 1 , ω 0 = ( 1 − υ 2 ) 2 / 5 , ω 1 = ( 4 / 5 ) 2 ( 1 − υ 2 ) 3 / 5 ∫ υ 1 ξ ( 1 − ξ ) d ξ ( 1 − ξ 2 ) 3 / 5 .
The substitution of (29) into Eq. (27) yields
τ m ≃ τ m 0 + ε c m τ , τ m 0 = 4 5 ∫ 0 1 d ξ ( 1 − ξ 2 ) 3 / 5 ,
c m τ = 2 4 5 2 ∫ 0 1 ( 1 − ξ ) d ξ ( 1 − ξ 2 ) 6 / 5 − 2 5 · 3 5 3 ∫ 0 1 1 ( 1 − υ 2 ) 8 / 5 ∫ υ 1 ξ ( 1 − ξ ) ( 1 − ξ 2 ) 3 / 5 d ξ d υ .
Moreover, in view of (29), we obtain
ω m ≃ 1 + ε c m ω , c m ω = 2 4 5 2 ∫ 0 1 ξ ( 1 − ξ ) ( 1 − ξ 2 ) 3 / 5 d ξ .
It can be easily verified numerically that the first-order approximations ( 30 ) 1 and ( 32 ) 1 completely agree with the corresponding results obtained by Hunter. At the same, the asymptotic formula ( 30 ) 1 disagrees with Forney’s result τ m − τ m 0 = O ( ε 1 / 2 ) as ε → 0 .
From a practical point of view, it is of interest to evaluate the maximum contact force, F M , and the corresponding time moment, t M , such that F M = F ( t M ) . In the case of a Maxwell solid, according to Eqs. (11), (17), (18), and (23), for τ ∈ ( 0 , τ m ) we have
w m 0 m V 0 2 F = 5 4 ω 3 / 2 + ε d ω d τ − 1 ≃ 5 4 ω 0 3 / 2 + ε 15 8 ω 0 1 / 2 ω 1 − 1 + υ ,
where ω 0 and ω 1 are given by ( 29 ) 2 and ( 29 ) 3 , respectively.
It can be shown that
w m 0 m V 0 2 F M ≃ 5 4 − ε 1 − 15 8 c m ω , V 0 w m 0 t M ≃ τ m 0 − ε 8 15 − c m τ ,
where c m τ and c m ω are given by (31) and ( 32 ) 2 , respectively.

2.4. Asymptotic Solution for the Unloading Stage

Now, we transform Eq. (25) as
υ d υ d ω = − 5 4 ω 3 / 2 + ε ( 3 υ + 1 ) , ω ∈ ( 0 , ω m ) , υ | ω = ω m = 0 .
The first-order approximate solution υ ≃ υ 0 + ε υ 1 to Eq. (35) is given by
υ 0 = − ω m 5 / 2 − ω 5 / 2 , υ 1 = − 1 ω m 5 / 2 − ω 5 / 2 ∫ ω ω m 3 ω m 5 / 2 − ϕ 5 / 2 − 1 d ϕ .
The end of the unloading stage is determined by the value
υ c = υ | ω = 0 ≃ − 1 + ε 1 − 5 4 c m ω − 3 ∫ 0 1 1 − ξ 5 / 2 d ξ ,
where c m ω is defined by formula ( 32 ) 1 .
The duration of the unloading stage can be evaluated as
τ c − τ m = ∫ 1 υ c d ω υ = − ∫ 0 ω m d ω υ ( ω ) ,
and, in view of (36), we find that
τ c − τ m ≃ τ m 0 − ε c c τ ,
where we have introduced the notation
c c τ = 1 4 τ m 0 c m ω + ∫ 0 1 1 ( 1 − ξ 5 / 2 ) 3 / 2 ∫ ξ 1 3 1 − ζ 5 / 2 − 1 d ζ d ξ .
Hence, the dimensional impact duration t c 0 = ( w m 0 / V 0 ) τ c 0 can be represented as
t c ≃ t c 0 1 + η t c 0 ( c m τ − c c τ ) ( τ c 0 ) 2 ,
where τ c 0 = 2 τ m 0 , and c c τ is given by (39).
Again, by numerical check for the involved integrals it can be easily established that formula (40) completely agrees with the corresponding Hunter’s result.
Finally, according to Eq. (21), the rebound velocity is found to be
V c = V 0 exp − 2 η ( t c − t m ) d ω d τ | τ = τ c ,
that is V c / V 0 ≃ 1 − ε ( τ c − τ m ) υ c , and, in view of (37) and (38), we arrive at the following Hunter’s result for the coefficient of restitution:
e ≃ 1 − 4 9 η t c 0 .
Thus, our calculations for w m , t c , and e have conformed those by Hunter, obtained by different method.

3. Comparison with the FEM Solution

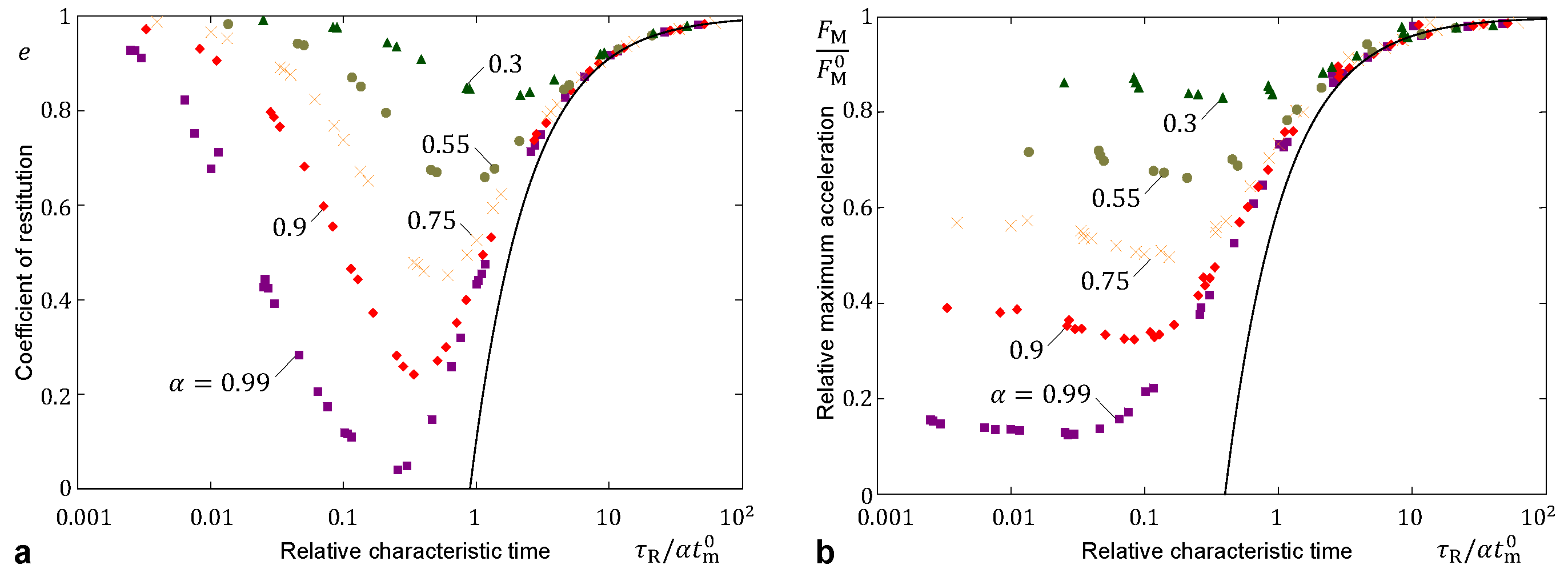
3.1. Impact for a Maxwell Solid

It is interesting that though numerical approaches for the viscoelastic Hertzian impact were developed in a number of papers [40,41,42], quite general numerical results were obtained not so long ago by Herrenbrück et al. [43] based on finite-element simulations for both the Maxwell model and the standard linear sold model. The numerical master curves were calculated for the maximum penetration w m scaled by the Hertzian elastic solution w m 0 , for the coefficient of restitution e as well as for the maximum acceleration, which coincides with the relative maximum contact force F M / m , also scaled by the Hertzian solution F M 0 / m , where
F M 0 = 5 4 m V 0 2 w m 0 .
In the case of a Maxwell solid, the creep function ( ) 2 is now represented as
μ − 1 ( t ) = 1 μ 0 1 + t τ R , τ R = 1 η ,
where τ R is the characteristic relaxation time, which is introduced instead of the inverse characteristic time η used before.
In view of ( 1 ) 1 , ( 23 ) 4 , and ( 43 ) 2 , we have
τ R t m 0 = 1 ε τ m 0 , ε = t m 0 τ m 0 τ R ,
where τ m 0 is given by ( 1 ) 2 .
According to relations ( 32 ) 1 , ( 34 ) 1 , and (41), the mentioned above impact parameters can be approximated as
w m w m 0 = 1 + ε c m ω , e = 1 − ε 8 9 τ m 0 , F M F M 0 = 1 − ε c M F ,
where F M 0 is given by (42), and we have introduced the notation
c M F = 4 5 − 3 2 c m ω .
As it is seen from Figure 2 and Figure 3 (see the inserts), the analytical approximations (45) can be used with less than 5% relative error for ε ≤ 0.2 .
We note that for a Maxwell solid, in view of (8), (9), and ( 17 ) 1 , we have μ ^ ( t ) = − η μ 0 exp ( − η t ) . It can be verified that Aksel [33] obtained the approximate formula e = 1 − 2.69 η w m 0 / V 0 , which can be transformed to the form (41) with the coefficient 0.914 instead of 4 / 9 ≈ 0.444 . Thus, Aksel’s asymptotic solution apparently contains a computational error, as it does not agree with the numerical solution shown in Figure 3b.

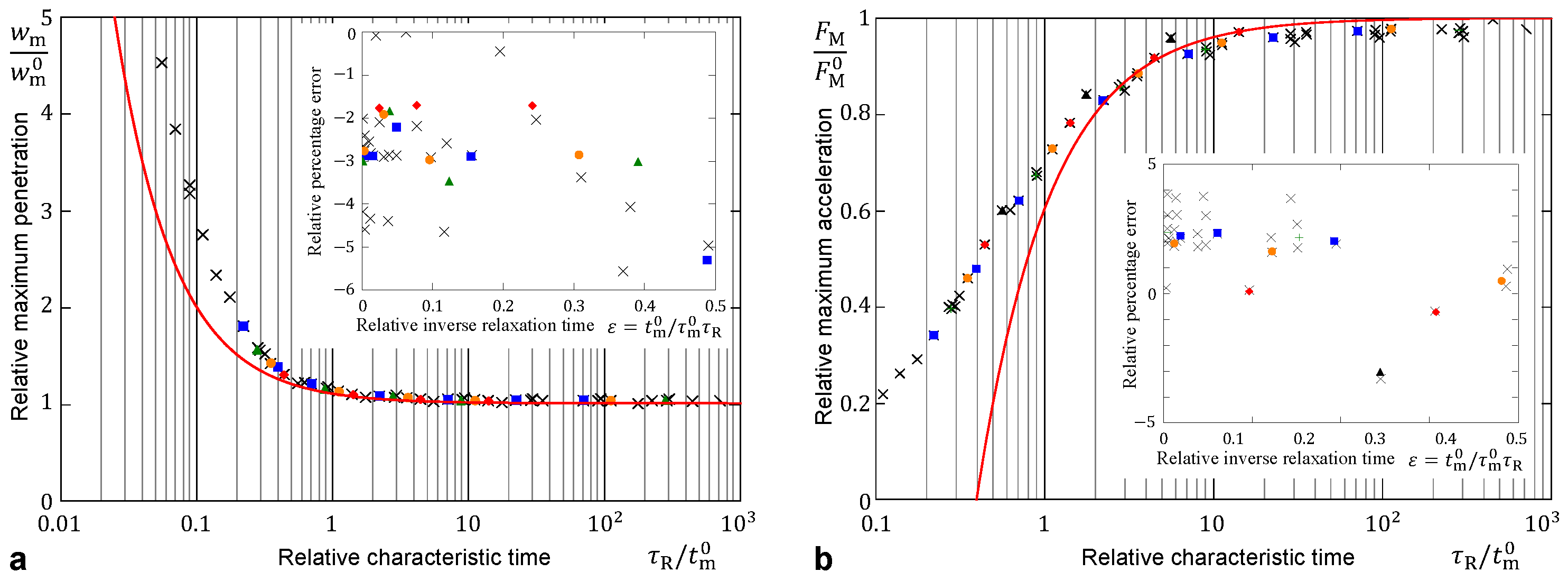
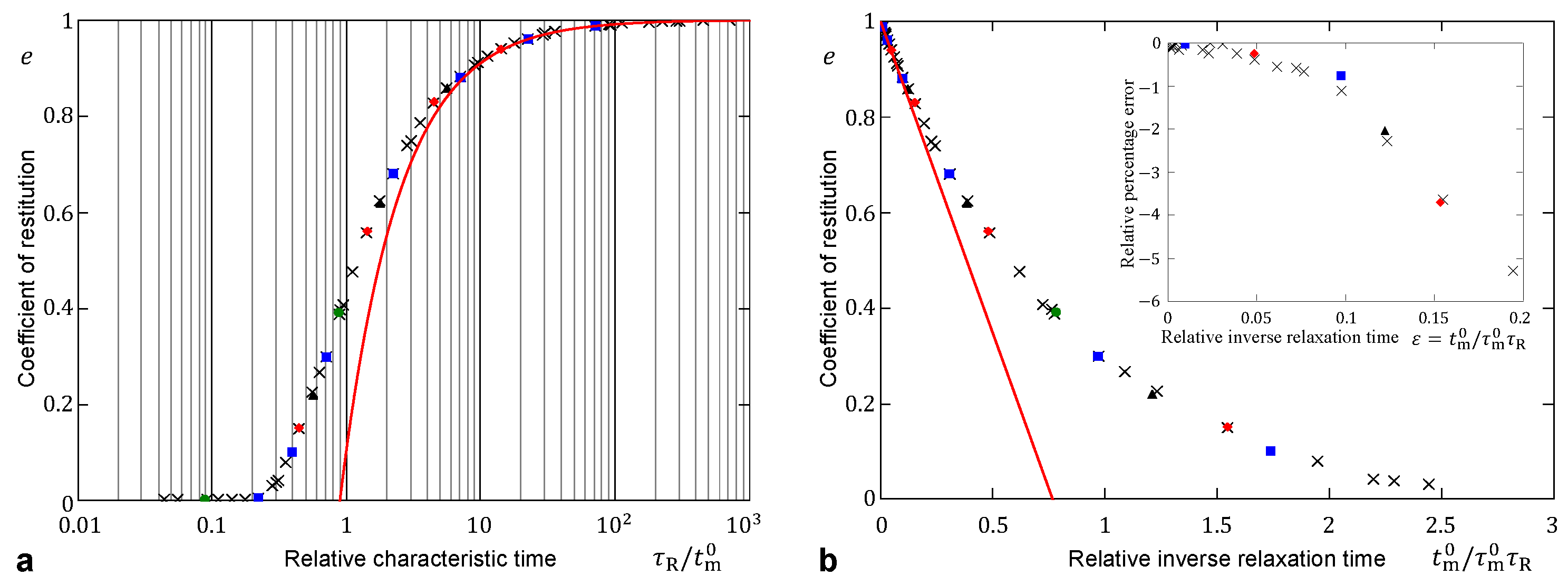
3.2. Impact for a Standard Linear Solid

By adopting the notation used in [43], the shear creep function in the case of a standard linear solid will be
μ − 1 ( t ) = 1 ( 1 − α ) μ 0 1 − α exp − ( 1 − α ) t τ ,
where α = ( μ 0 − μ ∞ ) / μ 0 , and μ ∞ is the relaxed shear modulus.
The short-time approximation (as t tends to zero) follows from (47) in the form
μ − 1 ( t ) ≃ 1 μ 0 1 + t τ / α .
By comparing formulas ( 43 ) 1 and (48), we conclude that the first-order approximations (45) still can be employed provided
ε = α t m 0 τ m 0 τ ,
where τ and α are the model parameters of a standard solid subjected to spherical impact.
As it may be seen from Figure 4, the short-time approximations can be utilized in a limited range of the dimensionless parameter ε . We note also that the Maxwell model (43) can be recovered from the standard linear solid model in the limit as α tends to zero (see also [44]).

4. Material Parameters Identification via Impact Testing

Let us recall that the analytical approximations for the characteristics of impact derived in the framework of the Maxwell viscoelastic model exploit the following expansions about t = 0 :
μ ( t ) = μ 0 ( 1 − η t + … ) , μ − 1 ( t ) = 1 μ 0 ( 1 + η t − … ) .
Moreover, the characteristic relaxation time 1 / η is assumed to be much larger than the impact duration, that is η t c ≪ 1 or, which is asymptotically the same, η t c 0 ≪ 1 .
The analytical approximations are given in terms of the small dimensionless parameter ε , which, in view of (1) and (23), is proportional to η t c 0 , where t c 0 is the Hertzian impact duration (see Eqs. (1) and ( 6 ) 2 ). Namely, Hertz’s theory of impact yields the characteristic time
w m 0 V 0 = C 0 m 2 R V 0 1 / 5 ,
where we have introduced the notation for the compliance coefficient
C 0 = 15 ( 1 − ν ) 32 μ 0 2 / 5 .
Now, we consider the approximate formulas (34), which can be recast as
F m m V 0 = V 0 w m 0 5 4 − ε c M F ,
t M = w m 0 V 0 τ m 0 − ε c M t ,
where we have introduced the short-hand notation
c M F = 1 − 15 8 c m ω , c M t = 8 15 − c m τ .
We recall that F M and t M denote the maximum contact force and the corresponding time moment. We assume that at least one of these parameters of impact can be measured experimentally. The problem is to evaluate the material parameters C 0 and η from the impact data collected from several tests characterized by the governing parameter
V = R V 0 m 2 1 / 5 .
In view of ( 23 ) 4 , (51), and (56), formulas (53) and (54) can be represented as follows:
F M m V 0 = 5 4 C 0 − 1 V − c M F η ,
t M = τ m 0 C 0 V − 1 − c M t η C 0 2 V − 2 .
First, we consider Eq. (57) and note that this formula represents a linear relation between the relative maximum contact force F m / ( m V 0 ) and the variable impact parameter V . Provided that both of them are measured in experiment, the material parameters C 0 − 1 and η can be evaluated via linear regression by means of fitting the linear formula (57) to the scaled experimental data. After that the instantaneous shear elastic modulus will be given by
μ 0 = 15 ( 1 − ν ) 32 C 0 − 5 / 2 ,
where the material Poisson’s ratio ν , as usual, is supposed to be known.
Second, in order to exhibit the method of linear regression, we transform Eq. (58) to the form
V t M = τ m 0 C 0 − c M τ η C 0 2 V − 1 .
By fitting Eq. (60) to the experimental data ( R V 0 / m 2 ) 1 / 5 t M versus ( m 2 / R V 0 ) 1 / 5 , we can evaluate C 0 and η C 0 2 , from where, in view of (59), we readily get μ 0 . Meanwhile, the inverse characteristic relaxation time η is simply determined from the ratio of the linear regression coefficients.
In the same way, formula (11) for the impact duration can be rewritten as
t c = w m 0 V 0 2 τ m 0 + ε c c t
and eventually transformed to the form
V t c = 2 τ m 0 C 0 + c c t η C 0 2 V − 1 .
By comparing Eqs. (60) and (62), we readily see that a similar linear regression method can be designed for evaluating the parameters μ 0 and η from the impact duration data.

5. Discussion

The Hertzian impact assumes a paraboloidal approximation φ ( r ) = r 2 / 2 R for the initial gap between two colliding elastic solids, which eventually leads to Hertz’s contact law F = k w 3 / 2 . Shtaerman [45] and Galin [46] obtained the force-displacement relations F = k n w ( 2 n + 1 ) / ( 2 n ) and F = k λ w ( λ + 1 ) / λ for the gap functions φ ( r ) = A n r 2 n (n is an integer) and φ ( r ) = A λ r λ ( λ ≥ 1 is a real number). The special case of a conical gap, φ ( r ) = A 1 r and F = k 1 w 2 , was earlier considered by Love [47]. The corresponding generalizations of the elastic Hertzian impact model was given by Kilchevsky [48]. However, to the best of the author’s knowledge, Hunter’s model of viscoelastic impact was not extended to the case of the Shtaerman–Galin contact law F = k λ w ( λ + 1 ) / λ .
Another open issue is to account for the target thickness, which is realized by a nonlinear force-displacement relation that looses the self-similarity scaling. In the case of quasi-static viscoelastic Hertzian contact, the thickness effect was considered by Argatov et al. [49]. It would be of undoubted interest to incorporate this effect even into the elastic Hertzian impact model (see, e.g., [35,50]).
Still a puzzle remains to be solved, and this concerns the inconsistency of Hunter’s prediction for the duration of impact ( t c < t c 0 ) with the experimental observations [35] that the effect of viscoelasticity increases the impact duration as compared to the elastic case (that is, t c > t c 0 ). For the linear viscoelastic Maxwell impact model (see, e.g., [44,51]), though the viscoelasticity effect increases the duration of impact, we have t m = t m 0 ( 1 + O ( ζ ) ) and t c = t c 0 ( 1 + O ( ζ 2 ) ) , where ζ is the loss factor, that is the effect on the duration of the loading stage is much stronger than the effect of the overall contact duration. Apparently, the answer to the raised question might be sought in the fact that Hunter’s approximation t 1 ≃ 2 t m − t is not asymptotically exact (strictly speaking, the sign ≃ should be replaced with ≈). At the same time, the approximate model (18) for the loading stage and the corresponding solutions (see Section 2.3) are asymptotically exact. It should be also noted that the FEM simulations performed by Diani et al. [37] for a generalized Maxwell model result in the impact duration smaller than that predicted by Hertz’s theory.
A remark should be made about numerical solutions to the unilateral viscoelastic impact problem, where the force-displacement relation in the unloading stage is given by the two nonlinear integral equations (15) and (16) with the function t 1 ( t ) being determined by the equation a ( t ) = a ( t 1 ) , where a ( t ) is the current contact radius in the unloading stage ( t > t m ), and a ( t 1 ) is the same value of contact radius in the loading stage ( t 1 < t m ). A number of numerical schemes have been designed in the literature [40,41,42], but still no in-depth numerical study of the impact problem (e.g., for a Maxwell solid) has been published. It is to note that the FEM simulations, while being very useful for the overall analysis [43], do not suit well for verifying asymptotic solutions, if the second order smallness effects should be spotlighted.
To conclude, in view of its practical significance, the problem of viscoelastic impact requires a further investigation.

Acknowledgments

We acknowledge support by the German Research Foundation and the Open Access Publication Fund of TU Berlin.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hertz, H. Ueber die Berührung fester elastischer Körper. Journal für die reine und angewandte Mathematik 1882, 92, 156–171. [Google Scholar]
  2. Argatov, I.; Kachanov, M.; Mishuris, G. On the concept of “far points” in Hertz contact problems. International Journal of Engineering Science 2017, 113, 20–36. [Google Scholar] [CrossRef]
  3. Willis, J.R. Hertzian contact of anisotropic bodies. Journal of the Mechanics and Physics of Solids 1966, 14, 163–176. [Google Scholar] [CrossRef]
  4. Bondareva, V.F. Contact problems for an elastic sphere. Journal of Applied Mathematics and Mechanics 1971, 35, 37–45. [Google Scholar] [CrossRef]
  5. Villaggio, P. The rebound of an elastic sphere against a rigid wall. Journal of Applied Mechanics 1996, 63, 259–263. [Google Scholar] [CrossRef]
  6. Hunter, S.C. Energy absorbed by elastic waves during impact. Journal of the Mechanics and Physics of Solids 1957, 5, 162–171. [Google Scholar] [CrossRef]
  7. Wu, C.Y.; Li, L.Y.; Thornton, C. Energy dissipation during normal impact of elastic and elastic–plastic spheres. International Journal of Impact Engineering 2005, 32, 593–604. [Google Scholar] [CrossRef]
  8. Argatov, I.I. Asymptotic modeling of the impact of a spherical indenter on an elastic half-space. International Journal of Solids and Structures 2008, 45, 5035–5048. [Google Scholar] [CrossRef]
  9. Miller, G.F.; Pursey, H. On the partition of energy between elastic waves in a semi-infinite solid. Proceedings of the Royal Society of London. Ser. A 1955, 233, 55–69. [Google Scholar]
  10. Argatov, I.I.; Fadin, Y.A. Excitation of the elastic half-space surface by normal rebounding impact of an indenter. Journal of Friction and Wear 2009, 30, 1–6. [Google Scholar] [CrossRef]
  11. Deresiewicz, H. A note on Hertz’s theory of impact. Acta Mechanica 1968, 6, 110–112. [Google Scholar] [CrossRef]
  12. Goldsmith, W. Impact – The Theory and Physical Behaviour of Colliding Solids; Edward Arnold Ltd: London, England, 1960. [Google Scholar]
  13. Borodich, F. The Hertz frictional contact between nonlinear elastic anisotropic bodies (the similarity approach). International journal of solids and structures 1993, 30, 1513–1526. [Google Scholar] [CrossRef]
  14. Willert, E. Ratio of loss and storage moduli determines restitution coefficient in low-velocity viscoelastic impacts. Frontiers in Mechanical Engineering 2020, 6, 3. [Google Scholar] [CrossRef]
  15. Jaeger, J. Analytical solutions of contact impact problems. Applied Mechanics Reviews 1994, 47, 35–54. [Google Scholar] [CrossRef]
  16. Lyashenko, I.A.; Popov, V.L. Impact of an elastic sphere with an elastic half space revisited: Numerical analysis based on the method of dimensionality reduction. Scientific Reports 2015, 5, 8479. [Google Scholar] [CrossRef]
  17. Willert, E.; Popov, V.L. Impact of an elastic sphere with an elastic half space with a constant coefficient of friction: Numerical analysis based on the method of dimensionality reduction. Zeitschrift für Angewandte Mathematik und Mechanik 2016, 96, 1089–1095. [Google Scholar] [CrossRef]
  18. Johnson, K.L.; Pollock, H.M. The role of adhesion in the impact of elastic spheres. Journal of Adhesion Science and Technology 1994, 8, 1323–1332. [Google Scholar] [CrossRef]
  19. Lyashenko, I.A.; Willert, E.; Popov, V.L. Adhesive impact of an elastic sphere with an elastic half space: Numerical analysis based on the method of dimensionality reduction. Mechanics of Materials 2016, 92, 155–163. [Google Scholar] [CrossRef]
  20. Love, A.E.H. Mathematical Theory of Elasticity; Dover Publications: New York, 1944. [Google Scholar]
  21. Reed, J. Energy losses due to elastic wave propagation during an elastic impact. Journal of Physics D: Applied Physics 1985, 18, 2329–2337. [Google Scholar] [CrossRef]
  22. Machado, M.; Moreira, P.; Flores, P.; Lankarani, H.M. Compliant contact force models in multibody dynamics: Evolution of the Hertz contact theory. Mechanism and Machine Theory 2012, 53, 99–121. [Google Scholar] [CrossRef]
  23. Boettcher, R.; Eichmann, S.; Mueller, P. Influence of viscous damping and elastic waves on energy dissipation during impacts. Chemical Engineering Science 2019, 199, 571–587. [Google Scholar] [CrossRef]
  24. Alves, J.; Peixinho, N.; da Silva, M.T.; Flores, P.; Lankarani, H.M. A comparative study of the viscoelastic constitutive models for frictionless contact interfaces in solids. Mechanism and Machine Theory 2015, 85, 172–188. [Google Scholar] [CrossRef]
  25. Goldobin, D.S.; Susloparov, E.A.; Pimenova, A.V.; Brilliantov, N.V. Collision of viscoelastic bodies: Rigorous derivation of dissipative force. The European Physical Journal E 2015, 38, 1–9. [Google Scholar] [CrossRef]
  26. He, A.; Wettlaufer, J.S. Hertz beyond belief. Soft matter 2014, 10, 2264–2269. [Google Scholar] [CrossRef] [PubMed]
  27. Hayakawa, H.; Kuninaka, H. Theory of the inelastic impact of elastic materials. Phase Transitions 2004, 77, 889–909. [Google Scholar] [CrossRef]
  28. Hunter, S.C. The Hertz problem for a rigid spherical indenter and a viscoelastic half-space. Journal of the Mechanics and Physics of Solids 1960, 8, 219–234. [Google Scholar] [CrossRef]
  29. Lee, E.H.; Radok, J.R.M. The contact problem for viscoelastic bodies. Journal of Applied Mechanics 1960, 27, 438–444. [Google Scholar] [CrossRef]
  30. Forney, L.J. On the duration of contact for the Hertzian impact of a spherical indenter on a Maxwell solid. International Journal of Solids and Structures 1974, 10, 621–624. [Google Scholar] [CrossRef]
  31. Khusid, B.M. Collision of polymer particle with rigid barrier. Journal of Engineering Physics 1986, 51, 1387–1393. [Google Scholar] [CrossRef]
  32. Wang, D.; de Boer, G.; Neville, A.; Ghanbarzadeh, A. A review on modelling of viscoelastic contact problems. Lubricants 2022, 10, 358. [Google Scholar] [CrossRef]
  33. Aksel, N. On the impact of a rigid sphere on a viscoelastic half-space. Ingenieur-Archiv 1986, 56, 38–54. [Google Scholar] [CrossRef]
  34. Calvit, H.H. Experiments on rebound of steel balls from blocks of polymer. Journal of the Mechanics and Physics of Solids 1967, 15, 141–150. [Google Scholar] [CrossRef]
  35. Southern, E.; Thomas, A.G. The impact of rigid spheres on rubber. Journal of Applied Polymer Science 1972, 16, 1641–1651. [Google Scholar] [CrossRef]
  36. Pouyet, J.; Lataillade, J.L. Dynamic investigation of hard viscoelastic materials by ball bouncing experiments. Journal of Materials Science 1975, 10, 2112–2116. [Google Scholar] [CrossRef]
  37. Diani, J.; Gilormini, P.; Agbobada, G. Experimental study and numerical simulation of the vertical bounce of a polymer ball over a wide temperature range. Journal of Materials Science 2014, 49, 2154–2163. [Google Scholar] [CrossRef]
  38. Kren, A.P.; Naumov, A.O. Determination of the relaxation function for viscoelastic materials at low velocity impact. International Journal of Impact Engineering 2010, 37, 170–176. [Google Scholar] [CrossRef]
  39. Kuwabara, G.; Kono, K. Restitution coefficient in a collision between two spheres. Japanese journal of applied physics 1987, 26, 1230. [Google Scholar] [CrossRef]
  40. Calvit, H.H. Numerical solution of the problem of impact of a rigid sphere onto a linear viscoelastic half-space and comparison with experiment. International Journal of Solids and Structures 1967, 3, 951–966. [Google Scholar] [CrossRef]
  41. Aboudi, J. The dynamic indentation and impact of a viscoelastic half-space by an axisymmetric rigid body. Computer Methods in Applied Mechanics and Engineering 1979, 20, 135–150. [Google Scholar] [CrossRef]
  42. Sabin, G.C.W. The impact of a rigid axisymmetric indentor on a viscoelastic half-space. International journal of engineering science 1987, 25, 235–251. [Google Scholar] [CrossRef]
  43. Herrenbrück, M.; Duddeck, F.; Lackner, R. Multifunctional optimization of viscoelastic materials subjected to spherical impact. Journal of Applied Mechanics 2015, 82, 121009. [Google Scholar] [CrossRef]
  44. Argatov, I.I. Mathematical modeling of linear viscoelastic impact: Application to drop impact testing of articular cartilage. Tribology International 2013, 63, 213–225. [Google Scholar] [CrossRef]
  45. Shtaerman, I.Y. On the Hertz theory of local deformations resulting from the pressure of elastic solids [in Russian]. Doklady Akad. Nauk SSSR 1939, 25, 360–362. [Google Scholar]
  46. Galin, L.A. Spatial contact problems of the theory of elasticity for punches of circular shape in planar projection [in Russian]. PMM Journal of Applied Mathematics and Mechanics 1946, 10, 425–448. [Google Scholar]
  47. Love, A.E.H. Boussinesq’s problem for a rigid cone. Quarterly Journal of Mathematics 1939, 10, 161–175. [Google Scholar] [CrossRef]
  48. Kilchevsky, N.A. The Theory of Solid Bodies Collision [in Russian]; Naukova Dumka: Kiev, 1969. [Google Scholar]
  49. Argatov, I.; Daniels, A.U.; Mishuris, G.; Ronken, S.; Wirz, D. Accounting for the thickness effect in dynamic spherical indentation of a viscoelastic layer: Application to non-destructive testing of articular cartilage. European Journal of Mechanics-A/Solids 2013, 37, 304–317. [Google Scholar] [CrossRef]
  50. Argatov, I.I. Asymptotic Models of Elastic Contact [in Russian]; Nauka: St. Petersburg, 2005. [Google Scholar]
  51. Butcher, E.A.; Segalman, D.J. Characterizing damping and restitution in compliant impacts via modified KV and higher-order linear viscoelastic models. Journal of Applied Mechanics 2000, 67, 831–834. [Google Scholar] [CrossRef]
Preprints 104143 g001
Figure 1. Initial impact configuration: (a) Collision of two elastic spheres; (b) Impact of a rigid sphere onto an elastic half-space.
Figure 1. Initial impact configuration: (a) Collision of two elastic spheres; (b) Impact of a rigid sphere onto an elastic half-space.
Preprints 104143 g001
Preprints 104143 g002
Figure 2. Master curves for the Maxwell model obtained by Herrenbrück et al. [43] using FEM simulations and the analytical approximations (45): Relative maximum penetration (a) and relative maximum acceleration (b) as functions of the scaled characteristic relaxation time.
Figure 2. Master curves for the Maxwell model obtained by Herrenbrück et al. [43] using FEM simulations and the analytical approximations (45): Relative maximum penetration (a) and relative maximum acceleration (b) as functions of the scaled characteristic relaxation time.
Preprints 104143 g002
Preprints 104143 g003
Figure 3. Master curves for the Maxwell model obtained by Herrenbrück et al. [43] using FEM simulations and the analytical approximations (45): Coefficient of restitution as a function of the scaled characteristic relaxation time (a) and the relative inverse relaxation time (b).
Figure 3. Master curves for the Maxwell model obtained by Herrenbrück et al. [43] using FEM simulations and the analytical approximations (45): Coefficient of restitution as a function of the scaled characteristic relaxation time (a) and the relative inverse relaxation time (b).
Preprints 104143 g003
Preprints 104143 g004
Figure 4. Rescaled master curves for the standard linear solid model obtained by Herrenbrück et al. [43] using FEM simulations and the analytical approximations (45): Coefficient of restitution (a) and relative maximum acceleration (b) as functions of the scaled characteristic relaxation time.
Figure 4. Rescaled master curves for the standard linear solid model obtained by Herrenbrück et al. [43] using FEM simulations and the analytical approximations (45): Coefficient of restitution (a) and relative maximum acceleration (b) as functions of the scaled characteristic relaxation time.
Preprints 104143 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated