Submitted:
18 April 2024
Posted:
18 April 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Experimental Design and Analysis
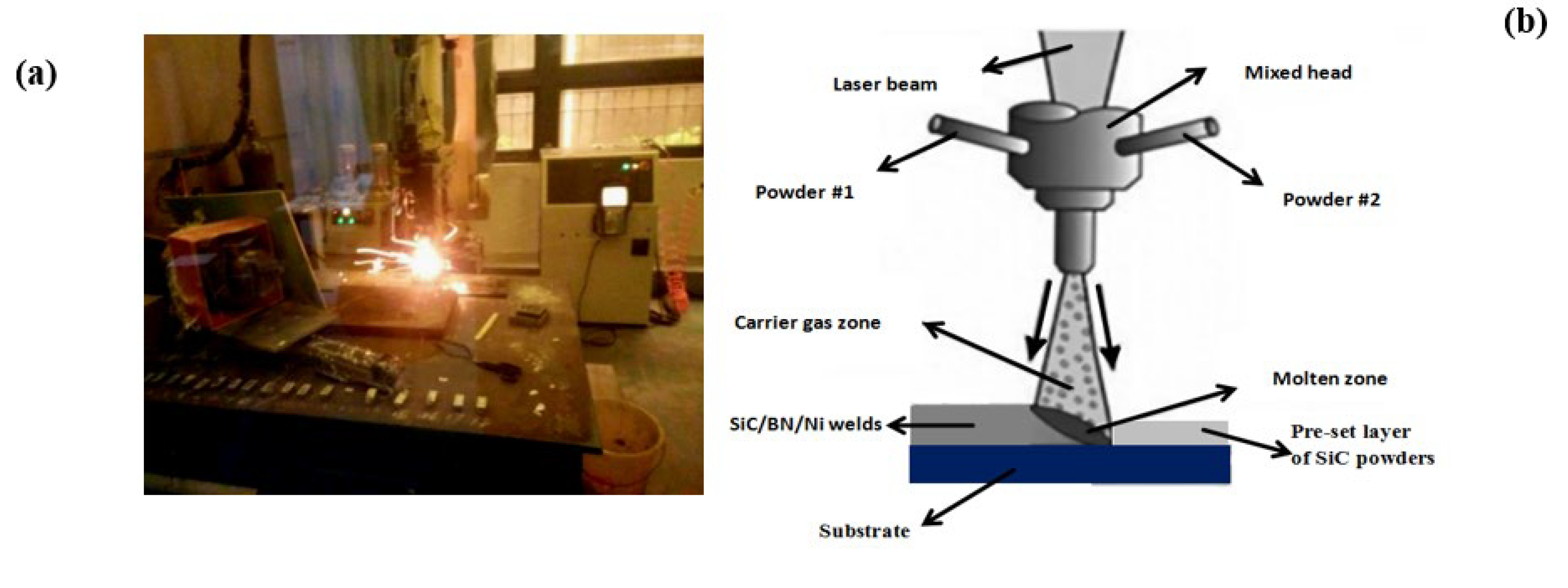
2.1. Materials and Preparations
2.2. Experimental Design and Layout
2.3. Adaptive Network Based Fuzzy Inference System
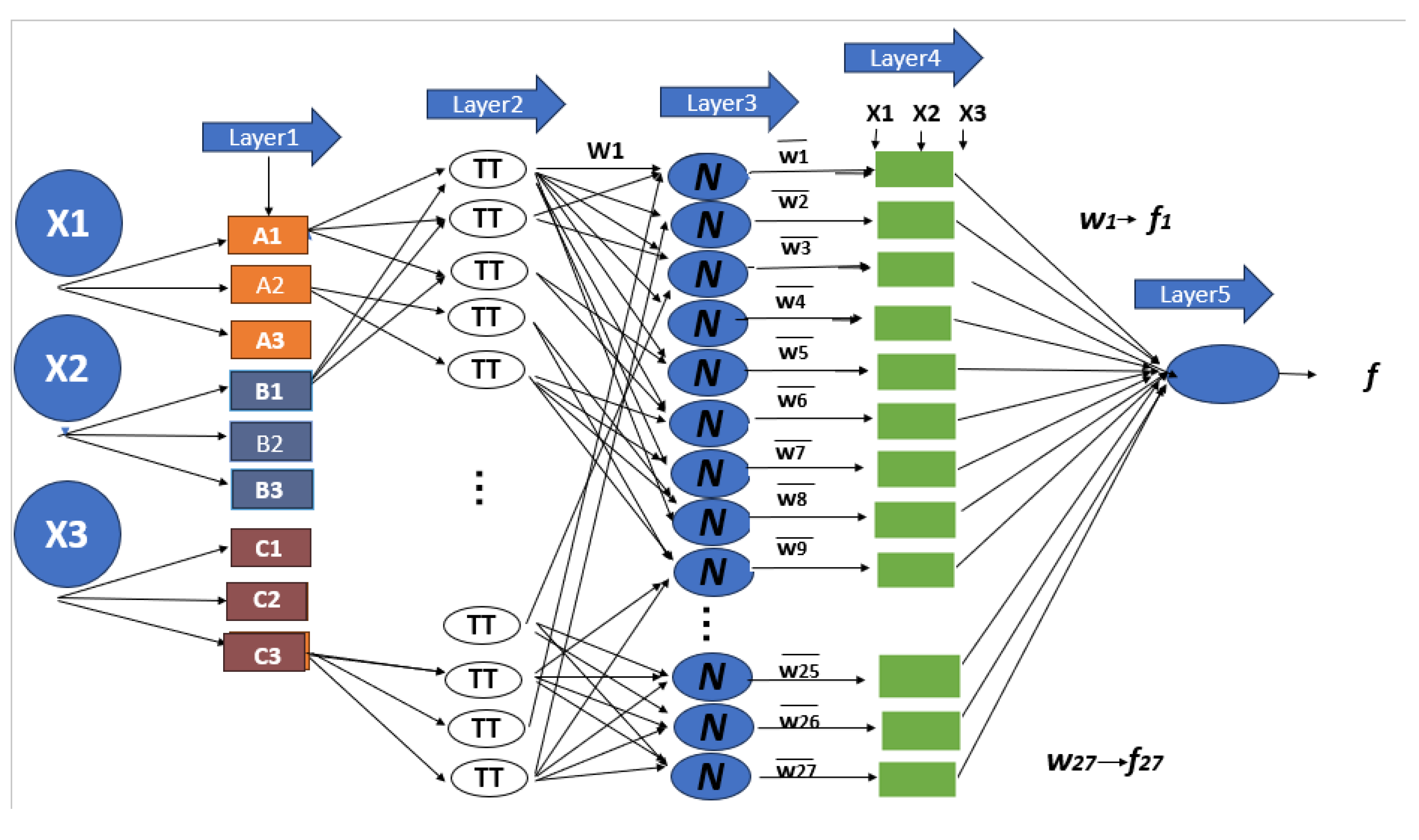
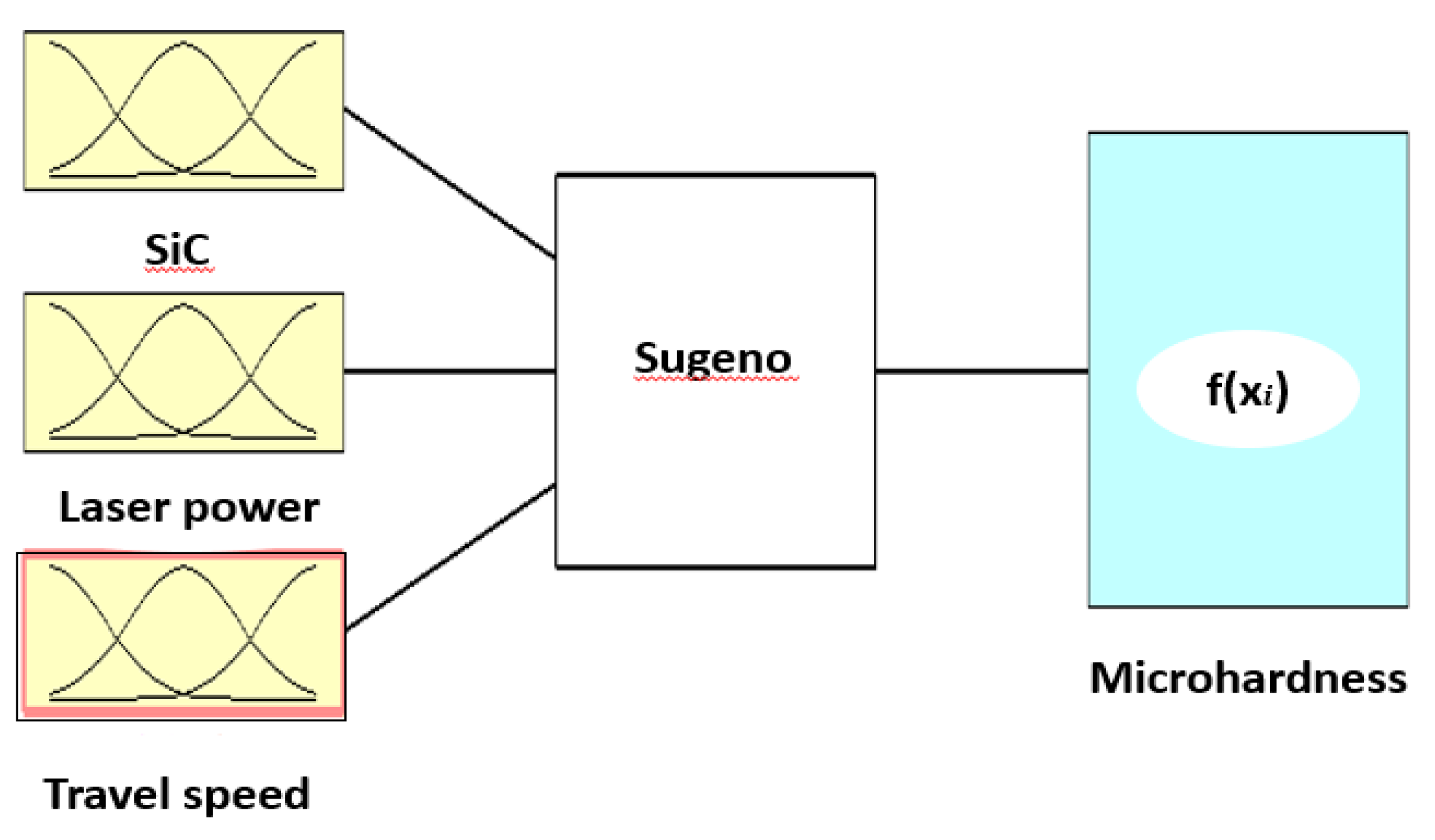
3. Experimental Results and Discussion
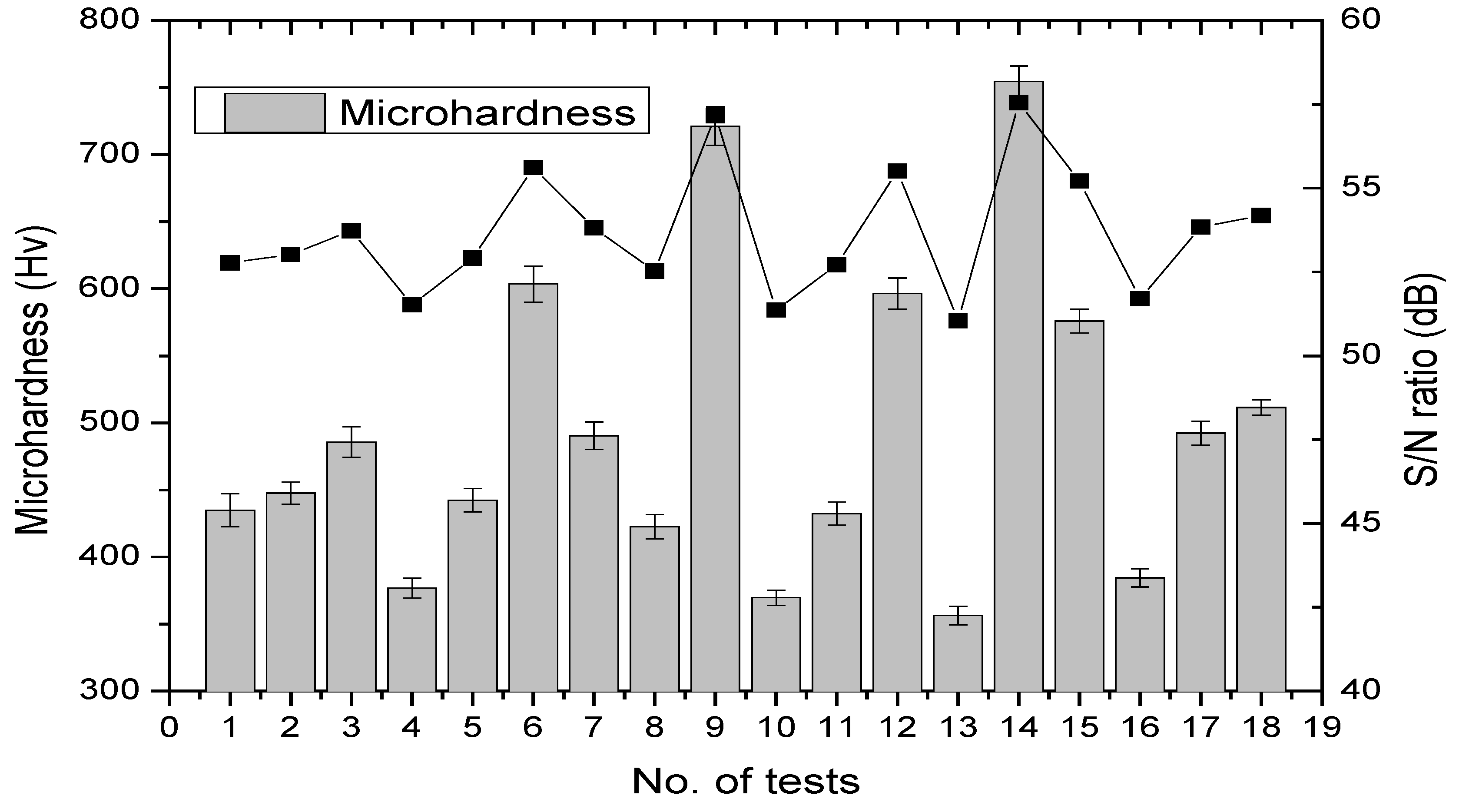
3.1. Experimental Design Based on Orthogonal Array
3.2. Microstructure of the Weld Zone for Laser-Coated NB/SiC/Ni Welds by Laser Cladding
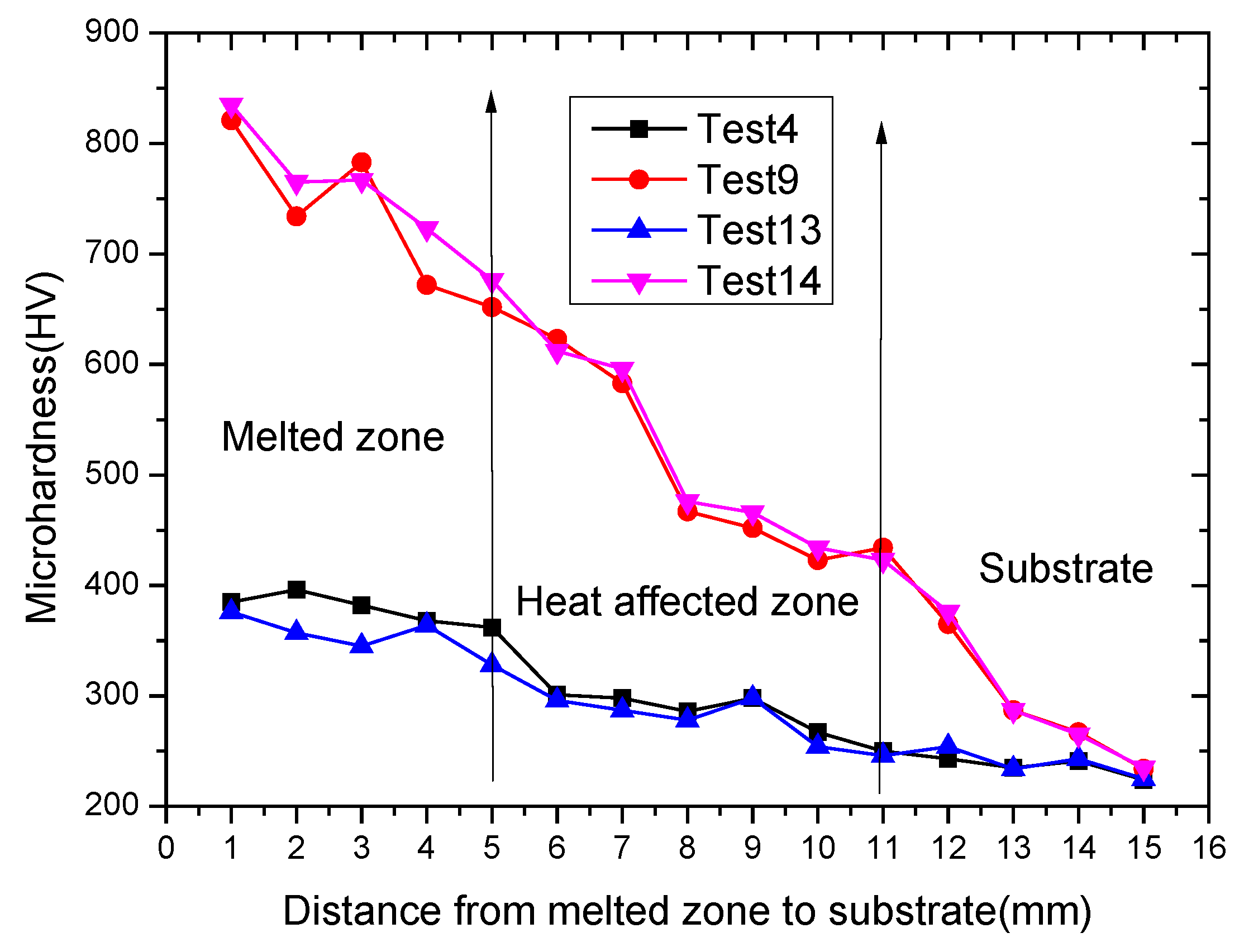

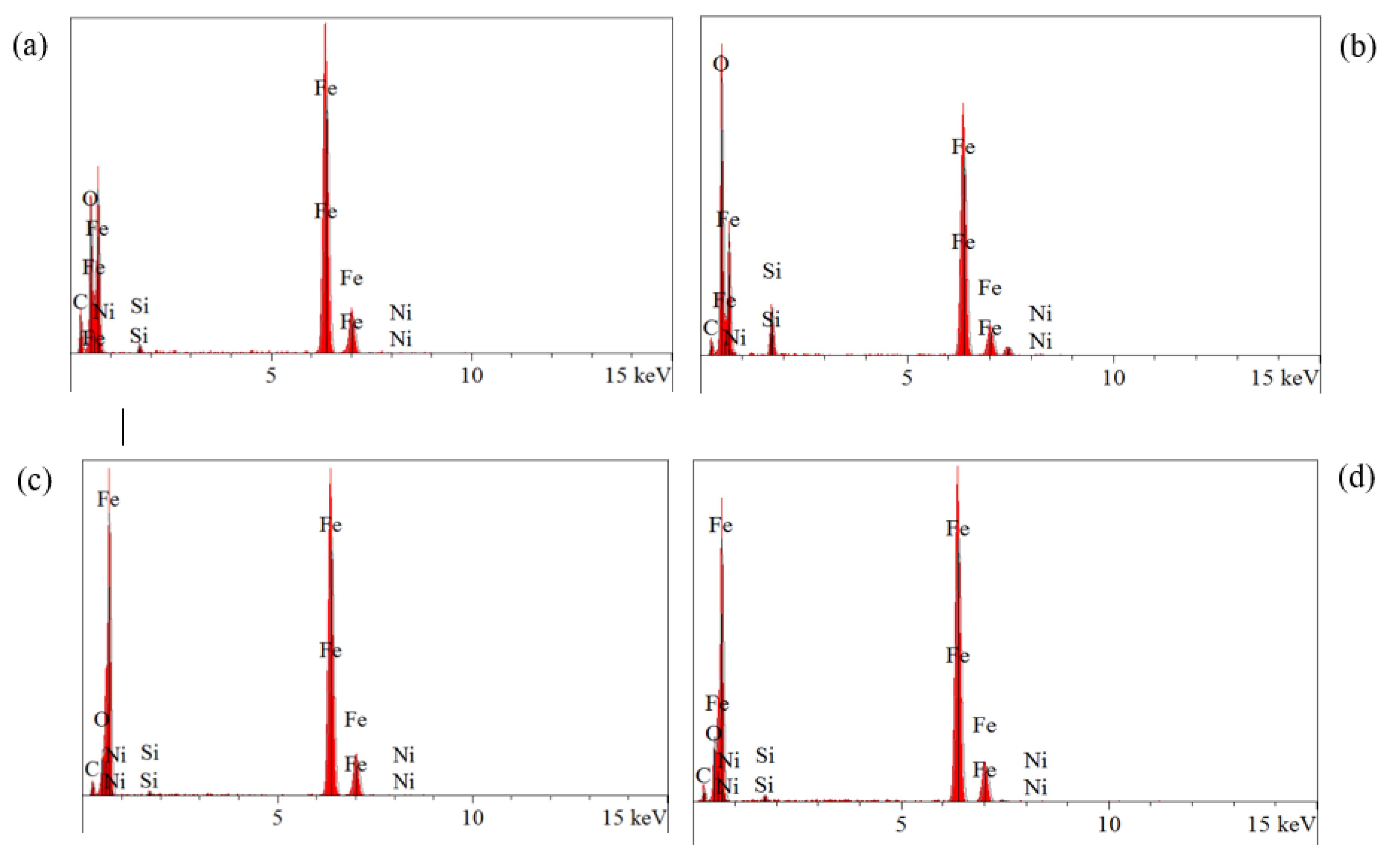
3.3. Effect of Designing with Ternary SiC/BN/Ni Mixtures on Hardness Yields
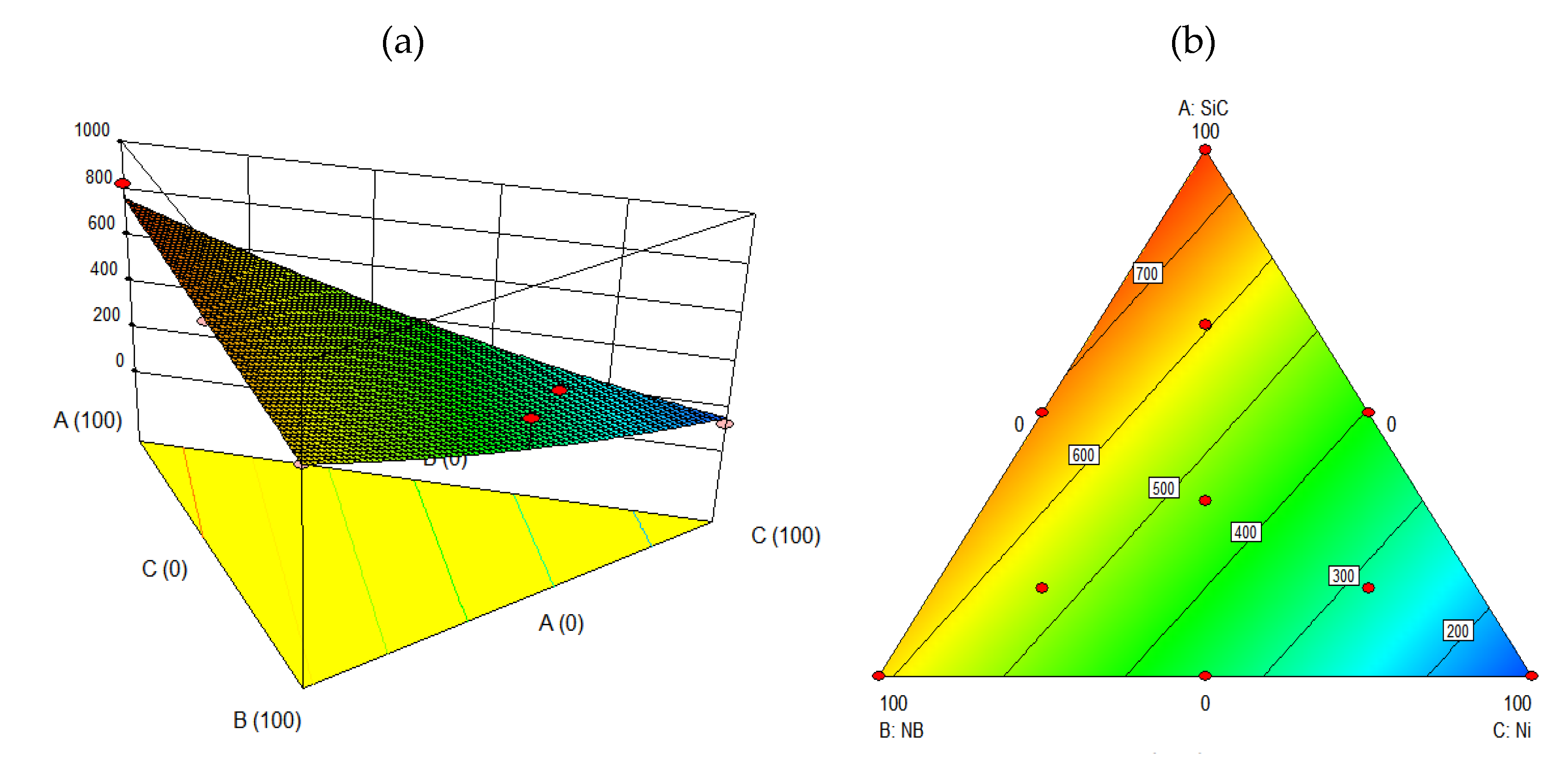
3.4. The Analysis of Variance of Laser-Coated BN/SiC/Ni Welds
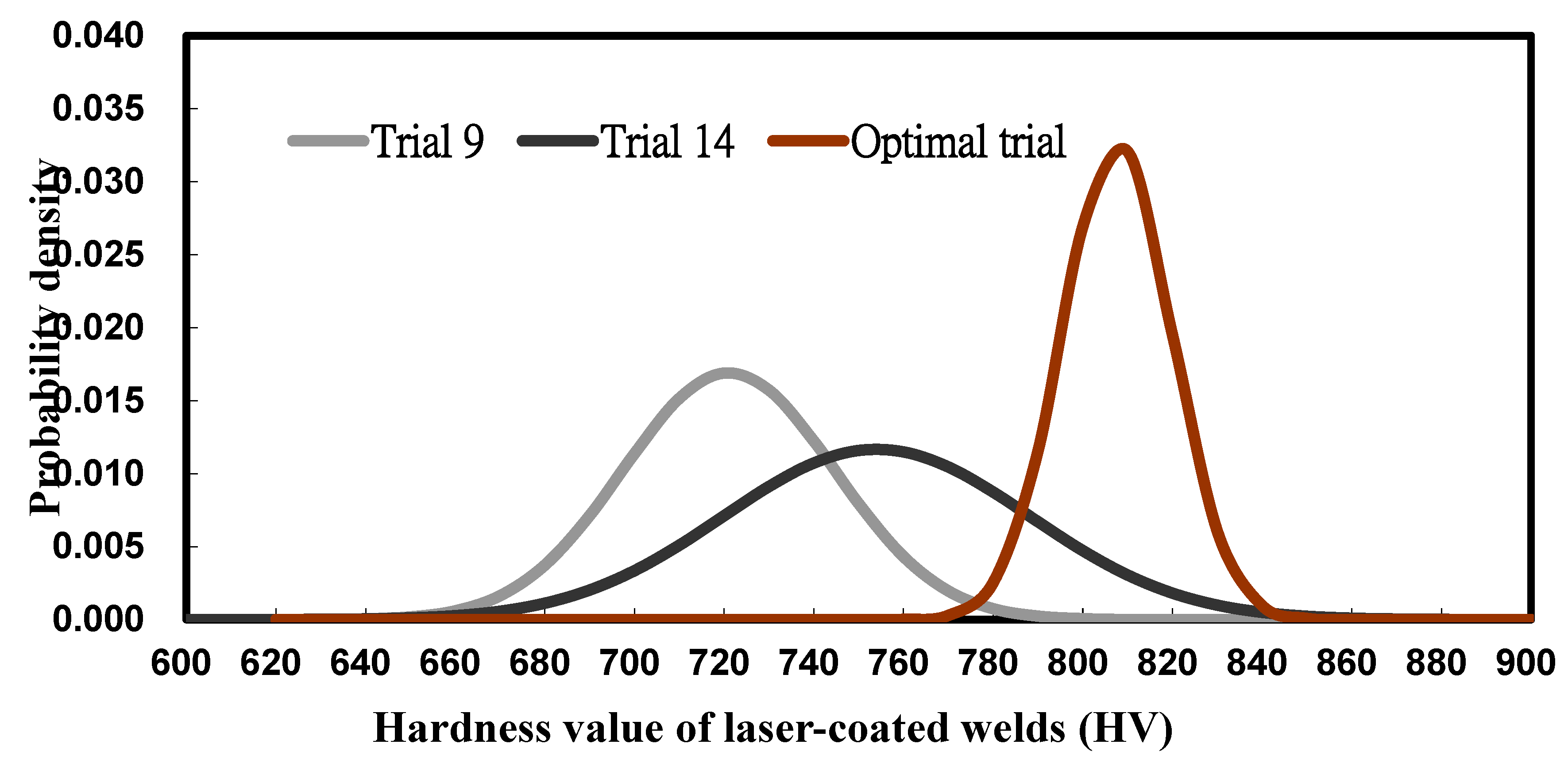
3.5. Confirm Run and Their Optimization on the Hardness Properties
4. Results and Discussion
4.1. Analysis of ANFIS Model
4.5. The Predictor of Surface Response Using an ANFIS
5. Concluding Remarks
Author Contributions
Acknowledgments
References
- Suryanarayanan, R. (1993). Plasma spraying: theory and applications. World scientific.
- Sun G, Zhou R, Lu J, et al. (2015). Evaluation of defect density, microstructure, residual stress, elastic modulus, hardness and strength of laser-deposited AISI 4340 steel. Acta Materialia, 84: 172-189. [CrossRef]
- W.L. Wang, J.Q. Bi, S.R. Wang, K.N. Sun, M. Du, N.N. Long, Y.J. Bai. Microstructure and mechanical properties of alumina ceramics reinforced by boron nitride nanotubes. Journal of the European Ceramic Society. 31(13), 2011, 2277-2284. [CrossRef]
- Li XC, Stampfl J, Prinz FB (2000) Mechanical and thermal expansion behavior of laser deposited metal matrix composites of Invar and TiC. Mater Sci Eng A Struct 282:86–90.
- Babout L, Brechet Y, Maire E, Fougeres R (2004) On the competition between particle fracture and particle decohesion in metal matrix composites. Acta Mater 52:4517–4525.
- Da Shu, Zhuguo Li, Ke Zhang, Chengwu Yao, Dayong Li, Zhenbang Dai. (2010). In situ synthesized high volume fraction WC reinforced Ni-based coating by laser cladding. Materials Letters 195 (2017) 178–181. [CrossRef]
- Zhang J, Lei J, Gu Z, et al. (2020). Effect of WC-12Co content on wear and electrochemical corrosion properties of Ni-Cu/WC-12Co composite coatings deposited by laser cladding. Surface and Coatings Technology, 393: 125807. [CrossRef]
- Chaokun Song, Xiaofei Liu, Fang Ye, Yongsheng Liu, Laifei Cheng. Mechanical and dielectric properties of SiCf/BN/SiBCN composites via different synthesis technologies. Journal of the European Ceramic Society. 39(14), 2019, 4417-4423. [CrossRef]
- Yu Pan, Yongsheng Liu, Mingxi Zhao, Ning Wang, Chenhao Wang, Sujun He, Fang Ye, Laifei Cheng. Effects of oxidation temperature on microstructure and EMI shielding performance of layered SiC/PyC porous ceramics. Journal of the European Ceramic Society. 39(15), 2019, 4527-4534. [CrossRef]
- Yamaguchi T, Hagino H. (2021). Effects of the ambient oxygen concentration on WC-12Co cermet coatings fabricated by laser cladding. Optics & Laser Technology, 139: 106922. [CrossRef]
- Cao Q, Fan L, Chen H, et al. (2022). Wear behavior of laser cladded WC-reinforced Ni-based coatings under low temperature. Tribology International, 176: 107939. [CrossRef]
- Chen Zishan, Li Hejun, Fu Qiangang, Qiang Xinfa.Tribological behaviors of SiC/h-BN composite coating at elevated temperatures. Tribology International 56 (2012) 58–65.
- Andre Contin, Getúlio de Vasconcelos, Danilo Maciel Barquete, Raonei Alves Campos, Vladimir Jesus Trava-Airoldi, Evaldo José Corat. Laser cladding of SiC multilayers for diamond deposition on steel substrates. Diamond & Related Materials 65 (2016) 105–114. [CrossRef]
- H. Zhuang, L. Zhang, T. Staedler, X. Jiang, Nanoscale integration of SiC/SiO2 core-shellnanocables in diamond through a simultaneous hybrid structure fabrication, Appl. Phys. Lett. 100 (2012). [CrossRef]
- Anjani Kumar, Anil Kumar Das. Evolution of microstructure and mechanical properties of Co-SiC tungsten inert gas cladded coating on 304 stainless steel. Engineering Science and Technology, an International Journal, 24(3), 2021, P 591-604.
- A. Kumar, R. Kumar Ram, A. Kumar Das. Mechanical characteristics of Ti-SiC metal matrix composite coating on AISI 304 steel by gas tungsten arc (GTA) coating process. Mater. Today: Proc., 17 (2019), pp. 111-117.
- Q. Li, G.M. Song, Y.Z. Zhang, T.C. Lei, W.Z. Chen, Microstructure and dry sliding wear behavior of laser clad Ni-based alloy coating with the addition of SiC, Wear. 254 (2003) 222-229. [CrossRef]
- S. Buytoz. Microstructural properties of SiC based hardfacing on low alloy steel. Surf. Coat. Technol., 200 (12-13) (2006), pp. 3734-3742. [CrossRef]
- F. Kretz, Z. F. Kretz, Z. Gácsi, J. Kovács, T. Pieczonka. The electroless deposition of nickel on SiC particles for aluminum matrix composites. Surf. Coat. Technol., 180-181 (2004), pp. 575-579.
- Maolin Chen, Ling Pan, Xiaodong Xia, Wei Zhou, Yang Li. Boron nitride (BN) and BN based multiple-layer interphase for SiCf/SiC composites: A review.Ceramics International 48(23), Part A, 2022, 34107-34127. [CrossRef]
- Richter J, Harabas K. (2019). Micro-abrasion investigations of conventional and experimental supercoarse WC-(Ni, Co, Mo) composites. International Journal of Refractory Metals and Hard Materials, 83: 104986. [CrossRef]
- A.K. Das et al. Effect of rare earth oxide (Y2O3) addition on alloyed layer synthesized on Ti-6Al-4V substrate with Ti+SiC+h-BN mixed precursor by laser surface engineering. Tribology International. 95, 2016, 35-43.
- Mingxi Zhao, Yongsheng Liu, Nan Chai, Hailong Qin, Xiaofei Liu, Fang Ye, Laifei Cheng, Litong Zhang. Effect of SiBCN content on the dielectric and EMW absorbing properties of SiBCN-Si3N4 composite ceramics. Journal of the European Ceramic Society 38(4), 2018,1334-1340. [CrossRef]
- S. Mahdavi, F. S. Mahdavi, F. Akhlaghi. Effect of the SiC particle size on the dry sliding wear behavior of SiC and SiC-Gr-reinforced Al6061 composites. J. Mater. Sci., 46 (24) (2011), pp. 7883-7894. [CrossRef]
- L. Li, H. Li, H. Lin, L. Zhuang, S. Wang, T. Feng, X. Yao, Q. Fu. Comparison of the oxidation behaviors of SiC coatings on C/C composites prepared by pack cementation and chemical vapor deposition. Surf. Coat. Technol., 302 (2016), pp. 56-64. [CrossRef]
- Xiangming Li, Litong Zhang, Xiaowei Yin, Liyun Feng, Quan Li. Effect of chemical vapor infiltration of SiC on the mechanical and electromagnetic properties of Si3N4–SiC ceramic.Scripta Materialia. 63(6), 2010, 657-660. [CrossRef]
- Yunyu Li, Lingjun Guo, Qiang Song, Hejun Li, Qiangang Fu, Kezhi Li. Oxidation pre-treatment and electrophoretic deposition of SiC nanowires to improve the thermal shock resistance of SiC coating for C/C composites. Journal of Alloys and Compounds. 636(5) 2015, 165-170. [CrossRef]
- Shuang Yin, Yuhang Jiang, Kai Su, Xia Fang, Yang Wang, Quan Li, Jian Yang. Preparation, mechanical, dielectric and microwave absorption properties of hierarchical porous SiCnw-Si3N4 composite ceramics. Journal of the European Ceramic Society. 42(9), 2022, 3820-3830.
- Wei Zhou, Lan Long, Yang Li. Mechanical and electromagnetic wave absorption properties of Cf-Si3N4 ceramics with PyC/SiC interphases. Journal of Materials Science & Technology. 35(12), 2019, 2809-2813. [CrossRef]
- Subhrojyoti Mazumder, Hendrik Simon Cornelis Metselaar, Nazatul Liana Sukiman, Nurin Wahidah Mohd Zulkifli. Friction and wear behavior of fluoride added Si3N4-SiC ceramic composites at elevated temperature. Ceramics International 49(8), 2023, 12787-12795. [CrossRef]
- F. Lusquiños, J. Pou, F. Quintero, M. Pérez-Amor. Laser cladding of SiC/Si composite coating on Si-SiC ceramic substrates. Surf. Coat. Technol., 202 (9) (2008), pp. 1588-1593.
- B.J. Zheng; X.M. Chen; J.S. Lian. Microstructure and wear property of laser cladding Al+SiC powders on AZ91D magnesium alloy. Optics and Lasers in Engineering.2010, 48 (5)526-532.
- Xiaoli Sun, Jiakai Zhang, Weiguo Pan, Wenhuan Wang, Congwei Tang. A review on the preparation and application of BN composite coatings. Ceramics International. 49(1), 2023,24-39. [CrossRef]
- Neng Li; Yi Xiong; Huaping Xiong; Gongqi Shi; Jon Blackburn;Wei Liu; Renyao Qin. Microstructure, formation mechanism and property characterization of Ti+SiC laser cladded coatings on Ti6Al4V alloy. Materials Characterization. 2019, 148, 43–51. [CrossRef]
- J.D. Majumdar, B.R. Chandra, A.K. Nath, I. Manna. Laser composite surfacing of stainless steel with SiC.Phys. Stat. Sol. (a), 203 (9) (2006), pp. 2260-2265. [CrossRef]
- S.P. Lee et al. Fabrication of liquid phase sintered SiC materials and their characterization. Fusion Engineering and Design. 81(8-14) 2006, 963-967. [CrossRef]
- Shu D, Li Z, Zhang K, et al. (2017). In situ synthesized high volume fraction WC reinforced Ni-based coating by laser cladding. Materials Letters, 195: 178-181. [CrossRef]
- F. Rebillat, J. Lamon, A. Guette, The concept of a strong interface applied to SiC/SiC composites with a BN interphase, Acta Mater. 48 (2000) 4609–4618. [CrossRef]
- Jens Eichler, Christoph Lesniak. Boron nitride (BN) and BN composites for high-temperature applications. Journal of the European Ceramic Society. 28(5), 2008, 1105-1109. [CrossRef]
- Lotfi A Zadeh. Fuzzy logica personal perspective. Fuzzy Sets and Systems, 281:4–20, 2015. [CrossRef]
- J Lee, K Um. A comparison in a back-bead prediction of gas metal arc welding using multiple regression analysis and artificial neural network. Optics and Lasers in Engineering,34(3) 2000, 149-158. [CrossRef]
- Sukhomay Pal, Surjya K. Pal, Arun K. Samantaray. Artificial neural network modeling of weld joint strength prediction of a pulsed metal inert gas welding process using arc signals. Journal of Materials Processing Technology. 202(1-3), 2008, 464-474. [CrossRef]
- D.S. Nagesh, G.L. Datta. Prediction of weld bead geometry and penetration in shielded metal-arc welding using artificial neural networks. Journal of Materials Processing Technology. 123(2) 2002, 303-312. [CrossRef]
- C.R.Wang, Z.Q. Zhong, M. D. Jean. Effect of ingredients proportions on mechanical properties in lasercoated WC-blend welds. Phys. Scr. 99 (2024) 035945. [CrossRef]
- Nicola Contuzzi; Giuseppe Casalino. On modelling Nd:Yag nanosecond laser milling process by neural network and multi response prediction methods. Optik - International Journal for Light and Electron Optics.2023,284: 170937. [CrossRef]
- Meng Liu; Chunzheng Duan; Guohe Li; Yujun Cai; Feng Wang; Lei Li. Multi-response optimization of Ni-based laser cladding via principal component analysis and grey relational analysis. Optik-International Journal for Light and Electron Optics. 2023.287. [CrossRef]
- Liu, J C;Ni, L B.Prediction of laser clad parameters based on neural network. Materials Technology: Advanced Performance Materials 012, 27 (1),11-14.
- Zhou, Zhijie; Du, Yanbin; He, Guohua; Xu, Lei; Shu, Linsen. Optimization and Characterization of Laser Cladding of 15-5PH Coating on 20Cr13 Stainless Steel. Journal of Materials Engineering and Performance. 2023, 32 (3) 962-977. [CrossRef]
- Gao, Jiali;Wang, Chi;Hao, Yunbo;Liang, Xudong;Zhao, Kai. Prediction of TC11 single-track geometry in laser metal deposition based on back propagation neural network and random forest. Journal of Mechanical Science and Technology. 2022, 36 (3)1417-1425. [CrossRef]
- Liaoyuan Chen, Tianbiao Yu, Xin Chen, Yu Zhao, Chuang Guan. Process optimization, microstructure and microhardness of coaxial laser cladding TiC reinforced Ni-based composite coatings. Optics & Laser Technology, 152, 2022, 108129. [CrossRef]
- Rasool Saeedi, Reza Shoja Razavi, Saeed Reza Bakhshi, Mohammad Erfanmanesh, Ahmad Ahmadi Bani. Optimization and characterization of laser cladding of NiCr and NiCr-TiC composite coatings on AISI 420 stainless steel. Ceramics International. 47(3), 2021, 4097-4110.
- Jang J S, R. ANFIS: Adaptive-Network–Based Fuzzy Inference System. IEEE Transactions on Systems, Man, and Cybernetics,1993, 23(3): 665–685.
- Lan-Ling Fu; Jin-Shui Yang; Shuang Li; Hao Luo; Jian-Hao Wu. Artificial neural network-based damage detection of composite material using laser ultrasonic technology. Measurement. 2023, 220, 113435. [CrossRef]
- Muhammad Arif Mahmood, Andrei C. Popescu, Mihai Oane, Asma Channa, Sabin Mihai, Carmen Ristoscu, Ion N. Mihailescu. Bridging the analytical and artificial neural network models for keyhole formation with experimental verification in laser melting deposition: Anovel approach. Results in Physics. 26, 2021, 104440.
- Andenson K‚Cook G E‚Karsai G et al. Artificial neural network applied to arc welding process modeling and control. IEEE Trans on Industry Application199026(5):824-830.
- S. Chowdhury, S. Anand. Artificial neural network based geometric compensation for thermal deformation in additive manufacturing processes. Int. Manuf. Sci. Eng. Conf, Blacksburg, VA, USA (2016).
- W. Sudnik, D. Radaj, W. Erofeew. Computerized simulation of laser beam welding, modelling and verification. J Phys D Appl Phys, 29 (11) 1996, 2811-2817. [CrossRef]
- Yuhang Zhang, Yifei Xu, Yaoning Sun and Wangjun Cheng. Surface quality optimization of laser cladding based on surface response and genetic neural network model. Surface Topography: Metrology and Properties, 10(4)2022, 10 044007. [CrossRef]
- S. Genna, E. Menna, G. Rubino, F. Trovalusci. Laser machining of silicon carbide: Experimental analysis and multiobjective optimization. Ceramics International 49(7), 2023,10682-10691. [CrossRef]
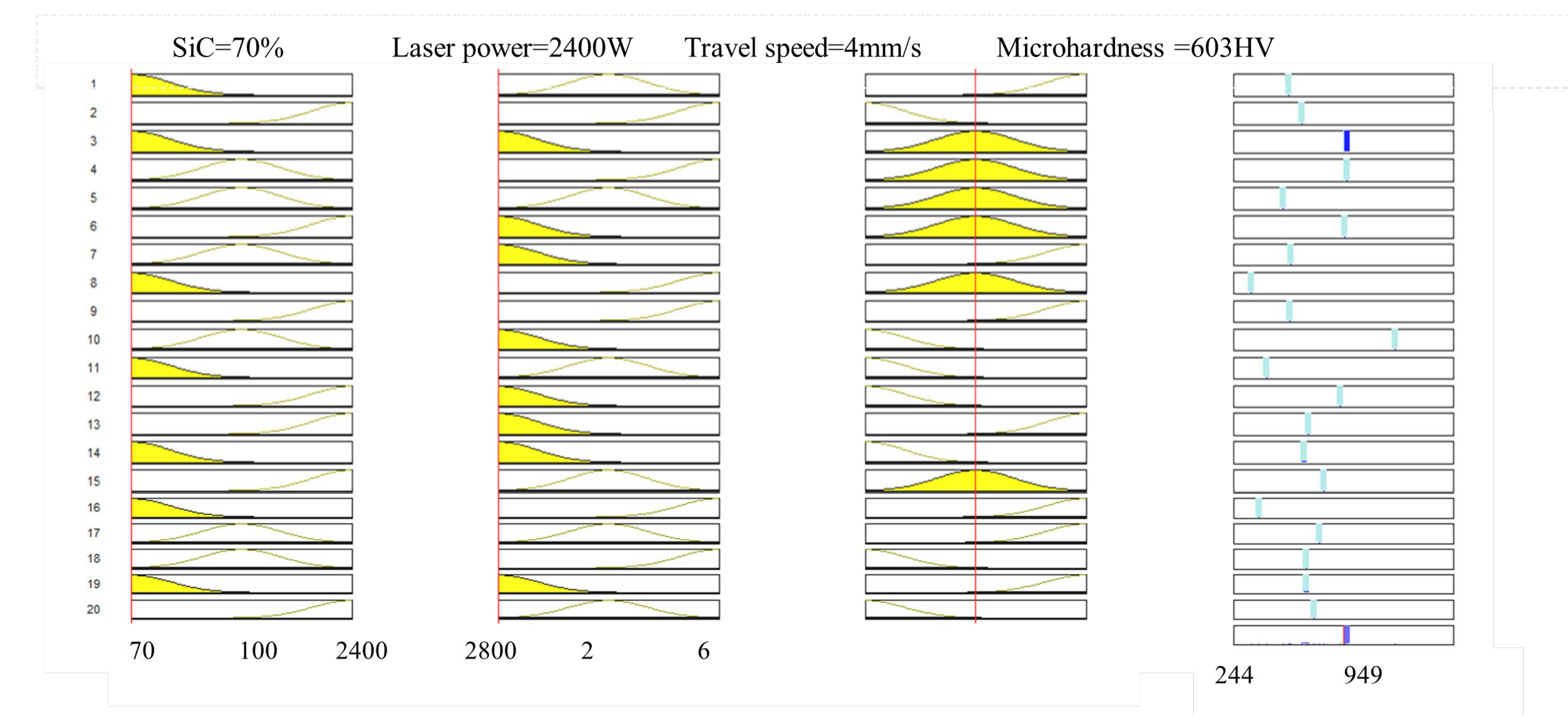
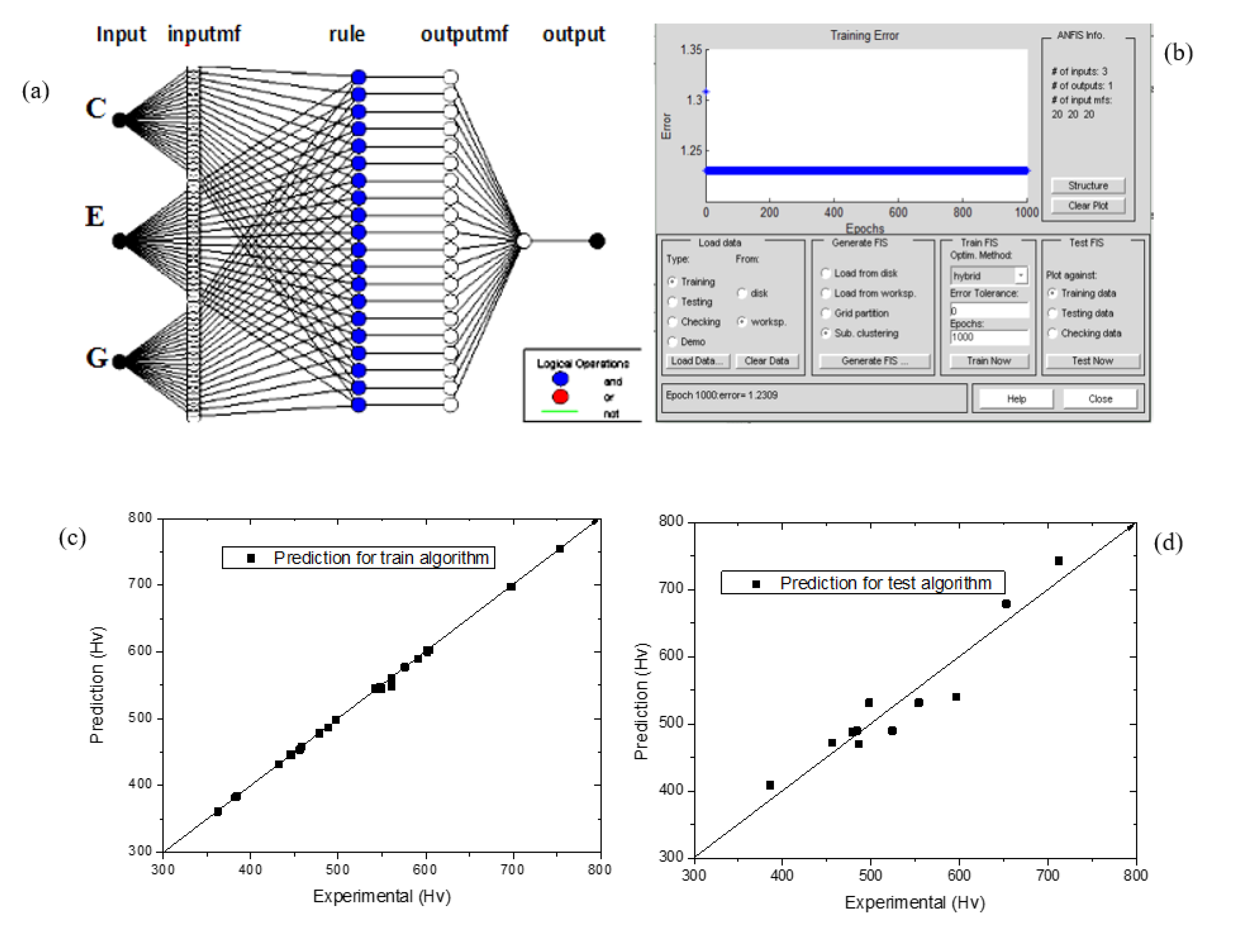
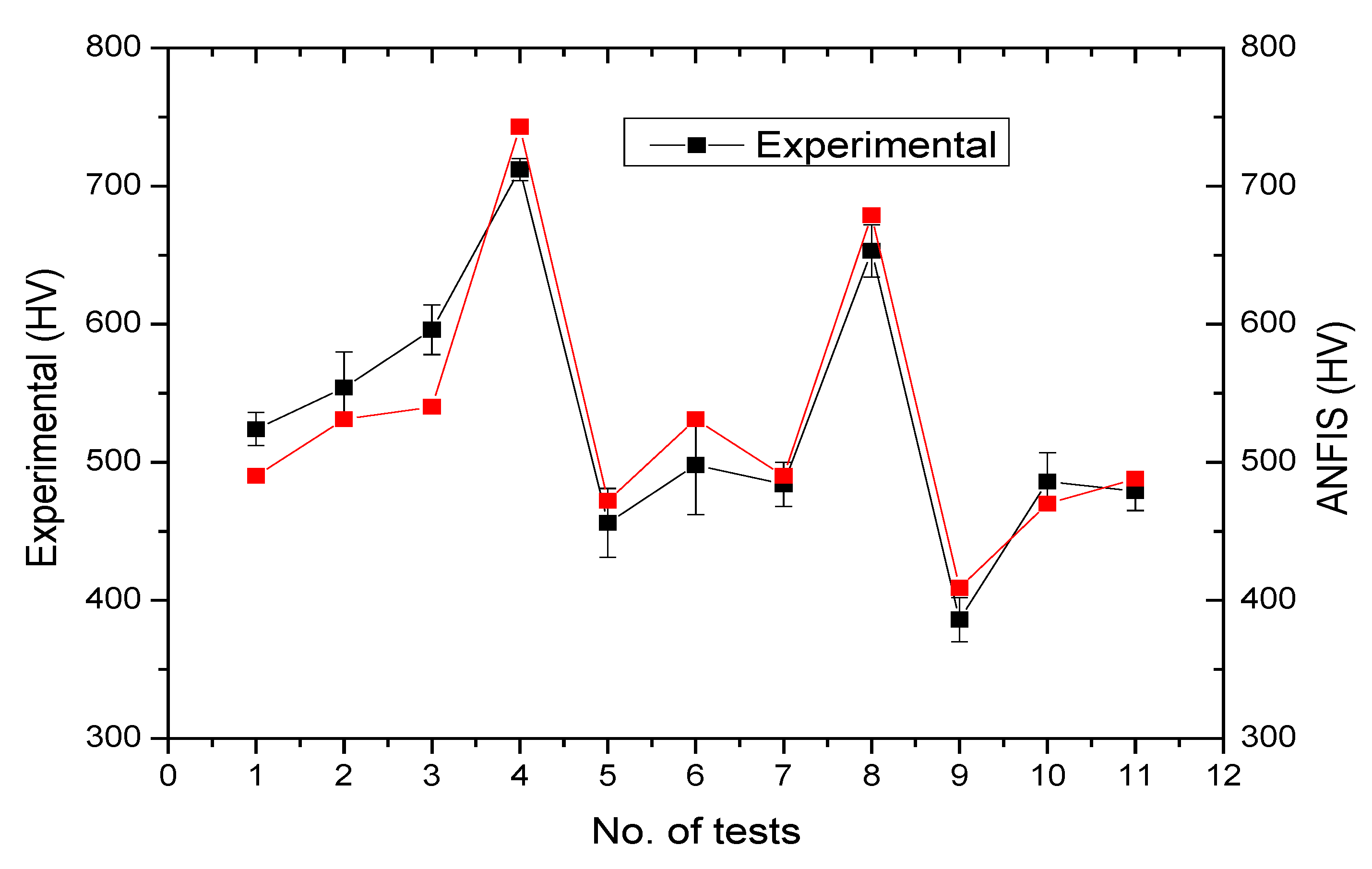
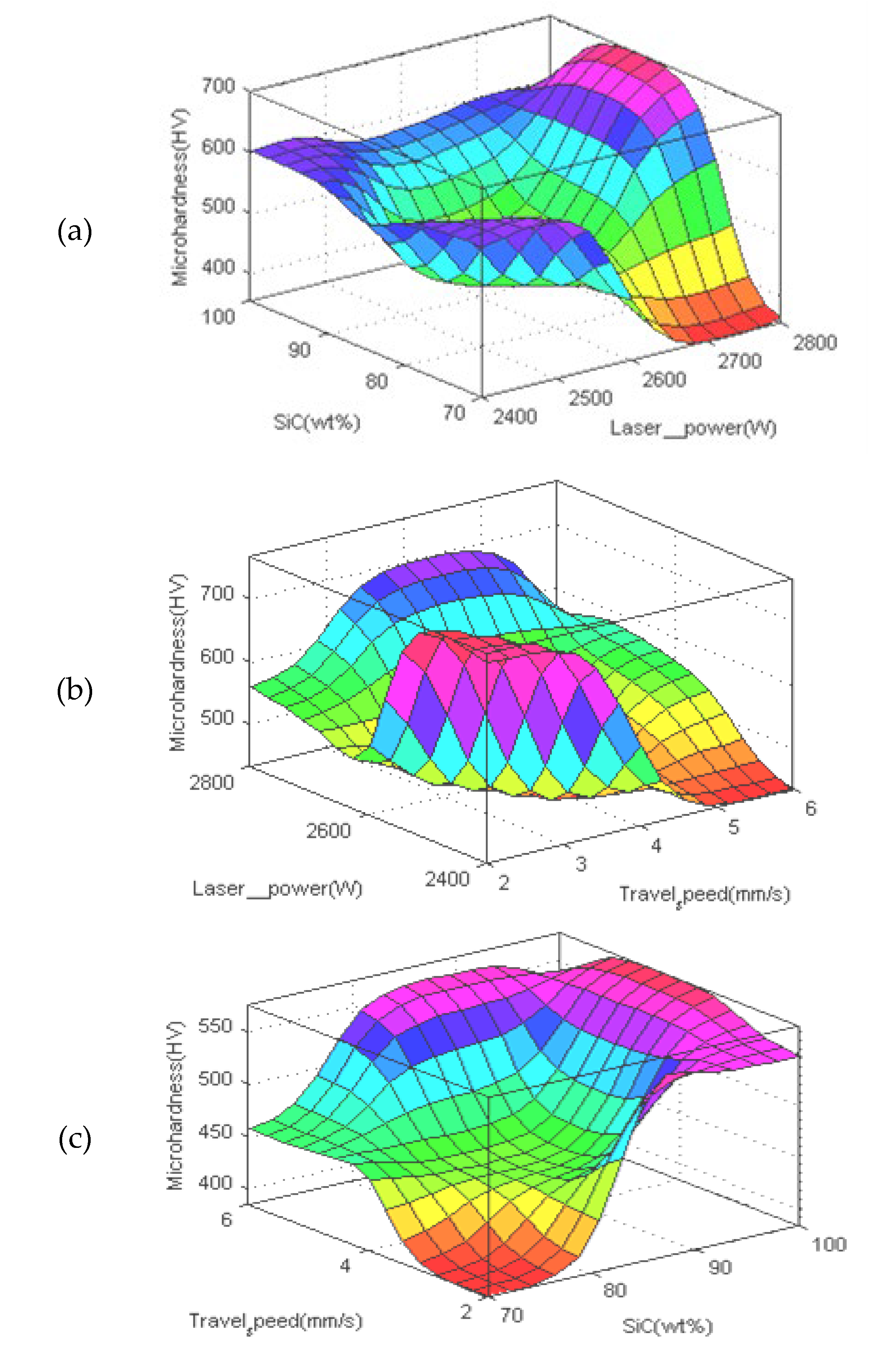
| Symbol | Controllable factors |
Level 1 | Level 2 | Level 3 |
|---|---|---|---|---|
| A | Base metal | 40Cr steel | #45 steel | - |
| B | BN(wt%) | 0 | 15 | 30 |
| C | SiC(wt%) | 100 | 85 | 70 |
| D | Ni(wt%) | 0 | 15 | 30 |
| E | Power of laser(W) | 2400 | 2600 | 2800 |
| F | Carrier gas(mL/min) | 1400 | 1600 | 1800 |
| G | Travel speed (mm/s) | 2 | 4 | 6 |
| H | Stand-off distance(mm) | 40 | 45 | 50 |
|
EXP |
A |
B |
C |
D |
E |
F |
G |
H |
Microhardness (HV) | S/N ratio (dB) |
||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H1 | H2 | H3 | Mean | St.Dev | ||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 423 | 442 | 440 | 434.9 | 8.5 | 52.77 |
| 2 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 437 | 434 | 472 | 447.6 | 17.2 | 53.02 |
| 3 | 1 | 1 | 3 | 3 | 3 | 3 | 3 | 3 | 478 | 479 | 500 | 485.7 | 10.2 | 53.73 |
| 4 | 1 | 2 | 1 | 1 | 2 | 2 | 3 | 3 | 367 | 386 | 377 | 376.8 | 7.8 | 51.52 |
| 5 | 1 | 2 | 2 | 2 | 3 | 3 | 1 | 1 | 431 | 453 | 443 | 442.3 | 9.0 | 52.91 |
| 6 | 1 | 2 | 3 | 3 | 1 | 1 | 2 | 2 | 596 | 589 | 626 | 603.5 | 15.8 | 55.61 |
| 7 | 1 | 3 | 1 | 2 | 1 | 3 | 2 | 3 | 484 | 499 | 488 | 490.4 | 6.3 | 53.81 |
| 8 | 1 | 3 | 2 | 3 | 2 | 1 | 3 | 1 | 412 | 432 | 424 | 422.5 | 8.2 | 52.52 |
| 9 | 1 | 3 | 3 | 1 | 3 | 2 | 1 | 2 | 712 | 698 | 754 | 721.2 | 23.6 | 57.16 |
| 10 | 2 | 1 | 1 | 3 | 3 | 2 | 2 | 1 | 353 | 376 | 380 | 369.7 | 11.9 | 51.36 |
| 11 | 2 | 1 | 2 | 1 | 1 | 3 | 3 | 2 | 412 | 443 | 442 | 432.4 | 14.4 | 52.72 |
| 12 | 2 | 1 | 3 | 2 | 2 | 1 | 1 | 3 | 578 | 602 | 609 | 596.4 | 13.3 | 55.51 |
| 13 | 2 | 2 | 1 | 2 | 3 | 1 | 3 | 2 | 345 | 376 | 348 | 356.4 | 13.9 | 51.04 |
| 14 | 2 | 2 | 2 | 3 | 1 | 2 | 1 | 3 | 712 | 756 | 796 | 754.6 | 34.2 | 57.55 |
| 15 | 2 | 2 | 3 | 1 | 2 | 3 | 2 | 1 | 567 | 586 | 575 | 575.9 | 7.8 | 55.21 |
| 16 | 2 | 3 | 1 | 3 | 2 | 3 | 1 | 2 | 375 | 396 | 382 | 384.4 | 8.7 | 51.70 |
| 17 | 2 | 3 | 2 | 1 | 3 | 1 | 2 | 3 | 479 | 470 | 528 | 492.3 | 25.4 | 53.84 |
| 18 | 2 | 3 | 3 | 2 | 1 | 2 | 3 | 1 | 493 | 512 | 529 | 511.4 | 14.7 | 54.18 |
| No. of trials |
Atomic concentration (%) | ||||
|---|---|---|---|---|---|
| C | O | Si | Fe | Ni | |
| Trial4 | 5.509 | 11.820 | 0.539 | 81.580 | 0.551 |
| Trial 9 | 2.051 | 24.967 | 0.383 | 69.031 | 3.568 |
| Trial 13 | 2.746 | 3.845 | 0.342 | 92,651 | 0.337 |
| Trial14 | 2.564 | 5.259 | 0.516 | 90.611 | 1.050 |
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| Level 1 | 53.67 | 53.18 | 52.03 | 53.87 | 54.44 | 53.55 | 54.60 | 53.16 |
| Level 2 | 53.68 | 53.98 | 53.76 | 53.41 | 53.24 | 54.13 | 53.81 | 53.54 |
| Level 3 | 0.00 | 53.87 | 55.23 | 53.74 | 53.34 | 53.35 | 52.62 | 54.33 |
| Effect | 0.01 | 0.79 | 3.20 | 0.46 | 1.19 | 0.79 | 1.98 | 1.17 |
| Rank | 8 | 5 | 1 | 7 | 3 | 6 | 2 | 4 |
| Control factors |
Sum of squares |
Degrees of freedom |
Mean square |
Test ratio |
Contribution |
|---|---|---|---|---|---|
| A | 0.00013 | 1.0 | 0.00013 | 0.00006 | 0.00 |
| B | 2.214 | 2.0 | 1.107 | 0.469 | 3.57 |
| C | 30.794 | 2.0 | 15.397 | 6.528 | 49.71 |
| D | 0.674 | 2.0 | 0.337 | 0.143 | 1.09 |
| E | 5.291 | 2.0 | 2.646 | 1.122 | 8.54 |
| F | 1.996 | 2.0 | 0.998 | 0.423 | 3.22 |
| G | 11.973 | 2.0 | 5.987 | 2.538 | 19.33 |
| H | 4.284 | 2.0 | 2.142 | 0.908 | 6.92 |
| Error | 4.717 | 2.0 | 2.359 | 1.000 | 7.62 |
| Total | 61.944 | 17.0 | 3.644 | 100.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




