Robust Wideband Interference Suppression Method for GNSS Array Antenna Receiver via Hybrid Beamforming Technique

Preprint

Article

Robust Wideband Interference Suppression Method for GNSS Array Antenna Receiver via Hybrid Beamforming Technique

Altmetrics

Downloads

200

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

17 April 2024

Posted:

18 April 2024

You are already at the latest version

Alerts

Abstract

Global navigation satellite system (GNSS) array antenna receivers are widely used to suppress wideband interference in navigation countermeasures. However, existing array antenna receivers all adopt digital array structure and digital beamforming technique, and it has limited analog-front-end (AFE) dynamic range. In strong interference scenarios, AFE saturation will occur, which limits the maximum interference suppression ability of the array receiver. Aiming at this issue, this paper proposes a robust wideband interference suppression method for GNSS array antenna receivers based on hybrid beamforming technique. Firstly, a novel fully connected hybrid array receiver structure is proposed; Secondly, the corresponding hybrid beamforming method is proposed at the same time, and it realizes the complete elimination of strong interference by jointly suppression in analog domain and digital domain. After mathematical simulation experiments, it is verified that compared to the digital beamforming-based anti-jamming technique, the proposed method can effectively suppress strong wideband interference, and the maximum interference suppression ability is improved by 36 dB.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

The global navigation satellite system (GNSS) has the characteristics of all-weather and all-time, and it is widely used in various fields of society to obtain position, velocity, and time (PVT) information [1]. Due to the low ground level of GNSS signals, they are highly susceptible to various intentional or unintentional interference [2]. In order to ensure the effective performance of GNSS receivers in harsh civilian and military environments, various anti-jamming techniques have been developed, which eliminate narrowband and wideband interference in the time domain and space domain [3,4].

However, various anti-jamming techniques can only be effectively implemented when the receiver analog-front-end (AFE, including the antenna, radio frequency (RF), and analog-to-digital converter (ADC) in a broad sense) responds linearly to the input combination of signal, noise, and interference [5]. As a weak link, the AFE of GNSS receivers is susceptible to nonlinear effects such as saturation that distort the input waveforms due to strong interference received [6,7]. AFE saturation is an extreme case of the interference effect in strong interference scenarios. The linear dynamic range of the AFE sets the maximum interference suppression ability of the anti-jamming techniques [8]. Therefore, how to relax the linear dynamic range of the receiver AFE to prevent saturation in strong interference scenarios is of great significance to improve the anti-jamming performance of the receiver.

In recent years, some techniques have been developed to deal with AFE saturation issues in GNSS receivers. Paper [9] proposed stopband filtering techniques to alleviate saturation caused by out-of-band and near-band interference. Paper [10] proposes two antenna modules composed of dynamically configured component topology networks. These two configurable antenna modules can detect, identify, and isolate potential interference. They switch modules with different gains based on the detected interference power to prevent AFE saturation. In paper [11], an ideal and very slow automatic gain control (AGC) is placed at the AFE to prevent AFE saturation when a continuous wave interference occurs. Paper [10,11] both ensure that the AFE does not experience saturation in strong interference scenarios by adaptively adjusting the AFE gain. However, all the methods mentioned above for dealing with AFE saturation focus on narrowband interference, and it is mainly applied to the single antenna receivers. The methods for dealing with saturation caused by strong wideband interference are rarely mentioned, and they are mainly applied to array antenna receivers. Firstly, wideband interference belongs to in band interference, and the stopband filtering technology in paper [8,9] cannot be used to prevent AFE saturation; Secondly, wideband interference is mostly intentional interference, and it has a greater interference power than narrowband interference which mostly belongs to unintentional interference. Excessive AFE gain adjustment in paper [10,11] may lead to insufficient amplification of GNSS weak signals, and the ADC sampled signal cannot obtain sufficient signal-to-noise ratio (SNR). Therefore, the existing AFE saturation processing methods cannot be used in the strong wideband interference scenario.

There is some literature on the AFE saturation processing methods caused by strong wideband interference in radar and communication field. Paper [12] proposes a hybrid beamforming method to filter out strong interference by adding a phase shifter array to the AFE of the antenna subarray and jointly suppressing interference in the analog domain and the digital domain. Paper [13,14] proposes a fully connected hybrid array chip design method for massive multiple-input multiple-output (MIMO) system, and it prevents AFE saturation by suppressing interference in the analog domain. Papers [15,16] propose a hybrid array form with a fully connected structure and a hybrid beamforming method to suppress high-power wideband self-interference signals in both analog and digital domains. However, the aforementioned hybrid beamforming method still cannot be used in GNSS array antennas. Firstly, the GNSS array is a small aperture array and it has a limited number of antennas [17], and the method proposed for antenna subarray in papers [12,13,14] is not applicable to GNSS array antennas; Secondly, the receiver only receives but does not transmit signals, and the prior information of the interference signal waveform cannot be obtained, so the method proposed in papers [15,16] cannot be adopted either.

Aiming at the AFE saturation caused by intentional strong wideband interference in the GNSS array antenna, a hybrid beamforming technique is proposed that simultaneously performs interference suppression in analog domain and digital domain. Firstly, a novel fully connected hybrid array anti-jamming receiver structure is proposed; Secondly, the corresponding hybrid beamforming technique is proposed at the same time. In the analog domain, multiple different 2D spatial analog notch filters are used to partially suppress interference to prevent AFE saturation; In the digital domain, the existing digital beamforming-based anti-jamming technique is calibrated and used to filter out residual interference.

The remainder of this paper is organized as follows: the second section briefly introduce the signal model and digital beamforming-based anti-jamming technique; the third section proposes the hybrid beamforming technique, which includes analog beamforming technique and digital beamforming technique; the fourth section gives the mathematical simulation results; the fifth section gives some conclusions of this paper.

2. Signal Model and Conventional Anti-Jamming Technique

In this section, the signal model of the anti-jamming receiver is firstly introduced, and then two conventional anti-jamming methods based on digital beamforming technique are introduced.

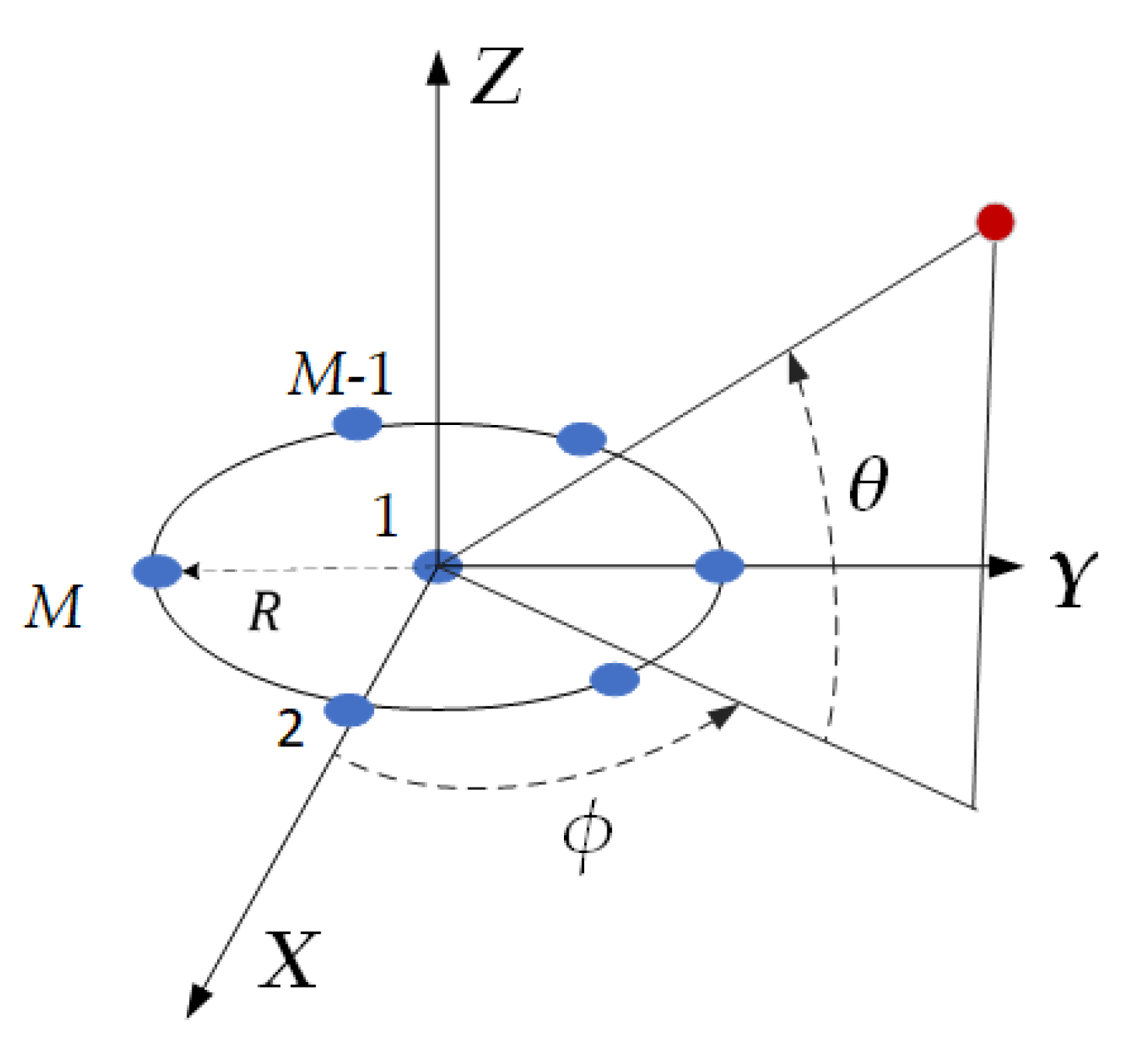
2.1. Signal Model

The GNSS array antenna receiver generally adopts small aperture circular array, as shown in Figure 1. The array is composed of M isotropic elements. Without loss of generality, assuming there is one GNSS signal and Q interference signals received by the array antenna, the array form of the received signal can be represented as

x (t) = a (Ω_{0}) s (t) + \sum_{q = 1}^{Q} a (Ω_{q}) j_{q} (t) + n (t)

(1)

where t is the time,

x (t) = {[x_{1} (t), x_{2} (t), \dots, x_{M} (t)]}^{Τ}

is the array snapshot with M-element array antennas.

s (t)

is the GNSS signal,

j_{q} (t)

is the q-th interference signal, Q is the number of interferences.

Ω

denotes the 2D angle

(θ, ϕ)

, i.e.

Ω = (θ, ϕ)

θ

and

ϕ

represent elevation and azimuth, respectively.

a (Ω_{0}) \in ℂ^{M \times 1}

and

a (Ω_{q}) \in ℂ^{M \times 1}

are the steering vectors of GNSS signal

s (t)

and interference signal

j_{q} (t)

, respectively, and

n (t) \in ℂ^{M \times 1}

is the additive white noise vector.

The steering vector of the array in Equation (1) can be represented as

a (Ω) = d (Ω) \cdot {[e^{- j ψ_{1}}, e^{- j ψ_{2}}, \dots, e^{- j ψ_{M}}]}^{T}

(2)

where

ψ_{m} = \frac{2 π}{λ} \cdot R \cdot \sin (θ) \cdot \cos [ϕ - \frac{2 π (m - 2)}{M - 1}], m = 2, 3, \dots M

(3)

Here,

ψ_{1} = 0

λ

represents the wavelength corresponding to GNSS signal center frequency f, i.e.

λ = c / f

, The

d (Ω)

denotes the pattern radiated by each element. Here, to simplify the derivation process,

d (Ω) = 1

is adopted.

2.2. Digital Beamforming Based Anti-Jamming Processing Technique

In order to suppress interference in Equation (1), a weight vector w is applied to the received signal vector, as shown below

y (n) = w^{H} x (n)

(4)

where

{(\cdot)}^{H}

is the conjugate transpose operation,

x (n)

denotes the signal

x (t)

after ADC.

In the field of conventional digital beamforming based anti-jamming processing technique, there are two techniques for obtaining the weight w: minimum variance distortionless response (MVDR) technique and power inversion (PI) technique [18,19].

The MVDR technique is widely used in various fields, and its objective function is as follow

{\begin{matrix} \min_{w} w^{H} R_{x x} w \\ s . t . w^{H} a (Ω_{0}) = 1 \end{matrix}

(5)

where

R_{x x} = \sum_{n = 1}^{N} {x (n) x^{H} (n)}

represents the covariance matrix of the received signal, N denotes the number of snapshots. The solution of Equation (5) is given by

w_{MVDR} = \frac{R_{x x}^{- 1} a (Ω_{0})}{a^{H} (Ω_{0}) R_{x x}^{- 1} a (Ω_{0})}

(6)

The objective function of the PI technique is as follow

{\begin{matrix} \min_{w} w^{H} R_{x x} w \\ s . t . w^{H} b = 1 \end{matrix}

(7)

where

b = {[1, 0, \dots, 0]}^{T}

is the constraint vector. The solution of Equation (7) is given by

w_{PI} = \frac{R_{x x}^{- 1} b}{b^{H} R_{x x}^{- 1} b}

(8)

Different anti-jamming techniques are adopted according to different application scenarios. However, both of the above techniques belong to digital beamforming technique. If there is signal distortion caused by AFE saturation in strong interference scenarios, both techniques cannot work, and interference suppression ultimately cannot be completed, and then the GNSS PVT solution cannot be performed.

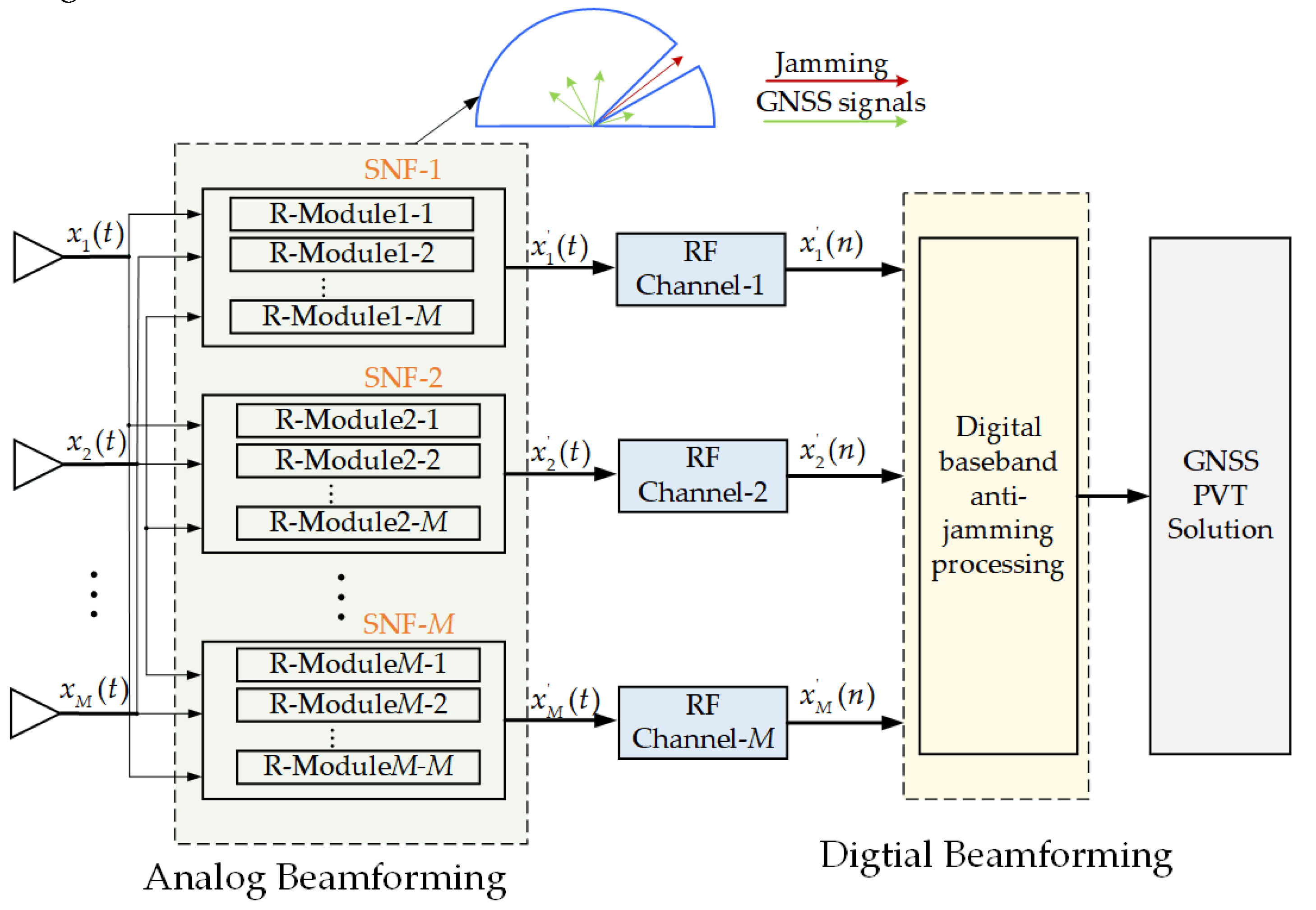
3. Proposed Technique

The proposed hybrid beamforming technique follows in this section. The hybrid array antenna receiver structure is shown in Figure 2. The receiver adopts a fully connected hybrid array structure containing multiple R-modules at the RFE. Each R-Module contains an attenuator and phase shifter as shown in Figure 3.

Hybrid beamforming technique includes analog beamforming technique and digital beamforming technique, as shown in Figure 2.

1) Analog beamforming technique. Taking the direction of arrival (DOA) of interference as a priori information, the multiple-notch-filter (MNF) composed of M different 2D spatial-notch-filters (SNF) are generated simultaneously in the baseband, as shown in Figure 2. The signal is filtered in the analog domain to partially suppress the strong interference and retain the original DOA distribution of the signal (including GNSS signal and interference signal).

2) Digital beamforming technique. After the data is filtered by the analog beamforming technique, and then it is sampled into the baseband through the RF channel and ADC. The original digital beamforming based anti-jamming processing technique, that is, Equation (6) and (8), need to be calibrated and then adopted to suppress interference in digital domain. In the end, the final suppression of interference is completed.

In this paper, the analog beamforming weights are represented by h, and the digital beamforming weights are represented by w.

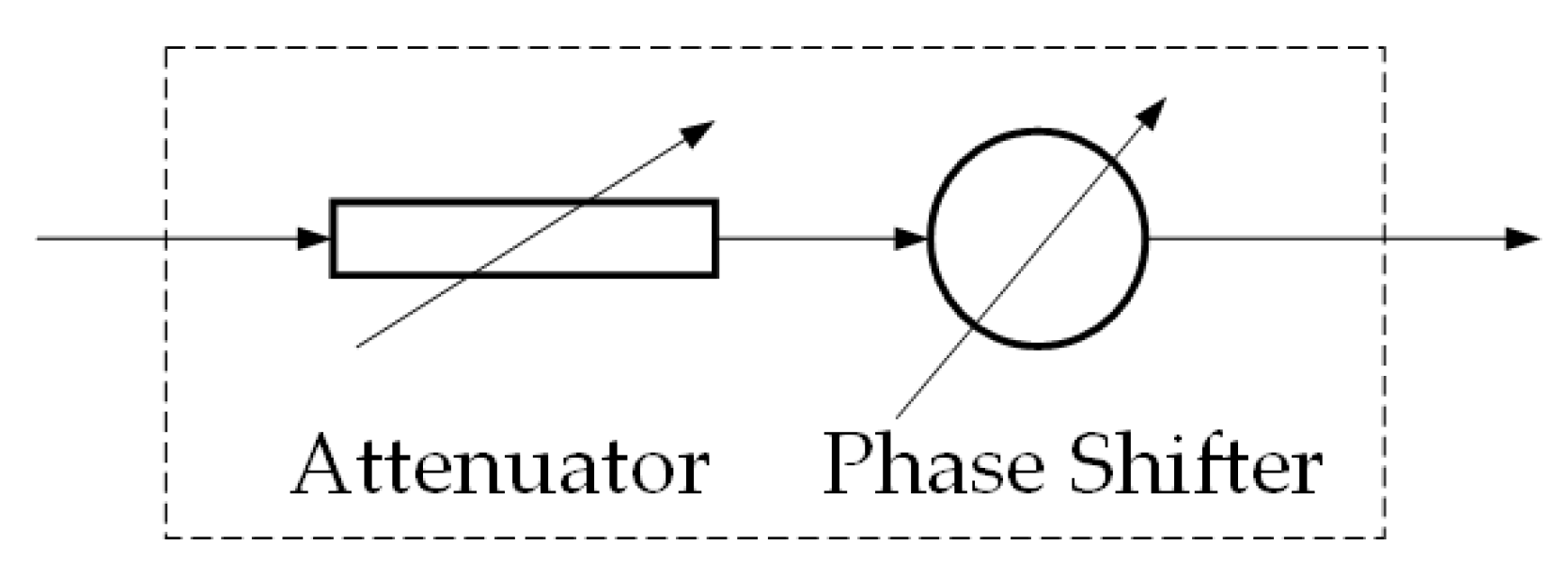
3.1. Analog Beamforming Technique

Firstly, analog beamforming technique is introduced. As shown in Figure 2, the GNSS hybrid array receiver includes a total of

M

SNFs, represented by

h_{m}, m = 1, 2, \dots, M

. Each SNF cannot be generated independently. The MNF not only need to achieve partial suppression of interference in the analog domain, but also strive to retain the original information of signal’s amplitude/phase as much as possible. After GNSS and interference signal are filtered by the MNF, the signal can continue to retain the original DOA distribution in the baseband. Therefore, effective implementation of subsequent baseband anti-jamming algorithms can be ensured. Beampattern synthesis method is used to generate the MNF [20].

In the synthesis process of the MNF, different steering vector forms are used as follow

a_{m} (Ω) = \frac{a (Ω)}{e^{- j ψ_{m}}}, m = 1, 2, \dots, M

(9)

Here,

a_{m} (Ω)

represents the steering vector corresponding to the m-th SNF, that is, the corresponding antenna is used as the reference antenna for each

h_{m}, m = 1, 2, \dots, M

The SNF and MNF constraints are simultaneously applied to the synthesized pattern. The first SNF

h_{1}

is generated by the SNF constraint. Then, using

h_{1}

as a reference mask, the other notch filters

h_{m}, m = 2, 3, \dots, M

are generated by the MNF constraints.

1) SNF Constraints

The SNF constraints include constraints on both non-interference and interference areas. The non-interference area and interference area are constrained separately. The 3 dB main lobe width of the interference spatial spectrum is used as a basis to distinguish between non-interference area and interference area. The area outside the 3 dB main lobe width of the interference spatial spectrum is the non-interference area, and the other area is the interference area.

The constraint for non-interference area is as

1 - δ \leq {| h_{1}^{H} a_{1} (Ω_{p}) |}^{2} \leq 1 + δ, Ω_{p} \in Θ, p = 1, 2, \dots, P

(10)

where the lower and upper magnitude bounds are applied [20]. In Equation (10), the non-interference area is divided into P uniformly spaced angles,

Θ

represents the set of P angles in the non-interference area, i.e.,

Θ ≜ {Ω_{1}, Ω_{2}, \dots, Ω_{P}}

, and

δ

is the ripple term.

The constraint for interference area is as

{| h_{1}^{H} {\bar{a}}_{1} (Ω_{q}) |}^{2} \leq ς, Ω_{q} \in Ψ, q = 1, 2, \dots, Q

(11)

In Equation (11), Q represents the number of interferences,

Ψ

represents the set of Q angles for Q interference areas, i.e.,

Ψ ≜ {Ω_{1}, Ω_{2}, \dots, Ω_{Q}}

, and

ς

is the nulling term.

As shown in Equations (10) and (11), P angles are used to constrain the non-interference area, but only one single angle is used to constrain each interference. This situation will lead to the inability of the objective function to converge and generate deep enough nulling that meet the requirements. To solve this problem, the method of virtual interference is adopted, and the K interferences at the same interference direction are assumed. In practice, the value of K should be greater than or equal to the number of non-interference area constraint angles P, that is, K ≥ P. And then, the Equation (11) are written as

{| h_{1}^{H} {\bar{a}}_{1} (Ω_{q, k}) |}^{2} \leq ς, q = 1, 2, \dots, Q, k = 1, 2, \dots, K

(12)

where

Ω_{q, 1} = Ω_{q, 2} = \dots = Ω_{q, K}, q = 1, 2, \dots, Q, k = 1, 2, \dots, K

(13)

2) MNF Constraints

After the first SNF

h_{1}

is generated based on the SNF constraints, the MNF constraints are used to generate

h_{m}, m = 2, 3, \dots, M

. The MNF constraints are used to partially suppress the interference and retain the original DOA distribution of the signal. Omitting the noise term

n (t)

in Equation (1), array input signal

x (t)

can be expressed as

x (t) = x (t) \cdot a (Ω)

(14)

Here,

x (t)

represents GNSS signal and interference signal. Substitute Equation (9) into Equation (14), the array input signal for each SNF in MNF can be represented as

x_{m} (t) = x (t) \cdot e^{- j ψ_{m}} \cdot a_{m} (Ω), m = 1, 2, \dots, M

(15)

The output of signal

x_{m}^{'} (t)

after being filtered by each SNF

h_{m}

x_{m}^{'} (t) = x (t) \cdot e^{- j ψ_{m}} \cdot h_{m}^{H} a_{m} (Ω), m = 1, 2, ..., M

(16)

where

G_{m} = h_{m}^{H} a_{m} (Ω), m = 1, 2, ..., M

G_{m}

represents the beampattern of the m-th SNF. Therefore, the vector form of the output signal after being filtered by the MNF is

x_{m}^{'} (t) = {[x_{1}^{'} (t), x_{2}^{'} (t), ..., x_{M}^{'} (t)]}^{T} = x (t) \cdot {[G_{1} (Ω) \cdot e^{- j ψ_{1}}, G_{2} (Ω) \cdot e^{- j ψ_{2}}, \dots, G_{M} (Ω) \cdot e^{- j ψ_{M}}]}^{T}

(17)

In the MNF beampattern synthesis, the below constraints are applied

G_{m} (Ω) \approx G_{1} (Ω), m = 2, 3, \dots, M

(18)

Then, Equation (17) can be written as

x_{m}^{'} (t) = x (t) \cdot G_{1} (Ω) \cdot {[e^{- j ψ_{1}}, e^{- j ψ_{2}}, \dots, e^{- j ψ_{M}}]}^{T}

(19)

Through the Equation (19), it can be seen that the output data of the MNF can retain the original DOA distribution.

The Equation (18) for the MNF constraints can be written as

\begin{matrix} \frac{1}{M - 1} \sum_{m = 2}^{M} {{| h_{1}^{H} a_{1} (Ω_{p}) - h_{m}^{H} a_{m} (Ω_{p}) |}^{2}} \leq η \\ Ω_{p} \in Θ, p = 1, 2, \dots, P \end{matrix}

(20)

\begin{matrix} \frac{1}{M - 1} \sum_{m = 2}^{M} {{| h_{1}^{H} {\bar{a}}_{1} (Ω_{q, k}) - h_{m}^{H} {\bar{a}}_{m} (Ω_{q, k}) |}^{2}} \leq ξ \\ Ω_{q, k} \in Ψ, q = 1, 2, \dots, Q; k = 1, 2, \dots K \end{matrix}

(21)

Here, Equations (20) and (21) represent the consistency constraints for non-interference and interference aeras between the m-th SNF and the first SNF, respectively.

η, ξ

represents the response error term.

The

l_{2}

norm of

h_{1}

is adopted as the objective function, which is used to receive useful signals with high gain. The objective function is shown below

{\begin{matrix} \min_{h_{1}} {‖ h_{1} ‖}^{2} \\ s . t . (10), (12), (20), and (21) \end{matrix}

(22)

Due to Equation (10), the objective function (22) is a nonconvex optimization problem, and the alternating directions method of multipliers (ADMM) optimization method is used to solve the objective function. It decomposes the problem into multiple sub problems, iteratively solves the sub problems in sequence, and obtains the final optimization result. The specific derivation process can refer to the papers [20,21]. The digital MNF

h_{m}, m = 1, 2, \dots, M

is obtained through Equation (22). After quantization, the analog beamforming coefficient

h_{Quan - m}, m = 1, 2, \dots, M

is solved.

3.2. Digital Beamforming Technique

Secondly, digital beamforming technique is introduced. The MVDR technique and PI technique in Equations (6) and (8) are still used in digital beamforming part. However, through Equations (20) and (21), it can be seen that although we have retained the DOA distribution of the original GNSS signal as much as possible, the small amount of amplitude/phase error is inevitably introduced. Therefore, in order to maximize the interference suppression ability of the digital domain anti-jamming technique, two processes should be added: amplitude/phase error calculation and calibration.

The beampattern

G_{m} (Ω)

corresponding to each analog SNF

h_{Quan - m}

should be firstly calculated as

G_{m} (Ω) = \frac{h_{Quan - m}^{H} a (Ω)}{\sqrt{h_{Quan - m}^{H} h_{Quan - m}}}, Ω \in Θ, m = 1, 2, \dots, M

(23)

Then, the calculation process of amplitude/phase error is as follow

Γ_{m} (Ω) = \frac{G_{1} (Ω)}{G_{m} (Ω)}, Ω \in Θ, m = 2, 3, \dots, M

(24)

Here,

Γ_{m} (Ω)

represents the amplitude/phase error between the m-th SNF

h_{Quan - m}

and the first SNF

h_{Quan - 1}

at angle

Ω

Finally, the updated MVDR algorithm was obtained

w_{MVDR} = \frac{R_{x x}^{- 1} \tilde{a} (Ω_{0})}{{\tilde{a}}^{H} (Ω_{0}) R_{x x}^{- 1} \tilde{a} (Ω_{0})}

(25)

where

\tilde{a} (Ω_{0}) = Γ (Ω_{0}) \cdot a (Ω_{0})

Γ (Ω_{0}) = diag {[1, Γ_{2} (Ω_{0}), \dots, Γ_{M} (Ω_{0})]}

, and

diag {\cdot}

represents the operation of transforming a vector into a diagonal matrix.

Due to the fact that the small amount of amplitude/phase error have no impact on the PI algorithm, Equation (8) is not updated in this section.

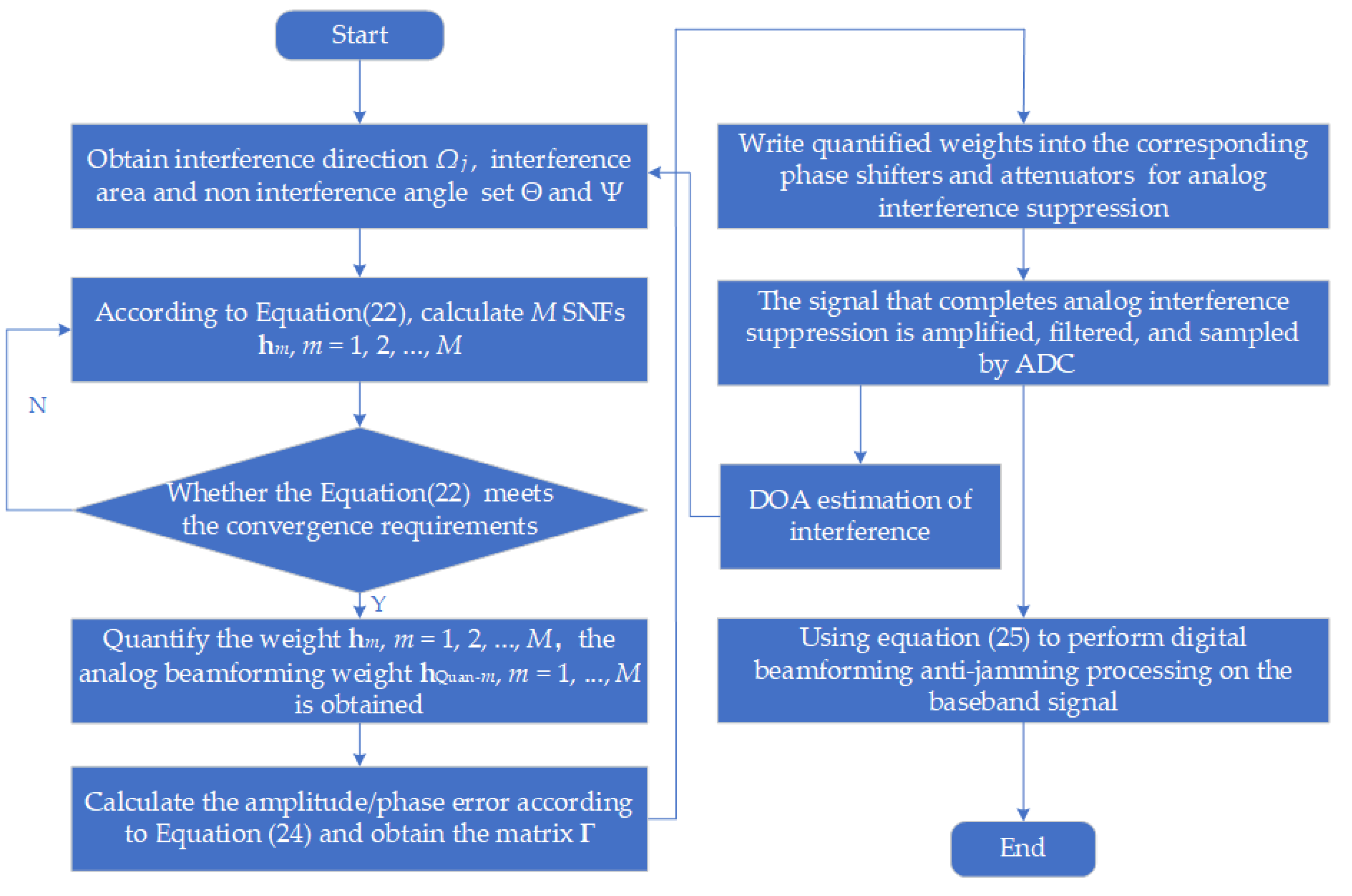
3.3. Implementation of Proposed Technique

Figure 4 illustrates the data processing flowchart of the robust wideband interference suppression method for GNSS array antenna receiver based on hybrid beamforming technique. The steps of the method are as follows:

Step 1: Analog beamforming is based on the prior information of interference direction. The prior information of interference direction is firstly obtained from DOA estimation and then the interference angle set

Ω_{q} \in Ψ, q = 1, 2, \dots, Q

and the non-interference angle set

Ω_{p} \in Θ, p = 1, 2, \dots, P

are determined based on the interference direction.

Step 2: Based on sets

Ψ

and

Θ

, analog beamforming technique in Section 3. 1 is run and M 2D spatial notch filters

h_{m}, m = 1, 2, \dots, M

are obtained through multiple iterations.

Step 3: Quantify the weight

h_{m}, m = 1, 2, \dots, M

, the analog beamforming coefficient

h_{Quan - m}, m = 1, 2, \dots, M

is obtained.

Step 4: Calculate the beampattern

G_{m}, m = 1, 2, \dots, M

for each SNF based on Equation (23). And then calculate the amplitude/phase error matrix

Γ_{m}, m = 2, 3, \dots, M

between each notch filter

h_{m}, m = 2, 3, \dots, M

and the first SNF

h_{1}

based on Equation (24).

Step 5: The analog MNF

h_{Quan - m}, m = 1, 2, \dots, M

are written down to the corresponding phase shifters and attenuators in the hybrid array anti-jamming receiver.

Step 6: After filtering through the analog MNF, the signal is amplified, filtered, and sampled to the digital baseband signal

x^{'} (n) = {[x_{1}^{'} (n), x_{2}^{'} (n), \dots, x_{M}^{'} (n)]}^{T}

Step 7: DOA estimation results can be obtained using multiple signal classification (MUSIC) algorithm [23] on baseband data and then DOA estimation results are sent to Step 1 in real-time.

Step 8: Using the Equation (25), digital beamforming technique is performed on the baseband data

x^{'} (n) = {[x_{1}^{'} (n), x_{2}^{'} (n), \dots, x_{M}^{'} (n)]}^{T}

The robust wideband interference suppression process based on hybrid beamforming technique is completed.

4. Simulations and Results

In this section, the performance of the proposed method in this paper is evaluated through simulations, which are performed using the MATLAB R2018b software platform. In Section 4.1, the simulation settings are presented. In Section 4.2, Experiment 1 analyzes the analog beamforming performance of the proposed method in two types of interference scenarios. In Section 4.3, Experiment 2 verifies the strong interference suppression performance. In Section 4.4, Experiment 3 verifies the maximum interference suppression ability of the proposed method. In Experiments 3 and 4, the performance of the proposed method is compared with the digital beamforming-based anti-jamming technique. In Experiments 3 and 4, in order to fully verify the interference suppression ability of the proposed technique, MVDR technique is used in hybrid beamforming and digital beamforming.

4.1. Simulation Settings

In the mathematical simulation verification experiment, we used a 7-element array antenna, as shown in Figure 1. The GNSS receiver simulation parameters are shown in Table 1. The interference distribution is shown in Table 2. The GNSS constellation distribution adopts the same uniform distribution scheme as in reference [22], which is shown in Table 3. The parameter settings of analog beamforming technique in Section 3.1 are shown in Table 4.

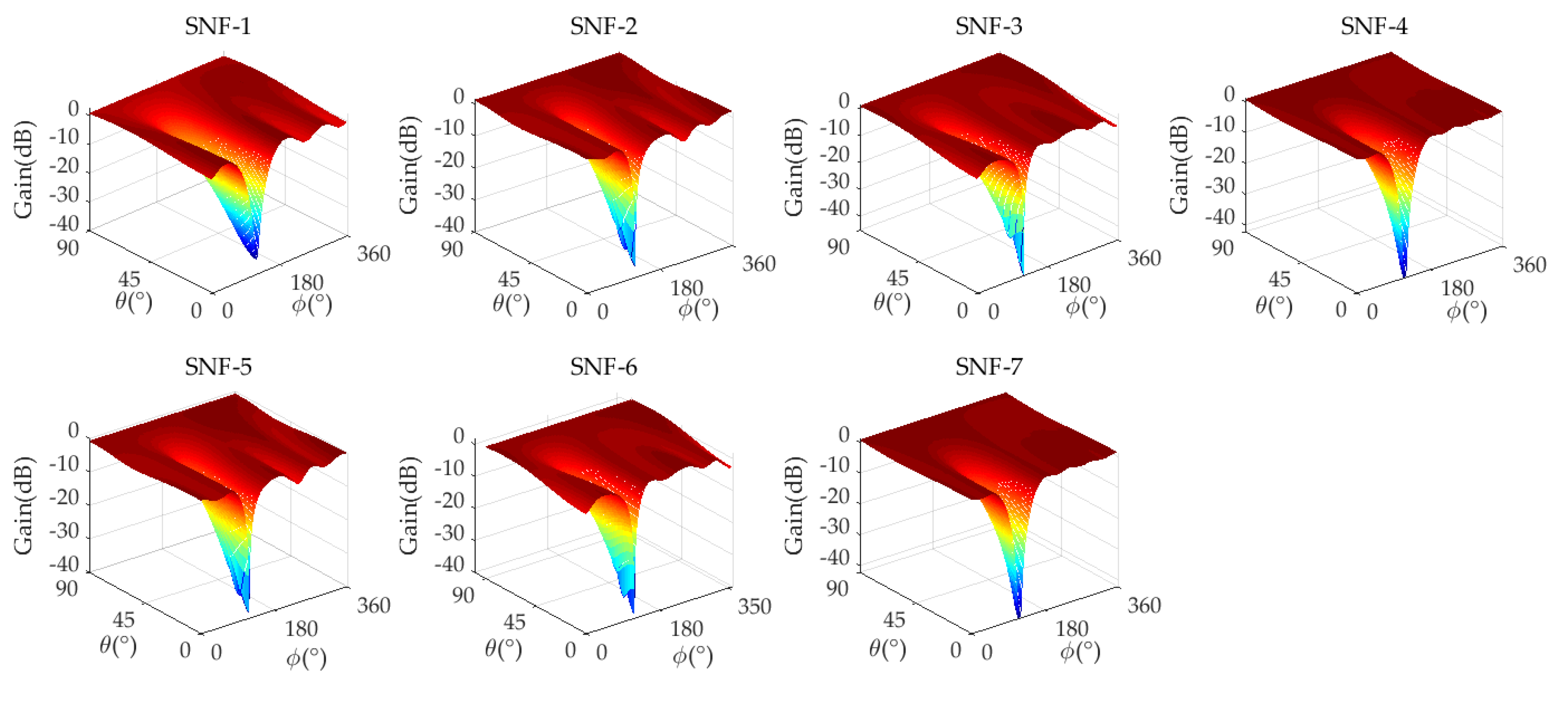
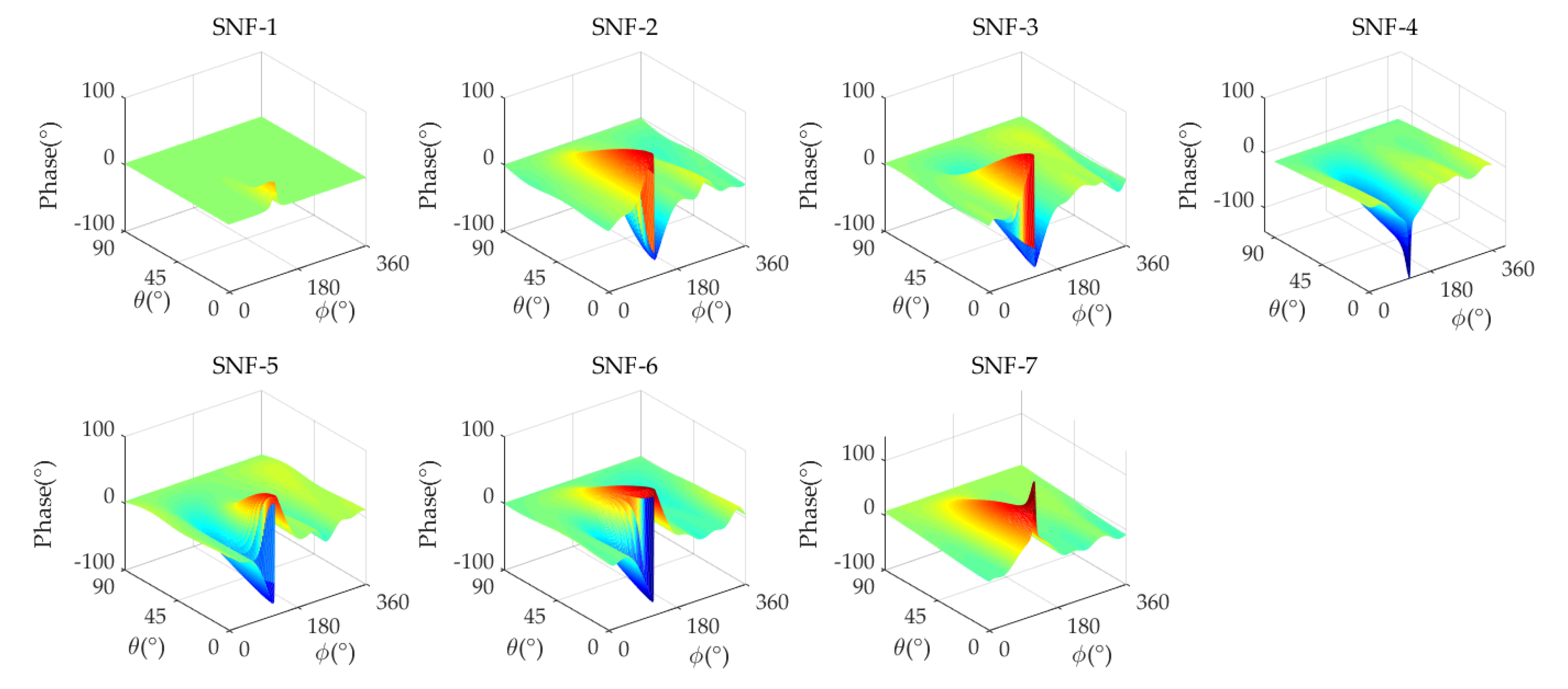
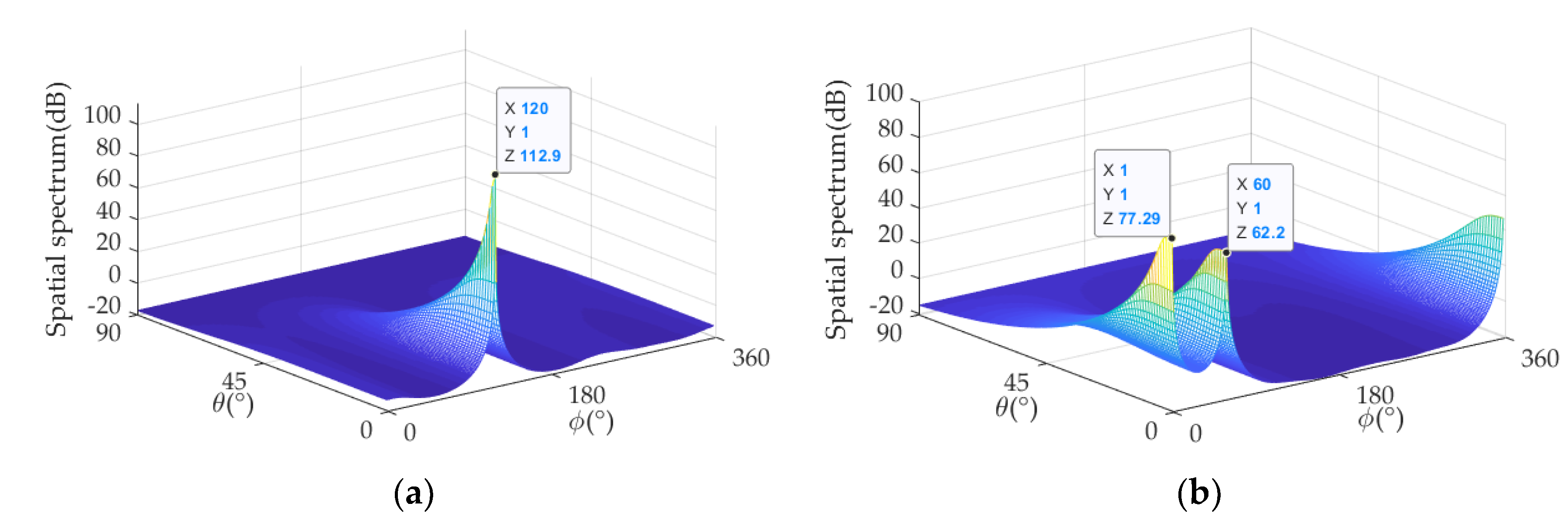
4.2. Experiment 1: Analog Beamforming Performance Analysis

The analog beamforming technique is the key part of the proposed method. In this section, the performance of the analog MNF is analyzed, including the performance analysis of each SNF and the consistency analysis between each SNF in MNF. The performance of each SNF is calculated by Equation (23). The gain G in the non-interference area and nulling depth D in the interference area are calculated. The calculation formulas of the amplitude error

A_{m}

and phase error

P_{m}

between each SNF and the first SNF in the non-interference area are as follows

A_{m} = | 20 \cdot \log 10 {G_{m} (Ω) / G_{1} (Ω)} |, Ω \in Θ, m = 2, 3, \dots, M

(26)

P_{m} (Ω) = | ∠ G_{m} (Ω) - ∠ G_{1} (Ω) |, Ω \in Θ, m = 2, 3, \dots, M

(27)

where

| \cdot |

represents the absolute value operation,

∠

represents the operation of taking complex phase.

Figure 5 and Figure 6 show the amplitude /phase response of the analog MNF. The performance of analog MNF is calculated, where

G_{\max}

G_{\min}

A_{m e a n}

A_{\max}

P_{m e a n}

, and

P_{\max}

represent the maximum gain, minimum gain, average amplitude error, maximum amplitude error, average phase error, and maximum phase error in the non-interference area, respectively, and D represent the nulling depth in the interference direction. The detailed performance results are shown in Table 5.

From Table 5, it can be seen that in the analog MNF, the maximum gain of all SNFs

G_{\max}

is 2.687 dB , the minimum gain

G_{\min}

is −4.683 dB, and the minimum nulling depth of each SNF in the analog MNF D is −35.07 dB. The amplitude/phase error between each SNF and reference SNF-1 in the analog MNF is: the maximum average amplitude error

A_{m e a n}

is 1.812 dB, the maximum amplitude error

A_{\max}

is 4.508 dB, the maximum average phase error

P_{m e a n}

is 3.96°, and the maximum phase error

P_{\max}

is 17.47°. This amplitude/phase error could meet the requirements of the array antenna.

Figure 7 and Figure 8 show the amplitude/phase response of the analog MNF in Scenario 2, and Table 6 presents the detailed performance of the analog MNF. In this scenario, the minimum nulling depth of each SNF in the analog MNF D is −34.22 dB, the maximum gain

G_{\max}

is 1.646 dB, the minimum gain

G_{\min}

is 0.687 dB, the maximum average amplitude error

A_{m e a n}

is 1.016 dB, the maximum amplitude error

A_{\max}

is 4.459 dB, the maximum average phase error

P_{m e a n}

is 3.451°, and the maximum phase error

P_{\max}

is 18.49°.

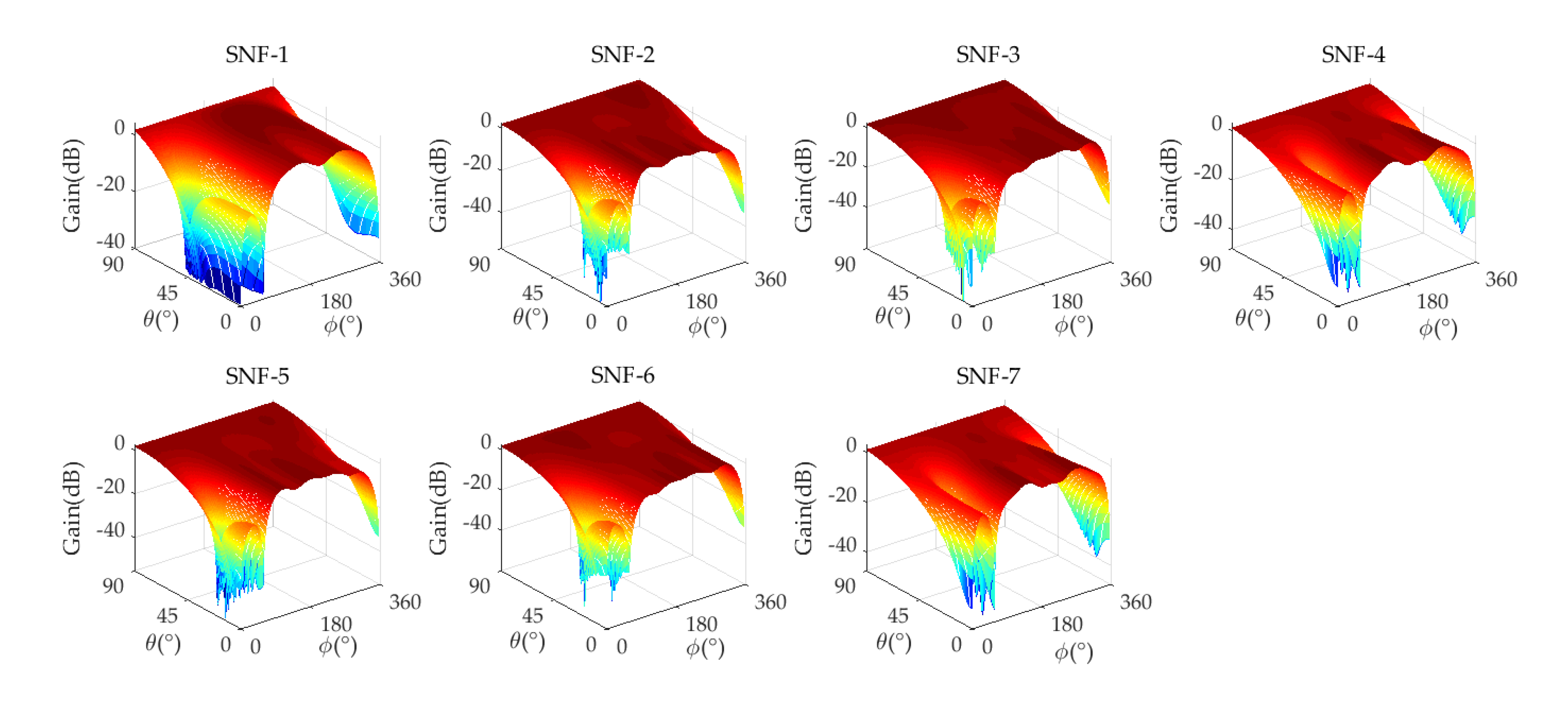
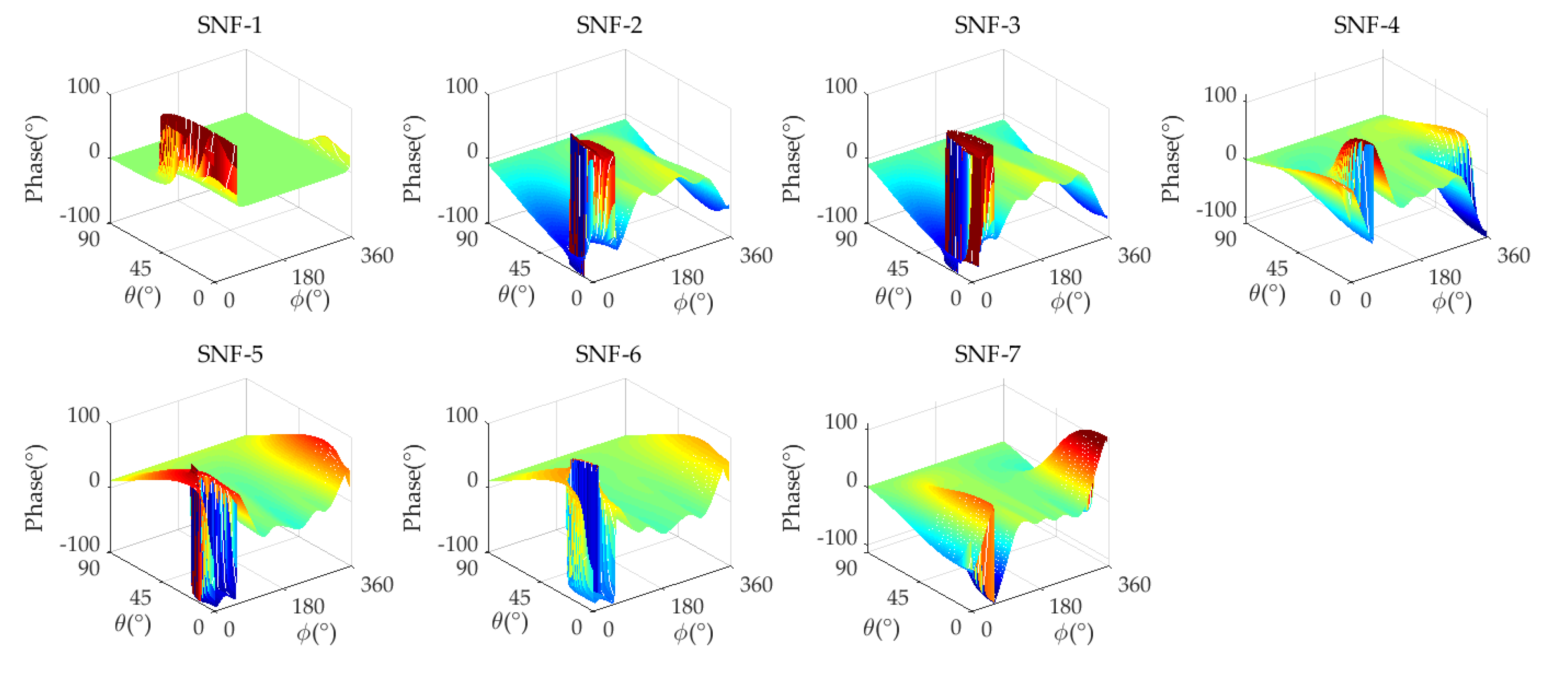
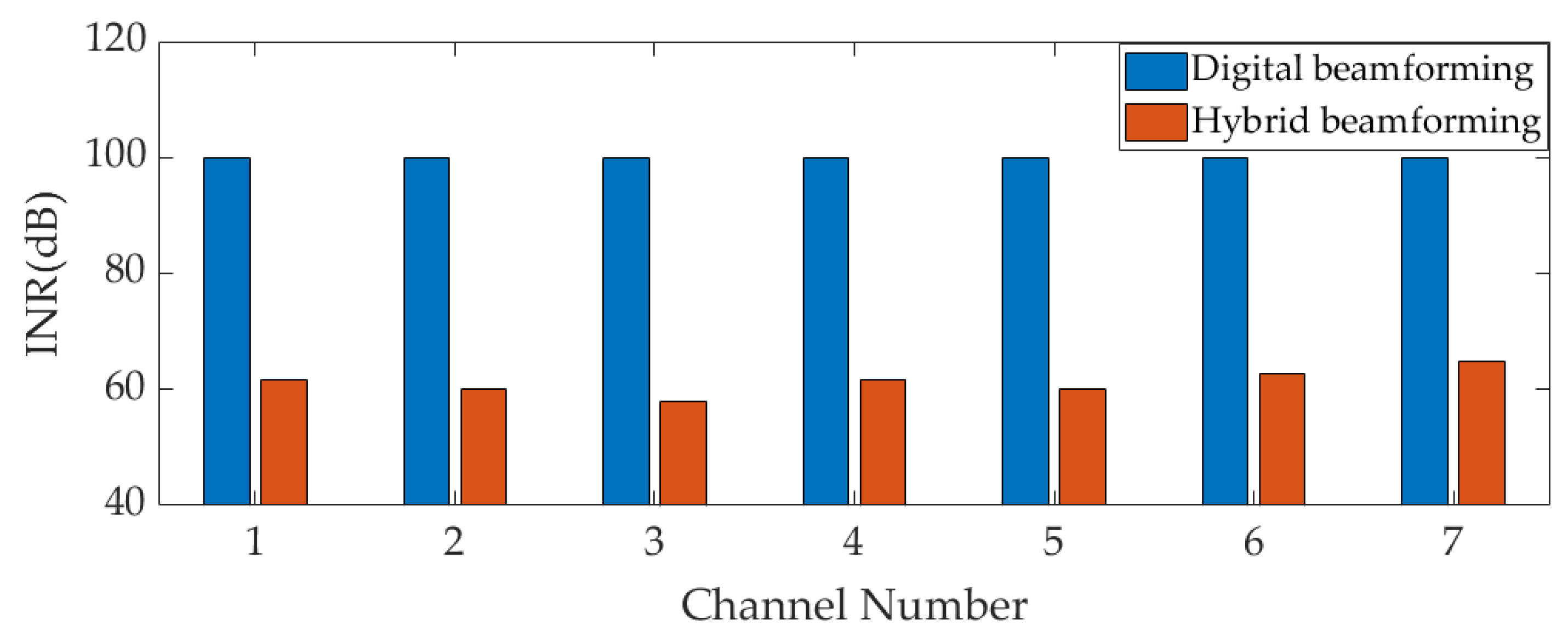
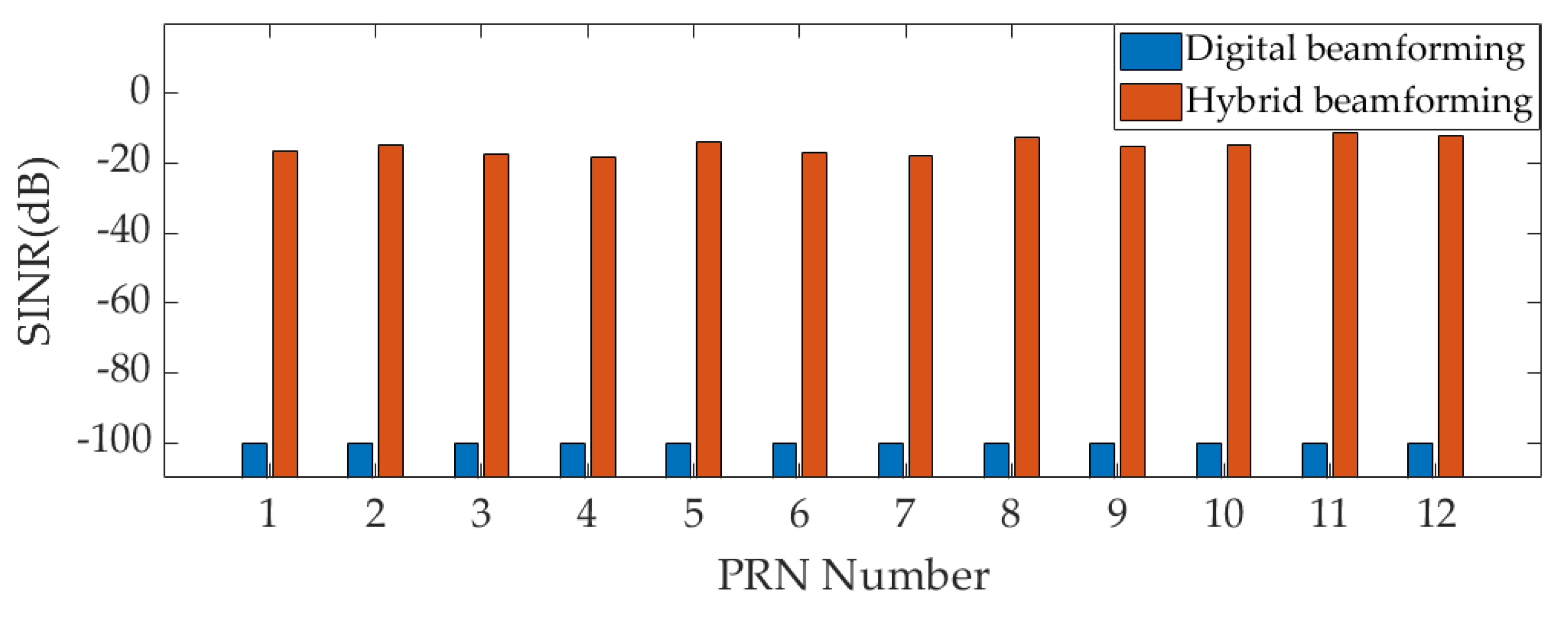
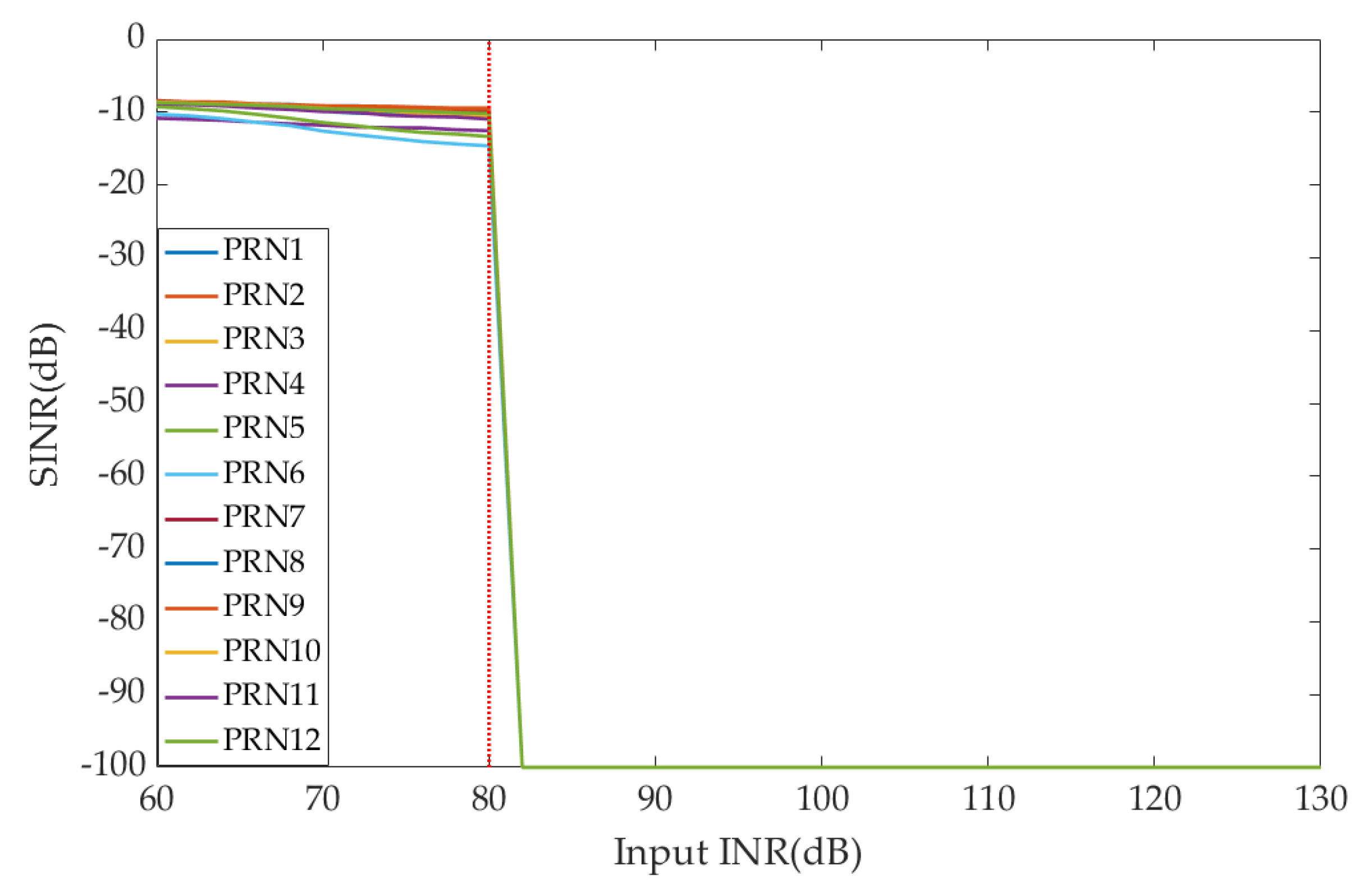
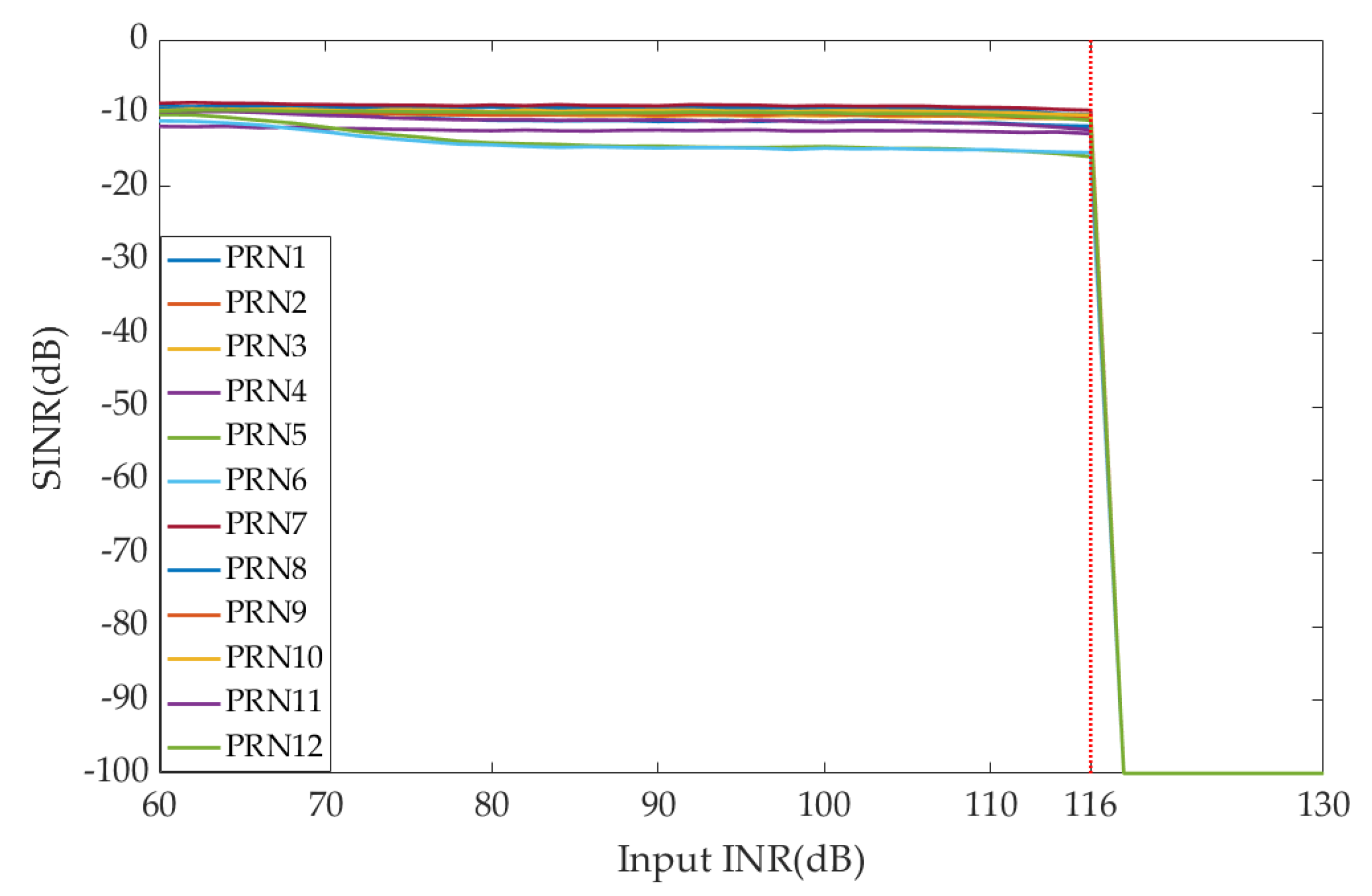
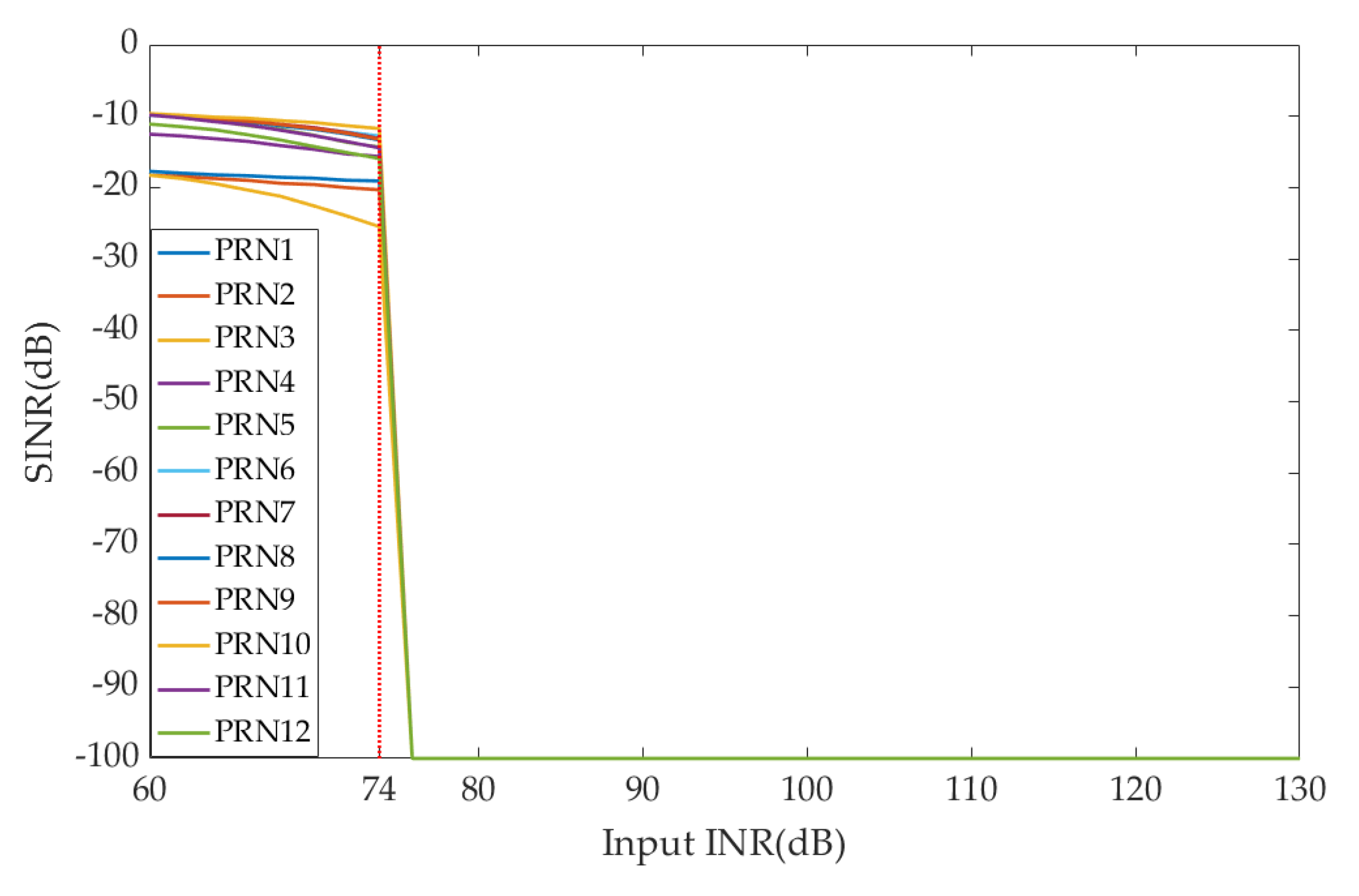
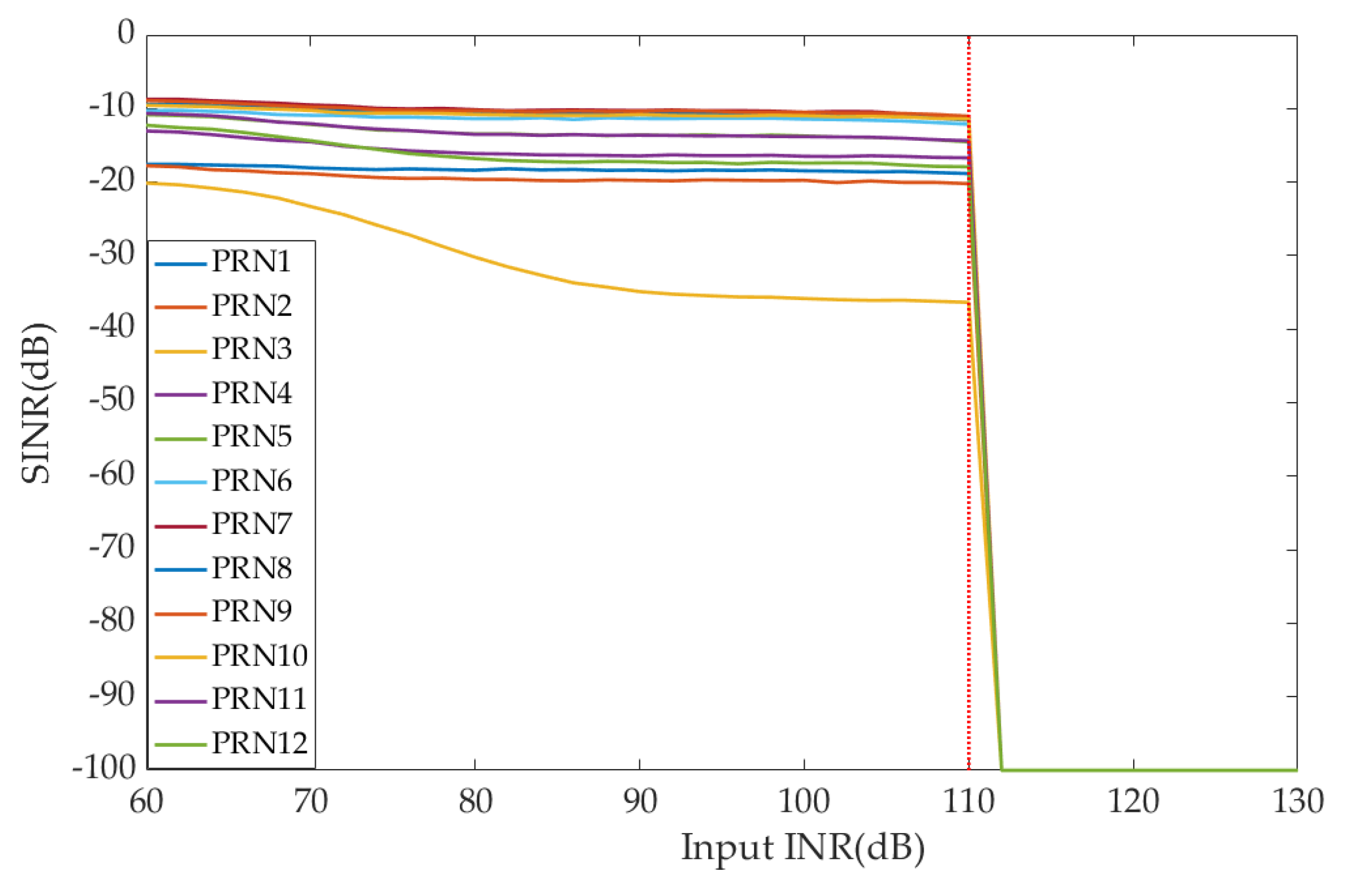
4.3. Experiment 2: Strong Interference Suppression Performance Analysis

In this section, the strong interference suppression performance of the proposed method is verified and compared with digital beamforming-based technique. The interference power is set to 0 dBm, that is, the input interference-to-noise ratio (INR) is 100dB.

Firstly, the interference suppression ability of the analog MNF in the analog domain is analyzed. The nulling depth values for two scenarios can be seen in Table 5 and Table 6, but it does not accurately reflect the interference suppression ability of the MNF. The interference suppression ability of the MNF is accurately demonstrated by comparing the input INR and INR before ADC sampling in the receiver. The INR of the two scenarios after their respective MNF is shown in the Figure 9 and Figure 10. In the figures, red represents the INR after the analog MNF, the blue color indicates the input INR, and both are also the INR before ADC sampling in two array forms. In Figure 9, it can be seen that, after the interference is filtered by the analog MNF, the input INR of hybrid array decays from 100 dB to 61.6 dB, 59.95 dB, 58.06 dB, 61.77 dB, 59.98 dB, 62.82 dB, and 64.8 dB, respectively. The wideband interference suppression ability of each SNF is 38.4 dB, 40.05 dB, 41.94 dB, 38.23 dB, 40.02 dB, 37.18 dB, and 35.2 dB, respectively. In Scenario 2, after two interferences enter the channel, the interference’s power should be the sum of the two interferences, so the input INR increases to 106dB. In Figure 10, the input INR of hybrid array decays from 106 dB to 64.91 dB, 60.5 dB, 60.49 dB, 67.1 dB, 63.31 dB, 64.61 dB, and 67.03 dB, respectively. The wideband interference suppression ability of each SNF is 41.09 dB, 45.95 dB, 45.51 dB, 38.9 dB, 42.69 dB, 41.39 dB, and 38.97 dB, respectively. The interference suppression ability of Scenario 2 is achieved through the combination of two nullings. From Figure 9 and Figure 10, it can be seen that due to the partial suppression of interference in the analog domain, the technique proposed in this paper can effectively relax the linear dynamic range of AFE to prevent saturation in strong interference scenarios. However, due to the presence of strong wideband interference, digital beamforming-based anti-jamming array antenna receiver will experience AFE saturation, and it results in signal distortion and inability to operate baseband processing. After the interference suppression ability of the analog MNF is analyzed, the interference suppression ability of hybrid beamforming-based array antenna receiver in strong interference scenarios will be analyzed.

The interference suppression ability of hybrid beamforming-based array antenna receiver is analyzed by comparing the input signal-to-interference-noise ratio (SINR) at the antenna entrance and the output SINR after anti-jamming baseband processing. Due to AFE saturation, the sampled signal is distorted, and the digital beamforming in two array forms is ineffective. Therefore, the statistics of SINR after AFE saturation are no longer meaningful. The SINR is uniformly set to −100 dB when AFE experiences saturation.

Figure 11 and Figure 12 respectively show the output SINR of the two scenarios in Table 2 under input INR = 100 dB. Due to AFE saturation in digital array at this INR, the output SINR of all GNSS signals is −100 dB. However, in the hybrid array, due to the partial suppression of interference by analog MNF in the analog domain, the AFE does not experience saturation, and digital beamforming of hybrid array can work normally. The output SINR of each GNSS signal is calculated after digital beamforming in hybrid array. As shown in Figure 11, the output SINR of GNSS signal in Scenario 1 are −16.39 dB, −14.75 dB, −17.41 dB, −18.45 dB, −13.72 dB, −17.05 dB, −17.9 dB, −12.53 dB, −15.12 dB, −14.72 dB, −11.13 dB, and −12.38 dB, respectively; As shown in Figure 12, the output SINR of GNSS signal in Scenario 2 are −18.56 dB, −19.85 dB, −35.86 dB, −16.43 dB, −13.8 dB, −11.48 dB, −10.41 dB, −10.74 dB, −10.51 dB, −10.93 dB, −13.75 dB, and −17.5 dB, respectively. In the two scenarios, after the signal is processed by hybrid beamforming technique, the number of GNSS signals with an output SINR greater than −20 dB is 12 and 11, respectively, which can be captured. The hybrid beamforming-based array antenna receiver can effectively complete GNSS PVT solution under input INR = 100 dB . However, due to AFE saturation, the digital beamforming-based array antenna receiver cannot work normally.

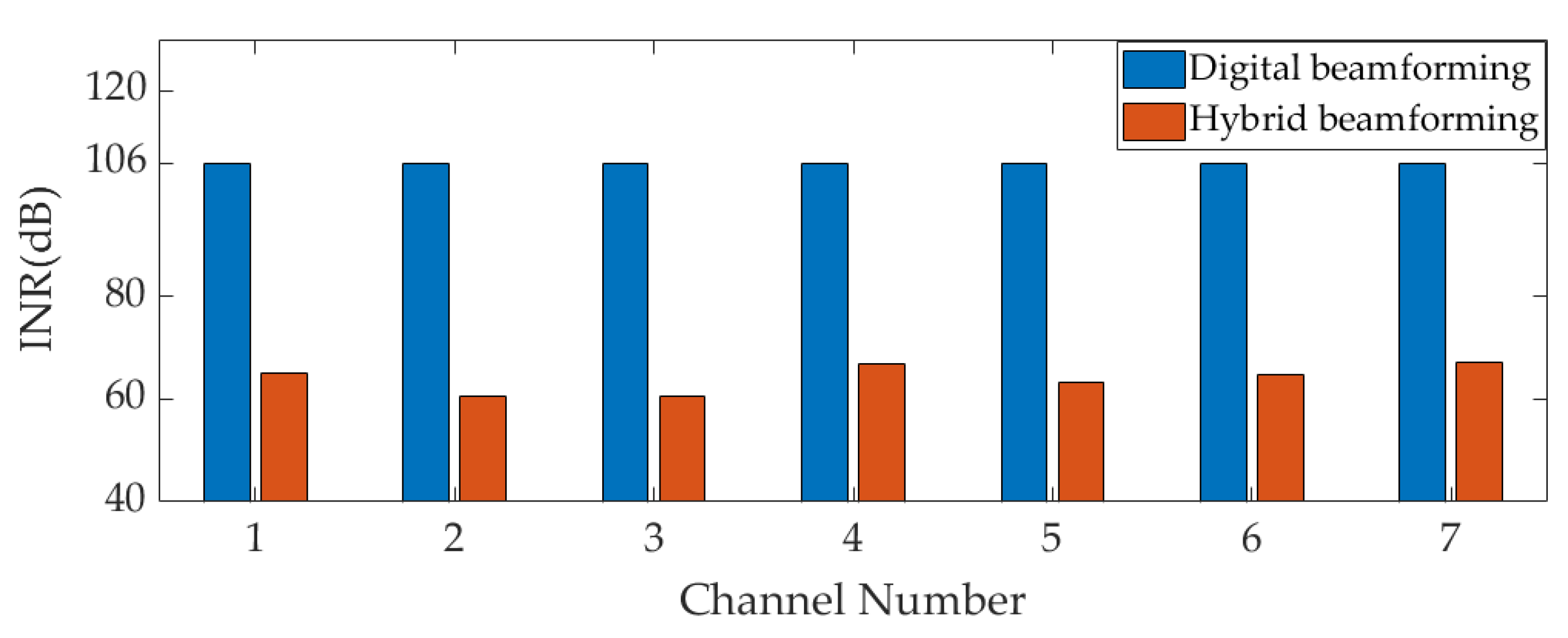
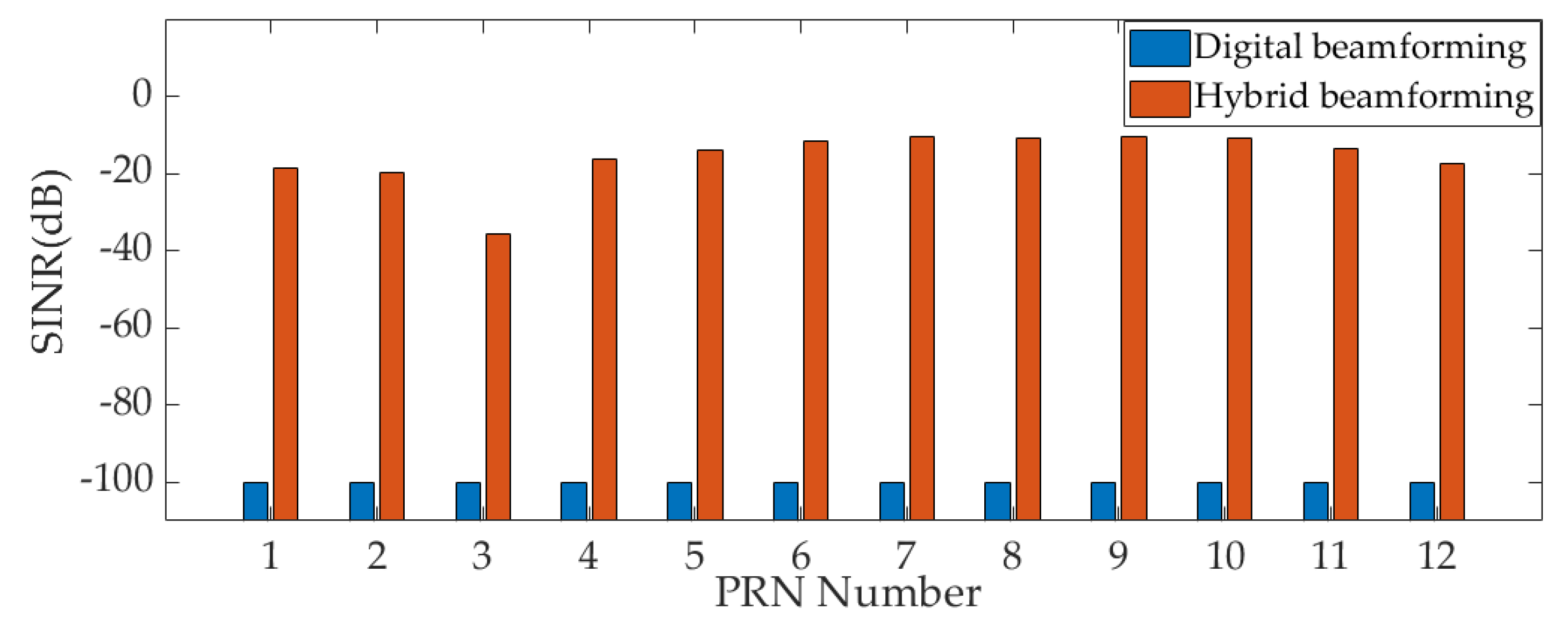
4.4. Experiment 3: Maximum Interference Suppression Abilty Performance Analysis

In this section, the maximum interference suppression ability of the proposed method is analyzed and compared with that based on digital beamforming technique.

To verify the improvement of the proposed technique in maximum interference suppression ability, the output SINR of all GNSS signals in Table 2 is calculated under different input INR conditions in two scenarios. The interference power is from −40 dBm to 30 dBm, and the step length of the interference power is 2 dBm, that is, the INR is from 60 dB to 130 dB.

Figure 13 and Figure 14 respectively show the output SINR curves of all GNSS signals under different INR conditions for the two beamforming techniques in Scenario 1. From Figure 13, it can be seen that when the input INR ≤ 80 dB, the digital beamforming-beased array antenna receiver can complete anti-jamming processing normally, and the output SINR of all GNSS signals is greater than −20 dB. The number of satellites that can be captured is 12. Therefore, GNSS PVT solution can be completed. When the input INR is greater than 100 dB, the digital beamforming-based array antenna receiver experiences AFE saturation. All GNSS signal’s output SINR are −100 dBm, and the number of available satellites is 0. The receiver is unable to complete the GNSS PVT solution. Therefore, the maximum interference suppression ability of the digital beamforming-based array antenna receiver is INR = 80 dB; From Figure 14, it can be seen that the AFE saturation of the hybrid beamforming-based array antenna receiver occurs when the input INR > 116 dB. When the input INR ≤ 116 dB, the number of satellites that can be captured is 12, and all GNSS signal’s output SINR are greater than −20 dBm. The receiver can complete the GNSS PVT solution normally. Therefore, the maximum interference suppression ability of hybrid beamforming-based array antenna receiver is INR = 116 dB. Therefore, in Scenario 1, compared with digital beamforming-based array antenna receiver, the maximum interference suppression ability of the hybrid beamforming-based anti-jamming receiver is improved by 36 dB.

Figure 15 and Figure 16 respectively show the output SINR curves of all GNSS signals under different INR conditions of the two beamforming techniques in Scenario 2. The AFE saturation position of digital beamforming-based array antenna receiver is input INR = 74 dB. However, the AFE saturation position of the hybrid beamforming-based array antenna receiver is input INR = 110 dB. Therefore, in Scenario 2, compared with digital beamforming-based array antenna receiver, the maximum interference suppression ability of the hybrid beamforming-based array antenna receiver is also improved by 36 dB. In Figure 15 and Figure 16, due to being close to the interference area, the output SINR of PRN3 satellite decreases below −20 dB as the interference power increases.

5. Discussions

In the present study, the method proposed in this paper takes interference’s DOA as prior information, which requires continuous tracking of interference direction from weak interference scenario to strong interference scenario. Figure 17 shows the DOA estimation results for two interference scenarios with INR = 100 dB. It can be seen that the interference after analog MNF still retains the original DOA distribution. The performance in retaining the DOA distribution of signals in the proposed technique is also verified.

6. Conclusions

Aiming at the AFE saturation problem caused by the strong wideband interference in array antenna receivers. The hybrid beamforming-based anti-jamming technique is proposed. The main contributions are as follows:

1): A novel fully connected hybrid array anti-jamming receiver structure is proposed, which is used for hybrid beamforming by adding the attenuator and phase shifter array to the AFE.
2): A hybrid beamforming method for GNSS array antenna receiver is proposed. In analog domain, the interference is partially suppressed (better than 30 dB) by analog MNF generated by the baseband, and it relaxes the linear dynamic range of AFE to prevent saturation under the strong interference scenarios. In digital domain, the calibrated MVDR algorithm is used for the final suppression of residual interference.
3): Through two interference scenarios, compared with the digital beamforming- based array antenna receiver, it is verified that the maximum interference suppression ability of the hybrid beamforming-based array antenna receiver are improved by 36 dB under the conditions of using 7-bit attenuators and 8-bit phase shifters.

There are several issues that should be consider in future works: (1) Space-time hybrid array structures should be considered. Firstly, it can provide higher interference suppression ability in the analog domain. Secondly, it can increase the degree of freedom to ensure that the signal has better amplitude consistency, especially the phase consistency, after it is filtered by the analog MNF. (2) The algorithm in this paper assumes that the array antenna is ideal and ignores the influence of amplitude/phase error in practical application. In the analog beamforming, the influence of non-ideal factors will be further considered, and the analog beamforming algorithm will be modified accordingly. (3) This article only verifies the improvement of anti-jamming ability under static conditions. The anti-jamming performance under dynamic conditions needs to be verified through field experiments, and further consideration needs to be given to the width parameter setting of nulling in analog beamforming.

Author Contributions

Conceptualization, Z.X. (Zhenxing Xu) and Q.D.; Data curation, M.W. and H.W.; Formal analysis, Z.X. (Zhenxing Xu); Funding acquisition, M.W. and F.Y.; Investigation, G.Z. and H.W.; Methodology, Z.X. (Zhenxing Xu)and M.W.; Project administration, S.L. and F.Y.; Software, Z.X. (Zhenxing Xu) and M.W.; Supervision, Q.D. and S.L.; Validation, Z.X. (Zhenxing Xu)and G.Z.; Visualization, S.Z.; Writing – original draft, Z.X. (Zhenxing Xu); Writing – review & editing, Z.X. ( Zhenghuan Xia), X.C. and M.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Key Research and Development Program of China (Grant No. 2023YFB3906500).

Conflicts of Interest

The authors declare no conflict of interest.

References

Chien, Y.R. Design of GPS Anti-Jamming Systems Using Adaptive Notch Filters. IEEE Syst J. 2015, 9, 451–460. [Google Scholar] [CrossRef]
Ni, G.; He, C.; Jin, R. Single-Channel Anti-Jamming Receiver With Harmonic-Based Space-Time Adaptive Processing. IEEE Wirel. Commun. Lett. 2022, 11, 776–780. [Google Scholar] [CrossRef]
Gioia, C.; Borio, D. Multi-layered Multi-Constellation Global Navigation Satellite System Interference Mitigation. Navigation. 2023, 70, 596. [Google Scholar] [CrossRef]
Borio, D.; Gioia, C. GNSS interference mitigation: A measurement and position domain assessment. Navigation. 2021, 68, 93–114. [Google Scholar] [CrossRef]
Kraus, T.; Pany, T.; Eissfeller, B. Maximum Theoretical Interference Mitigation Capability of a GNSS Receiver as Limited by the GNSS Frontend. Nat Microbiol. 2021, 6, 3471–3480. [Google Scholar]
Borio, D.; Gioia, C. Interference mitigation: impact on GNSS timing. GPS Solut. 2021, 25, 37. [Google Scholar] [CrossRef]
Borio, D.; Li, H.; Closas, P. Huber’s Non-Linearity for GNSS Interference Mitigation †. Sensors. 2018, 18, 2217. [Google Scholar] [CrossRef]
Dovis, F. GNSS Interference Threats and Countermeasures. Artech House: Boston, USA, 2015; pp.62-64.
9. Betz,J.W. Engineering Satellite-Based Navigation and Timing: Global Navigation Satellite Systems, Signals, and Receivers. Wiley: New York, USA, 2016; pp.39-42.
Li, Y.; Cervantes, J.; Shivaramaiah, N. C.; Akos, D. M.; Wang, M. Configurable GPS/GNSS Antenna Module Resistant to RFI Saturation. IEEE Trans. Aerosp. Eletron. 2020, 56, 381–392. [Google Scholar] [CrossRef]
Huo, S.; Nie, J.; Tang, X.; Wang, F. Minimum Energy Block Technique Against Pulsed and Narrowband Mixed Interferers for Single Antenna GNSS Receivers. IEEE Commun. Lett. 2015, 19, 1933–1936. [Google Scholar] [CrossRef]
Wu, K.; Zhang, J. A.; Huang, X.; Guo, Y. J.; Nguyen, D. N.; Kekirigoda, A.; Hui, K.P. Analog-Domain Suppression of Strong Interference Using Hybrid Antenna Array. Sensors. 2022, 22, 2417. [Google Scholar] [CrossRef] [PubMed]
Krishnaswamy, H.; Zhang, L. Analog and RF Interference Mitigation for Integrated MIMO Receiver Arrays. Proc IEEE. 2016, 104, 561–575. [Google Scholar] [CrossRef]
Golabighezelahmad, S.; Klumperink, E. A. M.; Nauta, B. A 0.7–5.7 GHz Reconfigurable MIMO Receiver Architecture for Analog Spatial Notch Filtering Using Orthogonal Beamforming. IEEE J. Solid-State. Circuits. 2021, 56, 1527–1540. [Google Scholar] [CrossRef]
Lin, T.; Wei, X.; Lai, J.; Xie, M. Transmit Beamforming Design Based on Multi-Receiver Power Suppression for STAR Digital Array. Sensors. 2024, 24, 622. [Google Scholar] [CrossRef] [PubMed]
Wang, G.; Yang, Z.; Gong, T. Hybrid Beamforming Design for Self-Interference Cancellation in Full-Duplex Millimeter-Wave MIMO Systems with Dynamic Subarrays. Entropy. 2022, 24, 1687. [Google Scholar] [CrossRef] [PubMed]
Sun, Y.; Chen, F.; Lu, Z.; Wang, F. Anti-Jamming Method and Implementation for GNSS Receiver Based on Array Antenna Rotation. Remote Sens. 2022, 14, 4774. [Google Scholar] [CrossRef]
Li, S.; Wang, F.; Tang, X.; Ni, S.; Lin, H. Anti-Jamming GNSS Antenna Array Receiver with Reduced Phase Distortions Using a Robust Phase Compensation Technique. Remote Sens. 2023, 15, 4344. [Google Scholar] [CrossRef]
Li, S.; Lin, H.; Tang, X.; Ma, C.; Wang, F. Noncoherent Channel Combining for GNSS Signal Tracking with an Adaptive Antenna Array. Remote Sens. 2024, 16, 213. [Google Scholar] [CrossRef]
Liang, J.; Zhang, X.; So, H. C.; Zhou, D. Sparse Array Beampattern Synthesis via Alternating Direction Method of Multipliers. IEEE Trans. Antennas. Propag. 2018, 66, 2333–2345. [Google Scholar] [CrossRef]
Liang, J.; Fan, X.; Fan, W.; Zhou, D.; Li, J. Phase-Only Pattern Synthesis for Linear Antenna Arrays. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 3232–3235. [Google Scholar] [CrossRef]
de Lorenzo, D. S.; Lo, S. C.; Enge, P. K.; Rife, J. Calibrating adaptive antenna arrays for high-integrity GPS. GPS Solut. 2012, 16, 221–230. [Google Scholar] [CrossRef]
Mills, K.; Ahmad, F.; Amin, M. G.; Himed, B. Mills, K.; Ahmad, F.; Amin, M. G.; Himed, B. Fast Iterative Interpolated Beamforming for Interference DOA Estimation in GNSS Receivers Using Fully Augmentable Arrays. 2019 IEEE Radar Conference (Radar Conf), Boston, MA, USA,22-26 April 2019.

Figure 1. GNSS array antenna receiver configuration.

Figure 2. The hybrid array receiver structure.

Figure 3. The components meaning of the R-module.

Figure 4. The flowchart of the proposed method.

Figure 5. The analog MNF amplitude response of 7-element antenna (Scenario 1).

Figure 6. The analog MNF phase response of 7-element antenna (Scenario 1).

Figure 7. The analog MNF amplitude response of 7-element antenna (Scenario 2).

Figure 8. The analog MNF phase response of 7-element antenna (Scenario 2).

Figure 9. The INR of each RF channel before ADC sampling (Scenario 1).

Figure 10. The INR of each RF channel before ADC sampling (Scenario 2).

Figure 11. The output SINR under INR = 100 dB (Scenario 1).

Figure 12. The output SINR under INR = 100 dB (Scenario 2).

Figure 13. The SINR curve under different INR - digital beamforming (Scenario 1).

Figure 14. The SINR curve under different INR - hybrid beamforming (Scenario 1).

Figure 15. The SINR curve under different INR - digital beamforming (Scenario 2).

Figure 16. The SINR curve under different INR - hybrid beamforming (Scenario 2).

Figure 17. DOA estimation results under hybrid beamforming (INR = 100 dB). (a) DOA estimation result in the Scenario 1. (b) DOA estimation result in the Scenario 2.

Table 1. Parameters of the GNSS receiver.

Parameters	Value
RF frequency f	1575.42 MHz
Number of antenna elements	M = 7
Array radius	R=λ/2
Signal bandwidth	20.46 MHz
Interference bandwidth	20.46 MHz
Bits of attenuator	7 bit
Bits of phase shifter	8 bit
Bits of ADC	16 bit
RF gain	30 dB
GNSS signal power	−120 dBm
Noise power	−100 dBm

Table 2. The interference distribution.

Scenario	Number of Interference	Interference’s DOA
Scenario 1	1	(1°,120°)
Scenario 2	2	(1°,1°), (1°,120°)

Table 3. The GNSS constellation distribution.

PRN	Azimuth( $ϕ$ )	Elevation ( $θ$ )
1	0°	40°
2	30°	30°
3	60°	40°
4	90°	30°
5	120°	80°
6	150°	60°
7	180°	20°
8	210°	70°
9	240°	20°
10	270°	30°
11	300°	80°
12	330°	60°

Table 4. Parameters of the analog beamforming.

Parameters	Value
$δ$	0.5
$ς$	$10^{- 10}$
$η$	0.15
$ξ$	$10^{- 10}$

Table 5. Performance statistics of analog MNF* (Scenario 1).

SNF Number	$G_{\min}$	$G_{\max}$	D	$A_{m e a n}$	$A_{\max}$	$P_{m e a n}$	$P_{\max}$
SNF-1	−1.345	2.687	−35.07	\	\	\	\
SNF-2	−2.776	1.727	−36.56	0.646	3.030	3.96	15.81
SNF-3	−2.912	1.809	−45.20	0.655	3.024	3.57	17.47
SNF-4	−0.716	1.221	−42.25	0.734	2.420	3.77	16.95
SNF-5	−4.683	−0.180	−38.47	1.812	4.508	3.69	17.29
SNF-6	−2.896	1.791	−38.90	0.652	3.008	3.86	16.21
SNF-7	−0.716	1.221	−42.25	0.734	2.420	3.67	15.50

* The units of

G_{\min}

G_{\max}

,D,

A_{m e a n}

and

A_{\max}

in the table are dB, and the units of

P_{m e a n}

and

P_{\max}

are degree.

Table 6. Performance statistics of analog MNF* (Scenario 2).

SNF Number	$G_{\min}$	$G_{\max}$	$D_{1}$	$D_{2}$	$A_{m e a n}$	$A_{\max}$	$P_{m e a n}$	$P_{\max}$
SNF-1	1.016	1.646	−39.40	−38.58	\	\	\	\
SNF-2	0.848	1.355	−44.43	−35.86	0.993	4.123	3.431	17.47
SNF-3	0.849	1.345	−50.99	−37.93	1.006	4.477	3.451	17.35
SNF-4	0.687	1.456	−42.92	−39.96	1.012	4.377	2.365	18.49
SNF-5	0.841	1.365	−37	−39.77	1.003	4.004	3.402	18.07
SNF-6	0.858	1.350	−34.22	−36.18	1.016	4.324	3.344	18.07
SNF-7	0.687	1.456	−39.96	−42.92	1.012	4.459	2.348	17.39

* The units of

G_{\min}

G_{\max}

,D,

A_{m e a n}

and

A_{\max}

in the table are dB, and the units of

P_{m e a n}

and

P_{\max}

are degree.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Robust Wideband Interference Suppression Method for GNSS Array Antenna Receiver via Hybrid Beamforming Technique

Abstract

1. Introduction

2. Signal Model and Conventional Anti-Jamming Technique

2.1. Signal Model

2.2. Digital Beamforming Based Anti-Jamming Processing Technique

3. Proposed Technique

3.1. Analog Beamforming Technique

3.2. Digital Beamforming Technique

3.3. Implementation of Proposed Technique

4. Simulations and Results

4.1. Simulation Settings

4.2. Experiment 1: Analog Beamforming Performance Analysis

4.3. Experiment 2: Strong Interference Suppression Performance Analysis

4.4. Experiment 3: Maximum Interference Suppression Abilty Performance Analysis

5. Discussions

6. Conclusions

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe