Mapping Petri Nets onto a Calculus of Context-Aware Ambients

1. Introduction

Over the years, a large number of mathematical formalisms for concurrency theory have been developed, each with its distinct features. Petri nets [1,2] were among the first formalisms for modelling interacting sequential processes. Then, Tony Hoare developed the calculus of Communicating Sequential Processes (CSP) [3], and Robin Milner the Calculus of Communicating Systems (CCS) [4]. These formalisms provided notations for modelling different forms of concurrency. Later on, the $\pi$-calculus was introduced to extend CCS with the notion of mobility. In the $\pi$-calculus, mobility is modelled using the mechanism of scope extrusion, i.e. a name sent through a receptor (i.e. a name that is used to receive messages) can also be used as a receptor. However, this makes the implementation of the $\pi$-calculus difficult in distributed systems. The join-calculus [5] was thus developed by Fournet and Gonthier to provide a formal basis for the design of distributed programming languages, by replacing the communication and mobility mechanisms of the $\pi$-calculus with the notion of join definition, which is much easier to implement in distributed systems. Recently, the Calculus of Context-aware Ambients (CCA) [6,7], inspired from the Calculus of Mobile Ambient (MA) [8], was developed to provide constructs for concurrency, mobility and context-awareness based on a single notion of ambient, which is an abstraction of a place where computation can happen. CCA emeges as a suitable formalism to reason about the behaviours of pervasive systems and the Internet of Things [9,10,11].

It is customary in formal methods to compare the expressive powers of formalisms, i.e. whether one formalism can be mapped onto another. In [12], Mennicke presents an operational Petri net semantics for the join-calculus. An approach to mapping Petri nets to concurrent programs in CC++ is proposed in [13], which establishes a link between Petri nets and object-oriented concurrent programming and forms a foundation for a Petri net based transformational software development methodology. Similarly, [14] proposes a mapping from Petri nets to the language of the B-Method in an effort to incorporate the Petri nets graphical notation in a software development method based on the B-language. A mapping of Petri nets to DEVS (Discrete Event System Specification) is presented in [15] so DEVS based platforms can be used to analyse systems specified in Petri nets.

This paper proposes an approach to mapping Petri nets onto CCA. This allows for the graphical language of Petri nets be used in combination with CCA for the modelling of complex pervasive and IoT systems. The contributions of the paper is fourfold:

• We propose an algorithm that transforms any Petri net into a CCA process (Sect 2.3). This demonstrates that CCA is at least as expressive as Petri nets, i.e. any system that can be specified in Petri nets can also be specified in CCA.
• We demonstrate that the proposed algorithm is efficient and scalable (Sect 2.3.3). Indeed, the time complexity of the algorithm is quadratic (i.e. the execution time is in the order of the square of the size of the Petri net in input) and the size of the CCA process generated in output grows linearly with the size of the Petri net in input.
• The proposed algorithm is implemented in Python so a Petri net can be translated into a CCA process automatically at a click of a button (Sect. 2.3.3 and Appendix A).
• We show through experiments that a Petri net and its corresponding CCA process behave the same way using the CCA simulator ccaPL. The proposed approach is illustrated using a case study of the dining cryptographers problem (Sect. 3).

The remaining of the paper is structured as follows. Section 2 presents the proposed algorithm for mapping Petri nets onto CCA and discusses the efficiency and the scalability of the algorithm. The experimental results and the case study are presented in Sect. 3. In Sect. 4, we discuss the results, highlight the limitations of the work, and propose future work. Section 5 concludes the paper.

2. Materials and Methods

2.1. Overview of Petri Nets

Petri nets are a graphical formalism to describe systems whose dynamics are characterised by concurrency, synchronisation, mutual exclusion and conflict [2,16]. A Petri net consists of places, transitions, and directed arcs. A place is represented by a circle and a transition by a rectangle. Arcs run from a place to a transition or vice versa, never between places or between transitions. A place may contain a discrete number of marks called tokens. An example of Petri net is depicted in Figure 1. Any distribution of tokens over the places will represent a configuration of the net called a marking.

The places from which an arc runs to a transition are called the input places of the transition; the places to which arcs run from a transition are called the output places of the transition. Similarly, the transitions from which an arc runs to a place are called the input transitions of the place; the transitions to which arcs run from a place are called the output transitions of the place. Therefore, a Petri net can be defined formally as a tuple $(P,T,I,O,m_0)$, where

• P is a finite set of places.
• T is a finite set of transitions, such that $P\cup T\ne \varnothing$ and $P\cap T=\varnothing$.
• $I:P\times T\to \mathbb{N}$ is an input function. $I(p,t)$ is the number of directed arcs from the place p to the transition t.
• $O:T\times P\to \mathbb{N}$ is an output function. $O(t,p)$ is the number of directed arcs from the transition t to the place p.
• $m_0:P\to \mathbb{N}$ is the initial marking, which defines the initial number of tokens in each place.

Example 1.

The Petri net of Figure 1 is formally defined as follows:

• $P=\{red,black\}$
• $T=\{bb,rb,rr\}$
• $I=\left\{\right(red,bb,0),(red,rb,1),(red,rr,2),(black,bb,2),(black,rb,1),(black,rr,0\left)\right\}$
• $O=\left\{\right(bb,red,0),(rb,red,1),(rr,red,0),(bb,black,1),(rb,black,0),(rr,black,1\left)\right\}$
• $m_0=\{(red,3),(black,2)\}$

Transitions are the active components of a Petri net. A transition t is enabled if each of its input places p contains at least $I(p,t)$ tockens. A transition may execute if it is enabled. The execution of a transition t is atomic and consumes $I(p,t)$ tokens from each input place p, and creates $O(t,p)$ tokens in each output place p. Therefore, the execution of a transition t updates the marking of each place p connected to it as in (1), where $m\left(p\right)$ is the marking of a place p.

$$m\left(p\right)=m\left(p\right)-I(p,t)+O(t,p).$$

(1)

For example, Figure 2 shows the marking of the Petri net of Figure 1 after the transition $rr$ is executed. The execution of Petri nets is non-deterministic: when multiple transitions are enabled at the same time, they will execute in any order.

2.2. Overview of CCA

CCA [6,7] is a process calculus for specifying and reasoning about the behaviour of context-aware, mobile, and concurrent systems. Table 1 depicts the syntax of $\mathtt{CCA}$, based on three syntactic categories: processes P (or Q), capabilities M, and context-expressions $\kappa$. The symbols n, x, y and z are names. Note that comments can be added anywhere in a specification using the prefix // for a single line comment or the pair /* and */ for a multiline comment.

2.2.1. Processes

The process $\mathbf{0}$, aka inactivity process, does nothing and terminates immediately. The process $P|Q$ denotes the parallel composition of the processes P and Q. A process of the form $\left\{P\right\}$ behaves just like P. The process $\left(\mathtt{new}n\right)P$ creates a new name n and the scope of that name is limited to the process P. The replication $!P$ denotes a process which can always create a new parallel copy of P, i.e. $!P$ is equivalent to $P|!P$. The process $n\left[P\right]$ denotes an ambient named n whose behaviour is described by the process P. A context expression $\kappa$ is a logical formula that specifies a property upon the state of the environment. A context-guarded prefix $<\kappa >M.P$ is a process that waits until the environment satisfies the context expression $\kappa$, then performs the capability M and continues like the process P. We let $M.P$ denote the process $<\mathtt{true}>M.P$. An if-then process $\mathtt{if}<{\kappa }_1>M_1.P_1\dots <{\kappa }_{\ell }>M_{\ell }.P_{\ell }\mathtt{fi}$ waits until at least one of the context-expressions ${\left({\kappa }_i\right)}_{1\le i\le \ell }$ holds; then proceeds non-deterministically like one of the processes $<{\kappa }_j>M_j.P_j$ for which ${\kappa }_j$ holds. An if-then-else process $\mathtt{if}<{\kappa }_1>M_1.P_1\dots <{\kappa }_{\ell }>M_{\ell }.P_{\ell }\mathtt{else}P\mathtt{fi}$ behaves like an if-then process, but does not wait and continues like the process P if none of the branches can be executed. A process $\mathtt{let}{x}_1=e_1,\dots ,y_{\ell }=e_{\ell }\mathtt{in}P$ behaves like the process P in which each occurrence of $x_i$ is substituted to the value of the arithmetic expression $e_i$, for $1\le i\le \ell$ and $\ell \ge 1$. A search process $\mathtt{find}{x}_1,\dots ,x_{\ell }:\kappa \mathtt{for}P$ looks for a list of names $n_1,\dots ,n_{\ell }$ in the context such that the context-expression $\kappa$ in which each occurrence of $x_i$ is replaced by $n_i$ holds, and continues like the process P in which each occurrence of $x_i$ is replaced by $n_i$, $1\le i\le \ell$ and $\ell \ge 1$. A process of the form $\mathtt{proc}x(y_1,\dots ,y_{\ell })P$ defines a process abstraction named x, whose behaviour is described by the process P. The names $y_1,\dots ,y_{\ell }$ are the formal parameters and the process abstraction, $\ell \ge 0$. A process abstraction is a mechanism to give a name say x to a process P and later use that name anywhere to refer to the process P, just the same way functions and procedures are used in programming languages.

2.2.2. Capabilities

A capability is an elementary action that an ambient can perform. The capability $\mathtt{skip}$ represents one transition, i.e. one execution step. An ambient can move into a sibling ambient n by performing the capability $\mathtt{in}n$; and move out of its parent ambient by executing the capability $\mathtt{out}$. An ambient can exchange messages with another ambient using the output capability $\alpha \mathtt{send}(z_1,\dots ,z_{\ell })$ to send a list of names $z_1,\dots ,z_{\ell }$ to a location $\alpha$, and the input capability $\alpha \mathtt{recv}(y_1,\dots ,y_{\ell })$ to receive a list of names from a location $\alpha$ into the variables $y_1,\dots ,y_{\ell }$, for some $\ell \ge 0$. The location $\alpha$ can be `@’ to mean any parent, `$n@$’ to mean a specific parent n, `#’ to mean any child ambient, `$n\#$’ to mean a specific child n, `$::$’ to mean any sibling, `$n::$’ to mean a specific sibling n, or $ϵ$ (empty string) to mean the executing ambient itself. A capability $\mathtt{del}n$ deletes an empty child ambient n (i.e. $n\left[\mathbf{0}\right]$). A capabilty of the form $\alpha x(z_1,\dots ,z_{\ell })$ calls the process abstraction x defined at the location $\alpha$ and the names $z_1,\dots ,z_{\ell }$ are the actual parameters, $\ell \ge 0$.

2.2.3. Context Model

In CCA, a context is modelled as a process with possibly a single hole in it. The hole (denoted by ⊙) in a context C represents the position of the process, which C is a context. For example, suppose a system is modelled by the process $P\left|n\right[Q\left|m\right[R\left|S\right]]$. So, the context of the process R in that system is $P\left|n\right[Q\left|m\right[\odot \left|S\right]]$, and that of the ambient named m is $P\left|n\right[Q|\odot ]$. Thus the context of a $\mathtt{CCA}$ process is described by the grammar in Table 2. A context-expression (CE, for short) is a formula representing some property over context.

2.2.4. Context-Expressions

The formal semantics of context-expressions (CEs) with respect to the context model of Table 2 is given in Table 3, where the notation $C\vDash \kappa$ means that the context C satisfies the context-expression $\kappa$. We also write $\vDash \kappa$ to mean that a context-expression $\kappa$ is valid, i.e. $\kappa$ is satisfied by all context.

The CE $\mathtt{true}$ holds for all context while the CE $\mathtt{false}$ holds for no context. A CE $n=m$ holds if the names n and m are identical. The CE $\mathbf{0}$ holds for the empty context $\mathbf{0}$. The CE $\mathtt{this}$ holds solely for the hole context, i.e. the position of the process evaluating that context expression. Propositional operators such as $\mathtt{not}$, $\mathtt{and}$ and $\mathtt{or}$ expand their usual semantics to context expressions. A CE ${\kappa }_1|{\kappa }_2$ holds for a context if that context is a parallel composition of two contexts such that ${\kappa }_1$ holds for one and ${\kappa }_2$ holds for the other. A CE $n\left[\kappa \right]$ holds for a context if that context is an ambient named n such that $\kappa$ holds inside that ambient. A CE $\mathtt{next}\kappa$ holds for a context if that context has a child context for which $\kappa$ holds. A CE $\mathtt{somewhere}\kappa$ holds for a context if there exists somewhere in that context a sub-context for which $\kappa$ holds. Some examples of context-expressions that are used later in this paper are given in Table 4.

Context-expressions are used in CCA to specified context-aware processes. We recall in Table 5 the formal semantics of context-aware processes, where $\sigma$ is a substitution of names and ⟶ is the reduction relation of processes. The complete formal semantics of CCA can be find in [6,7]. The next section presents an algorithm for generating from a Petri net a CCA process that behaves in a similar manner.

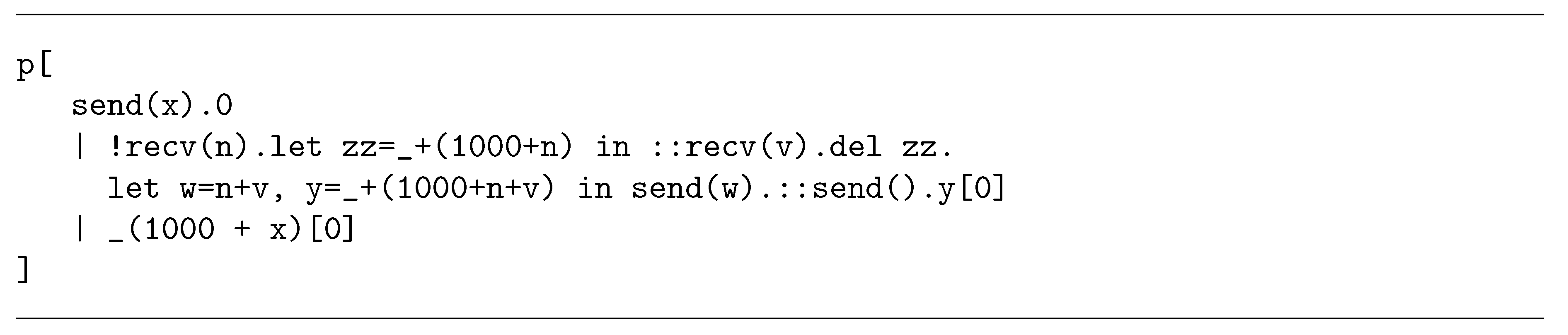
2.3. An Algorithm for Mapping a Petri Net onto a CCA Process

Algorithm 1 translates a Petri net (see Sect. 2.1) into a CCA process. The algorithm takes in input a Petri net $(P,T,I,O,m_0)$ and returns in output a CCA process in the variable $cca\_str$. The initial marking $m_0$ assigns to each place a number of tokens. The execution of a transition updates the number of tokens in the input places and the output places of the transition according to (1). A semaphore is used to guarantee that the execution of a transition is atomic, i.e. at most one transition can be executed at a time. In order to execute, a transition must obtain the semaphore, otherwise the transition must wait until the semaphore is released by another transition. This semaphore is described in CCA by the ambient $\mathtt{lock}$ defined in (2). The semaphore is in the obtained state if the ambient contains a child ambient $\mathtt{on}\left[\mathtt{0}\right]$ and is in the released state otherwise.

$$\begin{array}{c}\mathtt{lock}[\hfill \\ !\mathtt{recv}\left(\right).::\mathtt{recv}\left(\mathtt{t}\right).\left\{\mathtt{on}\right[\mathtt{0}\left]\right|\mathtt{t}::\mathtt{recv}\left(\right).\mathtt{del}\mathtt{on}.\mathtt{send}\left(\right).\mathtt{0}\}\hfill \\ \left|\mathtt{send}\right().\mathtt{0}\hfill \\ ]\hfill \end{array}$$

(2)

The behaviour of the ambient $\mathtt{lock}$ can be explained as follows. Initially, the semaphore is in the released state, i.e. no transition is being executed. The ambient waits (using the capability $::\mathtt{recv}\left(\mathtt{t}\right)$) until a transition t is willing to obtain the semaphore, then creates a child ambient $\mathtt{on}\left[\mathtt{0}\right]$ to indicate that the semaphore is obtained by the transition t. The semaphore remains in the obtained state until it is released by the transition t (using the capability $\mathtt{t}::\mathtt{recv}\left(\right)$), in which case the child ambient $\mathtt{on}\left[\mathtt{0}\right]$ is deleted. The context-expression $\mathtt{lockOn}\left(\right)$ defined in Table 4 holds if the semaphore $\mathtt{lock}$ is in the obtained state, i.e. it contains a child ambient $\mathtt{on}\left[\mathtt{0}\right]$.

In Algorithm 1, the declaration of the context expression $\mathtt{lockOn}\left(\right)$ is created in line 2, together with other simulation directives such as the execution mode and the simulation length. In ccaPL, these declarations appear between the keywords “BEGIN_DECLS” and “END_DECLS”. The semaphore $\mathtt{lock}$ is created in line 3 of Algorithm 1. The following subsections explain how places and transitions are modelled in CCA.

Algorithm 1: Mapping a Petri net onto a CCA process

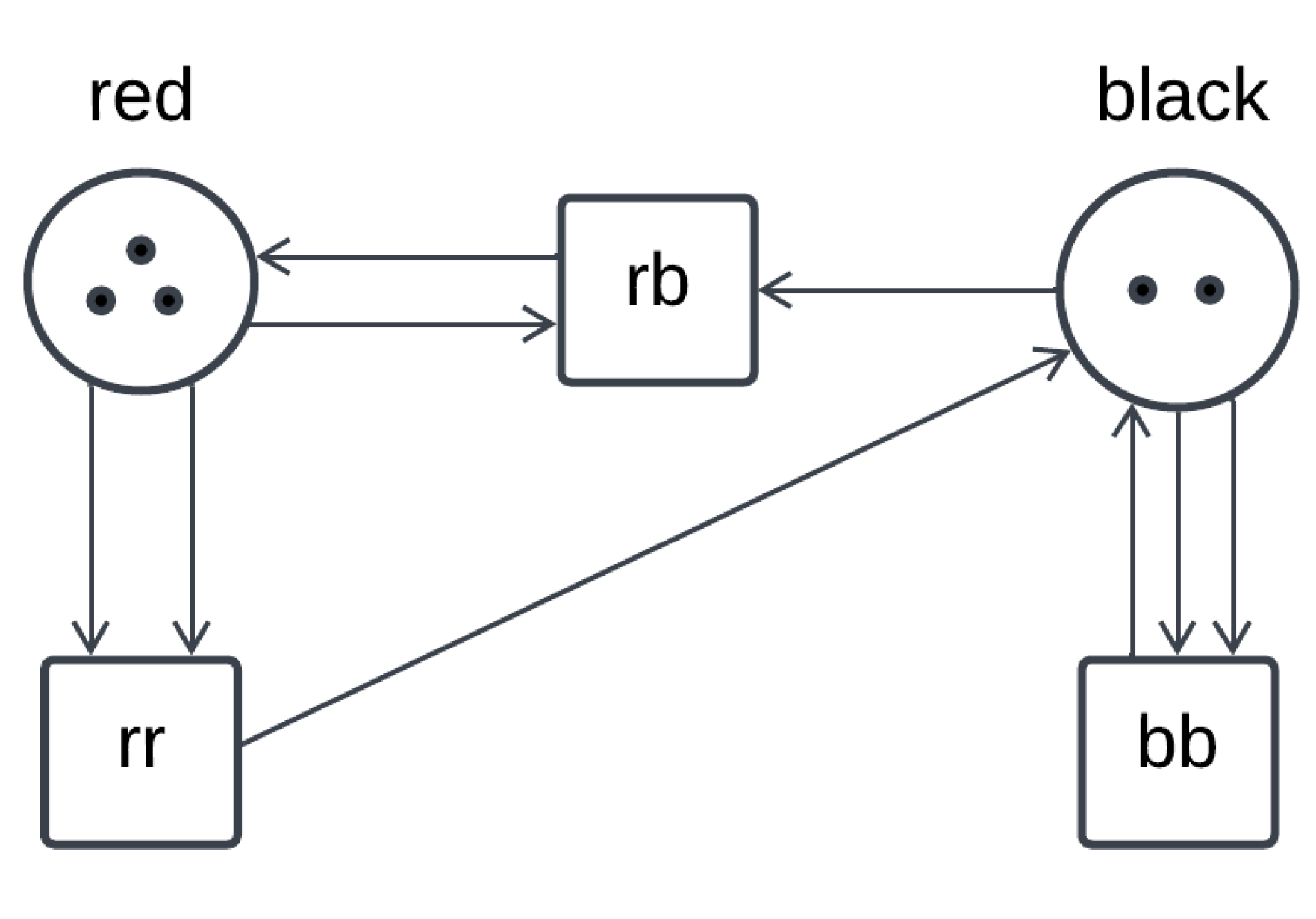
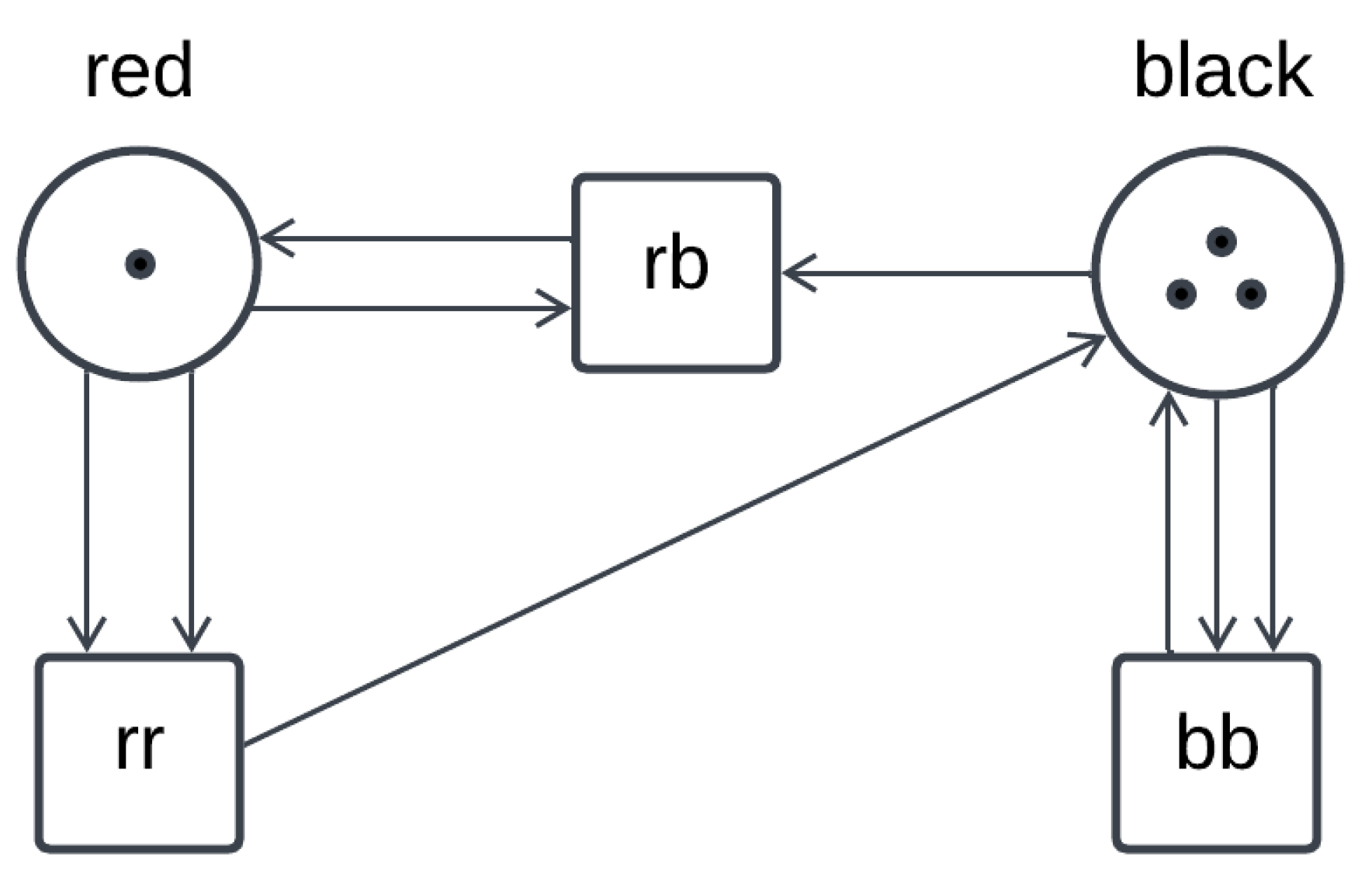
2.3.1. Modelling Places

In this section, we show how a place can be modelled as an ambient in CCA. For each place $p\in P$ an ambient of the same name is created in the line 7 of Algorithm 1. The general form of this ambient is given in Table 6. Initially, a place p contains $m_0\left(p\right)=x$ tokens. This is represented in Table 6 by the process “$\mathtt{send}\left(\mathtt{x}\right).\mathtt{0}$”. A child ambient to the ambient p is also created as “$\_(\mathtt{1000}+\mathtt{x})\left[\mathtt{0}\right]$”, e.g. if $\mathtt{x}=\mathtt{1}$ then the child ambient is “$\_\mathtt{1001}\left[\mathtt{0}\right]$”. This encoding reflects in the child ambient’s name the number of token in the ambient p and satisfies the property stated in Theorem 1. Therefore, the names of the child ambients of places can be compared instead of the number of tokens of these places. The behaviour of a place ambient p can be summarised as follows. A place ambient (see Table 6) waits until a transition it is connected to starts executing (see “$::\mathtt{recv}\left(\mathtt{v}\right)$”). It then deletes its current child ambient, updates its number of tokens according to (1) and creates a child ambient that reflects its new number of tokens. It also signals to the running transition that it has completed updating (see “$::\mathtt{send}\left(\right)$”). For example, the place ambients for the places red and black of the Petri net in Figure 1 are given in Table 7. The loop in line 5 of Algorithm 1 creates such a place ambient for each place $p\in P$ and composes them in parallel.

Definition 1.

Let $str\left(z\right)$ be the string representation of an integer value z. For example $str\left(0\right)=$“0” and $str\left(23\right)=$“23”.

Theorem 1.

Let n, x and y be 3 integers such that $n\ge 1$, $0\le x<{10}^n$, and $0\le y<{10}^n$. Then

$$x\ge y\iff str({10}^n+x)\ge str({10}^n+y).$$

The proof of Theorem 1 can be done by induction on n as follows.

Proof. 

Let $\parallel z\parallel$ denote the number of digit in a non-negative integer z. For example $\parallel 0\parallel =1$, $\parallel 23\parallel =2$, and $\parallel 100\parallel =3$.

Base case:

Prove that the theorem holds for $n=1$.

We have: $0\le x<10\Rightarrow \parallel x\parallel =1$. Similarly $\parallel y\parallel =1$. Therefore $x\ge y\Rightarrow str(10+x)=$“$1x$” $\ge str(10+y)=$“$1y$”.

Reversely, “$1x$” ≥“$1y$” ⇒ “x” ≥ “y”. And since $\parallel x\parallel =1$ and $\parallel y\parallel =1$, it follows that $x\ge y$.

Induction case:

Suppose that the theorem holds for n and prove that the theorem also holds for $n+1$.

• If $0\le x<{10}^n$, and $0\le y<{10}^n$, then $0\le x<{10}^{n+1}$, and $0\le y<{10}^{n+1}$. Let $str({10}^n+x)=$“$1\overline{x}$” and $str({10}^n+y)=$“$1\overline{y}$”, for some strings $\overline{x}$ and $\overline{y}$. It follows that $str({10}^{n+1}+x)=$“$10\overline{x}$” and $str({10}^{n+1}+y)=$“$10\overline{y}$”. In string comparison, “$1\overline{x}$” ≥ “$1\overline{y}$” ⇔ “$10\overline{x}$”≥ “$10\overline{y}$”. We conclude that $x\ge y\iff str({10}^{n+1}+x)\ge str({10}^{n+1}+y).$
• If ${10}^n\le x<{10}^{n+1}$, and $0\le y<{10}^n$, then $\parallel x\parallel \ge \parallel y\parallel +1$. Let $str({10}^{n+1}+x)=$“$1\sigma \overline{x}$” and $str({10}^{n+1}+y)=$“$10\overline{y}$”, for some digit $\sigma \ge 1$ and strings $\overline{x}$ and $\overline{y}$ of equal length n. Since $\sigma \ge 1$, “$1\sigma \overline{x}$” ≥ “$10\overline{y}$” is always true. Therefore we conclude that $x\ge y\iff str({10}^{n+1}+x)\ge str({10}^{n+1}+y).$
• If ${10}^n\le x<{10}^{n+1}$, and ${10}^n\le y<{10}^{n+1}$, then let $x=\sigma \times {10}^n+x^{\prime }$ and $y=\theta \times {10}^n+y^{\prime }$, for some integers $x^{\prime }<{10}^n$ and $y^{\prime }<{10}^n$, and digits $\sigma \ne 0$ and $\theta \ne 0$. There are 2 cases: $\sigma =\theta$ or $\sigma \ne \theta$.

  -

  If $\sigma =\theta$, then $x\ge y\iff (\sigma \times {10}^n+x^{\prime }\ge \sigma \times {10}^n+y^{\prime })\iff x^{\prime }\ge y^{\prime }\iff str({10}^n+x^{\prime })\ge str({10}^n+y^{\prime })\iff str(\sigma \times {10}^n+x^{\prime })\ge str(\sigma \times {10}^n+y^{\prime })\iff str({10}^{n+1}+\sigma \times {10}^n+x^{\prime })\ge str({10}^{n+1}+\sigma \times {10}^n+y^{\prime })\iff str({10}^{n+1}+x)\ge str({10}^{n+1}+y)$.

  -

  If $\sigma \ne \theta$, let $str({10}^{n+1}+x)=$ “ $1\sigma \overline{x^{\prime }}$” and $str({10}^{n+1}+y)=$ “$1\theta \overline{y^{\prime }}$”, for some strings $\overline{x^{\prime }}$ and $\overline{y^{\prime }}$. It follows that “$1\sigma \overline{x^{\prime }}$” > “$1\theta \overline{y^{\prime }}$” $\iff \sigma >\theta \iff \sigma \times {10}^n>\theta \times {10}^n\iff \sigma \times {10}^n+x^{\prime }>\theta \times {10}^n+y^{\prime }\iff x>y$.

  Therefore, we conclude that $x\ge y\iff str({10}^{n+1}+x)\ge str({10}^{n+1}+y)$.

  □

2.3.2. Modelling Transitions

Similarly to a place, a transition can be modelled as an ambient. Indeed, Algorithm 1, in the lines 9-25, creates for each transition $\mathtt{t}\in T$ an ambient named $\mathtt{t}$ of the form described in Table 8. The ambient uses the context-expression $state(p,x)$ defined in Table 4 to check if a place ambient p has a child ambient x. Note that the name of a child ambient of a place is encoded to reflect the number of tokens of that place and satisfies the property stated in Theorem 1. In Table 8, the variables p1, ..., pn denote the input places of the transition and q1, ..., qk denote the input and output places of the transition. The behaviour of the ambient is an iterative process, which waits until the semaphore $\mathtt{lock}$ is released, then obtains the semaphore $\mathtt{lock}$ (line 2 in Table 8). It then reads the markings of the transition’s input places (line 3) and checks if all the input places are enabled (line 4), in which case the number of tokens of each place connected to it is updated according to (1) (line 5). Finally, the process releases the semaphore $\mathtt{lock}$ and gets ready for further execution (lines 6 and 7). An example of transition ambient is given in Table 9 for the transition rr of the Petri net in Figure 1.

In summary, the CCA process generated by Algorithm 1 for a Petri net is the parallel composition of the semaphore $\mathtt{lock}$, all the place ambients and all the transition ambients. For example, the CCA process generated for the Petri net of Figure 1 is presented in Table 10.

2.3.3. Complexity of the Algorithm

It is important to discuss the complexity of the algorithm in terms of the execution time, and the size of the CCA process produced in output in comparison to the size of the Petri net received in input. For a Petri net of n places and m transitions, Algorithm 1 takes $O\left(n\right)$ time to generate the place ambients (see the loop in line 5) and $O\left(nm\right)$ time to generate the transition ambients (see the loop in line 9). Therefore the overall time complexity of Algorithm 1 is $O\left({\tilde{n}}^2\right)$, where $\tilde{n}=max(n,m)$; i.e. the execution time is in the order of the square of the size of the input. Besides, the algorithm creates for each place two ambients (see lin 5): a place ambient with a child ambient as depicted in Table 6. However, a single ambient is created for each transition in line 9 of Algorithm 1. The general form of a transition ambient is depicted in Table 8. Finally, a unique semaphore ambient named lock (see (2)) is created in line 3. Thus, the total number of ambients created is $2\times n+m+1$, and so the size of the CCA process generated by Algorithm 1 is in the order of $O\left(\tilde{n}\right)$, i.e. the size of the CCA process generated in output grows linearly with the size of the Petri net in input. The proposed algorithm is thus efficient and scalable. An implementation of the algorithm in Python (version 3.10.11) is given in Appendix A so the mapping of a Petri net onto a CCA process can be done automatically at a click of a button.

3. Results

In this section, the proposed algorithm is validated through experiments using a case study of the dining cryptographers problem. The experiments are carried out using the CCA simulator ccaPL.

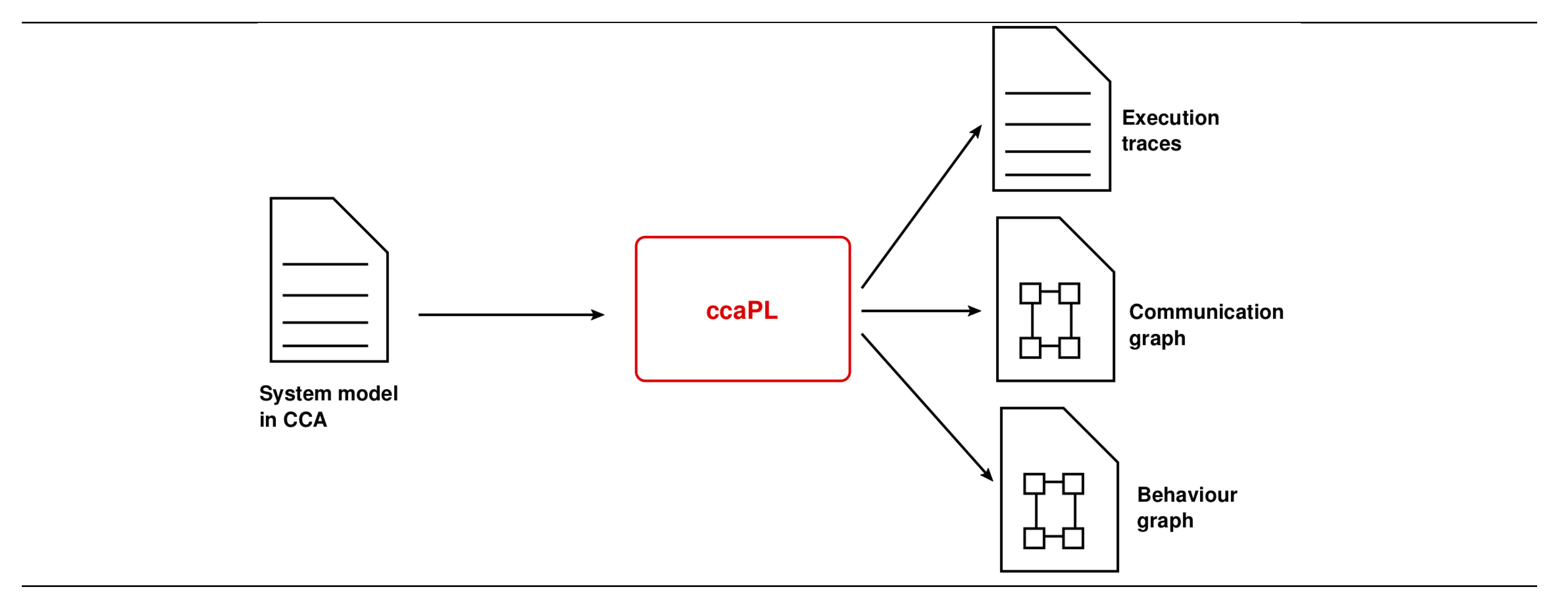
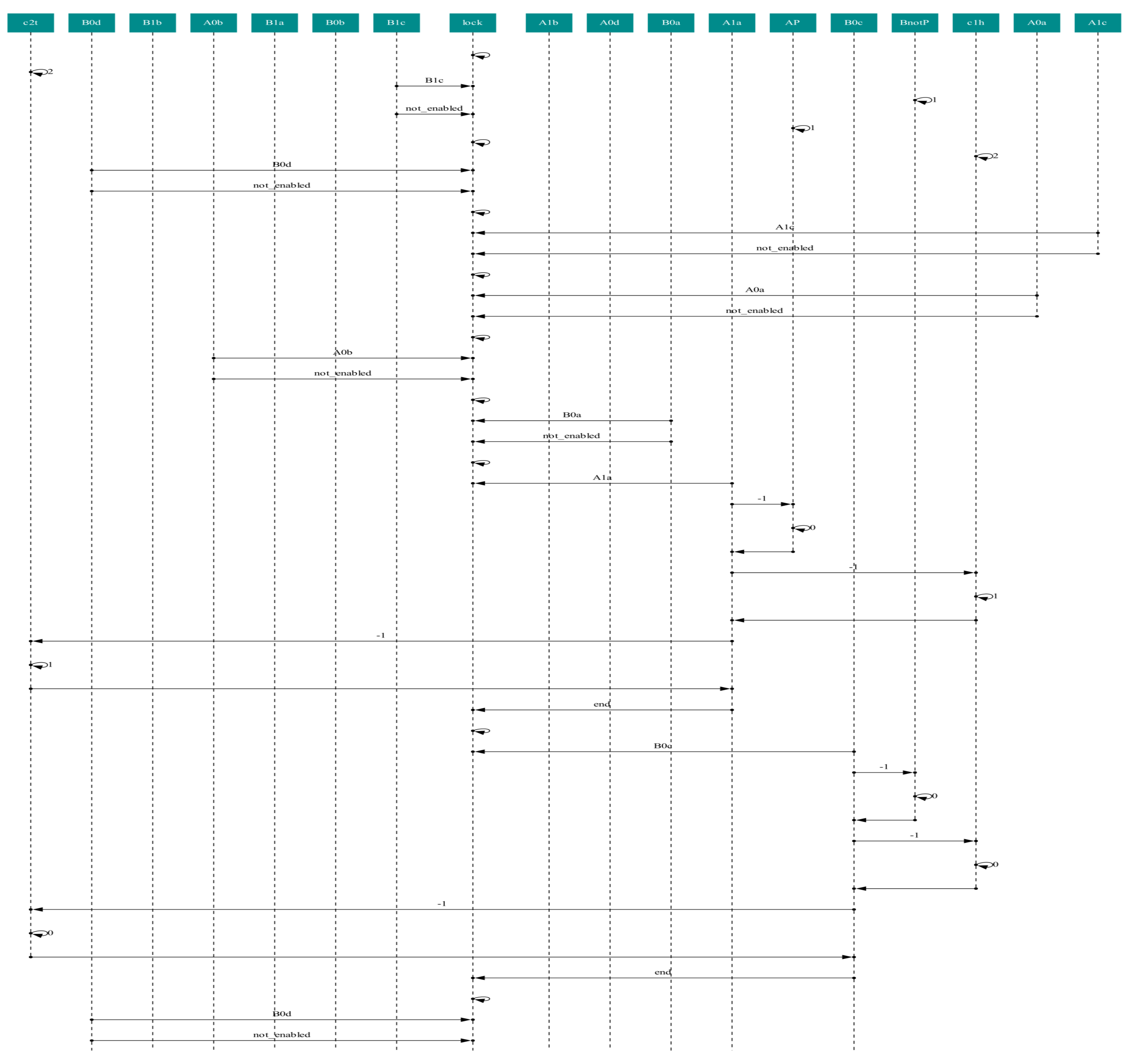
3.1. Overview of the CCA Simulator ccaPL

The syntax of a ccaPL program is given in Table 11, where P is a process and k is a context-expression defined in Table 1; <Id> stands for an identifier (i.e. a name), e for empty string, and <Val> is a non-negative integer number. It follows that a ccaPL program is composed of a declaration block (optional) and a body, which is a CCA process. The declaration block starts with the keyword BEGIN_DECLS and ends with the keyword END_DECLS. In between these keywords, one can add the definitions of context-expressions using the keyword def, and the declarations of execution directives. Note that ccaPL programs are case-sensitive. An example of ccaPL program is given in Table 10. The execution directives control how the parallel processes of a program are executed. By default, at each execution step the process to be executed is chosen deterministically based on two criteria: how long the process has been willing to execute (FIFO1), and in case of conflict the sequential order as they appear in the program text is used. The execution directive mode random changes the execution mode to a random selection of the processes to be executed. The directive display code forces the program code to be displayed after each execution step. By default, only reduction steps are shown in the execution traces; with the directive display congruence, the congruence steps are also shown in the execution traces. The directive length = xx stops the execution of the program after xx steps. Comments can be added anywhere in a program text using the prefix // for a single line comment or the pair /* and */ for a multiline comment, just like in the Java programming language. The ccaPL tool can generates three types of execution output as shown in Figure 3: a textual execution trace, a communication graph, and a behaviour graph.

3.1.1. Textual Execution Trace

The execution trace is a text describing the execution steps. An example of textual execution trace is given in Figure 4. Each execution step trace is prefixed by the symbol —> (resp. <—>) for a reduction step (resp. for a congruence step), followed by the explanation of the execution step between a pair of curly brackets { and }. For example, the explanation of a message passing step has the form {child to parent: A ===(X)===> B}, meaning that a message X is sent by a child ambient A to a parent ambient B. Notations such as Child to parent, Parent to child, Sibling to sibling, and local provide information about the relationship between the sender A and the receiver B. In particular, local means the sender is the receiver (i.e. A and B are the same ambient). An explanation of the form {binding: n -> X} corresponds to the execution of a statement of the form find n:k for P and means that the value (i.e. name) X has been found for the variable n such that the context-expression k holds in the current context. The variable n will then be replaced by the name X in the process P (see the semantic rule R5 in Table 5). The remaining execution step explanations are straightforward. To generate a textual execution trace, use the following command line, where myprog.cca is your program file.

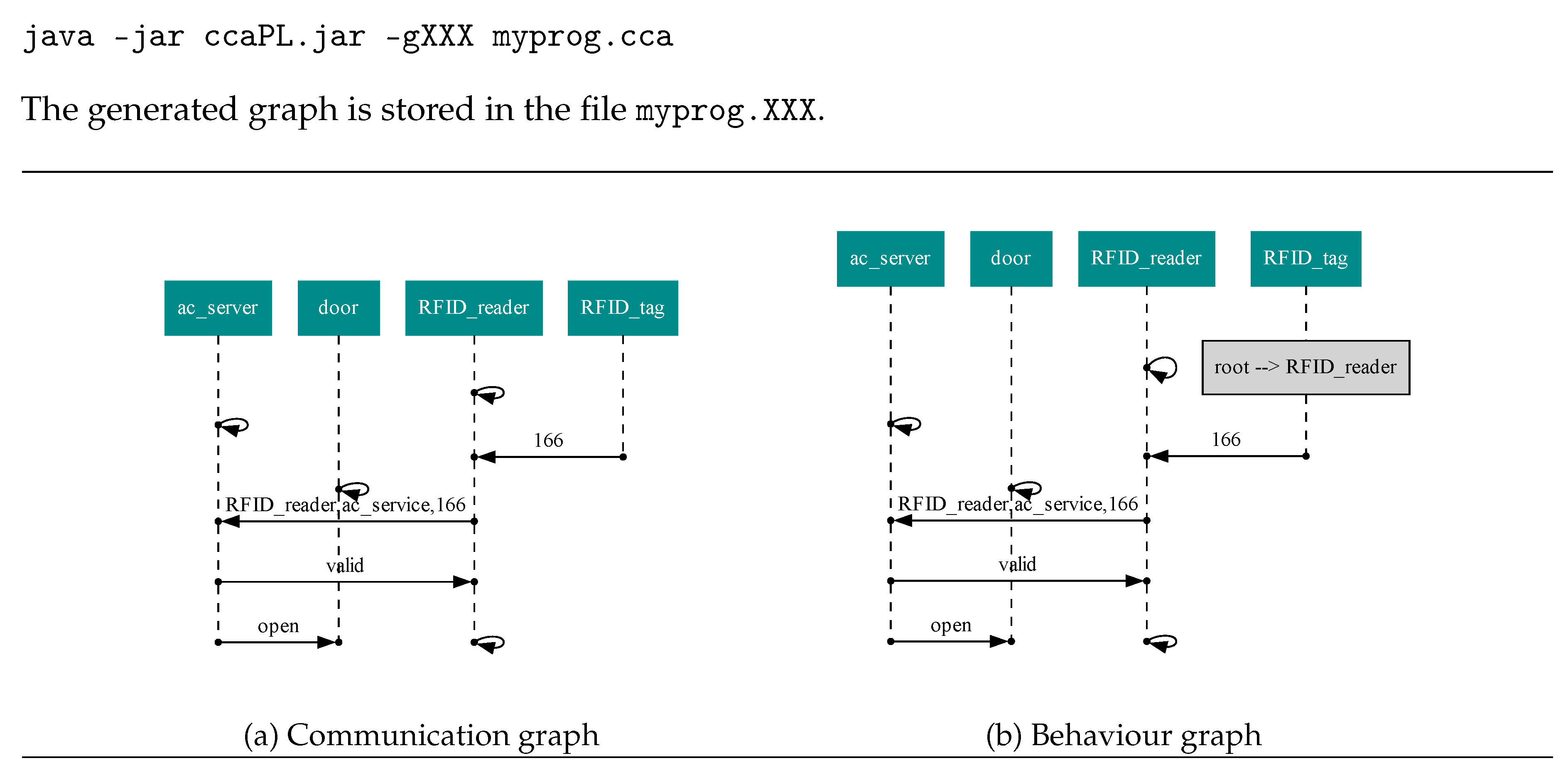
3.1.2. Communication Graph

The execution trace is a diagram showing the timeline of the communications between the ambients. An example of communication graph is given in Figure 5-a. The top row of the diagram is the list of the ambients being executed. The execution timeline of each ambient is denoted by a vertical dashed line, and the time increases from top to bottom. An arrow from one timeline (sender ambient) to another (receiver ambient) indicates a communication step between the corresponding ambients. This arrow is labelled with the message exchanged. A communication graph is created using the following command line, where XXX is the image format like ps, jpg, png, pdf, and so on.

3.1.3. Behaviour Graph

This is similar to a communication graph, but in addition it shows the movement steps using a grey box containing a text of the form A --> B on the timeline of an ambient to indicate that the ambient has moved from the location A to the location B. An example of behaviour graph is given in Figure 5-b. Recall that an ambient can move from one location to another by performing the capability in or the capability out (see Sect. 2.2). The following command line will generate a communication graph myprog_0.XXX and the corresponding behaviour graph myprog_1.XXX.

java -jar ccaPL.jar -gxXXX myprog.cca

Note that the generation of the graphical execution traces requires that the Graphviz package [18] be installed on your computer.

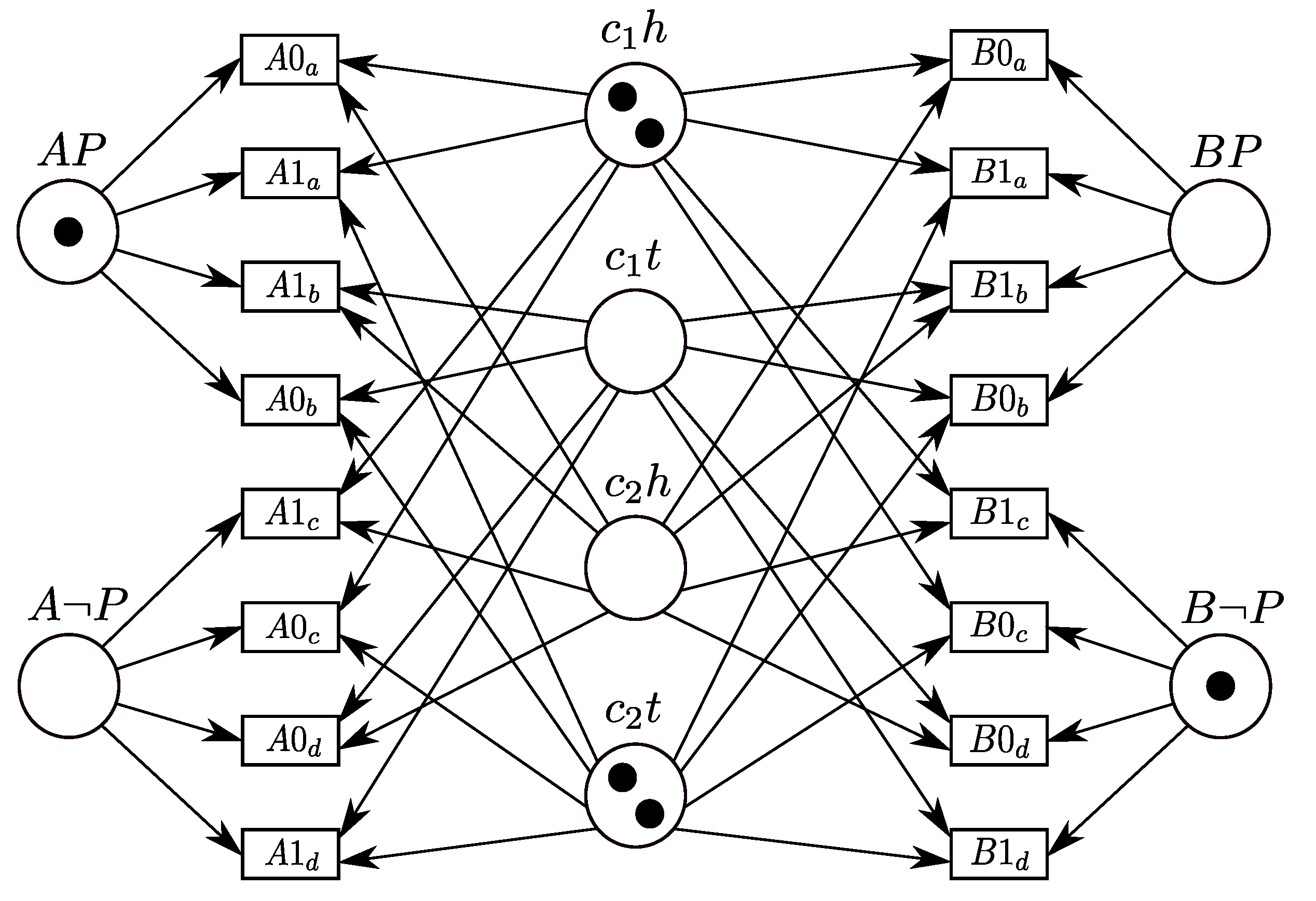
3.2. A Case Study: The Dining Cryptographers Problem

The standard dining cryptographers problem [19] consists of three diners and requires that the identity of the person who pays the bill (which may be one of the cryptographers or an external person) remains anonymous. In this section we consider a simplified version of the problem with just two diners. This version is also used in [20,21] and can be extended to three or more diners. Alice and Bob are two cryptographers who have a dinner in a restaurant. When it is time for the bill, they are informed by the waiter that the bill has already been paid. Both, Alice and Bob, would like to know whether the bill was paid by a third person, or it was one of them. However, if it is the second case, then they do not want an eavesdropper, Yves, on a neighbouring table to know which of them paid. Following is the protocol that they decided to use to solve this problem.

3.2.1. A Dining Cryptographers Protocol

Firstly, they toss two coins that are visible to both of them. At the same time, they ensure that Yves cannot see either of them. If Alice paid, she lies about the parity of the two coins i.e. she calls `agree’ if she sees a head and a tail, and `disagree’ otherwise. If Alice did not pay, she tells the truth about the parity of the coins. The same applies for Bob. Now Alice and Bob both know whether one of them paid. In case their calls are the same they know that a third person paid, otherwise it must have been one of them – in this example they actually both know which. On the other hand, Yves can only tell whether or not one of Alice and Bob paid, but not which one. It should be noted that Yves also knows about the protocol. A possible encoding of the protocol using a Petri net is depicted in Figure 6. The two places at the left of the net represent Alice’s initial state: having paid is shown by placing a single token in place $AP$, and having not paid is shown by placing a single token in place $A\neg P$. The initial state of Bob is represented by the places at the right. The three possible initial markings for Alice and Bob are given in (3).

$$\{AP,B\neg P\},\{A\neg P,BP\},\{A\neg P,B\neg P\}$$

(3)

The top two places in the centre of the net represent the first coin: head is represented by placing two tokens in the place $c_{1}h$, and tail is represented by placing two tokens in the place $c_{1}t$. The bottom two places, $c_{2}h$ and $c_{2}t$, represent the second coin. As it was mentioned, both Alice and Bob must see the coins. For this reason, the marked places must contain two tokens. As a result, the possible initial markings for the coins are the multi-sets in (4).

$$\begin{array}{c}\{c_{1}h,c_{1}h,c_{2}h,c_{2}h\},\{c_{1}h,c_{1}h,c_{2}t,c_{2}t\},\\ \{c_{1}t,c_{1}t,c_{2}h,c_{2}h\},\{c_{1}t,c_{1}t,c_{2}t,c_{2}t\}\end{array}$$

(4)

The cross product of the cryptographer markings in (3) and the coin markings in (4) denotes the set of all 12 possible initial markings. The eight transitions on the right represent the eight possible scenarios for Bob, given by two possibilities for each coin multiplied by the two possibilities for his own initial state. The transitions on the right represent Bob saying the coins `disagree’ ($B0$) or Bob saying the coins `agree’ ($B1$). Similarly for Alice on the left.

3.2.2. Mapping the Petri Net of the Dining Cryptographers Protocol onto a CCA Process

Algorithm 1 was applied to map the Petri net in Figure 6 onto a CCA process. In this section it is shown that the CCA process and the Petri net behave the same way. To achieve this, the CCA process is executed in ccaPL for each of the 12 possible initial markings. The result is summarised in Table 12. It follows that the transitions enabled in the Petri net correspond exactly to the transition ambients executed by the CCA process. A sample of the execution traces, in the form of a communication graph, is given in Figure 7. This corresponds to the simulation of the case where Alice paid the bill and Bob did not (i.e. $\{AP,B\neg P\}$), and the toss of the two coins shows head for coin 1 and tail for the other (i.e. $\{c_{1}h,c_{1}h,c_{2}t,c_{2}t\}$). The execution trace indicates with a pair of consecutive arrows a transition that is not enabled. The current number of tokens of each place is shown as a label to a loop-arrow along the execution timeline (i.e. the vertical dashed line) of the place ambients. The execution trace of an enabled transition starts with an arrow labelled with the name of the transition and terminates with an arrow labelled end. Therefore, in Figure 7 the simulation shows that the only enabled transitions, and thus executed, for this case are the transitions A1a and B0c. This experiment can be reproduced using the Python implementation of Algorithm 1 given in Appendix A to generate the CCA process for the dining cryptographers protocol and then execute the CCA process in the simulation too ccaPL.

4. Discussion

There has been a substantial amount of research that adapts and relates features of process algebras to Petri nets. Petri Box calculus [22,23], for instance, is a process algebra based on CCS that presents a compositional semantics for high level constructs of concurrent programming languages with regard to Petri nets. [24] proposed a translation from Condition/Event (C/E) nets to Circal process algebra based on a binary composition and hiding operators. Moreover, in [25,26,27], frameworks that endow Petri nets with labelled transition systems are presented, applying techniques come from process algebras. In particular, in [25], the theory of bigraphs has been applied to C/E nets, by converting C/E nets to bigraphs and examining their behavioural theory. Moreover, there has been a significant work on translating process algebras to Petri nets [28]; with application to the verification of mobile systems [29]. For instance, [30,31] proposed a translation of CCS into Petri nets, while [32] presented a distributed semantics for $\pi$-calculus, based on Petri nets.

Powerful, usable and flexible contemporary systems are characterised by features such as dynamic reconfigurability, where nodes in networks dynamically can appear or vanish; and logical mobility, where connections in ad-hoc networks can be formed dynamically. These systems are also called reference passing systems (RPS) [28]. As the number of such systems constantly is increased, the correct functionality of such systems is of paramount importance to eliminate potential costly errors in the design phase.

There is a number of formalisms that are suitable for modelling and verifying specifications that are characterised by concurrency and the ability to form dynamic logical connections between individual modules [33,34]. The major factors and trade-offs in selecting an appropriate formalism are its expressiveness and the tractability of the associated verification techniques. Formalisms that are expressive are Turing powerful and so not decidable in general. However, it is possible apply some restrictions (e.g., finiteness of the control) that would ensure decidability, while preserving a reasonable modelling power.

In [35], the authors present a number of equivalence notions on Petri nets that can be used in the construction of algebraic models. In [36], the authors proposed a new set of inference rules for a subclass of Calculus of Communicating Systems (CSS). This allows for a direct translation to a subclass of Petri nets, more particularly, to condition/event nets. Early work on translating Petri nets into CCA is presented in [37], but the proposed algorithm is limited to a subset of Petri nets without multiple arcs between a place and a transition. Our algorithm can handle Petri nets with multiple arcs between places and transitions, e.g. the Petri net in Figure 1. In [38], a notion of net calculus is introduced, which is defined through a place/transition Petri net. The authors proposed a calculus of nets, called SCONE. Based on this, relationships between SCONE and a subset of CCS are studied. In [39], different approaches for the modelling of parallel processes are examined. The work considers process algebras, like CCS and communicating sequential processes (CSP) as main representatives. It is shown that the construction of transition nets is possible for all CCS programs in which recursive calls start sequentially. In [33], Finite Control Processes (FCP), a subclass of $\pi$-calculus, have been proposed, where the system is defined as a parallel composition of sequential entities. In [28], the authors introduced a translation of FCP to safe Petri nets to formally verify mobile systems.

In formal methods it is customary to compare the expressive power of various languages and provide way of mapping one language to another. This paper has followed the same approach and proposes an algorithm that maps Petri nets onto CCA. The graphical language of Petri nets can then be combined uniformly with the text-based specification language of CCA to facilitate the specification and documentation of the design of complex distributed systems. The CCA tools such as ccaPL can also be used as additional tools to analyse the behaviours of Petri nets. The main limitation of this work is that the equivalence between a Petri net and its corresponding CCA process is not formally established, but through experiments. Thus in future work, we will investigate a formal proof of a behavioural equivalence between a Petri net and its corresponding CCA process. Reversely, we will also investigate whether CCA can be mapped onto Petri nets.

5. Conclusion

This paper demonstrates that any system that can be specified in Petri nets can also be specified in CCA. Therefore, CCA is at least as expressive as Petri nets. Indeed, an algorithm is proposed that transforms a Petri net into a process in CCA. It is established, through experiments, that a Petri net and its corresponding CCA process exhibit the same behaviours. The CCA process can then be analysed and verified using the CCA verification tools like the CCA simulator ccaPL. The algorithm is implemented in Python and therefore the translation of a Petri net into a CCA process can be done automatically at a click of a button. It follows from this work that the Petri net graphical notations can be used together with the CCA language in the specification of complex pervasive and IoT systems. A real-world case study of the dining cryptographers problem was used to illustrate the proposed approach.