Submitted:
23 April 2024
Posted:
24 April 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Typical Control and Disturbance Analyses of Grid-Forming Inverters
2.1. Typical Control Strategies for Grid-Forming Inverters
2.2. Disturbance Analysis after Considering Line Impedance Parameter Perturbation
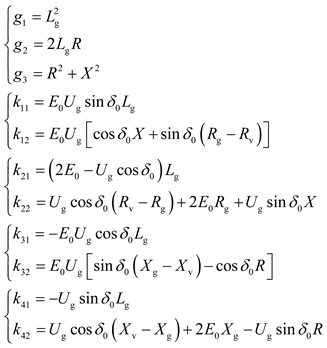
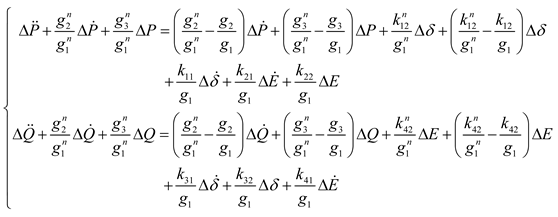
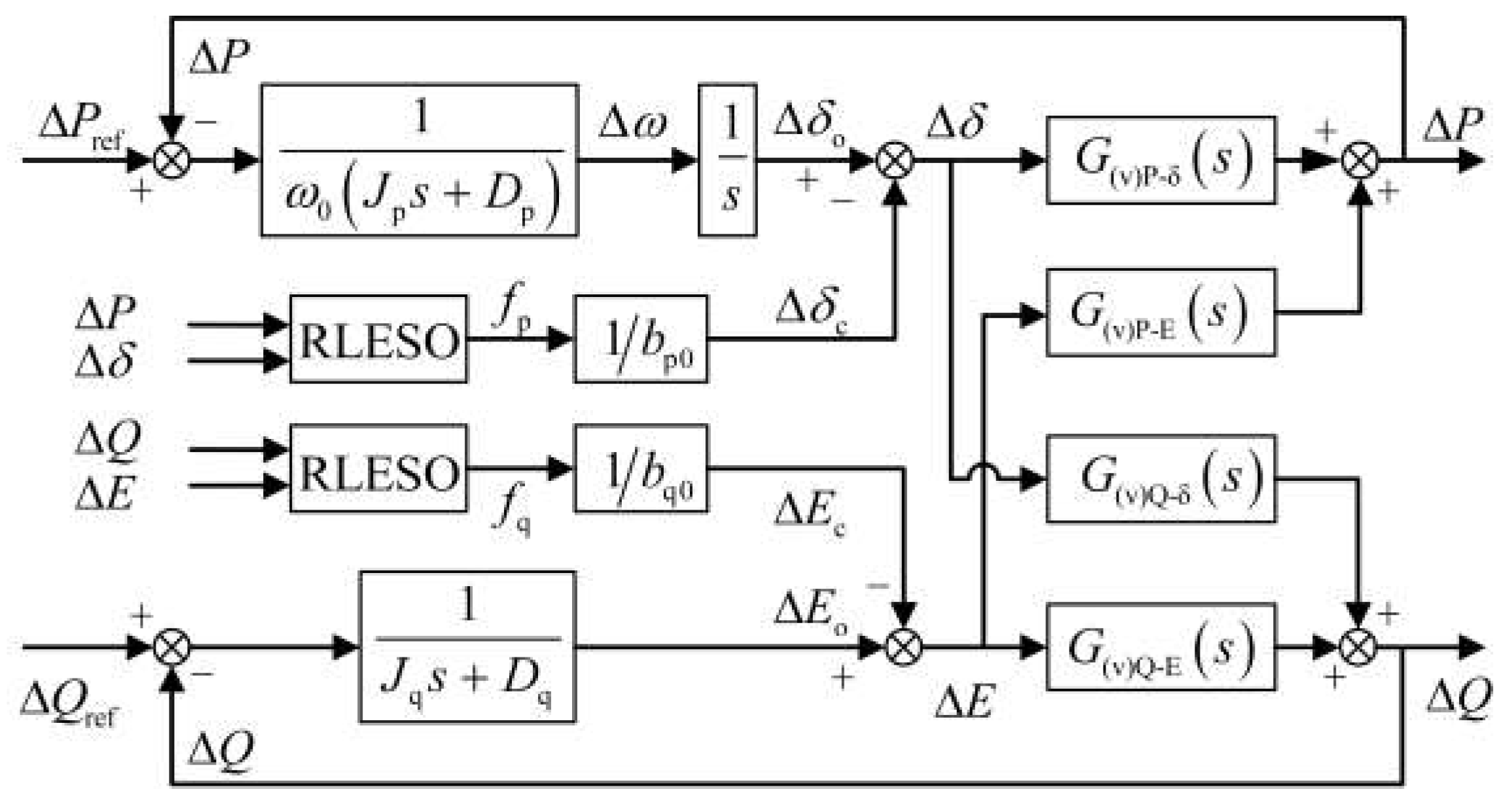
3. Decoupling Control Strategy of Grid-Forming Inverter Based on Reduced-Order ESO
3.1. Design of Reduced-Order ESO
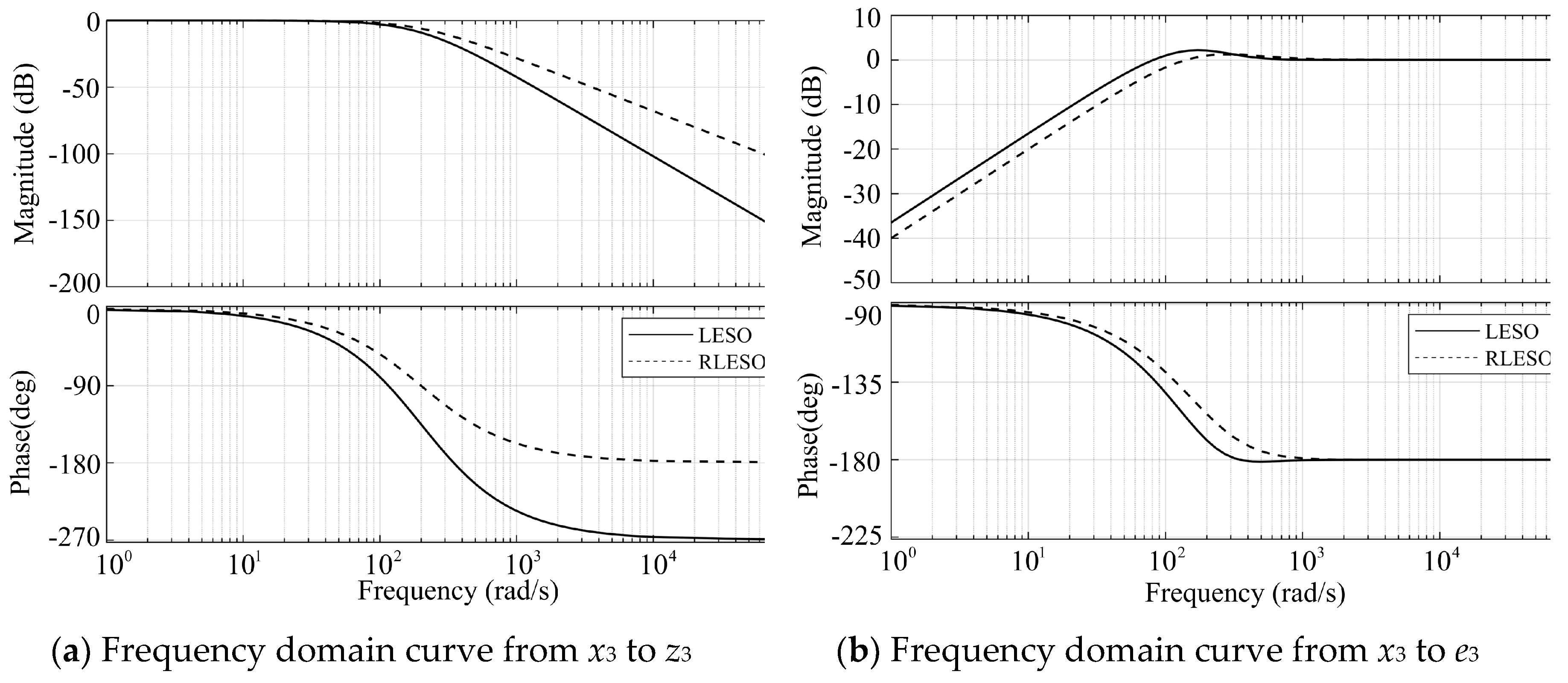
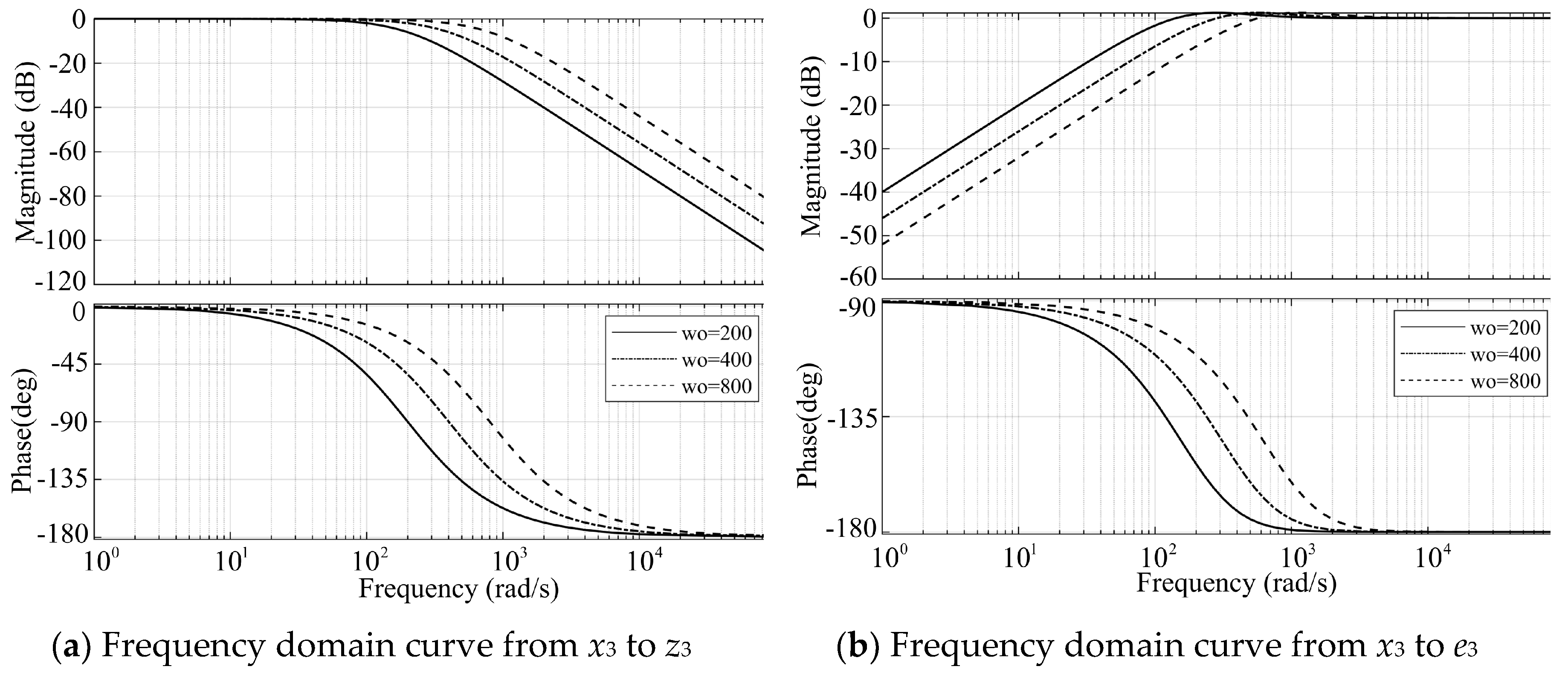
3.2. Frequency Domain Analysis of ESO Disturbance Estimation Performance
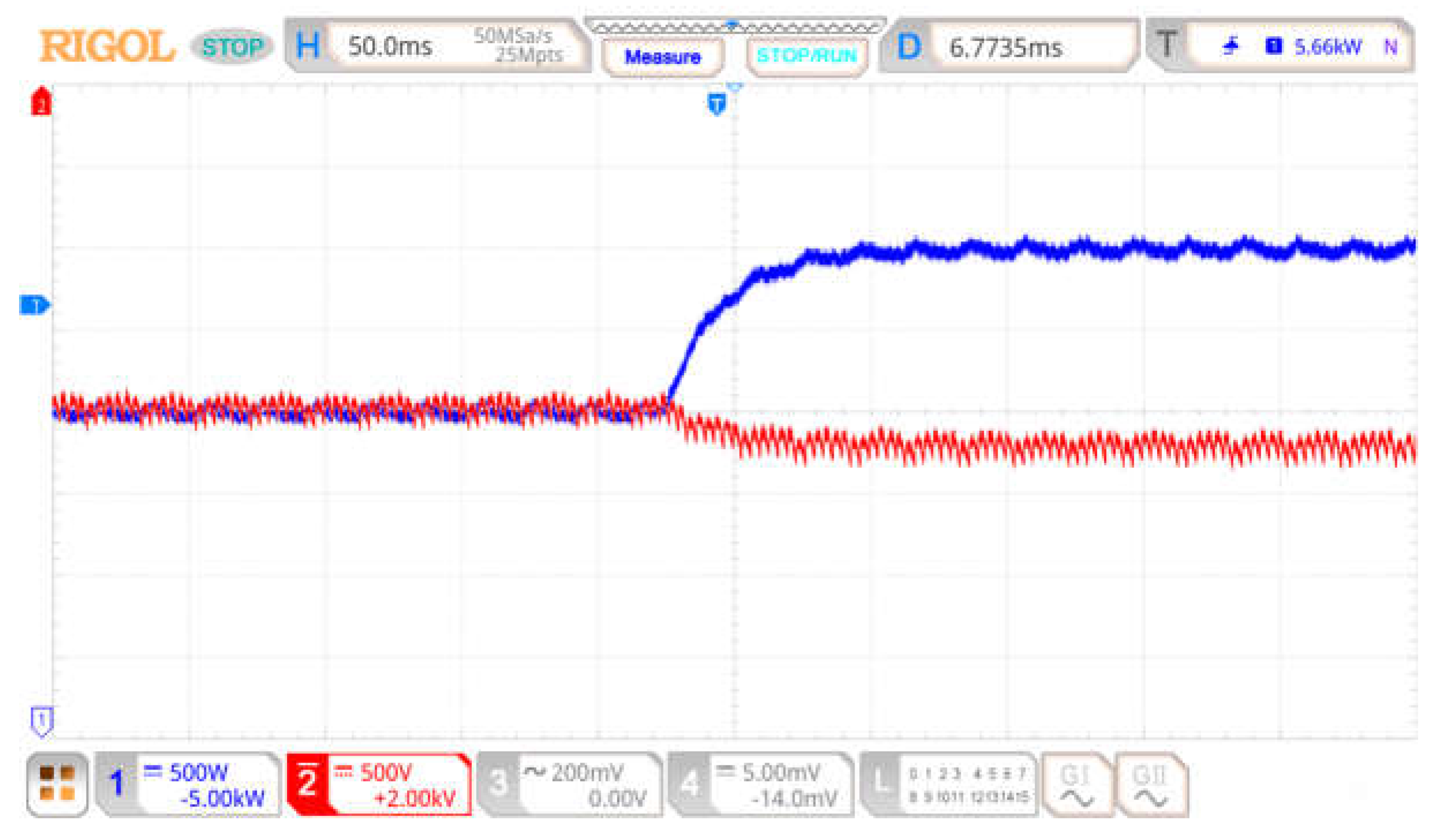
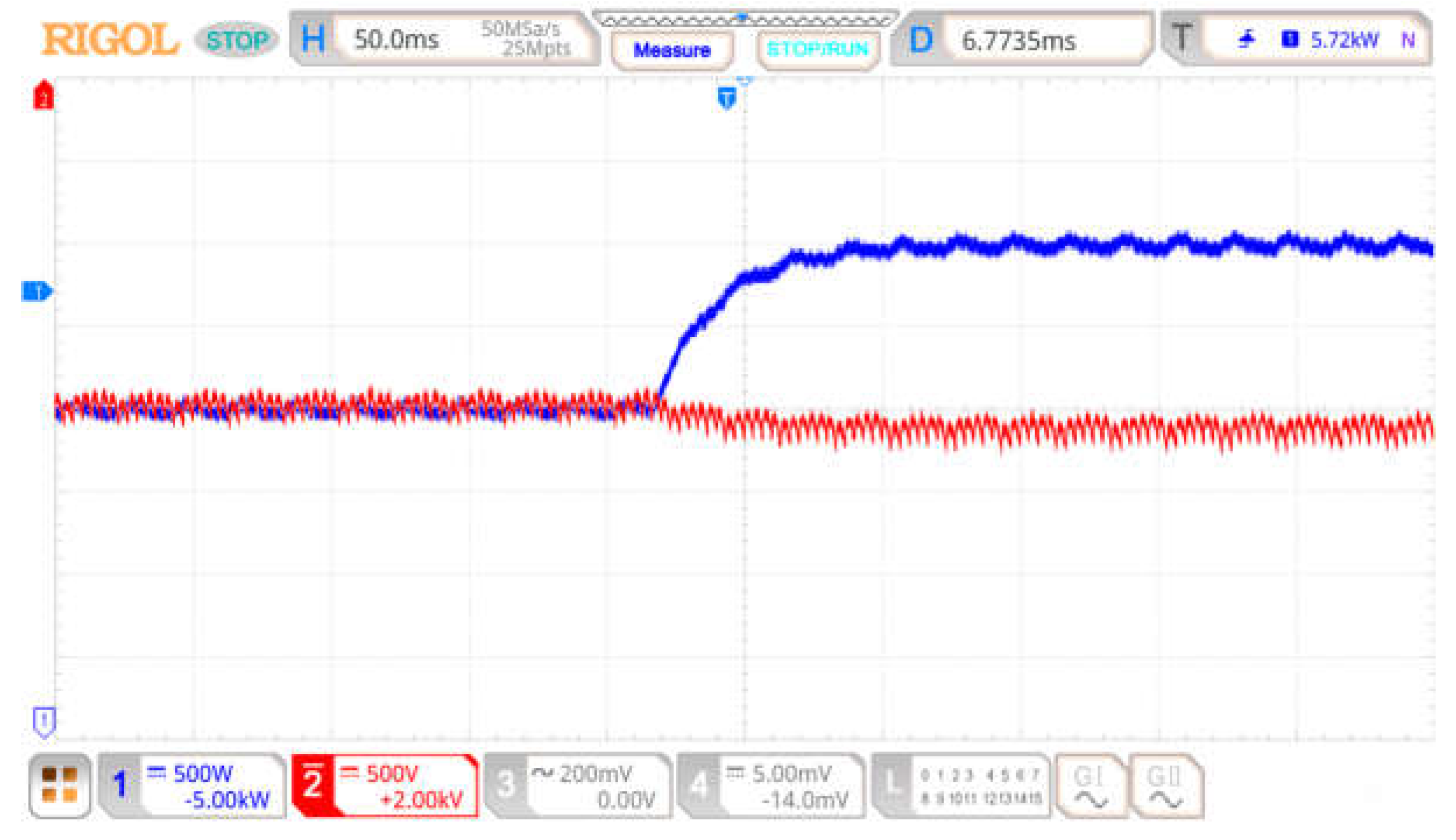
4. Hardware-in-the-Loop Experimental Verification
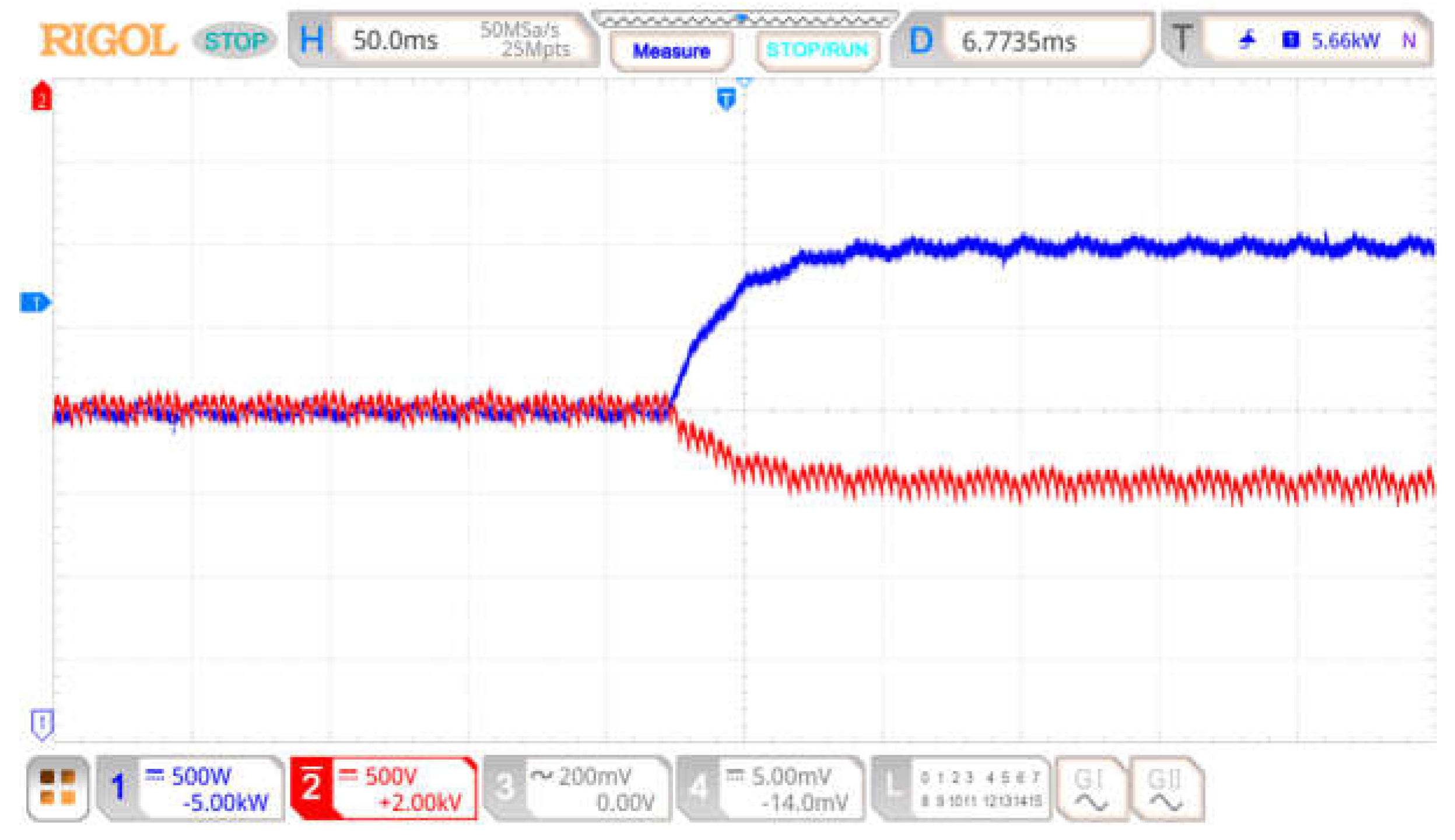
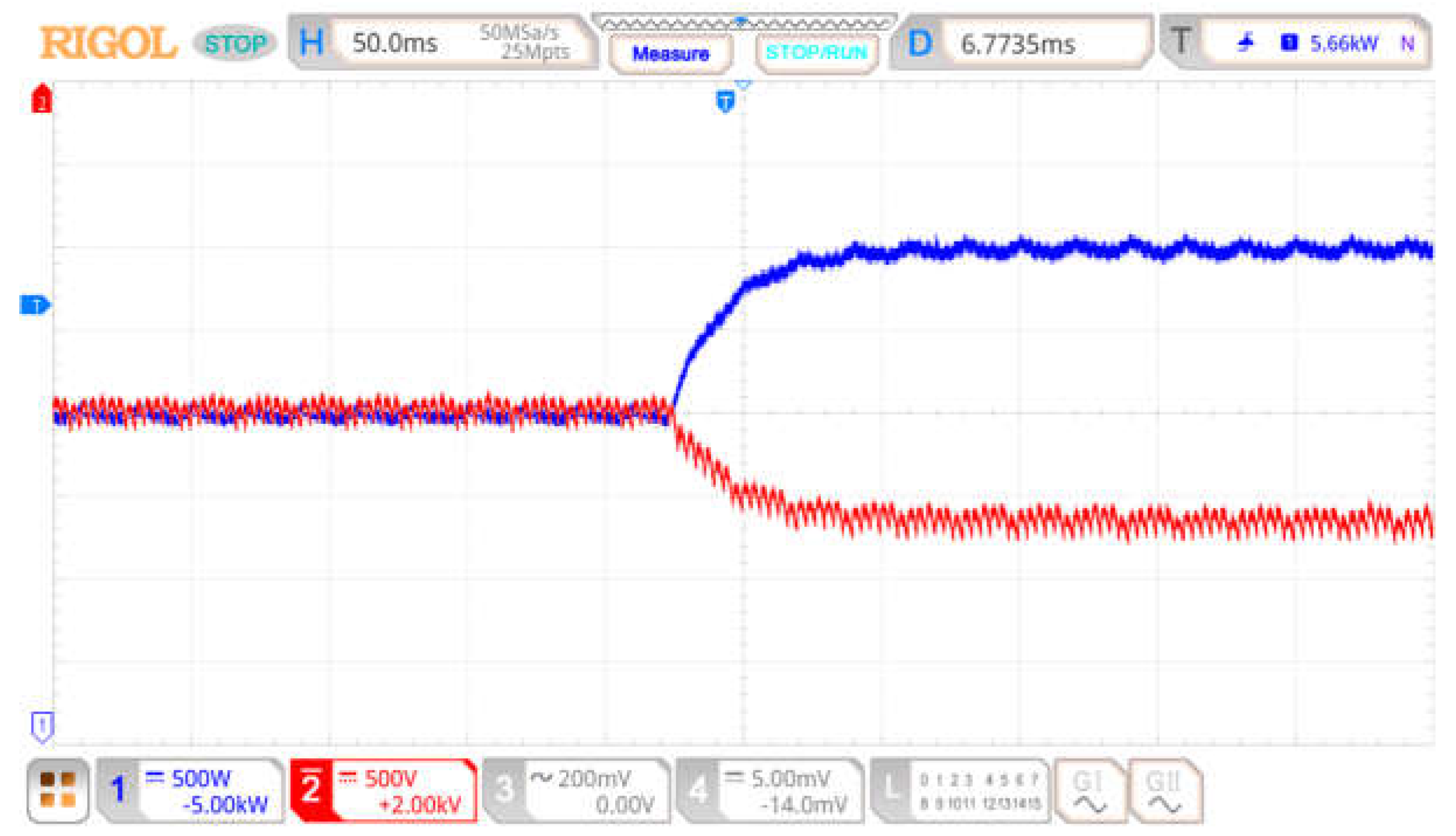
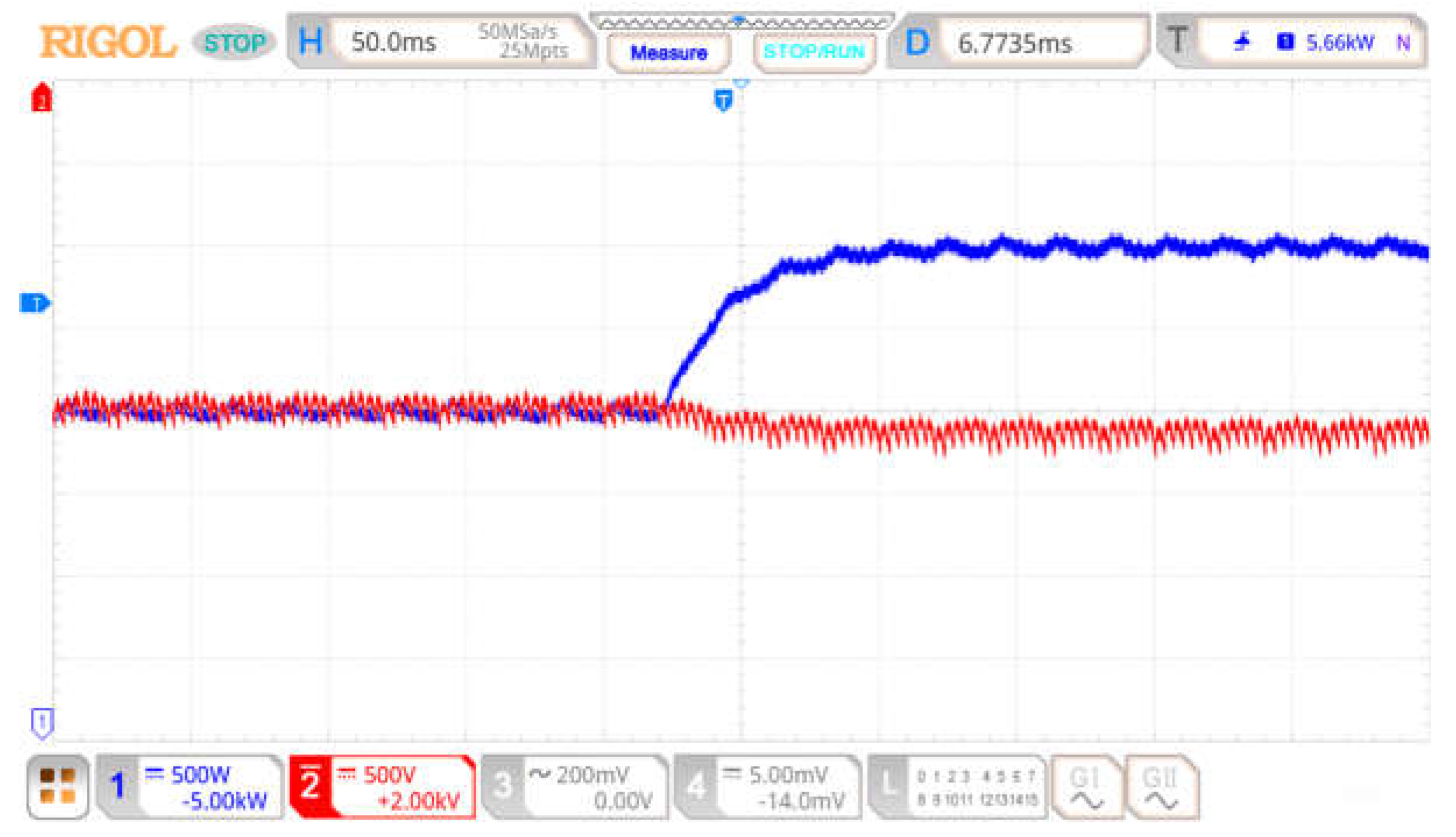
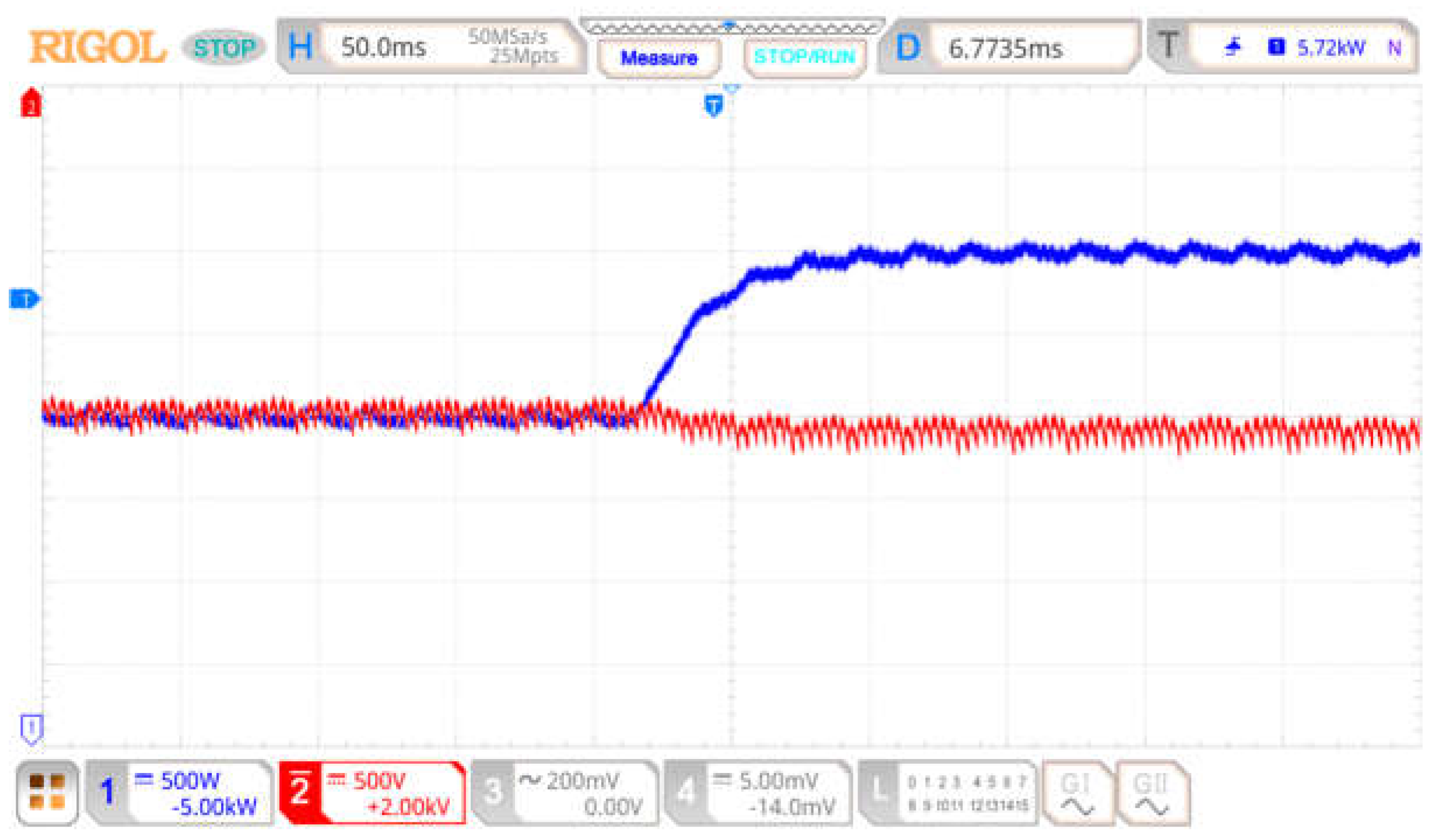
4.1. Verification of the Effect of Line Impedance Parameter Perturbation on Decoupling Ability
4.2. Verification of ESO-Based Power Decoupling Control Strategy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, G.; Yang, H. Parallel Control of Converters with Energy Storage Equipment in a Microgrid. Electronics 2019, 8, 1110. [Google Scholar] [CrossRef]
- Matevosyan, J.; Badrzadeh, B.; Prevost, T.; Quitmann, E.; Ramasubramanian, D.; Urdal, H.; Achilles, S.; MacDowell, J.; Hsien Huang, S.; Vital, V.; et al. Grid-Forming Inverters: Are They the Key for High Renewable Penetration? IEEE Power and Energy Magazine 2023, 21, 77–86. [Google Scholar] [CrossRef]
- Chen, Y.; Luo, J.; Zhang, X.; Li, X.; Wang, W.; Ding, S. A Virtual Synchronous Generator Secondary Frequency Modulation Control Method Based on Active Disturbance Rejection Controller. Electronics 2023, 12, 4587. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, H.; Hu, X.; Hou, X.; Su, C.; Sun, K. Adaptive Inertia and Damping Coordination (AIDC) Control for Grid-Forming VSG to Improve Transient Stability. Electronics 2023, 12, 2060. [Google Scholar] [CrossRef]
- Rosso, R.; Wang, X.; Liserre, M.; Lu, X.; Engelken, S. Grid-Forming Converters: Control Approaches, Grid-Synchronization, and Future Trends—A Review. IEEE Open Journal of Industry Applications 2021, 2, 93–109. [Google Scholar] [CrossRef]
- Arghir, C.; Jouini, T.; Dörfler, F. Grid-Forming Control for Power Converters Based on Matching of Synchronous Machines. Automatica 2018, 95, 273–282. [Google Scholar] [CrossRef]
- Garzon, O.D.; Nassif, A.B.; Rahmatian, M. Grid Forming Technologies to Improve Rate of Change in Frequency and Frequency Nadir: Analysis-Based Replicated Load Shedding Events. Electronics 2024, 13, 1120. [Google Scholar] [CrossRef]
- Johnson, B.B.; Sinha, M.; Ainsworth, N.G.; Dörfler, F.; Dhople, S.V. Synthesizing Virtual Oscillators to Control Islanded Inverters. IEEE Transactions on Power Electronics 2016, 31, 6002–6015. [Google Scholar] [CrossRef]
- Unruh, P.; Nuschke, M.; Strauß, P.; Welck, F. Overview on Grid-Forming Inverter Control Methods. Energies 2020, 13, 2589. [Google Scholar] [CrossRef]
- Hu, P.; Jiang, K.; Ji, X.; Cai, Y.; Wang, B.; Liu, D.; Cao, K.; Wang, W. A Novel Grid-Forming Strategy for Self-Synchronous PMSG under Nearly 100% Renewable Electricity. Energies 2023, 16, 6648. [Google Scholar] [CrossRef]
- Sun, Z.; Zhu, F.; Cao, X. Study on a Frequency Fluctuation Attenuation Method for the Parallel Multi-VSG System. Front. Energy Res. 2021, 9. [Google Scholar] [CrossRef]
- Shang, L.; Hu, J.; Yuan, X.; Chi, Y.; Tang, H. Modeling and Improved Control of Virtual Synchronous Generators Under Symmetrical Faults of Grid. Zhongguo Dianji Gongcheng Xuebao/Proceedings of the Chinese Society of Electrical Engineering 2017, 37, 403–411. [Google Scholar] [CrossRef]
- Jiang, K.; Liu, D.; Cao, K.; Xiong, P.; Ji, X. Small-Signal Modeling and Configuration Analysis of Grid-Forming Converter under 100% Renewable Electricity Systems. Electronics 2023, 12, 4078. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, J.; Tang, F.; Wu, M.; Lv, Z.; Sun, L.; Zhao, T. Small Signal Modeling and Parameter Design of Virtual Synchronous Generator to Weak Grid. In Proceedings of the 2018 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), May 2018; pp. 2618–2624. [Google Scholar]
- Wu, H.; Ruan, X.; Yang, D.; Chen, X.; Zhao, W.; Lv, Z.; Zhong, Q.-C. Small-Signal Modeling and Parameters Design for Virtual Synchronous Generators. IEEE Transactions on Industrial Electronics 2016, 63, 4292–4303. [Google Scholar] [CrossRef]
- Sarojini, R.K.; Palanisamy, K. Small Signal Modelling and Determination of Critical Value of Inertia for Virtual Synchronous Generator. In Proceedings of the 2019 Innovations in Power and Advanced Computing Technologies (i-PACT), March 2019; Vol. 1, pp. 1–6. [Google Scholar]
- Yu, J.; Qi, Y.; Deng, H.; Liu, X.; Tang, Y. Evaluating Small-Signal Synchronization Stability of Grid-Forming Converter: A Geometrical Approach. IEEE Transactions on Industrial Electronics 2022, 69, 9087–9098. [Google Scholar] [CrossRef]
- Zhang, L.; Harnefors, L.; Nee, H.-P. Power-Synchronization Control of Grid-Connected Voltage-Source Converters. IEEE Transactions on Power Systems 2010, 25, 809–820. [Google Scholar] [CrossRef]
- D’Arco, S.; Suul, J.A.; Fosso, O.B. Small-Signal Modelling and Parametric Sensitivity of a Virtual Synchronous Machine. In Proceedings of the 2014 Power Systems Computation Conference, August 2014; pp. 1–9. [Google Scholar]
- Stankovic, A.M.; Sanders, S.R.; Aydin, T. Dynamic Phasors in Modeling and Analysis of Unbalanced Polyphase AC Machines. IEEE Transactions on Energy Conversion 2002, 17, 107–113. [Google Scholar] [CrossRef]
- Wu, T.; Liu, Z.; Liu, J.; Wang, S.; You, Z. A Unified Virtual Power Decoupling Method for Droop-Controlled Parallel Inverters in Microgrids. IEEE Transactions on Power Electronics 2016, 31, 5587–5603. [Google Scholar] [CrossRef]
- De Brabandere, K.; Bolsens, B.; Van den Keybus, J.; Woyte, A.; Driesen, J.; Belmans, R. A Voltage and Frequency Droop Control Method for Parallel Inverters. IEEE Transactions on Power Electronics 2007, 22, 1107–1115. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.W. Power Management of Inverter Interfaced Autonomous Microgrid Based on Virtual Frequency-Voltage Frame. IEEE Transactions on Smart Grid 2011, 2, 30–40. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, J.; Bi, D.; Wen, Y.; Dai, Y.; Yin, X.; Shen, Z.J. Droop Control Strategy Incorporating Coupling Compensation and Virtual Impedance for Microgrid Application. IEEE Transactions on Energy Conversion 2019, 34, 277–291. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, J.; Wen, Y.; Bi, D.; Dai, Y.; Ning, Y. Virtual Synchronous Generator Control Strategy Incorporating Improved Governor Control and Coupling Compensation for AC Microgrid. IET Power Electronics 2019, 12. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Mijatovic, N.; Dragicevic, T. Frequency Stability Assessment of Grid-Forming VSG in Framework of MPME With Feedforward Decoupling Control Strategy. IEEE Transactions on Industrial Electronics 2022, 69, 6903–6913. [Google Scholar] [CrossRef]
- Rathnayake, D.B.; Bahrani, B. Multivariable Control Design for Grid-Forming Inverters With Decoupled Active and Reactive Power Loops. IEEE Transactions on Power Electronics 2023, 38, 1635–1649. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vicuna, L.G. de; Matas, J.; Castilla, M.; Miret, J. Output Impedance Design of Parallel-Connected UPS Inverters with Wireless Load-Sharing Control. IEEE Transactions on Industrial Electronics 2005, 52, 1126–1135. [Google Scholar] [CrossRef]
- Rodríguez-Cabero, A.; Roldán-Pérez, J.; Prodanovic, M. Virtual Impedance Design Considerations for Virtual Synchronous Machines in Weak Grids. IEEE Journal of Emerging and Selected Topics in Power Electronics 2020, 8, 1477–1489. [Google Scholar] [CrossRef]
- Wen, T.; Zhu, D.; Zou, X.; Jiang, B.; Peng, L.; Kang, Y. Power Coupling Mechanism Analysis and Improved Decoupling Control for Virtual Synchronous Generator. IEEE Transactions on Power Electronics 2021, 36, 3028–3041. [Google Scholar] [CrossRef]
- He, J.; Li, Y.W. Analysis, Design, and Implementation of Virtual Impedance for Power Electronics Interfaced Distributed Generation. IEEE Transactions on Industry Applications 2011, 47, 2525–2538. [Google Scholar] [CrossRef]
- Wang, Y.; Wai, R.-J. Newly-Designed Power Decoupling Strategy for Virtual Synchronous Generator in Micro-Grid. In Proceedings of the 2021 IEEE International Future Energy Electronics Conference (IFEEC), November 2021; pp. 1–6. [Google Scholar]
- Wang, Y.; Wai, R.-J. Adaptive Fuzzy-Neural-Network Power Decoupling Strategy for Virtual Synchronous Generator in Micro-Grid. IEEE Transactions on Power Electronics 2022, 37, 3878–3891. [Google Scholar] [CrossRef]
- Dong, N.; Li, M.; Chang, X.; Zhang, W.; Yang, H.; Zhao, R. Robust Power Decoupling Based on Feedforward Decoupling and Extended State Observers for Virtual Synchronous Generator in Weak Grid. IEEE Journal of Emerging and Selected Topics in Power Electronics 2023, 11, 576–587. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Transactions on Industrial Electronics 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Fu, C.; Tan, W. Parameters Tuning of Reduced-Order Active Disturbance Rejection Control. IEEE Access 2020, 8, 72528–72536. [Google Scholar] [CrossRef]
- Engler, A.; Soultanis, N. Droop Control in LV-Grids. In Proceedings of the 2005 International Conference on Future Power Systems, November 2005; p. 6. [Google Scholar]

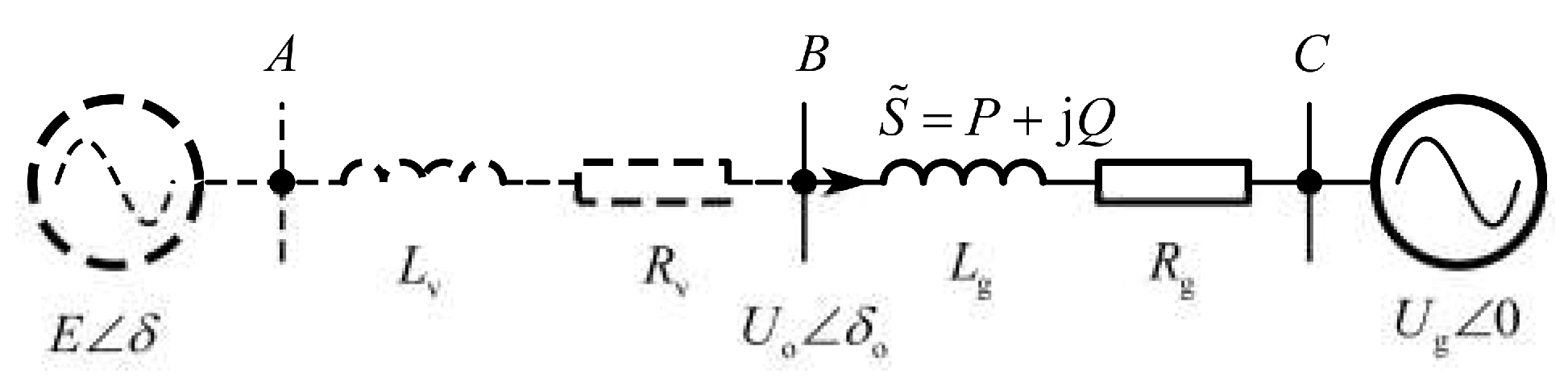
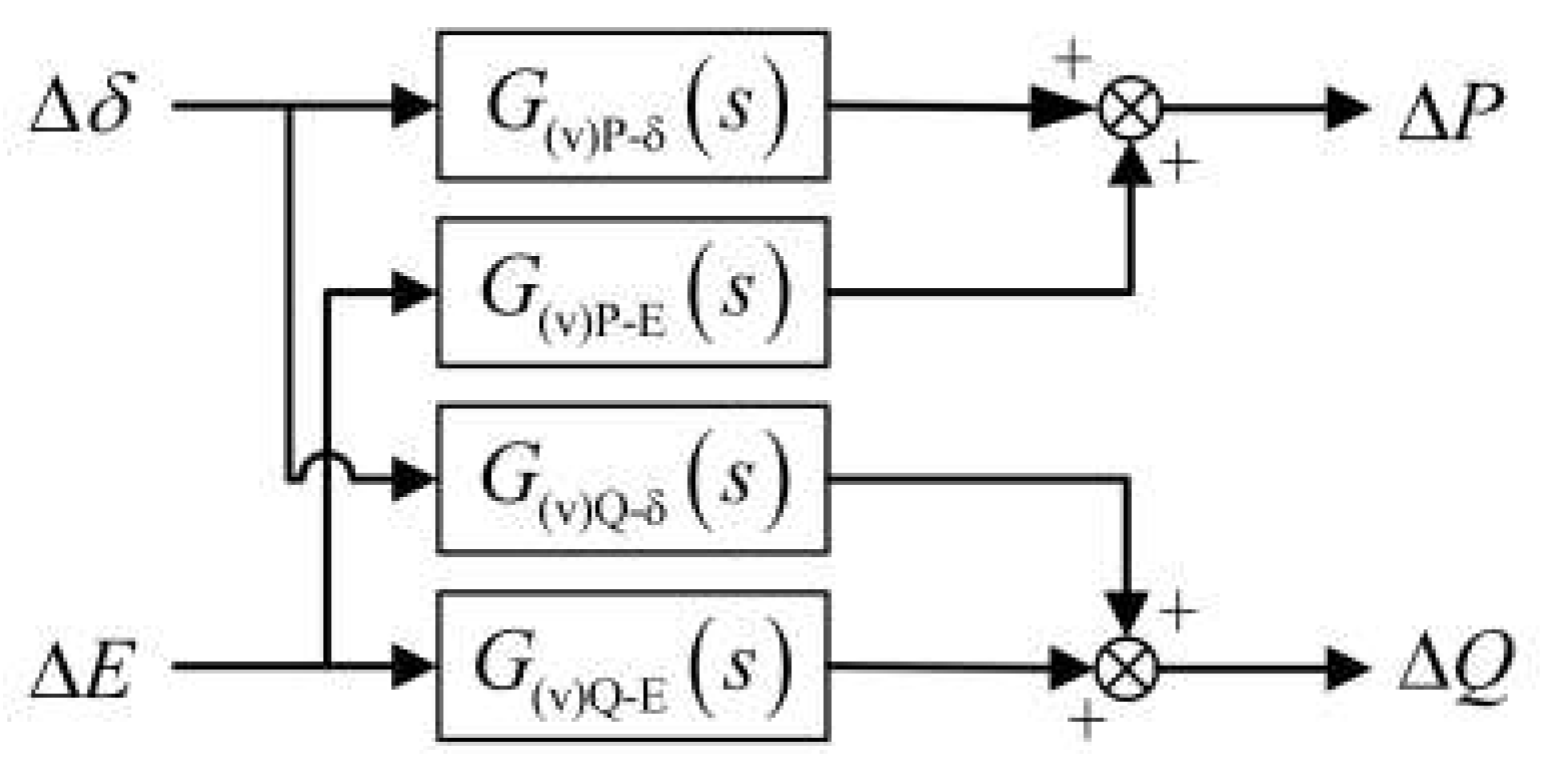



| Parameters | Value /unit |
|---|---|
| Grid phase voltage (RMS) | 220 V |
| DC bus voltage | 750 V |
| grid frequency | 50 Hz |
| Inverter side Inductance | 2 mH |
| Network side Inductance | 0.4 mH |
| filter capacitor | 2.2 uF |
| Nominal line Inductance | 1.32 mH |
| Nominal line resistance | 3.21 Ω |
| Virtual Inductors | 5 mH |
| Virtual Resistors | -3 Ω |
| switching frequency | 100 kHz |
| Plant discretization time-step | 500 ns |
| Parameters | Value |
|---|---|
| Current inner loop proportional gain | 5 |
| Voltage outer loop proportional gain | 0.01 |
| Voltage outer loop integration gain | 300 |
| Active power observer bandwidth | 700 rad/s |
| Reactive power observer bandwidth | 500 rad/s |
| Virtual Inductors | 5 mH |
| Virtual Resistors | -3 Ω |
| Virtual inertia factor for active power | 0.04 |
| Active droop factor | 10.07 |
| Virtual inertia factor for reactive power | 5 |
| Reactive droop factor | 321.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





