Modeling of Electrochemical Impedance of Fuel Cell Based on the Novel Nanocomposite Membrane

The new hybrid composite materials for PEM fuel cell were synthesized by UV-polymerization of acrylic monomers (acrylonitrile (AN), acrylic acid (AA), ethylene glycol dimethacrylate (EGDMA)) and sulfo aromatic monomer – sodium styrene sulfonate (SSS), and tetraethoxysilane/3-methacryloxypropyltrimethoxysilane (TEOS/MAPTMS)-based sol-gel system. By means of X-ray spectroscopy fractal structure of the obtained materials was characterized. Proton conductivity and viscoelastic properties of the materials were investigated depending on the content of inorganic component in nanocomposites. On the basis of impedance studies, an equivalent scheme is proposed that successfully describes the proton conductivity in the synthesized composite electrolyte membranes.

Keywords:

Subject: Chemistry and Materials Science - Electrochemistry

1. Introduction

Clean and efficient power is one of the sustainable development goals and a top priority for researchers. In recent years fuel cells are regarded as a promising and eco-friendly technology with high reliability and broad development prospects [1,2]. Proton conductive membrane is the main element of fuel cell, determining the effectiveness of its operating, and therefore must meet a number of requirements: high proton conductivity, low permeability to fuel, high chemical and thermal stability, good mechanical properties and low cost. Nowadays fuel cell technology is based mainly on the Nafion (Du Pont) membranes (perfluorosulfonic acid ionomer) due to their high proton conductivity and excellent durability and chemical stability, however, they are expensive and effective only at the temperatures up to 90°C because of the problem of their dehydration [3]. This limits the operating temperature below 90°C, since the conductivity sharply declines above this temperature. One more downside of the Nafion membrane is the use of highly toxic chemicals during production.

In order to reduce membrane cost and expand the operating temperature range for proton conductive membranes making their commercialization profitable scientists make efforts to develop novel materials. Among the alternatives to Nafion the non-fluorinated or partially-fluorinated hydrocarbon polymer membranes with aromatic backbone structures are developed [4,5]. Aromatic-based materials have an excellent thermal and mechanical strength, tailorable structures, tunable ionic conductivities, small methanol permeabilities, and low costs showing a great potential to be used as PEMs in fuel cells [5].

The backbones of these polymers comprise aromatic or phenyl rings with C-C, C=C and C-H bonds alongside with varying number of ether, ketone, imide, or benzimidazole functionalities in their structures. Due to the strong intramolecular π-π interactions SAP possess the film-forming properties, as well as high mechanical and chemical stability. To provide proton conductivity of membranes sulfonic acid groups (-SO3H) are introduced on the hydrophobic aromatic polymer chains through sulfonation reactions, producing sulfonated derivatives for application in PEMs [6,7,8]. Some common sulfonated aromatic polymers (SAP) are sulfonated polyether ether ketone (SPEEK) [9], polyether sulfone (SPES) [10], polyphenyl sulfone (SPPSU) [11]. To improve the properties of hydrocarbon-based PEMs a number of methods have been applied by researchers, including sol-gel technique, which is a convenient method of introduction of inorganic nanoparticles into polymeric matrix as it allows to form nanoparticles during the polymerization process in situ [12].

To analyze and predict the efficiency of the fuel cell operating, the ionic conduction mechanism is modeled using appropriate electrical circuits [13,14,15]. Impedance spectroscopy is an effective method for investigation of the charge transfer processes in fuel cells providing the highest accuracy for a wide range of operating signal frequencies and extensive information about the properties of the object under study. In order to determine different voltage loss contributions, appropriate models are required for the interpretation of the cell impedance. The analysis of the cell impedance allows to determine optimal operating conditions and to optimize the design of the cell components [16]. The development of this direction is hampered by the complexity of the processes in heterogeneous systems.

The goal of our work was to model the proton conducting behavior of the fuel cell with the new proton conductive membranes developed on the basis of cross-linked organic/inorganic materials synthesized by UV-polymerization of acrylic monomers including aromatic monomer (SSS) and sol-gel system prepared from the precursors TEOS/MAPTMS, and also to study the properties of the membranes.

2. Materials and Methods

Materials: Acrylonitrile (AN, 99%), acrylic acid (AA, 99%), sodium styrene sulfonate (SSS, 99%), ethylene glycol dimethacrylate (EGDMA, 99%), tetraethoxysilane (TEOS, 99%), 3-methacryloxypropyltrimethoxysilane (MAPTMS, 99%), photoinitiator 2,2-dimethoxy-2-phenylacetophenone (DMPA, 99%) were sourced from Sigma-Aldrich and used as received without further purification (unless otherwise noted). Phosphoric acid (85%, Sigma-Aldrich) (PhA) was used as a catalyst in sol–gel reaction. Milli-Q^® water, absolute ethanol (VWR), and acetone (Analytical Grade, Fisher Scientific) were used as solvents.

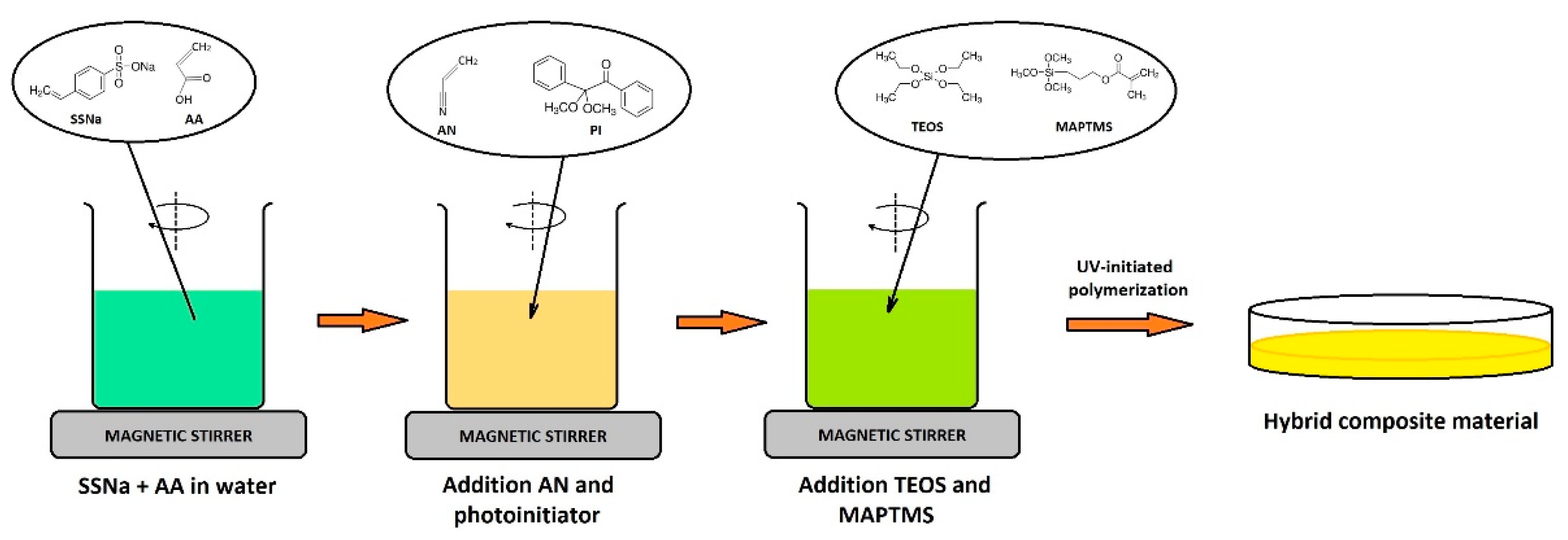
Synthesis of the hybrid composite material: The polymer material were synthesized by UV-initiated copolymerization of the mixture of monomers. A typical procedure according to [17] was as follows: a solution of water-soluble reagents was prepared by dissolving them in DW and then mixed with the appropriate amount of AN and DMPA under constant stirring (500 rpm) to form a homogeneous solution. Monomers that contained inhibitor upon purchase were purified through a basic alumina column to remove inhibitor prior to use. The resulting mixture was placed in a handmade glass mold. Polymerization was carried out under UV-irradiation (365 nm, 15 J·cm⁻²) using a multi-lamp BIO-LINK^® cross-linker (BLX-365, Witec AG, Switzerland) equipped with five UV lamps (8 W, output 0.8 W). To prevent the inhibiting effect of oxygen on polymerization process, the molds were covered with glass slides. After UV exposure, the obtained membranes were rinsed with acetone and then dried to the constant weight at the oven with temperature 323К. The feed compositions for the synthesis of polymer matrix of the material was as follows (wt. %): AN – 45; АA – 20; EGDMA – 20; SSS – 15. To obtain hybrid composite materials NSSA/SG3, NSSA/SG5, NSSA/SG7, NSSA/SG10 0, 3, 5, 7, 10 wt. % of the sol-gel system were added, relatively. The sol-gel procedure was similar to those described in [18]: TEOS and MAPTMS precursors, ethanol, distilled water and orthophosphoric acid were mixed in the following ratio: TEOS:MAPTMS:C₂H₅OH:H₂O:H₃PO₄ = 0.75:0.25:4:4:1.2 (mol). The system was continuously stirred at 500 rpm in a water bath at 323К for 180-200 min until the mixture became homogeneous. Then, a sol-gel precursor solution was added to the monomer mixture and stirring (500 rpm) to form a homogeneous solution.

Characterization:

Small-Angle X-ray Scattering (SAXS): SAXS measurements were conducted using a Ganesha 300 XL+ instrument (SAXSLAB ApS, Denmark/USA) equipped with a Pilatus 300 K 2D-detector, pixel size 172 × 172 mm². The X-ray beam from the monochromatic Cu-K_a radiation source (l-focus tube, 50 kV, 600 mA, monochromatization with bifocal Göbel mirror) had a wavelength of 0.1542 nm and a cross-section of 0.3 × 0.3 mm². During the measurements in vacuum, samples were kept enveloped in aluminum foil. The sample to detector distance was 1060 mm, which allows obtaining scattering data in the q-range from ca. 0.05 to 2.9 nm^-1. The scattering patterns were acquired for 3 h and radially averaged to obtain one-dimensional (1D) scattering intensity profiles. All scattering profiles were corrected for the scattering from the aluminum foil.

Proton conductivity: the conductivity of all synthesized materials was studied by impedance spectroscopy using the cell for the study of electrochemical systems shown in Figure 1. For the study, the membranes were cut into a circle with a diameter of 2 cm and placed between two steel electrodes, which were pressed with equal force by a spring located at the top of the cell. Before the measurement, the membranes were converted to acidic form by immersion in 0.1M HCl. Impedance spectra were measured using a measuring complex Autolab/FRA-2 (the Netherlands) in the frequency range of 0.1 – 10⁵ Hz.

Dynamic mechanical analysis: for the study of the viscoelastic properties of the hybrid composite materials dynamic mechanical analysis (DMA) was carried out by means of DMA Q800 (TA Instruments, USA) in the tensile mode at a frequency of 10 Hz. The experiments were performed within the temperature range of 293-473К at a heating rate of 3К/min.

3. Results

Feed composition for the hybrid material synthesis was choose to provide the resulting material with the required properties. SSS contains –SO₃H moiety in its structure which dissociate in wet conditions to form proton moving through the material from the anode to the cathode. In addition, SSS endows the polymer material with good mechanical and thermal properties [19]. AN is commercially available and inexpensive monomer. It is known for its excellent mechanical and film-forming properties. AA is also available and inexpensive monomer with ionic –COOH group which serves as an additional source of protons. EGDMA was used as a cross-linker. MAPTMS precursor has an acrylate moiety that allows it to be incorporated into the polymer chain. At the same time, MAPTMS contains methoxysilyl group that can be hydrolyzed to silanol [–Si(OH)₃] in aqueous medium and condensed into a cross-linked silica network [18]. Thus, organic and inorganic components are joined in the hybrid material by chemical bonds. As sol-gel transformation of MAPTMS occurs slowly we changed part of this precursor with TEOS. Amphiphilic structure of the obtained materials provides formation of channels for proton transport.

Figure 2 shows the formation of the cross-linked hybrid composite material. Polymeric matrix was formed as a result of UV-initiated copolymerization of acrylic monomers and SSS under UV-irradiation in the presence of the DMPA photoinitiator. The sol of inorganic nanoparticles previously formed from sol-gel precursors was added to the polymerization mixture before gelation. The process of gelation that forms silica network takes place in situ simultaneously with the polymerization.

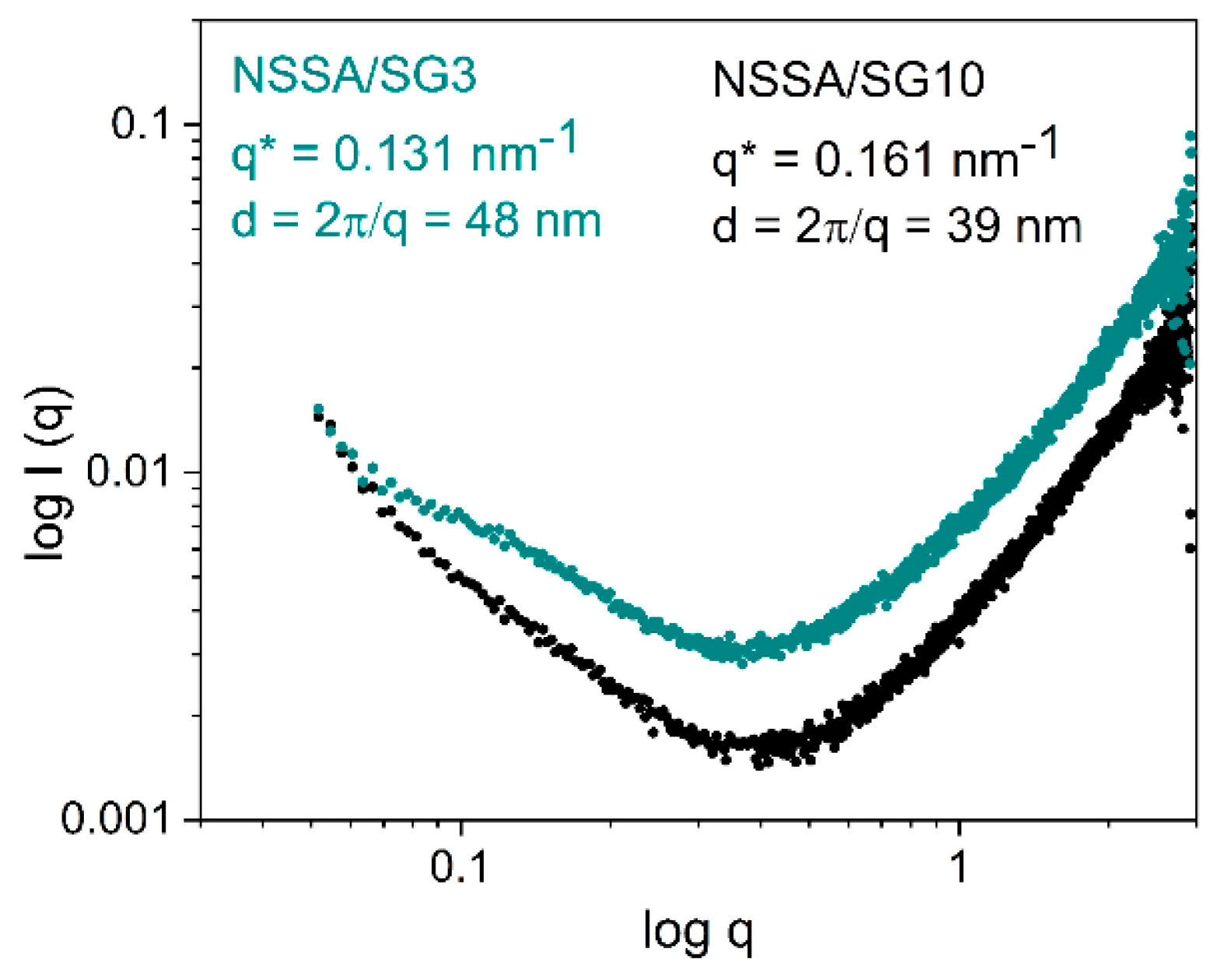
It is known that the final properties of the hybrid сomposite material depend on its morphology. Therefore, we aimed to reveal and investigate effect of the sol-gel system on morphology of the synthesized materials and for this the SAXS spectra for the hybrid materials NSSA/SG3 and NSSA/SG10 were obtained (Figure 3).

In the plot of scattering intensity I(q) vs scattering vector q in the logarithmic coordinates the Guinier region can be observed at very small angles. In this region the Eq. (Figure 3) is valid:

I (q) = G e x p (\frac{- q^{2} R g^{2}}{3})

(1)

where I(q) is scattering intensity, q is the Fourier spatial frequency, or scattering vector:

q = 4 π \sin (\frac{ϴ}{2}) / λ

(2)

where λ is the wavelength of the incident radiation.

The characteristic dimensions d of the domains (d = 2π/q) were calculated from the value of q (q = 0.131 nm^-1 for NSSA/SG3 and 0.161 nm^-1 for NSSA/SG10) (Table 1).

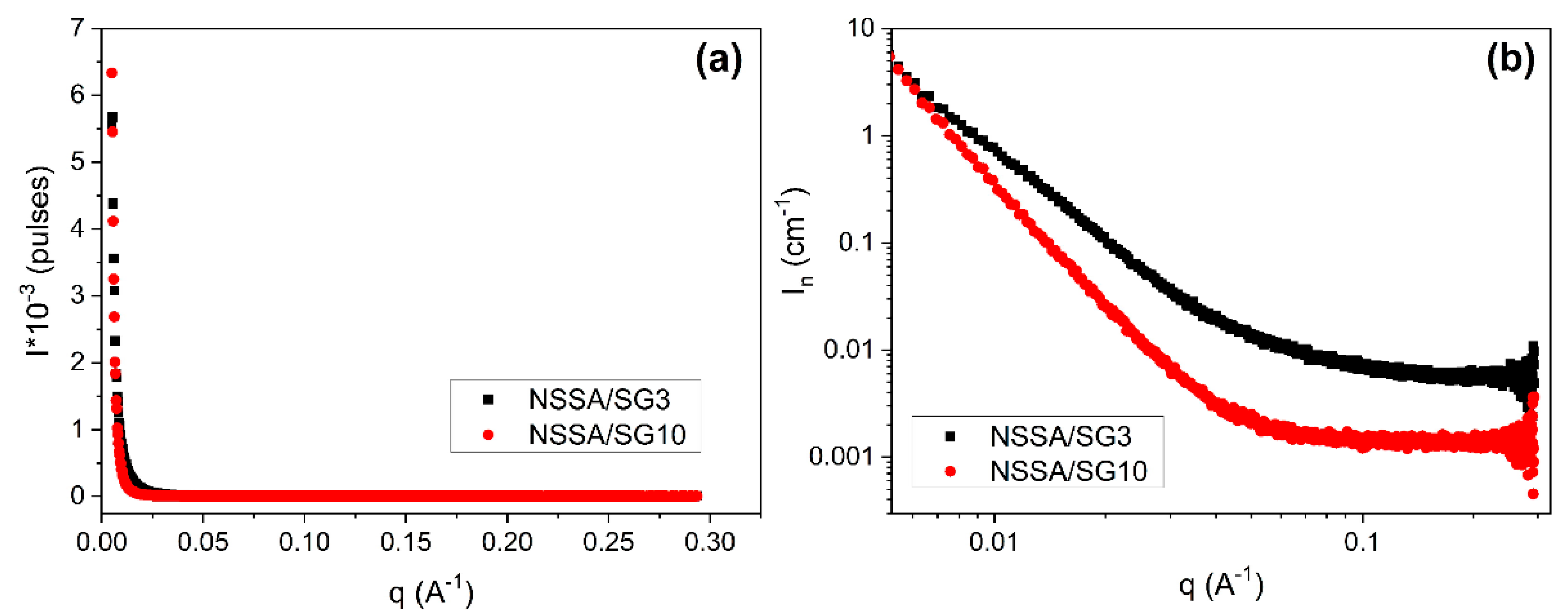
The radius of gyration R_g indicates a measure of the mean square distance of the scattering centers within inorganic domains from the center of gravity, hence, it is related to the size of inorganic domains. The value of R_g was calculated from the slope of a plot of ln(I(q)) vs q² in the linear region (Figure 4, Table 1).

The fractal dimensions D_f are power low exponent obtained from the slope in the linear region of the double logarithmic plot log I(q) – log q (so called the Porod plot):

I (q) = q^{- β}

(3)

This parameter is the measure of the compactness of the material [19]. For the NSSA/SG3 and NSSA/SG10 membrane samples the values of D_f were determined to be 2.9 and 2.7, relatively (Table 1). Since, if the absolute value of | β | is in the range from 1 to 3, then the fractal aggregates belong to the type of mass fractals, and the fractal dimension D_f = |β|. This indicates the formation of massive fractals in our case.

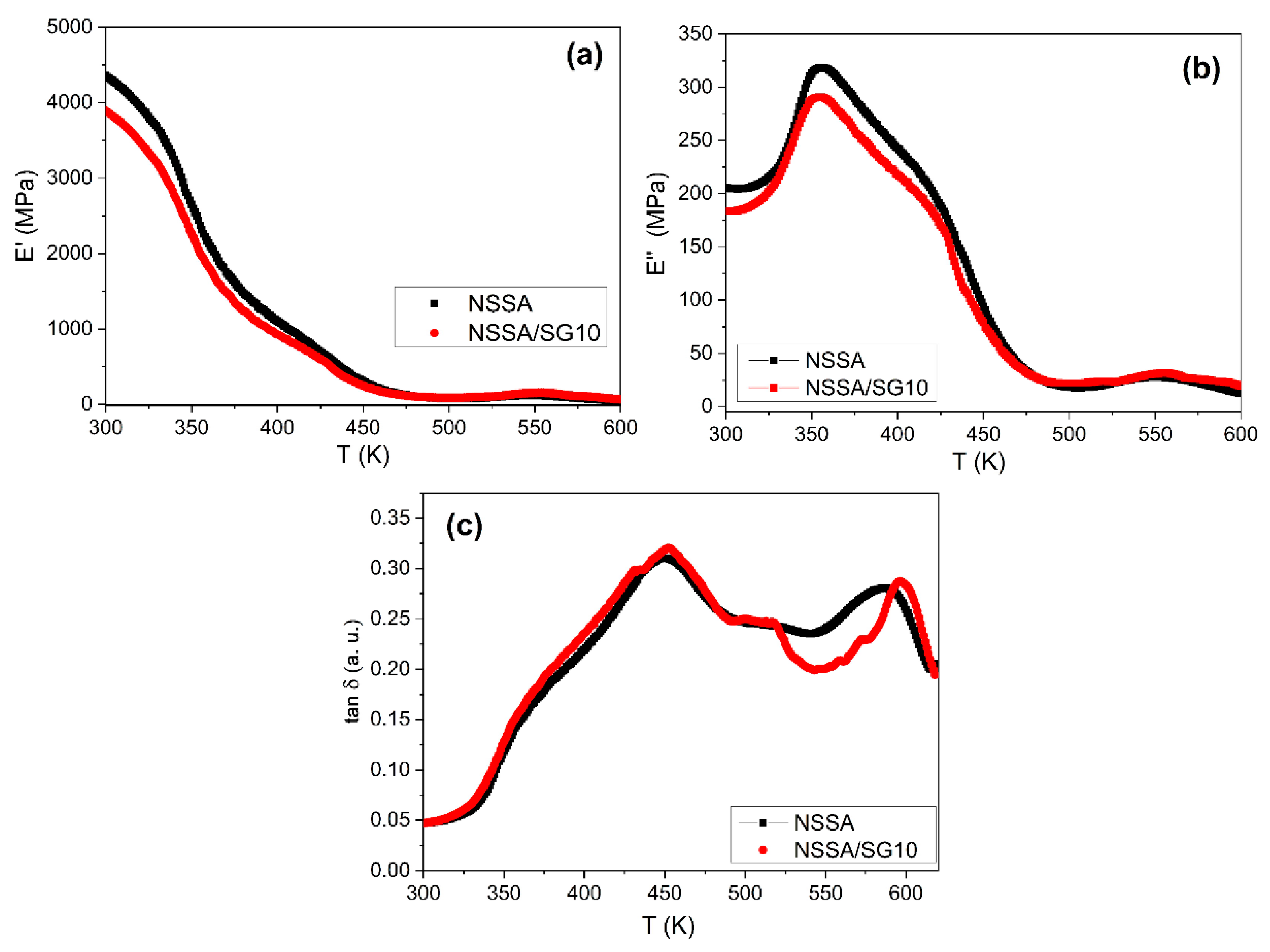
At the exploitation of the membrane as PEM for fuel cells an important characteristic is its viscoelastic behavior. Storage modulus (E’), loss modulus (E”), and mechanical loss factor (tan δ) as a function of temperature were determined using dynamic mechanical analysis (Figure 5).

Note that the viscoelastic dependences of the polymer NSSA membrane and the organic/inorganic NSSA/SG10 membrane are similar, as evidenced by the similar shape of the DMA curves, which reflects the phase morphology (Figure 5). For both membranes, two relaxation transitions are observed in the temperature range from 298 to 470 K, which indicates the two-phase structure of the obtained copolymers. These relaxation transitions are recorded as areas of a sharp decrease in the storage modulus on the temperature dependence of E’ (Figure 5a), as a maximum at T = 350 K and a shoulder in the region of 420 - 430 K on the temperature dependence of E’‘ (Figure 5b), and on dependence of tan δ(Т) – as a pronounced shoulder at temperatures of 350 - 380 K and a maximum at T = 450 K (Figure 5c).

Knowledge of storage modulus provides information about the material stiffness. Figure 5a) presents the E’ (T) plots of the NSSA and the NSSA/SG10 membranes. In comparison with the NSSA, a slight decrease in the storage modulus is observed for the NSSA/SG10 membrane. This can be interpreted as a weakening of the intermolecular bonds and a decrease in the packing density in the polymer matrix when 10 wt. % of SGS was added. As the temperature increases, the difference in E’ values between both membranes decreases (Table 2).

Therefore, DMA studies showed that the relaxation behavior and elastic properties of the proton conductive membranes do not change significantly at adding an inorganic component (silica) to their composition.

The proton conductivity of the membranes is the main characteristic for the use them in fuel cells. Accordingly, its definition was the subject of further research.

Under the measurement conditions described above in the “characterization” section, both electrodes can be considered reversible. In this case, the electrical conductivity is defined as the sum of electronic (σ_el) and ionic (σ_i) conductivities:

σ = σ_el + σ_i.

(4)

In this case, the membrane should behave not only as an ion conductor, but also as an electronic insulator. In practice, this means that the electronic conductivity should be low (≈10^-9 Sm/cm).

Electronic conductivity occurs due to the current carried by electrons (σ_e) and/or electron holes (σ_h):

σ_el = σ_e + σ_h.

(5)

Ionic conductivity of membranes is expected to arise solely from positively charged cations and negatively charged anions.

Under the conditions of measuring electrical conductivity on an alternating current, the total resistance Z is be equal to the sum of its real Z’ and imaginary Z” parts:

Z = Z’ – jZ”.

(6)

By measuring the total resistance in the frequency range, we get:

Z(ω) = Z’(ω) – jZ”(ω).

(7)

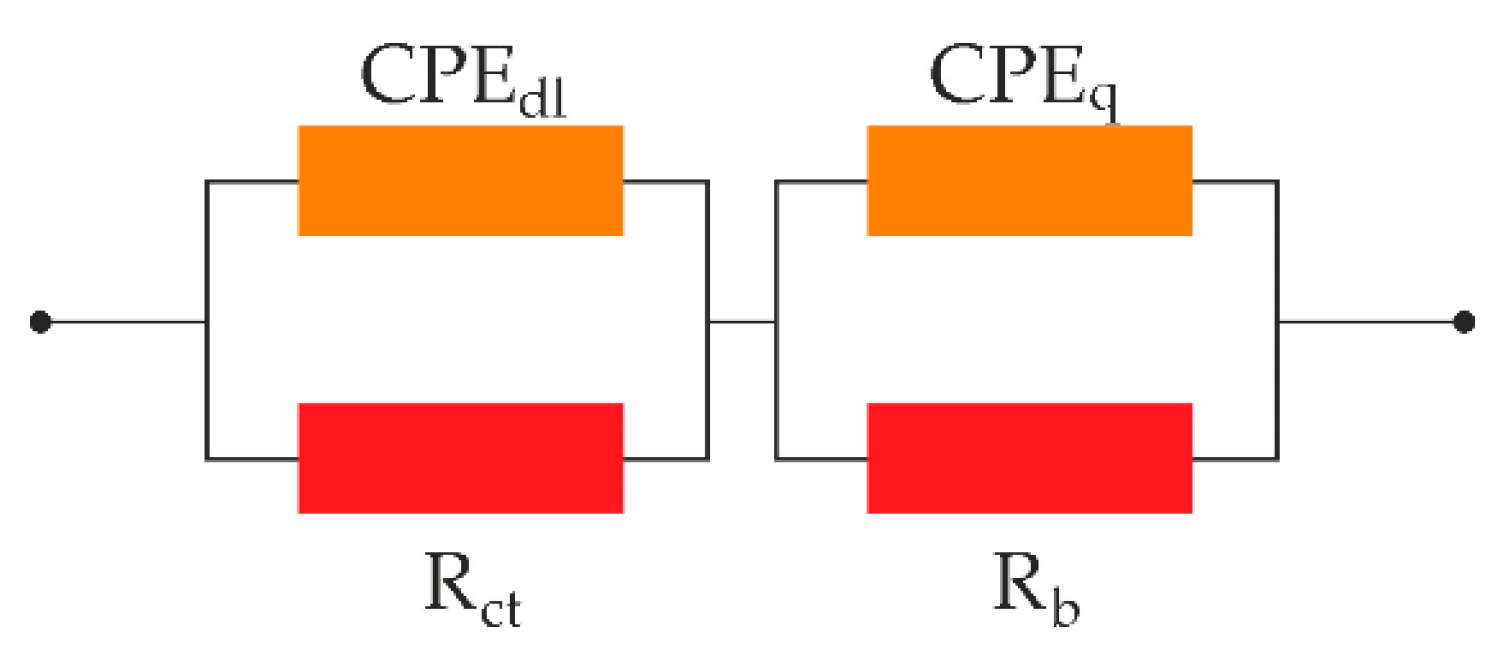
The test cell (Figure 1) included two electrodes in contact with the membrane, the conductivity of which we measured. The polymer/composite material acts as a resistor R_b, which is connected in series with the double-layer capacitor C_dl, at the interface, and in parallel with the geometric capacitance C_q. Since the electrodes are not blocking, a transfer of electric charge (both electrons and holes) between the electrode and the ions in the membrane takes place. The kinetics of this process are not infinitesimally easy, and therefore there is a resistance R_ct, associated with the charge transfer process. This results in a build-up of charge on both sides of the interface, which creates an associated, and quite large, charge transfer capacitance (C_dl) in parallel with the resistance (R_ct). An equivalent circuit for this situation contains a resistor R_ct that shunts the double layer capacitance (C_dl) (Figure 6).

Accepting this equivalent circuit, we get two semicircles on the Nyquist diagram. The high-frequency semicircle is associated with the bulk electrolyte, and the low-frequency semicircle, situated further from the origin of the coordinates, arises as a result of the processes at electrode-membrane interface.

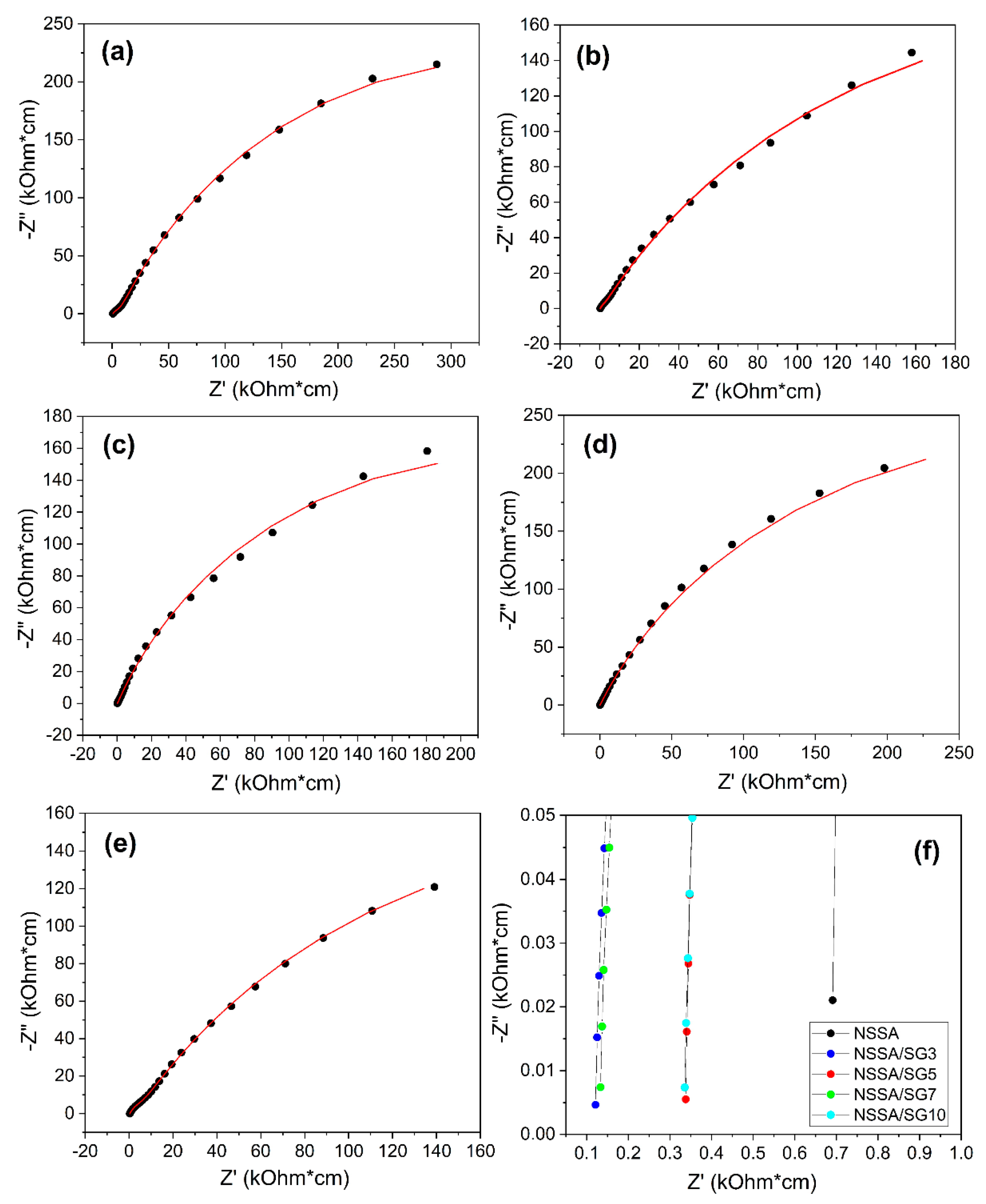
Considering the experimentally measured Nyquist diagrams presented in Figure 7, we can see that the real hodograph has a slightly deformed two-arc dependence, the center of the semicircles of which do not lie on the Z’ axis. In this case, the capacitors C_dl and C_q must be replaced by a constant phase elements CPE_dl and СРЕ_q, respectively. A constant-phase element is a hybrid between a resistor and a capacitor. This element is a generalized and universal tool for impedance modeling of a wide class of electrochemical and other systems [20]. The simplest description of the impedance of an element with a constant phase can be given as

Z_{C P E} = \frac{1}{A {(j ω)}^{n}}

(8)

where A is the coefficient of proportionality, n = 0, 1, -1 is the exponential coefficient that denotes the deviation phase.

For integer values of n, the CPE is combined with classical elements with lumped parameters R, C, and L, respectively. Accordingly, the values of the parameters of the elements of the equivalent circuit for all investigated membranes, determined by the simulation results, are given in the Table 3. The modeling error did not exceed 5%.

Proton conductivity values determined from experimental data are presented in Table 4. The corresponding values were calculated for the highest frequency point.

The measured values of proton conductivity of the synthesized materials are in the range of (1.45 – 8.26) × 10^-3 Sm/cm. As one can see the values of proton conductivity of the hybrid composite materials gradually increase with increase of the inorganic component content (from 2.96 ± 0.08 mSm/cm for the NSSA/SG3 membrane till 8.26 ± 0.22 mSm/cm for the NSSA/SG7 membrane) (Table 4).

If we look at the parameters of the low-frequency part of the impedance spectrum CPE_dl and R_ct, we can see that the change in capacitance is within 55%, and the change in resistance is within 33%, respectively. Such changes can be caused both by the properties of the electrode-membrane interface itself and by the presence of air, which was difficult to control under these conditions.

Much larger changes are observed in the high-frequency part of the impedance spectrum (Table 3). The corresponding parameters CPE_q and R_b change several times and by several orders of magnitude, respectively. The introduction of silica nanoparticles formed via sol-gel process of precursors is accompanied by the expansion of the pores and the corresponding expansion of the channels connecting them. Since the channels regulate the ion transport in the membrane, the proton conductivity increases. However, at the further increase in the content of inorganic component we observed sharp decreasing in the value of the proton conductivity of the membrane. The decrease in proton conductivity at a higher concentration of nanoparticles can be explained by the decrease in the pore space as a result of denser filling of the channels with nanoparticles [21]. It should also be noted that the introduction of silica nanoparticles leads to the transition of the geometric capacity from CPE_q to classical capacity, which is evidenced by the P parameter (Table 3), which is equal to 1.

As compared to the proton conductive organic/inorganic membranes based on aliphatic acrylic monomers the values of proton conductivity of the hybrid membranes including aromatic monomer are lower, in the same time the effect of the content of the inorganic component on proton conductivity value is similar.

4. Conclusions

The proton conductive organic/inorganic materials were synthesized by UV-initiated polymerization of acrylic monomers and sulfoaromatic monomer – sodium styrene sulfonate (SSS) with simultaneous sol-gel process of the sol-gel system. The content of the inorganic component was found to determine the properties of the obtained materials. The mass-fractal organization, determined by SAXS, provides the high level of proton transport, making the materials good candidates for proton exchange membranes in fuel cells. Introduction of silica to membrane structure does not lead to significant changes in its viscoelastic properties.

The equivalent scheme for the cell with the synthesized membranes was proposed. The scheme adequately describes the process of ion transfer in the membranes and through the interface electrode-membrane.

Author Contributions

Conceptualization, M.Z. and I.Y.; methodology, M.Z., F.I., N.B.; software, M.Z. and P.C.; formal analysis, M.Z., O.D., T.S.; investigation, M.Z., I.Y., F.I., P.C.; data curation, M.Z., I.Y., F.I., N.B; writing—original draft preparation M.Z. and I.Y.; writing—review and editing, M.Z., I.Y., F.I., N.B.; visualization, M.Z., O.D., P.C.; supervision, F.I.; funding acquisition, F.I. and P.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The authors declare no conflict of interest.

Acknowledgements

M.Z. acknowledges German Academic Exchange Service (DAAD) for financial support (Research Grants for Doctoral Candidates and Young Academics and Scientists 2019/20, program ID 57440918). The authors acknowledge the help extended by Mr. Michael Göbel at IPF Dresden for the SAXS measurements.

References

Cigolotti, V.; Genovese, M.; Fragiacomo, P. Comprehensive Review on Fuel Cell Technology for Stationary Applications as Sustainable and Efficient Poly-Generation Energy Systems. Energies 2021, 14, 4963–4991. [Google Scholar] [CrossRef]
Sharaf, O.Z.; Orhan, M.F. An overview of fuel cell technology: Fundamentals and applications. Renew. Sustain. Energy Rev. 2014, 32, 810–853. [Google Scholar] [CrossRef]
Zhang, Y. Chapter 12 - Nanomembranes in fuel cells. Nanotechnology in Fuel Cells. Micro and Nano Technologies 2022, 285–347. [Google Scholar] [CrossRef]
Gil, M.; Ji, X.; Li, X.; Na, H.; Hampsey, J.E.; Lu, Y. Direct synthesis of sulfonated aromatic poly (ether ether ketone) proton exchange membranes for fuel cell applications. Journal of Membrane Science 2004, 234, 75–81. [Google Scholar] [CrossRef]
Raja Rafidah, R.S.; Rashmi, W.; Khalid, M.; Khalid, M.; Wong, W.Y.; Priyanka, J. Recent Progress in the Development of Aromatic Polymer-Based Proton Exchange Membranes for Fuel Cell Applications. Polymers 2020, 12, 1061. [Google Scholar] [CrossRef]
Zhang, Z.; Wu, L.; Xu, T. Novel aromatic proton-exchange polyelectrolytes via polyacylation of pre-sulfonated monomers. J. Mater. Chem. 2012, 22, 13996–14000. [Google Scholar] [CrossRef]
Rajangam, P.; Dharmalingam, S. Design of novel SPEEK-based proton exchange membranes by self-assembly method for fuel cells. Ionics 2013, 19, 1423–1436. [Google Scholar] [CrossRef]
Gao, S.; Xu, H.; Fang, Z.; Ouadah, A.; Chen, H.; Chen, X.; Shi, L.; Ma, B.; Jing, C.; Zhu, C. Highly sulfonated poly (ether ether ketone) grafted on graphene oxide as nanohybrid proton exchange membrane applied in fuel cells. Electrochim. Acta 2018, 283, 428–437. [Google Scholar] [CrossRef]
Jun, M.-S.; Choi, Y.-W.; Kim, J.-D. Solvent casting effects of sulfonated poly (ether ether ketone) for Polymer electrolyte membrane fuel cell. J Memb. Sci. 2012, 396, 32–37. [Google Scholar] [CrossRef]
Mabrouk, W.; Ogier, L.; Vidal, S.; Sollogoub, C.; Matouss, F.; Fauvarque, J.F. Ion exchange membranes based upon crosslinked sulfonated polyethersulfone for electrochemical applications. J Memb. Sci. 2014, 452, 263–270. [Google Scholar] [CrossRef]
Matsushita, S.; Kim, J.-D. Organic solvent-free preparation of electrolyte membranes with high proton conductivity using aromatic hydrocarbon polymers and small cross-linker molecules. Solid State Ionics 2018, 316, 102–109. [Google Scholar] [CrossRef]
Klein, L. C. Sol-Gel Process for Proton Exchange Membranes. Key Engineering Materials 2008, 391, 159–168. [Google Scholar] [CrossRef]
Heimerdinger, P.; Rosin, A.; Danzer, M.A.; Gerdes, T. A Novel Method for Humidity-Dependent Through-Plane Impedance Measurement for Proton Conducting Polymer Membranes. Membranes 2019, 9, 62. [Google Scholar] [CrossRef] [PubMed]
Müller, F.; Ferreira, C.A.; Azambuja, D.S.; Alemán, C.; Armelin, E. Measuring the proton conductivity of ion-exchange membranes using electrochemical impedance spectroscopy and through-plane cell. J. Phys. Chem. B 2014, 118, 1102–1112. [Google Scholar] [CrossRef] [PubMed]
Cooper, K.R. Progress Toward Accurate Through-Plane Ion Transport Resistance Measurement of Thin Solid Electrolytes. J. Electrochem. Soc. 2010, 157, B1731–B1739. [Google Scholar] [CrossRef]
Yuan, X.; Wang, H.; Sun, J.C.; Zhang, J. AC impedance technique in PEM fuel cell diagnosis—A review. Int. J. of Hydrogen Energy 2007, 32, 4365–4380. [Google Scholar] [CrossRef]
Zhyhailo, М.; Demchyna, O.; Yevchuk, I.; Makota, O. Сo(ІІ) and Ni(II) Removal from Aqueous Solutions by Polymer and Polymer/Silica Adsorbents with Sulfo and Carboxyl groups. Acta Chimica Slovenica 2023, 70, 361–370. [Google Scholar] [CrossRef]
Zhyhailo, M.; Horechyy, A.; Meier-Haack, J.; Formanek, P.; Malanin, M.; Arnhold, K.; Schneider, K.; Yevchuk, I.; Fery, A. Proton conductive membranes from covalently cross-linked poly(acrylate)/silica interpenetrating networks. Macromol. Mater. Eng. 2021, 306, 2000776. [Google Scholar] [CrossRef]
Zheltonozhskaya, T.; Shembel, E.; Fedorchuk, S.; Kunitskaya, L.; Maksyuta, I.; Permyakova, N.; Gomza, Y. Nanostructured triblock copolymers with chemically complementary components and their ionic conductivity. Journal of Research Updates in Polymer Science 2013, 1, 84–95. [Google Scholar] [CrossRef]
Impedance Spectroscopy Theory, Experiment, and Applications. Edited by Evgenij Barsoukov and J. Ross Macdonald. John Wiley & Sons, Inc., Hoboken, New Jersey. Canada. 205. 595 p.
Zhyhailo, M.; Demchyna, O.; Rymsha, K.; Yevchuk, I.; Rachiy, B.; Kochubey, V. Proton Conductive Organic-Inorganic Nanocomposite Membranes Derived by Sol-Gel Method. Chemistry & Chemical Technology 2019, 13, 436–443. [Google Scholar] [CrossRef]

Figure 1. The cell in which the proton conductivity of the membrane was studied.

Figure 2. Scheme of the nanocomposite membrane synthesis.

Figure 3. SAXS profiles of the composite materials.

Figure 4. SAXS profiles of the hybrid composite materials.

Figure 5. DMA curves of the NSSA and the NSSA/SG10 materials.

Figure 6. Equivalent scheme for the test cell.

Figure 7. Nyquist plots for the membranes: a) NSSA; b) NSSA/SG3; c) NSSA/SG5; d) NSSA/SG7; e) NSSA/SG10; f) the high-frequency part is shown with high accuracy for all membranes.

Table 1. SAXS data of the nanocomposite membranes.

Sample	R_g, nm	d, nm	D_f
NSSA/SG3	24	48	2.9
NSSA/SG10	20	39	2.7

Table 2. Storage modulus of the NSSA and the NSSA/SG10 membranes.

Sample	E’, MPa
Sample	T=298 K	T=473 K	T=573 K
NSSA	4390	130	85
NSSA/SG10	3940	122	115

Table 3. The values of CPE and R_b for the tested cells.

Sample	СPE_q		R_b, Ohm	СPE_dl		R_ct, kOhm
Sample	T, μF	P	R_b, Ohm	T, μF	P	R_ct, kOhm
NSSA	1.95	0.63	6085.0	2.66	0.72	680.0
NSSA/SG3	1.89	1.00	757.3	4.78	0.67	546.8
NSSA/SG5	0.47	1.00	39.5	4.03	0.76	457.1
NSSA/SG7	0.71	1.00	19.2	3.37	0.76	680.5
NSSA/SG10	2.93	0.86	3356.0	5.97	0.68	487.7

Table 4. Conductive parameters for the studied materials.

Sample	σ, mSm/cm	∆σ, mSm/cm
NSSA	1.45	0.04
NSSA/SG3	2.96	0.08
NSSA/SG5	7.52	0.20
NSSA/SG7	8.26	0.22
NSSA/SG10	2.99	0.08

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer