Prerpints.org logo
Preprint
Article

Zonons Are Solitons Produced by Rossby Waves’ Ringing

Altmetrics

Downloads

82

Views

56

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

27 April 2024

Posted:

29 April 2024

You are already at the latest version

Alerts
Abstract
Along with the familiar Rossby–Haurwitz waves, two-dimensional flows on the surface of a rotating sphere in the regime of zonostrophic turbulence harbour another class of waves known as zonons. Zonons are wave packets produced by energetic large-scale Rossby–Haurwitz wave modes `enslaving’ other wave modes. They propagate westward with the phase speed of the enslaving modes. Zonons can be visualized as enslaving modes’ `ringing’ in the enslaved ones with the frequencies of the former, the property that renders zonons non-dispersive. Zonons reside in high-shear regions confined between the opposing zonal jets yet they are mainly attached to westward jets and sustained by the ensuing barotropic instability. They exchange energy with the mean flow while preserving their identity in a fully turbulent environment, a feature characteristic of solitary waves. The goal of this study is to deepen our understanding of zonons’ physics using direct numerical simulations, a weakly non-linear theory, and asymptotic analysis, and ascertain that zonons are indeed isomorphic to solitary waves in the Korteweg - de Vries framework. Having this isomorphism established, the analysis is extended to eddies detected in the atmospheres of Jupiter and Saturn based upon the observed mean zonal velocity profiles and earlier findings that circulations on both planets obey the regime of zonostrophic macroturbulence. Not only the analysis confirms that many eddies and eddy trains on both giant planets indeed possess properties of zonons, but the theory also correctly predicts latitudinal bands that confine zonal trajectories of the eddies.
Keywords: 
Subject: Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

The paper by Salmon and Pizzo in this Special Issue [1] refers to fundamental contributions of Jack Herring to the theories of two-dimensional (2D) and quasigeostrophic turbulence [2,3,4]. The authors notice that much of the theoretical developments in these areas were accomplished in planar geometry in the hope that the β -plane approximation would capture the most important features of flows in the spherical geometry. Their primary conclusion, however, was that this is not the case, and that 2D incompressible flows on the sphere are significantly different from 2D flows on a β -plane, even in the case of vanishing rotation.
The situation is different for fast rotating flows with a β -effect, however, as on the largest scales, β -effect becomes predominant, and the interaction of the Rossby waves, or Rossby-Haurwitz waves (RHWs) in the spherical geometry, and turbulence leads to strong turbulence anisotropization, establishment of the regime of zonostrophic turbulence, see e.g. [5,6], and formation of zonal jets. As was demonstrated in [7,8], various features of zonostrophic turbulence, including its spectral properties, are amicable to representation in both planar and spherical geometries. Many facets of this dynamics are detailed in the recent book [9].
An important feature of the zonostrophic regime is the excitation of non-dispersive nonlinear waves termed zonons first described in [10]. These waves coexist with the linear RHWs and their physics is at the focus of the present study. In [10] it was established that zonons are forced oscillations induced by RHWs in other modes via nonlinear interactions, and their dispersion relation differs from that of the RHWs. Zonons reside in regions with a strong shear between opposing jets acting as wave guides for the long-living coherent wave packets. In the physical space, as shown in [11], zonons form westward propagating coherent eddies with zonal velocity equal to the phase speed of the most energetic RHWs.
Zonons can be viewed as a product of the interaction between energetic, or “ringing” RHWs and their overtones excited in other modes, the phenomenon reminiscent of enslaved vibrations excited by forced, ringing strings of a musical instrument in quiescent, echoing strings. Once excited, the sound waves from the echoing strings blend with those from the ringing strings and form a specific chromatic signal slowly emanating from the body of the musical instrument as a virtually self-preserving “acoustic soliton”, see e.g. [12]. The underlying mechanism behind the integration of ringing and echoing vibrations is the nonlinear interaction between the energetic and enslaved modes.
Is there anything in common between zonons and another type of ringing waves, recently discovered in [13]? They found that randomly excited global-scale atmospheric modes may come to a resonance with the lunar and solar atmospheric tidal waves described by the Laplace equation. In their words, these resonant interactions can make the atmosphere “ring like a bell”.
While the resonant wave interactions are linear, the processes underlying the formation and maintenance of zonons are not. As they emerge from the typical for solitary waves non-linear interaction between wave packets and the shear, one may hypothesize that zonons are indeed solitary waves, such as those studied in [14,15]. The latter papers focused on long waves in a homogeneous atmosphere with a uniform zonal flow and small velocity shear and arrived at the Korteweg - de Vries (KdV) equation. Following up studies [16,17] and others developed a general theory of solitary waves in a planetary zonal shear flow and demonstrated that the amplitude of long Rossby waves is governed by either the KdV equation or the modified KdV (mKdV) equation, dependent on the density stratification, see e.g. [18]. Later, a multi-scale method utilized in [19,20] showed that the primitive governing equation can be reduced to the KdV equation controlling the evolution of long, small-amplitude Rossby waves.
In [11], the connection between the solitary Rossby waves (SRWs) and zonons was outlined in the framework of the 2D barotropic vorticity equation on a β -plane. That study was akin to [16] where SRWs were investigated on a β -plane using the vorticity equation expanded around latitude θ 0 in the absence of forcing and damping. A direct mathematical link between zonons and solitary Rossby waves was not established, however. Substantiating such link is one of the main goals of this paper.
Other studies were concerned with eddies’ energetics. In [21], this issue was considered through the prism of the zonal asymmetry of the Rossby wave propagation. The asymmetry prompts a sharp difference between the eastward and westward jets. The eastward jets are stable and sharp, while the westward ones are unstable and blunt. For Jupiter and Saturn, this asymmetry is illuminated in Figs. Figure 8 and Figure 9 below and also in [22]. Westward jets are prone to barotropic and baroclinic instabilities that lead to eddy shedding [23,24], mixing of the potential vorticity (PV), and flattening of its profile across the jets [25]. The instabilities not only evoke eddies but also sustain them. The coexistence of eddies and jets can be viewed as eddy-jet symbiosis. The continuous two-way energy exchange between jets and eddies is facilitated by upscale and downscale turbulent cascades [11,26,27,28].
The dynamics of giant planets’ atmospheres is strongly affected by the eddy - jet flow interaction [29,30,31,32]. For instance, almost all westward jets on Jupiter and Saturn are barotropically unstable [33,34,35] and shed cyclonic/anticyclonic eddies of various shapes and sizes.
Similar features are typical of the westward south-equatorial currents in all terrestrial oceans [21], where under the action of a seasonal forcing, the currents periodically become unstable and radiate the Tropical Instability Waves (TIWs), e.g. [36,37,38].
Do zonons and the SRWs [solitary Rossby-Haurwitz waves (SRHWs) on a sphere] represent different aspects of the same mathematical objects? This is an important non-trivial question as RHWs are spectral characteristics of a flow while zonons construe it in the physical space.
The purpose of the present study is to answer this question for flows in the zonostrophic regime and thereby extend the results in [11]. The RHWs in a zonal flow on a surface of a rotating sphere will be scrutinized using the asymptotic multi-scale analysis and the assumption of weak nonlinearity. This technique yields the KdV equation in the spherical geometry, the hallmark of the solitary Rossby waves. For a given zonal velocity profile, the SRHWs phase speeds will be estimated by solving the generalized eigenvalue problem pertinent to the KdV equation. The RHWs velocities for barotropic flows can be computed analytically. The quantitative agreement between the two will be taken as an indication that the SRHWs and zonons are indeed two sides of the same coin.
An important question arises regarding the consistency of a mathematical framework describing forced and dissipative regime of zonostrophic turbulence harbouring the inverse energy cascade and unforced and non-dissipative regime represented by the KdV equation featuring no cascades. We note that the backbone of both regimes is a quasi-steady zonal velocity profile that, while remaining intact, may develop shear instabilities.
In the KdV framework, the origin and the maintenance of the profile are immaterial yet the shear instabilities provide a waveguide for solitary waves [11]. In the zonostrophic regime, the profile is a product of a balance between the small-scale forcing and the large-scale energy withdrawal. As was noticed earlier, the profile may become barotropically unstable and instigate eddy shedding. As shown in [39], this process is sustained by the Available Rotational Kinetic Energy, or ARKE, which is a rotational equivalent of the available potential energy in flows with stable stratification. This energy, as well as the rate of the inverse cascade, can be estimated by a process of PV monotonizing in the horizontal plane [40] that is analogous to Thorpe’s vertical reshuffling of fluid particles in stably stratified flows [41]. In [42] it was shown that the method of PV monotonizing allows one to estimate the inverse cascade rate on Jupiter and Saturn using a limited amount of data and with no information about details of the forcing. The mean zonal velocity profile not only contains information on the rate of the inverse cascade, but, as was shown in [21] and in analogy to the KdV framework, it sustains the energy and guides the propagation of coherent eddies. As will be shown in Section 3, the profile also reveals potential locations of the SRHWs and their trains.
Establishing the duality between SRHWs and zonons has important practical implications. For instance, it was found in [43] that the KdV equation describes a flow adjacent to the African easterly jet and helps to understand the evolution of a proto-vortex [44] growing into tropical storm Debby over West Africa in August 2006. That study hints that zonons may help to explain the formation of tropical cyclones and shed light upon their dynamics and evolution, at least during the initial stages.
The most far reaching application of the theory of Rossby solitons goes back to [45] where it was suggested that the SRWs may explain some facets of the dynamics of the Great Red Spot (GRS) and other features of the Jovian atmosphere. The application of the soliton solutions to the GRS was revisited in [46] while an extensive review of possible manifestations of SRWs in various planetary and geophysical environments was given in [47]. We shall see later that using the observed zonal velocity profiles, the KdV equation can quite accurately predict the latitudinal locations of the major eddies on both Jupiter and Saturn, including the GRS.
The investigation of the similarity between RHWs and zonons will proceed in the following fashion. The next section provides description of direct numerical simulations of the regime of zonostrophic turbulence which will be followed by the derivation of the KdV equation in a 2D flow on the surface of a rotating sphere. The following up section elaborates the existence and the features of the SRHWs. Section 3 elucidates the connections between the zonons and the SRHWs, Section 4 investigates the relationship between zonons and large eddies on Jupiter and Saturn, and Section 5 is discussion and conclusions.

2. The Regime of Zonostrophic Turbulence in Barotropic Simulations in Spherical Coordinate System

The barotropization of planetary atmospheres, i.e., accumulation of a large portion of their kinetic energy in the barotropic mode, was discussed in [6,26]. Both the barotropization and flow two-dimensionalization escalate with the increasing rate of rotation. Major features of the emerging flow regime can be represented by a mathematical model emulating barotropic, externally forced, dissipative 2D turbulence on the surface of a rotating sphere [e.g. [6]. In a certain range of parameters, the flow attains the regime of zonostrophic turbulence with its inherent zonal jets and conjoined zonons. The model is based upon the vorticity evolution equation,
∂ ζ ∂ t + J ( ψ , q ) = ( − 1 ) p + 1 A 2 p ∇ 2 p ζ − λ ζ + ξ ,
where ζ is the absolute vorticity, ψ is the stream function; ∇ 2 ψ = ζ ; A 2 p is the hyperviscosity coefficient in which p was set to 4; f = 2 Ω sin θ is the Coriolis parameter; Ω is the angular velocity of sphere’s rotation; θ ∈ [ − π 2 , π 2 ] is the latitude, and q = ζ + f is the PV. Since f is time-independent, Equation (1) could also be written in terms of the PV conservation. The Jacobian, J ( ψ , q ) , defined as J ( A , B ) = ( R 2 cos θ ) − 1 ( A φ B θ − A θ B φ ) , with R and φ ∈ [ 0 , 2 π ] being sphere’s radius and longitude, respectively, represents the nonlinear term in (1).
The flow governed by (1) features a small-scale forcing, ξ , acting upon scales of the order of n ξ − 1 , and a large-scale energy withdrawal represented by a linear friction with the coefficient λ . The energy injected into the system by forcing drives the inverse cascade at a rate Π ϵ . This cascade is terminated on large scales, of the order of n fr − 1 , by the linear friction that dominates on scales for which n < n fr . Under the action of forcing and friction, the flow eventually attains a steady state.
The stream function is decomposed into a series of spherical harmonics, Y n m ( sin θ , φ ) ,
ψ ( θ , φ , t ) = ∑ n = 1 N ∑ m = − n n ψ n m ( t ) Y n m ( sin θ , φ ) .
They are eigenfunctions of the horizontal Laplacian operator, ∇ h 2 Y n m = − n ( n + 1 ) Y n m / R 2 , and depend on non-dimensional total and zonal indices, n and m, respectively.
Linearized Equation (1) that excludes forcing and dissipation admits a RHW solution whose dispersion relation is [6,48,49,50]
ω R H W ( n , m ) = − 2 β m n ( n + 1 )
yielding the phase speed
c R H W ( n ) = ω R H W ( n , m ) m = − 2 β n ( n + 1 ) ,
where β = Ω / R . Equation (3) is consistent with a β -plane approximation format [49,51,52,53].
Equation (1) with the decomposition (2) was used for numerical investigation of various aspects of the nonlinear dynamics. Details of the numerical scheme and the simulations are given in [54].
Employing a unit radius, R = 1 , eliminates the difference between the spherical harmonics’ indices and the wave numbers. The energy spectrum can be computed following [55,56],
E ( n ) = ∑ m = − n n E ( n , m ) = n ( n + 1 ) 4 ∑ m = − n n 〈 | ψ n m | 2 〉 ,
where the modal spectrum, E ( n , m ) , is the spectral energy density per mode ( n , m ) , and the angular brackets stand for ensemble or time average. The spectrum, E ( n ) , can be decomposed into a sum of zonal and nonzonal, i.e., residual components, E ( n ) = E Z ( n ) + E R ( n ) , where the zonal component is E Z ( n ) = E ( n , 0 ) .
In the regime of zonostrophic turbulence, the zonal and residual spectra acquire universal distributions [57] given by
E Z ( n ) = C Z β 2 n − 5 , C Z ≈ 0.5 ,
E R ( n ) = C R Π ϵ 2 / 3 n − 5 / 3 , C R ≈ 6 .
While the zonal spectrum (6a) develops a very steep slope, its residual counterpart (6b) closely follows the classical theory of isotropic 2D turbulence [58]. The intersection of (6a) and (6b) defines the transitional index, n β = ( β 3 / Π ϵ ) 1 / 5 . The strength of anisotropy is characterized by the zonostrophy index, R β = n β / n R [54,59], where n R is the Rhines index, n R = ( β / 2 U ) 1 / 2 , and U is the RMS zonal velocity. The threshold of the zonostrophic flow regime corresponds to R β ≳ 2 . 5 [6,26,54,59,60].
Figure 1 shows the zonal and residual kinetic energy spectra obtained in 2D simulation using Equation (1). The parameters in this simulation were Ω = 1 . 4 , R = 1 , and R β = 2 . 65 . The energy spectra in Figure 1 are in good agreement with Equations (6a) and (6b) and, thus, clearly demonstrate the signature of the zonostrophic regime. Both spectra attain their maxima at a scale close to n R − 1 . On larger scales, friction becomes a dominant factor that causes the spectral amplitudes to rapidly decrease.

3. Rossby-Haurwitz Waves, Zonons, and Solitons

The zonal mode with the maximum energy, approximately quantified by E Z ( n R ) , dominates the zonal velocity profile while n R divulges the corresponding number of alternating zonal jets [61]. Some of the westward jets are barotropically unstable [23,30,33,62] and feature a strong shear. Energized by incipient instabilities, nonlinear interactions between the RHWs lead to formation of nondispersive, westward propagating wave packets. In the physical space, these packets appear as coherent eddies termed zonons [10]. Zonons appear as eddies or trains of eddies riding on the most energetic RHWs [21,63], their speed being c R H W ( n R ) [10,11]. Later it will be shown that zonons’ dynamics is amenable to a description within the framework of the KdV equation, i.e., they possess properties of the solitary Rossby-Haurwitz waves (SRHWs). The congruity of RHWs, SRHWs and zonons will be demonstrated by exposing the consistency of their representations in the physical and Fourier spaces and closeness of their characteristic velocities. These issues will be addressed in the remainder of this section.

3.1. Flows on the Surface of a Rotating Sphere, the Mercator Projection, and the KdV Equation

As explained in the Introduction, the analysis of zonons is based upon consideration of a 2D flow on the surface of a rotating sphere absent external forcing, large-scale friction, and small-scale dissipation. The flow is governed by the barotropic vorticity equation (1) modified to express the PV conservation [52]:
q t + ψ φ q θ − ψ θ q φ R 2 cos θ = 0 ,
q = cos θ ψ θ cos θ θ + ψ θ θ R 2 cos 2 θ + f .
The variables in (7a), (7b) are nondimensionalized and marked by asterisks,
t = Ω − 1 t * , f = Ω f * , ψ = Ω R 2 ψ * , r = R r * , q = Ω q * .
In the nondimensional form, Equations (7a) and (7b) become
q t * * + ψ φ * q θ * − ψ θ * q φ * cos θ = 0 ,
q * = cos θ ψ θ * cos θ θ + ψ θ θ * cos 2 θ + f * .
Further derivations are performed in the Mercator projection developed by the Flemish geographer and cartographer Gerardus Mercator in 1569. In this approach, the geographic map is projected from the globe to a tangential cylindrical surface touching the globe at the equator. The cylindrical surface is then unrolled into a planar map.
Another way of mapping a spherical surface onto a plane is by using a stereographic projection as done in [1]. A detailed comparison between the Mercator and stereographic projections is elaborated in [64]. Briefly, both techniques belong in a family of conformal mappings of a sphere onto a plane that only involve elementary calculus and trigonometry. In both cases, the equations governing 2D turbulence on a sphere become quite similar to the corresponding equations in the Cartesian coordinate system on a β -plane, e.g. [43].
The nondimensional Mercator projection variables, x * and y * , are defined by
x * = r * φ , y * = r * arctanh ( sin θ ) = r * gd − 1 ( θ ) ,
where gd − 1 ( θ ) is the inverse Gudermannian, and r * = 1 on a sphere with the radius R.
The Gudermannian function, gd ( ψ ) = arcsin ( tanh ψ ) = arctan ( sinh ψ ) = ϕ , maps a hyperbolic angle ψ ∈ [ − π / 2 , π / 2 ] onto a circular angle ϕ ∈ ( − ∞ , ∞ ) (not to be confused with the stream function, ψ , and the latitude, ϕ , above). Correspondingly, the inverse Gudermannian in (10) maps θ ∈ [ − π / 2 , π / 2 ] onto y * ∈ ( − ∞ , ∞ ) . This function was introduced by Johann Heinrich Lambert circa 1760 and later named after Christoph Gudermann who derived the relationship between circular and hyperbolic functions in 1830 [65]. The Gudermannian is also called the hyperbolic amplitude as it describes the limiting case of the Jacobi elliptic amplitude. Both ψ and ϕ are used in the definition of the stereographic projection.
Using the new variables and dropping the asterisks, Equations (9a) and (9b) become
S 2 q t + ψ x q y − ψ y q x = 0 ,
q = 1 S 2 ψ y y + ψ x x + 2 Ω tanh y ,
where S ≡ cos θ = sech y .
Motivated by zonons’ properties, we employ the asymptotic multiscale method that focuses upon large-scale, long-time solutions of Equations (11a) and (11b) using a long spatial, X, and a slow temporal, T, scales,
X = ε 1 / 2 ( x − c 0 t ) , T = ε 3 / 2 t .
Here, c 0 is a free parameter representing the speed of a coherent structure, and ε is a small parameter, 0 < ε ≪ 1 , measuring the ratio of the fast and slow time scales. Using these notations, Equations (11a) and (11b) can be written in terms of X, y and T, and the stream function is then expanded in a series in powers of ε [11],
ψ ( X , y , T ) = ∑ i = 0 ∞ ε i ψ ( i ) .
Retaining a small O ( ε ) term in (13), ψ can be written as a sum of the basic mean stream function, ψ ( 0 ) , and a stream function of the coherent disturbance, ψ ( 1 ) ,
ψ ( X , y , T ) = ψ ( 0 ) + ε ψ ( 1 ) + O ε 2 .
A 2D velocity field on a sphere can be represented by its poloidal (meridional; θ ^ ) and toroidal (azimuthal, zonal; φ ^ ) components,
u = ∇ ⊥ ψ = 1 R cos θ ∂ ψ ∂ φ θ ^ − 1 R ∂ ψ ∂ θ φ ^ .
Numerical simulations presented in [26,54,59] indicate that the zonal flow is comprised of alternating zonal jets with the amplitude U j e t ( θ ) , where the mean velocity is 〈 u ( θ ) 〉 = U j e t ( θ ) φ ^ , and so the zero-order stream function can be expressed via
U j e t ( θ ) = − 1 R d ψ ( 0 ) d θ .
From (16) one infers that ψ ( 0 ) depends on θ only and can be computed by straightforward integration,
ψ ( 0 ) ( θ ) = − R ∫ 0 θ U j e t ( θ ′ ) d θ ′ .
In the Mercator projection, the zonal flow is V ( y ) , U j e t ( y ) = S V ( y ) , and
ψ ( 0 ) ( y ˜ ) = − ∫ 0 y ˜ S 2 V ( y ′ ) d y ′ ,
where y ˜ = arcsin ( tanh y ) = arctan ( sinh y ) = gd ( y ) .
We drop the tilde over y and seek a solution to ψ ( i ) , i > 0 , using the method of separation of variables,
ψ ( i ) ( X , y , T ) = A ( i ) ( X , T ) Φ ( i ) ( y ) ,
which yields a power-series representation of (13) in the form
ψ ( X , y , T ) = − ∫ 0 y S 2 V d y ′ + ∑ i = 1 ∞ ε i A ( i ) ( X , T ) Φ ( i ) ( y ) .
By rewriting Equations (11a) and (11b) in the new variables, X, y, T, substituting (13), and equating the terms with the same powers of the small parameter ε , we arrive at a system of coupled differential equations. In the leading order, O ( ε 3 / 2 ) , a second-order ordinary differential equation for Φ ( 1 ) is obtained,
Φ y y ( 1 ) + Γ y V − c 0 Φ ( 1 ) = 0 ,
Γ = f − S 2 V y S 2 .
Equations (21a) and (21b) have non-trivial solutions for a discrete set of values c 0 ( i ) , i = 0 , 1 , 2 , ⋯ , and so they form a generalized eigenvalue problem. The solution of this problem will be discussed later.
Equation (21a) underscores the usefulness of the Mercator projection as it is similar to Equation (17) derived in [11] in a planar geometry using a β -plane approximation in the vicinity of a latitude θ 0 . The differences appear, firstly, in the numerator, where the potential vorticity on a β -plane, f − U y , is replaced by the meridional gradient of (21b) and, secondly, in the denominator, where U j e t s is replaced by V. It is assumed that V − c 0 ≠ 0 in (21a), i.e., that the normal modes are non-singular.
The stationary Equations (21a) and (21b) along with Equation (19) describe the variation of ψ ( 1 ) in the latitudinal direction. The evolution of the amplitude, A ( 1 ) ( X , T ) , is determined by invoking the next-order approximation, O ( ε 5 / 2 ) , that yields the following equations:
Φ y y ( 2 ) + Γ y V − c 0 Φ ( 2 ) = − F A X ( 2 ) V − c 0 ,
F = A T ( 1 ) Φ y y ( 1 ) + κ A ( 1 ) A X ( 1 ) + A X X X ( 1 ) V − c 0 ,
κ = Φ ( 1 ) Φ y y ( 1 ) S 2 y − Φ y ( 1 ) Φ y y ( 1 ) S 2 .
Equation (22b) shows that the effect of a longitudinal dispersion represented by the term A X X X ( 1 ) and that of the nonlinearity, A ( 1 ) A X ( 1 ) , appear only in the order O ( ε 5 / 2 ) .
After multiplying (21a) by Φ ( 2 ) and (22a) by Φ ( 1 ) , subtracting the second product from the first one, and integrating the result over y in the interval y ∈ ( − ∞ , ∞ ) using the integration by parts while utilizing the boundary conditions Φ ( 1 ) ( ± ∞ ) = Φ ( 2 ) ( ± ∞ ) = 0 (vanishing velocity component in the direction y ^ at the poles), one finds:
− 1 A X ( 2 ) ∫ − ∞ ∞ F Φ ( 1 ) S 2 V − c 0 d y = 0 .
This equation implies that either A X ( 2 ) is infinite, or A ( 1 ) ( X , T ) satisfies the KdV equation,
A T ( 1 ) + μ A ( 1 ) A X ( 1 ) + δ A X X X ( 1 ) = 0 ,
where
I μ = ∫ − ∞ ∞ Γ y S 2 V − c 0 y Φ ( 1 ) 3 V − c 0 d y ,
I δ = − ∫ − ∞ ∞ Φ ( 1 ) 2 d y ,
I = ∫ − ∞ ∞ Γ y V − c 0 2 Φ ( 1 ) 2 d y .
This KdV equation is fully analogous to the one derived in the β -plane approximation [see e.g. [11] if Γ y = β − U y y is replaced by Γ y = f y − [ ( S 2 V ) y / S 2 ] y , U j e t s is replaced by V, and the metric coefficient, S 2 , appears in the expression for μ .
A well-known soliton solution of the KdV equation is
A ( 1 ) ( X , T ) = A * sech 2 X − c 1 T Δ * ,
A * = 3 c 1 μ ,
Δ * = 2 δ c 1 1 / 2 ,
This solution describes a solitary wave with a characteristic width Δ * that travels with a constant speed c 1 , the latter being a free parameter that represents the speed in the moving frame ( X , T ) .

3.2. Solitary Rossby waves in spherical coordinates

Computing the perturbation stream function, ψ ( 1 ) ( θ , φ , t ) , in spherical coordinates starts with its factorization,
ψ ( 1 ) ( θ , φ , t ) = A ( 1 ) ( φ , t ) Φ ( 1 ) ( θ ) ,
and follows up by evaluation of Φ ( 1 ) ( θ ) and A ( 1 ) ( φ , t ) using Equations (21a), (21b), and (26a) - (26c). These equations are cast in terms of the slow variables. Inverting (12) restores them back to the unscaled coordinates ( x , t ) . Next, by inverting (10), one restores the original spherical coordinates, ( θ , φ ) , and arrives at a boundary-value/eigenvalue problem for Φ ( 1 ) ( θ ) ,
Φ θ ( 1 ) cos θ θ + R Γ θ V − c 0 Φ ( 1 ) = 0 ,
Γ = 2 Ω sin θ − V cos 2 θ θ R cos θ ,
N . B . C . ∂ Φ ( 1 ) ∂ θ | θ = ± π / 2 = 0 .
Here, V ( θ ) is computed from a given zonal velocity profile, U j e t ( θ ) , and the Neumann boundary conditions, denoted N.B.C., follow from the requirement that both mean and coherent parts of the zonal velocity vanish at the poles.
The boundary value problem (28a) - (28c) possesses an infinite set of the eigenvalues, { c 0 } i , i = 1 , 2 , . . . . They define a set of the eigenfunctions, { Φ ( 1 ) } i , i = 1 , 2 , . . . . To simplify the notations, we shall use c i 0 and Φ i ( 1 ) instead of { c 0 } i and { Φ ( 1 ) } i while keeping in mind that the lower indexes are introduced for the bookkeeping and not to denote differentiation.
In a weakly-nonlinear approximation,
ψ ≅ ψ ( 0 ) + ε ψ ( 1 ) = ψ ( 0 ) + ε A ( 1 ) Φ ( 1 ) .
By multiplying (26a)-(26c) by ε , reverting the variables back to the unscaled coordinates ( x , t ) , and then to the original coordinates ( θ , φ ) using (12) and (10), one derives
ε A ( 1 ) ( φ , t ) = A 0 sech 2 R φ − c t Δ ,
A 0 = 3 ε c 1 μ ,
Δ = 2 δ ε c 1 1 / 2 ,
c = c 0 + ε c 1 ,
where Δ is soliton’s characteristic width, ε c 1 is the next order correction to c 0 that will be neglected, and the coefficients μ and δ are defined by
I μ R = 1 R 2 ∫ − π 2 π 2 Γ θ V − c 0 cos θ θ Φ ( 1 ) 3 V − c 0 d θ ,
I δ R 3 = − ∫ − π 2 π 2 Φ ( 1 ) 2 cos θ d θ ,
I = ∫ − π 2 π 2 Γ θ V − c 0 2 Φ ( 1 ) 2 d θ .
The parameters μ and δ depend on V ( θ ) and, thus, on the zonal velocity profile, U j e t ( θ ) . The other two parameters, ε and c 1 , can be varied in certain ranges such as to explore properties of the solution of the system (30a)-(31c).
A solitary wave appears stationary in a coordinate system moving along with it with the velocity c 0 . The solitary waves’ amplitudes, (30a), attain their maxima along the lines for which R φ − c 0 t = 0 . Figure 2 shows the normalized soliton solution, ε A ( 1 ) ( φ , t ) / A 0 , as given by (30a), for different values of c 1 with ε = 0 . 01 . The wave propagates in the zonal direction along a latitude isoline ( θ = const) while preserving meridional symmetry about that isoline. For small c 1 , ε A ( 1 ) ( φ , t ) / A 0 is nearly constant but with increasing c 1 , it gradually evolves into a sharp pulse. The limit c 1 → 0 brings on Δ → ∞ , and the soliton morphs into evanescent wave. Increase in c 1 raises wave’s amplitude, A 0 , while its characteristic width, Δ , decreases. Since the analytical solutions obtained on a rotating sphere and on a β -plane are practically identical, see e.g. [11] and [43], both panels in Figure 2 plotted here for a sphere are quite similar to Figs. 1 and 2 drawn in [43] for a β -plane.
A system of equations (30a)-(31c) can be used to diagnose whether or not a specific flow pattern gives rise to a solitary wave. The analysis is guided by the mean zonal velocity profile, U j e t ( θ ) , that produces the pattern at hand, and the pattern’s propagation speed, c 0 . The latitudinal structure of the SRHW is determined by the eigenfunction Φ ( 1 ) ( θ ) given by (28a). For ε ψ ( 1 ) , one derives a system of equations describing a wave with an amplitude A 0 ( θ ) traveling in the zonal direction with a constant speed c 0 ,
ε ψ ( 1 ) = ε A ( 1 ) Φ ( 1 ) ( θ ) = A 0 ( θ ) sech 2 R φ − c 0 t Δ ,
A 0 ( θ ) = 3 ε c 1 μ Φ ( 1 ) ( θ ) ,
Δ = 2 δ ε c 1 1 / 2 .
The initial system of equations can now be reduced to a single equation for the stream function ψ ( θ , φ , t ) [66] that yields an analytical expression for a SRHW,
ψ ( θ , φ , t ) = − R ∫ 0 θ U j e t θ ′ d θ ′ + A 0 ( θ ) sech 2 R φ − c 0 t Δ .
In [11] it was established that zonons are long-living coherent eddies that can survive in a flow even after the forcing and friction are turned off. In the vicinity of eddy’s center, the perturbation velocity inferred from ψ ( 1 ) approaches zero in both forced and unforced flows, or, equivalently, both ψ ( 1 ) and Φ ( 1 ) ( θ ) attain their extrema. These requirements imply that Φ ( 1 ) ( θ ) θ = 0 somewhere inside an eddy. Thus, the behaviors of Φ ( 1 ) ( θ ) and its derivative divulge not only zonon’s presence but also its latitudinal position.
The next subsection demonstrates how these results can be utilized to identify zonons in the physical space in the regime of zonostrophic turbulence as presented in Section 2 following [10].

3.3. Mean Zonal Velocity, Eigenfunctions, and Eigenvalues

The zonal velocity profile, U j e t ( θ ) , obtained in simulations described in Section 2, is used to solve the eigenvalue problem (28a) - (28c). A numerical solution of this problem, using Matlab, yields discrete sets of eigenvalues, c i 0 , and eigenfunctions, Φ i ( 1 ) ( θ ) , i = 1 , 2 , 3 , ⋯ . The normalized eigenfunctions, Φ i ( 1 ) ( θ ) / Φ i ( 1 ) ( θ = 0 ) , i = 1 , ⋯ , 11 , are shown in Figure 3.
Only Φ i ( 1 ) ( θ ) with i = 7 exhibits 6 extrema; those can be collocated with eddies emerging along both sides of the three westward jets shown in Figure 4. Figure 1 demonstrates that n = 7 is the most energetic zonal mode while the maximum energy RHW is at n = 5 . One infers that the closeness of the modes with most energy in either RHWs (residual spectrum) or zonal jets (zonal spectrum) may be a general feature of zonostrophic turbulence and so, in some situations where data is limited, one may be taken as a surrogate of the other.
Figure 4 also confirms that the extrema of Φ 7 ( 1 ) ( θ ) as well as the zeros of Φ 7 ( 1 ) ( θ ) θ coincide with the centers of the eddies as seen in the color maps of the potential vorticity perturbation, q ( 1 ) .
In addition, Figure 4 illuminates the fact that the vortices reside in the regions of maximum shear between zonal jets. These locations correspond to those at which the potential vorticity gradient crosses zero and which, according to the Charney-Stern stability criterion, are the epicenters of the barotropic instability.
Using a detailed analysis, such locations were associated with the hot spots of eddy formation in [21] where the propagation speed of the traveling structures inferred from the stream function was compared with that derived from the centroids of different types of clusters construed via the Okubo–Weiss analysis. The results were compared with the theoretical phase speed of Rossby waves. The congruity of these two characteristics at the locations of maximum shear was quite remarkable. An important conclusion drawn from this analysis was that “the Rossby waves and eddies are inseparable as the former maintain the instability that sustains the latter. This symbiosis visually resembles the Rossby soliton.” Note that a similar idea about the coexistence of eddies and Rossby waves was discussed in [63]. The hypothesis about the unity of Rossby waves and Rossby solitons, formulated in [21], has not yet been substantiated within the framework of the KdV equation. The validation of this hypothesis within the KdV framework and its various applications are presented in the forthcoming sections.

3.4. Numerical Simulations: Zonons and Eddies

Table 1 compares a set of the first 11 eigenvalues, c i 0 , i = 1 , ⋯ , 11 , of the boundary value problem (28a) - (28c) with a set of zonal phase speeds of the first 11 RHWs, c R H W ( n ) , n = 1 , ⋯ , 11 , given by (4). The two sets are in a close agreement, both in their enumerations, as the phase speeds of the possible solitary waves, c i 0 , are close to c R H W ( n ) for n = i , and in the proximity of their numerical values. For the most energetic RHW, n = 5 , the difference between c R H W and c i 0 is about 10%, and for the most energetic zonal mode, i = 7 , the difference is even smaller, only within 2%, blurring the contrast between waves and eddies. The eddy-wave duality was discussed in [21,44,63]. Proximity of c R H W and c i 0 for other wave numbers indicates that virtually all RHWs generate secondary, i.e., enslaved waves, see [10], but their energies are much lower than those of the predominant zonons, and so they are less amenable to detection and observation. In addition, turbulence intensity raises with increasing n causing turbulence-induced scrambling to overwhelm wave processes.
The eigenvalues obtained from the solution of the boundary value problem are used to evaluate the parameters I i , μ i and δ i needed to compute the coefficients of the KdV equations, and, ultimately, the amplitudes of the solitary waves.

3.5. Hovmöller Diagrams

The Hovmöller diagram technique highlights propagation of RHWs and SRHWs in the physical space. The diagram axes are usually chosen as longitude or latitude and time and the variable plotted is the velocity stream function relative to the zonal flow; its values are represented by a color table. The slopes of lines of the same color reveal the speed of propagating waves and structures, i.e., packets of RHWs and SRHWs, relative to the zonal flow.
Figure 5 reproduces Hovmöller diagrams for zonostrophic regime ( R β = 2 . 58 ) investigated in Sukoriansky et al. [11]. Figure 5(a) reveals westward propagation of zonons that were identified by their spectral properties and confirms that their speed along the latitude of the maximum shear coincides with the phase speed of the most energetic RHW with n = 5 . The same result was obtained for other latitudes (not shown) thereby reiterating that the westward propagating eddies can indeed be identified with zonons moving with a constant speed relative to the zonal flow. Moreover, Figure 5(b) underscores that zonons’ velocity in the meridional direction is zero. Figure 5(b),(c) and (d) combined indicate that zonons reside in areas where the zonal velocity exhibits strong shear. Figure 5(e-h) display similar results for the same flow 22000 days after the forcing and the large-scale drag were switched off. In this case, the energy of RHWs decreases while zonons preserve their energy and become the dominant feature of the flow.
In summary, zonons form long-living wave packets located between zonal jets. The shear exerted by opposing jets acts to tear the eddies apart while the nonlinearity opposes shear’s action and blocks eddies’ dispersion. As follows from the analysis employing the Hovmöller diagrams, whether the eddies are sustained by the shear instability or not, the summary action of two adjacent opposing jets results in their becoming a waveguide for the coherent wave packets. Such interaction between shear, nonlinearity, and wave propagation is typical of solitary waves, see e.g. [16], that include zonons.

4. Zonons in the Atmospheres of Jupiter and Saturn

The KdV framework developed in the previous sections will now be utilized to investigate eddies detected in the weather layers of Jupiter and Saturn. Both atmospheres feature the regime of zonostrophic macroturbulence as the values of the zonostrophy index, R β , are about 5 for Jupiter [26] and about 4 for Saturn [42]. The velocity profiles needed for this investigation were published in [67] for Jupiter and [68] for Saturn. The analysis is based upon the boundary value problem, Equations (28a) - (28c), that yields the eigenvalues and eigenfunctions pertinent to the respective planetary atmospheres. These results, along with the spectra in [61] and [26], were used to estimate likely locations of planetary eddies. The outcome of these estimates are summarized in Section 4.1 - Section 4.4.

4.1. A Brief Taxonomy of Jupiter’s Eddies

The zonal velocity profile for Jupiter was obtained from the upper cloud level data collected by Voyager in 1980-1981 [67]. As noted in [24], Jupiter’s mean zonal velocity, U j e t ( θ ) , has not significantly changed at least since 1979.
Numerous studies of Jovian vortices, e.g. [23,24,32,69] reveal that they reside at many latitudes outside the near-equatorial belt ± 15 ∘ . In line with the mentioned in the Introduction tendency, most vortices are aligned in rows bound to the westward jets [24]. The eddies are either anticyclonic or cyclonic when reside, respectively, on the poleward or equatorial flanks of a jet, as seen in Figure 6. Longitudinal interspersing of cyclones and anticyclones gives rise to a configuration termed `Jovian vortex street’ (JVS) [24,70]. A JVS may corrugate a westward jet and force it to meander between the cyclonic and anticyclonic eddies, just like a system of vortices wrinkles a zonal jet in the experiments on zonostrophic turbulence [21,39].
In [24], the JVSs were considered to be more fundamental coherent features of the Jovian atmosphere than the individual vortices. The dynamics of the JVS vortices implied quite elaborate yet bogus forcing and dissipation and it was unclear how they could affect the structure of turbulence. It was suggested that the JVS excludes the GRS because, due to its close proximity to the equator, the GRS does not possess a companion cyclonic vortex on its northern side while other anticyclonic vortices do.
After the GRS, the White Ovals (WOS) comprise the second in magnitude Jupiter’s vortex system. It is located at about − 33 ∘ , south of the GRS. The WOS formed in 1938 and then pinched off at six different longitudes labeled, alphabetically, as A, B, C, D, E, and F [69,71]. The vortices started moving towards each other while exhibiting signs of recirculation and eventually assumed oval shapes known today as BC, DE and FA. In 1998, the ovals BC and DE merged to a single storm, oval BE [72]. The new storm continued drifting along with oval FA and in the year 2000, the two storms merged into a single storm BA. This merger was described in [73] and, later on, in [69]. The oval BA is now the dominant vortex in its latitude. It has experienced various episodes of coloration changes.
The third longest-lived oval in Jupiter’s atmosphere is a large anticyclone formed in the year 2006 at the planetographic latitude of 19 ∘ N [74]. As most large vortices, it is also bound to a westward jet and located in a zone characterized by a strong latitudinal shear that is prone to formation of closely interspersed cyclones and anticyclones.
Yet another major Jupiter’s eddy is the so-called Jovian Ribbon. Located near 30 ∘ N, it is dynamically associated with a westward jet and exhibits irregular undulations in latitude [32], as seen in Figure 6.

4.2. Jupiter: Eddies or Zonons?

We now probe a congruence of Jupiter’s eddies and zonons. The boundary-value problem (28a) - (28c) is solved for the observed mean zonal velocity profile reported in [67]. Table 2 compares the RHWs’ phase speeds with the propagation velocities of the solitary waves. Similarly to the results of numerical simulations, there seems to be a good agreement between the propagation speeds of the corresponding zonons and RHWs (i.e., those for which i = n), they differ by less than 10% in the range of i between 17 and 23 although for several i from that range there was no convergence.
As explained earlier, the best visible zonons are produced by the most energetic RHWs, and to select proper modes, we need to scrutinize the residual energy spectrum. Figure 7 shows the zonal and residual energy spectra for Jupiter as estimated by the Cassini spacecraft during flyby in December 2000 [26]. The observed residual spectrum shows a peak at about n = 23 . This wave number coincides with the energy peak in the zonal spectrum and is also indicative of the number of zonal jets [61]. The closeness of the wave numbers of maximum zonal and residual kinetic energies as observed in numerical simulations was mentioned in Section 3.3.
The mode with n = 23 is a good candidate for producing energetic secondary waves that can form zonons. If this possibility indeed materializes, then the extrema of Φ 23 ( 1 ) ( θ ) would coincide with the locations of large coherent eddies observed on Jupiter’s disk.
Figure 8 collocates the observed large Jupiter’s eddies (left panel) and extrema of Φ 23 ( 1 ) ( θ ) (right panel). The figure corroborates the premise that the majority of the eddies are associated with the westward jets and are tightly connected to the locations of maximum shear and energetic instabilities. The figure also demonstrates close correspondence between the locations of the observed and anticipated eddies, including the GRS. Given that some properties of Jupiter’s eddies can be attributed to zonons, eddies’ appearance can be aptly characterized as ’zonon streets’. Zonon streets are inclusive of the GRS.
Preprints 105049 g008
Figure 8. Left panel: Jupiter’s zonal wind profile as measured by the HST [67] and used in [31] to trace large vortices. These vortices are represented by ovals and are scaled to their latitudinal size. Right panel: Jupiter’s zonal velocity profile from the Voyager data [67] (black line), the eigenfunction Φ 23 ( 1 ) ( θ ) (red line), and estimated locations of eddies, marked by small circles, at the extrema of the eigenfunction.
Figure 8. Left panel: Jupiter’s zonal wind profile as measured by the HST [67] and used in [31] to trace large vortices. These vortices are represented by ovals and are scaled to their latitudinal size. Right panel: Jupiter’s zonal velocity profile from the Voyager data [67] (black line), the eigenfunction Φ 23 ( 1 ) ( θ ) (red line), and estimated locations of eddies, marked by small circles, at the extrema of the eigenfunction.
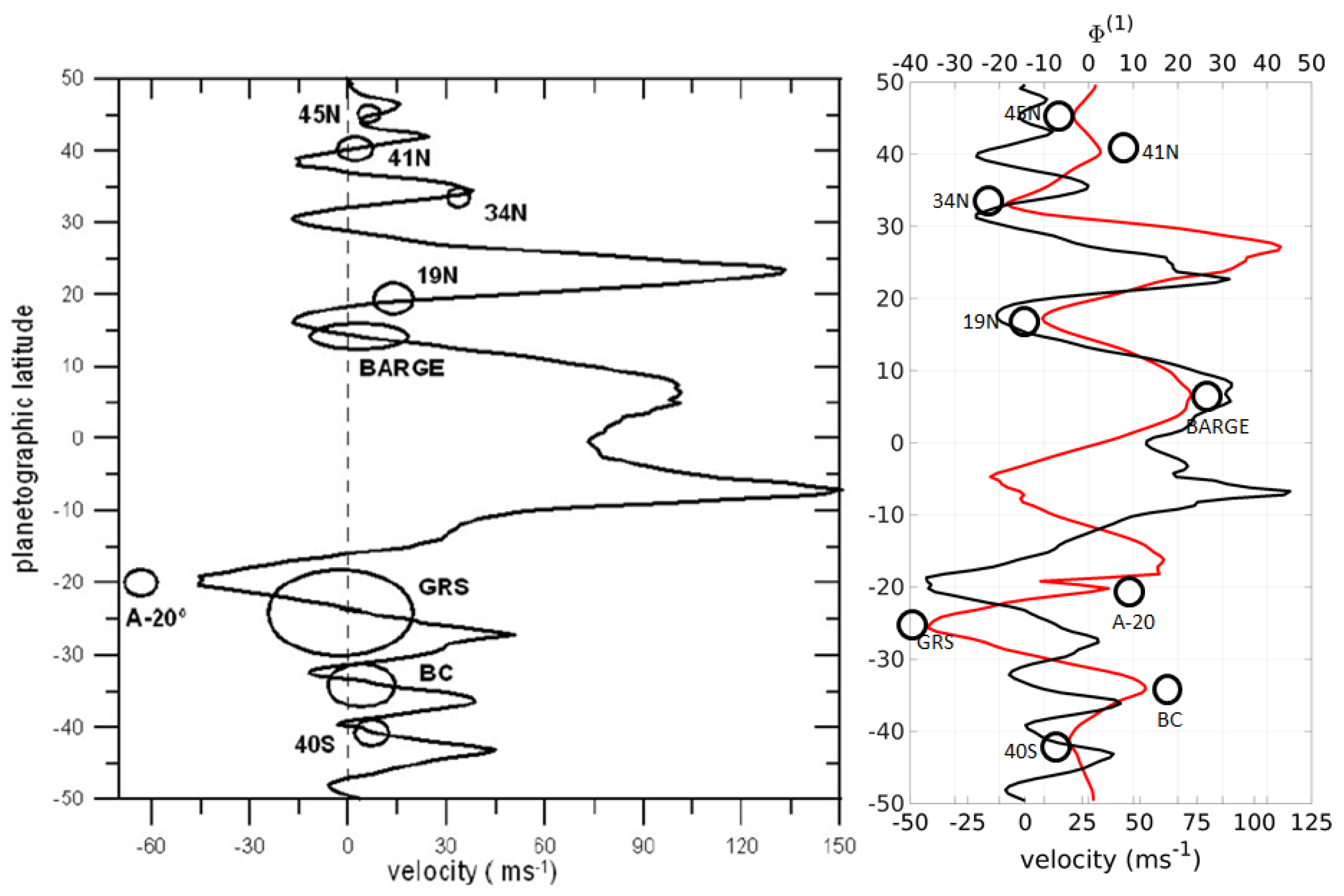
Preprints 105049 g008
The equatorial belt between the latitudes ± 10 ∘ features different dynamics [24] and was excluded from the analysis. For instance, new data obtained from the James Webb Space Telescope (JWST) observations of Jupiter reveals an intense narrow equatorial atmospheric jet located close to the tropopause [75]. The jet was extracted from the fast motions of equatorial hazes and is presumed to be a deep counterpart of equatorial oscillations in the stratosphere of Jupiter that are unrelated to the eddies.

4.3. A Brief Taxonomy of Saturn’s Eddies

The regime of zonostrophic macroturbulence on Saturn is distinguished by vortices and cloud structures forming alternating zonal jets that encircle the planet with their beautiful mottled textures [9]. The jets’ edges are wave-like but may become unstable and exhibit corrugation by turbulent eddies that may be evoked by either dynamic instabilities or moist convection [e.g., [76,77,78,79].
Similarly to the alternating jet pattern on Jupiter, jets on Saturn also form an east-west stencil that is important for identification of instabilities and locations of vortices and storms. This stencil appears asymmetric with a bias towards the eastward jets. The use of the reference frame termed System IIIw [80] renders the east-west pattern more symmetric and similar to that on Jupiter.
Observations of Saturnine southern hemisphere reported in [81] have revealed that, just like on Jupiter, its mean zonal velocity remains nearly time-independent outside the equatorial belt. In addition, also in similarity to Jupiter’s dynamics, eddies transfer momentum to eastward-going jets and remove momentum from their westward counterpart. On both planets, eddies are supplying the kinetic energy to the mean flow, i.e., the planets exhibit the inverse energy cascade. This cascade is terminated by a large-scale energy withdrawal due to the action of some large-scale drag. As elaborated in [61], the wave number associated with this drag on Saturn is about one half of that on Jupiter, and so the inverse cascade penetrates to wave numbers twice as small as those on Jupiter. As a result, in agreement with the tenets of the zonostrophic regime [26,61], the number of the zonal jets on Saturn is about one half of those on Jupiter, Saturnine total kinetic energy is about an order of magnitude larger than its Jupiter counterpart, and the velocity of its equatorial jet is about 4 times that of Jupiter. Fewer and broader zonal jets result in larger and more energetic storms on Saturn compared to Jupiter. However, while Jupiter’s storms are always present, storms on Saturn are intermittent. Similarly to Jupiter, many of Saturn’s vortices originate and propagate in close vicinity to its westward zonal jets. Although cloud structures on Jupiter and Saturn are similar, the cooler environment of Saturn (likely responsible for the smaller large-scale drag) causes its clouds to be seated deeper in its atmosphere.
Intense studies of Saturnine vortices and storms became possible with the emergence of satellite observations. Early evidence of its intermittent thunderstorms came from the Voyager flyby in 1980–1981. In 2004, the Cassini orbiter detected a series of storms at the narrow latitudinal band in the vicinity of 35 ∘ S known as the “Storm Alley” for its powerful lightning and thunderstorm activities [82]. Starting as localized bursts and cloud formations, the storms eventually develop into Dark Ovals. Similar dark spots were detected by Cassini in 2006 [83]. Most ovals resided in the shear zone, just to the south of the jet, and moved westward at speeds of about 25 m s−1. Other spots, detected several degrees to the south, were moving eastward at comparable speeds. They rotated counterclockwise (anticyclonic) and resembled ball bearings between conveyor belts while preserving the sense of rotation of the ambient shear flow. The westward- and eastward-moving vortices at adjacent latitudinal bands could interact and sometimes produced a merger or a near-merger, suddenly emitting bright material forming in the close-by area [82]. This system of vortices moving in opposite directions is quite different from the Jovian vortex street described in Section 4.1 in which the vortices are straddled on both sides of the same jet. The difference may be due to the more active role of the moist convection on Saturn as it injects large-scale vorticity at the cloud level [82].
A large, long-lived cyclonic vortex centered at 45 . 5 ∘ S was reported in [84]. This vortex was associated with a westward jet in the System IIIw coordinate frame. Observations and modeling efforts suggested that the vortex was sustained by the meridional shear of the zonal wind rather than the energy flux from the surrounding smaller-scale eddies.
Another large cyclonic vortex, located at 50 ∘ N and associated with a westward jet in the System IIIw frame, was reported in [85]. Between 2006 and 2010, this large typical Saturnine cyclone was surrounded by smaller-scale convective clouds. Eight smaller-scale convective storms erupted within the vortex during this period, the seventh one bringing significant disruption and the eighth one quenching it. The storms were quite similar to the storm observed at about the same latitude in the southern hemisphere and reported in [86]. The latter storm was also amalgamated with a westward jet, as well as a jet at 48 ∘ S if considered in the System IIIw coordinate frame. That jet exhibited phenomena similar to those in the Storm Alley, with anticyclonic vortices rolling in the anticyclonic shear zone to the south of the jet [82].
Saturn spotlights a train of vortices known as the String of Pearls (SoP). Observations on March 29, 2008 [87] showed the ‘pearls’ as a chain of 17 dark, featureless cyclonic spots occupying latitudes between, approximately, 32 . 5 ∘ N and 34 . 5 ∘ N and coinciding with a westward jet. The bright appearance of the SoPs has earned them the interpretation of being thermal radiation escape outlets from deep layers. The SoPs may be a precursor of the Great White Spots (GWS) [88], the largest observed vortex system on Saturn. As was shown in [35], the initial positions of the two storms coincided, and a new storm erupted from the SoPs. The SoPs was last detected on December 23, 2010, after which the new storm has filled the entire latitudinal belt and the SoPs became indistinguishable within it.
The GWSs appear in intervals of about 30 years whereas in the last 140 years, 6 cases were documented [88]. These giant storms occurred in the northern hemisphere at different latitudes: at the equatorial region, 15 ∘ S - 25 ∘ N; at mid-latitudes, 25 ∘ N - 47 ∘ N, and at subpolar latitudes, 48 ∘ N - 78 ∘ N. The heads, i.e., the leading bright spots of the storms, were found at 5 ∘ N, 12 ∘ N, 40 ∘ N, and 57 ∘ N. Aside from the near-equatorial storms, the other ones were located within the westward-propagating jets. Numerous studies converge on the idea that the onset stage of the GWS is driven by vigorous outbursts of moist convection [87,89].
Several weeks after formation of the GWS head, a chain of Dark Ovals (DOs) gradually formed in the storm’s tail. The ovals were centered at the latitude of 25 ∘ N and moved eastward at +65 ms − 1 . The SoPs moved westward, along the latitude 33 ∘ N, at -22.42 ms − 1 . At that time, the DOs and the SoPs coexisted while differing dynamically and morphologically. Their colors also had different appearances [87]. All DOs were extinguished by April 25.
As stated earlier, similar dark spots were detected in the southern hemisphere, around 35 ∘ S [82,83]. We note that most dark spots found on Saturn were previously located in anticyclonic shear zones. The spots in the vicinity of 25 ∘ N were formed in their cyclonic counterpart.

4.4. Saturn: Eddies or Zonons?

To ascertain whether or not Saturn’s vortices are congruent with zonons, we solve the eigenvalue problem (28a) - (28c) using the observed mean zonal velocity profile given in [68]. Our analysis extends between, approximately, the latitudes ± 60 ∘ . Since the planetary angular velocity in System IIIw differs from that in System III, it is important to verify the consistency of the eigenvalues and the RHWs’ phase speeds in both systems. For the System IIIw, we used the mean zonal velocity profile presented in [80]. Table 3 demonstrates that, in similarity to numerical simulations and computations for Jupiter, c R H W ( n ) = c i 0 for n = i . The values of c R H W ( n ) and c i 0 are mostly within 10% of each other in the range of i between 10 and 15 for both systems. For several values of i from that interval convergence in the System III was not achieved. The eigenfunctions in the System IIIw pointed to the same vortices as those found in the System III and so they are not shown.
To chose the wave number that may correspond to zonons, one needs to locate the wave number n at which a RHW has maximum energy. In principle, this wave number could be identified by scrutinizing the residual spectrum. For Saturn, however, this spectrum has not been established yet, and so the zonal spectrum computed in [61] was used as its surrogate. The zonal spectrum indicates that the mode n = 15 appears most likely candidate to contain the maximum energy. The corresponding eigenfunction, Φ 15 ( 1 ) ( θ ) , is shown in Figure 9. Evidently, its extrema provide a reasonably accurate representation of the solitary waves’ positions in the entire range of latitudes considered in this investigation.
In analogy to Jupiter, vortices on Saturn are usually coming in trains although their structure may differ from that on Jupiter as in addition to the Charney-Stern instability, the moist convection processes are playing significant role in vortex formation and maintenance. Our analysis indicates, however, that similarly to Jupiter, the nonlinear dynamical processes underscore the physics of vortex evolution on Saturn and so its vortices and their trains can also be characterized as `zonon streets’.
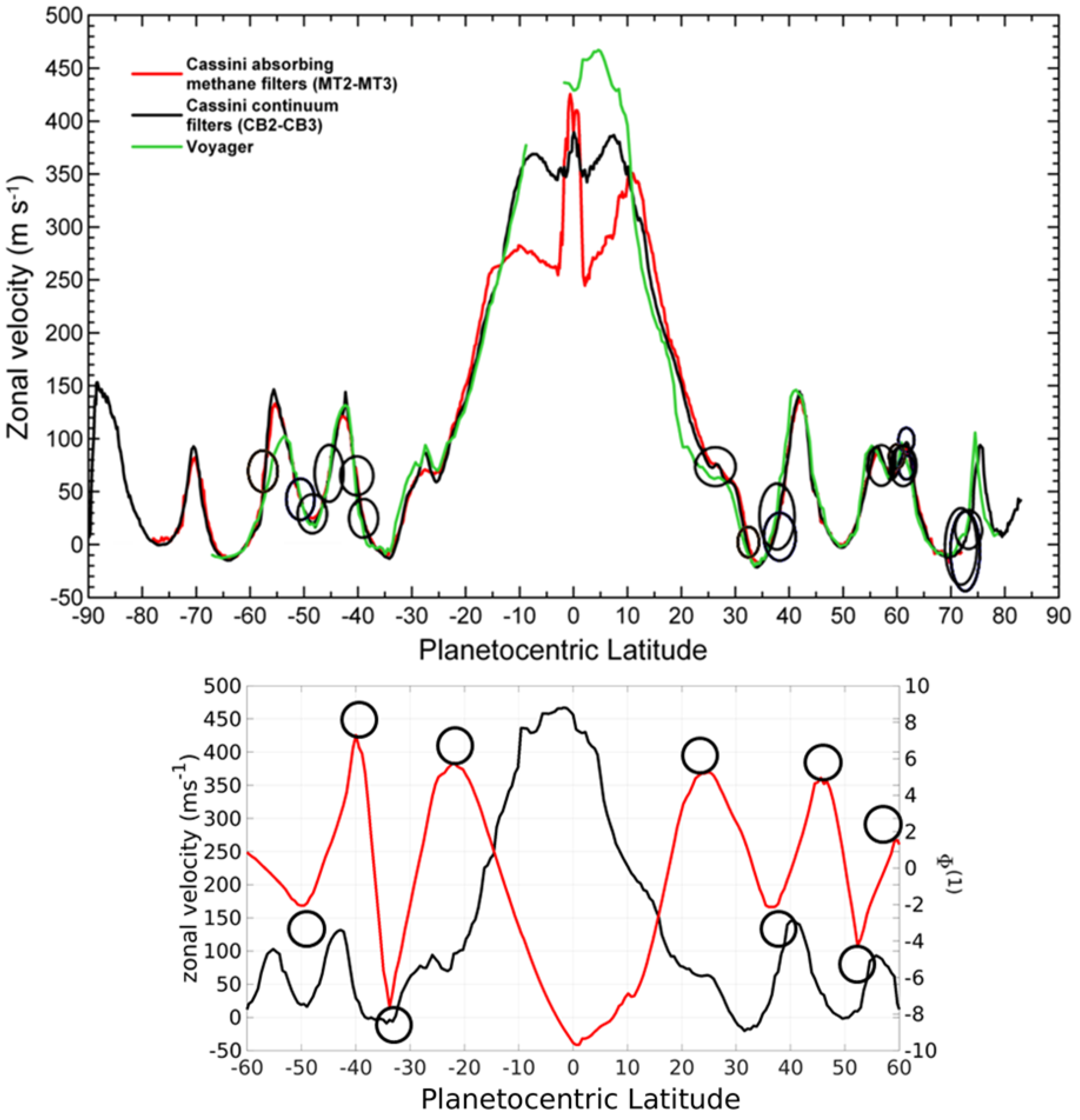
Preprints 105049 g009
Figure 9. Top panel: Three Saturn’s zonal wind profiles for two different epochs superimposed on each other. They reflect velocity fluctuations over the years [90]. The first epoch [68] is represented by the data for the upper cloud level was collected by Voyager in 1980-1981. The second epoch [91] embodies the data collected by Cassini spacecraft in 2004-2009 and encompassing the upper cloud level (CB-data) and upper haze (MT-data). There is a notable variability in the equatorial region compounded with the vertical wind shear likely coupled with the semiannual oscillation (SAO) [92,93] in the temperature and wind fields that occur in the stratosphere in the latitudinal belt ± 15 ∘ and affect Saturn’s equatorial dynamics [90]. This belt was not considered in the analysis. The observed vortices are marked by ovals drawn by Agustin Sánchez-Lavega. Most of the vortices are described in Section 4.3. Bottom panel: Saturn’s zonal velocity profile from the Voyager data [68] (black line), the eigenfunction Φ 15 ( 1 ) ( θ ) (red line), and estimated latitudinal locations of eddies, marked by small circles placed at the extrema of the eigenfunction.
Figure 9. Top panel: Three Saturn’s zonal wind profiles for two different epochs superimposed on each other. They reflect velocity fluctuations over the years [90]. The first epoch [68] is represented by the data for the upper cloud level was collected by Voyager in 1980-1981. The second epoch [91] embodies the data collected by Cassini spacecraft in 2004-2009 and encompassing the upper cloud level (CB-data) and upper haze (MT-data). There is a notable variability in the equatorial region compounded with the vertical wind shear likely coupled with the semiannual oscillation (SAO) [92,93] in the temperature and wind fields that occur in the stratosphere in the latitudinal belt ± 15 ∘ and affect Saturn’s equatorial dynamics [90]. This belt was not considered in the analysis. The observed vortices are marked by ovals drawn by Agustin Sánchez-Lavega. Most of the vortices are described in Section 4.3. Bottom panel: Saturn’s zonal velocity profile from the Voyager data [68] (black line), the eigenfunction Φ 15 ( 1 ) ( θ ) (red line), and estimated latitudinal locations of eddies, marked by small circles placed at the extrema of the eigenfunction.
Preprints 105049 g009

5. Discussion and Conclusions

This study outlines the connection between zonons and solitary Rossby-Haurwitz waves in the regime of zonostrophic turbulence. Zonons are ’slave’ waves excited by RHWs in other wave modes via non-linear interactions. One can also view zonons as a product of RHWs ringing in other wave modes. Zonons’ dispersion relation is different from that of the RHWs. They form long-lived, non-dispersive wave packets located between zonal jets that guide them around planets while replenishing their energy via shear instabilities. In the physical space, zonons form westward propagating coherent eddies whose zonal velocity is equal to the phase speed of the most energetic RHW.
Despite the dispersive action of the shear, the wave packets are being coagulated by the nonlinearity and preserve their identity. The balance between the effects of the shear and nonlinearity can be quantified within the KdV equation. The constructive interference between the effects of the shear and nonlinearity is typical of solitary waves [see e.g., [16] and so one infers that zonons are solitary Rossby-Haurwitz waves.
In the preceding study of zonons in [11], the solitary wave framework was established using the KdV equation in the Cartesian coordinate system. This framework was not validated against data, however. The present study goes farther and develops the KdV foundation for zonons in a spherical coordinate system. The derivations are performed in the Mercator projection that allows for smooth two-way transitions of the governing equations between spectral and physical space representations. This approach leads to a boundary value problem whose nontrivial solutions yield eigenvalues and eigenfunctions. The eigenvalues correspond to zonal velocities of zonons, while the respective eigenfunctions disclose their latitudinal locations.
This framework was tested and validated against the results of direct numerical simulations of two-dimensional turbulence on the surface of a rotating sphere. The main outcome of this initial study was that large coherent eddies emerging in the regime of zonostrophic turbulence, or zonons, can indeed be identified with the solitary Rossby-Haurwitz waves bound to westward zonal jets and propagating inside the rails formed by the opposing jets.
The KdV framework was then applied to probe coherent vortices on Jupiter and Saturn, the two giant planets that boast zonostrophic regime. These comparisons involved observed mean zonal winds and available kinetic energy spectra. Guided by the results deduced from direct numerical simulations, it was established that the zonal velocities of large coherent eddies on the planets are well represented by the eigenvalues of the boundary value problem and their latitudinal locations are disclosed by the extrema of the corresponding eigenfunctions.
One of the hallmarks of this theory is that much information on the planetary eddies can be deduced from the zonal velocity profile which is much easier to establish than other characteristics such as, for instance, the residual energy spectrum. Another hallmark of the theory is in the offering an analytical framework providing latitudinal locations of nearly all major eddies on a rotating planet given that its atmosphere obeys the zonostrophic regime. This framework may apply not only to our neighboring giant planets but also some of their satellites as the simulations presented in [94] point to the possibility that the zonostrophic regime may dominate the circulation of subsurface oceans of Ganymede, Europa, Enceladus, and Titan. The KdV frame may apply to eddies on some exoplanets as well. The finding that zonons may include the Great Red Spot elevates the possibility that they may also be relevant to great spots on other planets [95,96] provided that those obey the zonostrophic regime.
These results may also be applicable in the terrestrial atmospheric environments where the zonostrophic regime is marginal. In Section 1, for example, it was noted that the solitary Rossby waves may help to understand genesis and early evolution of the proto-vortices developing into tropical storms. Moreover, zonons may be helpful in clarifying the role of eddies and spirals in oceanic circulation [97,98,99,100] given that the oceanic turbulence is marginally zonostrophic [6].

Acknowledgments

Tov Elperin, who untimely passed away, played an important role in initial advising of Nimrod Cohen in his doctoral dissertation. Roger H. Grimshaw was instrumental in the development of the KdV framework in spherical geometry. Digitized profiles of the mean zonal velocities on Jupiter and Saturn used in Section 4 were made available to us by Agustin Sánchez-Lavega and Peter Read; they also provided editorial assistance. This study was supported by the Israel Science Foundation governed by Israeli Academy of Sciences (Grant No. 1037/11 and Grant No. 1210/15).

References

  1. Salmon, R.; Pizzo, N. Two-Dimensional Flow on the Sphere. MDPI Atmosphere 2023, 14, 747. [CrossRef]
  2. Herring, J.; Orszag, S.; Kraichnan, R.; Fox, D. Decay of two-dimensional homogeneous turbulence. J. Fluid Mech. 1974, 66, 417–444.
  3. Herring, J.R. On the Statistical Theory of Two-Dimensional Topographic Turbulence. J. Atmos. Sci. 1977, 34, 1731–1750.
  4. Herring, J.R. Statistical theory of quasi-geostrophic turbulence. J. Atmos. Sci. 1980, 37, 969–977.
  5. Galperin, B.; Sukoriansky, S. Zonostrophic turbulence. Phys. Scr. 2008, T132. [CrossRef]
  6. Galperin, B.; Sukoriansky, S.; Young, R.M.B.; Chemke, R.; Kaspi, Y.; Read, P.L.; Dikovskaya, N. Barotropic and Zonostrophic Turbulence. In Zonal Jets: Phenomenology, Genesis, and Physics; Galperin, B.; Read, P.L., Eds.; Cambridge University Press, 2019; pp. 220–237. [CrossRef]
  7. Chekhlov, A.; Orszag, S.; Sukoriansky, S.; Galperin, B.; Staroselsky, I. The effect of small-scale forcing on large-scale structures in two-dimensional flows. Physica D 1996, 98, 321–334.
  8. Huang, H.P.; Robinson, W. Two-dimensional turbulence and persistent zonal jets in a global barotropic model. J. Atmos. Sci. 1998, 55, 611–632.
  9. Galperin, B.; Read, P.L., Eds. Zonal Jets: Phenomenology, Genesis, and Physics; Cambridge University Press, 2019; p. 504. [CrossRef]
  10. Sukoriansky, S.; Dikovskaya, N.; Galperin, B. Nonlinear waves in zonostrophic turbulence. Phys. Rev. Lett. 2008, 101.
  11. Sukoriansky, S.; Dikovskaya, N.; Grimshaw, R.; Galperin, B. Rossby waves and zonons in zonostrophic turbulence. In AIP Conf. Proc.; American Institute of Physics, 2012; Vol. 1439, pp. 111–122. [CrossRef]
  12. Péronne, E.; Chuecos, N.; Thevenard, L.; Perrin, B. Acoustic solitons: A robust tool to investigate the generation and detection of ultrafast acoustic waves. Phys. Rev. B 2017, 95. [CrossRef]
  13. Sakazaki, T.; Hamilton, K. An Array of Ringing Global Free Modes Discovered in Tropical Surface Pressure Data. J. Atmos. Sci. 2020, 77, 2519–2539. [CrossRef]
  14. Long, R. Solitary waves in the westerlies. J. Atmos. Sci. 1964, 21, 197–200.
  15. Benney, D. Long nonlinear waves in fluid flows. J. Math. Phys. 1966, 45, 52–63.
  16. Redekopp, L. On the theory of solitary Rossby waves. J. Fluid Mech. 1977, 82, 725–745.
  17. Redekopp, L.; Weidman, P. Solitary Rossby waves in zonal shear flows and their interactions. J. Atmos. Sci. 1978, 35, 790–804.
  18. Wadati, M. The modified Korteweg–de Vries equation. J. Phys. Soc. Japan 1973, 34, 1289–1296.
  19. Boyd, J. Equatorial soliton waves, Part 1: Rossby solitons. J. Phys. Oceanogr. 1980, 10, 1699–1717.
  20. Boyd, J. The nonlinear equatorial Kelvin wave. J. Phys. Oceanogr. 1980, 10, 1–11.
  21. Espa, S.; Cabanes, S.; King, G.P.; Nitto, G.D.; Galperin, B. Eddy–wave duality in a rotating flow. Phys. Fluids 2020, 32. [CrossRef]
  22. Galperin, B.; Sukoriansky, S.; Espa, S.; Lacorata, G.; Dikovskaya, N.; Hoemann, J. Turbulence, Diffusion and Mixing Barriers in Flows with Zonal Jets. In Zonal Jets: Phenomenology, Genesis, and Physics; Galperin, B.; Read, P.L., Eds.; Cambridge University Press, 2019; pp. 450–460. [CrossRef]
  23. Limaye, S.S. Jupiter: New estimates of the mean zonal flow at the cloud level. Icarus 1986:, 65, 335–352.
  24. Humphreys, T.; Marcus, P.S. Vortex street dynamics: The selection mechanism for the areas and locations of Jupiter’s vortices. J. Atmos. Sci. 2007, 64, 1318–1333.
  25. Dritschel, G.; McIntyre, M.E. Multiple jets as PV staircases: The Phillips effect and the resilience of eddy-transport barriers. J. Atmos. Sci. 2008, 65, 855–874.
  26. Galperin, B.; Young, R.; Sukoriansky, S.; Dikovskaya, N.; Read, P.; Lancaster, A.; Armstrong, D. Cassini observations reveal a regime of zonostrophic macroturbulence on Jupiter. Icarus 2014, 229, 295–320. [CrossRef]
  27. Alexakis, A.; Biferale, L. Cascades and transitions in turbulent flows. Phys. Reports 2018, 767, 1–101.
  28. Ingersoll, A.P. Cassini exploration of the planet Saturn: A comprehensive review. Space Sci. Rev. 2020, 216. [CrossRef]
  29. Trammell, J.; Li, L.; Jiang, X.; Smith, M.; Hörst, S.; Vasavada, A. The global vortex analysis of Jupiter and Saturn based on Cassini imaging science subsystem. Icarus 2014, 242, 122–129.
  30. Li, L.; Ingersoll, A.P.; Vasavada, A.R.; Porco, C.C.; Del Genio, A.D.; Ewald, S.P. Life cycles of spots on Jupiter from Cassini images. Icarus 2004, 172, 9–23.
  31. Legarreta, J.; Sánchez-Lavega, A. Vertical structure of Jupiter’s troposphere from nonlinear simulations of long-lived vortices. Icarus 2008, 196, 184–201.
  32. Cosentino, G.; Simon, A.; Morales-Juberias, R.; Sayanagi, K.M. Observations and numerical modeling of the Jovian Ribbon. Astrophys. J. 2015, 810, L10.
  33. Ingersoll, A.P.; Beebe, R.F.; Mitchell, J.L.; Garneau, G.W.; Yagi, G.M.; Müller, J.P. Interaction of eddies and mean zonal flow on Jupiter as inferred from Voyager 1 and 2 images. J. Geophys. Res. 1981, A86, 8733–8743.
  34. Vasavada, A.R.; Hörst, S.M.; Kennedy, M.R.; Ingersoll, A.P.; Porco, C.C.; Del Genio, A.D.; West, R.A. Cassini imaging of Saturn: Southern hemisphere winds and vortices. J. Geophys. Res. 2006, 111, E05004.
  35. Sayanagi, K.M.; Dyudina, U.A.; Ewald, S.P.; Muro, G.D.; Ingersoll, A.P. Cassini ISS observation of Saturn’s string of pearls. Icarus 2014, 229, 170–180.
  36. Qiao, L.; Weisberg, R.H. Tropical instability wave kinematics: Observations from the tropical instability wave experiment. J. Geophys. Res.: Oceans 1995, 100, 8677–8693. [CrossRef]
  37. Chelton, D.B.; Wentz, F.J.; Gentemann, C.L.; de Szoeke, R.A.; Schla, M.G. Satellite microwave SST observations of transequatorial tropical instability waves. Geophys. Res. Lett. 2000, 27, 1239–1242. [CrossRef]
  38. Contreras, F. Long-term observations of tropical instability waves. J. Phys. Oceanogr. 2002, 32, 2715–2722.
  39. Galperin, B.; Hoemann, J.; Espa, S.; DiNitto, G.; Lacorata, G. Anisotropic macroturbulence and diffusion associated with a westward zonal jet - from laboratory to planetary atmospheres and oceans. Phys. Rev. E 2016, 94, 063102.
  40. Galperin, B.; Hoemann, J.; Espa, S.; Di Nitto, G. Anisotropic turbulence and Rossby waves in an easterly jet - An experimental study. Geophys. Res. Lett. 2014, 41, 6237–6243. [CrossRef]
  41. Thorpe, S. The Turbulent Ocean; Cambridge University Press, 2005.
  42. Cabanes, S.; Espa, S.; Galperin, B.; Young, R.M.B.; Read, P.L. Revealing the intensity of turbulent energy transfer in planetary atmospheres. Geophys. Res. Lett. 2020, 47. [CrossRef]
  43. Lenouo, A.; Nkankam, F.K. Solitary Rossby Waves in the Lower Tropical Troposphere. ISRN Atmos. Sci. 2013, 2013. [CrossRef]
  44. Dunkerton, T.J.; Montgomery, M.T.; Wang, Z. Tropical cyclogenesis in a tropical wave critical layer: easterly waves. Atmos. Chem. Phys. 2009, 9, 5587–5646. [CrossRef]
  45. Maxworthy, T.; Redekopp, L. A solitary wave theory of the Great Red Spot and other features in the Jovian atmosphere. Icarus 1976, 29, 261–271.
  46. Marcus, P. Jupiter’s Great Red Spot and other vortices. Annu. Rev. Astron. & Astrophys. 1993, 31, 523–573.
  47. Boyd, J.P. Chapter 6. Planetary solitary waves. In WIT Transactions on State of the Art in Science and Engineering; WIT Press, 2007; Vol. 9. [CrossRef]
  48. Holton, J. Dynamic Meteorology, 4th ed.; Elsevier, 2004.
  49. Sánchez-Lavega, A. An Introduction to Planetary Atmospheres; CRC Press, 2011.
  50. Zaqarashvili, T.V.; Albekioni, M.; Ballester, J.L.; Bekki, Y.; Biancofiore, L.; Birch, A.C.; Dikpati, M.; Gizon, L.; Gurgenashvili, E.; Heifetz, E.; Lanza, A.F.; McIntosh, S.W.; Ofman, L.; Oliver, R.; Proxauf, B.; Umurhan, O.M.; Yellin-Bergovoy, R. Rossby Waves in Astrophysics. Space Sci. Rev. 2021, 217:15, 1–93. [CrossRef]
  51. Pedlosky, J. Geophysical Fluid Dynamics, 2nd ed.; Springer–Verlag, 1987.
  52. Huang, H.P.; Galperin, B.; Sukoriansky, S. Anisotropic spectra in two-dimensional turbulence on the surface of a rotating sphere. Phys. Fluids 2001, 13, 225–240.
  53. Vallis, G. Atmospheric and Oceanic Fluid Dynamics; Cambridge University Press, 2006.
  54. Sukoriansky, S.; Dikovskaya, N.; Galperin, B. On the `arrest’ of the inverse energy cascade and the Rhines scale. J. Atmos. Sci. 2007, 64, 3312–3327.
  55. Boer, G. Homogeneous and isotropic turbulence on the sphere. J. Atmos. Sci. 1983, 40, 154–163.
  56. Boer, G.; Shepherd, T. Large-scale two-dimensional turbulence in the atmosphere. J. Atmos. Sci. 1983, 40, 164–184.
  57. Sukoriansky, S.; Galperin, B.; Dikovskaya, N. Universal spectrum of two-dimensional turbulence on a rotating sphere and some basic features of atmospheric circulation on giant planets. Phys. Rev. Lett. 2002, 89, 124501.
  58. Kraichnan, R. Inertial-range transfer in two- and three-dimensional turbulence. J. Fluid Mech. 1971, 47, 525–535.
  59. Galperin, B.; Sukoriansky, S.; Dikovskaya, N.; Read, P.; Yamazaki, Y.; Wordsworth, R. Anisotropic turbulence and zonal jets in rotating flows with a β-effect. Nonlinear Proc. Geophys. 2006, 13, 83–98.
  60. Lemasquerier, D.; Favier, B.; Le Bars, M. Zonal jets experiments in the gas giants’ zonostrophic regime. Icarus 2023, 390, 115292. [CrossRef]
  61. Galperin, B.; Sukoriansky, S.; Huang, H.P. Universal n-5 spectrum of zonal flows on giant planets. Phys. Fluids 2001, 13, 1545–1548.
  62. Li, L.; Ingersoll, A.; Huang, X. Interaction of moist convection with zonal jets on Jupiter and Saturn. Icarus 2006, 180, 113–123.
  63. Polito, S.; Sato, O.T. Do eddies ride on Rossby waves? J. Geophys. Res. Oceans 2015, 120, 5417–5435. [CrossRef]
  64. Daners, D. The Mercator and Stereographic Projections, and Many in Between. The Amer. Math. Monthly 2012, 119, 199–210. [CrossRef]
  65. Gudermannian Function. In CRC Standard Mathematical Tables and Formulae, 31 ed.; Zwillinger, D., Ed.; CRC Press: Boca Raton, FL, 1995; pp. 530–532.
  66. Crighton, D. Applications of KdV. Acta Applic. Math. 1995, 39, 39–67.
  67. García-Melendo, E.; Sánchez-Lavega, A. A study of the stability of Jovian zonal winds from HST Images: 1995-2000. Icarus 2001, 152, 316–330.
  68. Sánchez-Lavega, A.; Rojas, J.F.; Sada, P.V. Saturn’s zonal winds at cloud level. Icarus 2000, 147, 405–420. [CrossRef]
  69. Morales-Juberías, R.; Simon, A.A.; Cosentino, R.G. Analysis of the long-term drift rates and oscillations of Jupiter’s largest vortices. Icarus 2022, 372, 114732. [CrossRef]
  70. Marcus, P.S. Prediction of a global climate change on Jupiter. Nature 2004, 428, 828–831.
  71. Rogers, J.H. The giant planet Jupiter; Vol. 6, Cambridge University Press, 1995.
  72. Sánchez-Lavega, A.; Rojas, J.F.; Hueso, R.; Lecacheux, J.; Colas, F.; Acarreta, J.R.; Miyazaki, I.; Parker, D. Interaction of Jovian white ovals BC and DE in 1998 from Earth-based observations in the visual range. Icarus 1999, 142, 116–124. [CrossRef]
  73. Sánchez-Lavega, A.; Orton, G.S.; Morales, R.; Lecacheux, J.; Colas, F.; Fisher, B.; Fukumura-Sawada, P.; Golisch, W.; Griep, D.; Kaminski, C.; Baines, K.; Rages, K.; West, R. The merger of two giant anticyclones in the atmosphere of Jupiter. Icarus 2001, 149, 491–495. [CrossRef]
  74. Barrado-Izagirre, N.; Legarreta, J.; Sánchez-Lavega, A.; Pérez-Hoyos, S.; Hueso, R.; Iñurrigarro, P.; Rojas, J.F.; Mendikoa, I.; Ordonez-Etxeberria, I.; the IOPW Team. Jupiter’s third largest and longest-lived oval: Color changes and dynamics. Icarus 2021, 361, 114394. [CrossRef]
  75. Hueso, R.; Sánchez-Lavega, A.; Fouchet, T.; de Pater, I.; nano, A.A.; Fletcher, L.N.; Wong, M.H.; Rodríguez-Ovalle, P.; Sromovsky, L.A.; Fry, P.M.; Orton, G.S.; Guerlet, S.; Irwin, P.G.J.; Lellouch, E.; Harkett, J.; de Kleer, K.; Melin, H.; Hue, V.; Simon, A.A.; Luszcz-Cook, S.; Sayanagi, K.M. An intense narrow equatorial jet in Jupiter’s lower stratosphere observed by JWST. Nat. Astron. 2023. [CrossRef]
  76. Aurnou, J.M.; Heimpel, M.H. Zonal jets in rotating convection with mixed mechanical boundary conditions. Icarus 2004, 169, 492–498. [CrossRef]
  77. Sayanagi, K.M.; Showman, A.P. Effects of a large convective storm on Saturn’s equatorial jet. Icarus 2007, 187, 520–539. [CrossRef]
  78. Showman, A.P. Numerical simulations of forced shallow-water turbulence: Effects of moist convection on the large-scale circulation of Jupiter and Saturn. J. Atmos. Sci. 2007, 64, 3132–3157. [CrossRef]
  79. Palotai, C.; Brueshaber, S.; Sankar, R.; Sayanagi, K. Moist convection in the giant planet atmospheres. Remote Sens. 2023, 15, 219. [CrossRef]
  80. Read, P.L.; Dowling, T.E.; Schubert, G. Saturn’s rotation period from its atmospheric planetary-wave configuration. Nature 2009, 460, 608–610. [CrossRef]
  81. Del Genio, A.D.; Barbara, J.M.; Ferrier, J.; Ingersoll, A.P.; West, R.A.; Vasavada, A.R.; Spitale, J.; Porco, C.C. Saturn eddy momentum fluxes and convection: First estimates from Cassini images. Icarus 2007, 189, 479–492.
  82. Porco, C.C.; Baker, E.; Barbara, J.; Beurle, K.; Brahic, A.; Burns, J.A.; Charnoz, S.; Cooper, N.; Dawson, D.D.; Del Genio, A.D.; Denk, T.; Dones, L.; Dyudina, U.; Evans, M.W.; Giese, B.; Grazier, K.; Helfenstein, P.; Ingersoll, A.P.; Jacobson, R.A.; Johnson, T.V.; McEwen, A.; Murray, C.D.; Neukum, G.; Owen, W.M.; Perry, J.; Roatsch, T.; Spitale, J.; Squyres, S.; Thomas, P.; Tiscareno, M.; Turtle, E.; Vasavada, A.R.; Veverka, J.; Wagner, R.; West, R. Cassini imaging science: Initial results on Saturn’s atmosphere. Science 2005, 307, 1243–1247.
  83. Dyudina, U.A.; Ingersoll, A.P.; Ewald, S.P.; Porco, C.C.; Fischer, G.; Kurth, W.; Desch, M.; Del Genio, A.; Barbara, J.; Ferrier, J. Lightning storms on Saturn observed by Cassini ISS and RPWS during 2004-2006. Icarus 2007, 190, 545–555. [CrossRef]
  84. del Río-Gaztelurrutia, T.; Legarreta, J.; Hueso, R.; Pérez-Hoyos, S.; Sánchez-Lavega, A. A long-lived cyclone in Saturn’s atmosphere: Observations and models. Icarus 2010, 209, 665–681. [CrossRef]
  85. Gunnarson, J.L.; Sayanagi, K.M.; Fischer, G.; Barry, T.; Wesley, A.; Dyudina, U.A.; Ewald, S.P.; Ingersoll, A.P. Multiple convective storms within a single cyclone on Saturn. Icarus 2023, 389, 115228.
  86. Sánchez-Lavega, A.; Lecacheux, J.; Gomez, J.M.; Colas, F.; Laques, P.; Noll, K.; Gilmore, D.; Miyazaki, I.; Parker, D. Large-Scale Storms in Saturn’s Atmosphere During 1994. Science 1996, 271, 631–634, [https://www.science.org/doi/pdf/10.1126/science.271.5249.631]. [CrossRef]
  87. Sayanagi, K.M.; Dyudina, U.A.; Ewald, S.P.; Fischer, G.; Ingersoll, A.P.; Kurth, W.S.; Muro, G.D.; Porco, C.C.; West, R.A. Dynamics of Saturn’s great storm of 2010–2011 from Cassini ISS and RPWS. Icarus 2013, 223, 460–478. [CrossRef]
  88. García-Melendo, E.; Sánchez-Lavega, A. Shallow water simulations of Saturn’s giant storms at different latitudes. Icarus 2017, 286, 241–260.
  89. Sánchez-Lavega, A. Saturn’s Great White Spots. Chaos 1994, 4, 341–353. [CrossRef]
  90. Sánchez-Lavega, A.; García-Melendo, E.; Pérez-Hoyos, S.; Hueso, R.; Wong, M.H.; Simon, A.; Sanz-Requena, J.F.; Antuñano, A.; Barrado-Izagirre, N.; Garate-Lopez, I.; Rojas, J.F.; Del Río-Gaztelurrutia, T.; Gómez-Forrellad, J.M.; de Pater, I.; Li, L.; Barry, T. An enduring rapidly moving storm as a guide to Saturn’s Equatorial jet’s complex structure. Nat. Commun. 2016. [CrossRef]
  91. García-Melendo, E.; Pérez-Hoyos, S.; Sánchez-Lavega, A.; R., H. Saturn’s zonal wind profile in 2004 - 2009 from Cassini ISS images and its long-term variability. Icarus 2011, 215, 62–74.
  92. Orton, G.S.; Yanamandra-Fisher, P.A.; Fisher, B.M.; Friedson, A.J.; Parrish, P.D.; Nelson, J.F.; Bauermeister, A.S.; Fletcher, L.; Gezari, D.Y.; Varosi, F.; Tokunaga, A.T.; Caldwell, J.; Baines, K.H.; Hora, J.L.; Ressler, M.E.; Fujiyoshi, T.; Fuse, T.; Hagopian, H.; Martin, T.Z.; Bergstralh, J.T.; Howett, C.; Hoffmann, W.F.; Deutsch, L.K.; Cleve, J.E.V.; Noe, E.; Adams, J.D.; Kassis, M.; Tollestrup, E. Semi-annual oscillations in Saturn’s low-latitude stratospheric temperatures. Nature 2008, 453, 197–199. [CrossRef]
  93. Fouchet, T.; Guerlet, S.; Strobel, D.F.; Simon-Miller, A.A.; Bézard, B.; Flasar, F.M. An equatorial oscillation in Saturn’s middle atmosphere. Nature 2008, 453, 200–202. [CrossRef]
  94. Cabanes, S.; Gastine, T.; Fournier, A. Zonostrophic turbulence in the subsurface oceans of the Jovian and Saturnian moons. Icarus 2024, 415, 116047. [CrossRef]
  95. Kundt, W.; Lüttgens, G. Rings around planets, atmospheric super-rotation, and their great spots. Astrophys. Space Sci. 1998, 257, 33–47.
  96. Imamura, T.; Mitchell, J.; Lebonnois, S.; Kaspi, Y.; Showman, A.P.; Korablev, O. Superrotation in Planetary Atmospheres. Space Sci. Rev. 2020, 216. [CrossRef]
  97. Chelton, D.; Schlax, M.; Samelson, R.; deSzoeke, R. Global observation of large oceanic eddies. Geophys. Res. Lett. 2007, 34.
  98. Chelton, D.; Schlax, M.; Samelson, R. Global observations of nonlinear mesoscale eddies. Progr. Oceanogr. 2011, 91, 167–216.
  99. Early, J.; Samelson, R.; Chelton, D. The evolution and propagation of quasigeostrophic ocean eddies. J. Phys. Oceanogr. 2011, 41, 1535–1555.
  100. Wunsch, C. A time-average ocean: Thermal wind and flow spirals. Progress in Oceanography 2024, 221, 103206. [CrossRef]
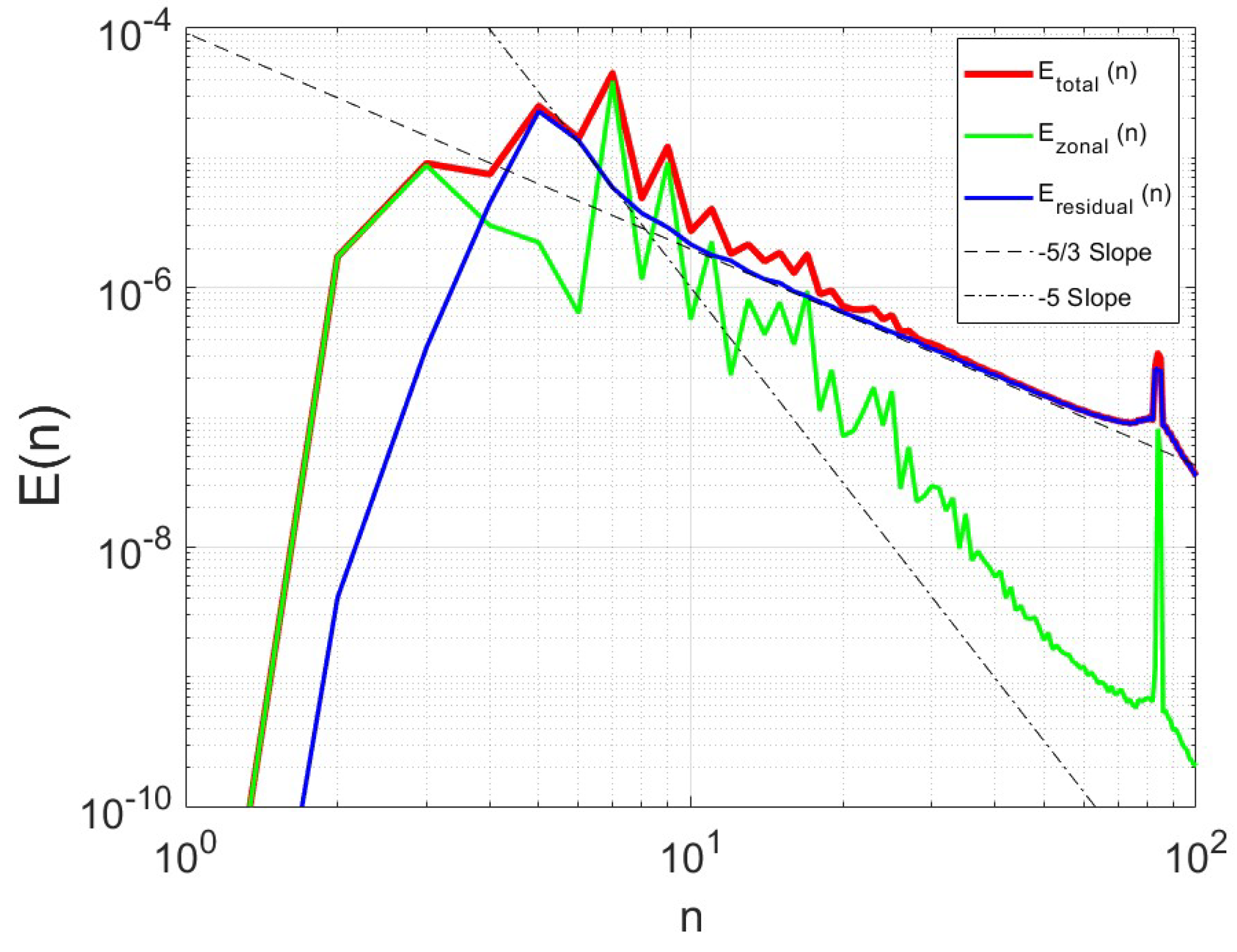
Preprints 105049 g001
Figure 1. The zonal, E Z ( n ) (green line), residual, E R ( n ) (blue line), and total, E ( n ) (red line) kinetic energy spectra obtained in numerical simulations of 2D turbulence on the surface of a rotating sphere in the zonostrophic regime ( R β = 2 . 65 ).
Figure 1. The zonal, E Z ( n ) (green line), residual, E R ( n ) (blue line), and total, E ( n ) (red line) kinetic energy spectra obtained in numerical simulations of 2D turbulence on the surface of a rotating sphere in the zonostrophic regime ( R β = 2 . 65 ).
Preprints 105049 g001
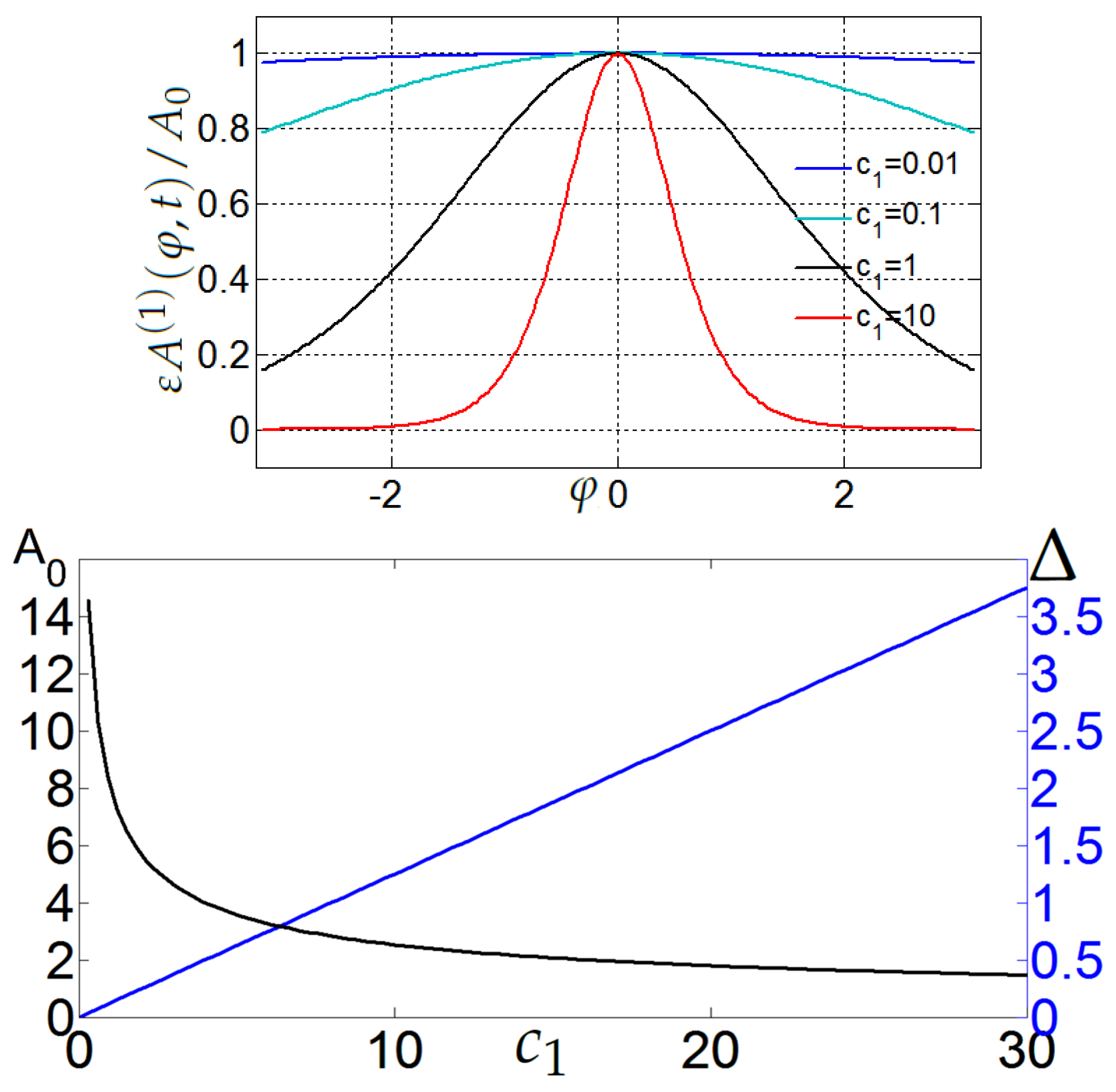
Preprints 105049 g002
Figure 2. Top panel: normalized soliton solution ε A ( 1 ) ( φ , t ) / A 0 in the propagation direction for different values of c 1 at t = 0 . The values of other parameters are: ε = 0 . 01 , c 0 = − 0 . 14 , and δ = 0 . 01 . Bottom panel: soliton’s amplitude, A 0 , (solid black line) and width, Δ , (solid blue line) as functions of c 1 .
Figure 2. Top panel: normalized soliton solution ε A ( 1 ) ( φ , t ) / A 0 in the propagation direction for different values of c 1 at t = 0 . The values of other parameters are: ε = 0 . 01 , c 0 = − 0 . 14 , and δ = 0 . 01 . Bottom panel: soliton’s amplitude, A 0 , (solid black line) and width, Δ , (solid blue line) as functions of c 1 .
Preprints 105049 g002
Preprints 105049 g003
Figure 3. The first 11 normalized eigenfunctions, Φ i ( 1 ) ( θ ) / Φ i ( 1 ) ( θ = 0 ) , shown from left to right and from top to bottom, from top left (i = 1) to bottom left (i = 11) corners.
Figure 3. The first 11 normalized eigenfunctions, Φ i ( 1 ) ( θ ) / Φ i ( 1 ) ( θ = 0 ) , shown from left to right and from top to bottom, from top left (i = 1) to bottom left (i = 11) corners.
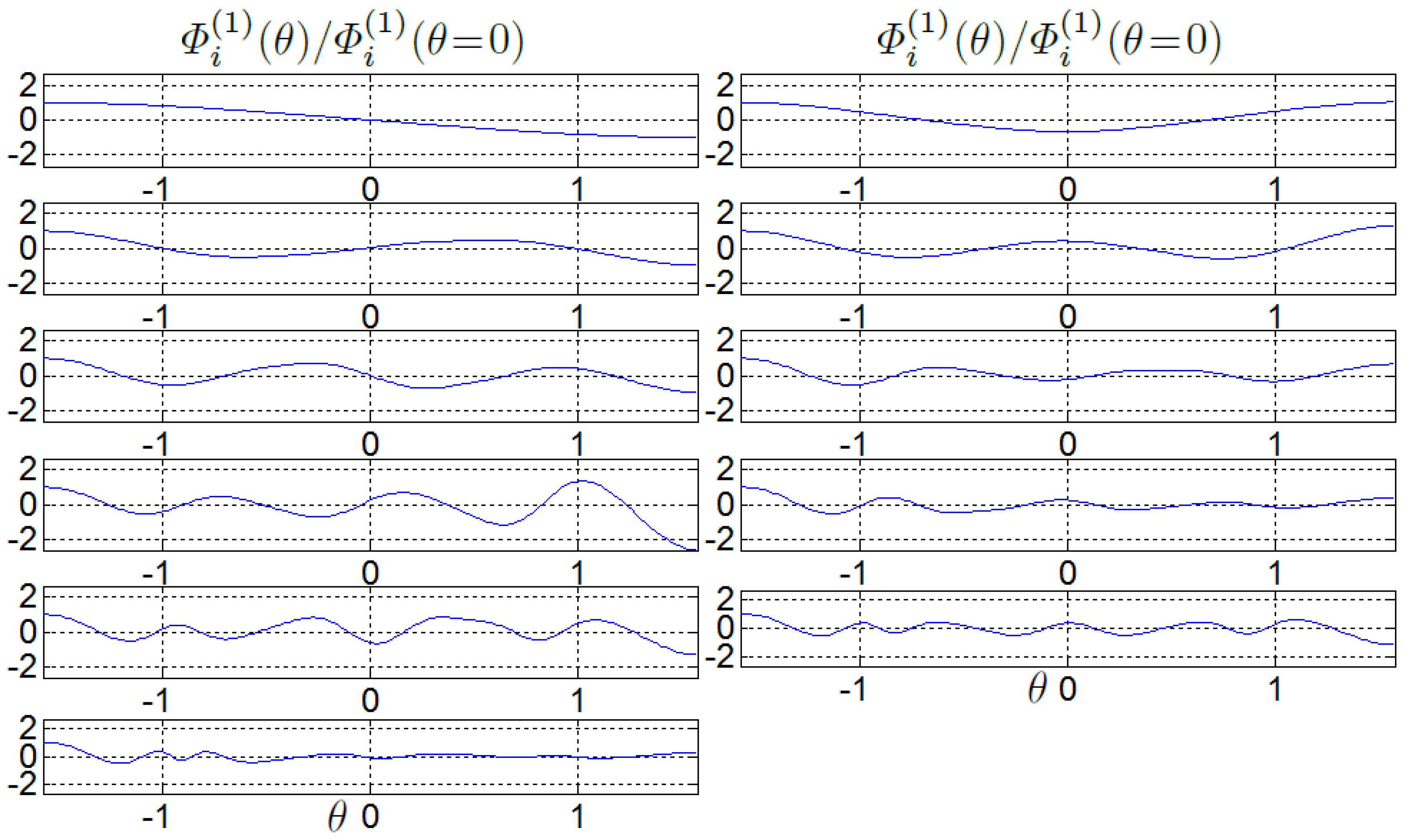
Preprints 105049 g003
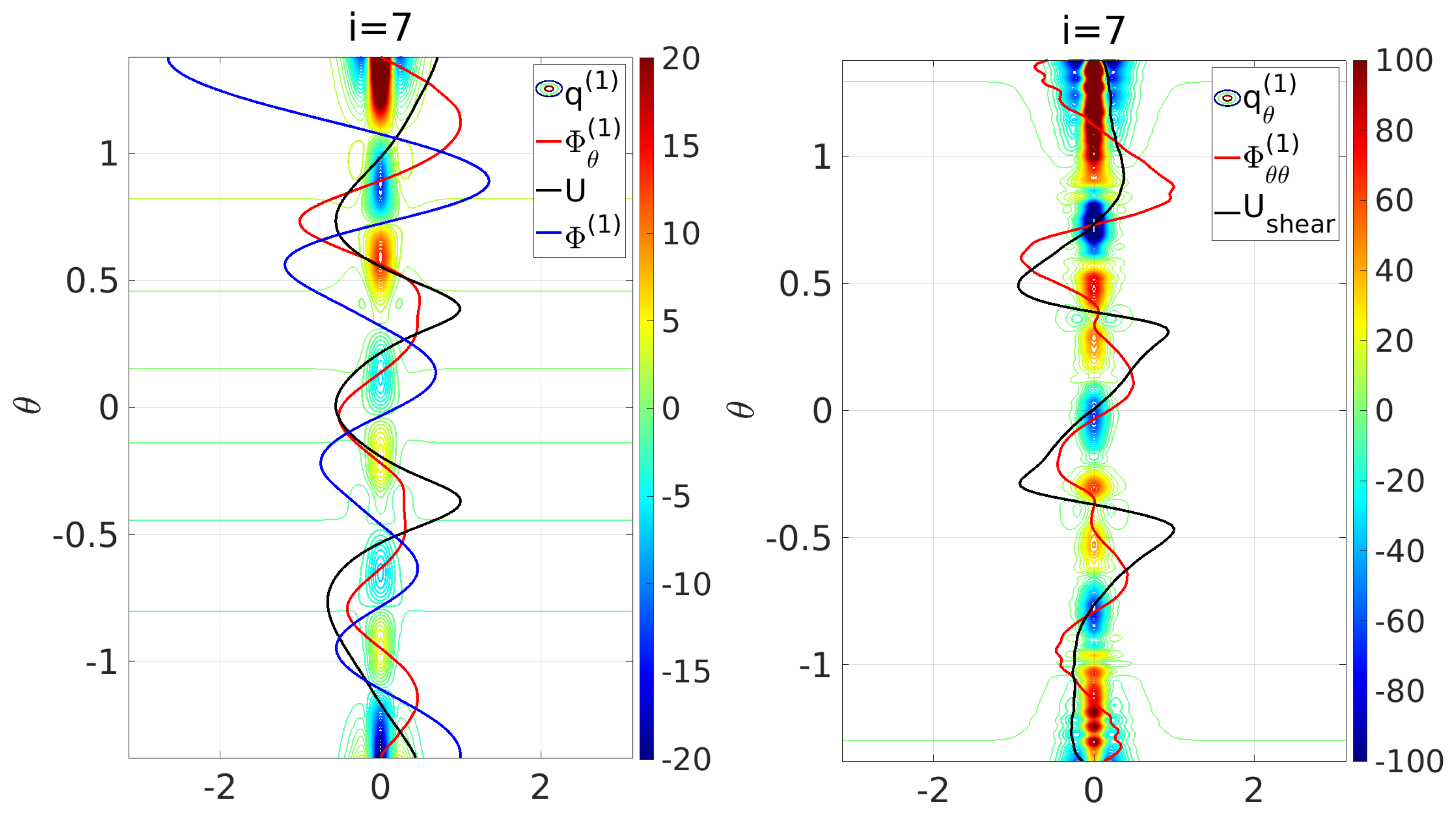
Preprints 105049 g004
Figure 4. Left panel shows normalized perturbation velocity eigenfunction, Φ i ( 1 ) ( θ ) , along with its gradient, [ Φ i ( 1 ) ( θ ) ] θ , and normalized mean zonal velocity profile, U j e t ( θ ) , vis-á-vis contours of the potential vorticity perturbation, q ( 1 ) . Right panel shows normalized second derivative of the perturbation velocity eigenfunction, [ Φ i ( 1 ) ( θ ) ] θ θ , and the normalized shear of the mean zonal velocity, U s h e a r ( θ ) , vis-á-vis contours of the perturbation potential vorticity gradient, q θ ( 1 ) . For both panels, i = 7 .
Figure 4. Left panel shows normalized perturbation velocity eigenfunction, Φ i ( 1 ) ( θ ) , along with its gradient, [ Φ i ( 1 ) ( θ ) ] θ , and normalized mean zonal velocity profile, U j e t ( θ ) , vis-á-vis contours of the potential vorticity perturbation, q ( 1 ) . Right panel shows normalized second derivative of the perturbation velocity eigenfunction, [ Φ i ( 1 ) ( θ ) ] θ θ , and the normalized shear of the mean zonal velocity, U s h e a r ( θ ) , vis-á-vis contours of the perturbation potential vorticity gradient, q θ ( 1 ) . For both panels, i = 7 .
Preprints 105049 g004
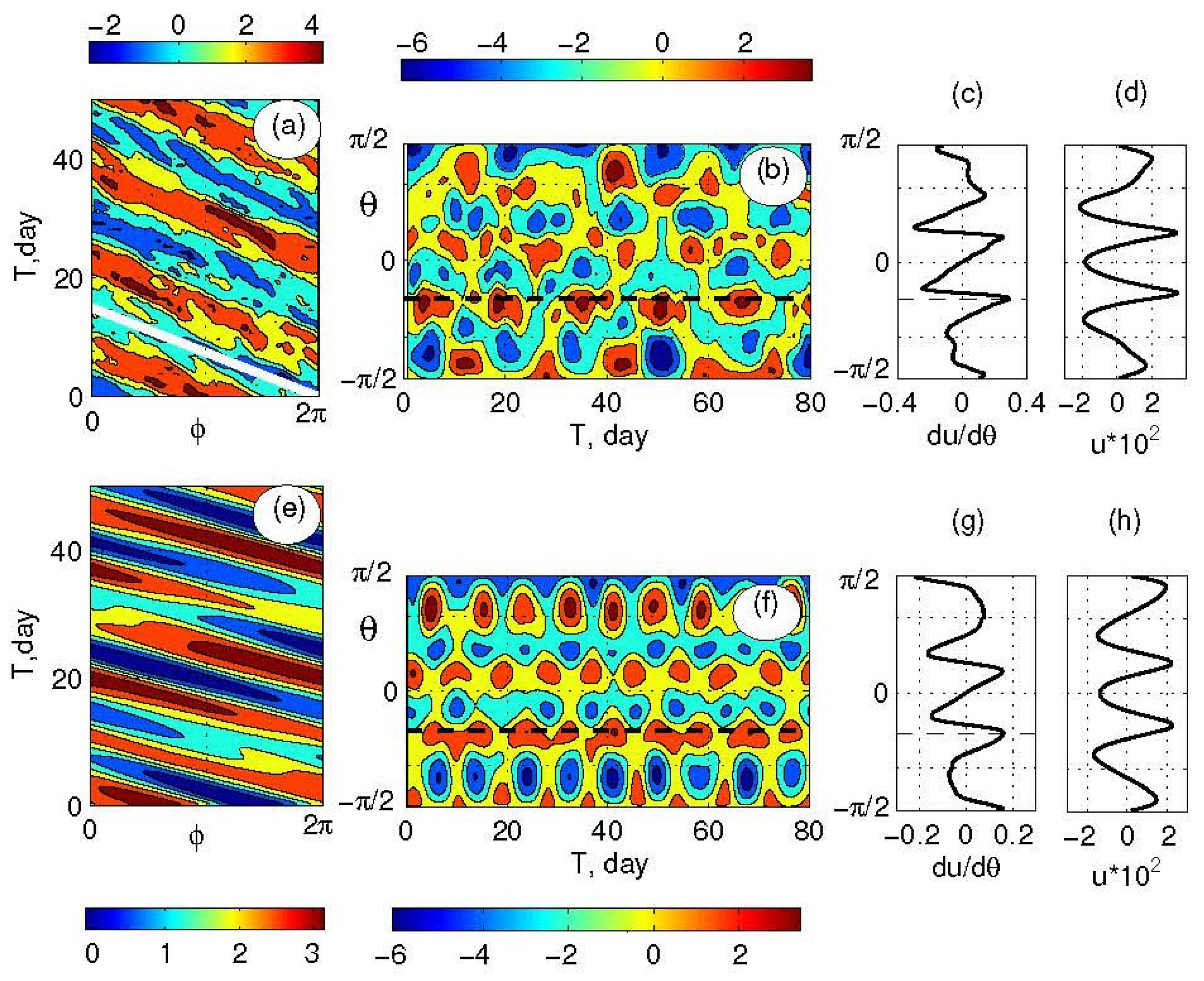
Preprints 105049 g005
Figure 5. Latitudinal (a,e) and longitudinal (b,f) Hovmöller diagrams for a flow in zonostrophic regime ( R β = 2 . 58 ) analyzed in Sukoriansky et al. [11]. The top and bottom rows represent forced and unforced flows, respectively. The white line on plate (a) corresponds to the phase speed of RHW with n = 5 . Plates (d) and (h) depict zonal velocity profiles while (c) and (g) show meridional shear of respective zonal velocities. The horizontal dashed lines on plates (b), (c) and (f), (g) correspond to the latitude of maximum shear that encompasses energetic zonons. After the forcing is switched off, the energy of velocity fluctuations decreases yet zonons retain their energy levels and integrity and become more apparent than RHWs.
Figure 5. Latitudinal (a,e) and longitudinal (b,f) Hovmöller diagrams for a flow in zonostrophic regime ( R β = 2 . 58 ) analyzed in Sukoriansky et al. [11]. The top and bottom rows represent forced and unforced flows, respectively. The white line on plate (a) corresponds to the phase speed of RHW with n = 5 . Plates (d) and (h) depict zonal velocity profiles while (c) and (g) show meridional shear of respective zonal velocities. The horizontal dashed lines on plates (b), (c) and (f), (g) correspond to the latitude of maximum shear that encompasses energetic zonons. After the forcing is switched off, the energy of velocity fluctuations decreases yet zonons retain their energy levels and integrity and become more apparent than RHWs.
Preprints 105049 g005
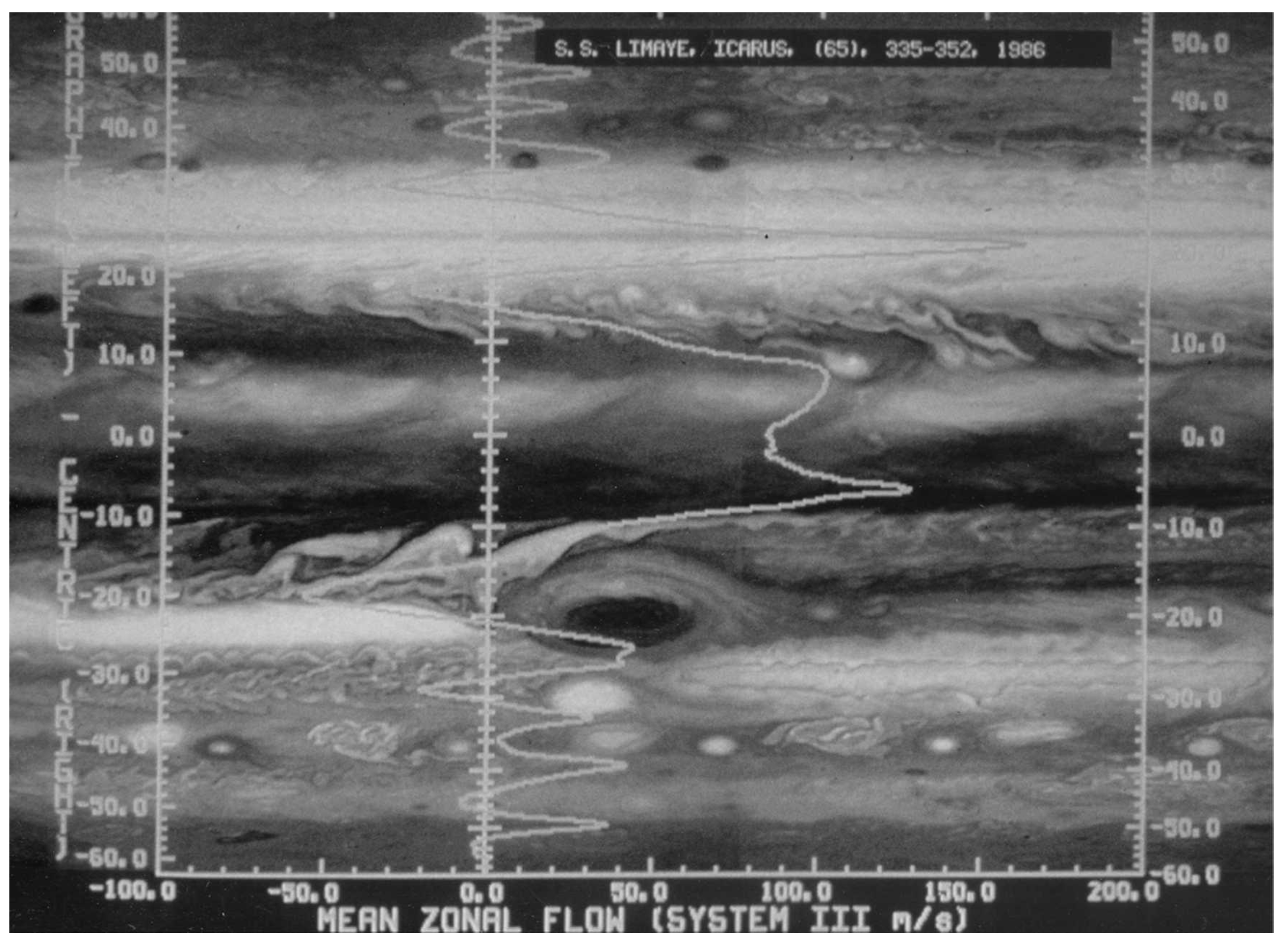
Preprints 105049 g006
Figure 6. Voyager mosaic used in [23] and [24]. The mean zonal velocity profile, U j e t ( θ ) , is represented by the white line. Rows of cyclones and anticyclones ride on the westward jets with the cyclones or anticyclones attached, respectively, to the equatorial or poleward sides. While the anticyclones are compact and bright, the cyclones appear as diffused filaments.
Figure 6. Voyager mosaic used in [23] and [24]. The mean zonal velocity profile, U j e t ( θ ) , is represented by the white line. Rows of cyclones and anticyclones ride on the westward jets with the cyclones or anticyclones attached, respectively, to the equatorial or poleward sides. While the anticyclones are compact and bright, the cyclones appear as diffused filaments.
Preprints 105049 g006
Preprints 105049 g007
Figure 7. Jupiter’s zonal (line 1) and residual (line 2) spectra estimated from the Cassini data [26]. The thick and thin dashed lines represent the zonostrophic n − 5 and Kolmogorov n − 5 / 3 spectra, Equations (6a) and (6b), respectively. At n = 23 , both spectra exhibit peaks whose coincidence was discussed earlier. The residual energy peak discloses the most energetic Rossby wave that generates zonons. These zonons may be identifiable with the observed eddies shown in Figure 8. The zonostrophy index for Jupiter is R β ≳ 5 such that its atmospheric circulation is in the zonostrophic regime [26].
Figure 7. Jupiter’s zonal (line 1) and residual (line 2) spectra estimated from the Cassini data [26]. The thick and thin dashed lines represent the zonostrophic n − 5 and Kolmogorov n − 5 / 3 spectra, Equations (6a) and (6b), respectively. At n = 23 , both spectra exhibit peaks whose coincidence was discussed earlier. The residual energy peak discloses the most energetic Rossby wave that generates zonons. These zonons may be identifiable with the observed eddies shown in Figure 8. The zonostrophy index for Jupiter is R β ≳ 5 such that its atmospheric circulation is in the zonostrophic regime [26].
Preprints 105049 g007
Table 1. The zonal phase speeds of the RHWs vis-à-vis the zonal phase speeds of the SRHWs on a rotating sphere. The highlighted index i = 7 corresponds to the eigenfunction Φ 7 ( 1 ) ( θ ) that divulges latitudinal locations of zonons.
Table 1. The zonal phase speeds of the RHWs vis-à-vis the zonal phase speeds of the SRHWs on a rotating sphere. The highlighted index i = 7 corresponds to the eigenfunction Φ 7 ( 1 ) ( θ ) that divulges latitudinal locations of zonons.
Rotating sphere
i or n c R H W ( n ) c i 0 Relative
difference [%]
1 − 1.4 − 1.445 3.2
2 − 0.466 − 0.465 0.2
3 − 0.233 − 0.2 14.1
4 − 0.14 − 0.144 2.8
5 − 0.0933 − 0.083 11
6 − 0.066 − 0.059 10.6
7 − 0.05 − 0.049 2
8 − 0.038 − 0.036 5.2
9 − 0.031 − 0.031 0
10 − 0.025 − 0.025 0
11 − 0.02121 − 0.023 8.4
Table 2. Zonal phase speeds of the RHWs vis-à-vis zonal phase speeds of the SRWs on Jupiter.
Table 2. Zonal phase speeds of the RHWs vis-à-vis zonal phase speeds of the SRWs on Jupiter.
Jupiter
i or n c R H W ( n ) c i 0 Relative
ms − 1 ms − 1 difference [%]
17 − 80.4 − 80.3 0.2
18 − 72.0
19 − 64.8 − 69.2 6.8
20 − 58.6
21 − 53.3
22 − 48.7 − 47.7 2.0
23 − 44.6 − 46.6 4.4
24 − 41.0
25 − 37.9
Table 3. Zonal phase speeds of the RHWs vis-à-vis zonal phase speeds of the SRWs on Saturn in Systems III and IIIw.
Table 3. Zonal phase speeds of the RHWs vis-à-vis zonal phase speeds of the SRWs on Saturn in Systems III and IIIw.
System III System IIIw
i or n c R H W ( n ) c i 0 Relative c R H W ( n ) c i 0 Relative
ms − 1 ms − 1 difference [%] ms − 1 ms − 1 difference [%]
9 − 232.6 − 235.3 1.1 − 221.3 − 233.9 5.4
10 − 190.3 − 182.5 4.1 − 181.0 − 156.1 13.8
11 − 158.6 − 143.9 9.3 − 150.9 − 140.6 6.8
12 − 134.2 − 127.6 − 124.3 2.6
13 − 115.0 − 109.4 − 105.7 3.4
14 − 99.7 − 101.8 2.1 − 94.8 − 94.1 0.7
15 − 87.2 − 90.2 3.4 − 83.0 − 87.3 4.9
16 − 77.0 − 73.2 − 75.3 2.8
17 − 68.4 − 65.1 − 63.8 2.0
18 − 61.2 − 58.2 − 58.9 1.2
19 − 55.1 − 52.4 − 54.2 3.3
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated