Prerpints.org logo
Preprint
Article

Numerical Analysis of Structural Vibrations in Masts. A Practical Study Applied to a 28-Meter Tugboat.

Altmetrics

Downloads

106

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 April 2024

Posted:

29 April 2024

You are already at the latest version

Alerts
Abstract
This article investigates the vibration analysis of the mast on the bridge top of a 28-meter tugboat, in the quasi-static regime. The study aims to determine the natural frequencies using an equivalent dynamic model of the mast and considers the accelerations of different degrees of freedom of the vessel. Practical design and reinforcement strategies for the local bridge top structure are proposed, utilizing numerical and analytical tools. The investigation explores various alternatives to optimize the structural arrangement. By analyzing the modal behavior, insights are provided for efficient design and reinforcement. The results contribute to understand the mast's vibration characteristics, offering guidance for similar structures. The study employs numerical and analytical methods, enhancing the optimization of the mast's behavior. It determines natural frequencies, proposes practical design strategies, and explores alternatives for structural optimization. The findings provide insights for shipbuilding and mast design applications in other vessels and industries such as radar mast, compass deck and guyed mast.
Keywords: 
Subject: Engineering  -   Marine Engineering

1. Introduction

Structural vibrations can arise from diverse sources and affect a variety of engineering systems. In the maritime industry, ship vibrations are a critical concern due to their influence on habitability and crew well-being. According to ISO 20283-5 guidelines [1], ship vibrations are typically analyzed within the frequency range of 1 to 80 Hz. At the higher end of this range structure-borne noise dominates, while at the lower end the natural frequencies of the global hull structures are located. Notably, local structures like deck-panel structures, masts, and deckhouse structures often possess natural frequencies within the middle of the frequency range [2]. To ensure optimal structural performance and mitigate vibration-related issues, the design of structures should avoid resonance with exciting frequencies, such as those generated by engines and propellers. However, due to variations in excitations and changing loading conditions, complete avoidance of resonance becomes challenging [2]. Four fundamental factors influence ship vibrations and vibration problems in general: excitation, stiffness, damping, and the frequency ratio. Altering these factors can help in reducing vibrations, especially near resonant conditions where the frequency ratio approaches unity.
During the concept design phase, two fundamental factors emerge as critical for significant vibration reduction: minimizing vibration excitations and avoiding excitation frequencies that coincide with the natural frequencies. Finite Element Analysis (FEA) has proven effective in evaluating the vibrational response of ships, incorporating all four influencing factors [3]. Moreover, it is recommended to design local structures with natural frequencies below 0.85 times the major exciting frequency or above 1.15 times the exciting frequency to mitigate vibrations associated with low-speed diesel engines and propeller excitations. In recent studies, researchers have made notable contributions to the field of structural vibrations in shipbuilding and mast design. Park et al. [4] focused on preventing resonance in radar masts through the utilization of diverse design of experiment (DOE) techniques. Kong et al. [5] pursued the objective of optimizing the size of stiffeners on compass deck structures to reduce vibration levels and decrease the overall weight of the ship's structure. Fukada et al. [6] presented calculation formulas for determining the lowest natural frequencies of frequently employed radar mast configurations.
Extensive research has been conducted on guyed masts, with a particular focus on wind-induced response and stability. Ngamkhanong et al. [7] analyzed the fundamental mode shapes, natural frequencies, and interactions with the soil for three-dimensional mast structures, considering soil-structure interaction effects. Lacarbonara and Ballerini [8] proposed a passive vibration mitigation architecture using tuned pendulum dampers for transverse vibrations in guyed masts. Yan-li et al. [9] investigated wind-induced response using a nonlinear discrete analysis method for random vibration, considering cable nonlinearity. The dynamic behavior and response of guyed masts under wind loading conditions have been extensively examined. Law et al. [10] studied the wind-induced acceleration responses of a 50m guyed mast, highlighting torsional vibrations in higher modes. Orlando et al. [11] focused on the analysis of the static and dynamic buckling behavior of a simplified cable-stayed tower model, emphasizing the influence of symmetries on buckling loads and post-buckling paths. Numar et al. [12] examined the behavior of cantilevered and linearly tapered thin-walled high masts under dynamic loadings, utilizing three different analysis methods.
Additional studies have explored numerical modeling and optimization techniques for mast design. Juozapaitis et al. [13] discussed the numerical analysis of masts using specialized computer-aided design packages, assessing stress and strain fields. Belevičius et al. [14,15] investigated the optimal schemes of tall guyed masts under wind loadings, simultaneously optimizing topology, shape, and sizing. Pezo et al. [16] focused on the non-linear behavior and stability of guyed masts under wind loads, employing numerical simulations and modal and stability analyses. The analysis of self-supporting antenna masts and communication towers has also been an area of interest. Luis García et al. [17] conducted an operational modal analysis on a self-supporting antenna mast, validating detailed finite element models through mode shape characterization. Alshurafa et al. [18,19,20] explored the design, dynamic characteristics, and optimization of glass fiber-reinforced polymer (GFRP) guyed towers, evaluating structural performance, vibration response, and material properties.
Furthermore, wind-induced vibration and stability analysis have been significant topics in the study of mast structures. Ahmad et al. [21] addressed vibration problems in ship masts by utilizing the effective mass participation factor criterion, which measures the energy in each resonant mode. Zhang et al. [22] examined the vibration characteristics of high-mast light poles using finite element models with and without spiral helical strakes. Ballaben et al. [23] investigated the sensitivity of the dynamic response of guyed masts to initial guy pretension. A three-dimensional mast model was used, considering nonlinear inclined cables and dynamic lateral loads. Finite element analysis and time domain algorithms were employed. Hulimka et al. [24] discussed the case of an 80-meter aluminum mast that collapsed shortly after being put into service. Investigations revealed design and execution errors, including incorrect calculations, omission of wind effects, and improper location and anchoring of guy ropes.
The main novelties of this research are related with the vibration study of the mast placed on bridge top, starting with the determination of eigenfrequencies and eigenmodes, followed by the assessment of load transfer on the local reinforcement and the establishment of design alternatives. The main objective of this research is the quantification of the structural behavior and then, the definition of design criteria and recommendations. The paper is structured as follows: Section 1 provides an introduction about the problem, Section 2 covers the mathematical basis, Section 3 presents the case study of the 28 m tugboat used in the numerical approach, and Section 4 details the numerical simulation procedure. Section 5 discusses the results derived from the previous sections, encompassing design load scenarios, optimal scantling of local reinforcement, modal analysis, structural assessment, and proposals for improvement. Finally, Section 6 presents the conclusions drawn from the study.

2. Free Vibration of a Ship Mast

The dynamic behavior of a ship mast approaches a cantilever beam, neglecting rotary inertia and shear effects, and can be described by a second-order differential equation system. In order to achieve this, a fourth-order partial differential equation is initially utilized, incorporating both x (distance) and t (time) as independent variables. However, this equation is subsequently reduced to a second-order ordinary differential equation with respect to t. The fourth-order differential equation governing the deflection y(x,t) of the beam is provided as follows [25]
E I ∂ 4 ∂ x 4 y ( x , t ) + m ∂ 2 ∂ t 2 y ( x , t ) = q ( x , t )
where E represents the Young's modulus of the beam material, and I is the area moment of inertia of the cross-section. Additionally, m represents the mass per unit length, and q(x,t) signifies the force per unit length acting in the y direction. Considering the free vibration of the beam, where q(x,t) is equal to zero, the given partial differential equation can be solved using a separation of variables method.
y ( x , t ) = Y ( x ) W ( t )
Consequently, the application of this method leads to the formulation of two separate ordinary differential equations. These equations serve as important components in the analysis and subsequent solution of the given problem.
d 2 W d t 2 + ω n 2 W = 0 d 4 Y d x 4 − β 4 Y = 0
where ω n 2 denotes the natural frequencies and β 4 = ω n 2 m E I , assuming in first approximation the non-consideration of damping effects. The natural deflection shapes or modes of the beam are obtained by solving the second part of Equation (3) with the relevant boundary conditions and the following general solution:
Y ( x ) = C 1 sin β x + C 2 cos β x + C 3 sinh β x + C 4 cosh β x
The constants C1, C2, C3, C4, and β in the general solution, are determined by imposing the appropriate boundary conditions to the cantilever beam,
Y ( 0 ) = 0   :   no   deflection   at   the   fixed   end
d d x Y ( x ) | x = 0 = 0   :   no   slope   at   the   fixed   end
M ( L ) = E I d 2 d x 2 Y ( x ) | x = L = 0   :   no   bending   moment   at   the   free   end
V ( L ) = E I d 3 d x 2 Y ( x ) | x = L = 0   :   no   shear   force   at   the   free   end
with L the length of the beam, which leads to the expression
cos ( β L ) cosh ( β L ) = − 1
In order to determine the allowable values of β, the transcendental equation must be solved numerically. This equation has an infinite number of numerical solutions, each representing to a specific mode of vibration. The first three natural frequencies of a cantilever beam are:
ω n 1 = 1.875 2 E I m L 4 ,   ω n 2 = 4.694 2 E I m L 4 ,   ω n 3 = 7.855 2 E I m L 4
The governing equation of modal analysis is obtained from the equation of 2D motion
[ M ] { u ¨ } + [ C ] { u ˙ } + [ K ] { u } = { f ( t ) }
where M is the mass, { u ¨ } is the acceleration, C is the damping, { u ˙ } is the velocity, K is the stiffness, { u } is the displacement and { f ( t ) } is the load. For modal analysis, a free and undamped system is considered
[ M ] { u ¨ } + [ K ] { u } = 0
which has a solution of the form { x ( t ) } = { X } e i ω t , then
( [ K ] − ω 2 [ M ] ) { X } e i ω t = { 0 }
The solutions of this last system other than the trivial one satisfy det ( [ K ] − ω 2 [ M ] ) = 0 , and from which the n values of ω 2 are obtained, which are the natural frequencies of the system without damping. Solving this equation for each of the eigenfrequencies gives its associated vector { ϕ } n , which represents the shape adopted by the structure at that particular frequency. From this concept, and with the eigenvector matrix, the well-known concepts of modal share factors and effective masses are employed to indicate the importance of each eigenfrequency.

3. Case Study

3.1. Main Particulars

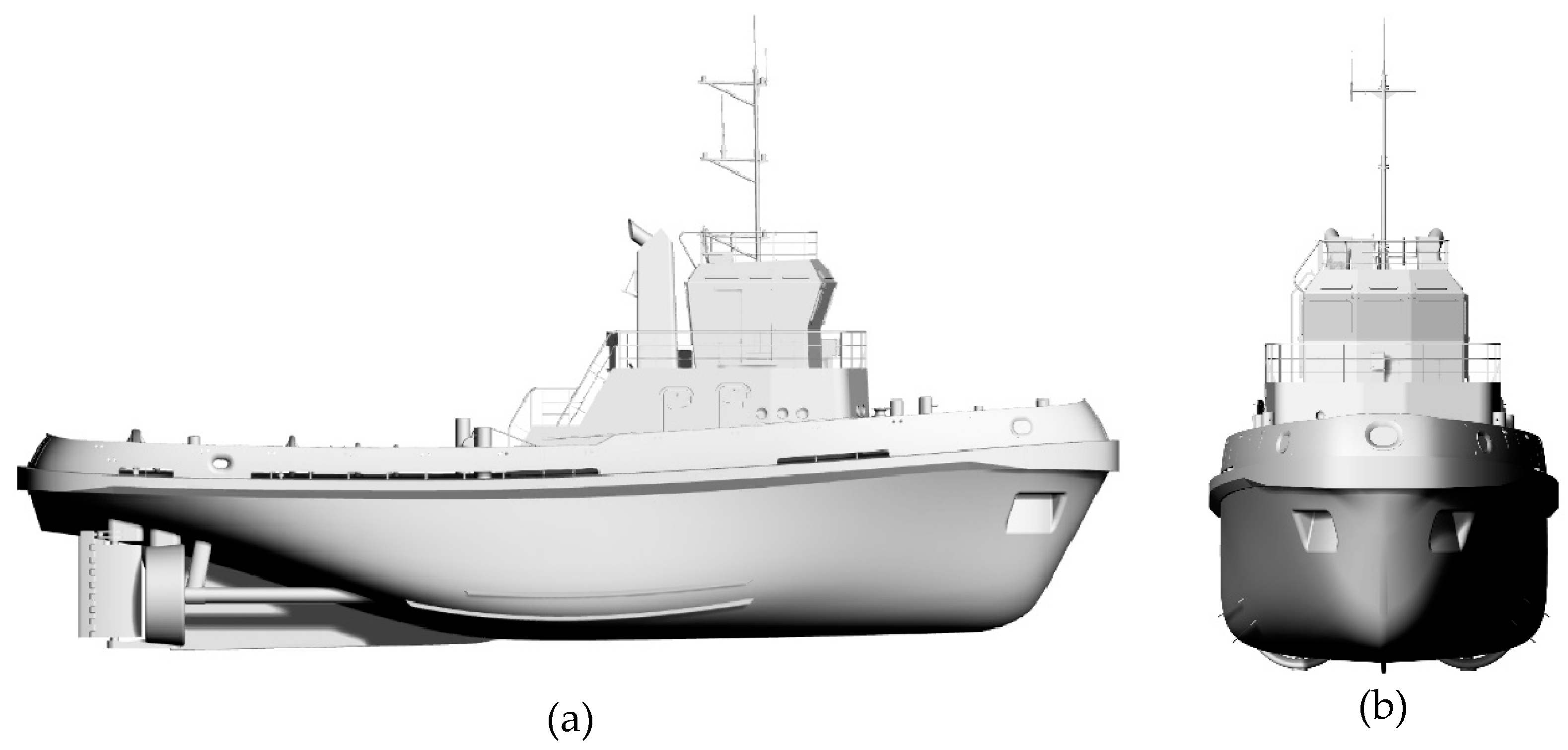
Figure 1 shows the general arrangement of the tugboat.
Table 1. presents the main dimensions of the tugboat.

3.2. Equivalent Dynamic Model

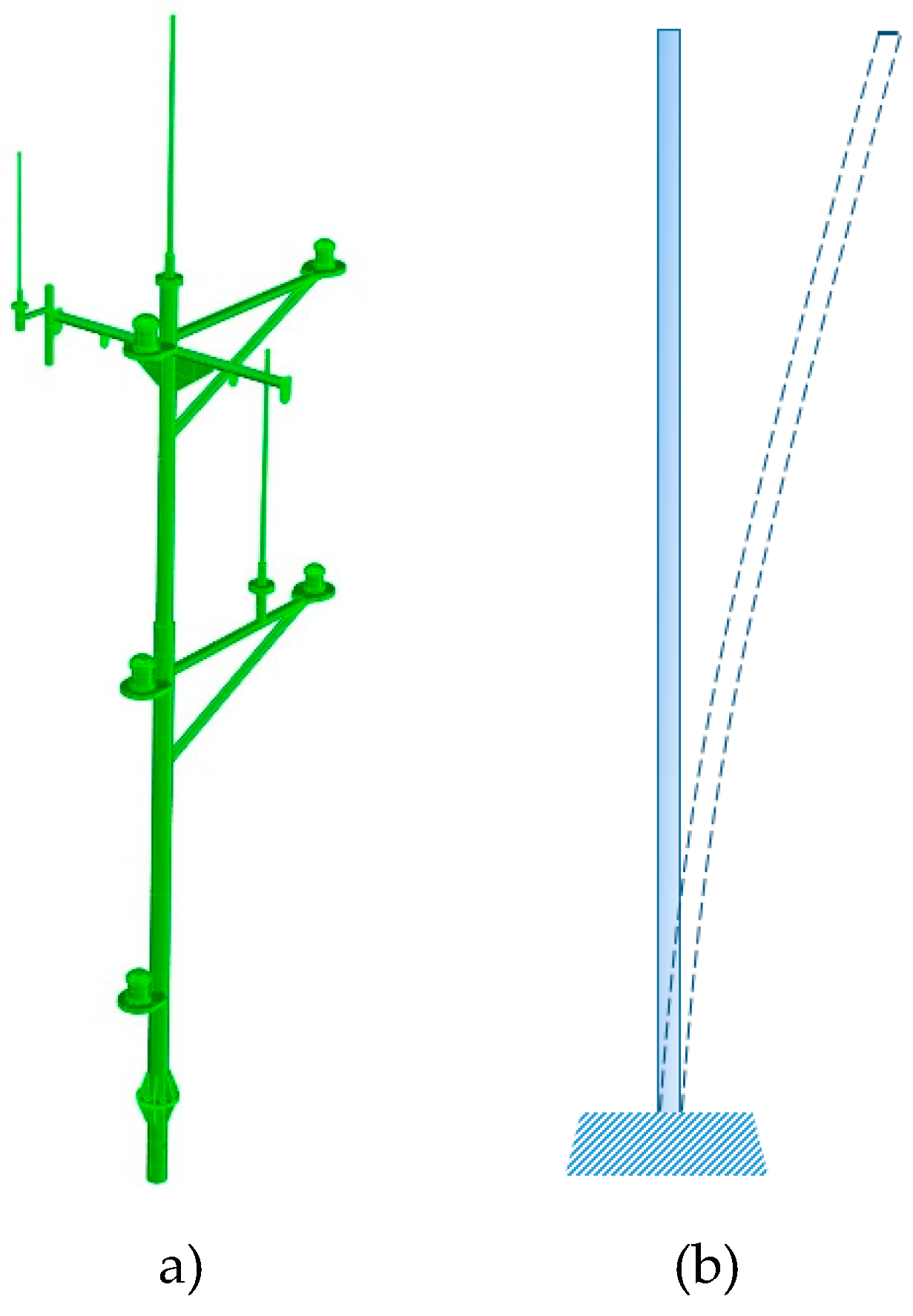
In general, a ship mast structure is often susceptible to vibrations due to its significant slenderness. This study models the ship mast structure, depicted in Figure 2, as a cantilever beam, following the same procedure that Zhao et al. [26]:
The material of the mast and deck house is steel, assuming elastic behavior (Table 2).
The mast has a constant tubular section with an outer radius of 200 mm and a thickness of 10 mm, a heigth of 10.55 m and a total weight of one ton. The location of the center of gravity is assumed in the mid point of the mast.

3.3. Bridge and Deckhouse Structure

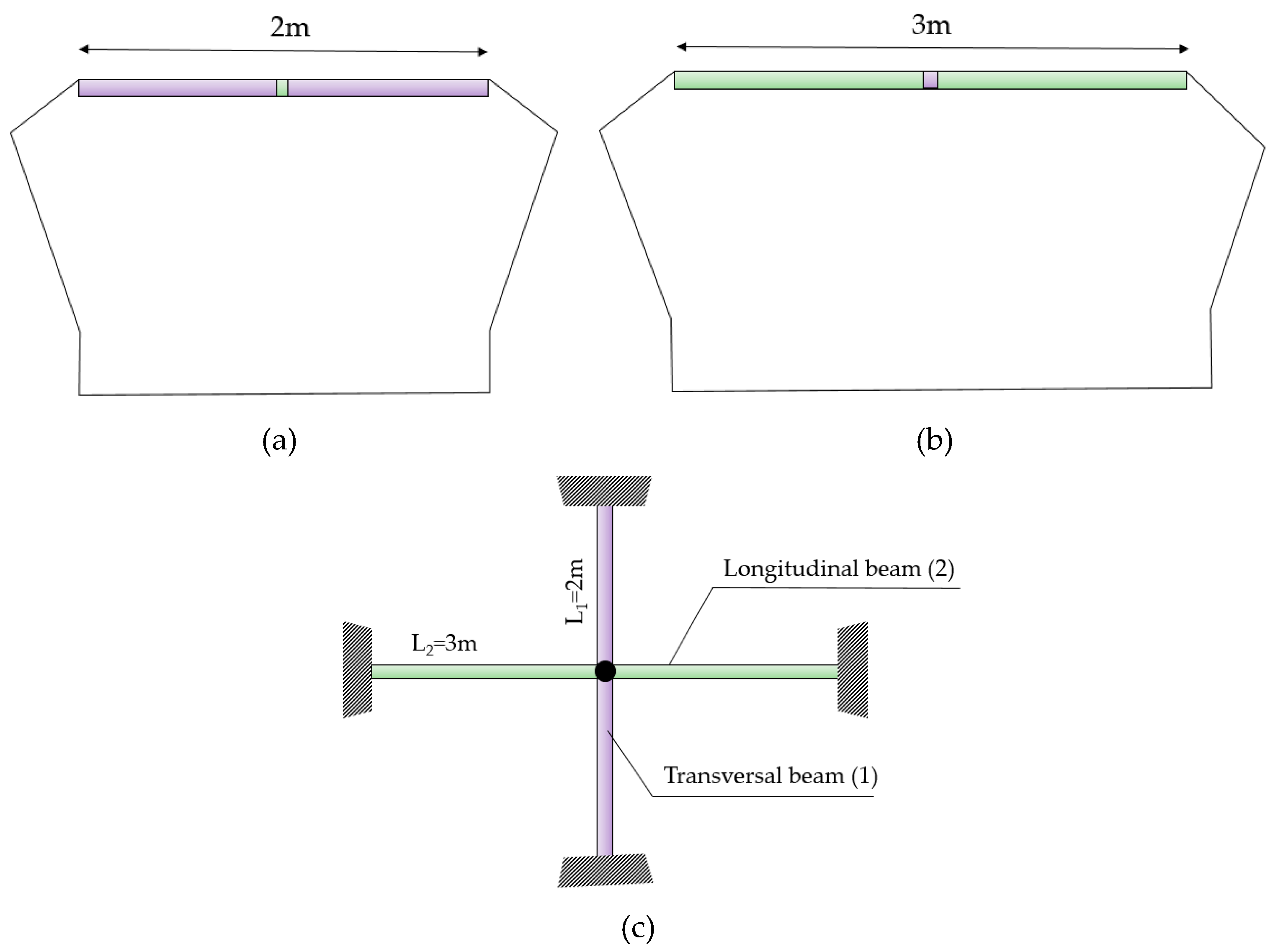
The base of the mast is welded against the bridge top, with a uniform thickness of 8 mm, and specifically in the crosshead joint between a transversal (1) and longitudinal (2) beam that form the reinforcement of the bridge top (Figure 3).
The cross section of the longitudinal and transversal beams is a T shape, with a web of 300×10 mm and a flange of 150×10 mm. The influence of the associated plate on the crosshead profiles is taken into account by including a double T-shaped profile whose upper flange with the indicated dimensions simulates this effect. The end of the beams (longitudinal and transversal) is welded against a beam that goes around the contour of the bridge top and simulates a fixed end, constraining all degrees of freedom at that point.

3.4. Ship Motions and Accelerations

The influence of ship motions on a vessel's forces is significant and necessitates their inclusion in calculations [27]. Neglecting to account for these motions can lead to severe consequences, affecting the stability, structural integrity, and material responses of the ship. The transverse acceleration due to sway, in m/s2, is to be taken from [28]:
a s w a y = 115 f R f S f n l H L f T L 0.15 f B L 0.5
where H is the wave parameter, fR is the routing factor, fS is the speed effect coefficient, fTL is the ratio between draught at the considered loading condition and rule length and fBL is the ratio between moulded breadth and rule length [28]. The vertical acceleration due to heave, in m/s2, is to be taken as:
a h e a v e = 350 f R f S f n l H L f B L 0.5
The summary of accelerations influencing the design of the mast is shown in Table 3.
The previous formulation from the rule [28], enable fast calculations and skips advanced seakeeping calculations with i.e. strip theories or panel methods. Nevertheless, these calculations might be developed in further stages of the ship design spiral in order to improve the previous calculations.

4. Finite Element Modeling

The ANSYS® Workbench 2023 software is utilized to implement an elastic and linear regime through solid elements. A mesh consisting of 20-node cubic elements is employed in this approach (Figure 4).
The mesh quality of the mast (21 elements) is assessed by comparing the results, in calculating the eigenfrequencies, obtained from analytical method outlined in section 2 with those obtained through finite element analysis (Table 4).
The evaluation of the quality of the mesh of the structural crosshead (33 elements) that forms the local reinforcement of the mast is obtained by comparing the displacement obtained at the midpoint of a doubly fixed beam between the analytical method and the finite element analysis, obtaining an error as low as 0.78%.

5. Results and Discussion

5.1. Design Load Scenarios

Two typical load conditions are established from the value of the accelerations mentioned above; the righting and heeling condition of the tugboat, with a standard heel angle of 20º following the Aalbers Ship Design B. V. procedure [29] (Figure 5).
Table 5 depicts the numerical values obtained for the vertical load and bending moment generated by the mast on the base for each load conditions presented.
It can be seen that the most unfavorable condition is the one corresponding to the heeled position, whatever the degree of heel, only the numerical value will be affected, but the load will always be lower in the upright condition.

5.2. Optimal Scantling of Local Reinforcement

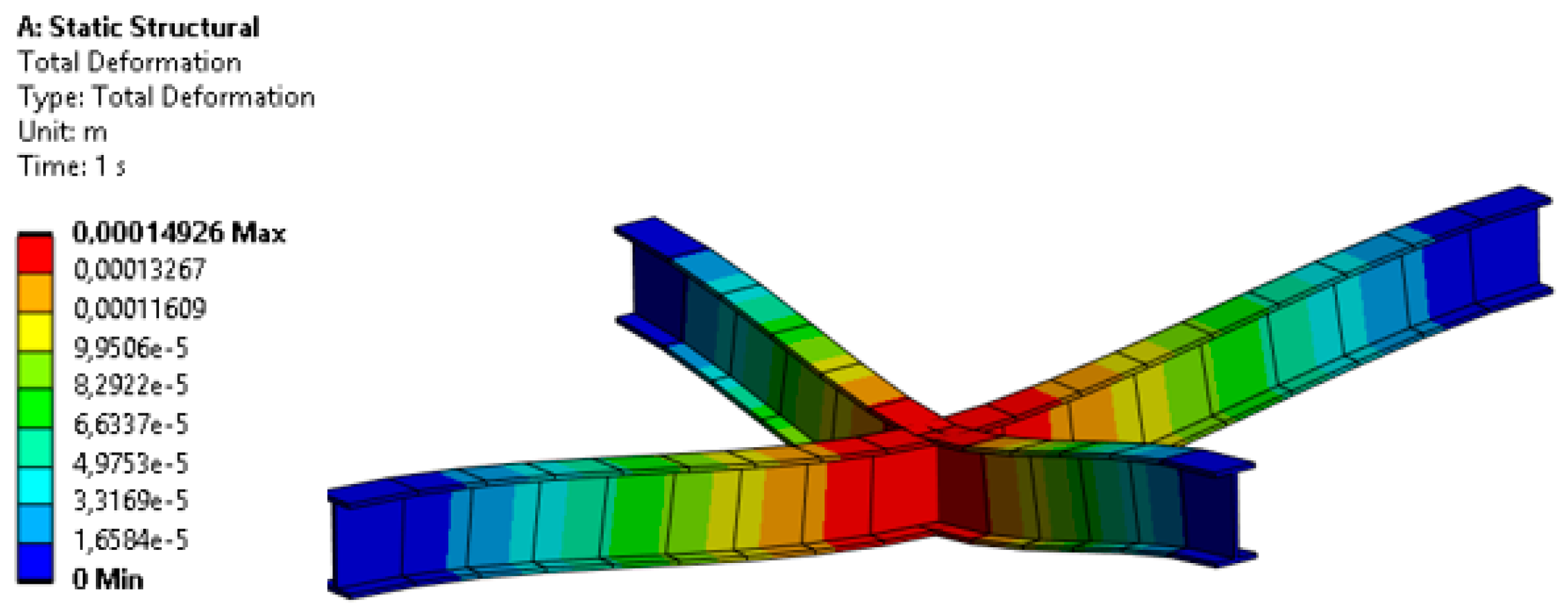
The scantling of the local reinforcement is carried out under the most unfavorable loading condition, the heeled one. The bending moment obtained above is decomposed into a bending moment in one of the beams forming the structural crosshead and into an a priori negligible torsional moment in the other beam (Figure 6).
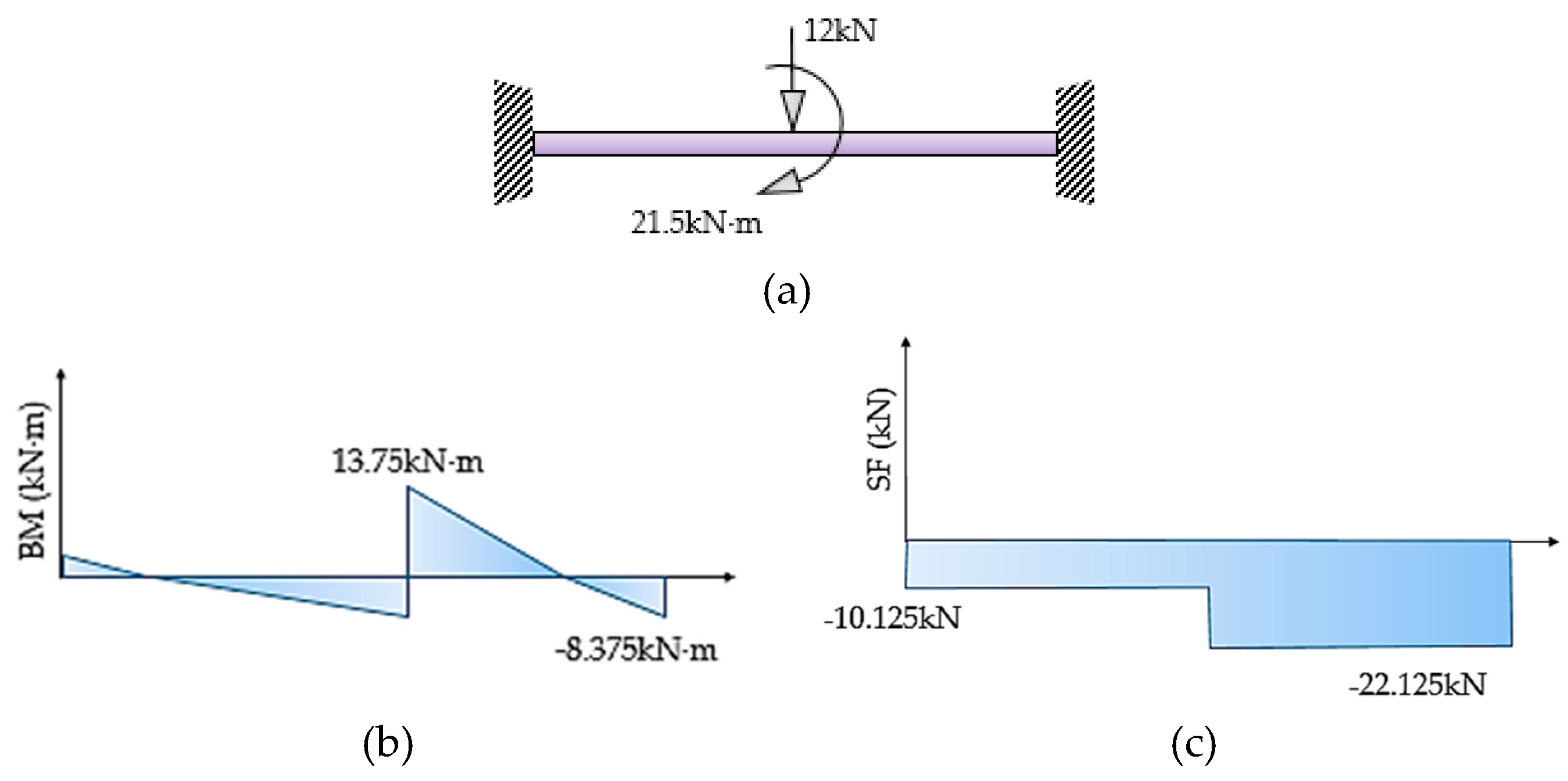
Once the loads of the mast placed on the bridge top have been established, it is necessary to quantify the strength contribution of each beam. As the cross section is identical for constructive and structural criteria, it will be sufficient to calculate the most unfavorable of the two and duplicate the result obtained in the other one. For this purpose, a system of two equations with two unknowns is used. The first arises from the so-called compatibility equation, which will be the equality of displacements at the midpoint of a beam with its two fixed ends and a load at its midpoint. If P1 is the load supported by the transverse beam, P2 is the load supported by the longitudinal beam, L1 is the length of the transverse beam, and L2 is the length of the longitudinal beam, then:
P 1 · L 1 3 192 E I = P 2 · L 2 3 192 E I ⇔ P 1 = ( 3 2 ) 3 · P 2
The second equation of the system of equations is related with the maximum vertical load:
P 1 + P 2 = 16 k N
Solving this system, the shortest beam (the transversal one) will be the most unfavorable with a 75% contribution (12kN) compared to a 25% contribution of the longitudinal one (4kN). Therefore, this will be the beam that sets the scantling of the local reinforcement of the mast (Figure 7).
The more similar the longitudinal and transverse beam lengths, the more homogeneous the stress distribution between them will be. If this is not the case and the difference between lengths is large, the possibility of reducing the scantling of the longitudinal beam, which will support considerably less amount of the total load, could be considered. If this option is chosen, it is advisable to have brackets at the intersection between the two beams to facilitate the transmission of loads from the mast to the bridge top deck.
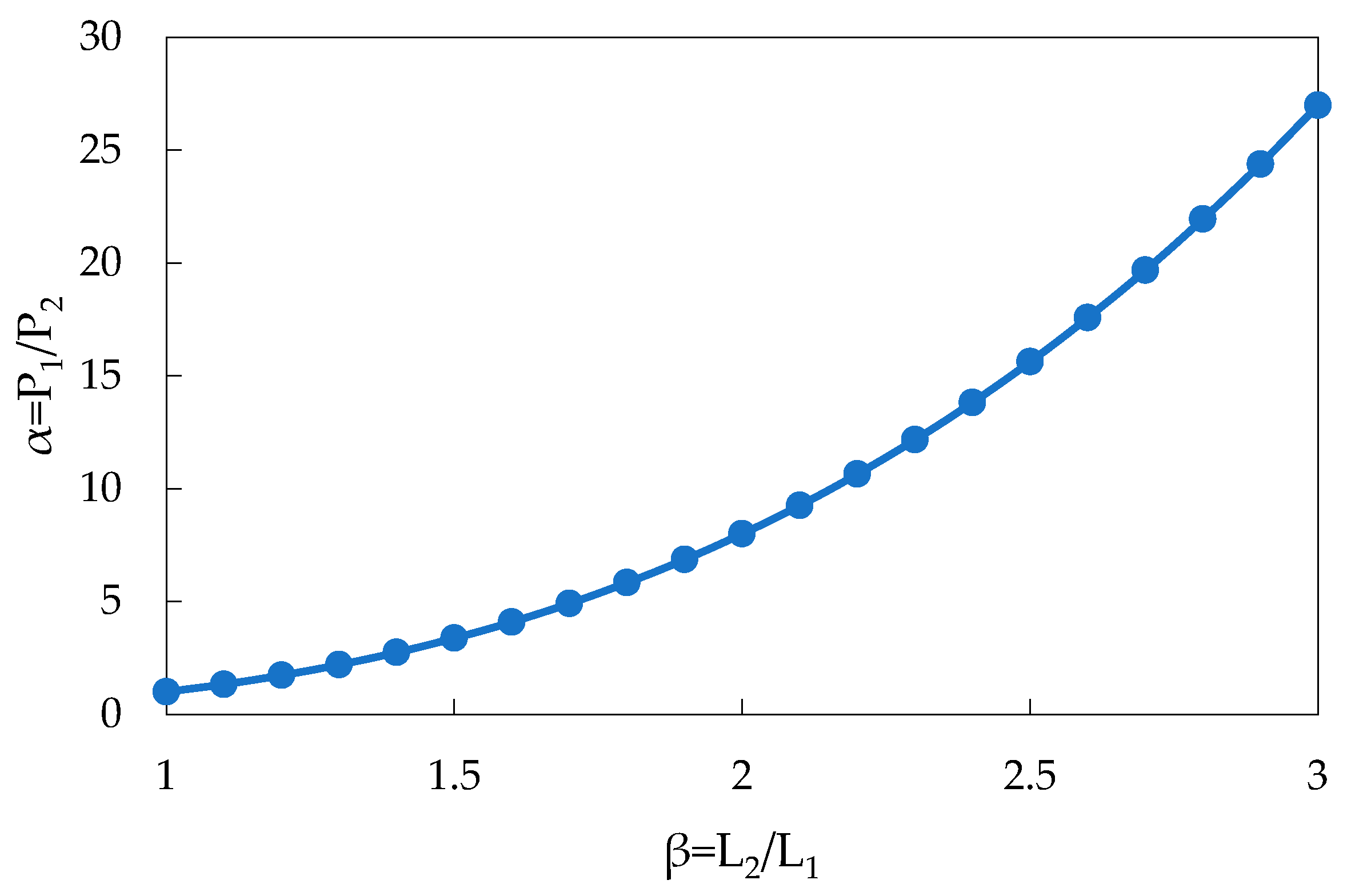
With α as the ratio between P1 and P2 and β the ratio between L2 and L1, where 1 and 2 are the lengths of the transverse (shorter) and longitudinal (longer) beams, a cubic parabola-type (α=β3) relationship is obtained between the two variables (Figure 8):
Figure 8 is applicable to the structural design process of the bridge top crosshead, once the bridge geometry has been determined to meet other construction or regulatory criteria.

5.3. Modal Analysis

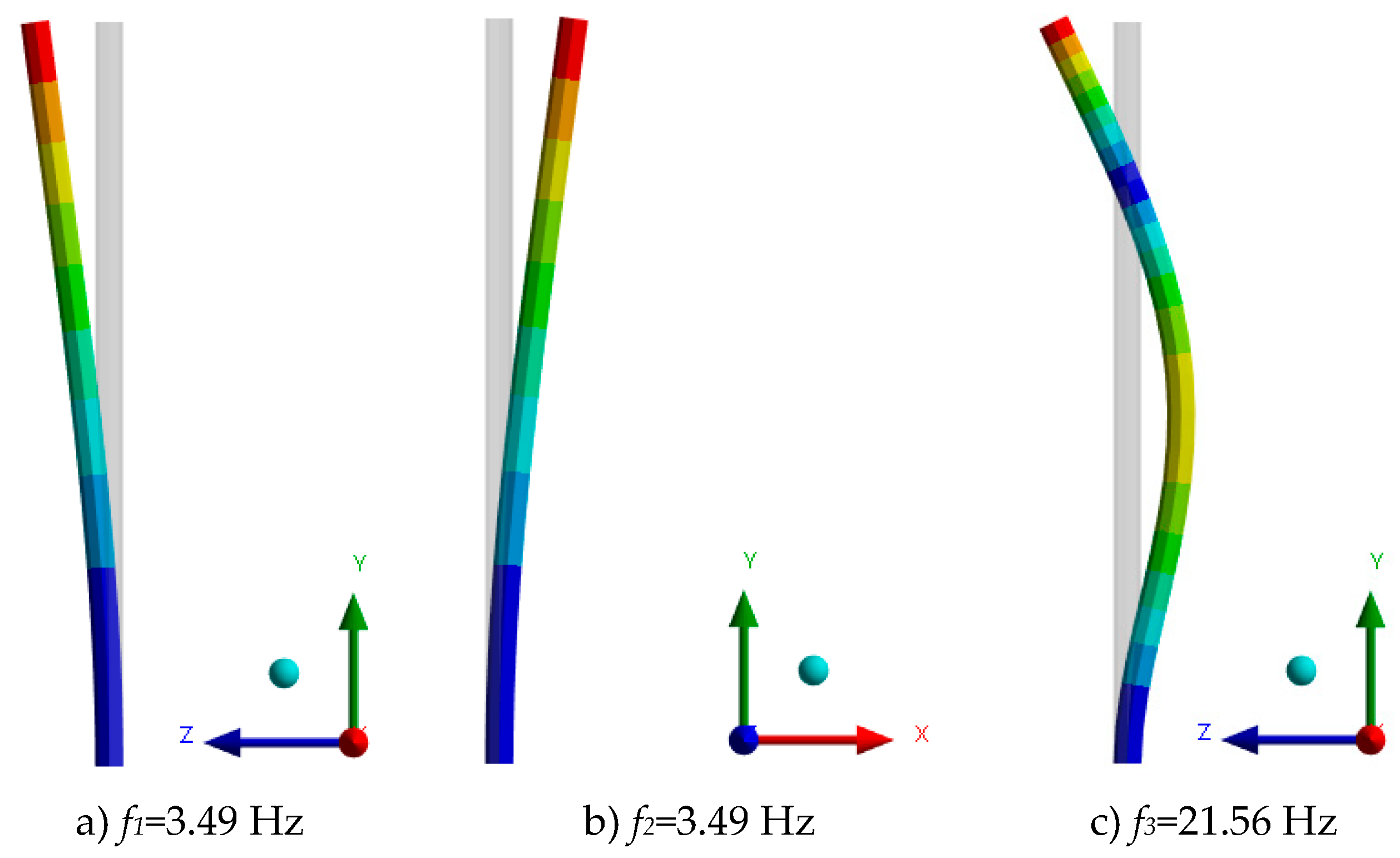
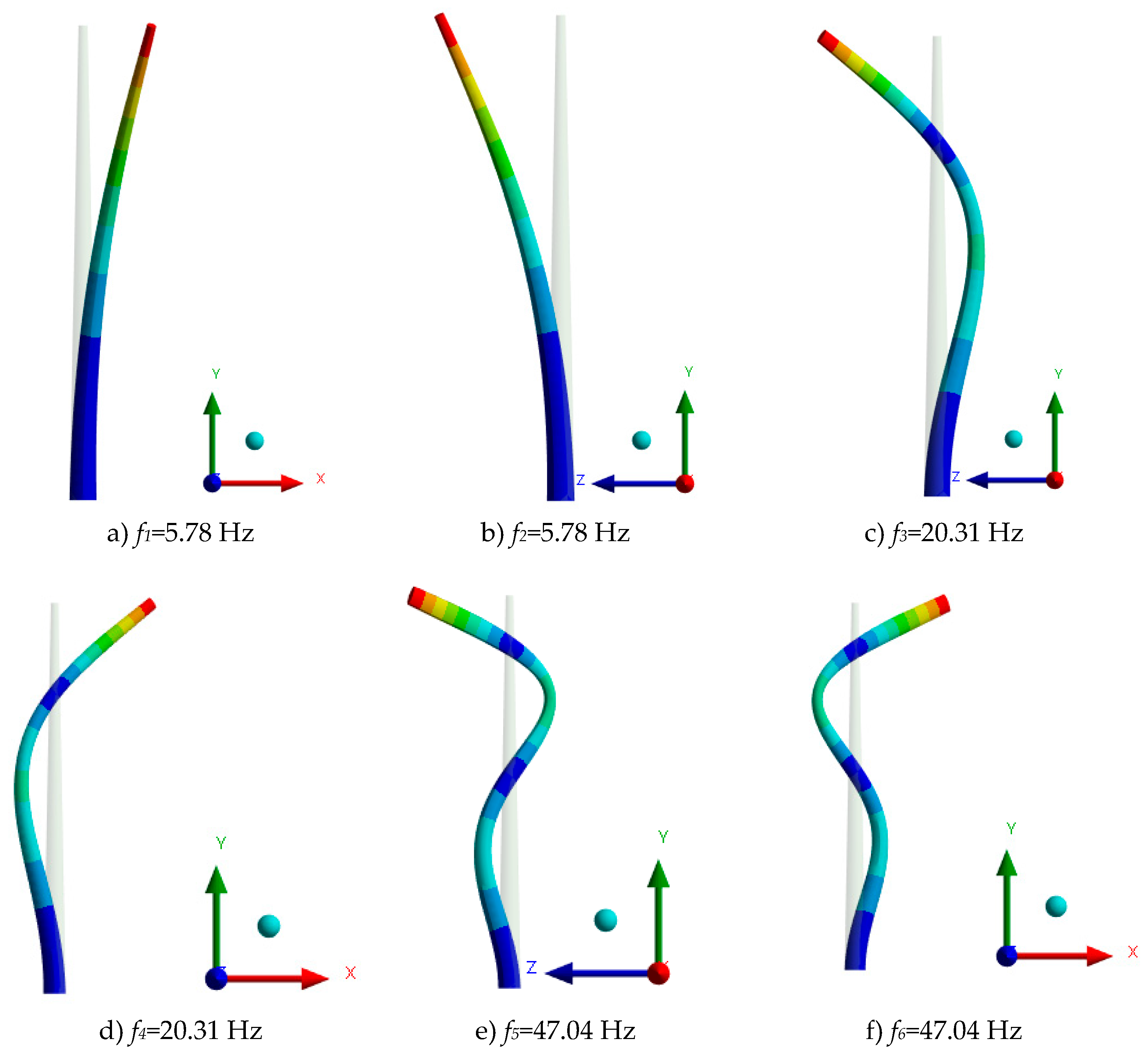
Modal analysis involves identifying the fundamental dynamic characteristics of the mast, including natural frequencies and mode shapes. These characteristics are then utilized to establish system's dynamic or quasi-static behavior. Figure 9 shows the first eigenfrequencies and eigenmodes of the mast in the initial condition.
Table 6 shows the effective masses in each of the directions according to the cartesian reference system shown in the figure above.
With the determination of the first six eigenfrequencies, a total of 86.97% of the total mass is captured. It is observed that the first mode is by far the most important, so it will be the one to pay attention in terms of structural design.
The influence of mass redistribution on the determination of the modal analysis translated, in terms of obtaining eigenfrequencies and eigenmodes, is studied. The alternative is a beam of variable section resembling a truncated cone (tapered beam), of the following dimensions: a lower radius of 300 mm, an upper radius of 100 mm for the same initial height. In order to generalize the structural behavior and not to condition it to the same cross-section, a solid circular cross-section with the same value as the outer radius for the tubular section is considered, in order to compare its structural behavior with its counterpart in terms of constant cross section.
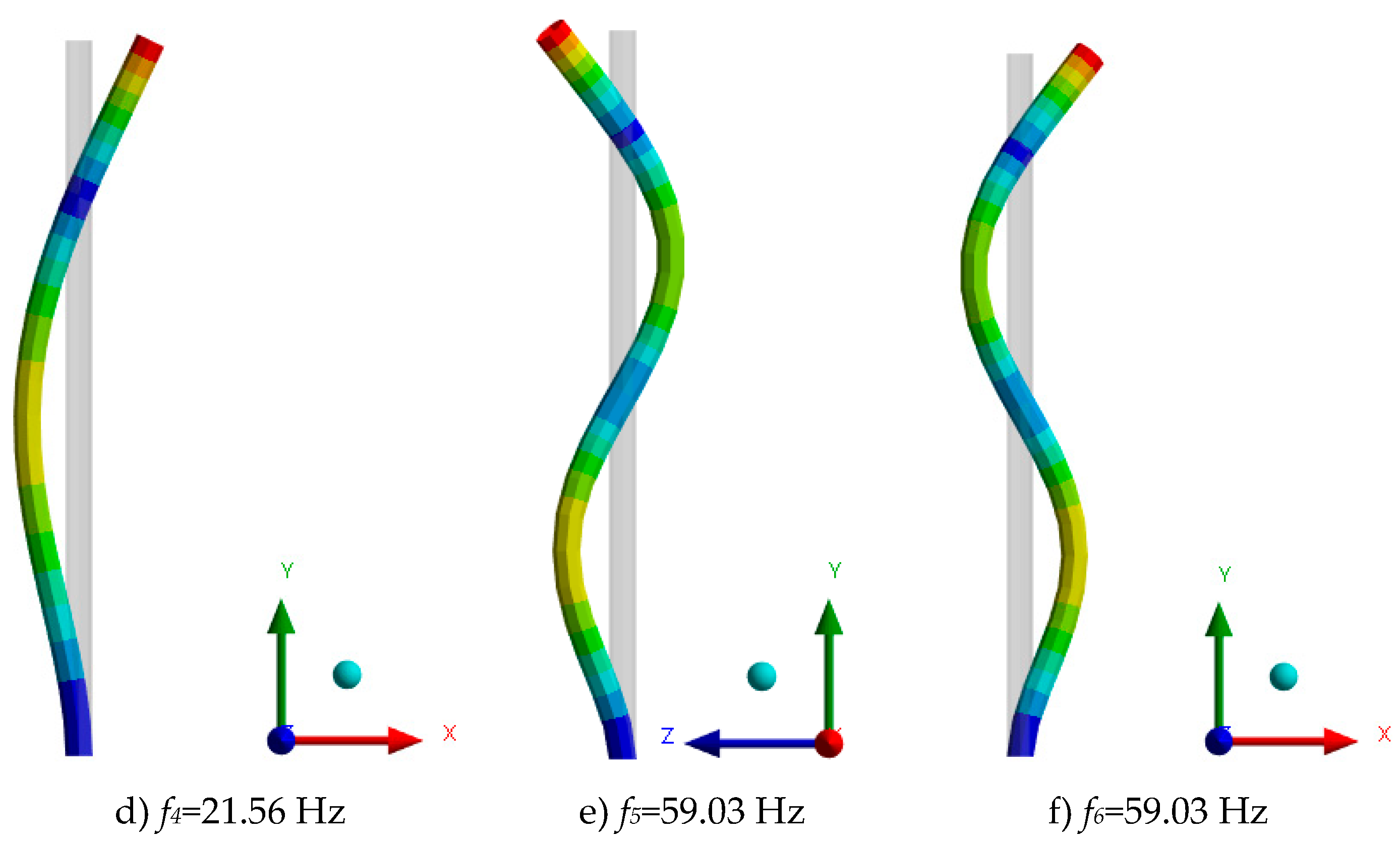
Figure 10 shows the eigenfrequencies and eigenmodes of the mast for the variable and solid cross section case.
Table 7 shows the comparison of the six eigenfrequencies between the constant solid section and the variable solid one.
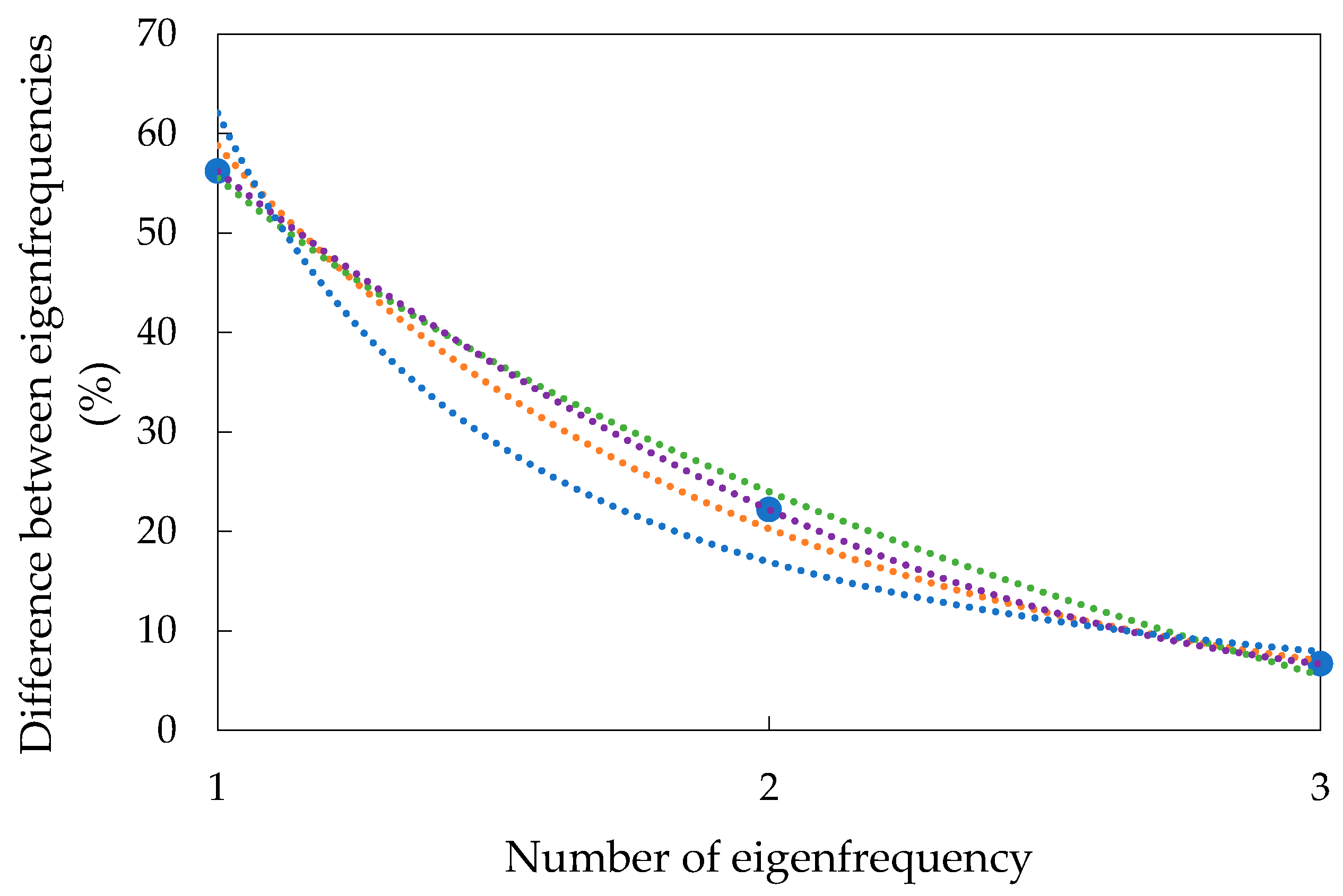
A difference of varying magnitude is observed between the eigenfrequencies of the solid circular cross sections, the constant and the variable ones. In the first case, there is a difference of 56.19%, in the second one 22.18% and in the third one 6.68%. A design tool, based on regression models is established in terms of structural design, which allows to establish the evaluation of the eigenfrequency of the constant or variable section mast from the knowledge of only one of them, with the advantages derived from this. Figure 11 shows graphically the percentage evolution of the differences between each of the eigenfrequencies previously calculated, for the constant and variable sections, with the comparison of different regression models. The potential regression is depicted by the blue line, while the orange line represents exponential regression. The purple line corresponds to a second-order polynomial regression, and lastly, the green line portrays logarithmic regression.
Table 8 shows the numerical difference, in terms of the correlation coefficient, of the different regression models.
Based on the above, it is considered that the most appropriate regression model to reflect the behavior between the two concepts, represented in the previous figure, is the polynomial regression model of order 2. Table 9 and Table 10 show the effective masses in each of the directions, for the variable and constant solid circular section.
It is observed that for the constant circular solid cross-section with the first six variable frequencies, a total of 86.7% of the total mass is captured. That coincides with the initial cross-section (constant tubular). However, when a variable cross-section is arranged, the total mass captured for the same number of natural frequencies decreases to 69.77% of the total mass, and also the individual percentage of each of the frequencies is more spread out, with a maximum of 28.55% versus 61.31% in the case of the constant solid cross-section.

5.4. Structural Assessment and Proposals for Improvement

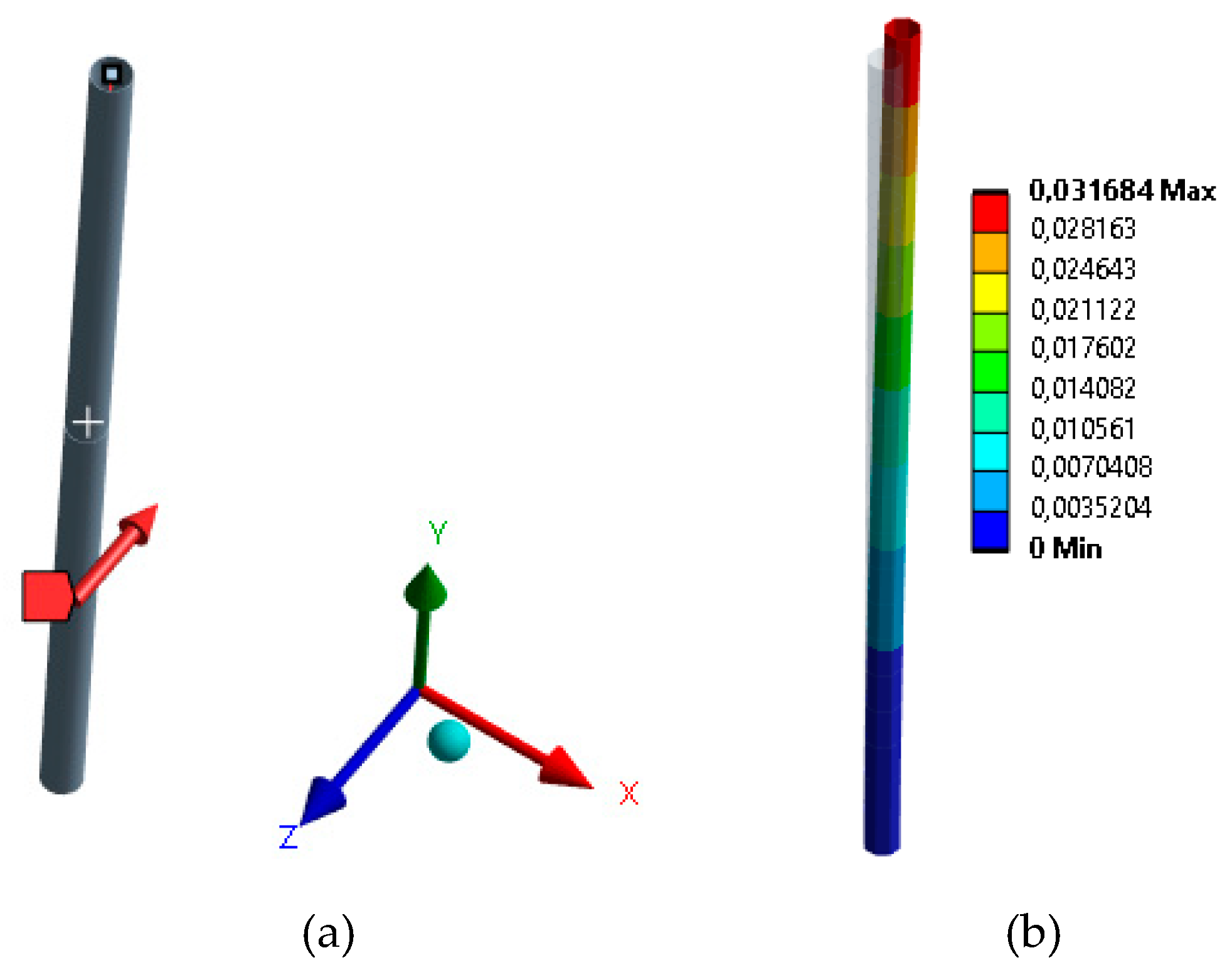
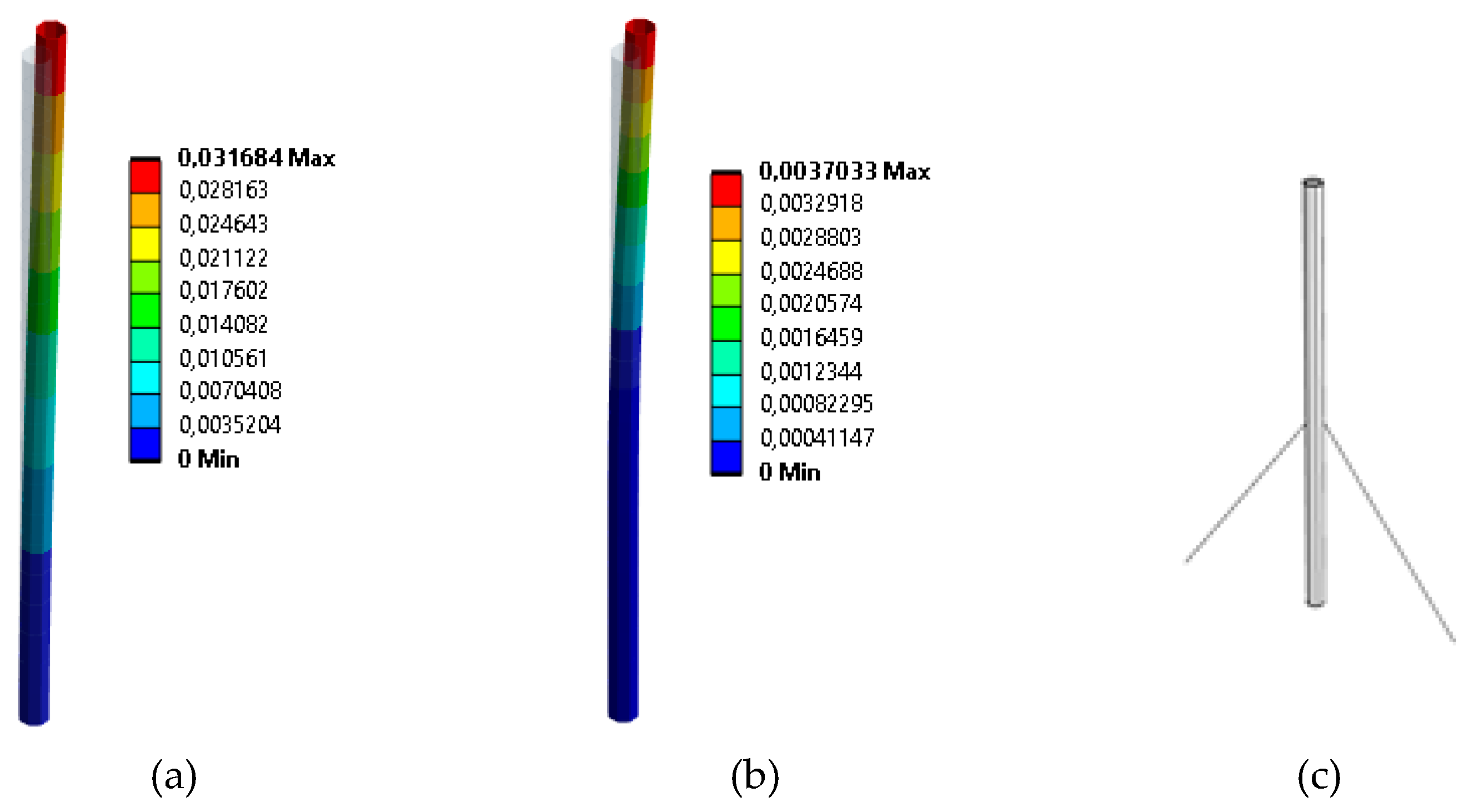
Different alternatives are evaluated to obtain a better structural behavior of the mast, with a generic standard wind load, applied perpendicularly and uniformly along the mast axis, with a maximum displacement of 31.68 mm (Figure 12).
It is decided to place two prestressed cables at the height of the midpoint of the mast, 180º out of phase with each other. The cables are simulated in the numerical model restricting the displacement and allowing the rotation at that point. Structural behavior varies depending it these cables are oriented along the x or z-axis. Figure 13 shows the maximum displacement, for the standard wind load, the two cable configurations, x-axis (31.68 mm) and z-axis (3.7 mm).
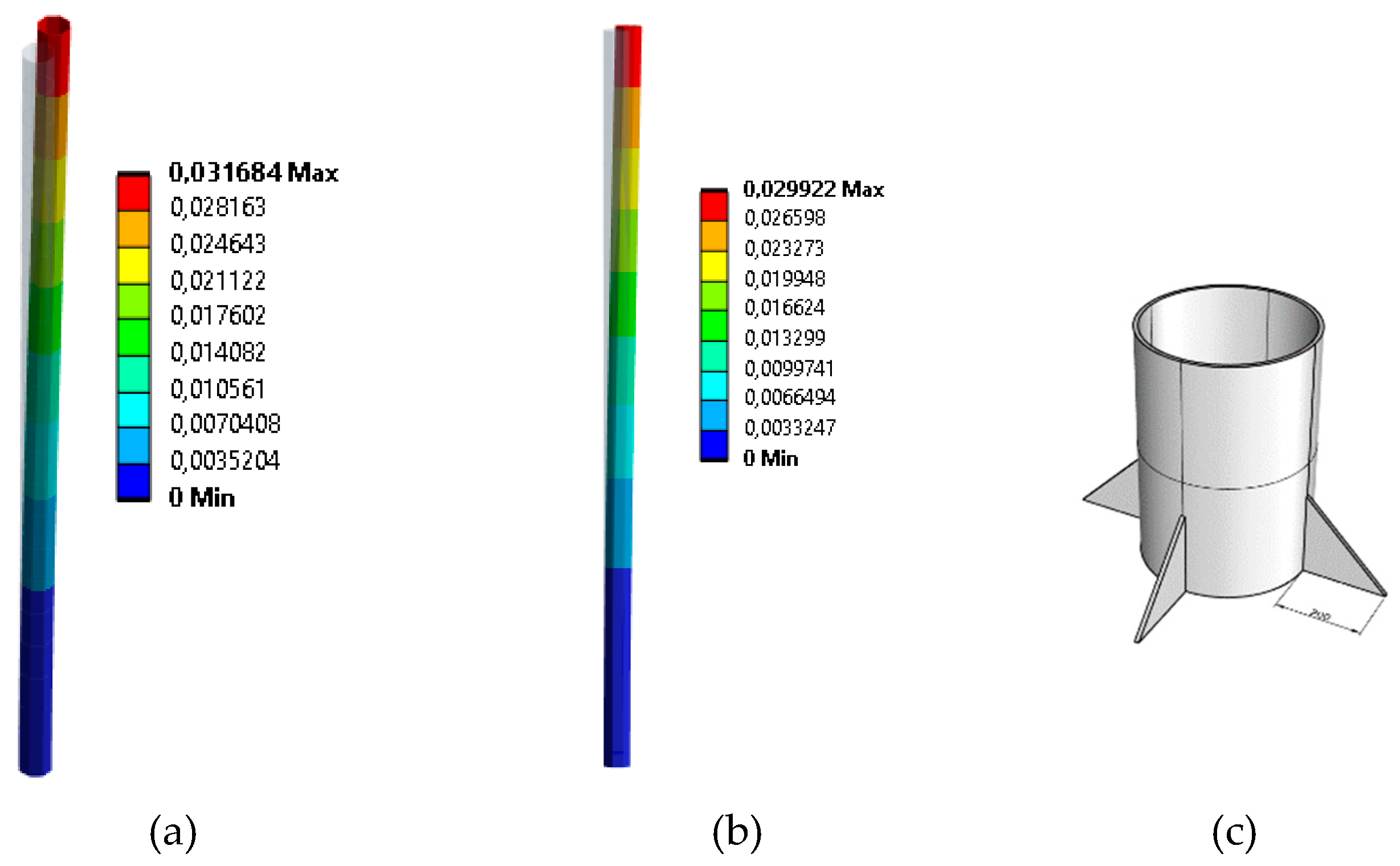
It is observed that the prestressed cables in the direction of the wind load decreases the maximum displacement by 88.3%, with a negligible effect when the location of the prestressed cables is perpendicular to the load direction. Therefore, it is recommended to use prestressed cables with a 90° offset in order to cover all possible load directions. On the other hand, the influence of the arrangement of brackets at the base of the mast, which are welded between it and the bridge top structure, is studied. The objective is the same as with the prestressed cables, but by means of a welding between elements that favors the transit of forces and moments on the local reinforcement. Figure 14 shows for the standard wind load with four triangular brackets (200×200 mm) influence, 90º out of phase.
An improvement of 5.55% is observed after the arrangement of four brackets at the base of the mast, a smaller improvement than the cable arrangement but sufficient depending on the structural requirements, with a minimum impact on the bridge top and improving the transmission of loads on the local reinforcement.
As a summary of this section, the different improvements tested that are aplicable to other type of masts, i.e. radar masts, compass decks or guyed masts in other vessels are:
-
Mass distribution (tapered sections)
-
Cables at 180º
-
Brackets at the base
-
The structural behavior, in terms of obtaining representative eigenmodes, for the constant cross section (up to the sixth natural frequency) and the variable cross section.
-
Structural design tools, as regression models, that relate the behavior of different masts.

6. Conclusions

This paper studies the vibration of the mast of a tugboat and its structural interaction with the local reinforcement (longitudinal and transverse beams) of the bridge top structure, from the determination of eigenfrequencies and eigenmodes, the assessment of load transfer on the local reinforcement and the establishment of design criteria and recommendations. It has been established that the load condition of the heeled ship predominates over the load condition of the upright ship, non depending of the degree of heel. This essential conclusion renders the structural check in the upright condition unnecessary during the mast's design process, significantly enhancing the efficiency of structural design.
A novel design tool has been introduced based on a cubic parabola relationship, enabling precise quantification of load transmission from the mast to the beams, depending on their respective lengths. Furthermore, the study emphasizes the critical role of local reinforcement on the bridge top, significantly influencing its overall structural behavior. Notably, the influence of cross-section variability on the dynamic behavior of the mast has been demonstrated. Constant cross sections exhibit clear structural behavior, while variable cross sections display a different dynamic response, making the option of varying the cross section viable for mitigating resonance risks from other sources of excitation on board (propeller or main engines). The study reveals a fascinating correlation between the structural behavior (eigenfrequencies) of the mast for two different cross sections.
A polynomial regression model is developed that allows deducing the structural behavior of one cross section from knowledge of the other, highlighting operational advantages. The study highlights the mast's susceptibility to wind loads, necessitating the reduction of wind effects through various structural elements. While tensioned cables in opposite directions provide the best solution in terms of minimal displacement of the mast's free end, their feasibility in design and operability is a challenge. Instead, a simpler solution with a few brackets has been proposed, offering sufficient improvement with minimal impact on on-board operations. Further exploration of the influence of load conditions, cross-section variability, and wind load reduction techniques will undoubtedly spark curiosity among scientists, engineers, and naval architects, driving innovation in the design and performance of vessels' mast system. The findings provide insights for shipbuilding and mast design applications in other vessels and industries such as radar mast, compass deck and guyed mast.
As future work, the degree of influence of different parameters on the presented initial results will be established, allowing for a better evaluation and comparison of the same, such as non-linear analysis of the elements under the action of permanent and cyclic loads (such as sea oscillation, wind gusts, etc.) and the prestressed cables as elastic elements. Experimental tests will also be included to validate the numerical model and to compare this tool with the validation tools presented in this manuscript. The effect of the tugboat dynamics under different operating regime and sea condition with resulting impact on the mast modal response will also be studied.

Author Contributions

Conceptualization, A.S-C. and F.P-A.; methodology, A.S-C. and F.P-A.; software, A.S-C; validation, F.P-A.; formal analysis, A.S-C. and F.P-A; investigation, A.S-C. and F.P-A; resources, A.S-C; data curation, F.P-A.; writing—original draft preparation, A.S-C; writing—review and editing, F.P-A; visualization, A.S-C. and F.P-A.; supervision, F.P-A.; project administration, A.S-C. and F.P-A;

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable

Acknowledgments

The authors would like to acknowledge the support received by the Universidad Politécnica de Madrid.

Informed Consent Statement

Not applicable.

Data Availability Statement

All data are presented in the paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. ISO 20283-5. Mechanical vibration -- Measurement of vibration on ships -- Part 5: Guidelines for measurement, evaluation and reporting of vibration with regard to habitability on passenger and merchant ships. 2017. Author 1, A.; Author 2, B. Book Title, 3rd ed.; Publisher: Publisher Location, Country, 2008; pp. 154–196.
  2. Bertram, V. Practical Ship Hydrodynamics; Elsevier: Oxford, 2012. [Google Scholar]
  3. American Bureau of Shipping. Guidance Notes on Ship Vibration. Houston, 2006.
  4. Park, J.H.; Lee, D.Y.; Yang, J.; Song, C.Y. Design Enhancement to Avoid Radar Mast Resonance in Large Ship using Design of Experiments. Journal of Ocean Engineering and Technology. 2019. [Google Scholar] [CrossRef]
  5. Kong, Y.; Choi, S.; Song, J. , Yang, B. Optimum Design for Vibration Reduction of Compass Deck Structure in Ship. Journal of The Society of Naval Architects of Korea 2005, 42, 249–258. [Google Scholar]
  6. Fukada, S.; Yu, J.; Zhao, L. Calculation Formula For Natural Frequency of Radar Mast. Proceedings of the Twentieth International Offshore and Polar Engineering Conference (ISOPE) 2010, Beijing, China, June 20-25.
  7. Ngamkhanong, C.; Kaewunruen, S.; Baniotopoulos, C.; Papaelias, M. Crossing Phenomena in Overhead Line Equipment (OHLE) Structure in 3D Space Considering Soil-Structure Interaction. IOP Conf. Series: Materials Science and Engineering 2017, 245, 032047. [Google Scholar] [CrossRef]
  8. Lacarbonara, W.; Ballerini, S. Vibration mitigation of guyed masts via tuned pendulum dampers. Structural Engineering and Mechanics 2009, 32, 517–529. [Google Scholar] [CrossRef]
  9. Yan-li, H.; Xing, M.; Zhao-min, W. Nonlinear discrete analysis method for random vibration of guyed masts under wind load. Journal of Wind Engineering and Industrial Aerodynamics 2003, 91, 513–525. [Google Scholar] [CrossRef]
  10. Law, S.; Bu, J.; Zhu, X.; Chan, S. Response prediction of a 50 m guyed mast under typhoon conditions. Wind and Structures 2006, 9, 397–412. [Google Scholar] [CrossRef]
  11. Orlando, D.; Gonçalves, P.; Rega, G.; Lenci, S. Nonlinear Dynamics and Instability as Important Design Concerns for a Guyed Mast. IUTAM Symposium on Nonlinear Dynamics for Advanced Technologies and Engineering Design 2013, 223–234. [Google Scholar]
  12. Numayr, K.; Mesmar, S.; Haddad, M. Dynamic analysis of tapered thin-walled masts. Journal of Engineering Science and Technology 2018, 13. [Google Scholar]
  13. Juozapaitis, A.; Kutas, R.; Jatulis, D. Mast behaviour analysis and peculiarities of numerical modelling. Journal of Civil Engineering and Management 2008, 14, 61–66. [Google Scholar] [CrossRef]
  14. Belevičius, R.; Jatulis, D.; Šešok, D. Some insights on the optimal schemes of tall guyed masts. Journal of Civil Engineering and Management 2013, 19, 749–758. [Google Scholar] [CrossRef]
  15. Belevičius, R.; Jatulis, D.; Rusakevičius, D.; Mačiunas, D. Optimization of rigidly supported guyed masts. Advances in Civil Engineering 2017, 4561376. [Google Scholar] [CrossRef]
  16. Pezo, M.; Bakic, V.; Markovic, Z. Structural analysis of guyed mast exposed to wind action. Thermal Science 2016, 20 (suppl. 5), 1473–1483. [Google Scholar] [CrossRef]
  17. Luis García, K.; Maes, K.; Parnás, V. E.; Lombaert, G. Operational modal analysis of a self-supporting antenna mast. Journal of Wind Engineering and Industrial Aerodynamics 2021, 209, 104490. [Google Scholar] [CrossRef]
  18. Alshurafa, S.; Alhayek, H.; Polyzois, D. Finite element method for the static and dynamic analysis of FRP guyed tower. Journal of Computational Design and Engineering 2019, 6, 436–446. [Google Scholar] [CrossRef]
  19. Alshurafa, S.; Alhayek, H.; Polyzois, D. Dynamic characteristics of an 8.6 m lightweight FRP tower supporting mass on its top. Marine Structures 2021, 79, 103052. [Google Scholar] [CrossRef]
  20. Alshurafa, S.; Alhayek, H.; Polyzois, D. Development of GFRP Monopole Guyed Communication Tower. Journal of Composites for Construction 2022, 27. [Google Scholar] [CrossRef]
  21. Ahmad, M.; Jamil, M.; Iqbal, J.; Khan, M.; Malik, M.; Butt, S. Modal Analysis of Ship’s Mast Structure using Effective Mass Participation Factor. Indian Journal of Science and Technology 2016, 9. [Google Scholar] [CrossRef]
  22. Zhang, M.; Li, T.; Wang, Y.; Chen, Y.; Zhao, G. Wind Induced Vibration and Vibration Suppression of High-Mast Light Poles with Spiral Helical Strakes. Buildings 2023, 13, 907. [Google Scholar] [CrossRef]
  23. Ballaben, J.; Rosales, M.; Preidikman, S. Nonlinear dynamic response of a three-dimensional guyed mast. Procedia Engineering 2017, 199, 814–819. [Google Scholar] [CrossRef]
  24. Hulimka, J.; Skwarek, M.; Kałuża, M. Collapse of aluminum lattice mast as an effect of design and executive errors. Engineering Failure Analysis 2023, 145, 107035. [Google Scholar] [CrossRef]
  25. Gritsenko, D.; Xu, J.; Paoli, R. Transverse vibrations of cantilever beams: Analytical solutions with general steady-state forcing. Applications in Engineering Science 2020, Volume 3, 100017. [Google Scholar] [CrossRef]
  26. Zhao, Y.; Lian, J.; Lian, C.; Dong, X.; Wang, H.; Liu, C.; Jiang, Q.; Wang, P. Stochastic Dynamic Analysis of an Offshore Wind Turbine Structure by the Path Integration Method. Energies 2019, 12, 3051. [Google Scholar] [CrossRef]
  27. Juncher, J.; Mansour, A.; Smærup, A. Estimation of ship motions using closed-form expressions. Ocean Engineering 2004, 31, 61–85. [Google Scholar]
  28. Bureau Veritas Rules. Part B, Chapter 5, Section 3. Edition 2023.
  29. Intact stability requirements for tugs with application to fairplay 22. ASD Ship Design B.V. Available online in: https://n9.cl/6dqzr.
Preprints 105148 g001
Figure 1. General arrangement. (a) Profile view, (b) Front view.
Figure 1. General arrangement. (a) Profile view, (b) Front view.
Preprints 105148 g001
Preprints 105148 g002
Figure 2. Mast on bridge top structural drawing. (a) 3D view, (b) equivalent dynamic model.
Figure 2. Mast on bridge top structural drawing. (a) 3D view, (b) equivalent dynamic model.
Preprints 105148 g002
Preprints 105148 g003
Figure 3. Bridge and deckhouse structure. (a) Front view, (b) Side view, (c) Top view.
Figure 3. Bridge and deckhouse structure. (a) Front view, (b) Side view, (c) Top view.
Preprints 105148 g003
Preprints 105148 g004
Figure 4. Mesh pattern. (a) Mast structure, (b) Local reinforcement.
Figure 4. Mesh pattern. (a) Mast structure, (b) Local reinforcement.
Preprints 105148 g004
Preprints 105148 g005
Figure 5. Modelling load conditions. (a) Upright condition, (b) Heeling condition.
Figure 5. Modelling load conditions. (a) Upright condition, (b) Heeling condition.
Preprints 105148 g005
Preprints 105148 g006
Figure 6. Deformed local reinforcement in the bridge top under the most unfavorable loading condition.
Figure 6. Deformed local reinforcement in the bridge top under the most unfavorable loading condition.
Preprints 105148 g006
Preprints 105148 g007
Figure 7. (a) Load condition and boundary condition (b) Bending moment (BM) diagram, (c) shear force (SF) diagram.
Figure 7. (a) Load condition and boundary condition (b) Bending moment (BM) diagram, (c) shear force (SF) diagram.
Preprints 105148 g007
Preprints 105148 g008
Figure 8. Relationship between variables α and β.
Figure 8. Relationship between variables α and β.
Preprints 105148 g008
Preprints 105148 g009aPreprints 105148 g009b
Figure 9. Natural modes and frequencies of the mast.
Figure 9. Natural modes and frequencies of the mast.
Preprints 105148 g009aPreprints 105148 g009b
Preprints 105148 g010
Figure 10. Natural modes and frequencies of the mast with variable and solid cross section.
Figure 10. Natural modes and frequencies of the mast with variable and solid cross section.
Preprints 105148 g010
Preprints 105148 g011
Figure 11. Comparative between regression models.
Figure 11. Comparative between regression models.
Preprints 105148 g011
Preprints 105148 g012
Figure 12. Maximum displacement of the mast under wind loading. (a) Force representation, (b) maximum displacement (m).
Figure 12. Maximum displacement of the mast under wind loading. (a) Force representation, (b) maximum displacement (m).
Preprints 105148 g012
Preprints 105148 g013
Figure 13. Maximum displacement (in meters) of the mast under wind loading with cables. (a) In the x-direction, (b) in the z-direction, (c) drawing of the mast with two cables at 180º.
Figure 13. Maximum displacement (in meters) of the mast under wind loading with cables. (a) In the x-direction, (b) in the z-direction, (c) drawing of the mast with two cables at 180º.
Preprints 105148 g013
Preprints 105148 g014
Figure 14. Maximum displacement (in meters) of the mast under wind loading. (a) Without brackets, (b) with brackets, (c) drawing of the four brackets on the mast base.
Figure 14. Maximum displacement (in meters) of the mast under wind loading. (a) Without brackets, (b) with brackets, (c) drawing of the four brackets on the mast base.
Preprints 105148 g014
Table 1. Main particulars of the tugboat.
Table 1. Main particulars of the tugboat.
Description Value
Scantling length, L 28 m
Breadth, B 8.5 m
Depth to the main deck, D 4.5 m
Scantling draught, T 3.75m
Service speed, V 12 knots
Table 2. Material properties of the steel.
Table 2. Material properties of the steel.
Young’s Modulus (GPa) Poisson’s Ratio Density (kg/m3)
200 0.3 7850
Table 3. Acceleration values.
Table 3. Acceleration values.
Movement Value (m/s2)
Sway 3.77
Heave 4.86
Table 4. Results comparison between analytical method and finite element analysis (FEA).
Table 4. Results comparison between analytical method and finite element analysis (FEA).
Output Analytical method (Hz) Finite element analysis (Hz)
Natural frequency, f1 3.4894 3.4895
Natural frequency, f2 21.551 21.556
Natural frequency, f3 58.99 59.032
Table 5. Comparison of values between load conditions.
Table 5. Comparison of values between load conditions.
Upright condition Heeling condition
Vertical load 15 kN 16 kN
Bending moment 20.2 kN·m 21,5 kN·m
Table 6. Effective mass in x, y and z-direction of the mast with constant and tubular cross section.
Table 6. Effective mass in x, y and z-direction of the mast with constant and tubular cross section.
Mode Frequency (Hz) Effective mass x-direction (%) Effective mass y-direction (%) Effective mass z-direction (%)
1 3.49 0 0 61.35
2 3.49 61.35 0 0
3 21.56 0 0 19.01
4 21.56 19.01 0 0
5 59.03 1.11 0 5.5
6 59.03 5.5 0 1.11
Table 7. Comparison of natural frequency between solid circular sections.
Table 7. Comparison of natural frequency between solid circular sections.
Natural frequency Constant section Variable section
f1 (Hz) 2.53 5.78
f2 (Hz) 2.53 5.78
f3 (Hz) 15.8 20.31
f4 (Hz) 15.8 20.31
f5 (Hz) 43.9 47.04
f6 (Hz) 43.9 47.034
Table 8. Comparison of natural frequency between solid circular sections.
Table 8. Comparison of natural frequency between solid circular sections.
Regression Equation Correlation coefficient (R2)
Exponential y=170.48e-1.065x 0.9946
Logarithmic y=-45.5ln(x)+55.523 0.9961
Polynomial of order 2 y=9.255x2-61.775x+108.71 1
Potential y=62.075x-1.874 0.951
Table 9. Effective mass in x, y and z-direction of the mast with variable and solid cross section.
Table 9. Effective mass in x, y and z-direction of the mast with variable and solid cross section.
Mode Frequency (Hz) Effective mass x-direction (%) Effective mass y-direction (%) Effective mass z-direction (%)
1 5.784 28.55 0 9.52
2 5.784 9.52 0 28.55
3 20.31 5.19 0 15.57
4 20.31 15.57 0 5.19
5 47.04 2.74 0 8.22
6 47.04 8.22 0 2.74
Table 10. Effective mass in x, y and z-direction of the mast with constant and solid cross section.
Table 10. Effective mass in x, y and z-direction of the mast with constant and solid cross section.
Mode Frequency (Hz) Effective mass x-direction (%) Effective mass y-direction (%) Effective mass z-direction (%)
1 2.534 61.31 0 0
2 2.534 0 0 61.31
3 15.8 18.87 0 0.01
4 15.8 0.01 0 18.87
5 43.9 0.14 0 6.37
6 43.9 6.37 0 0.14
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated