Submitted:
30 April 2024
Posted:
30 April 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. Objectives
2. Materials and Methods
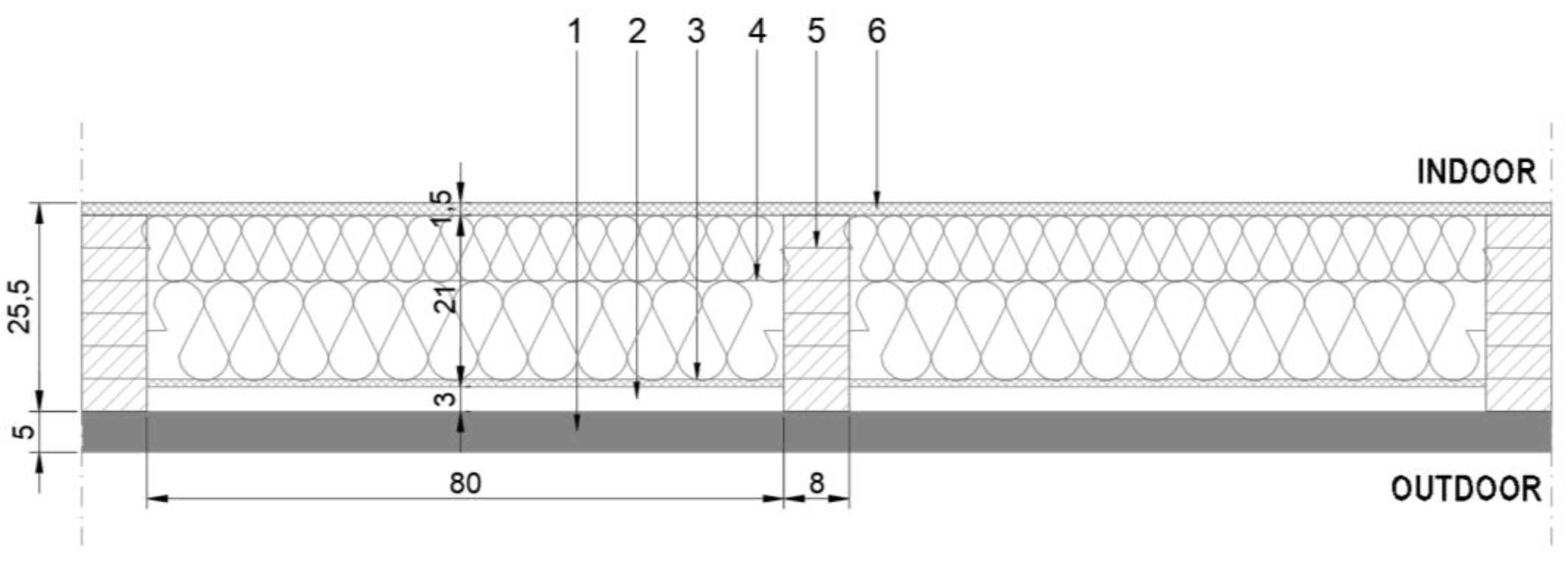
2.1. Geometry of the Model
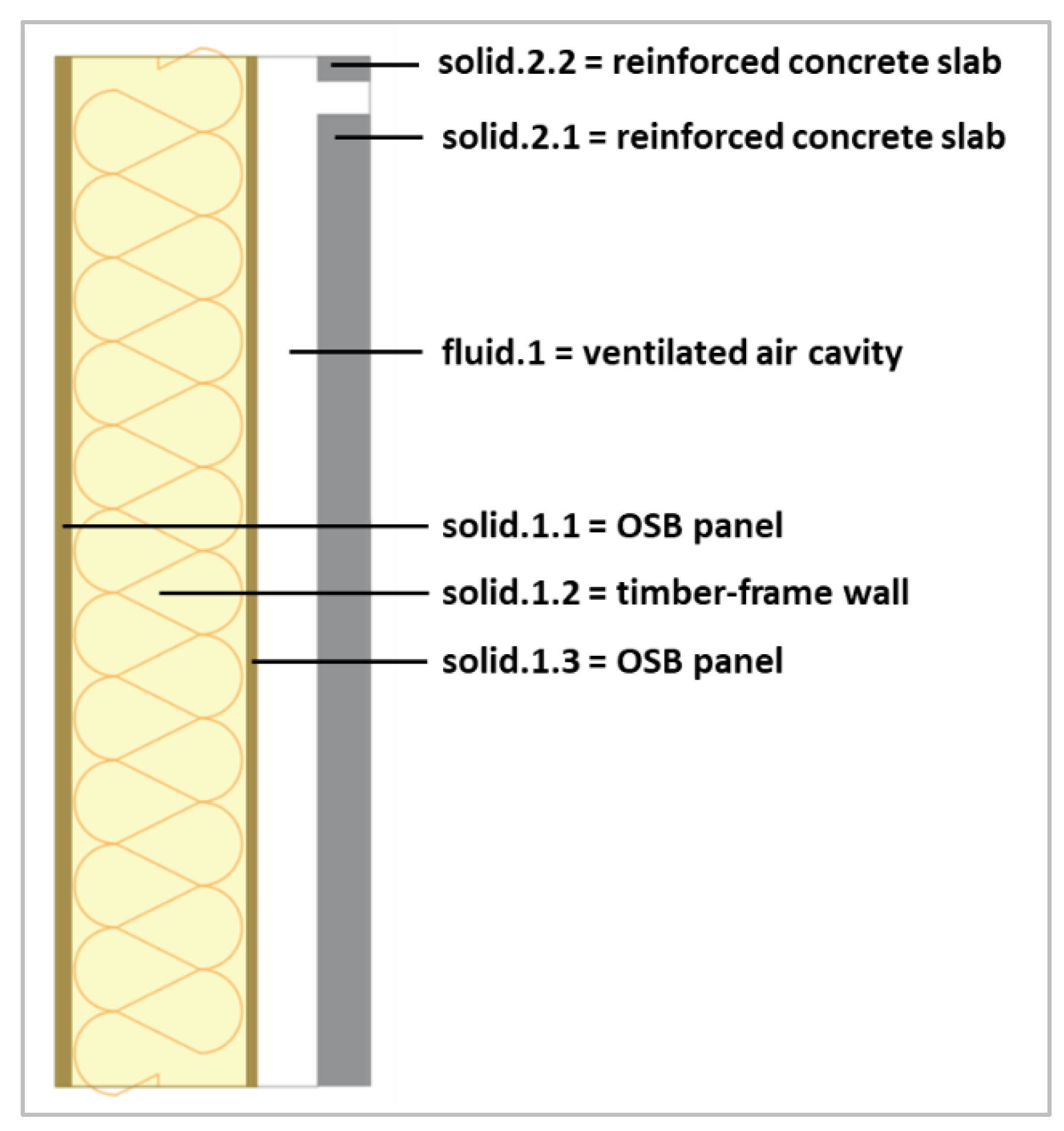
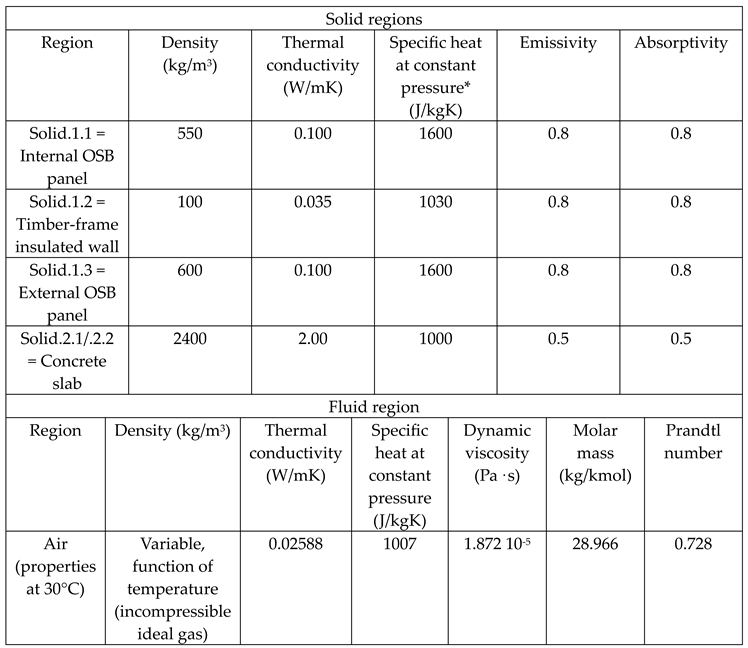
2.2. Physical Properties of the Model
2.3. Boundary Conditions
2.4. Mesh Refinement Study
- m0012_baseMesh
- m0013_baseMeshx1.5
- m0014_baseMeshx1.5x1.5
2.5. Solver
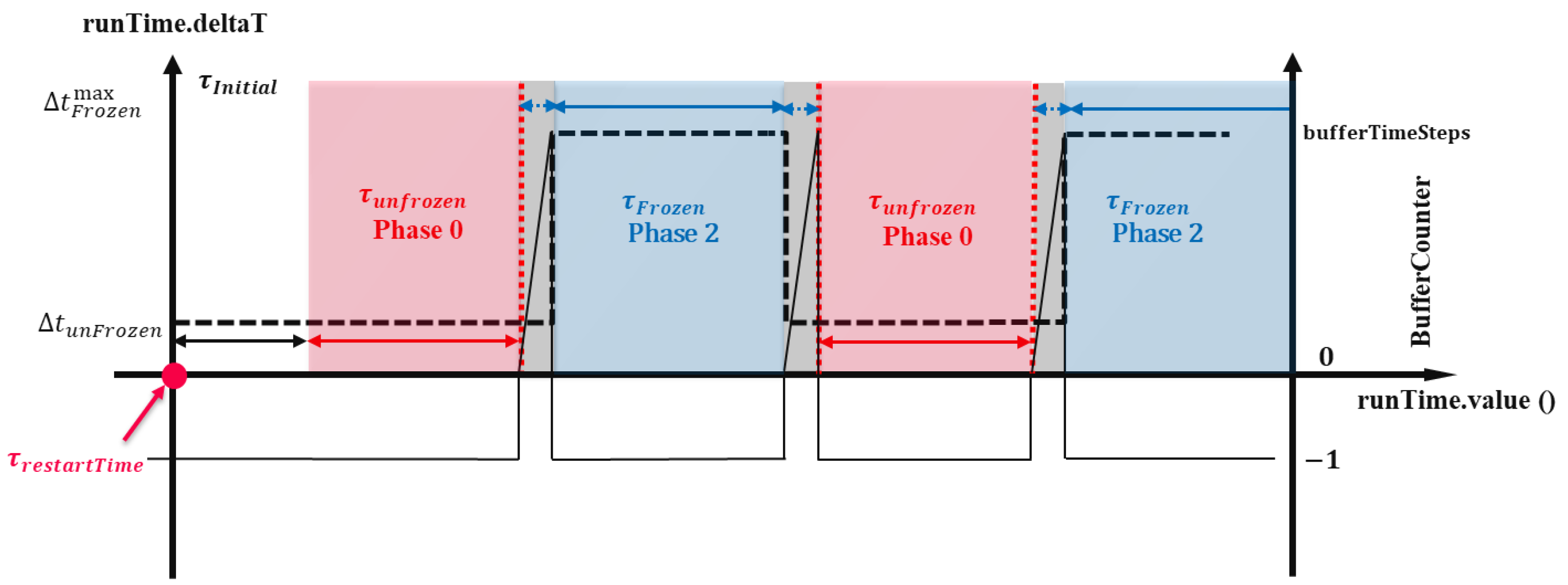
2.5.1. A New “Frozen-Unfrozen Flow” Solver
- “initial period”, when the fluid flow evolves according to time steps calculated based on Courant and solid diffusion numbers, to make the simulation stable at the beginning. It should be noted that the initial time not necessarily starts at time 0, since the algorithm is designed to work also in the case the simulation is re-started;
- “normal period”: in which the flow is sequentially set to frozen and unfrozen modes.
2.5.2. Solver Performance Evaluation
2.6. Model Calibration
2.7. Model Validation
3. Results
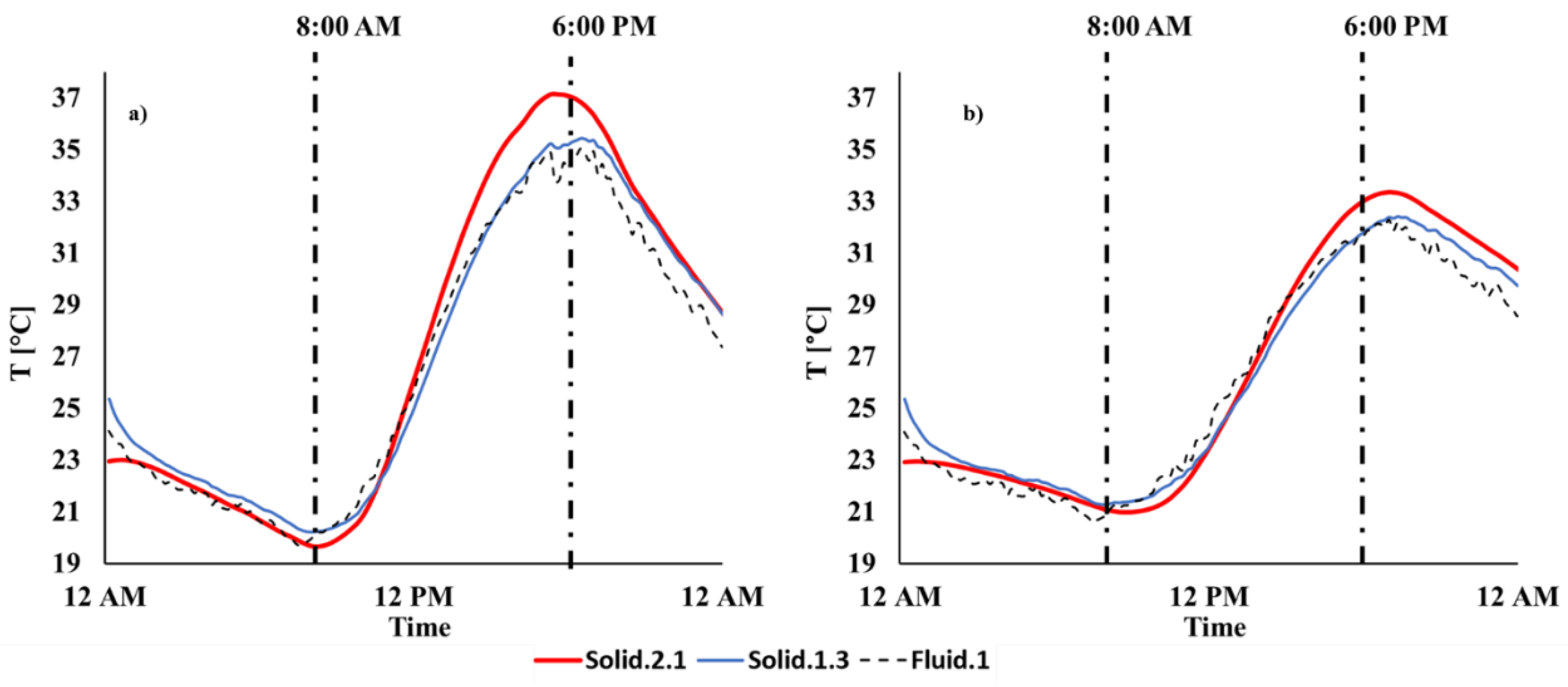
- TR: average temperature on the internal surface of the indoor OSB panel;
- TO: average temperature on the surface towards the cavity of the outdoor OSB panel;
- TC: average temperature on the concrete slab surface towards the ventilated cavity;
- TC_ext: average temperature on the external surface of the concrete slab.
3.1. Sensitivity Analysis
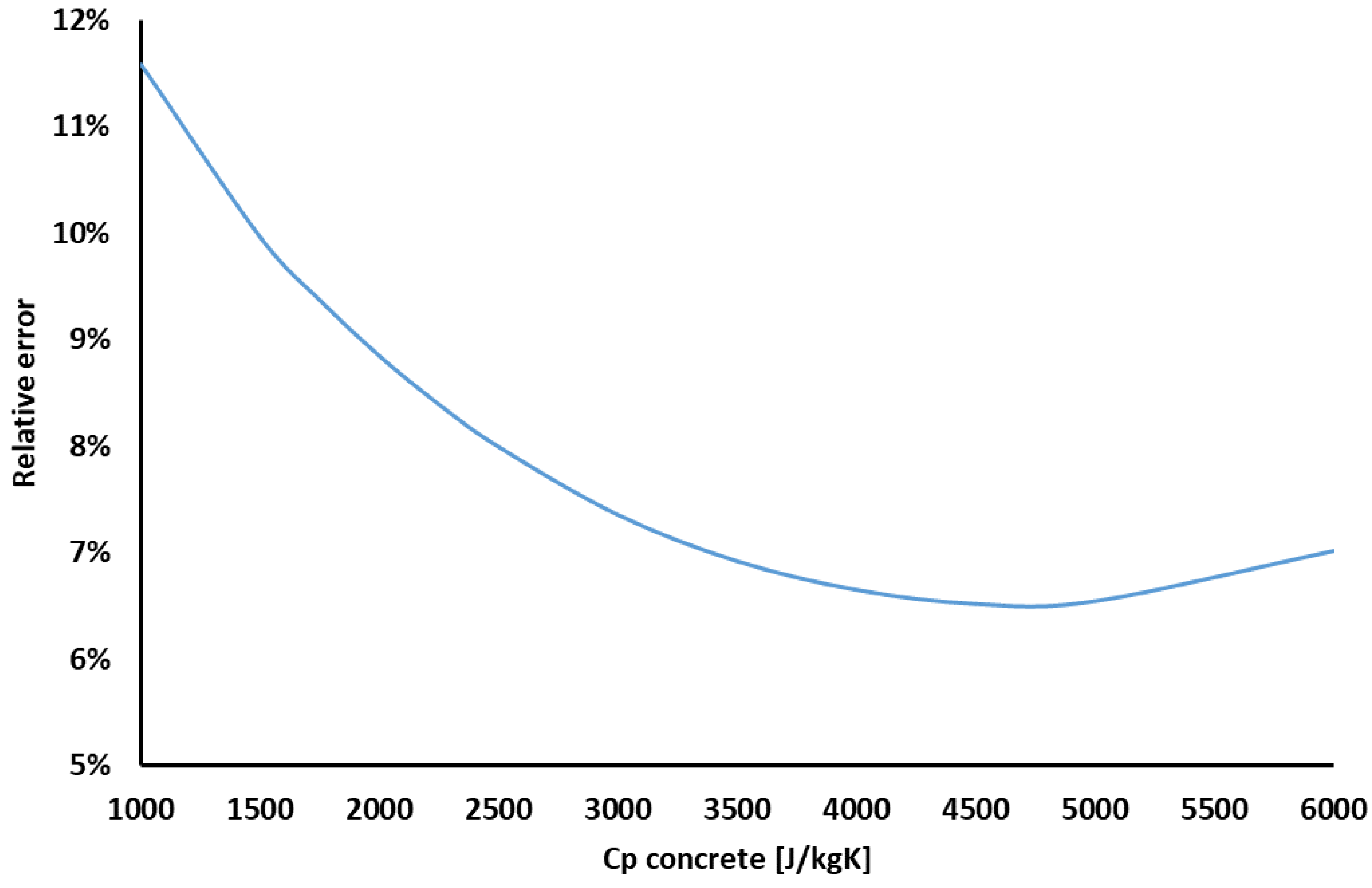
3.2. Calibration Process
| Results of calibration process | ||||
| Case | Description | Cp_concrete (J/kgK) |
Error of TO prediction |
Note |
| t1000 (= t0101) | 1xCp_concrete_base | 1000 | 11.59% | Cp value from EN ISO 10456:2007 |
| t1500 | 1.5xCp_concrete_base | 1500 | 9.97% | |
| t1750 | 1.75xCp_concrete_base | 1750 | 9.38% | |
| t2000 (= t0104) | 2xCp_concrete_base | 2000 | 8.85% | starting case |
| t2250 | 2.25xCp_concrete_base | 2250 | 8.40% | |
| t2500 | 2.5xCp_concrete_base | 2500 | 8.00% | |
| t3000 | 3xCp_concrete_base | 3000 | 7.36% | |
| t3500 | 3.5xCp_concrete_base | 3500 | 6.93% | |
| t4000 | 4xCp_concrete_base | 4000 | 6.66% | |
| t4500 | 4.5xCp_concrete_base | 4500 | 6.52% | best prediction |
| t5000 | 5xCp_concrete_base | 5000 | 6.55% | |
| t6000 | 6xCp_concrete_base | 6000 | 7.02% | |
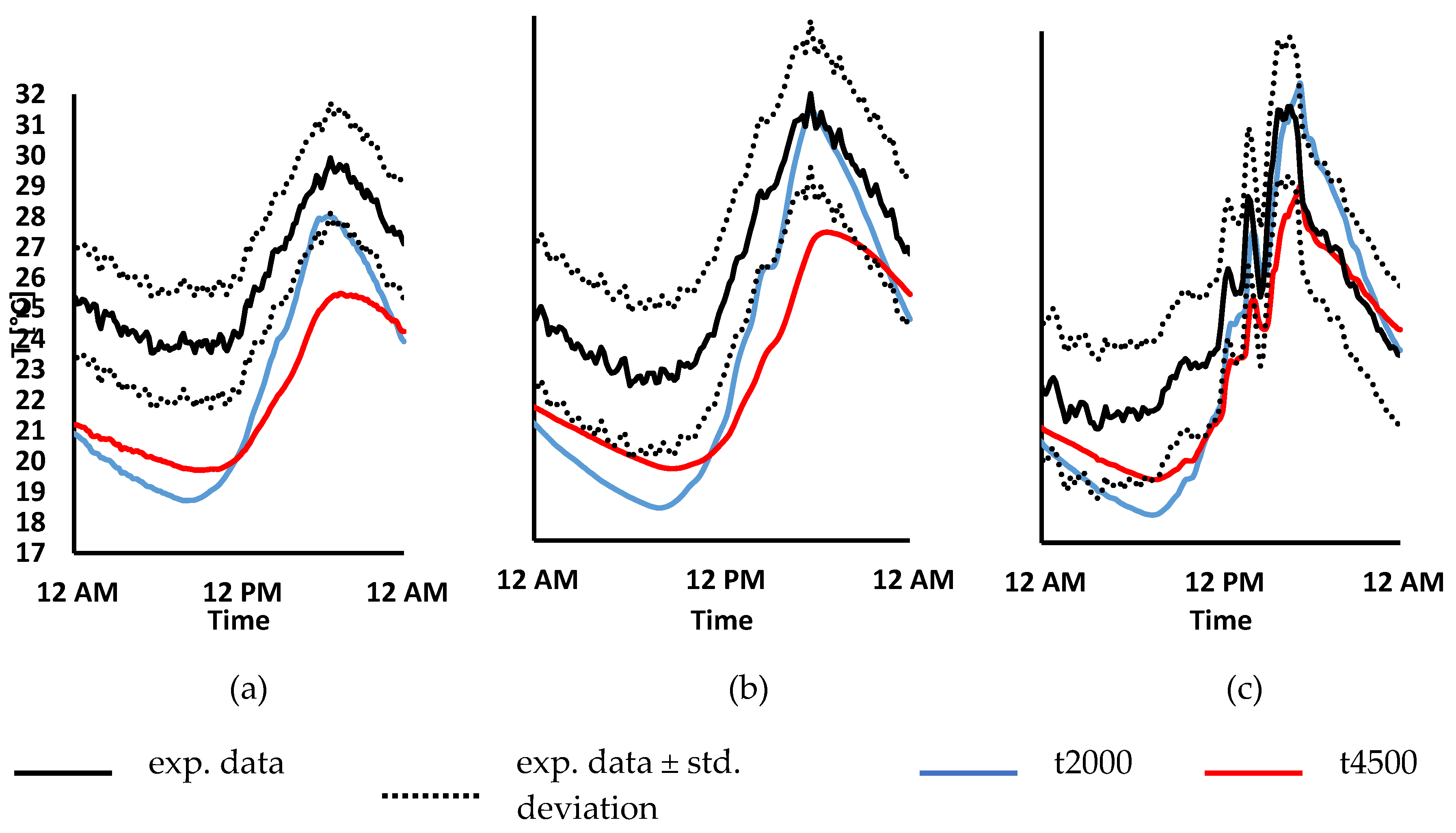
3.3. Validation Study
3.4. Discussion of Persistent Underprediction of Surface Temperatures Inside the Cavity
3.4.1. Relative Importance of Radiative Heat Transfer Inside the Cavity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Disclaimer
Conflicts of Interest
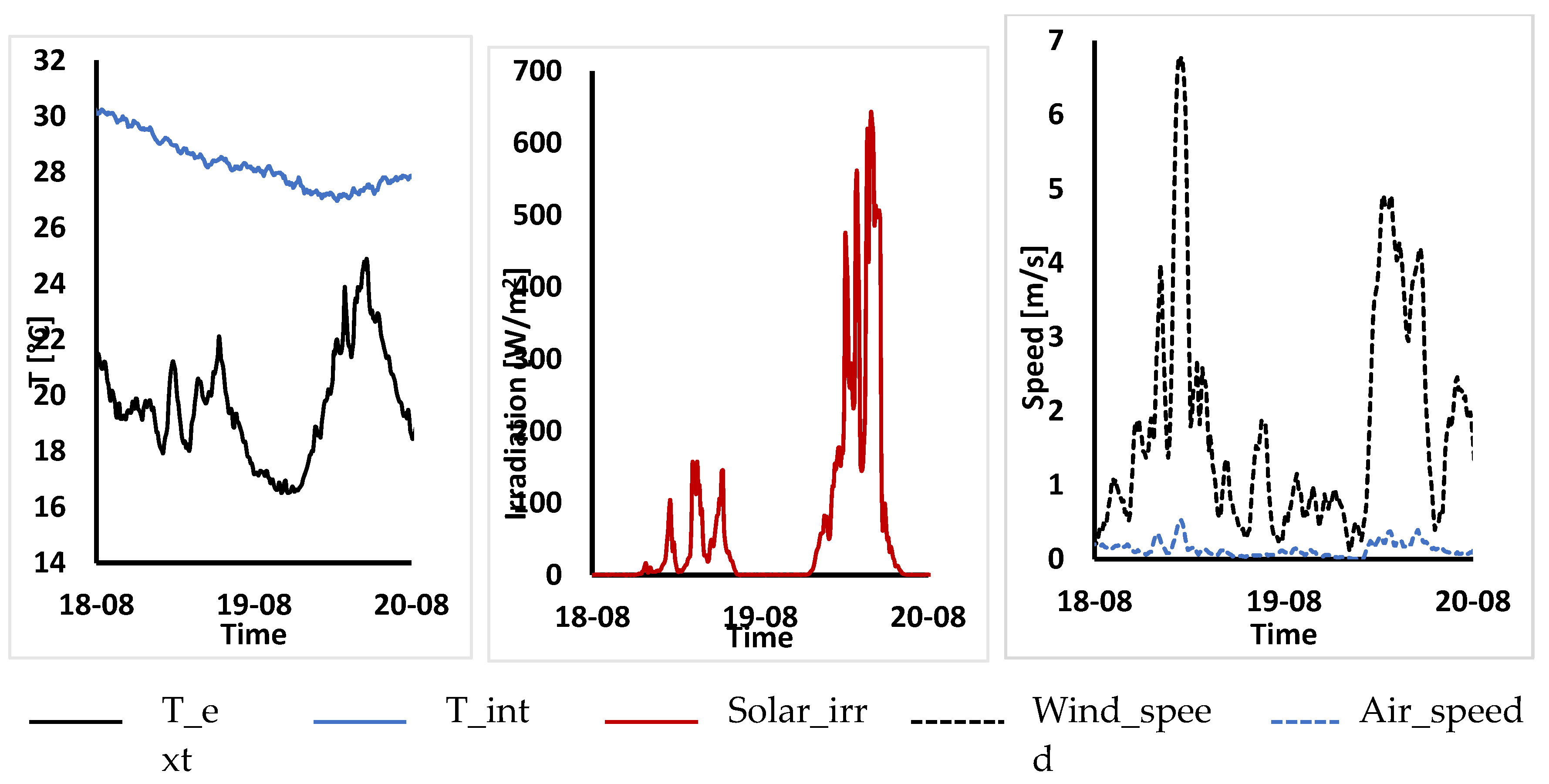
Appendix A – Settings of the CFD Solver & Boundary Conditions
| Region | Variable | Boundary conditions applied |
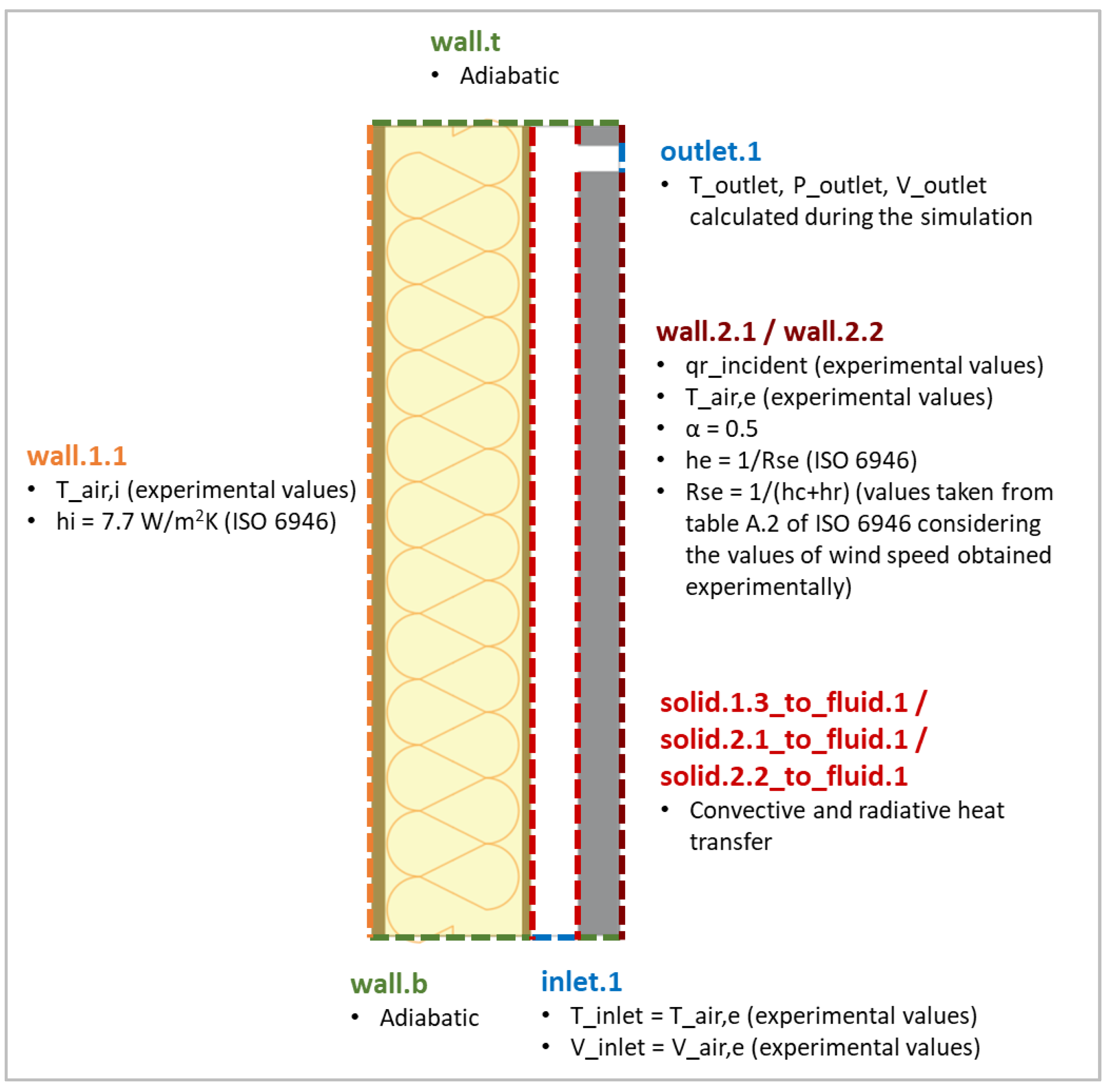
| wall.1.1 | Temperature | externalWallHeatFluxTemperatureIPPT (user defined) Ti: indoor air temperature, .csv file with values from experimental monitoring TiRad: off (i.e. indoor mean radiant temperature is switched off and only Ti is considered for the heat exchange between the wall and the indoor ambient) hInclRad: true (i.e. the radiation to indoor ambient lumped into the heat transfer coefficient hCoeffs taken from UNI EN ISO 6946) hCoeffs: heat transfer coefficient, .csv file with hCoeffs = 7.7 [W/m2K] (value for indoor ambient taken from UNI EN ISO 6946) |
| wall.2.* (wall.2.1 wall.2.2) |
Temperature | externalWallHeatFluxTemperatureIPPT Ta: outdoor air temperature, .csv file with monitored values TaRad: off (i.e. outdoor mean radiant temperature is switched off and only Ta is considered for the heat exchange between the wall and the outdoor environemnt) hInclRad: true (i.e. the radiation to outdoor ambient lumped into the heat transfer coefficient hCoeffs taken from UNI EN ISO 6946) hCoeffs: heat transfer coefficient, .csv file with h=1/Rse (Rse values taken from UNI EN ISO 6946, table A.2 according to the wind speed registered during the experimental monitoring) qr: incident solar irradiation on the wall, .csv file with values from experimental monitoring qrRelaxation: 1 |
| solid.1.*_to_solid.1.* (solid.1.1_to_solid.1.2 solid.1.2_to_solid.1.3) |
Temperature | compressible::turbulentTemperatureRadCoupledMixed kappaMethod: solidThermo (for values of thermophysical properties see Table 1 of main document) no radiative radiation model because of direct contact |
| solid.*_to_fluid.1 fluid.1_to_solid.* (solid.1.3_to_fluid.1 solid.2.1_to_fluid.1 solid.2.2_to_fluid.1 fluid.1_to_solid.1.3 fluid.1_to_solid.2.1 fluid.1_to_solid.2.2) |
Temperature | compressible::turbulentTemperatureRadCoupledMixed kappaMethod: solidThermo or fluidThermo (for values of thermophysical properties see Table 1 of main document) |
| Pressure | fixedFluxPressure p0: 105[Pa] |
|
| Radiation | greyDiffusiveRadiationViewFactor qro: uniform 0 for emissivity values see Table 1 of main document |
|
| Velocity | noSlip | |
| inlet.1 | Temperature | uniformFixedValue uniformValue: .csv file with Ta values |
| Pressure | zeroGradient | |
| Radiation | greyDiffusiveRadiationViewFactor qro: uniform 0 emissivity: 0.9 |
|
| Velocity | uniformFixedValue uniformValue: .csv file with values from experimental monitoring |
|
| outlet.1 | Temperature | inletOutlet inletValue: 297 [K] |
| Pressure | fixedValue value: 105 [Pa] |
|
| Radiation | greyDiffusiveRadiationViewFactor qro: uniform 0 emissivity: 0.9 |
|
| Velocity | inletOutlet inletValue: (0 0 0) [m/s] |
|
| wall.t wall.b |
Temperature | zeroGradient |

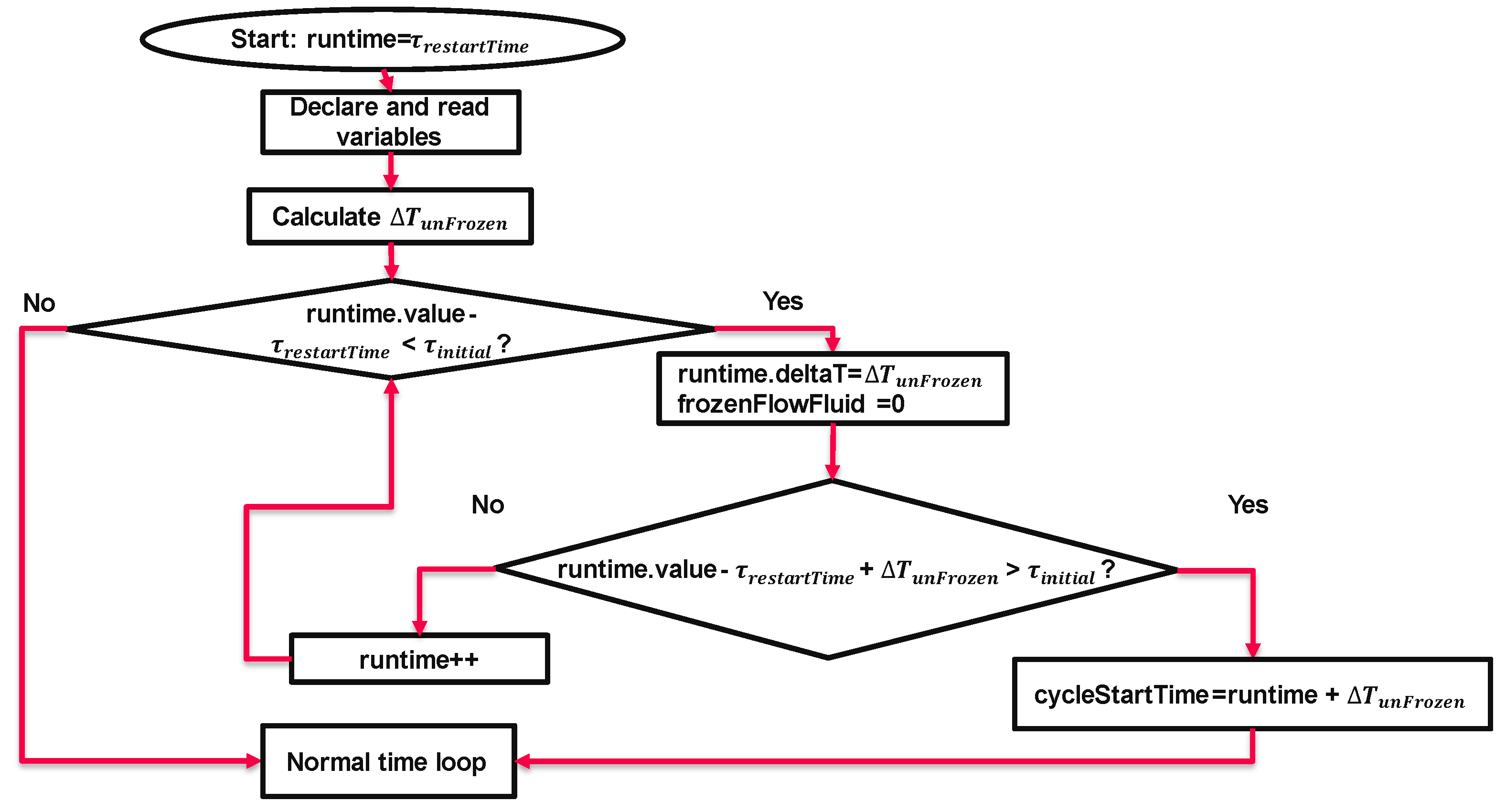
Appendix B – Algorithmic Details of the “Frozen Unfrozen Flow” Solver
- declaration of the variables;
- calculation of the time-step based on courant and solid diffusion numbers;
- setting the Unfrozen mode for the fluid flow;
- setting the “cycleStartTime” at the end of this period.
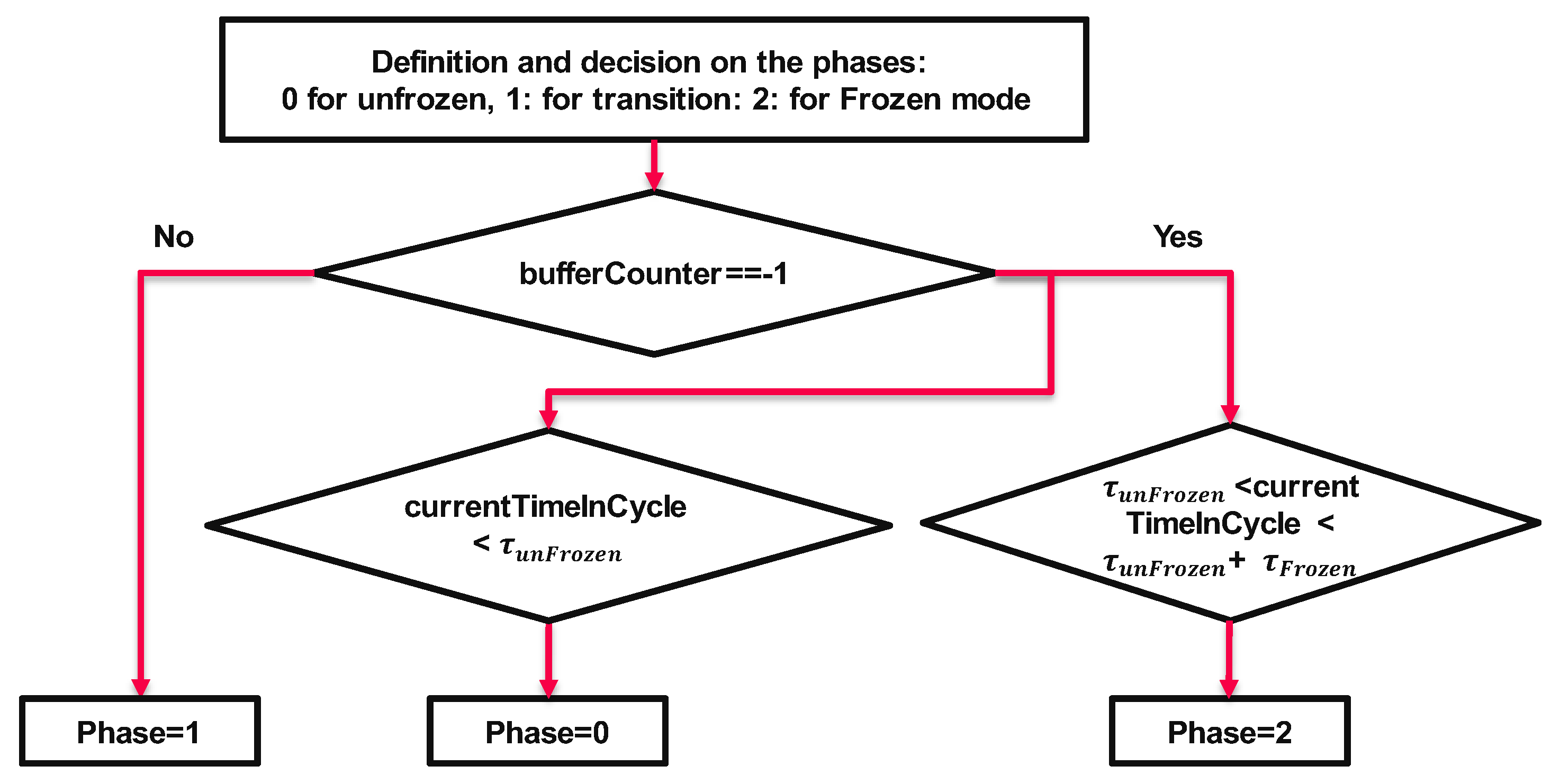
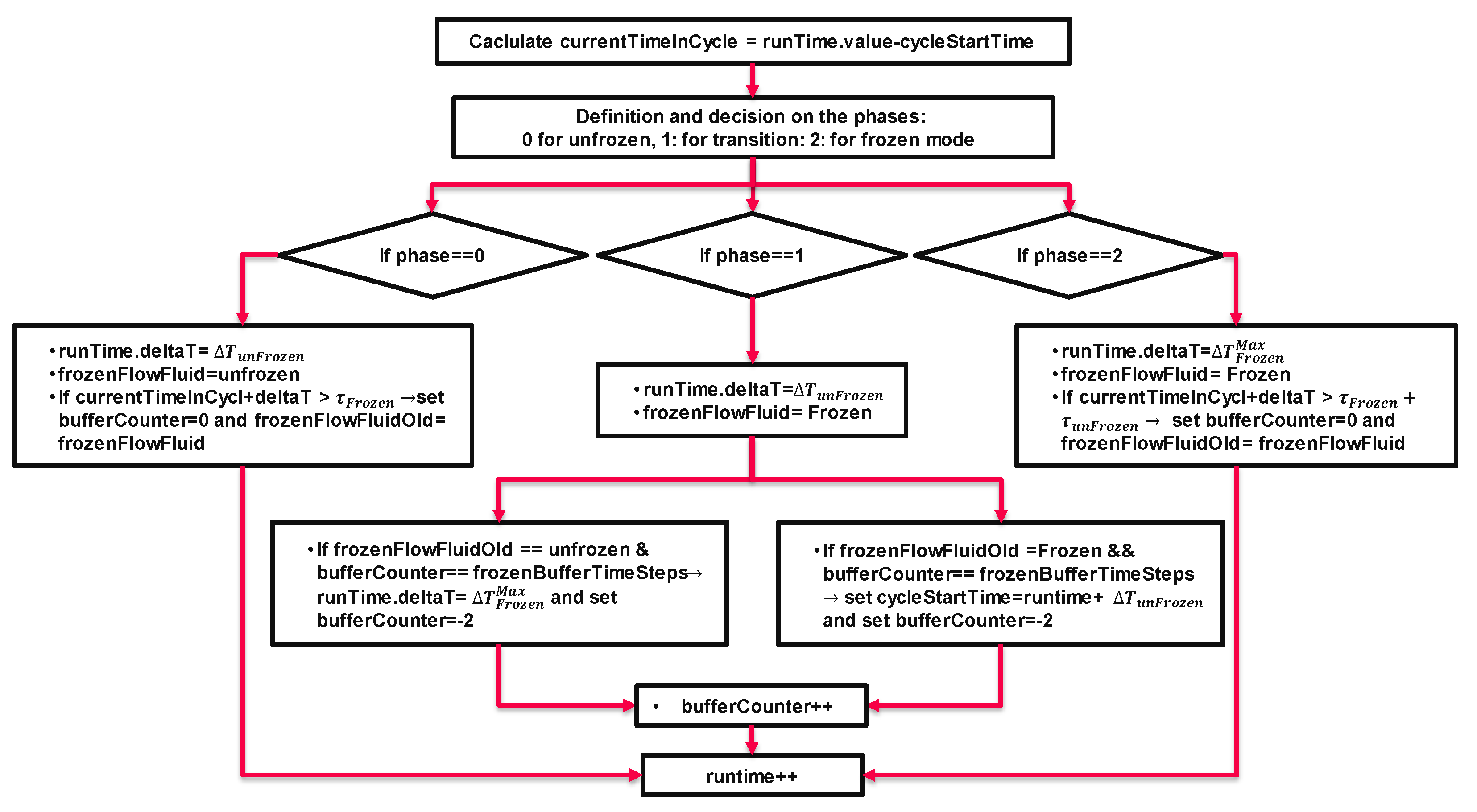
- it calculates the current time in a cycle (“currentTimeInCycle”), which is the difference between the current flow time and “cycleStartTime”;
-
it assigns the phases for frozen, unfrozen, or transition modes (see Error! Reference source not found.Error! Reference source not found.):
- ○
- if “bufferCounter” is equal to -1 and the runtime is in unfrozen mode, the phase is 0, otherwise, the phase is 2;
- ○
- if “bufferCounter” is not equal to -1, then set the phase to 1.
- if the phase is “0”, then set the time step to and the mode of the flow “unfrozen”. If the new flow time falls in a new phase, set “bufferCounter” to 0 and store the latest flow solution mode as “frozenFlowFluidOld”
-
if the phase is 1, then set the time step to , then decide based on the previous phase flow mode:
- ○
- if “frozenFlowFluidOld” is unfrozen and “bufferCounter” reaches the use input value (i.e. “bufferCounterSteps”), set the time step to and “bufferCounter” to -2;
- ○
- if “frozenFlowFluidOld” is frozen and “bufferCounter” reaches the use input value (i.e. “bufferCounterSteps”), then “bufferCounter”. to -2 and set “cycleStartTime” =current flow time + .
- if phase is 2 then, freeze the flow and set the time step to . Once the solution falls out of the cycle, set “bufferCounter” to 0 and store the latest flow solution mode as “frozenFlowFluidOld”
- repeat the above steps till the flow time reaches the end time of the simulation (defined in “controlDict”)
References
- Asdrubali, F.; Ferracuti, B.; Lombardi, L.; Guattari, C.; Evangelisti, L.; Grazieschi, G. A Review of Structural, Thermo-Physical, Acoustical, and Environmental Properties of Wooden Materials for Building Applications. . Build Environ 2017, 114, 307–332. [CrossRef]
- Janssen, H. Characterization of Hygrothermal Properties of Wood-Based Products – Impact of Moisture Content and Temperature. Constr Build Mater 2018, 185, 39–43. [CrossRef]
- Fortuna, S.; Mora, T.D.; Peron, F.; Romagnoni, P. Environmental Performances of a Timber-Concrete Prefabricated Composite Wall System. In Proceedings of the Energy Procedia; 2017; pp. 90–97.
- Pastori, S.; Mereu, R.; Mazzucchelli, E.S.; Passoni, S.; Dotelli, G. Energy Performance Evaluation of a Ventilated Façade System through Cfd Modeling and Comparison with International Standards. Energies (Basel) 2021, 14. [CrossRef]
- Destro, R.; Boscato, G.; Mazzali, U.; Russo, S.; Peron, F.; Romagnoni, P. Structural and Thermal Behaviour of a Timber-Concrete Prefabricated Composite Wall System. In Proceedings of the Energy Procedia; 2015; pp. 2730–2735.
- Patania, F.; Gagliano, A.; Nocera, F.; Ferlito, A.; Galesi, A. Thermofluid-Dynamic Analysis of Ventilated Facades. Energy Build 2010, 42, 1148–1155. [CrossRef]
- Fantucci, S.; Serra, V.; Carbonaro, C. An Experimental Sensitivity Analysis on the Summer Thermal Performance of an Opaque Ventilated Façade. Energy Build 2020, 225. [CrossRef]
- Marinosci, C.; Semprini, G.; Morini, G.L. Experimental Analysis of the Summer Thermal Performances of a Naturally Ventilated Rainscreen Façade Building. Energy Build 2014, 72, 280–287. [CrossRef]
- Melgaard, S.P.; Nikolaisson, I.T.; Zhang, C.; Johra, H.; Larsen, O.K. Double-Skin Façade Simulation with Computational Fluid Dynamics: A Review of Simulation Trends, Validation Methods and Research Gaps. Build Simul 2023, 16, 2307–2331. [CrossRef]
- Limane, A.; Fellouah, H.; Galanis, N. Thermo-Ventilation Study by OpenFOAM of the Airflow in a Cavity with Heated Floor. Build Simul 2015, 8, 271–283. [CrossRef]
- Horikiri, K.; Yao, Y.; Yao, J. Modelling Conjugate Flow and Heat Transfer in a Ventilated Room for Indoor Thermal Comfort Assessment. Build Environ 2014, 77, 135–147. [CrossRef]
- Brandl, D.; Mach, T.; Grobbauer, M.; Hochenauer, C. Analysis of Ventilation Effects and the Thermal Behaviour of Multifunctional Façade Elements with 3D CFD Models. Energy Build 2014, 85, 305–320. [CrossRef]
- Fantucci, S.; Marinosci, C.; Serra, V.; Carbonaro, C. Thermal Performance Assessment of an Opaque Ventilated Façade in the Summer Period: Calibration of a Simulation Model through in-Field Measurements. In Proceedings of the Energy Procedia; Elsevier Ltd, March 1 2017; Vol. 111, pp. 619–628.
- Chourdakis, G.; Schneider, D.; Uekermann, B. OpenFOAM-PreCICE: Coupling OpenFOAM with External Solvers for Multi-Physics Simulations. OpenFOAM® Journal 2023, 3, 1–25. [CrossRef]
- Laitinen, A.; Saari, K.; Kukko, K.; Peltonen, P.; Laurila, E.; Partanen, J.; Vuorinen, V. A Computational Fluid Dynamics Study by Conjugate Heat Transfer in OpenFOAM: A Liquid Cooling Concept for High Power Electronics. Int J Heat Fluid Flow 2020, 85. [CrossRef]
- Pastori, S. Timber-Concrete Composite Ventilated Envelope Systems. Experimental and Numerical Investigations for Thermal Performance Control and Optimization., Politecnico di Milano, 2024.
- EN ISO 10456:2007 Materials and Products - Hygrothermal Properties -Tabulated Design Values and Procedures for Determining Declared and Design Thermal Values.
- EN ISO 6946:2017 Components and Building Elements - Thermal Resistance and Thermal Transmittance - Calculation Methods.
- Kays, W.M.; Crawford, M.E. Convective Heat and Mass Transfer; McGraw-Hill, 1980;
- Tahmasebinia, F.; Lin, L.; Wu, S.; Kang, Y.; Sepasgozar, S. Exploring the Benefits and Limitations of Digital Twin Technology in Building Energy. Applied Sciences (Switzerland) 2023, 13. [CrossRef]

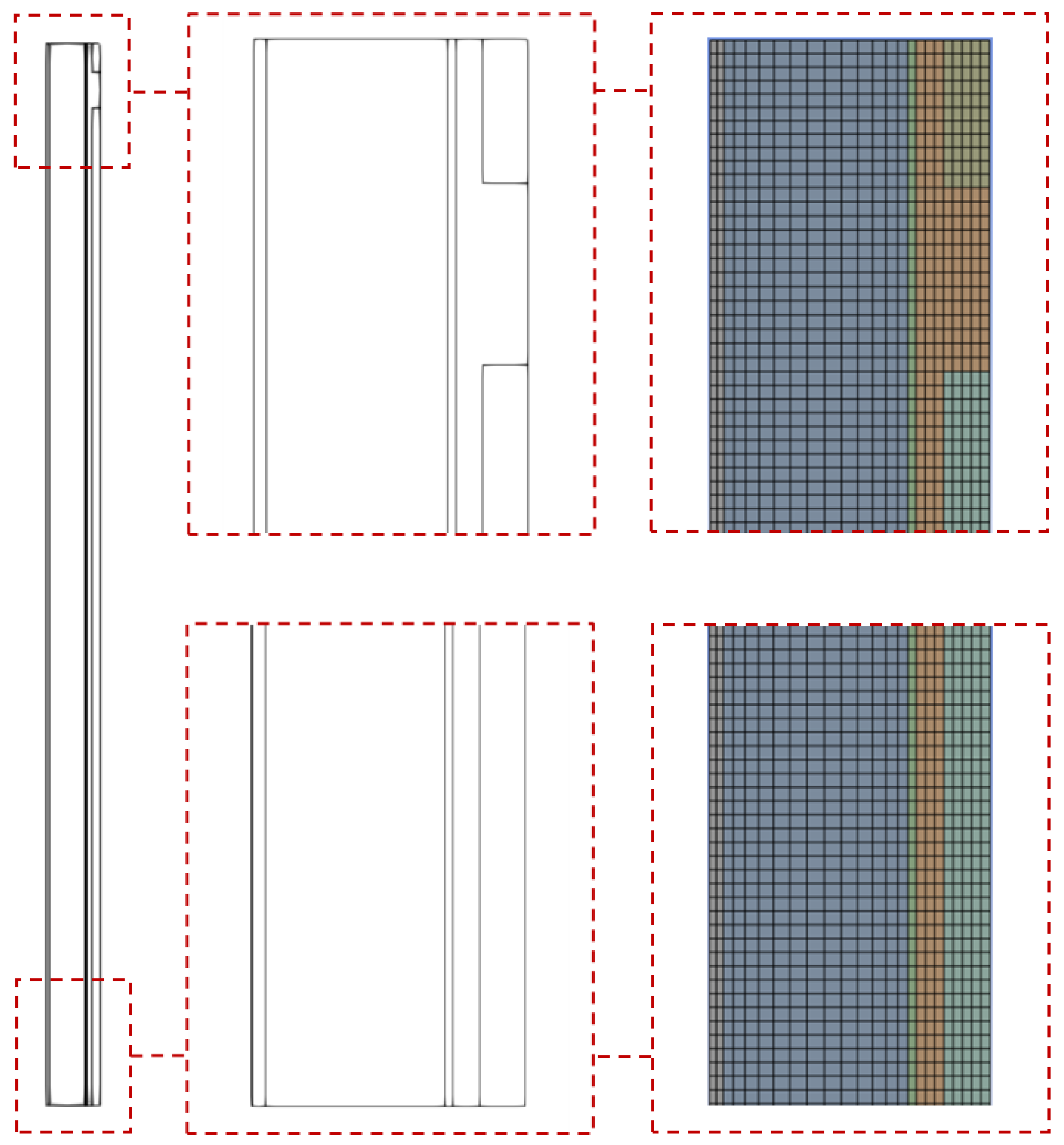
| Mesh refinement study | |||||
| Simulation | Mesh | Solver | Time simulated | Time needed for running simulation | Temperatures that differ more than 0.2K from base case (t0001) |
| t0001 | m0012_baseMesh (7152 cells) |
chtMultiRegionFoam | 96h (345000 s) |
67.5h |
- |
| t0002 | m0013_baseMeshx1.5 (14850 cells) |
chtMultiRegionFoam | 48h (172800 s) |
100h (+196% than t0001) |
1.4% |
| t0003 | m0014_baseMeshx1.5x1.5 (33075 cells) |
chtMultiRegionFoam | 24h (86400 s) |
314h (+1761% than t0001) |
5.7% |
| Comparison between “frozen-unfrozen flow” solver and old solver | |||||||
| Case | tauFrozen/ tauUnfrozen |
Simulation speedup (24h real time compared to base case t0001) | Relative performance | Max temperature difference (K) from t0001 | % of values that differ more than 0.2K from t0001 | % of values that differ more than 0.5K from t0001 | % of values that differ more than 1K from t0001 |
| t0011 | 5s/5s = 1 | x 1.8 | 90% | -2.61 (in outlet.1) | 12.9% | 7.6% | 3.9% |
| t0012 | 10s/5s = 2 | x 2.7 | 90% | 3.61 (in outlet.1) |
15.5% | 8.0% | 4.1% |
| t0013 | 15s/5s = 3 | x 3.5 | 88% | -2.87 (in outlet.1) | 16.6% | 7.7% | 4.3% |
| t0014 | 50s/5s = 10 | x 9.4 | 85% | 3.20 (in outlet.1) |
12.4% | 2.8% | 1.0% |
| t0015 | 100s/5s = 20 | x 16.5 | 79% | 2.66 (in outlet.1) |
12.6% | 2.9% | 1.3% |
| t0016 | 500s/5s = 100 | x 45 | 45% | 3.43 (in outlet.1) |
20.8% | 9.9% | 4.5% |
| Sensitivity analysis | |||
| Case | Goal | Physical parameters | Boundary conditions |
| t0101 |
Base case | Parameters reported in paragraph 3.2 | hToAmb = 1/Rse * hToAmbInt = 7.7 W/m2K qrIncident: summer sunny days, south Ta: summer sunny days TaRad: off (=Ta) Ti: summer sunny days U: summer sunny days |
| t0102 |
Change specific heat capacity for solid regions | 2xCp of solid regions | hToAmb = 1/Rse * hToAmbInt = 7.7 W/ m2K qrIncident: summer sunny days, south Ta: summer sunny days TaRad: off (=Ta) Ti: summer sunny days U: summer sunny days |
| t0103 |
Change solar irradiation values | 20% reduction of incident solar irradiation values | hToAmb = 1/Rse * hToAmbInt = 7.7 W/ m2K qrIncident: 0.8xqr,summer sunny days, south Ta: summer sunny days TaRad: off (=Ta) Ti: summer sunny days U: summer sunny days |
| t0104 |
Change of emissivity values for solid regions | 0.8xemissivity of solid regions | hToAmb = 1/Rse * hToAmbInt = 7.7 W/ m2K qrIncident: summer sunny days, south Ta: summer sunny days TaRad: off (=Ta) Ti: summer sunny days U: summer sunny days |
| t0105 |
Test how the model works with absence of solar irradiation | Incident solar irradiation switched off | hToAmb = 1/Rse * hToAmbInt = 7.7 W/ m2K qrIncident = 0 W/m2 Ta: summer sunny days TaRad: off (=Ta) Ti: summer sunny days U: summer sunny days |
| t0106 |
Change the type of heat exchange between the external surface of the wall and the outdoor environment, considering convective and radiative heat exchange separately. | Outdoor convective and radiative heat transfers are considered separately: qcv = hcv (Ta - TC_ext) qrd = ε σ Fw-sky (TC_ext4 - Tsky4) Tsky = 0.037536 Ta1.5 + 0.32 Ta |
hToAmb = 1/Rse * hToAmbInt = 7.7 W/ m2K qrIncident: summer sunny days, south Ta: summer sunny days TaRad: Tsky. csv Ti: summer sunny days U: summer sunny days |
| t0107 |
Change the type of heat exchange between the external surface of the wall and the outdoor environment, considering convective and radiative heat exchange separately. | Outdoor convective and radiative heat transfers are considered separately: qcv = hcv (Ta - TC_ext) qrd = ε σ Fw-sky (TC_ext4 - Tsky4) Tsky = 0.037536 Ta^1.5 + 0.32 Ta |
hcvToAmb =4+4v * hToAmbInt = 7.7 W/ m2K qrIncident: summer sunny days, south Ta: summer sunny days TaRad: Tsky. csv Ti: summer sunny days U: summer sunny days |
| t0108 |
Change the type of heat exchange between the external surface of the wall and the outdoor environment, considering convective and radiative heat exchange separately. | Option “hInclRad: false” | hToAmb = 1/Rse * hToAmbInt = 7.7 W/ m2K qrIncident: summer sunny days, south Ta: Ta,reduced.csv TaRad: off (=Ta) Ti: summer sunny days U: summer sunny days |
| t0109 |
Change specific heat capacity of solid regions | 1.5xCp for solid regions | hToAmb = 1/Rse * hToAmbInt = 7.7 W/ m2K qrIncident: summer sunny days, south Ta: summer sunny days TaRad: off (=Ta) Ti: summer sunny days U: summer sunny days |
| t0110 |
Change specific heat capacity of solid regions | 2xCp for solid region 2 1xCp for solid region 1 |
hToAmb = 1/Rse * hToAmbInt = 7.7 W/ m2K qrIncident: summer sunny days, south Ta: summer sunny days TaRad: off (=Ta) Ti: summer sunny days U: summer sunny days |
| t0111 |
Change thermal conductivity of solid regions | 2xCp for solid region 2 1xCp for solid region 1 0.5xlambda for solid regions |
hToAmb = 1/Rse * hToAmbInt = 7.7 W/ m2K qrIncident: summer sunny days, south Ta: summer sunny days TaRad: off (=Ta) Ti: summer sunny days U: summer sunny days |
| t0112 |
Change temperature values of outdoor air (Ta in °C) and specific heat capacity of solid regions | Ta,reduced = 0.6xTa 2xCp for solid region 2 1xCp for solid region 1 |
hToAmb = 1/Rse * hToAmbInt = 7.7 W/ m2K qrIncident: summer sunny days, south Ta: Ta,reduced TaRad: off (=Ta) Ti: summer sunny days, wall S3 U: summer sunny days, wall S3 |
| t0113 |
Change temperature values of outdoor air (Ta in °C) | TaReduced = 0.6xTa | hToAmb = 1/Rse * hToAmbInt = 7.7 W/ m2K qrIncident: summer sunny days, south Ta: Ta,reduced TaRad: off (=Ta) Ti: summer sunny days, wall S3 U: summer sunny days, wall S3 |
| t0114 |
Change temperature values of outdoor air (Ta in °C) | From 9am to 9pm: TaReduced,version2 = 0.6xTa From 9pm to 9am: TaReduced,version2 = 0.8xTa |
hToAmb = 1/Rse * hToAmbInt = 7.7 W/ m2K qrIncident: summer sunny days, south Ta: Ta,reduced,version2 TaRad: off (=Ta) Ti: summer sunny days, wall S3 U: summer sunny days, wall S3 |
| t0115 |
Change temperature values of outdoor air (Ta in °C), specific heat capacity and thermal conductivity of solid region 2 | TaReduced = 0.6xTa 1.5xCp for solid region 2 0.5xλ for solid region 2 |
hToAmb = 1/Rse * hToAmbInt = 7.7 W/ m2K qrIncident: summer sunny days, south Ta: Ta,reduced,version2 TaRad: off (=Ta) Ti: summer sunny days, wall S3 U: summer sunny days, wall S3 |
| t0116 |
Change temperature values of outdoor air (Ta in °C), specific heat capacity and thermal conductivity of solid region 2 | From 9am to 9pm: TaReduced,version2 = 0.6xTa From 9pm to 9am: TaReduced,version2 = 0.8xTa 1.5xCp for solid region 2 0.5xλ for solid region 2 |
hToAmb = 1/Rse * hToAmbInt = 7.7 W/ m2K qrIncident: summer sunny days, south Ta: Ta,reduced,version2 TaRad: off (=Ta) Ti: summer sunny days, wall S3 U: summer sunny days, wall S3 |
| Results of the sensitivity analysis | |||||
| Case | Time needed for running simulation with old solver (h) | TO: error % between experiment and CFD | TC: error % between experiment and CFD | TC_ext: error % between experiment and CFD | Average error % |
| t0101 | 37 | 12 | 10 | 9 | 10.33 |
| t0102 | 32.5 | 8.75 | 4.96 | 10.97 | 8.23 |
| t0103 | 36 | 13 | 10 | 7 | 10.00 |
| t0104 | 36 | 12 | 10 | 8 | 10.00 |
| t0105 | 41 | 19 | 18 | 13 | 16.67 |
| t0106 | 39 | 18 | 18 | 16 | 17.33 |
| t0107 | 39 | 18 | 18 | 18 | 18.00 |
| t0108 | 33.5 | 14 | 14 | 13 | 13.67 |
| t0109 | 32 | 10 | 7 | 9 | 8.67 |
| t0110 | 31.5 | 8.85 | 5.19 | 11.00 | 8.35 |
| t0111 | 30.5 | 9.41 | 5.49 | 12.57 | 9.16 |
| t0112 | 28.5 | 10 | 6 | 9 | 8.33 |
| t0113 | 30.5 | 12 | 8 | 5 | 8.33 |
| t0114 | 30.75 | 11 | 8 | 6 | 8.33 |
| t0115 | 27.25 | 12 | 7 | 9 | 9.33 |
| t0116 | 29 | 11 | 6 | 9 | 8.67 |
| Results of validation process | |||||
| Case | Error of TR prediction |
Error of TO prediction |
Error of TC prediction |
Error of TC_ext prediction |
Average error |
| t2000 (= t0104) | 0.73% | 13.99% | 10.06% | 8.14% | 8.23% |
| t4500 | 0.73% | 15.45% | 11.91% | 6.86% | 8.74% |
| Time (s) |
(°C) |
(°C) |
(°C) |
solid.1.3 to fluid.1 (W/m2) |
solid.2.1 to fluid.1 (W/m2) |
solid.1.3 (W/m2) |
solid.2.1 (W/m2) |
| case t0104 | |||||||
| 6:00 pm | 34.28 | 35.05 | 37.05 | 2.50 | 9.00 | -9.73 | |
| 8:00 am | 19.93 | 20.25 | 19.75 | 1.04 | -0.59 | -0.87 | 1.27 |
| case t4500 | |||||||
| 6:00 pm | 31.68 | 31.80 | 33.01 | 0.39 | 4.32 | 5.67 | - 6.09 |
| 8:00 am | 20.88 | 21.29 | 21.09 | 1.33 | 0.68 | 0.31 | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





