Submitted:
02 May 2024
Posted:
02 May 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
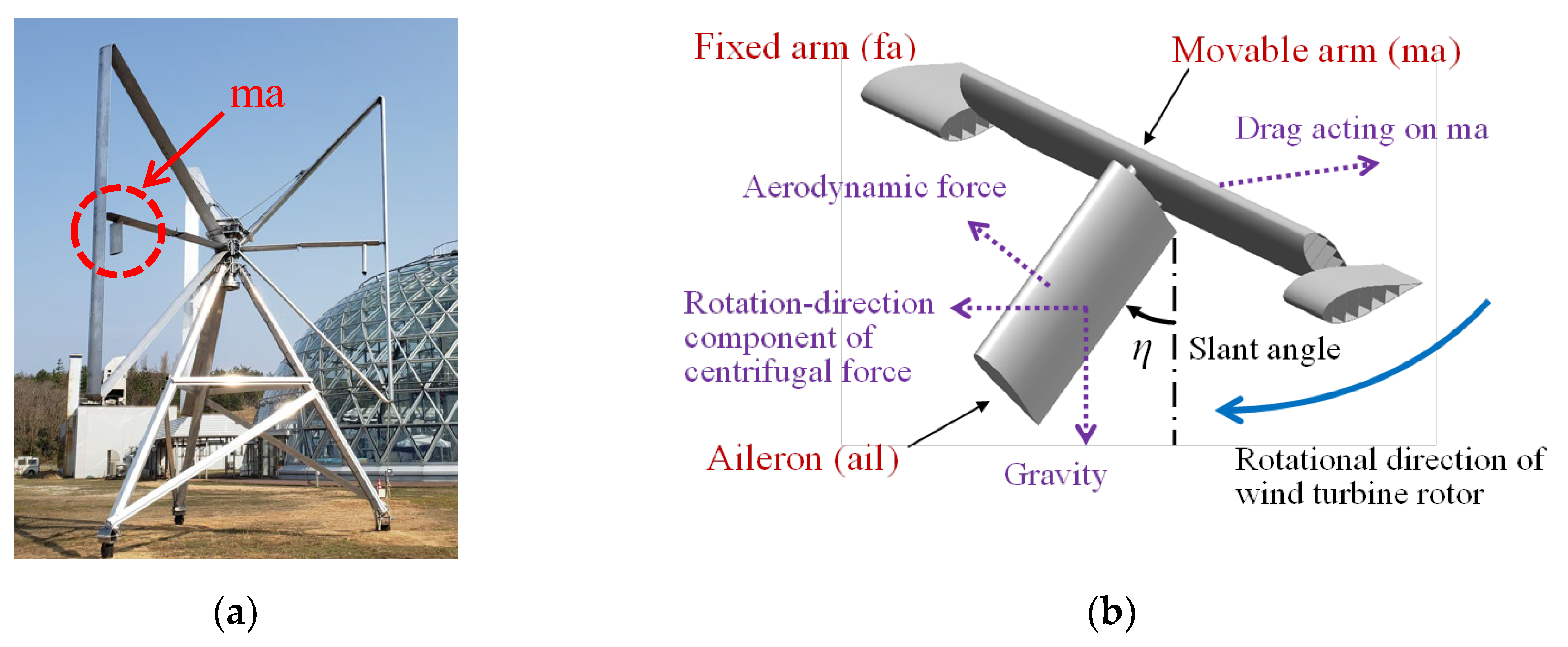
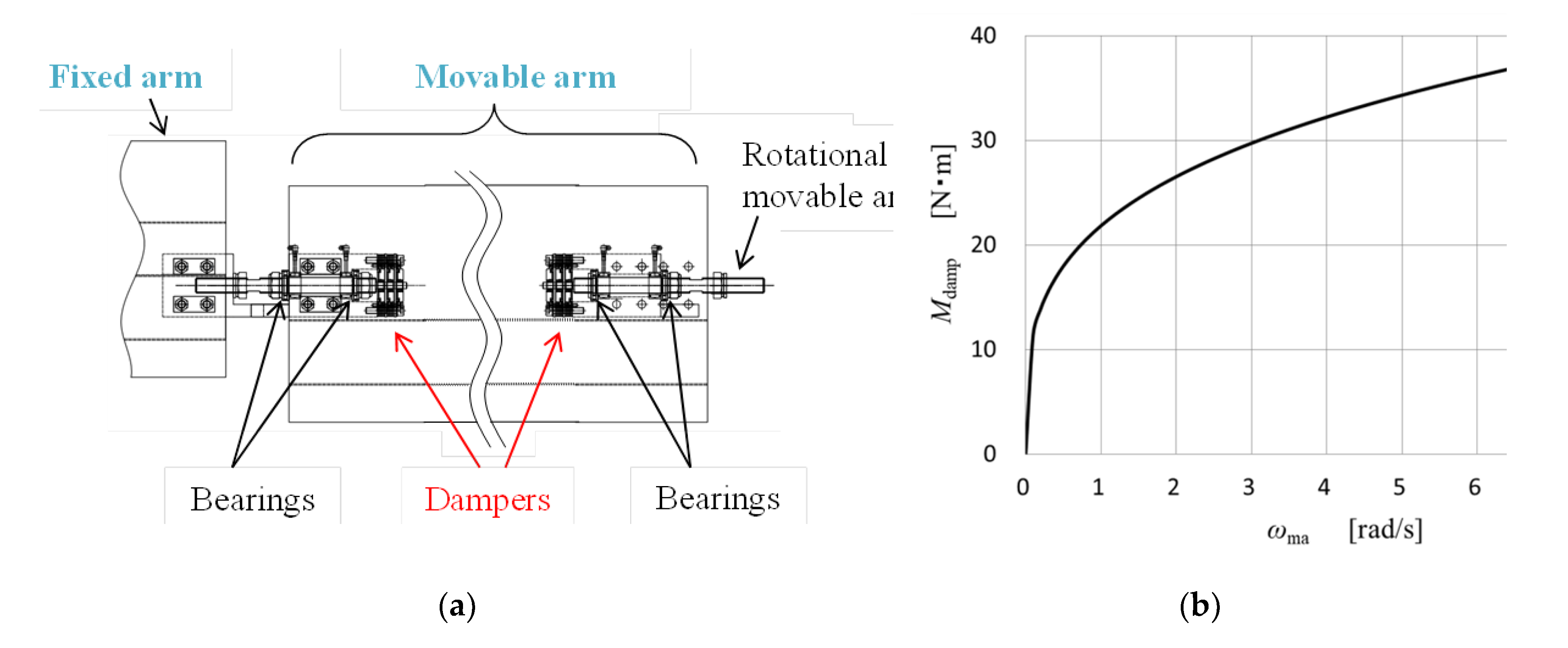
2. Prototype of Butterfly Wind Turbine Equipped with Over-Speed Control System
3. Theoretical Prediction
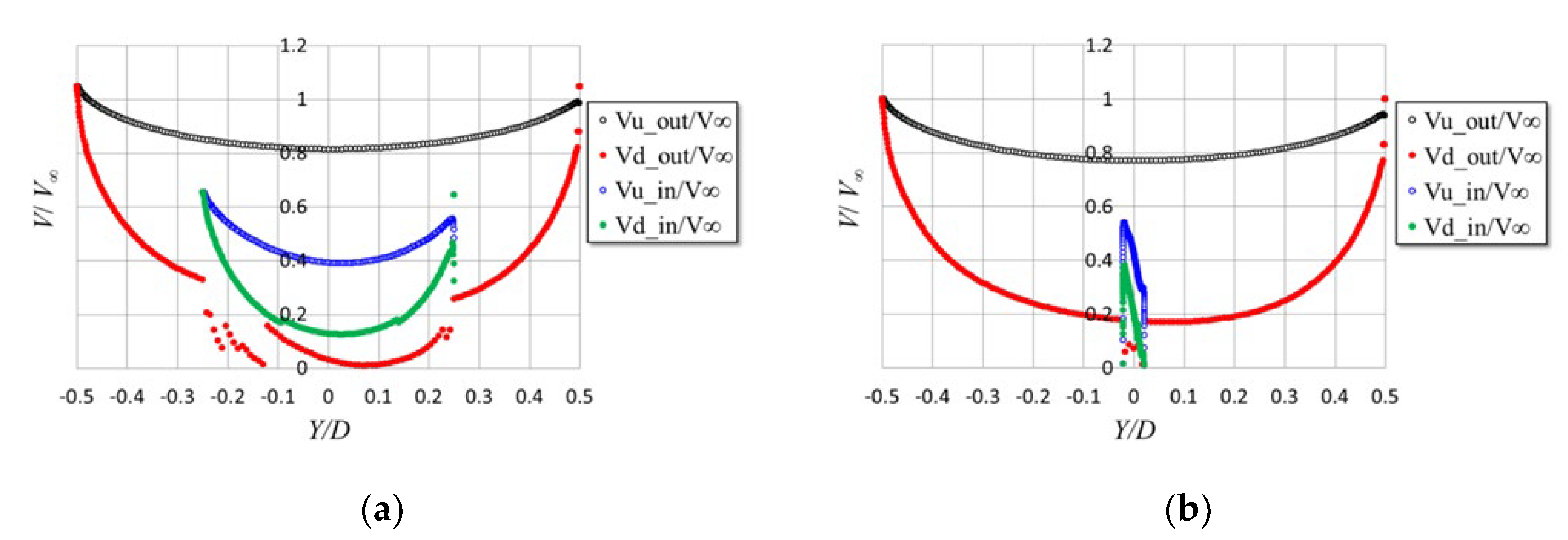
3.1. Prediction of Flow Speed Distribution
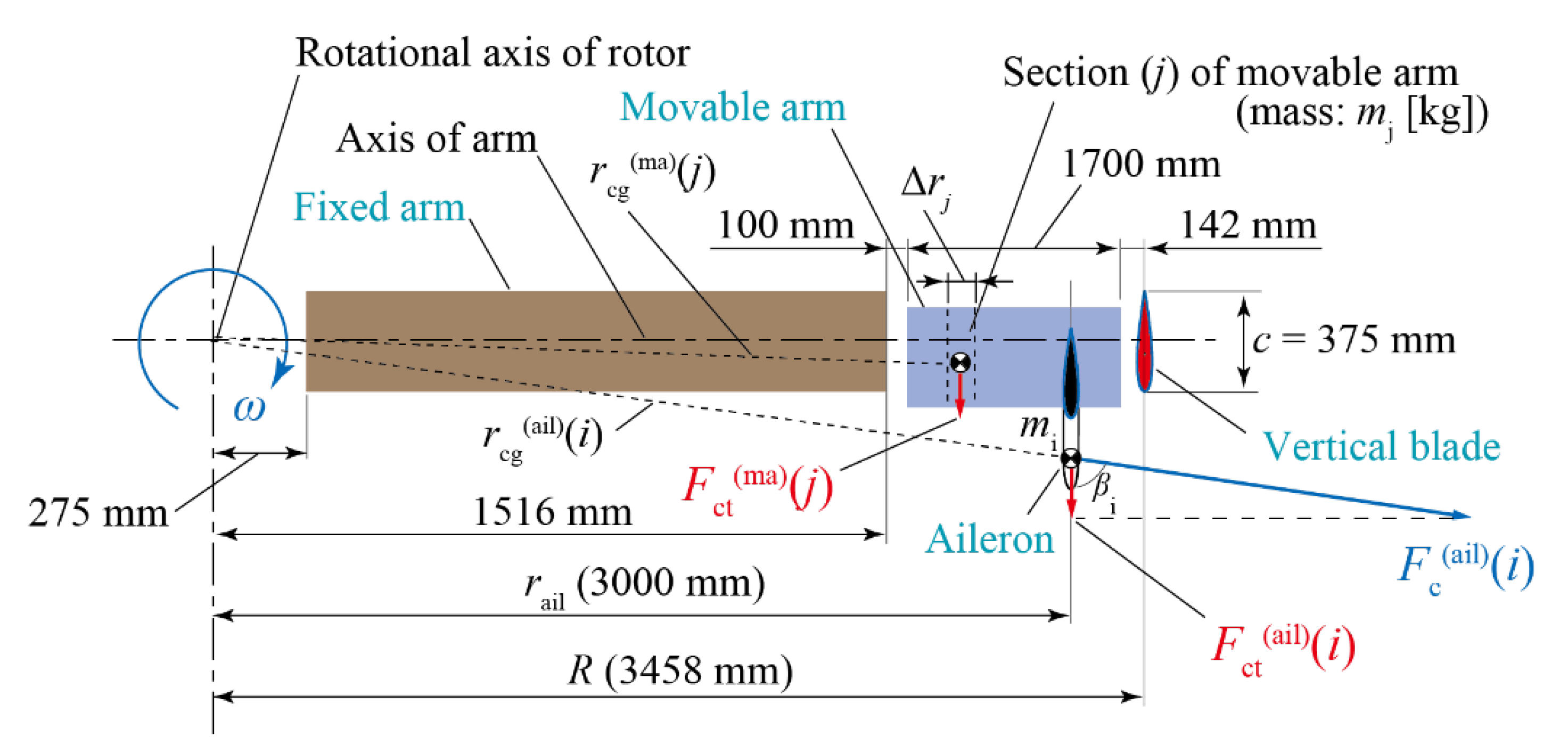
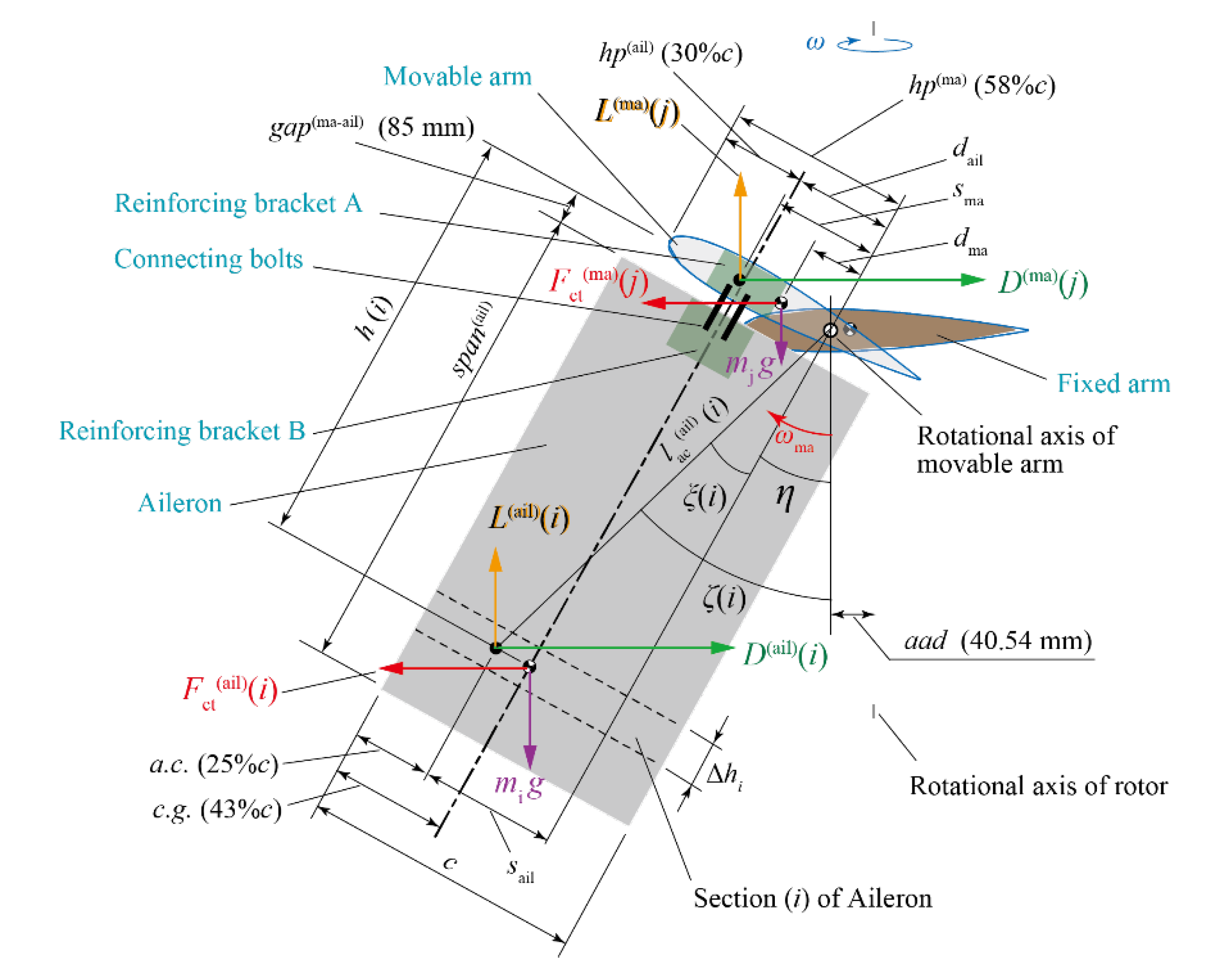
3.2. Equation of Motion of Movable Arm System
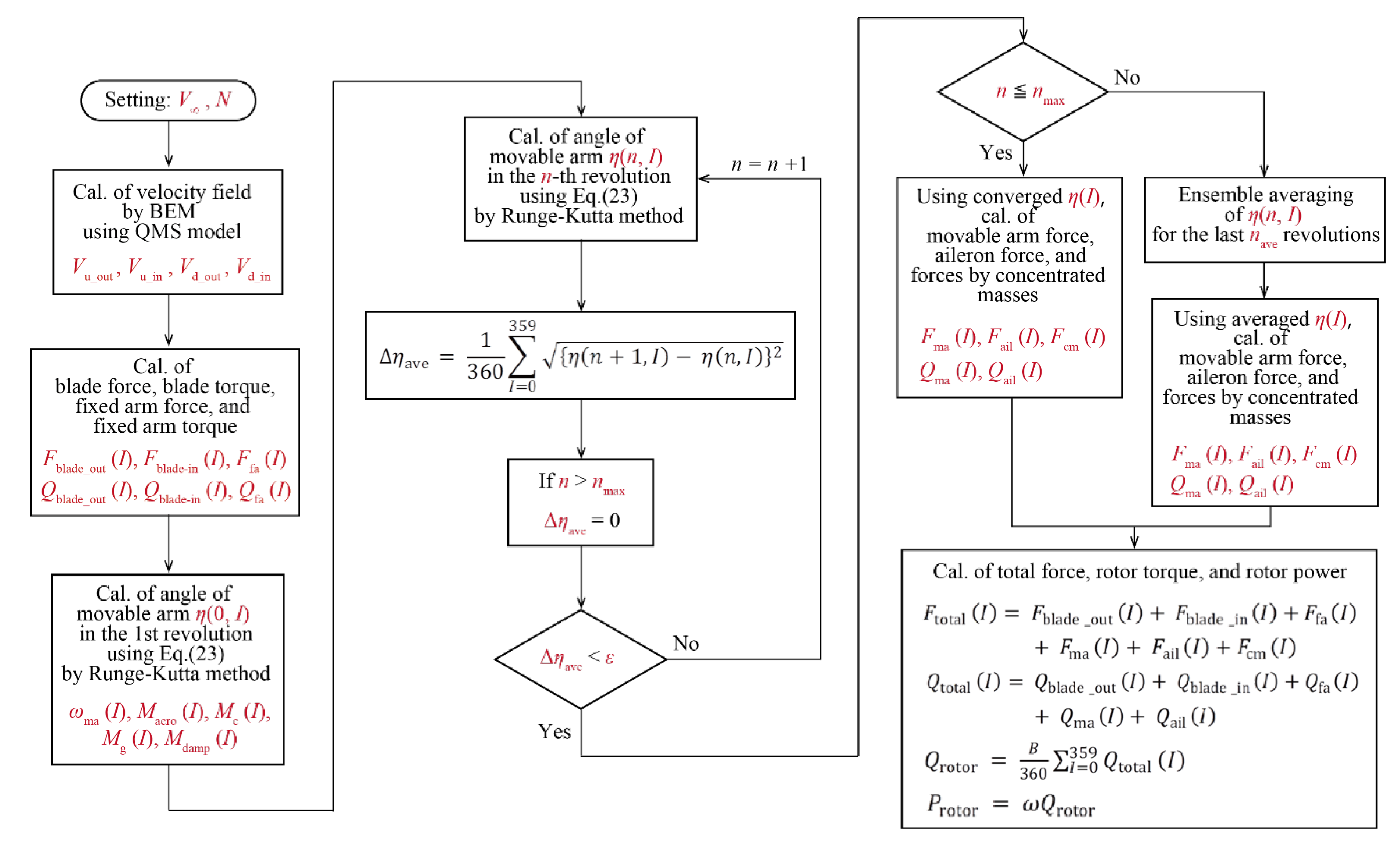
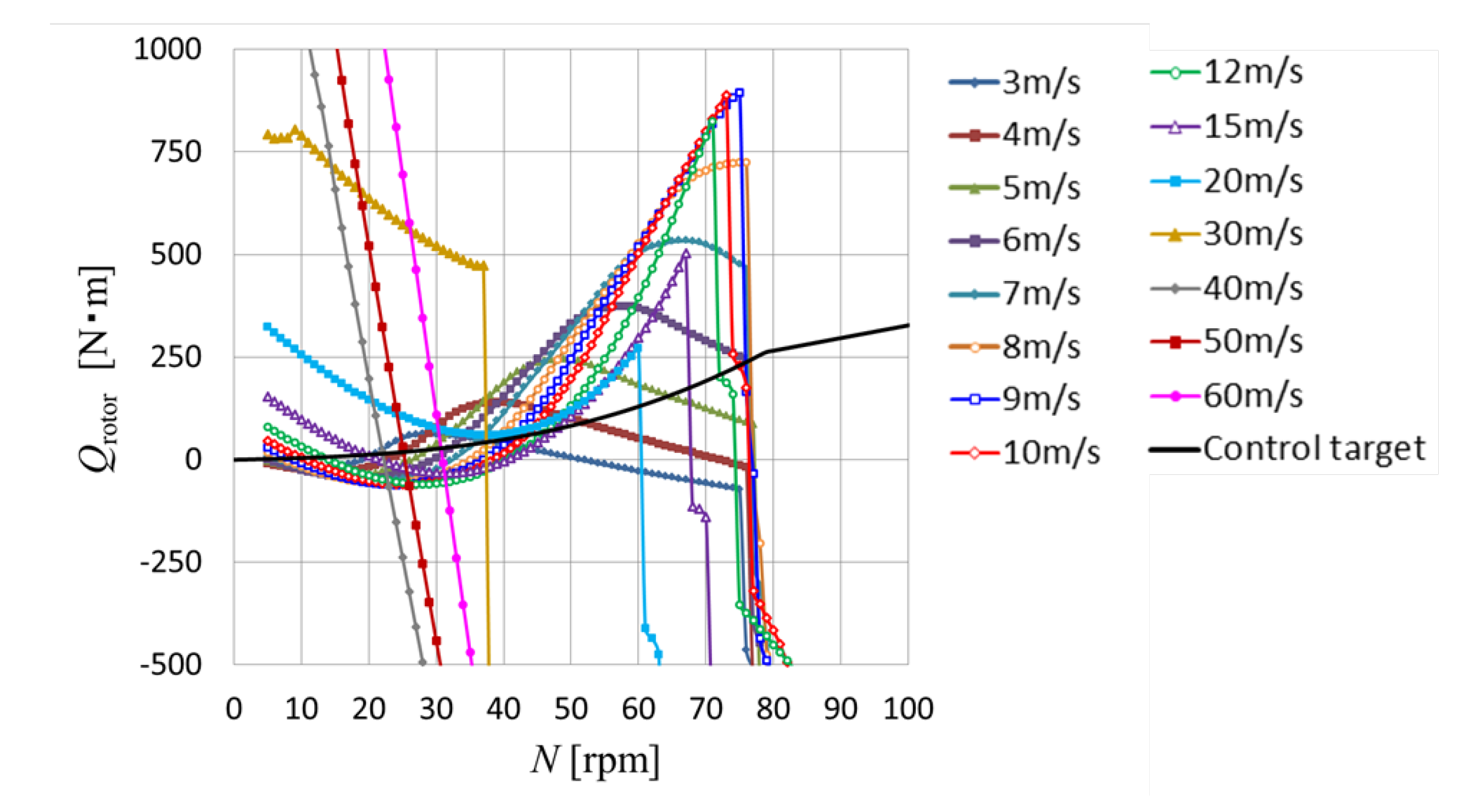
3.3. Prediction of Movable Arm Behavior and Rotor Performance
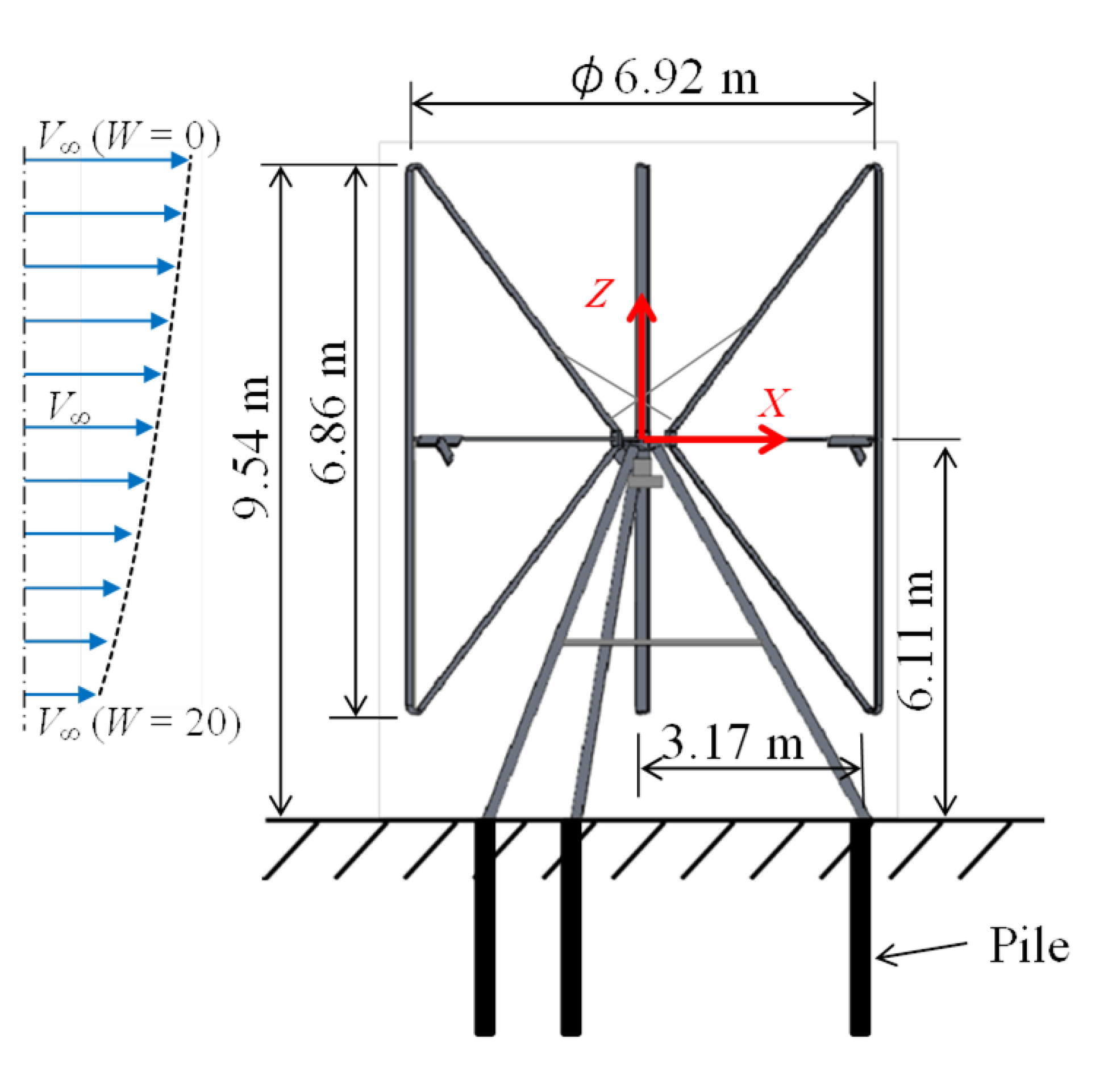
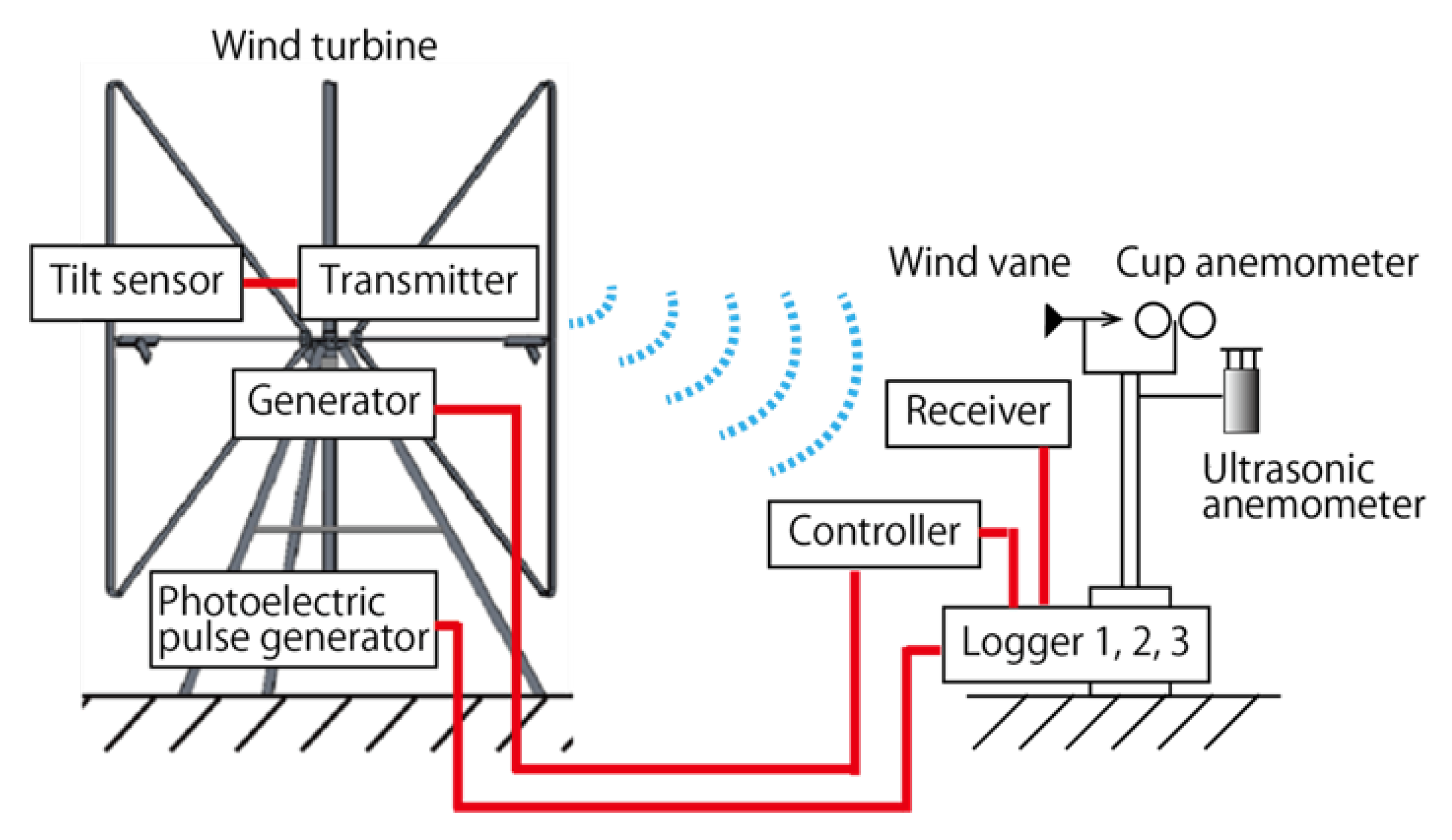
4. Experimental Setup
5. Results and Discussion
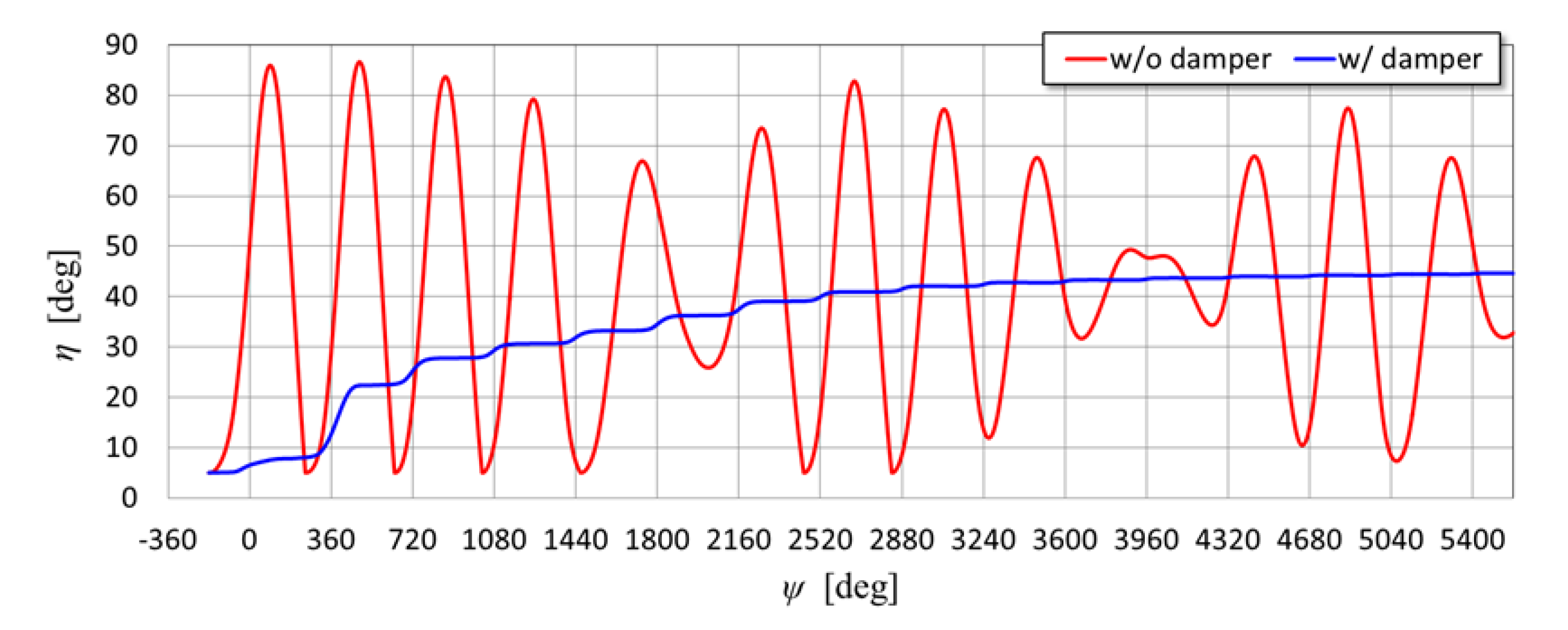
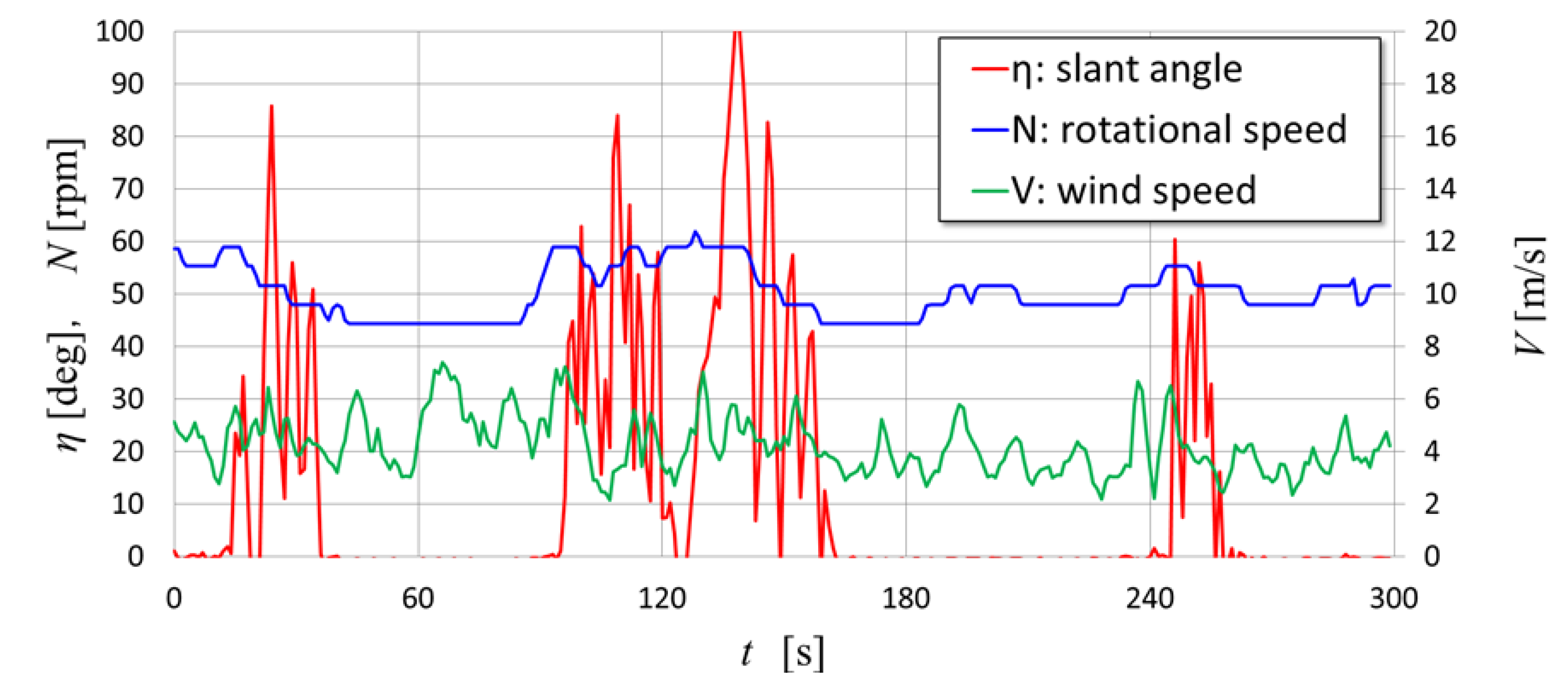
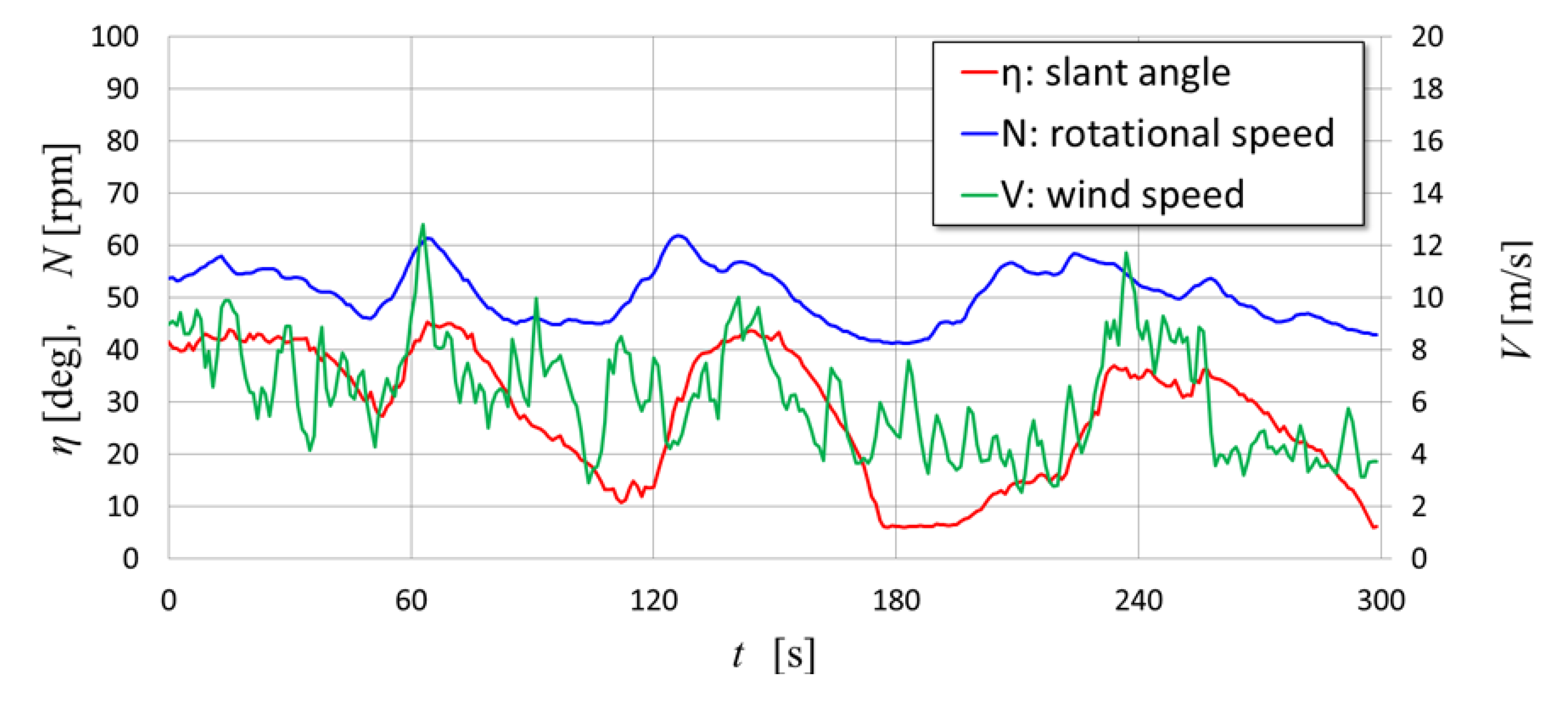
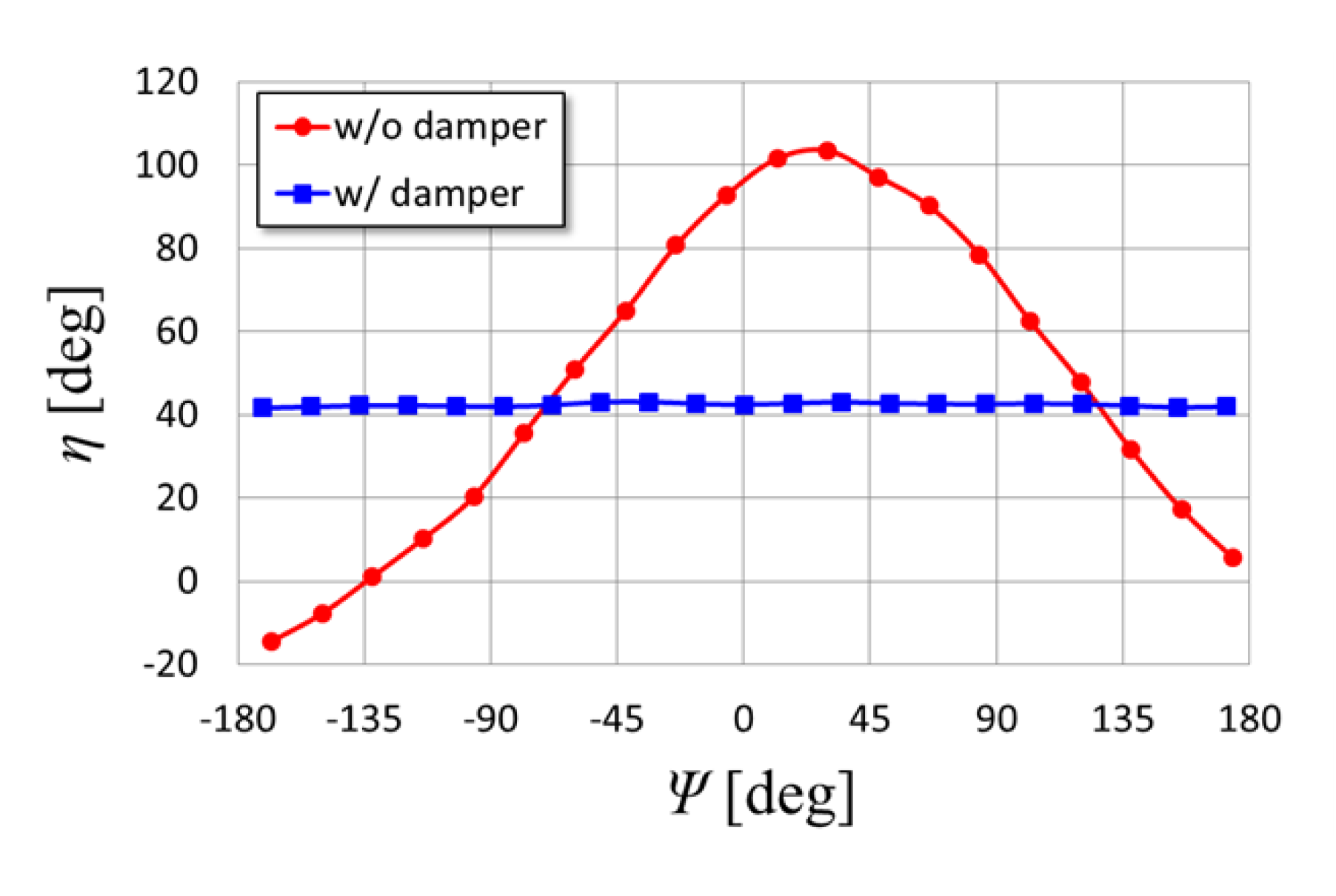
5.1. Comparison of Behavior of Movable Arm between with and Without Dampers
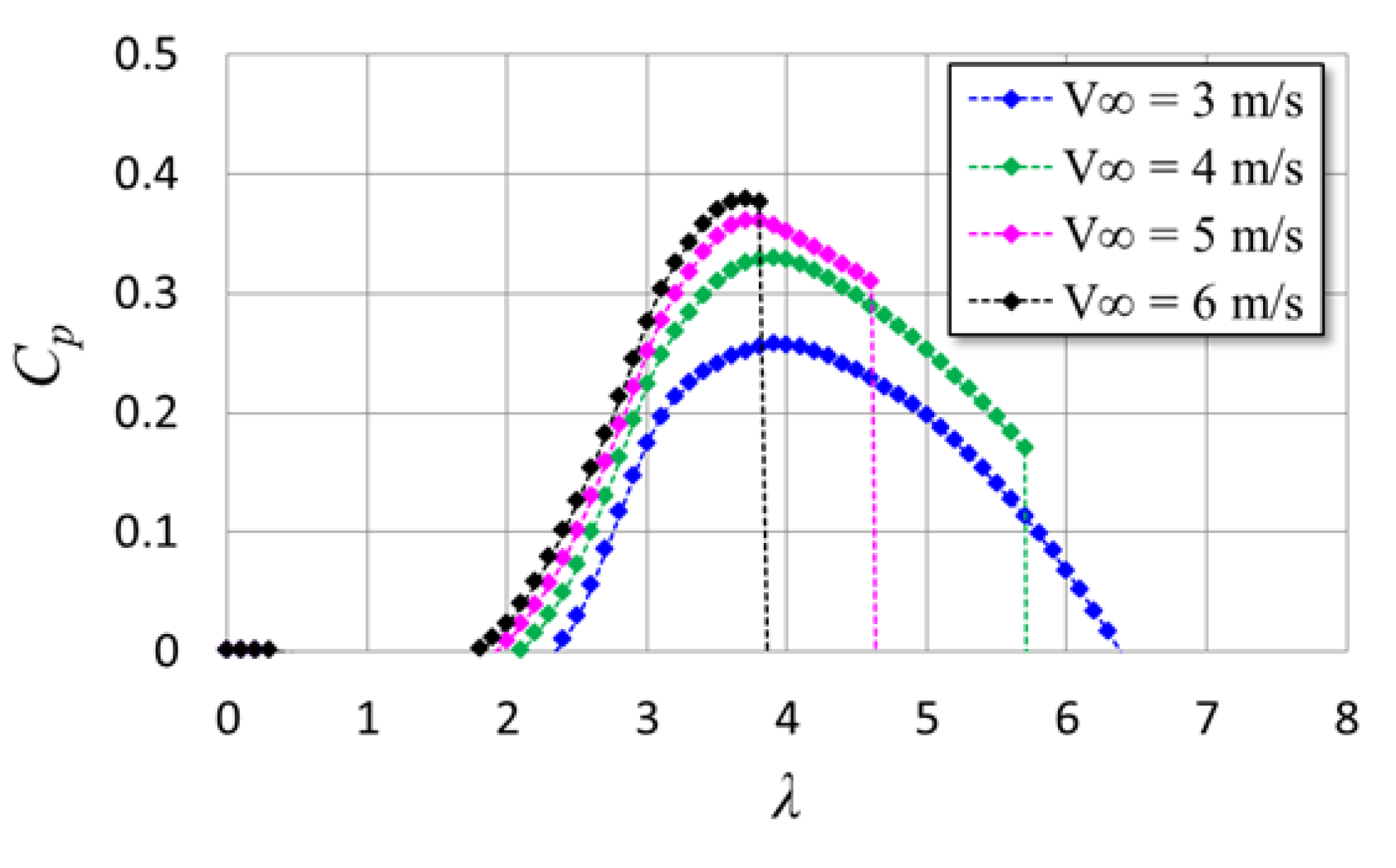
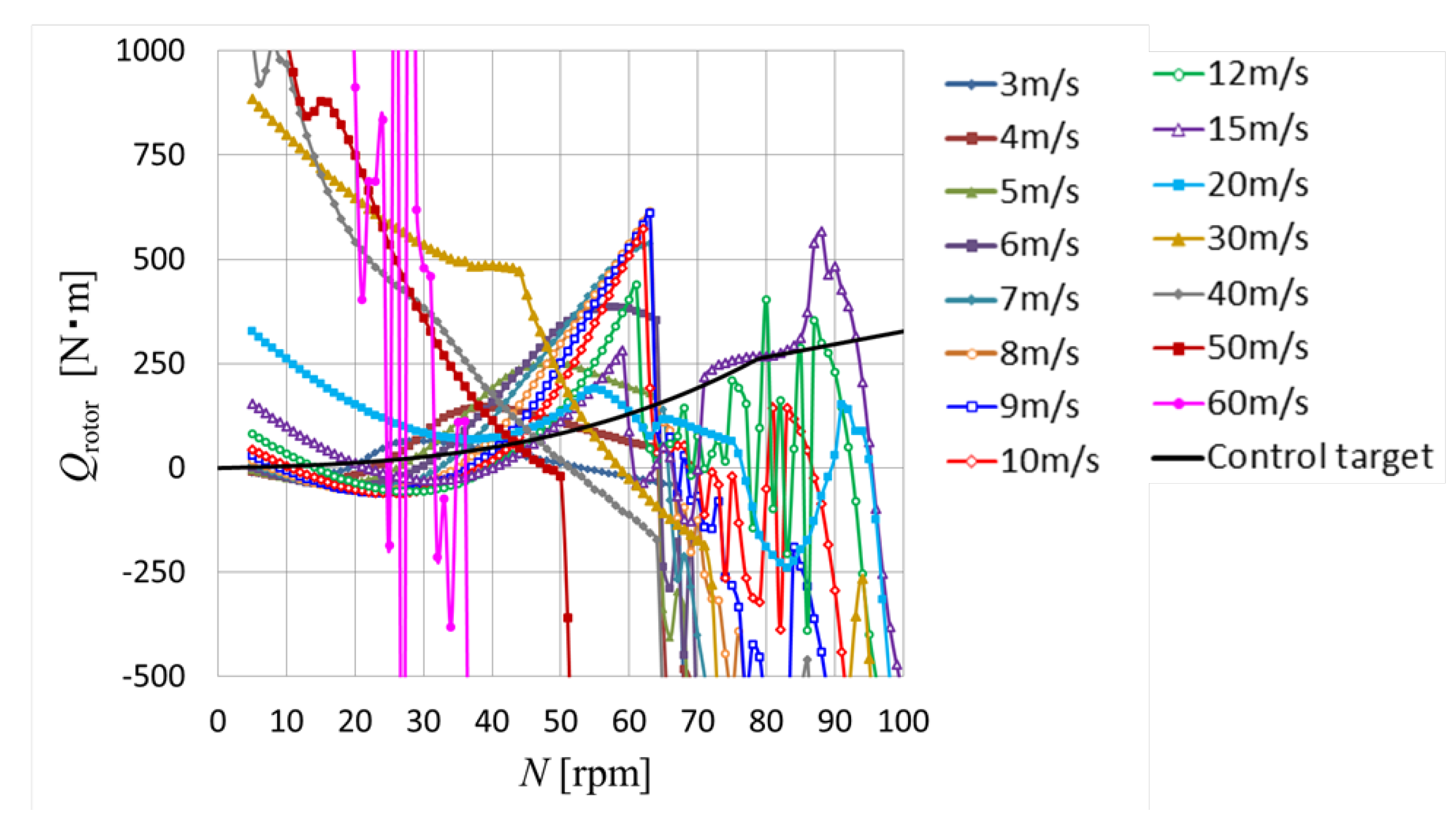
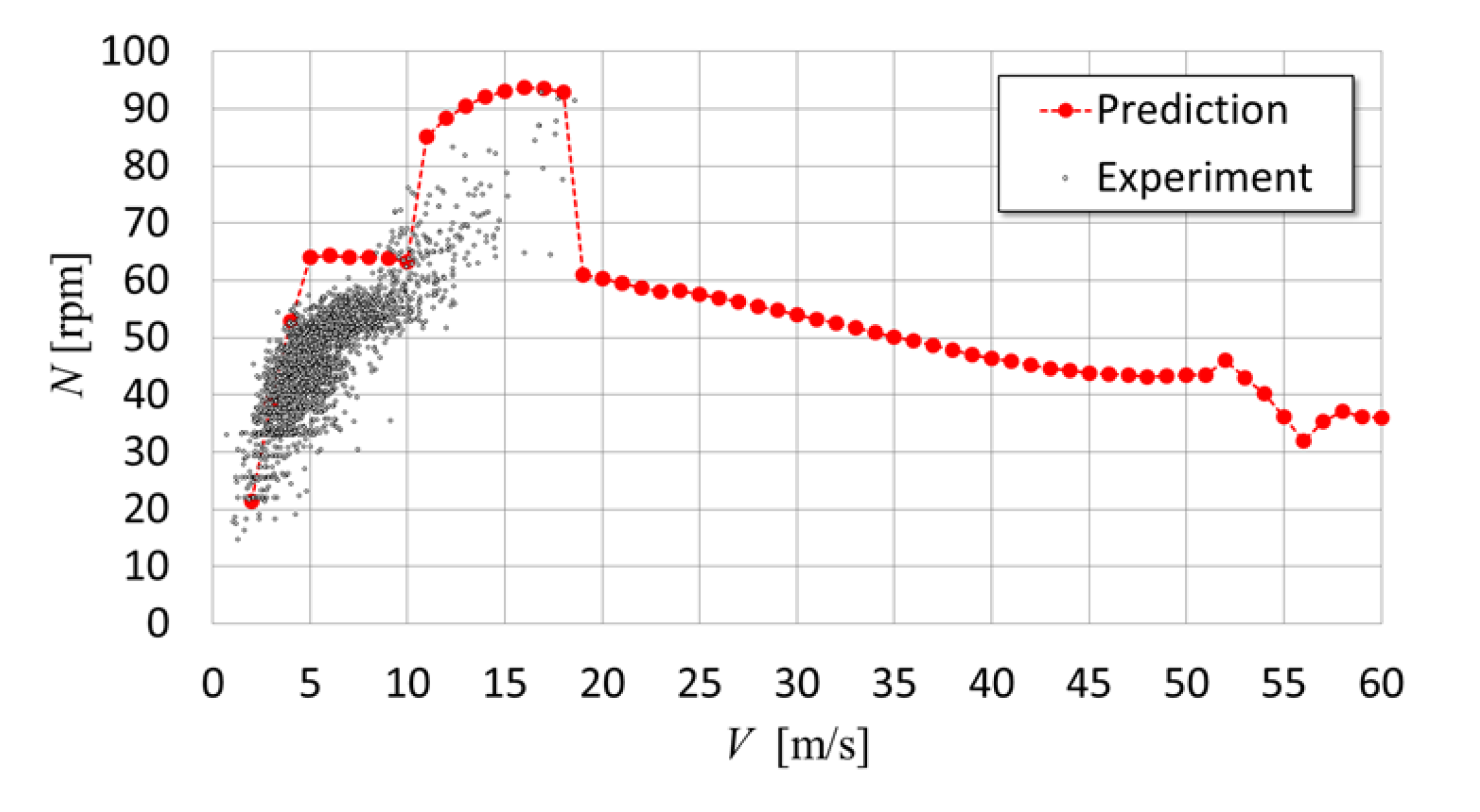
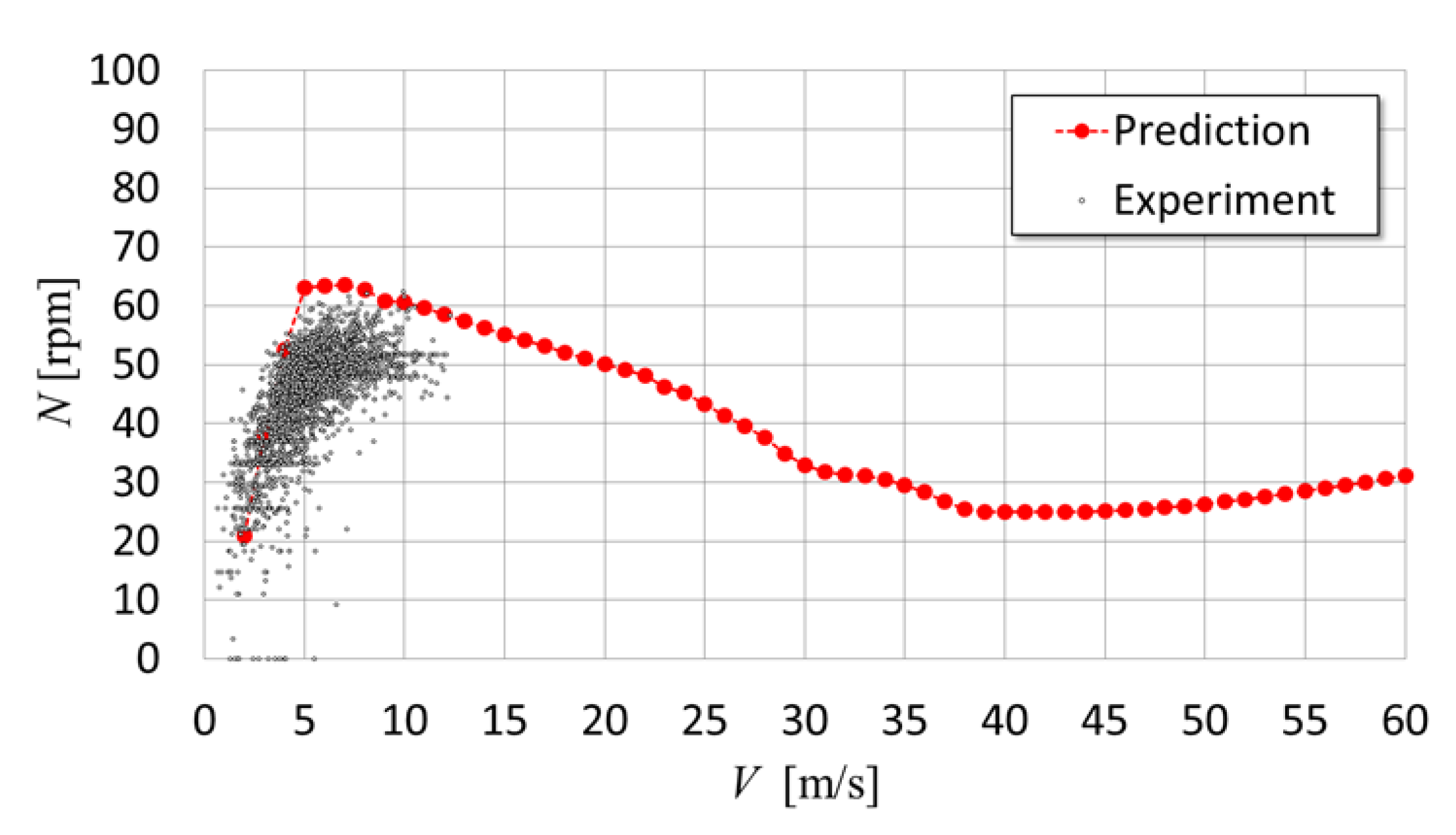
5.2. Comparison of Wind Speed Dependence of Rotational Speed between Prediction and Experiments
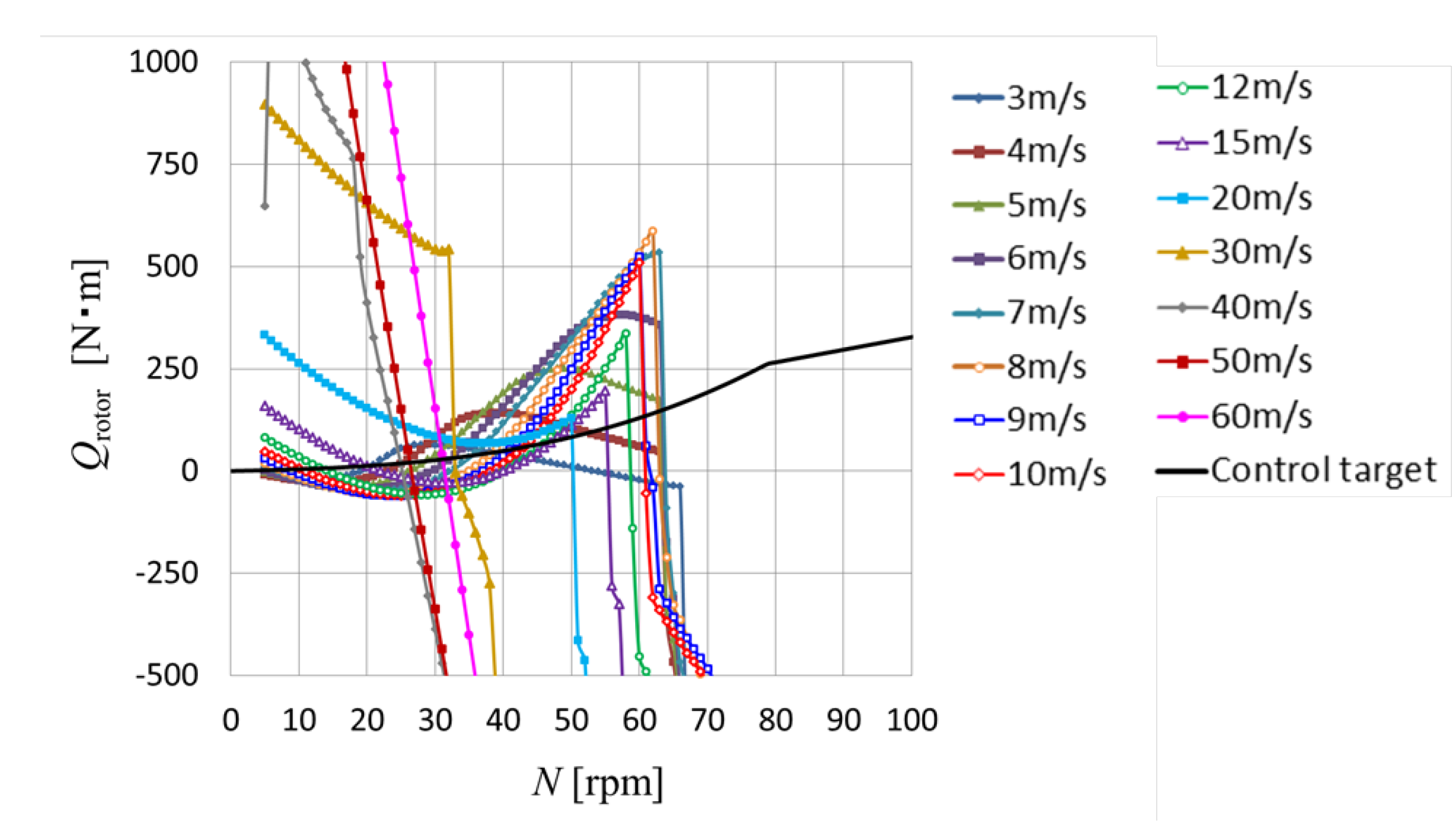
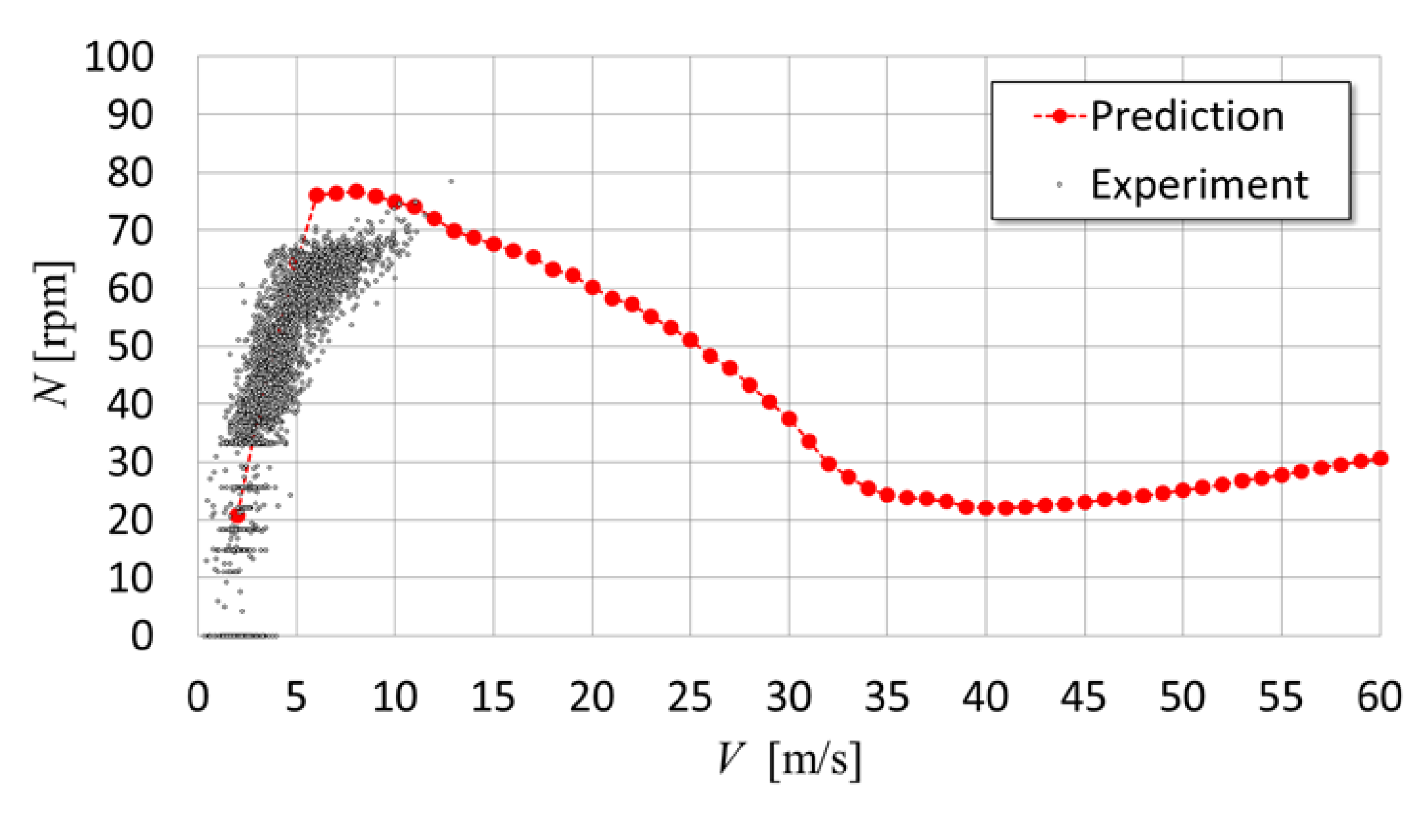
5.3. Prediction and Experimental Data after Replacement with Short Ailerons
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Rotor swept area [m2] |
| aad | Distance between rotor rotation axis and movable arm axis [m] |
| a.c.(i) | Aerodynamic center of section i of aileron [-] |
| a.c.(j) | Aerodynamic center of section j of movable arm [-] |
| B | Number of blades [-] |
| CD(αi, Re) | Drag coefficient of section i of aileron [-] |
| CD(αj, Re) | Drag coefficient of section j of movable arm [-] |
| CL(αi, Re) | Lift coefficient of section i of aileron [-] |
| CL(αj, Re) | Lift coefficient of section j of movable arm [-] |
| Cp | Power coefficient of wind turbine [-] |
| c | Chord length [m] |
| D | Diameter of wind turbine rotor [m] |
| D(ail)(i) | Horizontal aerodynamic force of section i of aileron [N] |
| D(ma)(j) | Horizontal aerodynamic force of section j of movable arm [N] |
| D(αi) | Drag force of section i of aileron [N] |
| D(αj) | Drag force of section j of movable arm [N] |
| dail | Chordwise distance between center of gravity of aileron and movable arm axis [m] |
| dma | Chordwise distance between center of gravity of movable arm and movable arm axis [m] |
| Fail(I) | Force acting on an aileron in azimuth I [N] |
| Fblade_in(I) | Force acting on an inner blade in azimuth I [N] |
| Fblade_out(I) | Force acting on an outer blade in azimuth I [N] |
| Fc(ail)(i) | Centrifugal force acting on section i of aileron [N] |
| Fc(ma)(j) | Centrifugal force acting on section j of movable arm [N] |
| Fcm(I) | Force acting on concentrated masses in azimuth I [N] |
| Fct(ail)(i) | Tangential component of centrifugal force acting on section i of aileron [N] |
| Fct(ma)(j) | Tangential component of centrifugal force acting on section j of movable arm [N] |
| Ffa(I) | Force acting on a fixed arm in azimuth I [N] |
| Fma(I) | Force acting on a movable arm in azimuth I [N] |
| Ftotal(I) | Total force acting on a blade in azimuth I [N] |
| g | Gravitational acceleration [m/s2] |
| gap(ma-ail) | Distance between aileron top end and movable arm axis [m] |
| H | Rotor height [m] |
| h(i) | Distance between aerodynamic center of section i of aileron and movable arm chord line [m] |
| hp(ail) | Holding point of aileron [m] |
| hp(ma) | Holding point of movable arm [m] |
| Δhi | Width of section i of aileron [m] |
| I | Integer parameter of azimuth [-] |
| Ima | Inertial moment of movable arm system around the axis [kgm2] |
| i | Integer parameter specifying a section of aileron [-] |
| j | Integer parameter specifying a section of movable arm [-] |
| L(ail)(i) | Vertical aerodynamic force of section i of aileron [N] |
| L(ma)(j) | Vertical aerodynamic force of section j of movable arm [N] |
| L(αi) | Lift force of section i of aileron [N] |
| L(αj) | Lift force of section j of movable arm [N] |
| lac(ail)(i) | Distance between aerodynamic center of section i of aileron and movable arm axis [m] |
| Maero | Total moment by aerodynamic forces acting on aileron and movable arm [N・m] |
| Maero(ail) | Moment by aerodynamic force acting on an aileron [N・m] |
| Maero(ma) | Moment by aerodynamic force acting on a movable arm [N・m] |
| Mc | Total moment by centrifugal forces acting on aileron, movable arm, and concentrated mass [N・m] |
| Mc(ail) | Moment by centrifugal force acting on an aileron [N・m] |
| Mc(cm) | Moment by centrifugal force acting on concentrated mass [N・m] |
| Mc(ma) | Moment by centrifugal force acting on a movable arm [N・m] |
| Mdamp | Resistant moment of dampers [N・m] |
| Mg | Total moment by gravity forces acting on aileron, movable arm, and concentrated mass [N・m] |
| Mg(ail) | Moment by gravity force acting on an aileron [N・m] |
| Mg(cm) | Moment by gravity force acting on concentrated mass [N・m] |
| Mg(ma) | Moment by gravity force acting on a movable arm [N・m] |
| mi | Mass of section i of aileron [kg] |
| mj | Mass of section j of movable arm [kg] |
| N | Rotor rotational speed [rpm] |
| n | Number of rotor rotations [-] |
| nave | Number of rotor rotations for ensemble averaging [-] |
| nmax | Maximum number of rotor rotations for calculation of movable arm behavior [-] |
| Protor | Power of wind turbine rotor [W] |
| p | Index of power law of vertical distribution of wind speed [-] |
| Qail(I) | Torque generated by an aileron in azimuth I [N・m] |
| Qblade_in(I) | Torque generated by an inner blade in azimuth I [N・m] |
| Qblade_out(I) | Torque generated by an outer blade in azimuth I [N・m] |
| Qfa(I) | Torque generated by a fixed arm in azimuth I [N・m] |
| Qma(I) | Torque generated by a movable arm in azimuth I [N・m] |
| Qrotor | Torque of wind turbine rotor [N・m] |
| Qtotal(I) | Total torque generated by a blade in azimuth I [N・m] |
| R | Radius of wind turbine rotor [m] |
| Re | Reynolds number based on chord length and relative wind speed [-] |
| rail | Distance between the installation position of aileron and rotational axis of rotor [m] |
| rcg(ail)(i) | Distance between the center of gravity of section i of aileron and rotational axis of rotor [m] |
| reff(ail)(i) | Distance between aerodynamic center of section i of aileron and rotational axis of rotor [m] |
| rma(j) | Distance between installation position of section j of movable arm and rotational axis of rotor [m] |
| Δrj | Width of section j of movable arm [m] |
| sail | Chordwise distance between aerodynamic center of aileron and movable arm axis [m] |
| sma | Chordwise distance between aerodynamic center of movable arm and movable arm axis [m] |
| span(ail) | Span length of aileron [m] |
| t | Time [s] |
| V | Wind speed [m/s] |
| V∞ | Upstream wind speed [m/s] |
| Vail | Rotational speed of aerodynamic center of each section of aileron around movable axis [m/s] |
| Vc | Relative wind velocity in cross section of aileron [m/s] |
| Vd_in | Wind speed through inner rotor in downwind side [m/s] |
| Vd_out | Wind speed through outer rotor in downwind side [m/s] |
| VH(ail) | Horizontal component of Vail [m/s] |
| VH(ma) | Horizontal component of Vma [m/s] |
| Vhub | Wind speed at hub height [m/s] |
| Vma | Rotational speed of aerodynamic center of movable arm around movable axis [m/s] |
| Vn(ail) | Normal component of Vrel in each section of aileron [m/s] |
| Vrel | Relative wind velocity in horizontal plane [m/s] |
| Vt(ail) | Tangential component of Vrel in each section of aileron [m/s] |
| Vt(ma) | Tangential component of Vrel in each section of movable arm [m/s] |
| Vu_in | Wind speed through inner rotor in upwind side [m/s] |
| Vu_out | Wind speed through outer rotor in upwind side [m/s] |
| VV(ail) | Vertical component of Vail [m/s] |
| VV(ma) | Vertical component of Vma [m/s] |
| Vz | Wind speed at altitude of z [m/s] |
| W | Integer parameter of height level in rotor [-] |
| Wc | Chord-wise component of We(ail) [m/s] |
| We(ail) | Relative wind velocity from Vt(ail) by considering Vail [m/s] |
| We(ma) | Relative wind velocity modified from Vt(ma) by considering Vma [m/s] |
| X, Y, Z | Absolute coordinate [m] |
| z | Coordinate in the vertical direction [m] |
| zhub | Hub height [m] |
| αi | Angle of attack defined in cross-section of section i of aileron [°] |
| αj | Angle of attack defined in cross-section of section j of movable arm [°] |
| Δαj | Angle between Vt(ma) and We(ma) [rad] |
| βi | Angle between Fc(ail)(i) and Fct(ail)(i) [rad] |
| βj | Angle between Fc(ma)(j) and Fct(ma)(j) [rad] |
| γi | Angle between Vt(ail) and We(ail) [rad] |
| δi | Angle between We(ail) and Wc [rad] |
| ε | Convergence judgment threshold of Δηave [°] |
| ζ(i) | Angle between lac(ail)(i) and vertical direction [rad] |
| η | Slant angle of movable arm [°] or [rad] |
| ηave | Averaged slant angle of movable arm in one rotor revolution [°] |
| η(I) | Converged or ensemble averaged slant angle of movable arm in azimuth I [°] or [rad] |
| η(n, I) | Slant angle of movable arm in azimuth I in n-th rotor rotation [°] or [rad] |
| ηini | Initial slant angle of movable arm [°] |
| Δηave | Evaluation value of convergence of slant angle variation [°] |
| λ | Tip speed ratio [-] |
| ξ(i) | Angle between lac(ail)(i) and span-wise direction of aileron [rad] |
| ρ | Air density [kg/m3] |
| Ψ | Azimuth angle [°] or [rad] |
| ΔΨ(i) | Difference in azimuth between rail and reff(ail)(i) [°] or [rad] |
| ω | Angular velocity of rotor rotation [rad/s] |
| ωma | Angular velocity of slant movement of movable arm [rad/s] |
Appendix A
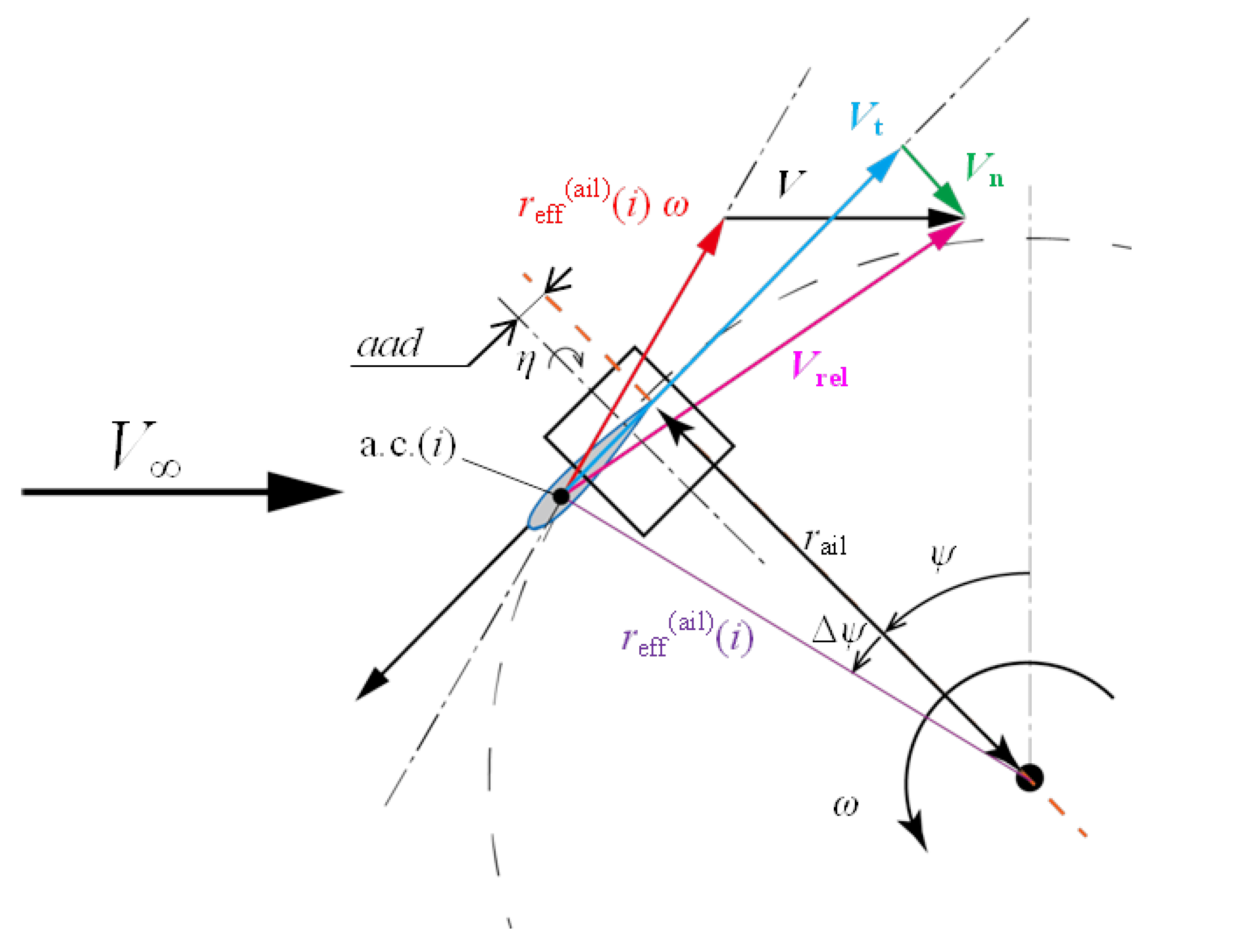
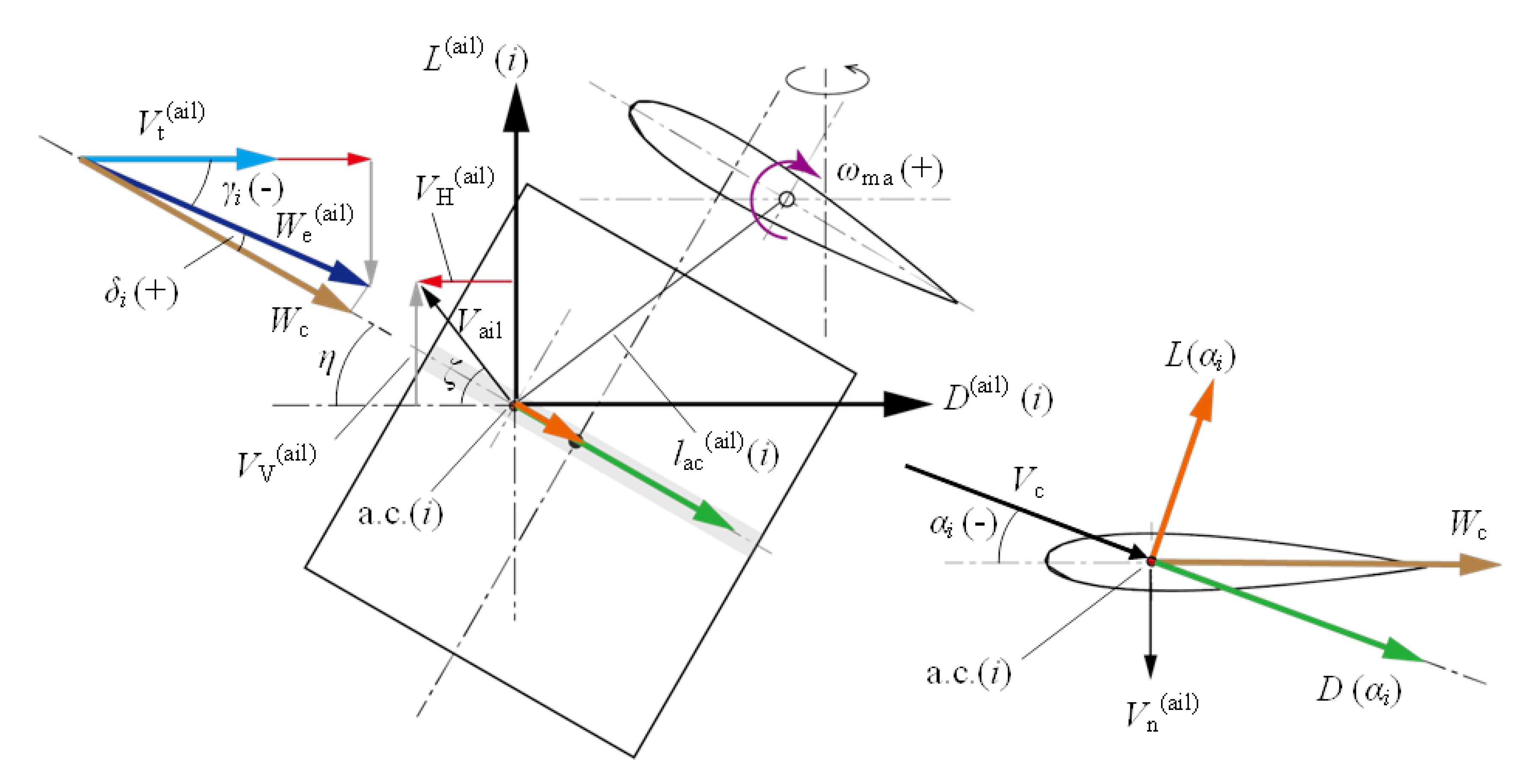
Appendix B
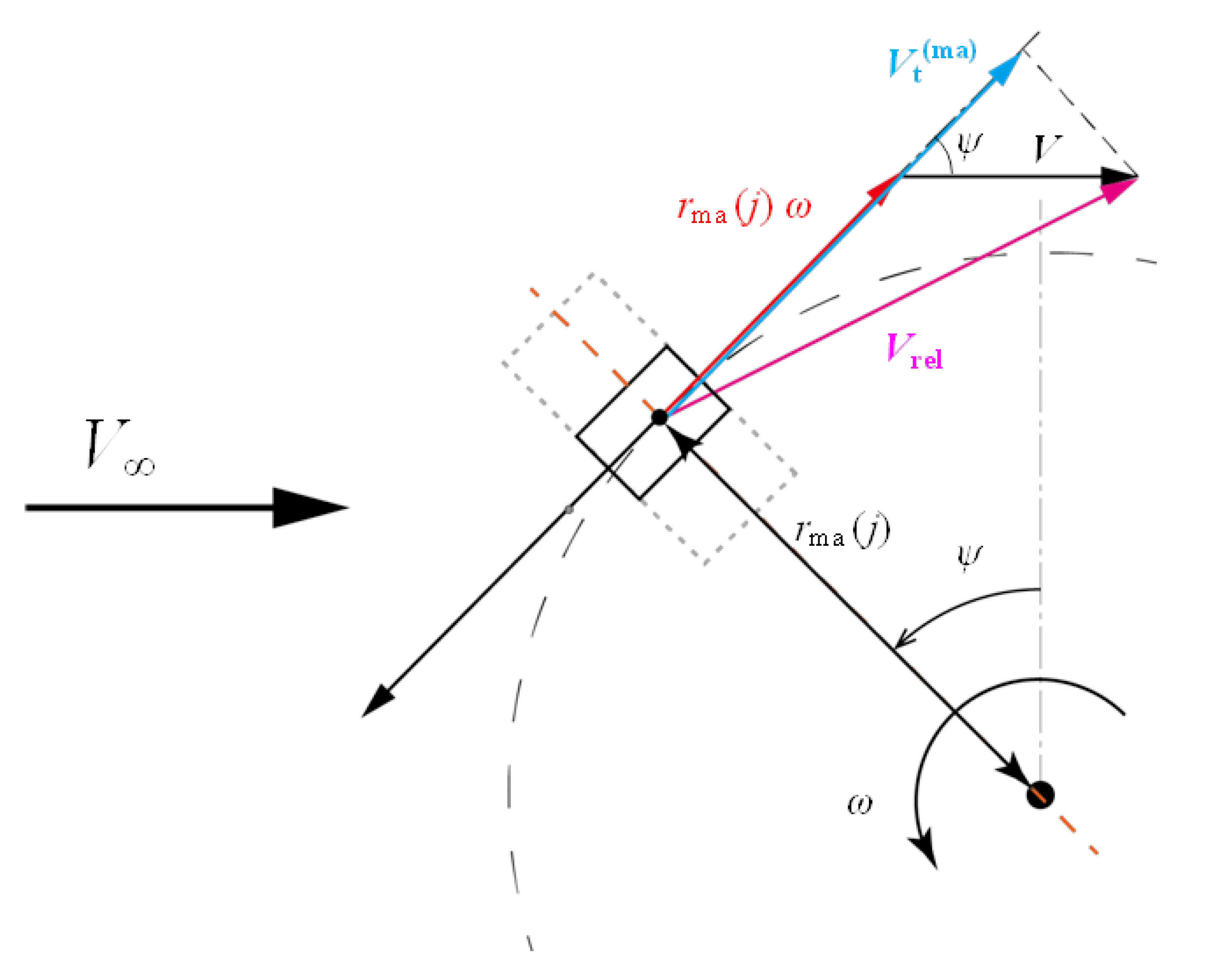
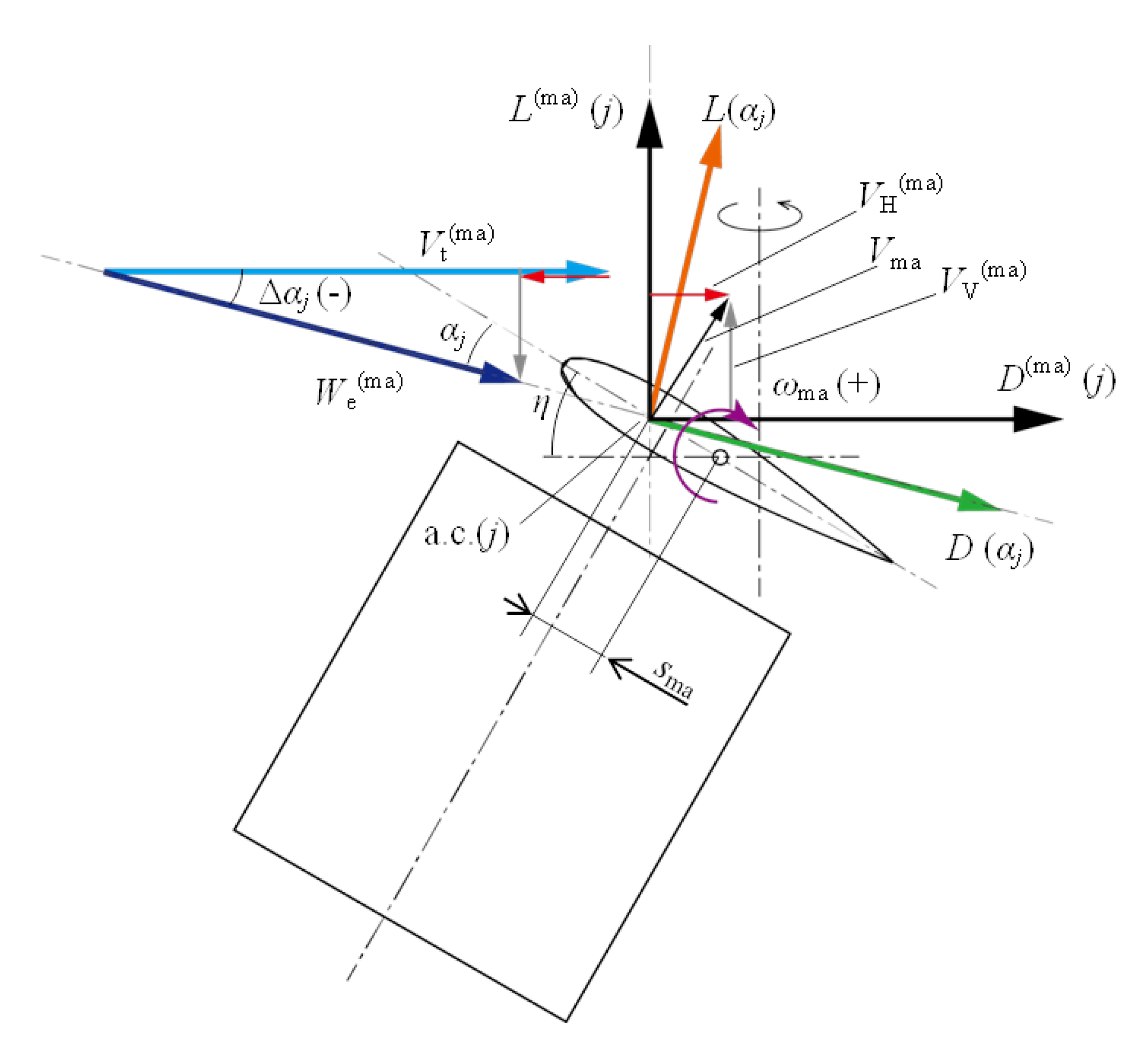
References
- Cheng, C.; Blakers, A.; Stocks, M.; Lu, B. 100% renewable energy in Japan. Energy Conversion and Management 2022, 255, 115299. [Google Scholar] [CrossRef]
- Motohashi, H.; Goto, M.; Tan, S. Development of over speed protector for small scale wind turbines, In Proceedings of the 26th Wind Energy Utilization Symposium, Tokyo, Japan, 26 Nov. 2004; pp. 413-416. [https://www.jstage.jst.go.jp/article/jweasympo1979/26/0/26_0_413/_pdf].
- Noda, M.; Nagao, F.; Shinomiya, A. Aerodynamic autonomous control of gyromill wind turbine, In Proceedings of the Annual Meeting of Japan Association for Wind Engineering, 30 April 2007; pp. 255-256. [https://www.jstage.jst.go.jp/article/jaweam/2007/0/2007_0_79/_article/-char/ja/].
- Noda, M.; Nagao, F.; Shinomiya, A.; Muneta, K. Rotation control of straight wing vertical axis wind turbine with inhibition mechanism of overspeed rotation, In Proceedings of the 20th National Symposium on Wind Engineering, 2008; pp. 133-138. [https://www.jstage.jst.go.jp/article/kazekosymp/20/0/20_0_23/_pdf].
- Kiwata, T.; Yamada, T.; Kita, T.; Takata, S.; Komatsu, N.; Kimura, S. Performance of a Vertical Axis Wind Turbine with Variable-Pitch Straight Blades utilizing a Linkage Mechanism. Journal of Environment and Engineering 2010, 5, 1, pp. 213-225. https://doi.org/10.1299/jee.5.213. [CrossRef]
- Yamada, T.; Kiwata, T.; Kita, T.; Hirai, M.; Komatsu, N.; Kono, T. Overspeed Control of a Variable-Pitch Vertical-Axis Wind Turbine by Means of Tail Vanes. Journal of Environment and Engineering 2012, 7, 1, pp. 39-52. [CrossRef]
- Tanzawa, Y.; Shimizu, S.; Inoue, Y.; Shimizu, Y. Study on the aerodynamic brake of small gyro-mill type vertical axis wind turbine (1st report, method of the rotational speed continuous control under the strong wind). Transactions of the Japan Society of Mechanical Engineers Part B 2013, 79, 797, pp. 12-21. [CrossRef]
- Hara, Y.; Tagawa, K.; Saito, S.; Shioya, K.; Ono, T.; Makino, K.; Toba, K.; Hirobayashi, T.; Tanaka, Y.; Takashima, K.; Sasaki, S.; Nojima, K.; Yoshida, S. Development of a Butterfly Wind Turbine with Mechanical Over-Speed Control System. Designs 2018, 2, 2. [CrossRef]
- Hara, Y.; Saito, S.; Park, O.; Ishikawa, H.; Ono, T.; Higami, H. Behavior analysis of 7m Butterfly Wind Turbine with over-speed control using movable arms, In Proceedings of the 26th National Symposium on Power and Energy Systems, Saga, Japan, 13-14 July 2022; C213.
- Ando, H.; Hara, Y.; Miura, T.; Yoshida, S. The selection of blade cross section of a vertical axis wind turbine with a diameter of 14 m and the evaluation of rotor performance, In Proceedings of the 50th Student Graduation Research Presentation Conference of the Japan Society of Mechanical Engineering Chugoku-Shikoku Branch, Hiroshima University, 5 March 2020; 04a1 [https://repository.lib.tottori-u.ac.jp/records/2000017].
- Paraschivoiu, I. Wind turbine design: with emphasis on Darrieus concept. Polytechnic International Press: 2002; pp. 147-264.
- Hara, Y.; Kawamura, T.; Akimoto, H.; Tanaka, K.; Nakamura, T.; Mizumukai, K. Predicting Double-Blade Vertical Axis Wind Turbine Performance by a Quadruple-Multiple Streamtube Model. International Journal of Fluid Machinery and Systems 2014, 7, 1, pp. 16-27. [CrossRef]
- Sheldahl, R. E.; Klimas, P. C. Aerodynamic characteristics of seven symmetrical airfoil sections through 180-degree angle of attack for use in aerodynamic analysis of vertical axis wind turbines; Sandia National Laboratories: 1981; 6548367 [https://www.osti.gov/biblio/6548367]. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




