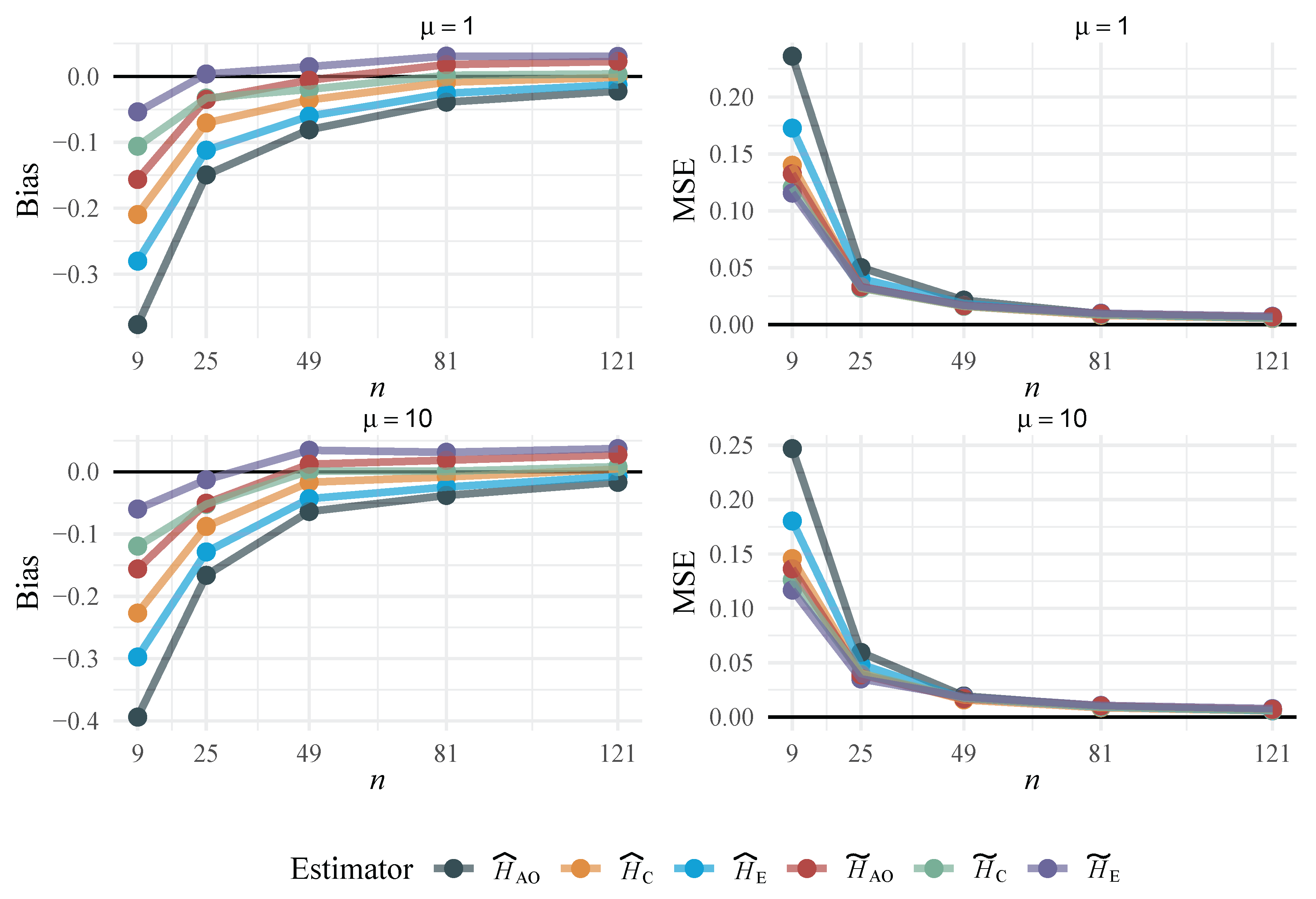
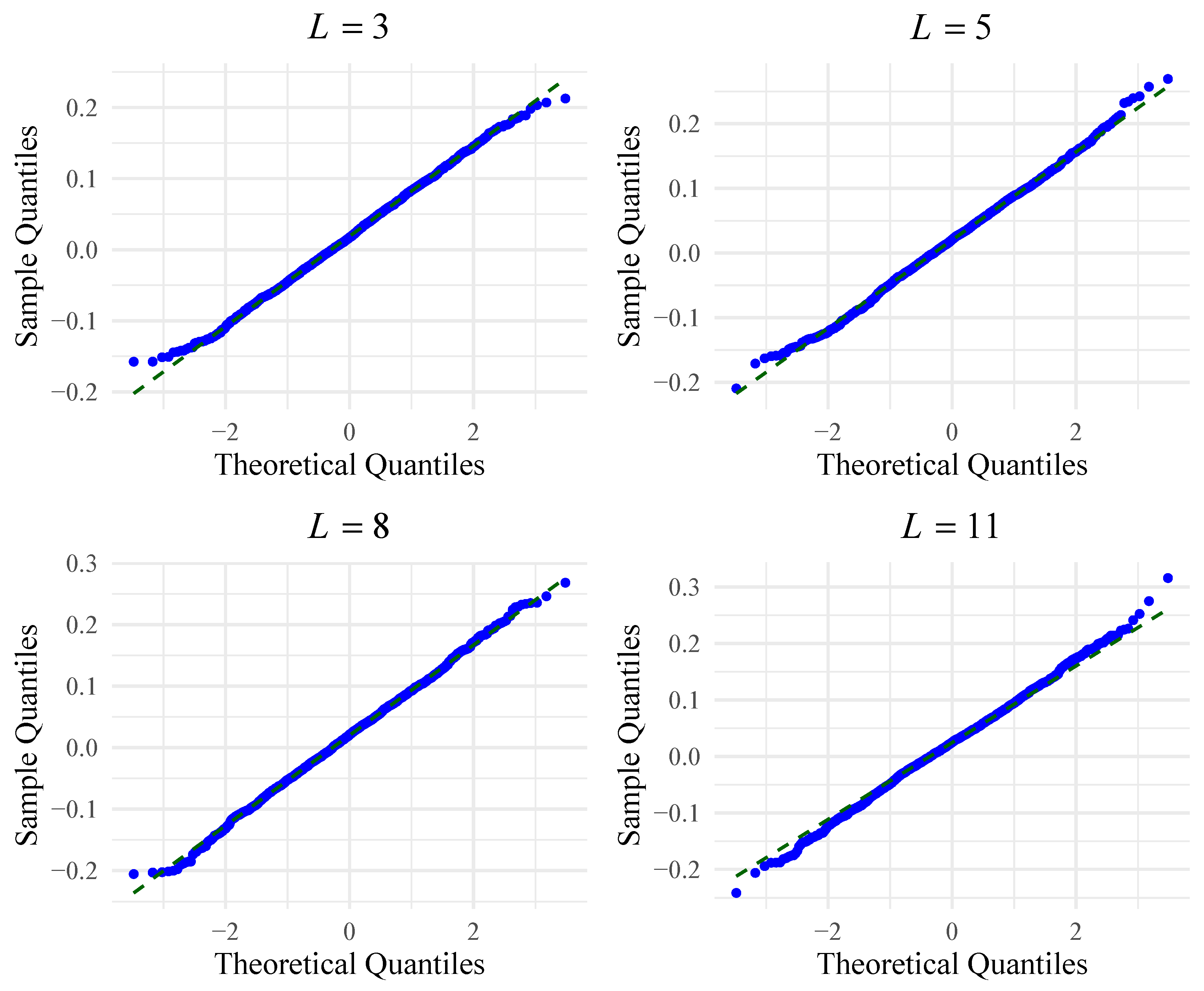
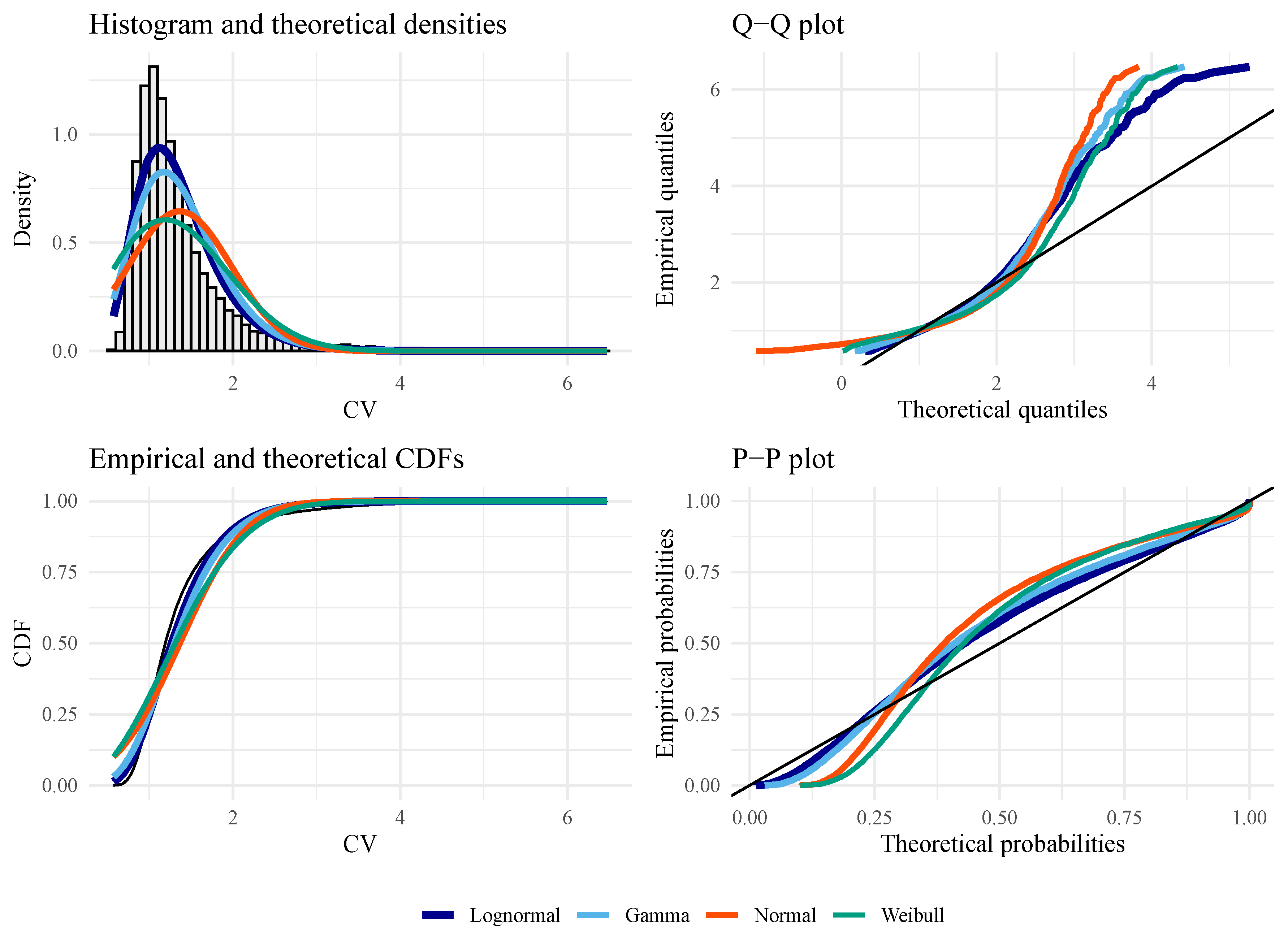
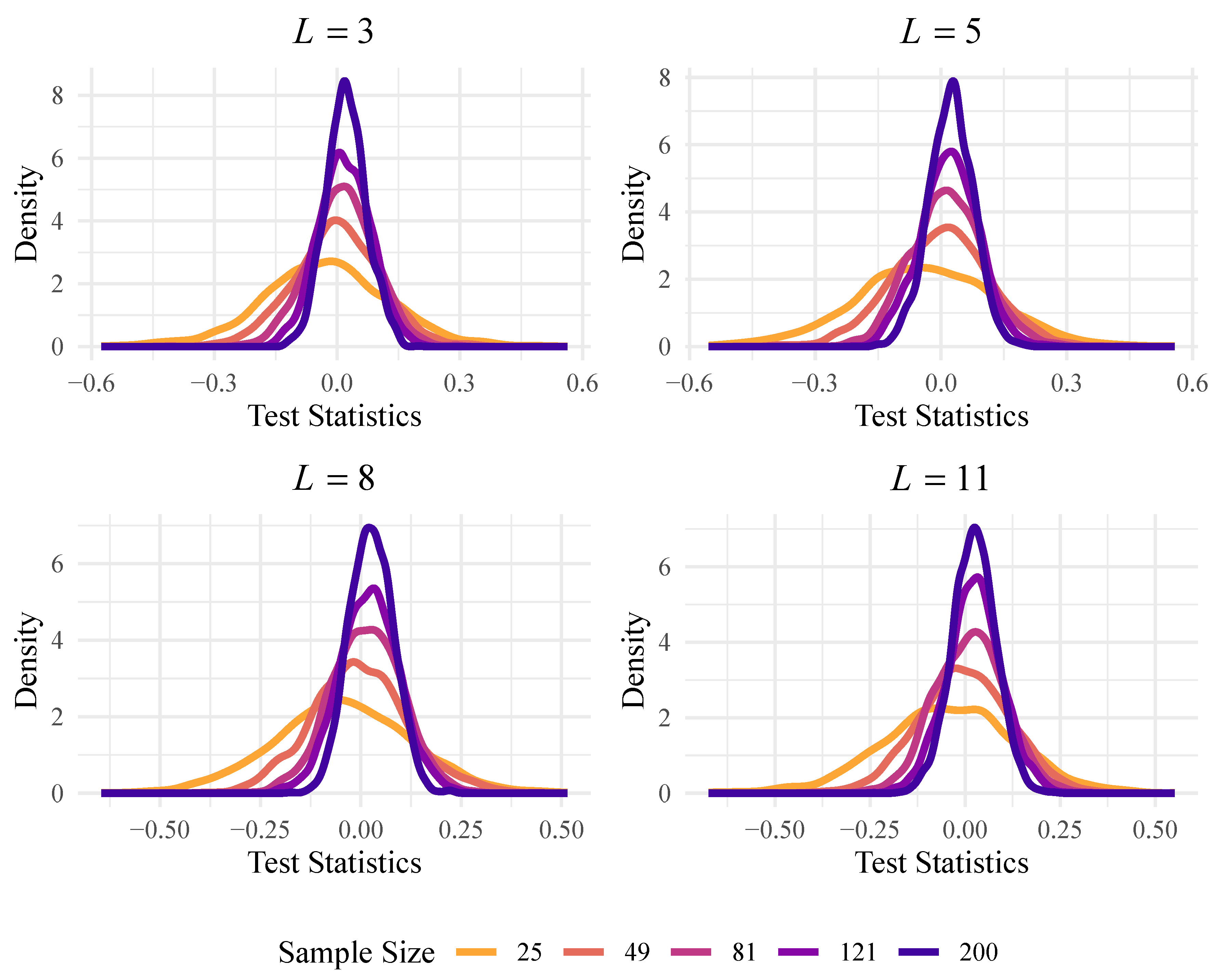This section presents the simulations we performed to evaluate the proposed test statistics’ performance, followed by applications to SAR data.
4.1. Simulated Data
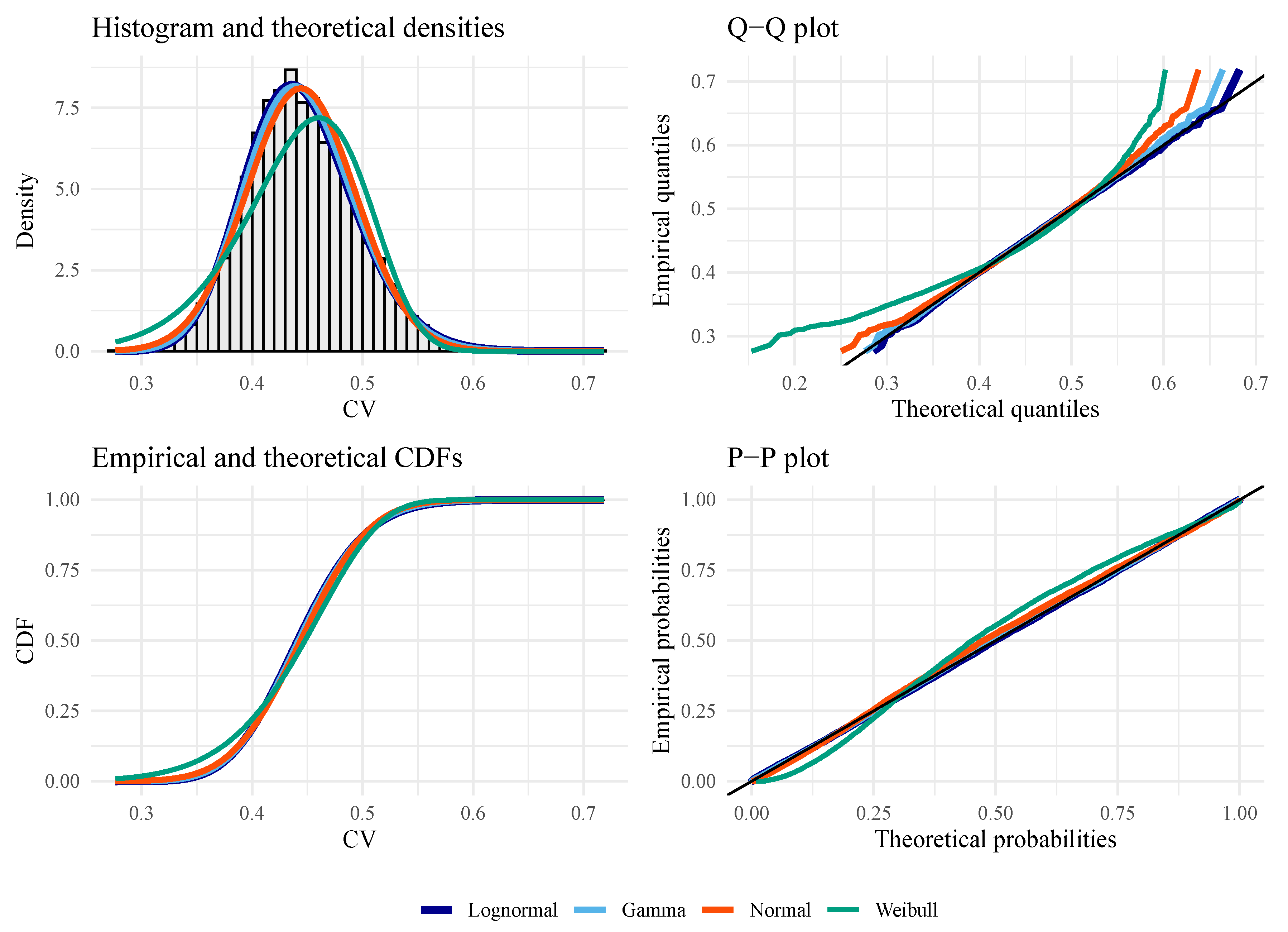
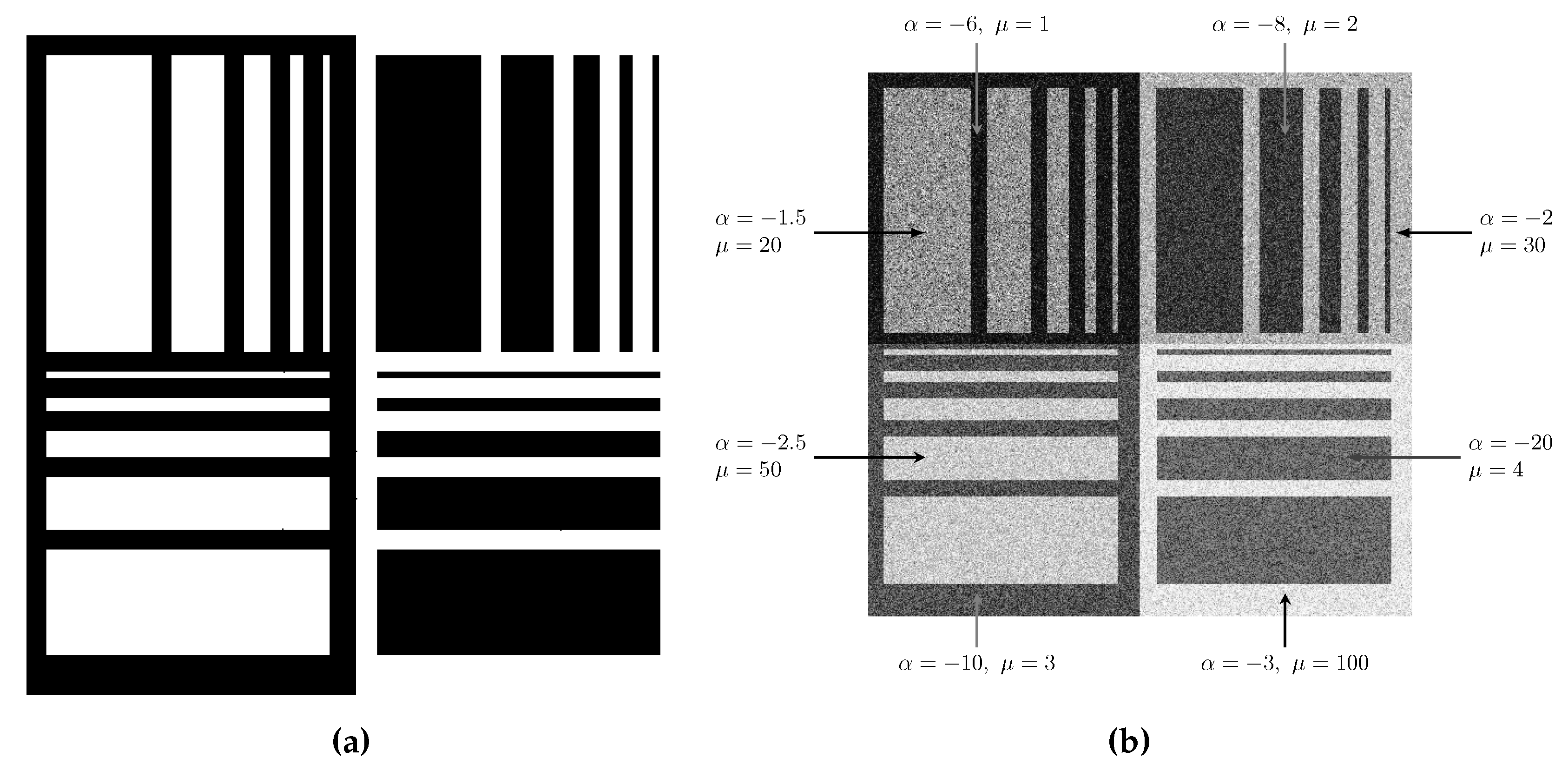
Figure 9(a) shows the phantom with dimensions of
pixels. It was proposed by Gomez et al. [
38] as a tool to assess the performance of speckle-reduction filters.
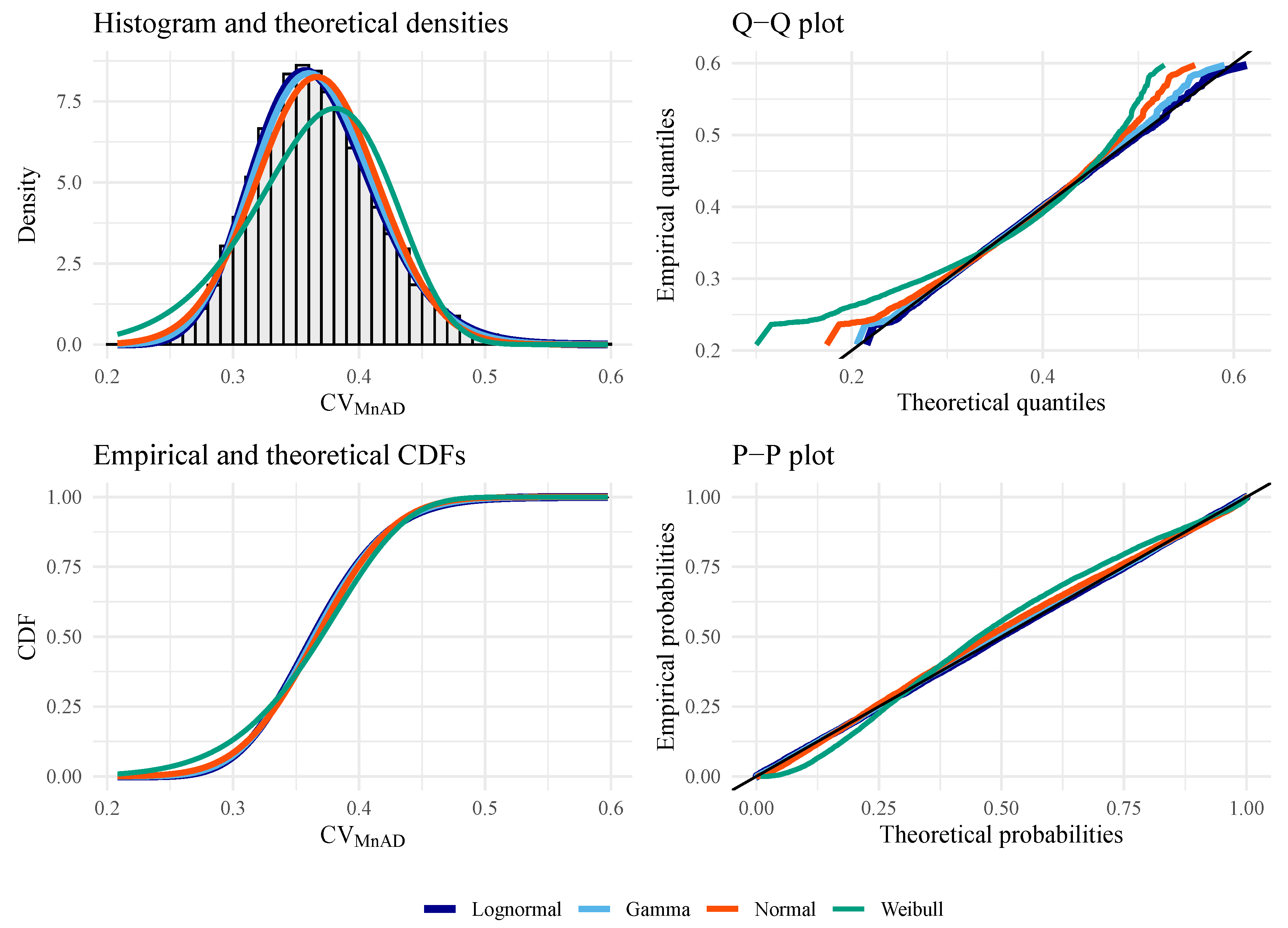
Figure 9(b) shows the simulated image, where each small phantom displaying texture variations. The observations are independent draws from the
distribution (
5), with
and varying
and
, annotated in the image for each quadrant. Light regions correspond to textured observations (heterogeneous), while darker regions represent textureless areas (homogeneous).
The
parameter of the
distribution is essential for interpreting texture characteristics. Values near zero greater than
suggest extremely textured targets, such as urban zones [
39]. As the value decreases, it indicates regions with moderate texture (in the
region), related to forest zones, while values below
correspond to textureless regions, such as pasture, agricultural fields, and water bodies [
40].
We applied the three test statistics, namely
,
, and
, to the simulated image using local sliding windows of size
, as shown in
Figure 10(a)–(c).
The resulting
p-values for each test are shown in
Figure 11(a)–(c). In
Figure 12(a)–(c), maps are depicted using a color table between black, gray levels, and white. All
p-values above
are represented in white (indicating no evidence to reject the null hypothesis), while those below
are shown in black (indicating evidence to reject the hypothesis). We notice that the
performs significantly better than the other tests in identifying heterogeneous areas in the simulated image.
4.2. SAR Data
We evaluated the proposed test statistics using three SAR images: one of the coast of Jalisco, Mexico (with a spatial resolution of 20 m both along azimuth and range directions) and two of Illinois, USA (with a spatial resolution of 10
both along azimuth and range directions), acquired by the Sentinel-1B satellite operating in C-band, with VV polarization and intensity format. The first two images have a size of
pixels, while the third has
pixels, and they contain mountainous areas, agricultural regions, water bodies, and urban areas, as shown in
Figure 13(a)–(c).
The three statistical tests are applied to the SAR images using
local sliding windows, as illustrated in
Figure 14,
Figure 17 and
Figure 20.
In
Figure 16,
Figure 19 and
Figure 22, the maps of
p-values composed of a linear gradient of black and white colors, represent the decisions at a 5 significance level. Dark areas represent values below
, indicating evidence to reject the null hypothesis and suggesting heterogeneity in these regions. In contrast, values above 0.05 are represented as white areas, indicating no evidence to reject the fully-developed speckle hypothesis.
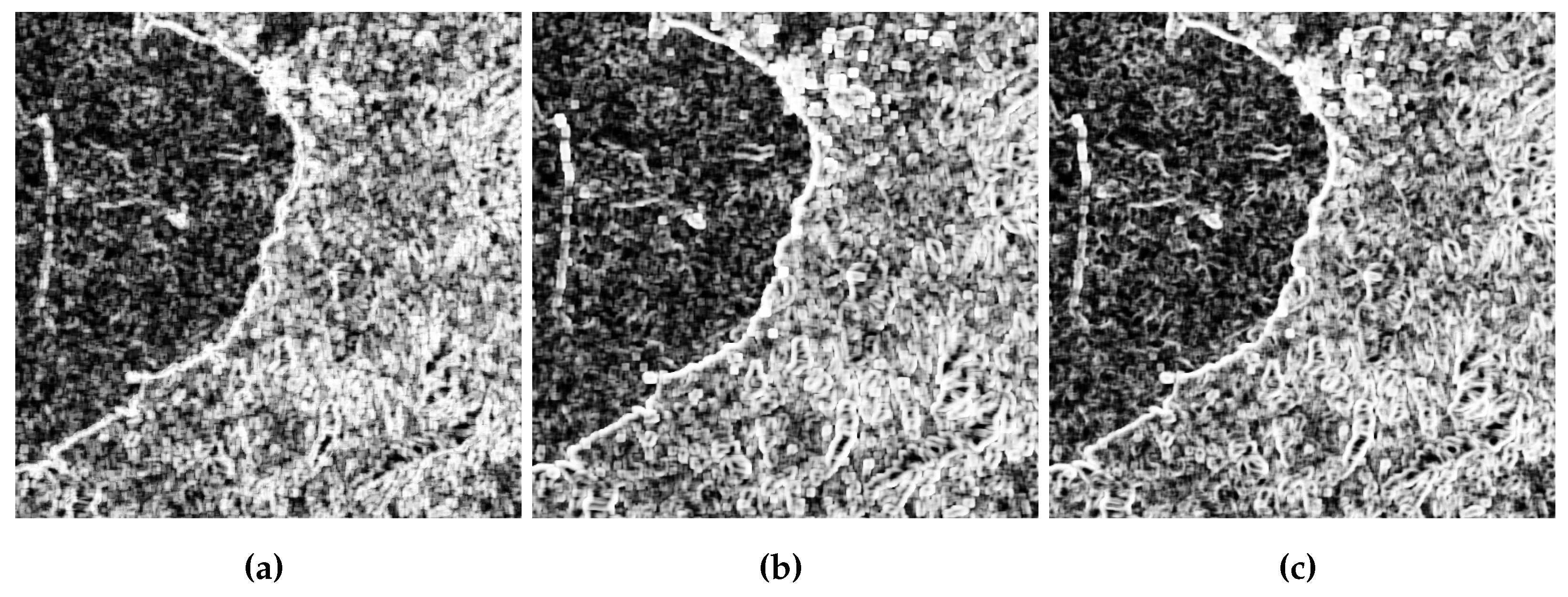
Figure 14.
Results of applying the test statistics, Coast of Jalisco: (a) , (b) , and (c) .
Figure 14.
Results of applying the test statistics, Coast of Jalisco: (a) , (b) , and (c) .
Figure 15.
Map of p-values, Coast of Jalisco: (a) . (b) . (c) .
Figure 15.
Map of p-values, Coast of Jalisco: (a) . (b) . (c) .
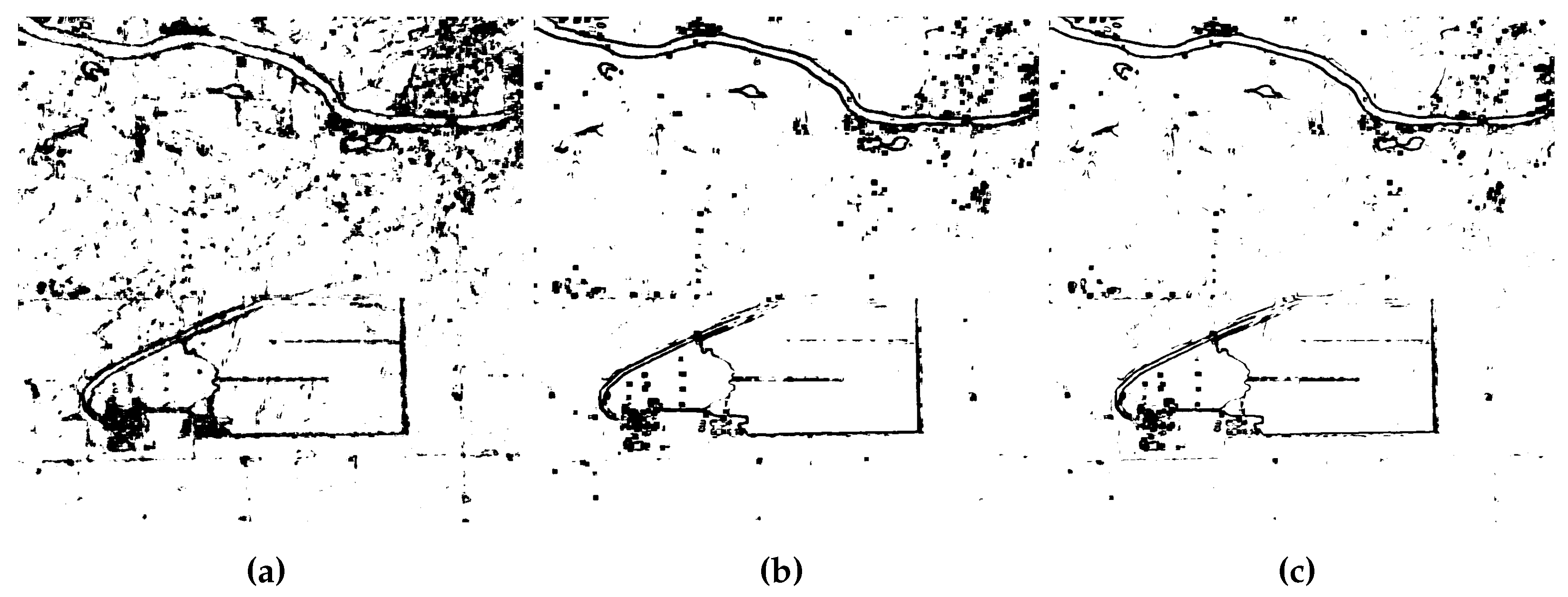
Figure 16.
Results for a threshold of of the p-value, Coast of Jalisco. (a) , (b) , and (c) .
Figure 16.
Results for a threshold of of the p-value, Coast of Jalisco. (a) , (b) , and (c) .
Figure 17.
Results of applying the test statistics, Illinois-Region 1: (a) , (b) , and (c) .
Figure 17.
Results of applying the test statistics, Illinois-Region 1: (a) , (b) , and (c) .
Figure 18.
Map of p-values, Illinois-Region 1: (a) , (b) , and (c) .
Figure 18.
Map of p-values, Illinois-Region 1: (a) , (b) , and (c) .
Figure 19.
Results for a threshold of of the p-value, Illinois-Region 1. (a) , (b) , and (c) .
Figure 19.
Results for a threshold of of the p-value, Illinois-Region 1. (a) , (b) , and (c) .
Using Shannon entropy is more meaningful than using the original and robust CV to capture heterogeneity. It is justified that the dark areas of the maps based on the and show coverage patterns similar to those reported for the map. This suggests that although CV-based tests may produce slightly less pronounced results than the entropy-based test, they still demonstrate a comparable ability to detect heterogeneity within SAR images.
Figure 20.
Results of applying the test statistics, Illinois-Region 2: (a) , (b) , and (c) .
Figure 20.
Results of applying the test statistics, Illinois-Region 2: (a) , (b) , and (c) .
Figure 21.
Map of p-values, Illinois-Region 2: (a) , (b) , and (c) .
Figure 21.
Map of p-values, Illinois-Region 2: (a) , (b) , and (c) .
Figure 22.
Results for a threshold of of the p-value, Illinois-Region 2. (a) , (b) , and (c) .
Figure 22.
Results for a threshold of of the p-value, Illinois-Region 2. (a) , (b) , and (c) .
It is noticeable that the entropy and CV-based tools predicted heterogeneity regions and boundaries where the statistical properties of texture vary. The test was shown to be an effective edge detector. It emerges as a robust alternative to the classical CV test, making it less susceptible to the influence of outliers and allowing it to produce more precise edges. Considering a higher significance level may increase the sensitivity to edge detection but also increase the risk of detecting false heterogeneous regions.
Additionally, assuming a 5 threshold for
p-values, in most cases, the heterogeneous regions detected by the
test were more extensive than those detected by the
and
tests. This was mainly observable in
Figure 12(a),
Figure 16(a), and
Figure 19(a).