On Efficiency of Two-Degree-of-Freedom Galloping Energy Harvesters with Two Transducers

Preprint

Article

On Efficiency of Two-Degree-of-Freedom Galloping Energy Harvesters with Two Transducers

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

10 May 2024

Posted:

12 May 2024

You are already at the latest version

Alerts

Abstract

This paper examines the energy efficiency of three variations of the two-degree-of-freedom transverse galloping energy harvester. These variants differ in the number and placement of electromechanical transducers. By utilizing the harmonic balance method, limit cycles of mathematical models of devices were determined. Analytical expressions derived from models were then used to formulate the efficiency of the systems. It was demonstrated that efficiency depends on flow speed and can be comprehensively characterized by four criteria parameters: peak efficiency, denoting the maximum efficiency of the system, and high efficiency bandwidth, which describes the range of flow velocities within which the efficiency remains at no less than 90% of peak efficiency. The values of these parameters are heavily reliant on the speed at which the system achieves peak efficiency—referred to as the nominal speed nominal speed, which in turn is related to the critical speed of the system. Comparative analysis revealed that only the two-degree-of-freedom device equipped with two electromechanical transducers can potentially outperform a simple one-degree-of-freedom system in terms of efficiency.

Keywords:

Subject: Engineering - Energy and Fuel Technology

1. Introduction

In the contemporary world, energy plays a pivotal role across all facets of human existence. Powering electronic gadgets, illuminating and heating homes, and propelling machinery all hinge on energy. However, as the population grow and technologies advance, we increasingly encounter challenges concerning energy production and distribution.

The energy crisis has become a pervasive issue demanding attention. Concurrently, with technological advancements, the concept of the Internet of Things (IoT) is burgeoning [1]. IoT delineates a network of interconnected devices that communicate and share data to enhance the daily lives of users. Smart home gadgets, vehicles, environmental sensors, and myriad other devices can interconnect, analyze data, and autonomously make decisions. Yet, as IoT devices proliferate, challenges in providing them with sustainable energy sources emerge. Conventional power methods such as batteries or power cords may prove inconvenient, have limited durability, or be impractical for distributed IoT networks.

Energy harvesting technologies, such as flow-induced vibration recovery, offer potential solutions. Notably, Bladeless Vortex power plants, activated by von Karman vortices, promise a cost reduction of up to 70% compared to traditional wind farms [3]. However, their dependence on specific flow conditions presents limitations.

Galloping emerges as an alternative vibration excitation method. Early studies explore its potential for energy recovery [4], emphasizing the crucial role of aerodynamic coefficients and the device's quasi-stationary nature. Subsequent research [5] delves into analytical, numerical, and experimental analyses of galloping energy harvesters (GEH), examining structural damping's impact and developing electromechanical models.

Due to the fundamental influence of flow body geometry [6], research focuses on optimizing shapes to enhance efficiency. While rhomboid geometries are prone to galloping instability, adding a stream splitter on the opposite side favors power generation [7,8]. Additionally, devices with irregular shapes demonstrate benefits [9,10].

Nonlinear elasticity's influence on GEH performance is extensively studied [11,12]. It is found to enhance efficiency at low flow rates, albeit potentially reducing operating speeds [13,14]. Various types of nonlinearities are assessed for their impact on device power [15], with duffing-type non-linear GEH variants analyzed for effectiveness [16].

Expanding GEH degrees of freedom shows promise [17], with series-connected mass systems and devices extended to multiple degrees explored [18,19]. Analytical solutions for mathematical models of such devices are developed [20], and experimental research on innovative designs, like magnetically coupled beams, shows increased power generation potential [21].

However, research on two-degree-of-freedom systems lacks exploration of utilizing two electromechanical transducers. Addressing this gap, this study aims to assess the efficiency of a GEH with two degrees of freedom. It considers transducer placement between the stationary base and lower mass and between masses, aiming to contribute to enhancing energy harvesting technologies.

2. Efficiency of Reference Variant

While the primary focus of this study lies in analyzing the efficiency of systems with two degrees of freedom (GEH2D), understanding the characteristics of this class of devices can be facilitated by comparing them with a system possessing well-established, as discussed in [3,4], properties - a linear device with one degree of freedom (GEH1D), hereafter referred to as the reference device. Therefore, it is justified to conduct an analysis of the efficiency of this system, particularly as we aim to highlight a certain intriguing feature of this variant, which has not been previously addressed in the literature. According the cited articles, the mathematical model of GEH1D takes the form (1) with parameters detailed in Table 1.

\hat{m} \ddot{z} + \hat{c} \dot{z} + \hat{k} z - θ ξ = F_{L} = - \frac{1}{2} \hat{ρ} {\hat{u}}^{2} \hat{h} (a_{1} \frac{\dot{z}}{\hat{u}} + a_{3} {(\frac{\dot{z}}{\hat{u}})}^{3}),

(1a)

\hat{C_{p}} \dot{ξ} + \frac{ξ}{\hat{R}} + \hat{θ} \dot{x} = 0 .

(1b)

The efficiency

η

of such a system is defined as the ratio of the average power generated by the device

\hat{P_{g}}

over a time period equal to the period

\hat{T}

of the voltage function ξ(τ) to the surface flow power density

\hat{P_{f}}

η^{L} = \frac{\hat{P_{g}}}{\hat{P_{f}}} = \frac{\frac{1}{\hat{T}} \int_{0}^{\hat{T}} \frac{ξ^{2} (τ)}{\hat{R}} d τ}{\frac{1}{2} \hat{ρ} \hat{h} {\hat{u}}^{3}},

(2)

y = \frac{z}{\hat{h}}, v = ξ \frac{\hat{θ}}{\hat{m} \hat{h} {\hat{ω}}_{n}^{2}}, {\hat{ω}}_{n} = \sqrt{\frac{\hat{k}}{\hat{m}}}, c = \frac{\hat{c}}{\hat{m} {\hat{ω}}_{n}}, u = \frac{\hat{u}}{\hat{h} {\hat{ω}}_{n}}, ρ = \hat{ρ} \frac{{\hat{h}}^{2}}{2 \hat{m}}, r = \hat{C_{p}} \hat{R} {\hat{ω}}_{n}, κ = \frac{{\hat{θ}}^{2}}{\hat{C_{p}} \hat{m} {\hat{ω}}_{n}^{2}}, t = τ {\hat{ω}}_{n},

(3)

the device dimensionless mathematical model can be written as:

\ddot{y} + c \dot{y} + y - v = ρ (a_{1} u \dot{y} + a_{3} \frac{{\dot{y}}^{3}}{u}),

(4a)

\dot{v} + \frac{v}{r} + κ \dot{y} = 0 .

(4b)

Assuming that

T_{c}

is the period of the function

v (t)

, efficiency in terms of dimensionless parameters can be expressed as:

η^{L} = \frac{\frac{1}{T_{c}} \int_{0}^{T_{c}} \frac{v^{2} (t)}{κ r} d t}{ρ u^{3}} .

(5)

To characterize the efficiency

η^{L}

of the system, it is essential to derive the voltage function

v (t)

generated by it, which can be accomplished using the harmonic balance method. Consequently, it was assumed that the limit cycle of the system would be described by a set of solutions in the form:

y = A_{y} c o s (ω t),

(6a)

v = A_{v} \cos (ω t + φ),

(6b)

where, the four unknown quantities

A_{y}

A_{v}

ω = \frac{\hat{ω}}{{\hat{ω}}_{n}}

φ

represent the dimensionless vibration amplitude, dimensionless voltage amplitude, dimensionless vibration frequency, and the phase shift between the oscillator vibrations and voltage oscillations, respectively. The parameter

\hat{ω}

denotes the unknown dimensional frequency of the system's vibrations. Substituting solutions of the form (6) into the model (1) leads to the transformation of the system of differential equations into a system of algebraic equations:

A_{y} (1 - ω^{2}) c o s (ω t) + A_{y}^{3} \frac{ρ ω^{3} a_{3}}{u} {s i n}^{3} (ω t) + A_{y} ω (u ρ a_{1} - c) s i n (ω t) - A_{v} c o s (ω t + φ) = 0,

(7a)

A_{v} (\frac{\cos (ω t + φ)}{r} - ω \sin (ω t + φ)) - A_{y} κ ω s i n (ω t) = 0 .

(7b)

This condition will be satisfied for every moment of time

t

if and only if the sum of the coefficients with corresponding time functions equals zero. From equation (7b), the following was deduced:

\frac{A_{v} (c o s (φ) - r ω s i n (φ))}{r} = 0,

(8a)

\frac{A_{v} (r ω c o s (φ) + s i n (φ)) + A_{y} κ r ω}{r} = 0 .

(8b)

Equation (8a) shows that:

t g (φ) = \frac{1}{ω r}, \sin (φ) = \frac{1}{\sqrt{{(ω r)}^{2} + 1}}, \cos (φ) = \frac{ω r}{\sqrt{{(ω r)}^{2} + 1}} .

(9)

Based on equations (8b) and (9), the expression describing the relationship between the vibration amplitude and the voltage amplitude can be derived:

A_{v} = {- A}_{y} \frac{r κ ω}{\sqrt{1 + r^{2} ω^{2}}} .

(10)

By balancing harmonics of equation (7a), the remaining two algebraic equations, necessary to determine an approximate solution of the device model are obtained. After taking into account the previously derived relations (9) and (10), they take the form:

A_{y} k_{e}^{L} ω - A_{y} (ω^{2} - 1) = 0,

(11a)

A_{y} u ρ ω a_{1} + A_{y}^{3} \frac{3 ρ ω^{3} a_{3}}{4 u} - A_{y} c ω - A_{y} e^{L} ω = 0,

(11b)

where

k_{e}^{L} = κ \frac{r^{2} ω^{2}}{1 + r^{2} ω^{2}}

and

e^{L} = κ \frac{r}{1 + r^{2} ω^{2}}

are the piezoelectric stiffness and electrical damping of the linear system. Based on the above system of equations, it can be shown that:

\begin{matrix} ω_{1}^{2} \\ ω_{2}^{2} \end{matrix} = \frac{r^{2} (1 + κ) - 1 \pm \sqrt{4 r^{2} + {(r^{2} (1 + κ) - 1)}^{2}}}{2 r^{2}},

(12a)

{A_{y}}^{2} = \frac{4 u (c + e^{L} - u ρ a_{1})}{3 ρ ω^{2} a_{3}} .

(12b)

Equation (12a) shows that

ω_{2}^{2} < 0

, regardless of the system parameters. Therefore, in the following part of the work notation

ω_{1} = ω

has been adopted. Returning now to the general definition of efficiency (5) and substituting the expressions (6b), (10), (12) into it, we obtain:

η^{L} = \frac{2 e^{L} (c + e^{L} - u ρ a_{1})}{3 u^{2} ρ^{2} a_{3}} .

(13)

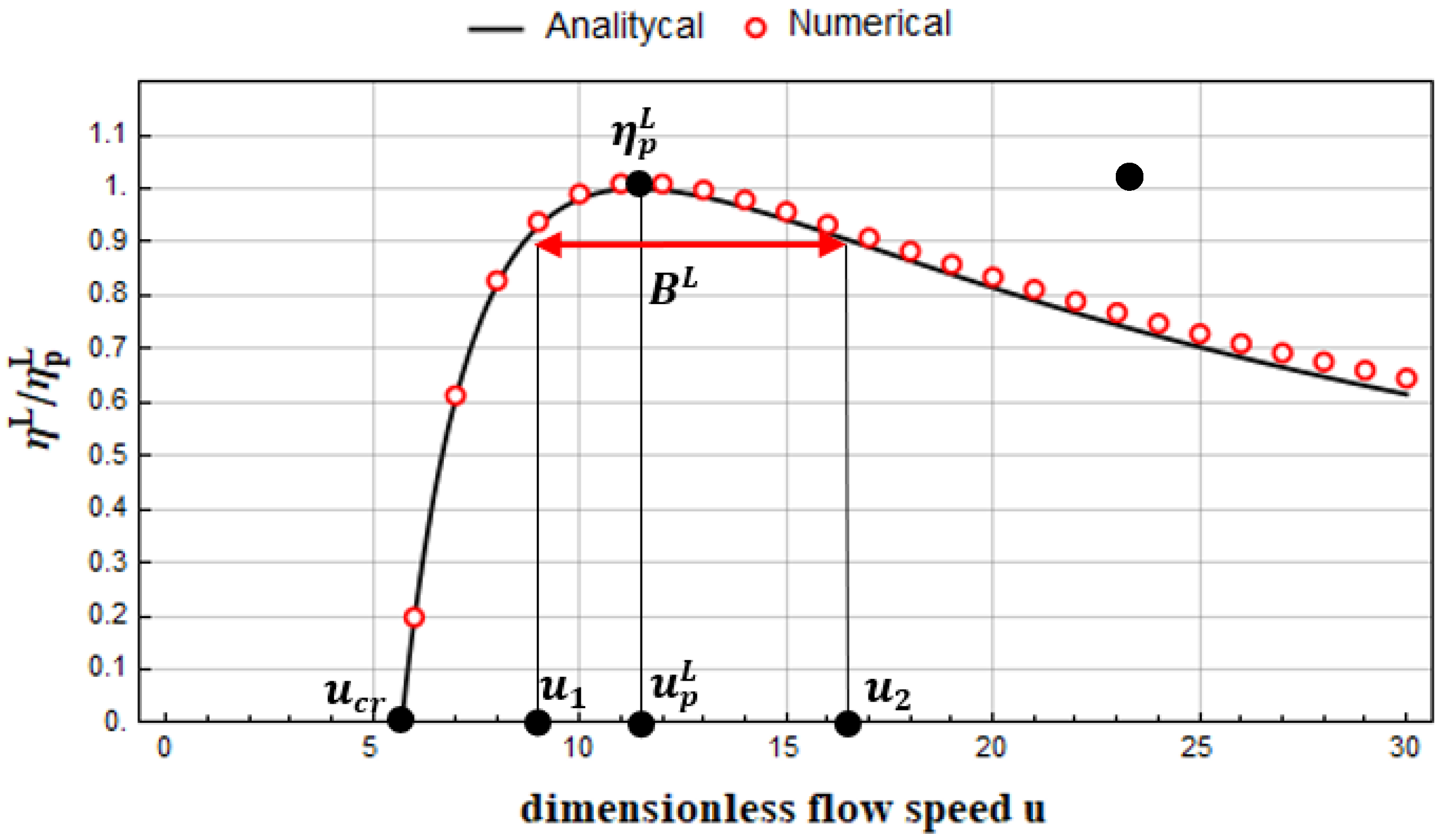
Figure 1 illustrates the efficiency characteristics of the system under discussion. The efficiency is depicted as the ratio

η^{L} / η_{p}^{L}

and such representation maintained throughout the study. The figure also includes the analogous characteristic obtained numerically for initial conditions

y (0) = 0.1

\dot{y} (0) = 0

n (0) = 0

, utilizing the fourth-order Runge-Kutta method. In this figure it can be observed that the system undergoes Hopf bifurcation at certain speed, from now on referred to as the critical flow speed

u_{c r}

,. Its value results directly from (13):

η^{L} = \frac{2 e^{L} (c + e^{L} - u ρ a_{1})}{3 u^{2} ρ^{2} a_{3}} = 0 \Rightarrow u = u_{c r} = \frac{c + e^{L}}{ρ a_{1}},

(14)

Another noteworthy observation from the same set of graphs is that irrespective of the parameter set, there exists a specific nominal flow speed

u = u_{p}^{L}

for which the efficiency

η^{L}

attains a maximum value, denoted as the peak efficiency

η_{p}^{L}

. These quantities are given by the expressions:

\frac{δ η^{L}}{δ u} = 0 \Rightarrow u = u_{p}^{L} = 2 \frac{c + e^{L}}{ρ a_{1}} = 2 u_{c r},

(15)

η_{p}^{L} = η^{L} (u_{p}^{L}) = \frac{- a_{1}^{2} e^{L}}{6 a_{3} (c + e^{L})} .

(16)

The aforementioned identities were previously derived in [3,4]. However, the remainder of the article discusses entirely original content. An unexplored property of GEH1D, which can be inferred from Figure 1 or deduced from the identity

u_{p}^{L} = 2 u_{c r}

, is noteworthy. A system with a low critical speed

u_{c r}

will experience a more pronounced decline in efficiency due to the deviation of the flow speed

u

at which it operates from the nominal speed

u_{p}^{L}

. Let the measure of this phenomenon be the flow speed bandwidth in which the system efficiency

η^{L}

does not fall below 90% of the maximum efficiency

η_{p}^{L}

, hereafter referred to as the high efficiency band

B^{L}

. According to the definition,

B^{L}

is given as:

η^{L} = 0.9 η_{p}^{L} \Rightarrow \begin{matrix} u_{2} \\ u_{1} \end{matrix} = \frac{ρ a_{1} (c + e^{L}) \pm \frac{\sqrt{0.4}}{0.9} ρ a_{1} (c + e^{L})}{\frac{0,9}{2} {(ρ a_{1})}^{2}},

(17)

B^{L} = u_{2} - u_{1} = \sqrt{\frac{160}{81}} \frac{(c + e^{L})}{ρ a_{1}} \approx 1.4 u_{c r} \approx 0.7 u_{p}^{L} .

(18)

The quantities: critical speed

u_{c r}

, nominal speed

u_{p}^{L}

, peak efficiency

η_{p}^{L}

and high efficiency bandwidth

B^{L}

will be further referred to as the criterion parameters. They have been labeled on Fig. 1.

3. Efficiency of Two Degree of Freedom System

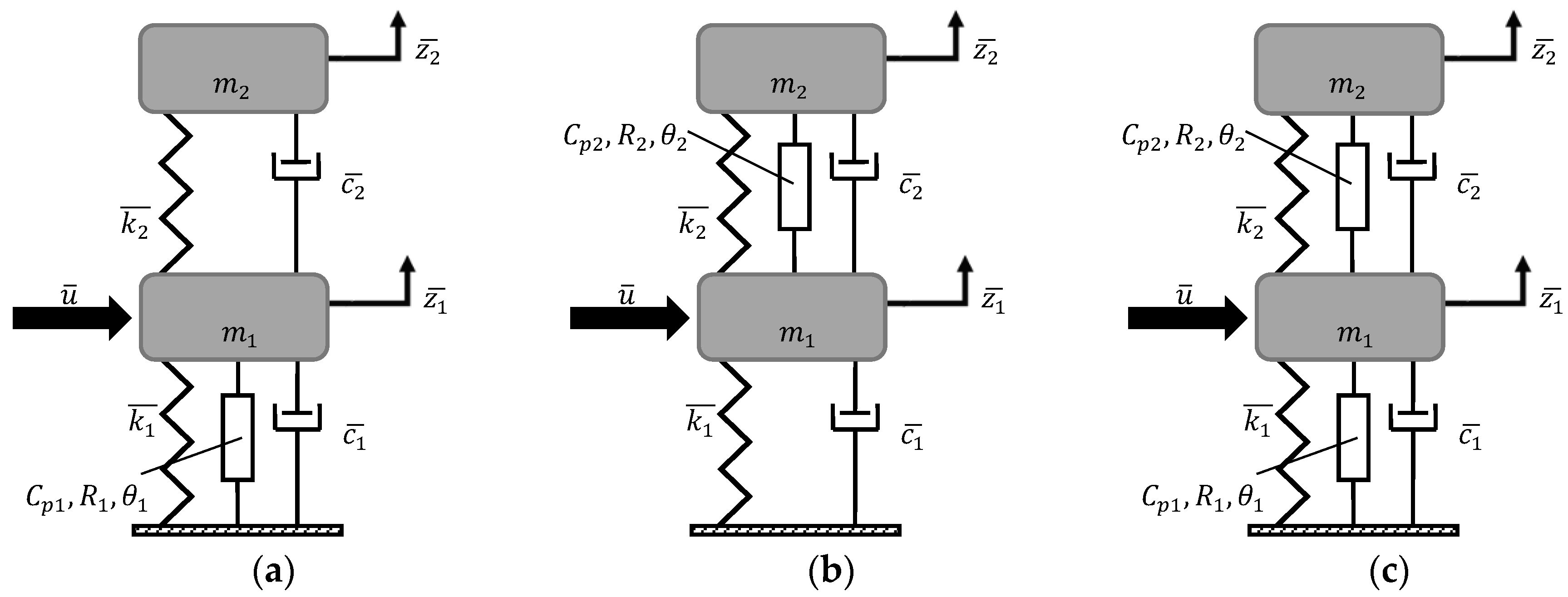
Based on the information provided in section 1, the presence of additional mass in systems with two degrees of freedom implies the necessity to consider the placement of the electromechanical transducer. It may be positioned between the main mass and the stationary base (Fig. 2a), between the masses (Fig. 2b), or in both of these locations (Fig. 2c).

Figure 2. Subvariants of two degree of freedom system.

To evaluate the influence of piezoelectric placement on efficiency, the efficiency characteristics of the variant with both transducers will be derived. Subsequently, the ramifications of removing one of them will be examined.

The dynamics of devices within the discussed category can be elucidated by a general dimensionless mathematical model of the form (20), where, in addition to the identities (3), the following also holds:

y_{i} = \frac{z_{i}}{\hat{h}}, v_{i} = ξ \frac{\hat{θ_{i}}}{\hat{m_{i}} \hat{h} {\hat{ω}}_{n}^{2}}, c_{i} = \frac{{\hat{c}}_{i}}{{\hat{m}}_{1} {\hat{ω}}_{n}}, k_{2} = \frac{{\hat{k}}_{2}}{{\hat{k}}_{1}}, κ = \frac{{\hat{θ_{i}}}^{2}}{\hat{C_{p i}} \hat{m_{1}} {\hat{ω}}_{n}^{2}}, θ = \frac{{\hat{θ}}_{1}}{{\hat{θ}}_{2}}, M = \frac{{\hat{m}}_{2}}{{\hat{m}}_{1}}, i = 1,2

(19)

{\ddot{y}}_{1} + y - k_{2} (y_{2} - y_{1}) + c_{1} {\dot{y}}_{1} - c_{2} ({\dot{y}}_{2} - {\dot{y}}_{1}) - v_{1} + v_{2} = ρ (a_{1} u {\dot{y}}_{1} + a_{3} \frac{{\dot{y}}_{1}^{3}}{u}),

(20a)

κ_{1} {\dot{v}}_{1} + \frac{v_{1}}{r_{1}} + {\dot{y}}_{1},

(20b)

{M \ddot{y}}_{2} + k_{2} (y_{2} - y_{1}) + c_{2} ({\dot{y}}_{2} - {\dot{y}}_{1}) - v_{2} = 0,

(20c)

κ_{2} {\dot{v}}_{2} + \frac{v_{2}}{r_{2}} + {\dot{y}}_{2} - {\dot{y}}_{1} = 0 .

(20d)

To derive the solutions of the GEH2D mathematical model, the procedure outlined in [20] was adapted. It was assumed that the approximate solution of the model (20) will have the following form:

y_{1} = A_{1} c o s (ω_{1} t) + B_{1} s i n (ω_{1} t) + G_{1} c o s (ω_{2} t) + H_{1} s i n (ω_{2} t),

(21a)

v_{1} = n_{1} c o s (ω_{1} t) + n_{2} s i n (ω_{1} t) + n_{3} c o s (ω_{2} t) + n_{4} s i n (ω_{2} t),

(21b)

y_{2} = A_{2} c o s (ω_{1} t) + B_{2} s i n (ω_{1} t) + G_{2} c o s (ω_{2} t) + H_{2} s i n (ω_{2} t),

(21c)

v_{2} = ϑ_{1} c o s (ω_{1} t) + ϑ_{2} s i n (ω_{1} t) + ϑ_{3} c o s (ω_{2} t) + ϑ_{4} s i n (ω_{2} t),

(21d)

Substituting the above identities into equations (20b) and (20d), and then balancing the harmonics

c o s (ω_{1} t)

s i n (ω_{1} t)

c o s (ω_{2} t)

s i n (ω_{2} t)

, allows for the derivation of the relationships between the amplitudes of voltage and the amplitudes of vibration.

n_{1} = B_{1} ω_{1} ε_{D 11} - A_{1} δ_{D 11}, n_{2} = - A_{1} ω_{1} ε_{D 11} - B_{1} δ_{D 11}, n_{3} = H_{1} ω_{2} ε_{D 12} - G_{1} δ_{D 12}, n_{4} = - G_{1} ω_{2} ε_{D 12} - H_{1} δ_{D 12},

(22a)

ϑ_{1} = θ (ε_{D 21} (θ B_{2} - B_{1}) ω_{1} + δ_{D 21} (A_{1} - θ A_{2})), ϑ_{2} = θ (ε_{D 21} (A_{1} - θ A_{2}) ω_{1} + δ_{D 21} (B_{1} - θ B_{2})), ϑ_{3} = θ (ε_{D 22} (θ H_{2} - H_{1}) ω_{2} + δ_{D 22} (G_{1} - θ G_{2})), ϑ_{4} = θ (ε_{D 22} (G_{1} - θ G_{2}) ω_{2} + δ_{D 22} (H_{1} - θ H_{2})) .

(22b)

where:

δ_{D i j} = κ_{i} \frac{r^{2} ω_{j}^{2}}{1 + r^{2} ω_{j}^{2}}

and

ε_{D i j} = κ_{i} \frac{r}{1 + r^{2} ω_{j}^{2}}

represent the piezoelectric stiffness and electric damping of the

i

-th piezoelectric for vibration with the

j

-th frequency. Harmonic balancing of

c o s (ω_{1} t)

and

s i n (ω_{1} t)

of the algebraic equation obtained by substituting the solutions (21) into equation (20c) and using the identities (22) leads to the system of equations:

A_{2} = B_{1} p_{1} + A_{1} q_{1},

(23a)

B_{2} = B_{1} q_{1} - A_{1} p_{1},

(23b)

where:

p_{1} = \frac{(k_{2} + θ δ_{D 21}) (c_{2} + θ^{2} ε_{D 21}) ω_{1} - (c_{2} + θ ε_{D 21}) (k_{2} + θ^{2} δ_{D 21} - M ω_{1}^{2}) ω_{1}}{{(c_{2} + θ^{2} ε_{D 21})}^{2} ω_{1}^{2} + {(k_{2} + θ^{2} δ_{D 21} - M ω_{1}^{2})}^{2}},

(23c)

q_{1} = \frac{(c_{2} + θ ε_{D 21}) (c_{2} + θ^{2} ε_{D 21}) ω_{1}^{2} + (k_{2} + θ δ_{D 21}) (k_{2} + θ^{2} δ_{T 21} - M ω_{1}^{2})}{{(c_{2} + θ^{2} ε_{D 21})}^{2} ω_{1}^{2} + {(k_{2} + θ^{2} δ_{D 21} - M ω_{1}^{2})}^{2}} .

(23d)

By substituting the above identities into the harmonic balance equations for

c o s (ω_{1} t)

and

s i n (ω_{1} t)

of expression (20a), the following identities can be formulated:

A_{1} α_{1} + B_{1} β_{1} - A_{1} \frac{3 ρ a_{3} ω_{1} ((A_{2}^{2} + B_{2}^{2}) ω_{1}^{2} + 2 (G_{2}^{2} + H_{2}^{2}) ω_{2}^{2})}{4 u} = 0,

(24a)

A_{1} β_{1} - B_{1} α_{1} + B_{1} \frac{3 ρ a_{3} ω_{1} ((A_{2}^{2} + B_{2}^{2}) ω_{1}^{2} + 2 (G_{2}^{2} + H_{2}^{2}) ω_{2}^{2})}{4 u} = 0,

(24b)

where:

α_{1} = (p_{1} (k_{2} + θ^{2} δ_{D 21}) + (c_{1} + ε_{T 11} + (c_{2} + ε_{D 21}) (1 - θ q_{1})) ω_{1} - u ρ ω_{1} a_{1}),

(25a)

β_{1} = 1 + δ_{T 11} + (δ_{D 21} θ + k_{2}) (1 - θ q_{1}) - ω_{1} (p_{1} (c_{2} + θ^{2} ε_{D 21}) + ω_{1}) .

(25b)

Adapting the above procedure to balance the harmonics

c o s (ω_{2} t)

and

s i n (ω_{2} t)

of equations (20c) and (20a) allows for the derivation of the following identities:

G_{2} = H_{1} p_{2} + G_{1} q_{2},

(26a)

H_{2} = H_{1} q_{2} - G_{1} p_{2},

(26b)

G_{1} α_{2} + H_{1} β_{2} - G_{1} \frac{3 ρ a_{3} ω_{2} (2 (A_{1}^{2} + B_{1}^{2}) ω_{1}^{2} + (G_{1}^{2} + H_{1}^{2}) ω_{2}^{2})}{4 u} = 0

(26c)

G_{1} β_{2} - H_{1} α_{2} + H_{1} \frac{3 ρ a_{3} ω_{2} (2 (A_{1}^{2} + B_{1}^{2}) ω_{2}^{2} + (G_{1}^{2} + H_{1}^{2}) ω_{2}^{2})}{4 u} = 0

(26d)

where:

p_{2} = \frac{(k_{2} + θ δ_{D 22}) (c_{2} + θ^{2} ε_{D 22}) ω_{2} - (c_{2} + θ ε_{D 22}) (k_{2} + θ^{2} δ_{D 22} - M ω_{2}^{2}) ω_{2}}{{(c_{2} + θ^{2} ε_{D 22})}^{2} ω_{2}^{2} + {(k_{2} + θ^{2} δ_{D 22} - M ω_{2}^{2})}^{2}},

(27a)

q_{2} = \frac{(c_{2} + θ ε_{T 22}) (c_{2} + θ^{2} ε_{D 22}) ω_{2}^{2} + (k_{2} + θ δ_{D 22}) (k_{2} + θ^{2} δ_{D 22} - M ω_{2}^{2})}{{(c_{2} + θ^{2} ε_{D 22})}^{2} ω_{2}^{2} + {(k_{2} + θ^{2} δ_{D 22} - M ω_{2}^{2})}^{2}},

(27b)

α_{2} = (p_{2} (k_{2} + θ^{2} δ_{D 22}) + (c_{1} + ε_{T 12} + (c_{2} + ε_{T 22}) (1 - θ q_{2})) ω_{2} - u ρ ω_{2} a_{1}),

(27c)

β_{2} = 1 + δ_{D 12} + (δ_{D 22} θ + k_{2}) (1 - θ q_{2}) - ω_{2} (p_{2} (c_{2} + θ^{2} ε_{D 22}) + ω_{2}) .

(27d)

By adding equation (24a) multiplied by

B_{1}

to equation (24b) multiplied by

A_{1}

, an expression was obtained that allows the frequency

ω_{1}

to be explicitly formulated:

1 + k_{2} + δ_{D 11} - k_{2} q_{1} + δ_{D 21} θ (1 - θ q_{1}) - p_{1} (c_{2} + θ^{2} ε_{D 21}) ω_{1} - ω_{1}^{2} = 0 .

(28)

Similarly, by adding equation (26c) multiplied by

H_{1}

to equation (26d) multiplied by

G_{1}

, an equation was obtained from which the frequency

ω_{2}

can be derived:

1 + k_{2} + δ_{D 12} - k_{2} q_{2} + δ_{D 22} θ (1 - θ q_{2}) - p_{2} (c_{2} + θ^{2} ε_{D 22}) ω_{2} - ω_{2}^{2} = 0 .

(29)

Note that in each pair of parameters ((

p_{1}

p_{2}

), (

q_{1}

q_{2}

), (

ε_{D 21}, ε_{D 22}

), (

δ_{D 11}, δ_{D 12}

), (

δ_{D 21}, δ_{D 22}

), the only difference is the frequency in their definition –

ω_{1}

ω_{2}

. Considering the similarity between equations (28) and (29), one can conclude that the frequencies

ω_{1}

and

ω_{2}

must be equal, thereby excluding the possibility of polymodal vibrations in the system. The expression describing the vibration frequency

ω_{2} = ω_{1}

can therefore be derived by solving only one of the above equations.

The relationship between the vibration amplitude and the system frequency remains unknown. The first of the equations necessary to determine this relationship was obtained by subtracting equation (24b) multiplied by

B_{1}

from equation (24a) multiplied by

A_{1}

. The second one is the difference of equation (26c) multiplied by

G_{1}

and equation (26d) multiplied by

H_{1}

\begin{array}{l} p_{1} (k_{2} + θ^{2} δ_{D 21}) + (c_{1} + c_{2} (1 - q_{1}) + ε_{D 11} + ε_{D 21} θ (1 - θ q_{1})) ω_{1} \\ - u ρ ω_{1} a_{1} - \frac{3 ρ ω_{1} (A_{y}^{2} ω_{1}^{2} + 2 G_{y}^{2} ω_{2}^{2}) a_{3}}{4 u} = 0, \end{array}

(30a)

\begin{array}{l} p_{2} (k_{2} + θ^{2} δ_{D 22}) + (c_{1} + c_{2} (1 - q_{1}) + ε_{D 12} + ε_{D 22} θ (1 - θ q_{2})) ω_{2} \\ - u ρ ω_{2} a_{1} - \frac{3 ρ ω_{2} (2 A_{y}^{2} ω_{1}^{2} + G_{y}^{2} ω_{2}^{2}) a_{3}}{4 u} = 0, \end{array}

(30b)

where

A_{y}^{2} = A_{1}^{2} + B_{1}^{2}

and

G_{y}^{2} = G_{1}^{2} + H_{1}^{2}

. Set of equations (30) has three non-trivial solutions in terms of

A_{y}^{2}

and

G_{y}^{2}

, which after recalling the

ω_{2} = ω_{1}

identity, take the form::

A_{y}^{2} = \frac{4 u (p_{1} (k_{2} + θ^{2} δ_{D 21}) + (c_{1} + c_{2} (1 - q_{1}) + ε_{D 11} + ε_{D 21} θ (1 - θ q_{1})) - u ρ a_{1})}{3 ρ {ω_{1}}^{3} a_{3}}, G_{y}^{2} = 0

(31a)

A_{y}^{2} = 0, G_{y}^{2} = \frac{4 u (p_{1} (k_{2} + θ^{2} δ_{D 21}) ω_{1} + (c_{1} + c_{2} (1 - q_{1}) + ε_{D 11} + ε_{D 21} θ (1 - θ q_{1})) - u ρ a_{1})}{3 ρ {ω_{1}}^{3} a_{3}},

(31b)

A_{y}^{2} = \frac{4 u (3 p_{1} (k_{2} + θ^{2} δ_{D 21}) ω_{1} + c_{1} + c_{2} (1 - q_{1}) + ε_{D 11} + ε_{D 21} θ (1 - θ q_{1})) - u ρ a_{1}}{9 ρ {ω_{1}}^{2} a_{3}}, G_{y}^{2} = \frac{4 u (- 3 p_{1} (k_{2} + θ^{2} δ_{D 21}) ω_{1} + c_{1} + c_{2} (1 - q_{1}) + ε_{T 11} + ε_{D 21} θ (1 - θ q_{1})) - u ρ a_{1}}{9 ρ {ω_{1}}^{2} a_{3}} .

(31c)

These expressions, along with the previously derived identities, enable the explicit formulation of solutions for the system (20) in the form (21). It should be noted that the identities given by equations (31a) and (31b) correspond to the same solution in the form (21); thus, only one of them, namely (31a), will be further analyzed. Moreover, no set of system parameters and initial conditions has been found that would lead to the excitation of vibrations with amplitude (31c). Therefore, this solution was considered unstable, and the efficiency has been derived based only on (31a):

η_{D} = \frac{\frac{1}{T_{c}} \int_{0}^{T_{c}} (\frac{{v_{1}}^{2} (t)}{r_{1} κ_{1}} + \frac{{v_{2}}^{2} (t)}{r_{2} κ_{2}}) d t}{ρ u^{3}} = \frac{2 λ (μ - u ρ a_{1})}{3 u^{2} ρ^{2} a_{3}},

(32)

where:

λ = (ε_{D 11} + ε_{D 12} θ^{2} (1 - 2 θ q_{1} + θ^{2} ({p_{1}}^{2} + {q_{1}}^{2}))),

(33a)

μ = (c_{1} + (c_{2} + θ ε_{D 11}) (1 - θ q_{1})) + \frac{p_{1} (k_{2} + θ^{2} δ_{T D 21})}{ω_{1}} .

(33b)

Critical speed

u_{c r}^{D}

and nominal speed

u_{p}^{D}

of GEH2D are given by the expressions:

η_{D} = γ_{1} \frac{2 λ (μ - u ρ a_{1})}{3 u^{2} ρ^{2} a_{3}} = 0 \Rightarrow u = u_{c r}^{D} = \frac{μ}{ρ a_{1}},

(34)

\frac{δ η_{D}}{δ u} = 0 \Rightarrow u = u_{p}^{D} = 2 \frac{μ}{ρ a_{1}} = 2 u_{c r}^{D} .

(35)

Now it is possible to derive peak efficiency of the system:

η_{p}^{D} = η^{D} (u_{p}^{D}) = \frac{- λ a_{1}^{2}}{6 γ_{2} a_{3}} .

(36)

To fully determine the features of the analyzed variant, it is necessary to define its high efficiency bandwidth

B^{D}

. It is:

η^{D} = 0,9 η_{p}^{D} \Rightarrow \begin{matrix} u_{2} \\ u_{1} \end{matrix} = \frac{\frac{2}{0.9} ρ a_{1} μ \pm \frac{\sqrt{0.4}}{0.9} ρ a_{1} μ}{{(ρ a_{1})}^{2}},

(37)

B^{D} = u_{2} - u_{1} = \sqrt{\frac{160}{81}} \frac{μ}{ρ a_{1}} \approx 1.4 u_{c r}^{D} \approx 0.7 u_{p}^{D} .

(38)

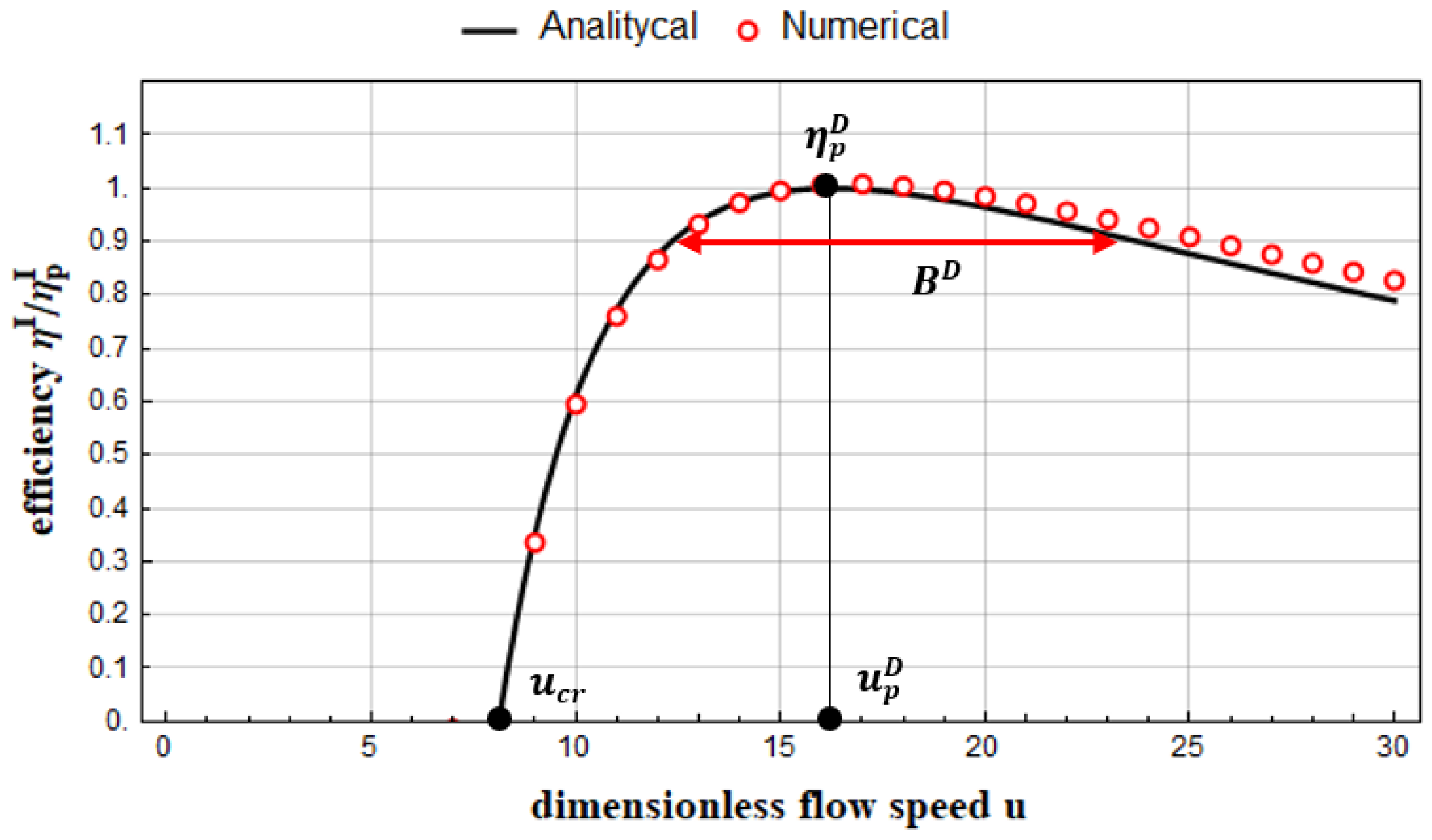
Figure 3 depicts the relationship between efficiency

η^{D}

and flow speed

u

, represented by the function (32), compared with an analogous relationship obtained through numerical integration of the model (20) for initial conditions:

y_{1} (0) = 0.1

{\dot{y}}_{1} (0) = 0

n_{1} (0) = 0

y_{2} (0) = 0

{\dot{y}}_{2} (0) = 0

n_{2} (0) = 0

. Moreover, the figure shows the values characterizing the efficiency of the variant -

u_{c r}^{D}

u_{p}^{D}

η_{p}^{D}

and

B^{I}

4. Comparison of Systems

As suggested by equations (34), (35), and (38), critical speeds, nominal speed, and high-efficiency bandwidths are interrelated in the same manner in both analyzed GEH variants. Consequently, comparing the efficiency of these systems can only be achieved by comparing their peak efficiencies. Since the efficiency of both devices depends on their nominal speeds, it is necessary to compare systems with the same nominal speeds. The electrical damping of the linear system

e^{L}

will therefore be selected in such a way that this condition is satisfied. In the following derivation, it is assumed that the structural damping of the linear system c is equal to the structural damping

c_{1}

of the damper connecting the lower mass of the GEH2D with the base, i.e.:

c = c_{1}

. The shape of the flowing body, represented by the coefficients

a_{1}

and

a_{3}

, and the density of the fluid remain the same for all variants.

u_{p}^{I} = u_{p}^{L},

(39a)

2 \frac{μ + γ_{2}}{ρ a_{1}} = 2 \frac{e^{L} + c_{1}}{ρ a_{1}},

(39b)

e^{L} = γ_{2} + μ - c_{1} .

(39c)

According to equations (16) and (39c), the efficiency of a system with one degree of freedom with a nominal speed equal to the nominal speed of the GEH2D is equal to:

η^{L} (u_{p}^{D}) = - \frac{(μ - c_{1}) a_{1}^{2}}{6 μ a_{3}} .

(40)

The ratio of peak efficiencies of compared systems with the same nominal speed is therefore given by:

\frac{η^{L} (u_{p}^{D})}{η^{D} (u_{p}^{D})} = \frac{s_{1} + s_{2}}{s_{1} + s_{3}},

(41)

where:

s_{1} = ε_{T 11} ((k_{2} + θ^{2} δ_{D 21}) (k_{2} + θ^{2} δ_{T 21} - 2 M {ω_{1}}^{2}) + {(c_{2} + θ^{2} ε_{D 21})}^{2} {ω_{1}}^{2} + M^{2} {ω_{1}}^{4}),

(42a)

s_{2} = M {ω_{1}}^{2} ((k_{2} ε_{D 21} - c_{2} δ_{D 21}) (θ - 1) θ + M {ω_{1}}^{2} (c_{2} + θ ε_{D 21})),

(42b)

s_{3} = θ^{2} ε_{D 21} (M {ω_{1}}^{2} (2 k_{2} (θ - 1) + M {ω_{1}}^{2}) + ({c_{2}}^{2} {ω_{1}}^{2} + {k_{2}}^{2}) {(θ - 1)}^{2}) .

(42c)

Clearly, according to (41), discussed system with two degree of freedom, will have greater efficiency than reference system if and only if

s_{3} > s_{2}

. For variant with only one, lower transducer (Fig. 2a), where

ε_{D 21} = δ_{D 21} = 0

, this inequality takes the form:

0 ≯ c_{2} M^{2} {ω_{1}}^{4},

(43)

what implies that such a device cannot be more efficient than the reference system, regardless of its parameters. This conclusion contradicts the results presented in [17]. The reason for this discrepancy lies in the fact that in the cited work, the operating conditions of the compared systems were not standardized - the devices had different critical speeds and, consequently, different nominal speeds. Despite the unquestionable value of this article, the conclusion stated therein can be subject to questioning. In the case of the variant with only the upper transducer (Fig. 2b), where

ε_{T 11} = δ_{T 11} = 0

, the condition for efficiency improvement takes the following form:

ε_{D 21} ≯ ε_{D 21} + c_{2},

(44)

what indicates that this variant does not offer efficiency enhancement. Similarly, an identical and impossible-to-satisfy requirement is associated with the special case of the third variant, where there are two identical transducers, meaning:

ε_{D 11} = ε_{T 21}

δ_{D 11} = δ_{D 21}

and

θ = 1

. However, the inequality

s_{3} > s_{2}

can be satisfied for the most general variant – the one equipped with two different transducers. In this case, it can be reduced to the condition:

(θ - 1) θ (ε_{D 21} {k_{2}}^{2} (θ - 1) θ + c_{2} δ_{D 21} M {ω_{1}}^{2} + {c_{2}}^{2} ε_{D 21} {ω_{1}}^{2} (θ - 1) θ + ε_{D 21} k_{2} M {ω_{1}}^{2} (2 θ - 1)) > M^{2} {ω_{1}}^{4} (c_{2} - ε_{D 21} (θ - 1) θ),

(45)

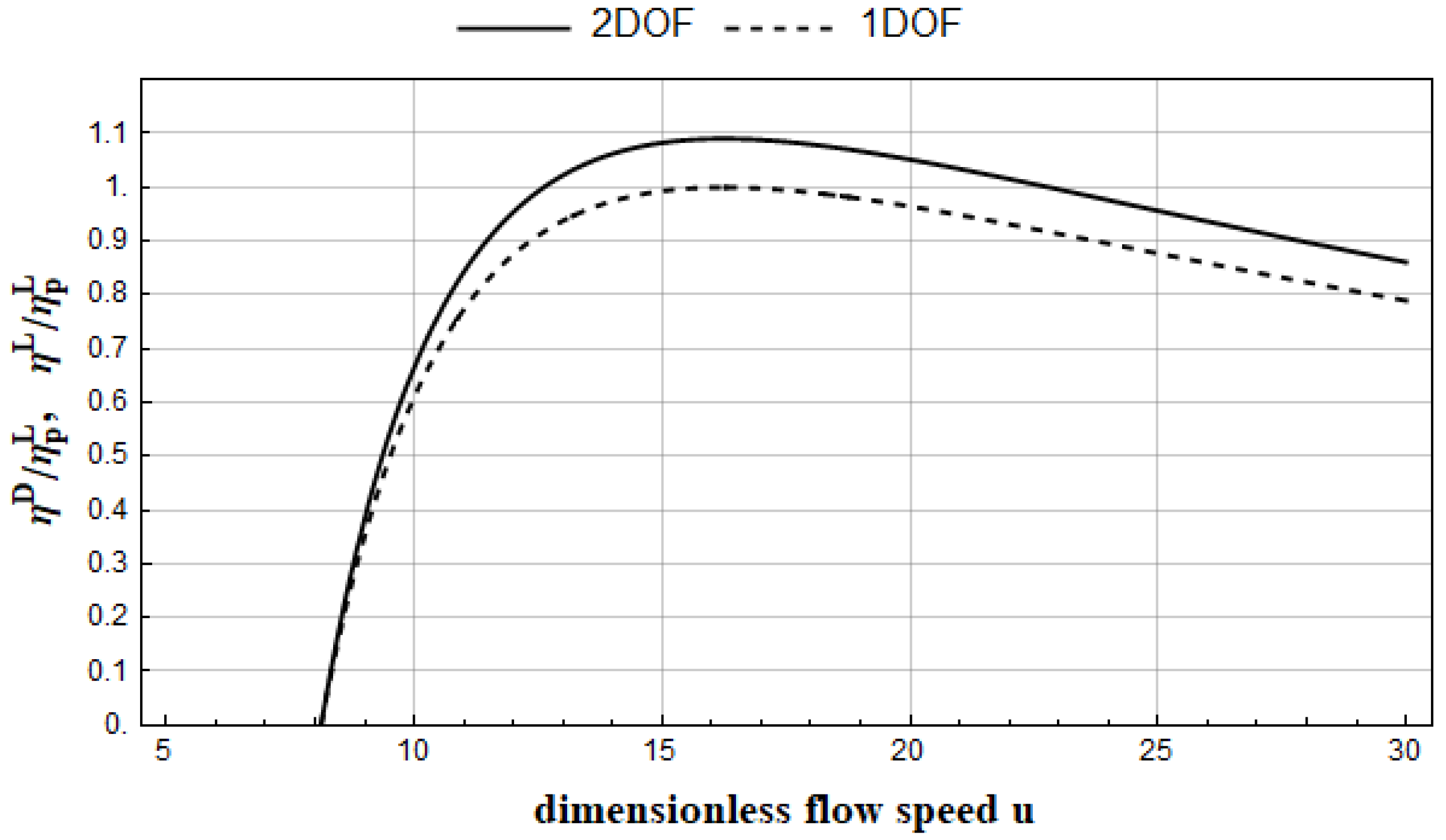
which, after substituting the solution of (27), can be solved numerically for a chosen parameter. For the parameters presented in Table 2, solving the above inequality for

θ

results in obtaining a threshold value of approximately

θ \approx 1.13

. An example of the efficiency characteristics of the GEH1D with

e^{L}

given by (39c) and GEH2D is shown in Figure 4, where condition (45) has been met by adopting parameters according to Table 2, with

θ = 1.3 > 1.13

5. Conclusions

The aim of the study was to investigate the efficiency of a galloping energy harvester with two degrees of freedom, considering its three variants, which differ in the number and location of electromechanical transducers. The realization of this objective commenced with the analysis of the reference variant with one degree of freedom. Utilizing the harmonic balance method, an approximate solution of the mathematical model of the system was derived, followed by the formulation of an expression describing the efficiency of the variant. Based on this, key criteria parameters were defined, providing comprehensive information about the variant's efficiency: peak efficiency, high efficiency bandwidth, critical speed, and nominal speed.

Subsequent sections of the study delineate the multitude of configurations that a system with two degrees of freedom can adopt: three different sub-variants of the device were characterized, differing from each other by the location and number of the electromechanical transducers. Parameters characterizing the efficiency of all subvariants were derived, demonstrating that the critical speed, nominal speed, and high efficiency bandwidth are related to each other in the same manner as in the case of the reference system. It was then demonstrated that among the three indicated subvariants of the two-degree-of-freedom system, only the one with two transducers can be more efficient than the reference system.

Funding

This research was funded by Polish Ministry of Higher Education, grant number 0612/SBAD/3628.

References

Kumar, S.; Tiwari, P.; Zymbler, M. Internet of Things is a revolutionary approach for future technology enhancement: a review. Journal of Big Data 2019, 6, 111. [Google Scholar] [CrossRef]
Bladeless Vortex Official Site. Available online: https://vortexbladeless.com (accessed on 01.05.2024).
Barrero-Gil, A.; Alonso, G. ,Sanz-Andrés A. Energy harvesting from transverse galloping. Journal of Sound and Vibration 2010, 329, 2873–2883. [Google Scholar] [CrossRef]
Ludlam D., V. Optimal energy harvesting form vortex induced vibration and transverse galloping vibrations. Doctoral Thesis, Universidad Politécnica de Madrid, Madrid, 2017. [Google Scholar]
Abdelkefi, A.; Hajj M., R.; Nayfeh A., H. Power harvesting from transverse galloping of square cylinder. Nonlinear Dynamics 2012, 70, 1355–1363. [Google Scholar] [CrossRef]
Ibarra, D.; Sorribes, F.; Alonso, G.; Meseguer, J. Transverse galloping of two-dimensional bodies having a rhombic cross-section. Journal of Sound and Vibration 2014, 333, 2855–2865. [Google Scholar] [CrossRef]
Noel, J.; Yadav, R.; Li, G. Daqaq M. Improving the performance of galloping micro-power generators by passively manipulating the trailing edge. Applied Physics Letters 2018, 12, 083503. [Google Scholar] [CrossRef]
Zhao, D.; Hu, X.; Tan, T.; Yan, Z.; Zhang, W. Piezoelectric galloping energy harvesting enhanced by topological equivalent aerodynamic design. Energy Conversion and Management 2022, 222, 113260. [Google Scholar] [CrossRef]
Zhao, K.; Zhang, Q.; Wang, W. Optimization of Galloping Piezoelectric Energy Harvester with V-Shaped Groove in Low Wind Speed. Energies 2019, 12, 4619. [Google Scholar] [CrossRef]
Zheng, J.; Li, Z.; Zhang, H. Low-Wind-Speed Galloping Wind Energy Harvester Based on a W-Shaped Bluff Body. Energies 2024, 17, 958. [Google Scholar] [CrossRef]
Abdelkefi, A.; Yan, Z.; Hajj M., R. Nonlinear dynamics of galloping-based piezoaeroelastic energy harvesters. The European Physical Journal Special Topics 2013, 222, 1483–1501. [Google Scholar] [CrossRef]
Abdelkefi, A.; Yan, Z.; Hajj M., R. Modeling and nonlinear analysis of piezoelectric energy harvesting from transverse galloping. Smart Materials and Structures 2013, 22, 025016. [Google Scholar] [CrossRef]
Li H., T.; Ren, H.; Cao, F.; Qin, W. Y. Improving the galloping energy harvesting performance with magnetic coupling. International Journal of Mechanical Sciences 2023, 237, 107785. [Google Scholar] [CrossRef]
Zhang, H.; Zhang, L.; Wang, Y.; Yang, X.; Song, R. Sui W. Modeling and experimental investigation of asymmetric distance with magnetic coupling based on galloping piezoelectric energy harvester. Smart Materials and Structures 2022, 31, 065007. [Google Scholar] [CrossRef]
Sarbinowski, F.; Starosta, R. Assessment of the role of structural nonlinearity in galloping energy harvesters. Vibrations in Physical Systems 2021, 32, 2021209. [Google Scholar]
Alhadidi, A.; Abderrahmane, H.; Daqaq, M. Exploiting stiffness nonlinearities to improve flow energy capture from the wake of a bluff body. Physica D: Nonlinear Phenomena 2016, 337, 30–42. [Google Scholar] [CrossRef]
Lan, C.; Tang, L.; Hu, G.; Qin, W. Dynamics and performance of a two degree-of-freedom galloping-based piezoelectric energy harvester. Smart Materials and Structures 2019, 28, 045018. [Google Scholar] [CrossRef]
Hu, G.; Wang, J.; Tang, L. A Comb-Like Beam based Piezoelectric System for Galloping Energy Harvesting. Mechanical Systems and Signal Processing 2021, 150, 107301. [Google Scholar] [CrossRef]
Hu, G.; Wang, J.; Qiao, H.; Zhao, L.; Li, Z.; Tang, L. An Experimental Study of a Two-Degree-of-Freedom Galloping Energy Harvester. International Journal of Energy Research 2020, 45. [Google Scholar] [CrossRef]
Hu, G.; Liang, J.; Tang, L.; Wang, J. Improved Theoretical Analysis and Design Guidelines of a Two-Degree-of-Freedom Galloping Piezoelectric Energy Harvester. Journal of Intelligent Material Systems and Structures 2021, 33. [Google Scholar] [CrossRef]
Zhao, L.; Tang, L.; Yang, Y. Enhanced piezoelectric galloping energy harvesting using 2 degree-of-freedom cut-out cantilever with magnetic interaction. Japanese Journal of Applied Physics 2014, 53, 060302. [Google Scholar] [CrossRef]

Figure 1. Efficiency characteristics of GEH1D for:

κ = 1.3

r = 3

c = 0.1

ρ = 0.02

a_{1} = 2.3

a_{3} = - 18

Figure 1. Efficiency characteristics of GEH1D for:

κ = 1.3

r = 3

c = 0.1

ρ = 0.02

a_{1} = 2.3

a_{3} = - 18

Figure 3. Efficiency characteristic of GEH2D for parameters values presented in Table 2.

Figure 4. Comparison of GEH1D and GEH2D having equal nominal speeds.

Table 1. List of GEH1D parameters.

Symbol	$P a r a m e t e r$	$U n i t$
$\hat{m}$	Mass	$k g$
$\hat{k}$	Stiffness coefficient	$N / m$
$\hat{c}$	Damping coefficient	$k g / s$
$\hat{u}$	Flow speed	$m / s$
$\hat{ρ}$	Planar fluid density	$k g / m^{2}$
$\hat{h}$	Characteristic dimension	$m$
$\hat{θ}$	Piezoelectric coefficient	$N / V$
$\hat{C_{p}}$	Equivalent capacity	$F$
$\hat{R}$	Circuit electrical resistance	$Ω$
$τ$	Time	$s$
$z = z (τ)$	Vibration vs time function	$m$
$ξ = ξ (τ)$	Voltage vs time function	$V$

Table 2. GEH2D system parameters values.

Parameter	Value
$M$	0.5
$k_{2}$	0.3
$c_{1}$	0.1
$c_{2}$	0.25
$κ_{1}$	0.9
$κ_{2}$	1.8
$r_{1}$	3
$r_{2}$	2
$θ$	1.3
$a_{1}$	2.3
$a_{3}$	-18
$ρ$	0.02

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On Efficiency of Two-Degree-of-Freedom Galloping Energy Harvesters with Two Transducers

Abstract

1. Introduction

2. Efficiency of Reference Variant

3. Efficiency of Two Degree of Freedom System

4. Comparison of Systems

5. Conclusions

Funding

References

MDPI Initiatives

Important Links

Subscribe