Prerpints.org logo
Preprint
Article

Polarization-dependent Plasmon Coupling in Gold Nanoparticles and Gold thin Film Systems

This is a preprint, it has not been peer-reviewed.

Submitted:

13 May 2024

Posted:

13 May 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
The characteristics of gap plasmon formed by nanoparticle-on-mirror (NPOM) structure composed of metal nanoparticles (MNP) and metal thin films have aroused the interest of various optoelectronic devices. The resonant spectrum obtained by the internal coupling effect of gap can be flexibly controlled by the polarization of incident light and the thickness of the dielectric layer between MNP and metal thin films. We have theoretically studied the resonance spectra of polarization-dependent gold ellipsoidal nanoparticles (GENP) and gold thin films in the gap region of NPOM structures. GENP and gold thin films are separated by a dielectric layer with a refractive index of 1.36. We observe that the intensity of the local electric field resonance peak in the gap region is inversely proportional to the polarization angle. Similarly, the intensity of the local electric field resonance peak in the gap region is inversely proportional to the thickness of the dielectric layer. We have obtained more than 2200 V/m local electric field intensity (dielectric layer thickness 0.3nm). Finally, the resonant peak wavelength of the electric field in the gap region of the NPOM structure is also controlled by the polarization angle of the incident light and the thickness of the dielectric layer.
Keywords: 
  -  

1. Introduction

The Localized surface plasmon resonance (LSPR) properties of metal nanoparticles (MNP) have attracted wide attention. It has potential applications in solar cells, catalysis, surface enhanced Raman scattering (SERS), fluorescence enhancement, biosensor, subwavelength imaging, random laser and many other fields [1,2,3,4,5,6,7]. This mainly makes use of the excitation of the incident light to the free electrons on the surface of the MNP. When the frequency of the incident light is consistent with the oscillation frequency of the electrons on the MNP surface, the surface plasmon resonance will occur [8,9,10]. The electric field on the surface of MNP will be greatly enhanced because of the resonance effect. The size and morphology of MNP have an important influence on the intensity of local electric field [11,12,13]. Therefore, based on the characteristics of local electric field on the surface of MNP, it has important applications in plasmon mode and surface structure of materials [14,15].
Compared with the size of MNP, the morphology of MNP has a greater influence on the local electric field on the surface of MNP. They can affect the intensity of the resonance spectrum, the wavelength of the resonance peak and the width of the resonance spectrum. Studies have shown that MNP with tip structure (nano-stars, nano-flowers, etc.) form a larger local electric field on their surface, which is due to the hot spot effect at the tip position [16,17]. In addition, when two MNP are close to each other, hot spots will also be formed in their sub-wavelength gap region. Due to the coupling effect between MNP, the local electric field intensity is higher than that on the surface of single tip MNP [18]. Similarly, when MNP and metal thin films are close to each other to form nanoparticle-on-mirror (NPOM) structures, hot spots with strong local electric field enhancement will appear in the gap space between them [19,20,21,22]. The electric field intensity in the gap region of the NPOM structure is greatly enhanced, at the same time, it is accompanied by the broadening of the resonant spectrum and the shift of the resonant wavelength. The preparation of NPOM structure does not depend on complex equipment, but also has good stability and tunability of resonance peak, which makes it have potential applications in many fields. At present, scholars' research on NPOM is mainly focused on the thickness of the dielectric layer between MNP and metal thin films. When the thickness of the dielectric layer is less than 4nm, there is only one gap mode in the NPOM structure. However, when the thickness is greater than 4nm, both gap mode and MNP mode will appear [19]. The morphology of MNP has a great influence on the electric field resonance in gap space. For example, when M. Lequeux studies [21] the NPOM structure composed of cylindrical nanoparticles, although the structural parameters of cylindrical nanoparticles are changed, the resonance peak wavelength in the gap region can only be controlled in a small range. Therefore, it can not be widely used in many application fields. And then, MNP with various morphologies (ellipse, mushroom, bowtie) have been proposed to study the optical enhancement properties of NPOM structures [23,24,25]. Among them, the most representative one is that Jubb [23] compared the NPOM SERS substrate composed of three kinds of ellipse, mushroom, bowtie nanoparticles. The results show that the Raman signal of ellipse nanoparticles is stronger than that of mushroom and bowtie nanoparticles. In fact, in addition to the thickness of the dielectric layer and the morphology of MNP, the polarization angle of the incident light also has an important influence on the local electric field optical enhancement properties of NPOM [26,27,28]. Although the coupling effect of two particles and the NPOM structure can produce a strong local electric field in the gap region. However, in the preparation of the two structures, the subwavelength distance between the two adjacent MNP needs to be accurately controlled by physical method. It not only needs to rely on complex equipment, but also has high cost and takes a long time. The thickness of the dielectric layer in NPOM structure can be accurately controlled by spin coating method, and various morphologies of MNP can be prepared by chemical synthesis. To sum up, the NPOM structure based on MNP and metal thin films has a greater prospect.
In this paper, the NPOM structure composed of gold nano-ellipsoid particles (GENP) and gold thin film will be studied theoretically with the help of finite element method. We keep the size of the GENP unchanged. Firstly, we compare and analyze the distribution characteristics of the electric field intensity on the surface of the GENP in the homogeneous medium and the electric field intensity in the gap space of NPOM structure. Then it is analyzed that the NPOM structures of three kinds of dielectric layer thickness are affected by the polarization angle of incident light. For each constant thickness of dielectric layer, the variation characteristics of local electric field intensity in gap region are studied by changing six different polarization angles of incident light. Finally, the influence of the thickness of the dielectric layer of NPOM structure on the intensity and wavelength of the local electric field resonance peak in the gap region is further studied. NPOM structure has strong optical enhancement properties because of its coupling effect, which has potential applications in the fields of SERS, fluorescence enhancement, catalysis and so on.

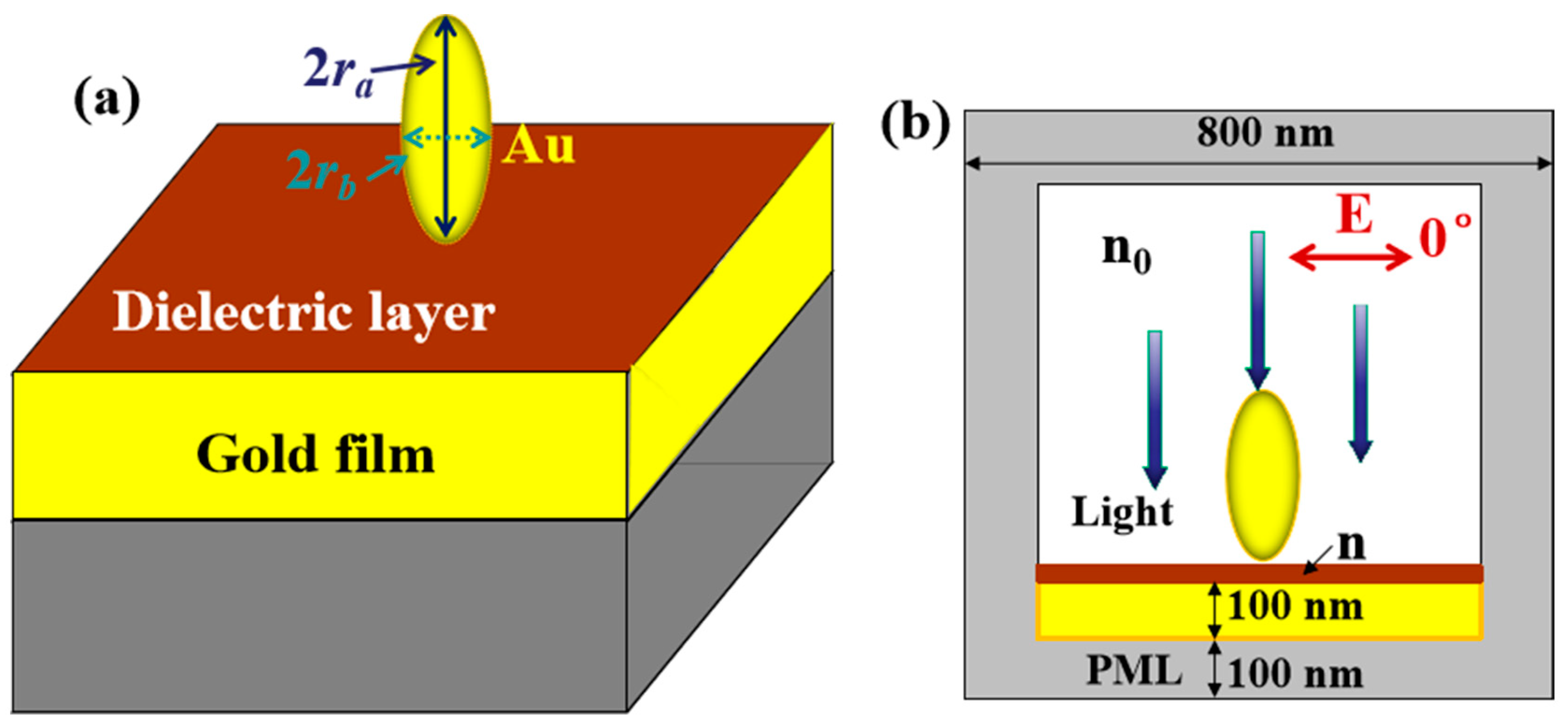
2. Simulation Model and Methods

The structural model diagram of the NPOM structure is shown in Figure 1a. The NPOM structure composed of GENP and gold thin film is separated by the dielectric layer, and the thickness of the dielectric layer t can be adjusted arbitrarily. The aspect ratio of GENP is 2, namely ra=2rb. Among them ra=30nm, rb=15nm. Throughout the article, the size and aspect ratio of GENP remain unchanged. As shown in Figure 1b, the refractive index n0 around the GENP is 1, and the refractive index n of the dielectric layer is 1.36. The thickness of the gold film is 100nm. GENP and gold thin films are composed of gold materials, and their optical parameters are from the literature [29]. The polarization angle of the incident light can be adjusted, in which the polarization angle in the horizontal direction is 0°, as shown in Figure 1b. After the completion of the theoretical model, we use the finite element method to simulate it. In the process of calculation, the model needs to be meshed. The smaller the mesh size is, the better the convergence of the calculation results is, and the more accurate the calculation results are. However, the smaller the grid size means the more the number of grids, the higher the performance requirements of the computing machine, but also requires more computing time. Therefore, under the premise that the performance of the calculation machine can meet the simulation calculation, in order to ensure the convergence of the calculation, and save the calculation time as much as possible. Our grid size is set to a maximum of no more than 2nm. In the gap region between the GENP and the gold film, the grid size is set to 0.2nm. In the process of calculation, some electromagnetic waves will be scattered into space. When they meet the surrounding boundary, they will reflect, thus interfering with the calculation results of the model. In order to solve this problem, we set up a perfect matching layer around the model, whose main function is to absorb scattered electromagnetic waves. Through many simulation calculations, the thickness of the perfectly matched layer is optimized. When it is 100nm, the scattered electromagnetic wave can be completely absorbed. In this paper, we calculate the electric field in the form of ratio, that is, E/E0. Where E0 represents the value of incident electric field, and E represents the value of electric field in the presence of particles. The near-field intensity we are studying all refers to the maximum value of E/E0.

3. Results and Discussion

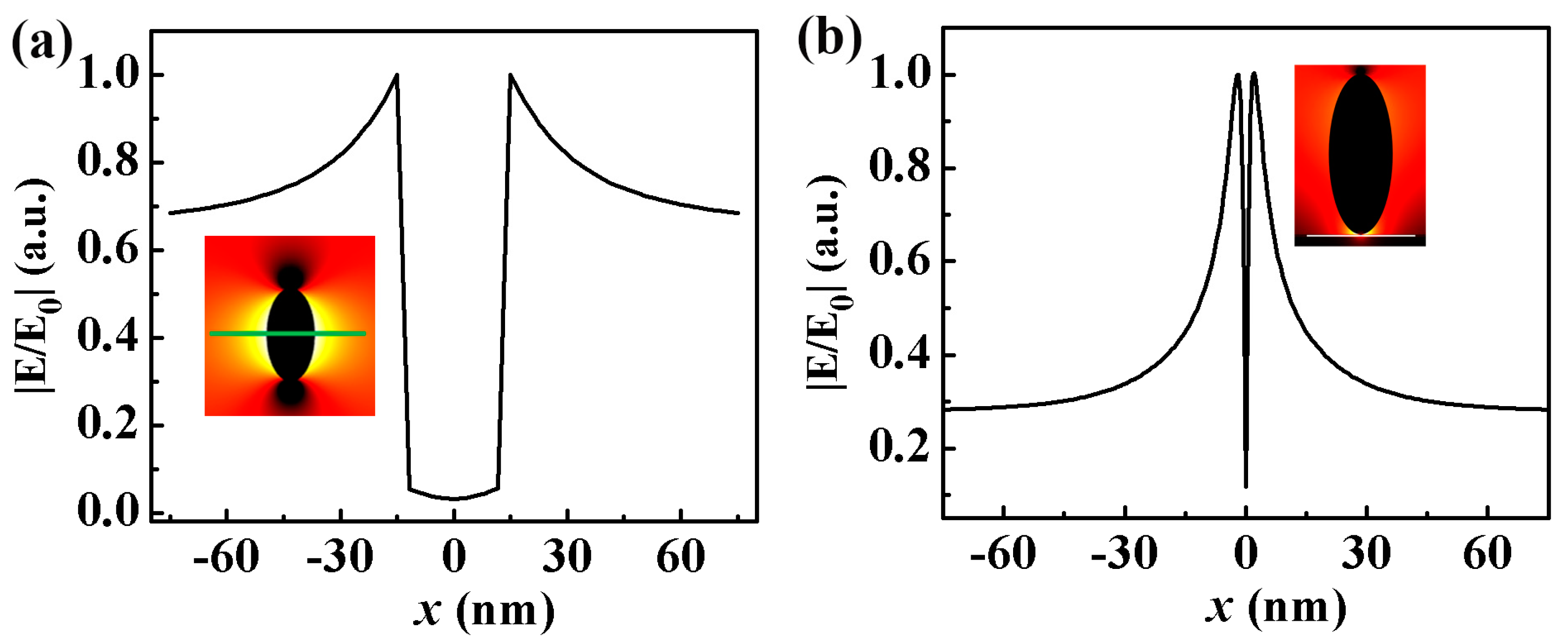
3.1. Electric Field Distribution on the Surface of GNEP and NPOM Structure

Under the excitation of incident light, the surface of MNP will form a local electric field. Similarly, there is a local electric field in the gap region of the NPOM structure composed of MNP and thin films. But their structures are different, so there must be some differences in the local electric field distribution. In order to obtain the distribution of the surface electric field between them, we select the position coordinates of the surface of the GENP (Figure 2a green line) and the interior of the gap of the NPOM structure (Figure 2b white line), and extract the electric field intensity E/E0 on each coordinate position. As shown in Figure 2a, the position coordinates of the surface of GENP are normalized. It can be seen from the figure that the largest position of the electric field is located on the surface of the GENP, and the electric field in the space attenuates rapidly with the increase of the distance from the surface of the GENP. At the distance from the 60nm on the surface of the GENP, the electric field intensity has decreased by 30%. Therefore, when using MNP for electric field enhancement applications, the control of the surface distance of MNP is very important. The normalized electric field values in the NPOM structure gap (along the white line) composed of GENP and gold thin films are shown in Figure 2b. We can see from Figure 2b that the electric field intensity in the gap region is the largest, but the electric field intensity in the central position is minimized. There is a pole in the central position. Then the electric field intensity decreased, and the decrease was much larger than that on the surface of GENP. Away from the center 30nm, the electric field strength decays by 70%. Finally, with the increase of the distance from gap, the electric field intensity tends to be stable. We can also see their electric field distribution from the illustrations in Figure 2a,b. Compared with GENP, the local electric field of NPOM structure is mainly concentrated in the gap region. Next, we will systematically study the optical enhancement properties in the gap region of the NPOM structure.

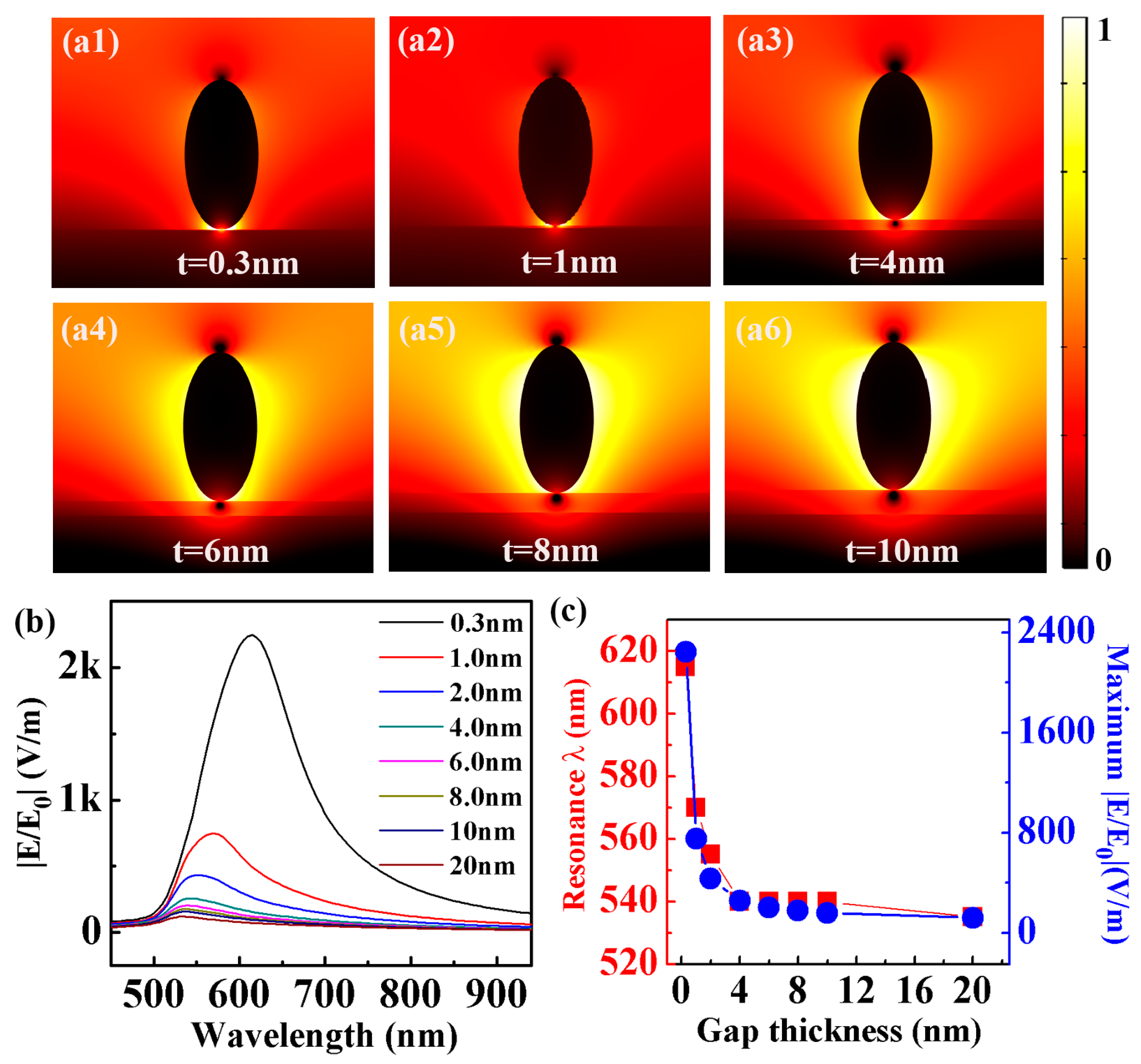
3.2. Electric Field Distribution of NPOM Structure at the Thickness of 0.3nm Dielectric Layer

Under the action of coupling effect, the local electric field intensity in the gap region of NPOM structure is much larger than that on the surface of single MNP. The main factors affecting the local electric field intensity in the gap region of NPOM structure are the polarization angle of the incident light, the thickness of the dielectric layer between the MNP and the film, the material of the dielectric layer, the morphology of the MNP and so on. The polarization angle of the incident light is a very important parameter. The resonance peak wavelength and intensity of the electric field in the gap region can be adjusted by changing the polarization angle. As shown in Figure 3, we keep the thickness of the dielectric layer 0.3nm and the refractive index of the dielectric layer 1.36. The effects of six different polarization angles of incident light (0°, 15°, 30°, 45°, 60°, 75°) on the local electric field intensity in the gap region are simulated systematically. As shown in Figure 3a1-a6, the surface electric field distribution of GENP under different incident light polarization angles is shown. It can be seen in Figure 3a1 that when the polarization angle is 0°, the electric field is mainly localized in the gap space and is symmetrically distributed. When the polarization angle increases to 15°, although the electric field is still localized in the gap space, it can be seen that the electric field has been asymmetrically distributed. Since then, as the polarization angle continues to increase, there will be more electric field distributed on the surface of the GENP, not just confined to the interior of the gap space. As shown in Figure 3a5, when the polarization angle increases to 60°, a weak electric field distribution appears at the top of the GENP. In Figure 3a6, we can clearly see a strong local electric field distributed on the top of the GENP (polarization angle 75°).
In order to quantitatively obtain the variation of the local electric field intensity with the polarization angle in the gap region of the NPOM structure, we further calculate the resonance spectrum of the electric field intensity in the gap region, as shown in Figure 3b. It can be seen from the figure that the electric field intensity decreases with the increase of polarization angle. At the same time, the wavelength of the resonance peak shows a red-shift with the increase of the polarization angle. In order to more intuitively see the change of the resonance peak intensity and wavelength with the increase of the polarization angle, we process the resonance peak intensity and wavelength position of the resonance spectrum in Figure 3b, as shown in Figure 3c. It can be seen from the figure that when the polarization angle is small, the wavelength of the resonance peak rapidly red-shifts with the increase of the angle. With the increase of polarization angle, the change trend of resonant wavelength becomes smaller and smaller. When the polarization angle increases from 60° to 70°, the wavelength of the resonance peak has almost no red-shift. However, the relationship between the electric field intensity of the resonant peak and the polarization angle is the opposite. When the polarization angle is small, the electric field intensity of the resonance peak changes little with the increase of the polarization angle. With the increase of polarization angle, the electric field intensity of the resonance peak begins to decrease rapidly. The electric field intensity of the resonance peak corresponding to the polarization angle of 60° is about 1550V/m, but when the polarization angle increases to 75°, the electric field intensity of the resonance peak has decreased to 1125V/m. The results show that the resonance peak intensity and wavelength of the electric field in the gap region of the NPOM structure can be accurately adjusted by changing the polarization angle of the incident light.

3.3. Electric Field Distribution of NPOM Structure at the Thickness of 1nm Dielectric Layer

The polarization angle of the incident light has an important influence on the resonance peak intensity and wavelength of the local electric field in the gap region of the NPOM structure. In addition, the thickness of the dielectric layer between the MNP and the thin film is also an important factor affecting the resonance peak intensity and wavelength of the local electric field in the gap region. We set the thickness of the dielectric layer to 0.3nm in Figure 3. Then we set the thickness of the dielectric layer to 1nm and keep other conditions unchanged to study the effect of polarization angle on the local electric field distribution in the gap region. The results are shown in Figure 4a1-a6. When the polarization angle is 0°, the electric field intensity is mainly localized in the gap space and still shows a symmetrical distribution. With the increase of polarization angle, the local electric field in gap space appears asymmetrical distribution, but the electric field is still localized in gap space. When the polarization angle increases to 60°, the local electric field in the NPOM structure is no longer only localized in the gap space. As the polarization angle continues to increase to 75°, we see an obvious local electric field at the top of the GENP. The distribution of local electric field on the surface of NPOM structure is similar to that when the thickness of dielectric layer is 0.3nm. However, for the specific numerical changes, it is also necessary to process the data of the electric field distribution map, and the result is shown in Figure 4b. In Figure 4b, we see the same trend as in Figure 3b. The electric field intensity in gap space decreases with the increase of polarization angle. The wavelength of the resonance peak is red-shifted with the increase of the polarization angle. However, the intensity and wavelength of the resonance peak have changed obviously. As shown in Figure 4c, when the polarization angle is 0°, the intensity and wavelength of the local electric field resonance peak are 800V/m and 570nm, respectively. When the thickness of the dielectric layer is 0.3nm, we can see from Figure 3c that the intensity and wavelength of the corresponding local electric field resonance peak are 2250V/m and 615nm, respectively. Similarly, it can be found from Figure 4c that the smaller the polarization angle is, the more obvious the wavelength of the resonance peak changes with the angle. With the increase of polarization angle, the change of resonant wavelength is no longer significant. On the contrary, the larger the polarization angle, the more obvious the change of the electric field intensity of the resonance peak with the polarization angle. However, when the polarization angle is small, the change of the electric field intensity of the resonance peak is no longer obvious with the increase of the polarization angle.

3.4. Electric Field Distribution of NPOM Structure at the Thickness of 4nm Dielectric Layer

The intensity of the local electric field in the gap space of the NPOM structure is mainly affected by the coupling effect between MNP and gold thin films. When the thickness of the dielectric layer is smaller than that of 2nm, the coupling effect is strong. With the increase of the thickness of the dielectric layer, the coupling effect decreases gradually. We further set the thickness of the dielectric layer to 4nm while keeping other conditions unchanged. The electric field distribution of NPOM structures with different polarization angles is shown in Figure 5a1-a6. It can be found from Figure 5a1 that even when the polarization angle is 0°, the surface electric field is no longer localized in the gap space, but also shows a weak electric field distribution on the surface of GENP. When the polarization angle increases to 15°, this situation is more obvious, and the electric field is mainly localized on the left side of the GENP. Until the polarization angle increases to 60°, the local electric field distribution begins to appear at the top of the GENP. When the polarization angle is 75°, a clear electric field distribution can be seen at the top of the GENP. The results show that with the increase of the thickness of the dielectric layer, the electric field appears on the surface of GENP. As shown in Figure 5b, we quantitatively calculate the local electric field intensity spectrum in the electric field distribution figure. It can be found in the figure that the variation of the resonance intensity of the local electric field in the gap space remains the same as that in 3b and 4b. However, the change of the resonant wavelength of the local electric field is obviously different. In order to see their changes more intuitively, we do further data processing in Figure 5b (as shown in Figure 5c). We can see more clearly from Figure 5c that when the polarization angle is greater than 15°, the local electric field resonance wavelength does not change. However, the resonance intensity of the local electric field still decreases rapidly with the increase of the polarization angle. What is more important is that the resonance peak intensity and wavelength of the local electric field change obviously at the same polarization angle. Corresponding to the case of polarization angle 0°, the intensity of the local electric field resonance peak has been reduced to 275V/m, and the resonant wavelength is 540nm. From the above analysis, it can be concluded that the thickness of the dielectric layer can also control the intensity and wavelength of the local electric field resonance peak in the gap region.

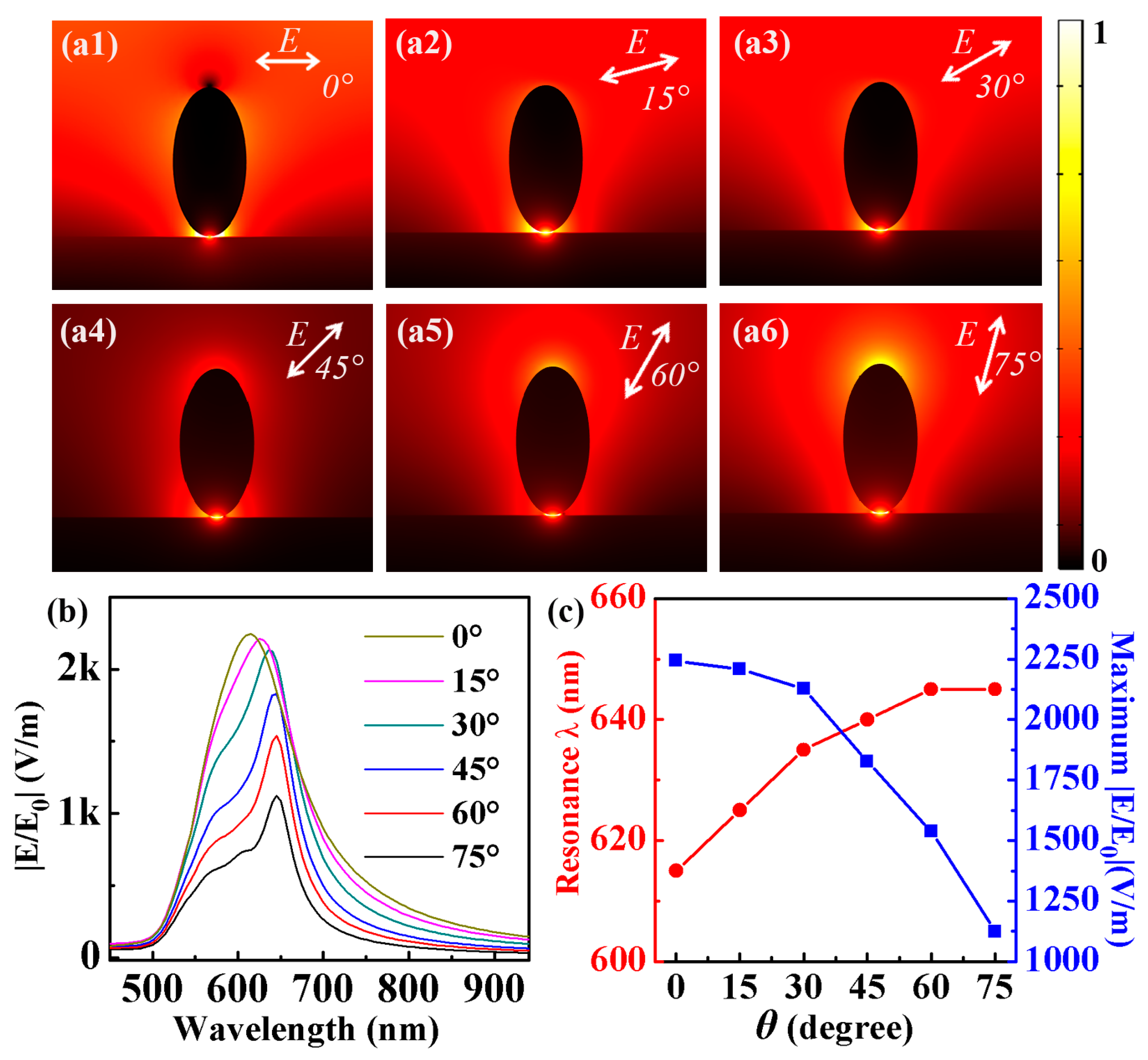
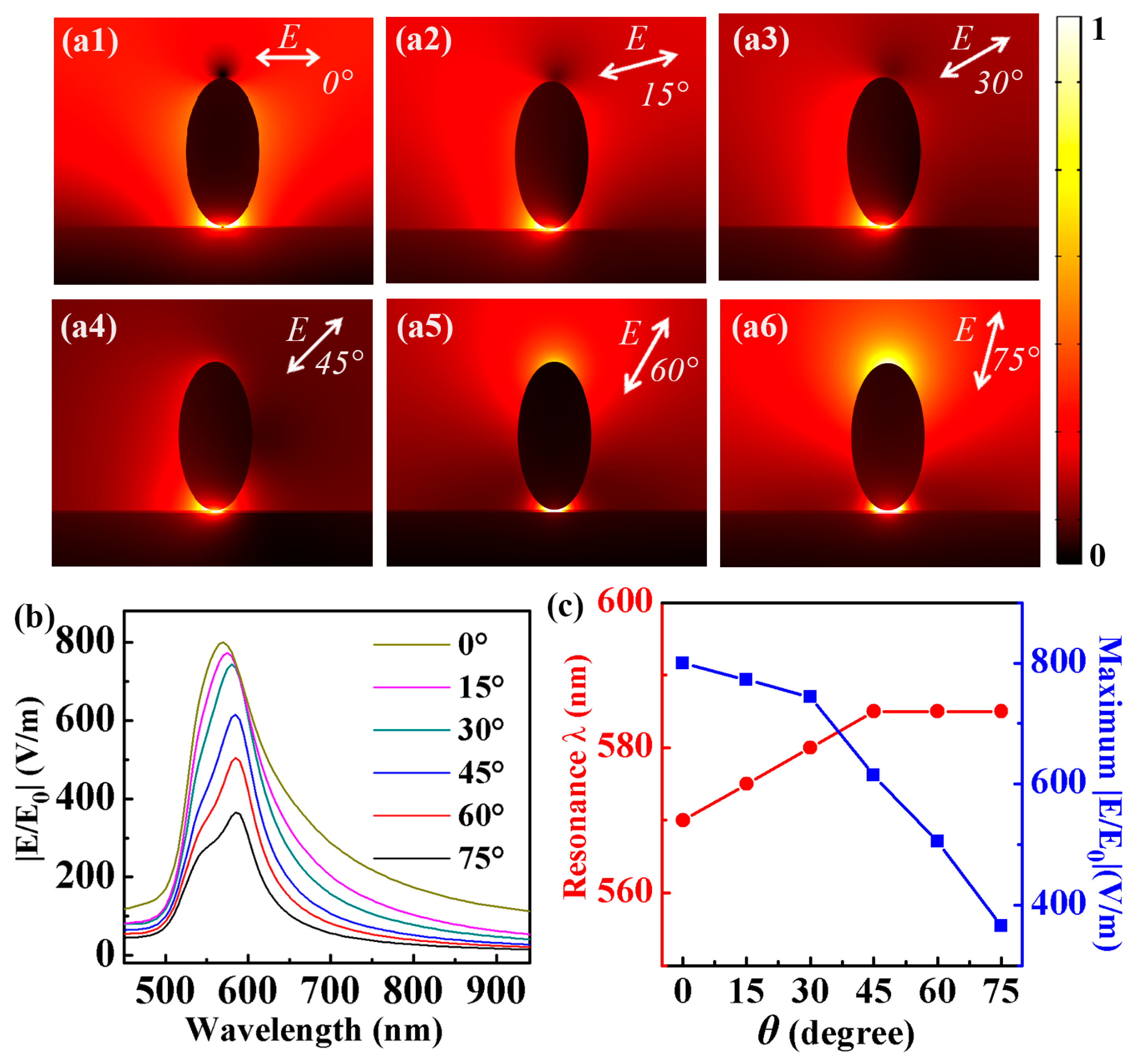
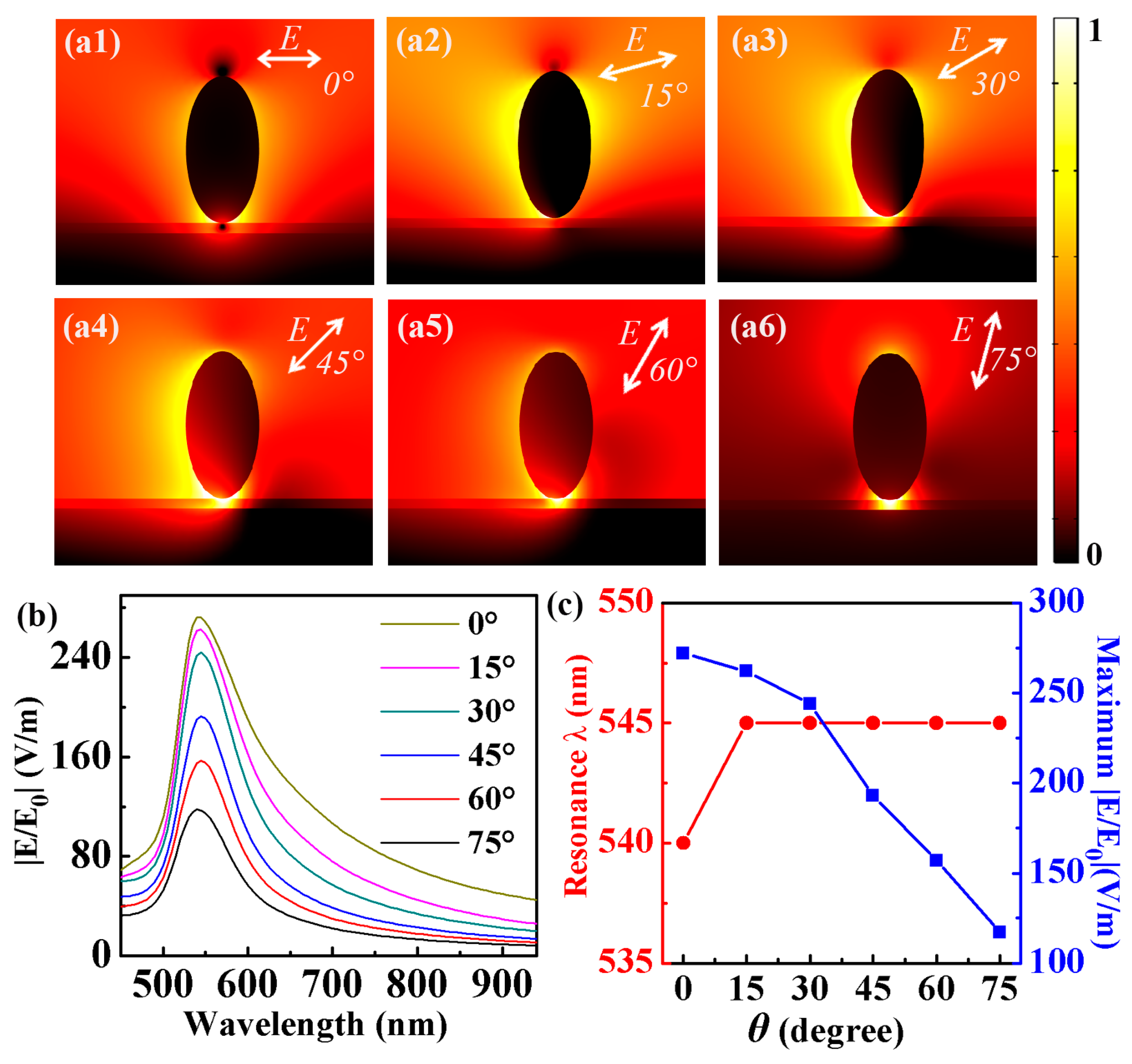
3.5. Electric Field Distribution of NPOM Structure at the Polarization Angles 0°

From Figure 3 to Figure 5, the variation of electric field intensity in the gap region of NPOM structure is studied when the thickness of dielectric layer is 0.3nm, 1nm and 4nm respectively. Through comparative analysis, it is found that the thickness of the dielectric layer has an important influence on the resonant peak intensity and wavelength of the electric field in the gap region. Under the condition of the same polarization angle 0°, the intensity of the resonance peak is 2250V/m, 800V/m and 275V/m respectively. The resonant peak wavelengths are 615nm, 570nm and 540nm respectively. Therefore, we can also accurately adjust the resonance peak intensity and wavelength of the electric field in the gap region by changing the thickness of the dielectric layer. Then we systematically studied the relationship between the electric field intensity in the gap region and the thickness of eight kinds of dielectric layer (0.3nm, 1nm, 2nm, 4nm, 6nm, 8nm, 10nm, 20nm). The surface electric field distribution of six kinds of dielectric layer thickness NPOM structures is shown in Figure 6a1-a6. It can be seen from the Figure 6a1 that the electric field is mainly localized in the gap region of the NPOM structure. With the increase of the thickness of the dielectric layer, the distribution of the electric field changes obviously. As shown in Figure 6a4, when the thickness of the dielectric layer is 6nm, there is an obvious electric field distribution on the surface of GNEP. With the increase of the thickness of the dielectric layer, this situation becomes more and more obvious. On this basis, we calculate the variation of the local electric field in the NPOM structure with each dielectric layer thickness, as shown in Figure 6b. It can be seen clearly from the resonance spectrum that the electric field intensity in the gap region is inversely proportional to the thickness of the dielectric layer. And the smaller the thickness of the dielectric layer is, the more obvious the change is. However, the resonance peak wavelength of the electric field in the gap region has a blue-shift with the increase of the thickness of the dielectric layer. Similarly, it can be seen that when the thickness of the dielectric layer is small, the change of the wavelength is more obvious. In order to see their changes more intuitively, we have processed the data in Figure 6b. The relationship between the resonant peak intensity and wavelength of the electric field in the gap region and the thickness of the dielectric layer is shown in Figure 6c. When the thickness of the dielectric layer is smaller than that of 4nm, the intensity and wavelength of the electric field resonance peak have an obvious change trend. When the thickness of the dielectric layer exceeds that of 4nm, the intensity and wavelength of the electric field resonance peak tend to be stable, and the range of change is very small. Therefore, only when the thickness of the dielectric layer is small, it is more meaningful to regulate the local electric field intensity in the NPOM structure.

4. Conclusion

The NPOM structure composed of GNEP and gold thin films is simulated theoretically by finite element method. The effects of the polarization angle of the incident light and the thickness of the dielectric layer on the local electric field in the gap region of the NPOM structure are studied systematically. The results show that the intensity of the local electric field in the gap region of the NPOM structure decreases with the increase of the polarization angle, while the wavelength of the resonance peak shows a red-shift with the increase of the polarization angle. When the polarization angle is small, the wavelength of the resonance peak shows a significant red-shift with the increase of the angle. But for the intensity of the resonance peak, the larger the polarization angle is, the more obvious the change is. Therefore, the resonance peak intensity and wavelength of the local electric field in the gap region of the NPOM structure can be accurately adjusted by changing the polarization angle of the incident angle. Finally, we also study the relationship between the thickness of the dielectric layer and the local electric field intensity in the gap region of the NPOM structure. From the resonance spectrum variation curve, it can be found that the electric field intensity in the gap region is inversely proportional to the thickness of the dielectric layer. When the thickness of the dielectric layer is smaller than that of 4nm, the electric field intensity in the gap region has a significant change trend. At the same time, the resonance peak wavelength of the electric field intensity in the gap region has a blue-shift with the increase of the thickness of the dielectric layer. Similarly, when the thickness of the dielectric layer is small, the change of wavelength is more obvious. When the thickness of the dielectric layer exceeds that of 4nm, the resonance peak wavelength remains stable. The proposed NPOM structure based on GNEP and gold thin film has potential applications in the fields of SERS, optical gain, catalysis and so on.

Author Contributions

F.S. planned and guided the simulation study; Y.Z. constructs the simulation model; The manuscript was written by J.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Funding Scheme for Key Scientifc Research Projects in Universities of Henan Province (Grant No. 22A140024).

Data Availability Statement

Raw data are available from the corresponding author upon request.

Conflicts of Interest

The authors declare no conflicts of interest.

Nomenclature

Abbreviation Definition
SERS Surface-enhanced Raman scattering
GENP gold ellipsoidal nanoparticles
MNP metal nanoparticles
NPOM nanoparticle-on-mirror

References

  1. Yanglin, Z.; Kaiwen, Z.; Jinyan, N.; Tao, X.; Shenghao, W. Plasmonics in Organic Solar Cells: Toward Versatile Applications. ACS Appl. Electron. Mater. 2023, 5, 631–641. [Google Scholar]
  2. Bipasha, B.; Pekham, C.; Najirul, H.; Swarbhanu, G.; Mitali, S.; Aslam, K.; Manirul, I. AgNPs Embedded in Porous Polymeric Framework: A Reusable Catalytic System for the Synthesis of α-Alkylidene Cyclic Carbonates and Oxazolidinones via Chemical Fixation of CO2. Catalysts 2023, 13, 1467. [Google Scholar] [CrossRef]
  3. Shan, F.; Zhang, X.Y.; Fu, X.C.; Zhang, L.J.; Su, D.; Wang, S.J.; Wu, J.Y.; Zhang, T. Investigation of simultaneously existed Raman scattering enhancement and inhibiting fuorescence using surface modifed gold nanostars as SERS probes. Sci. Rep. 2017, 7, 6813. [Google Scholar] [CrossRef] [PubMed]
  4. Battulga, M.; Johannes, Z.; Hannes, P.; Christian, W.; Dmitry, S.; Markus, C.S.; Thomas, A.K.; Calin, H. Hybrid Multilayered Plasmonic Nanostars for Coherent Random Lasing. J. Phys. Chem. C 2016, 120, 23707–23715. [Google Scholar]
  5. Yeshchenko, O.A.; Bondarchuk, I.S.; Malynych, S.Z.; Galabura, Y.; Chumanov, G.; Luzinov, I. Surface plasmon modes of sandwich-like metal–dielectric nanostructures. Plasmonics 2015, 12, 655–665. [Google Scholar] [CrossRef]
  6. Shan, F.; Zhang, X.Y.; Wu, J.Y.; Zhang, T. Hot spots enriched plasmonic nanostructure-induced random lasing of quantum dots thin film. Chin. Phys. B 2018, 27, 047804. [Google Scholar] [CrossRef]
  7. Armstrong, R.E.; Liempt, J.C.; Zijlstra, P. Effect of film thickness on the far- and near-field optical response of nanoparticle-on-film systems. J. Phys. Chem. C 2019, 123, 25801–25808. [Google Scholar] [CrossRef]
  8. Zhu, S.Q.; Zhang, T.; Guo, X.L.; Zhang, X.Y. Self-assembly of large-scale gold nanoparticle arrays and their application in SERS. Nanoscale Research Letters 2014, 9, 114. [Google Scholar] [CrossRef]
  9. Hu, P.; Zheng, L.; Zhan, L.; Li, J.; Zhen, S.; Liu, H.; Luo, L.; Xiao, G.; Huang, C. Metal-enhanced fluorescence of nano-core–shell structure used for sensitive detection of prion protein with a dual-aptamer strategy. Analytica Chimica Acta 2013, 787, 239–245. [Google Scholar] [CrossRef]
  10. Hiroyuki, N.; Akito, M.; Sadahiro, M.; Tsunenobu, O.; Hitoshi, K.; Hidetoshi, O. Highly Controlled Plasmonic Emission Enhancement from MetalSemiconductor Quantum Dot Complex Nanostructures. J. Phys. Chem. C 2013, 117, 2455–2459. [Google Scholar]
  11. Jiang, N.; Zhuo, X.; Wang, J. Active Plasmonics: Principles, Structures, and Applications. Chem. Rev. 2018, 118, 3054–3059. [Google Scholar] [CrossRef] [PubMed]
  12. Nielsen, M.G.; Bozhevolnyi, S.I. Highly confined gap surface plasmon modes in metal strip-gap-film configurations. J. Opt. Soc. Am. B 2015, 32, 462–467. [Google Scholar] [CrossRef]
  13. Kim, M.; Lee, J.; Nam, J. Plasmonic photothermal nanoparticles for biomedical applications. Adv. Sci. 2019, 6, 1900471. [Google Scholar] [CrossRef]
  14. Langer, J. Present and future of surface-enhanced Raman scattering. ACS Nano 2020, 14, 28–117. [Google Scholar] [CrossRef] [PubMed]
  15. Ratchford, D.C. Plasmon-induced charge transfer: Challenges and outlook. ACS Nano 2019, 13, 13610–13614. [Google Scholar] [CrossRef] [PubMed]
  16. Kim, W.; Kim, N.; Park, J.W.; Kim, Z.H. Nanostar probes for tip-enhanced spectroscopy. Nanoscale 2016, 8, 987–994. [Google Scholar] [CrossRef] [PubMed]
  17. Guo, Q.; Ma, X.; Xie, Y.; Tan, W.; Zhang, H. Green synthesis and formation mechanism of Ag nanofowers using lcysteine and the assessment of Ag nanofowers as SERS substrates. Colloids Surf A 2017, 530, 53–57. [Google Scholar]
  18. Khurana, K.; Jaggi, N. Localized surface plasmonic properties of Au and Ag nanoparticles for sensors: A review. Plasmonics 2021, 16, 981–999. [Google Scholar] [CrossRef]
  19. Vasanthan, D.; Jong, K.L.; Jin, W.O. Distinguishable Plasmonic Nanoparticle and Gap Mode Properties in a Silver Nanoparticle on a Gold Film System Using Three-Dimensional FDTD Simulations. Nanomaterials 2018, 8, 582. [Google Scholar] [CrossRef]
  20. Tanya, H.; Stephen, R.E.; Sumeet, M. Interaction of metallic nanoparticles with dielectric substrates: Effect of optical constants. Nanotechnology 2013, 24, 035201. [Google Scholar]
  21. Médéric, L.; David, M.; Priyamvada, V.; Gillibert, R.; Boujday, S.; Knoll, W.; Dostalek, J.; Chapelle, M.L. Plasmonic Properties of Gold Nanostructures on Gold Film. Plasmonics 2020, 15, 1653–1660. [Google Scholar]
  22. Vasanthan, D.; Hyun, L.; Minjun, K.; Thanh, M.N.; Jong, P.S.; Jong, M.L.; Lee, D.; Kim, K.H.; Oh, J.W. Unveiling facet effects in metallic nanoparticles to design an efficient plasmonic nanostructure. Current Applied Physics 2022, 44, 22–28. [Google Scholar]
  23. Jubb, K.M.; Jiao, Y.; Eres, G.; Retterer, S.T.; Gu, B. Elevated gold ellipse nanoantenna dimers as sensitive and tunable surface enhanced Raman spectroscopy substrates. Nanoscale 2016, 8, 5641–5648. [Google Scholar] [CrossRef]
  24. Near, R.; Tabor, C.; Duan, J.; Pachter, R.; El-Sayed, M. Pronounced effects of anisotropy on plasmonic properties of nanorings fabricated by electron beam lithography. Nano Lett 2012, 12, 2158–2164. [Google Scholar] [CrossRef] [PubMed]
  25. Hatab, N.A.; Hsueh, C.; Gaddis, A.L.; Retterer, S.T.; Li, J.H.; Eres, G.; et al. Freestanding optical gold bowtie nanoantenna with variable gap size for enhanced Raman spectroscopy. Nano Lett 2010, 10, 4952. [Google Scholar] [CrossRef] [PubMed]
  26. Vladimir, L.; Ronen, A.; Alket, A.; Ahmet, A.K.; Kai, C.; Thomas, H.J.; Shyamsunder, E.; Hatice, A. Angle-and polarization-dependent collective excitation of plasmonic nanoarrays for surface enhanced infrared spectroscopy. Optics Express. 2011, 19, 11202–11212. [Google Scholar]
  27. Oleg, A.Y.; Anastasiya, V.T.; Viktor, V.K.; Randal, J.K.; Michael, H.; Anatoliy, O.P. Angle and polarization dependent coupling of surface plasmon and gap modes in plasmonic gap metasurfaces. Optical Materials 2022, 132, 112884. [Google Scholar]
  28. Jiang, M.; Wang, G.; Xu, W.; Ji, W.; Zou, N.; Ho, H.P.; Zhang, X. Two-dimensional arbitrary nano-manipulation on a plasmonic metasurface. Optics Letters. 2018, 43, 1602–1605. [Google Scholar] [CrossRef]
  29. Palik, E.D. Handbook of optical constants of solids; Academic Press: Orlando, 1985. [Google Scholar]
Preprints 106347 g001
Figure 1. Schematic configuration (a) and calculation model (b) with NPOM structures separated by a dielectric layer.
Figure 1. Schematic configuration (a) and calculation model (b) with NPOM structures separated by a dielectric layer.
Preprints 106347 g001
Preprints 106347 g002
Figure 2. (a) The normalized electric field on the surface of GENP (along the green line) in a homogeneous medium, and (b) The normalized electric field value in the gap space of NPOM structure (along the white line) composed of GENP and gold thin films..
Figure 2. (a) The normalized electric field on the surface of GENP (along the green line) in a homogeneous medium, and (b) The normalized electric field value in the gap space of NPOM structure (along the white line) composed of GENP and gold thin films..
Preprints 106347 g002
Preprints 106347 g003
Figure 3. (a1-a6) Electric field distribution of NPOM structure with different polarization angles at the thickness of 0.3nm dielectric layer. (b) The resonance spectrum curve of the electric field intensity in the gap region under different polarization angles. (c) The relationship between the polarization angle and the electric field intensity.
Figure 3. (a1-a6) Electric field distribution of NPOM structure with different polarization angles at the thickness of 0.3nm dielectric layer. (b) The resonance spectrum curve of the electric field intensity in the gap region under different polarization angles. (c) The relationship between the polarization angle and the electric field intensity.
Preprints 106347 g003
Preprints 106347 g004
Figure 4. (a1-a6) Electric field distribution of NPOM structure with different polarization angles at the thickness of 1nm dielectric layer. (b) The resonance spectrum curve of the electric field intensity in the gap region under different polarization angles. (c) The relationship between the polarization angle and the electric field intensity.
Figure 4. (a1-a6) Electric field distribution of NPOM structure with different polarization angles at the thickness of 1nm dielectric layer. (b) The resonance spectrum curve of the electric field intensity in the gap region under different polarization angles. (c) The relationship between the polarization angle and the electric field intensity.
Preprints 106347 g004
Preprints 106347 g005
Figure 5. (a1-a6) Electric field distribution of NPOM structure with different polarization angles at the thickness of 4nm dielectric layer. (b) The resonance spectrum curve of the electric field intensity in the gap region under different polarization angles. (c) The relationship between the polarization angle and the electric field intensity.
Figure 5. (a1-a6) Electric field distribution of NPOM structure with different polarization angles at the thickness of 4nm dielectric layer. (b) The resonance spectrum curve of the electric field intensity in the gap region under different polarization angles. (c) The relationship between the polarization angle and the electric field intensity.
Preprints 106347 g005
Preprints 106347 g006
Figure 6. (a1-a6) Electric field distribution of NPOM structure with different thickness of the dielectric layer at polarization angles 0°. (b) The resonance spectrum curve of the electric field intensity in the gap region under different thickness of the dielectric layer. (c) The relationship between the thickness of the dielectric layer and the electric field intensity.
Figure 6. (a1-a6) Electric field distribution of NPOM structure with different thickness of the dielectric layer at polarization angles 0°. (b) The resonance spectrum curve of the electric field intensity in the gap region under different thickness of the dielectric layer. (c) The relationship between the thickness of the dielectric layer and the electric field intensity.
Preprints 106347 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated