1. Introduction
As economic development continues, the role of renewable energy sources (RES) is growing. This is largely due to the increasing environmental pollution caused by excessive use of fossil fuels [
1]. The rising cost of energy produced from fossil fuels, the ongoing technological advances and the increasingly stricter regional environmental regulations are also contributing to the growing importance of renewable energy [
2]. However, as studies indicate, the transition to renewable energy is currently a major challenge. It cannot be met effectively without understanding the factors that underlie such a transition [
3]. Based on a study of renewable energy consumption in the Eurozone in the years 2000-2019, the authors of [
3] showed a significant relationship between renewable energy consumption and the amount of electricity generation and energy production by other sources. They also concluded that energy transition issues should be research priorities for academia. The relevance of the energy transition is also confirmed by [
4], which contains research results concerning the relationship between the transition and the factors related to RES, construction and other sectors. Energy transition is supported by solar technologies, and the paper mentions solar collectors as one of them. The research presented therein mainly concerns the territory of France. It was pointed out that technical and socioeconomic factors were crucial for successful RES implementation.
Flat-plate solar collectors (FPSCs), being an important technology for harnessing solar energy, are clearly part of the energy transition issues analysed above. Due to their simple and reliable design, FSPCs find numerous applications in low- and medium-temperature systems. An interesting example of such an application is presented in the paper [
5], in which a techno-economic analysis of a prosumer installation was performed. The installation includes FPSCs, a heat pump, and a photovoltaic system. A methodology for selecting specific solutions based on operational data and mathematical models was proposed.
A significant number of works have been undertaken in recent years to improve the efficiency and performance of FPSCs. Among other problems, they focused on reducing heat losses, improving the heat exchange between the absorber and the solar fluid, and on new solutions for absorbers and solar cover coatings [
6]. Other efforts to increase the efficiency of FPSCs consisted in the analysis of the use of nanofluids, polymers, mini-channels, phase-changing materials (PCMs), and enhancement devices such as various types of inserts and reflectors [
7]. A new concept of FPSC was proposed by Zheng et al. [
8]. It involved the use of silica aerogel in the cover and transparent insulation materials. These solutions were successfully tested numerically and experimentally under steady-state conditions. Current design solutions for FPSCs are reviewed in [
9], taking into account the minimisation of heat losses from the collector front surface. Based on this review it was concluded that there was great potential for improving the FPSC thermal performance. This can contribute to increasing the competitiveness and expanding the range of applications of the collectors. Interesting FPSCs solutions were presented and analysed in [
10,
11,
12]. The main novelty of [
10] is the proposal for a stainless steel solar collector with micro channels. Based on numerical analysis and experimental studies, it was found that the collector thermal performance could be improved by increasing the width of the microchannel and the height of the corrugations. The advantage of the use of stainless steel is that a homogeneous temperature distribution can be maintained, which maximises heat absorption. In addition, the use of stainless steel extends the FPSC life. Mohseni-Gharyehsafa et al. [
11] carried out a sensitivity analysis and multi-objective optimisation for an FPSC fitted with twisted tapes. The aim of the optimisation was to find the collector most efficient design. Moreover, based on the Nusselt number, a generalised model of the collector efficiency was developed. The model makes it possible to integrate different fluid flows. The authors of [
12] present the first results of research on the use of FPSCs as cooling devices, exchanging heat at night by radiation, mainly with the sky. For this purpose, non-shielded solar collectors integrated with the building hydronic system were used (the same FPSCs are used during the day to produce domestic hot water, for example). An STC model based on the quasi-dynamic method according to the ISO 9806:2013 standard was used to predict the annual energy gain. This research and the analyses were carried out to establish the potential of the use of FPSCs to reduce the energy demand in the building sector in dry and hot areas.
In recent years, efforts have been made to study the effects of using nanofluids in devices intended for converting solar energy into other types of energy. Such devices include FPSCs, in which the use of nanofluids is an important field of research, numerical simulations and experiments. In [
13], the authors propose a hybrid nanofluid obtained by dispersing ZrO
2-SiC particles in distilled water (DW). The nanofluid was used in the FPSC to determine the collector efficiency. It was experimentally confirmed that the presence of this nanofluid resulted in an increase in energy and exergy efficiency compared to a system based on distilled water alone. The results of similar analyses and experimental studies are presented in [
14], in which SiC/DW was used as a nanofluid. The studies were conducted for different values of the fluid mass flow rate and different concentrations of nanoparticles. The conclusions from these studies are analogous to those presented in [
13]. In both cases, the thermophysical properties of the nanofluids were evaluated first. In their studies, Struchalin et al. [
15] used the concept of the direct-absorption solar collector (DASC), developed in the 1970s. Despite many promising results of research based on DASC nanofluids, the interest in this solution was lost due to environmental constraints and costly nanofluids. The authors of [
15] compared the results of research on a full-scale DASC with those obtained for the FPSC, finding higher average daily efficiency values for the former. An interesting thing is that the nanofluid was produced using instant coffee. Moreover, the DASC efficiency was compared with the efficiency of a commercial FPSC model. The results of research on the thermal output of FPSCs using advanced ionanofluids and nanofluids are presented in [
16]. The testing was carried out both in real conditions and using the FPSC theoretical model available in the literature. Hamdan et al. [
17] performed laboratory testing of the effect of a water-based Al
2O
3 nanofluid on thermal energy storage in a tank. The thermal fluid flowing in the tank coil, at different mass flow rates, was preheated in a flat-plate solar collector. The testing results were used to determine the fluid optimal mass flow rate, corresponding to the nanofluid maximum temperature in the tank, and the nanofluid optimal concentration.
In parallel with the research on new materials and nanofluids for the FPSC, new mathematical models are being developed to simulate the operation of the collectors. This is due to their great potential for industrial applications and small-scale heating systems [
11]. Solar collectors always operate in unsteady conditions. As indicated by Duffie and Beckman [
18], in most of the literature on the analysis of the FPSC performance, this unsteadiness is not taken into account. One of the first mathematical models of the FPSC was the model proposed by Cadafalch [
19]. It was an extension of the model presented in [
20], in which steady-state conditions were taken into account. The extension consisted in a more detailed approach to the calculation of the heat exchange of the collector cover and back. At the same time, it was emphasised that the heat exchange in the FPSC was essentially one-dimensional (1D). However, three-dimensional (3D) models can also be found in the literature. Cerón et al. [
21] developed a 3D model to predict the collector output curve. This model was based on the Reynolds-averaged Navier-Stokes (RANS) turbulence model, and a steady-state problem was considered. Many 3D models were created using computational fluid dynamics (CFD) and they also concern steady states, for example those presented in [
22,
23,
24]. An interesting FPSC concept is presented in [
22]. In order to increase the collector efficiency (by reducing heat losses), the integration of a polymethyl methacrylate (PMMA) sheet into a flat-plate collector was proposed. This solution is dedicated to FPSCs used in cold regions. Maji et al. [
23] simulated the operation of four FPSCs with similar dimensions. The aim of the simulations was to identify the impact of the channel geometry and turns on the collector performance. The results of similar analyses are presented in [
24]. The analyses concerned, among other things, the problem of increasing the heat transfer to the working fluid in the FPSC by using a cross-section different from the traditional circular shape. As highlighted in [
25], predicting the FPSC thermal performance is an important issue from the perspective of engineering applications. This prediction is complex and difficult, which is due to the thermal and operating parameters affecting the performance of the collectors. The authors of [
25] analysed the potential of various machine learning models to predict the performance of FPSCs with nanofluids as the working fluid. Studies have also been conducted for many years on predicting the FPSC performance using artificial neural networks (ANNs). Kalogirou [
26] presented six such prediction models, e.g. to predict the standard performance collector equation coefficients, the collector time constant, the incidence angle modifier coefficients, and the collector stagnation temperature. The use of ANNs is still relevant, as evidenced for example by [
27], in which the effect of an internally grooved absorber tube on the FPSC performance was analysed. The created ANN models were used to predict the collector performance and the outlet temperature. Just a few works on numerical modelling of the FPSC transient operation are also available in the literature at present. One of them is [
28], where a model of a typical FPSC is presented. The model, based on the solution of two-dimensional differential equations formulated for the absorber, was used to calculate the collector heat loss coefficient and efficiency. Constant values were assumed for all thermophysical properties. Freegah et al. [
29] performed a numerical and an experimental analysis of thermal responses of a traditional FPSC and its new model. The new model had elliptical tubes and wavy fins. Due to that, the surface area exposed to solar radiation was increased. The numerical models were created using the ANSYS Fluent software.
The analysis of the presented literature points to the relevance of issues related to experimental studies and modelling of the FPSC operation. The efforts of researchers concentrate mainly on improving the efficiency and performance of the collectors. Various nanofluids or new design solutions are proposed for this purpose. The effectiveness of these solutions is usually verified by measurements on real facilities. The attempts at numerical modelling are mainly limited to steady-state analyses, whereas solar collectors always operate under transient conditions. It should be emphasised that a large number of works are currently emerging to deal with the use of nanofluids. The impact of their application can be analysed numerically using the one-dimensional distributed parameter mathematical model of the FPSC proposed in the present paper. The basis for obtaining reliable results in this case is the correct determination of the dependence of the thermophysical properties of nanofluids on temperature. The developed model enables simulations of the FPSC operation at any variable boundary conditions (time-dependent intensity of solar radiation, and the solar fluid temperature and mass flow rate at the collector inlet). The outcome of the simulation calculations is the history of the fluid temperature at the outlet of the collector. One of the novelties of the presented study is the application of the developed model to determine the collector time constant, which was verified experimentally.
2. Brief Description of the Model Development
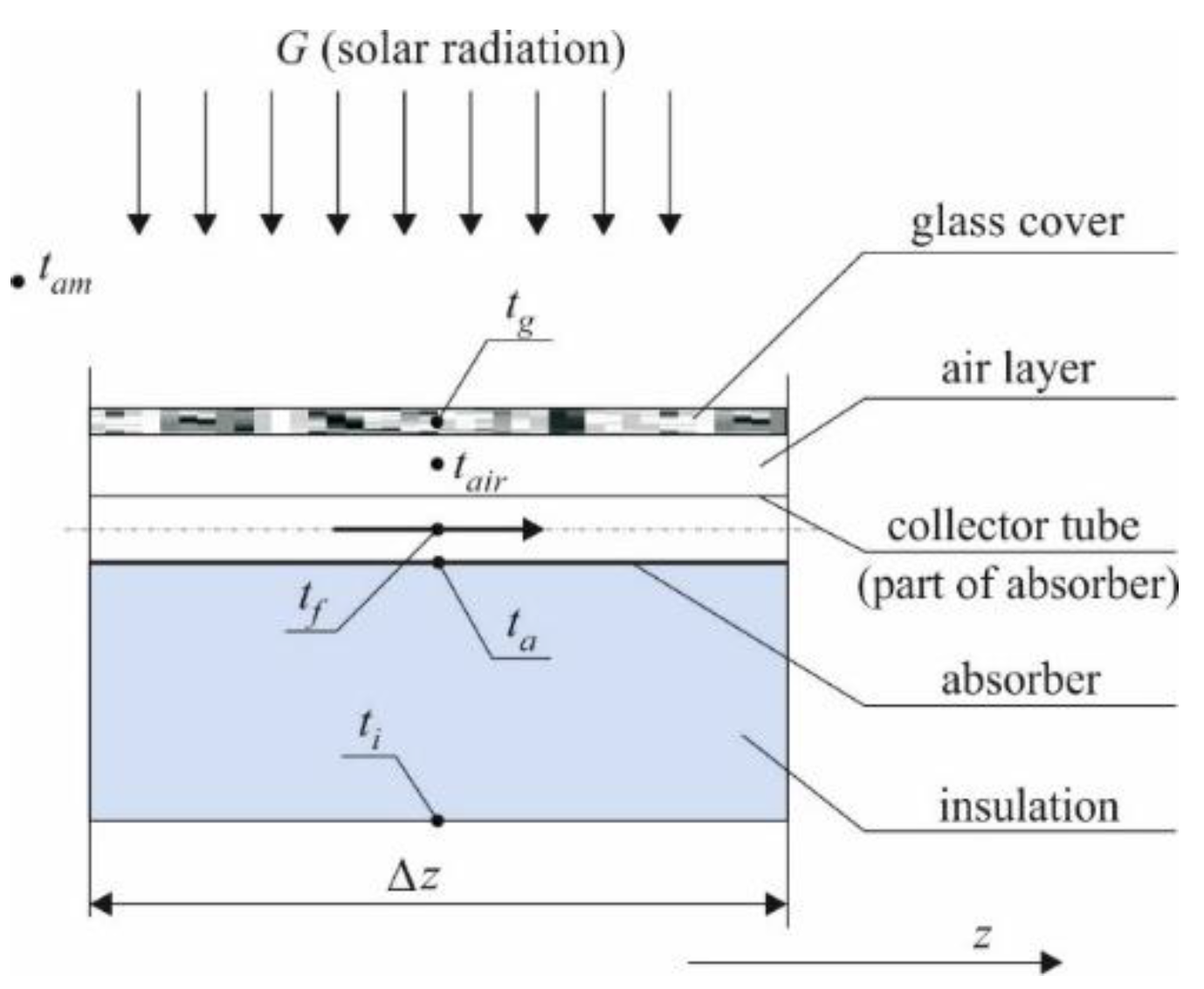
The proposed model, enabling simulation of the FPSC operation, is a one-dimensional distributed parameter model. It makes it possible to analyse the collector operation under transient conditions at any variable (time-dependent) boundary conditions. Five nodes located in the direction perpendicular to the fluid flow direction were considered in the model. The nodes are contained in the control volume shown in
Figure 1. They include the solar glass (
tg), the air layer between the glass and the absorber (
tair), the absorber (
ta), the working fluid (
tf) and the insulation (
ti). It is thus a 5×
N-model, where
N is the number of nodes (control volumes) in the fluid flow direction. The calculations are carried out along the path of the fluid flow in a single collector tube with dimensions as in the real facility.
The developed model basic assumptions are as follows:
- -
uniform fluid flow through all collector tubes,
- -
the thermophysical properties of the working fluid, the absorber material, and the air between the solar glass and the absorber are determined on an ongoing basis,
- -
the thermophysical properties of the solar glass and insulation are constant and temperature-independent,
- -
heat transfer coefficients are calculated in an on-line mode, based on the relations available in the literature,
- -
the collector loses heat to the environment through the solar glass and insulation (convection and radiation),
- -
the collector heat losses through the edges are not taken into account,
- -
all the collector elements contained in the control volume have dimensions as in the real facility.
The above assumptions, taken into account in the mathematical model, do not introduce any simplifications into the model and make it possible to preserve the physics of the phenomena occurring in the collector.
The following energy balance equations were formulated for the above-mentioned five components of the collector (
Figure 1):
Cg – thermal capacity of the glass cover, J/K
tg – temperature of the glass cover, oC
τ – time, s
Φg,am – heat flux lost through the glass cover to the environment, W
Φg,a – heat flux exchanged between the glass cover and the absorber due to radiation, W
Φg,air – heat flux exchanged between the glass cover and the air layer due to convection, W
Φg,G – heat flux absorbed by the glass cover due to solar radiation, W
Cair – thermal capacity of the air layer, J/K
tair – temperature of the air between glass cover and absorber, oC
Φair,g = - Φg,air, W
Φair,a – heat flux exchanged between the air layer and absorber due to convection, W
Ca – thermal capacity of the absorber, J/K
ta – temperature of the absorber, oC
Φa,g = - Φg,a, W
Φa,air = - Φair,a, W
Φa,i – heat flux exchanged between the absorber and the insulation due to thermal conductivity, W
Φa,f – heat flux exchanged between the absorber and the fluid due to convection, W
Φa,G – heat flux absorbed by the absorber due to solar radiation, W
Cf – thermal capacity of the working fluid, J/K
tf – temperature of the working fluid, oC
Φf,in – heat flux flowing into the control volume with the fluid, W
Φf,o – heat flux flowing out of the control volume with the fluid, W
Φf,a = - Φa,f, W
Ci – thermal capacity of the insulation, J/K
ti – temperature of the insulation, oC
Φi,a = - Φa,i, W
Φi,am – heat flux lost through the insulation to the environment, W
The relations presented above concern FPSCs with a single solar glass cover, operating in a parallel-channel configuration. The method is also suitable for collectors operating in a serpentine flow system and for collectors with a double solar glass cover. For collectors operating in a serpentine flow system, the presented method does not require modification. However, the use of a second solar glass cover requires the derivation of additional energy balance equations for the second cover and for the air layer between the covers.
The formulated differential equations (1) – (5) were solved iteratively using an implicit difference scheme (time derivatives were replaced by forward difference quotients). In this way, formulae were obtained that make it possible to calculate the time- and space-dependent temperature values at five nodes of each control volume. In this way, 5 × N differential equations are solved in every time instant.
The energy balance equation for the fluid (formula 4) takes account of the change in total energy in the control volume over time, the energy flux flowing into and out of the control volume and the heat flux flowing into it through its surface. Considering the slight effect of the other terms of the energy conservation equation (i.e. the heat flux flowing into the control volume due to conduction and the change in the work done by surface forces and friction forces over time), they are omitted. Also omitted are the momentum and mass balance equations. This resulted in fewer final equations and their more straightforward form, translating into a fast numerical calculation process. The omission of the above-mentioned balance equations is not a limitation of the proposed method, nor does it cause errors in numerical calculations, as demonstrated by the computational and experimental verification carried out in the next two sections below. The other details of the developed solution, the derived final formulae and the formulae used to describe the heat transfer coefficients are given in [
30].
3. Computational Verification
In order to obtain a stable solution of the derived differential equations, it was first necessary to estimate the values of the steps of the time and spatial division, i.e. the time step for the numerical calculations Δτ and the spatial size of the control volume Δ
z. They should satisfy the Courant-Friedrichs-Lewy condition for one-dimensional problems [
31]:
where:
wf – working fluid flow velocity in the solar collector tubes, m/s
By satisfying condition (6), it is possible to avoid the effects of dissipation and dispersion causing errors in numerical calculations.
The values of steps Δτ and Δ
z were estimated using an analytical solution available in the literature for the transient state [
32,
33]. The solution involves forcing a jump rise in heating on the outer surface of the tube (the case close to real conditions of the operation of solar collectors). The analytical solution in this case makes it possible to calculate the dimensionless increment in the fluid temperature caused by the forcing. In order to compare the results obtained from the proposed mathematical model of the collector with the results of the analytical solution, appropriate relations were derived in [
33], covering only the energy balance for one tube of the collector and for the fluid flowing inside the tube. These relationships are used in this section in the analysis of the effect of the time and spatial step values on the accuracy of obtained results.
An aqueous solution of propylene glycol is used as the working fluid. Because in analytical solutions it is impossible to take account of time-dependent changes in thermophysical properties, the following constant properties of the aqueous glycol solution (for the temperature of 40oC) were adopted for the calculations: density ρf = 1020 kg/m3, specific heat cf = 3750 J/(kg·K), thermal conductivity kf = 0.447 W/(m·K) and dynamic viscosity μf = 0.0013 kg/(s·m). It is also assumed that the 1.9 m-long collector tube with the outer diameter do = 0.01 m and the wall thickness gw = 0.0005 m is made of copper with the following properties: ρw = 8960 kg/m3 and cw = 390 J/(kg·K). The heat transfer coefficient on the wall inner surface is adopted as h = 185 W/(m2K). For verification purposes, the initial temperature of the flowing fluid and of the tube was assumed as tf = θ = 10oC. From the next time step on, an input step function appears on the tube outer surface in the form of heating with heat flux G = 500 W/m2. The tube pitch is p = 0.12 m.
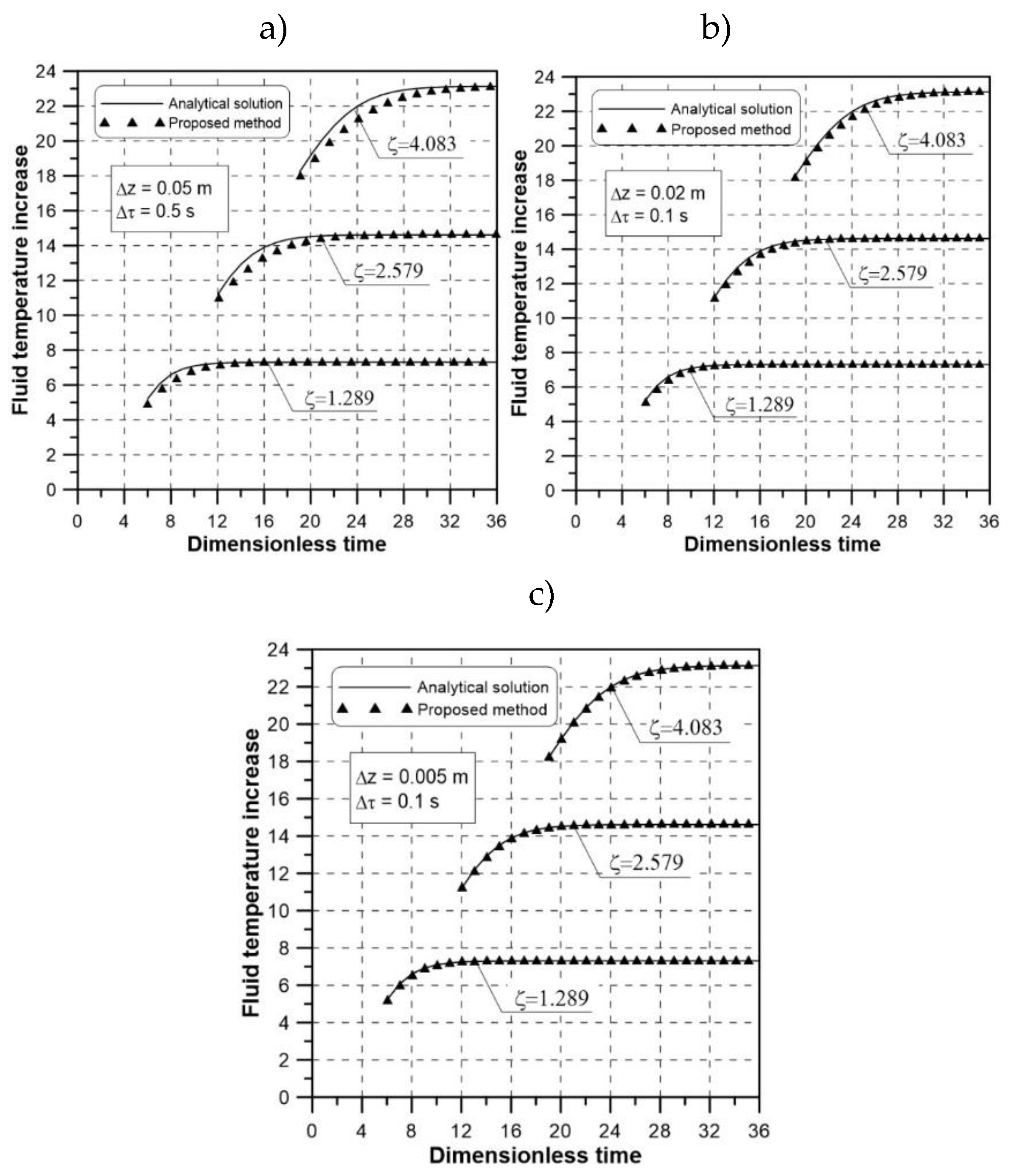
Three sets of steps of the time and spatial division were analysed, and the obtained results were compared with the analytical solution results (
Figure 2). The presented dimensionless coordinates ζ = 1.289, 2.579 and 4.083 correspond to the dimensional coordinates
z = 0.6 m, 1.2 m and 1.9 m, respectively.
The analysis of
Figure 2 indicates that in order to avoid dissipation and dispersion effects, numerical calculations should be carried out adopting the proposed time and space division shown in
Figure 2b or 2c (satisfactory agreement was obtained between the results of the numerical calculations and the analytical solution). It seems that the reasonable choice is to carry out calculations using the time and spatial steps shown in
Figure 2b, by means of which sufficient computing accuracy is obtained. If the values of the steps are taken according to
Figure 2c, the improvement in the accuracy of the calculations is not significant but the computing time is longer. The time shifts of the curves in individual cross-sections, visible in
Figure 2, are due to the fact that the analytical relations enable determination of time- and space-dependent increments in the fluid temperature in any cross-section
z, starting from the time when this cross-section is reached by a particle of the fluid flowing with velocity
wf. For example, if the velocity is 1m/s, analytical solutions make it possible to determine temperature changes in a cross-section which is, for example, 5 m away from the beginning of the tube only after 5 s.
4. Experimental Verification
This section presents the experimental verification of the developed mathematical model of the FPSC. The verification consisted in comparing the measured history of the fluid temperature at the collector outlet to the numerical calculation results. In order to carry out such verification, a test stand was built. The stand is described in detail in [
30].
Based on the computational verification presented in section 3, the following time and space division was adopted for the calculations: Δ
τ = 0.1 s and Δ
z = 0.02 m (
Figure 2b). For the absorber tube with length
L = 1.9 m,
N = 96 analysed cross-sections (control volumes) were obtained. This means that at every time instant 480 differential equations were solved (
M ×
N = 5 × 96-node model). The temperature histories of the solar glass cover, the air layer between the glass cover and the absorber, the absorber and the insulation were determined in each of the 96 cross-sections. The working fluid temperature history, on the other hand, was determined in cross-sections 2 through 96. For cross-section 1, the temperature history was known from the measurement. All heat transfer coefficients were calculated on-line, based on the relations given in [
34]. The thermophysical properties of the air layer, the absorber and the fluid were also calculated on-line. In the case of the solar glass cover and the insulation, the properties were adopted as constant. For the glass cover the following values were assumed:
cg = 720 J/(kgK) and
ρg = 2500 kg/m
3, whereas for the insulation layer:
ci = 1030 J/(kgK),
ρi = 70 kg/m
3 and
ki = 0.035 W/(mK). An aqueous solution of 50% by weight of propylene glycol C
3H
8O
2 was used as the working fluid. The computational program was created using the Fortran code [
35].
A view of the analysed collector is shown in
Figure 3, and selected results of the measurements, calculations and comparisons are presented in
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8 and
Figure 9. The figures refer to the measurements performed using the test stand of the Department of Energy of the Cracow University of Technology on a bright November day. The tested device was a liquid flat-plate collector with an absorber built of vertical copper tubes parallel to each other.
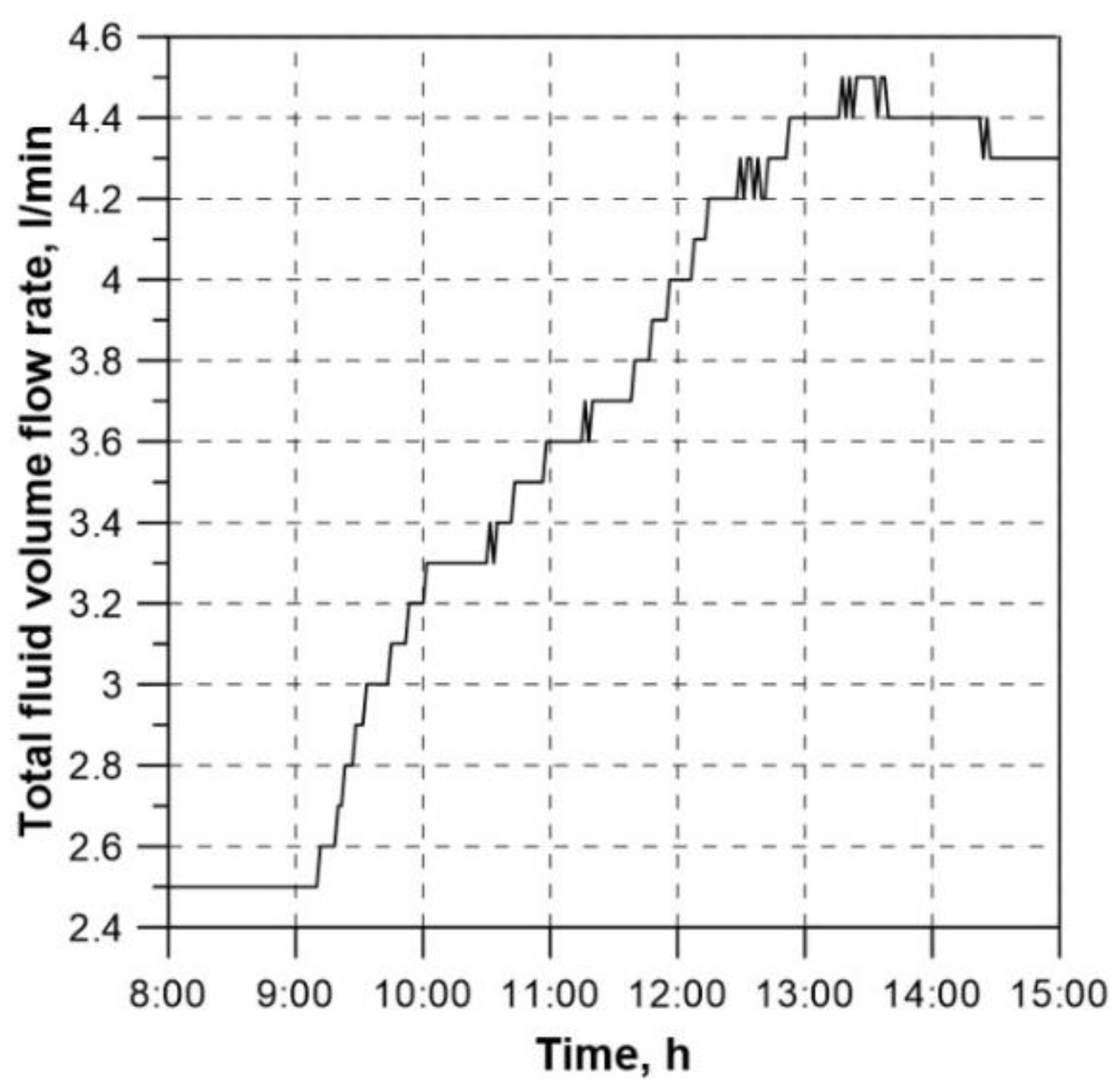
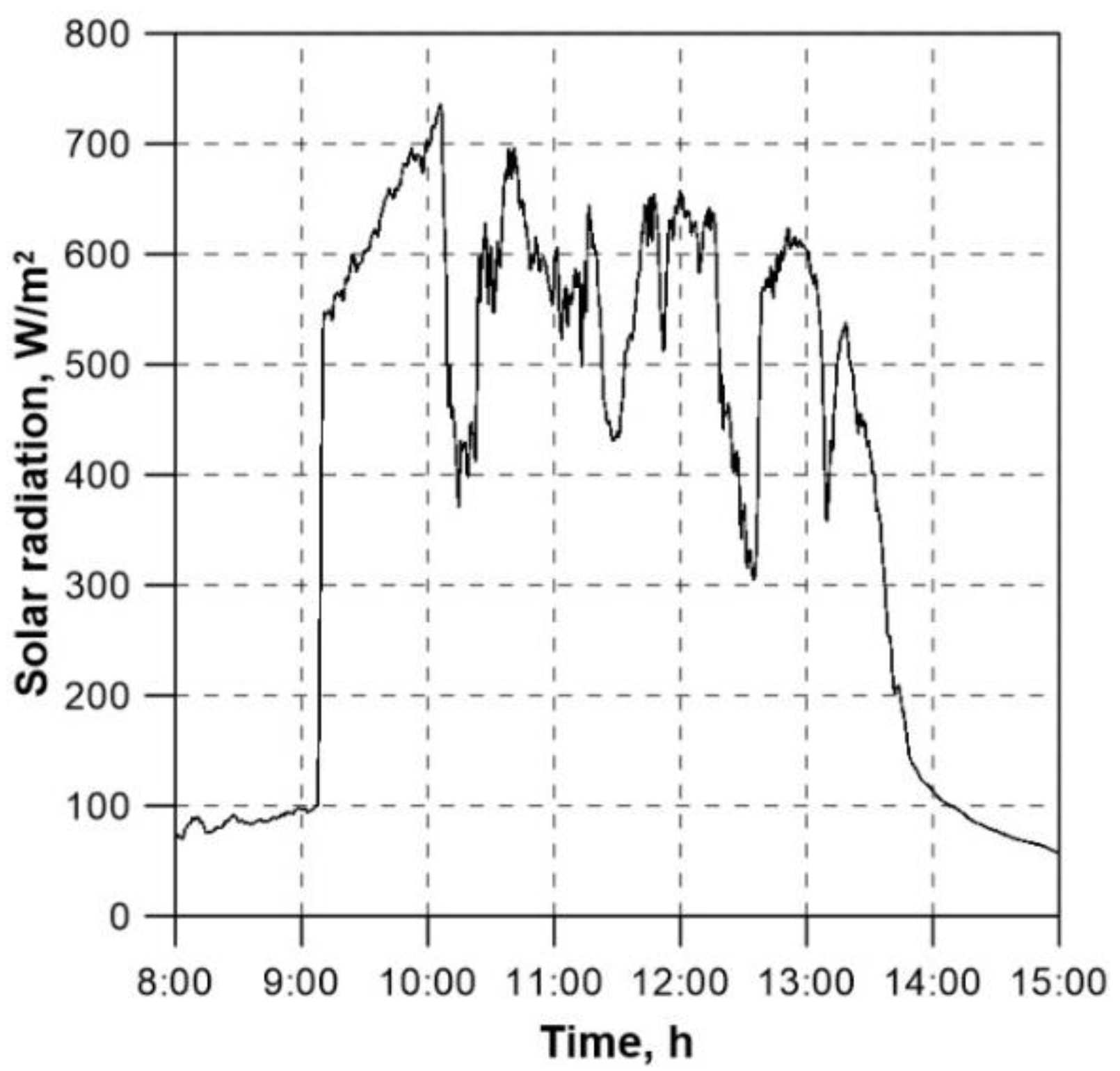
The following measured histories were the input data for the numerical calculations:
- -
the history of the fluid total volume flow rate (
Figure 4),
- -
the history of solar radiation intensity (
Figure 5),
- -
the history of the fluid temperature at the collector inlet (
Figure 6),
- -
the history of ambient temperature (
Figure 6).
The solar radiation intensity (
Figure 5) was measured using a pyranometer located in the plane of the collector aperture (
Figure 3). Due to this location of the pyranometer, it was not necessary to recalculate the solar radiation intensity values, measured for example on the horizontal plane (such measurements are carried out by meteorological stations). The collector was inclined at the angle of 45
o to the horizon and facing south.
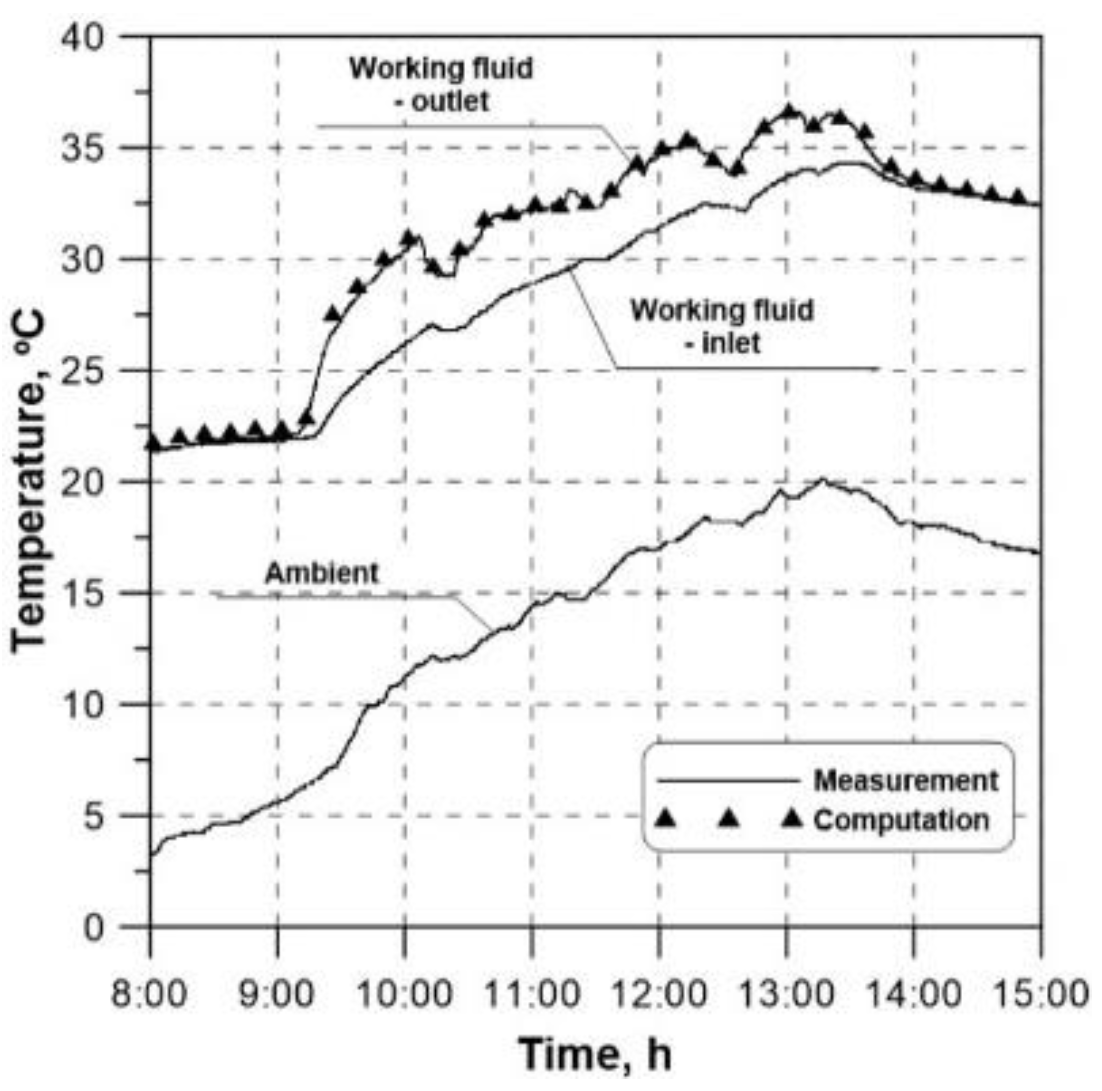
The comparison between the measured and the calculated history of the fluid temperature at the collector outlet is presented in
Figure 6. It follows from the figure that there is fully satisfactory agreement between the two curves, which indicates the effectiveness of the proposed mathematical model. In order to demonstrate the accuracy of reproducing the measured history of the fluid temperature in more detail,
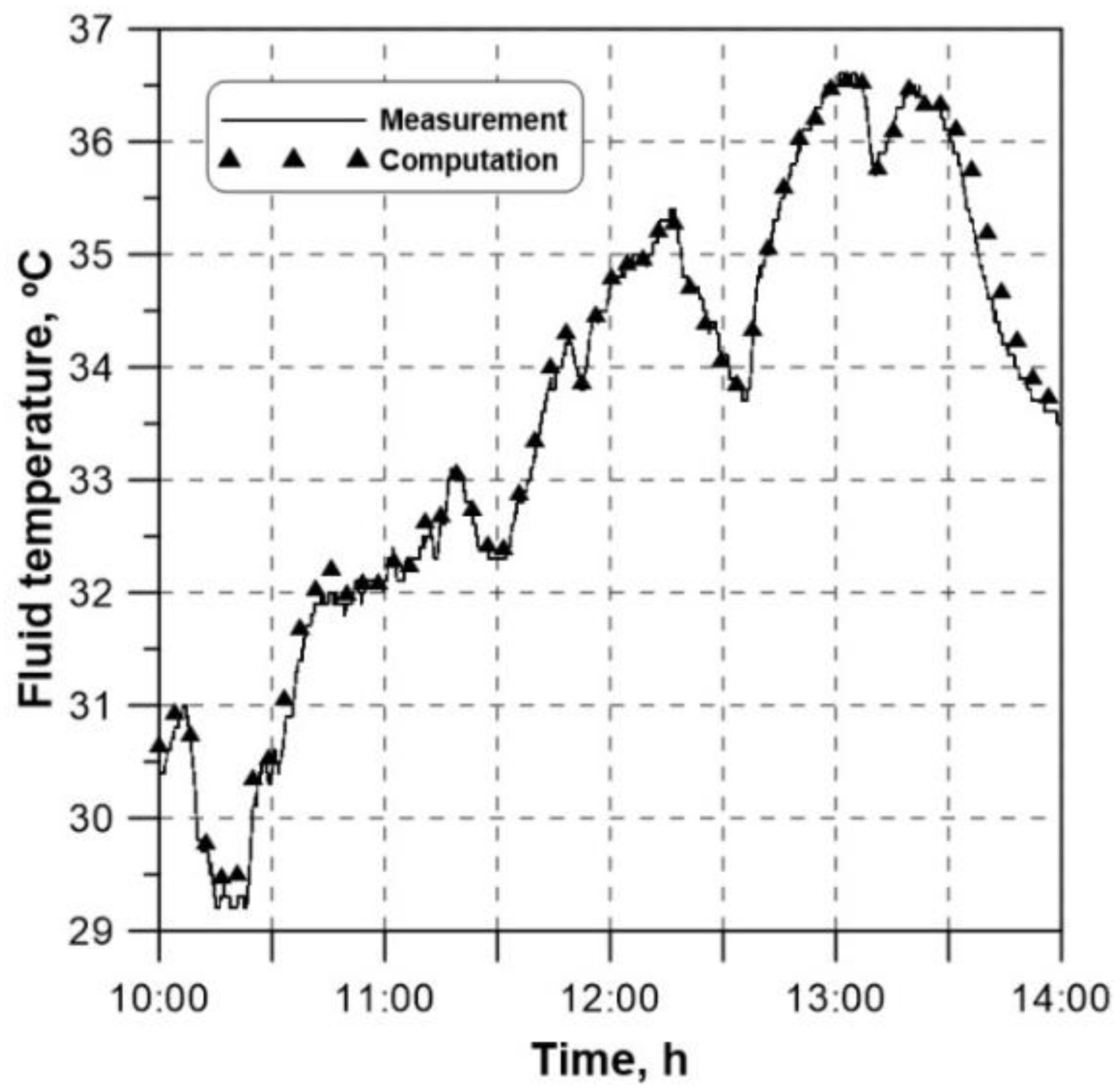
Figure 7 shows a fragment of
Figure 6 covering the time with the biggest temperature changes. An analysis of
Figure 7 also confirms the developed model effectiveness.
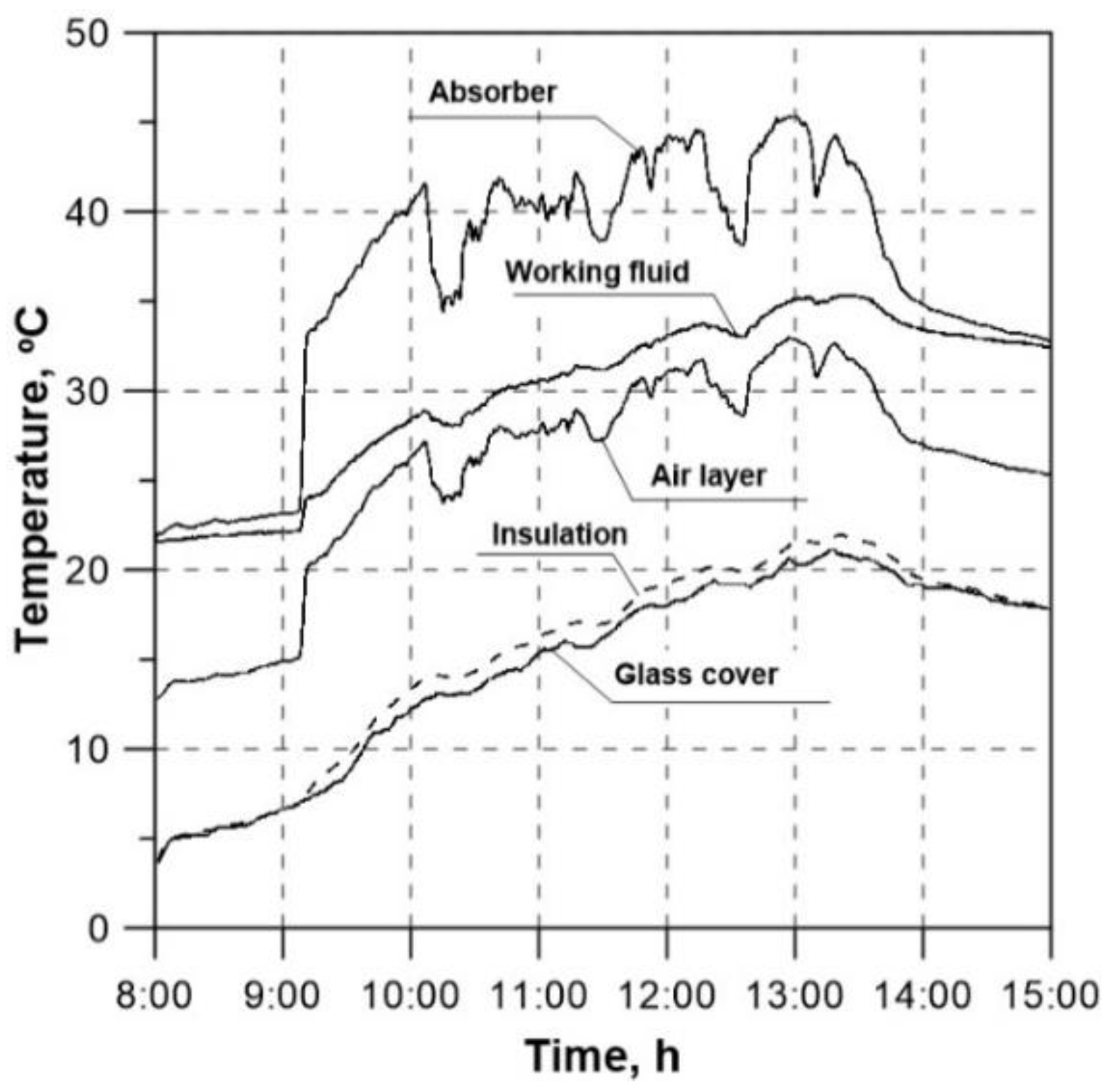
Figure 8 shows the calculated temperature histories for the collector individual elements (individual nodes of the collector in the direction transverse to the fluid flow) for the selected cross-section No. 48 (
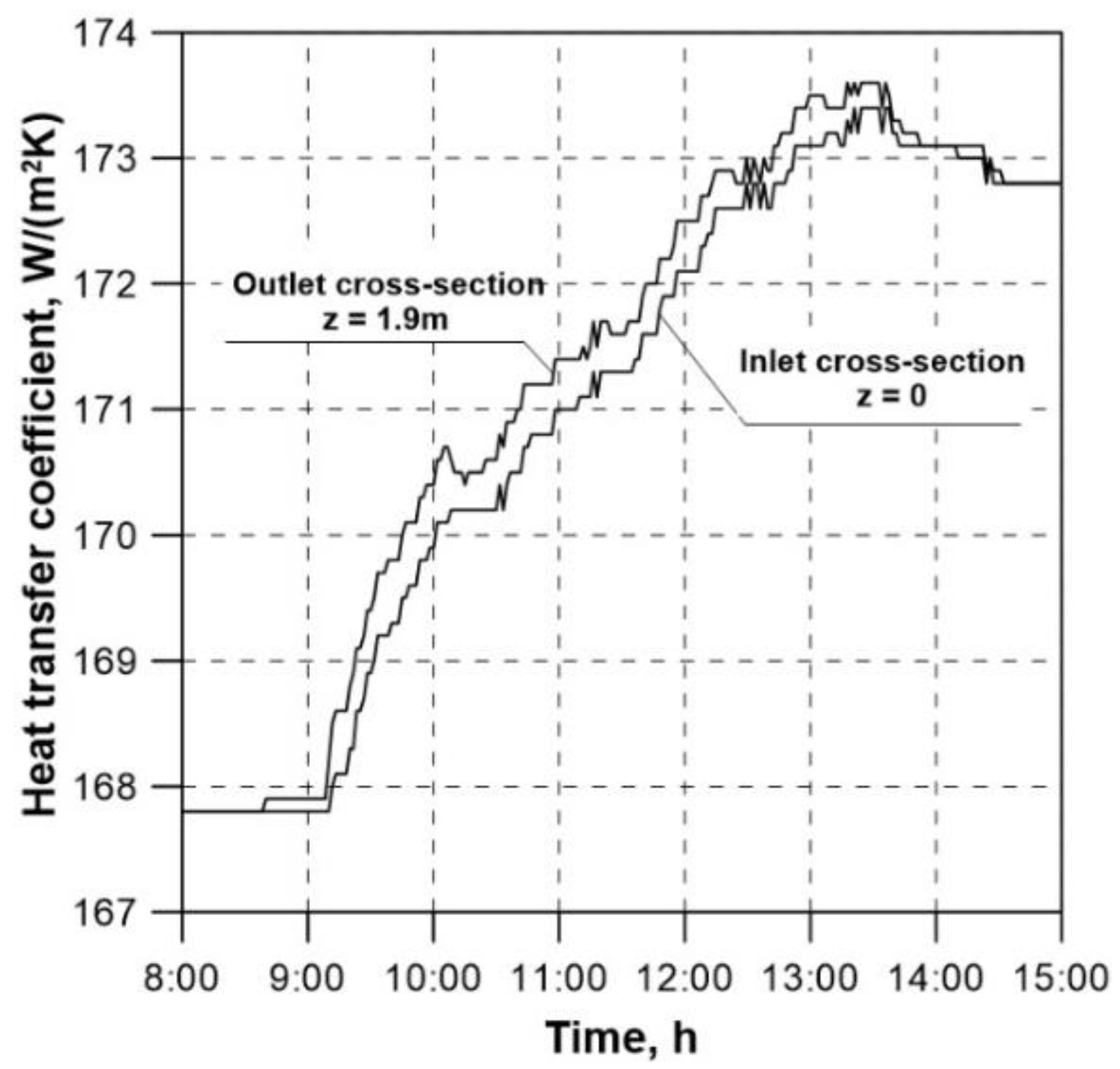
L = 0.94 m). Similar curves can be plotted for each of the 96 cross-sections under analysis. Example curves illustrating the changes in the heat transfer coefficient on the collector tube inner surface are shown in
Figure 9. These histories are calculated for the inlet and the outlet cross-section. The coefficient values were calculated using the Heaton empirical formula [
20]. This formula applies to laminar flows in short channels. The velocity of the fluid flowing through the collector tubes is small, from about a few mm/s to about a dozen cm/s. Given the small diameter of these tubes, the achieved Reynolds number values, ranging from about a dozen to several hundred, are much lower than the critical value Re
kr = 2300. The flow is therefore laminar in nature.
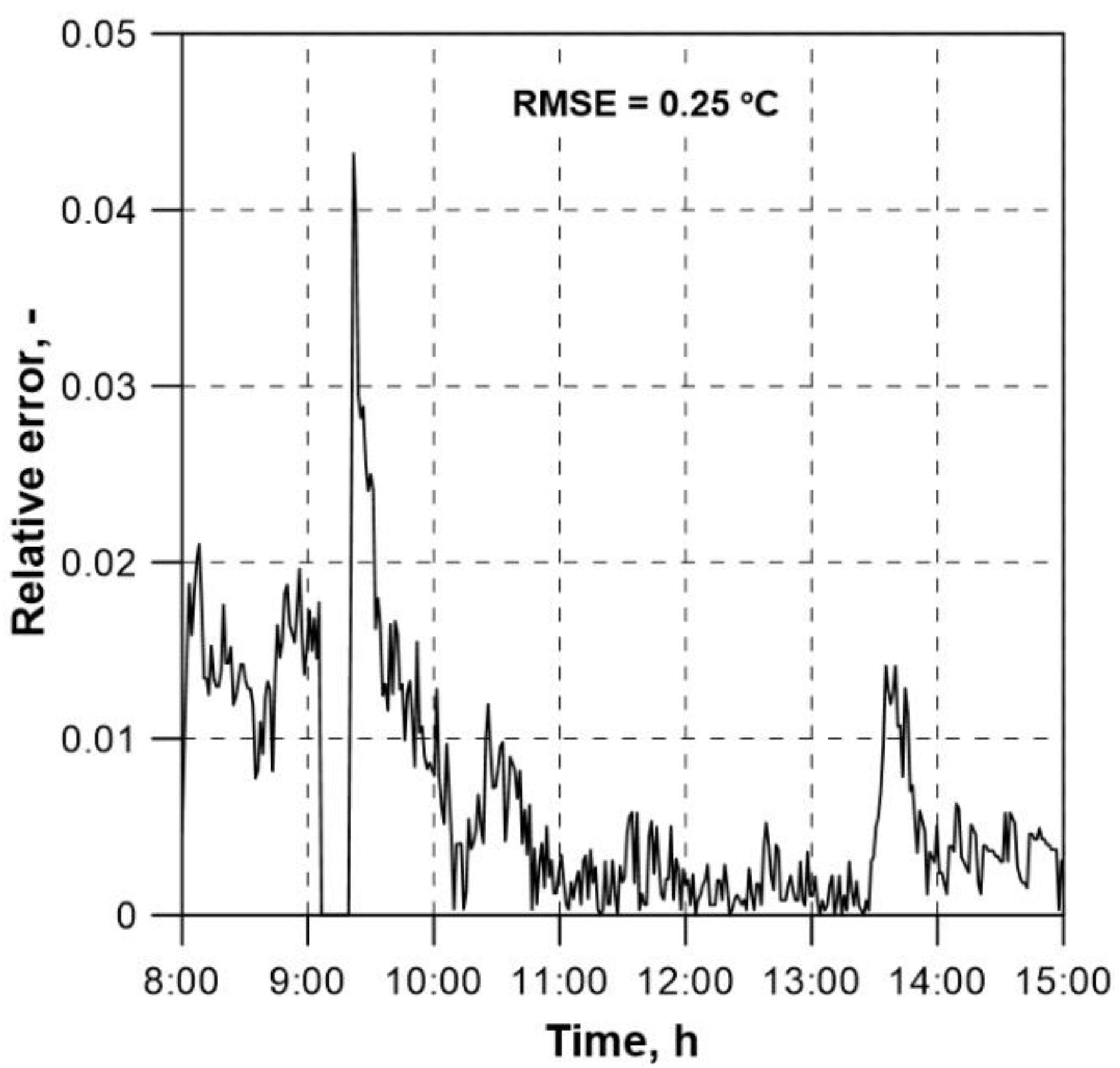
In order to further confirm the correctness of the results obtained from the developed mathematical model, the values of the relative error (RE) and the root-mean-square error (RMSE) are presented in
Figure 10. The values were calculated for the measured and the computed history of the fluid temperature at the collector outlet using the following formulae:
where:
N – number of measurements (N = 2520 measurements, performed every 10s),
tm – measured temperature,
tc – computed temperature.
The low values of the RE and the RMSE in
Figure 10 demonstrate high efficiency of the mathematical model under verification. They confirm the model suitability for simulating the FPSC operation under transient conditions.
The correctness of the proposed approach to the simulation of the transient operation of solar collectors is also confirmed by the mathematical model developed for the parabolic trough collector according to the principles given in section 2. The model is presented in [
36,
37], which also contain the results of the model computational and experimental verification. The versatility of the presented approach is evidenced by the findings presented in [
38], where a similar mathematical model was developed to study the effect of the use of phase-change materials on the performance of a passive solar still. The model was validated using experimental results.
5. Determination of the Collector Time Constant under Outdoor Conditions
Solar collectors always operate under transient conditions, while their thermal tests are very often performed using a stand equipped with a solar radiation simulator. The testing is then realised under steady-state conditions. At the request of manufacturers, specialised institutes and laboratories also carry out thermal tests on a stand placed outdoors using natural solar radiation. In both cases, the testing scope includes determination of thermal efficiency, heat capacity, the time constant and the incidence angle modifier. These quantities should be determined based on the guidelines specified in a relevant ISO standard [
39].
Owing to the fact that fully satisfactory convergence of the measured and the computed history of the fluid temperature at the collector outlet was obtained (see section 4), it is possible to use the developed mathematical model to determine the collector time constant numerically. The time constant is used to analyse the solar collector performance. The result of the time constant numerical computation was compared with the value obtained experimentally on the test stand. In order to confirm the correctness of the obtained values, the time constant numerical and experimental determination was carried out twice.
The procedure for determining the collector time constant is described in a relevant standard [
39], according to which the test should be carried out under outdoor conditions or using a simulator of solar radiation. In either case, the intensity of solar radiation onto the plane of the collector aperture should be higher than 700 W/m
2. At first, the aperture should be shielded from solar radiation using a solar reflective shield. The fluid temperature at the collector inlet should be set to a value almost equal to the ambient air temperature. When the steady state is reached, the shield should be removed and the measurements should be continued until a new steady state.
The following quantities should be measured:
- -
the fluid temperature at the collector inlet (tin),
- -
the fluid temperature at the collector outlet (te),
- -
the ambient air temperature(tam).
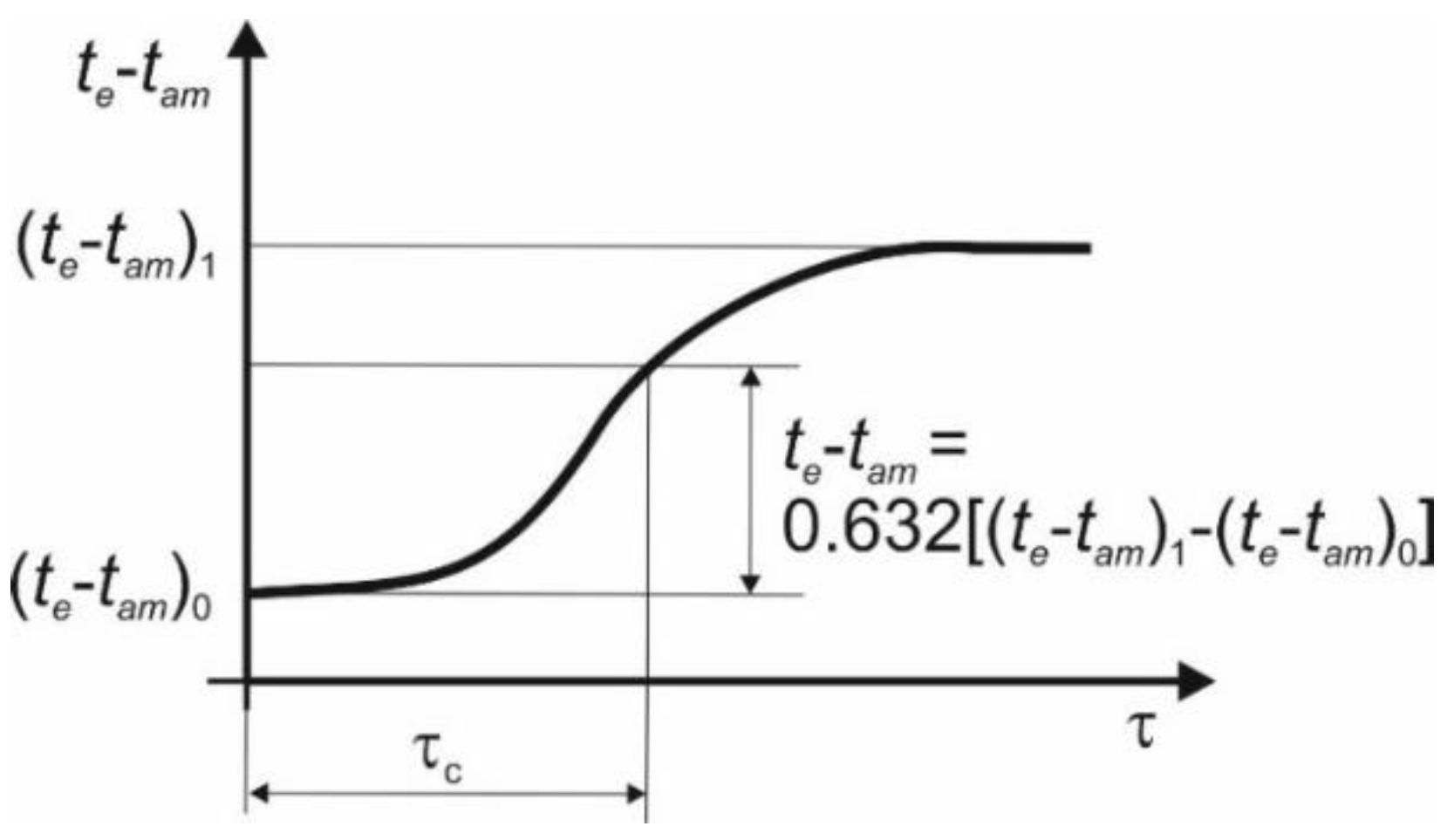
The differences between the fluid temperature at the collector outlet and the temperature of ambient air (
te –
tam) should be plotted as a function of time, starting from the first steady state (
te –
tam)
0 and continuing until the second steady state is reached in a higher temperature (
te –
tam)
1. The differences are shown in
Figure 11.
The collector time constant is defined as the time lasting from the moment the shield is taken off to the moment the temperature at the collector outlet rises by 63.2% of the total increment, from (te – tam)0 to (te – tam)1:
The time constant in this case is the time interval calculated from the moment of a change in a parameter after which the effect of the collector heat capacity on the collector balance can be omitted. In this paper, the parameter is the intensity of solar radiation. The time constant can also be defined as the time after which the collector reaches thermal equilibrium and begins to provide heat for collection in a stable manner, determined by momentary thermal conditions, such as the solar radiation intensity, ambient temperature or the wind speed.
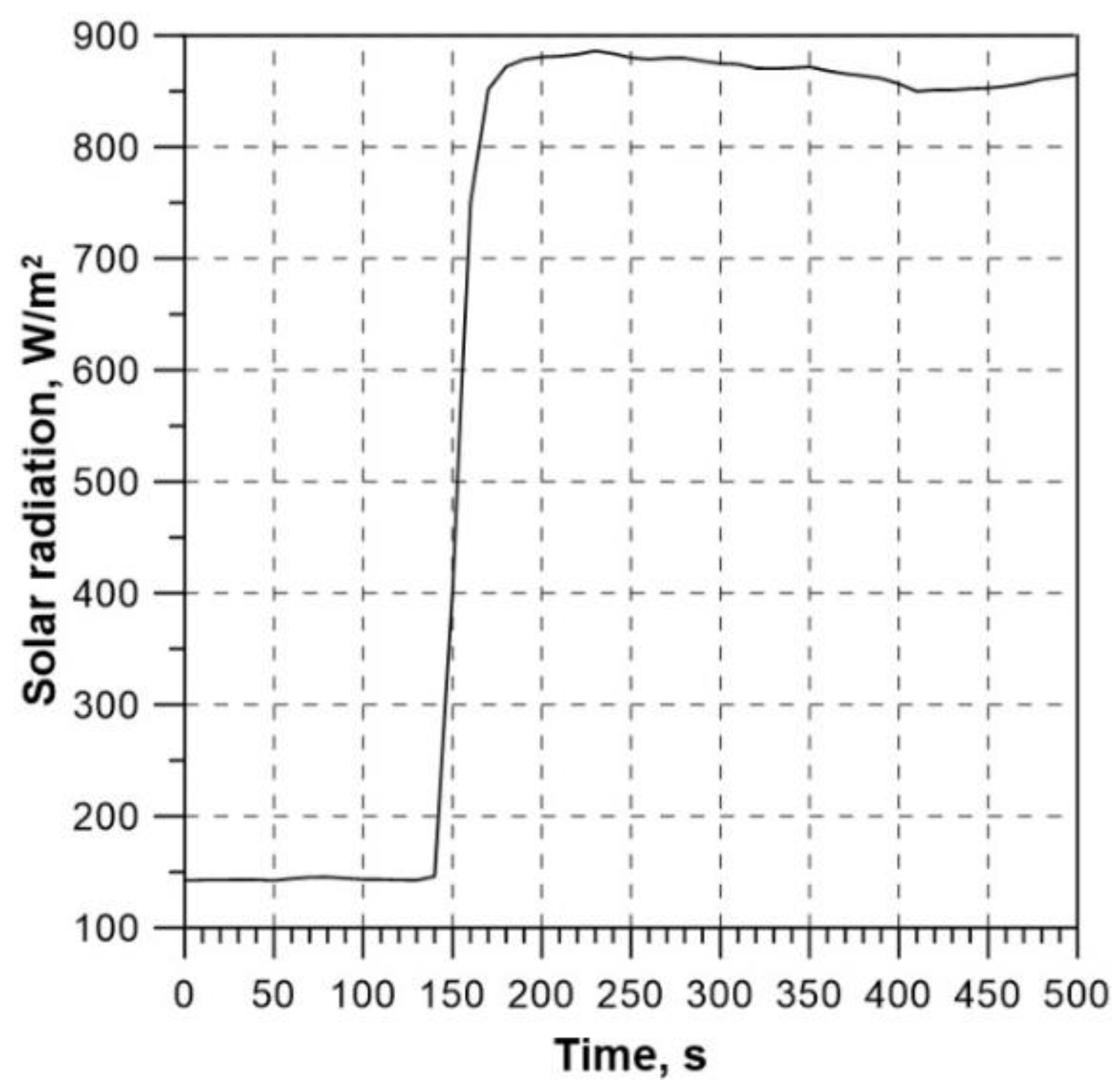
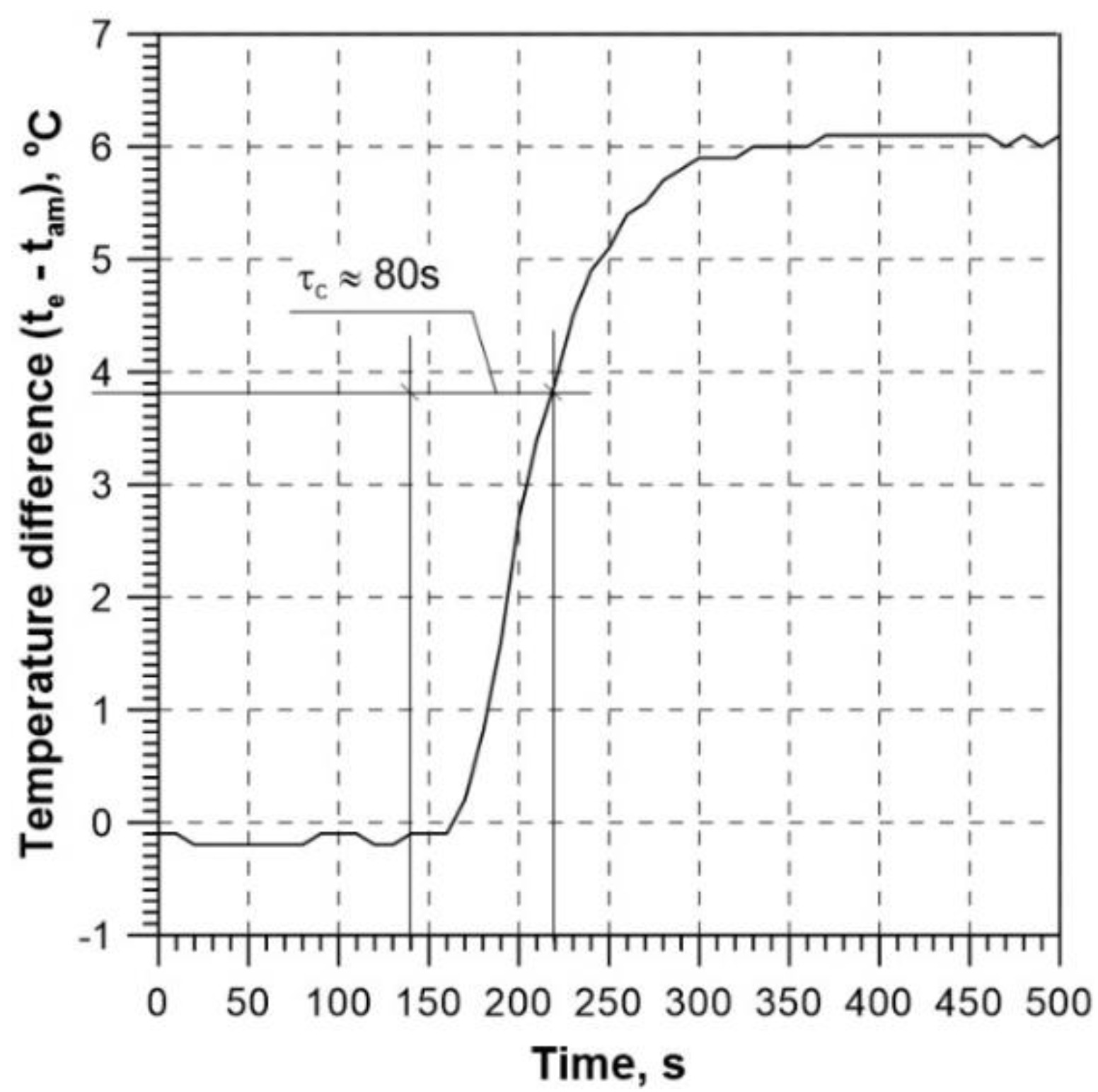
At first, two attempts were made at the time constant experimental determination for the solar collector under analysis. The testing was performed during the summer season in Cracow (Poland). In both cases, the requirements set out in the relevant standard [
39] were satisfied. The results of the first test are presented in
Figure 12 and
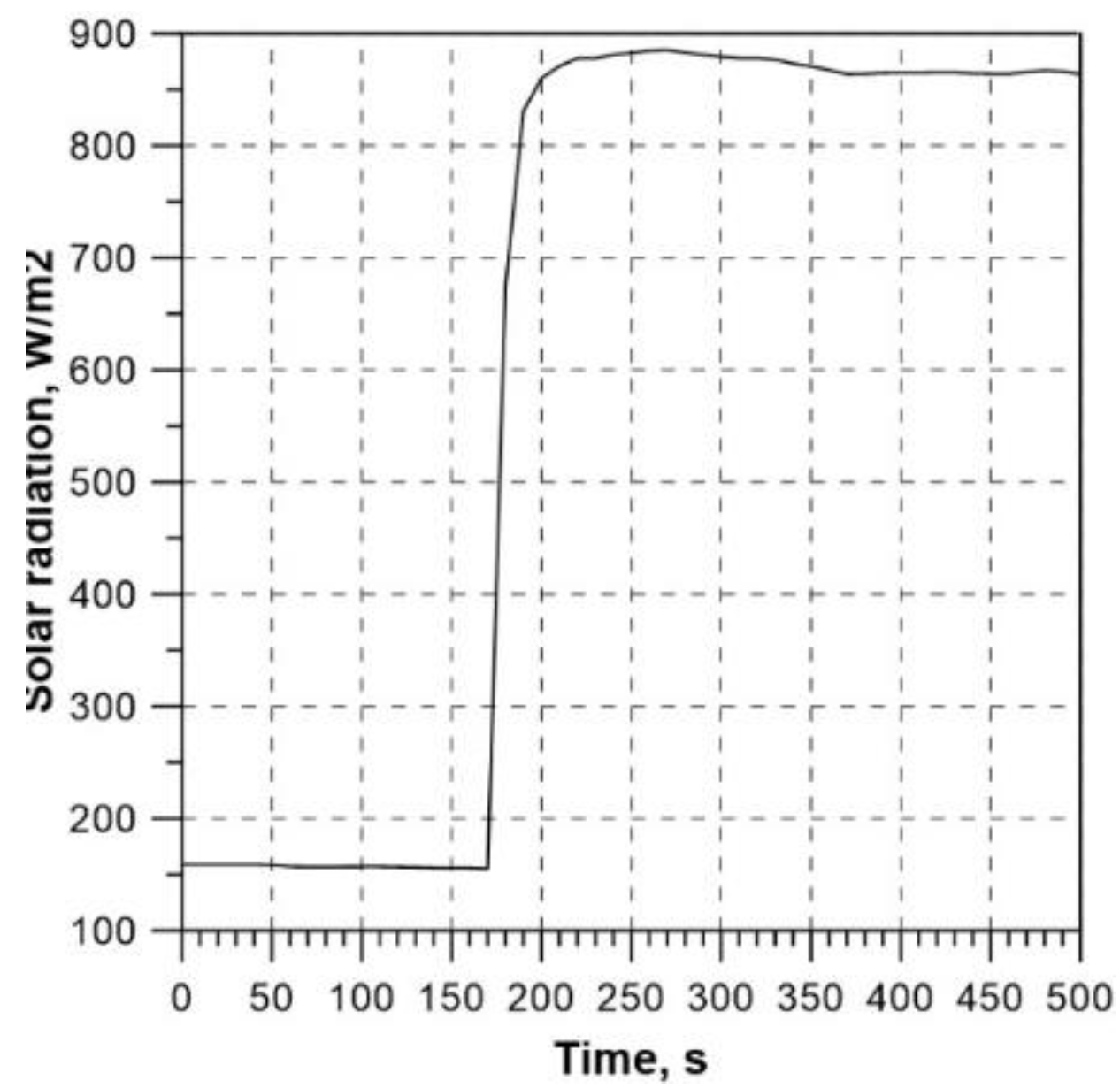
Figure 13. At first, the collector was shielded to reflect solar radiation. After the fluid temperature at the collector inlet became almost equal to the temperature of ambient air (the first steady state), the solar reflective shield was removed. The jump change in the solar radiation intensity due to the shield removal took place in the 140
th second (
Figure 12). As indicated by
Figure 13, the second steady state was reached for the time of about 310 s. The difference between the temperatures of the fluid at the collector outlet and of ambient air at that time totalled about 6
oC.
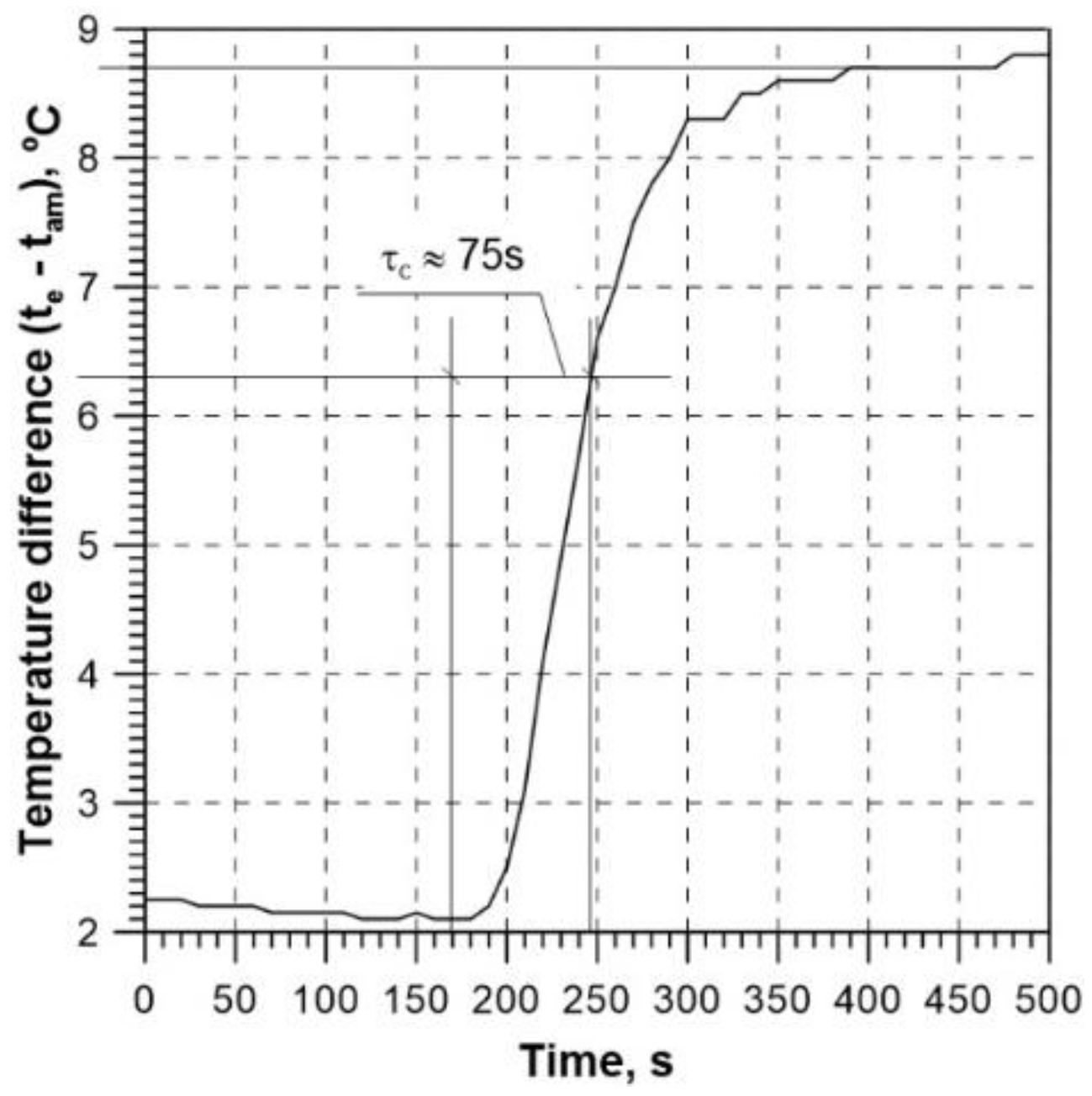
The increment in the temperature difference, to which the collector time constant corresponds, is: te – tam = 0.632 ⋅ [6 – (– 0.1)] = 3.9oC.
Considering the parameters of the first steady state, i.e. (
te –
tam)
0 = – 0.1
oC, the (experimentally determined) time constant thus totals
τc ≈ 80 s (
Figure 13).
In order to confirm this value, the measurements were repeated (test 2) on another day, using the same procedure as before. The results are presented in
Figure 14 and
Figure 15. The jump change in the solar radiation intensity due to the shield removal took place in the 170
th second (
Figure 14).
The increment in the temperature difference, to which the collector time constant corresponds, is (
Figure 15):
te – tam = 0.632 ⋅ (8.7 – 2.1) = 4.2
oC.
Because for the first steady state (
te –
tam)
0 = 2.1
oC, the experimentally determined time constant, read for (
te – tam) = 4.2
oC + 2.1
oC = 6.3
oC, totals
τc ≈ 75 s (
Figure 15). This value is very close to the value determined for the conditions of test 1. The agreement between the results proves the correctness of the testing. The experimentally determined time constant of the analysed collector is therefore about 75 – 80 s.
Below, the results of numerical determination of the collector time constant will be presented as an example of the application of the collector mathematical model. The numerical results are compared with the results of experimental testing. In order to numerically estimate the collector time constant (with the use of the mathematical model), calculations were performed for the above-described conditions of test 1 and test 2.
The following measured histories were the input data for the numerical calculations:
- -
the history of the fluid total volume flow rate,
- -
the history of solar radiation intensity,
- -
the history of the fluid temperature at the collector inlet,
- -
the history of ambient temperature.
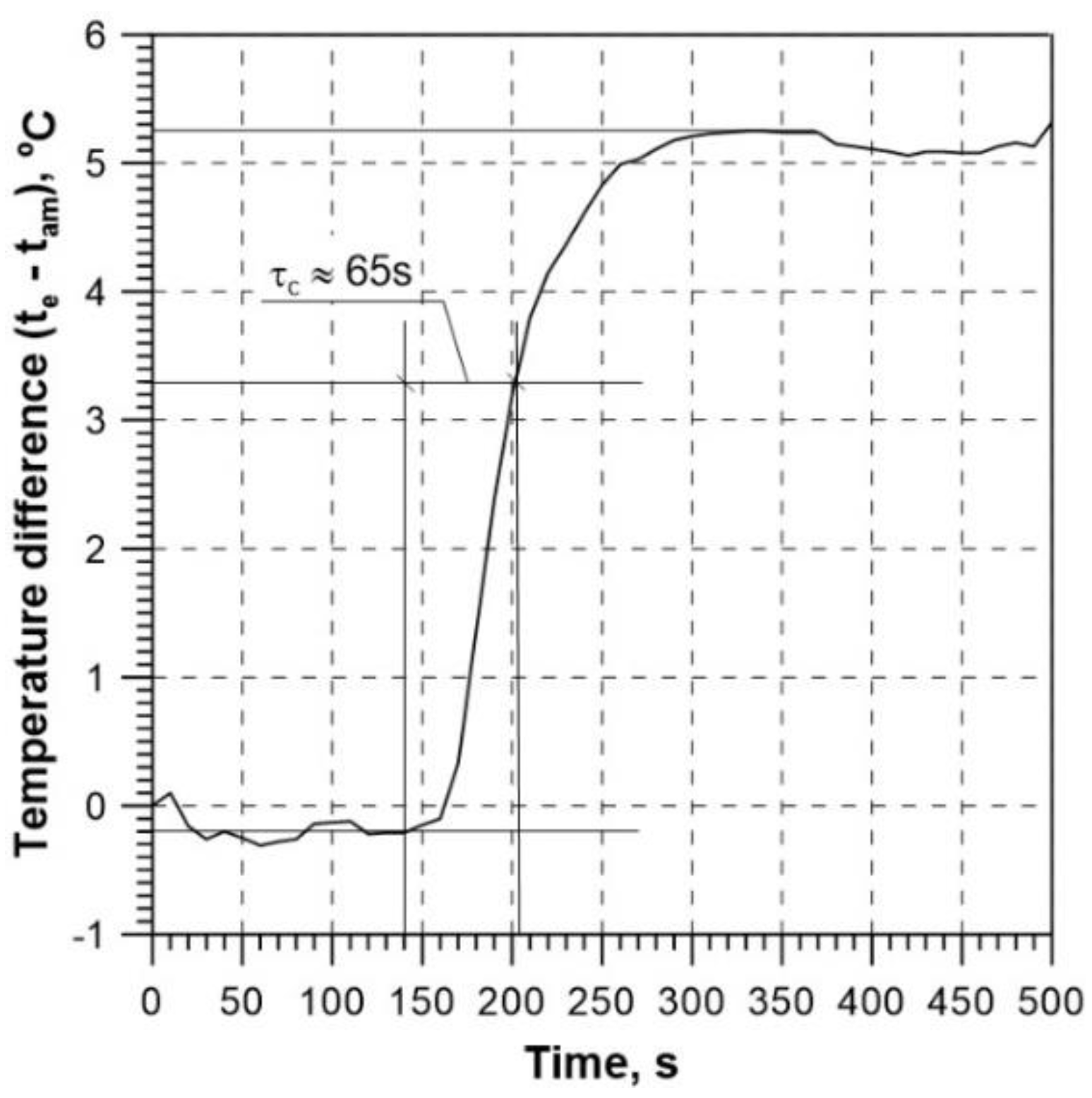
Assuming for the conditions of test 1 that the first steady state took place at the level of about – 0.2
oC (the difference between the fluid temperature at the collector outlet and the ambient temperature) and the second steady state (after the shield was removed) – at the level of 5.3
oC, a time constant of about 65 s was obtained (
Figure 16).
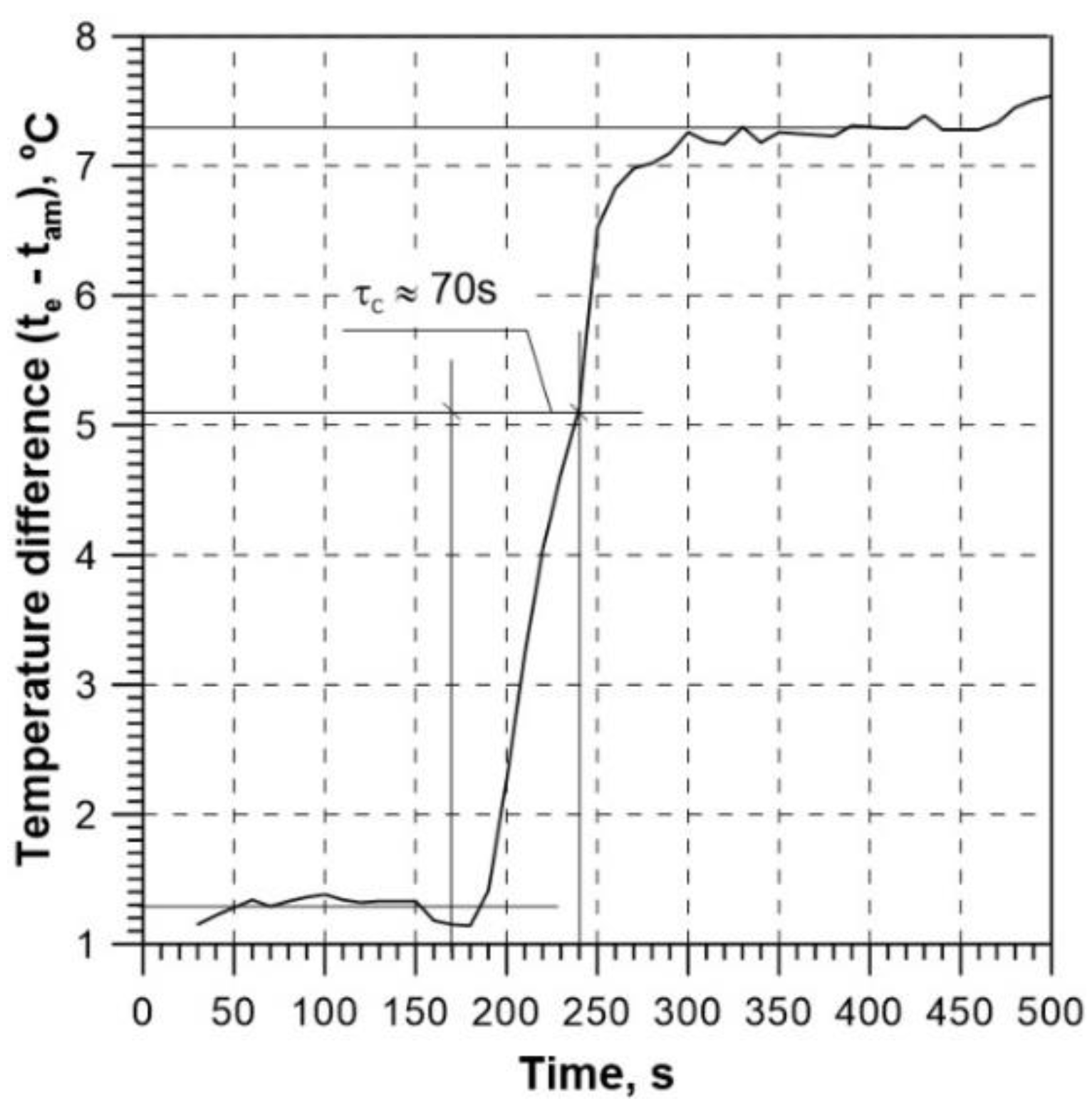
For the conditions of test 2 (
Figure 17), the first steady state was achieved for a temperature difference of about 1.3
oC, and the second – for a temperature difference of about 7.3
oC. The increment in the difference for which the time constant value should be read is thus (taking into account that the initial difference is 1.3
oC):
te – tam = 0.632 ⋅ (7.3 – 1.3) + 1.3 = 5.1
oC.
For this value of the difference between the temperature of the fluid at the collector outlet and the ambient temperature, the collector time constant read from
Figure 17 is about 70 s.
The results of the numerical determination of the collector time constant differ slightly from the time constant determined experimentally. Some differences were to be expected, even due to the fact that the initial conditions adopted in the numerical model differ slightly from the real ones. This mainly relates to the fact that the temperature of the fluid at the collector outlet was calculated using the developed mathematical model, while during the experiment it was measured. Nonetheless, taking account of the very big jump in the intensity of solar radiation that is required for the correct determination of the time constant, the obtained results of numerical calculations can be viewed as satisfactory, and the developed mathematical model can be considered a helpful tool in the case of the FPSC time constant determination.
6. Instantaneous Efficiency of the Collector under Outdoor Conditions
This section presents selected results of measurements and calculations related to the determination of the instantaneous efficiency of the FPSC installed on the test stand.
In order to calculate the collector instantaneous efficiency, the testing should be carried out under conditions meeting the requirements specified in [
39].
The collector instantaneous efficiency should be determined for a steady state. The efficiency is defined as:
where:
Gβ – total intensity of solar radiation reaching the collector surface, W/m2,
Aap – surface area of the collector aperture, m2,
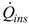
– instantaneous power collected by the fluid flowing through the collector channels, W.
Instantaneous power
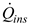
is calculated as:
Substituting expression (11) in formula (10), the following is obtained (steady-state instantaneous efficiency):
The conditions for which it is assumed that the steady state is achieved under outdoor conditions are described by standard [
39]. As specified by the standard, the period of testing steady-state measuring points should include an initial period of at least 15 minutes with an appropriate temperature at the inlet, followed by a period of steady-state measurements of at least 10 minutes. The collector is considered to have operated during the period of measurements under steady-state conditions if, during the measurements, none of the experimental parameters deviated from their mean values by more than the limit value given in
Table 1. In order to determine whether steady-state conditions have occurred, the mean values of each parameter (obtained for another interval of 30 s) should be compared with the mean values of the entire period of the measurements. During the testing, the solar radiation intensity onto the plane of the collector aperture should be higher than 700 W/m
2.
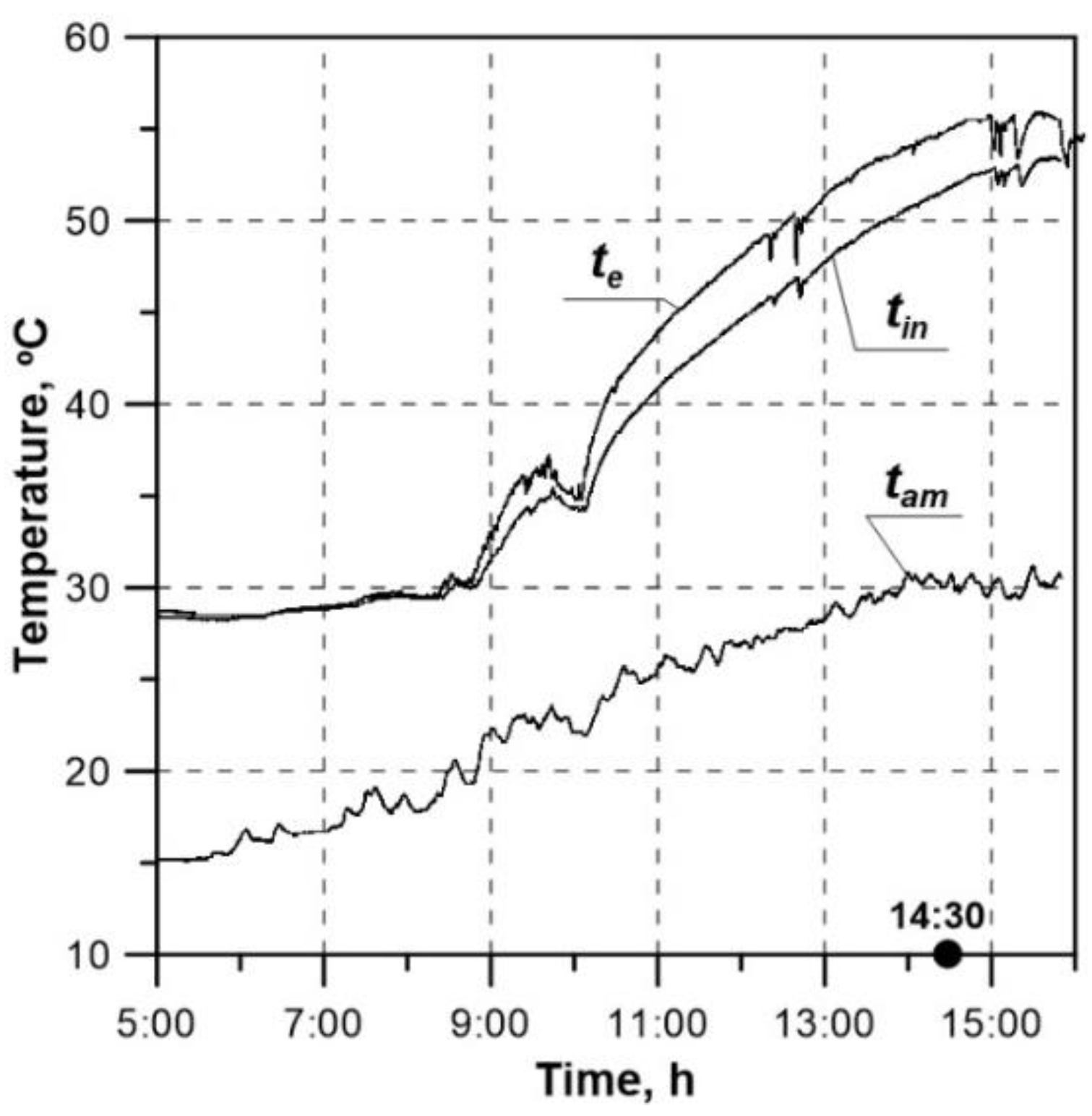
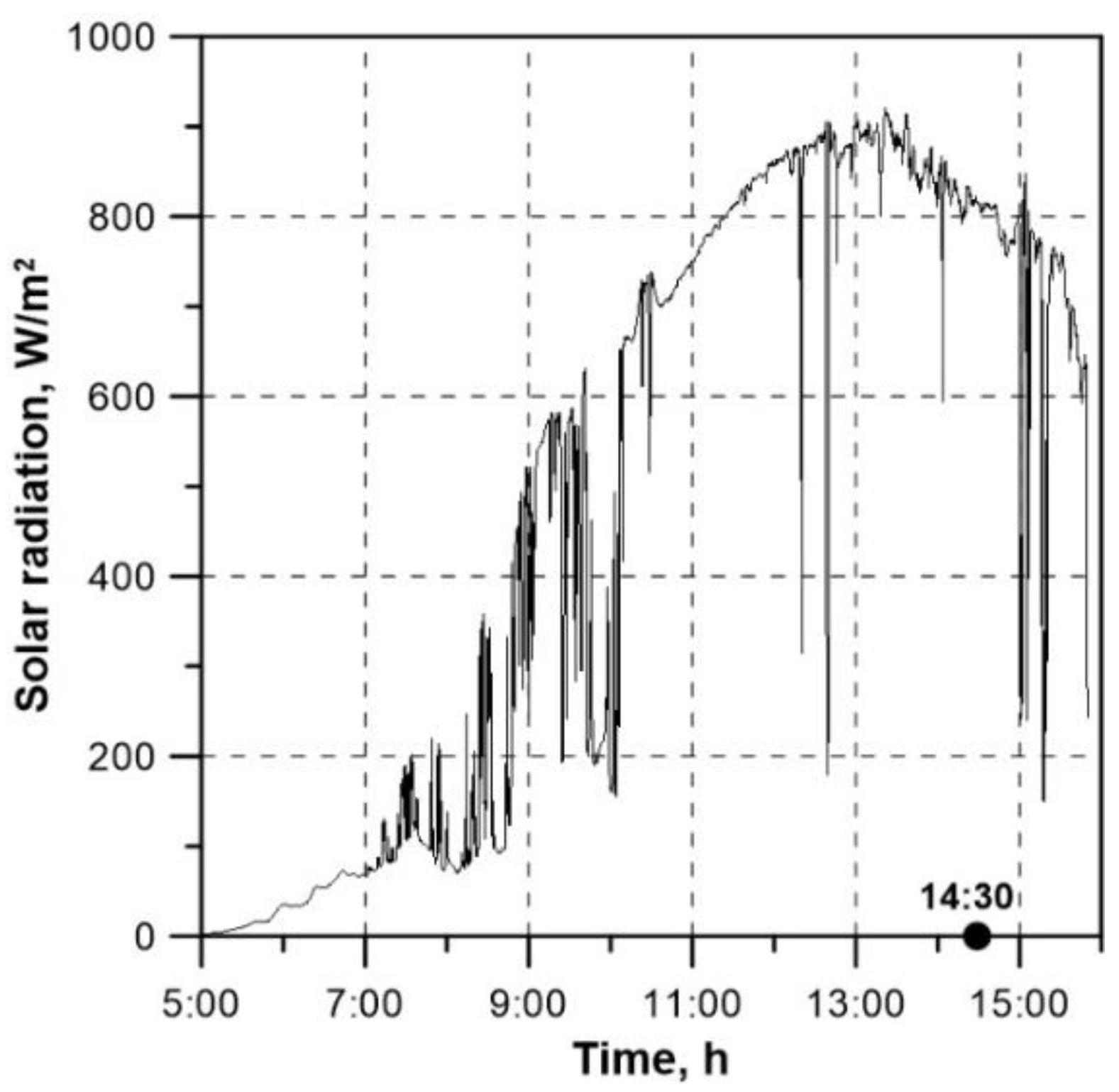
Figure 18 presents measured histories of ambient temperature (
tam) and of the fluid at the collector inlet (
tin) and outlet (
te) for a selected summer day in Cracow. The measured history of the total solar radiation intensity (
Gβ) for the day is illustrated in
Figure 19. The measurements cover the period from 5 a.m. to 4 p.m.
Based on the measurements, it was found that the requirements specified in the above-mentioned standard were satisfied at about 2.30 p.m. The collector instantaneous efficiency calculated using formula (12) was
η = 79.6 %. The calculations were carried out for the collector aperture surface area of
Aap = 1.83 m
2 and for the measured volume flow rate
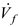
= 6.03 l/min (mass flow rate
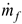
= 0.1027 kg/s).
Moreover, in order to establish the collector heat losses through the casing:
the following quantities were determined:
the collector optical losses:
The individual components of formula (13) for the analysed steady state total:
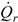
= 1485.6 W (for
Gβ = 811.8 W/m
2),
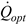
= 215.4 W (for the transmission-absorption coefficient
τα = 0.9⋅0.95 = 0.855),
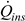
= 1183.1 W (for
cf = 3600 J/(kgK),
tin = 52
oC and
te = 55.2
oC),
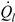
= 87.1 W.
Moreover, using the following relation:
the maximum measuring error was determined (one-off measurement) with the probability of 0.999. The measurements of the fluid mass flow rate
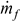
and of solar radiation intensity
Gβ were performed with the accuracy of ± 0.1 % of the measuring range. The measurement of the difference in the fluid temperature Δ
tf = (
te –
tin) was performed using error compensation of Pt100 sensors at both measuring points. The accuracy of the measurement in this case totalled ± 0.1
oC. This means that it was higher than the accuracy of a single Pt100 input, which is ± 0.5
oC. The maximum error calculated for the above data is 0.032. The collector real instantaneous efficiency thus totalled
ηins =
η + Δηmax = 79.6 % ± 3.2 %.
7. Conclusions
The paper presents a proposal for an in-house mathematical model of a liquid flat-plate solar collector enabling simulation of the collector transient-state operation. Differential equations, being the energy balance equations for all components of the collector, were formulated. Time and space derivatives were approximated using appropriate difference schemes. In this way, a one-dimensional distributed parameter model was obtained. From the perspective of the stability of numerical solutions, the important issue is the adoption of appropriate values of the time and spatial division steps. For this purpose, the analytical solution for the transient state, which takes account of the forcing of heating on the tube outer surface, was used. The established values of steps Δτ and Δz were then applied for experimental verification consisting in comparing the calculated and the measured history of the fluid temperature at the collector outlet. Fully satisfactory agreement between the histories was obtained, which is confirmed by low RE values and the RMSE (0.25 oC). An example of the model application was the presented determination of the collector time constant. The values of the time constant obtained for two cases were compared with the values determined experimentally. Satisfactory agreement was found between the results. The values of the time constant determined numerically and experimentally totalled about 65-70 s and about 75-80 s, respectively. The collector efficiency calculated next was 79.6 % ± 3.2 %. It should be noted that the efficiency value is high, but only momentary. It was calculated for the angle of the solar radiation falling on the receiver surface, measured between the direction of direct radiation and the normal to the receiver, of 30.7o. The radiation incidence angle was calculated using the formulae available in the literature, which is not presented in the paper.
The proposed mathematical model can prove useful in many cases, making it possible to simulate the obtained thermal and flow parameters without the need to carry out tests on real facilities. The collector time constant analysed in the paper can serve as an example. The model can also be used successfully to analyse the effectiveness of the application of the absorber new coatings, new collector covers (replacing traditional solar glass covers) or various nanofluids. For the collector user, the model can be useful in the diagnostics of the device correct operation. Systematic comparison of the fluid temperature measured at the collector outlet with the results of numerical computations makes it possible to draw conclusions about the technical state of the collector and the working fluid. If the values obtained from the fluid temperature measurement are lower than the numerical results, this may be the effect of fouling of the outer surface of the solar panel glass cover, or of deterioration in the fluid thermophysical properties due to glycol gelling or reduced efficiency of the absorber. The model can also be useful at the design stage of entire solar systems by making it possible to establish the necessary number of collectors, the fluid optimal volume flow rate or the appropriate arrangement of tubes inside the collector.
Further works on the mathematical model expansion may for example consider two solar glass covers to reduce the collector heat losses to the environment. The works presented in the paper were limited to the analysis of flows through parallel channels. However, the proposed model can also be used successfully for serpentine solar collectors. The serpentine arrangement of tubes is a common practice. Appropriate formulation of the energy balance equations also makes it possible to apply the model to concentrating and air collectors.
Author Contributions
Conceptualization, W.Z.; methodology, W.Z. and Ł.M.; software, K.S.; validation, W.Z., Ł.M. and K.S.; formal analysis, W.Z.; investigation, Ł.M. and K.S.; data curation, W.Z. and K.S.; writing - original draft preparation, W.Z.; writing - review and editing, W.Z., Ł.M. and K.S.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sharma, R.; Shahbaz, M.; Kautish, P.; Vo, X.V. Does energy consumption reinforce environmental pollution? Evidence from emerging Asian economies. Journal of Environmental Management 2021, 297, 113272. [CrossRef]
- Song, M.; Xu, H.; Shen, Z.; Pan, X. Energy market integration and renewable energy development: Evidence from the European Union countries. Journal of Environmental Management 2022, 317, 115464. [CrossRef]
- Estevão, J.; Lopes, J.D. SDG7 and renewable energy consumption: The influence of energy sources. Technological Forecasting & Social Change 2024, 198, 123004. [CrossRef]
- Lamnatou, Chr.; Cristofari, C,; Chemisana, D. Renewable energy sources as a catalyst for energy transition: Technological innovations and an example of the energy transition in France. Renewable Energy 2024, 221, 119600. [CrossRef]
- Kędzierski, A.; Bielecki, S. Comparative analysis of selected prosumer renewable energy solutions for a single-family residential house (in Polish). Rynek Energii 2023, 2(165), 23–33.
- Chopra, K.; Pathak, P.K.; Samykano, M.; Tyagi, V.V.; Pandey, A.K. Recent Advancements in Design of Flat Plate Solar Collectors. IOP Conference Series: Materials Science and Engineering 2021, 1127, 012007. [CrossRef]
- Pandey, K.M.; Chaurasiya, R. A review on analysis and development of solar flat plate collector. Renewable and Sustainable Energy Reviews 2017, 67, 641–650. [CrossRef]
- Zheng, J.; Febrer, R.; Castro, J.; Kizildag, D.; Rigola, J. A new high-performance flat plate solar collector. Numerical modelling and experimental validation. Applied Energy 2024, 355, 122221. [CrossRef]
- Shemelin, V.; Matuška, T. Quantitative review on recent developments of flat-plate solar collector design. Part 1: Front-side heat loss reduction. Energy Reports 2023, 9, 64–69. [CrossRef]
- He, Y.; Yu, H.; Duan, G.; Wang, Y.; Yang, Q.; Feng, L.; Zhang, J. Thermal performance and experimental analysis of stainless steel flat plate solar collector with full-flow channels. Heliyon 2024, 10, e28255. [CrossRef]
- Mohseni-Gharyehsafa, B.; Esfahani, J.A.; Kim, K.Ch.; Ouerdane, H. Soft computing analysis of thermohydraulic enhancement using twisted tapes in a flat-plate solar collector: Sensitivity analysis and multi-objective optimization. Journal of Cleaner Production 2021, 314, 127947. [CrossRef]
- Abdelnour, N.; Braun, R.; Torio, H.; Eicker, U. Testing of uncovered solar thermal collectors under dynamic conditions and identification of performance parameters - for nocturnal radiative cooling applications. Solar Energy Advances 2023, 3, 100038. [CrossRef]
- Ajeena, A.M.; Farkas, I.; Víg, P. Performance enhancement of flat plate solar collector using ZrO2-SiC/DW hybrid nanofluid: A comprehensive experimental study. Energy Conversion and Management: X 2023, 20, 100458. [CrossRef]
- Ajeena, A.M.; Farkas, I.; Víg, P. Energy and exergy assessment of a flat plate solar thermal collector by examine silicon carbide nanofluid: An experimental study for sustainable energy. Applied Thermal Engineering 2024, 236, 121844. [CrossRef]
- Struchalin, P.G.; Zhao, Y.; Balakin, B.V. Field study of a direct absorption solar collector with eco-friendly nanofluid. Applied Thermal Engineering 2024, 243, 122652. [CrossRef]
- Huminic, G.; Huminic A. Capabilities of advanced heat transfer fluids on the performance of flat plate solar collector. Energy Reports 2024, 11, 1945–1958. [CrossRef]
- Hamdan, M.; Abdelhafez, E.; Ajib, S.; Sukkariyh, M. Improving Thermal Energy Storage in Solar Collectors: A Study of Aluminum Oxide Nanoparticles and Flow Rate Optimization. Energies 2024, 17, 276. [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar engineering of thermal processes, 3rd edition, 2006 (Wiley Interscience, New York).
- Cadafalch, J. A detailed numerical model for flat-plate solar thermal devices. Solar Energy 2009, 83, 2157–2164. [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar engineering of thermal processes, 2nd edition, 1991 (Wiley Interscience, New York).
- Cerón, J.F.; Pérez-García, J.; Solano, J.P.; García, A.; Herrero-Martín, R. A coupled numerical model for tube-on-sheet flat-plate solar liquid collectors. Analysis and validation of the heat transfer mechanisms. Applied Energy 2015, 140, 275–287. [CrossRef]
- Zhou, L.; Wang, Y.; Huang, Q. CFD investigation of a new flat plate collector with additional front side transparent insulation for use in cold regions. Renewable Energy 2019, 138, 754–763. [CrossRef]
- Maji, A.; Deshamukhya, T.; Choubey, G. Numerical investigation and optimisation of flat plate solar collectors using two swarm-based metaheuristic algorithms. Engineering Analysis with Boundary Elements 2023, 156, 78–89. [CrossRef]
- Quitiaquez, W.; Estupiñán-Campos, J.; Nieto-Londoño, C.; Quitiaquez, P. CFD Analysis of Heat Transfer Enhancement in a Flat-Plate Solar Collector/Evaporator with Different Geometric Variations in the Cross Section. Energies 2023, 16, 5755. [CrossRef]
- Alawi, O.A.; Kamar, H.M.; Salih, S.Q.; Abba, S.I.; Ahmed, W.; Homod, R.Z.; Jamei, M.; Shafik, S.S.; Yaseen, Z.M. Development of optimized machine learning models for predicting flat plate solar collectors thermal efficiency associated with Al2O3-water nanofluids. Engineering Applications of Artificial Intelligence 2024, 133, 108158. [CrossRef]
- Kalogirou, S.A. Prediction of flat-plate collector performance parameters using artificial neural networks. Solar Energy 2006, 80, 248–259. [CrossRef]
- Chilambarasan, L.; Thangarasu, V.; Ramasamy, P. Solar flat plate collector's heat transfer enhancement using grooved tube configuration with alumina nanofluids: Prediction of outcomes through artificial neural network modelling. Energy 2024, 289, 129953. [CrossRef]
- Al-Tabbakh, A.A. Numerical transient modeling of a flat plate solar collector. Results in Engineering 2022, 15, 100580. [CrossRef]
- Freegah, B.; Alkhafaji, M.H.; Alhamdo, M.H. Study the thermal response of a solar flat-plate collector under transient solar radiation experimentally and numerically. Journal of Engineering Research 2024, In Press. [CrossRef]
- Zima, W.; Dziewa, P. Modelling of liquid flat-plate solar collector operation in transient states. Proc. Inst. Mech. Eng. Part A J. Power Energy 2011, 225, 53–62. [CrossRef]
- Gerald, C.F.; Wheatley, P.O. Applied Numerical Analysis; Addison-Wesley Publishing Company: New York, NY, USA, 1994.
- Serov, E. P. and Korolkov, B. P. Dynamics of steam generators (in Russian), 1981 (Energia, Moscow).
- Zima, W.; Dziewa, P. Mathematical modelling of heat transfer in liquid flat-plate solar collector tubes. Archives of Thermodynamics. Vol. 31(2010), No. 2, 45–62.
- Pluta, Z. Fundamentals of solar energy thermal conversion (in Polish); Warsaw University of Technology: Warszawa, Poland, 2000.
- Fortran PowerStation 4.0. Microsoft Developer Studio; Microsoft Corporation, 1995.
- Zima, W.; Cebula, A.; Cisek, P. Mathematical Model of a Sun-Tracked Parabolic Trough Collector and Its Verification. Energies 2020, 13, 4168. [CrossRef]
- Zima, W.; Cisek, P., Cebula, A. Mathematical model of an innovative double U-tube sun-tracked PTC and its experimental verification. Energy 2021, 235, 121293. [CrossRef]
- Radomska, E.; Mika, Ł.; Sztekler, K.; Kalawa, W.; Lis, Ł.; Pielichowska, K.; Szumera, M.; Rutkowski, P. Experimental and Theoretical Investigation of Single-Slope Passive Solar Still with Phase-Change Materials. Energies 2023, 16, 1188. [CrossRef]
- International Standard ISO 9806, Solar energy – Solar thermal collectors – Test Methods.
Figure 1.
FPSC control volume.
Figure 1.
FPSC control volume.
Figure 2.
Comparison of dimensionless histories of the fluid temperature increments.
Figure 2.
Comparison of dimensionless histories of the fluid temperature increments.
Figure 3.
View of the collector with a pyranometer on the test stand.
Figure 3.
View of the collector with a pyranometer on the test stand.
Figure 4.
Measured history of the fluid volume flow rate at the collector inlet.
Figure 4.
Measured history of the fluid volume flow rate at the collector inlet.
Figure 5.
Measured history of total solar radiation intensity.
Figure 5.
Measured history of total solar radiation intensity.
Figure 6.
Comparison between the measured and the calculated history of the fluid temperature at the collector outlet, and measured histories of the fluid temperature at the collector inlet and of ambient temperature.
Figure 6.
Comparison between the measured and the calculated history of the fluid temperature at the collector outlet, and measured histories of the fluid temperature at the collector inlet and of ambient temperature.
Figure 7.
Fragment of
Figure 6 for better visualisation of the time interval with the biggest changes in the measured values of the fluid temperature at the collector outlet.
Figure 7.
Fragment of
Figure 6 for better visualisation of the time interval with the biggest changes in the measured values of the fluid temperature at the collector outlet.
Figure 8.
Calculated temperature histories of the collector individual nodes in cross-section 48 (L = 0.94 m).
Figure 8.
Calculated temperature histories of the collector individual nodes in cross-section 48 (L = 0.94 m).
Figure 9.
Calculated histories of the heat transfer coefficient on the collector tube inner surface.
Figure 9.
Calculated histories of the heat transfer coefficient on the collector tube inner surface.
Figure 10.
History of the RE values and the RMSE for the fluid temperature at the collector outlet.
Figure 10.
History of the RE values and the RMSE for the fluid temperature at the collector outlet.
Figure 11.
Determination of the collector time constant τc.
Figure 11.
Determination of the collector time constant τc.
Figure 12.
Time-dependent changes in the measured solar radiation intensity (test 1).
Figure 12.
Time-dependent changes in the measured solar radiation intensity (test 1).
Figure 13.
Time-dependent changes in the measured difference between the temperature of the fluid at the collector outlet and the temperature of ambient air, along with the determined time constant of the collector (test 1).
Figure 13.
Time-dependent changes in the measured difference between the temperature of the fluid at the collector outlet and the temperature of ambient air, along with the determined time constant of the collector (test 1).
Figure 14.
Time-dependent changes in the measured solar radiation intensity (test 2).
Figure 14.
Time-dependent changes in the measured solar radiation intensity (test 2).
Figure 15.
Time-dependent changes in the measured difference between the temperature of the fluid at the collector outlet and the temperature of ambient air, along with the determined time constant of the collector (test 2).
Figure 15.
Time-dependent changes in the measured difference between the temperature of the fluid at the collector outlet and the temperature of ambient air, along with the determined time constant of the collector (test 2).
Figure 16.
Time-dependent changes in the calculated difference between the temperature of the fluid at the collector outlet and the measured temperature of ambient air, along with the collector time constant determined for the conditions of test 1.
Figure 16.
Time-dependent changes in the calculated difference between the temperature of the fluid at the collector outlet and the measured temperature of ambient air, along with the collector time constant determined for the conditions of test 1.
Figure 17.
Time-dependent changes in the calculated difference between the temperature of the fluid at the collector outlet and the measured temperature of ambient air, along with the collector time constant determined for the conditions of test 2.
Figure 17.
Time-dependent changes in the calculated difference between the temperature of the fluid at the collector outlet and the measured temperature of ambient air, along with the collector time constant determined for the conditions of test 2.
Figure 18.
Measured histories of the fluid temperature at the collector inlet (tin) and outlet (te) and of ambient temperature (tam).
Figure 18.
Measured histories of the fluid temperature at the collector inlet (tin) and outlet (te) and of ambient temperature (tam).
Figure 19.
Measured history of total solar radiation intensity Gβ.
Figure 19.
Measured history of total solar radiation intensity Gβ.
Table 1.
Permitted deviation of measured parameters during the measurement period [
39].
Table 1.
Permitted deviation of measured parameters during the measurement period [
39].
| Parameter |
Deviation from the mean value |
| Total solar radiation intensity |
± 50 W/m2
|
| Ambient air temperature |
± 1 K |
| Fluid mass flow rate |
± 1 % |
| Fluid temperature at the collector inlet |
± 0.1 K |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
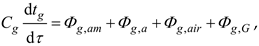
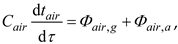
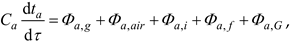
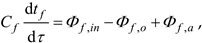
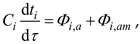
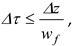
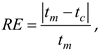
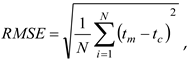
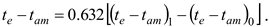
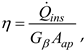
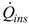 – instantaneous power collected by the fluid flowing through the collector channels, W.
– instantaneous power collected by the fluid flowing through the collector channels, W.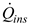 is calculated as:
is calculated as: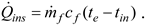
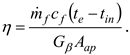
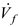 = 6.03 l/min (mass flow rate
= 6.03 l/min (mass flow rate 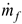 = 0.1027 kg/s).
= 0.1027 kg/s).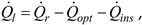
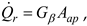
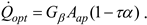
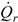 = 1485.6 W (for Gβ = 811.8 W/m2),
= 1485.6 W (for Gβ = 811.8 W/m2),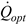 = 215.4 W (for the transmission-absorption coefficient τα = 0.9⋅0.95 = 0.855),
= 215.4 W (for the transmission-absorption coefficient τα = 0.9⋅0.95 = 0.855),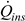 = 1183.1 W (for cf = 3600 J/(kgK), tin = 52oC and te = 55.2oC),
= 1183.1 W (for cf = 3600 J/(kgK), tin = 52oC and te = 55.2oC),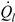 = 87.1 W.
= 87.1 W.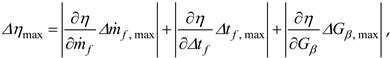
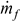 and of solar radiation intensity Gβ were performed with the accuracy of ± 0.1 % of the measuring range. The measurement of the difference in the fluid temperature Δtf = (te – tin) was performed using error compensation of Pt100 sensors at both measuring points. The accuracy of the measurement in this case totalled ± 0.1oC. This means that it was higher than the accuracy of a single Pt100 input, which is ± 0.5oC. The maximum error calculated for the above data is 0.032. The collector real instantaneous efficiency thus totalled ηins = η + Δηmax = 79.6 % ± 3.2 %.
and of solar radiation intensity Gβ were performed with the accuracy of ± 0.1 % of the measuring range. The measurement of the difference in the fluid temperature Δtf = (te – tin) was performed using error compensation of Pt100 sensors at both measuring points. The accuracy of the measurement in this case totalled ± 0.1oC. This means that it was higher than the accuracy of a single Pt100 input, which is ± 0.5oC. The maximum error calculated for the above data is 0.032. The collector real instantaneous efficiency thus totalled ηins = η + Δηmax = 79.6 % ± 3.2 %.