Raingauge vs IMERG Precipitation Data: Balancing Accuracy and Cost for a Reliable Hydrological Observatory in a Tropical River Basin

Reliable hydrological monitoring is crucial for effective water resource management, but establishing observatories in remote areas with extreme weather presents significant challenges. This study aimed at identifying cost-effective methods for streamflow estimation in such environments. We evaluated the performance of the Soil and Water Assessment Tool (SWAT) model using various precipitation data sources: ground-based rain gauge networks with different densities (one-gauge (1RG), two-gauge (2RG), and five-gauge (5RG) configurations) and satellite-derived Integrated Multi-satellite Retrievals for GPM (IMERG) data. The study focused on the Sahafihitry catchment, a 200 km² area in northeastern Madagascar. The results demonstrated that denser rain gauge networks (5RG and 2RG) captured the spatial variability of rainfall more effectively than a single gauge or IMERG data. This translated into superior SWAT model performance. Denser networks achieved higher statistical metrics (R², slope of regression a, Nash-Sutcliffe efficiency NSE, root mean square error RMSE, Kling-Gupta efficiency KGE) indicating a better fit between simulated and observed streamflow. Specifically, 5RG: R² = 0.84, a = 0.92, NSE = 0.83, RMSE = 3.33, KGE = 0.82; 2RG: R² = 0.85, a = 0.95, NSE = 0.83, RMSE = 3.36, KGE = 0.88; 1RG: R² = 0.73, a = 0.80, NSE = 0.72, RMSE = 4.28, KGE = 0.88; IMERG: R² = 0.48, a = 0.63, NSE = 0.37, RMSE = 6.46, KGE = 0.66. Furthermore, rain gauge data outperformed IMERG in simulating both flood events and low-flow periods. While IMERG offers low cost, readily available data, its lower performance introduces significant uncertainty into hydrological modeling. In contrast, the two-gauge network (2RG) achieved satisfactory streamflow simulations and represents the most cost-effective option for establishing reliable observatories within the specific characteristics of this study area.

Keywords:

Subject: Environmental and Earth Sciences - Remote Sensing

1. Introduction

The establishment of a reliable hydrological monitoring system is crucial for many applications, such as drought monitoring, flood prevention, water balance calculations and water resources management [1]. When properly installed and maintained, such monitoring systems can provide precise real-time data on hydrological variables, including precipitation, river discharge, and ground water levels [2]. However, given the high costs of maintaining accurate measurement networks, the implementation of such an observatory remains challenging, particularly in remote and hard-to-access sub-tropical regions that experience extreme weather conditions (WMO 2022, 1987 ; Sivakumar 2017; Sivapalan et al. 2003). These challenges are further exacerbated by the risk of infrastructure damage as well as insufficient public involvement in water resources monitoring, resulting in limited, fragmented, and discontinuous hydrological monitoring networks that impede a comprehensive understanding of the hydrological processes and hinder proper water resources management. Therefore, it is increasingly urgent to design easy-to-maintain and cost-effective observation systems that minimize field interventions while ensuring reliable operation of hydrological observatories.

Recent advances in remote sensing techniques have led to the emergence of satellite-based, data reanalysis-based, model-based products as a potential solution to meet the needs of hydrological observatories [7,8]. They offer an attractive alternative, especially to ground-based rain gauges [3]. Among recent satellite-based gridded precipitation products, the Global Precipitation Measurement Integrated Multi-satellitE Retrievals GPM IMERG v06 Final has garnered much attention due to its 20-year availability of precipitation data, fine spatial resolution (0.1° x 0.1° or ~11 x ~11 km²), and high temporal resolution (30 min) compared to other products (Huffman et al. 2020). Given their characteristics, IMERG products appear to be suitable data sources for forcing rainfall-runoff models used in a variety of hydrological applications, such as extreme event analysis and water resources management [9,10,11].

Despite their high potential, IMERG products are subject to errors arising from various factors, such as the nature of the precipitation measurement [12], sampling uncertainties [13], retrieval algorithms, and variations in land surface properties [14]. Furthermore, since IMERG incorporates ground-based rainfall measurements from the Global Precipitation Climatology Center (GPCC) through its multi-satellite algorithms, the product may be affected by greater uncertainties in tropical areas where there is a limited availability of rain gauges for calibration or validation [15]. In addition, several researchers have highlighted the limitations of IMERG, which include low accuracy representation of the spatial variability of rainfall, as well as both overestimation and underestimation of certain rainfall classes depending on the study area [16,17]. Despite these limitations, the research community continues to explore the applications of IMERG in the hydrological domain, especially in countries with poor rainfall monitoring networks.

While a significant amount of research has been conducted to quantify errors in IMERG products (e.g., Derin et al. 2021; Dezfuli et al. 2017), limited attention has been paid to understanding the implications of these errors on rainfall-runoff model forecasts. As hydrological models exhibit strong nonlinearity, errors in precipitation measurements can greatly affect the accuracy of flood simulations. The extent of this impact is contingent on the quality of input data and the interplay between different components of the model [20]. For instance, some studies indicate that, conditional upon recalibrating the hydrological model, IMERG can produce satisfactory flow simulations [10,18]. Some research even suggests that IMERG can be as effective as using ground-based rainfall data [21,22,23]. However, in other cases, hydrological models relying on IMERG products as input data exhibited inadequate performance despite repeated model calibration [24,25]. The main reasons for the lower performance of IMERG-data driven models have been attributed to significant biases between IMERG and ground-based observations. Hence, there is a need to recalibrate the hydrological model when using IMERG products to better account for IMERG rainfall-runoff model interactions. Furthermore, the inherently lower accuracy of IMERG rainfall data compared to those derived from ground-based networks exacerbates these challenges [26].

It is worth emphasizing that no rainfall product can ensure excellent performance in hydrology due to various factors such as study scale and spatial coverage of the rainfall data, location, time scale, basin characteristics, choice of hydrological model and process representation, and model calibration algorithms [27,28]. For instance, although satellite- and gauged-based products such as IMERG have demonstrated their efficacy in estimating rainfall patterns compared to ground-based measurements in remote areas [29], knowledge gaps remain regarding their reliability in hydrological applications, particularly in tropical areas with complex terrain and frequent extreme rainfall events. Moreover, most evaluations of the suitability of IMERG products for hydrological applications have focused on China, where extensive hydrometeorological monitoring equipment is available for conducting validation studies [24,25,27,28]. For the vast African continent, however, reliable data are scarce, and evaluations have often been conducted at large spatial (e.g., country level or larger) or temporal (e.g., annual or longer) scales, and on large river basins. Hence, given that many water management issues are addressed at smaller scales, it is crucial to also evaluate the effectiveness of rainfall products from different sources for hydrological observatory applications for small or meso-scale watersheds.

The overall aim of this study was therefore to evaluate the usefulness of ground-based rain gauge data (RG) and remote sensing IMERG products for streamflow estimation. More specifically, the study assesses the performance of the semi-distributed SWAT (Soil and Water Assessment Tool) model at predicting streamflow using either different configurations of a ground-based rain gauge network or the IMERG product. The study was conducted in the Sahafihitry watershed (ca. 200 km²) located in northeastern Madagascar. This tropical watershed experiences high seasonality in rainfall frequency, intensity and duration (Ramahaimandimby et al. 2022). Heavy precipitation, including those accompanying large cyclone events which tend to occur every other year on average, threatens human activity and causes natural disasters such as floods and landslides [30,31]. Data collection and measurement in this region are particularly challenging due to rugged terrain and impassable roads during the rainy season. Furthermore, a lack of awareness among the local population can make equipment vulnerable to vandalism. These factors complicate establishing and maintaining long-term hydrological observatories. By assessing different sources of rainfall data and considering the trade-offs between data cost and quality, this study can also help decision-makers select the most appropriate data sources and hydrological observatory designs for their specific needs, ultimately contributing to the sustainable management of water resources in Madagascar and other regions facing similar challenges.

2. Materials and Methods

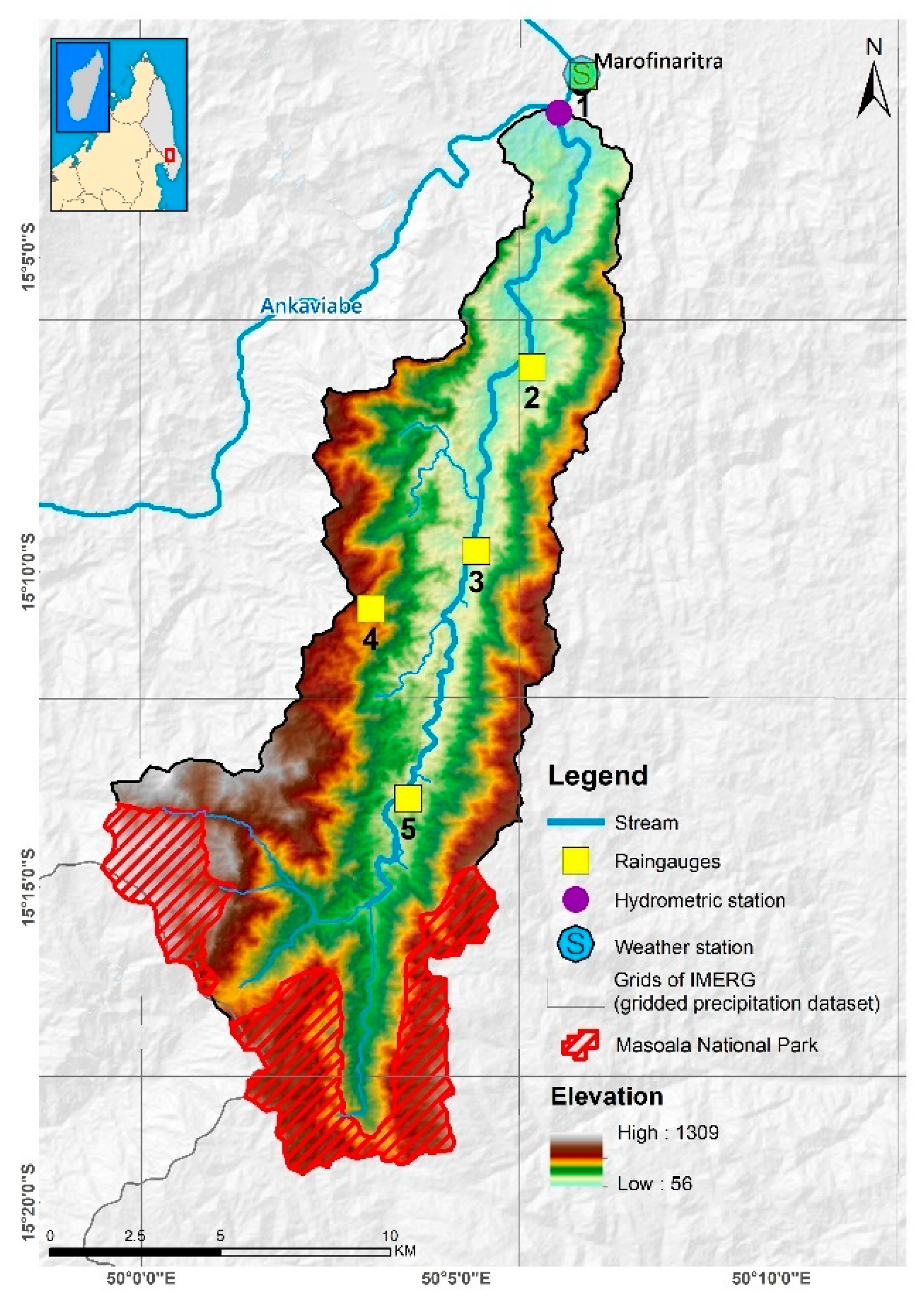
2.1. Study Area

The Sahafihitry river basin covers an area of 197 km² in the District of Antalaha, SAVA region, N-E of Madagascar (Figure 1). It lies between 15°00′ and 15°20′ South latitude and between 50°00’ and 50°10’ East longitude, with elevations ranging from 56 m to 1309 m a.m.s.l. The outlet is located at the confluence with the Ankaviabe river. The climate is humid-tropical with annual mean temperatures ranging from 22.3 to 27.7°C [30,32]. Annual precipitation is around 2240 mm (1960 – 2010), with high spatial variability [33]. Precipitation is unevenly distributed throughout the year, with a warm and rainy season from November to April and a cooler (less rainy) season from May to October [34]. Moreover, the region is often affected by storms and tropical cyclones, which frequently cause significant damage (Probst 2017).

The upstream part of the catchment is dominated by tropical rainforests and a mosaic of trees and shrubs, while the downstream part of the catchment is occupied by a mosaic of different types of natural vegetation. Also, the Masoala National Park, managed by the Madagascar National Park covers 18% of the total catchment area (Figure 1; CREAM 2013; Ormsby and Mannle 2006).

According to the World Reference Base, the dominant soils in the watershed are Ferralsols in the southern highlands and Acrisols in the downstream part of the watershed [37]. Ferralsols typically exhibit uniform profiles with high clay (kaolinite) and iron oxide contents, leading to a pseudo-sand structure that explains their high permeability in spite of the high clay content [38]. In contrast, Acrisols display more heterogeneous profiles with a lower permeability argillic horizon resulting from clay accumulation. These soils generally have lower clay content and are particularly susceptible to erosion [39].

2.2. Data Collection

A hydrometeorological network consisting of a weather station, 5 rainfall gauges and a water level gauging station was installed (Table S1). The network was fully operational as from August 2018. All data used in this study were collected from August 2018 to July 2021.

2.2.1. Weather Data

A meteorological station recording solar radiation, wind speed, relative humidity and maximum /minimum temperature was installed at Marofinaritra (Figure 1). Data were recorded with an hourly timestep using a Campbell Scientific^® CR300 series datalogger. Precipitation data were collected every 1 hour through a purposely installed network of five HOBO^® RG3M rain gauges (±1% accuracy) (Figure 1).

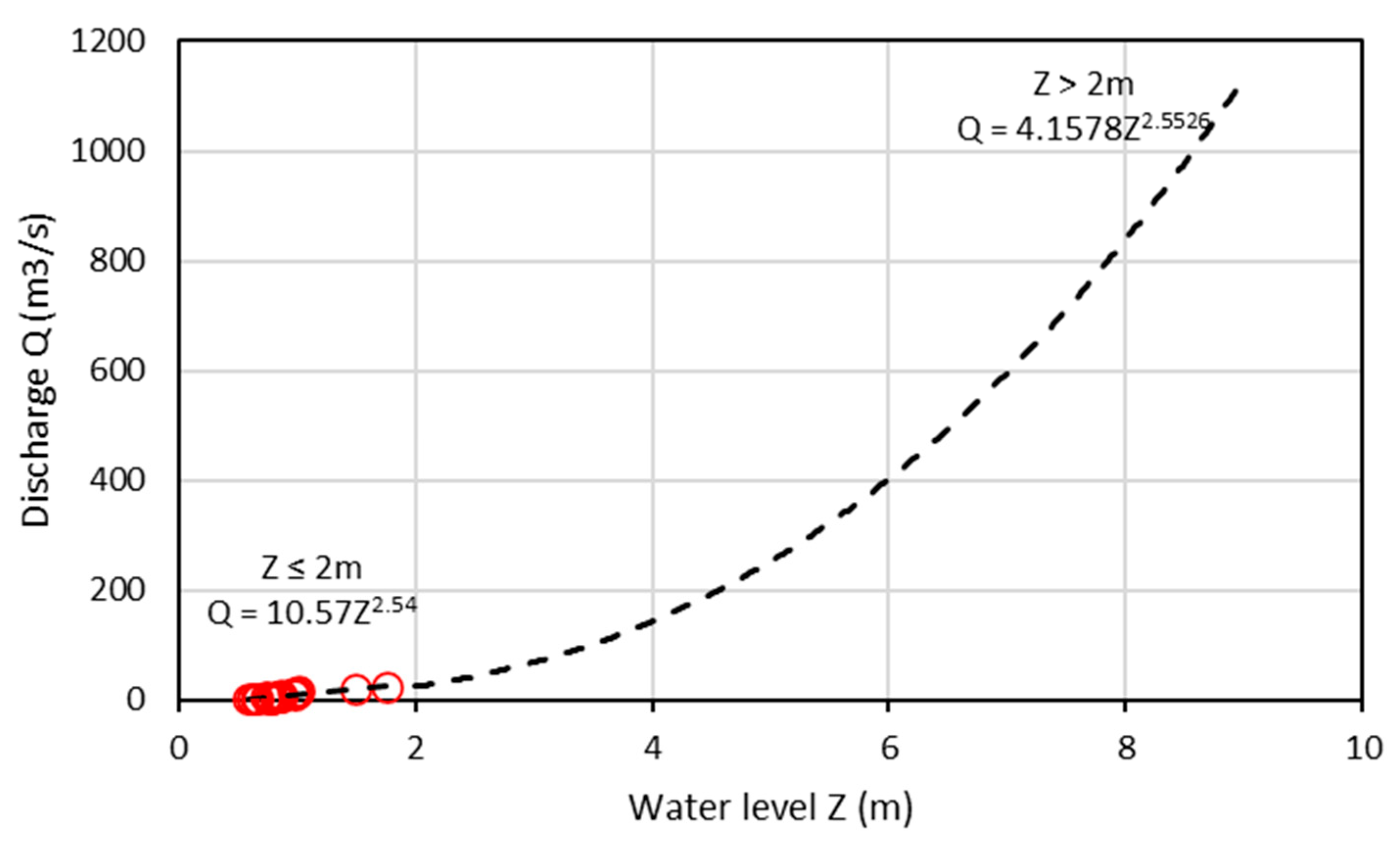
2.2.2. Discharge Data

Water levels at the outlet of the Sahafihitry river were monitored at hourly intervals using a Solinst^® LTC Levelogger Edge M5 C80 pressure sensor with an accuracy of ±0.3 cm. The water level data underwent correction for atmospheric pressure which were recorded by a Solinst^® 3001 LT Barologger Edge sensor with an accuracy of ±0.05 kPa. The atmospheric pressure data from the Marofinaritra weather station (Figure 1) were corrected using Equation (1) to take into account for elevation differences between the outlet and the weather station:

P(hi) = P(h₀) × e−Δh/hs,
with hs = R × T/M × g

(1)

where : P(hi) is the effective atmospheric pressure at the outlet at elevation hi [Pa],

P(h0) is the atmospheric pressure measured at the weather station at elevation h0 [Pa],

Δh is the difference in elevation between h_i and h₀ [m],

R is the molar gas constant [8.314 J K⁻¹ mol⁻¹],

T is the absolute temperature of the air, taken at the weather station [°K],

M is the average molar mass of gas in the atmosphere [0.02896 kg mol⁻¹],

g is the gravitational acceleration [9.81 m·s−²].

Subsequently, Equation (2) was applied to the levelogger data for deriving the water level:

Z = (Pi − P(hi))/ρ × g

(2)

where: Z represents the water level [m],

Pi denotes the measured water pressure [Pa] at the outlet, and ρ is the density of water (1000 kg/m³).

Discharge was determined by converting water level data into discharge using a rating curve. The OTT MF PRO magnetic induction current meter was used for gauging water velocity for low and medium flows (Q) with a measuring range of 0 to 6 m.s⁻¹ and an accuracy of ±2% (between 0 and 3 m.s⁻¹) and ±4% (between 3 and 5 m.s⁻¹). At least 20 gauging operations were conducted at the outlet to establish the rating curve, based on measured pairs of water level and discharge (Qi, Zi) for low and medium flow conditions (Figure A1). Subsequently, a power function (see Equation 3) was fitted to the water level discharge data:

Q = a × (Zi − Z₀)^b

(3)

where a and b represent fitting coefficients, Z_i is the water level [m] measured by the Levelogger, and Z₀ is the stage at zero discharge [m].

For safety reasons during high flow conditions and because of practical constraints, rating curves for high flows were extrapolated using an empirical method based on Manning’s equation (Equation 4):

Q = (1/n) × Cs × Hr^2/3 × Sl^1/2

(4)

where Cs denotes the flow cross-section [m²], and Hr represents the hydraulic radius [m]. Sl is the river slope (%) at the gauging station, which was estimated from a Digital Elevation Model (DEM) with a resolution of 30 m. The channel roughness coefficient n [s.m−1/3] was derived from stream gauging data for low and medium flow conditions by combining equations (3) and (4). However, when the water level exceeds 2.5 m, n is set at 0.08 for the left bank and 0.12 for the right bank, reflecting less dense vegetation cover on the left and more dense vegetation cover on the right [40].

2.2.3. Gridded Precipitation Data: IMERG

Given its good performance in estimating daily precipitation across the Sahafihitry watershed [16], IMERG precipitation data were used for forcing the hydrological model. GPM-IMERG, short for Integrated Multi-satellitE Retrievals for Global Precipitation Measurement, is a satellite-based precipitation product developed by the National Aeronautics and Space Administration Global Precipitation Measurement (GPM) mission. The IMERG product uses an algorithm that blends measurements from passive microwave sensors and infrared sensors to estimate precipitation. It incorporates data from ground-based rain gauges (GPCC) to calibrate and validate the satellite-derived estimates. The product is available with a spatial resolution of 0.1° × 0.1° and a temporal resolution of 30 minutes [15].

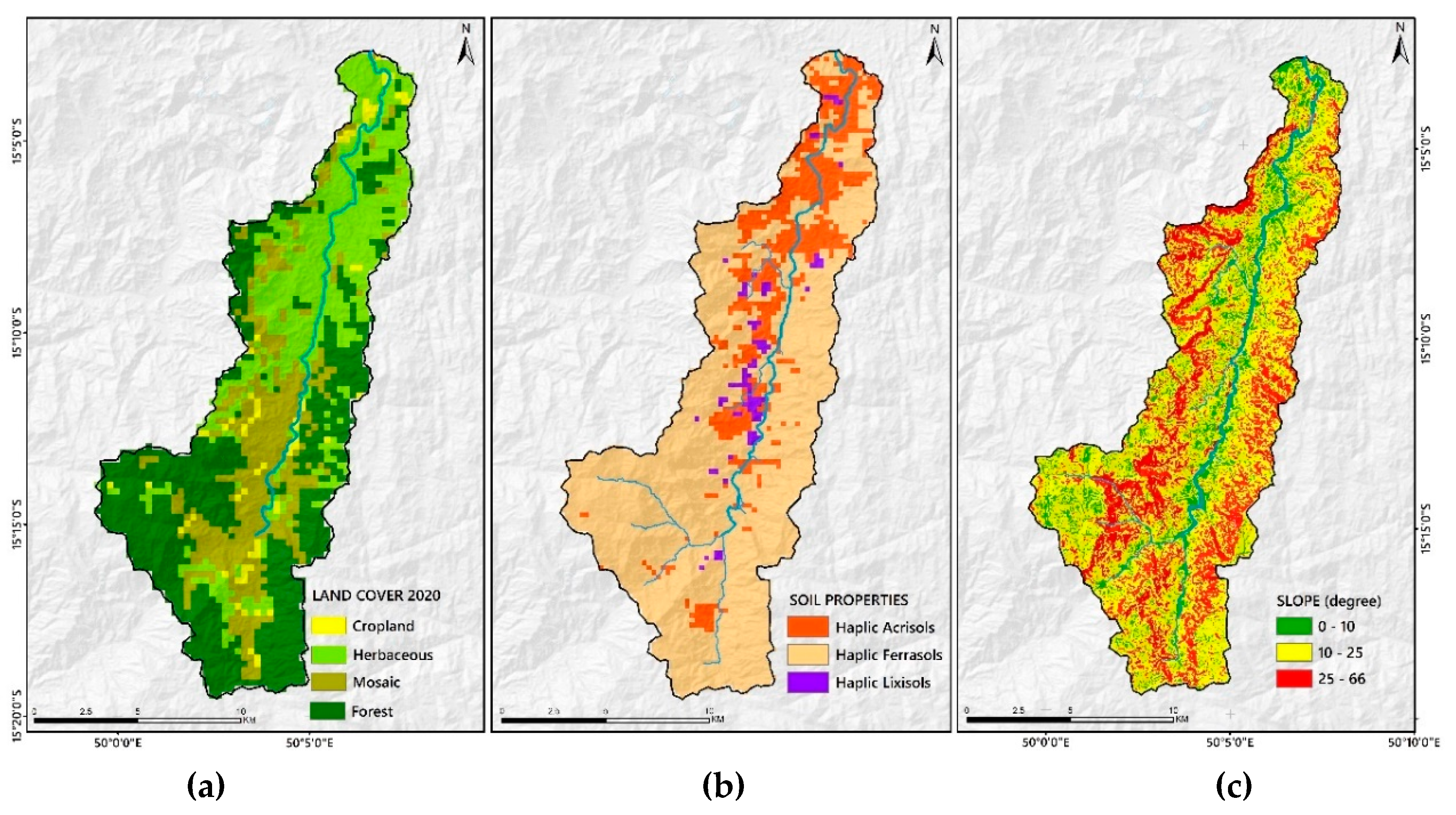
2.2.4. SPATIAL Data

The 2020 land cover map was generated based on the 300-m resolution GlobCover v.2 product (Bontemps et al. 2009; Figure 2A), while soil attributes were obtained from the 250-m resolution SoilGRID classification (Deckers et al. 2010; Figure 2B). The delineation of Sahafihitry catchment boundaries, hydrological structures, and slope information relied on a 30-m resolution DEM sourced from Shuttle Radar Topographic Mission (SRTM) (Earth Resources Observation And Science (EROS) Center 2017; Figure 2C).

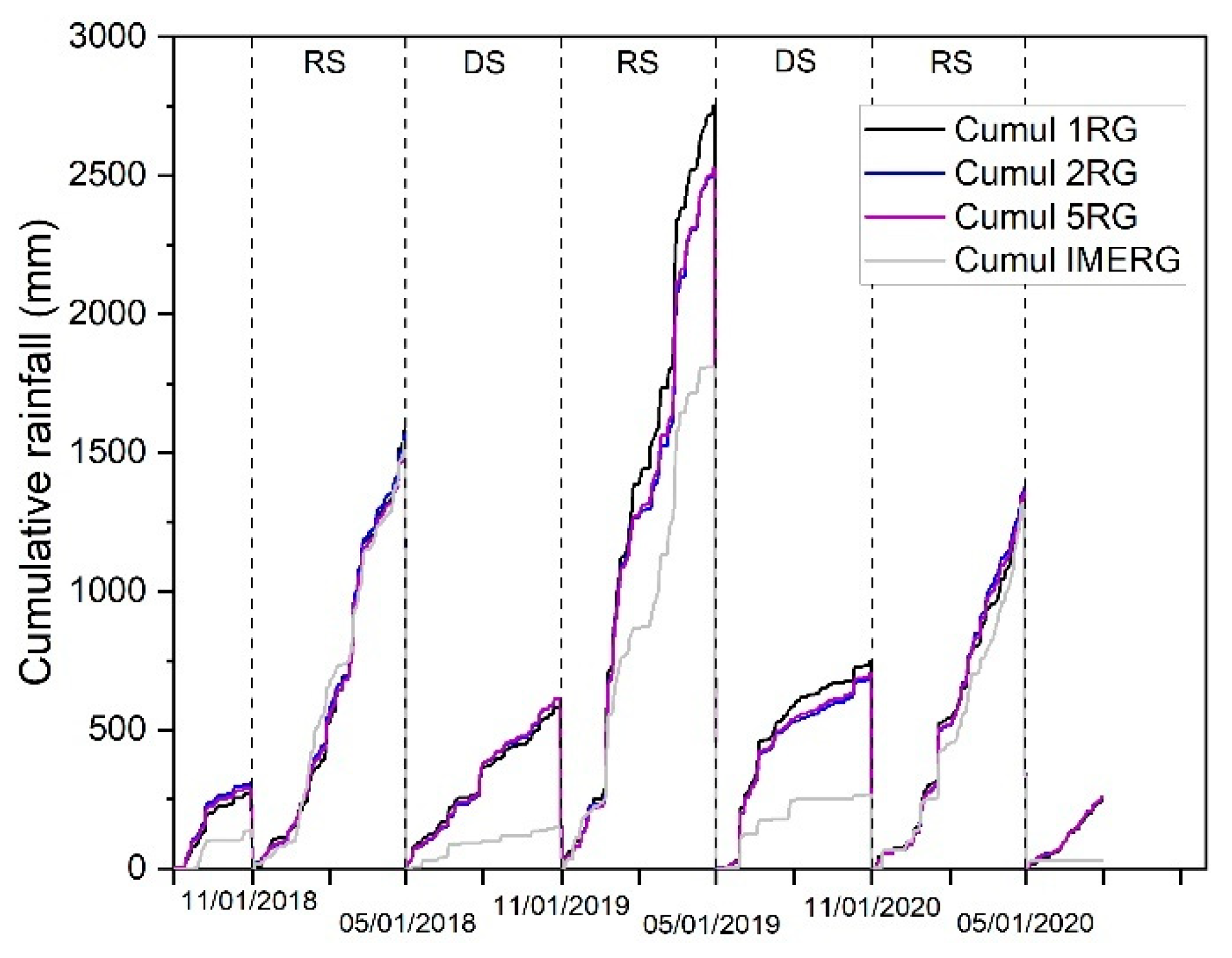
2.3. Rainfall Spatial Variability

An exploration of rainfall spatial variability in the Sahafihitry catchment was undertaken. Using the coefficient of variation as a key measure (Equations 5 and 6), the analysis aims to quantify the degree of variation in daily rainfall across the five rain gauges or the IMERG product grids for each of the three years of measurement. A high coefficient of variation (>70%) in rainfall indicates that the daily precipitation values within the dataset exhibit a substantial degree of spatial variability compared to the mean [44]. The coefficient of variation (CVi) was first calculated on a daily basis and subsequently averaged per year (CV; Equations 5 and 6):

C V = \frac{\sum_{i = 1}^{k} C V i}{k}

(5)

where CVi = (σi/µi) × 100

(6)

and where k represents the number of days in a given year, and CVi is the coefficient of variation for day i. µi and σi are the average precipitation for day i and the corresponding standard deviation. The calculations of daily CV (CVi) were performed by using either the five rain gauges or the eight IMERG grid cells comprising the catchment area (Figure 1).

2.4. Hydrological Modelling : SWAT Semi-Distributed Model

2.4.1. Model Description

The SWAT model is a widely used hydrological model that operates on a continuous daily time scale or greater [45]. It is a semi-distributed model that is coupled with a Geographic Information System interface. Besides daily weather and hydrological data (see Section 2.2.), SWAT uses data on land cover, soil, and slope properties (Figure 2). The watershed is then divided into Hydrologic Response Units (HRUs), which are composed of areas with homogeneous land cover, soil, and slope characteristics.

The hydrological components of the SWAT model are linked through the water balance equation (Equation 7), which serves as the foundation of the hydrological model:

S W t = S W o + \sum_{i = 1}^{t} (R d a y - Q s u r f - E a - W s e e p - Q g w)

(7)

where:

SWt and SWo are the final and initial soil water content [mm],

t is the time [days],

Rday is the amount of precipitation on day i [mm],

Qsurf is the amount of surface runoff on day i [mm], estimated using the runoff curve number (SCS CN) method,

Ea is the amount of evapotranspiration on day i [mm], calculated using the Penman–Monteith method,

Wseep is the amount of water seeping from the soil profile into the underlying vadose zone on day i [mm],

and Qgw is the amount of return (lateral subsurface) flow on day i [mm].

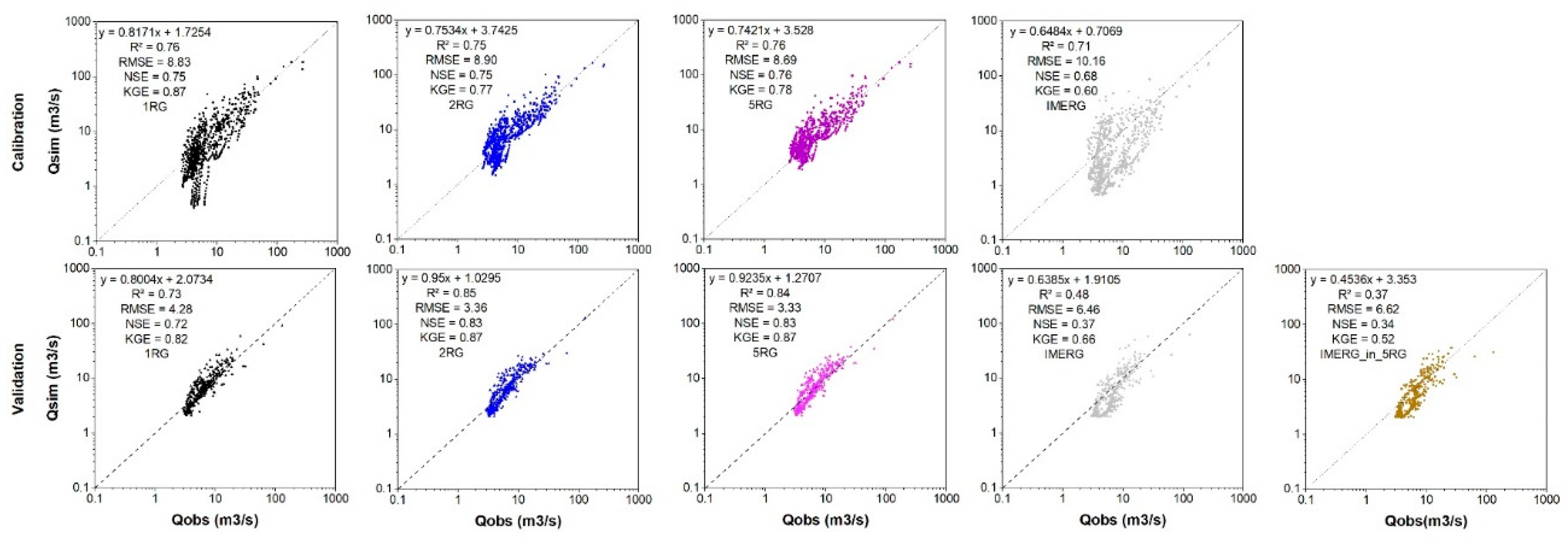
2.4.2. Sensitivity Analysis, Calibration and Validation

The Sequential Uncertainty Fitting version 2 (SUFI-2; Nkonge et al., 2014; Wu and Chen, 2015) available in the SWAT-Calibration and Uncertainty Programs (SWAT-CUP; Abbaspour, 2015) was used to calibrate the model for the diverse scenarios (see Section 2.4.3). The Nash-Sutcliffe efficiency (NSE) index was adopted as an objective function during the auto-calibration process (See Table 2.).

Model parameters were calibrated using observed streamflow data from August 2018 to July 2020, and the calibrated models were validated using streamflow data from August 2020 to July 2021. Since only three years of discharge data were available, the August 2020 – July 2021 data served as both the validation and warm-up period, although they were not used for calibration.

For each scenario, a set of 10 key parameters governing hydrological processes was selected for model calibration and validation. CN2 is associated with the runoff generation process, while SOL_AWC regulates soil water content. The parameter set related to groundwater flow includes GW_DELAY, GWQMN, SHALLST, DEEPST, GW_REVAP, RCHRG_DP, GWHT, and GW_SPYLD (Table 1). The initial parameter ranges and the selection of these parameters were determined through a comprehensive literature review and prior knowledge.

2.4.3. Scenarios

To assess the hydrological performance for different rainfall data sources, five rainfall scenarios were implemented in SWAT. The first three scenarios (1RG, 2RG, 5RG) utilize the ground-based rain gauges spatialized using the Thiessen method. Specifically, scenario 1RG relies on data from the catchment’s central rain gauge (No. 3; Figure 1), while scenario 2RG uses data from rain gauges No. 2 and No. 5. Scenario 5RG uses data from all five rain gauges. These scenarios seek to evaluate potential accuracy loss when reducing rain gauges from 5 to 2 and to 1. The fourth scenario relies on IMERG gridded precipitation products. For each of these four scenarios, all parameters are specifically calibrated. The final scenario, referred to as IMERG_in_5RG, involves the use of IMERG rainfall data using the optimized parameters derived from the 5RG scenario. This last scenario seeks to assess the possible loss in performance when using IMERG rainfall data in a model calibrated using ground-based data.

2.4.3. Hydrological Model Performance

The performance of the hydrological model was assessed using four continuous quantitative metrics: the coefficient of determination (R²), the slope of regression (a), Nash-Sutcliffe efficiency (NSE), the Root-Mean-Square Error (RMSE), and the Kling-Gupta Efficiency (KGE) (Table 2). These metrics, especially NSE, RMSE and KGE, were also applied to evaluate the ability of the model to reproduce different discharge classes (>5, >10, >15, >20, and >50 m3/s).

Table 2. Statistical metrics used for evaluating the SWAT model performance.

Name/Symbol	Formula	Optimal value
Coefficient of determination/ R²	$R^{2} = (\frac{\sum_{i = 1}^{n} [(Q m i - \bar{Q} m) (Q s i - \bar{Q} s)]}{\sqrt{\sum_{i = 1}^{n} (Q m i - \bar{Q} m) ² \sum_{i = 1}^{n} (Q s i - \bar{Q} s) ²}}) ²$	1
Slope of linear regression/ a	Qs=a(Qm) + b	1
Nash-Sutcliffe efficiency/ NSE	$N S E = 1 - \frac{\sum_{i = 1}^{n} (Q m i - \bar{Q} s i) ²}{\sum_{i = 1}^{n} (Q m i - \bar{Q} m) ²}$	1
Root-Mean-Square Error/ RMSE	$R M S E = \sqrt{\frac{\sum_{i = 1}^{n} (Q m i - Q s i) ²}{n}}$	0
Kling-Gupta Efficiency/ KGE	$K G E = 1 - \sqrt{{(C C - 1)}^{2} + {(\frac{σ s}{σ m} - 1)}^{2} + (\frac{\bar{Q} s i}{\bar{Q} m i} - 1) ²}$	1

Qm is the measured discharge, Qs is the simulated discharge,

\bar{Q}

m is the average measured discharge,

\bar{Q}

s is the average simulated discharge, σm is standard deviation of measured discharge, σs is standard deviation of simulated discharge, and CC = R is the Pearson coefficient value.

3. Results

3.1. Hydrological Modelling : SWAT Semi-Distributed Model

The coefficient of variation computed from 5RG data consistently exceeds that derived from IMERG for each of the three periods, indicating a greater degree of spatial variability in the 5RG data compared to the IMERG data.

The cumulative rainfall curves for 1RG, 2RG, and 5RG scenarios are very similar, reaching up to 7200 mm over the three-year study period. The cumulative IMERG curve is notably lower, especially as from 04/01, and totaling only 5000 mm over the three years.

Figure 3. Mean cumulative rainfall for one rain gauge (1RG), two rain gauges (2RG), five rain gauges (5RG) and IMERG satellite-based precipitation data. The date on the X-axis is in MM/DD/YYYY format.

Numerous events occurred in the region over the study period. The onset of extreme events is predominantly observed in January and extends until April. Less intense rainfall events are noted annually from April to November. When analyzing the cumulative curves seasonally, a consistent pattern emerges in the RG curves across all seasons (Figure 4). Throughout the ‘wet’ rainy season (November to April), the cumulative RG and IMERG rainfall curves are strikingly similar for the first and third rainy seasons. However, in the second ‘wet’ rainy season, the IMERG curve consistently underestimates rainfall by approximately 720 mm. Similarly, during the observed ‘dry’ rainy seasons throughout the study period, the IMERG data consistently underestimates rainfall, by around 440 mm on average.

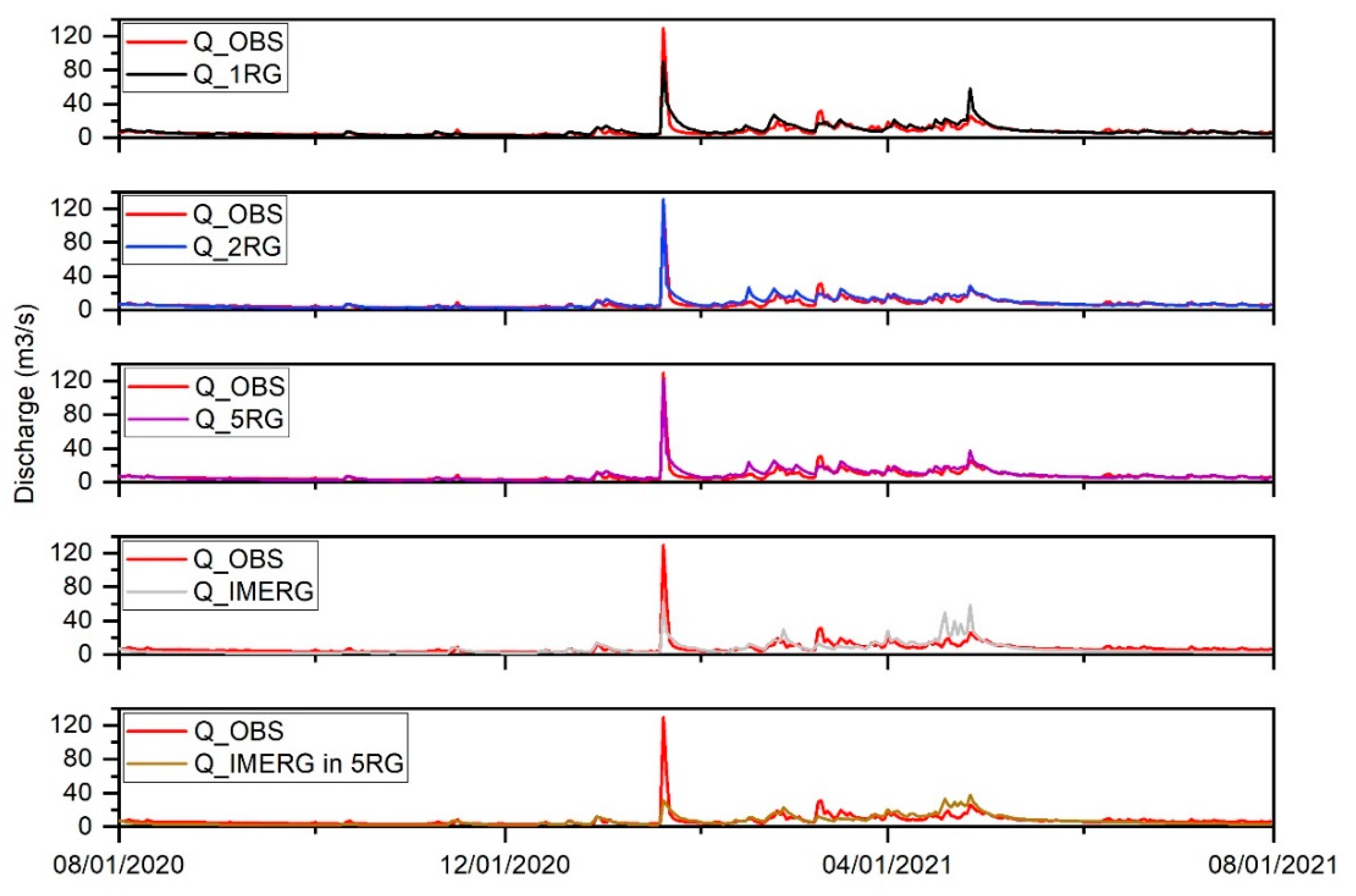
3.2. Streamfolw Characteristics

The cumulative discharge curve reached 4500 mm over the study period. The discharge curve rises in tandem with rainfall, except during period 1 when the rainfall escalates but the discharge exhibits a delayed ascent (Figure 5a). On a yearly basis, the difference between cumulative rainfall and cumulative discharge at the end of period 1 is 1320 mm, while for periods 2 and 3, it stands at 882 mm and 568 mm, respectively.

3.3. Rainfall-Runoff Model Performances

3.3.1. Overall Performance

Optimal parameter values for the 1RG, 2RG, 5RG and IMERG scenarios are provided in Table 1 following calibration. Overall, the observed vs. measured discharge data cloud exhibits greater dispersion for the 1RG scenario than for the 2RG and 5RG scenarios (Figure 6). In particular, the model has great difficulty in reproducing the low flows (< 10 m³/s) based on the rain gauge located at the center of the watershed (1RG scenario). In addition, there is a slight overestimation in the flow classes from 10 m³/s to 50 m³/s for the 1RG, 2RG, and 5RG scenarios.

There is also a much greater dispersion in the data for the IMERG scenario compared to the RG scenarios (Figure 6). The 1RG, 2RG, and 5RG scenarios outperform the IMERG scenario, as evidenced by their higher R² values, regression slopes closer to 1, NSE and KGE values closer to 1, and RMSE values closer to 0. The observed flows in the <10 m³/s flow class are underestimated when using 1RG and IMERG precipitation data.

For the validation period, the dispersion of data is less pronounced than during calibration, yet the 1RG/2RG/5RG scenarios still exhibit less scatter than the IMERG scenario. Additionally, the value of the statistical parameters (correlation coefficient, R², NSE, KGE approaching 1, and RMSE nearing 0) indicate that the 2RG/5RG scenarios outperform the 1RG and IMERG scenarios (Figure 6 and Figure 7). Running the model with IMERG data after calibration with 5RG data (IMERG_in_5RG) results in an overall degradation of the model performance compared to the 5RG and IMERG scenarios (Figure 6 and Figure 7).

3.3.2. Performance across Discharge Classes

RMSE values tend to rise as the flow rate class increases for both the calibration and validation periods (Figure 8). NSE and KGE values remain fairly constant for most scenarios except for discharges > 50 m³/s for which a sharp drop in these values is observed. For the IMERG and IMERG_in_5RG scenarios, NSE and KGE values tend to decline steadily as the flow rate class increases. In the calibration phase, RMSE and NSE values are generally comparable across all scenarios, but notable differences emerge during the validation phase (Figure 8). Conversely, KGE values for the 1RG scenario, while slightly outperforming 5RG and 2RG during calibration, noticeably decrease during validation periods compared to these scenarios. Additionally, KGE values for the IMERG remain distinctly lower than for RG scenarios. Based on RMSE and NSE values in the validation phase, the scenarios rank in decreasing order of performance as 5RG, 2RG, 1RG, IMERG, and IMERG_in_5RG. According to KGE values, the ranking is 2RG, 5RG, 1RG, IMERG, and IMERG_in_5RG.

4. Discussion

4.1. Rainfall Characteristics

During the study period, average rainfall aligned with the expected annual average of 2240 mm [33], although it was slightly below average in periods 1 and 3, and significantly above average in period 2 (Table 3). The study area displays also notable spatial variability in rainfall, as evidenced by the coefficients of variation observed across the five rain gauges. The spatial variability was most pronounced during the peak of the rainy season (period 2). Such variability was also observed in other parts of the region, particularly in the northeast of Madagascar [30,46].

The coefficients of variation derived from the rain gauge dataset consistently exceed those obtained from the IMERG dataset. This can partly be attributed to the inherent difference in data nature, with 5RG representing point-based observations and IMERG relying on gridded data [15,47]. While IMERG accurately captures rainfall during typical rainy seasons, its performance diminishes during exceptionally wet seasons due to challenges in detecting rainfall events exceeding 100 mm/day, leading to a significant underestimation of rainfall amounts [16,17]. Additionally, during less rainy periods like the ‘dry’ season, a notable gap emerges between observed cumulative rainfall and IMERG-reported values, attributed to IMERG’s tendency to underestimate the low-intensity rainfall events that prevail during that season [16,30,48].

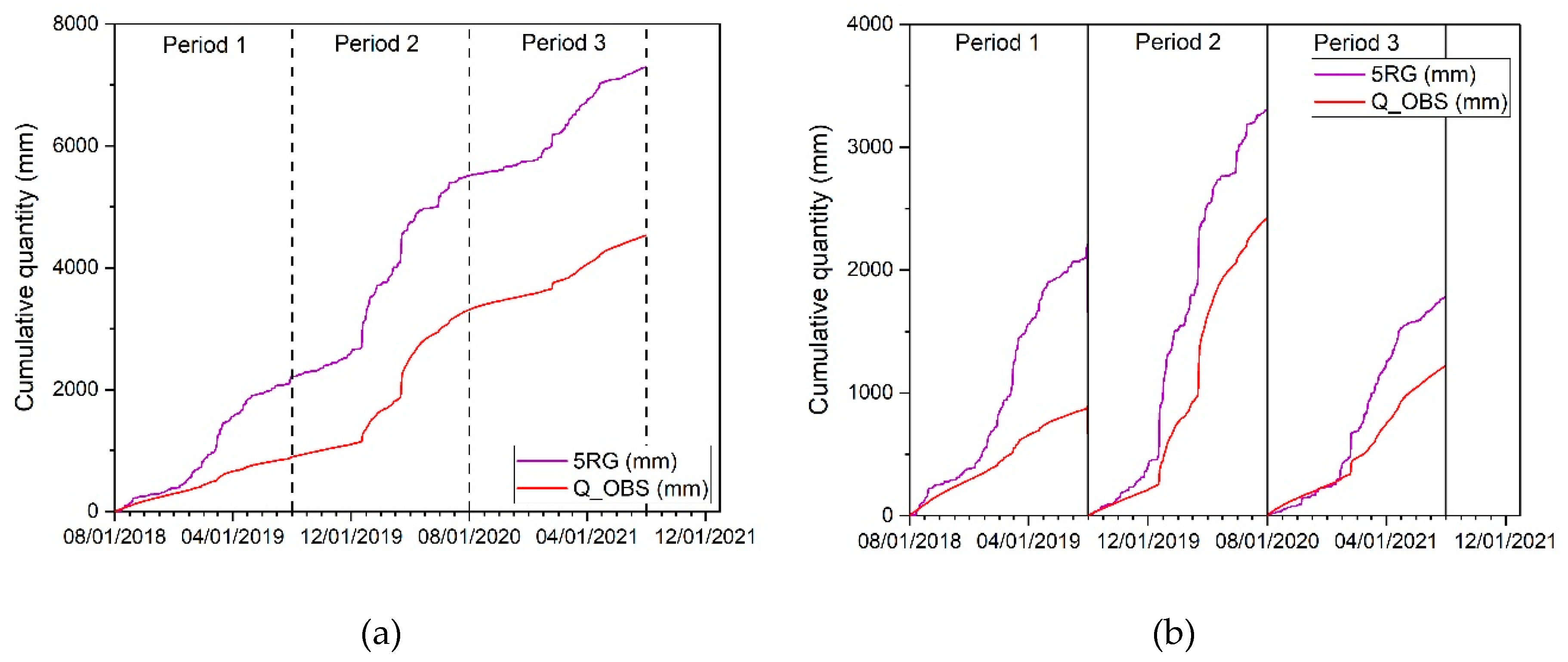
4.2. Hydrological Usefulness of Precipitation Data

In this study, we assessed the performance of four precipitation datasets in the SWAT model: data from 1, 2 or 5 rain gauges, or IMERG precipitation data. These datasets differ in their measurement methods, detection accuracy, and spatial representation of precipitation, which resulted in substantially different discharge simulation results.

In hydrological analyses involving RG scenarios, utilizing two or five RGs outweighs that of using a single RG for discharge simulation. With a single rain gauge, there is a tendency to underestimate flow classes < 10m3/s, a phenomenon not observed when multiple rain gauges are utilized (Figure 6, calibration). Similarly, the use of a single rain gauge leads to a decline in indicators (R², RMSE, NSE, KGE), which is largely attributable to the underestimation of high flow classes >100m3/s (Figure 6, validation). Integrating multiple RGs enhances spatial coverage, facilitating a comprehensive capture of rainfall variability across the study area. This is particularly crucial in tropical regions characterized by significant rainfall variation over short distances, attributed to factors like topography, land cover, and local weather patterns [46,49] (Section 4.1). Additionally, the use of multiple RGs offers a larger dataset, enabling the mitigation of errors or biases inherent in individual measurements, thereby providing more reliable estimates of rainfall inputs for hydrological models [11,50]. Conversely, sole reliance on a single RG may result in inaccurate representation of this variability, introducing uncertainties into hydrological modeling outcomes. This observation is supported by existing literature, where the spatial variability of precipitation input significantly influences the performance of runoff simulations [51].

The results obtained from the study highlight the superiority of ground-based rain gauge data, particularly from multiple gauges, over satellite-derived IMERG data in hydrological modelling. Other studies have also highlighted the limited applicability of IMERG satellite-based rainfall estimates in flood and low-water forecasting [52]. This limitation mainly arises from the tendency of IMERG products to underestimate rainfall rates by 12 - 35% (mostly for very low and very high rainfall intensities) and their low spatial variability at the catchment scale [15,16]. IMERG products tend to smooth precipitation values due to their gridded nature and size, which averages precipitation values within each grid cell [15].

The use of an extrapolated rating curve for high flows (Section 2.2.), combined with uncertainties in IMERG data, may also introduce significant biases in discharge estimations, particularly during extreme events like the 2020 rainy season (Figure 6b). This can lead to a decline in performance metrics (such as NSE and KGE) and inaccurate discharge simulations, especially during peak flows (Figure 8). Additionally, relying solely on Nash-Sutcliffe efficiency (NSE) during self-calibration might oversimplify model performance evaluation (Section 2.4.). While NSE helps mitigate mean errors and variances, it may overlook deviations during high and low flow periods, as highlighted by [53]. Consequently, the model may exhibit satisfactory statistical performance (acceptable NSE and KGE values) but fail to capture the intricacies of extreme events. This could lead to an underestimation of flood risks and inadequate preparedness measures for future events.

4.3. Implication of the Selection of Precipitations Datasets in Streamflow Simulation

The study underscores the crucial importance of adjusting model parameters before integrating rainfall data into the hydrological model, especially considering the diminished reliability of the IMERGin5RG scenario compared to the IMERG scenario. While calibration based on IMERG rainfall data yields improved results compared to IMERGin5RG, this raises concerns about the physical significance of these parameters. Ideally, hydrological model characteristics should not be contingent on rainfall data sources, emphasizing the necessity of ensuring that model parameters maintain their physical interpretation despite variations in rainfall input data [54]. However, there may be instances where the calibrated parameter values exceed their reasonable ranges [24,28]. Consequently, the recalibrated model may feature parameter values that do not accurately represent real-world features, potentially compromising the model’s predictive capability in internal basins.

5. Conclusions

Motivated by the need for a cost-effective and efficient system observatory that can provide reliable hydrological data, we investigated the performance of four configurations of precipitation datasets (1RG/2RG/5RG and IMERG) as inputs to the SWAT model for daily streamflow simulation. The study was conducted in the Sahafihitry watershed (~200 km²), a medium-sized tropical mountainous watershed in northeast Madagascar.

Our findings can be summarized as follows:
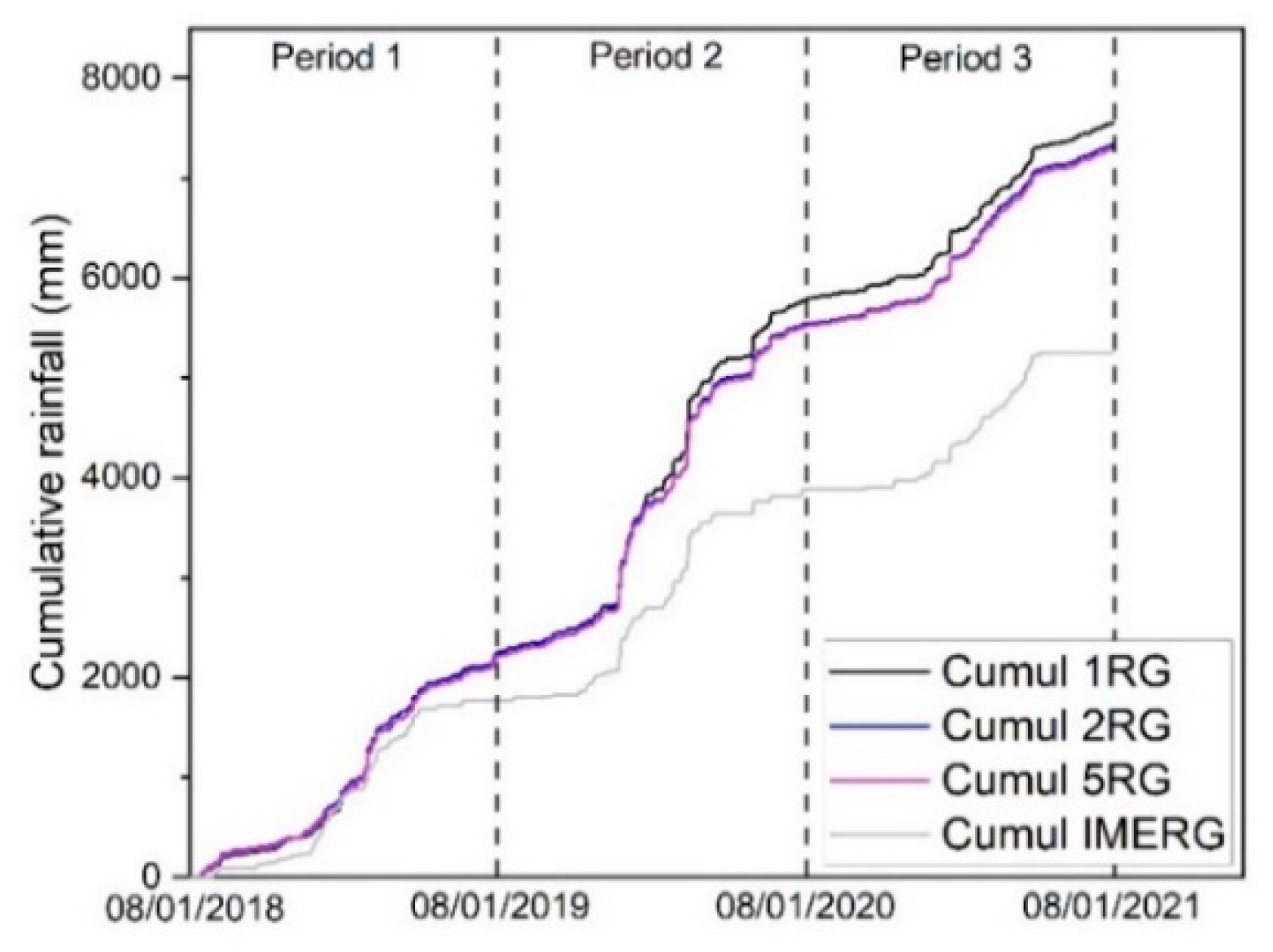
The utilization of a network of multiple rain gauges offers a more accurate depiction of the spatial variability of precipitation in tropical mountainous regions, surpassing the representation provided by a single rain gauge or IMERG satellite-based precipitation data.
The performance of the SWAT model, driven by four different precipitation datasets, decreased in the order 5RG > 2RG > 1RG > IMERG, indicating the effectiveness of a denser network for capturing rainfall variability in high-altitude watersheds.
Rain gauge scenarios performed better for accurate flood and low-flow forecasting.
Despite underestimating extreme precipitation and peak flow, IMERG achieved quite good performance based on statistical indicators. However, the use of IMERG rainfall as input data for hydrological applications comes with several limitations, including the physical significance of the parameters.
While IMERG data are readily available at low cost, its lower performance in hydrological modeling introduces significant uncertainty into the results. In comparison, the 2RG network configuration achieved satisfactory streamflow simulation and remains the most cost-effective option for establishing reliable hydrological observatories in this particular study area, considering its characteristics.

It is important to note that these results may only be applicable to watersheds with similar climatic conditions, soil properties, land cover, topography and scales as our study area. Therefore, caution should be exercised when applying these findings to other regions and it is recommended that further research be conducted in such areas to determine the most suitable configuration of rainfall networks for accurate streamflow modeling.

Author Contributions

Conceptualization, Z.R. and C.B.; Formal analysis, Z.R. and C.B.; Funding acquisition, M.V.; Investigation, Z.R.; Methodology, Z.R. and C.B.; Project administration, M.V.; Software, Z.R.; Supervision, A.R. and C.B.; Validation, Z.R., A.R. and C.B.; Visualization, Z.R., A.R., M.V. and C.B.; Writing—original draft, Z.R.; Writing—review and editing, Z.R., M.V. and C.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research and APC fees are funded by the Belgian Académie de Recherche d’Enseignement Supérieur (ARES-CCD: www.ares-ac.be) (accessed on 26 February 2022), through the 2017 Research Project for Development (PRD) in Madagascar, named: Renforcement des Capacités en Gestion Integrée des Ressources en Eau (GIRE-SAVA). More information on: https://www.ares-ac.be/fr/cooperation-au-developpement/pays-projets/projets-dans-le-monde/item/162-prd-renforcement-des-capacites-en-gestion-integree-des-ressources-en-eau-de-la-region-sava-gire-sava (accessed on 14 April 2022).

Acknowledgments

The authors acknowledge all those who gave their support for the accomplishment of this study. Our special thanks go to the south project coordinators Joseph Benitsiafantoka (2017–2021), Christophe Manjaribe (2021–2023), and their respective staff in the Centre Universitaire Régional de la SAVA (CURSA). We also acknowledge the contribution of the members of the Sambava regional direction of water, especially Tsirinasy (2017–2021), Carlos Totomalaza (since 2021), the heads of the surveyed communities, and the survey participants (technicians and research assistants).

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Appendix A

Figure A1. Rating curve of Sahafihitry river. Red circles indicate measured discharge.

References

Di Baldassarre, G.; Montanari, A.; Lins, H.; Koutsoyiannis, D.; Brandimarte, L.; Blöschl, G. Flood Fatalities in Africa: From Diagnosis to Mitigation. Geophysical Research Letters 2010, 37. [Google Scholar]
Carrière, S.D.; Health, T.; Rakotomandrindra, P.F.M.; Ollivier, C.; Rajaomahefasoa, R.E.; Rakoto, H.A.; Lapègue, J.; Rakotoarison, Y.E.; Mangin, M.; Kempf, J.; et al. Long-Term Groundwater Resource Observatory for Southwestern Madagascar. Hydrological Processes 2021, 35, e14108. [Google Scholar] [CrossRef]
WMO Climate Change Increased Extreme Rainfall in Southeast Africa Storms - Madagascar Available online:. https://reliefweb.int/report/madagascar/climate-change-increased-extreme-rainfall-southeast-africa-storms (accessed on 2 October 2022).
WMO Tropical Hydrology 1987.
Sivakumar, B. Chaos in Hydrology; Springer Netherlands: Dordrecht, 2017; ISBN 978-90-481-2551-7. [Google Scholar]
Sivapalan, M.; Takeuchi, K.; Franks, S.W.; Gupta, V.K.; Karambiri, H.; Lakshmi, V.; Liang, X.; McDONNELL, J.J.; Mendiondo, E.M.; O’Connell, P.E.; et al. IAHS Decade on Predictions in Ungauged Basins (PUB), 2003–2012: Shaping an Exciting Future for the Hydrological Sciences. Hydrological Sciences Journal 2003, 48, 857–880. [Google Scholar] [CrossRef]
Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
Tapiador, F.J.; Turk, F.J.; Petersen, W.; Hou, A.Y.; García-Ortega, E.; Machado, L.A.; Angelis, C.F.; Salio, P.; Kidd, C.; Huffman, G.J. Global Precipitation Measurement: Methods, Datasets and Applications. Atmospheric Research 2012, 104, 70–97. [Google Scholar]
Ombadi, M.; Nguyen, P.; Sorooshian, S.; Hsu, K. Developing Intensity-Duration-Frequency (IDF) Curves From Satellite-Based Precipitation: Methodology and Evaluation. Water Resources Research 2018, 54, 7752–7766. [Google Scholar] [CrossRef]
Maggioni, V.; Massari, C. On the Performance of Satellite Precipitation Products in Riverine Flood Modeling: A Review. Journal of hydrology 2018, 558, 214–224. [Google Scholar]
Gosset, M.; Viarre, J.; Quantin, G.; Alcoba, M. Evaluation of Several Rainfall Products Used for Hydrological Applications over West Africa Using Two High-Resolution Gauge Networks. Quarterly Journal of the Royal Meteorological Society 2013, 139, 923–940. [Google Scholar] [CrossRef]
Villarini, G.; Krajewski, W.F.; Ciach, G.J.; Zimmerman, D.L. Product-Error-Driven Generator of Probable Rainfall Conditioned on WSR-88D Precipitation Estimates. Water Resources Research 2009, 45. [Google Scholar]
Khan, S. Evaluating High-Resolution Satellite Precipitation Products Globally Over Land and Oceans. PhD Thesis, George Mason University, 2019.
Kummerow, C.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson, J. The Tropical Rainfall Measuring Mission (TRMM) Sensor Package. Journal of atmospheric and oceanic technology 1998, 15, 809–817. [Google Scholar]
Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.-L.; Joyce, R.J.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J. Integrated Multi-Satellite Retrievals for the Global Precipitation Measurement (GPM) Mission (IMERG). In Satellite Precipitation Measurement; Springer, 2020; pp. 343–353.
Ramahaimandimby, Z.; Randriamaherisoa, A.; Jonard, F.; Vanclooster, M.; Bielders, C.L. Reliability of Gridded Precipitation Products for Water Management Studies: The Case of the Ankavia River Basin in Madagascar. Remote Sensing 2022, 14, 3940. [Google Scholar] [CrossRef]
Tan, M.L.; Duan, Z. Assessment of GPM and TRMM Precipitation Products over Singapore. Remote Sensing 2017, 9, 720. [Google Scholar] [CrossRef]
Derin, Y.; Kirstetter, P.-E.; Gourley, J.J. Evaluation of IMERG Satellite Precipitation over the Land–Coast–Ocean Continuum. Part I: Detection. Journal of Hydrometeorology 2021, 22, 2843–2859. [Google Scholar] [CrossRef]
Dezfuli, A.K.; Ichoku, C.M.; Huffman, G.J.; Mohr, K.I.; Selker, J.S.; van de Giesen, N.; Hochreutener, R.; Annor, F.O. Validation of IMERG Precipitation in Africa. J. Hydrometeor. 2017, 18, 2817–2825. [Google Scholar] [CrossRef]
Sellami, H.; La Jeunesse, I.; Benabdallah, S.; Vanclooster, M. Parameter and Rating Curve Uncertainty Propagation Analysis of the SWAT Model for Two Small Mediterranean Catchments. Hydrological Sciences Journal 2013, 58, 1635–1657. [Google Scholar] [CrossRef]
Jiang, Q.; Li, W.; Fan, Z.; He, X.; Sun, W.; Chen, S.; Wen, J.; Gao, J.; Wang, J. Evaluation of the ERA5 Reanalysis Precipitation Dataset over Chinese Mainland. Journal of Hydrology 2021, 595, 125660. [Google Scholar] [CrossRef]
Li, N.; Tang, G.; Zhao, P.; Hong, Y.; Gou, Y.; Yang, K. Statistical Assessment and Hydrological Utility of the Latest Multi-Satellite Precipitation Analysis IMERG in Ganjiang River Basin. Atmospheric Research 2017, 183, 212–223. [Google Scholar] [CrossRef]
Tang, G.; Zeng, Z.; Long, D.; Guo, X.; Yong, B.; Zhang, W.; Hong, Y. Statistical and Hydrological Comparisons between TRMM and GPM Level-3 Products over a Midlatitude Basin: Is Day-1 IMERG a Good Successor for TMPA 3B42V7? Journal of Hydrometeorology 2016, 17, 121–137. [Google Scholar]
Jiang, S.; Ren, L.; Xu, C.-Y.; Yong, B.; Yuan, F.; Liu, Y.; Yang, X.; Zeng, X. Statistical and Hydrological Evaluation of the Latest Integrated Multi-satellitE Retrievals for GPM (IMERG) over a Midlatitude Humid Basin in South China. Atmospheric Research 2018, 214, 418–429. [Google Scholar] [CrossRef]
Wang, Z.; Zhong, R.; Lai, C.; Chen, J. Evaluation of the GPM IMERG Satellite-Based Precipitation Products and the Hydrological Utility. Atmospheric Research 2017, 196, 151–163. [Google Scholar] [CrossRef]
Su, J.; Li, X.; Ren, W.; Lü, H.; Zheng, D. How Reliable Are the Satellite-Based Precipitation Estimations in Guiding Hydrological Modelling in South China? Journal of Hydrology 2021, 602, 126705. [Google Scholar] [CrossRef]
Jiang, L.; Bauer-Gottwein, P. How Do GPM IMERG Precipitation Estimates Perform as Hydrological Model Forcing? Evaluation for 300 Catchments across Mainland China. Journal of Hydrology 2019, 572, 486–500. [Google Scholar] [CrossRef]
Yuan, F.; Wang, B.; Shi, C.; Cui, W.; Zhao, C.; Liu, Y.; Ren, L.; Zhang, L.; Zhu, Y.; Chen, T.; et al. Evaluation of Hydrological Utility of IMERG Final Run V05 and TMPA 3B42V7 Satellite Precipitation Products in the Yellow River Source Region, China. Journal of Hydrology 2018, 567, 696–711. [Google Scholar] [CrossRef]
Mahmoud, M.T.; Mohammed, S.A.; Hamouda, M.A.; Mohamed, M.M. Impact of Topography and Rainfall Intensity on the Accuracy of IMERG Precipitation Estimates in an Arid Region. Remote Sensing 2021, 13, 13. [Google Scholar] [CrossRef]
CREAM Monographie de La Région SAVA 2013. Available online: http://www.monographiemada.com/ (accessed on 23 July 2022).
Tadross, M.; Randriamarolaza, L.; Rabefitia, Z.; Zheng, K.Y. Climate Change in Madagascar; Recent Past and Future. Washington, DC: World Bank 2008, 18.
CPGU Atlas de La Vulnérabilité Sectorielle de La Région SAVA. Cellule de Prevention et de la Gestion des Urgences: Antananarivo, Madagascar. 2012.
Jury, M.R.; Parker, B.A.; Raholijao, N.; Nassor, A. Variability of Summer Rainfall over Madagascar: Climatic Determinants at Interannual Scales. International journal of climatology 1995, 15, 1323–1332. [Google Scholar] [CrossRef]
Chaperon, P.; Danloux, J.; Ferry, L. Fleuves et Rivières de Madagascar. Monographies hydrologiques ORSTOM 1993, 14–854. [Google Scholar]
Pamela Probst, C.P. Tropical Cyclone ENAWO Post-Event Report 2017.
Ormsby, A.; Mannle, K. Ecotourism Benefits and the Role of Local Guides at Masoala National Park, Madagascar. Journal of Sustainable Tourism 2006, 14, 271–287. [Google Scholar] [CrossRef]
Hengl, T.; Mendes de Jesus, J.; Heuvelink, G.B.M.; Ruiperez Gonzalez, M.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global Gridded Soil Information Based on Machine Learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef]
Martinez, P.; Souza, I.F. Genesis of Pseudo-Sand Structure in Oxisols from Brazil – A Review. Geoderma Regional 2020, 22, e00292. [Google Scholar] [CrossRef]
Rossi, G. L’érosion à Madagascar: L’importance Des Facteurs Humains. Cahiers d’outre-mer 1979, 32, 355–370. [Google Scholar] [CrossRef]
Phillips, J.V.; Tadayon, S. Selection of Manning’s Roughness Coefficient for Natural and Constructed Vegetated and Non-Vegetated Channels, and Vegetation Maintenance Plan Guidelines for Vegetated Channels in Central Arizona; US Geological Survey, 2006.
Bontemps, S.; Defourny, P.; Van Bogaert, E.; Team, E.S.A.; Arino, O.; Kalogirou, V.; Perez, J.R. GLOBCOVER 2009 Products Description and Validation Report. 2009.
Deckers, J.; Nachtergaele, F.; Spaargaren, O. Tropical Soils in the Classification Systems of USDA, FAO and WRB. Evolution of Tropical Soil Science 2010, 79. [Google Scholar]
Earth Resources Observation And Science (EROS) Center Shuttle Radar Topography Mission (SRTM) 1 Arc-Second Global. Available online: https://www.usgs.gov/centers/eros/science/usgs-eros-archive-digital-elevation-shuttle-radar-topography-mission-srtm-1 (accessed on 03 June 2022), 2017.
Jalilibal, Z.; Amiri, A.; Castagliola, P.; Khoo, M.B.C. Monitoring the Coefficient of Variation: A Literature Review. Computers & Industrial Engineering 2021, 161, 107600. [Google Scholar] [CrossRef]
Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; Van Griensven, A.; Van Liew, M.W. SWAT: Model Use, Calibration, and Validation. Transactions of the ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
Fleuves et Rivières de Madagascar; Chaperon et al. , C., Ed.; Monographies hydrologiques ORSTOM; Office de la recherche scientifique et technique outre-mer: Paris, 1974; ISBN 978-2-7099-0344-8. [Google Scholar]
Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. Integrated Multi-satellitE Retrievals for GPM (IMERG) Technical Documentation. NASA/GSFC Code 2015, 612, 47. [Google Scholar]
Randriatsara, H.H.-R.H.; Hu, Z.; Ayugi, B.; Makula, E.K.; Vuguziga, F.; Nkunzimana, A. Interannual Characteristics of Rainfall over Madagascar and Its Relationship with the Indian Ocean Sea Surface Temperature Variation. Theor Appl Climatol 2022. [Google Scholar] [CrossRef]
Leigh, E.G. Structure and Climate in Tropical Rain Forest. Annual review of ecology and systematics 1975, 67–86. [Google Scholar] [CrossRef]
Bayat, B.; Hosseini, K.; Nasseri, M.; Karami, H. Challenge of Rainfall Network Design Considering Spatial versus Spatiotemporal Variations. Journal of Hydrology 2019, 574, 990–1002. [Google Scholar] [CrossRef]
Hohmann, C.; Kirchengast, G.; O, S.; Rieger, W.; Foelsche, U. Runoff Sensitivity to Spatial Rainfall Variability: A Hydrological Modeling Study with Dense Rain Gauge Observations. Hydrology and Earth System Sciences Discussions 2020, 1–28. [Google Scholar] [CrossRef]
Getirana, A.; Kirschbaum, D.; Mandarino, F.; Ottoni, M.; Khan, S.; Arsenault, K. Potential of GPM IMERG Precipitation Estimates to Monitor Natural Disaster Triggers in Urban Areas: The Case of Rio de Janeiro, Brazil. Remote Sensing 2020, 12, 4095. [Google Scholar] [CrossRef]
Krause, P.; Boyle, D.P.; Bäse, F. Comparison of Different Efficiency Criteria for Hydrological Model Assessment. Advances in Geosciences 2005, 5, 89–97. [Google Scholar] [CrossRef]
Musy, A. Hydrology: A Science for Engineers. 2004, 583.

Figure 1. Geographical context of the Sahafihitry catchment in Northeastern Madagascar: topography and location of weather station, additional rain gauges and river discharge monitoring station within the watershed. Grids correspond to the grid of the IMERG gridded precipitation dataset.

Figure 2. Characteristics of the Sahafihitry catchment: (a) 2020 land cover, (b) soil type, (c) slope.

Figure 4. Cumulative rainfall for one rain gauge (1RG), two rain gauges (2RG), five rain gauges (5RG) and IMERG satellite-based precipitation data based on ‘wet’ rainy season (RS) and ‘dry’ rainy season (DS). The date on the X-axis is in MM/DD/YYYY format.

Figure 5. Cumulative rainfall (5RG) and discharge (Q_OBS) curves of the Sahafihitry watershed over the entire study period (a) and on an annual basis (b).

Figure 6. Plots of observed and simulated daily flows for the 5 rainfall-runoff scenarios (from the left to the right: 1RG, 2RG, 5RG, IMERG) for the calibration period (top, from 08/2018 to 07/2020) and validation period (bottom, 08/2020 – 07/2021). The last scenario (IMERG_in_5RG) corresponds to the model calibrated using 5 rain gauges but run with IMERG data for the validation period.

Figure 7. Comparison of observed (Q_OBS) and simulated hydrographs for the validation period (08/2020-07/2021) at the Sahafihitry station for the 5 rainfall-runoff scenarios. Model calibrated using one raingauge (Q_1RG), 2 gauges (Q_2RG), 5 gauges (Q_5RG) or IMERG data (Q_IMERG). The last scenario corresponds to the model calibrated using 5 rain gauges but run with IMERG data for the validation period (IMERG_in_5RG).

Figure 8. Root Mean Square Error (RMSE), Nash Sutcliffe Efficiency coefficient (NSE) and Kling-Gupta efficiency (KGE) for various classes of discharge for the 5 rainfall-runoff scenarios. Model calibrated using one rain gauge (1RG), 2 gauges (2RG), 5 gauges (5RG) or IMERG data (IMERG). The last scenario corresponds to the model calibrated using 5 rain gauges but run with IMERG data for the validation period (IMERG_in_5RG). Square markers refer to the calibration period, triangular markers refer to the validation period.

Table 1. Description of the parameters used in the calibration process, their possible range, the initial value as well as the optimum values after calibration using the 1RG, 2RG, 5RG and IMERG rainfall scenarios (see Section 2.4.3).

Parameters	Description	Range		Initial value	1RG	2RG	5RG	IMERG
Parameters	Description	Min	Max
1: CN2	Multiplication factor for SCS runoff curve number	0	1	0.5	0.506	0.563	0.545	0.834
2: SOL_AWC	Multiplication factor for available water capacity of the soil layer	0	1	1	0.774	0.649	0.686	0.879
3: GW_DELAY	Groundwater delay (days)	0	450	31	367	58	72	70
4: GWQMN	Threshold depth of water in the shallow aquifer required for return flow to occur (mm)	0	5000	1000	1097	922	4982	1572
5: SHALLST	Initial depth of water in the shallow aquifer (mm)	0	5000	1000	802	2442	1002	2697
6: DEEPST	Initial depth of water in the deep aquifer (mm)	0	10000	2000	8115	7725	5275	9555
7: GW_REVAP	Groundwater “revap” coefficient	0.02	0.2	0.02	0.081	0.105	0.113	0.120
8: RCHRG_DP	Deep aquifer percolation fraction	0	1	0.05	0.3	0.4	0.9	0.8
9: GWHT	Initial groundwater height (m)	0	25	1	6.4	22.0	12.0	6.3
10: GW_SPYLD	Specific yield of the shallow aquifer (m³/m³)	0	0.4	0.003	0.3	0.2	0.2	0.3

Table 3. Cumulative rainfall and average coefficients of variation (CV) between the five ground-based rain gauges (5RG) and eight IMERG grids across the Sahafihitry watershed for three successive years.

Period (MM/DD/YYYY)	CV 5RG (%)	Cumulative rainfall 5RG	CV IMERG (%)	Cumulative rainfall IMERG
Period 1 (08/01/2018 – 07/31/2019)	71.9	2100	70.2	1721
Period 2 (08/01/2019 – 07/31/2020)	73.8	3350	62.9	2121
Period 3 (08/01/2020 – 07/03/2021)	63.4	1806	60.3	1370

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer