Validation of Ground Based Solar Irradiance Measurements against Meteosat-Msg and Himawari-8 Satellite Data

The study conducts a comparative analysis of solar radiation estimation methods, assessing the efficacy of the Heliosat-2 algorithm against ground measurements across seven distinct countries: Netherlands, Spain, Japan, Namibia, South Africa, Saudi Arabia, and India. To achieve this, it utilizes two distinct satellite data sources—Himawari-8 for Japan and Metosat Second Generation-MSG for the rest of the countries—spanning the years Jan 2022 to April 2024. A robust methodology for determining albedo parameters specific to Heliosat-2 was developed. During cloudy days, the estimates provided by Heliosat-2 generally exceeded the ground measurements in all the countries. Conversely, on clear days, there was a tendency for underestimation, as indicated by the median value of the mean bias (MB) across most of the countries. The Heliosat-2 model slightly underestimates daily radiation values, with a median MB ranging from −27.5 to +10.2 W.m⁻². Notably, the median root mean squared error (RMSE) on clear days is significantly lower, with values ranging from 24.8 to 108.7 W.m⁻², compared to cloudy days where RMSE values lie between 75.3 and 180.2 W.m⁻². In terms of R² values, both satellites show a strong correlation between the estimated and actual values, with a median value consistently above 0.86 on a monthly scale and over 92% of daily data points falling within ±2 standard deviation.

Keywords:

Subject: Environmental and Earth Sciences - Remote Sensing

1. Introduction

Measuring solar radiation is crucial for various applications including climate monitoring, weather forecasting, and particularly for the development and optimization of renewable energy projects. Accurate solar radiation data is essential for optimizing solar energy applications and validating models that forecast long-term daily global radiation levels, aiding in the efficient deployment and management of solar energy systems [1,2]. Furthermore, accurate solar radiation data is indispensable for environmental and climate studies, impacting sustainable energy solutions aimed at mitigating climate change [3]. The importance of disseminating best practices in solar radiation measurement and modelling is emphasized, highlighting their significance in educational and operational contexts within the solar industry [4]. These efforts collectively facilitate the efficient deployment of solar technologies, enhancing energy management systems and contributing to sustainable development goals.

Solar radiation data is derived from various sources, including ground-based measurements, satellite observations, and reanalysis datasets, each offering unique insights into solar energy patterns and dynamics. Ground-based measurements, such as those obtained from pyranometers, pyrheliometers, and weather stations, provide direct and accurate assessments of solar radiation at specific locations. For example, the World Radiation Monitoring Center - Baseline Surface Radiation Network (WRMC-BSRN) operates globally distributed ground stations equipped with high-quality instruments to measure solar radiation parameters [5]. These measurements contribute valuable data for understanding regional variations in solar radiation and its impact on climate and energy systems. Within the realm of climate change research, BSRN data have been instrumental in investigating global phenomena such as solar dimming and brightening [6,7]. In the context of energy systems, these data have been crucial in validating the frequency and ramp distributions pertinent to studies focusing on low-voltage grid dynamics [8]. Satellite observations complement ground measurements by providing global coverage and continuous monitoring. Satellites like Himawari, Meteosat Second Generation (MSG), GOES (Geostationary Operational Environmental Satellites), and INSAT (Indian National Satellite System) offer geostationary perspectives, capturing solar radiation data over specific regions with high temporal resolution [9]. These satellites are instrumental in weather forecasting, solar energy planning, and monitoring meteorological phenomena. Reanalysis datasets, such as ECMWF-ERA5 (European Centre for Medium-Range Weather Forecasts - Fifth Generation Reanalysis), MERRA2 (Modern-Era Retrospective analysis for Research and Applications, version 2), merge observations with numerical models to offer consistent and gridded records of solar radiation and other meteorological parameters over time and space [10]. These datasets are invaluable for climate studies, renewable energy planning, and understanding historical solar radiation patterns.

Satellite data estimate solar radiation on Earth's surface via remote sensing [11]. While they offer broad coverage and frequent updates, ground-based data provide precise measurements but are limited to specific locations. Reanalysis data merge observations with models for historical records but may have biases and uncertainties [12]. Integrating these datasets requires validation, addressing uncertainties, and combining sources for reliable solar radiation estimates

Various methods are utilized to extract solar irradiance from satellite data, including empirical models that rely on historical data, physical models based on principles of physics, statistical methods analyzing data patterns, machine learning approaches trained on satellite-ground measurements, and radiative transfer (RT) models simulating solar radiation interaction with the atmosphere [13]. Each method offers unique advantages and limitations, catering to different data availability, computational resources, and accuracy requirements. Among the methods employed for extracting solar irradiance from satellite data, the Heliosat method [14,15] stands out for its unique approach to approximating cloud transmission based on satellite-observed digital counts or calibrated radiances. This method is particularly useful in converting satellite cloud index data to solar irradiance values, essential for solar radiation forecasting and energy applications. Case studies where the Heliosat method has been used include short-term forecasting of solar radiation [11,16,17], solar energy assessment using remote sensing technologies [18,19], and deriving shortwave solar radiation from satellite images [11,20]. The advantages of the Heliosat method include its ability to derive cloud transmission values from satellite data, its adaptability to different satellite sensors, and its capability to provide estimates of solar irradiance based on cloud cover information, contributing to improved solar energy forecasting and resource assessment.

The accuracy of solar irradiance data derived from the Meteosat Second Generation Spinning Enhanced Visible and Infrared Imager (SEVIRI) satellite over the European Union (EU), particularly in Southern Spain and Switzerland, was assessed for the year 2015 using a Heliosat-based method called HelioMont, with reference to in-situ measurements [21]. The results indicate that under all-sky conditions, the mean biases (MB) varied from approximately -5.0 W.m⁻² to 55.0 W.m⁻². The root mean squared error (RMSE) ranged between about 175.0 W.m⁻² and 195.0 W.m⁻². The validation approach employed revealed correlation coefficients (specifically Pearson’s correlation coefficient, r) between HelioMont and the in-situ data within the range of 0.79 to 0.92. This indicates a robust correlation between the satellite-derived solar irradiance data and the ground-based measurements.

In parts of the Indian subcontinent in South Asian region, the utilization of the Heliosat method indicates a general positive bias in the estimated daily Global Horizontal Irradiance (GHI) compared to ground measurements from 2000 to 2007, typically within a range of 5%, with a RMSE averaging around 12.0% [22]. Conversely, another study [23] conducted in the Indian subcontinent employed a remote sensing-based method known as the Indian Solar Irradiance Operational System (INSIOS) to assess ground GHI measurements for the year 2018. The GHI output through this method during clear sky conditions predominantly resulted in underestimations compared to ground measurements. The MB (and RMSE) ranged from −12.5 (and −19.7) to −143.3 (206.5) W.m^-2 across different seasons. Similarly, during cloudy conditions, the model tended to overestimate ground observations. The MB (and RMSE) varied from −35.7 (47.4) to 389.6 (427.3) W.m^-2.

Meanwhile, in parts of the Middle East region, the Heliosat method during 2011-2014 yields predominantly negative biases for the hourly data, ranging from −7.0% to 4.0% for all-sky conditions and from −8.0% to 3.0% for clear sky conditions. Under cloudy-sky conditions, biases vary significantly between stations, ranging from 16.0% to 85.0%. The relative root mean squared error (%RMSE) ranges between 12.0% to 20.0% for all-sky conditions and 8.0% to 12.0% for clear sky conditions, but notably increases to above 56.0% under cloudy-sky conditions [24].

In parts of the African region, a study [25] was conducted to evaluate the performance of the Heliosat-based validation method against hourly ground GHI across four typical climatic zones using entire year data from 2015. The study reported %RMSE values ranging from 10.4% to 12.7%, with nominal MB falling between -0.97% and 0.39%.

In parts of the East Asian region, the Heliosat-based estimation of GHI against observed data during 2011-2013 indicated overall relative mean bias deviations (%MB) and %RMSE in daily solar irradiance retrieval of about 5.0 and 15.0%, respectively. Seasonally, the largest %MB and %RMSE of retrieved daily solar irradiance occurred in spring (9.5 and 21.3% on average), while the least %MB (-0.3% on average) and %RMSE (9.7% on average) occurred in autumn and winter, respectively [26].

Validation studies of the Heliosat method play a crucial role in evaluating its accuracy in estimating solar irradiance, ensuring the reliability of its outputs, and pinpointing areas for algorithm enhancement. The present study endeavors to bridge several research gaps within the field.

Firstly, while prior validation studies of the BSRN predominantly utilized data predating 2022, our investigation focuses on a more recent timeframe, utilizing data spanning from 2023 to 2024. This temporal shift ensures that our analyses remain relevant and reflective of current conditions, including the potential impacts of climate change on solar radiation patterns.
Secondly, unlike previous studies which often relied solely on either Himawari-8 or MSG datasets for validation purposes, our study pioneers the simultaneous integration of both datasets. The Himawari-8 data was used to study the locations in Japan, while MSG data was used for the sites in EU, Africa, Middle East, and South Asian region.
Lastly, a key objective of our study is the development of a comprehensive and robust methodology for determining albedo parameters specific to Heliosat-2. By refining these parameters, we anticipate significant advancements in remote sensing techniques for more accurate and reliable estimation of solar radiation.

In Section 2, the study addresses the examination of study sites, utilization of various satellite and ground data, and the methodology employed for extracting GHI data from satellite images, alongside the validation process using different indices against ground datasets. Section 3 presents the obtained results, emphasizing the comparison between satellite and ground data across different sky conditions and assessing the performance of two satellites in capturing seasonal GHI values. Section 4 further discusses these findings, contextualizing them within previous research endeavors and elucidating any agreements or discrepancies encountered. Finally, Section 5 succinctly encapsulates the key conclusions drawn from the study's findings.

2. Materials and Methods

2.1. Study Area and Data Sets Used

In this study, data was collected from various solar monitoring stations located across different countries, including Cabauw in Netherlands, Cener in Spain, Abashiri and Tateno in Japan, Gobabeb in Namibia, USAid Venda in South Africa, and South Jeddah in Saudi Arabia. Ground data was sourced from different networks, such as the World Radiation Monitoring Center-Baseline Surface Radiation Network (BSRN ─ https://bsrn.awi.de/) [5] and the Southern African Universities Radiometric Network (SAURAN ─ https://sauran.ac.za/) [28], (https://dataportals.pangaea.de/bsrn/stations) while some stations utilized SCADA (Supervisory Control and Data Acquisition) systems for ground data collection. The details of metadata of the locations used in the present study has been given in Table 1.

Global positioning of the locations can be accessed from Figure 1. Quality controls undertaken for the SAURAN data can be assessed from [28]. Similarly Quality control information for the BSRN data is available in [5]. Besides, all irradiance data collected for this study undergo a quality control routine as described by [34], whereby irradiance data points are tested for their physical acceptability and extreme limits. We also remove any time step with zenith angles above 85° due to questionable accuracy of measured data at these times.

The choice of satellite data sources for these stations depended on the availability and coverage of satellite scans over the respective regions. In the case of locations in Japan, such as Abashiri (ABS) and Tateno (TAT), the Himawari-8 satellite system was utilized due to its comprehensive coverage and high-resolution imagery specifically tailored for East Asian regions. Conversely, for stations in other countries like Netherlands, Spain, Namibia, South Africa, Saudi Arabia, and India the MSG satellite system was employed, as its coverage extends to a broader geographical area outside of East Asia.

We leveraged the images from the 0.64 micrometer (μm) in the visible (red) channel of the “Advanced Himawari Imager (AHI)” on the Himawari-8 geostationary satellite, operated by the Japan Meteorological Agency (JMA), accessible at https://himawari8.nict.go.jp/. The VIS0.64 channel of the Himawari-8 AHI measures data in the spectral band ranging from 0.555 to 0.721 μm, with a central wavelength of 0.6399, accessible at https://www.data.jma.go.jp/mscweb/en/himawari89/space_segment/spsg_ahi.html.

Furthermore, we integrated Indian Ocean Data Coverage (IODC) imagery from the visible 0.6 μm channel of the “High Rate Spinning Enhanced Visible Infra-Red Imager (SEVIRI)” on the MSG satellite, operated by the European Organisation for the Exploitation of Meteorological Satellites (EUMETSAT), available at (https://view.meteosat.int/). Images captured before June 2022 were sourced from MSG-1 (Meteosat-8), while those from June 2022 onward were obtained from MSG-2 (Meteosat-9) following the conclusion of the MSG-1 mission on July 1, 2022. The VIS0.6 channel of MSG SEVIRI belongs to the Visible and Near Infrared spectrum, with a central wavelength of 0.635 μm and a spectral band ranging from 0.56 to 0.71 μm [35].

2.2. Methodology

This section delineates the Heliosat-2 algorithm, an advanced methodology for estimating solar irradiance from satellite imagery and ground observations. The approach integrates sophisticated image classification techniques using deep learning, rigorous statistical analyses, and empirical calculations to ensure precision in solar irradiance values. Additionally, the validation of this method employs robust statistical indices, which quantify the accuracy of the Heliosat-2 estimates in comparison to ground-based measurements.

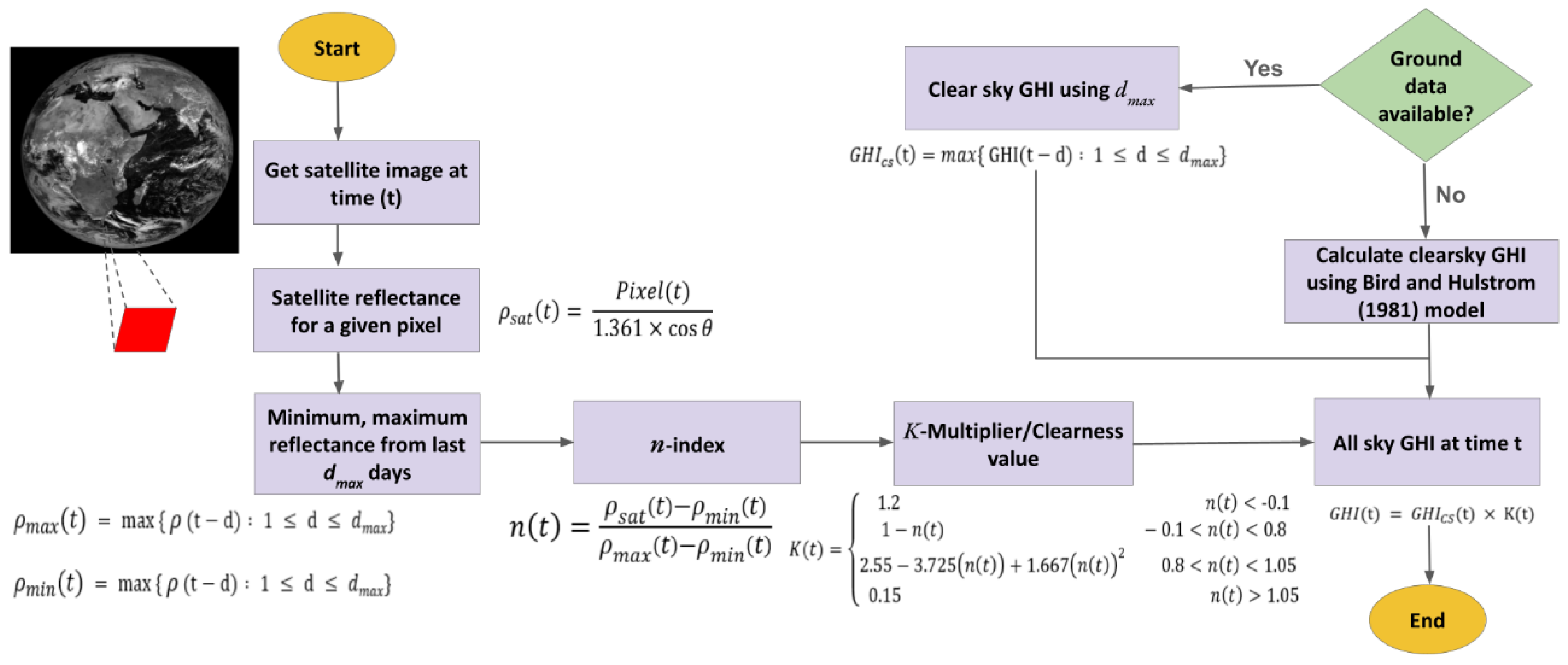
2.2.1. Heliosat-2

Below is a detailed explanation of the methodology and implementation of the Heliosat-2 algorithm for estimating solar irradiance, presenting a systematic approach to analyzing satellite imagery and ground observations to derive accurate solar irradiance values. Figure 2 shows the flowchart of the Heliosat-2 algorithm followed in this study.

Step 1: Generate Clear Sky Global Horizontal Irradiance ( ${G H I}_{c s}$ ):

Here the method utilizes the most recent ground GHI observations from the past to generate clear sky GHI for a specific timestamp (t)

{G H I}_{c s} (t) = m a x {G H I (t - d) : 1 \leq d \leq d_{m a x}}

(1)

Here,

d_{m a x}

is the number of days considered for calculating clear sky conditions.

Alternatively, a Bird clear sky model [36] can be used to calculate

{G H I}_{c s} (t)

depending on the availability of on-site clear sky solar radiation data set to estimate the coefficients in a solar radiation model [37]. Bird clear sky model takes into account factors such as the position of the sun, the solar zenith angle, atmospheric conditions (such as water vapor and aerosols), and surface albedo (reflectivity).

Step 2: Calculate Satellite Reflectance Value:

Determine the satellite reflectance value for the given timestamp (t) by analyzing the pixel value of the satellite image.

ρ_{s a t} (t) = \frac{P i x e l (t)}{1.361 \times \cos θ}

(2)

here,

ρ_{s a t} (t)

is the reflectance of the satellite,

P i x e l (t)

represents the pixel value, Here the solar constant is taken as 1.361 kW.m⁻², θ is the solar zenith angle.

Step 3: Calculate Minimum and Maximum Satellite Reflectance Values:

ρ_{m a x} (t) = m a x {ρ (t - d) : 1 \leq d \leq d_{m a x}}

(3)

ρ_{m i n} (t) = m a x {ρ (t - d) : 1 \leq d \leq d_{m a x}}

(4)

This helps in establishing the minimum and maximum satellite reflectance values to delineate the range of potential cloud cover.

In determining the albedo parameters, we take cues from both Bechet et al. [27] and Cros et al. [38].

The models developed by Bechet et al. and Cros et al. both represent significant advancements in the field of solar irradiance estimation, though they focus on different aspects of the issue. Model involved in Bechet et al. is primarily concerned with quantifying cloud cover through a cloudiness index labeled 'n', which is integral to understanding and predicting the solar irradiation that reaches the Earth's surface in a given area. The model operates on the principle that cloud cover significantly influences solar irradiance; by assessing the clarity of the sky through digital counts, it estimates the GHI. This methodology provides a focused approach to dealing with variability in cloud cover and its direct impact on solar energy reception. Conversely, method in Cros et al. broadens the scope by not only addressing cloud cover but also by integrating a comprehensive analysis of other atmospheric conditions, including aerosols, ozone, and water vapor, through RT modeling. Their technique retrieves a long time series of spectrally resolved all-sky radiance, enhancing the accuracy of irradiance data under both clear and cloudy sky conditions.

For

ρ_{m a x} (t)

, representing the maximum reflectance from cloudy pixels, we follow Cros et al.’s approach of selecting the 95^th percentile of reflectance values at local noon, ensuring robustness against outliers and changes in sensors. Local noon is when the sun is highest in the sky, marking its maximum altitude angle known as the solar zenith angle. It varies based on location and time of year due to factors like Earth's tilt and orbit. This is why the solar zenith angle is always at its minimum during local noon, making it distinct from surrounding times. As for

ρ_{m i n} (t)

, denoting ground albedo from a clear sky pixel, we blend methods, leaning towards the rationale in the study of Bechet et al. We opt for the second minimum albedo within a

d_{m a x}

time frame to mitigate potential image defects, ensuring reliability.

d_{m a x}

was fixed to a rolling window of 60-days in the current study.

Step 4: Calculate Cloudiness Index ( $n$ -index):

This step computes the cloudiness index or n-index or

n (t)

, where a higher value indicates a greater presence of clouds in the observed area.

n (t) = \frac{ρ_{s a t} (t) - ρ_{m i n} (t)}{ρ_{m a x} (t) - ρ_{m i n} (t)}

(5)

Step 5. Calculate $K$ -Multiplier or Clearness Value:

Here the

K

-multiplier, representing the clearness of the sky, based on the calculated cloudiness index is filtered out from an empirical set of values as given below.

K (t) = \{\begin{matrix} \begin{matrix} 1.2 n (t) < - 0.1 \\ 1 - n (t) - 0.1 < n (t) < 0.8 \\ 2.55 - 3.725 (n (t)) + 1.667 {(n (t))}^{2} 0.8 < n (t) < 1.05 \end{matrix} \\ 0.15 n (t) > 1.05 \end{matrix}

(6)

Step 6. Calculate GHI:

This step utilizes the previously determined clear sky GHI, along with the

K

-multiplier, to calculate the GHI for the given timestamp (t).

G H I (t) = {G H I}_{C S} (t) \times K (t)

(7)

2.2.2. Comparison Metrics

Three statistical indices were used to quantify degree of agreement/disagreement between the GHI estimates of Heliosat-2 (

\hat{y_{i}}

) and ground measurements (

y_{i}

): the Coefficient of Determination (R²), Mean Bias (MB), and Root Mean Squared Error (RMSE); whose equations are given below.

R^{2} = 1 - \frac{\sum_{i = 1}^{n} {(y}_{i} - {\hat{y_{i}})}^{2}}{\sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}

(8)

Here,

\bar{y}

represents the mean of the ground measurements.

M B = \frac{1}{n} \sum_{i = 1}^{n} (\hat{y_{i}} - y_{i})

(9)

R M S E = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} {(y_{i} - \hat{y_{i}})}^{2}}

(10)

R², quantifies the proportion of variability in the ground GHI measurement that is explained by the Heliosat-2 estimates, facilitating model evaluation regardless of scale. MB assesses the average error between Heliosat-2 and ground GHI values, providing insight into overall prediction accuracy. In contrast, RMSE, encapsulates the average magnitude of the differences between Heliosat-2 and ground GHI values, with lower values indicating better model performance. RMSE's sensitivity to large errors, interpretability in the units of the predicted variable, and robustness to outliers render it a versatile and informative metric for assessing predictive model accuracy.

3. Results

We conducted a thorough comparison between the solar radiation estimates generated by the Heliosat-2 model and ground measurements across diverse geographic locations: the Middle East, East Asia, and Africa. This analysis encompassed various categories, including hourly comparison, diurnal comparison (includes both clear sky and cloudy sky condition), month wise comparison, and season wise comparison.

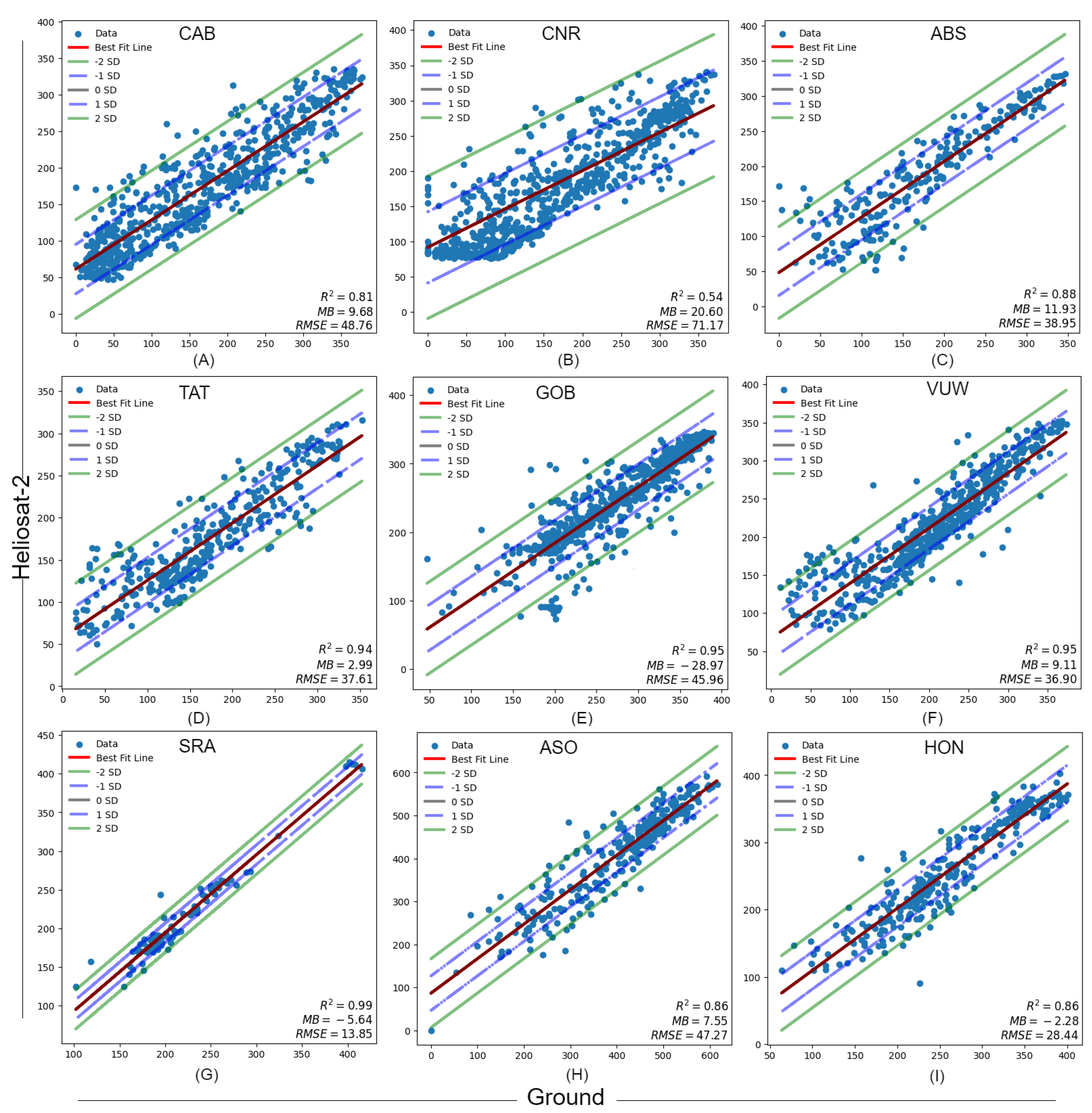
3.1. Validation of Mean Diurnal Radiation

Figure 3 illustrates the range of R² values, spanning from 0.54 to 0.99, across all locations. Specifically, the R² values for both EU locations were markedly different from each other. While the Cabauw (CAB) location demonstrated a fairly good agreement between satellite-derived and ground-based GHI estimates, with an R² value of 0.81 (Figure 3A), the Cener (CNR) location exhibited a poor comparison result with an R² value of 0.51 (Figure 3B). The R² value for Japanese sites employing Himawari-8 images [Abashiri (ABS) and Tateno (TAT)] stands at 0.91, as indicated in Figure 3C and Figure 3D. Conversely, Heliosat-2 estimates of GHI from MSG images exhibit a mean R² value of 0.95 for African locales [Gobabeb (GOB) and USAid Venda (VUW)], as depicted in Figure 3E and Figure 3F. Notably, the South Jeddah (SRA) location in Saudi Arabia boasts the highest R² value of 0.99, as evidenced in Figure 3G. The R² values for the Ashok Nagar (ASO) and Honnali (HON) locations in India were identical and shows a fairly good correlation (0.86) between the model and the ground GHI, as evident from Figure 3H and Figure 3I respectively. Across all locations, more than 92.4% of data points fell within the ±2 standard deviation (SD) range.

Regarding predicted GHI estimates, two EU locations shown an overestimation in terms of MB, ranging from +9.7 to +20.60 W.m^-2 (Figure 3A,B). Similarly, overestimations were also found for the two Japanese locations with MB, ranging from ~ 3.0 to 11.9 W.m^-2 (Figure 3C and 3D). Conversely, African sites in GOB and the Saudi Arabian location of SRA exhibit an underestimation ranging from -5.6 to ~ -29.0 W.m-². RMSE values range from a minimum of 13.8 W.m^-2 in the SRA location to a maximum of approximately 46.0 W.m-² in GOB. In India, the satellite GHI estimates shown a minor overestimation of +7.5 W.m^-2, while a nominal underestimation was observed in HON with a MB of -2.3 W.m^-2. The RMSE values across all the locations varies from a minimum of 13.8 W.m^-2 in SRA to a maximum of 71.2 in CNR.

3.2. Validation of Diurnal Radiation

Figure 4A displays the R² values depicting the correlation between the diurnal estimates of Heliosat-2 GHI and ground data. Meanwhile, Figure 4B and Figure 4C exhibit the MB and RMSE respectively. In Figure 4A, the median R² values exhibit a inclining trend as we transition from CAB to SRA locations and a declining nature from SRA to HON, with most values surpassing 0.8 except CAB and CNR. The Interquartile Range (IQR) for the SRA is the narrowest, followed by GOB and VUW, while its widest for CAB followed by CNR. The widest range of IQR in the two locations- CAB and CNR shows there are at least 25% of days when the estimated GHI and ground measurements had a R² value of less than 0.65 and 0.75 respectively.

The MB fluctuates significantly across the dataset, ranging from -130.7 to +145.2 W.m⁻² (Figure 4B). Analyzing the median MB, Heliosat-2's estimates show a nominal bias in CAB and CNR lying close to zero, while they have the highest range and IQR among all the other location in this study. Slight underestimation of daily radiation values, averaging -5.1 W.m⁻² was observed in TAT. Conversely, in ABS, there is an average overestimation of approximately +5.2 W.m⁻². Assessing the MB over African sites, Heliosat-2's estimates portray a tendency towards underestimation (-29.8 W.m⁻²) for the majority of daily radiation values in GOB, while in VUW, a minor overestimation (+3.4 W.m⁻²) is observed based on median values of MB throughout the study period (Figure 4B). The MB analysis in the SRA location of Saudi Arabia indicates that Heliosat-2 estimates slightly underestimate daily radiation values (clear + cloudy days) by a median value of approximately -10.5 W.m⁻². Both the Indian locations shown a nominal median MB close to zero. The HON location shows less uncertainty in terms of lower MB IQR and MB range across the study period for India.

Moreover, the RMSE data for Japan, depicted in Figure 4C, suggests relatively higher variability compared to the Middle East, with daily values ranging from 5.2 W.m⁻² to 195.0 W.m⁻² and an average median value of 71.9 W.m⁻², irrespective of sky conditions. Similarly, the analysis of RMSE data for the African region, as shown in Figure 4C, indicates a range of RMSE values between 9.6 W.m⁻² and 185.0 W.m⁻², with an average median value of 52.7 W.m⁻² on a daily time scale (inclusive of clear and cloudy days). The ASO location in India has the highest variability of RMSE values ranging from 0 to nearly 341.7 W.m⁻².

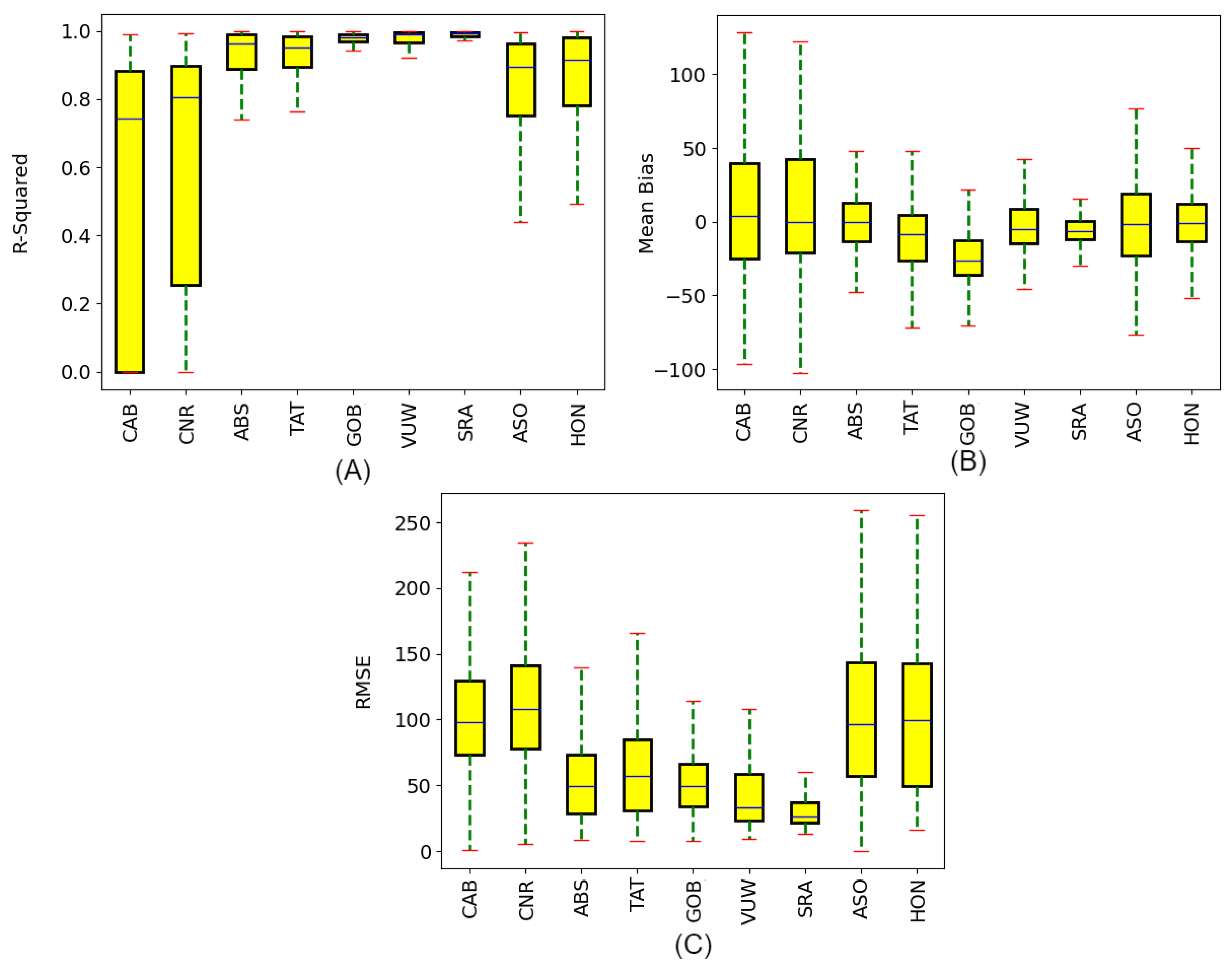
3.2.1. Validation under Daily Clear Sky Condition

On days classified as clear (as shown in Figure 5A), the median R² consistently exceeds 0.90 in all the regions except locations in EU (median R²>0.75), with African locations consistently surpassing 0.97. Under such conditions, the average median MB for both the EU locations were nearly Zero (though they have the highest variability among all the locations) while the average of the median MB for both the Japanese locations is −3.5 W.m⁻², ranging from −77.3 to +50.6 W.m⁻² (Figure 5B). Similarly, the median MB indicates an overall underestimation for both African locations, at −27.7 W.m⁻² in GOB and +7.6 W.m⁻² in VUW. In SRA location, the median value of the MB is −7.2 W.m⁻², with a range from −10.1 to −0.5 W.m⁻² for the 25^th to 75^th percentile of clear days' data. In India, the MB in clear days varies from -77.3 to 73.8 W.m⁻².

The highest RMSE for clear sky was observed in the CNR location with a median value of 108.6 W.m⁻². But the clear days presented lower RMSE values for both Japanese locations, averaging a median of 52.5 W.m⁻² (Figure 5C). In African locations, particularly on clear days, the median RMSE value hovers around 41.6 W.m⁻², with both GOB and VUW exhibiting similar error bars, ranging from approximately 7 to 115 W.m⁻². In SRA site, the RMSE values were notably lower, ranging from 16.2 W.m⁻² to 58.7 W.m⁻² (Figure 5C). The India locations shown the highest variability of RMSE values (0 to 250 W.m⁻²) under clear sky condition among all the locations analysed in this study.

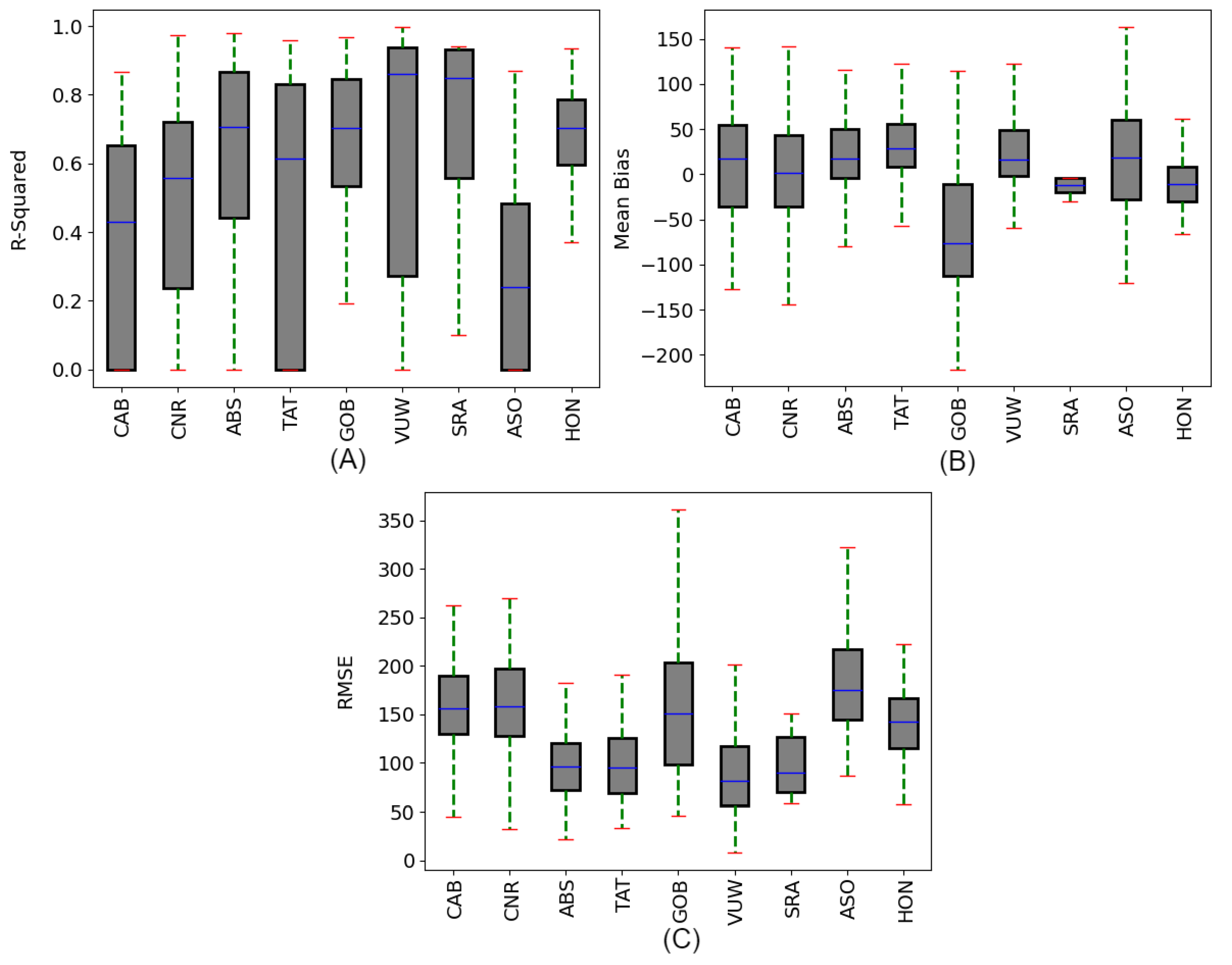
3.2.2. Validation under Daily Cloudy Sky Condition

In the overcast condition, the median values of R² across all the locations were remain less than 0.85. ASO location in India shows the lowest median R² value of approximately 0.23 (followed by 0.43 for CAB in the EU region), while it was highest for VUW. Under cloudy conditions, in Japanese sites, R² values drop to approximately 0.61 for TAT and 0.71 for ABS, as illustrated in Figure 6A. In contrast, the African region shows a less pronounced reduction under similar conditions, with median R² values falling to about 0.72 for GOB and 0.88 for VUW from a baseline of near perfect correlation (R²=0.98) on clear days. Similarly, in the SRA location, the decrease in R² value on cloudy days is to approximately 0.88, underscoring a universal trend of diminished solar radiation predictability during overcast weather.

Furthermore, the MB in solar radiation estimates under cloudy skies also varies significantly between these regions. In Japan, the MB indicates an average overestimation of +22.7 W.m^-2, with a wide range spanning from -80.9 to +125.2 W.m^-2. Conversely, the African sites display a diverse pattern of estimation errors; GOB records a median MB of -77.3 W.m^-2, suggesting a predominant underestimation, whereas VUW shows an overestimation with a median MB of +20.6 W.m^-2. The SRA location experiences a minimal underestimation with a median MB of -15.6 W.m^-2, ranging narrowly from -30.9 to -2.2 W.m^-2, as depicted in Figure 6B. The satellite estimates particularly performed well in SRA and HON locations as indicative from the lower IQR and range of MB in these locations (Figure 6B).

Additionally, the RMSE tends to increase across all locations during cloudy conditions, indicating greater variability in solar radiation estimates. Japan experiences a substantial spread in RMSE values from 23.7 to 185.9 W.m^-2, with a median of approximately 95.8 W.m^-2. For the African sites, GOB particularly shows higher RMSE values of 151.3 compared to VUW’s 84.9 W.m^-2, suggesting a higher error magnitude under cloudy skies at the GOB site. The SRA location also sees an elevation in RMSE, with values ranging from 62.3 to 148.2 W.m^-2 and a median of about 91.8 W.m^-2, reinforcing the global trend of increased uncertainty in solar radiation measurements during cloudier weather. Both the locations of EU, GOB, and ASO shows higher RMSE values consistently reaching up to 150.0 W.m^-2 under cloudy days.

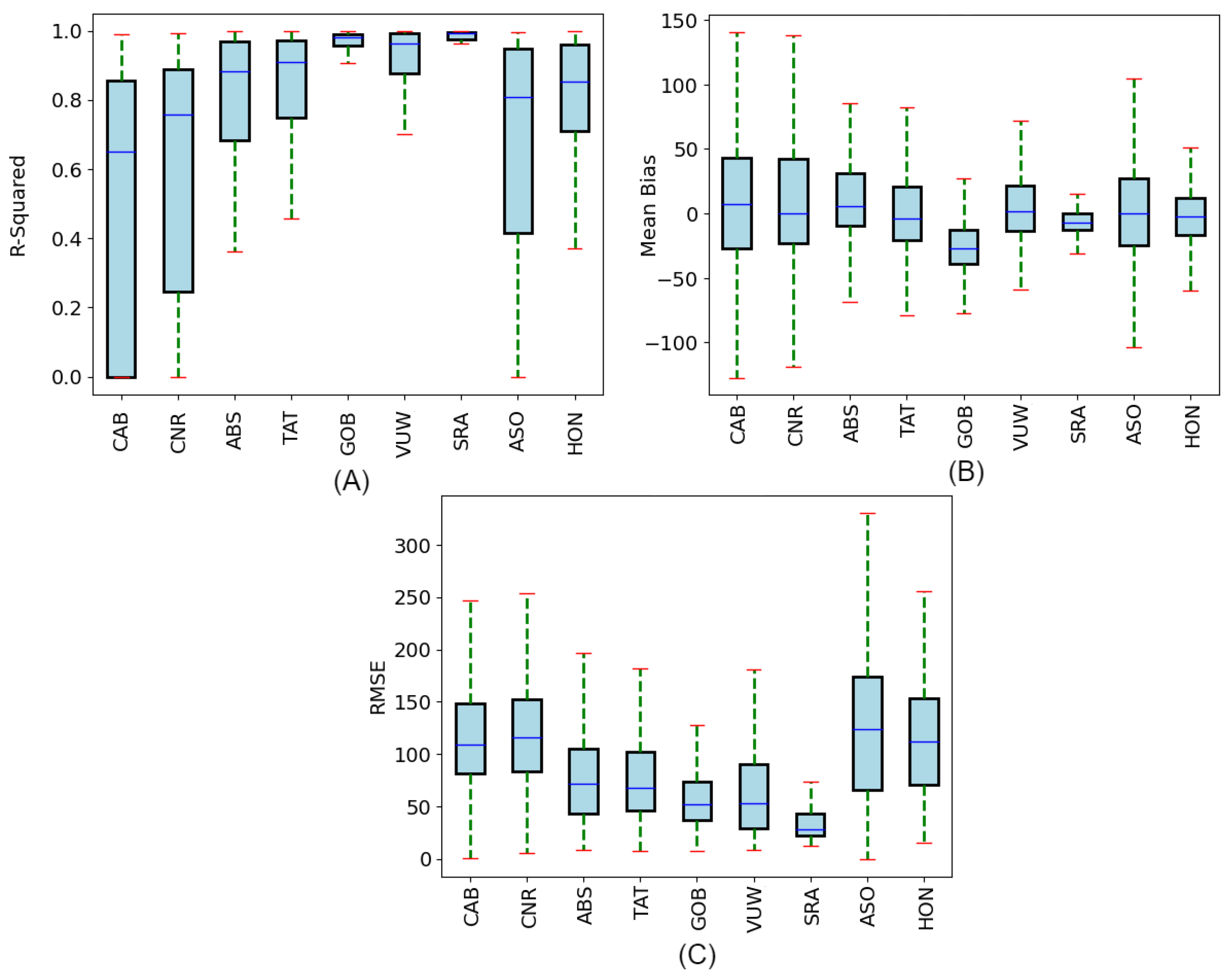
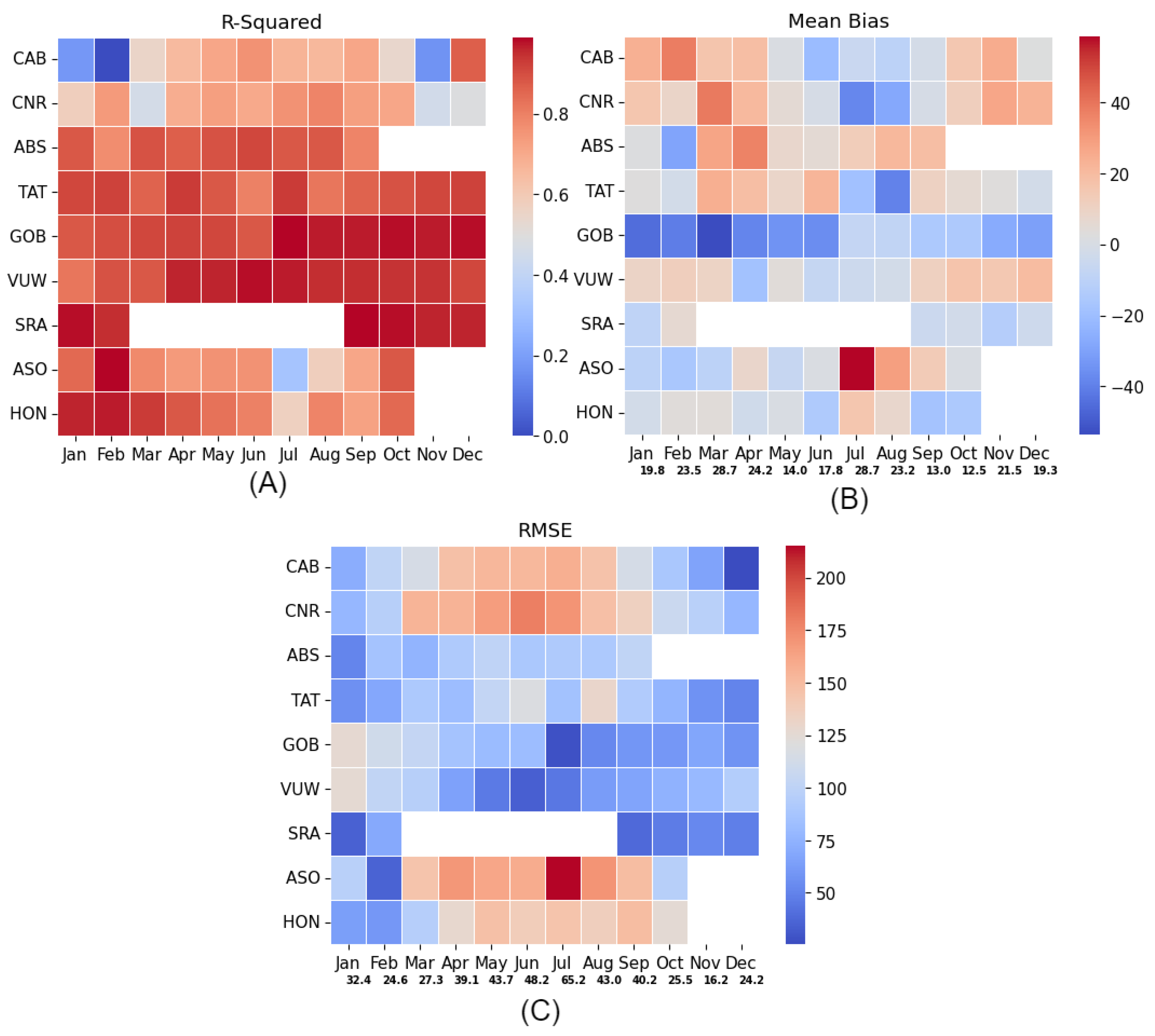
3.3. Validation of Diurnal Solar Radiation in Different Months

When evaluating GHI estimates from Heliosat-2 on a monthly basis, which includes both clear and cloudy days, the R² values in the EU locations were consistently lower than any other location in the study (< 0.65). Jan, Feb and Nov months in these locations were having very low R² values going below 0.3. In contrast, R² values in ABS and TAT locations of Japan remain impressively robust, consistently topping 0.75 (Figure 7A). Notably, in March, May, and June, these values often exceed 0.85. In African locations, R² values remain exceptionally high throughout the year, particularly from July through November, frequently surpassing 0.92. Similarly, in the SRA location, R² values are consistently high, generally exceeding 0.93, with peaks often above 0.97 during January, August, and September (Figure 7A). In Indian sites, during the monsoon months, the R² values were lower (< 0.7) compared to the non-monsoon months (>0.7).

EU sites, such as CAB and CNR, consistently display positive mean biases, indicating an overestimation of solar irradiance throughout the year, with CAB ranging from 15.91 to 37.96 W.m^-2 and CNR from 8.91 to 38.58 W.m^-2. On the monthly scale, MB values at Japanese sites fluctuate between −30.6 and +40.7 W.m^-2, with notable instances of overestimation, often exceeding +30.0 W.m^-2, particularly between March-April and August-September (Figure 7B). In contrast, at the African sites, GOB consistently shows a trend of underestimation, with values ranging from −11.1 to −50.0 W.m^-2, while VUW exhibits a general overestimation, with values ranging from 0 to +38.1 W.m^-2. The SRA location in Saudi Arabia sees MB values ranging from −13.5 to +12.2 W.m^-2, with a very slight underestimation typically observed during January, September, and November, ranging from −5.9 to +2.2 W.m^-2 (Figure 7B). In India, the performance of solar irradiance estimation using the Heliosate-2 method demonstrates a mixed pattern across the year. MB values for Indian sites, such as ASO and HON, vary notably, with ASO experiencing a range from -16.26 to 8.0 W.m^-2 and HON from -17.8 to 15.8 W.m^-2, indicating both overestimation and underestimation of solar irradiance.

In a monthly study, the RMSE values for EU sites are notably higher, with CAB and CNR recording values ranging from 72.0 to 166.0 W.m^-2 and 78.1 to 179.6 W.m^-2, respectively (Figure 7C). In the Japanese sites, notably lower RMSE values are observed between January-March and October-December, typically falling below 65.0 W.m^-2. African sites show a pattern of lower RMSE during the cooler months of July, August, and September (below 60.0 W.m^-2), whereas the warmer months of January, February, March, and December exhibit higher RMSE values, ranging from 95.0 to 130.0 W.m^-2, as illustrated in Figure 7C. At the SRA site in Saudi Arabia, RMSE values are exceptionally low, mostly below 50.2 W.m^-2, with January and September marking months where RMSE values are consistently below 30.0 W.m^-2. In India, the RMSE values remain relatively lower, with ASO and HON registering values ranging from 35.4 to 215.5 W.m^-2 and 60.1 to 146.8 W.m^-2, respectively.

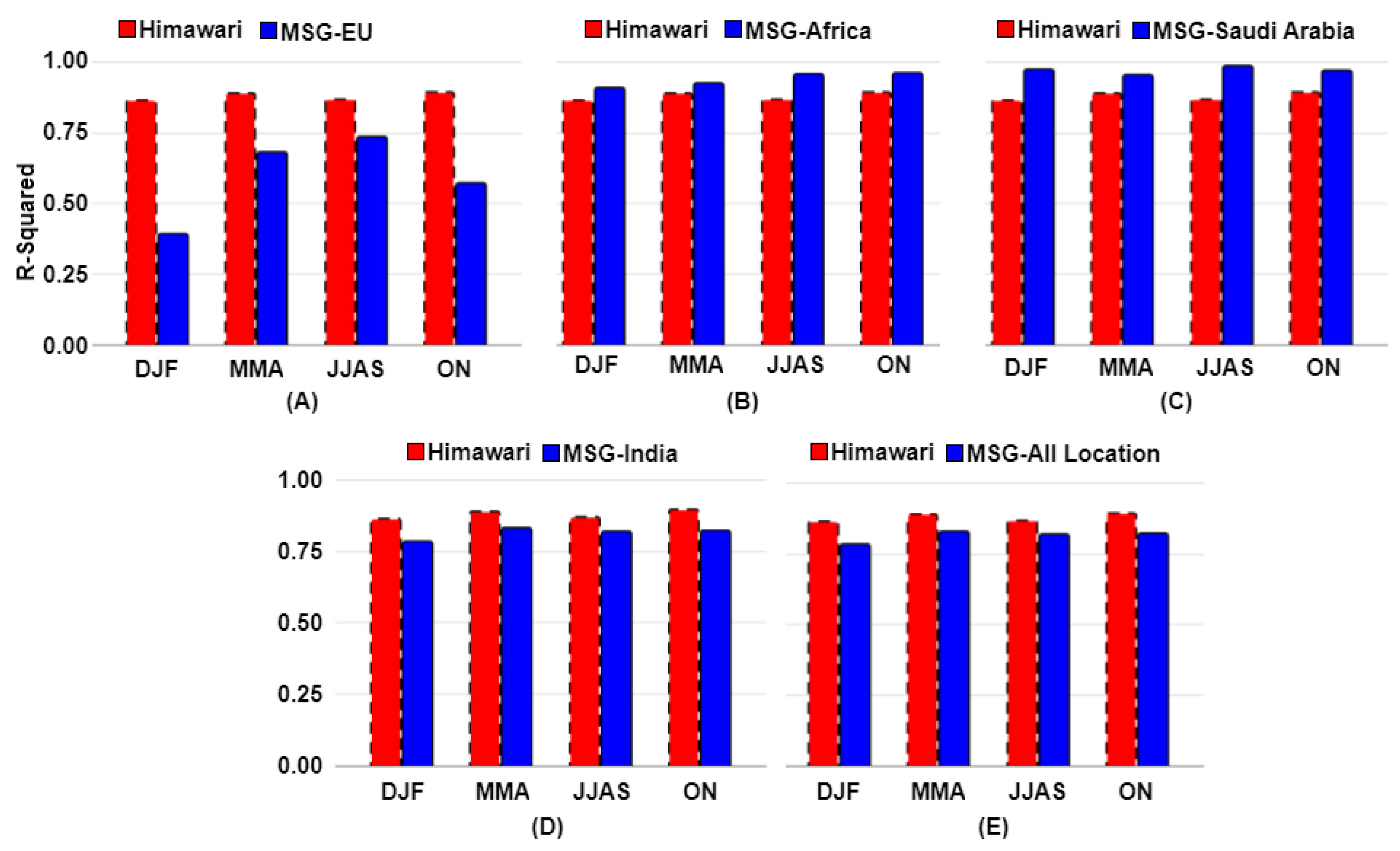
3.4. Validation of Diurnal Solar Radiation in Different Season

Figure 8 presents a comparative analysis of solar radiation estimates derived from the Himawari-8 and MSG satellites across various seasons, as represented by error and agreement indices. The study juxtaposes the satellite imagery by examining the magnitude of these indices within their respective geographical regions. Specifically, the Himawari-8 data originates from locations in East Asia, while the MSG data encompasses regions spanning EU, Middle East, Africa, and South Asia.

The R² values across all sub-images generally exhibit high levels, suggesting a strong correspondence between Himawari-8 and MSG-derived Global Horizontal Irradiance (GHI). Nonetheless, variations exist within the sub-images. In figure 8A, R² values for MSG-EU (< 0.75) region mostly lags behind Himawari-8 GHI estimates (>0.87) in most seasons. Conversely, figure 8B displays consistently higher R² values for MSG-Africa (>0.9) compared to Himawari-8. Subsequently, in Figure 8C, R² values for MSG-Saudi Arabia (>0.95) slightly surpassing those for Himawari. Similarly, in Figure 8D, MSG-India's R² values (~ 0.8) generally trail Himawari-8's, possibly due to heightened aerosol presence in MSG-India's locale. Lastly, in figure 8E, MSG-All (average) location's R² values (~ 0.8) generally fall short of Himawari-8’s estimates. Overall, while the R-squared values collectively indicate strong agreement between Himawari-8 and MSG-derived GHIs, disparities among different regions underscore the influence of satellite location, cloud cover, and aerosol levels.

4. Discussion

A blended method of estimation of all-sky GHI Heliosat-2 is proposed in this study adopted from Bechet et al. both [27] and Cros et al. [38] contribute significantly to the field of solar irradiance modeling, though they focus on different aspects. Bechet et al.'s H2-hybrid model emphasizes the importance of cloud cover in affecting solar irradiance, using a cloudiness index to estimate GHI. On the other hand, Cros et al.’s work enhances this approach by incorporating a wider range of atmospheric data including aerosols, ozone, and water vapor through radiative transfer modeling, enabling more precise calculations of spectrally resolved all-sky radiance. These methods complement each other by focusing on both specific and comprehensive atmospheric factors that influence solar irradiance, suggesting potential for integrated approaches to more accurately model and utilize solar energy data. Hence, we move into the following discussion to explore how these integrated approaches perform under varying weather conditions, particularly focusing on estimation biases during cloudy and clear days.

4.1. Estimation Bias Based on Weather: Cloudy vs. Clear

In our study, we observed that during cloudy days, the estimates provided by Heliosat-2 generally exceeded the ground measurements data in both Japanese and one African location. Conversely, on clear days, there was a tendency for underestimation, as indicated by the median value of the MB across all study locations. The proportion of cloudy days sampled (ranging from 19.9% to 41.23% across all regions in our study) was notably lower compared to the total sample of clear days (ranging from 58.77% to 81.1%), as demonstrated in Table 2. This result can be linked to the finding of [39] who employed FY-4A satellite images to derive GHI using the Heliosat-2 methodology across four locations in China from June 2018 to May 2019. Their findings mirrored ours, indicating a tendency to overestimate GHI in locations with limited ground-observed data and to underestimate it when such data were more abundant.

Studies [40,41,42] focusing on different versions of Heliosat, similarly noted a general underestimation of GHI values by the model during cloudy sky conditions. GHI estimation from SENSE2 (Solar Energy Nowcasting System) [43], also observed an overestimation of GHI under cloudy sky conditions. They attributed this to the uncertainties associated with cloud-related information within the satellite pixel. Additionally, they noted a relatively low underestimation linked with aerosol optical depth (AOD). In line with our findings, these studies underscore the influence of sky conditions and satellite data uncertainties on GHI estimation accuracy.

In the context of solar energy estimation, clear sky models provide estimates assuming cloudless conditions, considering factors like solar elevation angle, site altitude, and atmospheric properties. However, these models often underestimate the impact of cloud cover. Cloudy sky conditions, on the other hand, account for cloud scattering and absorption of sunlight, leading to overestimation due to clear sky assumptions. Real-world observations consider dynamic effects, resulting in differences between estimated and measured global horizontal irradiance (GHI). While clear sky models serve as useful benchmarks, understanding the complexities of cloud influence is crucial for accurate solar resource assessments

4.2. Comparison of GHI Studies

Study by [44] reported a RMSE of 73.8 W.m⁻² and an MB of −3.7 W.m⁻², indicating commendable accuracy but with a slight bias towards underestimation. Conversely, [45] exhibited a higher RMSE of 85.3 W.m⁻² and a significant bias (MB = 20.8 W.m⁻²), yet maintained a strong correlation with ground measurements (R² = 0.91). Our study surpassed both predecessors, boasting an RMSE of 65.0 W.m⁻², a minimal bias (MB = −5.1 W.m⁻²), and a similar R² value of 0.94. These results signify advancements in GHI estimation techniques, highlighting the efficacy of our methodological approach in achieving heightened precision and reliability.

In the TAT location of Japan, over the period from 2010 to 2014, the variability in MB highlights different challenges in the study of [46]. ERA5 shows a negative MB of −1.2 kW.m⁻², which may indicate underestimation of actual solar radiation levels. Both ERA-Interim and MERRA2 report positive biases (11.9 kW.m⁻² and 19.1 kW.m⁻², respectively), suggesting these models tend to overestimate solar radiation in this location. Our study indicates a MB of −5.1 kW.m⁻², further reinforcing the trend of underestimation observed in some datasets.

4.3. Performance Analysis of Heliosat-2 Estimates across Satellites

The accuracy of estimating Global Horizontal Irradiance (GHI) from satellite imagery using the Heliosat method hinges on understanding and mitigating various influencing factors. One such factor is the uncertainty associated with aerosol information, which plays a crucial role in GHI estimation accuracy [20]. Different regions exhibit varying levels of aerosol concentration, with India often experiencing higher pollution levels compared to regions like Africa, the Middle East, and East Asia. This discrepancy in aerosol levels introduces a significant source of uncertainty in GHI estimation, particularly in locations with elevated pollution levels like India. Consequently, accurately accounting for these uncertainties becomes imperative for improving GHI estimation accuracy, especially in regions prone to higher pollution levels.

Another critical factor impacting GHI estimation is the resolution of the satellite imagery used in the process [47]. Higher-resolution imagery, such as that provided by satellites like Himawari-8, enables more precise discrimination between cloudy and clear pixels, crucial for accurate GHI estimation. In contrast, lower-resolution imagery, such as that from MSG satellites, may struggle to discern such distinctions effectively. This limitation becomes particularly pronounced under conditions of moving clouds, which are prevalent in regions like Indian subcontinent in South Asia, especially during the monsoon season. As a result, the higher resolution of Himawari-8 compared to reference satellites like EUMETSAT positions it favorably for GHI estimation in India, offering better performance in resolving moving clouds and ultimately enhancing the accuracy of GHI estimation in the region.

5. Conclusions

In conclusion, the comparative analysis between the Heliosat-2 solar radiation estimates and ground measurements from diverse sources like BSRN, SAURAN, and SCADA across various geographic regions provides significant insights into the model's accuracy and reliability.

In the realm of solar energy estimation, clear sky models offer projections under the assumption of cloudless atmospheres, factoring in variables such as solar elevation angle, site altitude, and atmospheric characteristics. Nonetheless, these models often fall short in accurately assessing the influence of cloud cover. Conversely, cloudy sky conditions consider the scattering and absorption of sunlight by clouds, resulting in an overestimation attributable to the assumptions of clear sky scenarios. The study reveals a tendency for Heliosat-2 Global Horizontal Irradiance (GHI) estimates to overestimate during cloudy conditions and underestimate on clear days. This phenomenon can also be attributed to the lower sample size of the cloudy days compared to the clear days.

In EU regions, Heliosat-2 estimates exhibited poorer performance across all seasons compared to other regions, as indicated by lower MB, RMSE, and R² values, regardless of whether the days were clear or cloudy. Conversely, Africa and middle east regions demonstrated superior performance. In India and Japan, the performance was generally optimal, although India displayed higher variability in RMSE and lower R² values compared to Japan. The bias magnitude, derived from MSG estimates of Global Horizontal Irradiance (GHI), was lower in Africa and Saudi Arabia in contrast to India, Spain, and the Netherlands. This disparity is attributed to the higher resolution of Himawari-8 images, enabling the resolution of both cloudy and clear days with greater efficiency. Moreover, the presence of aerosol pollutants introduces uncertainty in GHI estimation, particularly in comparison to other regions.

The performance of Heliosat-2 in various locations demonstrates its efficacy in solar energy planning and radiation estimation. In Japan, despite notable variability in RMSE during cloudy days, the model achieves high median R² values on clear days, indicating robust performance. Similarly, in South Africa and Namibia, Heliosat-2 exhibits commendable accuracy, with a majority of data points falling within acceptable ranges. Although slight underestimations are observed in Saudi Arabia, particularly on cloudy days, the model consistently achieves high R² values, affirming its reliability in solar radiation estimation.

Overall, the study confirms the effectiveness of Heliosat-2 in providing reliable solar radiation estimates across diverse geographic regions and varying weather conditions. While slight deviations are noted under cloudy conditions, the model's ability to maintain high levels of accuracy during clear skies highlights its potential for widespread application in solar energy resource assessment and planning.

Author Contributions

Conceptualization, Syed Haider Abbas Rizvi and Ravi Choudhary; Data curation, Jitendra Kumar Meher and Ritesh Kumar; Formal analysis, Jitendra Kumar Meher; Investigation, Jitendra Kumar Meher; Methodology, Jitendra Kumar Meher; Project administration, Syed Haider Abbas Rizvi, Bhramar Choudhary and Ravi Choudhary; Resources, Ritesh Kumar; Software, Bhramar Choudhary and Yash Thakre; Supervision, Jitendra Kumar Meher and Syed Haider Abbas Rizvi; Validation, Jitendra Kumar Meher; Visualization, Jitendra Kumar Meher; Writing – original draft, Jitendra Kumar Meher; Writing – review & editing, Syed Haider Abbas Rizvi and Vikram Singh.

Funding

This research was fully funded by Solarad AI Private Limited. Solarad AI provided financial support and resources for the conduct of this research. The analysis and interpretation of data, as well as the decision to publish these findings, were carried out independently by the authors, ensuring the scientific rigor and integrity of the research.

Data Availability Statement

The BSRN datasets are publicly accessible via https://bsrn.awi.de/. SAURAN data can be retrieved from the public repository at https://sauran.ac.za/. Himawari-8 images, intended solely for research and educational purposes, are freely obtainable from https://himawari8.nict.go.jp/ following registration with the HIMAWARI administration. Similarly, images from MSG can be acquired from https://view.meteosat.int/. Heliosat-2 estimate datasets will be provided upon request. However, due to a Non-Disclosure Agreement (NDA) with the SRA, access to SCADA data is contingent upon signing an NDA with the requesting agency.

Acknowledgments

All the authors wish to express their gratitude to the administrators of BSRN, SAURAN, Himawari, EUMETSAT, and SRA SCADA data for generously providing access to their datasets, without which this research could not have been accomplished successfully. Additionally, the funding support extended by Solarad AI Private Limited is gratefully acknowledged.

Conflicts of Interest

The authors declare no conflicts of interest.” The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

Habte, A.; Sengupta, M.; Lopez, A. Evaluation of the National Solar Radiation Database (NSRDB): 1998-2015; No. NREL/TP-5D00-67722; National Renewable Energy Lab (NREL): Golden, CO, USA, 2017.
Zhang, J.; Zhao, L.; Deng, S.; Xu, W.; Zhang, Y. A Critical Review of the Models Used to Estimate Solar Radiation. Renew. Sustain. Energy Rev. 2017, 70, 314–329. [Google Scholar] [CrossRef]
Sen, Z. Solar Energy Fundamentals and Modeling Techniques: Atmosphere, Environment, Climate Change, and Renewable Energy; Springer Science & Business Media: 2008. [CrossRef]
Sengupta, M.; Habte, A.; Wilbert, S.; Gueymard, C.; Remund, J. Best Practices Handbook for the Collection and Use of Solar Resource Data for Solar Energy Applications; No. NREL/TP-5D00-77635; National Renewable Energy Lab (NREL): Golden, CO, USA, 2021.
Driemel, A.; Augustine, J.; Behrens, K.; Colle, S.; Cox, C.; Cuevas-Agulló, E.; Denn, F. M.; Duprat, T.; Fukuda, M.; Grobe, H.; Haeffelin, M.; Hodges, G.; Hyett, N.; Ijima, O.; Kallis, A.; Knap, W.; Kustov, V.; Long, C. N.; Longenecker, D.; Lupi, A.; Maturilli, M.; Mimouni, M.; Ntsangwane, L.; Ogihara, H.; Olano, X.; Olefs, M.; Omori, M.; Passamani, L.; Pereira, E. B.; Schmithüsen, H.; Schumacher, S.; Sieger, R.; Tamlyn, J.; Vogt, R.; Vuilleumier, L.; Xia, X.; Ohmura, A.; König-Langlo, G. Baseline Surface Radiation Network (BSRN): Structure and Data Description (1992–2017). Earth Syst. Sci. Data 2018, 10, 1491–1501. [Google Scholar] [CrossRef]
Hatzianastassiou, N.; Ioannidis, E.; Korras-Carraca, M.B.; Gavrouzou, M.; Papadimas, C.D.; Matsoukas, C.; Benas, N.; Fotiadi, A.; Wild, M.; Vardavas, I. Global Dimming and Brightening Features during the First Decade of the 21st Century. Atmosphere 2020, 11, 308. [Google Scholar] [CrossRef]
Stamatis, M.; Hatzianastassiou, N.; Korras-Carraca, M.B.; Matsoukas, C.; Wild, M.; Vardavas, I. Interdecadal Changes of the MERRA-2 Incoming Surface Solar Radiation (SSR) and Evaluation against GEBA & BSRN Stations. Appl. Sci. 2022, 12, 10176. [Google Scholar] [CrossRef]
Schreck, S.; Schroedter-Homscheidt, M.; Klein, M.; Cao, K.K. Satellite Image-Based Generation of High Frequency Solar Radiation Time Series for the Assessment of Solar Energy Systems. Meteorologische Zeitschrift 2020. [CrossRef]
Balsamo, G.; Agusti-Parareda, A.; Albergel, C.; Arduini, G.; Beljaars, A.; Bidlot, J.; Blyth, E.; Bousserez, N.; Boussetta, S.; Brown, A.; Buizza, R. Satellite and In Situ Observations for Advancing Global Earth Surface Modelling: A Review. Remote Sens. 2018, 10, 2038. [Google Scholar] [CrossRef]
Valipour, M.; Dietrich, J. Developing Ensemble Mean Models of Satellite Remote Sensing, Climate Reanalysis, and Land Surface Models. Theor. Appl. Climatol. 2022, 150, 909–926. [Google Scholar] [CrossRef]
Prasad, A. A.; Kay, M. Prediction of Solar Power Using Near-Real Time Satellite Data. Energies 2021, 14, 5865. [Google Scholar] [CrossRef]
Baatz, R.; Hendricks Franssen, H.J.; Euskirchen, E.; Sihi, D.; Dietze, M.; Ciavatta, S.; Fennel, K.; Beck, H.; De Lannoy, G.; Pauwels, V.R.N.; Raiho, A. Reanalysis in Earth System Science: Toward Terrestrial Ecosystem Reanalysis. Rev. Geophys. 2021, 59, e2020RG000715. [Google Scholar] [CrossRef]
Huang, G.; Li, Z.; Li, X.; Liang, S.; Yang, K.; Wang, D.; Zhang, Y. Estimating Surface Solar Irradiance from Satellites: Past, Present, and Future Perspectives. Remote Sens. Environ. 2019, 233, 111371. [Google Scholar] [CrossRef]
Cano, D.; Monget, J.M.; Albuisson, M.; Guillard, H.; Regas, N.; Wald, L. A Method for the Determination of the Global Solar Radiation from Meteorological Satellite Data. Solar Energy 1986, 37, 31–39. [Google Scholar] [CrossRef]
Rigollier, C.; Lefèvre, M.; Wald, L. The Method Heliosat-2 for Deriving Shortwave Solar Radiation from Satellite Images. Solar Energy 2004, 77, 159–169. [Google Scholar] [CrossRef]
Yang, L.; Gao, X.; Hua, J.; Wu, P.; Li, Z.; Jia, D. Very Short-Term Surface Solar Irradiance Forecasting Based on FengYun-4 Geostationary Satellite. Sensors 2020, 20, 2606. [Google Scholar] [CrossRef]
Thaker, J.; Höller, R.; Kapasi, M. Short-Term Solar Irradiance Prediction with a Hybrid Ensemble Model Using METEOSAT Satellite Images. Energies 2024, 17, 329. [Google Scholar] [CrossRef]
El Alani, O.; Ghennioui, H.; Abraim, M.; Ghennioui, A.; Blanc, P.; Saint-Drenan, Y.M.; Naimi, Z. Solar Energy Resource Assessment Using GHI and DNI Satellite Data for Moroccan Climate. In Proceedings of the International Conference on Advanced Technologies for Humanity, November 2021; Springer International Publishing: Cham, 275-285. [CrossRef]
Verma, P.; Patil, S. A Machine Learning Approach and Methodology for Solar Radiation Assessment Using Multispectral Satellite Images. Ann. Data Sci. 2023, 10, 907–932. [Google Scholar] [CrossRef]
Huang, C.; Shi, H.; Yang, D.; Gao, L.; Zhang, P.; Fu, D.; Chen, Q.; Yuan, Y.; Liu, M.; Hu, B.; Lin, K. Retrieval of Sub-Kilometer Resolution Solar Irradiance from Fengyun-4A Satellite Using a Region-Adapted Heliosat-2 Method. Solar Energy 2023, 264, 112038. [Google Scholar] [CrossRef]
Vuilleumier, L.; Meyer, A.; Stöckli, R.; Wilbert, S.; Zarzalejo, L.F. Accuracy of satellite-derived solar direct irradiance in Southern Spain and Switzerland. *Int. J. Remote Sens. 2020, 41, 8808–8838. [Google Scholar]
Polo, J.; Zarzalejo, L.F.; Cony, M.; Navarro, A.A.; Marchante, R.; Martin, L.; Romero, M. Solar Radiation Estimations over India Using Meteosat Satellite Images. Solar Energy 2011, 85, 2395–2406. [Google Scholar] [CrossRef]
Masoom, A.; Kosmopoulos, P.; Bansal, A.; Kazadzis, S. Solar Energy Estimations in India Using Remote Sensing Technologies and Validation with Sun Photometers in Urban Areas. Remote Sens. 2020, 12, 254. [Google Scholar] [CrossRef]
Ameen, B.; Balzter, H.; Jarvis, C.; Wey, E.; Thomas, C.; Marchand, M. Validation of Hourly Global Horizontal Irradiance for Two Satellite-Derived Datasets in Northeast Iraq. Remote Sens. 2018, 10, 1651. [Google Scholar] [CrossRef]
Sarr, A.; Kebe, C.M.F.; Ndiaye, A. Validation of Helioclim-3 irradiance with ground observations in Senegal using four typical climatic zones. Materials Today: Proceedings. 2022, 51, 1888–1895. [Google Scholar]
Syu, M.R.; Lee, P.H.; Leou, T.M.; Shen, Y. Solar Irradiance and Pan Evaporation Estimation from Meteorological Satellite Data. Terrestrial, Atmospheric & Oceanic Sciences 2016, 27. [Google Scholar]
Bechet, J.; Albarelo, T.; Macaire, J.; Salloum, M.; Zermani, S.; Primerose, A.; Linguet, L. Updated GOES-13 Heliosat-2 Method for Global Horizontal Irradiation in the Americas. Remote Sens. 2022, 14, 224. [Google Scholar] [CrossRef]
Brooks, M.J.; Du Clou, S.; Van Niekerk, W.L.; Gauché, P.; Leonard, C.; Mouzouris, M.J.; Meyer, R.; Van der Westhuizen, N.; Van Dyk, E.E.; Vorster, F.J. SAURAN: A New Resource for Solar Radiometric Data in Southern Africa. J. Energy Southern Africa 2015, 26, 2–10. [Google Scholar] [CrossRef]
Knap, Wouter. Basic and other measurements of radiation at station Cabauw (2005-02 et seq) [dataset publication series]. Koninklijk Nederlands Meteorologisch Instituut, De Bilt, PANGAEA, 2022. [CrossRef]
Olano, Xabier. Basic measurements of radiation at station Cener (2009-07 et seq) [dataset publication series]. National Renewable Energy Centre, PANGAEA, 2021. [CrossRef]
Ohtake, Jun. Basic measurements of radiation at station Abashiri (2021-04) [dataset]. Japan Meteorological Agency, Tokyo, PANGAEA. 2021. [CrossRef]
Ijima, Osamu. Basic and other measurements of radiation at station Tateno (2020-12) [dataset]. Aerological Observatory, Japan Meteorological Agency, PANGAEA. 2021. [CrossRef]
Vogt, R. Basic and Other Measurements of Radiation at Station Gobabeb (2013-09). [Online]. 2013. [CrossRef]
Long, C.N.; Shi, Y. The QCRad value added product: Surface radiation measurement quality control testing, including climatology configurable limits. Atmospheric Radiation Measurement Program Technical Report, 2006. [CrossRef]
Ouiqary, A.E.; Kheddioui, E.; Smiej, M.F. Evaluation of the Global Horizontal Irradiation (GHI) on the Ground from the Images of the Second Generation European Meteorological Satellites MSG. Journal of Computer and Communications 2023, 11, 1–11. [Google Scholar] [CrossRef]
Bird, R.E.; Hulstrom, R.L. Simplified clear sky model for direct and diffuse insolation on horizontal surfaces. Solar Energy Research Institute (SERI), Golden, CO, United States, 1981. (No. SERI/TR-642-761).
Annear, R.L.; Wells, S.A. A comparison of five models for estimating clear-sky solar radiation. Water Resources Research 2007, 43. [Google Scholar] [CrossRef]
Cros, S.; Badosa, J.; Szantaï, A.; Haeffelin, M. Reliability predictors for solar irradiance satellite-based forecast. Energies 2020, 13, 5566. [Google Scholar] [CrossRef]
Jia, D.; Hua, J.; Wang, L.; Guo, Y.; Guo, H.; Wu, P.; Liu, M.; Yang, L. Estimations of global horizontal irradiance and direct normal irradiance by using Fengyun-4A satellite data in northern China. Remote Sensing 2021, 13, 790. [Google Scholar] [CrossRef]
Oumbe, A.; Blanc, P.; Ranchin, T.; Homscheidt, M.S.; Wald, L. A new method for estimating solar energy resource. In Proceedings of the 33rd International Symposium on Remote Sensing of Environment (ISRSE 33), Joint Research Center, May 2009, paper-773.
Qu, Z.; Oumbe, A.; Blanc, P.; Espinar, B.; Gesell, G.; Gschwind, B.; Klüser, L.; Lefèvre, M.; Saboret, L.; Schroedter-Homscheidt, M.; Wald, L. Fast radiative transfer parameterisation for assessing the surface solar irradiance: The Heliosat-4 method. Meteorologische Zeitschrift 2017, 26, 33–57. [Google Scholar] [CrossRef]
Mouhamet, D.; Tommy, A.; Primerose, A.; Laurent, L. Improving the Heliosat-2 method for surface solar irradiation estimation under cloudy sky areas. Solar Energy 2018, 169, 565–576. [Google Scholar] [CrossRef]
Papachristopoulou, K.; Fountoulakis, I.; Bais, A.F.; Psiloglou, B.E.; Papadimitriou, N.; Raptis, I.P.; Kazantzidis, A.; Kontoes, C.; Hatzaki, M.; Kazadzis, S. Effects of clouds and aerosols on downwelling surface solar irradiance nowcasting and short-term forecasting. Atmospheric Measurement Techniques 2024, 17, 1851–1877. [Google Scholar] [CrossRef]
Li, J.; Tang, W.; Qi, J.; Yan, Z. Mapping high-resolution surface shortwave radiation over East Asia with the new generation geostationary meteorological satellite Himawari-8. International Journal of Digital Earth 2023, 16, 323–336. [Google Scholar] [CrossRef]
Yu, Y.; Shi, J.; Wang, T.; Letu, H.; Yuan, P.; Zhou, W.; Hu, L. Evaluation of the Himawari-8 shortwave downward radiation (SWDR) product and its comparison with the CERES-SYN, MERRA-2, and ERA-interim datasets. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2018, 12, 519–532. [Google Scholar] [CrossRef]
Urraca, R.; Huld, T.; Gracia-Amillo, A.; Martinez-de-Pison, F.J.; Kaspar, F.; Sanz-Garcia, A. Evaluation of global horizontal irradiance estimates from ERA5 and COSMO-REA6 reanalyses using ground and satellite-based data. Solar Energy 2018, 164, 339–354. [Google Scholar] [CrossRef]
Fountoulakis, I.; Kosmopoulos, P.; Papachristopoulou, K.; Raptis, I.P.; Mamouri, R.E.; Nisantzi, A.; Gkikas, A.; Witthuhn, J.; Bley, S.; Moustaka, A.; Buehl, J. Effects of Aerosols and Clouds on the Levels of Surface Solar Radiation and Solar Energy in Cyprus. Remote Sens. 2021, 13, 2319. [Google Scholar]

Figure 1. Global positioning of the locations taken in this study. The locations labels are the short names of the sites adopted from Table 1.

Figure 2. Flowchart showing the algorithms used for the all sky GHI estimation using Heliosat-2.

Figure 3. Comparison of mean diurnal ground and Heliosat-2 GHI estimates in terms of scatter plot for (A) CAB, (B) CNR, (C) ABS, (D) TAT, (E) GOB, (F) VUW, (G) SRA, (H) ASO, and (I) HON sites irrespective of clear and cloudy days.

Figure 4. Comparison of ground and Heliosat-2 GHI estimates in terms of (A) R² (B) MB (in W.m^-2) and (C) RMSE (in W.m^-2) values for the diurnal radiation irrespective of clear and cloudy days.

Figure 5. Comparison of ground and Heliosat-2 GHI estimates in terms of (A) R² (B) MB (in W.m^-2) and (C) RMSE (in W.m^-2) values for the diurnal radiation considering only clear sky condition.

Figure 6. Comparison of ground and Heliosat-2 GHI estimates in terms of (A) R² (B) MB (in W.m^-2) and (C) RMSE (in W.m^-2) values for the diurnal radiation considering only cloudy sky condition.

Figure 7. Comparison of ground and Heliosat-2 GHI estimates in terms of (A) R² (B) MB (in W.m^-2) and (C) RMSE (in W.m^-2) values for the diurnal radiation in different months.

Figure 8. The seasonal performance comparison between Himawari-8 retrieved GHI (red color bar) and that of GHI derived from MSG in (A) EU (B) Africa, (C) Saudi Arabia, (D) India and (E) All location. DJF represents December-January-February; MAM denotes March-April-May; JJAS signifies June-July-August-September, and ON stands for October-November.

Table 1. Metadata of locations taken. The ‘analysis period’ - column shows the time period where the statistical analysis was performed. For middle east and south Asia location, the ground data was taken from the site SCADA.

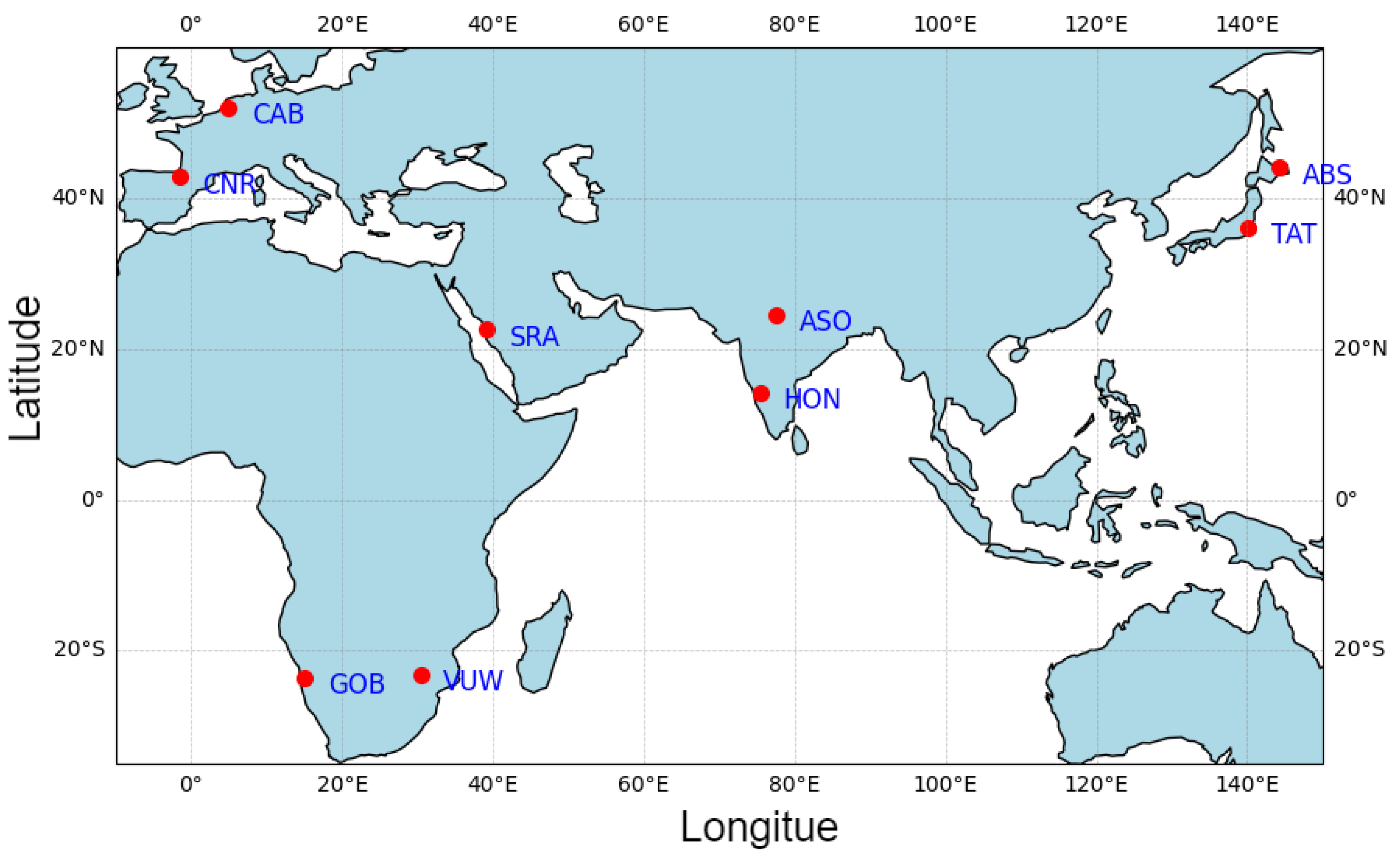
Station Name	Short Names	Lat (° N/S)	Lon (° E/W)	Country (Region)	Ground Data Source	Satellite Data source	Analysis Period	Reference
Cabauw	CAB	51.96	4.92	Netherlands (European Union)	BSRN	MSG-1 and 2	01/2022 - 02/2024	[29]
Cener	CNR	42.81	-1.60	Spain (European Union)	BSRN	MSG-1 and 2	01/2022 - 01/2024	[30]
Abashiri	ABS	44.01	144.27	Japan (East Asia)	BSRN	Himawari-8	01/2023 - 10/2023	[31]
Tateno	TAT	36.05	140.12	Japan (East Asia)	BSRN	Himawari-8	01/2023 - 02/2024	[32]
Gobabeb	GOB	−23.56	15.04	Namibia (Africa)	BSRN	MSG-1 and 2	01/2022 - 12/2023	[33]
USAid Venda	VUW	−23.13	30.42	South Africa (Africa)	SAURON	MSG-1 and 2	01/2022 - 12/2023	[28]
South Jeddah	SRA	22.58	39.16	Saudi Arabia (Middle East)	Ground SCADA	MSG-1 and 2	08/2023 - 01/2024 03/2024 - 04/2024	-
Ashok Nagar	ASO	24.52	77.62	India (South Asia)	Ground SCADA	MSG-1 and 2	01/2023 – 10/2023	-
Honnali	HON	14.20	75.56	India (South Asia)	Ground SCADA	MSG-1 and 2	01/2023 – 10/2023	-

Table 2. Represents the number of clear and cloudy days across all the locations in the current investigation. Here N_Clouds represent the number of cloudy days, N_Clear represents the number of clear sky days, % estimate of the number of cloudy and clear days were given in the last two columns.

Site	N_Cloudy	N_Clear	Total Days	% N_Cloudy	% N_Clear
CAB	167	596	763	21.89	78.12
CNR	136	624	760	17.89	82.11
ABS	132	140	272	48.53	51.47
TAT	143	252	395	36.20	63.80
GOB	88	642	730	12.05	87.95
VUW	240	490	730	32.88	67.12
SRA	55	150	205	26.83	73.17
ASO	74	229	303	24.42	75.58
HON	82	220	302	27.15	72.85
Region Wise (Sum)
Parts of Europe	303	1220	1523	19.9	81.1
Parts of East Asia	275	392	667	41.23	58.77
Part of Africa	328	1132	1460	22.47	77.53
Part of Middle East	55	150	205	26.83	73.17
Parts of South Asia	156	449	605	25.8	74.2

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer