Prerpints.org logo
Preprint
Article

Inversion of Left Ventricular Axial Shortening: In Silico Proof of Concept for Treatment of HFpEF

Altmetrics

Downloads

97

Views

36

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

16 May 2024

Posted:

17 May 2024

You are already at the latest version

Alerts
Abstract
Left ventricular (LV) longitudinal function is mechanically coupled to the elasticity of the ascending aorta (AA). The pathophysiologic link between stiff AA and reduced longitudinal strain and subsequent deterioration in longitudinal LV systolic function is likely relevant in heart failure with preserved ejection fraction (HFpEF). A proposed therapeutic effect of freeing the LV apex and allowing for LV inverse longitudinal shortening was studied in-silico utilizing Living Left Heart Human Model (Dassault Systémes Simulia Corporation). LV function was evaluated in a model with A) Elastic AA; B) Stiff AA; and C) Stiff AA with free LV apex. The cardiac model simulation demonstrated that freeing the apex caused inverse LV longitudinal shortening that can abolish the deleterious mechanical effect of a stiff AA on LV function. A stiff AA and impairment of LV longitudinal strain are common in patients HFpEF. The hypothesis-generating model strongly suggests that freeing the apex and inverse longitudinal shortening may improve LV function in HFpEF patients with a stiff AA.
Keywords: 
Subject: Biology and Life Sciences  -   Anatomy and Physiology

1. Introduction

Research indicates that atrioventricular plane displacement and LV longitudinal shortening are the primary contributor to heart pumping, accounting for 60% of the LV stroke volume and 80% of the right ventricular (RV) stroke volume [1]. Since LV longitudinal shortening is the major contributor to heart’s stroke volume [2] any alterations in AA elasticity and the subsequently increase in mechanical load on the LV may play an relevant role in heart failure, particularly for heart failure with preserved ejection fraction (HFpEF). During systolic longitudinal shortening of the heart the atrio-ventricular plane, which includes the aortic annulus, is displaced towards the apex of the heart by 16mm (range 14 to 19mm) [2,3,4]. As a result, the ascending aorta (AA) is stretched by 11.6±2.9mm, while the aortic arch at the level of the brachiocephalic artery and the apex are only displaced by 2.9±0.4mm (range 0 to 6mm) [5] and 1.9±0.5mm (range -0.1 to 5.1mm) respectively [2,6]. This longitudinal stretching of the AA requires force, which is a direct mechanical load on the LV that may have important implications for the relation between aortic stiffness and LV systolic longitudinal function [7]. Since the progressive deterioration of AA elasticity can hardly be changed, freeing the apex from the pericardial confinement, and letting the apex move freely towards the base could be an alternative mode of action to aid and restore left ventricular longitudinal shortening. The idea arose from observations during open heart surgery. With a closed pericardium, the base of the heart is drawn towards the cardiac apex. But once the pericardium is opened at the apical part, the heart’s mode of longitudinal contraction is reversed. Instead of stretching the AA during systolic contraction, the cardiac apex moves towards the heart’s base drawing air into the pericardial space but during diastolic and heart filling blowing air out of the pericardial space [8]. The present computational analysis was undertaken to mechanistically qualify and quantify the effects of releasing the apex from its pericardial confinement and allowing for inverse longitudinal shortening in a heart with a stiff ascending aorta, to better understand possible effects upon LV mechanics.

2. Methods

2.1. Computational Model

We utilized the Living Left Heart Human Model by Dassault Systémes Simulia Corporation (LLHH) which is capable of simulating LV performance, pressure-volume loops, and stress and strain analyses all of which correlate with clinical observations [9,10]. Our finite element model includes the AA, LV, left atrium, mitral valve, aortic root and the pericardium. The dynamic response is governed by realistic structural and blood flow physics, and the heart contraction is driven by electrical excitation. Blood is represented using a combination of three-dimensional hydrostatic fluid cavities for the heart chambers and system-level chambers to represent arterial and pulmonary compliances. Blood flow occurs inside a closed loop system between the chambers and the circulatory system through fluid link elements. Details of the model can be found under the “Simulation” and “Virtual Human” section at Dassault Systémes User Assistance, located at http://help.3ds.com/.
The passive material response of the cardiac tissue uses an anisotropic hyperelastic formulation proposed by Holzapfel and Ogden as described in Equation 1) [11]. The biaxial and triaxial experimental data published by Sommers et al. [12] were used for an initial calibration and diastolic filling tests were used to augment the calibration of the eight material parameters: a, b, af, bf, bs, as, bs, an, bn describing the ventricular passive material properties based on the methods described in Klotz et al. [13]
Ψ d e v = a 2 b e x p ⁡ [ b I 1 − 3 ) + ∑ i = f , s a i 2 b i e x p b i ( I 4 i − 1 ) 2 − 1 + a f s 2 b f s [ e x p ⁡ ( b f s I 8 f s 2 − 1 ]
Equation 1: Passive material response of cardiac tissue. Ψdev is the deviatoric strain energy. The parameters a, b, af, bf, bs, as, bs, an, bn describing the ventricular passive material parameters.
The active tissue response contains length-dependent considerations of regional sarcomere lengths, affecting the stress components in the fiber and sheet directions in the constitutive model. The active-tissue material model intended to capture the Frank-Starling effect (i.e., the strength of the heart’s systolic contraction is directly proportional to its diastolic expansion) [14]. The active contraction was simulated by adding stress in the direction of the muscle fiber defined by a time-varying model of elastance [15] as follows:
Equation 2). Tmax is the maximum isometric tension achieved at the longest sarcomere length and maximum peak intracellular calcium concentration. Tmax (N/mm2) is scalar factor representing the maximum active fiber stress or contractility in computational modeling.
σ a f t , E f f = T m a x 2 C a 0 2 C a 0 2 + E C a 50 2 E f f 1 − c o s ω t , E f f ,
where
E C a 50 2 E f f = C a 0 m a x e B l E f f − l 0 − 1 ω t , E f f = π t t 0   w h e n   0 ≤ t ≤ t 0 π t − t 0 + t r l E f f t r   w h e n   t 0 ≤ t ≤ t 0 + t r l E f f 0   w h e n   t ≥ t 0 + t r l E f f t r l = m l + b l E f f = l r 2 E f f + 1
Equation 2: Active Stress calculation. Tmax (N/mm2) is a scalar factor for myocardial contractility that represents the isometric tension achieved at the longest sarcomere length and maximum peak intracellular calcium concentration. Ca0max is the peak intercellular calcium concentration. B governs the shape of peak isometric tension and sarcomere length relation. l0 is the sarcomere length below which no active force develops. lr is the initial sarcomere length. t0 is time to reach the peak tension. m and b are coefficients that govern the relationship between of the linear relaxation duration and sarcomere length relaxation. Eff is Lagrangian strain tension component aligned with the local muscle fiber direction [15].
We simulated the mechanical constraints imposed by the pericardium by applying physiological boundary conditions on the ventricular epicardium to achieve realistic atrioventricular plane motion and radial inward motion of the epicardium as described in humans [2]. Forty-nine clusters of nodes, evenly distributed on the epicardium surface, were constrained via a spring with higher stiffness when closer to the apex and lower stiffness when closer to the base [16].
The heart was constrained via boundary conditions at the cut planes of the aortic root and pulmonary veins. Each cut plane was constrained relative to a central reference point and the reference point of the pulmonary veins was fixed. The aortic root was constrained from rotation but allowed to stretch. Aortic elasticity was modeled via a spring representing the AA stiffness. The stiffness of the spring was initially set at 0.5N/mm at baseline to achieve a realistic translation of the proximal aorta of 11.0mm during systole [17].
The spring stiffness was increased to 10N/mm to model a stiff AA until a stationary aorta (stationary plane of the sino-tubular junction) was achieved. We performed three simulations under the following conditions:
A) The effect of a mobile AA using normal AA stiffness as elastic spring stiffness to constrain the aortic root motion with an amplitude of 11.0mm. B) the effect of stiffening the AA by immobilizing the AA at the sino-tubular junction. C) To model the effect of removing the pericardial confinement at the apex of the heart, the apical boundary conditions of the distal half of the pericardial sack were eliminated in model B), allowing free movement of the LV apex. Apex displacement was determined from the coordinates of the epicardial apex and mitral annulus plane center at maximum length at end-diastole and minimum length at end-systole and displacement was computed along this apex-base axis.
Myocardial strain was calculated as the relative length change between the diastolic and the systolic states. The LV strains were measured along the radial, circumferential, and longitudinal directions at 12 locations (three axial and four circumferential locations) at both the epicardium and endocardium. The averages of tensile strains were reported with positive values. Compressive strains were reported with negative values (Table 1) and depicted as bar graphs (Figure 1 and Figure 2). Baseline values were in the reported range of normal human LV strains [18].
Volumetric-averaged myofiber stress was calculated at end-systole in MPa (N/mm2) (Table 3) and presented as a contour plot in LV parasternal long-axis cut planes (Figure 3 and Figure 4). Left ventricular pressures and volumes were computed (Table 4) and depicted as Pressure-Volume Loops (Figure 6). The area under the pressure-volume loop represents the total effective work (Joule) generated by ventricular shown in Equation 3:
S W = S V * M A P
Equation 3: Calculation of effective Stroke Work (SW) is area under the Pressure-Volume Loop, SV is Stroke Volume, and MAP is Mean Arterial Pressure.
Table 1. Average strain.
Table 1. Average strain.
Average strain Radial Circumferential Longitudinal
Baseline Tmax 0.2 0.63±0.11 -0.20±0.05 -0.16±0.01
Stiff AA Tmax 0.2 0.50±0.11 -0.18±0.03 -0.08±0.05
Stiff AA and free apex Tmax 0.2 0.72±0.16 -0.18±0.05 -0.21±0.02
Baseline Tmax 0.2 vs Stiff AA Tmax 0.2 -0.13±0.02 0.01±0.02 0.08±0.06
Baseline Tmax 0.2 vs Stiff AA Tmax 0.2 (%) -20.21±2.39% -6.78±10.86% -48.44±36.88%
Baseline Tmax 0.2 vs Stiff AA and free apex Tmax 0.2 0.09±0.06 0.02±0.04 -0.05±0.03
Baseline Tmax 0.2 vs Stiff AA and free apex Tmax 0.2 (%) 14.36±9.73% -10.17±18.31% 31.25±16.88%
Table 1: Average Radial, Circumferential and Longitudinal Strain at Baseline Tmax 0.2 N/mm2, Stiff AA Tmax 0.2 N/mm2, and stiff AA with free apex Tmax 0.2 N/mm2.
Table 2. Longitudinal strain.
Table 2. Longitudinal strain.
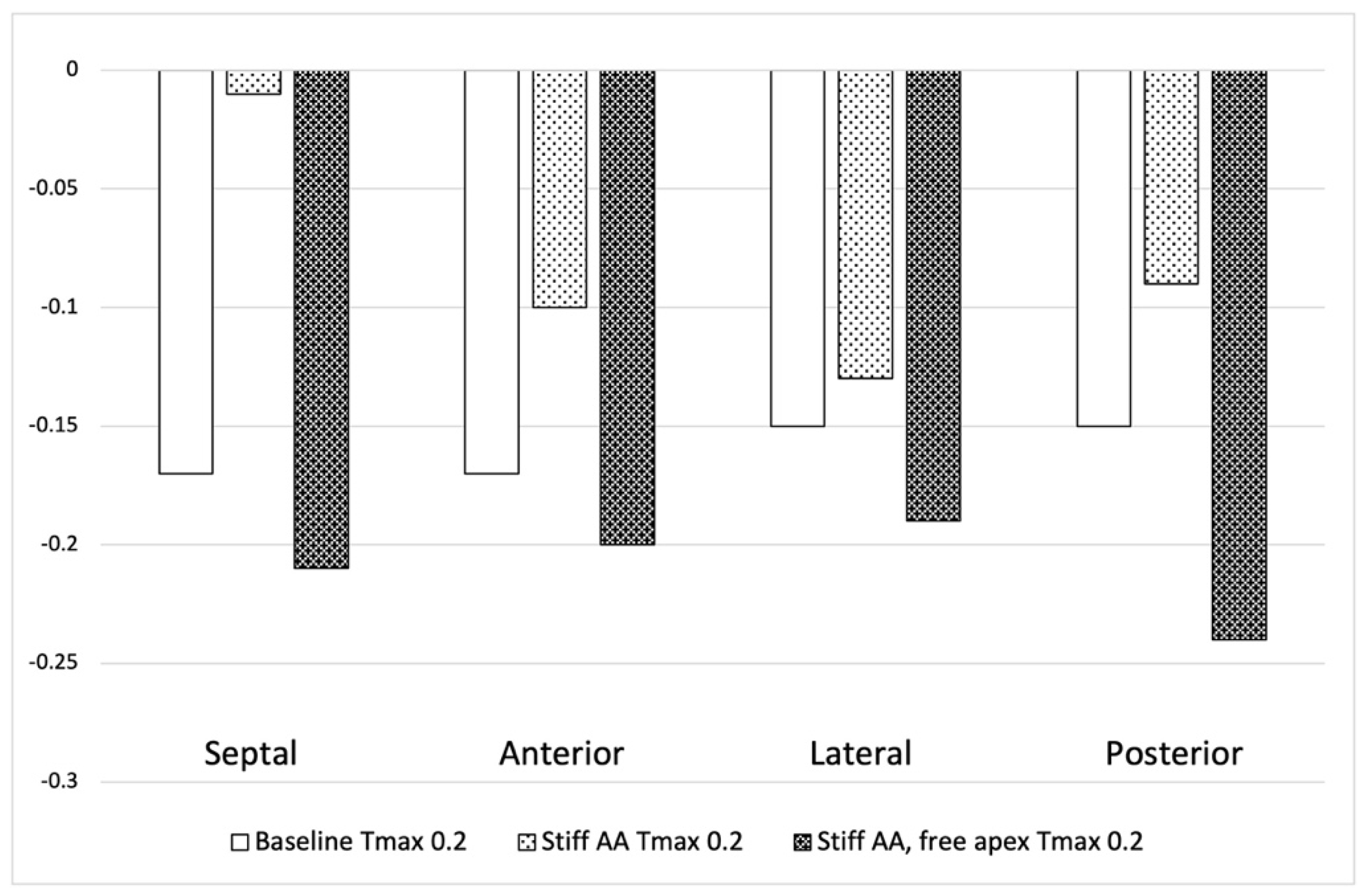
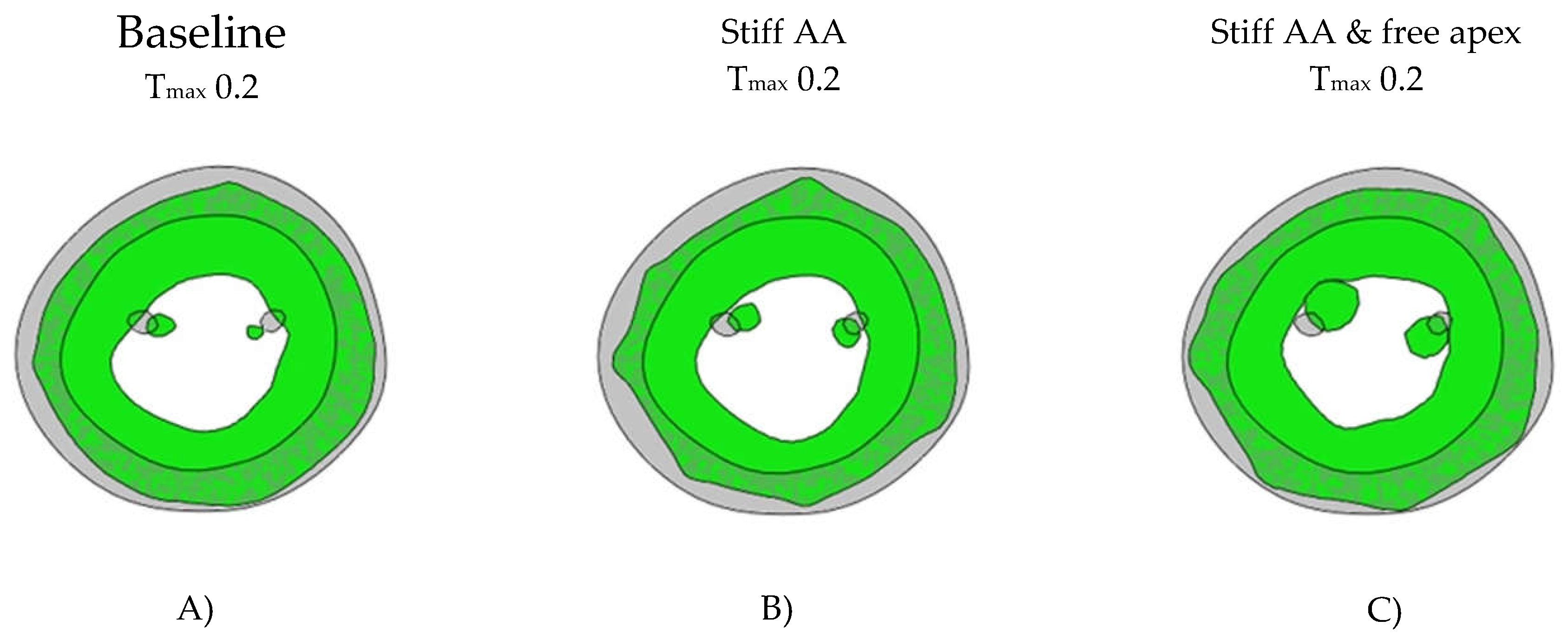
Longitudinal strain Septal Anterior Lateral Posterior
Baseline Tmax 0.2 -0.17 -0.17 -0.15 -0.15
Stiff AA Tmax 0.2 -0.01 -0.10 -0.13 -0.09
Stiff AA and free apex Tmax 0.2 -0.21 -0.2 -0.19 -0.24
Baseline Tmax 0.2 vs Stiff AA Tmax 0.2 0.16 0.07 0.02 0.06
Baseline Tmax 0.2 vs Stiff AA Tmax 0.2 (%) -94.12% -41.18% -13.33% -40.00%
Baseline Tmax 0.2 vs Stiff AA and free apex Tmax 0.2 -0.04 -0.03 -0.04 -0.09
Baseline Tmax 0.2 vs Stiff AA and free apex Tmax 0.2 (%) 23.53% 17.65% 26.67% 60.00%
Table 2: Longitudinal Strain in four regions, Septal, Anterior, Lateral, Posterior at Baseline Tmax 0.2 N/mm2, for stiff AA Tmax 0.2 N/mm2, and Stiff AA with free apex and Tmax 0.2 N/mm2.
Table 3. Myofiber stress.
Table 3. Myofiber stress.
Stress Baseline Stiff AA Stiff AA and free apex
Tmax 0.2 Tmax 0.2 Tmax 0.2
(MPa) 0.056±0.036 0.076±0.042 0.062±0.038
vs. Baseline 36.98±42.91% 12.03±42.19%
Table 3: Average myofiber stress at Baseline Tmax 0.2 N/mm2, Stiff AA Tmax 0.2 N/mm2 and Stiff AA with free apex Tmax 0.2 N/mm2. Comparison with Baseline.
Table 4. LV pressure and volume.
Table 4. LV pressure and volume.
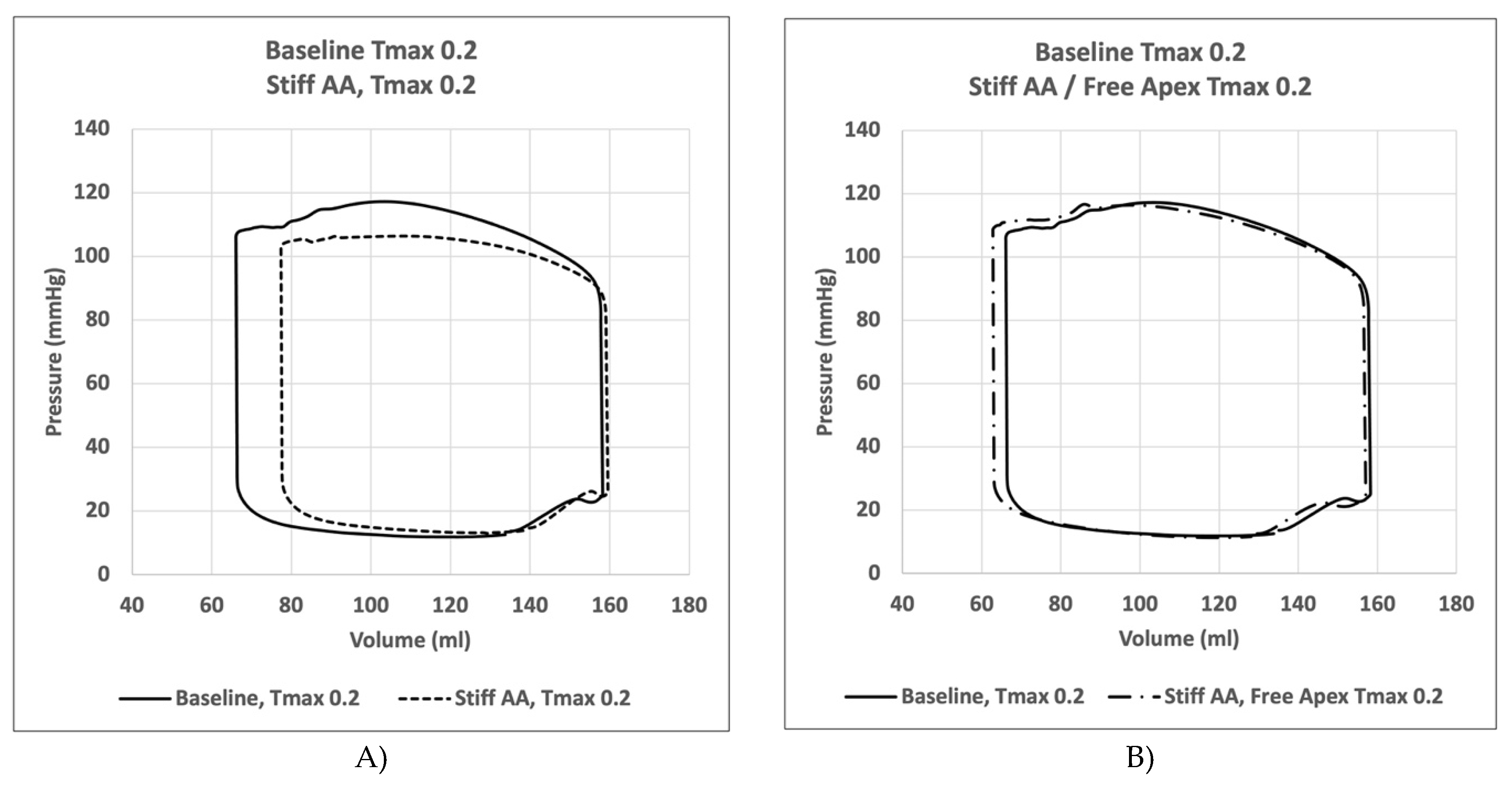
EDP EDV ESP ESV SVed-es SW
(mmHg) (ml) (mmHg) (ml) (ml) (Joule)
Baseline
Tmax 0.2		 11.85 158.30 117.10 66.10 92.20 8747.50
Stiff AA
Tmax 0.2		 12.86 159.60 106.40 77.40 82.20 7084.50
Stiff AA with free apex
Tmax 0.2		 11.25 157.00 116.60 62.86 94.14 8923.00
Baseline vs. Stiff AA
Tmax 0.2 vs. Tmax 0.2		 1.01 1.30 -10.70 11.30 -10.00 -1663.00
Baseline vs. Stiff AA
Tmax 0.2 vs. Tmax 0.2 (%)		 8.52% 0.82% -9.14% 17.10% -10.85% -19.01%
Baseline vs. Stiff AA with free apex
Tmax 0.2 vs. Tmax 0.2		 -0.60 -11.3 -0.50 -3.24 1.94 175.50
Baseline vs. Stiff AA with free apex
Tmax 0.2 vs. Tmax 0.2 (%)		 -5.06% -0.82% 0.43% -4.90% 2.10% 2.01%
Table 4: Computational simulation of LV pressure and volume, stroke volume and effective stroke work at Baseline Tmax 0.2 N/mm2, Stiff AA Tmax 0.2 N/mm2 and Stiff AA with free apex Tmax 0.2 N/mm2. (EDP: end-diastolic pressure; EDV: end-diastolic volume; ESP: end-systolic pressure; ESV: end-systolic volume; SVed-es: stroke volume; SW: stroke work).
Preprints 106699 g001
Figure 1. Left ventricular strains. Figure 1. Left ventricular strain for: baseline simulation Tmax 0.2 N/mm2, simulation with stiff AA Tmax 0.2 N/mm2 and simulation with stiff AA and free apex Tmax 0.2 N/mm2. A) Radial strain (three radial locations) is depicted positive when wall thickening from diastole to systole. B) Circumferential strain (three circumferential locations) is depicted negative when circumference is reduced from diastole to systole. C) Longitudinal strain (four longitudinal locations) is depicted negative when apex base length is reduced from diastole to systole.
Figure 1. Left ventricular strains. Figure 1. Left ventricular strain for: baseline simulation Tmax 0.2 N/mm2, simulation with stiff AA Tmax 0.2 N/mm2 and simulation with stiff AA and free apex Tmax 0.2 N/mm2. A) Radial strain (three radial locations) is depicted positive when wall thickening from diastole to systole. B) Circumferential strain (three circumferential locations) is depicted negative when circumference is reduced from diastole to systole. C) Longitudinal strain (four longitudinal locations) is depicted negative when apex base length is reduced from diastole to systole.
Preprints 106699 g001
Preprints 106699 g002
Figure 2. Left ventricular longitudinal strain in regions. Figure 2. Left ventricular longitudinal strain in four longitudinal regions (Septal, Anterior, Lateral and Posterior strain) at Baseline Tmax 0.2 N/mm2, Stiff AA Tmax 0.2 N/mm2 and stiff AA with free apex Tmax 0.2 N/mm2.
Figure 2. Left ventricular longitudinal strain in regions. Figure 2. Left ventricular longitudinal strain in four longitudinal regions (Septal, Anterior, Lateral and Posterior strain) at Baseline Tmax 0.2 N/mm2, Stiff AA Tmax 0.2 N/mm2 and stiff AA with free apex Tmax 0.2 N/mm2.
Preprints 106699 g002
Preprints 106699 g003
Figure 3. Myofiber stress. Figure 3. Long-axis profile of the LV at end of systole showing contours of myofiber stress at end-systole. A) Baseline Tmax 0.2 N/mm2, B) Stiff AA Tmax 0.2 N/mm2 and (C) Stiff AA and free apex Tmax 0.2 N/mm2. Dotted line indicates baseline level of ascending aorta at end-diastole and level of apex.
Figure 3. Myofiber stress. Figure 3. Long-axis profile of the LV at end of systole showing contours of myofiber stress at end-systole. A) Baseline Tmax 0.2 N/mm2, B) Stiff AA Tmax 0.2 N/mm2 and (C) Stiff AA and free apex Tmax 0.2 N/mm2. Dotted line indicates baseline level of ascending aorta at end-diastole and level of apex.
Preprints 106699 g003
Preprints 106699 g004
Figure 4. Cross-sectional LV profile. Figure 4. Cross-sectional profile of the LV at center of the longitudinal LV axis and base of the papillary muscles. Grey color showing the end-diastolic shape at Baseline, green color showing the end-systolic shape. A) Baseline Tmax 0.2 N/mm2, diameter 59mm, B) Stiff AA Tmax 0.2 N/mm2, diameter 57mm and (C) Stiff AA and free apex Tmax 0.2 N/mm2, diameter 63mm.
Figure 4. Cross-sectional LV profile. Figure 4. Cross-sectional profile of the LV at center of the longitudinal LV axis and base of the papillary muscles. Grey color showing the end-diastolic shape at Baseline, green color showing the end-systolic shape. A) Baseline Tmax 0.2 N/mm2, diameter 59mm, B) Stiff AA Tmax 0.2 N/mm2, diameter 57mm and (C) Stiff AA and free apex Tmax 0.2 N/mm2, diameter 63mm.
Preprints 106699 g004
Preprints 106699 g005
Figure 5. Pressure volume loops. Figure 5. A) Comparison of pressure volume loop of left ventricle for simulation with mobile aorta (Baseline) Tmax 0.2 N/mm2 against simulation with stiff AA Tmax 0.2 N/mm2, B) Comparison of pressure volume loop of the left ventricle for simulation with mobile aorta Tmax 0.2 N/mm2 against stiff AA and free apex Tmax 0.2 N/mm2.
Figure 5. Pressure volume loops. Figure 5. A) Comparison of pressure volume loop of left ventricle for simulation with mobile aorta (Baseline) Tmax 0.2 N/mm2 against simulation with stiff AA Tmax 0.2 N/mm2, B) Comparison of pressure volume loop of the left ventricle for simulation with mobile aorta Tmax 0.2 N/mm2 against stiff AA and free apex Tmax 0.2 N/mm2.
Preprints 106699 g005
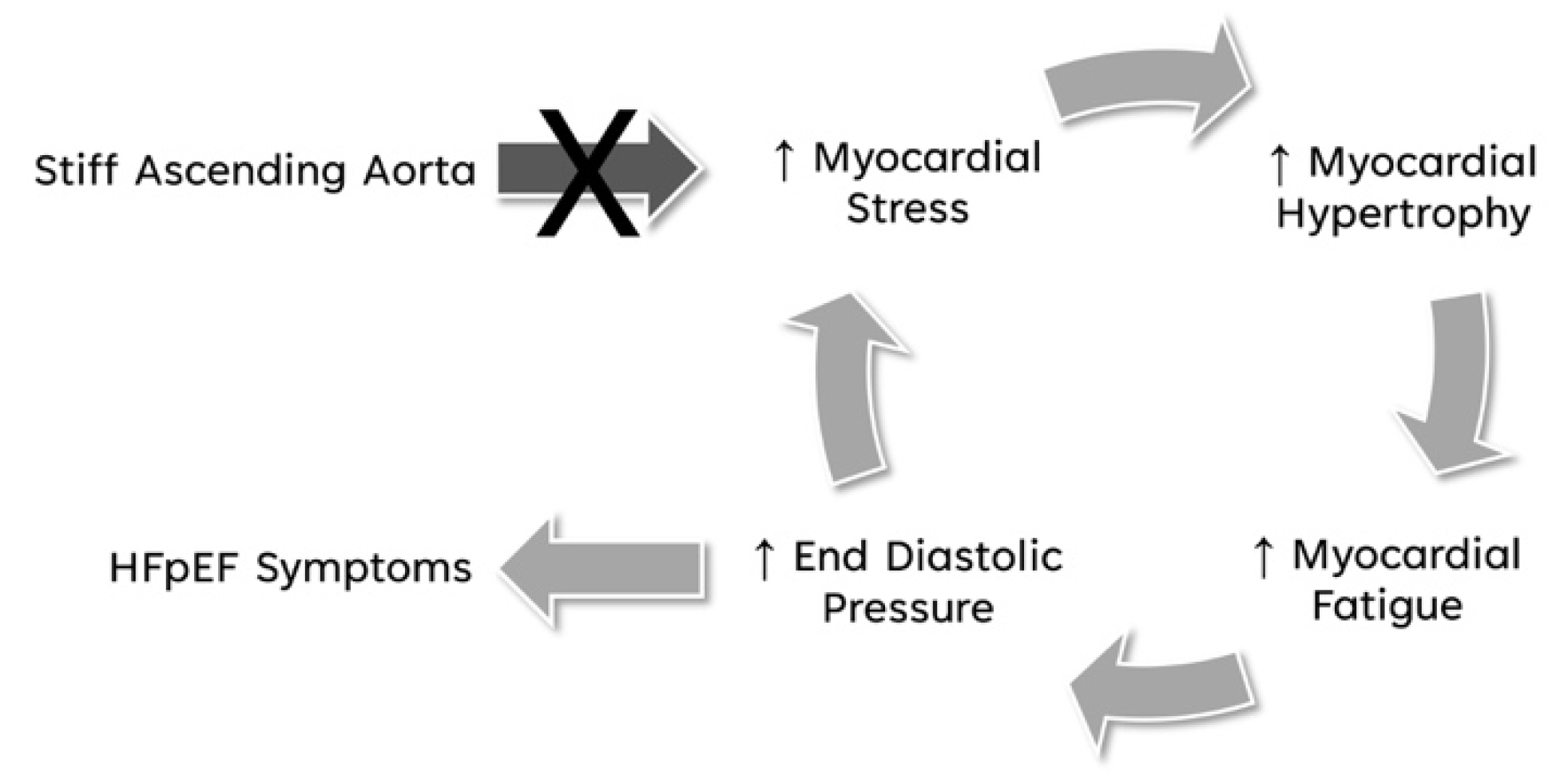
Preprints 106699 g006
Figure 6. Breaking the vicious cycle of stiffened AA to HFpEF symptoms.
Figure 6. Breaking the vicious cycle of stiffened AA to HFpEF symptoms.
Preprints 106699 g006

3. Results

3.1. Baseline Simulation

In the initial simulation (model A), with contractility Tmax of 0.2 N/mm2, the aortic root underwent a 11.0mm displacement towards the apex during systole, whereas the apex moved 1.9mm in the opposite direction [2]. The stroke volume and a stroke work calculated in this baseline simulation were 92.2 ml and 8,747 Joules, respectively (Table 4). A pressure-volume loop was generated, demonstrating the expected pattern (Figure 6A). The LV strain profiles at the end-systole are depicted in Figure 1 and Figure 2 and Table 1. Throughout systolic contraction, the wall exhibited thickening with a radial strain of 0.63±0.11, while the circumference displayed a reduction with a circumferential strain of-0.20±0.05 (Table 1, Figure 1). The average apex-base length shortened with an average longitudinal strain of -0.16±0.01 (Table 2, Figure 2). The calculated average myofiber stress was 0.056±0.036 MPa (Table 3).
A contour plot depicting systolic regional stress distribution at end-systole is shown in Figure 3A. Notably, the areas with highest myofiber stress appeared at the mitral annulus, the fibrous trigones, the aorto-mitral junction, and the papillary muscle tip.

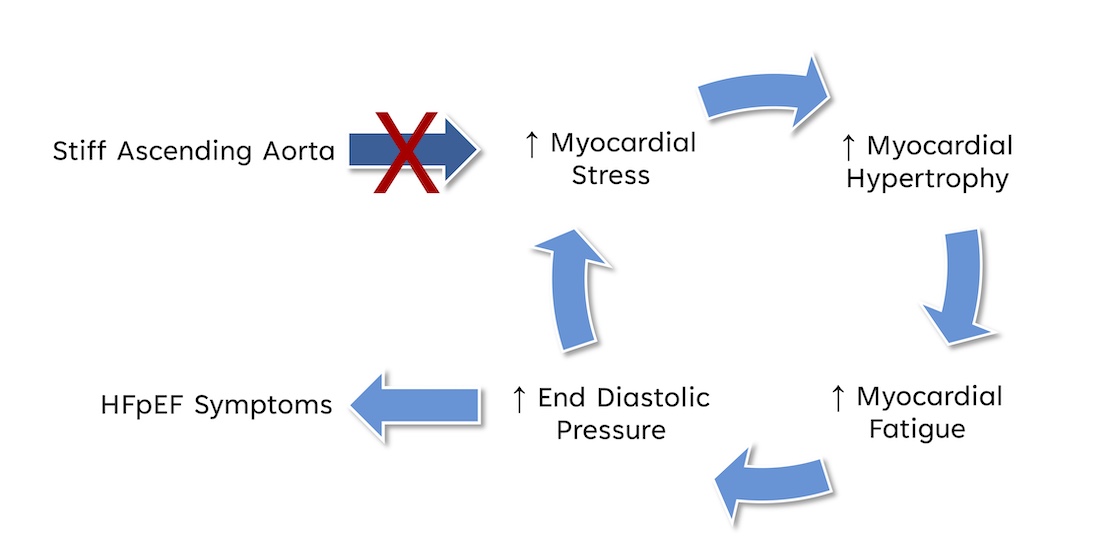
3.2. Effect of Stiff Ascending Aorta

In model B) with baseline contractility (Tmax 0.2 N/mm2) and with a stiff ascending aorta, the sino-tubular junction as well as the LV apex was stationary (Figure 3B and Figure 4B). At the level of the papillary muscle tip along the longitudinal axis of the LV, the transverse end-systolic diameter decreased from 59mm to 57mm, representing a reduction of 3.4% from the baseline value. (Figure 4). The cross-sectional profile of the LV shape demonstrated that LV tended to be more ovalized at end-systole.
Compared to baseline measurements, analysis of the pressure volume loop (Figure 5) demonstrated that end-diastolic pressure increased by 8.5% and end-systolic pressure showed a reduction of 9.1%. While end-diastolic volume remained nearly unchanged (1.3%) end-systolic volume increased by 17.1%, consequently the stroke volume was decreased by 10.9% and effective stroke work was reduced by 19.0% (Table 4). Analysis of the pressure volume loop showed a corresponding decrease of end-systolic LV pressure and increase in end-diastolic volume (Figure 5A)
The LV strain strains profiles at end-systole, along with their respective values (Table 1) are depicted in Figure 1 and Figure 2. The average radial strain, the circumferential strain and the longitudinal stain displayed a reduction of 20.2±2.4%, 6.8±10.9%, and 48.4±36.9%, respectively (Table 1, Figure 1). While the septal longitudinal strain was reduced greatest by 94.1%, the anterior, lateral and posterior strain measures were reduced by 41.2%, 13.3%, and 40.0%, respectively, indicating that AA stiffening exerts the greatest effect upon septal longitudinal stain (Table 2, Figure 2). The average myofiber stress increased 36.98±42.91% in comparison to the baseline from 0.056±0.036 to 0.076±0.042 MPa (Table 3). The systolic regional stress distribution at end-systole is presented as contour plot in Figure 3B. Stress increased overall in the LV with very high-stress areas noted at the septum, the papillary muscles, the mitral annulus, the fibrous trigones and the aorto-mitral junction.

3.3. Effect of Removing Pericardial Boundary Conditions at the Distal Half of the Pericardial Sack with Stiff Ascending Aorta

In model C, with stiff AA the pericardial boundary conditions were eliminated in the distal half of the pericardial sac, allowing for unrestricted movement of the LV apex. Systolic contraction with the same LV passive and active tissue properties and with the same contractility Tmax of 0.2 N/mm2 as in the previous models A) and B) caused the LV apex to move during systole towards the base of the heart by 15.4mm (Figure 3C).
Compared to baseline measurements, analysis of the pressure volume loop (Figure 5B) demonstrated that end-diastolic pressure, which was increased with stiffening of the AA by 8.5% dropped 5.1% below baseline value. End-systolic pressures which was reduced by 9.1% with stiffening the AA returned to 0.43% below baseline values. After stiffening the AA, stroke volume and effective stroke work had decreased by 10.9% and 19.0%, respectively. However, upon allowing for unrestricted movement of the LV apex, these values returned to 2.1% and 2.0% above of their respective baseline values (Table 4), and the overall visual aspect of the pressure volume loop returned to the baseline shape (Figure 5B). The transverse end-systolic diameter at the center of the longitudinal LV axis at the tip of the papillary muscles increased to 63mm, or 6.8% over baseline values (Figure 4C). The cross-sectional profile of the LV demonstrated increasing globalization of the LV shape. Average radial and longitudinal strain increased by 14.4±9.7% and 31.3±16.9%, respectively, while circumferential strain remained reduced by 10.2±18.3% below baseline values (Table 1, Figure 1). All reginal longitudinal strains recovered with septal, anterior, lateral, and posterior strains being 23.5%, 17.7%, 26.7% and 60.0% over baseline values (Table 2, Figure 2).
The calculated average myofiber stress, which was increased with stiffening of the AA to 0.076±0.042 MPa or 36.98±42.91% over baseline values deceased by 67.5% to 0.062±0.038 MPa or 12.0±42.2% over baseline values (Table 3). The systolic stress decreased overall in the LV with remarkably reduced stress-areas along the septum and the LV lateral wall, the papillary muscles, and the apex (Figure 3C).

4. Discussion

Throughout the cardiac cycle, the heart’s epicardial apex remains stationary within the fluid-tight pericardial sac, [1] which is anchored to the diaphragm. The pericardial sac’s apex is also connected to the caudal sternum by the sterno-pericardial ligament, effectively linking the caudal sternum to the LV-apex. This creates a relatively straight line of force that runs from the stationary LV-apex at the caudal end to the stationary aortic arch [5] at the cranial end, with the elastic AA situated in between. During the cardiac cycle, as the LV contracts longitudinally and AA is stretched, the aortic root moves up and down along this line of force. It is well-recognized that AA stiffening increases with age [7,19,20,21]. Numerous mechanisms have been suggested to account for this phenomenon, such as alterations in endothelial function, modification in the composition of structural proteins, collagen crosslinking, alterations in vascular geometry, and neurohumoral signaling [19,22,23]. Aortic stiffening is a well-known cause of reduced arterial compliance (i.e., elasticity) and impaired aorto-ventricular interaction. This can lead to significant reduction of longitudinal left ventricular function with reduced descent of the atrio-ventricular plane during systole and decreased average long axis strain, impaired early diastolic filling of the ventricle, higher left ventricular afterload and higher end-diastolic LV pressure [7,24,25,26]. With stiffening and reduced longitudinal elasticity of the aortic root, a higher load on the oblong-oriented myocardial fibers is expected and a stiff AA would be stretched and displaced less than a compliant aorta. The heart would have to contract with greater long-axis force to produce the same amount of aortic displacement and consequently, same stroke volume [6]. Studies in animals have demonstrated that a stiff aorta can cause significant 30% increase in myocardial oxygen consumption and a 20%-40% increase in the energy required by the heart to deliver a given stroke volume [27,28]. Similarly clinical studies in humans have shown that arterial stiffening raises myocardial oxygen consumption by over 50% for a given stroke volume [28]. The authors have concluded that although aortic stiffening may not have an impact on heart function at rest, it can limit reserve capacity under conditions of increased demand [27]. It was demonstrated in humans that increased aortic stiffness is associated with a reduction in global longitudinal strain, which supports the hypothesis that aortic stiffening imposes a direct mechanical load on long-axis LV function [7,19,29,30,31]. With aortic stiffening, the force required to stretch the ascending aorta increases, resulting in an increased load on the long axis of the LV and eventually lead to a decrease in LV long axis shortening [6].
In the present computational study, computational study stiffening and reduced longitudinal elasticity of the aortic root caused a greater load on the longitudinal myocardial fibers with increased myocardial stress (+37.0%) that led to reduced average LV longitudinal (-20.2%) and especially septal longitudinal strain (-94.1%), and subsequent deterioration of longitudinal LV function with decreased effective stroke work (-19.0%) and increased end-diastolic pressure (+8.5) compared to baseline values. Reduced longitudinal elasticity of the AA affects longitudinal myocardial shortening thus posing an additional load and stress upon the myofibers. This further adversely affects LV function, predisposing patients towards the HFpEF syndrome [28,29,30,31,32]. HFpEF is associated with significantly impaired LV global longitudinal strain [24,33,34] and longitudinal LV systolic function [28,32,35,36,37] while at the same time 65% of HFpEF patients harbor AA stiffening (beyond age-associated values).[34] The fact that HFpEF symptoms strongly correlate with increased arterial stiffness [7,19,29,30,31] suggests a possible pathophysiologic link between aortic stiffness, reduced AA stretching, decreased atrioventricular plane displacement and alterations in LV systolic longitudinal function, contributing to the pathophysiology of the HFpEF syndrome [7,29,34]. Consequently arterial stiffness has been proposed as a potential causative factor leading to HFpEF [7,29] and might be the pathologic mechanism which drives the progression from diastolic dysfunction to HFpEF [32].
Healthy women have shorter AA 79mm vs. 86mm and significantly greater AA longitudinal strain than men (8.5% vs. 6.7%) [6]. Postmenopausal women tend to have a higher arterial stiffness as compared to men [38]. Within one year of the final menstrual period women experience a rapid and significant increase in aortic stiffening independent of age [38], where black women having greater increase in arterial stiffness than white women [39]. While development of diastolic dysfunction of the left ventricle is equally common in women and men, women outnumber men with HFpEF by a 2:1 ratio [40,41], and women with HFpEF tend to show poorer prognosis, including a lower quality of life as compared to men [41]. The shorter AA with greater AA longitudinal strain and increased tendency for AA stiffening in women may create earlier and larger myocardial stress as compared to men and explain in part why women may be more predisposed to HFpEF [40].
The prevailing dogma that heart failure is an irreversible disease has been challenged by observations in some heart failure patients with myocardial recovery post-LVAD, offering support to the hypothesis of a mechanically exhausted myocardium that has the potential to recover [42,43,44]. A phenomenon also observed in reversible exercise induced cardiac fatigue [45,46,47]. Novel mechano-energetic concepts propose myocardial fatigue with impaired contractility and relaxation in the face of adverse load particularly caused by a stiffened arterial system [42,43,48,49]. Like skeletal muscles fatigued myocardium as proposed in HfpEF is largely structurally normal and should have the potential to recover, as long as its myocytes can be mechanically unloaded (e.g., with arterial vasodilators, or left ventricular assist devices in selected cases). In our in-silico study we mechanically unloaded the LV by removing the boundary condition of the pericardium at the apical part of the (Figure 3C), allowing the apex to become mobile. The apex moved to the heart’s base by 15.4mm instead of stretching the AA (11.0mm at baseline), achieving inverse longitudinal shortening. Beforehand reduced radial and longitudinal strain recovered beyond baseline, with overall reduced myocardial stress (-18.4%), increased effective stroke work (+26.0%) and stroke volume (+12.7%), and reduced end-diastolic pressure (-12.5%) compared to model B) with the stiff aorta. Freeing the apex from the pericardial confinement and allowing the apex to move freely made it easier for the simulated heart to shorten. By this recovered LV function, increased stroke volume, and reduced end-diastolic pressure.
We hypothesize that eliminating the high myocardial load created by a stiff AA by freeing the apex from its pericardial constrain, has the potential to break the vicious cycle of increased myocardial fiber stress, reactive myocardial hypertrophy, subsequent myocardial fatigue, and rising ventricular end-diastolic / left atrial pressure, further increasing myocardial fiber stress (Figure 6), and will prevent transition into irreversible myocardial damage where prolonged fatigue and ongoing inflammation may lead to myocardial fibrosis [34,42,43,48,50].
We propose a novel mode of action for treating HFpEF syndrome associated with a stiff AA. Freeing the apex from the pericardial confinement, and letting the apex move freely towards the base could be an alternative approach to reduce the heart’s mechanical load, make it easier for the heart to shorten, to restore LV function, and to recover from myocardial fatigue.
The effect of opening the pericardium and freeing the apex was studied in HFpEF patients who did undergo open heart surgery. Opening of the pericardium attenuated the increase in LV filling pressures that develop during volume loading in humans with HFpEF, demonstrating a potential therapeutic opportunity in HFpEF patients [51]. Freeing the apex by pericardiotomy alone has an immediate effect but will immediately create adhesions which, within a short period, again restrict the movement of the cardiac apex [52,53,54]. Illicit use of pericardiotomy to improve racing results in greyhound dogs was described, but the effect vanished after occurrence of adhesions [52,55]. We, therefore, propose the implantation of a passive pressure decompensation chamber that provides a fluid volume in the pericardial space in systole, allowing the apex to move towards the heart’s base, and that removes such volume from the pericardial space in diastole allowing the apex to move away from the heart’s base for cardiac filling.

5. Limitation of Study

Although the Living Left Heart Human (LLHH) Model has seen considerable use in cardiac modeling, several limitations apply [9,14]. The LLHH model includes the aortic arch, left ventricle, left atrium, mitral valve, aortic root, and pericardium, while the right heart is not captured in the model. As a result, potential effects, or influences of these structures on the left heart were not accounted for. Furthermore, the material properties of the ascending aorta remained unaltered, and the stiff aorta was simulated by immobilizing the arch at the level of the Sino-Tubular Junction, which may not fully simulate the mechanics of a stiffened aortic wall. In case of a stiff aorta, sympathetic nerves, and humoral regulation are expected to increase myocardial contractility to restore normal cardiac output. However, hemodynamic feedback control was not modeled to automatically regulate myocardial contractility to maintain cardiac output. Instead, contractility was uniformly increased in all myocytes, neglecting possible anisotropy and remodeling of the left ventricle. Noticeable surface irregularities (Figure 3 and Figure 4) were a result of the simplified representation of the pericardium, achieved through springs connected to forty-nine clusters of nodes evenly distributed on the epicardium surface. Employing more nodes with spring stiffness inversely proportional to the displacement, could potentially lead to a smoother surface but would not affect the overall results [16]. In summary, the LLHH model is a valuable tool for understanding the impact of stiffening of the ascending aorta on left ventricular function, However, it is essential to acknowledge its limitations, including the omission of certain heart structures, assumptions about material properties, and the obsenceof hemodynamic feedback control and simplified pericardium when interpreting the simulation results.

6. Conclusion

The findings of this study conducted in silico highlight the significant pathophysiological relationship between a stiff AA and reduced longitudinal strain, contributing to a deterioration of the longitudinal LV systolic function, often observed in patients suffering from heart failure with preserved ejection fraction (HFpEF). The simulations reveal that stiffening of the AA causes an increase in end-diastolic filling pressure and a decrease in end-systolic pressure, along with reductions in stroke volume and effective stroke work. In addition, average radial, circumferential, and longitudinal strains showed marked reduction while the average myofiber stress increased, indicating potential deleterious effects on LV function potentially leading to hypothesized myocardial fatigue. This in-silico study introduces a novel, theoretical therapeutic approach by suggesting that releasing the LV apex to enable inverse LV longitudinal shortening could mitigate the adverse mechanical effects induced by a stiff AA. Simulation of this condition showed promising results, with improvements in end-diastolic and end-systolic pressures, stroke volume, and effective stroke work, compared to the stiff AA scenario. Additionally, average radial and longitudinal strains increased. Most notably, the calculated average myofiber stress was significantly reduced, potentially allowing for recovery from myocardial fatigue.
Stiffness of the AA and the impairment of LV longitudinal strain are common in patients with HFpEF. Therefore, the promising results of this hypothesis-generating study provide a new direction for future experimental and clinical research aimed at new treatment options for this patient group. Pre-clinical and clinical studies are required to validate the proposed approach.

Acknowledgments

This research was funded in part by Artract Medical Inc., New York, USA, Dassault Systémes, Johnston RI, USA and Conrad Preby’s Foundation, San Diego, CA, USA.

Conflicts of Interest

Dr. Goetz is founder of Artract Medical Inc. Dr. Jiang Yao is employee of Dassault Systémes, Johnston RI, USA.

References

  1. Carlsson, M.; Ugander, M.; Heiberg, E.; Arheden, H. The quantitative relationship between longitudinal and radial function in left, right, and total heart pumping in humans. Am J Physiol Heart Circ Physiol 2007, 293, H636–H644. [Google Scholar] [CrossRef] [PubMed]
  2. Carlsson, M.; Ugander, M.; Mosen, H.; Buhre, T.; Arheden, H. Atrioventricular plane displacement is the major contributor to left ventricular pumping in healthy adults, athletes, and patients with dilated cardiomyopathy. Am J Physiol Heart Circ Physiol 2007, 292, H1452–H1459. [Google Scholar] [CrossRef] [PubMed]
  3. Buckberg, G.; Mahajan, A.; Saleh, S.; Hoffman, J.I.; Coghlan, C. Structure and function relationships of the helical ventricular myocardial band. J Thorac Cardiovasc Surg 2008, 136, 578–589. [Google Scholar] [CrossRef] [PubMed]
  4. Plonek, T.; Rylski, B.; Nawrocki, P.; Beyersdorf, F.; Jasinski, M.; Kuliczkowski, W. Systolic stretching of the ascending aorta. Arch Med Sci 2021, 17, 25–30. [Google Scholar] [CrossRef] [PubMed]
  5. Plonek, T.; Berezowski, M.; Kurcz, J.; Podgorski, P.; Sasiadek, M.; Rylski, B.; Mysiak, A.; Jasinski, M. The evaluation of the aortic annulus displacement during cardiac cycle using magnetic resonance imaging. BMC Cardiovasc Disord 2018, 18, 154. [Google Scholar] [CrossRef] [PubMed]
  6. Bell, V.; Mitchell, W.A.; Sigurethsson, S.; Westenberg, J.J.; Gotal, J.D.; Torjesen, A.A.; Aspelund, T.; Launer, L.J.; de Roos, A.; Gudnason, V.; et al. Longitudinal and circumferential strain of the proximal aorta. J Am Heart Assoc 2014, 3, e001536. [Google Scholar] [CrossRef] [PubMed]
  7. Bell, V.; McCabe, E.L.; Larson, M.G.; Rong, J.; Merz, A.A.; Osypiuk, E.; Lehman, B.T.; Stantchev, P.; Aragam, J.; Benjamin, E.J.; et al. Relations between aortic stiffness and left ventricular mechanical function in the community. J Am Heart Assoc 2017, 6. [Google Scholar] [CrossRef] [PubMed]
  8. Zhao, L.T.; Liu, L.; Meng, P.P.; Wang, Y.H.; Li, M.; Yang, J.; Gu, T.X.; Ma, C.Y. Effect of pericardial incision on left ventricular morphology and systolic function in patients during coronary artery bypass grafting. Cardiovasc Ultrasound 2020, 18, 27. [Google Scholar] [CrossRef] [PubMed]
  9. Baillargeon, B.; Rebelo, N.; Fox, D.D.; Taylor, R.L.; Kuhl, E. The living heart project: A robust and integrative simulator for human heart function. Eur J Mech A Solids 2014, 48, 38–47. [Google Scholar] [CrossRef]
  10. Wisneski, A.D.; Wang, Y.; Cutugno, S.; Pasta, S.; Stroh, A.; Yao, J.; Nguyen, T.C.; Mahadevan, V.S.; Guccione, J.M. Left ventricle biomechanics of low-flow, low-gradient aortic stenosis: A patient-specific computational model. Front Physiol 2022, 13, 848011. [Google Scholar] [CrossRef]
  11. Holzapfel, G.A.; Ogden, R.W. Constitutive modelling of passive myocardium: A structurally based framework for material characterization. Philos Trans A Math Phys Eng Sci 2009, 367, 3445–3475. [Google Scholar] [CrossRef] [PubMed]
  12. Sommer, G.; Schriefl, A.J.; Andra, M.; Sacherer, M.; Viertler, C.; Wolinski, H.; Holzapfel, G.A. Biomechanical properties and microstructure of human ventricular myocardium. Acta Biomater 2015, 24, 172–192. [Google Scholar] [CrossRef] [PubMed]
  13. Klotz, S.; Hay, I.; Dickstein, M.L.; Yi, G.H.; Wang, J.; Maurer, M.S.; Kass, D.A.; Burkhoff, D. Single-beat estimation of end-diastolic pressure-volume relationship: A novel method with potential for noninvasive application. Am J Physiol Heart Circ Physiol 2006, 291, H403–H412. [Google Scholar] [CrossRef] [PubMed]
  14. Sack, K.L.; Baillargeon, B.; Acevedo-Bolton, G.; Genet, M.; Rebelo, N.; Kuhl, E.; Klein, L.; Weiselthaler, G.M.; Burkhoff, D.; Franz, T.; et al. Partial lvad restores ventricular outputs and normalizes lv but not rv stress distributions in the acutely failing heart in silico. Int J Artif Organs 2016, 39, 421–430. [Google Scholar] [CrossRef] [PubMed]
  15. Walker, J.C.; Ratcliffe, M.B.; Zhang, P.; Wallace, A.W.; Fata, B.; Hsu, E.W.; Saloner, D.; Guccione, J.M. Mri-based finite-element analysis of left ventricular aneurysm. Am J Physiol Heart Circ Physiol 2005, 289, H692–H700. [Google Scholar] [CrossRef] [PubMed]
  16. Strocchi, M.; Gsell, M.A.F.; Augustin, C.M.; Razeghi, O.; Roney, C.H.; Prassl, A.J.; Vigmond, E.J.; Behar, J.M.; Gould, J.S.; Rinaldi, C.A.; et al. Simulating ventricular systolic motion in a four-chamber heart model with spatially varying robin boundary conditions to model the effect of the pericardium. J Biomech 2020, 101, 109645. [Google Scholar] [CrossRef] [PubMed]
  17. Pagoulatou, S.Z.; Ferraro, M.; Trachet, B.; Bikia, V.; Rovas, G.; Crowe, L.A.; Vallee, J.P.; Adamopoulos, D.; Stergiopulos, N. The effect of the elongation of the proximal aorta on the estimation of the aortic wall distensibility. Biomech Model Mechanobiol 2021, 20, 107–119. [Google Scholar] [CrossRef]
  18. Moore, C.C.; Lugo-Olivieri, C.H.; McVeigh, E.R.; Zerhouni, E.A. Three-dimensional systolic strain patterns in the normal human left ventricle: Characterization with tagged mr imaging. Radiology 2000, 214, 453–466. [Google Scholar] [CrossRef] [PubMed]
  19. Kohn, J.C.; Lampi, M.C.; Reinhart-King, C.A. Age-related vascular stiffening: Causes and consequences. Front Genet 2015, 6, 112. [Google Scholar] [CrossRef]
  20. Oishi, Y.; Miyoshi, H.; Mizuguchi, Y.; Iuchi, A.; Nagase, N.; Oki, T. Aortic stiffness is strikingly increased with age >/= 50 years in clinically normal individuals and preclinical patients with cardiovascular risk factors: Assessment by the new technique of 2d strain echocardiography. J Cardiol 2011, 57, 354–359. [Google Scholar] [CrossRef]
  21. Wuyts, F.L.; Vanhuyse, V.J.; Langewouters, G.J.; Decraemer, W.F.; Raman, E.R.; Buyle, S. Elastic properties of human aortas in relation to age and atherosclerosis: A structural model. Phys Med Biol 1995, 40, 1577–1597. [Google Scholar] [CrossRef] [PubMed]
  22. Safar, M.E.; Levy, B.I.; Struijker-Boudier, H. Current perspectives on arterial stiffness and pulse pressure in hypertension and cardiovascular diseases. Circulation 2003, 107, 2864–2869. [Google Scholar] [CrossRef] [PubMed]
  23. Zieman, S.J.; Melenovsky, V.; Kass, D.A. Mechanisms, pathophysiology, and therapy of arterial stiffness. Arterioscler Thromb Vasc Biol 2005, 25, 932–943. [Google Scholar] [CrossRef] [PubMed]
  24. Tan, Y.T.; Wenzelburger, F.; Lee, E.; Heatlie, G.; Leyva, F.; Patel, K.; Frenneaux, M.; Sanderson, J.E. The pathophysiology of heart failure with normal ejection fraction: Exercise echocardiography reveals complex abnormalities of both systolic and diastolic ventricular function involving torsion, untwist, and longitudinal motion. J Am Coll Cardiol 2009, 54, 36–46. [Google Scholar] [CrossRef] [PubMed]
  25. Thierry, C. Gillebert, M., PHD, Marc L. De Buyzere. Hfpef, diastolic suction, and exercise. JACC: CARDIOVASCULAR IMAGING 2012, 5, 871–873. [Google Scholar]
  26. Yotti, R.; Bermejo, J.; Antoranz, J.C.; Desco, M.M.; Cortina, C.; Rojo-Alvarez, J.L.; Allue, C.; Martin, L.; Moreno, M.; Serrano, J.A.; et al. A noninvasive method for assessing impaired diastolic suction in patients with dilated cardiomyopathy. Circulation 2005, 112, 2921–2929. [Google Scholar] [CrossRef]
  27. Kelly, R.P.; Tunin, R.; Kass, D.A. Effect of reduced aortic compliance on cardiac efficiency and contractile function of in situ canine left ventricle. Circ Res 1992, 71, 490–502. [Google Scholar] [CrossRef] [PubMed]
  28. Kawaguchi, M.; Hay, I.; Fetics, B.; Kass, D.A. Combined ventricular systolic and arterial stiffening in patients with heart failure and preserved ejection fraction: Implications for systolic and diastolic reserve limitations. Circulation 2003, 107, 714–720. [Google Scholar] [CrossRef]
  29. Chow, B.; Rabkin, S.W. The relationship between arterial stiffness and heart failure with preserved ejection fraction: A systemic meta-analysis. Heart Fail Rev 2015, 20, 291–303. [Google Scholar] [CrossRef]
  30. Hundley, W.G.; Kitzman, D.W.; Morgan, T.M.; Hamilton, C.A.; Darty, S.N.; Stewart, K.P.; Herrington, D.M.; Link, K.M.; Little, W.C. Cardiac cycle-dependent changes in aortic area and distensibility are reduced in older patients with isolated diastolic heart failure and correlate with exercise intolerance. J Am Coll Cardiol 2001, 38, 796–802. [Google Scholar] [CrossRef]
  31. Desai, A.S.; Mitchell, G.F.; Fang, J.C.; Creager, M.A. Central aortic stiffness is increased in patients with heart failure and preserved ejection fraction. J Card Fail 2009, 15, 658–664. [Google Scholar] [CrossRef]
  32. Karagodin, I.; Aba-Omer, O.; Sparapani, R.; Strande, J.L. Aortic stiffening precedes onset of heart failure with preserved ejection fraction in patients with asymptomatic diastolic dysfunction. BMC Cardiovasc Disord 2017, 17, 62. [Google Scholar] [CrossRef]
  33. Yip, G.; Wang, M.; Zhang, Y.; Fung, J.W.; Ho, P.Y.; Sanderson, J.E. Left ventricular long axis function in diastolic heart failure is reduced in both diastole and systole: Time for a redefinition? Heart 2002, 87, 121–125. [Google Scholar] [CrossRef]
  34. DeVore, A.D.; McNulty, S.; Alenezi, F.; Ersboll, M.; Vader, J.M.; Oh, J.K.; Lin, G.; Redfield, M.M.; Lewis, G.; Semigran, M.J.; et al. Impaired left ventricular global longitudinal strain in patients with heart failure with preserved ejection fraction: Insights from the relax trial. Eur J Heart Fail 2017, 19, 893–900. [Google Scholar] [CrossRef]
  35. Shah, A.M.; Claggett, B.; Sweitzer, N.K.; Shah, S.J.; Anand, I.S.; Liu, L.; Pitt, B.; Pfeffer, M.A.; Solomon, S.D. Prognostic importance of impaired systolic function in heart failure with preserved ejection fraction and the impact of spironolactone. Circulation 2015, 132, 402–414. [Google Scholar] [CrossRef]
  36. Morris, D.A.; Boldt, L.H.; Eichstadt, H.; Ozcelik, C.; Haverkamp, W. Myocardial systolic and diastolic performance derived by 2-dimensional speckle tracking echocardiography in heart failure with normal left ventricular ejection fraction. Circ Heart Fail 2012, 5, 610–620. [Google Scholar] [CrossRef]
  37. Wang, J.; Fang, F.; Wai-Kwok Yip, G.; Sanderson, J.E.; Feng, W.; Xie, J.M.; Luo, X.X.; Lee, A.P.; Lam, Y.Y. Left ventricular long-axis performance during exercise is an important prognosticator in patients with heart failure and preserved ejection fraction. Int J Cardiol 2015, 178, 131–135. [Google Scholar] [CrossRef] [PubMed]
  38. DuPont, J.J.; Kenney, R.M.; Patel, A.R.; Jaffe, I.Z. Sex differences in mechanisms of arterial stiffness. Br J Pharmacol 2019, 176, 4208–4225. [Google Scholar] [CrossRef]
  39. Samargandy, S.; Matthews, K.A.; Brooks, M.M.; Barinas-Mitchell, E.; Magnani, J.W.; Janssen, I.; Hollenberg, S.M.; El Khoudary, S.R. Arterial stiffness accelerates within 1 year of the final menstrual period: The swan heart study. Arterioscler Thromb Vasc Biol 2020, 40, 1001–1008. [Google Scholar] [CrossRef]
  40. Coutinho, T.; Borlaug, B.A.; Pellikka, P.A.; Turner, S.T.; Kullo, I.J. Sex differences in arterial stiffness and ventricular-arterial interactions. J Am Coll Cardiol 2013, 61, 96–103. [Google Scholar] [CrossRef]
  41. van Ommen, A.; Canto, E.D.; Cramer, M.J.; Rutten, F.H.; Onland-Moret, N.C.; Ruijter, H.M.D. Diastolic dysfunction and sex-specific progression to hfpef: Current gaps in knowledge and future directions. BMC Med 2022, 20, 496. [Google Scholar] [CrossRef]
  42. Tran, P.; Banerjee, P. Myocardial fatigue at a glance. Curr Heart Fail Rep 2023, 20, 191–193. [Google Scholar] [CrossRef] [PubMed]
  43. Tran, P.; Linekar, A.; Dandekar, U.; Barker, T.; Balasubramanian, S.; Bhaskara-Pillai, J.; Shelley, S.; Maddock, H.; Banerjee, P. Profiling the biomechanical responses to workload on the human myocyte to explore the concept of myocardial fatigue and reversibility: Rationale and design of the power heart failure study. J Cardiovasc Transl Res 2024, 17, 275–286. [Google Scholar] [CrossRef] [PubMed]
  44. Burkhoff, D.; Topkara, V.K.; Sayer, G.; Uriel, N. Reverse remodeling with left ventricular assist devices. Circ Res 2021, 128, 1594–1612. [Google Scholar] [CrossRef] [PubMed]
  45. Douglas, P.S.; O’Toole, M.L.; Hiller, W.D.; Hackney, K.; Reichek, N. Cardiac fatigue after prolonged exercise. Circulation 1987, 76, 1206–1213. [Google Scholar] [CrossRef] [PubMed]
  46. Kleinnibbelink, G.; van Dijk, A.P.J.; Fornasiero, A.; Speretta, G.F.; Johnson, C.; Hopman, M.T.E.; Sculthorpe, N.; George, K.P.; Somauroo, J.D.; Thijssen, D.H.J.; et al. Exercise-induced cardiac fatigue after a 45-minute bout of high-intensity running exercise is not altered under hypoxia. J Am Soc Echocardiogr 2021, 34, 511–521. [Google Scholar] [CrossRef] [PubMed]
  47. Oxborough, D.; Birch, K.; Shave, R.; George, K. “Exercise-induced cardiac fatigue”--a review of the echocardiographic literature. Echocardiography 2010, 27, 1130–1140. [Google Scholar] [CrossRef] [PubMed]
  48. Tran, P.; Maddock, H.; Banerjee, P. Myocardial fatigue: A mechano-energetic concept in heart failure. Curr Cardiol Rep 2022, 24, 711–730. [Google Scholar] [CrossRef] [PubMed]
  49. Ali, D.; Tran, P.; Ennis, S.; Powell, R.; McGuire, S.; McGregor, G.; Kimani, P.K.; Weickert, M.O.; Miller, M.A.; Cappuccio, F.P.; et al. Rising arterial stiffness with accumulating comorbidities associates with heart failure with preserved ejection fraction. ESC Heart Fail 2023, 10, 2487–2498. [Google Scholar] [CrossRef]
  50. Daou, D.; Gillette, T.G.; Hill, J.A. Inflammatory mechanisms in heart failure with preserved ejection fraction. Physiology (Bethesda) 2023, 38, 0. [Google Scholar] [CrossRef]
  51. Borlaug, B.A.; Carter, R.E.; Melenovsky, V.; DeSimone, C.V.; Gaba, P.; Killu, A.; Naksuk, N.; Lerman, L.; Asirvatham, S.J. Percutaneous pericardial resection: A novel potential treatment for heart failure with preserved ejection fraction. Circ Heart Fail 2017, 10, e003612. [Google Scholar] [CrossRef] [PubMed]
  52. Watkins, M.W.; LeWinter, M.M. Physiologic role of the normal pericardium. Annu Rev Med 1993, 44, 171–180. [Google Scholar] [CrossRef] [PubMed]
  53. Hill, M.A.; Walkowiak, O.A.; Head, W.T.; Kwon, J.H.; Kavarana, M.N.; Rajab, T.K. A review of animal models for post-operative pericardial adhesions. Front Surg 2022, 9, 966410. [Google Scholar] [CrossRef] [PubMed]
  54. Park, C.B.; Suri, R.M.; Burkhart, H.M.; Greason, K.L.; Dearani, J.A.; Schaff, H.V.; Sundt, T.M., 3rd. Identifying patients at particular risk of injury during repeat sternotomy: Analysis of 2555 cardiac reoperations. J Thorac Cardiovasc Surg 2010, 140, 1028–1035. [Google Scholar] [CrossRef] [PubMed]
  55. Shabetai, R. The pericardium; Grune & Stratton: New York, 1981. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated