1. Introduction
1.1. Renewable Energy Directives
The industrial revolution brought about the automation of numerous work tasks, leading to enhanced productivity and better standards of living. However, this progress came with the adverse consequence of increased
emissions due to fossil fuel consumption, contributing to an increase in Earth’s temperature of over
[
1]. Looking ahead, Germany’s energy infrastructure may confront various issues, particularly with the shift toward decentralized power generation. Policy changes at European and national levels have dismantled electricity grid monopolies, enabling consumers to choose their own power and gas suppliers in a competitive landscape. The fifth European energy package aims to align with the Paris Climate Agreement by advocating for the expansion of renewable energy and enhancing efficiency in industries such as manufacturing, transportation, and housing [
2]. Investment incentives are essential to achieve these objectives, and to this end, the Renewable Energy Directive (RED II) defines Renewable Energy Communities (REC) (Definition 1) [
3]. REC participants can share and utilize self-generated heat or electrical power at lower costs. Beyond regional growth, these initiatives allow for the optimization of local energy efficiency by coupling electricity, heating, and transport sectors [
4].
Definition 1 (Renewable Energy Community taken from [
3]).
Consists of at least 50 natural persons
At least 75% of the shares are held by natural persons who are located within one postal area and a radius of 50 kilometers
No member possess more than 10% of the shares
1.2. Renewable Energy Management Systems
Regulatory and legislative developments are reshaping the dynamics of the electricity market, with emerging opportunities for district energy management systems (DEMS) - coming potentially with seventeen principal roles and an innovative IT framework in this sector [
5]. Boundaries of districts are defined by either a local network transformer or a gas pressure regulator, setting them apart from neighboring districts, with each having its own unique spatial dimensions. These districts - whether located in urban, suburban, rural, or industrial settings, as well as those with mixed characteristics - have unique socio-economic and demographic features that influence their energy consumption [
6,
7]. Initiatives such as retrofitting buildings and modernizing heating systems can lead to lower energy consumptions. Leveraging smart demand-side management, flexible approaches in generating, consumption, and storing energy can diminish building heating demands by as much as 20% [
8]. As we move towards sustainable energy supply, the orchestrated operation of buildings is gaining importance [
7]. DEMS are instrumental in facilitating sector integration, minimizing electricity losses, enhancing supply reliability, and incorporating emergent technologies into the electrical grid [
4]. They additionally have to control and optimize energy generation, consumption and storage resources - satisfying demands of specific balancing groups [
9,
10]. REC energy management systems (REC-EMS) surpass DEMS by taking on the responsibility of monitoring energy distribution and fostering synergies among various districts.
1.3. Use Case
The growing complexity of decentralized energy networks necessitates for advanced REC-EMS that facilitate automated data management across distributed systems, intelligently linking components within a REC to foster synergies and leverage flexibilities between RECs [
7]. In addition to the rising use of heat pumps and electric vehicles, energy providers are obligated to provide customers with dynamic electricity pricing in accordance with EnWG (§41a) in Germany [
11]. As storage systems engage with dynamic pricing, a variety of feedback mechanisms may arise, potentially resulting in electricity consumption that is sensitive to price changes [
12]. To ensure the cost-effectiveness of REC-EMS, it is essential to develop REC energy consumption forecasting algorithms (REC-ECF) that are both scalable and transferable. With the energy market’s liberalization allowing prosumers freely to select their energy provider on a daily basis [
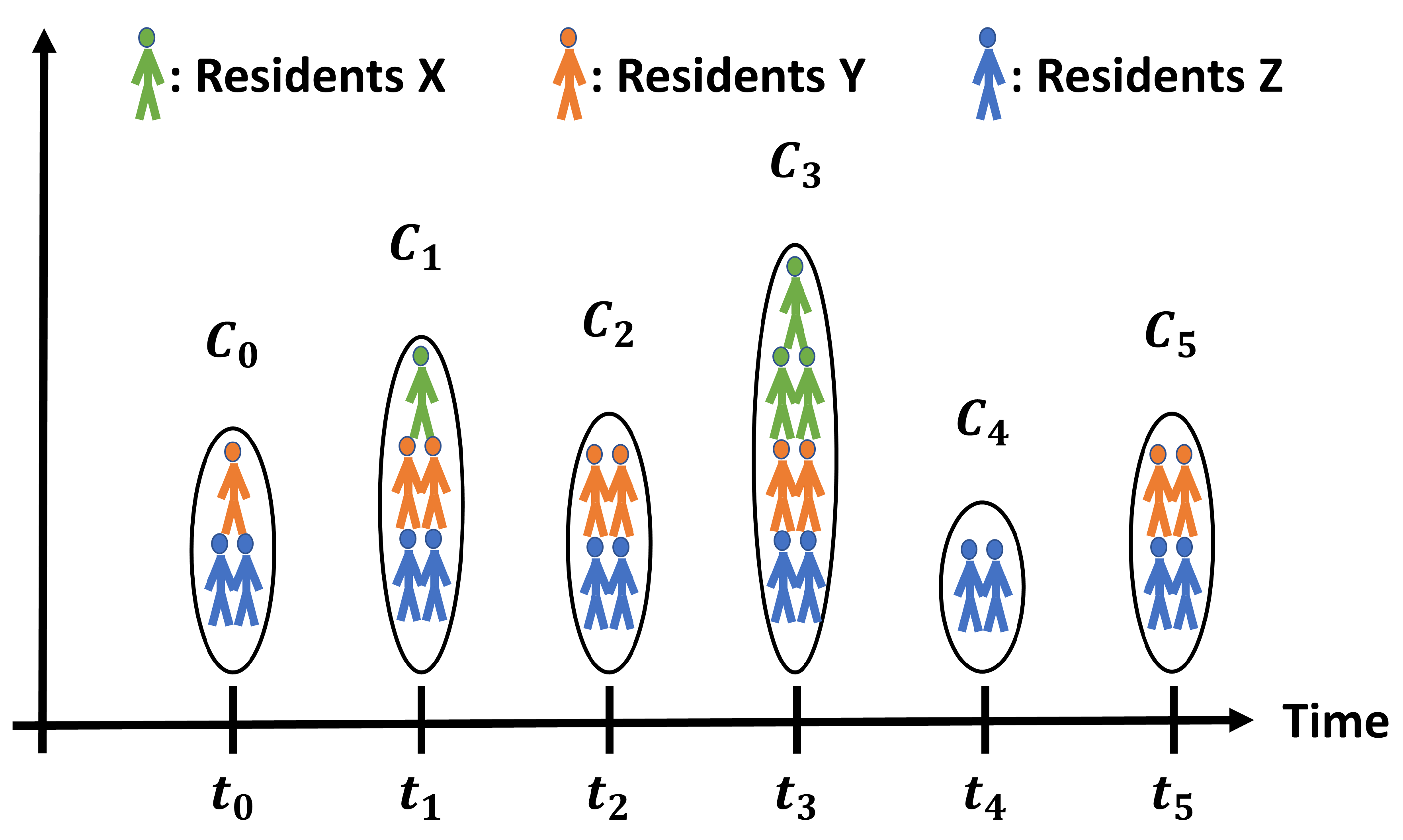
13], RECs possess a dynamic portfolio of their members, as depicted in
Figure 1. These members represent either particular residents of a specific REC or various elements of the energy system such as electric vehicles and heat pumps. Given that each has distinct consumption patterns, the consequent time series data tend to be non-stationary (Definition 2) and exhibit discontinuities (Definition 3). Under these circumstances, a predictive model must account for the varied member composition and be calibrated for a range of RECs. The essential objective is to uncover cross-domain as well as domain-invariant patterns within a forecasting model that can handle various time series characteristics and enhance systems with time-sensitive variations.
Definition 2 (Non-Stationarity, taken from [
14]).
A time series is considered stationary when its statistical characteristics remain consistent regardless of the observation time. In other words, the properties of a stationary time series do not change over time. On the contrary, if a time series exhibits trends or seasonality, it is considered non-stationary. The presence of trends or seasonality causes variations in the time series values at different points in time.
Definition 3 (Discontinuity).
Discontinuous time series possess bounds in the sequence of observations.
1.4. Contributions
There is extensive research on electrical load forecasting, with many studies claiming to outperform other algorithms. On the contrary, reviews of numerous works on this subject often conclude that they are not truly comparable due to differences in the level of aggregation, the dataset used, the forecast model applied, the data preprocessing step, the temporal resolution, and the forecast horizon. Moreover, a standard benchmark model for time series forecasting is lacking, the process behind time series is frequently under-detailed, the problem concerning model weight divergence in a non-identical and independently distributed (non-iid) setting is only inadequatly studied, issues such as non-stationarity and discontinuity are often ignored, and significant influences of the forecast execution time on forecast results is rarely considered [
15]. With respect to the explainability and interpretability of machine learning models designed for time series forecasting, there is still a deficiency [
16]. Investigations into the sensitivity to input features, uncertainties tied to conditionals, and the robustness to novel scenarios are still needed when utilizing machine learning (ML) models [
17]. Recent studies on time series forecasting analyze various use cases by training models with highly stochastic and distributed household data using federated learning (FL) (Definition 4). These studies primarily focus on comparing strategies for averaging model weights and clustering data, with a one-step-ahead forecast horizon, to tackle challenges associated with non-iid data [
18,
19,
20,
21,
22,
23]. Given the aforementioned research gaps, we propose a time series forecasting framework that aggregates knowledge from multiple clients and is simultaneously capable of handling non-stationary, discontinuous, and non-iid data. Our work is structured as follows (
Figure 2): (i) Analyze synthetic electrical load time series at the district scale, aggregate them to those of RECs with dynamic portfolios and prove non-stationarity, discontinuity and non-iid [
15], (ii) describe data pre-processing concerning the time series process, the resulting time series forecasting model architecture, and federated learning strategies regarding non-iid data and model weight divergence, (iii) define experimental setups, and (iv) evaluate and discuss the results.
Definition 4 (Federated Learning, inspired by [
24,
25]).
Federated learning is a machine learning technique where a central model is trained across multiple devices holding local data, without exchanging it, thus preserving privacy and reducing data transfer. Local models’ updates are aggregated to improve the central model.
2. Data
To address the research objective, to conduct various experiments, to evaluate results and lastly to discuss them (
Section 1.4), a huge amount of REC time series is essential, ones that encompass necessary attributes such as non-stationarity (Definition 2), discontinuity (Definition 3), stochasticity (Definition 5), autoregression (Definition 6), seasonality (Definition 7), trend (Definition 8), periodicity (Definition 9) and non-iid on various clients.
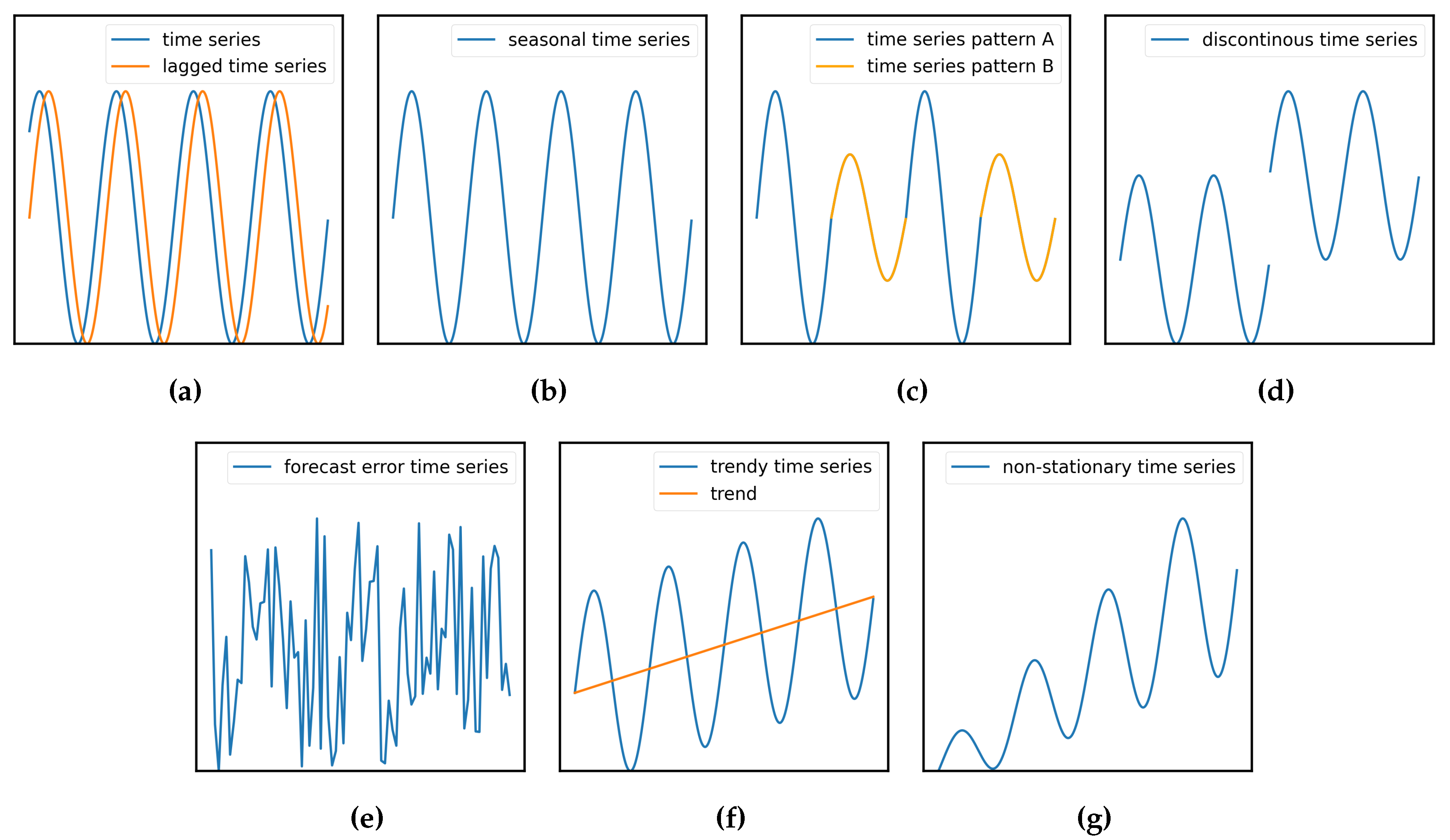
Figure 3 illustrates differences between these terms, where (a), (b), (c), (d), (f) and (g) are showing non-stationary characteristics (Definition 2). For simplicity, we assume that RECs are composed of various districts (
Section 1.2). Since no real dataset fulfills these requirements, we firstly generate stationary as well as distinctive district electricity consumption time series (DECTS) based on different socio-economic factors (
Section 2.1). Subsequently, we use these to construct RECs with dynamic portfolios, resulting in non-stationary and discontinous time series (
Section 2.2).
Definition 5 (Stochasticity).
The stochasticity of a time series refers to the inherent randomness or unpredictability in the data.
Definition 6 (Autoregression).
Autoregression is a time series modeling technique where future values are predicted based on past values of the same series.
Definition 7 (Seasonality).
Seasonality in time series is a long-term characteristic pattern that repeats at regular intervals (years).
Definition 8 (Trend).
The trend of a time series represents a long-term linear or even non-linear time-dependency in the data, typically showing sustained increase or decrease over time.
Definition 9 (Periodicity).
The periodicity of a time series refers to short-term, repetitive occurrences of specific patterns such as day of week or hour of day.
2.1. Synthesis And Analysis Of Synthetic Electrical Load Time Series At District Scale
We utilize a public dataset that provides more than 5500 household electricity consumption time series with a 30-minute temporal resolution, classified into 18 different ACORN groups (Definition 10), to handle the huge amount of DECTS with diverse characteristics. Since these time series are highly stochastic, we proceed as introduced in [
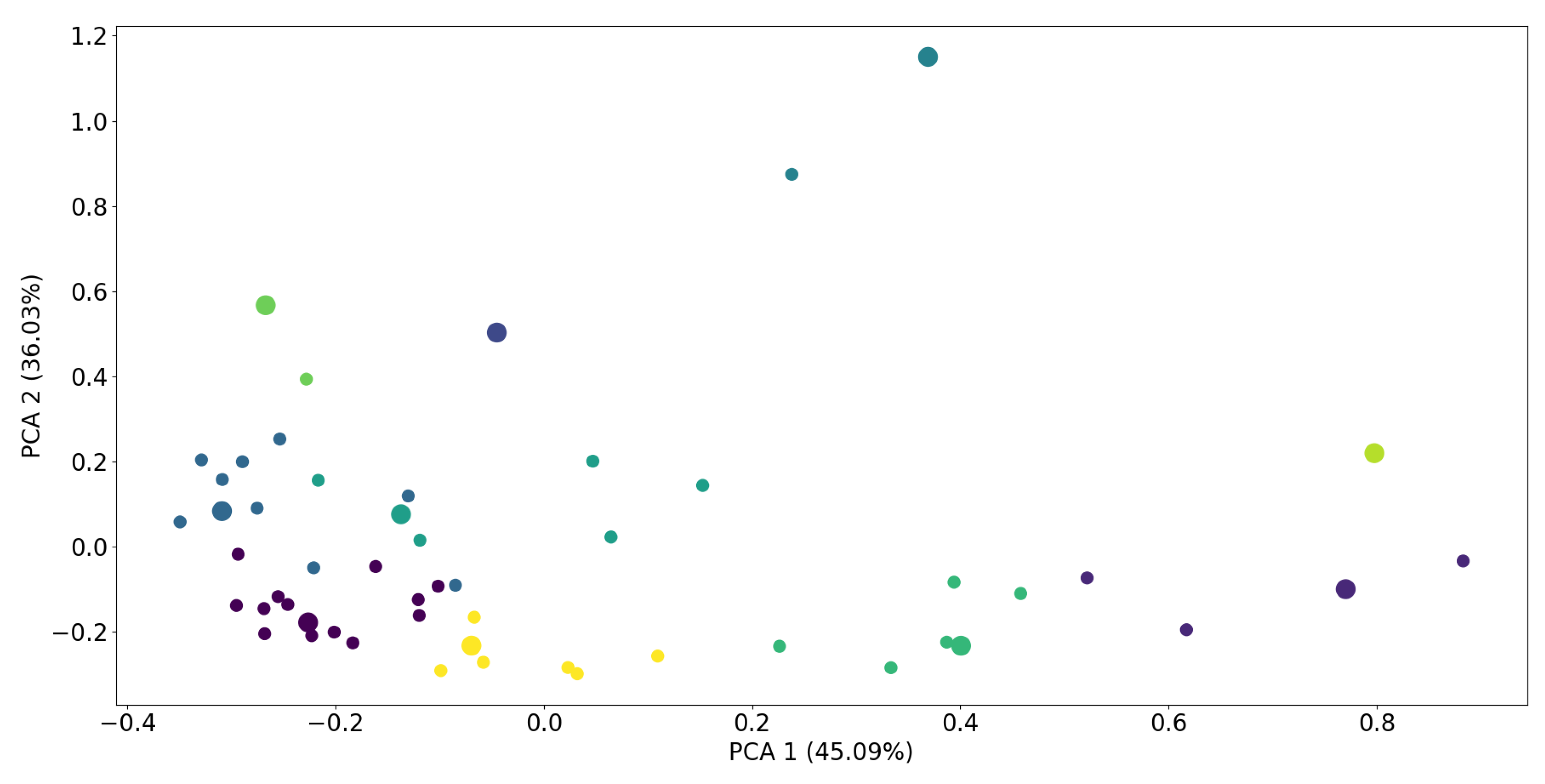
15]: (i) Clustering ACORN household electricity consumption time series, and transforming and scaling non-Gaussian distributed data, (ii) aggregating household data to the level of districts and extracting the time series process to ensure adequate sampling of training data, (iii) training a two-step probabilistic forecasting model to ensure both seasonal and short-term variations, and (iv) iterativly generate synthetic time series. This approach is applied in conjunction with weather data (temperature, relative humidity) of central Germany for the years 2018 and 2019. It results in a total of 55 distinct ACORN subgroups, each with specific time series characteristics influenced by socio-economic factors and household size. To gain a clearer understanding of the diversity of their characteristics, we firstly calculate a correlation matrix
to obtain correlations between all ACORN subgroups. We then perform principal component analysis to reduce the dimensions to two and to illustrate it with a scatter plot (
Figure 4). Since many ACORN subgroups possess similar electricity consumption characteristics, aggregating them to the level of a REC will not generate diverse time series. Therefore, we additionally apply K-means clustering with the number of clusters set to
, extracting the ten most distinctive subgroups. The effect of this filtering method is demonstrated in
Table 1, showing lower mean values and higher standard deviations of
for the ten most distinctive subgroups, resulting in a higher diversity.
Definition 10 (ACORN, taken from [
26]).
ACORN is a segmentation tool which categorizes UK’s population into demographic types.
2.2. Generate Dynamic Portfolios Of Renewable Energy Communities
Besides the general definition of non-stationarity (Definition 2), there even exist more refined ones named cyclostationarity (Definition 11) [
27]. Since synthetic REC time series (RECTS) should be constructed to satisfy a dynamic portfolio, they must not exhibit this characteristic. Keeping this in mind and given a set of 300 DECTS for each ACORN subgroup, we generate diverse RECTS from the ten most distintive ones (
Section 2.1) in respect of certain constraints (Algorithm 1):
No unique DECTS have to be used twice.
Each RECTS is composed of different DECTS in varying quantities
, depicting a time dependent residents composition vector
(Eq. (
1)) for each REC.
Since and only 300 DECTS exist for each ACORN subgroup, the quantity of RECTS is confined to 70.
Each REC is assigned both a random start and a random end with random various probabilities that is set to zero.
The residents composition of REC is linearly developed using start and end .
Every new day, one of ten ACORN subgroups is randomly chosen and either a new DECTS is added or an existing one is excluded, unless the linear development curve from start to end is undershot or exceeded by more than 1.
Quantity of specific ACORN subgroup at time t
Index of specific ACORN subgroup,
Index of time with a daily temporal resolution
Definition 11 (Cyclostationarity, taken from [
27]).
A time series may exhibit both seasonality as well as periodicity and can still remain predictable, as these cyclical patterns repeat at regular intervals. Removing these two components will strongly lead to a stationary time series.
|
Algorithm 1:Generation of non-stationary and discontinous RECTS |
 |
2.3. Analyze Time Series Of Renewable Energy Communities
While
Section 2.2 generates RECTS (examples of those can be found in
Appendix B and
Figure A1), we still have to test for required time series attributes. To address non-stationarity, we remove seasonality (week of the year), periodicity (day of the week, hour, minute), and even the long-term trend from the original time series by applying a Seasonal-Trend decomposition using LOESS of the Python statsmodels package. Subsequently, we apply the Augmented Dickey-Fuller (ADF) test on a representative RECTS, considering only timestamps at 12:00 (
Figure 5). The Dickey-Fuller test is a statistical method for testing whether a time series is non-stationary and contains a unit root. The null hypothesis is that there is a unit root, suggesting that the time series has a stochastic trend. The ADF test considers extra lagged terms (we use
to account for an entire week) of the time series’ first difference in the test regression to account for serial correlation. Since
, the null hypothesis can not be rejected, demonstrating non-stationarity of RECTS (
Table 2, for all RECTS see
Appendix A and
Table A1).
Discontinuity is often attributed to a change point, which indicates a transition from one state to another in the process generating the time series data. Various algorithms have been utilized to detect change points in data, including likelihood ratio, subspace model, probabilistic, kernal-based, graph-based and clustering methods [
28]. In contrary, a boxplot is easy to use and give overview about data distribution, skewness and outliers [
29]. In this, the box shows the interqurtile range (IQR) which is the distance between the first (Q1) and third (Q3) quartiles. The whiskers extend from the box to the highest and lowest values within
. The line in the middle of the box represents the median or the second quartile (Q2) of the data. Points outside the whiskers represent outliers. To analyze discontinuity in RECTS, we firstly calculate mean daily sequences for each week of the year. Subsequently, we compute differential time series (time series minus its lagged version with shift of 1). Considering that all 70 RECTS have varying magnitudes, we normalize them by utilizing Eq. (
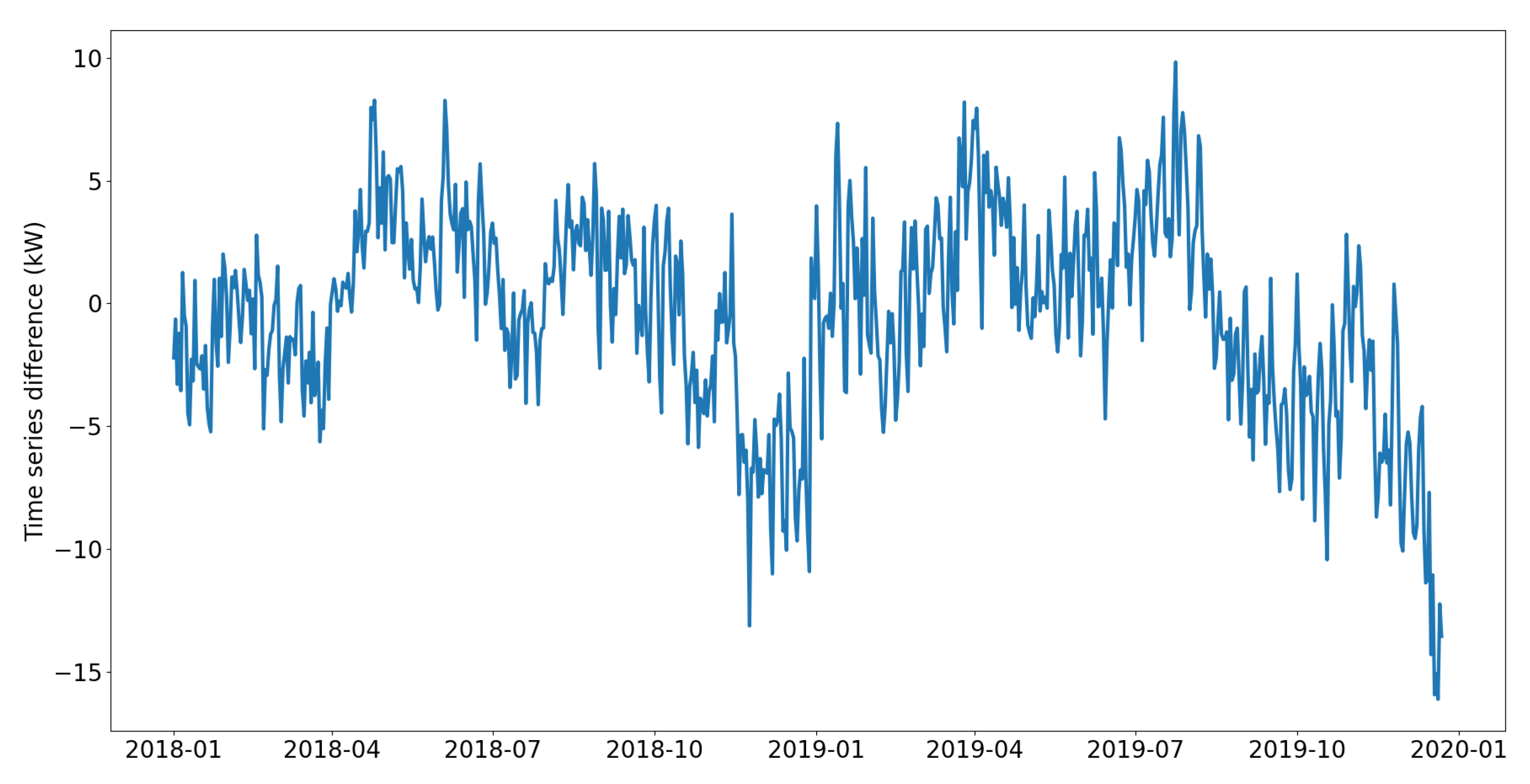
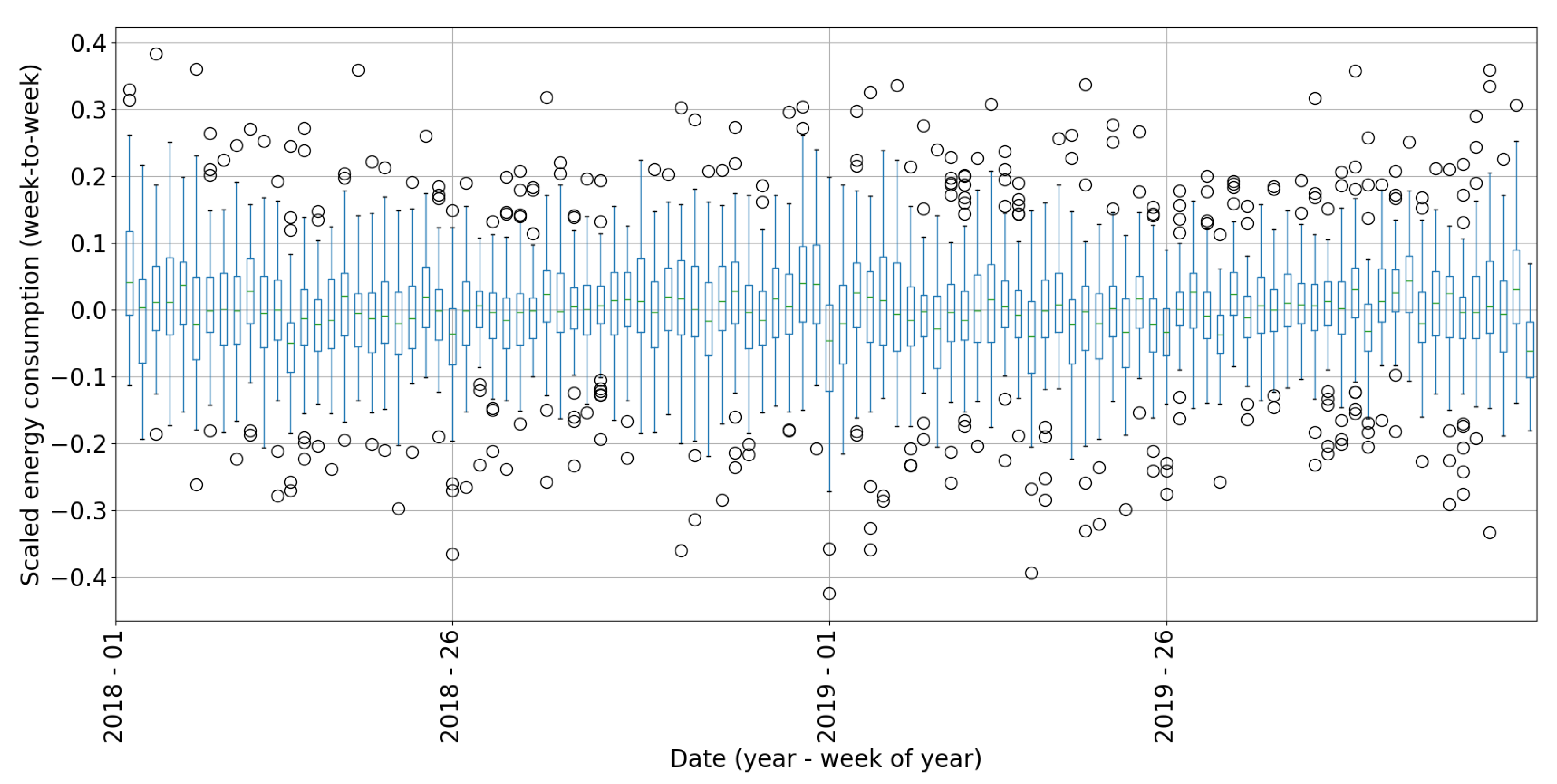
2). Then, we use a boxplot to illustrate the distribution of all generated RECTS for each week of the year (
Figure 6), showing a huge number of outliers and proving discontinuity in data.
Another requirement involves handling non-iid data across multiple clients, which can be simply demonstrated by illustrating correlations among all generated RECTS.
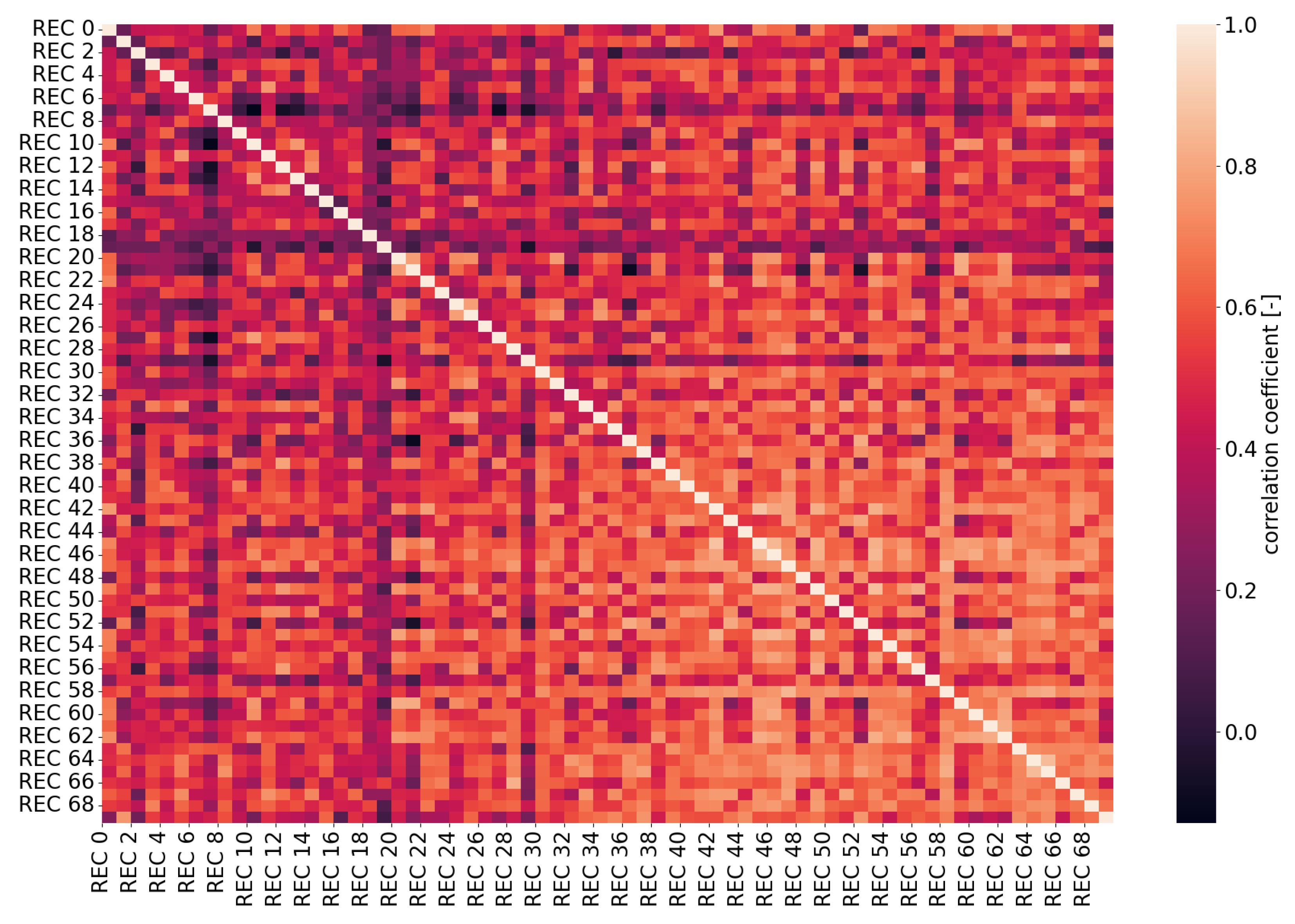
Figure 7 shows their correlation matrix
, with highest correlations on the diagonal - representing correlations of each RECTS to itself. Since each REC is individually developed using diverse
at start and end point, correlations are much lower than the ones of DECTS (compare
Table 1 with
Table 3). This strongly indicates, that RECTS possess a high degree of non-iid data, which must be adequatly considered within a time series forecasting model and FL.
2.4. Transformation
Time series data should be scaled before being used in machine learning, particularly because of algorithm performance and gradient descent optimization. In our work, we utilize Eq. (
3) to scale data within the range
by setting
and
. To rescale transformed data to its original magnitude, we use Eq. (
4)
3. Methodology
3.1. Problem Description
Time series are governed by a stochastic process, meaning that both past observations and random shocks directly influence future values . In terms of RECTS, the impact of autoregressive variables and on is dependent on temporal features like weekday or daytime and additionally varies from one RECTS to the next, resulting in individual forecast model parameters. The primary challenge is to create a forecast model that learns features which are consistent across different REC residents composition (domains) and can be generalized to a vast array of RECs, even those not included in model training. Moreover, this forecast model should account for non-stationarity and discontinuity with regard to dynamic portfolios of RECs. Since all RECTS are assumed to be located on distributed clients, the model training process must address privacy and security concerns through the application of FL, which must manage non-iid data and weight divergence.
3.2. Concept
Based on the problem description, we develop an approach that satisfies requirements and addresses unresolved challenges. Firstly, we provide a brief description of the time series process of RECTS by illustrating process equations. In addition to exogenous variables such as weather, we precisely incorporate the time-dependent residents composition
of RECs into these equations (
Section 3.3). Since these process equations reflect past, present, and future states, each with potentially different
, we take this into account during the development of the forecast model - feedforward neural network (FNN) (
Section 3.4). To train across multiple distributed clients, we also develop a FL framework that offers flexibility in forecast model parameterization (such as layer type, number of neurons, batch size, and optimizer type for gradient descent) and data sharing, aiming to overcome non-iid and model weight divergence issues (
Section 3.5). Finally, we set up meaningful experiments to distinguish between ineffective and effective settings (
Section 3.6). For this, we must make some assumptions:
All RECs are composed of the same distinct DECTS, as described in
Section 2.2.
All RECs are aware of the history of their .
For effective model training using FL, all RECs must share the minimum and maximum values of their RECTS to achieve consistent data scaling over all clients.
3.3. Time Series Process
RECTS, and time series in general, are composed of seasonal (regular long-term or annual variation), periodic (regular short-term or weekday variation), trend (long-term directional movement) and irregular (white noise, which can not be modeled) components. Time series can be predicted by extrapolating from past and present observations into the future, commonly utilizing an AutoRegressive Integrated with eXogenous variables (ARIX) model. In this context, AR is associated with present observations, I is associated with past observations, and X encompasses the impact of exogenous variables across past, present, and possible future (F) events. Then, a time series forecasting model should learn relationships between all variables (endogenous and exogenous) at past, present, and future timestamps. Within this framework, exogenous further variables include data of calendar, weather, and residents composition of REC
(
Table 4). In our approach, we encode calendar features using cyclical encodings (Definition 13), resulting in lower dimensions [
30,
31]. We determine the number of lagged values
that have a strong impact on subsequent values by following the Box-Jenkins method and utilizing the partial autocorrelation function [
32]. Since I is utilized to address short-term non-stationarities, we use reference values based on the type of day (such as day of the week, holiday, or bridge day), resulting in the following shifts
(
Figure 8):
monday → last friday ()
tuesday → yesterday ()
wednesday → yesterday ()
thursday → yesterday ()
friday → yesterday ()
saturday → last saturday ()
sunday → last sunday ()
holiday → last sunday ()
bridge day → last saturday ()
With this information, we can formulate regression equations for AR (Eq. (
5)), I (Eq. (
6)), and F (Eq. (
7)) within the context of an ARIX model to generate input data (
,
,
) for the purpose of model training purposes, while disregarding the difference filter. This subsequently yields the complete ARIX process equation (Eq. (
8)). Given that historical data of
is available for each REC and is also included in the input data, there is potential to extract cross-domain and domain-invariant features, a process known as domain adaptation [
33,
34,
35].
Definition 12 (One-Hot Encoding, taken from [
15]).
Within a one-hot encoding, each class is represented by a binary vector. In this encoding, each class occurrence assigns to 1 and otherwise to 0.
Definition 13 (Cyclical Encoding, inspired by [
15]).
Periodic encodings are transformations of one-hot encodings into more continuous variables by using sine and cosine functions. This can only be applied to periodic variables like daytime, day of the week or day of the year.
Example: For the cyclical transformation of all hours , we use both sinus and cosine transformations to create two new variables.
where:
| p
|
Number of past observations to be considered in AR |
| , ,
|
Regression parameters within an ARIX model |
| n
|
Number of variables used in regression equation (Table 4) |
| x
|
variable |
3.4. Time Series Forecast Model
In the context of time series forecasting, a huge amount of various neural network architectures have been studied [
16,
31]. While neural networks and ARIX regression models may utilize identical input data (refer to
Section 3.3), neural networks do not necessitate a predefined regression equation and are adept at discovering non-linear relationships and latent characteristics. This paper posits that the accuracy of forecasts is largely influenced by the choice of input features, the engineering of features (such as calendar data), and the manner in which past, present and future features are connected within the model’s architecture. A time series forecasting model is expected to discern the linkages between past, present and present endogenous and exogenous variables (see Eq. (
6), (
5)) and leverage this knowledge alongside future exogenous variables (Eq. (
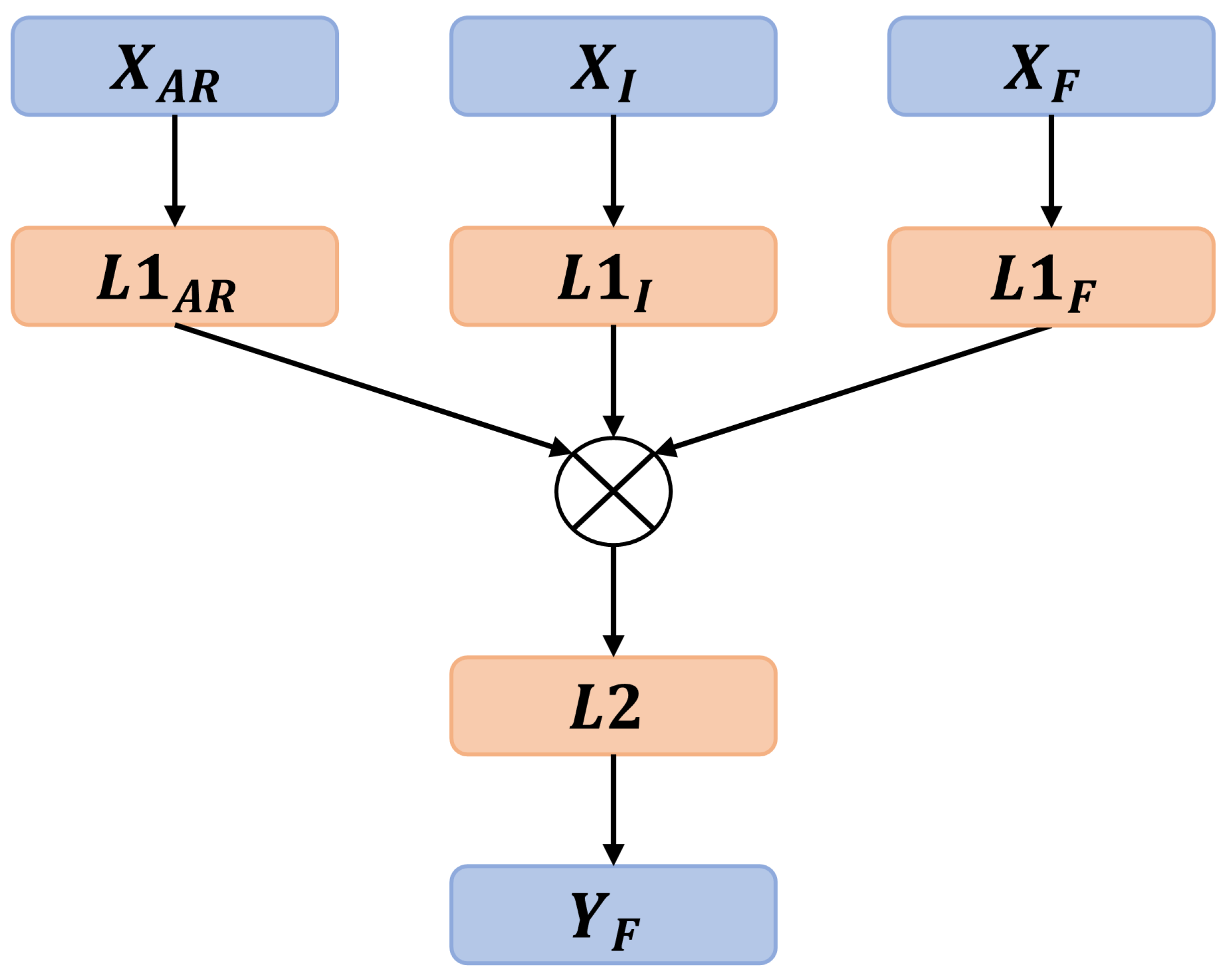
7)) to predict the target variable. To this end, we propose a neural network with distinct input layers
,
,
processing past
, present
, and future
data, each equipped with an equivalent neuron count to facilitate feature learning. Subsequent to this, latent features are combined following a principle of action (either concatenation or multiplication), and the resulting array is then processed within an output layer
, conforming to the target output dimensions (illustrated in
Figure 9). This architectural design can be implemented utilizing Dense-layers (FNN). In our work, we use three input layers, each with 30 neurons, and one output layer, with each layer equipped with a linear activation function.
3.5. Federated Learning
FL was introduced to train a high-quality global model while keeping training data distributed across multiple clients, thereby ensuring data privacy as well as security issues, and demonstrating robustness to non-iid data. Additionally, model performance can be improved by training a model with a diverse array of training data. To achieve this, the FederatedAveraging algorithm (Algorithm 2) applies stochastic gradient descent within local model training and averages each client’s model weights on a central server [
37]. In the context of energy time series forecasting, many publications have studied the application of FL at household level. Given that this data is highly stochastic and non-iid, they propose using a one-step-ahead forecast horizon and clustering similar clients into groups, resulting in multiple global forecast models, which are further fine-tuned by applying transfer learning [
24,
25,
38,
39,
40,
41]. While this approach overcomes issues with non-iid data, there is no one that attempts to unify heterogeneous time series data into a single global forecast model, addressing non-stationarity and discontinuity. The reason for doing so is that a non-iid data setting across multiple clients can lead to a divergence in model weights (
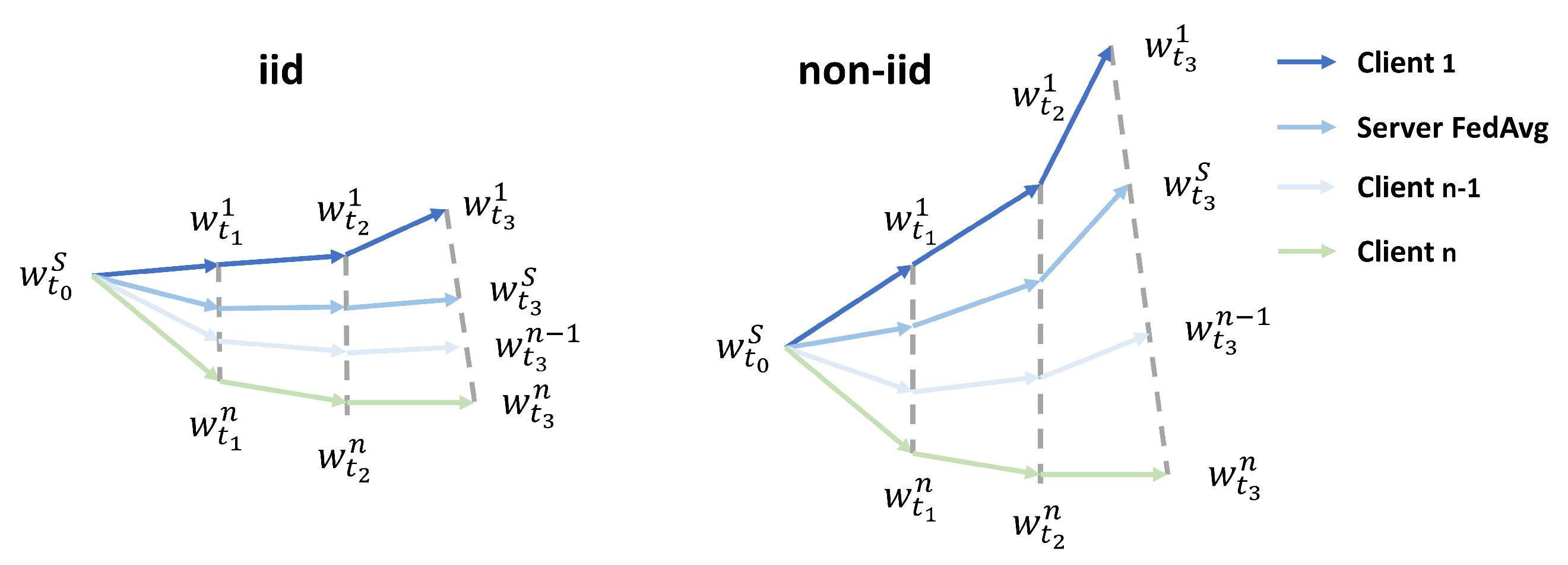
Figure 10). Moreover, the number of hidden neurons
N can significantly impact model convergence because gradients tend to increase when
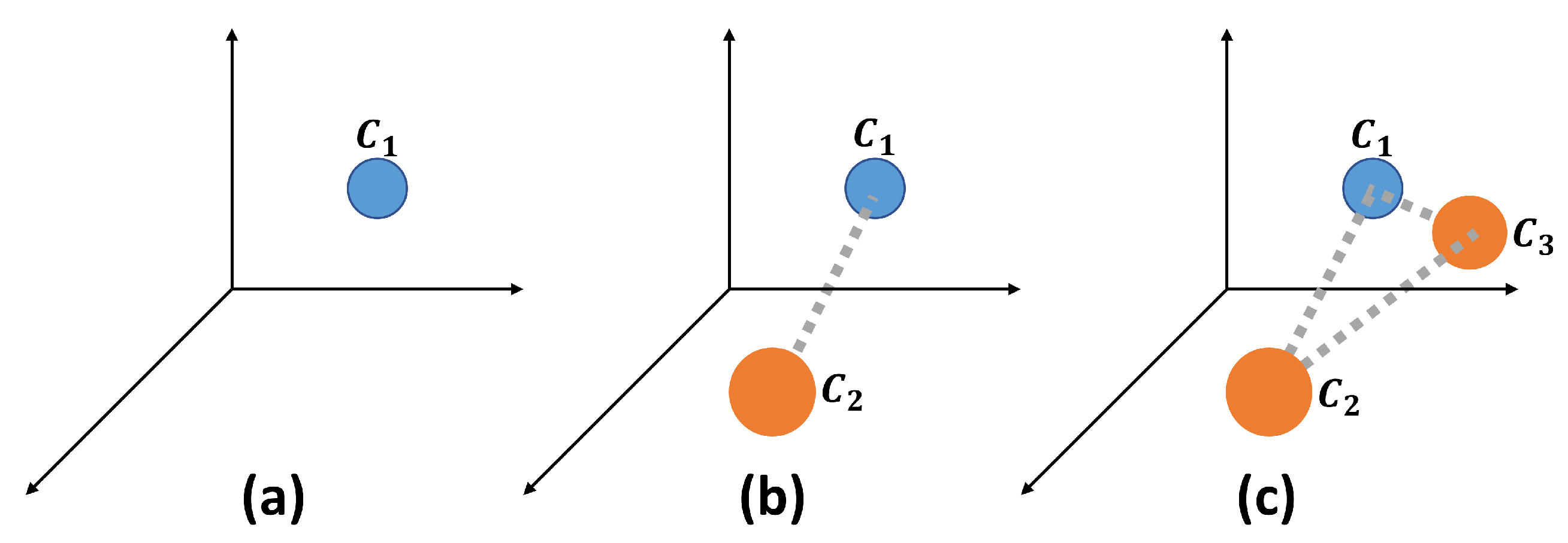
N is low. This effect can be observed during the optimization of model weights that do not align well with local data distributions and characteristics. A common practice, among others, for addressing this effect is to share data across multiple clients, which is beneficial for aggregating knowledge of relational behavior [
42] (
Figure 11).
|
Algorithm 2:FederatedAveraging |
 |
3.6. Experiments
Our work aims to bridge the research gap in training time series forecasting models using Federated Learning, addressing non-stationarity and discontinuity, as previously mentioned in
Section 1.4. For this purpose, we outline the time series process, including preprocessing of model input data (
Section 3.3), develop a generic neural network architecture that handles non-stationarities, discontinuities, and domain-specific characteristics across various observation times - including past, present, and future (
Section 3.4), and construct a FL framework to aggregate knowledge from a diverse set of clients by applying data sharing (
Section 3.5). In our experiments, we apply various model parameterizations (
Table 5) that include different values for the number of shared time series to each client (sts →extract relational behavior of RECTS with various
[
42]), the batch size (bs →generalize neural network [
44]) and the learning rate (lr →regularize model weight divergence [
43]), while maintaining the number of hidden neurons
, local training epochs
and FL training epochs
. While training local forecasting models with stochastic gradient descent, we use Federated Averaging (Algorithm 2) to update global model weights within the entire FL process. Training data is prepared for a subset of
clients with a small member size, considering the year 2018, and it is processed for a forecast execution time of 06:00 with a horizon spanning an entire day. To demonstrate our framework’s capability concerning domain-adaption, transferability, and performance, we need to design meaningful experiments (test data is a subset of
clients with large member size, considering the year 2019) that differentiate between ineffective and effective settings (
Table 6).
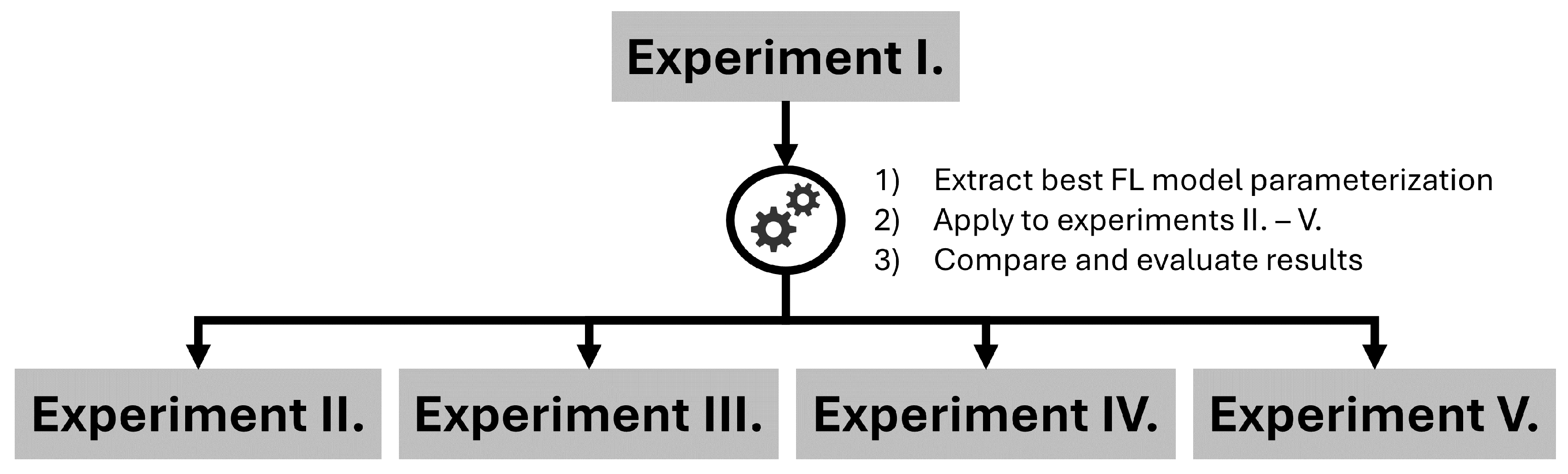
Figure 12 illustrates the process of conducting the various experiments. In
Appendix C,
Figure A2 illustrates the average number of members for each REC and their overall median value
. Regarding this,
refers to RECs smaller than
and
refers to RECs larger than
, dividing train and test dataset into two distinct subsets of time series, each with characteristic behaviors and magnitudes. We use TensorFlow [
45], an open-source machine learning framework, and
Stochastic Gradient Descent optimization algorithm.
4. Results
4.1. Experiment I.
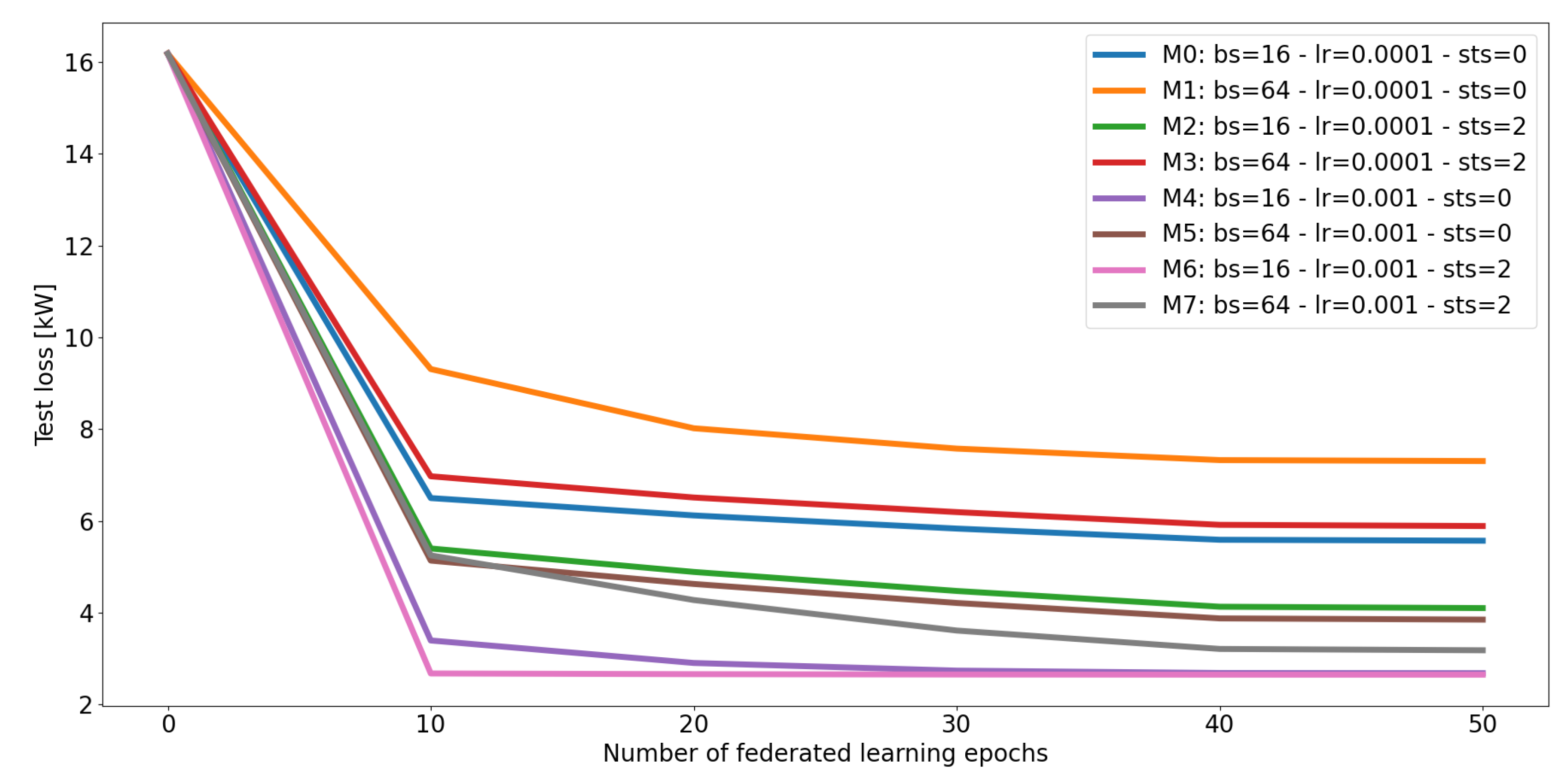
Experiment I is intended to identify the best model setting, which is then applied in subsequent experiments as well.
Table 7 displays the mean absolute error (MAE, see
Appendix D Eq. (
A1)) and the mean absolute percentage error (MAPE, see
Appendix D Eq. (
A2)) for each model applied to the test dataset (year 2019), showing strong dependencies on batch size, learning rate, and number of shared time series. The results propose to use a smaller batch size (compare error measurements between M0 and M1, between M2 and M3, between M4 and M5, or between M6 and M7), a higher number of shared RECTS with all clients (compare error measurements between M0 and M2, between M1 and M3, between M4 and M6, or between M5 and M7), and a bigger learning rate (compare error measurements between M0 and M4, between M1 and M5, between M2 and M6, or between M3 and M7). While models with higher learning rates converge faster and yield favorable error measurements, the others struggle to learn meaningful latent features necessary for transferable predictions. Moreover,
federated learning epochs are sufficient for the models to converge (see
Figure 13). Since these error measurements do not provide a clear overview of our forecasting framework’s capabilities, we further illustrate the predictions versus actual measurements in
Figure 14. The scatter plot (a) shows good agreement, except for some outliers that could possibly be caused by high variability during special events, and the line plot (b) confirms these findings. Since M6 provides best prediction results, we will use this setting within the experiments II. - V..
An optimal forecast model is achieved when the error time series (measurements minus predictions) can be proven to be equivalent to white noise [
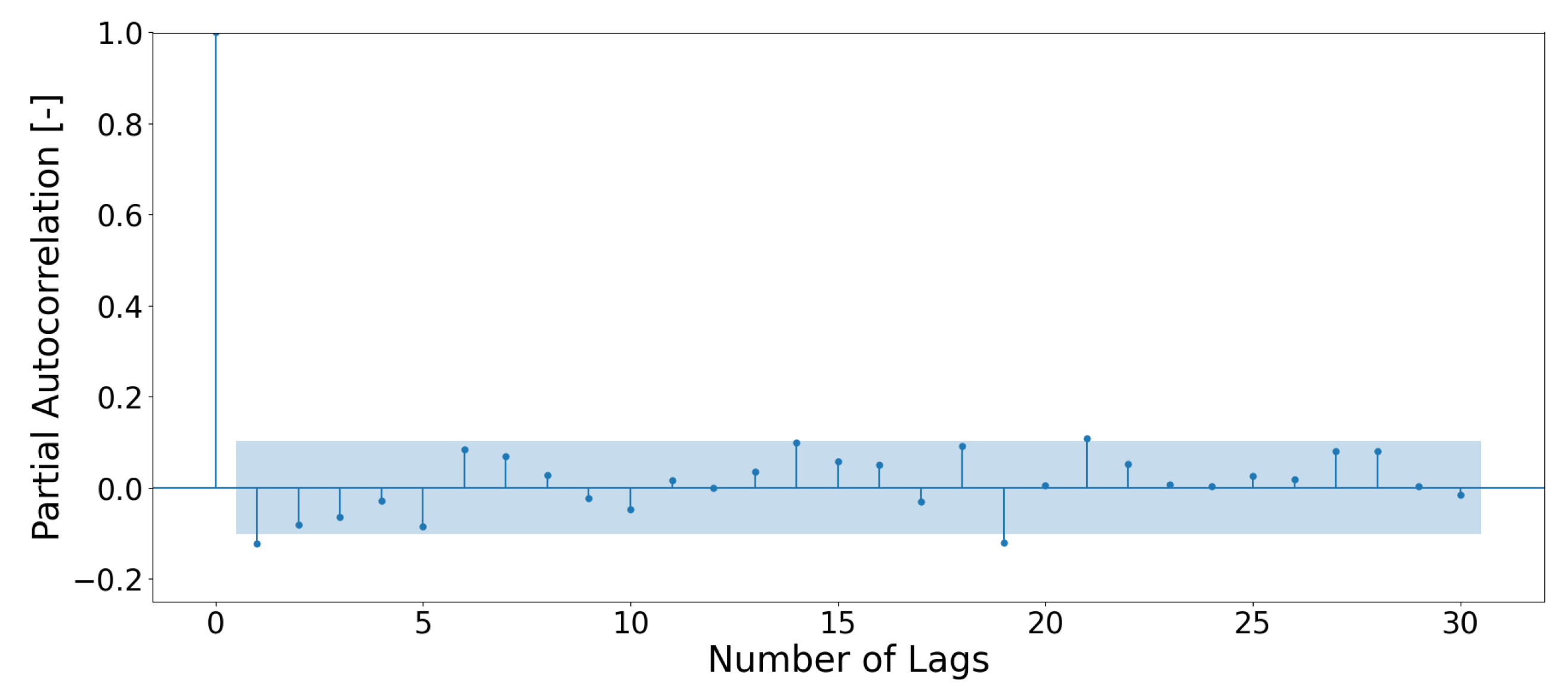
46]. Under such circumstances, the precision of the forecast is at its peak and further refinement is not possible, regardless of additional efforts. Since the partial autocorrelation is the correlation between a time series and its lagged version, excluding the influence of intervening lags, it can be used to determine temporal dependencies in the error time series.
Figure 15 illustrates this analysis by applying model M6 to forecast an exemplary RECTS for the year 2019 and using the 12:00 values of the error time series. It is observed that only the partial correlation at lag 0 is significant, indicating a strong self-correlation without temporal dependencies. This measurement can be used to test for white noise in the error time series, indicating no remaining information.
4.2. Experiment II.
This experiment uses the best model setting, M6 (
Table 5,
Section 4.1), trains a single forecast model for each REC using training data from the year 2018 and applies each one to the test data from the year 2019. Since forecast models are usually trained on single client without using auxiliary information like
, this procedure can be seen as a very good baseline for comparison. In particular, this analysis can determine the impact that including
and various RECs in the model input data has on forecast accuracy, specifically in terms of non-stationary and discontinuous time series. The results in
Table 8 show that forecast model performance greatly benefits from using
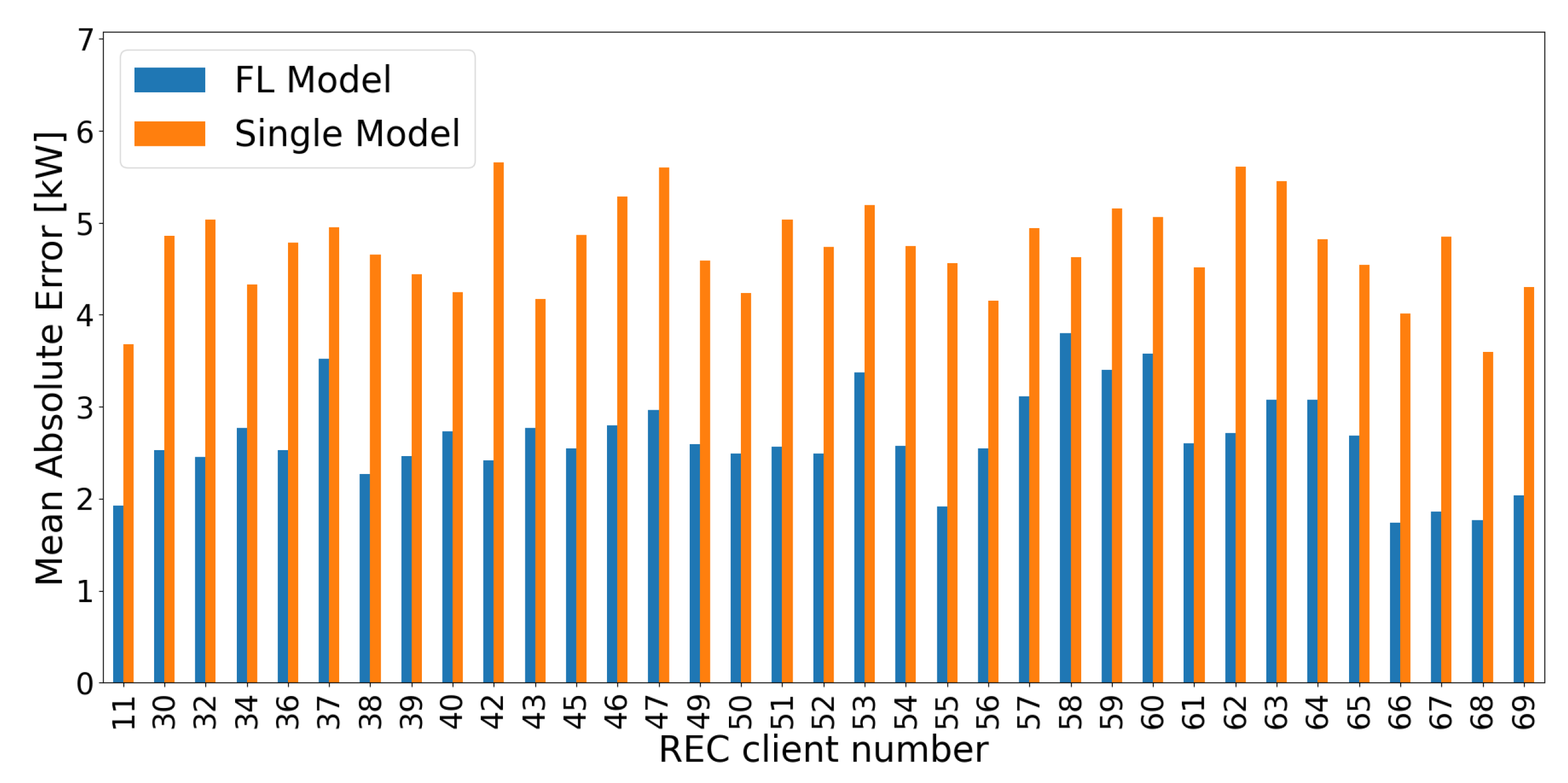
and a big amount of data during model training (federated learned forecast model - FL Model), while neglecting this leads to a significantly larger forecast error (single time series forecast model - Single Model). Moreover,
Figure 16 illustrates the distribution of MAE over multiple RECs with large member sizes for both, FL Model and Single Model. Regarding that training and test data are highly non-iid, only the FL Model is particularly capable of handling this circumstance. The reason for this is that the Single Model severely overfits to seasonality by considering doy in the model input data without taking the effect of
into account. This evaluation demonstrates the importance of model input data and the quantity of training data, and illustrates the capability of our framework to aggregate knowledge from different clients to improve forecast accuracy of RECTS.
4.3. Experiment III
After
Section 4.2 demonstrates bad forecast performances using Single Model, this experiment includes
as auxiliary information in the model input data to determin if it can benefit from it. Compared to
Table 8 and
Table 9 does not confirm this assumption, as the forecast error, in terms of MAE, increases from
to
.
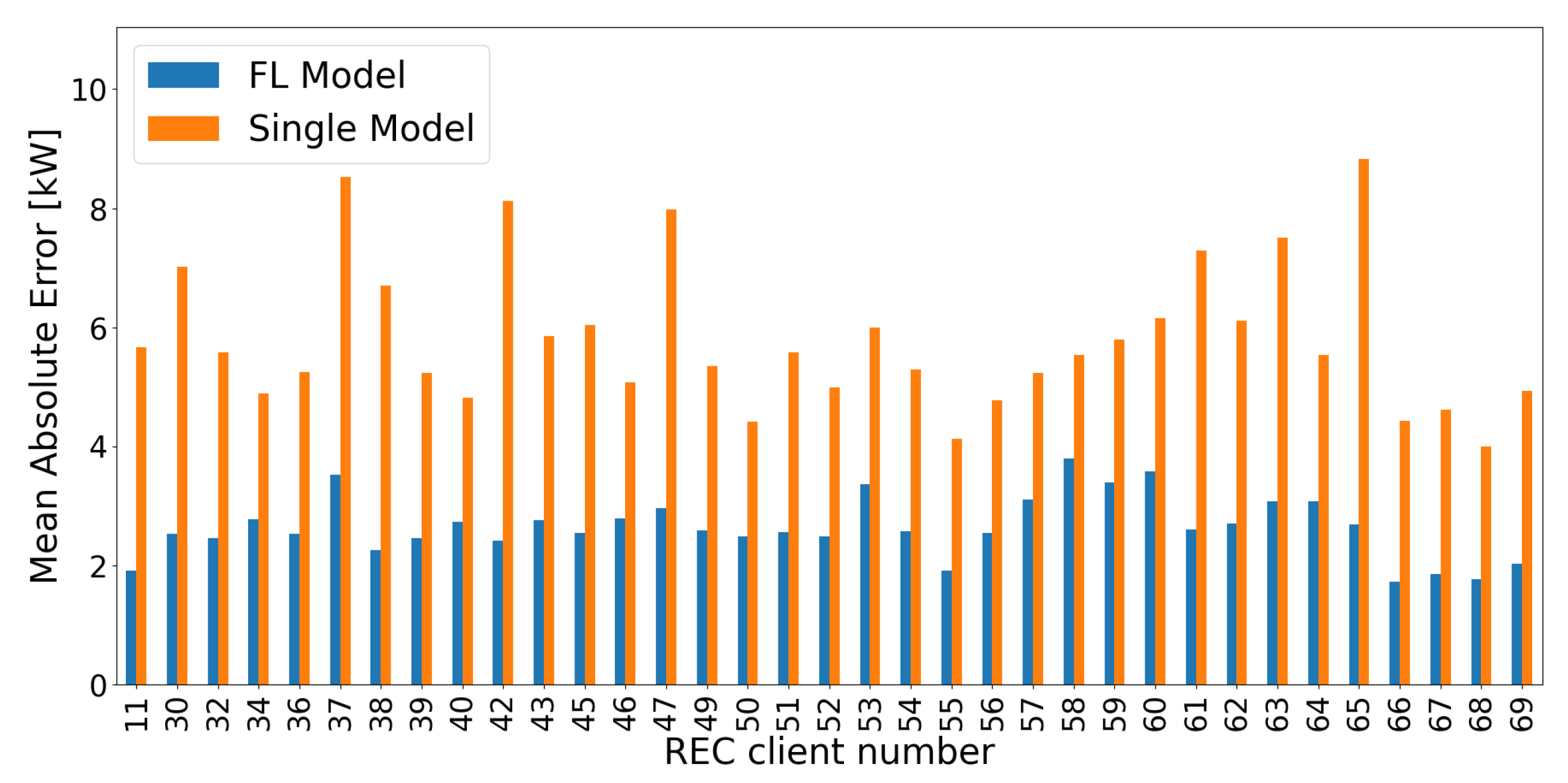
Figure 17 visually demonstrates this measurement, indicating a higher magnitude and higher variability of forecast errors. While the Single Model without
strongly overfit to the seasonality within the training dataset, the one considering
attemps to handle both, seasonality with regards to
. Since this further increases the complexity of data processing within the forecast model without providing a variety of samples for specific seasonalities and
, forecast accuracy even worsens. A reason for this is the dynamic evolution of
(
Section 2.2), whose impact on electricity consumption has not been adequately learned in model training due to a lack of data variety. This evaluation further shows that training a forecast model for each individual RECTS, whether using
or not, is unable to extract domain-invariant features as well as cross-domain behaviors in the context of non-stationary and discontinuous time series. Consequently, both Single Models are not transferable to unseen data. These results confirm that aggregating and extracting relational knowledge from a vast array of diverse data sources is essential to improve forecast accuracy of RECTS.
4.4. Experiment IV.
While
Section 4.2 and
Section 4.3 aim to compare forecast models trained on single data sources with those trained on multiple sources, Experiment IV evaluates forecast accuracies of a centrally learned forecast model (CL Model) against the best FL Model M6 (
Section 4.1) using identical data samples. In this case, the CL Model neglects
to obtain a baseline accuracy measurement for a forecast model, following common ARIX process equations.
Table 10 shows a strong improvement compared to Single Models (
Table 8 and
Table 9), but it still does not perform as well as the best FL Model M6 (
Section 4.1). Although FL Model is trained in a federated manner, it outperforms CL Model by over 18% in terms of MAE. This strongly suggests the usage of auxiliary data to forecast non-stationary and discontinuous RECTS -
Figure 18 demonstrates this behavior for every REC. This evaluation once again shows that FL Model can extract domain-invariant features and cross-domain behaviors by utilizing
, resulting in higher forecast accuracies compared to conventional forecast models.
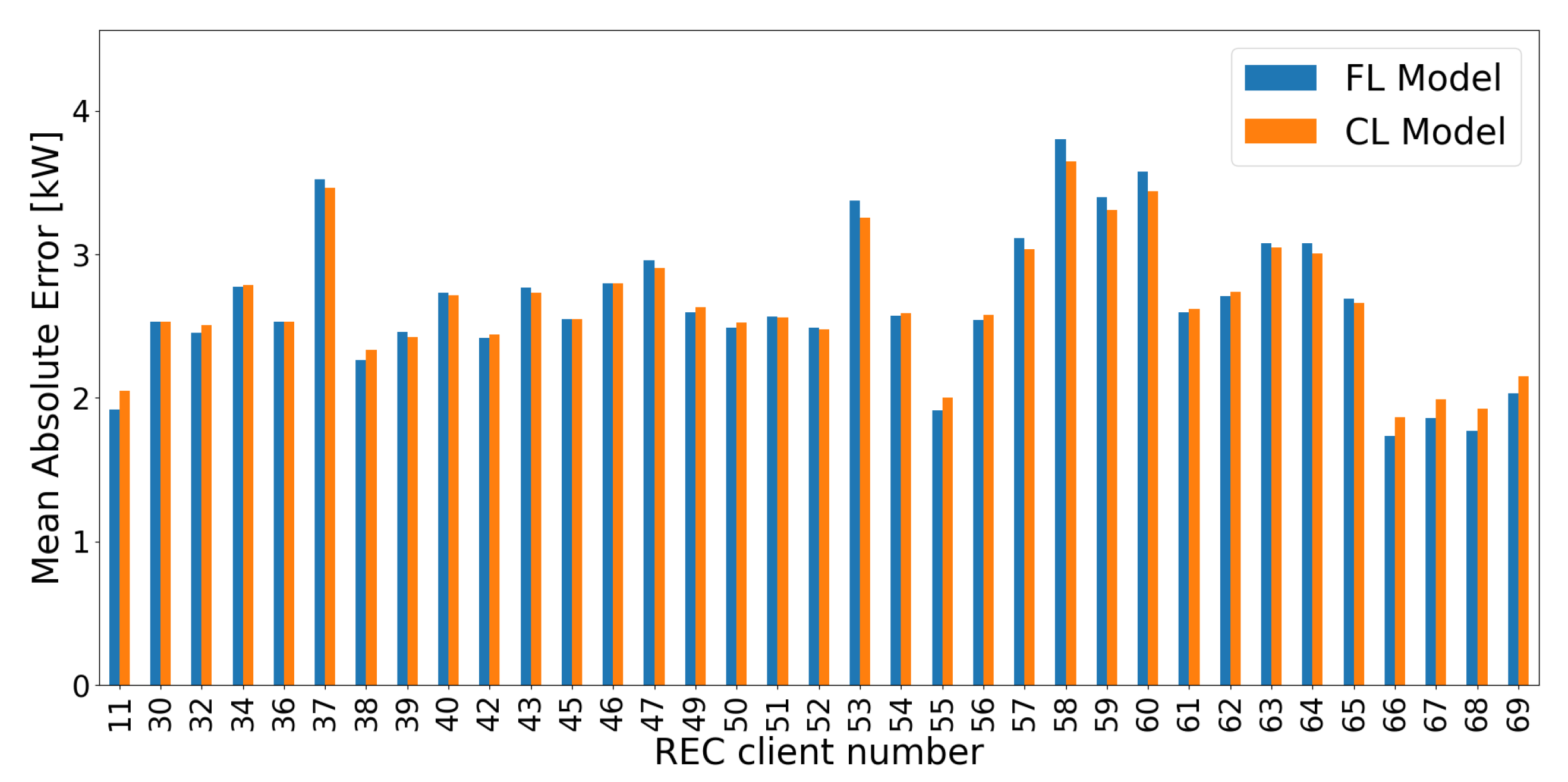
4.5. Experiment V.
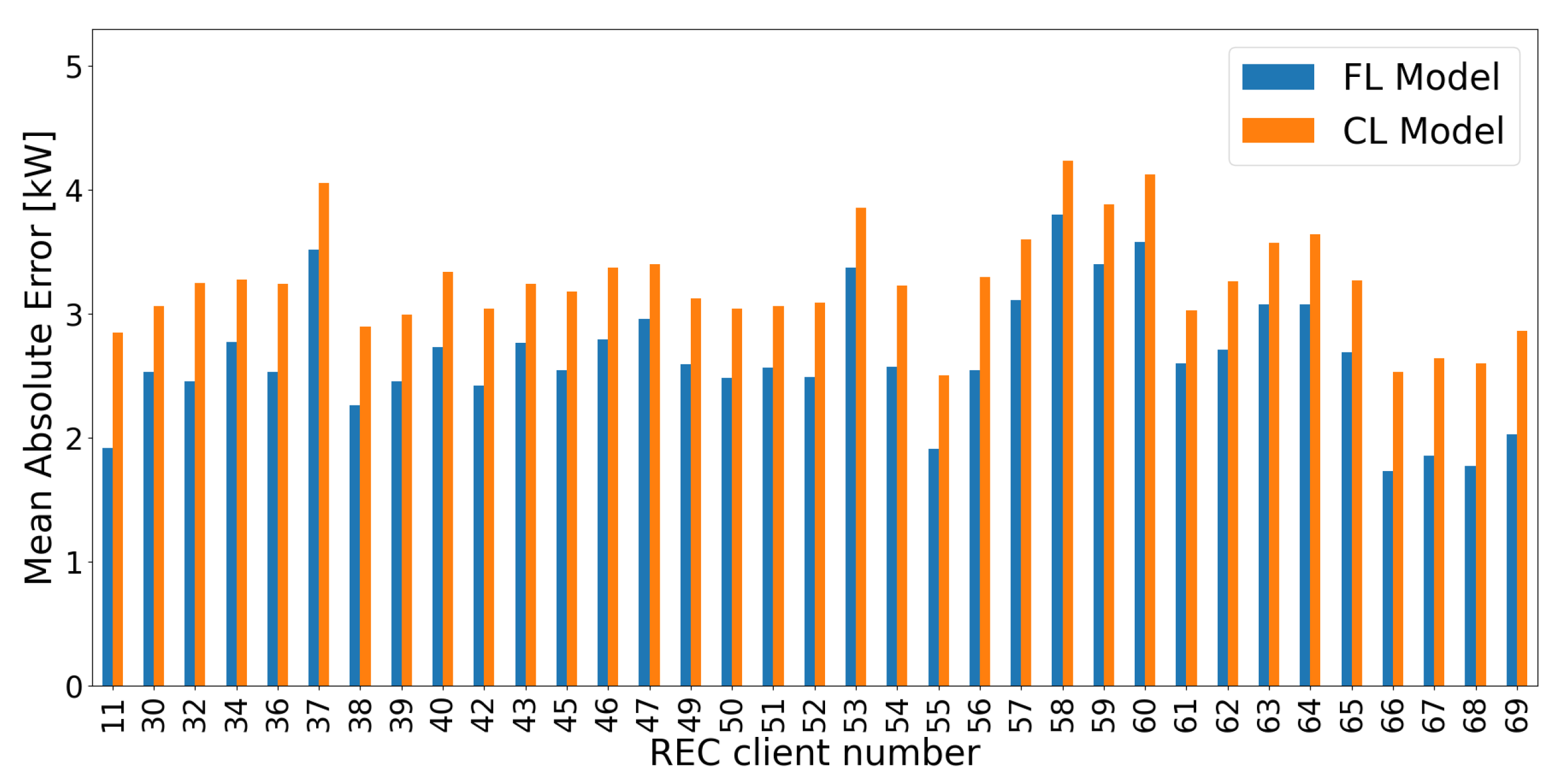
This section is intended to compare CL Model with FL Model using same training and testing samples, as well as same settings outlined in
Section 4.1. While
Table 11 shows slightly better results for FL Model,
Figure 19 illustrates no significant differences in error measurements. These results strongly prove the capability of our framework to forecast non-stationary and discontinous RECTS, when training a forecast model by applying FL. Moreover, it is able to extract domain-invariant features and cross-domain behaviors as good as a central learned model.
5. Discussion
This work introduces the European energy market, with a particular emphasis on dynamic portfolios of RECs, which have the potential to introduce new business models, enhance energy efficiency, and reduce electricity costs for their members. Besides fostering energy sharing (tenant electricity, electric vehicle charging, etc.), dynamic portfolios also contain risks concerning energy management tasks, e.g., forecasting energy demand or optimizing the energy system including demand side management, which could lead to financial losses, stress on the grid, operational inefficiencies, and member dissatisfaction. The goal of this work is to develop a forecast framework that overcomes non-stationary, discontinuous, and non-iid time series.
Since no real data is available, we synthesize RECTS by initially creating numerous district time series with diverse characteristics and subsequently aggregating them time-dependently. Given only this type of data, we can only simulate the forecasting of RECTS approximately. Various analyses confirm that the generated time series are non-stationary, discontinuous, and non-iid, as these attributes are prerequisites of the research question. Daily portfolio changes may appear extreme, but they can occur if there is a company whose business model involves automatically optimizing portfolios based on the day of the week, accounting for varying patterns of electricity consumption and generation.
To create model input arrays, we refer closely to ARIX time series processing equations, omitting the differencing filter, as neural networks are capable of automatically extracting this feature. Since the composition of residents in RECs might change daily, we divide these arrays into past, present, and future ones. Thereby, we clearly describe the engineering of calendar data to include temporal dependencies of RECTS. To determine the effect of residents composition on RECTS characteristics, we assume that we possess this information for all RECs and days. While such information does not actually exist, we must first label each member time series within a REC by using a sophisticated classification algorithm.
We then develop a forecasting model based on a FNN architecture with three input layers, each taking into account a separate input array representing a specific time interval within the time series process. As each layer extracts latent features across various time horizons, the forecasting model is capable of handling dynamic portfolios. As our primary objective is to analyze the feasibility of a forecasting model trained using FL, we omit considerations of other neural network architectures, such as sequence-to-sequence networks or temporal convolutional networks which might result in better forecast accuracies. Furthermore, we omit hyperparameter optimization regarding the activation function, the number of neurons, and the number of hidden layers to identify optimal settings.
To train a forecasting model across multiple clients with FL, we employ Federated Averaging exclusively for updating model weights, and use stochastic gradient descent for local model training. Additionally, we apply only one training epoch on each client and experiment with various configurations regarding data sharing, batch size, and learning rate to mitigate weight divergence issues. In contrast, we did not consider techniques such as FedProx [
47] and FedDyn [
48] that involve the regularization of model weight updates, learning rate degradation [
48,
49], layer-wise training [
50], and a varying quantity of training data samples [
49]. Since model convergence strongly depends on the interaction between sample size, batch size, and learning rate, this issue was be analyzed and by a more in-depth optimization, there could be significant potential for improvement in model convergence and performance.
Additionally, we perform multiple training sessions of the forecasting model using FL, taking into account various configurations related to the number of shared time series, the learning rate, and the batch size in order to determine the best setting. This one is subsequently applied in similar experiments to demonstrate the effectiveness of our framework, showing that the FL Model and the CL Model have nearly identical performance. Hence, our framework is capable of aggregating knowledge from multiple clients, learning domain-invariant features, and extracting cross-domain behaviors through the application of FL. Moreover, it is transferable to new unseen data. Nevertheless, more sensitivity studies on hyperparameter tuning must be conducted, e.g., testing the required quantity of RECTS to extract the relational knowledge necessary to cause failure, and the application in a real-world scenario should be analyzed. Since the number of RECs could potentially increase significantly, there could be advantages in using FL regarding training time.
6. Conclusion
This work examines various forecasting strategies to handle non-stationary, discontinous, and non-iid time series across distributed clients. After generating a sufficient number of electricity consumption time series for Renewable Energy Communities with dynamic customer portfolios, several data pre-processing methods are tested in conjunction with differently configured forecast model training on either single or multiple time series. Our novel forecasting framework demonstrates the effectiveness of data sharing to learn domain-invariant features and cross-domain behaviors by aggregating knowledge from various data sources using federated learning. Besides ensuring transferability to unseen data, the forecast accuracy is nearly identical to that of a centrally trained forecasting model. Our novel framework possesses the potential to revolutionize electricity demand forecasting for decentralized energy systems by identifying effective training settings. Future work will investigate the performance of more complex forecasting model architectures, as well as the development of appropriate classification algorithms to generate time series labels that can be used as auxiliary information in the model’s input data.
Author Contributions
Conceptualization, L.R.; Methodology, L.R.; Validation, L.R.; Formal analysis, S.L.; Writing—original draft, L.R.; Writing—review & editing, L.R. and S.L.; Visualization, L.R.; Supervision, S.L. and P.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Federal Ministry for Economic Affairs and Climate Action in Germany grant number 01MK20013A
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Dickey Fuller Test For All RECTS
Overall, there are 51 strong non-stationary, 8 medium non-stationary, 6 weak non-stationary, and 5 stationary RECTS (
Table A1).
Table A1.
Dickey fuller test statistics for all RECTS (eliminating seasonality, periodicity and trend): (i)

, (ii)
, (ii) medium non-stationary, (iv)

Table A1.
Dickey fuller test statistics for all RECTS (eliminating seasonality, periodicity and trend): (i)

, (ii)
, (ii) medium non-stationary, (iv)

|
RECTS |
Critical Value |
Pvalue |
1% |
5% |
10% |
|
0 |
-2.61 |
0.09 |
-3.44 |
-2.87 |
-2.57 |
|
1 |
-1.83 |
0.37 |
-3.44 |
-2.87 |
-2.57 |
|
2 |
-2.13 |
0.23 |
-3.44 |
-2.87 |
-2.57 |
|
3 |
-1.93 |
0.32 |
-3.44 |
-2.87 |
-2.57 |
|
4 |
-2.63 |
0.09 |
-3.44 |
-2.87 |
-2.57 |
|
5 |
-2.75 |
0.07 |
-3.44 |
-2.87 |
-2.57 |
|
6 |
-2.15 |
0.22 |
-3.44 |
-2.87 |
-2.57 |
|
7 |
-4.01 |
0.0 |
-3.44 |
-2.87 |
-2.57 |
|
8 |
-3.58 |
0.01 |
-3.44 |
-2.87 |
-2.57 |
|
9 |
-2.71 |
0.07 |
-3.44 |
-2.87 |
-2.57 |
|
10 |
-3.16 |
0.02 |
-3.44 |
-2.87 |
-2.57 |
|
11 |
-3.83 |
0.0 |
-3.44 |
-2.87 |
-2.57 |
|
12 |
-3.46 |
0.01 |
-3.44 |
-2.87 |
-2.57 |
|
13 |
-2.18 |
0.21 |
-3.44 |
-2.87 |
-2.57 |
|
14 |
-1.92 |
0.32 |
-3.44 |
-2.87 |
-2.57 |
|
15 |
-2.51 |
0.11 |
-3.44 |
-2.87 |
-2.57 |
|
16 |
-2.43 |
0.13 |
-3.44 |
-2.87 |
-2.57 |
|
17 |
-2.39 |
0.14 |
-3.44 |
-2.87 |
-2.57 |
|
18 |
-2.96 |
0.04 |
-3.44 |
-2.87 |
-2.57 |
|
19 |
-2.78 |
0.06 |
-3.44 |
-2.87 |
-2.57 |
|
20 |
-2.32 |
0.17 |
-3.44 |
-2.87 |
-2.57 |
|
21 |
-2.11 |
0.24 |
-3.44 |
-2.87 |
-2.57 |
|
22 |
-2.75 |
0.07 |
-3.44 |
-2.87 |
-2.57 |
|
23 |
-2.94 |
0.04 |
-3.44 |
-2.87 |
-2.57 |
|
24 |
-2.19 |
0.21 |
-3.44 |
-2.87 |
-2.57 |
|
25 |
-2.08 |
0.25 |
-3.44 |
-2.87 |
-2.57 |
|
26 |
-2.96 |
0.04 |
-3.44 |
-2.87 |
-2.57 |
|
27 |
-1.91 |
0.33 |
-3.44 |
-2.87 |
-2.57 |
|
28 |
-2.19 |
0.21 |
-3.44 |
-2.87 |
-2.57 |
|
29 |
-2.04 |
0.27 |
-3.44 |
-2.87 |
-2.57 |
|
30 |
-1.87 |
0.34 |
-3.44 |
-2.87 |
-2.57 |
|
31 |
-2.11 |
0.24 |
-3.44 |
-2.87 |
-2.57 |
|
32 |
-3.01 |
0.03 |
-3.44 |
-2.87 |
-2.57 |
|
33 |
-2.48 |
0.12 |
-3.44 |
-2.87 |
-2.57 |
|
34 |
-1.79 |
0.38 |
-3.44 |
-2.87 |
-2.57 |
|
35 |
-2.09 |
0.25 |
-3.44 |
-2.87 |
-2.57 |
|
36 |
-1.61 |
0.48 |
-3.44 |
-2.87 |
-2.57 |
|
37 |
-1.77 |
0.39 |
-3.44 |
-2.87 |
-2.57 |
|
38 |
-1.77 |
0.4 |
-3.44 |
-2.87 |
-2.57 |
|
39 |
-2.15 |
0.23 |
-3.44 |
-2.87 |
-2.57 |
|
40 |
-1.47 |
0.55 |
-3.44 |
-2.87 |
-2.57 |
|
41 |
-2.11 |
0.24 |
-3.44 |
-2.87 |
-2.57 |
|
42 |
-1.43 |
0.57 |
-3.44 |
-2.87 |
-2.57 |
|
43 |
-1.87 |
0.34 |
-3.44 |
-2.87 |
-2.57 |
|
44 |
-1.91 |
0.33 |
-3.44 |
-2.87 |
-2.57 |
|
45 |
-2.01 |
0.28 |
-3.44 |
-2.87 |
-2.57 |
|
46 |
-2.32 |
0.16 |
-3.44 |
-2.87 |
-2.57 |
|
47 |
-1.77 |
0.4 |
-3.44 |
-2.87 |
-2.57 |
|
48 |
-1.69 |
0.43 |
-3.44 |
-2.87 |
-2.57 |
|
49 |
-2.42 |
0.14 |
-3.44 |
-2.87 |
-2.57 |
|
50 |
-2.02 |
0.28 |
-3.44 |
-2.87 |
-2.57 |
|
51 |
-2.7 |
0.07 |
-3.44 |
-2.87 |
-2.57 |
|
52 |
-2.65 |
0.08 |
-3.44 |
-2.87 |
-2.57 |
|
53 |
-2.41 |
0.14 |
-3.44 |
-2.87 |
-2.57 |
|
54 |
-1.92 |
0.32 |
-3.44 |
-2.87 |
-2.57 |
|
55 |
-1.63 |
0.47 |
-3.44 |
-2.87 |
-2.57 |
|
56 |
-1.88 |
0.34 |
-3.44 |
-2.87 |
-2.57 |
|
57 |
-2.35 |
0.16 |
-3.44 |
-2.87 |
-2.57 |
|
58 |
-2.17 |
0.22 |
-3.44 |
-2.87 |
-2.57 |
|
59 |
-1.88 |
0.34 |
-3.44 |
-2.87 |
-2.57 |
|
60 |
-0.85 |
0.81 |
-3.44 |
-2.87 |
-2.57 |
|
61 |
-1.61 |
0.48 |
-3.44 |
-2.87 |
-2.57 |
|
62 |
-2.08 |
0.25 |
-3.44 |
-2.87 |
-2.57 |
|
63 |
-1.87 |
0.35 |
-3.44 |
-2.87 |
-2.57 |
|
64 |
-1.22 |
0.66 |
-3.44 |
-2.87 |
-2.57 |
|
65 |
-2.13 |
0.23 |
-3.44 |
-2.87 |
-2.57 |
|
66 |
-2.14 |
0.23 |
-3.44 |
-2.87 |
-2.57 |
|
67 |
-2.2 |
0.2 |
-3.44 |
-2.87 |
-2.57 |
|
68 |
-2.88 |
0.05 |
-3.44 |
-2.87 |
-2.57 |
|
69 |
-3.49 |
0.01 |
-3.44 |
-2.87 |
-2.57 |
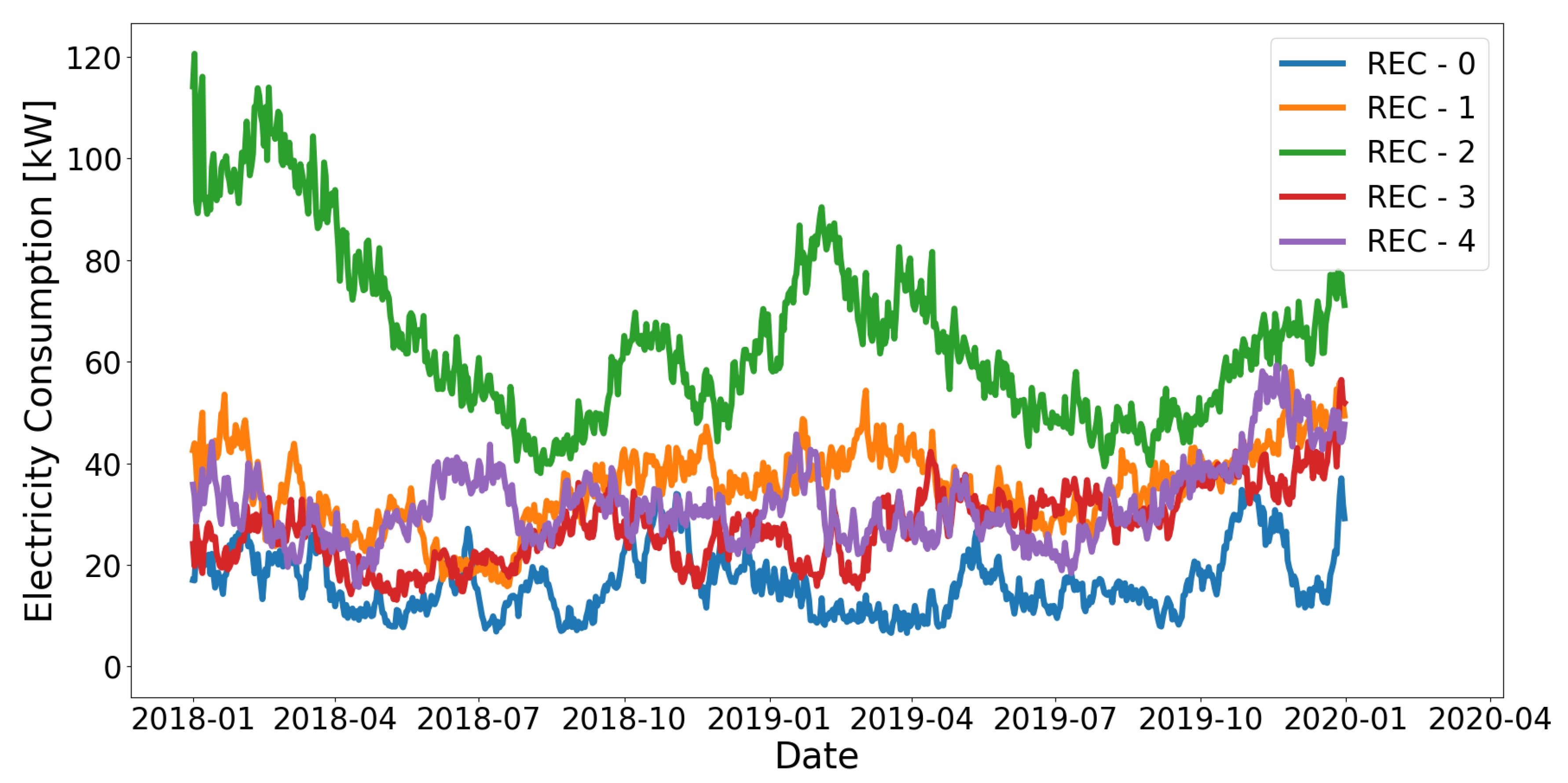
Appendix B. Example Time Series Of Renewable Energy Communities
Figure A1.
Exemplary RECTS showing non-stationarities.
Figure A1.
Exemplary RECTS showing non-stationarities.
Appendix C. Average Member Number Of Renewable Energy Communities
Figure A2.
Average size of individual REC members.
Figure A2.
Average size of individual REC members.
Appendix D. Error Metrics
where represents measurements and represents forecasts
Appendix E. Abbreviations
| ADF |
Augmented Dickey-Fuller test |
| AR |
AutoRegressive |
| ARIX |
AutoRegressive Integrated with eXogenous variables |
| bs |
Batch size |
| CL Model |
Centrally learned forecast model |
| DECTS |
District electricity consumption time series |
| DEMS |
District energy management systems |
| F |
Future part within ARIMA |
| FL |
Federated learning |
| FL Model |
Federated learned forecast model |
| FNN |
Feedforward neural network |
| I |
Integrated part within ARIMA |
| IQR |
Interqurtile range |
| lr |
Learning rate |
| MAE |
Mean absolute error |
| MAPE |
Mean absolute percentage error |
| ML |
Machine learning |
| non-iid |
Non-identical and independently distributed |
| Q1 |
First quartile |
| Q2 |
Second quartile |
| Q3 |
Third quartile |
| REC |
Renewable Energy Communities |
| RECTS |
REC time series |
| REC-ECF |
REC energy consumption forecasting algorithms |
| REC-EMS |
REC energy management systems |
| RED II |
Renewable Energy Directive |
| Single Model |
Single time series forecast model |
| sts |
Shared time series to each client |
References
- https://www.ipcc.ch/sr15/chapter/chapter-1/. visited on 2024-02-07.
- https://www.europarl.europa.eu/factsheets/de/sheet/45/energiebinnenmarkt. visited on 2023-01-05.
- https://eur-lex.europa.eu/legal-content/DE/TXT/PDF/?uri=CELEX:02018L2001-20181221&from=EN. visited on 2023-01-05.
- https://www.bmwk.de/Redaktion/DE/Publikationen/Energie/7-energieforschungsprogramm-der-bundesregierung.pdf?__blob=publicationFile&v=4. visited on 2023-01-05.
- Sauerbrey, J.; Bender, T.; Flemming, S.; Martin, A.; Naumann, S.; Warweg, O. Towards intelligent energy management in energy communities: Introducing the district energy manager and an IT reference architecture for district energy management systems. Energy Reports 2024, 11, 2255–2265. [Google Scholar] [CrossRef]
- Abrahamse, W.; Steg, L. Factors Related to Household Energy Use and Intention to Reduce It: The Role of Psychological and Socio-Demographic Variables. Human Ecology Review 2011, 18, 30–40. [Google Scholar]
- Flemming, S.; Bender, T.; Surmann, A.; Pelka, S.; Martin, A.; Kuehnbach, M. Vor-Ort-Systeme als flexibler Baustein im Energiesystem ? Eine cross-sektorale Potenzialanalyse 2023. [CrossRef]
- Beucker, S.; Bergesen, J.; Gibon, T. Building Energy Management Systems: Global Potentials and Environmental Implications of Deployment. Journal of Industrial Ecology 2015, 20, n/a–n/a. [Google Scholar] [CrossRef]
- https://wirtschaftslexikon.gabler.de/definition/energiemanagementsystem-53996. visited on 2023-01-06.
- Richter, L.; Lehna, M.; Marchand, S.; Scholz, C.; Dreher, A.; Klaiber, S.; Lenk, S. Artificial Intelligence for Electricity Supply Chain automation. Renewable and Sustainable Energy Reviews 2022, 163, 112459. [Google Scholar] [CrossRef]
- https://www.gesetze-im-internet.de/enwg_2005/__41a.html. visited on 2024-02-07.
- Klaiber, S. Analyse, Identifikation und Prognose preisbeeinflusster elektrischer Lastzeitreihen. PhD thesis, Technische Universität Ilmenau, 2020.
- https://eur-lex.europa.eu/legal-content/en/TXT/?uri=CELEX:32019L0944. visited on 2024-02-07.
- Hyndman, R.; Athanasopoulos, G. Forecasting: Principles and Practice, 2nd ed.; OTexts: Australia, 2018. [Google Scholar]
- Richter, L.; Bender, T.; Lenk, S.; Bretschneider, P. Generating Synthetic Electricity Load Time Series at District Scale Using Probabilistic Forecasts. Energies 2024, 17. [Google Scholar] [CrossRef]
- Han, Z.; Zhao, J.; Leung, H.; Ma, K.F.; Wang, W. A Review of Deep Learning Models for Time Series Prediction. IEEE Sensors Journal 2021, 21, 7833–7848. [Google Scholar] [CrossRef]
- Runge, J.; Zmeureanu, R. A Review of Deep Learning Techniques for Forecasting Energy Use in Buildings. Energies 2021, 14, 608. [Google Scholar] [CrossRef]
- Bot, K.; Ruano, A.; Ruano, M. , Forecasting Electricity Consumption in Residential Buildings for Home Energy Management Systems; 2020; pp. 313–326. [CrossRef]
- Wang, W.; Hussain, F.; Lian, Z.; Yin, Z.; Gadekallu, T.; Pham, Q.V.; Dev, K.; Su, C. Secure-Enhanced Federated Learning for AI-Empowered Electric Vehicle Energy Prediction. IEEE Consumer Electronics Magazine 2021. [Google Scholar] [CrossRef]
- Lu, Y.; Tian, Z.; Zhou, R.; Liu, W. A general transfer learning-based framework for thermal load prediction in regional energy system. Energy 2021, 217, 119322. [Google Scholar] [CrossRef]
- Suryanarayana, G.; Lago, J.; Geysen, D.; Aleksiejuk, P.; Johansson, C. Thermal load forecasting in district heating networks using deep learning and advanced feature selection methods. Energy 2018, 157. [Google Scholar] [CrossRef]
- Shirzadi, N.; Nizami, A.; Khazen, M.; Nik Bakht, M. Medium-Term Regional Electricity Load Forecasting through Machine Learning and Deep Learning. Designs 2021, 5, 27. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, X.; Shen, X.; Sun, H. A Federated Learning Framework for Smart Grids: Securing Power Traces in Collaborative Learning, 2021. [CrossRef]
- Taïk, A.; Cherkaoui, S. Electrical Load Forecasting Using Edge Computing and Federated Learning. ICC 2020 - 2020 IEEE International Conference on Communications (ICC), 2020, pp. 1–6. [CrossRef]
- Gholizadeh, N.; Musilek, P. Federated learning with hyperparameter-based clustering for electrical load forecasting. Internet of Things 2021, 17, 100470. [Google Scholar] [CrossRef]
- https://www.caci.co.uk/wp-content/uploads/2021/06/Acorn-User-Guide-2020.pdf. visited on 2024-05-16.
- Gardner, W.A.; Napolitano, A.; Paura, L. Cyclostationarity: Half a century of research. Signal Processing 2006, 86, 639–697. [Google Scholar] [CrossRef]
- Aminikhanghahi, S.; Cook, D. A Survey of Methods for Time Series Change Point Detection. Knowledge and Information Systems 2017, 51. [Google Scholar] [CrossRef]
- Schwertman, N.C.; Owens, M.A.; Adnan, R. A simple more general boxplot method for identifying outliers. Computational Statistics And Data Analysis 2004, 47, 165–174. [Google Scholar] [CrossRef]
- Pinheiro, M.; Madeira, S.; Francisco, A. Short-term electricity load forecasting - A systematic approach from system level to secondary substations. Applied Energy 2023, 332, 120493. [Google Scholar] [CrossRef]
- Gasparin, A.; Lukovic, S.; Alippi, C. Deep Learning for Time Series Forecasting: The Electric Load Case, 2019; arXiv:cs.LG/1907.09207].
- Tunnicliffe Wilson, G. Time Series Analysis: Forecasting and Control,5th Edition, by George E. P. Box, Gwilym M. Jenkins, Gregory C. Reinsel and Greta M. Ljung, 2015. Published by John Wiley and Sons Inc., Hoboken, New Jersey, pp. 712. ISBN: 978-1-118-67502-1. Journal of Time Series Analysis 2016, 37, n/a–n/a. [Google Scholar] [CrossRef]
- Shi, Y.; Ying, X.; Yang, J. Deep Unsupervised Domain Adaptation with Time Series Sensor Data: A Survey. Sensors 2022, 22. [Google Scholar] [CrossRef]
- Purushotham, S.; Carvalho, W.; Nilanon, T.; Liu, Y. Variational Recurrent Adversarial Deep Domain Adaptation. 2019.
- Arik, S.O.; Yoder, N.C.; Pfister, T. Self-Adaptive Forecasting for Improved Deep Learning on Non-Stationary Time-Series, 2022; arXiv:cs.LG/2202.02403].
- https://transparency.entsoe.eu. visited on 2023-11-28.
- McMahan, H.B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-Efficient Learning of Deep Networks from Decentralized Data, 2023; arXiv:cs.LG/1602.05629].
- Shi, Y.; Xu, X. Deep Federated Adaptation: An Adaptative Residential Load Forecasting Approach with Federated Learning. Sensors 2022, 22, 3264. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, N.; Hug, G. Personalized Federated Learning for Individual Consumer Load Forecasting. CSEE Journal of Power and Energy Systems 2023, 9, 326–330. [Google Scholar] [CrossRef]
- Chen, J.; Gao, T.; Si, R.; Dai, Y.; Jiang, Y.; Zhang, J. Residential Short Term Load Forecasting Based on Federated Learning. 2022 IEEE 2nd International Conference on Digital Twins and Parallel Intelligence (DTPI), 2022, pp. 1–6. [CrossRef]
- Savi, M.; Olivadese, F. Short-Term Energy Consumption Forecasting at the Edge: A Federated Learning Approach. IEEE Access 2021, 9, 1–21. [Google Scholar] [CrossRef]
- Zhu, H.; Xu, J.; Liu, S.; Jin, Y. Federated Learning on Non-IID Data: A Survey, 2021; arXiv:cs.LG/2106.06843].
- Zhao, Y.; Li, M.; Lai, L.; Suda, N.; Civin, D.; Chandra, V. Federated Learning with Non-IID Data 2018. [CrossRef]
- Keskar, N.S.; Mudigere, D.; Nocedal, J.; Smelyanskiy, M.; Tang, P.T.P. On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima, 2017; arXiv:cs.LG/1609.04836].
- https://www.tensorflow.org. visited on 2024-03-13.
- Schlittgen, R.; Streitberg, B.H. Zeitreihenanalyse; Oldenbourg Wissenschaftsverlag, 2001. [CrossRef]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated Optimization in Heterogeneous Networks, 2020; arXiv:cs.LG/1812.06127].
- Acar, D.A.E.; Zhao, Y.; Navarro, R.M.; Mattina, M.; Whatmough, P.N.; Saligrama, V. Federated Learning Based on Dynamic Regularization, 2021; arXiv:cs.LG/2111.04263].
- Li, X.; Huang, K.; Yang, W.; Wang, S.; Zhang, Z. On the Convergence of FedAvg on Non-IID Data, 2020; arXiv:stat.ML/1907.02189].
- Charles, Z.; Garrett, Z.; Huo, Z.; Shmulyian, S.; Smith, V. On Large-Cohort Training for Federated Learning, 2021; arXiv:cs.LG/2106.07820].
Figure 1.
Time-variant portfolios , , , , , of RECs.
Figure 1.
Time-variant portfolios , , , , , of RECs.
Figure 2.
Based on the research objective, non-stationary as well as discontinous time series of REC are firstly synthesized and subsequently validated for compliance with the required characteristics. Secondly, the process of electricity consumption time series, the equations related to data pre-processing, and the detailed description of the forecast model architecture are provided. With this in mind, the federated learning algorithm and research experiments are then presented. Following their execution, the results are shown and discussed in the final section to draw conclusions for future research.
Figure 2.
Based on the research objective, non-stationary as well as discontinous time series of REC are firstly synthesized and subsequently validated for compliance with the required characteristics. Secondly, the process of electricity consumption time series, the equations related to data pre-processing, and the detailed description of the forecast model architecture are provided. With this in mind, the federated learning algorithm and research experiments are then presented. Following their execution, the results are shown and discussed in the final section to draw conclusions for future research.
Figure 3.
Different time series characteristics: (a) autoregression illustrated by showing a time series to its lagged version, (b) seasonal time series with recurrent patterns, (c) periodic time series with different recurrent patterns, (d) discontinous time series with bounds in observations, (e) showing stochasticity referring to the time series forecast error, (f) seasonal time series with linear trend, (g) time series with linear and seasonal trend
Figure 3.
Different time series characteristics: (a) autoregression illustrated by showing a time series to its lagged version, (b) seasonal time series with recurrent patterns, (c) periodic time series with different recurrent patterns, (d) discontinous time series with bounds in observations, (e) showing stochasticity referring to the time series forecast error, (f) seasonal time series with linear trend, (g) time series with linear and seasonal trend
Figure 4.
Illustrating two dimensional principal components of , clustered with K-means and number of clusters . Each color represents subgroups belonging to one cluster, while thick points depict the central subgroups within each cluster.
Figure 4.
Illustrating two dimensional principal components of , clustered with K-means and number of clusters . Each color represents subgroups belonging to one cluster, while thick points depict the central subgroups within each cluster.
Figure 5.
Resulting time series after removing seasonality, periodicity and trend at 12:00.
Figure 5.
Resulting time series after removing seasonality, periodicity and trend at 12:00.
Figure 6.
Boxplot showing distributions of differential time series for every week of year in the dataset.
Figure 6.
Boxplot showing distributions of differential time series for every week of year in the dataset.
Figure 7.
Heatmap of correlation matrix using RECTS as input.
Figure 7.
Heatmap of correlation matrix using RECTS as input.
Figure 8.
Electricity load time series of 50Hertz [
36] showing exemplary temporal shifts (
: 7 days,
: 7 days, and
: 3 days) used in the itegrated part I (Eq. (
6)).
Figure 8.
Electricity load time series of 50Hertz [
36] showing exemplary temporal shifts (
: 7 days,
: 7 days, and
: 3 days) used in the itegrated part I (Eq. (
6)).
Figure 9.
Principle neural network architecture with three input-layers , , to handle past , present and future data separately and to fit future values of the target variable .
Figure 9.
Principle neural network architecture with three input-layers , , to handle past , present and future data separately and to fit future values of the target variable .
Figure 10.
The evolution of model weights across local training epochs
,
,
,
, under both independent and identically distributed (iid) and non-iid data scenarios, demonstrates diverging weight patterns (inspired by [
43]).
Figure 10.
The evolution of model weights across local training epochs
,
,
,
, under both independent and identically distributed (iid) and non-iid data scenarios, demonstrates diverging weight patterns (inspired by [
43]).
Figure 11.
Approaches to data sharing include: (a) not sharing any time series, (b) sharing one time series, and (c) sharing two time series.
Figure 11.
Approaches to data sharing include: (a) not sharing any time series, (b) sharing one time series, and (c) sharing two time series.
Figure 12.
Illustration of the process of conducting various experiments: 1) Conduct various FL runs within experiment I. using different configurations concerning shared time series, batch size, and learning rate, 2) extract best configuration from experiment I. and apply it within experiments II. - V., 3) compare and evaluate results.
Figure 12.
Illustration of the process of conducting various experiments: 1) Conduct various FL runs within experiment I. using different configurations concerning shared time series, batch size, and learning rate, 2) extract best configuration from experiment I. and apply it within experiments II. - V., 3) compare and evaluate results.
Figure 13.
Mean absolute error for models M0, M1, M2, M3, M4, M5, M6, M7 applied on test data, depending on the number of federated learning epochs.
Figure 13.
Mean absolute error for models M0, M1, M2, M3, M4, M5, M6, M7 applied on test data, depending on the number of federated learning epochs.
Figure 14.
Time series forecasts for an exemplary RECTS visualized as a scatter plot (a) and a line plot (b), using the best forecast model M6.
Figure 14.
Time series forecasts for an exemplary RECTS visualized as a scatter plot (a) and a line plot (b), using the best forecast model M6.
Figure 15.
Partial autocorrelation of the error series at time 12:00 analyzed using the Python statsmodels package.
Figure 15.
Partial autocorrelation of the error series at time 12:00 analyzed using the Python statsmodels package.
Figure 16.
MAE of forecast models referred to individual RECs neglecting
(orange - Single Model) compared to the best FL model M6 (blue - FL Model) from
Section 4.1.
Figure 16.
MAE of forecast models referred to individual RECs neglecting
(orange - Single Model) compared to the best FL model M6 (blue - FL Model) from
Section 4.1.
Figure 17.
MAE of forecast models referred to individual RECs taking
into account (orange - Single Model) compared to the best FL model M6 (blue - FL Model) from
Section 4.1.
Figure 17.
MAE of forecast models referred to individual RECs taking
into account (orange - Single Model) compared to the best FL model M6 (blue - FL Model) from
Section 4.1.
Figure 18.
MAE of a centralized learned forecast model neglecting
(orange - CL Model) compared to the best FL model M6 (blue - FL Model) from
Section 4.1.
Figure 18.
MAE of a centralized learned forecast model neglecting
(orange - CL Model) compared to the best FL model M6 (blue - FL Model) from
Section 4.1.
Figure 19.
MAE of a centralized learned forecast model taking
into account (orange - CL Model) compared to the best FL model M6 (blue - FL Model) from
Section 4.1.
Figure 19.
MAE of a centralized learned forecast model taking
into account (orange - CL Model) compared to the best FL model M6 (blue - FL Model) from
Section 4.1.
Table 1.
Statistics of unfiltered and filtered datasets, with respect to DECTS of various ACORN subgroups, indicating higher diversity for the filtered case.
Table 1.
Statistics of unfiltered and filtered datasets, with respect to DECTS of various ACORN subgroups, indicating higher diversity for the filtered case.
| |
|
|
| Unfiltered 55 ACORN subgroups |
0.88 |
0.08 |
| Filtered 10 ACORN subgroups |
0.82 |
0.12 |
Table 2.
Test statistics of ADF check if RECTS is non-stationary.
Table 2.
Test statistics of ADF check if RECTS is non-stationary.
| critical value |
pvalue |
|
|
|
| -1.58 |
0.49 |
-3.44 |
-2.87 |
-2.57 |
Table 3.
Statistics of the correlation matrix for all RECTS.
Table 3.
Statistics of the correlation matrix for all RECTS.
|
|
|
|
Table 4.
Description of endogenous and exogenous variables used in past (I), present (AR) and future (F) regression equations.
Table 4.
Description of endogenous and exogenous variables used in past (I), present (AR) and future (F) regression equations.
| data type |
variable |
description |
considered in |
| target |
RECTS |
provide target states |
AR, I |
| calendar |
day of year (doy) |
models annual seasonality |
AR, I, F |
| calendar |
day of week (dow) |
models short-term periodicity |
AR, I, F |
| calendar |
daytime (dt) |
models intraday periodicity |
AR, I, F |
| weather |
temperature (T) |
models T dependencies |
AR, I, F |
| weather |
relative humidity (RH) |
models RH dependencies |
AR, I, F |
| residents composition |
|
models dependencies
on RECTS stochasticity |
AR, I, F |
Table 5.
Various forecast model parameterizations in terms of batch size, the number of shared time series to each client, and the learning rate.
Table 5.
Various forecast model parameterizations in terms of batch size, the number of shared time series to each client, and the learning rate.
| Forecast Model |
Batch Size
|
Shared Time Series
|
Learning Rate
|
| M1 |
16 |
0 |
0.0001 |
| M1 |
64 |
0 |
0.0001 |
| M2 |
16 |
2 |
0.0001 |
| M3 |
64 |
2 |
0.0001 |
| M4 |
16 |
0 |
0.001 |
| M5 |
64 |
0 |
0.001 |
| M6 |
16 |
2 |
0.001 |
| M7 |
64 |
2 |
0.001 |
Table 6.
Experiments to be conducted, evaluated, and compared to gain knowledge about effective FL settings for non-stationary, discontinous, and non-iid RECTS.
Table 6.
Experiments to be conducted, evaluated, and compared to gain knowledge about effective FL settings for non-stationary, discontinous, and non-iid RECTS.
| No. |
Objective |
Setting |
| I. |
Train FNN for all RECs regarding
using federated learning (multi RECTS).
In this study, we use REC with a small
member size to illustrate the model’s transferability
to out-of-sample data. |
15em
share RECTS to each client
use multiple batch sizes
use multiple learning rates
|
| II. |
Train FNN for each REC neglecting
(single RECTS) and compare them |
15em
|
| III. |
Train FNN for each REC providing
(single RECTS) and compare them |
15em
|
| IV. |
Train a FNN for all RECs neglecting
(multi RECTS) and compare them |
15em
|
| V. |
Train a FNN for all RECs providing
(multi RECTS) and compare them |
15em
|
Table 7.
MAE and MAPE from various models trained with data from clients with a small member size and tested on clients with a large member size.
Table 7.
MAE and MAPE from various models trained with data from clients with a small member size and tested on clients with a large member size.
| |
M0 |
M1 |
M2 |
M3 |
M4 |
M5 |
M6 |
M7 |
| MAE [kW] |
5.57 |
7.30 |
4.10 |
5.89 |
2.68 |
3.85 |
2.65 |
3.18 |
| MAPE [%] |
17.18 |
22.70 |
12.40 |
18.23 |
8.10 |
12.04 |
8.03 |
9.77 |
Table 8.
Means
and standard deviations
of the errors from forecast models trained on individual RECs neglecting
(orange - Single Model) and best forecast model M6 trained on multiple RECs in a federated manner (
Table 5, blue - FL Model).
Table 8.
Means
and standard deviations
of the errors from forecast models trained on individual RECs neglecting
(orange - Single Model) and best forecast model M6 trained on multiple RECs in a federated manner (
Table 5, blue - FL Model).
| |
MAE-
|
MAE-
|
| FL Model |
2.65 |
0.5 |
| Single Model |
4.72 |
0.5 |
Table 9.
Means
and standard deviations
of the errors from forecast models trained on individual RECs taking
into account (Single Model) and best forecast model M6 trained on multiple RECs in a federated manner (
Table 5, FL Model).
Table 9.
Means
and standard deviations
of the errors from forecast models trained on individual RECs taking
into account (Single Model) and best forecast model M6 trained on multiple RECs in a federated manner (
Table 5, FL Model).
| |
MAE-
|
MAE-
|
| FL Model |
2.65 |
0.5 |
| Single Model |
5.81 |
1.22 |
Table 10.
Means
and standard deviations
of the errors from forecast models trained centrally on multiple RECs neglecting
(CL Model) and best forecast model M6 trained on multiple RECs in a federated manner (
Table 5, FL Model).
Table 10.
Means
and standard deviations
of the errors from forecast models trained centrally on multiple RECs neglecting
(CL Model) and best forecast model M6 trained on multiple RECs in a federated manner (
Table 5, FL Model).
| |
MAE-
|
MAE-
|
| FL Model |
2.65 |
0.5 |
| CL Model |
3.23 |
0.48 |
Table 11.
Means
and standard deviations
of the errors from forecast models trained centrally on multiple RECs taking
into account (CL Model) and best forecast model M6 trained on multiple RECs in a federated manner (
Table 5, FL Model).
Table 11.
Means
and standard deviations
of the errors from forecast models trained centrally on multiple RECs taking
into account (CL Model) and best forecast model M6 trained on multiple RECs in a federated manner (
Table 5, FL Model).
| |
MAE-
|
MAE-
|
| FL Model |
2.65 |
0.5 |
| CL Model |
2.86 |
0.43 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).


 , (ii)
, (ii)  , (ii) medium non-stationary, (iv)
, (ii) medium non-stationary, (iv) 
 , (ii)
, (ii) 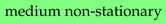 , (ii) medium non-stationary, (iv)
, (ii) medium non-stationary, (iv)