Entire-range Cooperative Trajectory Planning of Gliding-guided Projectiles with Weak Maneuverability

1. Introduction

Gliding-guided projectiles, also known as artillery-launched missiles, represent a new type of artillery weapon that combines the advantages of tactical missiles and conventional artillery projectiles. They not only offer low cost per shot, rapid response, and flexible usage but also provide a larger range and higher precision in striking, making them one of the key developmental directions in the field of weapons currently. Among the many critical technologies in the research of gliding-guided projectiles, trajectory planning remains a core and hot issue. Limited by the stringent requirements of the artillery-barrel launch platform and the harsh dynamic environment during launch, gliding projectiles have small volumes and control surfaces, and projectiles typically fly unpowered during the controlled trajectory phase. Consequently, gliding-guided projectiles have a low lift-to-drag ratio and limited maneuverability, the rationality of the trajectories designed under these conditions becomes particularly crucial[1].

Gliding-guided projectiles are equipped with rocket boosters and guidance control systems, and given the same battlefield environment and mission requirements, their flight schemes are often not unique. Therefore, rational planning performance indicators need to be designed. Existing literatures primarily address the range extension needs of gliding projectiles, designing various performance indicators from different perspectives such as maximizing the lift-to-drag ratio[2], minimizing control effort consumption[3] and minimizing the composite efficiency factor[4]. However, in modern warfare, gliding projectiles are not solely used for long-range precision strikes, and there is also a demand in engineering applications to explore the capabilities' boundaries of gliding projectiles (such as minimum range), which reduces the applicability of traditional studies assuming long ranges. Gliding projectiles operate in a large combat airspace, and the flight trajectories at different ranges exhibit different characteristics. Therefore, to achieve efficient attacks over the entire range and fully utilize the limited control capabilities of gliding projectiles, different planning focuses should be determined according to different range scopes, and on this basis, differentiated planning performance indicators should be designed.

With the advancement of science and technology and the innovation of combat concepts, the modes of confrontation between opposing forces have become more intense and complex. The diversification of defensive measures and multi-type interference poses severe challenges to the design of weapon systems. Emerging as a necessity, the cluster combat mode, which is centered around systems integration, information sharing, and overall coordination, has been developed, and cooperative attack has been introduced as a new constraint in the process of trajectory planning. Depending on the battlefield environment and mission requirements, there are different modes of cooperative combat, such as time cooperation, spatial cooperation[6,7], spatial-temporal cooperation[8–10], multi-target task allocation[11,12]. For gliding projectiles attacking fixed targets, the focus is on time coordination, specifically simultaneous impact, which typically involves scenarios of single-artillery multiple launches or multiple artilleries firing simultaneously. Against robust defensive fortifications, simultaneous hits from multiple projectiles launched by the same artillery can increase strike density and enhance the destructiveness of the projectiles. When facing heavily protected targets, projectiles launched from different directions hitting simultaneously can help disperse the defense system's firepower, improving the survivability of the projectiles. In a collaborative attack mode, multiple projectiles are not only independent entities but are also interlinked due to shared mission requirements[13,14]. Considering the limited control capabilities of gliding projectiles, to maximize combat effectiveness, research should be conducted on cooperative trajectory planning methods that consider the projectile group as a whole.

In the process of cooperative trajectory planning, coordinating the flight times of projectiles is crucial to meet the requirement of simultaneous impact. Existing literatures mainly present four flight time coordination strategies: open-loop coordination strategy, leader-follower strategy(LFS), distributed cooperation strategy(DCS), and centralized strategy. Among them, open-loop coordination refers to setting fixed projectile flight times before cooperative trajectory planning. Research on open-loop coordination was widespread in the 1990s, primarily applied to unguided conventional artillery projectiles, mainly adjusting flight times by changing the launching angle. In recent years, there have been a few research outcomes based on open-loop coordination strategies for guided projectiles[15–17]. However, this method of manually setting flight times heavily relies on experience, and if the preset values are unreasonable, it will significantly affect the combat effectiveness of the projectiles. Additionally, without information exchange between projectiles, this approach does not truly achieve coordination. LFS divides the projectile group into two categories: the leader projectile and follower projectiles. The projectile with the longest flight time serves as the leader, with the remaining projectiles acting as followers. The followers adjust their flight times by tracking the state of the leader projectile, thus achieving simultaneous attack[18–20]. This strategy places high demands on the control capabilities of follower projectiles and is less suitable for gliding projectiles. In scenarios involving simultaneous launching from multiple artilleries, the projectiles launched from different positions often have significant differences in flight times. Coordinating to match the longest flight time could exceed the control capabilities of some projectiles, leading to planning failures. For scenarios involving multiple launches from a single artillery where the launching frequency is not very low and the number of projectiles is not excessive, LFS can handle the planning task. However, coordinating to the longest flight time is overly conservative, usually resulting in unnecessary control effort consumption. DCS uses the flight time of the projectiles as the coordination variable. Coordination functions determine the desired values for these variables, allowing each launched projectile to control its flight time to converge towards the desired values, thereby achieving simultaneous impact. This strategy allows for different planning emphases among projectiles, offering considerable flexibility, and the planning process for individual projectiles is relatively simple, making it the most widely applied approach. Design methods for coordination functions include the semi-analytical method based on velocity prediction[21], the public flight time range method[22,23], and the average method[24]. The velocity prediction-based method, due to the need to estimate the remaining flight time of the projectiles, suffers from insufficient accuracy and considerable impact time errors (at least around 1 second). The public flight time range method requires at least two preliminary planning sessions for each projectile before formal planning to obtain the maximum and minimum flight times within the capabilities of the projectiles for specified mission requirements, making the algorithm process quite cumbersome. Moreover, for gliding projectiles with limited control capabilities, using numerical methods to solve for the maximum flight time is usually quite difficult. The average method independently plans for each projectile to determine their flight times and then calculates the average to determine the coordinated expected flight time. While averaging can eliminate differences in flight times among projectiles, this method may be overly arbitrary, and the coordinated flight times may still exceed the control capabilities of some projectiles, leading to planning failures. Even if the results are feasible, the average is typically not the optimal solution, leading to unnecessary consumption of control effort. All the above strategies involve artificially designed coordination processes, and the coordinated flight times usually represent feasible solutions, not optimal ones. The centralized strategy solves the system of dynamic equations for all projectiles with a unified independent variable, with flight times generated algorithmically, avoiding the process of manual coordination and ensuring optimality[25]. However, this approach not only limits the synchronization of launch and impact moments for the projectile group but also strongly binds all phases of the flight process. For single-phase UAV trajectory planning, this impact is minimal, but for gliding projectiles with multi-phase flight, using a unified independent variable results in simultaneous ignition and shutdown of booster rockets for all projectiles, and simultaneous deployment of control surfaces for all projectiles, which is clearly unreasonable and also fails to fully utilize the overall control capabilities of the projectile group. Based on the above analysis, adjusting the existing flight time coordination strategies to accommodate the limited control capabilities of gliding projectiles, or further integrating the advantages of existing strategies to design a flight time coordination strategy suitable for multi-phase planning tasks, would greatly facilitate research on cooperative trajectory planning for gliding projectiles.

In addressing the issue of simultaneous impact in cooperative trajectory planning, existing literatures predominantly focus on the improvement of planning algorithms and the study of flight time coordination strategies, often employing certain feasible operating conditions for simulations to verify the effectiveness of proposed methods. However, there is scarce mention of the process for selecting these feasible working conditions[26–30]. While planning the optimal cooperative trajectories for specific targets under particular conditions is crucial, the range of cooperative capabilities of projectiles is also a practical concern in engineering applications. Once the battlefield environment and mission requirements are established, if the single-artillery-multiple-launch attack approach is adopted, combat personnel typically focus on how many projectiles can achieve simultaneous impact at a given launching frequency. Conversely, if the multi-artillery-simultaneous-launch approach is used, the concern usually revolves around the extent to which projectiles launched from a current artillery position can collaborate with those in a broader range, thus aiding in the configuration of combat formations. Although theoretically straightforward, this work is sensitive to model specifics, and descriptions of such problems remain relatively rare in related researches to date. Therefore, designing a simple, universal method to determine the range of projectile cooperative capabilities could enhance the efficiency of cooperative trajectory planning and provide a reference for subsequent research and engineering applications.

In summary, this paper presents a study on cooperative trajectory planning methods using a certain type of gliding-guided projectile as a case study, targeting the task requirement of simultaneously impacting fixed targets. Firstly, the structure composition and flight trajectory principles of gliding projectiles are introduced, along with an explanation of the concept of 4-phase trajectory schemes. To reduce the complexity of the problem, the dimension of the dynamic model is simplified, and an artillery-target coordinate system specific to cooperative planning problems is proposed, along with the corresponding coordinate transformation method. Subsequently, addressing the uniqueness issue of optimal flight schemes within the entire range, the effective range of gliding projectiles is refined, and different battlefield zones are delineated. Considering the planning emphasis in different zones, distinct performance indicators are designed, and a zone-specific cooperative trajectory planning model is established. Furthermore, considering the limitations of existing flight time coordination strategies in cooperative trajectory planning applications of gliding projectiles, to enhance the planning success rate, improvements are made to LFS and DCS in scenarios of single-artillery-multiple-launch and multi-artillery-simultaneous-launch, respectively. Moreover, to fully exploit the control capabilities of the projectile group, a flight time coordination strategy applicable to multi-phase planning tasks and without human intervention, which combines the flexibility of DCS with the optimality of centralized strategy, is proposed. Additionally, for rapidly determining combat formations and other combat deployment issues, a simple, universal method for determining projectile cooperative capability ranges is proposed. Finally, based on the proposed methods, suitable feasible operating conditions are selected, and cooperative trajectory planning work is carried out using the proposed flight time coordination strategy, with a comparative analysis of the advantages and disadvantages of different methods.

2. Models and Methods

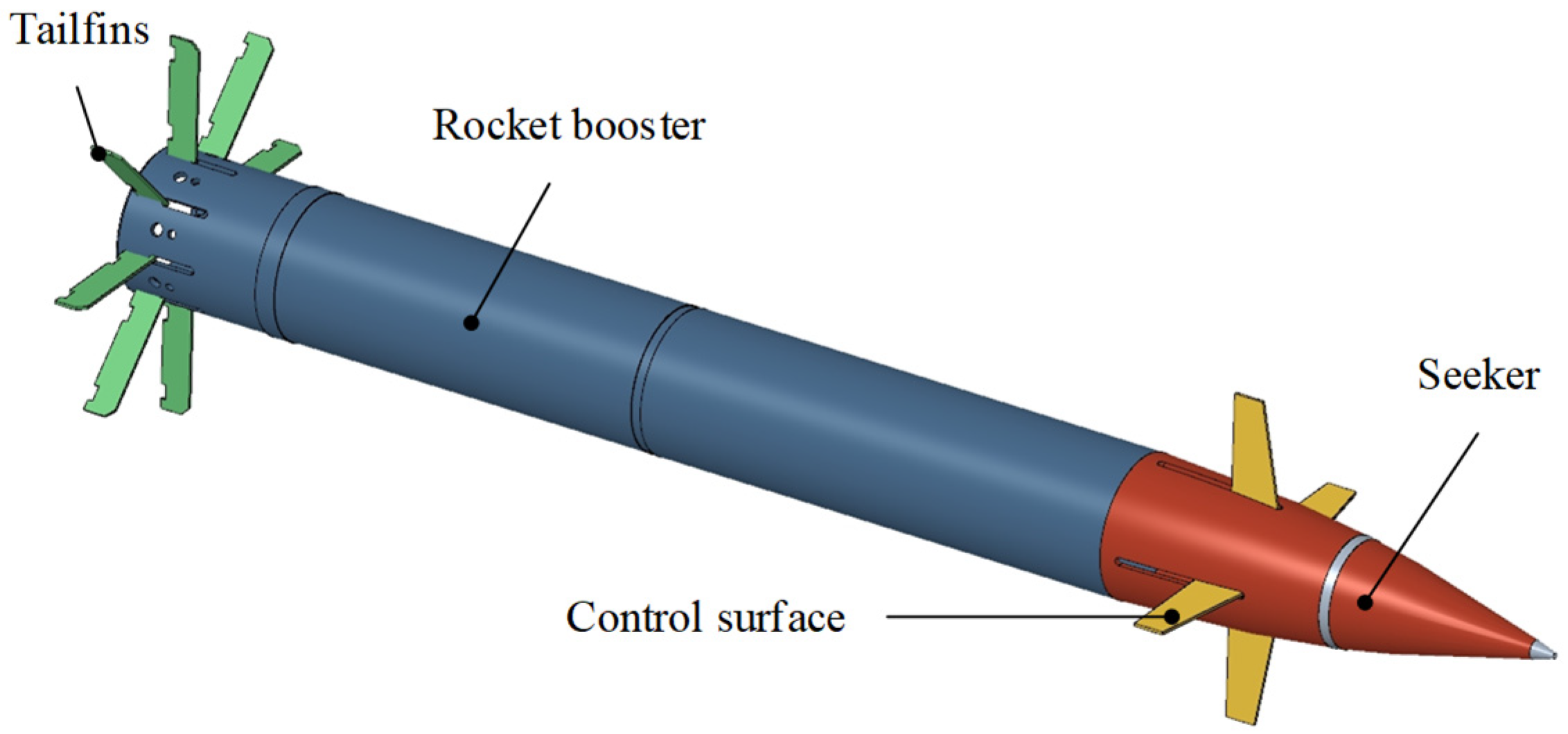
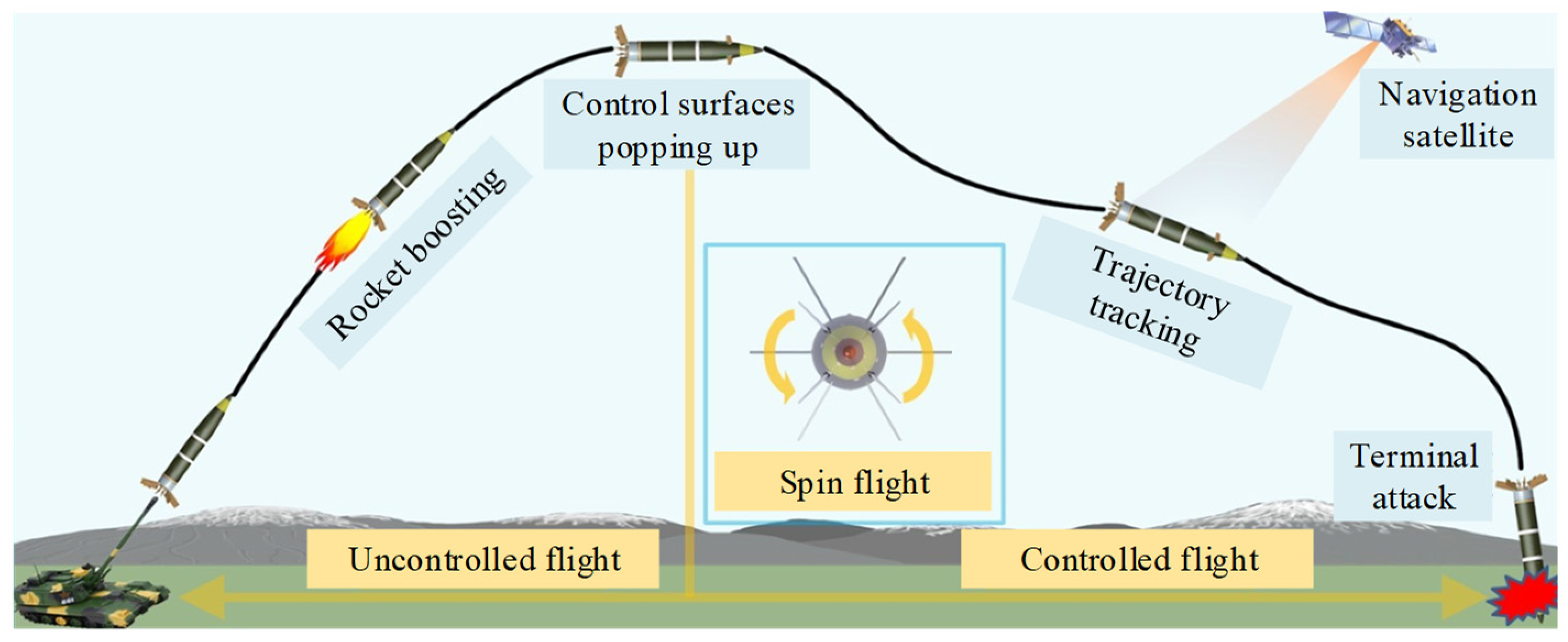
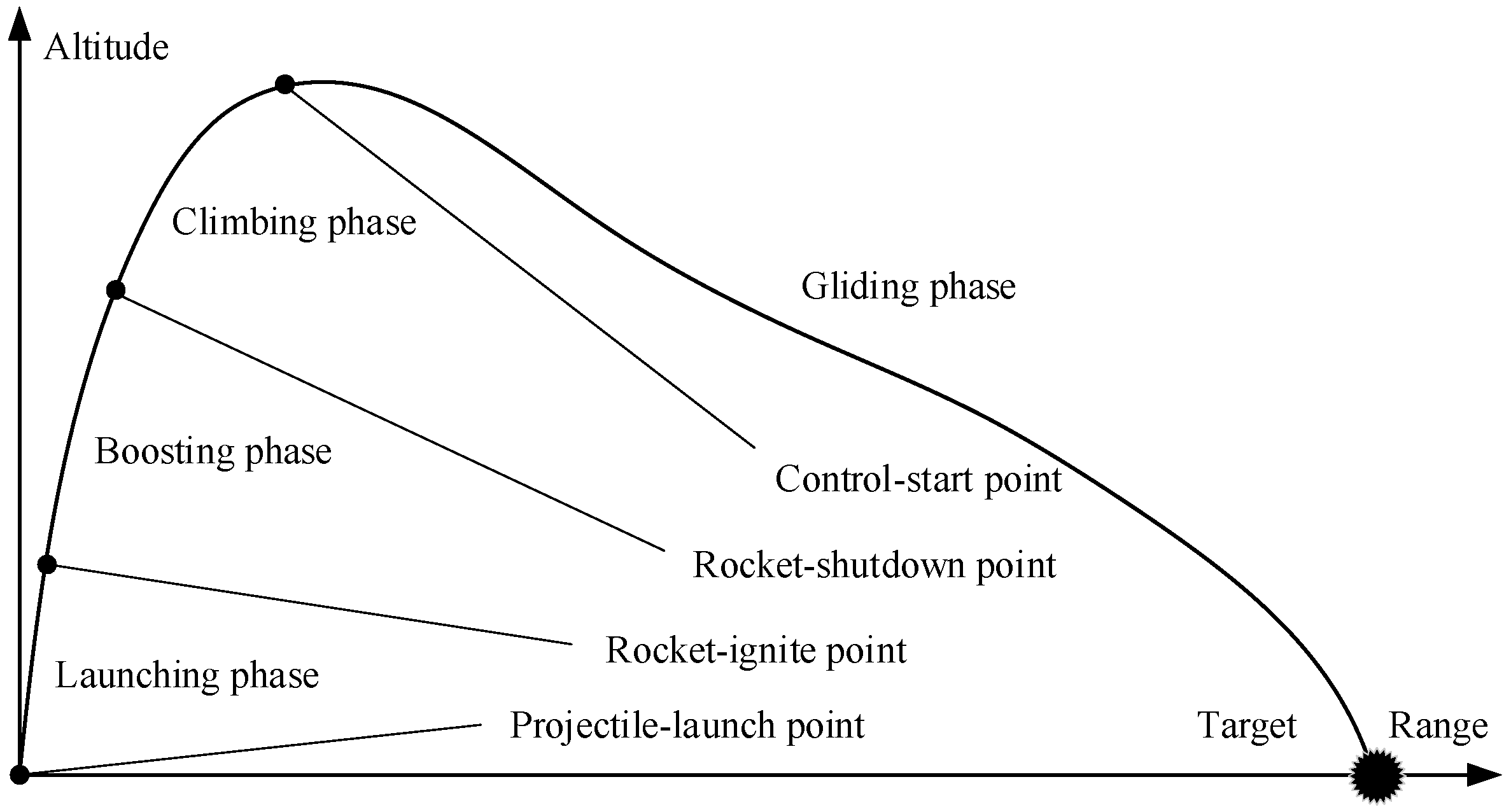
2.1. Structural Composition and Flight Trajectory Principle of Gliding-Guided Projectiles

The structural composition diagram of the gliding projectile is shown in Figure 1.

In Figure 1, Seeker is not an essential device, it typically operates in the terminal guidance phase, used for measuring the relative motion information between the projectile and the target, and generating guidance commands. The deflection of the Control surface produces control forces and moments, which are used to alter the projectile's flight trajectory. The Rocket booster is located at the rear of the projectile, usually functioning in the uncontrolled ascending arc phase, to compensate for velocity losses caused by aerodynamic drag. Tailfins are designed to deploy and are set at an angle, facilitating barrel launching and enabling the projectile to spin at a certain angular velocity. This design not only eliminates the need for additional stabilization control of the roll channel, thereby reducing the cost of the guidance control system, but also effectively mitigates the adverse effects caused by aerodynamic asymmetry and engine thrust eccentricity.

The flight trajectory principle of the gliding projectile is shown in Figure 2.

As shown in Figure 2, prior to the launch of the gliding projectile, the trajectory is pre-planned based on the current battlefield environment and operational task requirements, with related data set accordingly. Upon firing, the propellant generates high-pressure gas that propels the projectile through the barrel, the sliding sabot seals the bore and reduces spin, and the projectile's thermal battery activates under the stress of launch overload. The rocket motor's delayed ignition device is then triggered. After exiting the muzzle, the tail fins deploy and lock, stabilizing the flight of the projectile, at which point the onboard computer, satellite positioning device, and inertial navigation system commence operation. Once the delayed ignition device ignites the propellant, the booster rocket engine activates. Near the trajectory apex, the onboard computer sends fin deployment commands at the designated control moment, forms glide and trajectory tracking commands using preset guidance control laws and steers the projectile towards the target area along the pre-planned trajectory based on the real-time position and velocity data measured by the satellite positioning device and the projectile's attitude information measured by the inertial navigation system. In the terminal phase, if the projectile is not equipped with a seeker, generalized proportional guidance or other terminal control strategies are typically used against fixed targets to enhance impact precision. If equipped with a seeker, terminal guidance commences, capturing the target for a precise impact.

In the initial trajectory design phase, terminal guidance may be disregarded. Thus, from launch to impact, the projectile's trajectory is mainly divided into 4 phases: launching phase, boosting phase, climbing phase and gliding phase. The phases and their division points are illustrated in Figure 3.

For projectiles with a specified model, the muzzle velocity and the parameters of the rocket booster are often fixed or have limited options. The design parameters for the flight plan primarily include: the artillery launching angle, the rocket-ignite moment, the control-start moment, and the deflection laws of the control surfaces during the gliding phase. These dynamic and static parameters collectively influence the planned trajectory, and theoretically, once performance indicators are established, an optimal combination of these parameters is determined. Hence, the trajectory planning for gliding projectiles fundamentally constitutes a 4-phase optimal control problem that encompasses both parameter optimization and process optimization.

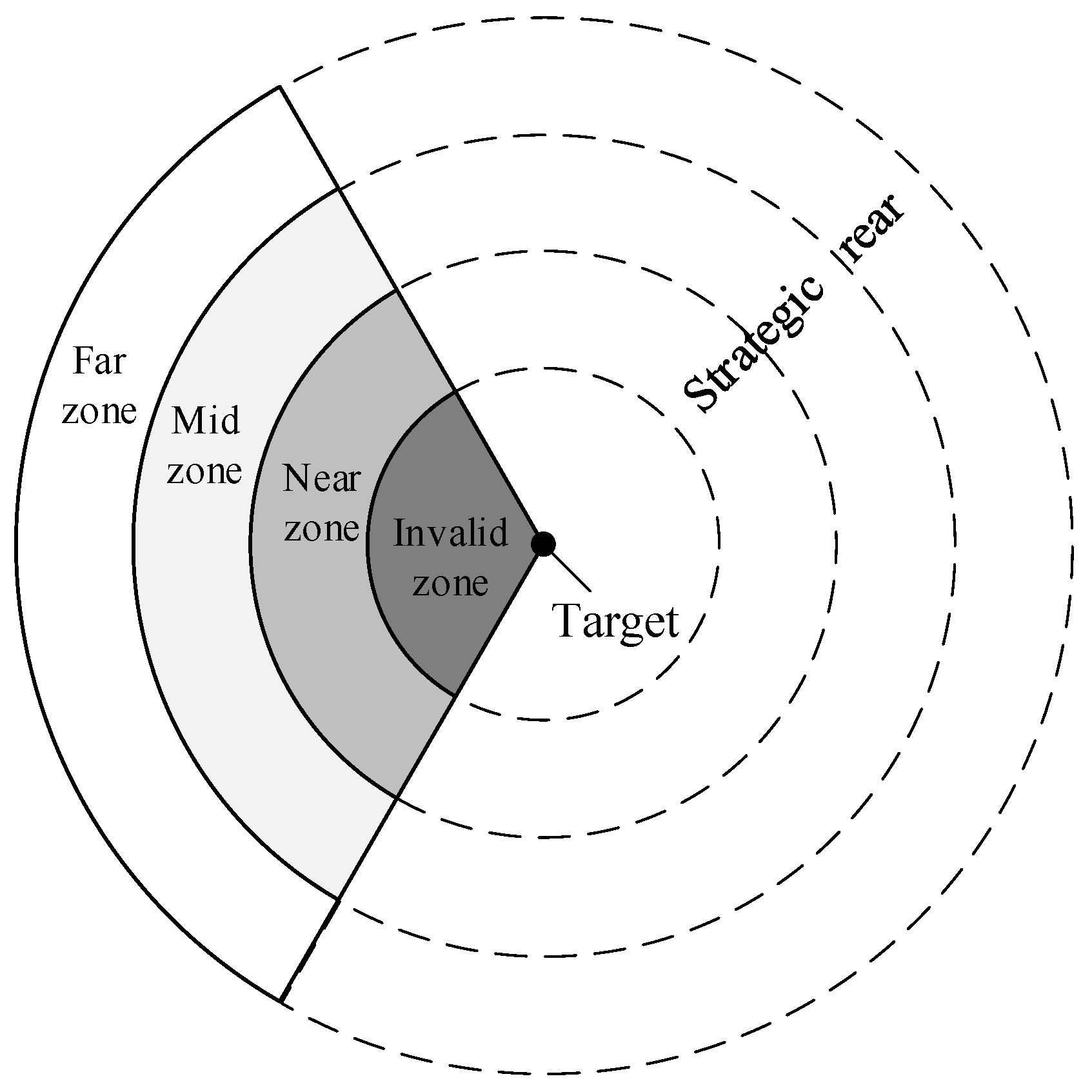
2.2. Division of Battlefield Areas of Gliding Guided Projectiles for Cooperative Attack

For traditional unguided artillery projectiles, once the amount of propellant(primarily affecting muzzle velocity) and battlefield conditions are set, the effective range is consequently determined. The projectile's range is mainly influenced by the artillery launching angle, with a trajectory resembling a parabola. Gliding projectiles introduce rocket boosters and guidance control systems on basis of the unguided ones, significantly extending the effective range (this extension is bidirectional, meaning not only is the maximum range extended beyond that of unguided projectiles, but the minimum range is also reduced). However, at the boundaries of the effective range, the control margins for projectiles are minimal and the flight times are essentially non-adjustable, making it unsuitable for cooperative attacks. Beyond the maximum range of unguided projectiles, both rocket boosting and fin deflection contribute to range extension, with the terminal trajectory appearing flatter due to the glide principle. Depending on the range, the control effort consumption for range extension varies, as does the control margin of the projectiles, thus necessitating different planning emphases. Within the effective range of unguided projectiles, due to rocket boosting (for the gliding projectiles studied in this article, the rocket will definitely operate with a fixed duration, only the timing of rocket ignition is adjustable), there is not only no need to extend range but actually a requirement to reduce it. The projectiles have a substantial control margin, thereby enabling pursuit of better destructive effects. Consequently, this paper divides the battlefield area of gliding projectiles for cooperative attacks into 4 zones, as illustrated in Figure 4.

Figure 4 depicts a target-centric top-down view. Considering the relationship between battlefield environment and offensive-defensive dynamics, this paper assumes that the target has the strategic rear and the operational deployment area for gliding projectiles is within a sector of 120° (indicated by solid lines in the figure). The definitions of each zone in the figure and the emphases of flight schemes are as follows.

• Invalid zone: this zone has a very short range, limited flight time, and minimal adjustability, making cooperative attacks inadvisable.
• Near zone: beyond the invalid zone, this zone lies between the minimum controlled flight range and the maximum unguided flight range. There is no need for range extension in this zone, with flight schemes primarily focusing on increasing terminal velocity to enhance destructive effects.
• Mid zone: beyond the near zone, this zone falls within the maximum controlled flight range with a 50% limit on control surface deflection. There is a certain requirement for range extension in this zone, but with sufficient control margin, flight schemes should balance between enhancing destructive effects and reducing control effort consumption.
• Far zone: beyond the mid zone, this zone falls within the maximum controlled flight range (within a certain distance from the boundary). There is an urgent need for range extension in this zone, shifting the emphasis of flight schemes to minimizing control effort consumption while ensuring the minimum terminal velocity of the projectiles.

It's worth noting that the 50% limit on control surface deflection for gliding projectiles is only to delineate the mid zone (for distinction from the far zone) and the limitation will not be applied during subsequent cooperative trajectory planning within mid zone.

2.3. Cooperative Trajectory Planning Model of Gliding-Guided Projectiles

2.3.1. The Artillery-Target Coordinate System

Drawing from extensive engineering and simulation experience, it is feasible to assume that for general combat missions without no-fly-zone or obstacle avoidance requirements, projectiles can be approximated to fly within a longitudinal plane. Given that the artillery positions corresponding to each launched projectile in a coordinated operation differ, this paper considers $n$ gliding projectiles, defining a distinct artillery-target coordinate system $O_i{x}_i{y}_i{z}_i,i=1,2,\dots ,n$ for each. As shown in Figure 5, the subscript $i$ denotes the projectile index, the origin $O_i$ represents the artillery position corresponding to each projectile, the $O_i{x}_i$-axis lies along the intersection of the ballistic plane and the horizontal plane, pointing towards the target as positive. The $O_i{y}_i$-axis, lies in the vertical plane and perpendicular to the $O_i{x}_i$-axis, points upwards as positive. The $O_i{z}_i$-axis is perpendicular to the other two axes and forms the coordinate system according to the right-hand rule.

The trajectory of each projectile is limited to its own ballistic plane, and the range is defined as the displacement in the $x$ direction in the respective artillery-target coordinate system. When the cooperation flight trajectories are subsequently displayed, the trajectories of all projectiles will be unified to the ground coordinate system through coordinate conversion. The conversion equations are as follows.

$$\{\begin{array}{l}{x}_{\mathrm{G}}=R_i+\left(x_i-R_i\right)\cos {\delta }_i\hfill \\ y_{\mathrm{G}}=y_i\hfill \\ z_{\mathrm{G}}=\left(x_i-R_i\right)\sin {\delta }_i\hfill \end{array}$$

(1)

In the equations, the subscript G represents the first letter of Ground, $R_i$ indicates the artillery-target distance of each projectile. $x$, $y$ and $z$ are respectively the range, altitude and lateral displacement of the projectile. ${\delta }_i$ denotes the angle between the artillery-target-line and the $x$-axis of the ground coordinate system. It is worth noting that in a single-artillery-multiple-shot scenario, ${\delta }_i=0$.

2.3.2. The Cooperation Flight Dynamics Model of Gliding Projectiles

In the initial design process, to facilitate the determination of the gliding projectile's flight trajectory and primary flight characteristics, the rotational motion around the center of mass is typically neglected, treating the projectile as a maneuverable mass point for analysis. It is also assumed that the moment acting on the projectile due to control surface deflection is in equilibrium at each instant. When the total angle of attack is small, the gliding projectile exhibits linear aerodynamic characteristics, meaning there is a linear relationship between the equilibrium control surface deflection angle and the equilibrium angle of attack. Therefore, the control variable during the gliding phase can be represented by the equilibrium angle of attack $\alpha$ to simplify the model. The flight dynamics model of each gliding projectile within its respective artillery-target coordinate system is as follows.

$$\{\begin{array}{l}{F}_{xi}=q_{i}S{C}_{x0}\left(1+k_{\mathrm{c}}{\alpha }_i^2\right)\hfill \\ F_{yi}=q_{i}S{C}_y^{\alpha }{\alpha }_i\hfill \\ {\dot{V}}_i=\frac{F_{\mathrm{P}}\cos {\alpha }_i-m_{i}g\sin {\theta }_{\mathrm{v},i}-F_{xi}}{m_i}\hfill \\ {\dot{\theta }}_i=\frac{F_{\mathrm{P}}\sin {\alpha }_i-mg\cos {\theta }_i+F_{yi}}{m_i{V}_i}\hfill \\ {\dot{x}}_i=V_i\cos {\theta }_i\hfill \\ {\dot{y}}_i=V_i\sin {\theta }_i\hfill \\ {\dot{m}}_i=-m_{\mathrm{c}}\hfill \end{array}$$

(2)

In the equations, $F_{xi}$ and $F_{yi}$ respectively represent the drag and lift acting on the i-th(the following will be omitted) projectile, $q_i=\rho V_i^2/2$ is the dynamic pressure, $\rho$ is the air density, $V_i$ is the projectile velocity, $S$ is the characteristic area of the projectile, $C_{x0}$ is the zero-lift drag coefficient, $k_{\mathrm{c}}$ is the induced drag coefficient, $C_y^{\alpha }$ is the derivative of lift coefficient with respect to equilibrium angle of attack, $m_i$ is the mass of the gliding projectile, $g$ is the gravity acceleration, ${\theta }_i$ is the ballistic inclination angle, $F_{\mathrm{p}}$ is the thrust of the rocket booster and $m_{\mathrm{c}}$ is the fuel mass flow rate.

2.3.3. Constraints

Take n gliding projectiles into consideration, remarking the launching moment of the i-th projectile as $t_{\mathrm{l},i}$, the rocket ignition moment as $t_{\mathrm{i},i}$, the rocket shutdown moment as $t_{\mathrm{s},i}$, the control-start moment as $t_{\mathrm{c},i}$ and the terminal impact moment as $t_{\mathrm{f},i}$. According to the working principle of the gliding projectiles, battlefield environment and combat mission requirements, the constraints that need to be met during the flight of the projectiles are as follows.

• Boundary constraints

The initial state constraints of the cooperation trajectories are

$$\{\begin{array}{l}{V}_i\left(t_{\mathrm{l},i}\right)=V_0\hfill \\ {\theta }_i\left(t_{\mathrm{l},i}\right)\in \left[{\theta }_{0\min },{\theta }_{0\max }\right]\hfill \\ x_i\left(t_{\mathrm{l},i}\right)=x_0\hfill \\ y_i\left(t_{\mathrm{l},i}\right)=y_0\hfill \\ m_i\left(t_{\mathrm{l},i}\right)=m_0\hfill \end{array}$$

(3)

Where $V_0$ is the muzzle velocity, ${\theta }_{0\min }$ and ${\theta }_{0\max }$ are the minimum and maximum launching angle of the artillery, respectively. $(x_0,y_0)$ is the origin of the artillery-target coordinate system and $m_0$ is the initial mass of the projectile(rocket fuel unburned).

In order to ensure the impact accuracy and damage effect, the terminal state constraints of the cooperation trajectories are

$$\{\begin{array}{l}{V}_i\left(t_{\mathrm{f},i}\right)⩾V_{\mathrm{f}\min }\hfill \\ x_i\left(t_{\mathrm{f},i}\right)=x_{\mathrm{T}}\hfill \\ y_i\left(t_{\mathrm{f},i}\right)=y_{\mathrm{T}}\hfill \\ m_i\left(t_{\mathrm{f},i}\right)=m_{\mathrm{b}}\hfill \end{array}$$

(4)

Where $V_{\mathrm{f}\min }$is the lower limit of terminal velocity of the projectile, $(x_{\mathrm{T}},y_{\mathrm{T}})$ is the target position and $m_{\mathrm{b}}$ is the body mass of the projectile(the rocket fuel has been exhausted).

2.

Path constraints

Remarking the 4 phases of the trajectory of the gliding projectiles as phase 1~phase 4, then the path constraints can be expressed as

$$\{\begin{array}{l}{F}_{\mathrm{P}}=\{\begin{array}{l}0,\mathrm{phase}1,3,4\\ {\overline{F}}_{\mathrm{P}},\mathrm{phase}2\end{array}\hfill \\ m_{\mathrm{c}}=\{\begin{array}{l}0,\mathrm{phase}1,3,4\\ \frac{m_{\mathrm{P}}}{t_{\mathrm{b}}},\mathrm{phase}2\end{array}\hfill & \\ {\alpha }_i=0,\mathrm{phase}1,2,3\hfill & \\ \left|{\alpha }_i\right|⩽{\alpha }_{\max },\mathrm{phase}4\hfill & \end{array}$$

(5)

In the equations, ${\overline{F}}_{\mathrm{P}}$ is the average thrust of the rocket booster, $m_{\mathrm{P}}$ is the mass of the rocket fuel, $t_{\mathrm{b}}$ is the working duration of the rocket and ${\alpha }_{\max }$ is the threshold value of the equilibrium angle of attack(it should be pointed out that when obtaining the range of mid zone, 50% of the design value is taken).

3.

Continuity constraints

Remarking the combination of all state variables of the gliding projectile in equation (2) as $S_i={[V_i,{\theta }_i,x_i,y_i,m_i]}^{\mathrm{T}}$, to ensure the trajectory continuity between the various phases of the projectile flight, the continuity constraint can be expressed as

$$\{\begin{array}{l}{S}_i(t_{\mathrm{i},i}^{-})=S_i(t_{\mathrm{i},i}^{+})\\ S_i(t_{\mathrm{s},i}^{-})=S_i(t_{\mathrm{s},i}^{+})\\ S_i(t_{\mathrm{c},i}^{-})=S_i(t_{\mathrm{c},i}^{+})\end{array}$$

(6)

In the formula, the symbols $-$ and $+$ respectively represent the end of the previous phase and the beginning of the next phase (refer to the symbolic understanding of left and right limits in mathematics). It should be pointed out that the working duration of the rocket in this article is fixed, so there is a correlation with $t_{\mathrm{i},i}$ and $t_{\mathrm{s},i}$, $t_{\mathrm{s},i}=t_{\mathrm{i},i}+t_{\mathrm{b}}$, therefore, only $t_{\mathrm{i},i}$ and $t_{\mathrm{c},i}$ need to be designed during trajectory planning (in order to ensure flight stability and reserve sufficient time for satellite and inertial navigation initialization, this article set $t_{\mathrm{i},i}⩾5\mathrm{s}$ and $t_{\mathrm{c},i}⩾30\mathrm{s}$).

4.

Cooperation constraint

For the purpose of simultaneous impact, the cooperation constraint can be expressed as

$$t_{\mathrm{f},i}=T_{\mathrm{f}}$$

(7)

Where $T_{\mathrm{f}}$ is the free terminal moment of the gliding projectile group.

2.3.4. Performance Indicators

To fully exploit the control ability of the projectile group at entire range and improve the impact effect, this article takes the whole as the planning object. Based on the discussion in Section 2.2, the performance indicators are designed for the trajectory planning in different battlefield zones as follows.

• Near zone: maximize overall terminal velocity.

  $$\min J_{\mathrm{near}}=-{\displaystyle \sum _{i=1}^n{V}_{\mathrm{f},i}}$$

  (8)
• Mid zone: taking into account both terminal velocity and control effort consumption.

  $$\min J_{\mathrm{mid}}=-{\displaystyle \sum _{i=1}^n\frac{V_{\mathrm{f},i}}{\overline{V}}+}{\displaystyle \sum _{i=1}^n\frac{{\displaystyle \underset{t_{\mathrm{l},i}}{\overset{T_{\mathrm{f}}}{\int }}{\alpha }_i^2}\mathrm{d}t}{\overline{E}}}$$

  (9)

In the formula, $\overline{V}$ and $\overline{E}$ respectively represent the average terminal velocity and average control effort consumption in the mid zone which are non-dimensional parameters introduced for multi-objective planning problems. The purpose is to keep the order of magnitude of the two terms consistent, ensuring that the both receive equal consideration. The so-called average is obtained by taking the mean value of the parameters at the two endpoints of the mid zone.

• Far zone: minimize overall control effort consumption.

  $$\min J_{\mathrm{far}}={\displaystyle \sum _{i=1}^n\left({\displaystyle \underset{t_{\mathrm{l},i}}{\overset{T_{\mathrm{f}}}{\int }}{\alpha }_i^2}\mathrm{d}t\right)}$$

  (10)

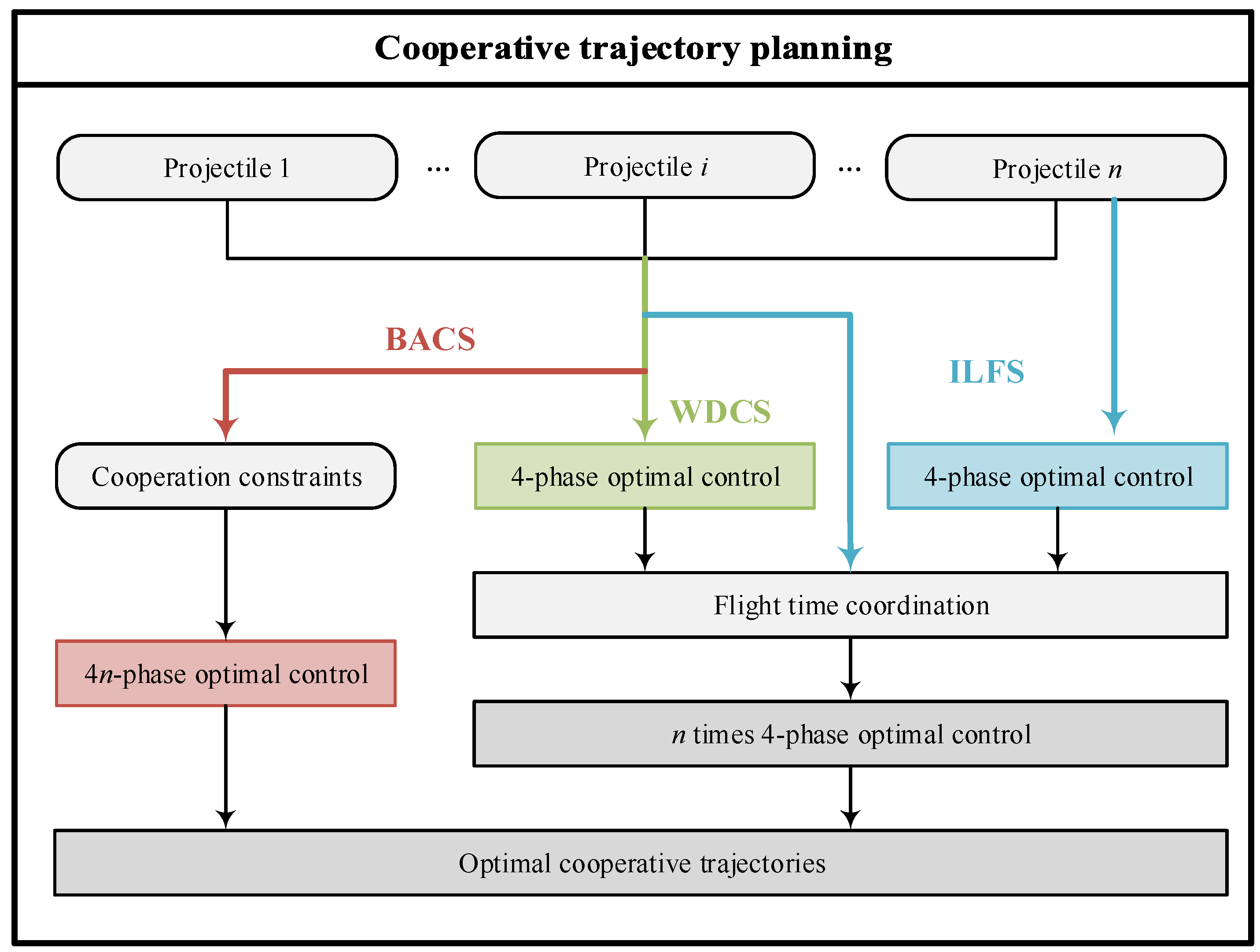
2.3.5. Cooperative Trajectory Planning Flow of Gliding Projectiles

To sum up, the cooperative trajectory planning flow of gliding projectiles aiming at a fixed target can be expressed as: considering the projectile cooperation flight dynamics model formula (2), according to the current battlefield environment and combat mission requirements, plan the initial launching angle ${\theta }_{0,i}$ of each artillery, the rocket ignition moment $t_{\mathrm{i},i}$, the control-start moment $t_{\mathrm{c},i}$ and the time-varying equilibrium angle of attack ${\alpha }_i(t_i)$ of the gliding phase within the time period to be determined $[t_{\mathrm{l},i},T_{\mathrm{f}}]$ for each projectile, and the best matching of these dynamic and static parameters are determined under the premise of satisfying the constraints (3) to (7). Depending on the current battlefield zone, the performance indicators shown in equations (8) to (10) are minimized.

2.4. Flight Time Coordination Strategy of Gliding Guided Projectiles

2.4.1. Improved Leader-Follower Strategy

Based on the analysis presented earlier, applying traditional LFS (Leader-Follower Strategy) to gliding-guided projectiles for coordinating flight times towards the longest duration requires relatively high launching frequency and a sufficiently small scale of cooperation projectiles. Otherwise, it can lead to insufficient control capability of the initially launched projectile, resulting in planning failure. To address this issue, this paper adjusts the conventional LFS and proposes an Improved Leader-Follower Strategy (ILFS) suitable for gliding projectiles. The main steps of ILFS are as follows.

Step 1. According to the established number of cooperation projectiles $n$ and the artillery launching frequency $f$, the initial launching moment of the last projectile $t_{\mathrm{l},n}$ is obtained.

$$t_{\mathrm{l},n}=\frac{n-1}{f}$$

(11)

Step 2. Taking $t_{\mathrm{l},n}$ as the launching moment and minimizing the flight time as the performance indicator, conduct trajectory planning for the final projectile to obtain the terminal impact time $t_{\mathrm{f},n}$.

Step 3. Taking $t_{\mathrm{f},n}$ as the coordinated flight time, plan the cooperative trajectory with a fixed terminal impact moment of the projectile group based on the original performance indicators.

Among the above 3 steps, step 2 is the most critical. The flight time of the last projectile is limited through an algorithm and the flight time of the first projectile is deduced according to the artillery launching frequency, thereby limiting the flight time of the first projectile in a disguised manner. As a result, the maximum flight time of the projectile group is within the capability of the gliding projectiles, thus improving the success rate of planning.

2.4.2. Weighted Distributed Cooperation Strategy

Based on the analysis in the previous sections, applying traditional DCS (Distributed Cooperation Strategy) to gliding-guided projectiles to coordinate flight times by averaging them requires that the range differences among the projectiles be sufficiently small. Otherwise, it may lead to insufficient control capability for projectiles with a large artillery-to-target distance, resulting in planning failure. To address this issue, this paper revises the traditional DCS and proposes a Weighted Distributed Cooperation Strategy (WDCS) suitable for gliding projectiles. The primary steps of WDCS are as follows.

Step 1. Carry out independent planning for $n$ projectiles and obtain each of the respective terminal impact time $t_{\mathrm{f},i}$.

Step 2. Sort all of the $t_{\mathrm{f},i}$ obtained in Step 1 and assign weights ${\omega }_i$ to them respectively.

$${\omega }_i=\frac{t_{\mathrm{f},i}}{{\displaystyle \sum _{i=1}^n{t}_{\mathrm{f},i}}}$$

(12)

Step 3. Calculate the weighted sum of $t_{\mathrm{f},i}$ as the coordinated flight time. Under the original performance indicators, cooperative trajectory planning with a fixed terminal impact moment is carried out for the projectile group.

$$T_{\mathrm{f}}={\displaystyle \sum _{i=1}^n{\omega }_i{t}_{\mathrm{f},i}}$$

(13)

Among them, step 2 is the most critical. By setting weights, the range differences of each projectile are fully considered, so that the coordinated weighted average flight time is within the capabilities of most projectiles, thus improving the success rate of planning.

2.4.3. Bi-Level Adaptive Cooperation Strategy

Based on the analysis presented earlier, employing the modified ILFS and WDCS in cooperation scenarios of single-artillery-multiple-launch and multi-artillery-simultaneous-launch respectively can effectively enhance the success rate of collaborative trajectory planning. However, both strategies involve manually set coordination functions (wherein ILFS aims to prevent excessively prolonged flight times post-coordination, whereas WDCS seeks to prevent overly short flight times), thus optimality cannot be guaranteed. To address this issue, this paper further combines the flexibility of DCS with the optimality of centralized strategy, introducing a Bi-level Adaptive Cooperation Strategy (BACS) tailored for multi-phase planning problems.

As discussed in Section 2.1, the trajectory planning problem for gliding-guided projectiles constitutes a 4-phase optimal control problem. As illustrated in Figure 6, considering $n$ gliding projectiles, the trajectory planning based on ILFS essentially involves initially solving a single 4-phase optimal control problem with a free terminal impact moment, followed by coordinating the flight times of the projectile group using a coordination function, and then jointly solving $n$ 4-phase optimal control problems with a fixed terminal impact moment to determine the optimal cooperative trajectories. In contrast, the trajectory planning based on WDCS fundamentally requires solving $n$ individual 4-phase optimal control problems with free terminal impact moments, followed by coordinating the flight times of the projectile group, and subsequently solving $n$ 4-phase optimal control problems with a fixed terminal impact moment jointly, thereby obtaining optimal cooperative trajectories. It is evident that under both strategies, the original problems are ultimately transformed into optimal control problems with fixed terminal times, which directly impacts the guarantee of optimality in the planning results. Addressing this, BACS adjusts the sequencing of planning, initially arranging the $n$ 4-phase optimal control problems in a specific order (might based on projectile numbering as well), augmenting the original problem into a single 4n-phase optimal control problem. Subsequently, by introducing a tolerance ${\epsilon }_{\mathrm{t}}$ for flight time, the cooperation constraint expressed in formula (7) is transformed into

$$\max (t_{\mathrm{f},j}-t_{\mathrm{f},k})⩽{\epsilon }_{\mathrm{t}},(j\ne k)\in [1,n]$$

(14)

In the formula, the $t_{\mathrm{f}}$ terms with subscripts j and k respectively represent the terminal independent variable values ​​in phase 4j and 4k of the augmented problem.

By setting the tolerance ${\epsilon }_{\mathrm{t}}$ approaching zero, the constraints among the originally n separate problems are transformed into constraints within a single problem, thereby allowing the solution of single 4n-phase optimal control problem to enable the flight times of each projectile to autonomously and gradually converge to the optimal solution during the algorithm's iterative process. Should the scale of the projectile group be large, a dynamically reduced tolerance can be set to improve the algorithm's convergence. Under the influence of BACS, the coordination of projectile flight times is adaptively generated by the algorithm without manual intervention, thus ensuring optimality. Meanwhile, the flight phases of each projectile remain independent of each other, thus ensuring flexibility. This approach fully exploits the control potential of the projectile group, achieving maximum efficiency. It is worth noting that while augmenting all sub-problems into one larger problem increases the computational difficulty and time required, by setting reasonable iterative initial values, the augmented problem can be properly solved. Moreover, this paper focuses on offline planning issues without rapidity requirements, and in cases where the size of the projectile group is not very large, the computational cost for the augmented problem is also not severe. Overall, it is anticipated that when dealing with multi-phase cooperative planning problems targeting the whole projectile group, BACS demonstrates superiority over ILFS, WDCS, and strategies mentioned in existing literatures.

2.5. Cooperation Capability Range of the Gliding-Guided Projectile

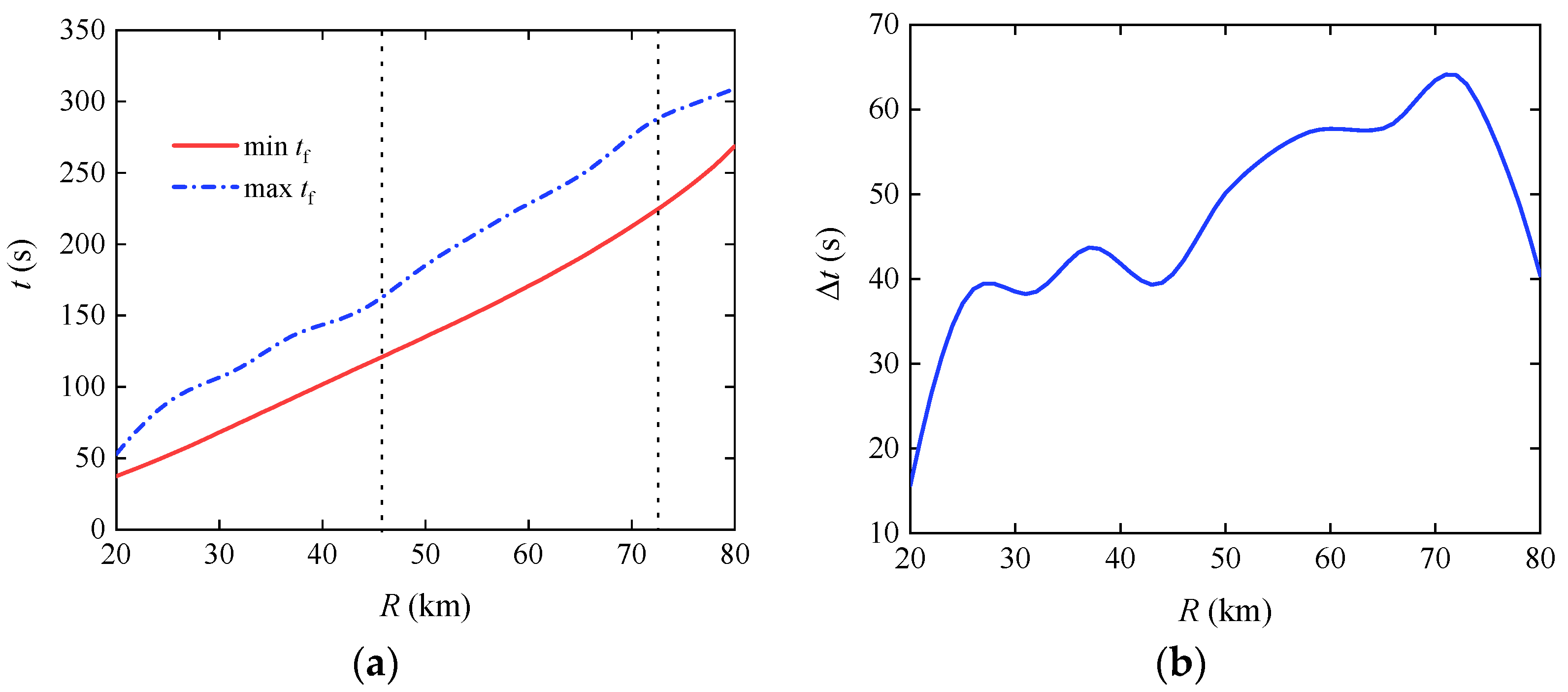
2.5.1. Flight Time Range of the Gliding Projectile at Different Ranges

Assuming the current distance between the artillery and the target is $R^{*}$(within the effective range of the gliding projectile), trajectory planning can be performed with the performance indicators of minimizing and maximizing flight time. This results in a feasible range of flight times $[t_{\min }^{*},t_{\max }^{*}]$ for the projectile at the current range $R^{*}$, that is, the capability range of coordinated flight time for the projectile when the range is specified. Extensive simulation experience indicates that when maximizing flight time as a performance indicator, the projectile control commands planned by numerical algorithms tend to exhibit high-frequency fluctuations, and this phenomenon is more likely to occur at shorter ranges. Therefore, during the planning process, the amplitude of control variables is dynamically adjusted with a coefficient $k^{*}$ to allow some margin.

$$\{\begin{array}{l}{k}^{*}=\frac{\left(1-\mathsf{\Phi }\right)\left(R^{*}-R_{\min }\right)}{R_{\max }-R_{\min }}+\mathsf{\Phi }\hfill \\ {\alpha }_{\max }^{*}=k^{*}{\alpha }_{\max }\hfill \end{array}$$

(15)

Where $\mathsf{\Phi }=0.618$ is the golden section number, $R_{\min }$ and $R_{\max }$ represent the lower and upper bounds of the effective range of the gliding projectile, respectively. Equation (15) indicates that the value of the dynamic coefficient is designed as a linear mapping of the interval [0.618, 1] to the effective range of the projectile.

After obtaining the maximum flight time $t_{\max }^{*}$ corresponding to the range $R^{*}$, it is added as a constraint to the planning model for verification, and unreasonable data is adjusted based on the principle that the control commands are smooth and not saturated. Through the above process, it can be theoretically ensured that the control capability of the gliding projectile is sufficient to cover this flight time range.

2.5.2. Cooperation Capability Range of the Gliding Projectile at Different Ranges

1.

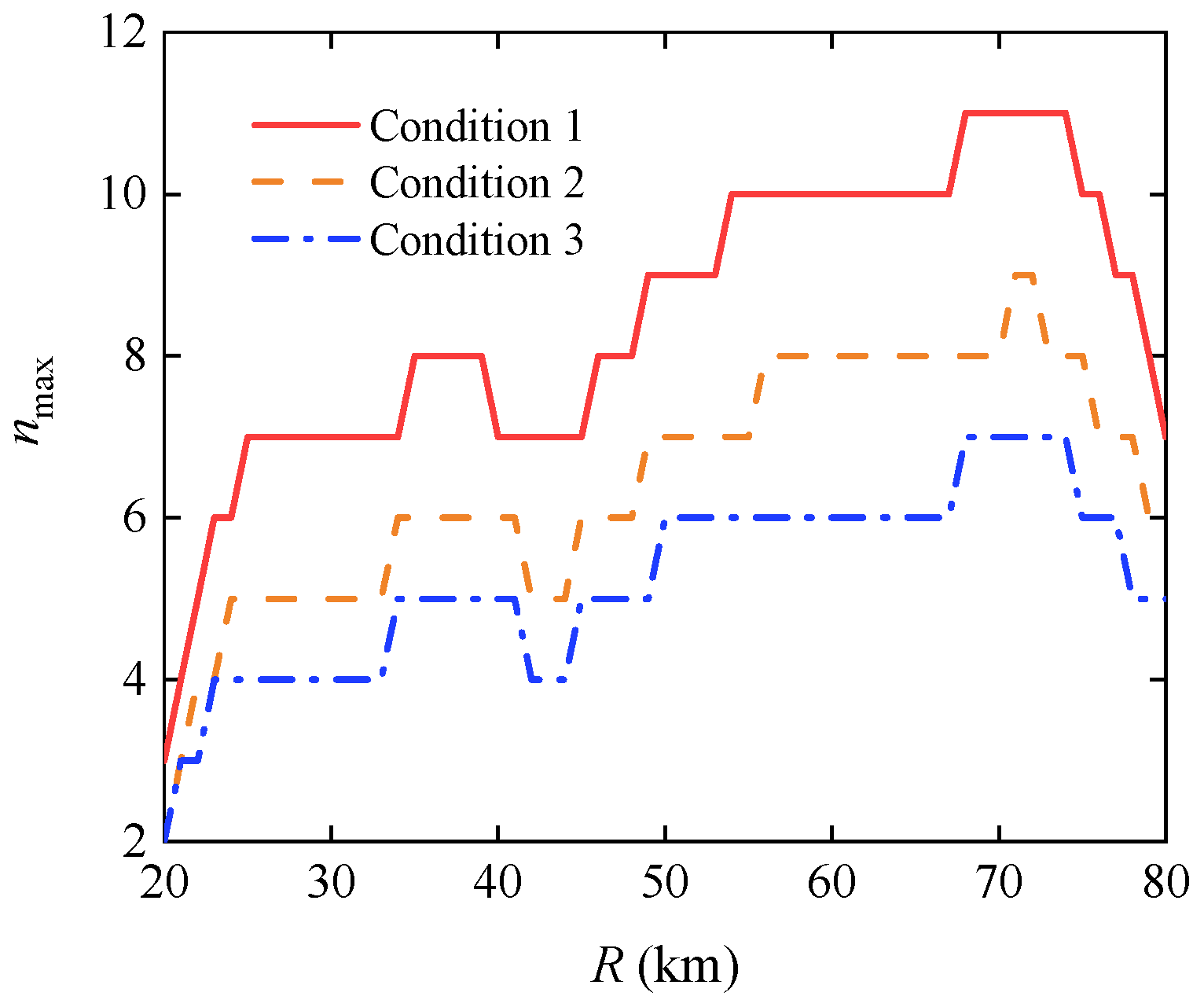
The number of cooperation projectiles in single-artillery-multiple-shot scenarios

Remarking the difference between the upper and lower bounds of the feasible flight time range of the projectile at the range $R^{*}$ is $\Delta t^{*}$, then the maximum number of cooperation projectiles at this range is

$$n_{\max }=\mathrm{floor}\left(\Delta t^{*}\times f\right)+1$$

(16)

In the formula, the operator $\mathrm{floor}(\cdot )$ represents rounding down.

2.

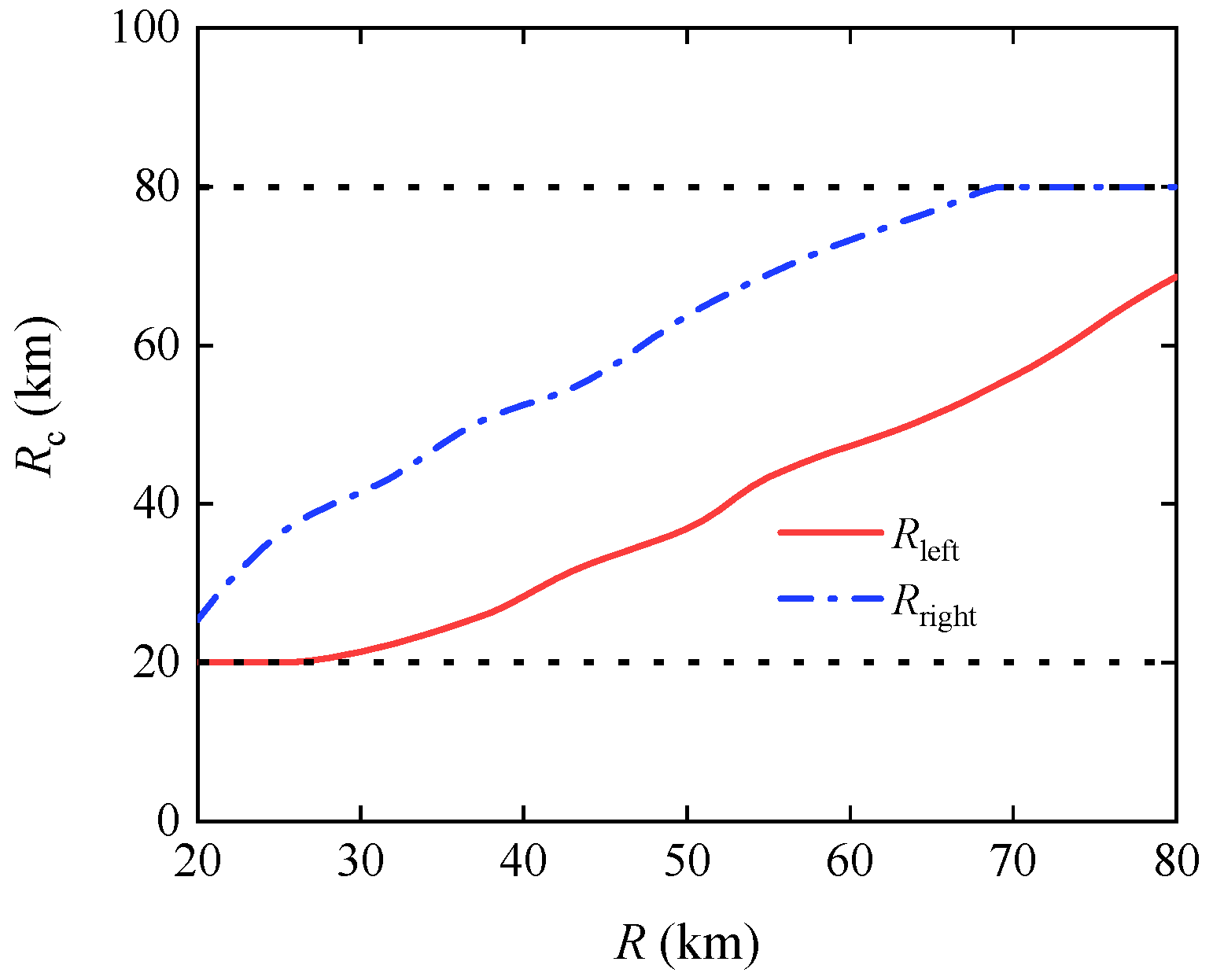
Feasible cooperative range extents in multi-artillery-simultaneous-launch scenarios

Considering n salvo projectiles with different ranges, as long as the relationship $\max (t_{\min }^i)\le \min (t_{\max }^i),i=1,2,\dots ,n$ is satisfied, that is, there is a common flight time range (this range has a certain margin and is not a extreme situation), then a cooperative salvo attack can definitely be achieved. Hence, for a projectile with a given range $R^{*}$, it is sufficient to calculate $R_{\mathrm{left}}^{*}$ and $R_{\mathrm{right}}^{*}$ within the effective range(taking boundary values if outside this range) to satisfy the relationship $t_{\min }^{*}=t_{\max }\left(R_{\mathrm{left}}^{*}\right),t_{\max }^{*}=t_{\min }\left(R_{\mathrm{right}}^{*}\right)$. This allows determination of the feasible cooperative range $[R_{\mathrm{left}}^{*},R_{\mathrm{right}}^{*}]$ for a projectile at the current range.

Through the above methods, the feasible working conditions for cooperative attack by gliding projectiles can be quickly determined. For different combat mission requirements, it is only necessary to modify the corresponding constraints and perform similar processing, showing certain versatility.

3. Simulation and Analysis

This paper uses a specific type of gliding-guided projectile as a case study, utilizing the Radau pseudo-spectral method to solve multi-phase optimal control problems. The simulations are conducted on the MATLAB 2022b platform using the GPOPS-II toolbox, with default values for relevant toolbox parameters. Aerodynamic parameters are interpolated from wind tunnel experimental data, and other simulation parameters are as shown in Table 1.

3.1. Division of Battlefield Areas of Gliding Guided Projectiles for Cooperative Attack

As discussed in Section 2.2, considering different constraints and using either maximization or minimization of range as performance indicators for trajectory planning (which will not be elaborated here in detail), it is possible to obtain the average velocity of the mid zone $\overline{V}=311.60(\mathrm{m}\cdot {\mathrm{s}}^{-1})$ and the average control effort consumption of the mid zone $\overline{E}=0.64({\mathrm{rad}}^2\cdot \mathrm{s})$, both nondimensionalization parameters. The scope of the invalid zone will be determined later, while the range extents for other zones are presented in Table 2.

3.2. Cooperation Capability Range of the Gliding-Guided Projectile

3.2.1. Flight Time Range of the Gliding Projectile at Different Ranges

According to the results in Section 3.1, the extreme range of the gliding-guided projectiles in this study is from 15.93 to 83.72 km. Considering the insufficient control margin of projectiles near the range boundaries during cooperative attacks, this paper appropriately reduces the extreme range, resulting in an effective range for cooperative attacks of approximately 20 to 80 km. For convenient and rapid determination of feasible operating conditions, the near, mid, and far zones are each divided into 4 equal parts, creating 13 nodes. The method proposed in Section 2.5.1 is employed to obtain the flight time ranges at each node, and the results are compiled into a table. By interpolating the table data (when the number of nodes is sufficient, interpolation results can be approximated as true values), the range of flight times at any position within the effective range can be determined. The simulation results are shown in Table 3 and Figure 7 (with black dotted lines indicating the boundaries between zones).

From the results in Figure 7, it is evident that the lower bound of the flight time for the gliding-guided projectiles changes approximately linearly with the range, whereas the upper bound experiences some fluctuations. These fluctuations are more pronounced within the near and mid zones, arising from the emphasis of the flight schemes not on extending range. In contrast, changes within the far zone are approximately linear. Overall, the flight time range first increases and then decreases with range, exhibiting a characteristic pattern that is low at both ends and high in the middle. This indicates that projectiles launched from the mid zone have stronger capabilities for coordinated flight timing and a broader range of cooperative ability. The results shown in Figure 7 can serve as a reference for subsequent work.

3.2.2. The Number of Cooperation Projectiles in Single-Artillery-Multiple-Shot Scenarios

For the gliding projectile studied in this article, the artillery launching frequency range $f\in [1/10,1/6]\mathrm{Hz}$. 3 working conditions are distinguished based on $f$ as follows.

• Condition 1: $f=1/6\mathrm{Hz}$
• Condition 2: $f=1/8\mathrm{Hz}$
• Condition 3: $f=1/10\mathrm{Hz}$

From equation (16), it can be obtained that the maximum number of cooperation projectiles for multiple rounds from a single artillery under different conditions is shown in Figure 8.

As indicated by the results in Figure 8, at the same range, the maximum number of cooperative projectiles is positively correlated with the launching frequency of the artillery, which is consistent with common sense. It should be noted that the curve in the figure is not smooth due to the floor operator executing a downward rounding calculation, which is a normal outcome. The results shown in the figure represent extreme cases and can serve as a theoretical reference for cooperative trajectory planning work. In practical engineering applications, the number of cooperative projectiles typically does not exceed 5.

3.2.3. Feasible Cooperative Range Extents in Multi-Artillery-Simultaneous-Launch Scenarios

Based on the results in Figure 7, using the method in Section 2.5.2, the cooperative range of the gliding projectile in multi-artillery-simultaneous-launch scenarios can be obtained, as shown in Figure 9 (the subscript c in the figure represents the initial letter of cooperative, and the black dotted line represents the effective range boundary of the gliding projectile).

The results shown in Figure 9 corroborate the analysis of Figure 7, from which it is evident that the cooperative range extents for projectiles at 20~26 km is small and varies dramatically, making it unsuitable for deployment in cooperative operations. Similar conclusions can be drawn from the results of Figure 8. Therefore, this paper sets the invalid zone range as 20~26 km and excludes this range from subsequent cooperative trajectory planning. In engineering practice, the results from Figure 9 can be used to quickly determine feasible salvo attack conditions, assisting in the configuration of combat formations.

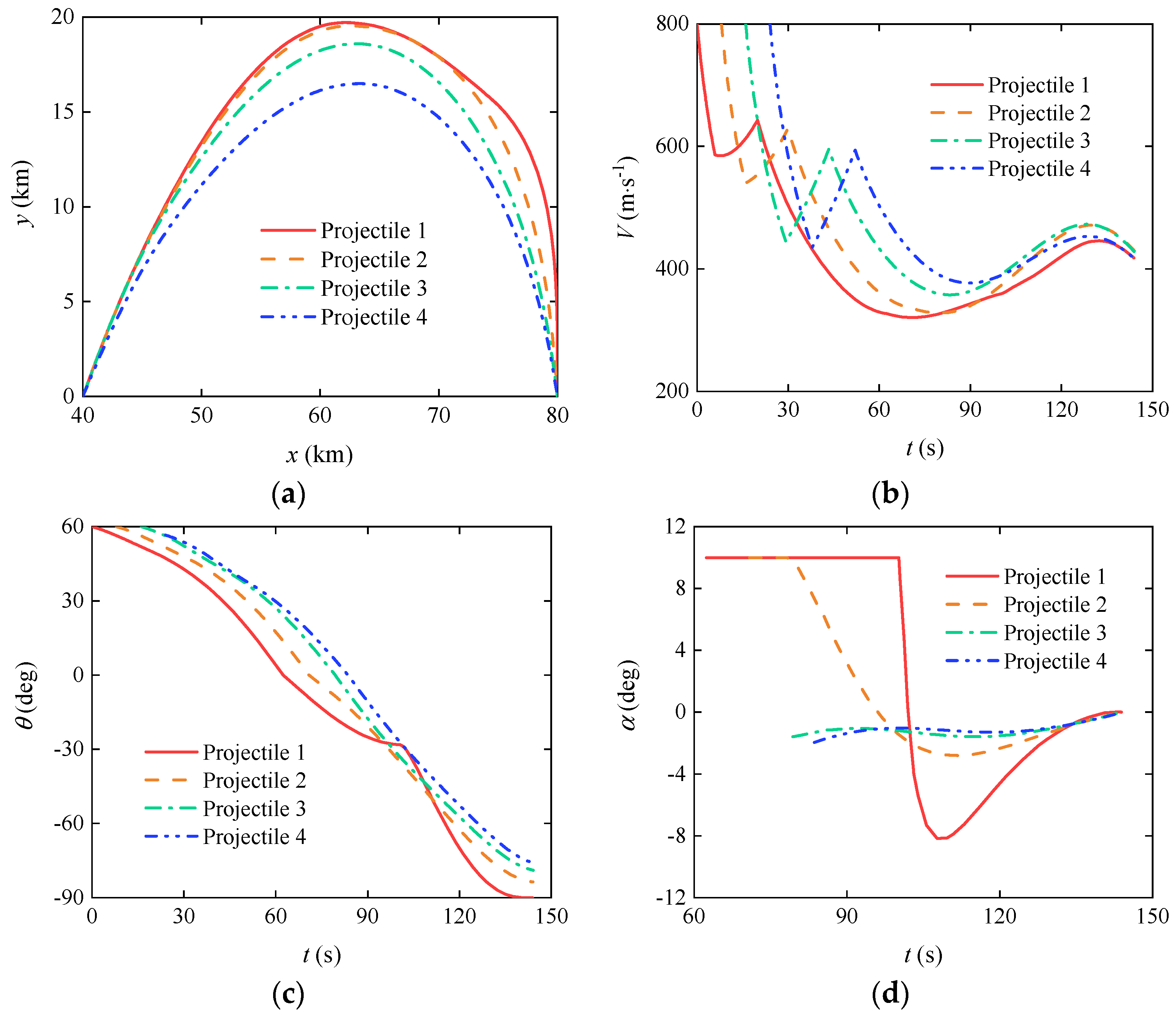
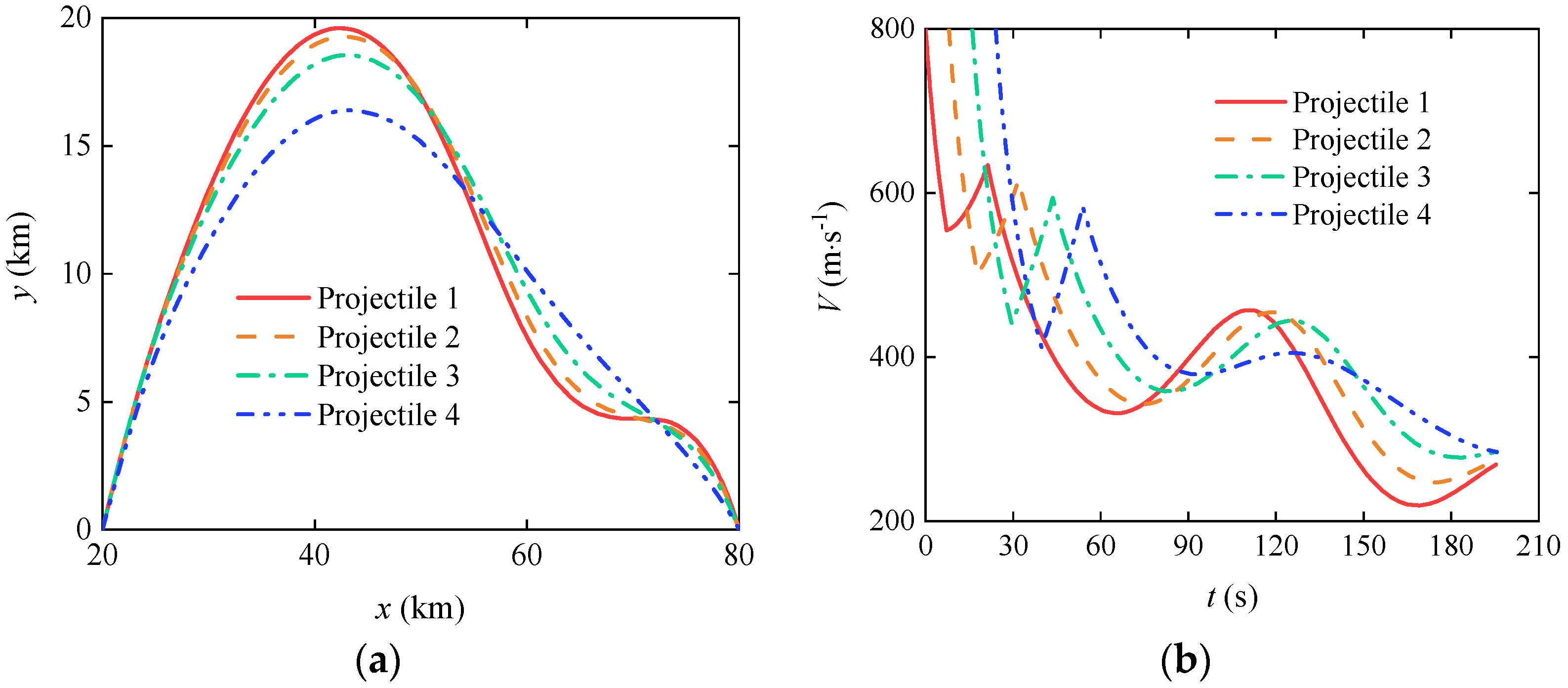
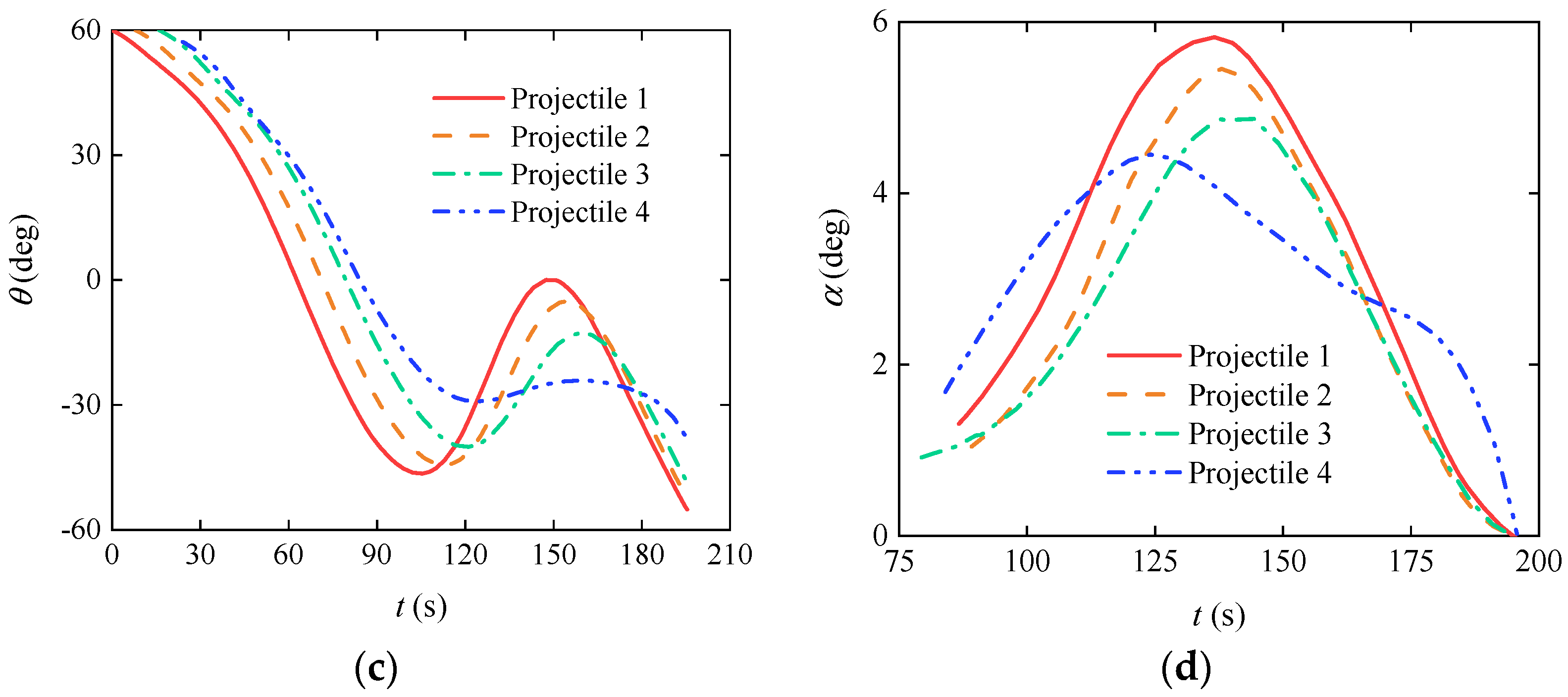
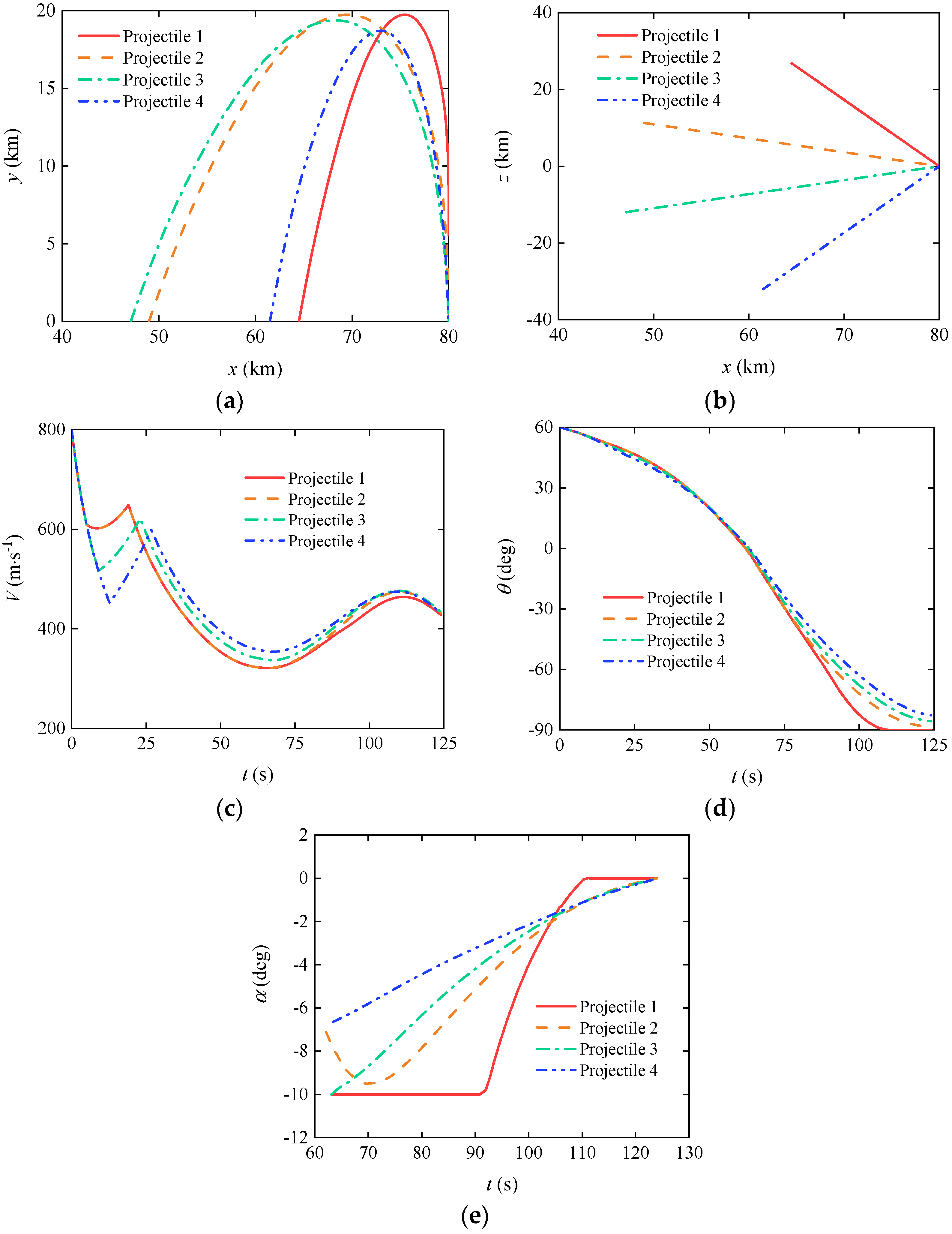
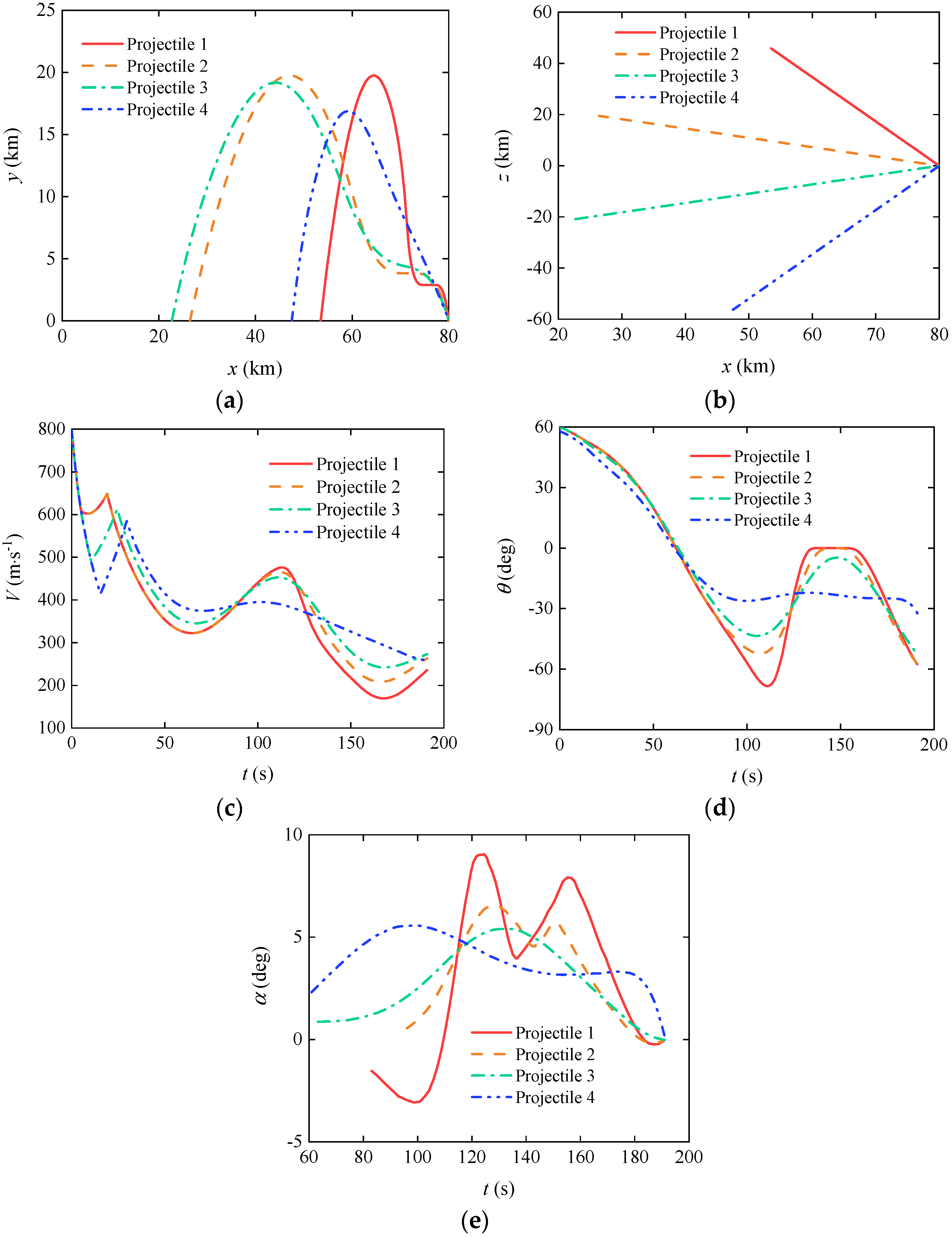
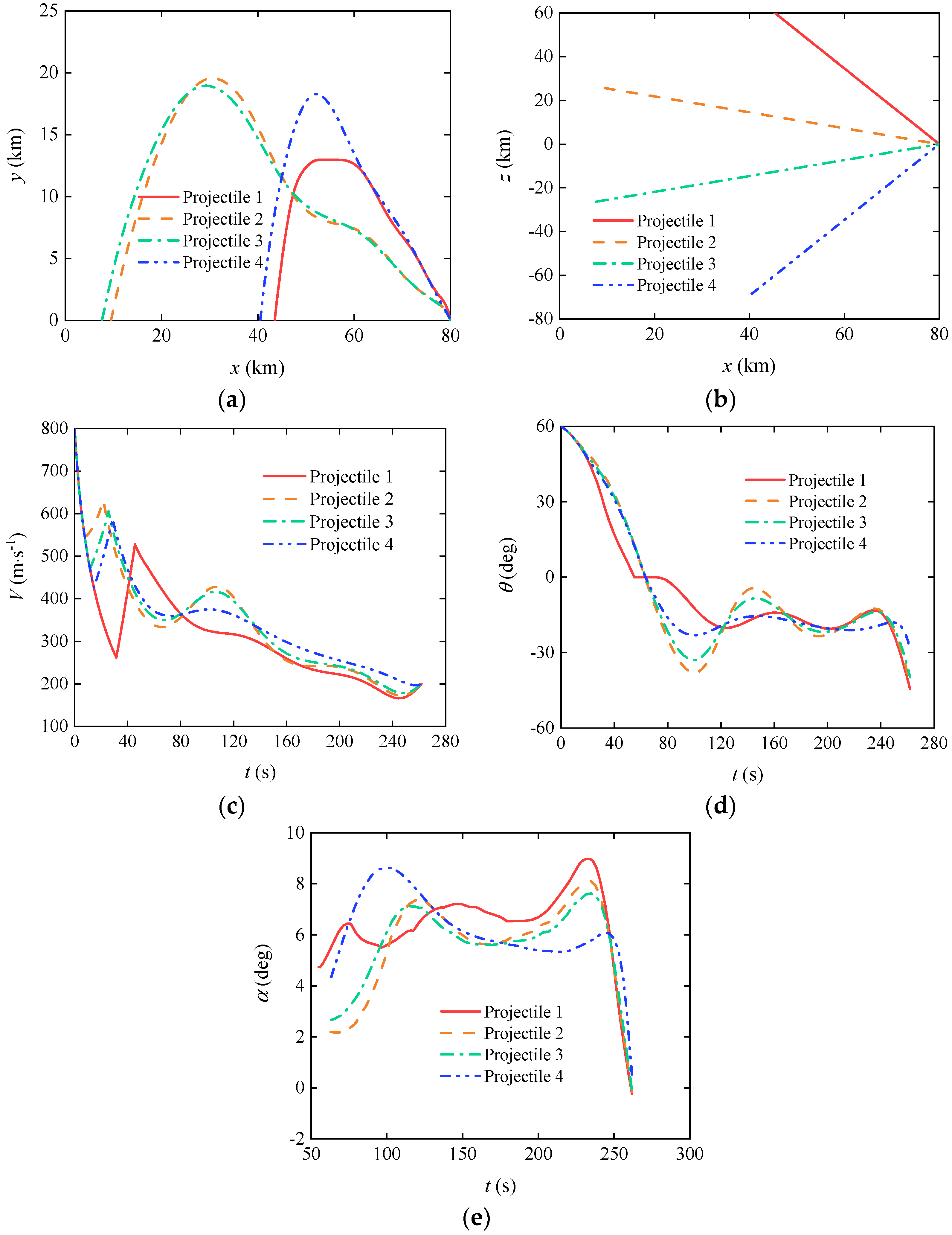
3.3. Cooperative Trajectory Planning of Gliding-Guided Projectiles in Single-Artillery-Multiple-Shot Scenarios

In order to facilitate comparative analysis without loss of generality, this article sets the number of cooperative projectiles $n=4$, and the target position in each artillery-target coordinate system $(x_{\mathrm{T}},y_{\mathrm{T}})=(80,0)\mathrm{km}$, artillery launching frequency $f=1/8\mathrm{Hz}$. Referring to the results in Figure 8, set the artillery-target distance $R_{\mathrm{near}}=40\mathrm{km}$ in the near zone, $R_{\mathrm{mid}}=60\mathrm{km}$ in the middle zone and $R_{\mathrm{far}}=75\mathrm{km}$ in the far zone. The cooperative trajectories planned based on BACS are shown in Figures 10 to 12.

From the results shown in Figure 10, under the influence of BACS, the cooperative trajectories within the near zone meet all constrains, demonstrating the effectiveness of the proposed flight time coordination strategy. Driven by the objective to maximize terminal velocity, each projectile's launching angle reaches its design upper limit, and the cooperative projectiles employ strategies to increase trajectory curvature, extend flight time, and enhance impact angles. The terminal velocities of the projectiles exceed 400 m/s, far surpassing the design threshold. The equilibrium attack angles of the projectiles not only serve the objective function but also coordinate flight times. Hence, projectiles launched earlier exhibit larger equilibrium attack angles, and consequently greater trajectory curvatures and impact angles. As observed in Figure 10(d), Projectile 1, being the first launched, reached control saturation during its flight.

From the results in Figure 11, under the influence of BACS, the cooperative trajectories within the mid zone satisfy all constraints, validating the effectiveness of the proposed flight time coordination strategy. With performance indicators balancing terminal velocity and control effort consumption, each projectile’s launching angle again reaches the design upper limit. Cooperative projectiles adopt strategies to increase trajectory height to mitigate air resistance, albeit sacrificing some terminal velocity to conserve control effort. Still, the projectiles' terminal velocities remain above the design threshold of 200 m/s, with reduced impact angles compared to those within the near zone. The equilibrium attack angles of the projectiles not only support the objective function but also facilitate the coordination of flight times. Thus, projectiles launched earlier have larger equilibrium attack angles.

Results from Figure 12 indicate that under the influence of BACS, the cooperative trajectories within the far zone meet all constraints, verifying the effectiveness of the flight time coordination strategy. Driven by the objective function to minimize control effort consumption, each projectile's launching angle reaches the design upper limit. Cooperative projectiles utilize increased trajectory heights to reduce the effect of air resistance. To ensure limited control capabilities serve the urgent need for extending range, terminal velocities are maintained at the design threshold, with further reduced impact angles compared to those within the mid zone, highlighting more pronounced gliding characteristics. The equilibrium attack angles of the projectiles serve both the objective function and the coordination of flight times. Therefore, projectiles launched earlier possess larger equilibrium attack angles.

Comparing the results from Figures 10 to 12, it can be inferred that increasing the impact angle helps improve the terminal velocity of the projectiles, but it also increases control effort consumption. In engineering applications, a trade-off should be made between terminal velocity and control effort consumption.

To further verify the superiority of BACS, traditional LFS and the proposed ILFS are used for cooperative trajectory planning under the same conditions, with simulation results of different strategies illustrated in Table 4 (the symbol × denotes planning failure).

The results from Table 4 indicate that, within different zones, the flight times coordinated by LFS are consistently longer compared to the strategy proposed in this paper. Consequently, in the near zone where overall flight time is relatively short, flight time coordinated by LFS exceeds the capability range of some projectiles, leading to planning failures. Conversely, ILFS enhances the success rate of planning by imposing restrictions on maximum flight time. In terms of performance indicators, cooperative schemes developed using BACS surpass those of ILFS, demonstrating the superiority of BACS. Specifically, in the near zone, ILFS limits flight time to avoid planning failures, resulting in a cooperative flight time that is 18.14 s shorter than that of BACS, thereby failing to fully utilize the control capacity of the projectile group and causing a 10.24% reduction in terminal velocity compared to BACS. In the mid zone, the algorithm makes trade-offs between terminal velocity and control effort consumption. The performance indicators show that ILFS differs from BACS by 19.44%, which is even more pronounced than in the near zone, suggesting that pursuing terminal velocity comes at a significant cost. In the far zone, since calculating control effort consumption requires integration over time t, and because the equilibrium angle of attack of projectiles at long ranges primarily serves the need for extending range, minimizing flight time and control effort consumption are essentially equivalent performance indicators. Thus, the cooperative schemes planned by ILFS and BACS are similar, with minimal differences in flight time and performance indicators.

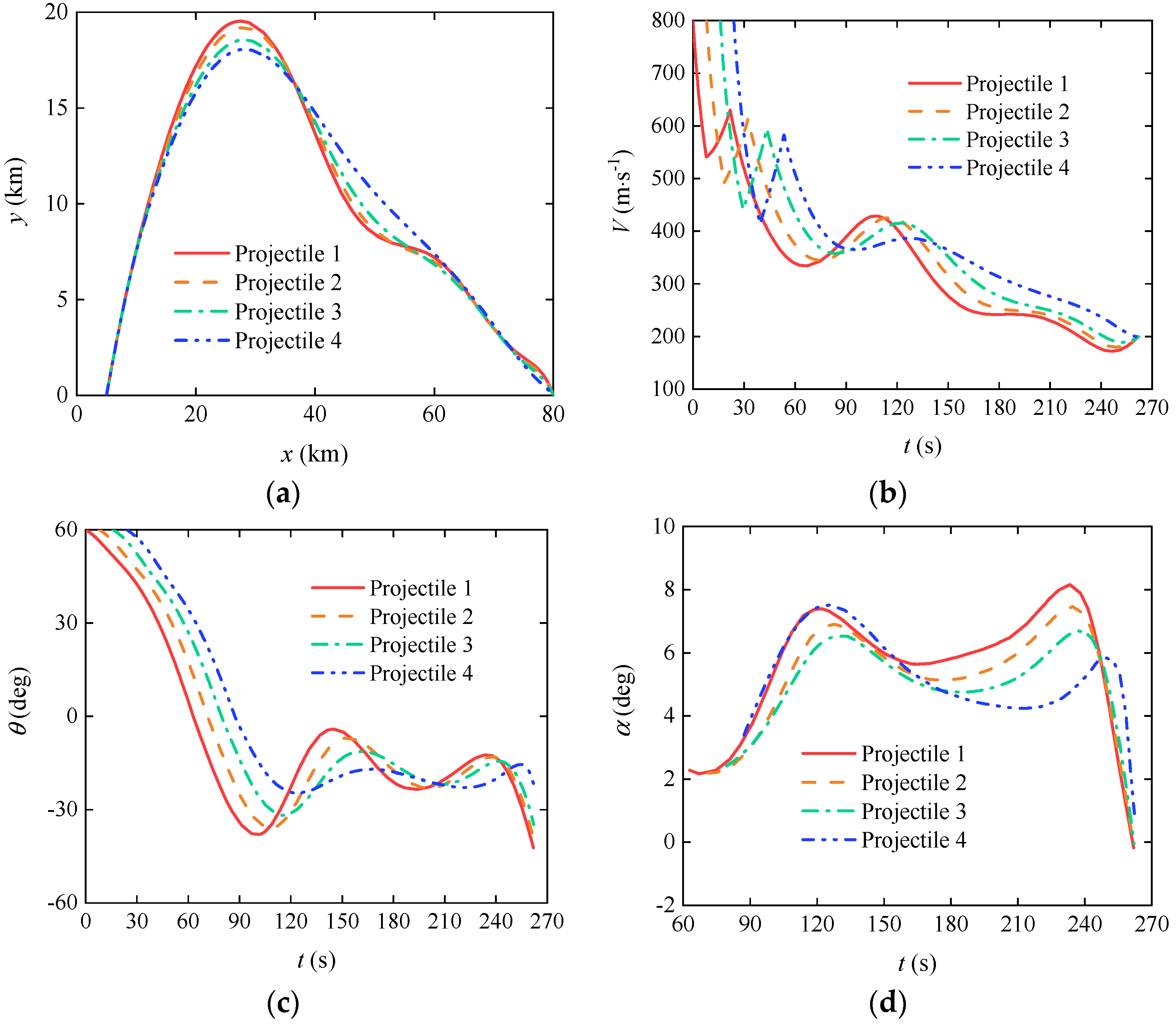
3.4. Cooperative Trajectory Planning of Gliding-Guided Projectiles in Multi-Artillery-Simultaneous-Launch Scenarios

To facilitate comparative analysis without loss of generality, this paper sets the number of cooperative projectiles $n=4$ and targets positioned in each artillery-target coordinate system $(x_{\mathrm{T}},y_{\mathrm{T}})=(80,0)\mathrm{km}$. Referencing Figure 4 and Figure 9, within a 120° sector in the near zone, positions for 4 artillery placements at distances of 31, 33, 35, and 37 km from the target are selected at 40° intervals to form a battle formation for salvo attacks(this approach theoretically achieves uniform coverage across the entire battlefield area). In the mid zone, 4 artillery positions are chosen at distances of 53, 57, 61, and 65 km from the target, and in the far zone, positions at 73, 75, 77, and 79 km are selected. The results of the cooperative schemes planned using BACS are illustrated in Figures 13 to 15, where the trajectories of the cooperative projectiles are unified to the ground coordinate system as outlined in Section 2.3.1, Equation (1).

The results from Figure 13 demonstrate that under the influence of BACS, the cooperative trajectories in the near zone satisfy all constraints, validating the efficacy of the proposed flight time coordination strategy. Driven by the goal of maximizing terminal velocity, each projectile adopts a maximum launching angle, with cooperative projectiles incorporating an increase in trajectory curvature, prolonging flight time, and enlarging the impact angle, resulting in terminal velocities exceeding 400 m/s, significantly surpassing the design threshold. The equilibrium angle of attack of the projectiles not only serves the objective function but also coordinates flight times. Consequently, projectiles with smaller artillery-target distances exhibit larger equilibrium angles of attack, and increased trajectory curvature and impact angles. Observation of Figure 13(d) reveals that projectile 1, with the smallest artillery-target distance, reaches control saturation during flight.

As shown in Figure 14, within the middle zone, the cooperative trajectories comply with all constraints under BACS, affirming the effectiveness of the proposed flight time coordination strategy. With objective functions balancing terminal velocity and control effort consumption, each projectile adopts a maximum launching angle. Cooperative projectiles employ increased trajectory height to minimize air resistance impact, sacrificing some terminal velocity to conserve control effort, yet still maintaining terminal velocities above the designed threshold of 200 m/s, with a reduced impact angle compared to flight schemes in the near zone. The equilibrium angle of attack of the projectiles serves both the objective function and flight time coordination, increasing with smaller artillery-target distances.

Figure 15 results indicate that in the near zone, cooperative trajectories meet all constraints under BACS, substantiating the proposed flight time coordination strategy's validity. Driven by minimizing control effort consumption, each projectile retains a maximum launching angle, employing higher trajectory heights to reduce air resistance impact. To ensure limited control capabilities cater to urgent range extension needs, terminal velocities are maintained at the design threshold, with further reduced impact angles compared to the mid zone, showcasing more pronounced gliding characteristics. The equilibrium angle of attack is pivotal for both serving the objective function and coordinating flight times, increasing with closer artillery-target distances.

Comparing results from Figures 13 to 15 suggests that in multi-artillery-simultaneous-launch scenarios, increasing the impact angle also can enhance terminal velocity but increases control effort consumption as well. Engineering applications should balance between velocity retention and control effort consumption.

To further validate the superiority of BACS, traditional DCS and proposed WDCS are employed for cooperative trajectory planning under identical conditions, with simulation results displayed in Table 5 (where a symbol × indicates planning failure).

Results from Table 5 indicate that within different zones, flight times coordinated using DCS are shorter compared to the strategy proposed in this paper. As observed in Figure 7(a), within the mid and far zones where there is a significant disparity in projectile ranges, the flight times coordinated by DCS exceed the capabilities of some projectiles, leading to planning failures. In the near zone, although feasible solutions were coordinated, the planning outcomes were suboptimal. WDCS, by employing a weighted averaging approach, accounts for the disparities in projectile ranges, thereby extending the coordinated flight times and enhancing the success rate of planning. However, from a performance indicator perspective, there is no apparent correlation between the duration of flight time and the quality of planning outcomes, and the flight times coordinated through weighted averaging are not optimal. The cooperative schemes planned using BACS outperform those by WDCS, demonstrating the superiority of BACS. In the near zone, where there is ample control margin for projectiles, the flight times coordinated by WDCS remain relatively conservative, failing to fully utilize the control capability of the projectile group, resulting in a terminal velocity 34.02 m/s lower compared to BACS. Beyond the near zone, since performance indicators consider the consumption of control effort, which requires integration over time t, the flight times coordinated by BACS turn out to be shorter. From a performance indicator standpoint, the advantages of BACS in the mid and far zones relative to WDCS are 84.72% and 25.30%, respectively. It should be noted that, to highlight the superiority of BACS, the examples in this paper involve substantial disparities in projectile ranges within harsh conditions, in actual applications for combat deployment, sufficient margins should be maintained.

4. Conclusions

This paper addresses the cooperative trajectory planning issue for weakly-maneuverable gliding-guided projectiles that attack a fixed target simultaneously. Aiming to fully utilize the limited control capabilities across the entire range to maximize overall efficiency, the effective range of gliding projectiles is refined, dividing the battlefield into 4 zones: the invalid zone, the near zone, the mid zone and the far zone. Considering the planning emphases in different zones, differentiated performance indicators are designed, and from this a zone-specific cooperative trajectory planning model is established. To enhance the planning success rate given the limitations in existing literatures on flight time coordination strategies applied to cooperative trajectory planning of gliding projectiles, improved ILFS and WDCS are proposed for scenarios involving single-artillery-multiple-shot and multi-artillery-simultaneous-launch scenarios, respectively. Furthermore, a BACS suitable for multi-phase planning problems that guarantees optimality is introduced. To rapidly determine combat formations and other operational deployments, a simple, universal method for determining the range of projectile cooperative capabilities is proposed. Using the multi-phase Radau pseudo-spectral method, numerical simulations were conducted based on these methods and strategies. The simulation results show that:

• Based on the proposed method for determining the range of projectile cooperative capabilities, feasible working conditions in different cooperation scenarios can be conveniently and effectively obtained, providing references for engineering applications.
• Compared to LFS and DCS in existing literatures, the flight times coordinated by the proposed ILFS and WDCS are within the capability range of most projectiles, offering higher compatibility to the problem. Therefore, ILFS and WDCS can ensure a high success rate even under stringent conditions, but due to the presence of manually designed coordination functions in the algorithms, optimality cannot be guaranteed.
• Under the influence of the proposed BACS, the cooperative flight times of projectiles are adaptively coordinated without manual intervention, ensuring optimality. Moreover, the flight phases of each projectile are independent of each other, enhancing flexibility and aiding in fully exploiting the control potential of the projectile group to achieve maximum efficiency. Consequently, BACS matches well with the study of weakly-maneuverable gliding-guided projectiles and the cooperative trajectory planning issues involving groups of projectiles.
• Increasing the impact angle helps to improve the terminal velocity of the projectiles, but also increases the consumption of control effort. In engineering applications, a trade-off should be made between terminal velocity and control effort consumption, with the pursuit of terminal velocity often coming at a higher cost.