Prerpints.org logo
Preprint
Article

Three-Dimensional Exploding Light Wave Packets

Altmetrics

Downloads

122

Views

50

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

22 May 2024

Posted:

23 May 2024

You are already at the latest version

Alerts
Abstract
We describe a family of paraxial and quasi-monochromatic optical wave packets with finite energy and smoothly shaped amplitude in space and time that develops a singularity in the intensity when spatiotemporally focused by imparting a converging spherical wave front and a negative temporal chirp. This singular behavior upon ideal focusing is manifested in actual focusing with finite apertures and in media with high-order dispersion in an "exploding" behavior featuring indefinitely increasing concentration of the energy when opening the aperture radius, thus exercising a continuous control on the focal intensity and spatial and temporal resolution. These wave packets offer a new way of focusing that outperforms what can be achieved with standard Gaussian wave packets in terms of focal intensity and resolution, and new possibilities in applications where energy concentration and its control are crucial.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

Structured light has gained attraction in the past decades, being now one of the central research directions in photonics. The ultimate goal is to explore all degrees of freedom of light to tailor arbitrary optical fields. In the basic scenario of monochromatic fields, complex amplitude and polarization manipulation is the domain of modern photonic technologies such as spatial light modulators [1], digital micromirror devices [2], metamaterials [3], etc. At its simplest, shaping amplitude and phase in a certain polarization state is essential to realize arbitrary scalar beams, where the vectorial feature of light plays no role. This is the case of the well known free-space eigenmodes such as Laguerre-Gaussian (LG) and Hermite-Gaussian beams [4], Airy beams [5], Ince-Gaussian beams [6] etc. By further combining orthogonal polarisation states, complex vector beams with inhomogeneous polarisation textures are obtained, such as radial/azimuthal cylindrical vector beams [7], full-Poincaré beams [8], optical skyrmions [9], etc.
The present work is in the broader context of spatio-temporal light shaping, which involves sculpturing the properties of light fields simultaneously in the spatial and temporal (spectral) domains. Compared to monochromatic fields, or space-time separable fields, non-separable spatio-temporal light fields feature radically different behaviours [10], which have been studied in various contexts such as toroidal electrodynamics and anapole radiation [11,12], spatio-temporal vortices [13,14], scalar hopfions [15], etc.
A recent trend in structured light are singular beams, initially monochromatic beam solutions of the Schrödinger equation for paraxial propagation in non-dispersive media that yield singular (infinite) focal intensity under ideal focusing conditions, mimicking focusing of a plane wave but with finite power. In this context, one-dimensional “concentrating" beams were first described in [16] and later observed in experiments in [17]. It was followed by two-dimensional exploding beams and vortex beams with cylindrical symmetry [18], and by their recently recent experimental realization using metasurfaces [19]. Although the singularity would appear only under ideal conditions, in real settings singular beams provide much larger peak intensities and finer spatial resolutions than other standard beams with the same power, which is of great interest in areas such as atom trapping [20], microscopy [21], material processing [22], etc. Indeed, concentrating the electromagnetic energy in minimal spots has been investigated since the invention of lasers and the development of beam shaping techniques [23], from binary optics [24], all the way to the present days with approaches such as superoscillatory fields [25]. Along with revolutionary pulse amplification techniques [26,27] with which modern pulsed laser systems have achieved powers up to 10 15 W and peak intensities of 10 23 W/cm2 [28], shaping the beam and pulse degrees of freedom is crucial to reach even larger levels.
In the present work we continue previous research on singular fields and extend the concept to the three-dimensional, spatiotemporal domain, describing what we call exploding wave packets (EWPs) with non-separable, spatiotemporal spherical symmetry. These EWPs are finite-energy analytical solutions to the paraxial diffraction integral, or to the linear Schrödinger equation in second-order dispersive media, that develop a singular (infinite) intensity when they are ideally spatiotemporally focused, i.e., focused spatially and compressed temporally. As for its predecessors, the ideal singularity disappears under real focusing conditions with finite apertures and in media with high-order dispersion. Nevertheless, the existence of the ideal singularity has physical manifestations such as a continuous increase of the focal intensity and a continuous diminution of the transversal spot size with increasing aperture radius that makes them to arbitrarily improve the focusing capabilities of standard Gaussian wave packets under similar conditions of peak intensity and energy. High-order dispersion sets a limit to the minimum duration; nevertheless this duration is substantially smaller than that achievable with Gaussian pulses.
Note that, as with preceding singular beams [16,17,18,19], we do not resort here to strong, non-paraxial focusing with large numerical apertures, but focus, however redundant, on paraxial focusing to emphasize the focusing properties of the spatiotemporally shaped exploding profile itself through its analytical properties. In fact, all our examples are fully paraxial. As pointed out in [19], non-paraxial focusing of exploding beams yields even stronger concentration of energy.

2. Methods

2.1. Propagation of Spatiotemporal Symmetric Wave Packets in Dispersive Media

We consider a quasi-monochromatic pulsed beam E = ψ e − i ω 0 t + i k 0 z of carrier frequency ω 0 and propagating along the z direction, whose complex envelope ψ is governed by the Schrödinger equation
∂ ψ ∂ z = i 2 k 0 Δ ⊥ ψ − i k 0 ″ 2 ∂ 2 ψ ∂ t ′ 2 ,
where Δ ⊥ = ∂ 2 / ∂ x 2 + ∂ 2 / ∂ y 2 , k 0 is the propagation constant at the carrier frequency, k 0 ′ ′ is the GVD, t ′ is the local time t ′ = t − k 0 ′ z , and 1 / k 0 ′ is the group velocity. Assuming anomalous dispersion ( k 0 ′ ′ < 0 ), we introduce the time τ = t ′ / k 0 | k 0 ′ ′ | with units of length, and Eq. (1) becomes
∂ ψ ∂ z = i 2 k 0 ∂ 2 ψ ∂ x 2 + ∂ 2 ψ ∂ y 2 + ∂ 2 ψ ∂ τ 2 ,
The propagator of Eq. (2) that yields the propagated envelope of an arbitrary illumination ψ ( x ′ , y ′ , τ ′ , 0 ) has a well-known analogous in the quantum mechanics of a free particle, and reads here as a Fresnel diffraction integral generalized to three dimensions,
ψ ( x , y , τ , z ) = k 0 2 π i z 3 / 2 ∫ R 3 ψ ( x ′ , y ′ , τ ′ , 0 ) e i k 0 2 z ( x − x ′ ) 2 + ( y − y ′ ) 2 + ( τ − τ ′ ) 2 d x ′ d y ′ d τ ′ = k 0 2 π i z 3 / 2 e i k 0 2 z ( x 2 + y 2 + τ 2 ) × ∫ R 3 ψ ( x ′ , y ′ , τ ′ , 0 ) e − i k 0 z ( x x ′ + y y ′ + τ τ ′ ) e i k 0 2 z ( x ′ 2 + y ′ 2 + τ ′ 2 ) d x ′ d y ′ d τ ′ .
We consider wave packets whose complex envelope only depends on r = ( x 2 + y 2 + τ 2 ) 1 / 2 , which we will call spatiotemporal spherically symmetric wave packet. For these wave packets the Schrödinger equation (2) can be written as
∂ ψ ∂ z = i 2 k 0 1 r 2 ∂ ∂ r r 2 ∂ ψ ∂ r ,
which in particular implies that this symmetry is preserved on propagation. The propagator in Eq. (3) can be accordingly simplified. We introduce spatiotemporal spherical coordinates x = r sin ϕ cos θ , y = r sin ϕ sin θ and τ = r cos ϕ , (and similar for x ′ , y ′ and τ ′ ) to rewrite Eq. (3) as
ψ ( r , z ) = k 0 2 π i z 3 / 2 e i k 0 2 z r 2 ∫ 0 ∞ ψ ( r ′ , 0 ) e i k 0 2 z r ′ 2 r ′ 2 d r ′ ∫ 0 π e − i k 0 z r r ′ cos ϕ cos ϕ ′ sin ϕ ′ d ϕ ′ × ∫ 0 2 π e − i k 0 z r r ′ sin ϕ sin ϕ ′ cos ( θ − θ ′ ) d θ ′ .
The integral in θ ′ is 2 π J 0 k 0 r r ′ sin ϕ sin ϕ ′ / z , where J 0 ( · ) is the Bessel function of the first kind and order zero, which introduced in Eq. (5) gives
ψ ( r , z ) = 2 π k 0 2 π i z 3 / 2 e i k 0 2 z r 2 ∫ 0 ∞ ψ ( r ′ , 0 ) e i k 0 2 z r ′ 2 r ′ 2 d r ′ × ∫ 0 π e − i k 0 z r r ′ cos ϕ cos ϕ ′ J 0 k 0 r r ′ z sin ϕ sin ϕ ′ sin ϕ ′ d ϕ ′ .
In the last integral, only the cosine of the exponential contributes. Since the spatiotemporal symmetry is preserved, the integral in ϕ ′ must be independent of ϕ , and it can conveniently be evaluated with ϕ = 0 , i.e.,
∫ 0 π cos k 0 z r r ′ cos ϕ ′ sin ϕ ′ d ϕ ′ = 2 z k 0 r r ′ sin k 0 r r ′ z .
Introducing Eq. (7) into Eq. (6) we obtain
ψ ( r , z ) = 4 π k 0 2 π i z 3 2 e i k 0 r 2 2 z ∫ 0 ∞ ψ ( r ′ , 0 ) e i k 0 2 z r ′ 2 sin c k 0 r r ′ z r ′ 2 d r ′
where sin c α ≡ sin α / α , and provides the simplified form of the propagator for spatiotemporal spherically symmetric wave packets in the dispersive medium.
Let us choose ψ ( r , 0 ) = ψ ( r ) e − i k 0 r 2 / 2 f , where ψ ( r ) is real. Displaying the exponential e − i k 0 r 2 / 2 f as e − i k 0 r 2 / 2 f = e − i k 0 ( x 2 + y 2 ) / 2 f e − i t ′ 2 / 2 f | k 0 ′ ′ | it is evident that ψ ( r ) e − i k 0 r 2 / 2 f represents focusing spatiotemporally the illumination ψ ( r ) with focal length f > 0 and a negative chirp − 1 / 2 f | k 0 ′ ′ | in such a way that the spatiotemporal spherical symmetry is preserved. Equation (8) then becomes
ψ ( r , z ) = 4 π k 0 2 π i z 3 2 e i k 0 r 2 2 z ∫ 0 ∞ ψ ( r ′ ) e i k 0 2 r ′ 2 1 z − 1 f sin c k 0 r r ′ z r ′ 2 d r ′ ,
and at the focal plane z = f ,
ψ ( r , f ) = 4 π k 0 2 π i f 3 2 e i k 0 r 2 2 f ∫ 0 ∞ ψ ( r ′ ) sin c k 0 r r ′ f r ′ 2 d r ′ ,
which provides the spatiotemporal focused field.

2.2. Exploding Wave Packets

Let the illuminating wave packet be
ψ ( r ) = E C 1 1 + r 2 / β 2 μ + 1 / 2 = E C 1 1 + ( x 2 + y 2 ) / β 2 + t ′ 2 / ( k 0 | k 0 ′ ′ | β 2 ) μ + 1 / 2 ,
where β determines the spatial size and temporal duration Δ t = k 0 | k 0 ′ ′ | β . If μ > 1 / 4 then the energy of this wave packet is finite. If we choose C = k 0 | k 0 ′ ′ | π 3 / 2 β 3 Γ ( 2 μ − 1 / 2 ) / Γ ( 2 μ + 1 ) in Eq. (11), where Γ ( · ) is the gamma function, it can be readily seen that E also in Eq. (11) coincides with the finite energy carried by the wave packet, i.e., E = ∫ d x d y d t ′ | ψ | 2 = 4 π k 0 k 0 ″ ∫ 0 ∞ d r r 2 | ψ ( r ) | 2 . Equation (11) into Eq. (10) yields the optical disturbance at the focal plane. The resulting integral can be performed analytically by using integral 3.251.2 in Ref. [29], obtaining, after some algebra,
ψ ( r , f ) = E C β μ + 2 2 π 1 i r 3 2 e i k 0 r 2 2 f k 0 r 2 f μ + 1 2 cos ( π μ ) Γ 1 2 − μ K 1 − μ k 0 β r f ,
where K ν ( · ) is the modified Bessel function of the second kind and order ν . Considering the asymptotic behaviour of K ν ( α ) ≃ ( 1 / 2 ) Γ ( ν ) ( α / 2 ) − ν for small values of α , the field at the focus r = 0 is seen to present a singularity, ψ → ∞ when r → 0 , if μ < 1 . In short, if we take the parameter μ in the range
1 / 4 < μ < 1 ,
the input illumination in Eq. (11) carries finite energy and produces a focused field with infinite intensity at the focus. Note that for μ = 1 / 2 , the singularity of the gamma function is removed by the zero of the cosine; indeed cos ( π μ ) Γ ( 1 / 2 − μ ) = π for μ = 1 / 2 . In addition, use of K 1 / 2 ( α ) = π / ( 2 α ) e − α leads to the simpler expression
ψ ( r , f ) = E C β 2 ( − i ) 3 / 2 π k 0 2 f e i k 0 r 2 2 f 1 r e − k 0 β r f
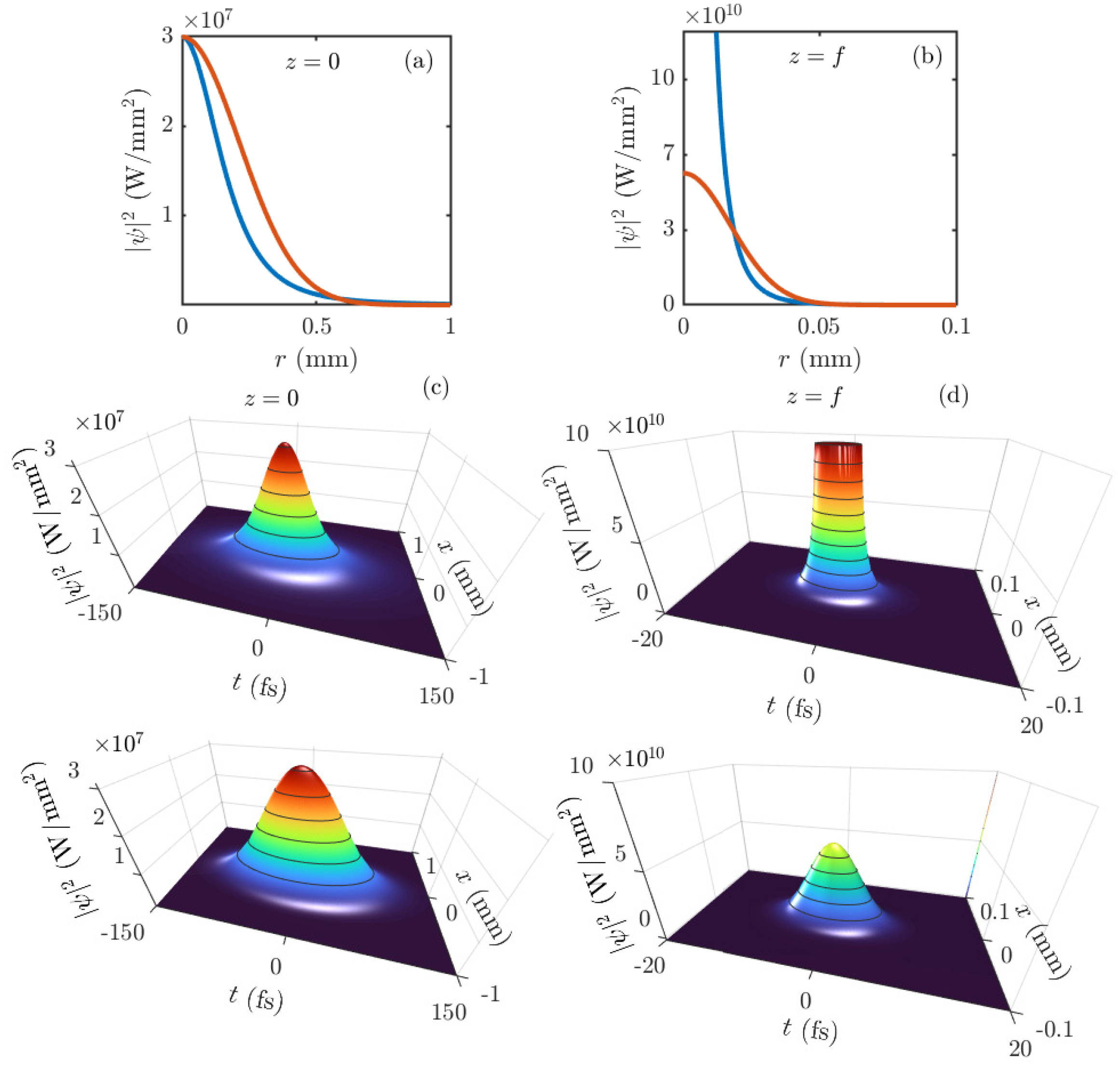
for μ = 1 / 2 . Figure 1(a) and (b) show an example of the EWP spatiotemporal radial profile in Eq. (11) at z = 0 and the focal plane in Eq. (14), respectively, in fused silica at a wavelength with anomalous dispersion. How it looks in real space-time is shown in Figure 1(c) and (d). They are compared with spatiotemporal spherically symmetric Gaussian wave packets of the same peak intensity and energy, ψ = E / C e − r 2 / w 2 e − i k 0 r 2 / 2 f , that are spatiotemporally focused in the same way, where the choice w 3 = 4 C / k 0 | k 0 ′ ′ | 2 π 3 equates the energies.
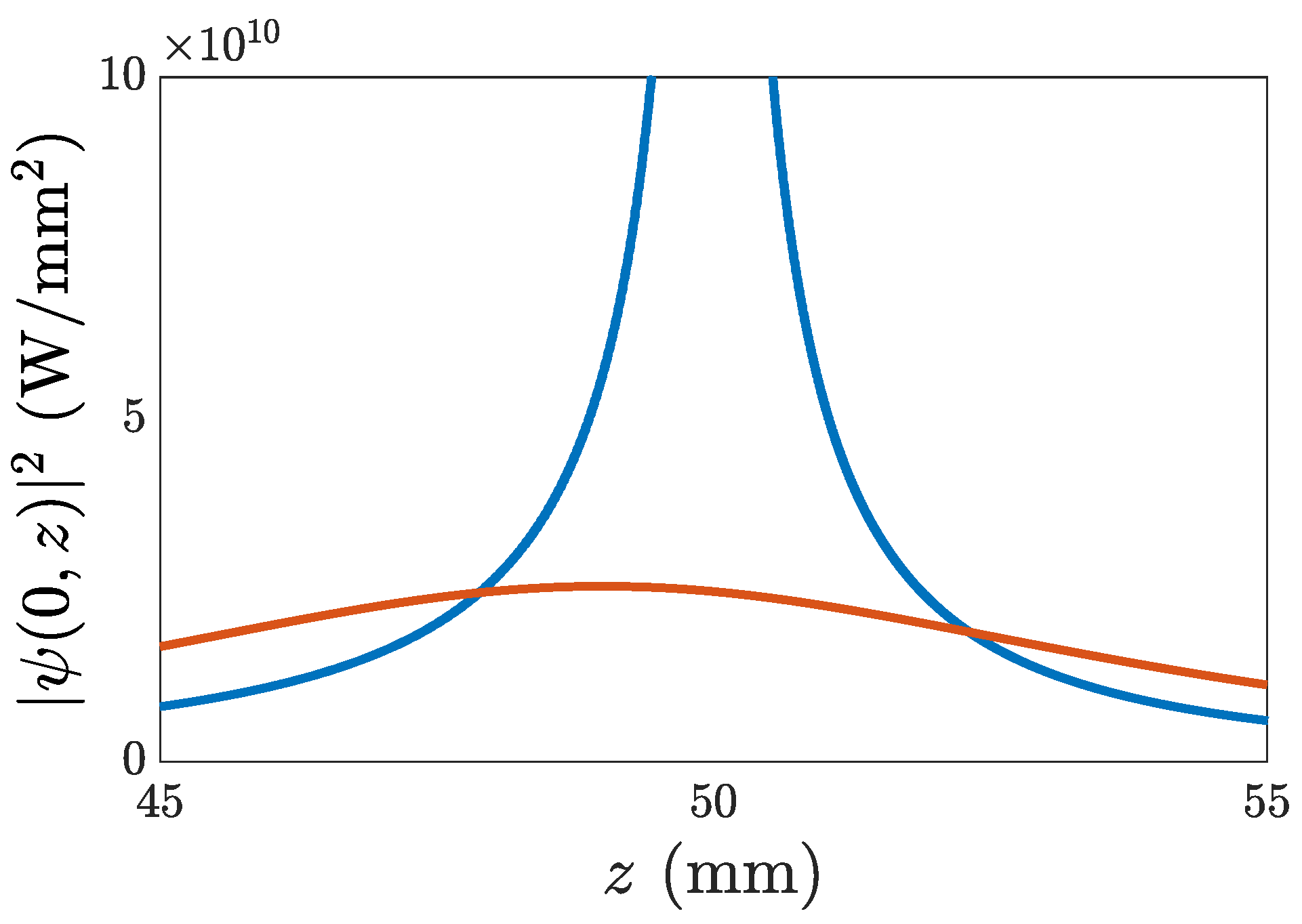
Figure 2 shows the on-axis intensity as it grows up to infinity to verify that the singularity is only formed at the focal plane, and to compare it with the on-axis intensity of the Gaussian wave packet of the same intensity and energy. We note that for the chosen parameters, there is a small focal shift for the Gaussian wave packet. The on-axis intensity of the EWP is also slightly asymmetric, but the singularity is only formed at the focal plane z = f .

3. Results

Of course the singularity is not observed in any real setting with a finite aperture. Also, high-order material dispersion has to be properly taken into account when the pulse shrinks in time without bound during propagation. However, the theoretical existence of the singularity has physical, observable consequences that makes EWPs to feature unconventional focusing properties. With increasing aperture, the peak intensity grows without bound towards the ideal singularity, and the transversal size diminishes without bound, always outperforming the focusing capabilities of standard, Gaussian-like wave packets, since the latter do not experience any change as the aperture increases above a certain value. Third and high-order dispersion sets a limit to the minimum achievable duration, but still our particular non-separable, spatiotemporal profile produces at the focus a pulse shape of significant shorter duration than a Gaussian pulse.
The circular aperture and high-order dispersion break the spatiotemporal spherical symmetry of the exploding illumination, and only cylindrical symmetry in space remains. To take into account their effects properly, we consider the temporal frequency spectrum E ^ ( ρ , ω , 0 ) = ( 1 / 2 π ) ∫ − ∞ ∞ E ( ρ , t , 0 ) e i ω t d t of the exploding illumination E ( ρ , t , 0 ) = ψ ( ρ , t , 0 ) e − i ω 0 t ,
ψ ( ρ , t , 0 ) = E C 1 1 + ρ 2 / β 2 + t 2 / ( k 0 | k 0 ′ ′ | β 2 ) μ + 1 / 2 e − i t 2 / 2 f | k 0 ″ | ,
where ρ = x 2 + y 2 , including the temporal chirp. Then we propagate each frequency from the focusing lens of finite radius R towards the focus as described by Fresnel diffraction integral for cylindrically symmetric beams [18] with the exact propagation constant k ( ω ) = n ( ω ) ( ω / c ) , where n ( ω ) is the refractive index of the medium, namely,
E ^ ( ρ , ω , z ) = e i k ( ω ) z k ( ω ) i z e i k ( ω ) ρ 2 2 z ∫ 0 R d ρ ′ ρ ′ E ^ ( ρ ′ , ω , 0 ) e i k ( ω ) ρ ′ 2 2 1 z − 1 f J 0 k ( ω ) ρ ρ ′ z ,
where focusing of each monochromatic component is accounted for by the factor e − i k ( ω ) ρ ′ 2 2 f , and then come back to time domain E ( ρ , t , z ) = ∫ − ∞ ∞ E ^ ( ρ , ω , z ) e − i ω t d ω .
For numerical computation it is convenient to evaluate the envelope ψ ( ρ , t ′ , z ) of E ( ρ , t , z ) = ψ ( ρ , t ′ , z ) e − i ω 0 t + i k 0 z in the local time, given by ψ ( ρ , t ′ , z ) = ∫ − ∞ ∞ d Ω ψ ^ ( ρ , Ω , z ) e − i Ω t ′ , where Ω = ω − ω 0 ,
ψ ^ ( ρ , Ω , z ) = e i [ k ( ω 0 + Ω ) − k 0 − k 0 ′ Ω ] z k ( ω 0 + Ω ) i z e i k ( ω 0 + Ω ) ρ 2 2 z × ∫ 0 R d ρ ′ ρ ′ ψ ^ ( ρ ′ , Ω , 0 ) e i k ( ω 0 + Ω ) ρ ′ 2 2 1 z − 1 f J 0 k ( ω 0 + Ω ) ρ ρ ′ z ,
and ψ ^ ( ρ , Ω , 0 ) = ( 1 / 2 π ) ∫ − ∞ ∞ d t ψ ( ρ , t , 0 ) e i Ω t .

3.1. Manifestations of the Singular Behaviour in Real Settings

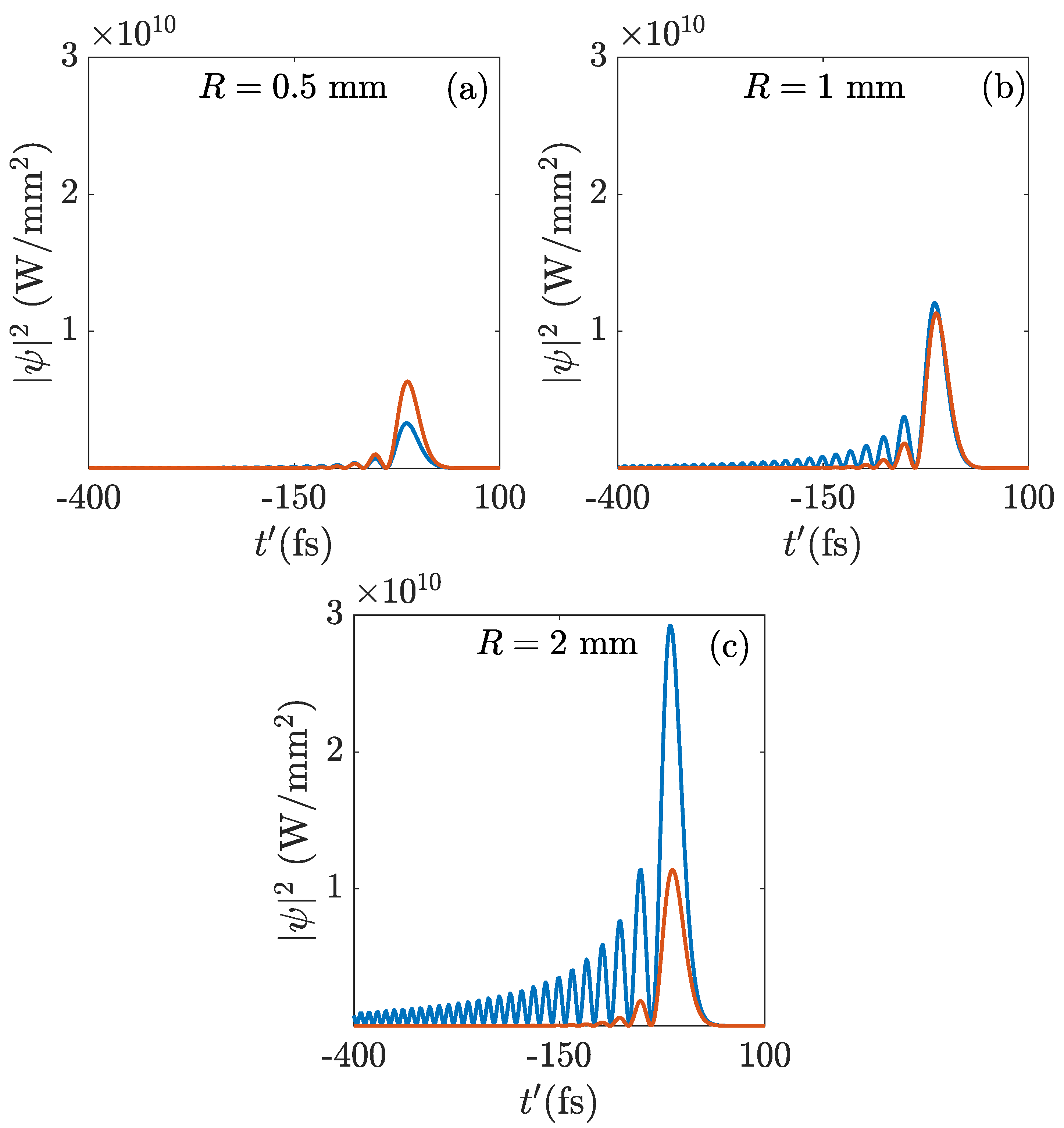
Figure 3 shows focal [ ( ρ , z ) = ( 0 , f ) ] pulse temporal shapes of an EWP (blue curves) and a Gaussian (orange) wave packets of the same peak intensity on the focusing system and carrying the same energy. From Figure 3(a) to Figure 3(c) the aperture radius increases. For strong the aperture truncation in (a) the peak intensity of the Gaussian wave packet is higher than that of the EWP since its tails are completely removed. As the aperture radius increases, larger volumes of the low, widespread EWP periphery is encircled and contributes to the focal intensity, which grows without bound and surpasses the peak intensity produced by the Gaussian wave packet, which does not experience any change in this process above a certain aperture radius. It is important to notice that the finiteness of the energy, or mathematically, the convergence of the integral E = ∫ d x d y d t ′ | ψ | 2 for the EWP, implies that the encircled energy does not significantly change when opening the aperture above several times β . The increase of the peak intensity originates instead from the constructive interference effect of the enlarging encircled EWP periphery carrying nevertheless increasingly negligible energy.
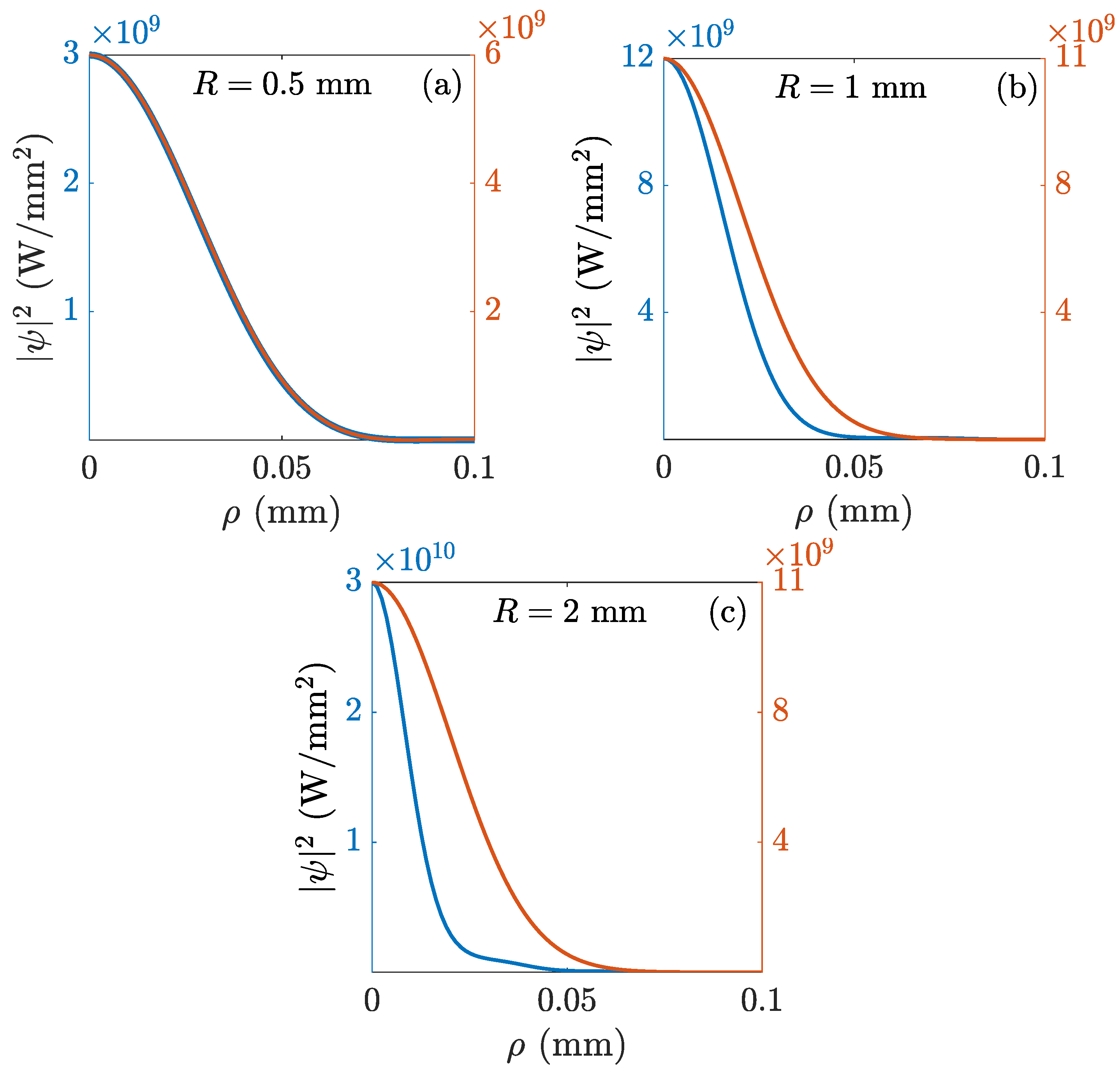
As another manifestation of the mathematical singularity on the focal concentration of the energy, we show in Figure 4 the transverse radial profiles of the same EWP and Gaussian wave packet at the instants of time of maximum intensity seen in Figure 3. The peak intensities have been equated for a better comparison of the widths. As the radius of the aperture increases, the EWP always becomes more and more concentrated radially at the focal plane, while increasing the aperture radius has no effect on the concentration of the Gaussian wave packet above a certain value.

4. Discussion and Conclusions

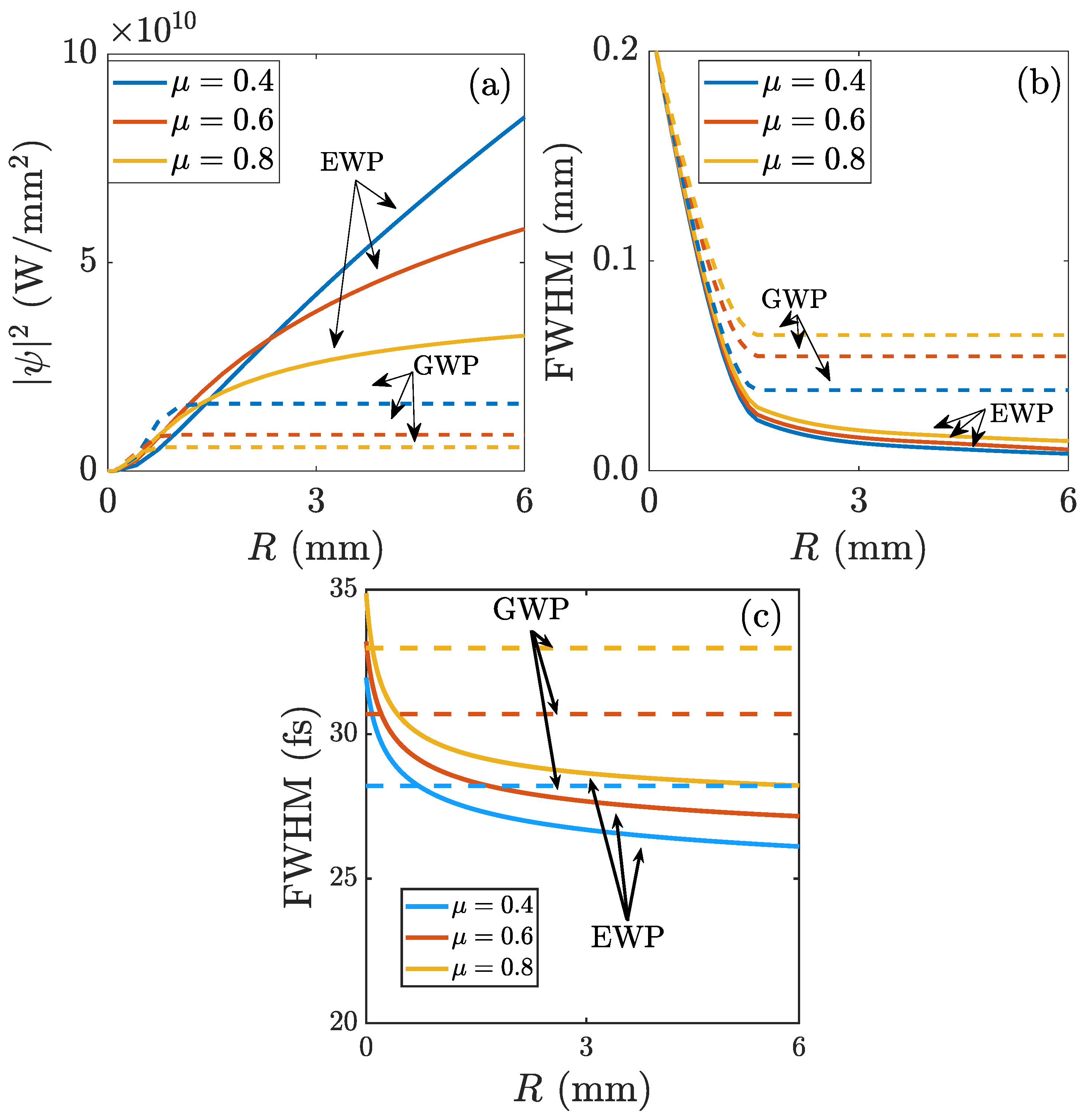
As a summary of the above properties, Figure 5 (a) and (b) represent the focal peak intensity and transversal size of EWPs with different values of the decaying parameter μ as functions of the aperture radius R (solid curves), compared to the same properties for standard Gaussian wave packets of the same peak intensity on the focusing system and the same energy. The slower the EWP decays (smaller μ ), the easier it is to achieve higher peak intensity and smaller width.
Also, Figure 5 (c) shows the pulse duration at the focus [ ( ρ , z ) = ( 0 , f ) ] as a function of the aperture radius R. As already seen in Figure 3, high-order dispersion, particularly third-order dispersion, sets a limit to the minimum achievable duration when increasing the aperture radius, which does not approach zero but a constant value, as for the Gaussian wave packets. However, also as a manifestation of the particular EWP profile, this minimum duration is seen in Figure 5 (c) to be significantly smaller than the minimum duration achievable with the Gaussian wave packets of the same peak intensity and energy.
In conclusion, we have described a spatiotemporal light wave packet carrying finite energy, and therefore a physically realizable wave packet, that ideally develops a singularity in its intensity when focused in space and time in a medium with anomalous group velocity dispersion, and have studied the real-world manifestations of such a singular behavior. The concentration of the focused energy can be increased as desired with the same illuminating wave packet just by increasing the aperture radius of the focusing system. In contrast to previous works, the concentration of the energy takes place in all dimensions, i.e., ( x , y , t ′ ) , or equivalently, ( x , y , z ) .
The spontaneous development of a singularity resembles the phenomenon of collapse in nonlinear Kerr-type media. However, this phenomenon occurs here in a linear medium, and therefore occurs independently of the energy of the wave packet. In fact, the exploding wave packet is a solution of the linear Schrödinger equation in three dimensions, and as such the same wave packet is of interest not only in optics but in other of fields of physics such as quantum mechanics or acoustics.

Acknowledgments

This work has been partially supported by the Spanish Ministry of Science and Innovation, Gobierno de España, under Contract No. PID2021-122711NB-C21. P.L. and M.H. acknowledge support from Grant No. D480 (Beca de colaboración de formación) of the Universidad Politécnica de Madrid.

Author Contributions

All authors contributed equally to this work

Funding

Spanish Ministry of Science and Innovation, Gobierno de España, Contract No. PID2021-122711NB-C21.

Data Availability Statement

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Efron, U. Spatial light modulator technology: materials, devices, and applications; Vol. 47, CRC press, 1994.
  2. Hu, X.B.; Rosales-Guzmán, C. Generation and characterization of complex vector modes with digital micromirror devices: a tutorial. Journal of Optics 2022, 24, 034001. [Google Scholar] [CrossRef]
  3. Brener, I.; Liu, S.; Staude, I.; Valentine, J.; Holloway, C. Dielectric metamaterials: fundamentals, designs and applications; Woodhead publishing, 2019.
  4. Saleh, B.E.; Teich, M.C. Fundamentals of photonics; john Wiley & sons, 2019.
  5. Siviloglou, G.; Broky, J.; Dogariu, A.; Christodoulides, D. Observation of accelerating airy beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef] [PubMed]
  6. Bandres, M.A.; Gutiérrez-Vega, J.C. Ince–gaussian beams. Optics letters 2004, 29, 144–146. [Google Scholar] [CrossRef] [PubMed]
  7. Zhan, Q. Cylindrical vector beams: from mathematical concepts to applications. Advances in Optics and Photonics 2009, 1, 1–57. [Google Scholar] [CrossRef]
  8. Beckley, A.M.; Brown, T.G.; Alonso, M.A. Full poincaré beams. Optics express 2010, 18, 10777–10785. [Google Scholar] [CrossRef] [PubMed]
  9. Shen, Y.; Zhang, Q.; Shi, P.; Du, L.; Yuan, X.; Zayats, A.V. Optical skyrmions and other topological quasiparticles of light. Nature Photonics 2024, 18, 15–25. [Google Scholar] [CrossRef]
  10. Shen, Y.; Zhan, Q.; Wright, L.G.; Christodoulides, D.N.; Wise, F.W.; Willner, A.E.; Zou, K.h.; Zhao, Z.; Porras, M.A.; Chong, A.; others. Roadmap on spatiotemporal light fields. Journal of Optics 2023, 25, 093001. [Google Scholar] [CrossRef]
  11. Papasimakis, N.; Fedotov, V.; Savinov, V.; Raybould, T.; Zheludev, N. Electromagnetic toroidal excitations in matter and free space. Nature materials 2016, 15, 263–271. [Google Scholar] [CrossRef] [PubMed]
  12. Zdagkas, A.; McDonnell, C.; Deng, J.; Shen, Y.; Li, G.; Ellenbogen, T.; Papasimakis, N.; Zheludev, N.I. Observation of toroidal pulses of light. Nature Photonics 2022, 16, 523–528. [Google Scholar] [CrossRef]
  13. Wan, C.; Chong, A.; Zhan, Q. Optical spatiotemporal vortices. eLight 2023, 3, 11. [Google Scholar] [CrossRef]
  14. Martín-Hernández, R.; Gui, G.; Plaja, L.; Kapteyn, H.K.; Murnane, M.M.; Porras, M.A.; Liao, C.T.; Hernández-García, C. Generation of high-order harmonic spatiotemporal optical vortices. High Intensity Lasers and High Field Phenomena. Optica Publishing Group, 2024, pp. HW5A–6.
  15. Wan, C.; Shen, Y.; Chong, A.; Zhan, Q. Scalar optical hopfions. eLight 2022, 2, 22. [Google Scholar] [CrossRef]
  16. Aiello, A. Spontaneous generation of singularities in paraxial optical fields. Opt. Lett. 2016, 41, 1668–1671. [Google Scholar] [CrossRef] [PubMed]
  17. Aiello, A.; Paúr, M.; Stoklasa, B.; Hradil, Z.; Řeháček, J.; Sánchez-Soto, L.L. Observation of concentrating paraxial beams. OSA Continuum 2020, 3, 2387–2394. [Google Scholar] [CrossRef]
  18. Porras, M.A. Exploding paraxial beams, vortex beams, and cylindrical beams of light with finite power in linear media, and their enhanced longitudinal field. Phys. Rev. A 2021, 103, 033506. [Google Scholar] [CrossRef]
  19. Mata-Cervera, N.; Sharma, D.; Veetil, R.; Mass, T.; Porras, M.; Paniagua-Dominguez, R. Observation of exploding vortex beams generated by amplitude and phase all-dielectric metasurfaces. ACS Photonics 2024. [Google Scholar]
  20. Yang, Y.; Ren, Y.X.; Chen, M.; Arita, Y.; Rosales-Guzmán, C. Optical trapping with structured light: a review. Adv. Photonics 2021, 3, 034001–034001. [Google Scholar] [CrossRef]
  21. Laskin, A.; Kaiser, P.; Laskin, V.; Ostrun, A. Laser beam shaping for biomedical microscopy techniques. Biophotonics: Photonic Solutions for Better Health Care V. SPIE, 2016, Vol. 9887, pp. 251–260.
  22. Dunsky, C.M. Beam shaping applications in laser micromachining for the microelectronics industry. Laser Beam Shaping II. SPIE, 2001, Vol. 4443, pp. 135–149.
  23. Dickey, F.M.; Lizotte, T. Laser beam shaping applications; Vol. 1, Crc Press, 2017.
  24. Wang, H.; Shi, L.; Lukyanchuk, B.; Sheppard, C.; Chong, C.T. Creation of a needle of longitudinally polarized light in vacuum using binary optics. Nature photonics 2008, 2, 501–505. [Google Scholar] [CrossRef]
  25. Rivy, H.M.; Aljunid, S.A.; Lassalle, E.; Zheludev, N.I.; Wilkowski, D. Single atom in a superoscillatory optical trap. Communications Physics 2023, 6, 155. [Google Scholar] [CrossRef]
  26. Strickland, D.; Mourou, G. Compression of amplified chirped optical pulses. Optics communications 1985, 55, 447–449. [Google Scholar] [CrossRef]
  27. Maine, P.; Strickland, D.; Bado, P.; Pessot, M.; Mourou, G. Generation of ultrahigh peak power pulses by chirped pulse amplification. IEEE Journal of Quantum electronics 1988, 24, 398–403. [Google Scholar] [CrossRef]
  28. Yoon, J.W.; Kim, Y.G.; Choi, I.W.; Sung, J.H.; Lee, H.W.; Lee, S.K.; Nam, C.H. Realization of laser intensity over 1023 W/cm2. Optica 2021, 8, 630–635. [Google Scholar] [CrossRef]
  29. Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; 1994.
Preprints 107196 g001
Figure 1. EWP at ω 0 = 1.4 rad/fs ( λ 0 = 1.346 μ m) ideally focused in fused silica ( k 0 = 6754 mm−1, k 0 ′ = 4876 fs mm−1, k 0 ′ ′ = − 6.508 fs1 mm−1). (a) Spatiotemporal radial intensity profile of the EWP (blue) with β = 0.25 mm and μ = 1 / 2 , and of Gaussian wave packet (orange) with w = 0.428 mm of the same peak intensity and energy E = 1 μ J. (b) Their focused intensity profiles with f = 50 mm. (c) The same EWP (top) and Gaussian wave packet (bottom) in space and real time, of width of duration Δ t = k 0 | k 0 ′ ′ | β = 104.8 fs. (d) Their focused intensity profiles.
Figure 1. EWP at ω 0 = 1.4 rad/fs ( λ 0 = 1.346 μ m) ideally focused in fused silica ( k 0 = 6754 mm−1, k 0 ′ = 4876 fs mm−1, k 0 ′ ′ = − 6.508 fs1 mm−1). (a) Spatiotemporal radial intensity profile of the EWP (blue) with β = 0.25 mm and μ = 1 / 2 , and of Gaussian wave packet (orange) with w = 0.428 mm of the same peak intensity and energy E = 1 μ J. (b) Their focused intensity profiles with f = 50 mm. (c) The same EWP (top) and Gaussian wave packet (bottom) in space and real time, of width of duration Δ t = k 0 | k 0 ′ ′ | β = 104.8 fs. (d) Their focused intensity profiles.
Preprints 107196 g001
Preprints 107196 g002
Figure 2. On-axis intensity of the same EWP (blue) and Gaussian wave packet (orange) as in Figure 1 as functions of propagation distance z.
Figure 2. On-axis intensity of the same EWP (blue) and Gaussian wave packet (orange) as in Figure 1 as functions of propagation distance z.
Preprints 107196 g002
Preprints 107196 g003
Figure 3. EWP at ω 0 = 1.2 rad/fs ( λ 0 = 1.57 μ m) focused in fused silica modelled by a Sellmeier relation with three resonances. Comparison between the temporal shape at the focus of the EWP with μ = 1 / 2 and β = 0.25 (blue) and a Gaussian wave packet (orange) of the same initial peak intensity and the same energy with ( w = 0.428 mm) when the raddi of the aperture are R = 0.5 mm (a), R = 1 mm (b) and R = 2 mm (c).
Figure 3. EWP at ω 0 = 1.2 rad/fs ( λ 0 = 1.57 μ m) focused in fused silica modelled by a Sellmeier relation with three resonances. Comparison between the temporal shape at the focus of the EWP with μ = 1 / 2 and β = 0.25 (blue) and a Gaussian wave packet (orange) of the same initial peak intensity and the same energy with ( w = 0.428 mm) when the raddi of the aperture are R = 0.5 mm (a), R = 1 mm (b) and R = 2 mm (c).
Preprints 107196 g003
Preprints 107196 g004
Figure 4. EWPs at ω 0 = 1.2 rad/fs ( λ = 1.57 μ m) focused in fused silica modelled by a Sellmeier relation with three resonances. Comparison between the radial profiles at the focal plane at instant of time of maximum intensity of the EWP with μ = 0.5 and β = 0.25 (blue) and of the Gaussian wave packet (orange) of the same initial peak intensity and energy when the aperture radii are R = 0.5 mm (a), R = 1 mm (b) and R = 2 mm (c).
Figure 4. EWPs at ω 0 = 1.2 rad/fs ( λ = 1.57 μ m) focused in fused silica modelled by a Sellmeier relation with three resonances. Comparison between the radial profiles at the focal plane at instant of time of maximum intensity of the EWP with μ = 0.5 and β = 0.25 (blue) and of the Gaussian wave packet (orange) of the same initial peak intensity and energy when the aperture radii are R = 0.5 mm (a), R = 1 mm (b) and R = 2 mm (c).
Preprints 107196 g004
Preprints 107196 g005
Figure 5. Properties of EWPs at ω 0 = 1.2 rad/fs ( λ = 1.57 μ m) and β = 0.25 mm focused in fused silica modelled by a Sellmeier relation with three resonances. (a) Peak intensity for the indicated values of the decay parameter μ as a function of the radius of the aperture R, compared to the same property for Gaussian wave packets of the same peak intensity and energy. (b) Radial FWHM of the same EWPs and Gaussian wave packets as functions of R. (c) Temporal FWHM of the EWPs and Gaussian wave packets as functions of R.
Figure 5. Properties of EWPs at ω 0 = 1.2 rad/fs ( λ = 1.57 μ m) and β = 0.25 mm focused in fused silica modelled by a Sellmeier relation with three resonances. (a) Peak intensity for the indicated values of the decay parameter μ as a function of the radius of the aperture R, compared to the same property for Gaussian wave packets of the same peak intensity and energy. (b) Radial FWHM of the same EWPs and Gaussian wave packets as functions of R. (c) Temporal FWHM of the EWPs and Gaussian wave packets as functions of R.
Preprints 107196 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated