Phase portraits of a class of Liénard equations

Preprint

Article

Phase portraits of a class of Liénard equations

Altmetrics

Downloads

144

Views

Comments

Rachid Cheurfa,

Jaume Llibre^*,Ahmed Bendjeddou

Rachid Cheurfa,

Jaume Llibre^*,Ahmed Bendjeddou

This version is not peer-reviewed

Submitted:

23 May 2024

Posted:

24 May 2024

You are already at the latest version

Alerts

Abstract

Recently several papers have been published on the Liénard equation x'' +L x+m x^3+n x^5=0, where the authors studied their explicit solutions and their applications. Here we describe the complete dynamics of these differential equations in the Poincar\'e disc. The Poincar\'e disc is the closed disc centered at the origin of coordinates of radius one, the whole plane R^2 is identified with the interior of this disc, and its boundary, the circle $\sss^1$ is identified with the infinity of R^2.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

1. Introduction and Statement of the Main Result

The differential Liénard equation of second order

\ddot{x} + ℓ x + m x^{3} + n x^{5} = 0,

(1)

or its equivalent differential system of first order

\begin{matrix} \dot{x} = y, \\ \dot{y} = - ℓ x - m x^{3} - n x^{5}, \end{matrix}

(2)

with

n \neq 0

has been studied in [4,5,6,11]. Kong in [6] was the first in consider the differential equation (1) in 1994. He studied their explicit solutions and applies these to the Rangwala-Rao differential equation, the Ablowitz differential equation and the Gerdjikov-Ivanov differential equation.

Later on Feng in [4,5] and Sun et al. in [11] continue studying some explicit solutions of the differential equation (1) and they apply them to the nonlinear Schrödinger differential equation and the Pochhammer-Chree differential equation.

The objective of this paper is to describe the complete dynamics of the differential system (2) in the Poincaré disc, see subSection 2.3 for details on the Poincaré compactification.

We note that the differential system (2) is invariant under the symmetries

(x, y, t) \to (- x, y, - t)

and

(x, y, t) \to (x, - y, - t)

. The first symmetry says that the phase portrait of the system is symmetric with respect to the y-axis, and the second one with respect to the x-axis. Therefore knowing the phase portrait of the differential system in the closed positive quadrant of the plane

R^{2}

, it is sufficient for determining the whole phase portrait of the system.

Our main result is the following theorem where we describe all topological distinct phase portraits of the differential system (2) in the Poincaré disc.

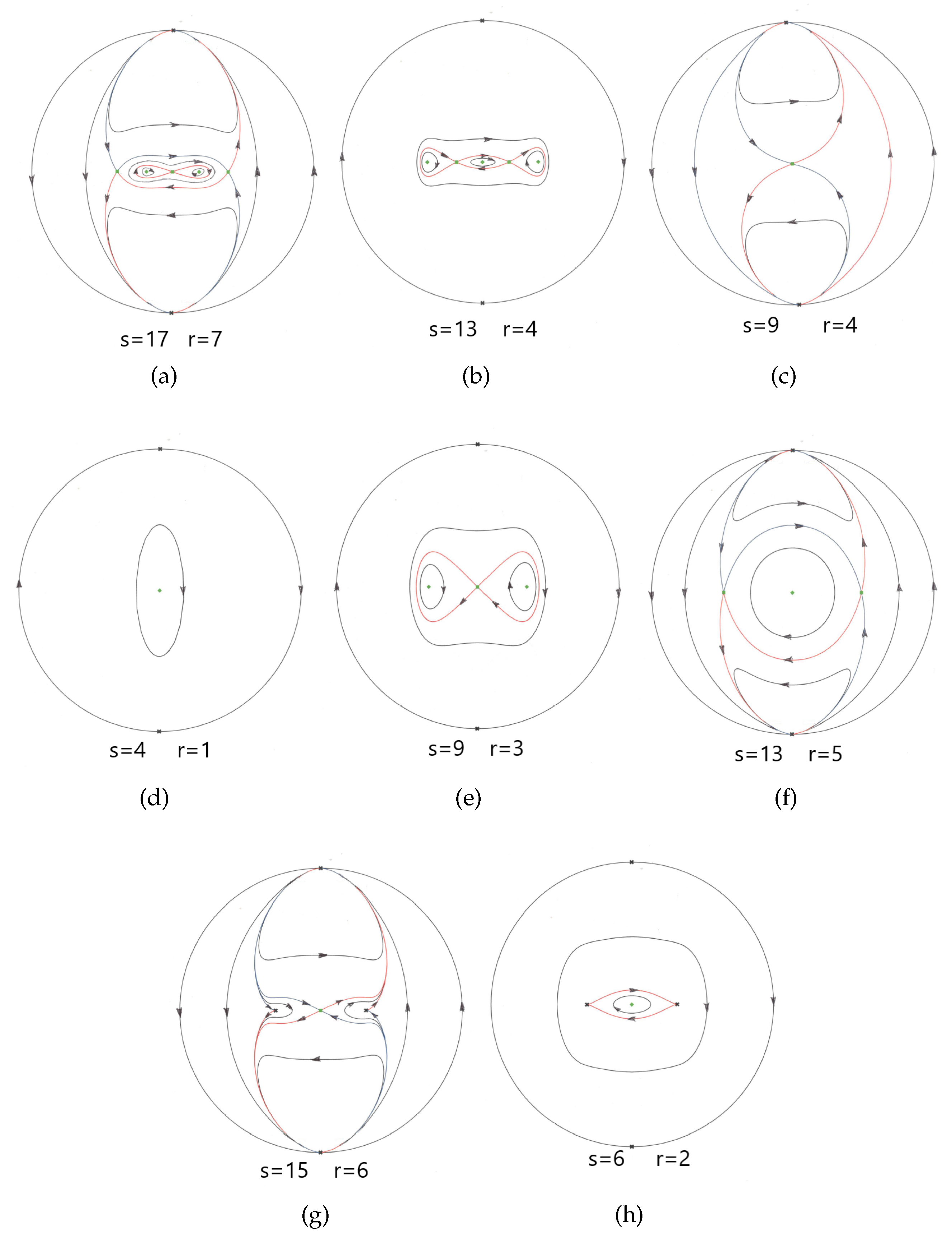
Theorem 1.

The differential system (2) has eight non-topological equivalent phase portraits on the Poincaré disc described in Figure 1.

See subSection 2.4 for the definition of topologically equivalent phase portraits of two polynomial differential systems in the Poincaré disc.

We remark that in the proof of Theorem 1, given in Section 5, we provide the explicit conditions on the coefficients ℓ, m and n of system (2) that determine each one of the eight distinct topological phase portraits of that differential system.

The paper is organized as follows. In Section 2 we recall the basic definitions and known results that we need for proving our Theorem 1, this section is divided in six subsections dedicated to the equilibrium points, the vertical blow ups, the Poincaré compactification, the phase portraits on the Poincaré disc, the topological index of an equilibrium point, and the Hamiltonian systems. The local phase portraits at the infinite and finite equilibria of system (2) are studied in Section 3 and Section 4, respectively. Finally in Section 5 we prove Theorem 1.

2. Preliminary Results

2.1. Equililbrium Points

Let

(x_{0}, y_{0})

be an equilibrium point of system (2), and denote by X the vector field associated to system (2). Let

λ_{1}

and

λ_{2}

be the eigenvalues of the Jacobian matrix

D X (x_{0}, y_{0})

. It is said that

(a): $(x_{0}, y_{0})$ is hyperbolic if $λ_{1}$ and $λ_{2}$ have no zero real parts;
(b): $(x_{0}, y_{0})$ is semi-hyperbolic if $λ_{1} λ_{2} = 0$ and $λ_{1}^{2} + λ_{2}^{2} \neq 0$ ;
(c): $(x_{0}, y_{0})$ is nilpotent if $λ_{1} = λ_{2} = 0$ and the matrix $D X (x_{0}, y_{0})$ is not the zero matrix;
(d): $(x_{0}, y_{0})$ is linearly zero if the matrix $D X (x_{0}, y_{0})$ is the zero matrix.

The hyperbolic and semi-hyperbolic equilibrium points are also called elementary equilibrium points, and their local phase portraits are well-known, see for instance Theorems 2.15 and 2.19 of [3]. Also the local phase portraits of the nilpotent singular points are well-known, see for example Theorem 3.5 of [3].

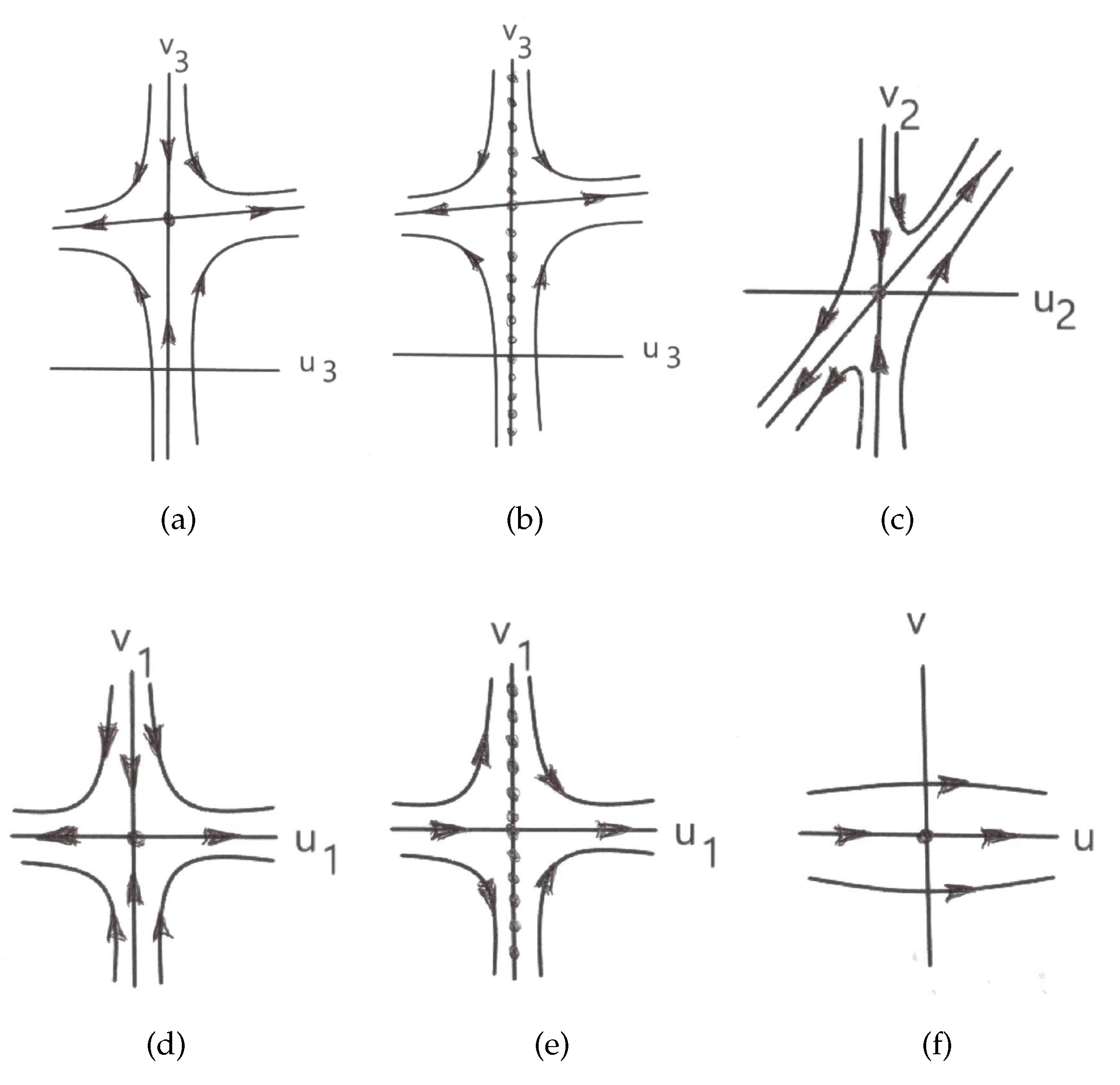
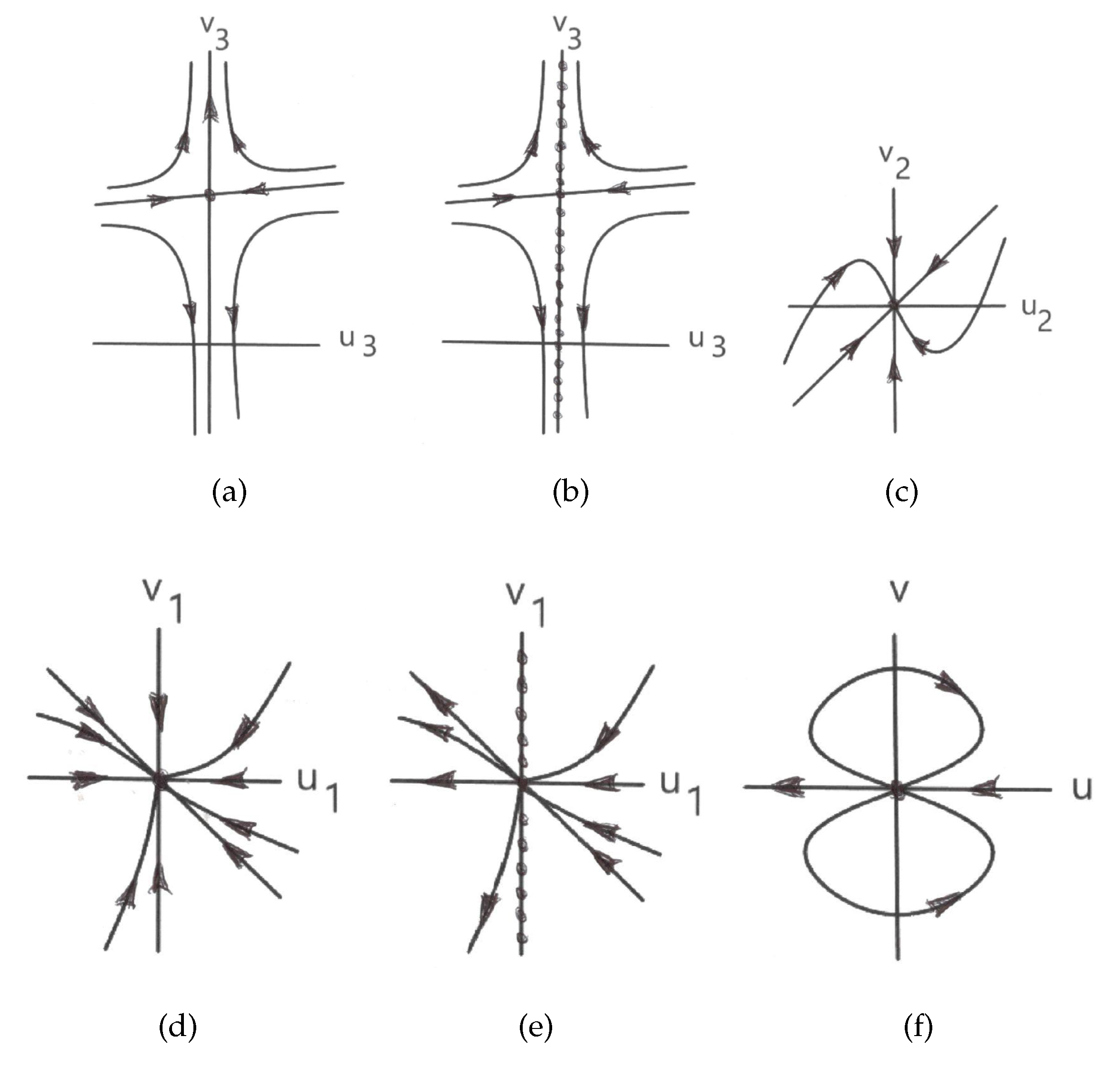
2.2. The Vertical Homogeneous Blow-Up

In the following we present a technique for determining the local phase portrait around an equilibrium point when it is linearly zero. This method determine the local phase portrait of an equilibrium point using changes of variables called vertical blow-ups. The idea of a blow-up is to turn an equilibrium point into the whole vertical axis and study the phase portrait in a neighborhood of this axis instead of studying it in the neigborhood of the equilibrium point, and repeating this process as many times if linearly zero equilibria appear on the vertical axes. In general, such equilibrium points are less degenerate. For more details see [3].

Consider the following analytical differential system

\dot{x} = P (x, y) = P_{m} (x, y) + \dots, \dot{y} = Q (x, y) = Q_{n} (x, y) + \dots,

(3)

where

P_{m}

and

Q_{n}

are homogeneous polynomials of degree

m \geq 1

and

n \geq 1

respectively, and the dots mean higher order terms in the variables x and y of m in

P (x, y)

and of n in

Q (x, y)

. Consider the polynomial

F (x_{1}, x_{2}) = \{\begin{matrix} x Q_{m} (x_{1}, x_{2}) - y P_{m} (x_{1}, x_{2}) & i f m = n \\ - y P_{m} (x_{1}, x_{2}) & i f m < n \\ x Q_{n} (x_{1}, x_{2}) & i f n < m \end{matrix} .

The homogeneous polynomial

F

is called the characteristic polynomial at the origin of system (3) and the straight lines through the origin defined by the real linear factors of the polynomial

F

are called the characteristic directions at the origin. It is known that if there are orbits starting or ending at the origin of coordinates of system (3) these at the origin are tangent to a characteristic direction. see for more details [1].

The vertical blow-up is the change of variables

(x_{1}, x_{2}) \to (u_{1}, u_{2})

where

(x_{1}, x_{2}) = (u_{1}, u_{1} u_{2})

. The new system in the variables

u_{1}

and

u_{2}

{\dot{u}}_{1} = P (u_{1}, u_{1} u_{2}), u_{2}^{'} = \frac{Q (u_{1}, u_{1} u_{2}) - u_{2} P (u_{1}, u_{1} u_{2})}{u_{1}} .

(4)

We only do a vertical blow-up when the vertical axis

x_{1} = 0

is not a characteristic direction of system (3), otherwise we can loss information on the orbits of system (3) tangent to the vertical axis.

The following result establishes relationships between the equilibrium at the origin of system (3) and the equilibrium points on the vertical axis

u_{1} = 0

of system (4), for more details see [1].

Theorem 2.

Let φ be an orbit of the differential system (3) tending to origin when

t ⟶ + \infty

(or

t ⟶ - \infty

) tangent to one of the two directions θ determined by

tan θ = w \neq \pm \infty

. Assume that

F \neg \equiv 0

. Then

(i): the straight line $(x_{1}, w x_{1})$ is a characteristic direction;
(ii): the point $(u_{1}, u_{2}) = (0, w)$ is an equilibrium point of system (4) and
(iii): an orbit φ as in the hypothesis is in biunivocal correspondence with an orbit of system (4) tending to the equilibrium point $(0, w)$ .

2.3. The Poincaré Compactification

In order to study the dynamics of a polynomial differential system in the plane

R^{2}

near infinity we need its Poincaré compactification. This tool was created by Poincaré in [10].

Consider the polynomial differential system

\dot{x} = P (x, y), \dot{y} = Q (x, y),

(5)

where P and Q are polynomial being d the maximum of the degrees of the polynomials P and Q.

We consider the plane

R^{2} \equiv {(x_{1}, x_{2}, 1); x_{1}, x_{2} \in R}

, the 2-dimensional sphere

S^{2} = {(x_{1}, x_{2}, x_{3}) \in R^{3}; x_{1}^{2} + x_{2}^{2} + x_{3}^{2} = 1}

, the northern hemisphere

H_{+} = {(x_{1}, x_{2}, x_{3}) \in S^{2}; x_{3} > 0}

, the southern hemisphere

H_{-} = {(x_{1}, x_{2}, x_{3}) \in S^{2}; x_{3} < 0}

and the equator

S^{1} \equiv {(x_{1}, x_{2}, x_{3}) \in S^{2}; x_{3} = 0}

of the sphere

S^{2}

In order to study a vector field over

S^{2}

we consider six local charts that cover the whole sphere

S^{2}

. So, for

i = 1, 2, 3

, let

U_{i} = {(x_{1}, x_{2}, x_{3}) \in S^{2}; x_{i} > 0} a n d V_{i} = {(x_{1}, x_{2}, x_{3}) \in S^{2}; x_{i} < 0} .

Consider the diffeomorphisms

φ_{i} : U_{i} ⟶ R^{2}

and

ψ_{i} : V_{i} ⟶ R^{2}

given by

φ_{i} (x_{1}, x_{2}, x_{3}) = ψ_{i} (x_{1}, x_{2}, x_{3}) = (\frac{x_{j}}{x_{i}}, \frac{x_{k}}{x_{i}})

with

j, k \neq i

and

j < k

. The sets

(U_{i}, φ_{i})

and

(V_{i}, ψ_{i})

are called the local charts over

S^{2}

Let

f^{\pm} : R^{2} ⟶ H_{\pm}

be the central projections from

R^{2}

S^{2}

given by

f^{\pm} (x_{1}, x_{2}) = \pm (\frac{x_{1}}{Δ (x_{1}, x_{2})}, \frac{x_{2}}{Δ (x_{1}, x_{2})}, \frac{1}{Δ (x_{1}, x_{2})})

where

Δ (x_{1}, x_{2}) = \sqrt{x_{1}^{2} + x_{2}^{2} + 1}

. In other words

f^{\pm} (x_{1}, x_{2})

is the intersection of the straight line through the points

(0, 0, 0)

and

(x_{1}, x_{2}, 1)

with

H_{\pm}

. Note that

f^{+} = φ_{3}^{- 1}

and

f^{-} = ψ_{3}^{- 1}

. Moreover, the maps

f^{\pm}

induces over

H_{\pm}

vector fields analytically conjugate with the differential system (5). Indeed,

f^{+}

induces on

H_{+} = U_{3}

the vector field

X_{1} (y) = D f^{+} (φ_{3} (y)) X (φ_{3} (y))

, and

f^{-}

induces on

H_{-} = V_{3}

the vector field

X_{2} (y) = D f^{-} (ψ_{3} (y)) X (ψ_{3} (y))

. Thus we obtain a vector field on

S^{2} ∖ S^{1}

that admits an analytic extension

p (X)

S^{2}

, see for more details [3]. The vector field

p (X)

S^{2}

is called the Poincaré compactification.

Denote

(u, v) = φ_{i} (x_{1}, x_{2}, x_{3}) = ψ_{i} (x_{1}, x_{2}, x_{3})

. Then the expression of the differential system associated to the vector field

p (X)

in the chart

U_{1}

u^{'} = v^{d} [Q (\frac{1}{v}, \frac{u}{v}) - u P (\frac{1}{v}, \frac{u}{v})], v^{'} = - v^{d + 1} P (\frac{1}{v}, \frac{u}{v}) .

The expression of

p (X)

U_{2}

u^{'} = v^{d} [P (\frac{u}{v}, \frac{1}{v}) - u Q (\frac{u}{v}, \frac{1}{v})], v^{'} = - v^{d + 1} Q (\frac{u}{v}, \frac{1}{v}) .

The expression of

p (X)

U_{3}

u^{'} = P (u, v), v^{'} = Q (u, v) .

For

i = 1, 2, 3

the expression of

p (X)

in the chart

V_{i}

differs of the expression in

U_{i}

only by the multiplicative constant

{(- 1)}^{d - 1}

Note that we can identify the infinity of

R^{2}

with the circle

S^{1}

. Two points for each direction in

R^{2}

provide two antipodal points of

S^{1}

. An equilibrium point of

p (X)

S^{1}

is called infinite equilibrium point and an equilibrium point on

S^{2} ∖ S^{1}

is called a finite equilibrium point. Observe that the coordinates of the infinite equilibrium points are of the form

(u, 0)

on the charts

U_{1}, V_{1}, U_{2}

and

V_{2}

. Thus, if

(x_{1}, x_{2}, 0) \in S^{1}

is an infinite equilibrium point, then its antipode

(- x_{1}, - x_{2}, 0)

is also a infinite equilibrium point.

The image of the closed northern hemisphere of

S^{2}

under the projection

(x_{1}, x_{2}, x_{3}) \to (x_{1}, x_{2}, 0)

is the Poincaré disc, denoted by

D^{2}

2.4. Phase Portraits on the Poincaré Disc

For the definition of separatrix of a differential system see for instance [8]. The separatrix of a vector field

p (X)

are all the orbits of the circle at the infinity, the equilibrium points, the limit cycles and the orbits which lie in the boundary of a hyperbolic sectors, i.e. the two separatrices of the hyperbolic sectors.

Neumann in [8] shown that the set of all separatrices

S (p (X))

of the vector field

p (X)

, is closed.

When there is an orientation preserving or reversing homeomorphism which maps the trajectories of

p (X)

into the trajectories of

p (Y)

we say that the two differential systems defined by

p (X)

and

p (Y)

in the Poincaré disc are topologically equivalent.

The canonical regions of

p (X)

are the open connected components of

D^{2} ∖ S (p (X))

. The set formed by the union of

S (p (X))

plus one orbit chosen from each canonical region is called a separatrix configuration of

p (X)

. When there is an orientation preserving or reversing homeomorphism which maps the trajectories of

S (p (X))

into the trajectories of

S (p (Y))

we say that the two separatrices configurations

S (p (X))

and

S (p (Y))

are topologically equivalent.

The next result is mainly due to Markus [7], Neumann [8] and Peixoto [9].

Theorem 3.

The phase portraits in the Poincaré disc of two compactified polynomial differential systems

p (X)

and

p (Y)

with finitely many separatrices are topologically equivalent if and only if their separatrix configurations

S (p (X))

and

S (p (Y))

are topologically equivalent.

2.5. The Differential System (2) is Hamiltonian

In all papers that we have found on the differential system (2) and that appear in our references is not mention that system (2) is Hamiltonian, i.e. that it can be written into the form

\dot{x} = \frac{\partial H}{\partial y}, \dot{y} = - \frac{\partial H}{\partial x},

with the Hamiltonian

H = H (x, y) = \frac{y^{2}}{2} + \frac{ℓ x^{2}}{2} + \frac{m x^{4}}{4} + \frac{n x^{6}}{6} .

(6)

We must mention that the first integral

6 H

also appears in the papers [11] of Sun et al. (2003), and also in the paper [5] of Feng (2004), but these authors did not mention that the differential system (2) is Hamiltonian.

The fact that the flow of the Hamiltonian systems preserves the area (see for details [2]) implies that system (2) has no limit cycles, and that its finite equilibrium points are either centers, or union of hyperbolic sectors.

2.6. On the Topological Indices of the Equilibrium Points

It is known that the local phase portrait of any equilibrium point of an analytic differential system in the plane

R^{2}

is either a focus, a center, or finite union of hyperbolic, elliptic and parabolic sectors, see [1] or [3].

The topological index or simply the index of an equililbrium point of an analytic differential system is an integer number which can be computed using the Poincaré Index Formula, i.e. if h, e and p are the number of hyperbolic, elliptic and parabolic sectors, respectively, of the local phase portrait of an equilibrium point its index is given by the formula

\frac{e - h}{2} + 1 .

For a proof of this formula see for instance [3]. Thus the index of a saddle is

- 1

, the index of a center is 1 because it has no sectors.

The next theorem shows that the sum of the indices of all equilibria of a compactified polynomial vector field

p (X)

in the Poincaré sphere

S^{2}

, having finitely many equilibria, does not depend on the polynomial vector field X.

Theorem 4

(Poincaré-Hopf Theorem). The sum of the indices of all equilibria of a compactified polynomial vector field

p (X)

in the Poincaré sphere

S^{2}

, having finitely many equilibria, is two.

For a simple proof of the Poincaré-Hopf Theorem on the sphere

S^{2}

see [3].

2.7. The Roots of a Polynomial of Degree 4

Consider the polynomial of degree 4

p (x) = b_{0} x^{4} + b_{1} x^{3} + b_{2} x^{2} + b_{3} x + b_{4},

b_{0} \neq 0

. Define

\begin{matrix} D_{2} = & 3 b_{1}^{2} - 8 b_{0} b_{2}, \\ D_{3} = & 16 b_{0}^{2} b_{2} b_{4} - 18 b_{0}^{2} b_{3}^{2} - 4 b_{0} b_{2}^{3} + 14 b_{0} b_{1} b_{2} b_{3} - 6 b_{0} b_{1}^{2} b_{4} + b_{1}^{2} b_{2}^{2} - 3 b_{1}^{3} b_{3}, \\ D_{4} = & 256 b_{0}^{3} b_{4}^{3} - 27 b_{0}^{2} b_{3}^{4} - 192 b_{0}^{2} b_{1} b_{3} b_{4}^{2} - 27 b_{1}^{4} b_{4}^{2} - 6 b_{0} b_{1}^{2} b_{3}^{2} b_{4} + b_{1}^{2} b_{2}^{2} b_{3}^{2} \\ - 4 b_{0} b_{2}^{3} b_{3}^{2} + 18 b_{1}^{3} b_{2} b_{3} b_{4} + 144 b_{0} b_{1}^{2} b_{2} b_{4}^{2} - 80 b_{0} b_{1} b_{2}^{2} b_{3} b_{4} + 18 b_{0} b_{1} b_{2} b_{3}^{3} \\ - 4 b_{1}^{2} b_{2}^{3} b_{4} - 4 b_{1}^{3} b_{3}^{3} + 16 b_{0} b_{2}^{4} b_{4} - 128 b_{0}^{2} b_{2}^{2} b_{4}^{2} + 144 b_{0}^{2} b_{2} b_{3}^{2} b_{4}, \\ E = & 8 b_{0}^{2} b_{3} + b_{1}^{3} - 4 b_{0} b_{1} b_{2} . \end{matrix}

Then the polynomial

p (x)

has the following roots:

four simple real roots if $D_{4} > 0$ , $D_{3} > 0$ and $D_{2} > 0$ ;
no real roots if $D_{4} < 0$ and $D_{3} \leq 0$ or $D_{2} \leq 0$ ;
two simple real roots and two complex roots if $D_{4} < 0$ ;
two simple real roots and one double real root if $D_{4} = 0$ and $D_{3} > 0$ ;
one double real root and two complex roots if $D_{4} = 0$ and $D_{3} < 0$ ;
two double real roots if $D_{4} = D_{3} = E = 0$ and $D_{2} > 0$ ;
one simple real root and one triple real root if $D_{4} = D_{3} = 0$ , $D_{2} > 0$ and $E \neq 0$ ;
no real roots if $D_{4} = D_{3} = 0$ and $D_{2} < 0$ ;
one quadruple real root if $D_{4} = D_{3} = D_{2} = 0$ .

For a proof see [12].

3. The Infinite Equilibria

From subSection 2.3 the expression of the differential system (2) in the local chart

U_{1}

\dot{u} = - n - m v^{2} - ℓ v^{4} - u^{2} v^{4}, \dot{v} = v (n + m v^{2} + ℓ v^{4}) .

Since

n \neq 0

there are no infinite equilibria on the chart

U_{1}

. Then the unique possible infinite equilibria can be the origins of the local charts

U_{2}

and

V_{2}

Again from subSection 2.3 the expression of the differential system (2) in the local chart

U_{2}

\dot{u} = v^{4} + n u^{6} + m u^{4} v^{2} + ℓ u^{2} v^{4}, \dot{v} = - v^{5} .

(7)

Hence the origin of the chart

U_{2}

is an infinite equilibrium. In the next proposition we characterize the local phase portrait at this equilibrium.

Proposition 1.

The following two statements hold.

(a): If $n > 0$ then the local phase portrait at the origin of the local chart $U_{2}$ is formed by two hyperbolic sectors, whose two separatrices are contained on the circle of the infinity, see Figure $(f)$ .
(b): If $n < 0$ then the local phase portrait at the origin of the local chart $U_{2}$ is formed by two elliptic sectors separated by two parabolic sectors, the line of the infinite pass through the two parabolic sectors, see Figure $(f)$ .

Proof.

The origin of the local chart

U_{2}

is a linearly zero equilibrium point, see system (7), we shall study its local phase portrait doing the changes of variables called vertical blow ups, see subSection 2.2. Since

u = 0

is not a characteristic direction at the origin of system (7) we do the vertical blow up

(u, v) = (u_{1}, u_{1} v_{1})

, then system (7) writes

\begin{matrix} {\dot{u}}_{1} = u_{1}^{4} (ℓ u_{1}^{2} v_{1}^{4} + m u_{1}^{2} v_{1}^{2} + n u_{1}^{2} + v_{1}^{4}), \\ {\dot{v}}_{1} = - u_{1}^{3} v_{1} (ℓ u_{1}^{2} v_{1}^{4} + m u_{1}^{2} v_{1}^{2} + n u_{1}^{2} + u_{1} v_{1}^{4} + v_{1}^{4}) . \end{matrix}

(8)

Rescaling the time by

u_{1}^{3}

the previous differential becomes

\begin{matrix} {\dot{u}}_{1} = u_{1} (ℓ u_{1}^{2} v_{1}^{4} + m u_{1}^{2} v_{1}^{2} + n u_{1}^{2} + v_{1}^{4}), \\ {\dot{v}}_{1} = - v_{1} (ℓ u_{1}^{2} v_{1}^{4} + m u_{1}^{2} v_{1}^{2} + n u_{1}^{2} + u_{1} v_{1}^{4} + v_{1}^{4}) . \end{matrix}

(9)

The unique equilibrium point of this differential system on the straight line

u_{1} = 0

is the origin, that again it is a linearly zero equilibrium. Since

u_{1} = 0

is a characteristic direction at the origin of system (9) we do the following twist

(u_{1}, v_{1}) = (u_{2}, u_{2} - v_{2})

. Thus in the variables

(u_{2}, v_{2})

system (9) writes

\begin{matrix} {\dot{u}}_{2} = & u_{2} (n u_{2}^{2} + (1 + m) u_{2}^{4} + ℓ u_{2}^{6} - 2 (2 + m) u_{2}^{3} v_{2} - 4 ℓ u_{2}^{5} v_{2} + (6 + m) u_{2}^{2} v_{2}^{2} + \\ 6 ℓ u_{2}^{4} v_{2}^{2} - 4 u_{2} v_{2}^{3} - 4 ℓ u_{2}^{3} v_{2}^{3} + v_{2}^{4} + ℓ u_{2}^{2} v_{2}^{4}), \\ {\dot{v}}_{2} = & 2 n u_{2}^{3} + 2 (1 + m) u_{2}^{5} + u_{2}^{6} + 2 ℓ u_{2}^{7} - n u_{2}^{2} v_{2} - (9 + 5 m) u_{2}^{4} v_{2} - 5 u_{2}^{5} v_{2} - \\ 9 ℓ u_{2}^{6} v_{2} + 4 (4 + m) u_{2}^{3} v_{2}^{2} + 10 u_{2}^{4} v_{2}^{2} + 16 ℓ u_{2}^{5} v_{2}^{2} - (14 + m) u_{2}^{2} v_{2}^{3} - 10 u_{2}^{3} v_{2}^{3} - \\ 14 ℓ u_{2}^{4} v_{2}^{3} + 6 u_{2} v_{2}^{4} + 5 u_{2}^{2} v_{2}^{4} + 6 ℓ u_{2}^{3} v_{2}^{4} - v_{2}^{5} - u_{2} v_{2}^{5} - ℓ u_{2}^{2} v_{2}^{5} . \end{matrix}

(10)

Now we do the blow

(u_{2}, v_{2}) = (u_{3}, u_{3} v_{3})

to system (10) obtaining the system

\begin{matrix} {\dot{u}}_{3} = & u_{3}^{3} (n + (1 + m) u_{3}^{2} + ℓ u_{3}^{4} - 2 (2 + m) u_{3}^{2} v_{3} - 4 ℓ u_{3}^{4} v_{3} + (6 + m) u_{3}^{2} v_{3}^{2} + \\ 6 ℓ u_{3}^{4} v_{3}^{2} - 4 u_{3}^{2} v_{3}^{3} - 4 ℓ u_{3}^{4} v_{3}^{3} + u_{3}^{2} v_{3}^{4} + ℓ u_{3}^{4} v_{3}^{4}), \\ {\dot{v}}_{3} = & - u_{3}^{2} (v_{3} - 1) (2 n + 2 (1 + m) u_{3}^{2} + u_{3}^{3} + 2 ℓ u_{3}^{4} - 4 (2 + m) u_{3}^{2} v_{3} - 4 u_{3}^{3} v_{3} - \\ 8 ℓ u_{3}^{4} v_{3} + 2 (6 + m) u_{3}^{2} v_{3}^{2} + 6 u_{3}^{3} v_{3}^{2} + 12 ℓ u_{3}^{4} v_{3}^{2} - 8 u_{3}^{2} v_{3}^{3} - 4 u_{3}^{3} v_{3}^{3} - 8 ℓ u_{3}^{4} v_{3}^{3} + \\ 2 u_{3}^{2} v_{3}^{4} + u_{3}^{3} v_{3}^{4} + 2 ℓ u_{3}^{4} v_{3}^{4}) . \end{matrix}

(11)

Now rescaling the time by

u_{3}^{2}

system (11) writes

\begin{matrix} {\dot{u}}_{3} = & u_{3} (n + (1 + m) u_{3}^{2} + ℓ u_{3}^{4} - 2 (2 + m) u_{3}^{2} v_{3} - 4 ℓ u_{3}^{4} v_{3} + (6 + m) u_{3}^{2} v_{3}^{2} + \\ 6 ℓ u_{3}^{4} v_{3}^{2} - 4 u_{3}^{2} v_{3}^{3} - 4 ℓ u_{3}^{4} v_{3}^{3} + u_{3}^{2} v_{3}^{4} + ℓ u_{3}^{4} v_{3}^{4}), \\ {\dot{v}}_{3} = & - (v_{3} - 1) (2 n + 2 (1 + m) u_{3}^{2} + u_{3}^{3} + 2 ℓ u_{3}^{4} - 4 (2 + m) u_{3}^{2} v_{3} - 4 u_{3}^{3} v_{3} - \\ 8 ℓ u_{3}^{4} v_{3} + 2 (6 + m) u_{3}^{2} v_{3}^{2} + 6 u_{3}^{3} v_{3}^{2} + 12 ℓ u_{3}^{4} v_{3}^{2} - 8 u_{3}^{2} v_{3}^{3} - 4 u_{3}^{3} v_{3}^{3} - 8 ℓ u_{3}^{4} v_{3}^{3} + \\ 2 u_{3}^{2} v_{3}^{4} + u_{3}^{3} v_{3}^{4} + 2 ℓ u_{3}^{4} v_{3}^{4}) . \end{matrix}

(12)

The unique equilibrium point of system (12) on the straight line

u_{3} = 0

is the

(0, 1)

, whose linear part has eigenvalues n and

- 2 n

, so it is a hyperbolic saddle.

(a):

n > 0

. The local phase portrait of system (12) in a neighborhood of the straight line

u_{3} = 0

is shown in Figure 2(a). Hence the local phase portrait of system (11) in a neighborhood of the straight line

u_{3} = 0

is shown in Figure 2(b). Going back through the blow up

(u_{2}, v_{2}) = (u_{3}, u_{3} v_{3})

and taking into account that

{\dot{v}}_{2} |_{v_{2} = 0} = 2 n u_{2}^{3} + h . o . t .

we obtain the local phase portrait at the origin of system (10) in Figure 2(c), as usual “h.o.t.” denotes higher order terms. Undoing the twist

(u_{1}, v_{1}) = (u_{2}, u_{2} - v_{2})

we get the local phase portrait at the origin of system (9) in Figure 2(d). Therefore the local phase portrait at the origin of system (8) is given in Figure 2(e). Undoing the blow up

(u, v) = (u_{1}, u_{1} v_{1})

and taking into account that

\dot{u} |_{u = 0} = v^{4}

we obtain the local phase portrait at the origin of the local chart

U_{2}

in Figure 2(f).

(b):

n < 0

. The local phase portrait of system (12) in a neighborhood of the straight line

u_{3} = 0

is shown in Figure 3(a). Hence the local phase portrait of system (11) in a neighborhood of the straight line

u_{3} = 0

is shown in Figure 3(b). Going back through the blow up

(u_{2}, v_{2}) = (u_{3}, u_{3} v_{3})

and taking into account that

{\dot{v}}_{2} |_{v_{2} = 0} = 2 n u_{2}^{3} + h . o . t .

we obtain the local phase portrait at the origin of system (10) in Figure 3(c). Undoing the twist

(u_{1}, v_{1}) = (u_{2}, u_{2} - v_{2})

we get the local phase portrait at the origin of system (9) in Figure 3(d). Therefore the local phase portrait at the origin of system (8) is given in Figure 3(e). Undoing the blow up

(u, v) = (u_{1}, u_{1} v_{1})

and taking into account that

\dot{u} |_{u = 0} = v^{4}

we obtain the local phase portrait at the origin of the local chart

U_{2}

in Figure 3(f). □

4. The Finite Equilibria

The finite equilibria of the differential system (2) are the points

(x_{0}, 0)

being

x_{0}

a real root of the polynomial

ℓ x + m x^{3} + n x^{5} = x (ℓ + m x^{2} + n x^{4}) = x p (x) .

Applying the results of subSection 2.6 to the polynomial

p (x)

we obtain

D_{2} = - 8 m n, D_{3} = - 4 m n (m^{2} - 4 ℓ n), D_{4} = 16 ℓ n {(- m^{2} + 4 ℓ n)}^{2}, E = 0 .

Then it is easy to prove the following ten paragraphs.

We have that

D_{4} > 0

D_{3} > 0

and

D_{2} > 0

if and only if

either (i)

ℓ < 0

m > 0

and

m^{2} / (4 ℓ) < n < 0

or (ii)

ℓ > 0

m < 0

and

0 < n < m^{2} / (4 ℓ)

We have that

D_{4} < 0

and

D_{3} \leq 0

if and only if

(iii) either

ℓ < 0

m < 0

and

m^{2} / (4 ℓ) < n < 0

(iv) or

ℓ < 0

m \geq 0

and

n < m^{2} / (4 ℓ)

(v) or

ℓ > 0

m \leq 0

and

n > m^{2} / (4 ℓ)

;

(vi) or

ℓ > 0

m > 0

and

0 < n < m^{2} / (4 ℓ)

We have that

D_{4} < 0

and

D_{2} \leq 0

if and only if

(vii) either

ℓ < 0

m \leq 0

and

n < m^{2} / (4 e l l)

(viii) or

ℓ < 0

m < 0

and

m^{2} / (4 ℓ) < n < 0

(ix) or

ℓ > 0

m > 0

and

0 < n < m^{2} / (4 ℓ)

(x) or

ℓ > 0

m = 0

and

n > m^{2} / (4 ℓ)

We have that

D_{4} < 0

if and only if

(xi) either

ℓ < 0

and

n > 0

;

(xii) or

ℓ > 0

and

n < 0

We have that

D_{4} = 0

and

D_{3} > 0

if and only if

(xiii) either

ℓ = 0

m < 0

and

n > 0

;

(xiv) or

ℓ = 0

m > 0

and

n < 0

We have that

D_{4} = 0

and

D_{3} < 0

if and only if

(xv) either

ℓ = 0

m < 0

and

n < 0

;

(xvi) or

ℓ = 0

m > 0

and

n > 0

We have that

D_{4} = D_{3} = E = 0

and

D_{2} > 0

if and only if

(xvii) either

ℓ < 0

m > 0

and

n = m^{2} / (4 ℓ)

;

(xviii) or

ℓ > 0

m < 0

and

n = m^{2} / (4 ℓ)

We have that the conditions

D_{4} = D_{3} = 0

D_{2} > 0

and

E \neq 0

do not hold.

We have that

D_{4} = D_{3} = 0

and

D_{2} < 0

if and only if

(xix) either

ℓ < 0

m < 0

and

n = m^{2} / (4 ℓ)

;

(xx) or

ℓ > 0

m > 0

and

n = m^{2} / (4 ℓ)

We have that

D_{4} = D_{3} = D_{2} = 0

if and only if

(xxi) either

ℓ = m = 0

and

n < 0

;

(xxii) or

ℓ = m = 0

and

n > 0

The next proposition classifies all finite equilibrium points of the differential system (2).

Proposition 2.

The finite equilibrium points of the differential system (2) under the assumptions:

(i)are

(- x_{-}, 0), (0, 0), (x_{-}, 0)

hyperbolic saddles and

(- x_{+}, 0), (x_{+}, 0)

centers, where

x_{\mp} = \sqrt{(- m \mp \sqrt{m^{2} - 4 ℓ n)} / (2 n)}

with

- x_{-} < - x_{+} < 0 < x_{+} < x_{-}

, see Figure

(a)

;

(ii)are

(- x_{+}, 0), (0, 0), (x_{+}, 0)

centers and

(- x_{-}, 0), (x_{-}, 0)

hyperbolic saddles with

- x_{+} < - x_{-} < 0 < x_{-} < x_{+}

, see Figure

(b)

;

(iii)-(iv)-(vii)-(viii)-(xv)-(xix)-(xxi)is a saddle at

(0, 0)

, see Figure

(c)

;

(v)-(vi)-(ix)-(x)-(xvi)-(xx)-(xxii)is a center at

(0, 0)

, see Figure

(d)

;

(xi)-(xiii)are

(- x_{+}, 0), (x_{+}, 0)

centers and

(0, 0)

a saddle, see Figure

(e)

;

(xii)-(xìv)are

(- x_{-}, 0), (x_{-}, 0)

hyperbolic saddles and

(0, 0)

a center, see Figure

(f)

;

(xvii)are

(- x_{-} = - x_{+}, 0), (x_{-} = x_{+}, 0)

formed by two hyperbolic sectors and the

(0, 0)

is a hyperbolic saddle, see Figure

(g)

;

(xviii)are

(- x_{-} = - x_{+}, 0), (x_{-} = x_{+}, 0)

formed by two hyperbolic sectors and the

(0, 0)

is a center, see Figure

(h)

;

Proof.

Under assumptions (i) an easy computation shows that system (2) has the five equilibria stated in statement (i) of the proposition. Due to the symmetry

(x, y, t) \to (- x, y, - t)

the local phase portraits of the equilibria

(- x_{-}, 0), (x_{-}, 0)

and

(- x_{+}, 0)

(x_{+}, 0)

are the same. By Theorem 2.15 of [3] it follows that

(- x_{-}, 0)

and

(0, 0)

are hyperbolic saddles because the determinant of its linear parts is negative. Since the eigenvalues of the linear part of the differential system (2) at the equilibria

(- x_{+}, 0)

are purely imaginary, these equilibria are either weak foci or centers, but since system (2) is Hamiltonian they are centers, see subSection 2.5.

Under the assumptions (ii) the proof of the proposition follows in a similar way than under the assumptions (i).

By subSection 2.7 under the assumptions either (iii), or (iv), of (vii), or (viii), or (xv) we have that

n < 0

. So the origins of the local charts

U_{2}

and

V_{2}

are formed by two elliptic sectors separated by two parabolic sectors, consequently by subSection 2.6 their indices are 2. Since the origin of coordinates is the unique finite equilibrium point, by the Poincaré-Hopf Theorem (see subSection 2.6) its index must be

- 1

. Therefore, since the differential system (2) is Hamiltonian the origin is a saddle.

By subSection 2.7 under the assumptions either (v), or (vi), or (ix), or (x), or (xvi), or (xix), we have that

n > 0

. So the origins of the local charts

U_{2}

and

V_{2}

are formed by two hyperbolic sectors, consequently by subSection 2.6 their indices are 0. Since the origin of coordinates is the unique finite equilibrium point, by the Poincaré-Hopf Theorem its index must be 1. Therefore, since the differential system (2) is Hamiltonian the origin is a center.

By subSection 2.7 under the assumptions either (xi), or (xiii), the unique finite equilibrium points are

(- x_{+}, 0), (0, 0), (x_{+}, 0)

. Since for (xi) the eigenvalues of the linear part of the differential system at

(0, 0)

are

\pm \sqrt{- ℓ}

and

ℓ < 0

, by Theorem 2.15 of [3] it is a hyperbolic saddle. But for (xiii) the linear part of the differential system (2) at

(0, 0)

is the matrix

(\begin{matrix} 0 & 1 \\ 0 & 0 \end{matrix}),

so the equilibrium

(0, 0)

is nilpotent, and by Theorem 3.5 it follows that it is saddle. By the symmetry

(x, y, t) \to (- x, y, - t)

the two equilibria

(- x_{+}, 0), (x_{+}, 0)

have the same local phase portrait. Since

n > 0

the two infinite equilibria at the origins of the local charts

U_{2}

and

V_{2}

have index 0, and the saddle

(0, 0)

has index

- 1

, by the Poincaré-Hopf Theorem it follows that the two equilibria

(- x_{+}, 0), (x_{+}, 0)

have index 1. Since the system is Hamiltonian, both are centers.

By subSection 2.7 under the assumptions either (xii) or (xiv), the unique finite equilibrium points are

(- x_{-}, 0), (0, 0), (x_{-}, 0)

. Since the linear part of the differential system at the equilibria

(- x_{-}, 0), (x_{-}, 0)

have negative determinant, by Theorem 2.15 of [3] they are hyperbolic saddles, and consequently their indices are

- 1

. Since

n < 0

the two infinite equilibria at the origins of the local charts

U_{2}

and

V_{2}

have index 2, by the Poincaré-Hopf Theorem we get that the equililbrium

(0, 0)

has index 0. Therefore, since the system is Hamiltonian, it is a center.

By subSection 2.7 under the assumptions either (xvii), the unique finite equilibrium point are

(- x_{-} = - x_{+}, 0), (0, 0), (x_{-} = x_{+}, 0)

. Since the eigenvalues of the linear part of the differential system at

(0, 0)

are

\pm \sqrt{- ℓ}

and

ℓ < 0

, by Theorem 2.15 of [3] it is a hyperbolic saddle with index

- 1

. Since

n < 0

the origins of the local charts

U_{2}

and

V_{2}

have index 2. By the symmetry

(x, y, t) \to (- x, y, - t)

the indices of

(- x_{-} = - x_{+}, 0)

and

(x_{-} = x_{+}, 0)

are equal. Then, by the Poincaré-Hopf Theorem these two indices are 0. Hence, since the differential system (2) is Hamiltonian these two equilibria are formed by two hyperbolic sectors.

By subSection 2.7 under the assumptions either (xviii), again the unique finite equilibrium points are

(- x_{-} = - x_{+}, 0), (0, 0), (x_{-} = x_{+}, 0)

. Since the eigenvalues of the linear part of the differential system at

(0, 0)

are

\pm \sqrt{- ℓ}

and

ℓ > 0

, the equilibrium

(0, 0)

is either a weak focus or a center, due to the fact that the differential system is Hamiltonian it is a center, so its index is 1. Since

n > 0

the origins of the local charts

U_{2}

and

V_{2}

have index 0. By the symmetry

(x, y, t) \to (- x, y, - t)

the indices of

(- x_{-} = - x_{+}, 0)

and

(x_{-} = x_{+}, 0)

are equal. Then, by the Poincaré-Hopf Theorem these two indices are 0. Hence, since the differential system (2) is Hamiltonian these two equilibria are formed by two hyperbolic sectors. □

5. Phase Portraits in the Poincaré Disc

From Propositions 1 and 2 we know all local phase portraits at the infinite and finite equilibria of the differential system (2). Moreover, since system (2) is Hamiltonian with the Hamiltonian

H = H (x, y)

given in (6). Evaluating

H (x, y)

on the finite equilibria having hyperbolic sectors, we know the behaviour of their separatrices, and consequently using Theorem 3 we can determine the phase portraits of system (2) in the Poincaré disc.

In summary, we obtain that the phase portraits of the differential system (2) under the assumptions

(i) is given in Figure 1(a);

(ii) is given in Figure 1(b);

(iii)-(iv)-(vii)-(viii)-(xv)-(xix)-(xxi) is given in Figure 1(c);

(v)-(vi)-(ix)-(x)-(xvi)-(xx)-(xxii) is a given in Figure 1(d);

(xi)-(xiii) is given in Figure 1(e);

(xii)-(xìv) is given in Figure 1(f);

(xvii) is given in Figure 1(g);

(xviii)is given in Figure 1(h).

This completes the proof of Theorem 1.

Funding

The first and third authors are partially supported by the Algerian Ministry of Higher Education and Scientific Research (MESRS) and the General Directorate of Scientific Research and Technological Development (DGRSDT) under projects: PRFUN COOLO3UN190120220004 and PRFUN COOLO3UN190120230015. The second author is partially supported by the Agencia Estatal de Investigación of Spain grant PID2022-136613NB-100, the H2020 European Research Council grant MSCA-RISE-2017-777911, AGAUR (Generalitat de Catalunya) grant 2021SGR00113, and by the Reial Acadèmia de Ciències i Arts de Barcelona.

References

Andronov,A. A., Gordon,I. I., Leontovich, E. A., Maier, A. G., Qualitative theory of 2nd order dynamic systems, J. Wiley Sons, 1973.
Arnold, V.I. , Mathematical Methods of Classical Mechanics, Graduate Texts in Mathematics, Vol. 60, 2nd Edition, Springer-Verlag, 2000.
Dumortier, F. , Llibre, J., Artés, J. C., Qualitative theory of planar differential systems, Springer-Verlag, 2006.
Feng, Z. On explicit exact solutions for the Lienard equation and its applications. Phys. Lett. A 2002, 293, 50–56. [Google Scholar] [CrossRef]
Feng, Z. Exact solutions to the Liénard equation and its applications, Chaos, Solitons and Fractals 21 (2004), 343–348.
Kong, D. Explicit exact solutions for the Liénard equation and its applications. Phys. Lett. A 1995, 196, 301–306. [Google Scholar] [CrossRef]
Markus, L. Quadratic differential equations and non-associative algebras, Annals of Mathematics Studies 45 (1960), 185–213.
Neumann, D. Classification of continuous flows on 2-manifolds. Proc. Amer. Math. Soc. 1975, 48, 73–81. [Google Scholar] [CrossRef]
Peixoto, L.M. , Dynamical Systems. Proceedings of a Symposium held at the University of Bahia: Acad. Press, New York, 1973, 389–420.
Poincaré, H. Mémoire sur les courbes définies par les équations différentielles, Journal de Mathématiques 37 (1881), 375–422; Oeuvres de Henri Poincaré, vol. I, Gauthier-Villars, Paris, 1951, pp 3–84.
Sun, J.; Wang, W.; Wu, L. A note on ´´On explicit exact solutions for the Liénard equation and its applications”. Phys. Lett. A 200, 318, 93–101. [Google Scholar] [CrossRef]
Yang, L. Recent advances on determining the number of real roots of parametric polynomials. J. Symbolic Computation 1999, 28, 225–242. [Google Scholar] [CrossRef]

Figure 1. The eight non-topologically equivalent phase portraits in the Poincaré disc of the differential system (2). Here s denotes the number of separatrices and r denotes the number of canonical regions of the phase portrait.

Figure 2. The blow up of the origin of the local chart

U_{2}

when

n > 0

Figure 2. The blow up of the origin of the local chart

U_{2}

when

n > 0

Figure 3. The blow up of the origin of the local chart

U_{2}

when

n < 0

Figure 3. The blow up of the origin of the local chart

U_{2}

when

n < 0

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Phase portraits of a class of Liénard equations

Abstract

1. Introduction and Statement of the Main Result

2. Preliminary Results

2.1. Equililbrium Points

2.2. The Vertical Homogeneous Blow-Up

2.3. The Poincaré Compactification

2.4. Phase Portraits on the Poincaré Disc

2.5. The Differential System (2) is Hamiltonian

2.6. On the Topological Indices of the Equilibrium Points

2.7. The Roots of a Polynomial of Degree 4

3. The Infinite Equilibria

4. The Finite Equilibria

5. Phase Portraits in the Poincaré Disc

Funding

References

MDPI Initiatives

Important Links

Subscribe