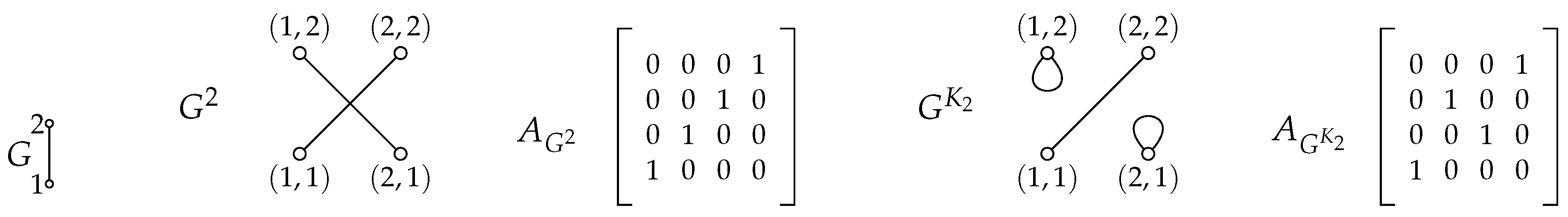In this paper, loops in an adjacency matrix are given a 1 along the diagonal. The direct power $G^x=G\times G\times \cdots$ is the direct product of G with itself x times. As is shown in [5], $G^x$ has connections to $G^K$ as seen in the adjacency matrices of both products. Let the adjacency matrix of graph G be $A_G$. Denoted $A_{G^x}$, the adjacency matrix for the direct power $G^x$ is the Kronecker product $A_G\otimes A_G\otimes \cdots$ of G with itself x times. The adjacency matrix for $G^K$ is given by $A_{G^K}$ as explained in [5] and in Section 3. Denote an all zero matrix as Z while J is a matrix of all ones.

The direct product $G\times H$ has vertex set that is the Cartesian product $V\left(G\right)\times V\left(H\right)$ producing ordered pair vertices $(g,h)$ where $g\in V\left(G\right)$ and $h\in V\left(H\right)$. An edge $\left((g,h)(g^{\prime },h^{\prime })\right)$ in $E(G\times H)$ is defined when $(g,g^{\prime })\in E\left(G\right)$ and $(h,h^{\prime })\in E\left(H\right)$. Thus, the edge structure of $G\times H$ is defined on homomorphisms that preserve the adjacency structures of G and H. Additional information on the direct product can be found in [3].

Depending on the edge structures of G and K, not all f function combinations generate edges in $G^K$. As an example, let K be $K_3$ with $V\left(G\right)=\{v_1,v_2,v_3\}$ and let G be $K_2$. Let $\sigma$ be a f combination. Although the set of $\sigma$ is $\mathrm{Aut}\left(K_3\right)$ that is the dihedral group on 3 (excluding the identity, $\mathrm{Aut}\left(K_3\right)$ is: $\left(v_2{v}_3{v}_1\right)$, $\left(v_3{v}_1{v}_2\right)$, $\left(v_2{v}_1{v}_3\right)$, $\left(v_1{v}_3{v}_2\right)$, $\left(v_3{v}_2{v}_1\right)$), any $\sigma$ function combination containing a fixed vertex is disregarded as these combinations of f cannot generate an edge in $G^K$. Thus, the f combinations in this case that generate edges in $G^K$ is set $\{\left(v_2{v}_3{v}_1\right),\left(v_3{v}_1{v}_2\right)\}$; and $K_2^{K_3}$ is the disjoint union $C_6+K_2$[4]. The edge-generating function combinations are also referred to in this note as the f combinations that apply to $G^K$.

As $K_1^{*}$ has one function that maps vertex v to v then $G^{K_1^{*}}=G$. Thus $K_1^{*}$ is the identity for this product.

Given graphs G, H and K plus direct product $G\times H$, the following hold as proved in [7].

Any G has a neighborhood multiset$\mathcal{N}\left(G\right)$ of the open neighborhoods $N\left(g\right)$ for $g\in V\left(G\right)$. For $K_2$ with $V\left(K_2\right)=\{0,1\}$, as $N\left(0\right)=1$ and $N\left(1\right)=0$, then $\mathcal{N}\left(K_2\right)=\{\left\{1\right\},\left\{0\right\}\}$. It is not always true that if $\mathcal{N}\left(G\right)=\mathcal{N}\left(H\right)$ then $G\cong H$. See [2] for a couple of examples. Graph G is said to be neighborhood reconstructible if $\mathcal{N}\left(G\right)=\mathcal{N}\left(H\right)$ implies that $G\cong H$[2]. In [2] it is shown that G is neighborhood reconstructible if and only if $G^{K_2}\cong H^{K_2}$ implies that $G\cong H$ for all H. This paper appears to be the only instance in which cancellation in $G^K$ is explored.

Most of the following material in this subsection is given in [5] and repeated here for completeness. As an overview, based on $|G^K{|=|G|}^{\left|K\right|}$, adjacency matrix $A_{G^K}$ is the Kronecker product matrix $A_{G\otimes }={\prod }_{i=1}^{\left(n_K\right)-1}{A}_G\otimes {\left(A_G\right)}_i$ of $A_G$ over $\left|K\right|$ that is row permuted by the $f_i$ function cmbinations that generate edges in the exponential.

Thus, when K is $K_2$, the exponential adjacency matrix $A_{G^{K_2}}$ is a single permutation of the adjacency matrix for $G^2$ as given by the following proposition from [5].

Examination of the adjacency matrices for the two graphs in Figure 1 gives an example for Proposition 1. Let $(g,g^{\prime })\in V\left(G^{K_2}\right)$ and $\pi$ be the permutation of $A_{G^2}$ to $A_{G^{K_2}}$. When $g=g^{\prime }$, as shown by the $(g,g^{\prime })$ row in $A_{G^2}$, $\pi$ fixes $N(g,g^{\prime })$. When $g\ne g^{\prime }$, $N(g,g^{\prime })\mapsto N(g^{\prime },g)$ due to the transposition action of $\pi$ on $A_{G^2}$ resulting in $A_{G^{K_2}}$.

Following are some definitions from [5]. Imagine set $\{{\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_k\}$ of $n_K$-tuple $f_j$ functions combinations where $f_j:V\left(K\right)\to V\left(G\right)$ and k is the number of ${\sigma }_i$ combinations of $f_j$ that apply to $G^K$. Let ${\pi }_i\in \mathsf{\Omega }$ be a ${\left|G\right|}^{\left|K\right|}\times {\left|G\right|}^{\left|K\right|}$ permutation matrix for each ${\sigma }_i$. Thus, based on the structures of G and K, ${\mathsf{\Omega }}_G$ contains only the k number of ${\pi }_i$ where the ${\sigma }_i$ produce edges in $G^K$.

Let $A_{G\otimes }$ be the Kronecker product of $A_G$ over $\left|K\right|$ where the Z blocks are maximized by having $A_G$ as the first multiplicand:

Define ${\mathsf{\Omega }}_{A_{\wedge }}$ as a collection of $|{\mathsf{\Omega }}_G|$ number of ${\left(A_{\wedge }\right)}_i={\pi }_i*A_{G\otimes }$. Thus, each ${\left(A_{\wedge }\right)}_i$ is associated with a distinct member ${\pi }_i$ of ${\mathsf{\Omega }}_G$; and each ${\left(A_{\wedge }\right)}_i$ member of ${\mathsf{\Omega }}_{A_{\wedge }}$ is a submatrix of $A_{G^K}$ based on a specific ${\pi }_i$, with set ${\mathsf{\Omega }}_{A_{\wedge }}$ over all ${\pi }_i$ in ${\mathsf{\Omega }}_G$.

Define ${\sum }_{\Delta }$ as a matrix sum of ${\left(A_{\wedge }\right)}_i$ such that $a_{ij}$ is changed to 1 for all $a_{ij}$ where $a_{ij}>1$. This eliminates the miscounting of redundantly generated neighbors in $G^K$.

Figure 2 contains a general $A_{G^K}$ construction algorithm while Theorem 1 discusses this matrix.

The proof of Theorem 1 is found in [5].

Weishcel’s Theorem (WT) [3] states that given any nontrivial connected G and H, if either G or H has an odd cycle, then $G\times H$ is connected. However, if both G and H are bipartite, WT states that $G\times H$ has exactly two components.

In addition to WT stating that bipartite G and H create exactly two components, it is also known that both of the two generated components are bipartite. Thus, the time-lapsed product $G_1\times G_2\times \cdots \times G_k={\times }_{i=1}^k{G}_i$ produces $2^{x-1}$ number of components where x is the number of bipartite factors.

In our case, as $G^{n_k}$ and $G^K$ are intimately linked, conisder when G is bipartite and $G^{n_k}$ produces $2^{\left(n_k\right)-1}$ bipartite graphs. In bipartite graphs, the two partite sets generate partitions of even and odd walks between vertex pairs based on the partite set members. As the edges in $G\times H$ are defined on the edges of G and H, the adjacency structures of both G and H are preserved in the product via homomorphisms that define the product edges. Let $(g,h),(g^{\prime },h^{\prime })\in V(G\times H)$. The proof of WT is based on the fact that if a $g,g^{\prime }$-walk of length n exists in G and a $h,h^{\prime }$-walk of length n is in H, then there is a length n$(g,h),(g^{\prime },h^{\prime })$-walk in $G\times H$. If no such length n walk exists for two vertices in $G\times H$, then the distance between the vertex pair is infinite and the two vertices must be in different components.

As G is bipartite in this subsection, then G has no loops. Let the two copies of G in $G^2$ be G and $G^{\prime }$. Let the partite sets of G be $V_1$ and $V_2$ with the parity vertex labeling scheme, and give the same assignment to the two partite sets of $G^{\prime }$. Based on the definition of the direct product, then one component $C_s$ has vertices $(g,g^{\prime })$ where g and $g^{\prime }$ have the same parity and there exists an even length walk between $(g,g^{\prime })$ and $(g^{\prime },g)$ for all same parity g and $g^{\prime }$ pairs in $C_s$. Note that $C_s$ includes when $g=g^{\prime }$. Component $C_d$ consists of $(g,g^{\prime })$ where g and $g^{\prime }$ have different parities resulting in $(g,g^{\prime })\sim (g^{\prime },g)$ for all g and $g^{\prime }$ in $C_d$.

Reiterated from earlier and as shown in [5], when K is $K_2$, the exponential adjacency matrix is found by colexicographically labeling the rows of $A_{G^2}$ to give $A_{G^2}^{*}$, followed by row permuting $A_{G^2}^{*}$ to lexicographic row order. Let $\pi$ be the permutation matrix that row permutes $A_{G^2}^{*}$ to lexicographic row order. The $\pi$ permutation fixes rows where $g=g^{\prime }$ but maps all other rows to their transpose. In other words, for all g and $g^{\prime }$, if $g\ne g^{\prime }$ then $(g,g^{\prime })$ in $A_{G^2}^{*}$ maps to row $(g^{\prime },g)$ in $A_{G^2}^{*}$ resulting in the $(g^{\prime },g)$ row of $A_{G^{K_2}}$. Component $C_s$ in $G^2$ has an isomorphic component $C_s^{*}$ in $G^{K_2}$ while $C_d$ becomes two components in the exponential as discussed in Proposition 2. First we give a general lemma that applies to all $G^K$ and is utilized in the proof of Proposition 2.

WT tells us that if connected G contains an odd cycle, then $G^2$ is connected. Thus, for any vertex pair in G containing an odd cycle there is a walk of some length n. As $G^2$ is connected, then there also exists a n length walk between vertex pairs in $G^2$. As $\pi$ merely row permutes, $A_{G^2}$ to give $A_{G^{K_2}}$, then the number of neighbors in $G^2$ for any $(g,g^{\prime })$ becomes the number of neighbors of $(g^{\prime },g)$. In particular, we refer to two specific situations: (1) $(g^{\prime },g)\in N(g,g^{\prime })$ in $G^2$ and (2) $(g,g^{\prime })$ is a pendant in $G^2$.

For (1), let $(g,g^{\prime })$ be such a vertex in $G^2$ so there exists edge $(g,g^{\prime })\in E\left(G\right)$. As G has an odd cycle, then the degree of both $(g,g^{\prime })$ and $(g^{\prime },g)$ in $G^2$ is at least 3. Then $\pi$ maps $N(g,g^{\prime })$ to the neighborhood of $(g^{\prime },g)$ in $G^{K_2}$; and edge $((g,g^{\prime }),(g^{\prime },g))$ is eliminated in $G^{K_2}$ and both vertices in $G^{K_2}$ gain loops. However, both neighborhoods in $G^2$ have degree at least 3, so $(g,g^{\prime })$ and $(g^{\prime },g)$ remain connected in $G^{K_2}$.

Now ponder situation (2). If $G^2$ contains a pendant vertex, then G must contain a pendant; so let the pendant in G be v. As G contains an odd cycle, then a neighbor of v must have degree at least 2. Given an arbitrary vertex x in G, then $vx$ and $xv$ both have degrees greater than 1 in $G^2$; and the only vertex with degree 1 in $G^2$ (and in $G^{K_2}$) is $vv$ which is fixed under $\pi$ so its degree is that of v. Hence, $G^{K_2}$ remains connected even if $G^2$ contains a pendant. Corollary 1 in the next section states that for all $K_n$ exponents, when G is connected and has an odd cycle, then $G^K$ has one component.

From WT it is a given that for any bipartite G, $G^{n_k}$ generates $2^{\left(n_k\right)-1}$ bipartite components. Based on the proof of WT and the parity vertex labeling scheme, one of the $2^{\left(n_k\right)-1}$ bipartite factors has vertex tuple elements that share the same parity. In this component, there are even length walks between the all-even vertex pairs and between the all-odd vertex pairs.

The other components of $G^{n_K}$ all have vertex elements with mixed parity. Denote an even element as e and let o indicate an odd element. Using shorthand notation and example $G^3$, since these components are bipartite, vertex $\left(\mathrm{eeo}\right)\sim \left(\mathrm{ooe}\right)$; but vertex pair (oeo)∼(eoe) is in a separate component from that of (eeo) and (ooe). In other words, given parity vertex labeling, the components of $G^{n_K}$ are constructed based on both the ratio of odd to even elements and their ordered arrangement in the vertex tuples. As the choices are binary and the tuple size is $n_K$, then there are $2^{n_k}$ ordered combinations of e and o over the $2^{\left(n_K\right)-1}$ components so each component has $\frac{2^{n_K}}{2^{\left(n_K\right)-1}}=2$ e-o ordered combinations.

A bipartite G implies that G is loopless; thus, the focus here is on the $(n_K-1)!$ directed Hamiltonian cycles (dH) of $K_n$ as K ($n>2$). Denote the tuple vertices by the number of even and odd elements so that $\left(n\right)e$ indicates that there are n number of even tuple elements in a particular tuple; and similarly for odd elements. Every set of $G^{n_K}$ components has a subset of components with tuples $((n_K-1)\mathrm{e},1\mathrm{o})\sim (1\mathrm{e},(n_K-1)\mathrm{o})$. For these components, in the set of dH, any repetition of a digit in a particular tuple position creates possibly redundant edges in $G^{K_n}$. As the regular degree for any $K_n$ is $n_K-1$, there are $(n_K-2)!$ listings of each digit d in a particular tuple position not indexed by d in the set of dH for $K_n$. This is based on the edge choices in each dH at each vertex that follow the initial vertex. Thus, excluding the component with same parity tuples, $\frac{(n_K-1)!}{(n_K-2)!}=n_K-1$ number of dH that generate distinct edges in $G^{K_n}$ for all of the mixed parity components. It needs to be noted that some subsets of components, such as those where $\left|\mathrm{e}\right|=\left|\mathrm{o}\right|$ in the tuples, have additional dH that create distinct edges in the exponential; but focus here is on the minimum number of dH that generate distinct exponential edges as these edges join components of $G^{n_K}$ to form the components of $G^{K_n}$.

To see the redundant dH, suppose that K is $K_4$ with $V\left(K_4\right)=\{1,2,3,4\}$ resulting in distinct dH of (2341), (4123), (4312), (3142), (2413), and (3421) excluding the identity. Imagine $K_2$ as G with $V\left(K_2\right)=\{\mathrm{e},\mathrm{o}\}$ so (eoee) is a vertex in ${\left(K_2\right)}^4$ and in $K_2^{K_4}$. Denote ${\pi }_1=\left(4123\right)$ and ${\pi }_2=\left(3142\right)$. Then ${\pi }_1·\left(\mathrm{eoee}\right)=\left(\mathrm{eooo}\right)={\pi }_2·\left(\mathrm{eoee}\right)$ as $2\mapsto 1$ in both ${\pi }_1$ and ${\pi }_2$.

When $G:=K_2$ has $V\left(K_2\right)=\{\mathrm{e},\mathrm{o}\}$, in the $2^{\left(n_K\right)-1}$ components, there are $2^{n_k}$ e-o ordered combinations that are also the vertices of $G^{n_K}$ since $\left|G\right|=2$. However, if G has $\left|G\right|>2$ such as $G:=C_4$ with $V\left(C_4\right)=\{1,2,3,4\}$ where $V_1=\{2,4\}$ while $V_2=\{1,3\}$, then e represents $\{2,4\}$ and o reflects $\{1,3\}$. In this case, there are still $2^{n_K}$ e-o ordered combinations but these combinations are over $4^{n_K}$ vertices of $C_4^{n_k}$ in $2^{\left(n_K\right)-1}$ components.

Again suppose $K_2$ is G with $V\left(K_2\right)=\{\mathrm{e},\mathrm{o}\}$, but now let K be $K_3$ with $V\left(K_3\right)=\{1,2,3\}$. Then the permutations that apply to G are ${\pi }_1=(2,3,1)$ and ${\pi }_2=(3,1,2)$. Thus, ${\pi }_1·\left(\mathrm{ooo}\right)=\left(\mathrm{e}\mathrm{e}\mathrm{e}\right)={\pi }_2·\left(\mathrm{ooo}\right)$ and ${\pi }_1·\left(\mathrm{oeo}\right)=\left(\mathrm{eeo}\right)$ and ${\pi }_2·\left(\mathrm{oeo}\right)=\left(\mathrm{oee}\right)$ as shown in Figure 3. As noted in the figure, the components in ${\left(K_2\right)}^3$ are derived from the e to o ratio plus the ordering of the e and o elements; however, the $K_2^{K_3}$ components are formed exclusively on the e to o ratio. In other words, the e and o element ordering does not matter in the $K_2^{K_3}$ components; only the e-o ratio is used in component formation. $K_2^{K_3}$ is $K_2+C_6$ [4].

When connected G has an odd cycle, then $G^{n_K}$ has a single component. Suppose K is $K_n$. Then the set of dH contains no reason that the single component in $G^{n_K}$ is partitioned. Hence, the rationale discussed for $K_2$ as K also applies to all $K_n$ as K when $n>2$ and G is connected with an odd cycle.