On the Lebesgue Constants

Preprint

Article

On the Lebesgue Constants

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Supplementary Material

supplementary.zip (470.96KB )

Manuel Duarte Ortigueira^*

Gabriel Bengochea

Manuel Duarte Ortigueira^*

Gabriel Bengochea

This version is not peer-reviewed

Submitted:

27 May 2024

Posted:

27 May 2024

You are already at the latest version

Alerts

Abstract

The obtention of simple formulae for the Lebesgue constants arising in the the classical Fourier series approximation is presented. Both even and odd cases are treated enlarging Fejér result. Asymptotic formulae are also obtained.

Keywords:

Subject: Computer Science and Mathematics - Other

MSC: 65T40

1. Introduction

There are many famous important constants in Mathematics, such as e (Napier’s constant or Euler’s number),

π

(Archimedes’ constant),

\sqrt{2}

(Pythagoras’ constant),

γ

(Euler’s constant) to cite a few [1]. In this article we shall be concerned with the Lebesgue constants which were introduced by H. Lebesgue as best possible upper bound for the approximation of functions through Fourier series [2,3,4]. These numbers are usually expressed in the form

I_{n} = \frac{1}{π} \int_{0}^{π} \frac{| sin ((n + 1 / 2) t) |}{sin (t / 2)} d t

(1)

where

n \in N .

Several famous mathematicians have worked on these constants, established some properties, namely asymptotic and proposed alternative expression. We list some of them.

Fejér [5] proved the formula

$I_{n} = \frac{1}{2 n + 1} + \frac{2}{π} \sum_{k = 1}^{n} \frac{1}{k} tan (\frac{k π}{2 n + 1}), n \in N;$

(2)
Szegö [6] contributed with the formula

$I_{n} = \frac{16}{π^{2}} \sum_{k = 1}^{\infty} \sum_{j = 1}^{(2 n + 1) k} \frac{1}{4 k^{2} - 1} \frac{1}{2 j - 1}, n \in N;$

(3)
Watson [7] established the following asymptotic formula

$lim_{n \to \infty} (I_{n} - \frac{4}{π^{2}} ln (2 n + 1)) = c$

(4)

where

$c = \frac{8}{π^{2}} \sum_{k = 1}^{\infty} \frac{ln (k)}{4 k^{2} - 1} - \frac{4}{π^{2}} ψ (\frac{1}{2}) = \frac{4}{π^{2}} (2.4413238136 \dots),$

(5)

and $ψ (x)$ is the digamma function;
Hardy [8] discovered two integral representations

$\begin{matrix} I_{n} & = 4 \int_{0}^{\infty} \frac{tanh ((2 n + 1) x)}{tanh (x)} \frac{1}{π 2 + 4 x^{2}} d x \\ = \int_{0}^{\infty} \frac{sinh ((2 n + 1) x)}{sinh (x)} ln (coth (\frac{2 n + 1}{2} x)) d x . \end{matrix}$

(6)

Later on, other mathematicians have contributed with two-sided estimates. Zhao [9] discovered two-sided inequalities which help to improve the Watson asymptotic expansion formulas. In [3], new inequalities were established for the Lebesgue constants

I_{n / 2}

which allowed obtaining an asymptotic expansion of

I_{n / 2}

in terms of

\frac{1}{n + 1}

. More recently, other contributions were published. Shakirov approximated the Lebesgue constant by a logarithmic function [10] and by means of logarithmic-fractional-rational function [4]. The asymptotic behaviour of

I_{n}

was also study in [11], although indirectly, since the authors studied the properties of the Dirichlet kernel that is related to the integrand function appearing in (7). It must be remarked that (1) can be rewritten in the form

I_{n} = \frac{2}{π} \int_{0}^{π / 2} \frac{| sin ((2 n + 1) t) |}{sin (t)} d t

(7)

where

n \in N .

2 n + 1, n \in N,

is an odd integer, we are motivated to consider the more general constants

I_{n} = \frac{2}{π} \int_{0}^{π / 2} \frac{| sin (n t) |}{sin (t)} d t

(8)

that we continue calling Lebesgue constants and where

n \in N .

In the following we will describe the steps involved in the obtention of the Fejér’s formula for the Lebesgue odd order numbers. The steps constitute a simple way that allow us to obtain formulae for any positive integer. We are going to consider and treat separately, even

n = 2 N,

and odd,

n = 2 N + 1,

cases (

N \in N

). Asymptotic formulae are also proposed.

2. The Way to the Lebesgue Constants

Lebesgue studied the approximation of periodic functions by the partial sum of the Fourier series [2] and obtained a formulation that can be stated as [11]

Theorem 1.

Let

f (t)

be a periodic continuous function on

[- π, π],

and

C_{k} = \frac{1}{2 π} \int_{- π}^{π} f (t) e^{- i k t} d t

the Fourier coefficients, where

i = \sqrt{- 1}

. If

S_{n} (f), n \in N

denotes the

n^{th}

partial sum of

f (t)

, that is

S_{n} (f) = \sum_{k = - n}^{n} C_{k} e^{i k t}

(9)

then

S_{n} (f) = \frac{1}{2 π} \int_{- π}^{π} D_{n} (τ) f (t - τ) d τ

(10)

where

D_{n} (t) = \{\begin{matrix} \frac{sin ((n + 1 / 2) t)}{sin (t / 2)} & t \neq 0 \\ 2 n + 1 & t = 0 \end{matrix}

(11)

is the so-called Dirichlet kernel.

This theorem shows the importance of the Dirichlet kernel and the relation with the Lebesgue constants. Lebesgue showed that,

Corollary 1.

max_{- π \leq t \leq π} |f (t)| \leq 1

then

max_{- π \leq t \leq π} | S_{n} (f) | \leq I_{n} = \frac{1}{2 π} \int_{- π}^{π} | D_{n} (t) | d t

(12)

where

I_{n}

is the best possible upper bound that can be rewritten as

I_{n} = \frac{1}{π} \int_{0}^{π} \frac{| sin ((n + 1 / 2) t) |}{sin (t / 2)} d t

(13)

The Dirichlet kernel verifies the following relation [11]

4 + \frac{8}{π} ln (n + \frac{1}{2}) \leq \int_{- π}^{π} |D_{n} (t)| d t \leq 2 π + 4 + \frac{8}{π} ln (2 n),

that can be used to find the asymptotic behaviour of the Lebesgue constants. We will consider a general version of (12)

I_{n} = \frac{2}{π} \int_{0}^{π / 2} \frac{| sin (n t) |}{sin (t)} d t

(14)

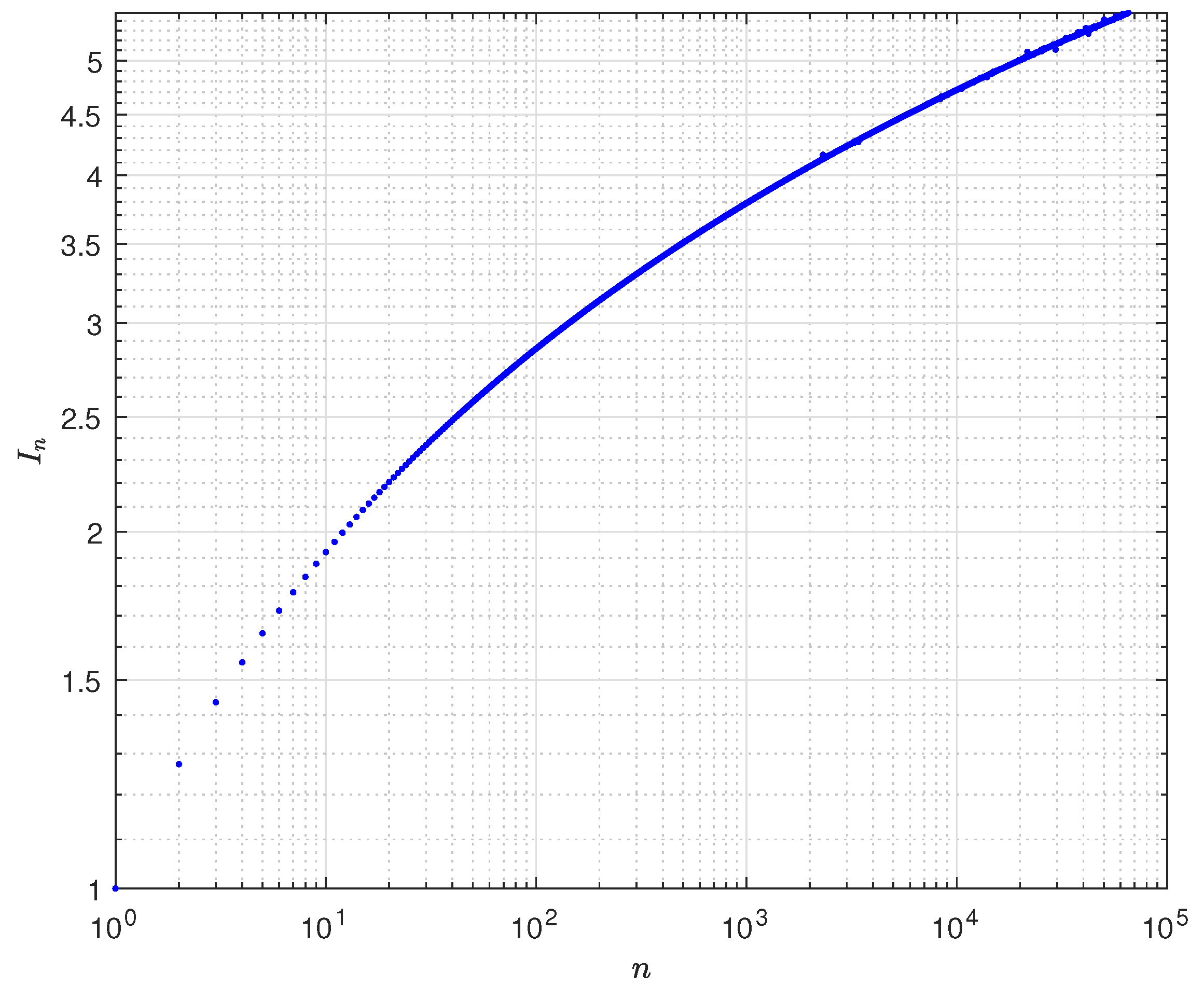
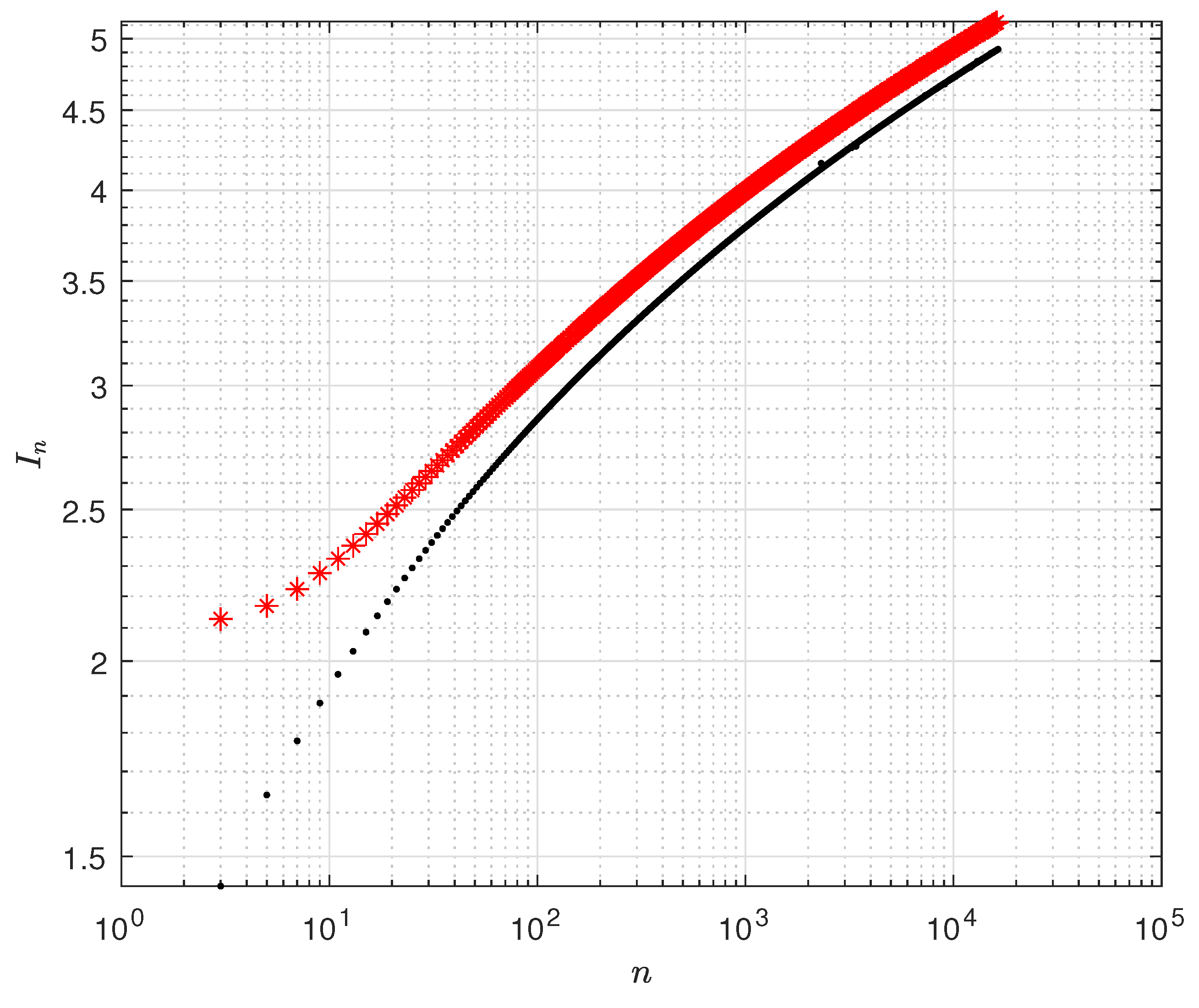
where n is any positive integer, even or odd. We will propose an alternative approach that leads to exact closed formulae corresponding any positive values of n. In the following picture we depict the result of numerical integration of (14) for

n = 1, 2, 3, \dots 2^{L}

, with

L = 16

. We used a log-scale.

Figure 1. Examples for

n = 1, 2, \dots

Figure 1. Examples for

n = 1, 2, \dots

We go on by establishing a result that will useful in a later Section. Let us define Dirichlet-like kernel given by

{\bar{D}}_{n} (t) = \frac{sin (n t)}{sin (t)}

Theorem 2.

We can show that

{\bar{D}}_{n} (t) = \frac{sin (n t)}{sin (t)} = e^{i (n - 1) t} + e^{i (n - 3) t} + \dots + e^{- i (n - 3) t} + e^{- i (n - 1) t}

(15)

The proof is immediate. We only need to note that

\frac{sin (n t)}{sin (t)} = \frac{e^{i n t} - e^{- i n t}}{e^{i t} - e^{- i t}} = e^{i (n - 1) t} \frac{1 - e^{- i 2 n t}}{1 - e^{- i 2 t}}

and apply the geometric sum rule.

As observed, the exponents have the generic form

i (n - (2 k - 1)) t, k = 1, 2, \dots

. If n is odd it can assume the value 0. Therefore

Corollary 2.

Let

N = \{\begin{matrix} \frac{n - 1}{2}, & if n is odd \\ \frac{n}{2}, & if n is even \end{matrix},

Then

{\bar{D}}_{n} (t) = \frac{sin (n t)}{sin (t)} = \{\begin{matrix} 1 + 2 \sum_{k = 1}^{N} cos (2 k t) & if n is odd \\ 2 \sum_{k = 1}^{N} cos ((2 k - 1) t) & if n is even \end{matrix}

(16)

This expression is suitable to obtain the primitive of

{\bar{D}}_{n} (t) .

3. New Formulation

3.1. Preliminaries

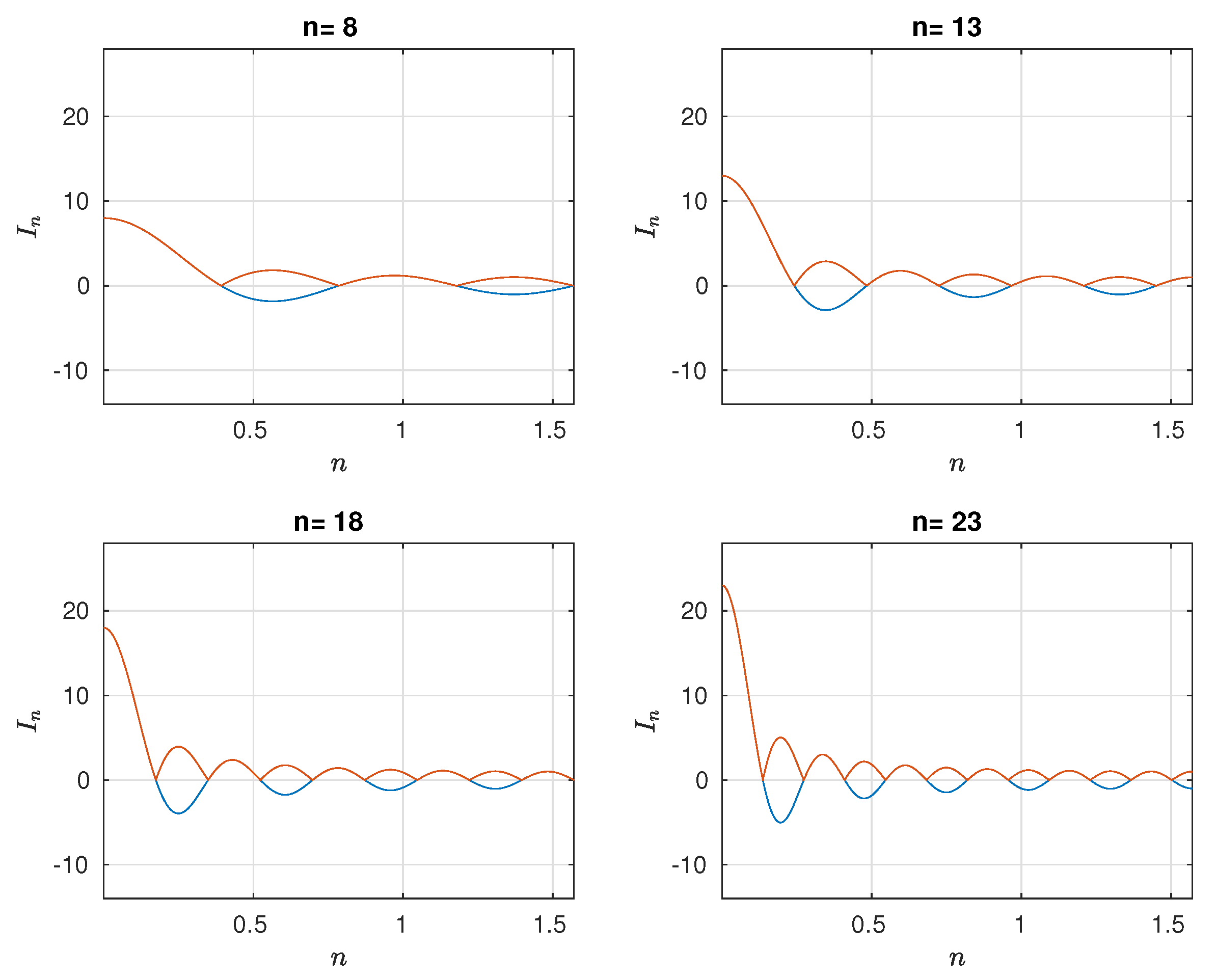
We are going to make a brief study of the kernel that makes easier the way into the solution we search. Consider the function

f (t) = | sin (n t) |, 0 \leq t \leq π / 2,

where the sinusoid

sin (n t)

has frequency

\frac{n}{2 π}

and half-period

T = \frac{π}{n}

. Therefore, in the interval

0 \leq t \leq π / 2

, there are N half periods. If n is odd, there is another quarter of period. In the half periods with orders

0, 2, 4, \dots

the function

sin (n t)

is positive. In the others, it is negative.

Figure 2. Examples for

n = 8, 13, 18, 23

Figure 2. Examples for

n = 8, 13, 18, 23

Therefore, the presence of the absolute value in

f (t)

allows us to write

f (t) = \sum_{m = 0}^{N} f_{m} (t),

where

f_{m} (t) = f_{m - 1} (t - T), m T \leq t < (m + 1) T, m = 1, 2, \dots N - 1,

with

f_{0} (t) = sin (n t), 0 \leq t < T,

and the last term

(m = N)

f_{N} (t) = \{\begin{matrix} f_{N - 1} (t - T), N T \leq t < N T + T / 2, & if N is odd \\ 0, & if N is even \end{matrix} .

This means that

f (t)

is obtained by juxtaposing N positive half periods of

sin (n t)

. If n is odd, we have to join another one quarter of a period.

3.2. The Even n Case

Theorem 3.

Let

n \in N

be an even number. Then

I_{n} = \frac{4}{π} \sum_{k = 1}^{n / 2} \frac{tan (\frac{(2 k - 1) π}{2 n})}{2 k - 1} .

(17)

Proof.

According to the structure of the numerator of our kernel, we can write We have

I_{n} = \frac{2}{π} \sum_{m = 0}^{N - 1} \int_{m T}^{(m + 1) T} \frac{sin (n (t - m T))}{sin (t)} d t

(18)

Attending to

sin (n t) = sin (n (t + m T - m T)) = sin (n (t + m T) - m π) = {(- 1)}^{m} sin (n (t + m T)),

we are led to

I_{n} = \frac{2}{π} \sum_{m = 0}^{N - 1} {(- 1)}^{m} [\int_{0}^{T} \frac{sin (n (t + m T))}{sin (t + m T)} d t],

(19)

that expresses the Lebesgue numbers in a new different way.

To continue, we need to find the primitive of the integrand which is not a big task. In fact, as seen above,

\frac{sin (n x)}{sin (x)} = 2 \sum_{k = 1}^{N} cos ((2 k - 1) x) .

It follows that

P_{n} (x) = \int \frac{sin (n x)}{sin x} d x = 2 \sum_{k = 1}^{N} \frac{sin ((2 k - 1) x)}{2 k - 1} .

(20)

For our application,

x = t + m T

, so that

P_{n} (t) = \int \frac{sin (n (t + m T))}{sin (t + m T)} d t = 2 \sum_{k = 1}^{n / 2} \frac{sin ((2 k - 1) (t + m T))}{2 k - 1} .

(21)

Let us denote the function in brackets in (19) by

J_{m} (n)

. We have

I_{n} = \frac{2}{π} \sum_{m = 0}^{N - 1} {(- 1)}^{m} J_{m} (n) .

(22)

with

J_{m} (n) = \int_{0}^{T} \frac{sin (n (t + m T))}{sin (t + m T)} d t = P_{n} (T) - P_{n} (0),

where

T = π / n

. Then

m T = \frac{π m}{n}

T + m T = \frac{(m + 1) π}{n}

, and

J_{m} (n) = 2 \sum_{k = 1}^{N} \frac{sin ((2 k - 1) (m + 1) π / n)}{2 k - 1} - 2 \sum_{k = 1}^{N} \frac{sin ((2 k - 1) m π / n)}{2 k - 1} .

Simplifying

J_{m} (n) = 2 \sum_{k = 1}^{N} \frac{sin ((2 k - 1) (m + 1) π / n) - sin ((2 k - 1) m π / n)}{2 k - 1},

using the trigonometric identity

sin (A) - sin (B) = 2 cos (\frac{A + B}{2}) sin (\frac{A - B}{2}),

we get

J_{m} (n) = 4 \sum_{k = 1}^{N} \frac{cos ((2 k - 1) (2 m + 1) π / (2 n)) sin ((2 k - 1) π / (2 n))}{2 k - 1} .

(23)

that inserted into (22) gives the expected result. However, we can go ahead and manipulate these formulae trying to obtain any simplification. We proceed to invert the summation order:

\begin{matrix} \sum_{m = 0}^{N - 1} {(- 1)}^{m} & (\sum_{k = 1}^{N} \frac{cos ((2 k - 1) (2 m + 1) π / (2 n)) sin ((2 k - 1) π / (2 n))}{2 k - 1}) = \\ \sum_{k = 1}^{N} \frac{sin ((2 k - 1) π / (2 n))}{2 k - 1} (\sum_{m = 0}^{N - 1} {(- 1)}^{m} cos ((2 k - 1) (2 m + 1) π / (2 n))) \end{matrix}

Substituting sinusoid by exponentials and using the rule for summing the geometric sequence, we can show that

\sum_{m = 0}^{N - 1} {(- 1)}^{m} cos ((2 k - 1) (2 m + 1) π / (2 n)) = \frac{1 - {(- 1)}^{N} cos (\frac{N}{n} (2 k - 1) π)}{2 cos (\frac{(2 k - 1) π}{2 n})}

Attending to the fact that

2 N = n

and

cos ((2 k - 1) π / 2) = 0

, we can write

\sum_{m = 0}^{N - 1} {(- 1)}^{m} cos ((2 k - 1) (2 m + 1) π / n) = \frac{1}{2 cos (\frac{(2 k - 1) π}{2 n})}

and finally,

I_{n} = \frac{4}{π} \sum_{k = 1}^{n / 2} \frac{tan (\frac{(2 k - 1) π}{2 n})}{2 k - 1} .

(24)

□

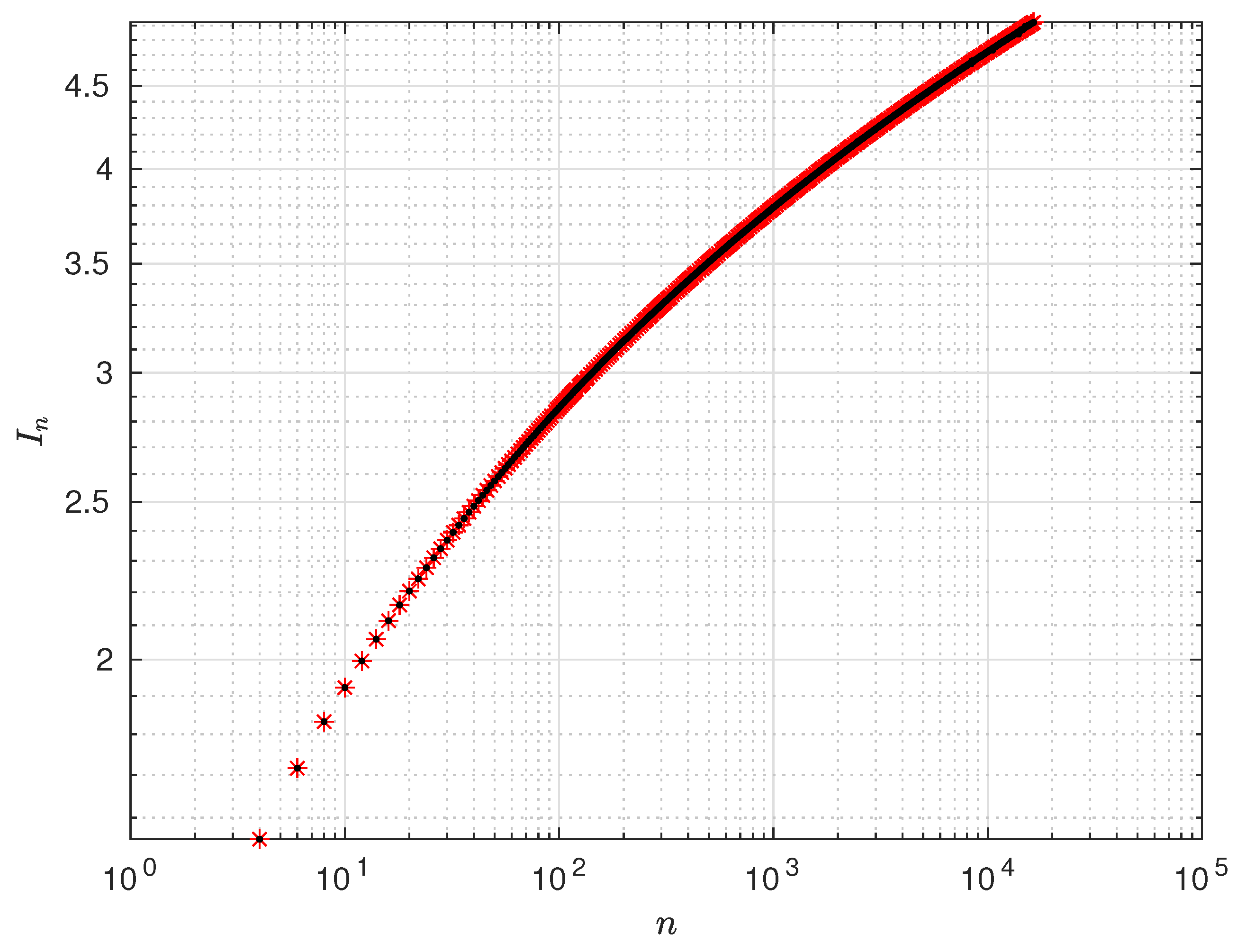
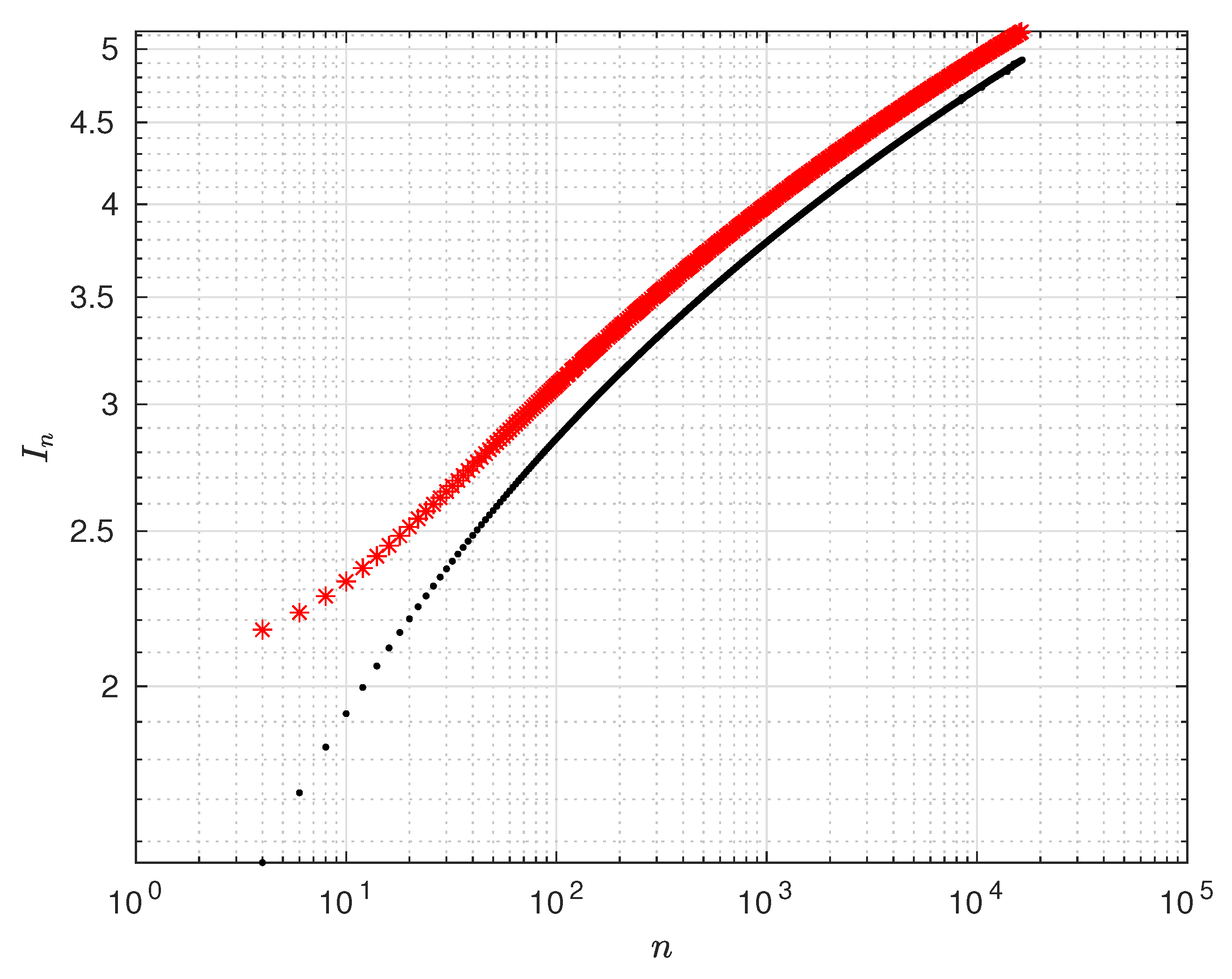
This formula was never proposed. In Figure 3 we compare the value of

I_{n}

obtained from (24) with the numerical integration of (14).

3.3. The Odd n Case

Theorem 4.

Let

n \in N

be an odd number. Then

I_{n} = \frac{2}{π} \sum_{k = 1}^{(n - 1) / 2} \frac{tan (k π / n)}{k} + \frac{1}{n}

(25)

This formula was proposed first by Fejér but deduced using a completely different procedure [5].

Proof.

Let

n = 2 N + 1

. Differently from the even n case, we have

I_{n} = \frac{2}{π} \sum_{m = 0}^{N - 1} \int_{m T}^{(m + 1) T} \frac{sin (n (t - m T))}{sin (t)} d t + \frac{2}{π} \int_{N T}^{N T + T / 2} \frac{sin (n (t - N T))}{sin (t)} d t .

(26)

We joined an extra quarter of a period.

We can write

sin (n t) = sin (n (t + m T - m T)) = sin (n (t + m T) - m π) = {(- 1)}^{m} sin (n (t + m T)) .

The second term on the right of the equality is

\int_{N T}^{N T + T / 2} \frac{sin (n (t - N T))}{sin (t)} d t = \int_{0}^{T / 2} \frac{sin (n t)}{sin (t + N T)} d t = \int_{0}^{T / 2} \frac{{(- 1)}^{N} sin (n (t + N T))}{sin (t + N T)} d t .

I_{n} = \frac{2}{π} [\sum_{m = 0}^{N - 1} {(- 1)}^{m} \int_{0}^{T} \frac{sin (n (t + m T))}{sin (t + m T)} d t + \int_{0}^{T / 2} {(- 1)}^{N} \frac{sin (n (t + N T))}{sin (t + N T)} d t],

(27)

that re-expresses the Lebesgue numbers in a new different way.

To continue, we need to find the primitive of the integrand which is not a big task attending to (15). In fact, we have

\frac{sin (n x)}{sin (x)} = 1 + 2 \sum_{k = 1}^{(n - 1) / 2} cos 2 k x,

It follows that

P_{n} (x) = \int \frac{sin (n x)}{sin x} d x = \sum_{k = 1}^{(n - 1) / 2} \frac{sin 2 k x}{k} + x .

For our application,

x = t + m T

, so that

P_{n} (t) = \int \frac{sin (n (t + m T))}{sin (t + m T)} d t = \sum_{k = 1}^{N} \frac{sin (2 k (t + m T))}{k} + (t + m T) .

(28)

As above, let us denote the function in brackets in (27) by

J_{m} (n)

and the second term by

J_{N} (n)

so that

I_{n} = \frac{2}{π} \sum_{m = 0}^{N - 1} {(- 1)}^{m} J_{m} (n) + \frac{2}{π} J_{N} (n)

(29)

with

J_{m} (n) = \int_{0}^{T} \frac{sin (n (t + m T))}{sin (t + m T)} d t = P_{n} (T) - P_{n} (0),

and

J_{N} (n) = \int_{0}^{T / 2} \frac{sin (n (t + m T))}{sin (t + m T)} d t = P_{n} (T / 2) - P_{n} (0) .

T = π / n

, then

m T = \frac{π m}{n}

T + m T = \frac{(m + 1) π}{n}

, and

J_{m} (n) = \sum_{k = 1}^{N} \frac{sin (2 k (m + 1) π / n)}{k} + \frac{(m + 1) π}{n} - \sum_{k = 1}^{N} \frac{sin (2 k m π / n)}{k} + \frac{m π}{n} .

We obtain

J_{m} (n) = \sum_{k = 1}^{N} \frac{sin (2 k (m + 1) π / n) - sin (2 k m π / n)}{k} + \frac{π}{n} .

Using the trigonometric identity

sin (A) - sin (B) = 2 cos (\frac{A + B}{2}) sin (\frac{A - B}{2}),

J_{m} (n) = 2 \sum_{k = 1}^{N} \frac{cos (k (2 m + 1) π / n) sin (k π / n)}{k} + \frac{π}{n} .

(30)

Concerning the other term,

J_{N} (n)

we have:

J_{N} (n) = \sum_{k = 1}^{N} \frac{sin (2 k (T / 2 + N T))}{k} + (T / 2 + N T) - \sum_{k = 1}^{N} \frac{sin (2 k N π / n)}{k} - N T .

But

n = 2 N + 1

and

T n = π

, allowing a simplification of the above expression:

J_{N} (n) = \sum_{k = 1}^{N} {(- 1)}^{k} \frac{sin (k π / n)}{k} + \frac{π}{2 n} .

(31)

Let us go ahead and manipulate these formulae trying to obtain simplifications. We turn our attention to (30), (31), and (29). Then

\begin{matrix} I_{n} = \frac{4}{π} & \sum_{m = 0}^{N - 1} {(- 1)}^{m} (\sum_{k = 1}^{N} \frac{cos (k (2 m + 1) π / n) sin (k π / n)}{k}) + \\ \frac{2}{π} {(- 1)}^{N} \sum_{k = 1}^{N} {(- 1)}^{k} \frac{sin (k π / n)}{k} + \frac{2}{n} \sum_{m = 0}^{N - 1} {(- 1)}^{m} + {(- 1)}^{N} \frac{1}{n} . \end{matrix}

\begin{matrix} I_{n} = \frac{4}{π} & \sum_{m = 0}^{N - 1} {(- 1)}^{m} (\sum_{k = 1}^{N} \frac{cos (k (2 m + 1) π / n) sin (k π / n)}{k}) + \\ \frac{2}{π} {(- 1)}^{N} \sum_{k = 1}^{N} {(- 1)}^{k} \frac{sin (k π / n)}{k} + \frac{1}{n} \end{matrix}

(32)

Let us change the summation order in the first term on the right in expression (32):

\begin{matrix} \sum_{m = 0}^{N - 1} {(- 1)}^{m} & (\sum_{k = 1}^{N} \frac{cos (k (2 m + 1) π / n) sin (k π / n)}{k}) = \\ \sum_{k = 1}^{N} \frac{sin (k π / n)}{k} (\sum_{m = 0}^{N - 1} {(- 1)}^{m} cos (k (2 m + 1) π / n)) . \end{matrix}

Observe that

\sum_{m = 0}^{N - 1} {(- 1)}^{m} cos (k (2 m + 1) π / n) = \frac{1 - {(- 1)}^{N} cos (\frac{2 N}{n} k π)}{2 cos (k \frac{π}{n})} .

(33)

But,

2 N = n - 1

, so that

cos (\frac{2 N}{n} k π) = cos ((1 - \frac{1}{n}) k π) = {(- 1)}^{k} cos (k \frac{π}{n}) .

Hence

\sum_{m = 0}^{N - 1} {(- 1)}^{m} cos (k (2 m + 1) π / n) = \frac{1 - {(- 1)}^{N + k} cos (k \frac{π}{n})}{2 cos (k \frac{π}{n})} = \frac{1}{2 cos (k \frac{π}{n})} - {(- 1)}^{N + k} \frac{1}{2},

that leads to

\begin{matrix} \sum_{m = 0}^{N - 1} {(- 1)}^{m} & (\sum_{k = 1}^{N} \frac{cos (k (2 m + 1) π / n) sin (k π / n)}{k}) = \\ \frac{1}{2} \sum_{k = 1}^{N} \frac{sin (k π / n)}{k} (\frac{1}{cos (k π / n)} - {(- 1)}^{N + k}) = \\ \frac{1}{2} \sum_{k = 1}^{N} \frac{tan (k π / n)}{k} - \frac{{(- 1)}^{N}}{2} \sum_{k = 1}^{N} {(- 1)}^{k} \frac{sin (k π / n)}{k} \end{matrix}

Inserting it into (32), we obtain

\begin{matrix} I_{n} = \frac{2}{π} & \sum_{k = 1}^{N} \frac{tan (k π / n)}{k} - \frac{2}{π} {(- 1)}^{N} \sum_{k = 1}^{N} {(- 1)}^{k} \frac{sin (k π / n)}{k} + \\ \frac{2}{π} {(- 1)}^{N} \sum_{k = 1}^{N} {(- 1)}^{k} \frac{sin (k π / n)}{k} + \frac{1}{n} \end{matrix}

(34)

Finally

I_{n} = \frac{2}{π} \sum_{k = 1}^{N} \frac{tan (k π / n)}{k} + \frac{1}{n} .

(35)

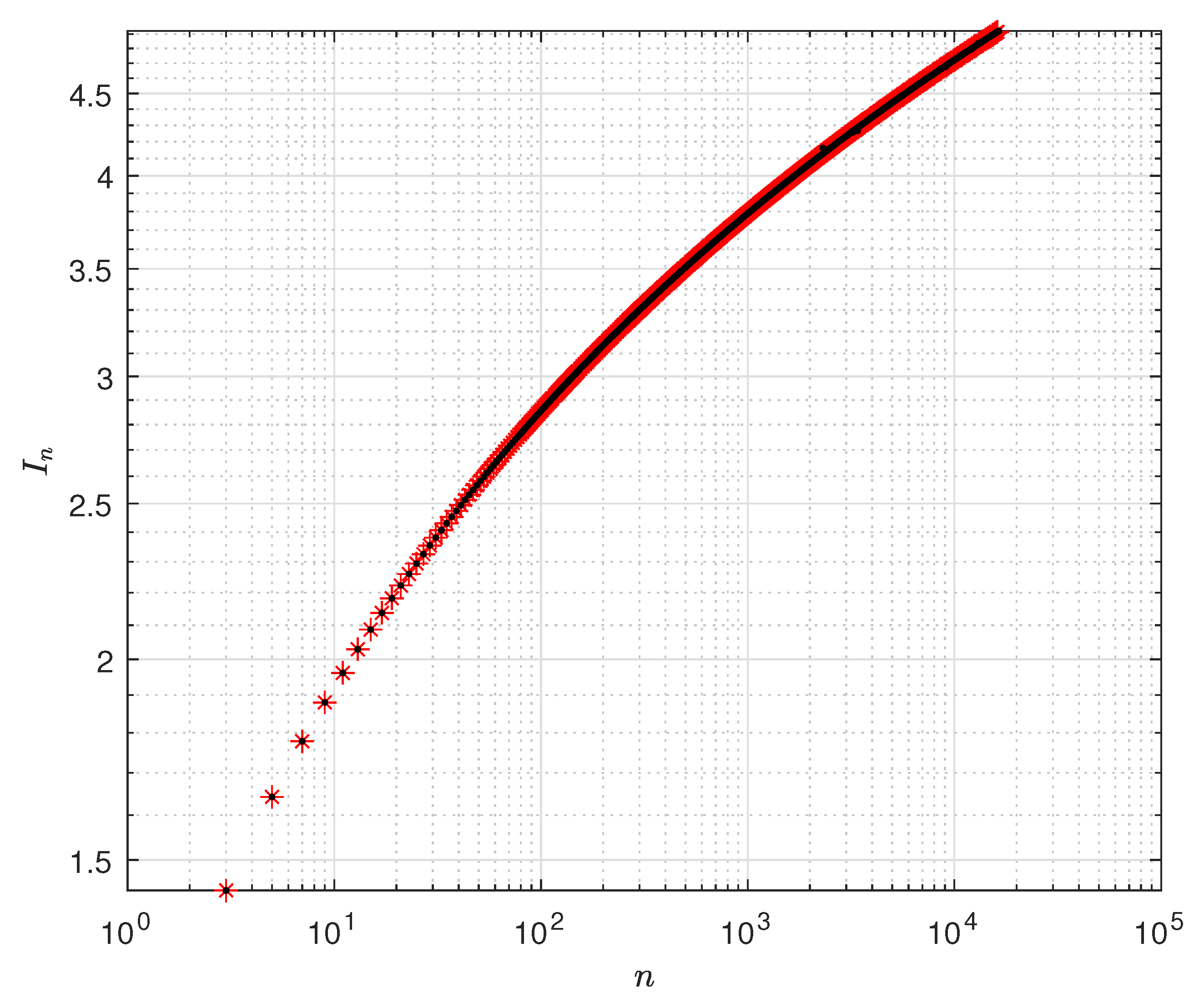
In Figure 4 we compare (35) with the integral representation of

I_{n}

(14). □

4. Asymptotic Behavior

We consider the odd n case. The even n case can be solved by relying on the odd case. Let us turn our attention to (29)

\begin{matrix} I_{n} = \frac{2}{π} \sum_{m = 0}^{N - 1} {(- 1)}^{m} & [\sum_{k = 1}^{N} \frac{sin (2 k (m + 1) π / n) - sin (2 k m π / n)}{k} + \frac{π}{n}] + \\ \frac{2}{π} [\sum_{k = 1}^{N} {(- 1)}^{k} \frac{sin (k π / n)}{k} + \frac{π}{2 n}] \end{matrix}

(36)

Using the formula [12]

\sum_{k = 1}^{N} \frac{sin (k x)}{k} = \frac{1}{2} \int_{0}^{x} (D_{N} (t) - 1) d t

(37)

where

D_{N} (t) = \frac{sin ((N + 1 / 2) t)}{sin (t / 2)},

we have

\sum_{k = 1}^{N} \frac{sin (2 k (m + 1) π / n) - sin (2 k m π / n)}{k} = \frac{1}{2} \int_{0}^{2 (m + 1) π / n} (D_{N} (t) - 1) d t - \frac{1}{2} \int_{0}^{2 m π / n} (D_{N} (t) - 1) d t .

It follows that

\begin{matrix} \sum_{m = 0}^{N - 1} {(- 1)}^{m} \sum_{k = 1}^{N} \frac{sin (2 k (m + 1) π / n) - sin (2 k m π / n)}{k} = \\ \frac{1}{2} \int_{0}^{2 π / n} (D_{N} (t) - 1) d t - \frac{1}{2} \int_{2 π / n}^{4 π / n} (D_{N} (t) - 1) d t + \dots + \frac{1}{2} {(- 1)}^{N - 1} \int_{2 (N - 1) π / n}^{2 N π / n} (D_{N} (t) - 1) d t = \\ \frac{1}{2} (\int_{0}^{2 π / n} D_{N} (t) d t - \int_{2 π / n}^{4 π / n} D_{N} (t) d t + \dots + {(- 1)}^{N - 1} \int_{2 (N - 1) π / n}^{2 N π / n} D_{N} (t) d t) + \\ min (0, {(- 1)}^{N - 1}) \frac{π}{n} \leq \frac{1}{2} \int_{0}^{2 N π / n} | D_{N} (t) | d t + min (0, {(- 1)}^{N - 1}) \frac{π}{n} \end{matrix}

(38)

It is not difficult to observe that

\begin{matrix} \int_{0}^{2 N π / n} | D_{N} (t) | d t \leq \frac{1}{2} \int_{- π}^{π} |D_{N} (t)| d t \end{matrix}

(39)

In [11], it is shown that

\frac{1}{2 π} \int_{- π}^{π} |D_{N} (t)| d t \leq 1 + \frac{2}{π} + \frac{4}{π^{2}} ln (2 N), n \geq 3 .

(40)

Hence

\begin{matrix} \sum_{m = 0}^{N - 1} {(- 1)}^{m} \sum_{k = 1}^{N} & \frac{sin (2 k (m + 1) π / n) - sin (2 k m π / n)}{k} \leq \\ \frac{π}{2} (1 + \frac{2}{π} + \frac{4}{π^{2}} ln (2 N)) + min (0, {(- 1)}^{N - 1}) \frac{π}{n} \end{matrix}

(41)

On the other hand, when

1 \leq k \leq N

0 \leq sin (k π / n) \leq 1

. So

\sum_{k = 1}^{N} {(- 1)}^{k} \frac{sin (k π / n)}{k} \leq - \sum_{k = 1}^{N} \frac{{(- 1)}^{k + 1}}{k} .

(42)

It is well-known that

\sum_{k = 1}^{\infty} \frac{{(- 1)}^{k + 1}}{k} = ln (2)

and

\sum_{k = 1}^{N} \frac{{(- 1)}^{k + 1}}{k} \geq ln (2) - 1 / (N + 1)

. Therefore

\sum_{k = 1}^{N} {(- 1)}^{k} \frac{sin (k π / n)}{k} \leq - ln (2) + 1 / (N + 1) .

(43)

Finally

I_{n} \leq 1 + \frac{2}{π} + \frac{4}{π^{2}} ln (n - 1) + \frac{2}{π} (- ln (2) + \frac{1}{N + 1}) + \frac{1}{n}

(44)

In Figure 5 we include a comparative illustration of (44) and (14).

For even n case we only need to observe that

I_{n}

is a increasing function [6], then

I_{n} \leq I_{n + 1}

with

n + 1

odd. From (44) we obtain that

I_{n} \leq 1 + \frac{2}{π} + \frac{4}{π^{2}} ln (n) + \frac{2}{π} (- ln (2) + \frac{2}{n + 2}) + \frac{1}{n + 1}

(45)

In Figure 6 a comparative illustration of (45) and (14) is depict.

Author Contributions

Conceptualization, M.O.; methodology, M.O and G.B.; formal analysis, M.O; investigation, M.O. and G.B.; writing—original draft preparation, M.O.; writing—review and editing, M.O. and G.B. Both authors have read and agreed to the published version of the manuscript.

Funding

The first author was partially funded by National Funds through the Foundation for Science and Technology of Portugal, under the projects UIDB/00066/2020. The second author was funded by the Autonomous University of Mexico City under the project UACM CCYT-CON-03.

Conflicts of Interest

The authors declare no conflict of interest.

References

Finch, S. Mathematical constants; Cambridge University Press, 2003.
Lebesgue, H. Sur la représentation trigonométrique approchée des fonctions satisfaisant à une condition de Lipschitz. Bulletin de la Société Mathématique de France 1910, 38, 184–210.
Chen, C.; Choi, J. Inequalities and asymptotic expansions for the constants of Landau and Lebesgue. Applied Mathematics and Computation 2014, 248, 610–624. [CrossRef]
Shakirov, I.A. Approximation of the Lebesgue constant of the Fourier operator by a logarithmic-fractional-rational function. Russian Mathematics 2023, 67, 64–74. [CrossRef]
Fejér, L. Sur les singularités de la série de Fourier des fonctions continues. Annales scientifiques de l’École Normale Supérieure, 1911, Vol. 28, pp. 63–104. [CrossRef]
Szego, G. Über die Lebesgueschen konstanten bei den Fourierschen reihen. Mathematische Zeitschrift 1921, 9, 163–166.
Watson, G. The constants of Landau and Lebesgue. Quart. J. Math. 1930, 1, 310–318. [CrossRef]
Hardy, G. Note on Lebesgue’s constants in the theory of Fourier series. Journal of the London Mathematical Society 1942, 1, 4–13. [CrossRef]
Zhao, D. Some sharp estimates of the constants of Landau and Lebesgue. Journal of Mathematical Analysis and Applications 2009, 349, 68–73. [CrossRef]
Shakirov, I. Approximation of the Lebesgue constant of the Fourier operator by a logarithmic function. Russian Mathematics 2022, 66, 70–76. [CrossRef]
Alvarez, J.; Guzmán-Partida, M. Properties of the Dirichlet kernel. Electronic Journal of Mathematical Analysis and Applications 2023, 11, 96–110. [CrossRef]
Stein, E.; Shakarchi, R. Fourier analysis: an introduction; Vol. 1, Princeton University Press, 2011.

Figure 3. Comparative of (24) (red) with (14) (black).

Figure 4. Comparative of (35) (red) with (14) (black).

Figure 5. Comparative of (44) (red) with (14) (black).

Figure 6. Comparative of (45) (red) with (14) (black).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On the Lebesgue Constants

Abstract

1. Introduction

2. The Way to the Lebesgue Constants

3. New Formulation

3.1. Preliminaries

3.2. The Even n Case

3.3. The Odd n Case

4. Asymptotic Behavior

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe