Prerpints.org logo
Preprint
Article

Enhanced Energy, Conversion Efficiency and Collimation of Protons Driven by High-Contrast and Ultra-Short Laser Pulses

Altmetrics

Downloads

298

Views

169

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

27 May 2024

Posted:

27 May 2024

You are already at the latest version

Alerts
Abstract
Progress in laser-driven proton acceleration requires increasing the proton maximum energy and laser-to-proton conversion efficiency, while reducing the divergence of the proton beam. However, achieving all these qualities simultaneously has proven challenging experimentally, the increase in beam energy often coming at the cost of beam quality. Numerical simulations suggest that coupling multi-PW laser pulses with ultrathin foils could offer a route for such simultaneous improvement. Yet experimental investigations have been limited by the scarcity of such lasers and the need for very stringent temporal contrast conditions to prevent premature target expansion before the pulse maximum. Here, combining the newly commissioned Apollon laser facility that delivers high-power ultrashort (∼24fs) pulses, with a double plasma mirror scheme to enhance its temporal contrast, we demonstrate the generation of up to 35 MeV protons with only 5 J of laser energy. This approach also achieves improved laser-to-proton energy conversion efficiency, reduced beam divergence, and optimized spatial beam profile. Therefore, despite the laser energy losses induced by the plasma mirror, the proton beams produced by this method are enhanced on all accounts compared to those obtained under standard conditions. Particle-in-cell simulations reveal that this improvement results from the intensified electrostatic field caused by a more compact hot-electron distribution.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

Since their inception in the early 2000s, laser-driven ion beams have opened novel pathways compared to those powered by traditional accelerators [1,2,3]. Owing to their very compact size ( ∼ 100 μ m ), ultrafast timescales ( ∼ ps ) and very high currents ( ∼ kA ) at the source, these beams enable a wide range of applications, spanning flash radiography [4], radiobiology [5], nuclear physics [6], and even ion therapy [7]. They can also be leveraged to generate bright neutron sources [8,9,10,11] which already outperform traditional neutron sources in terms of their intensity [12] and hold promise for material probing [13] and astrophysics [14].
Over the past 20 years, research has shown that laser pulses focused at relativistic intensities ( > 10 18 W cm − 2 ) onto thin solid foils (e.g. a few μ m thick) can generate fast (i.e., up to ∼ 150 MeV nowadays [15]) and highly directional ion beams. This process, named target normal sheath acceleration (TNSA) [16], relies on the strong ( ∼ 10 12 V m − 1 ) electrostatic sheath fields induced by the laser-generated hot electrons [17] at the target surfaces. Typically, TNSA is most efficient at the nonirradiated target backside [18,19,20], where it produces ion beams with a high particle flux (e.g., ∼ 10 10 – 10 12 particles exceeding a few MeV) and a relatively small angular divergence ( ∼ 15 –30 depending on the energy [21]) [22,23]. Moreover, different kinds of ions can be accelerated simply by changing the target material [24].
Now that we are at the dawn of the multi-petawatt (PW) laser era [25], the vast body of theoretical studies [1,2,26] tells us that further progress should be expected via little-explored, yet likely more efficient ion acceleration processes, i.e., radiation pressure acceleration (RPA) [27,28,29], breakout-afterburner (BOA) [30], and relativistically induced transparency (RIT) [31,32,33]. Numerical simulations predict better scaling of the maximum proton energy with laser intensity when utilizing ultrathin (nanometer-range) targets. In experiments, however, triggering the above mechanisms in a controlled way remains very challenging because the amplified spontaneous emission (ASE) pedestal, extending over picosecond or sometimes nanosecond scales ahead of the peak of the laser pulse, can easily preheat or even fully expand the thin target (less than few micron) [22], resulting in weak or no acceleration at all.
Plasma mirrors (PMs) are a well-known solution to eliminate the ASE, and hence to improve the temporal laser contrast, defined as the ratio of the peak intensity to the ASE intensity [34,35]. PMs are commonly made of polished glass slabs or liquid crystals [36] through which the low-intensity ASE light is transmitted. The subsequent rise in laser intensity eventually causes the irradiated PM surface to be ionized and, once the local electron density becomes overcritical, to reflect the main pulse. The resulting higher laser contrast can then allow ultrathin foils to survive until the intensity peak, leading to interaction conditions suitable for efficient proton acceleration.
For example, using a PM to achieve a high laser contrast of 10 10 , laser pulses of 40 fs duration and 1 J energy have been reported to drive protons up to 10 MeV energies from 20–30 nm thick foils [37,38]. Yet such ultrathin targets tend to result in filamentary proton beam profiles, as compared to the smooth profiles obtained with micrometer-range targets [34,39,40]. Concerning energy conversion efficiency, standard TNSA with ∼ μ m thick foils is typically limited to ∼ 1 % efficiency for joule-class lasers [3,39], which can be boosted up to ∼ 3 % if a hybrid TNSA/RPA regime is realized using thinner foils [41]. In the case of nanometer-range liquid crystal targets driven in the RIT regime by 3 J energy, 30 fs laser pulses, 20 MeV proton cutoff energies have been measured, but with degraded beam profile at low proton energy [42].
A general observation is that relatively long (a few 100 fs) pulse durations often lead to poor proton beam quality but higher conversion efficiency [34,40,41]. This is explained by the fact that the ASE-driven expansion of the target increases the plasma density scale-length seen by the main laser pulse. This tends to favor the laser absorption into hot electrons but also to disrupt the laser beam profile, entailing, in turn, a degraded imprint in the proton profile. When using a PM, the reduced preplasma due to the higher laser contrast is expected to improve the compactness of the hot-electron distribution and the proton beam quality, yet the associated laser energy loss, typically around 50 % , may detrimentally affect the achievable proton energies. Therefore, it is not clear whether the use of PMs systematically benefits or not proton acceleration.
In this study, we experimentally demonstrate that the combination of an ultrashort ( ∼ 24 fs ) and ultraintense ( > 10 21 W cm − 2 ) laser pulse with a double plasma mirror (DPM) [34] can significantly improve the maximum energy, conversion efficiency, beam profile, and divergence of the accelerated protons. Numerical particle-in-cell (PIC) simulations support these results, ascribing them to the more compact spatial distribution of hot electrons generated by the ASE-free laser pulse. Our findings have important implications for the development of high-quality proton beams for various applications.

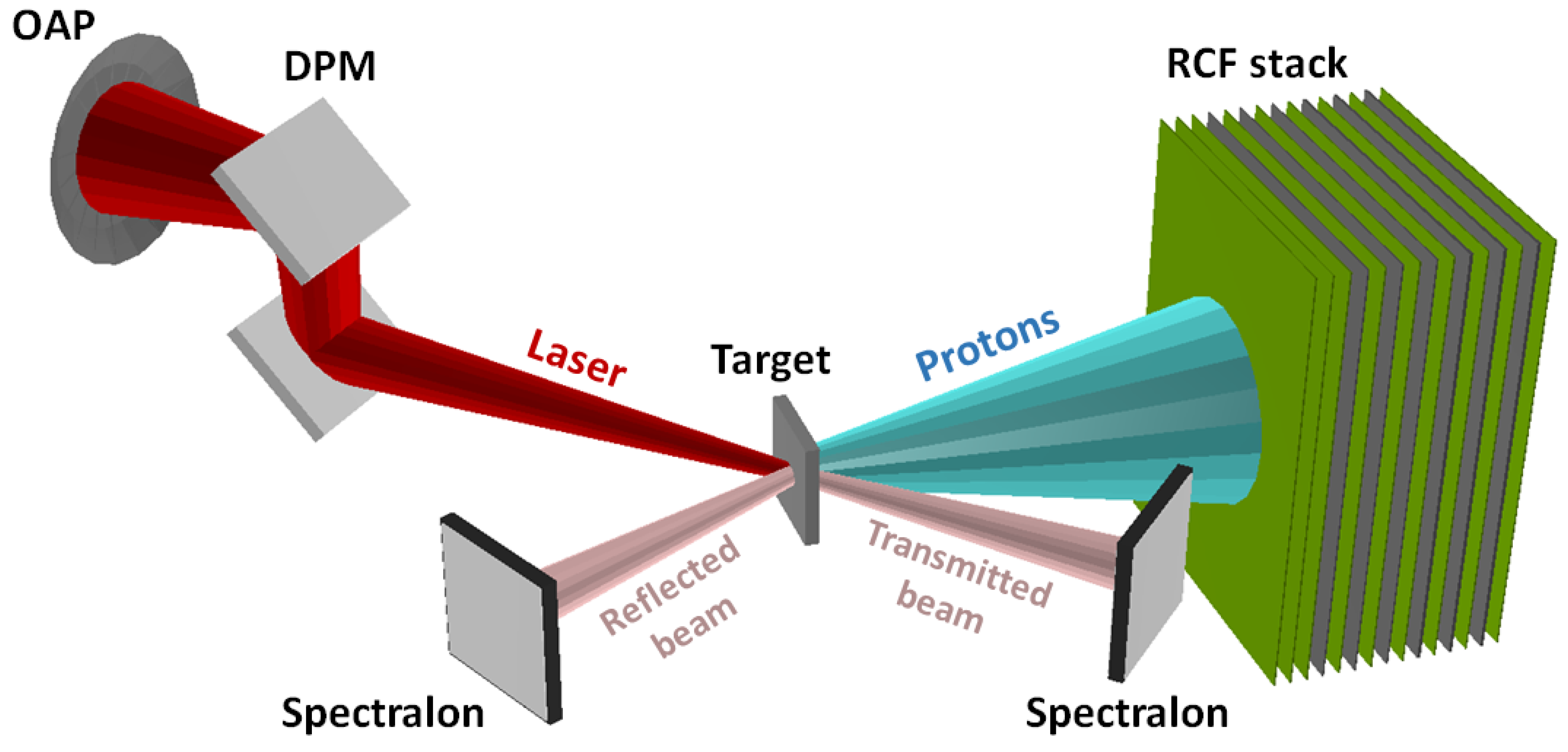
2. Experimental Setup

The experiment was performed at the short-focal area of the Apollon laser facility (Saclay, France), using its F2 secondary beam [43]. This beam utilizes a Ti:Sapphire laser, delivering pulses with a full-width-at-half-maximum (FWHM) duration of 24 fs, a mean on-target energy of 11 J and a central laser wavelength of 815 nm. Two configurations were tested: direct shots (without a DPM) and shots with a DPM [34], in which case the on-target laser energy was reduced to 5.7 J, due a measured DPM reflectivity of ∼ 52 % reflectivity.
The experimental setup is sketched in Figure 1. The DPM was placed inside the interaction chamber, between the f / 3 off-axis parabola (OAP) and the target. The beam was focused onto the target with a 45incidence angle. A camera recorded the image of the reflected laser beam on a Spectralon scatter plate positioned along the specular reflection axis. The transmitted light was monitored by another Spectralon plate placed along the laser transmission axis. Aluminum foils of 0.8 – 2 μ m thicknesses were used on direct shots, while thinner silicon foils, ranging from 10 nm to 300 nm (with, facing the incident laser, an additional coating of 50 nm of Al for some of them, in order to improve the laser absorption and the proton generation [44]), were used with the DPM. The proton spectra were measured using stacks of EBT3 Gafchromic radiochromic films (RCFs) interlaced with aluminum filters, placed at 25 mm from the target.
Figure 2 provides information on the focusing of the 140-mm-diameter, near-field laser beam. The focal spot was measured to be elliptical with 2.8 μ m × 3.7 μ m FWHM dimensions (see Figure 2a). It contained ∼ 47 % of the on-target laser energy, resulting in a peak intensity of ∼ 1.5 × 10 21 W cm − 2 . This peak intensity is derived directly from the focal spot image shown in Figure 2a (see caption). These values are very close to those obtained on direct shots during the commissioning of the F2 beam [43], demonstrating that the DPM did not deteriorate the laser focal spot. Figure 2b details the laser energy distribution within the laser spot. The graph plots the fraction of the laser energy within an encircled region as a function of the circle radius from the focal spot center.
The temporal intensity profile of the laser beam (measured without a DPM) is shown in Figure 3a. One can see that before the intensity peak (at time zero), there exists a 750 fs long plateau with a mean intensity of ∼ 10 18 W cm − 2 . This mildly relativistic intensity level is sufficient to destroy Al targets with thickness below 1 μ m [43].
The laser irradiated the PMs at 45 incidence angle, with elliptical spots of dimensions ∼ 4.5 mm × 6.3 mm on the PM closest to the focusing OAP and ∼ 3.5 mm × 5 mm on the second PM. The peak intensity on the PMs reached ∼ 5.3 × 10 13 W cm − 2 while the prepulse plateau intensity was of ∼ 2.6 × 10 10 W cm − 2 . These values are, respectively, well above and below the ionization threshold ( ∼ 2.5 × 10 12 W cm − 2 , considering the ∼ 750 fs prepulse duration) of the fused silica material of the PM [45]. The on-target intensity contrast between the prepulse plateau and pulse maximum was then increased by the square of the ratio between the reflection factor of the ionized PM ( ∼ 0.52 ) and the antireflection coating factor of each PM ( ∼ 10 − 3 ), i.e., by a factor of ∼ 2.7 × 10 5 . This would bring the prepulse plateau intensity down to ∼ 4 × 10 12 W cm − 2 , causing minimal, if any, disturbance to the foil targets. This prediction is supported by the observed smooth spatial profiles of the protons accelerated from targets as thin as 20 nm (see below). Note that the smooth spatial profiles we observe differ from previously reported results [34,39,40], which could be linked with the fact that the latter used longer laser pulses than in our case. Longer laser pulse leave indeed more time to induce deformation of the target surface during acceleration.
Figure 3b1 shows a typical image of the specularly reflected beam as obtained on the Spectralon plate without a DPM. The beam profile appears to be diffuse and of low intensity, meaning that the laser beam was reflected off an extended preplasma, as a result of the prepulse-induced target expansion. By contrast, the reflected beam profiles recorded on DPM shots (see Figure 3b2) were much more intense and collimated, suggesting that the laser interacted with a sharp target surface. This behavior is consistent with previous experiments using DPMs [38,42].
Figure 3c1 displays the transmitted laser beam profile measured with a DPM in the absence of a target. A very similar image (Figure 3c2), associated with a laser transmission rate of ∼ 88 % , was recorded when shooting at the thinnest (10 nm) Si foils, in which case no proton acceleration was detected. This indicates that, despite the enhanced contrast achieved by the DPM, such ultrathin targets remain vulnerable to the ASE. However, when the target thickness was increased to 50 nm, fast protons were measured up to ∼ 20 MeV while the laser transmission rate plummeted to ∼ 0.5 % (see Spectralon image in Figure 3c3).

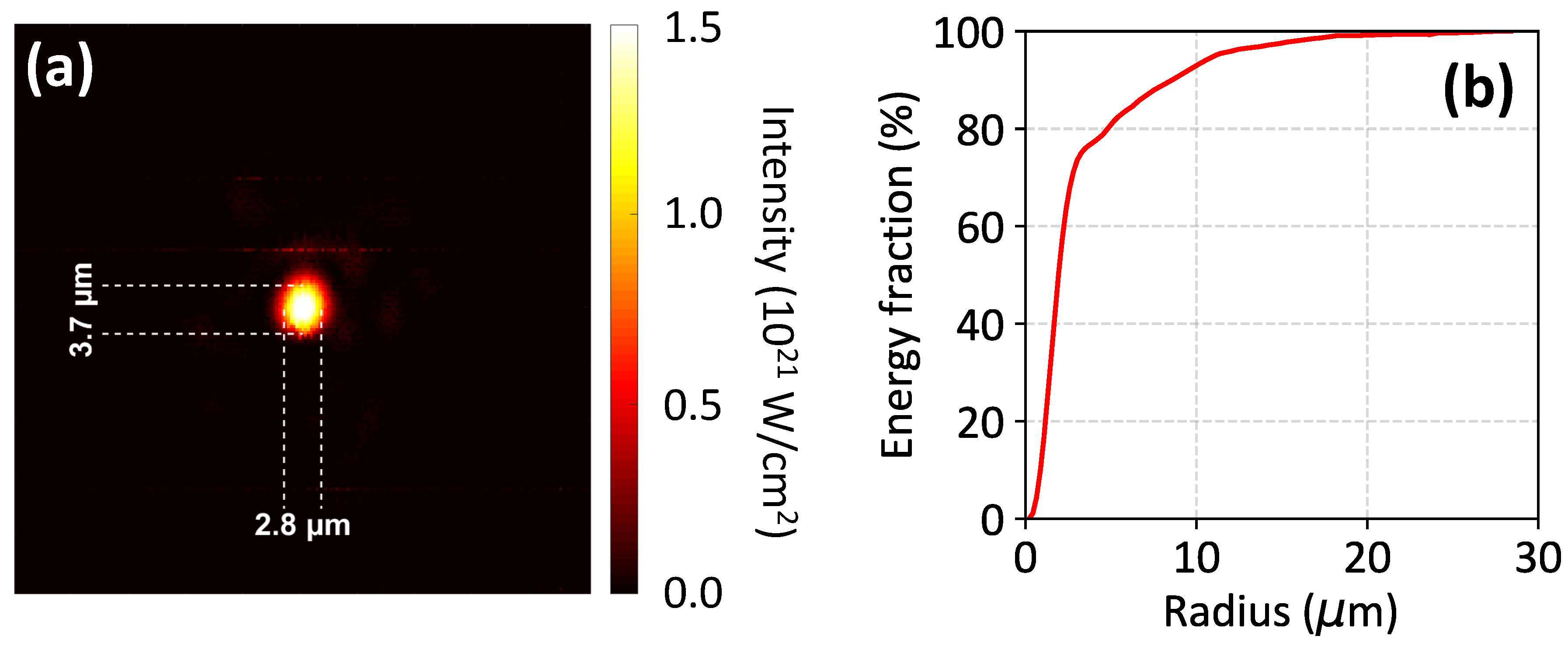
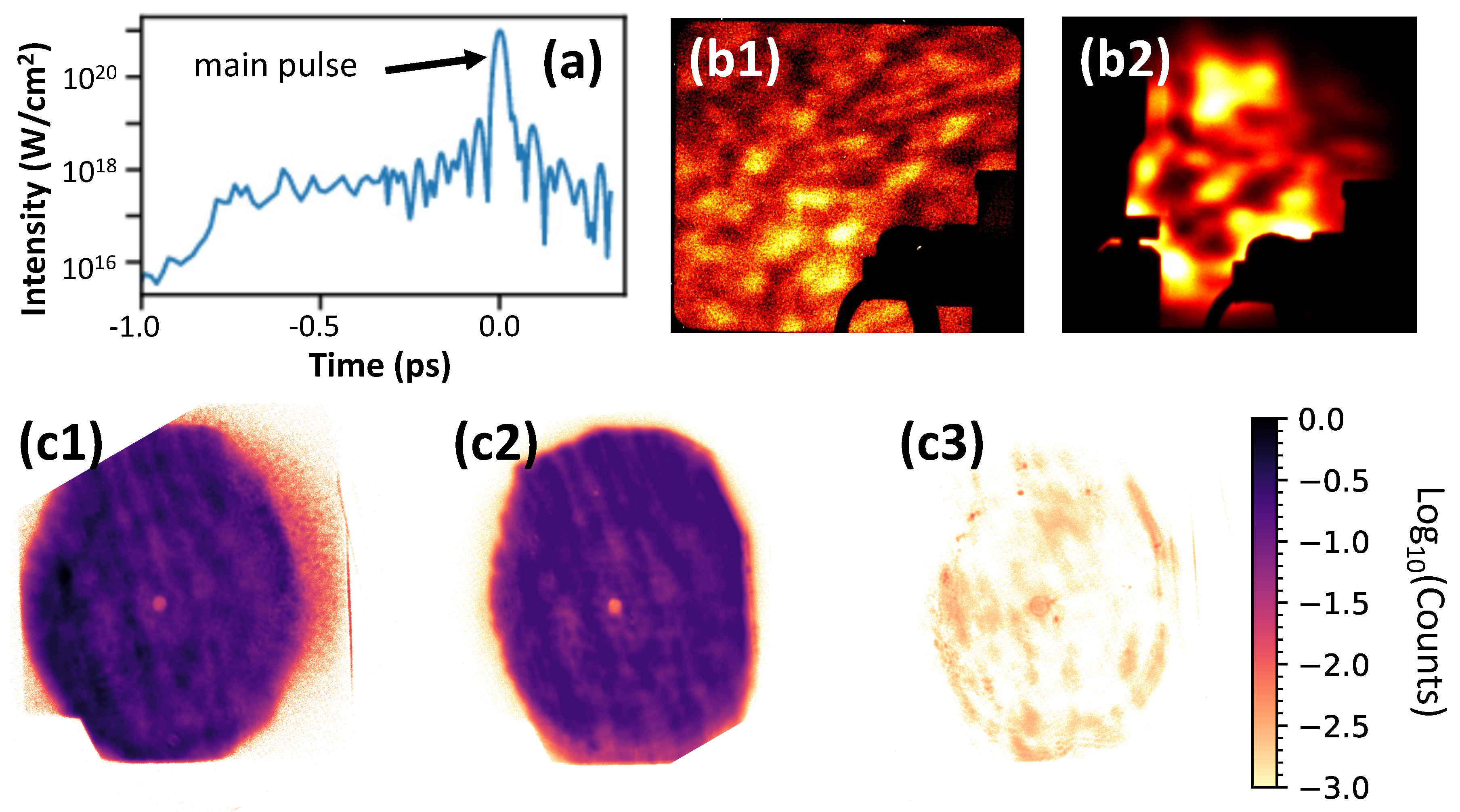
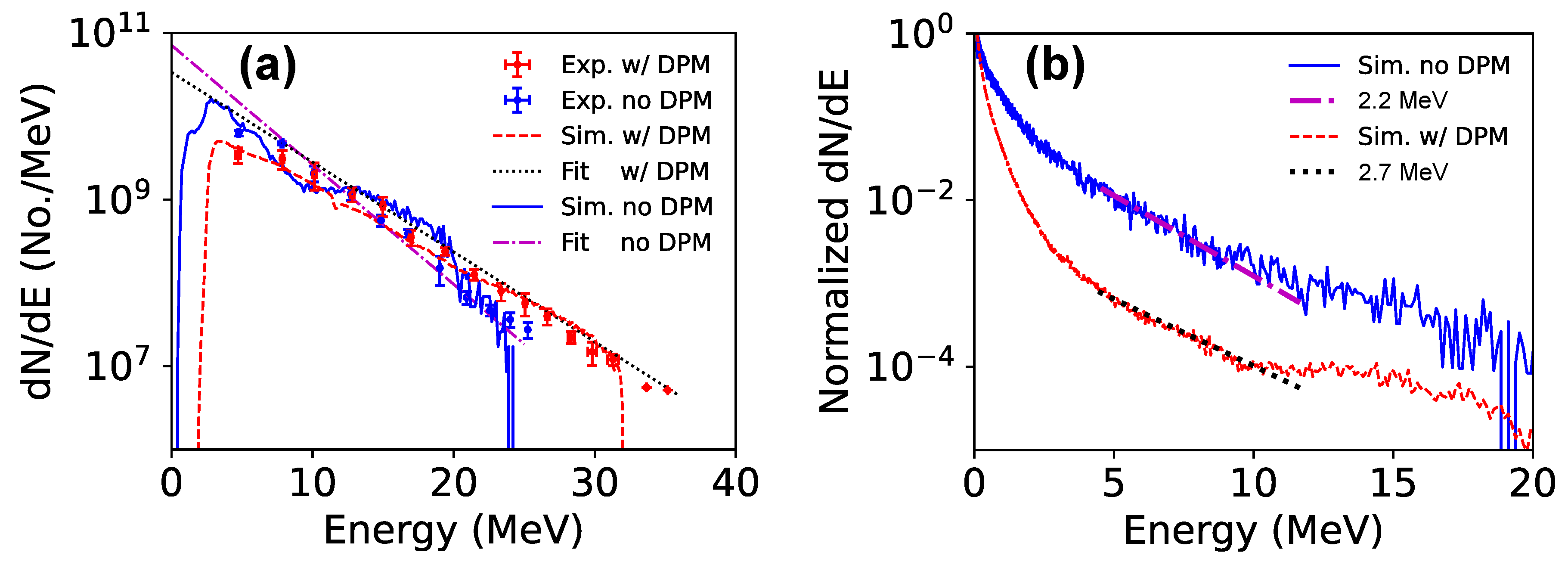
3. Experimental Results

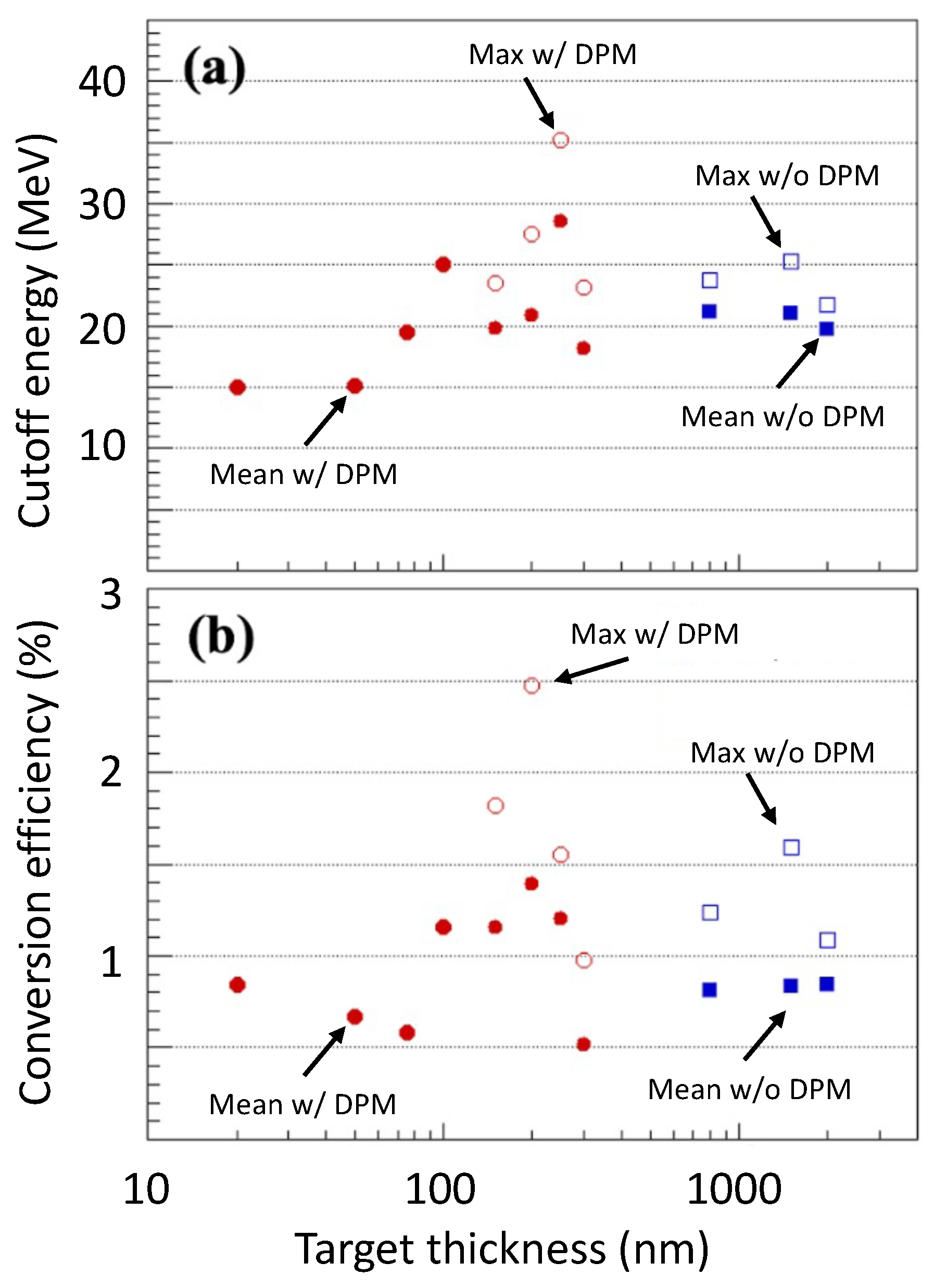
3.1. Increased Proton Energies

The proton energy spectra were inferred from the doses deposited into the RCF stack as detailed in Ref. [21]. Figure 4a shows two proton spectra for the target thicknesses maximizing the proton cutoff energy ( E max ) with or without a DPM. Overlaid are predictions from PIC simulations (see Section 4).
The best performance in the no-DPM case was recorded with a 1.5 μ m thick Al foil, yielding E max ≃ 25 MeV . The best DPM shot used a 250 nm (200 nm Si + 50 nm Al) thick foil, yielding E max ≃ 35 MeV , i.e., a ∼ 40 % enhancement. The proton spectra plotted in Figure 4a exhibit an exponential behavior of the form d N / d E = ( N p / T p ) exp ( − E / T p ) for E ≤ E max , where E is the proton energy, T p the effective temperature and N p the total proton number. The best-fitting parameters are N p = 2.1 × 10 11 and T p = 3.0 MeV without the DPM, and N p = 1.4 × 10 11 and T p = 4.0 MeV with the DPM. Note that the first RCFs were excluded from the analysis because their signal was saturated and they did not collect a fraction of the proton beam (the lateral extend of the protons goes beyond the size of the films for these first layers, as can be seen in the raw films shown below). The low-energy ( < 8 MeV ) component of the proton spectra not captured by the RCFs was characterized by a magnetic spectrometer in a previous campaign, conducted under similar interaction conditions, but without a DPM [46]. This measurement revealed a steeper proton spectrum ( T p ≃ 1.1 MeV ).
Figure 5a shows how the proton cutoff energy varies with target thickness (d).Empty and filled symbols represent the maximum and mean cutoff energies, respectively, from all shots with a given target thickness. Both quantities exhibit the same behavior, peaking around d = 250 nm with a DPM and at d = 1.5 μ m without. Notably, in the absence of a DPM, no detectable proton signal is observed from Al targets thinner than 800 nm. With a DPM, significant proton acceleration is achieved even in Si foils as thin as 20 nm, with a maximum proton energy of around 15 MeV.
Figure 5b shows the conversion efficiency of laser energy into protons, evaluated by integrating (over 0 ≤ E ≤ E max ) the exponential fit of each recorded proton spectrum (see Figure 4a). Note that (i) we use the fit of the spectrum, and not the actual spectrum since, as discussed above, the number of protons retrieved at low energy from the first films is underestimated (the films being saturated), thus the fit provides a better estimate of the actual spectrum, and (ii) the laser energy considered here is the on-target energy for each case, i.e. in the DPM case, the calculation takes into account the energy loss induced by the DPM. As in Figure 5a, we distinguish between the maximum and mean values obtained for a given target thickness. The dependence of both quantities on target thickness is similar to that observed for the proton energies, i.e., adding the DPM leads, for the best cases, to an increase in the maximum (resp. mean) conversion efficiency by 56% (resp. 75%), i.e., from 1.6% to 2.5% (from 0.8% to 1.4%).
Interestingly, for the DPM shots, the observed decrease of the proton cutoff energy and conversion efficiency when the target thickness decreases below d = 250 nm is gentler than in previous studies using longer laser pulses. Specifically, the decrease is ∼ 0.54 for the cutoff energy (from 30 MeV to 15 MeV) and ∼ 0.47 for the conversion efficiency (from 1.4% to 0.8%) as the target thickness is reduced from d = 250 nm to d = 20 nm . These values are comparable to those reported in Ref. [39] with a 35 fs pulse (0.31 for cutoff energy and 0.59 for efficiency, for thicknesses spanning from 20 to 100 nm) but significantly lower than those obtained with a 900 fs pulse in Ref. [41] (0.67 for cutoff energy and 0.79 for efficiency, for thicknesses spanning from 10 to 100 nm). The smaller decrease obtained with in our case of ultrahigh-contrast, ultrashort pulses indicate a more robust acceleration scheme, because even ultrathin targets (down to d = 20 nm under our conditions) do not have time to fully expand before the laser intensity peak, leading to a sustained “plateau” in the performance metrics, as well to a smooth proton spatial distribution, as shown in Figure 6. A similar plateau behavior in proton acceleration has been reported in Refs. [37,42].
To summarize this section, our main finding is that, despite reducing the on-target laser energy by almost a factor of 2, the use of a double plasma mirror (DPM) leads to a significantly (by ∼ 40 % ) higher proton cutoff energy, but is accompanied by a loss of protons at low energy, as shown in Figure 4a. As detailed in Ref. [11], we note that we measure very similar neutron yields from ( p , n ) nuclear reactions obtained from both direct and DPM shots in the same experiment.
As will be detailed below, the enhanced ion acceleration in high-contrast laser-foil interactions originates from a close overlap of the peak accelerating electric field with the proton bunch. A similar interpretation was put forward to explain the strong increase in the conversion efficiency observed when relatively thick ( d = 5 μ m ) targets were irradiated by two sequential ps-long laser pulses [47].

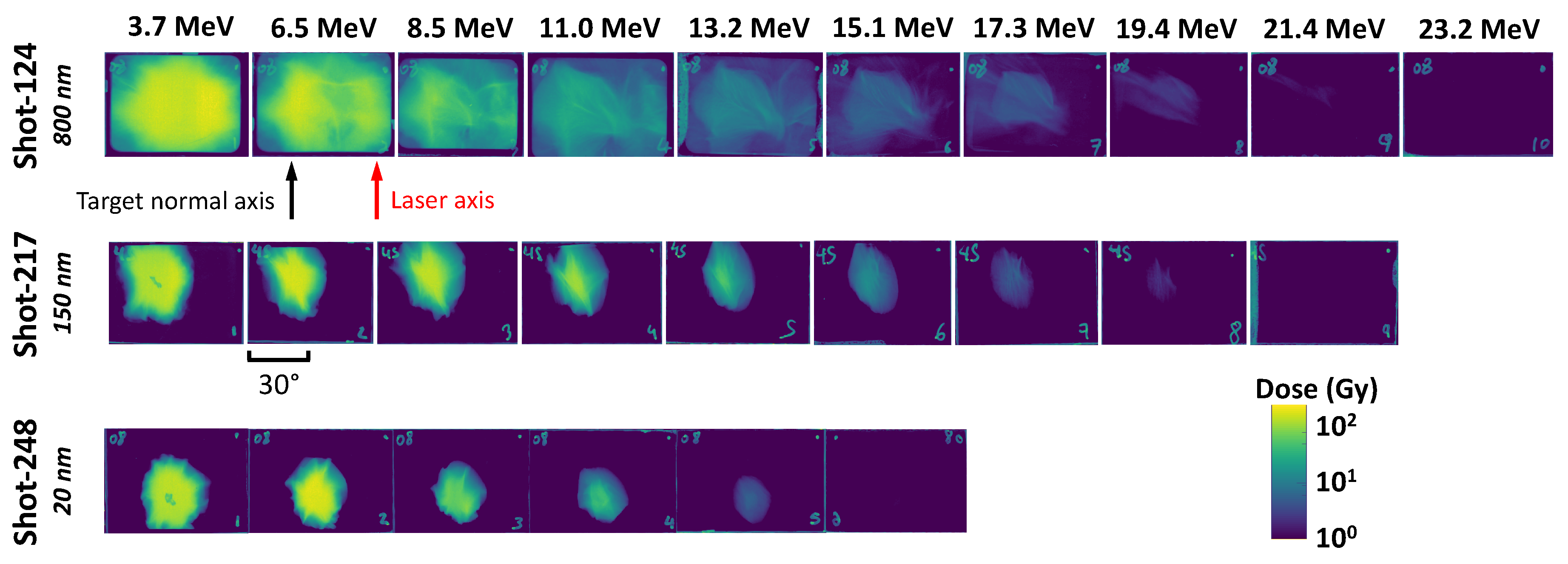
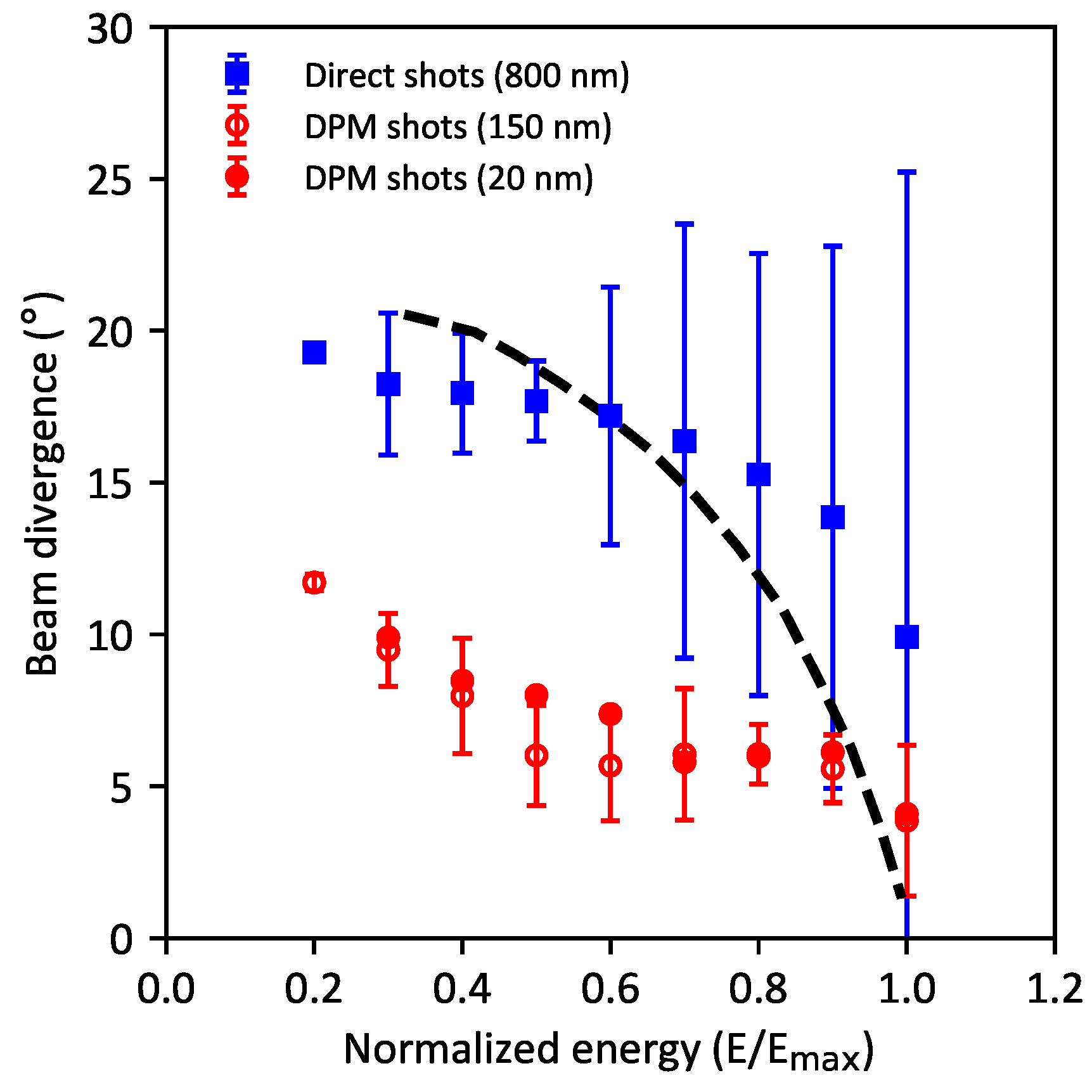
3.2. Improved Proton Beam Profile

Another benefit of the DPM is the significant improvement of the proton beam profile. Figure 6 compares the raw RCF data from direct and DPM shots. The spatial dose distribution at low proton energy ( ≲ 11 MeV ) proves to be much wider with a DPM (middle and bottom rows) than without it (top row). In the latter case, the distribution exhibits two components, one along the laser axis (red arrow) and one along the target normal (black arrow), as previously observed in Ref. [48]. With the DPM, however, the beam profile is preferentially concentrated around the target normal.
At higher proton energy, the beam profile becomes filamentary in the absence of a DPM, while it retains a rather collimated and round shape with a DPM. This trend, which contrasts with previous measurements [40], still holds in foils as thin as 20 nm (bottom row), likely a consequence of the shorter pulse duration used in our experiment, which minimizes the target pre-expansion. This may have important implications for proton radiography [4], where a smooth profile translates into better image quality, and for medical applications that necessitate homogeneous irradiation profiles [5,7].
The nonuniform profile of the proton beam produced without a DPM is attributed to the extended low-density plasma created by the laser prepulse. This preplasma causes the main pulse to filament, which affects the hot-electron distribution and ultimately the angular profile of the accelerated protons. In contrast, when a DPM is used, the laser interacts directly with the sharp surface of the solid target, likely resulting in a more homogeneous hot-electron profile.
Figure 7 quantifies the improved beam collimation achieved with the DPM. It shows the half-width of the beam angular distribution for the same shots discussed previously, as a function of energy normalized to the respective maximum cutoff energy. We observe a significantly wider divergence for direct shots, with angles exceeding 20 at low energies and remaining above 10 at high energies. The error bars of the data are compatible with the expected energy-dependent divergence of TNSA protons [21], plotted as a black curve. However, the DPM shots on 20 nm and 150 nm thick foils give to much smaller divergence angles, consistent with Ref. [37]. These angles decrease from ∼ 12 at low relative energy ( E / E max ∼ 0.2 ) down to ∼ 5 near the cutoff energy.

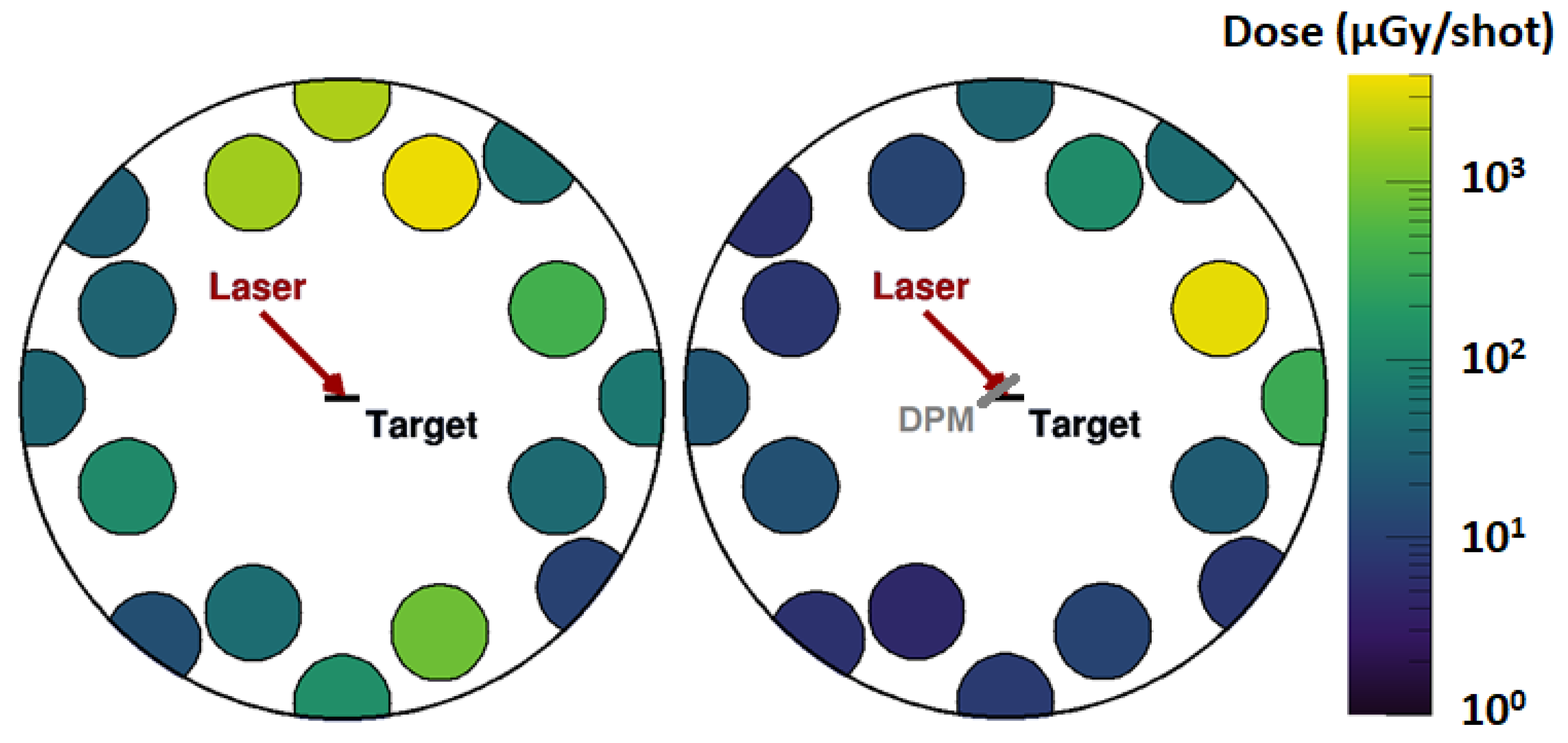
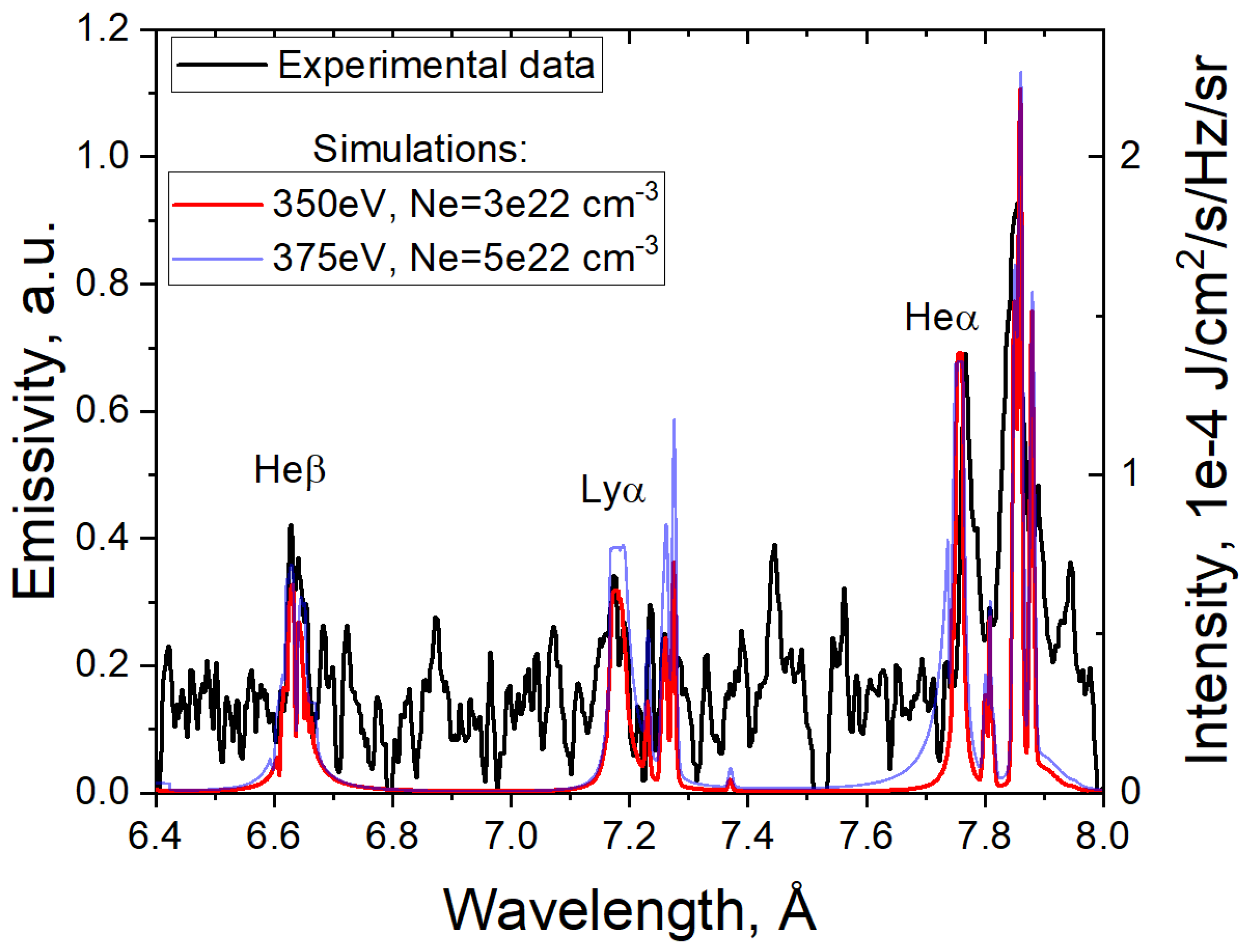
3.3. X-ray Emission

The X-ray emissions from the laser-foil interactions were measured with two diagnostics: a set of dosimeters with broad spectral sensitivity [49], and a spatially resolved spectrometer working in the keV range [50].
Twenty GD-351 radio-photo-luminescence dosimeters [49] were placed at various angles and positions inside the interaction chamber, at distances ranging from 87 cm and 115 cm from the target. The dosimeters were encapsuled in a 1.5 mm thick tin holder, making them sensitive to X rays in an energy range from around 30 keV to a few MeV, with an energy-independent response. The tin holder also served to protect the dosimeters from protons up to 23 MeV and electrons up to 1.5 MeV, by absorbing these particles and hence preventing them from depositing their energy into the dosimeters. However, in the absence of comparative measurements of the X-ray and electron energy spectra, we cannot exclude the possibility that higher-energy electrons contributed to the dosimeter signal.
Taking advantage of the high repetition rate of the Apollon laser, the dosimeter signals were accumulated over several shots (typically 20), enabling comparisons between different sessions by averaging out laser fluctuations. Figure 8 depicts two representative dose distributions obtained with direct and DPM shots, revealing strong differences between the two configurations. For direct shots (left panel), the doses are preferentially delivered in a broad lobe that extends between the target normal and the laser specular reflection axis. By contrast, the DPM shots (right panel) result in a much narrower emission cone centered along the laser specular direction. We also observe significant dose emission along the rear target normal in direct shots, which is absent with the DPM. Specifically, a factor of up to 130 is measured between the doses emitted in the backward direction for direct and DPM shots, with approximately 1670 μ Gy and 12.8 μ Gy per shot, respectively.
The broad angular distribution and high doses observed in the direct shots are consistent with dominant Bremsstrahlung emission. This is likely due to the presence of a significant preplasma at the target front, where laser-driven electrons can recirculate and radiate [51,52]. In contrast, the significant reduction in dose and the directional nature of the X-ray emission in the DPM case suggest a different radiation generation mechanism. The thinner targets used with the DPM reduce the hot-electron path length in matter, thereby decreasing the probability of Bremsstrahlung. Furthermore, in high-contrast, oblique laser-solid interactions such as those with the DPM, electrons can be accelerated along the target surface to high energies, radiating predominantly in the near-surface direction [53,54]. In addition, the laser beam reflected off the solid surface can directly accelerate some electrons [55], possibly leading to X-ray emission through synchrotron radiation induced by the energetic electrons propagating along the target surfaced and being bent in the TNSA field. Both mechanisms align well with the observed narrow cone of emission in the DPM case (Figure 8).
We now consider the spatially resolved measurements of the X-ray source. The focusing spectrometer [50], directed at the target front along the target normal, measured the K-shell emission of the plasma in the 1500–2000 eV range (wavelengths λ =6.4–8 Å). A mica crystal was used in the second order of reflection ( 2 d = 19.9419 Å) to measure the spectral lines of Aluminum (Ly α, Heβ and Heα with their satellites) and Silicon (Heα with its satellites if present). The emission was recorded on a TR-type image plate. The spatial resolution of the measurement was of 200 μ m , limited by the combined effects of the Fujifilm BAS-1800 II scanner resolution and the demagnification of the optical scheme. To protect the image plate from optical radiation, the detector holder was covered with an aluminized polypropylene foil ( 2 μ m PP + 80 nm Al).
Figure 9 shows a typical X-ray spectrum averaged over seven DPM shots on 200 nm Si foils with a 50 nm Al coating (on the laser-irradiated side). The spectra obtained with a DPM exhibited a higher signal-to-noise ratio than without it (not shown here). This improvement likely originates from a lower contribution from continuum emission, which can be attributed to both the higher laser contrast and the different X-ray generation mechanisms discussed above. The spectra contain mostly the X-ray emission of Aluminum with only a minor contribution from Silicon near the Al Heβ and Li-like emission (6.4–6.9 Å). Thus, the effective (i.e. temporally averaged over the plasma expansion and spatially averaged over the spectrometer’s line-of-sight) electron density ( n e ) and temperature ( T e ) of the emitting plasma can be inferred through comparison to flychk atomic physics calculations [56] of Aluminum. The best-fitting parameters are n e = 3 × 10 22 cm − 3 and T e = 350 eV . These values demonstrate the ability of the DPM to maintain the integrity of the ultrathin foils until the pulse maximum.

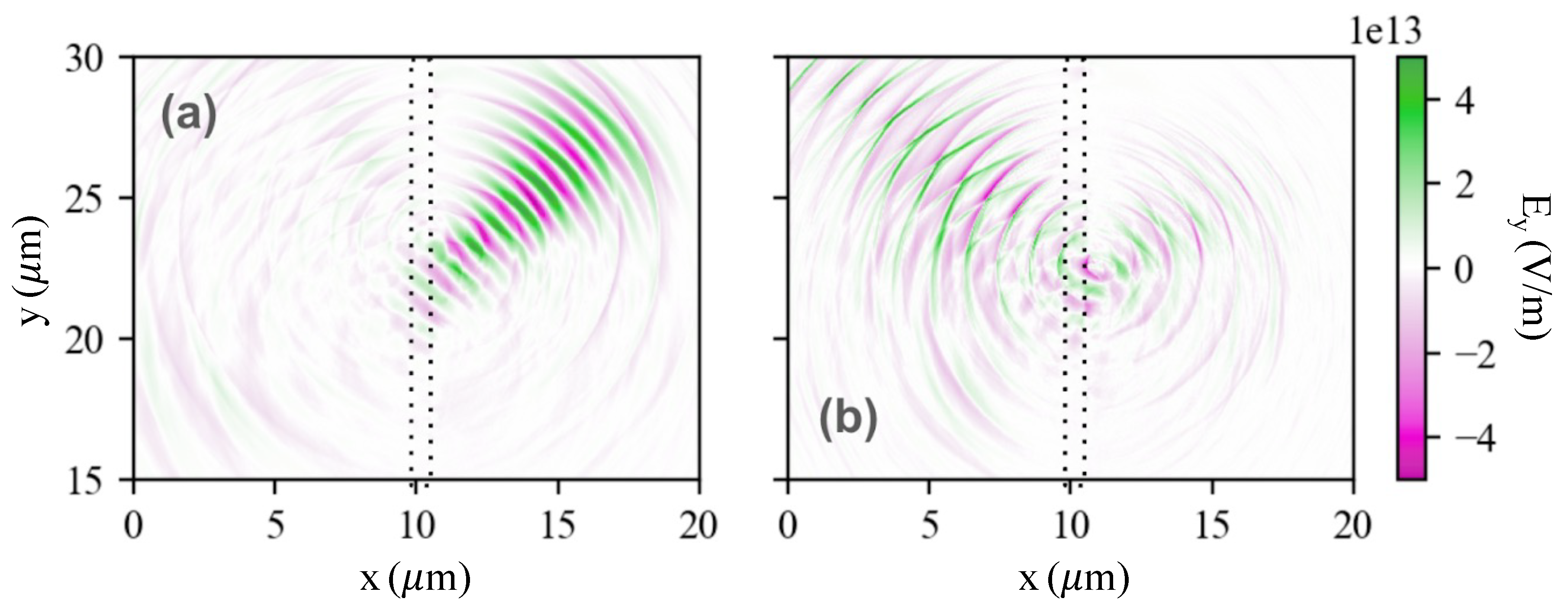
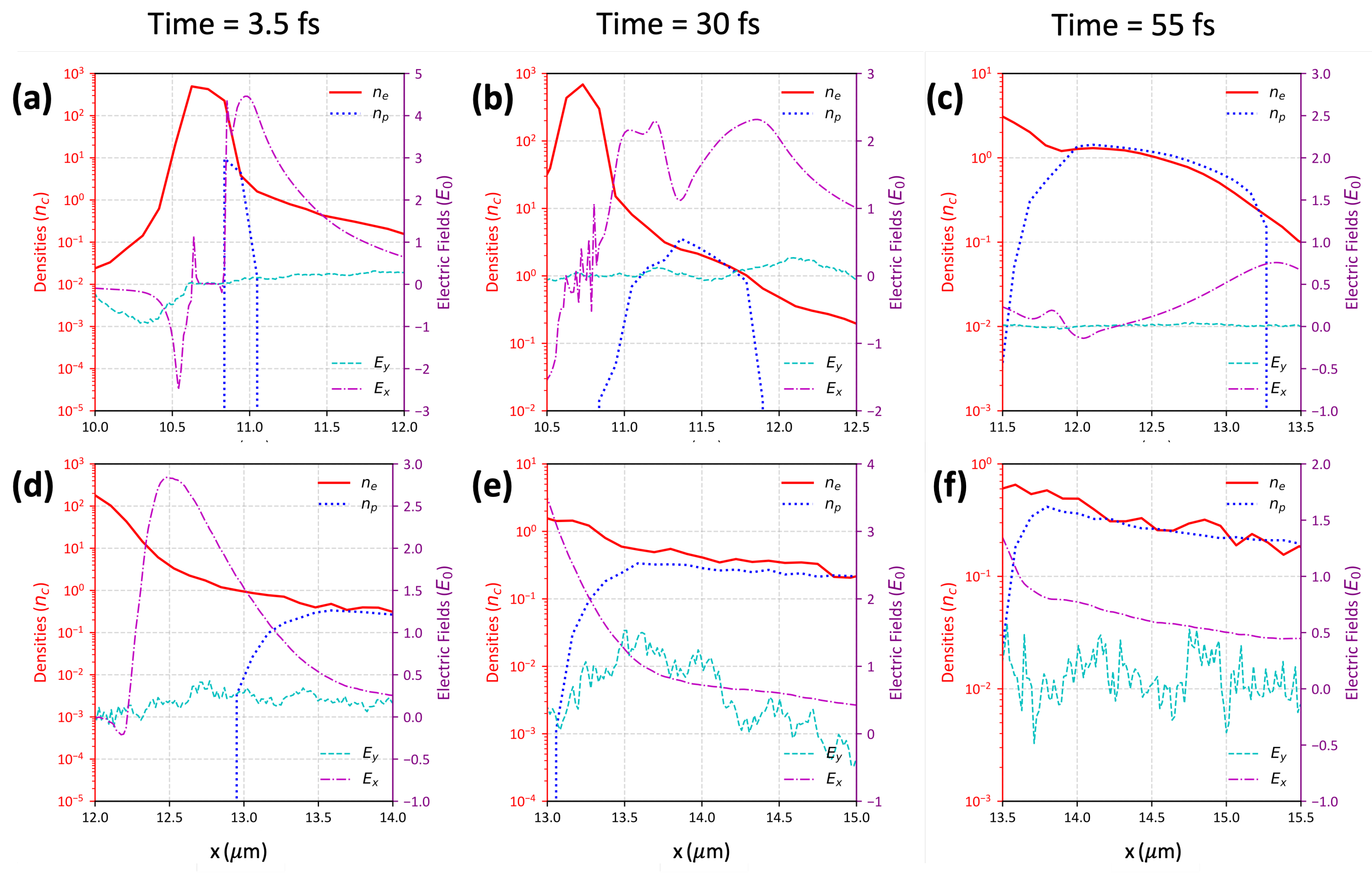
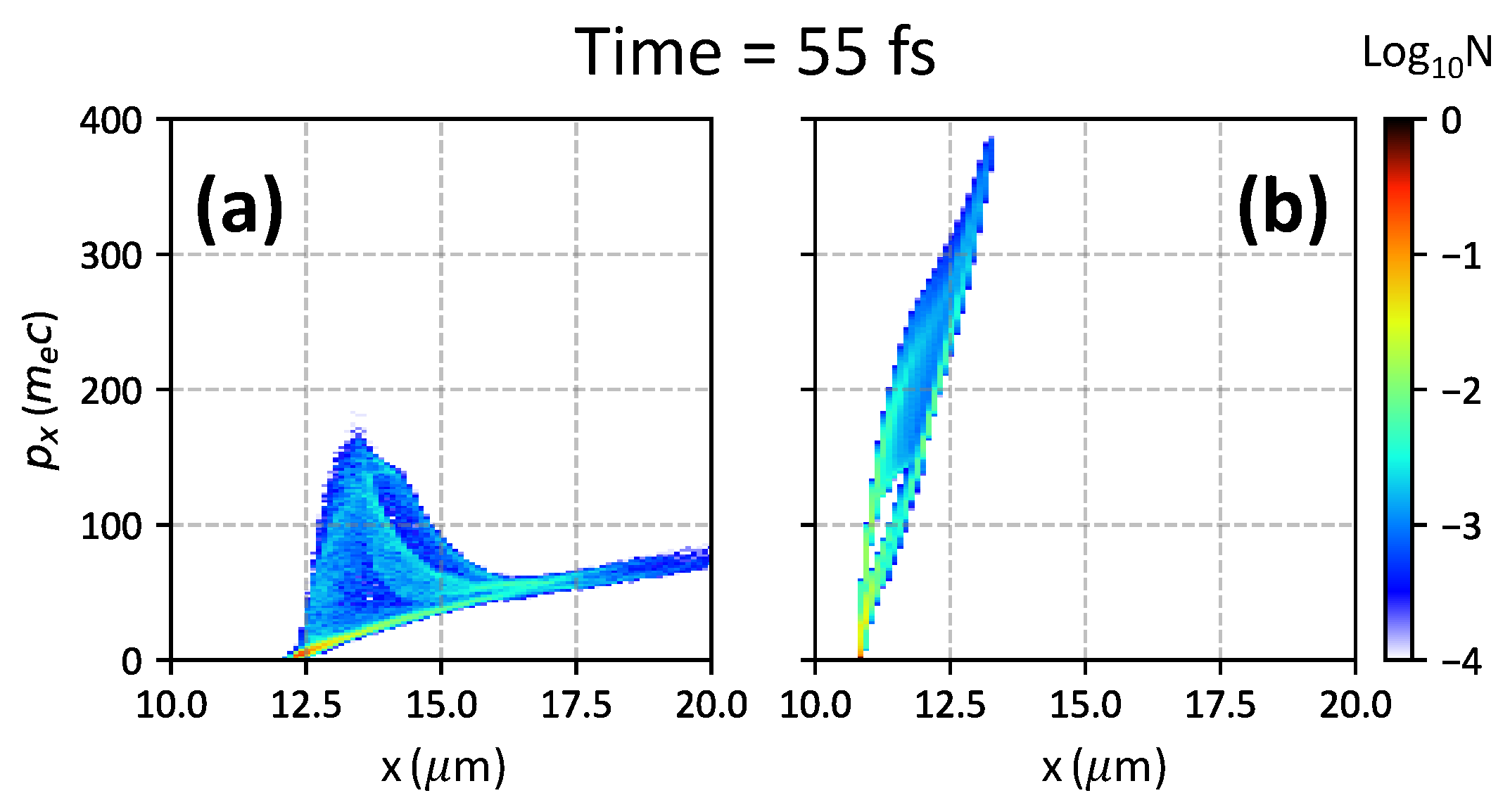
4. Numerical PIC Modeling

To elucidate the mechanism behind the enhanced proton acceleration with a DPM, we have carried 2D PIC simulations with the fully relativistic and electromagnetic smilei code [57]. The numerical domain has dimensions of L x × L y = 21 × 42 μ m 2 with a mesh size Δ x = Δ y = 7.8 nm , corresponding to 128 cells per micron. The time step is Δ t = 0.5 Δ x / c , where c is the speed of light. The laser beam, of wavelength λ 0 = 0.8 μ m , is injected from the lower left side ( x = 0 ) of the box at 45 incidence angle. It is focused with p-polarization onto the front side of the target (at x = 10 μ m and y = 21 μ m ). It has a Gaussian envelope with 3 μ m FWHM spot size and 24 fs FWHM duration. In the no-DPM case, the laser peak intensity is I 0 = 1.8 × 10 21 W cm − 2 , corresponding to a 0 = 29.2 . The laser beam also has a 1 ps long prepulse with the same spatial profile and a constant intensity.The intensity of the pre-pulse was adjusted so that the simulated proton energy spectrum matches the experimental one, see Figure 4a. In the DPM case, we consider only the main 24 fs pulse, with no pre-pulse, but with a reduced peak intensity of 9 × 10 20 W cm − 2 (corresponding to a 0 = 20.5 ) to take into account the energy loss associated with the DPM.
In the no-DPM case, the plasma targets consist of neutral Al foils with thickness d = 0.8 – 2 μ m . In the DPM case, we use neutral Si foils with d = 10 –300 nm, followed by a 50 nm thick neutral Al layer. All targets are coated with a 10 nm thick hydrogen contaminant layer on their backside. Due to computational limitations, their initial ion number density is capped at a sub-solid density value, i.e., n i = 60 n c , where n c = m e ϵ 0 ω 0 2 / e 2 = 1.75 × 10 21 cm − 3 is the critical density at the laser wavelength λ 0 ≡ 2 π c / ω 0 ( ϵ 0 is the vacuum permittivity, m e the electron mass, and e the elementary charge). Electron and ion species are represented by 256 macroparticles per cell, with a fourth-order shape-function. All simulations describe field and electron impact induced ionization. Boundary conditions for both particles and fields are open along both longitudinal (x) and transverse (y) directions. The integration time of the simulations is 500 fs after the laser peak.
To illustrate the coupling of the prepulse-free laser (DPM case) with two ultrathin Si foils as a function of their thickness, we display in Figure 10 the spatial distribution of the transverse electric field ( E y ). We observe near-complete laser transmission across the 10 nm target (Figure 10a) while the 20 nm target gives rise to partial transmission and reflection (Figure 10b). This behavior aligns with our experimental findings, i.e., high laser transmission across the 10 nm foil (Figure 3c2) and no detectable protons for targets thinner than 20 nm (Figure 5).
The simulated proton energy spectra, for a 200 nm Si + 50 nm Al target (DPM case, red dashed line) and a 1.5 μ m Al target (no-DPM case, blue solid line), are plotted alongside the experimental data in Figure 4a. Both simulation curves, integrated over the entire simulation duration (500 fs after peak laser impact), capture well the exponential shape of the distributions as well as their cutoff energies ( E max = 32 MeV and 24 MeV, respectively).
Moreover, the simulated electron spectra, plotted in Figure 4b, indicate that the no-DPM configuration generates hot electrons with energies similar to the DPM case, but in much larger numbers. However, these more energetic electron spectrum produced in the no-DPM case does not translate into better ion acceleration, as seen from Figure 4a. This paradox indicates that the stronger ion acceleration in the DPM case has a different origin, e.g. an enhanced E x field due to sharper density gradients at the time of the laser peak, as suggested in the following.
To explain the stronger proton acceleration achieved at high laser contrast, we plot in Figure 11 the evolution of longitudinal lineouts (across the center of the focal spot) of the particle (electron and proton) densities and electric ( E x and E y ) fields, respectively measured in units of n c and E 0 = m e c ω 0 / e . The time origin coincides with the on-target intensity peak. For a 200 nm Si + 50 nm Al target hit by the high-contrast pulse (top row), the accelerating E x field seen by the protons (the front of which is located at x ≃ 11 μ m ) reaches a maximum strength of ∼ 4 E 0 just after the laser maximum ( t = 3.5 fs ). This field decays over time (down to ∼ 0.75 E 0 at t = 55 fs ), but its spatial maximum always coincides with the outer edge of the proton bunch (Figure 11b,c), where the fastest protons reside (see Figure 12b). This spatial overlap of the peak electric field and the fastest protons maximizes the acceleration efficiency.
The situation is markedly different in the absence of a DPM, for a 1.5 μ m thick Al target (bottom row). As shown in Figure 11d, the prepulse-driven expansion of the target backside causes a significant reduction in the E x field [58] just after the laser peak ( E x ≃ 2.5 E 0 ). Another consequence of the pre-expanded density profile is that the spatial maximum of E x no longer coincides with the front of the proton bunch (see also in the phase space distribution in Figure 12a).
Another interesting point to notice is the significant E y field at t = 30 fs after the main pulse irradiation in the low laser contrast case (Figure 11e and f). On the contrary, in the high laser contrast case (Figure 11b), we see almost no E y at the location of the protons. Importantly, this field is mostly positive, and hence will bend the protons towards the y > 0 direction, i.e., towards the laser propagation axis [59]. This should contribute to the degraded beam profile seen in Figure 6a, where the high-energy protons show an elongated shape towards the laser axis. Note that here the E y field is not laser-cycle-averaged.

5. Conclusions

In summary, we demonstrate significant improvement in proton acceleration from thin solid targets using a double plasma mirror (DPM) [34] to enhance the temporal contrast of the ultrashort (24 fs), ultraintense ( > 10 21 W cm − 2 ) F2 Apollon laser beam. This improvement is observed simultaneously in terms of maximum energy, conversion efficiency, and beam quality. The DPM mitigates the impact of the ∼ 1 ps long, relativistic-intensity ( ∼ 10 3 contrast) laser pulse preceding the main pulse, thereby enabling solid foils as thin as 20 nm to be used. In contrast, the minimum target thickness exploitable under standard irradiation conditions is 800 nm. With the DPM, we were able to accelerate protons up to 15 MeV from a 20 nm thick foil, and achieved a peak proton energy of 35 MeV from a 250 nm foil, with only 5 J of laser energy. Remarkably, this maximum proton energy is ∼ 40 % higher than without the DPM, despite 50% less laser energy. 2D PIC simulations attribute the superior performance of the DPM configuration to a stronger longitudinal electrostatic field and its closer overlap with the expanding proton bunch when the main laser pulse interacts with the sharp-gradient solid foil. These results pave the way for optimizing laser-driven X-ray and neutron sources [11], opening new perspectives in nuclear material interrogation [60,61,62,63] and medicine [7]. Furthermore, we can expect even further improvements in laser-proton acceleration at higher intensities, such as with the upcoming 10 PW-scale F1 beam of the Apollon facility.

Author Contributions

Conceptualization, J.F.; methodology, J.F., F.M. and A.A..; software, W.Y., Y.Y., E.d’H., X.D. and L.G.; investigation, R.L., T.W., J.F., W.Y., I.C., A.B., E.C., C.G., I.P., D.P., D.M. and L.G.; data curation, P.K., F.T., W.Y., J.F., Q.D., E.F., S.P. and R.L.; writing—original draft preparation, W.Y., J.F., R.L., E.F. and L.G.; writing—review and editing, all. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by funding from the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation program (Grant Agreement No. 787539, Project GENESIS), by CNRS through the MITI interdisciplinary programs and by IRSN through its exploratory research program. The project was also made possible thanks to the credits of the Hubert Curien Maimonides program made available by the French Ministry of Europe and Foreign Affairs and the French Ministry of Higher Education and Research. We acknowledge the financial support of the IdEx University of Bordeaux / Grand Research Program "GPR LIGHT", and of the Pazy Foundation Grant No. 435/2023.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Acknowledgments

The authors acknowledge the national research infrastructure Apollon and the LULI staff for their technical assistance.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Daido, H.; Nishiuchi, M.; Pirozhkov, A.S. Review of laser-driven ion sources and their applications. Reports on progress in physics 2012, 75, 056401. [Google Scholar] [CrossRef] [PubMed]
  2. Macchi, A.; Borghesi, M.; Passoni, M. Ion acceleration by superintense laser-plasma interaction. Reviews of Modern Physics 2013, 85, 751. [Google Scholar] [CrossRef]
  3. Zimmer, M.; Scheuren, S.; Ebert, T.; Schaumann, G.; Schmitz, B.; Hornung, J.; Bagnoud, V.; Rödel, C.; Roth, M. Analysis of laser-proton acceleration experiments for development of empirical scaling laws. Physical Review E 2021, 104. [Google Scholar] [CrossRef] [PubMed]
  4. Schaeffer, D.B.; Bott, A.F.; Borghesi, M.; Flippo, K.A.; Fox, W.; Fuchs, J.; Li, C.; Séguin, F.H.; Park, H.S.; Tzeferacos, P.; et al. Proton imaging of high-energy-density laboratory plasmas. Reviews of Modern Physics 2023, 95. [Google Scholar] [CrossRef]
  5. Bin, J.; Obst-Huebl, L.; Mao, J.H.; Nakamura, K.; Geulig, L.D.; Chang, H.; Ji, Q.; He, L.; De Chant, J.; Kober, Z. A new platform for ultra-high dose rate radiobiological research using the BELLA PW laser proton beamline. Scientific reports 2022, 12, 1484. [Google Scholar] [CrossRef] [PubMed]
  6. Lelasseux, V.; Söderström, P.A.; Aogaki, S.; Burdonov, K.; Chen, S.; Cvetinovic, A.; Dechefdebien, E.; Dorard, S.; Fazzini, A.; Gremillet, L. Experimental investigation of the effect of ionization on the 51V (p, n) 51Cr reaction. arXiv 2023, arXiv:2309.16340 2023. [Google Scholar]
  7. Kroll, F.; Brack, F.E.; Bernert, C.; Bock, S.; Bodenstein, E.; Brüchner, K.; Cowan, T.E.; Gaus, L.; Gebhardt, R.; Helbig, U. Tumour irradiation in mice with a laser-accelerated proton beam. Nature Physics 2022, 18, 316–322. [Google Scholar] [CrossRef]
  8. Roth, M.; Jung, D.; Falk, K.; Guler, N.; Deppert, O.; Devlin, M.; Favalli, A.; Fernandez, J.; Gautier, D.; Geissel, M. Bright laser-driven neutron source based on the relativistic transparency of solids. Physical review letters 2013, 110, 044802. [Google Scholar] [CrossRef] [PubMed]
  9. Higginson, D.; Vassura, L.; Gugiu, M.; Antici, P.; Borghesi, M.; Brauckmann, S.; Diouf, C.; Green, A.; Palumbo, L.; Petrascu, H. Temporal narrowing of neutrons produced by high-intensity short-pulse lasers. Physical review letters 2015, 115, 054802. [Google Scholar] [CrossRef] [PubMed]
  10. Kleinschmidt, A.; Bagnoud, V.; Deppert, O.; Favalli, A.; Frydrych, S.; Hornung, J.; Jahn, D.; Schaumann, G.; Tebartz, A.; Wagner, F.; et al. Intense, directed neutron beams from a laser-driven neutron source at PHELIX. Physics of Plasmas 2018, 25. [Google Scholar] [CrossRef]
  11. Lelièvre, R.; Yao, W.; Waltenspiel, T.; Cohen, I.; Beck, A.; Cohen, E.; Michaeli, D.; Pomerantz, I.; Gautier, D.C.; Trompier, F. A Comprehensive Characterization of the Neutron Fields Produced by the Apollon Petawatt Laser. arXiv 2023, arXiv:2311.12653 2023. [Google Scholar]
  12. Martinez, B.; Chen, S.; Bolaños, S.; Blanchot, N.; Boutoux, G.; Cayzac, W.; Courtois, C.; Davoine, X.; Duval, A.; Horny, V. Numerical investigation of spallation neutrons generated from petawatt-scale laser-driven proton beams. Matter and Radiation at Extremes 2022, 7. [Google Scholar] [CrossRef]
  13. Yogo, A.; Lan, Z.; Arikawa, Y.; Abe, Y.; Mirfayzi, S.; Wei, T.; Mori, T.; Golovin, D.; Hayakawa, T.; Iwata, N. Laser-driven neutron generation realizing single-shot resonance spectroscopy. Physical Review X 2023, 13, 011011. [Google Scholar] [CrossRef]
  14. Hornỳ, V.; Chen, S.N.; Davoine, X.; Gremillet, L.; Fuchs, J. Quantitative feasibility study of sequential neutron captures using intense lasers. Physical Review C 2024, 109, 025802. [Google Scholar] [CrossRef]
  15. Ziegler, T.; Göthel, I.; Assenbaum, S.; Bernert, C.; Brack, F.E.; Cowan, T.E.; Dover, N.P.; Gaus, L.; Kluge, T.; Kraft, S.; et al. Laser-driven high-energy proton beams from cascaded acceleration regimes. Nature Physics 2024. [Google Scholar] [CrossRef]
  16. Wilks, S.; Langdon, A.; Cowan, T.; Roth, M.; Singh, M.; Hatchett, S.; Key, M.; Pennington, D.; MacKinnon, A.; Snavely, R. Energetic proton generation in ultra-intense laser–solid interactions. Physics of plasmas 2001, 8, 542–549. [Google Scholar] [CrossRef]
  17. Mora, P. Thin-foil expansion into a vacuum. Physical Review E 2005, 72, 056401. [Google Scholar] [CrossRef] [PubMed]
  18. Mackinnon, A.J.; Borghesi, M.; Hatchett, S.; Key, M.H.; Patel, P.K.; Campbell, H.; Schiavi, A.; Snavely, R.; Wilks, S.C.; Willi, O. Effect of Plasma Scale Length on Multi-MeV Proton Production by Intense Laser Pulses. Physical Review Letters 2001, 86, 1769–1772. [Google Scholar] [CrossRef] [PubMed]
  19. McKenna, P.; Ledingham, K.W.D.; Yang, J.M.; Robson, L.; McCanny, T.; Shimizu, S.; Clarke, R.J.; Neely, D.; Spohr, K.; Chapman, R.; et al. Characterization of proton and heavier ion acceleration in ultrahigh-intensity laser interactions with heated target foils. Physical Review E 2004, 70. [Google Scholar] [CrossRef] [PubMed]
  20. Fuchs, J.; Sentoku, Y.; Karsch, S.; Cobble, J.; Audebert, P.; Kemp, A.; Nikroo, A.; Antici, P.; Brambrink, E.; Blazevic, A.; et al. Comparison of Laser Ion Acceleration from the Front and Rear Surfaces of Thin Foils. Physical Review Letters 2005, 94. [Google Scholar] [CrossRef] [PubMed]
  21. Bolton, P.; Borghesi, M.; Brenner, C.; Carroll, D.; De Martinis, C.; Fiorini, F.; Flacco, A.; Floquet, V.; Fuchs, J.; Gallegos, P. Instrumentation for diagnostics and control of laser-accelerated proton (ion) beams. Physica Medica 2014, 30, 255–270. [Google Scholar] [CrossRef] [PubMed]
  22. Fuchs, J.; Antici, P.; d’Humières, E.; Lefebvre, E.; Borghesi, M.; Brambrink, E.; Cecchetti, C.; Kaluza, M.; Malka, V.; Manclossi, M. Laser-driven proton scaling laws and new paths towards energy increase. Nature physics 2006, 2, 48–54. [Google Scholar] [CrossRef]
  23. Dromey, B.; Coughlan, M.; Senje, L.; Taylor, M.; Kuschel, S.; Villagomez-Bernabe, B.; Stefanuik, R.; Nersisyan, G.; Stella, L.; Kohanoff, J.; et al. Picosecond metrology of laser-driven proton bursts. Nature Communications 2016, 7. [Google Scholar] [CrossRef] [PubMed]
  24. Ma, W.; Kim, I.J.; Yu, J.; Choi, I.W.; Singh, P.; Lee, H.W.; Sung, J.H.; Lee, S.K.; Lin, C.; Liao, Q. Laser acceleration of highly energetic carbon ions using a double-layer target composed of slightly underdense plasma and ultrathin foil. Physical Review Letters 2019, 122, 014803. [Google Scholar] [CrossRef] [PubMed]
  25. Danson, C.N.; Haefner, C.; Bromage, J.; Butcher, T.; Chanteloup, J.C.F.; Chowdhury, E.A.; Galvanauskas, A.; Gizzi, L.A.; Hein, J.; Hillier, D.I. Petawatt and exawatt class lasers worldwide. High Power Laser Science and Engineering 2019, 7, e54. [Google Scholar] [CrossRef]
  26. Stockem Novo, A.; Kaluza, M.; Fonseca, R.; Silva, L. Optimizing laser-driven proton acceleration from overdense targets. Scientific reports 2016, 6, 29402. [Google Scholar] [CrossRef] [PubMed]
  27. Yan, X.; Lin, C.; Sheng, Z.M.; Guo, Z.; Liu, B.; Lu, Y.; Fang, J.; Chen, J. Generating high-current monoenergetic proton beams by a circularlypolarized laser pulse in the phase-stableacceleration regime. Physical Review Letters 2008, 100, 135003. [Google Scholar] [CrossRef] [PubMed]
  28. Qiao, B.; Zepf, M.; Borghesi, M.; Dromey, B.; Geissler, M.; Karmakar, A.; Gibbon, P. Radiation-pressure acceleration of ion beams from nanofoil targets: The leaky light-sail regime. Physical review letters 2010, 105, 155002. [Google Scholar] [CrossRef] [PubMed]
  29. Martin, P.; Ahmed, H.; Doria, D.; Cerchez, M.; Hanton, F.; Gwynne, D.; Alejo, A.; Fernández-Tobías, J.; Green, J.; Macchi, A. Narrow-band acceleration of gold ions to GeV energies from ultra-thin foils. Communications Physics 2024, 7, 3. [Google Scholar] [CrossRef]
  30. Yin, L.; Albright, B.; Hegelich, B.; Bowers, K.J.; Flippo, K.; Kwan, T.; Fernández, J. Monoenergetic and GeV ion acceleration from the laser breakout afterburner using ultrathin targets. Physics of plasmas 2007, 14. [Google Scholar] [CrossRef]
  31. Palaniyappan, S.; Hegelich, B.M.; Wu, H.C.; Jung, D.; Gautier, D.C.; Yin, L.; Albright, B.J.; Johnson, R.P.; Shimada, T.; Letzring, S. Dynamics of relativistic transparency and optical shuttering in expanding overdense plasmas. Nature Physics 2012, 8, 763–769. [Google Scholar] [CrossRef]
  32. Chou, H.G.J.; Grassi, A.; Glenzer, S.H.; Fiuza, F. Radiation pressure acceleration of high-quality ion beams using ultrashort laser pulses. Physical Review Research 2022, 4, L022056. [Google Scholar] [CrossRef]
  33. Rehwald, M.; Assenbaum, S.; Bernert, C.; Brack, F.E.; Bussmann, M.; Cowan, T.E.; Curry, C.B.; Fiuza, F.; Garten, M.; Gaus, L. Ultra-short pulse laser acceleration of protons to 80 MeV from cryogenic hydrogen jets tailored to near-critical density. Nature communications 2023, 14, 4009. [Google Scholar] [CrossRef] [PubMed]
  34. Antici, P.; Fuchs, J.; d’Humières, E.; Lefebvre, E.; Borghesi, M.; Brambrink, E.; Cecchetti, C.; Gaillard, S.; Romagnani, L.; Sentoku, Y. Energetic protons generated by ultrahigh contrast laser pulses interacting with ultrathin targets. Physics of Plasmas 2007, 14. [Google Scholar] [CrossRef]
  35. Lévy, A.; Ceccotti, T.; D’Oliveira, P.; Réau, F.; Perdrix, M.; Quéré, F.; Monot, P.; Bougeard, M.; Lagadec, H.; Martin, P. Double plasma mirror for ultrahigh temporal contrast ultraintense laser pulses. Optics letters 2007, 32, 310–312. [Google Scholar] [CrossRef]
  36. Schumacher, D.W.; Zingale, A.; Czapla, N.; Nasir, D.; Cochran, G.E.; Poole, P.L. Liquid Crystal Targets And Plasma Mirrors For PW-Class Laser Experiments. OSA High-brightness Sources and Light-driven Interactions Congress 2020 (EUVXRAY, HILAS, MICS). Optica Publishing Group, 2020, HILAS. [CrossRef]
  37. Dollar, F.; Zulick, C.; Matsuoka, T.; McGuffey, C.; Bulanov, S.; Chvykov, V.; Davis, J.; Kalinchenko, G.; Petrov, G.; Willingale, L. High contrast ion acceleration at intensities exceeding 1021 Wcm-2. Physics of Plasmas 2013, 20. [Google Scholar] [CrossRef]
  38. Speicher, M.; Haffa, D.; Haug, M.A.; Bin, J.; Gao, Y.; Hartmann, J.; Hilz, P.; Kreuzer, C.; Lindner, F.H.; Ostermayr, T.M.; others. Integrated double-plasma-mirror targets for contrast enhancement in laser ion acceleration. Journal of Physics: Conference Series. IOP Publishing, 2018, Vol. 1079, p. 012002.
  39. Neely, D.; Foster, P.; Robinson, A.; Lindau, F.; Lundh, O.; Persson, A.; Wahlström, C.G.; McKenna, P. Enhanced proton beams from ultrathin targets driven by high contrast laser pulses. Applied Physics Letters 2006, 89. [Google Scholar] [CrossRef]
  40. Antici, P.; Fuchs, J.; d’Humières, E.; Robiche, J.; Brambrink, E.; Atzeni, S.; Schiavi, A.; Sentoku, Y.; Audebert, P.; Pépin, H. Laser acceleration of high-energy protons in variable density plasmas. New Journal of Physics 2009, 11, 023038. [Google Scholar] [CrossRef]
  41. Higginson, A.; Gray, R.; King, M.; Dance, R.; Williamson, S.; Butler, N.; Wilson, R.; Capdessus, R.; Armstrong, C.; Green, J. Near-100 MeV protons via a laser-driven transparency-enhanced hybrid acceleration scheme. Nature communications 2018, 9, 724. [Google Scholar] [CrossRef]
  42. Poole, P.L.; Obst, L.; Cochran, G.E.; Metzkes, J.; Schlenvoigt, H.P.; Prencipe, I.; Kluge, T.; Cowan, T.; Schramm, U.; Schumacher, D.W. Laser-driven ion acceleration via target normal sheath acceleration in the relativistic transparency regime. New Journal of Physics 2018, 20, 013019. [Google Scholar] [CrossRef]
  43. Burdonov, K.; Fazzini, A.; Lelasseux, V.; Albrecht, J.; Antici, P.; Ayoul, Y.; Beluze, A.; Cavanna, D.; Ceccotti, T.; Chabanis, M. Characterization and performance of the Apollon short-focal-area facility following its commissioning at 1 PW level. Matter and Radiation at Extremes 2021, 6. [Google Scholar] [CrossRef]
  44. Badziak, J.; Antici, P.; Fuchs, J.; Jabłoński, S.; Mancic, A.; Parys, P.; Rosiński, M.; Suchańska, R.; Szydłowski, A.; Wołowski, J. Laser-induced generation of ultraintense proton beams for high energy-density science. AIP Conference Proceedings. American Institute of Physics, 2008, Vol. 1024, pp. 63–77.
  45. Mirza, I.; Bulgakova, N.M.; Tomáštík, J.; Michálek, V.; Haderka, O.; Fekete, L.; Mocek, T. Ultrashort pulse laser ablation of dielectrics: Thresholds, mechanisms, role of breakdown. Scientific Reports 2016, 6. [Google Scholar] [CrossRef] [PubMed]
  46. Burdonov, K.; Lelièvre, R.; Forestier-Colleoni, P.; Ceccotti, T.; Cuciuc, M.; Lancia, L.; Yao, W.; Fuchs, J. Absolute calibration up to 20 MeV of an online readout CMOS system suitable to detect high-power lasers accelerated protons. Review of Scientific Instruments 2023, 94. [Google Scholar] [CrossRef] [PubMed]
  47. Brenner, C.M.; Robinson, A.P.L.; Markey, K.; Scott, R.H.H.; Gray, R.J.; Rosinski, M.; Deppert, O.; Badziak, J.; Batani, D.; Davies, J.R.; et al. High energy conversion efficiency in laser-proton acceleration by controlling laser-energy deposition onto thin foil targets. Applied Physics Letters 2014, 104. [Google Scholar] [CrossRef]
  48. Wagner, F.; Bedacht, S.; Bagnoud, V.; Deppert, O.; Geschwind, S.; Jaeger, R.; Ortner, A.; Tebartz, A.; Zielbauer, B.; Hoffmann, D.H.H.; et al. Simultaneous observation of angularly separated laser-driven proton beams accelerated via two different mechanisms. Physics of Plasmas 2015, 22. [Google Scholar] [CrossRef]
  49. Zhuo, W.; Liu, W.; Huang, G.; Zhu, G.; Ma, G. Comparisons of dosimetric properties between GD-300 series of radiophotoluminescent glass detectors and GR-200 series of thermoluminescent detectors. Nuclear Science and Techniques 2007, 18, 362–365. [Google Scholar]
  50. Faenov, A.Y.; Pikuz, S.A.; Erko, A.I.; Bryunetkin, B.A.; Dyakin, V.M.; Ivanenkov, G.V.; Mingaleev, A.R.; Pikuz, T.A.; Romanova, V.M.; Shelkovenko, T.A. High-performance x-ray spectroscopic devices for plasma microsources investigations. Physica Scripta 1994, 50, 333–338. [Google Scholar] [CrossRef]
  51. Vyskočil, J.; Klimo, O.; Weber, S. Simulations of bremsstrahlung emission in ultra-intense laser interactions with foil targets. Plasma Physics and Controlled Fusion 2018, 60, 054013. [Google Scholar] [CrossRef]
  52. Ryazantsev, S.N.; Martynenko, A.S.; Sedov, M.V.; Skobelev, I.Y.; Mishchenko, M.D.; Lavrinenko, Y.S.; Baird, C.D.; Booth, N.; Durey, P.; Döhl, L.N.K.; et al. Absolute keV x-ray yield and conversion efficiency in over dense Si sub-petawatt laser plasma. Plasma Physics and Controlled Fusion 2022, 64, 105016. [Google Scholar] [CrossRef]
  53. Chen, M.; Sheng, Z.M.; Zheng, J.; Ma, Y.Y.; Bari, M.; Li, Y.T.; Zhang, J. Surface electron acceleration in relativistic laser-solid interactions. Optics Express 2006, 14, 3093. [Google Scholar] [CrossRef] [PubMed]
  54. Serebryakov, D.A.; Nerush, E.N.; Kostyukov, I.Y. Near-surface electron acceleration during intense laser–solid interaction in the grazing incidence regime. Physics of Plasmas 2017, 24. [Google Scholar] [CrossRef]
  55. Thévenet, M.; Leblanc, A.; Kahaly, S.; Vincenti, H.; Vernier, A.; Quéré, F.; Faure, J. Vacuum laser acceleration of relativistic electrons using plasma mirror injectors. Nature Physics 2015, 12, 355–360. [Google Scholar] [CrossRef]
  56. Chung, H.K.; Chen, M.H.; Morgan, W.L.; Ralchenko, Y.; Lee, R.W. FLYCHK: Generalized population kinetics and spectral model for rapid spectroscopic analysis for all elements. High Energy Density Physics 2005, 1, 3–12. [Google Scholar] [CrossRef]
  57. Derouillat, J.; Beck, A.; Pérez, F.; Vinci, T.; Chiaramello, M.; Grassi, A.; Flé, M.; Bouchard, G.; Plotnikov, I.; Aunai, N. Smilei: A collaborative, open-source, multi-purpose particle-in-cell code for plasma simulation. Computer Physics Communications 2018, 222, 351–373. [Google Scholar] [CrossRef]
  58. Grismayer, T.; Mora, P. Influence of a finite initial ion density gradient on plasma expansion into a vacuum. Phys. Plasmas 2006, 13, 032103. [Google Scholar] [CrossRef]
  59. Hornỳ, V.; Burdonov, K.; Fazzini, A.; Lelasseux, V.; Antici, P.; Chen, S.N.; Ciardi, A.; Davoine, X.; d’Humières, E.; Gremillet, L. A" lighthouse" laser-driven staged proton accelerator allowing for ultrafast angular and spectral control. arXiv 2024, arXiv:2404.11321 2024. [Google Scholar]
  60. Favalli, A.; Aymond, F.; Bridgewater, J.S.; Croft, S.; Deppert, O.; Devlin, M.J.; Falk, K.; Fernandez, J.C.; Gautier, D.C.; Gonzales, M.A.; others. Nuclear material detection by one-short-pulse-laser-driven neutron source. Technical report, Los Alamos National Lab.(LANL), Los Alamos, NM (United States), 2015.
  61. Favalli, A.; Guler, N.; Henzlova, D.; Croft, S.; Falk, K.; Gautier, D.C.; Ianakiev, K.D.; Iliev, M.; Palaniyappan, S.; Roth, M. Characterizing laser-plasma ion accelerators driving an intense neutron beam via nuclear signatures. Scientific Reports 2019, 9, 2004. [Google Scholar] [CrossRef] [PubMed]
  62. Yogo, A.; Mirfayzi, S.R.; Arikawa, Y.; Abe, Y.; Wei, T.; Mori, T.; Lan, Z.; Hoonoki, Y.; Golovin, D.O.; Koga, K.; et al. Single shot radiography by a bright source of laser-driven thermal neutrons and x-rays. Applied Physics Express 2021, 14, 106001. [Google Scholar] [CrossRef]
  63. Yogo, A.; Lan, Z.; Arikawa, Y.; Abe, Y.; Mirfayzi, S.; Wei, T.; Mori, T.; Golovin, D.; Hayakawa, T.; Iwata, N.; et al. Laser-Driven Neutron Generation Realizing Single-Shot Resonance Spectroscopy. Physical Review X 2023, 13. [Google Scholar] [CrossRef]
Preprints 107558 g001
Figure 1. Experimental setup. The DPM was positioned between the f / 3 off-axis parabola (OAP) and the target. The laser beam hit the target at 45 relative to the target normal. Cameras outside the chamber captured images of the reflected and transmitted laser beams on Spectralon plates. A stack of RCFs (with aluminum filters) was used to measure the proton energy spectrum and spatial profile.
Figure 1. Experimental setup. The DPM was positioned between the f / 3 off-axis parabola (OAP) and the target. The laser beam hit the target at 45 relative to the target normal. Cameras outside the chamber captured images of the reflected and transmitted laser beams on Spectralon plates. A stack of RCFs (with aluminum filters) was used to measure the proton energy spectrum and spatial profile.
Preprints 107558 g001
Preprints 107558 g002
Figure 2. (a) Laser focal spot measurement (at low power) on a DPM shot. The intensity is calculated according to the spatial integration of the energy in each pixel, assuming that the full laser energy is contained in the image and taking into account the laser pulse duration. (b) Encircled laser energy distribution.
Figure 2. (a) Laser focal spot measurement (at low power) on a DPM shot. The intensity is calculated according to the spatial integration of the energy in each pixel, assuming that the full laser energy is contained in the image and taking into account the laser pulse duration. (b) Encircled laser energy distribution.
Preprints 107558 g002
Preprints 107558 g003
Figure 3. (a) Laser contrast measurement during direct (DPM-free) shots. (b) Images of the specularly reflected laser beam collected on a Spectralon plate during a direct shot on a 1.5 μ m thick Al target and (b1) a DPM shot on a 150 nm (100 nm Si + 50 nm Al) thick target (b2). The shadows present on the images come from objects placed between the target and the Spectralon plate. (c) Images of the transmitted laser beam on another Spectralon plate during DPM shots: (c1) calibration shot (without target), (c2) shot on a 10 nm Si foil, and (c3) shot on a 50 nm Si foil. Colormaps are normalized to the maximum count in the calibrated shot shown in (c1).
Figure 3. (a) Laser contrast measurement during direct (DPM-free) shots. (b) Images of the specularly reflected laser beam collected on a Spectralon plate during a direct shot on a 1.5 μ m thick Al target and (b1) a DPM shot on a 150 nm (100 nm Si + 50 nm Al) thick target (b2). The shadows present on the images come from objects placed between the target and the Spectralon plate. (c) Images of the transmitted laser beam on another Spectralon plate during DPM shots: (c1) calibration shot (without target), (c2) shot on a 10 nm Si foil, and (c3) shot on a 50 nm Si foil. Colormaps are normalized to the maximum count in the calibrated shot shown in (c1).
Preprints 107558 g003
Preprints 107558 g004
Figure 4. (a) Measured proton spectra, extracted from RCF data in the DPM case with a 250 nm (200 nm Si + 50 nm Al) thick target (red points, averaged over 3 shots) and in the no-DPM case with a 1.5 μ m thick Al target (blue points, averaged over 2 shots). Error bars represent the minimum and maximum values from different shots with the same target thickness. Exponential fits are shown as black dotted lines (DPM case) and purple dashed-dotted lines (no-DPM case). 2D PIC simulation results for both cases are plotted as red dashed and blue solid lines, respectively. (b) Simulated electron spectra together with exponential fits in the 4.5–11.5 MeV range. The line styles are the same as in panel (a).
Figure 4. (a) Measured proton spectra, extracted from RCF data in the DPM case with a 250 nm (200 nm Si + 50 nm Al) thick target (red points, averaged over 3 shots) and in the no-DPM case with a 1.5 μ m thick Al target (blue points, averaged over 2 shots). Error bars represent the minimum and maximum values from different shots with the same target thickness. Exponential fits are shown as black dotted lines (DPM case) and purple dashed-dotted lines (no-DPM case). 2D PIC simulation results for both cases are plotted as red dashed and blue solid lines, respectively. (b) Simulated electron spectra together with exponential fits in the 4.5–11.5 MeV range. The line styles are the same as in panel (a).
Preprints 107558 g004
Preprints 107558 g005
Figure 5. Target thickness dependence of the (a) proton cutoff energy and (b) laser-to-proton energy conversion efficiency (see text for definition). For both quantities, we distinguish between the maximum (empty symbols) and mean (filled symbols) values for all shots performed with the same target thickness. Direct and DPM shots are represented by squares and dots, respectively. The target thickness for DPM shots refers to the entire Si/Al target. For the thinnest targets, the results are single-shot, hence no mean is reported.
Figure 5. Target thickness dependence of the (a) proton cutoff energy and (b) laser-to-proton energy conversion efficiency (see text for definition). For both quantities, we distinguish between the maximum (empty symbols) and mean (filled symbols) values for all shots performed with the same target thickness. Direct and DPM shots are represented by squares and dots, respectively. The target thickness for DPM shots refers to the entire Si/Al target. For the thinnest targets, the results are single-shot, hence no mean is reported.
Preprints 107558 g005
Preprints 107558 g006
Figure 6. Spatial dose distribution on the RCF stack. Top row: no-DPM shot on a 800 nm thick Al target. Middle row: DPM shot on a 150 nm (100 nm+50 nm Al) thick target. Bottom row: DPM shot on a 20 nm thick Si target. The first two shots yield similar maximum proton energies, but different spatial beam profiles. The same colormap is used in all images. The arrows locate the laser propagation direction (red) and the target normal (black) direction.
Figure 6. Spatial dose distribution on the RCF stack. Top row: no-DPM shot on a 800 nm thick Al target. Middle row: DPM shot on a 150 nm (100 nm+50 nm Al) thick target. Bottom row: DPM shot on a 20 nm thick Si target. The first two shots yield similar maximum proton energies, but different spatial beam profiles. The same colormap is used in all images. The arrows locate the laser propagation direction (red) and the target normal (black) direction.
Preprints 107558 g006
Preprints 107558 g007
Figure 7. Measured half-width of the proton angular distribution as a function of proton energy (normalized to the cutoff energy). Filled blue squares: direct shots on 800 nm thick Al foils (symbols represent the average values and error bars the maximum and minimum values over the considered series of shots). Filled red circles: DPM shots on 150 nm (100 nm Si+50 nm Al) thick foils. Empty red circles: DPM shots on 20 nm thick Si foils. The black dashed curve represents the energy-dependent angular distribution observed in many experiments to be characteristic of TNSA protons [21].
Figure 7. Measured half-width of the proton angular distribution as a function of proton energy (normalized to the cutoff energy). Filled blue squares: direct shots on 800 nm thick Al foils (symbols represent the average values and error bars the maximum and minimum values over the considered series of shots). Filled red circles: DPM shots on 150 nm (100 nm Si+50 nm Al) thick foils. Empty red circles: DPM shots on 20 nm thick Si foils. The black dashed curve represents the energy-dependent angular distribution observed in many experiments to be characteristic of TNSA protons [21].
Preprints 107558 g007
Preprints 107558 g008
Figure 8. Spatial dose distribution recorded inside the interaction chamber by a set of dosimeters (details in text). Left panel: results for direct shots on Al foils of 0.8 μ m , 1.5 μ m and 2 μ m thicknesses. Right panel: results for DPM shots on Si/Al foils of 150 nm, 200 nm and 250 nm thicknesses. Each circle represents a dosimeter, and its color corresponds to the measured dose. The outer circle in both graphs represents the actual diameter of the target chamber. The grey bar representing the DPM in the right panel is to scale.
Figure 8. Spatial dose distribution recorded inside the interaction chamber by a set of dosimeters (details in text). Left panel: results for direct shots on Al foils of 0.8 μ m , 1.5 μ m and 2 μ m thicknesses. Right panel: results for DPM shots on Si/Al foils of 150 nm, 200 nm and 250 nm thicknesses. Each circle represents a dosimeter, and its color corresponds to the measured dose. The outer circle in both graphs represents the actual diameter of the target chamber. The grey bar representing the DPM in the right panel is to scale.
Preprints 107558 g008
Preprints 107558 g009
Figure 9. X-ray spectra averaged over seven DPM shots on a 200 nm Si foils with a 50 nm Al coating (on the laser-irradiated side) (black curve). The red and blue curves represent flychk atomic physics calculations for Al emission at n e = 3 × 10 22 cm − 3 and T e = 350 eV , and n e = 5 × 10 22 cm − 3 and T e = 375 eV , respectively.
Figure 9. X-ray spectra averaged over seven DPM shots on a 200 nm Si foils with a 50 nm Al coating (on the laser-irradiated side) (black curve). The red and blue curves represent flychk atomic physics calculations for Al emission at n e = 3 × 10 22 cm − 3 and T e = 350 eV , and n e = 5 × 10 22 cm − 3 and T e = 375 eV , respectively.
Preprints 107558 g009
Preprints 107558 g010
Figure 10. Spatial distribution of the transverse electric field E y (in V m − 1 units), in the DPM (no-prepulse) laser configuration with a Si target of (a) 10 nm and (b) 20 nm thickness. The black dotted box shows the target initial position.
Figure 10. Spatial distribution of the transverse electric field E y (in V m − 1 units), in the DPM (no-prepulse) laser configuration with a Si target of (a) 10 nm and (b) 20 nm thickness. The black dotted box shows the target initial position.
Preprints 107558 g010
Preprints 107558 g011
Figure 11. Simulations of a DPM shot on a 200 nm Si + 50 nm Al target (top row) and a direct shot on a 1.5 µm thick Al target (bottom row). Longitudinal cuts (across the center of the focal spot at y = 21 μ m ) of the electron density (red solid curves), proton density (blue dotted curves), E y electric field (cyan dashed curves) and E x (averaged over the laser cycle, purple dotted-dashed curves) are plotted at various times after the laser peak has struck the target ( t = 0 ). Particle densities are measured in units of n c while field strengths are shown in units of E 0 = m e c ω 0 / e ≃ 4 × 10 12 V m − 1 . The target rear side is initially located at x = 10.25 μ m with the DPM and x = 11.5 μ m without it.
Figure 11. Simulations of a DPM shot on a 200 nm Si + 50 nm Al target (top row) and a direct shot on a 1.5 µm thick Al target (bottom row). Longitudinal cuts (across the center of the focal spot at y = 21 μ m ) of the electron density (red solid curves), proton density (blue dotted curves), E y electric field (cyan dashed curves) and E x (averaged over the laser cycle, purple dotted-dashed curves) are plotted at various times after the laser peak has struck the target ( t = 0 ). Particle densities are measured in units of n c while field strengths are shown in units of E 0 = m e c ω 0 / e ≃ 4 × 10 12 V m − 1 . The target rear side is initially located at x = 10.25 μ m with the DPM and x = 11.5 μ m without it.
Preprints 107558 g011
Preprints 107558 g012
Figure 12. Phase space distribution ( x − p x ) of protons of (a) the direct shot on a 1.5 µm thick Al target and (b) the DPM shot on a 200 nm Si + 50 nm Al target.
Figure 12. Phase space distribution ( x − p x ) of protons of (a) the direct shot on a 1.5 µm thick Al target and (b) the DPM shot on a 200 nm Si + 50 nm Al target.
Preprints 107558 g012
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated