1. Introduction
Saudi Arabia, formally recognized as the Kingdom of Saudi Arabia (KSA), is located in the Middle East, occupying most of the Arabian Peninsula. With an area of approximately 2,150,000 square kilometers (830,000 square miles), it ranks as the fifth-largest nation in Asia and the biggest in the Middle East. The country shares its borders with the Red Sea to the west; Jordan, Iraq, and Kuwait to the north; the Persian Gulf, Qatar, and the United Arab Emirates to the east; Oman to the southeast; and Yemen to the south, with Bahrain lying as an island nation off its eastern shore. The Gulf of Aqaba to the northwest separates it from Egypt. Notably, Saudi Arabia is the sole nation featuring coastlines along both the Red Sea and the Arabian Gulf. The landscape predominantly comprises arid deserts, lowlands, steppes, and mountainous areas. Riyadh serves as its capital and largest city, and it is home to Mecca and Medina, the two most sacred cities in Islam.
Influenza represents a significant concern worldwide, highlighted by the World Health Organization's (WHO) Global Influenza Strategy for the years 2019 to 2030 [
1], which identifies it as a worldwide hazard. The strategy emphasizes the critical role of national prevention and control efforts in meeting its objectives. A key aspect of these efforts includes the enhancement of Influenza surveillance as a fundamental activity for control and preparedness against future pandemics. The Kingdom of Saudi Arabia (KSA) pays particular attention to the surveillance of such diseases prone to outbreaks [
2], especially considering the mass convergence of Muslims from across the globe for the annual Hajj and Umrah pilgrimages. Consequently, the Saudi Public Health Authority has set up a National Influenza Surveillance System. The ongoing assessment and initial review of these programs are crucial for enhancing their effectiveness and quality.
Saudi Arabia reported cases of Acute Lower Respiratory Tract Infection (ALRTI) affecting more than 5 million people, or 15.4% of its population in 2013. The spread, development, and patterns of respiratory virus transmission in the country are influenced by two primary factors. Firstly, the influx of over 11.9 million international workers from more than 100 countries, attracted by the Saudi's stable economic and welfare system; the frequent travel of such a large workforce between Saudi Arabia and their home countries potentially facilitates the introduction of new viral strains. Secondly, the annual convergence of over 10 million Muslims from around 184 countries to the holy cities of Mecca and Medina for the Hajj and Umrah pilgrimages is another critical factor. This gathering significantly impacts the epidemiology of respiratory viruses within the region [
3]. Further, Saudi Arabia belongs to Gulf Cooperation Council (GCC) countries, Gulf countries are centers for expatriates, who make up over half of the population, with a significant number coming from East and South-East Asia [
4].
A comprehensive study covers Middle East and North Africa (MENA) countries with cases reported from sixteen counties since April 2009 to December 2017 (total of 563,087 cases) indicated that the overall influenza positive cases accounted for 23% of all respiratory infections, with A/H1N1pdm09 being the dominant virus (50.8%) . The MENA region falls within West Asia and North Africa influenza transmission zones. Based on this classification, countries within the same geographical group show similar influenza transmission patterns ([
5], pp. 2009–2017).
Respiratory diseases linked to seasonal influenza are responsible for approximately 290,000 to 650,000 deaths worldwide each year [
6]. The rapid evolution of influenza viruses, due to mutations, enables them to evade the immune system's natural or vaccine-induced defenses. This process, known as antigenic drift, is a leading cause of the annual influenza outbreaks that significantly contribute to human morbidity and mortality, thus overwhelming healthcare services. Besides antigenic drift, influenza viruses also undergo genetic reassortment, which has led to the emergence of life-threatening pandemics on several occasions [
7]. The last century witnessed three pandemics caused by influenza A: the 1918 H1N1, 1957 H2N2, and 1968 H3N2. In June 2009, the WHO declared the first pandemic of the twenty-first century, triggered by a swine-origin H1N1 (A/H1N1pdm09) virus, accounting for over 250,000 deaths globally ([
5], pp. 2009–2017), [
7]. Since then, the A/H1N1pdm09 virus has supplanted the seasonal H1N1 virus and now circulates alongside H3N2 and influenza B viruses. Only influenza type A viruses are known to have caused pandemics [
6].
Every year, the World Health Organization (WHO) selects virus strains that are most likely to ensure the effectiveness of vaccines, announcing its recommendations for the northern hemisphere in February and for the southern hemisphere in September [
8]. In the wake of the 2009 pandemic, unparalleled surveillance initiatives were initiated to track influenza viruses from both a molecular and epidemiological standpoint. Since 2012, the Ministry of Health initiated the Health Electronic Surveillance Network (HESN), an online surveillance system that links together all healthcare facilities across the Kingdom [
2]. In 2017, Saudi Arabia expanded its surveillance program for influenza and other respiratory pathogens by lunching Sentinel Surveillance Program to monitor the influenza activities both locally and internationally, then planned its national influenza control strategies [
9]. This helped to enhance the healthcare system's readiness to combat seasonal, zoonotic, and pandemic influenza risks to both communities and individuals. Saudi Arabia implemented a number of vaccination policies.
Current seasonal influenza vaccines, depend largely on the WHO's annual forecasts and advice, formulated by influenza specialists. These predictions are grounded on the identification of circulating influenza strains worldwide, 6 to 9 months prior to the intended season. However, this approach has limitations, such as the potential for strain mismatches, which can significantly compromise the vaccine's effectiveness [
10]. A recently conducted research revealed that there were vaccine mismatches in approximately half of the influenza seasons from 2010 to 2020 [
11]. Differences in antibody specificity related to age are frequently observed among humans of various ages, who have unique immune system histories [
10].
The national influenza vaccination programs in Saudi Arabia recommend mass vaccination for all age groups. Saudi’s Health Minister lunched the influenza vaccination campaign in September until the ends of March of the following year. The season of 2019/2020 was among the critical and devastating seasons that witnessed the early stages of the COVID-19 pandemic, with uncertainty in influenza vaccine effectiveness (VE).
In this study, we investigate the impact of applying vaccination rate differently on the age groups. To the best of knowledge, this is the first study to propose the best vaccination policies for age groups based on the 2019/2020 influenza cases in the Kingdom of Saudi Arabia. We develop an age-structured SEIR model of the 2019/2020 influenza season based on published settings. Then, we divide the entire population into five age groups considering the age-specific incidence rate and life pattern. The age-dependent transmission rates are estimated using the epidemic data reported in a collection of published works covering the five main regions of Saudi Arabia. The contact matrix between age groups, describing the main characteristics of the influenza transmission, was projected from multiple contact matrices. The study conducts an in-depth analysis of three different vaccination scenarios: no vaccination, national vaccination, and an optimized vaccine allocation policy designed to minimize both the number of infections and the costs associated with a vaccination campaign. It explores how increasing vaccination coverage can help curb the spread of infection within the target population across various potential pandemic scenarios. The impact of these strategies is examined on different age groups and at both national and regional levels.
This paper is structured into several key sections to comprehensively present the research. Following this introduction, the Literature Review section reviews prior studies and sets the theoretical foundation for the current research. The Problem Statement section delves into the specifics of planning and allocating the seasonal influenza vaccine. The Materials and Methods section details the comparative analysis of three vaccination scenarios: no vaccination, national vaccination, and optimized vaccine allocation. Results and Discussion are combined to highlight the impacts of these strategies on various age groups and on both national and regional scales, while also interpreting these findings and discussing their implications for public health policy and pandemic management. Finally, the Conclusion summarizes the key findings and proposes directions for future research.
2. Literature Review
The distribution of vaccines, particularly influenza vaccines, based on age group population is a critical aspect of public health planning. Studies have shown that age-specific factors play a significant role in vaccine uptake and effectiveness. For instance, Galarce et al. [
12] found that A(H1N1) vaccination rates were strongly associated with age, urbanicity, and perceptions of vaccine safety. The literature on vaccination rates in Saudi Arabia spans various infectious diseases and age groups. Herzallah et al. [
13] found that influenza A H1N1 infection was more common in younger age groups and more severe among pregnant women in Eastern Saudi Arabian hospitals. Multiple studies analyzed the prevalence of A(H1N1) infection [
17,
18,
19] and vaccination coverage [
24,
25,
26] in different regions of Saudi Arabia, showing various infection characteristics and uptake rates among different age groups.
Prioritizing vaccine allocation among different age groups is addressed in the work of Galvani et al. [
30], who developed an optimization model for influenza vaccine distribution based on age groups. They stratified the population into 16 age groups and prioritized vaccine allocation accordingly. Enayati et al. [
31] contributed to optimizing vaccine distribution by proposing an equity constraint to ensure fairness in vaccine allocation decisions among heterogeneous populations. This approach is supported by the findings of Shim [
32], who emphasized the importance of considering age-specific factors such as contact rates and vaccine efficacy to minimize infections, deaths, and years of life lost in vaccine allocation strategies. Aro et al. [
33] observed age-specific HPV type distribution in cervical disease, highlighting the need for tailored vaccination strategies based on age groups. Worsham and Jena [
34] focused on optimizing vaccine allocation at different points in time, studying the optimal timing of influenza vaccination in young children to determine the most effective strategies for vaccine distribution. Additionally, Han et al. [
35] proposed time-varying optimization models for vaccine prioritization, where vaccines are allocated proportionally to the unvaccinated susceptible population in each age group to maximize the impact of vaccination efforts.
Various studies have explored the use of multi-objective optimization techniques to enhance vaccine distribution and allocation. Minoza et al. [
36] developed a multi-objective linear programming model to optimize vaccine distribution in an age-stratified population. Alkhamis and Hosny [
37] introduced a Controlled Elitism Non-Dominated Sorting Genetic Algorithm model in the context of influenza vaccination policies to optimize vaccine allocation. Additionally, Alkhamis and Hosny [
38] continued their research by using a Multi-objective simulated annealing algorithm to tackle the design of optimal vaccination sequences and distribution plans, aiming to improve overall vaccine effectiveness. In the context of COVID-19 vaccines, Briffoteaux et al. [
39] used multi-objective optimization approaches to distribute vaccines among age categories of the population, emphasizing the importance of equitable distribution based on age. Moreover, Mohammadi et al. [
40] developed mixed integer programming modelling to prioritize the population for vaccination based on limited vaccine supply.
Overall, optimizing flu vaccine distribution based on age group population requires a comprehensive understanding of age-specific factors, vaccine efficacy, and perceptions to maximize population benefits and ensure equitable access to vaccines. Utilizing advanced modelling techniques, such as multi-objective optimization can maximize the impact of vaccination campaigns and reduce the burden of influenza-related illnesses.
3. Problem Statement
The problem this research seeks to address is vaccination strategy planning and allocation for the seasonal influenza vaccine. The research follows the duration of influenza in the northern hemisphere, which commonly starts at the beginning of October and lasts until the end of May. The period of the influenza season lasts 30-35 weeks in total. In epidemiology, it corresponds to week 40 of the year, which roughly refers to the start of October as week 1 (t = 1) [
41]. Usually, vaccines are ready for distribution in July or August. However, the US Centre for Disease Control and Prevention (CDC) recommends that vaccination campaigns should begin early in the autumn (i.e., September, October, and November), before the flu season begins, which starts in October and peaks between December and February. As such, vaccination campaigns should begin in anticipation of waning immunity before the end of the flu season (i.e., as late as May).
1
Vaccination serves as the primary preventive strategy against seasonal influenza, aiding in curbing its spread. In Saudi Arabia, health authorities provide seasonal influenza vaccines (SIV) to all residents, including non-citizens, at no cost. Due to a significant rise in influenza cases and influenza-like illnesses (ILIs), the Ministry of Health (MOH) has encouraged the public to get vaccinated at primary healthcare centers (PHCs) [
22]. The MOH has noted a substantial increase in the number of influenza cases and ILIs in the 2022 flu season compared to previous years, suggesting an increased strain on the Kingdom's healthcare system [
42]. World Health Organization (WHO) surveillance reports show a dramatic increase in the percentage of positive influenza cases, and the numbers of ILIs and severe acute respiratory infections (SARIs) rose from 3.75%, 45, and 82 in 2021 to 25.11%, 344, and 303 in 2022, respectively [
43]. The decrease in ILI and SARI cases in 2021 is credited to successful campaigns for the simultaneous COVID-19 and seasonal influenza vaccinations during the pandemic. Conversely, the spike in ILI and SARI cases in 2022 is likely due to reduced adherence to preventive measures after COVID-19, and potentially, to an increased reluctance to receive the seasonal influenza vaccine (SIV) [
22].
Saudi Arabia initiated a large-scale vaccination drive, distributing 4.5 million doses during the 2019/2020 season. This period saw a notable rise in influenza activity from October to January in various Western Asian countries, including Saudi Arabia, primarily due to the widespread presence of the A(H1N1)pdm09 strain [
44]. Given that the A(H1N1)pdm09 strain was the cause of a global pandemic a decade ago, the possibility of a pandemic or outbreak remains significant. Since that time, the A(H1N1)pdm09 strain has been included in the Seasonal Influenza Vaccine (SIV) [
45]. The government's strategy ensures uniform vaccination coverage across all age groups and regions, with particular emphasis on high-risk populations such as children, pregnant women, the elderly over 65, and those with chronic conditions. However, this approach does not account for regional disparities, including areas recognized as holy, densely populated, hubs, and rural. Variations in climate and geographical landscape across regions influence social behaviors, people's interactions, the influx of international visitors or residents, and crucially the types of viruses circulating and the transmissibility of infections.
This research aims to investigate the impact of various vaccination campaigns on the total number of infections, as well as mortality and morbidity rates. It considers three different vaccination approaches: no vaccination, a government-led campaign, and an optimized campaign, across several basic reproduction number (R0) scenarios. The study is designed to address critical questions regarding the efficiency of optimal vaccination policies, including: (1) The effectiveness of the national influenza vaccination campaign, (2) The appropriate amount of vaccine distribution among different groups and the temporal adjustments required for vaccination rates, and (3) The efficacy of an optimal vaccination strategy across diverse geographical areas, or whether there is a necessity to tailor prioritization of age groups specifically for each region.
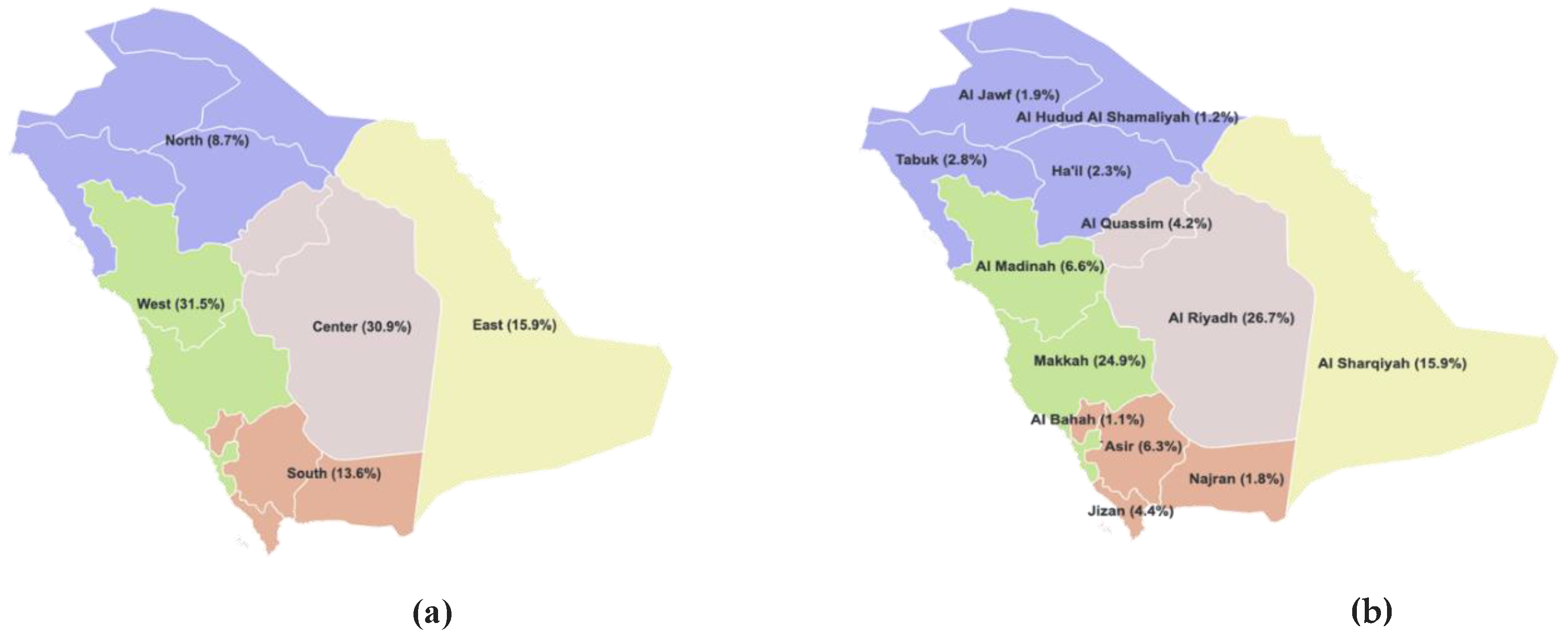
Figure 1.
Map of Saudi Arabia showing (a) Different regions and (b) Emirates.
Figure 1.
Map of Saudi Arabia showing (a) Different regions and (b) Emirates.
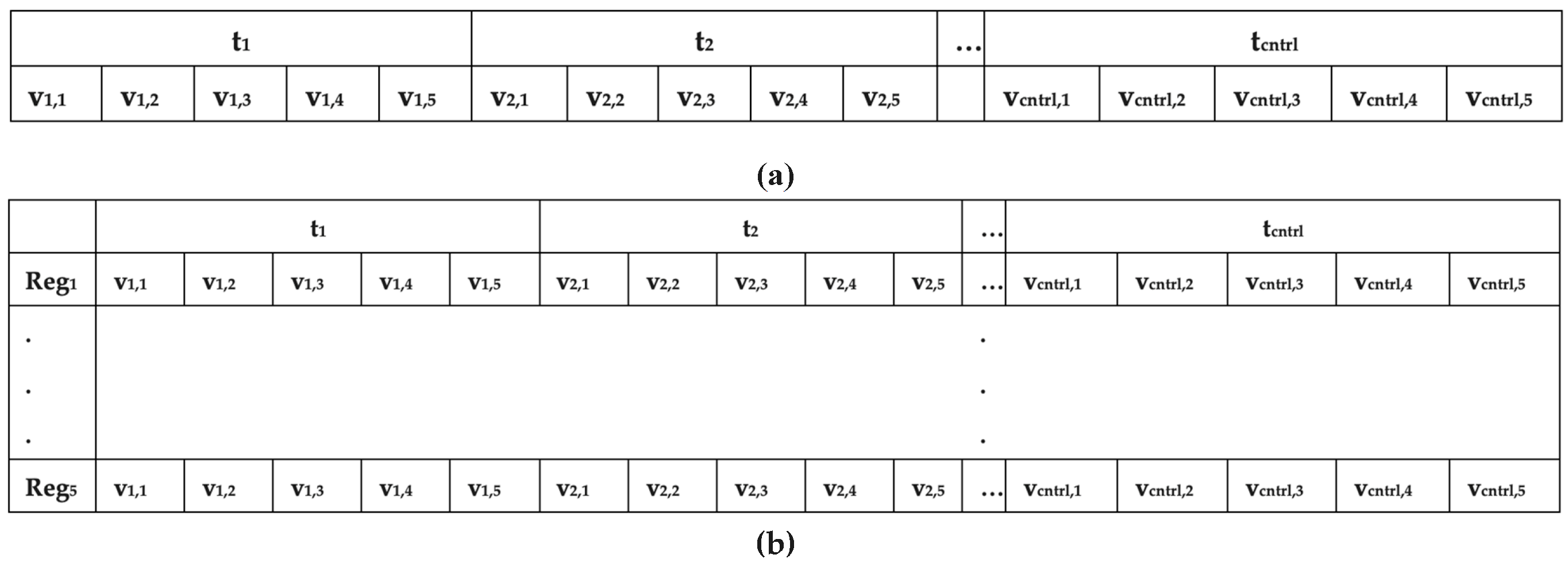
Figure 2.
Chromosome representation in general case (a) and regional cases (b).
Figure 2.
Chromosome representation in general case (a) and regional cases (b).
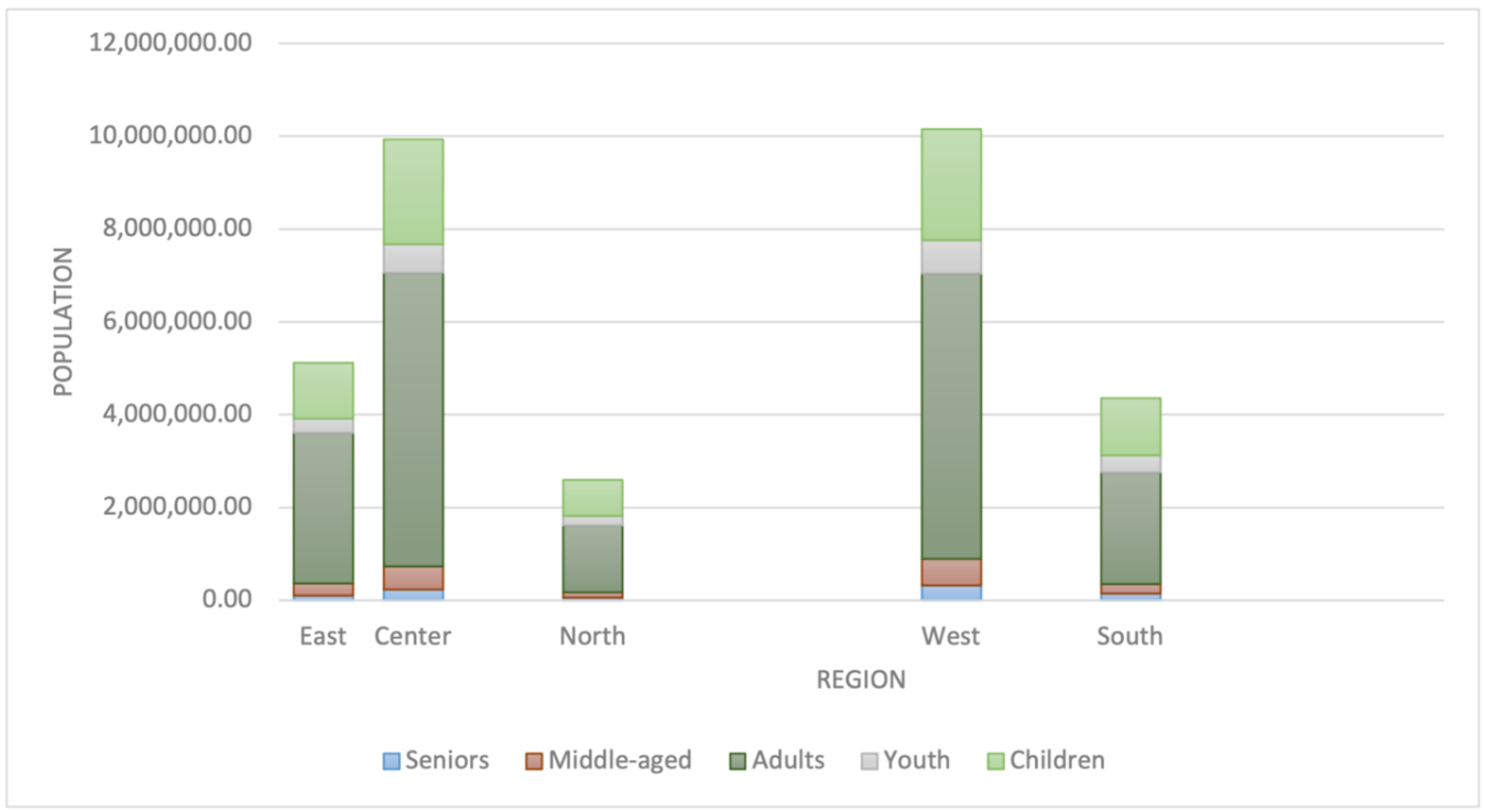
Figure 3.
Distribution of population among different age groups.
Figure 3.
Distribution of population among different age groups.
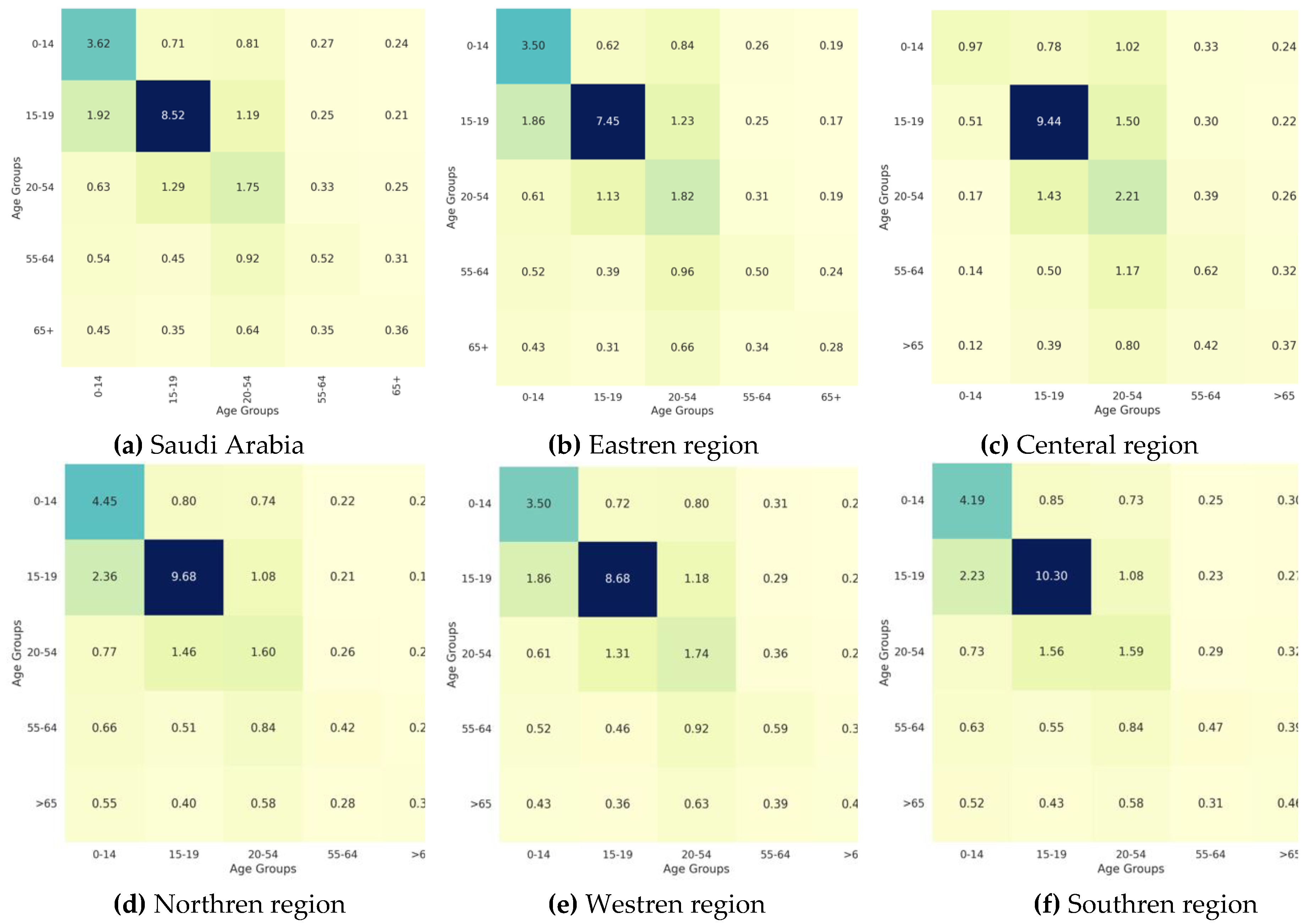
Figure 4.
Heatmaps representing reciporical contact patterns of all regions; (a) Saudi Arabia, (b) Eastren region, (c) entral region, (d) Northren region, I Westren region, and (f) Southren region.
Figure 4.
Heatmaps representing reciporical contact patterns of all regions; (a) Saudi Arabia, (b) Eastren region, (c) entral region, (d) Northren region, I Westren region, and (f) Southren region.
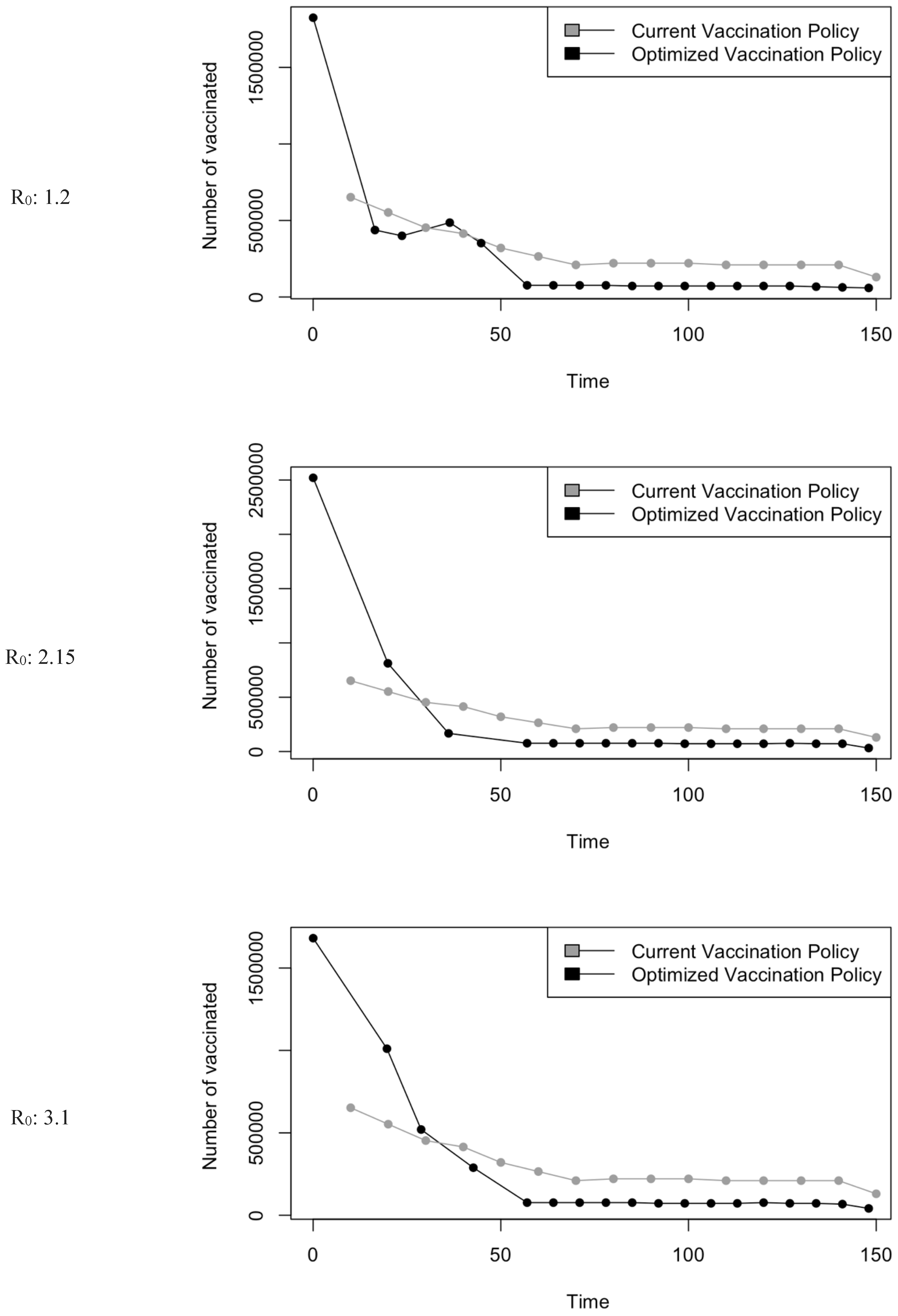
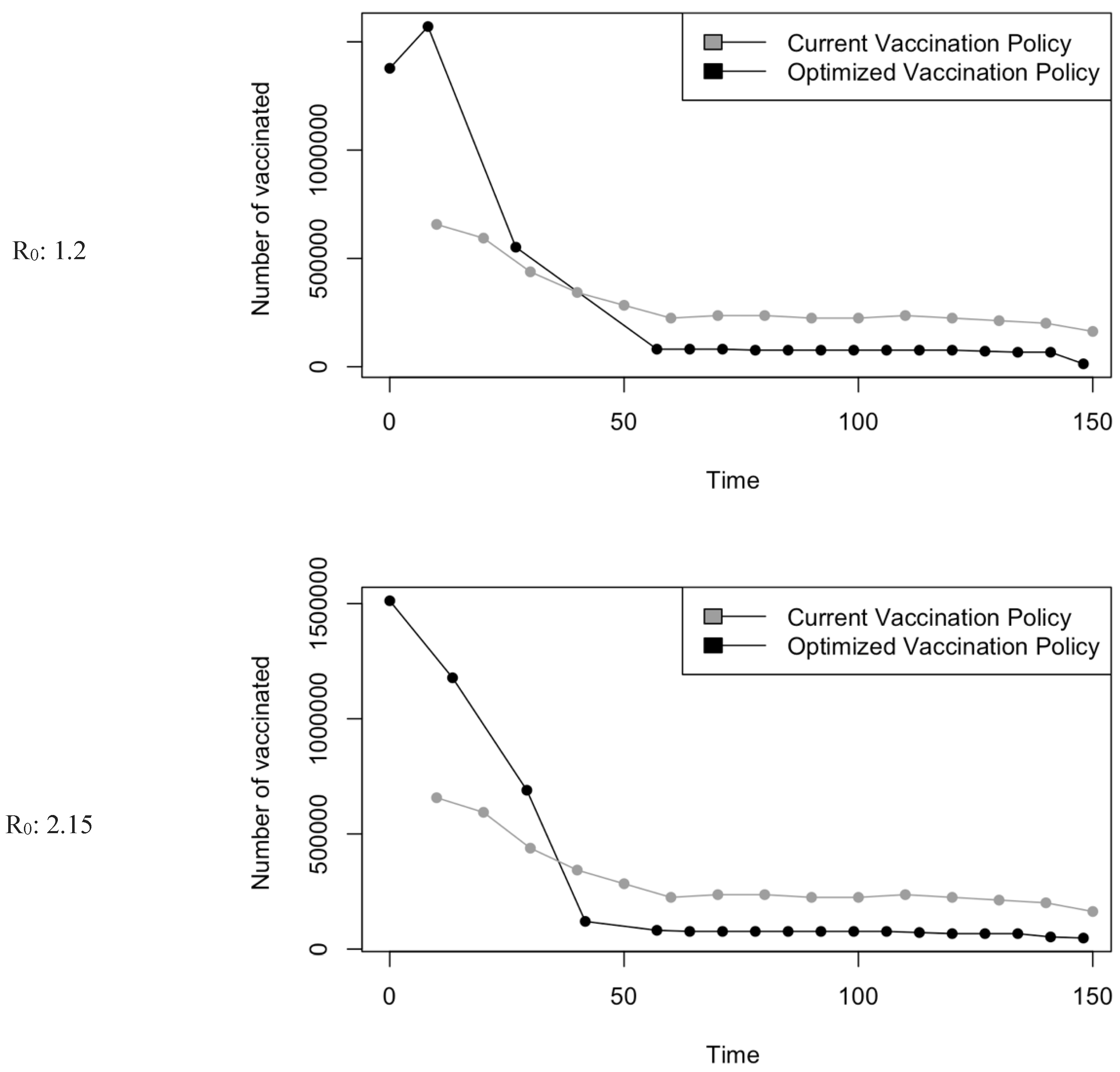
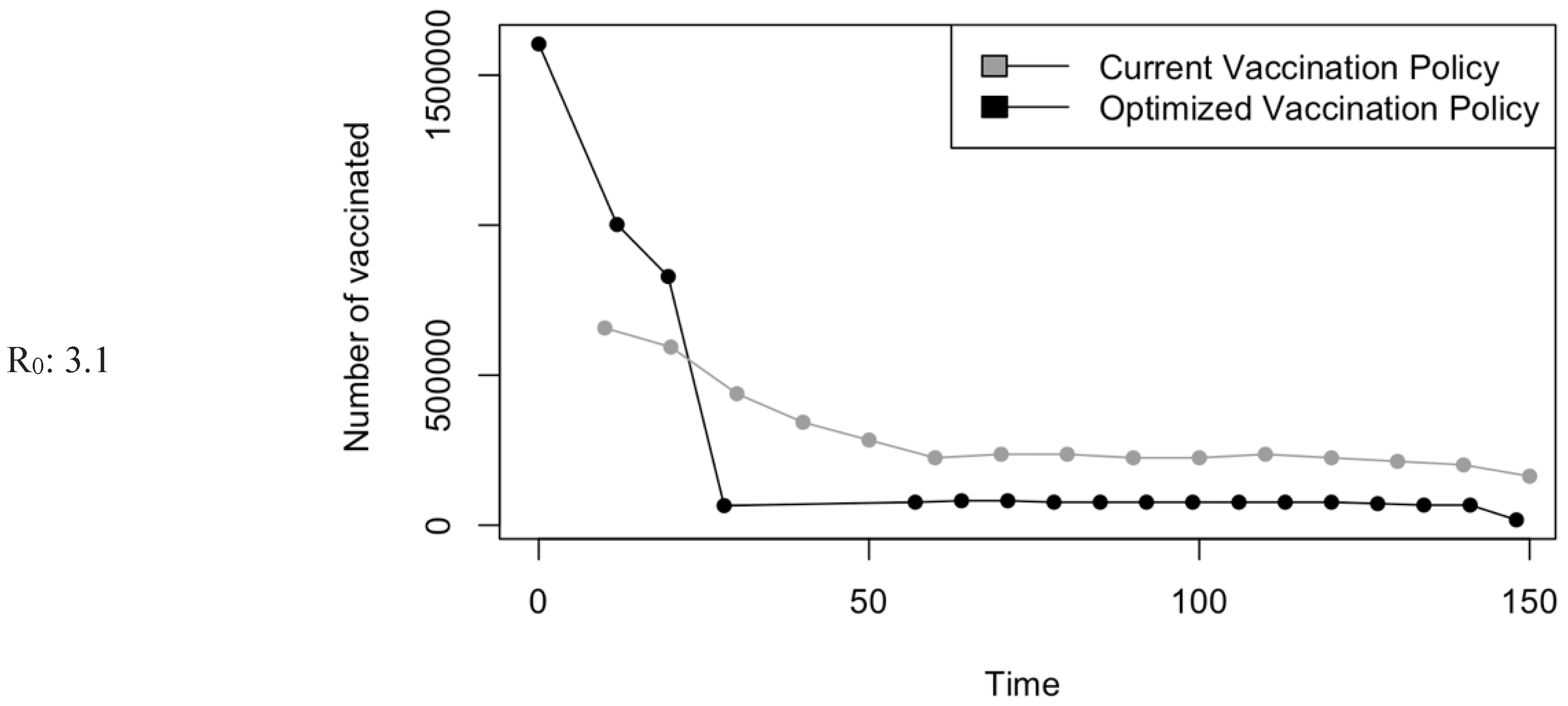
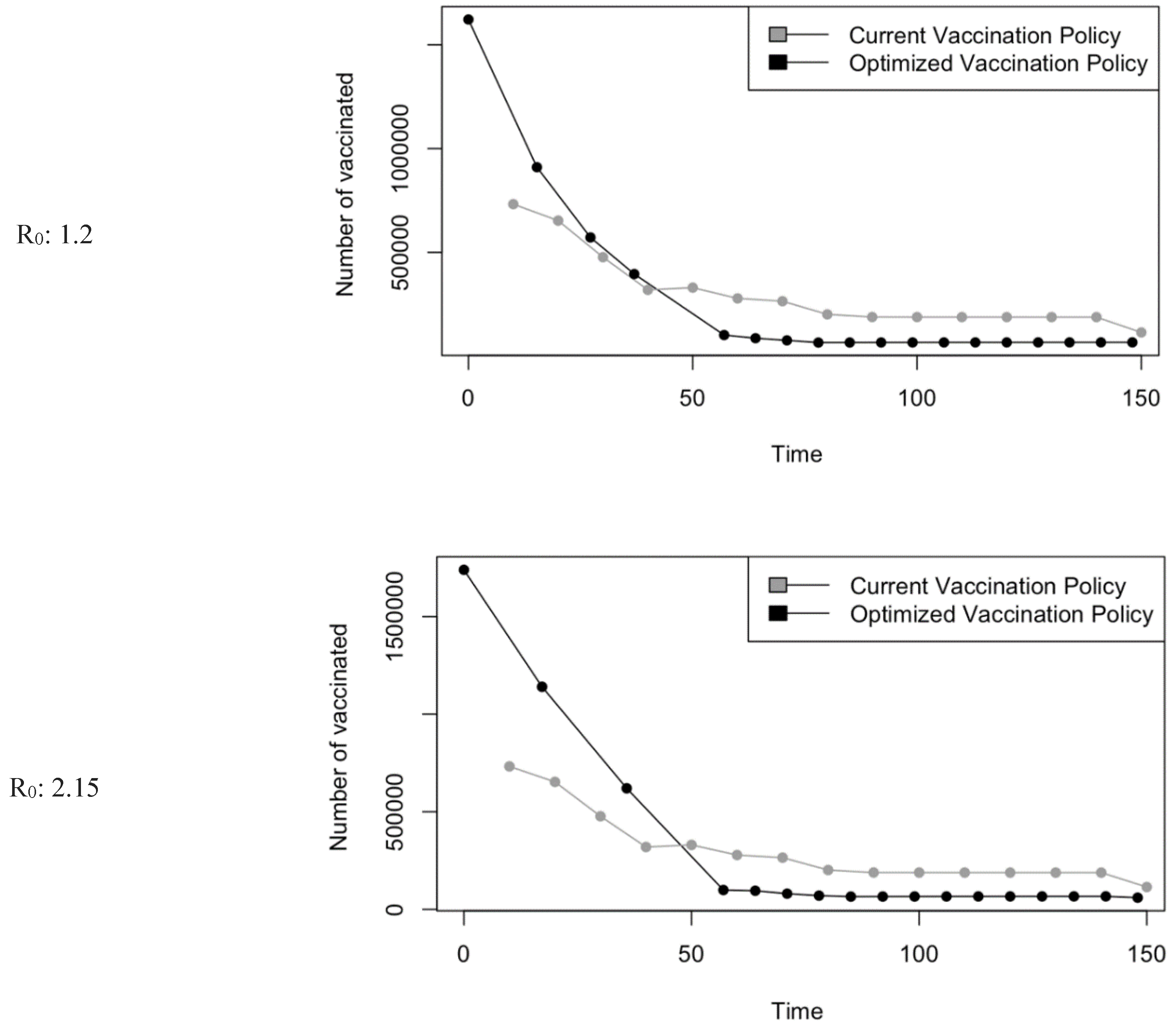
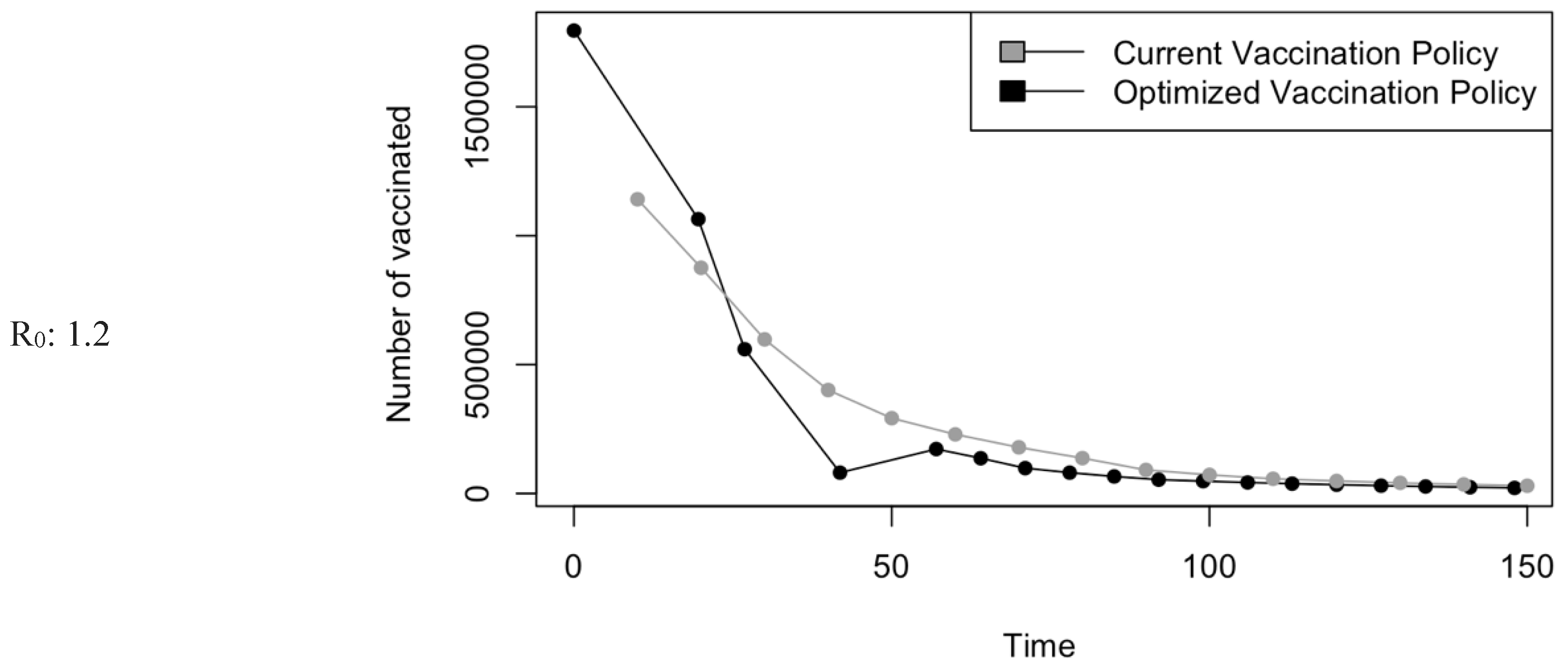
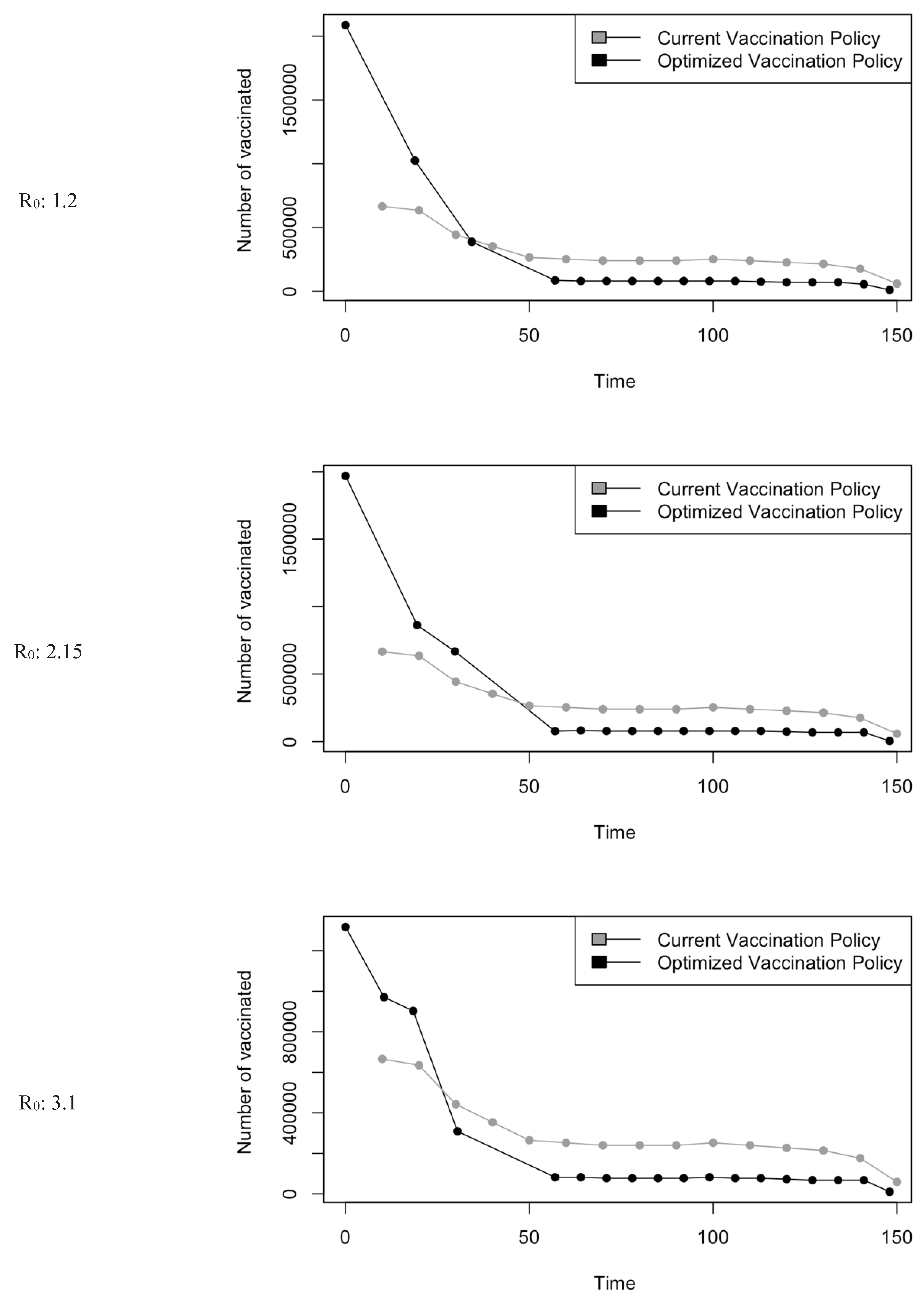
Figure 5.
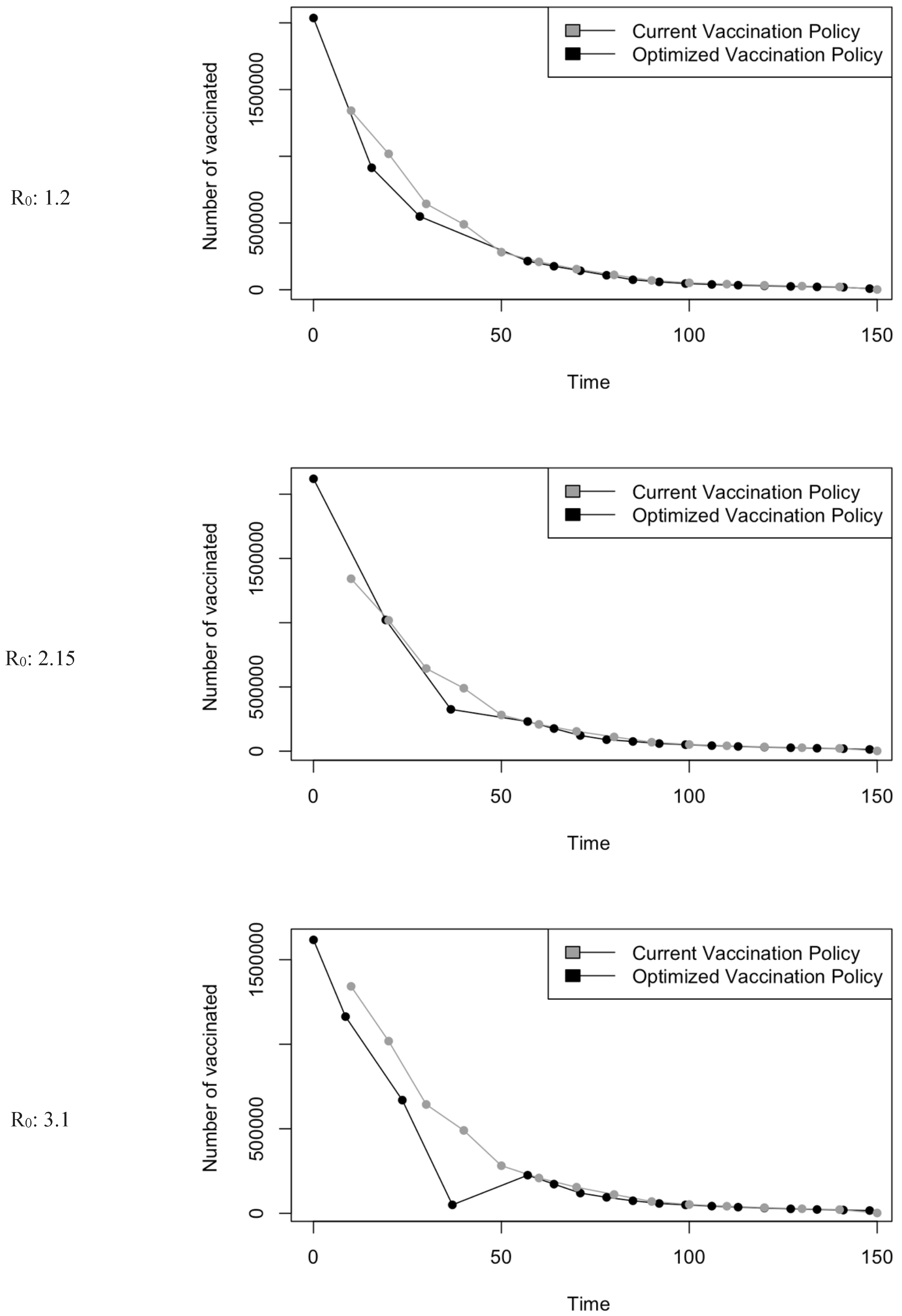
Vaccination Strategy for the Case of Saudi Arabia.
Figure 5.
Vaccination Strategy for the Case of Saudi Arabia.
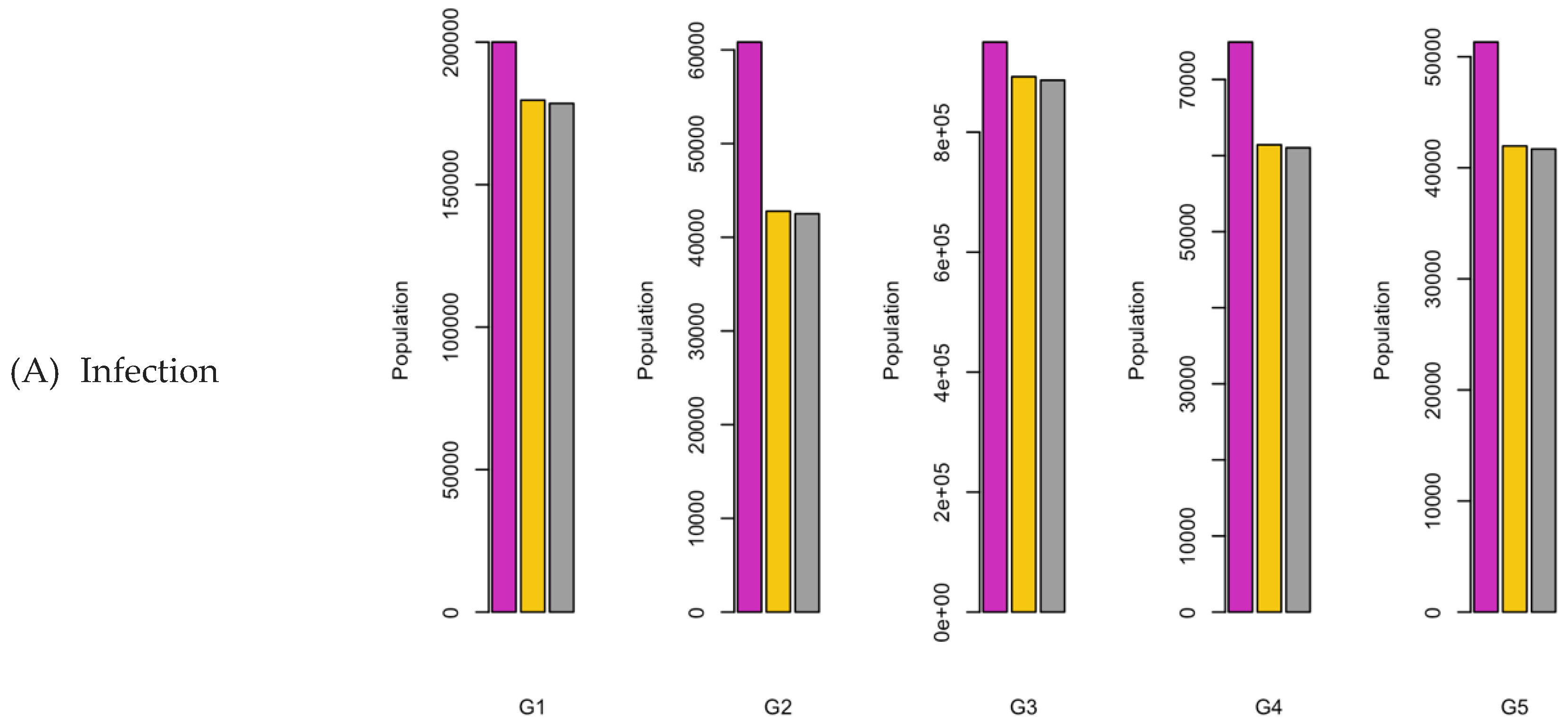
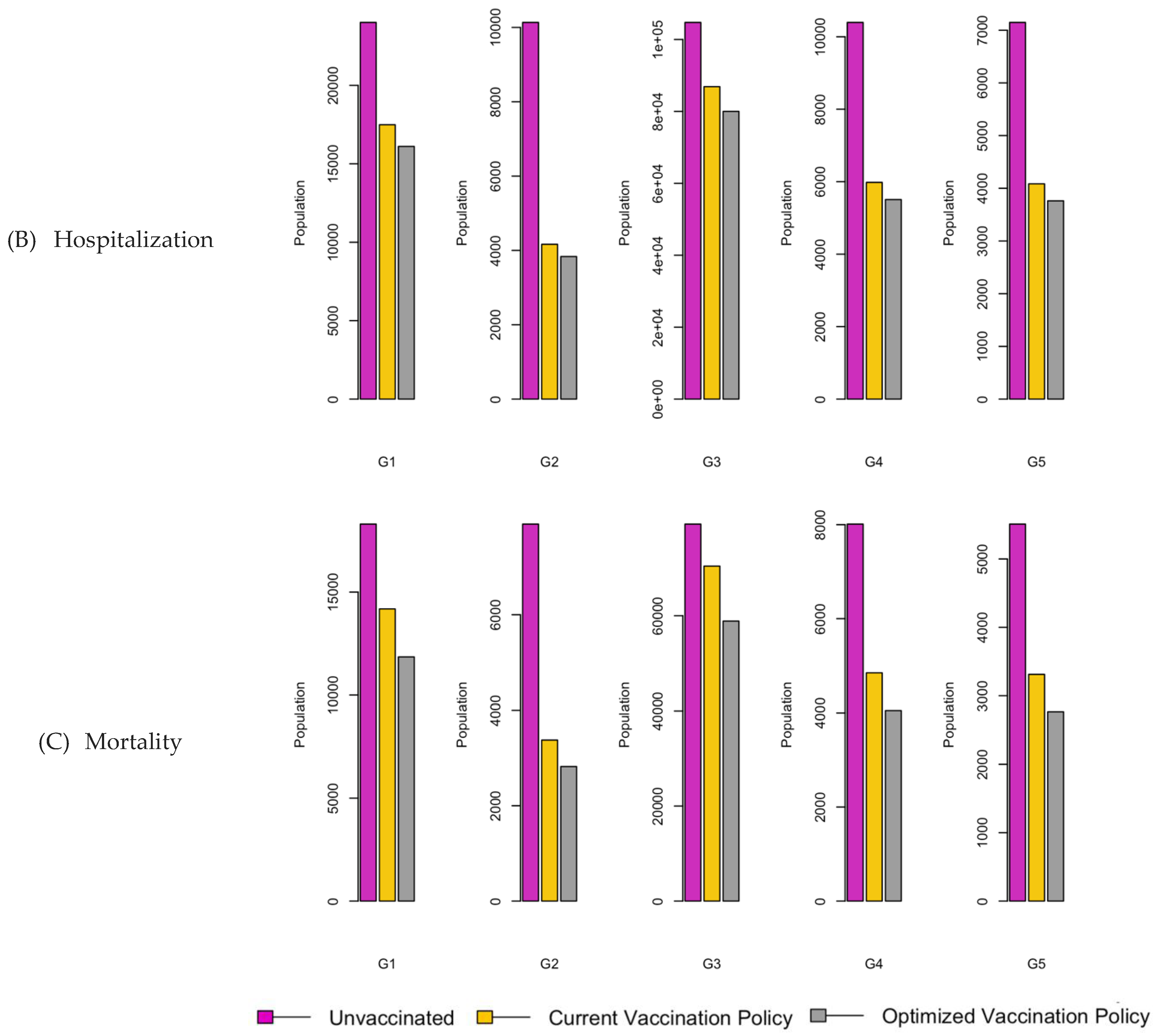
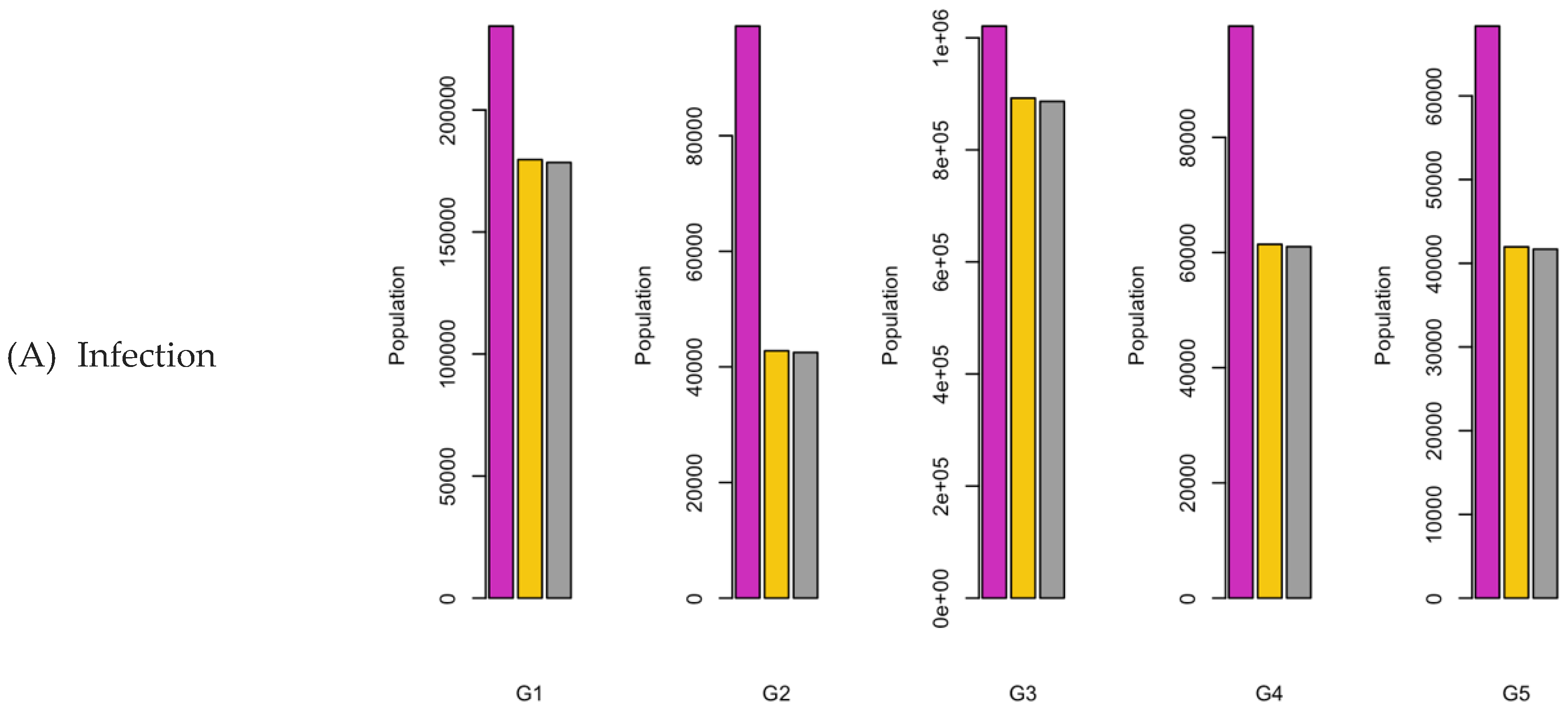
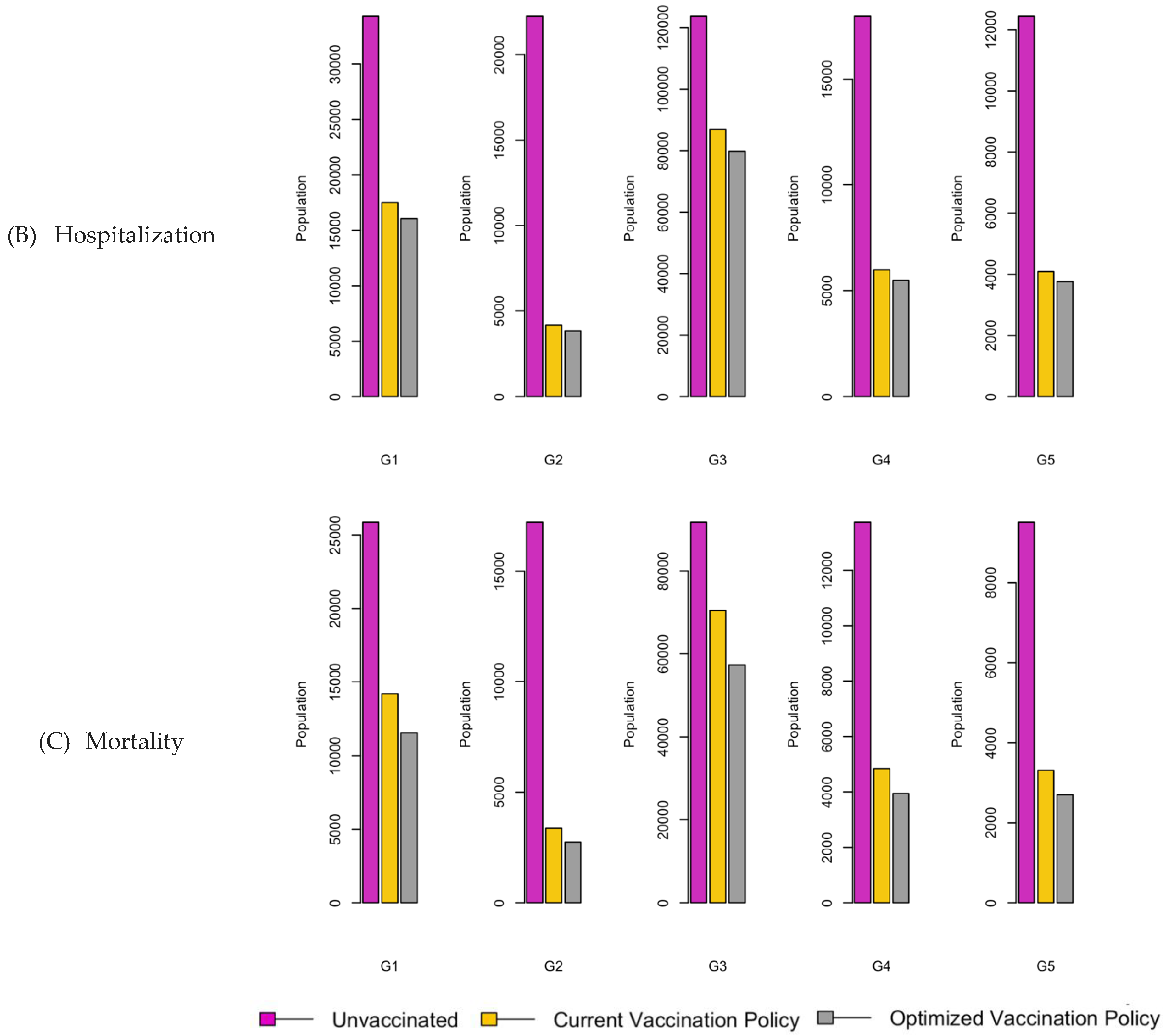
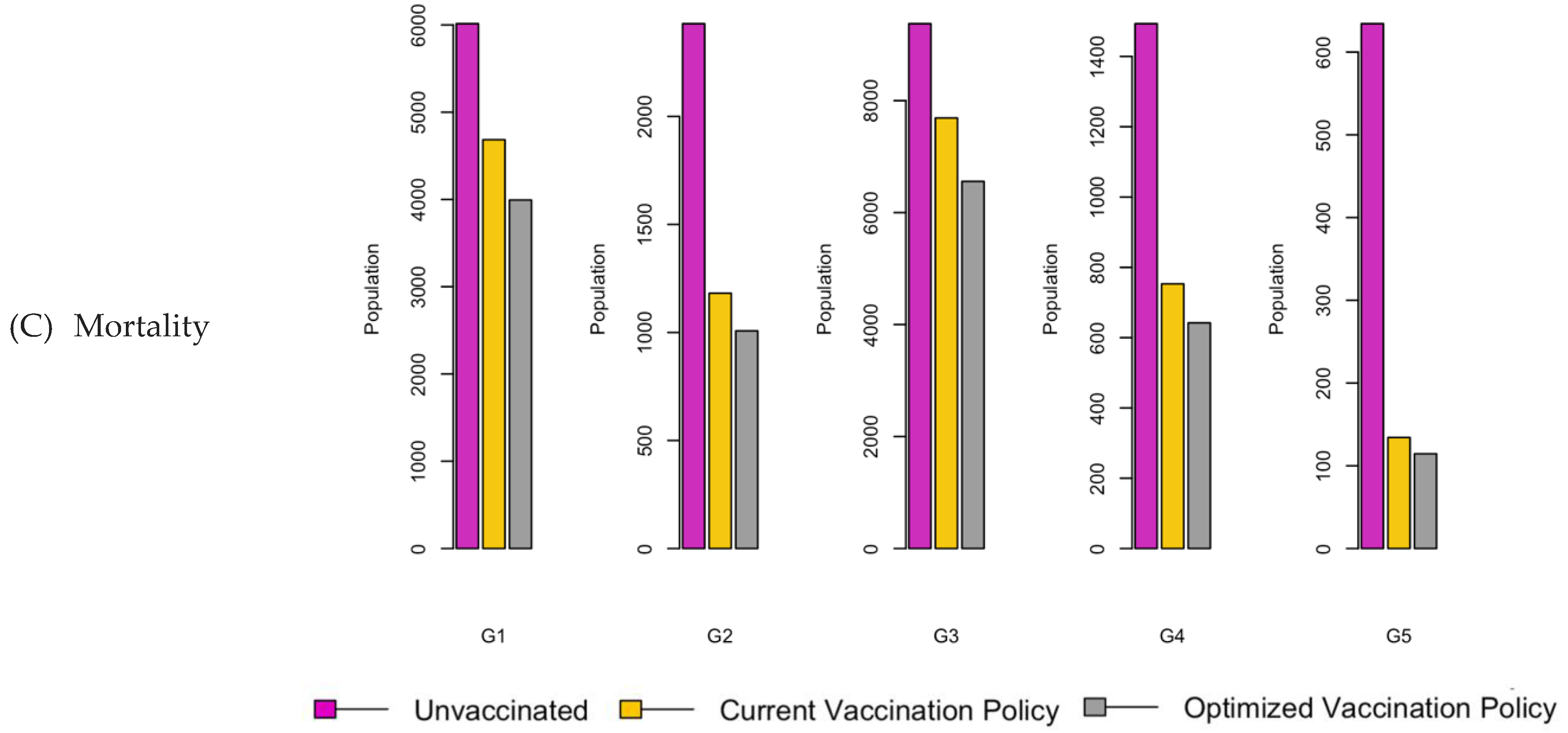
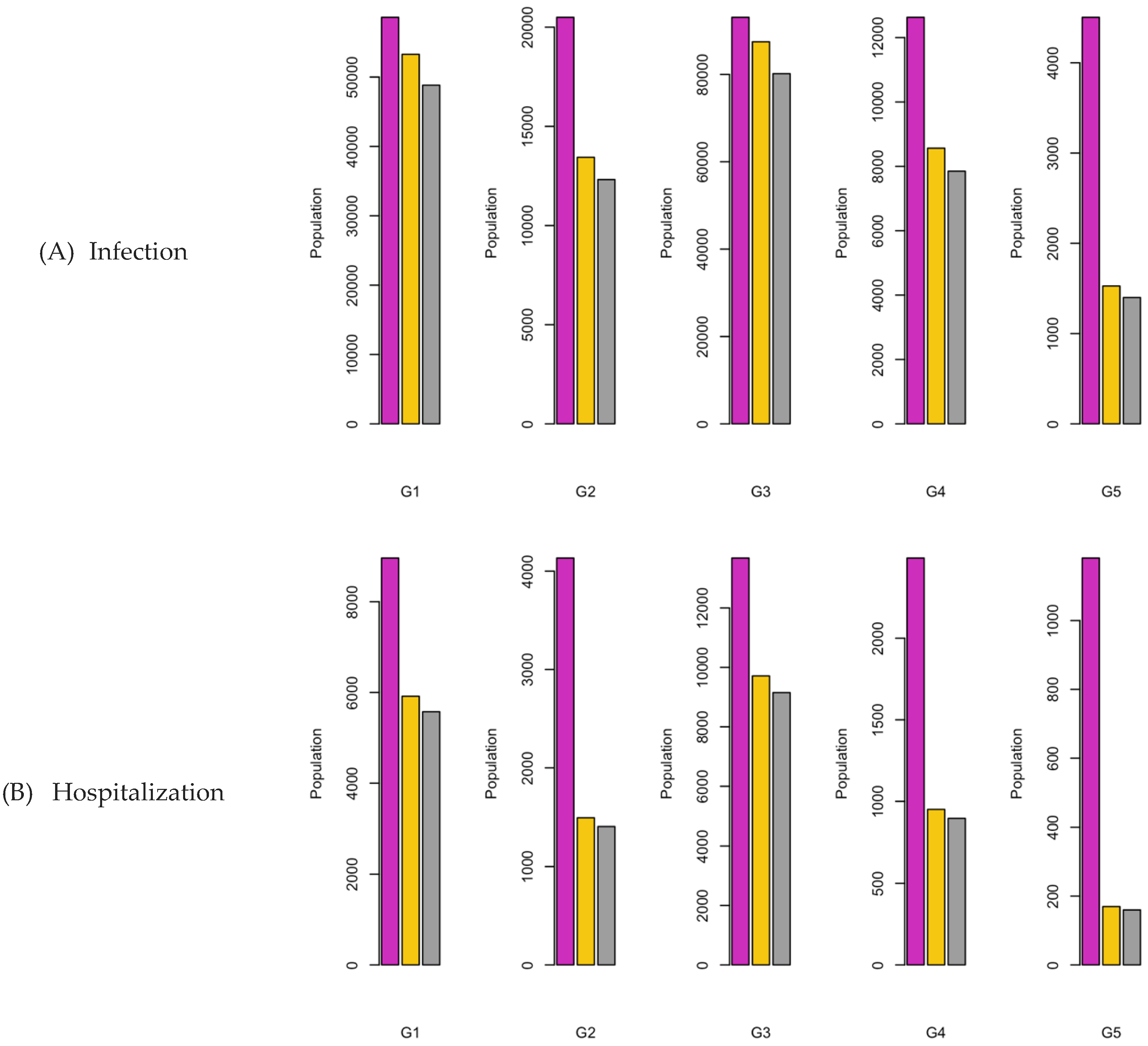
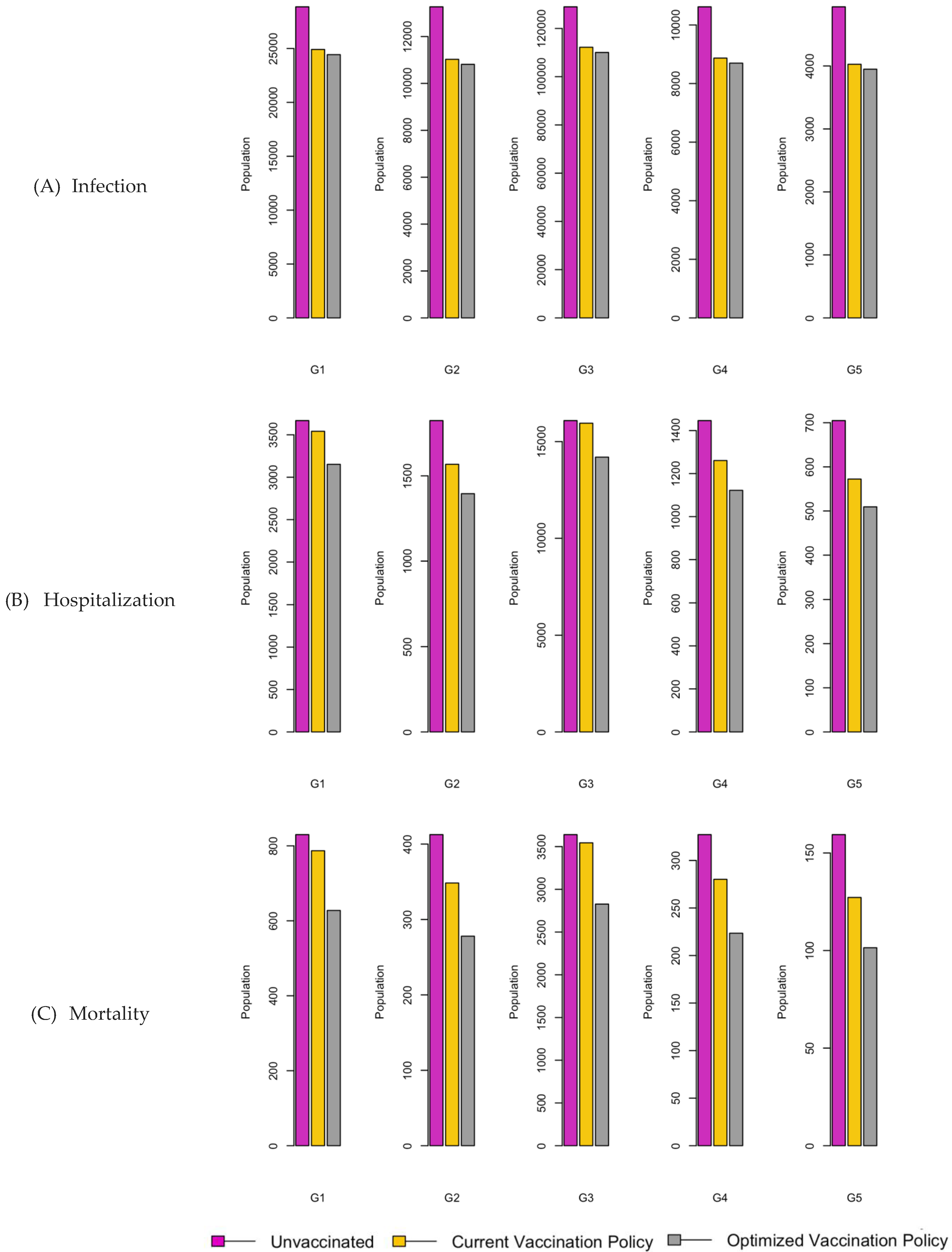
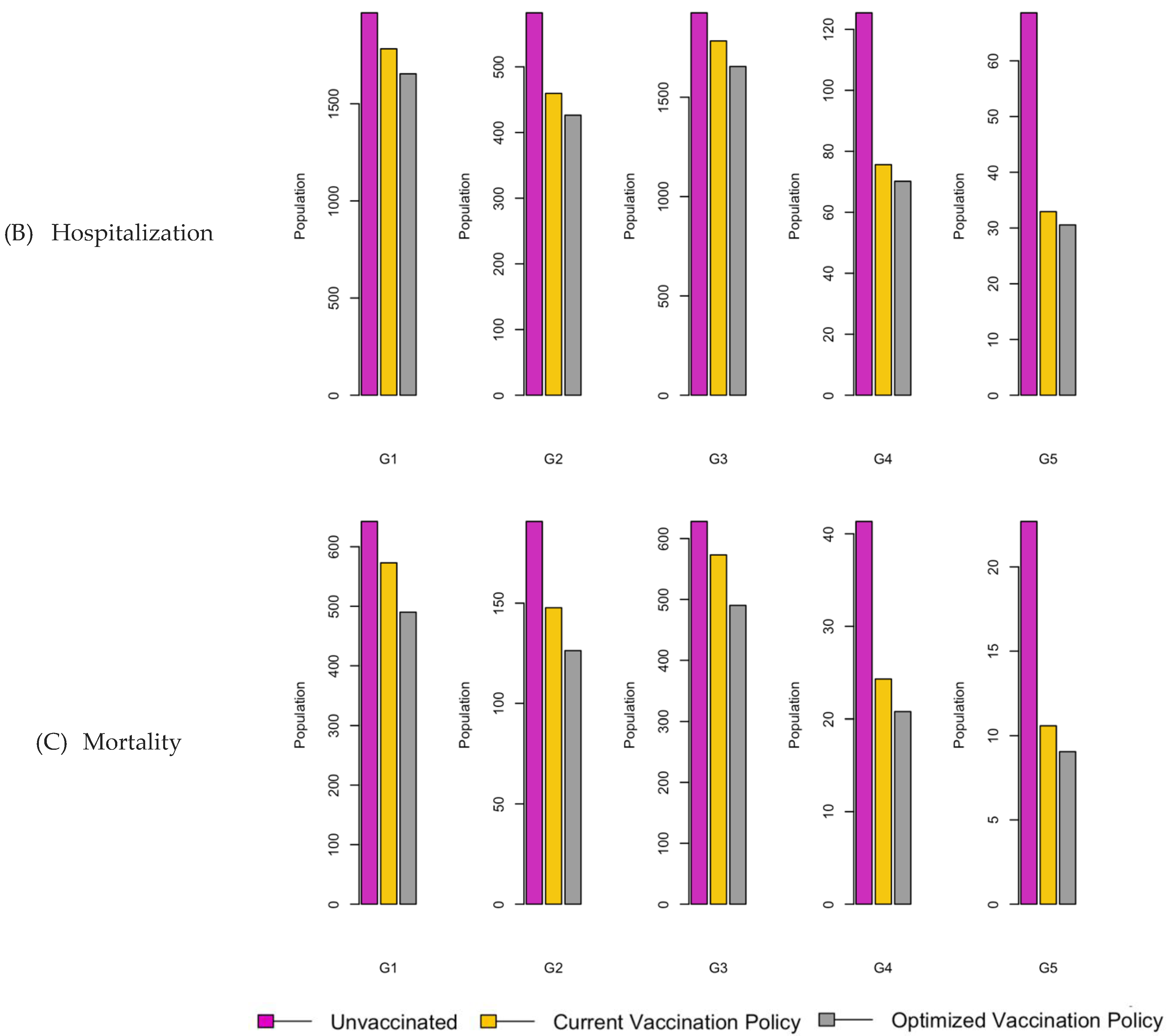
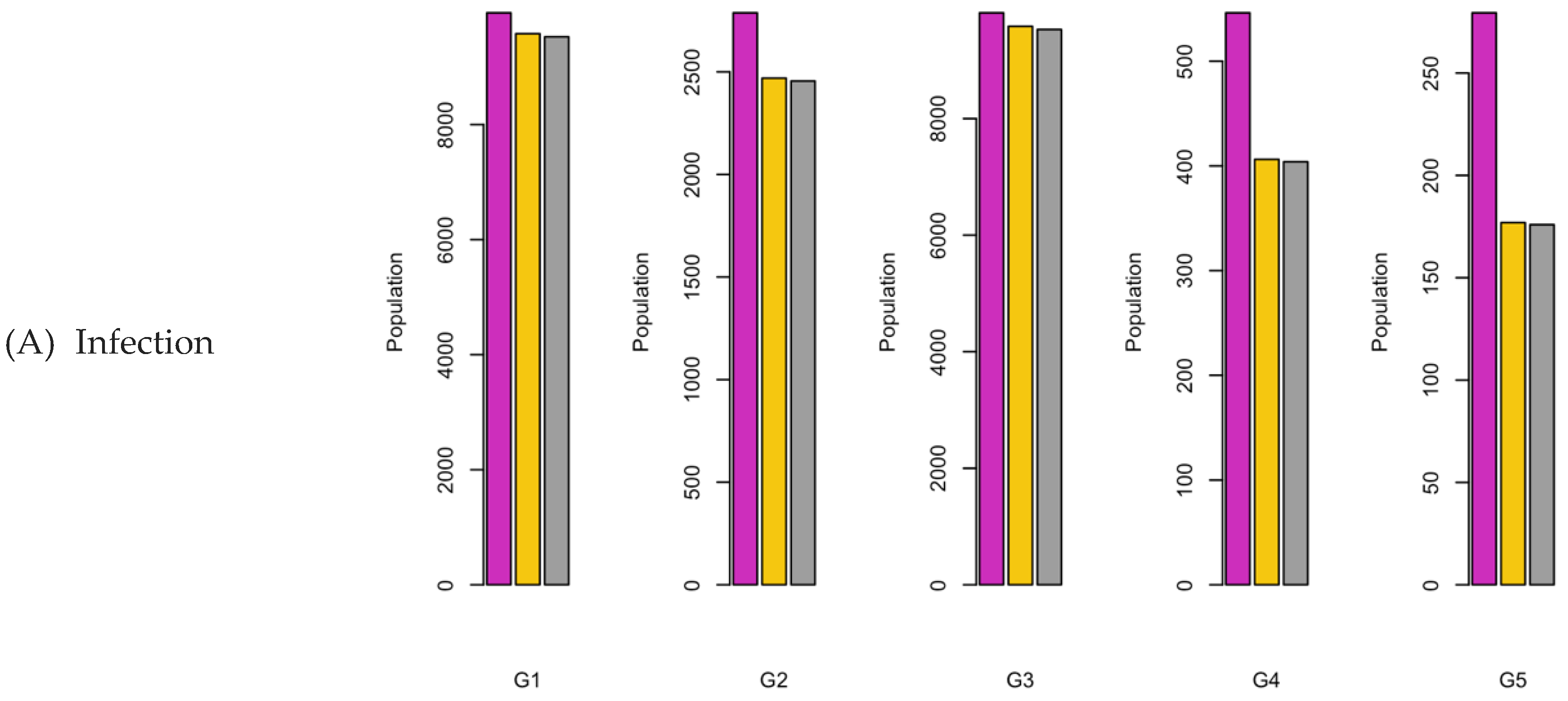
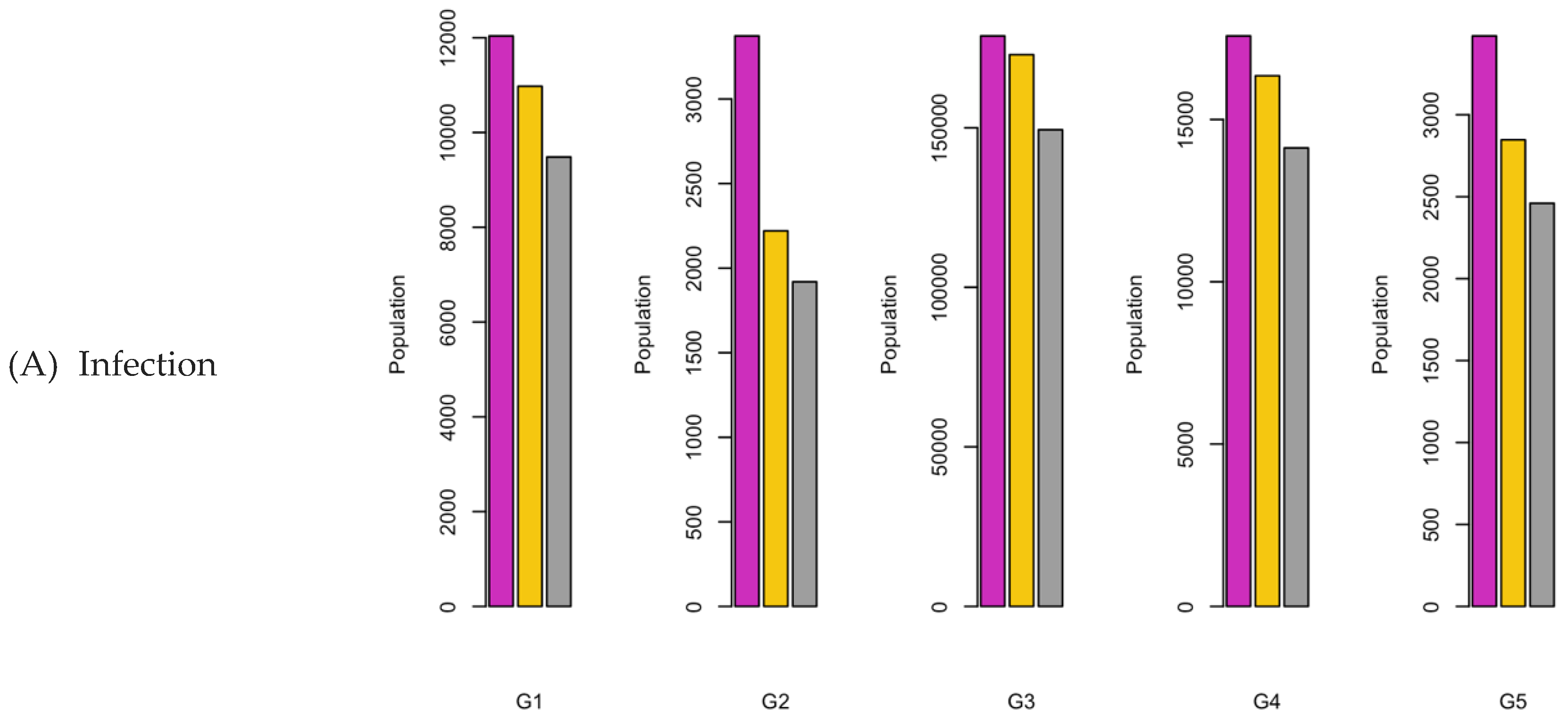
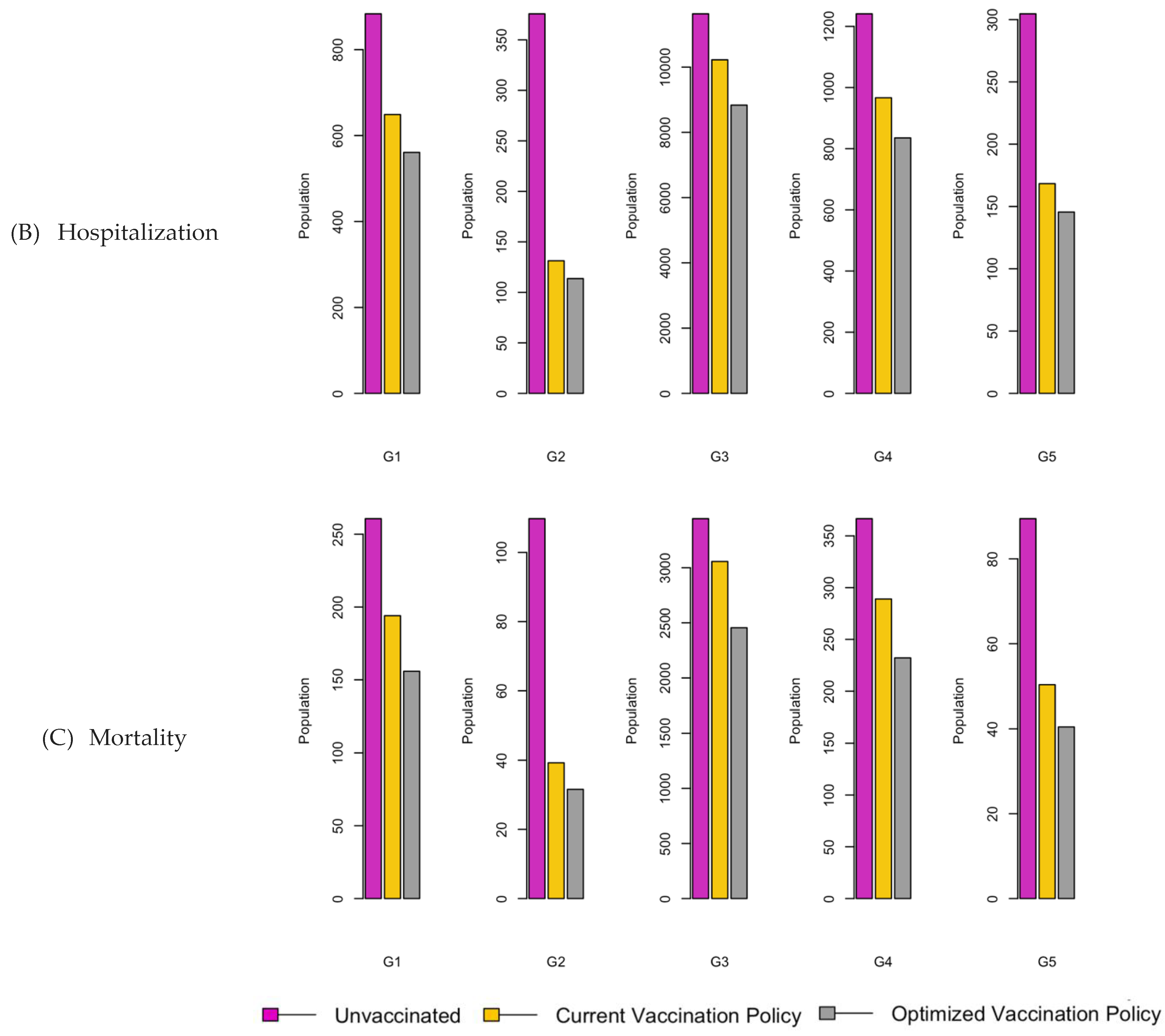
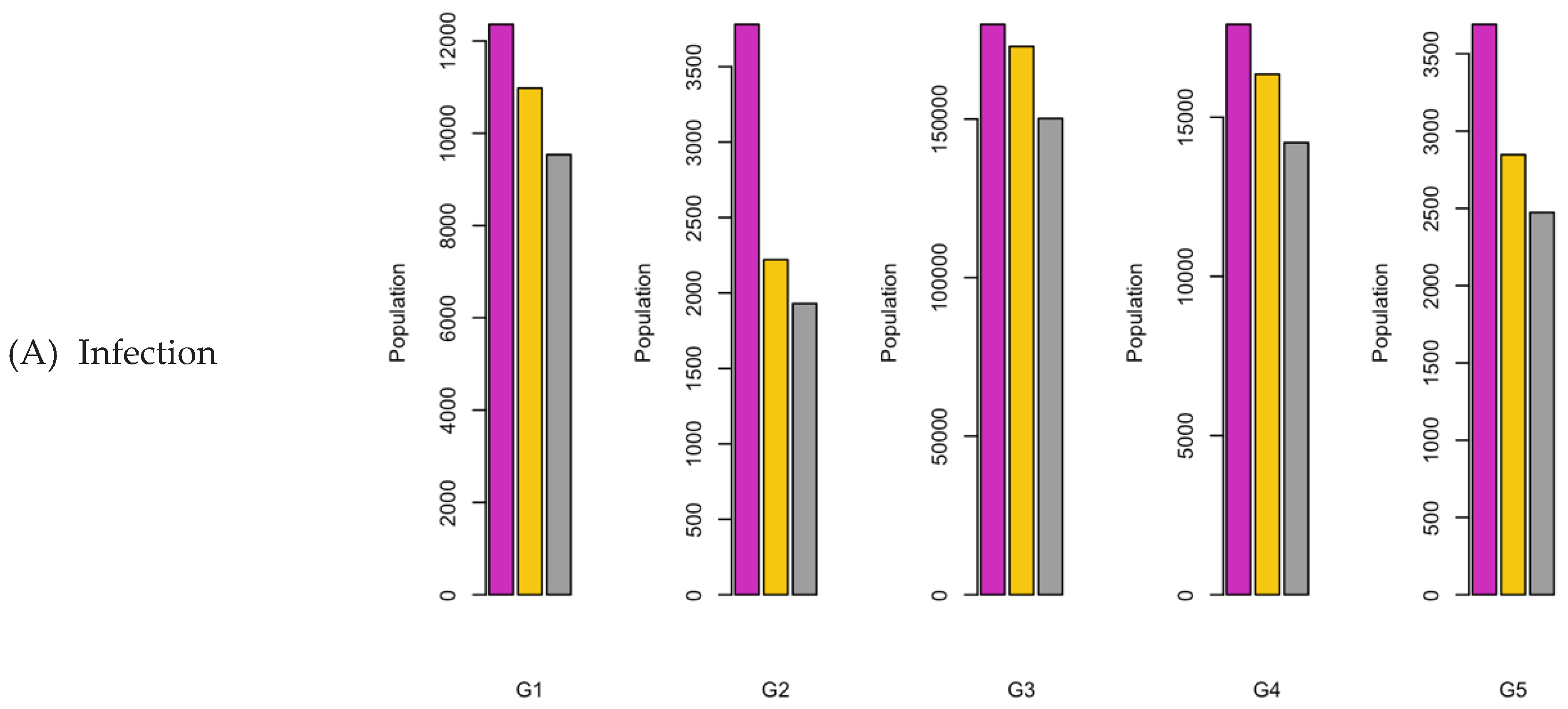
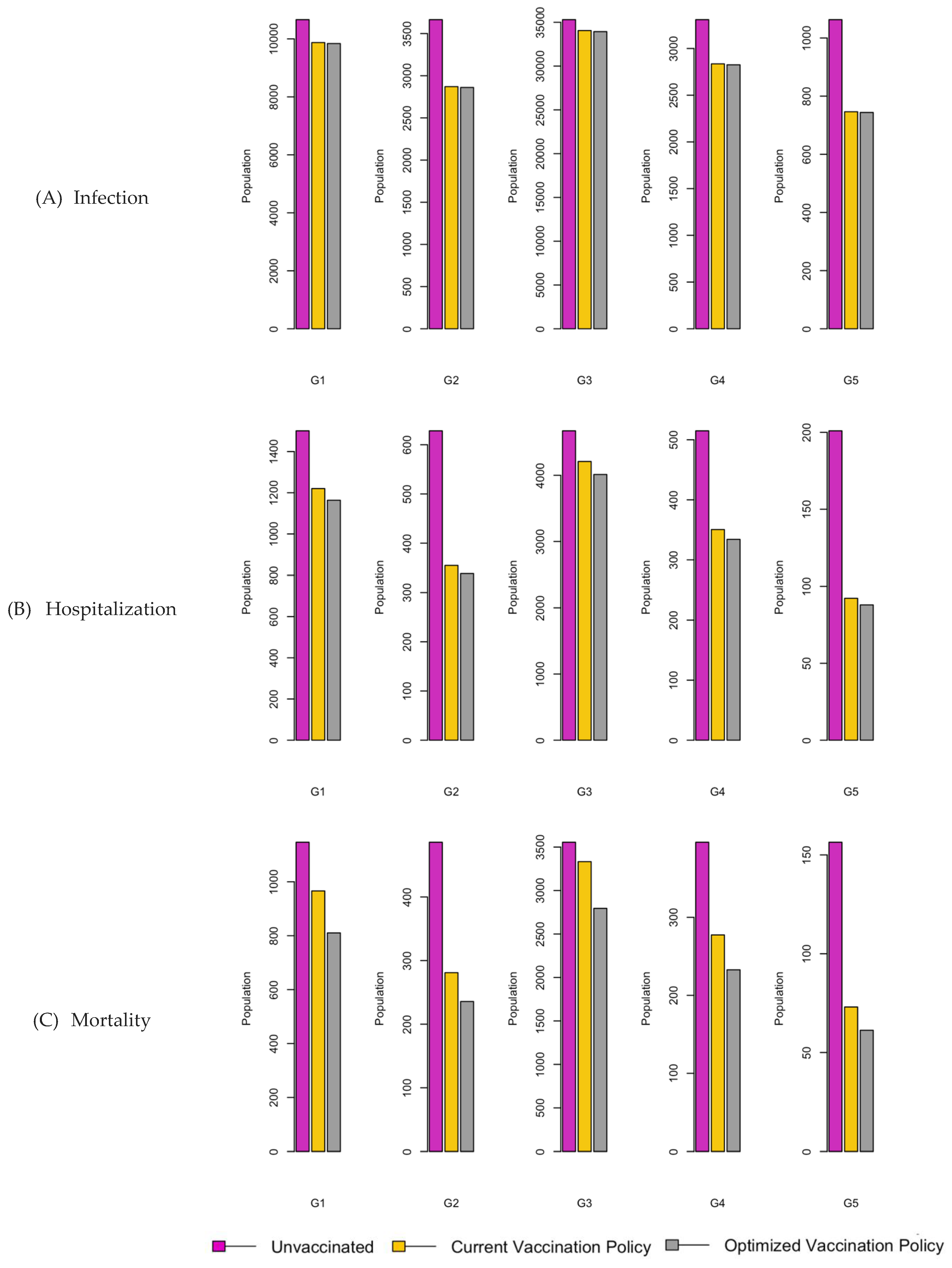
Figure 6.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 1.2.
Figure 6.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 1.2.
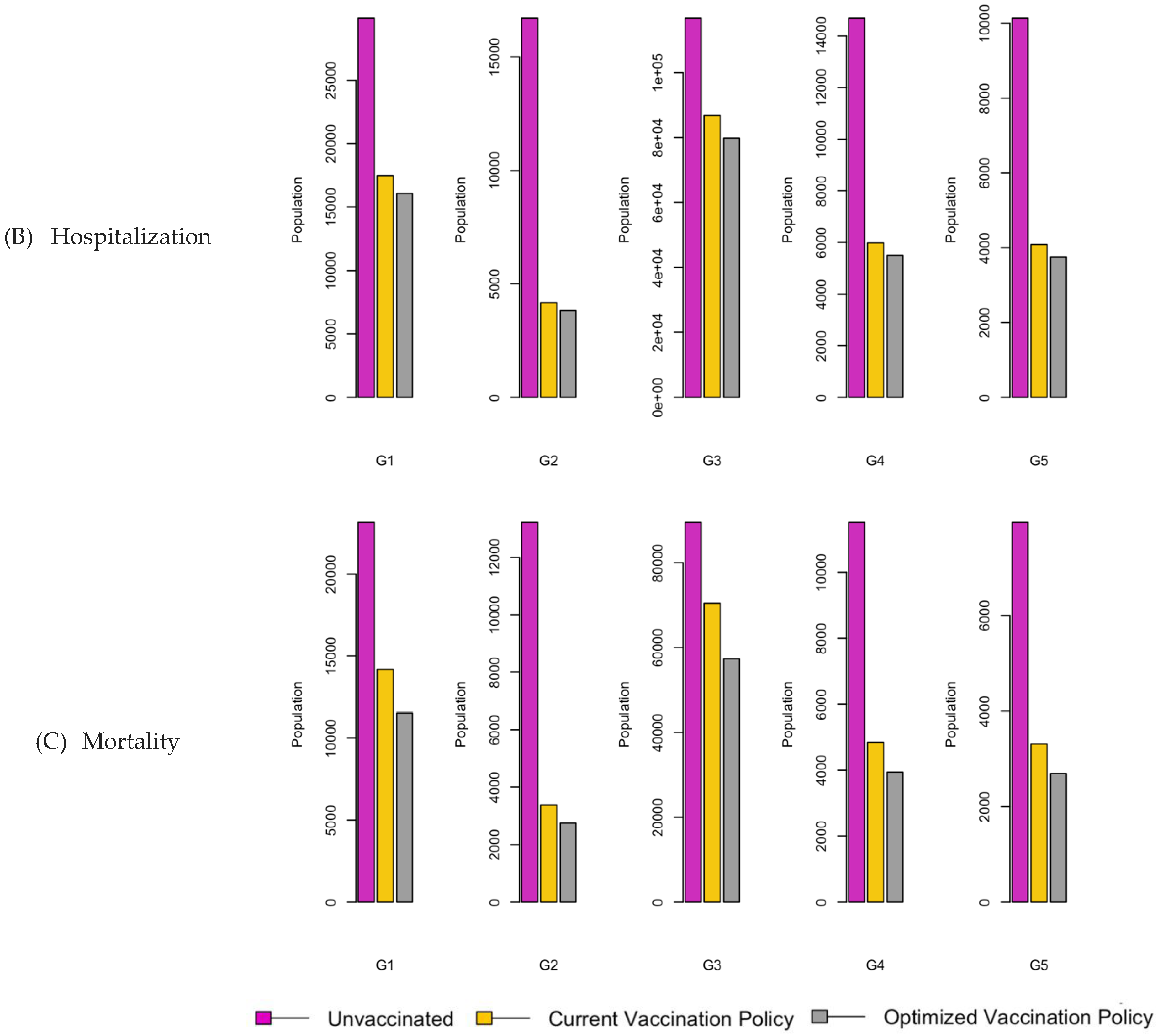
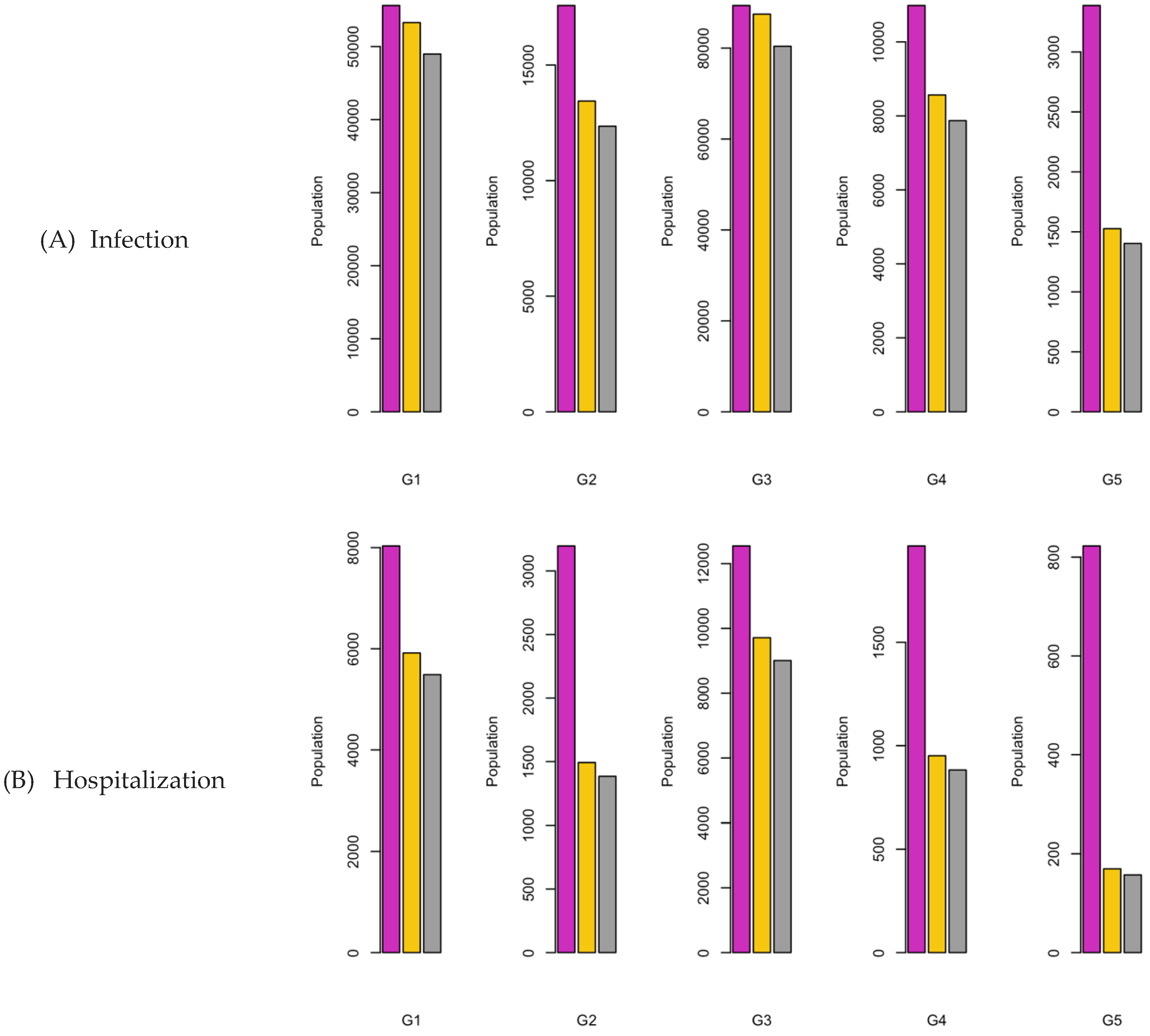
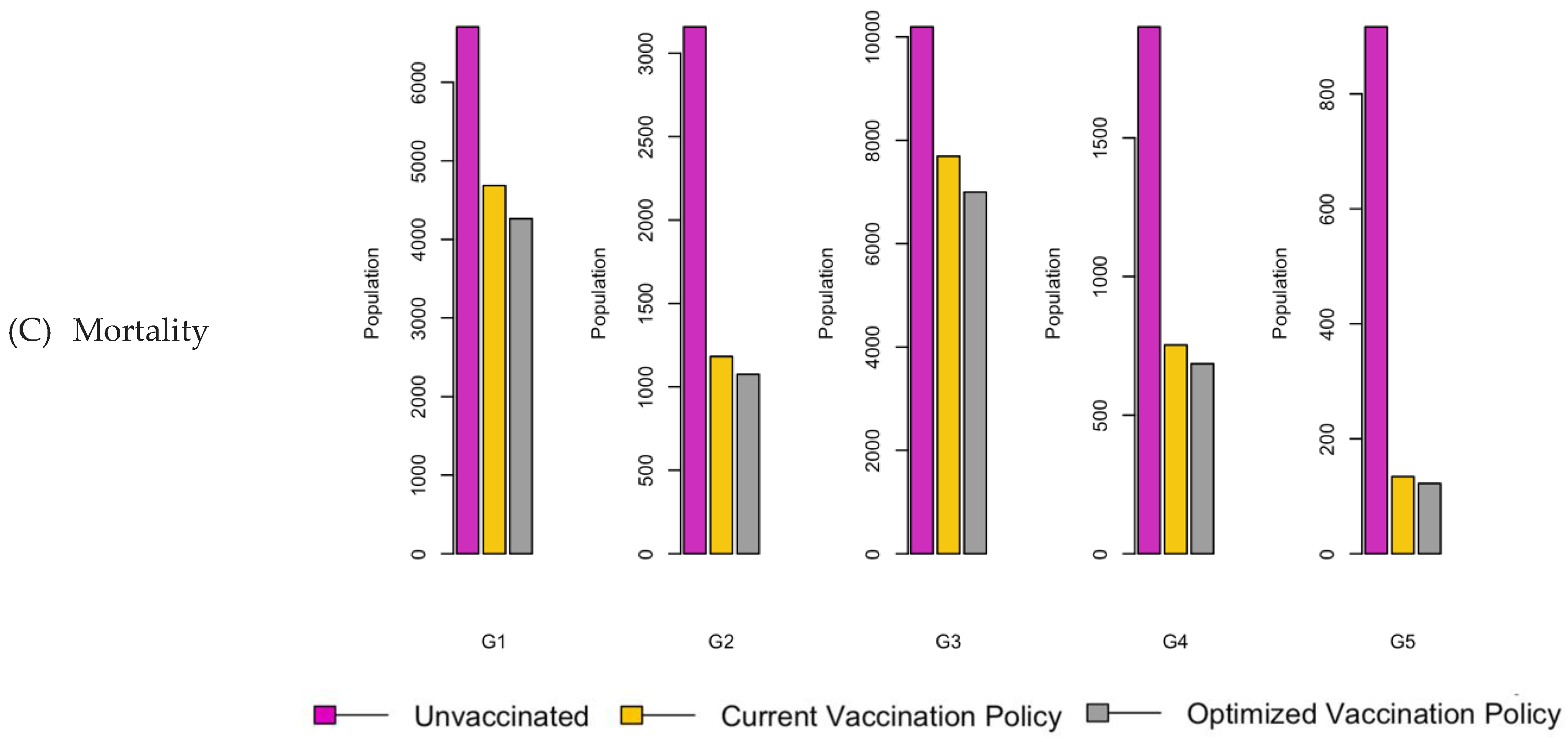
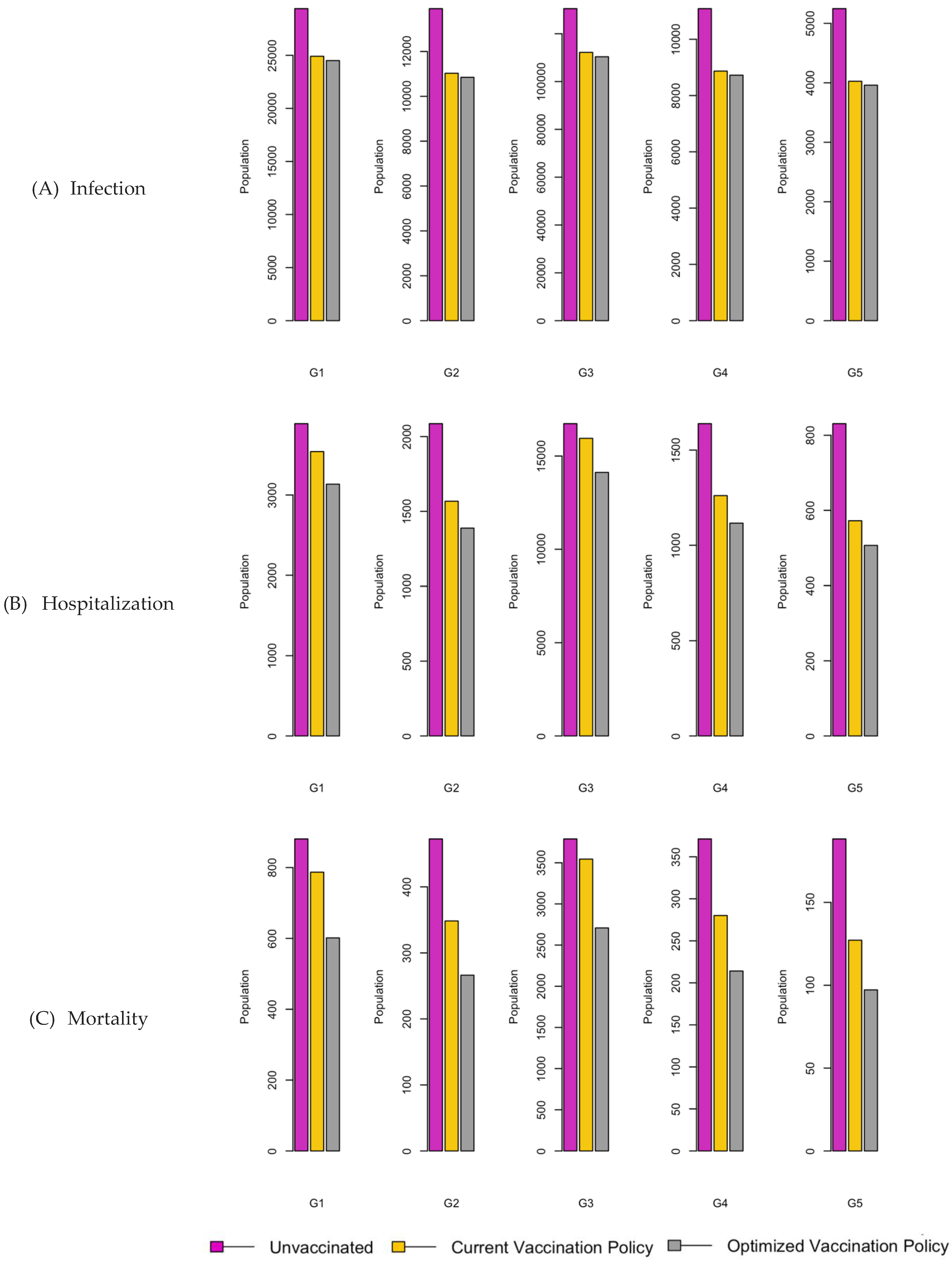
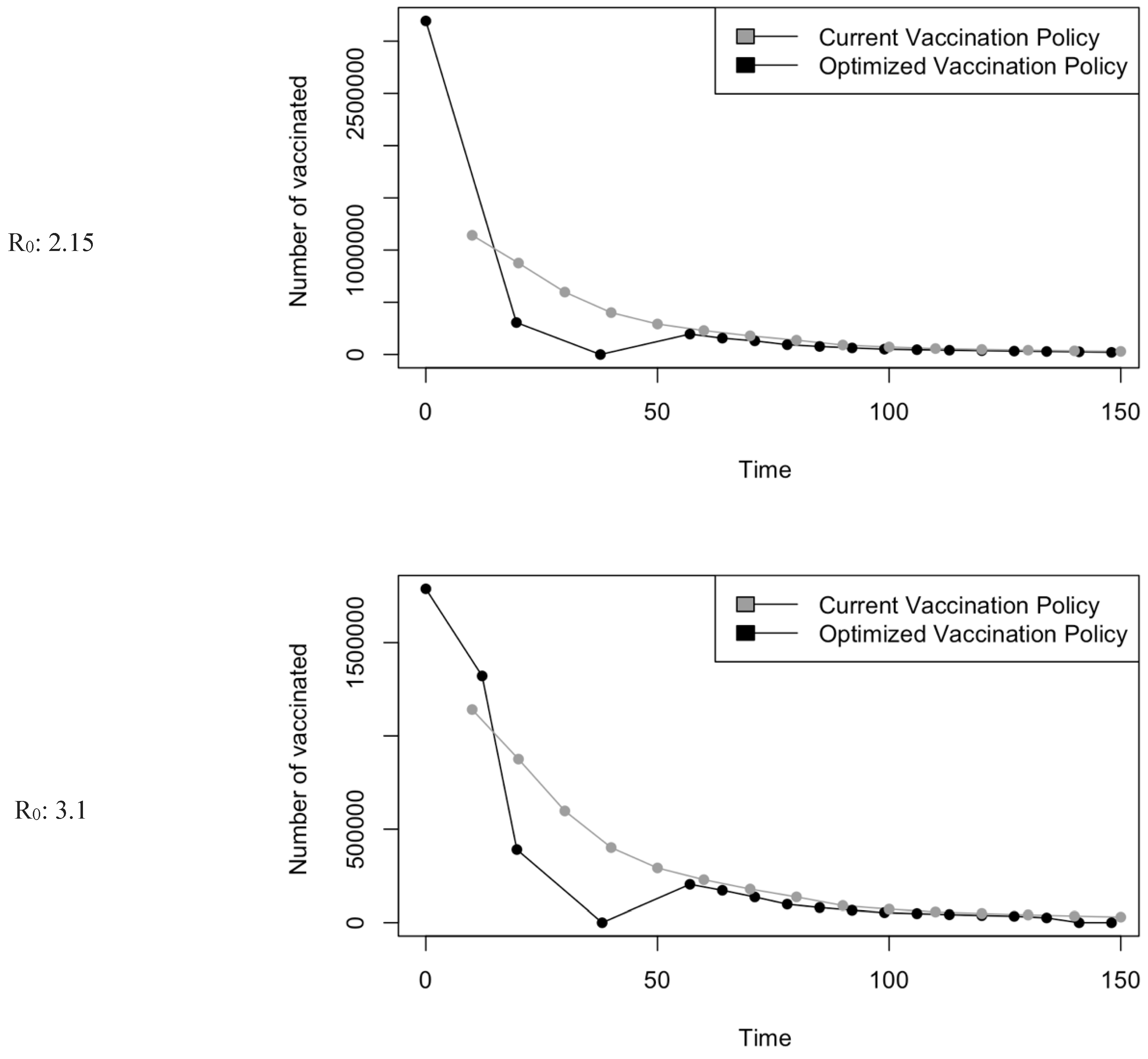
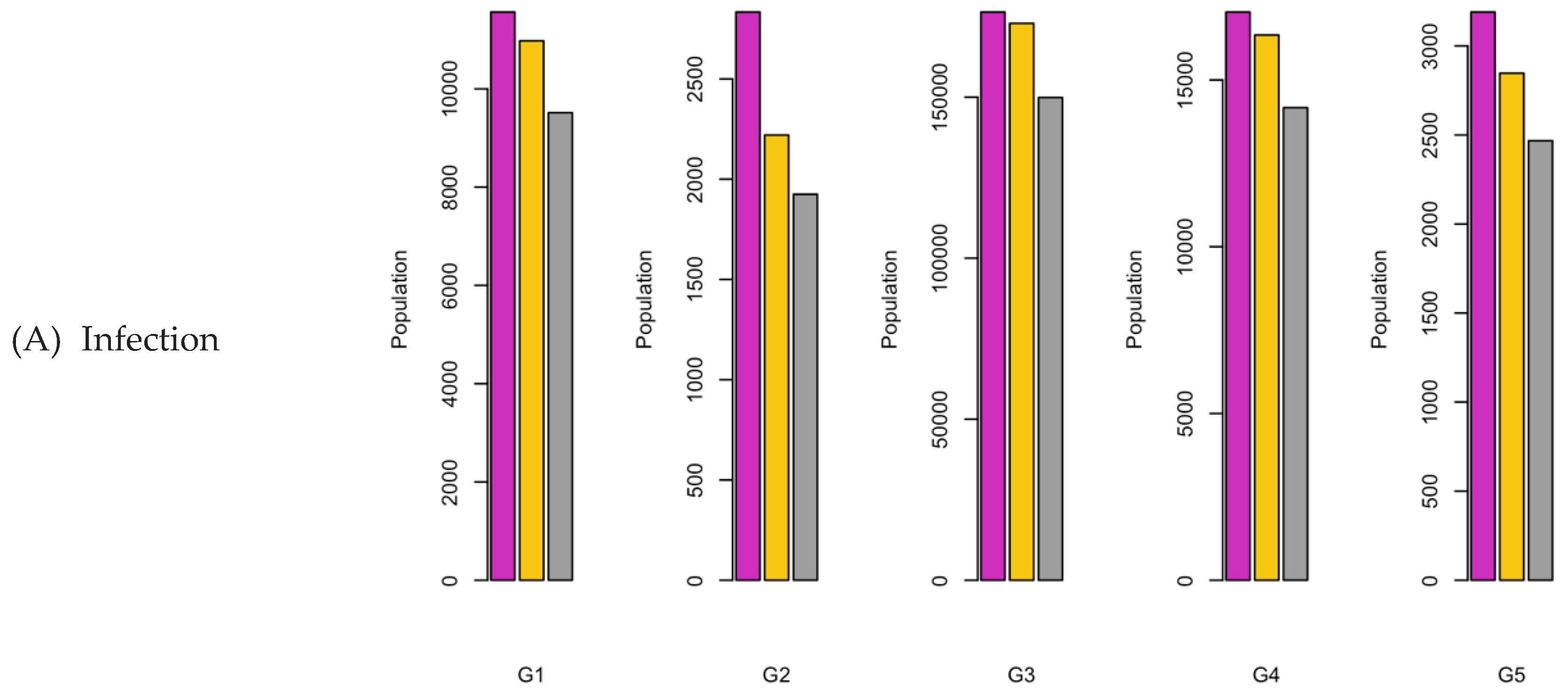
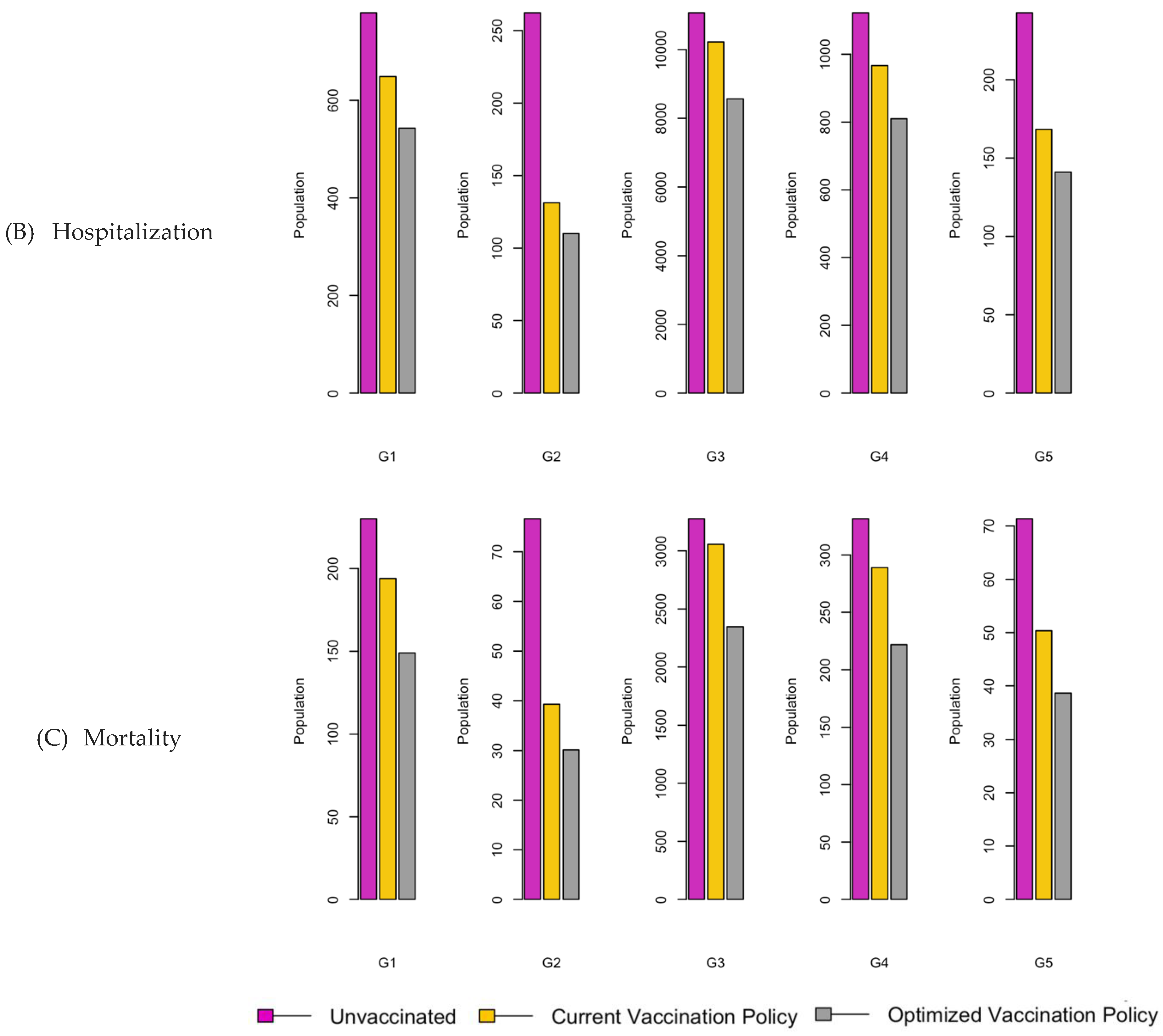
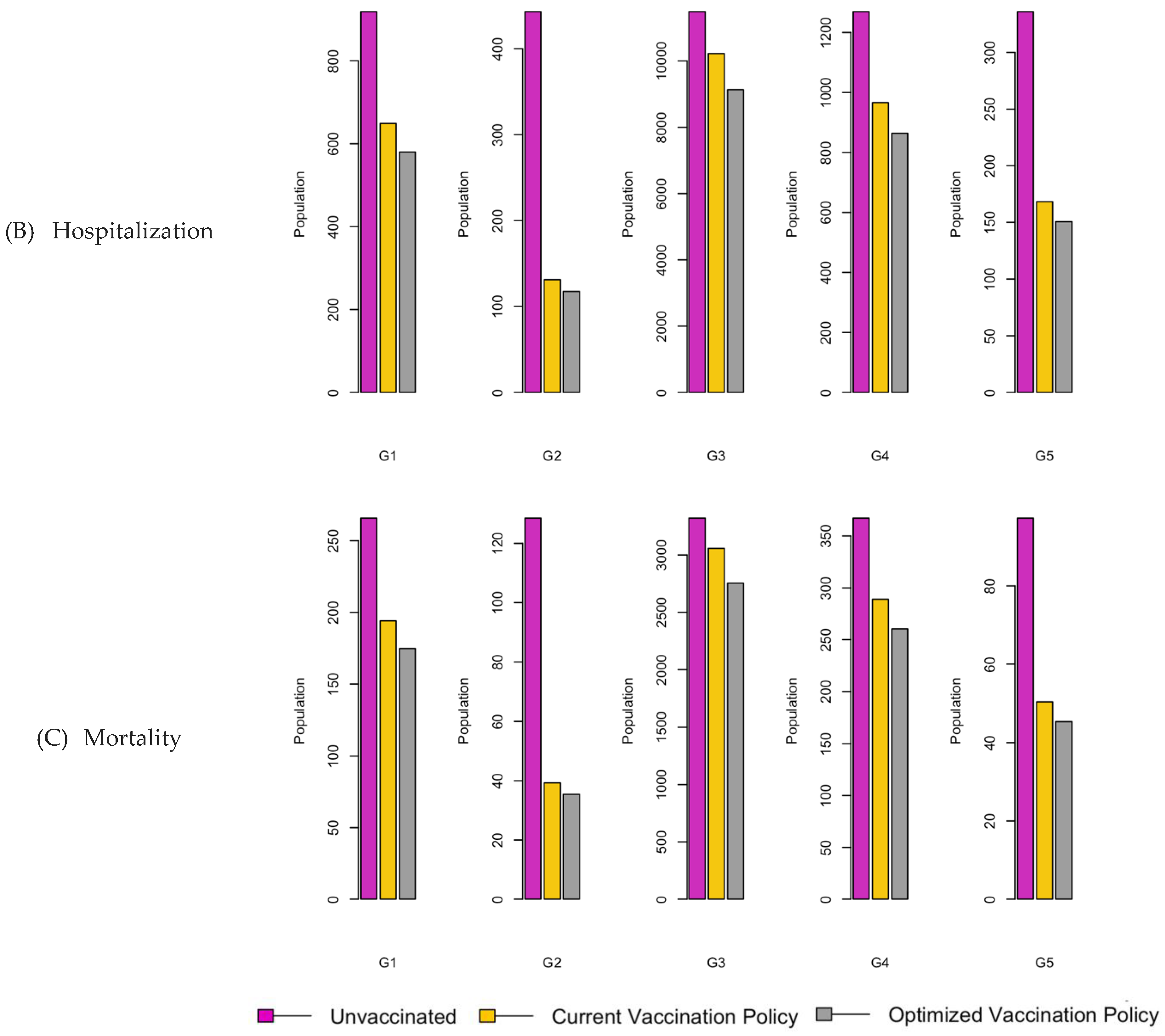
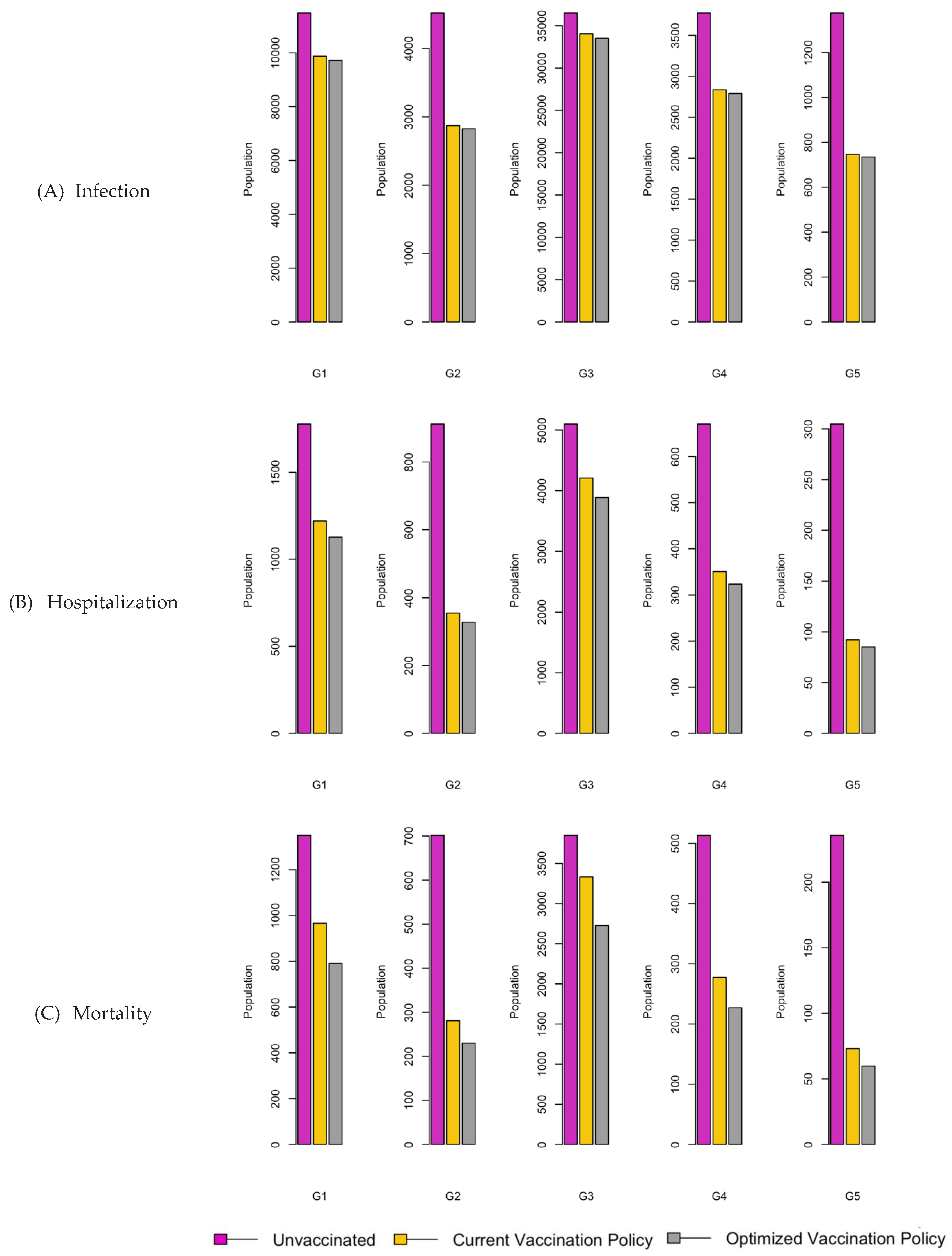
Figure 7.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 2.15.
Figure 7.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 2.15.
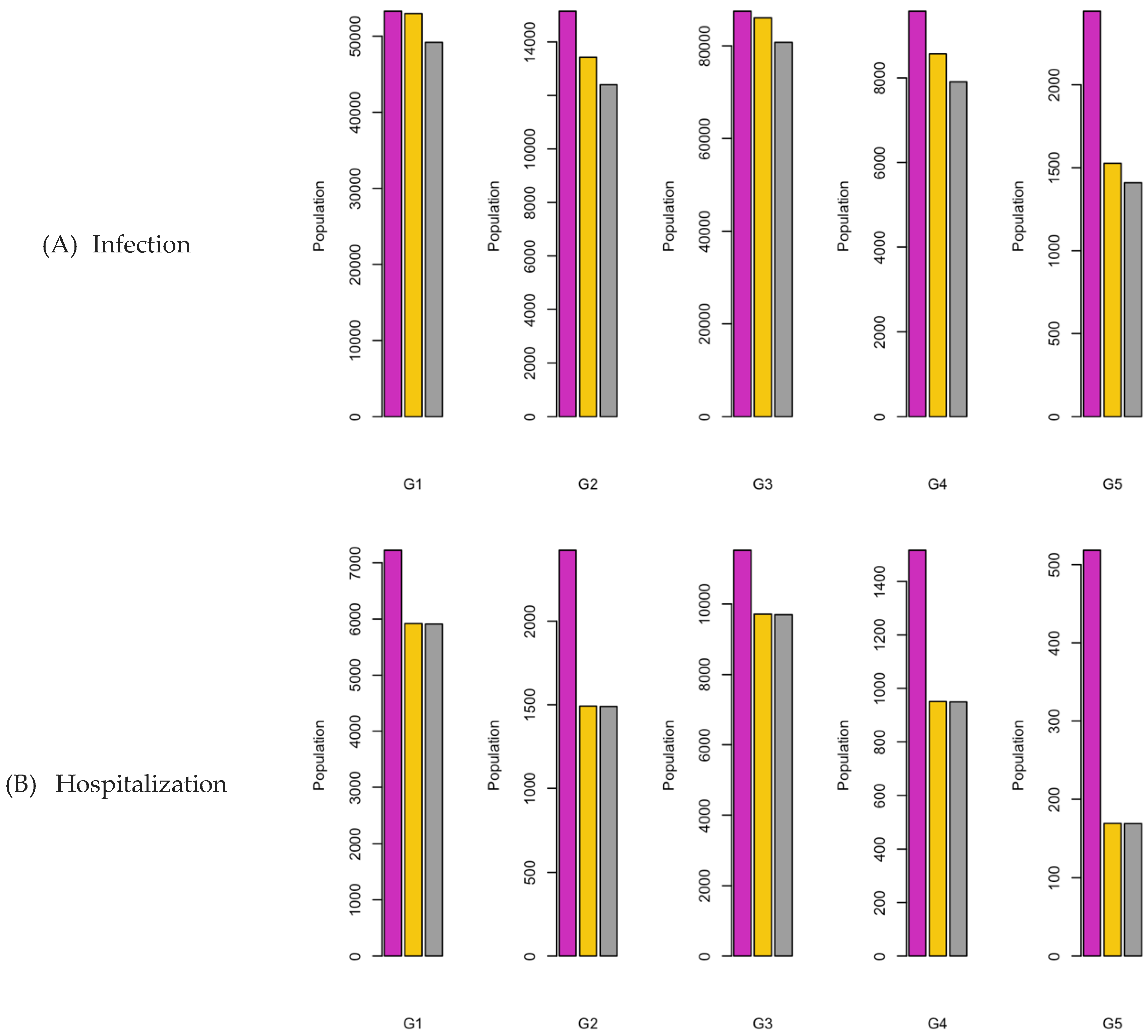
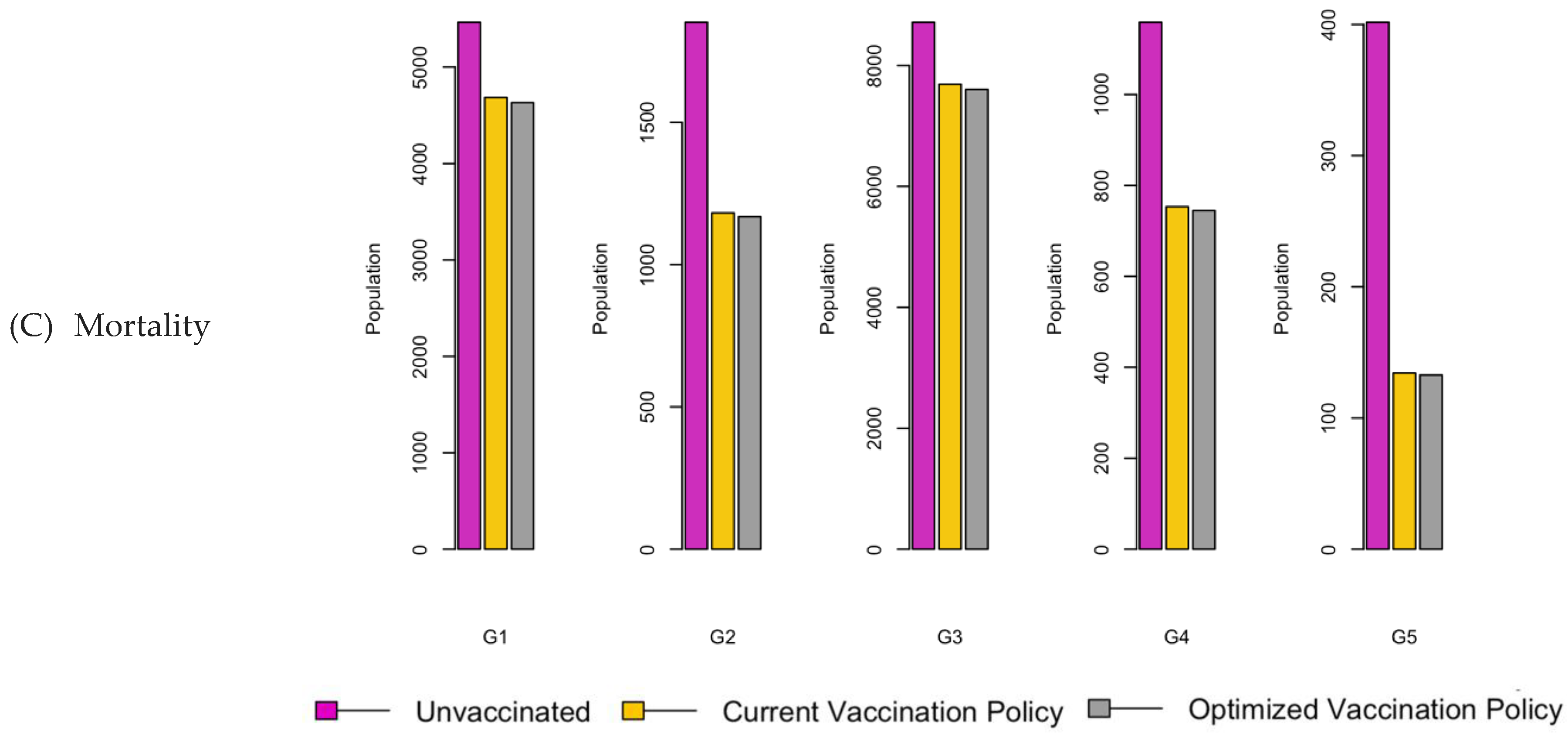
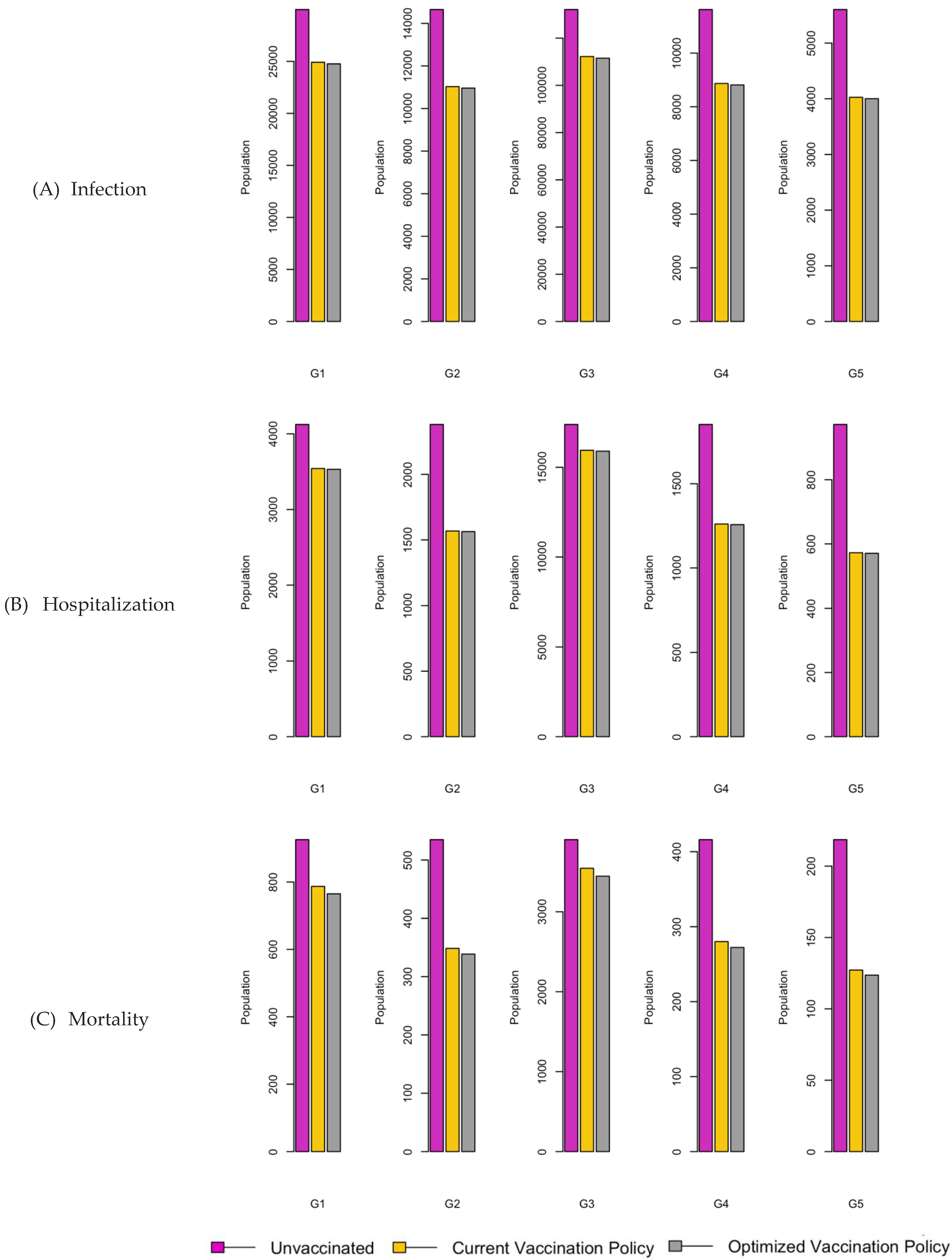
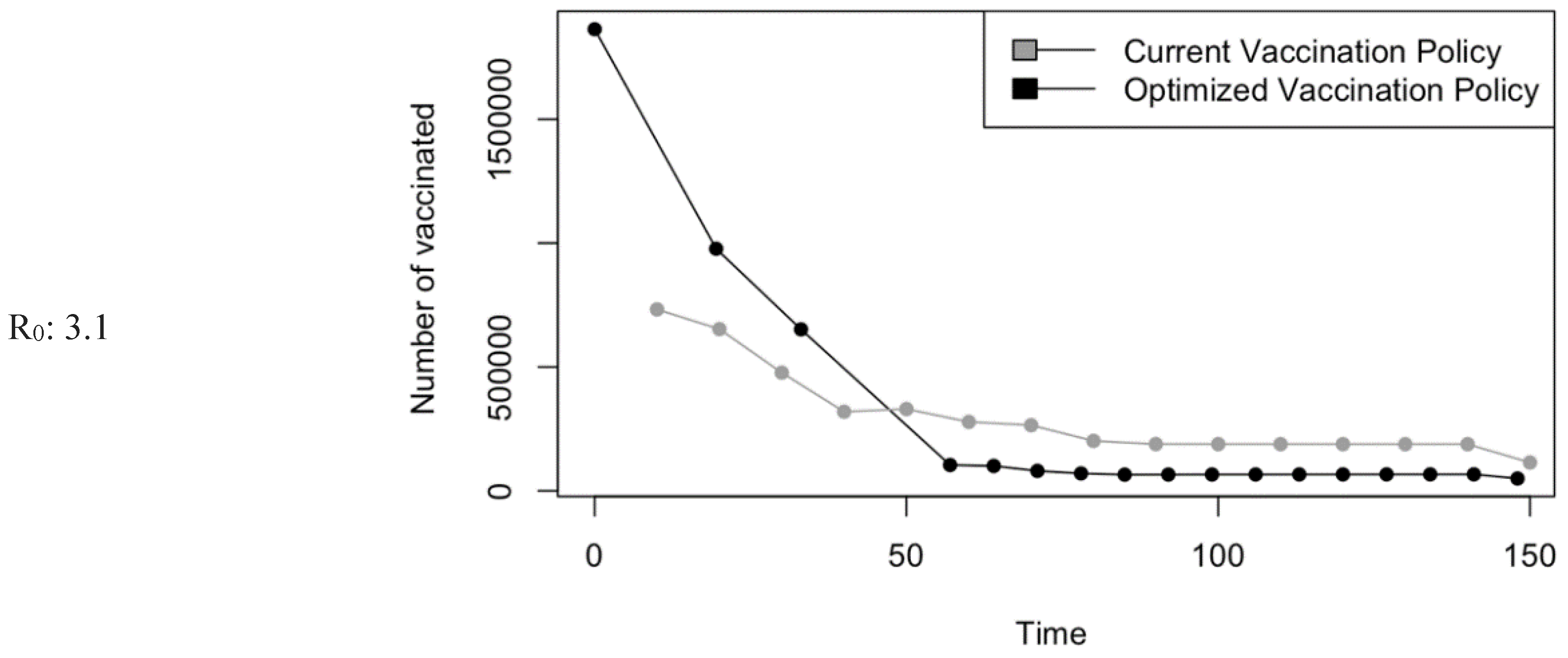
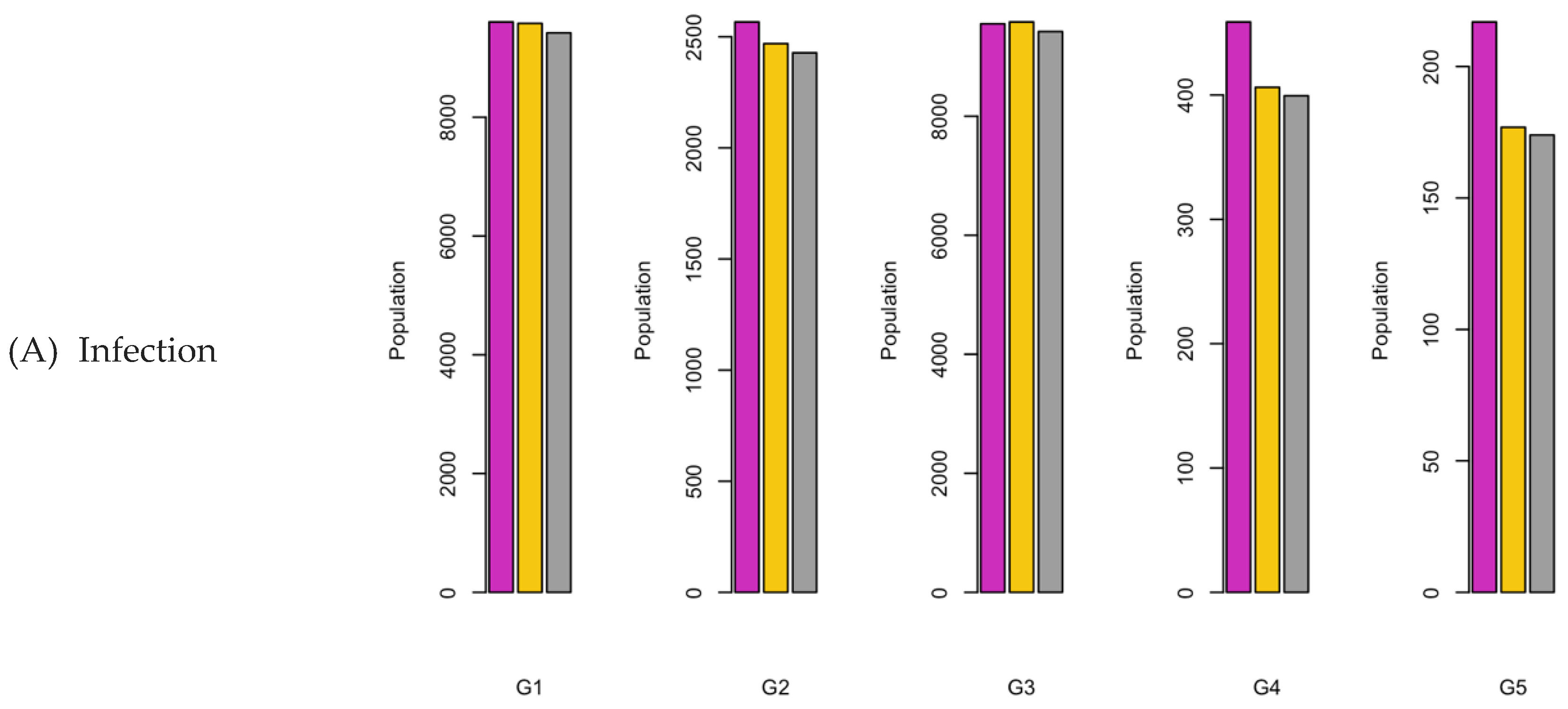
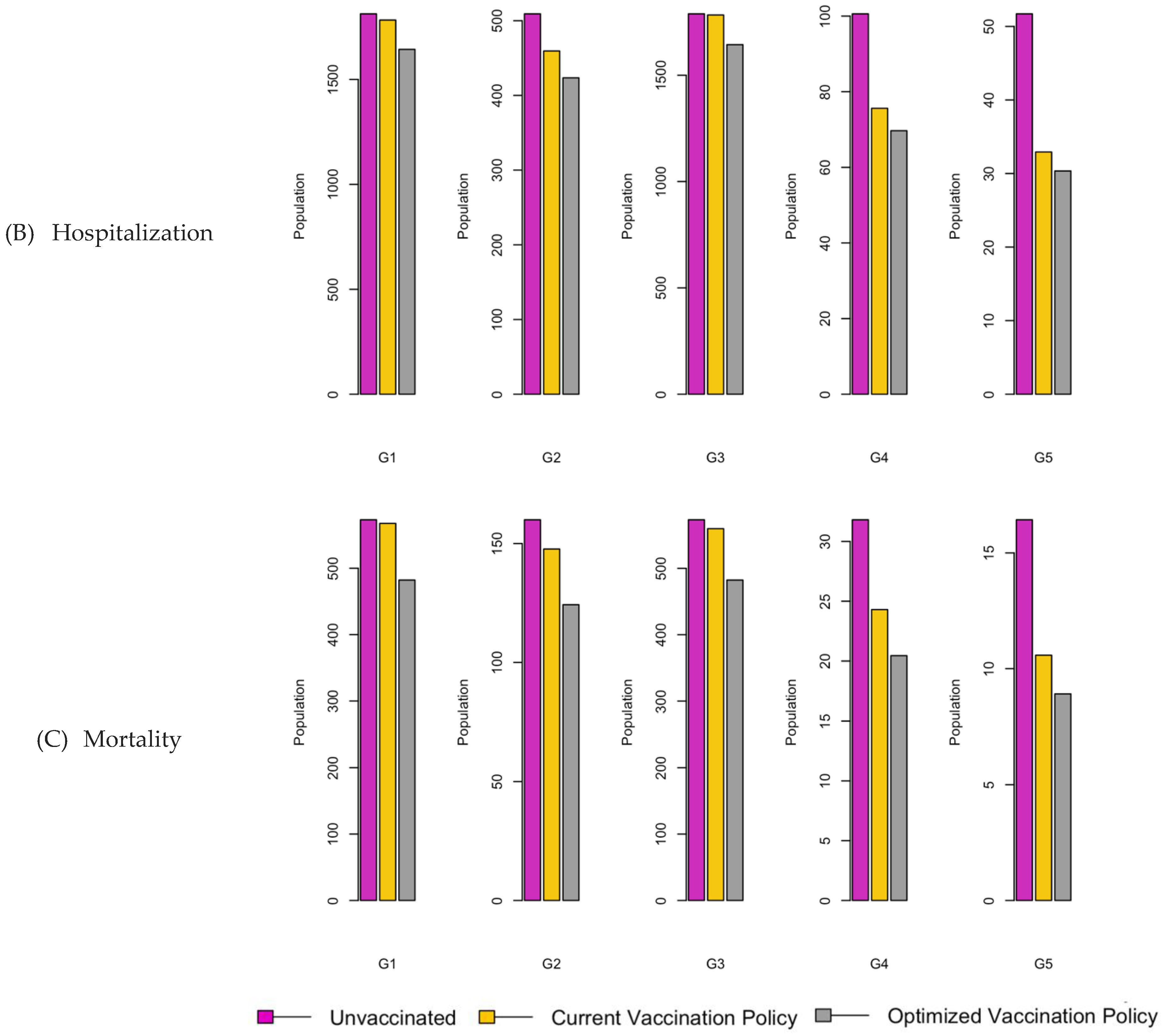
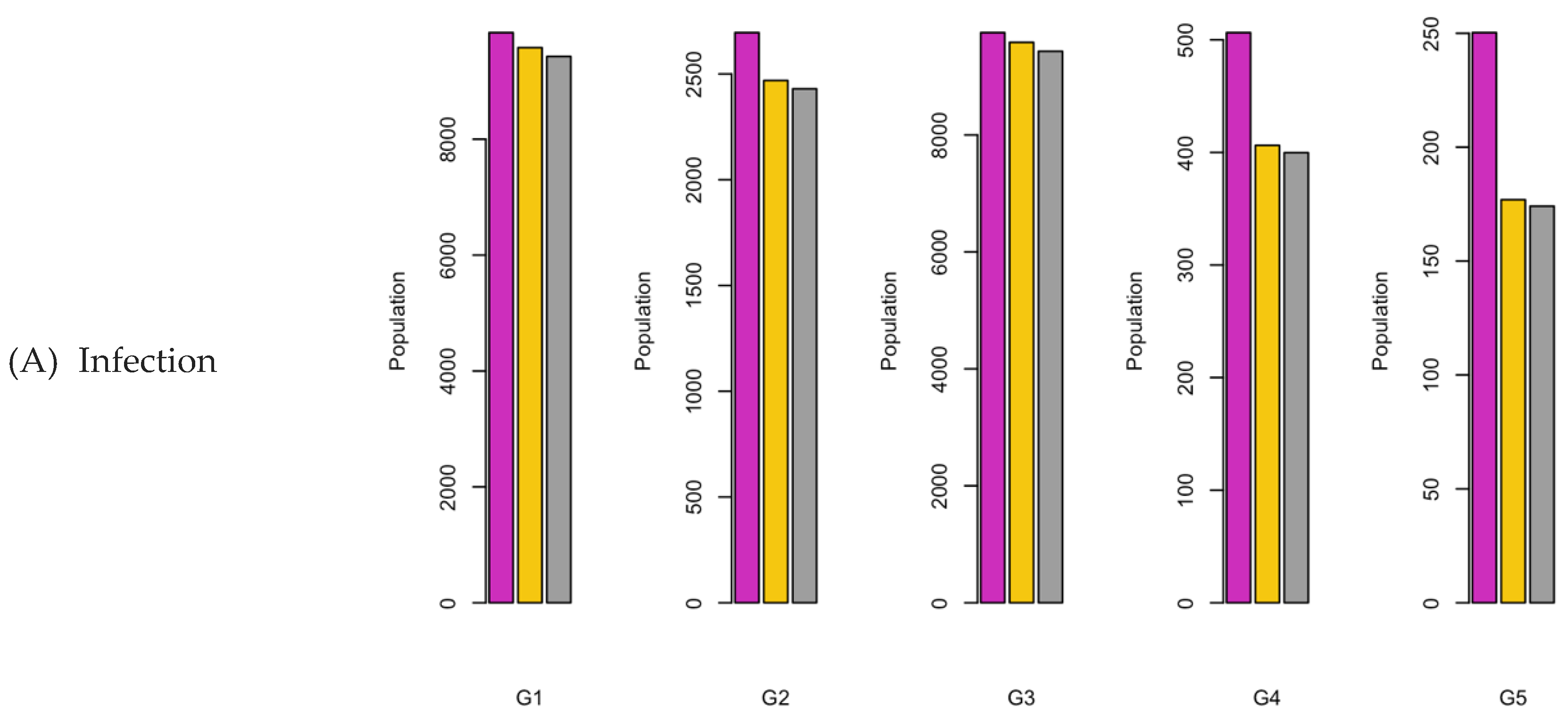
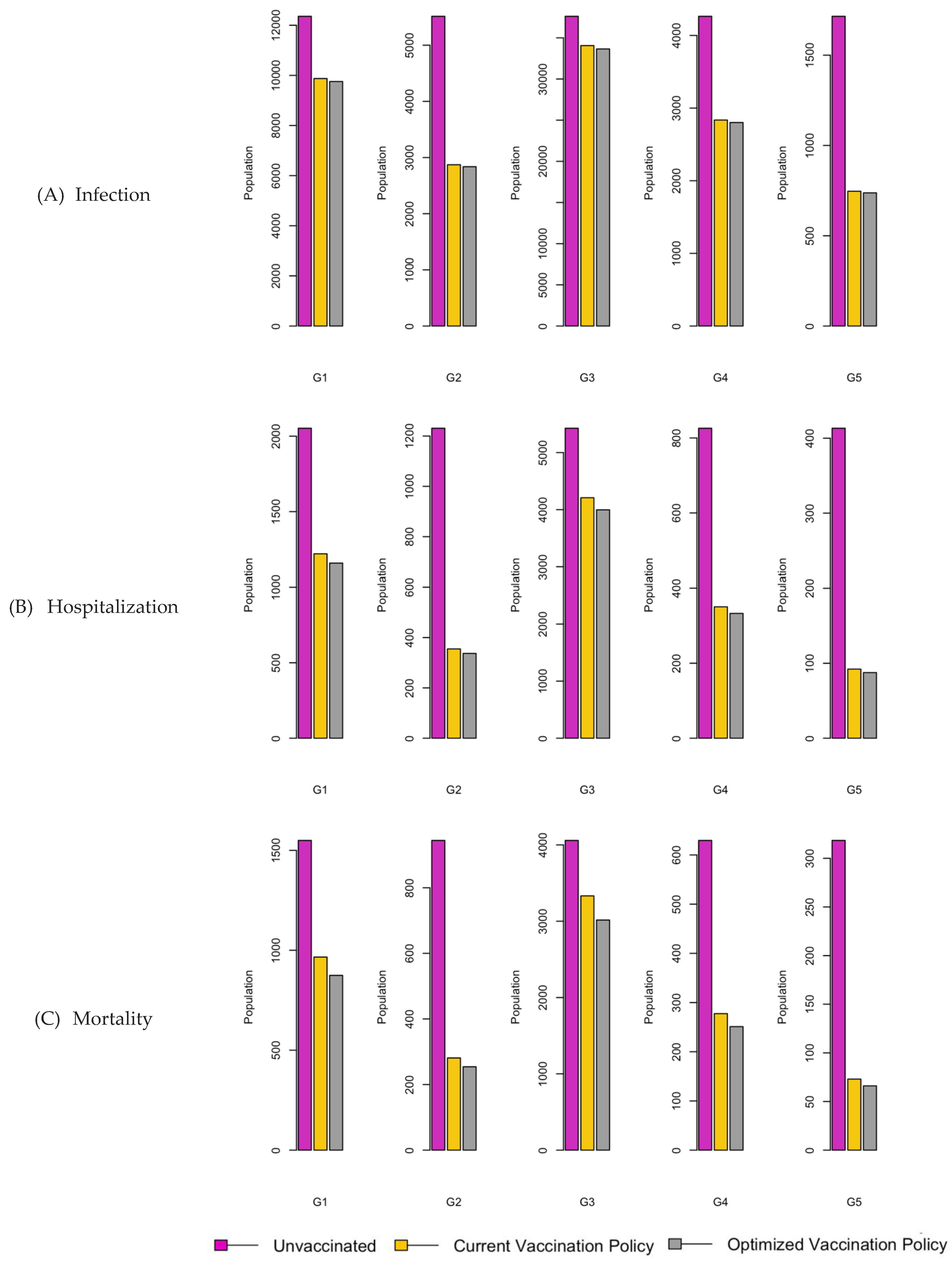
Figure 8.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 3.1.
Figure 8.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 3.1.
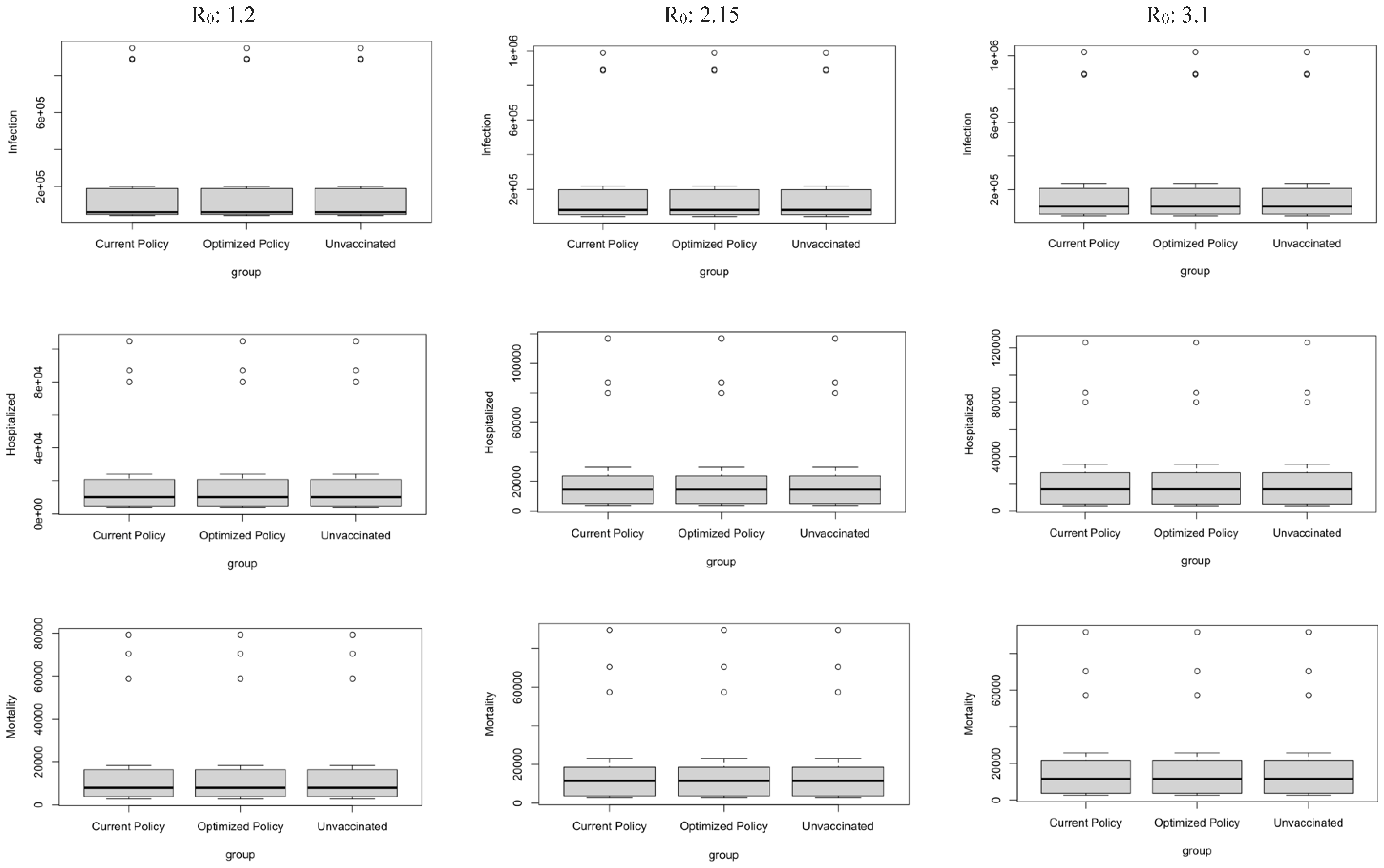
Figure 9.
Boxplot representing mean values of the three factors.
Figure 9.
Boxplot representing mean values of the three factors.
Figure 10.
Vaccination Strategy for the Case of Eastern region.
Figure 10.
Vaccination Strategy for the Case of Eastern region.
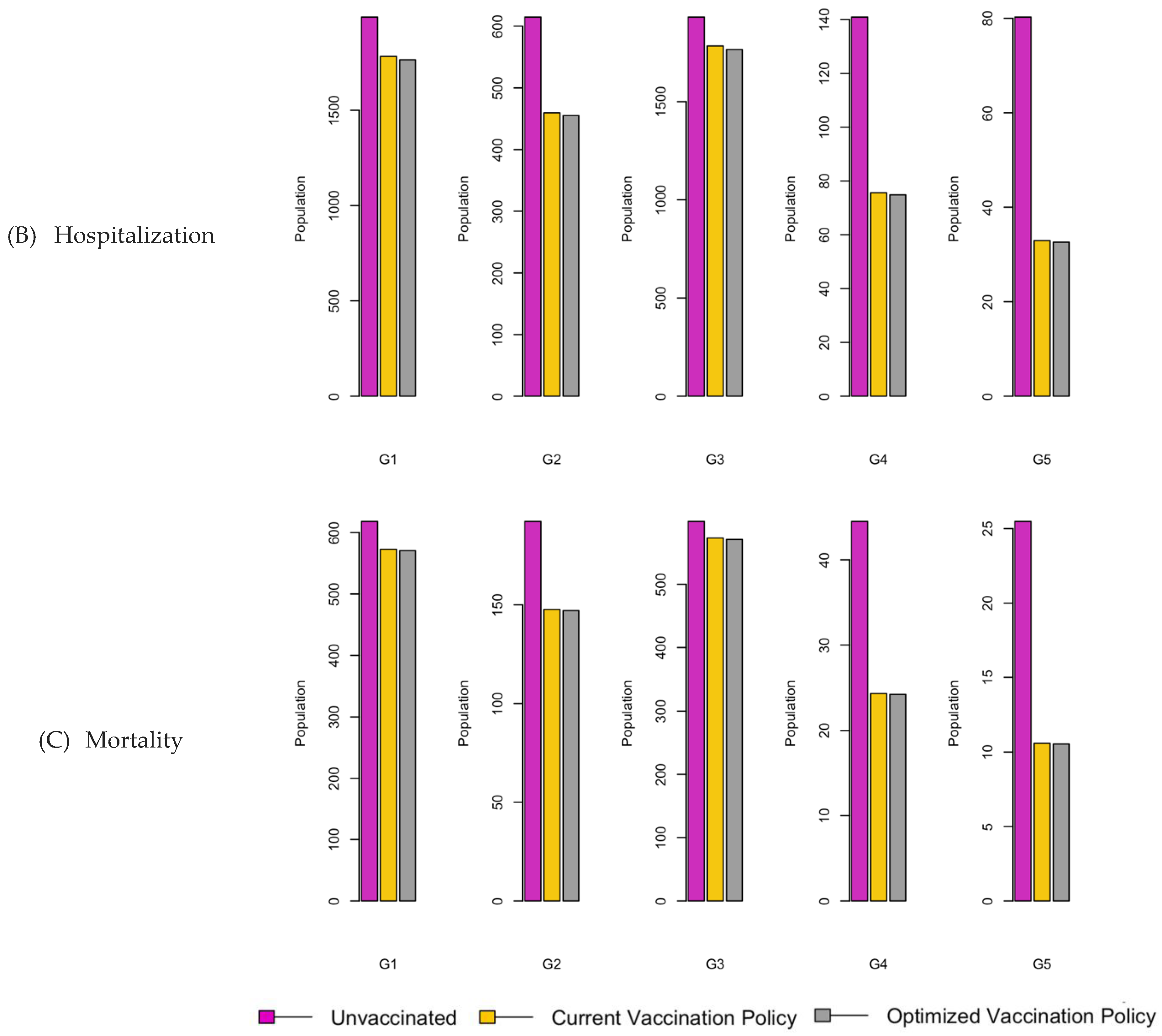
Figure 11.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 1.2.
Figure 11.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 1.2.
Figure 12.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 2.15.
Figure 12.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 2.15.
Figure 13.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 3.1.
Figure 13.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 3.1.
Figure 14.
Vaccination Strategy for the Case of Central region.
Figure 14.
Vaccination Strategy for the Case of Central region.
Figure 15.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 1.2.
Figure 15.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 1.2.
Figure 16.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 2.15.
Figure 16.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 2.15.
Figure 17.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 3.1.
Figure 17.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 3.1.
Figure 18.
Vaccination Strategy for the Case of Northern region.
Figure 18.
Vaccination Strategy for the Case of Northern region.
Figure 19.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 1.2.
Figure 19.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 1.2.
Figure 20.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 2.15.
Figure 20.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 2.15.
Figure 21.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 3.1.
Figure 21.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 3.1.
Figure 22.
Vaccination Strategy for the Case of Western region.
Figure 22.
Vaccination Strategy for the Case of Western region.
Figure 23.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 1.2.
Figure 23.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 1.2.
Figure 24.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 2.15.
Figure 24.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 2.15.
Figure 25.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 3.1.
Figure 25.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 3.1.
Figure 26.
Vaccination Strategy for the Case of Southern region.
Figure 26.
Vaccination Strategy for the Case of Southern region.
Figure 27.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 1.2.
Figure 27.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 1.2.
Figure 28.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 2.15.
Figure 28.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 2.15.
Figure 29.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 3.1.
Figure 29.
Bar charts showing the number of (A) Infection (B) Hospitalizations, and (C) Mortality over a given period for R0: 3.1.
Table 1.
Population characteristics of Saudi Arabia.
Table 1.
Population characteristics of Saudi Arabia.
| Region |
Children (G1) |
Youth (G2) |
Adults (G3) |
Middle-aged (G4) |
Seniors (G5) |
| Saudi |
7886890 |
2196700 |
19586914 |
1642871 |
861849 |
| East |
1213128 |
305980 |
3246567 |
252256 |
107323 |
| Center |
537799 |
622192 |
6330420 |
500358 |
227167 |
| North |
783017 |
201818 |
1446075 |
107843 |
63088 |
| West |
2404828 |
706681 |
6151106 |
581524 |
315307 |
| South |
1238127 |
360029 |
2412746 |
200890 |
148964 |
| West |
2404828 |
706681 |
6151106 |
581524 |
315307 |
Table 2.
Regional vaccine uptake by age groups.
Table 2.
Regional vaccine uptake by age groups.
| Region |
Age groups |
| 0-14 |
15-19 |
20-54 |
55-64 |
<65 |
| Saudi |
31.5% [21] |
31.5% [21] |
39.1% [23] |
31.5% [21] |
31.5% [21] |
| East |
22.9% [24] |
22.9% [24] |
16% [24] |
6.4% [24] |
6.4% [24] |
| Center |
18% [25] |
18% [25] |
28% [25] |
28% [25] |
28% [25] |
| North |
30.5% [26] |
30.5% [26] |
45% [27] |
45% [27] |
45% [27] |
| West |
48.8% [28] |
48.8% [28] |
52.2% [29] |
54.2% [58] |
54.2% [58] |
| South |
15.4% [22] |
15.4% [22] |
29.0% [22] |
2.5% [22] |
2.5% [22] |
Table 3.
Initial epidemic parameters categorized by age groups in various regions.
Table 3.
Initial epidemic parameters categorized by age groups in various regions.
| Region |
Age groups |
Infection rate |
Mortality |
Morbidity rate |
| Hospitalization rate |
Hospital stay |
| Saudi |
0-14 |
13.1% [14] |
19.6 % [14] |
7 [14] |
8.5% [14] |
| 15-19 |
11.2% [14] |
| 20-54 |
26.2% [14] |
| 55-64 |
21.5% [14] |
| <65 |
28.0% [14] |
| East |
0-14 |
27.94% [15] |
19.6 % [14] |
7 [14] |
8.5% [14] |
| 15-19 |
27.94% [15] |
| 20-54 |
17.14% [15] |
| 55-64 |
21.60% [15] |
| <65 |
9.05% [15] |
| Center |
0-14 |
31.1% [17] |
19.6 % [14] |
7 [16] |
2% [16] |
| 15-19 |
11.9% [17] |
| 20-54 |
11.9% [17] |
| 55-64 |
11.9% [17] |
| <65 |
11.9% [17] |
| North |
0-14 |
8.64% [18] |
27.8% [18] |
7 [18] |
3.7% [18] |
| 15-19 |
8.64% [18] |
| 20-54 |
4.68% [18] |
| 55-64 |
2.66% [18] |
| <65 |
1.98% [18] |
| West |
0-14 |
2.76% [19] |
7.6% [19] |
7 [14] |
1.5 [19] |
| 15-19 |
1.9% [19] |
| 20-54 |
17% [19] |
| 55-64 |
17% [19] |
| <65 |
5.46% [19] |
| South |
0-14 |
5.65% [20] |
19.6 % [14] |
7 [14] |
8.5% [14] |
| 15-19 |
5.65% [20] |
| 20-54 |
10% [20] |
| 55-64 |
10% [20] |
| <65 |
3.55% [20] |
Table 4.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 1.2.
Table 4.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 1.2.
| R0: 1.2 |
| |
Factors |
Age group |
#Infection (%) |
#Vaccine (%) |
#Hospitlized (%) |
#Death (%) |
| Scenarios |
|
| No vaccination |
G1 |
200020.33 (2.53%) |
0.0 (0%) |
24010.208 (0.31%) |
18304.891 (0.23%) |
| G2 |
60829.06 (2.77%) |
0.0 (0%) |
10134.604 (0.46%) |
7900.153 (0.36%) |
| G3 |
950114.20 (4.85%) |
0.0 (0%) |
104739.972 (0.54%) |
79281.039 (0.41%) |
| G4 |
74916.58 (4.56%) |
0.0 (0%) |
10394.412 (0.63%) |
8011.309 (0.49%) |
| G5 |
51319.10 (5.96%) |
0.0 (0%) |
7147.042 (0.83%) |
5509.852 (0.64%) |
| Total |
1337199 (4.16%) |
0.0 (0%) |
156426.2 (0.49%) |
119007.2 (0.37%) |
| Current Vaccination Policy |
G1 |
179663.01 (2.28%) |
963817.5 (21.4%) |
17491.014 (0.22%) |
14181.890 (0.18%) |
| G2 |
42782.94 (1.95%) |
268125.3 (5.96%) |
4165.121 (0.19%) |
3377.123 (0.15%) |
| G3 |
892377.70 (4.56%) |
2962333.5 (65.8%) |
86876.928 (0.44%) |
70440.685 (0.36%) |
| G4 |
61421.92 (3.74%) |
200499.7 (4.46%) |
5979.700 (0.36%) |
4848.401 (0.3%) |
| G5 |
41963.40 (4.87%) |
105173.3 (2.34%) |
4085.326 (0.47%) |
3312.424 (0.39%) |
| Total |
1218209 (3.79%) |
4499949 (99.99%) |
118598.1 (0.37%) |
96160.52 (0.3%) |
| Optimized Vaccination Policy |
G1 |
178506.65 (2.26%) |
1440239 (23.01%) |
16107.914 (0.2%) |
11852.206 (0.15%) |
| G2 |
42507.58 (1.94%) |
318928 (7.09%) |
3835.764 (0.18%) |
2822.357 (0.13%) |
| G3 |
886633.62 (4.53%) |
2323353 (51.63%) |
80006.993 (0.41%) |
58869.127 (0.3%) |
| G4 |
61026.58 (3.72%) |
312000 (6.93%) |
5506.852 (0.34%) |
4051.941 (0.25%) |
| G5 |
41693.30 (4.84%) |
105435 (2.34%) |
3762.275 (0.44%) |
2768.281 (0.32%) |
| Total |
1210368 (3.77%) |
4499955 (99.99%) |
109219.8 (0.34%) |
80363.91 (0.25%) |
Table 5.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 2.15.
Table 5.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 2.15.
| R0: 2.15 |
| |
Factors |
Age group |
#Infection (%) |
#Vaccine (%) |
#Hospitlized (%) |
#Death (%) |
| Scenarios |
|
| No vaccination |
G1 |
218029.46 (2.76%) |
0.0 (0%) |
29884.24 (0.38%) |
23139.691 (0.29%) |
| G2 |
80178.65 (3.65%) |
0.0 (0%) |
16708.75 (0.76%) |
13214.970 (0.6%) |
| G3 |
989569.50 (5.05%) |
0.0 (0%) |
116740.76 (0.6%) |
89484.770 (0.46%) |
| G4 |
87702.74 (5.34%) |
0.0 (0%) |
14687.06 (0.89%) |
11513.624 (0.7%) |
| G5 |
60225.81 (6.99%) |
0.0 (0%) |
10138.49 (1.18%) |
7949.642 (0.92%) |
| Total |
1435706 (4.46%) |
0.0 (0%) |
188159.3 (0.58%) |
145302.7 (0.45%) |
| Current Vaccination Policy |
G1 |
179663.67 (2.28%) |
963817.5 (21.42%) |
17491.052 (0.22%) |
14181.904 (0.18%) |
| G2 |
42783.12 (1.95%) |
268125.3 (5.96%) |
4165.138 (0.19%) |
3377.132 (0.15%) |
| G3 |
892380.64 (4.56%) |
2962333.5 (65.83%) |
86876.995(0.44%) |
70440.651 (0.36%) |
| G4 |
61422.13 (3.74%) |
200499.7 (4.46%) |
5979.708 (0.36%) |
4848.401 (0.3%) |
| G5 |
41963.55 (4.87%) |
105173.3 (2.34%) |
4085.332 (0.47%) |
3312.424 (0.38%) |
| Total |
1218213 (3.79%) |
4499949 (99.99%) |
118598.2 (0.37%) |
96160.51 (0.3%) |
| Optimized Vaccination Policy |
G1 |
178482.96 (2.26%) |
720647.9 (16.02%) |
16071.225 (0.2%) |
11537.265 (0.15%) |
| G2 |
42502.16 (1.93%) |
374838.1 (8.33%) |
3827.098 (0.17%) |
2747.417 (0.13%) |
| G3 |
886516.55 (4.53%) |
2944185 (65.43%) |
79824.968 (0.41%) |
57305.009 (0.29%) |
| G4 |
61018.55(3.71%) |
318097.6 (7.07%) |
5494.331 (0.33%) |
3944.290 (0.24%) |
| G5 |
41687.84 (4.84%) |
142186.5 (3.16%) |
3753.728 (0.44%) |
2694.740 (0.31%) |
| Total |
1210208 (3.76%) |
4499955 (99.99%) |
108971.4 (0.34%) |
78228.72 (0.24%) |
Table 6.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 3.1.
Table 6.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 3.1.
| R0: 3.1 |
| |
Factors |
Age group |
#Infection (%) |
#Vaccine (%) |
#Hospitlized (%) |
#Death (%) |
| Scenarios |
|
| No vaccination |
G1 |
234347.40 (2.97%) |
0.0 (0%) |
34327.51 (0.44%) |
25876.875 (0.33%) |
| G2 |
98965.42 (4.51%) |
0.0 (0%) |
22251.18 (1.01%) |
17224.329 (0.78%) |
| G3 |
1020792.15 (5.21%) |
0.0 (0%) |
123787.03 (0.63%) |
91813.560 (0.47%) |
| G4 |
99308.18 (4.06%) |
0.0 (0%) |
17976.81 (1.09%) |
13745.990 (0.84%) |
| G5 |
68334.11 (7.93%) |
0.0 (0%) |
12440.87 (1.44%) |
9516.397 (1.1%) |
| Total |
1521747 (4.73%) |
0.0 (0%) |
210783.4 (0.66%) |
158177.2 (0.49%) |
| Current Vaccination Policy |
G1 |
179661.18 (2.28%) |
963817.5 (21.42%) |
17491.024 (0.22%) |
14181.958 (0.18%) |
| G2 |
42782.55 (1.95%) |
268125.3 (5.96%) |
4165.139 (0.19%) |
3377.151 (0.15%) |
| G3 |
892367.94 (4.56%) |
2962333.5 (65.83%) |
86876.734 (0.44%) |
70440.818 (0.36%) |
| G4 |
61421.27 (3.74%) |
200499.7 (4.46%) |
5979.693 (0.36%) |
4848.416 (0.3%) |
| G5 |
41962.96 (4.87%) |
105173.3 (2.34%) |
4085.323 (0.47%) |
3312.435 (0.38%) |
| Total |
1218196 (3.79%) |
4499949 (99.99%) |
118597.9 (0.37%) |
96160.78 (0.3%) |
| Optimized Vaccination Policy |
G1 |
178481.68 (2.26%) |
1153255 (25.63%) |
16071.254 (0.2%) |
11543.032 (0.15%) |
| G2 |
42501.90 (1.93%) |
415796.9 (9.24%) |
3827.118 (0.17%) |
2748.801 (0.13%) |
| G3 |
886510 (4.53%) |
2475082 (55%) |
79825.041 (0.41%) |
57333.597 (0.29%) |
| G4 |
61018.14 (3.71%) |
359804 (8%) |
5494.349 (0.33%) |
3946.268 (0.24%) |
| G5 |
41687.49 (4.84%) |
96039.44 (2.13%) |
3753.718 (0.44%) |
2696.074 (0.31%) |
| Total |
1210199 (3.76%) |
4499978 (99.99%) |
108971.5 (0.34%) |
78267.77 (0.24%) |
Table 7.
p-values returned by Wilcoxon Rank Sum test for Infection factor.
Table 7.
p-values returned by Wilcoxon Rank Sum test for Infection factor.
| |
Compared Scenario |
Unvaccinated-National policy |
National-Optimized policy |
Unvaccinated-Optimized policy |
| R0 |
|
| 1.2 |
0.03125 |
0.03125 |
0.03125 |
| 2.15 |
0.03125 |
0.03125 |
0.03125 |
| 3.1 |
0.03125 |
0.03125 |
0.03125 |
Table 8.
p-values returned by Wilcoxon Rank Sum test for Hospitalization factor.
Table 8.
p-values returned by Wilcoxon Rank Sum test for Hospitalization factor.
| |
Compared Scenario |
Unvaccinated-National policy |
National-Optimized policy |
Unvaccinated-Optimized policy |
| R0 |
|
| 1.2 |
0.03125 |
0.03125 |
0.03125 |
| 2.15 |
0.03125 |
0.03125 |
0.03125 |
| 3.1 |
0.03125 |
0.03125 |
0.03125 |
Table 9.
p-values returned by Wilcoxon Rank Sum test for Mortality factor.
Table 9.
p-values returned by Wilcoxon Rank Sum test for Mortality factor.
| |
Compared Scenario |
Unvaccinated-National policy |
National-Optimized policy |
Unvaccinated-Optimized policy |
| R0 |
|
| 1.2 |
0.03125 |
0.03125 |
0.03125 |
| 2.15 |
0.03125 |
0.03125 |
0.03125 |
| 3.1 |
0.03125 |
0.03125 |
0.03125 |
Table 10.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 1.2.
Table 10.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 1.2.
| R0: 1.2 |
| |
Factors |
Age group |
#Infection (%) |
#Vaccine (%) |
#Hospitlized (%) |
#Death (%) |
| Scenarios |
|
| No vaccination |
G1 |
53283.93 (4.39%) |
0.0 (0%) |
7221.96 (0.6%) |
5464.93 (0.45%) |
| G2 |
15153.23 (4.95%) |
0.0 (0%) |
2422.85 (0.79%) |
1851.51 (0.61%) |
| G3 |
87477.50 (2.69%) |
0.0 (0%) |
11530.38 (0.36%) |
8715.39 (0.27%) |
| G4 |
9575.49 (3.8%) |
0.0 (0%) |
1516.71 (0.6%) |
1158.60 (0.46%) |
| G5 |
2444.214(2.28%) |
0.0 (0%) |
518.20 (0.48%) |
401.64 (0.37%) |
| Total |
166167.8 (3.24%) |
0.0 (0%) |
23210.1 (0.45%) |
17592.07 (0.34%) |
| Current Vaccination Policy |
G1 |
52982.59 (4.37%) |
1400730.96 (31.13%) |
5916.26 (0.49%) |
4684.70 (0.39%) |
| G2 |
13439.56 (4.39%) |
354224.85 (7.87%) |
1492.25 (0.49%) |
1181.62 (0.39%) |
| G3 |
86012.29 (2.65%) |
2627482.73 (58.39%) |
9712.76 (0.3%) |
7690.90 (0.24%) |
| G4 |
8565.581 (3.4%) |
82480.83 (1.83%) |
951.05 (0.38%) |
753.08 (0.3%) |
| G5 |
1526.881 (1.42%) |
35051.28 (0.78%) |
169.53 (0.16%) |
134.24 (0.13%) |
| Total |
164293.5 (3.21%) |
4499971 (99.99%) |
18241.85 (0.36%) |
14444.53 (0.28%) |
| Optimized Vaccination Policy |
G1 |
49170.152(4.05%) |
1117450 (24.83%) |
5906.90 (0.49%) |
4632.03 (0.38%) |
| G2 |
12401.99 (4.05%) |
287582.1 (6.39%) |
1489.90 (0.49%) |
1168.34 (0.38%) |
| G3 |
80723.52 (2.49%) |
2757575 (61.28%) |
9697.30 (0.3%) |
7604.35 (0.23%) |
| G4 |
7904.31(3.13%) |
240228.5 (5.34%) |
949.56 (0.38%) |
744.62 (0.3%) |
| G5 |
1409.03 (1.31%) |
97070.76 (2.16%) |
169.28 (0.16%) |
132.74 (0.12%) |
| Total |
151609 (2.96%) |
4499907 (99.99%) |
18212.94 (0.36%) |
14282.08 (0.28%) |
Table 11.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 2.15.
Table 11.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 2.15.
| R0: 2.15 |
| |
Factors |
Age group |
#Infection (%) |
#Vaccine (%) |
#Hospitlized (%) |
#Death (%) |
| Scenarios |
|
| No vaccination |
G1 |
55613.43 (4.58%) |
0.0 (0%) |
8032.06 (0.66%) |
6014.02 (0.5%) |
| G2 |
17571.34 (5.74%) |
0.0 (0%) |
3196.47 (1.04%) |
2429.11 (0.79%) |
| G3 |
89360.95 (2.75%) |
0.0 (0%) |
12545.42 (0.39%) |
9373.93 (0.29%) |
| G4 |
10983.37 (4.35%) |
0.0 (0%) |
1966.32 (0.78%) |
1493.25 (0.59%) |
| G5 |
3386.74 (3.16%) |
0.0 (0%) |
822.60 (0.77%) |
634.29 (0.59%) |
| Total |
176915.8 (3.45%) |
0.0 (0%) |
26562.87 (0.52%) |
19944.59 (0.39%) |
| Current Vaccination Policy |
G1 |
53284.14 (4.39%) |
1400730.95 (31.13%) |
5916.33 (0.49%) |
4684.76 (0.39%) |
| G2 |
13439.68 (4.39%) |
354224.85 (7.87%) |
1492.29 (0.49%) |
1181.65 (0.39%) |
| G3 |
87477.53 (2.69%) |
2627482.73 (58.39%) |
9712.77 (0.3%) |
7690.90 (0.24%) |
| G4 |
8565.59 (3.4%) |
82480.83 (1.83%) |
951.05 (0.38%) |
753.08 (0.3%) |
| G5 |
1526.89 (1.42%) |
35051.28 (0.78%) |
169.54 (0.16%) |
134.25 (0.13%) |
| Total |
164293.8 (3.21%) |
4499971 (99.99%) |
18241.98 (0.36%) |
14444.64 (0.28%) |
| Optimized Vaccination Policy |
G1 |
48977.32 (4.04%) |
1072186 (23.87%) |
5487.64 (0.45%) |
3994.24 (0.33%) |
| G2 |
12353.42 (4.04%) |
277914.2 (6.19%) |
1384.17 (0.45%) |
1007.49 (0.33%) |
| G3 |
80406.72 (2.48%) |
2801081 (62.36%) |
9008.95 (0.28%) |
6557.23 (0.2%) |
| G4 |
7873.3 (3.12%) |
240345.6 (5.35%) |
882.16 (0.35%) |
642.09 (0.25%) |
| G5 |
1403.53 (1.31%) |
100297.6 (2.23%) |
157.27 (0.15%) |
114.47 (0.11%) |
| Total |
151014.3 (2.95%) |
4491824 (99.82%) |
16920.19 (0.33%) |
12315.52 (0.24%) |
Table 12.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 3.1.
Table 12.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 3.1.
| R0: 3.1 |
| |
Factors |
Age group |
#Infection (%) |
#Vaccine (%) |
#Hospitlized (%) |
#Death (%) |
| Scenarios |
|
| No vaccination |
G1 |
58615.37 (4.83%) |
0.0 (0%) |
8963.14 (0.74%) |
6705.18 (0.55%) |
| G2 |
20497.55 (6.7%) |
0.0 (0%) |
4132.80 (1.35%) |
3158.11 (1.03%) |
| G3 |
93068.53 (2.87%) |
0.0 (0%) |
13678.69 (0.42%) |
10195.92 (0.31%) |
| G4 |
12630.50 (5.01%) |
0.0 (0%) |
2491.36 (0.99%) |
1900.81 (0.75%) |
| G5 |
4503.86 (4.2%) |
0.0 (0%) |
1181.78 (1.1%) |
916.73 (0.85%) |
| Total |
189315.8 (3.69%) |
0.0 (0%) |
30447.78 (0.59%) |
22876.74 (0.45%) |
| Current Vaccination Policy |
G1 |
53284.36 (4.39%) |
1400730.95 (31.13%) |
5916.41 (0.49%) |
4684.83 (0.39%) |
| G2 |
13439.79 (4.39%) |
354224.84 (7.87%) |
1492.33 (0.49%) |
1181.69 (0.39%) |
| G3 |
87477.56 (2.69%) |
2627482.73 (58.39%) |
9712.77 (0.3%) |
7690.91 (0.24%) |
| G4 |
8565.60 (3.4%) |
82480.83 (1.83%) |
951.06 (0.38%) |
753.08 (0.3%) |
| G5 |
1526.9 (1.42%) |
35051.28 (0.78%) |
169.54 (0.16%) |
134.25 (0.13%) |
| Total |
164294.2 (3.21%) |
4499971 (99.99%) |
18242.11 (0.36%) |
14444.75 (0.28%) |
| Optimized Vaccination Policy |
G1 |
48835.59 (4.03%) |
1080865 (24.02%) |
5574.91 (0.46%) |
4263.41 (0.35%) |
| G2 |
12317.74 (4.03%) |
272526.6 (6.06%) |
1406.20 (0.46%) |
1075.40 (0.35%) |
| G3 |
80173.43 (2.47%) |
2847669 (63.28%) |
9151.9822 (0.28%) |
6998.91 (0.22%) |
| G4 |
7850.5 (3.11%) |
201331.2 (4.47%) |
896.18 (0.36%) |
685.35 (0.27%) |
| G5 |
1399.51 (1.3%) |
97462.32 (2.17%) |
159.79 (0.15%) |
122.20 (0.11%) |
| Total |
150576.8 (2.94%) |
4499854 (99.99%) |
17189.06 (0.34%) |
13145.27 (0.26%) |
Table 13.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 1.2. .
Table 13.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 1.2. .
| R0: 1.2 |
| |
Factors |
Age group |
#Infection (%) |
#Vaccine (%) |
#Hospitlized (%) |
#Death (%) |
| Scenarios |
|
| No vaccination |
G1 |
28865.11 (5.37%) |
0.0 (0%) |
3667.51 (0.68%) |
832.21 (0.15%) |
| G2 |
13266.38 (2.13%) |
0.0 (0%) |
1823.92 (0.29%) |
417.85 (0.07%) |
| G3 |
128954.14 (2.04%) |
0.0 (0%) |
16085.52 (0.25%) |
3641.51 (0.06%) |
| G4 |
10618.61 (2.12%) |
0.0 (0%) |
1446.34 (0.29%) |
330.96 (0.07%) |
| G5 |
4938.26 (2.17%) |
0.0 (0%) |
704.82 (0.31%) |
162.13 (0.07%) |
| Total |
186642.5 (2.27%) |
0.0 (0%) |
23728.11 (0.29%) |
5384.67 (0.07%) |
| Current Vaccination Policy |
G1 |
24912.99 (4.63%) |
202049.3 (4.49%) |
3541.60 (0.66%) |
786.97 (0.15%) |
| G2 |
11028.51 (1.77%) |
234055.3 (5.2%) |
1567.80 (0.25%) |
348.38 (0.06%) |
| G3 |
112208.32 (1.77%) |
3644996.7 (81.0%) |
15951.37 (0.25%) |
3544.50 (0.06%) |
| G4 |
8868.98 (1.77%) |
288101.5 (6.4%) |
1260.80 (0.25%) |
280.16 (0.06%) |
| G5 |
4026.59 (1.77%) |
130797.0 (2.91%) |
572.42 (0.25%) |
127.19 (0.06%) |
| Total |
161045.4 (1.96%) |
4500000 (100.0%) |
22893.98 (0.28%) |
5087.19 (0.06%) |
| Optimized Vaccination Policy |
G1 |
24429.68 (4.54%) |
269717.2 (5.99%) |
3152.08 (0.59%) |
627.71 (0.12%) |
| G2 |
10814.56 (1.74%) |
298404.2 (6.63%) |
1395.37 (0.22%) |
277.87 (0.04%) |
| G3 |
110031.46 (1.74%) |
3531334 (78.47%) |
14196.99 (0.22%) |
2827.19 (0.04%) |
| G4 |
8696.92 (1.74%) |
278184.2 (6.18%) |
1122.13 (0.22%) |
223.46 (0.04%) |
| G5 |
3948.48 (1.74%) |
122318.7 (2.72%) |
509.46 (0.22%) |
101.45 (0.04%) |
| Total |
157921.1 (1.92%) |
4499958 (99.99%) |
20376.03 (0.25%) |
4057.68 (0.04%) |
Table 14.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 2.15.
Table 14.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 2.15.
| R0: 2.15 |
| |
Factors |
Age group |
#Infection (%) |
#Vaccine (%) |
#Hospitlized (%) |
#Death (%) |
| Scenarios |
|
| No vaccination |
G1 |
29423.38 (5.47%) |
0.0 (0%) |
3899.90 (0.73%) |
882.58 (0.16%) |
| G2 |
13942.21 (2.24%) |
0.0 (0%) |
2099.82 (0.34%) |
475.43 (0.08%) |
| G3 |
130557.24 (2.06%) |
0.0 (0%) |
16764.04 (0.26%) |
3793.19 (0.06%) |
| G4 |
11112.68 (2.22%) |
0.0 (0%) |
1648.40 (0.33%) |
373.27 (0.07%) |
| G5 |
5263.90 (2.32%) |
0.0 (0%) |
837.46 (0.37%) |
189.70 (0.08%) |
| Total |
190299.3 (2.32%) |
0.0 (0%) |
25249.62 (0.31%) |
5714.18 (0.07%) |
| Current Vaccination Policy |
G1 |
24912.99 (4.63%) |
202049.3 (4.49%) |
3541.60 (0.66%) |
786.97 (0.15%) |
| G2 |
11028.52 (1.77%) |
234055.3 (5.2%) |
1567.80 (0.25%) |
348.38 (0.06%) |
| G3 |
112208.32 (1.77%) |
3644996.7 (81.0%) |
15951.37 (0.25%) |
3544.50 (0.06%) |
| G4 |
8868.98 (1.77%) |
288101.5 (6.4%) |
1260.80 (0.25%) |
280.16 (0.06%) |
| G5 |
4026.59 (1.77%) |
130797.0 (2.91%) |
572.42 (0.25%) |
127.19 (0.06%) |
| Total |
161045.4 (1.96%) |
4500000 (100.0%) |
22893.98 (0.28%) |
5087.19 (0.06%) |
| Optimized Vaccination Policy |
G1 |
24505.97 (4.56%) |
263084.5 (5.89%) |
3135.50 (0.58%) |
601.40 (0.11%) |
| G2 |
10848.33 (1.74%) |
301372.9 (6.75%) |
1388.03 (0.22%) |
266.23 (0.04%) |
| G3 |
110375.04 (1.74%) |
3486407 (78.06%) |
14122.31 (0.22%) |
2708.72 (0.04%) |
| G4 |
8724.07 (1.74%) |
287516.8 (6.44%) |
1116.23 (0.22%) |
214.10 (0.04%) |
| G5 |
3960.81 (1.74%) |
128070.8 (2.87%) |
506.78 (0.22%) |
97.20 (0.04%) |
| Total |
158414.2 (1.93%) |
4466452 (99.25%) |
20268.85 (0.25%) |
3887.66 (0.05%) |
Table 15.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 3.1.
Table 15.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 3.1.
| R0: 3.1 |
| |
Factors |
Age group |
#Infection (%) |
#Vaccine (%) |
#Hospitlized (%) |
#Death (%) |
| Scenarios |
|
| No vaccination |
G1 |
29977.35 (5.57%) |
0.0 (0%) |
4123.36 (0.77%) |
925.60 (0.17%) |
| G2 |
14646.94 (2.35%) |
0.0 (0%) |
2380.68 (0.38%) |
534.82 (0.09%) |
| G3 |
132087.81 (2.09%) |
0.0 (0%) |
17388.11 (0.27%) |
3902.06 (0.06%) |
| G4 |
11621.74 (2.32%) |
0.0 (0%) |
1851.62 (0.37%) |
416.05 (0.08%) |
| G5 |
5601.91 (2.47%) |
0.0 (0%) |
972.14 (0.43%) |
218.55 (0.1%) |
| Total |
193935.8 (2.36%) |
0.0 (0%) |
26715.91 (%0.33) |
5997.08 (0.07%) |
| Current Vaccination Policy |
G1 |
24913.0 (4.63%) |
202049.3 (4.49%) |
3541.60 (0.66%) |
786.97 (0.15%) |
| G2 |
11028.52 (1.77%) |
234055.3 (5.2%) |
1567.80 (0.25%) |
348.38 (0.06%) |
| G3 |
112208.32 (1.77%) |
3644996.7 (81.0%) |
15951.37 (0.25%) |
3544.50 (0.06%) |
| G4 |
8868.98 (1.77%) |
288101.5 (6.4%) |
1260.80 (0.25%) |
280.16 (0.06%) |
| G5 |
4026.59 (1.77%) |
130797.0 (2.91%) |
572.42 (0.25%) |
127.19 (0.06%) |
| Total |
161045.4 (1.96%) |
4500000 (100.0%) |
22893.98 (0.28%) |
5087.19 (0.06%) |
| Optimized Vaccination Policy |
G1 |
24758.13 (4.6%) |
277026 (6.17%) |
3530.71 (0.66%) |
764.93 (0.14%) |
| G2 |
10959.96 (1.76%) |
339439.9 (7.56%) |
1562.98 (0.25%) |
338.62 (0.05%) |
| G3 |
111510.76 (1.76%) |
3476166 (77.4%) |
15902.34 (0.25%) |
3445.23 (0.05%) |
| G4 |
8813.84 (1.76%) |
266114.4 (5.93%) |
1256.93 (0.25%) |
272.31 (0.05%) |
| G5 |
4001.56 (1.76%) |
132597.9 (2.95%) |
570.66 (0.25%) |
123.63 (0.05%) |
| Total |
160044.2 (1.95%) |
4491345 (99.81%) |
22823.61 (0.28%) |
4944.72 (0.06%) |
Table 16.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 1.2.
Table 16.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 1.2.
| R0: 1.2 |
| |
Factors |
Age group |
#Infection (%) |
#Vaccine (%) |
#Hospitlized (%) |
#Death (%) |
| Scenarios |
|
| No vaccination |
G1 |
9603.08 (1.23%) |
0.0 (0%) |
1812.47 (0.23%) |
572.97 (0.07%) |
| G2 |
2566.52 (1.27%) |
0.0 (0%) |
509.18 (0.25%) |
159.99 (0.08%) |
| G3 |
9553.16 (0.66%) |
0.0 (0%) |
1788.61 (0.12%) |
573.16 (0.04%) |
| G4 |
458.75 (0.43%) |
0.0 (0%) |
100.58 (0.09%) |
31.81 (0.03%) |
| G5 |
216.94 (0.34%) |
0.0 (0%) |
51.70 (0.08%) |
16.43 (0.03%) |
| Total |
22398.45 (0.86%) |
0.0 (0%) |
4262.54 (0.16%) |
1335.59 (0.05%) |
| Current Vaccination Policy |
G1 |
9580.30 (1.22%) |
1057774.4 (23.93%) |
1782.90 (0.23%) |
567.58 (0.07%) |
| G2 |
2469.30 (1.22%) |
272635.1 (6.17%) |
459.55 (0.23%) |
147.69 (0.07%) |
| G3 |
9583.55 (0.66%) |
2762477.1 (62.51%) |
1783.48 (0.12%) |
559.79 (0.04%) |
| G4 |
406.25 (0.38%) |
206043.2 (4.66%) |
75.61 (0.07%) |
24.30 (0.02%) |
| G5 |
176.91 (0.28%) |
120540.4 (2.73%) |
32.93 (0.05%) |
10.58 (0.02%) |
| Total |
22216.31 (0.85%) |
4419470 (98.21%) |
4134.46 (0.16%) |
1328.70 (0.05%) |
| Optimized Vaccination Policy |
G1 |
9419.98 (1.2%) |
1314694 (29.26%) |
1643.38 (0.21%) |
482.19 (0.05%) |
| G2 |
2427.97 (1.2%) |
356192.3 (7.93%) |
423.58 (0.21%) |
124.29 (0.06%) |
| G3 |
9423.20 (0.65%) |
2522905 (56.16%) |
1643.93 (0.11%) |
482.34 (0.03%) |
| G4 |
399.44 (0.37%) |
187757.9 (4.18%) |
69.69 (0.06%) |
20.45 (0.02%) |
| G5 |
173.94 (0.28%) |
111039.3 (2.47%) |
30.35 (0.05%) |
8.91 (0.01%) |
| Total |
21844.52 (0.84%) |
4492589 (99.84%) |
3810.93 (0.15%) |
1118.16 (0.04%) |
Table 17.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 2.15.
Table 17.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 2.15.
| R0: 2.15 |
| |
Factors |
Age group |
#Infection (%) |
#Vaccine (%) |
#Hospitlized (%) |
#Death (%) |
| Scenarios |
|
| No vaccination |
G1 |
9838.75 (1.26%) |
0.0 (0%) |
1967.96 (0.25%) |
642.47 (0.08%) |
| G2 |
2695.37 (1.34%) |
0.0 (0%) |
582.21 (0.29%) |
190.72 (0.9%) |
| G3 |
9749.28 (0.67%) |
0.0 (0%) |
1924.98 (0.13%) |
628.05 (0.04%) |
| G4 |
506.38 (0.47%) |
0.0 (0%) |
125.41 (0.12%) |
41.33 (0.4%) |
| G5 |
250.26 (0.4%) |
0.0 (0%) |
68.61 (0.11%) |
22.70 (0.04%) |
| Total |
23040.04 (0.89%) |
0.0 (0%) |
4669.17 (0.18%) |
1525.27 (0.06%) |
| Current Vaccination Policy |
G1 |
9580.41 (1.22%) |
1057774.1 (23.93%) |
1782.95 (0.23%) |
572.99 (0.07%) |
| G2 |
2469.36 (1.22%) |
272635.0 (6.17%) |
459.57 (0.23%) |
47.70 (0.02%) |
| G3 |
9583.58 (0.66%) |
2762476.3 (62.51%) |
1783.49 (0.12%) |
573.16 (0.04%) |
| G4 |
406.27 (0.38%) |
206043.2 (4.66%) |
75.62 (0.07%) |
24.30 (0.02%) |
| G5 |
176.93 (0.28%) |
120540.4 (2.73%) |
32.94 (0.05%) |
10.59 (0.02%) |
| Total |
22216.54 (0.85%) |
4419469 (98.21%) |
4134.57 (0.16%) |
1328.73 (0.05%) |
| Optimized Vaccination Policy |
G1 |
9428.47 (1.2%) |
1349987 (30.0%) |
1654.30 (0.21%) |
490.07 (0.06%) |
| G2 |
2430.18 (1.2%) |
358068.5 (7.96%) |
426.41 (0.21%) |
126.32 (0.06%) |
| G3 |
9431.63 (0.65%) |
2487839 (55.29%) |
1654.82 (0.11%) |
490.22 (0.03%) |
| G4 |
399.81 (0.37%) |
191728.1 (4.26%) |
70.15 (0.07%) |
20.78 (0.02%) |
| G5 |
174.11 (0.28%) |
112117.8 (2.49%) |
30.55 (0.05%) |
9.05 (0.01%) |
| Total |
21864.19 (0.84%) |
4499740 (99.99%) |
3836.24(0.15%) |
1136.44 (0.04%) |
Table 18.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 3.1.
Table 18.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 3.1.
| R0: 3.1 |
| |
Factors |
Age group |
#Infection (%) |
#Vaccine (%) |
#Hospitlized (%) |
#Death (%) |
| Scenarios |
|
| No vaccination |
G1 |
9941.81 (1.27%) |
0.0 (0%) |
1989.03 (0.25%) |
618.27 (0.08%) |
| G2 |
2787.42 (1.38%) |
0.0 (0%) |
614.74 (0.3%) |
192.30 (0.01%) |
| G3 |
9814.34 (0.68%) |
0.0 (0%) |
1930.30 (0.13%) |
599.31 (0.04%) |
| G4 |
546.14 (0.51%) |
0.0 (0%) |
140.91 (0.13%) |
44.50 (0.04%) |
| G5 |
279.42 (0.44%) |
0.0 (0%) |
80.25 (0.13%) |
25.48 (0.04%) |
| Total |
23369.13 (0.9%) |
0.0 (0%) |
4755.22 (0.18%) |
1479.86 (0.06%) |
| Current Vaccination Policy |
G1 |
9580.51 (1.22%) |
1057773.9 (23.93%) |
1782.99 (0.23%) |
573.00 (0.07%) |
| G2 |
2469.41 (1.22%) |
272634.9 (6.17%) |
459.60 (0.23%) |
147.70 (0.07%) |
| G3 |
9583.62 (0.66%) |
2762475.6 (62.51%) |
1783.50 (0.12%) |
573.17 (0.04%) |
| G4 |
406.29 (0.38%) |
206043.1 (4.66%) |
75.63 (0.07%) |
24.31 (0.02%) |
| G5 |
176.95 (0.28%) |
120540.4 (2.73%) |
32.95 (0.05%) |
10.59 (0.02%) |
| Total |
22216.78 (0.85%) |
4419468 (98.21%) |
4134.67 (0.16%) |
1328.77 (0.05%) |
| Optimized Vaccination Policy |
G1 |
9526.33 (1.22%) |
1351268 (30.03%) |
1765.41 (0.23%) |
570.64 (0.07%) |
| G2 |
2455.43 (1.22%) |
352741.4 (7.84%) |
455.06 (0.23%) |
147.09 (0.07%) |
| G3 |
9529.42 (0.66%) |
2492424 (55.39%) |
1765.92 (0.12%) |
570.80 (0.04%) |
| G4 |
403.97 (0.37%) |
191864 (4.26%) |
74.87 (0.07%) |
24.20 (0.02%) |
| G5 |
175.93 (0.28%) |
111569.1 (2.48%) |
32.61 (0.05%) |
10.54 (0.02%) |
| Total |
22091.08 (0.85%) |
4499867 (99.99%) |
4093.88 (0.16%) |
1323.27 (0.05%) |
Table 19.
p-values returned by Wilcoxon Rank Sum test for Infection factor.
Table 19.
p-values returned by Wilcoxon Rank Sum test for Infection factor.
| |
Compared Scenario |
Unvaccinated-National policy |
National-Optimized policy |
Unvaccinated-Optimized policy |
| R0 |
|
| 1.2 |
0.09375 |
0.03125 |
0.03125 |
| 2.15 |
0.03125 |
0.03125 |
0.03125 |
| 3.1 |
0.03125 |
0.03125 |
0.03125 |
Table 20.
p-values returned by Wilcoxon Rank Sum test for Hospitalization factor.
Table 20.
p-values returned by Wilcoxon Rank Sum test for Hospitalization factor.
| |
Compared Scenario |
Unvaccinated-National policy |
National-Optimized policy |
Unvaccinated-Optimized policy |
| R0 |
|
| 1.2 |
0.03125 |
0.03125 |
0.03125 |
| 2.15 |
0.03125 |
0.03125 |
0.03125 |
| 3.1 |
0.03125 |
0.02895363 |
0.03125 |
Table 21.
p-values returned by Wilcoxon Rank Sum test for Mortality factor.
Table 21.
p-values returned by Wilcoxon Rank Sum test for Mortality factor.
| |
Compared Scenario |
Unvaccinated-National policy |
National-Optimized policy |
Unvaccinated-Optimized policy |
| R0 |
|
| 1.2 |
0.03125 |
0.03125 |
0.03125 |
| 2.15 |
0.03125 |
0.15625 |
0.03125 |
| 3.1 |
0.03125 |
0.03125 |
0.03125 |
Table 22.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 1.2.
Table 22.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 1.2.
| R0: 1.2 |
| |
Factors |
Age group |
#Infection (%) |
#Vaccine (%) |
#Hospitlized (%) |
#Death (%) |
| Scenarios |
|
| No vaccination |
G1 |
11561.46 (0.48%) |
0.0 (0%) |
779.71 (0.03%) |
230.21 (0.01%) |
| G2 |
2833.37 (0.4%) |
0.0 (0%) |
262.26 (0.04%) |
76.67 (0.01%) |
| G3 |
176414.05 (2.87%) |
0.0 (0%) |
11072.32 (0.18%) |
3277.99 (0.05%) |
| G4 |
17034.80 (2.93%) |
0.0 (0%) |
1122.23 (0.19%) |
331.63 (0.06%) |
| G5 |
3189.99 (1.01%) |
0.0 (0%) |
242.71 (0.08%) |
71.37 (0.02%) |
| Total |
211033.7 (2.08%) |
0.0 (0%) |
13479.23 (0.13%) |
3987.87 (0.04%) |
| Current Vaccination Policy |
G1 |
10976.25 (0.46%) |
953465.5 (22.55%) |
648.96 (0.03%) |
194.05 (0.01%) |
| G2 |
2220.44 (0.31%) |
280200.7 (6.63%) |
131.28 (0.02%) |
39.26 (0.01%) |
| G3 |
172927.02 (2.81%) |
2600458.6 (61.51%) |
10224.13 (0.17%) |
3057.17 (0.05%) |
| G4 |
16348.48 (20.81%) |
254934.2 (6.03%) |
966.59 (0.17%) |
289.02 (0.05%) |
| G5 |
2846.99 (0.9%) |
138333.9 (3.27%) |
168.33 (0.05%) |
50.33 (0.02%) |
| Total |
205319.2 (2.02%) |
4227393 (93.94%) |
12139.29 (0.12%) |
3629.83 (0.04%) |
| Optimized Vaccination Policy |
G1 |
9513.85 (0.4%) |
933013.6 (21.34%) |
543.46 (0.02%) |
148.97 (0.01%) |
| G2 |
1924.60 (0.27%) |
366738.1 (8.39%) |
109.94 (0.02%) |
30.14 (0.004%) |
| G3 |
149887.35 (2.44%) |
2715520 (62.11%) |
8562.01 (0.14%) |
2346.96 (0.04%) |
| G4 |
14170.31 (2.44%) |
230222 (5.27%) |
809.45 (0.14%) |
221.88 (0.04%) |
| G5 |
2467.68 (0.78%) |
126331.6 (2.89%) |
140.96 (0.04%) |
38.64 (0.01%) |
| Total |
177963.8 (1.75%) |
4371825 (97.15%) |
10165.82 (0.1%) |
2786.58 (0.03%) |
Table 23.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 2.15.
Table 23.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 2.15.
| R0: 2.15 |
| |
Factors |
Age group |
#Infection (%) |
#Vaccine (%) |
#Hospitlized (%) |
#Death (%) |
| Scenarios |
|
| No vaccination |
G1 |
12037.53 (0.5%) |
0.0 (0%) |
883.31 (0.04%) |
260.65 (0.01%) |
| G2 |
3372.78 (0.48%) |
0.0 (0%) |
375.75 (0.05%) |
109.76 (0.02%) |
| G3 |
178776.36 (2.91%) |
0.0 (0%) |
11631.71 (0.19%) |
3445.27 (0.06%) |
| G4 |
17572.52 (3.02%) |
0.0 (0%) |
1240.90 (0.21%) |
366.61 (0.06%) |
| G5 |
3480.76 (1.1%) |
0.0 (0%) |
304.62 (0.1%) |
89.47 (0.03%) |
| Total |
215239.9 (2.12%) |
0.0 (0%) |
14436.3 (0.14%) |
4271.75 (0.042%) |
| Current Vaccination Policy |
G1 |
10976.31 (0.46%) |
953465.5 (22.55%) |
648.96 (0.03%) |
194.05 (0.01%) |
| G2 |
2220.45 (0.31%) |
280200.7 (6.63%) |
131.28 (0.02%) |
39.26 (0.01%) |
| G3 |
172927.74 (2.81%) |
2600458.6 (61.51%) |
10224.14 (0.17%) |
3057.17 (0.05%) |
| G4 |
16348.55 (2.81%) |
254934.2 (6.03%) |
966.59 (0.17%) |
289.02 (0.05%) |
| G5 |
2847.01 (0.9%) |
138333.9 (3.27%) |
168.33 (0.05%) |
50.33 (0.02%) |
| Total |
205320.1 (2.02%) |
4227393 (93.94%) |
12139.3 (0.12%) |
3629.83 (0.0357%) |
| Optimized Vaccination Policy |
G1 |
9483.12 (0.39%) |
1058691 (23.53%) |
560.89 (0.02%) |
155.88 (0.01%) |
| G2 |
1919.37 (0.27%) |
323928.8 (7.2%) |
113.63 (0.016%) |
31.58 (0.004%) |
| G3 |
149391.61 (2.43%) |
2805230 (62.34%) |
8834.66 (0.14%) |
2455.34 (0.04%) |
| G4 |
14124.16 (2.43%) |
193090.4 (4.29%) |
835.34 (0.14%) |
232.16 (0.04%) |
| G5 |
2460.09 (0.78%) |
118852.4 (2.64%) |
145.54 (0.05%) |
40.45 (0.01%) |
| Total |
177378.3 (1.75%) |
4499793 (99.99%) |
10490.06 (0.1%) |
2915.42 (0.03%) |
Table 24.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 3.1.
Table 24.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 3.1.
| R0: 3.1 |
| |
Factors |
Age group |
#Infection (%) |
#Vaccine (%) |
#Hospitlized (%) |
#Death (%) |
| Scenarios |
|
| No vaccination |
G1 |
12358.58 (0.51%) |
0.0 (0%) |
918.67 (0.04%) |
265.83 (0.01%) |
| G2 |
3779.85 (0.53%) |
0.0 (0%) |
443.21 (0.06%) |
128.51 (0.02%) |
| G3 |
179865.98 (2.92%) |
0.0 (0%) |
11489.15 (0.19%) |
3321.50 (0.05%) |
| G4 |
17914.70 (3.08%) |
0.0 (0%) |
1269.39 (0.22%) |
367.22 (0.06%) |
| G5 |
3690.42 (1.17%) |
0.0 (0%) |
335.92 (0.11%) |
97.31 (0.03%) |
| Total |
217609.5 (2.14%) |
0.0 (0%) |
14456.32 (0.14%) |
4180.37 (0.04%) |
| Current Vaccination Policy |
G1 |
10976.29 (0.46%) |
953465.5 (22.55%) |
648.96 (0.03%) |
194.05 (0.01%) |
| G2 |
2220.45 (0.31%) |
280200.7 (6.63%) |
131.28 (0.02%) |
39.26 (0.01%) |
| G3 |
172927.41 (2.81%) |
2600458.6 (61.51%) |
10224.14 (0.17%) |
3057.17 (0.05%) |
| G4 |
16348.52 (2.81%) |
254934.2 (6.03%) |
966.59 (0.17%) |
289.02 (0.05%) |
| G5 |
2847.01 (0.9%) |
138333.9 (3.27%) |
168.33 (0.05%) |
50.33 (0.02%) |
| Total |
205319.7 (2.02%) |
4227393 (93.94%) |
12139.3 (0.12%) |
3629.83 (0.04%) |
| Optimized Vaccination Policy |
G1 |
9535.14 (0.4%) |
1053577 (23.41%) |
580.16 (0.02%) |
174.87 (0.01%) |
| G2 |
1930.00 (0.27%) |
393842.1 (8.75%) |
117.55 (0.017%) |
35.43 (0.005%) |
| G3 |
150209.87 (2.44%) |
2700216 (60.01%) |
9137.94 (0.15%) |
2754.40 (0.04%) |
| G4 |
14201.58 (2.44%) |
213136.8 (4.74%) |
864.03 (0.15%) |
260.44 (0.04%) |
| G5 |
2473.62 (0.78%) |
139082.3 (3.09%) |
150.55 (0.05%) |
45.38 (0.01%) |
| Total |
178350.2 (1.76%) |
4499854 (99.99%) |
10850.23 (0.11%) |
3270.53 (0.03%) |
Table 25.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 1.2.
Table 25.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 1.2.
| R0: 1.2 |
| |
Factors |
Age group |
#Infection (%) |
#Vaccine (%) |
#Hospitlized (%) |
#Death (%) |
| Scenarios |
|
| No vaccination |
G1 |
10663.39 (0.86%) |
0.0 (0%) |
1500.49 (0.12%) |
1146.72 (0.09%) |
| G2 |
3664.84 (1.02%) |
0.0 (0%) |
628.28 (0.17%) |
486.01 (0.13%) |
| G3 |
35300.87 (1.46%) |
0.0 (0%) |
4672.37 (0.19%) |
3555.38 (0.15%) |
| G4 |
3308.55 (1.65%) |
0.0 (0%) |
514.88 (0.26%) |
396.23 (0.2%) |
| G5 |
1062.99 (0.71%) |
0.0 (0%) |
200.98 (0.13%) |
156.40 (0.1%) |
| Total |
54000.64 (1.24%) |
0.0 (0%) |
7516.99 (0.17%) |
5740.74 (0.13%) |
| Current Vaccination Policy |
G1 |
9874.22 (0.8%) |
905235.36 (20.12%) |
1220.38 (0.1%) |
966.22 (0.08%) |
| G2 |
2871.29 (0.8%) |
263966.77 (5.87%) |
354.87 (0.1%) |
280.97 (0.08%) |
| G3 |
34056.39 (1.41%) |
3288823.80 (73.09%) |
4209.06 (0.17%) |
3332.48 (0.14%) |
| G4 |
2835.60 (1.41%) |
24105.77 (0.54%) |
350.46 (0.17%) |
277.47 (0.14%) |
| G5 |
746.44 (0.5%) |
17851.38 (0.4%) |
92.25 (0.06%) |
73.04 (0.05%) |
| Total |
50383.94 (1.16%) |
4499983 (99.99%) |
6227.02 (0.14%) |
4930.18 (0.11%) |
| Optimized Vaccination Policy |
G1 |
9839.29 (0.79%) |
1245020 (27.67%) |
1163.55 (0.09%) |
810.45 (0.07%) |
| G2 |
2861.14 (0.79%) |
349387.8 (7.76%) |
338.35 (0.09%) |
235.67 (0.07%) |
| G3 |
33935.70 (1.41%) |
2547427 (56.61%) |
4012.99 (0.17%) |
2795.19 (0.12%) |
| G4 |
2825.57 (1.41%) |
211195.5 (4.69%) |
334.14 (0.17%) |
232.74 (0.12%) |
| G5 |
743.81 (0.5%) |
146577.9 (3.26%) |
87.96 (0.06%) |
61.27 (0.04%) |
| Total |
50205.51 (1.15%) |
4499608 (99.99%) |
5936.98 (0.136%) |
4135.32 (0.09%) |
Table 26.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 2.15.
Table 26.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 2.15.
| R0: 2.15 |
| |
Factors |
Age group |
#Infection (%) |
#Vaccine (%) |
#Hospitlized (%) |
#Death (%) |
| Scenarios |
|
| No vaccination |
G1 |
11480.78 (0.93%) |
0.0 (0%) |
1777.79 (0.14%) |
1350.34 (0.11%) |
| G2 |
4519.03 (1.26%) |
0.0 (0%) |
911.80 (0.25%) |
701.53 (0.19%) |
| G3 |
36512.79 (1.51%) |
0.0 (0%) |
5099.83 (0.21%) |
3850.17 (0.16%) |
| G4 |
3773.84 (1.88%) |
0.0 (0%) |
670.54 (0.33%) |
513.31 (0.26%) |
| G5 |
1376.31 (0.92%) |
0.0 (0%) |
304.82 (0.2%) |
235.67 (0.16%) |
| Total |
57662.75 (1.32%) |
0.0 (0%) |
8764.77 (0.2%) |
6651.01 (0.15%) |
| Current Vaccination Policy |
G1 |
9874.26 (0.8%) |
905235.36 (20.12%) |
1220.39 (0.1%) |
966.23 (0.08%) |
| G2 |
2871.31 (0.8%) |
263966.77 (5.87%) |
354.88 (0.1%) |
280.97 (0.08%) |
| G3 |
34056.40 (1.41%) |
3288823.80 (73.09%) |
4209.07 (0.17%) |
3332.49 (0.14%) |
| G4 |
2835.60 (1.41%) |
24105.77 (0.54%) |
350.46 (0.17%) |
277.47 (0.14%) |
| G5 |
746.45 (0.5%) |
17851.38 (0.4%) |
92.25 (0.06%) |
73.04 (0.05%) |
| Total |
50384.02 (1.16%) |
4499983 (99.99%) |
6227.05 (0.14%) |
4930.20 (0.11%) |
| Optimized Vaccination Policy |
G1 |
9718.54 (0.78%) |
1268448 (28.19%) |
1127.01 (0.09%) |
790.52 (0.06%) |
| G2 |
2826.07 (0.78%) |
378464.6 (8.41%) |
327.74 (0.09%) |
229.89 (0.06%) |
| G3 |
33518.95 (1.39%) |
2491082 (55.36%) |
3886.90 (0.16%) |
2726.37 (0.11%) |
| G4 |
2790.88 (1.39%) |
211532.8 (4.7%) |
323.64 (0.16%) |
227.01 (0.11%) |
| G5 |
734.69 (0.49%) |
150247.5 (3.34%) |
85.20 (0.06%) |
59.76 (0.04%) |
| Total |
49589.14 (1.14%) |
4499776 (99.99%) |
5750.50 (0.13%) |
4033.55 (0.09%) |
Table 27.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 3.1.
Table 27.
Combination of number and ratio of infected, hospitalized, and dead individuals over a given period for R0= 3.1.
| R0: 3.1 |
| |
Factors |
Age group |
#Infection (%) |
#Vaccine (%) |
#Hospitlized (%) |
#Death (%) |
| Scenarios |
|
| No vaccination |
G1 |
12355.65 (0.99%) |
0.0 (0%) |
2052.37 (0.166%) |
1549.57 (0.125%) |
| G2 |
5514.14 (1.53%) |
0.0 (0%) |
1230.87 (0.34%) |
944.09 (0.26%) |
| G3 |
37607.99 (1.56%) |
0.0 (0%) |
5426.12 (0.22%) |
4058.25 (0.17%) |
| G4 |
4263.08 (2.12%) |
0.0 (0%) |
825.78 (0.41%) |
629.43 (0.31%) |
| G5 |
1715.03 (1.15%) |
0.0 (0%) |
413.26 (0.28%) |
318.36 (0.21%) |
| Total |
61455.89 (1.41%) |
0.0 (0%) |
9948.39 (0.23%) |
7499.69 (0.17%) |
| Current Vaccination Policy |
G1 |
9874.31 (0.8%) |
905235.36 (20.12%) |
1220.41 (0.1%) |
966.25 (0.08%) |
| G2 |
2871.34 (0.8%) |
263966.77 (5.87%) |
354.89 (0.1%) |
280.98 (0.08%) |
| G3 |
34056.42 (1.41%) |
3288823.80 (73.09%) |
4209.07 (0.17%) |
3332.49 (0.14%) |
| G4 |
2835.60 (1.41%) |
24105.77 (0.54%) |
350.46 (0.17%) |
277.47 (0.14%) |
| G5 |
746.45 (0.5%) |
17851.38 (0.4%) |
92.26 (0.06%) |
73.04 (0.05%) |
| Total |
50384.11 (1.16%) |
4499983 (99.99%) |
6227.08 (0.14%) |
4930.23 (0.11%) |
| Optimized Vaccination Policy |
G1 |
9755.79 (0.79%) |
1272933 (28.29%) |
1158.94 (0.09%) |
874.41 (0.07%) |
| G2 |
2836.91 (0.79%) |
370079.6 (8.22%) |
337.03 (0.09%) |
254.29 (0.07%) |
| G3 |
33647.09 (1.39%) |
2491113 (55.36%) |
3996.89 (0.17%) |
3015.58 (0.12%) |
| G4 |
2801.57 (1.39%) |
2491113 (55.36%) |
332.81 (0.17%) |
251.10 (0.12%) |
| G5 |
737.51 (0.5%) |
216707.5 (4.82%) |
87.62 (0.06%) |
66.11 (0.04%) |
| Total |
49778.86 (1.14%) |
4499843 (99.99%) |
5913.28 (0.136%) |
4461.47 (0.1%) |