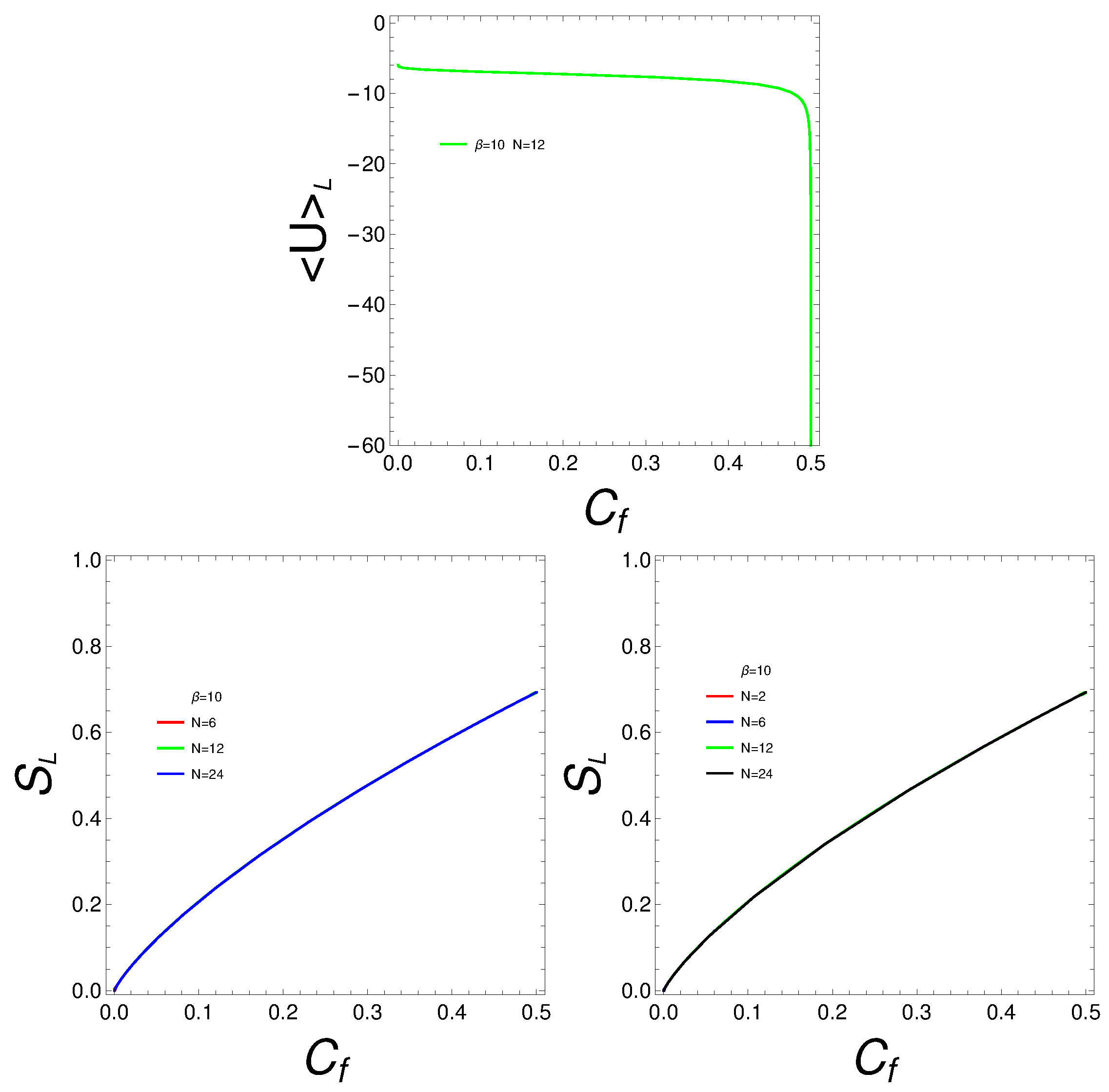1. Introduction
The Lipkin model, a cornerstone in the study of many-body quantum systems, offers a rich framework for exploring the complex interplay of quantum effects in fermionic systems. The literature on the Lipkin model and its applications is vast. A small illustrative sample is given by references [
1,
2,
3,
4,
5,
6,
7,
8]. In recent years, the intersection of quantum information theory and many-body physics has opened new avenues for understanding the intricate connections between different aspects of the Lipkin model, providing new insights. This study delves into the Lipkin model through the lens of information theory, focusing on the quantum degree of mixedness, particle number fluctuations, and temperature variations that characterize such systems.
Our investigation centers on the dependencies and behaviors of quantum mixedness as a function of the total fermion number, especially under varying temperature conditions. By recourse to a systematic numerical exploration of the system’s behavior we uncover notable trends trends that highlight the robustness of these phenomena, irrespective of the interaction strength among fermions, provided it is non-zero. The implications of our findings extend beyond theoretical interest, potentially impacting fields such as condensed matter physics and quantum information science, where understanding the fundamental properties of fermionic systems is crucial.
Through a detailed analysis, this study aims to provide deeper insights into the behavior of many-fermion systems, shedding light on how quantum mixedness and particle number fluctuations are intricately linked to temperature and system size. Our results not only enhance the theoretical framework of the Lipkin model but also offer practical perspectives for experimental applications in various quantum technologies.
2. The SU2-Angular Momentum Lipkin Quasi-Spin Formalism [1–8]
We deal with
N fermions and call
, that is, the Lipkin model consists of
fermions that occupy two different N-fold degenerate single-particle (sp) energy levels. The two levels are separated by an energy gap
. This entails
s.p. micro states. Two quantum numbers (called
and
p) are linked to a single micro state. The first one,
, takes the values
(lower level) and
(upper level). The remaining quantum number, is denominated the quasi spin
p pertaining to the
-fold degeneracy. The pair
p,
is viewed as a ”site” which can be occupied (by a fermion) or be empty. Lipkin fixes
Here
is a sort of angular momentum. Lipkin [
1] uses special angular momentum operators called quasi-spin ones. These are
together with the Casimir operator
The eigenvalues of
take form
and the Lipkin Hamiltonian reads (
v is a coupling constant)
For the Lipkin Hamiltonian one has the matrix [
1]
with
for
. Numerical diagonalization yields energy-eigenvalues
for our Hamiltonian. These eigenvalues are needed to build the partition function
Z in the canonical ensemble [
15].
All thermal quantities of interest are deduced from the partition function
Z[
15]. We construct
Z using probabilities assigned to the models’ microscopic states. Their energies are
[
15]. Some important macroscopic quantifiers are computed as in [
15]. These indicators, together with
Z, derive from the canonical probability distributions[
15].
.
is the inverse temperature. The pertinent expressions are given in [
15]. One has, if we call the mean energy
U and the free energy
F:
The thermal quantifiers above provide much more information than the one obtained via just the quantum resources of zero temperature
T[
15]. As stated above, taking a low enough
T, our quantifiers above yield a good representation of the
scenario [
15]. Below, we will adopt the high enough
value.
2.1. The State’s ’s Degree of Mixture
The concepts of purity and degree of mixedness are fundamental in quantum mechanics and play a crucial role in describing the behavior of quantum systems. They are particularly relevant in the study of quantum information, quantum computation, quantum entanglement, and quantum measurements. The distinction between pure states and mixed states allows for a comprehensive understanding of the coherence, superposition, and statistical behavior of quantum systems.
As well known in quantum mechanics, the degree of mixture
of a given state represented by
is given by [
36]
where,
is the so called ”Purity”
. Note that we have
and
for pure states.
is a very important quantity for us here.
In probability terms one has and .
3. First Results
3.1. versus Temperature
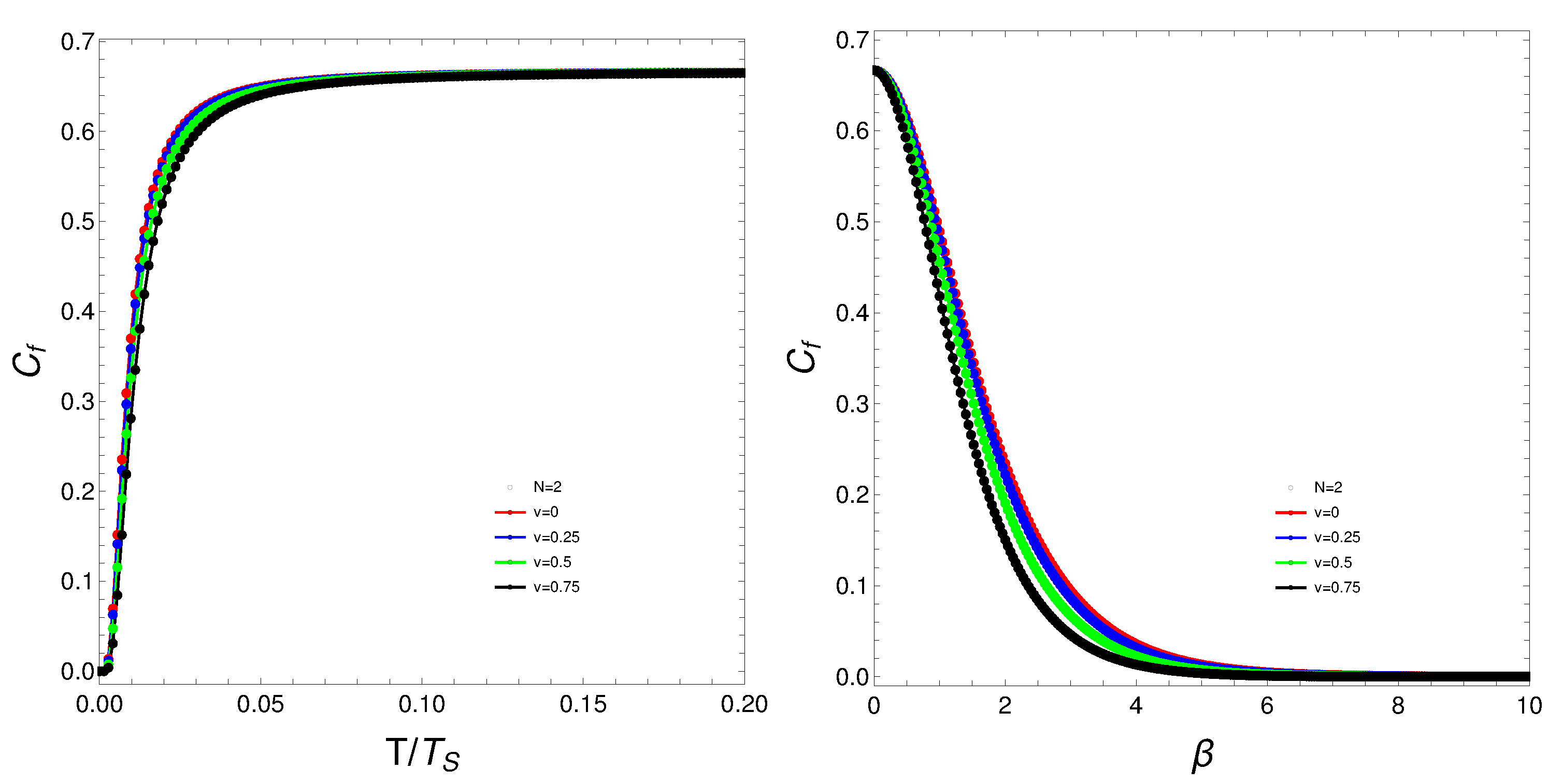
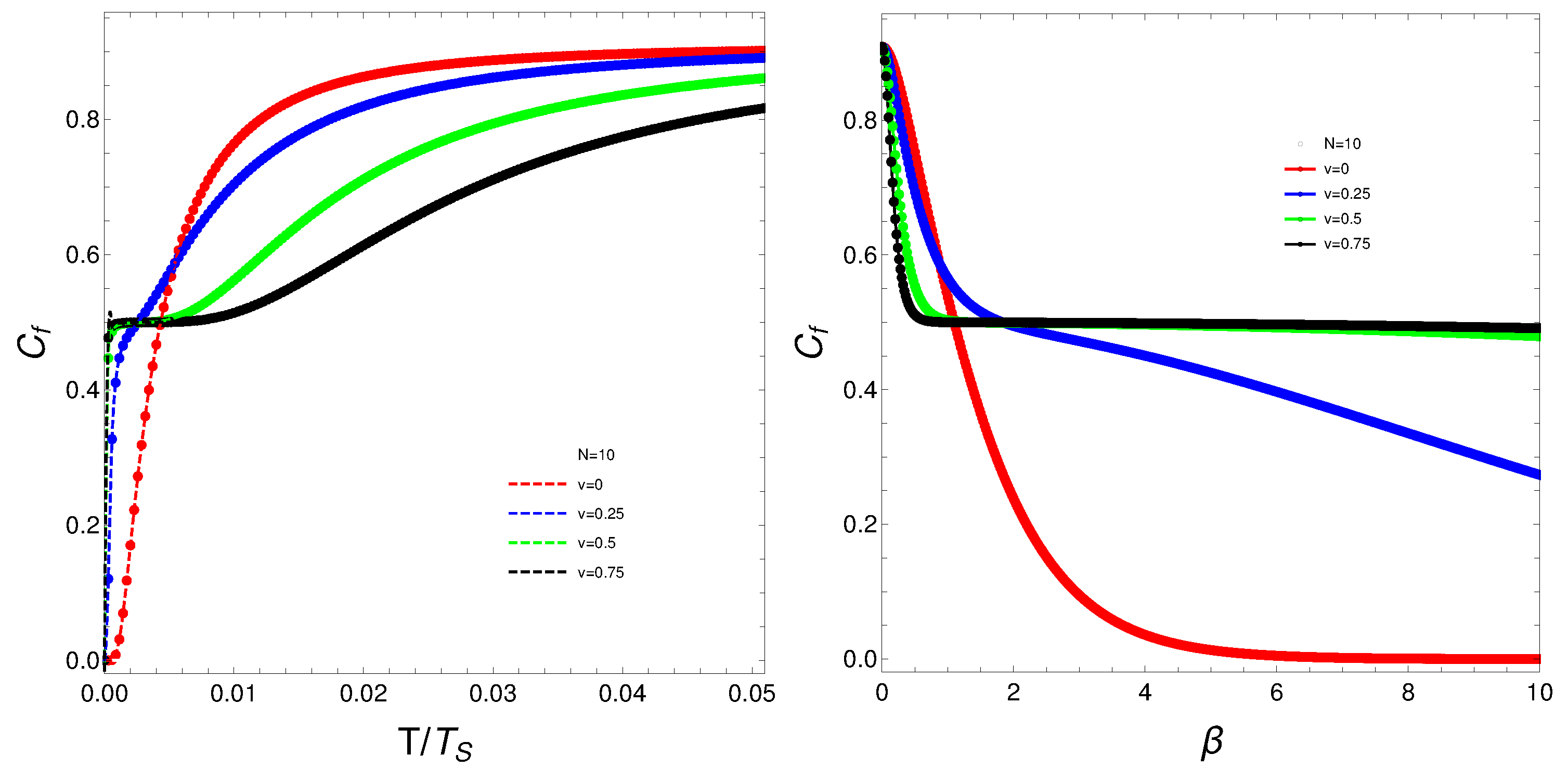
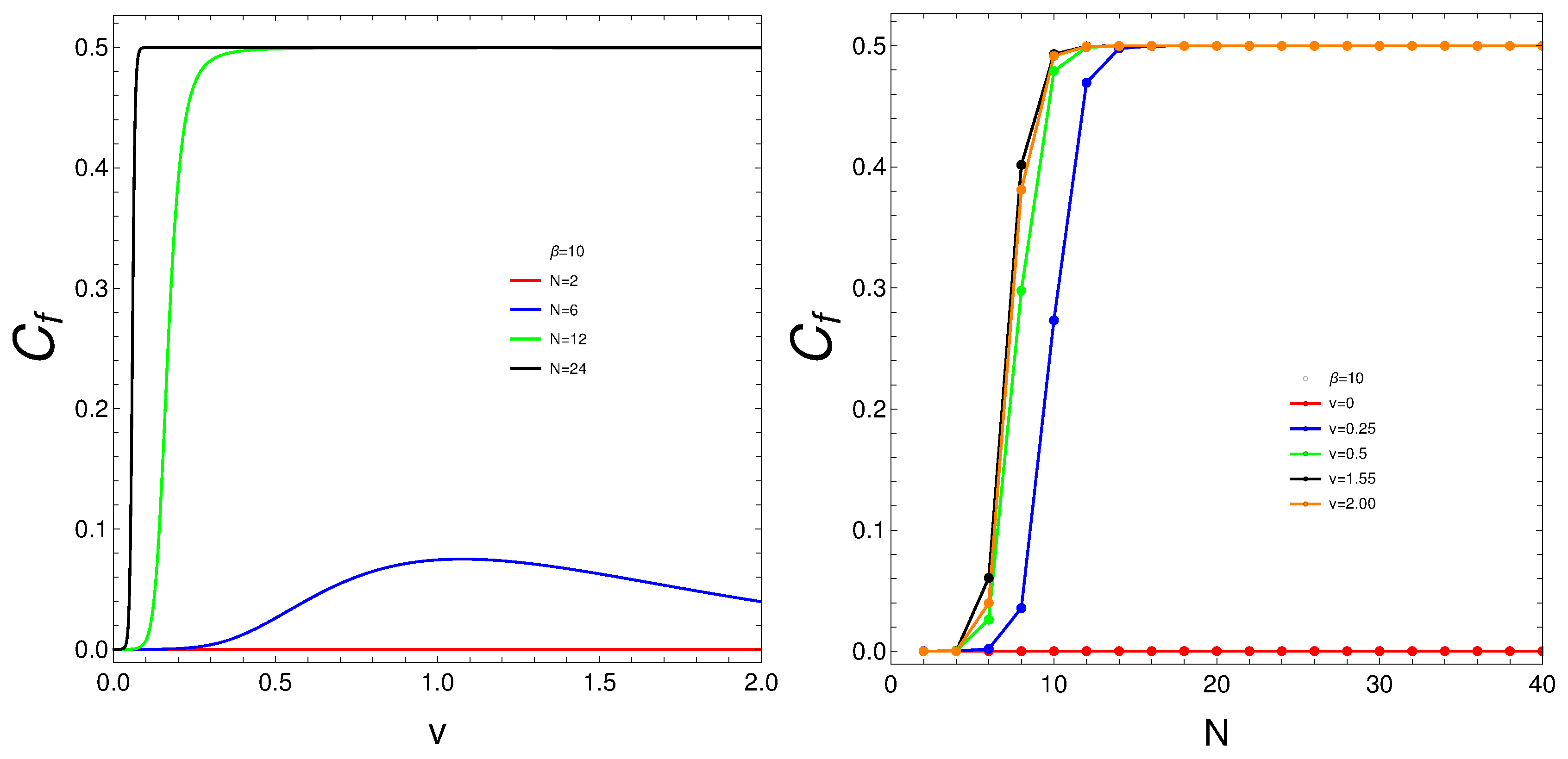
Strong changes in the system’s dynamics emerge as N grows, in plotting our degree of mixedness degree versus temperature. We plot below the mixing versus T and versus the inverse temperature . There seems to be a critical temperature at which stabilizes itself and ceases growing with temperature. It is clear that when N reaches the value six, the system’s behavior strongly changes, as multiple artifacts arise, whereas for the mixing grows smoothly with T.
Figure 1.
Left: vs where is that temperature for which the values of stabilizes. Right: vs . For both graphs N is fixed at and each curve correspond to a different v-value.
Figure 1.
Left: vs where is that temperature for which the values of stabilizes. Right: vs . For both graphs N is fixed at and each curve correspond to a different v-value.
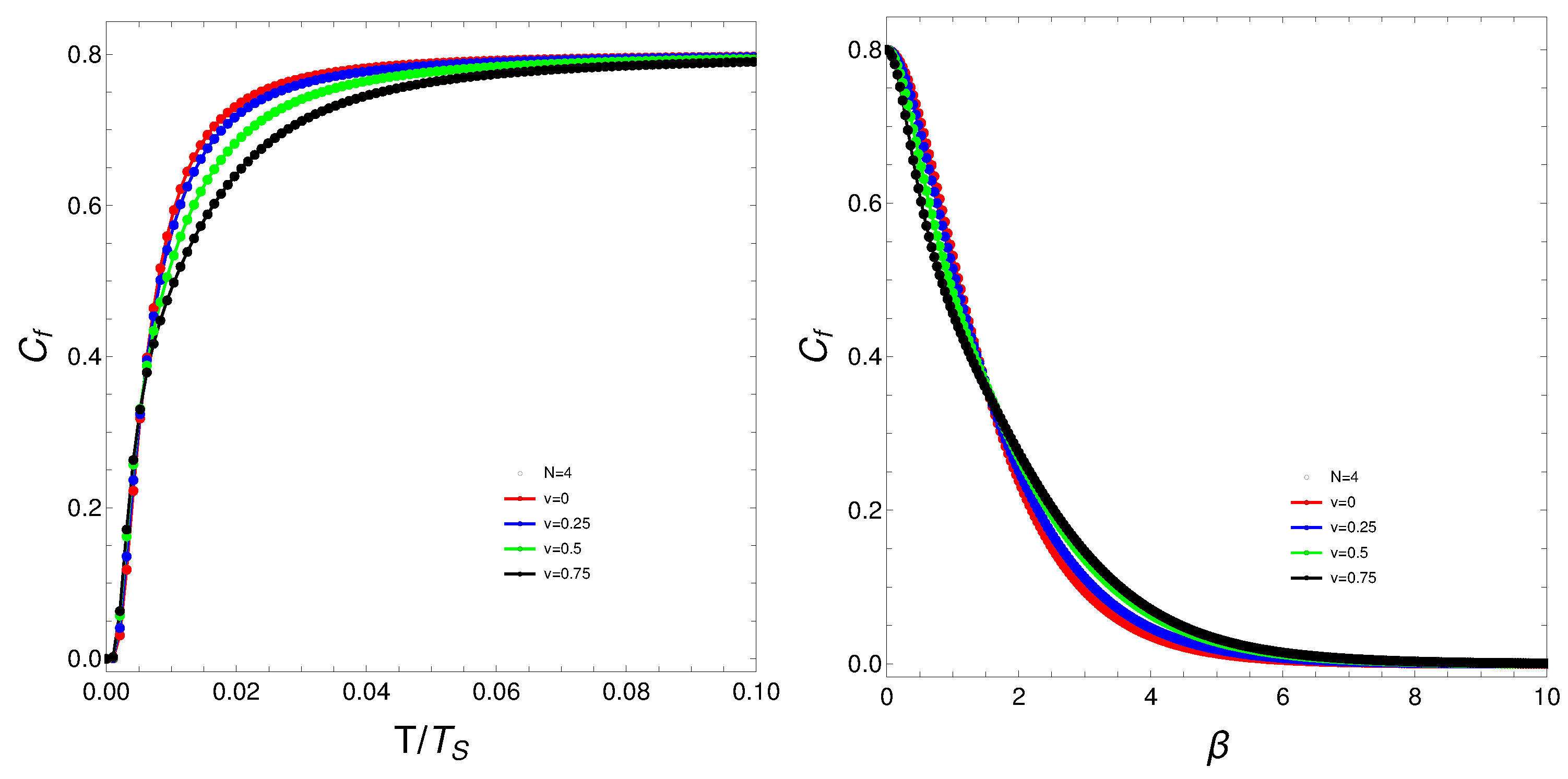
Figure 2.
Left: vs where is the temperature for which the values of stabilizes. Right: vs . For both graphs N is fixed at and each curve correspond to a different v-value.
Figure 2.
Left: vs where is the temperature for which the values of stabilizes. Right: vs . For both graphs N is fixed at and each curve correspond to a different v-value.
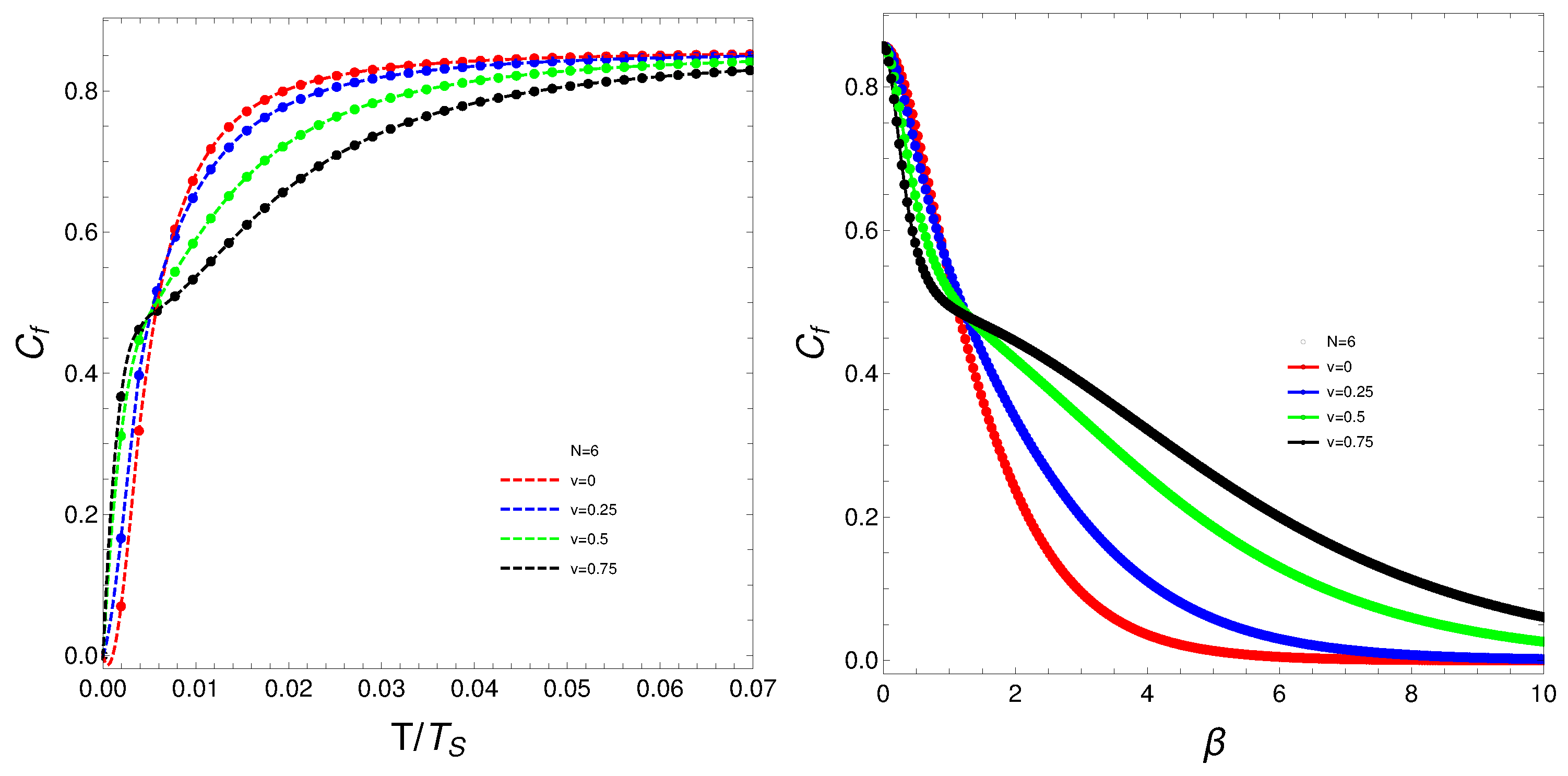
Figure 3.
Left: vs where is the temperature for which the values of stabilizes. Right: vs . For both graphs N is fixed at and each curve correspond to a different v-value.
Figure 3.
Left: vs where is the temperature for which the values of stabilizes. Right: vs . For both graphs N is fixed at and each curve correspond to a different v-value.
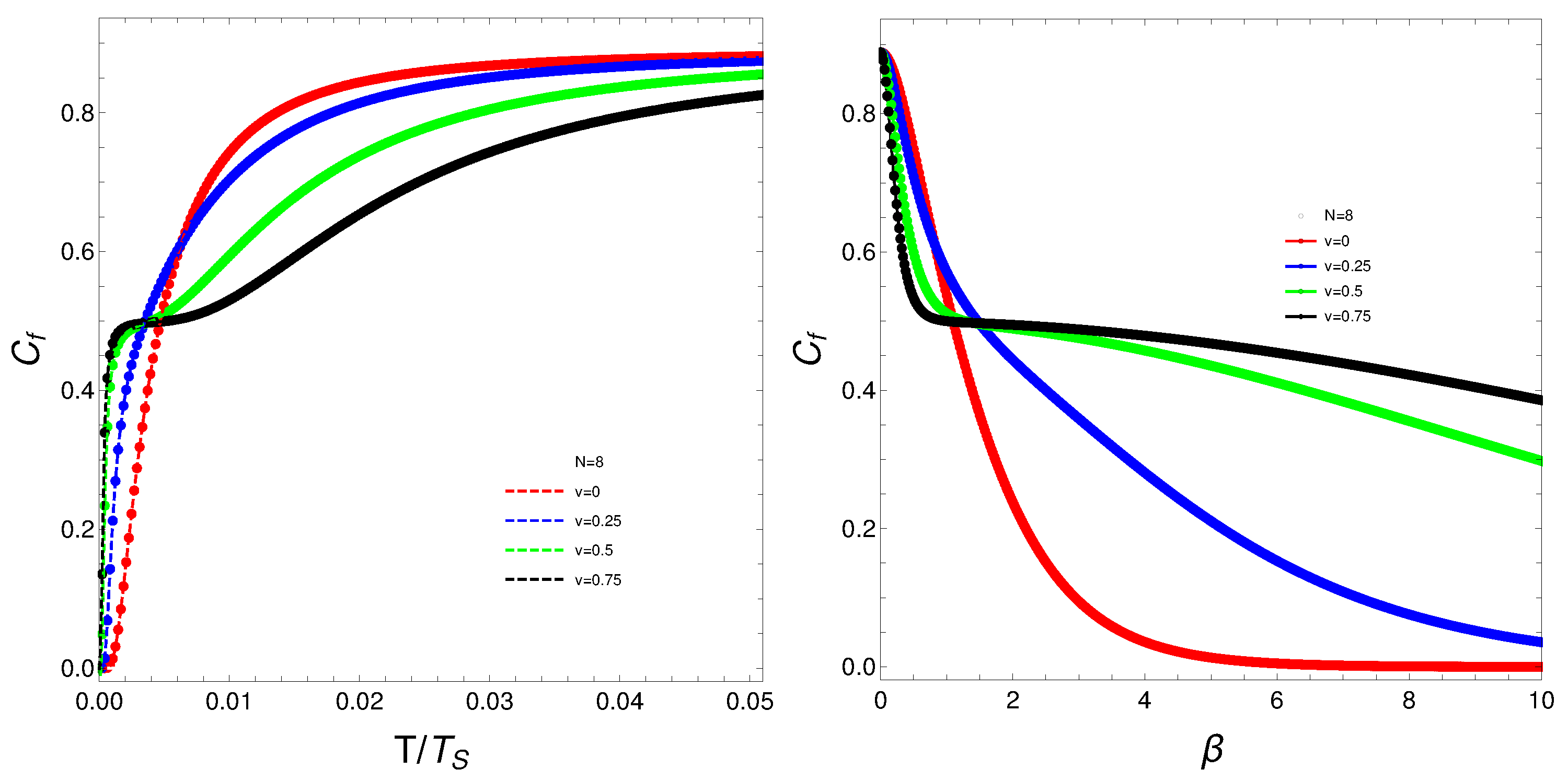
Figure 4.
Left: vs where is the temperature for which the values of stabilizes. Right: vs . For both graphs N is fixed at and each curve correspond to a different v-value.
Figure 4.
Left: vs where is the temperature for which the values of stabilizes. Right: vs . For both graphs N is fixed at and each curve correspond to a different v-value.
Figure 5.
Left: vs where is the temperature for which the values of stabilizes. Right: vs . For both graphs N is fixed at and each curve correspond to a different v-value.
Figure 5.
Left: vs where is the temperature for which the values of stabilizes. Right: vs . For both graphs N is fixed at and each curve correspond to a different v-value.
What do we learn from these graphs? That the mixing strongly depends not only on the temperature, but also, and in a very strong fashion, on the fermion-number and the coupling constant. In summary, the degree of quantum mixing in the Lipkin model is a multifaceted phenomenon influenced by temperature, fermion-number, and the coupling constant. Each of these factors contributes to the overall behavior of the system, determining how the quantum states are occupied and mixed. Understanding these dependencies is crucial for analyzing the dynamics and properties of many-fermion systems within the framework of the Lipkin model. Further analysis on these issues follows below.
3.2. Changes as Plotted versus v or versus N
The behavior of
in these circumstances is depicted in
Figure 6. We again detect a critical
v at which stability is reached. Same for
N. Here however we see quite abrupt jumps in the mixture-degree as the coupling constant grows for
N large enough or for
v finite.
Let us reflect upon the two above graphs. The interaction between fermions acts as a perturbation that drives the system through a quantum phase transition. Before the interaction is introduced, the system may be in a non-mixed, ordered phase with a degree of mixing at zero.
As soon as the interaction is turned on, it reaches a critical threshold where the system can no longer maintain this ordered phase, leading to an abrupt jump to a mixed phase with a degree of mixing at 0.5. This critical interaction threshold marks a point where the system’s energy landscape changes significantly.
At this critical point, the system’s ground state undergoes a reconfiguration. The abrupt jump in the degree of mixing suggests that the system transitions from a non-mixed state to a highly mixed state in which the particles are now in a superposition of states.
This reconfiguration minimizes the system’s free energy under the new interaction regime, as we will see below, leading to a more stable state with increased quantum coherence and entanglement among the fermions.
- -
The jump to a mixing of 0.5 indicates a sudden onset of quantum coherence. The system achieves a new equilibrium where the quantum states are coherently mixed, resulting in an optimal balance of energy.
- -
The high degree of mixing implies that the system has transitioned to a state where fermions are delocalized and strongly correlated, maximizing the entropy, as we will cinfirm below, Thus, introducing fermion interactions induces strong correlation effects that are not present in the non-interacting system. These correlations enhance the mixing of quantum states, leading to a robust mixed phase.
- -
The interactions cause the particles to collectively behave in a way that drastically alters the macroscopic properties of the system, reflected in the sudden change in the degree of mixing. The abrupt change in the degree of mixing highlights the robustness of the quantum phase transition. It demonstrates that even a small interaction can lead to significant changes in the system’s macroscopic properties when the number of particles is large enough.
- -
This robustness indicates that the system’s behavior is dominated by collective effects rather than individual particle properties, a hallmark of many-body quantum systems.
4. Connection between the Degree of Mixture and the Differences between Energy Levels
It is shown in reference [
38],
Figure 1, that the energy difference
between those for the ground state energy and the first excited state diminishes as
v grow, facilitating mixing.
Diminishing the energy difference between the first excited state and the ground state facilitates mixing in the system due to increased thermal population and enhanced quantum mechanical coupling.
In a system at thermal equilibrium, the population of states is governed by the Gibbs canonical distribution , where is the energy of state i, is the Boltzmann constant, and T is the temperature.
When the energy difference between the ground state and the first excited state decreases, the exponential factor exp() increases. This means that at a given temperature, more particles are thermally excited to the first excited state. Also, there is increased occupancy, as higher thermal population in the first excited state leads to a greater number of particles available to transition between these states, facilitating interactions and mixing. Additionally, the probability of quantum transitions between states depends on the overlap of their wavefunctions and the energy separation. A smaller energy gap can enhance the coupling between the ground state and the first excited state, increasing the transition rate between these states.
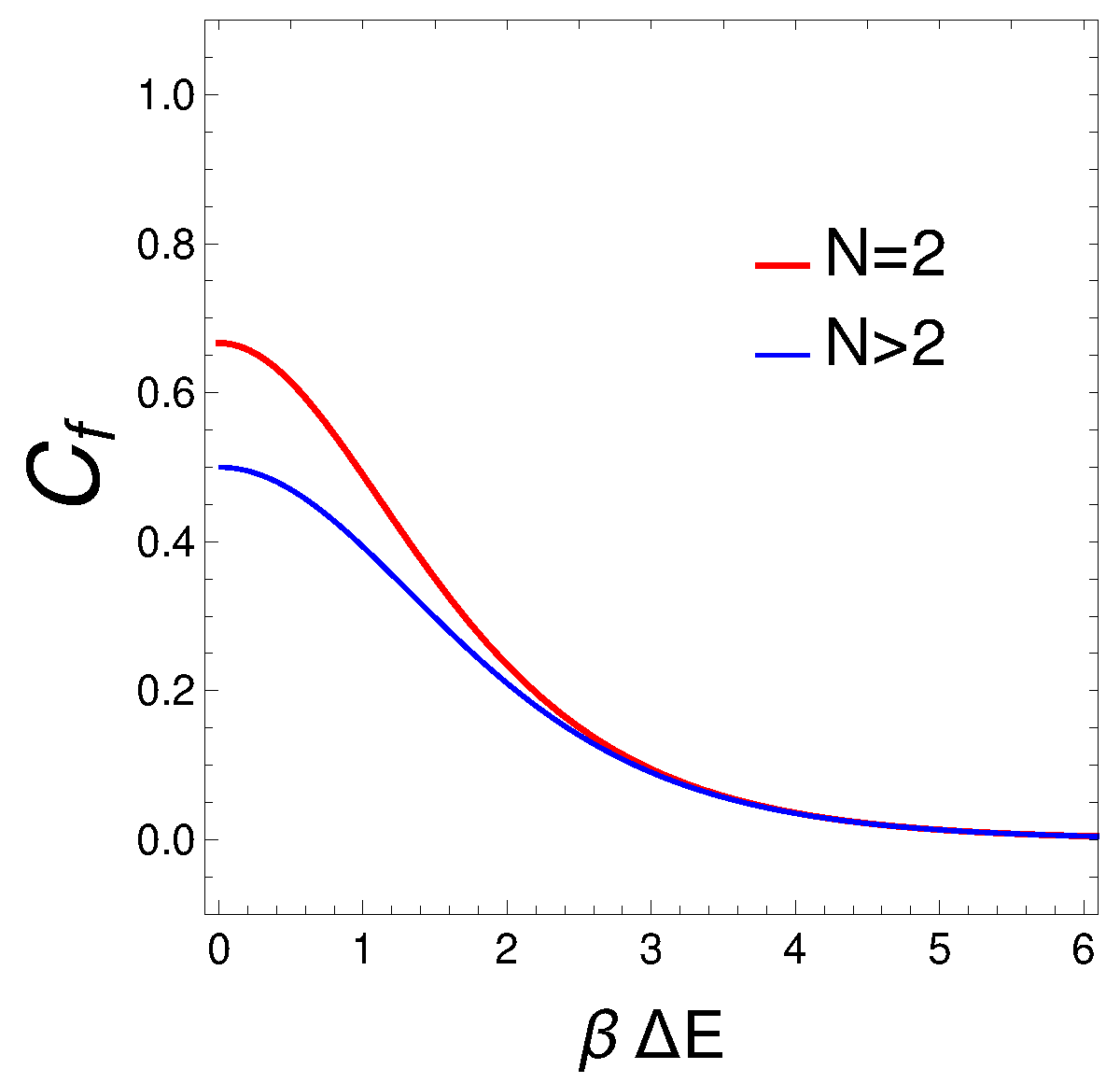
Let us see what happens for , involving diagonalization of a 3 x 3 matrix. We look for an analytical expression for as a function of v and the plot versus vor several values of v.
In diagonalizing the Hamiltonian
for
, the energies are
Accordingly
and
. The states’ probabilitis are
with
. As a consequence we have for
which is plotted in
Figure 7 (
vs ) for several numbers of fermions.
is a special instance. Other various of
N exhibit collapse into a single curve. As expected, the degree of mixing increases as
diminishes.
We can easily think on reasons as why in an interacting many-fermion system the degree of quantum mixing, or mixedness, tends to increase as the separation between energy levels diminishes. This phenomenon can be understood through several interrelated concepts in quantum mechanics and statistical mechanics.
Energy Level Density and Quantum States: As the separation between energy levels decreases, the density of available quantum states increases. When energy levels are closely spaced, fermions have a larger number of states to occupy within a small energy range. This increased state density enhances the probability of transitions between states, leading to greater mixing of quantum states.
Thermal Excitations: At low temperatures, fermions typically occupy the lowest available energy states due to the Pauli exclusion principle. However, as the energy level separation decreases, even small thermal excitations can cause fermions to transition between states. This results in a higher degree of occupation of excited states, contributing to quantum mixing.
Interaction-Induced Mixing: Interactions between fermions can lead to hybridization of states, where the eigenstates of the system become superpositions of non-interacting states. When energy levels are closely spaced, interactions more readily cause mixing because the energy required to couple states is lower. This leads to an increased degree of quantum mixedness as interactions redistribute the fermions among the available states.
Quantum Fluctuations: In systems with closely spaced energy levels, quantum fluctuations become more significant. These fluctuations can induce transitions between states, further enhancing quantum mixing. The reduced energy gap means that even small perturbations (thermal or quantum) can cause changes in the occupation of states.
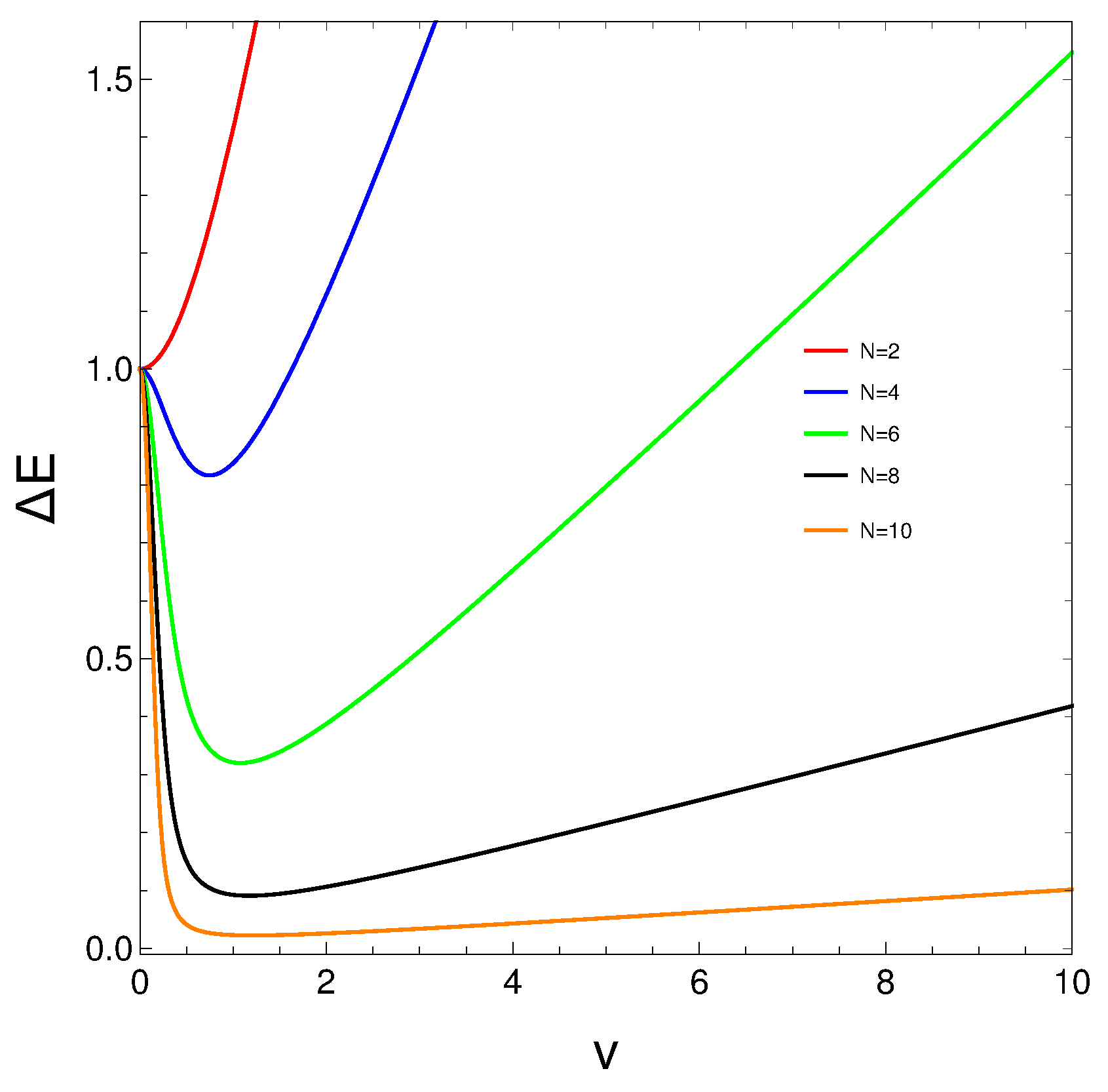
Now, let us take a look at the behavior of vs v for different N-value.
Figure 8.
vs v for different N’s.
Figure 8.
vs v for different N’s.
grows monotonously only for . We detect a local minimum for . The minima features for are clearly N-dependent.
5. Free Energy F vs
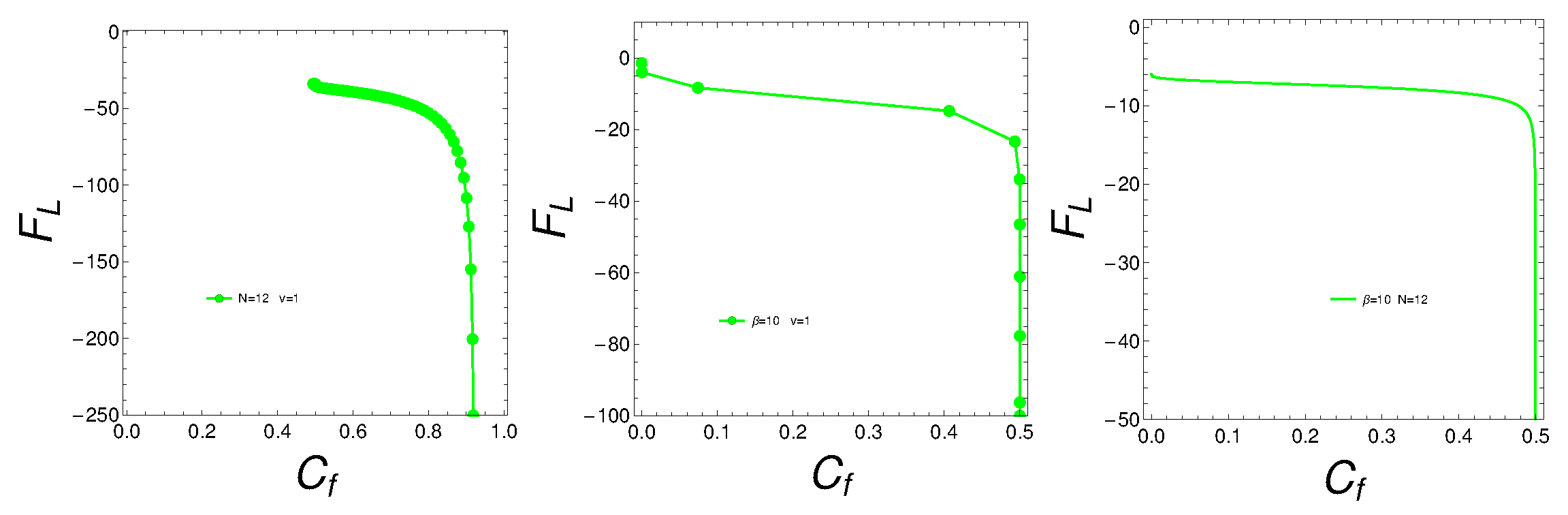
We pass to analyze the free energy behavior in reation to the mixture degree. We plot F vs considering either , N, or v as the varying parameter.
We plot then 1) left: ) vs with and ; 2) center: vs with and ; ) rigth: vs with and .
Figure 9.
vs in variegated conditions described in the text.
Figure 9.
vs in variegated conditions described in the text.
The observation that the free energy becomes more negative with a larger degree of quantum mixture in the Lipkin model can be attributed to increased entropy, lower effective energy, enhanced cooperative effects, and potential phase transitions. These factors collectively lead to a more energetically favorable state as the degree of quantum mixture increases, thus lowering the free energy. See the plots.
The increase in quantum mixing can enhance correlations between particles. When these correlations reach a critical level, the system can reorganize into a more energetically favorable configuration. This reorganization would manifest itself as an abrupt decrease in mean energy. This is what our plot indeed shows. At a mixing of 0.5, the system seems to achieve a state of enhanced quantum coherence, where the superposition of states leads to a lower energy configuration. This coherence can stabilize the system, resulting in a sharp decrease in energy. The abrupt change could signify that the system is reaching an optimal balance between the different quantum states, minimizing energy through constructive interference and optimal state mixing. We next present plots for the man energy and for the entropy, that confirm some assertions made above.
Figure 10.
U y S vs for and several N’s.
Figure 10.
U y S vs for and several N’s.
6. Conclusions
This study elucidates the intricate dynamics of quantum mixing, particle number fluctuations, and temperature variations within the Lipkin model, revealing profound insights into the behavior of many-fermion systems. Our findings underscore several key points:
The degree of quantum mixedness displays a strong dependency on the total number of fermions, highlighting distinct behaviors across different temperature regimes. This emphasizes the importance of considering fermion number in analyzing quantum systems, as it directly influences the system’s mixedness and overall state.
- Remarkably, the observed dependencies of quantum mixedness on fermion number and temperature are robust against variations in the fermion-fermion interaction strength, provided the interaction is non-zero. This robustness suggests that the fundamental properties of quantum mixing are intrinsic to the system’s structure rather than being heavily influenced by interaction specifics.
- The insights gained from this study have potential implications for various fields, including condensed matter physics and quantum information science. Understanding the dependencies and behaviors of quantum degree of mixedness in fermionic systems can inform the development of quantum technologies and enhance the theoretical models used to describe complex quantum systems.
Through a comprehensive numerical exploration of key features of the system we have provided a detailed analysis of the Lipkin model, offering valuable perspectives on the fundamental characteristics of many-fermion systems. Our results contribute to a deeper understanding of quantum phenomena in fermionic systems, paving the way for future research and practical applications in related fields.
Author Contributions
Investigation, D. M., A.P. and A.R.P..; Project administration, A.P.; Writing—original draft, D.M. A.P., and A.R.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by CONICET (Argentine Agency).
Data Availability Statement
Every thing needed is found in the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lipkin, H.J., N. Meshkov, and A.J. Glick. "Validity of many-body approximation methods for a solvable model: (I). Exact solutions and perturbation theory for the N = 3 case." Nuclear Physics, 62 (1965): 188-198. [CrossRef]
- Lipkin, H.J., N. Meshkov, and A.J. Glick. "Validity of many-body approximation methods for a solvable model: (II). Exact solutions and perturbation theory for the N = infinity case." Nuclear Physics, 62 (1965): 199-210.
- Lipkin, H.J., A. Abrikosov, and S. Meshkov. "Validity of many-body approximation methods for a solvable model: (III). Exact solutions and perturbation theory for the N = 2 case." Nuclear Physics, 62 (1965): 211-219.
- Lipkin, H.J., N. Meshkov, and A.J. Glick. "Validity of many-body approximation methods for a solvable model: (IV). Exact solutions and perturbation theory for the N = 1 case." Nuclear Physics, 62 (1965): 220-222.
- Rowe, D.J. "The Lipkin model." Reviews of Modern Physics, 40 (1968): 153-203.
- Schmid, K.W., and A. Bauer. "The Lipkin model." Physics Reports, 88 (1982): 251-334.
- Isacker, P.V., and S. Heinze. "The Lipkin model: a paradigm for a self-consistent theory of shape transitions." Physics Reports, 199 (1991): 67-144.
- Dukelsky, J., et al. "Quantum phase transitions in the Lipkin-Meshkov-Glick model." Reviews of Modern Physics, 76 (2004): 643-655.
- Kusnezov, D., et al. "Lipkin-Meshkov-Glick model, electron-nucleus scattering, and the Kondo problem." Physical Review Letters, 65 (1990): 1304-1307.
- Li, J., et al. "Quantum phase transition and phase diagram in the Lipkin-Meshkov-Glick model." Physical Review B, 95 (2017): 075139.
- I. Bengtsson and K. Zyczkowsi, Geometry of Quantum States: An Introduction to Quantum Entanglement, Cambridge University Press, 2006. [CrossRef]
- G. Jaeger, Qantum information: An Overview, Springer, 2007. [CrossRef]
- D. Giulini, et al., Decoherence and the Appearance of a Classical World in Quantum Theory, Springer, Berlin, 1996; M. Namiki, S. Pascazio, H. Nakazato, Decoherence and Quantum Measurements, World Scientific, Singapore, 1997. [CrossRef]
- P. Facchi, A. Mariano, S. Pascazio, Decoherence versus entropy in neutron interferometry, Phys. Rev. A 63 (2001) 052108. [CrossRef]
- A. R. Plastino, D. Monteoliva, A. Plastino, Information-theoretic features of many fermion systems: an exploration based on exactly solvable models, Entropy 23 (2021) 1488.
- Regine Frank, Quantum criticality and population trapping of fermions by non-equilibrium lattice modulations New Journal of Physics 15 (2013) 123030.
- Andreas Lubatsch and Regine Frank, Evolution of Floquet topological quantum states in driven semiconductors, Eur. Phys. J. B, 92 (2019) 215. [CrossRef]
- D. Otero, A. Proto, A. Plastino, Surprisal Approach to Cold Fission Processes, Physics Letters B 98 (1981) 225. [CrossRef]
- W. Satuła, J. Dobaczewski, W. Nazarewicz, Odd-Even Staggering of Nuclear Masses: Pairing or Shape Effect?, Phys. Rev. Lett. 81 (1998) 3599. [CrossRef]
- T. Dugett, P. Bonche, P. H. Heenen, J. Meyer, Pairing correlations. II. Microscopic analysis of odd-even mass staggering in nuclei, 65 (2001) 014311. [CrossRef]
- P. Ring, P. Schuck, The Nuclear Many-Body Problem (Springer, Berlin, 1980).
- H. Uys, H.G. Miller, F.C. Khanna, Phys. Lett. A, Generalized statistics and high-Tc superconductivity, 289 (2001) 264. [CrossRef]
- M. K. G. Kruse, H. G. Miller, A. R. Plastino, A. Plastino, S. Fujita, Landau-Ginzburg method applied to finite fermion systems: pairing in nuclei, European Journal of Physics A 25 (2005) 339. [CrossRef]
- M. de Llano, V.V. Tolmachev, Multiple phases in a new statistical boson fermion model of superconductivity, Physica A 317 (2003) 546. [CrossRef]
- F. R. Xu, R. Wyss, P. M. Walker, Mean-field and blocking effects on odd-even mass differences and rotational motion of nuclei Phys. Rev. C 60 (1999) 051301(R).
- H. Hakkinen et al., Phys. Rev. Lett., Universal Shapes of Small Fermion Clusters, 78 (1007) 1034. [CrossRef]
- J. Hubbard, Electron Correlations in Narrow Energy Bands. Proceedings of the Royal Society of London. 276 (1365) (1963) 237.
- Y. Liu, Exact solutions to nonlinear Schrodinger equation with variable coefficients Applied Mathematics and Computation 217 (2011) 5866.
- Giampaolo Co, Stefano De Leo, Analytical and numerical analysis of the complete Lipkin–Meshkov–Glick Hamiltonian, Int. J. Mod. Phys. E 27 (2018) 5.
- L. Arrachea, N. Canosa, A. Plastino, M. Portesi, R. Rossignol, Phys. Rev. A, Maximum Entropy Approach to Critical Phenomena in Finite Quantum Systems, 45 (1992) 44 (and references therein).
- S. M. Abecasis, A. Faessler, A. Plastino, Application of the Multi Configuration Hartree-Fock Theory to a Simple Model, Z. Phys. 218 (1969) 394. [CrossRef]
- D. H. Feng, R. G. Gilmore, , Phys. Rev. C 26 (1992) 1244.
- G. Bozzolo, M. C. Cambiaggio, A. Plastino, Maximum Overlap, Atomic Coherent States and the Generator Coordinate Method, Nucl. Phys. A 356 (1981) 48. [CrossRef]
- D. Monteoliva, Angelo Plastino, A. R. Plastino, Statistical Quantifiers Resolve a Nuclear Theory Controversy, Q. Reports 4 (2022) 127. [CrossRef]
- F. Reif, Fundamentals of statistical theoretic and Thermal Physics (McGraw Hill, New York, 1965).
- F. Pennini, A. Plastino, Thermal effects in quantum phase-space distributions, Phys. Lett. A 374 (2010) 1927-1932. [CrossRef]
- Angelo Plastino, Diana Monteoliva, Angel Ricardo Plastino, Quasi-Magical Fermion Numbers and Thermal Many-Body Dynamics, Axioms 12 (2023) 493. [CrossRef]
- M. C. Cambiaggio, A. Klar, F. J. Margetan, A. Plastino, J. P. Vary, Comparison of upper and lower bound methods using a soluble many-Fermion model , Phys. Rev. C 27 (1983) 2340. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).