Prerpints.org logo
Preprint
Article

Optimizing Fatigue Performance in Gradient Structural Steels by Manipulating Grain Size Gradient Rate

Altmetrics

Downloads

93

Views

53

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.zip (114.27KB )

Submitted:

29 May 2024

Posted:

29 May 2024

You are already at the latest version

Alerts
Abstract
As a new type of high-performance material, gradient structural steel is widely used in engineering fields due to its unique microstructure and excellent mechanical properties. For the prevalent fatigue failure problem, the rate of change of the local grain size gradients along the structure (referred to as the gradient rate) is a key parameter in the design of gradient structures, which significantly affects the fatigue performance of gradient structural steel. In this work, a method of ‘Voronoi primary + secondary modeling’ is adopted to successfully establish three typical high-strength steel models corresponding to the convex, linear, and concave type gradient rates for gradient structures, focusing on the stress-strain response and crack propagation in structural steel with different gradient rates under cyclic loading. It is found that the concave gradient rate structural model is dominated by finer grains with larger volume fraction, which is conducive to hindering fatigue crack propagation and has the longest fatigue life; the linear structure is the second one, and the convex structure is the shortest one. The simulation results in this work are consistent with the relevant experimental phenomena. Therefore, when regulating the gradient rate, priority should be given to increasing the volume fraction of fine grains and designing a gradient rate structure dominated by fine grains to improve the fatigue life of the material.
Keywords: 
Subject: Chemistry and Materials Science  -   Materials Science and Technology

1. Introduction

With the development of modern industrial technology, people are increasingly demanding the performance of engineering materials, gradient structural steel as a new type of high-performance material because of its unique microstructure and excellent mechanical properties has attracted widespread attention in the scientific research community [1,2]. Its internal grain size from one side to the other is a continuous change, forming unique ‘gradient’ characteristics [3,4,5,6], this characteristic directly affects the strength, plastic toughness, and fatigue properties of the material [7,8,9,10]. Among them, grain size gradient is one of the most common types of gradient-structured metallic materials [11,12].
According to statistics, more than 90% of metallic engineering materials fail due to fatigue [13,14]. Generated by surface induction [15,16], shot peening [17,18,19], heat treatment [20], mechanical grinding [21], and pre-deformation [22] can form gradient layers on material surfaces with thicknesses ranging from hundreds of nanometers to several millimeters. These surface gradient layers effectively reduce the incidence of surface damage, suppressing the failure behavior of materials and enhancing their fatigue properties. Since Fang et al. [8] first reported the preparation of gradient nano-grained (GNG) Cu through surface mechanical grinding treatment (SMGT), a series of related studies have shown that gradient structures enable materials to exhibit better combinations of strength and toughness [23,24,25], as well as improved fatigue resistance [26,27] and wear resistance [28]. Ding et al. [29] prepared grain size gradient Inconel 718 alloy using SMGT. Jiang et al. [5] prepared grain size gradient Inconel 718 alloy by ultrasonic surface rolling treatment (USRP). Theoretical models such as the low-cycle fatigue crack propagation model [30]; finite element simulation studies such as the results of Tilbrook [31], Zeng [25], Wang [32], Luo [26], and others reveal that gradient materials play an important role in crack propagation behavior, fatigue fracture characteristics, etc. Li and Soh [33] simulated the strengthening effect of samples containing tens of nanometres to tens of micrometers of grains by using the finite element method. Wu et al. [28] studied the deformation mechanism of gradient materials, and found that the grain size gradient under uniaxial stretching produces a macroscopic strain gradient due to the evolution of incompatible deformation along the depth of the gradient, which transforms the applied uniaxial stress into a multiaxial one, leading to a large number of dislocations accumulating and interacting with each other, and generating additional strain hardening.
In particular, the rate of change of the local grain size gradients along the structure (referred to as the gradient rate) is an important parameter describing the trend of grain size change [11], and in the process of gradient structure construction, different processing methods and different degrees of treatment can significantly affect the gradient rate of the structure. The concept of gradient rate makes it possible to quantitatively describe the relationship between the gradient structure and the mechanical properties of materials and also lays the foundation for a deeper understanding of the mechanisms related to gradient-structured metallic materials. Lin et al. [34] prepared pure Ni samples with gradient structure by electrodeposition technique and precisely controlled the grain size gradient to obtain the optimal grain size distribution, resulting in yield strength and uniform elongation superior to the coarse crystalline Ni. Wang et al. [32] demonstrated that the grain size gradient structure could improve the yield strength of the material without reducing its flexibility. As a key parameter in the design of gradient structures, the gradient rate delicately balances the distribution pattern of strength and toughness, so it is hoped that the gradient rate in the design of gradient structures can be used to more accurately control the fatigue crack initiation and extension, thus enhancing the reliability and durability of the materials under long-term service conditions.
However, although existing studies have revealed the positive effect of gradient structure on fatigue performance, there is still insufficient understanding of how gradient rate precisely regulates the fatigue life, crack initiation threshold, and cyclic deformation behavior, which undoubtedly constitutes a technological bottleneck restricting the further optimization and industrialization of its application [35,36]. Furthermore, with no sophisticated methods for controlling gradient rates [34], researchers urgently need to conduct more systematic and in-depth research to reveal the intrinsic law between the gradient rate and the key properties of gradient structural steel, establish accurate performance prediction models, and explore efficient and economical preparation processes to achieve precise control of gradient structure [37].
Therefore, this work establishes three-types of models of gradient structural steel under different gradient rates and simulates the stress-strain response and crack propagation behavior under fatigue loading by means of the finite element method. It is for the sake of systematically investigating the intrinsic connection between the gradient rate and the fatigue performance of gradient structural steel, further revealing the regulation strategy for the strength-toughness of gradient structural materials, and providing theoretical support for achieving the engineering of gradient structural materials for directional and the improvement of fatigue life of high-strength structural steel.

2. Materials and Methods

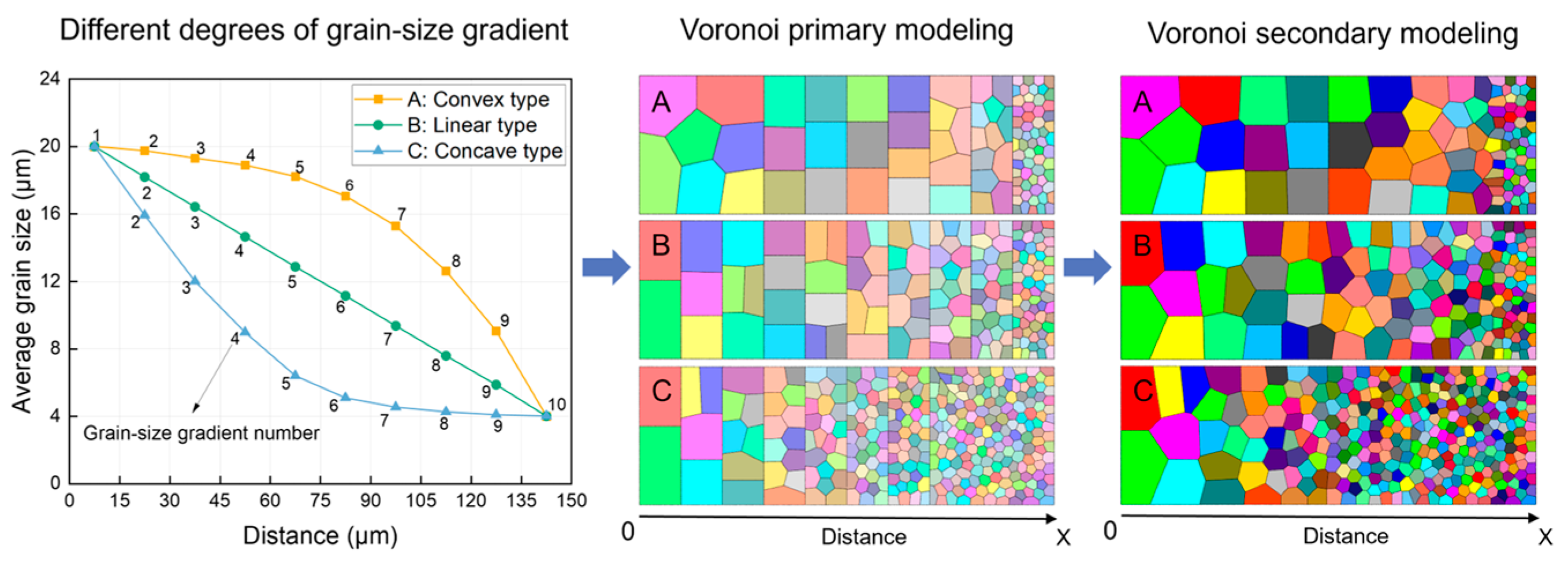
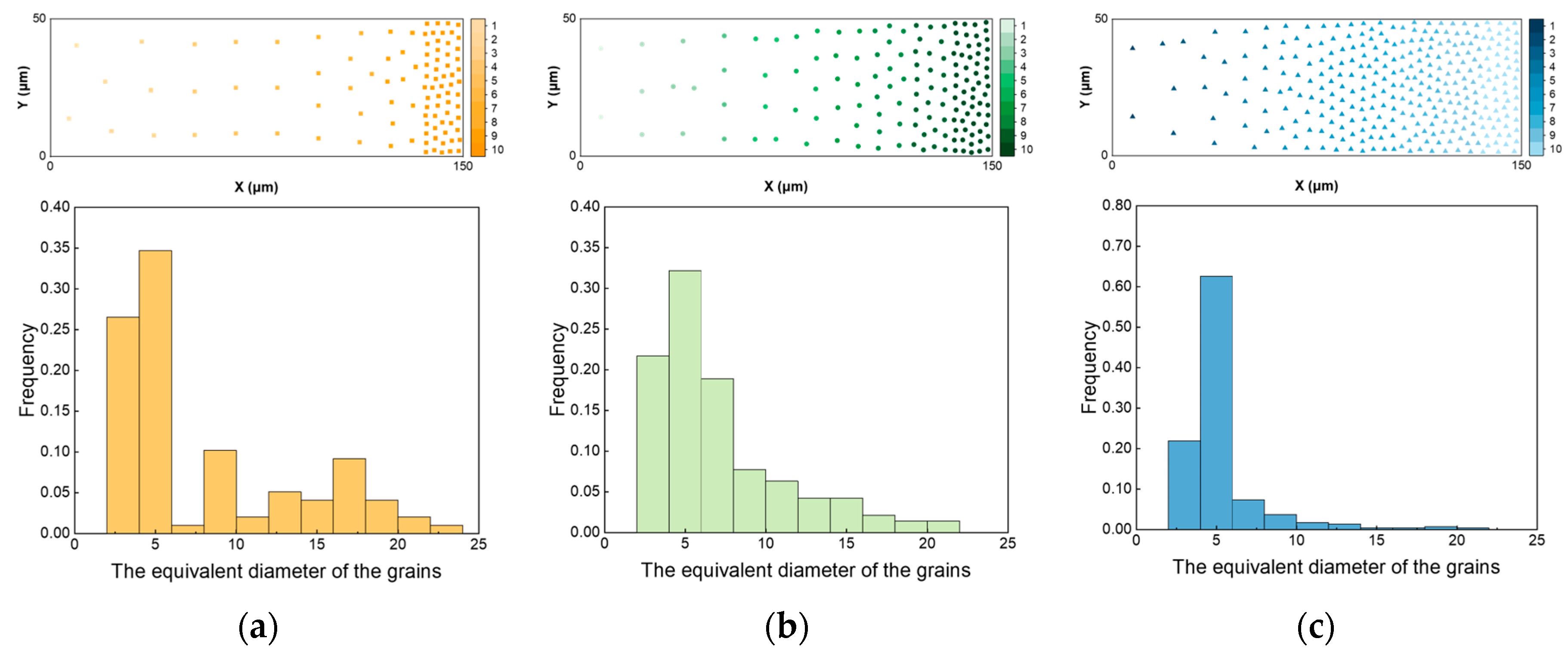
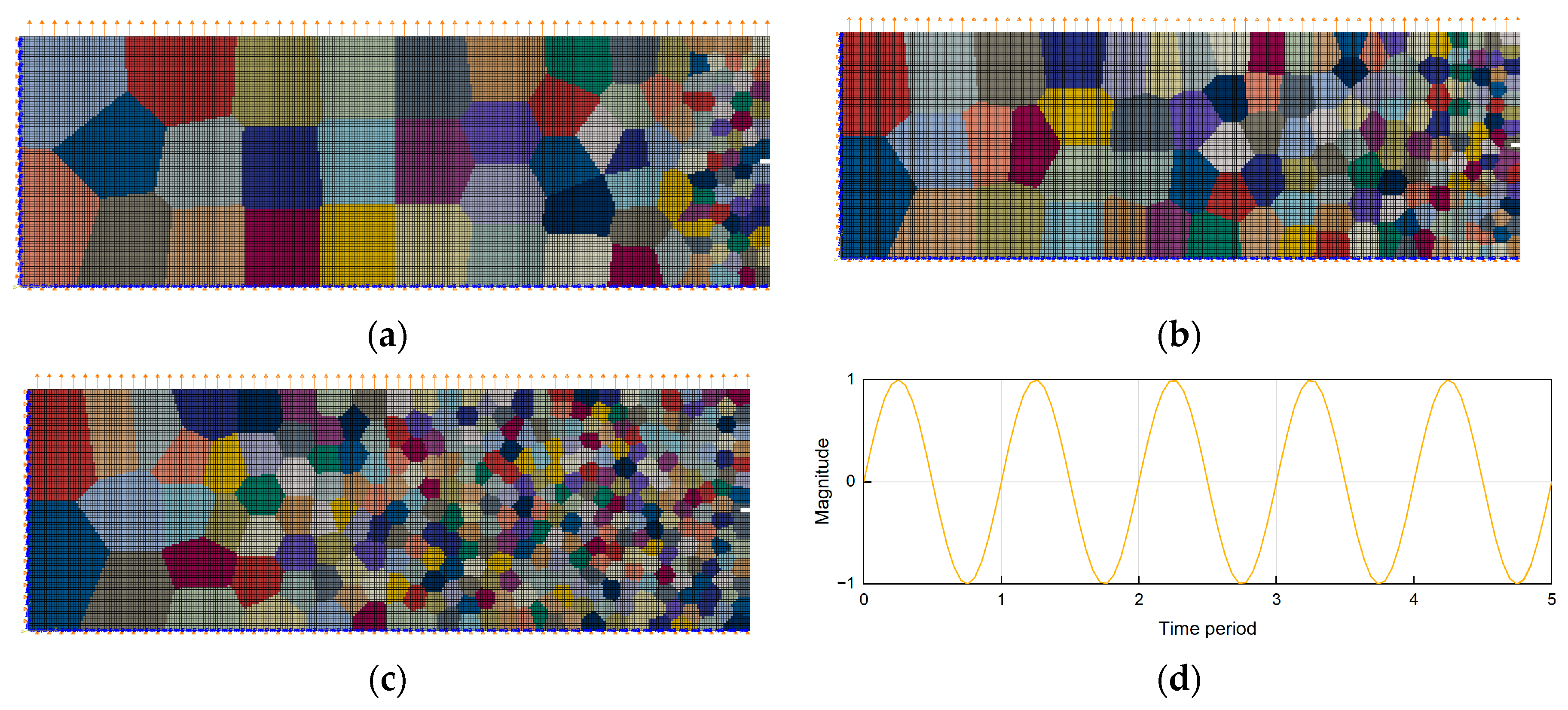
2.1. Three-Types of Gradient Rate Polycrystalline Models

This work focuses on a typical high-strength structural steel (Chinese grade Q690, 0.12C-2.24Mn-0.26Si-0.07Cr-0.05Nb-0.02Ni) with a yield strength of 690 MPa, tensile strength of 734 MPa, and fracture elongation of 15.4%. Table 1 lists the data obtained by the uniaxial tensile test of Q690 steel [38].
Typically, gradient rates consist of three types, namely convex (A), linear (B), and concave (C) type. Figure 1 shows a schematic of the position of the three-types of grain size gradients along the horizontal X direction. The maximum and minimum grain sizes remain constant under different circumstances, while the distribution of grain sizes varies greatly. Among them, the grain size change of gradient A is first flat and then steep, resulting in a larger volume fraction of coarse grains. The grain size change of gradient B is approximately constant, and the distribution of coarse-grained and fine-grained grains is relatively uniform. The grain size change of gradient C is steep and then flat, resulting in a greater volume fraction of fine grains (i.e., hard phase).
In this work, the "Voronoi primary + secondary modeling" method is used to construct a gradient polycrystalline geometry model with different gradient rates, and the Neper software [39] is open-source. Firstly, ten data points were taken on each of the three-types of gradient rate curves, and ten equal intervals (15k × 50k, scale bar k = actual structure size/model size, and k is a non-zero constant ) were used to compare in the simulated region (150k × 50k). The number of grains in each interval is converted according to the gradient rate in Figure 1, and then the coordinates of the gradient polycrystalline seed centroid of ten intervals are output, which is called the Voronoi primary modeling process. Next, the centroid coordinate file was used as a new input file, and Neper's Voronoi algorithm was used to model the whole region to obtain a two-dimensional gradient polycrystalline geometry model with a continuous gradient change in grain size, which was called the Voronoi secondary modeling process.
Through the above method, three-types of gradient polycrystalline models corresponding to different gradient rates can be constructed, as shown in Figure 1, the two-dimensional gradient structure geometry model along the X and Y directions are 150 μm and 50 μm. The total grain number of the three-types of gradient models is 98, 143, and 302, respectively, and the grain size varies from 20 μm to 4 μm. In addition, the meshing type is quadrilateral elements, the length of the grid edge is 0.5, and the total number of grids is 30, 000. Figure 2 shows the distribution of gradient polycrystalline seeds (top) and the equivalent grain size (bottom) for the three-types of gradient models.

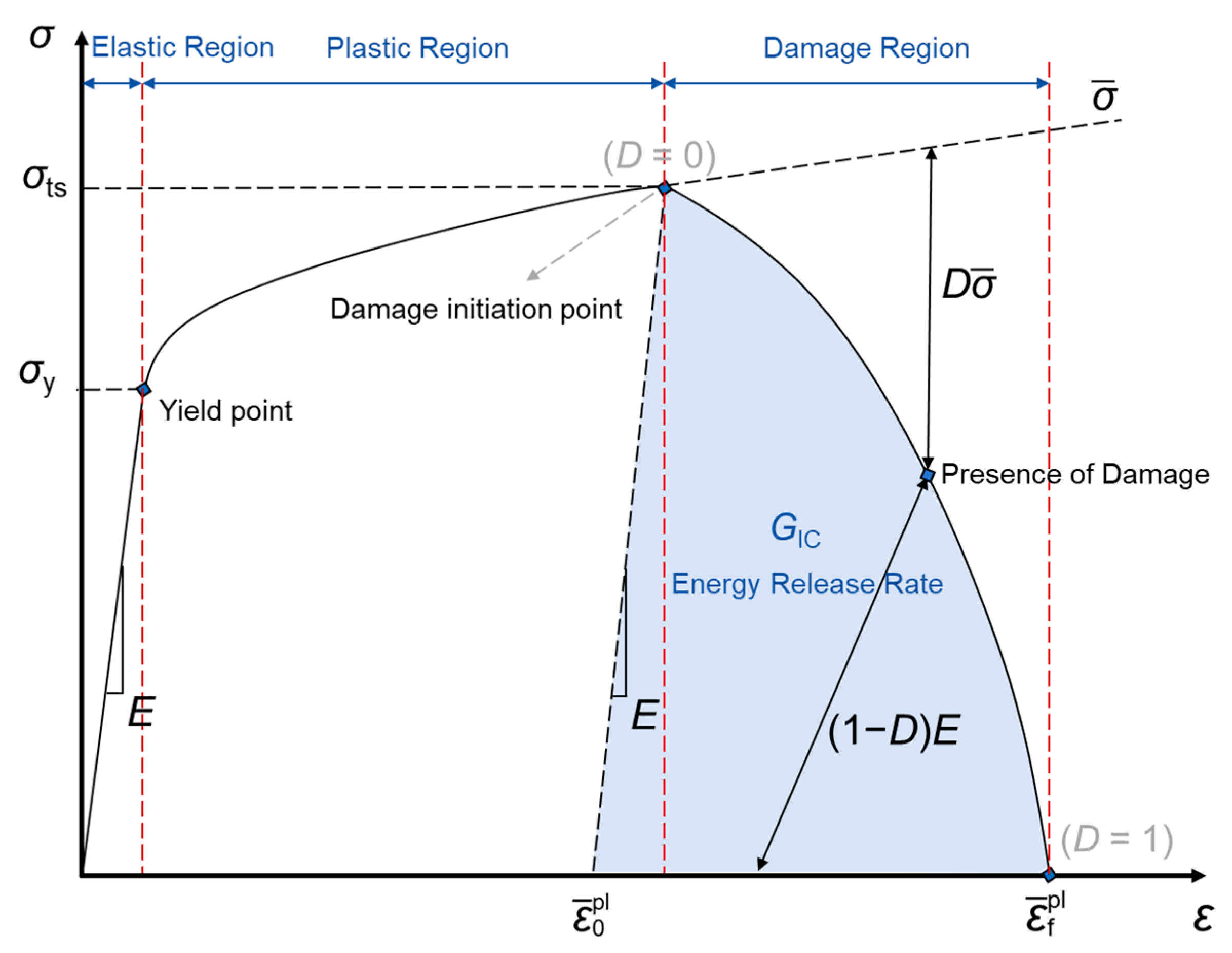
2.2. Elastoplastic and Damage Constitutive Equation

For the three-types of gradient models, we need to specify the elastic and hardening behavior of the gradient grains, respectively. In the present work, the modulus of elasticity is 207.0 GPa, the Poisson's ratio is 0.3, and the density of steel is 7.8 g/cm3 [40].
In addition, we can reasonably set the average size and yield strength of all grains in the model following the Hall-Petch equation [32,41]:
σ y = σ y 0 + k y d - 1 2
where σy is the yield strength of the material with an average grain size of d, σy0 is the constant related to the material itself, ky is the Hall-Petch coefficient (here the value of 632.456 MPa·μm1/2 [41]). In this work, when σy = 690.00 MPa, σy0 = 548.58 MPa. From this, σy0 and σy for different average grain sizes in the model can be calculated. Note that the term average grain size refers to the local values of grain sizes in the gradient microstructure. The regions in which these local grain sizes are evaluated are indicated by the numbers in Figure 1.
To simplify the model, and further assume that the tensile strength of the material is also dependent on the grain size, the tensile strength of the individual grains is assigned by a specific equation [32,41]:
σ ts = σ ts 0 + k y d - 1 2
where σts is the tensile strength, σts0 is the constant related to the material itself, ky is the Hall-Petch coefficient, and d is the average grain size. Similar to Equation (1), the σts0 and σts corresponding to the different average grain sizes in the model can be obtained.
Combined with the parameters listed in Equation (1) and Equation (2) above, the engineering tensile stress-strain curves of three-types of gradient rate structures (Figure 2a~c) can be obtained.
These engineering stress-strain curves are converted to true stress-strain curves by Equation (3) and Equation (4) [40]:
σ true = σ eng ( ε eng + 1 )
ε true = ln ( ε eng + 1 )
The engineering stress σeng and engineering strain εeng are converted into the true stress σtrue and the true strain εtrue, to obtain the corresponding true strain-stress curve, as shown in Figure 3d~f, and each sub-figure contains ten separate curves, some of which are very close to each other. The global stress-strain values (Table S1 and S2 in the Supplementary Materials) have been obtained by calculating the yield strength and tensile strength of different grains based on the Hall-Petch equation, thus assigning different material parameters to different gradient grains according to grain size.
In order to describe the material degradation during plastic deformation, a damage model has been employed in this work. For the sake of generality, this work choose the ductile damage evolution model embedded in Abaqus software as the damage constitutive model of the material. The damage evolution of elastoplastic materials includes the reduction of the flow stress and the degradation of elasticity, and the characteristic stress-strain behavior of the ductile metal subjected to damage is shown in Figure 4, where the solid black line represents the damaged stress-strain curve and the dashed line above the solid line represents the curve without damage. In Figure 4, E is the elastic modulus of the material, σy is the yield strength of the material, σts is the tensile strength of the material, and the stress of the material when it is damaged, ε - 0 p l is the equivalent plastic strain at the time of damage, and ε - f p l is the equivalent plastic strain at failure, i.e., when the overall damage variable reaches D = 1 [42]. The damage constitutive model specifies at least four ductile damage parameters, including stress triaxiality, fracture strain, strain rate, and fracture energy. In this work, the triaxiality of stress is taken as 0.33, the strain rate is taken as 0.00, and the formula for calculating the fracture energy [42]:
Gf = GIC × l
where Gf is the fracture energy, GIC is the area of the shaded blue part in Figure 4, the physical meaning is the critical energy release rate, l is the characteristic edge length of the element, and for the 2D model, l is the edge length of the mesh, i.e. l = 0.5. The main ductile damage parameters (the fracture strain and fracture energy) for three-types of gradient rate structures are shown in Table S3.

2.3. Pre-Processing and Abaqus/Explicit Calculation Method

The gradient models shown in Figure 1 have been imported into the commercial finite element package Abaqus in a pre-processing step. To simulate the conditions of uniaxial fatigue suited boundary conditions have been applied, where the nodes at the bottom and the left side have been fixed and the load is applied to the nodes on the top surface of the model, see Figure 5 a~c. The initial load amplitude is set to 500.00 MPa, which is converted into a displacement-controlled loading amplitude of 0.12 μm, resulting in a tension-compression amplitude ratio of R = −1, see Figure 5 d for a schematic diagram of the load amplitude. The nodes on the right-hand side, where the smallest grains are situated, are free of boundary conditions, mimicking the free surface of the material. Since the initial crack in the actual microstructure usually originates in this fine-grained region of the surface of the material, an initial microcrack is prefabricated at the center of the right end of the model to study the crack propagation behavior in the different microstructures. By comparing the fatigue crack propagation behavior in different gradient rate models, the optimal strategy to design a gradient rate for maximum fatigue performance of gradient materials is derived.
Based on the established gradient structure model under different gradient rates, the display analysis solver in Abaqus software. The single cycle length of the models is 1 second, and the total loading time set for the simulation is 200 seconds. At the same time, using reasonable quality scaling (quality scaling factor set to 1000, target time increment set to 0.0001) and time scaling (64-core parallel computation), a single case can be completed in 10-15 minutes to efficiently analyze the influence of gradient rate on the stress-strain response and fatigue crack propagation behavior.

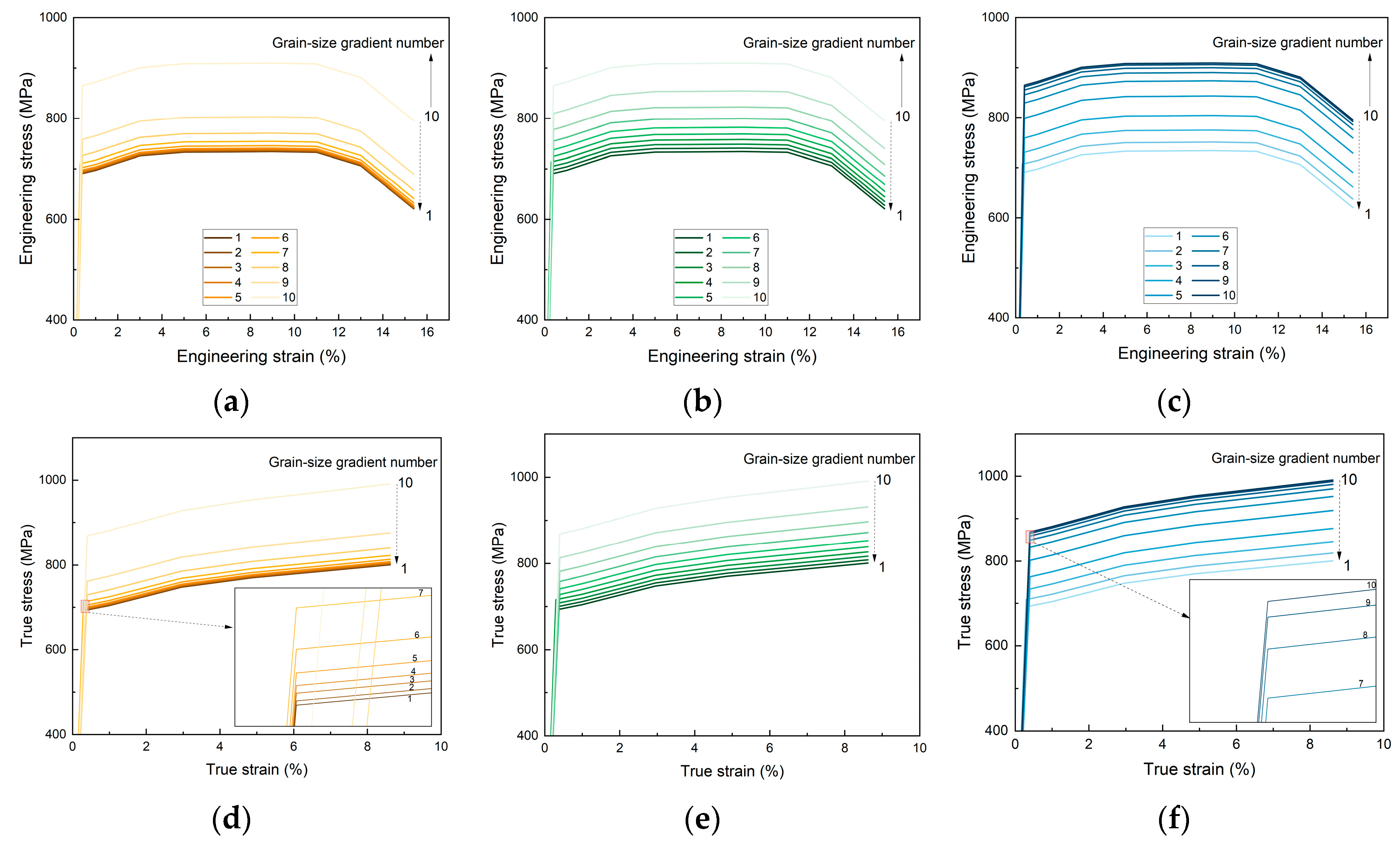
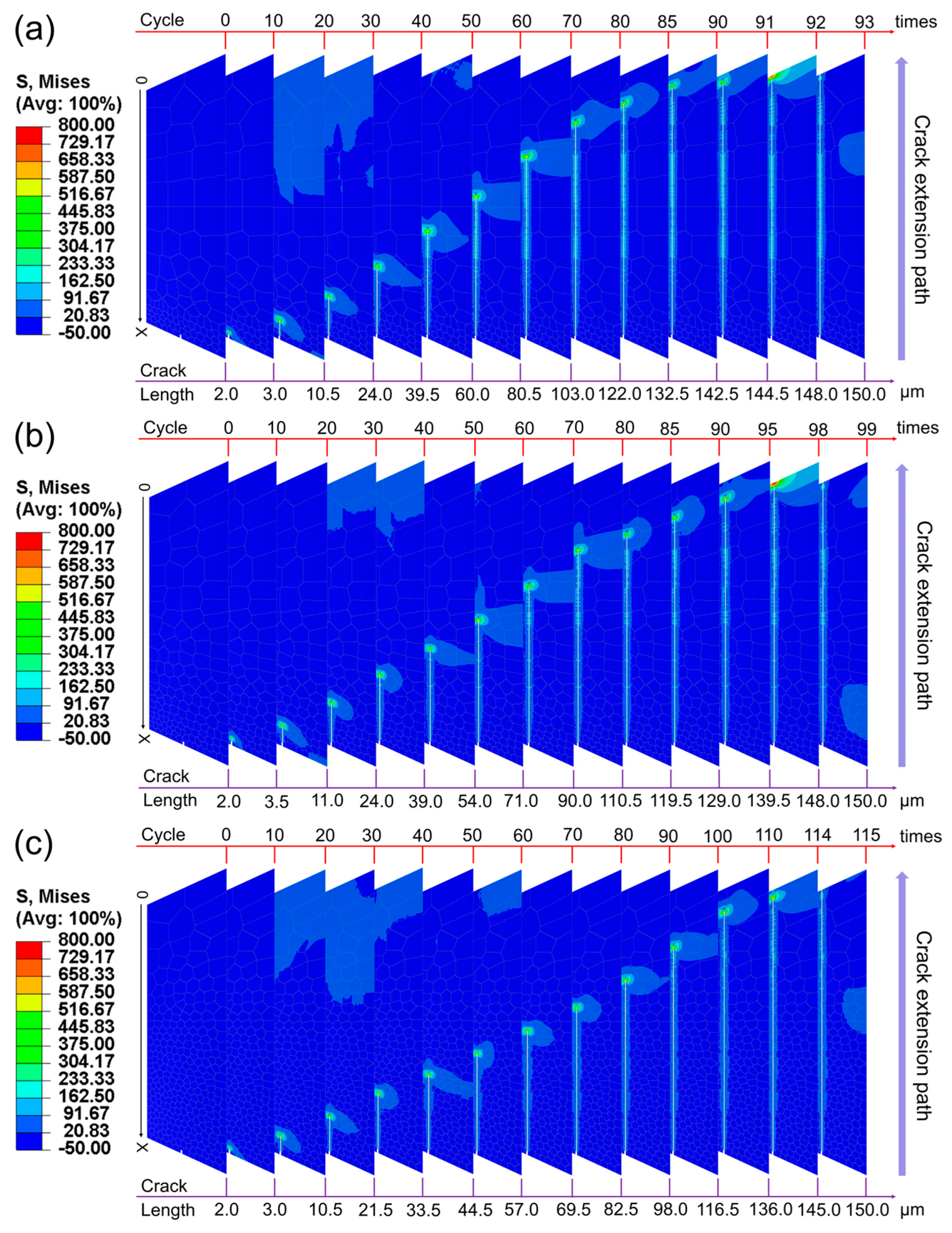
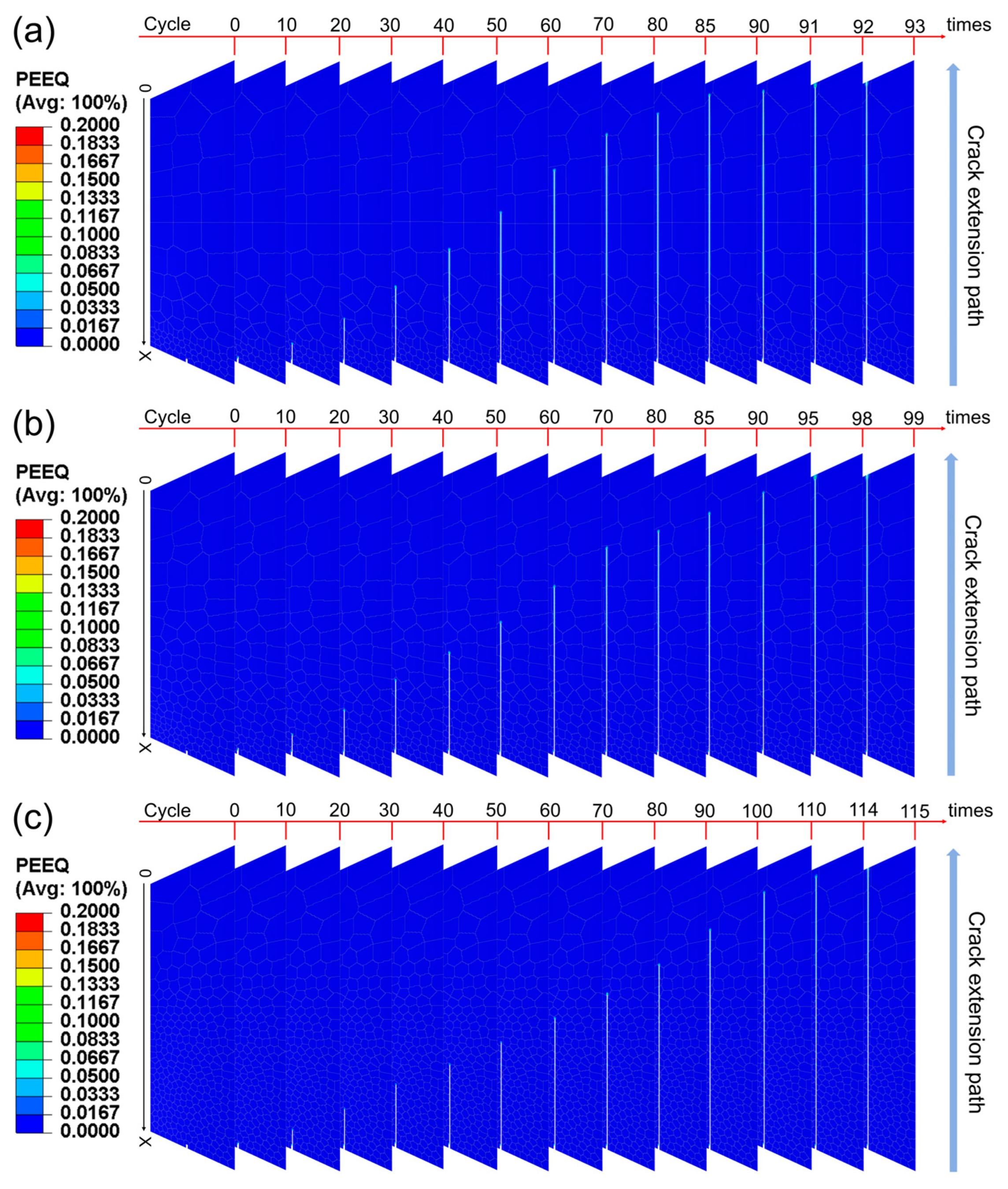
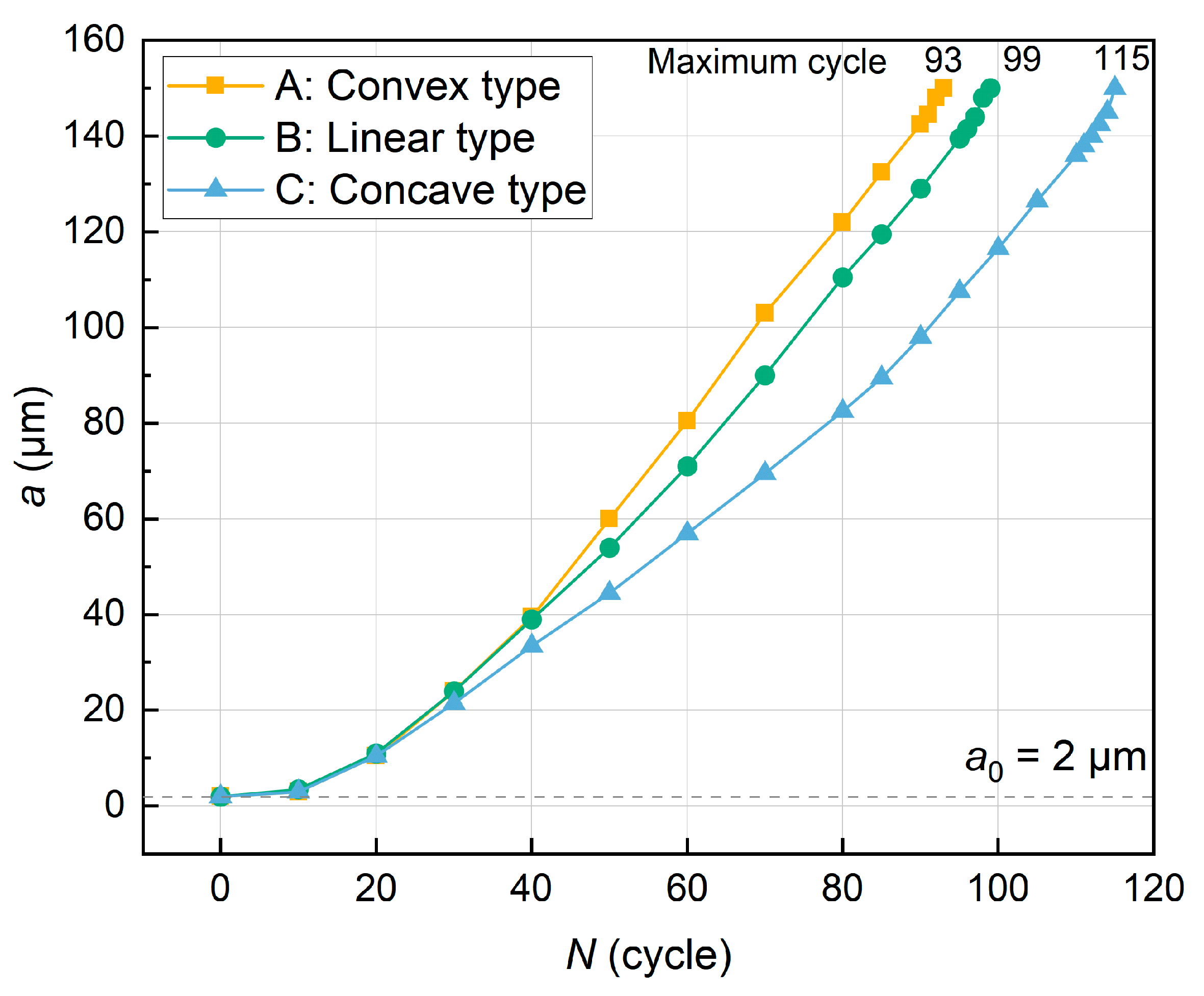
3. Results

By performing the finite element simulations under cyclic loading on the gradient structure high-strength steel models corresponding to three-types of gradient rates, the Mises stress values and equivalent plastic strain values under different loading cycles and the crack propagation length are obtained. Figure 6 and Figure 7 show the Mises stress and equivalent plastic strain (PEEQ) result contours for different gradient models, respectively, and the cycle numbers of different stages and their crack propagation lengths are marked in the diagrams to visually demonstrate the crack propagation process. The Mises stress varies from -50 MPa to 800 MPa in the contours with a more obvious change, and the equivalent plastic strain in the contours varies from 0 to 0.2 with a less obvious change.

4. Discussion

As can be seen from Figure 6 and Figure 7, as the number of load cycles increases, the crack propagates from the initial position in the direction perpendicular to the normal stress until a certain critical point is reached, and the crack completely penetrates the entire model, indicating that the material has completely failed. It is worth noting that even at the same cycle, the length of crack propagation in each gradient rate model shows significant differences. This phenomenon reveals the direct effect of the non-uniform variation of grain size and its spatial distribution on the crack propagation rate in the gradient structure. Hanlon et al. [43] investigated the effect of grain size on the fatigue response of nanocrystalline metals and found that an increase in grain size usually leads to a decrease in the fatigue endurance limit due to mechanisms such as periodic deflection of the fatigue crack path at grain boundaries during crystallographic fracture. In this work, the gradient distribution of grain size not only determines the mechanical properties of the local microzone but also regulates the stress field and strain energy release path at the crack tip at the relatively macroscopic level, significantly affecting the dynamic behavior of crack propagation.
In order to further reveal the quantitative relationship between crack propagation and the number of cycles, a graph of the variation of crack propagation length with the number of cycles was drawn based on the simulated data, as shown in Figure 8.
Figure 8 clearly shows the significant differences in fatigue life between the three-types of gradient structures. The C-type (concave type) gradient structure showed the most superior fatigue durability, with the slowest crack propagation rate and the longest fatigue life, while the B-type (linear type) structure was the second, and the A-type (convex type) structure had the shortest fatigue life. It is reasonable to infer that the C-type gradient structure has a stronger effect in inhibiting fatigue crack propagation.
An in-depth comparison of the A-type and C-type gradient structures shows that although the grain size of the coarsest grains and the finest grains are the same, the difference in gradient rate will still cause a large difference in the uniaxial tensile mechanical properties of the gradient structure materials. The coarse grains in the A-type structure have a relatively high integration number and show relatively weak yield strength and excellent plastic deformation ability. The C-type structure is dominated by fine grains with large volume fractions and shows stronger yield strength. This comparison reveals the importance of fine grain volume fraction in the grain size gradient structure to regulate the fatigue life of high-strength steels. Wang et al. [11] also specified that fine grains can withstand higher stress loading and coarse grains can carry more plastic deformation. Specifically, the wide presence and uniform distribution of fine grains in the C-type gradient structure can effectively hinder the initiation and propagation of fatigue cracks, and delay the energy accumulation and release process at the crack front by increasing the tortuosity of the crack path, enhancing the dislocation interaction, and improving the local plastic deformation ability, thereby significantly improving the fatigue life of the material. Conversely, A-type structures, although they have a higher potential for plastic deformation, result in lower yield strength and shortest fatigue life due to the high volume fraction of their coarse grains.
As for the B-type structure, the gradient rate of fine and coarse grains in the structure changes less, the grain size change transition is more uniform, and the volume fraction of coarse and fine grains is uniform, so the plasticity of the structure remains unchanged while increasing the strength. Compared with the A-type structure with poor performance and the C-type structure with high preparation difficulty, the B-type gradient structure can take into account the performance and preparation cost to a certain extent.
Next, the propagation behavior of fatigue cracks is further analyzed according to the Paris equation [44], which establishes the relationship between the stress intensity factor and crack propagation rate. It is the basis for predicting the fatigue crack propagation life theory in today's engineering applications, and it takes the form of:
da/dN = C (∆K)m
where a is the crack length, N is the number of stress cycles, da/dN is the crack propagation rate, ∆K is the amplitude of the stress intensity factor, C and m are the material constants, and environmental factors such as temperature, humidity, medium, loading frequency, etc. are implicit in the constants, which can be obtained by fitting the experimental data.
The stress intensity factor K and the stress intensity factor amplitude ∆K are expressed as [40]:
K = f σ π a  
Δ K = K max   - K min = f σ max π a   - f σ min π a = Δ f σ π a  
where σmax and σmin are the maximum stress and minimum stress, respectively, and the difference between the two is the stress amplitude ∆σ, f is the correction coefficient related to the geometry and size of the crack body, the load mode and the boundary conditions, etc., for the central crack wide plate f = 1, for the unilateral crack wide plate f = 1.12 [40].
Taking the common logarithm on both sides of Equation (6), the relationship between the fatigue crack propagation rate da/dN and the amplitude of the stress intensity factor ∆K can be obtained as follows:
lg(da/dN) = mlg(∆K) + lgC
However, the data obtained from the fatigue crack propagation simulation are the crack length a and the number of cycles N, so the appropriate data processing method must be used to calculate (da/dN)i and the corresponding (∆K)i. The double logarithmic coordinates were used for regression fitting, then the lg(da/dN)−lg(∆K) relationship curve and the m and C values of the material constant were obtained. The secant method used in this work is a simple and fast method for processing data, which is suitable for calculating the slope of a straight line connecting two adjacent data points on an a-N curve, which is calculated as [40]:
d a / d N a - = a i + 1   - a i / N i + 1 - N i
where d a / d N a - is the average rate of the increment (ai+1 - ai), so it is necessary to calculate the value of (∆K)i by substituting the average crack length a - = a i + 1   +   a i   /   2 into Equation (8). The derived (da/dN)i and the corresponding (∆K)i are plotted as shown in Figure 9a, Figure 9b shows the three sets of data points and their results after linear fitting based on the calculations in Equation (6)~(10), and the Paris equation for fatigue crack propagation for the three-types of gradient rate models are summarised in Table 2.
From the fitting results of Figure 10, it can be seen that the crack propagation rate of A-type structure is lower than that of B-type structure in the initial stage, and when a certain critical value is reached, the crack propagation rate completely exceeds that of B-type structure, while the crack propagation rate of type structure has always maintained the lowest crack propagation rate in this simulation due to the wide distribution of fine grains and its effective suppression of crack propagation, which verifies its high efficiency in inhibiting fatigue damage. As for whether there is a critical value between the B-type structure and the C-type structure, it is not possible to determine the value in this simulation, and it is necessary to further study the influence of coarse-grained integration number and fine-grained size to obtain the optimal critical coarse-grained grain volume fraction and critical fine-grained grain size.
Experiments have shown that different gradient distributions correspond to different proportions of fine grains (hard phase) and coarse grains (soft phase), and the interactions between the layers result in completely different mechanical properties [45]. Huang et al. [46] experimentally found that compared with the coarse-grained (CG) samples, the fatigue strength of SMRT (surface mechanical rolling treatment) samples was significantly enhanced in both low-cycle and high-cycle fatigue states, and the fatigue strength increased by 33% compared to that of the CG sample. Wang et al. [47] prepared gradient layers that showed a reduction in surface layer strength from 1600 MPa to about 400 MPa, with a corresponding increase in tensile ductility from 2% to 13%. In this work, the maximum fatigue life of the C-type gradient structure is increased by 23.66% compared with the A-type gradient structure, and 16.16% compared with the B-type structure. The C-type structure exhibits higher yield strength and tensile strength, while the change of plastic strain is smaller, which is the main reason for improved fatigue properties.

5. Conclusions

In this work, three models of high-strength steels with different types of gradient microstructures have been investigated under cyclic loading to quantify the effect of different gradient rates on the fatigue properties of the material. The corresponding types of microstructures gradients different in the gradient rate changed, where convex, linear, and concave type gradient rate models have been established. Comparing the stress-strain response and crack propagation in different gradient rate models, it is found that the concave gradient structure model is dominated by fine grains with a larger volume fraction, which is conducive to hindering the propagation of fatigue cracks and results in the longest fatigue life. In contrast, the convex type structure has a high plastic deformation potential, but the coarse grain volume fraction is higher, resulting in lower yield strength and the shortest fatigue life. The linear gradient structure has a better match between strength and plasticity, and the fatigue life is in between the other cases. When designing and controlling the gradient rate, priority should be given to increasing the volume fraction of fine grains, that is, selecting a concave gradient rate structure dominated by fine grains, to obtain structural materials with longer fatigue life. The computational simulation results in this study are consistent with the relevant experimental phenomena, and further show that structural materials with better fatigue properties can be obtained by adjusting the gradient rate in the gradient structure.
The findings of this work not only deepen the understanding of the fatigue mechanism of gradient structural materials, but also provide ideas and strategies for the design of engineering materials with higher durability, especially in those application scenarios that need to withstand cyclic loading for a long time, such as aerospace, bridge construction, and energy facilities.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Table S1: Engineering stress-strain data for three-types of gradient rate models; Table S2: True stress-strain data for three-types of gradient rate models; Table S3: The ductile damage parameters for three-types of gradient rate models.

Author Contributions

Simulation, Data curation, Writing—original draft, M.P.; Methodology, Investigation, Data curation, X.C., and M.H.; Writing—review & editing, Supervision, Y.K., and Y.D.; Methodology, Investigation, Conceptualization, A.H.; Software, Conceptualization, Results review, Writing—review, X.Z.; Supervision, Funding acquisition, Project administration, Conceptualization, Y.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (Grant Numbers: 52331002, 52101029, 52201010), and the Funds for International Cooperation and Exchange of the National Natural Science Foundation of China (Grant No. 51820105001).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

Yuling Liu and Yong Du are grateful for the backing of the State Key Laboratory of Powder Metallurgy from the Central South University of China. The authors would like to acknowledge the High-Performance Computing Center of Central South University and the Hefei Advanced Computing Center for assistance with computations.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Ji, W.M.; Zhou, R.H.; Vivegananthan, P.; Wu, M.S.; Gao, H.J.; Zhou, K. Recent progress in gradient-structured metals and alloys. Prog. Mater Sci. 2023, 140. [CrossRef]
  2. Wang, X.; Zhang, C.H.; Cui, X.; Zhang, S.; Chen, J.; Zhang, J.B. Novel gradient alloy steel with quasi-continuous ratios fabricated by SLM: Material microstructure and wear mechanism. Mater. Charact. 2021, 174, 111020. [CrossRef]
  3. Han, J.C.; Xu, L.; Wang, B.L.; Zhang, X.H. Progress and prospects of functional gradient materials. J. Solid. Rocket. Techno. 2004, 27, 207-215.
  4. Zhu, Y.T.; Wu, X.L. Heterostructured materials. Prog. Mater Sci. 2023, 131, 101019. [CrossRef]
  5. Jiang, W.; Xu, P.; Li, Y.; Wang, H.; Cai, Z.; Li, J.; Liang, Y.; Liang, Y. Effect of a gradient structure on the mechanical performance of Inconel 718 Ni-based superalloy at elevated temperatures. J. Mater. Res. Technol. 2023, 23, 2031-2042. [CrossRef]
  6. Cheng, Z.; Bu, L.; Zhang, Y.; Wu, H.; Zhu, T.; Gao, H.; Lu, L. Unraveling the origin of extra strengthening in gradient nanotwinned metals. Proceedings of the National Academy of Sciences 2022, 119, e2116808119. [CrossRef]
  7. Lu, K. Making strong nanomaterials ductile with gradients. Science 2014, 345, 1455-1456. [CrossRef]
  8. Fang, T.H.; Li, W.L.; Tao, N.R.; Lu, K. Revealing Extraordinary Intrinsic Tensile Plasticity in Gradient Nano-Grained Copper. Science 2011, 331, 1587-1590. [CrossRef]
  9. Ma, Z.W.; Liu, J.B.; Wang, G.; Wang, H.T.; Wei, Y.J.; Gao, H.J. Strength gradient enhances fatigue resistance of steels. Sci. Rep. 2016, 6, 22156. [CrossRef]
  10. Li, X.; Lu, L.; Li, J.; Zhang, X.; Gao, H. Mechanical properties and deformation mechanisms of gradient nanostructured metals and alloys. Nat. Rev. Mater. 2020, 5, 706-723. [CrossRef]
  11. Wang, Y. Numerical investigations on strengthening-toughening and failure mechanisms of metallic materials with gradient structure. PhD Dissertation, Beijing Jiaotong University, Beijing, 2019.
  12. Shuai, L.; Yinlei, G.; Dongdong, L.; Ziyue, L.; Yunli, F.; Fucheng, Z. Unusual grain-size effects on tensile deformation behavior of twinning-induced plasticity steel with low Mn content. J. Mater. Res. Technol. 2023, 24, 586-594. [CrossRef]
  13. Suresh, S. Fatigue of materials; Cambridge University Press: Cambridge, England, 1998.
  14. Fujii, T.; Muhamad Azmi, M.S.B.; Tohgo, K.; Shimamura, Y. Influence of Strain Gradient on Fatigue Life of Carbon Steel for Pressure Vessels in Low-Cycle and High-Cycle Fatigue Regimes. Materials 2022, 15, 445. [CrossRef]
  15. Zerbst, U.; Klinger, C.; Klingbeil, D. Structural assessment of railway axles–A critical review. Eng. Fail. Anal. 2013, 35, 54-65. [CrossRef]
  16. Liu, Z.P.; Zhang, H.X.; Yan, Z.F.; Dong, P. Enhanced fatigue performance of aluminum alloy through surface strengthening treatment. Mater. Lett. 2022, 306, 130864. [CrossRef]
  17. Liu, W.; Wu, G.; Zhai, C.; Ding, W.; Korsunsky, A.M. Grain refinement and fatigue strengthening mechanisms in as-extruded Mg–6Zn–0.5 Zr and Mg–10Gd–3Y–0.5 Zr magnesium alloys by shot peening. Int. J. Plast. 2013, 49, 16-35. [CrossRef]
  18. Pandey, V.; Chattopadhyay, K.; Santhi Srinivas, N.C.; Singh, V. Low Cycle Fatigue behavior of AA7075 with surface gradient structure produced by Ultrasonic Shot Peening. Procedia Struct. Integrity 2016, 2, 3288-3295. [CrossRef]
  19. Bagheri, S.; Guagliano, M. Review of shot peening processes to obtain nanocrystalline surfaces in metal alloys. Surf. Eng. 2009, 25, 3-14. [CrossRef]
  20. Li, W.; Tao, N.R.; Lu, K. Fabrication of a gradient nano-micro-structured surface layer on bulk copper by means of a surface mechanical grinding treatment. Scr. Mater. 2008, 59, 546-549. [CrossRef]
  21. Ke, L.; Jian, L. Surface nanocrystallization (SNC) of metallic materials-presentation of the concept behind a new approach. Journal of Materials Sciences and Technology 1999, 15, 193-197.
  22. Wei, Y.J.; Li, Y.Q.; Zhu, L.C.; Liu, Y.; Lei, X.Q.; Wang, G.; Wu, Y.X.; Mi, Z.L.; Liu, J.B.; Wang, H.T.; et al. Evading the strength–ductility trade-off dilemma in steel through gradient hierarchical nanotwins. Nat. Commun. 2014, 5, 3580. [CrossRef]
  23. Lin, Y.; Yu, Q.; Pan, J.; Duan, F.H.; Ritchie, R.O.; Li, Y. On the impact toughness of gradient-structured metals. Acta Mater. 2020, 193, 125-137. [CrossRef]
  24. Lu, K. Gradient nanostructured materials. Acta Metall Sin 2015, 51, 1-10. [CrossRef]
  25. Zeng, Z.; Li, X.Y.; Xu, D.S.; Lu, L.; Gao, H.J.; Zhu, T. Gradient plasticity in gradient nano-grained metals. Extreme Mech. Lett. 2016, 8, 213-219. [CrossRef]
  26. Luo, X.K.; Wang, Y.M.; Dang, N.; Tian, K.; Wang, K.; Zhao, C.L.; Zha, X.H.; Wang, X.; Yu, Y. Gradient microstructure and foreign-object-damaged fatigue properties of Ti6Al4V titanium alloy processed by the laser shock peening and subsequent shot peening. Mater. Sci. Eng., A 2022, 849, 143398. [CrossRef]
  27. Yang, M.X.; Li, R.G.; Jiang, P.; Yuan, F.P.; Wang, Y.D.; Zhu, Y.T.; Wu, X.L. Residual stress provides significant strengthening and ductility in gradient structured materials. Mater. Res. Lett. 2019, 7, 433-438. [CrossRef]
  28. Wu, X.L.; Jiang, P.; Chen, L.; Yuan, F.P.; Zhu, Y.T. Extraordinary strain hardening by gradient structure. Proc. Natl. Acad. Sci. U.S.A. 2014, 111, 7197-7201. [CrossRef]
  29. Ding, J.; Xue, S.; Shang, Z.; Li, J.; Zhang, Y.; Su, R.; Niu, T.; Wang, H.; Zhang, X. Characterization of precipitation in gradient Inconel 718 superalloy. Materials Science and Engineering: A 2021, 804, 140718. [CrossRef]
  30. Shao, C.W.; Zhang, X.Q.; Zhao, S.; Zhu, Y.K.; Yang, H.J.; Tian, Y.Z.; Zhang, Z.Z.; Zhang, P.; An, X.H.; Zhang, Z.F. Fatigue-resistant design in low-cycle regime by regulating the micro-structural gradient in a TWIP steel: Modelling and experiment. Int. J. Plast. 2022, 159, 103471. [CrossRef]
  31. Tilbrook, M.T.; Moon, R.J.; Hoffman, M. Finite element simulations of crack propagation in functionally graded materials under flexural loading. Eng. Fract. Mech. 2005, 72, 2444-2467. [CrossRef]
  32. Wang, Y.; Yang, G.; Wang, W.; Wang, X.; Li, Q.; Wei, Y. Optimal stress and deformation partition in gradient materials for better strength and tensile ductility: A numerical investigation. Sci. Rep. 2017, 7, 10954. [CrossRef]
  33. Li, J.; Soh, A.K. Modeling of the plastic deformation of nanostructured materials with grain size gradient. Int. J. Plast. 2012, 39, 88-102. [CrossRef]
  34. Lin, Y.; Pan, J.; Zhou, H.F.; Gao, H.J.; Li, Y. Mechanical properties and optimal grain size distribution profile of gradient grained nickel. Acta Mater. 2018, 153, 279-289. [CrossRef]
  35. Zhang, H.; Wu, S.; Ao, N.; Zhang, J.; Li, H.; Zhou, L.; Xu, P.; Su, Y. Fatigue crack non-propagation behavior of a gradient steel structure from induction hardened railway axles. Int. J. Fatigue 2023, 166, 107296. [CrossRef]
  36. Zhang, S.J.; Xie, J.J.; Jiang, Q.Q.; Zhang, X.L.; Sun, C.Q.; Hong, Y.S. Fatigue crack growth behavior in gradient microstructure of hardened surface layer for an axle steel. Mater. Sci. Eng., A 2017, 700, 66-74. [CrossRef]
  37. Du, Y.; Schmid-Fetzer, R.; Wang, J.C.; Liu, S.H.; Wang, J.C.; Jin, Z.P. Computational Design of Engineering Materials: Fundamentals and Case Studies; Cambridge University Press: Cambridge, England, 2023. [CrossRef]
  38. Wang, X.; Xiang, Y.X.; Zhu, W.J.; Ding, T.T.; Li, H.Y. Damage assessment in Q690 high strength structural steel using nonlinear Lamb waves. Constr. Build. Mater. 2020, 234, 117384. [CrossRef]
  39. Quey, R.; Kasemer, M. The Neper/FEPX Project: Free/Open-source Polycrystal Generation, Deformation Simulation, and Post-processing. IOP Conf. Ser.: Mater. Sci. Eng. 2022, 1249, 012021. [CrossRef]
  40. Bedford, A.; Liechti, K.M. Mechanics of materials; Springer Nature: Cham, Switzerland, 2019. [CrossRef]
  41. Seok, M.Y.; Choi, I.C.; Moon, J.; Kim, S.; Ramamurty, U.; Jang, J.-i. Estimation of the Hall–Petch strengthening coefficient of steels through nanoindentation. Scr. Mater. 2014, 87, 49-52. [CrossRef]
  42. Wagner, R. ABAQUS Tutorial: Damage for Ductile Metals–Material Model Explained–Ductile Damage. Available online: https://www.researchgate.net/publication/350124892 (accessed on 17 March 2021).
  43. Hanlon, T.; Kwon, Y.N.; Suresh, S. Grain size effects on the fatigue response of nanocrystalline metals. Scr. Mater. 2003, 49, 675-680. [CrossRef]
  44. Paris, P.C.; Marines-Garcia, I.; Hertzberg, R.; Donald, J.K. The relationship of effective stress intensity, elastic modulus and Burgers-vector on fatigue crack growth as associated with “fish eye” gigacycle fatigue phenomena. Proceedings of VHCF-3, Kyoto, Japan 2004, 1-13.
  45. Li, Y. Research Progress on Gradient Metallic Materials. Materials China 2016, 35, 658-665.
  46. Huang, H.W.; Wang, Z.B.; Lu, J.; Lu, K. Fatigue behaviors of AISI 316L stainless steel with a gradient nanostructured surface layer. Acta Mater. 2015, 87, 150-160. [CrossRef]
  47. Wang, Y.; Yuan, L.C.; Zhang, S.J.; Sun, C.Q.; Wang, W.J.; Yang, G.X.; Li, Q.; Wei, Y.J. The influence of combined gradient structure with residual stress on crack-growth behavior in medium carbon steel. Eng. Fract. Mech. 2019, 209, 369-381. [CrossRef]
Preprints 107767 g001
Figure 1. Schematic diagram of the modeling process of gradient polycrystalline models at the three-types of grain size gradient rates.
Figure 1. Schematic diagram of the modeling process of gradient polycrystalline models at the three-types of grain size gradient rates.
Preprints 107767 g001
Preprints 107767 g002
Figure 2. Schematic diagram of random distribution and grain size distribution in gradient polycrystalline seed intervals: (a) grain seed distribution (top) and particle size distribution (bottom) in the convex gradient rate model; (b) grain seed distribution (top) and particle size distribution (bottom) in the linear gradient rate model; (c) grain seed distribution (top) and particle size distribution (bottom) in the concave gradient rate model.
Figure 2. Schematic diagram of random distribution and grain size distribution in gradient polycrystalline seed intervals: (a) grain seed distribution (top) and particle size distribution (bottom) in the convex gradient rate model; (b) grain seed distribution (top) and particle size distribution (bottom) in the linear gradient rate model; (c) grain seed distribution (top) and particle size distribution (bottom) in the concave gradient rate model.
Preprints 107767 g002
Preprints 107767 g003
Figure 3. Engineering stress-strain curves and true stress-strain curves of materials: (a) the engineering stress-strain curves of materials in the convex gradient rate model; (b) the engineering stress-strain curves of materials in the linear gradient rate model; (c) the engineering stress-strain curves of materials in the concave gradient rate model; (d) the true stress-strain curves of materials in the convex gradient rate model; (e) the true stress-strain curves of materials in the linear gradient rate model; (f) the true stress-strain curves of materials in the concave gradient rate model.
Figure 3. Engineering stress-strain curves and true stress-strain curves of materials: (a) the engineering stress-strain curves of materials in the convex gradient rate model; (b) the engineering stress-strain curves of materials in the linear gradient rate model; (c) the engineering stress-strain curves of materials in the concave gradient rate model; (d) the true stress-strain curves of materials in the convex gradient rate model; (e) the true stress-strain curves of materials in the linear gradient rate model; (f) the true stress-strain curves of materials in the concave gradient rate model.
Preprints 107767 g003
Preprints 107767 g004
Figure 4. Stress-strain curves with progressive damage degradation.
Figure 4. Stress-strain curves with progressive damage degradation.
Preprints 107767 g004
Preprints 107767 g005
Figure 5. Schematic diagram of the model after applying boundary conditions and cyclic loads in Abaqus software: (a) the convex gradient rate model; (b) the linear gradient rate model; (c) the concave gradient rate model; (d) schematic diagram of the cyclic load amplitude curve applied to the model.
Figure 5. Schematic diagram of the model after applying boundary conditions and cyclic loads in Abaqus software: (a) the convex gradient rate model; (b) the linear gradient rate model; (c) the concave gradient rate model; (d) schematic diagram of the cyclic load amplitude curve applied to the model.
Preprints 107767 g005
Preprints 107767 g006
Figure 6. Figure 6. Mises stress results under cyclic loading for the three-types of gradient rate models: (a) the convex gradient rate model; (b) the linear gradient rate model; (c) the concave gradient rate model.
Figure 6. Figure 6. Mises stress results under cyclic loading for the three-types of gradient rate models: (a) the convex gradient rate model; (b) the linear gradient rate model; (c) the concave gradient rate model.
Preprints 107767 g006
Preprints 107767 g007
Figure 7. Equivalent plastic strain results under cyclic loading for three-types of gradient rate models: (a) the convex gradient rate model; (b) the linear gradient rate model; (c) the concave gradient rate model.
Figure 7. Equivalent plastic strain results under cyclic loading for three-types of gradient rate models: (a) the convex gradient rate model; (b) the linear gradient rate model; (c) the concave gradient rate model.
Preprints 107767 g007
Preprints 107767 g008
Figure 8. Fatigue life curves of three-types of gradient models under cyclic loads: curve A belongs to the convex gradient rate model, curve B belongs to the linear gradient rate model, and curve C belongs to the concave gradient rate model.
Figure 8. Fatigue life curves of three-types of gradient models under cyclic loads: curve A belongs to the convex gradient rate model, curve B belongs to the linear gradient rate model, and curve C belongs to the concave gradient rate model.
Preprints 107767 g008
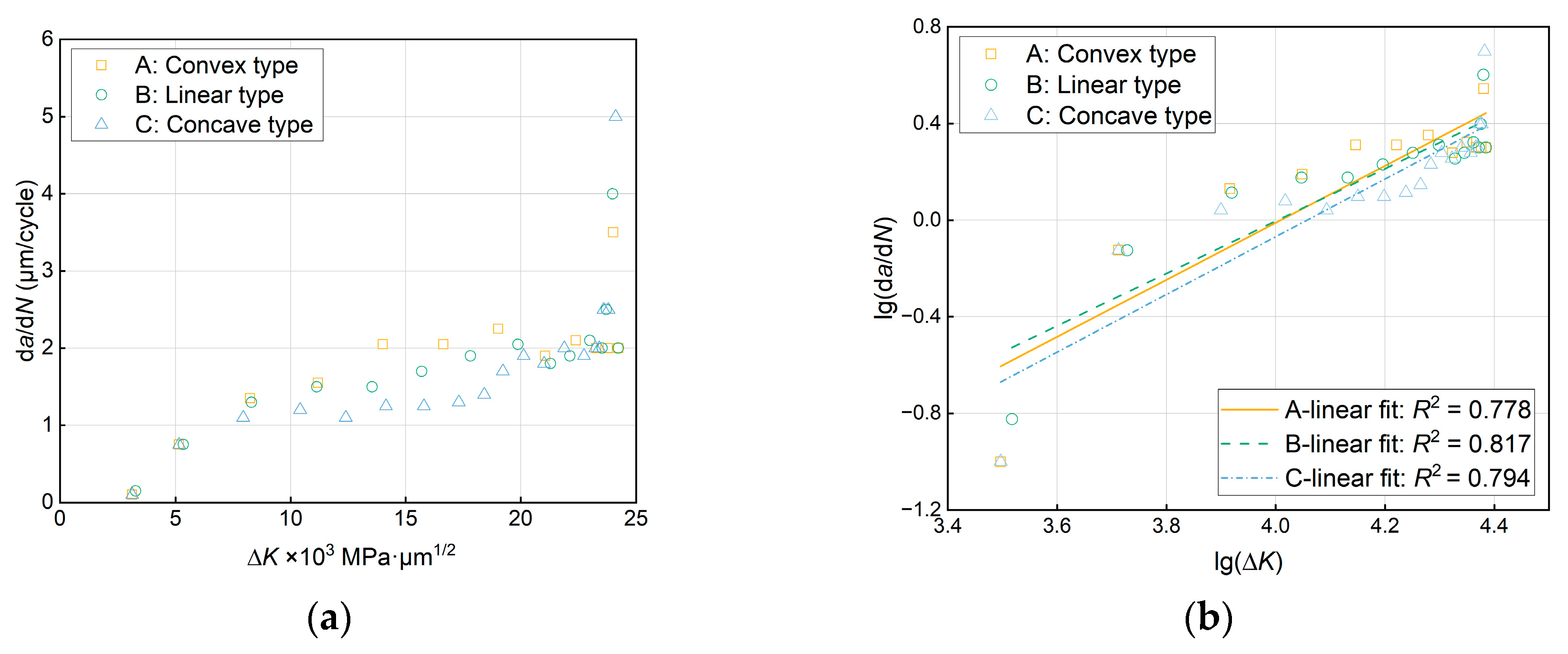
Preprints 107767 g009
Figure 9. Fatigue data scatter and fitting results: (a) data scatter of fatigue crack propagation rate da/dN and stress intensity factor amplitude ∆K; (b) data scatter and linear fitting results of double logarithmic lg(da/dN) and lg(∆K).
Figure 9. Fatigue data scatter and fitting results: (a) data scatter of fatigue crack propagation rate da/dN and stress intensity factor amplitude ∆K; (b) data scatter and linear fitting results of double logarithmic lg(da/dN) and lg(∆K).
Preprints 107767 g009
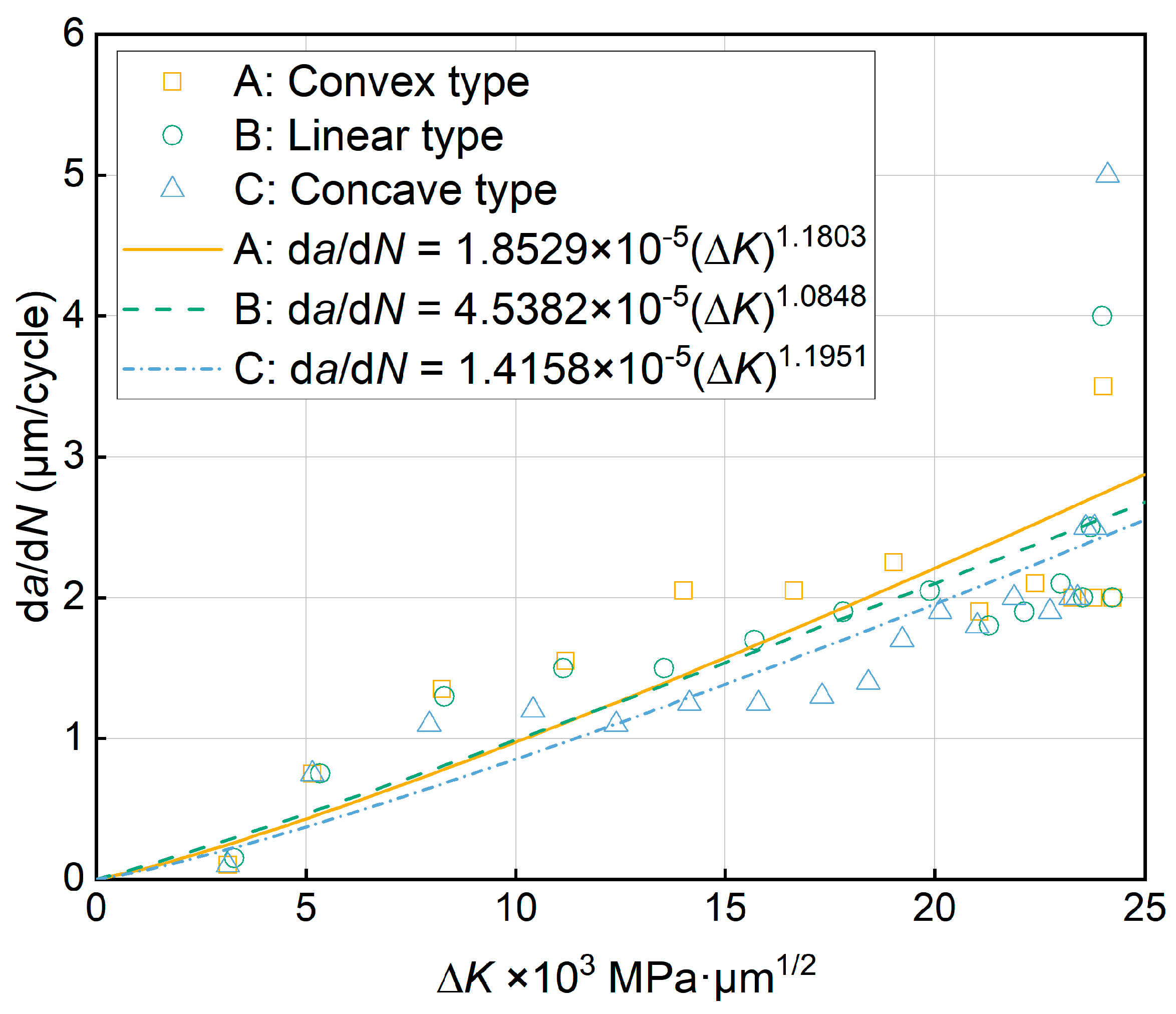
Preprints 107767 g010
Figure 10. Fitting curves of fatigue crack propagation rate da/dN and stress intensity factor amplitude ∆K.
Figure 10. Fitting curves of fatigue crack propagation rate da/dN and stress intensity factor amplitude ∆K.
Preprints 107767 g010
Table 1. The specific engineering stress-strain value of each tensile point [38].
Table 1. The specific engineering stress-strain value of each tensile point [38].
Point 1 2 3 4 5 6 7 8 9
Strain 0.10 0.20 0.30 0.50 0.70 0.90 0.11 0.13 0.15
Stress (MPa) 697.35 711.81 725.91 733.34 733.85 734.45 732.95 706.23 620.81
Table 2. Fitting results of three-grouped data points based on the secant method.
Table 2. Fitting results of three-grouped data points based on the secant method.
Model m lgC C R2
A 1.1803 -4.7322 1.8529×10-5 0.778
B 1.0848 -4.3431 4.5382×10-5 0.817
C 1.1951 -4.8490 1.4158×10-5 0.794
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated