Preprint

Communication

Creation of the Remote Spin Entanglement with a Nanomechanical Cantilever

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Vladimir I. Tsifrinovich^*

This version is not peer-reviewed

Submitted:

28 May 2024

Posted:

30 May 2024

You are already at the latest version

Alerts

Abstract

We consider creation of entanglement between the remote electron spins using a magnetic nanoparticle attached to a cantilever tip (CT). We assume that the frequency of the CT vibrations matches the Larmor frequency of the spin (the CT-spin resonance). In the conditions of the CT-spin resonance the CT-spin system is described by the exactly solvable Jaynes-Kummings model. In this work using the evolution operator of the Jaynes-Kummings model we show that a movable CT can create an entangled state between the remote spins. The most striking result is that the entanglement between the remote spins can be achieved without measurement of the vibrational state of the CT.

Keywords:

Subject: Physical Sciences - Applied Physics

1. Introduction

Entanglement between the remote particles is, probably, the most spectacular phenomenon in quantum physics. Since publication of the seminal article of Einstein, Podolsky, and Rosen [1] this phenomenon attracts unrelenting attention of physicists and general public. Today remote entanglement represents not only a deep philosophical meaning but also a profound practical importance. As an example, entanglement between the remote electron spins could be used for development secure quantum communication and quantum internet (see, for example a recent review [2]).

In this work we consider creation of the remote spin entanglement using a movable nanomechanical cantilever with the magnetic nanoparticle at the canteliver tip (CT). It was shown recently [3-5] that the Larmor frequency of the electron spin could be reduced to the fundamental frequency of the cantilever vibrations (the CT frequency). This situation was called the CT-spin resonance. It was shown that in the conditions of the CT-spin resonance the evolution of the CT-spin system is described by the exactly solvable Jaynes-Cummings model [6,7].

We use the evolution operator of the Jaynes-Cummings model to describe the creation of entanglement between the remote spins using the CT-spin resonance. To the best of our knowledge the entanglement between the remote qubits is always achieved by the measurement of the state of an intermediate object, e.g. the state of a photon which initially interacts with the first spin and later with the second spin (see, for rexample, [2]). We show that in our case, where the intermediate object is the CT, the entanglement can be created without measurement of the CT state.

2. Results

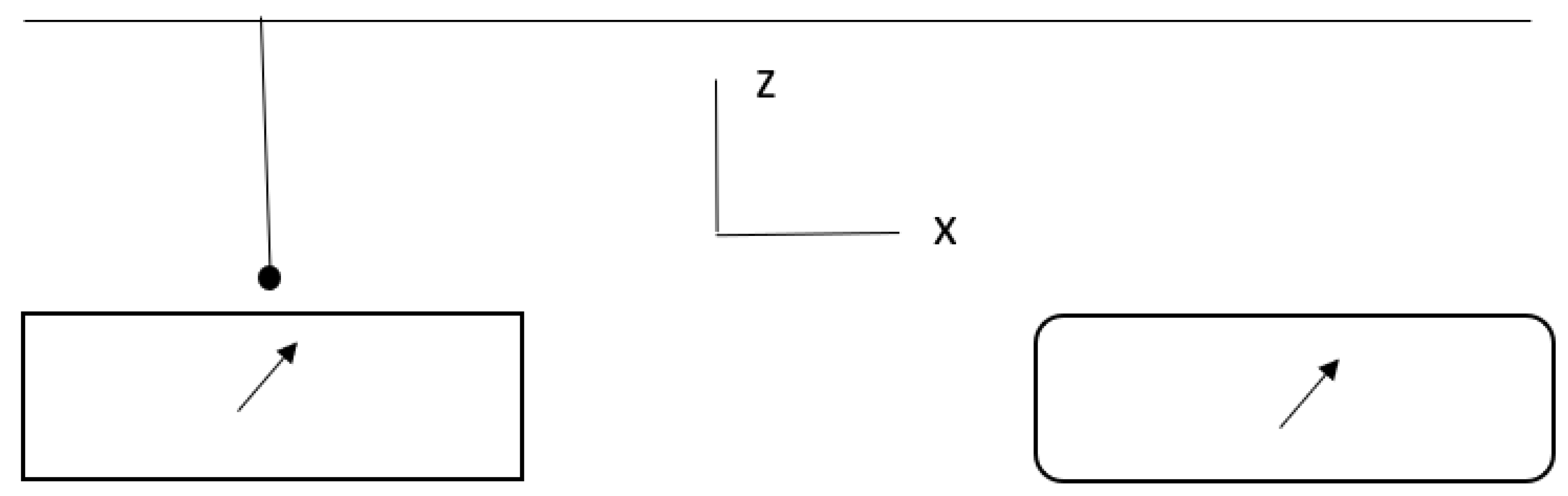
We consider two remote spins and a movable nanomechanical cantilever with a magnetic nanoparticle at the CT. (See Figure 1.) We assume that the CT can be placed at a small vertical distance from the first spin, or the second spin, or far away from both spins which we call the “neutral position”. The CT can oscillate along the horizontal x-axis. Both spins experience the external magnetic field which points in the positive z-direction and controls the Larmor frequency of the spin.

We assume that if the CT is placed near the first or the second spin the Larmor frequency of the corresponding spin matches the CT frequency (the CT-spin resonance) as it is described in refs [3-5]. Then, the Hamiltonian of the CT-spin system can be described by the Jaynes-Cummings model. Certainly, we assume that when the CT is placed near one spin we can ignore its interaction with the other one.

The evolution operator

{\hat{U}}_{k} (t)

in the Jaynes-Cummings model with a single spin

" k " (k = 1, 2)

can be written as a product of two operators [7]:

\begin{array}{l} {\hat{U}}_{k} (t) = {\hat{U}}_{0 k} (t) {\hat{U}}_{I k} (t) . \end{array}

(1)

Hear

{\hat{U}}_{0 k} (t)

describes the evolution of the CT-spin system with no CT-spin interaction:

\begin{array}{l} {\hat{U}}_{0 k} (t) = \exp {- i ω (\hat{n} + 1 / 2) + (- i ω_{k} {\hat{σ}}_{z k} t / 2)}, \end{array}

(2)

ω

is the CT frequency,

ω_{k}

is the Larmor frequency of spin

" k "

, which is equal to

ω

when the CT is placed near the spin,

\hat{n} = {\hat{a}}^{†} \hat{a}

{\hat{a}}^{†}

and

\hat{a}

are the creation and annihilation operators for the CT,

{\hat{σ}}_{z k}

is the Pauli operator for spin

" k "

. Operator

{\hat{U}}_{0 k} (t)

changes only the phase factors in the CT-spin state, and we will ignore it in our computations.

Operator

{\hat{U}}_{I k} (t)

describes the evolution caused by the CT-spin interaction in the condition of the CT-spin resonance when the CT is placed near the spin

" k "

\begin{array}{l} {\hat{U}}_{I k} (t) = \cos (λ_{k} t \sqrt{\hat{n} + 1}) X_{k}^{11} + i \hat{a} \frac{\sin (λ_{k} t \sqrt{{\hat{a}}^{†} \hat{a}})}{\sqrt{{\hat{a}}^{†} \hat{a}}} X_{k}^{10} \\ + i \frac{\sin (λ_{k} t \sqrt{{\hat{a}}^{†} \hat{a}})}{\sqrt{{\hat{a}}^{†} \hat{a}}} {\hat{a}}^{†} X_{k}^{01} + \cos (λ_{k} t \sqrt{{\hat{a}}^{†} \hat{a}}) X_{k}^{00} . \end{array}

(3)

Here

λ_{k}

is the CT-spin interaction constant for spin

" k "

, the Hubbard operator

X_{k}^{p q} = {(| p 〉 〈 q |)}_{k}

p, q = 0, 1

, the ground state

| 0 〉

corresponds to the spin direction “down” (the negative z-direction).

We assume that the interaction constant is the same for both spins, i.e. if the CT is placed near spin

" k "

then

λ_{k} = λ

. In the neutral position the interaction constant is equal to zero. For parameters suggested in [3] the value of the interaction constant

λ \approx 10^{4} rad / s .

Note that the operators

{\hat{U}}_{0 k} (t)

and

{\hat{U}}_{I k} (t)

commute.

Now we describe the protocol for creation of entanglement between the remote spins. The basis states for the CT-spin system are

| n, s_{1}, s_{2} 〉

where

n = 0, 1, 2, 3...

describes the CT state, and

s_{k} = 0_{k}, 1_{k}

describes the state of spin

" k "

. Let initially the CT is in a neutral position, and the CT-spin system is in its ground state

| ψ_{a} 〉 = | 0, 0_{1}, 0_{2} 〉

. Next, one drives the CT to the first excited state, so the vector of state changes to

| ψ_{b} 〉 = | 1, 0_{1}, 0_{2} 〉

. Then one quickly (during the time much smaller than

1 / λ

) moves the cantilever from a neutral position toward the first spin where the CT interacts with the spin in the conditions of the CT-spin resonance. After time interval

t_{1}

one quickly moves CT back to a neutral position. By direct computation we obtain vector of state after the interaction between the CT and the first spin:

\begin{array}{l} | ψ_{c} 〉 = U_{I 1} (t_{1}) | ψ_{b} 〉 \\ = \cos (λ t_{1}) | 1, 0_{1}, 0_{2} 〉 + i \sin (λ t_{1}) | 0, 1_{1}, 0_{2} 〉 \end{array}

(4)

Next, one quickly moves the cantilever toward the second spin so that the CT interacts with the second spin in the conditions of the CT-spin resonance. After time interval

t_{2}

one moves CT back to the neutral position. The resulting vector of state is

\begin{array}{l} | ψ_{d} 〉 = U_{I 2} (t_{2}) | ψ_{c} 〉 \\ = \cos (λ t_{1}) \cos (λ t_{2}) | 1, 0_{1}, 0_{2} 〉 + i \sin (λ t_{1}) | 0, 1_{1}, 0_{2} 〉 \\ + i \cos (λ t_{1}) \sin (λ t_{2}) | 0, 0_{1}, 1_{2} 〉 \end{array}

(5)

One can choose

t_{1} = π / 4 λ, t_{2} = π / 2 λ

in order to get an entangled state for the remote spins while the CT returns to its ground state:

\begin{array}{l} | ψ_{d} 〉 = (i / \sqrt{2}) (| 0, 1_{1}, 0_{2} 〉 + | 0, 0_{1}, 1_{2} 〉) \\ = | 0 〉 \otimes (i / \sqrt{2}) (| 1_{1}, 0_{2} 〉 + | 0_{1}, 1_{2} 〉) \end{array}

(6)

Note that the entanglement between the remote spins is achieved without measurement of the CT state.

3. Conclusions

In conclusion, in this work we study the creation of entanglement between the remote spins using the nanomechanical cantilever with the magnetic nanoparticle at the CT. The CT and a spin interact when the cantilever is moved toward the spin. The CT-spin interaction takes place in the condition of the CT-spin resonance when the CT frequency matches the frequency of the Larmor precession of the spin. In this case the evolution of the CT-spin system is described by the exactly solvable Jaynes-Kummings model. By direct computation we show that choosing the appropriate time of interaction one can create the remote spin entanglement without measurement of the CT state.

References

Einstein, A; Podolsky, B; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777-780.
Anderson, C.P.; Awschalom, D. D. Embracing imperfection for quantum technologies. Physics Today 2023, 76 (8), 26–33. [CrossRef]
Berman, G. P.; Gorshkov, V. N.; Tsifrinovich, V.I. Electron spin relaxation induced by a cantilever when the spin frequency matches the cantilever frequency. J. Appl. Phys. 2021, 130, 144402-144407. [CrossRef]
Berman, G. P.; Tsifrinovich, V.I. Magnetic resonance force microscopy with matching frequencies of cantilever and spin. J. Appl. Phys. 2022, 131, 044301-044301. [CrossRef]
Christou P.; Tsifrinovich, V.I. A Qubit represented by the oscillator’s quantum states in magnetic resonance force microscopy. Magnetochemistry, 2022, 8, 76-80. [CrossRef]
Jaynes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89-109. [CrossRef]
Stenholm, S. Quantum theory of electromagnetic fields interacting with atoms and molecules. Physics Reports (Section C of Physics Letter) 1973, 6, 1-121. [CrossRef]

Figure 1. Two samples (rectangles) each contain impurity atoms with the unpaired electron spins (arrows). A nanomechanical cantilever (the vertical line) with a magnetic nanoparticle (the black circle) at the CT is placed at a small vertical distance from the first spin. The cantilever is attached to the horizontal bar (the top horizontal line) and can be quickly moved (along the bar) from the first spin to the second spin or to a neutral position (far from both spins).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.