Prerpints.org logo
Preprint
Article

Characterization of Na0.5Bi0.5TiO3 Single Crystals by X-ray Diffraction, Scanning Electron Microscopy, X-ray Photoelectron Spectroscopy, Optical Absorption, Electric and Thermoelectric Properties Studies

Altmetrics

Downloads

142

Views

104

Comments

0

Submitted:

29 May 2024

Posted:

30 May 2024

You are already at the latest version

Alerts
Abstract
High-quality and large-size single crystals of lead-free Na0.5Bi0.5TiO3 were grown using the Czo-chralski technique. The crystals had pure perovskite structure with rhombohedral symmetry and were translucent in the visible and near infrared spectral ranges recorded in the interval 350-1050 nm. The energy gaps determined from the X-ray photoelectron spectroscopy (XPS) and optical measurements were approximately 2.92 eV. The current-voltage characteristics, depolarization current, dc (σdc) and ac (σac) electrical conductivity, and Seebeck coefficient of the crystals were investigated. The frequency/temperature-dependent electrical properties were also measured and analyzed through complex impedance spectroscopy. An overlapping reversible insulator-metal transition (resistive switching) on nanoscales, caused by the electric field, was detected. This was the first time that most of these investigations were performed for this material. The following conductivity mechanisms of NBT single crystals were identified: (i) quasi-free electron and hole conduction and hopping-charges mechanism at low temperatures, (ii) small polaron conductivity in the middle temperature range, and (iii) a significant contribution of the oxygen vacancies to conductivity in the high temperature range. The activation energy values determined from the conductivity data, the imaginary part of the electric impedance and the modulus indicate that the relaxation process in the high-temperature range is attributable to both single and double ionized oxygen vacancies, in combination with the hopping of electrons between Ti4+ and Ti3+. P-type electrical conductivity was also found. These discoveries create new possibilities of reducing the electrical conductivity of NBT and improving the process of effectively poling this material. The density of the electronic states was investigated using an ab initio method. The energy gap cal-culated for NBT (R3c) was 2.8 eV, and is well comparable to those determined from XPS and optical measurements. Our results indicate the possibility of tuning material properties by inten-tionally creating non-stoichiometry/structural defects (oxygen vacancies, cation excess and cation deficiency).
Keywords: 
Subject: Chemistry and Materials Science  -   Electronic, Optical and Magnetic Materials

1. Introduction

Lead-based materials, such as PZT, PMN, PFN, etc., have been widely used due to their excellent electromechanical properties [1,2,3,4]. However, the high toxicity and high volatility of lead oxide (PbO) results in environmental pollution, generates compositional inhomogeneities and the formation of an undesirable pyrochlore phase. For these reasons, it is strongly recommended that non-toxic materials are developed for use in various devices such as transducers, actuators, filters, multilayer capacitors, etc. [1,5]. One such important material is sodium-bismuth titanate, Na0.5Bi0.5TiO3 (NBT).
NBT has a perovskite (ABO3) structure with rhombohedral symmetry (R3c) with ion displacements along the [111] direction of the pseudocubic cell and with out-of-phase āāā octahedral tilting at room temperature, however monoclinic or rhombohedral/monoclinic mixtures have been also postulated [6,7]. NBT exhibits ferroelectric properties with remnant polarization Pr=20-35 μC/cm2 and coercive field Ec≈70-90 kV/cm at room temperature. On heating, it undergoes the following sequence of diffused structural transformations: rhombohedral (R3c) → tetragonal (P4bm) at TR-T=260-400°C →cubic (Pm3m) at TT-C=520-540°C. The tetragonal phase is non-polar or weakly polar. The results of transmission electron microscopy (TEM) studies [8,9] suggest that the rhombohedral-tetragonal phase transformation occurs in two steps: the disintegration of the rhombohedral R3c domains via a microtwinning process starts at the so-called “depolarization temperature” Td≈170-190oC, and the rhombohedral-tetragonal phase transition at approximately 279oC may proceed through the intermediate modulated orthorhombic Pnma phase [8]. The twin boundaries between ferroelectric rhombohedral micro-domains form the sheets of this intermediate phase. However, the existence of the orthorhombic phase has not been fully confirmed [10].
At Td, NBT loses its long-range ferroelectric state and transforms into a short-range relaxor-like state [5]. In the vicinity of Td, dielectric dispersion increases and a frequency dependent bump exists in the temperature evolution of electric permittivity ε(T). A broad maximum of electric permittivity is observed at Tm≈320°C, which does not correspond to any structural transformation and may originate from a dielectric relaxation attributed to an electromechanical interaction between polar regions and the non-polar matrix [11]. The existence of polar regions far above Tm was proved by Vakhrushev et al. [12] and confirmed by Suchanicz et al. [11,13,14]. These regions become the nuclei of the emerging ferroelectric phase.
Despite numerous studies to date, contradictory conclusions on the number, sequence and type of the electric order of the particular phases in NBT can be found in the literature and opposing opinions have been presented by various researchers. Particularly, the phase properties in the temperature interval 200-350°C have been the subject of some controversy, as either having a mixture of tetragonal and rhombohedral phases with polar regions [11] or being antiferroelectric [15]. Deviations from the average rhombohedral structure [16] and incommensurate [17] phase have been also postulated. Some of these discrepancies can be attributed to structural imperfections, arising from the impurity of the initial components and different technologies or sintering conditions of the ceramic and crystal. The too high electrical conductivity of NBT causes difficulties in poling it effectively. Therefore, understanding of the mechanisms behind the appearance this high conductivity is a priority.
As mentioned above, the available information concerning the properties of NBT is still incomplete and inconsistent. Most experimental results for NBT were obtained using ceramic samples. However, single crystals usually offer better properties than those of polycrystalline ceramics. The pore-free microstructure of single crystals positively influences the operating life of devices, since pores and other microstructural imperfections are usually responsible for material failures. Besides, the issues of grain size and porosity can be ignored for single crystals, which makes for easier, and more certain, interpretation of experimental data. However, the growth of high-quality and large-size Na0.5Bi0.5TiO3 single crystals continues to be a challenge.
The knowledge of the electronic structure of a material is key to understanding and modifying its physical and chemical behavior. Ab initio calculations and X-ray photoelectron spectroscopy (XPS) are powerful methods to study the electronic structure of matter. As electrical transport behavior influences other associated properties like dielectric losses, pyroelectricity, piezoelectricity, and also the strategy used for poling, the study of these behavior is extremely important. Moreover, these kinds of studies, particularly of NBT single crystals, are rare in the existing literature [18,19,20,21]. To our knowledge, there are no prior results on the depolarization current, current-voltage (I-U) characteristics, Seebeck coefficient and thermal conductivity for NBT single crystals.
In the present paper we report ab initio calculations, XPS, X-ray, depolarization current, I-U characteristics, Seebeck coefficient, dc/ac electrical conductivity and thermal conductivity results of the Na0.5Bi0.5TiO3 single crystals grown by the Czochralski method. To clarify the electrical conductivity phenomenon, the Electrochemical Impedance Spectroscopy (EIS) method was used.

2. Materials and Methods

Na0.5Bi0.5TiO3 single crystals were grown by the Czochralski method. Powder reagents NaHCO3 (99.7%), Bi2O3 (99.9%) and TiO2 (99.9%) were weighed in stoichiometric ratio and homogenized in an agate mortar for 24 h with ethanol. Using non-hygroscopic NaHCO3 instead of hygroscopic Na2CO3 allowed for careful adjustment of the stoichiometry during weighing. In addition, to eliminate of carbonate decomposition of Bi2O3, it was thermally treated at 400°C for 9h. Both treatments were intended to minimize the effect of uncertainties in the stoichiometry of the samples. The milled powders were then dried, calcined at 800°C for 2h and at 950°C for 5h. The calcined material was placed in a Pt crucible, heated to 1300ºC and then soaked for 2.5 h. The crystals growth was carried out at 1300°C in air. The crystal was pulled and rotated at rates of 5 mm/h and 20 rpm, respectively. Slightly yellowish, transparent cub-shaped single crystals of 1.5 cm in size and piezoelectric coefficients d33=91pC/N and k33=34% were obtained.
The XRD investigations were performed using a Philips X’Pert Pro MD diffractometer. Standard Bragg-Brentano geometry was applied with CuK α1,2 radiation (the Kβ line was suppressed by a Ni filter). All measurements were performed in air in the 2Θ scanning range 20°-100° with a step of 0.017º.
The microstructure analysis was undertaken by a scanning electron microscope (Hitachi S4700) with field emission and a Noran Vantage EDS system. The elemental distribution and composition were identified by elemental mapping and energy dispersive spectroscopy (EDS).
X-ray photoelectron spectroscopy (XPS) was used to determine the precise chemical compositions and oxidation states of the elements on the sample surface. The XPS measurements were performed using Omicron Nano-Science equipment with a hemispherical 128-channel Argus spectrometer. Experiments were conducted at room temperature under ultra-high vacuum conditions at pressure below 1.1 × 10−6 Pa. The obtained spectra were analysed by the CASA XPS software package, using Shirley background subtraction and the Gauss-Lorentz curve, GL (30), fitting algorithm through the least-squares method. To calibrate the results, a binding energy of 285.00 eV was established as the reference energy for the C1s signal (peak).
The dimensions of the samples were 4x4x0.3 mm with two main faces perpendicular to [001]c direction. The [001]c face of the samples were optically polished and coated with silver electrodes. The samples were annealed at a temperature above the tetragonal-cubic phase transition for 1h.
The direct electric conductivity (σdc) was measured over a temperature range from room temperature to 600°C using a Keithley 6517A electrometer. The alternating current electric conductivity (σac) and impedance spectroscopy were measured in a frequency/temperature range 100Hz-2MHz and from room temperature to 600°C for silver electrode samples using a GW 821LCR meter.
The depolarization currents and current-voltages (I-U) characteristics were measured using a Keithley 6517A electrometer. As these measurements require precise temperature stabilization to avoid the influence of pyrocurrents, stabilization within 0.1°C was maintained. In case of depolarization currents measurements, the sample was polarized at 5, 15 and 25 kV/cm for 1 or 2h at the chosen temperature. Next it was short-circuited and the depolarization current flowing from the sample was measured.
The Seebeck coefficient (α) was measured in the temperature range 50-370°C. The sample was placed in a thermostat between heated silver blocks, which made it possible to create a temperature gradient inside the sample (for more details see [22]). The temperature difference between the electrodes of the sample ∆T was varied from 0 to 10°C at each chosen temperature. Values of the Seebeck coefficient were determined from the slope of the linear dependencies of the electromotive force E vs. the temperature difference ∆T.
The density functional theory (DFT) calculations were performed without spin-polarization using the plane-wave pseudopotential method in the Vienna ab initio simulation package (VASP) [23,24]. Electron–ion interactions were represented by pseudopotentials as part of the projector-augmented wave (PAW) scheme. The valence electron configurations of the dataset were as follows: Na: 2p63s1, Bi: 6s26p3, Ti: 3d24s2, O: 2s22p4. The exchange–correlation potentials were handled by applying the Perdew–Burke–Ernzerhof (PBE) [25] form of generalized gradient approximation (GGA). Such functionals are sufficiently accurate for the description of the electronic properties of perovskite systems [26,27]. The sampling of Brillouin zones of Na0.5Bi0.5TiO3 unit cells was performed using 10×10×4 Monkhorst–Pack k-point meshes. The tested structure was completely relaxed with a mesh of 10 × 10 × 4. This k-space mesh was used to calculate the predicted state density. In the computations, a plane-wave basis with a cutoff energy ENCUT of 520 eV was used. The convergence criteria for the systems remaining forces and total energy were set to 10−4 eVÅ−1 and 10−5 eV. The structure for the rhombohedral phase is depicted in Figure 1.

3. Results and Discussion

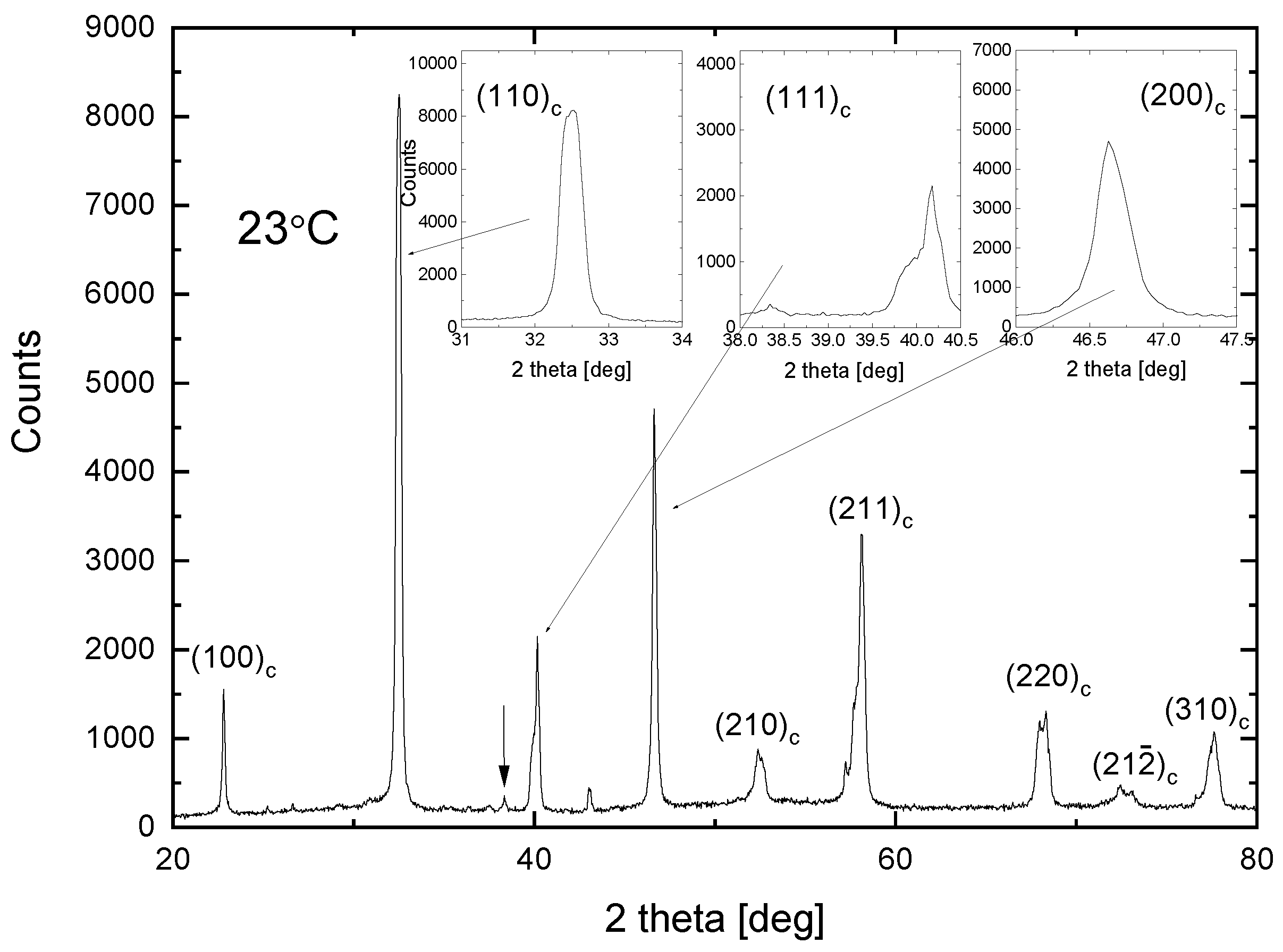
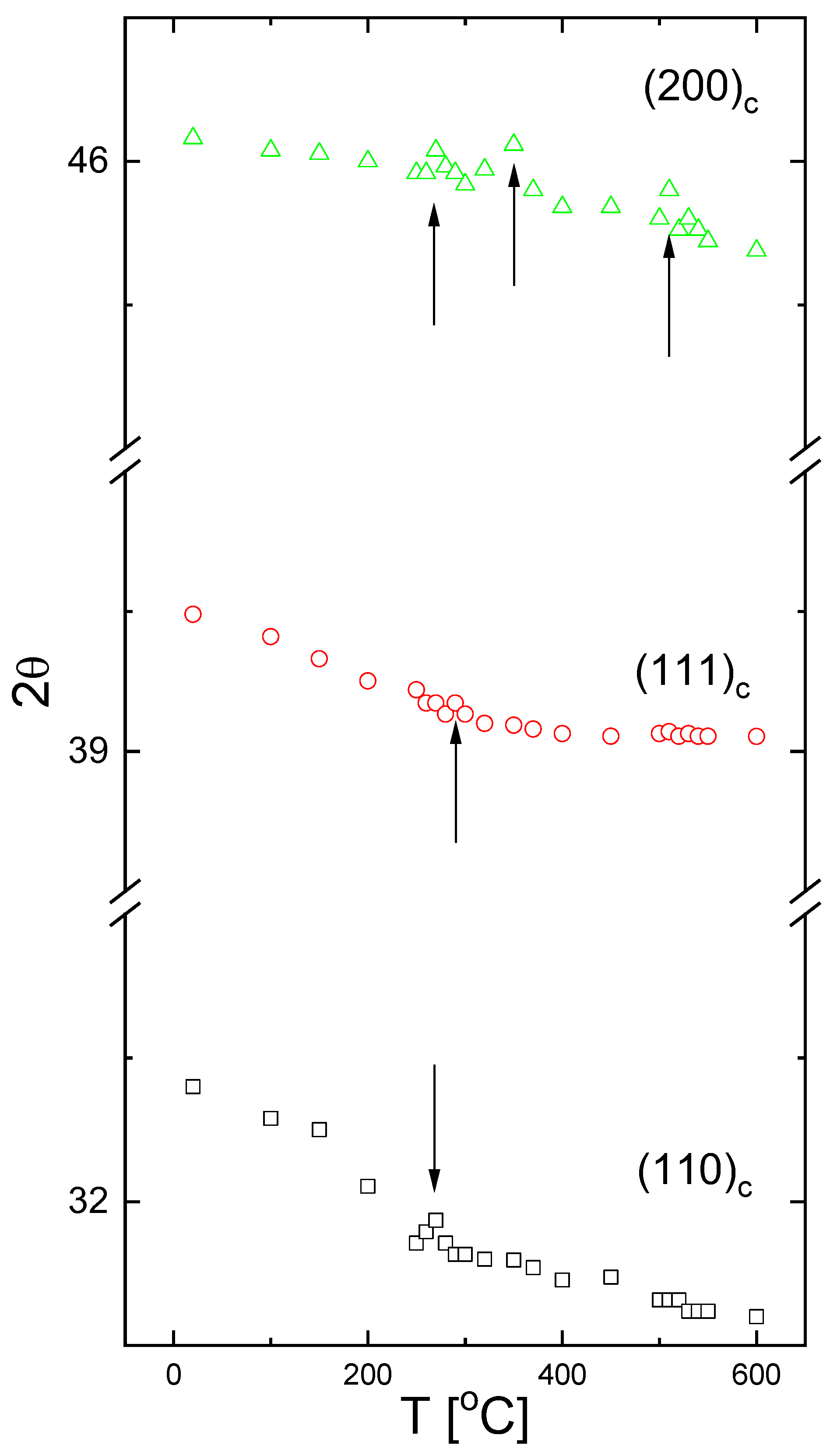
3.1. X-ray Results

Figure 2 shows the room-temperature X-ray pattern of NBT single crystals. X-ray spectrum does not contain reflections related to the second phases what points to high quality of studied crystals. As can be seen, the well-defined splitting of the (110)c and (111)c reflections, a small superreflection near 38° (indicated by an arrow) and the complex character of the (200)c reflections reveal rhombohedral (R3c) symmetry with a small content of tetragonal phase.
Figure 3 plots the central 2Θ-positions of the structure sensitive (110)c, (111)c and (200)c Bragg reflections (peaks) against temperature. As can be seen, a constant lower-angle shift exists and some anomalies of the 2Θ(T) curves at about 260°C (for (110)c, (111)c and (200)c peaks) and at about 350 and 520°C (for (200)c peak) are visible (indicated by arrows). The lower-angle shift of the peaks indicates a gradual increase of unit cell volume with rising temperature. The first and last anomaly is attributed to the transformation from rhombohedral to tetragonal phase, and from tetragonal to cubic phase, respectively. However, the second anomaly corresponds with Tm and reflects the dominance of the tetragonal phase in the range of coexistence of the rhombohedral and tetragonal phases. The phase transformation between the rhombohedral and tetragonal phases takes place successively in a wide range of temperatures, hence two anomalies are visible, the first one around 260°C, where the highest rate of growth of the tetragonal phase occurs at the expense of the rhombohedral phase, and the second one around 350°C, where the dominant phase is already the tetragonal phase.

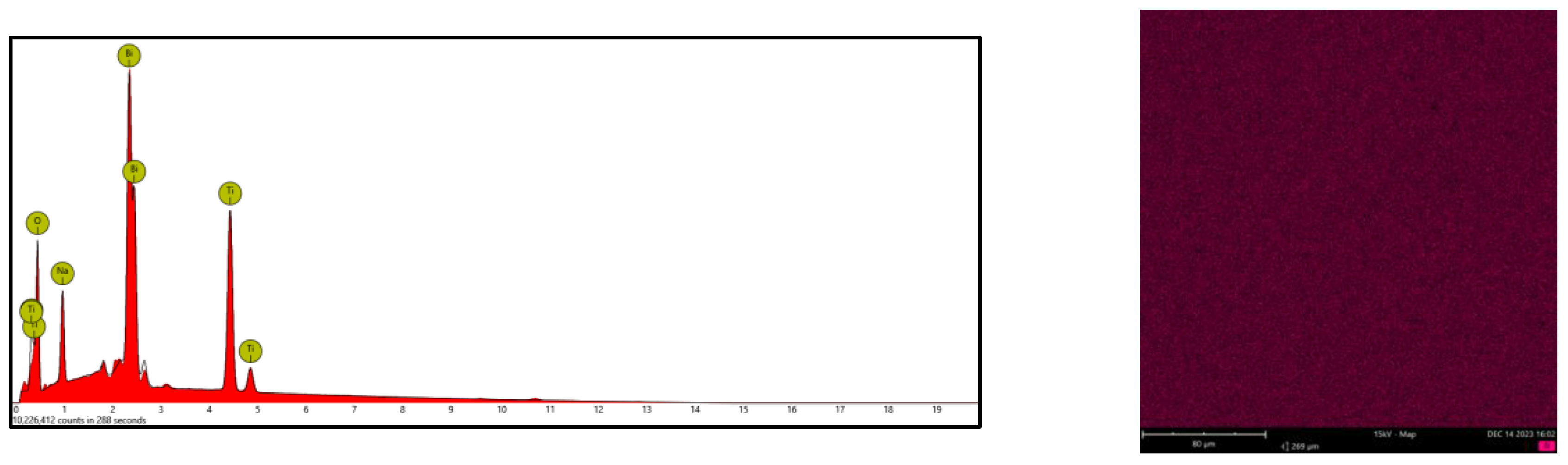
3.2. Microstructure Analysis

Figure 4 shows the EDS spectra and element mapping of the examined NBT sample. It can be clearly seen that crystals contain Na, Bi, Ti and O elements and exhibit a homogeneous distribution. The chemical formula of NBT obtained from EDS analysis is Na0.51Bi0.62TiO2.8 approximately close to the theoretical value.

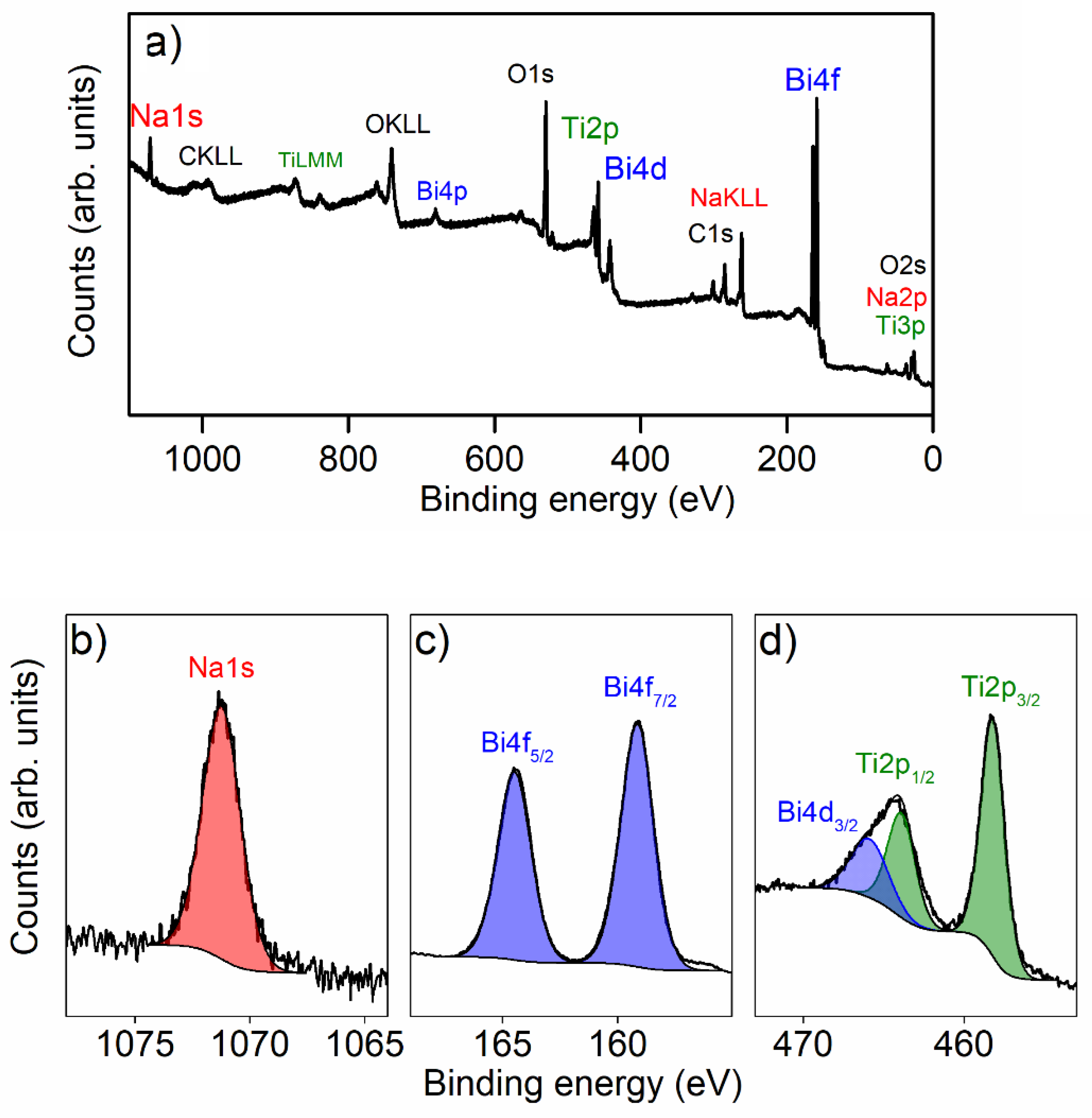
3.3. XPS Results

The XPS measurements of NBT single crystals were performed to analyse their chemical composition and the valence states of the particular elements. Figure 5a shows the survey spectrum. The average chemical composition calculated using the XPS spectra was estimated to be Na0.53Bi0.65TiO2.8 and it is approximately close to the nominal composition. There is an excess of sodium and bismuth and a deficiency of oxygen. These results confirm the crystal composition obtained from the EDS spectra. Additionally, carbon was detected, due to absorption from the atmosphere. In Figure 5b–d the high-resolution spectra for Na1s, Bi4f and Ti2p regions are presented. The signal recorded for Na1s is characteristic of the Na+ state [28,29], while the characteristic doublet visible in Figure 5c could be assigned to Bi3+ [30,31]. The spectrum recorded for the Ti2p region is more complicated due to overlapping of the Ti2p doublet and Bi4d singlet [32]. The curve was deconvolved into three peaks, corresponding to Bi4d3/2, Ti2p1/2 and Ti2p3/2. The positions of the peaks and the splitting energy, equal to 5.7 eV, is characteristic of the Ti4+ state [33].

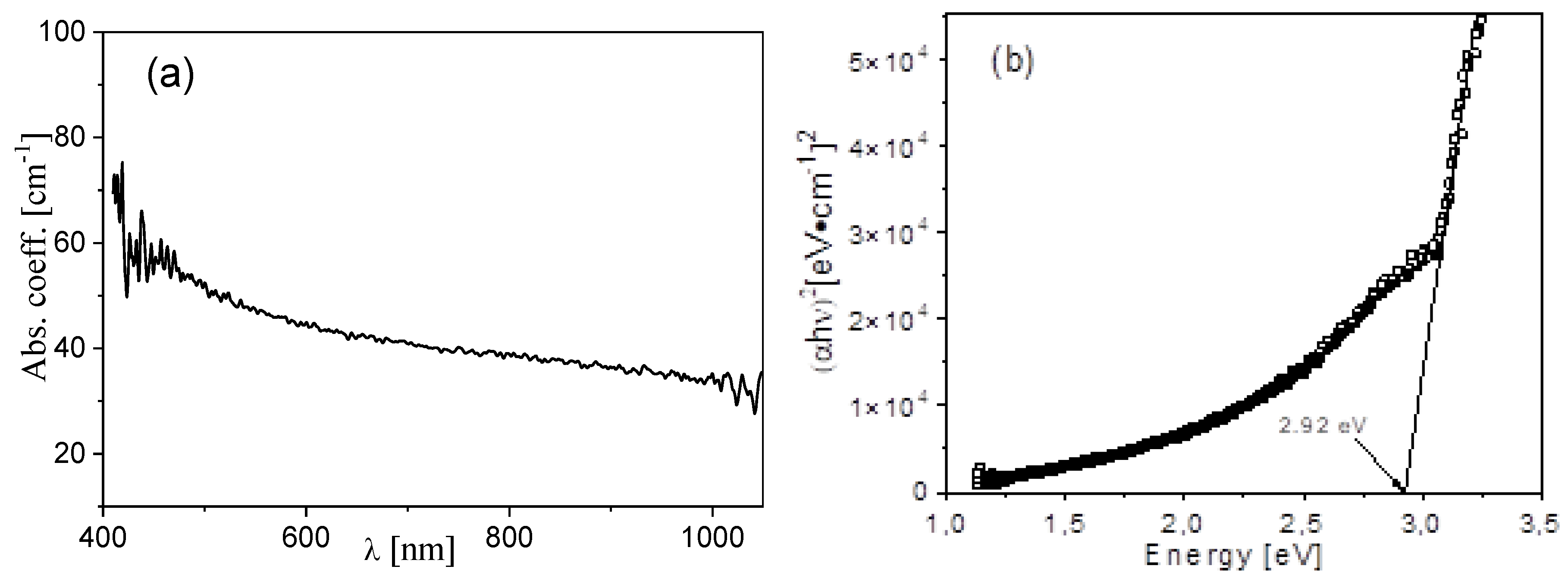
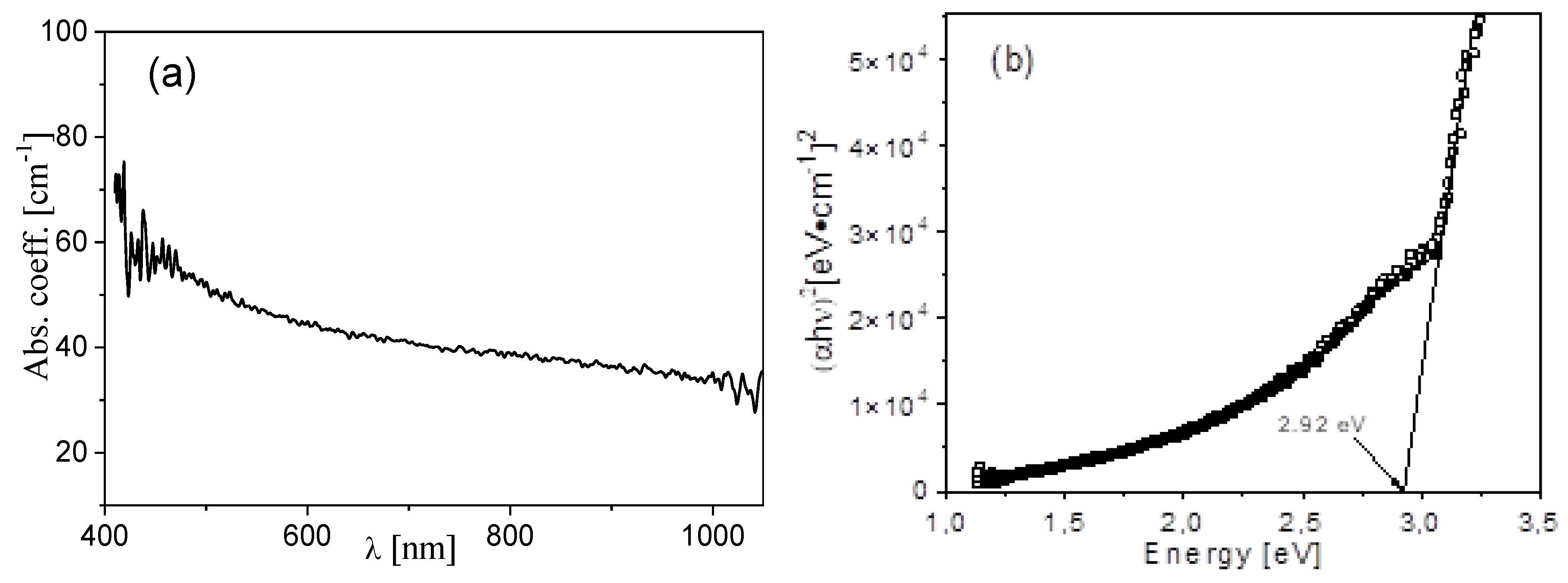
3.4. Optical Results

Figure 6a shown absorption coefficient spectra for NBT crystals. As can be seen, the examined materials are translucent in the visible and near infrared range. As the wavelength increases, a significant decrease in the material’s absorption coefficient is observed, which is consistent with the theory of light scattering on defects [34]. The absorption spectrum was fitted to the dependence expressed by [35]:
α = h v − E g 1 n h v
where α denotes the linear absorption coefficient of the material, hυ denotes the photon energy, Eg denotes the band gap energy. The n is ½ for direct allowed transitions, while n is equal to 2 for indirect allowed transitions. An extrapolation of a straight-line plot of αhυ vs. hυ intercepts a horizontal axis giving the value of Eg (Figure 6b). The best fit indicates that NBT has a direct band gap (n=½) of approximately 2.92±0.02 eV. This energy corresponds to a wavelength of approximately 400 nm, below which the incident light is completely absorbed. Literature data indicate a slightly higher energy gap from 3 to 3.2 eV for NBT single crystals [36,37] and doped ones [38], as well as for the epitaxial layer [39].

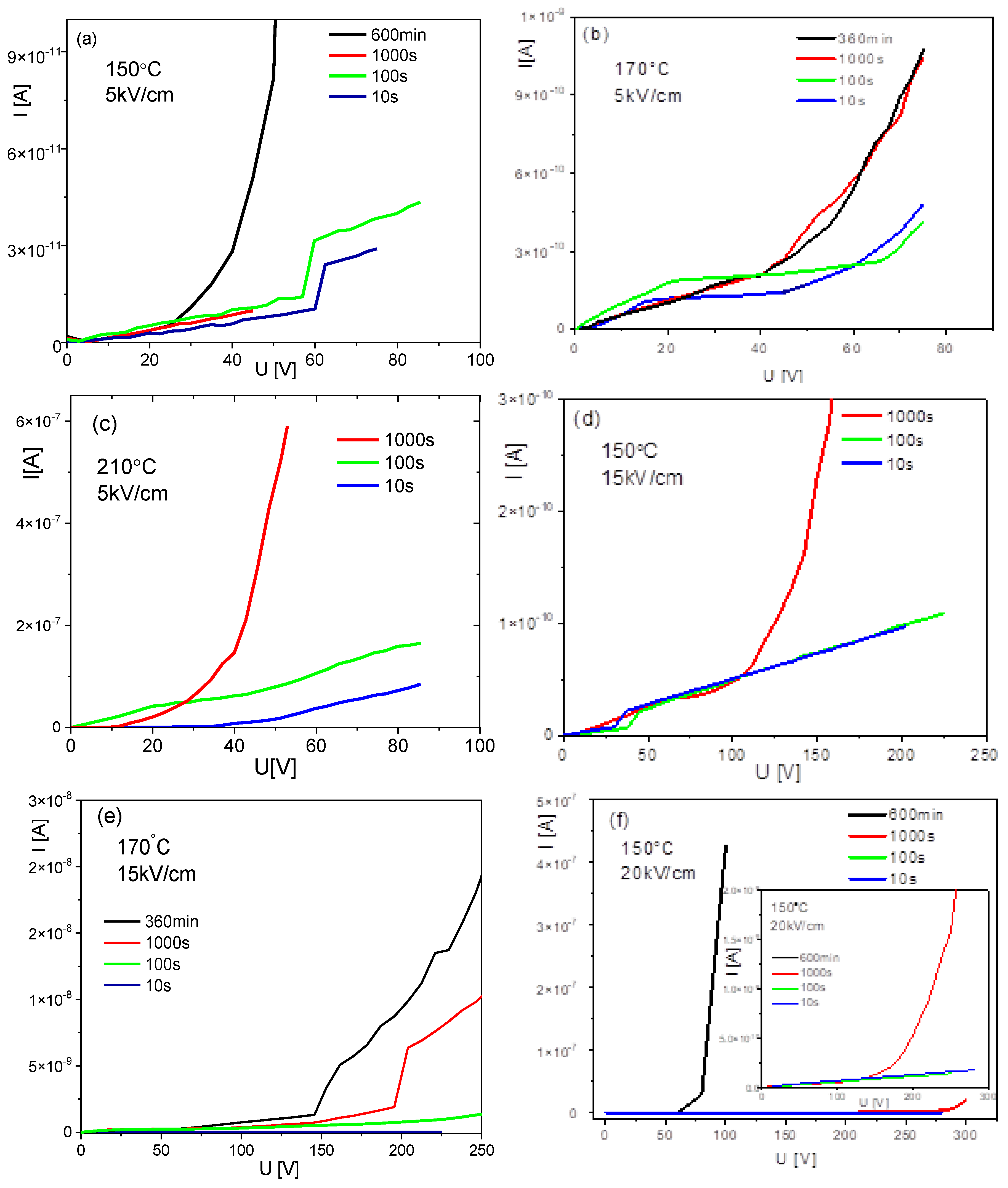
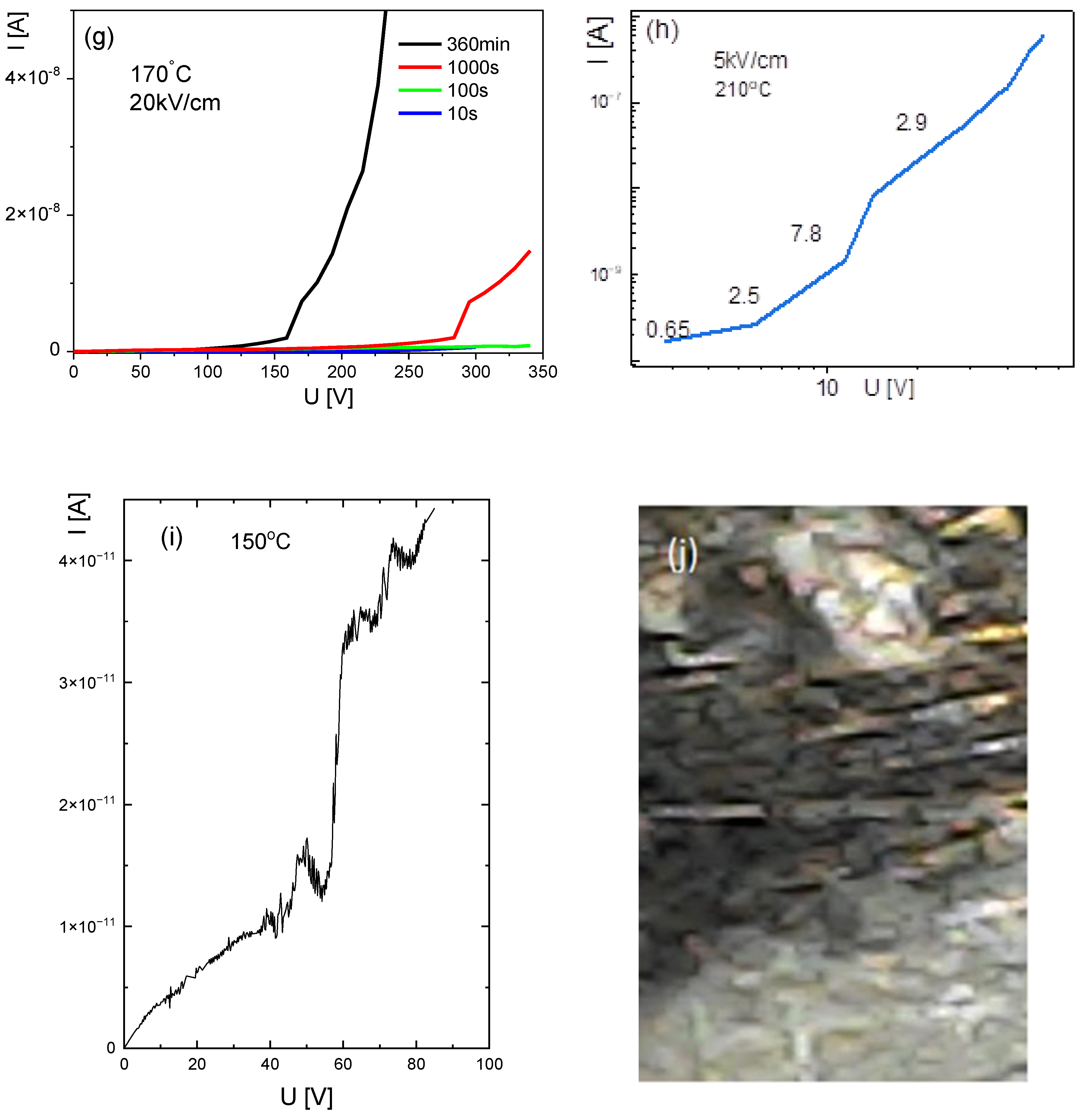
3.5. Current-Voltage Characteristics

Figure 7 presents the set of current-voltage I(U) characteristics for the NBT single crystals. For the longest duration of the applied electric field, we are dealing with so-called saturation. Analysis of the I(U) characteristics showed that the classical Ohm’s law was obeyed at low values of the applied electric field, and the range of its applicability strongly depends on the measurement duration. Linear fragments can be distinguished in I(U) curves with different slopes, satisfying the relationship [21]:
I ~ Un
Figure 7h shows as a “double” logarithmic (log-log) plot of the I(U) relationship at 210°C. The I(U) curve shows the adjustment values of the n parameter measured at a given voltage of 5kV/cm. As can be seen, approximately agreement with Ohm’s law has been ascertained at low electric field strength. When certain voltage limits are exceeded, the I(U) angle increases, which suggests a decrease in resistance and a change in the conduction mechanism. At higher temperatures and voltages, the material begins to exhibit semiconductor properties, which is related to the thermal activation of electric charge carriers and easier injection of carriers into the material. Further increasing the temperature and voltage leads to conduction, which agrees with the space-charge-limited current (SCLC) theory [40]. According to this theory, material defects are a source of trap states in which trapped charge carriers are excited only by a high external electric field and thermal energy. The concentration of excess injected charges at high electric field is greater that of thermal equilibrium charges. As the temperature increases, the concentration of equilibrium charges (holes and electrons) increases, which may lead to the appearance of SCLC space charge towards higher electric fields, which is confirmed by the results presented in Figure 7. When the electric field reaches the trap-filled limited (TFL), the electric current increases faster and the I(U) characteristics depend on the trap distribution according to the relationship I ~ Un (n = 2, 4 ...).
In order to determine the transition point between behavior consistent with Ohm’s law and the SCLC rule, the voltage value is introduced, as defined by the formula [21,41]:
V S C L S = e d 2 n 2 ε ε 0 θ
where e – electron charge, d – sample thickness, n – thermal equilibrium of the density of free carriers, ε – electrical permittivity of the material, ε0 – vacuum electrical permittivity, and θ – a coefficient determining the degree of charge trapping, given by the formula:
θ = n n t = N g N t e x p E t − E c k B T = N c g N t e x p − E t k B T
where nt – density of trapped charges, Nc – density of states in the conduction band, Nt – trap density, g = 2 – degradation coefficient, Et – trap energy below the edge of the conduction band Ec. From relation (3) we get:
θ = d 2 σ 2 ε ε 0 μ V S C L C
where: e – electron charge (1.602x10-19 C), d – sample thickness (0.0005m), ε=3746, ε0 =8.85*10-12 F/m, μ =10-10 m2/Vs, VSCLC = 60 V. The θ coefficient determined from the above equation is 1.97 ×10−2 for a temperature of 150°C (below Td). The estimated value is consistent with literature data for materials with a perovskite structure [21,42].
Based on the experimental data, the density of traps Nt and the trap-filled limited voltage VTFL was calculated for selected temperatures of 150, 170 and 210℃. The obtained values are summarized in Table 1. As the value of the applied electric field increases, the value of the VTFL voltage, at which the traps are filled, decreases. At a temperature of 170℃, a significant increase in the VTFL voltage is observed, resulting from the presence of the depolarization phenomenon. For 210℃, i.e., above the depolarization temperature, the same VTFL value is recorded as at 150℃, but for a much higher field E=20 kV/cm. Based on the analysis of these relationships, the presence of shallow traps in the discussed material is confirmed [21,42].
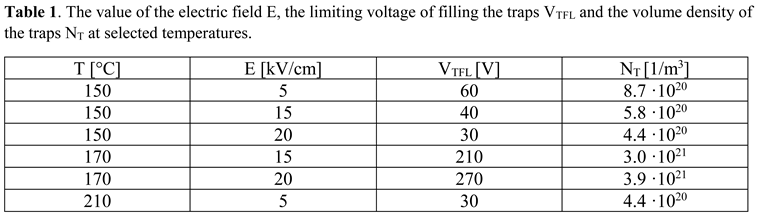
Preprints 107799 i001
Another explanation of the current-voltage characteristics is presented in paper [43], i.e., an overlapping reversible insulator-metal transition (resistive switching) on nanoscales caused by the electric field. As a result of non-stoichiometry, both point and extension defects (shear planes) may appear in perovskites. In our NBT single crystals non-stoichiometry exists (see SEM and XPS results). In particular, a deficiency of oxygen is observed. As shown in paper [43], a tendency toward vacancy clustering is observed. This ordering dominates in temperature range below the Tamman temperature, which is about half of the melting temperature (about 600°C for NBT single crystals), which included the temperature range over which the current-voltage characteristics were measured in the present paper. For low concentration of vacancies, the oxygen defects can be ordered along columns with different lengths of each segment and the segments (further called filaments) can be statistically distributed in the matrix [43]. Increasing oxygen nonstoichiometry leads to a rapid increase of the number of these filaments and introduces an additional parallel orientation between them lying close to each other. In consequence, oxygen defects are not randomly distributed but tend to arrange in regular patterns. Conduction of the filaments relative to the matrix is 4-5 orders of magnitude higher [43]. It was concluded, that reduction of the Ti valence as an effect of an enhanced local oxygen deficiency along the Ti-rich core of the edge shear planes (dislocations) causes the increase of the conductivity along the dislocations core with respect to the matrix i.e., electric transport is preferentially channeled along extension defects [43].
At least two factors indicate the possibility of resistive-switching occurring in NBT single crystals when performing current-voltage characteristics: (1) the occurrence of current oscillations, which can be classified as a kind of unipolar self-switching (Figure 7i), and (2) the presence of a network of dark stripes on the sample, which can be related to the carriers (oxygen) transport and current paths evolving throughout the sample [43] (Figure 7j).

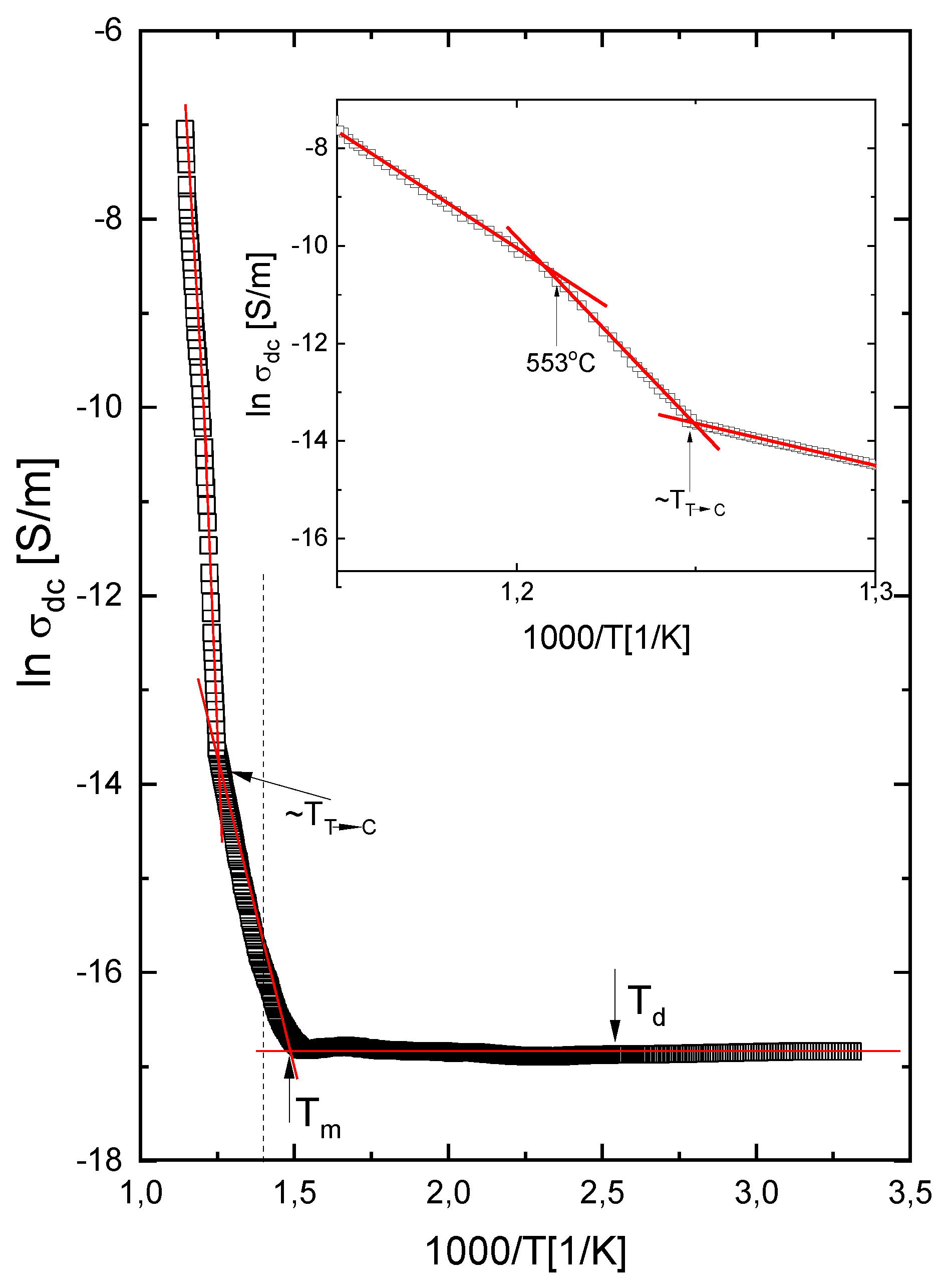
3.6. Direct Current Conductivity Results

Figure 8 shows direct current conductivity σdc vs.1000/T of NBT single crystals. As marked in this Figure, the σdc (1000/T) curve consists of five linear sections (ranges). The characteristic temperatures of NBT has been indicated by arrows. The activation energy Ea in these ranges was determined based on the Arrhenius equation:
σ d c = σ 0 exp ⁡ − E a k ⋅ T
where: σ0 – pre-exponential factor, k – Boltzmann constant, T – temperature. The obtained activation energies are presented in Table 2.
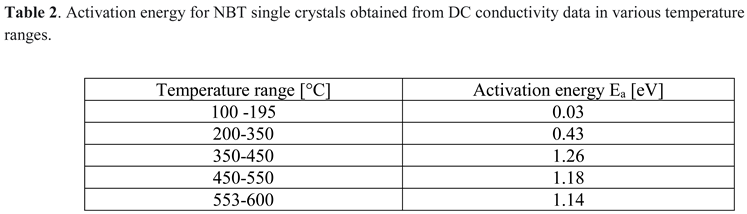
Preprints 107799 i002
The determined Ea values (Table 2) show that the electrical conductivity in NBT is complex and depends on the temperature range. At low temperatures, two competing conduction mechanisms coexist: the band model and the hopping model. The first one describes the phenomenon of conduction of quasi-free electrons and holes in the appropriate bands. The lowest Ea values recorded in the ferroelectric phase (up to about 200℃) result from the dominant mechanism of the conduction phenomenon of quasi-free electrons and holes, which is confirmed by studies of the thermoelectric properties of the Seebeck effect (see below). The change in the activation energy value around the depolarization temperature (Td≈190℃) indicates a change in the conduction mechanism [21]. The activation energy values (~0.4eV) occurring in the region of coexistence of the rhombohedral and tetragonal phases (200 - 350℃) can be associated with the increasing contribution to the conductivity of small polarons, as a result of their interaction with phonons, and eventually with a gradual change of oxygen vacancies from a neutral to a singly ionized state. Above Tm, the Ea value increases several times, which suggests that conduction at higher temperatures may occur through oxygen vacancies. In the highest range of temperatures tested, we observe a decrease in the Ea value, which suggests an increase of the electron conductivity contribution to total conductivity. To summarize, the NBT activation energy values in the presented temperature ranges are the result of various mechanisms of transport of electric charge carriers.

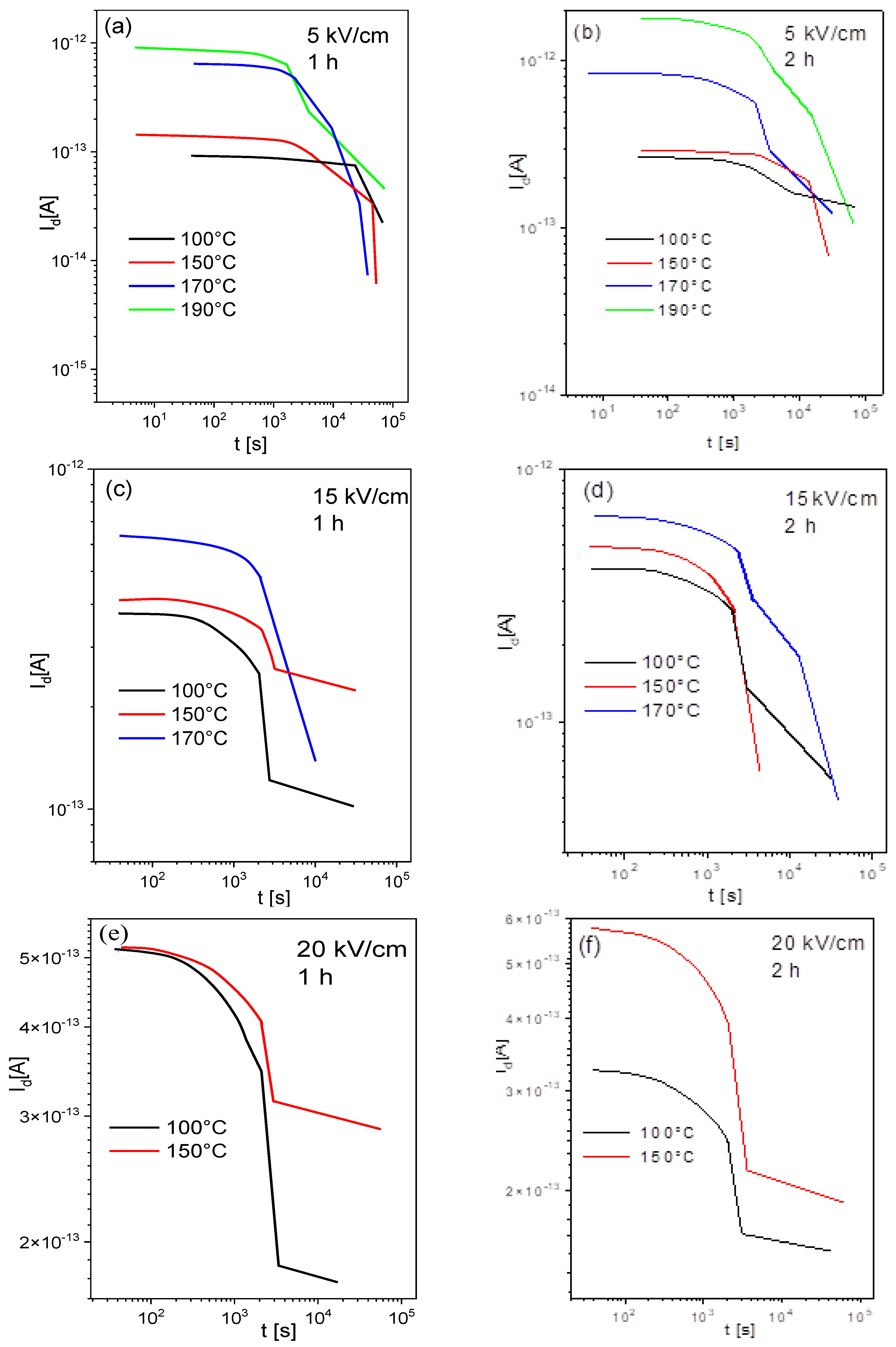
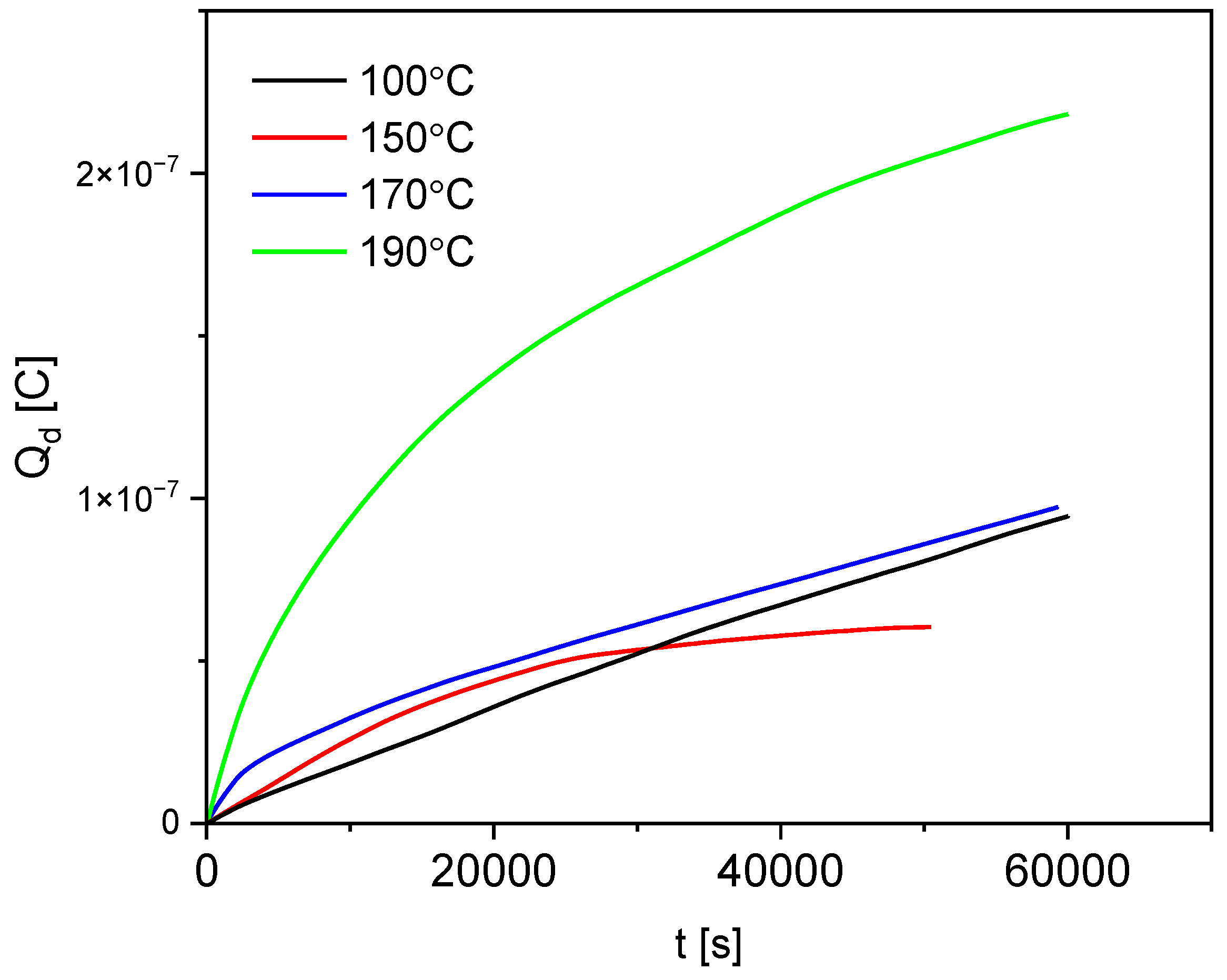
3.7. Depolarization Current Results

Depolarization currents for samples polarized at different temperatures, times and electric fields are shown in Figure 9. In general, three components with different angles of inclination and one nonlinear component can be distinguished, except Figure 9d, where four components are visible for temperature 170°C. The first nonlinear component which appears is directly related to the domain reorientation process, and the others are related to various types of polarization, including ionic, dipole and electronic [44]. Localized states (potential centers), e.g., ferroelectric/ferroelastic domain walls, point defects and inhomogeneity of the distribution of ions, which causes some occurrence of disorder in NBT. The latter is usual in perovskites with complex compositions such as NBT. Free charges as well as charges injected from electrodes at high electric field may be trapped on these centers. For example, an oxygen deficiency occurs in NBT (see EDS and XPS data), which leads to the appearance of long-range potential centers. After switching-off the applied electric field, charges which were trapped on localized states are released. This means that the sample is subjected to depolarization current flows through the sample [37]. Due to technical limitations, it was not possible to measure currents in the temperature range 200-300℃, where rhombohedral and tetragonal phases coexist. At higher temperatures, charge transport between potential centers will play a significant role in both polarization and depolarization processes, as well as electrical conduction [45].
The changes in discharge currents were described by the equation:
Id∼ t−s
where Id - depolarization (discharge) current intensity, t - time, s - exponent (dependent on polarization time and temperature) [46]. At the beginning of the depolarization process, the parameter s is approximately equal to zero, and then takes on larger values over time, eventually reaching or exceeding the value of one. The slope of the graph increases as the value of the polarization field increases, so the parameter s takes on larger and larger values. Similar results were obtained for NBT ceramics [46].
The course of changes in the value of the total depolarization charge Qd depending on the discharge time at selected temperatures is shown in Figure 10. The highest increase in the Qd value is recorded in the first seconds of the depolarization process. As the temperature increases, the charge Qd takes on higher values, which results mainly from the increased mobility of the charge.

3.8. Alternating Current Conductivity Results

The alternating current conductivity σac is related to the total conductivity σt and the direct current conductivity σdc by the relationship [18]:
σt(ω) = σac (ω) + σdc
where ω = 2πƒ is the angular frequency.
Figure 11a shows changes of the σac vs. 1000/T during heating. The ac conduction depends on the temperature and frequency of the electric field and is related to the movement of charge carriers at short-range scales. At low frequencies, the action of the electric field on charge carriers lasts for a long period of time. This favors the formation of localized states of these carriers and their elimination from the transport process, which results in lower conductivity in this frequency range. Anomalies of σac (1000/T) plot are visible around Td and Tm. The increase in the ac conductivity value may be caused by an increase in the concentration of electric charge carriers and/or an increase in their mobility. This indicates a thermally activated conduction process typical of the hopping mechanism of small polarons which proves the semiconductor features of NBT. Note that for frequencies f<2 kHz and for T>200°C conductivity grows rapidly (exponentially) on heating (a nearly linear interval appears in the Arrhenius plot), which reflects a growing contribution of thermally activated charges. The obtained conductivity values are consistent with literature data [21].
To better illustrate the temperature changes of ac conductivity, a graph of σac as a function of temperature for selected frequencies is presented in 11b. In the low temperature range up to approximately 140°C, a thermally activated increase in conductivity is observed, the rate of this increase depends on the frequency. The local increase in conductivity in the temperature range 170-190°C is related to the process of sample depolarization. Above a temperature of 190°C, there is a significant reduction in the conductivity value due to the coexistence of phases. Subsequently, an associated increase in σac is observed with the dominant thermally activated mechanism and the formation of a tetragonal phase. It should be mentioned that the local increase in the σac value observed in the temperature range of 320-330°C is correlated with the disappearance of the domain structure and the existence of the maximum of electric permittivity. The anomaly around the temperature of 400°C is related to the contribution of hopping conductivity and possibly an increase in the contribution of ionic conductivity. A σac(T) anomaly is also present around the temperature of 540°C, correlating with the T-C phase transition. In the above analysis, the following temperatures were once again distinguished: Td, Tm and TT-C. It should also be mentioned here, that comparison of both σac(T) and σdc (T) dependencies points to the contribution of dielectric losses to σac conductivity.

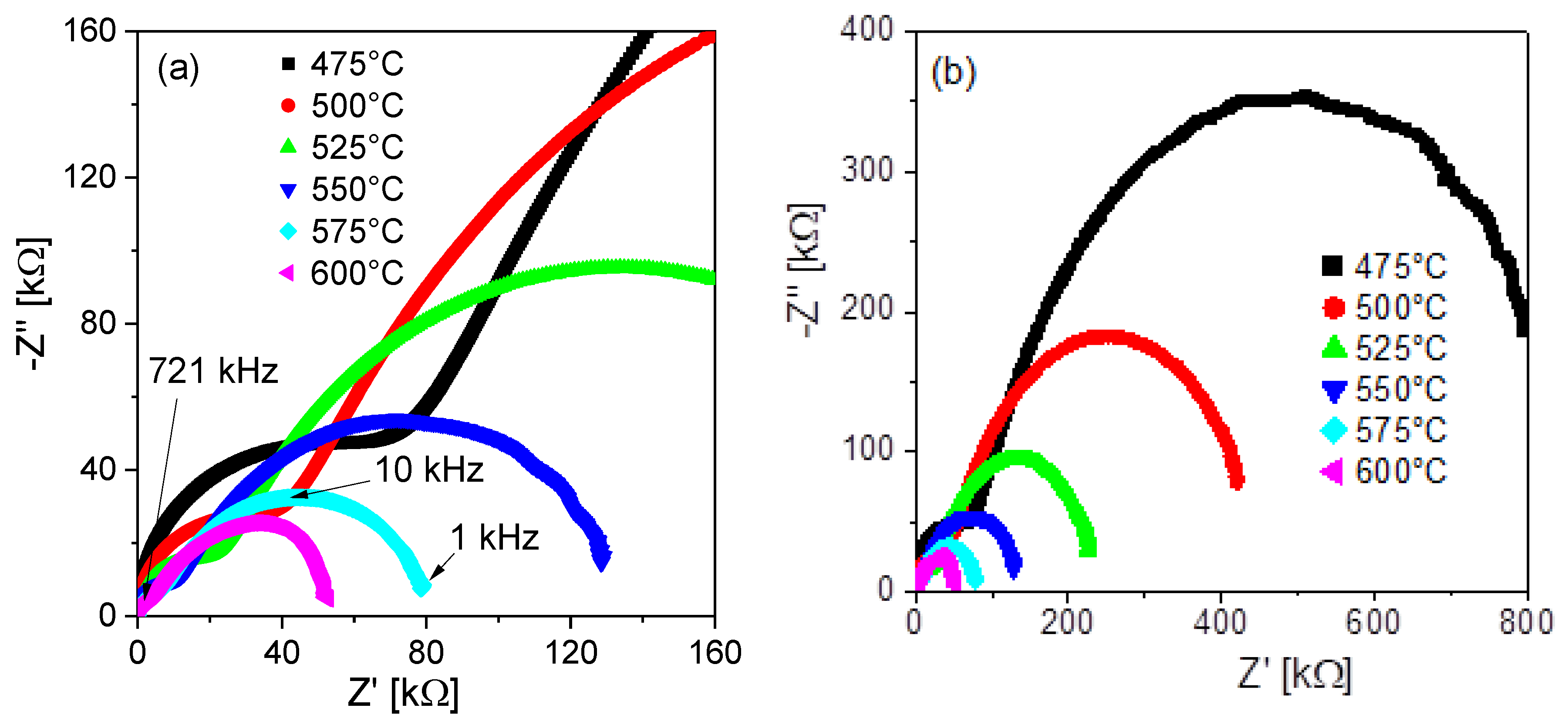
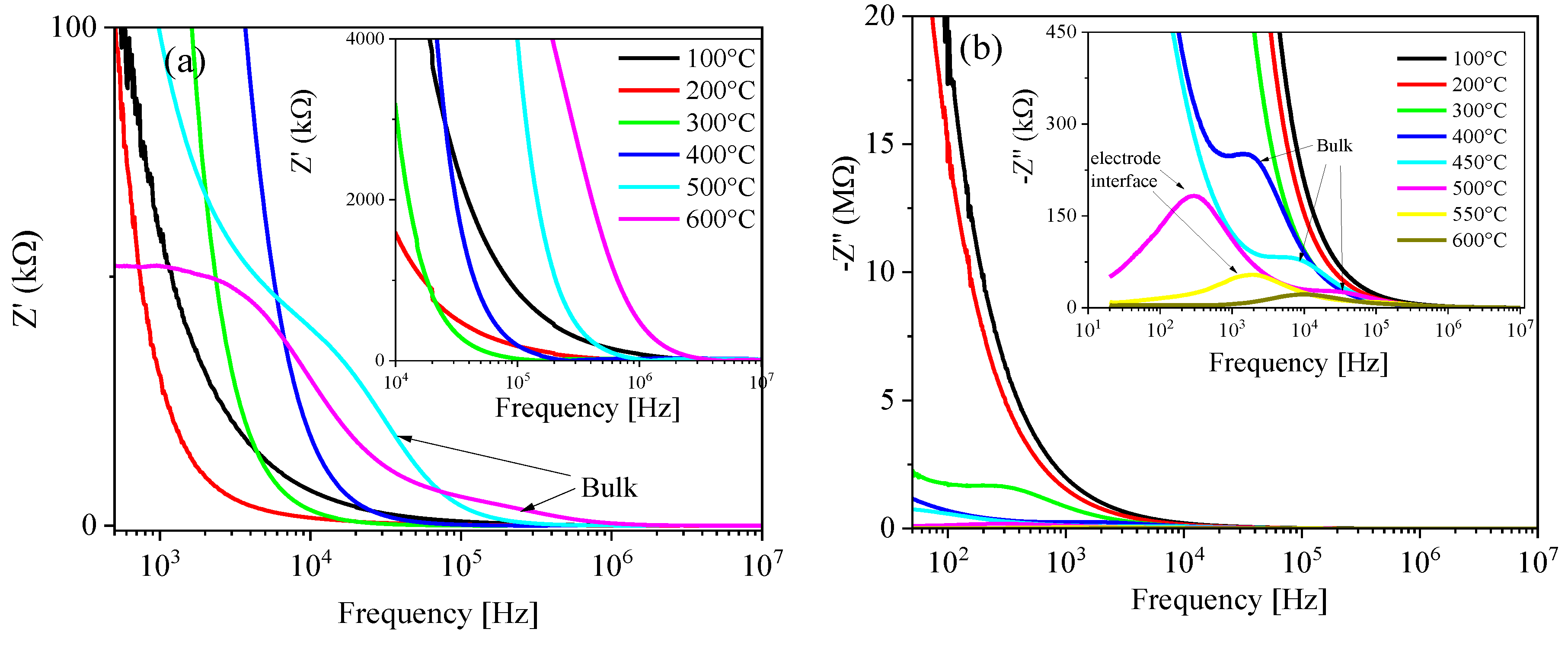
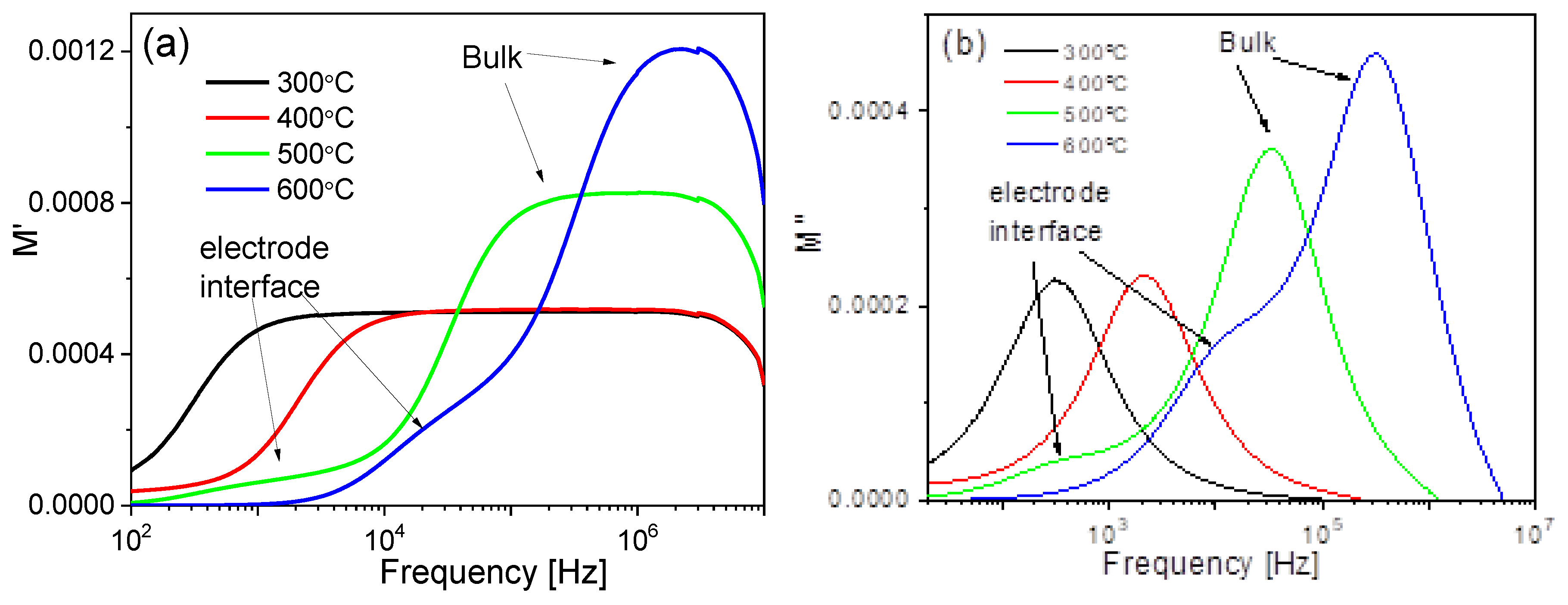
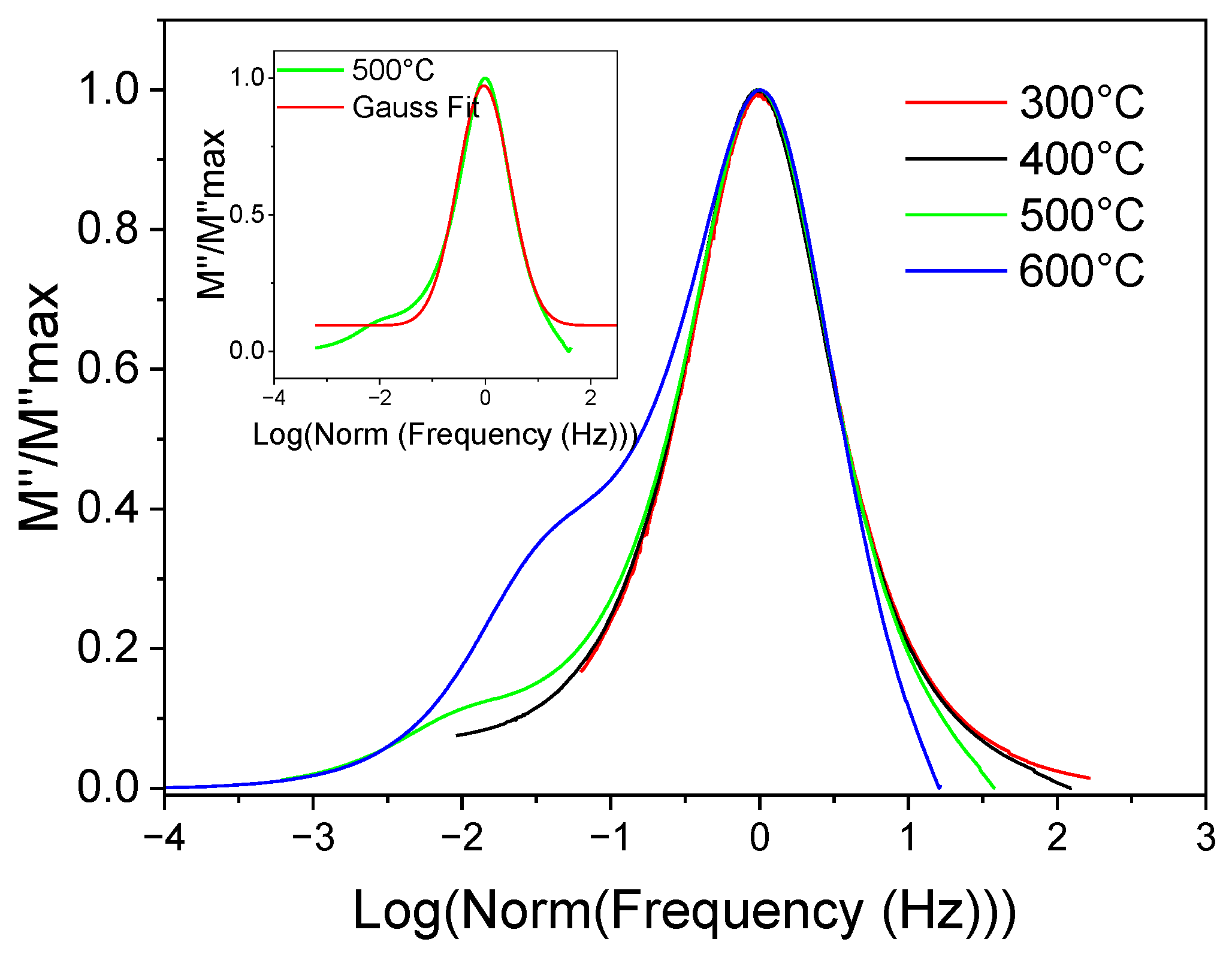
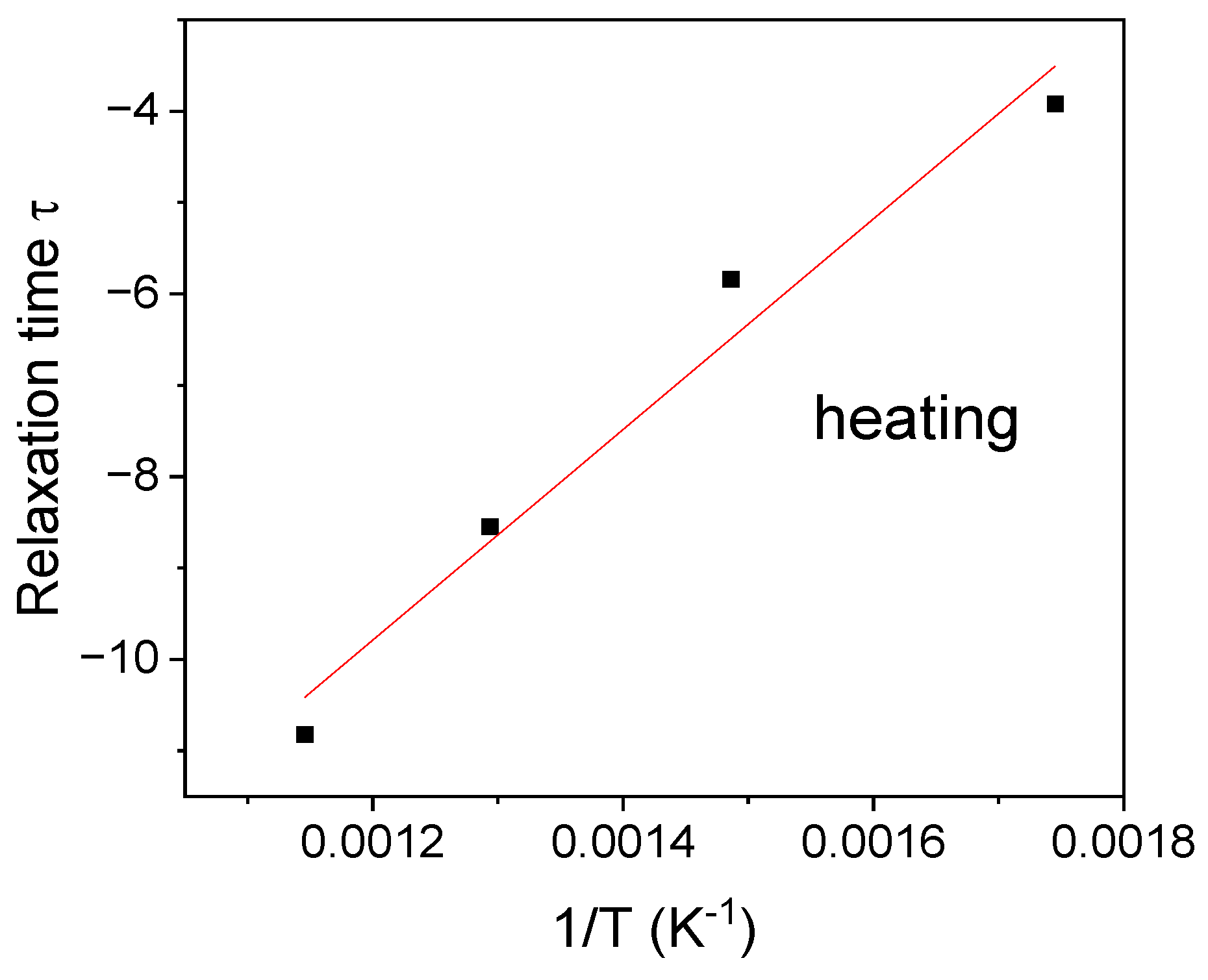
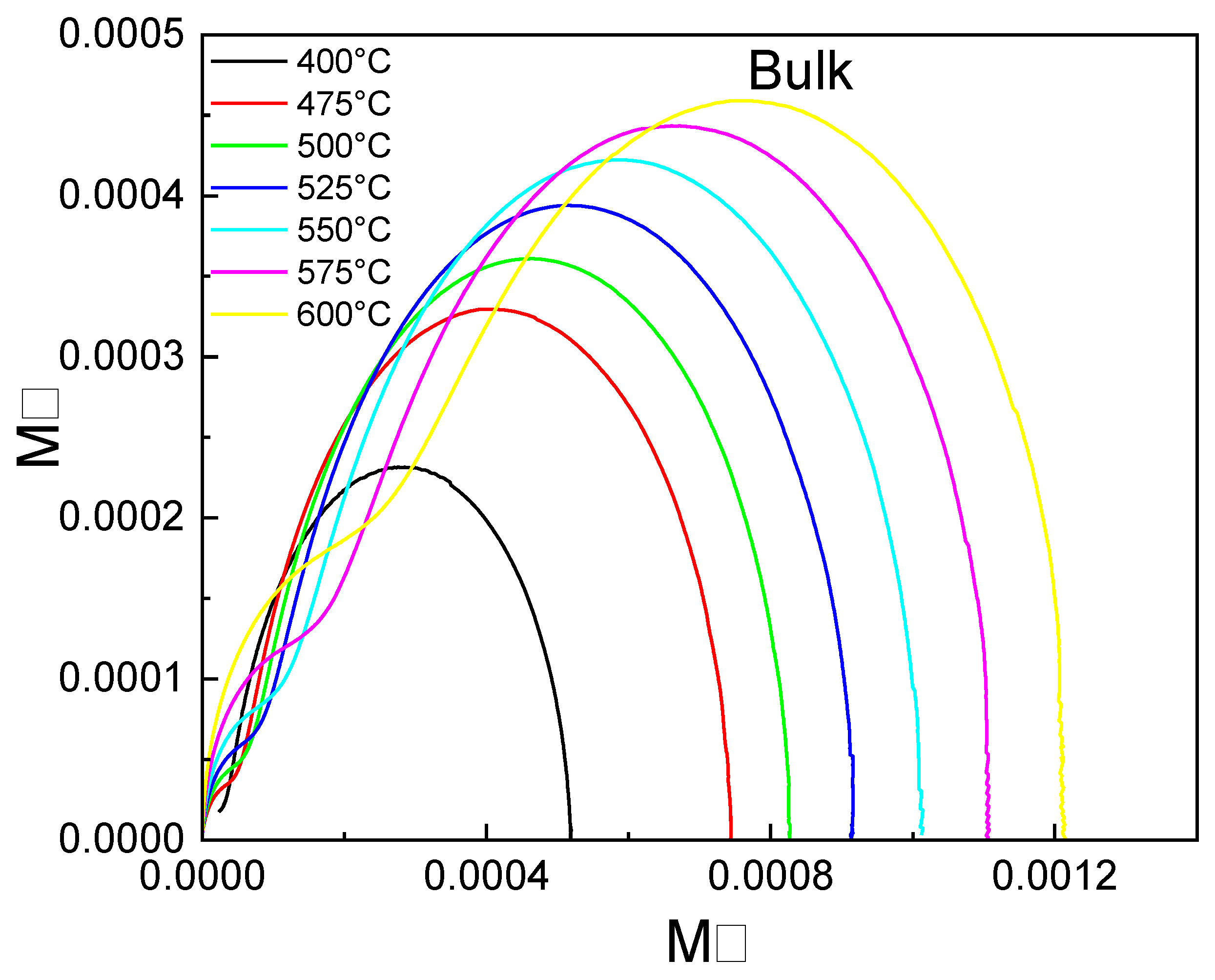
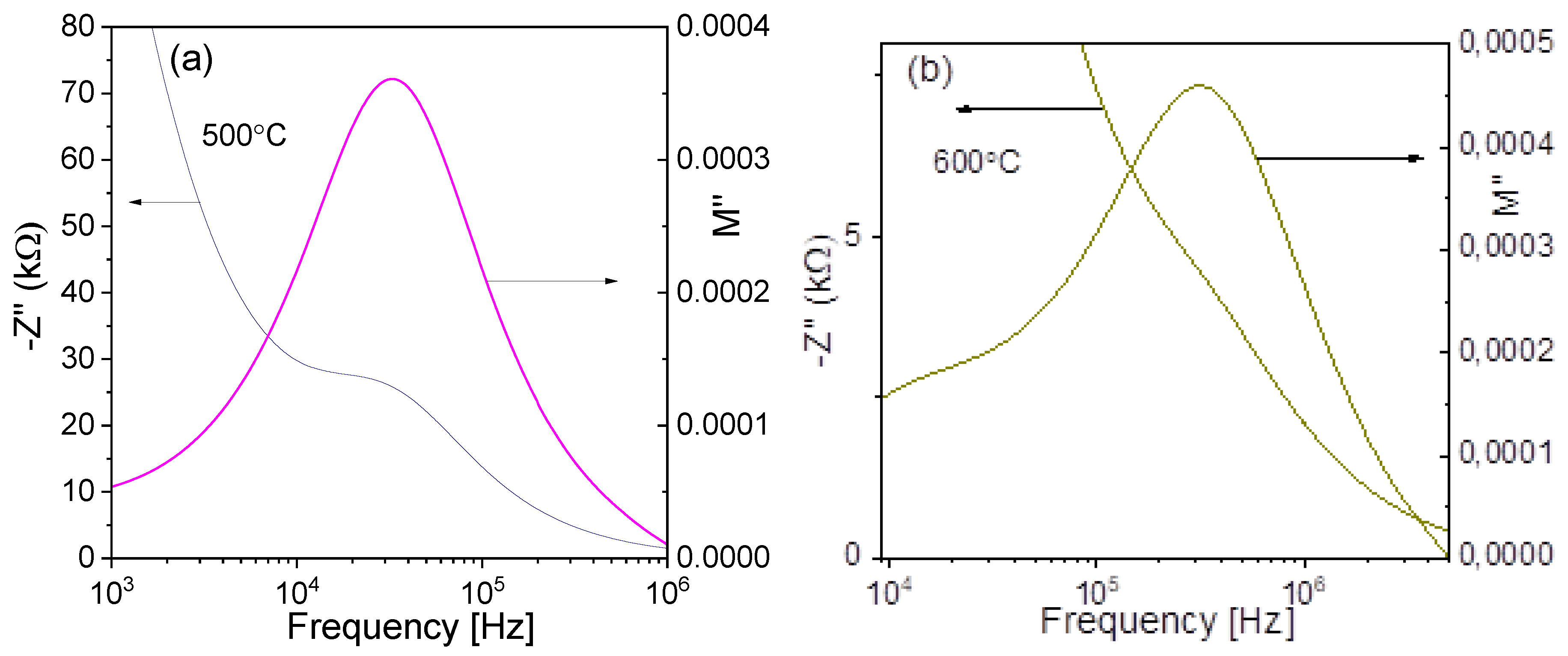
3.9. Complex Impedance Spectroscopy Analysis

Figure 12 shows Nyquist plots Z’‘(Z’), in which the -Z’‘ and Z’ axes refer to the imaginary and real parts of the impedance, respectively. The obtained spectra have an overall shape resembling two semicircles whose maximum radius decreases with increasing temperature. The specificity of changes in the Z’ value as a function of temperature is characteristic of semiconductor materials. Seen in detail, the EIS spectra have the form of two partially separated semicircles. The first semicircle present in the high-frequency region (0.1 -10 MHz) could come from the sample (Figure 12a) and the second one from double-layer capacitance occurring at the electrode-single crystal interface (Figure 12b) [47]. The second semicircle shows the highest impedance contribution and is located at medium and low frequencies between 10 kHz and 10 Hz. The analysis uses an electric equivalent circuit (EEC) composed of a parallel connection of a resistor R and a capacitor C or a constant model element (CPE) based on simple RC-RC model (EEC). The R1 value is responsible for the resistance of the single crystal, and C1 for its capacity, and R2 value is related to the resistance of the interface phenomena, and C2 for its capacitance at a given temperature [48]. The values of the total electric resistance of sample were estimated based on EEC model. The EEC fitting line is not shown for the sake of clarity of the image of the experimental spectra and since it is of little importance for the interpretation of the obtained results.
The activation energy Ea was determined (based on R1 data) as 1.1 eV using the Arrhenius formula in the temperature range from 475 to 600°C by fitting a straight line to the collected experimental data. The value of this activation energy and values of dc conductivity activation energies (1.18 and 1.14 eV) indicate that oxygen vacancies should be the most probable electric charge carriers in high-temperature range. On the other hand, the relationship between the width of the optical bandgap and the activation energy Eg∼2Ea, suggests that the conduction mechanism is consistent with intrinsic electronic conduction (i.e., the Fermi level is close to the midgap energy) in the analyzed temperature range. These results indicate two types of charge carriers i.e., oxygen vacancies and electrons in electric conductivity process. In turn, research conducted in papers [46,49] showed that an activation energy value above 2 eV is required for ion migration in NBT. However, this value of activation energy is valid for a stochiometric material, because any non-stoichiometry, particularly in the oxygen sublattice (oxygen loss) will lower this energy [50].
Further analysis of the conduction mechanism includes tracking changes in the real Z’ and imaginary component -Z’‘ as a function of frequency at selected temperatures (Figure 13). The real component Z’ (Figure 13a) shows a sigmoidal evolution vs. frequency in the low-frequency region followed by a saturation region in the high-frequency region. In the examined temperature region of 100-600°C, the Z’ values were observed to be greater at lower frequencies. In the low-frequency region (under 10 kHz), it was observed that Z’ values diminished as the temperature rises from 400°C to 600°C. It can be also observed that over 400°C, peak positions shift to higher frequencies with increasing temperature. This suggests a decrease in the resistance of the bulk and electrode interface, which in turn implies an enhancement in the sample conductivity. However, the curves from various temperatures converged to a nearly plateau region at higher frequencies (above 100 kHz) (the arch-like region progressively shrinks with increasing temperature for the temperature interval above 300°C and for high frequencies the creep-like region becomes predominant, insert in Figure 13a). This phenomenon can be attributed to release of point defects (space charge) [51]. The distinguishing features are the emerging modes (maxima) in the region of intermediate frequencies involved by the electrode-sample interface.
The imaginary part Z’‘ of impedance as a function of frequency at different temperatures is shown in Figure 13b. The plots exhibit two peaks: one at lower frequencies and a second one at higher frequencies. The major one is related to the electrode-surface phenomena, and the second peak originates from the sample bulk. The minor peak related to the crystal shifts towards high frequencies with increasing temperature, while its amplitude gradually diminishes. The peak indicates the maximum dielectric loss at the given frequency and attains a constant value in the high-frequency region. For frequencies below this peak, dipoles are completely polarized or aligned along the applied ac electric field and are in a stretched state. These observations show that the sample′s resistive properties were reduced and indicate the occurrence of relaxation processes in this temperature range. As temperature increased, thermal energy kBT provides driving force to the movement of charges. A detailed shape analysis suggests that we are dealing with only one relaxation process from the sample.
The complex electric modulus M (real component M’ and imaginary M’‘) is the inverse of the complex permittivity, which is used to study dielectric relaxation processes in materials. The frequency dependences of M’ process is shown in Figure 14a. M’ has very low values at lower frequencies and exhibits an increasing trend with the rise in frequency. When M′ approaches zero this behavior confirms the presence of an appreciable electrode and/or ionic polarization and represents an absence of the restoring energy for the mobile charge carriers in the studied temperature ranges. Generally, in the entire frequency range, the M’ values decrease with increasing temperature up to ~400°C. Above this temperature, the M’ values increase significantly with further temperature increase, especially in the high frequency range, resulting in a change in the dispersion image. This effect can be related to the increasing importance of ionic conductivity at high temperatures.
For high temperatures, a significant increase in M’ is observed with increasing frequency. Next, there is a “plateau” area where electrical processes are frequency independent. This area narrows as the samples are heated further. As the temperature increases, the slope of the M’(f) curves shifts towards higher frequencies, which is reflected in decreasing relaxation times. This phenomenon results from the increased activation of the short-range mobility of charge carriers or a gradual decrease in electron-lattice coupling [33,35].
M’ almost reaches zero at low frequencies due to the lack of electrical polarization and high dielectric losses and represents an absence of the restoring energy for the mobile charge carriers. M’ tends to reach a maximum (saturation) at high frequencies. This saturation can be connected to the fact that charge carriers move within a reducible range until the electric field changes become too rapid to induce the oscillation of charge carriers (vacancies).
Figure 14b shows the changes in the imaginary part of the electrical modulus M’‘ as a function of frequency, which denotes energy loss in the presence of an electric field. The evolution of M’‘ shows that with increasing temperature the maxima (peaks) shift to higher frequencies, which indicates that charge carriers become thermally stimulated with increasing temperature, resulting in a gradual movement (in other words: increasing temperature trigger faster ionic activity, which results in the peak shifting towards higher frequencies). The shorten the period and increase of the relaxation frequency, suggesting the presence of a temperature-dependent thermally activated relaxation process, dominated by the charge carrier hopping mechanism [52]. In the low-frequency interval below the maximum of M’‘(f), carriers can hop from one site to another site (i.e., long-distance hopping exists). In the high-frequency interval above the maximum of M’‘(f), charge carriers move over a short distance (i.e., localized movement inside potential wells). At the same time, the broadening of the asymmetric peak of M’‘(f), particularly at higher temperatures can be ascribed to non-Debye type relaxation (a stretched exponential character of the relaxation time exists) and is typical of hopping ion conductivity [53,54,55].
Figure 15 shows the normalized imaginary part of the M’‘/M’‘max modulus as a function of frequency (log norm(f/fmax)) in a wide temperature range. The frequency was normalized to the point where M’‘(f) reaches the maximum value M’‘max.. There is one overlapping relaxation curve (Figure 15) with left side perturbations in the low-frequency region originating from electrode-sample interface. This clearly suggests the same activation energy of oxygen vacancies occurring on different time scales and that the distribution of the relaxation times is temperature independent. A good fit of the experimental curves with a Gaussian function is also shown (insert in Figure 15). The value of FWHM evaluated from the normalized spectrum is greater than log[(2 + √3/(2 − √3)], and this indicates non-Debye-type behavior which is well supported by complex impedance and modulus plots.
The evolution of the conduction relaxation time as an inverse function of the inverse temperature is shown in Figure 16. The most probably relaxation time τ is estimated from the position of M’‘max. as a function of frequency, according to the relationship [51]:
τ = 1/2πf
where f is the relaxation frequency at the point M’‘max..
The activation energy (Ea-rel.) in the conductivity relaxation was calculated from the modified Arrhenius equation:
τ = τ0exp(Ea-rel./kT)
where: τ0 is the pre-exponential factor and is equal 5.6x10-11 s for NBT single crystals.
The activation energy for conductivity relaxation (Ea-rel.) is equal to the free energy of charge carrier migration (hopping) between adjacent positions in the lattice [37,56]. However, the activation energy obtained from dc conductivity is the sum of both the creation and migration free energy of charge carriers. It was found from eq. (10) that Ea-rel. is equal 0.99 eV. The closeness of this activation energy with those obtained from dc conductivity (1.18 and 1.14 eV) indicates that dispersion of the conductivity is attributable to the hopping of charge carriers. Based on these results, we can concluded that the creation free energy should be close to zero, which suggest that the carrier concentration is temperature independent, i.e., the carriers are almost dissociated from traps. These activation energies are comparable to the activation energy of 0.8-1.1 eV obtained for diffusion of oxygen vacancies in perovskite oxides [57,58]. Such values of the activation energy for NBT single crystals are indicative of the ionic nature of the electric relaxation involved in the process.
The next stage of the research was the analysis of the Argand chart (M’ vs. M’‘) and the results are shown in Figure 17. It is observed that the average radius of the arcs increases with increasing temperature, and the maximum values of M’‘max, shift to the higher frequency area. This confirms that relaxation is a thermally activated process dominated by the charge carrier hopping mechanism. As expected, only one semicircle dominates in the tested material, and the presence of small additional ones probably results from processes occurring at the crystal-electrode interface.
Figure 18 shows the combined diagram of Z’‘ and M’‘ versus frequency. The peak Z’‘(f) and M’‘(f) do not overlap, which indicates that the relaxation process is dominated by the short-range movement of charge carriers (relaxation time is temperature independent) and departs from the Debye type conduction mechanism found from Figure 14 [59,60,61]. This also suggests that the conduction process may be localized [62] in accordance with the above-mentioned prediction.
In oxide perovskites, oxygen vacancies (VO) are thought to be one of the mobile charge carriers. In the NBT crysta, oxygen vacancies are generated by trace impurities of the reagents as well as the evaporation of Bi ion during the material processing. In general, they can occur in three states: the neutral state VO (V0O), the singly ionized V⃰ O (V2+O) state, and the doubly ionized V⃰⃰ ⃰ O (V2+O) states. The neutral-state vacancies may be thermally ionized to singly (V⃰ O) and doubly (V⃰⃰ ⃰ O) ionized states according to:
VO ↔ V⃰ O + e′ ↔ V⃰⃰ ⃰ O+ 2e′′
Conduction electrons released from neutral oxygen vacancies may trapped (localized) by Ti4+
(Ti′Ti centers) and this generates a reduction of the valence following the relation:
Ti4++e ↔]Ti3+
Besides their association with Ti, these electrons can be weekly bonded (trapped) to oxygen vacancies, which can form a shallow level to trap electrons. However, it is difficult detect the precise location of the electrons, because this process can depend on local structure and temperature. Deficiency of electrons in p-type NBT (see below) favors the ionization of oxygen vacancies. The energy levels of Ti′Ti centers are also shallow, and the electrons can easily hop via titanium ions contributing to charge transport. The thermal activation of the electrons trapped by this Ti or by oxygen vacancies can increase conduction. The electron hopping may take two pathways (i) direct hopping in an oxidation-reduction process between Ti ions according to relation (12), and (ii) jumping through the bridging oxygen vacancies between Ti ions according to relation (11). Activation energies for singly and doubly ionized oxygen vacancies are in the ranges 0.3-0.5 and 0.6-1.2 eV, respectively [63,64,65], which suggested that, in our studies, double-ionized oxygen vacancies will be dominant way of generated in a higher temperature range than single ionized ones. The oxygen vacancies, electrons localized on titanium ion [66,67] and probably associated complexes based on them (Ti′Ti -V⃰⃰ ⃰ O) ⃰ could be the more likely charge carriers involved in the conduction process in the high-temperature range conductivity of NBT single crystals. The associated complexes are rather unstable and gradually decompose during heating, releasing their more mobile components, which participate in the charge transfer. We should also remember the possibility of the recapture of the previously emitted electrons by oxygen vacancies. This can be due to oxygen vacancies becoming metastable at high temperatures. Thus, the conduction process can occur due to the hopping of electrons between Ti4+ and Ti3+, leading to the contribution of both single and doubly ionized oxygen vacancies and to the contribution of the hopping energy between these localized centers to the activation energy in the high-temperature range. The decrease of the dc conductivity activation energy from 1.26 eV to 1.18 eV at 450°C and from 1.18 eV to 1.14 eV at 553°C can be related to an increased concentration of doubly ionized vacancies and/or to increased electrons content. In summary, these results show that oxygen vacancies and hopping electron mechanism coexist in NBT single crystals and make an important contribution to the electric conductivity and determine the conduction relaxation process in the high-temperature range.
The oxide-ion conduction in NBT may originates from (i) Bi deficiency and oxygen vacancies created during the material processing [21], and (ii) the highly polarizable Bi3+ ion, which provide pathways with low diffusion barriers, favoring the migration of oxygen ions [46,47,68]. In the low-temperature range, trapping of oxygen vacancies and their association with Bi vacancies makes their migration difficult or impossible and they do not contribute markedly to the long-range conduction process. In addition, most of the oxygen vacancies should be neutral in thermal equilibrium in this temperature interval due to the deep defect level, i.e., the Fermi level can be located above the defect level of the oxygen vacancy. However, as the temperature increases, due to the supplied thermal energy, the trapping energy gradually decreases and oxygen vacancies are released from the traps, gradually becoming ionized and releasing electrons. These vacancies and electrons contribute increasingly to electrical conductivity.
Complex impedance spectroscopy measured at high-temperatures captures the superposition of the electronic and ionic conductivity contributions. The contribution of electrons to charge carrier transfer, particularly in the high-temperature range can be related to the nonstoichiometry of NBT. As mentioned above, bismuth deficiency is one of the reasons for formation of oxygen vacancies in NBT. However, in our samples an excess of bismuth occurs. In this situation, a smaller number of oxygen vacancies and, consequently the emergence of electronic conductivity, should be expected. On the other hand, deficiency in sublattice O also occurs (see SEM/EDS and XPS results). The competitive influence of these non-stoichiometries may lead to an imbalance in the proportions between ionic and electronic conductivities. These results show that the possibility of modeling NBT single crystals with desired properties (particularly with expected electric conductivity) exists through careful control of stoichiometry, which can be achieved by minutely selection and examination of the precursors and in detail control/steering of crystal growth conditions.

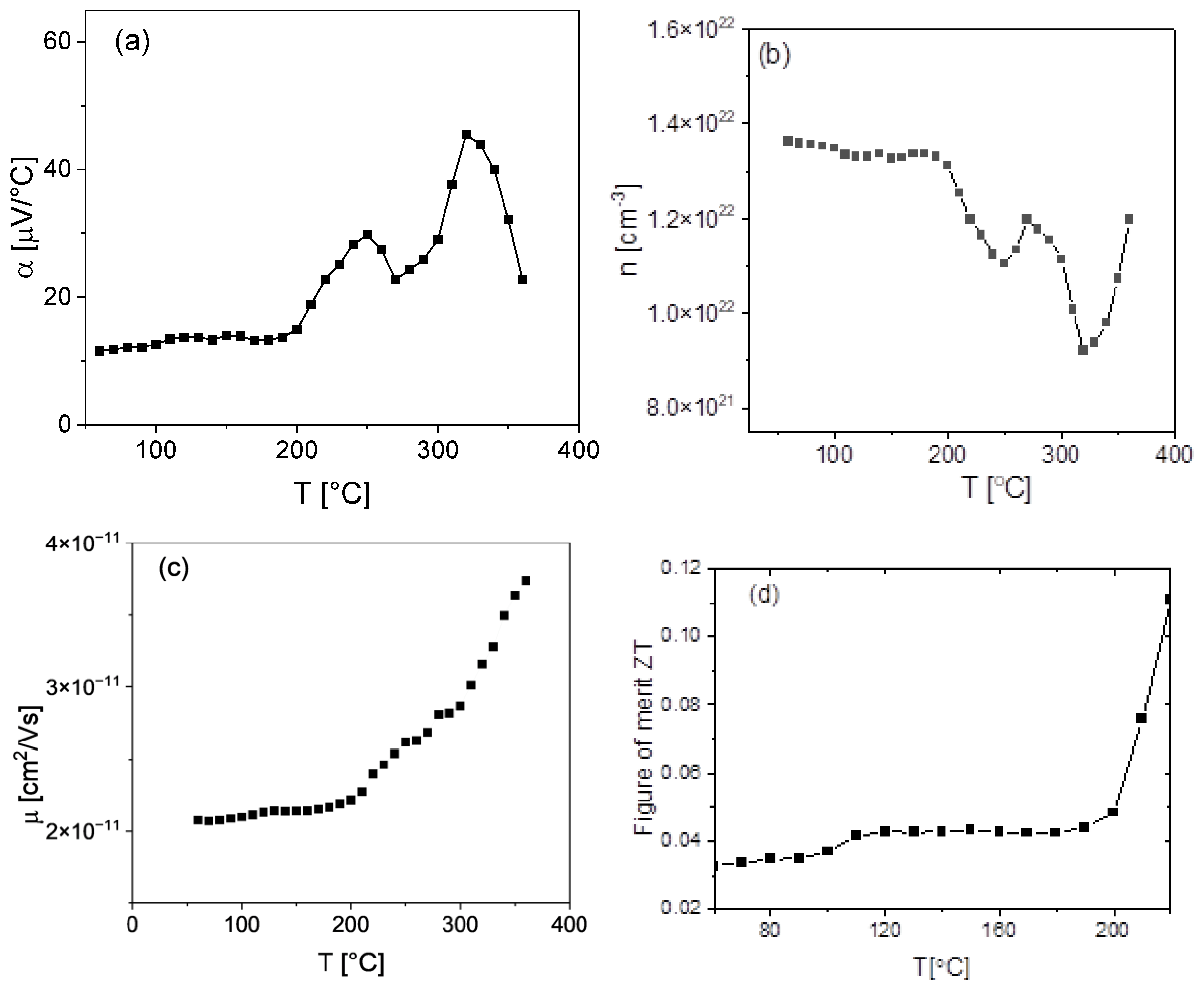
3.10. Thermoelectric Results

Figure 19a shows the temperature dependence of the Seebeck coefficient α. The α value generally increases with increasing temperature over the entire temperature range. The nearly temperature-independent Seebeck coefficient up to about 200°C suggests that the carrier mobility is thermally activated in this temperature range, which indicates the hopping process as discussed above. At higher temperatures, two distinct local maxima of α(T) is visible around the temperatures characteristic for NBT. The first anomaly visible around 190-220℃ is related to the disappearance of the long-range ferroelectric properties (depolarization process). The second maximum is visible in the temperature range of 220-350℃, in which rhombohedral and tetragonal phases coexist. At the same time, in this temperature range there is a gradual process of changing symmetry from rhombohedral to tetragonal. The positive sign of the Seebeck coefficient indicates the dominance of p-type conductivity. This can be due to creating of holes h• during cooling after growing or during the annealing step according to reaction:
½O2+ V⃰⃰ ⃰ O= V0O+2h•
The holes have higher mobility than oxygen vacancies.
Based on experimental data and on Equations (14) and (15), the carrier concentration n and carrier mobility μ were calculated [69,70] as:
α = kB/e ln(Nc/n)
where kB – Boltzmann constant, e –electric charge of the carrier, Nc - effective density of states in the conduction band (for NBT Nc = 1.56 x 1028 m-3), n - carrier concentration.
σ = enμ
where: e - electric charge of the carrier, and μ - mobility of the carrier. The results obtained are presented in Figure 19b,c.
The temperature dependence of thermoelectric power factor was determined in terms (α2σ)T/κ and shown in Figure 19d. As can be seen, the value of the power factor increases with increasing temperature. However, its values are too low (particularly in the low-temperature range) for actual use as a thermoelectric module. This may be due to the high resistivity (low electric conductivity) and high thermal conductivity. Although it is simple to increase the electric conductivity of NBT through introduction of non-stoichiometry (increased concentration of defects) [46,71], such a strategy usually also results in an undesirable increase of thermal conductivity. Thus, achieving a reasonable compromise between the value of both parameters in simple way is difficult in pure NBT.

1.11. Thermal Conductivity Results

Temperature variation (RT-220°C) of thermal conductivity (κ) is shown in Figure 20a. The small anomaly of κ(T) at about 140°C is visible (indicated by an arrow). Note that an anomaly in the DSC(T) plot was detected at similar temperature [71]. The thermal conductivity can be described as a sum of the lattice κl and electronic κe contributions:
κ=κl+κe
To separate κl from κe, the electronic thermal conductivity was calculated using Wiedemann-Franz law κe= LσT, where a Lorentz number of L=2.44x10-8WΩK-2 was taken, and σ is the electrical conductivity. The lattice thermal conductivity κl can then be derived by subtracting κe from κ. This estimation shows that the phonon thermal conductivity of NBT single crystals is predominant in the total thermal conductivity. Note that dc electric conductivity is in the range of 10-11-10-12Sm-1 in the investigated temperature interval. This indicates that the contribution of free electrons to the thermal conductivity is small, which confirms the predominantly phonon nature of the thermal conductivity of the investigated material. In general, thermal conductivity increases up to about 190°C (depolarization temperature) and then tends to stabilise with further temperature increase (Figure 20a). Assuming that the dominant contribution to thermal conductivity originates from phonons, their dispersion on domain walls (in the range in which the ferroelectric phase exists), interphase boundaries (in the range of coexistence of rhombohedral and tetragonal phases) may determine the total thermal conductivity. These perturbations of crystal structure lead to an increase of collisions of phonons travelling through the lattice (i.e., thermal phonon scattering increases) which can reduce the lattice thermal conductivity. Thermal conductivity (κ) directly depends on the concentration of carriers, i.e., when the carrier concentration increases, κ also increases. However, it is difficult to independently consider all factors, which influence the thermal conductivity, because they are interrelated.
It is expected that the perturbations of crystal structure can lead to a shortening of the phonon mean free path. The phonon mean free path was calculated using the relation:
κ=1/3Cυϑl
where Cυ is the heat capacity per unit volume [72], ϑ is the average sound velocity and l is the average phonon mean free path. Average sound velocity was measured using the usual pulse echo technique [14]. Temperature evolution of the calculated average mean free path is shown in Figure 20b. In general, the average phonon mean free path increases up to about 190°C (depolarization temperature) and then tends to stabilise with further temperature increase. The average phonon mean free path is comparable to the lattice parameters of NBT presented in papers [73,74].

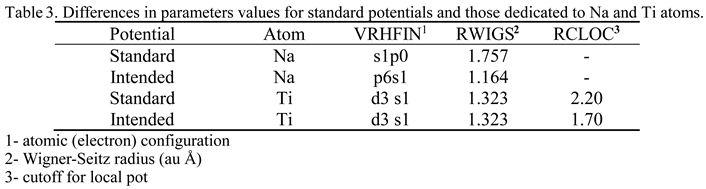
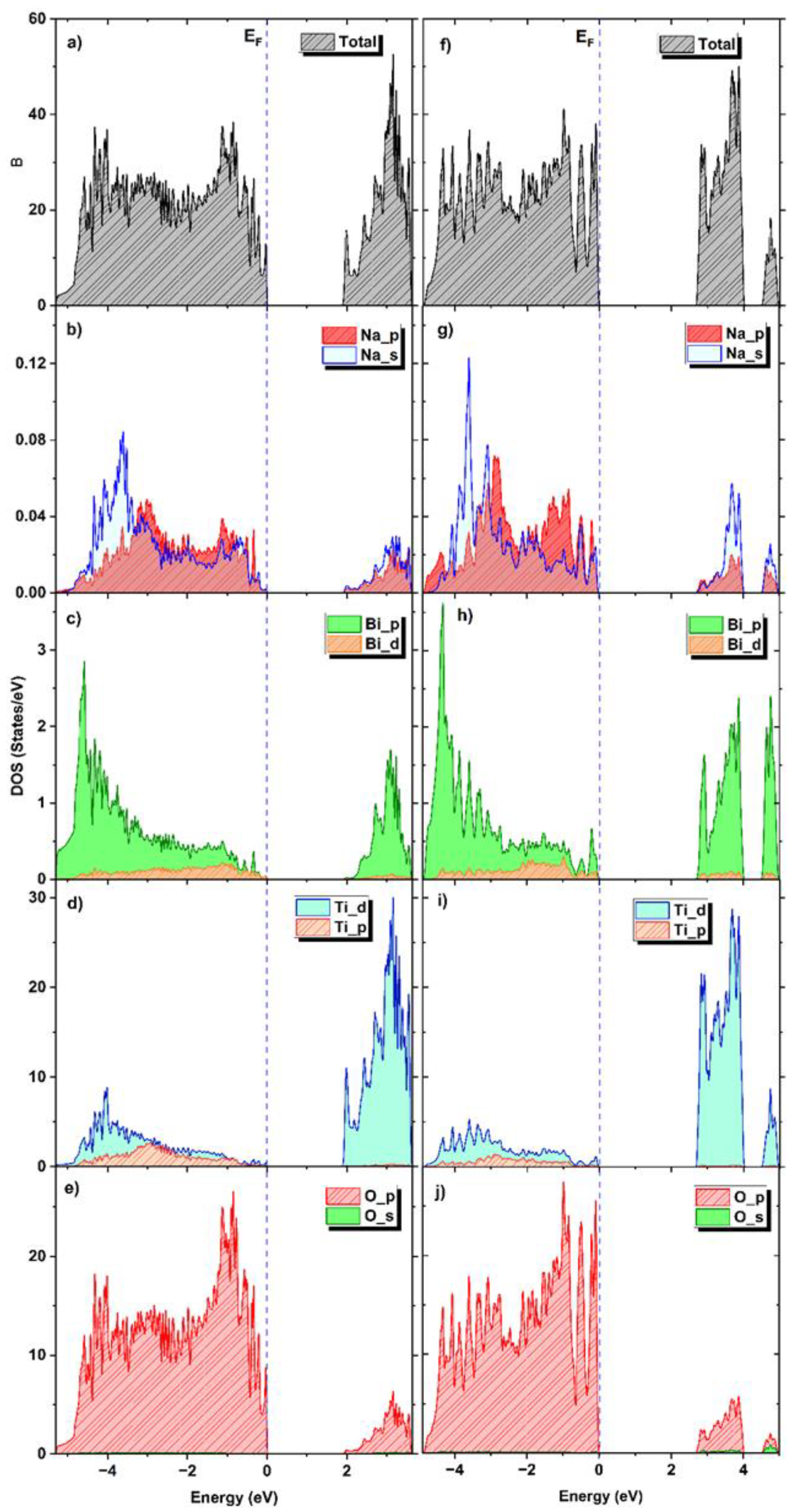
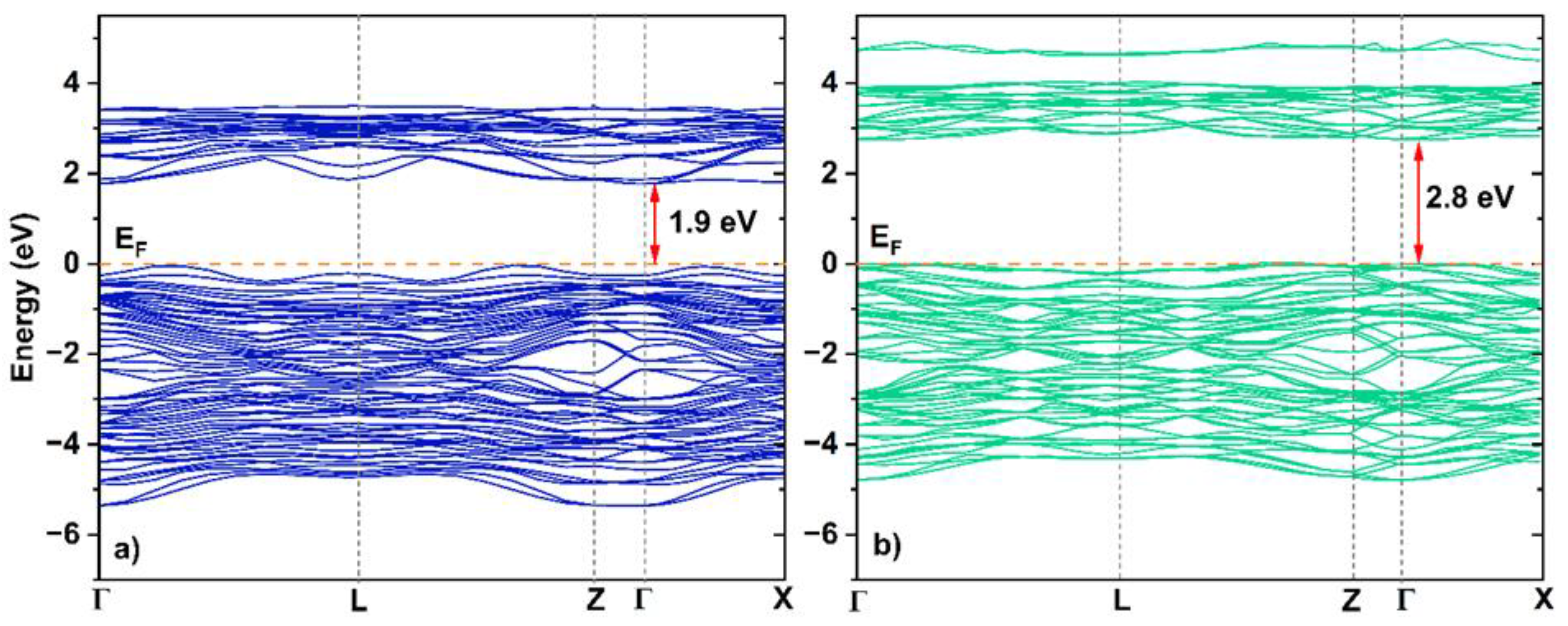
3.12. Ab Initio Calculations

The partial (PDOS) and total (TDOS) densities of the states of the Na0.5Bi0.5TiO3 system was computed. Figure 21 shows the calculated total and partial densities of the electronic states of selected orbitals of the atoms constituting the NBT for two different cases in which different potentials were used for the Na and Ti atoms. In the first case, standard potentials PAW PBE for all atoms constituting the NBT compound were used for calculations. In the second case, the potentials intended for the atoms forming perovskite structures were used in the calculations for Na and Ti atoms. For the first variant, the energy gap value was 1.9 eV, while for the second one it was 2.8 eV. As calculations have shown, when the potentials intended for perovskites are applied to Na and Ti atoms, the energy gap value increases by 68%. For comparison, in previous work [75] the energy gap value was set at 3.03 eV.
The results shown in Figure 21 confirm that the valence band of NBT is formed mainly by oxygen atoms, while the conduction band was determined by the titanium atoms for NBT. The Conduction Band (CB) consisted mainly of Ti (3d) and Bi (6p) orbitals and to a lesser extent of O (2p) states. The dominant contribution at the top of the conduction band originated from Ti (3d) electrons. The highest hybridization in the CB was observed in the middle region of the band formed by Ti (3d) and Bi (6p) states. The valence band (VB) is wider than the conduction band (CB) and was calculated to be 5.3 eV. The valence band consisted mostly of O (2p) states. Hybridization also occurred in the lower energy section of the VB and originated from the O (2p), Ti (3d) and Bi (6p) orbitals. The contribution from Na orbitals was relatively small, and it can be observed that both the conduction and valence band for sodium were determined by the s and p orbitals.
Figure 22 shows the calculated band structures of NBT along high-symmetric directions in the Brillouin zone. The bottom of the conduction band (CB) and the top of the valence band (VB) are both accurately located at highly symmetric positions relative to the Γ point. The calculated band gaps at the Γ point were 1.9 and 2.8 eV for case standard potentials Na, Ti and for case intended potentials Na, Ti, respectively. This difference in band gap values between the valence and conductivity bands was a consequence of using two different atomic potentials for Na and Ti (Table 3).
Preprints 107799 i003

4. Conclusions

High-quality and large size lead-free Na0.5Bi0.5TiO3 single crystals were successfully grown by the Czochralski technique. X-ray diffraction showed that the crystals do not contain any secondary phases and exhibit rhombohedral symmetry (R3c) at room temperature. Scanning electron microscopy SEM and energy dispersive spectra, X-ray photoelectron spectroscopy XPS studies showed that they are characterized by a homogeneous distribution of particular elements, and revealed that they exhibit nearly stochiometric composition. These results pointed to very high quality of the studied NBT single crystals.
An energy gap approximately 2.92 eV was found. Systematic studies of the thermoelectric effect (Seebeck coefficient), depolarization current, current-voltage characteristics, and direct (σdc) and alternating (σac) electrical conductivities for these crystals were performed. Impedance spectroscopy measurements provided a framework for creating an electric conductivity model for NBT. Most of these properties were measured for the first time. The occurrence of a reversible insulator-metal transition on nanoscales caused by the electric field, was revealed. It was shown that the electrical conductivity in NBT is complex and depends on temperature: (i) at low temperatures, two competing conduction mechanisms coexist: the band model and the hopping model (with dominance of the first mechanism), (ii) in the middle temperature interval, moving of small polarons, and (iii) in the high temperature interval, hopping of electrons thermally excited from oxygen vacancies. This gives useful pointers to strategies for optimizing the electrical conductivity for specific applications. The decrease of the activation energy in the high temperature range can be explained by an increase of the concentration of doubly ionized vacancies and/or an increased content of electrons. It is supposed that the relaxation process identified in the high-temperature interval was determined by a space charge polarization mechanism (i.e., oxygen vacancies and electrons localized on titanium ions) rather than by a dipolar one. The Seebeck coefficient measurements show that NBT single crystals have p-type conductivity. The measurements distinguished characteristic temperatures Td, Tm and TT-C. As calculations have shown, when the potentials intended for perovskites are applied to Na and Ti atoms, the energy gap value increases by 68% from 1.9 eV to 2.8 eV. The implications of the studies presented in this paper are twofold. First, they given further insight into the mechanisms responsible for electric conductivity of NBT and related perovskite materials. At the same time, they offer a pathway for creating lead-free perovskite materials with expected behaviors and thus enhances their usefulness in the industrial field.

Acknowledgments

We gratefully acknowledge Polish high-performance computing infrastructure PLGrid (HPC Centers: ACK Cyfronet AGH) for providing computer facilities and support within computational grants no. PLG/2022/015969 and PLG/2023/016854.

References

  1. Uchino K. Ferroelectric devices. New York, NY: Marcel Dekker; 2000.
  2. Zachariasz R, Bochenek D. Properties of the PZT type ceramics admixed with barium and niobium. Archives of Metallurgy and Materials. 2009; 54:895-902.
  3. Skulski R, Wawrzała P, Ćwikiel K, Bochenek D. Dielectric and electromechanical behaviors of PMN-PT ceramic samples. Journal of Intelligent Material Systems and Structures. 2007;18: 1049-1056. [CrossRef]
  4. Bochenek D. Magnetic and ferroelectric properties of PbFe1/2Nb1/2O3 synthesized by solution precipitation method. J.Alloys. Comp. 2010;504:508-513. [CrossRef]
  5. Suchanicz J, Kluczewska K, Czaja P, Kania A, Konieczny K, Handke B, Sokolowski M, Trubitsyn MP, Kruzina TV. Structural, thermal, dielectric and ferroelectric properties of poled Na0.5Bi0.5TiO3 ceramics. Ceramics International. 2017;43:17194-17201.
  6. Aksel E, Forrester JS, Jones JL, Thomas PA, Page K, Suchomel MR. Monoclinic crystal structure of polycrystalline Na0.5Bi0.5TiO3. Appl. Phys. Lett. 2011; 98: 152901 (1-5). [CrossRef]
  7. Rao BN, Fitch AN, Ranjan R. Ferroelectric-ferroelectric phase coexistence in Na1/2Bi1/2TiO3. Phys. Rev. 2013; B87: 060102 (1-8). [CrossRef]
  8. Dorcet V, Trolliard G, Boullay P. Reinvestigation of phase transitions in Na0.5Bi0.5TiO3 by TEM. Part I: First order rhombohedral to orthorhombic phase transition. Chem. Mater. 2008; 20: 5061-5073. [CrossRef]
  9. Trolliard G, Dorcet V. Reinvestigation of phase transitions in Na0.5Bi0.5TiO3 by TEM.Part II: Second order orthorhombic to tetragonal phase transition. Chem. Mater. 2008; 20: 5074-5082. [CrossRef]
  10. Aktas O, Duclere JR, Quignon S, Trolliard SG, Salje EKH. Polarity of modulated Na0.5Bi0.5TiO3 and its slow structural relaxation. Appl. Phys. Lett. 2018; 113: 032901(1-4). [CrossRef]
  11. Suchanicz J. Behaviour of Na0.5Bi0.5TiO3 ceramics in the ac electric field. Ferroelectrics. 1998;209:561-568. [CrossRef]
  12. Vakhrushev SB, Isupov VA, Kvyatkovsky BE, Okuneva NM, Pronin IP, Smolensky GA, Syrnikov PP. Phase transitions and soft modes in sodium bismuth titanate. Ferroelectrics.1985, 63: 153-160. [CrossRef]
  13. Suchanicz A, Roleder K, Kania A, Handerek J. Electrostrictive strain and pyroeffect in the region of phase coexistence in Na0.5Bi0.5TiO3. Ferroelectrics.1988; 77:107-110. [CrossRef]
  14. Suchanicz J. Elastic constants of Na0.5Bi0.5TiO3 single crystal. J.Mater.Sci. 2002; 37: 489-491. [CrossRef]
  15. Sakata K, Masuda Y. Ferroelectric and antiferroelectric properties of Na0.5Bi0.5TiO3-SrTiO3 solid solution ceramics. Ferroelectrics. 1974; 7, 347-349. [CrossRef]
  16. Aksel E, Forrester JS, Nino JC, Page K, Shoemaker P, Jones JL. Local atomic structure deviation from average structure of Na0.5Bi0.5TiO3: Combined x-ray and neutron total scattering study. Phys.Rev. 2013; B87:104113 (1-10). [CrossRef]
  17. Balagourov AM, Koroleva EY, Naberezhnov AA, Sakhnenko VP, Savenko BN, Ter-Oganessian AA, Vakhrushev SB. The rhombohedral phase with incommensurate modulation in Na0.5Bi0.5TiO3. Phase Transitions. 2006;79:163-173. [CrossRef]
  18. Barick BK, Mishra KK, Arora AK, Choudhary RNP, Pradhan DK. Impedance and Raman spectroscopic studies of Na0.5Bi0.5TiO3. J Phys D: Appl Phys. 2011;44:355402 (1-10). [CrossRef]
  19. East J, Sinclair DC. Characterization of (Bi1/2Na1/2)TiO3 using electric modulus spectroscopy. J Mater Sci. Lett. 1997;16:422-435. [CrossRef]
  20. Saradhi BVB, Srinivas K, Prasad G, Suryanarayana SV, Bhimasankaram T. Impedance spectroscopic studies in ferroelectric Na0.5Bi0.5TiO3. Mat. Sci. Eng. 2003;B98:10-16.
  21. Suchanicz J, Kluczewska-Chmielarz K, Sitko D, Jagło G. Electrical transport in lead-free Na0.5Bi0.5TiO3 ceramics. J.Adv.Ceram. 2021;10:152-156. [CrossRef]
  22. Karpierz M, Suchanicz J, Konieczny K, Smiga W, Czaja P, Sokolowski M. Effects of PbTiO3 doping on electric properties of Na0.5Bi0.5TiO3 ceramics. Phase Transitions. 2016;90:65-71. [CrossRef]
  23. Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a planewave basis set. Phys. Rev. B. 1996;54:11169-11186. [CrossRef]
  24. Kresse G, Furthmüller J. Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set. Computational Materials Science. Mater. Sci. 1996; 6: 15-50. [CrossRef]
  25. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996; 77: 3865-3868. [CrossRef]
  26. Lü H, Wang S, Wang X. The electronic properties and lattice dynamics of Na0.5Bi0.5TiO3: From cubic to tetragonal and rhombohedral phases. J. Appl. Phys. 2014; 115: 124107(1-7). [CrossRef]
  27. Berri S. Ab initio study of fundamental properties of XAIO3 (X=Cs, Rb and K) compounds. J. Sci. Adv. Mater. Devices. 2018; 3: 254–261. [CrossRef]
  28. Mandal, B., Thakur, A.K. Electrode response of NaFeTiO4 in aqueous supercapacitor cells. Ionics. 2021;27:1709-1721. [CrossRef]
  29. Siddiqui TAJ, Shaikh SF, Sangale SS, Raut SD, Mane RS, Ubaidullah M, Thamer BM, Al-Enizi AM, Totawar BB, Samdani MS. Mesoporous carbon of carbonized human urine waste: a valuable heterogeneous catalyst for chromone and xanthene derivative synthesis. Catalysts. 2020;10:1369(1-17). [CrossRef]
  30. Cheng L, Hu X, Hao L. Easily recycled Bi2O3 photocatalyst coatings prepared viaball milling followed by calcination. Appl. Phys. A. 2017;123:443(1-7). [CrossRef]
  31. https://doi.org/10.1007/s00339-017-1051-x.
  32. Zhou Z, Xiong P, Liu H, Peng M. Ultraviolet a persistent luminescence of a Bi3+- activated LiScGeO4 material. Inorg. Chem. 2020;59:12920-12927. [CrossRef]
  33. Hou D, Hu X, Wen Y, Shan B, Hu P, Xiong X, Qiaoa Y, Huanga Y. Electrospun sillenite Bi12MO20 (M = Ti, Ge, Si) nanofibers: general synthesis, band structure, and photocatalytic activity. Phys. Chem. Chem. Phys. 2013;15:20698-20705. [CrossRef]
  34. Łapiński M. Czubek J. Drozdowska K. Synak A. Sadowski W. Kościelska B. Plasmon-enhanced photoluminescence from TiO2 and TeO2 thin films doped by Eu3+ for optoelectronic applications. Beilstein J. Nanotechnol. 2021;12:1271–1278. [CrossRef]
  35. Horvath H. Gustav Mie and the scattering and absorption of light by particles: Historic developments and basics. Journal of Quantitative Spectroscopy & Radiative Transfer. 2009;110:787–799. [CrossRef]
  36. Stern F. Elementary theory of the optical properties of solids. Solid State Phys.1963;15:299-408. [CrossRef]
  37. Li L, Li M, Zhang H, Reaney IM, Sinclair DC. Controlling mixed conductivity inNa1/2Bi1/2TiO3 using A-site non-stoichiometry and Nb-donor doping. J. Mater. Chem.C. 2016;4: 5779 (1-8). [CrossRef]
  38. Andriyevsky B, Suchanicz J, Cobet C, Patryn A, Esser N, Kosturek B. Manifestation of phase transformations in optical spectra of Na0.5Bi0.5TiO3 crystals between 25oC and 350oC. Phase Transitions. 2009;82:567–575. [CrossRef]
  39. Zeng M, Or SW, Chan HL. First – principles study on the electronic and optical properties of Na0,5Bi0.5TiO3 lead free piezoelectrical crystal. J.Appl. Phys. 2010;107: 043513(1-8). [CrossRef]
  40. Bousquet M, Duclère J-R, Orhan E, Boulle A, Bachelet C. Optical properties of anepitaxial Na0,5Bi0.5TiO3 thin film grown by laser ablation: Experimental approach and density functional theory calculations. J. Appl. Phys. 2010;107:104107 (1-9). [CrossRef]
  41. Scott JF, Araujo CA, Melnick BM, McMillan LD, Zuleeg R. Quantitative measurement of space-charge effects in lead zirconate-titanate memories. J. Appl. Phys. 1991;70:382–385. [CrossRef]
  42. Lampert MA. Simplified theory of space-charge-limited currents in an insulator with traps. Phys. Rev. 1956;103: 1648-1656. [CrossRef]
  43. Huey RM, Taylor R McK. Anomalous discharges in ferroelectrics, J. Appl. Phys. 1963;34:1557-1560. [CrossRef]
  44. Szot K, Bihlmayer G, Speier W. Nature of the resistive switching phenomena in TiO2 and SrTiO3: origin of the reversible /insulator-metal transition. Solid State Physics. 2014;65:354-544. [CrossRef]
  45. Stanuch K, Sitko D, Kruk A, Suchanicz J, Nowakowska-Malczyk M, Wąs M, Konieczny K, Czaja P, Kluczewska-Chmielarz K, Stachowski G, Bik M, Łyszczarz K, Sokolowski M. Effects of Sr dopant and electric field poling on structural, thermal and dielectric properties of Ba(1-x )SrxTiO3 ceramics (x = 0, 0.3, 0.4 and 0.45). Phase Transitions. 2022; 95:456-465. [CrossRef]
  46. Bharti C, Sen A, Sinha TP. Enhanced dielectric and ferroelectric properties of Ca2+substituted sodium bismuth titanate. AIP Conference Proceedings. 2013;1512:1306-1307. [CrossRef]
  47. He X, Mo Y. Accelerated materials design of Na0.5Bi0.5TiO3 oxygen ionic conductors based on first principles calculations. Phys. Chem. Chem. Phys. 2015;17:18035-18044. [CrossRef]
  48. Li M, Pietrowski MJ, De Souza RA, Zhang H, Reaney IM, Cook SN, Kilner JA, Sinclair DC. A family of oxide ion conductors based on the ferroelectric perovskite Na0.5Bi0.5TiO3. Nature Materials. 2014;13:31-35. [CrossRef] [PubMed]
  49. Schönleber M, Klotz D, Ivers-Tiffée E. A Method for improving the robustness of linear Kramers-Krönig validity tests. Electrochimica Acta. 2014;131:20-27. [CrossRef]
  50. Steinsvik S, Bugge R, Gjonnes J, Tafto J, Norby T. The defect structure of SrTi1−xFexO3−y (x = 0–0.8) investigated by electrical conductivity measurements and electron energy loss spectroscopy (EELS). J.Phys.Chem.Solids. 1997;58:969-976. [CrossRef]
  51. Alaka P, Govindaraj R. Complex dielectric and impedance spectroscopic studies in a multiferroic composite of Bi2Fe4O9-BiFeO3. Condes.Matter Phys. 2018;3:44(1-15). [CrossRef]
  52. Gillot C, Michenaud JP. Electrical conductivity of similarly doped BaTiO3 single crystal and ceramics in the rhombohedral phase. Solid State Com. 1994;90:23-25. [CrossRef]
  53. Chandra Sekhar KSKR, Mahesh MLV, Sreenivasu T, Rama Krishna Y, Chandra Mouli K, Patri Tirupathi P. Structural evolution, dielectric relaxation and modulus spectroscopic studies in Dy substituted NBT-BT ferroelectric ceramics. J.Mat.Sci. 2021;32:8628–8647. [CrossRef]
  54. Almond D, Duncan GK, West AR. The determination of hopping rates and carrier concentrations in ionic conductors by a new analysis of ac conductivity. Sold State Ionics.1983;8:159- 164. [CrossRef]
  55. Chen RH, Yen CC, Shen CS, Fukami T. Impedance spectroscopy and dielectric analysis in KH2PO4 single crystal. Solid State Ionics. 2006;177:2857- 2864. [CrossRef]
  56. Macdonald JR. Note on the parametrization of the constant-phase admittance element. Solid State Ionics. 1984;13:147-149. [CrossRef]
  57. Hajra S, Sahoo S, Das R, Choudhary RNP. Structural, dielectric and impedance characteristics of Na0.5Bi0.5TiO3–BaTiO3 electronic system. J.Alloys Comp. 2018;750:507-514. [CrossRef]
  58. Ang C, Yu Z, Cross LE. Oxygen-vacancy-related low-frequency dielectric relaxation and electrical conduction in Bi:SrTiO3. Phys.Rev. 2000;B62:228-236. [CrossRef]
  59. Saha S, Krupanidhi SB. Dielectric response in pulsed laser ablated (Ba, Sr)TiO3 thin films. J.Appl.Phys. 2000;87: 849–854. [CrossRef]
  60. Rani R, Sharma S, Rai R, Kholkin AL. Investigation of dielectric and electrical properties of Mn doped sodium potassium niobate ceramic system using impedance spectroscopy. J.Appl.Phys. 2011;110:104102 (1-12). [CrossRef]
  61. Raymond O, Font R, Suárez-Almodover N, Portelles J, Siqueiros M. Frequency-temperature response of ferroelectromagnetic Pb(Fe1/2Nb1/2)O3 ceramics obtained by different precursors. Part II. Impedance spectroscopy characterization. J.Appl.Phys. 2005;97:084108 (1-8). [CrossRef]
  62. Pradhan DK, Choudhary RNP, Rinaldi C, Katiyar RS. Effect of Mn substitution on electrical and magnetic properties of Bi0.9La0.1FeO3.. J.Appl.Phys. 2009;106:024102 (1-10). [CrossRef]
  63. Peláiz-Barranco A, González-Abreu Y, López-Noda R. Dielectric relaxation and conductivity behavior in modified lead titanate ferroelectric ceramics. J.Phys.Condens.Matter. 2008;20:505208 (1-10). [CrossRef]
  64. Kang BS, Choi SK, Park CH. Diffuse dielectric anomaly in perovskite-type ferroelectric oxides in the temperature range of 400–700 °C. J.Appl.Phys. 2003;94:1904-k 1911. [CrossRef]
  65. Singh G, Tiwari V, Gupta P. Role of oxygen vacancies on relaxation and conduction behavior of KNbO3 ceramic. J.Appl.Phys. 2010;107:064103 (1-8). [CrossRef]
  66. Liu L, Huang Y, Li Y, Wu M, Fang L, Hu C, Wang Y. Oxygen-vacancy-related high temperature dielectric relaxation and electrical conduction in 0.95K0.5Na0.5NbO3-0.05BaZrO3 ceramic. Physica B: Condensed Matter. 2012;407:136-139. [CrossRef]
  67. Erdem E, Jakes P, Eichel R-A, Sinclair DC, Pasha M, Reaney IM. Formation of (Ti’Ti-VOˑˑ) defect dipoles in BaTiO3 ceramics heat-treated under reduced oxygen partial-pressure. Funct.Mater.Lett. 2010;3:65-68. [CrossRef]
  68. Yang F, Li M, Li L, Wu P, Velázquez E, Sinclair DC. Defect chemistry and electrical properties of sodium bismuth titanate perovskite. J.Mater.Chem. 2018; A6:5243-5254. [CrossRef]
  69. Davson JA, Chen H, Tanaka I. Crystal structure, defect chemistry and oxygen ion transport of the ferroelectric perovskite Na0.5Bi0.5TiO3: insights from first-principles calculations. J.Mater.Chem. 2015;A3:16574-16582. [CrossRef]
  70. Cox TA. Transition metal oxides. Oxford (UK): Oxford University Press, 1992.
  71. Austin IG, Mott NF. Polarons in crystalline and non-crystalline materials. Adv Phys.1969;18:41-102. [CrossRef]
  72. Li M, Zhang H, Cook SN, Li L, Kilner JA, Reaney IM, Sinclair DC. Dramatic influence of A-site nonstoichiometry on the electrical conductivity and conduction mechanisms in the perovskite oxide Na0.5Bi0.5TiO3. Chem.Mater. 2015;27:629-634. [CrossRef]
  73. Suchanicz J, Nowakowska-Malczyk M, Kania A, Budziak A, Kluczewska-Chmielarz K, Czaja P, Sitko D, Sokolowski M, Niewiadomski A, Kruzina TV. Effect of electric field poling on structural, thermal, vibrational, dielectric and ferroelectric properties of Na0.5Bi0.5TiO3 single crystals. J.Alloys Comp.2021; 854: 157227 (1-17). [CrossRef]
  74. Suchanicz J, Kwapulinski J. X-ray diffraction study of the phase transitions in Na0.5Bi0.5TiO3. Ferroelectrics. 1995;165:249-253. [CrossRef]
  75. Zvirgzds JA, Kapostins PP, Zvirgzde JV,Kruzina TV. X-ray study of phase transitions in ferroelectric Na0.5Bi0.5TiO3. Ferroelectrics. 1982;40:75-77. [CrossRef]
  76. Min Zeng, Siu Wing Or, and Helen Lai Wa Chan. First-principles study on the electronic and optical properties of Na0.5Bi0.5TiO3 lead-free piezoelectric crystal. J.Appl.Phys. 2010; 107: 043513; [CrossRef]
Preprints 107799 g001
Figure 1. Crystal structure of Na0.5Bi0.5TiO3 with a rhombohedral symmetry (R3c).
Figure 1. Crystal structure of Na0.5Bi0.5TiO3 with a rhombohedral symmetry (R3c).
Preprints 107799 g001
Preprints 107799 g002
Figure 2. Room-temperature X-ray pattern of NBT single crystals.
Figure 2. Room-temperature X-ray pattern of NBT single crystals.
Preprints 107799 g002
Preprints 107799 g003
Figure 3. The temperature dependence of the central 2Θ-positions of the (110)c, (111)c and (200)c Bragg reflections.
Figure 3. The temperature dependence of the central 2Θ-positions of the (110)c, (111)c and (200)c Bragg reflections.
Preprints 107799 g003
Preprints 107799 g004aPreprints 107799 g004b
Figure 4. EDS spectra and elemental mapping of NBT single crystals..
Figure 4. EDS spectra and elemental mapping of NBT single crystals..
Preprints 107799 g004aPreprints 107799 g004b
Preprints 107799 g005aPreprints 107799 g005b
Figure 5. XPS overview spectrum (a) and high-resolution Na1s (b), Bi4f (c), Bi4d and Ti2p (d) core level spectra of NBT single crystals.
Figure 5. XPS overview spectrum (a) and high-resolution Na1s (b), Bi4f (c), Bi4d and Ti2p (d) core level spectra of NBT single crystals.
Preprints 107799 g005aPreprints 107799 g005b
Preprints 107799 g006
Figure 6. Absorption coefficient spectra (a) and Tauc`s plot (b) for NBT single crystals.
Figure 6. Absorption coefficient spectra (a) and Tauc`s plot (b) for NBT single crystals.
Preprints 107799 g006
Preprints 107799 g007aPreprints 107799 g007b
Figure 7. Current-voltage characteristics (a-g) and double logarithmic relationship I(U) (h) for the NBT single crystals. Insert in Figure 7f shows an expanded part of this Figure. The numbers above the I(U) graph in Figure 7h indicate the values of the exponent n from the formula I ~ Un. Figure 7i shows an example of current oscillations. Figure 7j shows an example of the network of dark stripes on the sample.
Figure 7. Current-voltage characteristics (a-g) and double logarithmic relationship I(U) (h) for the NBT single crystals. Insert in Figure 7f shows an expanded part of this Figure. The numbers above the I(U) graph in Figure 7h indicate the values of the exponent n from the formula I ~ Un. Figure 7i shows an example of current oscillations. Figure 7j shows an example of the network of dark stripes on the sample.
Preprints 107799 g007aPreprints 107799 g007b
Preprints 107799 g008
Figure 8. Direct current conductivity σdc vs. 1000/T measured using 4-electrode method of NBT single crystals. Vertical dotted line indicates T= 400°C. Insert shows expanded part of this Figure.
Figure 8. Direct current conductivity σdc vs. 1000/T measured using 4-electrode method of NBT single crystals. Vertical dotted line indicates T= 400°C. Insert shows expanded part of this Figure.
Preprints 107799 g008
Preprints 107799 g009
Figure 9. Depolarization currents of NBT single crystals at several temperatures and for polarization time 1 and 2 hours.
Figure 9. Depolarization currents of NBT single crystals at several temperatures and for polarization time 1 and 2 hours.
Preprints 107799 g009
Preprints 107799 g010
Figure 10. The total depolarization charge Qd of NBT single crystals at different temperatures.
Figure 10. The total depolarization charge Qd of NBT single crystals at different temperatures.
Preprints 107799 g010
Preprints 107799 g011
Figure 11. ac conductivity σac vs. 1000/T (a) and ac conductivity σac vs. T (b) of NBT single crystals. Two vertical dotted lines in Figure 8b indicated the depolarization phenomenon (i.e., disappearance of polar (ferroelectric) properties).
Figure 11. ac conductivity σac vs. 1000/T (a) and ac conductivity σac vs. T (b) of NBT single crystals. Two vertical dotted lines in Figure 8b indicated the depolarization phenomenon (i.e., disappearance of polar (ferroelectric) properties).
Preprints 107799 g011
Preprints 107799 g012
Figure 12. Nyquist plot of NBT single crystals at selected temperatures, for small Z’, Z’ ranges (a) and for full Z’‘, Z’ ranges (b).
Figure 12. Nyquist plot of NBT single crystals at selected temperatures, for small Z’, Z’ ranges (a) and for full Z’‘, Z’ ranges (b).
Preprints 107799 g012
Preprints 107799 g013
Figure 13. Changes of Z` and Z’‘ as a function of frequency at selected temperatures.
Figure 13. Changes of Z` and Z’‘ as a function of frequency at selected temperatures.
Preprints 107799 g013
Preprints 107799 g014
Figure 14. The frequency dependence of the M’ and M’‘ modules of NBT single crystals for selected temperatures.
Figure 14. The frequency dependence of the M’ and M’‘ modules of NBT single crystals for selected temperatures.
Preprints 107799 g014
Preprints 107799 g015
Figure 15. The normalized imaginary part of the M’‘/M’‘max. module for NBT single crystals.
Figure 15. The normalized imaginary part of the M’‘/M’‘max. module for NBT single crystals.
Preprints 107799 g015
Preprints 107799 g016
Figure 16. Evolution of the conduction relaxation time as an inverse function of the temperature for NBT single crystals.
Figure 16. Evolution of the conduction relaxation time as an inverse function of the temperature for NBT single crystals.
Preprints 107799 g016
Preprints 107799 g017
Figure 17. M’ vs. M’‘ of NBT single crystals.
Figure 17. M’ vs. M’‘ of NBT single crystals.
Preprints 107799 g017
Preprints 107799 g018
Figure 18. Variation of Z’‘ and M’‘ with frequency of NBT single crystals (as a examples).
Figure 18. Variation of Z’‘ and M’‘ with frequency of NBT single crystals (as a examples).
Preprints 107799 g018
Preprints 107799 g019
Figure 19. The temperature dependence of (a) the Seebeck coefficient α, (b) carrier concentration n, (c) carrier mobility μ, and (d) figure of merit ZT of NBT single crystals.
Figure 19. The temperature dependence of (a) the Seebeck coefficient α, (b) carrier concentration n, (c) carrier mobility μ, and (d) figure of merit ZT of NBT single crystals.
Preprints 107799 g019
Preprints 107799 g020
Figure 20. Temperature evolution of (a) thermal conductivity and (b) average mean free path of NBT single crystals.
Figure 20. Temperature evolution of (a) thermal conductivity and (b) average mean free path of NBT single crystals.
Preprints 107799 g020
Preprints 107799 g021
Figure 21. Total and partial density of states in Na0.5Bi0.5TiO3 for two cases.
Figure 21. Total and partial density of states in Na0.5Bi0.5TiO3 for two cases.
Preprints 107799 g021
Preprints 107799 g022
Figure 22. Computed (GGA) energy band structures of Na0.5Bi0.5TiO3 along the high-symmetry directions in the Brillouin zone for two cases.
Figure 22. Computed (GGA) energy band structures of Na0.5Bi0.5TiO3 along the high-symmetry directions in the Brillouin zone for two cases.
Preprints 107799 g022
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated