Prerpints.org logo
Preprint
Article

Three DoF Cable Driven Parallel Manipulator with Self Sensing Nitinol Actuators

Altmetrics

Downloads

107

Views

66

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 May 2024

Posted:

30 May 2024

You are already at the latest version

Alerts
Abstract
This paper presents the design and analysis of a novel 3-degree-of-freedom (3-DOF) parallel ma-nipulator equipped with self-sensing Ni-Ti (Nitinol) actuators. The manipulator's architecture and mechanical design are elucidated, emphasizing the integration of Nitinol actuators. The self-sensing technique implemented in a previous work was extended to a 20 mm actuator length, and the actuator was used to design the 3 DOF manipulator. Kinematic analyses were conducted to eval-uate the manipulator's performance under various operating conditions. A dynamic model was implemented for the dynamic dimensioning of the actuators, which work synergistically with a bias spring. The manipulator was realized, and a control strategy was implemented. Experimental tests, although documenting some positioning accuracy issues, show the efficacy and potential applica-tions of the proposed manipulator in robotics and automation systems, highlighting the advantages of self-sensing Nitinol actuators in small parallel manipulator designs.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Parallel manipulators have gained significant attention in robotics due to their advantages such as high rigidity, accuracy, and payload capacity. In recent years, there has been a growing interest in integrating smart materials, particularly shape memory alloys (SMAs), into robotic systems to enhance their performance and capabilities. Among SMAs, nickel-titanium (Ni-Ti) alloys stand out for their unique properties, including high energy density, biocompatibility, and shape memory effect, making them ideal candidates as actuators [1,2,3,4,5,6,7] in many applications in different fields, such as aerospace [8,9,10,11,12], biomedical [13,14,15,16,17,18], wearables [19,20,21,22], micro-systems [23,24,25,26], robotics [27,28,29,30,31,32,33,34]. There are not many works in the literature regarding manipulators with parallel architecture with SMA actuators. In [35], a parallel device for the orientation of the platform connected to the base via a flexible central rod in superelastic Nitinol is described. Three Nitinol wires arranged at 120° are used as actuators. The flexible structure reflects a system with 2 DOF. The dimensions are contained in a cylinder of 65 mm in diameter and 75 mm in height. For the movement, a structural model allows position control through knowledge of the forces applied by the actuators which are detected using force sensors on each actuator. The experimental tests were carried out with the movement of just one actuator and the authors plan to use a position detection system additionally. [36] describes a parallel manipulator that uses actuators made by a carriage on a slide connected to an elastic plate that is bent by the actuator and shortens. The wires are kept in an eccentric configuration concerning the plate to amplify the shortening. Control is implemented with on-off commands based on feedback using a signal from linear variable displacement transducers (LVDTs), one for each actuator. The system has 3 DOF and good performance. Still, it is rather large given that the actuators are bulky to achieve the amplification effect, i.e., they have a length of approximately 220 mm and a transversal dimension of roughly 40 mm x 50 mm. The device is contained in a cylinder with a diameter of 230 mm and a height greater than 220 mm. In [37], the device BAPAMAN is presented. It is a module comprising a base and a platform connected by three legs arranged at 120°. Each includes two articulated segments, and all the connections between the two segments of the leg and between the leg with base and platform are made using flexible joints. There is a cylindrical hinge between the leg and the base and between the leg segments, while there is a universal joint between the leg and the platform. The platform has 5 DOF with respect to the base: three translational and two rotational. The system is designed to be organized into multiple serial modules to constitute more than a parallel manipulator, a snake robot. As for the movements, they are implemented in binary mode. Each leg features two actuators, giving the module 8 different configurations. The overall dimensions of the single module are contained in a cylinder with a diameter of 180 mm and a height of 200 mm. In [38], a parallel manipulator with a square base and platform that implements four SMA springs arranged at the vertices as actuators, each with a steel antagonist spring, is presented. The movements are implemented in binary mode. It features 3 DOFs for roll pitch and one along the vertical axis. The system has small dimensions, 30 mm x 30 mm x 34 mm, and performs large movements: a rotation of the platform of 30° and a stroke in the vertical direction of 12 mm, thanks to the high deformation of the SMA springs. Given the structure, it is probably not very rigid, losing a peculiar characteristic of parallel architecture robots. The biggest limit, however, is the actuators' binary operation, which leads to a limited number of possible configurations, placing the end effector discreetly in the working volume. [39] describes a system with a triangular base and platform connected with a universal joint and SMA springs at the vertices. Features 2 DOF Pich and Roll. The dimensions are contained in a cylinder with a diameter of 92 mm and a height of 114 mm. A position control with an on-off type command in the closed loop is implemented using an IMU sensor. In [40], a 3 DOF parallel manipulator with SMA wire actuators is presented. It features a base and a platform. The base and platform are connected with the actuators, which are constantly tensioned by a bias spring between the base and platform. The manipulator implements proportional position closed-loop control, using the signal generated by a potentiometer for each actuator. The project is well-functioning, but the system is rather bulky, given the presence of position sensors. The dimensions are contained in a cylinder with a diameter of 82 mm and a height of approximately 210 mm.
This paper presents the design and analysis of a novel 3 DOF parallel manipulator utilizing self-sensing Ni-Ti actuators. Integrating self-sensing capabilities within the actuation system eliminates the need for external sensors, simplifies the overall design, and reduces the system's complexity, size, and cost. Also, using Ni-Ti actuators allows for smooth and silent actuation mechanisms. The proposed parallel manipulator is compact and lightweight. It suits various tasks requiring positioning and manipulating small objects, such as pick-and-place operations, assembly tasks, and biomedical applications. The paper describes the design methodology, i.e., kinematic modeling and analysis of the manipulator's workspace, singularity conditions, error analysis, and dynamic modeling for the actuation system dimensioning of the proposed 3-DOF parallel manipulator and the investigation of dynamic performance characteristics, including integrating self-sensing Ni-Ti actuators. Furthermore, experimental validation of the realized manipulator prototype is conducted to assess its performance for positional accuracy. The results, except a limited area of the working volume in which positioning errors outside the expected range occur, prove the effectiveness of the project by demonstrating that for the creation of robots with parallel architecture, it is possible to use memory alloy wires which use of self-sensing allowing to obtain compact dimensions. Compared to the devices in scientific literature, the proposed manipulator is similar to the one described last. A comparison with that manipulator has been conducted to prove the actual project's performance.

2. Materials and Methods

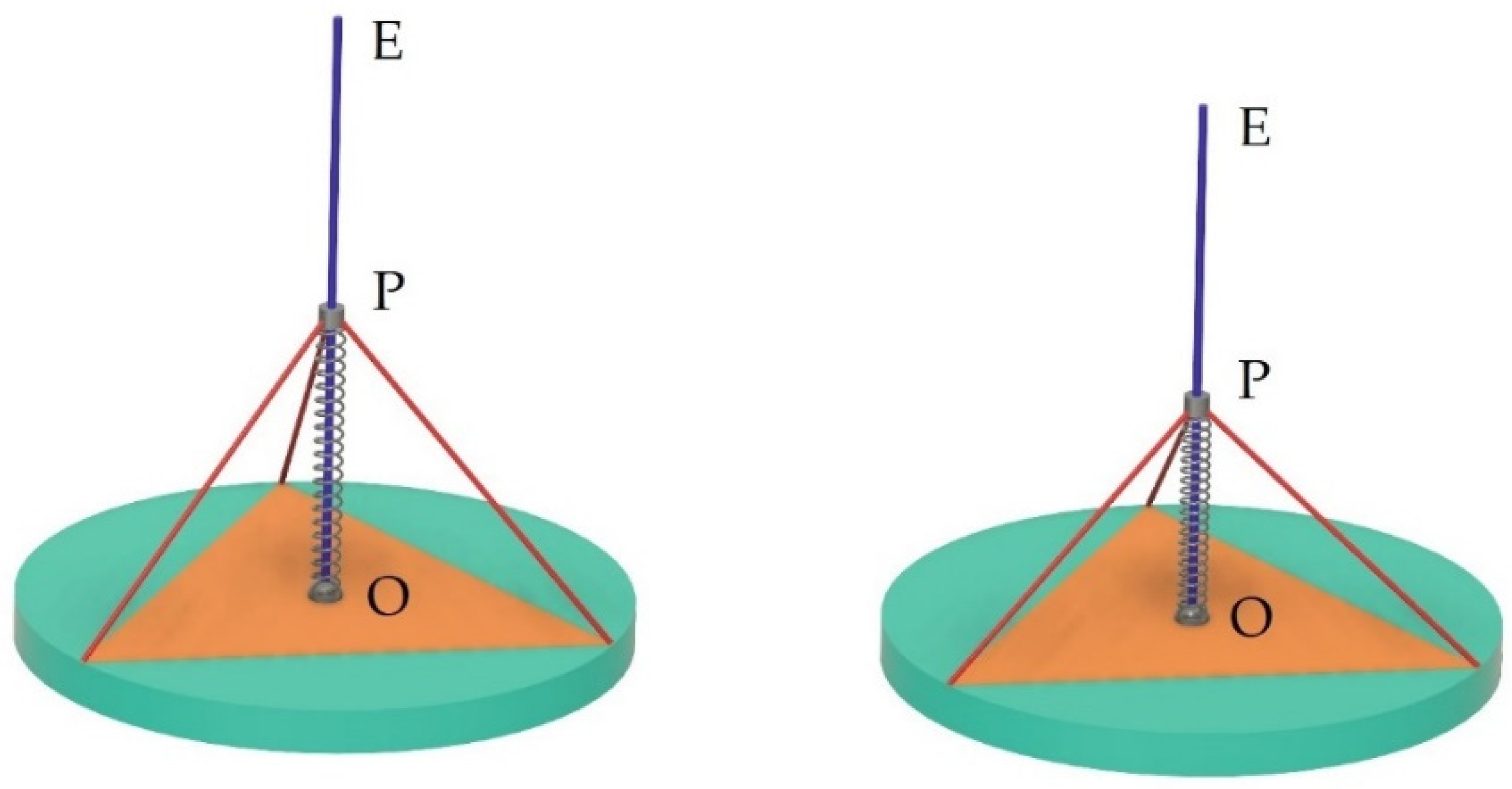
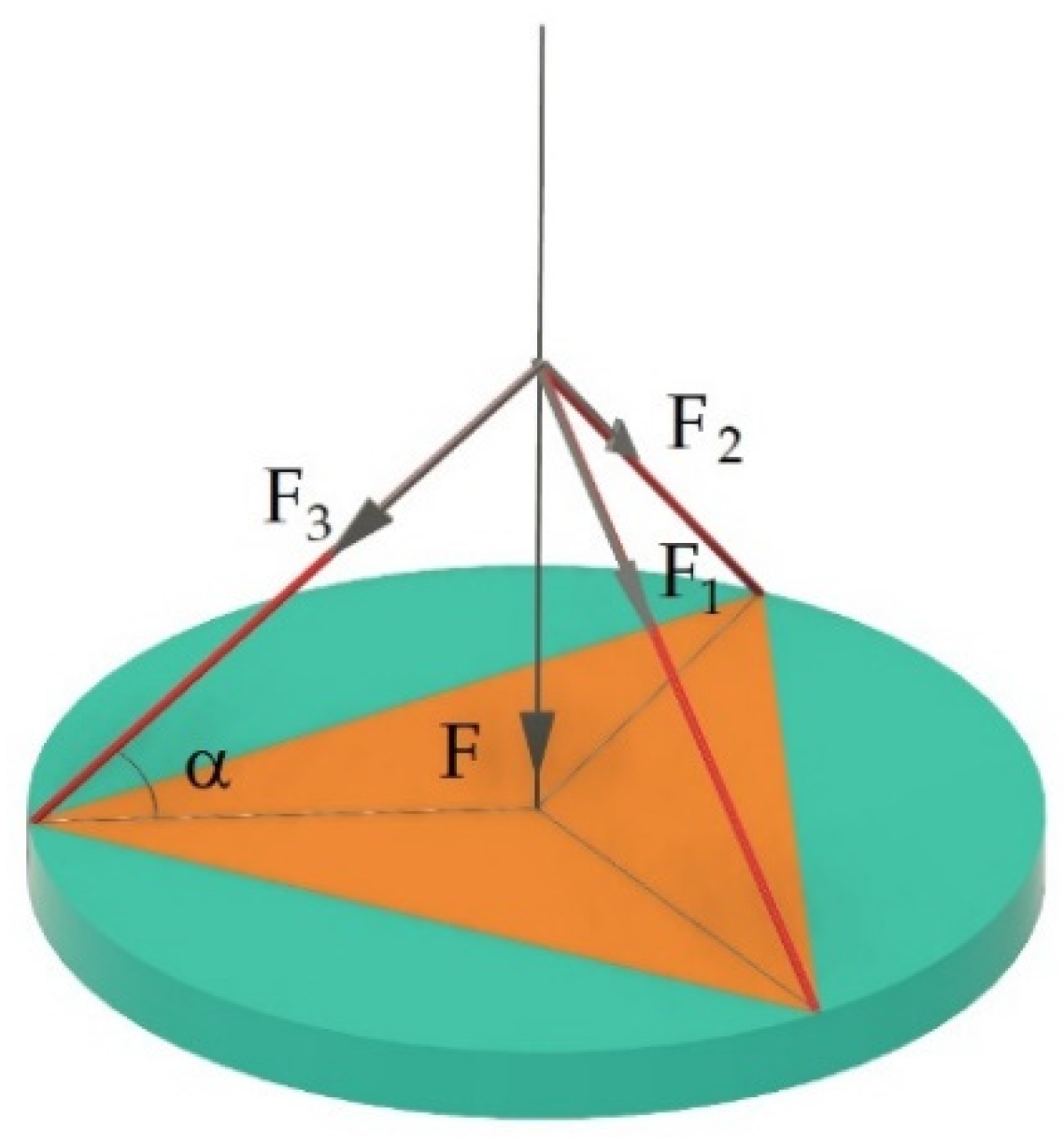
2.1. Mechanical Design of the Manipulator

2.1.1. Manipulator Technical Specification, Functional Design

The manipulator has to serve as a proof of concept for a small manipulator with parallel architecture, using shape memory alloy wires as actuators. Taking as a reference a Stewart platform, some preliminary analyses suggest it is convenient to consider technical specifications for the design of the device, as in the following:
  • Number of DOF: 3 without wrist and gripper;
  • overall dimensions, including actuators, contained in a cylinder with a diameter of 45 mm and a height of 140 mm;
  • diameter of the circle circumscribed to the plan projection of the working volume by height, in the range of 10 mm × 2 mm;
  • actuator’s block control volume not more than 20000 mm3;
  • overall mass without the electronics for control of not more than 0.05 kg;
  • the manipulator is intended to manipulate tiny mass objects. So, the considered load capability is 0.05 N.
Following the specifications above, a particular architecture of the Stewart platform is considered. A system consisting of a base and a platform is considered, with the dimensions of the platform theoretically reduced to zero [41] according to the scheme in Figure 1.
The proposed idea can be implemented using Ni-Ti wires as actuators, which use the self-sensing effect to avoid increasing the overall dimensions with external sensors. The actuators are anchored to the base, to the three vertices of an equilateral triangle each, and on the other side, to the platform, which is a tiny body. The actuators, which work only by traction, are constantly tensioned thanks to a compressed bias spring placed between the central point of the base, O, and the point P, representing the platform.
To amplify the movements, a small rod is used, which is coupled with the base via a joint consisting of a sphere articulated with the base and drilled to accommodate the end of the rod in a prismatic coupling. This joint allows the rod to rotate and slide along the direction of its axis relative to the base. To the other end, the rod is integral to the platform, P, and extends beyond it. The upper end of the rod, E, is at a fixed distance from the platform; it constitutes the end effector of the manipulator to which a tool can be applied.

2.1.2. Characterization of Actuators Using Self-Sensing Effect

Based on preliminary evaluations of the hypothesized architecture, a system with approximately 20 mm long actuators can satisfy the technical specification. The work [42] demonstrated that a Ni-Ti wire can work well as an actuator with a self-sensing effect. In that work, the effectiveness of a wire with a length of 200 mm was demonstrated. Here, the hypothesis is to work with a much shorter actuator. Therefore, before proceeding with the design of the manipulator, it is necessary to experimentally verify the effectiveness of the self-sensing process on a wire with a length of 20 mm.
The same Ni-Ti wire whose characteristics are in Table 1 was considered, and the same experimental setup described in [42] was used but with a modification of the index of the graduated scale, which has been brought to a greater length to amplify the movement generated by the actuator for better visualization. In this case, the actuator will have a total excursion equal to approximately 0.7 mm, considering a percentage shortening of 3.5%, so length variations of a hundredth of an mm must be detectable. Changes have been made to the electrical components of the control system to adapt them to the different electrical parameters of the shorter wire. The electrical measurement resistance was brought to 3.9 Ohm and the supply voltage to 1.1 V.
Tests were conducted to characterize the wire's unitary deformation (ε) relationship with electrical resistance (R) to obtain the model for self-sensing implementation. In particular, the model was obtained for the actuator in an antagonistic configuration with a bias spring. The resulting model was represented as a linear one:
ε = 26.374-17.419 R
whose relative graph is shown in Figure 2.
Positioning tests were conducted using the model and the setup described. A precision potentiometer connected to the pulley [42] was added to acquire the actual position by a data acquisition board. It turns out that the actuator works well over the entire operating range (0.7 mm) except for the value close to the minimum length, i.e., for an elongation equal to 0.1 mm. Figure 3 shows the system responses for stepped input signals. There is an error due to oscillations of approximately 0.04 mm.

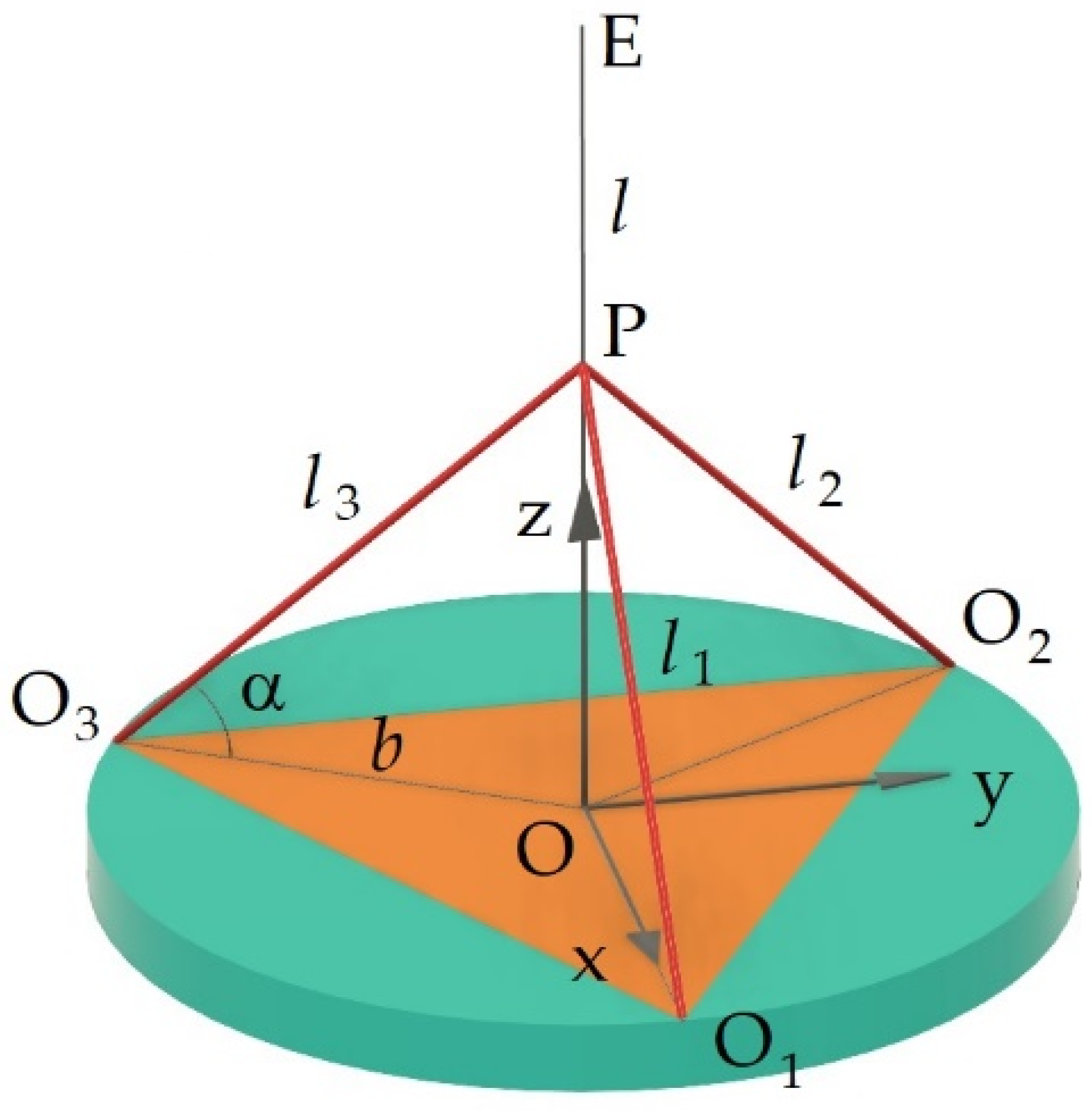
2.1.3. Direct Kinematic Model - Domain Analysis

For the working volume analysis, the direct kinematic model was considered. With reference to Figure 4, we name O1, O2, and O3 the three points where the actuators are attached to the base, everyone at a distance b from the center of the base, O. A fixed frame attached to the base, is considered such that the origin is located at the center of the base, the x-axis pointing toward the point O1, the z-axis pointing upward, and the y-axis pointing coherently with a right-handed reference. Each actuator is represented by a vector li (i = 1,2,3) from Oi to the point P, and all the actuators have the same initial length. The first step in determining the direct kinematic model is to solve for the position of the point P given the values of the actuator’s lengths, li. For each actuator, the loop closure equations can be written as:
OP-OOi = li  i = 1,2,3.
The vector OP is as follows:
OP = [xP, yP, zP]T
while OOi have a fixed magnitude and are as:
OO 1 = b ,   0 ,   0 T
OO 2 = − 1 2 b ,   3 2 b ,   0 T
OO 3 = − 1 2 b , − 3 2 b ,   0 T
We can substitute equations (3-6) into (2), thus resulting in three vector equations with three unknowns, the coordinates of the point P, for a given set of li. So, we have to solve the three equations with three unknowns simultaneously for the position of the platform (point P) to be determined.
Before solving equation (2), the values of the manipulator's design parameters, namely the actuators' rest length and the base's dimension b, must be defined. To do that, we can choose a resting length for the actuators and then derive the dimensions of the base from it.
The choice of these parameters derives from an optimization process between conflicting needs. In fact, for a given length of the actuators, the excursion of the end effector in the vertical direction is more extensive, and consequently, the same is for the working volume, the smaller the angle α, which involves a greater overall dimension of the basis, i.e., a bigger value for b.
From a quantitative point of view, the distance OP, given the size of the base b and the actual length of the actuators, li, is:
OP = l i   1 − b l i 2
Once the value b has also been hypothesized, with relation (7), it is possible to calculate the distance OP, considering the variation in the actuator's length and the end effector's vertical excursion. Therefore, based on what has been said, we will proceed by hypothesizing different values for b, evaluating the best compromise solution between the excursion of the end effector, which we want to be large, and the overall size of the base, which we wish to be small. Table 2 shows the results for the cases relating to the actuator with nominal length dimensions equal to 20 mm and different hypothesized values for dimension b. From the data observation, we chose to work with b = 16.5 mm as it constitutes a good compromise between the base's size and the end effector's excursion.
Once the geometric data characterizing the actuators were defined, the direct kinematic problem for determining the working volume was solved.
By substituting (3-6) into equations (2), then applying the norm, and squaring, we obtain the three equations:
x P − b 2 + y P − 0 2 + z P − 0 2 = l 1 2 x P + 1 2 b 2 + y P − 3 2 b 2 + z P − 0 2 = l 2 2 x P + 1 2 b 2 + y P + 3 2 b 2 + z P − 0 2 = l 3 2
These were solved with Mathematica code. An equation of the 16th order of xP is obtained:
a 1 ⋅ x P 16 + a 2 ⋅ x P 14 + a 3 ⋅ x P 12 + a 4 ⋅ x P 10 + a 5 ⋅ x P 8 + a 6 ⋅ x P 6 + a 7 ⋅ x P 4 + a 8 ⋅ x P 2 + a 9 = 0  
where the expressions of the coefficients ai are omitted because of their length.
This equation is in the 16th order of xP and leads to 16 solutions. Since the power is always even, the solution is facilitated because it is possible to solve an 8th-degree equation. Six of these solutions are coincident, while the remaining two are symmetric with respect to the xy plane. By substituting xP into the equations (8), it is possible to calculate yP and zP.
The second step concerns the calculation of the coordinates of the end-effector E (xE, yE, zE). The distance OP is a function of the coordinates of the point P:
O P = x P 2 + y P 2 + z P 2
Considering the distance of the end effector E from P is l, we have:
x E = x P O P + l O P
y E = y P O P + l O P
z E = z P O P + l O P
Thus the direct kinematic problem is solved.
A direct kinematic analysis was carried out using the model described to visualize the boundaries of the working volume. By a Matlab code, the lengths of the actuators were made to vary systematically in sequence, and the coordinates of the end effector in physical space were calculated. The actuators' lengths varied between 19.3 mm and 20 mm with variations of 0.035 mm for 1386 configurations. The size of the rod was considered equal to l = 120 mm. Figure 5 shows the working volume.
It results in a volume with a hexagonal shape in plan with an apothem equal to approximately 6 mm and with a maximum height equal to approximately 1.3 mm as per the project.

2.1.4. Inverse Kinematic Model

The inverse kinematic problem is very straightforward. Starting from a position of the end effector in the cartesian space, E(xE, yE, zE), it is possible to compute the coordinates of the point P by the equations (14)-(16)
x P = x E O E O E − l
y P = y E O E O E − l
z P = z E O E O E − l
Then by means of equations (8) it is possible to solve for the coordinates in the joint space, l1, l2, l3.

2.1.5. Jacobian and Singularity Analysis

Starting from equation (2), the differentiation must be carried out with respect to the time of both members. It should be considered that the derivative with respect to the time of the terms li has two components: the one represented by the variation in length and the other by the variation in orientation with respect to the reference system of the base. However, the derivative of the segments OOi is equal to zero since their lengths are constant. The OP vector also has two components, one due to the change in length and another due to the change in orientation (length and rotation variations of the spring with respect to the base reference). Both of these components contribute to determining the velocity of point P.
We have:
d d t O P − d d t O O i = d d t l i    
V P = l ˙ i s i + ω i × l i s i                           i = 1,2 , 3    
Where s i is the unit vector associated with the i-th actuator. To eliminate the angular velocities of actuators, we can dot multiply both members of the equation (18) by s i . We have:
s i · V P = l ˙ i s i · s i + ω i · l i s i × s i  
According to [43] two Jacobians can be individuated in (19). The first one (type I Jacobian) is the coefficient of the velocity vector V P , and the other (type II Jacobian) is the coefficient of the scalar l ˙ i
J q = I
J x = s 1 x s 1 y s 1 z s 2 x s 2 y s 2 z s 3 x s 3 y s 3 z    
The first Jacobian can give rise to the I type of singularities. After inversion, it can be useful for calculating joint speeds to obtain the assigned speeds of the end effector. It is, therefore, similar to the Jacobian that is determined for manipulators with serial architecture, and the singularities associated with it can be defined as inverse kinematic singularities. Since, in this case, it is equal to the identity matrix, there are no singularities in the inversion. Singularities, however, occur at the edge of the working volume when the spring is at its minimum and maximum lengths.
The second one can give rise to the II type of singularities. These can occur when the end effector is locally movable, even when all the actuated joints are locked. For this reason, we can refer to them as the forward kinematic singularities.
The singularities occur when
det   J x = 0
s 1 x s 2 y s 3 z + s 1 y s 2 z s 3 x + s 1 z s 2 x s 3 y − s 1 z s 2 y s 3 x + s 1 y s 2 x s 3 z + s 1 x s 2 z s 3 y = 0  
Then, the equation should be solved. Anyway, we can analyze two straightforward cases. The first occurs when all the z components of the unit vectors associated with the actuators are zero. This happens when the actuators and points P and E lie all in the plane of the base. Although theoretically possible, this condition never occurs because, in the current case, points P and E are always far from the base plane. The second occurs when the x, y, or both components of the unit vectors associated with actuators are zero. Moreover, this is a required but not sufficient condition since the actuators must be perpendicular to the upper base for the singularities to occur. This can be verified for an ideal architecture with a base and a platform of equal geometry. However, in the present case, where the platform is reduced to point P, the condition under the exam is never verified. The other type II singularities can also be excluded for the same reason.

2.1.6. Dynamic Analysis - Actuators Dimensioning

The following applies regarding the dynamic behavior of the actuators and their interaction with the bias spring. The spring has the task of keeping the wires permanently taut. In other words, it must guarantee that the wires, when at a low temperature in the martensite phase, can recover the maximum length, which requires the application of a force always at least equal to the deformation recovery force for all the actuators simultaneously. In this sense, the most critical condition is the one in which the wire is close to its maximum length both because the spring is in the conditions of minimal compression and because the angle α is at its maximum value, which involves a component of the force of the spring, useful for lengthening the wires, smaller. At the same time, the spring has to be sufficiently soft to be compressed by the actuators in the active work phase.
Concerning Figure 6, let Fi be the force developed by the i-th actuator and F the spring force that acts along the OP direction of the rod (end effector). The following relation is valid:
F = ∑ i F i × 1 − b l i 2
The chosen wire for the actuators requires a low-temperature recovery force of 0.6 N and develops a high-temperature transformation force of 3.2 N.
Based on preliminary evaluations, a spring with a stiffness of k = 0.22 N/mm is compatible with the bias spring utilized to obtain the actuators' ε-R relationship (1). The free length of the spring is equal to 15.7 mm, and by choosing to fix its upper end on the rod below the point P at a distance equal to 3.3 mm, the force exerted by the spring, in a generic configuration, is equal to:
F = k [15.7-(OP-3.3)]
A dynamic model is created to verify the correct tensioning of the actuators by the spring over the entire working volume.
The following relationships apply:
∑ F i j = F j
where:
F j = x j F O P
F i j = F i O i j − x j ∑ j O i j − x j 2  
with:
Fj = components of the force exerted by the spring
Fi = forces by the actuators
Fij = components of the forces exerted by the actuators
xj = coordinates of point P
Oij = coordinates of attaching points of the actuators to the base.
With this model, a dynamic analysis was carried out on the entire boundary of the working volume to verify the spring. Figure 7 shows the results obtained with the dynamic model. The actuator and spring system are well-sized and succeeded in the abovementioned task. Moreover, overcoming forces to those here documented result. They represent the capability of the robot to apply loads into the environment.

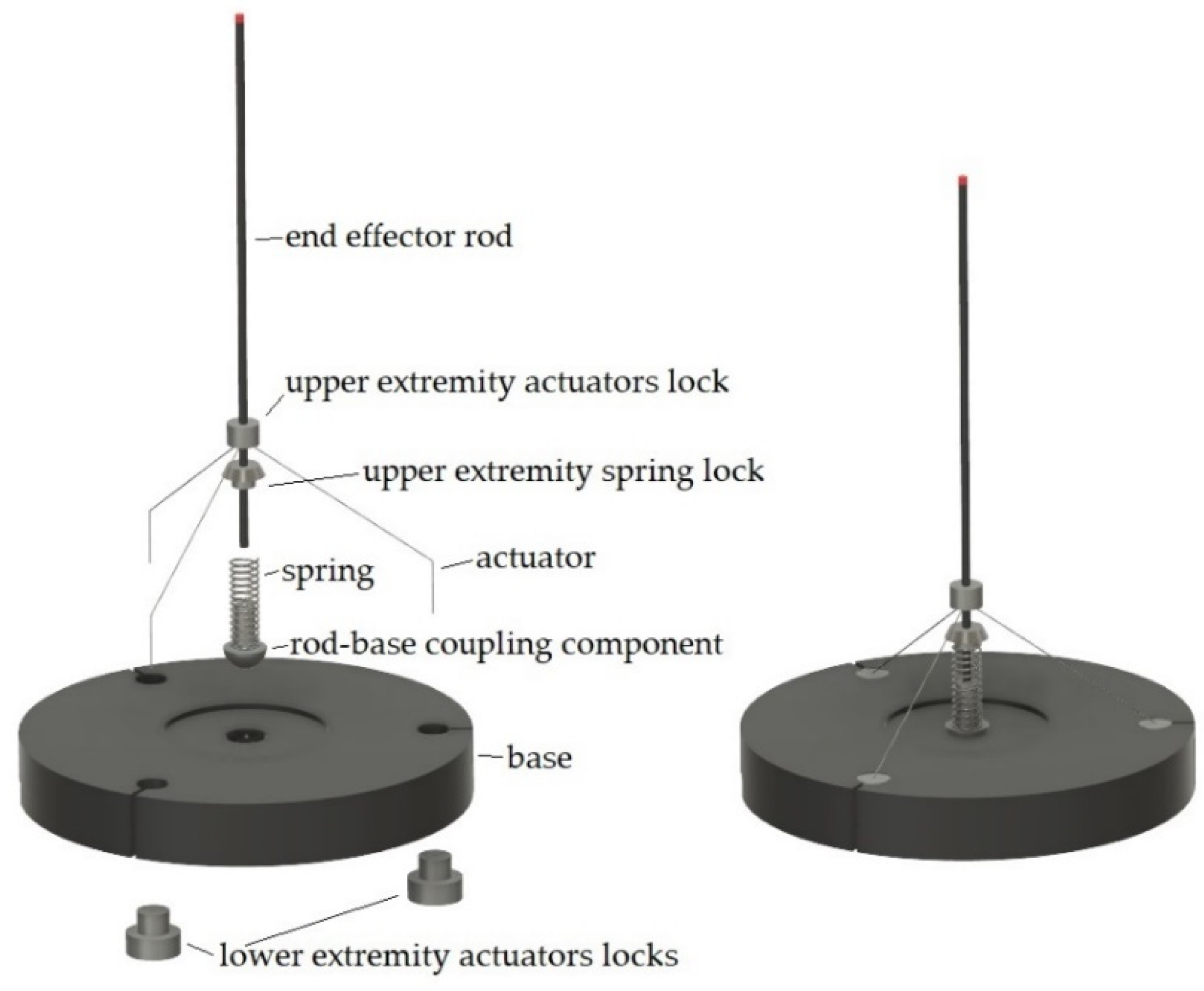
2.1.7. Detailed Design

The components were designed in detail. The base is circular with a thickness of 6 mm and a diameter of 40.8 mm, and it was realized in nylon. In the center, a spherical groove is present for the articulation with the rod. The joint is realized by a spherical component with a diameter of 4.5 mm for the articulation to the base side, with a diametral hole for the coupling with the rod. This one, with a diameter of 1 mm, can slide inside the hole to confer the robot a third degree of freedom. The spherical component presents, in the upper part, a plane surface, which constitutes the base on which rests the lower extremity of the spring. The rod presents a lock for the upper extremity of the spring formed by an axisymmetric component. Above it, there is a cylindrical component for the lock of the upper extremity of the actuators. Finally, on the base, there are three holes disposed at 120° angular distance, one from the other, where the locks are coupled for the lower extremity of the actuators. Figure 8 shows the CAD model of the designed prototype.

2.2. Control System

In the next paragraphs, we will discuss the hardware and strategy for the control implemented.

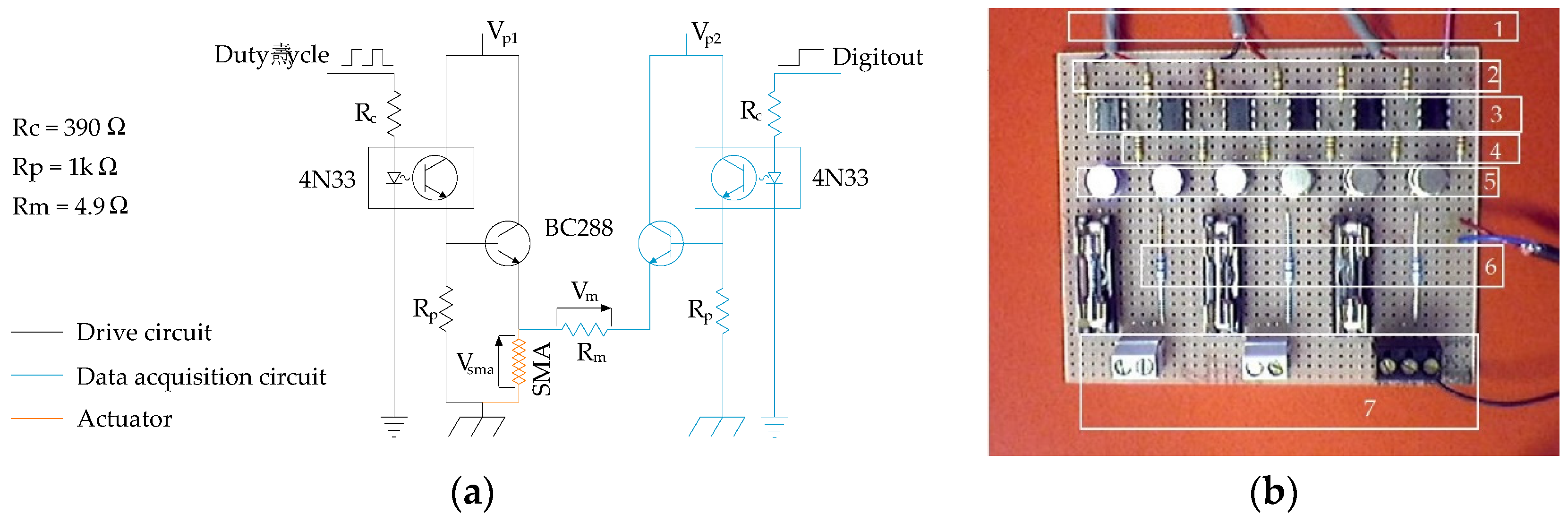
2.2.1. Hardware

The hardware for the control is derived from the one used and described in [42]. The single actuator is driven by a homemade board with a drive circuit to drive the actuator and a data acquisition circuit to measure the electrical resistance to estimate its actual length. The board used for the one actuator was replicated three times on a single board to drive the three actuators to control the manipulator. Figure 9 shows the homemade drive board for the manipulator.

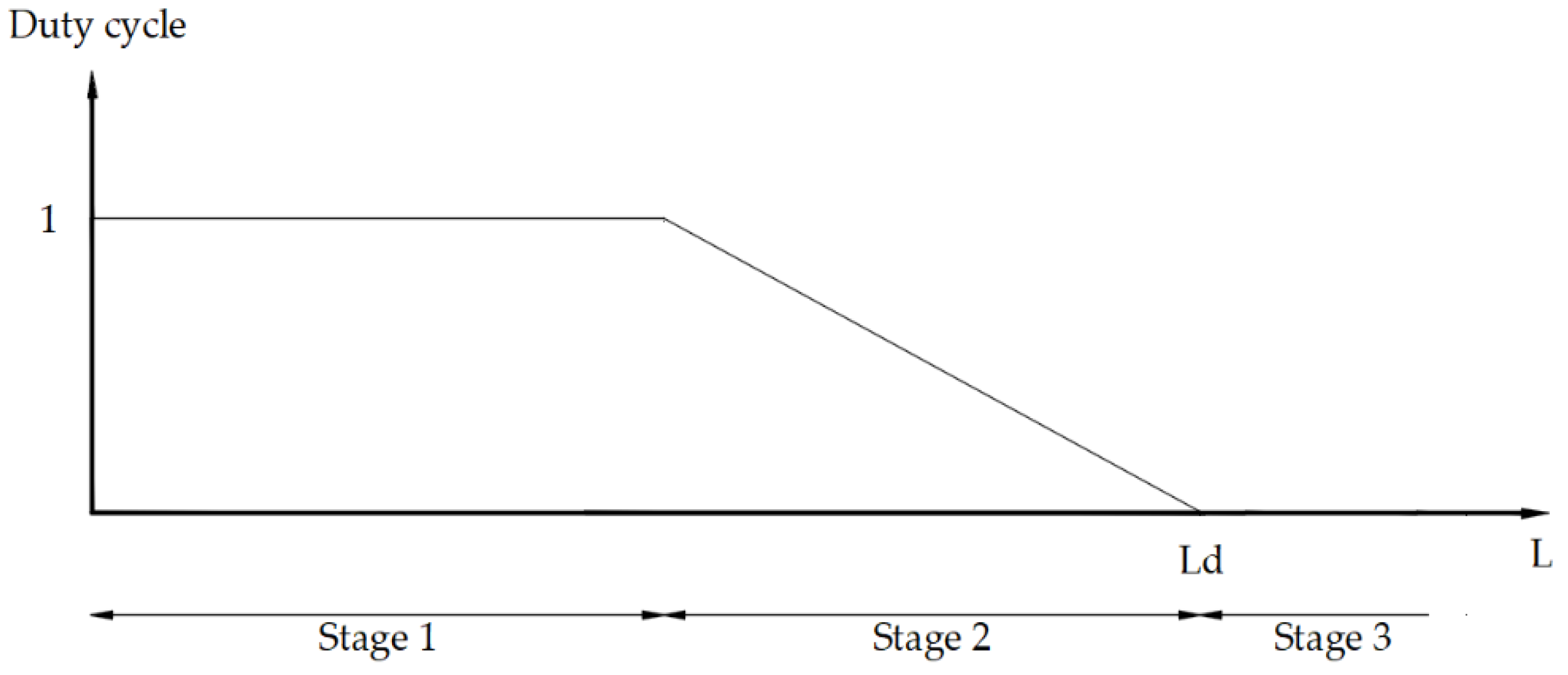
2.2.2. Control Strategy

As for control, we consider the command of the actuators in one direction and rely on the bias spring for movements in the opposite direction. The law adopted applies the maximum possible value of the signal when the actuator is far from the reference and becomes proportional (P) to the error near the reference according to the law shown in Figure 10.
This control logic allows a faster approach phase than a purely proportional one.
The power and measurement circuits are powered alternately to estimate the actual deformation by the measurement circuit to control the actuator. This logic is adopted similarly for every one of the three actuators.

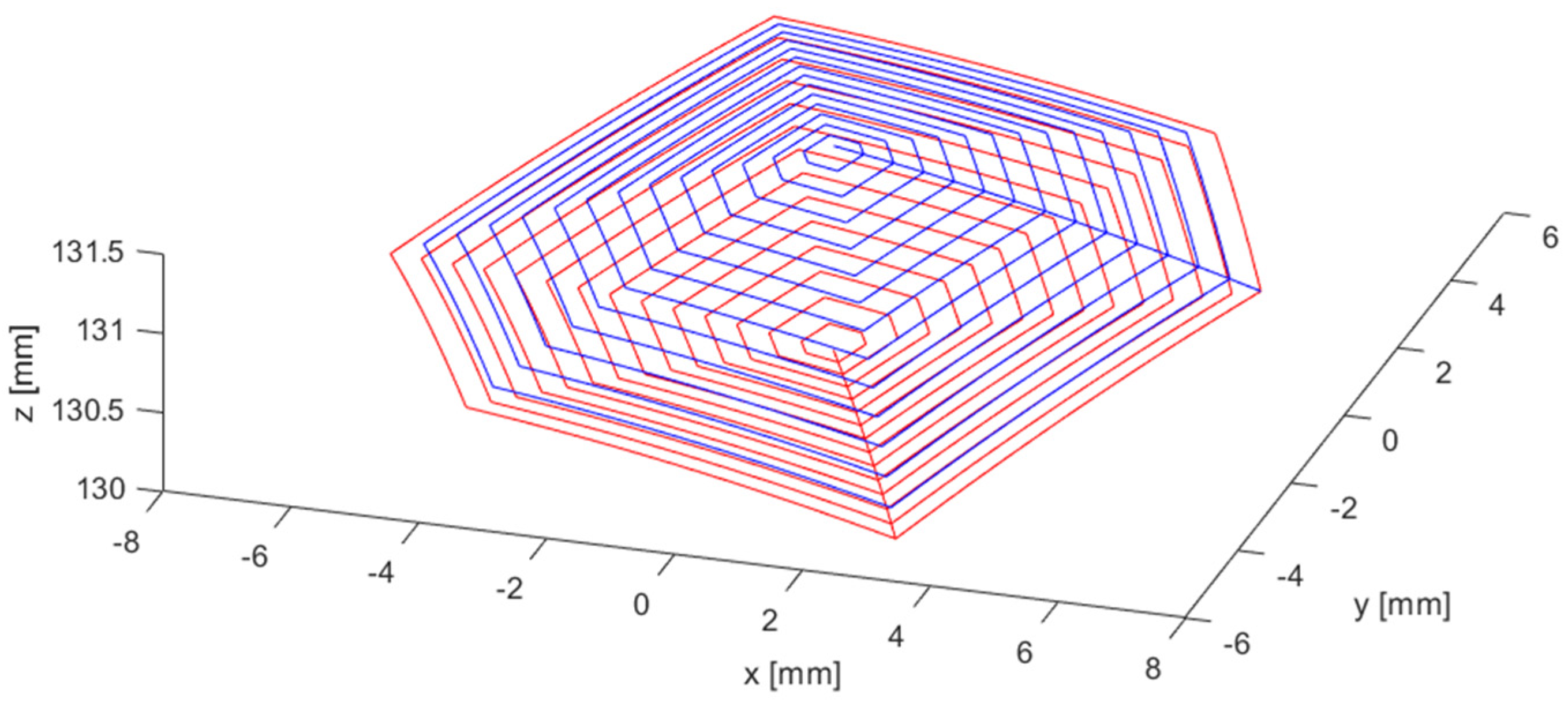
3. Results

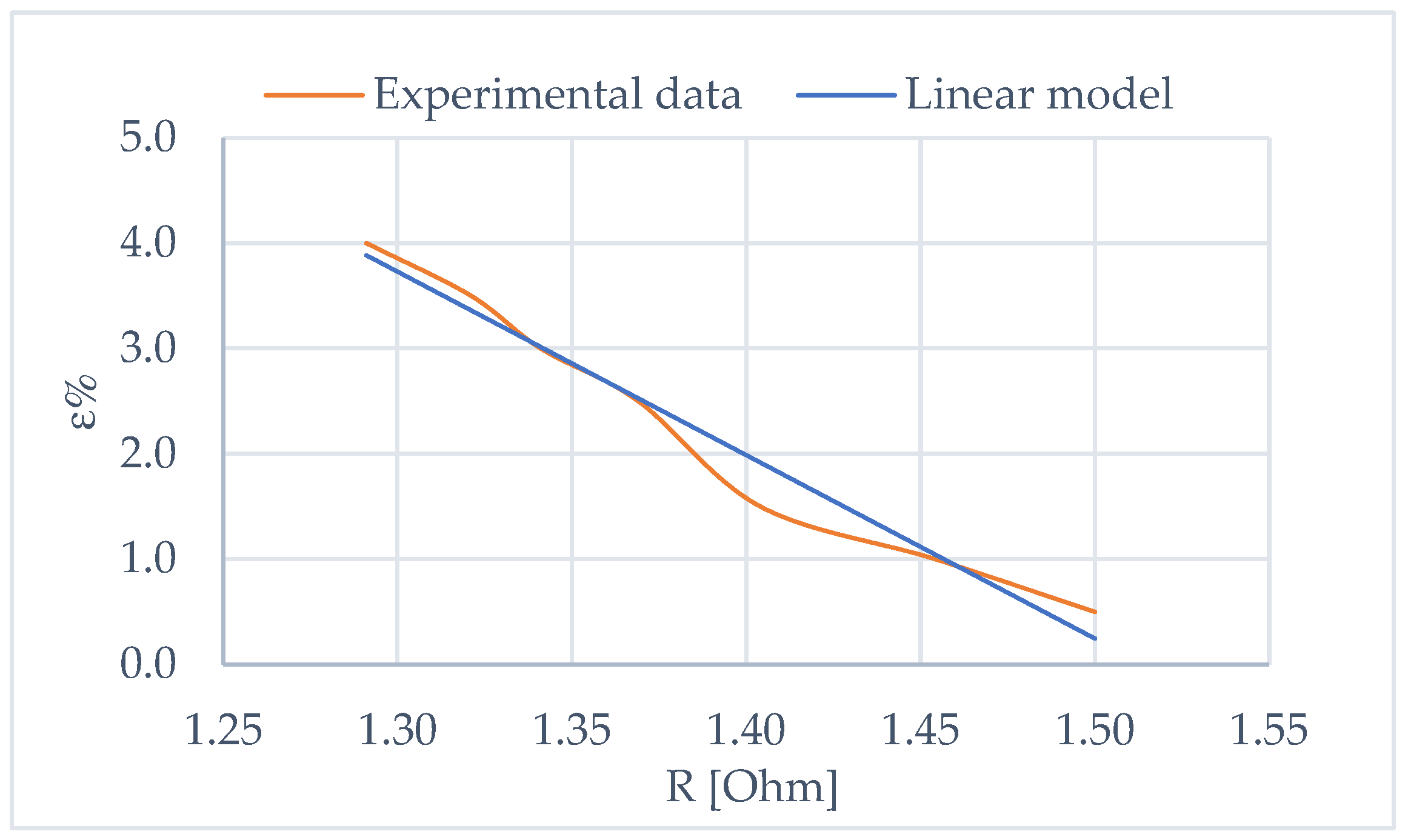
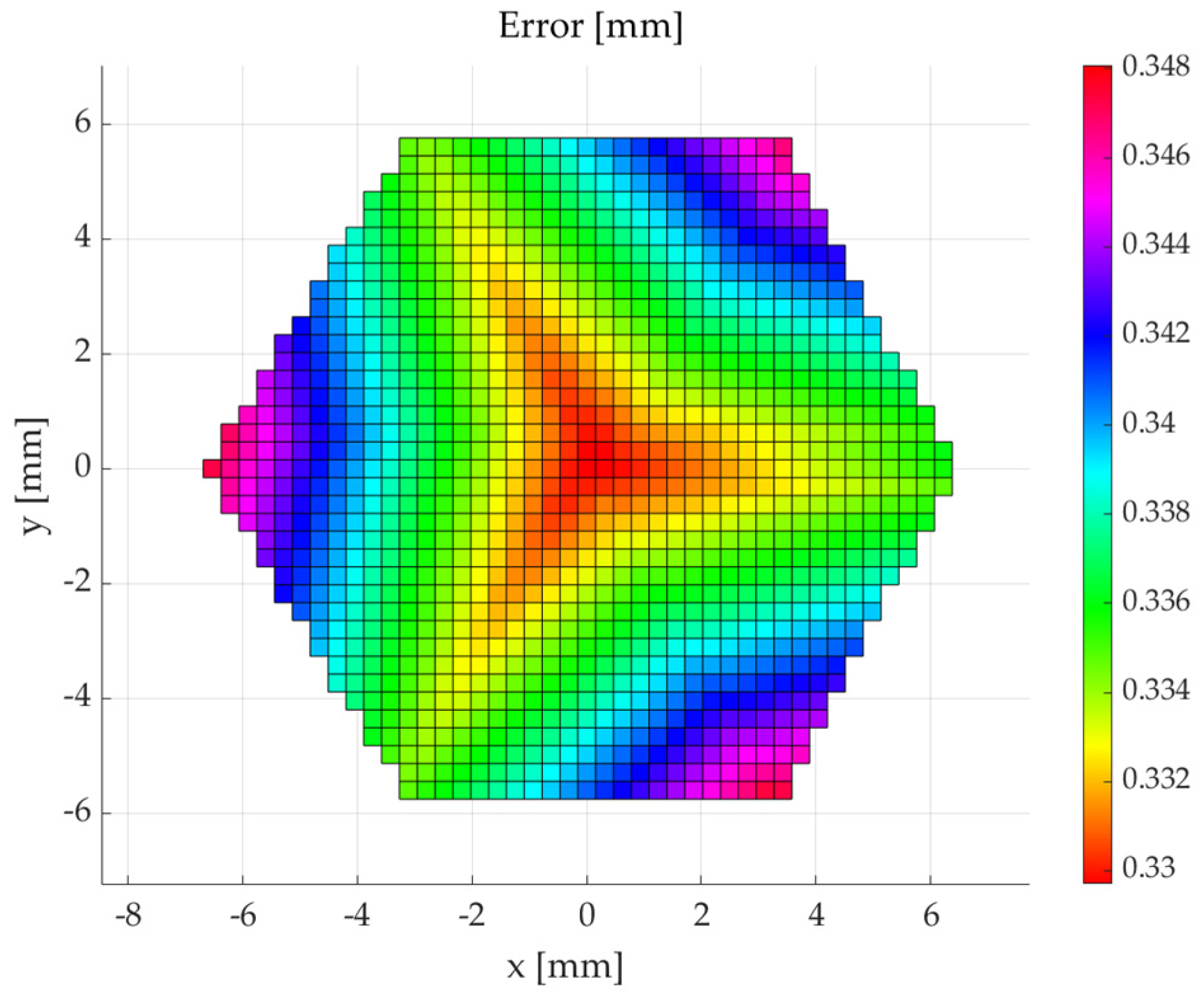
3.1. Analysis of the Influence of Actuator Errors on Working Volume Errors

In Figure 3, it was shown that the single actuator positioning error is about 0.02 mm. A mapping of the errors in the working volume was derived through an estimation of the influence of the errors of the three actuators using the direct kinematic model. The calculation was carried out by commanding movements equivalent to the documented errors and combining them in the worst combination of the three actuators, which corresponds to double the amplitude of the error of a single actuator. In Figure 11, the derived map is shown. It can be seen that the error is relatively constant over the working volume. The maximum values occur at three vertices where two actuators are near the maximum contraction, and the higher movement amplification effect of the cable system occurs.

3.2. Manipulator Prototype

The components were realized and assembled. Particular attention had to be paid to the realization of the actuators. They have to be of the same length of 20 mm. This goal was achieved using knots and mechanical end locks realized by machining. Figure 12 shows the realized prototype.

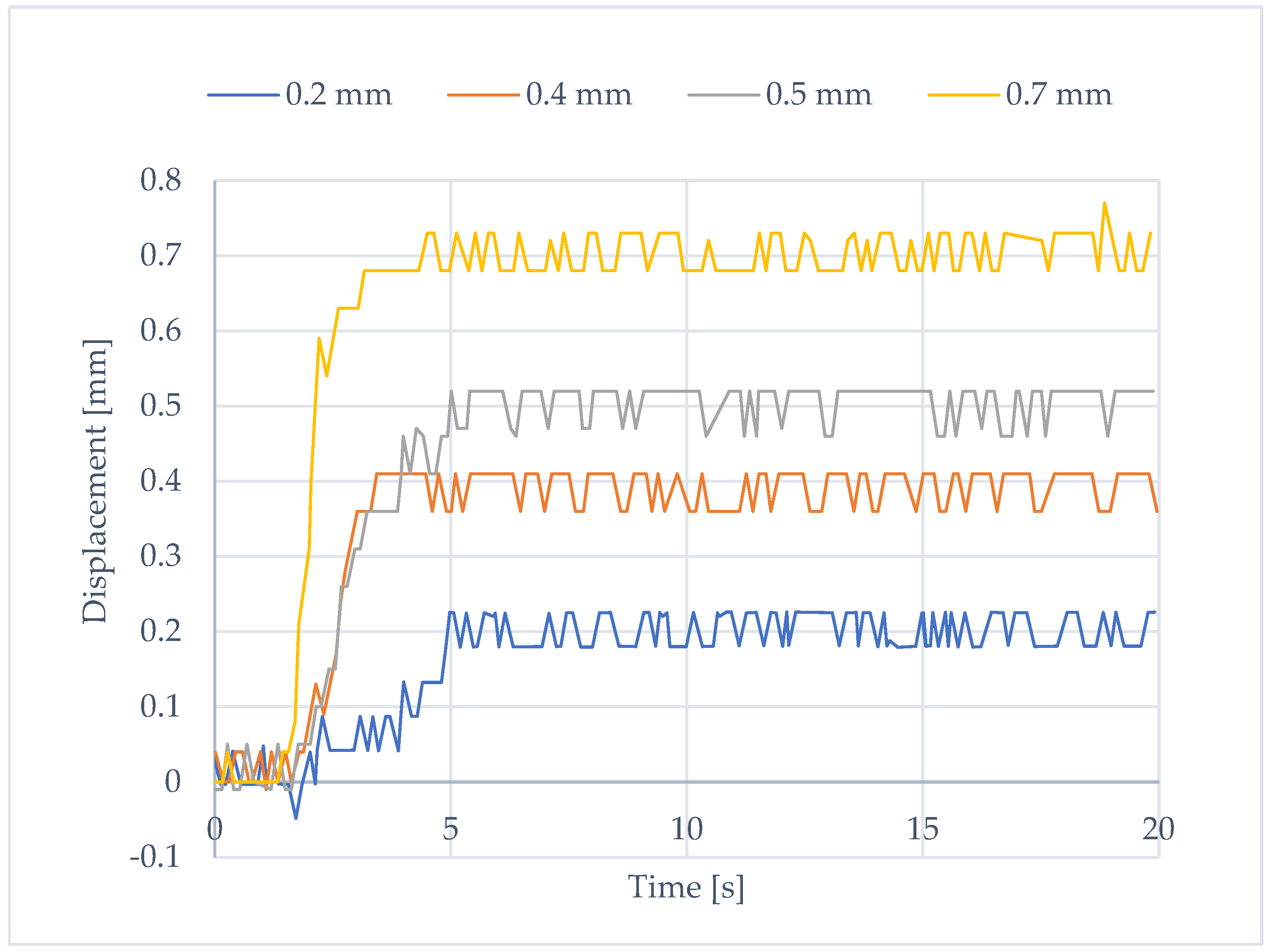
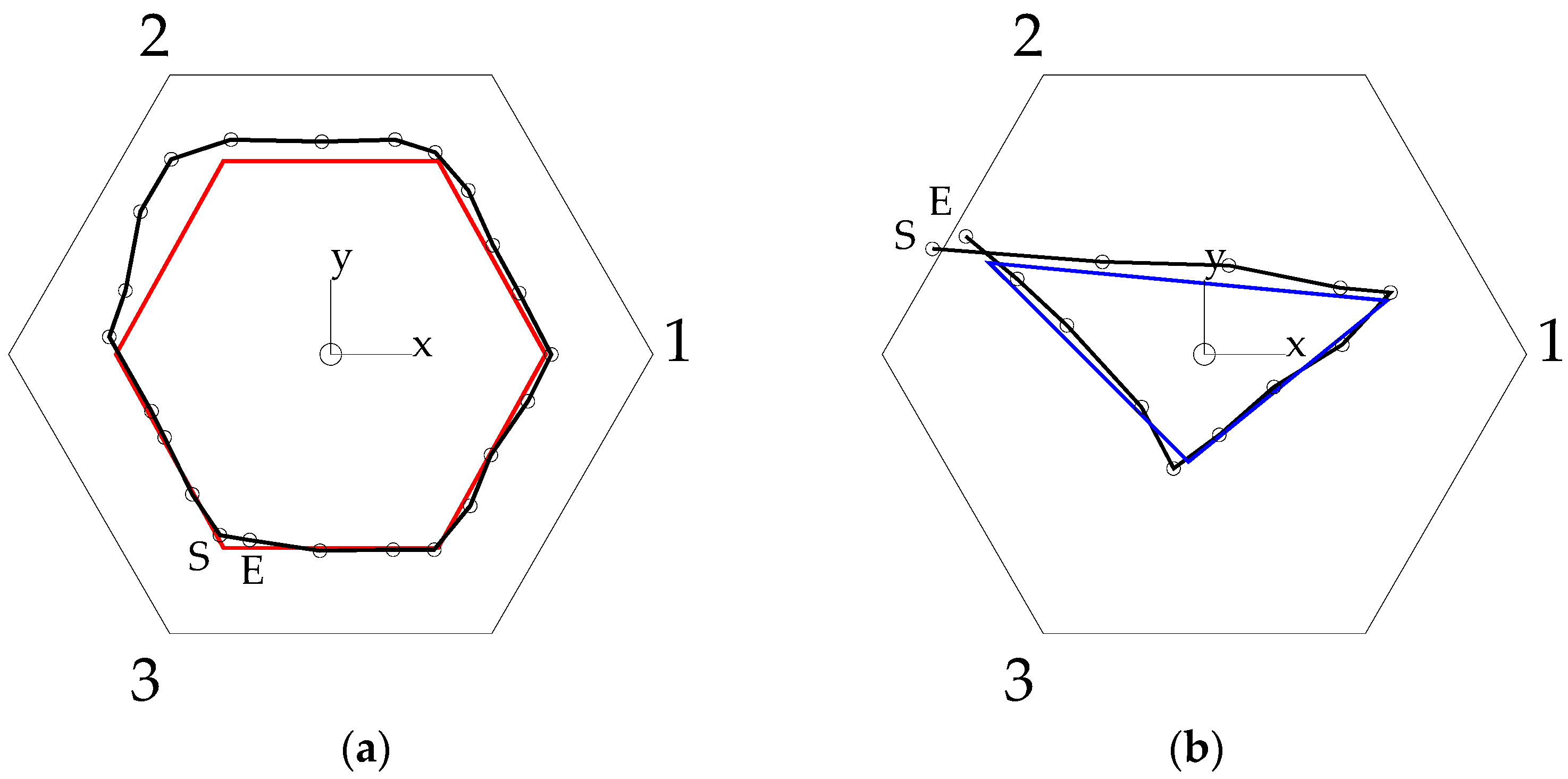
3.3. Experimental Tests

The first experimental tests were about movement involving one actuator at a time. Using lateral photography at a distance of about 4 m, it was possible to document the movements of the end effector on a graduated scale. The possibility of positioning by a single actuator one at a time was verified on the overall range of motion. Figure 13 shows the manipulator executing a single actuator movement (a) and the movement to the position (2, 0, 131.3) as viewed by the camera with the optic axis intersecting the z-axis and pointing toward the positive direction of the y-axis (b).
Once the functionality of the single actuators was demonstrated, some tests were conducted involving coordination between the actuators in trajectory control tasks. The first involved the end effector in describing a hexagonal trajectory centered on the working volume. Subsequently, trajectories arranged without particular symmetries with respect to the working volume were tested.
As for the measurement of the movements, a camera was placed above the robot, with its optical axis pointing downward and coincident with the manipulator's vertical axis. Video of the movement was recorded for every test. Subsequently, keyframes were extracted from the videos and analyzed in a CAD environment. To have a reference for the evaluations, a paper screen with a hexagonal hole, through which the robot's end effector can be seen, was placed centered with the vertical axis of the system and in the horizontal plane in which the motion of point E is expected to lie. By this setup, only trajectories in the horizontal planes can be analyzed. So, for a more complete characterization, there is a need for a more sophisticated setup and procedure to detect trajectories in planes different from the horizontal or with evolutions in tridimensional space.
The first trajectory tracking tests were related to hexagon trajectories centered on the working volume. Then, trajectories with less symmetry with respect to the working volume were considered as references. These were describing triangles whose vertices are chosen without particular conditions.
Figure 14 compares the reference trajectories and the achieved movements relating to representative cases of the tests described.
Figure 15 shows the errors of the trajectory tracking tests computed by the distance between the achieved positions, i.e., the black circles, and the reference trajectories, red line, and blue line for the relative tests documented in Figure 14.

4. Discussion and Conclusion

The manipulator responds well to positioning in a large part of the working volume, but there is a confined area where the error is considerably larger. In the area where the error is small, this is lower than the prediction based on the error detected for the single actuator. This is because the synergy between the three actuators ensures that the errors due to oscillations detected for the single actuator are dampened, reducing the error of the manipulator compared to what can be predicted based on a composition of the errors characterizing the individual actuators (Figure 11).
As for the area in which the error is most significant, it is clear that this derives from a discrepancy in the functioning of actuator number 2 compared to the others, which presents a more intense action than it should. It turns out that the positioning brings the end effector closer to the attack of actuator 2 than it should. This effect is noticeable in both trajectory tests.
Regarding the causes of this behavior, different lengths at rest can lead to this problem. Still, the authors believe this problem has a limited effect, given that particular care was taken in constructing the actuators.
Another possible cause, and more probable than the first, is that actuator number 2 responds differently than the others due to the physical composition of the alloy and that it needs a slightly different electrical resistance deformation model from the one implemented for all three actuators. A possibility that should, therefore, be investigated in the future is to characterize the actuators one by one and equip each with its strain-electric resistance model to implement the sensor effect.
Another possibility could be to calibrate the system on the area where the errors are most significant and create a lookup table that can make corrections to increase precision.
To provide evidence of the advantages of the proposed device, a comparison was carried out with a similar device. The comparison was based on the number of DOFs, working volume, the accuracy in the positioning, the overall dimensions, the actuator’s block control volume, and the mass. Figure 15 shows the considered device, and Table 3 compares the proposed device with the other under study.
From the comparison results, concerning the compared device, the proposed one has a smaller score just for the height of the working volume, which results in about 66% of the compared one and a lower accuracy due to the problem of the malfunctioning of the actuator number 2 as above discussed. In all the other indices, the proposed device outperforms the compared one. From the comparison, it can be concluded that the proposed device has a better score for the considered requirements.

Author Contributions

Conceptualization, FD; methodology, FD, PBZ and TR; validation, FD; formal analysis, FD, PBZ and TR; investigation, FD, PBZ and TR; data curation, FD; writing—original draft preparation, FD; writing—review and editing, FD; visualization, FD, PBZ and TR; supervision FD, PBZ and TR. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding

Data Availability Statement

Not applicable.

Acknowledgments

The authors gratefully acknowledge the contribution of dott. Emiliano Valentini in the experimental test reported in this paper.

Conflicts of Interest

The authors declare no conflict of interest

References

  1. Kittinanthapanya, R.; Sugahara, Y.; Matsuura, D.; Takeda, Y. Development of a Novel SMA-Driven Compliant Rotary Actuator Based on a Double Helical Structure. Robotics 2019, 8, 12. [Google Scholar] [CrossRef]
  2. Britz, R.; Motzki, P.; Seelecke, S. Scalable Bi-Directional SMA-Based Rotational Actuator. Actuators 2019, 8, 60. [Google Scholar] [CrossRef]
  3. Copaci, D.; Blanco, D.; Moreno, L. Flexible Shape-Memory Alloy-Based Actuator: Mechanical Design Optimization According to Application. Actuators 2019, 8, 63. [Google Scholar] [CrossRef]
  4. Schmelter, T.; Theren, B.; Fuchs, S.; Kuhlenkötter, B. Development of an Actuator for Translatory Movement by Means of a Detented Switching Shaft Based on a Shape Memory Alloy Wire for Repeatable Mechanical Positioning. Crystals 2021, 11, 163. [Google Scholar] [CrossRef]
  5. Ballester, C.; Copaci, D.; Arias, J.; Moreno, L.; Blanco, D. Hoist-Based Shape Memory Alloy Actuator with Multiple Wires for High-Displacement Applications. Actuators 2023, 12, 159. [Google Scholar] [CrossRef]
  6. Durante, F.; Beomonte Zobel, P.; Raparelli, T. The experience at University of L’Aquila on shape memory alloys actuators. In Advances in Service and Industrial Robotics; Mechanisms and Machine Science; Springer, Cham, Switzerland, 2018, Volume 49, pp. 638–645. [CrossRef]
  7. Dauksher, R.; Patterson, Z.; Majidi, C. Characterization and Analysis of a Flexural Shape Memory Alloy Actuator. Actuators 2021, 10, 202. [Google Scholar] [CrossRef]
  8. Ameduri, S.; Concilio, A.; Favaloro, N.; Pellone, L. A Shape Memory Alloy Application for Compact Unmanned Aerial Vehicles. Aerospace 2016, 3, 16. [Google Scholar] [CrossRef]
  9. Bovesecchi, G.; Corasaniti, S.; Costanza, G.; Tata, M. A Novel Self-Deployable Solar Sail System Activated by Shape Memory Alloys. Aerospace 2019, 6, 78. [Google Scholar] [CrossRef]
  10. Liu, M.; Wang, Z.; Ikeuchi, D.; Fu, J.; Wu, X. Design and Simulation of a Flexible Bending Actuator for Solar Sail Attitude Control. Aerospace 2021, 8, 372. [Google Scholar] [CrossRef]
  11. Costanza, G.; Delle Monache, G.; Tata, M.; Filosi, S. Development of SMA Spring Linear Actuator for an Autonomous Lock and Release Mechanism: Application for the Gravity-Assisted Pointing System in Moon to Earth Alignment of Directional Devices. Aerospace 2022, 9, 735. [Google Scholar] [CrossRef]
  12. Dimino, I.; Vendittozzi, C.; Reis Silva, W.; Ameduri, S.; Concilio, A. A Morphing Deployable Mechanism for Re-Entry Capsule Aeroshell. Appl. Sci. 2023, 13, 2783. [Google Scholar] [CrossRef]
  13. Braun, D.; Weik, D.; Elsner, S.; Hunger, S.; Werner, M.; Drossel, W. Position Control and Force Estimation Method for Surgical Forceps Using SMA Actuators and Sensors. Materials 2021, 14, 5111. [Google Scholar] [CrossRef] [PubMed]
  14. Kim, H.; Jang, S.; Do, P.; Lee, C.; Ahn, B.; Kwon, S.; Chang, H.; Kim, Y. Development of Wearable Finger Prosthesis with Pneumatic Actuator for Patients with Partial Amputations. Actuators 2023, 12, 434. [Google Scholar] [CrossRef]
  15. Deng, E.; Tadesse, Y. A Soft 3D-Printed Robotic Hand Actuated by Coiled SMA. Actuators 2021, 10, 6. [Google Scholar] [CrossRef]
  16. Kotb, Y.; Elgamal, I.; Serry, M. Shape Memory Alloy Capsule Micropump for Drug Delivery Applications. Micromachines 2021, 12, 520. [Google Scholar] [CrossRef] [PubMed]
  17. Shen, J.; Chen, Y.; Sawada, H. A Wearable Assistive Device for Blind Pedestrians Using Real-Time Object Detection and Tactile Presentation. Sensors 2022, 22, 4537. [Google Scholar] [CrossRef] [PubMed]
  18. Copaci, D.; Serrano, D.; Moreno, L.; Blanco, D. A High-Level Control Algorithm Based on sEMG Signalling for an Elbow Joint SMA Exoskeleton. Sensors 2018, 18, 2522. [Google Scholar] [CrossRef] [PubMed]
  19. He, J.; Lu, Y.; Wang, L.; Ma, N. On the Improvement of Thermal Protection for Temperature-Responsive Protective Clothing Incorporated with Shape Memory Alloy. Materials 2018, 11, 1932. [Google Scholar] [CrossRef] [PubMed]
  20. Srivastava, R.; Alsamhi, S.; Murray, N.; Devine, D. Shape Memory Alloy-Based Wearables: A Review, and Conceptual Frameworks on HCI and HRI in Industry 4.0. Sensors 2022, 22, 6802. [Google Scholar] [CrossRef] [PubMed]
  21. Lee, J.; Han, M. Design and Evaluation of Smart Textile Actuator with Chain Structure. Materials 2023, 16, 5517. [Google Scholar] [CrossRef]
  22. Helps, T.; Vivek, A.; Rossiter, J. Characterization and Lubrication of Tube-Guided Shape-Memory Alloy Actuators for Smart Textiles. Robotics 2019, 8, 94. [Google Scholar] [CrossRef]
  23. Raparelli, T.; Zobel, P.B.; Durante, F. A proposed methodology for the development of microgrippers: An application to a silicon device actuated by shape memory alloy wires. Int. J. Mech. Eng. Technol. 2018, 9, 235–249. [Google Scholar]
  24. Zainal, M.; Sahlan, S.; Ali, M. Micromachined Shape-Memory-Alloy Microactuators and Their Application in Biomedical Devices. Micromachines 2015, 6, 879–901. [Google Scholar] [CrossRef]
  25. Garcés-Schröder, M.; Hecht, L.; Vierheller, A.; Leester-Schädel, M.; Böl, M.; Dietzel, A. Micro-Grippers with Femtosecond-Laser Machined In-Plane Agonist-Antagonist SMA Actuators Integrated on Wafer-Level by Galvanic Riveting. Proceedings 2017, 1, 385. [Google Scholar] [CrossRef]
  26. Subendran, S.; Kang, C.; Chen, C. Comprehensive Hydrodynamic Investigation of Zebrafish Tail Beats in a Microfluidic Device with a Shape Memory Alloy. Micromachines 2021, 12, 68. [Google Scholar] [CrossRef]
  27. Maffiodo, D.; Raparelli, T. Flexible Fingers Based on Shape Memory Alloy Actuated Modules. Machines 2019, 7, 40. [Google Scholar] [CrossRef]
  28. Zeng, X.; Wu, Y.; Han, S.; Liu, Y.; Xiu, H.; Tian, F.; Ren, L. Theoretical and Experimental Investigations into a Crawling Robot Propelled by Piezoelectric Material. Micromachines 2021, 12, 1577. [Google Scholar] [CrossRef]
  29. Perez-Sanchez, V.; Garcia-Rubiales, F.; Nekoo, S.; Arrue, B.; Ollero, A. Modeling and Application of an SMA-Actuated Lightweight Human-Inspired Gripper for Aerial Manipulation. Machines 2023, 11, 859. [Google Scholar] [CrossRef]
  30. Raparelli T., Beomonte Zobel P., Durante F. Mechanical design of a 3-dof parallel robot actuated by smart wires. (2009) Proceedings of EUCOMES 2008 - The 2nd European Conference on Mechanism Science, pp. 271 - 278. [CrossRef]
  31. Shin, J.; Han, Y.; Lee, J.; Han, M. Shape Memory Alloys in Textile Platform: Smart Textile-Composite Actuator and Its Application to Soft Grippers. Sensors 2023, 23, 1518. [Google Scholar] [CrossRef]
  32. Shi, L.; Guo, S.; Li, M.; Mao, S.; Xiao, N.; Gao, B.; Song, Z.; Asaka, K. A Novel Soft Biomimetic Microrobot with Two Motion Attitudes. Sensors 2012, 12, 16732–16758. [Google Scholar] [CrossRef]
  33. Rajagopalan, R.; Petruska, A.; Howard, D. A Bi-State Shape Memory Material Composite Soft Actuator. Actuators 2022, 11, 86. [Google Scholar] [CrossRef]
  34. Maffiodo, D.; Raparelli, T. Three-fingered gripper with flexure hinges actuated by shape memory alloy wires. Int. J. Autom. Technol. 2017, 11, 355–360. [Google Scholar] [CrossRef]
  35. Sreekumar M., Singaperumal M., Nagarajan T., Zoppi M., Molfino R. A compliant miniature parallel manipulator with shape memory alloy actuators (2006) Proceedings of the IEEE International Conference on Industrial Technology, art. no. 4237692, pp. 848 - 853. [CrossRef]
  36. Elwaleed A.K., Mohamed N.A., Nor M.J.M., Mustafa M.M. A new method for actuating parallel manipulators (2008) Sensors and Actuators, A: Physical, 147 (2), pp. 593 - 599. [CrossRef]
  37. Giuseppe C. Experimental characterization of a binary actuated parallel manipulator (2016) Chinese Journal of Mechanical Engineering (English Edition), 29 (3), pp. 445 - 453. [CrossRef]
  38. AbuZaiter A., Ng E.L., Kazi S., Mohamed Ali M.S. Development of Miniature Stewart Platform Using TiNiCu Shape-Memory-Alloy Actuators (2015) Advances in Materials Science and Engineering, 2015, art. no. 928139. [CrossRef]
  39. Ranjith Pillai, R. , Ganesan M. Mechatronics Design and Kinematic Analysis of SMA Spring Actuated Parallel Manipulator (2021) Journal of Physics: Conference Series, 1969 (1), art. no. 012011. [CrossRef]
  40. Raparelli T., Zobel P.B., Durante F. Design of a parallel robot actuated by shape memory alloy wires. (2002) Materials Transactions, 43 (5), pp. 1015 - 1022. [CrossRef]
  41. Raparelli, T.; Beomonte Zobel, P.; Durante, F. A robot actuated by shape memory alloy wires. In Industrial Electronics, 2002. ISIE 2002, Proceedings of the 2002 IEEE International Symposium on, L’Aquila, Italy, 8–11 July 2002; IEEE: Piscataway, NJ, USA, 2002; Volume 2, pp. 420–423. [Google Scholar] [CrossRef]
  42. Durante F., Raparelli T., Beomonte Zobel P. Resistance Feedback of a Ni-Ti Alloy Actuator at Room Temperature in Still Air (2024) Micromachines, 15 (4), art. no. 545. [CrossRef]
  43. Gosselin C., Angeles J. Singularity Analysis of Closed-Loop Kinematic Chains (1990) IEEE Transactions on Robotics and Automation, 6 (3), pp. 281 - 290. [CrossRef]
Preprints 107817 g001
Figure 1. Concept of the manipulator.
Figure 1. Concept of the manipulator.
Preprints 107817 g001
Preprints 107817 g002
Figure 2. A linear mathematical model for the electrical resistance-deformation for the NiTi alloy wires is adopted for the control.
Figure 2. A linear mathematical model for the electrical resistance-deformation for the NiTi alloy wires is adopted for the control.
Preprints 107817 g002
Preprints 107817 g003
Figure 3. Responses of the 20 mm long actuator with the self-sensing process to step inputs of 0.2 mm, 0.4 mm, 0.5 mm, and 0.7 mm. The responses are quick with a precise mean value, but oscillations occur with an amplitude of less than 0.02 mm.
Figure 3. Responses of the 20 mm long actuator with the self-sensing process to step inputs of 0.2 mm, 0.4 mm, 0.5 mm, and 0.7 mm. The responses are quick with a precise mean value, but oscillations occur with an amplitude of less than 0.02 mm.
Preprints 107817 g003
Preprints 107817 g004
Figure 4. Parameters for the kinematic model of the Manipulator.
Figure 4. Parameters for the kinematic model of the Manipulator.
Preprints 107817 g004
Preprints 107817 g005
Figure 5. The boundaries of the working volume of the manipulator.
Figure 5. The boundaries of the working volume of the manipulator.
Preprints 107817 g005
Preprints 107817 g006
Figure 6. The force developed by the actuators Fi and their resultant F along the end effector rod axis. The spring has to apply a force opposite to F, as given by eq. (24).
Figure 6. The force developed by the actuators Fi and their resultant F along the end effector rod axis. The spring has to apply a force opposite to F, as given by eq. (24).
Preprints 107817 g006
Preprints 107817 g007
Figure 7. Forces applied by the actuators with the end effector lying on the upper working volume boundary (a) and lower working volume boundary (b) in contrast with the bias spring. The maximum force of the spring occurs in the lower boundary of the working volume and is equal to 1.98 N. In this case, the actuators must develop a maximum force equal to 1.26 N for equilibrium (b). Therefore, given that the wires develop a maximum force equal to 3.2 N, a large margin for the manipulator to apply loads externally occurs. On the upper boundary, the spring applies a minimum force of 1.69 N, and the wires develop a maximum force of 1.22 N (a). So, the spring can keep them taut and return them to their maximum length at low temperature since they require 0.6 N to be stretched. And, again, there is a margin to apply external forces.
Figure 7. Forces applied by the actuators with the end effector lying on the upper working volume boundary (a) and lower working volume boundary (b) in contrast with the bias spring. The maximum force of the spring occurs in the lower boundary of the working volume and is equal to 1.98 N. In this case, the actuators must develop a maximum force equal to 1.26 N for equilibrium (b). Therefore, given that the wires develop a maximum force equal to 3.2 N, a large margin for the manipulator to apply loads externally occurs. On the upper boundary, the spring applies a minimum force of 1.69 N, and the wires develop a maximum force of 1.22 N (a). So, the spring can keep them taut and return them to their maximum length at low temperature since they require 0.6 N to be stretched. And, again, there is a margin to apply external forces.
Preprints 107817 g007
Preprints 107817 g008
Figure 8. The CAD model of the manipulator.
Figure 8. The CAD model of the manipulator.
Preprints 107817 g008
Preprints 107817 g009
Figure 9. The board used for the measurement of the electrical resistance and the driving of the actuator. (a) the electric scheme, (b) the physical homemade board in which the electric scheme was replicated three times for the three actuators: (1) controller connector, (2) Rc electrical resistances, (3) 4N33 optocoupler, (4) Rp electrical resistances, (5) BC288 transistors, (6) Rm measuring electrical resistance, (7) Ni-Ti actuators connectors.
Figure 9. The board used for the measurement of the electrical resistance and the driving of the actuator. (a) the electric scheme, (b) the physical homemade board in which the electric scheme was replicated three times for the three actuators: (1) controller connector, (2) Rc electrical resistances, (3) 4N33 optocoupler, (4) Rp electrical resistances, (5) BC288 transistors, (6) Rm measuring electrical resistance, (7) Ni-Ti actuators connectors.
Preprints 107817 g009
Preprints 107817 g010
Figure 10. Control logic scheme: in stage 1, far from the target, the control supplies the maximum power. In stage 2, close to the target, the control becomes proportional. Stage 3, overcoming the target, the control cuts power off.
Figure 10. Control logic scheme: in stage 1, far from the target, the control supplies the maximum power. In stage 2, close to the target, the control becomes proportional. Stage 3, overcoming the target, the control cuts power off.
Preprints 107817 g010
Preprints 107817 g011
Figure 11. Sensitivity analysis of the error over the working volume domain due to the errors of the actuators (shown in Figure 3). It is possible to note a maximum absolute position error of 0.348 mm, corresponding to an error relative to the maximum transversal dimension of the working volume, equal to 2.7%.
Figure 11. Sensitivity analysis of the error over the working volume domain due to the errors of the actuators (shown in Figure 3). It is possible to note a maximum absolute position error of 0.348 mm, corresponding to an error relative to the maximum transversal dimension of the working volume, equal to 2.7%.
Preprints 107817 g011
Preprints 107817 g012
Figure 12. The realized prototype. An overall view showing the base and the end effector rod (a). A zoom on the base: it is possible to see the spherical joint between the end effector and the base, as well as the spring and the NiTi wires (b).
Figure 12. The realized prototype. An overall view showing the base and the end effector rod (a). A zoom on the base: it is possible to see the spherical joint between the end effector and the base, as well as the spring and the NiTi wires (b).
Preprints 107817 g012
Preprints 107817 g013
Figure 13. The first experimental tests were related to the positioning of an actuator at the time. A calibrated index indicates the actual position on a graduated scale where every notch corresponds to 1 mm (a). The positioning from the resting position to 2 mm (b).
Figure 13. The first experimental tests were related to the positioning of an actuator at the time. A calibrated index indicates the actual position on a graduated scale where every notch corresponds to 1 mm (a). The positioning from the resting position to 2 mm (b).
Preprints 107817 g013
Preprints 107817 g014
Figure 14. Trajectory tracking tests. The numbers 1, 2, and 3 represent the directions through which the action of the corresponding actuator is. The letters S and E represent the trajectory's start and end positions. The circles represent the points of the actual trajectory. (a) Representative case of the first trajectory-tracking test: the reference (red line) is an almost regular hexagon with an edge of 4 mm. Starting from the resting position with the end effector in (0, 0, 131.3), the trajectory reference was commanded to reach the vertices thru the own coordinates in the following sequence: (-2, -3.6, 130.7), (-4, 0, 130.7), (-2, 3.6, 130.7), (2, 3.6, 130.7), (4, 0, 130.7), (2, -3.6, 130.7), (-2, -3.6, 130.7); the comparison is made by 23 points of the actual trajectory. (b) Representative case of the second trajectory-tracking test: the reference is a general triangle (blue line). Starting from the resting position with the end effector in (0, 0, 131.3), the trajectory was commanded to reach the vertices through the own coordinates in the following sequence: (-0.3, -2, 130.7), (-4, 1.7, 130.7), (3.4, 1, 130.7); the comparison is made by 13 points of the actual trajectory.
Figure 14. Trajectory tracking tests. The numbers 1, 2, and 3 represent the directions through which the action of the corresponding actuator is. The letters S and E represent the trajectory's start and end positions. The circles represent the points of the actual trajectory. (a) Representative case of the first trajectory-tracking test: the reference (red line) is an almost regular hexagon with an edge of 4 mm. Starting from the resting position with the end effector in (0, 0, 131.3), the trajectory reference was commanded to reach the vertices thru the own coordinates in the following sequence: (-2, -3.6, 130.7), (-4, 0, 130.7), (-2, 3.6, 130.7), (2, 3.6, 130.7), (4, 0, 130.7), (2, -3.6, 130.7), (-2, -3.6, 130.7); the comparison is made by 23 points of the actual trajectory. (b) Representative case of the second trajectory-tracking test: the reference is a general triangle (blue line). Starting from the resting position with the end effector in (0, 0, 131.3), the trajectory was commanded to reach the vertices through the own coordinates in the following sequence: (-0.3, -2, 130.7), (-4, 1.7, 130.7), (3.4, 1, 130.7); the comparison is made by 13 points of the actual trajectory.
Preprints 107817 g014
Preprints 107817 g015
Figure 15. The hexagonal trajectory test shows a maximum error of almost 1 mm in a confined zone, while in the rest of the trajectory, the error is less than 0.2 mm. The triangular trajectory test shows similar maximum and minimum values for the errors.
Figure 15. The hexagonal trajectory test shows a maximum error of almost 1 mm in a confined zone, while in the rest of the trajectory, the error is less than 0.2 mm. The triangular trajectory test shows similar maximum and minimum values for the errors.
Preprints 107817 g015
Preprints 107817 g016
Figure 15. The manipulator used for comparison with the proposed device: (a) parallel manipulator with 3 DoF actuated by Ni-Ti wires and controlled by the use of potentiometers [40]; (b) the proposed manipulator.
Figure 15. The manipulator used for comparison with the proposed device: (a) parallel manipulator with 3 DoF actuated by Ni-Ti wires and controlled by the use of potentiometers [40]; (b) the proposed manipulator.
Preprints 107817 g016
Table 1. Technical specification of the wire.
Table 1. Technical specification of the wire.
Flexinol 150HT
Wire diameter: 150 µm
Linear resistance: 50 Ω/m
Maximum recovery force: 10.4 N
Recommended deformation ratio: 3-5 %
Austenite start temperature: 68°C
Austenite finish temperature: 78°C
Martensite start temperature: 52°C
Martensite finish temperature: 42°C
Table 2. Parameters’ comparison for the choice of the characteristic dimension of the robot, b.
Table 2. Parameters’ comparison for the choice of the characteristic dimension of the robot, b.
b (mm) aM (°) am (°) OPM (mm) OPm (mm) D(OP) (mm)
10.00 60.00 58.79 17.32 16.51 0.81
11.00 56.63 55.25 16.70 15.86 0.84
12.00 53.13 51.56 16.00 15.12 0.88
13.00 49.46 47.66 15.20 14.26 0.93
14.00 45.57 43.50 14.28 13.28 1.00
15.00 41.41 38.99 13.23 12.14 1.08
16.00 36.87 34.00 12.00 10.79 1.21
16.50 34.41 31.25 11.30 10.01 1.29
17.00 31.79 28.26 10.54 9.14 1.40
18.00 25.84 21.15 8.72 6.96 1.75
19.00 18.19 10.12 6.24 3.39 2.86
Table 3. Characteristics of the devices under comparison. DOF = degrees of freedom; WV = working volume dimensions as diameter of the circle circumscribed to the shape of the WV in plant by height [mm × mm]; PA = typical positioning accuracy [mm]; OD = overall dimensions intended as diameter by height of the smaller cylinder containing the device [mm × mm]; ABV = actuator’s block control volume [mm3]; M = mass of the device without electronics for control [kg]. Brackets (a)–(b) correspond to the devices shown in Figure 15; (c) represent the reference requirements.
Table 3. Characteristics of the devices under comparison. DOF = degrees of freedom; WV = working volume dimensions as diameter of the circle circumscribed to the shape of the WV in plant by height [mm × mm]; PA = typical positioning accuracy [mm]; OD = overall dimensions intended as diameter by height of the smaller cylinder containing the device [mm × mm]; ABV = actuator’s block control volume [mm3]; M = mass of the device without electronics for control [kg]. Brackets (a)–(b) correspond to the devices shown in Figure 15; (c) represent the reference requirements.
Device DOF WV PA OD ABV M
(a) 3 12 × 2 0.3 82 × 207 138600 0.245
(b) 3 12 × 1.3 1/0.3 40.8 × 120 7844 0.012
(c) 3 10 × 2 0.1 45 × 140 20000 0.050
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated