Quantum Cosmology Part I: The Integration of Special Relativity and Quantum Mechanics

Preprint

Article

Quantum Cosmology Part I: The Integration of Special Relativity and Quantum Mechanics

Altmetrics

Downloads

457

Views

227

Comments

Dennis Kahan^*

This version is not peer-reviewed

Submitted:

09 August 2024

Posted:

09 August 2024

Read the latest preprint version here

Alerts

Abstract

The inability to delineate a unified physical ontology that accounts simultaneously for the laws of special relativity and the results of quantum experiments has been a defining problem in physics for more than 100 years. This analysis addresses the problem by positing a novel mixed ontology composed of a “discrete” 4D spacetime and a physical, ultra-high dimensional (3 x N) “Planck Space.” Together, Planck Space and the three spatial dimensions of 4D spacetime form a tightly integrated ((3 x N) + 3) hyperspace (the “Dual Ontology”).Critically, the Dual Ontology’s structure replaces 1) the continuous, differentiable manifold of 4D spacetime with a discrete, background-independent 4D spacetime that is intrinsically curved and 2) mathematical spaces with a physical (3 x N) Planck Space. Moreover, the Dual Ontology is structurally and dynamically predicated on the one-to-one mapping and identity between the discrete spatial units that simultaneously form 4D spacetime and Planck Space. The one-to-one mapping and identity of the discrete spatial units support an integrated quantum dynamics based upon the dynamic evolution of single and N-body quantum states in 4D spacetime in full compliance with the laws of special relativity and the instantaneous collapse of all quantum states in an ontic Planck Space, where special and general relativity and more generally, 4D spacetime’s laws of physics, do not apply.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. The Dual Ontology

1.1. Introduction

Ontological premises have profound theoretical implications. When Albert Einstein developed the laws of special relativity (“SR”) in 1905, he did so without regard to whether 4D spacetime was continuous or discrete. However, Einstein’s subsequent publication of the theory of general relativity (“GR”) in 1915 established the predominance of a continuous, differentiable 4D spacetime manifold as part of the fundamental physical structure of 4D spacetime. Mathematically based upon Riemannian and differential geometries, the concept of a continuous 4D spacetime manifold has been directly or indirectly incorporated into the Standard Model of Physics, Quantum Field Theory (“QFT”), Hilbert space, the non-relativistic Schrödinger wave equation, and both mathematical and ontic 3N configuration spaces. Many quantum theories, including primitive ontologies¹ (including Bohmian pilot wave,² spontaneous and objective collapse theories³), wave function ontologies,⁴ the many-worlds interpretation,⁵ and multi-field theories,⁶ have been directly or indirectly influenced by the concept of a continuous 4D spacetime.

For almost 100 years, physicists and philosophers of physics have also used Schrödinger’s non-relativistic wave equation to describe the dynamic motion of N-body quantum states over time in a mathematical 3N configuration space.⁷ Nevertheless, not only is the equation non-relativistic, but without a one-to-one correspondence between a low-dimensional 4D spacetime and a high-dimensional, mathematical, or ontic 3N configuration space based on a continuous manifold,⁸ it is impossible for an N-body quantum state’s mathematical wavefunction to simultaneously represent a quantum state in 4D spacetime and a 3N configuration or ontic space. ^{9 10}

1.2. The Dual Ontology Conjecture

Notwithstanding the diligent efforts of many physicists and philosophers of physics, the ontological and dynamic tension between SR and quantum mechanics will not be resolved if it is premised upon a continuous, differentiable 4D spacetime and a mathematical or ontic 3N configuration space.

Accordingly, this analysis adopts a novel alternative ontology and dynamics. In order to ontologically and dynamically unite SR with quantum mechanics, this analysis posits a physical ((3 x N) + 3) hyperspace (the “Dual Ontology”) composed of a discrete, curved, low-dimensional 4D spacetime and a physical, ultra-high-dimensional (3 x N) “Planck Space.”^{11 12} The ontology not only sets the foundation for the dynamic evolution of all quantum states in a background-independent 4D spacetime based on the laws of GR under a discrete Quantum Field Theory on Curved Spacetime but also the dynamic collapse of all quantum states in a Planck Space where the laws of SR and GR (collectively “Relativity”), and more generally the 4D spacetime laws of physics, do not apply.¹³

Critically, the three spatial dimensions of 4D spacetime and an ultra-high-dimensional Planck Space are composed of two ontic rather than physically salient or mathematical substructures: Planck Spheres and a State of Absolute Nothingness (the “SOAN”). Planck Spheres are discrete, three-dimensional, quantized units of space with a spherical volume of approximately 2.2 ×10⁻¹⁰⁸ cubic meters. On the other hand, the sole characteristic of the SOAN is onticness. It has no other positive physical characteristics.

The introduction of discrete, quantized Planck Spheres and an ontic SOAN not only alters current conceptions of 4D spacetime as a continuous, differentiable manifold but also replaces mathematical spaces with a physical ultra-high-dimensional (3 x N) space in the form of an N-tuple of ordered triples, where each N forms a separate dimension.¹⁴ 15 Neither the discreteness of Planck Spheres nor the SOAN’s existence in 4D spacetime alters the laws of SR. However, a (3 x N) Planck Space does not have a time dimension or the physical properties of space or volume and the physical laws of 4D spacetime are not applicable.

Ontologically, the SOAN is the non-temporal, non-spatial link between the Planck Spheres that simultaneously form 4D spacetime and Planck Space. More specifically, the link ensures that the same set of x, y, z coordinates that map to and identify the physical characteristics of every Planck Sphere in 4D spacetime physically and mathematically map to and identify the characteristics of the same Planck Sphere in Planck Space (the “Planck Identity”). The Planck Identity can be mathematically formulated as a function f that maps from 4D spacetime R⁴ to a (3 x N) dimensional Planck Space R^3×N and is defined as: f: R⁴→R^3×N. For a given set of coordinates in 4D spacetime (x_i,y_i,z_i,t_i), the function f maps these coordinates to f((x_i,y_i,z_i,t_i)) = ((x_i1,y_i1,z_i1),(x_i2,y_i2,z_i2),…,(x_iN,y_iN,z_iN)).¹⁶ As a result, the Planck Identity not only creates the unified ontological framework for the Dual Ontology’s tightly integrated ((3 x N + 3) hyperspace, but it also supports a fully integrated and simultaneous quantum dynamics based upon the dynamic evolution of all single and N-body quantum states in 4D spacetime in full compliance with the laws of SR and the instantaneous collapse of all quantum states in Planck Space, where the 4D spacetime laws of physics do not apply.¹⁷

Although the tightly integrated ((3 x N) + 3) hyperspace formed by a (3 x N) Planck Space, the three discrete spatial dimensions of 4D spacetime and the SOAN appear to be an imposing physical structure with a complex mathematical description, from a non-technical perspective, the Dual Ontology’s hyperspace is much less complicated. 4D spacetime and Planck Space are physically and mathematically interrelated ontological entities that form a single, integrated universal structure in the same physical space in which 4D spacetime is located. More proverbially, 4D spacetime does not exist “here,” and Planck Space does not exist “there.” They co-exist in the same physical space.

For example, assume that a discrete 4D spacetime is composed of Planck Spheres and that the SOAN is ontic within the interstices of Planck Spheres. Next, assume there are five Planck Spheres, one each on Venus, Mars, the Milky Way Galaxy, the Andromeda Galaxy, and the Orion Constellation. In 4D spacetime, each Planck Sphere has three spatial dimensions, and a unique set of x, y, z coordinates. Since the SOAN, rather than “space,” is located in the interstices between Planck Spheres, when viewed from the perspective of Planck Space rather than 4D spacetime, the SOAN does not separate the five Planck spheres by time, space, or volume. Instead, the same five Planck Spheres physically located in 4D spacetime simultaneously form a single 15-dimensional point (3 x 5) in Planck Space, where the number 3 represents the three x, y, z dimensions of an individual Planck Sphere in 4D spacetime, and the number 5 represents the five individual Planck Spheres.

The total number of Planck Spheres that comprise Planck Space can be represented by “N,” and the total number of dimensions in Planck Space can be represented by (3 x N), where “3” represents the three x, y, z dimensions of each Planck Sphere. The Dual Ontology’s structure integrates a (3 x N) Planck Space and the 3 spatial dimensions of 4D spacetime into a ((3 x N) + 3) hyperspace linked ontologically by the Planck Identity’s one-to-one identity and mapping of Planck Spheres in 4D spacetime and Planck Space.

Several preliminary points regarding the Dual Ontology conjecture are noted. First, the analysis does not attempt to determine the origin of the SOAN, Planck Spheres, 4D spacetime, Planck Space, or the energy content of the Dual Ontology. Second, the ontological existence of the SOAN and Planck Spheres is coeval, as is the ontological existence of 4D spacetime and Planck Space. Third, although the SOAN is ontic in 4D spacetime and Planck Space, it can never be directly observed or measured. Fourth, Planck Spheres are posited as the smallest structural units in the universe, but whether individual Planck Spheres can be directly observed or measured is unlikely. Fifth, subatomic entities are “quantum states,” not “particles.” All quantum states are ontic, but the mathematical wavefunctions that describe the dynamic evolution of all quantum states in 4D spacetime and their instantaneous collapse in Planck Space are not.^{18 19}

1.3. Analytical Structure

The specific sections of the analysis are structured as follows. Section 1 introduces the Dual Ontology conjecture. Section 2 introduces the ontological structure of the SOAN, Planck Spheres, 4D spacetime, and Planck Space. Section 3 re-examines the Einstein/de Broglie Boxes thought experiment, the double-slit experiment, the EPR thought experiment, and a which-way experiment and explains why all quantum states dynamically evolve in 4D spacetime subject to the laws of SR but instantaneously collapse in Planck Space, where Relativity does not apply. Section 4 reviews the physical implications of the Dual Ontology conjecture with regard to quantum indeterminacy, quantum state emergence and annihilation, the physical triggers of quantum state collapse, the generalized localization of a quantum state, quantum tunneling, and the Born Rule. Section 5 resolves the historical tension between SR and quantum mechanics by providing physical explanations for the 4D spacetime concepts of space-like separation, non-separability, instantaneity, the quantum connection, Bell’s theorem and non-locality, the Relativity of Simultaneity and Relativistic Energy Increase. Section 6 concludes with a review of the Dual Ontology conjecture, its implications, and open issues. Appendix A contains the mathematical formalisms supporting the Dual Ontology conjecture.

2. The ((3 x N) + 3) Dual Ontology

2.1. The SOAN and Planck Spheres

The Western tradition has long regarded an absolute state of “nothingness” with skepticism as logically inconsistent or ontologically impossible.²⁰ In this analysis, a state of “nothingness” has no relationship to the terms “nothing” or “void,” as those terms are used in current quantum or cosmological theory. A state of nothingness is not a “quantum vacuum state,” has no “fluctuating energy fields,” and is not governed by or subject to the physical laws of 4D spacetime or Planck Space.²¹

Although the non-technical term “nothing” occasionally appears in physics, it generally means “not anything” rather than an ontic state of nothingness.²² For example, in GR, the term “nothing,” as in “not anything,” is used as a visual aid to describe what 4D spacetime expands into after its inception at t = 0. The term has no independent physical reality. Similarly, in the context of quantum mechanics and discrete space, the term “nothing,” as in “not anything,” has been used to describe the area beyond the smallest divisible area of space:

“…[Q]uantum mechanics and general relativity, taken together, imply that there is a limit to the divisibility of space. Below a certain scale, nothing more is accessible. More precisely, nothing exists there.”²³ (Emphasis added).

Cosmologically, the term “nothing” has also been used conditionally to describe a scenario where space and time do not exist:

“Empty space is a very interesting place in modern physics; there’s a lot going on, whereas, if it were nothing, there would be nothing going on…. [S]o it’s probably better to think of nothing as the absence of even space and time, rather than space and time without anything in them There’s a big difference between empty space and nothing.”²⁴ (Emphasis added).

Despite the conceptual difficulties associated with the SOAN, this analysis posits that the SOAN is ontic and that its ontological existence is required to resolve the tension between the laws of SR and the results of quantum experiments. As used in this analysis, in a State of Absolute Nothingness:²⁵

“There is no spacetime, dimension, boundary, size, structure, volume, gravity, energy, pressure, temperature, force, fields, ground states, vacuum states, virtual particles, quantum fluctuations, dynamical properties, frame of reference, matter, strings, information, mathematical entities, potentials, concepts, abstractions, consciousness, positive physical laws, possibilities, or entropy.”

The SOAN’s highly restrictive definition means it is a passive ontological entity with no active role in the universe. Since the SOAN is devoid of physical attributes other than onticness, neither the physical laws of 4D spacetime nor Planck Space apply. Nevertheless, the absence of physical attributes other than onticness is a feature, not a bug. The very absence of physical characteristics and laws creates a physical environment within which an ontic SOAN fundamentally alters the physical structure and dynamics of the universe.

In contrast to the SOAN, Planck Spheres are defined as discrete quanta of space, with each quantum of space assumed to have the same shape and volume.²⁶ More specifically, Planck Spheres are posited as the smallest physical structures in the universe, with a spherical volume of approximately 2.2 ×10⁻¹⁰⁸ meters.²⁷ As the smallest independent structural unit in the universe, no smaller space units exist within the interstices of Planck Spheres. Like the SOAN, individual Planck Spheres are passive ontological units. However, unlike the SOAN, individual Planck Spheres can physically hold energy, and in the aggregate, Planck Spheres contain all of the universe’s energy.

2.2. Discrete 4D Spacetime and Planck Space

In order to resolve theoretical problems associated with a continuous 4D spacetime manifold and a mathematical 3N configuration space or an ontic 3N space, the Dual Ontology conjecture posits that 4D spacetime and a physical (3 x N) Planck Space are composed of discrete Planck Spheres and the SOAN. Although Planck Spheres and the SOAN form a universal substructure, when combined, Planck Spheres and the SOAN structurally form 1) the three spatial dimensions of a discrete 4D spacetime and 2) an ultra-high dimensional (3 x N) Planck Space. In turn, 4D spacetime and Planck Space form the universe’s ((3 x N) +3) Dual Ontology.

Although a discrete 4D spacetime differs from Relativity’s continuous differentiable manifold, discreteness is not difficult to grasp. On the other hand, a discrete 4D spacetime that includes the SOAN is difficult to understand and even more difficult to accept. The SOAN is a passive ontological entity. It cannot be directly observed or measured, does not have structure or boundaries, does not occupy space, does not have a time dimension, nor is it governed by the physical laws that apply to 4D spacetime or Planck Space.

Nevertheless, as counterintuitive as it may seem, it is precisely because the SOAN’s only physical attribute is onticness that the combination of discrete Planck Spheres and the SOAN create the Planck Identity’s one-to-one mapping and identity between the Planck Spheres that form 4D spacetime and Planck Space. In the context of 4D spacetime,

“The concept of a true void, apart from inducing a queasy feeling, strikes many people as preposterous or even meaningless. If two bodies are separated by nothing, should they not be in contact? How can ‘emptiness’ keep things apart or have properties such as size or boundaries?” ²⁸ (Emphasis added).

Viewed solely from the perspective of 4D spacetime, the SOAN does not add spatial dimensions or volume. Nevertheless, the SOAN’s ontic status as a state of nothingness is the physical, non-spatial, and non-temporal link between Planck Spheres in a low-dimensional 4D spacetime and the same Planck Spheres in an ultra-high-dimensional (3 x N) Planck Space. In other words, the one-to-one identity and mapping between the Planck Spheres of a discrete 4D spacetime and Planck Space is physically dependent on the link created by the SOAN. Based on the link, the Planck Identity ensures that the x, y, z coordinates of Planck Spheres in 4D spacetime also map to and identify the physical characteristics of the same Planck Sphere in Planck Space.

Planck Space is the second of the two ontological structures that comprise the Dual Ontology. Like 4D spacetime, Planck Space is composed of discrete Planck Spheres and the SOAN. However, unlike the 3 spatial dimensions of a discrete 4D spacetime, Planck Spheres and the SOAN form an ultra-high dimensional (3 x N) Planck Space. Fundamental ontological and dynamic differences exist between a low-dimensional 4D spacetime and ultra-high-dimensional (3 x N) Planck Space. More specifically, a physical (3 x N) Planck Space does not have a time dimension, nor the physical properties of space or volume, and the laws of Relativity (including gravity), the strong nuclear force, the electro-weak force, the second law of thermodynamics, kinetic and potential energy and the concept of entropy do not apply to it.²⁹

Mathematically, Planck Space is composed of N-tuples of ordered triples; Q_n = {(x₁,y₁,z₁)_,(x₂,y₂,z₂),...,(x_n, y_n, z_n)}where each N-tuple represents the coordinates of a Planck Sphere in Planck Space. Every N-tuple represents a dimension in Planck Space, and all of the N-tuples collectively represent the total number of dimensions in Planck Space. Accordingly, unlike a mathematical, continuous manifold 3N configuration or ontic space composed of mutually orthogonal vectors, in a physical, high dimensional (3 x N) Planck Space, the “N” Planck Spheres that comprise Planck Space form a single “Planck Hyper-Point” composed of N dimensions.³⁰ More generally, for any “N” Planck Spheres, the “N” Planck Spheres form a single Planck Hyper-Point of (3 x N). In the case of the 5.58 x 10¹⁸⁶ Planck Spheres that comprise the observable portion of a discrete 4D spacetime, the Planck Spheres form a single Planck Hyper-Point composed of (3 x 5.58 x 10¹⁸⁶) dimensions.³¹

3. Quantum State Evolution and Collapse in Discrete 4D Spacetime and Planck Space

3.1. The Dynamic Evolution of a Single Quantum State

The analysis begins with the dynamic evolution of a single quantum state in a discrete 4D spacetime composed of Planck Spheres and the SOAN. As we have already seen, the Planck Identity holds that the x, y, z coordinates of every Planck Sphere in 4D spacetime identify and map to the same Planck Sphere in Planck Space. As a single quantum state dynamically evolves in a discrete 4D spacetime, its field will occupy an extremely large number of individual Planck Spheres. Since individual Planck Spheres occupied by a quantum state contain a quantized amount of energy, the combination of a Planck Sphere with the quantized energy it contains is referred to as a “Bell Quantum Sphere.” Given the Planck Identity, a one-to-one mapping and identity exists between a Bell Quantum Sphere in 4D spacetime and the same Bell Quantum Sphere in Planck Space (the “Bell Identity”). Consequently, the Bell Identity holds that the x, y, z coordinates of a Bell Quantum Sphere not only map to the same Bell Quantum Sphere in 4D spacetime and Planck Space but also identify the physical attributes of the Bell Quantum Sphere in both spaces.³²

The Bell Identity can be mathematically formulated as a function g that maps from 4D spacetime R⁴ to a (3 x N) dimensional Planck Space R^3×N. The function g is defined as: g: R⁴→R^3×N. For a given set of coordinates in 4D spacetime (x_i,y_i,z_i,t_i), occupied by a single quantum state the function g maps these coordinates to: g((x_i,y_i,z_i,t_i)) = ((x_i1,y_i1,z_i1),(x_i2,y_i2,z_i2),…,(x_iN,y_iN,z_iN)) where each Bell Quantum Sphere of the quantum state represents a separate 3-dimensional space in Planck Space.

Cumulatively, all the Bell Quantum Spheres occupied by a quantum state simultaneously form the quantum state’s “Bell Quantum Field” in 4D spacetime and its ultra-high dimensional “Bell Quantum Hyper-Point” in Planck Space. For example, in the case of an electron in the ground state of a hydrogen atom, the 1.92 x 10⁷⁴ Bell Quantum Spheres that comprise the electron’s Bell Quantum Field in 4D spacetime simultaneously form a single, ultra-high dimensional (3 x 1.92 x 10⁷⁴) Bell Quantum Hyper-Point in Planck Space. Consequently, the physical attributes of a quantum state, including its energy content, are simultaneously represented by the Bell Quantum Spheres that comprise the quantum state’s Bell Quantum Field in 4D spacetime and its Bell Quantum Hyper-Point in Planck Space. ^{33 34}

As a quantum state spreads in 4D spacetime, the number of Bell Quantum Spheres occupied by the quantum state increases. The Bell Identity ensures that the increase in the number of Bell Quantum Spheres that comprise the quantum state’s Bell Quantum Field in 4D spacetime is simultaneously reflected in an increase in the number of Bell Quantum Spheres that comprise the quantum state’s Bell Quantum Hyper-Point in Planck Space. Accordingly, on a one-to-one basis, as the number of Bell Quantum Spheres occupied by the quantum state in 4D spacetime increases, the number of Bell Quantum Spheres comprising the quantum state’s Bell Quantum Hyper-Point also increases.

3.2. The Collapse of a Single Quantum State

The Bell Identity not only links the dynamic evolution of a quantum state’s Bell Quantum Field in 4D spacetime with its Bell Quantum Hyper-Point in Planck Space, but it also links the instantaneous collapse of a quantum state’s Bell Quantum Hyper-Point in Planck Space with its Bell Quantum Field in 4D spacetime.^{35 36} More specifically, the Bell Identity links the instantaneous decrease in the number of Bell Quantum Spheres that comprise a quantum state’s Bell Quantum Hyper-Point in Planck Space with a simultaneous reduction in the number of Bell Quantum Spheres that comprise the quantum state’s Bell Quantum Field in 4D spacetime.³⁷

For example, assume Box A is a three-dimensional box with impenetrable walls. Box A is 2 inches wide, 1 inch deep, and 1 inch tall. There is zero potential inside Box A. The instant a single quantum state (“quantum state A”) is generated, it simultaneously forms Bell Quantum Field A in 4D spacetime and Bell Quantum Hyper-Point A in Planck Space. Quantum state A is inserted into Box A, where it spreads but will never have zero energy.

As quantum state A spreads, the Bell Identity ensures that the increase in the number of Bell Quantum Spheres that comprise Bell Quantum Field A is simultaneously mirrored in a one-to-one increase in the number of Bell Quantum Spheres that comprise Bell Quantum Hyper-Point A. The opening of Box A triggers the instantaneous collapse of Bell Quantum Hyper-Point A. The collapse instantaneously reduces the number of Bell Quantum Spheres that formerly composed Bell Quantum Hyper-Point A, and the Bell Identity ensures that the collapse is simultaneously linked to the instantaneous reduction in the number of Bell Quantum Spheres that now comprise Bell Quantum Field A. Quantum state A is now generally localized in Box A.^{38 39} Nevertheless, SR has not been violated.^{40 41} The generalized localization of quantum state A is an event extraneous to 4D spacetime caused by 1) the collapse of the quantum state’s Bell Quantum Hyper-Point, 2) the instantaneous reduction in the number of Bell Quantum Spheres that comprise the quantum state’s Bell Quantum Hyper-Point following its collapse, and 3) the simultaneous decrease in the number of Bell Quantum Spheres that comprise the quantum’s state’s generally localized Bell Quantum Field in 4D spacetime.

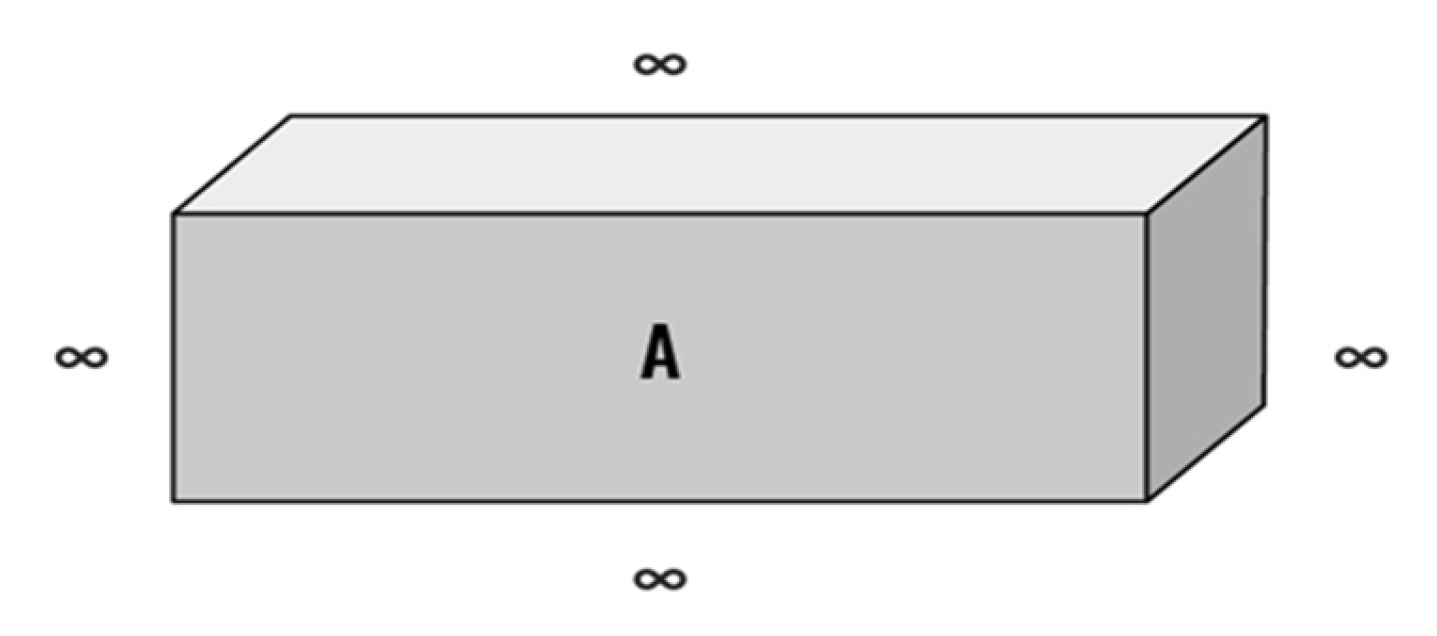
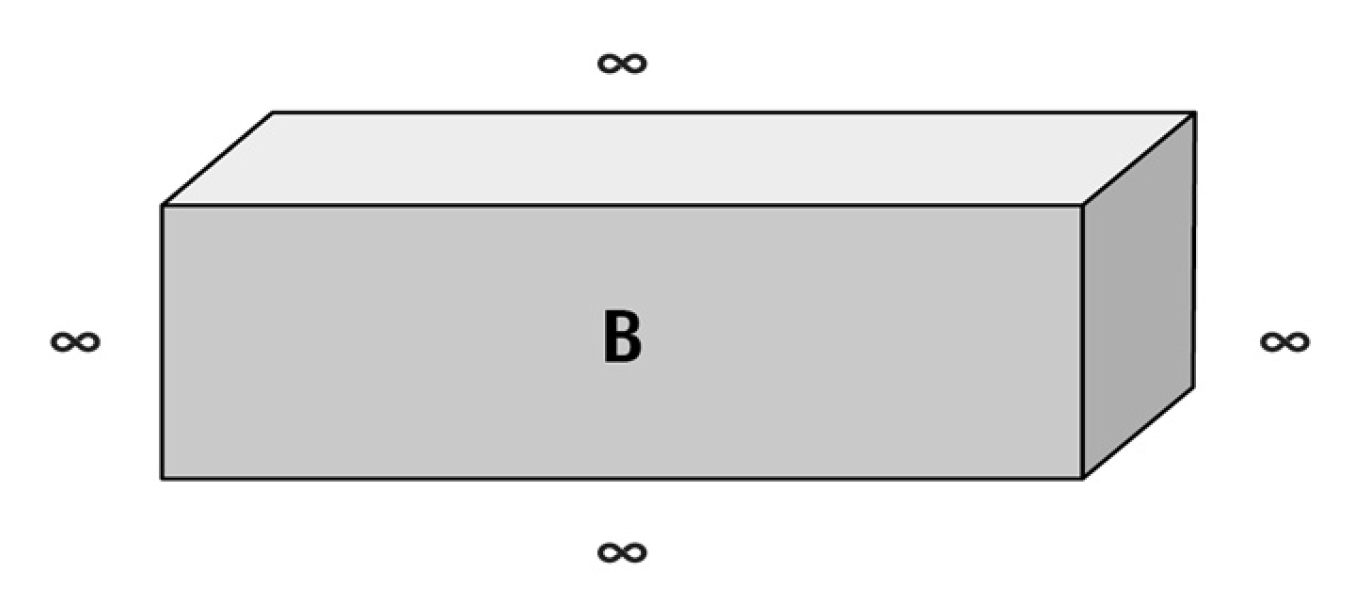
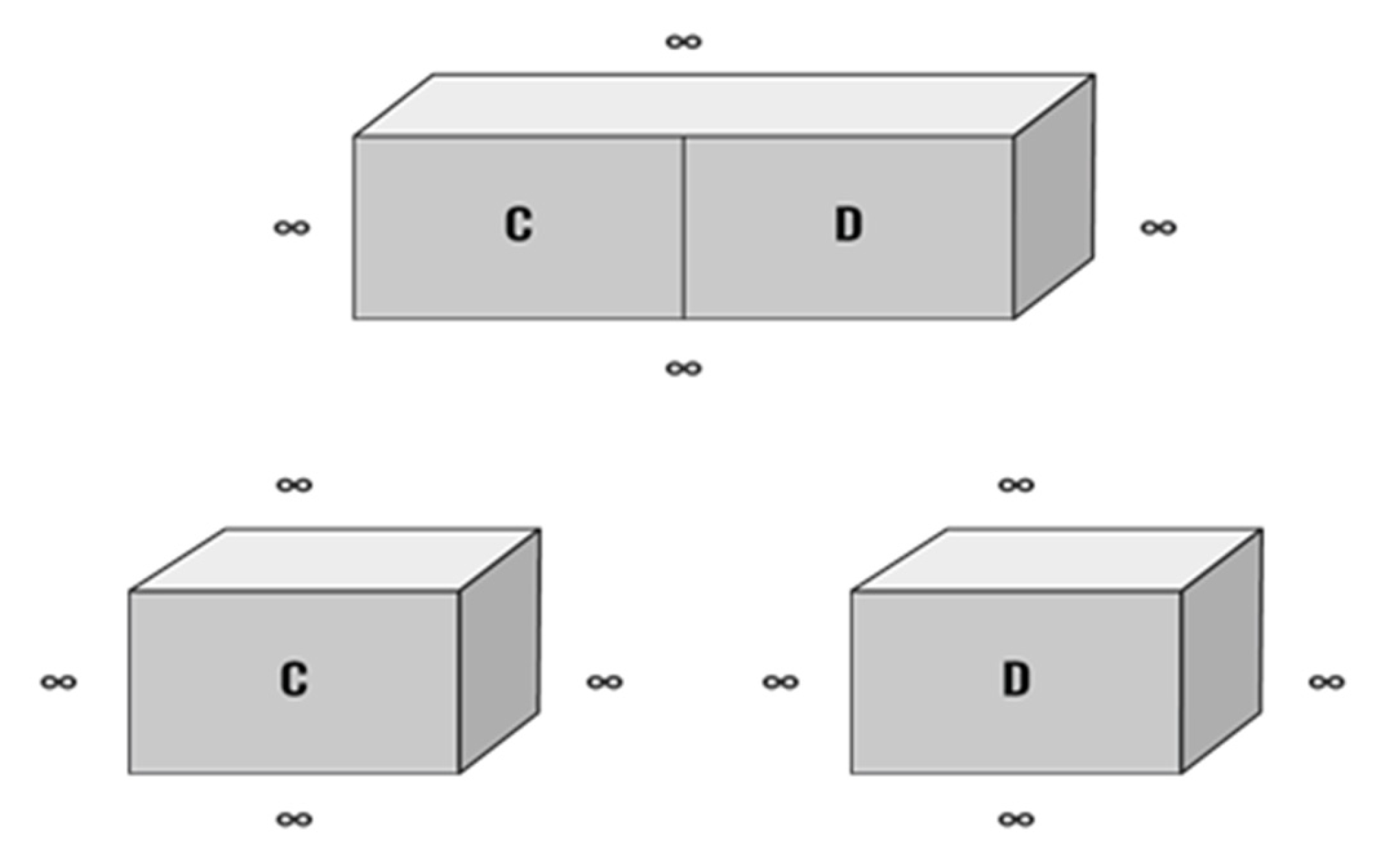
3.2.1. The Einstein/de Broglie Boxes Thought Experiment

The Einstein/de Broglie Boxes thought experiment is a more complex example of the dynamics of a single quantum state.⁴² Assume Box B is initially identical to Box A. A single quantum state (“quantum state B”) is generated, simultaneously forming Bell Quantum Field B in 4D spacetime and Bell Quantum Hyper-Point B in Planck Space. Quantum state B is inserted into Box B and begins to spread. As quantum state B spreads, the number of Bell Quantum Spheres that comprise Bell Quantum Field B within Box B increases, and so does the number of Bell Quantum Spheres that form Bell Quantum Hyper-Point B in Planck Space.

Without becoming entangled with quantum state B, an impenetrable divider is inserted into the middle of Box B, separating it into two identical boxes, C and D. Ignoring the physical dimensions of the divider, Box C and Box D are now 1 inch wide, 1 inch deep, and 1inch tall. Inside Boxes C and D, the potential energy remains zero.

The insertion of the impenetrable divider has separated the quantum state into two equal Bell Quantum Fields in 4D spacetime: Bell Quantum Field C and Bell Quantum Field D. Nevertheless, the quantum state continues to form a single Bell Quantum Hyper-Point in Planck Space, now designated as “Bell Quantum Hyper-Point CD.” The mathematical wave function

Ψ_{C, D} = \frac{1}{\sqrt{2}} (Ψ_{C} + Ψ_{D})

indicates that the quantum state is in a superposition of location with a 50% chance that following the quantum state’s collapse, the quantum state is found in Box B and a 50% chance that the quantum state is found in Box C. ⁴³

Box C remains in Princeton, and Box D is shipped to Copenhagen, 6,252 kilometers away. Although the movement of Box D’s physical location has altered the x, y, z coordinates of the Bell Quantum Spheres that comprise Bell Quantum Field D in 4D spacetime, the Bell Quantum Spheres that comprise Bell Quantum Field C and Bell Quantum Field D continue to comprise Bell Quantum Hyper-Point CD. In other words, so long as Bell Quantum Hyper-Point CD does not collapse, the quantum state remains in a superposition of location with a 50% chance of being found in Box C and a 50% chance of being found in Box D.

Regardless of whether Box B or Box C is opened first, the opening of either box is the physical trigger that causes the collapse of Bell Quantum Hyper-Point CD. In turn, the collapse instantaneously reduces the number of Planck Spheres that formerly composed Bell Quantum Hyper-Point CD. The reduction in the number of Planck Spheres that formerly composed Bell Quantum Hyper-Point CD has several significant ramifications. ⁴⁴

If Box C is opened first and the entire quantum state ψ_c (x₁,y₁,z₁)_c is found in Box C, 1) the number of Planck Spheres that comprise Bell Quantum Field C and Bell Quantum Hyper-Point C have been instantaneously reduced, 2) Bell Quantum Field C is generally localized in Box C, and 3) there is a one to one mapping and identity between the Bell Quantum Spheres that comprise Bell Quantum Field C in 4D spacetime and Bell Quantum Hyper-Point C in Planck Space. In addition, the mathematical wave function formerly representing Bell Quantum Field D and Bell Quantum Hyper-Point D no longer has meaning. A similar analysis applies if Box C is opened and the quantum state is not found in Box C or if Box D is opened first and the quantum state is or is not found in Box D.⁴⁵

Finally, the collapse of Bell Quantum Hyper-Point CD is not a “quantum jump” in 4D spacetime.⁴⁶ Recall that a Bell Quantum Hyper-Point is an ultra-high dimensional point in a Planck Space where time, space, and volume do not exist. When Bell Quantum Hyper-Point CD collapses, there is a reduction in the number of dimensions that comprise the quantum state’s new Bell Quantum Hyper-Point, and the Bell Identity ensures that there is a simultaneous reduction in the number of Bell Quantum Spheres that comprise the quantum state’s new Bell Quantum Field. What appears to be a “jump” in 4D spacetime is the collapse of Bell Quantum Hyper-Point CD in Planck Space and the reduction in the number of Bell Quantum Spheres that comprise the quantum state’s Bell Quantum Field. ⁴⁷

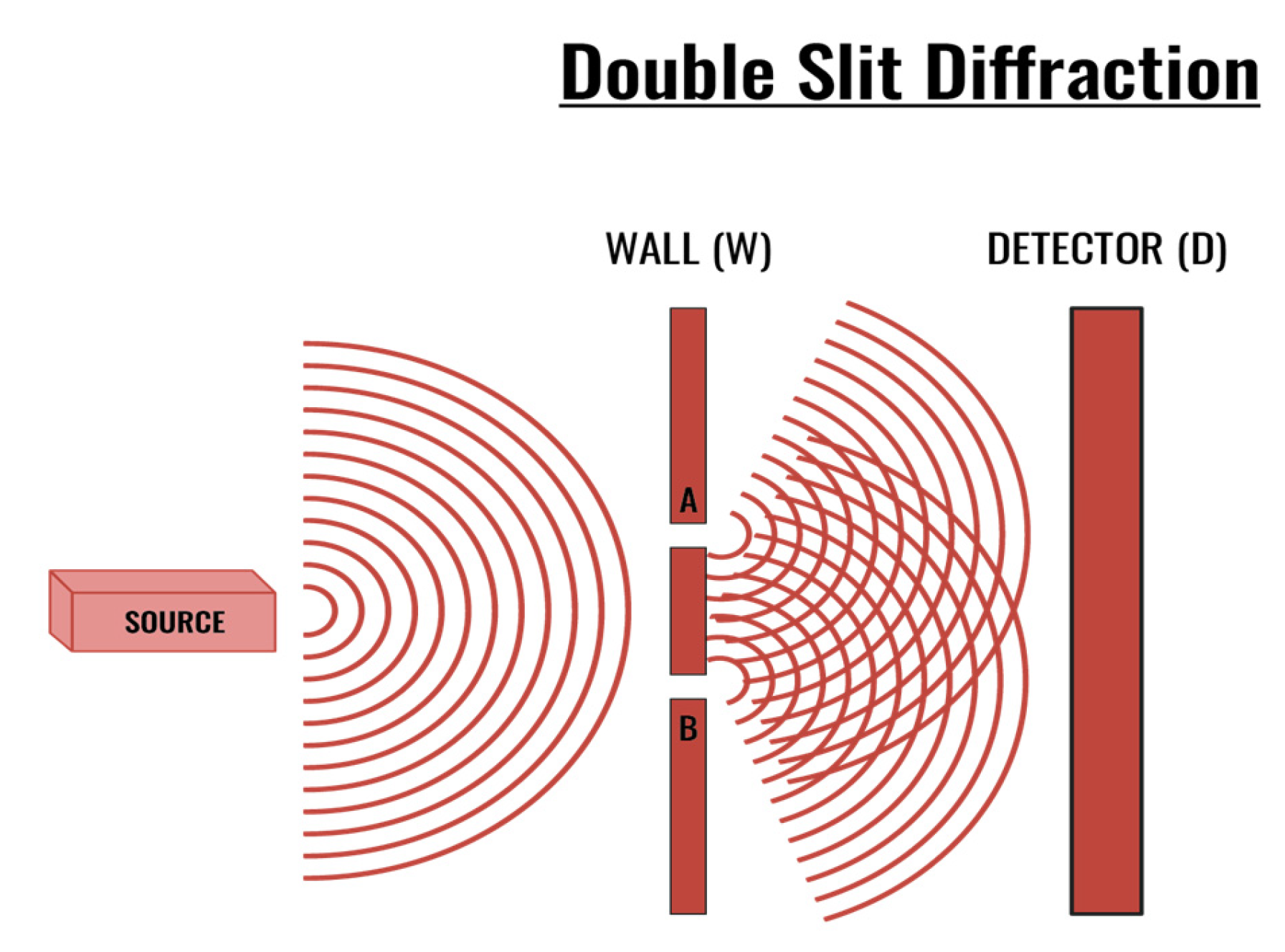
3.2.2. The Double-Slit Experiment

The double-slit experiment and its multiple incarnations have been reviewed extensively by physicists and philosophers. Notwithstanding the numerous controversies surrounding it, the experimental results of the various double-slit experiments are subject to the same ontological structure and dynamic laws that govern the dynamic spreading and the instantaneous collapse of all quantum states under the Dual Ontology conjecture.

Individual electrons (“quantum states”) are sent one at a time towards “Wall (W)” with two narrow Gaussian slits (A) and (B). In comparison with a quantum state’s wavelength, slits (A) and (B) are sufficiently narrow so that a quantum state diffracts if it passes through slits (A) and (B). Some of the individual quantum states that move towards Wall (W) hit the wall, while others pass through slits (A) and (B).⁴⁸ Once a quantum state passes through slit (A), it spreads uniformly as a spherical wave toward a detector “Detector (D).” Similarly, as the quantum state passes through slit (B), it too spreads uniformly as a spherical wave toward Detector (D). The two spherical waves interfere as they spread toward Detector (D). A single flash occurs whenever a quantum state hits Detector (D). Only one flash is detected per quantum state. After many flashes, Detector (D) indicates an interference pattern.⁴⁹

When each quantum state is generated, it forms a Bell Quantum Field in 4D spacetime and an ultra-high dimensional Bell Quantum Hyper-Point in Planck Space. Accordingly, when a quantum state is fired toward Wall W, the quantum state is simultaneously composed of a Bell Quantum Field in 4D spacetime and a Bell Quantum Hyper-Point in Planck Space. As the quantum state travels toward Wall W, it spreads spherically in 4D spacetime but continuously forms a single Bell Quantum Hyper-Point in Planck Space. A one-to-one mapping and identity exists between the Bell Quantum Spheres that comprise the quantum state’s Bell Quantum Field in 4D spacetime and the quantum state’s Bell Quantum Hyper-Point in Planck Space.

As the quantum state passes through slits (A) and (B), both slits independently diffract the quantum state, and the quantum state begins to spread from both slits towards Detector D in a spherical pattern. The Bell Quantum Spheres of the quantum state that passes through slit A forms Bell Quantum Field A in 4D spacetime, and the Bell Quantum Spheres of the quantum state that passes through slit B forms Bell Quantum Field B in 4D spacetime. The quantum state forms a single Bell Quantum Hyper-Point AB in Planck Space. Mathematically, the quantum state’s wavefunction is typically described as

Ψ_{A + B} = \frac{1}{\sqrt{2}} (Ψ_{A} + Ψ_{B})

.⁵⁰

Before reaching Detector D, the two wave functions combine linearly, and the linear combination causes interference. The modulus squared of the mathematical wavefunction is greater where the linear combination is constructive and approaches zero where the interference is destructive. Whether the mathematical wavefunction forms a peak or a trough, the quantum state always continues to form Bell Quantum Hyper-Point AB in Planck Space.

In 4D spacetime, a flash anywhere on Detector (D) indicates that a quantum state’s single Bell Quantum Hyper-Point has instantaneously collapsed. Upon its collapse, the number of Bell Quantum Spheres that comprise the quantum state’s Bell Hyper-Point is reduced to a subset of the Bell Quantum Spheres that composed its Bell Quantum Hyper-Point prior to the collapse. Simultaneously, the Bell Identity ensures that the collapse of the quantum state’s Bell Quantum Hyper-Point is, on a one-to-one basis, linked to an instantaneous reduction in the number of Bell Quantum Spheres that now comprise the quantum state’s single Bell Quantum Field in 4D spacetime.

Regardless of how spread out a quantum state’s Bell Quantum Field may have been in 4D spacetime before its collapse, and regardless of the interference caused by the interaction of the diffracted waves spreading from slits (A) and (B), the collapse of a quantum state’s Bell Quantum Hyper-Point ensures that the entire quantum state is generally localized in 4D spacetime. The collapse of the quantum state to a generally localized position anywhere on Detector (D) is instantaneous, and the mathematical wave function of Bell Quantum Spheres that are no longer occupied by the quantum state following its collapse has no meaning.

Following many flashes caused by the collapse of individual electrons, an interference pattern emerges on the Detector (D). The interference pattern is the combined result of the collapse of individual Bell Quantum Hyper-Points in Planck Space and the simultaneous reduction in the number of Bell Quantum Spheres that comprise each quantum state’s Bell Quantum Field.

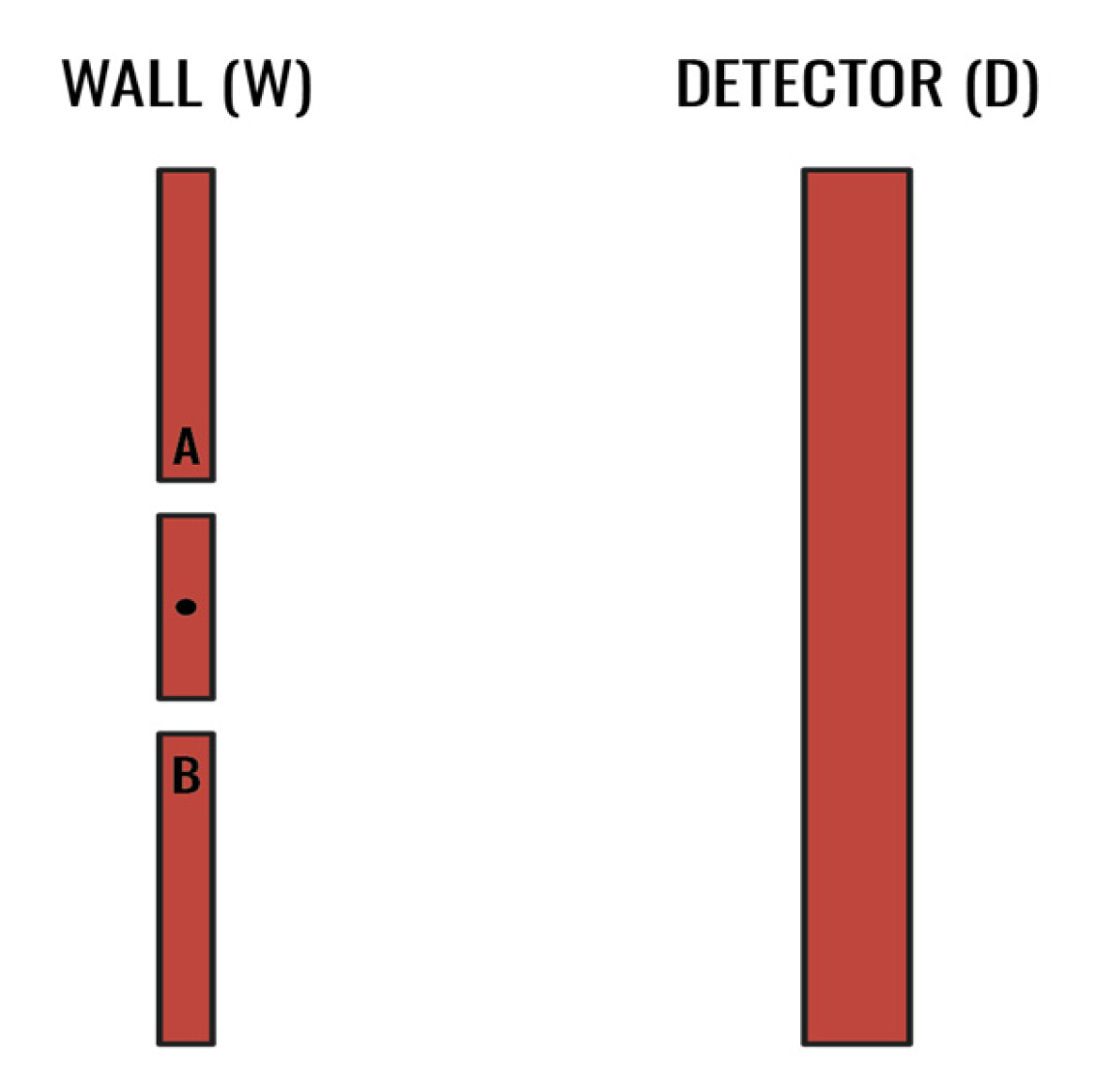
3.2.3. A Which-Way Experiment

Historically, “which way” experiments have compounded the theoretical issues of double-slit experiments. Once again, however, from the perspective of the Dual Ontology conjecture, the theoretical analysis of a which-way experiment is the same as it is for all other collapse-based quantum events.

The baseline experiment repeats the double-slit example in section 3.2.2 but is modified by inserting a proton into an empty rectangular box at the center of Wall (W).⁵¹ The proton is positively charged, and each electron (“quantum state”) fired towards Wall (W) is negatively charged. Assuming the experiment is 100% reliable, slit (A) flashes if the proton is attracted towards slit (A), and slit (B) flashes if the proton is attracted towards slit (B). Experimentally, 50% of the flashes are recorded at slit (A) and 50% at slit (B) 50%.

As an electron spreads in 4D spacetime, it forms a Bell Quantum Field in 4D spacetime and simultaneously forms a single Bell Quantum Hyper-Point in Planck Space. If slit (A) flashes, the electron’s Bell Quantum Hyper-Point collapses, and the number of Bell Quantum Spheres that comprise the electron’s Bell Quantum Hyper-Point is reduced. Simultaneously, on a one-to-one basis, the Bell Identity ensures that the number of Bell Quantum Spheres comprising the electron’s Bell Quantum Field is reduced. The electron is now generally localized at slit A. The analysis is the same if slit B flashes rather than slit A.

Once the electron is generally localized at either slit (A) or slit (B), it will once again continue to spread towards Detector (D). Critically, however, since the electron passed through either slit (A) or slit (B), but not both, an interference pattern is not formed at detector D. Conversely, if neither slit (A) nor slit (B) flashes, as the electron passes through slits (A) and (B) the analysis of the double-slit experiment described in Section 3.2.2 above is once again applicable.

3.3. N-Body Quantum State Evolution and Collapse

The Dual Ontology conjecture examines the ontic status of N-body quantum states based on the principle that the same theoretical and physical laws must apply equally to single and N-body quantum states. Instead of relying on a mathematical or ontic 3N configuration space to describe the dynamic motion of N-body quantum states, the Dual Ontology conjecture posits that all N-body quantum states are physical entities that dynamically evolve in a discrete 4D spacetime subject to the laws of SR and collapse in a (3 x N) Planck Space.⁵²

For an N-body quantum state, the Bell Identity can be mathematically formulated as a function h that maps from 4D spacetime R⁴ to a (3 x N) dimensional Planck Space R^3×N. The function h is defined as: h: R⁴→R^3×N. For a given set of coordinates in 4D spacetime (x_j1,y_j1,z_j1,t_j1), (x_j2,y_j2,z_j2,t_j2),…,(x_jk,y_jk,z_jk,t_jk), occupied by an N-body quantum state the function h maps these coordinates to: h((x_j1,y_j1,z_j1,t_j1), (x_j2,y_j2,z_j2,t_j2),…, (x_jk,y_jk,z_jk,t_jk)) = ((x_j1,y_j1,z_j1), (x_j2,y_j2,z_j2),…,(x_jk,y_jk,z_jk)) where each Bell Quantum Sphere of a quantum state represents a separate 3-dimensional space in Planck Space.

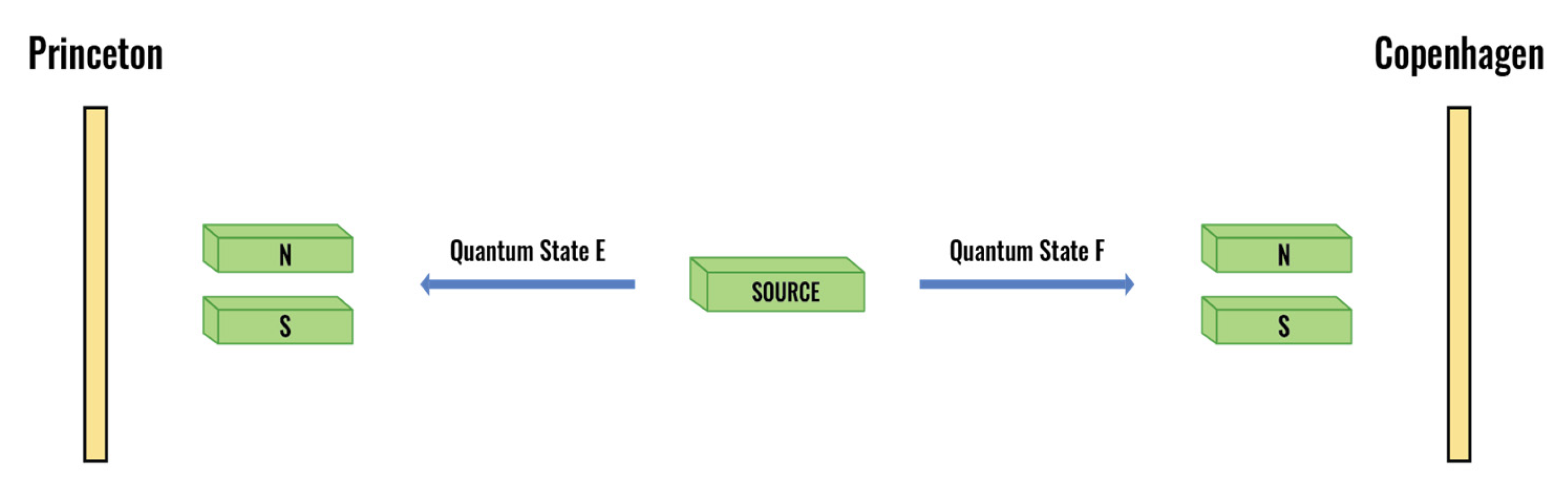
The Bohm-EPR Thought Experiment

The Bohm version of the EPR experiment highlights the issues raised by the dynamic evolution of an N-body quantum state in 4D spacetime and its collapse in Planck Space.⁵³ A pair of electrons is prepared in the singlet state. The wave function of the entangled quantum state is in a superposition, and its combined angular momentum is 0. The instant the entangled quantum state is generated, the quantum state simultaneously forms two Bell Quantum Fields in 4D spacetime (Bell Quantum Fields E and F, respectively) and a single ultra-high dimensional Bell Quantum Hyper-Point (“Bell Quantum Hyper-Point EF”) in Planck Space. Quantum state E is sent toward Princeton, and quantum state F is sent toward Copenhagen. Testing equipment is configured to conduct a Stern-Gerlach experiment in the z direction on either Bell Quantum Field E or Bell Quantum Field F.

Regardless of the space-like separation or dynamic motion of Bell Quantum Fields E and F in 4D spacetime, the Bell Identity ensures that the Bell Quantum Spheres that comprise Bell Quantum Fields E and F also comprise Bell Quantum Hyper-Point EF. As Bell Quantum Fields E and F dynamically spread in 4D spacetime, the number of Bell Quantum Spheres that comprise their respective Bell Quantum Fields increases, as does the number of Bell Quantum Spheres that comprise Bell Quantum Hyper-Point EF.⁵⁴

Bell Quantum Hyper-Point EF collapses following a Stern-Gerlach experiment in the z direction in either Princeton or Copenhagen.⁵⁵ The collapse instantaneously reduces the number of Bell Quantum Spheres that formerly composed Bell Quantum Hyper-Point EF. The Bell Identity ensures that the collapse is simultaneously linked to the reduced number of Bell Quantum Spheres that comprise Bell Quantum Field E and Bell Quantum Field F, respectively.⁵⁶ Unlike the case with a single Bell Quantum Hyper-Point, Bell Quantum Hyper-Point EF now forms two independent Bell Quantum Hyper-Points designated as Bell Quantum Hyper-Point E and Bell Quantum Hyper-Point F. Bell Quantum Hyper-Point E shares a one-to-one mapping and identity with the Bell Quantum Spheres that now form Bell Quantum Field E, and Bell Quantum Hyper-Point F shares a one-to-one mapping and identity with the Bell Quantum Spheres that now form Bell Quantum Field F.

Following the collapse of Bell Quantum Hyper-Point EF, Bell Quantum Hyper-Point E and Bell Quantum Hyper-Point F form a product state rather than an entangled state. Using a notation based on a physical (3 x N) Planck Space rather than a mathematical 3N space, the transition would be ψ_1,2((x₁,y₁,z₁)_1,(x₂,y₂,z₂)₂) → ψ₁(x₁,y₁,z₁)₁ ⊗ ψ₂(x₂,y₂,z₂)₂.⁵⁷ The reduction in the number of Bell Quantum Spheres that comprise Bell Quantum Field E and Bell Quantum Field F instantaneously causes the generalized localization of both Bell Quantum Field E and Bell Quantum Field F on the detectors in Princeton and Copenhagen, respectively. Nevertheless, regardless of how spread out each of the individual Bell Quantum Fields may have been before the collapse of Bell Quantum Hyper-Point EF, SR has not been violated.

If the Stern-Gerlach experiment in the z direction is conducted in Princeton on quantum state E, and the quantum state is found in the z spin-up direction, quantum state F is instantly in the z spin-down direction in Copenhagen. Conversely, if the Stern-Gerlach experiment in the z direction is conducted in Princeton on quantum state E and the quantum state is found in the z spin-down direction, quantum state F is instantly in the z spin-up direction in Copenhagen. The same analysis applies if the Stern-Gerlach experiment in the z direction is conducted on quantum state F in Copenhagen instead of quantum state E in Princeton.

4. Physical Implications of the Dual Ontology Conjecture

4.1. Indeterminacy

Indeterminacy, like many other quantum terms, has disparate meanings. This analysis adopts a simple definition: Indeterminacy occurs when a quantum system “has a determinable property, but no determinate value for the determinable.”⁵⁸ For a singlet state in the z-direction, spin is a determinable property, and spin in the z spin-up and z spin-down directions are determinant values. Assuming quantum states z₁ and z₂ form a singlet state in the z-direction, the mathematical representation would be ψ =

\frac{1}{\sqrt 2}

(↑z₁↓z₂ −↓z₁↑z₂).

Regardless of whether the singlet state is space-like separated in 4D spacetime, the Bell Identity ensures that the singlet state forms a single Bell Quantum Hyper-Point in Planck Space and two Bell Quantum Fields in 4D spacetime. Although the singlet state’s spin is physically indeterminate, both in Planck Space and in 4D spacetime, the singlet state’s ultra-high dimensional Bell Quantum Hyper-Point is not space-like separated. After the collapse of the singlet state, the system transitions to a product state, and the spins of the z₁ and z₂ quantum states become determinate rather than indeterminate ψ =

\frac{1}{\sqrt 2}

(↑z₁↓z₂ −↓z₁↑z₂)→↑z₁↓z₂ in both 4D spacetime and Planck Space. The z₁ and z₂ quantum states now form independent Bell Quantum Hyper-Points in Planck Space and two generally localized Bell Quantum Fields in 4D spacetime.⁵⁹ The z₁ quantum state is spin up, and the z₂ quantum state is spin down.

4.2. Quantum State Emergence and Annihilation

Quantum state emergence and annihilation have been well-documented experimentally. Nevertheless, the physical acts of quantum state emergence and annihilation have been theoretically problematic when viewed from the perspective of the non-relativistic Schrödinger equation because of the fixed nature of mathematical quantum configuration spaces.⁶⁰ Since the size of the configuration space is based on the number of quantum states it represents, the number of quantum states is typically conserved. As a result, it is difficult to account for either the decrease or increase in the number of quantum states in a given system. Relativistic QFT, unlike non-relativistic quantum theory, targets both quantum state emergence and annihilation, and within QFT, the number of quantum states may vary.

The Dual Ontology provides a physical, ultra-high dimensional ontological solution to the issue of quantum state annihilation and emergence, even though the number of dimensions in Planck Space is potentially finite.⁶¹ As we have seen, the Bell Identity links a quantum state’s Bell Quantum Spheres in 4D spacetime with the same Bell Quantum Spheres in Planck Space. Given that there are approximately 10⁹⁰ quantum states in the observable universe, the aggregate number of Bell Quantum Spheres occupied by all quantum states in the observable universe at any one moment depends upon the spread of their respective Bell Quantum Fields. To put this number into perspective, if a single quantum’s state’s field is limited to the ground state of a hydrogen atom, that field would be composed of approximately 1.92E+74 Bell Quantum Spheres, an incredibly large number under ordinary circumstances, but an incredibly small number compared to the 5.58E+186 Planck Spheres in the observable universe. Ignoring the Pauli exclusionary principle, the number of Planck Spheres in the observable universe is a tiny fraction of the 2^5.58186-1 unique combinations formed by the 10⁹⁰ quantum states in the observable universe. Since the number of unique quantum combinations of Planck Spheres in the observable universe is orders of magnitude greater than the total number of quantum states, there is no apparent physical or mathematical reason that the number of Planck Spheres occupied by quantum states must remain constant.

During the process of quantum annihilation, a quantum state’s Bell Quantum Hyper-Point instantaneously collapses. The quantum state’s Bell Quantum Hyper-Point and Bell Quantum Field no longer exist, and the mathematical wave function describing the quantum state no longer has any meaning. Conversely, when a quantum state is generated, the quantum state forms a Bell Quantum Field in 4D spacetime and a Bell Quantum Hyper-Point in Planck Space.

4.3. Physical Triggers

The Dual Ontology conjecture analysis does not identify the precise physical cause or causes in 4D spacetime that precipitate quantum state collapse. Nevertheless, the analysis provides a physical framework to investigate the role of physical triggers in quantum collapse.⁶² The starting point is the dynamic, physical evolution of all quantum states in a 4D spacetime governed by the three known fundamental forces: electromagnetism, the strong nuclear force, and the weak nuclear force, as well as the warping of spacetime by gravity (the “Fundamental Forces.”)^{63 64} Consequently, not only do the Fundamental Forces underlie all quantum state motion in 4D spacetime, but they are also the cause of all known physical interactions (“Physical Interactions”) between quantum states, including all physical triggers that precede the collapse of a quantum system.⁶⁵

The Dual Ontology conjecture does not rely upon ad hoc parameters, fine-tuning, or perturbation techniques. All triggers in 4D spacetime are independent time and location events.⁶⁶ Physical triggers occur with varying frequency, depending on time and location. Heat and cold will, for example, affect the rate of Physical Interactions.⁶⁷ Human beings can not only trigger Physical Interactions or be the proximate cause of a physical trigger, but they can also determine the time and location of such triggers.⁶⁸ Individual Physical Interactions are not based upon human consciousness or observation, do not give any special significance to human beings or human action, are not based upon a single universal cause, a single white or non-white noise source,⁶⁹ nor are they spontaneous,⁷⁰ universally continuous or discontinuous, and are not predicated upon rules governing the frequency or probability of occurrence.

4.4. Quantum State Localization

Although the Bell Identity links the collapse of a quantum state to the simultaneous reduction in the number of Bell Quantum Spheres that comprise a quantum state’s Bell Quantum Hyper-Point in Planck Space and its Bell Quantum Field in 4D spacetime, nothing in the Dual Ontology conjecture provides a physical basis to determine the precise localization of a quantum state in 4D spacetime. Nevertheless, the Dual Ontology provides a possible structural framework for further analysis that differs considerably from current theoretical approaches to quantum localization.^{71 72}

As we have seen, the Bell Identity ensures a one-to-one mapping and identity between Bell Quantum Spheres in 4D spacetime and Planck Space. The collapse of a Bell Quantum Hyper-Point must be to a subset of the Bell Quantum Spheres that had previously represented the quantum state’s original Bell Quantum Hyper-Point in Planck Space and its Bell Quantum Field in 4D spacetime. In this sense, the Bell Identity is always restrictive. It places a strict boundary on the collapse outcome. A quantum state’s Bell Quantum Hyper-Point cannot collapse anywhere in the universe; instead, it is a linked collapse restricted to the Bell Quantum Spheres that comprise the quantum state before its collapse.

Although the Bell Identity places strict boundaries on the generalized location of a quantum state immediately following its collapse in Planck Space, it does not set a specific limit on the size or location of a quantum state’s Bell Quantum Field in 4D spacetime following a collapse. The generalized location of a quantum state may be related to the physical trigger that initiated collapse in the first instance. The size of a quantum state’s Bell Quantum Field may also vary based on the physical composition of the quantum state in question. Photons, neutrinos, electrons, muons, and other sub-atomic quantum states may localize to Bell Quantum Fields of varying sizes. In addition, high or low-energy collapses may have different localization characteristics, and a quantum state’s momentum in 4D spacetime may also affect its localization.

4.5. Time and Instantaneous Collapse

Neither Planck Space nor 4D spacetime alone supports the concept of instantaneous collapse. Planck Space does not have a time dimension, and except for the collapse process, Planck Space does not have an independent concept of dynamic movement. 4D spacetime, on the other hand, has dynamic movement and a time dimension, but SR constrains the time dimension. Since the instantaneous collapse process in 4D spacetime is a single point in time, the event occurs in the three spatial dimensions of 4D spacetime. However, there is no movement in 4D spacetime’s time dimension.

The Dual Ontology’s integrated structure and mixed dynamics provide a physical explanation for the “instantaneous” nature of quantum collapse. Since the Bell Identity posits a one-to-one mapping and identity between each Bell Quantum Sphere in 4D spacetime and Planck Space, dynamic motion in 4D spacetime is always reflected simultaneously in the Bell Quantum Spheres that comprise a Bell Quantum Hyper-Point in Planck Space. When a Physical Interaction in 4D spacetime triggers the collapse of a quantum state, the trigger directly affects the quantum state’s Bell Quantum Hyper-Point in Planck Space, where Relativity does not apply. Since neither time, space, volume, nor the 4D space laws of physics are applicable in Planck Space, the collapse of the Bell Quantum Hyper-Point is instantaneous. Once again, the Bell Identity ensures that the collapse of the Bell Quantum Spheres in Planck Space is instantly reflected in the reduction in the number of Bell Quantum Spheres that comprise the quantum state’s Bell Energy Field in 4D spacetime.

4.6. Quantum Tunneling

Despite the usefulness of the “quantum tunneling” concept, the physical process by which a quantum state is found on the other side of a classically impenetrable barrier is not a tunneling process in 4D spacetime.⁷³ Although the probability that the leading edge of a quantum state penetrates an otherwise impenetrable barrier is currently based upon the Schrödinger equation and the exponential decay of the quantum state’s wave function, the collapse of a quantum state reflects the instantaneous collapse of the quantum state’s Bell Quantum Hyper-Point in Planck Space, not the tunneling of the entire quantum state through an otherwise impassible barrier in 4D spacetime. Stated slightly differently, concurrently with the instantaneous reduction in the number of Bell Quantum Spheres that comprise the quantum state’s Bell Quantum Hyper-Point in Planck Space following its collapse, the Bell Identity ensures that there is a one-to-one reduction in the number of Bell Quantum Spheres that comprise the quantum state’s new Bell Quantum Field in 4D spacetime. Although the quantum state is generally localized on the other side of a classically impenetrable barrier, the quantum state did not tunnel through the barrier, and the laws of SR are not violated.⁷⁴

4.7. The Born Rule Revisited

The Dual Ontology’s ontological structure and dynamics are physically at odds with the Born Rule⁷⁵ and its probability density interpretation of wave-function collapse for continuous variables.⁷⁶ In contrast to the Born Rule, the Dual Ontology conjecture holds that a quantum state cannot instantaneously appear anywhere in 4D spacetime following its collapse, even if the probability of doing so is infinitesimally small. Instead, the collapse of a quantum state’s Bell Quantum Hyper-Point in Planck Space and the generalized localization of a quantum state’s Bell Quantum Field in 4D spacetime must be to a discrete subset of the Bell Quantum Spheres occupied by the quantum state prior to its collapse. Accordingly, rather than integrating a density function of the quantum state over a continuous space, the likelihood of generally locating a quantum state in a “discrete, constrained space” is a probability based on the square modulus of the quantum state’s wave function.⁷⁷ For example, in the case of quantum tunneling, a quantum state’s collapse on the other side of an otherwise classically impenetrable barrier is based on a probability, not a probability density.

5. Resolving the Tension Between SR and Quantum Mechanics

The theoretical conflict between SR and quantum mechanics has had a long and unresolved history. John Bell, for example, recognized that the conflict was at the forefront of theoretical physics:

“…I think, any sharp formulation of quantum mechanics, has a very surprising feature: the consequences of events at one place propagate to other places faster than light…For me then this is the real problem with quantum theory: the apparently essential conflict between any sharp formulation and fundamental relativity. That is to say, we have an apparent incompatibility, at the deepest level, between the two fundamental pillars of contemporary theory.”⁷⁸

The apparent incompatibility is typically described by a set of terms and concepts derived from 4D spacetime rather than Planck Space or the Dual Ontology. Despite their usefulness in the context of a closed 4D spacetime, the use of common terms such as space-like separated, non-separability, entangled, instantaneous, superluminal, faster than light, local and non-local, discrimination, and unattenuation, as well as more complex concepts such as the Relativity of Simultaneity and Relativistic Energy Increase have had the unintended effect of magnifying a theoretical and experimental conflict that does not exist.⁷⁹

5.1. Space-Like Separated

The term “space-like separated” is based upon a 4D spacetime structure composed of three dimensions of space and one dimension of time. The term is directly related to the concepts of space and time, the theory of SR, and the spatial distance between two or more events outside of one another’s light cones. Nevertheless, the term has no meaning in conjunction with an ultra-high dimensional Bell Quantum Hyper-Point in Planck Space. Planck Space does not have a time dimension, space, or volume, and Relativity concepts have no meaning.

5.2. Non-separability

Einstein may have been the first physicist to raise concerns regarding the theoretical implications of separability. His primary concern was based upon the conjunction of two assumptions related to his incompleteness argument: that spatially separate systems are ontic states and that the physical effects of space-like separated quantum systems could not communicate faster than the speed of light.⁸⁰

In 4D spacetime, a singlet state in the z-direction ψ =

\frac{1}{\sqrt 2}

(↑z₁↓z₂ −↓z₁↑z₂ ) is non-separable, even though it is often considered an abstract mathematical concept. Key attributes of a non-separable singlet state are 1) the spatial separation of the z₁ and z₂ states, 2) the temporal separation of z₁ and z₂ states, and 3) the existence of a single system.

Without time, space, or volume, an ultra-high dimensional Bell Quantum Hyper-Point is not spatially or temporally separated in Planck Space.⁸¹ Instead, the Bell Quantum Hyper-Point is a single, non-separable entity linked by the Bell Identity to the Bell Quantum Spheres that comprise the quantum state’s Bell Quantum Field(s) in 4D spacetime. Although the issue of non-separability raises significant theoretical issues in 4D spacetime, the non-separability of a Bell Quantum Hyper-Point in Planck Space does not challenge SR. Instead, it reinforces the integrated status of the Dual Ontology’s structure and the importance of the Bell Identity as an explanatory tool that simultaneously links a quantum state’s Bell Quantum Field(s) in 4D spacetime and its Bell Quantum Hyper-Point in Planck Space.⁸²

5.3. Instantaneous, Superluminal, and Faster than Light

The temporal terms instantaneous, superluminal, and faster than light are often used to describe the collapse of a quantum state in 4D spacetime and the apparent violation of the laws of SR. The terms are closely associated with space and time and are directly related to the maximum speed of light in a vacuum. Following the collapse of a quantum state, the terms instantaneous, superluminal, and faster are typically used to describe the quantum state’s speed of 1) communication, 2) signaling or the absence of signaling, 3) information transmission, and 4) matter and energy transfer.

In contrast, the instantaneous collapse of a Bell Quantum Hyper-Point is an event that has physical ramifications in both Planck Space and 4D spacetime. The Dual Ontology’s ontological structure and the Bell Identity ensure that the reduction in the number of Bell Quantum Spheres that comprise a quantum state’s Bell Quantum Hyper-Point in Planck Space is simultaneously reflected in the reduction in the number of Bell Quantum Spheres that comprise the quantum state’s new Bell Quantum Field in 4D spacetime. Although that reduction is, in fact, instantaneous, it does not violate SR.

5.4. The Quantum Connection

In 4D spacetime, quantum discrimination describes a quantum state’s ability to maintain an exclusive “connection” to the exclusion of all other quantum states, and unattenuated denotes the strength (or non-attenuation) of a quantum state’s connection.⁸³ The terms are typically used to denote the connection between space-like separated entangled states in 4D spacetime. Moreover, discrimination and non-attenuation imply an instantaneous and continuous connection that violates the maximum speed of light.

In the context of the Dual Ontology, quantum discrimination and non-attenuation are directly related to the Bell Identity and the one-to-one mapping and identity between each of the Bell Quantum Spheres that comprise a quantum state’s Bell Quantum Field(s) in 4D spacetime and its Bell Quantum Hyper-Point in Planck Space. There is nothing in either the structure of the Dual Ontology or in the dynamics of a quantum state’s spreading or collapse that suggests that the ability to discriminate or the lack of attenuation implies a violation of Einstein’s theory of SR. On the contrary, the Dual Ontology conjecture explains why a quantum state’s ability to discriminate and its non-attenuation are physical phenomena that do not violate SR.^{84 85}

5.5. Bell’s Theorem and Locality

No development in quantum theory in the latter half of the 20th century has been more important than John Bell’s inequality theorem.⁸⁶ The theorem posits that relativistic local causation theories cannot physically account for the statistical predictions of quantum theory (for spin experiments of entangled quantum states in the singlet state).⁸⁷ More generally, Bell’s theorem posits that theories that conform with the statistical results of quantum experiments cannot be local. Although numerous attempts have been made to describe the precise meaning and import of “locality” and “non-locality,” those discussions are well beyond the scope of this analysis.⁸⁸ As used in this analysis, the terms local and non-local are causal concepts connected with the 4D spacetime concepts of time, space, and the maximum speed of light.⁸⁹

Despite the importance of the local vs. non-local debate in 4D spacetime, the concepts of time, space, and volume do not apply to Planck Space. In Planck Space, a quantum state’s Bell Quantum Hyper-Point is neither space-like separated nor separable.⁹⁰ Accordingly, the Dual Ontology alters the 4D spacetime local causality vs. non-local causality discussion, but it does not alter the import of Bell’s inequality theorem. Recall that Bell’s inequality theory posits that relativistic local causation theories cannot physically account for the statistical predictions of quantum theory (for spin experiments in the singlet state), and more generally, theories that conform with the statistical results of quantum experiments cannot be local. Neither the existence nor the collapse of a quantum state’s Bell Quantum Hyper-Point alters the correctness of either of these statements.⁹¹

Nevertheless, the Dual Ontology conjecture alters the assumption that quantum state collapse is evidence of non-local causality in 4D spacetime. Quantum state collapse is evidence of a physical event external to 4D spacetime. Accordingly, the Dual Ontology conjecture strengthens rather than weakens the core of the Bell Inequality theorem.⁹² Instead of a theoretically troublesome non-local event in 4D spacetime, the collapse of a Bell Quantum Hyper-Point in Planck Space and the generalized localization of a quantum state in 4D spacetime by-passes the non-locality issue.⁹³ Perhaps even more satisfying to John Bell, the Dual Ontology conjecture eliminates “…the real problem with quantum theory: the apparently essential conflict between any sharp formulation and fundamental relativity.”⁹⁴

5.6. The Relativity of Simultaneity

The historical tension between SR and quantum mechanics extends to Einstein’s Relativity of Simultaneity theory. The theory of SR holds that 1) there are no privileged frames of reference—all inertial reference frames (frames that move relative to one another at a constant speed) are equally valid, and 2) for all observers in inertial frames, the speed of light in a vacuum is invariant. Consequently, Einstein’s Relativity of Simultaneity theory posits that 1) whether two events that are spatially separated occur at the same time depends on an inertial observer‘s frame of reference, and 2) two observers with different inertial reference frames will conclude that the same event occurred at two separate times.

In the case of space-like separated entangled electrons in the singlet state in the z-direction

ψ = \frac{1}{\sqrt 2}

(↑z₁↓z₂ −↓z₁↑z₂), an experiment that causes the instantaneous collapse of the z₁ electron simultaneously causes the instantaneous collapse of the z₂ electron. Since the Relativity of Simultaneity theory posits that whether a cause (the collapse of the z₁ electron) precedes an effect (the collapse of the z₂ electron) is dependent upon an inertial observer’s frame of reference, the simultaneous nature of the experiment appears to violate Einstein’s Relativity of Simultaneity theory. It implies both a violation of Lorentz Invariance and a preferred frame of reference.⁹⁵

However, based on the Dual Ontology conjecture, the instantaneous collapse of a quantum state is a physical event but does not violate the 4D spacetime concept of Relativity of Simultaneity. In the case of an entangled pair of electrons in the singlet state in the z-direction, it does not matter whether a quantum experiment in 4D spacetime is first conducted on the z₁ electron or the z₂ electron, nor does it matter whether the z₁ and z₂ electrons are space-like separated in 4D spacetime. The Bell Identity automatically ensures that an experiment on either the z₁ or z₂ electron in 4D spacetime is conducted simultaneously on the entangled quantum state’s single Bell Quantum Hyper-Point. Moreover, the Bell Identity simultaneously links the instantaneous collapse of the Bell Quantum Spheres that comprise the quantum state’s single Bell Quantum Hyper-Point in Planck Space with a reduction in the number of Bell Quantum Spheres that comprise the now generally localized Bell Quantum Fields of both the z₁ and z₂ electrons in 4D spacetime. The formerly entangled electrons now form a product state; the collapse was instantaneous and simultaneous, but the 4D spacetime laws of SR have not been violated.

5.7. Relativistic Energy Increase

The instantaneous nature of quantum state collapse also appears to violate the concept of Relativistic Energy Increase. Einstein’s theory posits that the relativistic energy of a body in motion relative to an observer or another body increases as its velocity accelerates. Since the velocity of an object accelerates as it approaches the speed of light, its relativistic kinetic energy theoretically approaches infinity, but SR limits its speed. In quantum mechanics, momentum is a more commonly used term than velocity. Accordingly, as the momentum of a quantum state increases, its associated energy increases. For a quantum state to reach or exceed the speed of light, as with instantaneous collapse, the energy required would be infinite.

Although the collapse of a quantum state’s Bell Quantum Hyper-Point in Planck Space is instantaneous, the collapse is a physical event extraneous to 4D spacetime. The Dual Ontology and the Bell Identity ensure that the instantaneous collapse of a Bell Quantum Hyper-Point decreases the number of Bell Quantum Spheres that comprise a quantum state’s Bell Quantum Hyper-Point and its Bell Quantum Field(s). As a result, the reduction in the number of Bell Quantum Spheres that comprise a Bell Quantum Field is instantaneous. However, there is no Relativistic Energy Increase of the quantum state in 4D spacetime or Planck Space.

6. Conclusion

The Dual Ontology conjecture posits a physical, tightly integrated ((3 x N) +3) hyperspace composed of a discrete, curved 4D spacetime and an ontic, ultra-high dimensional (3 x N) Planck Space. The Dual Ontology’s structure, supported by a substructure composed of the SOAN and Planck Spheres, creates a unified physical ontology and dynamics that resolves the tension between SR and the results of quantum experiments. Critically, all single and N-body quantum states dynamically evolve in a discrete 4D spacetime in full compliance with SR, with the instantaneous collapse of all quantum states in Planck Space where the laws of 4D spacetime, including the laws of Relativity, do not apply.

The conjecture replaces the assumption of a closed 4D spacetime with a physical ((3 x N) + 3) hyperspace and GR’s assumption of a continuous, differentiable 4D spacetime manifold with a discrete, curved 4D spacetime. The conjecture supports theoretical and physical alternatives to quantum mechanics’ core concepts, including the state space, observable, projection, and unitary evolution postulates. These differences include the Dual Ontology’s interpretation of the non-locality/locality debate, the nature of entanglement, the meaning of space-like separation and non-separability, the physical basis for the “quantum connection” and indeterminism, the generalized localization of quantum states following quantum state collapse, the relativity of simultaneity and relativistic energy increase.

The Dual Ontology re-interprets the Einstein/de Broglie Boxes thought experiment, a double-slit experiment, a simple which-way experiment, and the Bohm-EPR thought experiment by applying the same laws of physics to both single and N-body quantum states. The conjecture replaces the Born Rule’s probability density with a probability, the 4D spacetime concept of quantum tunneling with the instantaneous collapse of a Bell Hyper-Point in Planck Space and describes the trigger for all quantum state collapses in Planck Space as physically random time and location events in 4D spacetime. The Dual Ontology conjecture replaces the linear, non-relativistic Schrödinger equation, Hilbert Space, Hamiltonians, and quantum mechanical operators with mathematical formalisms that support the non-linear, dynamic evolution of all quantum states in 4D spacetime and their instantaneous collapse in Planck Space. The conjecture also replaces the flat Minkowski spacetime of QFT with a curved 4D spacetime.

The Dual Ontology conjecture is compatible with a discrete Quantum Field Theory on Curved Spacetime. Appendix A sets forth mathematical formalisms for discrete Maxwell, Dirac, and Klein-Gordan equations, a modified Regge Calculus for a discrete 4D spacetime, discrete Einstein field equations, modified Dirac and Klein-Gordon equations for a discrete, curved 4D spacetime, and functional notations for the general law of quantum state evolution in 4D spacetime and collapse in Planck Space as well as specific evolution and collapse laws for single quantum states, N-body quantum states, and the special case of the Bohm version of the EPR experiment.⁹⁶

The theoretical and physical implications of the Dual Ontology’s structure and dynamics extend well beyond the unification of SR and quantum mechanics and include cosmology, the nature of time, 4D spacetime’s second law of thermodynamics and the meaning of entropy, the nature of gravity, and the structure and dynamics of black holes. Based on a universal substructure composed of Planck Spheres and the SOAN, together with the presence of energy within Planck Spheres, the Dual Ontology also suggests that both a discrete, curved 4D spacetime and Planck Space are emergent ontological structures and that time, space, and volume, as well as the physical laws that govern 4D spacetime and Planck Space, are emergent properties.

Part II of the analysis expands the scope of the Dual Ontology conjecture by addressing a number of physical and theoretical issues associated with 4D spacetime’s cosmogony and cosmology. Without relying upon ad hoc parameters, fine-tuning, or perturbation techniques, these include a physical explanation for the instantaneous collapse of the Planck Hyper-Point at or near the heat death of 4D spacetime and the resulting re-inception of a homogeneous and isotropic 4D spacetime at t = 0.⁹⁷ Additionally, Part II addresses current theoretical issues regarding quantum gravity, including issues related to singularities, renormalization, non-locality, quantum entanglement, gravity, time, the black hole information paradox, and the cosmological constant problem. The conjecture also offers a new physical interpretation for quantum path irreversibility and the arrow of time and explores the second law of thermodynamics and entropy in the context of a closed ((3 x N) + 3) Dual Ontology.

Acknowledgments

This analysis benefited immeasurably from lengthy and vigorous debates and penetrating criticism from Dr. Stanley Kahan and Mr. Joseph Atsmon. Over many years, Dr. Kahan’s intuitive insights and Mr. Atsmon’s analytical probing not only helped shape the analysis but also explored all of its fundamental topics, from the nature of the SOAN and Planck Space and their relationship to 4D spacetime and quantum mechanics to the collapse of quantum states in Planck Space. I still cannot thank them enough. Once again, I would also like to express a special thanks to Ms. Naomi Kahan for her patience and technical expertise in preparing this manuscript.

Appendix A. Mathematical Formalisms

The following mathematical formalisms are based upon the ontological structure and fully integrated dynamics of the Dual Ontology’s ((3 x N) + 3) hyperspace. SR governs the dynamic evolution of all single and N-body quantum states’ Bell Field(s) in a discrete 4D spacetime but is not applicable to the instantaneous collapse of all single and N-body quantum states’ Bell Quantum Hyper-Points in Planck Space. A discrete Quantum Field Theory on Curved Spacetime ensures compatibility with GR and background independence.

1. Special Relativity

Einstein’s theory of Special Relativity is modified to conform with a discrete 4D spacetime.

1.1. Discrete Maxwell Equations

Purpose:

Maxwell’s equations use discrete differential equations to describe electric and magnetic fields for discrete Planck Spheres in 4D spacetime.

Equations:

A. Gauss’s Law for Electricity:

\nabla \cdot E_{i j k l} = \frac{ρ_{i j k l}}{ϵ_{0}}

B. Gauss’s Law for Magnetism:

\nabla \cdot B_{i j k l} = 0

C. Faraday’s Law of Induction:

\nabla \times E_{i j k l} = - \frac{\partial B_{i j k l}}{\partial t}

D. Ampère’s Law (with Maxwell’s correction):

\nabla \times B_{i j k l} = μ_{0} J_{i j k l} + μ_{0} ϵ_{0} \frac{\partial E_{i j k l}}{\partial t}

1.2. Discrete Dirac Equation

Purpose:

The Dirac equation uses discrete spinor fields and gamma matrices to describe fermion behavior, including spin and relativistic fields.

Equation:

i γ^{0} \frac{ψ_{i, j + 1} - ψ_{i, j}}{Δ t} + i \sum_{k = 1}^{3} γ^{k} \frac{ψ_{i + k, j} - ψ_{i - k, j}}{2 Δ x} - m ψ_{i, j} = 0

The equation for an N-body quantum state:

i ℏ \frac{\partial Ψ_{n} (t)}{\partial t} = \sum_{j = 1}^{N} (c α_{j} Δ_{j} + β_{j} m_{j} c^{2}) Ψ_{n} (t)

1.3. Discrete Klein-Gordon Equation

Purpose:

The Klein-Gordon equation uses second-order differential equations to model spin-0 particles in a relativistic context and to describe scalar field evolution.

Equation:

\frac{ϕ_{i + 1, j} - 2 ϕ_{i, j} + ϕ_{i - 1, j}}{Δ x^{2}} + \frac{ϕ_{i, j + 1} - 2 ϕ_{i, j} + ϕ_{i, j - 1}}{Δ t^{2}} + m^{2} ϕ_{i, j} = 0

The equation for an N-body quantum state:

\sum_{n = 1}^{N} (\frac{ϕ_{i_{n} + 1, j} - 2 ϕ_{i_{n}, j} + ϕ_{i_{n} - 1, j}}{Δ x^{2}} + \frac{ϕ_{i_{n}, j + 1} - 2 ϕ_{i_{n}, j} + ϕ_{i_{n}, j - 1}}{Δ t^{2}} + m^{2} ϕ_{i_{n}, j}) = 0

2. General Relativity

The laws of GR are predicated on a continuous differentiable 4D spacetime manifold. Accordingly, the following equations integrate GR within the context of the Dual Ontology’s discrete 4D spacetime.

2.1. Modified Regge Calculus for a Discrete 4D Spacetime

Purpose:

The Modified Regge calculus describes GR’s spacetime curvature within the Dual Ontology’s discrete Planck Sphere framework. In this context, spacetime is composed of Planck Spheres rather than a continuous manifold. Deficit angles at each Planck Sphere represent the curvature of 4D spacetime.

Equation:

\sum_{Planck Spheres} V_{PS} δ_{PS} + Λ V_{PS} = 2 κ \sum_{Planck Spheres} T_{PS} + ρ Λ V_{PS}

2.2. Discrete Einstein Field Equations

Purpose:

The discretization of Einstein’s Field Equations describes how mass and energy influence the curvature of discrete spacetime.

Equation:

\sum_{j} V_{j} δ_{j} = 2 κ \sum_{j} T_{j} V_{j}

2.3. Modified Dirac Equation for Curved Discrete 4D Spacetime:

Purpose:

The Dirac equation has been modified for a curved spacetime in a discrete 4D spacetime framework to ensure accurate descriptions of fermionic fields in a relativistic context.

Equation:

i γ^{μ} D_{μ} ψ - m ψ = 0

The equation for an N-body quantum state:

\sum_{n = 1}^{N} (i γ^{0} \frac{ψ_{i_{n}, j + 1} - ψ_{i_{n}, j}}{Δ t} + i \sum_{k = 1}^{3} γ^{k} \frac{ψ_{i_{n} + k, j} - ψ_{i_{n} - k, j}}{2 Δ x} - m ψ_{i_{n}, j}) = 0

2.4. Modified Klein-Gordon Equation for Curved Discrete 4D Spacetime:

Purpose:

The Klein-Gordon equation has been modified for curved spacetime in a discrete 4D spacetime framework to ensure spin-0 particles are properly modeled in a relativistic context.

\sum_{μ, ν} g_{i, j}^{μ ν} (\frac{ϕ_{i + \hat{μ}, j} - 2 ϕ_{i, j} + ϕ_{i - \hat{μ}, j}}{Δ x^{2}} + \frac{ϕ_{i, j + \hat{ν}} - 2 ϕ_{i, j} + ϕ_{i, j - \hat{ν}}}{Δ t^{2}}) + \frac{m^{2} c^{2}}{ℏ^{2}} ϕ_{i, j} = 0

The equation for an N-body quantum state:

\sum_{k = 1}^{N} (\sum_{μ, ν} g_{i, j, k}^{μ ν} (\frac{ϕ_{i + \hat{μ}, j, k} - 2 ϕ_{i, j, k} + ϕ_{i - \hat{μ}, j, k}}{Δ x^{2}} + \frac{ϕ_{i, j + \hat{ν}, k} - 2 ϕ_{i, j, k} + ϕ_{i, j - \hat{ν}, k}}{Δ t^{2}}) + \frac{m_{k}^{2} c^{2}}{ℏ^{2}} ϕ_{i, j, k}) = 0

3. Dynamic Evolution of Single and N-Body Quantum States in 4D Spacetime

Purpose:

The dynamic evolution of single and N-body quantum states in a discrete 4D spacetime and the Bell Identity’s continuous mapping of quantum states in 4D spacetime and Planck Space ensures quantum coherence and unitarity. Changes in a quantum state’s Bell Field(s) in 4D spacetime are instantaneously mirrored by corresponding changes in the quantum state’s single Bell Quantum Hyper-Point in Planck Space.

3.1. General Law of Quantum State Evolution

Equations:

D E : ϕ_{i, n}^{4 D} \leftrightarrow Bell Identity ψ_{n}^{PS}

δ ϕ_{i, n}^{4 D} = (ϕ_{i, n}^{4 D}, ϕ_{i, n + 1}^{4 D}, \dots, t)

δ ψ_{n}^{PS} = (ψ_{n}^{PS}, ψ_{n + 1}^{PS}, \dots, t)

Dynamic Process:

D E : (ϕ_{i, n}^{1, 4 D}, ϕ_{i, n}^{2, 4 D}, \dots) \leftrightarrow Bell Identity ψ_{n}^{PS}

D E : (ϕ_{i, n}^{A, 4 D}, ϕ_{i, n}^{B, 4 D}, \dots) \leftrightarrow Bell Identity ψ_{n}^{PS}

Definitions:

DE: The dynamic evolution of single or N-body quantum state in 4D spacetime.

Bell Identity: The one-to-one identity and mapping between a Bell Quantum Sphere in 4D spacetime and Planck Space. The same Bell Quantum Spheres that form a quantum state’s Bell Field(s) in 4D spacetime and also form its single Bell Quantum Hyper-Point in Planck Space.

(i): "Time variable in 4D spacetime."

(n): The number of Bell Fields that comprise a quantum state in 4D spacetime.

(ϕ_{i, n}^{4 D})

: Represents the number of Bell Fields that comprise a single or N-body quantum state at any given moment of time in 4D spacetime.

(ϕ_{i}^{1, 4 D}) :

Represents Bell Field 1 in connection with a single body quantum state at any given moment in time in 4D spacetime.

(ϕ_{i}^{2, 4 D}) :

Represents Bell Field 2 in connection with a single body quantum state at any given moment in time in 4D spacetime.

(ϕ_{i}^{A, 4 D})

: Represents Bell Field A in connection with an N-body quantum state in 4D spacetime

(ϕ_{i}^{B, 4 D})

: Represents Bell Field B in connection with an N-body quantum state in 4D spacetime.

(ψ^{PS})

: Represents a single or N-body quantum state’s single Bell Quantum Hyper-Point in Planck space.

3.2. General Law of Single Quantum State Evolution

Equation:

D E : ϕ_{i}^{4 D} \leftrightarrow Bell Identity ψ^{PS}

Dynamic Process

D E : (ϕ_{i}^{1, 4 D}, ϕ_{i}^{2, 4 D}, \dots) \leftrightarrow Bell Identity ψ^{PS}

3.3 General Law of N-body Quantum State Evolution

Equation:

D E : (ϕ_{i}^{A, 4 D}, ϕ_{i}^{B, 4 D}, \dots) \leftrightarrow Bell Identity ψ^{PS}

Dynamic Process:

D E : (ϕ_{i}^{A, 4 D}, ϕ_{i}^{B, 4 D}, \dots) \to (ϕ_{i + 1}^{A, 4 D}, ϕ_{i + 1}^{B, 4 D}, \dots) \leftrightarrow Bell Identity ψ_{i + 1}^{PS}

3.4 Dynamic Evolution—Bohm/EPR Experiment

Equation:

D E : (ϕ_{i}^{A, 4 D}, ϕ_{i}^{B, 4 D}) \leftrightarrow Bell Identity ψ^{PS}

Dynamic Process:

D E : (ϕ_{i}^{A, 4 D}, ϕ_{i}^{B, 4 D}) \to (ϕ_{i + 1}^{A, 4 D}, ϕ_{i + 1}^{B, 4 D}) \leftrightarrow Bell Identity ψ_{i + 1}^{PS}

4. Planck Space Collapse Operator

Purpose:

Section 4 of the mathematical formalism addresses the physical mechanisms underlying the instantaneous collapse of all single and N-body quantum states’ single Bell Quantum Hyper-Point within the Dual Ontology’s ((3 x N) + 3) hyperspace and the simultaneous reduction in the number of Planck Sphere’s that form all quantum state’s new Bell Field(s) in 4D spacetime.

4.1 General Law of Quantum State Collapse

Equations:

C : ψ_{j}^{PS} \leftrightarrow Bell Identity ϕ_{i, j}^{4 D}

δ (ψ_{j}^{PS} - ψ_{j^{'}}^{PS})

δ (ϕ_{i, j}^{4 D} - ϕ_{i, j^{'}}^{4 D})

If Collapse Process:

T \to ψ_{j}^{PS} \to ψ_{j^{'}}^{PS} \to (ϕ_{i, j^{'}}^{4 D})

T \to ψ_{j}^{PS} \to ψ_{j^{'}}^{PS} \to (ϕ_{i, j^{'}}^{4 D})

T \to ψ_{j}^{PS} \to (ψ_{j_{1}^{'}}^{PS}, ψ_{j_{2}^{'}}^{PS}, \dots, ψ_{j_{N}^{'}}^{PS}) \to (ϕ_{i, j_{1}^{'}}^{4 D}, ϕ_{i, j_{2}^{'}}^{4 D}, \dots, ϕ_{i, j_{N}^{'}}^{4 D})

Definitions:

C: The collapse operator describes the process initiated by a 4D spacetime trigger that leads to the instantaneous collapse of a single or N-body quantum state’s Bell Quantum Hyper-Point in Planck Space. Following the collapse:

A single quantum state will form a single Bell Quantum Hyper-Point in Planck Space and a single Bell Field in 4D spacetime.

An N-body quantum state will form multiple independent Bell Quantum Hyper-Points in Planck Space and multiple corresponding Bell Fields in 4D spacetime.

Each resulting Bell Quantum Hyper-Point and corresponding Bell Field will be a subset of the original Bell Quantum Hyper-Point and Bell Field(s).

The operator also reflects the effect of the Bell Identity, which ensures an instantaneous and simultaneous reduction in the number of Bell Quantum Spheres that comprise the single or N-body quantum state’s new Bell Field(s) in 4D spacetime, causing the generalized localization of the new Bell Field(s).

T: The 4D spacetime trigger that initiates the collapse of the quantum state’s Bell Quantum Hyper-Point in Planck Space.

Bell Identity: Ensures a one-to-one correspondence between the Bell Quantum Spheres that form a Bell Quantum Hyper-Point in Planck Space and one or more Bell Fields in 4D spacetime.

For a single quantum state, the Bell Identity ensures an instantaneous reduction in the number of Bell Quantum Spheres that form a single new Bell Quantum Hyper-Point and Bell Field.

For an N-body quantum state, the Bell Identity ensures an instantaneous reduction in the number of Bell Quantum Spheres that form multiple Bell Quantum Hyper-Points and corresponding Bell Fields.

(ψ) :

The wave function of the quantum state.

(j)

: Represents the initial number of Bell Quantum Spheres that comprise the quantum state before collapse.

(j')

: Represents the reduced number of Bell Quantum Spheres that comprise the quantum state after collapse.

(i) : Time variable in 4 D spacetime .

(ϕ)

Represents the quantum state’s Bell Field(s) in 4D spacetime.

(δ) :

"Delta function indicating the change or difference."

(PS)

: Planck Space

(4D): "4D spacetime"

{(ψ}_{j}^{PS})

: The quantum state before the collapse of its single Bell Quantum Hyper-Point.

{(ψ}_{j'}^{PS})

: The quantum state’s collapsed state following the collapse of its Bell Quantum Hyper-Point. Following the collapse, a single quantum state will form a single new Bell Quantum Hyper-Point, and an N-body quantum state will form two or more new Bell Quantum Hyper-Points. Each new Bell Quantum Hyper-Point is a subset of the initial Bell Quantum Spheres that formerly comprised the quantum state’s single Bell Quantum Hyper-Point.

(ϕ_{i, j}^{4 D})

: The quantum state’s Bell Field in 4D spacetime before collapse.

(ϕ_{i, j^{'}}^{4 D})

: Following the collapse of the quantum state’s Bell Quantum Hyper-Point, a single quantum state will form a single new Bell Field in 4D spacetime, and an N-body quantum state will form two or more new Bell Fields in 4D spacetime. The new Bell Field(s) are generally localized in 4D spacetime and are subsets of the original Bell Fields that comprised the quantum state.

Delta Function (

δ

– The first delta function represents the precise reduction in the number of Bell Quantum Spheres that form one or more of the quantum state’s Bell Quantum Hyper-Points in Planck Space following the quantum state’s collapse.

– The second delta function indicates the identical reduction in the number of Bell Quantum Spheres that form one or more of the quantum state’s Bell Fields in 4D spacetime following the generalized localization of the new Bell Field(s).

4.2 General Law of Single Quantum State Collapse

Equation:

C : ψ_{j}^{PS} \leftrightarrow Bell Identity φ_{i, j}^{4 D}

δ (ψ_{j}^{PS} - ψ_{j'}^{PS})

δ (φ_{i, j}^{4 D} - φ_{i, j'}^{4 D})

Collapse Process:

T \to ψ_{j}^{PS} \to ψ_{j^{'}}^{PS} \to (ϕ_{i, j^{'}}^{4 D})

4.3 General Law of N-Body Quantum State Collapse

Equation:

C : ψ_{j}^{PS} \leftrightarrow Bell Identity φ_{i, j}^{4 D}

δ (ψ_{j}^{PS} - ψ_{j'}^{PS})

δ (φ_{i, j}^{4 D} - φ_{i, j'}^{4 D})

Collapse Process:

T \to ψ_{j}^{PS} \to (ψ_{j_{1}^{'}}^{PS}, ψ_{j_{2}^{'}}^{PS}, \dots, ψ_{j_{N}^{'}}^{PS}) \to (ϕ_{i, j_{1}^{'}}^{4 D}, ϕ_{i, j_{2}^{'}}^{4 D}, \dots, ϕ_{i, j_{N}^{'}}^{4 D})

4. Quantum State Collapse—Bohm/EPR Experiment

Equation:

C : ψ_{A B}^{PS} \leftrightarrow Bell Identity φ_{i, j}^{A, B, 4 D}

C : ψ_{A B}^{P S} \leftrightarrow Bell Identity φ_{i, j}^{A, B, 4 D}

δ (ψ_{A B}^{P S} - ψ_{A' B'}^{P S})

δ (φ_{i, j}^{A, B, 4 D} - φ_{i, j}^{A' B', 4 D})

Collapse Process:

T \to ψ_{A B}^{PS} \to (ψ_{A^{'}}^{PS}, ψ_{B^{'}}^{PS}) \to (ϕ_{i, j^{'}}^{A, 4 D}, ϕ_{i, j^{'}}^{B, 4 D})

References

Adams, F. C. (2019). The degree of fine-tuning in our universe — and others. Physics Reports, 807, 1–111. [CrossRef]
Albert, D. Z. (1992). Quantum mechanics and experience. Harvard University Press. https://www.jstor.org/stable/j.ctv1bzfptv.
Albert, D. (2013). Wave Function Realism. In D. Albert & A. Ney (Eds.), The Wave Function: Essays on the Metaphysics of Quantum Mechanics (pp. 51–56). [CrossRef]
Albert, D. Z., & Ney, A. (2013). The wave function: Essays on the metaphysics of quantum mechanics. Oxford University Press. https://philpapers.org/rec/ALBTWF.
Allori, V. (2013b). Primitive ontology and the structure of fundamental physical theories. In A. Ney & D. Alberts (Eds.), The Wave Function: Essays on the Metaphysics of Quantum Mechanic (pp. 58–75). Oxford University Press. https://philarchive.org/rec/ALLPOA.
Allori, V. (2015). Primitive ontology in a nutshell. International Journal of Quantum Foundations, 1(3), 107–122. https://philsci-archive.pitt.edu/11651/.
Allori, V. (2016). How to make sense of quantum mechanics: Fundamental physical theories and primitive ontology. PhilPapers. https://philpapers.org/rec/ALLQTM.
Allori, V. (2021). Primitive beables are not local ontology: On the relation between primitive ontology and local beables. Crítica (México D. F. En Línea), 53(159). [CrossRef]
Allori, V. (2022). Spontaneous localization theories. In G. Bacciagaluppi & O. Freire Jr. (Eds.), Oxford Handbook of the History of Interpretations and Foundations of Quantum Mechanics (pp. 1103–1134). Oxford University Press. https://philpapers.org/rec/ALLSLT-3.
Allori, V. (2023). What if we lived in the best of all possible (quantum) worlds? PhilSci-Archive. http://philsci-archive.pitt.edu/21840/1/what-if-latest.pdf.
Allori, V., Bassi, A., Durr, D., & Zanghi, N. (2021). Do wave functions jump?: Perspectives of the work of GianCarlo Ghirardi. Springer. https://link.springer.com/book/10.1007/978-3-030-46777-7.
Allori, V., Goldstein, S., Tumulka, R., & Zanghi, N. (2008). On the common structure of Bohmian mechanics and the Ghirardi-Rimini-Weber theory. The British Journal for the Philosophy of Science, 59(3), 353–389. [CrossRef]
Bacciagaluppi, G., & Valentini, A. (2009). Quantum theory at the crossroads: Reconsidering the 1927 Solvay conference. ArXiv (Cornell University. https://arxiv.org/abs/quant-ph/0609184.
Banerjee, S., Bera, S., & Singh, T. P. (2016). Quantum nonlocality and the end of classical spacetime. International Journal of Modern Physics D, 25(12), 1644005–1644005. [CrossRef]
Barrow, J. D. (2001). The book of nothing. Vintage. https://philpapers.org/rec/BARTBO-11.
Bassi, A., & Ghirardi, G. (2003). Dynamical reduction models. Physics Reports, 379(5-6), 257–426. [CrossRef]
Bassi, A., Lochan, K., Satin, S., Singh, T. P., & Ulbricht, H. (2012). Models of wave-function collapse, underlying theories, and experimental tests. Reviews of Modern Physics, 85(2), 471–527. [CrossRef]
Bassi, A., & Ulbricht, H. (2014). Collapse models: From theoretical foundations to experimental verifications. Journal of Physics: Conference Series, 504. [CrossRef]
Becker, A. (2018). What is real? Basic Books. Kindle Edition.
Bedingham, D. (2021). Collapse models, relativity, and discrete spacetime. In V. Allori, A. Bassi, D. Durr, & N. Zanghi (Eds.), Do Wave Functions Jump? Perspectives of the Work of GianCarlo Ghirardi (pp. 191–203). Springer. [CrossRef]
Bell, J. S. (2004). Speakable and unspeakable in quantum mechanics: collected papers on quantum philosophy. Cambridge University Press. Kindle Edition.
Bell, M., & Gao, S. (2016). Quantum nonlocality and reality: 50 years of Bell’s theorem. Cambridge University Press. Kindle Edition.
Belot, G. (2012). Quantum states for primitive ontologists. European Journal for Philosophy of Science, 2(1), 67–83. [CrossRef]
Bohm, D. (1952b). A suggested interpretation of the quantum theory in terms of “hidden” variables. I. Physical Review, 85(2), 166–179. [CrossRef]
Bricmont, J. (2016). Making sense of quantum mechanics. Springer. https://philpapers.org/rec/BRIMSO.
Brunner, N., Cavalcanti, D., Pironio, S., Scarani, V., & Wehner, S. (2014). Bell nonlocality. Reviews of Modern Physics, 86(2), 419–478. [CrossRef]
Broglie, L. de. (1964). The current interpretation of wave mechanics. Elsevier Publishing Company.
Carroll, S. (2018, October 31). What is nothing? Vice Magazine Online. https://www.vice.com/en/article/vbk5va/what-is-nothing.
Carroll, S. M., & Singh, A. (2018). Mad-dog Everettianism: Quantum mechanics at its most minimal. ArXiv. [CrossRef]
Castro, P., Gatta, M., Croca, J. R., & Moreira, R. N. (2018). Spacetime as an emergent phenomenon: A possible way to explain entanglement and the tunnel effect. Journal of Applied Mathematics and Physics, 6, 2107–2118. [CrossRef]
Chen, E. K. (2019). Realism about the wave function. Philosophy Compass, 14(7). [CrossRef]
Crouse, D. T. (2016). On the nature of discrete space-time: The atomic theory of space-time and its effects on Pythagoras’s theorem, time versus duration, inertial anomalies of astronomical bodies, and special relativity at the Planck scale. ArXiv. [CrossRef]
Crouse, D., & Skufca, J. (2018). On the nature of discrete space-time: Part 1: The distance formula, relativistic time dilation, and length contraction in discrete space-time. [CrossRef]
Davies, P. (2014). The turbulent life of empty space. In J. Webb (Ed.), Nothing : Surprising Insights Everywhere from Zero to Oblivion. The Experiment.
Dürr, D., Goldstein, S., & Zanghi, N. (1995). Bohmian mechanics as the foundation of quantum mechanics. ArXiv.org. [CrossRef]
Einstein, A., Przibram, K., & Klein, M. J. (2011). Letters on wave mechanics: Correspondence with H. A. Lorentz, Max Planck, and Erwin Schrödinger. Philosophical Library/Open Road. Kindle Edition.
Feynman, R. P. (1985). The character of physical law. The MIT Press. https://www.ling.upenn.edu/~kroch/courses/lx550/readings/feynman1-4.pdf (Original work published 1967).
Gao, S. (2016). The meaning of the wave function: In search of the ontology of quantum mechanics. Cambridge University Press. ArXiv. https://arxiv.org/abs/1611.02738.
hypothesis. Foundations of Science, 23(1), 145–157. [CrossRef]
Gao, S. (2018). Collapse of the wave function: Models, ontology, origin, and implications. Cambridge University Press.
Gao, S. (2019). Quantum theory is incompatible with relativity: A new proof beyond Bell’s theorem and a test of unitary quantum theories. PhilSci Archive. http://philsci-archive.pitt.edu/16155/.
Gao, S. (2020). A puzzle for the field ontologists. Foundations of Physics, 50(11), 1541–1553. [CrossRef]
Gao, S. (2024). Locality implies reality of the wave function: Hardy’s theorem revisited. Philsci-Archive.pitt.edu. https://philsci-archive.pitt.edu/23005/.
Genovese, M. (2023). Can quantum non-locality be connected to extra-dimensions? International Journal of Quantum Information, 21(07), 2340003. [CrossRef]
Genovese, M., & Gramegna, M. (2019). Quantum correlations and quantum non-locality: A review and a few new ideas. Applied Sciences, 9(24), 5406. [CrossRef]
Ghirardi, G. (2004). Sneaking a look at god’s cards. Princeton University Press.
Goldstein, S., & Zanghi, N. (2011). Reality and the role of the wavefunction in quantum theory. ArXiv (Cornell University).
Grünbaum, A. (2009). Why is there a world AT ALL, rather than just nothing? Ontology Studies, 9, 7–19.
Hagar, A. (2015). Discrete or continuous?: The quest for fundamental length in modern physics. Cambridge University Press. Kindle Edition.
Holt, J. (2012). Why does the world exist?: An existential detective story. Liveright. Kindle Edition.
Hossenfelder, S. (2013). Minimal length scale scenarios for quantum gravity. Living Reviews in Relativity, 16(1). [CrossRef]
Hossenfelder, S. (2014). Theory and phenomenology of space-time defects. Advances in High Energy Physics, 2014, 1–6. [CrossRef]
Hossenfelder, S. (2018). Lost in math. Basic Books.
Howard, D. (1985). Einstein on locality and separability. Studies in History and Philosophy of Science, 16(3), 171–201. [CrossRef]
Howard, D. (1989). Holism, separability, and the metaphysical implications of the Bell experiments. In E. McMullin (Ed.), Philosophical consequences of quantum theory: Reflections on Bell’s theorem (pp. 224–253). University of Notre Dame Press. https://philpapers.org/rec/HOWHSA-2.
Howard, D. (1990). “Nicht sein kann was nicht sein darf,” or the prehistory of EPR, 1909–1935: Einstein’s early worries about the quantum mechanics of composite systems. In A. I. Miller (Ed.), Sixty-Two Years of Uncertainty (pp. 61–111). Cambridge University. [CrossRef]
Hubert, M., & Romano, D. (2018). The wave-function as a multi-field. European Journal for Philosophy of Science, 8(3), 521–537. [CrossRef]
Huggett, N., & Wüthrich, C. (2013). Emergent spacetime and empirical (in)coherence. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 44(3), 276–285. [CrossRef]
Kahan, D. (2024). On the Dual Ontological Structure and Mixed Dynamics of the Universe. [CrossRef]
Kastner, R. (2023). Quantum theory needs (and probably has) real reduction. ArXiv.org. [CrossRef]
Krauss, L. M. (2012). A universe from nothing: Why is there something rather than nothing? Free Press.
Leslie, J., & Kuhn, R. L. (2013). The mystery of existence. John Wiley & Sons.
Lewis, P. J. (2013). Dimension and illusion. In A. Ney & D. Albert (Eds.), The Wave Function: Essays on the Metaphysics of Quantum Mechanics (pp. 110–125). Oxford University Press. http://philsci-archive.pitt.edu/8841/.
Lewis, P. J. (2016). Quantum ontology: A guide to the metaphysics of quantum mechanics. Oxford University Press. Kindle Edition.
Licata, I., & Chiatti, L. (2019). Event-Based quantum mechanics: A context for the emergence of classical information. Symmetry, 11(2), 181–181. [CrossRef]
Maudlin, T. (2007). Completeness, supervenience, and ontology. Journal of Physics A, 40(12), 3151–3171. [CrossRef]
Maudlin, T. (2011). Quantum non-locality & relativity : Metaphysical intimations of modern physics. (3rd ed.). John Wiley. Kindle Edition.
Maudlin, T. (2013a). Philosophy of physics: Space and time (Princeton foundations of contemporary philosophy book 11). Princeton University Press. Kindle Edition.
Maudlin, T. (2013b). The nature of the quantum state. In D. Albert & A. Ney (Eds.), The Wave Function: Essays on the Metaphysics of Quantum Mechanics (pp. 126–153). [CrossRef]
Maudlin, T. (2014). What Bell did. Journal of Physics A: Mathematical and Theoretical, 47(42), 424010. [CrossRef]
Maudlin, T. (2019). Philosophy of physics: Quantum theory (Princeton foundations of contemporary philosophy book 19) Princeton University Press. Kindle Edition.
McQueen, K. J. (2015). Four tails problems for dynamical collapse theories. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 49, 10–18. [CrossRef]
Moghri, M. (2020). Much ado about nothingness? Kriterion (Salzburg), 34(3), 79–98. [CrossRef]
Monton, B. (2002). Wave function ontology. Synthese, 130(2), 265–277. https://philarchive.org/rec/MONWFO-2.
Monton, B. (2006). Quantum mechanics and 3N-Dimensional Space. Philosophy of Science, 73(5), 778–789. [CrossRef]
Ney, A. (2016). Separability, locality, and higher dimensions in quantum mechanics. Philarchive.org. https://philarchive.org/rec/NEYSLA.
Ney, A. (2021). The world in the wave function : A metaphysics for quantum physics. Oxford University Press. Kindle Edition.
Ney, A. (2023). Three arguments for wave function realism. European Journal for Philosophy of Science, 13(4). [CrossRef]
Norsen, T. (2005). Einstein’s boxes. American Journal of Physics, 73(2), 164–176. [CrossRef]
Norsen, T. (2011). John S. Bell’s concept of local causality. American Journal of Physics, 79(12), 1261–1275. [CrossRef]
Norsen, T., Marian, D., & X. Oriols. (2015). Can the wave function in configuration space be replaced by single-particle wave functions in physical space? Synthese, 192(10), 3125–3151. [CrossRef]
Penrose, R. (1997). Physics and the mind. In M. Longair (Ed.), The Large, the Small and the Human Mind (pp. 93–143). Cambridge University Press.
Pusey, M. F., Barrett, J., & Rudolph, T. (2012). On the reality of the quantum state. Nature Physics, 8(6), 475–478. [CrossRef]
Romano, D. (2020). Multi-field and Bohm’s theory. Synthese, 198(11), 10587–10609. [CrossRef]
Rovelli, C. (2017). Reality is not what it seems: The journey to quantum gravity. Penguin Publishing Group. Kindle Edition.
Sebens, C. T. (2021). Electron charge density: A clue from quantum chemistry for quantum foundations. Foundations of Physics, 51(4). [CrossRef]
Sebens, C. T. (2023). Eliminating electron self-repulsion. Foundations of Physics, 53(4). [CrossRef]
Smolin, L. (2004). Atoms of space and time. Scientific American, 290(1), 66–75. https://www.jstor.org/stable/26172656.
Vaidman, L. (2021a). Many-Worlds interpretation of quantum mechanics. The Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/archives/fall2021/entries/qm-manyworlds.
Vaidman, L. (2021b). Wave function realism and three dimensions. In V. Allori (Ed.), Quantum Mechanics and Fundamentality; Naturalizing Quantum Theory between Scientific Realism and Ontological Indeterminacy. Springer. http://philsci-archive.pitt.edu/19979/.
Wechsler, S. (2021). About the nature of the quantum system—an examination of the random discontinuous motion interpretation of the quantum mechanics. Journal of Quantum Information Science, 11(03), 99–111. [CrossRef]
Wiseman, H. M. (2006). From Einstein’s theorem to Bell’s theorem: a history of quantum non-locality. Contemporary Physics, 47(2), 79–88. [CrossRef]
Wittgenstein, L., & Russell, B. (2021). Tractatus logico-philosophicus (C. K. Ogden, Trans.). Routledge. https://www.gutenberg.org/files/5740/5740-pdf.pdf (Original work published 1921).

1	(Allori et al., 2008); (Allori, 2013b, 2015, 2016).
2	(Dürr et al., 1995); (Goldstein & Zanghi, 2011).
3	(Bassi & Ghirardi, 2003); (Bassi et al., 2012).
4	(Gao, 2016, 2024); (Ney, 2021).
5	(Carroll & Singh, 2018); (Vaidman, 2021a and 2021b).
6	(Belot, 2012); (Hubert & Romano, 2018); (Norsen et al., 2015); (Romano, 2020).
7	The Dual Ontology conjecture replaces the linear, non-relativistic Schrodinger equation with mathematical formalisms for discrete Maxwell, Dirac, and Klein-Gordon equations, a modified Regge Calculus for a discrete 4D spacetime, discrete Einstein Field equations, modified Dirac and Klein Gordon equations for a curved, discrete 4D spacetime and a functional notation for the dynamic evolution of all quantum states in 4D spacetime and their instantaneous collapse in an ultra-high-dimensional Planck Space. See Appendix A.
8	The theoretical problems of a mathematical 3N configuration space were well understood in the early days of quantum mechanics. (Einstein et al., 2011, p. 48); (Howard, 1990); (Bacciagaluppi & Valentini, 2009, p.447).
9	See Monton, 2002, p. 207, 2006) regarding the critical importance of one-to-one mapping between 3D space and ultra-high dimensional spaces. See also (Albert, 2013, p. 54); (Maudlin, 2007 p. 3161, 2013b); (Ney, 2021, pp. 207-215).
10	See (Ney, 2021, 2023).
11	Despite the Dual Ontology’s unique structure, “It may be that a real synthesis of quantum and relativity theories requires not just technical developments but radical conceptual renewal.” (Bell, 2004, p. 171). See also (Maudlin, 2014, p. 24): “My own view is that…belief in the completeness of Relativity as an account of space-time structure has been irrationally fetishized just as belief in the completeness of the quantum-mechanical description had been by Bohr and company.”
12	See (Howard, 1989, pp. 247-253) for an early consideration of higher dimensional spaces. See also (Monton, 2002, 2006).
13	See Appendix A for the mathematical formalisms supporting the Dual Ontology conjecture.
14	(Lewis, 2013, p. 116) for the early use of an ultra-high dimensional (3 x N) space.
15	See generally (Huggett & Wüthrich, 2013) regarding emergent spacetime and empirical coherence.
16	Planck Space does not have an independent time parameter. The function f describes the instantaneous state of Planck Spheres at any given moment in time in 4D spacetime. Changes in the energy content and configuration of Planck Spheres over time in 4D spacetime are mirrored instantaneously in the corresponding Planck Spheres in Planck Space without an independent temporal dimension in Planck Space.
17	“A physical theory should clearly and forthrightly address two fundamental questions: what there is, and what it does. The answer to the first question is provided by the ontology of the theory, and the answer to the second by its dynamics.” (Maudlin, 2019, p. 3).
18	See (Maudlin, 2013b, 2019, pp. 36-37 and 79-93); (Monton, 2006); (Pusey et al., 2012). See (Ney, 2021, p.11) for an alternate view of quantum states.
19	In order to avoid confusion, the term “quantum state” is used in this analysis rather than John Bell‘s now famous term “beables.” See (Allori, 2021); (Ney, 2021, p. 42).
20	20. (Barrow, 2002); (Grunbaum, 2009); (Holt, 2012). An ontological SOAN turns one of the greatest philosophical questions of all time on its head. The question is not, “Why is there something rather than nothing?” Rather, it is, “Why is there something AND nothing?”
21	See (Krauss, 2012).
22	(Holt, 2012). See also (Moghri, 2020, p. 81): “Another move is to coin the term ‘nothingness’ as a name that refers to a state empty of every concrete thing. Using that term, one can better distinguish between the two meanings of the statement ‘There is nothing:’ one that uses a negative quantifier and means that there is no concrete thing; another that uses a positive quantifier and means that there is an abstract thing (the state of nothingness). Thus, the statement ‘There is nothingness’ can be meaningful and coherent without referring to concrete things.”
23	(Rovelli, 2017, p. 152).
24	Interview with Sean Carroll, Vice Magazine On Line. What is Nothing? with Nick Rose, October 31, 2018.
25	For extensive discussions on the issues associated with a physical state of nothingness, see (Holt, 2012); (Barrow, 2002); (Leslie & Kuhn, 2013).
26	See generally (Bedingham, 2021); (Gao, 2018, pp. 248-253); (Smolin, 2004). Whether 4D spacetime is a continuous or discrete space is a controversial subject. In addition to preventing singularities upon the initial emergence of the 4D spacetime at t = 0 or the center of black holes, space discretization prevents the infinities that appear in the quantization of Relativity. Arguments in favor of the discretization of space have been proposed based upon mathematics, electrodynamics, quantum electrodynamics, loop quantum gravity, loop quantum cosmology, string theory, discrete lattice, asymptotic safe gravity, causal sets, spin foams, deformed special relativity, causal dynamical triangulation, quantum graphity, and black hole theory among others. (Crouse, 2016); (Crouse & Skufca, 2018); (Hagar, 2015); (Hossenfelder, 2013, 2014).
27	The precise shape and size of Planck Spheres is unknown, and the description of “Planck Spheres” is illustrative only.
28	(Davies, 2014, p. 126).
29	See (Adams, 2019, p. 158). “We first note that most authors agree that habitable universes should have only one-time dimension… If space-time had more than one temporal dimension, then closed time-like loops could be constructed. Such loops, in turn, allow for observers to revisit the “past” and thereby affect causality.”
30	See also (Albert 1992, 2013), (Chen, 2019), and (Ney, 2021, 2023) for alternative arguments regarding a wave function in higher-dimensional 3N spaces.
31	Although the complexity differs, a single Planck Hyper-Point and a single 3-dimensional point in a discrete 4D spacetime are analogous. In a discrete 4D spacetime, a single, 3-dimensional point in 4D spacetime can be described by its 3 spatial coordinates in the x, y, z dimensions. Similarly, a single Planck Hyper-Point is defined by the coordinates of its individual dimensions in a (3 x N) Planck Space.
32	For an alternative approach, see (Norsen et al., 2015).
33	See Appendix A, sections 3.1 and 3.2, for the mathematical formalisms applicable to the dynamic evolution of a single quantum state’s Bell Field in 4D spacetime.
34	See section 5.4 for additional information on the “quantum connection.”
35	See Appendix A, sections 4.1 and 4.2, for the mathematical formalisms applicable to the collapse of a single quantum state’s Bell Quantum Hyper-Point in Planck Space.
36	See also (Genovese, 2023) and (Genovese & Gramenga, 2022) regarding non-locality and ultra-high dimensions.
37	The preferred basis for all observations of a quantum state is the position basis. (Bell, 204, p. 161); (Maudlin, 2019, pp. 48-50).
38	Significantly, the Bell Identity ensures unitarity throughout the dynamic evolution of all quantum states in 4D spacetime and their collapse in Planck Space, and as a direct consequence, solves the “tails” problem. See McQueen (2015).
39	Following the quantum state’s generalized localization, it once again begins to spread. See section 4.4 for additional information on the meaning of “generalized localization.”
40	The 4D spacetime laws of special relativity, including the maximum speed of light, c, the invariance of the speed of light, time dilation, length contraction, the equivalence of mass and energy, the relativity of simultaneity, and relativistic energy increase, apply in all circumstances except for the instantaneous collapse of a quantum state in Planck Space.
41	See (Gao, 2019) regarding the incompatibility of unitary quantum theories and relativity.
42	See (Allori, 2022); (Bricmont, 2016); (Broglie, 1964); (Norsen, 2005).
43	See Appendix A, sections 3.1 and 3.2, for the mathematical formalisms applicable to the dynamic evolution of a single quantum state’s Bell Field(s) in 4D spacetime based on the Einstein/de Broglie boxes thought experiment.
44	See Appendix A, sections 4.1 and 4.2, for the mathematical formalisms applicable to the collapse of a single quantum state’s Bell Quantum Hyper-Point in Planck Space based on the Einstein/de Broglie boxes thought experiment.
45	If the walls of Boxes B, C, and D are “impenetrable,” there must be a physical explanation for the presence of the entire quantum state in Box C or Box D following the collapse of the quantum state. The explanation lies at the heart of the Dual Ontology conjecture. Recall that a quantum state is always composed of a Bell Quantum Field in 4D spacetime and a single Bell Quantum Hyper-Point in Planck Space. When a quantum state is inserted into “impenetrable” Box B, it will be composed of Bell Quantum Field B in Box B and Bell Quantum Hyper-Point B in Planck Space. Similarly, when the divider is inserted into Box B and Box B is separated into Boxes C and D, Bell Quantum Field C, and Bell Quantum Field D not only continue to form a single Bell Quantum Hyper-Point (Bell Quantum Hyper-Point CD) but also the Bell Identity simultaneously links Bell Quantum Hyper-Point CD to Bell Quantum Field C inside Box C and Bell Quantum Field D inside Box D. The collapse of Bell Quantum Hyper-Point CD is an event in an ultra-high dimensional Planck Space that is extraneous to 4D spacetime. Accordingly, the physical existence of an ultra-high dimensional Planck Space ensures that Bell Quantum Hyper-Point B and Bell Quantum Hyper-Point CD were never physically constrained by the three spatial dimensions of 4D spacetime or “impenetrable” Boxes B, C, or D in the first instance.
46	For alternative views, see generally (Allori et al., 2021).
47	See also section 4.6 on quantum tunneling.
48	See Appendix A, sections 3.1 and 3.2, for the mathematical formalisms applicable to the dynamic evolution of a single quantum state’s Bell Fields in 4D spacetime based on a double-slit experiment.
49	See Appendix A, sections 4.1 and 4.2, for the mathematical formalisms applicable to the collapse of a single quantum state’s Bell Quantum Hyper-Point in Planck Space based on the double-slit experiment.
50	Double-slit experiments describe a quantum state by its wave function rather than the considerably more amorphous terms “charge density” or “energy content.” Nevertheless, since all quantum states are real if an electron passes through slits A and B, the charge density, and the energy content of the electron, however ill-defined after it has passed through slits A and B, must also do so. See (Sebens C. T., 2021).
51	The “which way” monitoring experiment is based upon the example presented in Maudlin, 2019, pp. 14-16.
52	See Appendix A, sections 3.1 and 3.3, for the mathematical formalisms applicable to the dynamic evolution of N-body quantum states’ Bell Fields in 4D spacetime and sections 4.1 and 4.3, for the mathematical formalisms applicable to the collapse of an N-body quantum state’s Bell Quantum Hyper-Point in Planck Space.
53	(Bohm, 1951, pp. 611-619).
54	See Appendix A, sections 3.1 and 3.4, for the mathematical formalisms applicable to the dynamic evolution of the singlet state’s Bell Fields in 4D spacetime based on the Bohm version of the EPR experiment.
55	Although the Stern-Gerlach experiment in the z direction is conducted in 4D spacetime on either Bell Quantum Field E in Princeton or Bell Quantum Field F in Copenhagen, the Bell Identity ensures that the experiment is simultaneously reflected on Bell Quantum Hyper-Point EF in Planck Space. More generally, any quantum experiment in 4D spacetime is always reflected simultaneously on the quantum state’s Bell Quantum Hyper-Point in Planck Space.
56	See Appendix A, sections 4.1 and 4.4, for the mathematical formalisms applicable to the collapse of the singlet state’s Bell Quantum Hyper-Point in Planck Space based on the Bohm version of the EPR experiment.
57	For a mathematical 3N notation the transition would be ∣ψ 1,2⟩→∣ψ 1⟩⊗∣ψ 2⟩.
58	(Lewis, 2016, pp. 72-107).
59	In Planck Space, a single Bell Quantum Hyper-Point is neither space-like separated nor a separable system. See Sections 5.1 and 5.2 below. See also (Ney, 2021, pp. 112-128); (Howard, 1985, p. 197).
60	For a detailed discussion, see (Ney, 2021).
61	The unobservable universe is considerably larger than the observable universe and may be infinite.
62	Although decoherence extensively considers environmental triggers and the loss of coherence rather than a specific quantum collapse mechanism, the Dual Ontology conjecture supports a very specific collapse mechanism initiated by 4D spacetime Physical Interactions.
63	The concepts of gravity, the strong nuclear force, and the electro-weak force do not exist in Planck Space.
64	No specific assumptions are made regarding dark matter or dark energy.
65	See also (Licata & Chiatti, 2019).
66	Physical triggers such as nuclear interactions on the sun may be statistically determinable, but individual quantum state collapses are still time and location-dependent.
67	The collapse rate of individual quantum states on the sun directly relates to temperature and location.
68	Humans can control and precisely vary the collapse rate of electrons at will using a scanning tunneling microscope.
69	(Bassi & Ulbricht, 2014).
70	(Ghirardi, 2004, p. 406).
71	The Dual Ontology conjecture conflicts with mathematical models that describe quantum state collapse to a single dimensionless point, a Dirac delta function, or an eigenstate of position with a single discrete value.
72	From the perspective of the Dual Ontology conjecture, "The problem is that mathematics has become too dominant in physics. We have become so focused on finding mathematical descriptions of nature that we have forgotten to ask if these descriptions are actually true. We have become so entranced by the beauty of mathematics that we have lost sight of the goal of physics, which is to understand the real world." (Hossenfelder, 2018, p. 8). “Physics is not mathematics, and mathematics is not physics.” (Feynman, 1985, p. 55). See also (Allori, 2016).
73	See footnote 45 regarding “impenetrable boxes” and section 4.7 below regarding the Born Rule.
74	In the context of pilot wave theory, see (Castro et al., 2018).
75	For a discussion on the Born Rule, see (Maudlin, 2019); (Ney, 2021, pp. 4-11).
76	See (Bacciagaluppi & Valentini, 2009, p. 136) regarding the debates between Schrödinger and Born and the probability density rule.
77	Under the Dual Ontology conjecture, the probability of finding the location of a quantum state in a generalized location must be one.
78	(Bell, 2004, p. 171); See also (Norsen, 2011, p. 1216).
79	The terminology that describes 4D spacetime may confirm Ludwig Wittgenstein’s concern that “The limits of my language mean the limits of my world.” (Wittgenstein, 1922, p. 74).
80	Although the term “non-separable” has multiple definitions, a stronger version of that term holds that “…the non-separability of states is the claim that spatio-temporal separation is not a sufficient condition for the individuating systems themselves, that under certain circumstances the contents of two spatio-temporally separated regions of space-time constitute just a single system”. (Howard, 1989). For a slightly different perspective, see (Ney, 2016). Einstein’s primary concern was not with non-separability per se but with the possibility that non-separability implied a violation of his theory of special relativity. (Howard, 1985, pp. 172-173); (Howard, 1989, p. 232). See also (Maudlin, 2011, pp. 88-89).
81	See also (Ney, 2016, 2021).
82	The non-separability of a Bell Quantum Hyper-Point addresses a concern raised by Einstein. Einstein questioned whether spatially separated quantum states in 4D spacetime had an independent reality. (Wiseman, 2006). The existence of a single ultra-high dimensional Bell Quantum Hyper-Point would help to prove two points. First, space-like quantum states separated in 4D spacetime are ontic, and second, they are not physically independent.
83	See (Maudlin, 2011, pp. 21-2 ).
84	The ability of a Bell Quantum Hyper-Point to maintain a “quantum connection” also answers the self-interference puzzle outlined in (Gao, 2020). An electron’s Bell Quantum Hyper-Point contains all of the information regarding an electron’s charge distribution regardless of whether the electron is space-like separated in 4D spacetime. The electron’s Bell Quantum Hyper-Point also quantum discriminates and is non-attenuated, but it does not interfere with itself. In this sense, all electrons (and all quantum states) are not the same; they are all different. See also (Sebens, 2021, 2023); (Wechsler, 2021).
85	Future theoretical work and testing may very well prove that electrons are, in fact, unique rather than indistinguishable.
86	(Brunner et al., 2014).
87	(Goldstein et al., 2011); (Maudlin, 2014, p. 21); See also (Bell & Gao, 2016).
88	See (Maudlin, 2011, pp. 53, Note 1).
89	(Ney, 2021, p. 96). See (Allori, 2022) regarding different uses of the term “non-local” in Einstein/de Broglie Box experiments.
90	See (Banerjee et al., 2016): “We conclude that the problem of time in quantum theory is intimately connected with the vexing issue of quantum non-locality and acausality in entangled states. Addressing the former compels us to revise our notions of space-time structure, which in turn provides a resolution for the latter.”
91	See also (Genovese, 2023).
92	See also (Ney, 2021, pp. 104-119).
93	See generally (Allori, 2023): “In any case, I think that the result of Bell’s theorem is the true quantum revolution: not the paradigm shift in terms of the type of understating one can achieve, but a new feature of the world. The natural question then is how to combine quantum nonlocality with relativity.”
94	(Bell, 2004, p. 171). See also (Penrose, 1997, p. 137): “My own view is that, to understand quantum non-locality, we shall require a radical new theory. This theory will not just be a slight modification of quantum mechanics but something as different from standard quantum mechanics as general relativity is different from Newtonian gravity. It would have to be something which has a completely different conceptual framework. In this picture, quantum non-locality would be built into the theory”. See also (Kastner, 2023).
95	(Maudlin. 2011, p. 185).
96	See Appendix A – Mathematical Formalisms.
97	For an earlier version of this paper and a discussion of material to be included in Part II, see Kahan (2024)."

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Quantum Cosmology Part I: The Integration of Special Relativity and Quantum Mechanics

Abstract

1. The Dual Ontology

1.1. Introduction

1.2. The Dual Ontology Conjecture

1.3. Analytical Structure

2. The ((3 x N) + 3) Dual Ontology

2.1. The SOAN and Planck Spheres

2.2. Discrete 4D Spacetime and Planck Space

3. Quantum State Evolution and Collapse in Discrete 4D Spacetime and Planck Space

3.1. The Dynamic Evolution of a Single Quantum State

3.2. The Collapse of a Single Quantum State

3.2.1. The Einstein/de Broglie Boxes Thought Experiment

3.2.2. The Double-Slit Experiment

3.2.3. A Which-Way Experiment

3.3. N-Body Quantum State Evolution and Collapse

The Bohm-EPR Thought Experiment

4. Physical Implications of the Dual Ontology Conjecture

4.1. Indeterminacy

4.2. Quantum State Emergence and Annihilation

4.3. Physical Triggers

4.4. Quantum State Localization

4.5. Time and Instantaneous Collapse

4.6. Quantum Tunneling

4.7. The Born Rule Revisited

5. Resolving the Tension Between SR and Quantum Mechanics

5.1. Space-Like Separated

5.2. Non-separability

5.3. Instantaneous, Superluminal, and Faster than Light

5.4. The Quantum Connection

5.5. Bell’s Theorem and Locality

5.6. The Relativity of Simultaneity

5.7. Relativistic Energy Increase

6. Conclusion

Acknowledgments

Appendix A. Mathematical Formalisms

References

MDPI Initiatives

Important Links

Subscribe