Weighted Ranked Set Sampling for Skew Distributions

1. Introduction

The Ranked Set Sampling (RSS) procedure has been used advantageously in agriculture, forestry, environmental, ecological and recently in human studies where the exact measurement of units is either difficult or expensive. For example, in forestry, the measurement of stem volume of standing trees is difficult but the ranking of the trees using their height and diameter at breast height is rather easy. For such situations, McIntyre (1952) introduced RSS to estimate the population mean. The RSS is a cost-efficient alternative to simple random sampling (SRS) if observations can be ranked according to the characteristic under investigation by means of visual inspection or other methods not requiring actual measurements. McIntyre (1952) indicated that the RSS procedure is superior to SRS procedure to estimate the population mean. However, Dell and Clutter (1972) and Takahasi and Wakimoto (1968) provided mathematical foundation for RSS. Dell and Clutter (1972) also showed that the estimator for population mean based on RSS is at least as efficient as the estimator based on SRS with the same number of measurements even though when there are ranking errors. Bhoj (2001) introduced RSS with unequal samples. Bhoj and Kushary (2016) proposed RSS with unequal samples for positively skew distributions with heavy right tails. RSS is a nonparametric procedure. However, recently, RSS has also been used in the parametric setup (see Bhoj and Ahsanullah (1996); Bhoj (1997a, 1997b); Lam et al. (1994); Stokes (1995).

The selection of ranked set sample of size k involves drawing k random samples with k units in each sample. The units in each sample are ranked by using judgment or other methods not requiring actual measurements. The unit with lowest rank is measured from the first sample, the unit with second lowest rank is measured from the second sample, and the procedure is continued until the unit with the highest rank is measured from the last sample. The k² ordered observations in k samples can be displayed in the matrix form as:

$$\begin{gathered} y_{\left(11\right)},y_{\left(12\right)},\dots ,y_{\left(1k\right)} \\ {y}_{\left(21\right)},y_{\left(22\right)},\dots ,y_{\left(2k\right)} \\ \dots \\ {y}_{\left(k1\right)},y_{\left(k2\right)},\mathrm{...},y_{\left(kk\right)} \end{gathered}$$

We measure only k$\left(y_{\left(ii\right)},i=1,\mathrm{2...},k\right)$ diagonal observations, and they constitute the RSS. We note that these k observations are independently but not identically distributed. In RSS, k is usually small to reduce the ranking errors and therefore, to increase the sample size, the above procedure is repeated$m\ge 2$times to get the sample of size $n=mk$. In this paper, we assume m=1.

In the present paper, our main interest is to estimate the population mean for positively skew distributions with longer right tail. We propose estimators based on weighted ranked set sampling (WRSS) and compare their performance with the ones based on the usual RSS procedure and Neyman’s optimal allocation model. In section 2, we summarize the estimators of population mean based on RSS procedure and Neyman’s optimal solution. In section 3, we propose our WRSS procedure to estimate the population mean of skew distributions. First, we introduce WRSS procedure where we assign one low weight to the highest order statistics and calculated the relative precisions of the estimator based on WRSS, RSS and Neyman’s optimal procedure with respect to the estimator based on SRS. The procedures are used to obtain the relative precisions by using the four positively skew distributions. We also computed one set of weights for all four distributions for each k. In section 4, we derived optimal weights for the lowest and highest order statistics for the chosen distributions for each k. We then obtained one set of weights for the lowest and highest order statistics for each k which will maximize the sum of relative precisions of four distributions. In section 5, we generalize the use of all optimal weights for all order statistics for k=4 and k=5 for each distribution. We also obtained one set of weights for each k for the four chosen distributions. In section 6, to see the effect of increasing skewness, the relative precisions of estimators for lognormal family of distributions have been compared. In section 7, we summarize the results with recommendations.

2. Estimation of Mean

We consider first the usual RSS to estimate the population mean. Let $y_{\left(ii\right)}, i=1,2,\dots ,k$ denote the value of characteristic under study of $i^{th}$ order statistic. The mean and variance of the $i^{th}$ rank order statistic for set size k are denoted by ${\mu }_{\left(ii\right)}$ and ${\sigma }_{\left(ii\right)}^2$, respectively. We denote the population mean and variance by $\mu$ and ${\sigma }^2$, respectively. Then the unbiased estimator for $\mu$ based on RSS is given by

$$\overline{\mu }=\frac{1}{k}{{\displaystyle \sum }}_{i=1}^k{y}_{\left(ii\right)},$$

with the variance

$$Var\left(\overline{\mu }\right)=\frac{1}{k^2}{{\displaystyle \sum }}_{i=1}^k{\sigma }_{\left(ii\right)}^2.$$

The relative precision of $\overline{\mu }$ compared to the estimator based on SRS with the same number of observations k (Bhoj and Chandra, 2019) is

$$R{P}_1=\frac{{\sigma }^2}{\overline{{\sigma }^2}},$$

(2.1)

where $\overline{{\sigma }^2}=\frac{1}{k}{{\displaystyle \sum }}_{i=1}^k{\sigma }_{\left(ii\right)}^2$ is the average within-rank variance.

For the skewed distribution, Neyman’s allocation $m_i=\frac{n{\sigma }_{\left(ii\right)}}{{{\displaystyle \sum }}_{i=1}^k{\sigma }_{\left(ii\right)}}$ provides the optimal allocation and the relative precision of the unbiased estimator of $\mu$ based on this model with respect of SRS with the same number of observations n and is given by (Bhoj and Chandra, 2019).

$$R{P}_3=\frac{{\sigma }^2}{{\overline{\sigma }}^2},$$

(2.2)

where, $\overline{\sigma }=\frac{1}{k}{{\displaystyle \sum }}_{i=1}^k{\sigma }_{\left(ii\right)}$is the average within-rank standard deviation.

There are some unequal allocation models for the skew distributions in the literature (see, ‘t’ and ‘s, t’ model (Kaur et al., 1997); Systematic model (Tiwari and Chandra, 2011) and simple model (Chandra et al., 2018 and Bhoj and Chandra, 2019)). The Neyman’s allocation does not provide the integer values of $m_i$ which are necessary for any application. The procedure of making them integer is shown in Bhoj and Chandra (2019) and used in this paper. It is noted that the inequality $R{P}_3>R{P}_1$ always holds for the skew distributions.

3. WRSS with One Optimal Weight

In this section, we propose a weighted ranked set sampling (WRSS) with the optimal weight for the largest order statistic since the largest order statistic has the highest variance and higher bias of the estimator for the mean when we deal with the positively skew distributions. We define that the weights $w_i$ $\left(with 0\le w_i\le 1 and {{\displaystyle \sum }}_{i=1}^k{w}_i=1\right)$ as,

$$w_i\propto 1,\mathrm{for}i=1, 2, \dots ,k-1$$

$$w_k\propto \frac{1}{C_k},$$

The exact values of weights are proposed as follows:

$$w_i=\frac{1}{\left(k-1\right)+\frac{1}{C_k}},\mathrm{for}i=1, 2, \dots ,k-1,$$

$$w_k=\frac{1}{C_k\left(\left(k-1\right)+\frac{1}{C_k}\right)}$$

Our weighted estimator for the population mean $\mu$ is

$${\overline{\mu }}_{W_1}={{\displaystyle \sum }}_{i=1}^k{w}_i{y}_{\left(ii\right)},$$

(3.1)

The relative precision of our biased estimator ${\overline{\mu }}_{W_1}$with respect to the estimator based on SRS is

$$R{P}_2=\frac{{\sigma }^2{\left[1+C_k\left(k-1\right)\right]}^2}{k\left[C_k^2{{\displaystyle \sum }}_{i=1}^{k-1}{\sigma }_{\left(ii\right)}^2+{\sigma }_{\left(kk\right)}^2+{\left\{\mu \left(1+C_k\left(k-1\right)\right)-C_k{{\displaystyle \sum }}_{i=1}^{k-1}{\mu }_{\left(ii\right)}-{\mu }_{\left(kk\right)}\right\}}^2\right]}$$

(3.2)

The value of $C_k$ is to be chosen such that the $R{P}_2$ is maximum. To find the optimum value of $C_k$ (for each k), the excel program of $R{P}_2$ was developed and using the different iterations on $C_k$, the values of $R{P}_2$ was tested until it gets maximum. All the other values above and below from this optimal $C_k$, $R{P}_2$ starts decreasing.

We computed $C_k$ for all four chosen distributions lognormal (LN(0, 1)), Pareto (P(3.5) and P(4.5)) and Weibull (W(0.5)) and k=2(1)5. The values of $R{P}_2$, $C_k$, $R{P}_3$ and $R{P}_1$ for these distributions and k=2(1)5 are presented in Table 1. The values of $R{P}_2$ are much higher than $R{P}_1$, i.e., the relative precisions of the estimator based on RSS procedure. Furthermore, the $R{P}_2$ are higher than $R{P}_3$, i.e., those based on Neyman’s optimal allocation model for all four distributions when $k\le 4$. All relative precisions increase as k increases for LN(0,1), P(3.5) and P(4.5). However, for W(0.5), $R{P}_2$ decreases as k increases. This may be because the distribution W(0.5) has extremely large skewness and kurtosis.

Now we attempt to compute one set of values of $C_k$ for four values of sample sizes, which will work well for all chosen four distributions. In these computations, $C_k$ was determined so that the sum of $R{P}_2$ for the four distributions is close to the maximum. This optimum value of $C_k$ was found using the same iteration procedure in the developed excel program.

The values of optimum $C_k$, and $R{P}_2$ for the chosen four distributions and four sample sizes are presented in Table 2. The values of $R{P}_2$ in Table 2 are slightly smaller than the ones in Table 1 as is expected. However, the pattern of $R{P}_2$ remained the same.

4. WRSS with Two Optimal Weights

In this Section, we propose a WRSS with two optimal weights for the two extreme order statistics. Here the weights $w_i$ $\left(with 0\le w_i\le 1 and {{\displaystyle \sum }}_{i=1}^k{w}_i=1\right)$ for k>2 are defined as

$$w_1\propto \frac{1}{C_1},$$

$$w_i\propto 1,\mathrm{for}i=2, 3, \dots ,k-1$$

$$w_k\propto \frac{1}{C_k},$$

The proposed exact weights are as follows:

$$w_1=\frac{1}{D{C}_1},$$

$$w_i=\frac{1}{D}, \mathrm{for}\mathrm{i}=2,3,\dots ,k-1$$

$$w_k=\frac{1}{D{C}_k},$$

where $D=\left(k-2\right)+\frac{1}{C_1}+\frac{1}{C_k}$.

Our estimator of population mean is

$${\overline{\mu }}_{W_2}={{\displaystyle \sum }}_{i=1}^k{w}_i{y}_{\left(ii\right)}$$

(4.1)

The relative precision of ${\overline{\mu }}_{W_2}$with respect to the estimator based on SRS is

$$R{P}_2=\frac{{\sigma }^2{D}^2}{k\left[{{\displaystyle \sum }}_{i=2}^{k-1}{\sigma }_{\left(ii\right)}^2+\frac{{\sigma }_{\left(11\right)}^2}{C_1^2}+\frac{{\sigma }_{\left(kk\right)}^2}{C_k^2}+{\left\{\mu D-{{\displaystyle \sum }}_{i=2}^{k-1}{\mu }_{\left(ii\right)}-\frac{{\mu }_{\left(11\right)}}{C_1}-\frac{{\mu }_{\left(kk\right)}}{C_k}\right\}}^2\right]}$$

(4.2)

We calculate the optimal values of $C_k$ and $C_1$ using the iteration method. Based on these values, we computed $R{P}_2$ along with $R{P}_1$ and $R{P}_3$for chosen four distributions and sample sizes k=3, 4 and 5 are presented in Table 3. The gains in precisions of the estimator ${\overline{\mu }}_{W_2}$ over ${\overline{\mu }}_{W_1}$ are marginal. The gains of $R{P}_2$ based on ${\overline{\mu }}_{W_2}$ are substantially higher than the estimator based on RSS. ${\overline{\mu }}_{W_2}$ is superior to the estimator based on Neyman’s optimal allocation model for all k for the LN(0,1) and P(3.5) distributions. The values of $R{P}_2$ are higher than those of $R{P}_3$ for the other two distributions for k=3 and 4. The gains of $R{P}_3$ over $R{P}_2$ for k=5 for these two distributions are marginal.

As we did in case of ${\overline{\mu }}_{W_1},$we attempt to compute one set of values of $C_k$ and $C_1$ for three values of sample sizes which will work well for all chosen four distributions. In these computations, $C_k$ and $C_1$ were determined so that the sum of relative precisions of ${\overline{\mu }}_{W_2}$ for the four distributions is close to the maximum relative precision. The values of $C_k$ and $C_1$, $R{P}_1$,$R{P}_2$and $R{P}_3$ for three sample sizes and four chosen distributions are presented in Table 4. The relative precisions of ${\overline{\mu }}_{W_2}$ in Table 4 are higher than those of ${\overline{\mu }}_{W_1}$for each k in Table 2. The pattern of relative precisions are same as seen in Table 3.

5. WRSS with All Optimal Weights

Now, we extend WRSS with optimal weights for all order statistics for k=4 and 5. We take $C=w_1+w_k$, and determine the optimal values of C and $w_k$ by minimizing MSE of the estimator by using $w_i\propto 1$, $\mathrm{for}i=2, \dots ,k-1$.

In the next step we use

$$w_i=\left(1-C\right)f_i,i=2, \dots ,k-1\mathrm{with}{\displaystyle \sum }_{i=2}^{k-1}{f}_i=1.$$

The values of $f_i$ are chosen so that the value of $R{P}_2$ is maximized. Then we repeat the procedure of computing the optimal values of C and $w_k$with these new $w_i\text{'}s$. The procedure is repeated until the value of $R{P}_2$ achieves the maximum value. We did this by using the developed computer program in Excel.

The values of $R{P}_2$ are presented in Table 5. We observe that the values of $R{P}_2$ presented in Table 4 are higher than the values of $R{P}_2$ based on one or two optimal weights which are given in Table 1 and Table 3.

As we did in section 3 and 4, we computed one set of values of C, $w_k$ and different fractions $f_i$ for k=4 and k=5 which work well for all chosen four distributions. In these computations, these values were determined so that the sum of $R{P}_2\text{'}s$ for the four distributions is close to the maximum relative precision. These values along with $R{P}_1$,$R{P}_2$and $R{P}_3$ for k=4 and k=5 and four chosen distributions are presented in Table 6. As we expected the values of $R{P}_2$ are smaller in Table 6 when compared to the values of $R{P}_2$ in Table 5. However, the pattern of relative precisions remains the same.

6. WRSS with Increasing Skewness

In this section, we wish to study the performance of the three methods, RSS, WRSS and Neyman’s optimum allocation model with increasing values of skewness of a family of distributions. For this purpose, the lognormal distribution, $LN\left(0,b\right)$ has been considered. The pdf of $LN\left(a,b\right)$ is given by

$$f\left(x\right)=\frac{1}{xb\sqrt{2\pi }}\exp \left[\frac{-1}{2}{\left(\frac{\log x-a}{b}\right)}^2\right],forx>0,a>0,b>0,\mathrm{with}\mathrm{population}\mathrm{mean}=\exp \left(a+{\frac{b}{2}}^2\right)\mathrm{and}\mathrm{variance}=\exp \left(2a+2b^2\right)-\exp \left(2a+b^2\right)$$

Then skewness (Sk) and shape parameter (p) are given by

$$Sk=\sqrt{{\beta }_1}=\sqrt{\exp \left(b^2\right)-1}\left(\exp \left(b^2\right)+2\right)$$

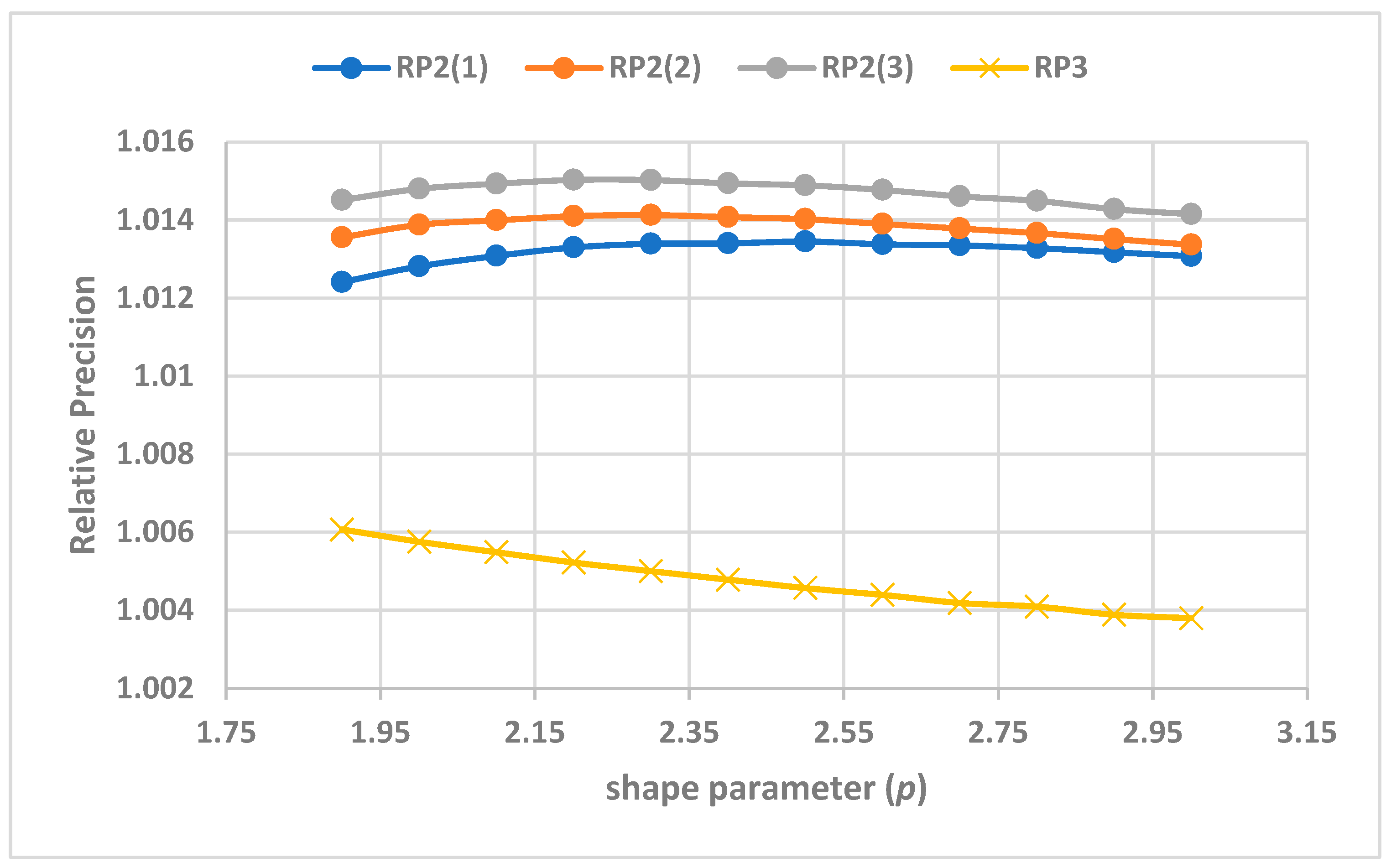
The performance of these three methods relative to SRS with k=4 is presented in Table 7 for lognormal family of distributions for a range of values of population standard deviation. The variances of the order statistics of the family of distributions were computed by using the variances of order statistics for different values of shape parameter (p) which are readily available in Balakrishnan and Chen (1999). From Table 7, we observe that as skewness increases the performance of (i) RSS method decreases, and (ii) Neyman’s and WRSS methods increases. The values of $R{P}_2$based on all and two optimal weights are higher than$R{P}_3$ for all values of shape parameters, However, $R{P}_2$based on one optimal weight is higher than $R{P}_3$ for all p>1.9. The rate of increase of relative precisions of the proposed estimators based on WRSS are more than that of estimator based on Neyman’s method (See Figure 1).

7. Conclusions and Discussion

In this paper, we proposed weighted ranked set sampling procedure to estimate the population mean of the distributions which are positively skew with heavy right tail. We chose four distributions: lognormal (LN(0, 1)), Pareto (P(3.5) and P(4.5)) and Weibull (W(0.5)). The means and variances of order statistics for these distributions are readily available in Harter and Balakrishnan (1996). We proposed three weighted ranked set sampling procedures. The first procedure is based on one optimal weight for the largest order statistics, the second procedure is to use the two optimal weights for the two extreme order statistics, and the third is the one which is based on k optimal weights. We calculated the relative precisions for each of these four distributions by using the WRSS procedure for each sample size. These relative precisions are much higher than the relative precisions of RSS estimator of mean. Furthermore, relative precisions of our estimators are higher than those which are based on Neyman’s optimal procedures for $k\le 4$. The relative precisions of our estimator are even higher than Neyman’s procedure for k=5 for some distributions. Furthermore, we attempted to compute one set of weight(s) for each k for all the distributions and compared the relative precisions of our estimator with those of RSS and Neyman’s estimators. Although there is slight loss in the values of relative precisions, they are still higher than those of Neyman’s model for $k\le 4$ for all four distributions and either more than or very close to Neyman’s model for k=5. In general, as is expected, the relative precisions of our estimator based on all optimal weights are higher than the relative precisions of our estimator based on two and one optimal weight(s). The gain in relative precisions is however marginal.

We studied the performance of our proposed estimators for increasing skewness of a family of lognormal distributions. The relative precision of our estimator based on one optimal weight is higher than those of Neyman’s estimator when the shape parameter exceeds 1.9. The relative precisions of our estimator based on two and k optimal weights is uniformly higher than those of Neyman’s estimator for all values of shape parameter considered in Table 7. From Figure 1, we see that with the increasing values of skewness, the rate of increase of relative precisions of our proposed estimators based on WRSS are more than that of estimator based on Neyman’s method.

Based on the numerical computations of relative precisions, we recommend our estimator based on WRSS procedures for estimator of population mean of skew distributions with heavy right tail for small values of set sizes.