Prerpints.org logo
Preprint
Article

A Proposal to Change the Leap-Second Adjustments to UTC

Altmetrics

Downloads

170

Views

81

Comments

0

This version is not peer-reviewed

Submitted:

01 June 2024

Posted:

03 June 2024

You are already at the latest version

Alerts
Abstract
The definition of UTC in 1972 balanced the needs of the time and frequency community for a universal time scale that was traceable to the definition of frequency in the SI system of units with the needs of the astronomical community for a time scale that was closely linked to UT1, a time scale related to the rotation of Earth. The balance between these two considerations has changed very significantly since 1972, and there is widespread agreement that the method of relating UTC to UT1 should be changed by increasing the maximum tolerance between the two scales to more than the current limit of 0.9 s. I propose to realize this decision by means of an algorithmic adjustment process based on the variation in the length of the day over the previous centuries. I use these historical data to extrapolate the length of the day for a century into the future, and to compute a periodic rate adjustment to UTC based on this extrapolation. The adjustment process will not use time steps. The magnitude of the periodic rate adjustment will be re-considered every century, but the basic adjustment algorithm will not change. I suggest a maximum tolerance between UT1 and UTC that is large enough to absorb the irregular and unpredictable variations in the length of the day with respect to the long-term average increase in this value but plays no role in determining the parameters of the adjustment process that is proposed. I also propose that the adjustment be implemented at 12 UTC on 1 January since that is closest to a universal holiday in all time zones.
Keywords: 
Subject: Physical Sciences  -   Atomic and Molecular Physics

Introduction

1. UTC and UT1

The international reference time scale is Coordinated Universal Time (UTC). It is computed by the International Bureau of Weights and Measures (BIPM) using data from atomic clocks maintained in more than 80 institutions. The rate of this time scale is adjusted by using data from primary frequency standards, and the resulting time scale is International Atomic Time, TAI. Since 1972, the UTC time scale is derived from TAI by adding “leap seconds” as needed so that the magnitude of the difference between UTC and UT1, a time scale based on the rotation of Earth, is not greater than 0.9 s. The difference between UTC and TAI is an exact integral number of seconds, and the two scales are equivalent otherwise. [1,2] The difference between UTC and UT1 is monitored by the International Earth Rotation and Reference Service (IERS), and this organization publishes this difference periodically and also announces the need for a leap second several months in advance. [3] Thirty-seven leap seconds have been added to UTC with respect to TAI since 1972 (ten seconds were added when the current definition of UTC was initialized in 1972, and the remaining 27 seconds have been added since that time). The most recent leap second was added at the end of 2016.
The definition of UTC in 1972 balanced the needs of the time and frequency community for a universal time scale that was traceable to the definition of frequency in the SI system of units with the needs of the astronomical community for a time scale that was closely linked to UT1. The balance between these two considerations has changed very significantly since 1972, and discussions to change the method of linking UT1 and UTC have been ongoing since 1999. There is general agreement that the current leap-second method is increasingly problematic, and that the method of adjusting UTC should be modified by increasing the maximum tolerances between UT1 and UTC. [4]
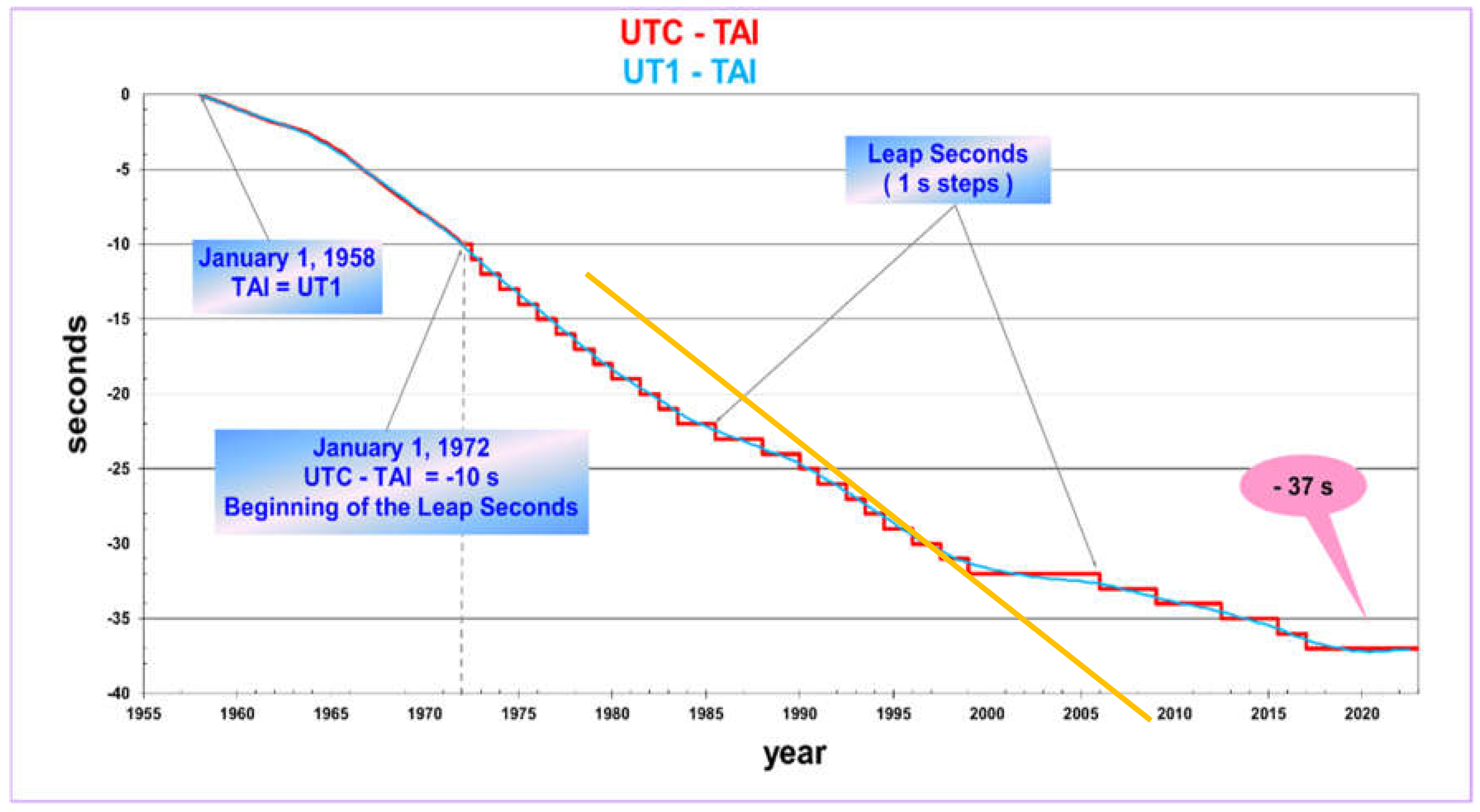
The rate of UTC has been systematically greater than the rate of UT1 for many years, and only positive leap seconds have been added up until now. See Fig. 1, which displays UT1 and UTC with leap seconds inserted with respect to TAI. (The UTC time scale was adjusted by using both frequency adjustments and time steps from 1958 to 1972.)
Preprints 108132 g001
Figure 1. The difference UT1-TAI (blue) and UTC-TAI (red) from 1958 to the present. The time steps in UTC are the leap second adjustments. The positive leap second is an extra second that is inserted into the UTC time scale, which slows its advance relative to TAI and UT1. The yellow line shows the evolution of UT1-TAI that would result from a rate of -1.0 s/year, which was typical for the 13 years following 1972.
Figure 1. The difference UT1-TAI (blue) and UTC-TAI (red) from 1958 to the present. The time steps in UTC are the leap second adjustments. The positive leap second is an extra second that is inserted into the UTC time scale, which slows its advance relative to TAI and UT1. The yellow line shows the evolution of UT1-TAI that would result from a rate of -1.0 s/year, which was typical for the 13 years following 1972.
Preprints 108132 g001
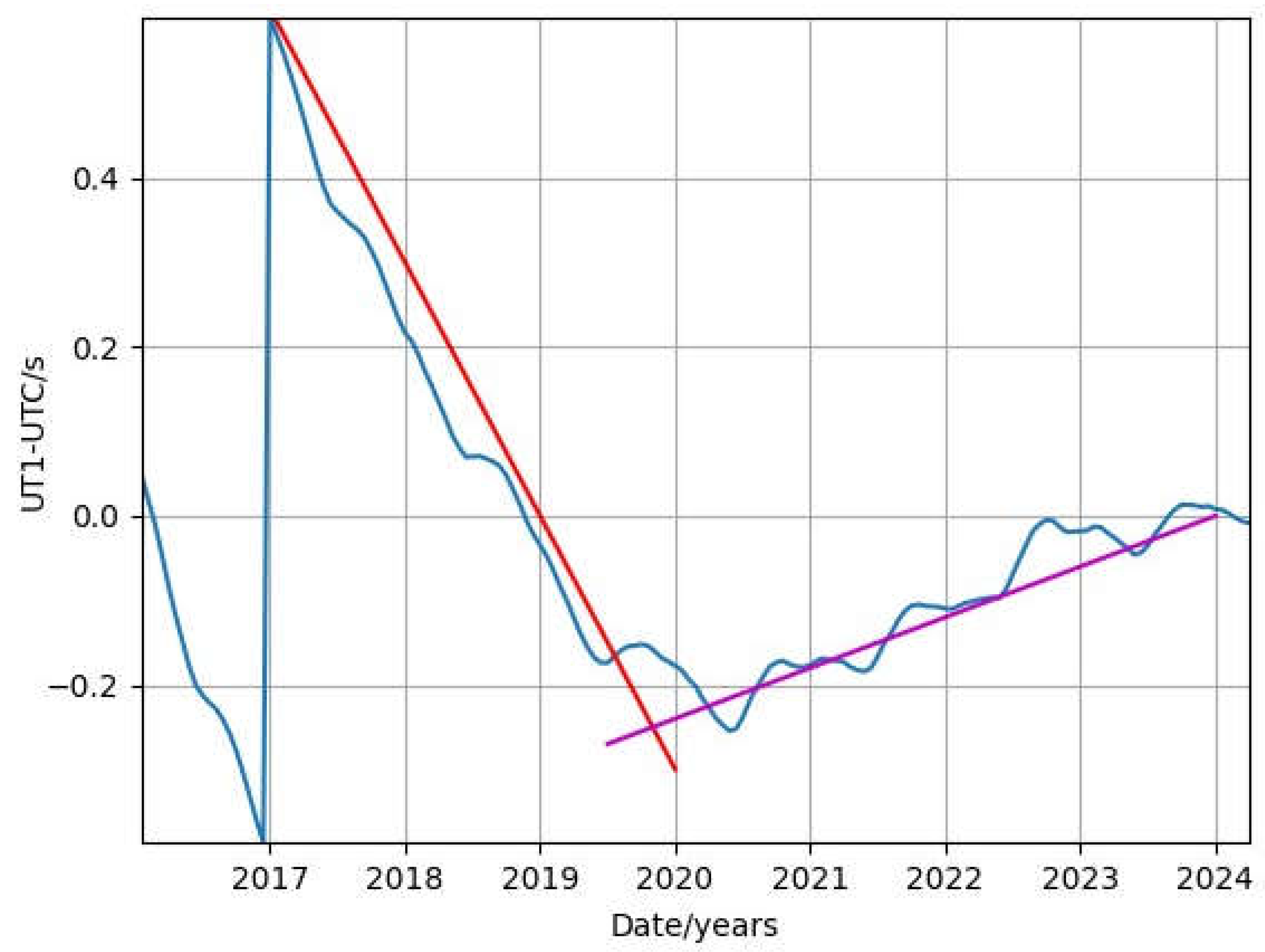
The effect of the positive leap second is to slow the advance of UTC so that UT1 time can catch up. However, the rotation rate of Earth has been increasing in the last few years, so that the difference, UT1-UTC, which has been negative since November, 2018, is increasing and crossed zero in August, 2023. [3] See fig. 2, which shows UT1-UTC from 2016 to April, 2024, including the leap second at the end of 2016.. [3]
Preprints 108132 g002
Figure 2. The blue curve shows UT1-UTC from 2016 to April, 2024. A positive leap second was added at the end of 2016. The red line shows the differences that would result from a constant rate of -0.3 s/year, and the magenta line shows the differences that would result from a constant rate of +0.06 s/year.
Figure 2. The blue curve shows UT1-UTC from 2016 to April, 2024. A positive leap second was added at the end of 2016. The red line shows the differences that would result from a constant rate of -0.3 s/year, and the magenta line shows the differences that would result from a constant rate of +0.06 s/year.
Preprints 108132 g002
If this trend continues, UT1-UTC will become increasingly positive, and a negative leap second may be needed when the integrated difference of UT1-UTC approaches +0.9 s in about 2030.
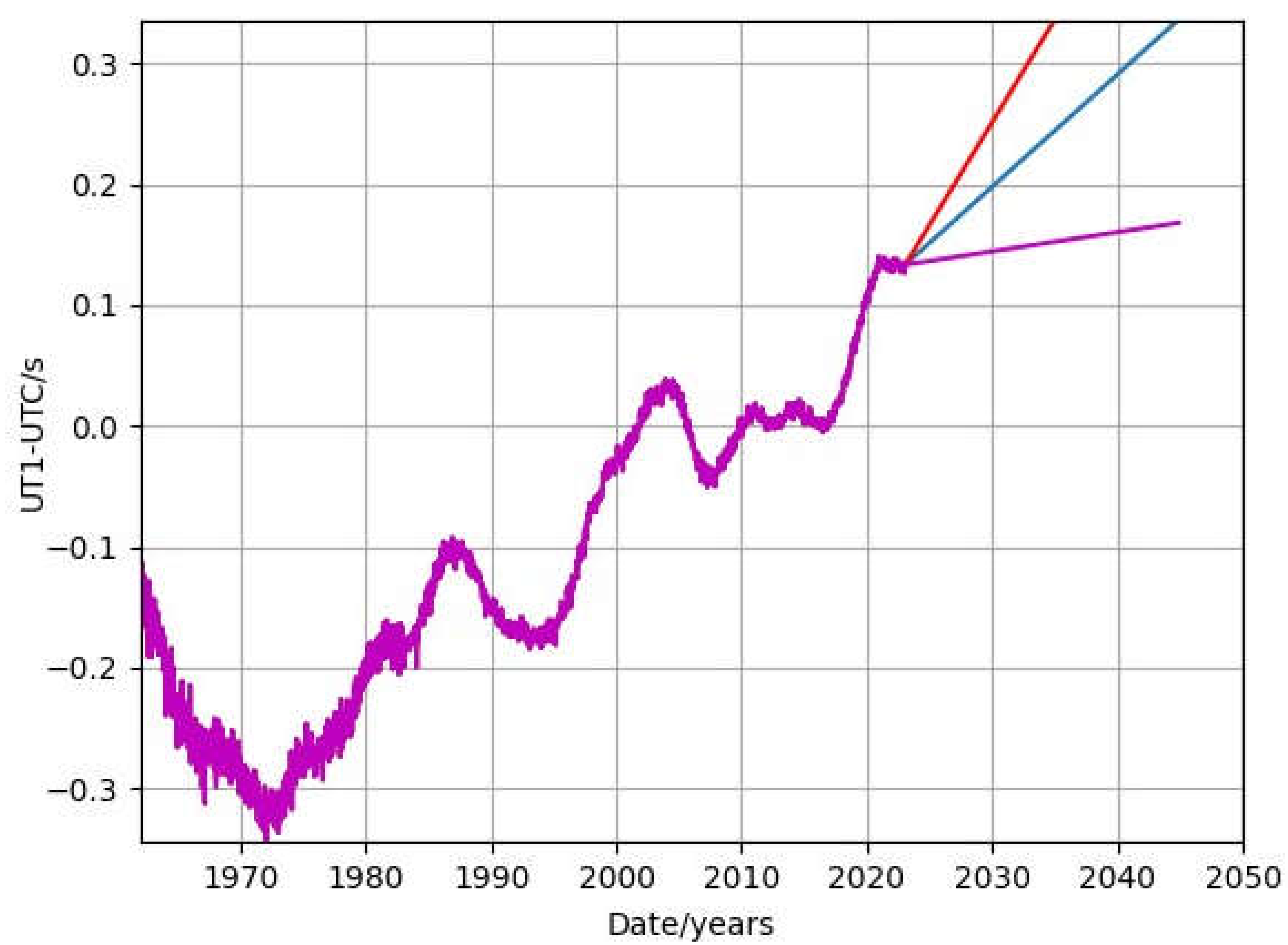
Agnew [5] discusses the geophysical effects that contribute to variations in UT1. Fig. 3, adapted from fig. 2c in that report includes an extrapolation of UT1-UTC. The data in the reference have been converted to seconds and the sense of the plot has been inverted. The thicker purple line shows the residual, unmodeled difference between UT1 and UTC from 1962 to 2024, and the thinner lines show extrapolations based on the data to that point (blue) and computed based on data ± 2σ (red and purple, respectively). The extrapolations predict that UT1-UTC will increase by 0.09 +0.086 -0.074 s/year starting in 2024. If the rate of change of 0.09 s/year continues, then negative leap second will be needed in about the year 2029. The extrapolation shown in fig. 2, which is based solely on the data without the geophysical context, is consistent with this prediction.
As will be discussed below, the current decision is that there will be no change to the current method of inserting leap seconds before 2035. Both of these analyses suggest that there is a significant probability that a negative leap second will be required before then.
Preprints 108132 g003
Figure 3. adapted from Agnew [5]. The data in that report have been converted from fractional angular speed to time and the sense of the plot has been inverted to conform to the rest of this text. The thicker line shows the residual data from 1962 to the present and the thinner lines show an extrapolation of UT1-UTC based on the previous data (blue) and the previous data ±2σ (red and purple, respectively).
Figure 3. adapted from Agnew [5]. The data in that report have been converted from fractional angular speed to time and the sense of the plot has been inverted to conform to the rest of this text. The thicker line shows the residual data from 1962 to the present and the thinner lines show an extrapolation of UT1-UTC based on the previous data (blue) and the previous data ±2σ (red and purple, respectively).
Preprints 108132 g003
The extrapolation that predicts the need for a negative leap second has a large uncertainty, so that the need for a negative leap second should be considered as something that might happen rather than something that will definitely happen. There is some indication that the rate of increase of UT1-UTC is smaller than either of the previous estimates. The most recent prediction of the IERS [3, Bulletin A, 23 May 2024] is that UT1-UTC will increase by only 28 ms until May 2025. This is close to the minimum rate deduced from the data in fig. 3. (Also, see Method and Results sections.) Although the probability that a negative leap second will be needed cannot be accurately predicted, it will have very serious consequences should it be required because this possibility has never occurred before so that the method of applying a negative leap second has never been tested.

2. UTC and the ITU

In 1972, the Radio Communications Sector of the International Telecommunications Union (ITU-R) recommended the transmission code that should be used to transmit the difference between UT1 and UTC, ITU-R TF.460-6 [6]. The difference, DUT1, is published by the IERS with a resolution of 0.1 s in Bulletin D [3] and is transmitted by many radio time-services.
A draft revision of Recommendation ITU-R TF.460-6 was reviewed by the Radiocommunication Assembly 2012 (RA-12), and RA-12 decided to postpone the decision and consider an agenda item on this topic for the World Radio Conference in 2015 (WRC-15). WRC-15 adopted agenda item 1.14 and the ITU-R was invited to carry out the relevant studies in accordance with Resolution 653 (WRC-12). [7]
WRC-15 agreed to Resolution 655 (WRC-15) [8] that resolves to study the issue more widely in cooperation with the relevant international organizations. It also instructs the Director of the Radiocommunications Bureau (BR) to report on the progress of the studies to the World Radiocommunication Conference 2023 (WRC-23), and that there should be no change to the method of adjusting UTC until the question is considered by WRC-23.
The UTC question was referred to ITU-R Study Group 7 and Working Party 7A, and they prepared a report for the BR, which was presented by the BR to WRC-23. WRC-23 resolved to amend resolution 655, and the revised resolution is included in the report of the conference. [9]. The amended version of resolution 655 resolves that the ITU-R collaborate with the BIPM to define a new maximum value for the difference between UT1 and UTC, and that the maximum value should be not less than 100 s. The choice of this limit is not explained, and the details of the method for realizing the changed relationship between UT1 and UTC and the required changes to the broadcast format that is currently specified in ITU-R TF.460-6 are not specified. Since the resolution specifies a maximum tolerance for the difference between UT1 and UTC, the resolution implicitly assumes that a link between UT1 and UTC should be maintained in some form.

3. UTC and the BIPM

The BIPM had extensive discussions on the topic, and the results of these discussions were formulated in resolutions that were considered by the General Conference on Weights and Measures (CGPM), the governing body of the BIPM.
At its 26th meeting in 2018 the CGPM stated that [10]
“UTC is a time scale produced by the BIPM with the same rate as TAI, but differing from TAI only by an integral number of seconds” and“UTC is the only recommended time scale for international reference and is the basis of civil time in most countries”. And “all relevant unions and organizations work together to develop a common understanding on reference time scales, their realization and dissemination with a view to consider the present limitation on the maximum magnitude of UT1 – UTC, so as to meet the needs of the current and future user communities”.
The relationship between the ITU and the BIPM with regards to the definition of UTC was clarified by a Memorandum of Understanding in 2020 [11], which explained that The ITU-R set standards concerning time signals and frequency standard emissions, protocols, and dissemination procedure The BIPM defines and realizes measurement standards and reference time-scales
Resolution 4 of the CGPM meeting of 2022 [12] resolved that the maximum value for the difference (UT1-UTC) will be increased in, or before, 2035, and requests that the CIPM[1] consult with the ITU, and other organizations that may be impacted by this decision in order to propose a new maximum value for the difference (UT1-UTC) that will ensure the continuity of UTC for at least a century, and prepare a plan to implement by, or before, 2035 the proposed new maximum value for the difference (UT1-UTC), The ITU and BIPM resolutions agree that the maximum difference between UT1 and UTC should be increased. Since both resolutions mention a maximum tolerance for the difference between UT1 and UTC, they both implicitly assume that a link between UT1 and UTC should be maintained.
The resolutions of both the BIPM and the ITU do not capture the lengthy discussions about the future relationship between UT1 and UTC, which have been ongoing for more than 20 years. An important aspect of these discussions is that it is important to maintain a link between UT1 and UTC because time and time interval have been related to astronomy since antiquity, and completely removing this link is likely to face opposition in principle, even if the difference between the two time scales was not large at the start. [14,15] The implicit assumption that a link between UT1 and UTC should be maintained is important.
The ITU resolution includes a suggestion for a maximum tolerance not less than 100 s, and the BIPM resolution stipulates that the new maximum value should ensure the continuity of UTC for at least a century. The next sections present specific proposals that could satisfy these resolutions. We also present other considerations, which are important in constraining the solution.

Method

The resolution of the BIPM presented in the previous section requires a new maximum tolerance that will ensure a continuous UTC for at least a century, and the first step is to understand how this requirement constrains the adjustment process to maintain the link between UT1 and UTC.
The method proposed in the text estimates the variation in the length of the day for the next century by extrapolating the variation in the length of the day over the previous centuries. This extrapolation is based on the long-term variation in the length of the day to attenuate the uncertainty and the short-term variations in the evolution of UT1-UTC that we discussed in the previous section. It uses these long-term data to construct an algorithmic adjustment process that uses only periodic rate adjustments to UTC that are derived from the average increase in the length of the day over centuries. The procedure does not use time steps and is continuous and monotonic.
In addition, the historical deviations in the length of the day from a constant rate of change are used to estimate a maximum tolerance between UT1 and UTC, which must be large enough to absorb these irregular and unpredictable changes, which can persist for many years, without requiring a change to the constant algorithmic adjustments.

Results

1. The Short-Term Variation in UT1

The data presented in fig. 1 show that the difference between UT1 and TAI changed by -37 s in the 59 years from 1958 to 2017, and that this difference has been applied to UTC by the leap second process. If this long-term trend in the evolution of UT1-TAI were to continue for 41 more years, the difference between UT1 and TAI would be predicted to be about -63 s a century (-0.63 s/yr) after 1958. The ITU and BIPM resolutions would both have been satisfied by having made no leap-second adjustments to UTC from 1958 to 2024 and continuing to do nothing until 2058. If this trend were to continue after 2058, then the difference between UT1 and UTC would increase by about one minute per century. If the maximum tolerance was set to 100 s to conform to the ITU resolution, then this extrapolation would predict that a leap event would occur approximately every 160 years, and the next leap event would be in the year 2176 (2016 + 160).
This extrapolation has very significant uncertainties because the rate of change of UT1-TAI varies. The yellow line in fig. 1 shows that the rate was about -1.0 s/year for the years immediately after 1972, and fig. 2 shows that the rate was much smaller following 2016, and that it changed sign in about 2020. (The change in sign is what has prompted the concern for the possibility that a negative leap second would be needed in the future.) This variability in the rate of UT1-TAI introduces significant uncertainties into any extrapolation based on the relatively short data span from 1958 to 2024. It is important to examine the longer-term variation in the length of the day to construct an adjustment process that is algorithmic in the long term and is not sensitive to these short-term variations. This proposed solution is designed to address a weakness with the current adjust process that the interval between adjustments is irregular and unpredictable.

2. The Long-Term Variation in UT1

There are three aspects to this longer-term variation: (1) a steady deceleration, (2) random fluctuations, and (3) periodic effects. [16]. Studies by Stephenson and Morrison [17,18] imply an average rate of increase in the length of the day of 1.7 ms/cy. This increase in the length of the day includes an increase due to tidal friction of about 2.3 ms/cy and a decrease of -0.6 ms/cy due to the change in the moment of inertia of Earth. The periodic effects have a peak-to-peak amplitude of order 60 ms, [18] and are not large enough to be important in this discussion because they do not affect the long-term variation.
There is significant variability in the estimates of the long-term increase in the length of the day because the irregular variations are large and last for many years and a simple linear fit to the data does not capture them. However, the estimates all agree that the long-term length of the day has been increasing for centuries, and there is no reason to assume that this long-term behavior will change.
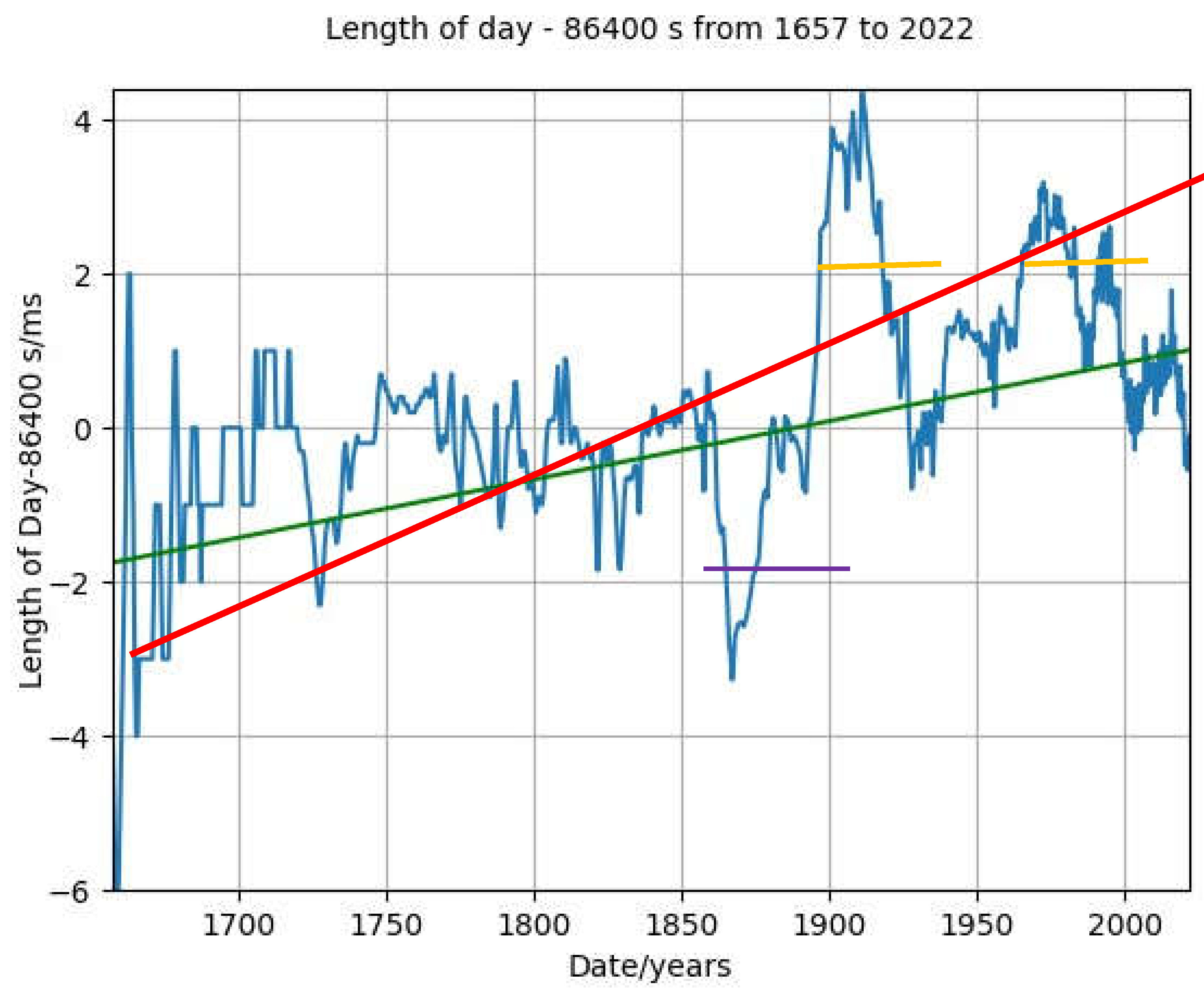
Figure 4 shows the variation in the length of the day over the last 4 centuries. [17].
The red line shows the effect of the Stephenson and Morrison rate of 1.7 ms/cy; the green line shows a constant slope of 0.76 (±0.1, 1 σ) ms/cy, which is more consistent with the data in a least-squares sense. However, there are deviations from this smaller constant rate that limit the accuracy and reliability of long-term predictions, and account for the variation in the different estimates of the long-term rate of change. Although the different linear models of the length of the day vary somewhat, all of them agree that the length of the UT1 day was 86 400 s in about 1830 (± 10 years) and that the UT1 day in 2022 was significantly longer by at least 1 ms.
The constant increase in the length of the day implies a quadratic variation in the UT1 time relative to a uniform time scale. Stephenson and Morrison [17, p.188] show that the variation in the UT1 time scale over the last 2700 years can be expressed by
∆ T = R T 2 − 20   s
where the drift, R, is 31 s/cy2 and the elapsed time, T, is in centuries from 1820. The time difference, ΔT, is in s. They caution that no single quadratic expression can satisfactorily represent both modern and historical data. [16, also, fig. 1 and fig. 2 of 19].
For example, eq. 1 predicts that the difference between UT1 and atomic time would have been 39.036 s in 1958, the origin epoch of TAI, whereas the actual value was 32.184 s, which suggests a smaller average long-term rate of about 27 s/cy2. If we use R=31 s/cy2, Eq. 1 predicts that the difference between UT1 and atomic time would have increased by about 60 s from 1958 to the end of 2016, when the most recent leap second was added, but the actual increase was only 37 s. From eq. 1, the observed increase of 69 s (32 s + 37 s) from 1820 to 2017 is consistent with an even smaller average rate, R, of about 23 s/cy2. If we include the 7 years from 2017 to 2024 in the previous calculation, then the long-term rate is closer to 21 s/cy2. The much smaller estimate of the long-term rate results from including the very much smaller variation in UT1-TAI since 2017, which may be an anomalous event and may not indicate a change in the long-term rate.
Other analyses also conclude that the Stephen and Morrison value of 1.7 ms/cy2 is too large. For example, McCarthy and Babcock [19] estimate that the increase in the length of the day is 0.73 ms/cy, which is in good agreement with the simple least-squares fit to the data in fig. 4 discussed above. Maeder and Gueorguiv [20] estimate at rate of 1.09 ms/cy based on observations of lunar occultations. They also present the rate estimates based on various other methods [20, table 2] The smaller estimate of McCarthy and Babcock gives a value of R of about 13 s/cy2 [19, eq. 11] which is somewhat smaller than the value estimated above based on contemporary data. Although the magnitudes of the various estimates are different, all of them agree that the long-term variation in the length of the day is positive, and there is no suggestion that the long-term rate will change sign, with the caution that deviations from the long-term rate are not rare and often persist for many years.
The differences in the different predictions of the evolution of UT1-UTC over a century are of order tens of seconds, which are much smaller than the proposed maximum tolerance of at least 100 s mentioned in the ITU resolution. Therefore, the actual rate used in the following discussion is arbitrary and is likely to disagree with the actual evolution of UT1-UTC over the next century.
If we arbitrarily assume that the long-term variation in UT1 given by eq. 1 will continue with R = 23 s/cy2, then eq. 1 predicts that the difference between UT1 and TAI will be about -160 s in 2100 and -312 s in 2200 relative to 1820, with the cautions that other analyses suggest that this rate is too large, and that the stochastic variations in the length of the day are significant and may persist for many years. Therefore, these estimates have significant uncertainties. For example, the decrease in the length of the day of about 2ms, which was not consistent with the long-period variation, and which persisted for about 30 years (purple line, fig. 4) changed UT1-TAI by about -0.002 s × 365.25 ×30= -22 s.
In the next sections, a solution is proposed that adjusts UTC relative to TAI to match the predicted long-term evolution of UT1-TAI, with a tolerance between UTC and UT1 that is sufficiently large so that UT1-UTC does not exceed the tolerance even if the length of the UT1 day has variations that are comparable to those that have been observed in the historical record (fig. 4). In addition, the solution addresses other problems with the current leap-second adjustment procedure.

3. Algorithmic Adjustments

A serious deficiency in the current method of adding leap seconds to UTC is that the leap seconds are added at irregular and unpredictable intervals, and this causes many problems that were documented in a previous publication. [4]
The solution to the unpredictable and irregular interval between leap events is to choose a maximum tolerance for the difference between UT1 and UTC and then implement an algorithmic process that uses regular and predictable adjustments that are a fraction of this maximum tolerance. This hides the unavoidable impossibility of designing an algorithmic process to correct for the irregular and unpredictable variation in UT1- UTC.
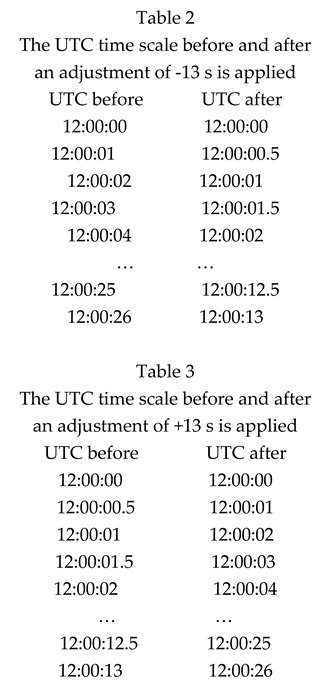
The previous discussion predicts that UT1-TAI = -160 s in 2100 (relative to 1820), so that UTC must be adjusted by an additional -91 s (-160 + 69) by that date. Instead of waiting until 2100 to make this adjustment, we could make a smaller adjustment of -13 s every 10 years on 1 January starting in 2035, the date specified in the BIPM resolution. The details are shown in Table 1.
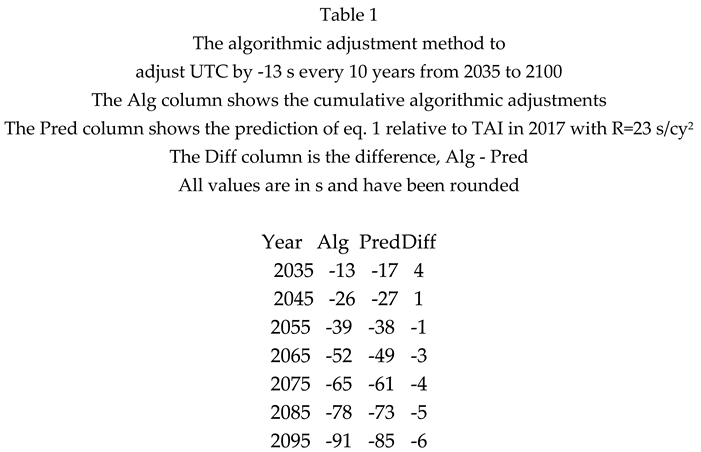
Preprints 108132 i001
The largest deviations from a constant increase in the length of the day from 1657 to the present was about -2 ms/day in about 1860 and about +2 ms/day in about 1900(Fig. 3). If those rates persisted for 40 years, and if the algorithm were not modified to compensate for them, they would modify the predicted value of UT1-TAI by about ±0.002×365.25×40 = ±30 s. If the maximum tolerance between UT1 and UTC were chosen to be 100 s, and if the algorithmic method were used to adjust UTC, the resulting UTC time scale would differ from the prediction of the long-term quadratic variation (eq. 1) by significantly less than the maximum tolerance of 100 s even if the largest deviation from the linear trend in fig. 4 were to occur and persist for longer than has ever happened.
The algorithmic adjustment principle does not tightly constrain the constant interval between adjustments. Any adjustment process introduces a burden on the timekeeping community, and this burden would be minimized with a long interval between adjustments. On the other hand, the method depends on the assumption that the adjustment is much smaller than the maximum tolerance to maximize the capacity of the tolerance to absorb a change in the length of the day that deviates from the long-term average and persists for an appreciable number of years. This consideration favors a shorter interval between adjustments. Finally, there is a programming advantage to having an adjustment that occurs predictably and algorithmically. For example, in every year with the same least-significant digit. These considerations suggest (but do not uniquely specify) an interval of 10 years, starting from 2035, the year mentioned in the BIPM resolution.
If the algorithmic adjustment process was adopted, the magnitude of the maximum tolerance is not critical since it is very unlikely that the difference between UT1 and UTC would ever reach it. It must only be large enough to absorb the impact of the largest deviation of the rate of evolution of UT1 that has been observed in the historical record without requiring a change to the long-term rate, R for at least a century. Any value larger than 60 s would be adequate in this situation.
The algorithmic method would be modified in 2100 by adjusting the R parameter in eq. 1 to compensate UTC for the predicted evolution of UT1-TAI from 2100 to 2200. The modified adjustment would be based on both the historical data and the additional observations of the length of the day from now until 2100; it would also add a term that would amortize the difference between the algorithmic adjustments that had been applied to UTC between now and 2100 and the actual value of UT1-UTC in 2100.
With no change in the value of R, the discussion above predicts a change of -152 s in the century starting in 2100 relative to 1820, and this prediction would be amortized in ten equal installments of -15 s in 2105, 2115, … 2185, 2195. This calculation is only for illustrative purposes. It is very unlikely that this magnitude would actually be used starting in 2100. The magnitude of each installment would be decided in 2100 based on an updated prediction equation and might also include an additional adjustment to compensate for the difference between the evolution of the difference between UT1 and UTC that is predicted now and what happens to the difference between 2035 and 2100. The magnitude would remain constant for the century.
The algorithmic method would be implemented once; the magnitude of the periodic adjustment might need to be changed once per century, but the algorithm itself would not be altered.

4. The Adjustment Process

The previous discussion presented an algorithmic method for adjusting UTC to maintain a connection between UTC and UT1. There are two additional considerations that will specify when and how the adjustments should be made.
a. The time for a UTC adjustment
The adjustment for a leap second is now at 23:59:59 UTC, which is an awkward time in the Pacific time zone of the US (UTC-8), where it is late in the afternoon and in Asia and Australia, where it is the next morning (UTC + 10). In both cases, the adjustment time can be in the normal business day, which introduces extra complications in the commercial and financial applications that use UTC time stamps. Although there is no perfect way to avoid this problem, scheduling the leap adjustment at 12 UTC on 1 January would be a better alternative, because it is the closest thing to a universal holiday in all time zones, and many financial and commercial users of UTC time stamps are closed on that day.
b. The process of applying the adjustment
The adjustment process should implement the leap event by using an internationally defined and universally adopted adjustment to the rate of advance of the clock rather than a time step [21], so that UTC is continuous, the time stamps are monotonically increasing, and the time-ordering of events can be unambiguously determined both before, during, and after the leap event. In addition, the adjustment to the rate of advance of UTC should be digitally-defined so that it can be easily removed by a user either in hardware or in software to recover the unmodified time scale. (Compare the adjustment method described in [22], which does not satisfy this requirement.)
An adjustment to the rate of advance of exactly a factor of 2 is particularly easy to apply and to remove either in hardware or in software, and this method is illustrated in the following text by using timestamps that advance every second. The actual adjustment process would be the same for time stamps that are specified at any resolution.
For example, table 2 shows the details of the adjustment of -13 s that would be used every 10 years from 2035 to 2095 as described in table 1. This table illustrates the adjustment method. The magnitude used at each step would be chosen to amortize the adjustment over an interval twice as long as the adjustment for a positive adjustment.
The discussion in the previous sections concluded that a negative leap adjustment will never be required because of the long-term increase in the length of the day and because the maximum tolerance of the difference between UT1 and UTC will absorb the shorter-term decreases without requiring an explicit adjustment. Nevertheless, it is straightforward to describe the method that would be used to insert a negative adjustment to UTC by an increase in the rate of the advance of the clock by a factor of 2. See Table 3, which also illustrates how a positive leap adjustment could be removed by a user should it be necessary or desirable to do this.
The entries in the tables are tabulated at 1 s intervals, but the actual adjustments could be implemented with a shorter-period signal, such as a period of 200 ns (frequency of 5 MHz). The adjustment method does not constrain the method of implementing it. This input signal would be divided by a factor of 2 for a positive adjustment or multiplied by a factor of 2 for a negative adjustment. These operations could be implemented by using well-known analog or digital methods, and the “ticks” of the modified signal would be used to advance the time.
Preprints 108132 i002

Discussion

The resolutions of the ITU and the BIPM recognize the consensus that there are serious problems with the current method of linking UTC to UT1. The method proposed here is a significant improvement over the current leap-second adjustment process and is even better than simply increasing the tolerance between UT1 and UTC because simply increasing the tolerance would not address the other weaknesses of the current process.
The method replaces the error-prone and irregular method of adding leap seconds on an ad-hoc basis with an algorithmic method that need be realized once and with an adjustment parameter that would change at most only once per century. The change would modify the method by changing the magnitude of the periodic adjustment but would not change the overall structure of the process.
The method uses a simple frequency adjustment process that can be implemented in a straightforward way either in hardware or in software. It does not use time steps and is therefore monotonic and always single-valued. It would assign a unique timestamp to all events. This avoids the difficulties and ambiguities with adjusting UTC by using time steps, no matter how the steps are realized. The frequency adjustments can be removed in a simple procedure either in hardware or in software if recovering the underlying TAI time scale is needed.
Applications that required an accurate knowledge of UT1-UTC would continue to use the data from the IERS, and it is important that these data be easily available. This would be important no matter what increase in the tolerance is adopted or how it is applied. However, applications with more modest needs could maintain the link between UT1 and UTC by realizing the algorithmic method without the need to reference external data. The results in table 1 and the extrapolation examples in the text show that the algorithmic method would have been expected to predict UT1-UTC with an error of a few seconds over at least several decades. However, the accuracy of the algorithmic method depends on the accuracy of the extrapolation of the drift parameter, R, and the accuracy of the method will be degraded if the actual value of the drift parameter for the next century is significantly different from the value based on data from the previous century. The drift parameter has been systematically decreasing since 1820, and this has contributed to the offset between the predicted difference between UT1 and UTC and the actual difference observed in the 20th century. The quadratic depends on the elapsed time since 1820 in eq. 1 magnifies this effect.
The effect of the secular decrease in the drift parameter that we discussed above can be illustrated by considering how the algorithm would have performed from 1820 to the present. The discussion is only qualitative because it uses estimates of the rate of evolution of UT1-UTC that were not available at the time.
Starting in 1820, the first step in the algorithmic method would be to define the parameter that will set the magnitude of the adjustment for the first century starting in 1820. (We choose to begin the example in 1820 because the length of the day was 86400 s at that time.) Eq. 1 predicts that the time difference between UT1 and UTC would be 31 s-20 s = 11 s in 1920, a century after 1820, and this prediction agrees within 1 s with the integration of the length-of-day data in fig. 4 from 1820 to 1920. The algorithmic method would have implemented the 11 s adjustment with 10 1-second adjustments in 1830,1840, …, 1910, 1920, and the algorithmic method would have agreed with the actual data within 1 s. The integration of the data in Fig. 3 from 1820 to 1920 gives a value for R of 29.5 s/cy2 instead of the 31 s/cy2 used in the prediction starting from 1820. By using this value for R, eq. 1 would predict that the difference between UT1 and UTC would be 98 s a century later in 2020 so that UT1-UTC would increase by 98 s – 11 s = 89 s. The algorithmic method would have implemented this difference by 10 9-second adjustments to UTC in 1930, 1940, and 1950, so that the difference in 1950 would be 27+10= 37 s, about 5 s more than the difference of 32.184 s in 1958, the next date for which we have an independent estimate of UT1-UTC. As was shown in a previous section, the magnitude of R derived from the length-of-day data has been decreasing for most of the 20th century, so that a prediction of the difference between UT1 and UTC that uses a value of R based on the data to 1920 would have increasingly diverged from the observations. The algorithmic method would have continued for the rest of the century and would have made an adjustment of 54 s (6 adjustments of 9 s each) in 1960, 1970, …, 2000, 2010, about 17 s more than the actual evolution of 37 s. In the two centuries from 1820 to 2020, the algorithmic method would have made a total adjustment of 100 s, about 31 s more than the actual evolution of the difference between UT1 and UTC of 69 s (32.184 s+ 37 s).
The over-correction of about 31 s is implicit in the previous discussion, which concluded that the value of R has been decreasing for much of the 20th century, and that the two centuries of data from 1820 to 2020 were consistent with a much smaller value for R of about 23 s/cy2. The over-correction would have been larger if we had used to results of McCarthy and Babcock [19, eq. 11], which concluded that the long-term evolution of UT1-TAI was closer to 13 s/cy2 and would have predicted that the difference between UT1 and TAI would be about 59 s in 2020. There was no basis for predicting this decrease from the vantage point of 1820 or even 1920. Both of these over-corrections are smaller than the maximum tolerance of 100 s, and both of them would be amortized by adjusting the rate for the next century.
The data in fig. 4 show that there are significant deviations in the length of the day from the long-term average, and these deviations can last for years or even decades. There is no basis for concluding that the smaller drift that has characterized the data over the last few decades represents a fundamental change in the evolution of the length of the day. The over-correction of 31 s (or even 41 s) is smaller than the maximum tolerance in the ITU resolution and there is no compelling reason to change the fundamental algorithmic method for the next adjustment period, which will start in or before 2035. The analysis in the text suggests a value of R =13 s/cy2 and that the estimate of 23 s/cy2 based on the earlier data, is too large. Since any adjustment protocol will not be implemented for several years from now, there will be additional data that may modify the value for R that will be used to compute the adjustment for the next century starting in or before 2035.
The method proposes to adjust UTC at 12 hours rather than at 0 as at present. This change recognizes the importance of timekeeping in Asia, Australia and even the Pacific time zone of the US. This change is independent of the rest of the proposal and should be implemented no matter what adjustment process is finally adopted.
The method defines an adjustment process that is derived from the long-term variation of the length of the day, and the maximum tolerance need only be large enough to accommodate the deviations of this variation from a long-term constant rate increase. It would be unlikely that the maximum tolerance was ever reached. A maximum tolerance on the order of one minute would be adequate, but a tolerance of 100 s or even a larger value could be chosen because the choice would almost certainly make no difference in practice.

Conclusions

The accuracy of the adjustment process discussed in the text depends on an accurate estimate of the long-term variation in the length of the day, and especially on the magnitudes of the deviations of this variation from a constant rate of increase. The long-term accuracy of the adjustment algorithm would be improved with a better prediction for the long-term variation in the length of the day, and the maximum tolerance could be decreased if the deviations from a constant rate of increase could be predicted or at least understood. The deviations in the constant rate of increase often persist for many years and this increases the difficulty and reduces the accuracy of an estimate of the long-term rate of change. The variation in the rotation rate of Earth is affected by many complex factors, so that improving the prediction of this variation will not be a simple task.
Applications that depend on an accurate knowledge of UT1-UTC will continue to use the data from the IERS, and it is important that these data be widely and easily available in machine-readable formats. This requirement is independent of any change to the method of linking UT1 to UTC.
Although extrapolations have significant uncertainties, there is a significant probability that a negative leap second will be needed before the current adjustment process is modified in 2035. This transition date should be re-considered if a shorter extrapolation, which will have a smaller uncertainty, confirms the current prediction that the negative leap second will be needed before 2035.

References

  1. BIPM Annual report, https://webtai.bipm.org/ftp/pub/tai/annual-reports/bipm-annual-report/annual_report_2020.pdf.
  2. Panfilo G, Arias F, Metrologia 56, 042001 (2019).
  3. IERS Bulletins A, C, and D, www.iers.org/iers/en/publications/bulletins/bulletins.html.
  4. Levine, J, Tavella, P and Milton, M., Metrologia, 60, 04001 (2023). https://doi.org/10.1088/1681-7575/ac9da5. [CrossRef]
  5. Agnew, D. C., Nature, https://doi.org/10.1038/s41586-024-07170-O, 2024. Also private communication from the author. [CrossRef]
  6. 2002 ITU-R, recommendation TF.460–6, Standard-frequency and time-signal emissions (https://itu.int/rec/R-REC-TF.460/en).
  7. https://studylib.net/doc/13875859/resolution-653--wrc-12--future-of-the-coordinated-universal time time-scale.
  8. https://www.itu.int/dms_pub/itu-r/oth/0C/0A/R0C0A00000F00135PDFE.pdf.
  9. World Radiocommunication Conference 2023 (WRC-23), Final Acts, R-ACT-WRC.15-2023.pdf, pp. 398 – 399.
  10. Conference generale des poids et mesures (CGPM) 2018 Resolution 2 of the 26th CGPM (2018), on the definition of time scales (https://bipm.org/en/committees/cg/cgpm/26-2018).
  11. https://www.bipm.org/documents/20126/42177518/BIPM-ITU+MoU.pdf/d5ae968b-28ba-3a2b-611b-a7ca9b2a2111.
  12. On the use and future development of UTC, CGPM 2022, Resolution 4, DOI : 10.59161/CGPM2022RES4E. [CrossRef]
  13. CIPM-election-process-EN.pdf, at www.bipm.org.
  14. Gabor P 2017 The leap second debate: rational arguments vs unspoken unease The Science of Time 2016. Astrophysics and Space Science Proceedings vol 50 ed. E Arias, L Combrinck,.
  15. P Gabor, C Hohenkerk, and P Seidelmann (Berlin: Springer). Report of the ITU/BIPM Workshop on the future of the international time scale, ITU Document R12-WP7A-C-0056!N02!MSW-E (Annex to 7A/51E), 20 April 2014. See also fig. 10 in the presentation of Peter Whibberley, The Future of UTC – A British Perspective at www.itu.int/ITU-R/go/itu-bipm-worshop-13.
  16. Jones H. Spencer, Dimensions and Rotations, The Solar System, Vol. II, The Earth as a Planet, Chicago, University of Chicago Press, 1954, Chap. 1.
  17. F. R. Stephenson and L. V. Morrison, Phil. Trans. Roy. Soc. London, Vol. A313, pp. 47-70, 1984.
  18. F. R. Stephenson and L. V. Morrison, Phil. Trans. Roy. Soc. London, Vol. A351, pp. 166-202, 1995.
  19. D. D. McCarthy and A. K. Babcock, Physics of Earth and Planetary Interiors, 44, 281-292 (1986).
  20. Maeder and V. G. Gueorguiev, ARxiv: 2110.09037v1, 18 October 2021.
  21. The network time protocol (NTP), https://www.rfc-editor.org/rfc/rfc1305.txt.
  22. Google public NTP guides, LeapSmear, https://developers.google.com/time/smear?hl=en and Facebook, https://engineering.fb.com/2022/07/25/production-engineering/its-time-to-leave-the-leap-second-in-the-past/.
Preprints 108132 g004
Figure 4. The length of the day from 1657 to 2022 relative to exactly 86 400 s. The red line shows the effect of a constant rate of 1.7 ms/cy, and the green line shows the effect of a constant rate of 0.76 ms/cy, which is more consistent with these data in a formal, least-squares sense, although neither rate fits the entire data set very well. Additional estimates of the long-term variation of the length of the day are in the text. There are significant deviations from these long-term average rates (orange and purple lines), which persist for many years.
Figure 4. The length of the day from 1657 to 2022 relative to exactly 86 400 s. The red line shows the effect of a constant rate of 1.7 ms/cy, and the green line shows the effect of a constant rate of 0.76 ms/cy, which is more consistent with these data in a formal, least-squares sense, although neither rate fits the entire data set very well. Additional estimates of the long-term variation of the length of the day are in the text. There are significant deviations from these long-term average rates (orange and purple lines), which persist for many years.
Preprints 108132 g004

Notes

1
The CIPM is a group of 18 individuals from different member states. They are elected by the CGPM, and the details are in [13]).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated