God’s Certainty-Uncertainty Principle versus Heisenberg’s Uncertainty Principle: Leading to Unification of Gravity and Quantum Mechanics

1. Two Steps in the Wrong Direction Seems to be the Reason Gravity and Quantum Mechanics Not Was Unified until Now

Einstein [1] already in 1916 in one of his most famous general relativity papers suggested that the next step in gravity would be quantum gravity or in his own words:

Because of the intra-atomic movement of electrons, the atom must radiate not only electromagnetic but also gravitational energy, if only in minute amounts. Since, in reality, this cannot be the case in nature, then it appears that the quantum theory must modify not only Maxwell’s electrodynamics but also the new theory of gravitation. —A. Einstein

It is important to remember that when Einstein discussed how a quantum theory must lead to a new quantum gravity theory, it was years before the development of key concepts in today’s quantum mechanics, such as Heisenberg’s uncertainty principle. It is often forgotten that Einstein was one of the first to be part of developing quantum theory. Einstein in 1905 proposed that light is also propagated and absorbed in quanta, today called photons. These photons came with energy according to the Planck–Einstein relation: $E=hf=h\frac{c}{\lambda }$. This was experimentally confirmed already in 1912 by Richardson and Compton [2] (the brother of Arthur Compton that we soon will come to).

Einstein was actually very skeptical of certain aspects of the developments in quantum mechanics that occurred in the 1920s. Therefore, unifying gravity with quantum mechanics could clearly involve modifying quantum mechanics. Einstein spent much of his remaining life trying to develop a new theory of gravity that could unify it with quantum theory, but he had very limited success. Many of the most brilliant physicists and mathematicians have been working on this unification for over a century with little success. If developing a unified theory of quantum gravity and quantum mechanics were simply a matter of solving or formulating some very complex equations, it likely would have already been accomplished and borne fruit.

Indeed, there have been multiple interesting ideas and models, such as Superstring Theory and Loop Quantum Gravity (LQG). However, after they have been explored for many years they do not seem very promising; some even consider them failed theories, while others continue to work on them, hoping they will ultimately provide the answer, see [3,4,5] .

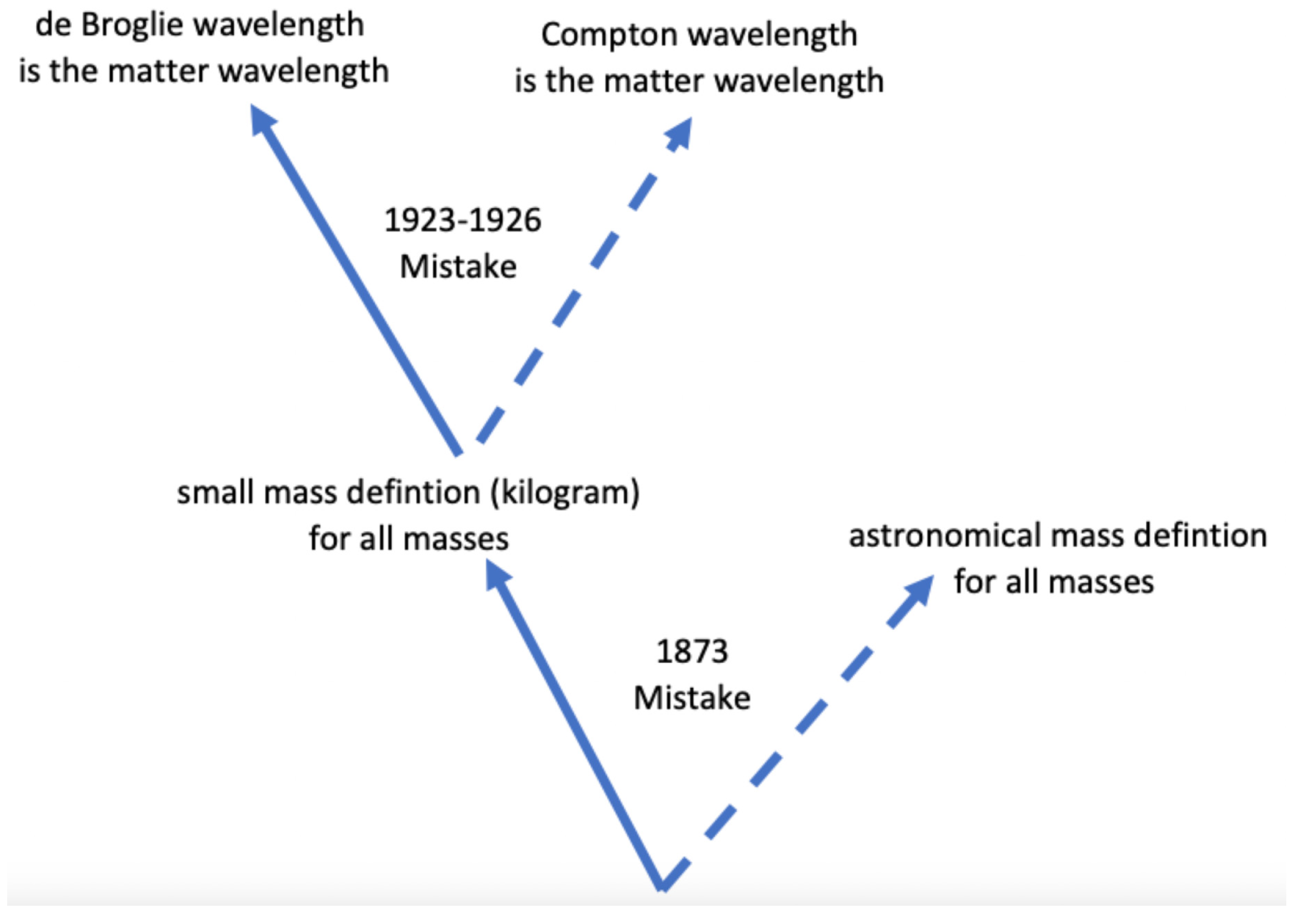
Given the extensive efforts by numerous brilliant minds to unify gravity with quantum mechanics and other aspects of physics, it’s worth considering the possibility that the scientific community may have taken the wrong path at certain junctures in the history of physics. A thorough examination of the history of physics reveals several instances where crucial decisions led to the exploration of one path while leaving others unexplored or underexplored. We believe we have identified two such points where the physics community veered off course, resulting in unnecessary complexity and hindering efforts to unify gravity with quantum mechanics. By revisiting these junctures and exploring the alternative paths, along with deriving further insights from them, we are led to a remarkably simple and overlooked approach to unify gravity with quantum mechanics.

The first step in the wrong direction occurred in 1873 when the gravitational constant was introduced essentially ad hoc to make Newton’s formula work when the kilogram mass was used in gravitational equations. We will discuss this further in section 4. In short, Newton had never introduced nor attempted to introduce what is known today as Newton’s gravitational constant. His formula was $F=\frac{M_n{m}_n}{r^2}$, which worked just as well as the modern formula $F=G\frac{Mm}{r^2}$. The key question is: what does the gravitational constant then truly represent?

The second step in the wrong direction happened around 1923 to 1924 when it was assumed that the de Broglie wavelength was the matter wavelength, instead of the Compton wavelength. This topic will be explored in the next section. Figure 1 illustrates these two missteps, which have made it almost impossible to unify gravity with quantum mechanics. Understanding that the Compton wavelength is the true matter wavelength, and comprehending why the gravitational constant was needed and what it truly represents, are crucial steps forward.

2. De Broglie Wavelength versus Compton Wavelength

Modern physics and quantum mechanics assume the de Broglie wavelength is the real matter wavelength. It was already known that light had particle-wave duality, so de Broglie [6] in his 1924 breakthrough PhD thesis suggested that matter also had to have wave properties in addition to particle properties. In addition, de Broglie in the same thesis presents the following formula for this matter wavelength, which today is known as the de Broglie wavelength:

$${\lambda }_b=\frac{h}{mv}$$

(1)

The formula above is actually a good approximation when $v\ll c$. Broglie [7] extended it also for relativistic effects and gave the formula

$${\lambda }_b=\frac{h}{mv\gamma }$$

(2)

Davisson and Germer [8], in 1927, published their paper on Diffraction of Electrons, which experimentally strongly supported the idea that matter also had wave properties. The de Broglie hypothesis was therefore quickly accepted and praised after this experiment. However, one had not measured the de Broglie wavelength as predicted by the formulas above, just that the matter had wavelike properties. We will not question that matter has wavelike properties in addition to particle properties as this is fully in line also with out view. What we will question is if the mathematical de Broglie wavelength is the real matter wavelength. From the de Broglie matter wavelength formulas, we can clearly see that the formula cannot be valid for $v=0$, as this means division by zero, which is not allowed in mathematics. Further, even when v is just very close to zero, then the de Broglie wavelength for even an electron can become longer than the radius of the Hubble sphere. In our view, this is simply absurd. Proponents and specialists in quantum mechanics will defend that the de Broglie wavelength formula is not valid for $v=0$ with the claim that the Heisenberg [9] uncertainty principle forbids particles to be fully at rest, so then the case of $v=0$ is not relevant. They will even claim that the de Broglie wavelength going beyond the Hubble radius is avoided in this way as one has not been able to measure velocities as low as one needs to get this to happen.

However, we will claim that it is the Compton wavelength that is the real matter wavelength. Compton [10] in 1924 was describing what today is known as Compton scattering and based on this predicted what today is known as the Compton wavelength, given by:

$${\lambda }_c=\frac{h}{mc}$$

(3)

Even if his theory was relativistic in the sense that he took into account that light moves at a speed of c when colliding with the electron, Compton still assumed that the electron when hit was standing still. So the Compton wavelength of the electron is related to the rest of the electron. The Compton wavelength has not only been discussed in relation to the electron, but the Compton wavelength of the proton has also been discussed, for example by Levitt [11] in 1958, who claimed the Compton wavelength of the proton was essential to understand the proton. In recent years, Bohr and Trinhammer [12] have indirectly pointed out that the current best estimates of the classical proton radius are exactly equal to four times the reduced Compton wavelength of the proton, $R_P=4{\overline{\lambda }}_{c,P}$. We doubt this is a pure coincidence, even if that cannot be fully excluded.

Haug has shown in a series of publications that the Compton wavelength can be found for basically any mass without any knowledge of the Planck constant. The Compton wavelength for a mass larger than the Planck mass is shorter than the Planck length, so such a Compton wavelength can likely not exist physically. However, masses larger than the Planck mass, and many masses also smaller than the Planck mass, such as the Proton, are composite masses. The Compton wavelength of these masses is simply the aggregate of the Compton wavelength of their individual elementary particles, including photon-like elements as the photon wavelength of a rest mass particle is identical to the Compton wavelength. We have that the Compton wavelength of a composite mass must be given by:

$$\begin{array}{ccc}\hfill m& =& \sum _i^n{m}_i\pm \sum _j^N\frac{E_j}{c^2}\hfill \\ \hfill \frac{h}{{\lambda }_c}\frac{1}{c}& =& \sum _{i=1}^n\frac{h}{{\lambda }_{c,i}}\frac{1}{c}\pm \sum _{j=1}^N\frac{h\frac{c}{{\lambda }_{c,i}}}{c^2}\hfill \\ \hfill {\lambda }_c& =& \frac{1}{{\sum }_{i=1}^n\frac{1}{{\lambda }_{c,i}}\pm {\sum }_{j=1}^N\frac{1}{{\lambda }_{c,j}}}.\hfill \end{array}$$

(4)

The reason for the plus-minus sign in front of energies is that the mass of composite particles can be both smaller than the mass of their composites due to binding energy released when the masses are bound. This formula holds for any composite mass as well as for any composite structure of photons, see also [13,14].

Unlike the de Broglie wavelength, the Compton wavelength is always valid, even when the particle is at rest. The Compton wavelength also does not become macroscopically large even if the velocity of the particle is small or at any velocity of the particle. The Compton wavelength always has a length we would associate with what simple logic would tell us about the lengths of the atomic and subatomic quantum world, that such a length simply has to be incredibly small. This again is in strong contrast to the de Broglie wavelength that, if we take the predictions from the de Broglie formula as given, can spread out on a macroscopic scale even for a single electron. Again, we will claim the latter is absurd.

As pointed out earlier, Compton derived his formula based on the assumption that the mass is at rest. Haug [15] has recently extended the work on Compton to derive a full relativistic Compton wavelength, also taking into account that the mass is initially moving. This simply leads to:

$${\lambda }_c=\frac{h}{mc\gamma }$$

(5)

where $\gamma =1/\sqrt{1-v^2/c^2}$. This means the de Broglie wavelength is always equal to the Compton wavelength times $\frac{c}{v}$. However, again, we see the de Broglie wavelength is not defined for $v=0$ while the Compton wavelength is.

We will conjecture that the de Broglie wavelength is not a real matter wavelength but, in reality, a pure mathematical derivative of the Compton wavelength. Further, we can summarize this section from a pure logical common-sense perspective that the Compton wavelength seems to make more sense than the de Broglie wavelength. Still, some will protest here as they will think this could not be the case, as the de Broglie wavelength and Compton wavelength have been studied so well that there cannot suddenly be a new and very different interpretation of the de Broglie wavelength. However, we will soon see that general relativity theory can easily be quantized if we rely on the Compton wavelength and not when relying on the de Broglie wavelength. Further, we will see how quantum mechanics needs to be reformulated or extended to achieve a nice and simple unification of gravity and quantum mechanics.

3. Domain Validity of Matter Wavelengths

Even if there is some repetition in this section from the previous section, we feel it is necessary to point out and precisely define the domain range of the de Broglie wavelength versus the Compton wavelength.

The de Broglie wavelength formula is not valid for $v=0$, and we have defined its valid domain for v below:

$${\lambda }_b=\frac{h}{mv\gamma }=\frac{h}{p} \mathrm{when} 0<v<c$$

(6)

where p is the relativistic momentum $p=mv\gamma$ that was first introduced by Max Planck [16] in 1906. And also, from ${\lambda }_b={\lambda }_c\frac{c}{v}$, we can see the de Broglie wavelength is not valid for $v=0$. This is very important, as a model that assumes the de Broglie wavelength is the real matter wavelength will not be able to model rest mass properly. Again, most physicists will think this is not needed due to the Heisenberg uncertainty principle that we will soon get back to. This means the valid domain for the de Broglie wavelength is $0<v<c$.

On the other hand, the Compton wavelength for a particle at rest is:

$${\lambda }_c=\frac{h}{mc} \mathrm{when} v=0$$

(7)

and in the more general formula also taking into account $v>0$, we have:

$${\lambda }_c=\frac{h}{mc\gamma }\mathrm{when}0\le v<c$$

(8)

That is, the valid domain for the Compton wavelength is $0\le v<c$.

The relation between the de Broglie wavelength and the Compton wavelength is only valid where the domains of the two overlap. So we have:

$${\lambda }_b={\lambda }_c\frac{c}{v}\mathrm{when}0<v<c$$

(9)

and

$${\lambda }_c={\lambda }_b\frac{v}{c}\mathrm{when}0<v<c$$

(10)

In this latter equation, we do not encounter the problem of setting $v=0$ directly. However, since the de Broglie wavelength is not valid for $v=0$, the domain for this equation is indeed $0<v<c$.

We can conclude that the Compton wavelength is valid in the full domain as the de Broglie wavelength and can likely be used to model all that the de Broglie wavelength can model related to what can be checked with real observations. However, the de Broglie wavelength cannot be used to model all that the Compton wavelength can predict, simply because the de Broglie wavelength cannot account for rest. As we will soon see, rest seems to play a central role in quantum gravity. Switching from the de Broglie wavelength as the matter wavelength to the Compton wavelength as the true matter wavelength can be mathematically seen as a form of domain stretching of existing concepts in quantum mechanics. As we will soon discuss, this likely has major implications and even seems to lead to the unification of gravity and quantum mechanics.

4. Quantization of Gravity and How It Is Linked to the Reduced Compton Frequency

Before delving into Heisenberg’s uncertainty principle and quantum mechanics, it’s worth noting a relatively new approach to quantize both Newton’s gravitational theory and Einstein’s general relativity, as well as other gravity theories. We’ll discover that gravity, when understood at a deeper level, is rooted in the reduced Compton frequency over the Planck time. This leads to the quantization of gravity and establishes a connection to the Planck scale, essentially forming a quantum gravity theory. We’ll also explore how this theory can be seamlessly unified with quantum mechanics. However, before that, we need to make slight modifications to quantum mechanics.

Newton introduced his gravity theory in 1686 [17]. It’s essential to recognize that his original gravitational force formula was:

$$F=\frac{M_n{m}_n}{r^2}$$

(11)

Newton only expressed his formulas in words, but this was clearly the formula he stated. We use the symbols for mass $M_n$ and $m_n$ because Newton had a quite different view on mass compared to modern gravitational physics. Newton said mass was the quantity of matter and mentioned that matter consisted of indivisible particles. Newton also referred to indivisible time interval (see [18]).

Newton’s original gravity formula and its derivations were successfully used to predict phenomena such as the orbital velocity of moons and planets, and the relative size of planets, for several hundred years and still hold to this day [19,20]. In 1784, Michell [21] used Newton’s theory to calculate the radius of a gravitational object with a field so strong that not even light could escape. This radius was identical to today’s Schwarzschild radius. Again, Michell stated his calculations in words, but they led to a radius of $r=\frac{2M_n}{c^2}$, which in modern notation would be $r=\frac{2GM}{c^2}$, indeed identical to the Schwarzschild radius [22].

Michell was the first to design an apparatus that could measure the gravitational field from a small macroscopic object on Earth. However, Michell died before he could build and use it. Cavendish [23] accomplished this task and published his work in 1798, where he measured the density of the Earth relative to a macroscopic object on Earth with known density. A series of books and papers incorrectly claim that Cavendish measured Newton’s gravitational constant. This is not true. Cavendish did not know about any gravitational constant nor tried to measure it, as pointed out by multiple researchers that carefully have studied this in detail: [24,25].

Maxwell [26] used the original Newton formula as late as early 1873. At that time, there were two different mass standards. For small, manageable masses, one used kilograms in France and pounds in Great Britain. For astronomical masses, one used the Newtonian mass, which had dimensions of length cubed divided by time squared: $[L^3·T^{-2}]$. For a considerable time, researchers had wished to unify the mass units used for astronomical masses and small masses. They ended up choosing the kilogram. When switching to the kilogram, Newton’s original gravitational force formula and formulas derived from it would no longer work. To fix this, a constant had to be introduced.

So first, in 1873, Cornu and Baille [27] changed Newton’s gravitational force formula to $F=f\frac{Mm}{r^2}$, where M and m were now masses in kilograms, and the gravity constant was f. In 1894, Boys [28] changed the symbol of the gravity constant to G. Einstein, however, used the symbol k. Naturally, the symbol used for the constant is purely cosmetic. What is important to understand is that the gravity constant was introduced to make Newton’s formula work after the mass definition was changed. The kilogram mass, as well as the pound mass, are arbitrary, human-selected clumps of matter. Gravity does not care if humans declare a certain amount of matter as a kilogram or a pound.

Thüring [29], as late as 1961, pointed out that the gravity constant had been somehow ad hoc inserted. Further, he pointed out that the gravity constant could not be associated with a unique physical property of nature. Despite the gravity constant being ad hoc inserted to make Newton’s gravity formula work after the mass dimensions and units were changed, it was brought over into general relativity theory without question. It is important to note that changing from the Newton mass to the kilogram mass was more than just changing units. To change the mass unit from, for example, kilograms to pounds or from pounds to kilograms is a trivial switch between units; it is a matter of choice. On the other hand, changing from the Newton mass to kilograms means going from just length and time units in the mass to something more diffuse, namely kilograms. This means even the dimensions have changed.

To make a long story short, the gravitational constant that Newton never invented, sought to invent, or tried to find was carried over into general relativity theory and plays an important role in a series of gravity theories. As long as one uses kilograms for mass, one indeed needs to use the gravitational constant. A gravitational constant would also be needed if we switched the mass definition to pounds. However, the gravitational constant would not be needed if one used the original Newtonian mass definition, where mass has units $[L^3·T^{-2}]$. The main point to understand here is that there is no deep theory behind the gravitational constant; it was basically ad hoc inserted to make Newton’s formula still work when switching to kilograms. Clearly, kilograms did not contain enough information about the mass in relation to gravity to be used on their own; they had to be multiplied by a constant that could be found by calibration.

Further, it is important to be aware that the gravitational force itself has never been measured directly, only indirectly through how it affects objects in the gravitational field, such as: light, clocks and satellites. The gravitational force formula is used to derive observable gravitational formulas. In all these observable gravitational phenomena, one has $GM$ and not $GMm$ in the prediction formulas. That is, the kilogram mass must always be corrected by multiplying it by the gravitational constant to make the formula work. If the small mass m is large enough to have a significant contribution to the observed gravitational phenomena, a real two-body problem, the gravitational parameter is $\mu =GM+Gm$ and never $GMm$. Actually, in modern notation, Newton’s original gravitational force formula corresponds to:

$$\frac{M_n{m}_n}{r^2}=\frac{GMGm}{r^2}$$

(12)

However the formula $F=\frac{GMGm}{r^2}$ can only be used if one in derivations assume the small mass also is corrected by G. For example if we are going to derive the escape velocity we now have

$$\frac{1}{2}Gm{v}^2-\frac{GMGm}{r}=0$$

(13)

which solved for v gives the standard formula:

$$v=\sqrt{\frac{2GM}{r}}$$

(14)

We could naturally also have this directly from Newtons original formula, as we then have

$$\frac{1}{2}{m}_n{v}^2-\frac{M_n{m}_n}{r}=0$$

(15)

which solved for v gives the standard formula:

$$v=\sqrt{\frac{2M_n}{r}}$$

(16)

and since $M_n=GM$, it gives the same formula as in modern notation. The modern notation involving a gravitational constant G is, however, in reality, confusing. Most physicists will likely think that including G is not confusing and is how it must be, but that is almost certainly because they are used to always including a gravitational constant. The important point to understand at this point is that we can make all the predictions with Newton’s original formula just as we can with the 1873 version of the formula that is used today. Further, G was needed to put back into the mass something that was removed when switching from the Newtonian mass to the kilogram mass. Still, what exactly is G and the mass M from a deeper perspective?

Max Planck [30,31], only a few years after the gravitational constant was introduced, assumed there were three important universal constants: the gravitational constant G, the Planck constant ℏ, and the speed of light c. Combining this with dimensional analysis, he derived what he called natural units: a unique length $l_p=\sqrt{\frac{G\hslash }{c^3}}$, time $t_p=\sqrt{\frac{G\hslash }{c^5}}$, mass $m_p=\sqrt{\frac{\hslash c}{G}}$, and temperature $T_p=\frac{1}{k_B}\sqrt{\frac{\hslash c^5}{G}}$, today known as the Planck units.

Eddington in 1918 [32] pointed out that a future quantum gravity theory would likely need to be linked to the Planck length. As we know, Newton never introduced the gravitational constant; it was first introduced ad hoc in 1873. It is worth asking if the gravitational constant could have a deeper meaning and even be derived from more fundamental entities. Cahill [33,34] in 1984 suggested that the Planck units were more central than the gravitational constant and that one could simply express the gravitational constant by solving the Planck mass formula for G, which gives $G=\frac{\hslash c}{m_p^2}$. However, Cohen [35] in 1987 pointed out that expressing the gravitational constant in terms of Planck units and claiming the Planck units were more essential would lead to a circular problem, as no one knew how to find the Planck units without first finding G. This has changed in recent years, as it has been clearly demonstrated how to find the Planck length independently of any knowledge of G[13,36,37]. This means that we indeed can write G in terms of Planck units. We can solve the Planck length formula for G, which gives:

$$G=\frac{l_p^2{c}^3}{\hslash }$$

(17)

In addition, we can solve the Compton wavelength formula ${\lambda }_c=\frac{h}{Mc}$ for M, which gives:

$$M=\frac{h}{{\lambda }_c}\frac{1}{c}=\frac{\hslash }{{\overline{\lambda }}_c}\frac{1}{c}$$

(18)

Since in all formulas used to predict observable gravitational phenomena we have either $GM$ or $GM+Gm$ and never $GMm$, this means we always have:

$$GM=\frac{l_p^2{c}^3}{\hslash }\frac{\hslash }{{\overline{\lambda }}_c}\frac{1}{c}=c^2{l}_p\frac{l_p}{{\overline{\lambda }}_c}$$

(19)

That is, the Planck constant always cancels out. The term $\frac{l_p}{{\overline{\lambda }}_c}$ is the reduced Compton frequency per Planck time.

This also means Einstein’s field equation can be rewritten as [38,39,40]:

$$\begin{array}{ccc}\hfill R_{\mu \nu }-\frac{1}{2}R{g}_{\mu \nu }& =& \frac{8\pi G}{c^4}{T}_{\mu \nu }\hfill \\ \hfill R_{\mu \nu }-\frac{1}{2}R{g}_{\mu \nu }& =& \frac{8\pi l_p^2}{c\hslash }{T}_{\mu \nu }\hfill \end{array}$$

(20)

The reason the Planck constant is there is to be canceled with the Planck constant in the energy tensor.

However, Einstein’s field equation itself says little; it needs to be solved for chosen boundary conditions. If we, for example, look at the Schwarzschild metric, we have:

$$\begin{array}{ccc}\hfill d{s}^2& =& -\left(1-\frac{2GM}{c^{2}r}\right)c^{2}d{t}^2+{\left(1-\frac{2GM}{r{c}^2}\right)}^{-1}d{r}^2-r^{2}d{\Omega }^2\hfill \\ \hfill d{s}^2& =& -\left(1-\frac{2l_p}{r}\frac{l_p}{{\overline{\lambda }}_{c,M}}\right)c^{2}d{t}^2+{\left(1-\frac{2l_p}{r}\frac{l_p}{{\overline{\lambda }}_{c,M}}\right)}^{-1}d{r}^2-r^{2}d{\Omega }^2\hfill \end{array}$$

(21)

That is, again, the Schwarzschild metric at a deeper level contains the term $\frac{l_p}{{\overline{\lambda }}_{c,M}}$, which is the reduced Compton frequency per Planck time. The Planck constant is nowhere to be seen. Importantly, the de Broglie wavelength is also nowhere to be seen. It is the reduced Compton wavelength, together with the Planck length and the speed of light (gravity), that are the keys to gravity at the deeper level. In this way, one introduces both quantization by the reduced Compton frequency per Planck time and also links to the Planck scale through the Planck length.

The reduced Compton wavelength in the Schwarzschild metric is the rest-mass wavelength. This cannot be accomplished by the de Broglie wavelength. Even if the Compton wavelength is equal to the de Broglie wavelength multiplied by $\frac{v}{c}$, it is not valid for $v=0$ as the de Broglie wavelength is not defined for $v=0$.

In addition, we have recently proposed unifying a series of solutions from Einstein’s field equations into one solution. The extremal solution of the Reissner-Nordström [41,42] metric as well as the minimal solution of the Haug-Spavieri [43] metric is given by:

$$\begin{array}{ccc}\hfill d{s}^2& =& -\left(1-\frac{2GM}{c^{2}r}+\frac{G^2{M}^2}{c^4{r}^2}\right)c^{2}d{t}^2+{\left(1-\frac{2GM}{c^{2}r}+\frac{G^2{M}^2}{c^4{r}^2}\right)}^{-1}d{r}^2+r^2{\Omega }^2\hfill \\ \hfill d{s}^2& =& -\left(1-\frac{2\frac{l_p^2{c}^3}{\hslash }\frac{\hslash }{{\overline{\lambda }}_{c,M}}\frac{1}{c}}{c^{2}r}+\frac{\frac{l_p^4{c}^6}{{\hslash }^2}\frac{{\hslash }^2}{{\overline{\lambda }}_{c,M}^2}\frac{1}{c^2}}{c^4{r}^2}\right)c^{2}d{t}^2+{\left(1-\frac{2\frac{l_p^2{c}^3}{\hslash }\frac{\hslash }{{\overline{\lambda }}_{c,M}}\frac{1}{c}}{c^{2}r}+\frac{\frac{l_p^4{c}^6}{{\hslash }^2}\frac{{\hslash }^2}{{\overline{\lambda }}_{c,M}^2}\frac{1}{c^2}}{c^4{r}^2}\right)}^{-1}d{r}^2+r^2{\Omega }^2\hfill \\ \hfill d{s}^2& =& -\left(1-\frac{2l_p}{r}\frac{l_p}{{\overline{\lambda }}_{c,M}}+\frac{l_p^2}{r^2}\frac{l_p^2}{{\overline{\lambda }}_{c,M}^2}\right)c^{2}d{t}^2+{\left(1-\frac{2l_p}{r}\frac{l_p}{{\overline{\lambda }}_{c,M}}+\frac{l_p^2}{r^2}\frac{l_p^2}{{\overline{\lambda }}_{c,M}^2}\right)}^{-1}d{r}^2+r^2{\Omega }^2.\hfill \end{array}$$

(22)

That is, now gravity is quantized. The reduced Compton frequency per Planck time, $\frac{c}{\overline{\lambda }}{t}_p=\frac{l_p}{\overline{\lambda }}$, is the number of Planck mass events per Planck time in the mass M. The rest mass Compton wavelength plays a central role here. If the reduced Compton wavelength is the true matter wavelength, then gravity is linked to rest mass. Rest mass, from mathematics, is strictly related to when a mass is at rest relative to the laboratory frame (the frame one observes from).

This extremal metric above be rewritten in multiple different forms that are the same, for example:

$$\begin{array}{ccc}\hfill d{s}^2& =& -\left(1-\frac{2G{n}_p{m}_p}{c^{2}r}+k_e\frac{n_p{q}_p{n}_p{q}_p}{r^2}\frac{G}{c^4}\right)c^{2}d{t}^2\hfill \\ & & +{\left(1-\frac{2G{n}_p{m}_p}{c^{2}r}+k_e\frac{n_p{q}_p{n}_p{q}_p}{r^2}\frac{G}{c^4}\right)}^{-1}d{r}^2+r^2{\Omega }^2.\hfill \end{array}$$

(23)

We now see the last term $k_e\frac{n_p{q}_p{n}_p{q}_p}{r^2}\frac{G}{c^4}$ is quantized charge, where the quanta comes in Planck charge. The $\frac{G}{c^4}$ is just a conversion factor needed to get the Joule energy into collision-length energy [44,45]. As we have $\frac{F_c}{F}=\frac{k_e\frac{q_p{q}_p}{r^2}}{\frac{m_p{m}_p}{r^2}}=1$, the metric above can again be rewritten as:

$$\begin{array}{ccc}\hfill d{s}^2& =& -\left(1-\frac{2G{n}_p{m}_p}{c^{2}r}+k_e\frac{n_p{q}_p{n}_p{q}_p}{r^2}\frac{G}{c^4}\right)c^{2}d{t}^2\hfill \\ & & +{\left(1-\frac{2G{n}_p{m}_p}{c^{2}r}+k_e\frac{n_p{q}_p{n}_p{q}_p}{r^2}\frac{G}{c^4}\right)}^{-1}d{r}^2+r^2{\Omega }^2.\hfill \end{array}$$

(24)

That is, again, all gravity is now quantized. However, the deepest level is when we write it in the Compton wavelength form further up: Eq. (22). Also, the Schwarzschild metric is now the weak field solution of this metric. The Schwarzschild metric is normally considered to be valid also in strong gravitational fields, but it is unexplained why it gives the same radius of a black hole as plain Newton gives for a dark star $r_s=2\frac{GM}{c^2}$ and the same escape velocity formula $v_e=\sqrt{\frac{2GM}{r}}$. We will claim Newton in reality is a weak field approximation. This happens as one calibrates the Schwarzschild solution to Newton before one gets out a practically useful metric. In the extremal solution above, we get an escape velocity of $v_e=\sqrt{\frac{2GM}{c^2}-\frac{G^2{M}^2}{c^4{r}^2}}$, where the Schwarzschild escape velocity is the weak field approximation when ignoring the higher-order term needed to properly work in strong gravitational fields. This is not the main topic of this paper, but we mention it.

The most important takeaway from this section is that we can indeed quantize general relativity and other gravity theories in a very simple form by understanding that G is needed to fix an incomplete kilogram mass. Additionally, the gravitational constant, from a deeper perspective, can be represented by $G=\frac{l_p^2{c}^3}{\hslash }$. Furthermore, any kilogram mass can be expressed as $M=\frac{\hslash }{{\overline{\lambda }}_{c,M}}\frac{1}{c}$, and in all predictive gravity phenomena (involving one body), we have $GM=\frac{l_p^2{c}^3}{\hslash }\frac{\hslash }{{\overline{\lambda }}_{c,M}}\frac{1}{c}=c^2{l}_p\frac{l_p}{{\overline{\lambda }}_{c,M}}$, meaning the Planck constant cancels out and is not needed in quantum gravity, and further we incorporate the reduced Compton frequency per Planck time $\frac{l_p}{{\overline{\lambda }}_{c,M}}$ and thereby get quantum gravity.

Gravity can be seen as Planck mass particles that fit the mathematics of micro black holes, emerging and vanishing at the reduced Compton frequency. These particles endure only for the Planck time and possess a radius equal to the Planck length. How does this tie into quantum mechanics? We’ll delve into that in the following section.

5. From Heisenberg’s Uncertainty Principle to the Certainty-Uncertainty Principle

In 1927, Heisenberg [9] published his uncertainty principle1. He also wrote extensively about it in his book The Physical Principles of Quantum Theory," published in 1930 [47]. Here he states, Defining momentum as $p_x=m{v}_x$ (where $m=$ mass of electron, $v_x=$ x component of velocity), this uncertainty in velocity causes an uncertainty in $p_x$ of an amount $\Delta p_x$; from which simple laws of optics, together with the empirically established law $\lambda =\frac{h}{p}$, it can readily be shown that

$$\Delta x\Delta p_x\ge h.$$

(25)

This is naturally correct under Heisenberg’s assumptions, but again he based the uncertainty principle on the matter wavelength being the de Broglie wavelength: $\lambda =\frac{h}{p}$. We will here explore the uncertainty principle more in depth if we relate it to the Compton wavelength instead of the de Broglie wavelength. We will first write:

$$x{p}_t\ge h$$

(26)

where x is the area in which the particle element of an elementary particle can be, and $p_t$ is what we will call the total Compton momentum, $p_t=mc\gamma$. That is, we have replaced the standard momentum that is linked to the de Broglie wavelength with a momentum linked to the Compton wavelength, what we before have coined the Compton momentum [44].

Next, we replace x with the Compton wavelength, then we get:

$$\begin{array}{c}\hfill {\lambda }_c{p}_t\ge h\\ \hfill {\lambda }_{c}mc\gamma \ge h\\ \hfill {\lambda }_c\frac{mc}{\sqrt{1-\frac{{(\Delta v)}^2}{c^2}}}\ge h\end{array}$$

This we will call the Certainty-Uncertainty principle. That is, it takes into account both the uncertainty in where the particle can be observed but has a special case for a special particle, namely the Planck mass particle, that gives certainty in position. This will first become clear as we dive deeper into the equation above.

Further, if we solve the Compton wavelength formula $\lambda =\frac{h}{mc}$ with respect to the mass m, we can express the kilogram mass as $m=\frac{h}{\lambda }\frac{1}{c}$. Replacing this back into our Certainty-Uncertainty principle (see also [14]), we get:

$$\begin{array}{c}\hfill {\lambda }_c\frac{h}{\lambda }\frac{1}{c}c\gamma \ge h\\ \hfill \gamma \ge 1\\ \hfill \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\ge 1\end{array}$$

(27)

That is, as long as there is uncertainty in v, the left-hand side is greater than 1 and uncertain. However, as we have stated in the previous sections, the Planck mass particle is unique. It is a photon-photon collision that gives rise to mass lasting the Planck time. The maximum velocity of any particle with mass is $v\ge c\sqrt{1-\frac{l_p^2}{{\overline{\lambda }}^2}}$. The maximum velocity formula for any elementary particle with mass we get from simply assuming the reduced Compton wavelength is the matter wavelength and that relativistic length contraction of this length is limited by the Planck length is the shortest possible even contracted length, this gives [48]:

$$\begin{array}{ccc}\hfill l_p& \ge & \overline{\lambda }\sqrt{1-\frac{v^2}{c^2}}\hfill \\ \hfill v& \le & c\sqrt{1-\frac{l_p^2}{l_p^2}}.\hfill \end{array}$$

(28)

The reduced Compton wavelength of the Planck mass particle is the Planck length: ${\overline{\lambda }}_c=\frac{\hslash }{m_{p}c}=l_p$, so the maximum velocity for the Planck mass particle is remarkably always $v\ge c\sqrt{1-\frac{l_p^2}{l_p^2}}=0$, see [49]. Again, this sounds absurd, but only until one realizes this particle lasts only the Planck time and has a radius equal to the Planck length. To observe the Planck mass particle directly, one must therefore be part of the particle itself. In other words, one must be part of the same reference frame where all is at rest relative to one, but since the reference frame only lasts the Planck time, this causes no problems. It is impossible to observe a particle with a radius of the Planck length that lasts the Planck time if one, for example, is one Planck length away from it. This as even light would then need a Planck time to travel that distance, and in the Planck time the Planck mass particle dissolve into pure energy again, photons.

Next, let’s try to do similarly, but now with the de Broglie wavelength. We then get:

$$\begin{array}{c}\hfill {\lambda }_{b}p\ge h\\ \hfill {\lambda }_{b}mv\gamma \ge h\end{array}$$

(29)

Next, as the rest mass m can only be expressed from the Compton wavelength formula and not from the de Broglie wavelength formula, we replace m with $m=\frac{h}{{\lambda }_c}\frac{1}{c}$. This gives:

$$\begin{array}{c}\hfill {\lambda }_b\frac{h}{{\lambda }_c}\frac{1}{c}v\gamma \ge h\\ \hfill \frac{{\lambda }_b}{{\lambda }_c}\frac{v}{c}\gamma \ge 1\end{array}$$

(30)

As the de Broglie wavelength is not defined when $v=0$, this will not allow us to have a particle at absolute rest. Going through the de Broglie wavelength instead of the Compton wavelength therefore does not allow for $v=0$. The uncertainty in Heisenberg’s uncertainty principle indeed comes from uncertainty in v as Heisenberg himself stated, but Heisenberg’s uncertainty principle does not allow for $v=0$. This is even obvious from Heisenberg’s uncertainty principle itself. If $v=0$ and also the uncertainty in $\Delta v=0$ (for the Planck time) then the momentum $p=mv\gamma =0$ and also the uncertainty in the momentum is then zero, so it will not be correct that $\Delta x\Delta p\ge h$, then one will have $0\ge h$ which is not correct. So yes indeed Heisenberg’s uncertainty principle does not allow for $v=0$ (which also means $\Delta v=0$ as is the case for the Planck mass particle and the Heisenberg uncertainty principle without modifications is therefore not compatible with the simple way to get quantum gravity as described above.

There are many possible implications from this. For example, the current interpretation of entanglement could even be wrong. We are fully aware that entanglement has been experimentally tested; however, the interpretation is based on certain assumptions. Einstein, Podolsky, and Rosen [50] suggested hidden variables could be the explanation behind it. Bell [51] disproved that Einstein, Podolsky, and Rosen could be right, and this led to rejection of hidden variables as an explanatory hypothesis. However, Bell’s theorem is based on the assumption that Heisenberg’s uncertainty principle always holds, see Clover [52,53]. If we switch to the view that the Compton wavelength is the true matter wavelength and that the de Broglie wavelength is only derivative, then we can transition from Heisenberg’s uncertainty principle to a certainty-Uncertainty principle. Bell’s theorem may no longer hold necessarily, and even the interpretation of entanglement can the possibly be rooted in some type of hidden variable hypothesis. At least, this should be investigated, as we now have a simple way to unify gravity and quantum mechanics that involves replacing the uncertainty principle with a certainty-uncertainty principle.

6. Conclusion

We’ve demonstrated in a series of papers that it’s possible to quantize general relativity and other gravity theories in a straightforward manner while incorporating the Planck scale. This quantization arises from the reduced Compton frequency per Planck time, which can only be observed in integers, representing the number of Planck mass events. These events correspond to the number of Planck mass particles per Planck time in the gravitational mass of interest. However, aligning it with quantum mechanics requires modifications. For example, principles like Heisenberg’s uncertainty principle, initially derived under the assumption that matter wavelength was the de Broglie wavelength, need to be adjusted to a Certainty-Uncertainty principle rooted in the Compton wavelength as the true matter wavelength.

This suggests that Einstein’s skepticism towards quantum mechanics as a complete theory was justified. Even his assertion that there must be some underlying certainty in the system, famously expressed as "God does not play dice with the universe," seems to hold weight.