Prerpints.org logo
Preprint
Article

Spin–Orbit Coupling Free Nonlinear Spin Hall Effect in a Triangle-Unit Collinear Antiferromagnet with Magnetic Toroidal Dipole

Altmetrics

Downloads

177

Views

87

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 June 2024

Posted:

06 June 2024

You are already at the latest version

Alerts
Abstract
We investigate emergent conductive phenomena triggered by collinear antiferromagnetic orderings. We show that an up-down-zero spin configuration in a triangle cluster leads to linear and nonlinear spin conductivities even without the relativistic spin–orbit coupling; the linear spin conductivity is characterized by the Drude-type one, while the nonlinear spin conductivity is characterized by the Hall-type one. We demonstrate the emergence of both spin conductivities in the breathing kagome system consisting of a triangle cluster. The nonlinear spin conductivity becomes larger than the linear one when the Fermi level lies near the region where a small partial band gap opens. Our results indicate that collinear antiferromagnets with the triangle geometry give rise to rich spin conductive phenomena.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

Antiferromagnetic orderings and their related physical phenomena have been long studied in condensed matter physics [1,2,3]. Depending on spin patterns under lattice structures, a variety of symmetry lowerings are caused by the antiferromagnetic phase transition. Based on Neumann’s principle that connects symmetry and the appearance of physical phenomena, functional materials have been discovered. One of the examples is a multiferroic property as a consequence of both spatial inversion and time-reversal symmetry breakings, which results in the linear magnetoelectric effect by the coupling between electric and magnetic degrees of freedom [4,5,6,7,8,9,10]. Another example is the anomalous Hall effect without a net magnetization when the time-reversal symmetry and other crystal symmetries are broken so that the antiferromagnetic structure belongs to the same irreducible representation as the ferromagnetic state [11,12,13,14,15,16,17,18,19,20,21,22]. The complicated noncollinear/noncoplanar antiferromagnetic structures have often been studied as the origin of these physical phenomena since they lead to the lowering of the crystal symmetry.
Meanwhile, collinear antiferromagnetic structures can also lead to the same physical phenomena by considering the lattice structures with multiple sublattices. For example, the multiferroic property can be engineered by the staggered collinear antiferromagnetic orderings on the one-dimensional zigzag chain [23,24,25,26,27,28,29,30], two-dimensional honeycomb structure [31,32,33,34,35], and three-dimensional diamond structure [36,37,38,39,40,41]. In addition, the anomalous Hall effect is also induced in collinear antiferromagnets [42,43,44,45,46,47,48,49,50]. Since the number of materials with collinear antiferromagnetic structures is larger than that with noncollinear/noncoplanar ones, it is desired to explore further functionalities in collinear antiferromagnets from the fundamental viewpoint.
In this context, emergent spin–orbit coupling (SOC) in antiferromagnets has recently attracted growing interest in both theory and experiments [51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73], which is sometimes referred to as “altermagnetism" [74,75]. There, collinear antiferromagnets exhibit the symmetric momentum-dependent spin-split band structure even without the relativistic SOC. Owing to the momentum dependence of the spin splitting, the directional-dependent spin current generation by an external electric field can be expected [54,76,77,78,79]. As the SOC is not necessary to generate such spin current, this type of collinear antiferromagnet can be a potential candidate for highly efficient spintronics devices that are not limited to the heavy-element materials.
In the present study, we investigate the spin current generation in SOC-free collinear antiferromagnets by focusing on the effect of the cluster geometry. We show that the collinear antiferromagnetic structure in a triangle cluster gives rise to both linear and nonlinear spin conductivities owing to the lack of spatial inversion symmetry in the triangle unit, which differs from the square cluster case. We discuss their emergence from the viewpoint of the group theory and cluster multipole theory. We also study the behavior of both conductivities by analyzing the tight-binding model in the breathing kagome structure formed by triangle clusters. Our results indicate that the cluster structure plays an important role in discussing the spin current generation in SOC-free antiferromagnets.
The rest of this paper is organized as follows. In Section 2, we show the relationship between the collinear antiferromagnetic structures and magnetic toroidal multipoles in the square and triangle clusters. We also introduce the tight-binding model in the breathing kagome system. Then, we show the linear and nonlinear spin conductivities under the collinear antiferromagnetic ordering in Section 3. We compare the linear and nonlinear spin conductivities in Section 4. Section 5 concludes the result of the present paper.

2. Model

2.1. Magnetic Toroidal Multipoles in a Cluster

First, let us discuss the physical properties of antiferromagnetic structures by introducing the magnetic toroidal multipole T l m [80,81,82], which is defined as
T l m = ∑ j r j l + 1 × 2 l j l + 2 + σ j · ∇ O l m ( r j ) ,
where l j and σ j / 2 are the dimensionless orbital and spin angular-momentum operators of an electron at r j . l and m represent the azimuthal and magnetic quantum numbers, respectively. O l m ( r ) is proportional to the spherical harmonics Y l m ( r ^ ) as a function of angle r ^ = r / | r | , Y l m ( r ^ ) , which is given by
O l m ( r ) = 4 π 2 l + 1 r l Y l m * ( r ^ ) .
The magnetic toroidal multipole T l m is characterized by time-reversal-odd polar tensor; even(odd)-rank T l m has the even(odd) parity for the spatial inversion. When Equation (1) applies to the antiferromagnetic structure, one needs to read r j with the position of the jth atom R j in a magnetic unit cell [20,83].
The l = 1 component of T l m corresponds to the magnetic toroidal dipole, which appears when both the spatial inversion and time-reversal symmetries are broken. The expression of T 1 m , i.e., T = ( T x , T y , T z ) , is proportional to ( R × σ ) j when the orbital angular momentum operator is neglected. Thus, the magnetic toroidal dipole T exists in the vortex-type antiferromagnetic structure; it is noted that T is also induced in the collinear antiferromagnetic structure, as shown later. When the antiferromagnetic structure accompanies such a magnetic toroidal dipole, the system exhibits parity-violating physical phenomena, such as the linear magnetoelectric effect [84,85,86,87] and nonreciprocal transport [28,88,89,90,91]. Especially, in the case of collinear antiferromagnets without the relativistic SOC, the nonlinear spin Hall effect can be expected in the presence of the magnetic toroidal dipole [92].
The l = 2 component of T l m corresponds to the magnetic toroidal quadrupole, whose spatial inversion parity is + 1 , while the time-reversal parity is − 1 . There are five components of the magnetic toroidal quadrupole, whose expressions are given by [82]
T u = 3 ( Z X σ x − Y Z σ y ) ,
T v = − 3 ( Z X σ y + Y Z σ x − X Y σ z ) ,
T y z = 3 [ − ( Y 2 − Z 2 ) σ x + X Y σ y − Z X σ z ] ,
T z x = 3 [ − X Y σ x − ( Z 2 − X 2 ) σ y + Y Z σ z ] ,
T x y = 3 [ Z X σ x − Y Z σ y − ( X 2 − Y 2 ) σ z ] ,
where we omit the numerical coefficient and the contribution from the orbital angular momentum for simplicity; we also omit the subscript j, where R j = ( X j , Y j , Z j ) . When the antiferromagnetic structure has the magnetic toroidal quadrupole, the system exhibits the symmetric spin splitting in the electronic band structure. The functional form of the symmetric spin splitting in momentum space is obtained by replacing R j with the wave vector k = ( k x , k y , k z ) , which is given by [93]
T u ( k ) = 3 ( k x k x σ x − k y k z σ y ) ,
T v ( k ) = − 3 ( k z k x σ y + k y k z σ x − k x k y σ z ) ,
T y z ( k ) = 3 [ − ( k y 2 − k z 2 ) σ x + k x k y σ y − k z k x σ z ] ,
T z x ( k ) = 3 [ − k x k y σ x − ( k z 2 − k x 2 ) σ y + k y k z σ z ] ,
T x y ( k ) = 3 [ k z k x σ x − k y k z σ y − ( k x 2 − k y 2 ) σ z ] ,
where the subscript u and v correspond to 3 z 2 − r 2 and x 2 − y 2 , respectively. Such a symmetric spin splitting becomes the origin of the linear spin current generation when the electric field or thermal gradient is applied [54,78]. This spin-split band structure and resultant linear spin current generation occur even without the SOC.
The magnetic toroidal dipole and quadrupole appear in a simple collinear antiferromagnetic structure. To show this, we consider the collinear antiferromagnetic spin configurations in the square and triangle clusters, as shown in Figure 1, where we suppose that the antiferromagnetic spin moments point along the ± z direction. By using the expression in Equation (3) and setting R A = ( − 1 , − 1 , 0 ) , R B = ( 1 , 1 , 0 ) , R C = ( 1 , − 1 , 0 ) , and R D = ( − 1 , 1 , 0 ) , one finds that the antiferromagnetic structure in Figure 1a accompanies T v . Meanwhile, T = 0 owing to the presence of the spatial inversion symmetry. Such emergence of T v is intuitively understood from the distribution of the magnetic toroidal dipole on the bond. When calculating the magnetic toroidal dipole on the i j bond defined by R i × σ i + R j × σ j , one obtains the x 2 − y 2 -type distribution of the magnetic toroidal dipole, i.e., T v , as shown by the purple arrows in Figure 1a. Thus, the antiferromagnetic ordering in Figure 1a leads to the symmetric spin splitting in the form of k x k y σ z for k z = 0 when the lattice structure is formed by the square clusters, which results in the linear spin current generation [55].
Meanwhile, when the spin polarizations for sublattices A and C are reversed in Figure 1b, the magnetic toroidal dipole T y becomes nonzero, whereas T v = 0 . Then, this type of antiferromagnetic structure does not show symmetric spin splitting in the band structure. On the other hand, this magnetic structure gives rise to the nonlinear spin Hall effect owing to a nonzero dipole component, which is irrespective of the SOC [92].
In contrast to the square cluster, the collinear up-down-zero spin configuration in the triangle cluster accompanies both the magnetic toroidal dipole T y and the magnetic toroidal quadrupole T v , where the distribution of the magnetic toroidal dipole on the bond is shown in Figure 1c 1. Thus, the antiferromagnetic ordering consisting of the triangle cluster exhibits both linear and nonlinear spin current generation even without the SOC. In the following, we focus on such a situation by exemplifying the breathing kagome model. We summarize the correspondence between magnetic toroidal multipoles and antiferromagnetic structures in square and triangle clusters in Table 1.

2.2. Breathing Kagome Model

To investigate the spin current generation in the collinear antiferromagnetic systems with the triangle cluster, we adopt the two-dimensional breathing kagome structure, whose point group symmetry is the same as the triangle cluster D 3 h . The breathing kagome structure consists of three sublattices A–C at R A = ( 0 , 0 , 0 ) , R B = a ( 1 , 0 , 0 ) , and R C = a ( 1 / 2 , 3 / 2 , 0 ) ; we set the lattice constant a + b as unity. The tight-binding Hamiltonian is given by
H = − t ∑ σ , 〈 i j 〉 ∈ ▵ + t ′ ∑ σ , 〈 i j 〉 ∈ ▽ c i σ † c j σ   − ∑ i h i ( c i ↑ † c i ↑ ′   − c i ↓ † c i ↓ ′   ) ,
where c i σ † ( c i σ   ) is the creation (annihilation) operator at site i and spin σ = ↑ , ↓ . The first term represents the hoppings within upward triangles t and downward triangles t ′ . We set t = 1 and t ′ = 0.5 in the following calculations. The second term represents the antiferromagnetic mean-field term to induce the up-down-zero spin order; h A = − h , h B = h , and h C = 0 . The schematic spin configurations in the presence of h are shown in Figure 2.

3. Results

3.1. Linear Spin Conductivity

We investigate the linear spin conductivity J ν s = ∑ μ σ μ ; ν s E μ in the model in Equation (13) by using the linear response theory; J ν s = J ν σ z represents the ν -directional spin current with the z-spin component and E μ represents the electric field for the μ = x , y direction. We evaluate σ μ ; ν s from the J ν η ( s ) – J μ correlation function within the Kubo formula following Refs. [78,95] with the scattering rate τ − 1 = 10 − 2 and the temperature T = 10 − 2 . The number of grid points in the Brillouin zone is N k = 2400 2 . Nonzero tensor components in the collinear antiferromagnetic structure in Figure 2 are given by σ x ; y s = σ y ; x s .
Figure 3a shows σ y ; x s while the electron filling per site n e and h are varied, where n e = ∑ k l σ 〈 c k l σ † c k l σ 〉 / ( 3 N k ) ; c k l σ † is the momentum-space representation of c i σ † at the wave vector k and the sublattice l. We also show the data at h = 0.5 in Figure 3b for reference. In all the regions except for n e = 0 and 2 or h = 0 , σ y ; x s becomes nonzero. For σ y ; x s , the intraband process is dominant, which means that σ y ; x s is proportional to τ . This indicates that the symmetric spin splitting at the Fermi level plays an important role; σ y ; x s tends to be enhanced for a large spin splitting. We show the band structure in Figure 4a, which are plotted along the high-symmetric lines in the Brillouin zone in Figure 4b; the color map in Figure 4a represents the z-spin polarization at each wave vector. As shown in Figure 4a, the symmetric spin-split band dispersion appears in the M   2 – Γ –M   3 line, while it does not in the M   1 – Γ and Γ –K lines; this spin-split tendency is consistent with the functional form of k x k y σ z . For h = 0.5 , σ y ; x s becomes larger when the Fermi level lies in the middle or top two bands in Figure 4a, where the symmetric spin splitting becomes larger than that in the bottom two bands.

3.2. Nonlinear Spin Hall Conductivity

We calculate the nonlinear spin Hall conductivity J γ s = ∑ μ ν σ γ ; μ ν s E μ E ν by using the second-order Kubo formula with the relaxation time approximation. The specific expression is given by [92,96]
σ γ ; μ ν s = e 3 τ 2 ℏ 2 N k ∑ k , n f n k ϵ γ μ λ D n ν λ ( s ) ( k ) + ( μ ↔ ν ) ,
where ϵ η μ λ represents the Levi-Civita tensor. We take the electric charge e, the reduced Planck constant ℏ, and the relaxation time τ as unity, i.e., e = ℏ = τ = 1 . f n k is the Fermi distribution function with the band index n and D n μ ν ( s ) ( k ) denotes the spin-dependent Berry curvature dipole, which is related to the spin-dependent Berry curvature Ω n ν ( s ) ( k ) as D n μ ν ( s ) ( k ) = ∂ μ Ω n ν ( s ) ( k ) [96,97]. In the case of the collinear antiferromagnetic structure in Figure 2, the nonzero tensor components of σ γ ; μ ν s is given by σ x ; y y z ( s ) = − 2 σ y ; x y z ( s ) . In contrast to the noncentrosymmetric systems with the relativistic SOC [98,99,100,101,102], the present mechanism is driven by magnetic order, which does not require the SOC.
Figure 5a shows the behavior of σ y ; x y s in the plane of n e and h. Similarly to the linear spin conductivity σ y ; x s , σ y ; x y s becomes nonzero except for n e = 0 and 2 or h = 0 , although almost all of the regions except around the area with 1.3 ≲ n e ≲ 1.5 and 0 < h ≲ 1 take small values. We show the n e dependence of σ y ; x y s at h = 0.5 in Figure 5b, where σ y ; x y s takes the minimum and maximum values at n e ≃ 1.28 and 1.38 , respectively.
The enhancement of σ y ; x y s in the specific region is understood from the fact that both intraband and interband processes contribute to σ y ; x y s . Since the interband process also contributes to σ y ; x y s , the small band gap leading to the small energy denominator included in the spin-dependent Berry curvature dipole is important. Indeed, one finds that the small band gap appears close to the Fermi level, as shown by the band structure in Figure 4(a); the upper (lower) horizontal line represents the chemical potential that gives the maximum (minimum) of σ y ; x y s .

4. Discussion

Finally, let us compare the behavior of the linear spin conductivity σ y ; x s and nonlinear spin Hall conductivity σ y ; x y s in the collinear antiferromagnets with triangle clusters. Although their relaxation time dependence proportional to τ is the same, their symmetry and microscopic conditions are different from each other; the linear spin conductivity appears when the magnetic toroidal quadrupole is activated, while the nonlinear spin Hall conductivity appears when the magnetic toroidal dipole is activated. Reflecting such a difference, the linear spin conductivity is dominated by the intraband process originating from the symmetric spin-split band structure, while the nonlinear spin conductivity is relevant to both intraband and interband processes and is not relevant to the symmetric spin splitting. Accordingly, the model parameter dependence is different, as shown in Figure 3a and Figure 5a, where the linear spin conductivity tends to be larger than the nonlinear spin conductivity.
Meanwhile, the nonlinear spin conductivity becomes larger than the linear spin conductivity when the Fermi level is located near the band gap. Figure 6a shows the ratio of two spin conductivities, R = σ y ; x y s / σ y ; x s , in the plane of n e and h, where τ − 1 = 10 − 2 is taken for both conductivities. We also show the absolute value | R | for different contour ranges in Figure 6b for reference. In the region where the nonlinear spin conductivity is enhanced for 1.3 ≲ n e ≲ 1.5 and 0 < h ≲ 1 , the nonlinear spin conductivity can give the comparable contribution to the linear one. In other words, the contribution from the nonlinear spin conductivity is non-negligible depending on the chemical potential.

5. Conclusions

In conclusion, we have investigated the spin current generation in collinear antiferromagnets without the relativistic SOC. By focusing on the cluster geometry, we have shown that the collinear antiferromagnetic spin configuration in the triangle cluster is qualitatively different from that in the square cluster. In the case of the square cluster, either linear spin conductivity or nonlinear spin conductivity is induced depending on the type of antiferromagnetic spin configuration, while both spin conductivities occur in the up-down-zero spin configuration in the case of the triangle cluster. We have demonstrated the emergence of linear and nonlinear spin conductivities by taking the two-dimensional breathing kagome structure. When the Fermi level lies near the band gap, the contribution from the nonlinear spin conductivity is comparable to that from the linear spin conductivity. Our results indicate that the different cluster geometry gives rise to different behaviors of spin conductivity in SOC-free antiferromagnets, which would be useful for future spintronics applications.

Funding

This research was supported by JSPS KAKENHI Grants Numbers JP21H01037, JP22H00101, JP22H01183, JP23H04869, JP23K03288, JP23K20827, and by JST CREST (JPMJCR23O4).

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Diep, H.T. Frustrated spin systems; World Scientific, 2004.
  2. Lacroix, C.; Mendels, P.; Mila, F., Eds. Introduction to Frustrated Magnetism:Materials, Experiments, Theory (Springer Series in Solid-State Sciences). Springer, 2011.
  3. Bulaevskii, L.N.; Batista, C.D.; Mostovoy, M.V.; Khomskii, D.I. Electronic orbital currents and polarization in Mott insulators. Phys. Rev. B 2008, 78, 024402. [Google Scholar] [CrossRef]
  4. Kimura, T.; Goto, T.; Shintani, H.; Ishizaka, K.; Arima, T.; Tokura, Y. Magnetic control of ferroelectric polarization. Nature 2003, 426, 55–58. [Google Scholar] [CrossRef] [PubMed]
  5. Fiebig, M. Revival of the magnetoelectric effect. J. Phys. D: Appl. Phys. 2005, 38, R123. [Google Scholar] [CrossRef]
  6. Spaldin, N.A.; Fiebig, M. The renaissance of magnetoelectric multiferroics. Science 2005, 309, 391–392. [Google Scholar] [CrossRef] [PubMed]
  7. Ramesh, R.; Spaldin, N.A. Multiferroics: Progress and prospects in thin films. Nat. Mater. 2007, 6, 21. [Google Scholar] [CrossRef] [PubMed]
  8. Khomskii, D. Classifying multiferroics: Mechanisms and effects. Physics 2009, 2, 20. [Google Scholar] [CrossRef]
  9. Tokura, Y.; Seki, S.; Nagaosa, N. Multiferroics of spin origin. Rep. Prog. Phys. 2014, 77, 076501. [Google Scholar] [CrossRef] [PubMed]
  10. Fiebig, M.; Lottermoser, T.; Meier, D.; Trassin, M. The evolution of multiferroics. Nat. Rev. Mater. 2016, 1, 16046. [Google Scholar] [CrossRef]
  11. Ohgushi, K.; Murakami, S.; Nagaosa, N. Spin anisotropy and quantum Hall effect in the kagomé lattice: Chiral spin state based on a ferromagnet. Phys. Rev. B 2000, 62, R6065–R6068. [Google Scholar] [CrossRef]
  12. Shindou, R.; Nagaosa, N. Orbital Ferromagnetism and Anomalous Hall Effect in Antiferromagnets on the Distorted fcc Lattice. Phys. Rev. Lett. 2001, 87, 116801. [Google Scholar] [CrossRef]
  13. Taguchi, Y.; Oohara, Y.; Yoshizawa, H.; Nagaosa, N.; Tokura, Y. Spin chirality, Berry phase, and anomalous Hall effect in a frustrated ferromagnet. Science 2001, 291, 2573–2576. [Google Scholar] [CrossRef] [PubMed]
  14. Tomizawa, T.; Kontani, H. Anomalous Hall effect in the t2g orbital kagome lattice due to noncollinearity: Significance of the orbital Aharonov-Bohm effect. Phys. Rev. B 2009, 80, 100401. [Google Scholar] [CrossRef]
  15. Neubauer, A.; Pfleiderer, C.; Binz, B.; Rosch, A.; Ritz, R.; Niklowitz, P.G.; Böni, P. Topological Hall Effect in the A Phase of MnSi. Phys. Rev. Lett. 2009, 102, 186602. [Google Scholar] [CrossRef] [PubMed]
  16. Nagaosa, N.; Sinova, J.; Onoda, S.; MacDonald, A.H.; Ong, N.P. Anomalous Hall effect. Rev. Mod. Phys. 2010, 82, 1539–1592. [Google Scholar] [CrossRef]
  17. Xiao, D.; Chang, M.C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959–2007. [Google Scholar] [CrossRef]
  18. Chen, H.; Niu, Q.; MacDonald, A.H. Anomalous Hall Effect Arising from Noncollinear Antiferromagnetism. Phys. Rev. Lett. 2014, 112, 017205. [Google Scholar] [CrossRef] [PubMed]
  19. Nakatsuji, S.; Kiyohara, N.; Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 2015, 527, 212. [Google Scholar] [CrossRef] [PubMed]
  20. Suzuki, M.T.; Koretsune, T.; Ochi, M.; Arita, R. Cluster multipole theory for anomalous Hall effect in antiferromagnets. Phys. Rev. B 2017, 95, 094406. [Google Scholar] [CrossRef]
  21. Chen, H.; Wang, T.C.; Xiao, D.; Guo, G.Y.; Niu, Q.; MacDonald, A.H. Manipulating anomalous Hall antiferromagnets with magnetic fields. Phys. Rev. B 2020, 101, 104418. [Google Scholar] [CrossRef]
  22. Feng, W.; Hanke, J.P.; Zhou, X.; Guo, G.Y.; Blügel, S.; Mokrousov, Y.; Yao, Y. Topological magneto-optical effects and their quantization in noncoplanar antiferromagnets. Nat. Commun. 2020, 11, 118. [Google Scholar] [CrossRef]
  23. Yanase, Y. Magneto-Electric Effect in Three-Dimensional Coupled Zigzag Chains. J. Phys. Soc. Jpn. 2014, 83, 014703. [Google Scholar] [CrossRef]
  24. Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous Multipole Ordering by Local Parity Mixing. J. Phys. Soc. Jpn. 2015, 84, 064717. [Google Scholar] [CrossRef]
  25. Sumita, S.; Yanase, Y. Superconductivity in magnetic multipole states. Phys. Rev. B 2016, 93, 224507. [Google Scholar] [CrossRef]
  26. Matsumura, T.; Yamamoto, T.; Tanida, H.; Sera, M. Temperature-Dependent Cycloidal Magnetic Structure in GdRu2Al10 Studied by Resonant X-ray Diffraction. J. Phys. Soc. Jpn. 2017, 86, 094709. [Google Scholar] [CrossRef]
  27. Cysne, T.P.; Guimarães, F.S.M.; Canonico, L.M.; Rappoport, T.G.; Muniz, R.B. Orbital magnetoelectric effect in zigzag nanoribbons of p-band systems. Phys. Rev. B 2021, 104, 165403. [Google Scholar] [CrossRef]
  28. Yatsushiro, M.; Oiwa, R.; Kusunose, H.; Hayami, S. Analysis of model-parameter dependences on the second-order nonlinear conductivity in PT-symmetric collinear antiferromagnetic metals with magnetic toroidal moment on zigzag chains. Phys. Rev. B 2022, 105, 155157. [Google Scholar] [CrossRef]
  29. Suzuki, Y. Tunneling spin current in systems with spin degeneracy. Phys. Rev. B 2022, 105, 075201. [Google Scholar] [CrossRef]
  30. Li, D.X.; Honda, F.; Miyake, A.; Homma, Y.; Haga, Y.; Nakamura, A.; Shimizu, Y.; Maurya, A.; Sato, Y.J.; Tokunaga, M.; Aoki, D. Magnetic and electrical properties of the ternary compound U2Ir3Si5 with one-dimensional uranium zigzag chains. Phys. Rev. B 2019, 99, 054408. [Google Scholar] [CrossRef]
  31. Li, X.; Cao, T.; Niu, Q.; Shi, J.; Feng, J. Coupling the valley degree of freedom to antiferromagnetic order. Proc. Natl. Acad. Sci. U.S.A. 2013, 110, 3738–3742. [Google Scholar] [CrossRef]
  32. Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous parity breaking in spin-orbital coupled systems. Phys. Rev. B 2014, 90, 081115. [Google Scholar] [CrossRef]
  33. Hayami, S.; Kusunose, H.; Motome, Y. Emergent spin-valley-orbital physics by spontaneous parity breaking. J. Phys.: Condens. Matter 2016, 28, 395601. [Google Scholar] [CrossRef] [PubMed]
  34. Yanagi, Y.; Kusunose, H. Optical Selection Rules in Spin–Orbit Coupled Systems on Honeycomb Lattice. J. Phys. Soc. Jpn. 2017, 86, 083703. [Google Scholar] [CrossRef]
  35. Oishi, R.; Umeo, K.; Shimura, Y.; Onimaru, T.; Strydom, A.M.; Takabatake, T. Antiferromagnetic order in the honeycomb Kondo lattice CePt6Al3 induced by Pd substitution. Phys. Rev. B 2021, 104, 104411. [Google Scholar] [CrossRef]
  36. Hayami, S.; Kusunose, H.; Motome, Y. Emergent odd-parity multipoles and magnetoelectric effects on a diamond structure: Implication for the 5d transition metal oxides AOsO44pt0ex(A=K,Rb,andCs). Phys. Rev. B 2018, 97, 024414. [Google Scholar] [CrossRef]
  37. Ishitobi, T.; Hattori, K. Magnetoelectric Effects and Charge-Imbalanced Solenoids: Antiferro Quadrupole Orders in a Diamond Structure. J. Phys. Soc. Jpn. 2019, 88, 063708. [Google Scholar] [CrossRef]
  38. Yamaura, J.i.; Hiroi, Z. Crystal structure and magnetic properties of the 5d transition metal oxides AOsO4(A=K,0.28em0exRb,0.28em0exCs). Phys. Rev. B 2019, 99, 155113. [Google Scholar] [CrossRef]
  39. Paramekanti, A.; Maharaj, D.D.; Gaulin, B.D. Octupolar order in d-orbital Mott insulators. Phys. Rev. B 2020, 101, 054439. [Google Scholar] [CrossRef]
  40. Maharaj, D.D.; Sala, G.; Stone, M.B.; Kermarrec, E.; Ritter, C.; Fauth, F.; Marjerrison, C.A.; Greedan, J.E.; Paramekanti, A.; Gaulin, B.D. Octupolar versus Néel Order in Cubic 5d2 Double Perovskites. Phys. Rev. Lett. 2020, 124, 087206. [Google Scholar] [CrossRef] [PubMed]
  41. Winkler, R.; Zülicke, U. Theory of electric, magnetic, and toroidal polarizations in crystalline solids with applications to hexagonal lonsdaleite and cubic diamond. Phys. Rev. B 2023, 107, 155201. [Google Scholar] [CrossRef]
  42. Solovyev, I.V. Magneto-optical effect in the weak ferromagnets LaMO3 (M= Cr, Mn, and Fe). Phys. Rev. B 1997, 55, 8060–8063. [Google Scholar] [CrossRef]
  43. Sivadas, N.; Okamoto, S.; Xiao, D. Gate-Controllable Magneto-optic Kerr Effect in Layered Collinear Antiferromagnets. Phys. Rev. Lett. 2016, 117, 267203. [Google Scholar] [CrossRef]
  44. Yamasaki, Y.; Nakao, H.; Arima, T.h. Augmented Magnetic Octupole in Kagomé 120-degree Antiferromagnets Detectable via X-ray Magnetic Circular Dichroism. J. Phys. Soc. Jpn. 2020, 89, 083703. [Google Scholar] [CrossRef]
  45. Šmejkal, L.; González-Hernández, R.; Jungwirth, T.; Sinova, J. Crystal time-reversal symmetry breaking and spontaneous Hall effect in collinear antiferromagnets. Sci. Adv. 2020, 6, eaaz8809. [Google Scholar] [CrossRef] [PubMed]
  46. Naka, M.; Hayami, S.; Kusunose, H.; Yanagi, Y.; Motome, Y.; Seo, H. Anomalous Hall effect in κ-type organic antiferromagnets. Phys. Rev. B 2020, 102, 075112. [Google Scholar] [CrossRef]
  47. Hayami, S.; Kusunose, H. Essential role of the anisotropic magnetic dipole in the anomalous Hall effect. Phys. Rev. B 2021, 103, L180407. [Google Scholar] [CrossRef]
  48. Kimata, M.; Sasabe, N.; Kurita, K.; Yamasaki, Y.; Tabata, C.; Yokoyama, Y.; Kotani, Y.; Ikhlas, M.; Tomita, T.; Amemiya, K.; Nojiri, H.; Nakatsuji, S.; Koretsune, T.; Nakao, H.; Arima, T.h.; Nakamura, T. X-ray study of ferroic octupole order producing anomalous Hall effect. Nat. Commun. 2021, 12, 5582. [Google Scholar] [CrossRef] [PubMed]
  49. Chen, H. Electronic chiralization as an indicator of the anomalous Hall effect in unconventional magnetic systems. Phys. Rev. B 2022, 106, 024421. [Google Scholar] [CrossRef]
  50. Sasabe, N.; Kimata, M.; Nakamura, T. Presence of X-Ray Magnetic Circular Dichroism Signal for Zero-Magnetization Antiferromagnetic State. Phys. Rev. Lett. 2021, 126, 157402. [Google Scholar] [CrossRef] [PubMed]
  51. Noda, Y.; Ohno, K.; Nakamura, S. Momentum-dependent band spin splitting in semiconducting MnO 2: A density functional calculation. Phys. Chem. Chem. Phys. 2016, 18, 13294–13303. [Google Scholar] [CrossRef]
  52. Okugawa, T.; Ohno, K.; Noda, Y.; Nakamura, S. Weakly spin-dependent band structures of antiferromagnetic perovskite LaMO3 (M= Cr, Mn, Fe). J. Phys.: Condens. Matter 2018, 30, 075502. [Google Scholar] [CrossRef]
  53. Ahn, K.H.; Hariki, A.; Lee, K.W.; Kuneš, J. Antiferromagnetism in RuO2 as d-wave Pomeranchuk instability. Phys. Rev. B 2019, 99, 184432. [Google Scholar] [CrossRef]
  54. Naka, M.; Hayami, S.; Kusunose, H.; Yanagi, Y.; Motome, Y.; Seo, H. Spin current generation in organic antiferromagnets. Nat. Commun. 2019, 10, 4305. [Google Scholar] [CrossRef] [PubMed]
  55. Hayami, S.; Yanagi, Y.; Kusunose, H. Momentum-Dependent Spin Splitting by Collinear Antiferromagnetic Ordering. J. Phys. Soc. Jpn. 2019, 88, 123702. [Google Scholar] [CrossRef]
  56. Hayami, S.; Yanagi, Y.; Kusunose, H. Spontaneous antisymmetric spin splitting in noncollinear antiferromagnets without spin-orbit coupling. Phys. Rev. B 2020, 101, 220403. [Google Scholar] [CrossRef]
  57. Hayami, S.; Yanagi, Y.; Kusunose, H. Bottom-up design of spin-split and reshaped electronic band structures in antiferromagnets without spin-orbit coupling: Procedure on the basis of augmented multipoles. Phys. Rev. B 2020, 102, 144441. [Google Scholar] [CrossRef]
  58. Yuan, L.D.; Wang, Z.; Luo, J.W.; Rashba, E.I.; Zunger, A. Giant momentum-dependent spin splitting in centrosymmetric low-Z antiferromagnets. Phys. Rev. B 2020, 102, 014422. [Google Scholar] [CrossRef]
  59. Egorov, S.A.; Evarestov, R.A. Colossal Spin Splitting in the Monolayer of the Collinear Antiferromagnet MnF2. J. Phys. Chem. Lett. 2021, 12, 2363–2369. [Google Scholar] [CrossRef] [PubMed]
  60. Yuan, L.D.; Wang, Z.; Luo, J.W.; Zunger, A. Strong influence of nonmagnetic ligands on the momentum-dependent spin splitting in antiferromagnets. Phys. Rev. B 2021, 103, 224410. [Google Scholar] [CrossRef]
  61. Yuan, L.D.; Wang, Z.; Luo, J.W.; Zunger, A. Prediction of low-Z collinear and noncollinear antiferromagnetic compounds having momentum-dependent spin splitting even without spin-orbit coupling. Phys. Rev. Materials 2021, 5, 014409. [Google Scholar] [CrossRef]
  62. Mazin, I.I. Altermagnetism in MnTe: Origin, predicted manifestations, and routes to detwinning. Phys. Rev. B 2023, 107, L100418. [Google Scholar] [CrossRef]
  63. Lovesey, S.W.; Khalyavin, D.D.; van der Laan, G. Templates for magnetic symmetry and altermagnetism in hexagonal MnTe. Phys. Rev. B 2023, 108, 174437. [Google Scholar] [CrossRef]
  64. Yuan, L.D.; Zunger, A. Degeneracy Removal of Spin Bands in Collinear Antiferromagnets with Non-Interconvertible Spin-Structure Motif Pair. Adv. Mater. 2023, 35, 2211966. [Google Scholar] [CrossRef] [PubMed]
  65. Yuan, L.D.; Zhang, X.; Acosta, C.M.; Zunger, A. Uncovering spin-orbit coupling-independent hidden spin polarization of energy bands in antiferromagnets. Nat. Commun. 2023, 14, 5301. [Google Scholar] [CrossRef]
  66. Gonzalez Betancourt, R.D.; Zubáč, J.; Gonzalez-Hernandez, R.; Geishendorf, K.; Šobáň, Z.; Springholz, G.; Olejník, K.; Šmejkal, L.; Sinova, J.; Jungwirth, T.; Goennenwein, S.T.B.; Thomas, A.; Reichlová, H.; Železný, J.; Kriegner, D. Spontaneous Anomalous Hall Effect Arising from an Unconventional Compensated Magnetic Phase in a Semiconductor. Phys. Rev. Lett. 2023, 130, 036702. [Google Scholar] [CrossRef]
  67. Ouassou, J.A.; Brataas, A.; Linder, J. dc Josephson Effect in Altermagnets. Phys. Rev. Lett. 2023, 131, 076003. [Google Scholar] [CrossRef] [PubMed]
  68. Cui, Q.; Zeng, B.; Cui, P.; Yu, T.; Yang, H. Efficient spin Seebeck and spin Nernst effects of magnons in altermagnets. Phys. Rev. B 2023, 108, L180401. [Google Scholar] [CrossRef]
  69. Brekke, B.; Brataas, A.; Sudbø, A. Two-dimensional altermagnets: Superconductivity in a minimal microscopic model. Phys. Rev. B 2023, 108, 224421. [Google Scholar] [CrossRef]
  70. Aoyama, T.; Ohgushi, K. Piezomagnetic properties in altermagnetic MnTe. Phys. Rev. Mater. 2024, 8, L041402. [Google Scholar] [CrossRef]
  71. Hariki, A.; Takahashi, Y.; Kuneš, J. X-ray magnetic circular dichroism in RuO2. Phys. Rev. B 2024, 109, 094413. [Google Scholar] [CrossRef]
  72. Osumi, T.; Souma, S.; Aoyama, T.; Yamauchi, K.; Honma, A.; Nakayama, K.; Takahashi, T.; Ohgushi, K.; Sato, T. Observation of a giant band splitting in altermagnetic MnTe. Phys. Rev. B 2024, 109, 115102. [Google Scholar] [CrossRef]
  73. Hariki, A.; Dal Din, A.; Amin, O.J.; Yamaguchi, T.; Badura, A.; Kriegner, D.; Edmonds, K.W.; Campion, R.P.; Wadley, P.; Backes, D.; Veiga, L.S.I.; Dhesi, S.S.; Springholz, G.; Šmejkal, L.; Výborný, K.; Jungwirth, T.; Kuneš, J. X-Ray Magnetic Circular Dichroism in Altermagnetic α-MnTe. Phys. Rev. Lett. 2024, 132, 176701. [Google Scholar] [CrossRef]
  74. Šmejkal, L.; Sinova, J.; Jungwirth, T. Beyond Conventional Ferromagnetism and Antiferromagnetism: A Phase with Nonrelativistic Spin and Crystal Rotation Symmetry. Phys. Rev. X 2022, 12, 031042. [Google Scholar] [CrossRef]
  75. Šmejkal, L.; Sinova, J.; Jungwirth, T. Emerging Research Landscape of Altermagnetism. Phys. Rev. X 2022, 12, 040501. [Google Scholar] [CrossRef]
  76. Shao, D.F.; Zhang, S.H.; Li, M.; Eom, C.B.; Tsymbal, E.Y. Spin-neutral currents for spintronics. Nat. Commun. 2021, 12, 7061. [Google Scholar] [CrossRef]
  77. González-Hernández, R.; Šmejkal, L.; Výborný, K.; Yahagi, Y.; Sinova, J.; Jungwirth, T.; Železný, J. Efficient Electrical Spin Splitter Based on Nonrelativistic Collinear Antiferromagnetism. Phys. Rev. Lett. 2021, 126, 127701. [Google Scholar] [CrossRef]
  78. Hayami, S.; Yatsushiro, M. Spin Conductivity Based on Magnetic Toroidal Quadrupole Hidden in Antiferromagnets. J. Phys. Soc. Jpn. 2022, 91, 063702. [Google Scholar] [CrossRef]
  79. Bai, H.; Zhang, Y.C.; Zhou, Y.J.; Chen, P.; Wan, C.H.; Han, L.; Zhu, W.X.; Liang, S.X.; Su, Y.C.; Han, X.F.; Pan, F.; Song, C. Efficient Spin-to-Charge Conversion via Altermagnetic Spin Splitting Effect in Antiferromagnet RuO2. Phys. Rev. Lett. 2023, 130, 216701. [Google Scholar] [CrossRef]
  80. Spaldin, N.A.; Fiebig, M.; Mostovoy, M. The toroidal moment in condensed-matter physics and its relation to the magnetoelectric effect. J. Phys.: Condens. Matter 2008, 20, 434203. [Google Scholar] [CrossRef]
  81. Kopaev, Y.V. Toroidal ordering in crystals. Physics-Uspekhi 2009, 52, 1111–1125. [Google Scholar] [CrossRef]
  82. Hayami, S.; Kusunose, H. Microscopic Description of Electric and Magnetic Toroidal Multipoles in Hybrid Orbitals. J. Phys. Soc. Jpn. 2018, 87, 033709. [Google Scholar] [CrossRef]
  83. Suzuki, M.T.; Nomoto, T.; Arita, R.; Yanagi, Y.; Hayami, S.; Kusunose, H. Multipole expansion for magnetic structures: A generation scheme for a symmetry-adapted orthonormal basis set in the crystallographic point group. Phys. Rev. B 2019, 99, 174407. [Google Scholar] [CrossRef]
  84. Popov, Y.F.; Kadomtseva, A.; Belov, D.; Vorob’ev, G.; Zvezdin, A. Magnetic-field-induced toroidal moment in the magnetoelectric Cr2O3. J. Exp. Theor. Phys. Lett. 1999, 69, 330–335. [Google Scholar] [CrossRef]
  85. Schmid, H. On ferrotoroidics and electrotoroidic, magnetotoroidic and piezotoroidic effects*. Ferroelectrics 2001, 252, 41–50. [Google Scholar] [CrossRef]
  86. Ederer, C.; Spaldin, N.A. Towards a microscopic theory of toroidal moments in bulk periodic crystals. Phys. Rev. B 2007, 76, 214404. [Google Scholar] [CrossRef]
  87. Thöle, F.; Spaldin, N.A. Magnetoelectric multipoles in metals. Philos. Trans. R. Soc. A 2018, 376, 20170450. [Google Scholar] [CrossRef]
  88. Sawada, K.; Nagaosa, N. Optical Magnetoelectric Effect in Multiferroic Materials: Evidence for a Lorentz Force Acting on a Ray of Light. Phys. Rev. Lett. 2005, 95, 237402. [Google Scholar] [CrossRef]
  89. Miyahara, S.; Furukawa, N. Nonreciprocal Directional Dichroism and Toroidalmagnons in Helical Magnets. J. Phys. Soc. Jpn. 2012, 81, 023712. [Google Scholar] [CrossRef]
  90. Miyahara, S.; Furukawa, N. Theory of magneto-optical effects in helical multiferroic materials via toroidal magnon excitation. Phys. Rev. B 2014, 89, 195145. [Google Scholar] [CrossRef]
  91. Hayami, S.; Kusunose, H.; Motome, Y. Asymmetric Magnon Excitation by Spontaneous Toroidal Ordering. J. Phys. Soc. Jpn. 2016, 85, 053705. [Google Scholar] [CrossRef]
  92. Hayami, S.; Yatsushiro, M.; Kusunose, H. Nonlinear spin Hall effect in PT-symmetric collinear magnets. Phys. Rev. B 2022, 106, 024405. [Google Scholar] [CrossRef]
  93. Hayami, S.; Yatsushiro, M.; Yanagi, Y.; Kusunose, H. Classification of atomic-scale multipoles under crystallographic point groups and application to linear response tensors. Phys. Rev. B 2018, 98, 165110. [Google Scholar] [CrossRef]
  94. Yatsushiro, M.; Kusunose, H.; Hayami, S. Multipole classification in 122 magnetic point groups for unified understanding of multiferroic responses and transport phenomena. Phys. Rev. B 2021, 104, 054412. [Google Scholar] [CrossRef]
  95. Mook, A.; Neumann, R.R.; Johansson, A.; Henk, J.; Mertig, I. Origin of the magnetic spin Hall effect: Spin current vorticity in the Fermi sea. Phys. Rev. Research 2020, 2, 023065. [Google Scholar] [CrossRef]
  96. Sodemann, I.; Fu, L. Quantum Nonlinear Hall Effect Induced by Berry Curvature Dipole in Time-Reversal Invariant Materials. Phys. Rev. Lett. 2015, 115, 216806. [Google Scholar] [CrossRef] [PubMed]
  97. Kondo, H.; Akagi, Y. Nonlinear magnon spin Nernst effect in antiferromagnets and strain-tunable pure spin current. Phys. Rev. Research 2022, 4, 013186. [Google Scholar] [CrossRef]
  98. Yu, H.; Wu, Y.; Liu, G.B.; Xu, X.; Yao, W. Nonlinear Valley and Spin Currents from Fermi Pocket Anisotropy in 2D Crystals. Phys. Rev. Lett. 2014, 113, 156603. [Google Scholar] [CrossRef] [PubMed]
  99. Hamamoto, K.; Ezawa, M.; Kim, K.W.; Morimoto, T.; Nagaosa, N. Nonlinear spin current generation in noncentrosymmetric spin-orbit coupled systems. Phys. Rev. B 2017, 95, 224430. [Google Scholar] [CrossRef]
  100. Araki, Y. Strain-induced nonlinear spin Hall effect in topological Dirac semimetal. Sci. Rep. 2018, 8, 15236. [Google Scholar] [CrossRef]
  101. Pan, A.; Marinescu, D.C. Nonlinear spin-current generation in quantum wells with arbitrary Rashba-Dresselhaus spin-orbit interactions. Phys. Rev. B 2019, 99, 245204. [Google Scholar] [CrossRef]
  102. Zhang, Z.F.; Zhu, Z.G.; Su, G. Theory of nonlinear response for charge and spin currents. Phys. Rev. B 2021, 104, 115140. [Google Scholar] [CrossRef]
1
Although the magnetic toroidal quadrupole T u also belongs to the totally symmetric irreducible representation [94], it is not activated within the two-dimensional system.
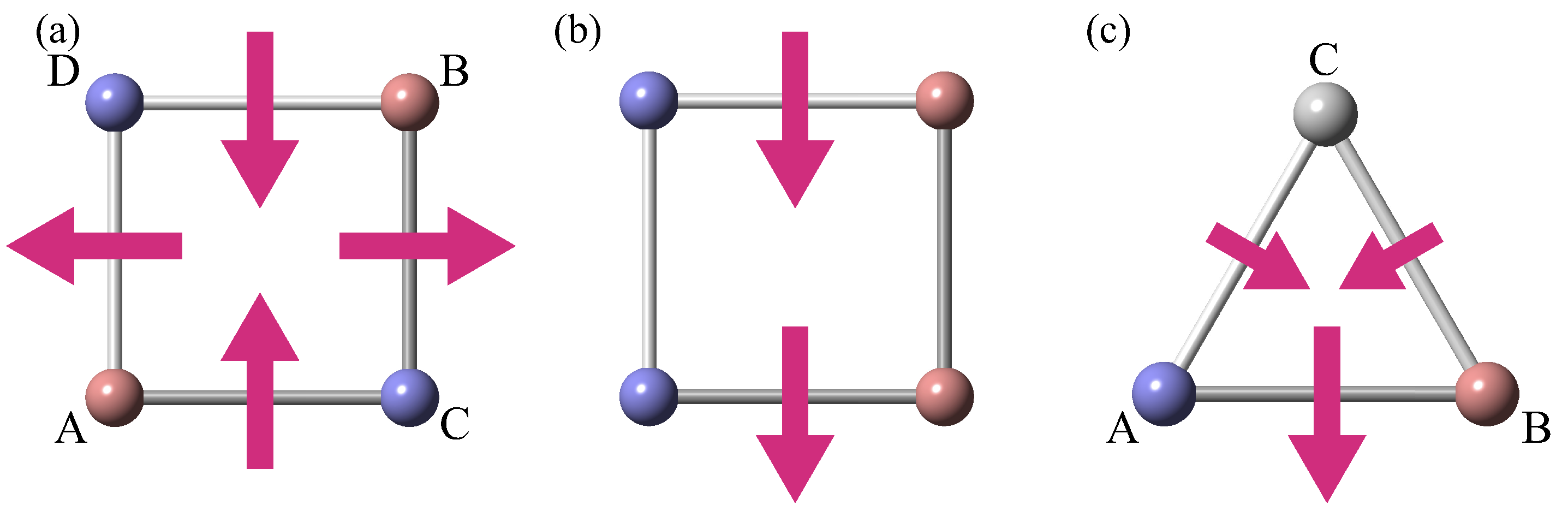
Preprints 108412 g001
Figure 1. Schematic configurations of the spins and magnetic toroidal dipoles in (a,b) the square cluster and (c) the triangle cluster. The red and blue spheres represent the collinear spin moments along the z direction. The purple arrows on the bond represent the magnetic toroidal dipoles. In (b,c), the uniform component of the magnetic toroidal dipole is present.
Figure 1. Schematic configurations of the spins and magnetic toroidal dipoles in (a,b) the square cluster and (c) the triangle cluster. The red and blue spheres represent the collinear spin moments along the z direction. The purple arrows on the bond represent the magnetic toroidal dipoles. In (b,c), the uniform component of the magnetic toroidal dipole is present.
Preprints 108412 g001
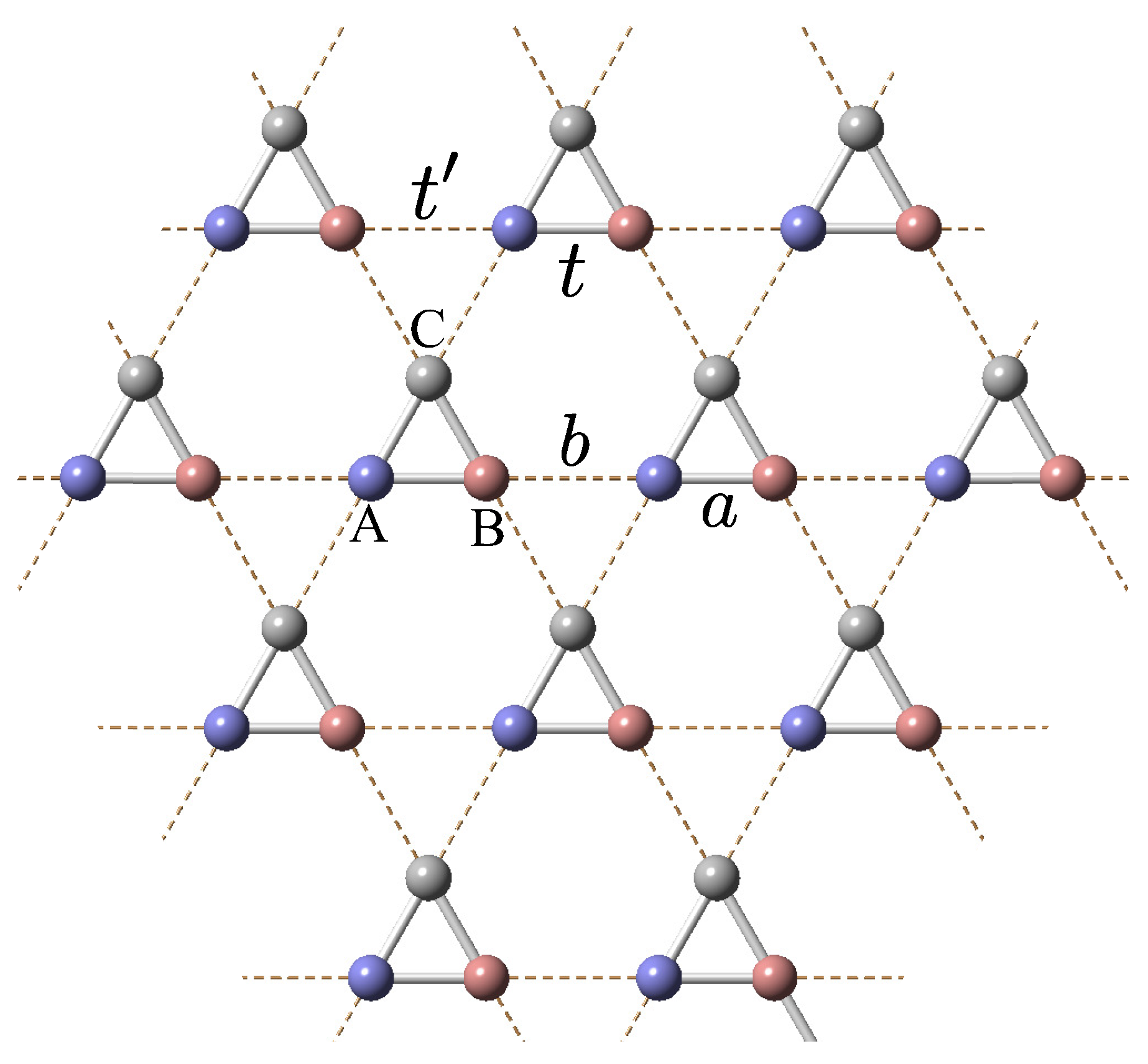
Preprints 108412 g002
Figure 2. Two-dimensional breathing kagome structure with the lattice constant a + b . The red and blue spheres represent the collinear spin moments along the z direction. t and t ′ stand for the intra- and inter-sublattice hoppings, respectively.
Figure 2. Two-dimensional breathing kagome structure with the lattice constant a + b . The red and blue spheres represent the collinear spin moments along the z direction. t and t ′ stand for the intra- and inter-sublattice hoppings, respectively.
Preprints 108412 g002
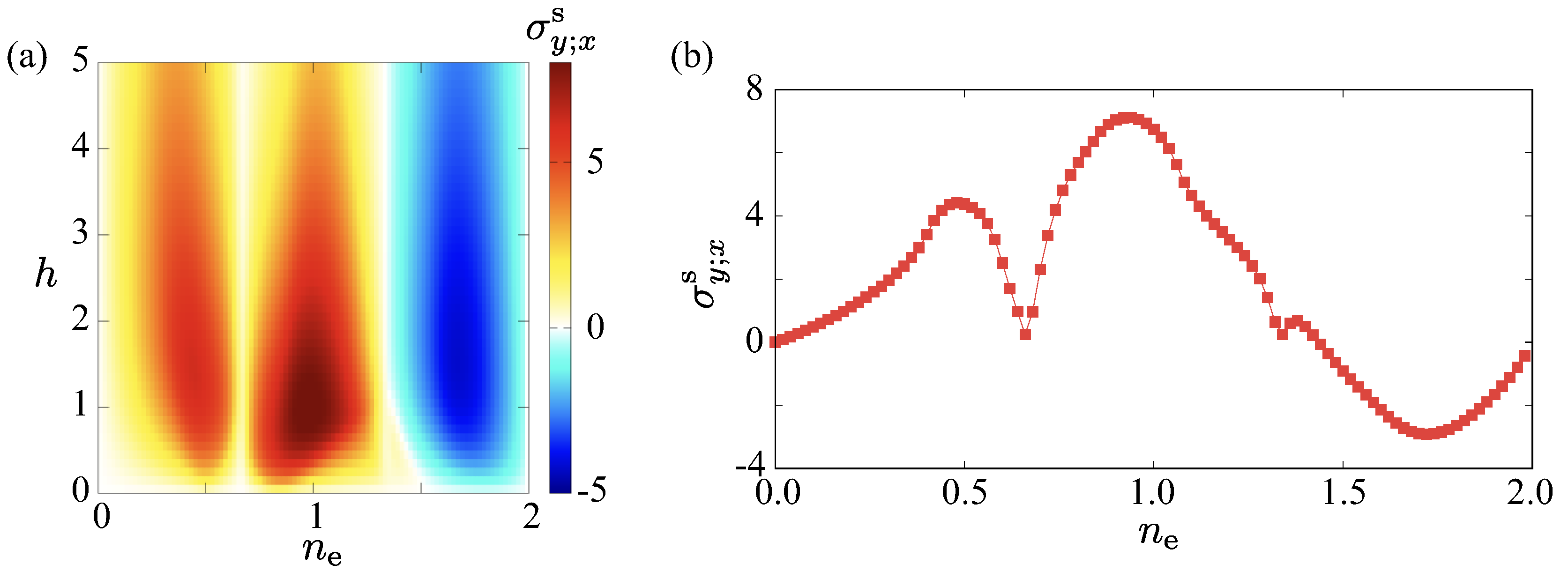
Preprints 108412 g003
Figure 3. (a) Contour plot of the linear spin conductivity σ y ; x s in the plane of the electron filling n e and the molecular field h at t = 1 and t ′ = 0.5 . (b) n e dependence of σ y ; x s at h = 0.5 .
Figure 3. (a) Contour plot of the linear spin conductivity σ y ; x s in the plane of the electron filling n e and the molecular field h at t = 1 and t ′ = 0.5 . (b) n e dependence of σ y ; x s at h = 0.5 .
Preprints 108412 g003
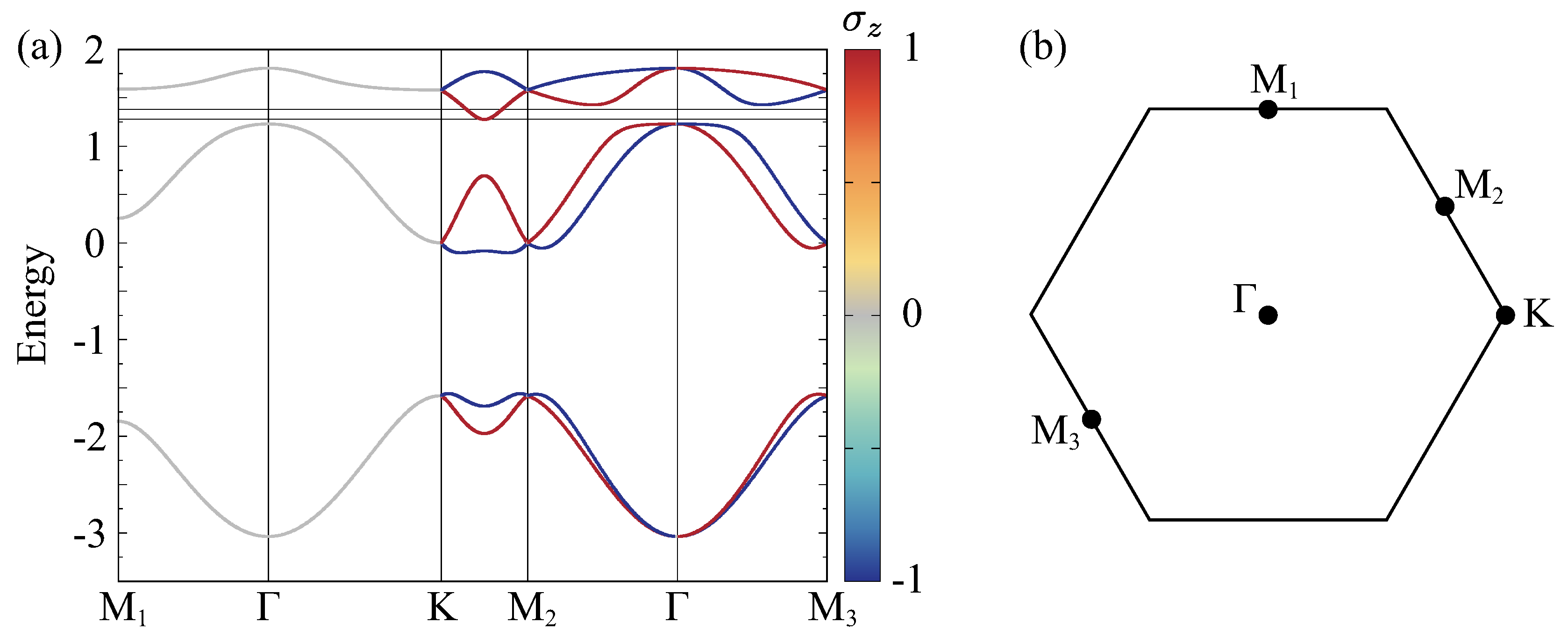
Preprints 108412 g004
Figure 4. (a) Electronic band structure in the breathing kagome system under the collinear AFM structure at t = 1 , t ′ = 0.5 , and h = 0.5 . The contour represents the spin polarization in terms of the z component, σ z . The upper (lower) horizontal line stands for the chemical potential that maximizes (minimizes) σ y ; x y s in Figure 5b. (b) The Brillouin zone in the breathing kagome system.
Figure 4. (a) Electronic band structure in the breathing kagome system under the collinear AFM structure at t = 1 , t ′ = 0.5 , and h = 0.5 . The contour represents the spin polarization in terms of the z component, σ z . The upper (lower) horizontal line stands for the chemical potential that maximizes (minimizes) σ y ; x y s in Figure 5b. (b) The Brillouin zone in the breathing kagome system.
Preprints 108412 g004
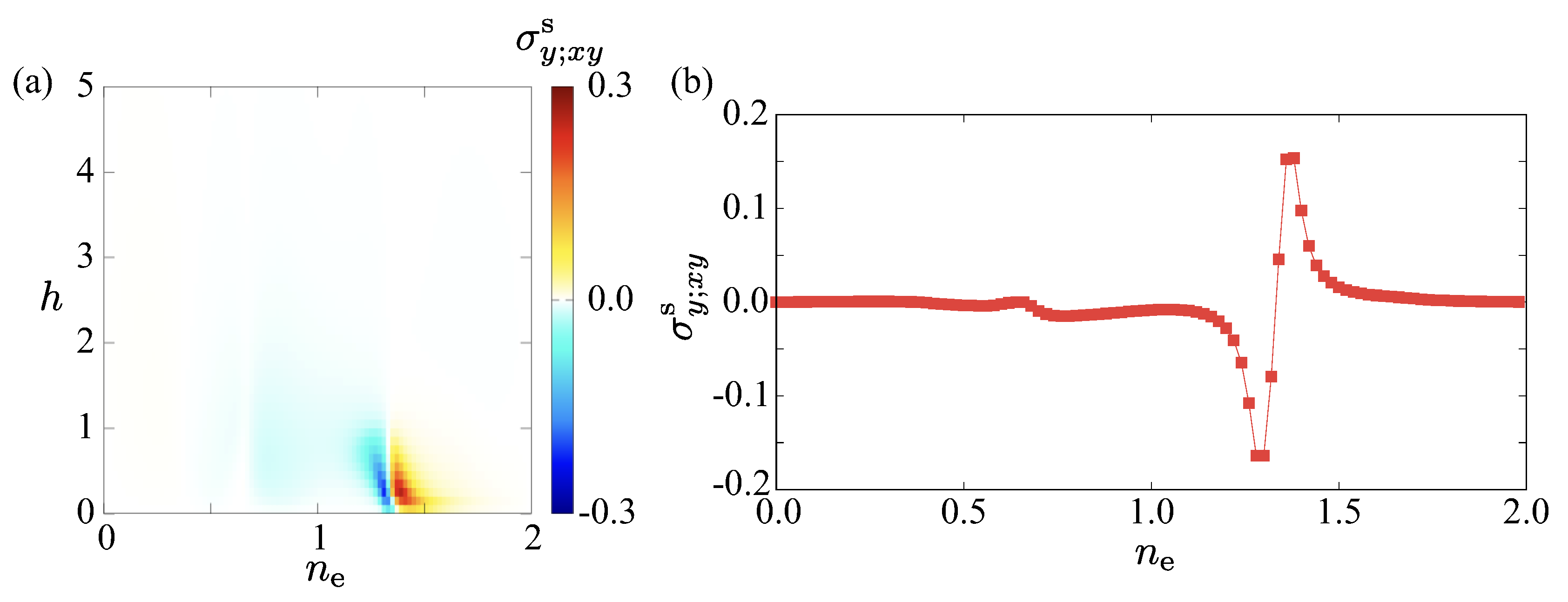
Preprints 108412 g005
Figure 5. (a) Contour plot of the nonlinear spin Hall conductivity σ y ; x y s in the plane of the electron filling n e and the molecular field h at t = 1 and t ′ = 0.5 . (b) n e dependence of σ y ; x y s at h = 0.5 .
Figure 5. (a) Contour plot of the nonlinear spin Hall conductivity σ y ; x y s in the plane of the electron filling n e and the molecular field h at t = 1 and t ′ = 0.5 . (b) n e dependence of σ y ; x y s at h = 0.5 .
Preprints 108412 g005
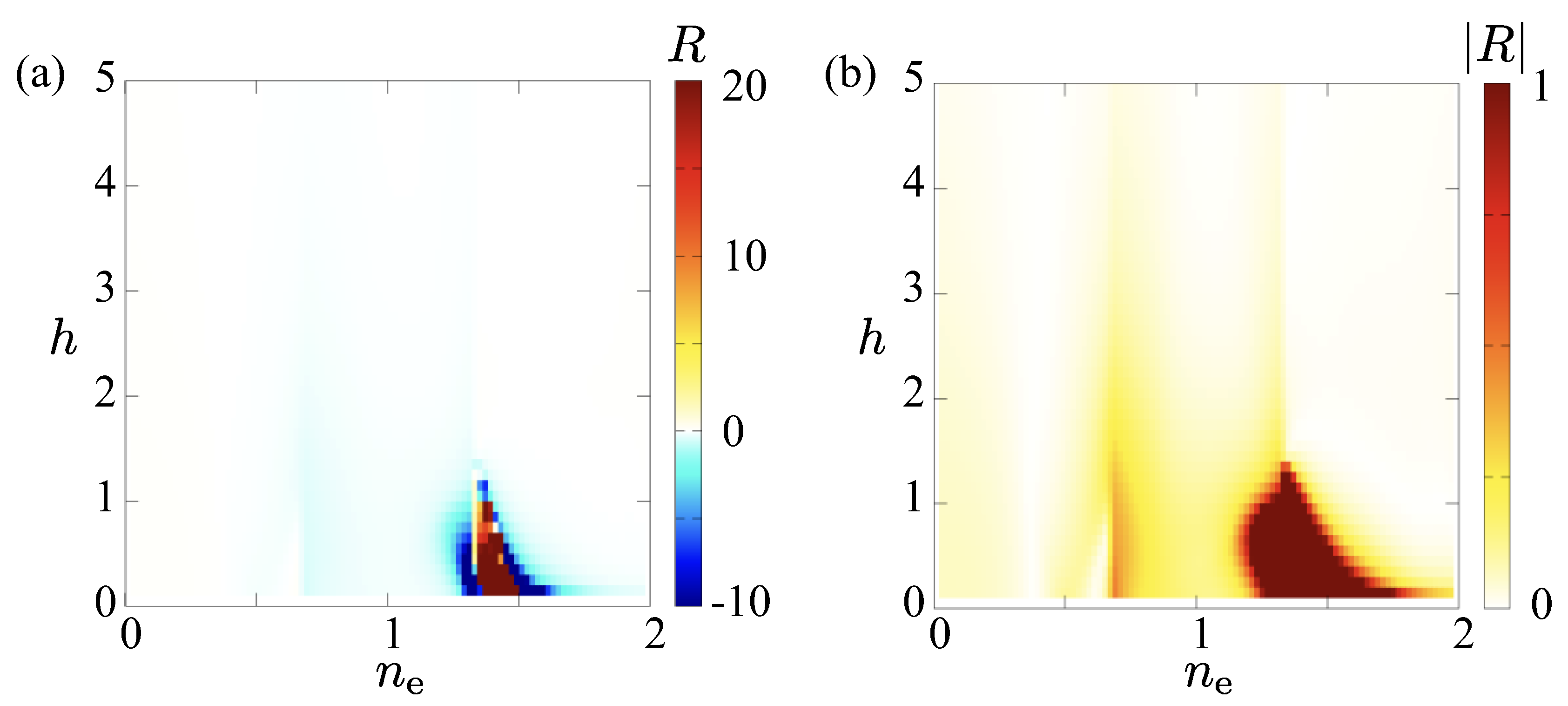
Preprints 108412 g006
Figure 6. (a) n e and h dependence of the ratio R = σ y ; x y s / σ y ; x s at t = 1 , t ′ = 0.5 , and τ − 1 = 0.01 . (b) Enlarged figure of (a) for 0 ≤ | R | ≤ 1 .
Figure 6. (a) n e and h dependence of the ratio R = σ y ; x y s / σ y ; x s at t = 1 , t ′ = 0.5 , and τ − 1 = 0.01 . (b) Enlarged figure of (a) for 0 ≤ | R | ≤ 1 .
Preprints 108412 g006
Table 1. The correspondence among the magnetic point group (MPG), induced rank-1 and rank-2 magnetic toroidal (MT) multipoles, and the emergence of the spin-split band structure (SS) and nonlinear spin Hall conductivity (NSHC) in the collinear antiferromagnets without the spin–orbit coupling. The antiferromagnetic patterns correspond to those in Figure 1a–c from the top row. The parent point group (PG) and the irreducible representation (Irrep.) are also shown; the superscript − in the Irrep. represents the odd parity with respect to the time-reversal operation.
Table 1. The correspondence among the magnetic point group (MPG), induced rank-1 and rank-2 magnetic toroidal (MT) multipoles, and the emergence of the spin-split band structure (SS) and nonlinear spin Hall conductivity (NSHC) in the collinear antiferromagnets without the spin–orbit coupling. The antiferromagnetic patterns correspond to those in Figure 1a–c from the top row. The parent point group (PG) and the irreducible representation (Irrep.) are also shown; the superscript − in the Irrep. represents the odd parity with respect to the time-reversal operation.
PG Irrep. MPG MT multipole SS NSHC
square D 4 h B 1 g − 4 ′ / m m m ′ T v –
square D 4 h E u − m m ′ m T y –
triangle D 3 h E ′ − m 2 m T y , T v
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated