A Survey of Computationally Efficient Graph Neural Networks for Reconfigurable Systems

Preprint

Review

A Survey of Computationally Efficient Graph Neural Networks for Reconfigurable Systems

Altmetrics

Downloads

220

Views

132

Comments

A peer-reviewed article of this preprint also exists.

Habib Taha Kose

Jose Nunez-Yanez^*,Robert Piechocki,James Pope

Habib Taha Kose

Jose Nunez-Yanez^*,Robert Piechocki,James Pope

This version is not peer-reviewed

Submitted:

02 June 2024

Posted:

05 June 2024

You are already at the latest version

Alerts

Abstract

Graph Neural Networks (GNNs) are powerful models capable of managing intricate connections in non-Euclidean data, such as social networks, physical systems, chemical structures, and communication networks. Despite their effectiveness, the large-scale and complex nature of graph data demands substantial computational resources and high performance during both training and inference stages, presenting significant challenges, particularly in the context of embedded systems. Recent studies on GNNs have investigated both software and hardware solutions to enhance computational efficiency. Earlier studies on Deep Neural Networks (DNNs) have indicated that methods like reconfigurable hardware and quantization are beneficial in addressing these issues. Unlike DNN research, studies on efficient computational methods for GNNs are less developed and require more exploration. This survey reviews the latest developments in quantization and FPGA-based acceleration for GNNs, showcasing the capabilities of reconfigurable systems (often FPGAs) to offer customized solutions in environments marked by significant sparsity and the necessity for dynamic load management. It also emphasizes the role of quantization in reducing both computational and memory demands through the use of fixed-point arithmetic and streamlined vector formats. This paper concentrates on low-power, resource-limited devices over general hardware accelerators and reviews research applicable to embedded systems. Additionally, it provides a detailed discussion of potential research gaps, foundational knowledge, obstacles, and prospective future directions.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Recent scientific research has witnessed remarkable strides in deep learning methodologies and neural network architectures. These advances have garnered considerable attention from researchers due to their extensive applicability in the academic and commercial domains [1]. Deep learning techniques have demonstrated efficacy across diverse domains such as computer vision, natural language processing, medical imaging, and communication systems. The key to this success lies in the adept use of large datasets with significant computing resources by specialized network models. Therefore, both software and hardware-based applications have been the subject of extensive research aimed at enhancing the prospects of deep learning and facilitating its widespread adoption.

Deep learning is a process of learning complex input data using simple parts [1]. In common machine learning and deep learning applications, these input data are typically represented by Euclidean structures. In contrast, graph data with complex relationships, such as physical phenomena, chemical bonds, protein structures, and diseases, are represented by non-Euclidean data and require specialized models [2]. Current machine learning methods for non-Euclidean data have limited performance due to their high computational cost and implementation inflexibility. Although deep learning models have proven successful on vector-based inputs, Graph Neural Networks (GNNs) have attracted the attention of researchers due to their ability to learn complicated relationships between nodes and edges in a graph [1]. Research has shown that GNNs outperform classical deep learning models when dealing with non-Euclidean data [2].

GNNs are high-accuracy neural network models that can be trained on graph data and used for inference. Graph datasets often have complex relationships between their nodes, and GNNs can use these relationships to successfully learn local and global information. The unique structure of GNNs demonstrates impressive performance in social networks [3], friend recommendations, molecular bonding [4], e-commerce [5], and product recommendation systems [6]. Successful results have been achieved in various fields, including particle physics [7,8], natural language processing [9], traffic applications [10], anomaly detection [11], and many academic studies [12,13,14]. In addition, GNN technology has attracted the attention of technology companies and major corporations such as Google [15], Amazon [16], Facebook [17], and Alibaba [6], which have started to include it in their strategic plans. Current research shows that GNNs will have wide-ranging applications in various areas of life, and it is foreseen that this technology will play an important role in various applications such as information processing analysis, science, industry, and daily life.

Compared to the Euclidean data used in classical neural network models, graph data require more computationally intensive resources [1]. The massive size of the data and the complexity of the connections increase the effectiveness of the GNN on graph datasets [18,19]. In addition, the irregular nature and instability of graph data pose several computational challenges [20]. Current GNN implementations for learning these complex datasets use frameworks such as the Deep Graph Library (DGL) [16], PyTorch Geometric (PyG) [21], and TensorFlow GNN [22]. These frameworks provide software support for graph neural networks on CPUs and GPUs, which are often used for Convolutional Neural Networks (CNNs) and other well-known methods [23,24]. However, for embedded device applications such as edge devices, IoT, and mobile applications, generic frameworks are insufficient in terms of integration and efficiency. To overcome this problem, there are several works in the literature to build lightweight and fast GNN models. While these studies cover both traditional and embedded hardware, GPU and CPU implementations form a large part of the overall topic. Although the use of low-bit precision and FPGA-based accelerators to derive low-dimensional and real-time models is a well-known research topic in Neural Networks (NNs) [25] and Convolutional Neural Networks [26], there has been insufficient research on GNNs [20,24,27,28]. Therefore, the study of quantized GNN models for accelerators is a promising potential research topic.

Developments in GNNs have increased the range of applications of the models, and specialized GNN implementations require specialized hardware techniques [20]. In previous neural network studies, hardware accelerators based on FPGAs have often been the preferred solution when classical neural networks face challenging situations. In the same spirit, these specialized accelerators are seen as crucial in improving the performance of GNN models and making them more suitable for use on embedded devices [29]. However, there has not yet been enough research conducted on this topic in GNNs [30]. Due to their high computational power, FPGAs are known as ideal candidates for efficient processing of complex algorithms and fast application execution. Furthermore, the flexibility of FPGA hardware components allows customization to meet the unique requirements of users, enabling neural network models to be optimized to suit specific demands, ultimately leading to increased performance. In addition, specially designed and optimized hardware reduces power consumption by significantly reducing computational costs [31]. Low power consumption can increase the energy efficiency of embedded devices, making it advantageous for mobile applications. FPGAs offer flexibility, which opens up innovative possibilities for researchers and developers [32]. The research community aims to utilize FPGA-based accelerators to address issues such as load imbalance, memory requirements, and computing power [30]. Improved performance in GNN-based applications can be achieved through the effective optimization of FPGAs. However, for larger models, additional approaches are required to achieve performance improvements due to limited storage and computing power.

Neural network quantization constitutes an essential technique for the scaling of network models, as well as the efficient computation on hardware such as FPGAs. It serves as a means to enhance computational efficiency and alleviate memory demands by representing the model parameters with reduced bit precision [33]. The core objective underlying quantization is the minimization of bit usage, achieved through the mapping of real numbers to lower-precision equivalents while upholding accuracy standards [34]. This process holds significant promise for facilitating high-performance applications in the future by enabling a streamlined representation of the parameters crucial for matrix multiplication operations. A notable advantage of quantization is its capacity to accommodate lightweight neural networks by employing fewer bits for both activation and model weights. Integer-based representations, which are central to quantization, offer enhanced processing efficiency on FPGAs compared with floating-point numbers [20]. Although floating-point calculations often entail intricate operations, integer computations can be executed more straightforwardly and with greater efficiency [35]. This attribute is particularly advantageous for the development of efficient systems tailored for embedded devices, especially when coupled with specialized hardware, such as FPGAs. The significance of quantization techniques transcends mere computational efficiency; they play a pivotal role in optimizing the performance of FPGA-based hardware accelerators in GNN systems.

The literature examines Graph Neural Networks (GNNs) in-depth, covering general knowledge, network structures, potential gaps, and perspectives through various surveys [1,2,12,15,18,19,36,37,38,39,40,41,42,43,44,45,46,47]. In addition, the existing literature includes surveys and reviews focusing on specific applications [48,49,50,51]. For instance, Lamb et al. [52] conducted a study on the use of GNNs as a neural-symbolic computing tool, whereas Malekzadeh et al. [53] analyzed their use in text classification. Ahmad et al. [54] examined the use of Graph Convolutional Neural Networks (GCNs) in human action recognition and proposed a taxonomy of studies in this area. Other studies have provided detailed insights into the use of GNNs in various applications such as the Internet of Things (IoT) [55], network science [56], and language processing [57]. There are also general information on accelerators and efficient GNNs [29,58,59]. Liu et al. [60] approach current and future GNN work from an algorithmic perspective, while Abadal et al. [61] provide a comprehensive overview of the acceleration algorithms and GNN fundamentals. As shown in Figure 1, we review hardware-based accelerators and quantization approaches for computationally efficient GNNs, with a particular focus on energy-constrained embedded device applications.

This survey explores quantization methods and FPGA-based hardware accelerators to reduce the computational cost and model complexity of GNNs. The paper focuses on quantization approaches that can be applied directly to embedded devices or may be compatible with such hardware in the future, FPGA-based hardware accelerators, and efficient system designs using these two complementary methods together. Moreover, we provide an overview of work on FPGA-based quantized GNNs and a review of other work on medium-large scale FPGA accelerators and quantization methods for researchers investigating GNNs/GCNs, embedded systems with accelerated/reconfigurable hardware (FPGA), and quantization techniques. The motivation behind this survey is twofold. First, to provide a comprehensive study on GNN quantization, which is a promising complementary method for FPGA accelerators. Second, it aims to update the existing literature which is outdated due to the recent increase in research on FPGA-based GNN accelerators. This research makes the following contributions to the academic community:

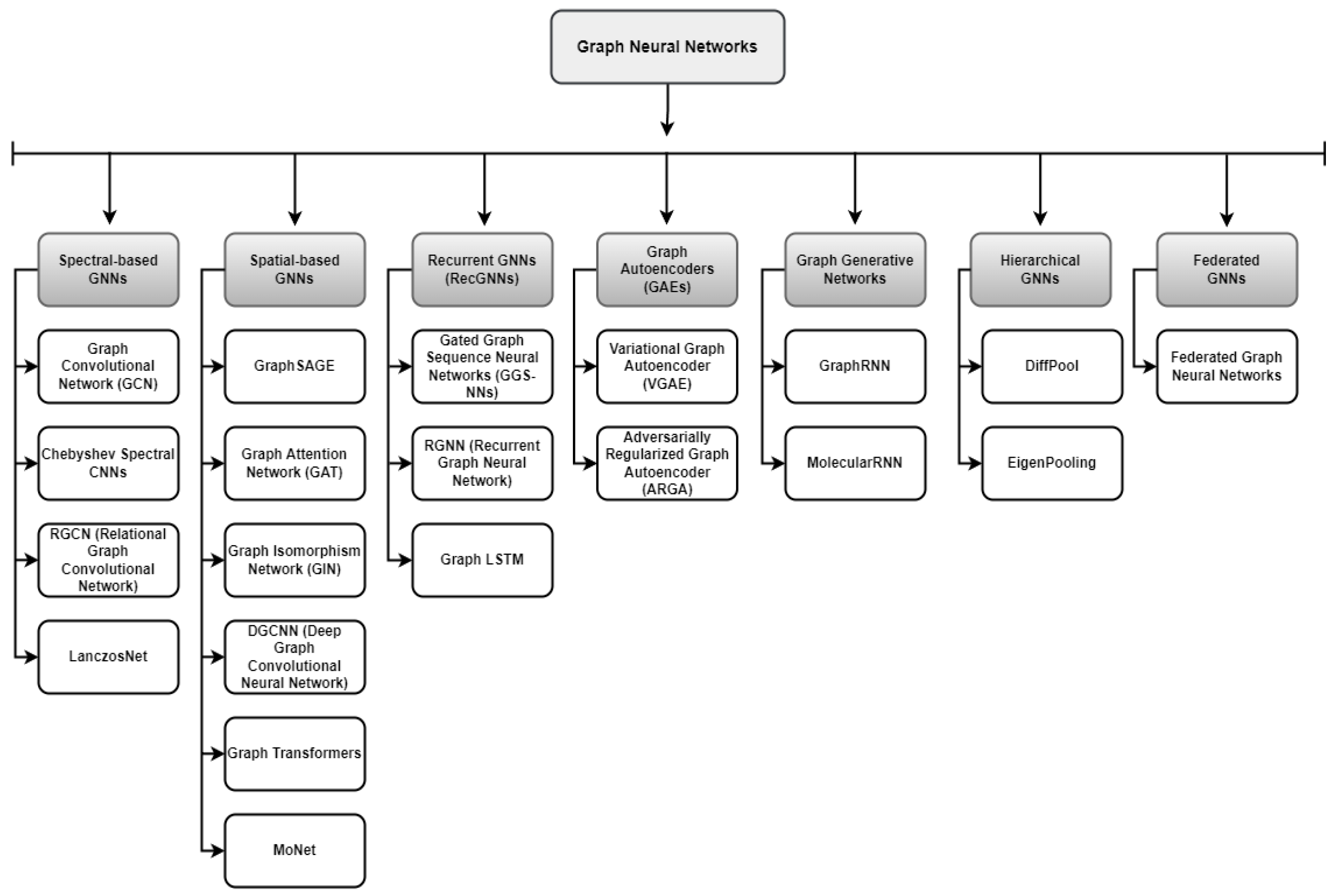
GNN Basics and Theories: This paper presents the basic concepts of GNNs and their layers. Furthermore, Figure 2, proposes a taxonomy of GNNs according to their variations.
Quantization Methods and Lightweight Models: This survey includes reviews of quantization methods aimed at building lightweight GNN models for embedded systems or GPU, CPU based applications.
FPGA Based Hardware Accelerators: Our research describes in detail the work being done on hardware-based accelerators (typically FPGAs) that can be used in current or future embedded device applications.
Discussion and Future Research Directions: The study discusses study outcomes for future research based on the findings and provides insights about possible research gaps.

The following sections provide a background with general information about GNN models, GNN quantization including quantization methods and studies, and FPGA-based hardware accelerator approaches. The paper finishes with future directions and a conclusion.

Figure 2. Proposed taxonomy based on variants of GNNs.

2. Background

Designed to uncover patterns within graph data by scrutinizing the relationships between nodes and edges, GNN models offer an effective means of extracting insights from intricate network structures. Various GNN models with different characteristics are documented in the literature [62,63,64,65,66,67,68,69,70,71]. Figure 2 illustrates an updated taxonomy that categorizes GNN variants based on their intended applications, as delineated in the existing literature.

Variations of GNNs, including Graph Convolutional Networks (GCN), Graph Isomorphism Network (GIN), Graph Attention Network (GAT), and GraphSAGE, are widely employed in this domain, serving as fundamental building blocks for graph-based applications. This section provides an overview of GNNs, encompassing their foundational principles, mathematical formulations, and commonly used layers.

2.1. Graph Neural Networks

A graph is defined by its vertices and edges, expressed as

G = (V, E)

, where V represents the vertices and E represents the edges. Graph neural network (GNN) models that utilize these edges and vertices to learn the network structure typically involve two main phases: aggregation and combination phases. The aggregation phase, as shown in Equation 1, involves the computation of a new feature vector by aggregating the features of neighbour nodes. Several techniques are used to compute these feature vectors, including weighted averages, maximum values, or summations. It is important to emphasize that the aggregation process operates on the set

N (v)

of neighbour nodes and serves as an essential component in extracting contextual information for each node.

a_{v}^{l} = Aggregation (h_{u}^{(l - 1)} : u \in N (v))

(1)

Subsequently, the combination phase, as represented by Equation 2, combines these derived feature vectors to construct a high-level feature matrix. Here, the new feature vector of each node is fused with the original feature matrix, resulting in a comprehensive representation of high-level features that can be leveraged for classification or regression applications.

h_{v}^{l} = Combination (a_{v}^{l})

(2)

In equations 1 and 2,

h_{v}^{l}

symbolizes the feature vector of a node, and

N (v)

denotes the set of neighboring nodes. The sequencing of aggregation and combination phases has been the focus of research into system efficiency [20,72]. Experimental proofs show that changing the order of aggregation and combination phases has an impact on the system efficiency. In their study, Tian et al. show that the adoption of CoAg ordering improves system efficiency [24]. This research finding highlights the importance of strategic stage sequencing in optimizing the computational efficiency of GNNs.

2.2. Graph Convolutional Networks

GCNs [73] are a specialized type of GNNs. These models apply the convolution operations of classical neural networks on graph data. GCNs can be expressed locally for a single edge and vertex or globally for all edges and vertices. Equation 3 shows the global representation of GNNs.

H^{(l + 1)} = σ (A H^{(l)} W^{(l)})

(3)

In Equation 3,

H^{(l + 1)}

represents the input feature matrix for layer l, A denotes the adjacency matrix, and

σ

denotes the nonlinear activation function. The term

A H

corresponds to the aggregation phase, while

H W

refers to the combination phase. Note that in this equation, only the features of neighbouring nodes are combined, while the nodes themselves aren’t considered. Furthermore, multiplication by the adjacency matrix changes the scale of the feature vector. As a result, higher-degree nodes exert more influence on the aggregation process because they have more neighbours, while the influence of low-degree nodes is reduced. To address these issues, the Equation 4 is proposed.

H^{(l + 1)} = σ ({\tilde{D}}^{- \frac{1}{2}} \tilde{A} {\tilde{D}}^{- \frac{1}{2}} H^{(l)} W^{(l)})

(4)

To acquire the normalized matrix

\tilde{A}

, the identity matrix I is added to the adjacency matrix A. Here,

\tilde{D}

denotes the diagonal node degree matrix.

2.3. Graph Isomorphism Networks

In 2019, Xu et al. [74] introduced Graph Isomorphism Networks (GIN) as a solution to the analytical challenges posed by Graph Convolutional Networks (GCN) and GraphSAGE, particularly in the context of certain straightforward graph structures. GIN is a recent addition to the Graph Neural Network (GNN) domain and takes a distinctive approach compared to its counterparts.

Equation 5 shows the mathematical formula for GIN. Where

h_{v}^{(k)}

is the feature vector of node v.

M L P

is a multi-layer perceptron and

ϵ

represents the learnable parameter.

h_{v}^{(k)} = M L P^{(k)} ((1 + ϵ^{(i)}) \cdot h_{v}^{(k - 1)} \sum_{u \in N (v)} h_{u}^{(k - 1)})

(5)

In contrast to conventional models, GIN provides a separate representation of isomorphic and non-isomorphic graphs. This unique feature provides GIN with mathematical robustness, which is advantageous. In particular, GIN is an important achievement by enabling the convergence of the graph to the Weisfeiler-Lehman isomorphism test under certain conditions. The unique feature of GIN enhances its ability to recognize and distinguish effectively non-isomorphic graphs characterized by topological non-identity. GIN’s mathematical ability and the ability to provide a variety of representations contribute to its ability to address the challenges posed by certain graphical structures and make it a remarkable model in the landscape of graphical neural networks.

2.4. Graph Attention Networks

Graph Attention Networks (GAT) [75] is one of the leading models in the GNN family, proposed by Velickovic et al. in 2018. Unlike traditional GNN models, GAT focuses on learning the importance of neighbouring nodes using an attention mechanism and directing information propagation according to this importance. In this way, GAT can improve the learning performance of the model by giving more weight to information from important neighbouring nodes. Similar to GCNs, this model computes a representation vector for each node and a weight vector for each edge. However, in GAT, the hidden representation vectors of neighbouring nodes and the weight vectors of edges are used to compute attention.

a_{i j} = \frac{exp (LeakyReLU ({\vec{a}}^{T} [W \vec{h_{i}} | | W \vec{h_{j}}]))}{\sum_{k \in N_{i}} exp (LeakyReLU ({\vec{a}}^{T} [W \vec{h_{i}} | | W \vec{h_{k}}]))}

(6)

For each node, GAT calculates the attention coefficients for its neighbouring nodes Equation 6. These coefficients are an indication of how important a neighbour node is. For the calculation of the attention coefficients, the node’s hidden representation vector and the hidden representation vector of the neighbouring node are used. Equation 6 utilises

a_{i j}

as attention coefficients, T for transpose, and

| |

for concatenation. Equation 7 shows the mathematical formula for GAT. Here K is the number of heads and

W^{k}

is the linear transformation weight matrix.

{\vec{h}}_{i}^{'} = σ (\frac{1}{K} \sum_{k = 1}^{K} \sum_{j \in N_{i}} α_{i j}^{k} W^{k} \vec{h_{j}})

(7)

2.5. GraphSAGE

GraphSAGE [12] offers a general inductive learning framework that is especially useful for large and complex graphs. The GraphSAGE model, proposed by William L. Hamilton et al., learns hidden representations solely for nodes in the training data. This enables the model to generalize effectively to previously unseen nodes. GraphSAGE is a scalable framework that enables the inclusion of other models by using various aggregation and combination functions.

GraphSAGE creates an adjacency matrix for each node based on its own features and those of its neighbors. An aggregation function is used to combine the information in the neighbour feature matrix for each neighbour. The authors analyzed three different aggregation functions and found no significant difference between max and mean pooling. Therefore, max-pooling was used in this study. Additionally, the LSTM aggregator was also analyzed. Equation 8 shows the max-pooling aggregation function, where ’max’ is the maximum operator and sigma is the activation function.

{AGGREGATE}_{k}^{p o o l} = \max ({σ (W_{p o o l} h_{u_{i}}^{k} + b), \forall u_{i} \in N (v)})

(8)

In the combination stage, the information obtained from the aggregation functions is combined with a learnable model parameter. This combination allows for the weighting of the node’s own features and neighbour information.

3. Graph Neural Network Quantization

3.1. Quantization

GNNs, particularly in extensive graph applications, may encounter constraints due to their intricate model complexity and size. Quantization methods present a promising remedy to tackle these issues by reducing the model’s size and computational demands. Quantization entails condensing model parameters into smaller dimensions, a pivotal step for implementing GNNs on hardware platforms such as FPGAs. However, it’s crucial to recognize and handle the challenges linked with these techniques through thorough parameter adjustment procedures to optimize their advantages. This section provides an overview of the fundamental concepts of scalar and vector quantization and reviews quantization strategies developed for GNNs.

3.1.1. Scalar Quantization

Scalar quantization is a method designed to decrease the number of bits required to represent values within data. In this technique, each feature or parameter is depicted using a limited number of bits falling within a particular range. Scalar quantization encompasses diverse methods such as uniform, non-uniform, signed, unsigned, symmetric, asymmetric, dynamic, and static quantization. These varied strategies offer adaptability in customizing the quantization process to specific needs and enhancing performance across various applications. Nevertheless, each approach comes with its own set of trade-offs.

The network’s real-valued input parameters are transformed into a discrete space by mapping them to quantization levels, which are evenly or unevenly divided using scalar quantization. Figure 3 illustrates the quantization levels generated by uniform and non-uniform quantization. In non-uniform quantization, the distribution of the data determines the quantization levels. Although this method yields improved quantization points, it is more complicated to execute compared to uniform quantization.

For scalar quantization, decisions must be made about the type of quantization to use, such as signed or unsigned, and symmetric or asymmetric. These decisions are typically influenced by the data distributions within the datasets and can vary accordingly. Signed quantization creates both negative and positive quantization points in the quantization domain. Unsigned quantization uses only the positive side of the number line. Additionally, symmetric and asymmetric quantization refers to the treatment of the positive and negative sides of the quantization domain. However, implementing asymmetric quantization is more challenging due to the additional processing involved. Figure 4 illustrates the methods of symmetric-signed and asymmetric-unsigned quantization.

Similar to asymmetric quantization, dynamic quantization offers another option that increases both implementation and computational complexities. Unlike static quantization, dynamic quantization recalibrates the quantization ranges for input parameters each time, enabling each input data to be quantized within the range that best represents it. Consequently, this approach improves the accuracy of the model. However, due to the dense nature of input data in Graph Neural Networks, dynamic quantization is anticipated to incur significant computational overhead. Nevertheless, despite its computational demands, it may be preferred in applications where the highest accuracy is crucial.

3.1.2. Vector Quantization

The core elements of vector quantization are codebooks and codewords. A codebook comprises vectors containing all possible codewords. Vector quantization typically involves identifying the closest codeword based on a distance metric and associating the input vector with that codeword. Mathematically, given an input vector (

x

) and a codebook (

C

), vector quantization is expressed as in Equation 9. Here, the function ( Q(

x

) ) ensures that the vector (

x

) is matched to its nearest codeword in the codebook (

C

). Euclidean distance is commonly employed as the distance metric.

Figure 5 illustrates a vector quantization map, where Voronoi diagrams, depicted by dashed lines, play a crucial role in the quantization process. Each input vector is quantized relative to its Voronoi cell, with each x-point within these areas representing the vectors therein. The circles in the figure signify the codewords that most accurately represent the vectors in each region.

Q (x) = arg min_{w \in C} {∥ x - w ∥}^{2}

(9)

Vector quantization involves grouping values together and mapping them to a set of prototype vectors, typically in a high-dimensional space. Because of this, vector quantization is more effective than scalar quantization in preserving the structure and relationships of data, making it preferable for processing more complex data structures. In FPGA based applications, both scalar and vector quantization techniques can be utilized. Although scalar quantization offers a simpler and less resource-intensive implementation of FPGAs, vector quantization can handle more intricate data structures and relationships. However, it generally requires more resources and is more complex to implement on FPGAs. When designing FPGA-based applications, it is important to choose the optimal solution by considering the advantages and limitations of both quantization methods.

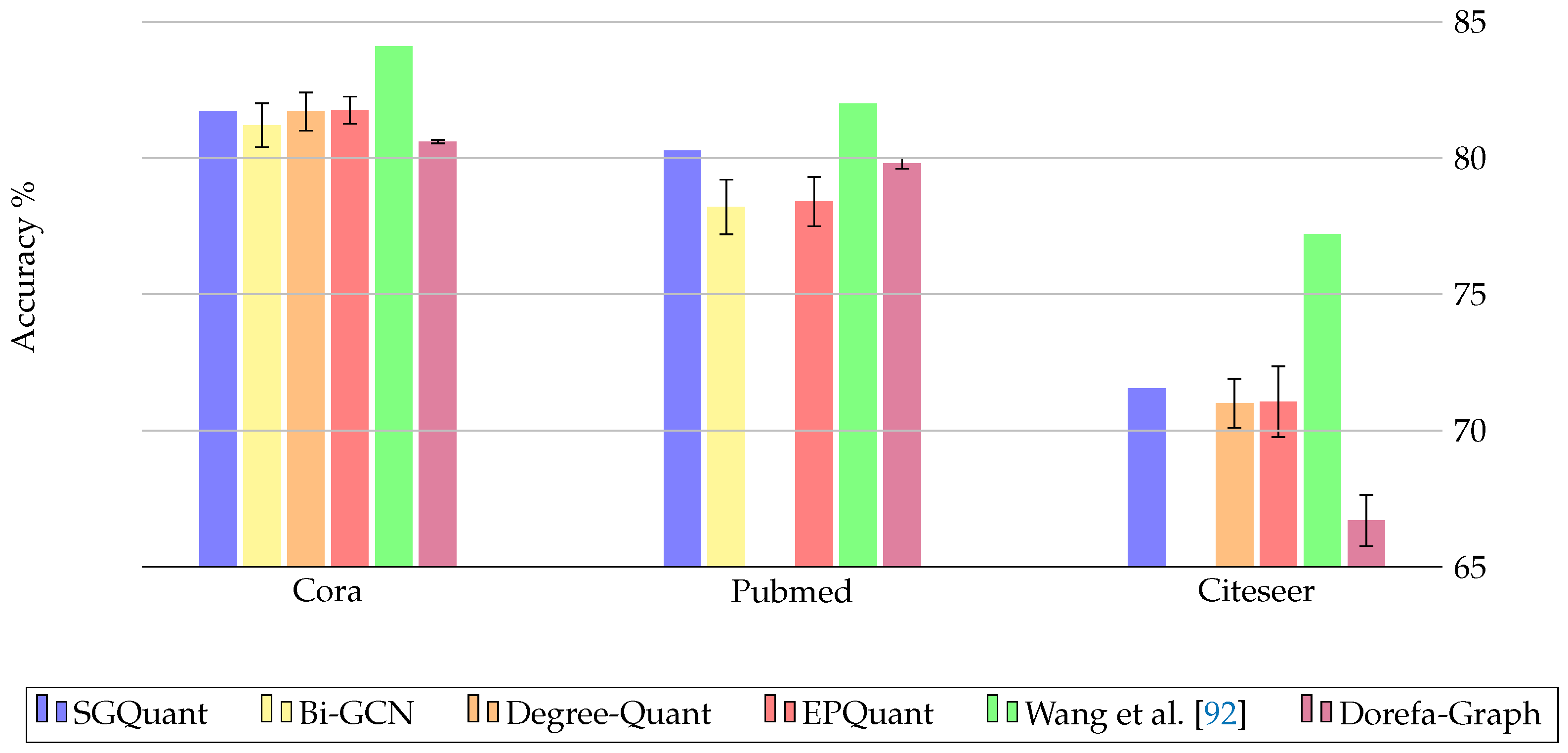
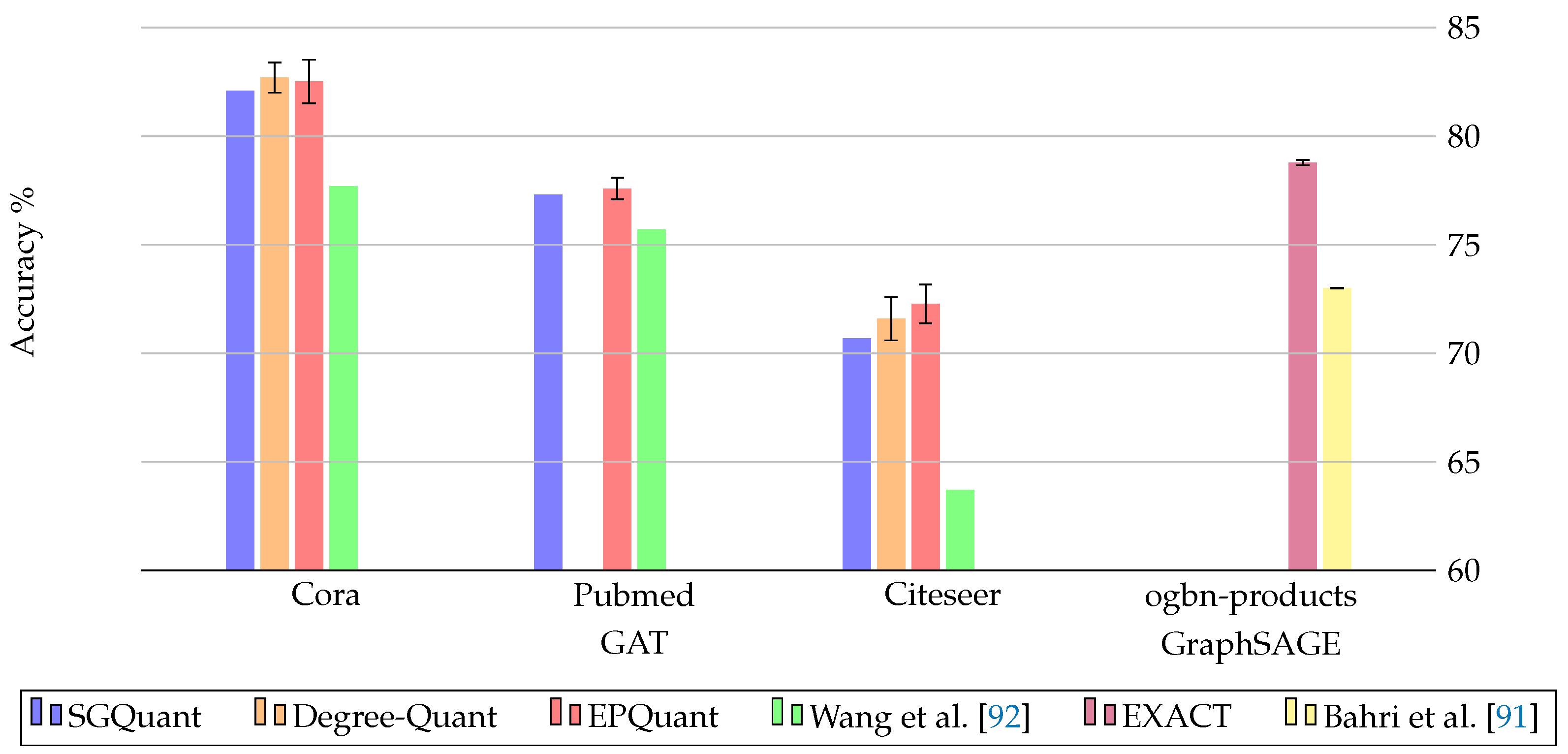
3.2. Quantization Approaches for GNNs

Quantization emerges as a powerful approach capable of supporting the efficiency of GNN models across both the training and inference phases. By reducing the memory footprint and reducing the usage of computational resources, quantization methods offer a viable solution to improve the efficiency of GNN. Quantization techniques are commonly used to improve efficiency across various hardware platforms, including large-scale systems such as GPUs and CPUs, as well as small-scale devices such as IoT and edge devices. This preference stems from their ability to achieve high compression rates and deliver computational speed advantages, making them indispensable tools in the quest for streamlined GNN deployment in real-world scenarios.

This section provides a review of the quantization studies for GNNs in the literature. Details of some studies are listed in Table 1. The reviewed works use different datasets and GNN layers. To ensure a fair comparison, accuracy graphs based on the results of studies with common datasets and layers are presented in Figure 6 and Figure 7.

Quantization is an effective approach to overcome the challenges posed by graph data, not only for embedded devices but also for GPU-based applications. Tango [76] aims to accelerate GNN training on GPU systems using techniques such as GEMM, SPMM, and SDDMM. The authors propose a set of rules and stochastic rounding for GPUs to speed up training without compromising accuracy. In addition, on-the-fly quantization and dequantization techniques are used to reduce the GNN training time. Tango can be integrated with DGL for performance enhancement without requiring any modifications. Novkin et al. [77] propose in their study a QAT approach that simulates approximate multiplication operations using CUDA kernels. The method aims to maintain the overall accuracy of the system by quantizing the model’s weights and activations into different bit numbers, incorporating quantization and approximation-aware training. The authors share their experimental results with layers such as GAT, GIN, SAGE, and GCN on different datasets using the PyTorch Geometric framework. Another GPU-based study, AdaQP [78], takes advantage of integer quantization to reduce communication traffic between devices during distributed training. The authors propose two approaches to address this issue in their new system. The first approach involves reducing communication traffic by lowering the precision of transmitted messages through stochastic integer quantization. The second approach is to optimize resource usage by parallelizing computations of central nodes and message communication of nodes on the edge.

GCINT [79] proposes an alternative QAT method for INT tensor cores of GPUs. This method quantizes all model parameters, including weights, activations, gradients, errors, and loss, to INT 8-bits. The dynamic structure of this method establishes an architecture that is independent of datasets and weight distributions by adaptively adjusting the quantization range. Another study, that aims to accelerate GNNs on GPU tensor cores using CUDA kernels, is QGTC [80]. QGTC provides a flexible structure capable of performing various bit widths and computation optimizations. The authors demonstrate the integration of their approach with PyTorch, showcasing fast results with popular frameworks by using quantized adjacency matrices, weight matrices, and node embedding matrices.

Scalar and vector quantization can be used separately, although there are instances in the literature where they are used together to achieve high compression rates and computational efficiency using integer arithmetic. BiFeat [81] proposes feature quantization in GNNs by combining the quantization approaches BiFeat, BiFeat-SQ, and BiFeat-VQ. The authors claim that this approach resolves GPU memory and bottleneck issues with an acceptable loss of accuracy, providing up to a threefold acceleration.

Quantization is a robust method for making GNNs applicable to energy-constrained devices. Eliasof et al. [82] note in their study that the complex and large structure of GNNs is not suitable for resource-constrained devices. The authors demonstrate in their research that the adverse effects of using very low bit counts on accuracy can be mitigated through Haar Wavelet transformation. As a result of this QAT approach, it is shown that the use of 4 and 8-bit values provides gains with minimal loss in both memory and computation, offering a potential solution to the bottleneck issues in devices used in real-world applications. Another study in this area is the segmented quantization method proposed by Dai et al. [83] with the aim of high accuracy and low cost of computation. This research reduces the error caused by linear quantization through the creation of segments. Furthermore, the study introduces a hardware design that utilizes the benefits of quantization for GNN accelerators.

Dissatisfied with current mixed-precision use in CPUs and GPUs, Zhu et al. [84] propose a scalable hardware accelerator for learning quantization parameters using their proposed addition-aware mixed-precision quantization method. The authors recommend using different bit-widths for each node, local gradient, and Nearest Neighbor Strategy to address the significant accuracy losses resulting from the utilization of quantization methods that overlook the overall structure of GNNs. Another study, proposed by Wang et al. [85] aims at an efficient GNN structure for resource-constrained embedded systems. This paper presents a GNN architecture that considers quantization effects throughout all its stages, including QLR-BT (Quantization Learn Range - Skewness-aware Bitwise Truncation) and SMP (Smoothness-aware Message Propagation). QLR aims to reduce the model size, while SMP aims to maintain accuracy by preventing excessive smoothing.

EXACT [86] is proposed by Liu et al. as a method to obtain lighter GNN models through random projection and quantization. The authors provide a GPU implementation and use random projection to represent activations in a low-dimensional space while compressing activations with integer quantization. They note that there is an effect between the random projection method and quantization and that quantization after random projection has a limited effect. However, it is emphasized that this method yields better results in terms of time compared to single use. In this method, only activations are quantized, while gradients are computed using their dequantized versions, and all multiplications are performed with full precision due to the GPU hardware used. The study results demonstrate an improvement in memory space and time overhead with acceptable accuracy losses. The study proposes using the EXACT framework as an extension of PyTorch and PyTorch Geometric in combination with various GNN models.

In addition, Eliassen et al. [87] present an improved EXACT version. This application reduces memory consumption and training time through block-based quantization, resulting in a memory gain of over 15% compared to the original EXACT method. The authors achieve both memory savings and model acceleration by quantizing node embeddings in larger pieces rather than individually. While the original EXACT method limits quantization boundaries to integer values, assuming a uniform distribution of activations, Eliassen et al. show that activation maps should be expressed with a normal distribution. This approach improves the quantization process by providing variance estimates for the distribution of intermediate activations.

Table 1. Quantization studies on Graph Neural Networks.

Publication	Year	Targetted Problem	Quantized Parameters	Datasets
EXACT [86]	2021	High memory need for training	Activations	Reddit, Flicker, Yelp, obgn-arxiv, obgn-products
VQ-GNN [88]	2021	Challenges of sampling based techniques	Convolution matrix, Node feature matrix	ogbn-arxiv, Reddit, PPI, ogbl-collab
SGQuant [89]	2020	High memory footprint for energy-limited devices	Feature matrix	Cora, Citeseer, Pubmed, Amazon-computer, Reddit
LPGNAS [90]	2020	Insufficient optimization research in the field	Weights, Activations	Cora, Citeseer, Pubmed, Amazon-Computers and Photos, Flicker, CoraFull, Yelp
Bahri et al. [91]	2021	Challenges in real-world applications due to model size and energy requirements	Weights, Feature matrix	obgn-Products, obgn-Protein
Wang et al. [92]	2021	Model inefficiency and scaling problems with inefficient real-valued parameters	Weights, Attention coefficients, Node embeddings	Cora, Citeseer, Pubmed, Facebook, wiki-vote, Brazil, USA
Degree-Quant [35]	2020	Inefficient training/inference time	Weights, Activations	Cora, Citeseer, ZINC, MNIST, CIFAR10, Reddit-Binary
EPQuant [93]	2022	Limited availability on edge devices due to high requirements	Input embeddings, Weights, Learnable parameters	Cora, Citeseer, Pubmed, Reddit, Amazon2M
Bi-GCN [94]	2021	High memory requirements of GNNs	Weights, Node features	Cora, Pubmed, Flicker, Reddit
Dorefa-Graph [95]	2024	Cost-effective computing on embedded systems	Feature matrix, Weights, Adjacency matrix, Activations	Cora, Pubmed, Citeseer

Figure 6. Accuracy results of quantization methods using GCN layer for three datasets. Result parameters from the studies: SGQuant (average reduced precision), Bi-GCN (1-bit int), Degree-Quant (8-bit int weights and activations), EPQuant (ap_wf - quantized features and full precision parameters), Wang et al. [92] (1-bit int), Dorefa-Graph (8-bit int features, weight and adjacency matrices).

Figure 7. Accuracy results of quantization methods using GAT layer for three datasets (Left). Accuracy results of quantization methods using GraphSage layer for ogbn-products datasets (Right). Result parameters from the studies: SGQuant (average reduced precision), Degree-Quant (8-bit int weights and activations), EPQuant (ap_wf - quantized features and full precision parameters), Wang et al. [92] (1-bit int), EXACT (2-bit int), Bahri et al. [91] (1-bit int).

VQ-GNN [88] proposes a vector quantization approach to prevent neighbor explosion when scaling large GNNs. Instead of using sampling methods, Ding et al. introduce reference vectors that learn and update the messages passed in each mini-batch. The proposed message passing and backpropagation algorithm of VQ-GNN provides a robust framework against neighborhood explosion. The paper clearly outlines the challenges faced by Neighborhood-sampling, Layer-sampling, and Subgraph-sampling approaches. VQ-GNN offers vector quantization of convolution and node feature matrices to reduce the size of GNNs. The paper distinguishes between intra-mini-batch messages and out-of-mini-batch messages as the two ways in which the quantized messages are expressed. The authors state that their proposed method enables training and inference operations in large GNNs to be performed similarly to normal neural networks. The study focuses on performance analysis and memory size assessments. Based on the results obtained, the proposed model performed as well as or better than the other models. The authors also acknowledge that VQ-GNN may require additional memory in certain scenarios and emphasize that it should be supported by complementary techniques.

SGQuant [89] proposes a scalar quantization method to address the efficiency issues caused by the high memory utilization of Graph Neural Network (GNN) systems, particularly in IoT and edge devices. To solve this problem, Feng et al. implement a multi-granular quantization scheme that includes layer-wise, component-wise, and topology-aware functions to express node embeddings with a low number of bits. In this process, the proposed algorithm is used to automatically select the appropriate number of bits. The paper highlights that aggressive quantization practices can result in high accuracy loss, while more lenient approaches offer no gain. The input features are quantized, rather than other network parameters, as they comprise the majority (99%) of the network. SGQuant utilizes a straight-through estimator for gradients and a specialized layer from the PyTorch Geometric library for quantized inference and backpropagation. The automatic bit selection algorithm aims to achieve the maximum compression ratio with minimal loss of accuracy by selecting the optimal bit value. This algorithm comprises two essential components: the machine learning cost model and the discovery scheme. The study utilized two distinct groups of datasets. The first group represented relatively small graph data, while the second group represented larger datasets. These datasets were passed through three different GNN layers: GCN, AGNN, and GAT.

Degree-Quant [35] proposes an integer quantization method that supports acceleration in Graph Neural Networks (GNNs) and can be used efficiently on low-energy consumption hardware. In this work, Tailor et al. aim to efficiently utilize GNN applications on energy-limited devices such as smartphones, regardless of the architecture. The approach uses uniform quantization levels of 8 and 4 bits over message-passing neural networks (MPNNs) to achieve acceptable accuracy and speedup while taking advantage of the ease with which integer quantization can be applied to models. Three different GNN models are used in the study (GCN, GAT, GIN). The authors focus on inaccurate weight updates and unrepresentative quantization weights to deal with error sources. In the approach, protection masks are stochastically generated at each layer during training, and mask-protected nodes are represented with full precision at each stage. During the inference phase, all operations are performed with low bit values. A preprocessing phase is required to generate and compute the masks. For testing, different datasets are used for three different tasks (Node classification, Graph classification, and Graph regression). According to the results obtained, the DQ-8 bit provides equal or more accuracy compared to fully fine-tuned base models, while the DQ-4 bit provides 8x compression. These results demonstrate the effective applicability of the Degree-Quant method in GNNs at low bit levels and its potential to improve model performance.

Several other works propose quantization architectures using node degrees in addition to the Degree-Quant study. Chen et al. [96] emphasize the need for efficient systems and the scarcity of computations when using GNN models on energy-constrained devices. They present a topology-based quantization strategy using Personalized PageRank (TQPP) to address this issue. TQPP analyzes the structure of the graph, determines node importance, and creates masks to preserve sensitive nodes based on their importance. This quantization approach accelerates computations and saves memory by separating nodes according to their sensitivities while maintaining accuracy. The study examines the Degree-Quant baseline and shows higher accuracy values at the same bit levels compared to the baseline. Guo et al. [97] propose a degree-based study to address the challenge of applying GNNs to resource-constrained devices. The study suggests protecting sensitive nodes with a sensitivity determiner mask while applying dynamic mixed-precision quantization to other nodes to reduce the model size without compromising accuracy. The proposed method is implemented using GCN, GAT, and GAT layers on four different datasets.

Bahri et al. [91] propose a binary quantized GNN that can operate on energy-constrained devices. The authors highlight that although the use of non-Euclidean data makes GNNs challenging in several aspects compared to CNN models, small network sizes can be achieved through a controlled training process and model design. The paper demonstrates the application of various approaches, including Hamming space, knowledge distillation, and XNOR-Net for GNNs, and presents the results obtained on an ARM device. The quantization method follows a multi-stage structure, beginning with the use of a trained base model where real numbers are used for the parameters. The quantization process is then replaced by the

t a n h

function. During the second stage, the trained model serves as a teacher for the training of the second model. Binary activations and real number weights are used in this stage. The quantization process is structured based on the sign operator. However, this can result in continuous zero gradients, so the system employs a straight-through estimator. In the following stage, the new model becomes the teacher in the same way, and both weights and activations are binary during the next training. The paper introduces the Dynamic Graph CNN model and compares it to other approaches, such as direct binarization. The authors demonstrate the speedup effects of the work using a Raspberry Pi 4B board.

Another binary quantization approach is Bi-GCN [94]. The method proposed by Wang et al. attempts to overcome the problems of loading the entire graph into memory by quantizing weights, network parameters, and input features. Additionally, it aims to accelerate multiplication operations within the network using binary operations. The authors reduce quantization errors by adding a scalar value to weights and features after the binarization process. Furthermore, an efficient training phase is provided with the created back propagation method. Wang et al. recommend BGN [92], a graph attention mechanism-based approach where weights and activations are quantized as binary. In their study, an attention mask is applied to preserve the structural information of the model, and the resulting attention coefficients are expressed in binary. The authors explore two different estimators, the Straight Through Estimator and Reinforce, to overcome the problem of untrainable parameters caused by zero gradients, preferring the STE due to its advantages.

EPQuant [93] is a method proposed by Huang et al. that combines product quantization and scalar quantization approaches to obtain viable GNN models for energy-constrained devices. The authors investigate the vector quantization approach and exploit the efficient structure of integer arithmetic with scalar quantization while achieving high compression with advanced product quantization. Vector quantization offers higher compression rates than scalar quantization by quantizing multiple vectors together. However, this clustering process can lead to longer processing times and increased memory requirements. To address these issues, the authors suggest using index-based and hash-based batching. The study introduces EPQ and SQ blocks that not only quantize the input data but also perform quantization of weights and other learnable parameters within these blocks. The PyG architecture is utilized in the proposed method to replace layers with quantized versions. The study’s results test various cases where vector and scalar quantization are performed on different layers and datasets.

Kose et al. propose Dorefa-Graph [95], a fully quantized network model, to enhance GCN performance on embedded devices. The authors apply the Dorefa-Net algorithm designed for CNN models to build a lightweight GCN model, and present a modified version of Dorefa-Graph to adapt to the data structure. The paper focuses on creating a fully quantized model using scalar quantization on model parameters such as model weights, weighted adjacency matrix, input features, and activations. The study employs scalar quantization methods due to their ease of computation in FPGA applications and simple implementation in embedded devices. Dorefa-Graph offers a GCN model suitable for embedded devices. However, the results are demonstrated through simulation experiments on GPUs. The impact of quantization error and dequantization effects on accuracy during inference is analyzed by the authors in several cases. The study examined the accuracy values by testing various bit values for two GNN layers and three quantization approaches. The authors demonstrate that their proposed method outperforms the original Dorefa-Net algorithm on GNNs, particularly at low bit levels. They also show that quantization can be carried out at higher bit levels with acceptable accuracy losses.

Zhao et al. propose LPGNAS [90], an approach to systematically quantize GNNs using Network Architecture Search (NAS). The authors create a NAS structure that includes different quantization approaches for different blocks at the micro-architecture level. This structure has single-path, one-shot, and gradient-based features. The quantization function is applied by LPGNAS after labeling the possible parameters to be quantized. The LPGNAS algorithm applies the quantization function to both learnable parameters and activations, as well as input data due to its ease of multiplication and size. The study uses a large set of datasets, with one group consisting of relatively small networks and the other group consisting of larger datasets. The study shows that the LPGNAS method selects binary and ternary levels for weight quantization, while it prefers higher bit numbers, such as 8-bit, for activations. Previous studies have typically quantized networks with 4-bit weights and 8-bit activations.

4. Graph Neural Network Acceleration

The intricate and computationally demanding nature of GNNs, especially when operating on large graphs, often leads to time-consuming processes and efficiency constraints. This is further compounded by performance limitations encountered on conventional CPUs and GPUs. In this regard, hardware accelerators are emerging as pivotal components to facilitate the swift and efficient processing of GNNs.

The major challenges in accelerating GNNs revolve around their complex structure and significant data sizes. Both training and inference tasks require significant computational power and memory resources. Conventional hardware may prove inadequate for such computations, thereby prolonging the overall processes. Conversely, hardware accelerators, leveraging their parallel processing capabilities and tailored computing units, expedite the training and inference processes of GNNs. They offer the requisite low latency crucial for real-time applications.

4.1. Hardware-Based Accelerator Approaches

In the existing literature, various accelerator designs proposed for diverse hardware platforms such as GPU-CPU [98,99,100], ASIC [28,101,102,103,104,105,106,107], and FPGA [20,30,33,108], among others, contribute valuable insights to this domain. This chapter provides a brief overview of other hardware-based accelerators before an in-depth review of FPGA-based accelerators. Additionally, Figure 8 presents a comparison of different hardware accelerators using HyGCN as a baseline.

HyGCN [101] is introduced as a solution to tackle the challenges posed by hybrid execution models of GCNs, which involve a combination of irregular aggregation stages and regular combination stages. To effectively handle the dynamic and irregular nature of the aggregation process, as well as exploit the static and regular properties of the combination process in GCNs, the proposed accelerator adopts a hybrid architecture. In order to ensure parallelism in both the aggregation and combination phases, the authors devise a programming model. Additionally, they propose a hardware design that incorporates dedicated Aggregation and Combination Engines. HyGCN achieves significant speedup and energy reduction on both CPU and GPU platforms, highlighting its effectiveness in enhancing the execution of GCNs.

EnGN [28] is proposed for the efficient processing of large-scale GNNs in real-world applications as a dimension-aware accelerator architecture that optimizes GNN computations based on input and output feature sizes and eliminates the need for external memory accesses. The authors present a dimension-aware stage reordering (DASR) strategy for partitioning large graphs into intervals and shards. The work achieves on-chip memory efficiency using graph tiling and scheduling techniques and minimizes data dependencies between tiles. The accelerator uses a ring-edge-reduction (RER) dataflow to address irregular memory access patterns in GNN propagation, improving computational efficiency.

GRIP [107] is proposed with the aim of improving the efficiency of GNNs by addressing the problems of delay and energy consumption. Kiningham et al. show improvements in latency reduction and energy efficiency for GNN inference tasks by exploiting special architectural features. The study evaluates the performance of GRIP on various GNN models and datasets, analyses the impact of architecture and model parameter tuning, and assesses the effectiveness of GNN optimizations integrated into GRIP.

Rubik [104] addresses the challenge of learning from graphs by optimizing software and hardware accelerations in GCN learning to improve energy efficiency and performance. In this work, the authors present a hierarchical computing paradigm that separates graph-level and node-level computation for specific optimizations. The paper includes a lightweight graph reordering technique to improve graph-level data reuse and a custom GCN accelerator architecture with a hierarchical spatial design for efficient data locality utilization. Furthermore, the authors propose a hierarchical mapping methodology that optimizes both graph-level and node-level computations to improve data reuse and task-level parallelism.

GCNAX [105] is proposed as an accelerator designed to address irregularity in the aggregation phase and exploit regularity in the combination phase of GCNs. The authors present a systematic design space exploration to optimize performance and minimize off-chip data accesses, and use a cycle-accurate simulator for evaluation and ASIC synthesis for area and power estimation. The baseline hardware used for comparison includes two GCN accelerators and one SpMM accelerator. The benchmark is used to evaluate the efficiency of flexible data streaming.

H-GCN [109] proposes a hybrid accelerator design that utilizes Xilinx Versal ACAPs to enhance GNN inference performance. The paper explores graph heterogeneity and utilizes a hybrid PL and AIE architecture to fully exploit the computational capabilities of ACAPs for GNN computations. The H-HCN involves graph partitioning, the utilization of PL and AIE components, exploring sparsity support in the AIE, and creating an effective approach for mapping sparse matrix-matrix products to the systolic tensor array. Using the Xilinx Versal VCK5000 platform, the paper demonstrates the positives of H-GCN over CPU and GPU platforms on various graphics datasets by comparing speedups, energy efficiency, and inference latency with existing GCN accelerators.

4.2. FPGA-Based Accelerators Approaches

FPGA-based accelerators are advantageous over alternative hardware accelerators due to their inherent flexibility in handling variable states. They are equipped with configurable logic and memory blocks, making them adaptable to specific computing requirements. Additionally, they offer parallel processing capabilities and low power consumption, distinguishing them from fixed-architecture accelerators like GPUs. The flexibility of FPGAs is particularly valuable in scenarios that involve variable graph structures and dynamic data flows. Furthermore, FPGAs often outperform other accelerators in terms of energy efficiency and performance, offering low power consumption at high data processing speeds. However, programming and optimizing FPGAs can be complex and time-consuming, which may limit their widespread adoption. Accessing relevant information about FPGAs can be challenging due to their comparatively lower usage prevalence compared to GPUs.

The literature presents software and hardware architectures that address different scales of FPGA applications, ranging from small to large deployments. Some studies focus exclusively on FPGA research, while others provide insight into heterogeneous system architectures that encompass larger-scale applications.

AWB-GCN, proposed by Geng et al. [20], endeavors to tackle the challenge of workload imbalance encountered in real-world graph inference scenarios. By dynamically redistributing tasks among processing elements, AWB-GCN aims to optimize hardware resource utilization and enhance performance. The authors employ hardware-based automatic tuning techniques to adaptively rebalance workloads in real-time, thus improving the efficiency of GCN inference across diverse graph structures. In their study, Geng et al. conducted an evaluation focusing on several key aspects, including processing element (PE) utilization, performance metrics, energy efficiency, and hardware consumption. Through analysis, the research compares the PE utilization, performance metrics, energy efficiency, and hardware resource consumption of the Intel D5005 platform across different datasets. Overall, the findings presented by Geng et al. shed light on the significance of dynamic workload distribution in improving the efficiency and effectiveness of real-world graphics inference tasks, particularly within the context of GCN inference optimization.

ACE-GCN [110] is proposed by Romero et al. for the efficient processing of graph-structured data by exploiting the sparsity and power law distribution in real-world graph datasets for efficient graph convolutional embedding. The authors effectively utilize first-order subgraph similarity, feature exchangeability, and structure redundancy to improve graph convolutional embedding. This addresses performance and resource scalability issues in graph neural network accelerators. The task at hand is to transfer computational complexity to storage capacity while maintaining high accuracy, resulting in speedup gains compared to baseline methods. ACE-GCN optimizes on-chip memory utilization and computational efficiency by customizing configurations for different datasets and using an auxiliary similarity estimation circuit. The results demonstrate that the proposed method provides speedup on datasets compared to baseline models, and in some cases outperforms other FPGA accelerators.

I-GCN [111] aims to improve data locality and reduce redundant computation in GCNs, particularly for efficient inference on large-scale graphs. According to Geng et al., current hardware accelerators for GCNs face challenges in dealing with the irregular non-zero distribution, high sparsity, and significant size of real-world graphs, leading to inefficiencies in data processing and computation. This paper presents the islanding algorithm, which identifies clusters of nodes with strong internal connections. This enables graph data to be processed at the level of centers and islands rather than individual nodes, resulting in improved data reuse and reduced redundant computation. The islanding process of the research identifies clusters of nodes with strong internal connections, which leads to improved data locality and a reduction in the movement of data off-chip.

Lin et al. [112] aim to efficiently accelerate GCN inference on FPGA platforms for cloud-based applications, such as e-commerce and recommender systems. They address the challenges of existing solutions, such as high latency inference and energy inefficiency. The paper proposes a new approach to GCN inference acceleration on FPGA. The paper suggests using a partition-centric mapping strategy and HLS-based core design to reduce memory access overhead, leverage data reuse, and achieve significant data parallelism. The authors utilize kernel designs in Vitis-HLS and OpenCL on the Xilinx Alveo U200 platform. They evaluate the performance of the designs using large-scale datasets such as Reddit, Yelp, and Amazon-2M. To do this, they use a two-layer Vanilla-GCN model with detailed specifications about GCN layer sizes and operations.

Figure 9. Comparison of latency (ms) and energy efficiency (graph/kJ) of 3 different methods using the same hardware (Intel Stratix 10 SX, 330 MHz) on the same datasets.

Zhang et al. [113] propose an accelerator approach to address the problem of limited on-chip memory when dealing with massive node-attributed graphs with static topologies and to improve GCN inference efficiency on FPGA. Their algorithm-architecture co-optimization approach uses data partitioning, decomposition, and node reordering, which distinguishes it from traditional methods. The article describes a hardware architecture pipeline that supports aggregation and transformation kernels, along with a flexible bus and scheduling strategy that is tailored for various GCN models. Additionally, it includes a mathematical analysis of data communication costs to optimize memory traffic. The article also proposes a two-stage preprocessing algorithm to increase data reuse and reduce external memory access.

SPA-GCN [114] integrates deep pipelining and customized levels of parallelization to efficiently process small graphs. SPA-GCN uses a very deep pipeline with nested parallelization, customized compute units, and efficient utilisation of FPGA resources. The paper optimizes data flow through FIFOs and dynamic process scheduling. The study compares SPA-GCN’s performance on Xilinx FPGAs with that of Intel Xeon CPUs and NVIDIA GPUs. SPA-GCN highlights the efficiency of the proposed architecture in accelerating GCN computations on small graphics.

BlockGNN addresses the problem of increasing computational complexity in GNNs by proposing a software-hardware co-design strategy using block circulating weight matrices for efficient GNN acceleration, reducing computational complexity from

O (n^{2})

O (n l o g n)

with minimal loss of accuracy. The authors suggest compressing GNN models by using block-entangled weight matrices at the algorithm level and implementing a pipelined CirCore architecture at the hardware level. They also propose using the Fast Fourier Transform (FFT) during inference to enhance efficiency. Additionally, they introduce a performance and resource model to automatically optimize hardware parameters for various GNN tasks and improve overall acceleration.

Gui et al. [115] aims to enhance the efficiency of sampling algorithms in GNNs by utilizing hardware acceleration to reduce sampling time while maintaining high test accuracy on large datasets. The paper presents the CONCAT Sampler, an algorithm that merges sample graphs to simplify hardware acceleration and ensure accuracy in GNN models. The authors suggest utilizing the CONCAT Sampler on FPGA hardware. This involves using parallel sampling modules to independently sample from partitioned datasets and combining the results for faster sampling.

Li et al. [116] present an FPGA-based hardware architecture designed to address the challenges of implementing Large Scale Distributed Graph Neural Networks (LSD-GNNs) in hyperscale environments, with a focus on memory access acceleration and scalability. This work highlights the obstacles faced by LSD-GNNs in hyperscale environments and discusses custom heterogeneous hardware solutions to improve memory access and sampling performance. This work involves the implementation of a domain-specific hardware architecture with an access engine (AxE) to optimize memory access and a RISC-V control interface to implement a memory-on-fabric (MoF) system for near-data processing, with the goals of scalability, and programmability.

Graph-OPU [117] addresses the need for efficient acceleration methods for GNNs due to their widespread applications and provides a solution to the challenge of time-consuming FPGA reconfiguration when switching between GNN models. The authors present this work as a novel FPGA-based overlay processor adapted to mainstream GNNs, with software programmability that enables fast model switching. Graph-OPU includes instruction set customization, design of a fully pipelined microarchitecture, implementation of unified matrix multiplication, and testing with various datasets on the Xilinx Alveo U50.

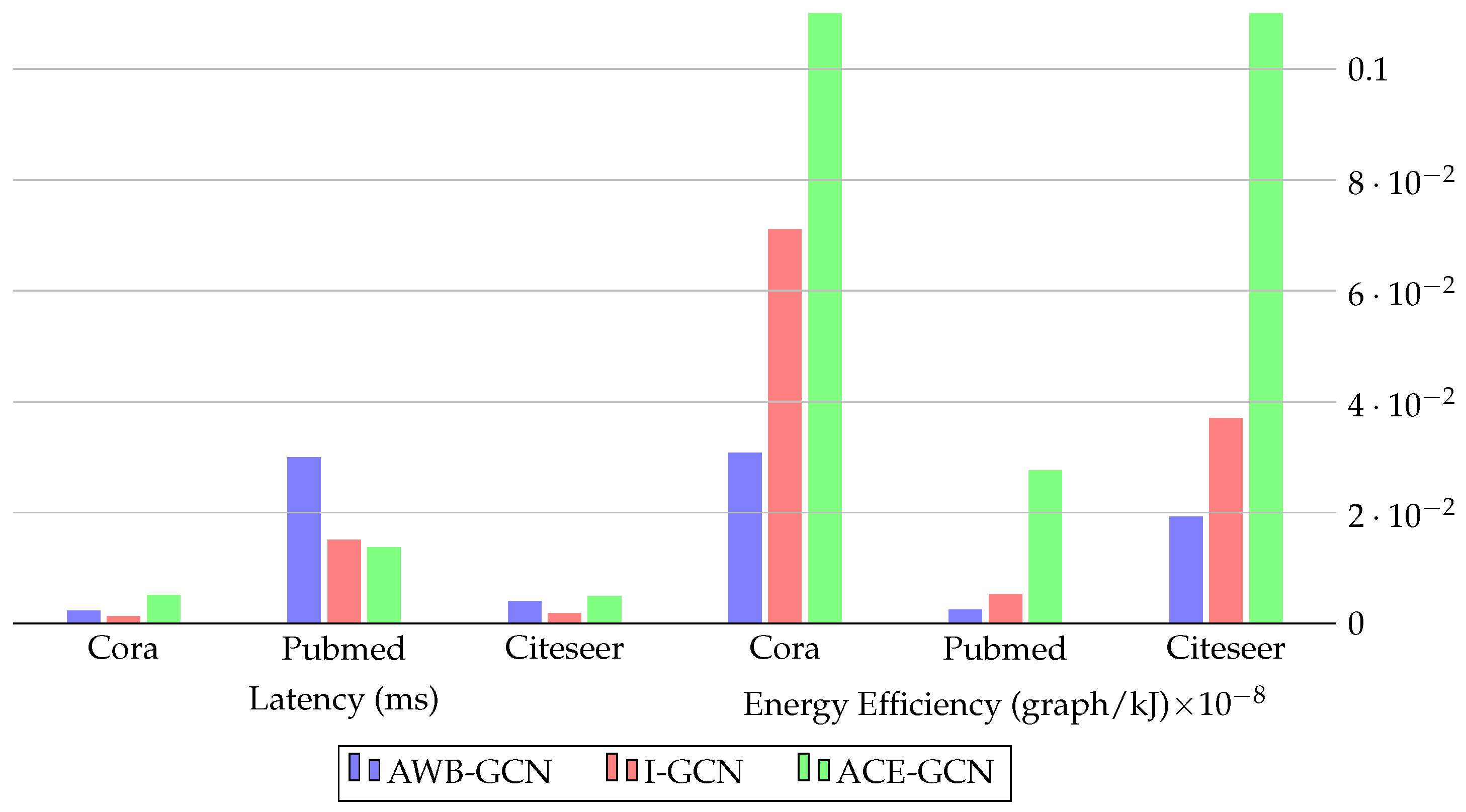
4.3. FPGA-Based Heterogeneous Approaches

Heterogeneous computing architectures combine different types of processors to create powerful and flexible systems. CPU-FPGA heterogeneous approaches, in particular, offer solutions for applications requiring high levels of parallelism and customizability. By combining the general-purpose processing capability of the CPU with the specialized hardware advantages of the FPGA, these approaches enable the faster and more energy-efficient performance of complex computational tasks [27]. Although these structures are not applicable to embedded systems, they are preferred for large-scale applications. This section reviews some proposed heterogeneous FPGA approaches for GNNs.

Zhang et al. [27] recommend a method for training GNNs on large-scale graphs using a CPU-FPGA heterogeneous platform. The method uses neighbor sampling to address scalability and overfitting challenges. The authors discuss the computational challenges associated with neighbour sampling and feature aggregation, which impact the overall execution time of NS GNN training, thereby impeding scalability and efficiency. The work involves implementing a parallel neighbor sampling algorithm on the main processor and an FPGA accelerator optimized for GNN operations. It also proposes to leverage optimizations such as neighbor sharing and task pipelining to improve memory performance and computational efficiency, ultimately increasing training throughput and accelerating NS GNN training.

GraphACT [30] proposes a heterogeneous approach to address memory access and load balancing challenges in accelerating the training of GCNs on CPU-FPGA platforms due to significant data communication issues. GraphACT optimizes the FPGA design through a graph-theoretic pre-processing step to balance the load across on-chip compute modules and various FPGA devices. Additionally, it features a systolic array-based design that improves weight update efficiency. The authors evaluated this work using a 40-core Xeon server with a Xilinx Alveo U200 board and demonstrated the strengths of the proposed method with parameters such as convergence time and test set accuracy on datasets such as PPI, Reddit, and Yelp.

Zhang et al. [118] aim to improve the efficiency and speed of GNNs in real-time applications. They address the challenge of achieving low-latency mini-batch inference on CPU-FPGA platforms. The hardware accelerator design presented in this paper uses the Adaptive Computing Kernel (ACK) architecture to run different GNN computing cores with low latency. It provides a unified solution for different GNN models on FPGA platforms without the need for runtime reconfiguration. The methodology involves identifying GNN compute kernels, designing the flexible ACK architecture, and using a design space exploration algorithm to create a single hardware design point for different GNN models and optimize it for low-latency inference without reconfiguration.

HP-GNN [119] targets to address inefficiencies in full-graph GNN training on large graphs. It aims to reduce the high memory footprint and increase the frequency of model updates per epoch on CPU-FPGA heterogeneous platforms. In contrast to previous work that focused on specific GNN models or algorithms, HP-GNN provides a general framework for GNN training on CPU-FPGA platforms. Hardware templates are optimized for efficient accelerator generation. Lin et al. suggest a design space exploration engine to improve throughput and generate accelerators automatically. They also provide software APIs to simplify building a high-level abstraction for sampling-based mini-batch GNN training, developing optimized hardware templates, and simplifying development without requiring hardware expertise.

4.4. Frameworks for FPGA-Based Accelerators

In the field of high-performance computing, FPGA accelerator frameworks facilitate the integration between hardware and software, enabling algorithms to run efficiently on hardware. Frameworks allow researchers to quickly and efficiently prototype customized hardware designs. They can be used to develop power-efficient systems that can perform complex data processing tasks in real-time. Customized FPGA frameworks provide performance advantages to designers, particularly in areas such as big data analysis, artificial intelligence applications, and deep learning models. This section reviews frameworks for FPGA-based accelerators designed for GNNs.

BoostGCN [108] aims to optimize the inference of GCNs on FPGA platforms by proposing a Hardware-aware Partition-Centric Feature Aggregation (PCFA) scheme to overcome inefficiencies and adaptability challenges in memory accesses encountered by GCNs. The authors state that the issues arise from different graph sizes, sparsity levels, and complexities of GCN models. Zhang et al. propose a framework that can adapt to these variations to enhance performance and efficiency. The PCFA scheme in BoostGCN performs three-dimensional graph partitioning considering data reuse on the chip and external memory architecture. Additionally, a central load balancing scheme is employed to effectively address workload imbalance. This study enables important data parallelism through optimized RTL templates and a task scheduling strategy aimed at minimizing pipeline stalls.

FlowGNN [120] is proposed to support generic GNN models for real-time inference applications. By introducing explicit message passing and multi-level parallelism, the authors provide a comprehensive solution for GNN acceleration without sacrificing adaptability. FlowGNN includes the compiling of each GNN model into the FPGA kernel, allowing easy updates for new architectures and the creation of custom accelerators through modular components. Using the Xilinx Alveo U50 FPGA, FlowGNN outperforms existing baselines such as CPU, GPU, and I-GCN, achieving speedup and energy efficiency on a variety of datasets and GNN models.

DeepBurning-GL addresses the growing need for efficient and specialized accelerators for GNNs due to their complexity and computational demands in various applications. Liang et al. [121] present an automated framework for designing custom GNN accelerators that can meet performance requirements while satisfying resource constraints and user-specific design goals. By focusing on automating the customization of GNN accelerators, this work stands out for streamlining the design process by providing end-to-end solutions tailored to specific applications without manual intervention. DeepBurning-GL includes a systematic approach that starts with a performance analysis of GNN models to identify bottlenecks, selects templates based on model requirements, combines templates into a unified accelerator design, and fine-tunes design parameters using a simulated annealing algorithm combined with model-based design space pruning for optimization.

DGNN-Booster is proposed by Chen et al. [122] as an FPGA accelerator framework designed for real-time Dynamic Graph Neural Networks (DGNN) inference with HLS, offering high-speed performance and low energy consumption. DGNNs pose challenges in hardware deployment due to low parallelism and a lack of general accelerator frameworks for dynamic graphs. DGNN-Booster employs two FPGA accelerator designs, V1 and V2, each optimized for different levels of parallelism and computational intensity. V1 focuses on parallelizing the GNN and RNN in adjacent time steps, while V2 emphasizes parallelization in a single time step. The designs incorporate graph renumbering, format conversion, multi-level parallelism, and task scheduling to improve hardware efficiency and performance.

GNNBuilder [123] is a framework that enables the automatic generation of GNN accelerators for different models, providing design flexibility and optimization strategies. The authors propose using serialized trained direct fit models for efficient design space exploration, facilitating fast performance evaluation compared to traditional HLS synthesis. The framework demonstrates predictive capabilities for runtime and BRAM models based on a database of 400 synthesized designs, using a random forest regressor with 10 predictors and 5-fold cross-validation. The evaluation is performed on FPGA-based parallel implementations and shows speedups over PyG CPU, PyG GPU, and C++ CPU runtimes for various GNN models.

FGNAS [124] is proposed as a hardware/software co-exploration framework that uses FPGA platforms to optimize hardware accelerators for GNNs, aiming at efficient GNN deployment. FGNAS is differentiated by its holistic approach in integrating hardware and software considerations to improve accuracy and speedup in GNN architectures on FPGAs. The methodology uses reinforcement learning to sequentially sample hardware and software parameters, analyze FPGA model performance, and update the controller using policy gradients for optimized design. By partitioning the search space into architectural and hardware parameters such as embedding size, attention type, aggregation type, and group sizes, FGNAS efficiently explores the design space to determine the optimal GNN architecture and FPGA design.

4.5. FPGA-Based Accelerator Approaches with Quantization

By reducing the dimension of data representations and using hardware resources more efficiently, quantization allows FPGA accelerators to reduce energy consumption and increase processing speed. Quantization is especially important for embedded systems that have limited computational resources due to energy constraints. FPGA accelerators designed using quantization increase the usability of GNNs in real-time applications and scenarios requiring energy efficiency. This section explores in detail the integration of quantization techniques with FPGA-based accelerators.

FPGAN [125] proposes an FPGA-based accelerator to improve the performance and energy efficiency of Graph Attention Networks (GATs) while maintaining accuracy. The study demonstrates the effectiveness of the software-hardware co-optimized approach in accelerating inference and highlights the potential of FPGA accelerators in this area. The authors integrate model optimization and software hardware co-design to create a dedicated accelerator for GATs. The FPGAN involves process fusion, quantization, data reconfiguration, model tuning, and architecture optimization. Process fusion simplifies the self-attention mechanism, while data reconfiguration improves data storage and access efficiency. Model tuning optimizes activation functions, and architecture design focuses on software and hardware co-design for efficient inference operations. The study demonstrates improvements in performance and energy efficiency without sacrificing accuracy.

SkeletonGCN [126] addresses the growing demand for efficient training of GCNs on FPGA platforms, due to their computational and memory requirements. The authors present the work as a solution that optimizes data representation, simplifies operations, and uses a unified hardware architecture to achieve significant speedup without trade-offs in accuracy. The methodology involves quantizing data to SINT16 to reduce computation and storage requirements, simplifying non-linear operations, using a compression algorithm for sparse matrices, and designing a unified hardware architecture to improve DSP efficiency for various matrix operations in GCN training.

Table 2. Quantization studies on FPGA-based accelerators.

Publication	Hardware	Resource Consumption	Quantized Parameters	Baselines
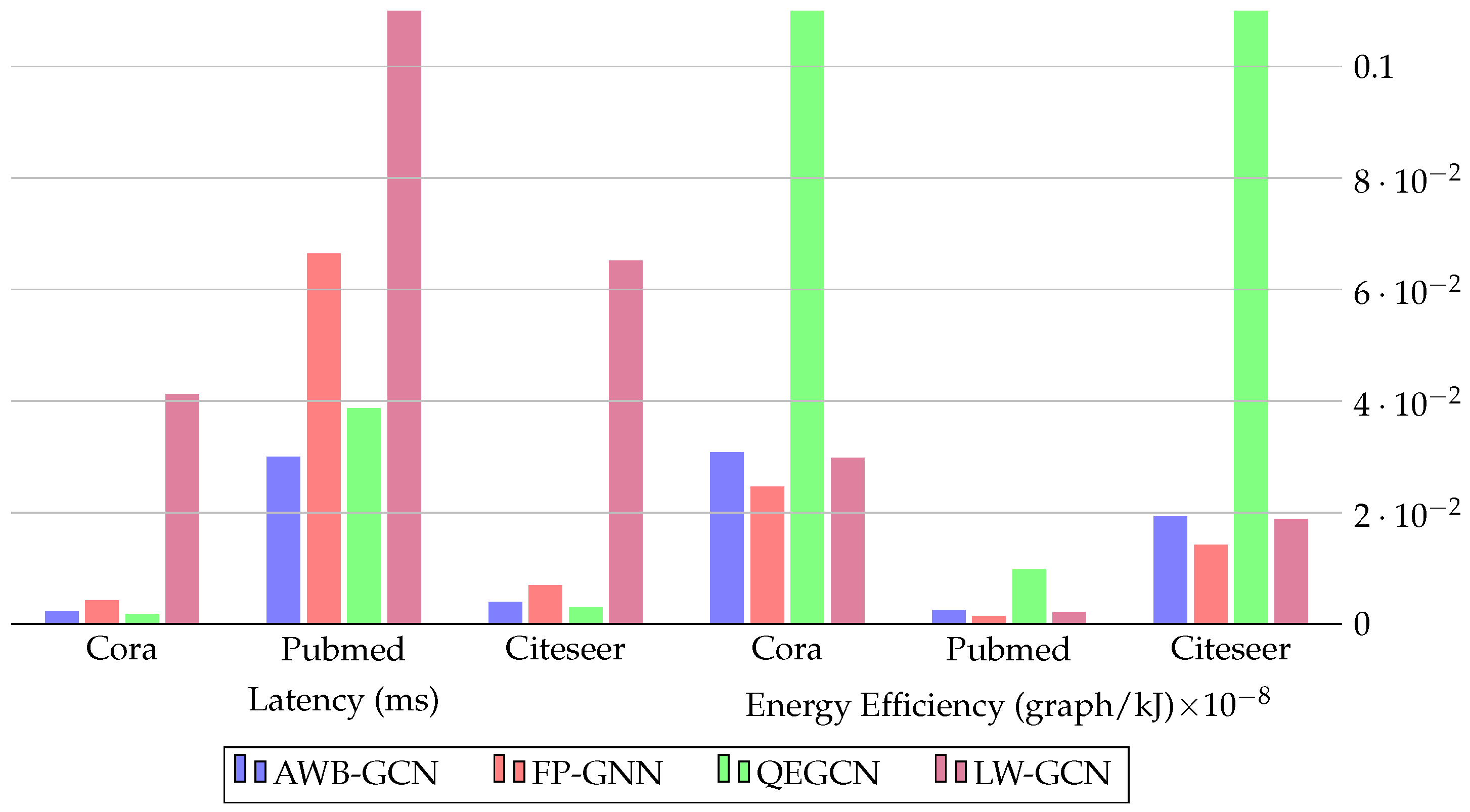
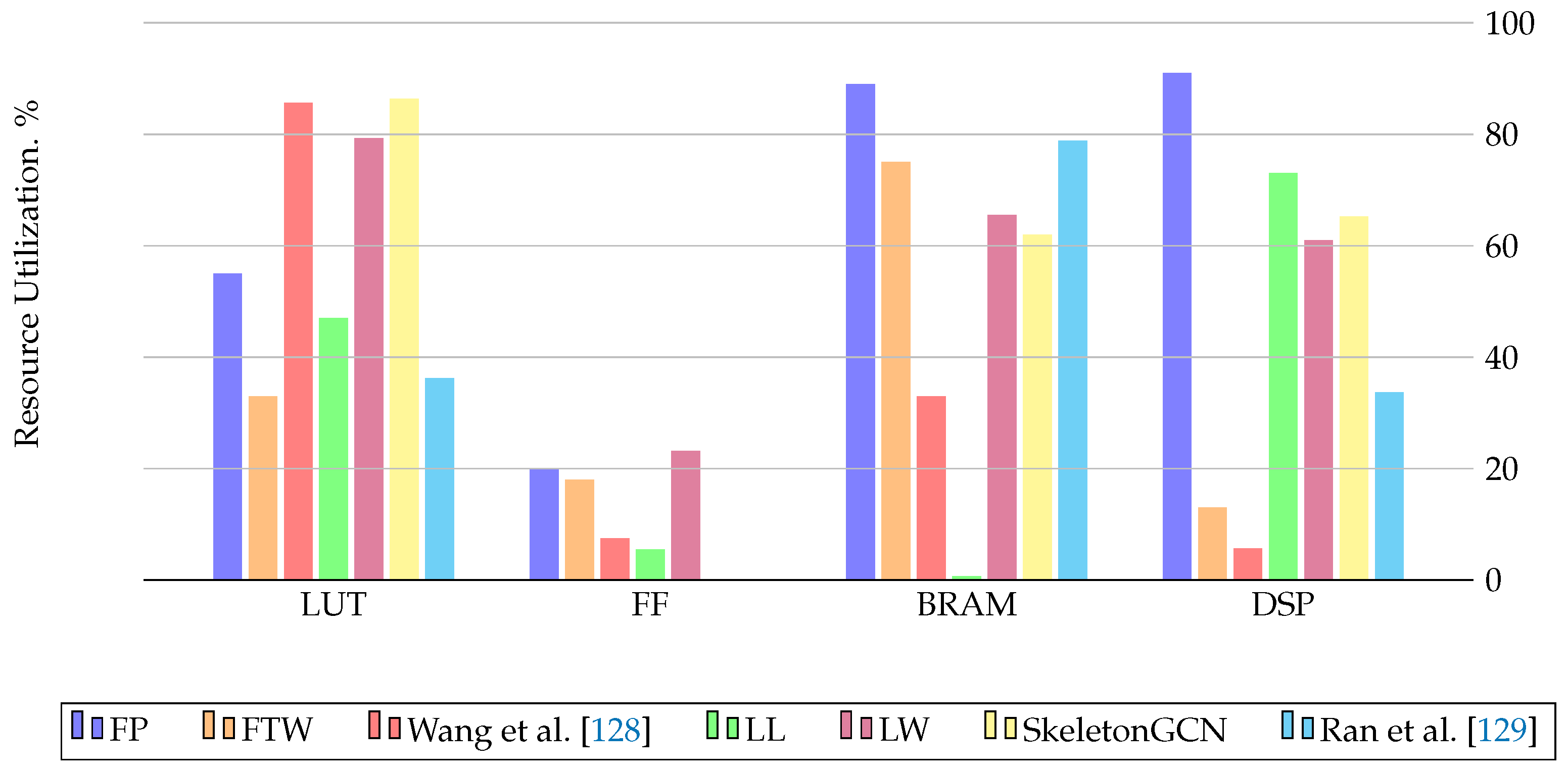
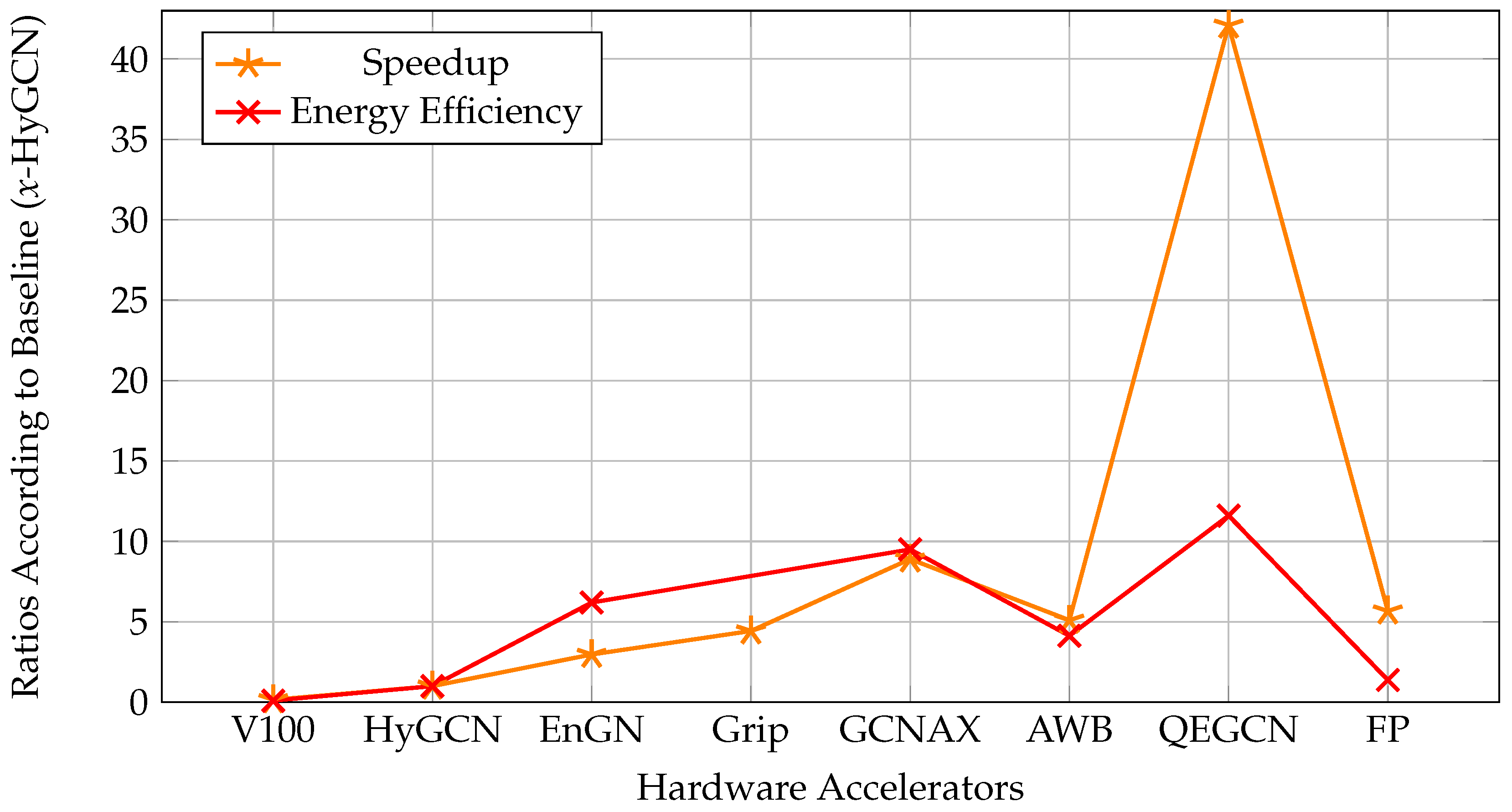
FP-GNN [24]	VCU128 Freq:225 MHz	LUT: 717,578 FF: 517,428 BRAM: 1,792 DSP: 8,192	Features, Weights 32-bit fixed point	PyG-CPU-GPU, HyGCN, GCNAX, AWB-GCN, I-GCN
FTW-GAT [127]	VCU128 Freq:225 MHz	LUT: 436.657 FF: 470,222 BRAM: 1,502 DSP: 1,216	8-bit int Features3-bit int Weights	PyG-CPU-GPU, FP-GNN
Wang et al. [128]	Alveo U200 Freq:250 MHz	LUT: 1,010,00 FF: 117,00 BRAM: 1,430 DSP: 392	1-bit integer Features, Weights 32-bit integer Adjacency matrix	PyG-CPU-GPU, ASAP [113]
LL-GNN [32]	Alveo U250 Freq:200 MHz	LUT: 815,000 FF: 139,000 BRAM: 37 DSP: 8,986	Model Parameters 12-bit fixed point	PyG-CPU-GPU
Ran et al. [129]	Alveo U200 Freq:250 MHz	LUT: 427,438 FF: NI BRAM: 1,702 DSP: 33.7	Features, Weights	PyG-CPU-GPU, HyGCN, ASAP [113], AWB-GCN, LW-GCN
SkeletonGCN [126]	Alveo U200 Freq:250 MHz	LUT: 1,021,386 FF: NI BRAM: 1,338 DSP: 960	Feature, Adjacency matrices, Trainable parameters 16-bit signed integer	PyG-CPU-GPU, GraphACT
QEGCN [130]	VCU128 Freq:225 MHz	LUT: 21,935 FF: 9,201 BRAM: 22 DSP: 0	Features, Weights 8-bit fixed point	PyG-CPU-GPU, DGL-CPU-GPU, HyGCN, EnGN, AWB-GCN, ACE-GCN
Yuan et al. [131]	VCU128 Freq:300 MHz	LUT: 3,244 FF: 345 BRAM: 102.5 DSP: 64	Features, Weights 32-bit fixed point	PyG-CPU-GPU
FPGAN [125]	Arria10 GX1150 Freq:216 MHz	LUT: 250,570 FF: 338,490 BRAM: NI DSP: 148	Features, Weights fixed point	PyG-CPU-GPU
LW-GCN [132]	Kintex-7 K325T Freq:200 MHz	LUT: 161,529 FF: 94,369 BRAM: 291.5 DSP: 512	Features, Weights 16-bit signed fixed point	PyG-CPU-GPU, AWB-GCN

¹ NI: The dataset in the study does not provide any information about this value.

QEGCN [130] is an instance of efficient hardware accelerators to improve GCN performance. The research proposes an FPGA-based accelerator that uses edge-level parallelism. The authors aim to optimize the execution of quantized GCNs and distinguish themselves from existing graph-level parallelism approaches. The paper emphasizes edge-level parallelism, stating that it enables more efficient processing of graph data compared to traditional methods. QEGCN investigates the impact of data quantization on GCN accuracy, evaluates energy efficiency at different quantization levels, and analyses performance on various benchmark platforms.

FTW-GAT [127] accelerator tackles the difficulties presented by intricate data dependencies and irregular structures of graph attention networks (GATs) by quantizing GAT weights to ternary values. This simplifies processing elements, eliminates the need for digital signal processors (DSPs), and reduces power consumption. This paper presents a methodology that combines ternary-weight quantization with additional techniques such as process fusion, multi-level pipelining, and graph partitioning to increase parallelism in the GAT inference acceleration process. The aim is to improve efficiency and performance. The authors indicate that the proposed model achieves accuracy values similar to full-precision models with quantization, and outperforms baselines in terms of latency and energy efficiency.

LL-GNN [32] aims to minimize latency in processing GNNs on FPGA for real-time applications in high-energy physics, especially in collider triggering systems where ultra-low latency is crucial for timely event selection. Que et al. propose a design combining quantization and FPGAs that offers low latency when processing small graphs and can be used in scenarios requiring sub-microsecond latency and high throughput, such as particle identification in fundamental physics experiments. LL-GNN involves a co-design approach that optimizes both the algorithm and hardware for GNNs on FPGAs, including defining delay thresholds, rebalancing Multilayer Perceptron (MLP) sizes, exploring parallelism parameters, and implementing sublayer fusion to improve performance and reduce latency. The authors show that they have achieved low latency as a result of this work and that it is possible to embed GNNs in FPGAs with sub-microsecond latency.

HuGraph [33] aims to address the increasing demand for efficient and scalable GCN training on large and irregular graphs using heterogeneous FPGA clusters. The paper employs a load-balanced mapping strategy and a scheduling method to optimize GCN training. HuGraph focuses on adapting various large graphs to FPGAs while achieving significant speedups with minimal loss of accuracy compared to traditional platforms. The authors state that they use 8-bit integer quantized adjacency coefficients, features, weights, and error values for efficient computation. HuGraph allocates hardware resources, configures samplers, and simulates training performance for each FPGA and dataset configuration to achieve workload balance across heterogeneous FPGAs.

Figure 10. Latency (ms) and energy efficiency (graph/kJ) comparison of 4 different methods on the same datasets. Compared to the 3 approaches with quantization, AWB-GCN represents an approach without quantization.

Ran et al. [129] developed a software-hardware co-design to achieve low-latency GCN inference on FPGA platforms. The paper presents an integrated approach that combines algorithm-level attention mechanism-based graph parsing with a two-phase hardware architecture and achieves speedups compared to existing accelerators. This work includes the use of attention mechanisms for graph parsing, designing a pipelined two-stage accelerator for efficient aggregation and merging phases, exploiting edge-level and feature-level parallelism, and implementing a graph partitioning strategy to improve data reuse efficiency. The authors emphasize the use of fixed-point representation in the study, as floating-point representation is more resource-intensive.

FP-GNN [24] is suggested as a unified processing module that can perform both the aggregation and combination phases simultaneously. This allows for flexible execution orders and supports various GNN models. The authors provide a customizable hardware architecture with components such as a Workflow Controller and Processing Modules, enabling high-performance computing and efficient resource utilization. The Adaptive GNN Accelerator (AGA) framework and Adaptive Graph Partitioning (AGP) strategy in FP-GNN optimize parallelism and memory management, enabling improved performance efficiency in GNN inference tasks. In this work, weights and input features are quantized as 32-bit fixed-point to take advantage of the integer artifacts while avoiding accuracy loss.

Yuan et al. [131] use a 32-bit fixed-point representation for efficient computation without loss of accuracy, as in FP-GNN. The paper aims to enhance the performance and energy efficiency of GNNs by developing a dedicated accelerator for the Gathering phase on FPGA platforms. This addresses the inefficiencies of CPUs and GPUs in handling dynamic and irregular data access patterns of GNNs. This research presents an architecture that optimizes the execution order of the Apply and Gather phases, reducing operations and improving performance, while leveraging FPGA technology to design an efficient accelerator for the Gather phase of GNNs.

Wang et al. [128] introduce a customizable FPGA-based accelerator for BiGCNs. The hardware optimizations include fine-grained pipelining, sparse matrix multiplication, and partial unrolling, which significantly improve performance. The work also includes overlapping data transfer with computation, using COO format storage for the adjacency matrix, and sparse matrix multiplication to improve hardware efficiency. The focus is on deep customization to support various GCNs. The results indicate that the proposed FPGA-based accelerator outperforms a previous FPGA-based GCN accelerator by achieving four times faster throughput while consuming fewer DSP resources.

Figure 11. Resource utilization demonstration for FPGA-based hardware accelerators combined with quantization. Here FP is denoted as FP-GNN, FTW as FTW-GAT, LL as LL-GNN, LW as LW-GCN.

4.6. FPGA-Based Accelerators for Embedded Applications

Efficient system designs for embedded devices are critical for applications that require efficient data processing and fast response times due to their limited computational resources. In this scope, FPGA-based accelerators have the potential to improve the performance of embedded systems, optimizing energy consumption and handling more complex computational tasks. In particular, the implementation of advanced machine learning models such as GNNs in embedded systems is made possible by the flexibility and reconfigurability of FPGA accelerators. This chapter provides a detailed review of the work on FPGA-based accelerators designed for embedded systems.

Table 3. FPGA-based GNN accelerator works for embedded devices.

Study	Target Device	Datasets	Fixed-point representation
LW-GCN [132]	Xilinx Kintex-7	Cora, Citeseer, Pubmed	✔
Zhou et al. [133]	Xilinx ZCU104, Alveo U200	Wikipedia, Reddit, GDELT	-
gFADES [72]	Zynq Ultrascale+ XCZU28DR	Cora, Citeseer, Pubmed	-
Hansson et al. [134]	Xilinx Zynq UltraScale+	Cora, Citeseer, Pubmed	✔

LW-GCN is proposed by Tao et al. [132] to improve the efficiency of Graph Convolutional Networks (GCNs) on edge devices with limited resources by addressing irregular computation and memory access challenges. LW-GCN addresses irregular computation and memory access challenges and achieves improvements in storage utilization and computation time. This is accomplished through a software-hardware co-design approach and a PCOO compression format that efficiently pre-processes sparse data. The authors present a versatile approach that includes post-training quantization with 16-bit signed fixed-point representation for features and weights, and 4-bit signed fixed-point quantization for non-zero elements in sparse matrices. Additionally, they use an external product tiling technique to balance the workload and reduce the data volume during computation. LW-GCN achieves important reductions in latency and improvements in power efficiency, demonstrating its effectiveness in improving GCN inference performance on edge devices.

Zhou et al. [133] aims to improve the accuracy and speed of inference over dynamic graphs by addressing the challenge of efficiently processing temporal information in graph neural networks. They investigate the optimization of temporal graph neural networks through a model-architecture co-design approach and exploit batch processing, pipelining, and prefetching techniques for improved performance. This paper presents a co-design methodology for temporal graph neural networks that optimizes both the model and the hardware architecture. The methodology enables efficient processing of evolving temporal information on FPGA platforms. The paper includes proposing a hardware mechanism to enable chronological vertex updates without compromising computational parallelism. The methodology reduces computational complexity and memory access while maintaining an accuracy loss of less than 0.33%. The study compared the performance of embedded-scale and large-scale hardware platforms using parameters such as latency, throughput, and batch size.

gFADES [72], discusses the complex data access and processing requirements of GNNs combining both dense and sparse data representations, which makes hardware acceleration crucial for efficient computation. The focus of the paper is on hardware acceleration for GNNs, with a particular emphasis on performance optimization for GCNs. This paper stands out due to its approach that utilizes a dataflow architecture of data streams to optimize dense and sparse tensor processing, resulting in high-performance execution of GNNs. The methodology of the study involves developing the gFADES accelerator using a dataflow of dataflows (DoD) approach, optimizing the High-Level Synthesis (HLS) description for extreme sparsity in GNNs, scaling performance with multiple hardware threads and compute units, and integrating the accelerator with Pytorch for edge computing devices. In the study, the Zynq device, known for its resource-constrained structure, was used as the base hardware with the PYNQ overlay. Results of the study show performance improvements of up to 140x with multithreaded hardware configurations compared to optimized software implementations in Pytorch, demonstrating the effectiveness of the gFADES accelerator in improving GNN processing on resource-constrained devices.

Hansson et al. [134] extend the gFADES architecture and focus on optimizing hardware designs for Graph Convolutional Networks (GCNs) by exploring deep quantization strategies to improve performance and energy efficiency. The authors state that the challenge is to meet the computational requirements of GCNs on resource-constrained embedded hardware while maintaining accuracy. This paper provides runtime hardware-aware training for GCNs by embedding a mixed-precision design in the forward pass of the PyTorch backpropagation training loop, enabling significant speedups without trade-offs in accuracy. The methodology involves integrating a hardware accelerator into the PyTorch training loop to explore various hardware configurations with different bit precision levels of up to four bits and evaluate their impact on classification accuracy and performance. The work focuses on optimizing the quantization of features, adjacencies, weights, and intermediate data to increase hardware efficiency and throughput while minimizing logic requirements. The results of the study are evaluated with classification accuracy, execution time, and speedup metrics for different cases obtained with hardware configurations. The authors state that optimized hardware design with deep quantization can provide significant speedup while maintaining classification accuracy.

5. Discussion and Future Research Directions

Following our examination of quantization techniques and reconfigurable (FPGA) hardware accelerators that enhance the computational efficiency in GNNs from the standpoint of embedded devices, we identify the variances and parallels among current methods based on their techniques. This section addresses the existing voids, similarities, obstacles, and potential areas in the literature that could be investigated further for future studies.

5.1. Quantization and Future Directions

The studies reviewed underscore the significance of quantization techniques in optimizing embedded systems, striking a balance between computational efficiency and model accuracy. Quantization methods employed during both the training and inference phases offer effective solutions to challenges such as computational complexity and memory demands in GNN models. The findings of our research on quantization methods can be summarized as follows:

Scalar quantization methods are prevalent in embedded systems due to their ease of implementation and the computational efficiency of integer arithmetic.
Vector quantization provides higher compression ratios compared to scalar quantization by grouping multiple vectors together.
Combining vector and scalar quantization offers the benefits of both integer arithmetic computational power and the high compression ratio of vector quantization, crucial for developing highly efficient low-dimensional models for hardware applications.
Achieving a delicate balance between energy efficiency, training-output speed, and accuracy in unified approaches requires careful customization during the design phase according to the specific requirements of particular applications, highlighting the important role of future efforts in achieving this balance.
Mixed precision approaches show the potential to maintain accuracy while reducing model size. However, different bit representations can introduce computational complexity from a hardware standpoint. As a result, there is growing interest in the development of fully quantized GNN models specifically designed for embedded system applications.
Research shows that the accuracy achieved with 16-bit and 8-bit quantization values can be achieved with lower-bit numbers such as 4-bit and 2-bit. In this context, the adoption of aggressive methods involving low-bit representations to integrate large GNN models into embedded device applications will begin to attract the attention of more researchers.

5.2. Hardware Accelerators and Future Directions

Despite increasing interest in machine learning models, there is a noticeable gap in the literature on the exploration of FPGA-based GNN accelerators designed specifically for embedded systems. This lack of research highlights the importance of investigating FPGA implementations in this domain. In addressing this gap, several key themes emerge:

The current body of FPGA studies related to Graph Neural Network (GNN) models is still insufficient to comprehensively address the complexities of embedded system applications, and it underscores a significant research gap in the field of FPGA.
While a significant portion of research efforts concentrate on GNN inference, there exists a critical need to expedite the training phase, particularly for dynamic graph structures, necessitating further exploration in this realm.
The adaptive nature of FPGA accelerators exhibits notable efficacy in accommodating diverse application requirements, demonstrating their potential for widespread adoption in various domains.
While the utilization of common datasets and network models provides an initial benchmark for researchers, the limited extension of studies to diverse application domains and the absence of the establishment of distinct baselines pose significant challenges requiring resolution.
Although this work is focused on quantization and FPGA-based accelerators, additional techniques such as sampling, reordering, simplification, and knowledge distillation are currently being used with promising results. It is anticipated that interest in additional methods such as quantization and other approaches will grow in hardware-based applications.

6. Conclusions

In this paper, we provide an overview of FPGA-based accelerator approaches for computationally efficient Graph Neural Networks (GNNs) with a focus on embedded hardware. In addition, we explore quantization as an additional method. To the best of our knowledge, for the first time in the existing literature, we present a survey of quantization methods developed for GNNs and assess common fundamentals by comparing these methods with results from published papers. Furthermore, with this survey, we update the work on FPGA-based accelerators for GNNs and provide a taxonomy of existing GNN models.

Our results indicate a growing need for lightweight and computationally efficient GNN models. Quantization studies enable the development of models that run on embedded hardware due to their high compression ratios. Additionally, hardware-based accelerators for GNNs are gaining popularity, and we demonstrate promising results for future work, emphasizing that FPGA accelerators combined with quantization are under-explored when embedded device applications are the focus of research.

Given these findings, we suggest that future work should further investigate the integration of quantization and FPGA-based accelerators to improve the computational efficiency of GNNs. Specifically, studies evaluating the effectiveness of these techniques in real-world scenarios and on large datasets can expand the practical applications of GNNs and promote their use in industrial applications. Moreover, the combination of quantization and accelerator technologies could unlock new research opportunities to optimize energy efficiency and performance in embedded systems.

Author Contributions

Investigation, H.T.K; writing—original draft preparation, H.T.K.; writing—review and editing, H.T.K., J.N.Y., R.P. and J.P.; visualization, H.T.K.; supervision, J.N.Y., R.P. and J.P. All authors have read and agreed to the published version of the manuscript.

Funding

Mr. Kose’s PhD program at the University of Bristol is funded by the Republic of Turkiye Ministry of National Education. Professor Nunez-Yanez position at the Wallenberg AI autonomous systems and software (WASP) program is funded by the Knut and Alice Wallenberg Foundation.

Data Availability Statement

All the materials used in the study are mentioned within the article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Bronstein, M.M.; Bruna, J.; LeCun, Y.; Szlam, A.; Vandergheynst, P. Geometric deep learning: going beyond euclidean data. IEEE Signal Processing Magazine 2017, 34, 18–42. [Google Scholar] [CrossRef]
Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI open 2020, 1, 57–81. [Google Scholar] [CrossRef]
Gama, F.; Isufi, E.; Leus, G.; Ribeiro, A. Graphs, convolutions, and neural networks: From graph filters to graph neural networks. IEEE Signal Processing Magazine 2020, 37, 128–138. [Google Scholar] [CrossRef]
Coutino, M.; Isufi, E.; Leus, G. Advances in distributed graph filtering. IEEE Transactions on Signal Processing 2019, 67, 2320–2333. [Google Scholar] [CrossRef]
Saad, L.B.; Beferull-Lozano, B. Quantization in graph convolutional neural networks. 2021 29th European Signal Processing Conference (EUSIPCO). IEEE, 2021, pp. 1855–1859.
Zhu, R.; Zhao, K.; Yang, H.; Lin, W.; Zhou, C.; Ai, B.; Li, Y.; Zhou, J. Aligraph: A comprehensive graph neural network platform. arXiv preprint 2019, arXiv:1902.08730. [Google Scholar] [CrossRef]
Ju, X.; Farrell, S.; Calafiura, P.; Murnane, D.; Gray, L.; Klijnsma, T.; Pedro, K.; Cerati, G.; Kowalkowski, J.; Perdue, G.; others. Graph neural networks for particle reconstruction in high energy physics detectors. arXiv preprint 2020, arXiv:2003.11603. [Google Scholar]
Ju, X.; Murnane, D.; Calafiura, P.; Choma, N.; Conlon, S.; Farrell, S.; Xu, Y.; Spiropulu, M.; Vlimant, J.R.; Aurisano, A.; others. Performance of a geometric deep learning pipeline for HL-LHC particle tracking. The European Physical Journal C 2021, 81, 1–14. [Google Scholar] [CrossRef]
Wu, L.; Chen, Y.; Shen, K.; Guo, X.; Gao, H.; Li, S.; Pei, J.; Long, B.; others. Graph neural networks for natural language processing: A survey. Foundations and Trends® in Machine Learning 2023, 16, 119–328. [Google Scholar] [CrossRef]
Jiang, W.; Luo, J. Graph neural network for traffic forecasting: A survey. Expert Systems with Applications, 2022; 117921. [Google Scholar]
Pope, J.; Liang, J.; Kumar, V.; Raimondo, F.; Sun, X.; McConville, R.; Pasquier, T.; Piechocki, R.; Oikonomou, G.; Luo, B.; others. Resource-Interaction Graph: Efficient Graph Representation for Anomaly Detection. arXiv preprint 2022, arXiv:2212.08525. [Google Scholar]
Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. Advances in neural information processing systems 2017, 30. [Google Scholar]
Huang, W.; Zhang, T.; Rong, Y.; Huang, J. Adaptive sampling towards fast graph representation learning. Advances in neural information processing systems 2018, 31. [Google Scholar]
Ying, R.; He, R.; Chen, K.; Eksombatchai, P.; Hamilton, W.L.; Leskovec, J. Graph convolutional neural networks for web-scale recommender systems. Proceedings of the 24th ACM SIGKDD international conference on knowledge discovery & data mining, 2018, pp. 974–983.
Battaglia, P.W.; Hamrick, J.B.; Bapst, V.; Sanchez-Gonzalez, A.; Zambaldi, V.; Malinowski, M.; Tacchetti, A.; Raposo, D.; Santoro, A.; Faulkner, R.; others. Relational inductive biases, deep learning, and graph networks. arXiv preprint 2018, arXiv:1806.01261. [Google Scholar]
Wang, M.Y. Deep graph library: Towards efficient and scalable deep learning on graphs. ICLR workshop on representation learning on graphs and manifolds, 2019.
Lerer, A.; Wu, L.; Shen, J.; Lacroix, T.; Wehrstedt, L.; Bose, A.; Peysakhovich, A. Pytorch-biggraph: A large scale graph embedding system. Proceedings of Machine Learning and Systems 2019, 1, 120–131. [Google Scholar]
Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE transactions on neural networks and learning systems 2020, 32, 4–24. [Google Scholar] [CrossRef] [PubMed]
Zhang, Z.; Cui, P.; Zhu, W. Deep learning on graphs: A survey. IEEE Transactions on Knowledge and Data Engineering 2020, 34, 249–270. [Google Scholar] [CrossRef]
Geng, T.; Li, A.; Shi, R.; Wu, C.; Wang, T.; Li, Y.; Haghi, P.; Tumeo, A.; Che, S.; Reinhardt, S.; others. AWB-GCN: A graph convolutional network accelerator with runtime workload rebalancing. 2020 53rd Annual IEEE/ACM International Symposium on Microarchitecture (MICRO). IEEE, 2020, pp. 922–936.
Fey, M.; Lenssen, J.E. Fast graph representation learning with PyTorch Geometric. arXiv preprint 2019, arXiv:1903.02428. [Google Scholar]
Ferludin, O.; Eigenwillig, A.; Blais, M.; Zelle, D.; Pfeifer, J.; Sanchez-Gonzalez, A.; Li, S.; Abu-El-Haija, S.; Battaglia, P.; Bulut, N.; others. TF-GNN: graph neural networks in TensorFlow. arXiv preprint 2022, arXiv:2207.03522. [Google Scholar]
Yazdanbakhsh, A.; Park, J.; Sharma, H.; Lotfi-Kamran, P.; Esmaeilzadeh, H. Neural acceleration for GPU throughput processors. Proceedings of the 48th international symposium on microarchitecture, 2015, pp. 482–493.
Tian, T.; Zhao, L.; Wang, X.; Wu, Q.; Yuan, W.; Jin, X. FP-GNN: adaptive FPGA accelerator for graph neural networks. Future Generation Computer Systems 2022, 136, 294–310. [Google Scholar] [CrossRef]
Nunez-Yanez, J.; Hosseinabady, M. Sparse and dense matrix multiplication hardware for heterogeneous multi-precision neural networks. Array 2021, 12, 100101. [Google Scholar] [CrossRef]
Sit, M.; Kazami, R.; Amano, H. FPGA-based accelerator for losslessly quantized convolutional neural networks. 2017 International Conference on Field Programmable Technology (ICFPT). IEEE, 2017, pp. 295–298.
Zhang, B.; Kuppannagari, S.R.; Kannan, R.; Prasanna, V. Efficient neighbor-sampling-based gnn training on cpu-fpga heterogeneous platform. 2021 IEEE High Performance Extreme Computing Conference (HPEC). IEEE, 2021, pp. 1–7.
Liang, S.; Wang, Y.; Liu, C.; He, L.; Huawei, L.; Xu, D.; Li, X. Engn: A high-throughput and energy-efficient accelerator for large graph neural networks. IEEE Transactions on Computers 2020, 70, 1511–1525. [Google Scholar] [CrossRef]
Zhang, S.; Sohrabizadeh, A.; Wan, C.; Huang, Z.; Hu, Z.; Wang, Y.; Cong, J.; Sun, Y.; others. A Survey on Graph Neural Network Acceleration: Algorithms, Systems, and Customized Hardware. arXiv preprint 2023, arXiv:2306.14052. [Google Scholar]
Zeng, H.; Prasanna, V. GraphACT: Accelerating GCN training on CPU-FPGA heterogeneous platforms. Proceedings of the 2020 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, 2020, pp. 255–265.
Kiningham, K.; Levis, P.; Ré, C. GReTA: Hardware optimized graph processing for GNNs. Proceedings of the Workshop on Resource-Constrained Machine Learning (ReCoML 2020), 2020.
Que, Z.; Loo, M.; Fan, H.; Blott, M.; Pierini, M.; Tapper, A.D.; Luk, W. LL-GNN: low latency graph neural networks on FPGAs for particle detectors. arXiv preprint 2022, arXiv:2209.14065. [Google Scholar]
Zhao, L.; Wu, Q.; Wang, X.; Tian, T.; Wu, W.; Jin, X. HuGraph: Acceleration of GCN Training on Heterogeneous FPGA Clusters with Quantization. 2022 IEEE High Performance Extreme Computing Conference (HPEC). IEEE, 2022, pp. 1–7.
Gholami, A.; Kim, S.; Dong, Z.; Yao, Z.; Mahoney, M.W.; Keutzer, K. A survey of quantization methods for efficient neural network inference. In Low-Power Computer Vision; Chapman and Hall/CRC, 2022; pp. 291–326.
Tailor, S.A.; Fernandez-Marques, J.; Lane, N.D. Degree-quant: Quantization-aware training for graph neural networks. arXiv preprint 2020, arXiv:2008.05000. [Google Scholar]
Goyal, P.; Ferrara, E. Graph embedding techniques, applications, and performance: A survey. Knowledge-Based Systems 2018, 151, 78–94. [Google Scholar] [CrossRef]
Zhang, S.; Tong, H.; Xu, J.; Maciejewski, R. Graph convolutional networks: a comprehensive review. Computational Social Networks 2019, 6, 1–23. [Google Scholar] [CrossRef] [PubMed]
Zhang, S.; Tong, H.; Xu, J.; Maciejewski, R. Graph convolutional networks: Algorithms, applications and open challenges. Computational Data and Social Networks: 7th International Conference, CSoNet 2018, Shanghai, China, December 18–20, 2018, Proceedings 7. Springer, 2018, pp. 79–91.
Quan, P.; Shi, Y.; Lei, M.; Leng, J.; Zhang, T.; Niu, L. A brief review of receptive fields in graph convolutional networks. IEEE/WIC/ACM International Conference on Web Intelligence-Companion Volume, 2019, pp. 106–110.
Asif, N.A.; Sarker, Y.; Chakrabortty, R.K.; Ryan, M.J.; Ahamed, M.H.; Saha, D.K.; Badal, F.R.; Das, S.K.; Ali, M.F.; Moyeen, S.I.; others. Graph neural network: A comprehensive review on non-euclidean space. IEEE Access 2021, 9, 60588–60606. [Google Scholar] [CrossRef]
Chami, I.; Abu-El-Haija, S.; Perozzi, B.; Ré, C.; Murphy, K. Machine learning on graphs: A model and comprehensive taxonomy. The Journal of Machine Learning Research 2022, 23, 3840–3903. [Google Scholar]
Veličković, P. Everything is connected: Graph neural networks. Current Opinion in Structural Biology 2023, 79, 102538. [Google Scholar] [CrossRef] [PubMed]
Bhatti, U.A.; Tang, H.; Wu, G.; Marjan, S.; Hussain, A. Deep learning with graph convolutional networks: An overview and latest applications in computational intelligence. International Journal of Intelligent Systems 2023, 2023, 1–28. [Google Scholar] [CrossRef]
Xu, X.; Zhao, X.; Wei, M.; Li, Z. A comprehensive review of graph convolutional networks: approaches and applications. Electronic Research Archive 2023, 31, 4185–4215. [Google Scholar] [CrossRef]
Shabani, N.; Wu, J.; Beheshti, A.; Sheng, Q.Z.; Foo, J.; Haghighi, V.; Hanif, A.; Shahabikargar, M. A comprehensive survey on graph summarization with graph neural networks. IEEE Transactions on Artificial Intelligence 2024. [Google Scholar] [CrossRef]
Ju, W.; Fang, Z.; Gu, Y.; Liu, Z.; Long, Q.; Qiao, Z.; Qin, Y.; Shen, J.; Sun, F.; Xiao, Z.; others. A comprehensive survey on deep graph representation learning. Neural Networks 2024, 106207. [Google Scholar] [CrossRef] [PubMed]
Liu, R.; Xing, P.; Deng, Z.; Li, A.; Guan, C.; Yu, H. Federated Graph Neural Networks: Overview, Techniques, and Challenges. IEEE Transactions on Neural Networks and Learning Systems 2024. [Google Scholar] [CrossRef] [PubMed]
Lopera, D.S.; Servadei, L.; Kiprit, G.N.; Hazra, S.; Wille, R.; Ecker, W. A survey of graph neural networks for electronic design automation. 2021 ACM/IEEE 3rd Workshop on Machine Learning for CAD (MLCAD). IEEE, 2021, pp. 1–6.
Liu, X.; Yan, M.; Deng, L.; Li, G.; Ye, X.; Fan, D. Sampling methods for efficient training of graph convolutional networks: A survey. IEEE/CAA Journal of Automatica Sinica 2021, 9, 205–234. [Google Scholar] [CrossRef]
Varlamis, I.; Michail, D.; Glykou, F.; Tsantilas, P. A survey on the use of graph convolutional networks for combating fake news. Future Internet 2022, 14, 70. [Google Scholar] [CrossRef]
Li, H.; Zhao, Y.; Mao, Z.; Qin, Y.; Xiao, Z.; Feng, J.; Gu, Y.; Ju, W.; Luo, X.; Zhang, M. A survey on graph neural networks in intelligent transportation systems. arXiv preprint 2024, arXiv:2401.00713. [Google Scholar]
Lamb, L.C.; Garcez, A.; Gori, M.; Prates, M.; Avelar, P.; Vardi, M. Graph neural networks meet neural-symbolic computing: A survey and perspective. arXiv preprint 2020, arXiv:2003.00330. [Google Scholar]
Malekzadeh, M.; Hajibabaee, P.; Heidari, M.; Zad, S.; Uzuner, O.; Jones, J.H. Review of graph neural network in text classification. In 2021 IEEE 12th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), 2021.
Ahmad, T.; Jin, L.; Zhang, X.; Lai, S.; Tang, G.; Lin, L. Graph convolutional neural network for human action recognition: A comprehensive survey. IEEE Transactions on Artificial Intelligence 2021, 2, 128–145. [Google Scholar] [CrossRef]
Dong, G.; Tang, M.; Wang, Z.; Gao, J.; Guo, S.; Cai, L.; Gutierrez, R.; Campbel, B.; Barnes, L.E.; Boukhechba, M. Graph neural networks in IoT: a survey. ACM Transactions on Sensor Networks 2023, 19, 1–50. [Google Scholar] [CrossRef]
Jia, M.; Gabrys, B.; Musial, K. A Network Science perspective of Graph Convolutional Networks: A survey. IEEE Access 2023. [Google Scholar] [CrossRef]
Ren, H.; Lu, W.; Xiao, Y.; Chang, X.; Wang, X.; Dong, Z.; Fang, D. Graph convolutional networks in language and vision: A survey. Knowledge-Based Systems 2022, 251, 109250. [Google Scholar] [CrossRef]
Garg, R.; Qin, E.; Martínez, F.M.; Guirado, R.; Jain, A.; Abadal, S.; Abellán, J.L.; Acacio, M.E.; Alarcón, E.; Rajamanickam, S.; others. A taxonomy for classification and comparison of dataflows for gnn accelerators. Technical report, Sandia National Lab.(SNL-NM), Albuquerque, NM (United States), 2021.
Li, S.; Tao, Y.; Tang, E.; Xie, T.; Chen, R. A survey of field programmable gate array (FPGA)-based graph convolutional neural network accelerators: challenges and opportunities. PeerJ Computer Science 2022, 8, e1166. [Google Scholar] [CrossRef] [PubMed]
Liu, X.; Yan, M.; Deng, L.; Li, G.; Ye, X.; Fan, D.; Pan, S.; Xie, Y. Survey on graph neural network acceleration: An algorithmic perspective. arXiv preprint 2022, arXiv:2202.04822. [Google Scholar]
Abadal, S.; Jain, A.; Guirado, R.; López-Alonso, J.; Alarcón, E. Computing graph neural networks: A survey from algorithms to accelerators. ACM Computing Surveys (CSUR) 2021, 54, 1–38. [Google Scholar] [CrossRef]
Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. Advances in neural information processing systems 2016, 29. [Google Scholar]
Liao, R.; Zhao, Z.; Urtasun, R.; Zemel, R.S. Lanczosnet: Multi-scale deep graph convolutional networks. arXiv preprint 2019, arXiv:1901.01484. [Google Scholar]
Dwivedi, V.P.; Bresson, X. A generalization of transformer networks to graphs. arXiv. arXiv preprint 2020, arXiv:2012.09699. [Google Scholar]
Monti, F.; Boscaini, D.; Masci, J.; Rodola, E.; Svoboda, J.; Bronstein, M.M. Geometric deep learning on graphs and manifolds using mixture model cnns (2016). Available online: https://arxiv.org/abs/1611.08402.
Li, Y.; Tarlow, D.; Brockschmidt, M.; Zemel, R. Gated graph sequence neural networks. arXiv preprint 2015, arXiv:1511.05493. [Google Scholar]
Kipf, T.N.; Welling, M. Variational graph auto-encoders. arXiv preprint 2016, arXiv:1611.07308. [Google Scholar]
Pan, S.; Hu, R.; Long, G.; Jiang, J.; Yao, L.; Zhang, C. Adversarially regularized graph autoencoder for graph embedding. arXiv preprint 2018, arXiv:1802.04407. [Google Scholar]
You, J.; Ying, R.; Ren, X.; Hamilton, W.; Leskovec, J. Graphrnn: Generating realistic graphs with deep auto-regressive models. International conference on machine learning. PMLR, 2018, pp. 5708–5717.
Ying, Z.; You, J.; Morris, C.; Ren, X.; Hamilton, W.; Leskovec, J. Hierarchical graph representation learning with differentiable pooling. Advances in neural information processing systems 2018, 31. [Google Scholar]
Ma, Y.; Wang, S.; Aggarwal, C.C.; Tang, J. Graph convolutional networks with eigenpooling. Proceedings of the 25th ACM SIGKDD international conference on knowledge discovery & data mining, 2019, pp. 723–731.
Nunez-Yanez, J. Accelerating Graph Neural Networks in Pytorch with HLS and Deep Dataflows. International Symposium on Applied Reconfigurable Computing. Springer, 2023, pp. 131–145.
Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv preprint 2016, arXiv:1609.02907. [Google Scholar]
Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How powerful are graph neural networks? arXiv preprint 2018, arXiv:1810.00826. [Google Scholar]
Veličkovič, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv preprint 2017, arXiv:1710.10903. [Google Scholar]
Chen, R.; Zhang, H.; Li, S.; Tang, E.; Yu, J.; Wang, K. Graph-OPU: A Highly Integrated FPGA-Based Overlay Processor for Graph Neural Networks. 2023 33rd International Conference on Field-Programmable Logic and Applications (FPL). IEEE, 2023, pp. 228–234.
Novkin, R.; Amrouch, H.; Klemme, F. Approximation-aware and quantization-aware training for graph neural networks. Authorea Preprints 2023. [Google Scholar] [CrossRef]
Wan, B.; Zhao, J.; Wu, C. Adaptive Message Quantization and Parallelization for Distributed Full-graph GNN Training. Proceedings of Machine Learning and Systems 2023, 5. [Google Scholar]
Wu, Q.; Zhao, L.; Liang, H.; Wang, X.; Tao, L.; Tian, T.; Wang, T.; He, Z.; Wu, W.; Jin, X. GCINT: Dynamic Quantization Algorithm for Training Graph Convolution Neural Networks Using Only Integers 2022.
Wang, Y.; Feng, B.; Ding, Y. QGTC: accelerating quantized graph neural networks via GPU tensor core. Proceedings of the 27th ACM SIGPLAN symposium on principles and practice of parallel programming, 2022, pp. 107–119.
Ma, Y.; Gong, P.; Yi, J.; Yao, Z.; Li, C.; He, Y.; Yan, F. Bifeat: Supercharge gnn training via graph feature quantization. arXiv preprint 2022, arXiv:2207.14696. [Google Scholar]
Eliasof, M.; Bodner, B.J.; Treister, E. Haar wavelet feature compression for quantized graph convolutional networks. IEEE Transactions on Neural Networks and Learning Systems 2023. [Google Scholar] [CrossRef] [PubMed]
Dai, Y.; Tang, X.; Zhang, Y. An efficient segmented quantization for graph neural networks. CCF Transactions on High Performance Computing 2022, 4, 461–473. [Google Scholar] [CrossRef]
Zhu, Z.; Li, F.; Mo, Z.; Hu, Q.; Li, G.; Liu, Z.; Liang, X.; Cheng, J. A²Q: Aggregation-Aware Quantization for Graph Neural Networks. arXiv preprint 2023, arXiv:2302.00193. [Google Scholar]
Wang, S.; Eravci, B.; Guliyev, R.; Ferhatosmanoglu, H. Low-bit quantization for deep graph neural networks with smoothness-aware message propagation. Proceedings of the 32nd ACM International Conference on Information and Knowledge Management, 2023, pp. 2626–2636.
Liu, Z.; Zhou, K.; Yang, F.; Li, L.; Chen, R.; Hu, X. EXACT: Scalable graph neural networks training via extreme activation compression. International Conference on Learning Representations, 2021.
Eliassen, S.; Selvan, R. Activation Compression of Graph Neural Networks using Block-wise Quantization with Improved Variance Minimization. arXiv preprint 2023, arXiv:2309.11856. [Google Scholar]
Ding, M.; Kong, K.; Li, J.; Zhu, C.; Dickerson, J.; Huang, F.; Goldstein, T. VQ-GNN: A universal framework to scale up graph neural networks using vector quantization. Advances in Neural Information Processing Systems 2021, 34, 6733–6746. [Google Scholar]
Feng, B.; Wang, Y.; Li, X.; Yang, S.; Peng, X.; Ding, Y. Sgquant: Squeezing the last bit on graph neural networks with specialized quantization. 2020 IEEE 32nd International Conference on Tools with Artificial Intelligence (ICTAI). IEEE, 2020, pp. 1044–1052.
Zhao, Y.; Wang, D.; Bates, D.; Mullins, R.; Jamnik, M.; Lio, P. Learned low precision graph neural networks. arXiv preprint 2020, arXiv:2009.09232. [Google Scholar]
Bahri, M.; Bahl, G.; Zafeiriou, S. Binary graph neural networks. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2021, pp. 9492–9501.
Wang, H.; Lian, D.; Zhang, Y.; Qin, L.; He, X.; Lin, Y.; Lin, X. Binarized graph neural network. World Wide Web 2021, 24, 825–848. [Google Scholar] [CrossRef]
Huang, L.; Zhang, Z.; Du, Z.; Li, S.; Zheng, H.; Xie, Y.; Tan, N. EPQuant: A Graph Neural Network compression approach based on product quantization. Neurocomputing 2022, 503, 49–61. [Google Scholar] [CrossRef]
Wang, J.; Wang, Y.; Yang, Z.; Yang, L.; Guo, Y. Bi-gcn: Binary graph convolutional network. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021, pp. 1561–1570.
Kose, H.T.; Nunez-Yanez, J.; Piechocki, R.; Pope, J. Fully Quantized Graph Convolutional Networks for Embedded Applications.
Chen, Y.; Guo, Y.; Zeng, Z.; Zou, X.; Li, Y.; Chen, C. Topology-Aware Quantization Strategy via Personalized PageRank for Graph Neural Networks. 2022 IEEE Smartworld, Ubiquitous Intelligence & Computing, Scalable Computing & Communications, Digital Twin, Privacy Computing, Metaverse, Autonomous & Trusted Vehicles (SmartWorld/UIC/ScalCom/DigitalTwin/PriComp/Meta). IEEE, 2022, pp. 961–968.
Guo, Y.; Chen, Y.; Zou, X.; Yang, X.; Gu, Y. Algorithms and architecture support of degree-based quantization for graph neural networks. Journal of Systems Architecture 2022, 129, 102578. [Google Scholar] [CrossRef]
Xie, X.; Peng, H.; Hasan, A.; Huang, S.; Zhao, J.; Fang, H.; Zhang, W.; Geng, T.; Khan, O.; Ding, C. Accel-gcn: High-performance gpu accelerator design for graph convolution networks. 2023 IEEE/ACM International Conference on Computer Aided Design (ICCAD). IEEE, 2023, pp. 01–09.
Ma, L.; Yang, Z.; Miao, Y.; Xue, J.; Wu, M.; Zhou, L.; Dai, Y. {NeuGraph}: Parallel deep neural network computation on large graphs. 2019 USENIX Annual Technical Conference (USENIX ATC 19), 2019, pp. 443–458.
Peng, H.; Xie, X.; Shivdikar, K.; Hasan, M.; Zhao, J.; Huang, S.; Khan, O.; Kaeli, D.; Ding, C. Maxk-gnn: Towards theoretical speed limits for accelerating graph neural networks training. arXiv preprint 2023, arXiv:2312.08656. [Google Scholar]
Yan, M.; Deng, L.; Hu, X.; Liang, L.; Feng, Y.; Ye, X.; Zhang, Z.; Fan, D.; Xie, Y. Hygcn: A gcn accelerator with hybrid architecture. 2020 IEEE International Symposium on High Performance Computer Architecture (HPCA). IEEE, 2020, pp. 15–29.
Yin, L.; Wang, J.; Zheng, H. Exploring architecture, dataflow, and sparsity for gcn accelerators: A holistic framework. Proceedings of the Great Lakes Symposium on VLSI 2023, 2023, pp. 489–495. [Google Scholar]
Auten, A.; Tomei, M.; Kumar, R. Hardware acceleration of graph neural networks. 2020 57th ACM/IEEE Design Automation Conference (DAC). IEEE, 2020, pp. 1–6.
Chen, X.; Wang, Y.; Xie, X.; Hu, X.; Basak, A.; Liang, L.; Yan, M.; Deng, L.; Ding, Y.; Du, Z.; others. Rubik: A hierarchical architecture for efficient graph neural network training. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 2021, 41, 936–949. [Google Scholar] [CrossRef]
Li, J.; Louri, A.; Karanth, A.; Bunescu, R. GCNAX: A flexible and energy-efficient accelerator for graph convolutional neural networks. 2021 IEEE International Symposium on High-Performance Computer Architecture (HPCA). IEEE, 2021, pp. 775–788.
Li, J.; Zheng, H.; Wang, K.; Louri, A. SGCNAX: A scalable graph convolutional neural network accelerator with workload balancing. IEEE Transactions on Parallel and Distributed Systems 2021, 33, 2834–2845. [Google Scholar] [CrossRef]
Kiningham, K.; Levis, P.; Ré, C. GRIP: A graph neural network accelerator architecture. IEEE Transactions on Computers 2022, 72, 914–925. [Google Scholar] [CrossRef]
Zhang, B.; Kannan, R.; Prasanna, V. BoostGCN: A framework for optimizing GCN inference on FPGA. 2021 IEEE 29th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM). IEEE, 2021, pp. 29–39.
Zhang, C.; Geng, T.; Guo, A.; Tian, J.; Herbordt, M.; Li, A.; Tao, D. H-gcn: A graph convolutional network accelerator on versal acap architecture. 2022 32nd International Conference on Field-Programmable Logic and Applications (FPL). IEEE, 2022, pp. 200–208.
Romero Hung, J.; Li, C.; Wang, P.; Shao, C.; Guo, J.; Wang, J.; Shi, G. ACE-GCN: A Fast data-driven FPGA accelerator for GCN embedding. ACM Transactions on Reconfigurable Technology and Systems (TRETS) 2021, 14, 1–23. [Google Scholar] [CrossRef]
Geng, T.; Wu, C.; Zhang, Y.; Tan, C.; Xie, C.; You, H.; Herbordt, M.; Lin, Y.; Li, A. I-GCN: A graph convolutional network accelerator with runtime locality enhancement through islandization. MICRO-54: 54th annual IEEE/ACM international symposium on microarchitecture, 2021, pp. 1051–1063.
Lin, Y.C.; Zhang, B.; Prasanna, V. Gcn inference acceleration using high-level synthesis. 2021 IEEE High Performance Extreme Computing Conference (HPEC). IEEE, 2021, pp. 1–6.
Zhang, B.; Zeng, H.; Prasanna, V. Hardware acceleration of large scale gcn inference. 2020 IEEE 31st International Conference on Application-specific Systems, Architectures and Processors (ASAP). IEEE, 2020, pp. 61–68.
Sohrabizadeh, A.; Chi, Y.; Cong, J. SPA-GCN: Efficient and Flexible GCN Accelerator with an Application for Graph Similarity Computation. arXiv preprint 2021, arXiv:2111.05936. [Google Scholar]
Gui, Y.; Wei, B.; Yuan, W.; Jin, X. Hardware Acceleration of Sampling Algorithms in Sample and Aggregate Graph Neural Networks. arXiv preprint 2022, arXiv:2209.02916. [Google Scholar]
Li, S.; Niu, D.; Wang, Y.; Han, W.; Zhang, Z.; Guan, T.; Guan, Y.; Liu, H.; Huang, L.; Du, Z.; others. Hyperscale FPGA-as-a-service architecture for large-scale distributed graph neural network. Proceedings of the 49th Annual International Symposium on Computer Architecture, 2022, pp. 946–961.
Chen, S.; Zheng, D.; Ding, C.; Huan, C.; Ji, Y.; Liu, H. TANGO: re-thinking quantization for graph neural network training on GPUs. Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, 2023, pp. 1–14.
Zhang, B.; Zeng, H.; Prasanna, V. Low-latency mini-batch gnn inference on cpu-fpga heterogeneous platform. 2022 IEEE 29th International Conference on High Performance Computing, Data, and Analytics (HiPC). IEEE, 2022, pp. 11–21.
Lin, Y.C.; Zhang, B.; Prasanna, V. Hp-gnn: Generating high throughput gnn training implementation on cpu-fpga heterogeneous platform. Proceedings of the 2022 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, 2022, pp. 123–133.
Sarkar, R.; Abi-Karam, S.; He, Y.; Sathidevi, L.; Hao, C. FlowGNN: A Dataflow Architecture for Real-Time Workload-Agnostic Graph Neural Network Inference. 2023 IEEE International Symposium on High-Performance Computer Architecture (HPCA). IEEE, 2023, pp. 1099–1112.
Liang, S.; Liu, C.; Wang, Y.; Li, H.; Li, X. Deepburning-gl: an automated framework for generating graph neural network accelerators. Proceedings of the 39th International Conference on Computer-Aided Design, 2020, pp. 1–9.
Chen, H.; Hao, C. Dgnn-booster: A generic fpga accelerator framework for dynamic graph neural network inference. 2023 IEEE 31st Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM). IEEE, 2023, pp. 195–201.
Abi-Karam, S.; Hao, C. Gnnbuilder: An automated framework for generic graph neural network accelerator generation, simulation, and optimization. 2023 33rd International Conference on Field-Programmable Logic and Applications (FPL). IEEE, 2023, pp. 212–218.
Lu, Q.; Jiang, W.; Jiang, M.; Hu, J.; Shi, Y. Hardware/Software Co-Exploration for Graph Neural Architectures on FPGAs. 2022 IEEE Computer Society Annual Symposium on VLSI (ISVLSI). IEEE, 2022, pp. 358–362.
Yan, W.; Tong, W.; Zhi, X. FPGAN: an FPGA accelerator for graph attention networks with software and hardware co-optimization. IEEE Access 2020, 8, 171608–171620. [Google Scholar] [CrossRef]
Wu, C.; Tao, Z.; Wang, K.; He, L. Skeletongcn: a simple yet effective accelerator for gcn training. 2022 32nd International Conference on Field-Programmable Logic and Applications (FPL). IEEE, 2022, pp. 445–451.
He, Z.; Tian, T.; Wu, Q.; Jin, X. FTW-GAT: An FPGA-based accelerator for graph attention networks with ternary weights. IEEE Transactions on Circuits and Systems II: Express Briefs 2023. [Google Scholar] [CrossRef]
Wang, Z.; Que, Z.; Luk, W.; Fan, H. Customizable FPGA-based Accelerator for Binarized Graph Neural Networks. 2022 IEEE International Symposium on Circuits and Systems (ISCAS). IEEE, 2022, pp. 1968–1972.
Ran, S.; Zhao, B.; Dai, X.; Cheng, C.; Zhang, Y. Software-hardware co-design for accelerating large-scale graph convolutional network inference on FPGA. Neurocomputing 2023, 532, 129–140. [Google Scholar] [CrossRef]
Yuan, W.; Tian, T.; Wu, Q.; Jin, X. QEGCN: An FPGA-based accelerator for quantized GCNs with edge-level parallelism. Journal of Systems Architecture 2022, 129, 102596. [Google Scholar] [CrossRef]
Yuan, W.; Tian, T.; Liang, H.; Jin, X. A gather accelerator for GNNs on FPGA platform. 2021 IEEE 27th International Conference on Parallel and Distributed Systems (ICPADS). IEEE, 2021, pp. 74–81.
Tao, Z.; Wu, C.; Liang, Y.; Wang, K.; He, L. LW-GCN: A lightweight FPGA-based graph convolutional network accelerator. ACM Transactions on Reconfigurable Technology and Systems 2022, 16, 1–19. [Google Scholar] [CrossRef]
Zhou, H.; Zhang, B.; Kannan, R.; Prasanna, V.; Busart, C. Model-architecture co-design for high performance temporal gnn inference on fpga. 2022 IEEE International Parallel and Distributed Processing Symposium (IPDPS). IEEE, 2022, pp. 1108–1117.
Hansson, O.; Grailoo, M.; Gustafsson, O.; Nunez-Yanez, J. Deep Quantization of Graph Neural Networks with Run-Time Hardware-Aware Training. International Symposium on Applied Reconfigurable Computing. Springer, 2024, pp. 33–47.

Figure 1. Diagram showing the key areas forming the basis of the survey.

Figure 3. Uniform quantization (left) with equally ranged quantization levels and Non-Uniform quantization (right) with quantization levels based on the data distribution. Here, y denotes the input data and x the quantized value representations.

Figure 4. Illustration of symmetric and signed quantization (left) and asymmetric and unsigned quantization (right).

Figure 5. Vector quantization map, vectors, codewords and Voronoi regions.

Figure 8. Illustration of speedup and energy efficiency comparison for hardware-based accelerators (GPU, ASIC, FPGA). The results of the HyGCN study are used as a baseline (1x). The y-axis is presented as a factor, indicating the degree of improvement achieved by the studies in comparison to HyGCN. In the chart, V100 represents the GPU baseline, AWB represents AWB-GCN and FP represents FP-GNN.The results are used directly as presented in the papers.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Survey of Computationally Efficient Graph Neural Networks for Reconfigurable Systems

Abstract

1. Introduction

2. Background

2.1. Graph Neural Networks

2.2. Graph Convolutional Networks

2.3. Graph Isomorphism Networks

2.4. Graph Attention Networks

2.5. GraphSAGE

3. Graph Neural Network Quantization

3.1. Quantization

3.1.1. Scalar Quantization

3.1.2. Vector Quantization

3.2. Quantization Approaches for GNNs

4. Graph Neural Network Acceleration

4.1. Hardware-Based Accelerator Approaches

4.2. FPGA-Based Accelerators Approaches

4.3. FPGA-Based Heterogeneous Approaches

4.4. Frameworks for FPGA-Based Accelerators

4.5. FPGA-Based Accelerator Approaches with Quantization

4.6. FPGA-Based Accelerators for Embedded Applications

5. Discussion and Future Research Directions

5.1. Quantization and Future Directions

5.2. Hardware Accelerators and Future Directions

6. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe