Prerpints.org logo
Preprint
Article

Quantum Mechanics Characterization of Non-Covalent Interaction in Nucleotides Fragments

Altmetrics

Downloads

113

Views

40

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

04 June 2024

Posted:

06 June 2024

You are already at the latest version

Alerts
Abstract
Accurate calculation of non-covalent interaction energies in nucleotides is crucial for understanding the driving forces governing nucleic acid structures and functions, as well as developing advanced molecular mechanics forcefields or machine learning potentials tailored to nucleic acids. Here, we dissect the nucleotides’ structure into three main constituents: nucleobases (A, G, C, T, and U), sugar moieties (ribose and deoxyribose), and phosphate group. The interactions among these fragments and between fragment and water were analyzed. Different quantum mechanical methods were compared for their accuracy in captuing the interaction energy. The non-covalent interaction energy was decomposed into electrostatics, exchange-repulsion, dispersion, and induction using two ab-initio methods: Symmetry-Adapted Perturbation Theory (SAPT) and Absolutely Localized Molecular Orbitals (ALMO). These caculations provide the benchmark for different QM methods while providing valuable understanding of the roles of various interamolecular forces in hydrogen bonding and aromatic stacking.
Keywords: 
Subject: Chemistry and Materials Science  -   Physical Chemistry

1. Introduction

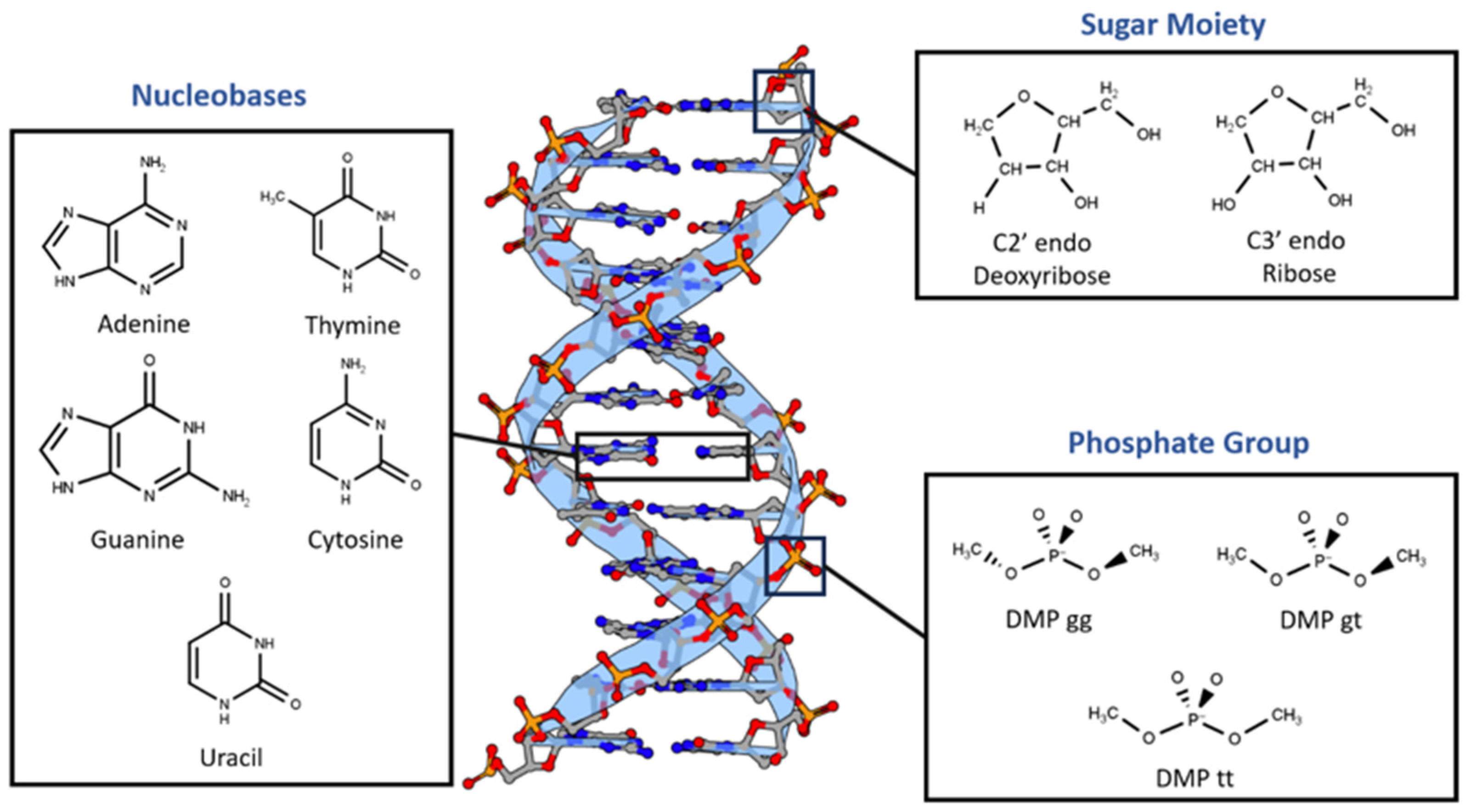
Nucleotides are the main building blocks of nucleic acid, either DNA or RNA. Nucleotides are composed of neutral sugar moiety (deoxyribose in DNA or ribose in RNA), negatively charged phosphate group, and nucleobase. Nucleobases are either purine (Adenine (A) or Guanine (G) or pyrimidine (Cytosine (C), Thymine (T), or Uracil (U)) [1]. Nucleic acids are not only essential for the storage of genetic material, transcription, and translation but also for various cellular processes as ligand binding, enzymatic function, regulation of different metabolic activities, genomic instability, apoptosis, and stress response [2,3,4,5].
The most common configuration of DNA is the B-DNA duplex [6,7]. Transition from B-DNA geometry to A-DNA geometry is observed upon adding solvents or interacting with other proteins or drug molecules [8,9,10]. Z-DNA form was detected in crystal structures and environments with high-salt concentration [11,12,13]. A-form helix is the dominant configuration for RNA as well as hairpins loops and tertiary structures depending on the sequence and the number of strands [14]. Depending on the B-DNA or A-DNA geometry, the sugar moiety adopts either C2’ endo conformation or C3’ endo conformation, respectively [15]. On the other hand, RNAs typically exist in A form. These complex and different configurations of nucleic acids are maintained and stabilized by the non-covalent interactions among the three main components of the nucleotides. Two main types of non-covalent interactions are present in the nucleic acid hydrogen bond and stacking interactions.
Due to the complex nature of DNA and RNA molecules with the dominance of non-covalent interactions, molecular simulations using the current molecular mechanics (MM) forcefields have been challenging. Current nucleic acid forcefields treat the non-covalent interactions as a sum of electrostatics interactions between fixed atomic charges and van-der-Waals interactions accounted for by Lennard-Jones potentials [16]. AMOEBA (atomic multipole optimized energetics for biomolecular applications) employs polarizable atomic multipoles to improve the representation of electrostatics [17,18,19]. Drude NA force fields account for polarization in NAs based on classical Drude oscillators [20,21,22]. These efforts significantly improved our ability to describe many-body polarizations. Nonetheless, challenges remain. For example, in the case of stacked aromatic molecules, any point charge or multipole models are unable to capture electrostatic interactions between the atomic rings [23]. This is attributed to the lack of charge penetration effect needed to account for the π-stacking interactions due to the overlapping of the π-electron clouds and atomic nuclei [24,25,26]. The improvement in the accuracy of atomic potentials and force field parameters depends on the quality of the underlying QM benchmarks used.
Here we applied five different high-quality QM methods to the non-covalent interactions of nucleic acid based on Symmetry-Adapted Perturbation Theory (SAPT) and Absolutely Localized Molecular Orbitals (ALMO): SAPT0 with jun-cc-pVDZ, SAPT2+ with aug-cc-pVDZ, SAPT2+(3)/dmp2 with aug-cc-pVDZ, SAPT2+(3)/dmp2 with aug-cc-pVTZ, and ALMO EDA2 (original energy decomposition) with B97M-V and aug-cc-pVTZ. Nucleotides were divided into three main components based on the difference in the chemical structure and charge (Figure 1). First, the three most probable configurations of the negatively charged dimethyl phosphate: DMP gg, DMP gt, and DMP tt. Second, the neutral C 2’endo deoxyribose sugar moiety, the most common in B-DNA structure, and the neutral C3’endo ribose sugar moiety, the most common structure in the RNA and the A-DNA. The main non-covalent interaction that governs the bonding of the last two moieties is the hydrogen bond. The third component of nucleotides are the nucleobases, which interact with both hydrogen bonds and stacking interactions. The interaction of the three main components of the nucleotides with the water molecule over a wide range of locations and distances was studied to probe the hydrogen bond interaction aspect of the nucleotides. Besides the interaction with the water molecule, the stacked nucleobases (intrastrand) and the hydrogen-bonding nucleobases (interstrand) were examined. ALMO EDA2 was found to be consistent among selected DFT methods and independent of the basis sets used. On the other hand, the three levels of SAPT investigated (SAPT0, SAPT2+, and SAPT2+(3)/dmp2) showed high dependence on the basis set used. Upon studying the interactions of the intrastrand stacked nucleobases, interstrand nucleobases, and the three main fragments with water and nucleobases, the two of the best ab-initio methods for the nucleotides are ALMO EDA2 (B97M-V) with aug-cc-pVTZ basis set with original energy decomposition scheme and SAPT2+(3)/dmp2 with aug-cc-pVTZ. By examining the energy components of the interactions among the various constituents of nucleotides, it was found that exchange-repulsion dominates within the neutral sugar moiety. Electrostatic attraction is also strong, largely offsetting the repulsion. Similar trends were observed for neutral nucleobases’ interaction with water. As expected, electrostatics were more significant in the charged DMP interaction with water molecules. In all these cases, there is a large cancellation between the electrostatic attraction and exchange-repulsion, and as a result the attractive induction and dispersion are responsible for stabilizing the molecular complexes with water, highlighting the significance of explicit consideration of induction effect. For interstrand or intrastrand nucleobase dimers, however, dispersion was found to be the most important while electrostatics is slightly attractive, and induction is insignificant.

2. Results

2.1. Benchmarking of Small Molecules

2.1.1. Various Theoretical Methods

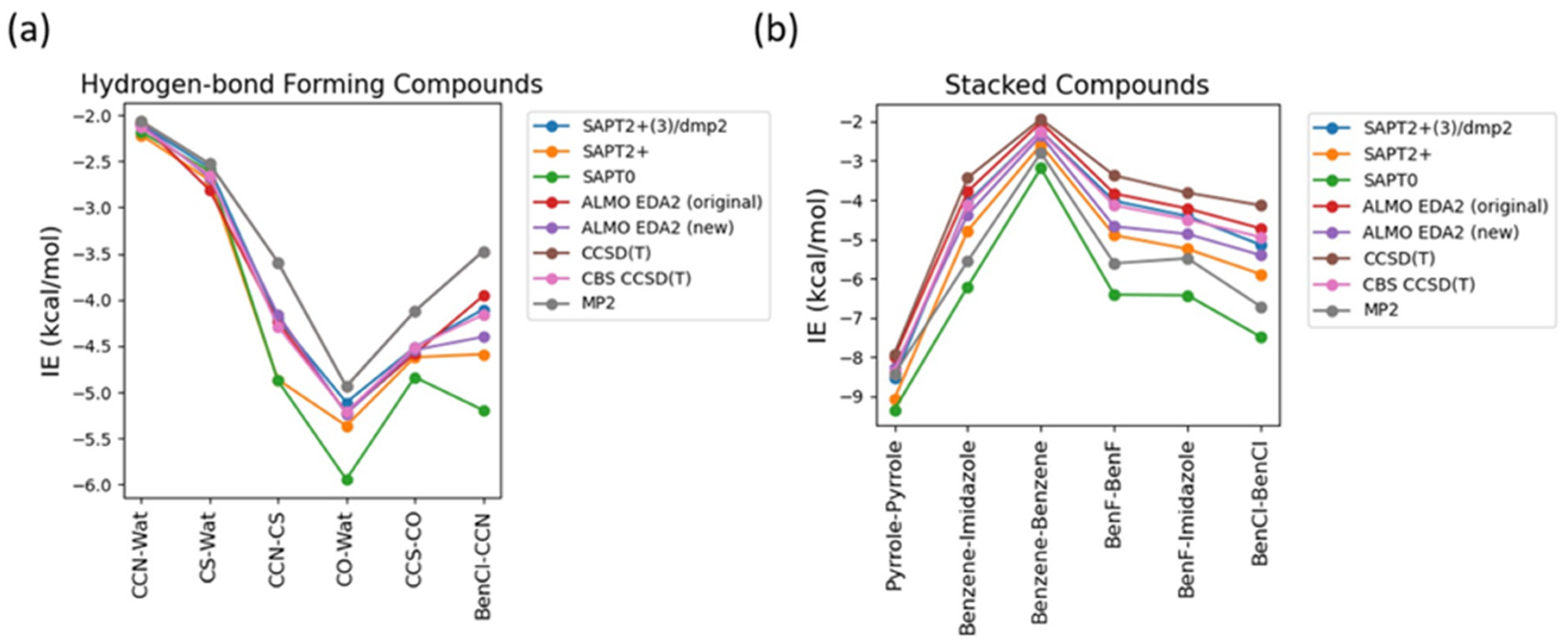
Nucleotides mainly compromise two types of interactions: stacking interactions between the nucleobases and hydrogen bond interactions involving nucleobases, sugar moiety, phosphate group and water solvent. To determine the best theoretical method to study the interaction energies in such a complex system, benchmarking was done on 6 hydrogen-bond forming compounds, Ethylamine-water (CCN-Wat), Methanethiol-Water (CS-Wat), Ethylamine-Methanethiol (CCN-CS), Methanol-Water (CO-Wat), Methanol-Ethanethiol (CCS-CO), and Chlorobenzene-Ethylamine (BenCl-CCN), and 6 stacked molecular dimers, Pyrrole-Pyrrole, Benzene-Imidazole, Benzene-Benzene, Fluorobenzene-Fluorobenzene, Fluorobenzene-Imidazole, Chlorobenzene-Chlorobenzene. For these dimers, interactions energy at the MP2 (Møller−Plesset perturbation), CCSD(T) Coupled Cluster Theory through perturbative triples and Complete Basis Set CBS CCSD(T) were previously reported in the DE Shaw database [27]. Here we compared these methods with 1) DFT based Absolutely Localized Molecular Orbitals Energy Decomposition Analysis, ALMO EDA2, with the original and the new energy decomposition schemes [28,29,30,31] and 2) different level of theory of Symmetry-Adapted Perturbation Theory (SAPT): SAPT0, SAPT2+, and SAPT2+(3)/dmp2 [32,33,34]. The aug-cc-pVTZ basis set was used for both ALMO and SAPT calculations. These methods also offer value interaction energy components that allows us better understanding the driving force for intra- and intermolecular complexes and developing accurate atomic potentials for molecular simulations. The most accurate method here, CBS CCSD(T), is used as the benchmark. The interaction energies of the hydrogen-bond forming compounds from the different methods were comparably similar with most deviation observed in SAPT0 and MP2 methods (Figure 2a). MP2 method was found to underestimate the interaction energies compared to CBS CCSD(T), with most difference of 0.7 kcal/mol observed in the interaction energy of CCN-CS dimer. SAPT0 overestimated the interaction energies with the biggest deviation from CBS CCSD(T), -1.0 kcal/mol, in BenCl-CCN. SAPT2+ performed well for most of the hydrogen-bond forming dimers except for CCN-CS, where the difference from CBS CCSD(T) was -0.57 kcal/mol. In summary, all the tested methods showed relatively small deviation compared to CBS CCSD(T). The best performance was given by SAPT2+(3)/dmp2 and ALMO EDA2 with both old and new energy decomposition scheme – the maximum deviation from CBS CCSD(T) is 0.1 kcal/mol (Figure 2a).
The interaction energies obtained from the various theoretical methods were found to vary much more significantly for the stacked complexes (Figure 2b) compared to the hydrogen-bond forming complexes. CCSD(T), MP2, SAPT0, and SAPT2+ overestimated the interaction energies compared to CBS CCSD(T) with most deviation observed for SAPT0. The interaction energy of BenCl-BenCl dimer obtained from the various methods was found to be associated with the maximum difference compared to CBS CCSD(T) interaction energies. For example, SAPT0 interaction energy deviated from the CBS CCSD(T) value by 2.54 kcal/mol and for MP2 method the deviation was 1.77 kcal/mol. BenF-BenF and BenF-Imidazole interaction energies also showed large variations among different methods. This showcases the limitation of these methods with the halogen substituted aromatic systems in general. The best theoretical method with the least deviation from CBS CCSD(T) for the stacked molecules was found to be SAPT2+(3)/dmp2, with maximum of 0.2 kcal/mol observed in BenCl-BenCl, followed by ALMO EDA2 with the original energy decomposition with maximum deviation of 0.36 kcal/mol observed in BenCl-BenCl, and then ALMO EDA2 with the new energy decomposition with maximum difference of 0.54 kcal/mol observed in BenF-BenF (Figure 2b).

2.1.2. Comparison of DFT Methods

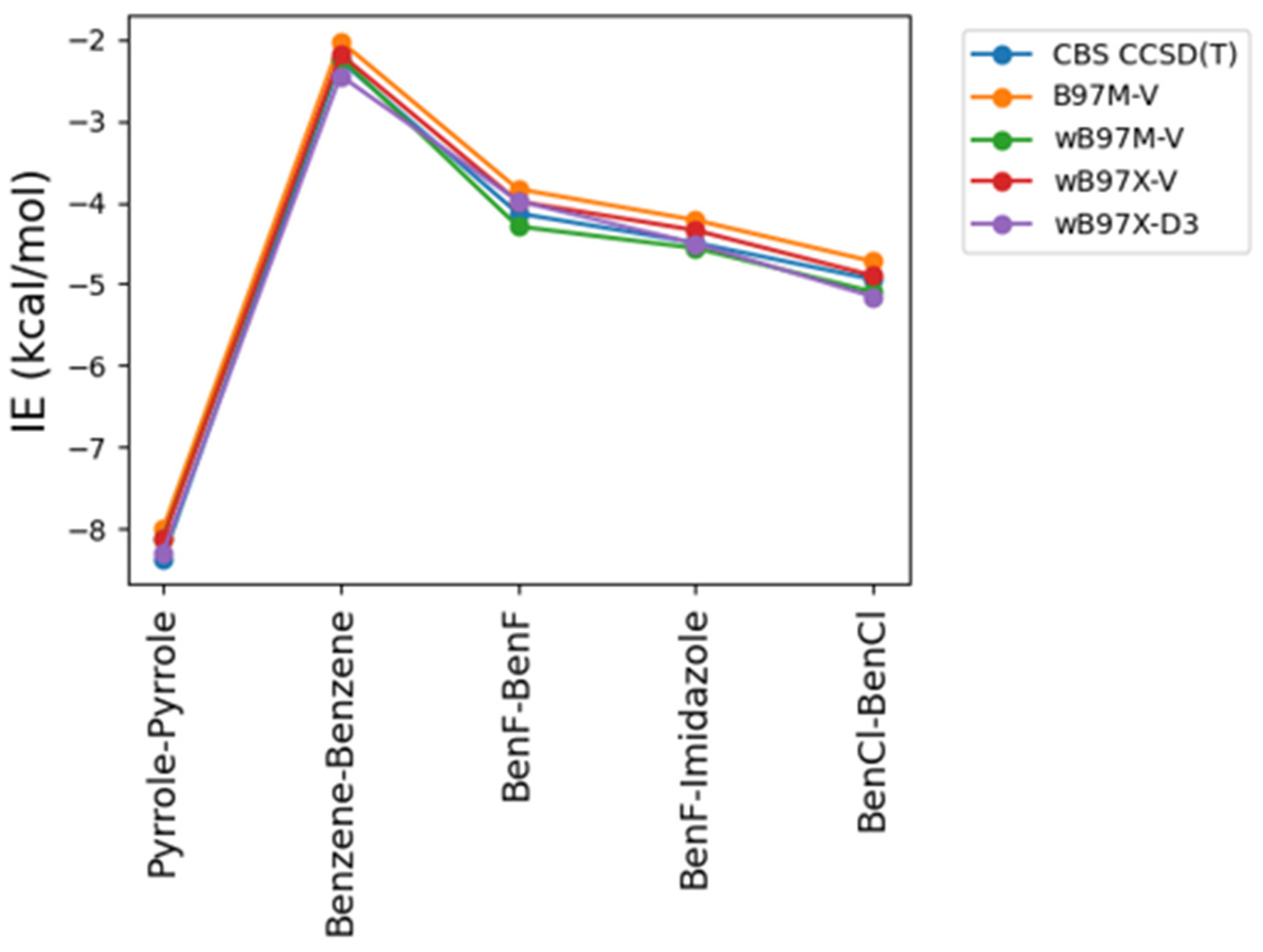
As some of the tested theoretical methods were inconsistent in the case of the stacked complexes compared to the hydrogen-bond forming complexes, further analysis was performed on the stacked compounds using different DFT levels of theory. Four different DFT methods B97M-V, ωB97M-V, ωB97X-V, and ωB97X-D3 were tested and contrasted with CBS CCSD(T) and DLPNO/CCSD(T) an approximate CBS CCSD(T) method. This additional comparison is also performed due to the superior performance of both the original and the new energy decomposition schemes of ALMO EDA2, based on DFT calculation, for the hydrogen-bonding and stacked complexes. The interaction energies obtained from the four tested DFT level of theory were found to be very similar to each other and to CBS CCSD(T) interaction energies for the stacked molecule (Figure 3). B97M-V showed the most deviation from the CBS CCSD(T) method, and yet the maximum error (pyrrole-pyrrole) is only 0.36 kcal/mol. Interestingly, pyrrole-pyrrole was the dimer showing the largest variation among the different DFT methods, except for ωB97X-D3 where the largest error was associated with BenCl-BenCl molecule. ωB97X-D3 method was found to be the most consistent with CBS CCSD(T) with maximum difference of 0.21 kcal/mol among the test sets. Overall, the results indicate that all these DFT methods tested here produce satisfying interaction energies that closely match the CBS CCSD(T) results (Figure 3).

2.1.3. Basis Set Dependence

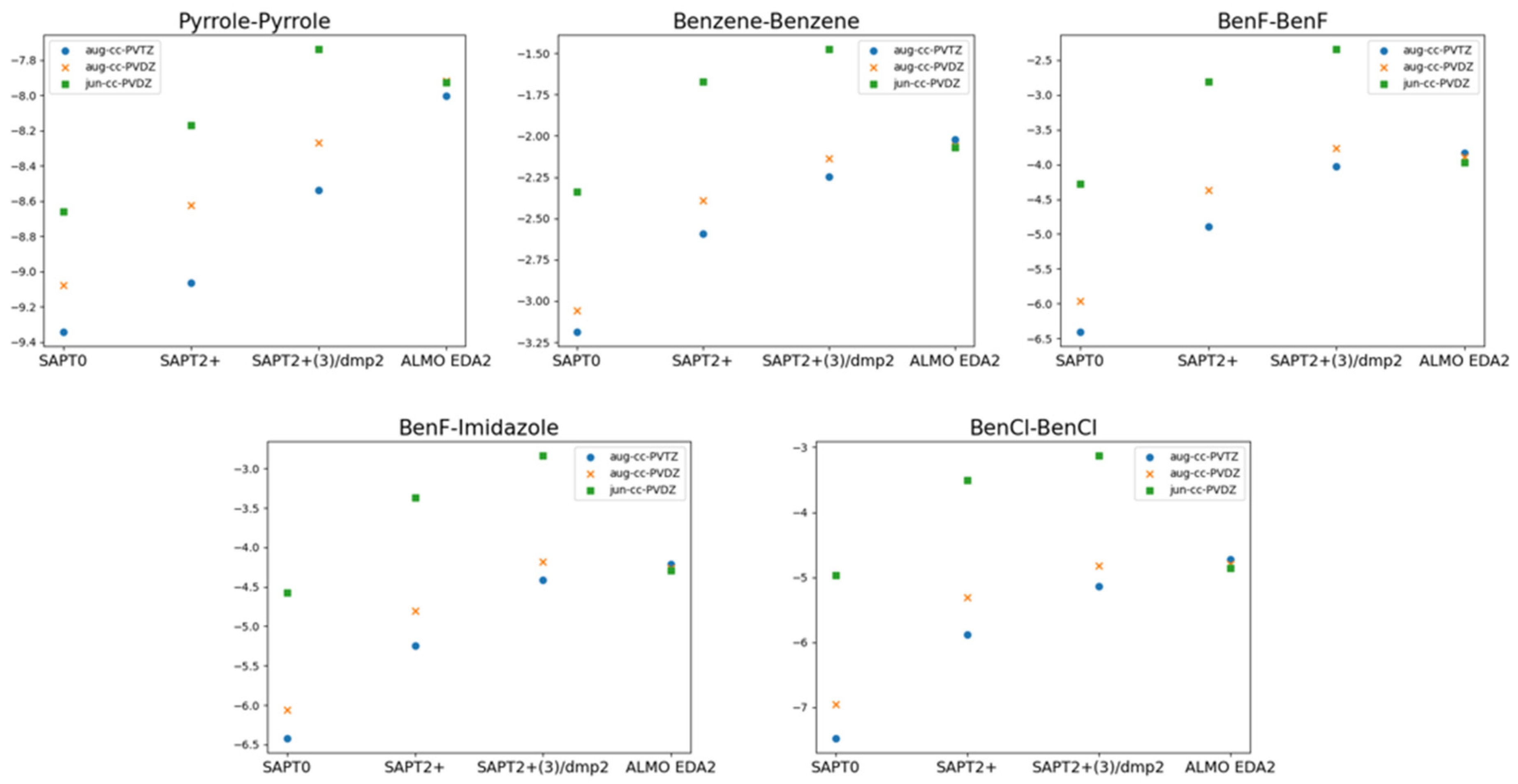
The superior performance of ALMO EDA2 (B97M-V) with original energy decomposition scheme and SAPT2+(3)/dmp2 methods for both stacked and hydrogen-bond forming compounds was based on using aug-cc-pVTZ basis set. Benchmarking of the basis set dependence of both ALMO and SAPT methods is also crucial. Three different basis sets of aug-cc-PVTZ, aug-cc-PVDZ, and jun-cc-PVDZ were used for the five stacked molecules using different levels of theory: SAPT0, SAPT2+, SAPT2+(3)/dmp2, and ALMO EDA2 (Figure 4).
ALMO EDA2 was found to be independent of the basis set used, where the maximum difference in the interaction values for all 5 stacked molecules obtained from different basis sets is around 0.1 kcal/mol. This reflects the robustness of the DFT methods such as B97M-V.
The situation with SAPT is complicated. Using the larger basis sets aug-cc-pVTZ and aug-cc-pVDZ with SAPT0 resulted in overestimation of the interaction energy by 3.0 kcal/mol on average, especially for halogen substituted benzene molecules, compared to SAPT0 with the smallest basis set jun-cc-pVDZ. Surprisingly, SAPT0 with jun-cc-pVDZ resulted in interaction energies that are more consistent with those obtained from ALMO EDA2. In higher levels of SAPT, SAPT2+ and SAPT2+(3)/dmp2, using jun-cc-pVDZ resulted in underestimation of the interaction energy for all the stacked molecules, by ~2.0 kcal/mol for the 5 stacked dimers. The interaction energies from using aug-cc-pVDZ with SAPT2+ were closer to those obtained from ALMO compared to using aug-cc-pVTZ basis set. The maximum difference of using the two basis sets is around 0.58 kcal/mol, observed in BenCl-BenCl molecule. The performance of SAPT2+(3)/dmp2 with aug-cc-pVDZ was slightly better, compared to ALMO energies, than with aug-cc-pVTZ. The difference between the two basis sets aug-cc-pVTZ and aug-cc-pVDZ in the highest level of theory SAPT2+(3)/dmp2 was found to be less compared to SAPT2+.

2.2. Total Interaction Energies of The Main Three Constituents of Nucleotides

Based on the benchmarking so far, we applied the following five protocols to examine the interaction energies of nucleotide fragments: ALMO EDA2 (B97M-V, original scheme), SAPT0 with jun-cc-pVDZ, SAPT2+ with aug-cc-pVDZ, and SAPT2+(3)/dmp2 with either aug-cc-pVTZ or aug-cc-pVDZ.

2.2.1. Sugar Moiety

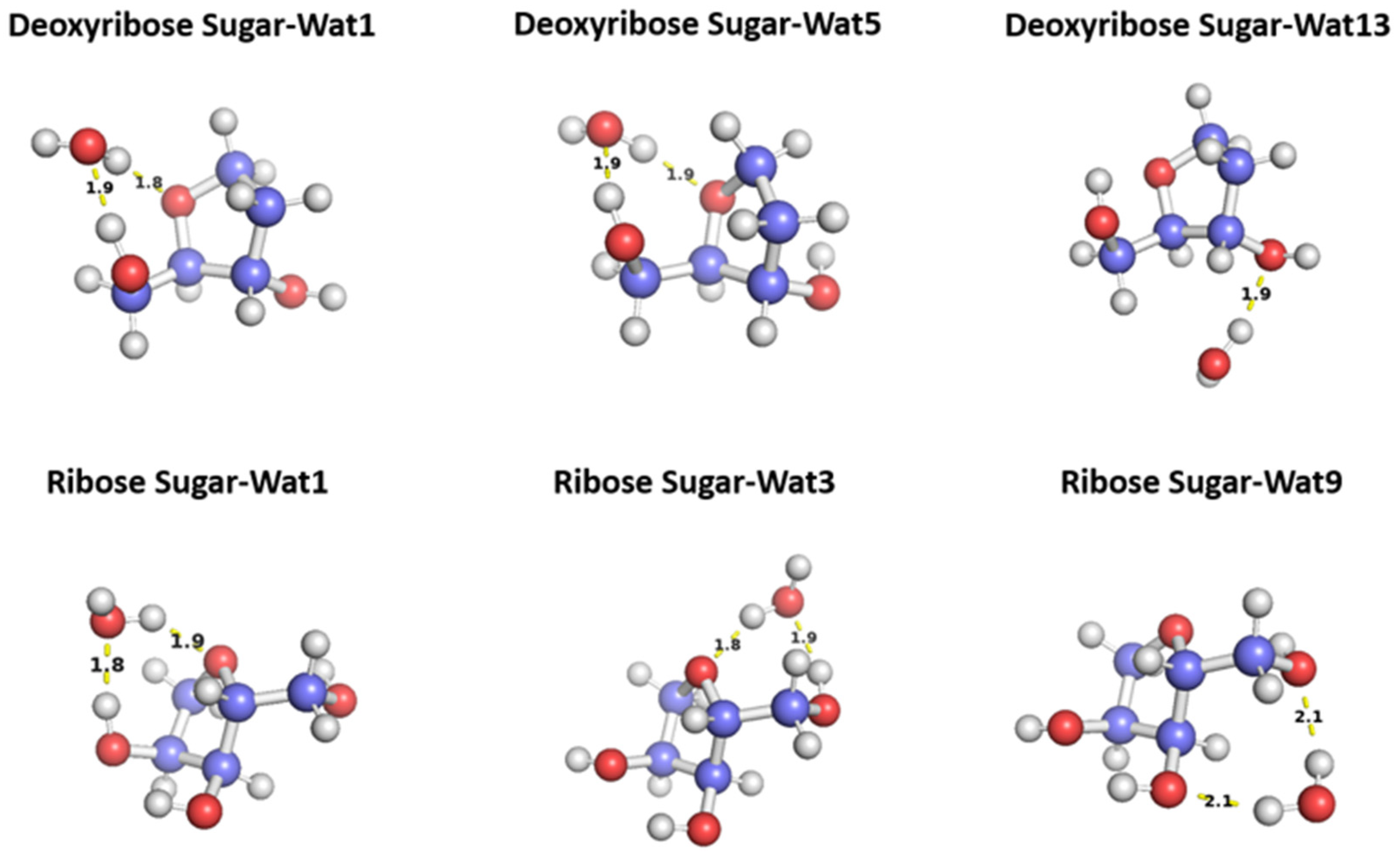
To probe the hydrogen binding interaction around the sugar moiety, three different configurations of a water molecule interacting with C2 ‘endo deoxyribose was selected based on the optimal docking scores obtained from aISS workflow [35] and on the uniqueness of the water position (Figure 5). In Wat1 and Wat5 configurations, the water molecules form hydrogen bond with the oxygen moiety of the 5-membered ring sugar moiety and with the terminal hydroxyl group. Both configurations interact with different angles with the sugar moiety but with the similar distances 1.8 or 1.9 Å. Wat13 configuration forms a single hydrogen bond with the hydroxyl group attached to C3’ at 1.9 Å. Similarly, three different configurations of the water molecule interacting with C3’ endo ribose sugar moiety were selected (Figure 5). Wat 1 configuration forms hydrogen bond with the oxygen of the 5-membered ring and the hydroxyl group attached to the C3’, Wat 3 configuration forms hydrogen bond with the oxygen in the ring and the terminal hydroxyl group, and Wat 9 configuration forms hydrogen bond with the terminal hydroxyl group and the hydroxyl group attached to C2’. To probe the interaction energy surface, the water probe was moved away from the minimum energy distance along the vector connecting the two molecular centers of mass. For each distance, the single point interaction energy of sugar-water was calculated.
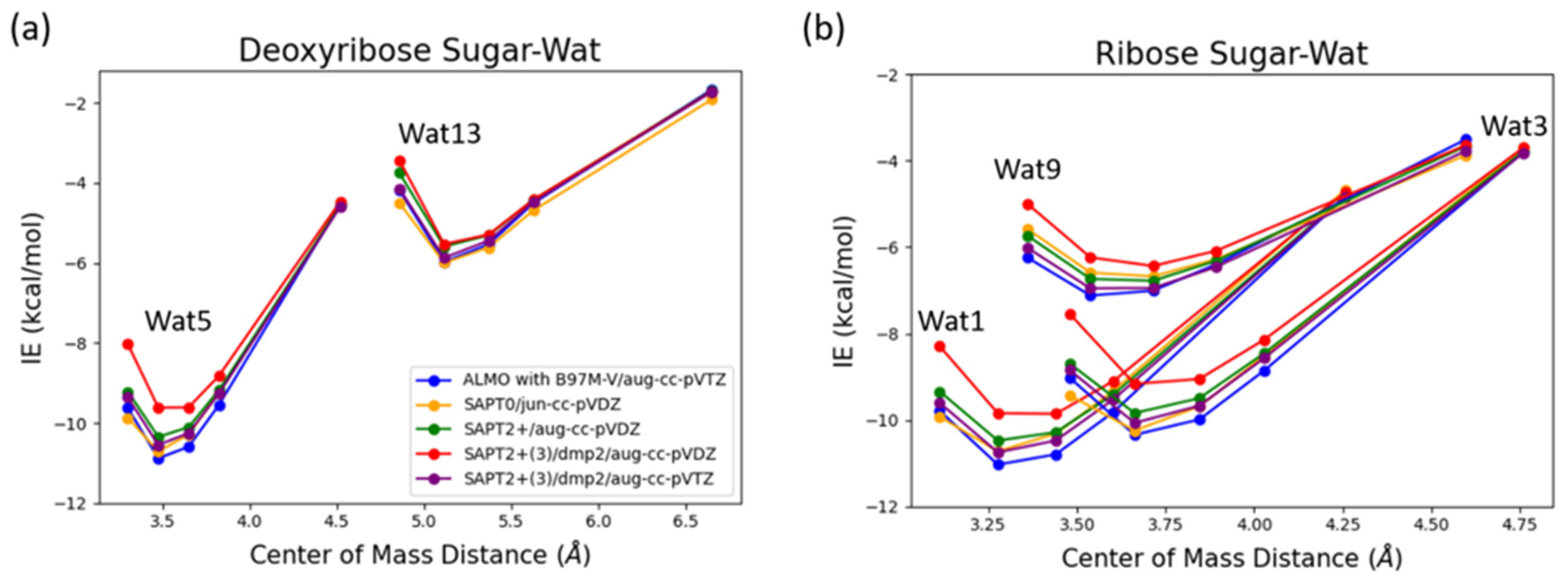
Deoxyribose Wat1 and Wat5 configurations were found to have lower energy compared to Wat13 configuration due to the additional hydrogen bond formed. Wat5 configuration has slightly lower energy than Wat1 configuration by about 0.6 kcal/mol. For clarify, only Wat 1 and Wat13 energy profiles are shown in Figure 6a.
Ribose Wat1 configuration was associated with the lowest energy followed by Wat3 configuration then Wat9 configuration. This indicates that forming hydrogen bond with the oxygen of the ring is crucial to have the lowest energy configurations. SAPT2+(3)/dmp2 with aug-cc-pVDZ resulted in the most inconsistent interaction energies compared to the other methods with an average difference of 1.2 kcal/mol at the equilibrium distance for all three configurations. This suggests that SAPT2+(3)/dmp2 with aug-cc-pVDZ should not be recommended for QM benchmark for the nucleic acid, even though the stacking calculations above indicated this protocol was “reasonable.” Similar to deoxyribose-water interaction curve, SAPT0 with jun-cc-pVDZ, SAPT2+(3)/dmp2 with aug-cc-pVTZ, and ALMO EDA2 generation were found to be very consistent in the predicted interaction energies, except in Wat9 configuration (Figure 6b). The stabilization energy is about –6 or -7 kcal/mol for a single hydrogen-bond and about –11 kcal/mol for double hydrogen-bonds. The only exception was observed in Wat9 configuration, SAPT2+ with aug-cc-pVDZ was found to be more consistent with the other protocols compared to SAPT0, with average difference of 0.2 kcal/mol between the two protocols for the different distances.
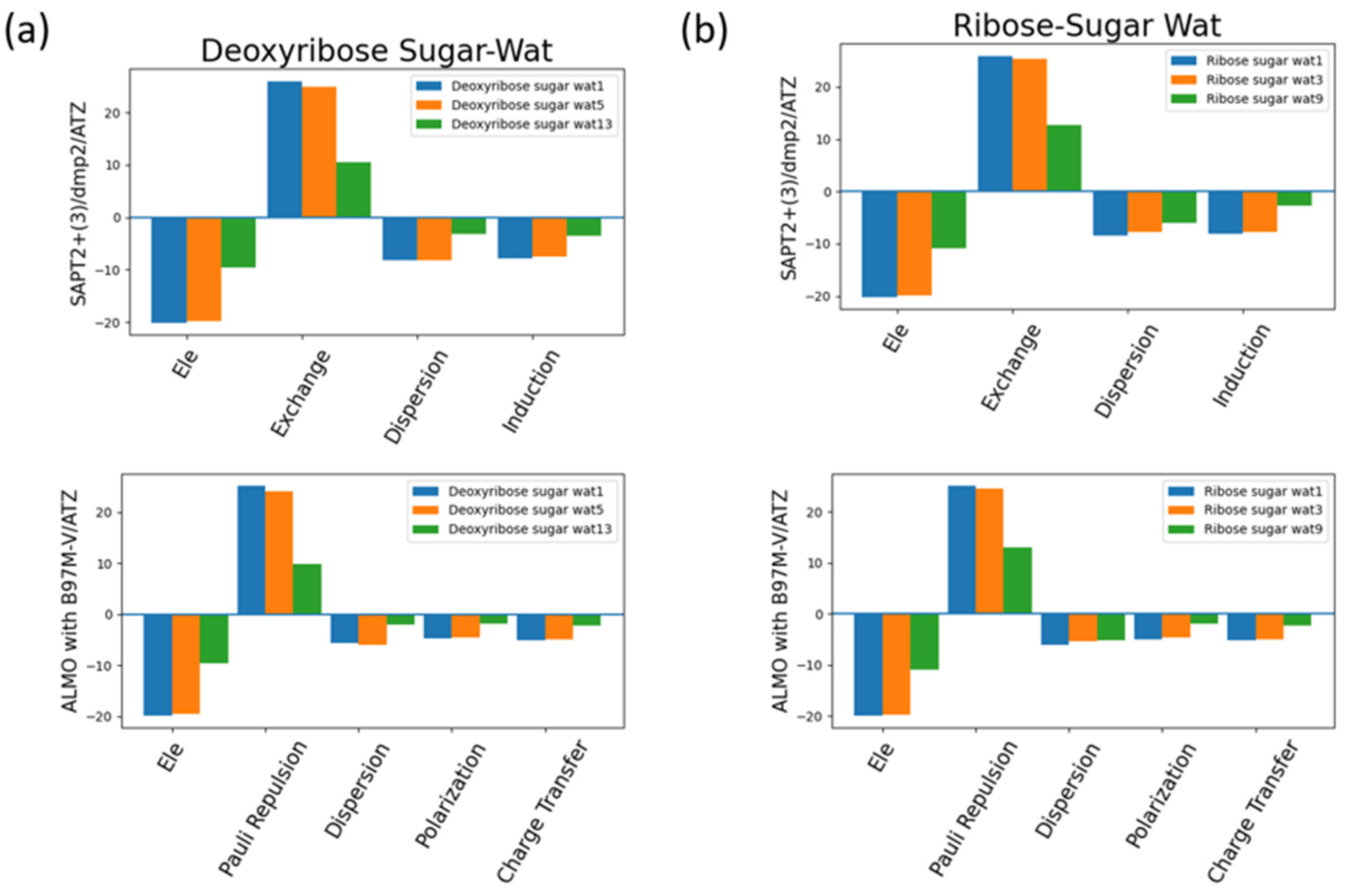
The interaction energy components were obtained from SAPT2+(3)/dmp2 and ALMO EDA2 (original scheme) B97M-V aug-cc-pVTZ (ATZ) for the equilibrium structures of deoxyribose and ribose sugar moieties with the water probe (Figure 7). Overall, the EDA results from SAPT and ALMO are quite consistent with each other. The exchange repulsion is the most dominant positive component. Typically, the repulsion is ~25 kcal/mol for double h-bond complexes, ~10 kcal/mol for a single h-bond complex. The electrostatic, dispersion and induction (polarization + charge transfer in ALMO) make the attractive contributions. The electrostatic is clearly the major stabilizing force, contributing ~-20 kcal/mol in double h-bond complexes, and ~ -9 kcal/mol in single h-bond complexes. The separation among dispersion and induction is slightly different between SAPT and ALMO. In SAPT, the dispersion is about –7 and –3 kcal/mol for double and single h-bond complexes, respectively. In ALMO, the dispersion is about 1-2 kcal/mol less negative than that of SAPT. Nonetheless the sum of polarization and charge transfer in ALMO is slightly more negative that the induction in SAPT but a similar amount. Thus, the total interaction energies are still consistent. Both EDA methods show that induction is significant, amounting to ~30-40% of the electrostatic energy. This again highlights the importance of explicit consideration of electronic polarization in classical force fields.

2.2.2. DMP

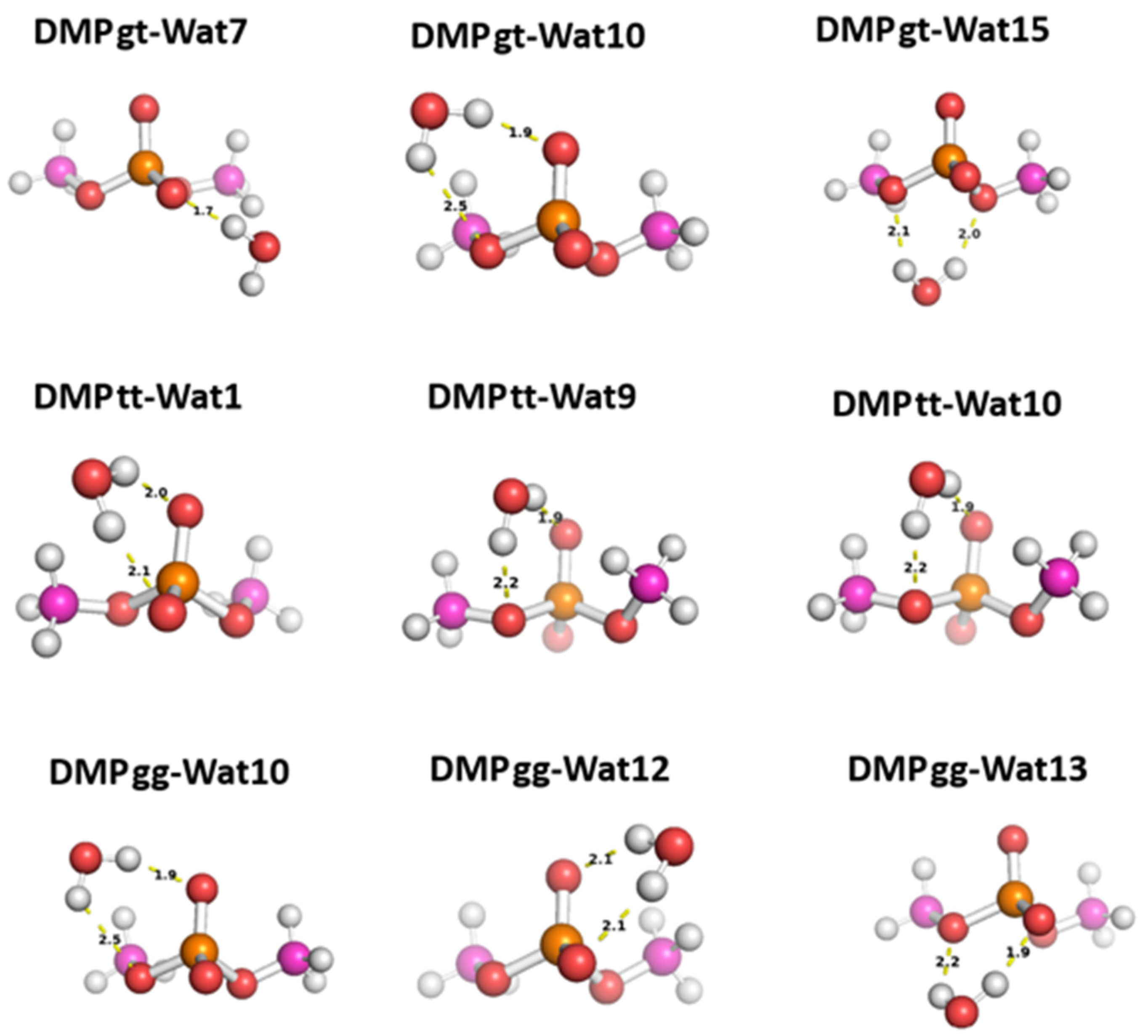
Three different positions for the water molecules surrounding the low energy configurations of DMP [17]were selected to probe the hey functional groups of DMP molecule. In Wat1 DMP tt configuration, the water molecule forms two hydrogen bonds with the phosphate group, While in Wat 9 and Wat10 configurations the water molecule forms a single hydrogen bond with different oxygen atoms of the phosphate group and with the oxygen of the -OCH3 groups attached to the phosphate group (Figure8). For DMP gt configuration, Wat7 forms a single hydrogen bond with the oxygen atom of the phosphate group, Wat10 configuration forms a hydrogen bond with the phosphate group and with the oxygen of the -OCH3 group, and Wat15 configuration forms two hydrogen bonds with the oxygens of the two -OCH3 groups attached to the phosphate group (Figure 8). In Wat10 of DMP gg configuration, water molecule forms hydrogen bond with the phosphate group and with the oxygen of -OCH3 group attached to it, Wat 12 and Wat13 configurations form two hydrogen bonds with the phosphate group (Figure 8).
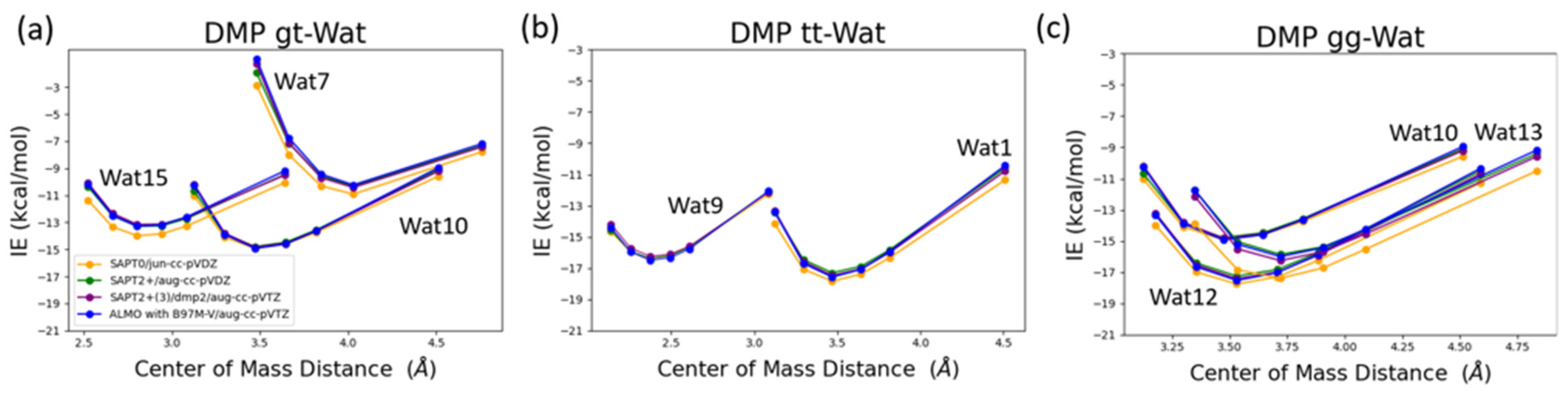
The interaction energy of DMP tt-Wat1 configuration was found the most favorable among the three configurations of DMP tt-water, followed by Wat9 and Wat10 configurations that have similar interaction energy (Figure 9). For clarity, Wat10 profiles are not shown here since it largely overlaps with those of Wat9. The two hydrogen bonds involving the two charged oxygen atoms in the phosphate group in Wat1 configuration resulted in higher interaction energy of ~-2 kcal/mol near the equilibrium distances compared to those where a hydrogen bond is with the sp3 oxygen of the phosphate group. Wat10 and Wat 15 in DMP gt configuration followed a similar trend except that the interaction energy is slightly less favorable than those in the DMP tt conformation. DMP gt-Wat7 has only one hydrogen bond and the interaction energy is much weaker as expected. Water interaction energies with the DMP gg conformer are in general similar to those observed for DMP gt conformation (Figure 9). The results suggest that interaction of DMP with water has a nonnegligible conformational dependence, with the tt conformation being preferred.
Again, the different QM methods resulted in consistent interaction energies except SAPT0 with jun-cc-pVDZ basis set (Figure 9). Therefore, SAPT0 with jun-cc-pVDZ is not recommended as a general method for evaluating nonvalent interactions.
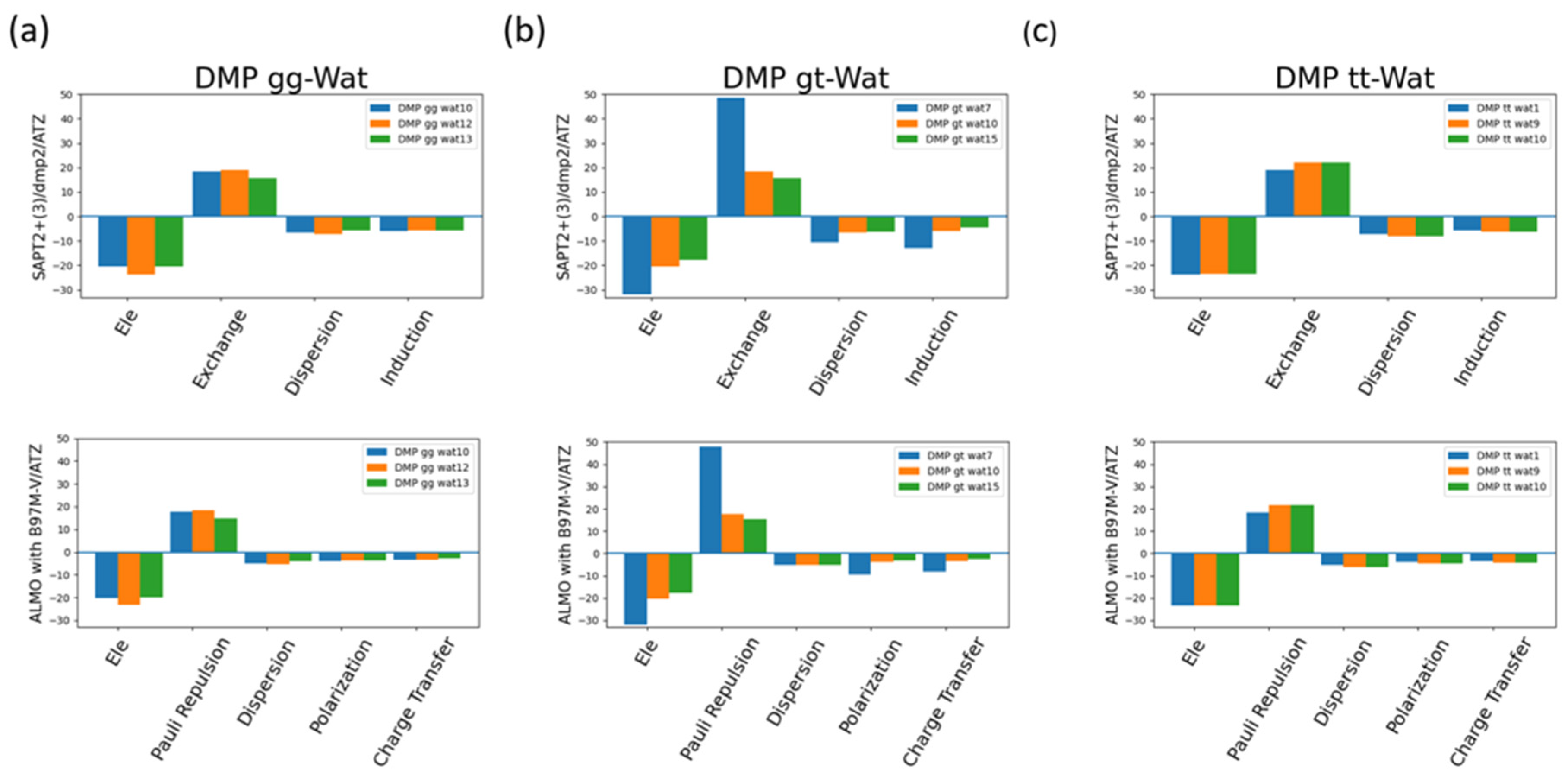
The EDA of the interaction of the negatively charged DMP gg with water molecule at the equilibrium distance showed that the attractive electrostatics is counterbalanced with the positive exchange-repulsion, similar to what was observed for sugar-water (Figure 10a). The main difference here is electrostatic is A similar pattern was observed in ALMO energy decomposition where the dominant electrostatics component, with an average contribution of -22 kcal/mol for all three configurations, was counterbalanced with the Pauli repulsion, with average of 17 kcal/mol for the three configurations, (Figure 10a). Electrostatics components were found to be dominant in both DMP gt-Wat and DMP tt-Wat configurations with an average contribution of -23.5 kcal/mol and -23.7 kcal/mol for SAPT2+(3)/dmp2 and with average of -23.3 kcal/mol for both in ALMO energy decomposition, respectively (Figure 10b, 10c). DMP gt 7 was the only exception where the exchange component had the largest contribution to the total energy with 48.5 kcal/mol followed by the electrostatics component with a contribution of -32.1 kcal/mol (Figure 10b). Also, the contribution of the induction and dispersion in DMP gt-Wat7 in SAPT2+(3)/dmp2 scheme was found to be double of that of the remaining configurations. This was similar to what observed in the ALMO energy decomposition where polarization and charge transfer was also twice as high as in the remaining configurations (Figure 10b). This high contribution of the polarization and energy transfer may be contributed to the small distance of 1.7Å between the water molecule and the oxygen molecule of the phosphate group of the DMP gt molecule compared to 1.9Å in DMP gt-Wat10 (Figure 8). Besides DMP gt-Wat7 configuration, the contribution of the induction and dispersion components in the SAPT2+(3)/dmp2 decomposition were found to be less compared to the electrostatics and exchange. This was also observed in the ALMO energy decomposition, the dispersion, polarization, and charge transfer were found to be contributing less than the electrostatics and the Pauli repulsion for all DMP configurations (Figure 10).

2.2.3. Nucleobases

2.2.3.1. Nucleobase-Water

aISS workflow [35]was used to generate 15 different conformations of purine (A and G) and pyrimidine (U, T, and C) nucleobases interacting with water probes at different positions. 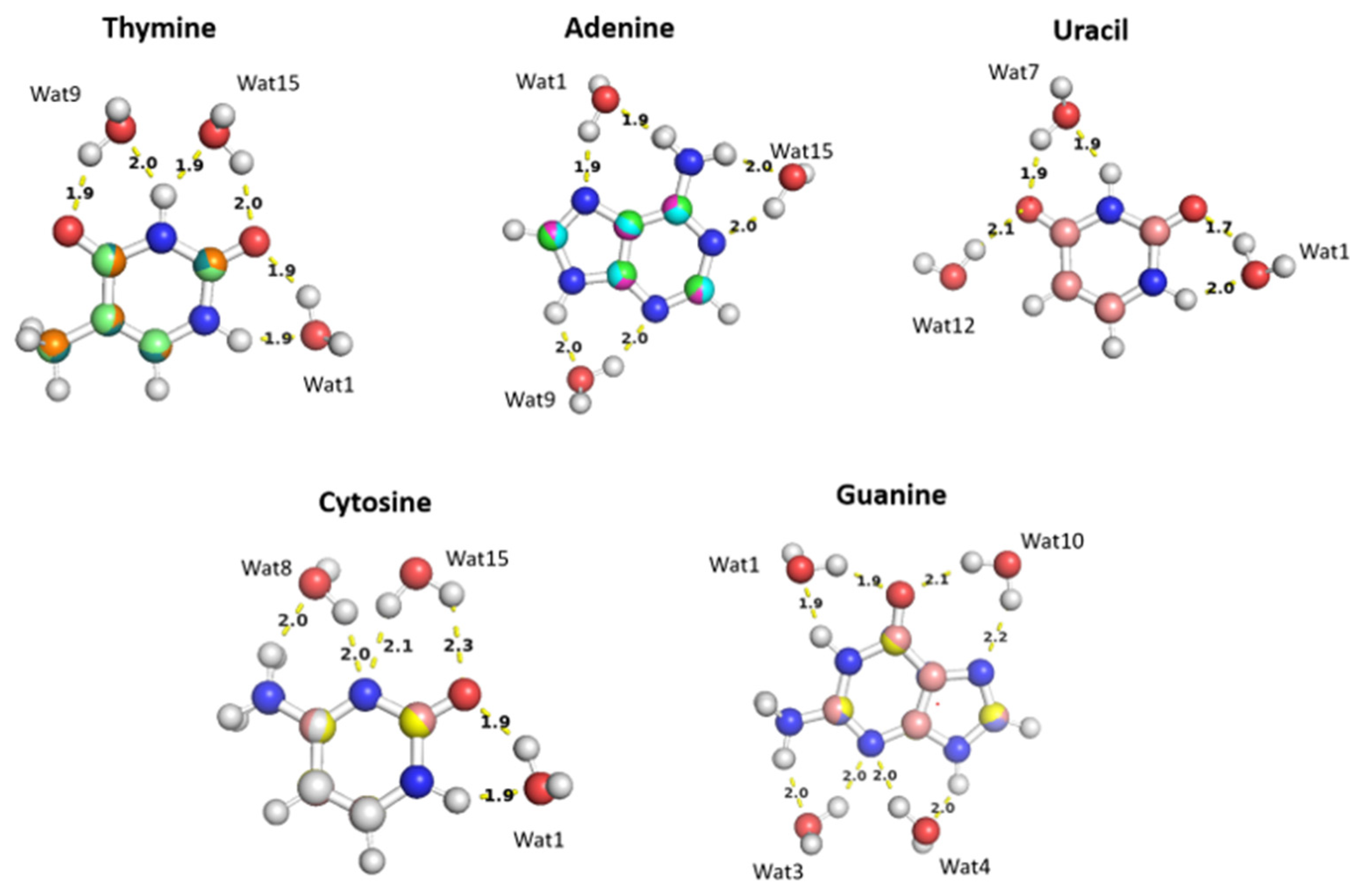Three different positions of the water molecule probe around A, U, T, and C nucleobases and four positions around G nucleobase were selected to cover the interactions of the water molecule with all the corresponding polarizable groups of the nucleobases (Figure 11). Optimization of the selected nucleobase-water structures was performed using MP2/6-31G* basis to obtain the equilibrium distances of the interaction of the nucleobases with the water probe at various positions.
The water molecules interacting with the Thymine nucleobase form two hydrogen ; one with the hydrogen atom of amine group and the other with the oxygen of the carbonyl group at different positions and at various distances. T-Wat1 interacts with N1 (1.9 Å) and oxygen at C2 (1.9 Å), T-Wat9 interacts with N3 (2.0 Å) and oxygen at C4 (1.9 Å), and T-Wat15 interacts with N3 (1.9 Å) and the oxygen atom at C2 (2.0 Å). Adenine-Wat1 (A-Wat1) interacts with the terminal NH2 group at 1.9Å and N7 of the purine ring, A-Wat9 interacts with N3 and N9 at equal distance of 2.0 Å, and A-Wat15 interacts with N1 of the purine ring at 2.0 Å and with the terminal NH2 group. Uracil-Wat1 and Uracil-Wat7 show similar interaction patterns, where U-Wat1 interacts with N1 and with the carbonyl group at C2 at 1.9Å and 1.7Å, respectively. U-Wat7 interacts with N3 and the carbonyl of C4 at 1.9Å each. On the other hand, U-Wat12 forms a single hydrogen bond with the carbonyl group of C4. All the water molecules interact with the Cytosine nucleobase share the same interaction pattern of forming two hydrogen bonds with the hydrogen of NH2 and the oxygen of the carbonyl group at different positions. Cytosine-Wat1 interacts with N1 and the oxygen atom at of the carbonyl group at C2, C-Wat9 interacts with N3 and the oxygen of the carbonyl group at C4, and C-Wat15 interacts with N3 and the oxygen atom of the carbonyl group at C2. Four water probes were needed to cover all the polarizable groups of the Guanine nucleobase. G-Wat1 and G-Wat10 interact in a similar manner to each other and to the other water probes interacting with the other nucleobases. Both Wat1 (hydrogen atom of N1 and oxygen atom at carbonyl group of C6) and Wat10 (N7 oxygen atom at carbonyl group of C6) interact with an amine group and with the oxygen atom of the carbonyl group. G-Wat3 and G-Wat4 interact with amine groups. Wat3 and Wat4 interact with equal distances of 2Å with N3 and NH2 attached at C2 and with N3 and N9, respectively (Figure11).
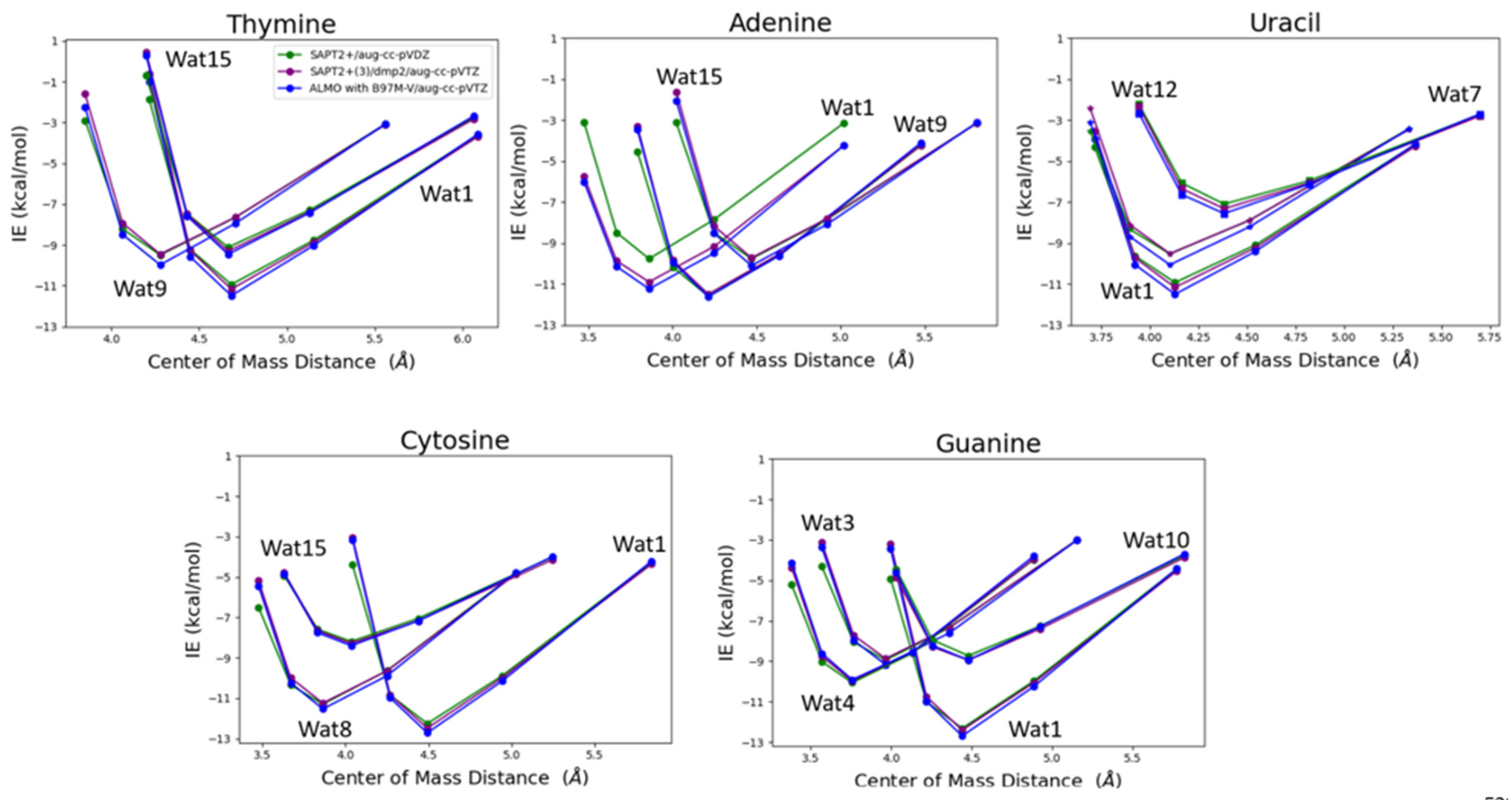
The water probe interacting with the nucleobases at different positions was transitioned at 0.90, 0.95, 1.0, 1.1, and 1.3 percent of the equilibrium distance between the center of mass of the two molecules, water and nucleobase, obtained from the optimized structures to get an interaction energy curve of the nucleobases with the water probes. T-Wat1 was found to have the lowest energy among the three conformations of T-Wat interacting complexes (Figure 12). This may be attributed to the shorter distance of the two hydrogen bonds formed by Wat1 probe at 1.9Å of compared to the other two Wat probes at 1.9Å and 2.0Å (Figure 11). A-Wat9 was found to have the lowest energy conformation followed by A-Wat1. A-Wat15 was found to have the highest energy among the three conformations. This is attributed to the difference in the hydrogen bonding pattern of the different water probes. Wat12 interacting with Uracil nucleobase was found to be the least energetically stable as it forms a single hydrogen bond compared to Wat1 and Wat7 that form two hydrogen bonds (Figure 11). Wat1 probe has lower interaction energy with Uracil compared to Wat7 probe due to the shorter distances of the hydrogen bonds formed. C-Wat15 had the lowest interaction energies due to the large distances of the two formed hydrogen bonds at 2.1Å and 2.3Å compared to C-Wat1 (1.9Å) and C-Wat8 (2.0Å) interaction energies. G-Wat1 was found to have the lowest energy among the four G-Wat conformations due to the short hydrogen bond formed unlike Wat10 probe that was found to have the lowest interaction energy despite having nearly similar interaction of Wat1 probe. G-Wat3 and G-Wat4 complexes were found to have higher energy compared to G-Wat1 (Figure 12). This indicates that the interaction with the oxygen of the carbonyl group at short distance resulted in stronger interaction. Wat4, forms two bonds with the amine of the Guanine ring, was found to have higher interaction energy than Wat3 probe, one amine in the ring and one terminal amine, due to the resonance effect found in the purine ring.
SAPT2+(3)/dmp2 with aug-cc-pVTZ and ALMO EDA2 generation with B97M-V were found to be in good agreement with each other for studying the interaction energy of the water probe with the different nucleobases (Figure 12). A maximum difference of -1.2 kcal/mol between ALMO EDA2 generation and SAPT2+ with aug-cc-pVDZ was observed at the smallest interacting distance of Wat 15 probe with Adenine (A-Wat15), where RMSE was found to be 0.52. This reflects that SAPT2+ with aug-cc-pVDZ falls behind when the interacting molecules are so close to each other. That is why this protocol was dropped as a possible QM benchmark to study the interaction energy of the different components of nucleic acid.
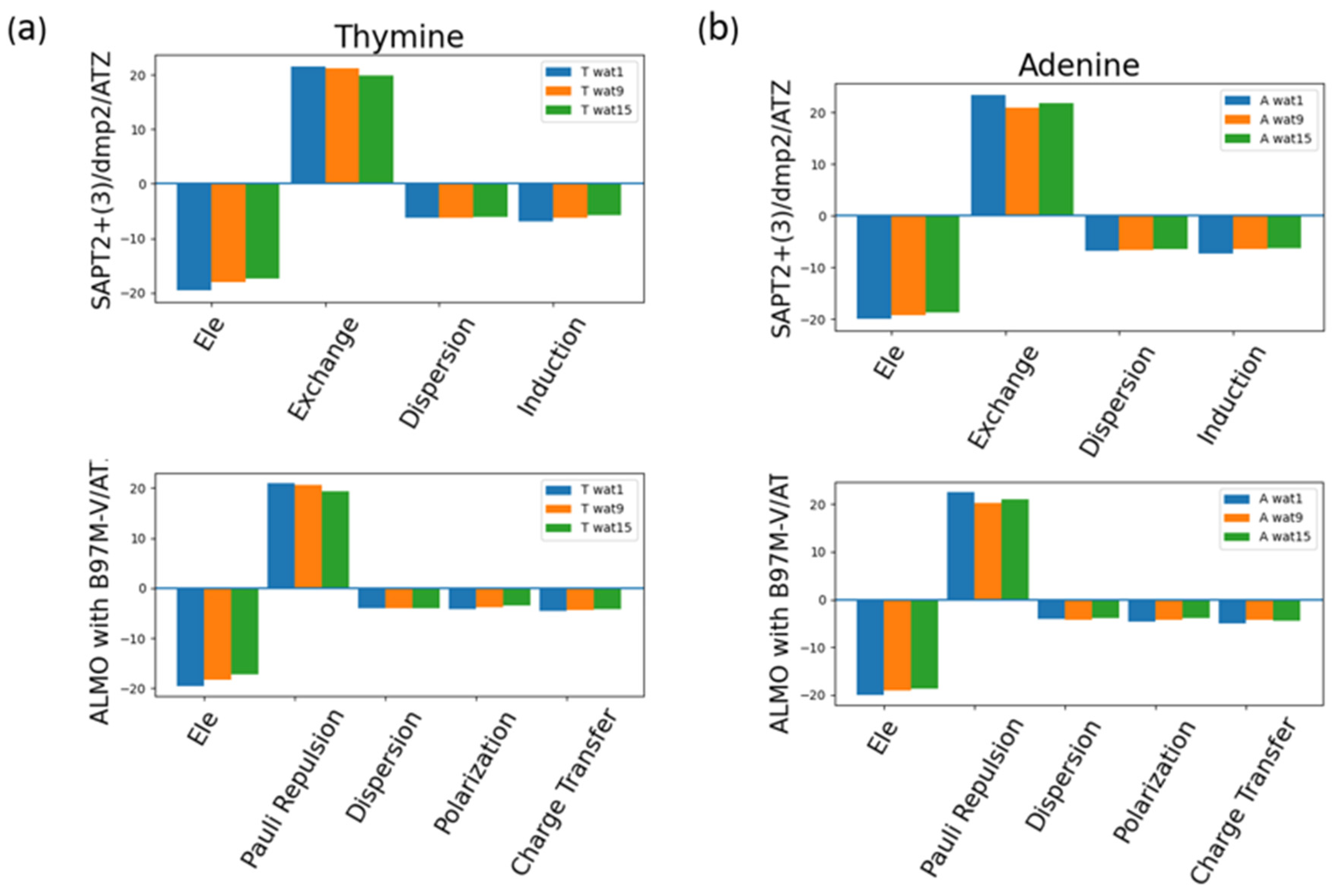
The energy components of Thymine total interaction energy and of Adenine total interaction energy were investigated as an example of pyrimidine and purine interactions with water (Figure 13). Similar to the neutral sugar moiety (Figure 7), exchange in SAPT2+(3)/dmp2 scheme and Pauli repulsion in ALMO EDA2 generation scheme were found to be the most dominant component, which was counterbalanced with the attractive electrostatics’ component. Dispersion, Induction, and Charge transfer were found to be contributing less with an average of -6.5 kcal/mol for each component in the different Nucleobase-Wat configurations. In other words, induction and dispersion are the main contributing forces to stabilize the nucleobase-water interactions. The difference in the purine and pyrimidine structure did not make a difference in the contribution of the different energy components to the total interaction energy.

2.2.3.2. Intrastrand and Interstrand Nucleobases

Another important non-covalent interaction to consider in the nucleic acid structure is the π-stacking interaction. That is why the interaction energies of the intrastrand stacked nucleobases and the interstrand nucleobases were studied using SAPT2+(3)/dmp2 and ALMO EDA2 with B97M-V (Figure 14). The structures of the of B-DNA geometry nucleobases were obtained from Sherill paper following the same nomenclature for the interstrand and intrastrand nucleobases [26]. 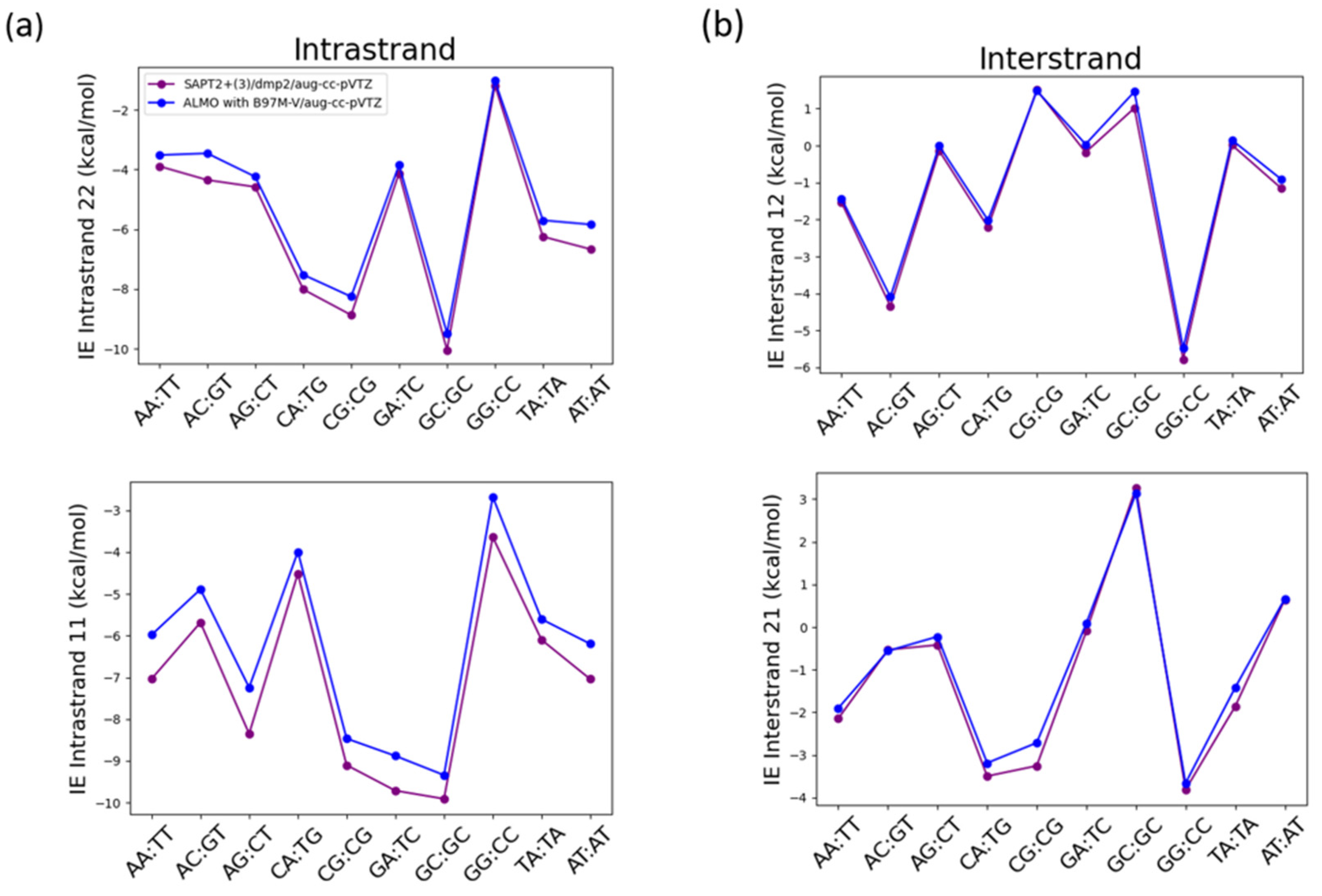The two methods were found to result in different interaction energies for the stacked intrastand nucleobases (Figure 14a), however both methods were in good agreement with each other for the interstrand nucleobases (Figure 14b). The average root-mean-square-error (RMSE) for both 11 and 22 intrastrand nucleobases was 0.68, while the average RMSE for both 12 and 21 interstrand nucleobases was found to be 0.25.
The maximum difference in the intrastrand 11 nucleobases of -1.11 kcal/mol between SAPT2+(3)/dmp2 and ALMO with B97M-V was observed in the stacked AG base pair followed by stacked AA base pair with a difference of -1.06 kcal/mol (Figure 14a). The maximum difference in the intrastrand 22 nucleobases was observed in GT base pair (-0.89 kcal/mol) followed by AT base pair with a difference of -0.83 kcal/mol (Figure 14a). A much smaller difference was observed in the interstrand nucleobases, where the maximum difference observed in interstrand 12 nucleobases between the two methods was -0.25 kcal/mol in AC base pair followed by AT base pair at -0.24 kcal/mol (Figure 14b). The maximum difference of -0.54 kcal/mol observed in 21 interstrand nucleobases was observed in CG base pair followed by TA base pair with a difference of -0.44 kcal/mol.
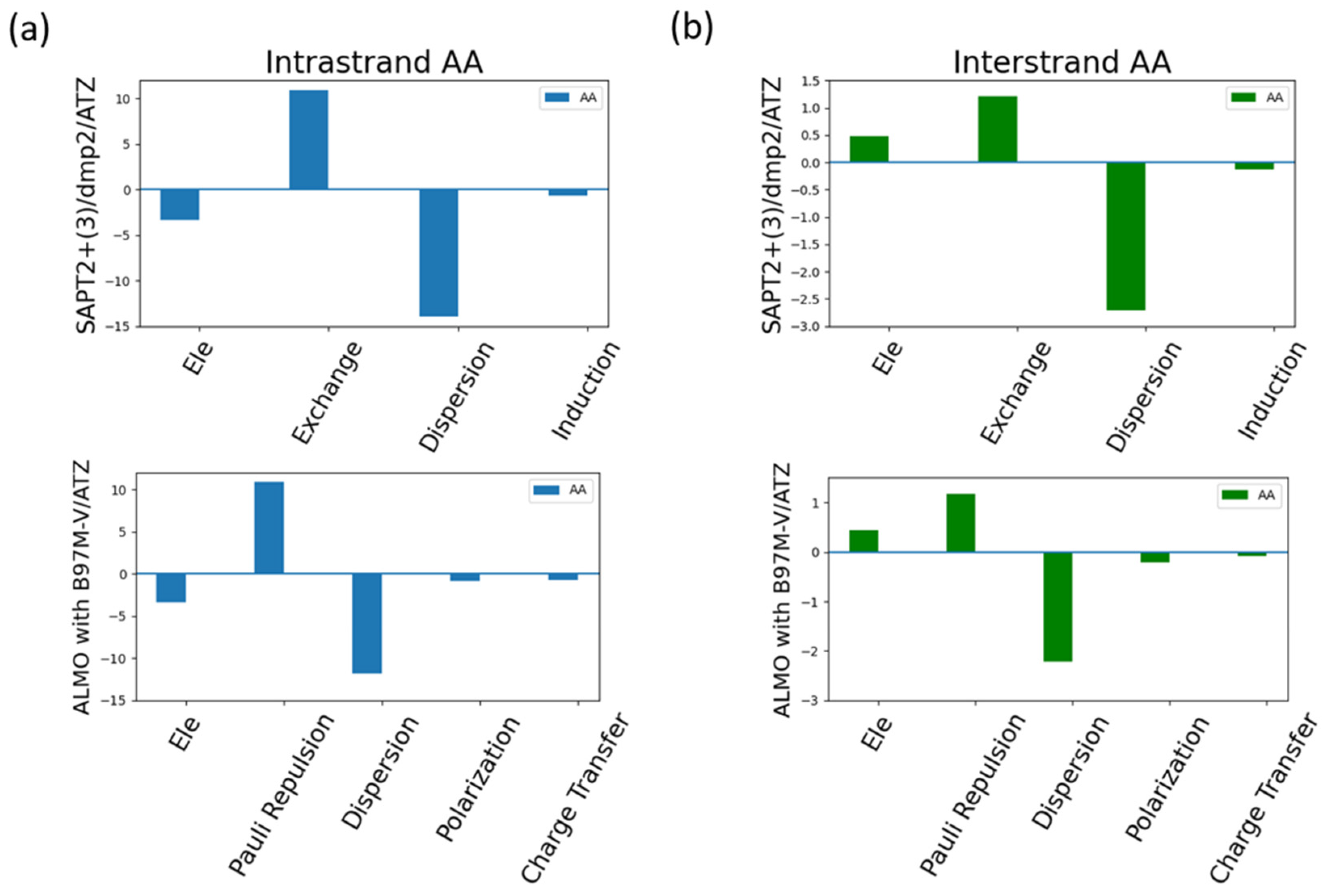
Analyzing the energy components of the intrastrand AA and interstand AA as an example for the π-stacking interactions in the nucleic acid (Figure 15). Dispersion was found to be the most contributing component in the intrastrand AA (Figure 15a) as expected due to the dominating π-stacking interaction. Exchange-Pauli Repulsion was found to be the second most dominant contributor to the total energy, followed by a much lesser extent attractive electrostatics components.
Figure 15b showed that dispersion was also the most dominating factor, to a much lesser extent compared to intrastrand AA, to the interaction of the interstrand AA. This was surprising as the dominating type of interaction in the intrastrand AA is the hydrogen bond. The second most dominating factor in the interstrand interaction was found to be the Exchange-Pauli Repulsion similar to what observed in the intrastrand AA. Unlike the intrastrand AA base pair, the electrostatics component was found to be repulsive, having a positive contribution, rather than attractive.

3. Discussion

Nucleic acid plays a vital role in several biological processes from contributing to the central dogma of the cell to functioning as an enzyme or binding as a ligand. With the current limitations of the MM forcefields in dealing with the non-covalent interactions dominating the nucleic acid, especially the π-stacking interactions due to the lack of charge penetration factor, accurate description of the non-covalent interactions will help in developing better forcefields tailored for the nucleic acid.
Benchmarking of SAPT0, SAPT2+, SAPT2+(3)/dmp2, ALMO EDA2 with the original and the new energy decomposition, MP2, and CCSD(T) on a set of small molecules with available CBS CCSD(T) interaction energies was performed. The small molecules compromised the two types of interactions prevalent in the nucleic acid structure: hydrogen bond and π-stacking interactions. Based on the benchmarking results, ALMO EDA2 was found to be independent of the DFT method, or the basis set used. On the other hand, the level of SAPT was highly dependent on the basis set used. The approximate CCSD(T), DLPNO/CCSD(T), was found to be less reliable compared to the DFT methods due to the large deviation from the CBS CCSD(T) interaction energies, especially for the halogen substituted benzene molecules. The interaction energy of BenCl-BenCl complex was the most challenging to the various theoretical methods. Further analysis for this deviation is needed to tackle the inconsistent and inaccurate interaction energy for the halogen substituted benzene and heterocycles in general, especially BenCl.
After testing the different theoretical methods along with dependence on DFT method and basis set, five different protocols were selected to be tested on the three main components of the nucleotides’ structure. SAPT0 with jun-cc-pVDZ, SAPT2+ with aug-cc-pVDZ, SAPT2+(3)/dmp2 with aug-cc-pVDZ, SAPT2+(3)/dmp2 with aug-cc-pVTZ, ALMO EDA2 (B97M-V) with the original energy decomposition and aug-cc-pVTZ. The five protocols were tested on the interaction of neutral sugar moiety (C2’endo deoxyribose sugar and C3’ endo ribose sugar) with water, the negatively charged DMP (DMP gg, DMPgt, and DMP tt) with water, nucleobases with water, and the interstrand and intrastrand nucleobases to govern the two types of interactions found in the structure of the nucleic acid. SAPT2+(3)/dmp2 and ALMO EDA2 were found to be the most consistent with each other with respect to the obtained interaction energies. Most of the difference observed between the two methods was in the stacked interaction energies of the nucleobases. Another important point to consider is the computational cost of the calculations, ALMO EDA2 is faster on average than SAPT2+(3)/dmp2 with similar accuracy.
Analyzing the energy components of the total interaction energies obtained from the ALMO EDA2 and SAPT2+(3)/dmp2 schemes showed that Exchange-Pauli repulsion, the dominating contributor to the total interaction energy of the neutral molecules (sugar moiety and nucleobases) with water was counterbalanced with the attractive electrostatics component, resulting in making the induction and dispersion the stabilizing factors for these interactions. In the negatively charged DMP interaction with water, electrostatics components were found to be associated with the largest contribution to the total energy. In the interstrand and intrastrand nucleobases, dispersion was found to be the dominating factor in this type of π-stacking and hydrogen bond interactions.

4. Materials and Methods

4.1. Preparation of Structures

The canonical structures of the nucleotides were constructed using Nucleic.exe implemented in Tinker8 [36,37]. C2’endo deoxyribose sugar was extracted from B-DNA geometry, while C3’ endo ribose sugar was extracted from A-DNA geometry. The purine and pyrimidine nucleobases were obtained from B-DNA geometry of the nucleic acid as indicated by Tinker8 [36,37]. The three dominant conformations of DMP: DMP gg, DMP gt, and DMP tt were constructed using Pymol [17]. The structures of the B-DNA interstrand and intrastrand nucleobases were obtained from Sherill paper following the same nomenclature [26].
After obtaining the canonical structures of the nucleotides’ components, water molecules were placed at various positions surrounding the structures following aISS workflow [35]. aISS workflow is based on searching for the lowest energy conformation of two fragments interacting non-covalently. The first step in the workflow is to calculate the electronic structure properties using semi-empirical GFNn-xTB [38,39] followed by grid-search based on xTB-IFF [40] interaction energies of the two fragments. In other words, several geometries are generated for the two interacting fragments by moving the first fragment around the second one. Then, the interaction energy is evaluated using xTB-IFF interaction energies. The generated structures from the grid-search are subjected to genetic optimization followed by final GFNn-xTB or GFN-FF optimization.
15 different conformations of the water molecule interacting with the different constituents were generated (nucleobase-water, sugar moiety-water, and DMP-water). Three different conformations of the water molecule probe were selected based on the docking score and the uniqueness of the water molecule position. In other words, the position of the water molecule was chosen to cover the entire conformational space around the counter interacting moieties and to interact with all the polarizable groups present in the structure.
The selected three complexes with the water molecule probe were subjected to energy minimization using MP2/6-31G* in GAUSSIAN16 [41]. This was followed by translation of the water molecule probe along the center of mass of the water molecule. The translation distances corresponded to percents of the equilibrium distance of the optimized structures. The water molecule was translated to five or six positions corresponding to 0.90, 0.95, 1.0, 1.05, 1.1, and 1.3 of the equilibrium distance between the center of mass of the water molecule and the center of mass of the counter interacting moiety. These distances do not reflect the interacting distances between the two molecules. This translation of the water probe helped us to generate an interaction energy curve of the nucleobase-water, sugar moiety-water, and DMP-water, which helped us in identifying the local minimum of each structure.

4.2. Ab-Initio Calculations

The interaction energies of the generated nucleobase-water, sugar moiety-water, DMP-water complexes, and interstrand and intrastrand base pairs were computed using the original and the new decomposition energy scheme of ALMO (Absolutely Localized Molecular Orbital) ALMO EDA2 [29,30,31] implemented in QCHEM 6.1 package [28]. ALMO EDA decomposes the interaction energy into three main terms: frozen density component, polarization, and charge transfer. The frozen density core includes the electrostatics, pauli-repulsion, and dispersion. ALMO EDA2 resolved the shortcomings of ALMO EDA as the dependence of the polarization term on the basis set used. It was found by the larger basis set utilized the more contaminated the polarization term become by the charge transfer term. Two energy decomposition schemes are popular while using ALMO EDA2: the first is the original energy decomposition scheme which includes the Frozen energy decomposition with ALMO polarization (AO-block-based), the new energy decomposition scheme involves Frozen energy decomposition with nDQ-FERF polarization. Both were tested on a set of small molecules to determine which will be better for computing the interaction energies of the nucleotides.
Different levels of SAPT (Symmetry-Adapted Perturbation Theory): SAPT0, SAPT2+, and SAPT2+(3)/dmp2 [34,42,43,44,45] implemented in psi4 package [32] were also used to compute the interaction energies. SAPT determines the interaction energy between two fragments directly by decomposing the energy into four physically meaningful terms: electrostatics, exchange, induction, and dispersion. SAPT0 mainly depends on error cancellation. Higher-order SAPT depends on including several corrections, for example SAPT2+. involves second-order correction for the monomeric fluctuations and dispersion energy correction by adding the effect of the intramolecular correlation [33]. SAPT2+(3)/dmp2 includes higher-order perturbative terms and variational correction terms.

5. Conclusions

QM benchmarks for nucleotides, the monomeric structure of nucleic acid, is essential to develop better forcefields with improved parameters for the non-covalent interactions preserving the complex structure of the nucleic acid. Upon testing five different protocols, we recommend using SAPT2+(3)/dmp2 with aug-cc-pVTZ and ALMO EDA2 with B97M-V and aug-cc-pVTZ as high-quality ab-initio methods for studying the non-covalent interactions of the nucleic acid. The attractive induction and dispersion were found to be responsible for stabilizing the interactions of the neutral moieties (sugar moiety and nucleobase) with water due to the cancellation of the large Exchange-Pauli repulsion component with the attractive electrostatics’ components. Dispersion was found to be the most important in the interstrand and intrastrand base pairs.

Author Contributions

Conceptualization, Mayar Tarek Ibrahim and Pengyu Ren; methodology, Mayar Tarek Ibrahim and Pengyu Ren; validation, Mayar Tarek Ibrahim, Elizabeth Wait and Pengyu Ren; formal analysis, Mayar Tarek Ibrahim and Pengyu Ren; investigation, Mayar Tarek Ibrahim, Elizabeth Wait, and Pengyu Ren; resources, Pengyu Ren.; data curation, Mayar Tarek Ibrahim.; writing—original draft preparation, Mayar Tarek Ibrahim, Elizabeth Wait, and Pengyu Ren; writing—review and editing, Mayar Tarek Ibrahim, Elizaebeth Wait, and Pengyu Ren.; visualization, Mayar Tarek Ibrahim.; supervision, Pengyu Ren; funding acquisition, Pengyu Ren. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Institutes of Health, grant number R01GM106137 and R01GM114237, the Welch Foundation (F-2120), and the Cancer Prevention and Research Institute of Texas grant (RP210088).

Data Availability Statement

SAPT2+(3)/dmp2 and ALMO EDA2 with original energy decomposition scheme interaction energies for all the complexes are provided in separate excel sheet.

Acknowledgments

The authors are grateful for support from the National Institutes of Health (R01GM106137 and R01GM114237), the Welch Foundation (F-2120), and the Cancer Prevention and Research Institute of Texas grant (RP210088).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Rudolph, F.B. The Biochemistry and Physiology of Nucleotides. J. Nutr. 1994, 124, 124S–127S, . [CrossRef]
  2. Breaker, R.R.; Joyce, G.F. The Expanding View of RNA and DNA Function. Chem. Biol. 2014, 21, 1059–1065, . [CrossRef]
  3. Hudson, W.; Ortlund, E. The structure, function and evolution of proteins that bind DNA and RNA. Nat. Rev. Mol. Cell Biol. 2014, 15, 749–760, . [CrossRef]
  4. Varshney, D.; Spiegel, J.; Zyner, K.; Tannahill, D.; Balasubramanian, S. The regulation and functions of DNA and RNA G-quadruplexes. Nat. Rev. Mol. Cell Biol. 2020, 21, 459–474, . [CrossRef]
  5. Carthew, R.W.; Sontheimer, E.J. Origins and Mechanisms of miRNAs and siRNAs. Cell 2009, 136, 642–655, . [CrossRef]
  6. Hays, F.A.; Teegarden, A.; Jones, Z.J.R.; Harms, M.; Raup, D.; Watson, J.; Cavaliere, E.; Ho, P.S. How sequence defines structure: A crystallographic map of DNA structure and conformation. Proc. Natl. Acad. Sci. 2005, 102, 7157–7162, . [CrossRef]
  7. Svozil, D.; Kalina, J.; Omelka, M.; Schneider, B. DNA conformations and their sequence preferences. Nucleic Acids Res. 2008, 36, 3690–3706, . [CrossRef]
  8. Minchenkova, L.E.; Schyolkina, A.K.; Chernov, B.K.; Ivanov, V.I. CC/GG Contacts Facilitate the B to A Transition of DMA in Solution. J. Biomol. Struct. Dyn. 1986, 4, 463–476, . [CrossRef]
  9. Jose, D.; Porschke, D. The Dynamics of the B−A Transition of Natural DNA Double Helices. J. Am. Chem. Soc. 2005, 127, 16120–16128, . [CrossRef]
  10. Whelan, D.R.; Hiscox, T.J.; Rood, J.I.; Bambery, K.R.; McNaughton, D.; Wood, B.R.; R., W.D.; J., H.T.; I., R.J.; R., B.K.; et al. Detection of an en masse and reversible B- to A-DNA conformational transition in prokaryotes in response to desiccation. J. R. Soc. Interface 2014, 11, 20140454, . [CrossRef]
  11. Zhang, C.; Lu, C.; Jing, Z.; Wu, C.; Piquemal, J.-P.; Ponder, J.W.; Ren, P. AMOEBA Polarizable Atomic Multipole Force Field for Nucleic Acids. J. Chem. Theory Comput. 2018, 14, 2084–2108, . [CrossRef]
  12. A. Herbert and A. Rich, “The Biology of Left-handed Z-DNA (∗),” Journal of Biological Chemistry, vol. 271, no. 20, pp. 11595–11598, 1996.
  13. R. V Gessner, C. A. Frederick, G. J. Quigley, A. Rich, and A. H. J. Wang, “The molecular structure of the left-handed Z-DNA double helix at 1.0-Å atomic resolution: Geometry, conformation, and ionic interactions of d (CGCGCG),” Journal of Biological chemistry, vol. 264, no. 14, pp. 7921–7935, 1989.
  14. N. Leontis and E. Westhof, RNA 3D structure analysis and prediction, vol. 27. Springer Science & Business Media, 2012.
  15. Rao, S.N.; Kollman, P. On the role of uniform and mixed sugar puckers in DNA double-helical structures. J. Am. Chem. Soc. 1985, 107, 1611–1617, . [CrossRef]
  16. Galindo-Murillo, R.; Robertson, J.C.; Zgarbová, M.; Šponer, J.; Otyepka, M.; Jurečka, P.; Cheatham, T.E. Assessing the Current State of Amber Force Field Modifications for DNA. J. Chem. Theory Comput. 2016, 12, 4114–4127, . [CrossRef]
  17. Zhang, C.; Lu, C.; Wang, Q.; Ponder, J.W.; Ren, P. Polarizable Multipole-Based Force Field for Dimethyl and Trimethyl Phosphate. J. Chem. Theory Comput. 2015, 11, 5326–5339, . [CrossRef]
  18. Zhang, C.; Bell, D.; Harger, M.; Ren, P. Polarizable Multipole-Based Force Field for Aromatic Molecules and Nucleobases. J. Chem. Theory Comput. 2016, 13, 666–678, . [CrossRef]
  19. Zhang, C.; Lu, C.; Jing, Z.; Wu, C.; Piquemal, J.-P.; Ponder, J.W.; Ren, P. AMOEBA Polarizable Atomic Multipole Force Field for Nucleic Acids. J. Chem. Theory Comput. 2018, 14, 2084–2108, . [CrossRef]
  20. J. A. Lemkul and A. D. MacKerell Jr, “Polarizable force field for DNA based on the classical Drude oscillator: II. Microsecond molecular dynamics simulations of duplex DNA,” J Chem Theory Comput, vol. 13, no. 5, pp. 2072–2085, 2017.
  21. Lemkul, J.A.; MacKerell, A.D. Polarizable Force Field for DNA Based on the Classical Drude Oscillator: I. Refinement Using Quantum Mechanical Base Stacking and Conformational Energetics. J. Chem. Theory Comput. 2017, 13, 2053–2071, . [CrossRef]
  22. Lemkul, J.A.; MacKerell, A.D. Polarizable force field for RNA based on the classical drude oscillator. J. Comput. Chem. 2018, 39, 2624–2646, . [CrossRef]
  23. C. D. Sherrill et al., “Assessment of standard force field models against high-quality ab initio potential curves for prototypes of π–π, CH/π, and SH/π interactions,” J Comput Chem, vol. 30, no. 14, pp. 2187–2193, 2009.
  24. Hohenstein, E.G.; Duan, J.; Sherrill, C.D. Origin of the Surprising Enhancement of Electrostatic Energies by Electron-Donating Substituents in Substituted Sandwich Benzene Dimers. J. Am. Chem. Soc. 2011, 133, 13244–13247, . [CrossRef]
  25. Stone, A.J.; Price, S.L. Some new ideas in the theory of intermolecular forces: anisotropic atom-atom potentials. J. Phys. Chem. 1988, 92, 3325–3335, . [CrossRef]
  26. Parker, T.M.; Sherrill, C.D. Assessment of Empirical Models versus High-Accuracy Ab Initio Methods for Nucleobase Stacking: Evaluating the Importance of Charge Penetration. J. Chem. Theory Comput. 2015, 11, 4197–4204, . [CrossRef]
  27. Donchev, A.G.; Taube, A.G.; Decolvenaere, E.; Hargus, C.; McGibbon, R.T.; Law, K.-H.; Gregersen, B.A.; Li, J.-L.; Palmo, K.; Siva, K.; et al. Quantum chemical benchmark databases of gold-standard dimer interaction energies. Sci. Data 2021, 8, 1–9, . [CrossRef]
  28. Khaliullin, R.Z.; Cobar, E.A.; Lochan, R.C.; Bell, A.T.; Head-Gordon, M. Unravelling the Origin of Intermolecular Interactions Using Absolutely Localized Molecular Orbitals. J. Phys. Chem. A 2007, 111, 8753–8765, . [CrossRef]
  29. Horn, P.R.; Mao, Y.; Head-Gordon, M. Defining the contributions of permanent electrostatics, Pauli repulsion, and dispersion in density functional theory calculations of intermolecular interaction energies. J. Chem. Phys. 2016, 144, 114107–114107, . [CrossRef]
  30. Horn, P.R.; Mao, Y.; Head-Gordon, M. Probing non-covalent interactions with a second generation energy decomposition analysis using absolutely localized molecular orbitals. Phys. Chem. Chem. Phys. 2016, 18, 23067–23079, . [CrossRef]
  31. Horn, P.R.; Head-Gordon, M. Polarization contributions to intermolecular interactions revisited with fragment electric-field response functions. J. Chem. Phys. 2015, 143, 114111, . [CrossRef]
  32. Smith, D.G.A.; Burns, L.A.; Simmonett, A.C.; Parrish, R.M.; Schieber, M.C.; Galvelis, R.; Kraus, P.; Kruse, H.; Di Remigio, R.; Alenaizan, A.; et al. PSI4 1.4: Open-source software for high-throughput quantum chemistry. J. Chem. Phys. 2020, 152, 184108, . [CrossRef]
  33. McDaniel, J.G.; Schmidt, J. Next-Generation Force Fields from Symmetry-Adapted Perturbation Theory. Annu. Rev. Phys. Chem. 2016, 67, 467–488, . [CrossRef]
  34. Hohenstein, E.G.; Sherrill, C.D. Density fitting and Cholesky decomposition approximations in symmetry-adapted perturbation theory: Implementation and application to probe the nature of π-π interactions in linear acenes. J. Chem. Phys. 2010, 132, . [CrossRef]
  35. Plett, C.; Grimme, S. Automated and Efficient Generation of General Molecular Aggregate Structures. Angew. Chem. Int. Ed. 2022, 62, . [CrossRef]
  36. J. W. Ponder, “TINKER: Software tools for molecular design,” Washington University School of Medicine, Saint Louis, MO, vol. 3, p. 116, 2004.
  37. Rackers, J.A.; Wang, Z.; Lu, C.; Laury, M.L.; Lagardère, L.; Schnieders, M.J.; Piquemal, J.-P.; Ren, P.; Ponder, J.W. Tinker 8: Software Tools for Molecular Design. J. Chem. Theory Comput. 2018, 14, 5273–5289, . [CrossRef]
  38. C. Bannwarth et al., “Extended tight-binding quantum chemistry methods,” Wiley Interdiscip Rev Comput Mol Sci, vol. 11, no. 2, p. e1493, 2021.
  39. S. Grimme, “Semiempirical Extended Tight-Binding Program Package.” 2019.
  40. Grimme, S.; Bannwarth, C.; Caldeweyher, E.; Pisarek, J.; Hansen, A. A general intermolecular force field based on tight-binding quantum chemical calculations. J. Chem. Phys. 2017, 147, 161708–161708, . [CrossRef]
  41. M. J. ea Frisch et al., “Gaussian 16.” Gaussian, Inc. Wallingford, CT, 2016.
  42. Hohenstein, E.G.; Parrish, R.M.; Sherrill, C.D.; Turney, J.M.; Schaefer, H.F. Large-scale symmetry-adapted perturbation theory computations via density fitting and Laplace transformation techniques: Investigating the fundamental forces of DNA-intercalator interactions. J. Chem. Phys. 2011, 135, 174107, . [CrossRef]
  43. Hohenstein, E.G.; Sherrill, C.D. Density fitting of intramonomer correlation effects in symmetry-adapted perturbation theory. J. Chem. Phys. 2010, 133, 014101, . [CrossRef]
  44. Hohenstein, E.G.; Sherrill, C.D. Efficient evaluation of triple excitations in symmetry-adapted perturbation theory via second-order Møller–Plesset perturbation theory natural orbitals. J. Chem. Phys. 2010, 133, 104107, . [CrossRef]
  45. Jeziorski, B.; Moszynski, R.; Szalewicz, K. Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of van der Waals Complexes. Chem. Rev. 1994, 94, 1887–1930, . [CrossRef]
Preprints 108374 g001
Figure 1. Nucleotides dissected into three main constituents based on the difference in the chemical nature: Dimethyl phosphate, Sugar Moiety, and Nucleobases.
Figure 1. Nucleotides dissected into three main constituents based on the difference in the chemical nature: Dimethyl phosphate, Sugar Moiety, and Nucleobases.
Preprints 108374 g001
Preprints 108374 g002
Figure 2. Benchmarking of the interaction energies of different small molecules using various theoretical methods, mainly different levels of SAPT (SAPT0, SAPT2+, and SAPT2+(3)/dmp2) and ALMO EDA2 (B97M-V) with original and new energy decomposition against CBS CCSD(T). All the calculations were performed using aug-cc-pVTZ basis set. (a) Interaction energies of hydrogen-bond forming compounds as obtained from different methods; (b) Interaction energies of stacked compounds.
Figure 2. Benchmarking of the interaction energies of different small molecules using various theoretical methods, mainly different levels of SAPT (SAPT0, SAPT2+, and SAPT2+(3)/dmp2) and ALMO EDA2 (B97M-V) with original and new energy decomposition against CBS CCSD(T). All the calculations were performed using aug-cc-pVTZ basis set. (a) Interaction energies of hydrogen-bond forming compounds as obtained from different methods; (b) Interaction energies of stacked compounds.
Preprints 108374 g002
Preprints 108374 g003
Figure 3. Benchmarking of different levels of DFT theory (B97M-V, ωB97M-V, ωB97X-V, and ωB97X-D3) for the stacked molecules against CBS CCSD(T) method.
Figure 3. Benchmarking of different levels of DFT theory (B97M-V, ωB97M-V, ωB97X-V, and ωB97X-D3) for the stacked molecules against CBS CCSD(T) method.
Preprints 108374 g003
Preprints 108374 g004
Figure 4. Basis set dependence of ALMO EDA2 generation with B97M-V, SAPT0, SAPT2+, and SAPT2+(3)/dmp2 in the stacked molecules using jun-cc-PVDZ, aug-cc-PVDZ, and aug-cc-PVTZ. Thus, using higher level of SAPT or large basis set do not guarantee better accuracy. Empirically, it was determined that SAPT0 with jun-cc-pVDZ basis and SAPT2+ and SAPT2+(3)/dmp2 with aug-cc-pVDZ are in reasonable agreement with ALMO EDA2, with an average deviation of 0.2 kcal/mol for all stacking energies. The maximum difference among the three SAPT methods was 0.3 kcal/mol, observed for BenCl-BenCl.
Figure 4. Basis set dependence of ALMO EDA2 generation with B97M-V, SAPT0, SAPT2+, and SAPT2+(3)/dmp2 in the stacked molecules using jun-cc-PVDZ, aug-cc-PVDZ, and aug-cc-PVTZ. Thus, using higher level of SAPT or large basis set do not guarantee better accuracy. Empirically, it was determined that SAPT0 with jun-cc-pVDZ basis and SAPT2+ and SAPT2+(3)/dmp2 with aug-cc-pVDZ are in reasonable agreement with ALMO EDA2, with an average deviation of 0.2 kcal/mol for all stacking energies. The maximum difference among the three SAPT methods was 0.3 kcal/mol, observed for BenCl-BenCl.
Preprints 108374 g004
Preprints 108374 g005
Figure 5. Representative structures for the C2’ endo deoxyribose sugar and C3’ endo ribose sugar interact with water probe at different positions. The distances correspond to the equilibrium distance obtained from MP2 optimization of the structures with 6-31G* basis.
Figure 5. Representative structures for the C2’ endo deoxyribose sugar and C3’ endo ribose sugar interact with water probe at different positions. The distances correspond to the equilibrium distance obtained from MP2 optimization of the structures with 6-31G* basis.
Preprints 108374 g005
Preprints 108374 g006
Figure 6. Interaction energy curve of the sugar moiety with different positions of water molecule at various percents of the equilibrium COM distance (0.95, 1.0, 1.0, 1.05, 1.1, and 1.3 times of equilibrium separation). (a) Interaction energy curve of C2’ endo deoxyribose sugar with water; (b) Interaction energy curve of C3’ endo ribose sugar with water.
Figure 6. Interaction energy curve of the sugar moiety with different positions of water molecule at various percents of the equilibrium COM distance (0.95, 1.0, 1.0, 1.05, 1.1, and 1.3 times of equilibrium separation). (a) Interaction energy curve of C2’ endo deoxyribose sugar with water; (b) Interaction energy curve of C3’ endo ribose sugar with water.
Preprints 108374 g006
Preprints 108374 g007
Figure 7. Analysis of total energy components using SAPT2+(3)/dmp2 and ALMO EDA2 generation scheme for sugar moiety-water configurations. (a) Energy components of C2’ endo deoxyribose sugar-water configurations; (b) Energy components of C3’ endo ribose sugar-water configurations.
Figure 7. Analysis of total energy components using SAPT2+(3)/dmp2 and ALMO EDA2 generation scheme for sugar moiety-water configurations. (a) Energy components of C2’ endo deoxyribose sugar-water configurations; (b) Energy components of C3’ endo ribose sugar-water configurations.
Preprints 108374 g007
Preprints 108374 g008
Figure 8. The optimized structures of the three dominant conformations of DMP [17]: DMP gg, DMP gt, and DMP tt interact with water molecules in various positions. The distances between DMP and water moieties shown on the structures correspond to the equilibrium distances retrieved from MP2/6-31G* optimization.
Figure 8. The optimized structures of the three dominant conformations of DMP [17]: DMP gg, DMP gt, and DMP tt interact with water molecules in various positions. The distances between DMP and water moieties shown on the structures correspond to the equilibrium distances retrieved from MP2/6-31G* optimization.
Preprints 108374 g008
Preprints 108374 g009
Figure 9. Interaction energy curve of the DMP with different positions of water molecule at various percents of the equilibrium COM distance (0.9, 0.95, 1.0, 1.0, 1.0, 1.0, 1.05, 1.1, and 1.3). (a) DMP tt-Wat configurations; (b) DMP gt-Wat configurations; (c) DMP gg-Wat configurations.
Figure 9. Interaction energy curve of the DMP with different positions of water molecule at various percents of the equilibrium COM distance (0.9, 0.95, 1.0, 1.0, 1.0, 1.0, 1.05, 1.1, and 1.3). (a) DMP tt-Wat configurations; (b) DMP gt-Wat configurations; (c) DMP gg-Wat configurations.
Preprints 108374 g009
Preprints 108374 g010
Figure 10. Analysis of total energy components using SAPT2+(3)/dmp2 and ALMO EDA2 generation scheme for DMP-water configurations. (a) Energy components of DMP gg-Wat; (b) Energy components of DMP gt-Wat; (c) Energy components of DMP tt-Wat.
Figure 10. Analysis of total energy components using SAPT2+(3)/dmp2 and ALMO EDA2 generation scheme for DMP-water configurations. (a) Energy components of DMP gg-Wat; (b) Energy components of DMP gt-Wat; (c) Energy components of DMP tt-Wat.
Preprints 108374 g010
Preprints 108374 g011
Figure 11. The optimized structures of the nucleobases: A, G, U, T, and C interact with water molecules in various positions. The distances between the purine and pyrimidine nucleobases and water moieties shown on the structures correspond to the equilibrium distances retrieved from MP2/6-31G* optimization.
Figure 11. The optimized structures of the nucleobases: A, G, U, T, and C interact with water molecules in various positions. The distances between the purine and pyrimidine nucleobases and water moieties shown on the structures correspond to the equilibrium distances retrieved from MP2/6-31G* optimization.
Preprints 108374 g011
Preprints 108374 g012
Figure 12. Interaction energy curve of the purine and pyrimidine nucleobases with a water probe molecule over various distances. The distance between center of mass of the two molecules (nucleobase and water in this case), correspond to various percents of the equilibrium distance (0.9, 0.95, 1.0, 1.1, and 1.3). The distance between the center of mass shown in the plot does not reflect the interaction distance between the water probe and the nucleobase.
Figure 12. Interaction energy curve of the purine and pyrimidine nucleobases with a water probe molecule over various distances. The distance between center of mass of the two molecules (nucleobase and water in this case), correspond to various percents of the equilibrium distance (0.9, 0.95, 1.0, 1.1, and 1.3). The distance between the center of mass shown in the plot does not reflect the interaction distance between the water probe and the nucleobase.
Preprints 108374 g012
Preprints 108374 g013
Figure 13. Analysis of total energy components using SAPT2+(3)/dmp2 and ALMO EDA2 generation scheme for Nucleobase-water configurations. (a) Energy components of Thymine-Wat; (b) Energy components of Adenine-Wat.
Figure 13. Analysis of total energy components using SAPT2+(3)/dmp2 and ALMO EDA2 generation scheme for Nucleobase-water configurations. (a) Energy components of Thymine-Wat; (b) Energy components of Adenine-Wat.
Preprints 108374 g013
Preprints 108374 g014
Figure 14. Interaction energies of the nucleobases with each other using SAPT2+(3)/dmp2 and ALMO with B97M-Vgeneration scheme (a) Interaction energies of intrastrand nucleobases governed by π-stacking interactions; (b) Interaction energies of interstrand nucleobases governed by hydrogen bond.
Figure 14. Interaction energies of the nucleobases with each other using SAPT2+(3)/dmp2 and ALMO with B97M-Vgeneration scheme (a) Interaction energies of intrastrand nucleobases governed by π-stacking interactions; (b) Interaction energies of interstrand nucleobases governed by hydrogen bond.
Preprints 108374 g014
Preprints 108374 g015
Figure 15. Analysis of total energy components using SAPT2+(3)/dmp2 and ALMO EDA2 with B97MV generation scheme for interstanded and intrastranded AA base pair. (a) Energy components of Intrastranded AA nucleobases; (b) Energy components of interstranded AA nucleobase.
Figure 15. Analysis of total energy components using SAPT2+(3)/dmp2 and ALMO EDA2 with B97MV generation scheme for interstanded and intrastranded AA base pair. (a) Energy components of Intrastranded AA nucleobases; (b) Energy components of interstranded AA nucleobase.
Preprints 108374 g015
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated