Preprint

Article

Atmospheric Aircraft Conceptual Design Based on Multidisciplinary Optimization with Differential Evolution Algorithm and Neural Networks

Altmetrics

Downloads

106

Views

Comments

A peer-reviewed article of this preprint also exists.

Oleg Lukyanov^*,

Van Hung Hoang,

Evgenii Kurkin

Jose Gabriel Quijada-Pioquinto

Oleg Lukyanov^*,

Van Hung Hoang,

Evgenii Kurkin

Jose Gabriel Quijada-Pioquinto

This version is not peer-reviewed

Submitted:

05 June 2024

Posted:

10 June 2024

You are already at the latest version

Alerts

Abstract

A methodology for selecting rational parameters of atmospheric aircrafts at the initial stages of design using an optimization algorithm of differential evolution and numerical mathematical modeling of aerodynamics problems is proposed. The technique involves the implementation of weight and aerodynamic balance in the main flight modes, has the ability to consider atmospheric aircrafts with one or two lifting surfaces, apply parallel calculations and automatically generate a three-dimensional geometric model of aircraft appearance based on the optimization results. A method for accelerating the process of optimizing the parameters of an aircraft in terms of take-off weight by more than three times by introducing a objective function into a set of design variables is proposed and demonstrated. The results of assessing the reliability of the used mathematical models of aerodynamics and the correctness of the calculation the objective function, taking into account various constraints, are presented. A comprehensive test of the performance and efficiency of the methodology is considered by solving demonstration problems to optimize more than ten main design parameters the appearance of two existing heavy-class unmanned aerial vehicles with known characteristics from open sources.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

The growing importance of aviation technology in various fields of human activity today requires the emergence of new, more effective manned and unmanned aerial vehicles (UAVs). A key role in ensuring the competitiveness of newly created models or modifications of existing aircraft is played by the initial stages of design, during which up to three-quarters of the main technical decisions are made. The success of the project as a whole depends on the correctness of these decisions [1,2,3,4,5,6,7].

Traditional methods of aircraft design [1,2,3,4,5,6,7,8] involve a sequential consideration of the problems of aerodynamics, flight dynamics, strength, weight calculations and a number of other disciplines. This determines the iterative character of the initial stages of design, which requires repeated execution of computational approximations in each discipline. Many solutions are based on the experience of the designer and the established traditions in the development team.

The development of high-performance computing technology has made possible the emergence of a new design paradigm of "concurrent design" [9,10,11], which involves parallel consideration of weight, energy and aerodynamic efficiency indicators at the early stages of design through the use of multidisciplinary optimization (MDO) methods and numerical mathematical modeling. This approach is already being introduced into the practice of designing manned [12,13,14,15,16,17,18] and unmanned aerial vehicles [19,20,21,22,23,24,25,26,27]. The use of MDO at the initial stages of design for UAVs is of particular importance, since the unmanned aerial vehicles being created today cover almost the entire variety of existing and possible unusual aerodynamic configurations [28] and require consideration of a larger number of design variables across various types. The key requirements of the paradigm “concurrent design” for the design methods used are the high accuracy of mathematical models and the quick impact of optimization algorithms that allow considering a large number of design variables in the limited time at the initial design stages.

A monograph [29] should be considered a certain stage in the development of automation of aircraft design processes, in which it is proposed to use the formulation and solution of design problems in terms of nonlinear mathematical programming (NLP), including the problems of choosing the appearance of aircraft of various types and configurations [30].

In a number of works on optimizing the appearance of aircraft, various search methods are used, in particular, gradient [24,25,31], but they require the calculation of partial derivatives of the objective function, including the refinement of the calculation of take-off weight according to the sizing equation at each iteration. An additional difficulty in solving problems of choosing a design is the heterogeneity and discreteness of design variables. For example, a hybrid power plants may include a heat engine and an electric motor in various combinations. Therefore, to solve such problems, metaheuristic search methods are being developed, in particular, evolutionary methods borrowed from the natural environment are considered the main idea. In the beginning, these were relatively simple algorithms and programs that solved combinatorial optimization problems from homogeneous elements, for example, the choice of orientation and number of layers of composite material in different parts of the wing skin [32] or the optimization of the structural and geometric parameters of complex composite parts [33,34]. At present, algorithms and programs in this area are intensively developed and implemented in the field of preliminary design of aviation technology, [22,35,36]. Two main components of any evolutionary algorithm are: the selection of the best solutions and randomization. The selection of the best ones ensures that the solutions will converge to the optimal values, while randomization prevents the solutions from getting trapped in the local optima and, at the same time, increases the diversity of the solutions. The good combination of these two components will usually ensure that the overall optimization can be achieved. One of the most used evolutionary algorithms in engineering problems is the differential evolution (DE) algorithm. DE optimizes a problem by maintaining a population of candidate solutions and creating new candidate solutions by combining existing ones according to their simple operators, and then maintaining the candidate solution that has the best score or aptitude in the optimization problem in question. In this way, the optimization problem is treated as a black box that simply provides a measure of quality given a candidate solution. In addition, it presents a great flexibility to incorporate adaptive methods, use different forms of vector coding and to work with different surrogate methods (especially with methods based on deep learning models) [37,38,39,40]. However, the potential of this optimization method in the field of conceptual design of aircraft has so far been demonstrated in a limited number of publications.

The purpose of this work is to show the possibilities of the DE algorithm with certain adaptability in solving multidisciplinary optimization problems of aircraft-type aerial vehicles with many design variables, including structural ones. In addition, the use of the DE algorithm and neural networks for the optimal selection of the wing airfoil of the aircraft is shown.

2. Methods and Models

2.1. Formulation of the Conceptual Design Problem

The problem of choosing the optimal parameters of the appearance of an aircraft-type UAV will be considered in terms of NLP, following [7,29,41] and most recent works in this area. In canonical form, the problem of NLP is formulated as follows [42]:

F (x^{o p t}) \leq F (x) \forall x \in Ω,

Ω = \{x : q_{j} (x) \leq 0, h_{k} (x) = 0\}

(1)

where:

x

) - objective function;

x = \{x_{1}, x_{2}, . . ., x_{n}\}

- vector of design variables;

x^{o p t}

- optimal solution of the problem;

Ω - area of permissible design variables;

q_j(

x

)

\leq

0, j = 1, …, p- constraints in the form of inequalities;

h_k(

x

)=0, k = 1, …, k- constraints in the form of equations;

n, m, l - the number of variables and constraints.

In the proposed methodology, various technical characteristics of UAVs that are of interest to developers can be declared as a objective function. However, due to the complexity of formulating and solving the problem in a fairly general form, the features of the methodology are further considered through the problem of improving technical characteristics - minimizing weight take-off - of two existing heavy drones with different aerodynamic configurations, the U-40 [43] and MQ-1 [44] (see Figure 1).

2.2. Digital UAV Model

When solving problems using NLP methods, the mathematical model of the optimization object must answer two questions:

- What is the value of the objective function at the considered point in the space of the design variables, defined by the vector x?

- Does this point belong to the area of permissible design variables or not? And if “no,” then to what area should the value of the objective function be degraded – increased in minimization problems using a penalty?

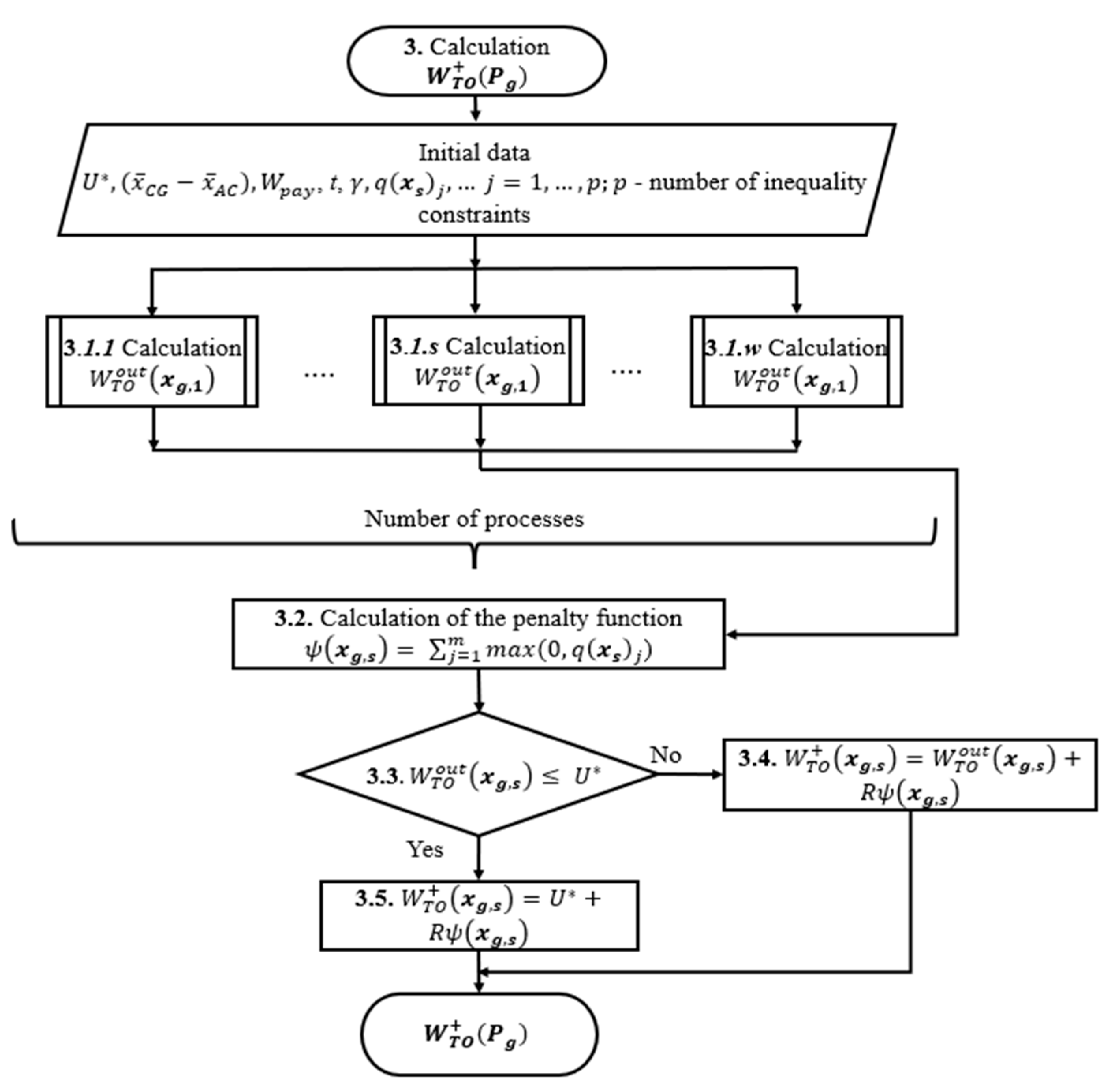
2.2.1. Objective Function

In the considered tasks, the take-off weight f(

x

) =

W_{T O}

is chosen as the objective function. If another indicator (energy or transport efficiency, etc.) is selected as the objective function, a sufficiently accurate calculation of the take-off weight is required in any case, since on the basis of this value, the aircraft is balanced, the weight and energy balance is calculated, and absolute geometric parameters are determined. The take-off weight of an aircraft depends on almost all design parameters. To determine it, an iterative solution of the sizing equation is used – the balance of weight [45,46].Interventionary studies involving animals or humans, and other studies that require ethical approval, must list the authority that provided approval and the corresponding ethical approval code.

2.2.2. Constraints

In solving NLP problems, it is convenient to divide restrictions into three groups:

The first is restrictions on the maximum and minimum values of the design variables of the form a_i ≤ x_i ≤ b_i. These constraints determine the range of values of the corresponding variable and are called geometric regardless of their nature. They can be linear, angular, specific wing load, etc.

The second group in the form of inequalities q_j(x) ≤ 0 and the third group in the form of equations h_k(x) = 0 determine the technical requirements for the operation of the aircraft. As a rule, they cannot be expressed explicitly through design variables. To assess the fulfillment of functional constraints, special algorithms are used, in some cases quite complex, such as the vortex-lattice method (VLM) in aerodynamics, statistical data or criteria “Force coefficient” [46] in weight calculation, etc.

Among the second and third groups of restrictions, the following are used in the work:

- UAV equilibrium condition in the vertical plane with a given static stability margin:

h_{1} (x) = C_{m} (x) = 0

(2)

h_{2} (x) = C_{L_bal} (x) – C_{L} (x) = 0

(3)

q_{1} (x) = C_{L} (x) \leq C_{L}^{*};

(4)

- Constraint on the value of the horizontal tail volume coefficient to ensure the required characteristics of UAV controllability influencing the size of the horizontal tail arm and its relative area:

q_{2} (x) = c_{H T} (x) ∈ [c_{H T_m i n}, c_{H T_m a x}]

(5)

Here: C_m – the coefficient of pitch moment relative to the center mass; C_L – the lift coefficient; C_{L_bal} – lift the coefficient in the equilibrium condition;

C_{L}^{*}

- permissible lift coefficient in a given flight mode;

c_{H T}

– the horizontal tail volume coefficient.

2.2.3. Design Variables

The vector of design variables x includes the geometric and specific energy parameters of the aircraft appearance, as well as the kinematic parameters of the considered flight modes.

A feature of this work is the addition of the input value (preliminary approximation) of the take-off mass

W_{T O}^{i n}

into the vector x. On the basis

W_{T O}^{i n}

, the output (refined) value of the take-off weight

W_{T O}^{o u t}

is calculated and then the value of the objective function

W_{T O}^{+}

W_{T O}^{o u t}

+ ψ, where ψ is the value of the penalty function that implements the requirements of the constraints. Convergence of the optimization process is ensured when

W_{T O}^{i n}

≈

W_{T O}^{o u t}

W_{T O}^{+}

. For the variable

W_{T O}^{i n}

, the first index in the vector x should be used, so in this work the proposed vector x consists of 14 design variables: x = [

W_{T O}^{i n}

, AR₁, AR₂,

Λ_{1}

Λ_{2}

λ_{1}

λ_{2}

, δ₁,

{\bar{L}}_{2}

{\bar{S}}_{2}

, V, W/S, δ₂, α], where

W_{T O}^{i n}

- the input value of the take-off weight, [kg]; AR₁, AR₂ - the aspect ratio of the forward lift surface and the aftward lift surface, respectively;

Λ_{1}

Λ_{2}

– sweep angle the leading edge of the forward lift surface and the aftward lift surface, respectively, [^o];

λ_{1}

λ_{2}

– taper ratio of the forward lift surface and the aftward lift surface, respectively; δ₁ – incidence angle of the forward lift surface, [^o];

{\bar{L}}_{2} = \frac{L_{2}}{\bar{c}}

– the relative distance between the lift surfaces;

{\bar{S}}_{2} = \frac{S_{2}}{S_{1}}

– the relative area of the aftward lift surface compared to the forward lifting surface; V – the flight speed, [m/s] and W/S – lift system loading, [kg/m²]. The selection of the values incidence angle δ₂ of the aftward lift surface and the angle of attack α of the aircraft is carried out by the balancing algorithm within the general optimization cycle.

A set of tools for calculating the value of the take-off weight of an aircraft at certain values of design variables and assessing the level of compliance with constraints is an information model of the optimization object in NLP problems.

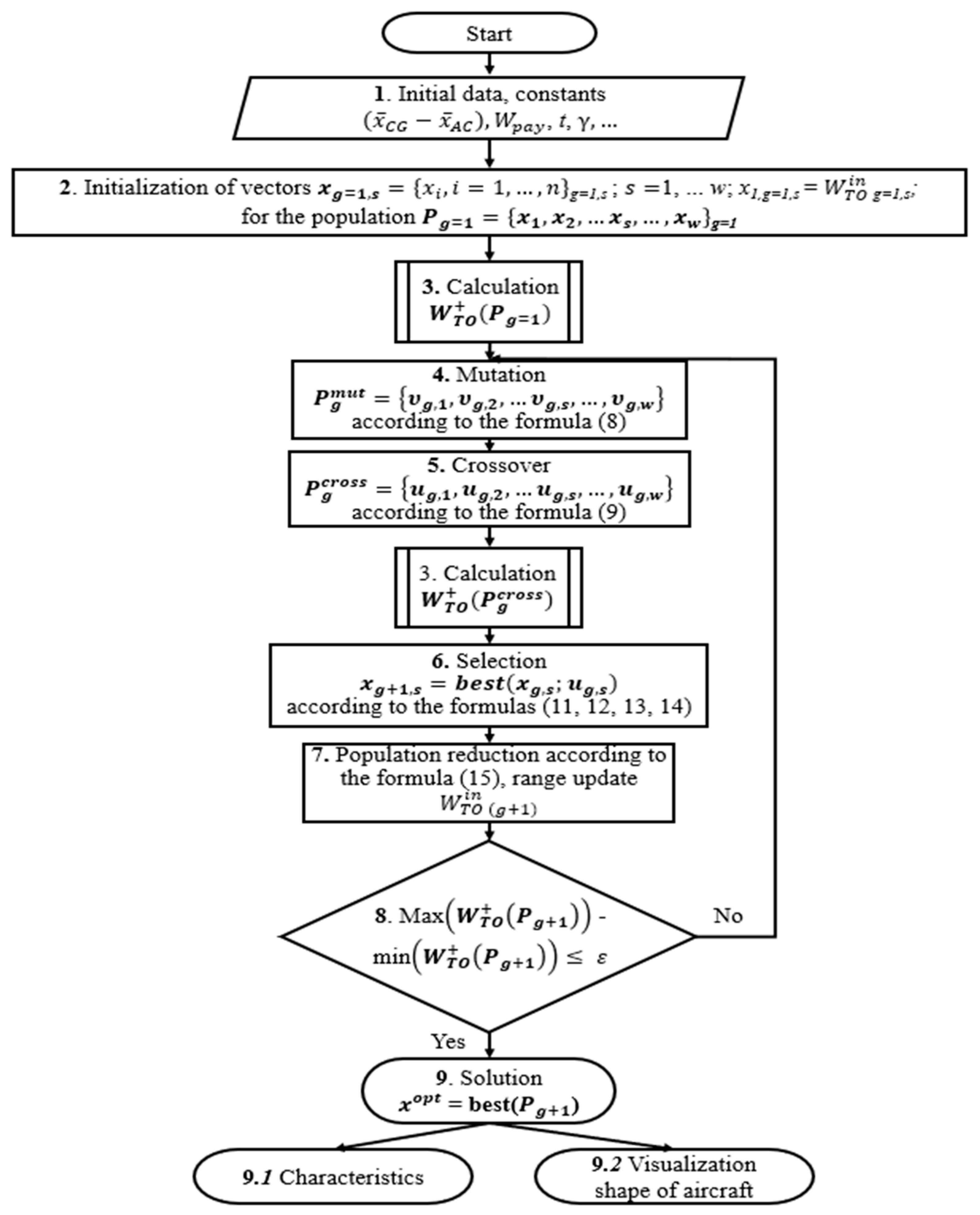
2.3. Methodology for Selecting the Optimal Parameters of an Aircraft-Type UAV

The proposed method is based on the use of the differential evolutionary optimization algorithm “Successful-History based Adaptive Differential Evolution” (SHADE) [47,48,49] with the use of penalty functions [50,51,52], method of population size reduction [53,54,55] and numerical mathematical modeling. The optimization method used (SHADE) involves the transformation of information contained in populations of individuals.

In the considered problems, an individual is one of the possible variants of the project – vector x_s, the components of which are certain values of the design variables of the designed aircraft x_i:

x_{s} = {[x_{1}, x_{2}, … x_{i}, … x_{n}]}_{s}, s = 1, \dots w

x_{s}

– the vector design variables of the individual s in the population P_g;

s – index of the individual;

w – number of individuals in the population;

i and n – index and number of design variables in the individual s.

A population P_g is a set of individuals s at an iteration of optimization (generation) g, includes vectors of individuals

x_{s}

P_{g} = {\{x_{1}, x_{2}, \dots x_{s}, \dots, x_{w}\}}_{g}, g = 1, \dots, m .

Where: g – the index of population.

The methodology of this work is based on an algorithm of [56], but have new approach with significant improvements that allow:

- consider various aerodynamic configurations of UAVs with one or two lift surfaces (flying-wing, normal, duck, tandem);

- design UAVs of different dimensions;

- use various types of power plants on UAVs;

- increase the performance of calculations through the use of an analytical tools and parallel calculations.

The methodology is implemented on the Python platform with the connection of the AVL open source code for aerodynamic calculations [57].

A block-scheme of the methodology is presented in Figure 2.

In general, the methodology includes a number of basic blocks.

Block 1

the process of entering initial data, design constants, entering the settings of the optimization method, choosing the size of the first NP population, assigning the value of the stop criterion ε, setting the ranges of values for the design variables [x_i_(min)… x_i_(max)], the values of constraints q_j ≤ 0 as well as specifying the range of possible values of the input take-off weight of the individuals of the initial approximation at the first iteration [

W_{T O g = 1}^{i n}

_(min)...

W_{T O g = 1}^{i n}

_(max)].

Block 2

the process of initialization of the first populations P_g=1, consisting of vectors

x_{s}

of individuals. The selection of the values of the design variables x_g=1,i in the vectors of each individual x_g=1,s is carried out randomly from the user-defined range of values design variables [x_i_(min)… x_i_(max)], using the Latin Hypercube Sampling (LHS) method [58], including the initial take-off weight approximation

W_{T O}^{i n}

_g=1,s taking into account a given range [

W_{T O g = 1}^{i n}

_(min)...

W_{T O g = 1}^{i n}

_(max)]. The size of the first population should be at least NP_g=1 = 10⋅n, where n is the number of design variables.

Block 3

Block 3 is designed to calculate the values of the objective function

W_{T O}^{+} (x_{g, s})

of individuals

x_{s}

of the population P_g based on the values of their design variables x_i, including the input take-off weight of the initial approximation

W_{T O}^{i n}

_g,s.The value of the objective function of each individual is the value of the output (refined) take-off weight

W_{T O}^{o u t}

(x_g,s), calculated using the sizing equation (see Figure 3, blocks 3.1.s) and supplemented by the value of the penaltyψ (see Figure 3, block 3.2):

W_{T O}^{+} (x_{g, s}) = \{\begin{matrix} W_{T O}^{o u t} (x_{g, s}) i f ψ (x_{g, s}) = 0 \\ R ψ (x_{g, s}) + U^{*} i f ψ (x_{g, s}) > 0 ⋀ W_{T O}^{o u t} (x_{g, s}) \leq U^{*} \\ R ψ (x_{g, s}) + W_{T O}^{o u t} (x_{g, s}) i f ψ (x_{g, s}) > 0 ⋀ W_{T O}^{o u t} (x_{g, s}) > U^{*} \end{matrix}

(6)

Where is:

ψ (x_{g, s}) = ψ_{1} (x_{g, s}) + ψ_{2} (x_{g, s})

(7)

ψ_{1} (x_{g, s}) = \{\begin{matrix} 0 i f C_{L} (x_{g, s}) \leq C_{L}^{*} \\ C_{L} (x_{g, s}) - C_{L}^{*} i f C_{L} (x_{g, s}) > C_{L}^{*} \end{matrix}

ψ_{2} (x_{g, s}) = \{\begin{matrix} \begin{matrix} 0 i f c_{H T} (x_{g, s}) [c_{H T_m i n}, c_{H T_m a x}] \\ c_{H T} (x_{g, s}) - c_{H T_m a x} i f c_{H T} (x_{g, s}) > c_{H T_m a x} \end{matrix} \\ {c_{H T_m i n} - c}_{H T} (x_{g, s}) i f c_{H T} (x_{g, s}) < c_{H T_m i n} \end{matrix}

ψ (x)

– penalty function;

U^{*}

- upper limit of the possible take-off weight; R – the penalty amplification parameter that matches the dimensions and orders of the penalty function and take-off weight values. The value of this parameter is selected expertly taking into account the take-off weight.

The result of block 3 is a vector of values of objective functions

W_{T O}^{+} (x_{g, s})

for each individual x_s in the population P_g (see Figure 3).

The use of the differential evolution method allows the calculation process

W_{T O}^{o u t}

(x_g,s) to be performed using parallel calculations (see Figure 3, blocks 3.1.s) using the Joblib library [59] in order to improve performance, since the vectors of the design variables of each individual do not depend on each other.

Blocks 4-7 are responsible for the process of generating new populations.

A new population P_g+1 of individuals x_g+1,s at each subsequent step of optimization is formed on the basis of the selection of the best individuals x_g,s from the previous populations P_g = {x_1, x _2,… x _{s, …} x _w}_g and crossover populations

P_{g}^{c r o s s}

= {u_1, u_{2, …} u_{s, …} u_w}_gwhich is obtained by crossing a population of P_g and a mutant population

P_{g}^{m u t}

= {v_1, v_2,…v_{s, …} v_w}_g.

Block 4 – Mutation

A population

P_{g}^{m u t}

includes mutated vectors of individuals

P_{g}^{m u t}

= {v_1, v_2,…v_{s, …} v_w}_g, each of which is calculated by the formula:

v_{s} = x_{s} + F_{s} (x_{p b e s t} - x_{s}) + F_{s} (x_{r 1} - x_{r 2})

(8)

Where:

x_{p b e s t}

– a randomly selected vector from the group of the best vectors of the population P_g. The group of best vectors is formed according to the principle of the minimum value of the objective function

W_{T O}^{+} (x_{g, s})

, and the size of the group of best vectors is determined by the settings of the algorithm [47].

x_{r 1}

– a random vector from the population P_g, except

x_{s}

;

x_{r 2}

– a random vector from the combined population P_g and the archive of worst solutions A [47].

The value of the scaling factor F_s is determined by the algorithm settings [47].

Block 5 – Crossover

Vectors u_s = (u_1, u_2,… u_{i, …} u_n)_s of crossover population

P_{g}^{c r o s s}

= {u_1, u_{2, …} u_{s, …} u_w}_gis formed by crossing the values of mutant vectors v_s =(v_1, v_2,…v_{i, …} v_n)_s of mutant populations

P_{g}^{m u t}

= {v_1, v_2,…v_{s, …} v_w}_gand vectors x_s = (x_1, x _2,… x _{i, …} x_n)_s of the current population P_g = {x_1, x _2,… x _{s, …} x _w}_g.

Crossing is carried out randomly according to the condition:

u_{i, s} = \{\begin{matrix} v_{i, s} i f U [0,1] \leq {C R}_{s} o r i = i_{r a n d} \\ x_{i, s} i f o t h e r w i s e \end{matrix}

(9)

{C R}_{s}

– the value of the crossover speed;

U [0,1]

– random number range.

In the event that after the mutation and crossover operations, the new values of the design variables of any individual go beyond the range of variables, they will be reassigned according to the condition:

u_{i} = \{\begin{matrix} \min (x_{i}) i f u_{i} < \min (x_{i}) \\ ma x (x_{i}) i f u_{i} > ma x (x_{i}) \end{matrix}

(10)

Block 6 – Selection of individuals and the formation of new population

The values of the objective functions

W_{T O}^{+} (u_{g, s})

of the crossover vectors u_s are calculated using block 3 (see Figure 2) and their values are compared with the values of the objective functions

{W_{T O}^{+} (x}_{g, s})

of the vectors x_s of the current population P_g. The selection of individuals of the new population P_g+1 for the next optimization step is carried out according to the condition:

x_{g + 1, s} = \{\begin{matrix} u_{g, s} i f W_{T O}^{+} (u_{g, s}) \leq W_{T O}^{+} (x_{g, s}) \\ x_{g, s} i f o t h e r w i s e \end{matrix}

(11)

Accordingly, the values of the objective functions, penalty functions, and input values of the take-off weight of each individual will be obtained for the new population according to the following conditions:

W_{T O}^{o u t} (x_{g + 1, s}) = \{\begin{matrix} W_{T O}^{o u t} (u_{g, s}) i f W_{T O}^{+} (u_{g, s}) \leq W_{T O}^{+} (x_{g, s}) \\ W_{T O}^{o u t} (x_{g, s}) i f o t h e r w i s e \end{matrix}

(12)

W_{T O}^{+} (x_{g + 1, s}) = \{\begin{matrix} W_{T O}^{+} (u_{g, s}) i f W_{T O}^{+} (u_{g, s}) \leq W_{T O}^{+} (x_{g, s}) \\ W_{T O}^{+} (x_{g, s}) i f o t h e r w i s e \end{matrix}

(13)

ψ (x_{g + 1, s}) = \{\begin{matrix} ψ (u_{g, s}) i f W_{T O}^{+} (u_{g, s}) \leq W_{T O}^{+} (x_{g, s}) \\ ψ (x_{g, s}) i f o t h e r w i s e \end{matrix}

(14)

At this stage, an archive of the worst individuals is also formed, which are used for mutation in subsequent optimization iterations:

A_{g + 1} A + x_{g, s} i f W_{T O}^{+} (u_{g, s}) \leq W_{T O}^{+} (x_{g, s})

In this case, a set of vectors of individuals is formed, the value of the penalty function of which is equal to zero ψ = 0 according to the following condition:

{Mxf}_{g} = Ø + x_{g + 1, s} i f ψ (x_{g + 1, s}) = 0

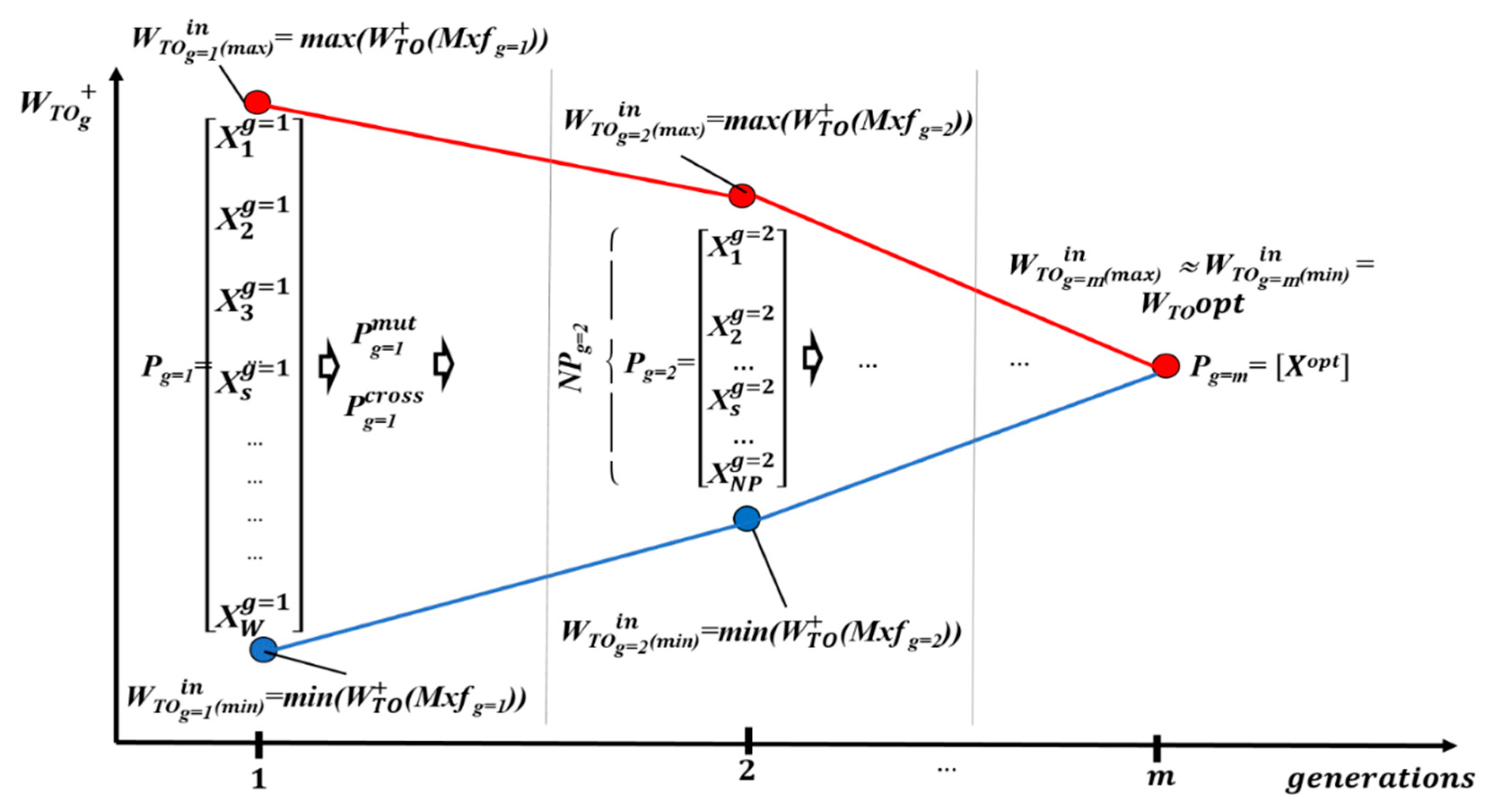
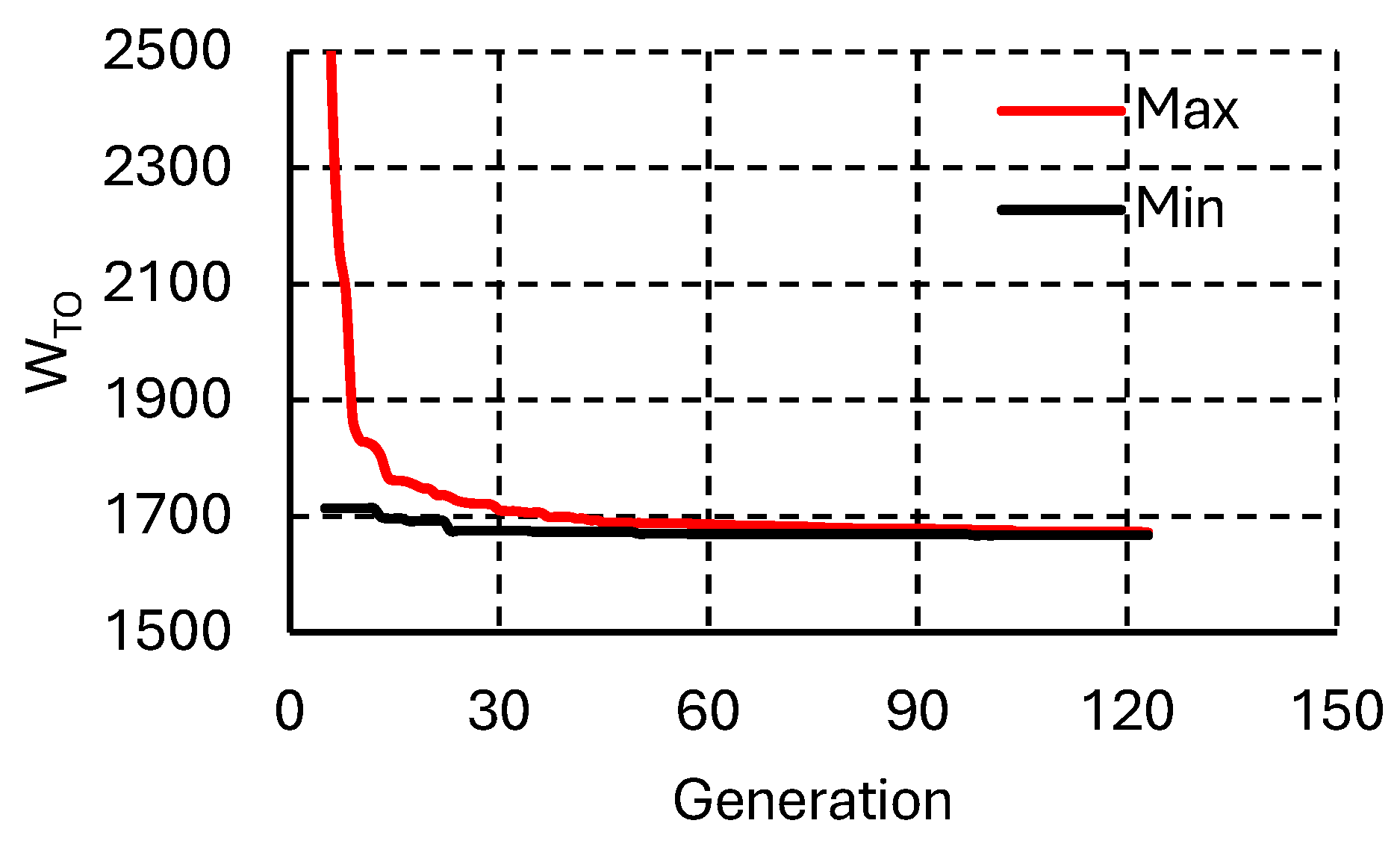
Block 7 – Population reduction and convergence of the sizing equation

The convergence of the sizing equation is ensured by narrowing the range of values [

W_{T O}^{i n}

_(min)...

W_{T O}^{i n}

_(max)] at each subsequent optimization step according to the condition:

W_{T O g + 1}^{i n} \min ({Mxf}_{g})

W_{T O g + 1}^{i n} \max ({Mxf}_{g})

That is, new boundaries [

W_{T O g + 1}^{i n}

_(min)...

W_{T O g + 1}^{i n}

_(max)] for the next generation are determined by the most successful individuals (ψ = 0).

If the set of individuals with ψ = 0 at the previous optimization step is empty Mxf_g = ∅ (that is, all

ψ (x_{g, s})

>0), then the new range of values [

W_{T O}^{i n}

_(min)...

W_{T O}^{i n}

_(max)] remains the same as in the previous generation:

{W_{T O g + 1}^{i n}}_{(\min)} = W_{T O g}^{i n} \min

{W_{T O g + 1}^{i n}}_{(\max)} = W_{T O g}^{i n} \max

At each optimization step, the population size is reduced by excluding the worst individuals with the highest values of the objective function

W_{T O}^{+}

(ψ >> 0). The population size of the next generation is defined by an exponential population size reduction method:

{N P}_{g + 1} = r o u n d [{N P}_{0} {(\frac{{N P}_{m i n}}{{N P}_{0}})}^{\frac{N F E}{{N F E}_{m a x}}}]

(15)

where: NP_min – the minimum population, NP₀ – the initial population, NFE_max – the maximum number of evaluated functions, NFE is the current number of evaluated functions. The NP_g+1 individuals with the best fitness are selected..

If the size of the new population is greater than the number of individuals with ψ = 0, then the population will be supplemented by individuals with the lowest values of the objective function of those with ψ ≠ 0.

The input value of the take-off weight of the next approximation

W_{T O g + 1, s}^{i n}

for any individual is a product of the mutation and crossing process of population at the previous step. If these actions result in the input take-off weight value

W_{T O g + 1, s}^{i n}

of an individual of the new generation going beyond the boundary of the new value range [

W_{T O g + 1}^{i n}

_(min)…

W_{T O g + 1}^{i n}

_(max)], then this individual will be reassigned a boundary value from this range.

Therefore, individuals with ψ ≠ 0 will be gradually eliminated in accordance with the process of population reduction, and the boundaries [

W_{T O}^{i n}

_(min)...

W_{T O}^{i n}

_(max)] will narrow until the convergence of the sizing equation

W_{T O}^{i n}

_≈

W_{T O}^{o u t}

W_{T O}^{+}

together with the convergence of the overall optimization process max

(W_{T O}^{+} (P_{g + 1}))

- min

(W_{T O}^{+} (P_{g + 1})) \leq ε

The convergence of objective function when solving the sizing equation is shown schematically in Figure 4.

Block 8

Evaluation the convergence condition max

(W_{T O}^{+} (P_{g + 1}))

- min

(W_{T O}^{+} (P_{g + 1})) \leq ε

. If this condition is not met, blocks of algorithm 3-7 are executed until it converges.

Block 9

Selects the best individual from the final population

x^{o p t}

and the corresponding value of the objective function

W_{T O}^{+}

(

x^{o p t}

) (as a result,

W_{T O}^{+}

(

x^{o p t}

) =

{W_{T O}^{o u t}}^{o p t}

). In addition, the result of the algorithm is other output values that are important for comparing the result with alternative solutions and for carrying out further design stages, including the weights of UAV parts, the value of its take-off weight, flight technical, energy, aerodynamic characteristics and appearance (see Figure 2, blocks 9.1-9.2).

The pseudocode of the algorithm (see Figure 2) is presented in Appendix A.

The algorithm for calculating the output (refined) take-off weight

W_{T O}^{o u t}

(x_g,s) (see Figure 3, blocks 3.1.s) is one of the cycles of the general optimization algorithm and is presented in more detail in Figure 5:

Blockm1 – receives as input the initial data from Block 1 and the vector of the design variables of the individual х_g,s on the generation g, which also includes the initial approximation (input value) of the take-off weight

W_{T O g, s}^{i n}

Blockm2 is used to calculate the absolute geometric characteristics of the aircraft based on the input value of the take-off weight

W_{T O g, s}^{i n}

and the specific load on the lift surface (W/S)_g,s, the value of which is in the vector of the design variables of the considered individual х_g,s.

Geometric characteristics are used in the algorithm to:

- automated generation of three-dimensional geometric models of UAVs;

- generation of numerical models for calculating the aerodynamic characteristics of UAVs;

- application of engineering formulas for aerodynamics, taking into account compressibility and viscous friction;

- calculation of the weight of the UAV airframe structure.

Blockm3 – calculates the aerodynamic characteristics of the UAV in order to determine the lift-to-drag ratio.

Unitm4 – checks the balancing condition of the UAV in the vertical plane.

Blockm5 – implements the process of balancing the UAV by selecting the angle of attack α and the incidence angle δ₂ of the balancing surface, taking into account the specified static margin of longitudinal stability.

Blockm6 – calculates the required power characteristics of the power plants and the required amount of energy carrier at all stages of the flight.

Blockm7 – calculates the weights of the main parts of the UAV.

Blockm8 – calculates the output take-off weight

W_{T O}^{o u t} (x_{g, s})

using the sizing equation (16) based on the values of the parameters x_i and the input take-off weight value

W_{T O g, s}^{i n}

Calculation of the weights of aircraft parts

Taking into account the features of the optimization algorithm, the take-off weight is calculated using formula (16) for each individual x_g,s of the current generation g.

W_{T O}^{o u t} (x_{g, s}) = \frac{W_{p a y}}{1 - (\frac{W_{p o w}}{W_{T O}}) - (\frac{W_{f u e l}}{W_{T O}}) - (\frac{W_{s t r u c t}}{W_{T O}}) - (\frac{W_{e q u i p}}{W_{T O}})}

(16)

where:

W_{p a y}

– payload;

(\frac{W_{p o w}}{W_{T O}})

– relative weight of the power plants;

(\frac{W_{f u e l}}{W_{T O}})

– relative weight of fuel (or

(\frac{W_{b a t}}{W_{T O}})

– relative weight of batteries in the case of an electric power plants);

(\frac{W_{s t r u c t}}{W_{T O}})

– relative weight of structure;

(\frac{W_{e q u i p}}{W_{T O}})

– relative weight of equipment and control.

1.: Weight of energy carrier

In the case of the use of an internal combustion engine UAV (or other type of fuel engine), the relative weight of the fuel is determined by the formula:

(\frac{W_{f u e l}}{W_{T O}}) = (\frac{P}{W_{T O}}) C t

(17)

where:

(\frac{P}{W_{T O}})

– power-to-weight ratio [kW/daN]; C – specific fuel consumption [kg/(kW.h)]; t – the flight endurance [h].

In the case of using an electric motor UAV, the relative weight of the batteries will be equal to:

\frac{W_{b a t}}{W_{T O}} = \frac{g (\frac{P}{W_{T O}}) t}{E η_{p o w} S o c}

(18)

where:

η_{p o w}

– efficiency of the power plants; SoC – the state of charge of the battery; E – the specific energy capacity of the battery [kg/(kW.h)]; g – the acceleration of gravity [m/s²].

2.: The weight of the power plants

The weight of the power plants includes the weight of the propellers and the engine with performance support systems – a fuel system for the internal combustion engine and controllers of electric motors in the case of their use as a power unit. The relative weight of the engine is calculated according to the formula:

(\frac{W_{p o w}}{W_{T O}}) = k (\frac{P}{W_{T O}}) γ

(19)

where: k – coefficient takes into account the increase in the weight of the power plants due to the systems;

γ

– the specific weight of the engine.

3.: Weight of structure and on-board equipment

The weight of the UAV airframe structure, which includes the weights of the wing, tail, fuselage, landing gear, as well as the weight of the onboard equipment, is determined using weight formulas presented in the specialized literature [2,4,6,7,8].

The values included in the denominator in (16) directly or indirectly depend on the take-off weight and vice versa. Equation (16) is solved by successive approximations: it requires the value of the take-off weight of the initial approximation

W_{T O}^{i n}

as an input and gives a refined value

W_{T O}^{o u t}

at the output. The convergence of the solution (16) is achieved with a given accuracy

W_{T O}^{i n}

_≈

W_{T O}^{o u t}

. The process of convergence of the sizing equation is organized in the general optimization cycle and is described in detail above.

The pseudocode of the take-off weight calculation algorithm is presented in Appendix B.

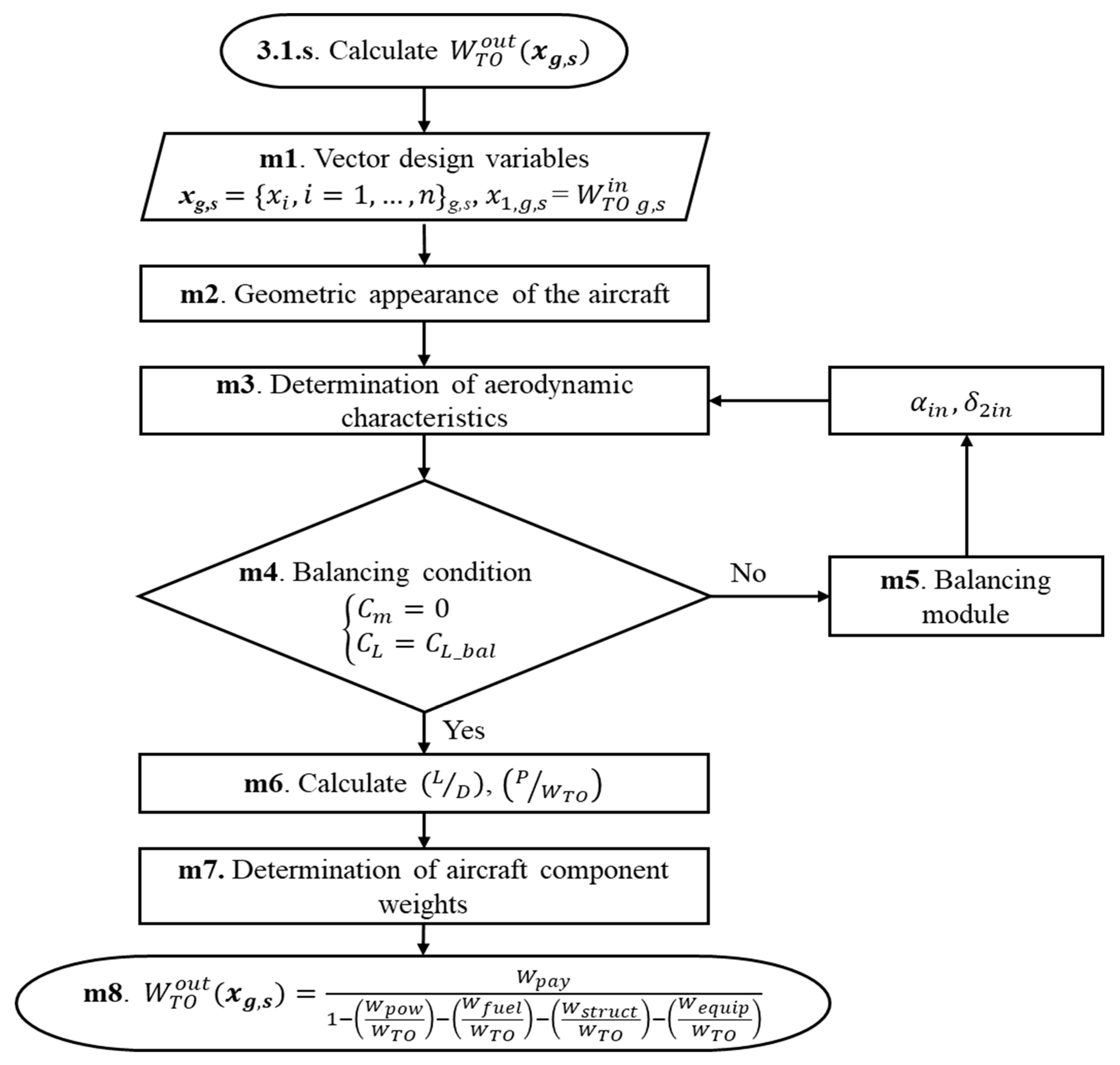
Geometric characteristics (see Figure 5, Block m2)

The geometric characteristics of each individual of the current generation x_g,s (see Figure 5, Block m2) are calculated on the basis of the input value of the take-off weight

W_{T O g, s}^{i n}

, the lift system loading (W/S)_g,s and other relative geometric parameters from the vector of the individual x_g,s generated by the optimization cycle.

The total area of the lift surfaces of the UAV S_Σ is determined by the formula:

S_{\sum} = \frac{W_{T O}}{(W / S)}

(20)

where: W_TO – take-off weight [kg];

W / S

– the lift system loading [daN/m²].

The remaining absolute geometric characteristics of each lift surface are found by the relationships:

S_{\sum} = S_{1} + S_{2}

(21)

b_{j} = \sqrt{{A R}_{j} S_{j}}

(22)

c_{t j} = \frac{2 S_{j}}{b_{j} (1 + λ_{j})}

(23)

c_{r j} = \frac{c_{t j}}{λ_{j}}

(24)

\bar{c} = \frac{2}{3} c_{r} \frac{1 + λ + λ^{2}}{1 + λ}

(25)

where: S₁ – the area of the forward lift surface [m²]; S₂ – the area of the aftward lift surface [m²]; b – the span [m];

A R

– aspect ratio; j – the index (j = 1 or 2); c_r – root chord [m]; c_t – tip chord [m];

λ

– taper ratio;

\bar{c}

– the mean aerodynamic chord [m]. The geometric twist

τ

is determined by the law of distribution of the incidence angles of the flow sections of the wing.

The geometry of the fuselage is described by relative and absolute parameters: fuselage aspect ratio

{A R}_{f}

; aspect ratio of the nose and tail fuselage

{A R}_{n}

{A R}_{t}

; equivalent mid-section diameter

d_{m f}^{э}

, loading on mid-section (W/S)_mf.

The scientific novelty of the proposed method is the use of geometric parameters

S_{\sum}

and

\bar{S_{2}}

S_{2} / S_{1}

, which allow considering aerodynamic configurations of one or two lift surfaces without dividing them into a normal, a duck, a tandem or a flying-wing. The value

\bar{S_{2}}

is a variable parameter during optimization. In the case

\bar{S_{2}}

< 1, UAV has a normal configuration, in the case

\bar{S_{2}}

> 1 – duck configuration, if

\bar{S_{2}}

~ 1 – tandem and

\bar{S_{2}}

= 0 – this is the flying-wing or tailless configuration.

In this case, the main lift surface is distinguished: the forward if

S_{1}

S_{2}

and otherwise, the aftward if

S_{1} <

S_{2}

. Normalization of aerodynamic coefficients and relative geometric characteristics is carried out relative to the mean aerodynamic chord of the main surface.

Calculation of the aerodynamic characteristics of the UAV (see Figure 5, Block m3)

The calculation of the aerodynamic characteristics of the UAV (see Figure 5, Block m3) is carried out for the aerodynamic configuration of the UAV obtained for each individual x_g,s. Determination of the main properties and the inductive component of drag is carried out using the method VLM [60,61,62] using open software AVL [57] in conjunction with Python, and taking into account the compressibility and calculating the viscous friction forces is carried out on the basis of engineering methods.

Pseudocode for creating a calculation file for AVL and determining aerodynamic characteristics is presented in Appendix C.

The main problem of the aerodynamics model used is to determine the lift-to-drag ratio at each of the stages of flight in order to assess the required energy characteristics of the power plants and the amount of energy carrier, determined by the required power-to-weight ratio at various stages of flight (26).

The lift-to-drag ratio, which determines the energy costs at each stage of flight, is determined by the ratio of the lift coefficient C_L and drag coefficient C_D corresponding to this flight mode.

The energy balance is provided at each of the stages of flight by the expression:

(\frac{P}{W_{T O}}) = \frac{V}{η_{v i n t}} \frac{\frac{L}{D} s i n γ + c o s γ}{s i n α + \frac{L}{D} c o s α}

(26)

where:

γ

– flight path angle [^o]; α - angle of attack [^o];

\frac{L}{D}

– lift-to-drag ratio; V – flight speed [m/s];

η_{v i n t}

– efficiency of the propeller.

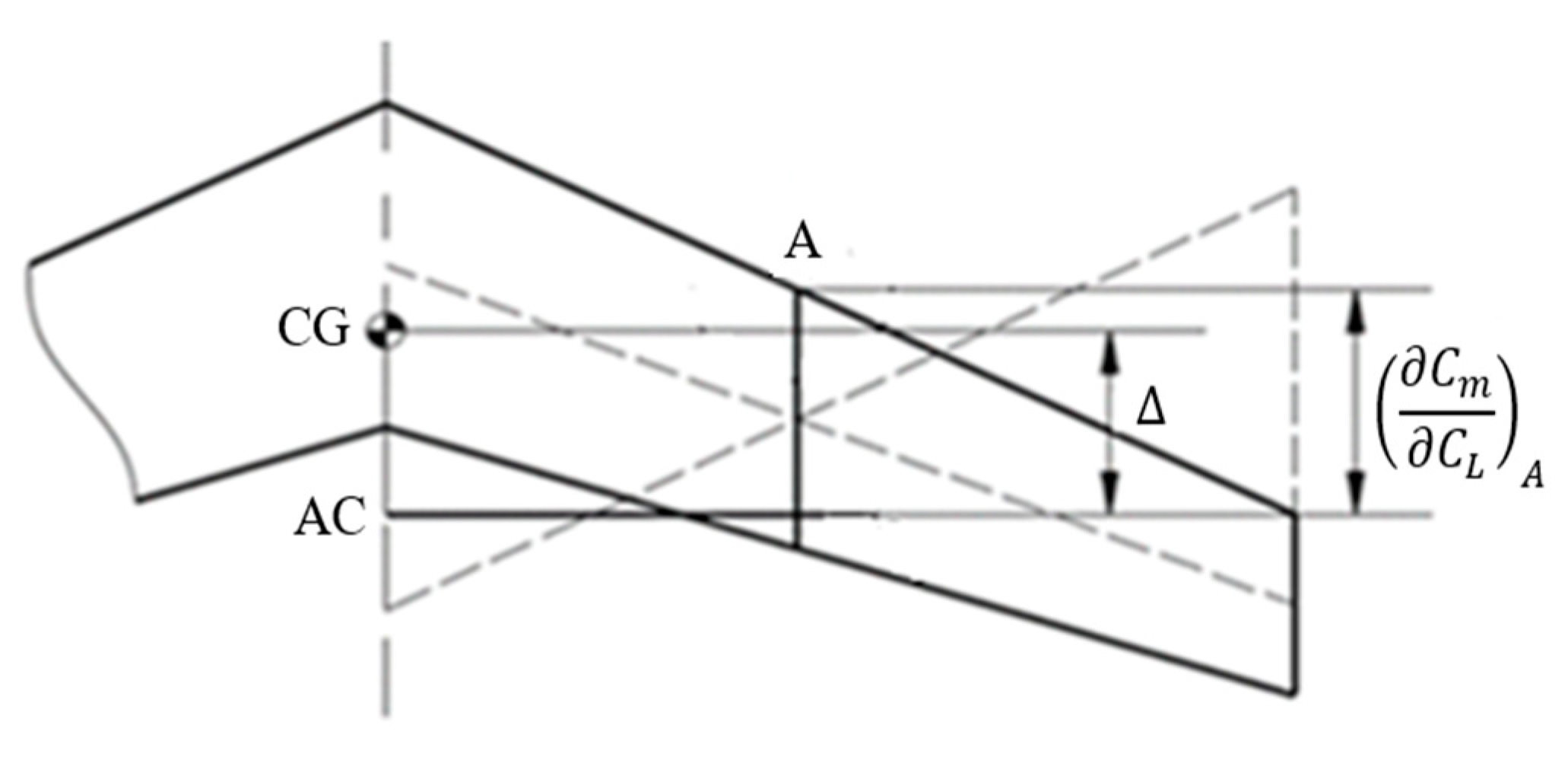
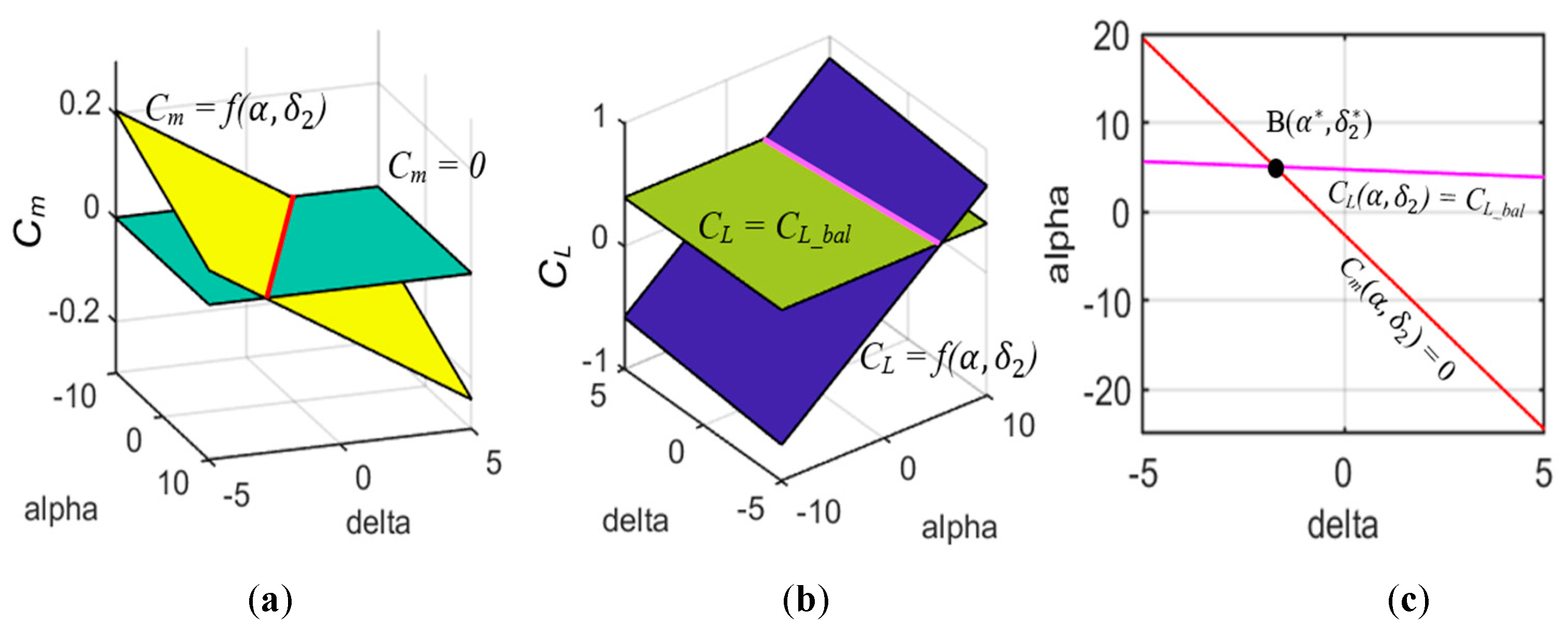
UAV balancing (see Figure 5, Block m4)

Determination of the lift-to-drag ratio and required energy characteristics of the UAV is carried out when the UAV equilibrium is ensured in the vertical plane, that is, the condition is met:

\{\begin{matrix} M = 0 (a) \\ L = L_{b a l} (b) \\ D = T c o s + W s i n γ (c) \end{matrix}

(27)

where: M – the pitch moment relative to the centre mass; L – lift force;

L_{b a l}

– lift required for equilibrium along the axis z_w of the wind coordinate frame; D – drag force and T – the thrust of the power plants; W – the weight of the UAV.

Condition (27) is fulfilled at the expense of (26). The values of forces and moments in equations (27a) and (27b) are more conveniently converted into coefficients.

The value of the lift coefficient

C_{L_b a l}

required to ensure equilibrium on the axis z_w is determined by the formula:

C_{L_b a l} = \frac{g (W / S) c o s γ}{\frac{1}{2} ρ V^{2}}

(28)

where: g – the acceleration of gravity [m/s²];

\frac{W}{S}

– the lift system loading [kg/m²];

γ

– flight path angle [^o];

ρ

– air density [kg/m³]; V – the flight speed [m/s].

The lift coefficient

C_{L}

of the aircraft depends on the angle of attack and the angular location of the lift surfaces relative to each other, and the coefficient of pitch moment relative to the center mass also depends on the selected static margin of longitudinal stability.

The equilibrium problem (27) is an optimization problem to ensure equations (27a) and (27b) with two variables:

\{\begin{matrix} C_{m} (α, δ_{2}) = 0 (а) \\ C_{L} (α, δ_{2}) - C_{L_b a l} = 0 (b) \end{matrix}

(29)

where: α - angle of attack [^o];

δ_{2}

– the incidence angle of the balancing aerodynamic surface [^o].

The aerodynamic models used determine the linear characteristic of the dependencies in (29), so it is proposed to use the following algorithm with the wide use of analytical methods in order to increase the speed of solving this problem:

- Calculation of the characteristics

C_{L}

and

C_{m A}

by numerical method VLM in the AVL software regarding the leading edge of mean aerolynamic chord of the main lift surface for two different combinations α and

δ_{2}

;

- Based on the data obtained, a linear approximation of the analytical dependencies

С_{L} (α, δ_{2})

\frac{\partial C_{L}}{\partial α} (α - α_{0} + δ_{2})

and

C_{m A} (α, δ_{2})

C_{m 0} + {(\frac{\partial C_{m}}{\partial C_{L}})}_{A} С_{L} (α, δ_{2})

is performed;

- The position of the aerodynamic focus is calculated by the angle of attack relative to the leading edge of mean aerolynamic chord of the main lift surface

x_{A C}^{α} = - \frac{\partial C_{m}}{\partial C_{L}}

and the required position of the center mass is calculated, which will provide a given static margin of longitudinal stability:

{\bar{x}}_{A C} + ({\bar{x}}_{C G} - {\bar{x}}_{A C})

, where

({\bar{x}}_{C G} - {\bar{x}}_{A C})

= Δ - the required static margin of longitudinal stability;

- the dependence is recalculated

C_{m_C G} (α, δ_{2})

relative to the required position of the center mass (see Figure 6):

C_{m_{C G}} = C_{m 0} + C_{L} = C_{m 0} + \frac{C_{m A} - C_{m 0}}{{(\frac{\partial C_{m}}{\partial C_{L}})}_{A}} \cdot Δ

(30)

- analytical expressions of two lines obtained by the intersection of plane

C_{L} = C_{L} (α, δ_{2})

with plane

C_{L} = C_{L_b a l}

and plane

C_{m_C G} = C_{m_C G} (α, δ_{2})

with plane

C_{m_C G}

= 0 are found, solutions (29a) and (29b) are found independently of each other (see Figure 7);

- the solution of the problem (27) is analytically calculated, which is the point B = (

α^{*}, δ_{2}^{*}

) of the intersection of two lines

C_{L} (α, δ_{2}) = C_{L_b a l}

and

C_{m_C G} (α, δ_{2}) = 0

(see Figure 7).

- Values

C_{L} (α^{*}, δ_{2}^{*})

and

C_{m_C G} (α^{*}, δ_{2}^{*})

are also calculated based on the models of the method VLM in the AVL software to verify the balancing conditions.

The pseudocode of the algorithm is presented in Appendix D.

and

δ_{2}

; (b) Dependence of C_L from

α

and

δ_{2}

; (c) Solution of the condition UAV balancing.

2.4. Visualization of Optimization Results in the Form of a Planned Projection of the Optimal Option and Its Three-Dimensional Model

After the optimization cycle is completed, a file *.xlsx containing all the geometric parameters of the last generation is saved.

At the end of the main optimization program, an additional module is added to run the FreeCAD program [63]. Through a Python subprocess package.

3D models are built using macro files written in Python. This macro file creates a 3D model based on the geometric parameters contained in the *.xlsx file, saves the model image in .png format, closes the FreeCAD program after the task is completed, and places it in the FreeCAD installation folder. With the “run macro on startup” feature, FreeCAD automatically runs the macro file and the whole process happens in the background on the system.

2.5. Selection of the Wing Airfoil with Multilayer Perceptron

Returning to the

C_{L}^{*}

condition used for the optimization of the prototypes. The selection of the wing airfoil of the aircraft is mathematically defined as:

f ({x'}^{o p t}) \geq f (x^{'}) = \frac{C_{l}^{1.5}}{C_{d}} \forall x' \in Ω_{1},

Ω_{1} = \{x^{'} : C_{l}^{*} (x^{'}) - C_{l} \geq 0, y_{t} (x^{'}) - y_{t, m i n} \geq 0\}

(31)

where C_l and C_d are the lift and drag coefficients of the profile;

C_{l}^{*}

is the maximum permissible lift coefficient for the given flight condition (

C_{l}^{*}

C_{L}^{*}

); y_t is the maximum thickness of the profile; y_t,min is the minimum allowable value of y_t;

x^{'}

is the vector of design parameters. The objective function of maximizing the

\frac{C_{l}^{1.5}}{C_{d}}

parameter was selected in order to improve the endurance of the aircraft [64].

For the resolution of this optimization problem, the same optimization algorithm described in the previous section was used, only adapting it for this optimization task. The design parameters are determined by the Bezier-PARSEC (BP) parameters [65]. The parameters used to create the profiles are the following: r_le – radius of the leading edge; α_te – angle of the camber line at the trailing edge; β_te – angle of the thickness line at the trailing edge; z_te – vertical displacement of the trailing edge; γ_le – angle of the camber line at the leading edge; (x_c, y_c) – position of the maximum value of the camber line; k_c – curvature at the maximum point of the thickness line; (x_t, y_t) – position of the maximum value of the thickness line; k_t – curvature at the maximum point of the thickness line; dz_te – half the thickness of the trailing edge; α is added to these parameters, which is the angle of attack of the airfoil.

Figure 8. BP parameters and Bezier reference points for: (a) thickness line; (b) camber line.

To determine the aerodynamic coefficients of the profile, a multilayer perceptron (MLP) was used. The MLP is in charge of performing a non-linear mapping of the vector that indicates the aerodynamic coefficients and the design parameters (the BP parameters and the angle of attack) [66]. The MLP used has the following architecture: an input layer with 13 neurons, an output layer with two neurons, and 6 hidden layers (256, 128, 64, 32, 16, 8 neurons, respectively) [40]. The input and output values were normalized with values between 0 and 1, for a better training. The hidden layers have as activation function the RELU function, while the output layer has the sigmoid function. For the training the ADAM optimizer was used and the loss function was the mean square error (MSE). The database used for MLP training was created from tests carried out in XFOIL.

3. Assessment of the Reliability of Models and Methods

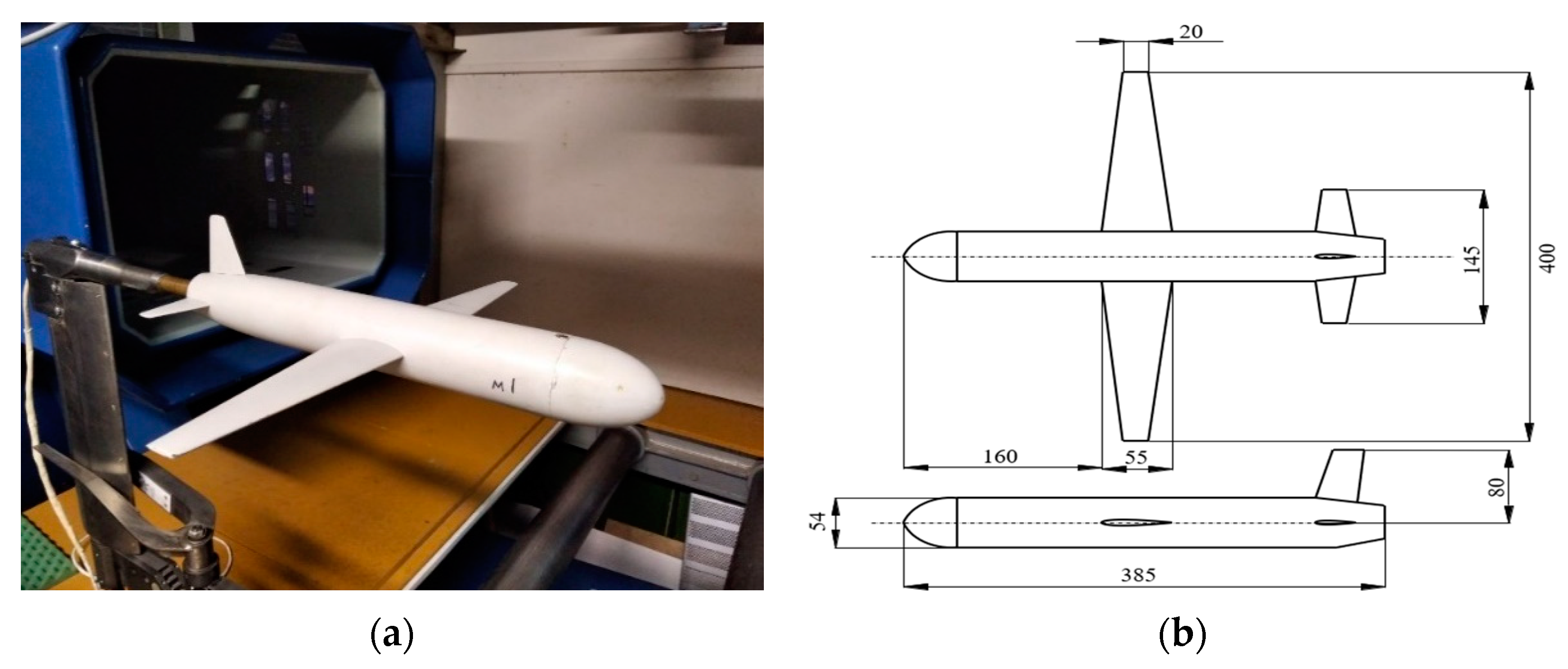
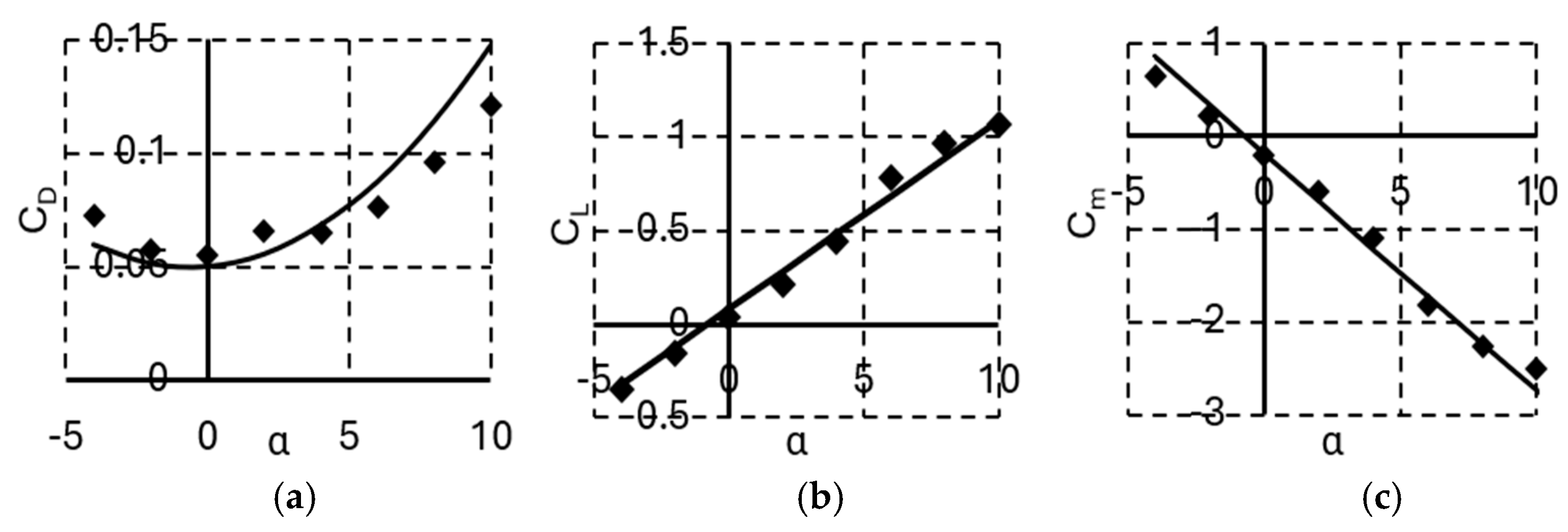
3.1. Validation of Mathematical Models of Aerodynamics

The aerodynamic characteristics of the UAV according to the specified parameters are calculated based on the method VLM with the connection of AVL software in combination with the formulas of engineering methods on the Python platform. Validation of the obtained calculation results was carried out on the basis of comparison with experimental data obtained in the T-3 wind tunnel of Samara University by the weight method. A description of the experimental setup is presented in [67,68]. The object of the study is a model with geometric characteristics presented in Figure 9.

For validation, the integral aerodynamic coefficients C_D, C_L, C_m depending on the angle of attack were considered.

Figure 10 present the results of a comparison of experimental data and calculation results.

The validation results showed a good correspondence between the calculation results using the mathematical models and experimental data. The coefficient of variation in the deviation of data on the coefficients C_D, C_L and C_m was 6.8%, 6.1%, and 7.3%, respectively.

3.2. Validation of Models and Algorithm for Calculating the Objective Function

To assess the reliability of the calculation of the objective function and the characteristics obtained from the results of the take-off weight calculation cycle, the calculation of the main characteristics of existing UAVs with known data was carried out using the proposed models: U-40 [43] and MQ-1 [44]. Both UAVs are equipped with Rotax 914 engines. Some characteristics of these devices (geometric, kinematic, specific energy) used in the calculations are given in Table 1.

The convergence of the solution of the sizing equation in the proposed conceptual design methodology is provided in the general optimization cycle. Therefore, to solve the sizing equation in a direct one-time calculation of the objective function with the initial data from Table 1, Table 2 and Table 4, a regular iterative cycle is used. The stages of the flight are considered: take-off, climb, cruise, descent and landing. Taking into account the balancing of the UAV in the vertical plane in all flight modes.

Table 1 shows the results of calculating the objective function - take-off weight, as well as empty UAV weight, fuel weight, engine weight and their maximum power. Similar characteristics of existing considered UAVs [43,44] are also given in Table 1, 4 for comparison with the results of calculations.

The difference in the results of calculating the take-off weight, as well as the weights of the main parts of the two existing UAVs according to the proposed methodology, did not exceed 3-4%. The estimated required power of the power plants and the actual maximum power of the UAV power plants are in the range of 4-5%. The comparison results from Table 1 allow to assess the accuracy of the calculation the main characteristics of the UAV using the proposed methodology, as sufficient for design.

4. Solving Applied Optimization Problems

Using the proposed optimization methodology, the solution of problems for possible improvement of the characteristics of two existing UAVs U-40 and MQ-1 by optimizing a number of their main parameters is considered.

These examples use the general statement of problem (1) presented in Section 2 and use functional constraints (2)-(5).

The objective function is the take-off weight

W_{T O}

A number of values used as initial data are taken from Table 1, Table 2 and Table 4. Table 3 shows some of the optimization algorithm settings.

Table 3. Some optimization algorithm settings.

Parameters	Value
Lift coefficient constraint (C_L)	< 0.6
Constraint of the horizontal tail volume coefficient (c_HT)	[0.2…0.6]
Initial value of penalty (U*) [kg]	60000
Optimization stopping criterion: max $(W_{T O}^{+} (P_{g + 1}))$ - min $(W_{T O}^{+} (P_{g + 1})) \leq ε$	1
Number of design variables (D)	12
Number of initial population (NP0)	10D
Minimum number of generations	12

Table 4. Results of optimization of UAV U-40 and MQ-1 parameters.

	Parameters	Optimization
		Min value	Max value	Optimal value		Initial values
		Min value	Max value	U-40	MQ-1	U-40	MQ-1
1	${A R}_{1}$	4	20	14	7.6	20	19
2	$Λ_{1}$ [o]	0	25	2.7	0	1	7.22
3	$λ_{1}$	0.3	1	0.53	0.34	0.33	0.36
4	$δ_{1}$ [o]	0	5	2.5	0	2,5	2.5
5	${A R}_{2}$	4	20	4	18.7	20	6.75
6	$Λ_{2}$ [o]	0	25	0	3	1	0
7	$λ_{2}$	0.3	1	0.63	0.62	0.33	1
8	$δ_{2}$ [o]	-10	+10	-2.2	-2.0	2.2	-2.62
9	${\bar{L}}_{2}$	3	8	5.1	4.6	5.55	4.37
10	${\bar{S}}_{2}$	0.2	5	0.2	4.9	1	0.26
11	α [o]	-10	+10	2.8	5.2	-	-
12	V [m/s]	40	90	50	45	55	47
13	W/S [kg/m2]	20	110	92	75	90	73.2
14	WTO [kg]	500	3000	1687	914	2000	1020

The number of individuals of the initial population was 120.

The convergence of the optimization was achieved after 123 generations and spent 62 minutes on a computer with Windows 10, an Intel(R) Core i7-6700 processor @ 3.40 GHz, 64 GB of RAM. The number of the last generation was 22 individuals. Figure 11 shows the convergence of take-off weight calculation during the optimization process using the algorithm used.

Table 4 shows the results of the parameters optimization. For a visual assessment of the improvements in the characteristics obtained as a result of optimization, the initial characteristics of the considered aircrafts are entered in Table 4.

Table 5. Results of calculating the weight of components and aerodynamic characteristics of the UAV as a result of optimization.

Parameters		U-40					MQ-1
Parameters		Initial values	Optimal value		$ξ$ , %		Initial values		Optimal value		$ξ$ , %
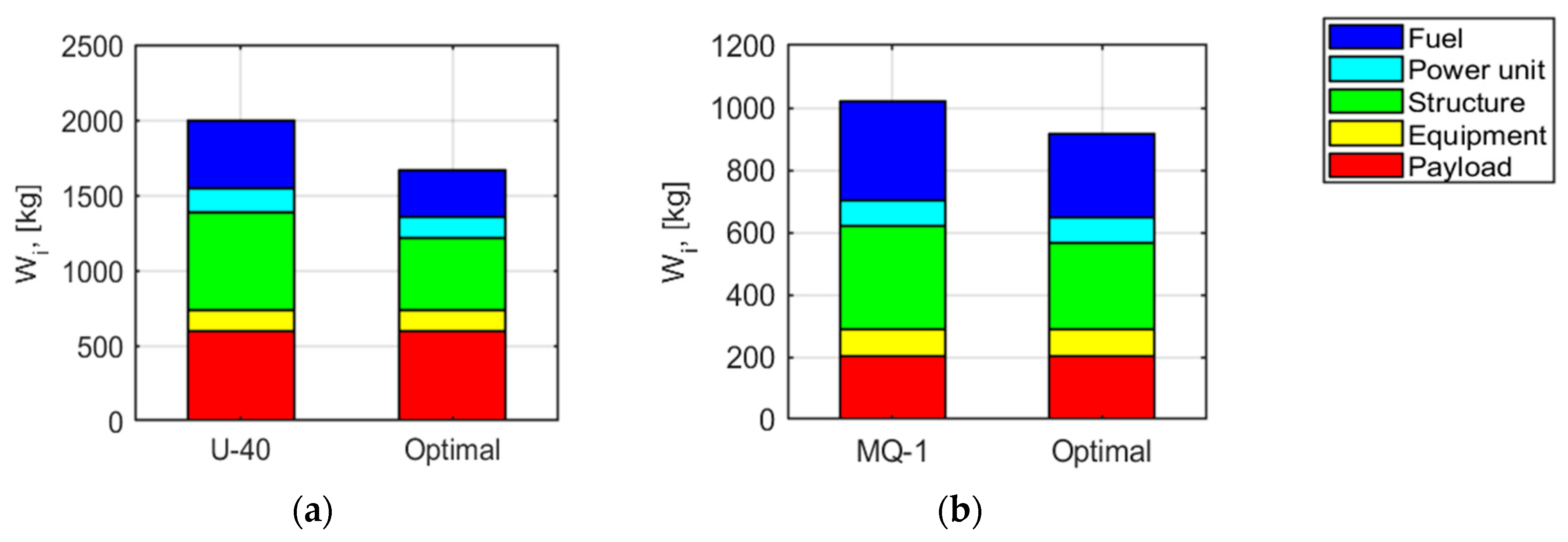
Take-off weight [kg]		2000	1667		16.7		1020		914		10.4
Payload [kg]		600	600		0		204		204		0
Equipment weight [kg]		n/a	137		-		n/a		84.1		-
Weights [kg]	forward lift surface	n/a		181.7		-		n/a		22.4		-
	aftward lift surface	n/a		25.2		-		n/a		123.4		-
	vertical tail	n/a		13.5		-		n/a		19.6		-
	fuselage	n/a		171.6		-		n/a		77.6		-
	landing gear	n/a		84.1		-		n/a		36.5		-
Engine weight [kg]		152	132		13.2		76		76		0
Fuel weight [kg]		450	313.5		30.3		302		266.6		11.7
Propeller weight [kg]		n/a	8.4		-		n/a		3.8		-

Table 5. cont.

Parameters	U-40			MQ-1
Parameters	Initial values	Optimal value	$ξ$ , %	Initial values	Optimal value	$ξ$ , %
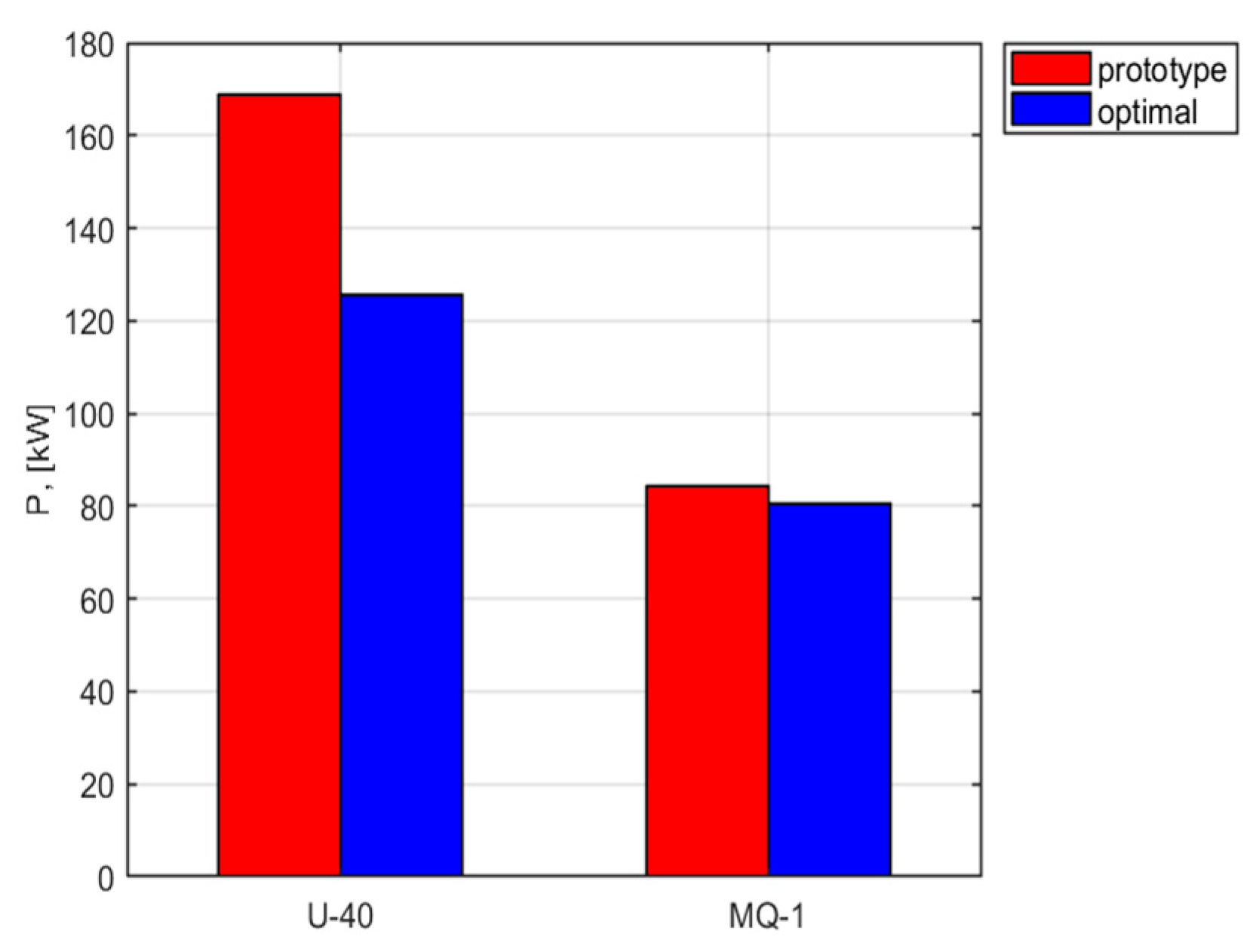
Engine power [kW]	2х84.5	2х62.9	25.6	1х84.5	1х80.6	4.6
Relative position of the center mass $({\bar{x}}_{C G} = \frac{x_{C G}}{M A C})$	n/a	0.54	-	n/a	-0.651	-
Cruise lift coefficient	n/a	0.59	-	n/a	0.59	-
Cruise lift-to-drag ratio	n/a	26	-	n/a	24.7	-

Figure 12 and Figure 13 show histograms of the weight distribution of the UAV main parts and a comparison of the required engine power before and after optimization.

Changes in the geometric parameters of the considered UAVs appearance as a result of optimization are shown in Figure 14, the appearance of the prototype is shown in red, and the appearance after optimization is shown in blue.

The figures are obtained automatically using the FreeCAD application, which is used in Batch mode to automatically render the general view of the last population of optimization individuals.

The following design constraints were taken to make the airfoil selection: C_l = 0.59, y_t,min = 11%. For the optimization process, NP₀ = 10*D (D = 11 because z_te and dz_te are kept constant), 100 generations and U* = 0.2 were considered. The ranges of each design parameter are shown in Table 6.

The optimization test was performed 2 times. The results are shown in Table 7 and Figure 15.

Each test required 72 seconds of computing time.

Table 5 shows that the result of optimization allowed to reduce the take-off weight of the considered UAVs and reduce the required power of the power plants.

The UAV U-40 was developed according to the aerodynamic configuration tandem. The results of optimizing its appearance showed that the proposed methodology makes it possible to perform parametric optimization not only of a specific aerodynamic layout, but also to partially solve the problems of circuit synthesis. The tandem configuration with an equal distribution of areas between the wings, all other things being equal, will have the lowest lift-to-drag ratio and the largest weight of the structure. This circumstance is due to the fact that the aftward wing in cruising flight mode (the main mode for long-range UAVs) is "underloaded": in the example considered at

{\bar{S}}_{2}

= 1, the forward wing creates 64% of the lift, and the aftward wing - 36%. Attempts to load the rear fender result in a normal or a duck configuration. The increase in the weight of the U-40 structure is also associated with the greater aspect ratio of both wings. The proposed algorithm redistributed the air load more rationally and reduced the solution to a normal configuration with the relative areas

{\bar{S}}_{2}

= 0.2. This solution allowed to slightly reduce the aspect ratio of the main wing and thereby reduce the weight of the wing structure and the UAV as a whole. Due to the increase in lift-to-drag ratio by 3.84% and a decrease in the take-off weight of the UAV by 16.7%, the required power of the power plants was reduced by 25.6%. This would allow the UAV U-40 to replace the existing engines of the power plants (Rotax 914) with less powerful ones, such as the Rotax 912, which would further reduce the weight of the power plants and the UAV as a whole.

The aerodynamic layout of the UAV MQ-1 was chosen by the developers more successfully, but the placement of the heavy power plants in the rear fuselage shifted the center mass back, which required the wing to be shifted back closer to the tail. In order to maintain the required coefficient of the horizontal tail volume coefficient, due to the reduction of the horizontal tail arm, its area was forced to be increased and the dynamic characteristics of the UAV in the longitudinal channel were worsened.

The proposed algorithm made it possible to obtain a different layout - a forward horizontal tail with a smaller area and a longer arm. The forward horizontal tail creates a positive lift and thus somewhat unloads the wing. Thus, the wing area has been reduced and the lift-to-drag ratio of the UAV has been increased. Taken together, this resulted in a 10.4% reduction in take-off weight and 4.6% in the required power of the power plants.

5. Conclusion

A methodology for optimizing the appearance of UAVs is proposed. The problem statement is presented in terms of nonlinear mathematical programming. Certain features of the methodology related to the conceptual design of the aircraft are considered on two real examples of heavy-class UAVs with fundamentally different aerodynamic configurations.

The main attention in the technique is paid to ensuring high accuracy in predicting the take-off weight of an aircraft. For this purpose, the method VLM used in aerodynamic calculations has been tested by our own full-scale experiment in a wind tunnel. The peculiarity of the proposed approach also lies in taking into account and ensuring longitudinal balancing in algorithm for determining the take-off weight. Integrally, the accuracy of the mathematical models, algorithms and programs used in the methodology was tested by a single calculation of the take-off weight, power-to-weight ratio and fuel weight of each of the considered UAVs according to their geometric characteristics. The discrepancy between the published main parameters and those obtained by the calculation is within the range of 3-4%.

Estimation of the accuracy of optimization algorithms in complex multidisciplinary technical problems deserves special consideration and, apparently, does not have any general methods, except for test functions, test models and specially designed problems with a known optimal solution.

The solution of the optimization take-off weight problems of two UAVs using 14 design variables with a given payload and flight endurance, characteristic of the U-40 and MQ-1, helping to significant reduce the take-off weight of these vehicles by making certain changes in appearance and geometric parameters. The obtained results can be considered as a test of the reliability and effectiveness of the methodology as a whole.

When developing the methodology, certain attention was paid to its speed. For this purpose, the optimization algorithm provides the possibility of parallel calculation of the take-off weight of each individual in the population and a one-time calculation of

W_{T O}

and several other measures. Particularly noteworthy are the results of a computational experiment, in which the current value of the objective function - take-off weight - was added to the number of design variables. According to preliminary studies, this measure speeds up the optimization process by approximately three times, obtaining an equivalent result when compared with the traditional method of convergence of the sizing equation at each optimization step. The analysis of the reasons for such acceleration is of certain scientific interest. Using these accelerations, the time to obtain a solution with 12 design variables is about one hour on a personal computer with an Intel(R) Core i7-6700 @ 3.40 GHz processor, 64 GB of RAM, which, taking into account the complexity of the multidisciplinary combinatorial problem, seems quite acceptable.

The development of a methodology and software for the conceptual design of UAVs with the achieved parameters of accuracy and speed can be considered as a certain step towards concurrent design technology.

The proposed methodology, based on the considered examples, showed the possibility of obtaining new competitive models of unmanned aviation technical or improving the characteristics of existing modifications in terms of the required energy of the power plants and the take-off weight of the device as a whole.

At the moment only the wing profile selection was made using neural networks in the future, it is intended that the proposed methodology makes use of neural networks to predict the aerodynamic characteristics of the aircraft in the balance problem and determine the lift-to-drag ratio instead of the mathematical models used to significantly increase the performance of the algorithm.

Author Contributions

Conceptualization, O.E.L.; methodology, O.E.L., V.H.H., E.I.K.; software, V.H.H., E.I.K. J.G.Q.P.; validation, V.H.H., O.E.L.; formal analysis, V.H.H.; investigation, O.E.L.; resources, O.E.L., E.I.K.; data curation, V.H.H., J.G.Q.P.; writing—original draft preparation, V.H.H., O.E.L.; writing—review and editing, O.E.L. V.H.H., E.I.K. J.G.Q.P.; visualization, O.E.L., V.H.H.; supervision, E.I.K.; project administration, O.E.L.; funding acquisition, O.E.L., E.I.K.. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Analytical Center for the Government of the Russian Federation (agreement identifier 000000D730324P540002, grant No 70-2023-001317 dated 28.12.2023).

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s O.E.L.

Acknowledgments

We would like to thank Prof. Valery Komarov for valuable discussions during the preparation of the manuscript.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Appendix A

Module 1: Optimization Algorithm.

1	// Initialization phase
2	Input design constants;
3	Input the interval of design variables [x_min, x_max];
4	Input optimization algorithm parameters G, NP, NP_min, NP_max, ε, U*, H, p, g=1;
5	Initialize the initial population P using LHS;
6	// Parallel loop using Joblib
7	for s = 1 to w do
8		Determine take-off weight with module 2;
9	end for;
10	Determine ψ(x_g=1,s) according to (7) and $W_{T O}^{+}$ (x_g=1,s) according to (6);
11	Update U*;
12	Save $W_{T O}^{+}$ (x_g=1,s);
13	Save data of generation g;
14	Set all values in M_CR, M_F to 0.5;
15	Archive A = ∅;
16	Index counter g = 2;
17	Index counter k = 1;
18	// Main loop
19	while Stop criteria not met do
20		S_CR = ∅, S_F = ∅;
21		for s = 1 to w do
22				r_s = select from [1, H] randomly;
23				Determine F_g,s; Determine CR_g,s;
24				Determine the mutation vector v_g,s;
25				Define the crossover vector u_g,s;
26		end for;
27		// Parallel loop using Joblib
28		for s = 1 to w do
29				Determine take-off weight with module 2;
30		end for;
31		Determine ψ(x_g,s) according to (7) and $W_{T O}^{+}$ (x_g,s) according to (6);
32		Update U*;
33		for s = 1 to w do
34				if $W_{T O}^{+}$ (u_g,s) ≤ $W_{T O}^{+}$ (x_g,s) then
35					x_g+1,s = u_g,s;
36					x_g,s → A;
37					CR_g,s → S_CR, F_g,s → S_F;
38				else
39					x_g+1,s = x_g,s;
40				end if;
41		end for;
42		// UpdateM_CR,k, M_F,k based on S_CR, S_F;
43		if S_CR = ∅ and S_F= ∅ then
44				M_F,g+1,k = mean_WL(S_F);
45				if M_CR,g,k = -1 or max(S_CR) = 0 then
46					M_CR,(g+1),k = -1;
47				else
48					M_CR,(g+1),k = mean_WL(S_CR);
49				end if;
50				if k > H then
51					k = 1;
52				else
53					k++;
54				end if;
55		else
56				M_CR,g+1,k = M_CR,g,k;
57				M_F,g+1,k = M_F,g,k;
58		end if;
59		Save $W_{T O}^{+}$ (x_g+1,s);
60		// Update range $W_{T O (g + 1)}^{i n}$
61		Mxf = [];
62		For s =1 to NP do
63			if ψ(x_g+1,s) = 0 then
64					Mxf = append(Mxf, x_g,s)
65			end if;
66		end for;
67		if size(Mxf) = 0 then
68			$W_{T O g + 1}^{i n} [0] = W_{T O g}^{i n} [0]$ ;
69			$W_{T O g + 1}^{i n} [1] = W_{T O g}^{i n} [1]$ ;
70		else
71			$W_{T O g + 1}^{i n} [0]$ = min(Mxf);
72			$W_{T O g + 1}^{i n} [1]$ = max(Mxf);
73		end if;
74		if g ≥ 3 then
75			Determine NP_g+1;
76			(NP_g – NP_g+1)-th worst vector→ A;
77			Delete (NP_g – NP_g+1)-th worst vector from P_g+1;
78		end if;
79		Save data of generation (g+1);
80		if (max( $W_{T O}^{+}$ (P_g+1))– min( $W_{T O}^{+}$ (P_g+1)) then
83			break;
81		end if;
82		g++;
83	end while;
84	Output x^opt, $W_{T O}^{+}$ (x^opt);

Appendix B

Module 2: Determining take-off weight $W_{T O}^{o u t}$

1	Input: ${A R}_{1}$ , $Λ_{1}$ , $λ_{1}$ , ${A R}_{2}$ , $Λ_{2}$ , $λ_{2}$ , ${\bar{L}}_{2}$ , ${\bar{S}}_{2}$ , W/S, V, $W_{T O}^{i n}$ ;
2	Create input files for AVL software to determine aerodynamic characteristics with module 3;
3	Determine α_bal and δ_2bal with module 4;
4	c_xi, c_ya, m_z = runAVL( ${A R}_{1}$ , $Λ_{1}$ , $λ_{1}$ , ${A R}_{2}$ , $Λ_{2}$ , $λ_{2}$ , ${\bar{L}}_{2}$ , ${\bar{S}}_{2}$ , W/S, V, α_bal, δ_2bal);
5	Determine с_х0 according to empirical formulas;
6	Determine the lift-to-drag ratio $\frac{L}{D}$ ;
7	Determine ${\bar{W}}_{s t r u c t}$ ;
8	Determine C_D;
9	Determine T;
10	// Determine weight components during climb, cruise, and descent phases
11	Determine $\bar{N}$ according to (26);
12	${\bar{W}}_{p o w_i}$ according to (19);
13	if type_motor == ‘eltr’ then
14		${\bar{W}}_{b a t_i}$ according to (18);
15		${\bar{W}}_{b a t} = \sum_{i = 1}^{3} {\bar{W}}_{b a t_i}$ ;
16	else
17		${\bar{W}}_{f u e l_i}$ according to (17);
18		${\bar{W}}_{f u e l} = \sum_{i = 1}^{3} {\bar{W}}_{f u e l_i}$ ;
19	end if;
20	$W_{v i n t_i};$
21	${\bar{W}}_{p o w}$ = max ( ${\bar{W}}_{p o w_i}$ );
22	$W_{v i n t}$ = max ( $W_{v i n t_i}$ );
23	Determine $W_{T O}^{o u t}$ according to (16);

Appendix C

Module 3: Creating an input file for AVL software and determining aerodynamic characteristics

1	Input: ${A R}_{1}$ , $Λ_{1}$ , $λ_{1}$ , S₁, ${A R}_{2}$ , $Λ_{2}$ , $λ_{2}$ , S₂, L₂, V, $α$ ;
2	Determine $S_{Σ}$ , $b$ , MACaccording to (29), (22), (25);
3	Write input file for AVL;
4	Determine C_Di, C_L, $C_{m A}$ by AVL;

Appendix D

Module 4: Determination of the condition for longitudinal balancing of the UAV

1	Input: ${A R}_{1}$ , $Λ_{1}$ , $λ_{1}$ , ${A R}_{2}$ , $Λ_{2}$ , $λ_{2}, {\bar{L}}_{2}$ , ${\bar{S}}_{2}$ , W/S, V, $W_{T O}^{i n}$ ;
2	Create input files for AVL software and determine aerodynamic characteristics with module 3;
3	Determine $C_{L_b a l}$ according to (28);
4	for i in range(2) do
5		for j in range(2) do
6			$δ_{2}$ = $δ_{2}$ [i];
7			$C_{m A} (α, δ_{2})$ , $C_{L} (α, δ_{2}) =$ runAVL( ${A R}_{1}$ , $Λ_{1}$ , $λ_{1}$ , ${A R}_{2}$ , $Λ_{2}$ , $λ_{2}$ , ${\bar{L}}_{2}$ , ${\bar{S}}_{2}$ , W/S, V, $W_{T O}^{i n}$ );
8			C_m0 = interpolation(0, $C_{L} (α, δ_{2})$ , $C_{m A} (α, δ_{2})$ );
9			Determine C_m( $α, δ_{2}$ ) according to (30);
10		end for;
11	end for;
12	Determine α_bal и δ_2bal according to (29);

References

Komarov, V.A.; Borgest, N.M.; Vislov, I.P.; Vlasov, N.V.; Kozlov, D.M.; Korolkov, O.N.; Mainskov, V.N. Kontseptual'noe proektirovanie samoleta [Aircraft concept design]; Samara National Research University: Samara, Russia, 2013; ISBN 978-5-7883-0921-7. [Google Scholar]
Raymer, D.P. Aircraft Design: A Conceptual Approach, 2nd ed.; American Institute of Aeronautics and Astronautics, Inc.: Washington, USA, 2018; ISBN 0-930403-51-7. [Google Scholar]
Nicolai, L.M.; Carichner, G.E. Fundamentals of Aircraft and Airship Design; American Institute of Aeronautics and Astronautics: Columbia, LL, USA, 2010; ISBN 978-1-60086-751-4. [Google Scholar]
Torenbeek, E. Advanced Aircraft Design: Conceptual Design, Technology and Optimization of Subsonic Civil Airplanes; Wiley: Hoboken, NJ, USA, 2013; ISBN 978-1-118-56811-8. [Google Scholar]
Kroo, I.; Altus, S.; Braun, R.; Gage, P.; Sobieski, I. Multidisciplinary Optimization Methods for Aircraft Preliminary Design. In Proceedings of the 5th Symposium on Multidisciplinary Analysis and Optimization, Panama, FL, USA, 7–9 September 1994; pp. 697–707. [Google Scholar]
Badyagin, A.A.; Mukhamedov, F.A. Proektirovanie legkikh samoletov [Design of light aircraft]; Mashinostroenie Publ: Moscow, Russia, 1978. [Google Scholar]
Eger, S.M.; Mishin, V.F.; Liseytsev, N.K.; Badyagin, A.A.; Rotin, V.E.; Sklyansky, F.I.; Kondrashov, N.A.; Kiselev, V.A.; Fomin, N.A. Proektirovanie samoletov [Aircraft design]; Mashinostroenie Publ: Moscow, Russia, 1983. [Google Scholar]
Sheinin, V.M.; Kozlovsky, V.I. Vesovoye proektirovanie i effektivnost' passazhirskikh samoletov [Weight design and efficiency of passenger aircraft]; Mashinostroenie Publ: Moscow, Russia, 1977. [Google Scholar]
Komarov, V.A. Tochnoe proektirovanie [Concurrent design]. Ontology of Design 2012, 3, 8–23. [Google Scholar]
Weishaar, T.A.; Komarov, V.A. Chelovecheskii faktor v proektirovanii aviatsionnykh konstruktsii [Human Factor in the Design of Aviation Structures]. All-Russian Scientific and Technical Journal "Flight" 1998, 1, 17–23. [Google Scholar]
Komarov, V.A.; Weisshaar, T.A. New Approach to Improving the Aircraft Structural Design process. Journal of Aircraft 2002, 39(2), p. 227-233. [CrossRef]
Manning, V.M. High Speed Civil Transport Design Using Collaborative Optimization and Approximate Models; Northern Trust Corporation: Chicago, LL, USA, 1997. [Google Scholar]
Lukyanov, O. Razrabotka Metodiki Vybora Oblika Gruzovykh Samolotov s Ispol’zovaniyem Mnogodistsiplinarnoy Optimizatsii [Development of a Methodology for Selecting the Shape of Cargo Aircraft Using Multidisciplinary Optimization]. Candidate of engineering sciences thesis, Samara National Research University, Samara, Russia, 2019.
Komarov, V.; Lukyanov, O. Multidisciplinary Optimization of the Cargo Airplane Wing Parameters. All-Russ. Sci.-Tech. J. Polet 2018, 3, 3–15. [Google Scholar]
Martins, J.R.R.A.; Kenway, G.; Brooks, T. Multidisciplinary Design Optimization of Aircraft Configurations Part 2: High-Fidelity Aerostructural Optimization; University of Michigan: Ann Arbor, MI, USA, 2016. [Google Scholar]
Wunderlich, T.; Dähne, S.; Heinrich, L.; Reimer, L. Multidisciplinary Optimization of an NLF Forward Swept Wing in Combination with Aeroelastic Tailoring Using CFRP. CEAS Aeronaut. J 2017, 8, 673–690. [Google Scholar] [CrossRef]
Sgueglia, A.; Schmollgruber, P.; Bartoli, N.; Benard, E.; Morlier, J.; Jasa, J.; Martins, J.R.R.A.; Hwang, J.T.; Gray, J.S. Multidisciplinary Design Optimization Framework with Coupled Derivative Computation for Hybrid Aircraft Journal of Aircraft, 2020, 57(4), p. 715–729. [CrossRef]
Leifsson, L. Multidisciplinary Design Optimization of Low-Noise Transport Aircraft [Electronic Resource]. Ph.D. thesis, Virginia Polytechnic Institute and State University, Virginia, Montgomery, 2005.
Champasak, P.; Panagant, N.; Pholdee, N.; Bureerat, S.; Yildiz, A.R. Self-Adaptive Many-Objective Meta-Heuristic Based on Decomposition for Many-Objective Conceptual Design of a Fixed Wing Unmanned Aerial Vehicle. Aerosp. Sci. Technol 2020, 100, 105783. [Google Scholar] [CrossRef]
Escobar-Ruiz, A.G.; Lopez-Botello, O.; Reyes-Osorio, L.; Zambrano-Robledo, P.; Amezquita-Brooks, L.; Garcia-Salazar, O. Conceptual Design of an Unmanned Fixed-Wing Aerial Vehicle Based on Alternative Energy. International Journal of Aerospace Engineering 2019, 2019, 8104927. [Google Scholar] [CrossRef]
Chung, P.H.; Ma, D.M.; Shiau, J.K. Design, Manufacturing, and Flight Testing of an Experimental Flying Wing UAV. Appl. Sci. 2019, 9(15), 3043. [Google Scholar] [CrossRef]
Boutemedjet, A.; Samardžic´, M.; Rebhi, L.; Rajic´, Z.; Mouada, T. UAV aerodynamic design involving genetic algorithm and artificial neural network for wing preliminary computation. Aerospace Science and Technology 2019, 84, 464–483. [Google Scholar] [CrossRef]
Aksugur, M.; Inalhan, G. Design Methodology of a Hybrid Propulsion Driven Electric Powered Miniature Tailsitter Unmanned Aerial Vehicle. Journal of Intelligent & Robotic Systems, 2010; 57, 505–529. [Google Scholar] [CrossRef]
Gu, H.; Lyu, X.; Li, Z.; Zhang, F. Coordinate Descent Optimization for Winged-UAV Design. Journal of Intelligent & Robotic Systems 2020, 97, 109–124. [Google Scholar] [CrossRef]
Ming, L.; Junqiang, B.; Li, L.; Xiaoxuan, M.; Qian, L.; Bao, C. A gradient-based aero-stealth optimization design method for flying wing aircraft. Aerospace Science and Technology 2019, 92, 156–169. [Google Scholar] [CrossRef]
Parada, L.M.A. Conceptual and Preliminary Design of a Long Endurance Electric UAV. Master’s Thesis, University of Lisbon, Lisbon, Portugal, 2016. [Google Scholar]
Papageorgiou, A. Design Optimization of Unmanned Aerial Vehicles: A System of Systems Approach. Ph.D. dissertation, Linköping studies in science and technology, Linköping, Sweden, 2019.
Bowers, P.M. Unconventional aircraft; Blue Ridge Summit, PA: TAB Books: New York, USA, 1984; 323p. [Google Scholar]
Eger, S.M.; Liseytsev, N.K.; Samoilovich, O.S. Osnovyi avtomatizirovannovo proektirovaniya samoletov [Fundamentals of Automated Design of Aircraft]; Mashinostroenie Publ: Moscow, Russia, 1986; 232p. [Google Scholar]
Malchevskiy, V.V. Matrichno-topologicheskii metod sinteza i komponovki samoleta (opyt avtomatizatsii tvorcheskoy deyatel'nosti konstruktora) [Matrix-topological method of synthesis and aircraft layout (experience of automation of the designer's creative activity)]; Monograph, Moscow Aviation Institute: Moscow, Russia, 2011; 356p. [Google Scholar]
Safavi, E.; Tarkian, M.; Gavel, H.; Ölvander, J. Collaborative Multidisciplinary Design Optimization. A Framework Applied on Aircraft Conceptual System Design. Concurrent Engineering, 2015; 23, 236–249. [Google Scholar] [CrossRef]
Cherniaev, A.; Komarov, V. Multistep Optimization of Composite Drive Shaft Subject to Strength, Buckling, Vibration and Manufacturing Constraints. Applied Composite Materials, 2015; 22, 475–487. [Google Scholar] [CrossRef]
Komarov, V.A.; Pavlov, A.A.; Pavlova, S.A. Designing, manufacturing and testing of complex form structures from layered polymer composite materials. Deformation and destruction of composite materials and structures, 2018; 64–66. [Google Scholar]
Kurkin, E.; Kishov, E.; Espinosa Barcenas, O.U.; Chertykovtseva, V. Gate Location Optimization of Injection Molded Aerospace Brackets Using Metaheuristic Algorithms. In Proceedings of the 2021 International Scientific and Technical Engine Conference (EC), Samara, Russian Federation; 2021; pp. 1–6. [Google Scholar] [CrossRef]
Simanowitsch, D.; Theiss, A.; Sudhi, A.; Badrya, C. Comparison of Gradient-Based and Genetic Algorithms for Laminar Airfoil Shape Optimization. In: AIAA SciTech 2022 Forum, pp. 1-21. ARC. AIAA Scitech Forum 2022, 3.-7. Jan. 2022, San Diego, USA. ISBN 978-162410631-6. [CrossRef]
Zingg, D.W.; Nemec, M.; Pulliam, T.H. A comparative evaluation of genetic and gradient-based algorithms applied to aerodynamic optimization. European Journal of Computational Mechanics 2008, 17, 2008. [Google Scholar] [CrossRef]
Xin-She, Y. Engineering optimization: a introduction with metaheuristic applications; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2010; 376p, ISBN 978-0-470-58246-6. [Google Scholar] [CrossRef]
Blum, C.; Roli, A. Metaheuristics in combinatorial optimization: overview and conceptual comparison. ACM computing surveys, 2001; 35, 268–308. [Google Scholar] [CrossRef]
Almufti, S.M.; Shaban, A.A.; Ali, Z.A.; Ali, R.I.; Fuente, J.A.D. Overview of metaheuristic algorithms. Polaris Global Journal of Scholarly Research and Trends, 2023; 2, 10–32. [Google Scholar] [CrossRef]
Pioquinto, J.G.Q.; Moreno, R.A.F. Methods for increasing the efficiency of the differential evolution algorithm for aerodynamic shape optimization applications. In Proceedings of the XXVI All-Russian Seminar on motion Control and Navigation of Aircraft., Russia, 14-16 June 2023; pp. 166–171. [Google Scholar]
Lazarev, I.B. Osnovy optimal'nogo proektirovaniya konstruktsii [Fundamentals of optimal design of structures]; Siberian State Academy of Railway Engineering: Novosibirsk, Russia, 1995; 295p. [Google Scholar]
Malkov, V.P.; Ugodchikov, A.G. Optimization of elastic systems; Nauka Publ: Moscow, Russia, 1981. [Google Scholar]
Srednevysonyi bespilotnyi letatel’nyi apparat bol’šoi prodolžiten’nosti polota United 40 [Medium-altitude long-endurance unmanned aerial vehicle United 40]. Available online: https://vpk.name/library/f/united-40.html (accessed on 2 December 2023).
The General Atomics "Predator MQ-1" UAS. Available online: https://barnardmicrosystems.com/UAV/uav_list/predator.html (accessed on 2 December 2023).
Bolkhovitinov, V.F. Puti razvitiya letatelnykh apparatov [Ways of development of flying apparatus]; Oborongiz Publ.: Moscow, Russia, 1962; 132p. [Google Scholar]
Komarov, V.A. Vesovoy analiz aviatsionnykh konstruktsii: teoreticheskie osnovy [Weight analysis of aviation structures: theoretical foundations]. All-Russian Scientific and Technical Journal “Flight” 2000, 1, 31–39. [Google Scholar]
Tanabe, R.; Fukunaga, A. Success-history based parameter adaptation for Differential Evolution. 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 2013, 71–78. [CrossRef]
Jin, R.; Chen, W. An efficient algorithm for constructing optimal design of computer experiments. Proceedings of DETC’03 ASME 2003 Design Engineering Technical Conferences and Computers and Information in Engineering Conference Chicago, Illinois, USA, 2-6 September 2003. [Google Scholar]
Viktorin, A.; Senkerik, R.; Pluhacek, M.; Kadavy, T.; Jasek, R. A Lightweight SHADE-Based Algorithm for Global Optimization - liteSHADE. Lecture Notes in Electrical Engineering 2020, 554, 197–206. [Google Scholar] [CrossRef] [PubMed]
Storn, R.; Price, K. Differential Evolution - A Simple and Efficient Adaptive Scheme for Global Optimization Over Continuous Spaces. Journal of Global Optimization, 1995; 23. [Google Scholar]
Storn, R.; Price, K. Differential evolution - A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. Journal of Global Optimization, 1997; 11, 341–359. [Google Scholar] [CrossRef]
Ali, M.M.; Zhu, W.X. A penalty function-based differential evolution algorithm for constrained global optimization. Comput Optim Appl, 2013; 54, 707–739. [Google Scholar] [CrossRef]
Pioquinto, J.G.Q.; Shakhov, V.G. Acceleration of Evolutionary Optimization for Airfoils Design with Population Size Reduction Methods. In Proceedings of 20 Int. Conf. on the Aviation and Cosmonautics. Samara, Russia, 2021; pp. 22–26. [Google Scholar]
Wong, I.; Liu, W.; Ho, C.H.; Ding, X. Continuous adaptive population reduction (CAPR) for differential evolution optimization. SLAS Technology, 2017; 22, 289–305. [Google Scholar] [CrossRef]
Tanabe, R.; Fukunaga, A.S. Improving the search performance of SHADE using linear population size reduction. Proceedings of 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China; 2014; pp. 1658–1665. [Google Scholar] [CrossRef]
Barcenas, O.U.E.; Pioquinto, J.G.Q.; Kurkina, E.; Lukyanov, O. Multidisciplinary Analysis and Optimization Method for Conceptually Designing of Electric Flying-Wing Unmanned Aerial Vehicles. Drones 2022, 6(10), 307. [Google Scholar] [CrossRef]
AVL Overview. Available online: https://web.mit.edu/drela/Public/web/avl/ (accessed on 13 October 2023).
Viana, F.A. A tutorial on Latin hypercube design of experiments. Quality and reliability engineering international, 2015; 32, 1975–1985. [Google Scholar] [CrossRef]
Sharma, H. Lightweight Pipelining in Python. Using Joblib for Storing the Machine Learning Pipeline to a File. Available online: https://towardsdatascience.com/lightweight-pipelining-in-python-1c7a874794f4 (accessed on 2 November 2023).
Belotserkovsky, S.M. Thin carrying surface in the subsonic flow of gas. Ed. by N.I. Rozalskaya, I.Sh. Axelrod, T.D. Doverman. Nauka Publ: Moscow, Russia, 1965; 244 p.
Katz, J.; Allen, P. Low-Speed Aerodynamics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2001; 126p. [Google Scholar] [CrossRef]
Budziak, K. Aerodynamic Analysis with Athena Vortex Lattice (AVL); Hamburg university of applied sciences: Hamburg, Germany, 2015. [Google Scholar]
FreeCAD. Available online: https://www.freecad.org/ (accessed on 21 January 2024).
Nikolaev, N.V. Optimization of airfoils along high-aspect-ratio wing of long-endurance aircraft in trimmed flight. Journal of Aerospace Engineering 2019, 32(6). 32(6). [CrossRef]
Derksen, R.W.; Rogalsky, T. Bezier-PARSEC: An optimized aerofoil parameterization for design. Advances in Engineering Software, 2010; 41, 923–930. [Google Scholar] [CrossRef]
Espinosa Barcenas, O.U.; Quijada Pioquinto, J.G.; Kurkina, E.; Lukyanov, O. Surrogate aerodynamic wing modeling based on a multilayer perceptron. Aerospace, 2023; 10, 149. [Google Scholar] [CrossRef]
Lukyanov, O.E.; Tarasova, E.V.; Martynova, V.A. Remote control of experimental installation and automation of experimental data processing. In Proceedings of the Samara Scientific Center of the Russian Academy of Sciences, Samara, Russia; 2017; pp. 128–132. [Google Scholar]
Lukyanov, O.E.; Martynova, V.A. Eksperimental'nye issledovaniya aerodinamicheskikh kharakteristiki modeli korpusha nesushchey forma [Experimental studies of the aerodynamic characteristics of the model of the hull of the bearing form]. In Proceedings of the Samara Scientific Center of the Russian Academy of Sciences; 2016; pp. 83–89. [Google Scholar]

Figure 1. View in the plan of the heavy-class considered UAVs: (a) U-40; (b) MQ-1.

Figure 2. Block-scheme of algorithm of the proposed methodology for optimizing the design parameters of UAVs.

Figure 3. Block-scheme of calculation for objective function.

Figure 4. Simulation of the convergence process of the objective function.

Figure 5. Block-scheme of the take-off weight calculation algorithm based on the iterative solution of the sizing equation with the UAV balancing cycle in the vertical plane.

Figure 6. Determination of the pitch moment coefficient relative to the center mass.

Figure 7. Solve the balancing problem: (a) Dependence of C_m from

α

Figure 7. Solve the balancing problem: (a) Dependence of C_m from

α

Figure 9. Validation of mathematical models of aerodynamics: (a) Experimental model in a wind tunnel; (b) Geometric parameters of an experimental model in a wind tunnel.

Figure 10. Results of aerodynamic properties: (a) Dependence of C_D from α; (b) Dependence of C_L from α; (c) Dependence of C_m from α; by AVL; ◆ by experiment.

Figure 11. Example of calculating take-off weight by generations of the proposed algorithm.

Figure 12. Weight summary of the design assignment for UAV modernization: (a) U-40; (b) MQ-1.

Figure 13. Comparison engine power of prototypes and after optimization.

Figure 14. Appearance of UAV prototypes (red) and after optimization (blue): (a) U-40; (b) MQ-1.

Figure 15. Optimal profiles for the provided design conditions.

Table 1. Calculation results.

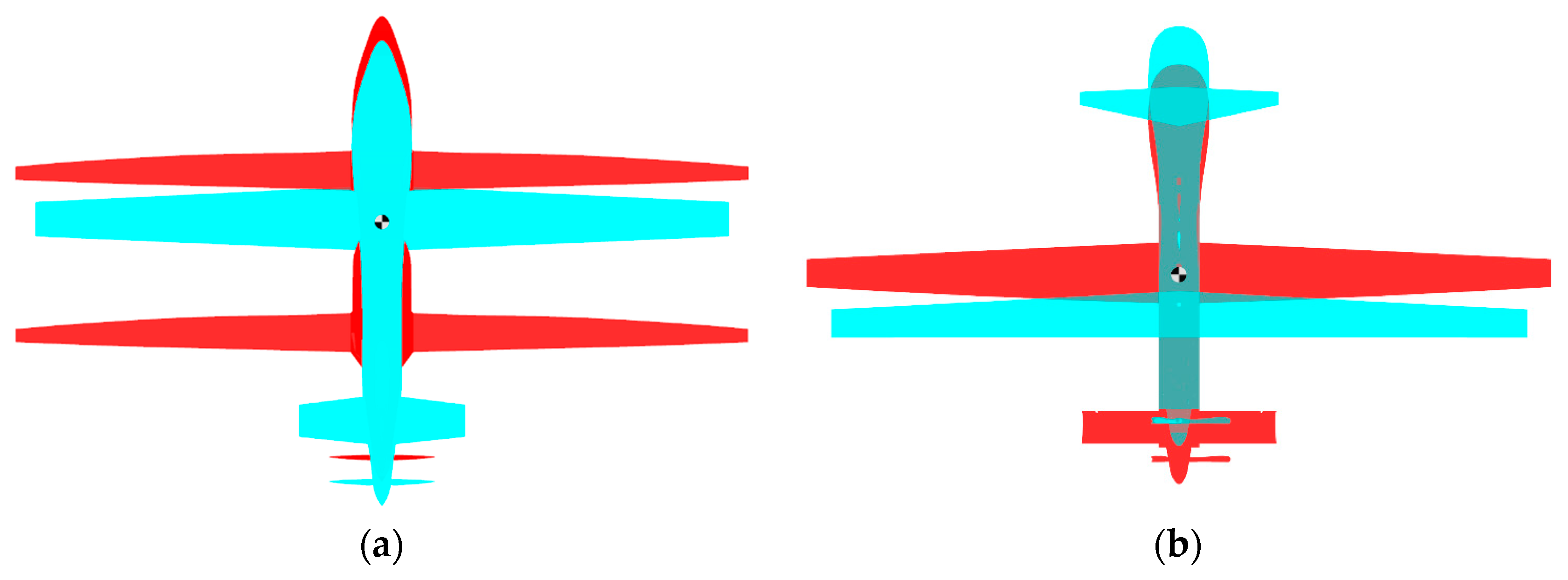
Parameters	U-40	Calculation	%	MQ-1	Calculation	%
Take-off weight [kg]	2000	2055	2.68	1020	1015	0.49
Payload [kg]	600	600	0	204	204	0
Engine weight [kg]	152	150	1.3	76	79	3.9
Fuel weight [kg]	450	458	1.8	302	316	4.4
Empty weight [kg]	950	997	4.7	514	495	3.7
Max engine power [kW]	2х84.5	2х84.1	0.01	84.5	88.3	4.3
Cruise lift-to-drag ratio	n/a	24.8	-	n/a	23.2	-

Table 2. Design constants.

Parameters		U-40	MQ-1
Flight endurance [h]		24	35
Static margin longitudinal stability		-0.1
Specific fuel consumption [kg/(kW.h)]	Climb	0.285
Specific fuel consumption [kg/(kW.h)]	Cruise	0.27
Flight path angle [^o]	Climb	+5
	Cruise	0
	Declimb	-5
Propeller efficiency		0.75
Payload [kg]		600	204
Specific weight engine $ϑ_{e n} = \frac{W_{e n} . g}{10 . N_{0}}$ [dаN/kW]		0.87

Table 6. Design intervals to define the wing airfoil of UAVs.

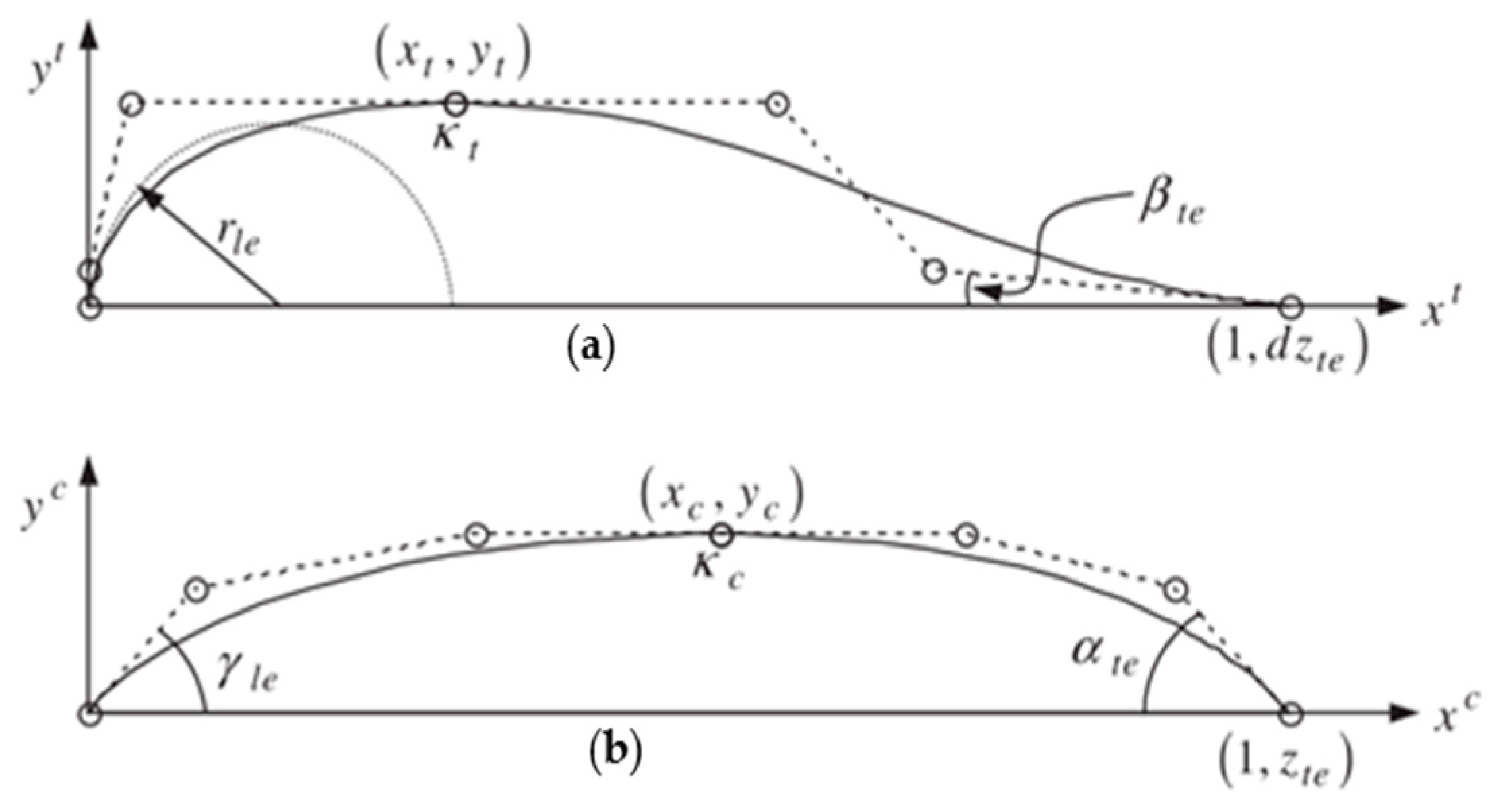
Parameter	Design interval	Parameter	Design interval
r_le	[-0.030, -0.001]	γ_le	[-0.01, 0.32]
x_t	[0.23, 0.50]	x_c	[0.20, 0.85]
y_t	[0.030, 0.095]	y_c	[0.010, 0.065]
k_t	[-0.9, -0.2]	k_c	[-1.000, 0.025]
β_te	[0.01, 0.40]	α_te	[0.01, 0.70]
dz_te	[0, 0]	z_te	[0, 0]
α	[0, 4]°

Table 7. Aerodynamic characteristics of the optimized airfoils.

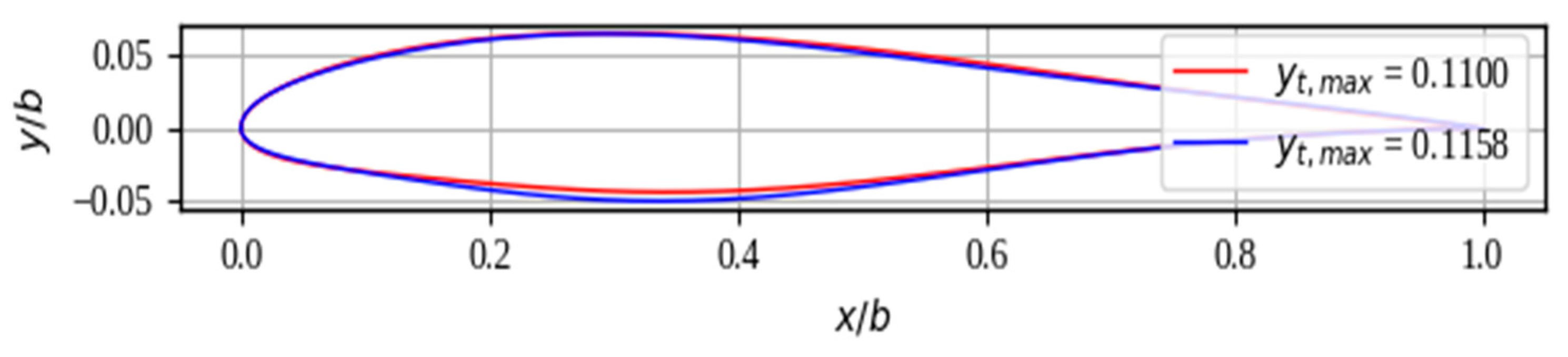
Airfoil	α [°]	c_l	c_d	c_l^1.5/c_d	y_t,max
1	3.9	0.59	0.0106	42.7059	0.1100
2	3.9	0.59	0.0106	42.7059	0.1158

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Atmospheric Aircraft Conceptual Design Based on Multidisciplinary Optimization with Differential Evolution Algorithm and Neural Networks

Abstract

1. Introduction

2. Methods and Models

2.1. Formulation of the Conceptual Design Problem

2.2. Digital UAV Model

2.2.1. Objective Function

2.2.2. Constraints

2.2.3. Design Variables

2.3. Methodology for Selecting the Optimal Parameters of an Aircraft-Type UAV

2.4. Visualization of Optimization Results in the Form of a Planned Projection of the Optimal Option and Its Three-Dimensional Model

2.5. Selection of the Wing Airfoil with Multilayer Perceptron

3. Assessment of the Reliability of Models and Methods

3.1. Validation of Mathematical Models of Aerodynamics

3.2. Validation of Models and Algorithm for Calculating the Objective Function

4. Solving Applied Optimization Problems

5. Conclusion

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

Appendix A

Appendix B

Appendix C

Appendix D

References

MDPI Initiatives

Important Links

Subscribe