Prerpints.org logo
Preprint
Article

Insights on the Bonding Mechanism, Electronic and Optical Properties of Diamond Nanothread—Polymer and Cement—Boron Nitride Nanotube Composites

Altmetrics

Downloads

110

Views

158

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

06 June 2024

Posted:

07 June 2024

You are already at the latest version

Alerts
Abstract
The success of composite materials is attributed to the nature of bonding at the nanoscale and the resulting structure-related properties. This study reports the interaction, electronic, and optical properties of diamond nanothread/polymers (cellulose and epoxy) and boron nitride nanotube/calcium silicate hydrate composites using density functional theory modeling. Our findings indicate that the interaction between the nanothread and polymer is due to van der Waals-type bonding. Minor modifications in the electronic structures and absorption spectra are noticed. Conversely, the boron nitride nanotube and calcium silicate hydrate composite display an electron-shared type of interaction. The electronic structure and optical absorption spectra of the diamond nanothread and boron nitride nanotube in all configurations studied in the aforementioned composite systems are well maintained. Our findings offer an electronic-level perspective into the bonding characteristics and electronic-optical properties of diamond nanothread/polymer and boron nitride nanotube/calcium silicate hydrate composites for developing next-generation materials.
Keywords: 
Subject: Chemistry and Materials Science  -   Materials Science and Technology

1. Introduction

To advance existing technology usually boils down to engineering materials at the nanoscale[1]. Incorporating advanced materials into traditional materials, such as nanomaterial, and integrating it into polymer and ceramic matrices can significantly improve the resulting mechanical properties and introduce new functionalities to the composites[2,3]. The potential applications of composites are in diverse fields, ranging from aerospace to construction materials[4,5,6]. Among the list of composites, polymer-based and cement-based composites are the most influential and have great economic value due to their high volume of utilization.
Polymer composites with carbon-based nanomaterials (CNMs) have been a subject of interest due to the remarkable ability of CNMs like carbon nanotubes (CNTs) and graphene to reinforce, significantly improving mechanical properties and adding new functionalities to polymer composites[7,8,9,10,11,12]. For instance, an investigation of the mechanical properties of CNT-reinforced polymer composites using a closed-form micromechanical interphase model considering the diameter of CNT, the thickness of interphase, and the mechanical properties of CNT and polymer reveals that the elastic modulus of CNT/polymer composite increase by up to 108% with the addition of CNT [13]. However, despite these benefits, poor interface adherence is still one of the interface-level issues that CNMs in polymer composites confront. Research is increasingly focusing on addressing this problem to maximize the reinforcing efficiency of CNMs in polymer composites, and this includes looking into substitute reinforcements with better interfacial interaction.
Recently, a new class of carbon nanomaterial known as the diamond nanothread (DNT) has been gaining attention due to its unique geometrical structure and outstanding properties. This nanomaterial is typically produced by controlled compression/decompression of aromatics such as benzene, aniline, pyridine, thiophene, furan, etc. [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. A DNT consists of a one-dimensional chain of sp3-bonded carbon atoms, which can be arranged in several ways [29,30,31], with their outer surface functionalized by hydrogen atoms. This bonding pattern of DNT produces a robust structure with an ultralight density. DNTs have been reported to possess an ideal strength of 26.4 nN (134 GPa), Young's modulus of 850 GPa, specific strength of 2.6 × 10 7 N∙m/kg and specific stiffness of 2.8 × 10 8 N∙m/kg [32]. These outstanding mechanical properties of DNTs make them ideal reinforcements for nanocomposites [33,34,35,36]. Previous reports have demonstrated that DNTs even outperform CNTs as a reinforcing material for enhancing the thermal-mechanical properties of polymer composites [33,35,36]. Zhan et al. reported that DNT demonstrates remarkable torsional stiffness, nearly three times greater than that of CNT, and the interfacial shear strength (ISS) in DNT bundles surpasses that observed in CNT bundles [37]. Further study revealed that the ISS at the DNT-polyethylene (PE) interface is comparable to that observed in the CNT-PE interface [33]. Additionally, a simulation study on mechanical properties of bulk poly (methyl methacrylate) (PMMA), CNT/PMMA composite, and DNT/PMMA composite under uniaxial tension reveal that the Young’s modulus and yield stress of DNT/PMMA composite are 85% and 15% higher than those of PMMA matrix [34].
While the mechanical properties of DNT and its effectiveness as a reinforcement in polymer composites have been investigated, the electronic behavior of DNT with polymer composites has not been elucidated. Exploring the electronic properties of DNT combined with polymer matrices (i.e., biopolymers, epoxies, thermoplastics, etc.) may provide insights into their interaction and offer alternative means to design high-strength polymer composites. Among these polymers, cellulose is the most abundant natural polymer on earth, with molecular formula ( C 6 H 10 O 5 ) n and is known for its hydrophilicity, biodegradability, biocompatibility, nontoxicity, low cost, etc. [38,39]. Studies on cellulose with CNMs have been actively conducted and demonstrated to enhance composite properties such as Young’s modulus, tensile strength, adsorption rate, porosity, etc. [40,41]. In addition to cellulose, epoxy, one of the most widely used polymer resins, has become widely utilized in the development of polymer composites due to their exceptional properties including excellent chemical and corrosion resistance, high adhesion strength, and good thermal, electrical, and adhesive properties [42]. Several reports on CNMs/epoxy combined material have revealed improved thermal, electrical, and mechanical properties [43,44,45,46,47,48,49,50,51]. For these reasons, delving into the interaction of cellulose and epoxy with DNT is also noteworthy.
Another research field of interest is smart cement-based composites, which show promise in revolutionizing the construction industry. Unlike conventional cement-based composites, smart cement incorporates advanced nanomaterials to improve its mechanical properties and add functionalities such as piezoelectric, thermoelectric, self-cleaning, self-sensing, and electromagnetic interference shielding properties[52,53,54,55]. This emerging technology has the potential to enhance the durability, safety, and sustainability of infrastructure projects, making it a promising solution for the challenges of modern construction and the environment as a whole.
In the recent past, graphene, CNTs, metal-oxides nanoparticles, and polymers have been the topic of nanoreinforcement in cement-based composites[56,57,58]. For instance, combining a small percentage of graphene oxide into a calcium silicate hydrate (C-S-H) matrix enhances flexural and compressive strength by 50% and 28%[59]. Several papers obtained similar conclusions communicated in the following works[60,61,62,63]. The improvement in the macroscopic mechanical properties is attributed to the nanomaterials, which served as a seeding nanomaterial for the growth of C-S-H, thus producing more C-S-H in the composite[64]. A similar trend is observed in the mechanical performance of cement and CNT composite [65]. The carbon nanostructures as filler materials reduced the composite's porosity, thus shielding it from the penetration of chloride ions [66]. The application of nanotechnology in cement composites holds great promise as the building material for smart cities. However, the diversity of nanomaterials for cement-based composite makes the study challenging. Currently, most research is focused on graphene-based nanostructures, with minimal attention paid to boron nitride nanomaterials, which perform similarly to graphene-based nanomaterials.
Boron nitride nanomaterials are remarkable nanomaterials with a wide range of applications, including their potential use in cement composites[67,68,69,70]. These nanotubes are structurally similar to carbon nanotubes but comprise boron and nitrogen atoms. The mechanical properties of the Boron Nitride sheet are also comparable with that of carbon-based nanomaterials, with Young's modulus and fracture strength of 0.865 TPa and 70.5 Gpa, respectively[71]. Meanwhile, BNNT has Young's modulus and tensile strength of 1.3 GPa and 33 GPa, respectively[72]. Its incorporation into the C-S-H matrix at the electronic level has not yet been investigated, at least at the electronic level. This information is crucial for understanding the bonding characteristics of the BNNT and C-S-H layers.
This work examines the bonding mechanism, electronic structure, and optical properties of DNT/cellulose, DNT/epoxy, and BNNT/C-S-H nanocomposites using density functional theory (DFT) calculations. Results indicate weak interactions between the DNT and polymers with minimal charge transfer. Thus, only minor alterations in the electronic and optical properties of the nanothread are observed. On the one hand, the C-S-H/BNNT composite demonstrates the bonding with electrons overlapping between the BNNT and the prototype C-S-H. The wide bandgap of the BNNT is well maintained in the composite structure, as well as the electronic and optical properties. The results presented here will serve as a reference for developing advanced polymer-based composites and cement-based composites.

2. Materials and Methods

The DFT calculations are performed using the Quantum ESPRESSO package [73,74]. In all calculations, the optimized norm-conserving pseudopotential [75], generalized gradient approximation (GGA) within Perdew–Burke–Ernzerhof parametrization [76], and plane-wave basis sets are used. The energy and charge density cutoff are set at 60 Ry and 240 Ry, respectively. The energy and force tolerance is set to 10 − 8 Ry and 10 − 4 Ry/Bohr. The standard semi-empirical Grimme-D3 [77] van der Waals (vdW) correction is utilized to take into account the weak interaction between subsystems.
Gamma-point-specific algorithms are used for structural optimization calculations on DNT/polymer composites. The well-established sp3 tube (3,0) nanothread (corresponding to 123456 structure [29]) is utilized in our calculations. This DNT type was theoretically proposed [60] even before the experimental demonstration of nanothreads. It is also classified as the lowest energy achiral nanothread [29] and has a uniform and regular structure. The DNT/Cellulose composites are modeled by considering three orientations of cellulose with respect to the nanothread and are labeled as DNT/cellulose – 1, DNT/cellulose – 2, and DNT/cellulose – 3. The dimension of the simulation box is 20.00 Å x 20.00 Å x 17.34 Å. Similarly, three orientations of epoxy with respect to the DNT are constructed and labeled as DNT/epoxy – 1, DNT/epoxy – 2, and DNT/epoxy – 3. The simulation box for each of the DNT/epoxy composites has the dimensions 22.00 Å x 22.00 Å x 17.34 Å (DNT/epoxy – 1), 26.00 Å x 22.00 Å x 17.34 Å (DNT/epoxy – 2), and 28.00 Å x 20.00 Å x 17.34 Å (DNT/epoxy – 3). For the C-S-H/BNNT complex system, a 3 x 4 x 1 Monkhorst-Pack grid [78] is used for the optimization calculation, and the dimensions of the simulation box are 11.16 Å x 7.39 Å x 30.00 Å.
To examine the stability of the composites, binding energy ( E b ) is also calculated using the expression:
E b = E C o m p o s i t e − ∑ E S u b s y s t e m s
where E C o m p o s i t e and E S u b s y s t e m s denotes the total energy of the combined structure and isolated subsystems, respectively. Charge density distribution (CDD) and electron localization function (ELF) are also obtained for all structures to visualize the electron redistributions. Both provide descriptive insights into the redistribution of the electronic distribution, thus essential in distinguishing the nature of bonds in the complex structure, as demonstrated in our previous works on similar systems [79,80,81]. The CDD and ELF images are visualized using VESTA [82]. Bader charge transfer analysis [83,84,85,86], which implements the zero-flux approach in dividing atoms in many-body electronic systems, is performed, and the charge transfer is calculated using the expression:
∆ ρ = ρ c o m p o s i t e − ρ i s o l a t e d
where ρ c o m p o s i t e and ρ i s o l a t e d are the charges of the atoms of interest in the composite and isolated systems. Refined 1 x 1 x 29 and 10 x 14 x 1 Monkhorst-Pack grids are utilized for the electronic structure and optical properties calculations of DNT/polymer and C-S-H/BNNT systems, respectively.

3. Results and Discussion

In this section, we present the atomic configurations, electronic band structures and density of states, and optical absorption spectra of DNT/cellulose, DNT/epoxy, and C-S-H/BNNT composites.

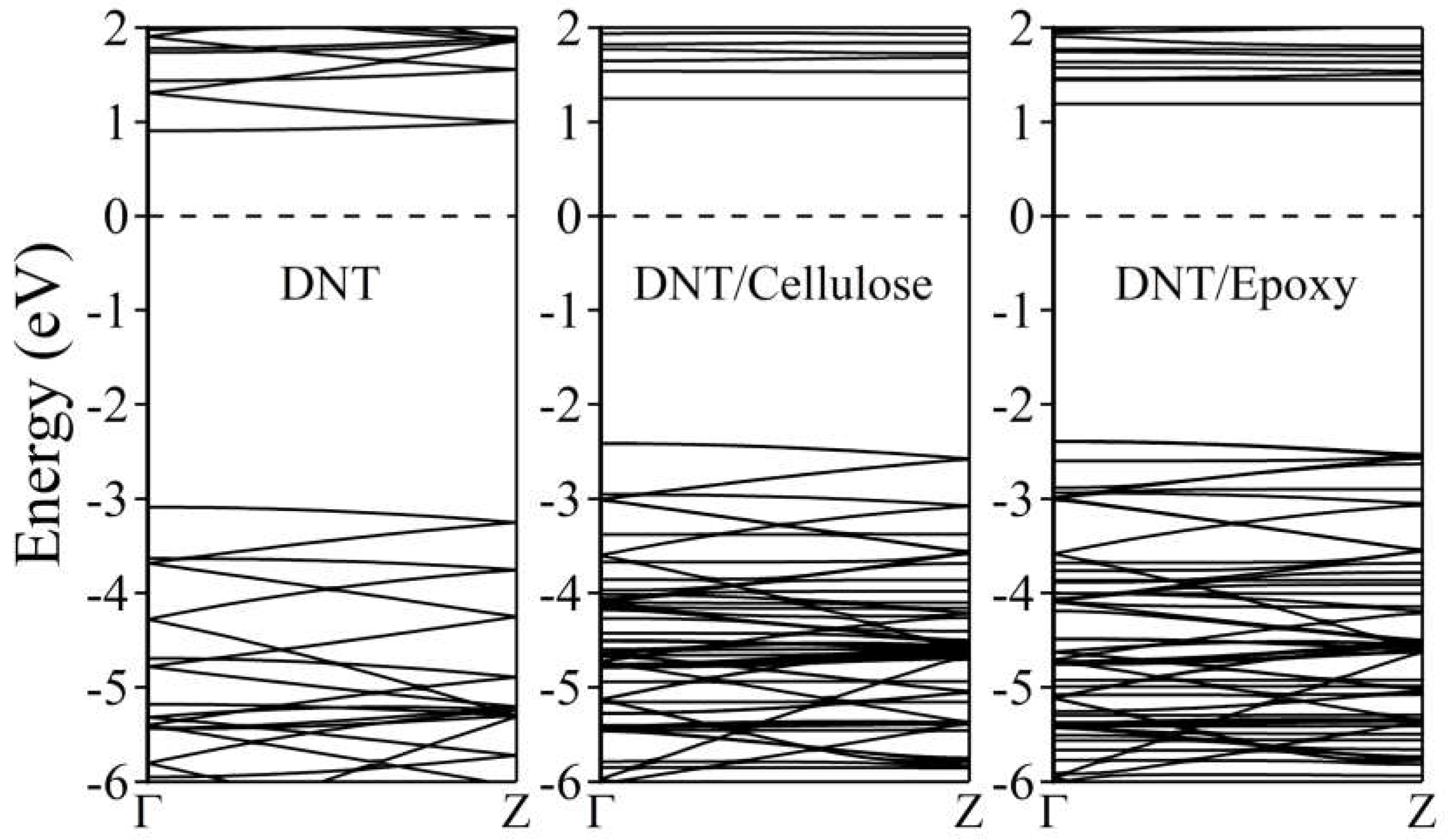
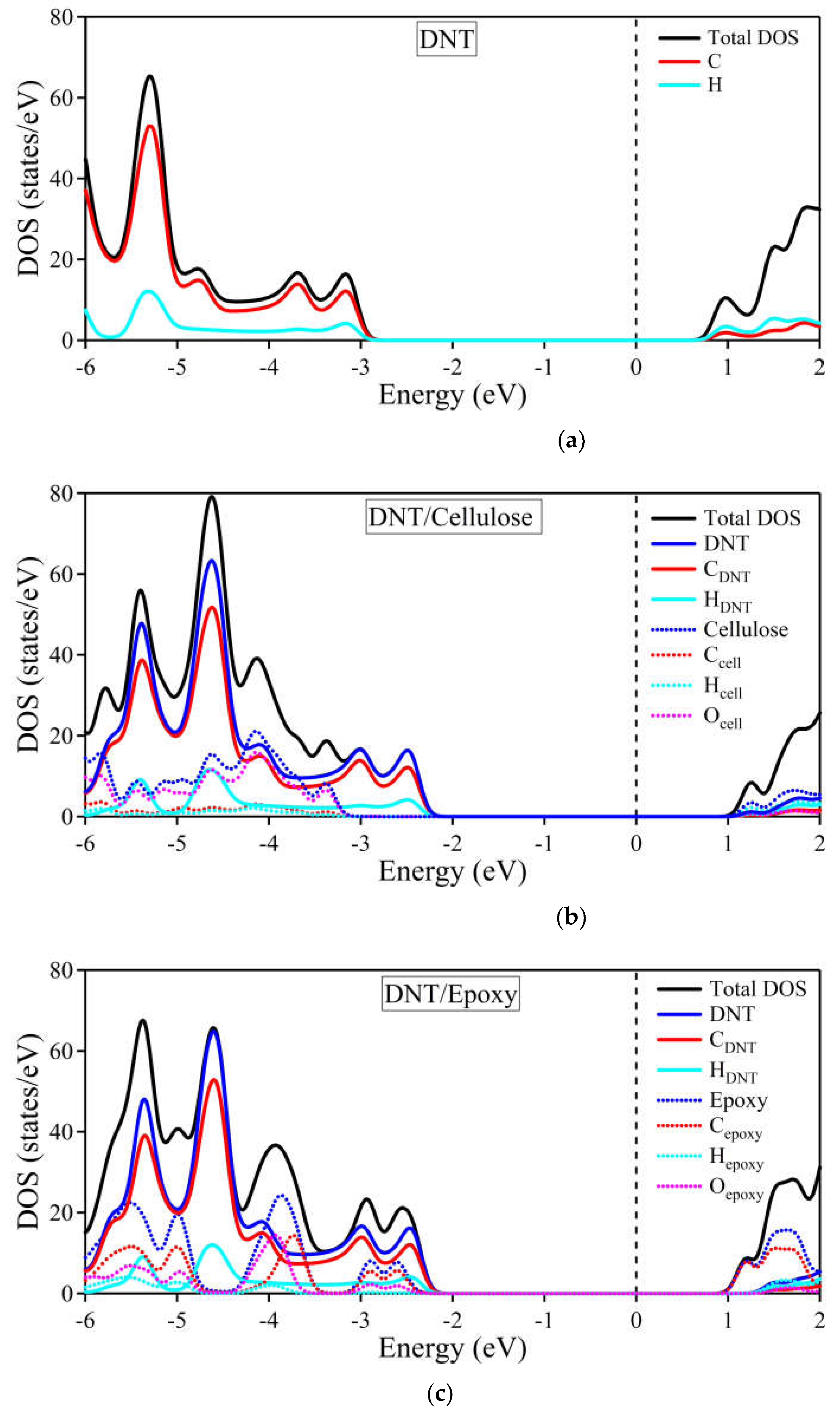
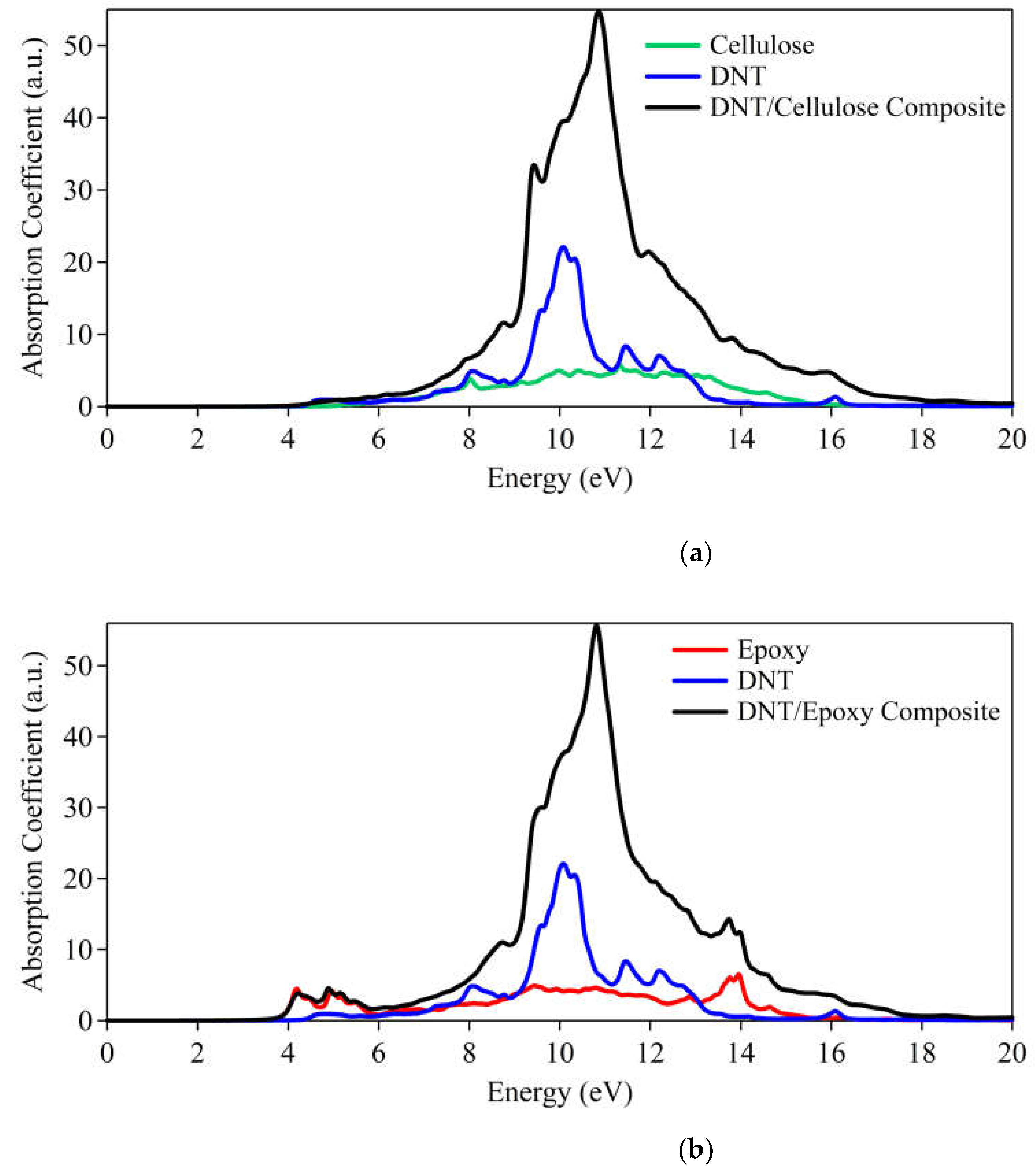
3.1. DNT/Cellulose and DNT/Epoxy Nanocomposites

The optimized atomic configurations of the sp3 tube (3,0) DNT, cellulose chain, and epoxy are illustrated in Figure 1. The DNT shown in Figure 1a consists of 96 total atoms which can be viewed as stacked benzene rings forming a one-dimensional thread. The C – H bond length is measured to be 1.10 Å. The C – C bond length between the carbon atoms in a benzene ring is 1.54 Å, while those between the adjacent benzene rings are 1.58 Å. These measured C – C bond lengths of the DNT are in good agreement with the computed values (1.54 Å – 1.57 Å) from the previous report [29]. The modeled cellulose chain has 45 total atoms, as presented in Figure 1b. Its C – C, C – H, and C – O bond lengths range from 1.52 Å – 1.54 Å, 1.10 Å – 1.11 Å, and 1.40 Å – 1.43 Å, respectively, while O – H bond has a length of ~ 0.97 Å. In Figure 1c, the selected epoxy model is illustrated and consists of 55 total atoms. The C – C, C – H, C – O, and O – H bond lengths range from 1.39 Å – 1.54 Å, 1.10 Å – 1.11 Å, 1.37 Å – 1.43 Å, and 0.96 Å – 0.97 Å, respectively.
The optimized structures of DNT/cellulose nanocomposites are displayed in Figure 2. The minimum interaction distances d m i n ( Å ) between DNT and cellulose, calculated binding energies E b , and the results of Bader charge transfer analyses ∆ ρ are obtained and summarized in Table 1. The first configuration illustrated in Fig. 2a, where the backbone of the cellulose lies parallel to the nanothread, yields the strongest interaction relative to the interaction energies of the DNT/cellulose complex systems. This is attributed to the orientation of cellulose on DNT, which leads to a more expansive interface. The shortest distance between the non-hydrogen atoms of the nanothread and cellulose is 3.67 Å (C – O), and the calculated binding energy is –0.797 eV. In Fig. 2b, the cellulose is oriented perpendicular to the tube, and the minimum distance between their non-hydrogen atoms is measured to be 3.42 Å (C – O), and the binding energy is –0.730 eV. In Fig. 2c, the minimum distance and binding energy are calculated to be 3.48 Å (C – O) and –0.726 eV, respectively. In all structures, negative values of the binding energies indicate an exothermic process. The non-bonded interaction between the DNT and cellulose and the obtained values of d m i n suggests a physical type of adsorption dominated by vdW forces.
To further examine the interaction of the DNT and cellulose composites, the CDD and ELF are obtained for all structures. The CDD is calculated by taking the difference between the charge density of the composites and the charge densities of the isolated constituents. The CDD isosurfaces presented in Figure 3 (a, d, g) show that the charges are mainly distributed along the nanothread interface. The yellow and cyan isosurface implies gain and loss of charge, respectively. To inspect charge transfer, a Bader charge transfer analysis is performed. A 0.008 e (DNT/cellulose – 1) and 0.006 e (DNT/cellulose – 3) charge transfer from the cellulose to the DNT are acquired. In contrast, a 0.004 e charge transfer from the DNT to cellulose is obtained for DNT/cellulose – 2 composite. The ELF isosurface and 2D ELF contour are displayed in Fig. 3 (b, e, h) and Fig. 3 (c, f, i). ELF [87] is a measurement of electron localization in atomic and molecular systems and is represented on a scale from 0 to 1. When ELF values exceed 0.7, electrons are considered localized, indicating the presence of core or bonding regions or lone pairs. Meanwhile, when ELF values fall between 0.7 and 0.2, electron localization resembles that of an electron gas and is typical of metallic bonds [88]. The ELF isosurface illustrated in Fig. 3 (b, e, h) shows a relatively uniform electron density across the composites. The 2D ELF contour displayed in Fig. 3 (c, f, i) further confirms the non-bonding interactions between cellulose and DNT. No overlapping of ELF is observed, as evident in the distinct blue region between the cellulose and nanothreads.
The optimized atomic configurations of DNT/epoxy composites are displayed in Figure 4. Calculated minimum interaction distance d m i n , binding energy E b , and charge transfer ∆ ρ are summarized in Table 2. The first configuration illustrated in Fig. 4a (DNT/epoxy – 1), where the epoxy wraps around the thread, has –0.224 eV binding energy and the minimum distance between the non-hydrogen atoms is measured to be 3.56 Å (C – O). In the second configuration (DNT/epoxy – 2), where the backbone of the epoxy is oriented slightly perpendicular to the thread, as displayed in Fig. 4b, the closest distance between their atoms is 3.64 Å (C – O). Also, the binding energy is –0.236 eV, which is relatively higher than the interaction energy of DNT/epoxy – 1. In Fig. 4c (DNT/epoxy – 3), the epoxy is aligned parallel to the DNT with a minimum distance of 3.60 Å (C – O) and a binding energy of –0.168 eV, which is the lowest among the three configurations of DNT/epoxy composites. Similar to the discussions above, all structures display noncovalent interactions, and the negative values of binding energies indicate an exothermic reaction. The non-bonded interactions between the DNT and epoxy as well as the measured minimum interaction distances, demonstrate physisorption mainly governed by weak vdW forces.
The CDD and ELF calculations are also performed for DNT/epoxy composites and are presented in Figure 5. Our results yield similar behavior to those of DNT/cellulose composites. The CDD isosurface shows accumulation and depletion of charges mainly distributed along the nanothread interface. Bader charge transfer analysis reveals 0.003 e (DNT/epoxy – 1) and 0.019 e (DNT/epoxy – 2) charge transfer from the epoxy to the nanothread. A 0.002 e charge transfer from the DNT to epoxy is obtained for the DNT/epoxy – 3 composite. The DNT/epoxy complex systems' ELF isosurface shows uniform electron density across the composites. The 2D ELF plots confirm the non-bonded interactions with the visible blue region between the epoxy and nanothread. Owing to the hydrogenated surface of DNT, the vdW interactions between polymer and nanothread are weaker than those with similar systems. This behavior is consistent with previously reported interactions of diamond nanothreads with other polymers [33,34,35,36,89,90,91].
Figure 6 illustrates the calculated electronic band structure of (3,0) tube DNT. According to GGA/PBE DFT calculations, benzene-derived diamond nanothreads are insulators with at least a 3.5 eV energy band gap, which is expected due to the intrinsic sp3 bonding of carbon atoms just like diamond [29,30,92,93,94,95,96]. Our result shows that pure sp3 – (3,0) DNT has a direct band gap of 3.99 eV at the Γ point, which is close to the previously calculated value (3.98 eV) [96]. The complex systems, meanwhile, show a slightly lower band gap. We observe a shift of bands at the higher energy level, resulting in DNT/cellulose – 1 and DNT/epoxy – 1 composites having a direct band gap of ~3.7 eV and ~3.6 eV, respectively. These minor modifications in the energy band gap are attributed to the weak interaction between the nanothread and polymers and the minimal charge transfer previously mentioned. This, in turn, leads to the realignment of the energy states. As discussed above, the interaction energies of DNT/cellulose – 1 and DNT/epoxy – 1 composites are 0.797 eV and 0.224 eV, respectively. The charge transfer from the cellulose to the nanothread is calculated to be 0.008 e while the charge transfer from the epoxy to DNT is 0.003 e. However, it is also noteworthy that GGA usually underestimates the band gap of materials.
To further inspect the composites' electronic band structures, the total and partial density of states are provided in Figure 7. The black solid line depicts the total DOS, while the DNT and cellulose/epoxy contributions are represented by blue solid and dotted lines, respectively. The DOS of carbon and hydrogen atoms of DNT are outlined by red and cyan solid lines, respectively. Also, the carbon, hydrogen, and oxygen atoms of the cellulose/epoxy are depicted by red, cyan, and magenta dotted lines, respectively. In Figure 7a, the density of states of the DNT/cellulose composite shows that at the lower energy range [~ −2.3 eV, −6 eV], most contribution to the total DOS of the composite, comes from DNT, specifically from the carbon atoms of the nanothread. The cellulose shows a significant contribution at ~ −3.1 eV to −6 eV, with its oxygen atoms having the highest DOS relative to the total contribution of the cellulose.
Similarly, the DOS of DNT/epoxy nanocomposite presented in Figure 7b shows that most contribution to the total DOS still comes from the DNT, specifically from its carbon atoms. The contributions of the epoxy in the valence band are observed at –2.5 eV to –3.0 eV, –3.5 eV to 4.5 eV, and –4.8 eV to –6.0 eV, mostly coming from its carbon and oxygen atoms. At around –3.5 eV to –4.5 eV, higher contributions of the atoms from epoxy are observed compared to those of DNT. Overall, it can be noticed that in both complex systems, the primary features of the pure (3,0) DNT are reproduced, suggesting that the electronic properties of the nanothread are preserved. Besides, we notice no strong hybridization between atoms of the nanothread and polymer. These observations further support our claim that DNT and cellulose/epoxy only interact weakly.
We have also explored the optical absorption spectra of the DNT/cellulose and DNT/epoxy composites. As illustrated in Figure 8a, the adsorption of DNT onsets at ~4.4 eV and the cellulose at ~5.2 eV indicates insulating behavior (i.e., wide bandgap). The combined system produces the same characteristics as cellulose and DNT. On the other hand, the absorption spectra of DNT/epoxy presented in Figure 8b reveal that the epoxy has absorption starting at ~3.6 eV while the DNT appears at ~4.4 eV, similar to the observation made in Fig. 8a. These results further confirm the large energy band gaps of the composites illustrated on their electronic structures.

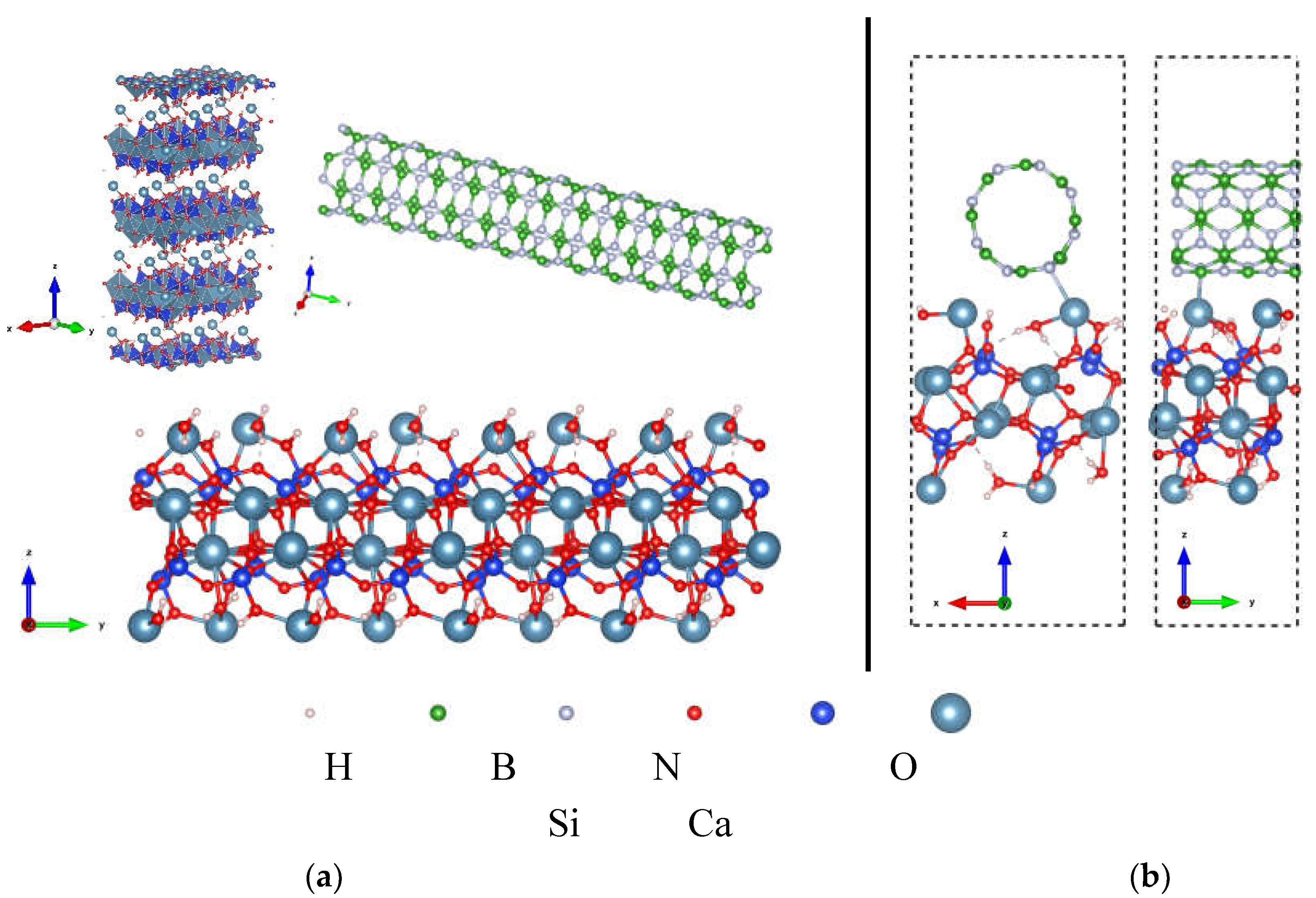
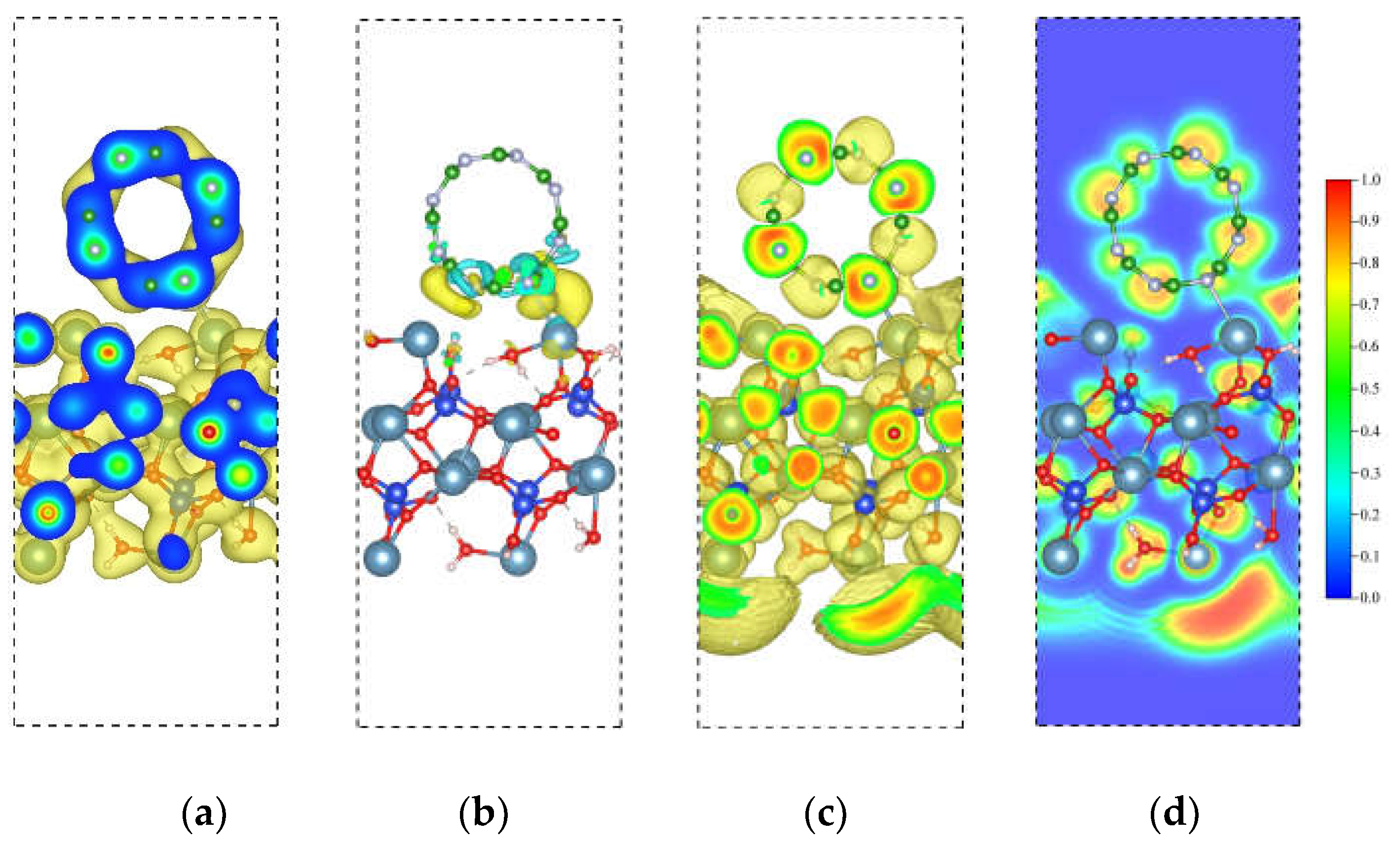
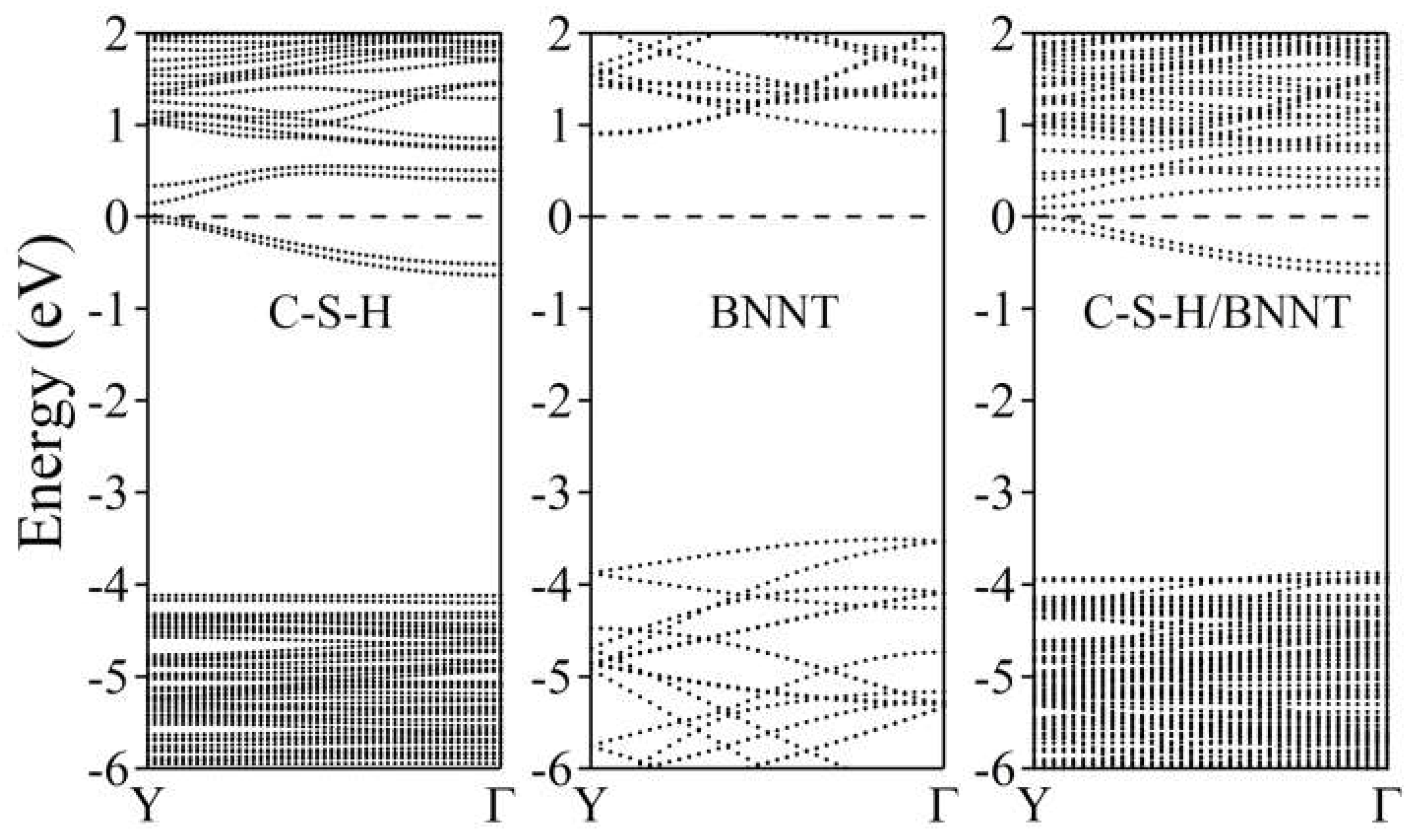
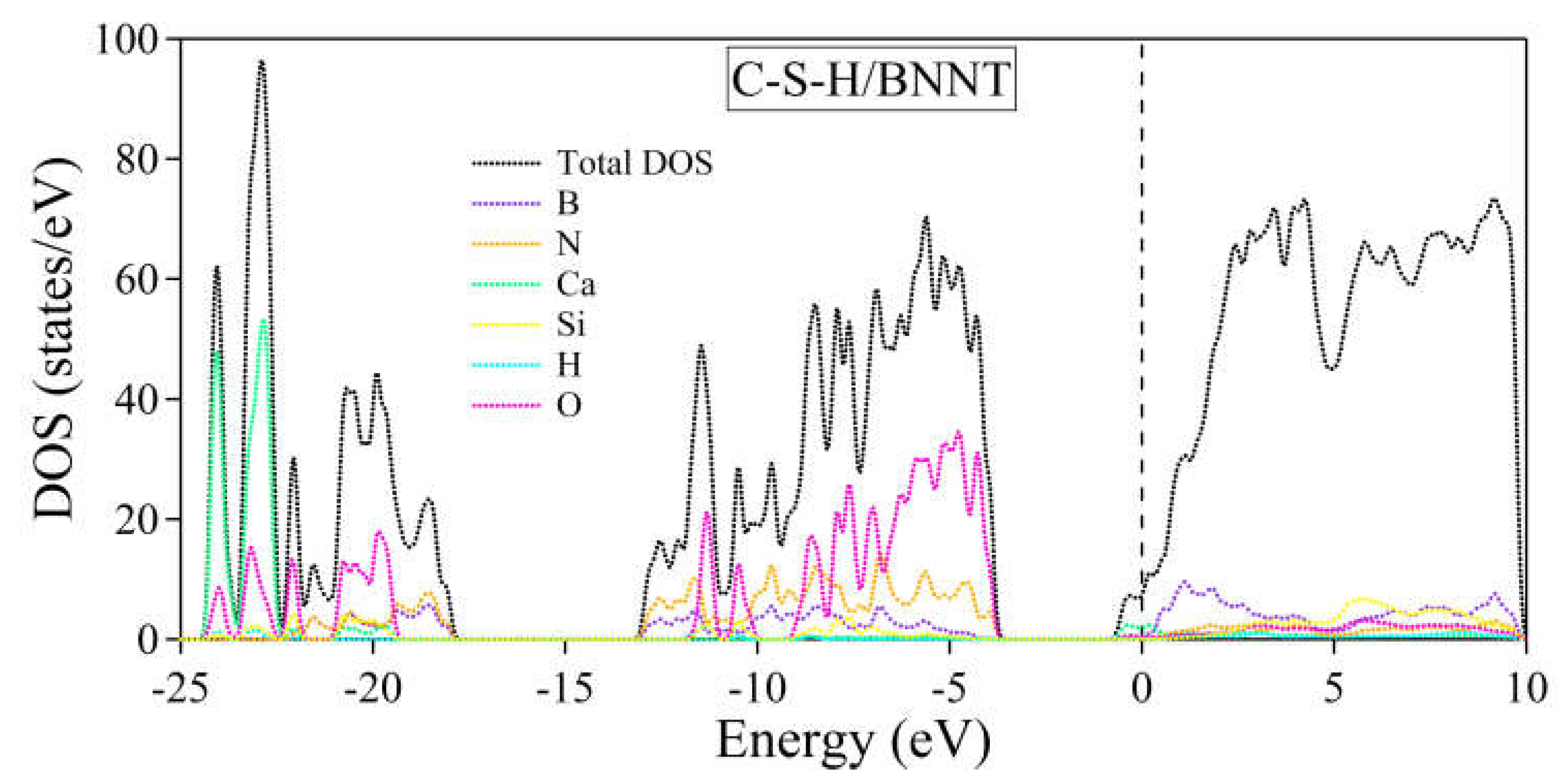
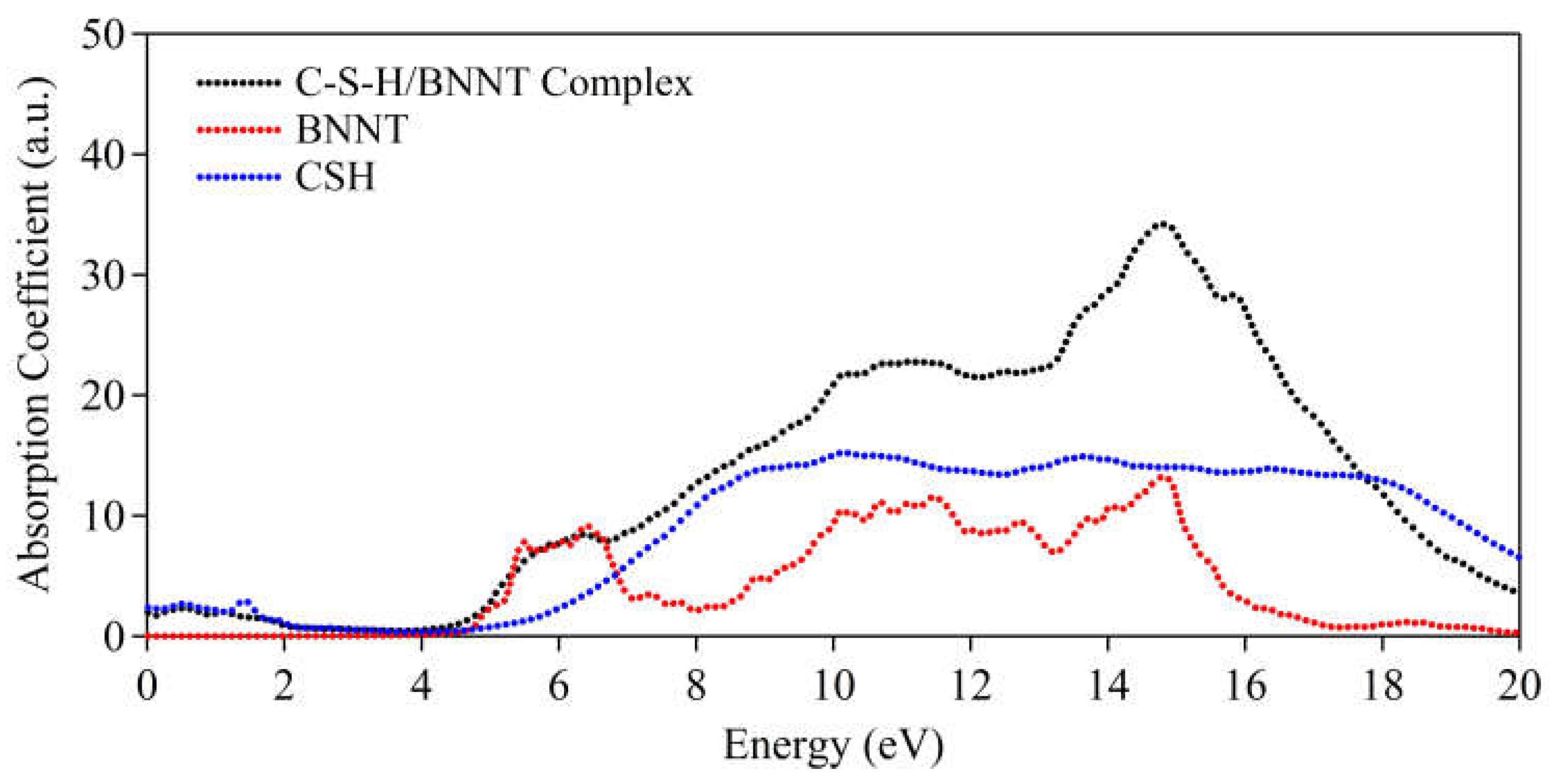
3.2. Calcium-Silicate-Hydrates and Boron Nitride Nanotube Nanocomposites

The optimized atomic structure of the C-S-H model, single layer C-S-H, BNNT(4,4), and the optimized configuration of the C-S-H/BNNT(4,4) composite are presented in Figure 9. To simulate the interface of the C-S-H with the BNNT, a single layer of the C-S-H taken from the molecular dynamics results is utilized [97]. The intralayer of prototype C-S-H has a 1:1 Ca to Si ratio, while two Ca ions and two water molecules are placed at the surfaces of the C-S-H. This model parallels the recent research showing that the surface of C-S-H is rich in Ca ions [98]. Both the tendency of the Ca ions to diffuse in the system and the variability of the Ca:Si ratio are probable [99]. These situations will not be covered in this work.
The prototype C-S-H here is adapted to our recent work that describes the interface of graphene-nanoribbon and SWCNT with the C-S-H[81]. The isolated C-S-H has Ca–H2O, Ca–O, and Si–O bonds ranging from 2.35-2.43 Å, 2.39-2.70 Å, and 1.62 –1.70 Å, respectively. The bond lengths are in agreement with experimental data[98]. Turning to the isolated BNNT, the B-N bond in the tube direction is measured to be 1.44 Å, while in the circumferential direction, the B-N bond is 1.46 Å. These measured bond lengths here are close to the BNNT's report [100]. The deviation is attributed to the fixed unit cell considered here and the overall method limitation.
The minimum interaction distance of C-S-H and BNNT is 2.68 Å (Ca–N). On the one hand, the interaction distance of the H2O – BNNT is 3.10 Å (O–B), and the Si-OH – BNNT distance is 2.40 Å and 3.21 Å for H-N and O-N, respectively. In the composite, minor changes to the Ca-O and Si-OH of the C-S-H at the interface are lower than 0.005 Å. The most observable change in the atomic structure of the C-S-H in the complex structure is the orientation of the confined H2O, in which the H points toward the O atoms, establishing a hydrogen bond. This minor structural change is mainly a signal of weakly bonded systems similar to the discussion in the preceding section.
The interaction strength is quantified by calculating the binding energy per unit cell. The binding energy of the C-S-H/BNNT is -0.89 eV, which is lower in magnitude compared to the binding energy of the C-S-H/SWCNT (-5.0 eV) and C-S-H/graphene-nanoribbon (-3.24 eV) [81]. Furthermore, the calculated binding energy here is much lower than the binding energy of graphene-based material with the monomer of C-S-H[101].
The CDD and ELF are also provided to understand the interaction of BNNT and C-S-H composite. At the isosurface value of 0.02/Å3, it is noticeable that Ca and N bonds overlapped, indicative of a shared electron type of interaction. We further confirm this result by calculating the CDD isosurface, showing an accumulation of electronic charge at the bond region. The overall charge transfer from C-S-H to the BNNT is 0.47 e. The total electron depletion of the Ca ions at the interface is 0.37 e. The total contribution of the Si-OH and H2O is ~0.10 e, which is way lower owing to the size of the system considered. These results indicate that major charge transfer is attributed to the Ca ions at the interface, which drives the interaction of nanocomposites. This further confirms the findings in our recent work on the Ca ions at the interface, which drives the bonding between the C-S-H layer with the graphene-nanoribbon and SWCNT. The ELF isosurface and 2D contour are displayed in Figure 10c and Figure 10d, respectively. The result shows that the BNNT tends to interact with the lone pair of the Ca ions of the C-S-H. This is contrary to our previous work, where the Ca ion's lone pair vanishes upon adsorption of the graphene-nanoribbon and SWCNT.
The electronic band structures of the C-S-H, BNNT, and C-S-H/BNNT complexes are further calculated to reveal the composites' metallicity, as shown in Figure 11. Our results show that the dispersive bands appear near the Fermi energy due to the lone pair of the Ca ions, as discussed here [81]. On the one hand, the BNNT shows insulating properties having a bandgap of 3.77 eV located at the Γ point. This is in agreement with the reports presented in ref. [102] with a bandgap of 3.87 eV and 4.11 eV calculated using PBE and BLYP functionals, respectively. The PBE functional is well-known for underestimating the bandgap of semiconductors and insulators. Moreover, the theoretical length of the BNNT (3.695Å) is used here to match the size of the unit cell of the C-S-H, while ref. [102] allowing cell relaxation, giving 2.560 Å leads to minor disagreement with the bandgap of BNNT, aside from intrinsic error of the theory and approximations combined. The composite electronic band structure can be considered superimposed on the constituents, except for the minor shift of bands of the BNNT to lower energy due to charge accumulations. This is the usual result of weakly bonded systems, as demonstrated in the following references [79,80,103,104,105]. We further provide the system's total and partial density of states shown in Figure 12. The black dotted line depicts the total DOS, while the total contributions of the B, N, Ca, Si, H, and O atoms are depicted by purple, orange, green, yellow, cyan, and magenta dotted lines, respectively. The decomposed DOS of BNNT and C-S-H shows no strong hybridization indicative of weakly bonded systems, confirming our previous conclusions.
The absorption spectra are further calculated to provide reference to observables. Here, as can be observed in Figure 13, the BNNT tends to have abrupt absorption at ~4.5 eV, indicative of insulating properties (i.e. wide bandgap nature). Meanwhile, the single C-S-H layer shows metallic characteristics having minor absorption at energy region < 3.0 eV. This is attributed to the dispersive bands at the vicinity of the Fermi level. In the complex structure, both the characteristics of BNNT and C-S-H absorption spectra are reproduced except for minor deviation owing to the realignment of bands. It should be noted that in a bulk system of C-S-H, the dispersive bands may vanish due to the presence of bulk H2O in the interface.

4. Conclusions

We have studied the interactions, electronic structures, and optical properties of DNT/cellulose, DNT/epoxy, and C-S-H/BNNT composites through density functional theory calculations. Various orientations of DNT/cellulose and DNT/epoxy composites have been considered. Our results reveal wide minimum interaction distances between non-hydrogen atoms of the nanothread and polymers, less binding energies, and minimal charge transfer, indicating physical adsorption and weakly interacting systems mainly of vdW type, as further discerned from the CDD and ELF plots. Consequently, only minor modifications to the electronic properties of the nanothread occurred. The electronic band structures of DNT/polymer systems show a slight shift of bands at the higher energy level relative to that of DNT. The density of states displays no hybridization between atoms of the nanothread and polymer, confirming their weak interactions. The optical absorption spectra of the composites indicate insulating behavior.
On the other hand, the BNNT and C-S-H composite show a shared type of interaction as indicated by the formed Ca – N bond and accumulation of electronic charge at the bond region. Bader charge transfer analysis further confirms that most charge transfer from C-S-H to the BNNT comes from the Ca ions. The electronic band structure of the complex system shows superimposed bands of BNNT and C-S-H. The density of states reveals no hybridization, which further confirms the weak interaction between the subsystems. The absorption spectra of the C-S-H/ BNNT complex show metallic characteristics.
Overall, this work provides fundamental information on the bonding characteristics and electronic-optical properties of the DNT/polymer (cellulose and epoxy) and BNNT/C-S-H composites, otherwise not readily known in experiments. This information is useful in giving experimentalists an electronic-level perspective for tuning the nanomaterials-reinforced composites' properties for targeted applications.

Author Contributions

Conceptualization, D.C.D., A.A.Z.M., and L.C.C.A.; methodology, D.C.D., A.A.Z.M., and L.C.C.A.; validation, D.C.D., A.A.Z.M., N.J.P.J., D.R.T.F., and L.C.C.A.; formal analysis, D.C.D., A.A.Z.M., and L.C.C.A.; investigation, D.C.D. and A.A.Z.M.; resources, D.C.D., A.A.Z.M., and L.C.C.A.; data curation, D.C.D. and A.A.Z.M.; writing—original draft preparation, D.C.D. and A.A.Z.M.; writing—review and editing, D.C.D., A.A.Z.M., N.J.P.J., and L.C.C.A.; visualization, D.C.D. and A.A.Z.M.; supervision, L.C.C.A.; project administration, L.C.C.A. and D.R.T.F.; funding acquisition, L.C.C.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Office of the Vice Chancellor for Research and Enterprise (OVCRE) of Mindanao State University – Iligan Institute of Technology (MSU-IIT) (S.O. No. 01020-IIT S. of 2023, S.O. No. 00362-IIT S. of 2024, and S.O. No. 00232-IIT S. of 2024).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors acknowledge the support of Mindanao State University – Iligan Institute of Technology and Jose Rizal Memorial State University. The authors are also grateful for the allocation of computational resources at the Computing and Archiving Research Environment (COARE) facility at the Department of Science and Technology – Advanced Science and Technology Institute, Republic of the Philippines.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Egbo, M.K. A Fundamental Review on Composite Materials and Some of Their Applications in Biomedical Engineering. Journal of King Saud University - Engineering Sciences 2020. [Google Scholar] [CrossRef]
  2. Li, W.; Dong, W.; Guo, Y.; Wang, K.; Shah, S.P. Advances in Multifunctional Cementitious Composites with Conductive Carbon Nanomaterials for Smart Infrastructure. Cement and Concrete Composites 2022, 128, 104454. [Google Scholar] [CrossRef]
  3. Umar, K.; Yaqoob, A.A.; Ibrahim, M.N.M.; Parveen, T.; Safian, M.T. Chapter Thirteen - Environmental Applications of Smart Polymer Composites. In Smart Polymer Nanocomposites; Bhawani, S.A., Khan, A., Jawaid, , M., Eds.; Woodhead Publishing Series in Composites Science and Engineering; Woodhead Publishing, 2021; pp. 295–312. ISBN 978-0-12-819961-9. [Google Scholar]
  4. Ali, A.; Andriyana, A. Properties of Multifunctional Composite Materials Based on Nanomaterials: A Review. RSC Advances 2020, 10, 16390–16403. [Google Scholar] [CrossRef] [PubMed]
  5. Bekzhanova, Z.; Memon, S.A.; Kim, J.R. Self-Sensing Cementitious Composites: Review and Perspective. Nanomaterials 2021, 11, 2355. [Google Scholar] [CrossRef] [PubMed]
  6. Basquiroto de Souza, F.; Yao, X.; Lin, J.; Naseem, Z.; Tang, Z.Q.; Hu, Y.; Gao, W.; Sagoe-Crentsil, K.; Duan, W. Effective Strategies to Realize High-Performance Graphene-Reinforced Cement Composites. Construction and Building Materials 2022, 324, 126636. [Google Scholar] [CrossRef]
  7. Sreenivasulu, B.; Ramji, Br.; Nagaral, M. A Review on Graphene Reinforced Polymer Matrix Composites. Materials Today: Proceedings 2018, 5, 2419–2428. [Google Scholar] [CrossRef]
  8. Díez-Pascual, A.M. Carbon-Based Polymer Nanocomposites for High-Performance Applications. Polymers 2020, 12, 872. [Google Scholar] [CrossRef] [PubMed]
  9. Harussani, M.M.; Sapuan, S.M.; Nadeem, G.; Rafin, T.; Kirubaanand, W. Recent Applications of Carbon-Based Composites in Defence Industry: A Review. Defence Technology 2022, 18, 1281–1300. [Google Scholar] [CrossRef]
  10. Wang, Z.; Liu, L.; Zhang, Y.; Huang, Y.; Liu, J.; Zhang, X.; Liu, X.; Teng, H.; Zhang, X.; Zhang, J.; et al. A Review of Graphene-Based Materials/Polymer Composite Aerogels. Polymers (Basel) 2023, 15, 1888. [Google Scholar] [CrossRef] [PubMed]
  11. Seydibeyoğlu, M.Ö.; Dogru, A.; Wang, J.; Rencheck, M.; Han, Y.; Wang, L.; Seydibeyoğlu, E.A.; Zhao, X.; Ong, K.; Shatkin, J.A.; et al. Review on Hybrid Reinforced Polymer Matrix Composites with Nanocellulose, Nanomaterials, and Other Fibers. Polymers 2023, 15, 984. [Google Scholar] [CrossRef]
  12. Latif, Z.; Ali, M.; Lee, E.-J.; Zubair, Z.; Lee, K.H. Thermal and Mechanical Properties of Nano-Carbon-Reinforced Polymeric Nanocomposites: A Review. J. Compos. Sci. 2023, 7, 441. [Google Scholar] [CrossRef]
  13. Amraei, J.; Jam, J.E.; Arab, B.; Firouz-Abadi, R.D. Modeling the Interphase Region in Carbon Nanotube-reinforced Polymer Nanocomposites. Polymer Composites 2019, 40. [Google Scholar] [CrossRef]
  14. Fitzgibbons, T.C.; Guthrie, M.; Xu, E.; Crespi, V.H.; Davidowski, S.K.; Cody, G.D.; Alem, N.; Badding, J.V. Benzene-Derived Carbon Nanothreads. Nature Mater 2015, 14, 43–47. [Google Scholar] [CrossRef]
  15. Li, X.; Baldini, M.; Wang, T.; Chen, B.; Xu, E.; Vermilyea, B.; Crespi, V.H.; Hoffmann, R.; Molaison, J.J.; Tulk, C.A.; et al. Mechanochemical Synthesis of Carbon Nanothread Single Crystals. J. Am. Chem. Soc. 2017, 139, 16343–16349. [Google Scholar] [CrossRef]
  16. Duan, P.; Li, X.; Wang, T.; Chen, B.; Juhl, S.J.; Koeplinger, D.; Crespi, V.H.; Badding, J.V.; Schmidt-Rohr, K. The Chemical Structure of Carbon Nanothreads Analyzed by Advanced Solid-State NMR. J. Am. Chem. Soc. 2018. [Google Scholar] [CrossRef]
  17. Wang, T.; Duan, P.; Xu, E.-S.; Vermilyea, B.; Chen, B.; Li, X.; Badding, J.V.; Schmidt-Rohr, K.; Crespi, V.H. Constraining Carbon Nanothread Structures by Experimental and Calculated Nuclear Magnetic Resonance Spectra. Nano Lett. 2018, 18, 4934–4942. [Google Scholar] [CrossRef]
  18. Nobrega, M.M.; Teixeira-Neto, E.; Cairns, A.B.; Temperini, M.L.A.; Bini, R. One-Dimensional Diamondoid Polyaniline-like Nanothreads from Compressed Crystal Aniline. Chem. Sci. 2018, 9, 254–260. [Google Scholar] [CrossRef]
  19. Fanetti, S.; Nobrega, M.M.; Teixeira-Neto, E.; Temperini, M.L.A.; Bini, R. Effect of Structural Anisotropy in High-Pressure Reaction of Aniline. J. Phys. Chem. C 2018, 122, 29158–29164. [Google Scholar] [CrossRef]
  20. Li, X.; Wang, T.; Duan, P.; Baldini, M.; Huang, H.-T.; Chen, B.; Juhl, S.J.; Koeplinger, D.; Crespi, V.H.; Schmidt-Rohr, K.; et al. Carbon Nitride Nanothread Crystals Derived from Pyridine. J. Am. Chem. Soc. 2018, 140, 4969–4972. [Google Scholar] [CrossRef]
  21. Fanetti, S.; Santoro, M.; Alabarse, F.; Enrico, B.; Bini, R. Modulating the H-Bond Strength by Varying the Temperature for the High Pressure Synthesis of Nitrogen Rich Carbon Nanothreads. Nanoscale 2020, 12, 5233–5242. [Google Scholar] [CrossRef]
  22. Oburn, S.M.; Huss, S.; Cox, J.; Gerthoffer, M.C.; Wu, S.; Biswas, A.; Murphy, M.; Crespi, V.H.; Badding, J.V.; Lopez, S.A.; et al. Photochemically Mediated Polymerization of Molecular Furan and Pyridine: Synthesis of Nanothreads at Reduced Pressures. J. Am. Chem. Soc. 2022. [Google Scholar] [CrossRef]
  23. Biswas, A.; Ward, M.D.; Wang, T.; Zhu, L.; Huang, H.-T.; Badding, J.V.; Crespi, V.H.; Strobel, T.A. Evidence for Orientational Order in Nanothreads Derived from Thiophene. J. Phys. Chem. Lett. 2019, 10, 7164–7171. [Google Scholar] [CrossRef]
  24. Huss, S.; Wu, S.; Chen, B.; Wang, T.; Gerthoffer, M.C.; Ryan, D.J.; Smith, S.E.; Crespi, V.H.; Badding, J.V.; Elacqua, E. Scalable Synthesis of Crystalline One-Dimensional Carbon Nanothreads through Modest-Pressure Polymerization of Furan. ACS Nano 2021, 15, 4134–4143. [Google Scholar] [CrossRef]
  25. Ward, M.D.; Tang, W.S.; Zhu, L.; Popov, D.; Cody, G.D.; Strobel, T.A. Controlled Single-Crystalline Polymerization of C 10 H 8 ·C 10 F 8 under Pressure. Macromolecules 2019, 52, 7557–7563. [Google Scholar] [CrossRef]
  26. Friedrich, A.; Collings, I.E.; Dziubek, K.F.; Fanetti, S.; Radacki, K.; Ruiz-Fuertes, J.; Pellicer-Porres, J.; Hanfland, M.; Sieh, D.; Bini, R.; et al. Pressure-Induced Polymerization of Polycyclic Arene–Perfluoroarene Cocrystals: Single Crystal X-Ray Diffraction Studies, Reaction Kinetics, and Design of Columnar Hydrofluorocarbons. J. Am. Chem. Soc. 2020, 142, 18907–18923. [Google Scholar] [CrossRef]
  27. Gao, D.; Tang, X.; Xu, J.; Yang, X.; Zhang, P.; Che, G.; Wang, Y.; Chen, Y.; Gao, X.; Dong, X.; et al. Crystalline C 3 N 3 H 3 Tube (3,0) Nanothreads. Proc. Natl. Acad. Sci. U.S.A. 2022, 119, e2201165119. [Google Scholar] [CrossRef]
  28. Dunning, S.G.; Zhu, L.; Chen, B.; Chariton, S.; Prakapenka, V.B.; Somayazulu, M.; Strobel, T.A. Solid-State Pathway Control via Reaction-Directing Heteroatoms: Ordered Pyridazine Nanothreads through Selective Cycloaddition. J. Am. Chem. Soc. 2022, 144, 2073–2078. [Google Scholar] [CrossRef]
  29. Xu, E.; Lammert, P.E.; Crespi, V.H. Systematic Enumeration of Sp 3 Nanothreads. Nano Lett. 2015, 15, 5124–5130. [Google Scholar] [CrossRef]
  30. Silveira, J.F.R.V.; Muniz, A.R. Functionalized Diamond Nanothreads from Benzene Derivatives. Phys. Chem. Chem. Phys. 2017, 19, 7132–7137. [Google Scholar] [CrossRef]
  31. Chen, B.; Wang, T.; Crespi, V.H.; Li, X.; Badding, J.; Hoffmann, R. All the Ways To Have Substituted Nanothreads. J. Chem. Theory Comput. 2018, 14, 1131–1140. [Google Scholar] [CrossRef]
  32. Roman, R.E.; Kwan, K.; Cranford, S.W. Mechanical Properties and Defect Sensitivity of Diamond Nanothreads. Nano Lett. 2015. [Google Scholar] [CrossRef]
  33. Zhan, H.; Zhang, G.; Tan, V.B.C.; Cheng, Y.; Bell, J.M.; Zhang, Y.; Gu, Y. Diamond Nanothread as a New Reinforcement for Nanocomposites. Adv Funct Materials 2016, 26, 5279–5283. [Google Scholar] [CrossRef]
  34. Zhang, L.W.; Ji, W.M.; Liew, K.M. Mechanical Properties of Diamond Nanothread Reinforced Polymer Composites. Carbon 2018, 132, 232–240. [Google Scholar] [CrossRef]
  35. Ji, W.M.; Zhang, L.W. Diamond Nanothread Reinforced Polymer Composites: Ultra-High Glass Transition Temperature and Low Density. Composites Science and Technology 2019, 183, 107789. [Google Scholar] [CrossRef]
  36. Duan, K.; Zhang, J.; Li, L.; Hu, Y.; Zhu, W.; Wang, X. Diamond Nanothreads as Novel Nanofillers for Cross-Linked Epoxy Nanocomposites. Composites Science and Technology 2019, 174, 84–93. [Google Scholar] [CrossRef]
  37. Zhan, H.; Zhang, G.; Tan, V.B.C.; Gu, Y. The Best Features of Diamond Nanothread for Nanofibre Applications. Nat Commun 2017, 8, 14863. [Google Scholar] [CrossRef]
  38. Klemm, D.; Heublein, B.; Fink, H.; Bohn, A. Cellulose: Fascinating Biopolymer and Sustainable Raw Material. Angew Chem Int Ed 2005, 44, 3358–3393. [Google Scholar] [CrossRef]
  39. Tapia-Orozco, N.; Ibarra-Cabrera, R.; Tecante, A.; Gimeno, M.; Parra, R.; Garcia-Arrazola, R. Removal Strategies for Endocrine Disrupting Chemicals Using Cellulose-Based Materials as Adsorbents: A Review. Journal of Environmental Chemical Engineering 2016, 4, 3122–3142. [Google Scholar] [CrossRef]
  40. Miyashiro, D.; Hamano, R.; Umemura, K. A Review of Applications Using Mixed Materials of Cellulose, Nanocellulose and Carbon Nanotubes. Nanomaterials 2020, 10, 186. [Google Scholar] [CrossRef]
  41. Dong, Y.-D.; Zhang, H.; Zhong, G.-J.; Yao, G.; Lai, B. Cellulose/Carbon Composites and Their Applications in Water Treatment – a Review. Chemical Engineering Journal 2021, 405, 126980. [Google Scholar] [CrossRef]
  42. Yang, K.; Yazawa, K.; Tsuchiya, K.; Numata, K.; Guan, J. Molecular Interactions and Toughening Mechanisms in Silk Fibroin–Epoxy Resin Blend Films. Biomacromolecules 2019, 20, 2295–2304. [Google Scholar] [CrossRef]
  43. Yu, A.; Itkis, M.E.; Bekyarova, E.; Haddon, R.C. Effect of Single-Walled Carbon Nanotube Purity on the Thermal Conductivity of Carbon Nanotube-Based Composites. Applied Physics Letters 2006, 89, 133102. [Google Scholar] [CrossRef]
  44. Rana, S.; Alagirusamy, R.; Joshi, M. A Review on Carbon Epoxy Nanocomposites. Journal of Reinforced Plastics and Composites 2009, 28, 461–487. [Google Scholar] [CrossRef]
  45. Gantayat, S.; Rout, D.; Swain, S.K. Carbon Nanomaterial–Reinforced Epoxy Composites: A Review. Polymer-Plastics Technology and Engineering 2018, 57, 1–16. [Google Scholar] [CrossRef]
  46. Singh, N.P.; Gupta, V.K.; Singh, A.P. Graphene and Carbon Nanotube Reinforced Epoxy Nanocomposites: A Review. Polymer 2019, 180, 121724. [Google Scholar] [CrossRef]
  47. Khostavan, S.; Fazli, M.; Ahangari, M.G.; Rostamiyan, Y. The Effect of Interaction between Nanofillers and Epoxy on Mechanical and Thermal Properties of Nanocomposites: Theoretical Prediction and Experimental Analysis. Advances in Polymer Technology 2019, 2019, 1–10. [Google Scholar] [CrossRef]
  48. Prasanthi, P.P.; Kumar, M.S.R.N.; Chowdary, M.S.; Madhav, V.V.V.; Saxena, K.K.; Mohammed, K.A.; Khan, M.I.; Upadhyay, G.; Eldin, S.M. Mechanical Properties of Carbon Fiber Reinforced with Carbon Nanotubes and Graphene Filled Epoxy Composites: Experimental and Numerical Investigations. Mater. Res. Express 2023, 10, 025308. [Google Scholar] [CrossRef]
  49. Zeng, K.; Jibril Ibrahim, A.; Muter Saleh, Z.; Altimari, U.S.; Turki Jalil, A.; Kadhim, M.M.; Hussain Dilfy, S.; Taheri Andani, M.; Alizadeh, A.; Hekmatifar, M. Investigation of Mechanical and Thermal Characteristics of Epoxy/Graphene Oxide Nanocomposites by Molecular Dynamics Simulation. Materials Science and Engineering: B 2023, 287, 116087. [Google Scholar] [CrossRef]
  50. Khalid, M.Y.; Kamal, A.; Otabil, A.; Mamoun, O.; Liao, K. Graphene/Epoxy Nanocomposites for Improved Fracture Toughness: A Focused Review on Toughening Mechanism. Chemical Engineering Journal Advances 2023, 16, 100537. [Google Scholar] [CrossRef]
  51. Hu, P.; Alizadeh, A.; Jasim, D.J.; Nasajpour-Esfahani, N.; Shamsborhan, M.; Sabetvand, R. The Effect of Graphene Oxide Nanosheet Size and Initial Temperature on the Mechanical and Thermal Properties of Epoxy/Graphene Oxide Structure Using Molecular Dynamics Simulation. Journal of Physics and Chemistry of Solids 2024, 184, 111713. [Google Scholar] [CrossRef]
  52. Cassese, P.; Rainieri, C.; Occhiuzzi, A. Applications of Cement-Based Smart Composites to Civil Structural Health Monitoring: A Review. Applied Sciences 2021, 11, 8530. [Google Scholar] [CrossRef]
  53. Rao, R.K.; Sasmal, S. Nanoengineered Smart Cement Composite for Electrical Impedance-Based Monitoring of Corrosion Progression in Structures. Cement and Concrete Composites 2022, 126, 104348. [Google Scholar] [CrossRef]
  54. Suryanto, B.; McCarter, W.J.; Starrs, G.; Wilson, S.A.; Traynor, R.M. Smart Cement Composites for Durable and Intelligent Infrastructure. Procedia Engineering 2015, 125, 796–803. [Google Scholar] [CrossRef]
  55. Yang, H.; Cui, H.; Tang, W.; Li, Z.; Han, N.; Xing, F. A Critical Review on Research Progress of Graphene/Cement Based Composites. Composites Part A: Applied Science and Manufacturing 2017, 102, 273–296. [Google Scholar] [CrossRef]
  56. Huseien, G. A Review on Concrete Composites Modified with Nanoparticles. Journal of Composites Science 2023, 7, 67. [Google Scholar] [CrossRef]
  57. Kedir, A.; Gamachu, M.; Alex, A.G. Cement-Based Graphene Oxide Composites: A Review on Their Mechanical and Microstructure Properties. Journal of Nanomaterials 2023, 2023, e6741000. [Google Scholar] [CrossRef]
  58. Zhang, P.; Wang, M.; Han, X.; Zheng, Y. A Review on Properties of Cement-Based Composites Doped with Graphene. Journal of Building Engineering 2023, 70, 106367. [Google Scholar] [CrossRef]
  59. Bagheri, A.; Negahban, E.; Asad, A.; Ali Abbasi, H.; Muhammad Raza, S. Graphene Oxide-Incorporated Cementitious Composites: A Thorough Investigation. Materials Advances 2022, 3, 9040–9051. [Google Scholar] [CrossRef]
  60. Cho, B.H.; Nam, B.H. Concrete Composites Reinforced with Graphene Oxide Nanoflake (GONF) and Steel Fiber for Application in Rigid Pavement. Case Studies in Construction Materials 2022, 17, e01346. [Google Scholar] [CrossRef]
  61. Murali, M.; Alaloul, W.S.; Mohammed, B.S.; Musarat, M.A.; Salaheen, M.A.; Al-Sabaeei, A.M.; Isyaka, A. Utilizing Graphene Oxide in Cementitious Composites: A Systematic Review. Case Studies in Construction Materials 2022, 17, e01359. [Google Scholar] [CrossRef]
  62. Xu, Y.; Zeng, J.; Chen, W.; Jin, R.; Li, B.; Pan, Z. A Holistic Review of Cement Composites Reinforced with Graphene Oxide. Construction and Building Materials 2018, 171, 291–302. [Google Scholar] [CrossRef]
  63. Du, M.; Jing, H.; Gao, Y.; Su, H.; Fang, H. Carbon Nanomaterials Enhanced Cement-Based Composites: Advances and Challenges. Nanotechnology Reviews 2020, 9, 115–135. [Google Scholar] [CrossRef]
  64. Cho, B.H.; Chung, W.; Nam, B.H. Molecular Dynamics Simulation of Calcium-Silicate-Hydrate for Nano-Engineered Cement Composites—A Review. Nanomaterials 2020, 10, 2158. [Google Scholar] [CrossRef]
  65. Lu, D.; Zhong, J. Carbon-Based Nanomaterials Engineered Cement Composites: A Review. Journal of Infrastructure Preservation and Resilience 2022, 3, 2. [Google Scholar] [CrossRef]
  66. Du, H.; Pang, S. Transport of Water and Chloride Ion in Cement Composites Modified with Graphene Nanoplatelet. Key Engineering Materials 2015, 629, 162–167. [Google Scholar] [CrossRef]
  67. Maselugbo, A.O.; Harrison, H.B.; Alston, J.R. Boron Nitride Nanotubes: A Review of Recent Progress on Purification Methods and Techniques. Journal of Materials Research 2022, 37, 4438–4458. [Google Scholar] [CrossRef]
  68. Xu, T.; Zhang, K.; Cai, Q.; Wang, N.; Wu, L.; He, Q.; Wang, H.; Zhang, Y.; Xie, Y.; Yao, Y.; et al. Advances in Synthesis and Applications of Boron Nitride Nanotubes: A Review. Chemical Engineering Journal 2022, 431, 134118. [Google Scholar] [CrossRef]
  69. Roudi, M.R.R.; Ranjkesh, M.; Korayem, A.H.; Shahsavary, R. Review of Boron Nitride Nanosheet-Based Composites for Construction Applications. ACS Appl. Nano Mater. 2022, 5, 17356–17372. [Google Scholar] [CrossRef]
  70. Liu, J.; Jian, W.; Lau, D. Boron Nitride Nanosheet as a Promising Reinforcement for Cementitious Composites. Applied Surface Science 2022, 572, 151395. [Google Scholar] [CrossRef]
  71. Falin, A.; Cai, Q.; Santos, E.J.G.; Scullion, D.; Qian, D.; Zhang, R.; Yang, Z.; Huang, S.; Watanabe, K.; Taniguchi, T.; et al. Mechanical Properties of Atomically Thin Boron Nitride and the Role of Interlayer Interactions. Nat Commun 2017, 8, 15815. [Google Scholar] [CrossRef]
  72. Chen, X.; Dmuchowski, C.M.; Park, C.; Fay, C.C.; Ke, C. Quantitative Characterization of Structural and Mechanical Properties of Boron Nitride Nanotubes in High Temperature Environments. Sci Rep 2017, 7, 11388. [Google Scholar] [CrossRef]
  73. Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys.: Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
  74. Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced Capabilities for Materials Modelling with Quantum ESPRESSO. J. Phys.: Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
  75. Hamann, D.R. Optimized Norm-Conserving Vanderbilt Pseudopotentials. Phys. Rev. B 2013, 88, 085117. [Google Scholar] [CrossRef]
  76. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
  77. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. The Journal of Chemical Physics 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
  78. Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
  79. Munio, A.A.Z.; Domato, D.C.; Pido, A.A.G. Non-Covalent Functionalization of Biphenylene Network by Cellulose and Nylon-6: A First-Principles Study.
  80. Munio, A.A.Z.; Pido, A.A.G.; Ambolode Ii, L.C.C. First-Principles Insights on the Bonding Mechanism and Electronic Structure of SWCNT and Oxygenated-SWCNT Functionalized by Cellulose Biopolymer. NHC 2023, 40, 51–63. [Google Scholar] [CrossRef]
  81. Munio, A.A.Z.; Domato, D.C.; Pido, A.A.G.; Ambolode Ii, L.C.C. On the Nanoscale Interface, Electronic Structure, and Optical Properties of Nanocarbon-Reinforced Calcium Silicate Hydrates. Phys. Scr. 2024, 99, 015927. [Google Scholar] [CrossRef]
  82. Momma, K.; Izumi, F. VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data. J Appl Crystallogr 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
  83. Henkelman, G.; Arnaldsson, A.; Jónsson, H. A Fast and Robust Algorithm for Bader Decomposition of Charge Density. Computational Materials Science 2006, 36, 354–360. [Google Scholar] [CrossRef]
  84. Sanville, E.; Kenny, S.D.; Smith, R.; Henkelman, G. Improved Grid-based Algorithm for Bader Charge Allocation. J Comput Chem 2007, 28, 899–908. [Google Scholar] [CrossRef]
  85. Tang, W.; Sanville, E.; Henkelman, G. A Grid-Based Bader Analysis Algorithm without Lattice Bias. J. Phys.: Condens. Matter 2009, 21, 084204. [Google Scholar] [CrossRef]
  86. Yu, M.; Trinkle, D.R. Accurate and Efficient Algorithm for Bader Charge Integration. The Journal of Chemical Physics 2011, 134, 064111. [Google Scholar] [CrossRef]
  87. Becke, A.D.; Edgecombe, K.E. A Simple Measure of Electron Localization in Atomic and Molecular Systems. The Journal of Chemical Physics 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
  88. Koumpouras, K.; Larsson, J.A. Distinguishing between Chemical Bonding and Physical Binding Using Electron Localization Function (ELF). J. Phys.: Condens. Matter 2020, 32, 315502. [Google Scholar] [CrossRef]
  89. Zhang, L.-W.; Ji, W.-M.; Hu, Y.; Liew, K.M. Atomistic Insights into the Tunable Transition from Cavitation to Crazing in Diamond Nanothread-Reinforced Polymer Composites. Research 2020, 2020, 2020–7815462. [Google Scholar] [CrossRef]
  90. Li, C.; Zhou, Y.; Zhan, H.; Bai, J.; Gu, Y. Effective Enhancement of a Carbon Nanothread on the Mechanical Properties of the Polyethylene Nanocomposite. J. Phys. Chem. C 2021, 125, 5781–5792. [Google Scholar] [CrossRef]
  91. Zhan, H.; Zhou, Y.; Zhang, G.; Zhu, J.; Zhang, W.; Lü, C.; Gu, Y. Carbon Nanothreads Enable Remarkable Enhancement in the Thermal Conductivity of Polyethylene. Nanoscale 2021, 13, 6934–6943. [Google Scholar] [CrossRef]
  92. Wu, W.; Tai, B.; Guan, S.; Yang, S.A.; Zhang, G. Hybrid Structures and Strain-Tunable Electronic Properties of Carbon Nanothreads. J. Phys. Chem. C 2018, 122, 3101–3106. [Google Scholar] [CrossRef]
  93. Chen, M.-M.; Xiao, J.; Cao, C.; Zhang, D.; Cui, L.-L.; Xu, X.-M.; Long, M.-Q. Theoretical Prediction Electronic Properties of Group-IV Diamond Nanothreads. AIP Advances 2018, 8, 075107. [Google Scholar] [CrossRef]
  94. Demingos, P.G.; Muniz, A.R. Electronic and Mechanical Properties of Partially Saturated Carbon and Carbon Nitride Nanothreads. J. Phys. Chem. C 2019, 123, 3886–3891. [Google Scholar] [CrossRef]
  95. Xiao, J.; Chen, M.-M.; Liu, W.-J.; He, J.; Pan, C.-N.; Long, M.-Q. Perfect Mechanical and Robust Electronic Properties of New Carbon Nanothreads: A First Principles Study. Physica E: Low-dimensional Systems and Nanostructures 2019, 111, 37–43. [Google Scholar] [CrossRef]
  96. Miao, Z.; Cao, C.; Zhang, B.; Duan, H.; Long, M. First-Principles Study on the Effects of Doping and Adsorption on the Electronic and Magnetic Properties of Diamond Nanothreads. Physica E: Low-dimensional Systems and Nanostructures 2020, 118, 113949. [Google Scholar] [CrossRef]
  97. Selvam, R.P.; Subramani, V.J.; Murray, S. Potential Application of Nanotechnology on Cement Based Materials.
  98. Soyer-Uzun, S.; Chae, S.R.; Benmore, C.J.; Wenk, H.; Monteiro, P.J.M. Compositional Evolution of Calcium Silicate Hydrate ( C–S–H ) Structures by Total X-Ray Scattering. J. Am. Ceram. Soc. 2012, 95, 793–798. [Google Scholar] [CrossRef]
  99. Cho, B.H.; Chung, W.; Nam, B.H. Molecular Dynamics Simulation of Calcium-Silicate-Hydrate for Nano-Engineered Cement Composites—A Review. Nanomaterials 2020, 10, 2158. [Google Scholar] [CrossRef] [PubMed]
  100. Ju, S.-P.; Wang, Y.-C.; Lien, T.-W. Tuning the Electronic Properties of Boron Nitride Nanotube by Mechanical Uni-Axial Deformation: A DFT Study. Nanoscale Res Lett 2011, 6, 160. [Google Scholar] [CrossRef] [PubMed]
  101. Izadifar, M.; Dolado, J.S.; Thissen, P.; Ayuela, A. Interactions between Reduced Graphene Oxide with Monomers of (Calcium) Silicate Hydrates: A First-Principles Study. Nanomaterials 2021, 11, 2248. [Google Scholar] [CrossRef] [PubMed]
  102. Movlarooy, T.; Minaie, B. First Principles Study of Structural and Electronic Properties of BNNTs. J Comput Electron 2018, 17, 1441–1449. [Google Scholar] [CrossRef]
  103. Pido, A.A.G.; Munio, A.A.Z.; Ambolode Ii, L.C.C. Ab Initio Calculations of the Atomic Structure, Stability, and Electronic Properties of (C6H10O5)2 Encapsulation into Hydrogen-Doped Carbon Nanotube. NHC 2023, 38, 53–62. [Google Scholar] [CrossRef]
  104. Jilili, J.; Abdurahman, A.; Gülseren, O.; Schwingenschlögl, U. Non-Covalent Functionalization of Single Wall Carbon Nanotubes and Graphene by a Conjugated Polymer. Applied Physics Letters 2014, 105, 013103. [Google Scholar] [CrossRef]
  105. Shen, Y.; Yang, X.; Bian, Y.; Nie, K.; Liu, S.; Tang, K.; Zhang, R.; Zheng, Y.; Gu, S. First-Principles Insights on the Electronic and Optical Properties of ZnO@CNT Core@shell Nanostructure. Sci Rep 2018, 8, 15464. [Google Scholar] [CrossRef] [PubMed]
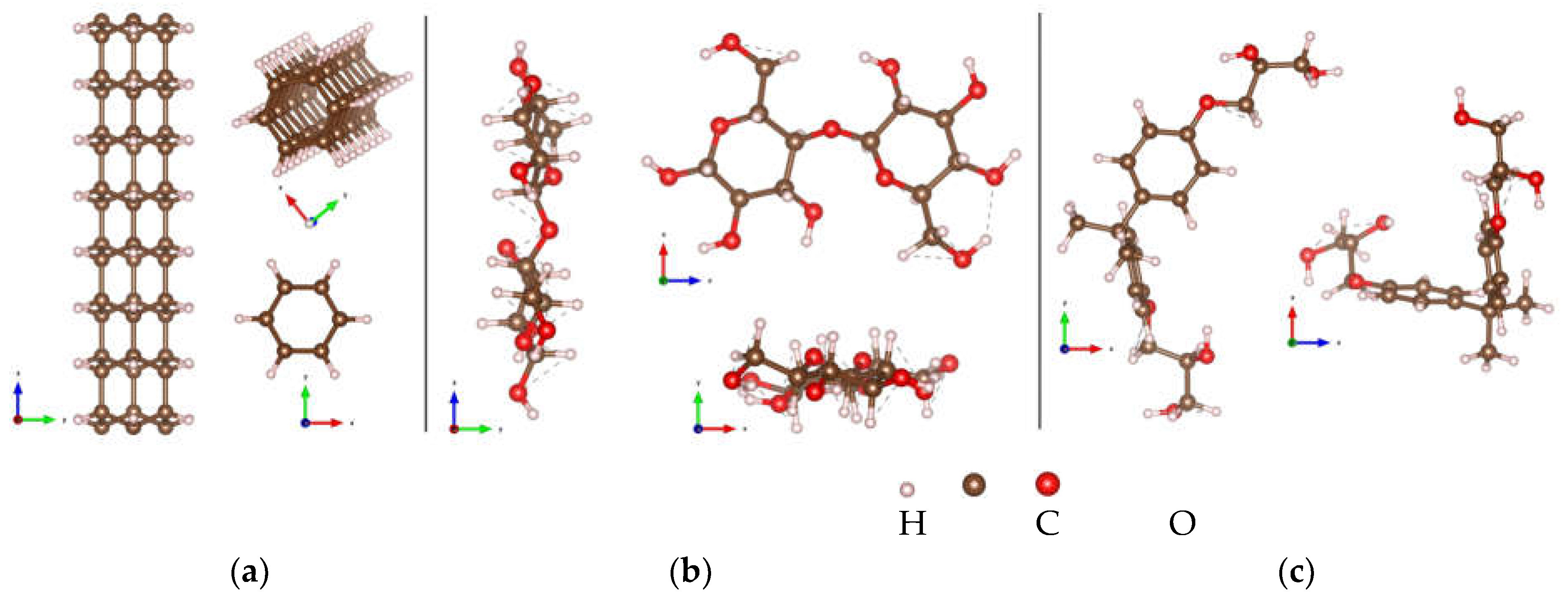
Preprints 108576 g001
Figure 1. Atomic configurations of (a) tube (3,0) diamond nanothread; (b) cellulose chain; (c) epoxy.
Figure 1. Atomic configurations of (a) tube (3,0) diamond nanothread; (b) cellulose chain; (c) epoxy.
Preprints 108576 g001
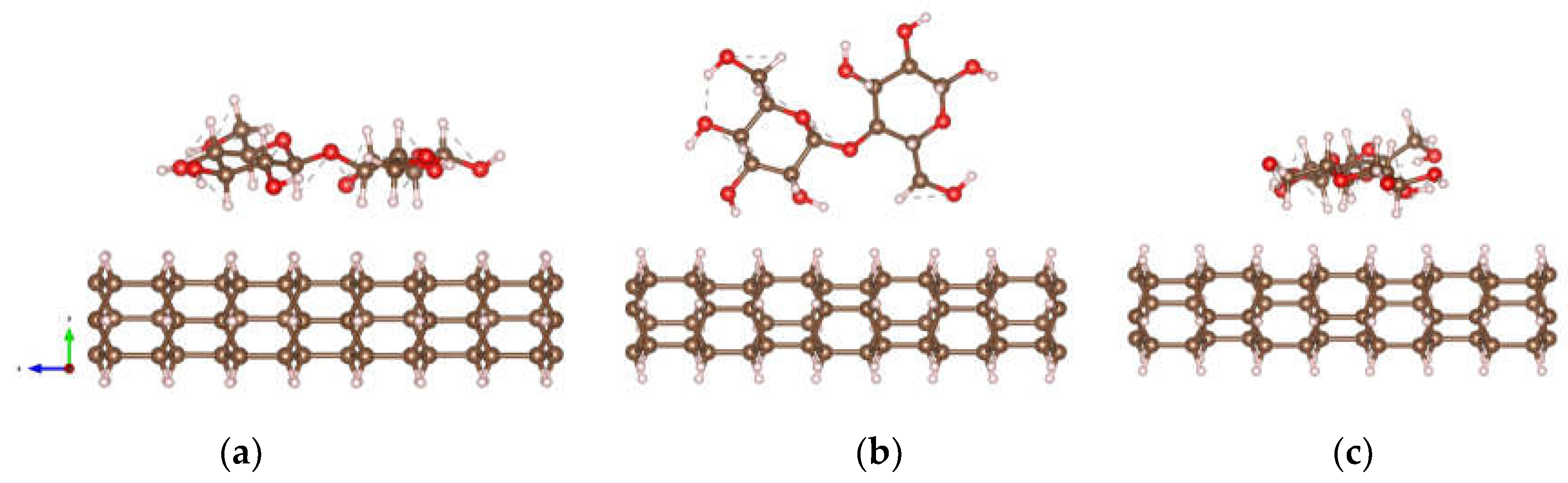
Preprints 108576 g002
Figure 2. Optimized structures of DNT/cellulose composites with varying orientations of cellulose on the nanothread, labeled as: (a) DNT/cellulose – 1; (b) DNT/cellulose – 2; (c) DNT/cellulose – 3. The carbon, hydrogen, and oxygen atoms are represented by brown, off-white, and red spheres, respectively.
Figure 2. Optimized structures of DNT/cellulose composites with varying orientations of cellulose on the nanothread, labeled as: (a) DNT/cellulose – 1; (b) DNT/cellulose – 2; (c) DNT/cellulose – 3. The carbon, hydrogen, and oxygen atoms are represented by brown, off-white, and red spheres, respectively.
Preprints 108576 g002
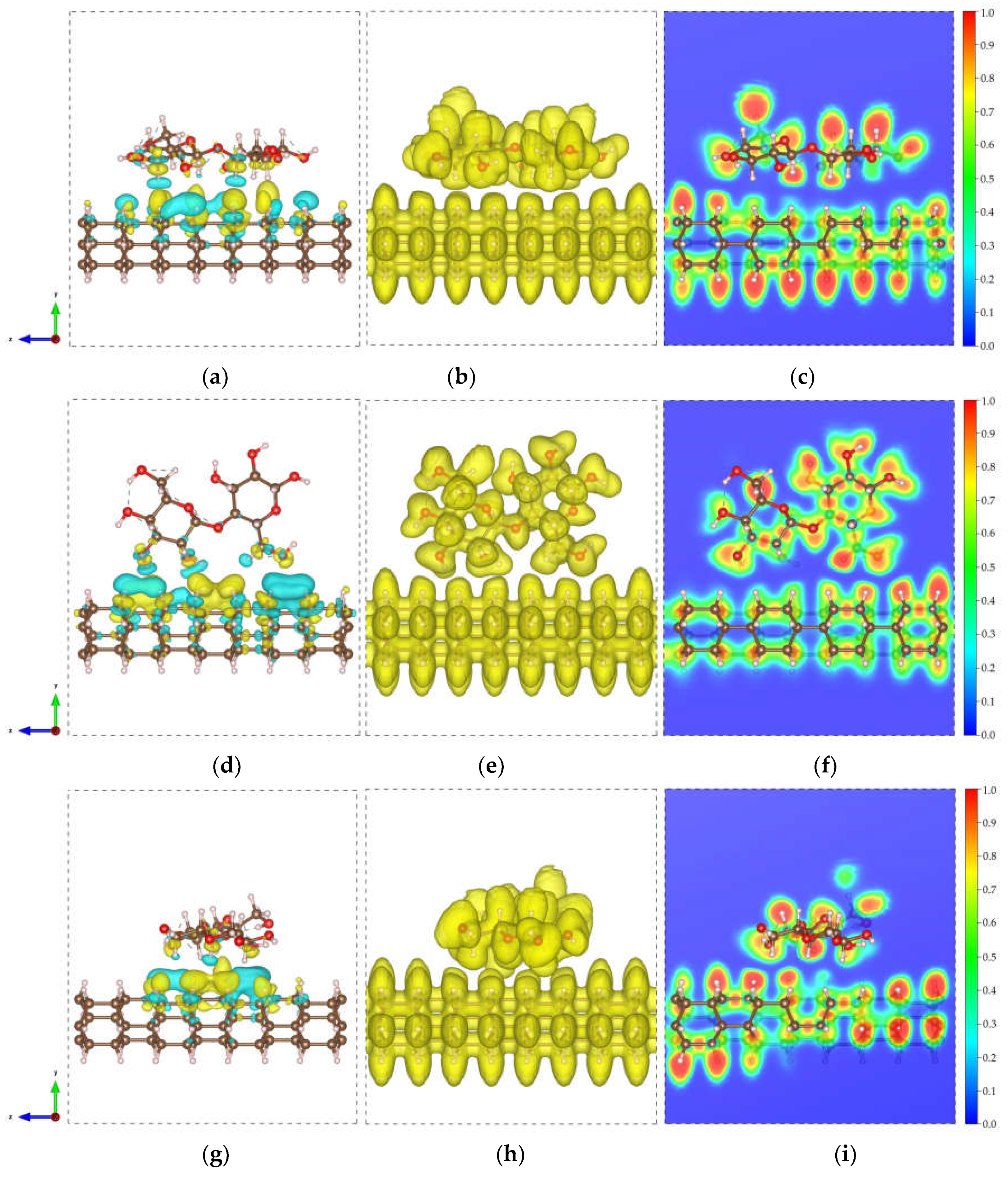
Preprints 108576 g003
Figure 3. Electronic visualization of the DNT/cellulose composites: (a, d, g) charge density difference (CDD) (0.0002 e/Å3); (b, e, h) ELF isosurface (0.4); (c, f, i) 2D ELF contour of (a-c) DNT/cellulose – 1, (d – f) DNT/cellulose – 2, and (g – i) DNT/cellulose – 3. The yellow and cyan isosurface denote the accumulation and depletion of the electronic charge, respectively.
Figure 3. Electronic visualization of the DNT/cellulose composites: (a, d, g) charge density difference (CDD) (0.0002 e/Å3); (b, e, h) ELF isosurface (0.4); (c, f, i) 2D ELF contour of (a-c) DNT/cellulose – 1, (d – f) DNT/cellulose – 2, and (g – i) DNT/cellulose – 3. The yellow and cyan isosurface denote the accumulation and depletion of the electronic charge, respectively.
Preprints 108576 g003
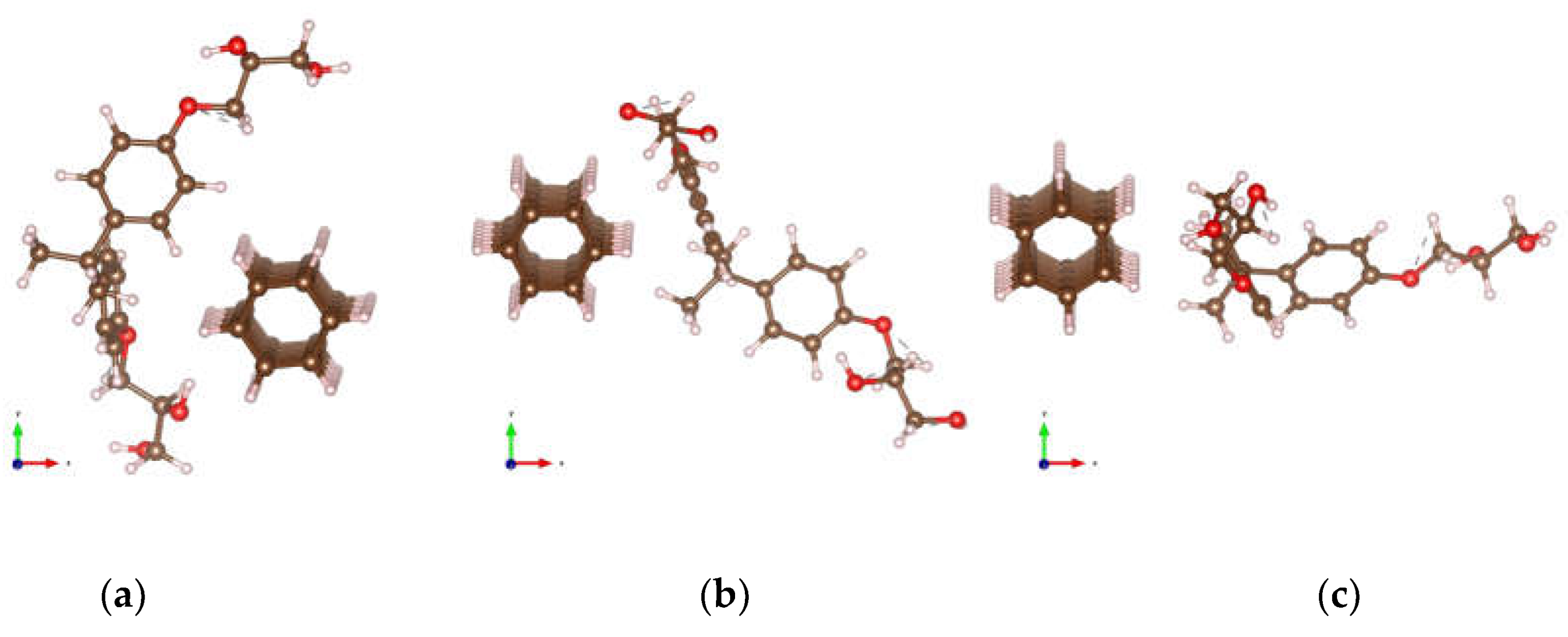
Preprints 108576 g004
Figure 4. Optimized structures of DNT/epoxy composites with varying orientations of epoxy on the nanothread: (a) DNT/epoxy – 1; (b) DNT/epoxy – 2; (c) DNT/epoxy – 3. The carbon, hydrogen, and oxygen atoms are represented by brown, off-white, and red spheres, respectively.
Figure 4. Optimized structures of DNT/epoxy composites with varying orientations of epoxy on the nanothread: (a) DNT/epoxy – 1; (b) DNT/epoxy – 2; (c) DNT/epoxy – 3. The carbon, hydrogen, and oxygen atoms are represented by brown, off-white, and red spheres, respectively.
Preprints 108576 g004
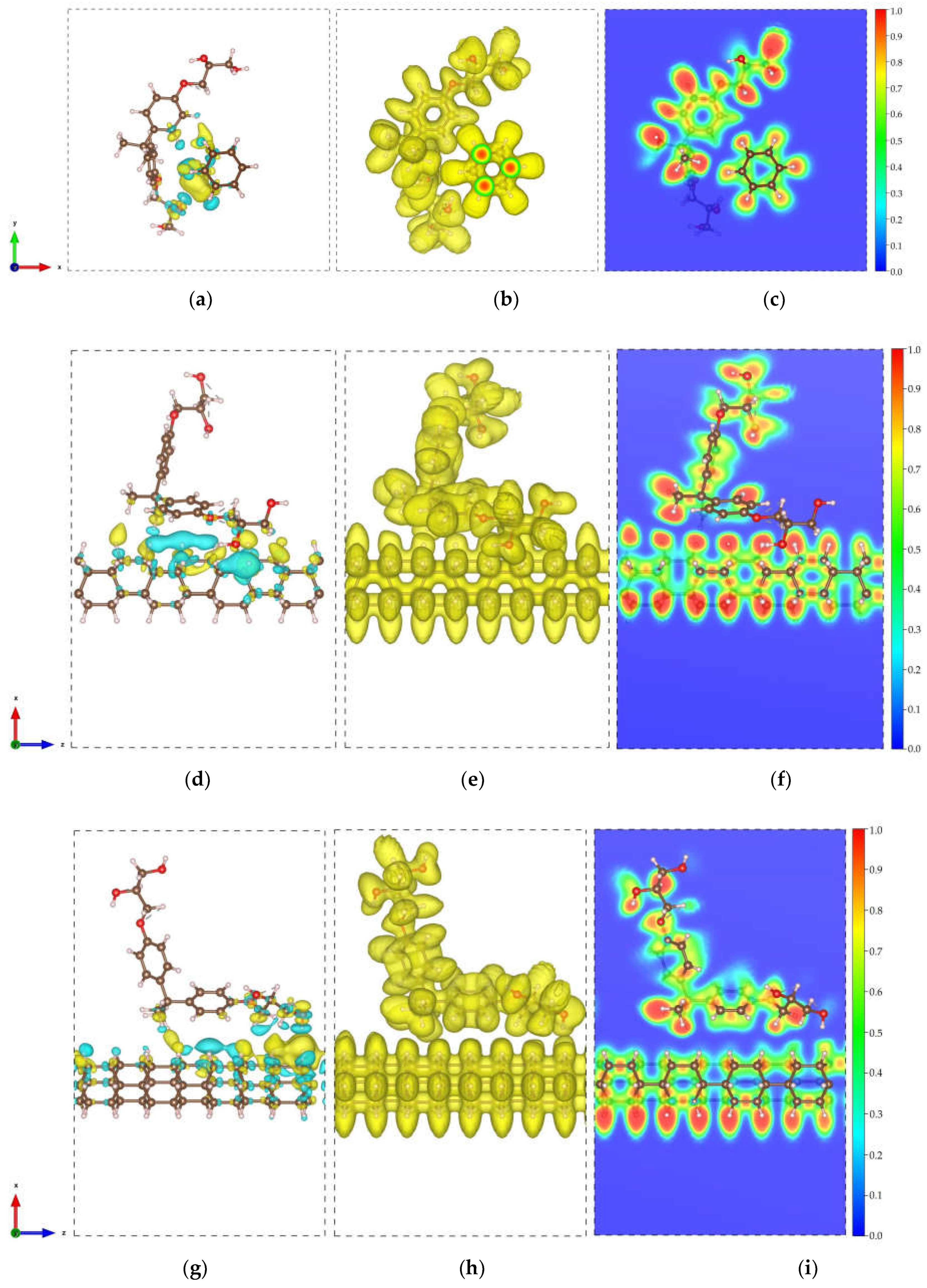
Preprints 108576 g005
Figure 5. Electronic visualization of the DNT/epoxy composites: (a, d, g) charge density difference (CDD) (0.0002 e/Å3); (b, e, h) ELF isosurface (0.4); (c, f, i) 2D ELF contour of (a-c) DNT/epoxy – 1, (d – f) DNT/epoxy – 2, and (g – i) DNT/epoxy – 3. The yellow and cyan isosurface denote the accumulation and depletion of the electronic charge, respectively.
Figure 5. Electronic visualization of the DNT/epoxy composites: (a, d, g) charge density difference (CDD) (0.0002 e/Å3); (b, e, h) ELF isosurface (0.4); (c, f, i) 2D ELF contour of (a-c) DNT/epoxy – 1, (d – f) DNT/epoxy – 2, and (g – i) DNT/epoxy – 3. The yellow and cyan isosurface denote the accumulation and depletion of the electronic charge, respectively.
Preprints 108576 g005
Preprints 108576 g006
Figure 6. Electronic band structures of (3,0) DNT, DNT/cellulose – 1, and DNT/epoxy – 1 composite. The Fermi level is set to zero and is designated by the horizontal dashed line at 0 eV.
Figure 6. Electronic band structures of (3,0) DNT, DNT/cellulose – 1, and DNT/epoxy – 1 composite. The Fermi level is set to zero and is designated by the horizontal dashed line at 0 eV.
Preprints 108576 g006
Preprints 108576 g007
Figure 7. Total and partial density of states of (a) (3,0) DNT (b) DNT/cellulose – 1; (c) DNT/epoxy – 1 composite. The Fermi level is set to zero and is designated by the vertical dashed line at 0 eV.
Figure 7. Total and partial density of states of (a) (3,0) DNT (b) DNT/cellulose – 1; (c) DNT/epoxy – 1 composite. The Fermi level is set to zero and is designated by the vertical dashed line at 0 eV.
Preprints 108576 g007
Preprints 108576 g008
Figure 8. Absorption spectra of (a) DNT/cellulose and (b) DNT/epoxy composites.
Figure 8. Absorption spectra of (a) DNT/cellulose and (b) DNT/epoxy composites.
Preprints 108576 g008
Preprints 108576 g009
Figure 9. (a) Crystal structure of C-S-H model, single layer C-S-H, and BNNT(4,4); (b) Optimized configuration C-S-H/BNNT(4,4) nanocomposite showing the unit cell. .
Figure 9. (a) Crystal structure of C-S-H model, single layer C-S-H, and BNNT(4,4); (b) Optimized configuration C-S-H/BNNT(4,4) nanocomposite showing the unit cell. .
Preprints 108576 g009
Preprints 108576 g010
Figure 10. Electronic visualization of the C-S-H/BNNT (4,4) nanocomposite: (a) pseudo-charge density (0.02 e/Å3); (b) charge density difference (CDD) (10-3 e/Å3); (c) ELF isosurface (0.4); (d) 2D ELF contour.
Figure 10. Electronic visualization of the C-S-H/BNNT (4,4) nanocomposite: (a) pseudo-charge density (0.02 e/Å3); (b) charge density difference (CDD) (10-3 e/Å3); (c) ELF isosurface (0.4); (d) 2D ELF contour.
Preprints 108576 g010
Preprints 108576 g011
Figure 11. Electronic band structure of C-S-H, BNNT (5,5), and C-S-H/BNNT complex. The Fermi level is set to zero and is designated by the horizontal dashed line at 0 eV.
Figure 11. Electronic band structure of C-S-H, BNNT (5,5), and C-S-H/BNNT complex. The Fermi level is set to zero and is designated by the horizontal dashed line at 0 eV.
Preprints 108576 g011
Preprints 108576 g012
Figure 12. Total and partial density of states of the C-S-H/BNNT complex. The Fermi level is set to zero and is designated by the vertical dashed line at 0 eV.
Figure 12. Total and partial density of states of the C-S-H/BNNT complex. The Fermi level is set to zero and is designated by the vertical dashed line at 0 eV.
Preprints 108576 g012
Preprints 108576 g013
Figure 13. Absorption spectra of C-S-H/BNNT complex.
Figure 13. Absorption spectra of C-S-H/BNNT complex.
Preprints 108576 g013
Table 1. Calculated minimum distances ( d m i n ), binding energies ( E b ), and charge transfer ( ∆ ρ ) of the DNT/cellulose composites.
Table 1. Calculated minimum distances ( d m i n ), binding energies ( E b ), and charge transfer ( ∆ ρ ) of the DNT/cellulose composites.
System d m i n (Å) E b (eV) Δ ρ (e)
DNT/cellulose – 1 3.67 – 0.797 – 0.008
DNT/cellulose – 2 3.42 – 0.730 0.004
DNT/cellulose – 3 3.48 – 0.726 – 0.006
Table 2. Calculated minimum distances ( d m i n ), binding energies ( E b ), and charge transfer ( ∆ ρ ) of the DNT/epoxy composites.
Table 2. Calculated minimum distances ( d m i n ), binding energies ( E b ), and charge transfer ( ∆ ρ ) of the DNT/epoxy composites.
System d m i n (Å) E b (eV) Δ ρ
DNT/Epoxy – 1 3.56 – 0.224 – 0.003
DNT/Epoxy – 2 3.64 – 0.236 – 0.019
DNT/Epoxy – 3 3.60 – 0.168 0.002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated