Compact, Ultra-Wideband Butler Matrix Beamformers for the Advanced 5G Band FR3

Preprint

Article

Compact, Ultra-Wideband Butler Matrix Beamformers for the Advanced 5G Band FR3 – Part I

Altmetrics

Downloads

162

Views

113

Comments

A peer-reviewed article of this preprint also exists.

Submitted:

07 June 2024

Posted:

10 June 2024

You are already at the latest version

Alerts

Abstract

Butler matrix networks are well established as beam forming networks for phased antenna arrays. The challenge we address in this work is to cover the entire, (advanced 5G or 6G), FR3 band (7-24 GHz) with a single network, while retaining low losses and minimal size. The employed multilayer topology is also well established, however, the matching between the utilized hybrid couplers and the phase shifters constitutes a major challenge for such a wideband operation. This is achieved herein employing meander lines with appropriate curvature and introducing two distinct design methods for the Butler Matrix. The first method focuses on designing individual components separately, followed by their integration into the overall Butler Matrix structure. This approach is demonstrated through the design, prototyping, measurements and validation of an 8x8 Butler Matrix beamformer, which operates across the 6-16 GHz band (FR3 Low). The second method introduces a wideband matching technique, which simplifies the implementation process by designing the Butler Matrix as a single, unified structure. This technique is applied to both 4x4 and 8x8 Butler Matrices, which are implemented and simulated for the low FR3 band. Both design methods result in wideband operation, compact size, and meet the desired performance criteria.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction – FR3 Use for eMMB via Analog Beamformers

It is anticipated that the mid band spectrum FR3 (spectrum between FR1 and FR2) would be the Urban Extreme Capacity for 6G, [1,2]. A simple examination of the 5G occupied bands shows that the FR3 band is the only one left for enhanced Mobile Brodaband (eMMB) use and, thus, it has an enormous potential in terms of coverage and capacity. This frequency band facilitates co-deployment, enabling 5G, advanced 5G, and 6G cellular infrastructure to operate at the same cell sites, thereby minimizing deployment costs to practically zero. While the eMBB demands significant increase in Capacity, Throughput and Spectral Efficiency, massive multiple-input-multiple-output (MIMO) or GIGA MIMO will be the key enabling technologies for the realization of advanced 5G and 6G wireless communication, [3,4]. Massive MIMO exploits the advantages of beamforming technologies to enhance the efficiency of wireless communication. To fulfill the requirements of modern wireless systems, the deployment of multibeam antenna arrays, employing either passive beamforming with fixed beams or active beamforming with flexible beams, emerges as the optimal solution. Thus, the essential part of multibeam antenna arrays is the beamforming network (BFN), which in general, is classified into digital BFN, [5], analogue BFN, [6] and the combination of two as hybrid BFN, [7]. Analogue BFNs, compared to digital BFNs are cost effective more energy-efficient and preferable in large-scale applications due to their simplicity, [8].

Popular analogue BFNs or RF-type BFNs are Blass [9], Nolen [10] and Butler Matrix (BM), [11]. BMs are the most widely used BFNs for feeding antenna arrays due to their easy fabrication, low cost and low profile [12] and they may offer Ultra-Wideband (UWB) characteristics given certain topologies.

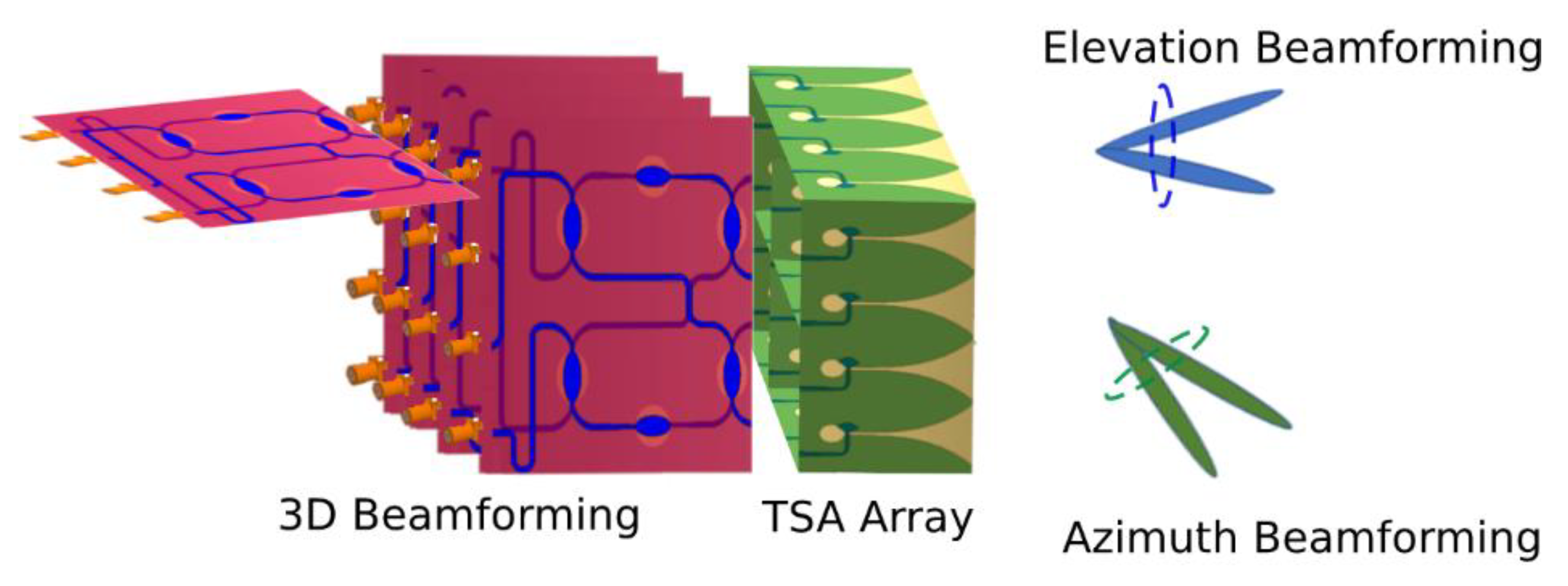
Figure 1 depicts an example of a 3D beamforming topology which could increase the capacity and efficiency of a system, supporting both transmit and receive functions with narrow beams in both azimuth and elevation angles. The analog three dimensional beamformer is build using a stack of vertical BMs driven by either a single or a stack of horizontal BMs. Ultra-wideband planar printed Vivaldi antenna elements are forming the planar array. It is clear from the above discussion that to deliver a fully functional and efficient BFN for currently anticipated 6G enhanced mobile broadband use case, we need to develop an UWB system covering the 7-24GHz band. Moreover, the RF-BFN, the BM in our case should be of compact size with UWB characteristics providing fixed radiation pattern through amplitude and phase accuracy. Thus, the miniaturization of the BM, while preserving or achieving the needed performance, is the most critical point for the realization of a multibeam antenna array similar to that of Figure 1.

Numerous miniaturization efforts for the BM are reported in the literature and reviewed next. The recent advancements in 4×4 BM are summarized in Table 1 and those of 8×8 BM are depicted in Table 2. These approaches are grouped into single-layer (SL) [13,14,15,16,17,18,19] and multilayer (ML) [20,21,22,23,24,25,26,27,28,29] configurations. In [13,14] artificial transmission line branch line coupler (BLC) and swapped ports coupled line coupler, respectively, are utilized to achieve a reduction in the size of the BM from 21% to 10% (0.11λ² – 0.05 λ²) when compared to the conventional BM, while maintaining a fractional bandwidth (FBW) of 30%. In [15,16,17], elimination of phase shifter and crossovers approach is enforced, using 45° and 90° couplers only, to build the BM. Therein, an improvement on the FBW is reported (45% - 63%) with miniaturized sizes ranging from 1.41

λ_{0}^{2}

-1.22

λ_{0}^{2}

. While works [13,14,15,16,17] refer to 4×4 BM, in [18] a conventional 8×8 BLC BM, printed in glass substrate was presented with narrow FWB of 2.6% and large size of 33.5

λ_{0}^{2}

. Nevertheless in [19] two asymmetrical 4×4 BMs consisting of BLCs are employed to form an 8×8 BM with reduced size of 4.14

λ_{0}^{2}

and FBW equal to 24%.

Regarding multilayer configurations, a folded 4×4 BM with eliminated crossovers couplers was newly proposed in [20]. Stacking half components of the BM on different layers, while combining them with multilayer transition scheme achieved a Footprint Area (FA) of 7.67

λ_{0}^{2}

and an FBW of 14%. Similar FBW is achieved in [21] where the components of a conventional 4×4 BM are stacked up in four different layers using the low temperature co-fired ceramics (LTCC) process, thus achieving significantly reduced size with FA of 1.12

λ_{0}^{2}

. An increase in the FBW to 26.5% is reported in [22], adopting the grounded coplanar waveguide (GCPW) technology. Using bent hybrid couplers, curved line phase shifter and multilayer transitioned crossovers, a size with FA of 5.04

λ_{0}^{2}

is obtained. A good compromise between size and BW is reported in [23,24]. In [23] a BM composed of forward wave directional couplers (FWDC) combined with microstrip line phase shifters and via crossovers, is proposed, resulting in a compact size of 1.19

λ_{0}^{2}

and FBW of 47%. In [24], dual transmission line couplers and circular patched phase shifters combined with elliptic and circular slots respectively, resulted in a compact BM with FA of 0.78

λ_{0}^{2}

and FBW of 40%. Concerning 8×8 BM designs, slot-line transition and magic tees are utilized in [25], where a 8×8 BM with 3 dB 180° couplers and several phase shifters (PS) is proposed. The achieved FBW is 60% and FA equal to 15.04

λ_{0}^{2}

. A conventional 8×8 BM comprised of BLCs and Schiffman phase shifters is proposed in [26]. The multilayered configuration is achieved using vias to connect the components at different layers, achieving size with FA of 4.4

λ_{0}^{2}

and a FBW of 32%. Stripline technology is employed in [27,28,29] for the implementation of compact 8×8 BMs. Specifically, in [27], two 4×4 BM using both 90° and 180° couplers combined with an output network of the same couplers and several different PSs are proposed. Despite the reduced number of crossovers, the inclusion of output network and multiple PSs increase the complexity of the proposed design and the size (FA=2.56

λ_{0}^{2}

), while the FBW is only 5.5%. In [28], an 8×8 BM composed of coupled line quadrature directional couplers and coupled line Schiffman C-sections PS is proposed. The designs feature reduced number of crossovers and thus the obtained size is 2.46

λ_{0}^{2}

and a significantly enhanced FBW of 73% is achieved. An optimal trade-off between BW and size is reported in [29]. Therein, a 8×8 BM with single section 3 dB/90° directional couplers and PSs realized in tandem connection of two 3 dB/90° coupler, is proposed. The achieved size is 1.3

λ_{0}^{2}

and FBW of 66%.

In this paper we propose two different design approaches for the BM beamformers, targeting the FR-3 band and utilizing the microstrip to slot technology. The BMs are realized using multilayer 3 dB/90° hybrid couplers (HC) and PS with elliptical geometry. The first design approach focuses on designing the components comprising the BM (HC, PS, etc.) separately and then integrating them to form the overall BM structure. Thus, an 8×8 BM operating in the 6 GHz – 16 GHz band was successfully designed and prototyped. Except the UWB characteristics where an FBW of 92% were achieved, a compact size was delivered, replacing the reference microstrip lines associated with the PSs and required for the appropriate differential phase, with meander lines (ML). The second method introduces a novel design approach utilizing the wideband matching technique. This technique simplifies the implementation process by designing the BM as a single, unified structure and contributes to further reduction of the size of the BM while maintaining the same and even higher FBW. For this case, a 4×4 and 8×8 BMs, were successfully implemented and simulated for the FR3 band, achieving compact size and UWB operation while meeting the desired performance criteria. Table 1 and 2 provide a comprehensive summary of the performance metrics for the mentioned multilayer designs concerning the 4×4 and 8×8 BMs respectively. Therein, except the size and FBW, various characteristics including technology, amplitude imbalance and phase accuracy are listed in comparison with the herein contributed designs.

As shown from Table 1 and Table 2, our proposed designs exhibit the best performance in terms of BW and offer comparable size with the reported works. Concerning the phase accuracy, the deviation listed especially in Table 2, is expected given the large BW of operation. Notably, our proposed BM topologies integrate an equiphased transmission line (TL) network leading in a significant increase in the overall size of the BMs. The size of the BMs alone (excluding the TL network) is provided in parenthesis in Table 2 for clarity.

The rest of the paper is organized as follows: Section 2 demonstrates the BM design methods, while Section 3 presents the results of the implemented and prototyped designs. Finally, Section 4 draws conclusions regarding the proposed work.

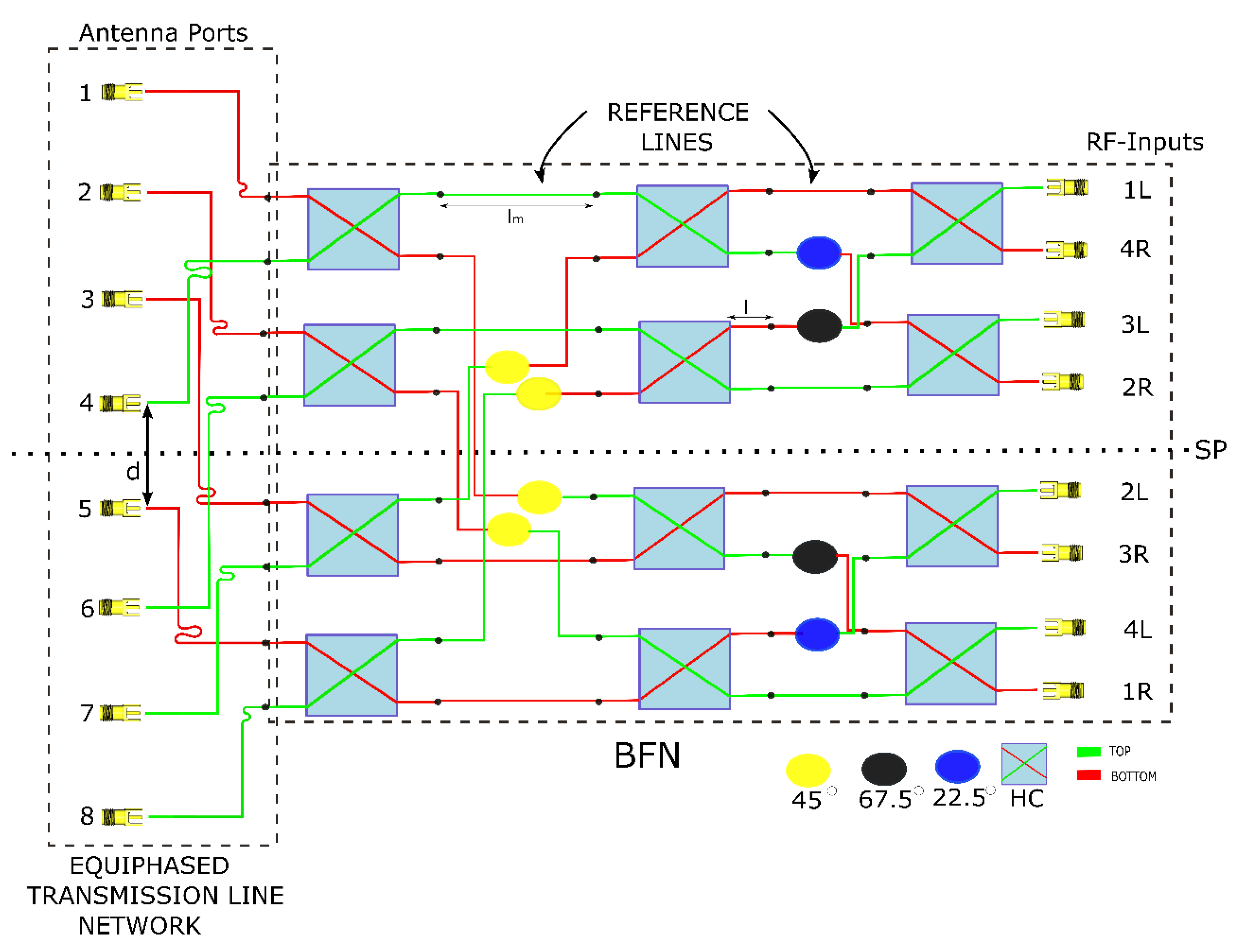
2. Butler Matrix Design

Figure 2 depicts the topology of the proposed BM, which consists of N=2ⁿ=8 (n=3) input ports or excitation ports and N=2ⁿ=8 output ports or antenna ports. Since each input port is electrically connected to the output ports, exciting one of its N inputs produce uniform amplitudes at the outputs with phase difference Δφ. Thus, for every input port excitation there is a different Δφ between the output ports and hence a different beam is produced in the desired direction. Exciting the 8 input ports separately, 8 orthogonal beams are produced at the output, where their radiation field is in the form of sinx/x. The phase difference Δφ at the output ports is calculated as:

Δ φ = \pm \frac{2 p - 1}{N} \times 180^{o}

(1)

where N=8, p=1,2,…..,(n+1) n=7 for 8X8 BM. The beam angular direction θ_p is given as:

\sin θ_{p} = \frac{λ}{d} \times \frac{Δ φ}{360^{ο}}

(2)

where λ is the free space wavelength of the operating frequency and d is the distance of antenna elements at the output ports. Using equation (2) and with respect to Figure 2 the phase relations between input and output ports and produced beam’s angle are easily derived which are given in Table 3.

Referring again to the BM topology in Figure 2, it is comprised of the BFN and the equiphased TL network. The BFN is composed of 12 HCs 3dB/90°, 8 PSs (values shown in Figure 2) and their corresponding reference lines. The TL network is used to align and order in sequence the BM outputs ports to match to the linear array ports enabling their integration.

The BM design is initially carried out estimating the theoretical dimensions of the HC and PSs following the methodology outlined in our previous works [30,31,32]. Subsequently, we introduce two distinct design approaches for the BM. The first approach involves the design of each component (HC, PSs, TL network) of the 8×8 BM separately and then integrating them to form the overall BM structure. The second approach incorporates the wideband matching technique, as adopted from our preceding work [33]. With this technique the separate design of each component is avoided since the BM is implemented as a single structure using the theoretical values of the core components and the estimated geometrical characteristic of the interconnecting TLs between them. Moreover, this technique not only facilitates the further miniaturization of the BM by using only the appropriate interconnecting TLs, but also demonstrates adaptability to various passive devices, including six-port networks and beyond.

2.1. Butler Matrix Components Design

2.1.1. 3 dB/90˚ Hybrid Coupler

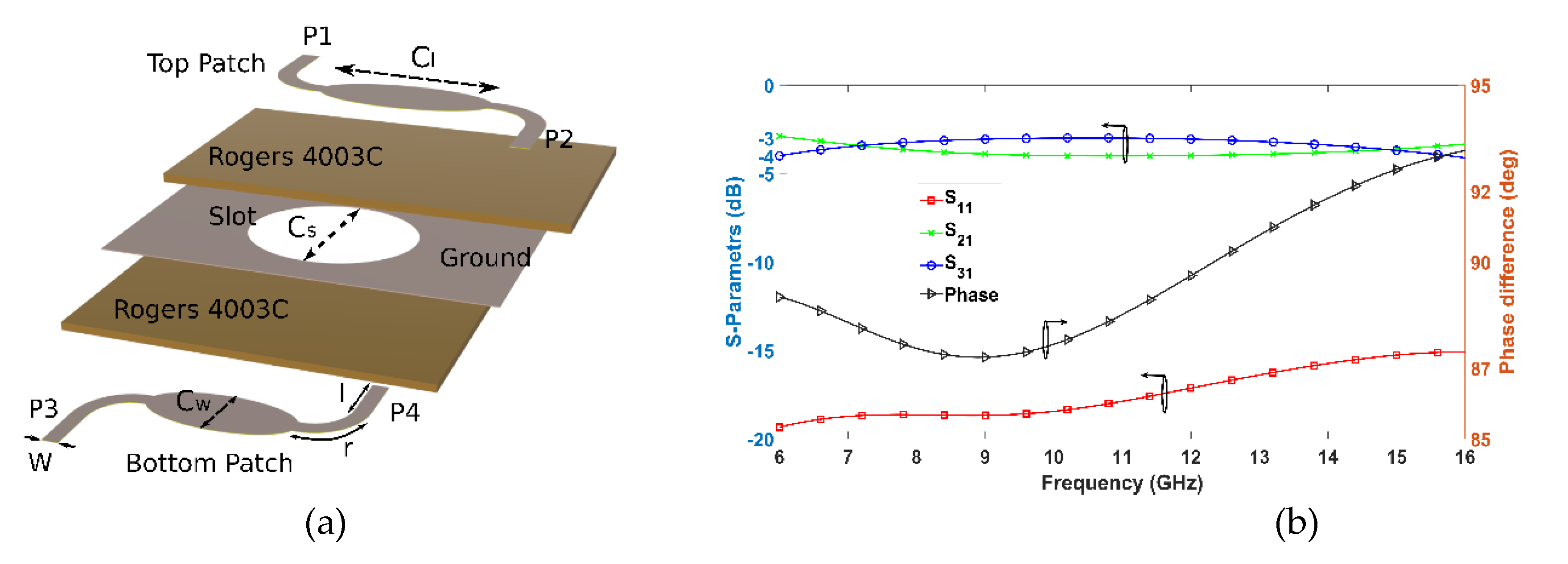
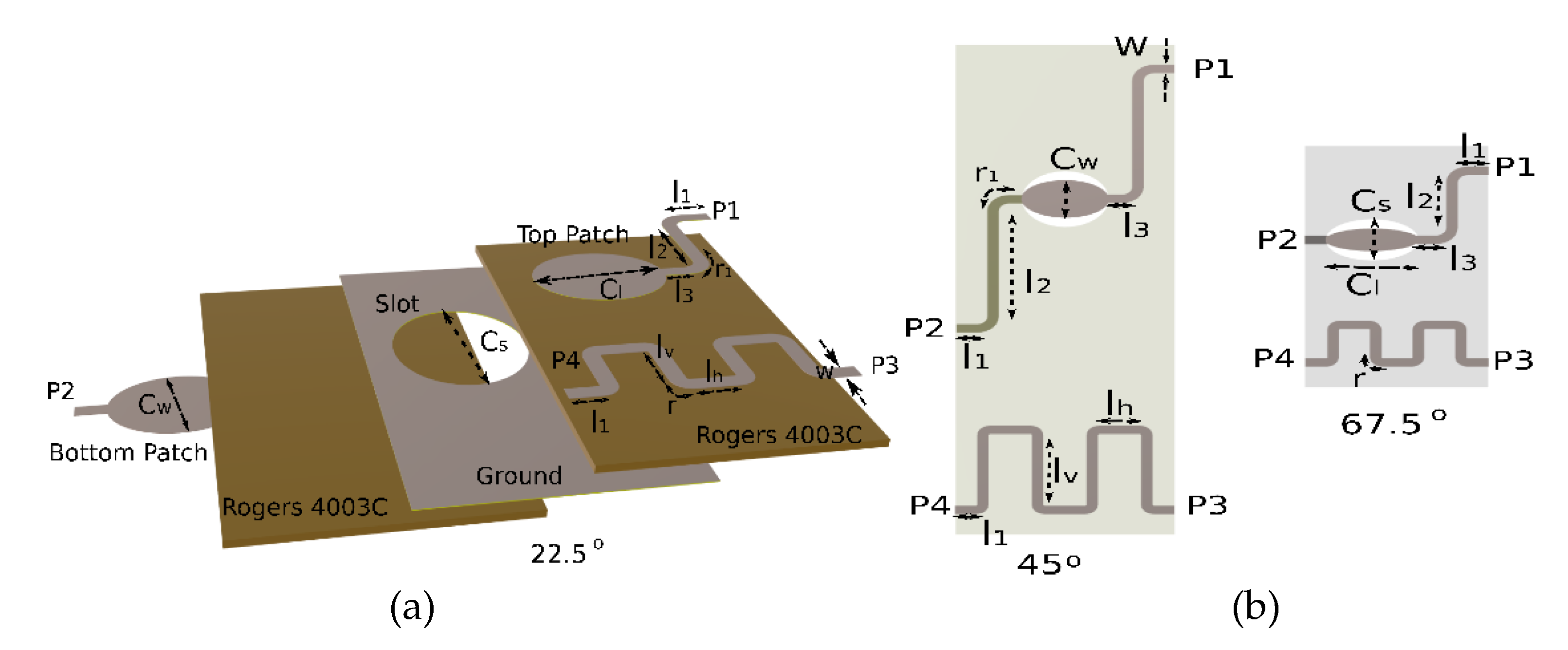
Figure 3a depicts the multilayer structure of the adopted HC, which consists of three conductive layers interleaved with two Rogers 4003C dielectric layers. Elliptically shaped patches are printed on the top and bottom layers, which are coupled through an elliptical slot etched on the middle metallic (ground) layer. Thus, as shown in Figure 3a, a signal applied to input port P1 is equally divided between output P2 and coupled port P3 with a phase shift of −90°. Ideally there is no signal at the isolated port P4, which is not illustrated in Figure 3b as it is below -20 dB, with an average value of -20.12 dB.

The coupling C between the P1 input and P3 output as well as the UBW operation of the HC are totally controlled by its geometrical characteristics (Figure 3a), which are the widths C_w, C_s of the elliptical patch and slot, respectively, and the coupler length C_l. In the design process of the HC, the desired coupling coefficient C=S₃₁ is initially chosen which defines the outputs power ratio K=P₂/P₃. For an ideal coupler with perfect isolation (S₄₁=0) and ignoring the presence of small loses, the conservation of power yields (K+1)C²=1, and therefore it is |S₂₁|²=K/(K+1). From the coupling coefficient the even and odd impedances are derived, since the HC of Figure 3a exhibits a symmetry between ports, thus, supporting the even and odd modes. Subsequently, the parameters C_w, C_s and C_l are calculated using formulas outlined in our previous work, [30], where a detailed design methodology of the HC and PSs and the calculation of their geometrical characteristics is given. The theoretically estimated and optimized values of the HCs parameters are depicted in Table 4. The performance of the HC in terms of S-parameters and phase accuracy is illustrated in Figure 3b. As shown, the transmission parameters S21 and S31 are -3.5 dB for the entire frequency range (6 GHz – 16 GHz) with a negligible deviation of ±0.5 dB, while the reflection coefficient at the input ports is below -15 dB at the same frequency range. Concerning the phase difference between P2 and P3 it is stable at 90° with an acceptable deviation of ±3°.

2.1.2. Phase Shifter and Meander Lines

The same multilayer technology used for the HC is applied to the PSs, with the exception of open-ended ports and the removal of the TLs from ports P2 and P4 of the HC shown in Figure 3a. The obtained two port PS is shown in Figure 4a. It consists of top and bottom elliptical patches coupled through an elliptical slot located in the middle layer

The phase shift φ_p inserted by the PS is referenced to the phase shift φ_m of a corresponding microstrip line of length l_m=2×l₁+3×l_h+4×l_v+8×(w+r) in order to achieve the desired differential phase Δφ.

Δ φ = ∠ φ_{p} - ∠ φ_{m}

(3)

The differential phase is influenced by both the coupling coefficient C of the PS and the length of the microstrip line which is also shown in Figure 4a. The coupling coefficient, in turn, is selected based on the required length dictated by the layout. Consequently, the lengths of the patches and slots are set equal to a quarter of the effective wavelength (λ_eff/4), while the widths (Cw and Cs) of the patches and slots, respectively, are determined using again the formulas provided in [30,31,32]. The lengths of the remaining TLs at ports P1 and P2 are adjusted to align with the length of the reference transmission line. In this work, the reference TLs are intentionally meandered to shrink the size of the BM without sacrificing its performance. As outlined in our previous work [33], when a microstrip line is meandered, it achieves wideband matching characteristics through conjugate matching and admittance compensation, just treating the ML as a shunt component. 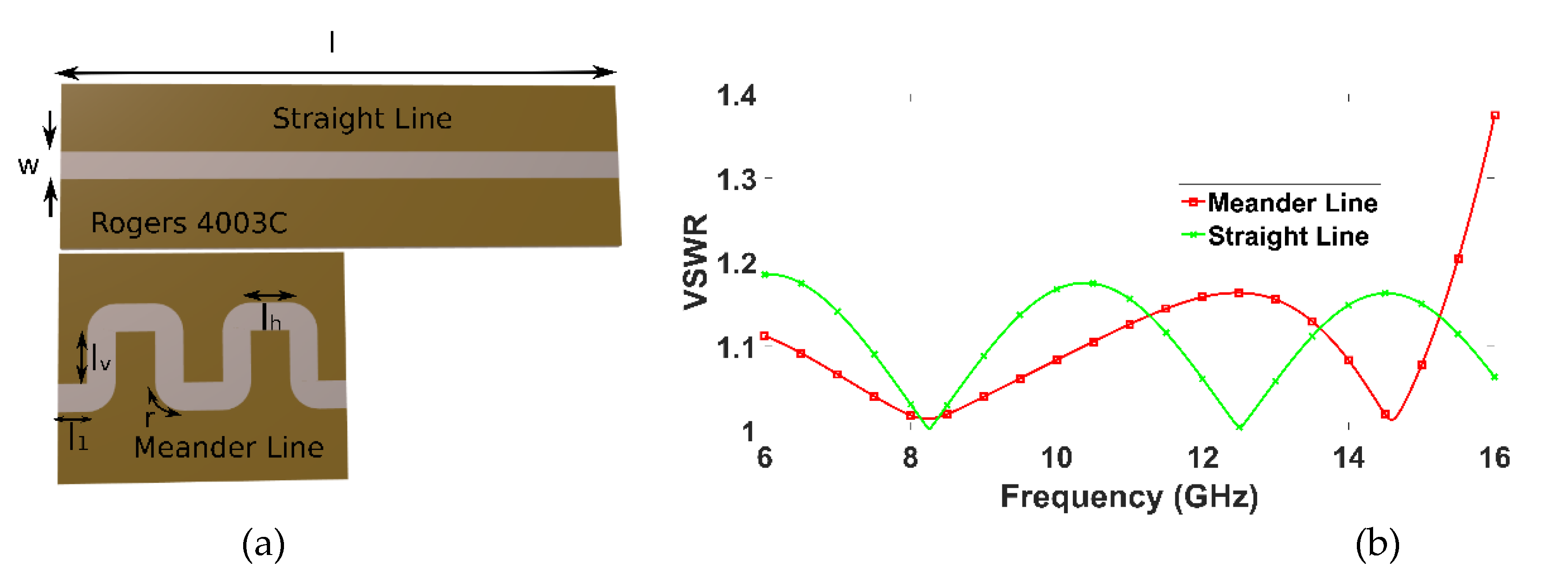Figure 5a illustrates a TL with a length l alongside its meandered counterpart, which maintains the same length while reducing its footprint to nearly half. In Figure 5b, the simulated Voltage Standing Wave Ratio (VSWR) of both lines is depicted. Notably, the ML demonstrates equivalent or even superior response within the 6 GHz to 15 GHz range compared to the straight-line configuration, while it remains well below the limit of VSWR=2 over the entire band of 6-16 GHz.

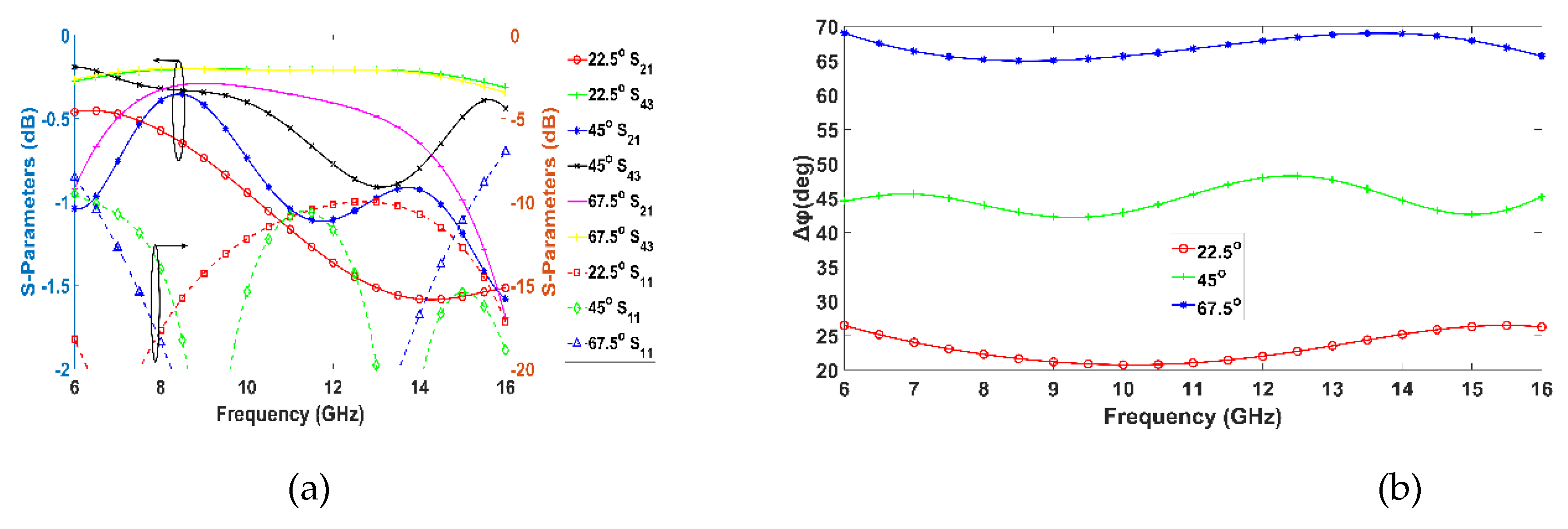
Thus, all the required PSs are designed in conjunction with the MLs while the required coupling and differential phase are achieved tuning the PS elliptic geometry and the vertical length of the MLs. At the same time, the footprint of the PS is effectively reduced resulting further in the compactness of the overall BM as will be shown in section 4. Three PSs were designed and simulated herein. A 22.5° PS shown in exploded view (Figure 4a) followed by a 45° and a 67.5° PS shown in a layout view (Figure 4b) both sharing the same layer stack as the 22.5° PS. All parameters depicted in Figure 4 and their corresponding values for the three PSs are listed in Table 4, while Figure 6 illustrates the performance of the PSs in terms of S-parameters accuracy and differential phase, between the PS path and the corresponding microstrip line or ML. As shown in Figure 6a the transmission coefficient (S₂₁) for the PSs as expected exhibits an insertion loss of -1 dB or less, with a maximum deviation of 0.6 dB at 16 GHz, while the reflection coefficient (S₁₁) is below -10 dB for almost the whole frequency range. The maximum deviation for the transmission coefficient (S₄₃) of MLs is 0.5 dB at 13 GHz from the expected value of -0.3 dB. Excellent agreement between the ideal - theoretical and the simulated differential phase is achieved for the three PSs as shown in Figure 6b, where a maximum deviation of 3° for the 22.5° PS is observed.

Table 5. Final values of the parameters of the three PSs. T denotes theoretical and S denotes simulated.

	C_w		C_s		C_l		W	l₁	l₂	l₃	l_h	l_v	r	r₁
	T	S	T	S	T	S	W	l₁	l₂	l₃	l_h	l_v	r	r₁
22.5°	4.21	3.72	5.21	5.32	5.01	4.5	0.54	1	3	0.807	1.372	1.705	0.06	0.5
45°	3.4	2.7	3.9	3.7	4.7	4.2	0.54	1	7.024	0.643	1.953	4.63	0.06	0.5
67.5°	2.5	1.47	2.75	2.76	4.59	4.5	0.54	1	3	0.807	1.372	1.801	0.06	0.5

2.1.3. Equiphased Transmission Line Network

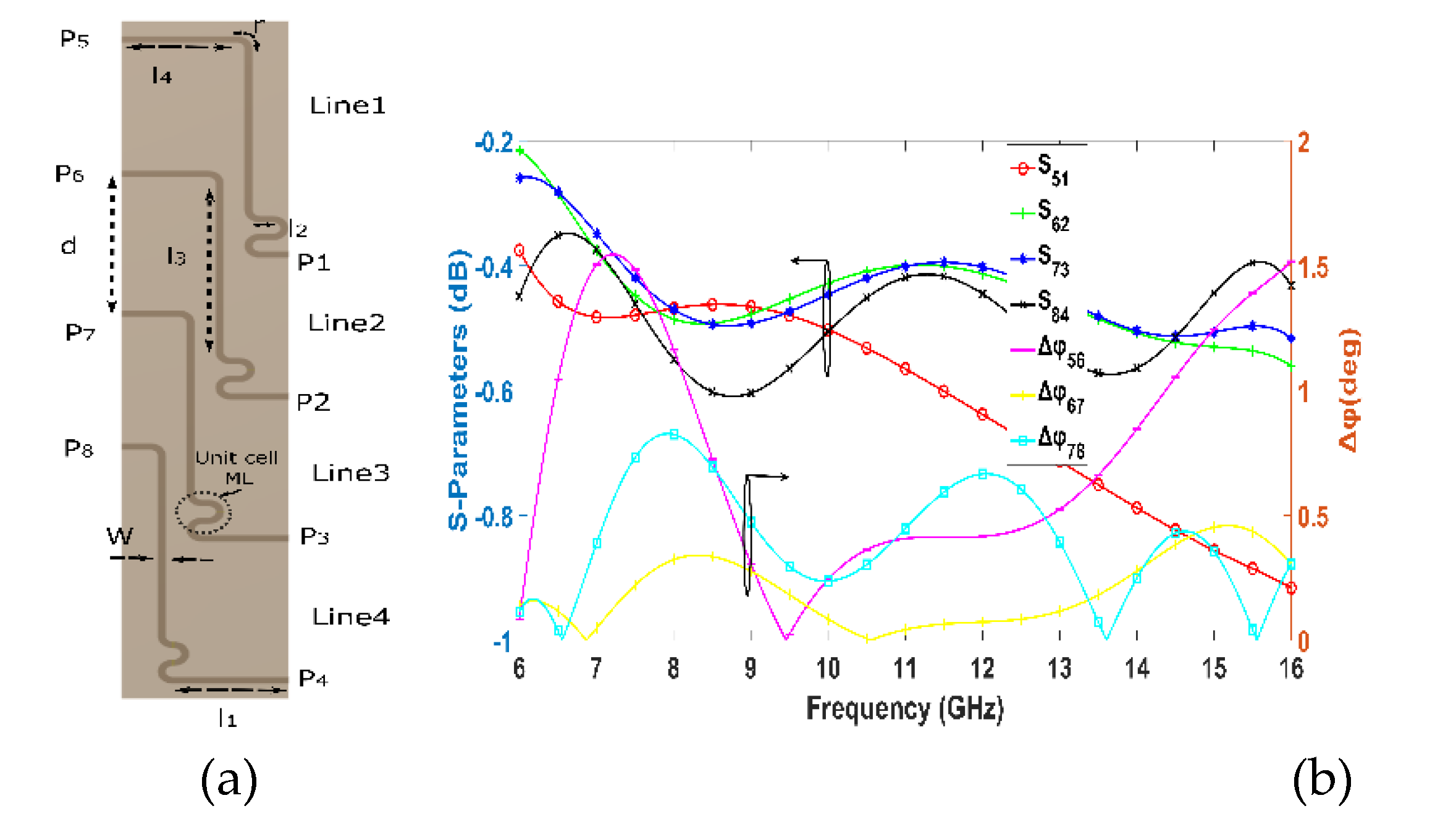
Figure 7a illustrates the equiphased TLs network which is employed to rearrange the outputs ports of the BM to achieve the desired phase shift Δφ (Table 3) between them and to facilitate the integration of the linear Vivaldi antenna array. Only the four out of the eight lines are depicted in Figure 7a, since our BM exhibit symmetry as shown in Figure 2. Those lines are structured in a reversed ‘S’ shape configuration and positioned at distance d, where d=0.6×λ_min=0.6×c/f_max. This distance allows for a direct connection to the corresponding antenna ports. It is selected to ensure the avoidance of grating lobes in the radiation pattern even for the two far end steered beams expected at angles θ_max=±45^° from broadside. According to Balanis [34] this restriction reads:

d ≤ \frac{λ_{\min}}{1 + |\sin θ_{\max}|} ⃒_{θ_{m a x} = 45^{o}} ≅ \frac{λ_{m i n}}{1.7}

(4)

Additionally, each of the four lines integrate a unit cell ML which serves to equalize their physical lengths, thereby compensating - zeroing the phase difference between them.

The parameters for the four TLs shown in Figure 7a and their values are listed in Table 6, while Figure 7b depicts the transmission S-parameters and phase difference of the TLs. A maximum loss is observed for the first line where the S₅₁ transmission parameter is -0.9 dB at 16 GHz. Maximum phase deviation of 1.5° from zero is observed between lines 5 and 6.

2.2. BM Design Employing Wideband Matching Technique

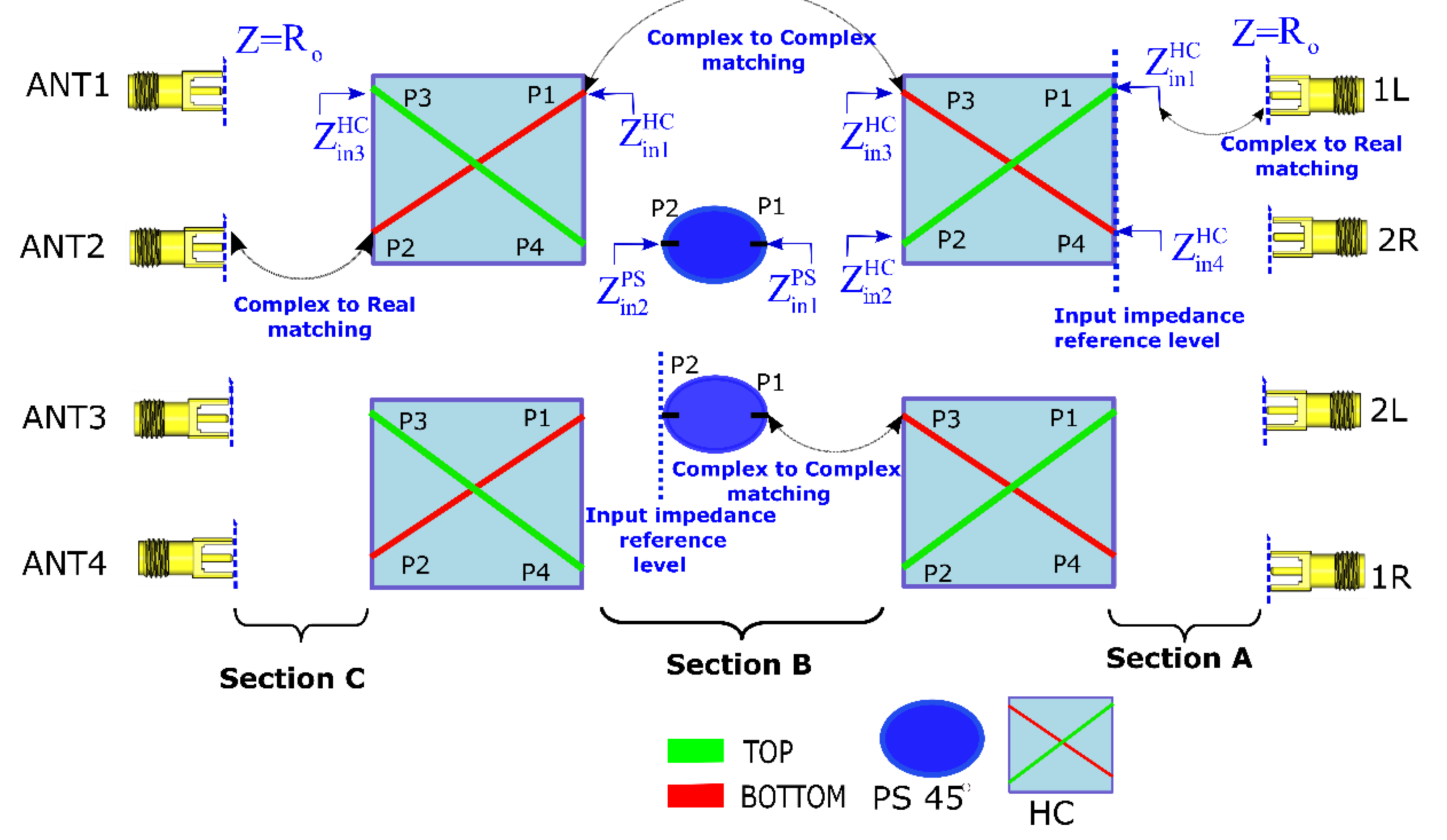
The second approach elaborating on the design of BM as a single unified structure is now presented. Figure 8 illustrates the concept of the wideband matching technique utilized to design a BM in the 6 – 16 GHz band. For illustrative purposes, the design of a 4×4 BM is presented here, however, the method is identical for the design of an 8×8 BM. The 4×4 BM is the classical BM consisting of four HCs and two 45° PSs. As shown in Figure 8 the TLs connecting the HCs ports to the input and output ports are removed (Sections A and C). Additionally, the interconnecting TLs and those connecting the PSs ports to the HCs ports (Section B), are also eliminated leaving only the HCs and PSs as the core components. The theoretical parameters related to the geometry of the core components are given in Table 4 (Section 3.1) for the HC and in Table 5 (Section 3.2) for the PS. 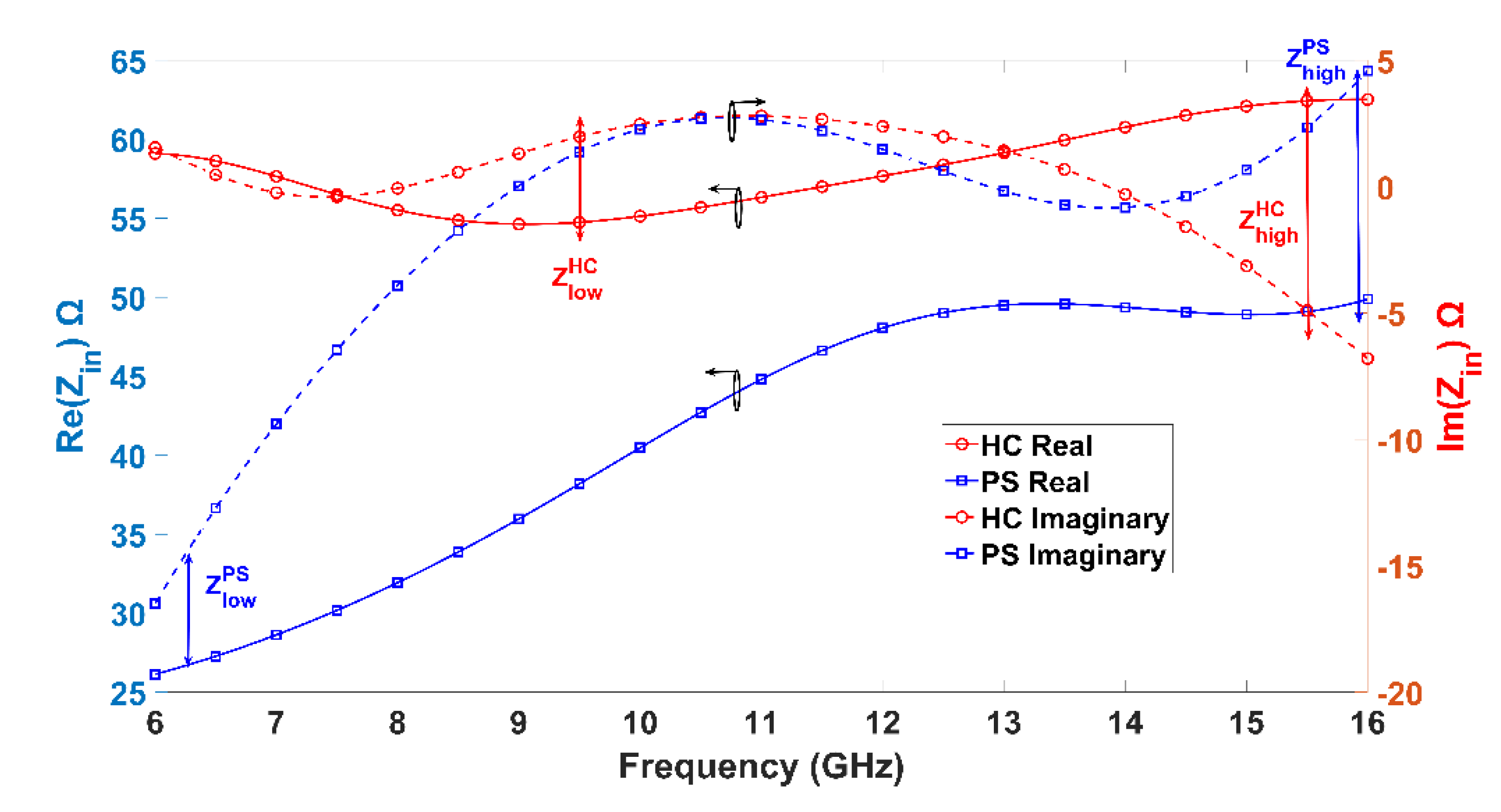Thus, the input impedance at the reference plane, depicted in Figure 8, is initially estimated through simulation for each core component. The simulated input impedance for the HC and for the PS is depicted in Figure 9 where the real and the imaginary parts are plotted. Form the input impedances, the low - min and high - max impedances for each component are easily obtained from the plots as Z_low=R_low+jX_low and Z_high=R_high+jX_high. Subsequently, the hyperbolic mean impedance Z_m=R_m+jX_m is computed for the HC and PS from the relation given in our previous work, [33]. Due to the symmetry and reciprocity inherent in the core components it is evident that the hyperbolic mean impedance will be identical for all ports of both the HC and PS. Therefore, we have Z^HC_m1= Z^HC_m2= Z^HC_m3= Z^HC_m4 and Z^PS_m1= Z^PS_m2. The next step is to determine the appropriate characteristic impedance Z_o of the interconnecting TLs between the core components and between the input and output ports using equation (5) taken from [33] and repeated herein in order to clarify the procedure.

Z_{o} = \sqrt{\frac{r e a l {(Z_{A}^{*} Z_{B}^{*}) (Z_{A} - Z_{B})}}{r e a l (Z_{A} - Z_{B})}}

(5)

In equation (5) Z_A and Z_B represent the hyperbolic mean impedances of the components to be matched. Thus, to compute for example, the characteristic impedance of the TL connecting the HC’s port P1 to connector port 1L (Figure 8), a complex to real matching is applied, since it is connected to 50 Ω connector and hence, in equation (5), Z_A=50 Ω and Z_B= Z^HC_m1. A complex to real matching is applied also for the estimation of TLs connecting the HC ports to the output connector ports (ANT1 – ANT4). A complex-to-complex matching is applied for the interstage components. Specifically, to match for example, PS port P1 to HC port P2 (Figure 8) it should be Z_A= Z^HC_m2 and Z_B= Z^PS_m1, while to estimate the matching reference line connecting the HC’s port P3 to the next HC’s port P1 it should be Z_A= Z^HC_m3 and Z_B= Z^HC_m1. Except the characteristic impedance of the TLs, the electrical length of them is also estimated using equation (17) given in [33]. However, for the BM in Figure 8 only the length of the TLs connecting the HCs ports to the input connectors (1L, 2R, 2L and 1R) is determined. This is because the lengths of the interstage TLs, as well as those at the output ports, are dictated by the required differential phase and the geometry of the equiphased TL network, respectively. Therefore, their estimation is omitted herein. The last step is to compute the appropriate width (W) and length (L) of the interconnecting TLs using well known equations found in [35]. Table 7 depicts the Z_low, Z_high and the estimated Z_m of the HC and PS ports as well as the geometrical characteristics of their corresponding interconnecting TLs.

Thus, using the theoretical values for the core components and the estimated geometrical characteristics (width and length) of the interconnecting TLs, a 4×4 BM is designed as will be shown in section 3.2. The same design approach is employed to design an 8×8 BM operating again in the 6 – 16 GHz band.

3. Butler Matrix Results

3.1. 8×8. BM Results of the 1^st Design Approach

Figure 8 shows a schematic view of our proposed BM. The multilayer structure is comprised of three conductive layers interleaved with two dielectric layers. Notably, the dielectric layers are not shown here to provide a clear view of the top and bottom patches as well as the ground layer. It is worth mentioning that each key component was individually designed as demonstrated in section 2.1 with a 50 Ω characteristic impedance for both input and output lines - connectors. Consequently, when these components are assembled to create the overall structure, there is a degree of mismatch at the connection points due to slight deviations from the exact 50 Ω characteristic impedance at the input and output connectors of each component. This mismatch results in a slight variation in transmission coefficient for each path altering the phase as well. Hence, the parameters denoted in Figure 8 which are related to PSs and MLs geometry are further tuned to get their final optimized values listed in Table 8. Specifically, the vertical lengths l_22.5v, l_45v and l_67.5v are tuned to keep the differential phase between output ports around the target value, while the widths C_w and C_s for each PS are tuned to reduce the ripples of each Δφ. 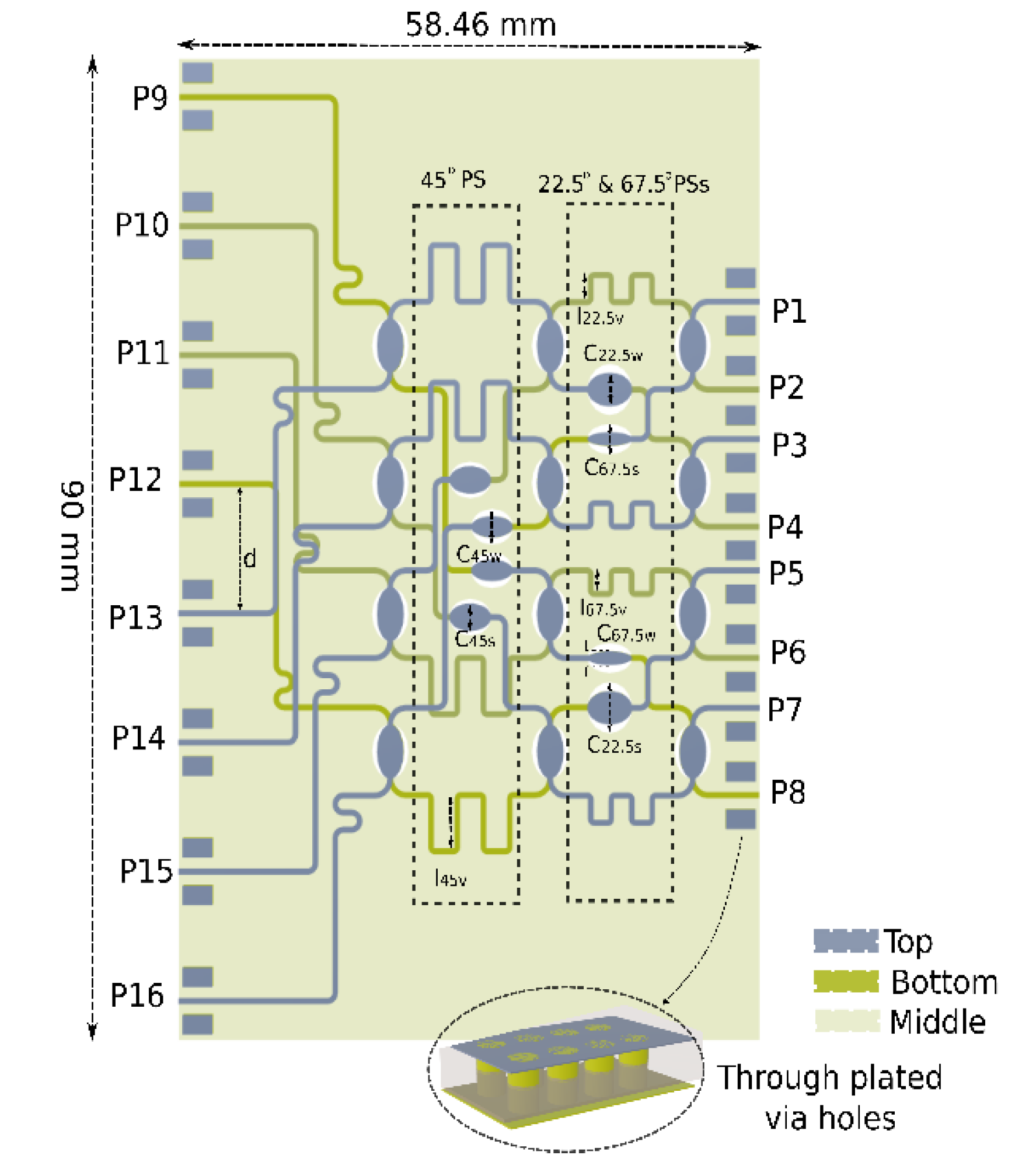As shown in Table 8, the maximum percentage change occurs for the vertical length l_67.5v which is 17%. For adequate grounding and to minimize parasitic effects, additional 4 mm long lines with 0.4 mm diameter through-plated via holes have been placed at each port, as shown in Figure 8. These modifications facilitate measurements using SMA or SMP connectors. The total achieved size of the BM is 58.46 mm × 90 mm or 5.6

λ_{0}^{2}

FA. Notably, since the length of the vertical side of the BM is defined by the length of the TLs network, miniaturization achieved (through the integration of the MLs) on the horizontal side of the BM effectively reducing its FA.

Figure 8. Designed 8×8 BM.

Figure 9. Fabricated 8×8 BM prototype. (a) Top view and (b) bottom view.

The fabricated BM prototype is depicted in Figure 9, printed into separated boards which are aligned appropriately and bonded together in a back-to-back configuration. Due to the limited amount of space at the input side of the BM, the SMA connectors that corresponds to the input ports (right side of Figure 9b) of the bottom layer were attached vertically. Rogers 4350B with ε_r=3.34 and thickness h of 0.25 mm was utilized for the two dielectric layers.

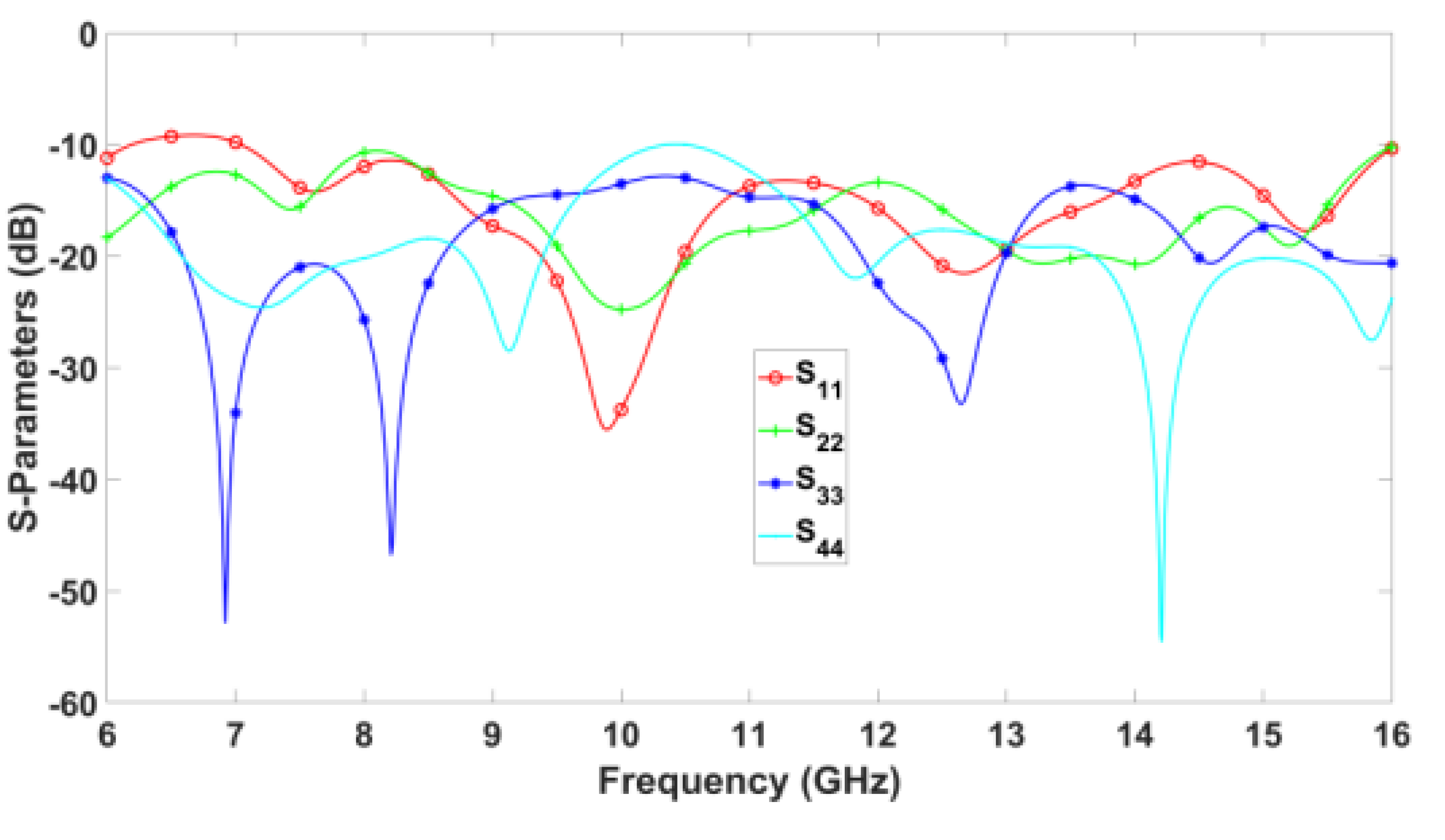
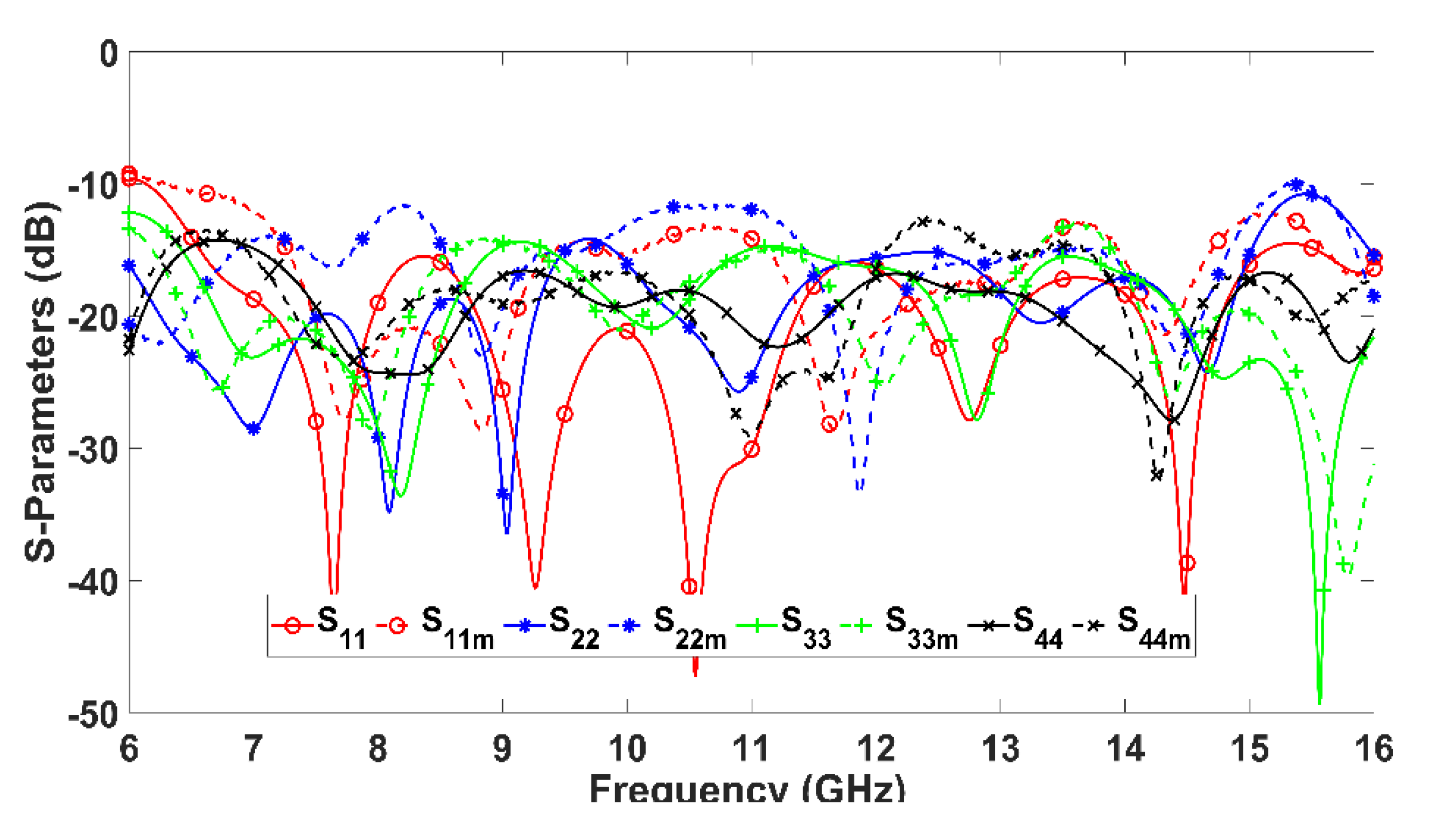
Figure 10 illustrates the simulated and measured reflection coefficient of the input ports for the 8×8 BM of Figure 8 and Figure 9. Given the symmetry of the BM’s topology shown in Figure 2, the response from four out of eight ports suffices for illustration purposes. Consequently, the responses of the remaining ports is identical. Hence, S₁₁=S₈₈, S₂₂=S₇₇, S₃₃=S₆₆ and S₄₄=S₅₅. As shown in Figure 10, both the simulated and measured reflection coefficient remains below -10 dB for the entire frequency range from 6 to 16 GHz.

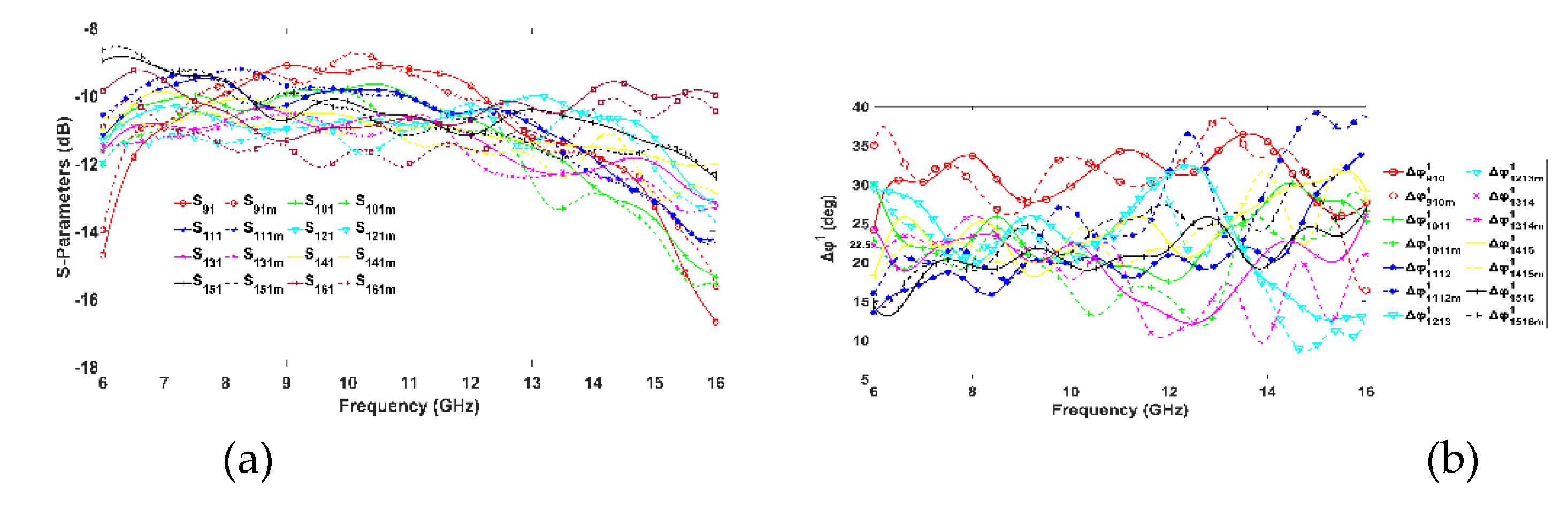
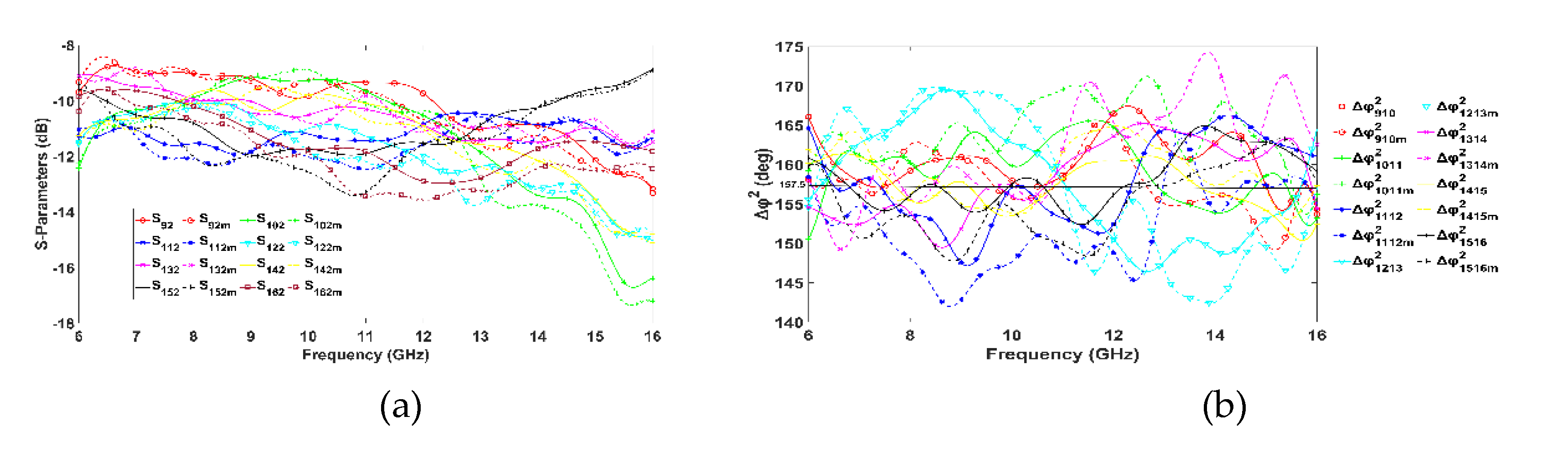
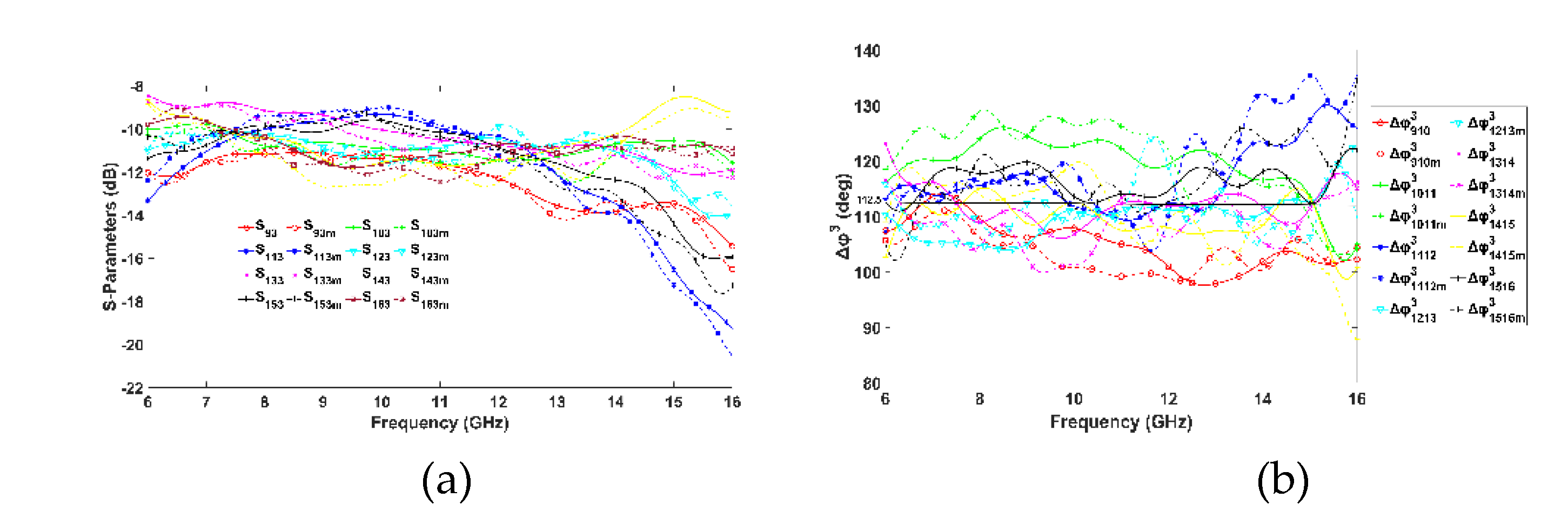
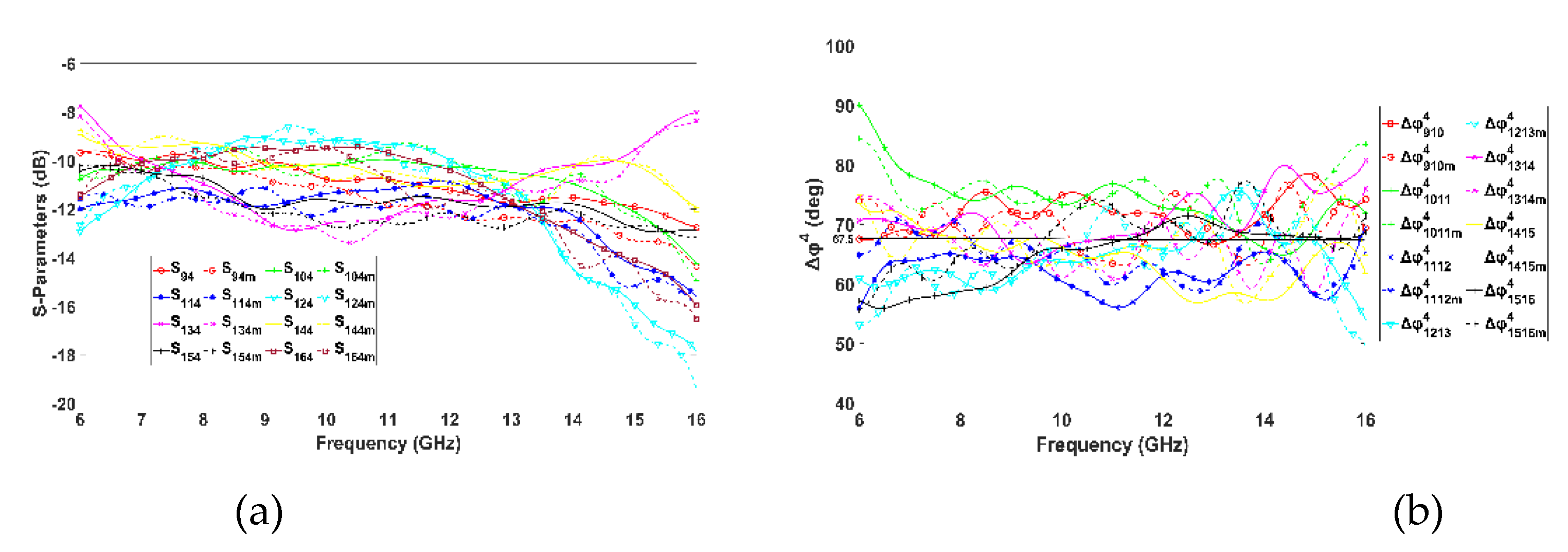
Figure 11, Figure 12, Figure 13 and Figure 14 illustrate the simulated and measured transmission responses and phase differences obtained at the output ports when input ports 1, 2, 3, and 4 are excited. Due to the symmetrical design, the responses for ports 5, 6, 7, and 8 are identical. The expected transmission coefficients to the output ports are around -12 dB. This is because a signal applied to the input ports will traverse three HCs and two PSs, or a PS with an ML, or two MLs to reach the output ports. Notably, an ideal 8×8 BM divides the input power equally to its 8 output ports, thus, an S₂₁ of -9 dB would result. Hence, the measured -12 dB observed includes 3 dB losses across the entire path. Observing Figure 11a to Figure 14a, there is a good agreement between simulated and measured transmission coefficients from input to output ports when input ports 1 to 4 are excited, respectively. Their magnitude is around -12 dB with a ±3 dB deviation across the frequency range from 6 to 15 GHz. Considering the 6 GHz – 15 GHz range as the band of operation, the achieved FBW of the proposed BM is 92% which is the highest as compared against related works in Table 2.

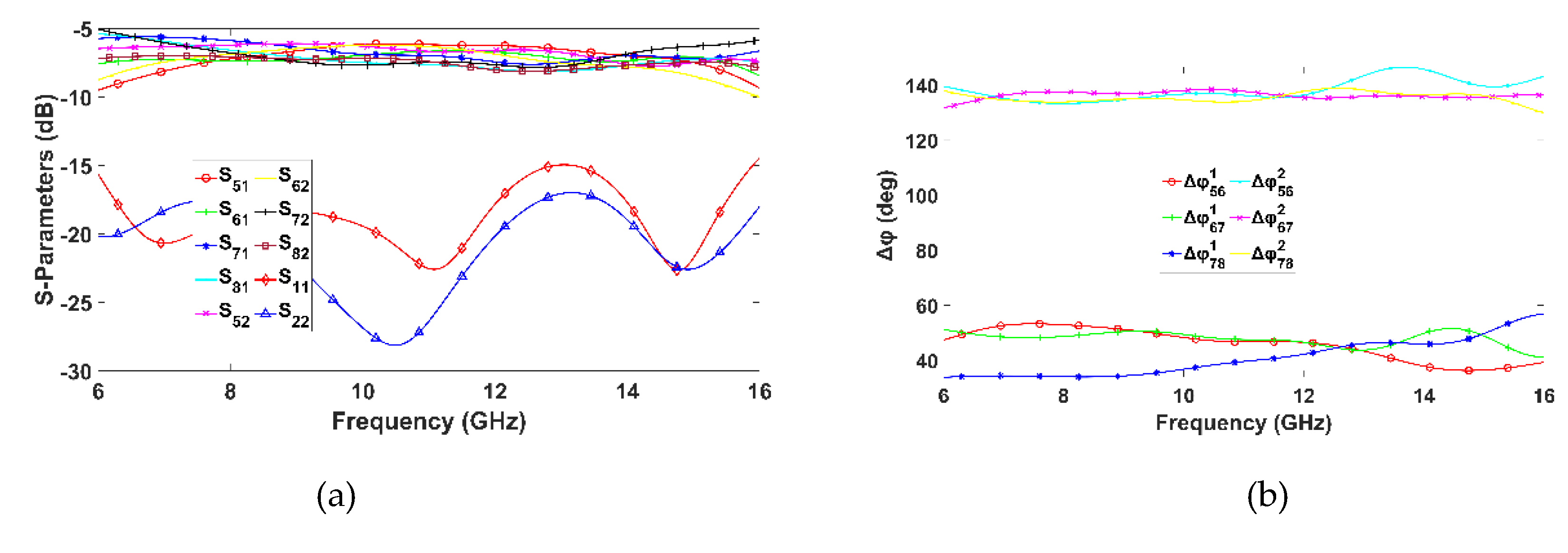
Regarding the phase difference at output ports for each input ports excitation, as depicted from Figure 11b to Figure 14b, the maximum deviation Δφ from the ideal values occurs for the measured phase differences. Specifically, for port 1 its phase deviation is Δφ¹=15°, for port 2 Δφ²=16°, for port 3 Δφ³=20° and for port 4 Δφ⁴=21.5°. The phase variations of the proposed BM are relatively high, which was anticipated given the UWB operation. Phase accuracy tends to vary linearly with BW, hence, the wider the BW, the more significant the phase variations.

Moreover, despite the phase variations, the generated beam pattern of the BM experiences minimal impact, as illustrated in Figure 15. This figure illustrates the gain of each beam when the output ports of the BM feed into a uniform linear array. For this purpose, the simulated and measured S-parameters were imported in an antenna array simulation tool representing the excitation amplitude and phase. As shown in Figure 15, a very good agreement is obtained between the theoretical (Table 3), the simulated and the measured beam angles.

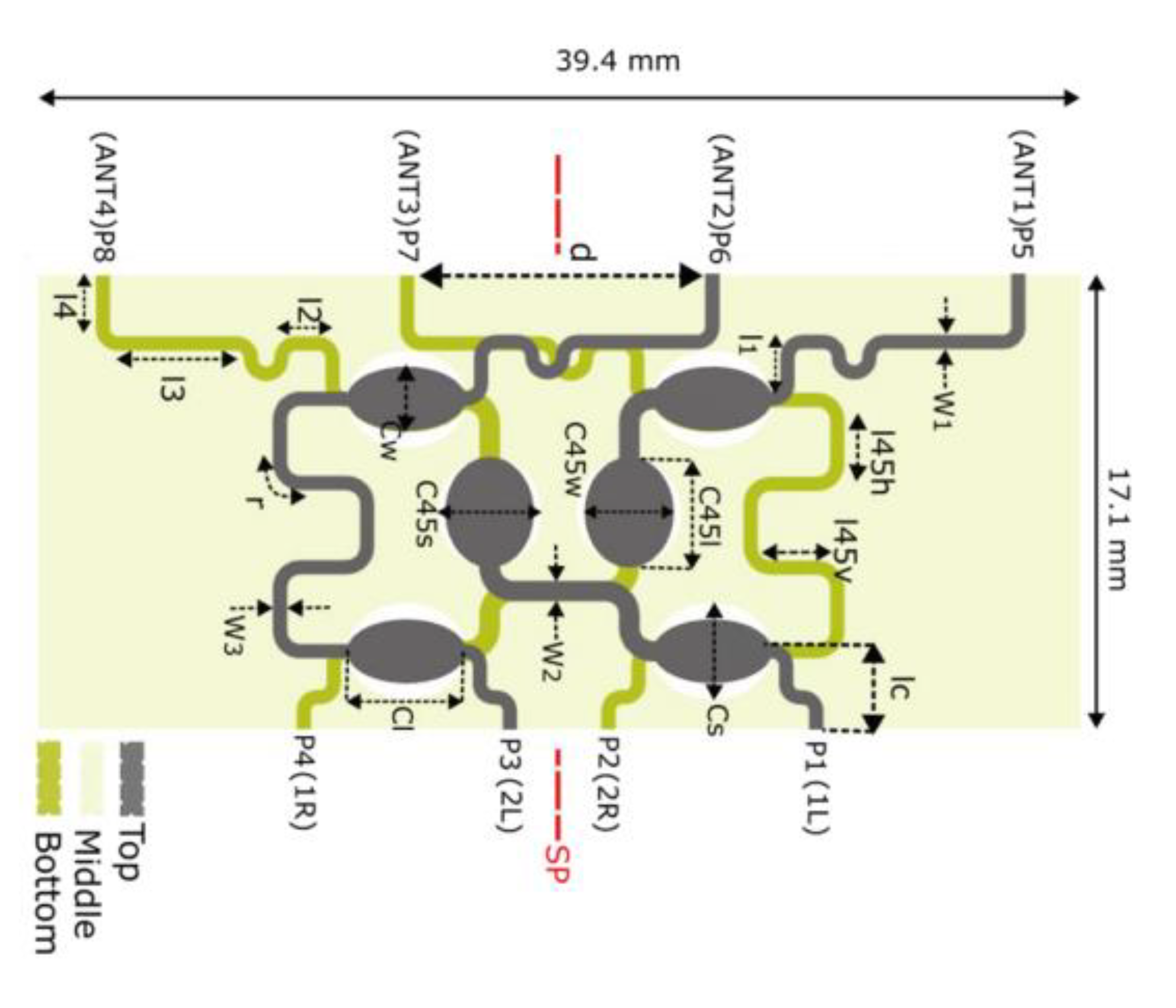
3.2. BM Results of the 2^nd Design Approach

Using the estimated geometrical characteristics of the interconnecting TLs from Table 7, a 4×4 BM was implemented as shown in Figure 16. Each section (input, output and interstage) is designed given the widths tabulated in Table 7. Additionally, the reference TLs connecting the HCs are meandered once again resulting in a BM size of 39.4 mm × 17.1 mm or 0.74

λ^{2}

. The theoretical parameters of the HC and 45° PS (shown in the parenthesis of Table 9) are optimized with their final values provided in Table 9. Figure 17 depicts the performance of the 4×4 BM in terms of S-parameters and phase accuracy. Since the network is symmetric, result for ports 1 and 2 only are illustrated. As shown in Figure 17a the insertion loss of the BM exciting ports P1 and P2 is as expected around -7 dB with a ±2 dB deviation in the entire 6 GHz -16 GHz band. The reflection coefficient of the BM is below -10 dB for the entire band of operation. Regarding the phase difference at the output ports, Δφ=45° is expected between them when port P1 is excited, while Δφ=135° is expected when port P2 is excited. Indeed, as shown in Figure 17b the obtained phase difference is around 45° and 135° exciting P1 and P2, respectively, with maximum deviation of 9° for P1 excitation. Considering the S-parameter and phase response of the 4×4 BM the achieved FBW is 102% which is the highest compared to the works reported in Table 1. Additionally, the design maintains a compact size, comparable to or even smaller than those reported in Table 1.

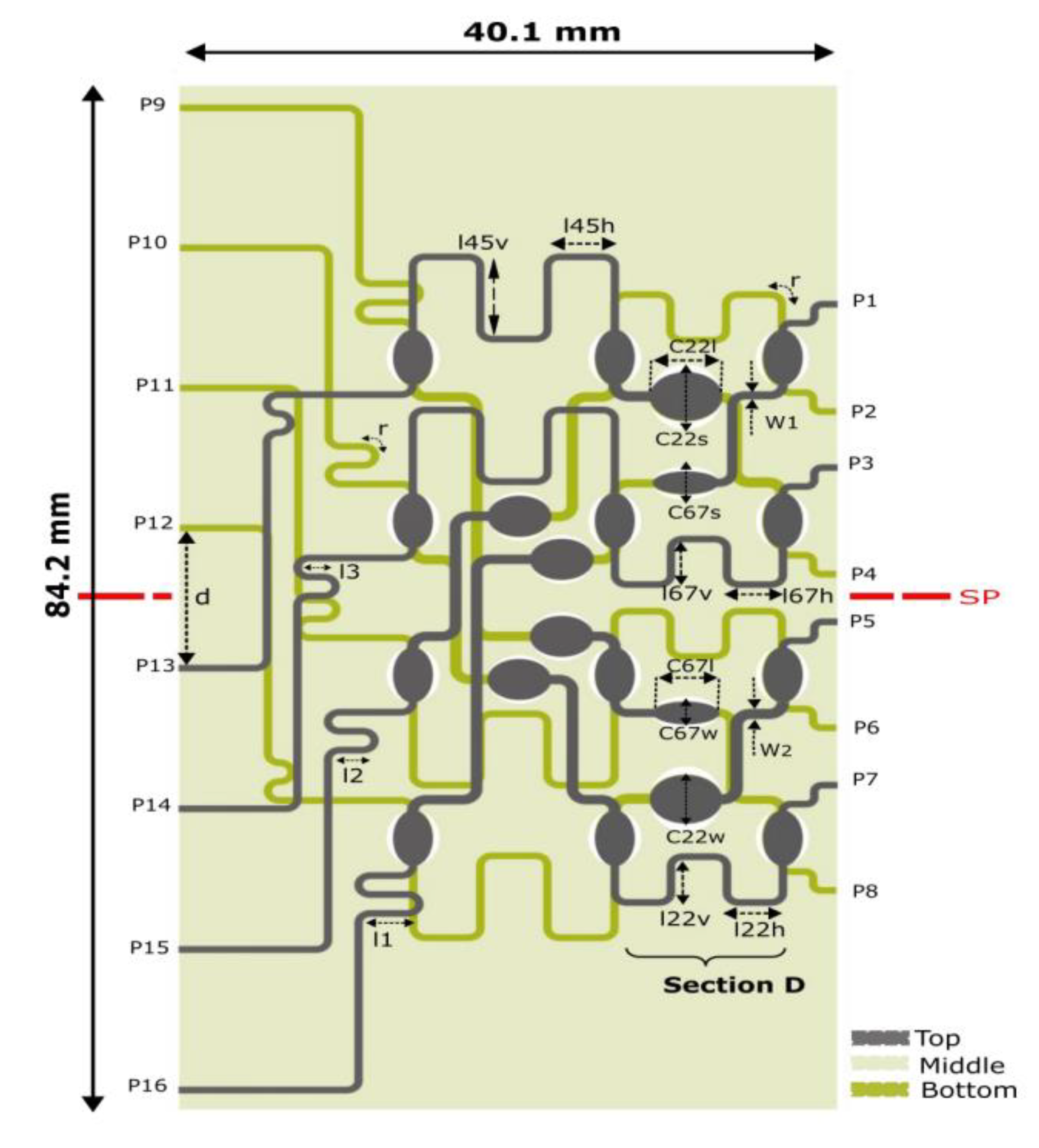
Following the same procedure used for the 4×4 BM, an 8×8 BM was designed utilizing the wideband matching technique described in Section 2.2. Herein, in the estimation of the geometrical characteristics of interconnecting TLs an extra section (Section D) is added as shown in Figure 18 which contains the 22.5° and 67.5° PSs and their related reference TLs. The estimated widths are given in the caption of Figure 18. The theoretical parameters (shown in the parenthesis of Table 10) of the 22.5° and 67.5° PSs are optimized with their final dimensions provided in Table 10. Since BM is designed as a single – unified structure using only the appropriate TLs to interconnect the core components, the total achieved size is 84.2 mm × 40.1 mm or 3.57

λ^{2}

. This design represents an approximate 20% miniaturization compared to the previous 8×8 BM design outlined in Section 2.1.

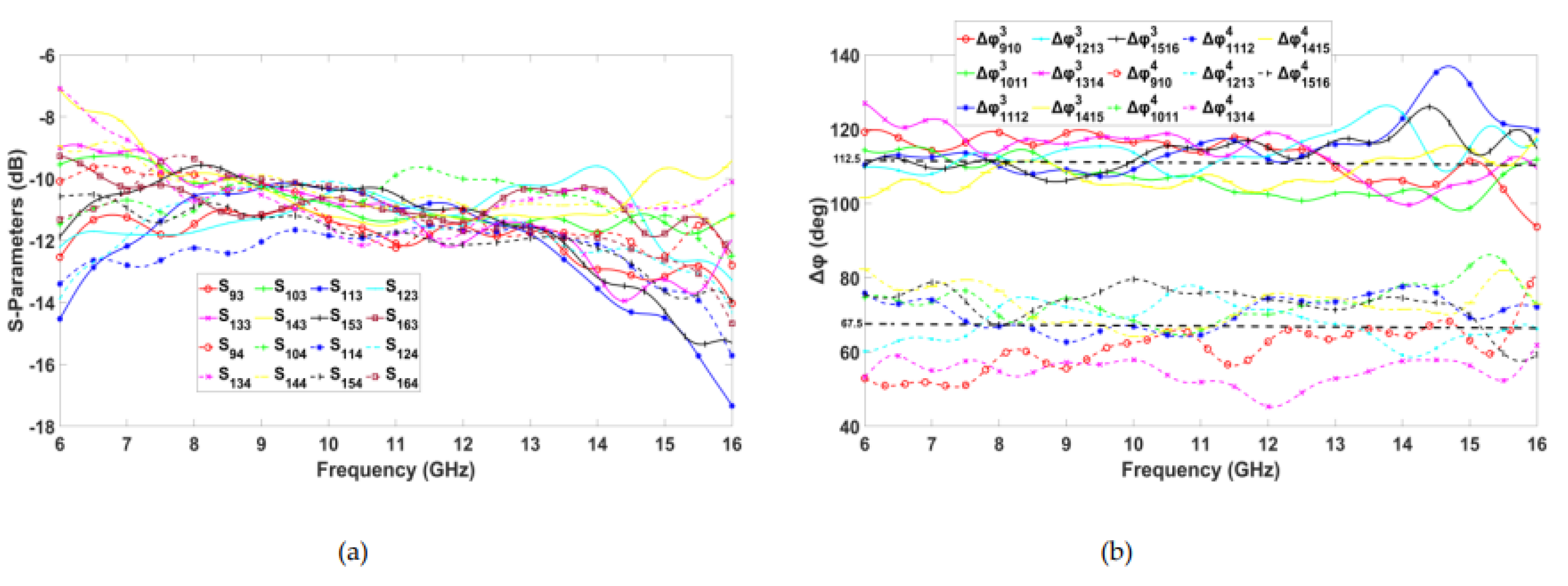
Figure 19 depicts the simulated reflection coefficient at the input ports of the 8×8 BM presented in Figure 18. As shown, the reflection coefficient is maintained below -10 dB across the entire operational bandwidth. Figure 20 and Figure 21 illustrate the simulated transmission responses and phase differences obtained at the output ports when input ports 1, 2, 3, and 4 are excited. Due to the symmetrical design, the responses for ports 5, 6, 7, and 8 are identical. The simulated transmission coefficients from input to output ports for each port excitation are approximately -12 dB with a deviation of a ±3 dB within the frequency range of 6 to 15 GHz, as demonstrated in Figure 20a and Figure 21a. Considering its ideal value of -9 dB resulting from the 1 to 8 power division, the additional -3 dB corresponds to power losses. Concerning the phase difference Δφ at output ports for each input ports excitation, as illustrated in Figure 20b and Figure 21b, a maximum deviation of 21° from the ideal values occurs between output ports P11-P12 when port P3 is excited. The same FBW is achieved as the BM designed in Section 2.1. Notably, a reduction in footprint area (FA) by 36% is attained in this design, resulting in the best compromise between FBW and size compared to the reported works in Table 2

4. Conclusion

This paper introduced two distinct design approaches for Butler Matrix beamformers operating in the low FR3 (6-16 GHz) band. The first approach is based on designing individual components and utilizing the advantages of MLs. This method led to the successful design and construction of an 8×8 BM, operating in the 6 GHz to 16 GHz frequency range. Both simulated and measured results demonstrate UWB operation and a remarkably compact size, surpassing previously reported works in the literature. The second approach simplifies the implementation process by using wideband matching techniques to design the BM as a single, unified structure. Using this method, 4×4 and 8×8 BMs were successfully implemented and simulated for the FR3 band, achieving further size reduction while maintaining consistent performance and FBW.

Acknowledgments

The authors would like to thank Dr. A. Koutinos and Mr. D. Lialios from Florida International University for their efforts in constructing the Butler matrix prototype and conducting the measurements.

Conflicts of Interest

The authors declare no conflict of interest.

References

L. -H. He, Y. -L. Ban, F. -Q. Yan and G. Wu, "Dual-Polarized Two-Dimensional Multibeam Antenna Array With Hybrid Beamforming and its Planarization," in IEEE Access, vol. 9, pp. 54951-54961, 2021. [CrossRef]
S. Payami et al., "Developing the First mmWave Fully-Connected Hybrid Beamformer With a Large Antenna Array," in IEEE Access, vol. 8, pp. 141282-141291, 2020. [CrossRef]
Y. Hu, J. Zhan, Z. Hao Jiang, C. Yu, and W. Hong, ``An orthogonal hybrid analog-digital multibeam antenna array for millimeter-wave massive MIMO systems,'' IEEE Trans. Antennas Propag., vol. 69, no. 3, pp. 1393_1403, Mar. 2021.
E. G. Larsson, O. Edfors, F. Tufvesson, and T. L. Marzetta, “Massive MIMO for next generation wireless systems,” IEEE Commun. Mag., vol. 52, no. 2, pp. 186–195, Feb. 2014.
G. Babur, G. O. Manokhin, A. A. Geltser and A. A. Shibelgut, "Low-Cost Digital Beamforming on Receive in Phased Array Radar," in IEEE Transactions on Aerospace and Electronic Systems, vol. 53, no. 3, pp. 1355-1364, June 2017. [CrossRef]
V. Venkateswaran and A. -J. van der Veen, "Analog Beamforming in MIMO Communications With Phase Shift Networks and Online Channel Estimation," in IEEE Transactions on Signal Processing, vol. 58, no. 8, pp. 4131-4143, Aug. 2010. [CrossRef]
I. Ahmed et al., "A Survey on Hybrid Beamforming Techniques in 5G: Architecture and System Model Perspectives," in IEEE Communications Surveys & Tutorials, vol. 20, no. 4, pp. 3060-3097, Fourthquarter 2018. [CrossRef]
B. Shallah et al., "Recent Developments of Butler Matrix From Components Design Evolution to System Integration for 5G Beamforming Applications: A Survey," in IEEE Access, vol. 10, pp. 88434-88456, 2022. [CrossRef]
Lialios, D.I.; Ntetsikas, N.; Paschaloudis, K.D.; Zekios, C.L.; Georgakopoulos, S.V.; Kyriacou, G.A. Design of True Time Delay Millimeter Wave Beamformers for 5G Multibeam Phased Arrays. Electronics 2020, 9, 1331. [Google Scholar] [CrossRef]
F. E. Fakoukakis and G. A. Kyriacou, ‘‘Novel Nolen matrix based beamforming networks for series-fed low SLL multibeam antennas,’’ Prog. Electromagn. Res. B, vol. 51, pp. 33–64, Apr. 2013.
Butler, J. . “Beam-forming matrix simplifies design of electronically scanned antennas.” Electronic Design 9 (1961): 170-173.
K. Vallappil, M. K. A. Rahim, B. A. Khawaja, N. A. Murad and M. G. Mustapha, "Butler Matrix Based Beamforming Networks for Phased Array Antenna Systems: A Comprehensive Review and Future Directions for 5G Applications," in IEEE Access, vol. 9, pp. 3970-3987, 2021. [CrossRef]
A.-W. Wang, T. -G. Ma and C. -F. Yang, "A New Planar Artificial Transmission Line and Its Applications to a Miniaturized Butler Matrix," in IEEE Transactions on Microwave Theory and Techniques, vol. 55, no. 12, pp. 2792-2801, Dec. 2007. [CrossRef]
Y. S. Jeong and T. W. Kim, "Design and Analysis of Swapped Port Coupler and Its Application in a Miniaturized Butler Matrix," in IEEE Transactions on Microwave Theory and Techniques, vol. 58, no. 4, pp. 764-770, April 2010. [CrossRef]
G. Tian, J. -P. Yang and W. Wu, "A Novel Compact Butler Matrix Without Phase Shifter," in IEEE Microwave and Wireless Components Letters, vol. 24, no. 5, pp. 306-308, May 2014. [CrossRef]
J. M. Wen, C. K. Wang, W. Hong, Y. M. Pan and S. Y. Zheng, "A Wideband Switched-Beam Antenna Array Fed by Compact Single-Layer Butler Matrix," in IEEE Transactions on Antennas and Propagation, vol. 69, no. 8, pp. 5130-5135, Aug. 2021. [CrossRef]
Aicha Bembarka, Larbi Setti, Abdelwahed Tribak, Hafid Tizyi, and Mohssine El Ouahabi, "A Novel Wideband Beamforming Antenna for 5G Applications by Eliminating the Phase Shifters and Crossovers from the Butler Matrix," Progress In Electromagnetics Research C, Vol. 133, 51-63, 2023. [CrossRef]
Sakhiya, R.; Chowdhury, S. A Low-Loss, 77 GHz, 8 × 8 Microstrip Butler Matrix on a High-Purity Fused-Silica (HPFS) Glass Substrate. Sensors 2023, 23, 1418. [Google Scholar] [CrossRef]
A. Tajik, A. Shafiei Alavijeh and M. Fakharzadeh, "Asymmetrical 4×4 Butler Matrix and its Application for Single Layer 8×8 Butler Matrix," in IEEE Transactions on Antennas and Propagation, vol. 67, no. 8, pp. 5372-5379, Aug. 2019. [CrossRef]
M. O. Shady and A. A. Kishk, "Compact 4 × 4 Multilayer Butler Matrix With Four-Slot Array," in IEEE Transactions on Microwave Theory and Techniques. [CrossRef]
J. Jung, J. Ryu and K. -Y. Jung, "Multi-Beam 5G Antenna With Miniaturized Butler Matrix Using Stacked LTCC," in IEEE Access, vol. 11, pp. 125519-125528, 2023. [CrossRef]
L. Van Messem et al., "A 4 × 4 Millimeterwave-Frequency Butler Matrix in Grounded Co-Planar Waveguide Technology for Compact Integration With 5G Antenna Arrays," in IEEE Transactions on Microwave Theory and Techniques, vol. 71, no. 1, pp. 122-134, Jan. 2023. [CrossRef]
T. -H. Lin, S. -K. Hsu and T. -L. Wu, "Bandwidth Enhancement of 4 ×4 Butler Matrix Using Broadband Forward-Wave Directional Coupler and Phase Difference Compensation," in IEEE Transactions on Microwave Theory and Techniques, vol. 61, no. 12, pp. 4099-4109, Dec. 2013. [CrossRef]
Ausordin, S.F. , Abdul Rahim, S.K., Seman, N., Dewan, R. and Sa'ad, B. (2014), A compact 4 × 4 butler matrix on double-layer substrate. Microw. Opt. Technol. Lett., 56: 223-229. [CrossRef]
Fanyaev I, Faniayeu I. Synthesis of novel 8 × 8 beam-forming network for broadband multibeam antenna array. Int J RF Microw Comput Aided Eng. 2022; 32(2):e22970. [CrossRef]
Zhai, Yu & Fang, Xiaoxing & Ding, Kejia & He, Fei. (2014). Miniaturization Design for 8 × 8 Butler Matrix Based on Back-to-Back Bilayer Microstrip. International Journal of Antennas and Propagation. 2014. 1-7. 10.1155/2014/583903.
Q. Shao, F. -C. Chen, Y. Wang and Q. -X. Chu, "Design of 4 × 4 and 8 × 8 Filtering Butler Matrices Utilizing Combined 90° and 180° Couplers," in IEEE Transactions on Microwave Theory and Techniques, vol. 69, no. 8, pp. 3842-3852, Aug. 2021. [CrossRef]
K. Wincza and S. Gruszczynski, "Broadband Integrated 8×8 Butler Matrix Utilizing Quadrature Couplers and Schiffman Phase Shifters for Multibeam Antennas With Broadside Beam," in IEEE Transactions on Microwave Theory and Techniques, vol. 64, no. 8, pp. 2596-2604, Aug. 2016. [CrossRef]
K. Wincza, S. Gruszczynski and K. Sachse, "Broadband Planar Fully Integrated 8 ×8 Butler Matrix Using Coupled-Line Directional Couplers," in IEEE Transactions on Microwave Theory and Techniques, vol. 59, no. 10, pp. 2441-2446, Oct. 2011. [CrossRef]
P. I. Bantavis, C. I. Kolitsidas, T. Empliouk, M. Le Roy, B. L. G. Jonsson and G. A. Kyriacou, "A Cost-Effective Wideband Switched Beam Antenna System for a Small Cell Base Station," in IEEE Transactions on Antennas and Propagation, vol. 66, no. 12, pp. 6851-6861, Dec. 2018. [CrossRef]
F. E. Fakoukakis, T. N. Kaifas, E. E. Vafiadis, G. A. Kyriacou, Design and implementation of Butler matrix-based beam-forming networks for low sidelobe level electronically scanned arrays, International Journal of Microwave and Wireless Technologies 7 (1), 69-79.
T. N. Kaifas, J. N. Sahalos, A 4× 4 Butler matrix optimized for umts applications, Microwave and Optical Technology Letters 49 (3), 585-588.
Empliouk TM, Bantavis PI, Koltsidas CI, Kaifas TNF, Kyriacou GA. Ultra-Wideband Six-Port Network Miniaturization—Matching. International Journal of Microwave and Wireless Technologies. 2023;15(10):1676-1688. [CrossRef]
C. A. Balanis, “Antenna Theory Analysis and Design,” 2nd Edition, John Wiley & Sons, Inc., New York, 1997.
Pozar DM, Microwave Engineering, 3rd ed. New York: Wiley, 2011.

Figure 1. Multibeam antenna array exploiting 3D Beamformer based on Butler matrix feeding Tapered Slot Antenna Array.

Figure 2. 8×8 Butler Matrix Topology. SP denotes symmetry plane.

Figure 3. (a) Hybrid Coupler layers stack up. W=0.54, l=1.66 and r=1.26 (Dimensions are in mm). (b) Simulated S-Parameters and phase difference between ports 2 and 3, for an RF-input at port-1.

Figure 4. (a) Layers stack of 22.5° PS. (b) Layout of 45° and 67.5° PSs.

Figure 5. (a) Straight line and its equivalent ML, l=20, w=1, l1=0.5, lv=1.7, lh=1.3 and r=0.01, (Dimensions are in mm). (b) VSWR plot of the two lines.

Figure 6. (a) S-parameters and (b) differential phase for the three PSs.

Figure 7. (a) Layout of the equiphased TLs network. (b) Transmission S-parameters and differential phase between the lines.

Figure 8. Wideband matching technique utilized to design a 4×4 BM. All interconnecting TLs are initially removed to be replaced by appropriate MLs.

Figure 9. Real and imaginary parts of the input impedances of the HC and PS at input reference level.

Figure 10. Reflection coefficient of input ports of our proposed 8×8 BM. m denotes measurements.

Figure 11. Port 1 excitation. (a) Transmission coefficients S_i1 from input port 1 to output ports, i=9,..,16. (b) Phase difference

{Δ φ}_{i j}^{1}

of output ports (ideal 22.5˚). Superscript 1 denotes the input port and subscript ij denotes the consecutive output ports, m denotes measurements.

Figure 11. Port 1 excitation. (a) Transmission coefficients S_i1 from input port 1 to output ports, i=9,..,16. (b) Phase difference

{Δ φ}_{i j}^{1}

of output ports (ideal 22.5˚). Superscript 1 denotes the input port and subscript ij denotes the consecutive output ports, m denotes measurements.

Figure 12. Port 2 excitation. (a) Transmission coefficients S_i2 from input port 2 to output ports, i=9,..,16. (b) Phase difference

{Δ φ}_{i j}^{2}

of output ports (ideal 157.5˚), superscript 2 denotes the input port and subscript ij denotes the consecutive output ports, m denotes measurements.

Figure 12. Port 2 excitation. (a) Transmission coefficients S_i2 from input port 2 to output ports, i=9,..,16. (b) Phase difference

{Δ φ}_{i j}^{2}

of output ports (ideal 157.5˚), superscript 2 denotes the input port and subscript ij denotes the consecutive output ports, m denotes measurements.

Figure 13. Port 3 excitation. (a) Transmission coefficients S_i3 from input port 3 to output ports, i=9,..,16. (b) Phase difference

{Δ φ}_{i j}^{3}

of output ports (ideal 122.5˚). Superscript 3 denotes the input port and subscript ij denotes the consecutive output ports, m denotes measurements.

Figure 13. Port 3 excitation. (a) Transmission coefficients S_i3 from input port 3 to output ports, i=9,..,16. (b) Phase difference

{Δ φ}_{i j}^{3}

of output ports (ideal 122.5˚). Superscript 3 denotes the input port and subscript ij denotes the consecutive output ports, m denotes measurements.

Figure 14. Port 4 excitation. (a) Transmission coefficients S_i4 from input port 4 to output ports, i=9,..,16. (b) Phase difference

{Δ φ}_{i j}^{4}

of output ports (ideal 67.5˚). Superscript 4 denotes the input port and subscript ij denotes the consecutive output ports, m denotes measurements.

Figure 14. Port 4 excitation. (a) Transmission coefficients S_i4 from input port 4 to output ports, i=9,..,16. (b) Phase difference

{Δ φ}_{i j}^{4}

of output ports (ideal 67.5˚). Superscript 4 denotes the input port and subscript ij denotes the consecutive output ports, m denotes measurements.

Figure 15. Simulated and measured radiation pattern of the 8×8 BM, d=0.6λ_min. The corresponding theoretical beam directions are ±46˚, ±31˚, ±18˚ and ±6˚ respectively.

Figure 16. Implemented 4×4 BM. W₁=0.49, W₂=0.68, W₃=0.41, lc=5.48, l45v=1.74, l45h=1.63, l1=1, l2=0.8, l3=4.5, l4=2 and r=0.5. All dimensions are in mm.

Figure 17. (a) S-parameters of the 4×4 BM. (b) Phase difference

{Δ φ}_{i j}^{n}

of output ports, superscript n=1,2 denotes the input port and subscript ij denotes the consecutive output ports.

Figure 17. (a) S-parameters of the 4×4 BM. (b) Phase difference

{Δ φ}_{i j}^{n}

of output ports, superscript n=1,2 denotes the input port and subscript ij denotes the consecutive output ports.

Figure 18. Schematic view of our proposed 8×8 BM. W₁=0.67, W₂=0.84, l22v=2.21, l22h=2.11, l67v=2.18, l67h=2.11, l45v=5.2, l45h=2.85, l1=2.42, l2=1.49, l3=0.94 and r=0.5. All dimensions are in mm.

Figure 19. Reflection coefficient at the input ports of the 8×8 BM of Figure 18.

Figure 20. (a) Transmission coefficients S_in from input ports n=1,2 to output ports, i=9,..,16. of the 8×8 BM of Figure 20. (b) Phase difference

{Δ φ}_{i j}^{n}

of output ports. Superscript n=1,2 denotes the input port and subscript ij denotes the consecutive output ports.

Figure 20. (a) Transmission coefficients S_in from input ports n=1,2 to output ports, i=9,..,16. of the 8×8 BM of Figure 20. (b) Phase difference

{Δ φ}_{i j}^{n}

of output ports. Superscript n=1,2 denotes the input port and subscript ij denotes the consecutive output ports.

Figure 21. (a) Transmission coefficients S_in from input ports n=3,4 to output ports, i=9,..,16. of the 8×8 BM of Figure 20. (b) Phase difference

{Δ φ}_{i j}^{n}

of output ports, superscript n=3,4 denotes the input port and subscript ij denotes the consecutive output ports.

Figure 21. (a) Transmission coefficients S_in from input ports n=3,4 to output ports, i=9,..,16. of the 8×8 BM of Figure 20. (b) Phase difference

{Δ φ}_{i j}^{n}

of output ports, superscript n=3,4 denotes the input port and subscript ij denotes the consecutive output ports.

Table 1. Performance summary of state-of-the-art multilayer 4×4 BM. Note: The acronyms are denoted as follow: OB, operating band, NS, normalized size, FA, footprint area; ILAv ± ΔA, average insertion loss with amplitude deviation, PA, phase accuracy.

Work	Technology	OB (GHz)	f₀ (GHz)	FBW (%)	Size (mm²)	NS (λ)	FA (λ²)	IL_Av±ΔA (dB)	PA(˚)
[20]	Microstrip to Slot	27 – 31	29	13.8		3.49 × 2.2	7.67	-9±1.4	±8
[21]	LTCC	26-30	28	14	22.02 × 5.93	2.05 × 0.55	1.12	-9±3.5	±9
[22]	GCPW	23.75 –31	27	26.5	19.2 × 29.84	1.8 × 2.8	5.04	-9±4	-
[23]	FWDC	1.9-3.1	2.5	47	81.65 × 71.56	0.68 × 0.59	0.4	-7±3	±6
[24]	Microstrip to Slot	2-3	2.45	40	100 × 120	0.8 × 0.98	0.78	-7±3	±7
This Work	Microstrip to Slot	6-16	9.8	102	39.4 × 17.9	1.28 × 0.58	0.74	-7±3	±9

Table 2. Performance summary of state-of-the-art multilayer 8×8 BM. Note: The acronyms are denoted as follow: OB, operating band, NS, normalized size, FA, footprint area; ILAv ± ΔA, average insertion loss with amplitude deviation, PA, phase accuracy.

Work	Technology	OB (GHz)	f₀ (GHz)	FBW (%)	Size (mm²)	NS (λ)	FA (λ²)	IL_Av±ΔA (dB)	PA(˚)

[25]	Slotline Transition – Magit T	7-13	10	85	140 × 97	4.7 × 3.2	15.04	-12±2.5	±20
[26]	Microstrip	3.6-4.7	4.2	26	160 × 160	2.1 × 2.1	4.4	-12±3	±15
[27]	Stripline	2.3-2.5	2.4	5.5	250 × 160	2 × 1.28	2.56	-12±1.9	±12
[28]	Stripline		3	33	170 × 145	1.7 × 1.45	2.46	±0.5	±10
[29]	Stripline	2.5-3.5	3	33	130 × 100	1.3 × 1	1.3	±0.45	±7.5
This Work	Microstrip to Slot	6-16	9.8	92	58.46 × 90 (39.9 × 53.52)	1.91 × 2.94 (1.3 × 1.74)	5.6 (2.26)	-12±3	±21.5
This Work	Microstrip to Slot	6-16	9.8	92	40.1 × 84.26 (29.55 × 53.6)	1.3 × 2.75 (0.96 × 1.75)	3.57 (1.68)	-12±3	±21

Table 3. Excitation phase distribution in an ideal 8×8 BM.

Antenna Ports	Beam Ports
Antenna Ports	1L	4R	3L	2R	2L	3R	4L	1R
1	90	-180	157.5	-112.5	135	-135	157.5	-112.5
2	112.5	22.5	-90	-180	-157.5	112.5	-45	-135
3	135	-135	22.5	112.5	90	0	112.5	-157.5
4	157.5	67.5	135	45	-22.5	-112.5	-90	-180
5	-180	-90	-112.5	-22.5	45	135	67.5	157.5
6	-157.5	112.5	0	-90	112.5	22.5	-135	135
7	-135	-45	112.5	-157.5	-180	-90	22.5	112.5
8	-112.5	157.5	-135	135	-112.5	157.5	-180	90
Δφ	22.5	-157.5	112.5	-67.5	67.5	-112.5	157.5	-22.5
Beam Angle	-6°	46°	-31°	18°	-18°	31°	-46°	6°

Table 4. Theoretical and simulated values of the HCs parameters of Figure 3a.

HC	C_l	C_w	C_s
Theoretical Value	4.57	2.29	3.44
Simulated Value	4.97	2.35	3.6

Table 6. Final values of the parameters of the four TLs (Dimensions are in mm).

	L1	L2	L3	L4	w	r
Line1	2	0.92	14.34	8	0.54	0.5
Line2	4	0.6	15	6	0.54	0.5
Line3	6	0.469	15.2	4	0.54	0.5
Line4	8	0.06	16	2	0.54	0.5

Table 7. Estimated hyperbolic mean impedance for the HC and PS and their corresponding TL’s geometrical characteristics.

	Section	Z_low (Ω)	Z_high (Ω)	Z_m (Ω)	Matching TL
	Section	Z_low (Ω)	Z_high (Ω)	Z_m (Ω)	Z_o (Ω)	θ (deg)	W (mm)	L (mm)
HC	A & C	54.63+j1.56	62.52-j6.46	58.57-j2.18	54.3	103	0.49	5.48
HC	B	54.63+j1.56	62.52-j6.46	58.57-j2.18	58.51	-	0.42	-
PS	B	26.13-j16.5	49.6+j4.1	37.3-j9.4	44.16	-	0.68	-

Table 8. Final Optimized parameters for the 8×8 Butler Matrix (Dimensions are in mm). PD denotes percent difference.

	C_22.5w C_45w C_67.5w			C_22.5s C_45s C_67.5s			l_22.5v l_45v l_67.5v
	Initial	Final	PD (%)	Initial	Final	PD (%)	Initial	Final	PD (%)
22.5°	3.72	3.4	8.6	5.32	4.68	12	1.705	1.816	6.5
45°	2.7	2.52	6.6	3.7	3.4	8	4.63	4.47	3.4
67.5°	1.47	1.23	16.3	2.76	2.77	0.36	1.801	1.48	17.8

Table 9. Final parameters of the HC and PS. Dimensions are in mm.

	C_w C_45w	C_s C_45s	Cl C_45l
HC	2.42 (2.29)	3.63 (3.44)	4.5 (4.56)
PS 45°	3.39 (3.4)	3.7 (3.9)	4.2 (4.7)

Table 10. Final parameters of the 22.5° and 67.5° PSs. Dimensions are in mm.

	C22_w C67_w	C22_s C67_s	C22l C67_l
PS 22.5°	5.19 (4.21)	5.82 (5.21)	4.5 (4.5)
PS 67.5°	1.87 (2.5)	2.76 (2.75)	4.5 (4.5)

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer