Prerpints.org logo
Preprint
Article

Approximations in Mean Square Analysis of Stochastically Forced Equilibria for Nonlinear Dynamical Systems

Altmetrics

Downloads

83

Views

13

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

07 June 2024

Posted:

11 June 2024

You are already at the latest version

Alerts
Abstract
Motivated by important applications to the analysis of complex noise-induced phenomena, a problem of the constructive description of randomly forced equilibria for nonlinear systems with multiplicative noise is considered. Using apparatus of the first approximation systems, we construct an approximation of mean square deviations that explicitly takes into account the presence of multiplicative noise. This approximation is compared with the widely used approximation based on the stochastic sensitivity technique. The general mathematical results are illustrated with the example of the van der Pol oscillator with hard excitement.
Keywords: 
Subject: Computer Science and Mathematics  -   Probability and Statistics

MSC:  37H10; 37H20

1. Introduction

Currently, nonlinear stochastic phenomena such as noise-induced transitions [1,2], stochastic excitement [3,4,5], noise-induced crisis [6,7], stochastic bifurcations [8,9], noise-induced chaos [10,11], stochastic and coherence resonances [12,13,14] are being actively studied in various fields of natural sciences. One of the key mechanisms of such effects is associated with the transition of random trajectories through separatrices detaching basins of coexisting attractors. For the parametric analysis of the conditions causing such transitions and the estimation of the corresponding critical values of the intensity of random disturbances that generate them, a new fairly general geometric approach has been used, based on the method of confidence domains [15,16,17].
The main idea of this approach is as follows. As the noise intensity increases, the size of the confidence domain increases. The critical value of the noise intensity is found from the condition of the intersection of the confidence domain and the separatrix. The key parameter that determines the configuration of the confidence domain is the stochastic sensitivity of the attractor [18,19]. Initially, the stochastic sensitivity technique was introduced in connection with the approximation [20] of a quasipotential [21] in the vicinity of an attractor. Currently, this technique has been developed for regular and chaotic attractors of both continuous and discrete systems (see, e.g. [22,23,24]). The stochastic sensitivity technique and the associated confidence domains method are actively used in the analysis of nonlinear stochastic phenomena [25,26,27,28] and control problems [29,30].
Using the stochastic sensitivity technique, an approximation of the mean square deviations of random states of a stochastic system from the deterministic attractor is constructed. Although formally this technique is applicable to both the case of additive and parametric noise, however, in the case of parametric noise, the error in the corresponding approximations may be such that the prediction made on the basis of this approximation may turn out to be incorrect.
This paper is devoted to the problem of approximation of probabilistic distributions of random states around stable equilibria of stochastic differential Ito’s equations with general multiplicative noise. Using first approximation systems, we construct an approximation of mean square deviations that explicitly takes into account the presence of parametric noise. This more accurate approximation is compared with an approximation based on the stochastic sensitivity technique. General mathematical results are illustrated with examples.

2. Mean Square Analysis of Stochastic Equilibria

Consider a nonlinear autonomous system of ordinary differential equations
d x = f ( x ) d t ,
where x is an n-dimensional vector and f ( x ) is a sufficiently smooth n-vector function. It is assumed that the system (1) has an exponentially stable equilibrium x ¯ .
Definition 1. The equilibrium x ¯ is called exponentially stable in system (1) if for some neighborhood U of x ¯ there exist constants K > 0 , l > 0 such that for all t ⩾ 0 it holds that
∥ x ( t ) − x ¯ ∥ ⩽ K e − l t ∥ x 0 − x ¯ ∥ ,
where x ( t ) is a solution of the system (1) with the initial condition x ( 0 ) = x 0 ∈ U . Here, ∥ · ∥ is the Euclidean norm.
Along with the deterministic system (1), let us consider the stochastic Ito system
d x = f ( x ) d t + ∑ i = 1 k σ i ( x ) d w i ( t ) ,
where σ i ( x ) are sufficiently smooth n-vector functions, w i ( t ) are scalar standard independent Wiener processes. The functions σ i ( x ) model the dependence of multiplicative disturbances on the system state.
Solutions of the stochastic system (2), leaving the deterministic equilibrium x ¯ under the influence of random disturbances, form some probability distribution. It is assumed that the probabilistic distribution of the states of system (2) stabilizes. The corresponding stable stationary distribution density satisfies the Fokker-Planck-Kolmogorov equation [21,31]. It is known that in the general case it is very difficult to directly use this equation to describe probability distributions, even for two-dimensional systems. Here, the apparatus of first approximation systems is useful.

2.1. First Approximation System and Its Mean Square Analysis

Let us consider the deviation z = x − x ¯ of the random state x of the system (2) from the exponentially stable equilibrium x ¯ of the system (1). Dynamics of the variable z is governed by the following first approximation linear system:
d z = F z d t + ∑ i = 1 k ( S 0 , i + S 1 , i z ) d w i ,
where
F = ∂ f ∂ x ( x ¯ ) , S 0 , i = σ i ( x ¯ ) , S 1 , i = ∂ σ i ∂ x ( x ¯ ) .
In our mean square analysis of the system (3) solutions, we will use first (m) and second (M) moments: m = E ( z ) , M = E ( z z ⊤ ) . Dynamics of these deterministic characteristics is described by the following equations:
m ˙ = F m ,
M ˙ = F M + M F ⊤ + ∑ i = 1 k S 0 , i S 0 , i ⊤ + S 0 , i m ⊤ S 1 , i ⊤ + S 1 , i m S 0 , i ⊤ + S 1 , i M S 1 , i ⊤ .
To find an approximation of the dispersion of stationary distributed random states of the nonlinear stochastic system (2) around the deterministic equilibrium x ¯ , we will use stationary solutions of the system (4), (5).
Due to exponential stability of the equilibrium x ¯ , it holds that Re λ i ( F ) < 0 , where λ i ( F ) , i = 1 , … , n , are eigenvalues of the matrix F. In these circumstances, the system (4) has a unique stationary stable solution m ¯ = 0 . Substituting m ¯ = 0 into (5), we get
M ˙ = F M + M F ⊤ + ∑ i = 1 k S 0 , i S 0 , i ⊤ + S 1 , i M S 1 , i ⊤ .
So, the matrix M ¯ of the stationary solution of the equation (6) satisfies the following algebraic equation:
F M ¯ + M ¯ F ⊤ + ∑ i = 1 k S 0 , i S 0 , i ⊤ + S 1 , i M ¯ S 1 , i ⊤ = 0 .
Let us consider a deviation Δ ( t ) = M ( t ) − M ¯ where M ( t ) is a solution of the equation (6). For the function Δ ( t ) , one get the homogeneous equation
Δ ˙ = F Δ + Δ F ⊤ + ∑ i = 1 k S 1 , i Δ S 1 , i ⊤ .
The matrix Δ ( t ) is the matrix of second moments Δ ( t ) = E y ( t ) y ( t ) ⊤ for solutions y ( t ) of linear homogeneous stochastic equation
d y = F y d t + ∑ i = 1 k S 1 , i y d w i .
Thus, the question about stability of the stationary solution M ¯ of the equation (6) is reduced to the equivalent question about the exponential mean square stability of the trivial solution y = 0 of the stochastic system (9).
Definition 2. Solution y ≡ 0 of the stochastic system (9) is called exponentially stable in mean square, if there exist constants K > 0 , l > 0 such that for all t ⩾ 0 it holds that
E ∥ y ( t ) ∥ 2 ⩽ K e − l t E ∥ y 0 ∥ 2 ,
where y ( t ) is a solution of the system (9) with the initial condition y ( 0 ) = y 0 .
Let us consider the matrix S 0 = ∑ i = 1 k S 0 , i S 0 , i ⊤ and operators
A [ M ] = F M + M F ⊤ , S [ M ] = ∑ i = 1 k S 1 , i M S 1 , i ⊤ , P = − A − 1 S .
Rewrite equations (6), (7), and (8) as follows:
M ˙ = A [ M ] + S ( M ) + S 0 ,
A [ M ¯ ] + S [ M ¯ ] + S 0 = 0 ,
Δ ˙ = A [ Δ ] + S [ Δ ] .
Note that the existence of the operator A − 1 follows from the condition Re λ i ( F ) < 0 .
Basic theoretical connections are presented in the following theorem.
Theorem 1. 
The following statements are equivalent:
(a) System (10) has a stationary exponentially stable solution M ¯ satisfying (11);
(b) The solution Δ ≡ 0 of the system (12) is exponentially stable;
(c) The solution y ≡ 0 of the stochastic system (9) is exponentially stable in mean square;
(d) It holds that Re λ i ( F ) < 0 ( i = 1 , . . . , n ) and ρ ( P ) < 1 , where ρ ( P ) is the spectral radius of the operator P .
The statements of this theorem were proven or follow from more general results presented in [32,33,34,35].
Remark. 
In the one-dimensional case ( n = 1 ), we have
S 0 = ∑ i = 1 k σ i 2 ( x ¯ ) , A [ M ] = 2 f ′ ( x ¯ ) M , S [ M ] = ∑ i = 1 k σ i ′ ( x ¯ ) 2 M ,
and the condition ρ ( P ) < 1 has an explicit parametric representation:
ρ ( P ) = − 1 2 f ′ ( x ¯ ) ∑ i = 1 k σ i ′ ( x ¯ ) 2 < 1 .
In this case, for the mean square variance of random states around the equilibrium x ¯ the following estimation can be written:
M = − ∑ i = 1 k σ i 2 ( x ¯ ) 2 f ′ ( x ¯ ) + ∑ i = 1 k σ i ′ ( x ¯ ) 2 .

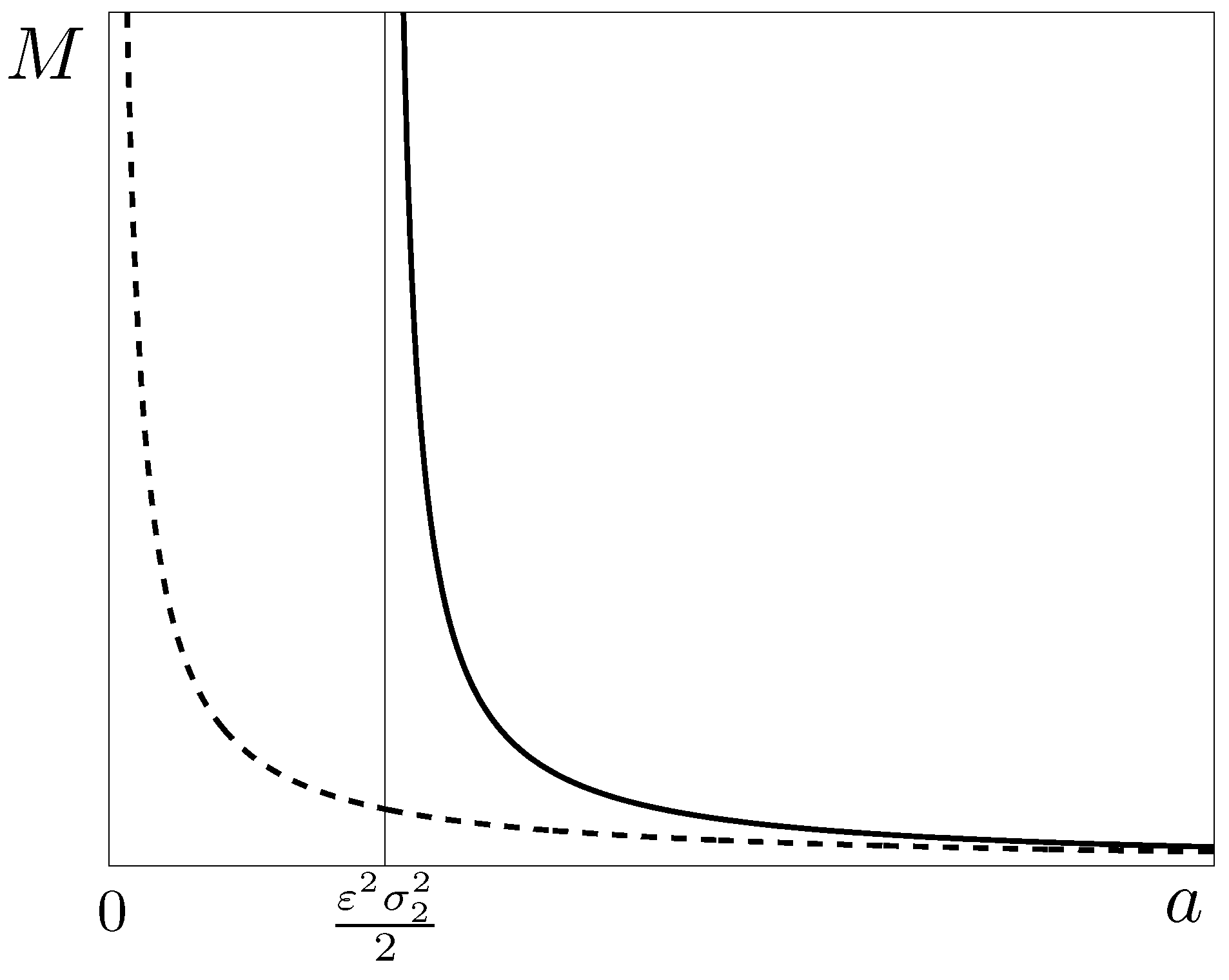
2.2. Asymptotics for the Case of Weak Noise, Stochastic Sensitivity of the Equilibrium

Consider the stochastic system
d x = f ( x ) d t + ε ∑ i = 1 k σ i ( x ) d w i ( t ) ,
where ε is a scalar small parameter of the disturbance intensity. For this system, the equation (11) for the covariance matrix M of the equilibrium x ¯ has the form
A [ M ] + ε 2 S [ M ] + ε 2 S 0 = 0 .
Let us study the dependence of the solution M ( ε ) of this equation on the parameter ε . Let W ( ε ) be the solution to the equation
A [ W ] + ε 2 S [ W ] + S 0 = 0 .
Then M ( ε ) = ε 2 W ( ε ) . For W ( ε ) , one can write the following decomposition:
W ( ε ) = − ( A + ε 2 S ) − 1 [ S 0 ] = − I + ε 2 A − 1 S − 1 A − 1 [ S 0 ] =
= I − ε 2 P − 1 [ W ( 0 ) ] .
For small ε , it holds that
W ( ε ) = ∑ m = 0 ∞ ε 2 m P m [ W ( 0 ) ] = W ( 0 ) + ε 2 P [ W ( 0 ) ] + ε 4 P 2 [ W ( 0 ) ] + …
As a result, for the matrix function M ( ε ) we get the expansion in powers of the small parameter:
M ( ε ) = ∑ m = 0 ∞ ε 2 m + 2 P m [ W ( 0 ) ] = ε 2 W ( 0 ) + ε 4 P [ W ( 0 ) ] + ε 6 P 2 [ W ( 0 ) ] …
In this series, the matrix W ( 0 ) plays an important role in the asymptotic analysis of the spread of random states around the equilibrium. Because of W ( 0 ) = lim ε → 0 1 ε 2 M ( ε ) , this matrix characterizes the stochastic sensitivity of the equilibrium to the impact of weak noise. Thus, in the first approximation, we have
M ( ε ) ≈ M ( 1 ) ( ε ) = ε 2 W ,
where W is a solution of the following equation
F W + W F ⊤ + S 0 = 0 .
If the noise in the system (14) does not depend on the state, then P = 0 and the first approximation coincides with the exact value: M ( ε ) = ε 2 W . In general, using W as an approximation for M ( ε ) one get an underestimation of the covariance of random states. Indeed, since the operator P is positive, the inequality M ( ε ) ⪰ ε 2 W is valid.
In one-dimensional case, the stochastic sensitivity of the equilibrium x ¯ for the system (14) is given by the formula
W = − ∑ i = 1 k σ i 2 ( x ¯ ) 2 f ′ ( x ¯ ) .

3. Examples

Let us consider how these theoretical results can be applied to the approximation of mean square deviation of random states from the equilibrium in some stochastic systems.
Example 1. 
Consider a simple one-dimensional stochastic system
d x = − a x d t + ε ( σ 1 d w 1 ( t ) + σ 2 x d w 2 ( t ) ) ,
where a , σ 1 , and σ 2 are non-negative parameters, ε is the intensity of random disturbances, w i ( t ) are uncorrelated scalar Wiener processes. The parameters σ 1 and σ 2 specify the weights of additive and multiplicative disturbances, accordingly.
For a > 0 , the corresponding deterministic system (with ε = 0 ) has an exponentially stable equilibrium x ¯ = 0 . Second moments M ( t ) = E ( x ( t ) − x ¯ ) 2 of deviations of solutions x ( t ) from the equilibrium satisfy the equation
M ˙ = − 2 a M + ε 2 ( σ 1 2 + σ 2 2 M ) .
This equation has a stationary solution
M ( ε ) = ε 2 σ 1 2 2 a − ε 2 σ 2 2 .
Following the decomposition (16), for weak noise M ( ε ) has the following asymptotics
M ( ε ) = ε 2 W + O ( ε 4 ) ,
where W characterizes the stochastic sensitivity of the equilibrium x ¯ . Here, Wy satisfies (see (18)) the equation:
− 2 a W + σ 1 2 = 0 .
Using W one can write the first approximation for the function M ( ε ) :
M ( 1 ) ( ε ) = ε 2 W = ε 2 σ 1 2 2 a .
Formally, the approximation M ( 1 ) ( ε ) is defined for any a > 0 while the approximated function M ( ε ) is defined only for a > ε 2 σ 2 2 2 . In absence of multiplicative noise ( σ 2 = 0 ), the values M ( 1 ) and M are identical. At σ 2 ≠ 0 , they can essentially differ.
This difference is clearly seen in Figure 1 where plots of the functions M (solid line) and M ( 1 ) (dashed line) are shown versus parameter a. Note that the approximation M ( 1 ) is always less than M (this fact was shown above for the general case). Moreover, in the interval 0 < a < ε 2 σ 2 2 2 , where the approximation gives finite values, the original function is not defined at all: the second moments M ( t ) tend to infinity. In the interval a > ε 2 σ 2 2 2 , the approximation error monotonically increases and tends to infinity as it approaches the bifurcation value a * = ε 2 σ 2 2 2 . For the relative error, an explicit representation can be written:
M − M ( 1 ) M = ε 2 σ 2 2 2 a .
Let us continue the comparison of these two methods for estimating the dispersion of random states around the equilibrium using the two-dimensional system as an example.
Example 2. 
Consider the van der Pol model with hard excitation of self-oscillations:
d x = y d t d y = ( − x + ( a + b x 2 − x 4 ) y ) d t + σ 1 d w 1 + σ 2 y d w 2 .
Here, σ 1 is the intensity of the additive noise, σ 2 is the intensity of the multiplicative noise, and w 1 ( t ) , w 2 ( t ) are scalar standard independent Wiener processes.
Let us fix a = − 0.1 , b = 2 . For this set of parameters, the deterministic system (20) with σ 1 = σ 2 = 0 is bistable and exhibits the coexisting attractors: the stable equilibrium x ¯ = 0 , y ¯ = 0 and stable limit cycle. Basins of these attractors are separated by the orbit of the unstable limit cycle. In Figure 2a and Figure 3a, the equilibrium is shown by black filled circle, the stable cycle is plotted by blue curve, and the unstable cycle (the separatrix) is shown by red curve.
Let us consider the behavior of trajectories of the stochastic system (20) solutions starting at the equilibrium ( 0 , 0 ) . Under the influence of weak random disturbances, trajectories leave the stable equilibrium and form a stationary probability distribution concentrated in a small neighborhood of the origin. This type of dynamics corresponds to the unexcited mode of the oscillator (see Figure 2 for σ 1 = 0.02 , σ 2 = 0.2 ).
As the noise intensity increases, random trajectories cross the separatrix (unstable limit cycle) and continue to oscillate near the stable cycle. This means a transition to the excitation mode (see Figure 2 for σ 1 = 0.05 , σ 2 = 0.4 ).
For the analytical approximation of the dispersion of random states, we will use theory presented above.
For the system (20), parameters of the equation (7) are following:
F = 0 1 − 1 a , M = m 11 m 12 m 21 m 22 ,
S 0 , 1 = σ 1 0 1 , S 0 , 2 = 0 0 , S 1 , 1 = 0 0 0 0 , S 1 , 2 = σ 2 0 0 0 1 .
Now, we can write the matrix equation (7) as the following system for the elements m i j of the symmetric matrix M:
− m 11 + a m 12 + m 22 = 0 , m 12 = m 21 = 0 , − 2 m 12 + 2 a m 22 + σ 1 2 + σ 2 2 m 22 = 0 .
From this system, we have solution
m 11 = m 22 = − σ 1 2 2 a + σ 2 2 , m 12 = m 21 = 0 .
Thus, the matrix M that defines mean square deviation of random states from the equilibrium ( 0 , 0 ) is
M = − σ 1 2 2 a + σ 2 2 1 0 0 1 .
Note that the asymptotic method of stochastic sensitivity gives for mean square deviation another approximation:
M ( 1 ) = − σ 1 2 2 a 1 0 0 1 .
The difference in these approximations can lead to the qualitative differences in the prediction of the results of the noise influence. Let us consider how these two estimations work in the context of the confidence domains method. For diagonal 2 × 2 -matrices, the equation of the confidence ellipse is written as
x 2 m 11 + y 2 m 22 = − 2 ln ( 1 − P ) .
Here, P is fiducial probability.
Confidence ellipses are effectively used in predicting noise-induced transitions through the separatrix. Figure 4 shows two confidence ellipses constructed using the matrices M (larger ellipse) and M ( 1 ) (smaller ellipse) for the stochastic system (20) with a = − 1 , σ 1 = 0.05 , σ 2 = 0.4 . The larger ellipse captures the basin of attraction of the limit cycle, which allows us to make a prediction about the generation of large-amplitude oscillations (excitation mode). The smaller ellipse is entirely contained in the basin of attraction of the stable equilibrium and therefore predicts the unexcited mode of the oscillator. 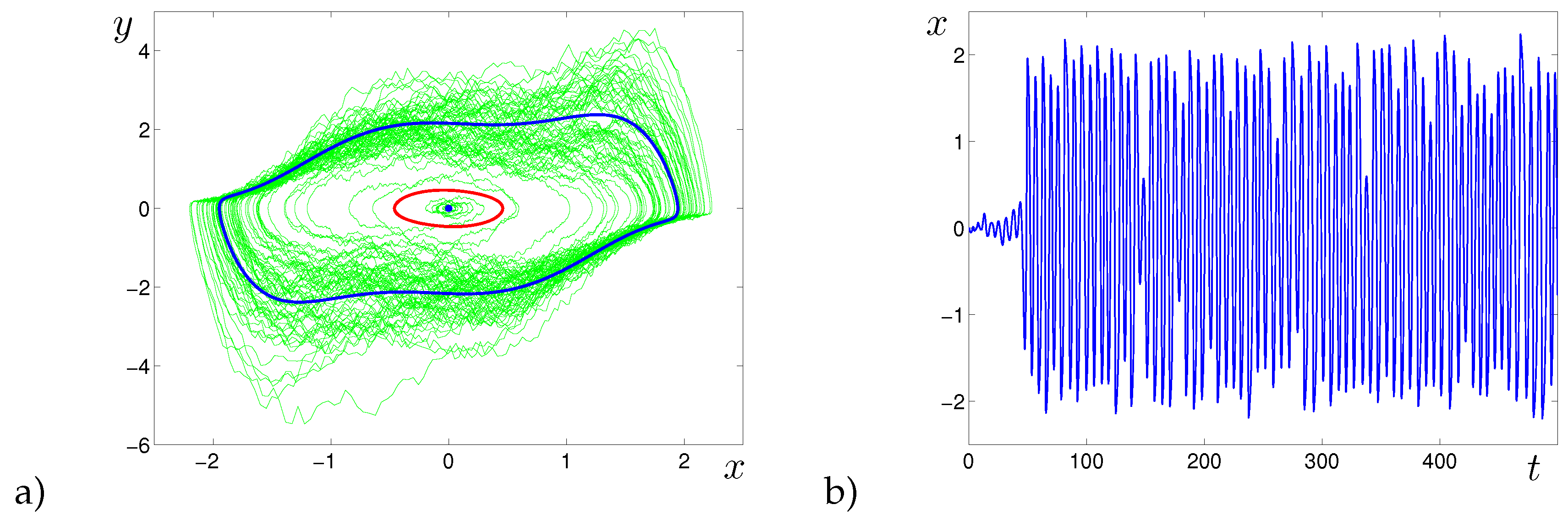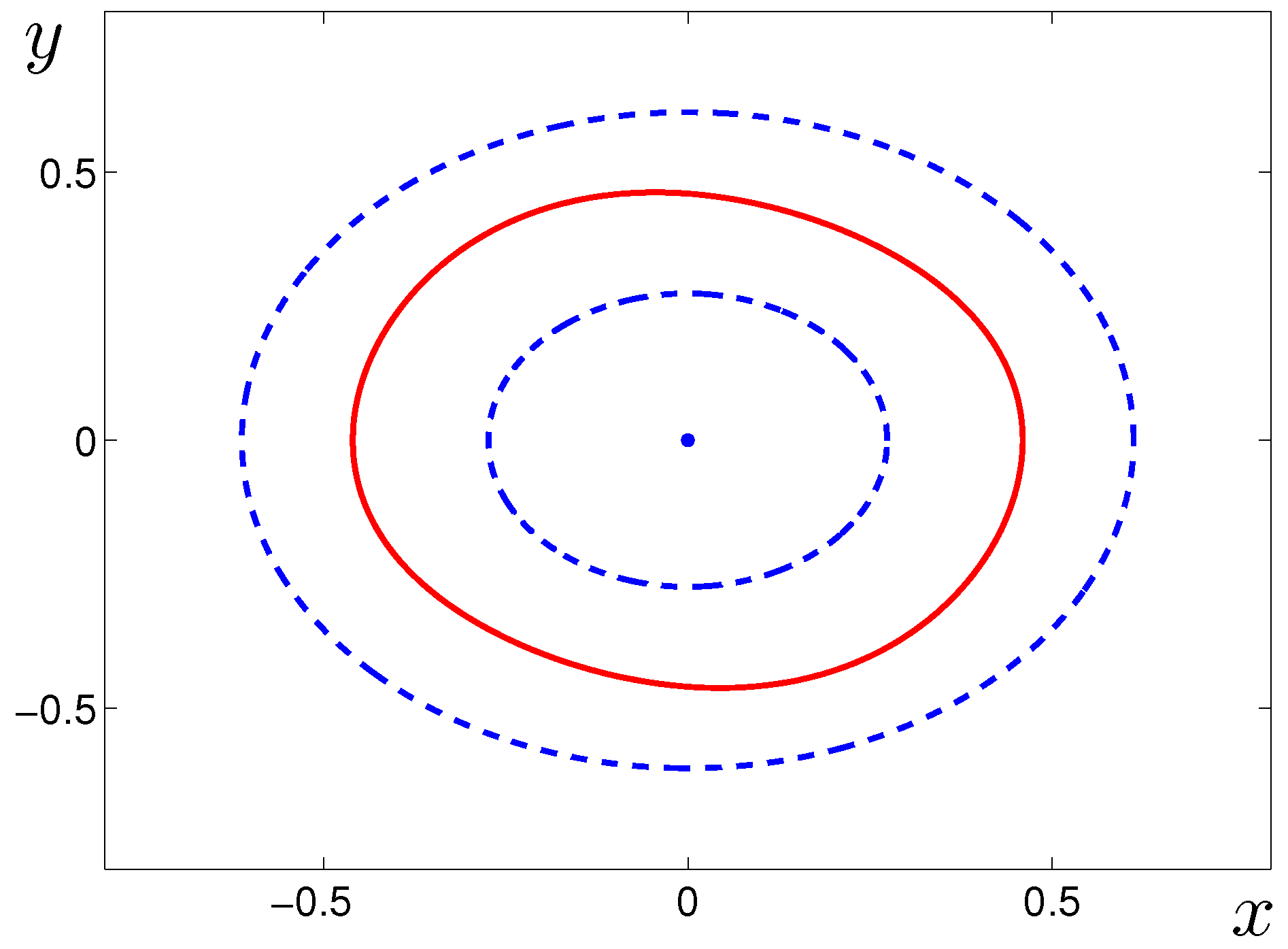As we see, an error in estimating the second moments can lead to qualitative errors in solving important prediction problems.

4. Conclusions

The paper is devoted to the problem of approximation of probability distributions of random states near the equilibrium of the stochastic system with multiplicative noise. The system of nonlinear stochastic differential Ito’s equations is used as a basic mathematical model. For the linear first approximation system, we present conditions of existence of the mean square stable stationary distribution. For mean square deviation, an expansion in powers of the small parameter of noise intensity is derived. These approximations are compared with the widely used approximation based on the stochastic sensitivity technique. The general mathematical results are applied to the analysis of noise-induced generation of large-amplitude oscillations in the van der Pol oscillator with hard excitement.

Funding

The work was supported by Russian Science Foundation (N 24-11-00097).

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Horsthemke, W.; Lefever, R. Noise-Induced Transitions; Springer: Berlin, 1984; p. 338. [Google Scholar]
  2. Anishchenko, V.S.; Astakhov, V.V.; Neiman, A.B.; Vadivasova, T.E.; Schimansky-Geier, L. Nonlinear Dynamics of Chaotic and Stochastic Systems. Tutorial and Modern Development; Springer-Verlag: Berlin, Heidelberg, 2007; p. 535. [Google Scholar]
  3. Lindner, B.; Garcia-Ojalvo, J.; Neiman, A.; Schimansky-Geier, L. Effects of noise in excitable systems. Physics Reports 2004, 392, 321–424. [Google Scholar] [CrossRef]
  4. Chen, Z.; Zhu, J. Non-differentiability of quasi-potential and non-smooth dynamics of optimal paths in the stochastic Morris-Lecar model: Type I and II excitability. Nonlinear dynamics 2019, 96, 2293–2305. [Google Scholar] [CrossRef]
  5. Lima Dias Pinto, I.; Copelli, M. Oscillations and collective excitability in a model of stochastic neurons under excitatory and inhibitory coupling. Phys. Rev. E 2019, 100, 062416. [Google Scholar] [CrossRef] [PubMed]
  6. Anishchenko, V.S.; Khairulin, M.E. Effect of noise-induced crisis of attractor on characteristics of Poincaré recurrence. Technical Physics Letters 2011, 37, 561–564. [Google Scholar] [CrossRef]
  7. Cisternas, J.; Descalzi, O. Intermittent explosions of dissipative solitons and noise-induced crisis. Phys. Rev. E 2013, 88, 022903. [Google Scholar] [CrossRef]
  8. Arnold, L. Random Dynamical Systems; Springer-Verlag: Berlin, 1998; p. 600. [Google Scholar]
  9. Zakharova, A.; Kurths, J.; Vadivasova, T.; Koseska, A. Analysing dynamical behavior of cellular networks via stochastic bifurcations. PLoS ONE 2011, 6, e19696. [Google Scholar] [CrossRef] [PubMed]
  10. Gao, J.B.; Hwang, S.K.; Liu, J.M. When can noise induce chaos? Phys. Rev. Lett. 1999, 82, 1132–1135. [Google Scholar] [CrossRef]
  11. Lai, Y.C.; Tel, T. Transient Chaos. Complex Dynamics on Finite Time Scales; Springer-Verlag: New York, 2011; p. 502. [Google Scholar]
  12. Pikovsky, A.S.; Kurths, J. Coherence resonance in a noise-driven excitable system. Phys. Rev. Lett. 1997, 78, 775–778. [Google Scholar] [CrossRef]
  13. Schmid, G.; Hänggi, P. Intrinsic coherence resonance in excitable membrane patches. Math. Biosci. 2007, 207, 235–245. [Google Scholar] [CrossRef] [PubMed]
  14. McDonnell, M.D.; Stocks, N.G.; Pearce, C.E.M.; Abbott, D. Stochastic Resonance: From Suprathreshold Stochastic Resonance to Stochastic Signal Quantization; Cambridge University Press, 2008; p. 446.
  15. Bashkirtseva, I.; Chen, G.; Ryashko, L. Stabilizing stochastically-forced oscillation generators with hard excitement: a confidence-domain control approach. European Physical Journal B 2013, 86, 437. [Google Scholar] [CrossRef]
  16. Xu, C.; Yuan, S.; Zhang, T. Confidence domain in the stochastic competition chemostat model with feedback control. Appl. Math. J. Chinese Univ. 2018, 33, 379–389. [Google Scholar] [CrossRef]
  17. Bashkirtseva, I.; Ryazanova, T.; Ryashko, L. Confidence domains in the analysis of noise-induced transition to chaos for Goodwin model of business cycles. International Journal of Bifurcation and Chaos 2014, 24, 1440020. [Google Scholar] [CrossRef]
  18. Bashkirtseva, I. Stochastic sensitivity analysis: theory and numerical algorithms. IOP Conf. Ser.: Mater. Sci. Eng. 2017, 192, 012024. [Google Scholar] [CrossRef]
  19. Bashkirtseva, I.; Ryashko, L. Stochastic Sensitivity Analysis of Noise-Induced Phenomena in Discrete Systems. In Recent Trends in Chaotic, Nonlinear and Complex Dynamics; World Scientific Series on Nonlinear Science Series B, 2021; chapter 8, pp. 173–192. [CrossRef]
  20. Mil’shtein, G.; Ryashko, L. A first approximation of the quasipotential in problems of the stability of systems with random non-degenerate perturbations. Journal of Applied Mathematics and Mechanics 1995, 59, 47–56. [Google Scholar] [CrossRef]
  21. Freidlin, M.I.; Wentzell, A.D. Random Perturbations of Dynamical Systems; Springer: New York, 1984. [Google Scholar]
  22. Sun, Y.; Hong, L.; Jiang, J. Stochastic sensitivity analysis of nonautonomous nonlinear systems subjected to Poisson white noise. Chaos, Solitons & Fractals 2017, 104, 508–515. [Google Scholar] [CrossRef]
  23. Bashkirtseva, I.; Ryashko, L. Stochastic sensitivity analysis of chaotic attractors in 2D non-invertible maps. Chaos, Solitons and Fractals 2019, 126, 78–84. [Google Scholar] [CrossRef]
  24. Kolinichenko, A.; Bashkirtseva, I.; Ryashko, L. Self-organization in randomly forced diffusion systems: A stochastic sensitivity technique. Mathematics 2023, 11. [Google Scholar] [CrossRef]
  25. Alexandrov, D.V.; Bashkirtseva, I.A.; Crucifix, M.; Ryashko, L.B. Nonlinear climate dynamics: From deterministic behaviour to stochastic excitability and chaos. Physics Reports 2021, 902, 1–60. [Google Scholar] [CrossRef]
  26. Garain, K.; Sarathi Mandal, P. Stochastic sensitivity analysis and early warning signals of critical transitions in a tri-stable prey-predator system with noise. Chaos 2022, 32, 033115. [Google Scholar] [CrossRef] [PubMed]
  27. Ryashko, L.; Bashkirtseva, I. Stochastic bifurcations and excitement in the ZS-model of a thermochemical reaction. Mathematics 2022, 10, 960. [Google Scholar] [CrossRef]
  28. Slepukhina, E.; Bashkirtseva, I.; Ryashko, L.; Kügler, P. Stochastic mixed-mode oscillations in the canards region of a cardiac action potential model. Chaos, Solitons & Fractals 2022, 164, 112640. [Google Scholar] [CrossRef]
  29. Bashkirtseva, I.; Ryashko, L.; Chen, G. Stochastic sensitivity synthesis in nonlinear systems with incomplete information. Journal of the Franklin Institute 2020, 357, 5187–5198. [Google Scholar] [CrossRef]
  30. Huang, M.; Yang, A.; Yuan, S.; Zhang, T. Stochastic sensitivity analysis and feedback control of noise-induced transitions in a predator-prey model with anti-predator behavior. Mathematical Biosciences and Engineering 2023, 20, 4219–4242. [Google Scholar] [CrossRef] [PubMed]
  31. Risken, H. The Fokker-Planck Equation: Methods of Solution and Applications; Springer: Berlin, 1984. [Google Scholar]
  32. Ryashko, L. Stabilization of linear stochastic systems with state and control dependent perturbations. Journal of Applied Mathematics and Mechanics 1981, 43, 655–663. [Google Scholar] [CrossRef]
  33. Mao, X. Exponential Stability of Stochastic Differential Equations; Marcel Dekker, 1994; p. 307.
  34. Ryashko, L.; Bashkirtseva, I. Exponential Mean Square Stability Analysis of Invariant Manifolds for Nonlinear SDE’s. In Stochastic Differential Equations, Ed. N. Halidias, Series: Mathematics Research Developments; Nova Science Publishers, 2011; chapter 4, pp. 67–95.
  35. Khasminskii, R. Stochastic Stability of Differential Equations; Springer: Berlin, 2012. [Google Scholar]
Preprints 108659 g001
Figure 1. Stationary second moments M (solid line) and approximation M ( 1 ) (dashed) versus parameter a.
Figure 1. Stationary second moments M (solid line) and approximation M ( 1 ) (dashed) versus parameter a.
Preprints 108659 g001
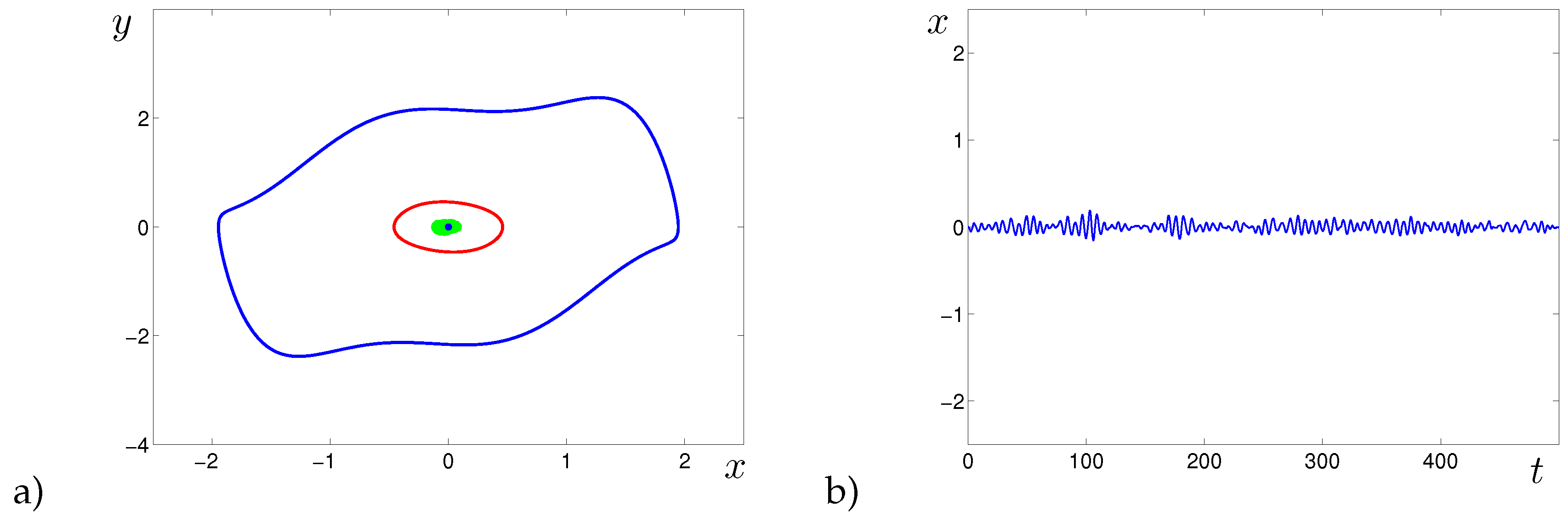
Preprints 108659 g002
Figure 2. Stochastic system (20) with σ 1 = 0.02 , σ 2 = 0.2 : a) random trajectory (green) of the solution starting at the equilibrium ( 0 , 0 ) ; b) time series.
Figure 2. Stochastic system (20) with σ 1 = 0.02 , σ 2 = 0.2 : a) random trajectory (green) of the solution starting at the equilibrium ( 0 , 0 ) ; b) time series.
Preprints 108659 g002
Preprints 108659 g003
Figure 3. Stochastic system (20) with σ 1 = 0.05 , σ 2 = 0.4 : a) random trajectory (green) of the solution starting at the equilibrium ( 0 , 0 ) ; b) time series.
Figure 3. Stochastic system (20) with σ 1 = 0.05 , σ 2 = 0.4 : a) random trajectory (green) of the solution starting at the equilibrium ( 0 , 0 ) ; b) time series.
Preprints 108659 g003
Preprints 108659 g004
Figure 4. Confidence ellipses (dashed) and unstable cycle (red solid) for the system (20) with a = − 1 , σ 1 = 0.05 , σ 2 = 0.4 . The internal ellipse is constructed using the matrix M ( 1 ) , and the external ellipse is constructed using the matrix M. Here, fiducial probability P = 0.99 .
Figure 4. Confidence ellipses (dashed) and unstable cycle (red solid) for the system (20) with a = − 1 , σ 1 = 0.05 , σ 2 = 0.4 . The internal ellipse is constructed using the matrix M ( 1 ) , and the external ellipse is constructed using the matrix M. Here, fiducial probability P = 0.99 .
Preprints 108659 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated